Automorphism groups and signatures of smooth septic curves

Abstract

We determine the list of automorphism groups for smooth plane septic curves over an algebraically closed field 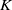$K$ of characteristic 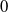$0$, as well as their signatures. For each group, we also provide a geometrically complete family over 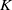$K$, which consists of a generic defining polynomial equation describing each locus up to 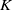$K$-projective equivalence. Notably, we present two distinct examples of what we refer to as final strata of smooth plane curves.

1. Introduction

The classification of isomorphism classes for smooth algebraic curves of a fixed genus $g$ is a classic challenge in algebraic geometry, with significant implications for both algebraic and arithmetic geometry. Achieving these classifications requires a solid understanding of the automorphism groups associated with these curves. Below we recall some motivating examples and connections.

First, when examining smooth curves over algebraically closed fields $K$ , one can determine whether a curve $C$ with certain properties is unique up to $K$ -isomorphism. One such property of interest is having a maximal automorphism group. For example, the Klein quartic ${\mathcal{K}}_{4}: X^3Y+Y^3Z+Z^3X=0$ has the largest automorphism group for a curve with that genus, namely the Klein group $\textrm {PSL}(2,7)$ of order $168$ . This remarkable curve is a central subject of study in number theory, physics, and beyond (see [10, 17, 18]). For quintic curves of genus $g=6$ , the Fermat curve ${\mathcal{F}}_5:X^5+Y^5+Z^5=0$ is notable for its maximal symmetries, characterized by an automorphism group of order $150$ , $(\mathbb{Z}/5\mathbb{Z})^2\rtimes {\textrm {S}}_3$ (see [3]). In the realm of sextic curves with genus $g=10$ , the Wiman curve

\begin{equation*} {\mathcal{W}}_6\,:\,7X^6+9X(Y^5+Z^5)-135X^4YZ-45X^2Y^{2}Z^{2}+10Y^3Z^3=0 \end{equation*}

is the one with maximal symmetries, having an automorphism group ${\textrm {A}}_6$ , the alternating group of order $360$ , as first shown in [15] and confirmed in [6]. For $g=15$ septic curves, we the Fermat septic curve ${\mathcal{F}}_7:X^7+Y^7+Z^7=0$ exhibits the most symmetries, with an automorphism group of order 294, $(\mathbb{Z}/7\mathbb{Z})^2\rtimes {\textrm {S}}_3$ , as established in [[30],Theorem 5].

Next, when considering non-algebraically closed fields $k$ in the context of arithmetic geometry, understanding the automorphism group of $C\otimes _kk^s$ can significantly streamline the realization of various models (or twists) of $C$ . The set of isomorphism classes of twists, $\textrm {Twist}(C)$ , is in one-to-one correspondence with ${\textrm {H}}^1\left (\textrm {Gal}(k^s/k),\textrm {Aut}(C\otimes _kk^s)\right )$ , where $k^s$ denotes a separable closure of $k$ , and $\textrm {Gal}(k^s/k)$ is its Galois group (see [[40], Chapitre III]). Additionally, the forms of automorphisms of $C$ as projective transformations in the plane ${{\mathbb{P}}}^2(k^s)$ influence the defining equations of its twists, guiding the search for solutions to Galois embedding problems associated with these twists. More details can be found in [32, 33, 35].

Third, smooth plane curves of degree $d\geq 4$ with non-trivial automorphism groups play a crucial role in studying the algebraic geometry of the Cremona group $\textrm {Bir}\left ({{\mathbb{P}}}^2(\mathbb{C})\right )$ , particularly in examining the dynamics of its elements. The collection of birational classes of curves with a fixed genus is a vital invariant, leading to the discovery of infinitely many conjugacy classes of elements of order $2n$ in $\textrm {Bir}\left ({\mathbb{P}}^2(\mathbb{C})\right )$ for any integer $n$ (see [8, 9] for more information).

The main aim of the present work is to identify all possible automorphism groups for smooth plane septic curves and to explore the relationships among them. This work builds on the efforts of the first author and Bars as detailed in [3–6], where the cases of smooth plane quintics and sextics were addressed. We hope that examining various cases in depth will unveil underlying patterns, ultimately leading to general algorithms for determining automorphism groups and models once the degree $d$ is specified.

The organization of the sections is as follows. In section 2, we categorize smooth plane curves of degree $d \geq 4$ , focusing on large automorphism orders $m$ , by automorphism order and presents a theorem summarizing automorphism groups for specific values of $m$ , along with cyclic subgroups and equations for septic curves. Section 3 introduces key concepts, referencing H. Mitchell’s classification [37] of finite subgroups of ${\textrm {PGL}}_3(K)$ , and T. Harui’s classification [25] for smooth plane curves. In section 4, we analyze the nonexistence of certain finite groups as automorphism groups for septic curves, proving that $\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}$ and $\mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/3\mathbb{Z}$ cannot be automorphism subgroups. In section 5, we study the automorphism groups of descendants of Fermat and Klein septic curves. In sections 6 and 7, we explore smooth plane curves with cyclic and noncyclic automorphism groups, showing that some curve types have cyclic automorphisms, while others, like descendants of the Fermat curve, have larger groups. In section 8, we study the signatures of the quotient curves of a smooth plane septic by its autmorphism group and connect that to the corresponding study of all genus 15 curves whose quotient by their automorphism group is of genus zero, as catalogued in the L-functions and modular forms database (LMFDB) [34]. This provides criteria that can be used to prove that certain of those genus 15 curves are not smooth planar (cf. Table 5).

We shall state our main results below.

Theorem 1. Let $K$ be an algebraically closed field $K$ of characteristic zero. The listing of nontrivial automorphism groups of smooth plane septic curves over $K$ , accompanied by geometrically complete defining polynomial equation $F(X,Y,Z)=0$ over $K$ for each stratum, is provided in Table 1 .

We follow the standard indexing convention from the atlas for small finite groups [23]. In this context, “SmallGroup(n, m)” refers to the finite group of order $n$ that appears in the $m$ -th position of that atlas. See also GroupNames [16]. When two isomorphic but non-conjugate groups $G$ serve as the automorphism groups of smooth plane septic curves, we use the $\varrho$ prefix to differentiate between them.

Table 1. Automorphism groups and defining equations

Here $L_{i,*}$ denotes the generic homogeneous polynomial of degree $i$ in the variables $\{X,Y,Z\}-\{*\}$ , $\zeta _m$ is a fixed primitive $m$ th root of unity in $K$ , and a projective linear transformation $A=(a_{i,j})\in {\textrm {PGL}}_3(K)$ is written as

\begin{equation*}[a_{1,1}X+a_{1,2}Y+a_{1,3}Z:a_{2,1}X+a_{2,2}Y+a_{2,3}Z:a_{3,1}X+a_{3,2}Y+a_{3,3}Z].\end{equation*}

The following diagram illustrates the stratification of smooth plane septic curves by their automorphism groups.

Let $G$ be a finite subgroup of ${\textrm {PGL}}_3(K)$ , and let $\widetilde {\mathcal{M}^{\textrm {pl}}_d(G)}$ represents the set of $K$ -isomorphism classes of smooth plane curves $C$ of degree $d$ over $K$ for which $\textrm {Aut}(C)$ is ${\textrm {PGL}}_3(K)$ -conjugate to $G$ . We refer to $\widetilde {\mathcal{M}^{\textrm {pl}}_d(G)}$ as a final stratum if it has nonzero dimension and is not properly contained in any other stratum.

The existence of a final stratum is considered a noteworthy phenomenon, as one might expect that imposing additional restrictions on the parameters would lead to larger automorphism groups, ultimately resulting in a zero-dimensional stratum. The first known example of final strata was identified for $d=5$ and $G=\mathbb{Z}/4\mathbb{Z}$ by Badr and García [7], who effectively illustrated this phenomenon using a family of canonical models in ${\mathbb{P}}^{g-1}(K)$ . They demonstrated that this situation typically arises when $d=1\,\textrm {mod}\,4$ . In contrast, Badr ans Bars [6] showed that final strata do not exist for $d=6$ .

For $d=7$ , as a result of Theorem1, we conclude that:

Corollary 1. The strata $\widetilde {\mathcal{M}^{\textrm {pl}}_{7}(\varrho _{1,2}(\mathbb{Z}/6\mathbb{Z}))}$ and $\widetilde {\mathcal{M}^{\textrm {pl}}_{7}(\varrho _{2,3}(\mathbb{Z}/6\mathbb{Z}))}$ are final strata.

2. Full automorphism groups of very large types $m,(a,b)$

Let $C$ be a smooth plane curve of degree $d\geq 4$ . According to [[4],Corollary 33], the automorphisms of $C$ have orders that divide $d-1,\,\,d,\,\,(d-1)^2,\,\,d(d-2),\,\,d(d-1)$ or $d^2-3d+3$ . Moreover, we define $C$ to be of Type $m, (a,b)$ if it possesses an automorphism of maximal order $m$ , represented as $\textrm {diag}(1,\zeta _m^a,\zeta _m^b)$ acting on a fixed smooth plane model $F(X,Y,Z)=0$ for $C$ . Here $a,b$ are integers with $0\leq a\lt b\lt m$ . Additionally, we categorize $C$ as a very large type if $m=d(d-1),\,(d-1)^2,\,d(d-2),\,d^2-3d+3$ or $q(d-1)$ with $q\geq 2$ .

For a fixed degree $d\geq 4$ , the findings in [4] provide a constructive approach to generate all possible Types $m,\,(a,b)$ for which there exists a smooth plane curve $C$ of degree $d$ having an automorphism of order $m$ , assigning a generic polynomial equation $F_{m,\,(a,b)}(X,Y,Z)=0$ of degree $d$ over $K$ that describe those plane curves of Type $m,\,(a,b)$ . Particularly relevant to the present work is the case $d=7$ which we now recall:

Proposition 1. Let $C$ be a smooth plane septic curve over an algebraically closed field $K$ of characteristic $0$ . Then, $C$ falls into one of the following types:

Proof. This is Table A.4 in [4], we refer the reader to that paper for the details.

The results in [4, 25] provide a detailed characterization of ${\textrm {Aut}}(C)$ when $C$ is classified as a very large type. In particular, we have that

Theorem 2. Let $C$ be a smooth plane degree $d$ curve of Type $m,\,(a,b)$ .

1. 1. If $m=d(d-1)$ , then $\textrm {Aut}(C)$ is cyclic of order $d(d-1)$ . In this scenario, $C$ is $K$ -isomorphic to $C:X^d+Y^d+XZ^{d-1}=0$ , where ${\textrm {Aut}}(C)=\langle \sigma \rangle$ with $\sigma =\textrm {diag}(1,\zeta _{d(d-1)}^{d-1},\zeta _{d(d-1)}^d)$ .

2. 2. If $m=(d-1)^2$ , then $\textrm {Aut}(C)$ is cyclic of order $(d-1)^2$ . In this scenario, $C$ is $K$ -isomorphic to $C:X^d+Y^{d-1}Z+XZ^{d-1}=0$ , where ${\textrm {Aut}}(C)=\langle \sigma \rangle$ with $\sigma =\textrm {diag}(1,\zeta _{(d-1)^2},\zeta _{(d-1)^2}^{-(d-1)})$ .

3. 3. If $m=d(d-2)$ , then $C$ is $K$ -isomorphic to $C:X^d+Y^{d-1}Z+YZ^{d-1}=0$ . For $d\neq 4,6$ , ${\textrm {Aut}}(C)$ is a central extension of the dihedral group ${\textrm {D}}_{2(d-2)}$ by $\mathbb{Z}/d\mathbb{Z}$ . More precisely,

   \begin{equation*}\textrm {Aut}(C)=\langle \sigma, \,\tau \,|\,\sigma ^{d(d-2)}=\tau ^2=1,\, \tau \sigma \tau =\sigma ^{-(d-1)},\ldots \rangle, \end{equation*}
   with $\sigma =\textrm {diag}(1,\zeta _{d(d-2)},\zeta _{d(d-2)}^{-(d-1)})$ and $\tau =[X:Z:Y]$ . Thus, it has order $2d(d-2)$ .

4. 4. If $m=d^2-3d+3$ , then $C$ is $K$ -isomorphic to the Klein curve defined by $\mathcal{K}_d:X^{d-1}Y+Y^{d-1}Z+Z^{d-1}X=0$ . Moreover, for $d\geq 5$ , we have

   \begin{equation*}\textrm {Aut}(C)=\langle \sigma, \tau |\sigma ^{d^2-3d+3}=\tau ^3=1,\,\tau ^{-1}\sigma \tau =\sigma ^{-(d-1)}\rangle, \end{equation*}
   with $\sigma =\textrm {diag}(1,\zeta _{d^2-3d+3},\zeta _{d^2-3d+3}^{-(d-2)})$ and $\tau =[Y:Z:X]$ . Consequently, $\textrm {Aut}(C)$ has order $3(d^2-3d+3)$ .

5. 5. If $m=q(d-1)$ for some $q\geq 2$ , then we guarantee that $\textrm {Aut}(C)$ is cyclic.

Substituting $d=7$ in Theorem2 yields:

Corollary 2. Suppose that $C$ is a smooth plane septic curve over $K$ that possesses an automorphism of very large order $m\in \{42,36,35,31,18,12\}$ . Below, we outline the full automorphism groups and the corresponding defining equations, up to $K$ -isomorphism.

Proof. Everything is clear from Theorem2, except possibly for the last two cases. When $C$ is of Type $12,\,(1,6)$ , the automorphism group is cyclic of order $12m$ with $m=1$ or $3$ , as established in Theorem2-(5) and Proposition1. If ${\textrm {Aut}}(C)$ has order $36$ , then $C$ is $K$ -isomorphic to $X^{7} + Y^{6} Z+X Z^{6}=0$ via some $\phi \in {\textrm {PGL}}_3(K)$ . Moreover, we can choose $\phi$ in the normalizer of $\langle \textrm {diag}(1,\zeta _{12},-1)\rangle$ , since $\mathbb{Z}/12\mathbb{Z}$ forms a single conjugacy class within $\mathbb{Z}/36\mathbb{Z}$ . Direct calculations reveal that $\phi =\textrm {diag}(1,a,b)$ for some $a,\,b \in K^{*}$ . This implies that $a^6b=b^6=1$ and $\beta _{2,0}=\beta _{4,0}=0$ .

A similar approach can be applied to the Type $18,(1,12)$ .

3. Preliminaries about automorphism groups

Using purely geometric methods applied to the projective plane ${\mathbb{P}}^2_K$ over the field $K$ , H. Mitchell [37] compiled a list of finite subgroups $G\subset {\textrm {PGL}}_3(K)$ . Specifically, he demonstrated that $G$ fixes either a point, a line, or a triangle, unless it is primitive and conjugate to a group from a particular list.

We will employ the following notations throughout the paper.

3.1 Notation

The exponent of a nonzero monomial $cX^{i_1}Y^{i_2}Z^{i_3}$ with $c\in K^*$ is defined as the maximum of $i_1,\,i_2,\,i_3$ . The core of a homogeneous polynomial $F(X,Y,Z)$ in $K[X,Y,Z]$ refers to the sum of all terms in $F(X,Y,Z)$ that have the largest exponent.

A descendent of a smooth plane curve $C_0\,:\,F(X,Y,Z)=0$ of degree $d$ over $K$ is a pair $(C,G)$ , where $C$ is a smooth plane curve of degree $d$ that admits a smooth plane model $\widetilde {F}(X,Y,Z)=0$ over $K$ whose core matches $F(X,Y,Z)$ . This means that

\begin{equation*}\widetilde {F}(X,Y,Z)=F(X,Y,Z)\,+\, \text{lower order terms}.\end{equation*}

Moreover, $G\leq {\textrm {Aut}}(C)$ is ${\textrm {PGL}}_3(K)$ -conjugate to a subgroup of $\textrm {Aut}(C_0)$ .

Let $ \textrm {PBD}(2,1)$ be the set of all elements in $ {\textrm {PGL}}_3(K)$ that have the form:

\begin{equation*}\left ( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0\\ 0 & \ast & \ast \\ 0 & \ast & \ast \\ \end{array} \right )\end{equation*}

An element in $ {\textrm {PGL}}_3(K)$ is called intransitive if it is conjugate to an element in $ \textrm {PBD}(2,1)$ . The natural group homomorphism

\begin{equation*}\left ( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0\\ 0 & \ast & \ast \\ 0 & \ast & \ast \\ \end{array} \right )\in \textrm {PBD}(2,1)\mapsto \left ( \begin{array}{c@{\quad}c} \ast & \ast \\ \ast & \ast \\ \end{array} \right )\in {\textrm {PGL}}_2(K)\end{equation*}

is denoted by $\Lambda .$

Now we present Theorem3 below, attributed to T. Harui [[25],Theorem 2.1]. This theorem is essential for our investigation of the automorphism groups of smooth plane curves when the degree is fixed. It serves as a detailed extension of Mitchell’s classification applied to smooth plane curves.

Theorem 3. Let $C$ be a smooth plane curve of degree $d\geq 4$ defined over an algebraically closed field $K$ of characteristic $0$ . Then, one of the following scenarios applies

1. 1. $\textrm {Aut}(C)$ fixes a point on $C$ , so it is cyclic.

2. 2. $\textrm {Aut}(C)$ fixes a point not lying on $C$ . This situation can be understood through the following commutative diagram, with exact rows and vertical injective morphisms:

   

   where $N$ is a cyclic group such that $|N|\,|\,d$ , and $G'$ , a subgroup of ${\textrm {PGL}}_2(K)$ , can be

   1. (i) A cyclic group $\mathbb{Z}/m\mathbb{Z}$ of order $m$ with $m\leq d-1$ ,

   2. (ii) A Dihedral group ${\textrm {D}}_{2m}$ of order $2m$ such that $|N|=1$ or $m\,|\,(d-2)$ ,

   3. (iii) One of the alternating groups $\textrm {A}_4$ , $\textrm {A}_5$ , or the symmetry group ${\textrm {S}}_4$ .

   In fact, $N$ represents the component of $\textrm {Aut}(C)$ that acts on the variable $B\in \{X,Y,Z\}$ while fixing the other two variables. In contrast, $G'$ is the component that acts on $\{X,Y,Z\}\setminus \{B\}$ and fixes $B$ . For example, if $B=Y$ , then every automorphism in $N$ takes the form $\textrm {diag}(1,\zeta _n,1)$ for some $n$ th root of unity $\zeta _n$ ; moreover, any automorphism of $C$ would have the form:

   \begin{equation*}\left ( \begin{array}{c@{\quad}c@{\quad}c} \ast & 0 & \ast \\ 0 & 1 & 0\\ \ast & 0 & \ast \\ \end{array} \right ).\end{equation*}
   Thus, $\textrm {Aut}(C)$ can be embedded into $\textrm {PBD}(2,1)$ as $^{\phi }\textrm {Aut}(C)$ , where $\phi =[Y:X:Z]$ . In this context, we will use $\Lambda (\textrm {Aut}(C))$ to refer to the image of $^{\phi }\textrm {Aut}(C)$ under $\Lambda$ , by an abuse of notation. Similarly, when $B=Z$ .

3. 3. $\textrm {Aut}(C)$ is conjugate to a subgroup $G$ of $\textrm {Aut}(\mathcal{F}_d)$ , where $\mathcal{F}_d$ is the Fermat curve $X^d+Y^d+Z^d=0$ . Here, $|G|$ divides $|\textrm {Aut}(\mathcal{F}_d)|=6d^2$ , and $(C,G)$ is a descendant of $\mathcal{F}_d$ .

4. 4. $\textrm {Aut}(C)$ is conjugate to a subgroup $G$ of $\textrm {Aut}(\mathcal{K}_d)$ , where $\mathcal{K}_d$ is the Klein curve curve $XY^{d-1}+YZ^{d-1}+ZX^{d-1}$ . In this instance, $|\textrm {Aut}(C)|$ divides $|\textrm {Aut}(\mathcal{K}_d)|=3(d^2-3d+3)$ , and $(C,G)$ is a descendant of $\mathcal{K}_d$ .

5. 5. $\textrm {Aut}(C)$ is conjugate to one of the finite primitive subgroup of ${\textrm {PGL}}_3(K)$ namely, the Klein group $\textrm {PSL}(2,7)$ , the icosahedral group $\textrm {A}_5$ , the alternating group $\textrm {A}_6$ , or to one of the Hessian groups $\textrm {Hess}_{*}$ with $*\in \{36,\,72,\,216\}$ .

Following Mitchell [37], we classify finite-order automorphisms of the projective plane ${\mathbb{P}}^2_K$ into two categories: homologies and non-homologies. An homology of period $n$ is defined as a projective linear transformation in ${\textrm {PGL}}_3(K)$ that is conjugate to $\textrm {diag}(1,1,\zeta _n)$ . Such a transformation fixes point-wise a line $\mathcal{L}$ (its axis) and a point $P$ located off this line (its center). In its canonical form, this is represented by $\mathcal{L}:Z=0$ and $P=(0:0:1)$ .

The existence of homologies can confer additional desirable geometric properties, as demonstrated by the following fact due to H. Mitchell [37].

Theorem 4. Let $G$ be a finite subgroup of ${\textrm {PGL}}_3(K)$ . The following statements hold:

1. 1. If $G$ contains an homology of period $n\geq 4$ , then it fixes a point, a line or a triangle.

2. 2. The Hessian group $\textrm {Hess}_{216}$ is the unique finite subgroup of ${\textrm {PGL}}_3(K)$ that contains homologies of period $n=3$ but does not leave invariant a point, a line or a triangle.

3. 3. Inside $G$ , a transformation that leaves invariant the center of an homology must leave invariant its axis and vice versa.

Furthermore, the existence of homologies is closely related to the concept of Galois points, first introduced by H. Yoshihara in 1996 (to the best of our knowledge) and further explored by several mathematicians, including [19–22, 27, 36, 43].

Definition 5. A Galois point for a plane curve $C$ is a point $P \in {\mathbb{P}}^2_K$ such that the natural projection $\pi _P$ morphism from $C$ to a line $\mathcal{L}$ with center $P$ constitutes a Galois covering.

A Galois point $P$ for $C$ is termed inner if $P \in C$ ; otherwise, $P$ is an outer Galois point.

As a consequence of [[25],Lemma 3.8], we find that

Proposition 2. Let $C$ be a smooth plane curve of degree $d\geq 5$ over an algebraically closed field $K$ of characteristic $0$ , and let $\sigma \in \textrm {Aut}(C)$ be an homology with center $P$ . Then, the order of $\sigma$ divides $d-1$ if $P\in C$ , and it divides $d$ when $P\notin C$ . Moreover, the order of $\sigma$ equals $d-1$ if and only if $P$ is an inner Galois point for $C$ , and it equals $d$ if and only if $P$ is an outer Galois point for $C$ .

4. Finite primitive groups never occur for smooth septic curves

For smooth plane septic curves $C$ , we first show that $\textrm {Aut}(C)$ is not one of the finite primitve subgroups; $\textrm {PSL}(2,7),\,\textrm {A}_5,\,A_6$ , and $\textrm {Hess}_*$ for $*\in \{36,\,72,\,216\}$ .

Proposition 3. The group $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$ is never an automorphism subgroup for a smooth plane septic curve $C$ . In particular, $\textrm {Aut}(C)\neq \textrm {PSL}(2,7),\,\textrm {A}_5$ and $\textrm {A}_6$ .

Proof. Assume that $\sigma$ and $\tau$ are involutions for $C$ that commute. There is no loss of generality to take $\sigma =\textrm {diag}(-1,1,1)$ , up to ${\textrm {PGL}}_3(K)$ -equivalence. In particular,

\begin{equation*}\tau = \begin{pmatrix} 1&0&0\\ 0&*&*\\ 0&*&*\\ \end{pmatrix}\in \textrm {PBD}(2,1),\end{equation*}

since $\sigma \tau =\tau \sigma$ . Another change of variables $\phi \in \textrm {PBD}(2,1)$ would reduce $\tau$ to $\textrm {diag}(1,-1,1)$ . This does not change $\sigma$ as $\textrm {PBD}(2,1)$ is the normalizer of $\langle \sigma \rangle$ in ${\textrm {PGL}}_3(K)$ . Second, to ensure smoothness, the defining equation for $C$ should have degree $\geq 6$ in each variable, as indicated in [[2],Lemma 2.1.1]. In particular, since $C$ is invariant under the action of $\sigma$ and $\tau$ , it should have degree $7$ in exactly one of the variables and be defined by an equation of one of the following forms:

\begin{equation*} X^7+\sum _{i=0}^2 \alpha _i X^{2i+1}L_{7-(2i+1),X}=0 \end{equation*}

or

\begin{equation*} X^{6}L_{1,X}+\sum _{i=0}^2 \alpha _i X^{2i}L_{7-2i,X}=0 \end{equation*}

We discard the first form because it factors as $X\cdot G(X,Y,Z)=0$ , making $C$ reducible and singular. Additionally, in the second form, the equation should have degree $7$ in either $Y$ or $Z$ (but not both), as it is invariant under $\tau$ and $\sigma \tau$ . Therefore, it also reduces to a reducible defining equation, divisible by $Y$ or $Z$ , which contradicts the smoothness of $C$ .

The rest is straightforward, as any of the groups $\textrm {PSL}(2,7),\,\textrm {A}_5$ and $\textrm {A}_6$ has a subgroup isomorphic to $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$ .

Proposition 4. The group $\mathbb{Z}/3\mathbb{Z}\times \mathbb{Z}/3\mathbb{Z}$ is never an automorphism subgroup for a smooth plane septic curve $C$ . In particular, $\textrm {Aut}(C)\neq \textrm {Hess}_{*}$ for $*=36,\,72,\,216$ .

Proof. Assume that $\sigma$ and $\tau$ are automorphisms of order $3$ for $C$ that commute. Up to ${\textrm {PGL}}_3(K)$ -equivalence, $\sigma$ is either $\textrm {diag}(\zeta _3,1,1)$ , an homology, or $\textrm {diag}(1,\zeta _3,\zeta _3^{-1})$ , a non-homology.

- If $\sigma =\textrm {diag}(\zeta _3,1,1)$ , then relation $\sigma \,\tau =\tau \,\sigma$ implies that

\begin{equation*} \tau =\begin{pmatrix} 1&0&0\\ 0&*&*\\ 0&*&*\\ \end{pmatrix}\in \textrm {PBD}(2,1). \end{equation*}

Again, we can apply an extra change of variables $\phi \in \textrm {PBD}(2,1)$ that reduces $\tau$ to $\tau =\textrm {diag}(1,\zeta _3,1)$ or $\tau =\textrm {diag}(1,\zeta _3,\zeta _3^{-1})$ . Obviously, such $\phi$ does not change $\sigma =\textrm {diag}(\zeta _3,1,1)$ as it belongs to $\textrm {PBD}(2,1)$ the normalizer of $\langle \sigma \rangle$ in ${\textrm {PGL}}_3(K)$ . Therefore, $C_3\times C_3=\langle \textrm {diag}(\zeta _3,1,1),\,\textrm {diag}(1,\zeta _3,1)\rangle$ .

- If $\sigma =\textrm {diag}(1,\zeta _3,\zeta _3^{-1})$ , then the relation $\sigma \,\tau =\tau \,\sigma$ implies that

\begin{equation*} \tau =\textrm {diag}(1,a,b),\,[Y:a Z:bX],\,\,\text{or}\,\,[Z:aX:bY]. \end{equation*}

for some $a,b\in K^*$ . In the worst case, we may require a change of variables $\phi =\textrm {diag}(1,\lambda, \nu )$ , again in the normalizer of $\langle \sigma \rangle$ in ${\textrm {PGL}}_3(K)$ , to reduce to one of the following situations: either $C_3\times C_3=\langle \textrm {diag}(1,\zeta _3,1),\,\textrm {diag}(1,1,\zeta _3)\rangle$ or $C_3\times C_3=\langle \textrm {diag}(1,\zeta _3,\zeta _3^{-1}),\,[Y:Z:X]\rangle$ .

Now, for $\tau =[Y:Z:X]$ to be an automorphism, the core of $C$ should be $X^7+Y^7+Z^7,\,$ $X^6Y+Y^6Z+Z^6X$ or $X^6Z+Z^6Y+Y^6X$ . However, none of these cores is preserved under the action of $\sigma =\textrm {diag}(1,\zeta _3,\zeta _3^{-1})$ , a contradiction.

On the other hand, for $\sigma =\textrm {diag}(\zeta _3,1,1)$ and $\tau =\textrm {diag}(1,\zeta _3,1)$ to be automorphisms, the defining equation of $C$ must be $F(X^3,Y^3,Z^3)=0$ , which is absurd because $3$ does not divide $d=7$ .

The rest is straightforward, as any of the Hessian groups contains a subgroup isomorphic to $\mathbb{Z}/3\mathbb{Z}\times \mathbb{Z}/3\mathbb{Z}$ .

5. On septic descendants of $\mathcal{F}_7$ and $\mathcal{K}_7$

In this section, we state and prove some observations about smooth plane septic curves $C$ that are descendants of either the Fermat curve $\mathcal{F}_7$ or the Klein curve $\mathcal{K}_7$ .

Proposition 5. For the Fermat septic curve $\mathcal{F}_7\,:\,X^7+Y^7+Z^7=0$ , we have that Aut( $\mathcal{F}_7$ )=SmallGroup(294,7). In particular, a Fermat’s septic descendant is one of the following types: $3,\, (1,2),\,7,\, (a,b),\,14,\,(2,7)$ .

Proof. We know that $\textrm {Aut}(\mathcal{F}_7)$ is of order $6d^2=294$ , moreover, it is generated by the four automorphisms

\begin{equation*}\eta _1=[X:Z:Y],\,\eta _2=[Y:Z:X],\,\eta _3=\textrm {diag}(1,\zeta _{7},1),\, \eta _4\,:\!=\,\textrm {diag}(1,1,\zeta _{7}). \end{equation*}

We identify ${\textrm {Aut}}(\mathcal{F}_7)$ with SmallGroup(294,7), since

\begin{equation*} (\eta _1\eta _2)^2=1,\,\eta _1\eta _3\eta _1= \eta _4,\, \eta _3\eta _4=\eta _4\eta _3,\,(\eta _1 \eta _4)^2=\eta _3 \eta _4,\, \eta _2\eta _3\eta _2^{-1}= (\eta _3\eta _4)^{-1}. \end{equation*}

Corollary 3. If a smooth septic curve $C$ is a descendant of the Fermat curve $\mathcal{F}_7$ such that $\textrm {Aut}(C)$ contains a $\mathbb{Z}/7\mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}$ , then $C$ is $K$ -isomorphic to the Fermat curve $\mathcal{F}_7$ itself.

Proof. The subgroups of Aut( $\mathcal{F}_7$ )=SmallGroup(294,7) that are isomorphic to $\mathbb{Z}/7\mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}$ are all $\textrm {Aut}(\mathcal{F}_7)$ -conjugate to $ \langle \textrm {diag}(1,\zeta _7,1),\,\textrm {diag}(1,1,\zeta _7)\rangle .$ Hence, we deduce by [[25],Lemma 6.5-(1)] that $C$ should be the Fermat curve as claimed.

Corollary 4. If a smooth plane septic curve $C$ is a descendent of the Fermat curve $\mathcal{F}_7$ such that $\textrm {Aut}(C)$ contains a $\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ as a subgroup, then $C$ is $K$ -isomorphic to

\begin{equation*} C^{'}:X^7+Y^7+Z^7+\alpha \left (X^4YZ^2+X^2Y^4Z+XY^2Z^4\right )=0 \end{equation*}

for some $\alpha \in K$ . In particular, $\textrm {Aut}(C)$ is either $\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ or SmallGroup(294,7).

Proof. Any $\mathbb{Z}/7\mathbb{Z} \rtimes \mathbb{Z}/3\mathbb{Z}$ inside Aut( $\mathcal{F}_7$ )= SmallGroup(294,7) is $\textrm {Aut}(\mathcal{F}_7)$ -conjugate to

\begin{equation*} \mathcal{G}\,:\!=\,\langle \textrm {diag}(1,\zeta _7,\zeta _7^{-4}),\,[Y:Z:X]\rangle . \end{equation*}

A plane curve $C':X^7+Y^7+Z^7+\text{lower order terms in}\,\,X,Y,Z$ is invariant under the action of $\mathcal{G}$ if and only if

\begin{equation*} C'\,:\,X^7+Y^7+Z^7+\sum _{7\,|\,4j-i}\,\alpha _{i,j}\left (X^{7-i-j}Y^iZ^{j}+X^jY^{7-i-j}Z^i+X^iY^jZ^{7-i-j}\right )\,=\,0, \end{equation*}

So $(i,j)=(1,2),\,(2,4)$ or $(4,1)$ , which gives us the prescribed equation for $C'$ .

Now, for all values $\alpha \in K^{*}$ , ${\textrm {Aut}}(C^{'})=\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ . Indeed, if $\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ is a proper subgroup of automorphisms, then ${\textrm {Aut}}(C)=(\mathbb{Z}/7\mathbb{Z})^2\rtimes \mathbb{Z}/3\mathbb{Z}$ or SmallGroup(294,7), see Group structure of SmallGroup(294,7) [16]. In either way, $\mathbb{Z}/7\mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}$ would be a subgroup of automorphisms, which means that $C'$ is the Fermat curve by Corollary3. However, the defining equation for $C'$ is not invariant under the action of $\eta _1=[X:Z:Y]$ .

Proposition 6. For the Klein septic curve $\mathcal{K}_7\,:\,X^6Y+Y^6Z+Z^6X=0$ , we have that Aut( $\mathcal{K}_7$ )= SmallGroup(93,1).

Proof. We know that $\textrm {Aut}(\mathcal{K}_7)$ has order $3(d^2-3d+3)=93$ and is generated by the two automorphisms

\begin{equation*}\sigma =\textrm {diag}(1,\zeta _{31},\zeta _{31}^{-5}),\, \tau =[Y:Z:X].\end{equation*}

We identify ${\textrm {Aut}}(\mathcal{K}_7)$ with SmallGroup(93,1), since $\sigma ^{31}=\tau ^3=1,\, \tau \sigma \tau ^{-1}=\sigma ^{-6}.$

Corollary 5. Let $C$ be a descendant of the Klein septic curve $K_7$ . Then, $C$ is the Klein curve $\mathcal{K}_7$ or $\textrm {Aut}(C)=\mathbb{Z}/3\mathbb{Z}$ .

Proof. Since Aut( $\mathcal{K} _7$ )= SmallGroup(93,1) by Proposition5, then it is necessary for $C$ to be a descendant of $\mathcal{K}_7$ that $C$ is of Type $31, (1,26)$ or Type $3, (1,2)$ . If $C$ is of Type $31, (1,26)$ , then it is $K$ -isomorphic to $\mathcal{K}_7$ and $\textrm {Aut}(C)=\textrm {SmallGroup}(93,1)$ by Proposition1 and Corollary2. On the other hand, if $C$ is of Type $3, (1,2)$ then $\textrm {Aut}(C)$ should be $\mathbb{Z}/3\mathbb{Z}$ because $\mathbb{Z}/3\mathbb{Z}$ is maximal in SmallGroup(93,1), see Group structure of SmallGroup(93,1) [16].

6. More curves whose automorphism groups are cyclic

We aim here to show that any of the types $21, (3,7)$ , $9, (1,3)$ , $7, (0,1)$ , $6, (a,b)$ , $4, (1,2)$ , $3, (0,1)$ , and $2, (0,1)$ has cyclic automorphism group.

6.1. Type $21,(3,7),$ type $9,\,(1,3)$ and type $4,\,(1,2)$

A smooth septic curve $C$ of Type $21,(3,7)$ is given by an equation of the form

\begin{equation*}C:X^{7} + Y^{7}+X Z^{6}+{\beta _{3,0}} X^{4} Z^{3} =0,\end{equation*}

for some $\beta _{3,0}\in K^*$ , where $\sigma =\textrm {diag}(1,\zeta _{21}^3,\zeta _{21}^7)$ is an automorphism of maximal order $21$ . We claim to show that $\textrm {Aut}(C)=\langle \sigma \rangle$ .

The results in sections 4 and 5 assure that ${\textrm {Aut}}(C)=\langle \sigma \rangle$ as desired or that ${\textrm {Aut}}(C)$ is a subgroup of $\textrm {PBD}(2,1)$ . The latter case is absurd, since

- if $N$ acts on $X$ (respectively $Z$ ), then $N=1$ and $\Lambda (\sigma )=\textrm {diag}(\zeta _{21}^3,\zeta _{21}^7)$ (respectively $\textrm {diag}(\zeta _{21}^{-7},\zeta _{21}^{-4}))$ has order $21\gt 6$ . This violates Theorem3-(2).

- if $N$ acts on $Y$ , then $N=\langle \sigma ^3\rangle$ . Again $\Lambda (\sigma )=\textrm {diag}(\zeta _{21}^{-3},\zeta _{21}^4)$ has order $21\gt 6$ , which contradicts Theorem3-(2).

This proves our claim that $\textrm {Aut}(C)$ is cyclic of order $21$ for Type $21,\,(3,7)$ . On the other hand, the same argument applies to Type $9,\,(1,3)$ and Type $4,\,(1,2)$ . But two remarks are to be noted here.

• • First, always $N=1$ whenever ${\textrm {Aut}}(C)$ is a subgroup of $\textrm {PBD}(2,1)$ .

• • Second, for Type $4,\,(1,2)$ , if $\textrm {Aut}(C)\hookrightarrow \textrm {PBD}(2,1)$ , then $\langle \textrm {diag}(\zeta _4,\zeta _4^2)\rangle$ is a $\mathbb{Z}/4\mathbb{Z}$ subgroup of $\Lambda (\textrm {Aut}(C))$ . By applying Proposition3 and then Theorem3-(2), we deduce that $\Lambda ({\textrm {Aut}}(C))$ cannot exceed $\mathbb{Z}/4\mathbb{Z}$ , as asserted.

6.2. Type $7,(0,1)$

A smooth septic curve $C$ of Type $7, (0, 1)$ is given by an equation of the form

\begin{equation*}C:Z^{7} + {L_{7,Z}}=0,\end{equation*}

where $\sigma \,:\!=\,\textrm {diag}(1,1,\zeta _{7})$ is an automorphism of maximal order $7$ . We claim to show that $\textrm {Aut}(C)=\langle \sigma \rangle$ .

Since $\sigma \in \textrm {Aut}(C)$ is an homology of period $d=7$ with center $P=(0:0:1)$ and axis $\mathcal{L}:Z=0$ , then Proposition2 guarantees us that $P$ is an outer Galois point for $C$ . By Theorem [[43],Theorem 4’], we also can say that $P=(0:0:1)$ is the unique outer Galois point for $C$ because $C$ is not $K$ -equivalent to the Fermat curve $\mathcal{F}_7$ from our assumption that automorphisms of $C$ have orders $7$ or less. Hence, $\textrm {Aut}(C)$ should leave invariant the point $P=(0:0:1)$ and also the line $\mathcal{L}:Z=0$ are invariant under the action of ${\textrm {Aut}}(C)$ as a result of Theorem4-(2). In particular, the automorphisms of $C$ must be of the form

\begin{equation*}\left (\begin{array}{c@{\quad}c@{\quad}c} *&*&0\\ *&*&0\\ 0&0&1 \end{array}\right). \end{equation*}

The results in sections 4 and 5 tell us that we can think about $\textrm {Aut}(C)$ as in Theorem3, (1)–(3). We are going to tackle each of these situations.

Assume first that $C$ is a descendant of $\mathcal{F}_7$ with a bigger automorphism group than $\mathbb{Z}/7\mathbb{Z}=\langle \sigma \rangle$ . From Group structure of SmallGroup294,7(294,7) we can verify that any $\mathbb{Z}/7\mathbb{Z}$ generated by a homology inside $\textrm {Aut}(\mathcal{F}_7)$ is contained in a $(\mathbb{Z}/7\mathbb{Z})^2$ or a $\mathbb{Z}/14\mathbb{Z}$ . We reject $\mathbb{Z}/14\mathbb{Z}$ by the maximality of order $\sigma$ inside ${\textrm {Aut}}(C)$ . Therefore, $\textrm {Aut}(C)$ should have $(\mathbb{Z}/7\mathbb{Z})^2$ as a subgroup. But then $C$ would be the Fermat curve $\mathcal{F}_7$ by applying Corollary3, a contradiction. Thus $\textrm {Aut}(C)=\langle \sigma \rangle$ in this situation.

Otherwise, we can suppose that $\textrm {Aut}(C)$ satisfies a short exact sequence

\begin{equation*}1\rightarrow N=\langle \sigma \rangle \rightarrow {\textrm {Aut}}(C)\rightarrow \Lambda (\textrm {Aut}(C))\rightarrow 1,\end{equation*}

where $\Lambda (\textrm {Aut}(C))$ equals $\mathbb{Z}/m\mathbb{Z}$ for some $m \leq 6$ , ${\textrm {D}}_{2m}$ for some $m\in \{1,5\}$ , $\textrm {A}_4,\,\textrm {A}_5$ or ${\textrm {S}}_4$ . Unless $\Lambda (\textrm {Aut}(C))=1$ , $C$ would have an automorphism $\tau$ of order $m=2,3$ or $5$ . So $\sigma \tau \in \textrm {Aut}(C)$ is an element of order $7m\gt 7$ , a contradiction. Therefore, it must be the case that $\textrm {Aut}(C)=\langle \sigma \rangle$ .

This proves the claim.

6.3. Types $6, (a,b)$

Suppose that $C$ is a smooth plane septic curve of Type $6, (a,b)$ with $(a,b)=(1,2)$ or $(2,3)$ as in Table 2, and let $\sigma =\textrm {diag}(1,\zeta _6^a,\zeta _6^b)$ be an automorphism of maximal order $6$ .

Table 2. Cyclic subgroups and defining equations

Clearly, $C$ is not a descendant of the Fermat curve $\mathcal{F}_7$ or the Klein curve $\mathcal{K}_6$ since neither $\mathcal{F}_7$ nor $\mathcal{K}_7$ admits automorphisms of order $6$ . Moreover, $\textrm {Aut}(C)$ cannot be one of the finite primitive subgroups in ${\textrm {PGL}}_3(K)$ , see section 4 for details. On the other hand, if $\textrm {Aut}(C)$ satisfies Theorem3-(2), then $N=1$ and $\Lambda (\sigma )$ would be an element of order $6$ in ${\textrm {PGL}}_2(K)$ . Consequently, $\Lambda (\textrm {Aut}(C))=\mathbb{Z}/6\mathbb{Z}$ , so $\textrm {Aut}(C)=\langle \sigma \rangle$ as claimed.

6.4. Type $6,(0,1)$

A smooth septic curve $C$ of Type $6,(0,1)$ is given by an equation of the form

\begin{equation*}C: Z^{6} Y+L_{7,Z}=0 \end{equation*}

where $\sigma \,:\!=\,\textrm {diag}(1,1,\zeta _{6})$ is an automorphism of maximal order $6$ . Again, we claim to show that $\textrm {Aut}(C)=\langle \sigma \rangle$ .

In this case, $\textrm {Aut}(C)$ contains a homology $\sigma$ of period $d-1=6$ with center $P=(0:0:1)$ . Then by Proposition2 we have that $P=(0:0:1)$ is an inner Galois point for $C$ . Moreover, by [[43],Theorem 4, Proposition5], we ensure that $P=(0:0:1)$ is the unique inner Galois point for $C$ . Thus, it must be fixed by $\textrm {Aut}(C)$ , which in turn implies that $\textrm {Aut}(C)$ is cyclic as it fixes a point on $C$ . Finally, we deduce that $\textrm {Aut}(C)$ is generated by $\sigma$ as desired as the order of $\sigma$ is maximal.

6.5. Type $3,(0,1)$

Let $C$ be a smooth plane septic curve of Type $3,(0,1)$ , that is, $\sigma =\textrm {diag}(1,1,\zeta _3)$ is a homology of maximal order $3$ in $\textrm {Aut}(C)$ .

Neither $\textrm {Aut}(\mathcal{F}_7)$ nor $\textrm {Aut}(\mathcal{K}_7)$ has homologies of period $3$ , hence $C$ is never a descendant of $\mathcal{F}_7$ or $\mathcal{K}_7$ . On the other hand, if we think about $\textrm {Aut}(C)$ as in Theorem3-(2), we must have $N=1$ and $\Lambda (\textrm {Aut}(C))=\mathbb{Z}/3\mathbb{Z}$ . Otherwise, $\textrm {Aut}(C)$ would contain a $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$ , which contradicts Proposition3, or it would have elements of order $\gt 3$ , which contradicts the maximality of order $\sigma$ . Thus, we are left with $\textrm {Aut}(C)=\langle \sigma \rangle$ as we wanted to show.

6.6. Type $2, (0,1)$

The automorphism group of any smooth plane septic curve $C$ of Type $2,\,(0,1)$ is always cyclic of order $2$ . To see this, we first note that $C$ is not a descendant of $\mathcal{K}_7$ as $2\nmid |\textrm {Aut}(\mathcal{K}_7)|$ . On the other hand, if $C$ is a descendant of $\mathcal{F}_7$ with bigger automorphism group than $\mathbb{Z}/2\mathbb{Z}$ , then the Group structure of SmallGroup(294,7) assures that $\textrm {Aut}(C)$ would contain an element of order $3$ or $7$ , which contradicts the assumption that $\sigma \,:\!=\,\textrm {diag}(1,1,-1)\in \textrm {Aut}(C)$ is of maximal order $2$ . Lastly, if $\textrm {Aut}(C)$ is as Theorem3-(2), then it should be the case that $N=1$ and $\Lambda (\textrm {Aut}(C))=\mathbb{Z}/2\mathbb{Z}$ . For otherwise, $\textrm {Aut}(C)$ would contain a $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$ , which contradicts Proposition3, or it would have elements of order $\gt 2$ , which contradicts the maximality of order $\sigma$ .

Table 3. $\textrm {Aut}(C)$ for very large types $m, (a,b)$

7. When $ \textbf{Aut}(C)$ is not necessarily cyclic

Throughout this section, the full description of the automorphism groups of smooth plane septic curves of Type $14, (2,7)$ , $7, (1,2)$ , $7, (1,3)$ , $5, (1,4)$ , or $3, (1,2)$ will be investigated.

7.1. Type $14,(2,7)$

A smooth plane septic curve $C$ of Type $14,(2,7)$ is given by an equation of the form

\begin{equation*}C:X^{7} + Y^{7}+X Z^{6}+ {\beta _{2,0}}X^{5} Z^{2} + {\beta _{4,0}}X^{3} Z^{4}=0,\end{equation*}

for some $\beta _{2,0}, \beta _{4,0}\in K^*$ , where $\sigma \,:\!=\,\textrm {diag}(1,\zeta _{14}^2,-1)$ is an automorphism of maximal order $14$ .

Clearly $C$ cannot be a descendant of the Klein curve $\mathcal{K}_7$ as $14\nmid |\textrm {Aut}(\mathcal{K}_7)|$ . On the other hand, $\Lambda (\sigma )$ has order $\geq 7$ , so $\textrm {Aut}(C)$ does not appear as in Theorem3-(2). From this, we can see that either $\textrm {Aut}(C)=\langle \sigma \rangle$ or $C$ is a descendant of the Fermat curve $\mathcal{F}_7$ with a bigger automorphism group than $\mathbb{Z}/14\mathbb{Z}$ . Now, the Group structure of SmallGroup(294,7) tells us that for $C$ to be a descendant of $\mathcal{F}_7$ such that $\langle \sigma \rangle \subset \textrm {Aut}(C)$ it is necessary that $\textrm {Aut}(C)$ contains another homology $\sigma '$ of order $7$ that commutes with $\sigma ^2$ . In particular, $C$ is $K$ -isomorphic to the Fermat curve itself as a result of Corollary3.

Thus we conclude:

Proposition 7. If $C$ is a smooth septic curve of Type $14, (2,7)$ , then $\textrm {Aut}(C)$ equals $\mathbb{Z}/14\mathbb{Z}$ or $C$ is $K$ -isomorphic to the Fermat curve $\mathcal{F}_7$ .

It then remains to specify the conditions on the parameters $\beta _{2,0}$ and $\beta _{4,0}$ so that $^{\phi }C$ becomes $X^7+Y^7+Z^7$ for some change of variables $\phi \in {\textrm {PGL}}_3(K)$ . Since any $\mathbb{Z}/14\mathbb{Z}$ inside $\textrm {Aut}(\mathcal{F}_7)$ is $\textrm {Aut}(\mathcal{F}_7)$ -conjugated to $\langle [X:\zeta _7Z:Y]\rangle$ , then we can assume that $\phi ^{-1}{\sigma }\phi =[X:\zeta _7^{s+1}Z:\zeta _7^sY]$ for some $s\in \{0,1,2,4,5,6\}$ . Using direct calculations, we obtain that

\begin{equation*} \phi =\left ( \begin{array}{ccc} 0 & \zeta _7^3b & b \\ 1 & 0 & 0 \\ 0 & -\zeta _7^3c & c \\ \end{array} \right )\text{and}\,\,\,s=2. \end{equation*}

The transformed equation $^{\phi }C$ has the form:

\begin{equation*} X^7+A(Y^7+Z^7)+BYZ(\zeta _7Y^5+Z^5)+CY^2Z^2(Y^3+\zeta _7^5Z^3)+DY^3Z^3(Y+\zeta _7^{-3}Z)=0, \end{equation*}

where

\begin{eqnarray*} A&:=&b \left (b^6+\beta _{20} b^4 c^2+\beta _{40} b^2 c^4+c^6\right ),\\ B&\,:\!=\,&b \zeta _7^3 \left (7 b^6+3 \beta _{20} b^4 c^2-\beta _{40} b^2 c^4-5 c^6\right ),\\ C&\,:\!=\,&b \zeta _7 \left (21 b^6+\beta _{20} b^4 c^2-3 \beta _{40} b^2 c^4+9 c^6\right ),\\ D&\,:\!=\,&b \zeta _7 ^5 \left (35 b^6-5 \beta _{20} b^4 c^2+3 \beta _{40} b^2 c^4-5 c^6\right ). \end{eqnarray*}

Eliminating $a$ and $b$ from the system of equations $A=1,\,B=C=D=0$ , we get $\beta _{20}=\frac {3}{25}\beta _{40}$ such that $\beta _{40}^3=875$ .

Summing up, we can say that

Corollary 6. Let $C$ be a smooth plane septic curve of Type $14,(2,7)$ as above. Then, $\textrm {Aut}(C)$ is always cyclic of order $14$ , generated by $\sigma =\textrm {diag}(1,\zeta _{14}^2,-1)$ , unless $\beta _{20}=\frac {3}{25}\beta _{40}$ such that $\beta _{40}^3=875$ . In this situation, $C$ is $K$ -isomorphic to the Fermat curve $\mathcal{F}_7$ .

7.2. Type $7,(1,2)$

A smooth plane septic curve $C$ of Type $7,(1,2)$ is given by an equation of the form

\begin{equation*}C:X^{7}+Y^{7}+ Z^{7}+{{\beta _{4,1}}} X^{3}Y Z^{3}+{{\beta _{5,3}}} X^{2} Y^{3} Z^{2}+{{\beta _{6,5}}} X Y^{5} Z=0,\end{equation*}

where $\sigma \,:\!=\,\textrm {diag}(1,\zeta _{7},\zeta _{7}^2)$ is an automorphism of maximal order $7$ .

Obviously, $\textrm {Aut}(C)$ always contains the dihedral group ${\textrm {D}}_{14}$ generated by $\sigma$ and $\tau \,:\!=\,[Z:Y:X]$ . Thus, $\textrm {Aut}(C)$ is not cyclic, and $C$ is never a descendant of the Klein curve $\mathcal{K}_7$ . On the other hand, $\Lambda (\sigma )=\textrm {diag}(\zeta _7^{-1},\zeta _7)$ and $\Lambda (\tau )=[Z:X]$ generate ${\textrm {D}}_{14}$ inside ${\textrm {PGL}}_2(K)$ . So if $\textrm {Aut}(C)$ is as in Theorem3-(2), then $\Lambda (\sigma )={\textrm {D}}_{2m}$ with $m=7$ and $N=1$ , since none of the other options for $\Lambda (\textrm {Aut}(C))$ has ${\textrm {D}}_{14}$ as a subgroup and elements of orders $\leq 7$ .

Finally, assume that $C$ is a descendant of the Fermat curve $\mathcal{F}_7$ . This implies that $\textrm {Aut}(C)$ is exactly ${\textrm {D}}_{14}$ . For otherwise, $\textrm {Aut}(C)$ would contain a $\mathbb{Z}/7\mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}$ from the Group structure of SmallGroup(294,7), which means by Corollary3 that $C$ is $K$ -isomorphic to $\mathcal{F}_7$ contradicting the fact that automorphisms of $C$ have orders at most $7$ .

As a result, we deduce that

Corollary 7. For any smooth plane septic curve $C$ of Type $7, (1,2)$ as above, we have that $\textrm {Aut}(C)=\langle \textrm {diag}(1,\zeta _7,\zeta _7^2), [Z:Y:X]\rangle ={\textrm {D}}_{14}$ .

7.3. Type $5, (1,4)$

Now assume that $C$ is a smooth septic curve of Type $5, (1,4)$ . Then, $C$ is defined by an equation of the form

\begin{equation*}C:X^{7} +Y^{6} Z+Y Z^{6} + {\beta _{2,1}}X^{5} Y Z+ {\beta _{4,2}}X^{3} Y^{2} Z^{2}+{\beta _{6,3}} X Y^{3} Z^{3}+X^{2} \left ({\beta _{5,0}} Z^{5}+{\beta _{5,5}}Y^{5}\right )=0,\end{equation*}

where $\sigma \,:\!=\,\textrm {diag}(1,\zeta _{5},\zeta _{5}^{-1})$ is an automorphism of maximal order $5$ .

Since $5$ does not divide $|\textrm {Aut}(\mathcal{F}_7)|$ or $|\textrm {Aut}(\mathcal{K}_7)|$ , $C$ cannot be a descendant of $\mathcal{F}_7$ or $\mathcal{K}_7$ . Thus, it must be the case that $\textrm {Aut}(C)$ is as Theorem3-(2). More precisely, $N=1$ by the maximality of order $\sigma$ , and $\Lambda (\textrm {Aut}(C))=\mathbb{Z}/5\mathbb{Z},\,{\textrm {D}}_{10}$ or $\textrm {A}_5$ as it contains the element $\Lambda (\sigma )=\textrm {daig}(\zeta _5,\zeta _5^{-1})$ of order $5$ . Equivalently, $\textrm {Aut}(C)$ equals $\mathbb{Z}/5\mathbb{Z},\,{\textrm {D}}_{10}$ or $\textrm {A}_5$ . The latter case is absurd or $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$ would be a subgroup of automorphisms for $C$ , which violates Proposition3. For $\textrm {Aut}(C)={\textrm {D}}_{10}$ , the curve $C$ should have an extra involution, say $\tau$ , such that $\tau \sigma \tau =\sigma ^{-1}$ . Solving this equation in ${\textrm {PGL}}_3(K)$ leads to $\tau =[X:aZ:a^{-1}Y],\,[aZ:Y:a^{-1}X]$ or $[aY:a^{-1}X:Z]$ for some $a\in K^*$ . The core of $C$ only allows $\tau =[X:aZ:a^{-1}Y]$ to be an automorphism under the assumptions that $a^5=1$ and $\beta _{5,0}=\beta _{5,5}$ .

As a result, we deduce that:

Corollary 8. For any smooth plane septic curve $C$ of Type $5, (1,4)$ as above, $\textrm {Aut}(C)$ is always cyclic generated by $\sigma =\textrm {diag}(1,\zeta _5,\zeta _5^{-1})$ unless $\beta _{5,0}=\beta _{5,5}$ . In this case, it becomes the ${\textrm {D}}_{10}$ generated by $\sigma$ and $\tau =[X:Z:Y]$ .

7.4. Type $7,(1,3)$

A smooth plane septic curve $C$ of Type $7,(1,3)$ is given by an equation of the form

\begin{equation*}C:X^{7} + Y^{7} + Z^{7}+{\beta _{3,1}}X^{4} Y Z^{2} + {\beta _{5,4}}X^{2} Y^{4} Z+ {\beta _{6,2}}X Y^{2} Z^{4}=0,\end{equation*}

where $\sigma \,:\!=\,\textrm {diag}(1,\zeta _{7},\zeta _{7}^3)$ is an automorphism of maximal order $7$ .

If $\textrm {Aut}(C)$ is cyclic, then it equals $\langle \sigma \rangle$ by the maximality of order $\sigma$ inside $\textrm {Aut}(C)$ . So from now on we may assume that $\textrm {Aut}(C)$ is not cyclic.

Again $7$ does not divide $\textrm {Aut}(\mathcal{K}_7)=93$ , so $C$ is not a descendant of $\mathcal{K}_7$ . On the other hand, $\Lambda (\sigma )$ always has order $7$ inside ${\textrm {PGL}}_2(K)$ , which means that $\textrm {Aut}(C)$ is ${\textrm {D}}_{14}$ if it behaves as in Theorem3-(2), since $N=1$ in this situation. Therefore, $C$ must have an extra involution $\tau$ such that $\tau \sigma \tau =\sigma ^{-1}$ . One can easily verify that the last equation is inconsistent in ${\textrm {PGL}}_{3}(K)$ , from which we discard this scenario.

Finally, assume that $C$ is a descendant of $\mathcal{F}_7$ with a noncyclic automorphism group. The assumption on $7$ being the maximal order of the elements of $\textrm {Aut}(C)$ and the fact that $\mathbb{Z}/7\mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}$ is never a subgroup of automorphisms (Proposition3) imply that $\textrm {Aut}(C)$ equals ${\textrm {D}}_{14}$ or $\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ , see the Group structure of SmallGroup(294,7). As before, ${\textrm {D}}_{14}$ is absurd. To get $\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ , we should be able to find an automorphism $\sigma '$ for $C$ of order $3$ such that $\sigma '\sigma (\sigma ')^{-1}=\sigma ^4$ . Direct calculations in ${\textrm {PGL}}_3(K)$ assure that $\sigma '=\left ( \begin{array}{ccc} 0 & 0 & 1 \\ a & 0 & 0 \\ 0 & b & 0 \\ \end{array} \right )$ for some $a,\,b \in K^*$ . Imposing $\sigma '\in \textrm {Aut}(C)$ we obtain that $a^7=b^7=1,\,\beta _{3,1}=\beta _{5,4}a^4b,\,\beta _{6,2}=\beta _{5,4}a^5b^3$ , in particular, the defining equation for $C$ becomes $K$ -isomorphic via $\phi =\textrm {diag}(a^2b^2,a^5b^4,1)$ to the curve

\begin{equation*}C^{'}: X^7+Y^7+Z^7+a^3 b^6 \beta _{5,4} \left (X^4 Y Z^2+X^2 Y^4 Z+X Y^2 Z^4\right )\end{equation*}

with $\textrm {Aut}(C')=\langle \sigma, \,[Z:X:Y]\rangle =\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ .

As a result, we deduce that

Corollary 9. For any smooth plane septic curve $C$ of Type $7, (1,3)$ as above, we classify $\textrm {Aut}(C)$ as follows.

1. (1) If $\beta _{3,1}=\beta _{5,4}a^4b,\,\beta _{6,2}=\beta _{5,4}a^5b^3$ for some $a,b,\,\beta _{5,4}\in K^*$ such that $a^7=b^7=1$ , then $C$ is $K$ -isomorphic to

   \begin{equation*} C': X^7+Y^7+Z^7+a^3 b^6 \beta _{5,4} \left (X^4 Y Z^2+X^2 Y^4 Z+X Y^2 Z^4\right )=0,\end{equation*}
   where $\textrm {Aut}(C')$ equals $\mathbb{Z}/7\mathbb{Z}\rtimes \mathbb{Z}/3\mathbb{Z}$ , generated by $\textrm {diag}(1,\zeta _7,\zeta _7^{3})$ and $[Z:X:Y]$ .

2. (2) Otherwise, $\textrm {Aut}(C)$ equals $\mathbb{Z}/7\mathbb{Z}$ generated by $\textrm {diag}(1,\zeta _7,\zeta _7^3)$ .

7.5. Type $3,(1,2)$

A smooth plane septic curve $C$ of Type $3,(1,2)$ is given by an equation of the form

\begin{equation*}C:X^{7}+X Z^{6}+X Y^{6}+{\beta _{2,1}} X^{5} Y Z+{\beta _{4,2}} X^{3} Y^{2} Z^{2}+{\beta _{6,3}} X Y^{3} Z^{3}+{\beta _{7,2}} Y^{2} Z^{5}\end{equation*}

\begin{equation*}{+\beta _{7,5}} Y^{5} Z^{2}+X^{4} {\left ({\beta _{3,0}}Z^{3}+{\beta _{3,3}}Y^{3} \right )}+X^{2}YZ{\left ({\beta _{5,1}}Z^3+{\beta _{5,4}}Y^3 \right )}=0,\end{equation*}

where $\sigma \,:\!=\,\textrm {diag}(1,\zeta _{3},\zeta _{3}^{-1})$ is an automorphism of maximal order $3$ .

Suppose first that $C$ is a descendant of $\mathcal{K}_7$ . Then, $\textrm {Aut}(C)=\mathbb{Z}/3\mathbb{Z}$ generated by $\sigma$ or $C$ would be $K$ -isomorphic to the $\mathcal{K}_7$ , see the Group structure of SmallGroup(93,1). We reject the latter case as $\sigma$ is of maximal order in $\textrm {Aut}(C)$ . Hence, $\textrm {Aut}(C)=\langle \sigma \rangle$ in this case.

Second, assume that $C$ is a descendant of $\mathcal{F}_7$ . Then, $\textrm {Aut}(C)=\mathbb{Z}/3\mathbb{Z}$ generated by $\sigma$ or $\textrm {Aut}(C)={\textrm {S}}_3$ , see the Group structure of SmallGroup(294,7). For $\textrm {Aut}(C)$ to be an ${\textrm {S}}_3$ , $C$ should admit an extra involution $\tau$ such that $\tau \sigma \tau =\sigma ^{-1}$ . Similarly as above (Type $5, (1,4)$ ), we can reduce to $\tau =[X:aZ:a^{-1}Y]$ such that $a^6=1$ (hence, $a^3=\pm 1$ ), $\beta _{7,5}=\pm \beta _{7,2},\,\beta _{3,3}=\pm \beta _{3,0}$ , and $\beta _{5,4}=\pm \beta _{5,1}$ .

Thus $C$ is $K$ -isomorphic, via $\phi =\textrm {diag}(1,a,1)$ , to

\begin{equation*}C':X^{7}+X Z^{6}+X Y^{6}+\beta _{2,1}a X^{5} Y Z+\beta _{4,2}a^2 X^{3} Y^{2} Z^{2}+\beta _{6,3}a^3 X Y^{3} Z^{3}+\beta _{7,2}a^2Y^2Z^2(Y^{3}+Z^3)\end{equation*}

\begin{equation*}+\beta _{3,0}X^{4}(Y^{3}+Z^3)+\beta _{5,1}aX^{2}YZ(Y^3+ Z^3)=0,\end{equation*}

with $\textrm {Aut}(C')=\langle \sigma, [X:Z:Y]\rangle ={\textrm {S}}_3$ .

Finally, assume that $\textrm {Aut}(C)$ appears as in Theorem3-(2). That is, $N=1$ from the core of $C$ and $\Lambda (\textrm {Aut}(C))$ always contains $\Lambda (\sigma )$ as an element of order $3$ . Applying Proposition3 would eliminate $\,\textrm {A}_4,\,\textrm {A}_5$ , and ${\textrm {S}}_4$ from the list, in particular, $\textrm {Aut}(C)$ equals $\mathbb{Z}/3\mathbb{Z}$ or ${\textrm {S}}_3.$ We treat the case $\textrm {Aut}(C)={\textrm {S}}_3$ as before.

As a result, we deduce that

Proposition 8. For any smooth plane septic curve $C$ of Type $3, (1,2)$ as above, we classify $\textrm {Aut}(C)$ as follows.

1. (1) If $\beta _{7,5}=\pm \beta _{7,2},\,\beta _{3,3}=\pm \beta _{3,0}$ and $\beta _{5,4}=\pm \beta _{5,1}$ , then $C$ is $K$ -isomorphic to

   \begin{equation*}C':X^{7}+X Z^{6}+X Y^{6}+\beta _{2,1}aX^{5} Y Z+\beta _{4,2}a^2 X^{3} Y^{2} Z^{2}+\beta _{6,3}a^3 X Y^{3} Z^{3}+\beta _{7,2}a^2Y^2Z^2(Y^{3}+Z^3)\end{equation*}
   \begin{equation*}+\beta _{3,0}X^{4}(Y^{3}+Z^3)+\beta _{5,1}aX^{2}YZ(Y^3+ Z^3)=0,\end{equation*}
   for some $a^6=1$ . In that case, $\textrm {Aut}(C')=\langle \textrm {diag}(1,\zeta _3\zeta _3^{-1}),[X:Z:Y]\rangle ={\textrm {S}}_3$ .

2. (2) Otherwise, $\textrm {Aut}(C)$ equals $\mathbb{Z}/3\mathbb{Z}$ generated by $\textrm {diag}(1,\zeta _3,\zeta _3^{-1})$ .

8. Determining the possible signatures of smooth plane septics

In this section, we explicitly evaluate the possible signatures of the smooth plane septic curves studied above and connect them to the data available on the $L$ -Functions and Modular Forms Database (LMFDB) [34]. The LMFDB (https://www.lmfdb.org/) is an ever-expanding valuable resource for studying fundamental objects in number theory, algebraic geometry, and related fields. Of interest to us is the section on higher genus curves, which currently contains all groups $G$ acting as automorphisms of curves $X$ over $\mathbb{C}$ of genus 2 to 15 such that $X/G$ has genus 0 (as well as genus 2 through 4 with quotient genus greater than 0). Attached to each such curve is a signature (whose definition is recalled below) and by computing all the possible signatures of plane septics, we obtain a criterion that can be used to exclude whether a given genus 15 curve in the database can be realized as a smooth plane septic.

We now recall the definition and basic properties of the signature of a curve (see [13] for additional background and details). Consider $ C$ , a compact Riemann surface with genus $ g \geq 2$ , and let $ G = {\textrm {Aut}}(C)$ be its automorphism group. Define the natural mapping $ \phi : C \to Y = C/G$ , where $ Y$ is the orbit space of $ C$ under the action of $ G$ . This map $ \phi$ assigns each point $ x \in C$ to its orbit under $ G$ . Let $ g_0$ denote the genus of the quotient curve $ Y$ . The map $ \phi$ may branch at several points in $ Y$ , forming a set $ B \subset Y$ of size $ r$ . If we denote the preimage of these points as $ \phi ^{-1}(B) \subset C$ , then the map from $ C - \phi ^{-1}(B)$ to $ Y - B$ is a degree $ d$ covering for some positive integer $ d$ .

Choose a base point $ y_0 \in Y - B$ . The preimage $ \phi ^{-1}(y_0)$ consists of $ d = |G|$ points in $ C - \phi ^{-1}(B)$ , denoted $ \phi ^{-1}(y_0) = \{x_1, \ldots, x_d\} \subset X$ . Consider a loop starting at $ y_0$ that winds once around a branch point in $ B$ . For each $ x_i$ in $ \phi ^{-1}(y_0)$ , this loop uniquely lifts to a path in $ C$ that starts at $ x_i$ and ends at some $ x_j \in \phi ^{-1}(y_0)$ . This process defines a permutation on the $ d$ elements of $ \phi ^{-1}(y_0)$ , mapping $ i$ to the index of the endpoint $ x_j$ of the lifted path starting at $ x_i$ .

These $ r$ permutations induce a map $ \rho : \pi _1(Y - B, y_0) \to S_d$ , where $ S_d$ is the symmetric group on $ d$ elements and $ \pi _1(Y - B, y_0)$ denotes the fundamental group. Its standard generators are obtained by considering the homotopy classes of loops indexed by $ b \in B$ that begin at $ y_0$ and make a counterclockwise loop around $ b$ without enclosing any other elements of $ B$ . The order of each permutation corresponding to a loop around an element of $ B$ is denoted $ m_i$ for $ 1 \leq i \leq r$ .

Let $ \mathbb{H} = \{ z \in \mathbb{C} : \text{Im}(z) \gt 0 \}$ be the complex upper half-plane. It is well known that it has automorphism group $\text{PSL}(2, \mathbb{R})$ , and that $\mathbb{H}$ is a universal cover for any compact Riemann surface of genus $\geq 2$ . A Fuchsian group $ \Gamma$ is a discrete subgroup of $\text{PSL}(2, \mathbb{R})$ . Such a group is well known (see [[13],Theorem 3.2] for instance) to have a presentation as

\begin{equation*} \Gamma =\langle \alpha _1, \beta _1, \cdots, \alpha _{g_0}, \beta _{g_0},\gamma _{1}, \cdots, \gamma _{r} : \prod _{i=1}^{g_0}[\alpha _{i},\beta _{i}] \prod _{j=1}^{r} \gamma _{j}=1, \,\, \gamma _{j}^{m_{j}}=1\rangle \end{equation*}

(where $[\alpha _{i},\beta _{i}]$ is the commutator of $\alpha _{i}$ and $\beta _i$ ). The signature of $ \Gamma$ is the tuple $[g_0; m_1, m_2, \ldots, m_n]$ . In order to compute the signature of a smooth plane curve $ C$ of genus $ g \geq 2$ with automorphism group $ G$ , we implement the following steps (see [[13], Chapter 3] for more details):

1. 1. Determine the points $ p \in C$ for which the stabilizer subgroup $ G_{p}$ is non-trivial and compute the order of $G_p$ . For such points, $ \phi (p)$ is a branch point of the natural projection $ \phi : C \to C/ G$ .

2. 2. Compute the genus of the quotient curve $ C / G$ using the Riemann–Hurwitz formula:

   (A) \begin{align} 2 g_{C} - 2 = |G|\left (2 g_{C/ G} - 2 \right )+ \sum _{p \in C} (|G_{p}| - 1). \end{align}

3. 3. By rewriting the Riemann–Hurwitz formula in the form:

   (B) \begin{align} 2g_{C} - 2 = |G| \left ( 2g_{C/G} - 2 \right ) + |G| \sum _{i=1}^{r} \left ( 1 - \frac {1}{m_i} \right ) \end{align}
   (where $ r$ is the number of branch points), we obtain the signature $ [g_{C /G}; m_1, \ldots, m_r]$ of the Fuchsian group $ \Gamma$ such that $ C / G \cong \mathbb{H} / \Gamma$ .

Performing those steps on all the curves from Table 1, we obtain the following result:

Proposition 9. The signature of every smooth plane septic curve is outlined in Table 4 .

Example 1. In the following example, we apply the steps outlined before Proposition 9 to the curve of type $5, (1,4)$ .

\begin{equation*}C:X^{7} +Y^{6} Z+Y Z^{6} + {\beta _{2,1}}X^{5} Y Z+ {\beta _{4,2}}X^{3} Y^{2} Z^{2}+{\beta _{6,3}} X Y^{3} Z^{3}+X^{2} \left ({\beta _{5,0}} Z^{5}{\beta _{5,5}}Y^{5}\right )=0 \end{equation*}

The automorphism group of the curve $C$ is $\textrm {Aut}(C)$ is generated by the non-homology $\textrm {diag}(1,\zeta _5,\zeta _5^{-1})$ . Thus, the fixed points are precisely the three reference points, namely $(1:0:0), (0:1:0)$ and $(0:0:1)$ . However, only $(0:1:0)$ and $(0:0:1)$ lie on $C$ . Substituting in (A) yields

\begin{equation*}2 (15) - 2 = 5 (2 g_{C/G} - 2) + 5 - 1 + 5 - 1,\end{equation*}

hence $g_{C/G} = 3$ . Using (B) , we get

\begin{equation*} 2(g-1)=5(2g_{C/G}-2)+5 \sum _{i=1}^2(1-\frac {1}{5}). \end{equation*}

Consequently, the curve $C$ has signature $[3;\,5,5]$ .

In the case where the genus of a curve $ C$ is $ g = 15$ , the LMFDB catalogs all the various curves and their signatures. Utilizing the results above, we can deduce that those curves whose automorphism group or signature do not appear in Table 4 are not smooth plane septics. For instance, if the automorphism group $ {\textrm {Aut}}(C)$ is isomorphic to $ \mathbb{Z}/18\mathbb{Z}$ , then the signature of $C$ has to be one of the following: $ [ 0;\, 6, 6, 18, 18 ]$ , $ [ 0;\, 6, 9, 9, 18 ]$ , and $ [ 0;\, 2, 2, 3, 18, 18 ]$ . By Proposition9, we deduce that curves with signatures $ [ 0;\, 6, 9, 9, 18 ]$ or $ [ 0;\, 2, 2, 3, 18, 18 ]$ are not smooth plane septic curves.

We conclude with Table 5, which identifies the subset of signatures of genus $0$ quotients of smooth plane septics in comparison to all the LMFDB signatures of genus $0$ quotient curves of genus $15$ .

Table 4. Automorphism groups and signature

Table 5. Automorphism groups and signatures of genus $15$ curves with genus $0$ quotients