Hostname: page-component-5b777bbd6c-sbgtn Total loading time: 0 Render date: 2025-06-21T15:29:17.470Z Has data issue: false hasContentIssue false
  • English
  • Français

Percolation in lattice k-neighbor graphs

Part of: Special processes Equilibrium statistical mechanics

Published online by Cambridge University Press:  03 June 2025

Benedikt Jahnel Open the ORCID record for Benedikt Jahnel [Opens in a new window] ,
Jonas Köppl Open the ORCID record for Jonas Köppl [Opens in a new window] ,
Bas Lodewijks Open the ORCID record for Bas Lodewijks [Opens in a new window]  and
András Tóbiás Open the ORCID record for András Tóbiás [Opens in a new window]
Benedikt Jahnel*
Affiliation:
Technische Universität Braunschweig
Jonas Köppl*
Affiliation:
Weierstrass Institute for Applied Analysis and Stochastics
Bas Lodewijks*
Affiliation:
Universität Augsburg
András Tóbiás*
Affiliation:
Budapest University of Technology and Economics, and Alfréd Rényi Institute of Mathematics
*
*Postal address: Institut für Mathematische Stochastik, Technische Universität Braunschweig Universitätsplatz 2, 38106 Braunschweig, Germany, and Weierstrass Institute for Applied Analysis and Stochastics, Mohrenstraße 39, 10117 Berlin, Germany. Email: benedikt.jahnel@tu-braunschweig.de
**Postal address: Weierstrass Institute for Applied Analysis and Stochastics, Mohrenstraße 39, 10117 Berlin, Germany. Email: jonas.koeppl@wias-berlin.de
***Postal address: Mathematical Department, Universität Augsburg, Universitätsstraße 2, 86159 Augsburg, Germany. Email: bas.lodewijks@uni-a.de
****Postal address: Department of Computer Science and Information Theory, Budapest University of Technology and Economics, Műegyetem rkp. 3., H-1111 Budapest, Hungary, and HUN-REN Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13-15, H-1053 Budapest, Hungary. Email: tobias@cs.bme.hu
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a random graph obtained by connecting each point of 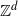$\mathbb{Z}^d$ independently and uniformly to a fixed number $1 \leq k \leq 2d$ of its nearest neighbors via a directed edge. We call this graph the directed k-neighbor graph. Two natural associated undirected graphs are the undirected and the bidirectional k-neighbor graph, where we connect two vertices by an undirected edge whenever there is a directed edge in the directed k-neighbor graph between the vertices in at least one, respectively precisely two, directions. For these graphs we study the question of percolation, i.e. the existence of an infinite self-avoiding path. Using different kinds of proof techniques for different classes of cases, we show that for $k=1$ even the undirected k-neighbor graph never percolates, while the directed k-neighbor graph percolates whenever 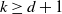$k \geq d+1$, 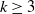$k \geq 3$, and 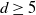$d \geq 5$, or 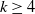$k \geq 4$ and $d=4$. We also show that the undirected 2-neighbor graph percolates for 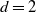$d=2$, the undirected 3-neighbor graph percolates for $d=3$, and we provide some positive and negative percolation results regarding the bidirectional graph as well. A heuristic argument for high dimensions indicates that this class of models is a natural discrete analogue of the k-nearest-neighbor graphs studied in continuum percolation, and our results support this interpretation.

Keywords

Lattice k-neighbor graphsdirected k-neighbor graphundirected k-neighbor graphbidirectional k-neighbor graph1-dependent percolationoriented percolationnegatively correlated percolation modelsconnective constantplanar dualitycoexistence of phases

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 82B43: Percolation
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 18
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amir, G., Heydenreich, M. and Hirsch, C. (2024). Planar reinforced k-out percolation. Preprint, arXiv:2407.12484.Google Scholar
Balister, P. and Bollobás, B. (2013). Percolation in the k-nearest neighbor graph. In Recent Results in Designs and Graphs: A Tribute to Lucia Gionfriddo, Quaderni di Matematica, eds. M. Buratti, C. Lindner, F. Mazzocca and N. Melone. Vol. 28, pp. 83–100.Google Scholar
Balister, P., Johnston, T., Savery, M. and Scott, A. (2025). Improved bounds for 1-independent percolation on $\mathbb{Z}^n$ . Electron. J. Prob. 30, 1–26.10.1214/25-EJP1341CrossRefGoogle Scholar
Coupier, D., Henry, B., Jahnel, B. and Köppl, J. (2024). The planar lattice two-neighbor graph percolates. Preprint, arXiv:2412.20781.Google Scholar
Cox, T. and Durrett, R. (1983). Oriented percolation in dimensions $d \geq 4$ : Bounds and asymptotic formulas. Math. Proc. Camb. Phil. Soc. 93, 151–162.10.1017/S0305004100060436CrossRefGoogle Scholar
Grimmett, G. (2006). The Random-Cluster Model. Springer, New York.10.1007/978-3-540-32891-9CrossRefGoogle Scholar
Häggström, O. and Meester, R. (1996). Nearest neighbor and hard sphere models in continuum percolation. Random Structures Algorithms 9, 295–315.10.1002/(SICI)1098-2418(199610)9:3<295::AID-RSA3>3.0.CO;2-S3.0.CO;2-S>CrossRefGoogle Scholar
Hara, T., Slade, G. and Sokal, A. D. (1993). New lower bounds on the self-avoiding-walk connective constant. J. Statist. Phys. 72, 479–517.10.1007/BF01048021CrossRefGoogle Scholar
Hirsch, C., Holmes, M. and Kleptsyn, V. (2021). Absence of warm percolation in the very strong reinforcement regime. Ann. Appl. Prob. 31, 199–217.10.1214/20-AAP1587CrossRefGoogle Scholar
Holmes, M. and Salisbury, T. S. (2014). Degenerate random environments. Random Structures Algorithms 45, 111–137.10.1002/rsa.20473CrossRefGoogle Scholar
Holmes, M. and Salisbury, T. S. (2016). Forward clusters for degenerate random environments. Combinatorics Prob. Comput. 25, 744–765.10.1017/S0963548316000158CrossRefGoogle Scholar
Holmes, M. and Salisbury, T. S. (2021). Phase transitions for degenerate random environments. Lat. Am. J. Prob. Math. Statist. 18, 707–725.10.30757/ALEA.v18-26CrossRefGoogle Scholar
Holmes, M. and Salisbury, T. S. (2021). A shape theorem for the orthant model. Ann. Prob. 49, 1237–1256.10.1214/20-AOP1476CrossRefGoogle Scholar
Holmes, M. and Salisbury, T. S. (2025). Percolation of terraces, and enhancements for the orthant model. Trans. Amer. Math. Soc. Ser. B 12, 237–275.10.1090/btran/220CrossRefGoogle Scholar
Jahnel, B. and Tóbiás, A. (2022). Absence of percolation in graphs based on stationary point processes with degrees bounded by two. Random Structures Algorithms 62, 240–255.10.1002/rsa.21084CrossRefGoogle Scholar
Lyons, R. and Peres, Y. (2017). Probability on Trees and Networks. Cambridge University Press.Google Scholar
Pönitz, A. and Tittmann, P. (2000). Improved upper bounds for self-avoiding walks in $\mathbb{Z}^d$ . Electron. J. Combinatorics 7, R21–R21.10.37236/1499CrossRefGoogle Scholar
Swart, J. (2017). A course in interacting particle systems 2017. Preprint, arXiv:1703.10007.Google Scholar