Hostname: page-component-5b777bbd6c-5mwv9 Total loading time: 0 Render date: 2025-06-21T07:36:27.361Z Has data issue: false hasContentIssue false
  • English
  • Français

Branching processes in nearly degenerate varying environment

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  10 May 2024

Péter Kevei  and
Kata Kubatovics
Péter Kevei*
Affiliation:
University of Szeged
Kata Kubatovics*
Affiliation:
University of Szeged
*
*Postal address: Bolyai Institute, University of Szeged, Aradi vértanúk tere 1, 6720 Szeged, Hungary.
*Postal address: Bolyai Institute, University of Szeged, Aradi vértanúk tere 1, 6720 Szeged, Hungary.
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate branching processes in varying environment, for which 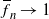$\overline{f}_n \to 1$ and 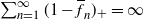$\sum_{n=1}^\infty (1-\overline{f}_n)_+ = \infty$, 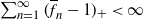$\sum_{n=1}^\infty (\overline{f}_n - 1)_+ < \infty$, where 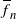$\overline{f}_n$ stands for the offspring mean in generation n. Since subcritical regimes dominate, such processes die out almost surely, therefore to obtain a nontrivial limit we consider two scenarios: conditioning on nonextinction, and adding immigration. In both cases we show that the process converges in distribution without normalization to a nondegenerate compound-Poisson limit law. The proofs rely on the shape function technique, worked out by Kersting (2020).

Keywords

Branching process in varying environmentYaglom-type limit theoremimmigrationshape function

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60F05: Central limit and other weak theorems
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 4 , December 2024 , pp. 1107 - 1126
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Athreya, K. B. and Ney, P. E. (1972). Branching Processes. Springer, New York.CrossRefGoogle Scholar
Bhattacharya, N. and Perlman, M. (2017). Time-inhomogeneous branching processes conditioned on non-extinction. Preprint, arXiv:1703.00337.Google Scholar
Cardona-Tobón, N. and Palau, S. (2021). Yaglom’s limit for critical Galton–Watson processes in varying environment: A probabilistic approach. Bernoulli 27, 1643–1665.CrossRefGoogle Scholar
Church, J. D. (1971). On infinite composition products of probability generating functions. Z. Wahrscheinlichkeitsth. 19, 243–256.CrossRefGoogle Scholar
Dolgopyat, D., Hebbar, P., Koralov, L. and Perlman, M. (2018). Multi-type branching processes with time-dependent branching rates. J. Appl. Prob. 55, 701–727.CrossRefGoogle Scholar
Fearn, D. H. (1972). Galton–Watson processes with generation dependence. In Proc. Sixth Berkeley Symp. Math. Statist. Prob., Vol. IV. University of California Press, Berkeley, CA, pp. 159–172.Google Scholar
Feller, W. (1968). An Introduction to Probability Theory and its Applications, Vol. I, 3rd edn. John Wiley, New York.Google Scholar
Gao, Z. and Zhang, Y. (2015). Limit theorems for a Galton–Watson process with immigration in varying environments. Bull. Malays. Math. Sci. Soc. 38, 1551–1573.CrossRefGoogle Scholar
González, M., Kersting, G., Minuesa, C. and del Puerto, I. (2019). Branching processes in varying environment with generation-dependent immigration. Stoch. Models 35, 148–166.CrossRefGoogle Scholar
Graham, R. L., Knuth, D. E. and Patashnik, O. (1994). Concrete Mathematics, 2nd edn. Addison-Wesley, Reading, MA.Google Scholar
Györfi, L., Ispány, M., Kevei, P. and Pap, G. (2015). Asymptotic behavior of multitype nearly critical Galton–Watson processes with immigration. Theory Prob. Appl. 59, 590–610.CrossRefGoogle Scholar
Györfi, L., Ispány, M., Pap, G. and Varga, K. (2007). Poisson limit of an inhomogeneous nearly critical $\textrm{INAR}(1)$ model. Acta Sci. Math. (Szeged) 73, 789–815.Google Scholar
Ispány, M. (2016). Some asymptotic results for strongly critical branching processes with immigration in varying environment. In Branching Processes and their Applications (Lect. Notes Statist. 219), eds. I. M. del Puerto et al. Springer, Cham, pp. 77–95.CrossRefGoogle Scholar
Jagers, P. (1974). Galton–Watson processes in varying environments. J. Appl. Prob. 11, 174–178.CrossRefGoogle Scholar
Kersting, G. (2020). A unifying approach to branching processes in a varying environment. J. Appl. Prob. 57, 196–220.CrossRefGoogle Scholar
Kersting, G. and Vatutin, V. (2017). Discrete Time Branching Processes in Random Environment. ISTE Ltd, London, and John Wiley, Hoboken, NJ.CrossRefGoogle Scholar
Kevei, P. (2011). Asymptotics of nearly critical Galton–Watson processes with immigration. Acta Sci. Math. (Szeged) 77, 681–702.CrossRefGoogle Scholar
Simon, B. (2015). Real Analysis. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
Steutel, F. W. and van Harn, K. (2004). Infinite Divisibility of Probability Distributions on the Real Line (Monographs and Textbooks in Pure and Applied Math. 259). Marcel Dekker, New York.Google Scholar
Weiß, C. H. (2008). Thinning operations for modeling time series of counts—a survey. AStA Adv. Stat. Anal. 92, 319–341.CrossRefGoogle Scholar
Yaglom, A. M. (1947). Certain limit theorems of the theory of branching random processes. Doklady Akad. Nauk SSSR (N.S.) 56, 795–798.Google Scholar