Hostname: page-component-5b777bbd6c-5mwv9 Total loading time: 0 Render date: 2025-06-19T05:37:03.684Z Has data issue: false hasContentIssue false
  • English
  • Français

The effects of double diffusive convection on the basal melting of solid ice in seawater

Published online by Cambridge University Press:  18 June 2025

Rongfu Guo  and
Yantao Yang Open the ORCID record for Yantao Yang [Opens in a new window]
Rongfu Guo
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, PR China
Yantao Yang*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, PR China Laoshan Laboratory, Qingdao, Shandong 266299, PR China
*
Corresponding author: Yantao Yang, yantao.yang@pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

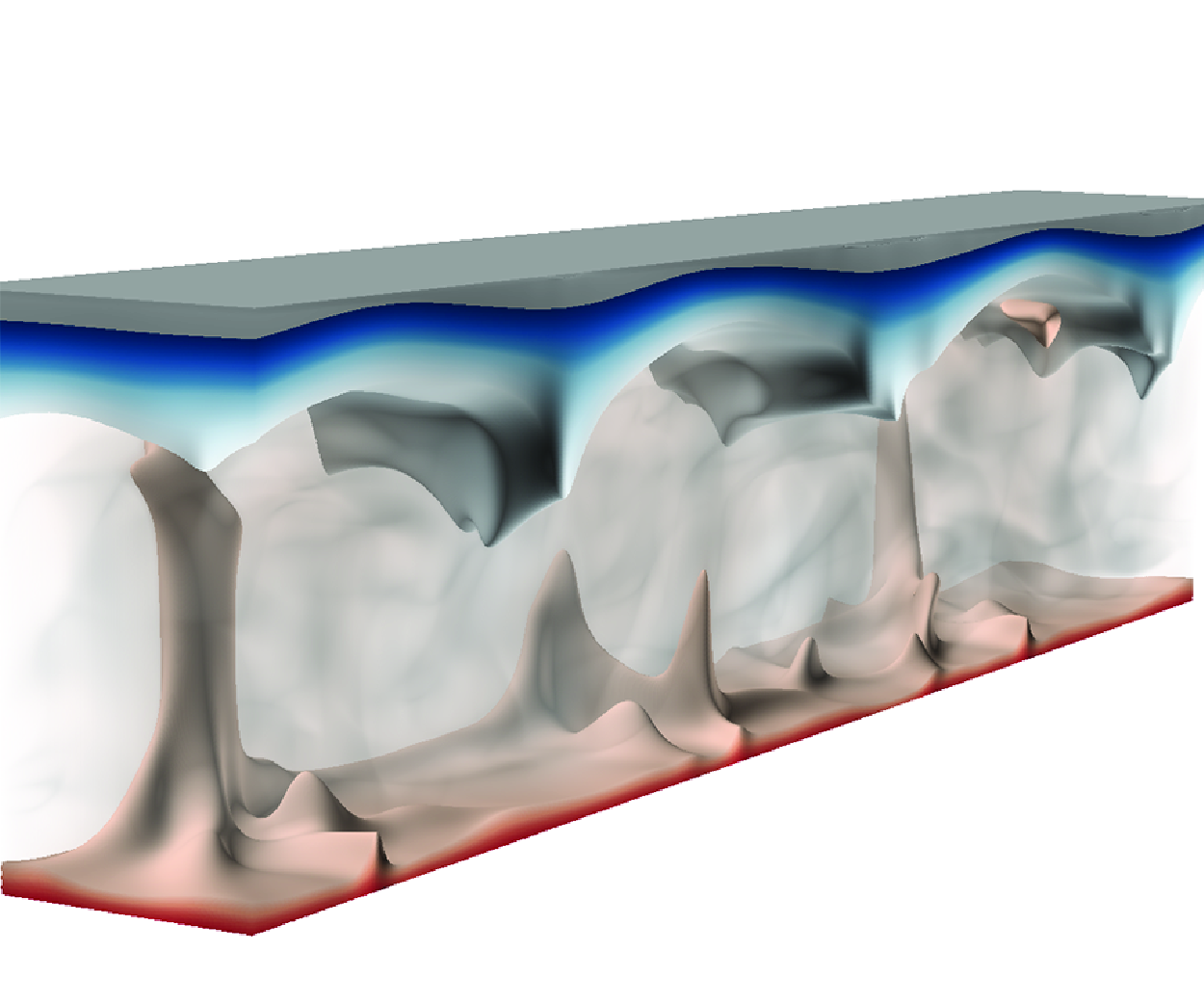
The dynamics of ice basal melting in seawater is one of the key factors in understanding and modelling the ice–seawater interaction in the polar oceans. In this work we study the basal melting of solid ice in seawater, and focus on the interaction between the melting process and the double diffusive convection developed in the seawater layer. Different temperatures and salinity differences are systematically simulated, and two different flow regimes are identified. For a relatively weak salinity difference, the convection layer occupies most of the liquid layer and grows in height as the ice melts. When the salinity difference is strong enough, the convection layer shrinks with time and a stably stratified layer grows between the ice layer and convection layer. When the dynamics is dominated by the convection layer, the global heat and salinity transfer rates follow a power-law scaling. Theoretical models are developed for the local mean salinity at the ice–water interface and the melting rates, and the critical density ratio corresponding to the transition between the two regimes, which all agree with the numerical results. Density inversion happens consistently adjacent to the ice–seawater interface, which has a profound influence on the ice surface shape. All these findings provide useful insights into the detailed dynamics of ice basal melting in oceans.

JFM classification

Convection: Double diffusive convection Geophysical and Geological Flows: Sea ice Turbulent Flows: Stratified turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , A24
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bhatia, M.P., Kujawinski, E.B., Das, S.B., Breier, C.F., Henderson, P.B. & Charette, M.A. 2013 Greenland meltwater as a significant and potentially bioavailable source of iron to the ocean. Nat. Geosci. 6 (4), 274–278.10.1038/ngeo1746CrossRefGoogle Scholar
Bigg, G.R. 2016 Icebergs: Their Science and Links to Global Change. Cambridge University Press Press.Google Scholar
Bintanja, R. & van de Wal, R.S.W. 2008 North American ice-sheet dynamics and the onset of 100,000-year glacial cycles. Nature 454 (869), 869–872.10.1038/nature07158CrossRefGoogle ScholarPubMed
Carey, V.P. & Gebhart, B. 1981 Visualization of the flow adjacent to a vertical ice surface melting in cold pure water. J. Fluid Mech. 107 (37), 37.10.1017/S0022112081001663CrossRefGoogle Scholar
Carey, V.P., Gebhart, B. & Mollendorf, J.C. 1980 Buoyancy force reversals in vertical natural convection flows in cold water. J. Fluid Mech. 97 (279), 279.10.1017/S002211208000256XCrossRefGoogle Scholar
Cenedese, C. & Straneo, F. 2023 Icebergs melting. Annu. Rev. Fluid Mech. 55 (1), 377–402.10.1146/annurev-fluid-032522-100734CrossRefGoogle Scholar
Clark, P.U., Alley, R.B. & Pollard, D. 1999 Northern hemisphere ice-sheet influences on global climate change. Science 286 (5442), 1104–1111.10.1126/science.286.5442.1104CrossRefGoogle Scholar
Couston, L.-A. 2021 Turbulent convection in subglacial lakes. J. Fluid Mech. 915 (A31), 1–31.10.1017/jfm.2021.38CrossRefGoogle Scholar
Couston, L.-A., Hester, E., Favier, B., Taylor, J.R., Holland, P.R. & Jenkins, A. 2021 Topography generation by melting and freezing in a turbulent shear flow. J. Fluid Mech. 911 (A44), 1–37.10.1017/jfm.2020.1064CrossRefGoogle Scholar
Du, Y., Calzavarini, E. & Sun, C. 2024 The physics of freezing and melting in the presence of flows. Nat. Rev. Phys. 381 (10), 676–690.10.1038/s42254-024-00766-5CrossRefGoogle Scholar
Du, Y., Wang, Z., Jiang, L., Calzavarini, E. & Sun, C. 2023 Sea water freezing modes in a natural convection system. J. Fluid Mech. 960 (A35), 1–21.10.1017/jfm.2023.215CrossRefGoogle Scholar
Dumore, J.M., Merk, H.J. & Prins, J.A. 1953 Heat transfer from water to ice by thermal convection. Nature 172 (460), 460–461.10.1038/172460b0CrossRefGoogle Scholar
Duprat, L.P.A.M., Bigg, G.R. & Wilton, D.J. 2016 Enhanced southern ocean marine productivity due to fertilization by giant icebergs. Nat. Geosci 9 (3), 219–221.10.1038/ngeo2633CrossRefGoogle Scholar
Edwards, T.L. et al. 2021 Projected land ice contributions to twenty-first-century sea level rise. Nature 593 (7857), 74–82.10.1038/s41586-021-03302-yCrossRefGoogle ScholarPubMed
Enderlin, E.M., Hamilton, G.S., FStraneo, & Sutherland, D.A. 2016 Iceberg meltwater fluxes dominate the freshwater budget in Greenland’s iceberg-congested glacial fjords. Geophys. Res. Lett. 43 (11), 287–294.10.1002/2016GL070718CrossRefGoogle Scholar
England, M.R., Wagner, T.J.W. & Eisenman, I. 2020 Modeling the breakup of tabular icebergs. Sci. Adv. 6 (51), 1–8.10.1126/sciadv.abd1273CrossRefGoogle ScholarPubMed
Esfahani, B.R., Hirata, S.C., Berti, S. & Calzavarini, E. 2018 Basal melting driven by turbulent thermal convection. Phys. Rev. Fluids 3 (053501), 1–24.Google Scholar
Favier, B., Purseed, J. & Duchemin, L. 2019 Rayleigh–Bénard convection with a melting boundary. J. Fluid Mech. 858, 437–473.10.1017/jfm.2018.773CrossRefGoogle Scholar
Gayen, B., Griffiths, R.W. & Kerr, R.C. 2016 Simulation of convection at a vertical ice face dissolving into saline water. J. Fluid Mech. 798, 284–298.10.1017/jfm.2016.315CrossRefGoogle Scholar
Golledge, N.R., Keller, E.D., Gomez, N., Naughten, K.A., Bernales, J., Trusel, L.D.> & Edwards, T.L. 2019 Global environmental consequences of twenty-first-century ice-sheet melt. Nature 566 (65), 65–72.10.1038/s41586-019-0889-9CrossRefGoogle ScholarPubMed
Hanna, E. et al. 2013 Ice-sheet mass balance and climate change. Nature 498 (51), 51–59.10.1038/nature12238CrossRefGoogle ScholarPubMed
Hester, E.W., McConnochie, C.D., Cenedese, C., Couston, L.-A. & Vasil, G. 2021 Aspect ratio affects iceberg melting. Phys. Rev. Fluids 6 (023802), 1–20.10.1103/PhysRevFluids.6.023802CrossRefGoogle Scholar
Huppert, H.E. & Turner, J.S. 1978 On melting icebergs. Nature 271 (5640), 46–48.10.1038/271046a0CrossRefGoogle Scholar
Huppert, H.E. & Turner, J.S. 1980 Ice blocks melting into a salinity gradient. J. Fluid Mech. 100 (2), 367–384.10.1017/S0022112080001206CrossRefGoogle Scholar
IOC, SCOR & IAPSO 2010 The International Thermodynamic Equation of Seawater – 2010: Calculation and Use of Thermodynamic Properties Oceans (IAPSO). UNESCO.Google Scholar
Jenkins, A. 2011 Convection-driven melting near the grounding lines of ice shelves and tidewater glaciers. J. Phys. Oceanogr. 41 (12), 2279–2294.10.1175/JPO-D-11-03.1CrossRefGoogle Scholar
Jenkins, A., Nicholls, K.W. & Corr, H.F.J. 2010 Observation and parameterization of ablation at the base of Ronne ice shelf, Antarctica. J. Phys. Oceanogr. 40 (10), 2298–2312.10.1175/2010JPO4317.1CrossRefGoogle Scholar
Kang, W., Mittal, T., Bire, S., Campin, J.M. & Marshall, J. 2022 How does salinity shape ocean circulation and ice geometry on Enceladus and other icy satellites. Sci. Adv. 8 (29), 1–16.10.1126/sciadv.abm4665CrossRefGoogle ScholarPubMed
Linden, P.F. & Shirtcliffe, T.G.L. 1978 The diffusive interface in double-diffusive convection. J. Fluid Mech. 87 (03), 417–432.10.1017/S002211207800169XCrossRefGoogle Scholar
Lu, C., Zhang, M., Luo, K., Wu, J. &Yi, H. 2022, Rayleigh–Bénard instability in the presence of phase boundary and shear. J. Fluid Mech. 948 (A46), 1–26.10.1017/jfm.2022.723CrossRefGoogle Scholar
Middleton, L., Vreugdenhil, C.A., Holland, P.R. & Taylor, J.R. 2021 Numerical simulations of melt-driven double-diffusive fluxes in a turbulent boundary layer beneath an ice shelf. J. Phys. Oceanogr. 51 (2), 403–418.10.1175/JPO-D-20-0114.1CrossRefGoogle Scholar
Mondal, M., Gayen, B., Griffiths, R.W. & Kerr, R.C. 2019 Ablation of sloping ice faces into polar seawater. J. Fluid Mech. 863, 545–571.10.1017/jfm.2018.970CrossRefGoogle Scholar
Musman, S. 1968 Penetrative convection. J. Fluid Mech. 31 (343), 343–360.10.1017/S0022112068000194CrossRefGoogle Scholar
Notz, D. 2009 The future of ice sheets and sea ice: between reversible retreat and unstoppable loss. Proc. Natl Acad. Sci. USA 106 (20590), 20590–20595.10.1073/pnas.0902356106CrossRefGoogle ScholarPubMed
Ostilla-Monico, R., Yang, Y., van der Poel, E.P., Lohse, D. & Verzicco, R. 2015 A multiple-resolution strategy for direct numerical simulation of scalar turbulence. J. Comput. Phys. 301, 308–321.10.1016/j.jcp.2015.08.031CrossRefGoogle Scholar
Rignot, E., Jacobs, S., Mouginot, J. & Scheuchl, B. 2013 Ice-shelf melting around Antarctica. Science 341 (266), 266–270.10.1126/science.1235798CrossRefGoogle ScholarPubMed
Roquet, F., Madec, G., Brodeau, L. & Nycander, J. 2015 Defining a simplified yet ‘realistic’ equation of state for seawater. J. Phys. Oceanogr. 45 (10), 2564–2579.10.1175/JPO-D-15-0080.1CrossRefGoogle Scholar
Rosevear, M.G., Gayen, B. & Galton-Fenzi, B.K. 2021 The role of double-diffusive convection in basal melting of Antarctic ice shelves. Proc. Nati Acad. Sci. USA 118 (6), e2007541118.10.1073/pnas.2007541118CrossRefGoogle ScholarPubMed
Rosevear, M.G., Gayen, B., Vreugdenhil, C.A. & Galton-Fenzi, B.K. 2025 How does the ocean melt Antarctic ice shelves? Annu. Rev. Mar. Sci. 17 (1), 325–353.10.1146/annurev-marine-040323-074354CrossRefGoogle ScholarPubMed
Shepherd, A., Hubbard, A., Nienow, P., King, M., McMillan, M. & Joughin, I. 2009 Greenland ice sheet motion coupled with daily melting in late summer. Geophys. Res. Lett. 36 (1), L01501.10.1029/2008GL035758CrossRefGoogle Scholar
Silva, T.A.M., Bigg, G.R. & Nicholls, K.W. 2006 Contribution of giant icebergs to the southern ocean freshwater flux. J. Geophys. Res. Oceans 111, C03004.10.1029/2004JC002843CrossRefGoogle Scholar
Smith, K.L. Jr., Sherman, A.D., Shaw, T.J. & Sprintall, J. 2013 Icebergs as unique Lagrangian ecosystems in polar seas. Annu. Rev. Mar. Sci. 5 (1), 269–287.10.1146/annurev-marine-121211-172317CrossRefGoogle ScholarPubMed
Sugawara, M., Ishikura, T. & Beer, H. 2005 Effect of cavity inclination on a temperature and concentration controlled double diffusive convection at ice plate melting. Heat Mass Transfer 41 (5), 432–441.10.1007/s00231-004-0557-xCrossRefGoogle Scholar
Sugawara, M., Tamura, E., Satoh, Y., Komatsu, Y., Tago, M. & Beer, H. 2007 Visual observations of flow structure and melting front morphology in horizontal ice plate melting from above into a mixture. Heat Mass Transfer 43 (10), 1009–1018.10.1007/s00231-006-0175-xCrossRefGoogle Scholar
Tietsche, S., Notz, D., Jungclaus, J.H. & Marotzke, J. 2011 Recovery mechanisms of Arctic summer sea ice. Geophys. Res. Lett. 38 (2), L02707.10.1029/2010GL045698CrossRefGoogle Scholar
Toppaladoddi, S. 2021 Nonlinear interactions between an unstably stratified shear flow and a phase boundary. J. Fluid Mech. 919 (A28), 1–25.10.1017/jfm.2021.396CrossRefGoogle Scholar
Toppaladoddi, S. & Wettlaufer, J.S. 2019 The combined effects of shear and buoyancy on phase boundary stability. J. Fluid Mech. 868, 648–665.10.1017/jfm.2019.153CrossRefGoogle Scholar
Townsend, A.A. 1964 Natural convection in water over an ice surface. Q. J. R. Meteorol. Soc. 90 (385), 248–259.10.1002/qj.49709038503CrossRefGoogle Scholar
Tsai, C.W., Yang, S.J. & Hwang, G.J. 1998 Maximum density effect on laminar water pipe flow solidification. Intl J. Heat Mass Transfer 41 (24), 4251–4257.10.1016/S0017-9310(98)00129-XCrossRefGoogle Scholar
Veronis, G. 1963 Penetrative convection. Astrophys. J. 137 (641), 641.10.1086/147538CrossRefGoogle Scholar
Vreugdenhil, C.A. & Taylor, J.R. 2019 Stratification effects in the turbulent boundary layer beneath a melting ice shelf: insights from resolved large-eddy simulations. J. Phys. Oceanogr. 49 (7), 1905–1925.10.1175/JPO-D-18-0252.1CrossRefGoogle Scholar
Wang, Q., Reiter, P., Lohse, D. & Shishkina, O. 2021 a Universal properties of penetrative turbulent Rayleigh–Bénard convection. Phys. Rev. Fluids 6 (063502), 1–15.10.1103/PhysRevFluids.6.063502CrossRefGoogle Scholar
Wang, Z., Calzavarini, E. & Sun, C. 2021 b Equilibrium states of the ice-water front in a differentially heated rectangular cell. Europhys. Lett. 135 (54001), 54001.10.1209/0295-5075/ac30e7CrossRefGoogle Scholar
Wang, Z., Calzavarini, E., Sun, C. & Toschi, F. 2021 c How the growth of ice depends on the fluid dynamics underneath. Proc. Natl Acad. Sci. USA 118 (10), 1–8.Google ScholarPubMed
Wang, Z., Jiang, L., Du, Y. & Sun, C. 2021 d Ice front shaping by upward convective current. Phys. Rev. Fluids 6 (9), L091501.10.1103/PhysRevFluids.6.L091501CrossRefGoogle Scholar
Weady, S., Tong, J., Zidovska, A. & Ristroph, L. 2022 Anomalous convective flows carve pinnacles and scallops in melting ice. Phys. Rev. Lett. 128 (4), 044502.10.1103/PhysRevLett.128.044502CrossRefGoogle ScholarPubMed
Wells, A.J. & Worster, M.G. 2011 Melting and dissolving of a vertical solid surface with laminar compositional convection. J. Fluid Mech. 687, 118–140.10.1017/jfm.2011.322CrossRefGoogle Scholar
Wilson, N.J., Vreugdenhil, C.A., Gayen, B. & Hester, E.W. 2023 Double-diffusive layer and meltwater plume effects on ice face scalloping in phase-change simulations. Geophys. Res. Lett. 50 (17),e2023GL104396.10.1029/2023GL104396CrossRefGoogle Scholar
Xue, Z.-H., Zhang, J. & Ni, M.-J. 2024 Flow regimes in a melting system composed of binary fluid: transition from penetrative convection to diffusion. J. Fluid Mech. 998 (A14), 1–29.10.1017/jfm.2024.905CrossRefGoogle Scholar
Yang, R., Chong, K.L., Liu, H.R., Verzicco, R. & Lohse, D. 2022 Abrupt transition from slow to fast melting of ice. Phys. Rev. Fluids 7 (8), 083503.10.1103/PhysRevFluids.7.083503CrossRefGoogle Scholar
Yang, R., Howland, C.J., Liu, H.-R., Verzicco, R. & Lohse, D. 2023 a Ice melting in salty water: layering and non-monotonic dependence on the mean salinity. J. Fluid Mech. 969 (2), 1–12.10.1017/jfm.2023.582CrossRefGoogle Scholar
Yang, R., Howland, C.J., Liu, H.-R., Verzicco, R. & Lohse, D. 2023 b Morphology evolution of a melting solid layer above its melt heated from below. J. Fluid Mech. 956 (A23), 1–19.10.1017/jfm.2023.15CrossRefGoogle Scholar