Hostname: page-component-5b777bbd6c-w9n4q Total loading time: 0 Render date: 2025-06-20T16:18:45.435Z Has data issue: false hasContentIssue false
  • English
  • Français

Liquid states in horizontal plate-inserted slits

Published online by Cambridge University Press:  26 May 2025

Dongwen Tan Open the ORCID record for Dongwen Tan [Opens in a new window] ,
Qi Zhang Open the ORCID record for Qi Zhang [Opens in a new window]  and
Xinping Zhou Open the ORCID record for Xinping Zhou [Opens in a new window]
Dongwen Tan
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China
Qi Zhang
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China
Xinping Zhou*
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China State Key Laboratory of Intelligent Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, PR China
*
Corresponding author: Xinping Zhou, xpzhou08@hust.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

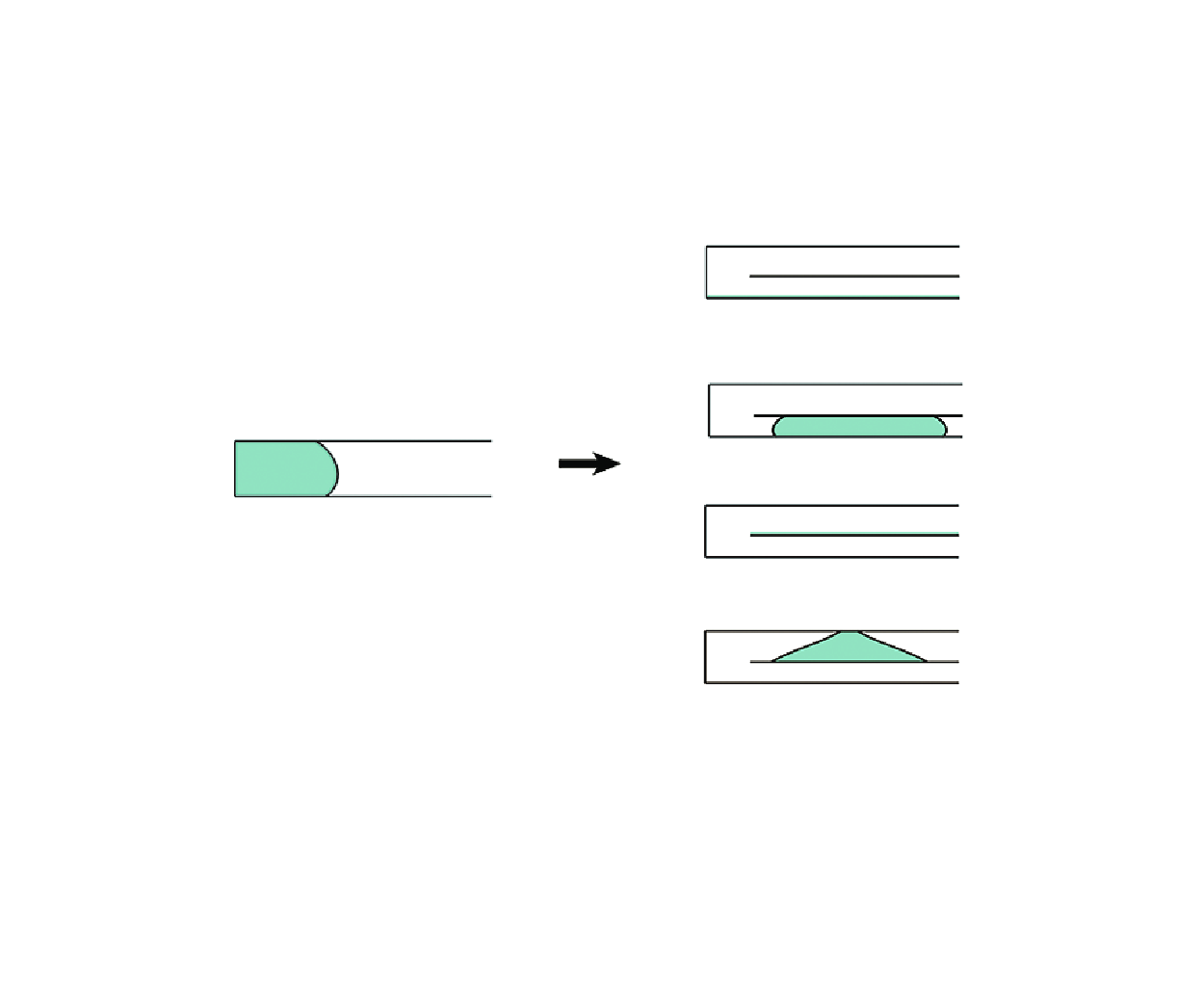
Removing liquid from a channel is an important process. In a horizontal slit in the presence of a downward gravity field, two distinct liquid states were commonly observed: gravity-driven liquid non-occlusion and liquid plug (Parry et al. 2012 Phys. Rev. Lett. 108, 246101). A wetting-driven non-occlusion at some contact angles was induced by insertion of a rod into a horizontal tube at an eccentric position (Tan et al. 2022 J. Fluid Mech. 946, A7). Insertion of a plate into a horizontal slit may enhance the capacity of removing liquid. This situation is theoretically investigated, and the theoretical results are mutually verified by a computational fluid dynamics (CFD) numerical method that is first employed to determine the critical non-occlusion conditions. Four types of liquid states are observed. The effects of contact angles, plate position and Bond number (measured by downward gravitational force relative to surface tension force) on different types of liquid states are analysed. This paper additionally provides a CFD numerical method for understanding the conditions for the stability and existence of the liquid plugs in complex situations (e.g. considering the effect of the sidewalls, or when a rod or plate is inserted into a circular, elliptical or polygonal tube) in the future.

JFM classification

Interfacial Flows (free surface): Capillary flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1012 , 10 June 2025 , A2
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bhatnagar, R. & Finn, R. 2016 On the capillarity equation in two dimensions. J. Math. Fluid Mech. 18 (4), 731–738.10.1007/s00021-016-0257-6CrossRefGoogle Scholar
Bradley, A.T., Box, F., Hewitt, I.J. & Vella, D. 2019 Wettability-independent droplet transport by Bendotaxis . Phys. Rev. Lett. 122 (7), 074503.10.1103/PhysRevLett.122.074503CrossRefGoogle ScholarPubMed
Brakke, K.A. 1992 The surface evolver. Expl Maths 1 (2), 141–165.10.1080/10586458.1992.10504253CrossRefGoogle Scholar
Cahn, J.W. & Hilliard, J.E. 1958 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267.10.1063/1.1744102CrossRefGoogle Scholar
Chen, Y. & Collicott, S.H. 2004 Investigation of the symmetric wetting of vane-wall gaps in propellant. AIAA J. 42 (2), 305–314.10.2514/1.915CrossRefGoogle Scholar
Concus, P. & Finn, R. 1969 On the behavior of a capillary surface in a wedge. Proc. Natl Acad. Sci. USA 63 (2), 292–299.10.1073/pnas.63.2.292CrossRefGoogle Scholar
Elcrat, A., Kim, T.-E. & Treinen, R. 2004 Annular capillary surfaces. Arch. Math. 82 (5), 449–467.10.1007/s00013-003-0101-0CrossRefGoogle Scholar
Finn, R. 1986 Equilibrium Capillary Surfaces. Springer.10.1007/978-1-4613-8584-4CrossRefGoogle Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.10.1007/978-0-387-21656-0CrossRefGoogle Scholar
Gordon, J. & Siegel, D. 2010 a Properties of annular capillary surfaces with equal contact angles. Pac. J. Maths 247 (2), 353–370.10.2140/pjm.2010.247.353CrossRefGoogle Scholar
Gordon, J. & Siegel, D. 2010 b Approximating annular capillary surfaces with equal contact angles. Pac. J. Maths 247 (2), 371–387.10.2140/pjm.2010.247.371CrossRefGoogle Scholar
Holló, G., Suematsu, N.J., Ginder, E. & Lagzi, I. 2021 Electric field assisted motion of a mercury droplet. Sci. Rep. 11 (1), 2753.10.1038/s41598-020-80375-1CrossRefGoogle ScholarPubMed
Litterst, C., Eccarius, S., Hebling, C., Zengerle, R. & Koltay, P. 2006 Increasing $\mathrm{\mu }$ DMFC efficiency by passive CO $_{2}$ bubble removal and discontinuous operation. J. Micromech. Microengng 16, S248.10.1088/0960-1317/16/9/S12CrossRefGoogle Scholar
Manning, R., Collicott, S. & Finn, R. 2011 Occlusion criteria in tubes under transverse body forces. J. Fluid Mech. 682, 397–414.10.1017/jfm.2011.230CrossRefGoogle Scholar
Oesterle, A. 2015 Pipette Cookbook 2015 p-97 and p-1000 Micropipette Pullers. Sutter Instrument.Google Scholar
Parry, A.O., Rascón, C., Jamie, E.A.G. & Aarts, D.G.A.L. 2012 Capillary emptying and short-range wetting. Phys. Rev. Lett. 108 (24), 246101.10.1103/PhysRevLett.108.246101CrossRefGoogle ScholarPubMed
Parry, A.O., Rascón, C. & Wood, A.J. 2000 Critical effects at 3 $\mathrm{{D}}$ wedge wetting. Phys. Rev. Lett. 85, 345–348.10.1103/PhysRevLett.85.345CrossRefGoogle Scholar
Pour, N.B. & Thiessen, D.B. 2019 Equilibrium configurations of drops or bubbles in an eccentric annulus. J. Fluid Mech. 863, 364–385.10.1017/jfm.2018.1010CrossRefGoogle Scholar
Rascón, C., Parry, A.O. & Aarts, D.G.A.L. 2016 Geometry-induced capillary emptying. Proc. Natl Acad. Sci. USA 113 (45), 12633–12636.10.1073/pnas.1606217113CrossRefGoogle ScholarPubMed
Smedley, G. 1990 Containments for liquids at zero gravity. Microgravity Sci. Technol. 3, 13–23.Google Scholar
Tan, D. & Zhou, X. 2024 a Multistability of a long droplet in a capillary tube under transverse body force. J. Fluid Mech. 996, A28.10.1017/jfm.2024.689CrossRefGoogle Scholar
Tan, D. & Zhou, X. 2024 b Rounded-corners-induced re-entrant non-occlusion in a horizontal tube. J. Fluid Mech. 979, A49.10.1017/jfm.2023.1014CrossRefGoogle Scholar
Tan, D., Zhou, X., Zhang, G., Zhu, C. & Fu, C. 2022 Eccentricity effect on horizontal capillary emptying. J. Fluid Mech. 946, A7.10.1017/jfm.2022.567CrossRefGoogle Scholar
Treinen, R. 2012 Extended annular capillary surfaces. J. Math. Fluid Mech. 14 (4), 619–632.10.1007/s00021-012-0100-7CrossRefGoogle Scholar
Verma, G., Saraj, C.S., Yadav, G., Singh, S.C. & Guo, C. 2020 Generalized emptying criteria for finite-lengthed capillary. Phys. Rev. Fluids 5 (11), 112201(R).10.1103/PhysRevFluids.5.112201CrossRefGoogle Scholar
Zhang, F.Y., Yang, X.G. & Wang, C.Y. 2006 Liquid water removal from a polymer electrolyte fuel cell. J. Electrochem. Soc. 153 (2), A225–A232.10.1149/1.2138675CrossRefGoogle Scholar
Zhou, X. & Zhang, F. 2017 Bifurcation of a partially immersed plate between two parallel plates. J. Fluid Mech. 817, 122–137.10.1017/jfm.2017.105CrossRefGoogle Scholar
Zhou, X., Zhang, G., Zhu, C., Tan, D. & Fu, C. 2021 Inside rod induced horizontal capillary emptying. J. Fluid Mech. 924, A23.10.1017/jfm.2021.634CrossRefGoogle Scholar
Zhu, C., Zhou, X. & Zhang, G. 2020 Capillary plugs in horizontal rectangular tubes with non-uniform contact angles. J. Fluid Mech. 901, R1.10.1017/jfm.2020.598CrossRefGoogle Scholar