Hostname: page-component-5b777bbd6c-2hk6m Total loading time: 0 Render date: 2025-06-26T00:11:08.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Aerodynamic heating in hypersonic shock wave and turbulent boundary layer interaction

Published online by Cambridge University Press:  18 November 2024

Zhenyuan Tang Open the ORCID record for Zhenyuan Tang [Opens in a new window] ,
Haonan Xu ,
Xueying Li  and
Jing Ren
Zhenyuan Tang
Affiliation:
Department of Energy and Power Engineering, Tsinghua University, Beijing, PR China
Haonan Xu
Affiliation:
Department of Energy and Power Engineering, Tsinghua University, Beijing, PR China
Xueying Li*
Affiliation:
Department of Energy and Power Engineering, Tsinghua University, Beijing, PR China
Jing Ren
Affiliation:
Department of Energy and Power Engineering, Tsinghua University, Beijing, PR China
*
†Email address for correspondence: li_xy@tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

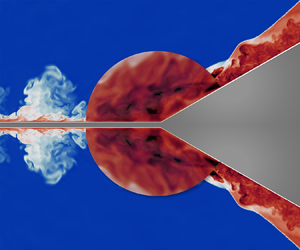
In hypersonic flight the shock wave and turbulent boundary layer interaction (STBLI) sharply increases wall heat transfer that intensifies the aerodynamic heating problems. In this work the STBLI is modelled by compression ramp flow with a Mach number of 5, a Reynolds number based on momentum thickness of 4652 and a wall to recovery temperature ratio of 0.5. The aerodynamic heat generation and transport mechanisms are investigated in the interaction based on theoretical analysis and direct numerical simulation (DNS) that agrees with previous studies. A prediction correlation of wall heat flux in STBLI is deduced theoretically and validated by some representative data including the present DNS, which improves the prediction accuracy and can be applied to a wider $Ma$ range compared with the canonical Q-P theory. The correlation indicates that the sharp increase of wall heat transfer in the STBLI can be explained by the boundary layer compression and the convection transport enhancement. Based on the DNS results, the aerodynamic heat generation and transport mechanisms are revealed in the separation, recirculation and reattachment zones in the STBLI. From this perspective, the peak heat flux can be further explained by the enhancement of near-wall turbulent energy dissipation, compression aerodynamic heat generation and the near-wall turbulent transport. The generation and transport of compression aerodynamic heat reveal the underlying mechanism of the strong correlation between the peak heat flux ratios and the pressure ratios in STBLIs.

JFM classification

Compressible Flows: Hypersonic Flow Turbulent Flows: Turbulent boundary layers Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 999 , 25 November 2024 , A66
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adler, M.C. & Gaitonde, D.V. 2019 Flow similarity in strong swept-shock/turbulent-boundary-layer interactions. AIAA J. 57 (4), 1–15.CrossRefGoogle Scholar
Andreopoulos, Y., Agui, J.H. & Briassulis, G. 1987 Some new aspects of the shock-wave boundary layer interaction. J. Fluid Mech. 180, 405–428.CrossRefGoogle Scholar
Andreopoulos, Y., Agui, J.H. & Briassulis, G. 2000 Shock wave-turbulence interactions. Annu. Rev. Fluid Mech. 32 (1), 309–345.CrossRefGoogle Scholar
Babinsky, H. & Harvey, J.K. 2011 Shock Wave-Boundary-Layer Interactions. Cambridge University Press.CrossRefGoogle Scholar
Back, L.H. & Cuffel, R.F. 1970 Changes in heat transfer from turbulent boundary layers interacting with shock waves and expansion waves. AIAA J. 8 (10), 1871–1873.CrossRefGoogle Scholar
Bernardini, M., Asproulias, I., Larsson, J., Pirozzoli, S. & Grasso, F. 2016 Heat transfer and wall temperature effects in shock wave turbulent boundary layer interactions. Phys. Rev. Fluids 1, 084403.CrossRefGoogle Scholar
Bhagwandin, V.A., Helm, C.M. & Martin, P. 2019 Shock wave-turbulent boundary layer interactions in separated compression corners at Mach 10. In AIAA Scitech 2019 Forum, p. 1129.Google Scholar
Bookey, P., Wyckham, C., Smits, A. & Martin, P. 2005 New experimental data of STBLI at DNS/LES accessible Reynolds numbers. In 43rd AIAA Aerospace Sciences Meeting and Exhibit, p. 309.Google Scholar
Brown, G.L. & Roshco, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
Cebeci, T. 2012 Analysis of Turbulent Boundary Layers. Elsevier.Google Scholar
Chu, Y.-B., Zhuang, Y.-Q. & Lu, X.-Y. 2013 Effect of wall temperature on hypersonic turbulent boundary layer. J. Turbul. 14 (12), 37–57.CrossRefGoogle Scholar
Clemens, N.T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.CrossRefGoogle Scholar
Coleman, G.T. & Stollery, J.L. 1972 Heat transfer from hypersonic turbulent flow at a wedge compression corner. J. Fluid Mech. 56 (4), 741–752.CrossRefGoogle Scholar
Delery, J. & Coet, M.-C. 1991 Experiments on shock-wave boundary-layer interactions produced by two-dimensional ramps and three-dimensional obstacles. In Hypersonic Flows for Reentry Problems: Volume II: Test Cases—Experiments and Computations Proceedings of a Workshop Held in Antibes, France, 22–25 January 1990, pp. 97–128. Springer.CrossRefGoogle Scholar
Dolling, D.S. 2001 Fifty years of shock-wave boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
van Driest, E.R. 1956 The Problem of Aerodynamic Heating. Institute of the Aeronautical Sciences.Google Scholar
Duan, L., Beekman, I. & Martin, M.P. 2010 Direct numerical simulation of hypersonic turbulent boundary layers. Part 2. Effect of wall temperature. J. Fluid Mech. 655, 419–445.CrossRefGoogle Scholar
Duan, L., Beekman, I. & Martin, M.P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part 3. Effect of Mach number. J. Fluid Mech. 672, 245–267.CrossRefGoogle Scholar
Eckert, E.R.G. 1955 Engineering relations for friction and heat transfer to surfaces in high velocity flow. J. Aeronaut. Sci. 22 (8), 585–587.Google Scholar
Eckert, E.R.G. 1960 Survey of Boundary Layer Heat Transfer at High Velocities and High Temperatures, vol. 59. Wright Air Development Center.Google Scholar
Erengil, M.E. & Dolling, D.S. 1991 Unsteady wave structure near separation in a Mach 5 compression ramp interaction. AIAA J. 29 (5), 728–735.CrossRefGoogle Scholar
Erengil, M.E. & Dolling, D.S. 1993 Physical causes of separation shock unsteadiness in shock wave turbulent boundary layer interactions. In 24th AIAA Fluid Dynamics Conference, Orlando, FL, pp. 1993–3134.Google Scholar
Fan, X.-H., Tang, Z.-G., Wang, G. & Yang, Y.-G. 2022 Review of low-frequency unsteadiness in shock wave turbulent boundary layer interaction. Acta Aeronaut. Astronaut. Sin. 43, 9–29.Google Scholar
Fang, J., Zheltovodov, A.A., Yao, Y.-F., Moulinec, C. & Emerson, D.R. 2020 On the turbulence amplification in shock-wave/turbulent boundary layer interaction. J. Fluid Mech. 897, A32.CrossRefGoogle Scholar
Fu, D.-X., Ma, Y.-W. & Li, X.-L. 2010 Direct Numerical Simulation of Compressible Turbulence. China Science Press.Google Scholar
Gaitonde, D.V. 2015 Progress in shock wave/boundary layer interactions. Prog. Aerosp. Sci. 72, 80–99.CrossRefGoogle Scholar
Ganapathisubramani, B., Clemenn, N.T. & Dolling, D.S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–94.CrossRefGoogle Scholar
Gaviglio, J. 1987 Reynolds analogies and experimental study of heat transfer in the supersonic boundary layer. Intl J. Heat Mass Transfer 30 (5), 911–926.CrossRefGoogle Scholar
Georgiadis, N.J., Rizzetta, D.P. & Fureby, C. 2010 Large-eddy simulation: current capabilities, recommended practices, and future research. AIAA J. 48 (8), 1772–1784.CrossRefGoogle Scholar
Hayashi, M., Aso, S. & Tan, A. 1989 Fluctuation of heat transfer in shock wave turbulent boundary layer interaction. AIAA J. 27 (4), 399–404.CrossRefGoogle Scholar
Hayashi, M., Sakurai, A. & Aso, S. 1986 Measurement of heat-transfer coefficients in shock wave-turbulent boundary layer interaction regions with a multi-layered thin film heat transfer gauge. Tech. Rep. NASA.Google Scholar
Helm, C.M. & Martín, M.P. 2022 Large eddy simulation of two separated hypersonic shock/turbulent boundary layer interactions. Phys. Rev. Fluids 7 (7), 074601.CrossRefGoogle Scholar
Holden, M.S. 1972 Shock wave-turbulent boundary layer interaction in hypersonic flow. In 10th Aerospace Sciences Meeting, p. 74.Google Scholar
Holden, M.S. 1977 Shock wave-turbulent boundary layer interaction in hypersonic flow. In 15th Aerospace Sciences Meeting, p. 45.Google Scholar
Hong, Y.-T., Li, Z.-F. & Yang, J.-M. 2021 Scaling of interaction lengths for hypersonic shock wave turbulent boundary layer interactions. Chin. J. Aeronaut. 34 (5), 504–509.CrossRefGoogle Scholar
Huang, J.-J., Lian, D. & Choudhari, M.M. 2022 Direct numerical simulation of hypersonic turbulent boundary layers: effect of spatial evolution and Reynolds number. J. Fluid Mech. 937, A3.CrossRefGoogle Scholar
Huang, P.-G., Coleman, G.N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.CrossRefGoogle Scholar
Humble, R.A., Elsinga, G.E., Scarano, F. & van Oudheusde, B.W. 2009 Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.CrossRefGoogle Scholar
Hung, F. & Barnett, D. 1973 Shockwave-boundary layer interference heating analysis. In 11th Aerospace Sciences Meeting, p. 237.Google Scholar
Jameson, A., Schmidt, W. & Turkel, E. 1981 Numerical solutions of the euler equations by finite volume methods using Runge–Kutta time stepping. In 14th Fluid and Plasma Dynamics Conference, Palo Alto, CA, USA.CrossRefGoogle Scholar
Jaunet, V., Debieve, J.F. & Dupont, P. 2014 Length scales and time scales of a heated shock-wave/boundary-layer interaction. AIAA J. 52 (11), 2524–2532.CrossRefGoogle Scholar
Levin, V. & Fabish, T.J. 1962 Thermal effects of shock wave turbulent boundary layer interaction at Mach numbers 3 and 5. Tech. Rep. North American Aviation.CrossRefGoogle Scholar
Li, S.-X. 2007 Complex Flows Dominated by Shock Waves and Boundary Layers. China Science Press.Google Scholar
Li, X.-L., Fu, D.-X., Ma, Y.-W. & Liang, X. 2010 Direct numerical simulation of shock wave turbulent boundary layer interaction. Sci. Sin. 40, 791–799.Google Scholar
Liang, X., Li, X.-L., Fu, D.-X. & Ma, Y.-W. 2012 DNS and analysis of a spatially evolving hypersonic turbulent boundary layer over a flat plate at Mach 8. Sci. Sin. 42, 82–293.Google Scholar
Longo, J.M. 2003 Aerothermodynamics – a critical review at DLR. Aerosp. Sci. Technol. 7 (6), 429–438.CrossRefGoogle Scholar
Ma, C.-L. & Liu, J.-Y. 2023 Effect of grid strategy on numerical simulation results of aerothermal heating loads over hypersonic blunt bodies. Acta Aeronaut. Astronaut. Sin. 44 (05), 73–86.Google Scholar
Magnan, J.D. & Spurlin, C.J. 1966 Investigation of flow field interference caused by shock impingement on a flat plate at Mach numbers of 6, 8 and 10. Tech. Rep. Arnold Engineering Development Center, Arnold Air Force Base.Google Scholar
Markarian, C.F. 1968 Heat transfer in shock wave-boundary layer interaction regions. Tech. Rep. Naval Weapons Center.Google Scholar
Morkovin, M.V. 1962 Effects of compressibility on turbulent flows. Méc. Turbul. 367 (380), 26.Google Scholar
Murray, N., Hillier, R. & Williams, S. 2013 Experimental investigation of axisymmetric hypersonic shock-wave/turbulent-boundary-layer interactions. J. Fluid Mech. 714, 152–189.CrossRefGoogle Scholar
Padmanabhan, S., Maldonado, J.C., Threadgill, J.A. & Little, J.C. 2021 Experimental study of swept impinging oblique shock/boundary-layer interactions. AIAA J. 59 (1), 140–149.CrossRefGoogle Scholar
Piponniau, S., Dussauge, J.P., Debieve, J.F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.CrossRefGoogle Scholar
Pirozzoli, S., Grasso, F. & Gatski, T.B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at $M= 2.25$. Phys. Fluids 16 (3), 530–545.CrossRefGoogle Scholar
Priebe, S. & Martin, M.P. 2012 Low-frequency unsteadiness in shock wave-turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.CrossRefGoogle Scholar
Priebe, S. & Martín, M.P. 2021 Turbulence in a hypersonic compression ramp flow. Phys. Rev. Fluids 6 (3), 034601.CrossRefGoogle Scholar
Qu, Z.-H., Liu, W., Zeng, M. & Liu, J. 2001 Hypersonic Aerodynamics. National University of Defense Technology Press.Google Scholar
Roshco, A. 1976 Structure of turbulent shear flows: a new look. AIAA J. 14, 1349–1357.CrossRefGoogle Scholar
Rubesin, M.W. 1990 Extra compressibility terms for Favre-averaged two-equation models of inhomogeneous turbulent flows. Tech. Rep. NASA.Google Scholar
Sayano, S., Bausch, H.P. & Donnelly, R.J. 1962 Aerodynamic heating due to shock impingement on a flat plate. Tech. Rep. McDonnell-Douglas Aircraft Co..Google Scholar
Schreyer, A.M., Sahoo, D., Williams, O.J.H. & Smits, A.J. 2018 Experimental investigation of two hypersonic shock/turbulent boundary-layer interactions. AIAA J. 56 (12), 4830–4844.CrossRefGoogle Scholar
Schülein, E. 2006 Skin friction and heat flux measurements in shock/boundary layer interaction flows. AIAA J. 44 (8), 1732–1741.CrossRefGoogle Scholar
Schülein, E., Krogmann, P. & Stanewsky, E. 1996 Documentation of two-dimensional impinging shock/turbulent boundary layer interaction flows. Tech. Rep. DLR, German Aerospace Research Center.Google Scholar
Sillero, J.A., Jimenez, J. & Moser, R.D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to delta+ 2000. Phys. Fluids 25 (10), 133–166.CrossRefGoogle Scholar
Souverein, L.J., Bakker, P.G. & Dupont, P. 2013 A scaling analysis for turbulent shock-wave boundary-layer interactions. J. Fluid Mech. 714, 505–535.CrossRefGoogle Scholar
Spaid, F.W. & Frishett, J.C. 1972 Incipient separation of a supersonic, turbulent boundary layer, including effect of heat transfer. AIAA J. 10 (7), 915–922.CrossRefGoogle Scholar
Spalart, P.R. 1988 Direct simulation of a turbulent boundary layer up to $R_\theta =1410$. J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
Sun, D., Guo, Q.-L., Yuan, X.-X., Zhang, H.-Y., Li, C. & Liu, P.-X. 2021 A decomposition formula for the wall heat flux of a compressible boundary layer. Adv. Aerodyn. 3 (1), 33.CrossRefGoogle Scholar
Thomas, F.O., Putnam, C.M. & Chu, H.-C. 1994 On the mechanism of unsteady shock oscillation in shock wave/turbulent boundary layer interactions. Exp. Fluids 18, 69–81.CrossRefGoogle Scholar
Tong, F.-L., Dong, S.-W., Lai, J., Yuan, X.-X. & Li, X.-X. 2022 a Wall shear stress and wall heat flux in a supersonic turbulent boundary layer. Phys. Fluids 34 (1), 015127.CrossRefGoogle Scholar
Tong, F.-L., Duan, J.-Y. & Li, X.-L. 2021 Shock wave and turbulent boundary layer interaction in a double compression ramp. Comput. Fluids 229, 105087.CrossRefGoogle Scholar
Tong, F.-L., Li, X., Yu, C.-P. & Li, X.-L. 2018 Direct numerical simulation of hypersonic shock wave and turbulent boundary layer interactions. Chin. J. Theor. Appl. Mech. 50 (2), 197–208.Google Scholar
Tong, F.-L., Yuan, X.-X., Lai, J., Duan, J.-Y., Sun, D. & Dong, S.-W. 2022 b Wall heat flux in a supersonic shock wave turbulent boundary layer interaction. Phys. Fluids 34 (6), 065104.CrossRefGoogle Scholar
Vanstone & Clemens 2019 Proper orthogonal decomposition analysis of swept-ramp shockwave/boundary-layer unsteadiness at Mach 2. AIAA J. 57 (8), 3395–3409.CrossRefGoogle Scholar
Volpiani, P.S., Bernardini, M. & Larsson, J. 2018 Effects of a nonadiabatic wall on supersonic shock/boundary-layer interactions. Phys. Rev. Fluids 3 (1), 083401.CrossRefGoogle Scholar
Volpiani, P.S., Bernardini, M. & Larsson, J. 2020 Effects of a nonadiabatic wall on hypersonic shock/boundary-layer interactions. Phys. Rev. Fluids 5 (1), 014602.CrossRefGoogle Scholar
Wagner, A., Schramm, J.M., Hannemann, K., Whitside, R. & Hickey, J.-P. 2017 Hypersonic shock wave boundary layer interaction studies on a flat plate at elevated surface temperature. In International Conference on RailNewcastle Talks, pp. 231–243.Google Scholar
Walz, A. & Oser, H.J. 1969 Boundary Layers of Flow and Temperature. M.I.T. Press.Google Scholar
Wenzel, C., Selent, B., Kloker, M. & Rist, U. 2018 DNS of compressible turbulent boundary layers and assessment of data/scaling-law quality. J. Fluid Mech. 842, 428–468.CrossRefGoogle Scholar
White, F.M. & Majdalani, J. 2006 Viscous Fluid Flow, vol. 3. McGraw-Hill Higher Education New York.Google Scholar
Wu, M. & Martin, M.P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.CrossRefGoogle Scholar
Zhang, C., Duan, L. & Choudhari, M.M. 2018 Direct numerical simulation database for supersonic and hypersonic turbulent boundary layers. AIAA J. 56 (11), 4297–4311.CrossRefGoogle Scholar
Zhang, Y.-S., Bi, W.-T., Hussain, F. & She, Z.-S. 2014 A generalized Reynolds analogy for compressible wall-bounded turbulent flows. J. Fluid Mech. 739, 392–420.CrossRefGoogle Scholar
Zhang, Z.-S., Ciu, G.-X., Xu, C.-X. & Huang, W.-X. 2017 Theory and Modeling of Turbulence. Tsinghua University Press.Google Scholar
Zhu, X.-K., Yu, C.-P., Tong, F.-L. & Li, X.-L. 2017 Numerical study on wall temperature effects on shock wave turbulent boundary-layer interaction. AIAA J. 55 (1), 131–140.CrossRefGoogle Scholar
Zuo, F.-Y. 2023 Hypersonic shock wave/turbulent boundary layer interaction over a compression ramp. AIAA J. 61 (4), 1579–1595.CrossRefGoogle Scholar
Zuo, F.-Y., Wei, J.-R., Hu, S.-L. & Pirozzoli, S. 2022 Effects of wall temperature on hypersonic impinging shock-wave/turbulent-boundary-layer interactions. AIAA J. 60 (9), 5109–5122.CrossRefGoogle Scholar