Hostname: page-component-5b777bbd6c-v47t2 Total loading time: 0 Render date: 2025-06-23T17:57:56.169Z Has data issue: false hasContentIssue false
  • English
  • Français

Bulge evolution on shallow water

Published online by Cambridge University Press:  16 June 2025

Shuo-Jun Teng ,
Jun-Hua Pan Open the ORCID record for Jun-Hua Pan [Opens in a new window]  and
Ming-Jiu Ni Open the ORCID record for Ming-Jiu Ni [Opens in a new window]
Shuo-Jun Teng
Affiliation:
Sino-Danish College, University of Chinese Academy of Sciences, Beijing 101408, PR China
Jun-Hua Pan
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics and University of Chinese Academy of Sciences, Beijing 100190, PR China
Ming-Jiu Ni*
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics and University of Chinese Academy of Sciences, Beijing 100190, PR China
*
Corresponding author: Ming-Jiu Ni, mjni@ucas.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

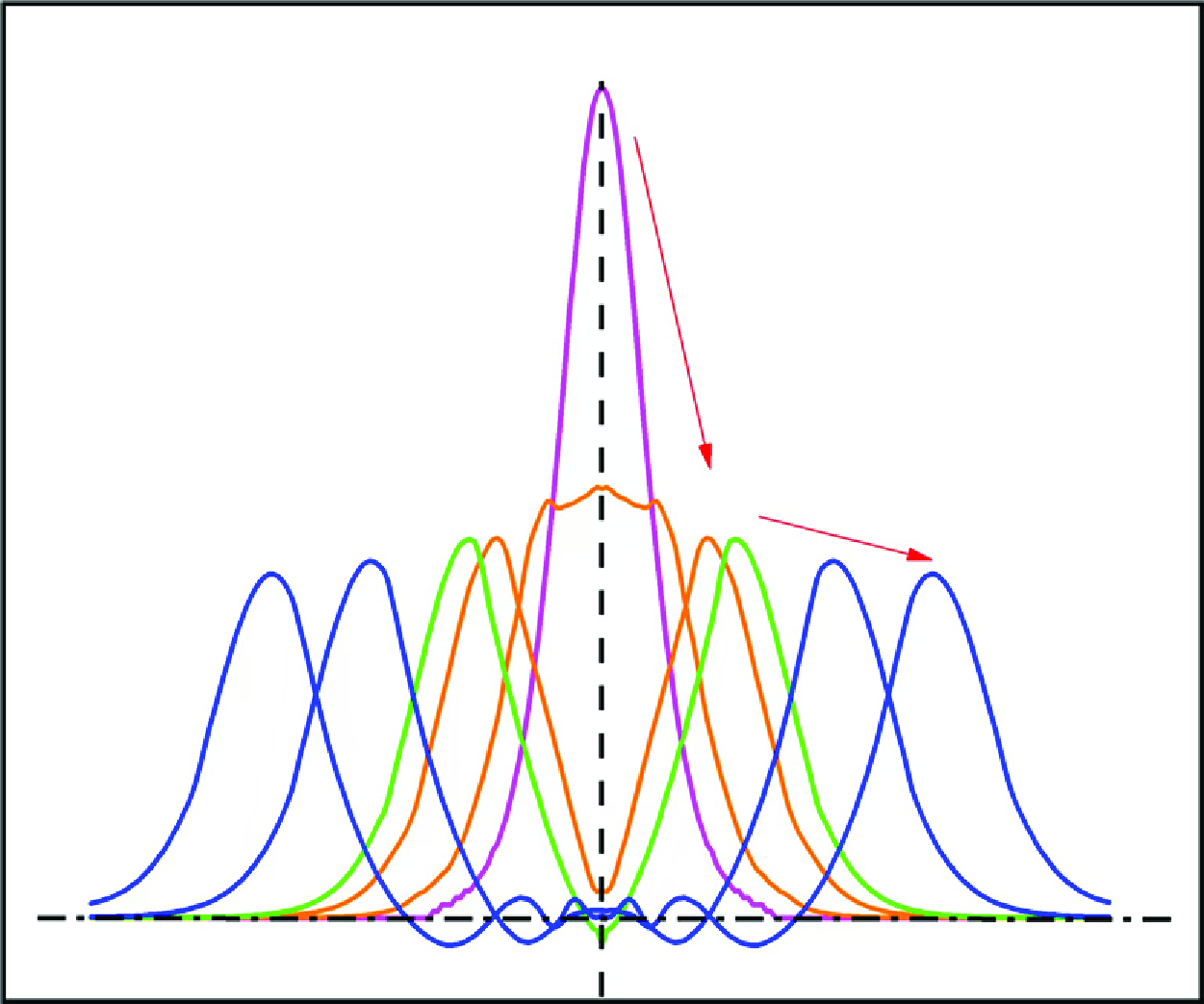
The phenomenon of bulge evolution under the action of gravity on shallow water is prevalent both in natural occurrences and engineering industries. However, despite its ubiquity, its physical process remains largely unexplored. The evolution of bulge contains two fundamental physical processes: collapse and propagation. The collapse process can be further divided into two sub-processes: squeezing process and diffusion process. Based on the weakly nonlinear shallow water assumption with the classical perturbation method, the governing equations controlling the surface elevations in the diffusion process and the propagation process have been theoretically derived, where a bulge-induced surface pressure is modeled for the propagation process. Moreover, their scaling laws for the decay of wave height are also established, which have been validated by direct numerical simulation results. The derived scaling laws for wave height attenuation of bulge evolution provide profound insights, which hold the potential to applications in the engineering industry.

JFM classification

Geophysical and Geological Flows: Shallow water flows Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , A15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

These authors contributed equally to this work and should be considered co-first authors.

References

Allain, J.P., Ruzic, D.N. & Hendricks, M.R. 2001 D, He and Li sputtering of liquid eutectic Sn–Li. J. Nucl. Mater 290, 33–37.10.1016/S0022-3115(00)00504-3CrossRefGoogle Scholar
Brackbill, J.U., Kothe, D.B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100 (2), 335–354.10.1016/0021-9991(92)90240-YCrossRefGoogle Scholar
Craster, R.V. & Matar, O.K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81 (3), 1131–1198.10.1103/RevModPhys.81.1131CrossRefGoogle Scholar
Deshpande, S.S., Anumolu, L. & Trujillo, M.F. 2012 Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 5 (1), 014016.10.1088/1749-4699/5/1/014016CrossRefGoogle Scholar
Dhar, M., Das, G. & Das, P.K. 2020 Planar hydraulic jumps in thin film flow. J. Fluid Mech. 884, A11.10.1017/jfm.2019.833CrossRefGoogle Scholar
Francois, M.M., Cummins, S.J., Dendy, E.D., Kothe, D.B., Sicilian, J.M. & Williams, M.W. 2006 A balanced-force algorithm for continuous and sharp interfacial surface tension models within a volume tracking framework. J. Comput. Phys. 213 (1), 141–173.10.1016/j.jcp.2005.08.004CrossRefGoogle Scholar
Grimshaw, R. 2019 Initial conditions for the cylindrical Korteweg‐de Vries equation. Stud. Appl. Maths 143 (2), 176–191.10.1111/sapm.12272CrossRefGoogle Scholar
Hinton, E.M. & Slim, A.C. 2023 Dynamics and containment of a viscous liquid atop a granular bed. J. Fluid Mech. 969, R3.10.1017/jfm.2023.604CrossRefGoogle Scholar
Johnson, R.S. 1980 Water waves and Korteweg–de Vries equations. J. Fluid Mech. 97 (4), 701–719.10.1017/S0022112080002765CrossRefGoogle Scholar
Kakutani, T. & Matsuuchi, K. 1975 Effect of viscosity on long gravity waves. J. Phys. Soc. Japan 39 (1), 237–246.10.1143/JPSJ.39.237CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M.G. 2012 Falling Liquid Films. 1st edn. Springer.10.1007/978-1-84882-367-9CrossRefGoogle Scholar
Korteweg, D.J. & De Vries, G. 1895 On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. 39 (240), 422–443.10.1080/14786449508620739CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics. 6th edn. Cambridge University Press.Google Scholar
Landau, L.D. & Lifshitz, E.M. 1987 Fluid Mechanics. 2nd edn. Course of Theoretical Physics, Elsevier. Pergamon Press.Google Scholar
Lee, J.J., Skjelbreia, J.E. & Raichlen, F. 1982 Measurement of velocities in solitary waves. J. Waterw. Port Coast. Ocean Div. 108 (2), 200–218.10.1061/JWPCDX.0000293CrossRefGoogle Scholar
Lighthill, T.B.B.J., Benjaminm, J. 1954 On conoidal waves and bores. Proc. R. Soc. Lond. Series A. Math. Phys. Sci. 224 (1159), 448–460.Google Scholar
Longuet-Higgins, M.S. 1957 The statistical analysis of a random, moving surface. Phil. Trans. R. Soc. Lond. 249 (966), 321–387.Google Scholar
Lunz, D. & Howell, P.D. 2019 Flow of a thin liquid-metal film in a toroidal magnetic field. J. Fluid Mech. 867, 835–876.10.1017/jfm.2019.173CrossRefGoogle Scholar
Mandi, L., Roy, K. & Chatterjee, P. 2020 Approximate analytical solution of nonlinear evolution equations. In Selected Topics in Plasma Physics (ed. S. Singh), pp. 111. IntechOpen.Google Scholar
Miles, J.W. 1977 Note on a solitary wave in a slowly varying channel. J. Fluid Mech. 80 (1), 149–152.10.1017/S0022112077001578CrossRefGoogle Scholar
Miles, J.W. 1978 An axisymmetric Boussinesq wave. J. Fluid Mech. 84 (1), 181–191.10.1017/S0022112078000105CrossRefGoogle Scholar
Mirjalili, S., Jain, S.S. & Dodd, M. 2017 Interface-capturing methods for two-phase flows: An overview and recent developments, Tech. Rep, Center for Turbulence Research, Stanford University. 2017 (117–135), 13.Google Scholar
Moss, A.J., Walker, P.H. & Hutka, J. 1979 Raindrop-stimulated transportation in shallow water flows: an experimental study. Sediment. Geol. 22 (3–4), 165–184.10.1016/0037-0738(79)90051-4CrossRefGoogle Scholar
Nakaya, C. 1974 Spread of fluid drops over a horizontal plane. J. Phys. Soc. Japan 37 (2), 539–543.10.1143/JPSJ.37.539CrossRefGoogle Scholar
Ott, E. & Sudan, R.N. 1969 Nonlinear theory of ion acoustic waves with landau damping. Phys. Fluids 12 (11), 2388–2394.10.1063/1.1692358CrossRefGoogle Scholar
Pan, J.-H. & Ni, M.-J. 2022 The development of the MHD film flow numerical simulation platform. Sci. Sin.-Phys. Mech. Astron. 52 (10), 104712.10.1360/SSPMA-2022-0240CrossRefGoogle Scholar
Shemilt, J.D., Horsley, A., Jensen, O.E., Thompson, A.B. & Whitfield, C.A. 2023 Surfactant amplifies yield-stress effects in the capillary instability of a film coating a tube. J. Fluid Mech. 971, A24.10.1017/jfm.2023.588CrossRefGoogle ScholarPubMed
Weidman, P.D. & Zakhem, R. 1988 Cylindrical solitary waves. J.Fluid Mech. 191 (-1), 557–573.10.1017/S0022112088001703CrossRefGoogle Scholar
Wellens, P.R. 2012 Wave simulation in truncated domains for offshore applications. Ph.D. thesis, Delft University of Technology.Google Scholar
Xie, B. & Xiao, F. 2017 Toward efficient and accurate interface capturing on arbitrary hybrid unstructured grids: The THINC method with quadratic surface representation and Gaussian quadrature. J. Comput. Phys. 349, 415–440.10.1016/j.jcp.2017.08.028CrossRefGoogle Scholar
Yang, J.-C., Qi, T.-Y., Ni, M.-J. & Wang, Z.-H. 2016 Flow patterns of GaInSn liquid on inclined stainless steel plate under a range of magnetic field. Fusion Engng Des. 109, 861–865.10.1016/j.fusengdes.2016.01.061CrossRefGoogle Scholar
Zdyrski, T. & Feddersen, F. 2021 Wind-induced changes to surface gravity wave shape in shallow water. J. Fluid Mech. 913, A27.10.1017/jfm.2021.15CrossRefGoogle Scholar