Hostname: page-component-5b777bbd6c-5mwv9 Total loading time: 0 Render date: 2025-06-19T09:48:30.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of rotating helices in a viscous fluid

Published online by Cambridge University Press:  13 June 2025

Chijing Zang ,
Luke Omodt ,
Moumita Dasgupta  and
Xiang Cheng Open the ORCID record for Xiang Cheng [Opens in a new window]
Chijing Zang
Affiliation:
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA
Luke Omodt
Affiliation:
Department of Physics, Augsburg University, Minneapolis, MN 55455, USA
Moumita Dasgupta
Affiliation:
Department of Physics, Augsburg University, Minneapolis, MN 55455, USA
Xiang Cheng*
Affiliation:
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA Saint Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
*
Corresponding author: Xiang Cheng, xcheng@umn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

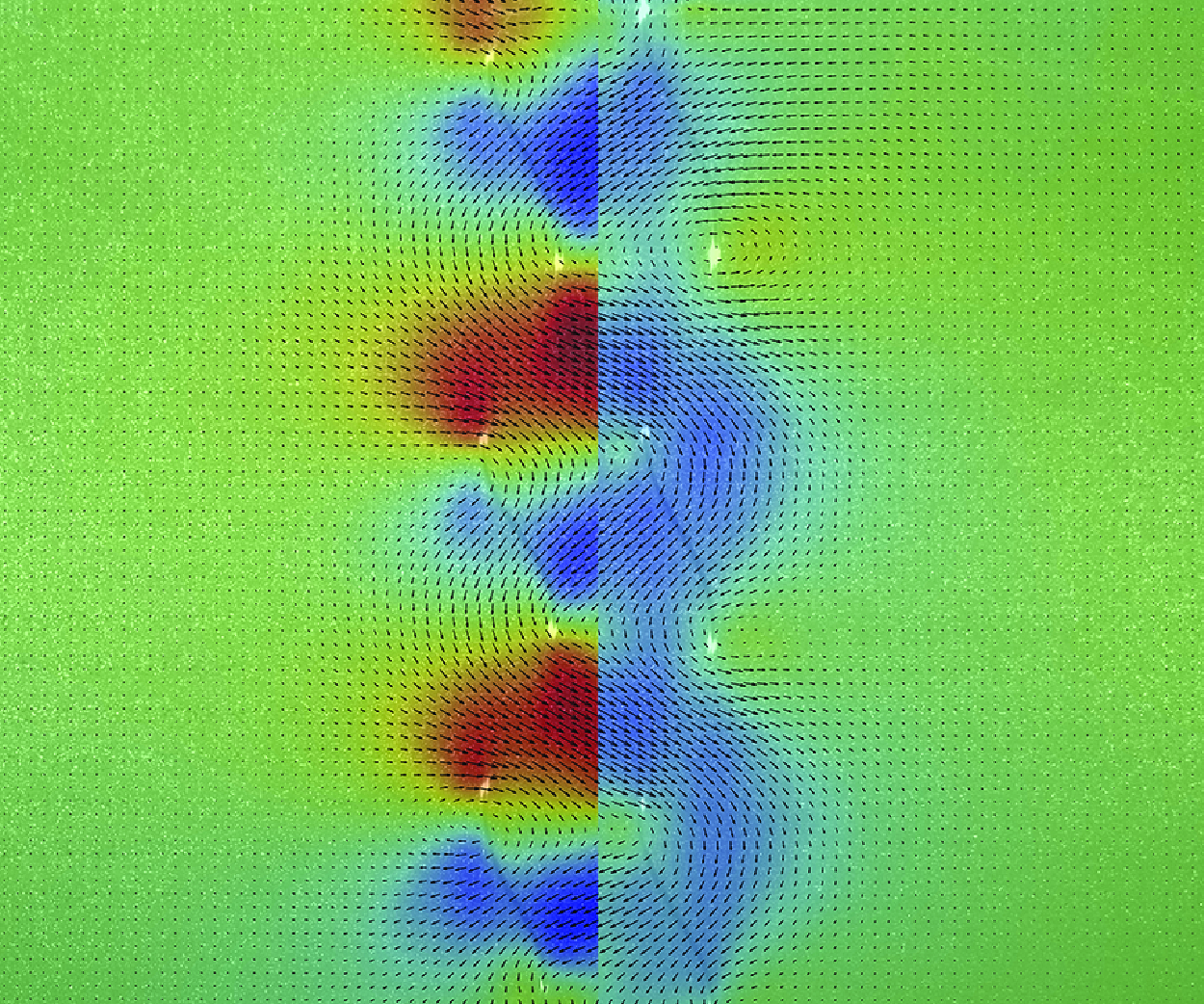
We investigate the dynamics of a pair of rigid rotating helices in a viscous fluid, as a model for bacterial flagellar bundle and a prototype of microfluidic pumps. Combining experiments with hydrodynamic modelling, we examine how spacing and phase difference between the two helices affect their torque, flow field and fluid transport capacity at low Reynolds numbers. Hydrodynamic coupling reduces the torque when the helices rotate in phase at constant angular speed, but increases the torque when they rotate out of phase. We identify a critical phase difference, at which the hydrodynamic coupling vanishes despite the close spacing between the helices. A simple model, based on the flow characteristics and positioning of a single helix, is constructed, which quantitatively predicts the torque of the helical pair in both unbounded and confined systems. Finally, we show the influence of spacing and phase difference on the axial flux and the pump efficiency of the helices. Our findings shed light on the function of bacterial flagella and provide design principles for efficient low-Reynolds-number pumps.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Low-Reynolds-number flows: Slender-body theory Biological Fluid Dynamics: Propulsion
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , R1
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barrett, A., Fogelson, A.L., Forest, M.G., Gruninger, C., Lim, S. & Griffith, B.E. 2024 Flagellum pumping efficiency in shear-thinning viscoelastic fluids. J. Fluid Mech. 999, A2.10.1017/jfm.2024.666CrossRefGoogle ScholarPubMed
Berg, H.C. 2004 E. coli in Motion. Springer.10.1007/b97370CrossRefGoogle Scholar
Bianchi, S., Saglimbeni, F., Frangipane, G., Cannarsa, M.C. & Di Leonardo, R. 2023 Light-driven flagella elucidate the role of hook and cell body kinematics in bundle formation. PRX Life 1 (1), 013016.10.1103/PRXLife.1.013016CrossRefGoogle Scholar
Buchmann, A., Fauci, L.J., Leiderman, K., Strawbridge, E. & Zhao, L. 2018 Mixing and pumping by pairs of helices in a viscous fluid. Phys. Rev. E 97 (2), 023101.10.1103/PhysRevE.97.023101CrossRefGoogle Scholar
Chamolly, A. & Lauga, E. 2020 Direct versus indirect hydrodynamic interactions during bundle formation of bacterial flagella. Phys. Rev. Fluids 5 (12), 123102.10.1103/PhysRevFluids.5.123102CrossRefGoogle Scholar
Danis, U., Rasooli, R., Chen, C.Y., Dur, O., Sitti, M. & Pekkan, K. 2019 Thrust and hydrodynamic efficiency of the bundled flagella. Micromachines (Basel) 10 (7), 449.10.3390/mi10070449CrossRefGoogle ScholarPubMed
Darnton, N., Turner, L., Breuer, K. & Berg, H.C. 2004 Moving fluid with bacterial carpets. Biophys. J. 86 (3), 1863–1870.10.1016/S0006-3495(04)74253-8CrossRefGoogle ScholarPubMed
Dauparas, J., Das, D. & Lauga, E. 2018 Helical micropumps near surfaces. Biomicrofluidics 12 (1), 014108.10.1063/1.5012070CrossRefGoogle ScholarPubMed
Flores, H., Lobaton, E., Méndez-Diez, S., Tlupova, S. & Cortez, R. 2005 A study of bacterial flagellar bundling. Bull. Math. Biol. 67 (1), 137–168.10.1016/j.bulm.2004.06.006CrossRefGoogle ScholarPubMed
Gao, Z., Li, H., Chen, X. & Zhang, H.P. 2015 Using confined bacteria as building blocks to generate fluid flow. Lab Chip 15 (24), 4555–4562.10.1039/C5LC01093DCrossRefGoogle ScholarPubMed
Guo, H., Man, Y. & Zhu, H. 2024 Hydrodynamic bound states of rotating microcylinders in a confining geometry. Phys. Rev. Fluids 9 (1), 014102.10.1103/PhysRevFluids.9.014102CrossRefGoogle Scholar
Janssen, P.J.A. & Graham, M.D. 2011 Coexistence of tight and loose bundled states in a model of bacterial flagellar dynamics. Phys. Rev. E 84 (1), 011910.10.1103/PhysRevE.84.011910CrossRefGoogle Scholar
Jeffery, G.B. 1922 The rotation of two circular cylinders in a viscous fluid. Proc. R. Soc. Lond. A 101 (709), 169–174.Google Scholar
Kamdar, S., et al. 2023 Multiflagellarity leads to the size-independent swimming speed of peritrichous bacteria. Proc. Natl Acad. Sci. USA 120 (48), e2310952120.10.1073/pnas.2310952120CrossRefGoogle Scholar
Kamdar, S., Shin, S., Leishangthem, P., Francis, L.F., Xu, X. & Cheng, X. 2022 The colloidal nature of complex fluids enhances bacterial motility. Nature 603 (7903), 819–823.10.1038/s41586-022-04509-3CrossRefGoogle ScholarPubMed
Kanehl, P. & Ishikawa, T. 2014 Fluid mechanics of swimming bacteria with multiple flagella. Phys. Rev. E 89 (4), 042704.10.1103/PhysRevE.89.042704CrossRefGoogle ScholarPubMed
Kim, M.J., Bird, J.C., Van Parys, A.J., Breuer, K.S. & Powers, T.R. 2003 A macroscopic scale model of bacterial flagellar bundling. Proc. Natl Acad. Sci. USA 100 (26), 15481–15485.10.1073/pnas.2633596100CrossRefGoogle ScholarPubMed
Kim, M.J. & Breuer, K.S. 2008 Microfluidic pump powered by self-organizing bacteria. Small 4 (1), 111–118.10.1002/smll.200700641CrossRefGoogle ScholarPubMed
Kim, M.J., Kim, M.J., Bird, J.C., Park, J., Powers, T.R. & Breuer, K.S. 2004 Particle image velocimetry experiments on a macro-scale model for bacterial flagellar bundling. Exp. Fluids 37 (6), 782–788.10.1007/s00348-004-0848-5CrossRefGoogle Scholar
Kim, M.J. & Powers, T.R. 2004 Hydrodynamic interactions between rotating helices. Phys. Rev. E 69 (6), 061910.10.1103/PhysRevE.69.061910CrossRefGoogle ScholarPubMed
Lauga, E. 2020 The Fluid Dynamics of Cell Motility. Cambridge University Press.10.1017/9781316796047CrossRefGoogle Scholar
Lighthill, J. 1976 Flagellar hydrodynamics. SIAM Rev. 18 (2), 161–230.10.1137/1018040CrossRefGoogle Scholar
Lim, S., Yadunandan, A. & Khalid Jawed, M. 2023 Bacteria-inspired robotic propulsion from bundling of soft helical filaments at low Reynolds number. Soft Matter 19 (12), 2254–2264.10.1039/D2SM01398CCrossRefGoogle ScholarPubMed
Liu, B., Breuer, K.S. & Powers, T.R. 2014 Propulsion by a helical flagellum in a capillary tube. Phys. Fluids 26 (1), 011701.10.1063/1.4861026CrossRefGoogle Scholar
Macnab, R.M. 1977 Bacterial flagella rotating in bundles: a study in helical geometry. Proc. Natl Acad. Sci. USA 74 (1), 221–225.10.1073/pnas.74.1.221CrossRefGoogle ScholarPubMed
Man, Y., Page, W., Poole, R.J. & Lauga, E. 2017 Bundling of elastic filaments induced by hydrodynamic interactions. Phys. Rev. Fluids 2 (12), 123101.10.1103/PhysRevFluids.2.123101CrossRefGoogle Scholar
Martindale, J.D. & Fu, H.C. 2017 Autonomously responsive pumping by a bacterial flagellar forest: a mean-field approach. Phys. Rev. E 96 (3), 033107.10.1103/PhysRevE.96.033107CrossRefGoogle Scholar
Martindale, J.D., Jabbarzadeh, M. & Fu, H.C. 2016 Choice of computational method for swimming and pumping with nonslender helical filaments at low Reynolds number. Phys. Fluids 28 (2), 021901.10.1063/1.4940904CrossRefGoogle Scholar
Park, J., Kim, Y., Lee, W., Pfeifer, V., Muraveva, V., Beta, C. & Lim, S. 2024 Bundling instability of lophotrichous bacteria. Phys. Fluids 36 (10), 101917.10.1063/5.0228395CrossRefGoogle Scholar
Raz, O. & Avron, J. 2007 Swimming, pumping and gliding at low Reynolds numbers. New J. Phys. 9 (12), 437–437.10.1088/1367-2630/9/12/437CrossRefGoogle Scholar
Reichert, M. & Stark, H. 2005 Synchronization of rotating helices by hydrodynamic interactions. Eur. Phys. J. E 17 (4), 493–500.10.1140/epje/i2004-10152-7CrossRefGoogle ScholarPubMed
Reigh, S.Y., Winkler, R.G. & Gompper, G. 2012 Synchronization and bundling of anchored bacterial flagella. Soft Matter 8 (16), 4363–4372.10.1039/c2sm07378aCrossRefGoogle Scholar
Rodenborn, B., Chen, C.H., Swinney, H.L., Liu, B. & Zhang, H.P. 2013 Propulsion of microorganisms by a helical flagellum. Proc. Natl Acad. Sci. USA 110 (5), E338–E347.10.1073/pnas.1219831110CrossRefGoogle ScholarPubMed
Rostami, M.W., Liu, W., Buchmann, A., Strawbridge, E. & Zhao, L. 2022 Optimal design of bacterial carpets for fluid pumping. Fluids 7 (1), 25.10.3390/fluids7010025CrossRefGoogle Scholar
Taylor, G. 1951 Analysis of the swimming of microscopic organisms. Proc. R. Soc. Lond. A 209 (1099), 447–461.Google Scholar
Tottori, S., Zhang, L., Qiu, F., Krawczyk, K.K., Franco-Obregõn, A. & Nelson, B.J. 2012 Magnetic helical micromachines: fabrication, controlled swimming, and cargo transport. Adv. Mater. 24 (6), 811–816.10.1002/adma.201103818CrossRefGoogle ScholarPubMed
Turner, L., Ryu, W.S. & Berg, H.C. 2000 Real-time imaging of fluorescent flagellar filaments. J. Bacteriol. 182 (10), 2793–2801.10.1128/JB.182.10.2793-2801.2000CrossRefGoogle ScholarPubMed
Tătulea-Codrean, M. & Lauga, E. 2021 Asymptotic theory of hydrodynamic interactions between slender filaments. Phys. Rev. Fluids 6 (7), 074103.10.1103/PhysRevFluids.6.074103CrossRefGoogle Scholar
Tătulea-Codrean, M. & Lauga, E. 2022 Elastohydrodynamic synchronization of rotating bacterial flagella. Phys. Rev. Lett. 128 (20), 208101.10.1103/PhysRevLett.128.208101CrossRefGoogle ScholarPubMed
Vizsnyiczai, G., Frangipane, G., Bianchi, S., Saglimbeni, F., Dell’Arciprete, D. & Di Leonardo, R. 2020 A transition to stable one-dimensional swimming enhances E. coli motility through narrow channels. Nat. Commun. 11 (1), 2340.10.1038/s41467-020-15711-0CrossRefGoogle ScholarPubMed
Yamagata, Y. 1970 Torque exerted on a cylinder by viscous flow between non-coaxial cylinders. Japan. J. Appl. Phys. 9 (1), 139–149.10.1143/JJAP.9.139CrossRefGoogle Scholar
Zhang, L., Peyer, K.E. & Nelson, B.J. 2010 Artificial bacterial flagella for micromanipulation. Lab Chip 10 (17), 2203–2215.10.1039/c004450bCrossRefGoogle ScholarPubMed
Supplementary material: File

Zang et al. supplementary material movie 1

Flow field of two rotating helices at a separation $d/R = 5$ and a phase difference $\\Delta \\phi=0$ in the axial plane ($x$-$z$ plane with $y=0$). The top row shows the experimental flow field obtained via PIV, while the bottom row presents results from SBT simulations. The left column illustrates the $z$-component of velocity ($v_z$), and the right column depicts the $r$-component of velocity ($v_r$). Velocities are normalized by $\\omega R$. White lines and arrows are streamlines. Notably, experiments reveal an upward flow $(+z)$ near the wall, whereas SBT simulations in an unbounded fluid consistently show flow in the $-z$ direction. The movie shows one rotation period $2\\pi/\\omega = 12.5$ s.
Download Zang et al. supplementary material movie 1(File)
File 2.3 MB
Supplementary material: File

Zang et al. supplementary material movie 2

Flow field of two rotating helices at a separation $d/R = 5$ and a phase difference $\\Delta \\phi=0$ in the meridional plane ($x$-$y$ plane). The color indicates the magnitude of the in-plane velocity $v_{x-y} = \\sqrt{v_x^2+v_y^2}$ normalized by the rotation speed $\\omega R$. The top row shows the experimental flow field obtained via PIV, while the bottom row presents results from SBT simulations. White lines and arrows are streamlines. The movie shows one rotation period $2\\pi/\\omega = 12.5$ s.
Download Zang et al. supplementary material movie 2(File)
File 2.6 MB