Electro-osmotic flow of semi-dilute polyelectrolyte solutions in nanochannels

Abstract

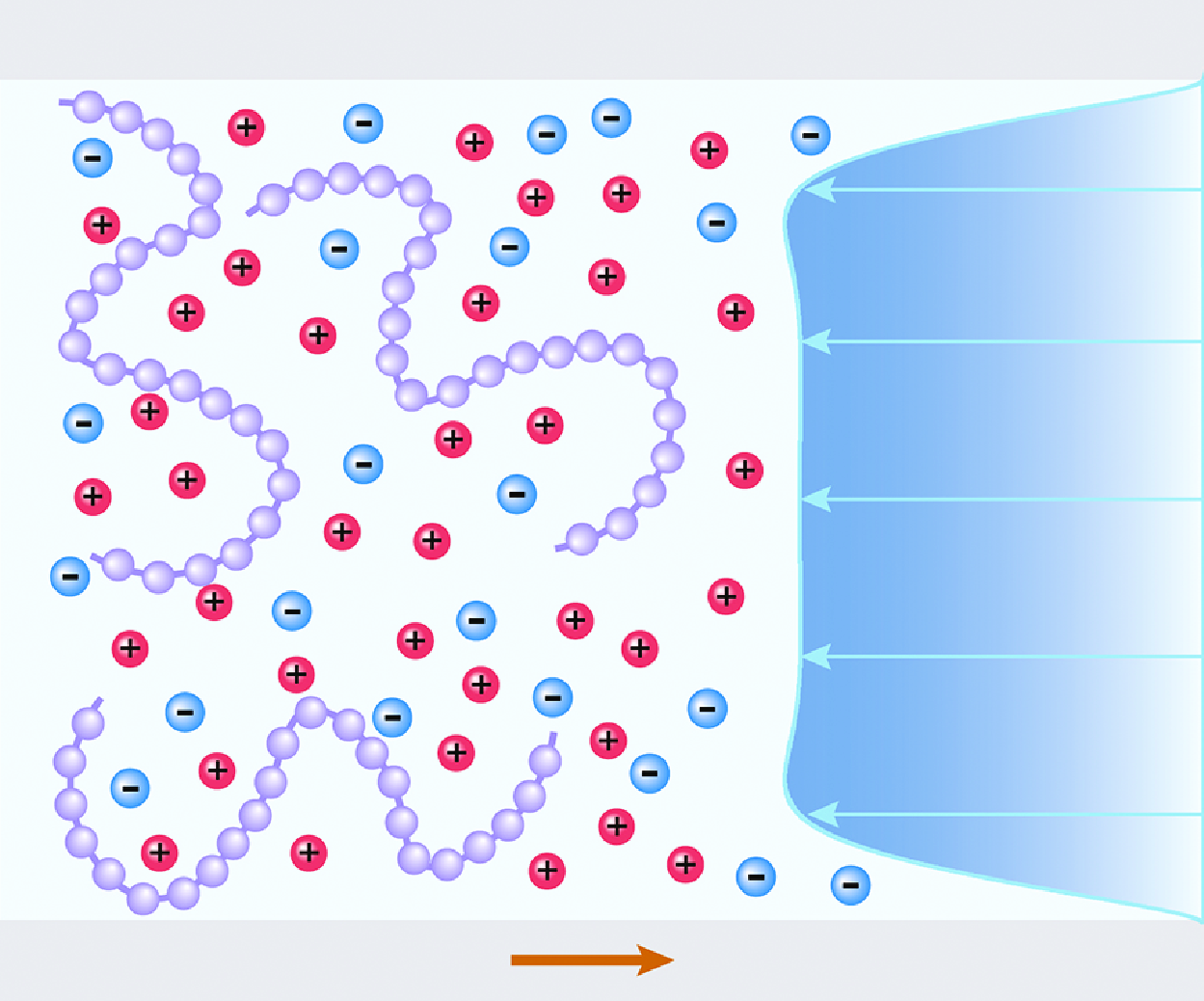
This paper presents a theoretical model for the electro-osmotic flow (EOF) of semi-dilute polyelectrolyte (PE) solutions in nanochannels. We use mean-field theories to describe the properties of electric double layer and viscosity of PE solutions that are prerequisites for constructing the EOF model. The EOF model is validated via a good match to the existing experimental results. Based on the validated EOF model, we conduct a comprehensive analysis of EOF of semi-dilute PE solutions in nanochannels. First, we observe considerable EOF of PE solutions in the uncharged nanochannels, which is in stark contrast to EOF of simple electrolyte solutions. The analyses show that the EOF of PE solutions in uncharged nanochannels is triggered by the external electric field acting on the near-wall non-electroneutral regions resulting from the confinement-induced inhomogeneous distribution of PE monomers. Although the solutions are electroneutral as a whole, the presence of local non-electroneutral regions and the mismatch between non-electroneutral regions and high-viscosity regions lead to the net EOF in uncharged nanochannels. Furthermore, we reveal that the EOF mobility $\mu _{{eof}}$ in uncharged nanochannels exhibits a scaling law $\mu _{{eof}} \propto a^{-0.44}$ (wherein $a$ denotes monomer Kuhn length) and is inversely proportional to the PE chain length, while it decreases nonlinearly with the charge fraction of the PE chains. Moreover, the EOF mobility reaches its maximum at specific bulk monomer concentration, and increases with the nanochannel height before converging to that under no confinement. Second, we analyse the EOF of PE solutions in nanochannels with various wall effects, such as surface charge density, slip length and adsorption length. When the surface charge is absent, the adsorption length significantly influences the direction and magnitude of the EOF, whereas the slip length has no effect. When the wall becomes increasingly charged, the influence of adsorption length on EOF gradually diminishes, while the importance of the slip length progressively intensifies and the EOF is highly influenced by the co-action of various wall effects in a complicated manner. When the surface wall is oppositely charged to polymer monomers, the EOF mobility varies nonlinearly with the surface charge density, while a zero net flow of EOF followed by a direction reversal is discovered when the wall is likely charged to polymer monomers.