No CrossRef data available.
Published online by Cambridge University Press: 07 July 2025
A drop of an electrically conducting non-magnetic fluid of radius  $R$, electrical conductivity
$R$, electrical conductivity  $\kappa$, density
$\kappa$, density  $\rho _i$ and viscosity
$\rho _i$ and viscosity  $\eta _i$ is suspended in a non-conducting medium of density
$\eta _i$ is suspended in a non-conducting medium of density  $\rho _o$, viscosity
$\rho _o$, viscosity  $\eta _o$ and subject to an oscillating magnetic field of magnitude
$\eta _o$ and subject to an oscillating magnetic field of magnitude  $H_0$ and angular frequency
$H_0$ and angular frequency  $\omega$. Oscillating eddy currents are induced in the drop due to Faraday’s law. The Lorentz force density, the cross product of the current density and the magnetic field, is the superposition of a steady component and an oscillating component with frequency
$\omega$. Oscillating eddy currents are induced in the drop due to Faraday’s law. The Lorentz force density, the cross product of the current density and the magnetic field, is the superposition of a steady component and an oscillating component with frequency  $2 \omega$. The characteristic velocity due to the Lorentz force density is
$2 \omega$. The characteristic velocity due to the Lorentz force density is  $(\mu _0 H_0^2 R/\eta _i)$ times a function of the dimensionless parameter
$(\mu _0 H_0^2 R/\eta _i)$ times a function of the dimensionless parameter  $\beta = \sqrt {\mu _0 \kappa \omega R^2}$, the square root of the ratio of the frequency and the current relaxation rate. Here,
$\beta = \sqrt {\mu _0 \kappa \omega R^2}$, the square root of the ratio of the frequency and the current relaxation rate. Here,  $\mu _0$ is the magnetic permeability. The characteristic velocities for the steady and oscillatory components increase proportional to
$\mu _0$ is the magnetic permeability. The characteristic velocities for the steady and oscillatory components increase proportional to  $\beta ^{4}$ for
$\beta ^{4}$ for  $\beta \ll 1$, and decrease proportional to
$\beta \ll 1$, and decrease proportional to  $\beta ^{-1}$ for
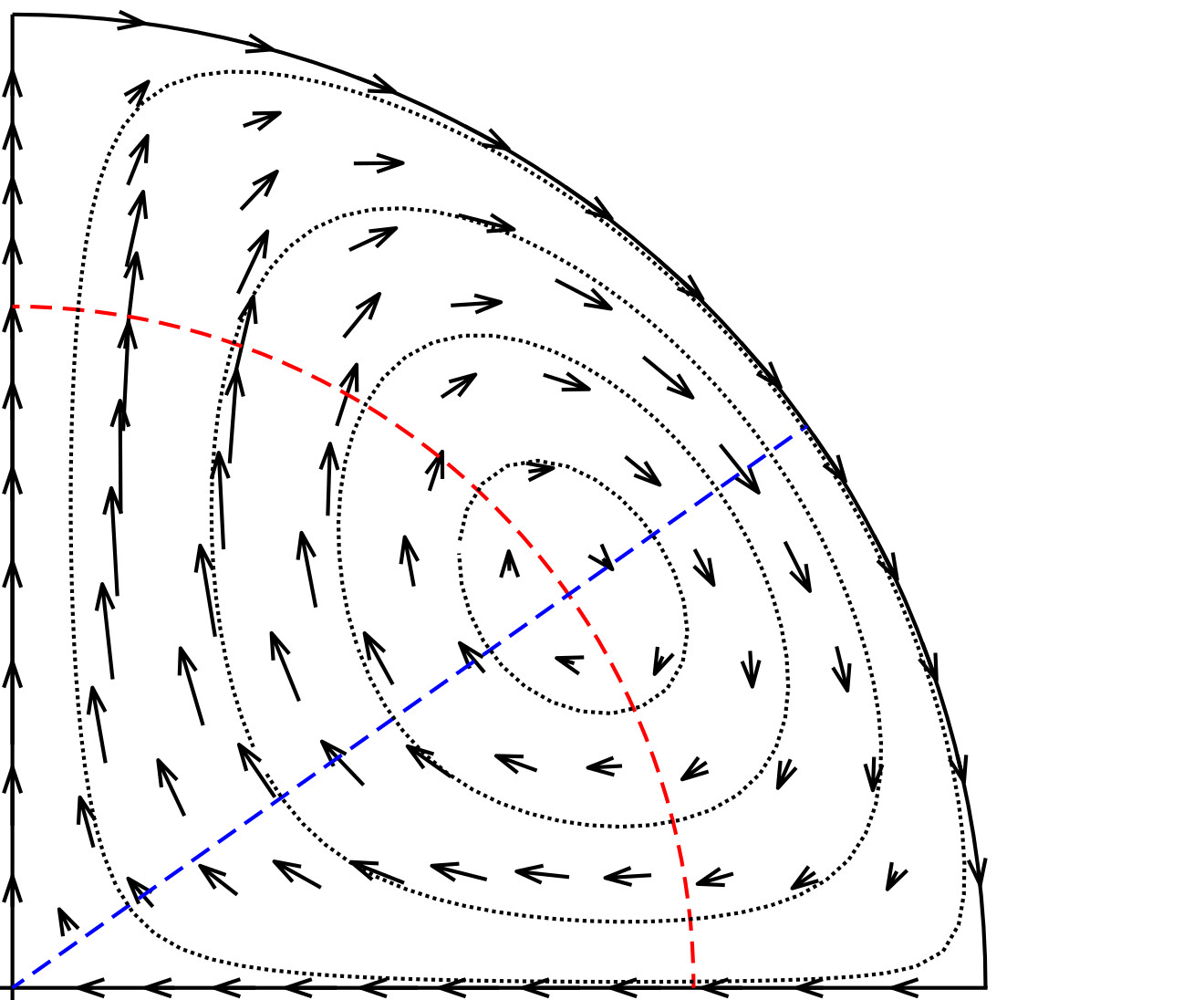
$\beta ^{-1}$ for  $\beta \gg 1$. The steady flow field consists of two axisymmetric eddies in the two hemispheres with flow outwards along the magnetic field axis and inwards along the equator. The flow in the drop induces a biaxial extensional flow in the surrounding medium, with compression along the magnetic axis and extension along the equatorial plane. The oscillating component of the velocity depends on
$\beta \gg 1$. The steady flow field consists of two axisymmetric eddies in the two hemispheres with flow outwards along the magnetic field axis and inwards along the equator. The flow in the drop induces a biaxial extensional flow in the surrounding medium, with compression along the magnetic axis and extension along the equatorial plane. The oscillating component of the velocity depends on  $\beta$ and the Reynolds number
$\beta$ and the Reynolds number  ${Re}_\omega$ based on the frequency of oscillations. For
${Re}_\omega$ based on the frequency of oscillations. For  ${Re}_\omega \gg 1$, the amplitude of the oscillatory velocity decreases proportional to
${Re}_\omega \gg 1$, the amplitude of the oscillatory velocity decreases proportional to  ${Re}_\omega ^{-1}$ for
${Re}_\omega ^{-1}$ for  $\beta \ll 1$, and proportional to
$\beta \ll 1$, and proportional to  ${Re}_\omega ^{-1/2}$ for
${Re}_\omega ^{-1/2}$ for  $\beta \gg 1$.
$\beta \gg 1$.