Hostname: page-component-5b777bbd6c-rbv74 Total loading time: 0 Render date: 2025-06-18T22:07:21.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypersonic boundary-layer receptivity to free-stream acoustic waves with thermochemical non-equilibrium effects

Published online by Cambridge University Press:  17 June 2025

Anand Rama Varma Open the ORCID record for Anand Rama Varma [Opens in a new window]  and
Xiaolin Zhong
Anand Rama Varma*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California Los Angeles, Los Angeles, CA 90095, USA
Xiaolin Zhong
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California Los Angeles, Los Angeles, CA 90095, USA
*
Corresponding author: Anand Rama Varma, varmaar@ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

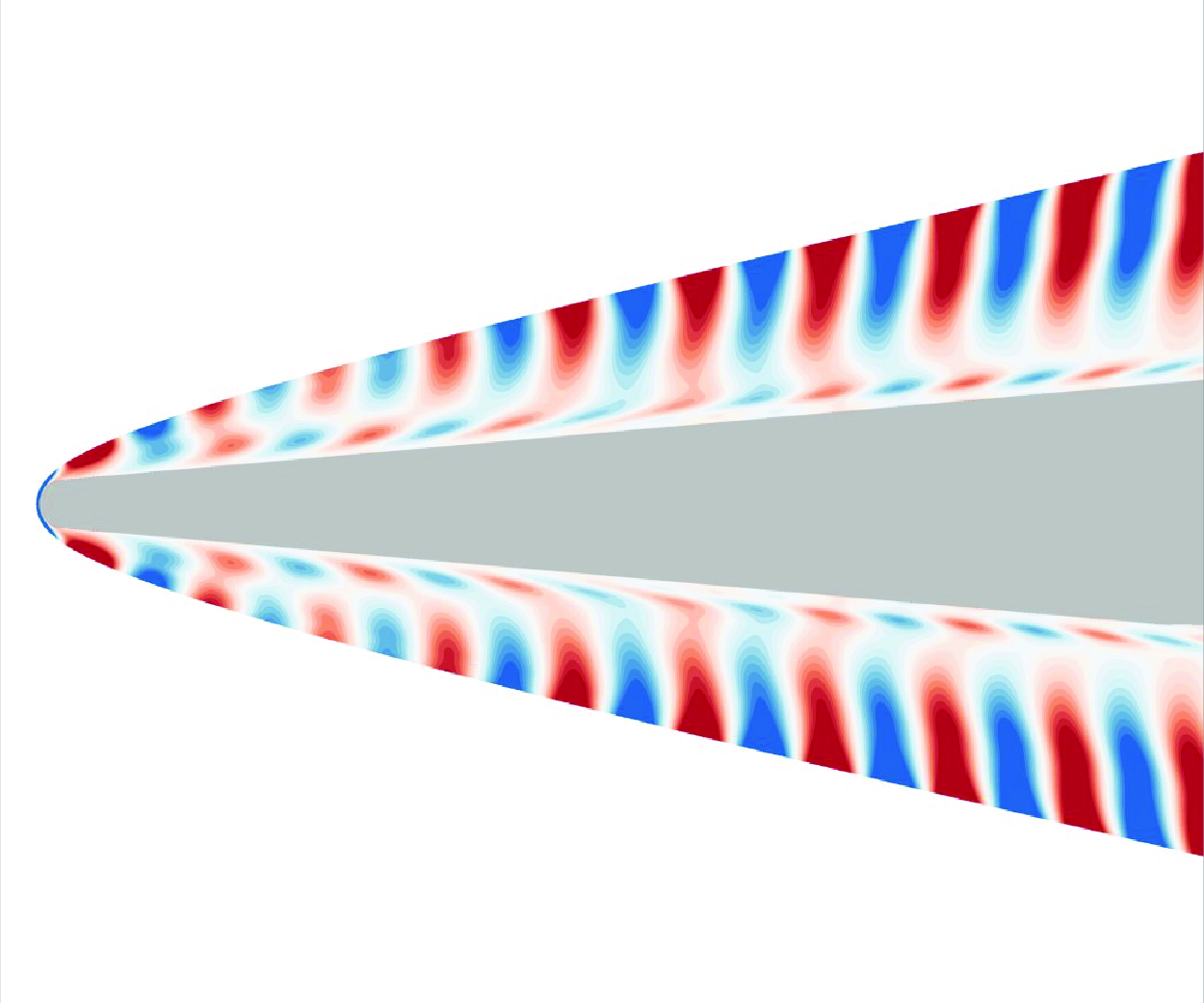
Many hypersonic flows of interest feature high free-stream stagnation enthalpies, which lead to high flow-field temperatures and thermochemical non-equilibrium (TCNE) effects, such as finite-rate chemistry and vibrational excitation. However, very few studies have considered receptivity for high-enthalpy flows. In this paper, we investigate the receptivity of a high-enthalpy Mach 5 straight-cone boundary layer to slow and fast acoustic free-stream waves using direct numerical simulation alongside linear stability theory and the linear parabolised stability equations. In addition, we investigate the TCNE effect on receptivity by comparing results between the TCNE gas model and a thermochemically frozen gas model. The dominant instability mechanism for this flow configuration is found to be Mack’s second mode, with the unstable mode being the fast mode. Second-mode receptivity coefficients are obtained for a number of frequencies. For free-stream slow acoustic waves, these receptivity coefficients are found to generally increase with frequency. For a small subset of the considered frequency range, the receptivity coefficients corresponding to free-stream fast acoustic waves are found to be several times larger than for free-stream slow acoustic waves. The TCNE effects are found to lead to higher peak $N$-factors while also reducing second-mode receptivity coefficients, indicating that TCNE effects have competing impacts on receptivity versus stability for the considered frequencies.

JFM classification

Boundary Layers: Boundary layer receptivity Compressible Flows: Hypersonic Flow Boundary Layers: Boundary layer stability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , A16
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anderson, J.D. 2006 Hypersonic and High-Temperature Gas Dynamics. 2nd edn. AIAA.10.2514/4.861956CrossRefGoogle Scholar
Balakumar, P. & Chou, A. 2018 Transition prediction in hypersonic boundary layers using receptivity and freestream spectra. AIAA J. 56 (1), 193–208.10.2514/1.J056040CrossRefGoogle ScholarPubMed
Balakumar, P. & Kegerise, M.A. 2011 Receptivity of hypersonic boundary layers to acoustic and vortical disturbances. In 49th AIAA Aerosciences Meeting, AIAA 2011-371.Google Scholar
Beyak, E.S. 2022 Transition physics and boundary-layer stability: computational modeling in compressible flow. PhD thesis, Texas AM University, USA.Google Scholar
Bitter, N.P. & Shepherd, J.E. 2015 Stability of highly cooled hypervelocity boundary layers. J. Fluid Mech. 778, 586–620.CrossRefGoogle Scholar
Blottner, F., Johnson, M. & Ellis, M. 1971 Chemically reacting gas viscous flow program for multi-component gas mixtures, Tech. Rep. SC-RR–70-754. Sandia National Laboratories.10.2172/4658539CrossRefGoogle Scholar
Cerminara, A. & Sandham, N.D. 2017 Acoustic leading-edge receptivity for supersonic/Hypersonic flows over a blunt wedge. AIAA J. 77 (12), 4234–4244.10.2514/1.J055749CrossRefGoogle Scholar
Chang, C.-L., Kline, H. & Li, F. 2021 Wall cooling effect on high-enthalpy supersonic modes over a cone. AIAA J. 59 (10), 3831–3844.10.2514/1.J060161CrossRefGoogle Scholar
Chang, C.-L. & Malik, M.R. 1994 Oblique-mode breakdown and secondary instability in supersonic boundary layers. J. Fluid Mech. 273, 323–359.10.1017/S0022112094001965CrossRefGoogle Scholar
Chang, C.-L., Vinh, H. & Malik, M.R. 1997 Hypersonic boundary-layer stability with chemical reactions using PSE. In 28th AIAA Fluid Dynamics Conference, AIAA 1997-2012.Google Scholar
Chen, X., Wang, L. & Fu, S. 2021 Parabolized stability analysis of hypersonic thermal–Chemical nonequilibrium boundary-layer flows. AIAA J. 59 (7), 2382–2395.CrossRefGoogle Scholar
Cleveland, W.S. & Devlin, S.J. 1986 Locally weighted regression: an approach to regression analysis by local fitting. J. Am. Stat. Assoc. 83 (403), 596–610.10.1080/01621459.1988.10478639CrossRefGoogle Scholar
De Tullio, N. & Sandham, N.D. 2015 Influence of boundary-layer disturbances on the instability of a roughness wake in a high-speed boundary layer. J. Fluid Mech. 763, 136–165.10.1017/jfm.2014.663CrossRefGoogle Scholar
Duan, L., Choudhari, M.M. & Wu, M. 2014 Numerical study of acoustic radiation due to a supersonic turbulent boundary layer. J. Fluid Mech. 746, 165–192.10.1017/jfm.2014.116CrossRefGoogle Scholar
Eucken, A. 1913 Über das wärmeleitvermögen, die spezifische wärme und die innere reibung der gase (in german). Physikalische Zeitschrift XIV, 324–332.Google Scholar
Fedorov, A. & Khokhlov, A. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14 (6), 359–375.10.1007/s001620100038CrossRefGoogle Scholar
Fedorov, A.V., Ryzhov, A.A., Soudakov, V.G. & Utyuzhnikov, S.V. 2013 Receptivity of a high-speed boundary layer to temperature spottiness. J. Fluid Mech. 722, 533–553.10.1017/jfm.2013.111CrossRefGoogle Scholar
Fedorov, A.V. & Tumin, A. 2003 Initial-value problem for hypersonic boundary-layer flows. AIAA J. 41 (3), 379–389.10.2514/2.1988CrossRefGoogle Scholar
Fedorov, A.V. & Tumin, A. 2011 High-speed boundary-layer instability: old terminology and a new framework. AIAA J. 49 (8), 1647–1657.CrossRefGoogle Scholar
Gaydos, P. & Tumin, A. 2004 Multimode decomposition in compressible boundary layers. AIAA J. 42 (6), 1115–1121.10.2514/1.2289CrossRefGoogle Scholar
He, S. & Zhong, X. 2022 The effects of nose bluntness on broadband disturbance receptivity in hypersonic flow. Phys. Fluids 34 (5).10.1063/5.0088236CrossRefGoogle Scholar
Hollis, B.R. 2012 Blunt-body entry vehicle aerothermodynamics: transition and turbulent heating. J. Spacecr. Rockets 49 (3), 435–449.10.2514/1.51864CrossRefGoogle Scholar
Huang, Y. & Zhong, X. 2014 Parametric study of boundary-layer receptivity to freestream hot-spot perturbation over a blunt compression cone. In 52nd AIAA Aerosciences Meeting, AIAA 2014-0774.Google Scholar
Hudson, M.L., Chokani, N. & Candler, G.V. 1997 Linear stability of hypersonic flow in thermochemical nonequilibrium. AIAA J. 35 (6), 958–964.10.2514/2.204CrossRefGoogle Scholar
van Ingen, J.L. 1956 A suggested semi-empirical method for the calculation of the boundary layer transition region, Delft University of Technology, Tech. Rep. VTH-74. Delft University of Technology.Google Scholar
Johnson, C., Stainback, P., Wicker, K. & Boney, L. 1972 Boundary-layer edge conditions and transition reynolds number data for a flight test at mach 20 (reentry f), Tech. Rep. NASA-TM-X-2584. NASA.Google Scholar
Johnson, H.B., Seipp, T.G. & Candler, G.V. 1998 Numerical study of hypersonic reacting boundary layer transition on cones. Phys. Fluids 10 (10), 2676–2685.10.1063/1.869781CrossRefGoogle Scholar
Kara, K., Balakumar, P. & Kandil, O. 2008 Effects of wall cooling on hypersonic boundary layer receptivity over a cone. In 38th AIAA Fluid Dynamics Conference and Exhibit, AIAA 2008-3734.Google Scholar
Kara, K., Balakumar, P. & Kandil, O. 2011 Effects of nose bluntness on hypersonic boundary-layer receptivity and stability over cones. AIAA J. 49 (12), 2593–2606.10.2514/1.J050032CrossRefGoogle Scholar
Kline, H.L., Chang, C.-L. & Li, F. 2018 Hypersonic chemically reacting boundary-layer stability using LASTRAC. In AIAA 2018 Fluid Dynamics Conference, AIAA 2018-3699.Google Scholar
Knisely, C.P. & Zhong, X. 2017 An investigation of sound radiation by supersonic unstable modes in hypersonic boundary layers. In 47th AIAA Fluid Dynamics Conference, AIAA 2018-4516.Google Scholar
Knisely, C. & Zhong, X. 2019 a Significant supersonic modes and the wall temperature effect in hypersonic boundary layers. AIAA J. 57 (4), 1552–1566.10.2514/1.J057775CrossRefGoogle Scholar
Knisely, C.P. & Zhong, X. 2019 Sound radiation by supersonic unstable modes in hypersonic blunt cone boundary layers. i. linear stability theory. Phys. Fluids 31.Google Scholar
Knisely, C.P. & Zhong, X. 2019 c Sound radiation by supersonic unstable modes in hypersonic blunt cone boundary layers. ii. direct numerical simulation. Phys. Fluids 31.Google Scholar
Knisely, C.P. & Zhong, X. 2020 Impact of vibrational nonequilibrium on the supersonic mode in hypersonic boundary layers. AIAA J. 58 (4), 1704–1714.10.2514/1.J058758CrossRefGoogle Scholar
Laufer, J. 1961 Aerodynamic noise in supersonic wind tunnels. J. Aerosp. Sci. 29 (9), 685–692.10.2514/8.9150CrossRefGoogle Scholar
Lee, J. 1985 Basic governing equations for the flight regimes of aeroassisted orbital transfer vehicles. In Thermal Design of Aeroassisted Orbital Transfer Vehicles, (ed. Nelson, H.F.), vol. 96, pp. 3–53. AIAA.Google Scholar
Ma, Y. & Zhong, X. 2003 a Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions. J. Fluid Mech. 488, 31–78.10.1017/S0022112003004786CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2003 b Receptivity of a supersonic boundary layer over a flat plate. Part 2. Wave structures and interactions. J. Fluid Mech. 488, 31–78.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2004 Receptivity to freestream disturbances of a Mach 10 nonequilibrium reacting oxygen flow over a flat plate. In 42nd AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2004-0256.Google Scholar
Mack, L.M. 1977 Transition and laminar instability. Tech. Rep. NASA-CP-153203. NASA.Google Scholar
Mack, L.M. 1984 Boundary layer linear stability theory. Tech. Rep. AGARD Rep. No. 709. AGARD.Google Scholar
Malik, M.R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86 (2), 376–413.CrossRefGoogle Scholar
Marineau, E. 2017 Prediction methodology for second-mode-dominated boundary-layer transition in wind tunnels. AIAA J. 55 (2), 484–499.10.2514/1.J055061CrossRefGoogle Scholar
Marxen, O., Magin, T.E., Shaqfeh, E.S.G. & Iaccarino, G. 2013 A method for the direct numerical simulation of hypersonic boundary-layer instability with finite-rate chemistry. J. Comput. Phys. 255 (1), 572–589.CrossRefGoogle Scholar
McBride, B., Heimel, S., Ehlers, J. & Gordon, S. 1963 Thermodynamic properties to 6000∘ for 210 substances involving the first 18 elements, Tech. Rep. NASA-SP-3001. NASA.Google Scholar
McKenzie, J.F. & Westphal, K.O. 1968 Interaction of linear waves with oblique shock waves. Phys. Fluids 11 (11), 2350–2362.10.1063/1.1691825CrossRefGoogle Scholar
Miró Miró, F., Beyak, E.S., Pinna, F. & Reed, H.L. 2020 Ionization and dissociation effects on boundary-layer stability. J. Fluid Mech. 907 (A13).Google Scholar
Miselis, M., Huang, Y. & Zhong, X. 2016 Modal analysis of receptivity mechanisms for a freestream hot-spot perturbation on a blunt compression-cone boundary layer. In 46th AIAA Fluid Dynamics Conference, AIAA 2016-3345.Google Scholar
Mortensen, C.H. 2018 Toward an understanding of supersonic modes in boundary-alyer transition for hypersonic flow over blunt cones. J. Fluid Mech. 846, 789–814.10.1017/jfm.2018.246CrossRefGoogle Scholar
Mortensen, C.H. 2015 Effects of thermochemical nonequilibrium on hypersonic boundary-layer instability in the presence of surface ablation and isolated two-dimensional roughness. PhD thesis, University of California Los Angeles, USA.Google Scholar
Mortensen, C.H. & Zhong, X. 2013 Numerical simulation of graphite ablation induced outgassing effects on hypersonic boundary layer receptivity over a cone frustum. In 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA 2013-0522.Google Scholar
Mortensen, C.H. & Zhong, X. 2014 Simulation of second-mode instability in a real-gas hypersonic flow with graphite ablation. AIAA J. 52 (8), 1632–1652.10.2514/1.J052659CrossRefGoogle Scholar
Mortensen, C.H. & Zhong, X. 2016 Real-gas and surface-ablation effects on hypersonic boundary-layer instability over a blunt cone. AIAA J. 54 (3), 980–998.10.2514/1.J054404CrossRefGoogle Scholar
Park, C. 1985 On convergence of computation of chemically reacting flows. In 23rd AIAA Aerosciences Meeting, AIAA 1985-0247.Google Scholar
Park, C. 1990 Nonequilibrium Hypersonic Aerothermodynamics. John Wiley & Sons Inc.Google Scholar
Prakash, A. & Zhong, X. 2012 Numerical simulation of receptivity of freestream disturbances to hypersonic boundary layers with thermochemical nonequilibrium. In 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA 2012-1085.Google Scholar
Roache, P.J. 2009 Fundamentals of Verification and Validation. Hermosa Publishers.Google Scholar
Schneider, S. 2001 Effects of high-speed tunnel noise on laminar-turbulent transition. J. Spacecr. Rockets 38 (3), 323–333.10.2514/2.3705CrossRefGoogle Scholar
Shu, C.-W. & Osher, S. 1988 Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77 (2), 439–471.10.1016/0021-9991(88)90177-5CrossRefGoogle Scholar
Spiteri, R.J. & Ruuth, S.J. 2002 A new class of optimal high-order strong-stability preserving time discretization methods. SIAM J. Numer. Anal. 40 (2), 469–491.10.1137/S0036142901389025CrossRefGoogle Scholar
Stuckert, G. & Reed, H. 1994 Linear disturbances in hypersonic, chemically reacting shock layers. AIAA J. 32 (7), 1384–1393.10.2514/3.12206CrossRefGoogle Scholar
Varma, A.R. & Zhong, X. 2022 Real-gas effects on hypersonic boundary-layer receptivity to freestream acoustic disturbances. In AIAA SciTech 2022 Forum, AIAA 2022-0735.10.2514/6.2022-0735CrossRefGoogle Scholar
Vigneron, Y.C., Rakich, J.V. & Tannehill, J.C. 1978 Calculation of supersonic viscous flow over delta wings with sharp supersonic leading edges. In 11th AIAA Fluid and Plasma Dynamics Conference, AIAA 1978-1337.Google Scholar
Vincenti, W.G. & Kruger, C.H. 1967 Introduction to Physical Gas Dynamics. John Wiley and Sons.Google Scholar
Wagner, A., Schülein, E., Petervari, R., Hannemann, K., Ali, S.R.C., Cerminara, A. & Sandham, N.D. 2018 Combined free-stream disturbance measurements and receptivity studies in hypersonic wind tunnels by means of a slender wedge probe and direct numerical simulation. J. Fluid Mech. 842, 495–531.10.1017/jfm.2018.132CrossRefGoogle Scholar
Wagnild, R.M. 2012 High enthalpy effects on two boundary layer disturbances in supersonic and hypersonic flow. PhD thesis, University of Minnesota, USA.Google Scholar
Wang, X. 2017 Non-equilibrium effects on the stability of a mach 10 flat-plate boundary layer. In 8th AIAA Theoretical Fluid Mechanics Conference, AIAA 2017-3162.Google Scholar
Wilke, C. 1950 A viscosity equation for gas mixtures. J. Chem. Phys. 18 (4), 517–519.10.1063/1.1747673CrossRefGoogle Scholar
Zanus, L., Knisely, C.P., Miró Miró, F. & Pinna, F. 2020 a Multiple-tool stability analysis of supersonic modes in thermo-chemical nonequilibrium boundary layers. In AIAA Aviation 2020 Forum, AIAA 2020-3067.Google Scholar
Zanus, L., Miró Miró, F. & Pinna, F. 2020 b Parabolized stability analysis of chemically reacting boundary-layer flows in equilibrium conditions. Proc. Inst. Mech. Engrs G: J. Aerosp. Engng 234 (1), 79–95.10.1177/0954410019839894CrossRefGoogle Scholar
Zhong, X. 1998 High-order finite-difference schemes for numerical simulation of hypersonic boundary-layer transition. J. Comput. Phys. 144 (2), 662–709.10.1006/jcph.1998.6010CrossRefGoogle Scholar
Zhong, X. & Ma, Y. 2006 Boundary-layer receptivity of Mach 7.99 flow over a blunt cone to free-stream acoustic waves. J. Fluid Mech. 556, 55–103.10.1017/S0022112006009293CrossRefGoogle Scholar
Zou, Z. & Zhong, X. 2023 A high-order finite-difference method for linear stability analysis and bi-orthogonal decomposition of hypersonic boundary layer flow. In AIAA Scitech 2023 Forum, AIAA 2023-1043.10.2514/6.2023-1043CrossRefGoogle Scholar