Major role and longitudinal nature of stochastic resonance in promoting chaotic states in viscoelastic channel flow with low inlet perturbations

Abstract

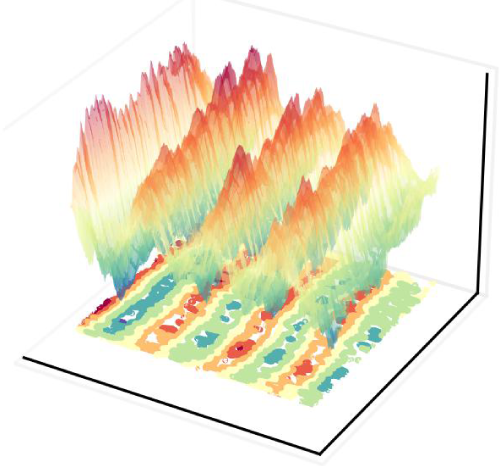
Stochastic resonance (SR) is universal phenomenon, where noise amplifies a weak periodic signal in bistable nonlinear systems, with wide applications in biology, climate science, engineering etc., although in fluid dynamics it remains underexplored. Recently, we unexpectedly found SR above non-modal elastic instability onset in an inertialess viscoelastic channel flow, where it emerges on the top of a chaotic streamwise velocity power spectrum $E_u$ due to its interaction with white-noise spanwise velocity power spectrum $E_w$ and weak elastic waves. These three conditions necessary for SR emergence differ from those required for the classical SR emergence mentioned above. Here, we consider SR in an inertialess viscoelastic channel flow with a smoothed inlet causing order of magnitude lower noise intensity than in our former studies. Our observations reveal that SR appears at the same conditions mentioned above, where SR is found just upon the instability onset in a lower subrange of a transition regime, in contrast, here, SR persists across all flow regimes – transition, elastic turbulence and drag reduction. Furthermore, we provide experimental evidence that SR, presented by a sharp peak in $E_u$, manifests as either a standing or propagating wave in the $x$-direction, with a rather uniform amplitude of streamwise velocity fluctuations and zero propagation velocity in the $z$-direction. These findings reveal a new mechanism underpinning the transition to a chaotic channel flow of viscoelastic fluids and establish SR as a robust framework for understanding complex flow dynamics. This work opens new avenues for exploring SR in other nonlinear systems and practical applications such as mixing enhancement and flow control in industrial and biological contexts.