Measurements of turbulent decay in a von Kármán flow at high Reynolds numbers

Abstract

We present the measurements of the decay of stationary turbulence at Reynolds numbers based on the Taylor microscale $Re_{\lambda }=493, 599, 689$ produced in a large-scale von Kármán flow using stereoscopic particle image velocimetry. First, steady-state conditions were established, after which the impellers were simultaneously and abruptly stopped, and the turbulent decay was measured over 10–20 impeller rotation periods. A total of 258 decay experiments were performed. The temporal evolution of the ensemble-averaged turbulent kinetic energy (TKE) showed excellent agreement over all $Re_{\lambda }$ and exhibited two distinct phases: a short, initial transition phase where the TKE remained almost constant due to the inertia of the flow and lasted approximately $0.4$ impeller rotations, followed by a classical power-law decay. To extract the decay exponent $n$, a curve-fitting function based on a one-dimensional energy spectrum was used, and successfully captured the entire measured decay process. A value $n=1.62$ was obtained based on ensemble-averaged TKE. However, different decay exponents were found for individual velocity components: $n=1.38$ for the axial component consistent with various reports in the literature and Loitsiansky’s prediction ($n=1.43$), and $n=1.99$ for the radial and circumferential components indicating saturation/confinement effects. Similarly, the longitudinal integral length scale in the axial direction grew as $L\propto t^{2/7}$, whereas it remained nearly constant in the radial direction. Finally, the evolution of the ensemble-averaged velocity gradients showed that after the impellers were stopped, the mean flow pattern persisted for a short time before undergoing a large-scale reversal before the onset of the turbulent decay.

1. Introduction

The energy cascade, which describes the transfer of kinetic energy from the largest scales of fluid motion to smaller scales until it is eventually converted to heat by viscous dissipation, is a central principle of turbulence theory (Richardson 1926; Kolmogorov 1941a ). In freely decaying homogeneous isotropic turbulence, the dissipation of turbulent kinetic energy (TKE) simplifies to

(1.1) \begin{equation} \textrm{d}k(t)/\textrm{d}t = -\langle \epsilon \rangle , \end{equation}

where $\langle \epsilon \rangle$ is the ensemble-averaged dissipation, and $k(t)= ({1}/{2})\langle u_iu_i \rangle$ is the TKE, with $u_i$ being fluctuating velocity components (Pope 2000). However, there is no exact solution for this simple equation as the relationship between $\langle \epsilon \rangle$ and $u_i$ or $k$ is not known a priori.

However, it is well established that the decay of kinetic energy of freely decaying homogeneous isotropic turbulence is self-similar and follows a power law in time of the form $k(t)\propto t^{-n}$ . The decay in $k$ is accompanied by the growth of the integral length scale $L$ , which also follows a power law, $L(t)\propto t^m$ . There are two well-known theoretical predictions for $n$ and $m$ based on the assumption that the turbulence should contain some invariants of motion. Considering the conservation of angular momentum (Loitsiansky’s integral) yields $k\propto t^{-10/7}$ and $L\propto t^{2/7}$ (Kolmogorov 1941b ), while considering the conservation of linear momentum results in $k\propto t^{-6/5}$ and $L\propto t^{2/5}$ (Birkhoff 1954; Saffman 1967). Early studies of grid turbulence by Batchelor & Townsend (1948) and Comte-Bellot & Corrsin (1966) verified the power-law scaling, after an initial transition period close to the grid, finding that values of $n$ varied in the range $1.15\leqslant n \leqslant 1.29$ . Many grid turbulence studies have been carried out since, including Hak & Corrsin (1974), Warhaft & Lumley (1978), Lavoie & Antonia (2007), Krogstad & Davidson (2009) and Sinhuber et al. (2015), to name a few, and have reported values of $n$ close to both thoeretical predictions. More recent studies by Hurst & Vassilicos (2007), Krogstad & Davidson (2011), Valente & Vassilicos (2011) and Hearst & Lavoie (2014) have examined turbulence produced by complex grids, such as fractal or multi-scale grids, which have also been found to exhibit similar values of $n$ in the far field. Overall, there is no conclusive evidence supporting $n=10/7$ or $6/5$ , but there appears to be broad agreement that the values of $n$ vary in the range $1\leqslant n \leqslant 1.6$ .

The physical size of the facility can also affect the turbulent decay rate due to the continuous growth of the integral length scale to saturation, increasing values of $n\rightarrow 2$ or greater (Smith et al. 1993; Skrbek & Stalp 2000; Hwang & Eaton 2004; Esteban et al. 2019; Panickacheril John et al. 2022). Exemplary examples of saturation are found in the towed grid study by Smith et al. (1993) and box turbulence by Hwang & Eaton (2004) and Esteban et al. (2019). These high values of $n$ observed in experiments have also been derived by invoking scaling arguments. Lohse (1994) derived expressions for the dimensionless energy dissipation rate based on different Reynolds number scalings, $Re$ and $Re_{\lambda }$ , which captured the decay rate of mean vorticity observed in the towed grid experiments of Smith et al. (1993). Using a similar approach, Panickacheril John et al. (2022) also used the mean energy dissipation $\langle \epsilon \rangle =C_{\epsilon }\,\mathcal{U}^{3}/\mathcal{L}$ , where $\mathcal{U}$ and $\mathcal{L}$ are the velocity and length scales characteristic of the energy injection, and $C_{\epsilon }$ is a constant, to show that the decay in a confined turbulent flow varies as $k(t)\propto t^{-2}$ . This is in contrast to the self-similarity argument of freely decaying turbulence that leads to $k(t)\propto t^{-1}$ (Batchelor 1953). We emphasise the difference between the final period of decay and saturation. The former is associated only with very low Reynolds numbers, while the latter can happen at any Reynolds number, depending on the size of the facility.

Measurements of turbulent decay within closed vessels are comparatively fewer than grid turbulence in wind tunnels or water channels (Hwang & Eaton 2004; Verschoof et al. 2016; Ostilla-Mónico et al. 2014, 2016, 2017; Esteban et al. 2019). A recent study by Esteban et al. (2019) investigated the temporal decay of homogeneous anisotropic turbulence generated in a box by a random jet array with zero mean flow, and reported the evolution of $n$ . They observed a decay exponent $n=2.3$ during the initial period typical of values in the near-field region of grid turbulence, which reduced to $n=1.4$ , which is close to $10/7$ and similar to values found in the far-field region of grid turbulence. After some time, the final decay regime emerged with decay exponent $n=1.8$ due to saturation as the growth of the integral length scale approaches the size of the box. A similarly high value $n=1.86$ was reported by Hwang & Eaton (2004) for the same reasons.

In this paper, we present measurements of the decay of high Reynolds number stationary turbulence in a von Kármán flow. This configuration produces a large turbulent shear flow at the midplane between two counter-rotating impellers within a closed cylindrical vessel, and has been a subject of interest in turbulence research since the original work of Batchelor (1951), Stewartson (1953), Picha & Eckert (1958) and Zandbergen & Dijkstra (1987). Von Kármán flows have been particularly well suited to the experimental study of the structure and dynamics of small-scale turbulence due to their ability to produce high Reynolds number homogeneous turbulent fluctuations in the central region of the vessel, as demonstrated by Ouellette et al. (2006), Worth & Nickels (2011), Lawson & Dawson (2015), Huck et al. (2017), Knutsen et al. (2020), Debue et al. (2021) and Aligolzadeh et al. (2023) to name but a few. However, to the best of the authors’ knowledge, no measurements of turbulent decay have yet been reported in von Kármán flows.

To address this gap, the decay of TKE of the velocity fluctuations at Reynolds numbers based on the Taylor microscale ( $\lambda$ ) of $Re_{\lambda }=493, 599, 689$ produced in a von Kármán flow was investigated using stereoscopic particle image velocimetry (PIV). Access to all three velocity components allows for separate and cumulative analysis of the decay rates. Measurements of the turbulent decay begin immediately after abruptly stopping the impellers, and continue for 10, 15 or 20 impeller revolution periods, depending on the initial rotation speed. We introduce a fitting function based on a one-dimensional energy spectrum to determine the evolution of the decay exponent, which includes an initial transition phase where the TKE remains constant for a short time after the impellers are stopped due to inertia. Evidence is also presented of a large-scale inversion of the flow before the onset of the turbulent decay rate.

2. Experiments

2.1. Apparatus and measurements

Experiments were carried out in a large dodecagonal Perspex water tank which is $2$ m high with radius $1$ m, as shown in figure 1. Two counter-rotating impellers, $R=0.8$ m, are driven by stepper motors located at the top and bottom of the tank. The large size of the facility was designed to facilitate resolved measurements by producing time and length scales exploited in previous studies focusing on the dynamics and structure of small-scale turbulence (Worth & Nickels 2011; Cardesa et al. 2013; Lawson & Dawson 2014, 2015; Aligolzadeh et al. 2023). However, in the decay experiments presented herein, the baffles were removed as this produces higher turbulence intensities for the same impeller rotation speed.

Operating the impellers with equal but opposite rotational speeds generates a shear flow at the midplane and induces secondary poloidal flow patterns above and below the midplane along the axis of rotation of the tank. Figure 1(a) illustrates schematically the primary toroidal (green) and secondary poloidal (red) motions. In the central region of the tank, a mean stagnation flow is produced, resulting in a region of homogeneous velocity fluctuations with a negligible mean velocity (Lawson & Dawson 2015). To measure the temporal decay of the turbulent fluctuations, steady-state flow conditions were first established before the impellers were simultaneously and abruptly stopped. Velocity fields in the middle of the tank with a field of view (FoV) $18\: \textrm{cm}\times 18\:\textrm{cm}$ centred were measured during the decay process using stereoscopic PIV whose set-up is described in the next subsection.

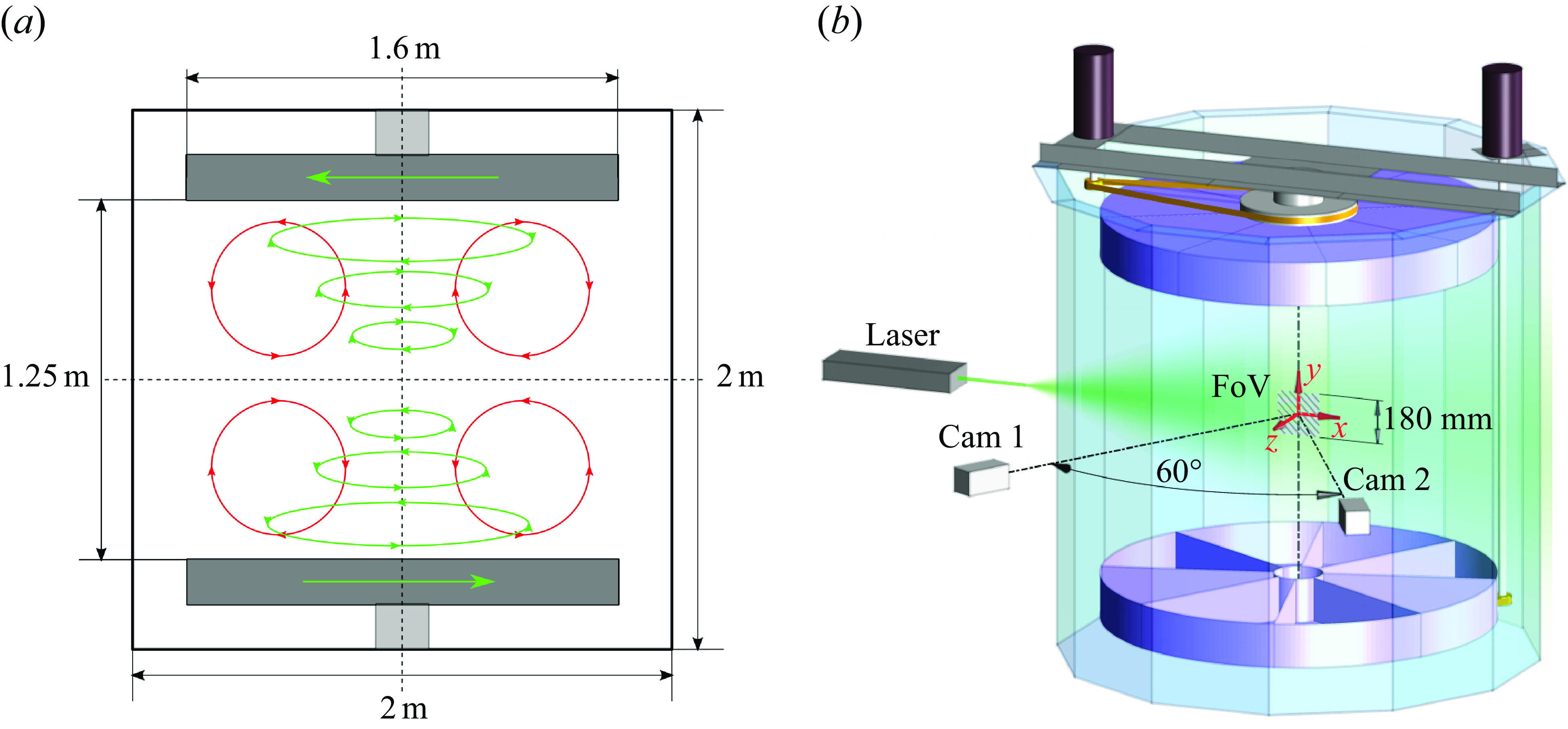
Figure 1. The von Kármán swirling flow facility used in this study. (a) The key dimensions and the mean flow pattern presented as a superposition of the primary shearing toroidal (green) and the secondary induced poloidal (red) motions. (b) Schematic of the stereoscopic PIV measurement set-up.

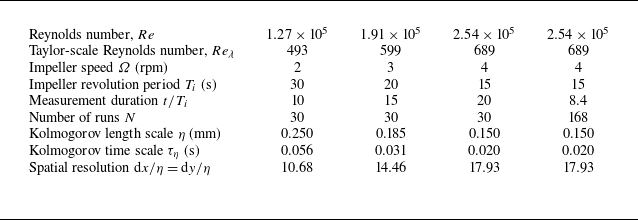
A summary of the experimental conditions for the decay measurements is provided in table 1. Velocity measurements were conducted for different initial impeller rotation rates 2, 3 and 4 rpm, corresponding to Reynolds numbers $Re=R^2\Omega /\nu =1.27\times 10^5$ , $1.91\times 10^5$ and $2.54\times 10^5$ , respectively, where $R$ is the impeller radius, $\Omega$ is the angular velocity, and $\nu =1.11\times 10^{-6}\ \textrm{m}^2\, \textrm{s}^{-1}$ is the kinematic viscosity of water at $16\ ^{\circ }\textrm{C}$ . The change in water temperature during the measurements was less than $0.1\ ^{\circ }\textrm{C}$ . Each measurement was repeated a minimum of 30 times. The average measurement time was $t=300$ s, corresponding to 10, 15 and 20 impeller revolutions at 2, 3 and 4 rpm, respectively, with 400 velocity fields acquired per run. To test for convergence, 168 additional decay experiments were performed at 4 rpm, acquiring 180 velocity fields over a shorter duration $t=126$ s (8.4 revolutions). The comparison confirmed excellent consistency across all 258 tests. Steady-state flows at 2, 3 and 4 rpm were also measured to characterise the initial conditions of the turbulence, with 3000 velocity fields acquired for each case at 1.5 Hz.

Table 1. Experimental conditions.

2.2. Measurement technique

A schematic of the stereoscopic PIV set-up is shown in figure 1(b). The coordinate system $(x, y, z)$ corresponds to the radial, axial and circumferential directions, with velocity components $(U, V, W)$ . Two 16-bit LaVision Imager sCMOS cameras (2560 $\times$ 2160 pixels, with physical pixel size $6.5\,\unicode{x03BC} \textrm{m} \times 6.5\,\unicode{x03BC} \textrm{m}$ ) fitted with Zeiss Milvus 2/100M lenses and Scheimpflug adapters were positioned $60^\circ$ apart on the same side of the laser sheet in a backward–forward scattering configuration. A dual-cavity pulsed ND:YAG laser (Litron Nano L 200-15 PIV, 200 mJ per pulse) served as the light source. Spherical particles (80 $\unicode{x03BC}$ m diameter, 1.05 kg m^– $^3$ density) were used for seeding, with average size $3 \times 3$ pixels in the images to minimise pixel locking. To measure the decaying flow, the time delay ${\rm d}t$ between camera frames and laser pulses was systematically increased to achieve particle displacement of approximately $1/4$ of the interrogation window in each snapshot. This was done by cumulative increases of $0.15$ ms to the starting ${\rm d}t$ of 5, 3.5 and $2$ ms for 2, 3 and $4$ rpm until $400$ vector fields were recorded. A similar approach was used by Esteban et al. (2019). It is worth noting that the maximum ${\rm d}t$ possible for the experimental set-up was limited by the interframe transfer time of the cameras. The data were processed using LaVision Davis 10, using multi-pass cross-correlation with final interrogation window size $32\times 32$ and $75\, \%$ window overlap and self-calibration. This gave a spatial resolution, based on the interrogation window size, $2.67\:\textrm{mm}\times 2.67\:\textrm{mm}$ corresponding to normalised resolution 10 $\eta$ –18 $\eta$ as shown in table 1. The effective magnification of the cameras was 0.083 mm pixel^–1. Estimating the spatial resolution following the approach of Foucaut et al. (2004) based on a $3\ \textrm{dB}$ attenuation of the spectral response due to the applied windowing was $5.99$ mm.

3. Results

3.1. Stationary turbulence

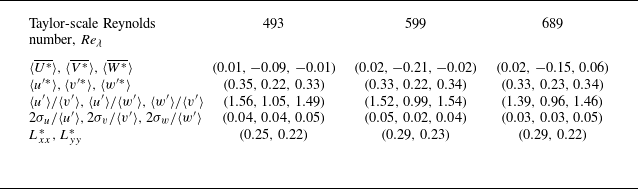
Steady-state conditions were first established before abruptly stopping the impellers to measure the turbulent decay rates. These form the initial conditions of the decay experiments and are therefore described briefly. The normalised mean flow and velocity fluctuations of the highest Reynolds number case (4 rpm) are shown in figure 2, with associated turbulent statistics in table 2. As the measurements were insufficiently resolved for direct calculation of the small scales, the fits $Re_{\lambda }=1.75\,Re^{0.482}$ and $\eta /R = 1.98\, Re^{-0.748}$ from volumetric measurements provided in Worth (2010) were used. These fits have been well characterised in later experiments via spherical correlations from the volumetric measurements of Lawson & Dawson (2014, 2015) in the same apparatus.

Table 2. Turbulence statistics of the stationary flow (initial conditions).

We denote ensemble averages over repeated measurements at the same normalised time step with an overline, spatial averages over the PIV field of view with angle brackets ( $\langle \cdot \rangle$ ) and normalised quantities with an asterisk ( $ ^\ast$ ), where units of length are normalised by the impeller radius $R$ , and velocities are normalised by the impeller tip velocity $R\Omega$ . The prime symbol ( $^\prime$ ) is used to denote the root mean square (r.m.s.) of the component velocity fluctuations such that $u_i^\prime = (\overline {u_i^2})^{1/2}$ .

Figure 2(a) presents a larger field of view than used in the decay experiments to highlight the mean flow pattern. The streamlines show the inward radial flow and outward axial flow from the centre of the tank resembling a stagnation flow where the mean velocity is negligible and the flow is dominated by turbulent fluctuations that were previously shown to be homogeneous via resolved volumetric measurements (Lawson & Dawson 2014, 2015). The colour-filled contours correspond to the mean out-of-plane velocity component in the circumferential direction of the tank, $\overline {W^*}$ , which captures part of the large-scale toroidal and poloidal flow motions. The values of the mean component velocities and fluctuations are shown in table 2. Figures 2(b), 2(c) and 2(d) plot fields of the normalised velocity fluctuations r.m.s. in the radial, axial and circumferential directions, respectively. The normalised r.m.s. fluctuations are close to 1, which indicates that the turbulence is reasonably homogeneous. Further confirmation of the homogeneity for each $Re_{\lambda }$ in the decay experiments is evaluated using the ratio $2\sigma _{u_i}/\langle u'_i \rangle$ , where the pre-factor ensures a 95 % confidence interval (Esteban et al. 2019), as well as the level of isotropy, evaluated via r.m.s. ratios, shown in table 2. These show that the radial and circumferential components are nearly isotropic, $\langle u' \rangle /\langle w' \rangle =0.96$ , but deviations appear when axial components $\langle v' \rangle$ are included. The longitudinal integral length scales of the flow ( $L_{ii}^*$ ) in the $x$ and $y$ directions at the start of the decay experiments were calculated from the PIV data by evaluating the area under the curve of the normalised autocorrelation functions as described in Pope (2000).

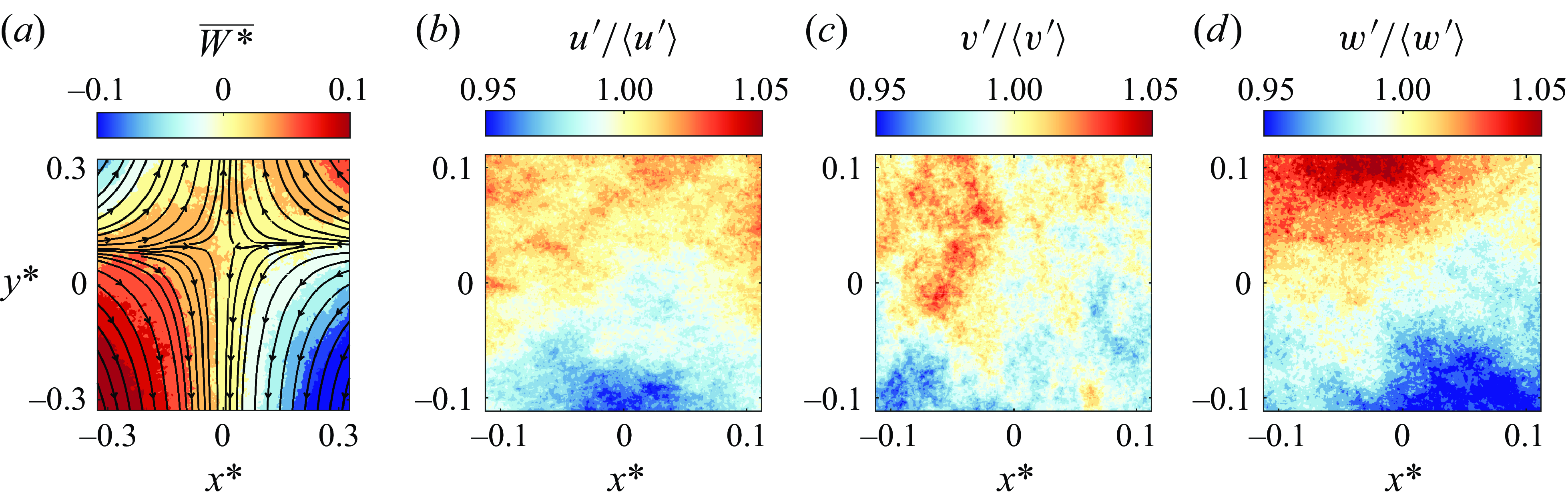
Figure 2. (a) Normalised mean velocities of the stationary flow, where $\overline {U^*}$ and $\overline {V^*}$ vectors are shown as the streamlines, while $\overline {W^*}$ is shown as colour-filled contours. (b–d) Normalised ensemble-averaged contours of the r.m.s. of the component velocity fluctuations $u'_i/\langle u'_i\rangle$ .

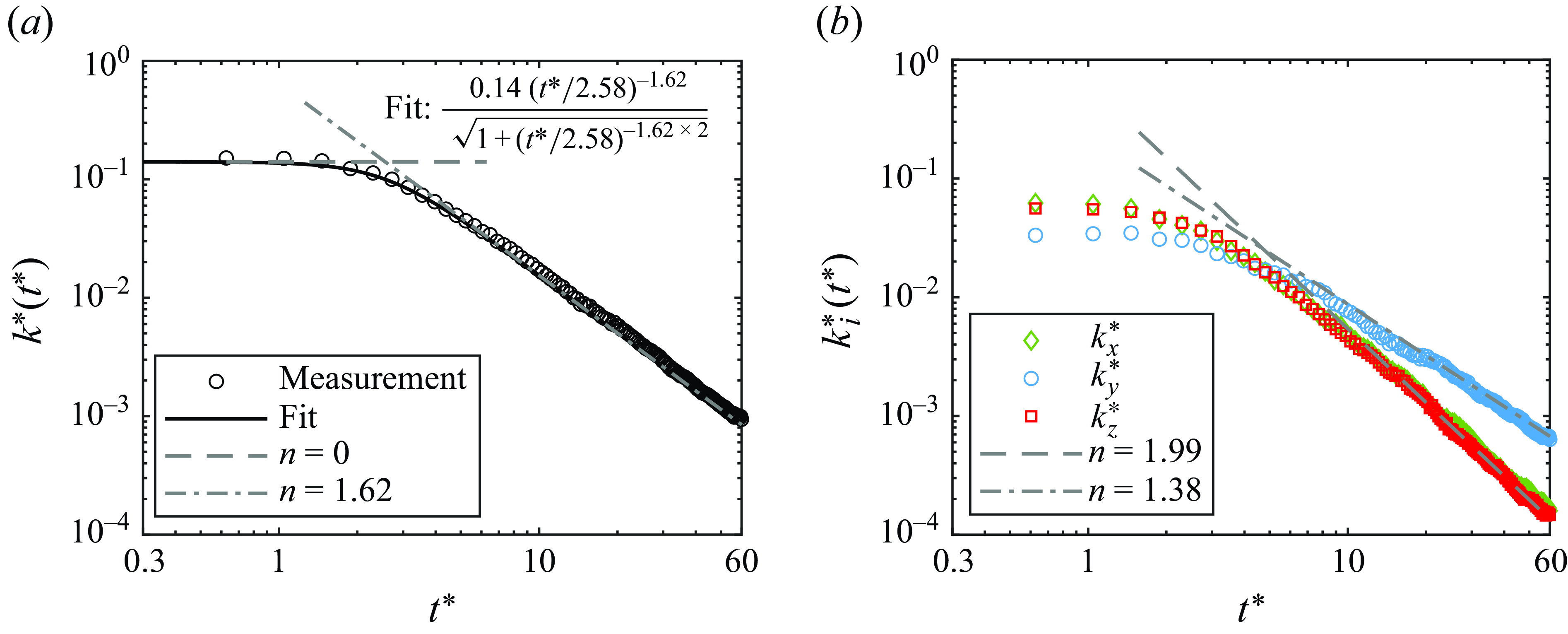
Figure 3. Temporal decay of (a) the TKE $k^*(t^*)$ and (b) the contribution from different velocity components  $k_i^*(t^*)$ .

3.2. Decaying turbulence

In this subsection, we present the results of the temporal decay measurements after abruptly stopping the impellers. For each Reynolds number shown in table 1, we first calculate an ensemble-averaged velocity field $\overline {U_i^*}(\boldsymbol{x}^*,t^*)$ over each of the 30 runs for each non-dimensional time step during the decay. We then perform a Reynolds decomposition to obtain component fluctuation fields for $u^*, v^*, w^*$ at each non-dimensional time step. Finally, we calculate the TKE by ensemble averaging the component fluctuation square fields, and then spatial averaging them to get a single value at each time step using the expression $k^*(t^*)=0.5\langle \overline {u^{*2}+v^{*2}+w^{*2}}\rangle$ . Similarly, we evaluated the decay in TKE for each of the velocity components $k^*_x(t^*)=0.5\langle \overline {u^{*2}}\rangle$ , $k^*_y(t^*)=0.5\langle \overline {v^{*2}}\rangle$ and $k^*_z(t^*)=0.5\langle \overline {w^{*2}}\rangle$ , where $k^*(t^*) = k^*_x(t^*) + k^*_y(t^*) + k^*_z(t^*)$ . When plotting the decay curves for each Reynolds number, it was found that they collapsed when plotted using normalised values of $k^*$ and $t^*$ . In other words, the decay of TKE was found to be independent of the Reynolds numbers tested. We therefore plot the temporal evolution of the total and component TKE averaged over all cases in figure 3 on a log-log scale.

Figure 3(a) shows that the total $k^*(t^*)$ follows a clear and smooth pattern of decay covering more than two decades after the impellers are stopped. The decay process is preceded by an initial phase where $k^*$ is approximately constant followed by a short transition before reaching a negative exponent power-law decay rate. As the figure is very similar to the form of a one-dimensional energy spectrum, it was found that we could represent this behaviour by a single fit by adopting a similar approach to modelling the one-dimensional energy spectrum at small wavenumbers as described in Pope (2000) using the equation

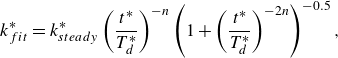(3.1) \begin{equation} k^*_{{fit}} = k^*_{{steady}} \left (\frac {t^*}{T^*_{{d}}}\right )^{-n}\left (1+\left (\frac {t^*}{T^*_{{d}}}\right )^{-2n}\right )^{-0.5}, \end{equation}

where the fit coefficients $k^*_{{steady}}$ , $n$ and $T^*_{{d}}$ represent the steady-state energy, power-law decay exponent and initial transition time, respectively. This ansatz eliminates the ambiguity of the virtual origin position (Panickacheril John et al. 2022), enabling consistent estimation of the decay exponent $n$ . For small $t^*$ , the function simplifies to $k^*_{fit} = k^*_{{steady}}$ , whilst for large $t^*$ , it follows a classical power-law decay: $k^*_{fit} = k^*_{{steady}}(t^*/T^*_{{d}})^{-n}$ . Fitting this function to the measured data shown by the solid line in figure 3(a) yields decay exponent $n=1.62$ and transition time $T^*_{\textrm{d}}=2.58$ , which corresponds to $2.58/2\unicode{x03C0} =0.41$ impeller rotations. The decay exponent $n=1.62$ indicates a faster decay than the theoretical predictions by Birkhoff and Saffman ( $n=6/5=1.2$ ) and Loitsiansky ( $n=10/7\approx 1.43$ ), but it lies within the range of self-similarity ( $n=1$ ) and scaling arguments ( $n=2$ ).

By decomposing the decay of TKE into contributions from individual velocity components, we can assess whether the decay rate is isotropic or anisotropic. Figure 3(b) shows the temporal decay of radial, axial and circumferential components. The axial component ( $k^*_y$ ) decays more slowly than the radial ( $k^*_x$ ) and circumferential ( $k^*_z$ ) components, which have similar decay rates. The corresponding decay exponents were found to be $n_y=1.38$ and $n_x=n_z=1.99$ . The value $n_y=1.38$ is in good agreement with Loitsiansky’s prediction and values reported in grid turbulence studies (Comte-Bellot & Corrsin 1966; Van Atta & Chen 1969; Sirivat & Warhaft 1983; Mohamed & Larue 1990; Hearst & Lavoie 2014), stationary turbulence (Esteban et al. 2019), and numerical simulations (Ishida et al. 2006; Thornber et al. 2007; Meldi et al. 2011; Meldi & Sagaut 2017; Yu et al. 2021). In contrast, $n_x=n_z=1.99$ closely matches the saturation decay exponent ( $n=2$ ) predicted by Skrbek & Stalp (2000) and observed in the experiment of Esteban et al. (2019), which was attributed to confinement effects. The decay exponents for different velocity components indicate a classical unsaturated decay regime in the axial direction, where the component flow is moving away in the normal direction relative to the shear layer produced by the large poloidal vortices, and a saturated decay regime in the radial and circumferential directions, where the component flow is moving parallel to the shear layer. It is worth further comment that the turbulent decay rate along the symmetry axis of rotation follows Loitsiansky’s prediction, which is based on the conservation of angular momentum. Although Loitsiansky assumed isotropy, our results in figure 3(b) suggest that rate of turbulent decay in von Kármán flows may feature a preferred direction (the axial direction) that is normal to the applied angular momentum of the impellers. A possible explanation for this is that the geometry may impose a directional preference that selectively conserves of angular momentum in specific component directions, leading to different decay exponents.

The evolutions of the longitudinal integral length scales in the radial ( $L^*_{xx}$ ) and axial ( $L^*_{yy}$ ) directions are plotted in Figure 4(a). The autocorrelation function $\rho _{i}(\boldsymbol{r}^{*}, t^*)=\int _{{FoV}} u_i^{*}(\boldsymbol{x}^{*},t^*)\, u_i^{*}(\boldsymbol{x}^{*}+\boldsymbol{r}^{*},t^*)\,\textrm{d}\boldsymbol{x}^{*}{\Big/\int _{{FoV}} u_i^{*}(\boldsymbol{x}^{*},t^*)\, u_i^{*}(\boldsymbol{x}^{*},t^*)\,\textrm{d}\boldsymbol{x}^{*}}$ was calculated for each snapshot, where $\boldsymbol{r}^{*}$ is the normalised separation vector. An exponential function of the form $\exp (-r^*/L_{ii}^*)$ was fitted to the ensemble-averaged autocorrelation function $\overline {\rho _i}$ along the $i$ direction of the separation vector to estimate $L_{ii}^*$ (Reynolds & Castro 2008). During the initial phase, the length scales are preserved, after which the growth in the axial direction follows a power law with exponent $m_y \approx 2/7 = 0.29$ , which is also consistent with Loitsiansky’s prediction $m = 2/7 = 0.286$ . This is in contrast to the radial integral length scale, which remains nearly constant, $m_x \approx 0$ . Both the decay rates and growth of integral length scales demonstrate classical behaviour in axial components, while the radial direction exhibits a saturation or confinement effect.

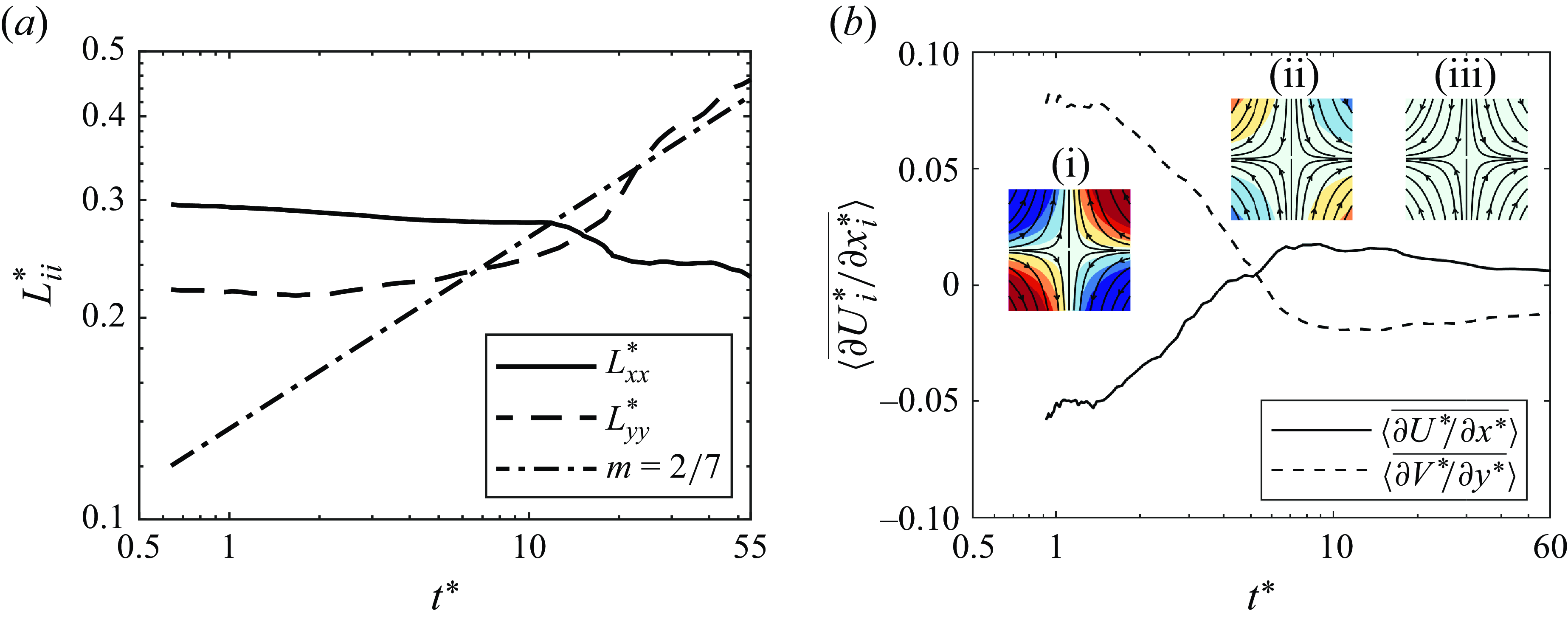
Figure 4. (a) Temporal evolution of longitudinal integral length scales $L^*_{xx}$ and $L^*_{yy}$ from the PIV data. (b) Temporal decay of the mean velocity gradients.

Finally, we examine the evolution of the mean velocity gradients. Near the stagnation point, the stationary mean flow can be approximated by uniform velocity gradients: $ \overline {U_i^*}(x^*,y^*) = \langle \overline {\partial U_i^*/\partial x^*}\rangle (x^*-x_0^*) + \langle \overline {\partial U_i^*/\partial y^*}\rangle (y^*-y_0^*)$ , where $(x_0^*,y_0^*)$ is the stagnation point (Lawson & Dawson 2015; Knutsen et al. 2020). In figure 4(b), we plot the normalised decay of the ensemble-averaged velocity gradients $\langle \overline {\partial U^* /\partial x^*}\rangle (t^*)$ and $\langle \overline {\partial V^* /\partial y^*}\rangle (t^*)$ . 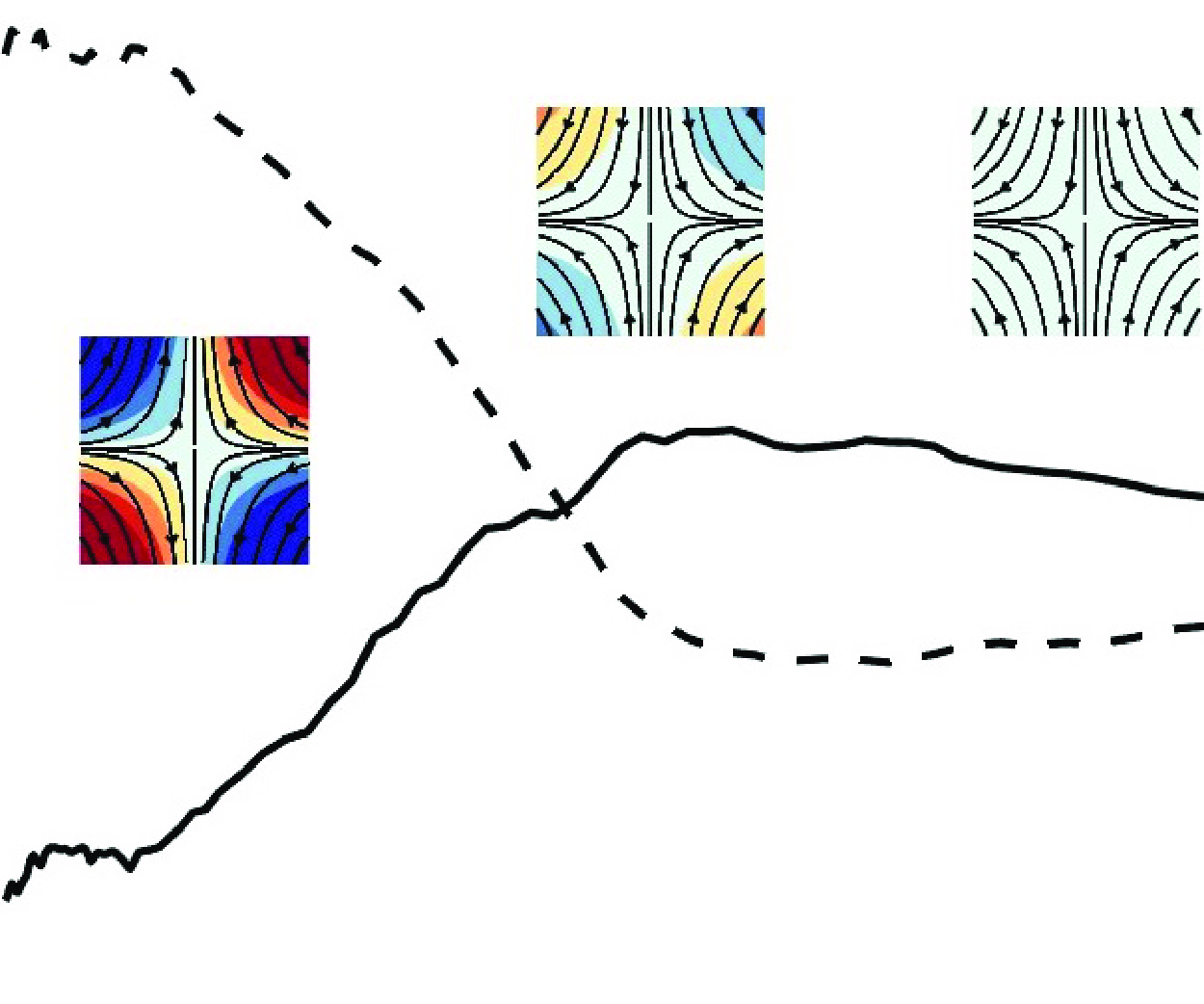During the initial phase (early $t^*$ ), the gradient signs match the stationary flow pattern under steady flow conditions (inset i) and their magnitudes decrease until $t^* \approx 4$ , after which the gradients then reverse sign (inset ii) implying a large-scale flow inversion. The gradients then reach a local maximum and decay towards zero (inset iii). These results show that after the impellers are stopped, the stationary mean flow persists due to inertia, undergoes a flow reversal, and then decays. Comparing the timing of these transitions with the decay rates in figure 3 strongly suggests that the power-law decay begins only after the large-scale flow reversal. The underlying mechanisms of this reversal currently remain unclear. However, it is conjectured that the flow reversal is likely triggered by the interaction between the inertia of the upper and lower toroidal flows when the impellers are suddenly stopped, and the viscous drag imparted by the stationary impellers to ensure conservation of angular momentum.

4. Conclusion

In this paper, the decay of stationary turbulence at Reynolds numbers based on the Taylor microscale $Re_{\lambda }=493, 599, 689$ produced in a von Kármán flow was investigated using stereoscopic PIV. To characterise the initial conditions of the decay experiments, measurements were obtained to characterise the turbulence under steady flow conditions (constant impeller rotation speeds). To initiate the decay experiments, the impellers were stopped and the turbulent decay was measured over 10–20 impeller rotation periods. A total of 258 decay experiments were performed. To the best of the authors’ knowledge, this is the first reporting of turbulent decay measured in a von Kármán flow.

The decay in TKE showed excellent agreement over all $Re_{\lambda }$ and exhibited two distinct phases. After stopping the impellers, the inertia of the flow resulting in an initial plateau where the TKE was constant and lasted $\approx 0.4$ impeller rotations, followed by a transition to a power-law decay. A fitting function, based on a one-dimensional energy spectrum, was used and successfully captured the entire measured decay process, eliminating any ambiguities encountered when defining the virtual start point. A power-law decay exponent $n=1.62$ was obtained for the ensemble average at all $Re_{\lambda }$ . However, different decay exponents were found when considering the velocity components. The decay exponent of the axial velocity component, which is normal to the applied angular momentum of the impellers, was $n_y=1.38$ , consistent with various reports in the literature and Loitsiansky’s theoretical prediction $n=1.43$ , which is based on the conservation of angular momentum. The radial and circumferential components yielded $n_x=n_z=1.99$ , indicative of saturation/confinement effects. This raises the possibility that the geometry of von Kármán flows may impose a directional preference in the turbulent decay rate that selectively conserves angular momentum in specific component directions, leading to different decay exponents. Similar behaviour in the growth of the longitudinal integral length scales was also observed as $L^*_{yy} \propto t^{*2/7}$ ( $m_y=2/7$ ), whilst $L^*_{xx}$ remained nearly constant.

Finally, the evolution of the ensemble-averaged velocity gradients showed that after the impellers were stopped, the mean flow pattern persisted for a short time before undergoing a large-scale reversal before the turbulent decay. Although the mechanisms behind this large-scale flow reversal remain unclear, we conjecture that it is likely triggered by the interaction between the inertia of the upper and lower toroidal flows and the viscous drag imparted by the stationary impellers to conserve angular momentum. Further studies are needed to identify whether such large scale reorganisations observed herein are a general feature of not only von Kármán flows but also other rotating flows such as toroidal flows or Ekman flow.