Hostname: page-component-5b777bbd6c-cp4x8 Total loading time: 0 Render date: 2025-06-24T12:05:14.557Z Has data issue: false hasContentIssue false
  • English
  • Français

Molecular kinetic modelling of nanoscale confined flows

Published online by Cambridge University Press:  05 June 2025

Baochao Shan ,
Manuel Torrilhon ,
Zhaoli Guo  and
Yonghao Zhang Open the ORCID record for Yonghao Zhang [Opens in a new window]
Baochao Shan
Affiliation:
Applied and Computational Mathematics, RWTH Aachen University, Aachen 52062, Germany
Manuel Torrilhon*
Affiliation:
Applied and Computational Mathematics, RWTH Aachen University, Aachen 52062, Germany
Zhaoli Guo*
Affiliation:
Institute of Interdisciplinary Research for Mathematics and Applied Science, Huazhong University of Science and Technology, Wuhan 430074, PR China
Yonghao Zhang*
Affiliation:
Centre for Interdisciplinary Research in Fluids, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
*
Corresponding authors: Yonghao Zhang, yonghao.zhang@imech.ac.cn; Manuel Torrilhon, mt@acom.rwth-aachen.de; Zhaoli Guo, zlguo@hust.edu.cn
Corresponding authors: Yonghao Zhang, yonghao.zhang@imech.ac.cn; Manuel Torrilhon, mt@acom.rwth-aachen.de; Zhaoli Guo, zlguo@hust.edu.cn
Corresponding authors: Yonghao Zhang, yonghao.zhang@imech.ac.cn; Manuel Torrilhon, mt@acom.rwth-aachen.de; Zhaoli Guo, zlguo@hust.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

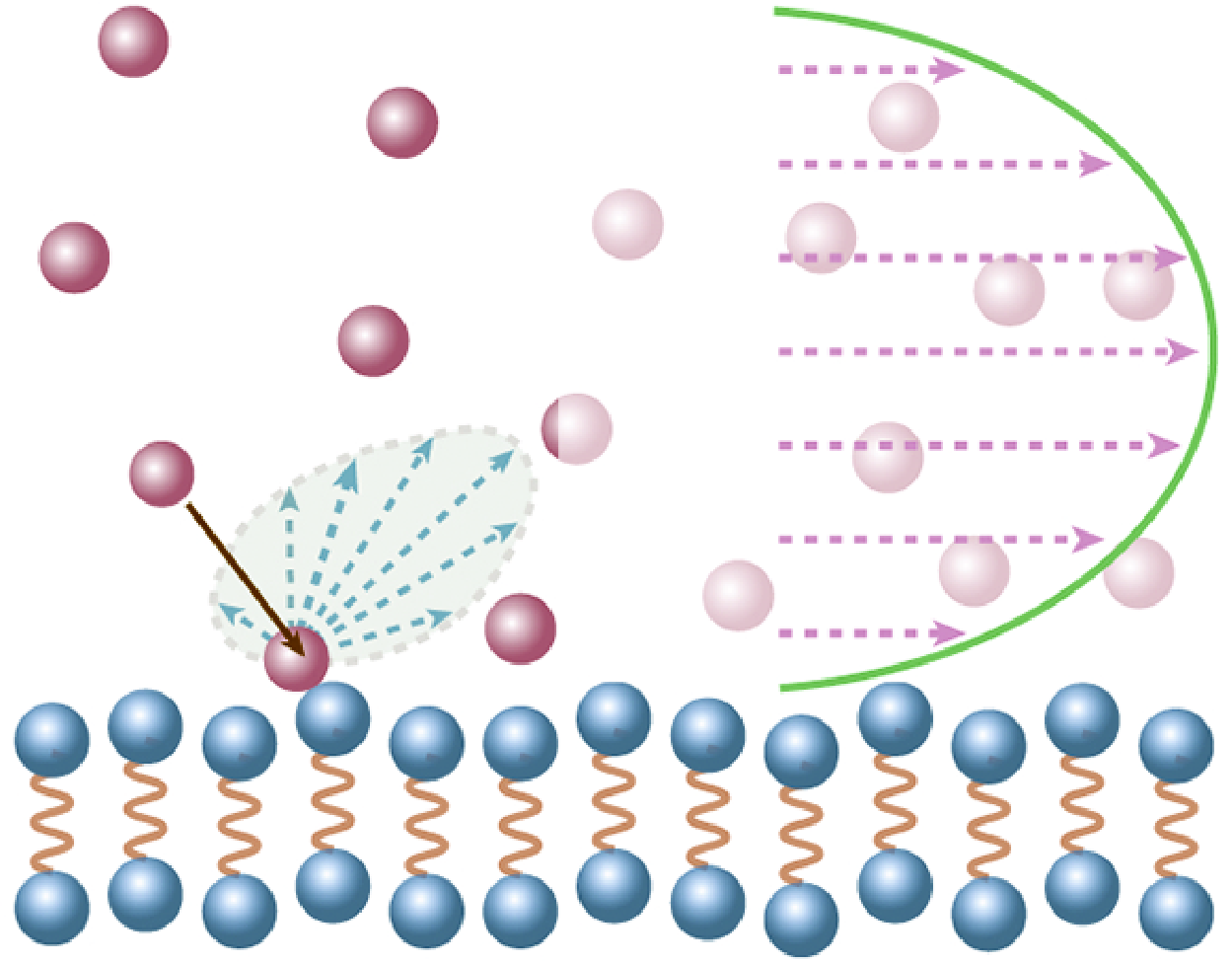
We have established a novel molecular kinetic model that addresses fundamental challenges in the non-equilibrium transport of nanoscale confined fluids, such as rarefaction and fluid inhomogeneities, which are crucial to a range of scientific and engineering fields. The proposed model explicitly considers fluid–solid molecular interactions in the transport equations, eliminating the reliance on predefined boundary conditions. By consistently accounting for molecular interactions between fluids and solids, the unified model captures both intrinsic and apparent non-hydrodynamic effects, as well as real fluid behaviours. Rigorous comparisons with molecular dynamics simulations demonstrate that the present model accurately predicts unique features of strongly inhomogeneous fluid flows, including fluid adsorption, solvation force, velocity slip and temperature jump. Therefore, this mesoscopic model bridges the gap between molecular-scale dynamics and macroscopic hydrodynamics, enabling a practical simulation tool for nanoscale surface-confined flows. Moreover, it offers valuable insights into the molecular mechanisms underlying anomalous transport phenomena observed in confined flows, such as the disappearance and re-emergence of the Knudsen minimum.

JFM classification

Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Rarefied Gas Flow: Kinetic theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1012 , 10 June 2025 , A20
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anderson, D.M., McFadden, G.B. & Wheeler, A.A. 1998 Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30 (1), 139–165.10.1146/annurev.fluid.30.1.139CrossRefGoogle Scholar
Aoki, K., Giovangigli, V. & Kosuge, S. 2022 Boundary conditions for the Boltzmann equation from gas-surface interaction kinetic models. Phys. Rev. E 106 (3), 035306.10.1103/PhysRevE.106.035306CrossRefGoogle ScholarPubMed
Barisik, M. & Beskok, A. 2011 Equilibrium molecular dynamics studies on nanoscale-confined fluids. Microfluid. Nanofluid. 11 (3), 269–282.10.1007/s10404-011-0794-5CrossRefGoogle Scholar
Barrat, J.-L. & Bocquet, L. 1999 Large slip effect at a nonwetting fluid-solid interface. Phys. Rev. Lett. 82 (23), 4671–4674.10.1103/PhysRevLett.82.4671CrossRefGoogle Scholar
Beenakker, J.J.M., Borman, V.D. & Krylov, S.Y. 1994 Molecular transport in the nanometer regime. Phys. Rev. Lett. 72 (4), 514–517.10.1103/PhysRevLett.72.514CrossRefGoogle ScholarPubMed
Berthelot, D. 1898, Sur le mélange des gaz. Compt. Rendus 126 (3), 15.Google Scholar
Bhadauria, R. & Aluru, N.R. 2017 A multiscale transport model for non-classical nanochannel electroosmosis. J. Chem. Phys. 147 (21), 214105.10.1063/1.5005127CrossRefGoogle ScholarPubMed
Bhadauria, R., Sanghi, T. & Aluru, N.R. 2015 Interfacial friction based quasi-continuum hydrodynamical model for nanofluidic transport of water. J. Chem. Phys. 143 (17), 174702.10.1063/1.4934678CrossRefGoogle ScholarPubMed
Bhatnagar, P.L., Gross, E.P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525.10.1103/PhysRev.94.511CrossRefGoogle Scholar
Bocquet, L. & Barrat, J.-L. 1994 Hydrodynamic boundary conditions, correlation functions, and Kubo relations for confined fluids. Phys. Rev. E 49 (4), 3079–3092.10.1103/PhysRevE.49.3079CrossRefGoogle ScholarPubMed
Born, M. & Huang, K. 1996 Dynamical Theory of Crystal Lattices. Oxford University Press.10.1093/oso/9780192670083.001.0001CrossRefGoogle Scholar
Brancher, R., Johansson, M.V., Perrier, P. & Graur, I. 2021 Measurements of pressure gradient and temperature gradient driven flows in a rectangular channel. J. Fluid Mech. 923, A35.10.1017/jfm.2021.586CrossRefGoogle Scholar
Carnahan, N.F. & Starling, K.E. 1969 Equation of state for nonattracting rigid spheres. J. Chem. Phys. 51 (2), 635–636.10.1063/1.1672048CrossRefGoogle Scholar
Cercignani, C. 1988 The Boltzmann Equation. Springer.10.1007/978-1-4612-1039-9CrossRefGoogle Scholar
Chapman, S. & Cowling, T. 1990 The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases. Cambridge University Press.Google Scholar
Chen, Y., Gibelli, L., Li, J. & Borg, M.K. 2023 Impact of surface physisorption on gas scattering dynamics. J. Fluid Mech. 968, A4.10.1017/jfm.2023.496CrossRefGoogle Scholar
Chubynsky, M.V., Belousov, K.I., Lockerby, D.A. & Sprittles, J.E. 2020 Bouncing off the walls: the influence of gas-kinetic and van der Waals effects in drop impact. Phys. Rev. Lett. 124 (8), 084501.10.1103/PhysRevLett.124.084501CrossRefGoogle Scholar
Chung, T.H., Ajlan, M., Lee, L.L. & Starling, K.E. 1988 Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Engng Chem. Res. 27 (4), 671–679.10.1021/ie00076a024CrossRefGoogle Scholar
Corral-Casas, C., Li, J., Borg, M.K. & Gibelli, L. 2022 Knudsen minimum disappearance in molecular-confined flows. J. Fluid Mech. 945, A28.10.1017/jfm.2022.563CrossRefGoogle Scholar
Davis, H.T., Rice, S.A. & Sengers, J.V. 1961 On the kinetic theory of dense fluids. IX. The fluid of rigid spheres with a square-well attraction. J. Chem. Phys. 35 (6), 2210–2233.10.1063/1.1732234CrossRefGoogle Scholar
de la Torre, J A., Duque-Zumajo, D., Camargo, D. & Español, P. 2019 Microscopic slip boundary conditions in unsteady fluid flows. Phys. Rev. Lett. 123 (26), 264501.10.1103/PhysRevLett.123.264501CrossRefGoogle ScholarPubMed
van Erp, R., Soleimanzadeh, R., Nela, L., Kampitsis, G. & Matioli, E. 2020 Co-designing electronics with microfluidics for more sustainable cooling. Nature 585 (7824), 211–216.10.1038/s41586-020-2666-1CrossRefGoogle ScholarPubMed
Ewart, T., Perrier, P., Graur, I.A. & Méolans, J.G. 2007 Mass flow rate measurements in a microchannel, from hydrodynamic to near free molecular regimes. J. Fluid Mech. 584, 337–356.10.1017/S0022112007006374CrossRefGoogle Scholar
Fan, J., De Coninck, J., Wu, H. & Wang, F.C. 2020 a Microscopic origin of capillary force balance at contact line. Phys. Rev. Lett. 124 (12), 125502.10.1103/PhysRevLett.124.125502CrossRefGoogle ScholarPubMed
Fan, J.C., Wu, H. & Wang, F.C. 2020 b Evaporation-driven liquid flow through nanochannels. Phys. Fluids 32 (1), 012001.10.1063/1.5137803CrossRefGoogle Scholar
Fernández-Toledano, J.C., Braeckeveldt Bertrand, M.M. & De Coninck, J. 2020 How wettability controls nanoprinting. Phys. Rev. Lett. 124 (22), 224503.10.1103/PhysRevLett.124.224503CrossRefGoogle ScholarPubMed
Frezzotti, A. & Gibelli, L. 2008 A kinetic model for fluid – wall interaction. Proc. Inst. Mech. Engnrs Part C: J. Mech. Engng Sci. 222 (5), 787–795.10.1243/09544062JMES718CrossRefGoogle Scholar
Ghasemi, H., Ni, G., Marconnet, A.M., Loomis, J., Yerci, S., Miljkovic, N. & Chen, G. 2014 Solar steam generation by heat localization. Nat. Commun. 5 (1), 4449.10.1038/ncomms5449CrossRefGoogle ScholarPubMed
Guo, Z., Wang, R., Xu, K. 2015 Discrete unified gas kinetic scheme for all Knudsen number flows. II. Thermal compressible case. Phys. Rev. E 91 (3), 033313.10.1103/PhysRevE.91.033313CrossRefGoogle ScholarPubMed
Guo, Z., Xu, K. & Wang, R. 2013 Discrete unified gas kinetic scheme for all Knudsen number flows: low-speed isothermal case. Phys. Rev. E 88 (3), 033305.10.1103/PhysRevE.88.033305CrossRefGoogle ScholarPubMed
Guo, Z., Zhao, T.S. & Shi, Y. 2005 Simple kinetic model for fluid flows in the nanometer scale. Phys. Rev. E 71 (3), 035301.10.1103/PhysRevE.71.035301CrossRefGoogle ScholarPubMed
Guo, Z., Zhao, T.S. & Shi, Y. 2006 Generalized hydrodynamic model for fluid flows: from nanoscale to macroscale. Phys. Fluids 18 (6), 067107.10.1063/1.2214367CrossRefGoogle Scholar
Hadjiconstantinou, N.G. 2024 Molecular mechanics of liquid and gas slip flow. Annu. Rev. Fluid Mech. 56 (1), 435–461.10.1146/annurev-fluid-121021-014808CrossRefGoogle Scholar
Han, Q., Liu, Y., Li, Z., Zhang, Y. & Chen, Y. 2022 Investigation of energy accommodation coefficient at gas-solid interface of a hypersonic flying vehicle. Aerosp. Sci. Technol. 126, 107585.10.1016/j.ast.2022.107585CrossRefGoogle Scholar
Han, Q., Xia, H., Chen, W., Wu, G., Li, J., Wei, Z., Zheng, F. & Ma, C. 2025 Non-equilibrium molecular motion and interface heat transfer in supersonic rarefied flows. Phys. Fluids 37 (3), 037132.10.1063/5.0256301CrossRefGoogle Scholar
Hattori, M. 2023 Poiseuille and thermal transpiration flows of a dense gas between two parallel plates. J. Fluid Mech. 962, A20.10.1017/jfm.2023.270CrossRefGoogle Scholar
Iftimia, I. & Manson, J.R. 2001 Theory of molecule-surface scattering at thermal and hyperthermal energies. Phys. Rev. Lett. 87 (9), 093201.10.1103/PhysRevLett.87.093201CrossRefGoogle ScholarPubMed
Joseph, S. & Aluru, N.R. 2008 Why are carbon nanotubes fast transporters of water? Nano Lett. 8 (2), 452–458.10.1021/nl072385qCrossRefGoogle ScholarPubMed
Keerthi, A. et al. 2018 Ballistic molecular transport through two-dimensional channels. Nature 558 (7710), 420–424.10.1038/s41586-018-0203-2CrossRefGoogle ScholarPubMed
Kobryn, A.E. & Kovalenko, A. 2008 Molecular theory of hydrodynamic boundary conditions in nanofluidics. J. Chem. Phys. 129 (13), 134701.10.1063/1.2972978CrossRefGoogle ScholarPubMed
Li, S., Su, W., Shan, B., Li, Z., Gibelli, L. & Zhang, Y. 2024 a Molecular kinetic modelling of non-equilibrium evaporative flows. J. Fluid Mech. 994, A16.10.1017/jfm.2024.605CrossRefGoogle Scholar
Li, S., Zhao, Z., Zhang, A.-M. & Han, R. 2024 b Cavitation bubble dynamics inside a droplet suspended in a different host fluid. J. Fluid Mech. 979, A47.10.1017/jfm.2023.1076CrossRefGoogle Scholar
Li, Y., Xu, J. & Li, D. 2010 Molecular dynamics simulation of nanoscale liquid flows. Microfluid. Nanofluid. 9 (6), 1011–1031.10.1007/s10404-010-0612-5CrossRefGoogle Scholar
Lichter, S., Martini, A., Snurr, R.Q. & Wang, Q. 2007 Liquid slip in nanoscale channels as a rate process. Phys. Rev. Lett. 98 (22), 226001.10.1103/PhysRevLett.98.226001CrossRefGoogle ScholarPubMed
Logan, R.M. & Stickney, R.E. 1966 Simple classical model for the scattering of gas atoms from a solid surface. J. Chem. Phys. 44 (1), 195–201.10.1063/1.1726446CrossRefGoogle Scholar
Lorentz, H.A. 1881 Ueber die anwendung des satzes vom virial in der kinetischen theorie der gase. Ann. Phys. 248 (1), 127–136.10.1002/andp.18812480110CrossRefGoogle Scholar
Lu, Z., Kinefuchi, I., Wilke, K.L., Vaartstra, G. & Wang, E.N. 2019 A unified relationship for evaporation kinetics at low Mach numbers. Nat. Commun. 10 (1), 2368.10.1038/s41467-019-10209-wCrossRefGoogle ScholarPubMed
Martini, A., Hsu, H.-Y., Patankar, N.A. & Lichter, S. 2008 a Slip at High Shear Rates. Phys. Rev. Lett. 100 (20), 206001.10.1103/PhysRevLett.100.206001CrossRefGoogle ScholarPubMed
Martini, A., Roxin, A., Snurr, R.Q., Wang, Q. & Lichter, S. 2008 b Molecular mechanisms of liquid slip. J. Fluid Mech. 600, 257–269.10.1017/S0022112008000475CrossRefGoogle Scholar
Navaid, H.B., Emadi, H. & Watson, M. 2023 A comprehensive literature review on the challenges associated with underground hydrogen storage. Intl J. Hydrogen Energy 48 (28), 10603–10635.10.1016/j.ijhydene.2022.11.225CrossRefGoogle Scholar
Ohwada, T., Sone, Y. & Aoki, K. 1989 Numerical analysis of the Poiseuille and thermal transpiration flows between two parallel plates on the basis of the Boltzmann equation for hard-sphere molecules. Phys. Fluids 1 (12), 2042–2049.10.1063/1.857478CrossRefGoogle Scholar
Perumanath, S., Chubynsky, M.V., Pillai, R., Borg, M.K. & Sprittles, J.E. 2023 Rolling and sliding modes of nanodroplet spreading: molecular simulations and a continuum approach. Phys. Rev. Lett. 131 (16), 164001.10.1103/PhysRevLett.131.164001CrossRefGoogle Scholar
Qian, J.H., Wu, H.A. & Wang, F.C. 2023 A generalized Knudsen theory for gas transport with specular and diffuse reflections. Nat. Commun. 14 (1), 7386.10.1038/s41467-023-43104-6CrossRefGoogle ScholarPubMed
Rahman, A. 1964 Correlations in the motion of atoms in liquid argon. Phys. Rev. 136 (2A), A405–A411.10.1103/PhysRev.136.A405CrossRefGoogle Scholar
Sadr, M., Pfeiffer, M. & Gorji, M.H. 2021 Fokker–Planck–Poisson kinetics: multi-phase flow beyond equilibrium. J. Fluid Mech. 920, A46.10.1017/jfm.2021.461CrossRefGoogle Scholar
Shakhov, E.M. 1968 Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 3 (5), 95–96.10.1007/BF01029546CrossRefGoogle Scholar
Shan, B., Ju, L., Su, W., Guo, Z. & Zhang, Y. 2023 a Non-equilibrium flow of van der Waals fluids in nano-channels. Phys. Fluids 35 (5), 052004.Google Scholar
Shan, B., Su, W., Gibelli, L. & Zhang, Y. 2023 Molecular kinetic modelling of non-equilibrium transport of confined van der Waals fluids. J. Fluid Mech. 976, A7.10.1017/jfm.2023.893CrossRefGoogle Scholar
Shan, B., Wang, P., Wang, R., Zhang, Y. & Guo, Z. 2022 Molecular kinetic modelling of nanoscale slip flow using a continuum approach. J. Fluid Mech. 939, A9.10.1017/jfm.2022.186CrossRefGoogle Scholar
Shan, B., Wang, P., Zhang, Y. & Guo, Z. Discrete unified gas kinetic scheme for all Knudsen number flows. IV. Strongly inhomogeneous fluids. Phys. Rev. E 101 (4), 043303.10.1103/PhysRevE.101.043303CrossRefGoogle Scholar
Sheng, Q., Gibelli, L., Li, J., Borg, M.K. & Zhang, Y. 2020, Dense gas flow simulations in ultra-tight confinement. Phys. Fluids 32 (9), 092003.10.1063/5.0019559CrossRefGoogle Scholar
Snook, I.K. & van Megen, W. 1980 Solvation forces in simple dense fluids. I. J. Chem. Phys. 72 (5), 2907–2913.10.1063/1.439489CrossRefGoogle Scholar
Sprittles, J.E. 2015 Air entrainment in dynamic wetting: Knudsen effects and the influence of ambient air pressure. J. Fluid Mech. 769, 444–481.10.1017/jfm.2015.121CrossRefGoogle Scholar
Steele, W.A. 1973 The physical interaction of gases with crystalline solids: i. Gas-solid energies and properties of isolated adsorbed atoms. Surf. Sci. 36 (1), 317–352.10.1016/0039-6028(73)90264-1CrossRefGoogle Scholar
Struchtrup, H. 2013 Maxwell boundary condition and velocity dependent accommodation coefficient. Phys. Fluids 25 (11), 112001.10.1063/1.4829907CrossRefGoogle Scholar
Struchtrup, H., Frezzotti, A. 2022 Twenty-six moment equations for the Enskog–Vlasov equation. J. Fluid Mech. 940, A40.10.1017/jfm.2022.98CrossRefGoogle Scholar
Su, W., Gibelli, L., Li, J., Borg, M.K. & Zhang, Y. 2023 Kinetic modeling of nonequilibrium flow of hard-sphere dense gases. Phys. Rev. Fluids 8 (1), 013401.10.1103/PhysRevFluids.8.013401CrossRefGoogle Scholar
Tarazona, P. 1985 Free-energy density functional for hard spheres. Phys. Rev. A 31 (4), 2672–2679.10.1103/PhysRevA.31.2672CrossRefGoogle ScholarPubMed
Tarazona, P., Marconi, U.M.B. & Evans, R. 1987 Phase equilibria of fluid interfaces and confined fluids: non-local versus local density functionals. Mol. Phys. 60 (3), 573–595.10.1080/00268978700100381CrossRefGoogle Scholar
Thompson, A.P. et al. 2022 LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171.10.1016/j.cpc.2021.108171CrossRefGoogle Scholar
Torrilhon, M. 2016 Modeling nonequilibrium gas flow based on moment equations. Annu. Rev. Fluid Mech. 48 (1), 429–458.10.1146/annurev-fluid-122414-034259CrossRefGoogle Scholar
Vanderlick, T.K., Scriven, L.E. & Davis, H.T. 1989 Molecular theories of confined fluids. J. Chem. Phys. 90 (4), 2422–2436.10.1063/1.455985CrossRefGoogle Scholar
Wang, P., Wu, L., Ho, M.T., Li, J., Li, Z.H & Zhang, Y. 2020 The kinetic Shakhov–Enskog model for non-equilibrium flow of dense gases. J. Fluid Mech. 883, A48.10.1017/jfm.2019.915CrossRefGoogle Scholar
Woods, L.C. 1993 An Introduction to the Kinetic Theory of Gases and Magnetoplasmas. Oxford University Press.10.1093/oso/9780198563938.001.0001CrossRefGoogle Scholar
Wu, L., Liu, H., Reese, J.M. & Zhang, Y. 2016 Non-equilibrium dynamics of dense gas under tight confinement. J. Fluid Mech. 794, 252–266.10.1017/jfm.2016.173CrossRefGoogle Scholar
Yamaguchi, H., Matsuda, Y. & Niimi, T. 2017 Molecular-dynamics study on characteristics of energy and tangential momentum accommodation coefficients. Phys. Rev. E 96 (1), 013116.10.1103/PhysRevE.96.013116CrossRefGoogle Scholar
Zhang, Y., Zhu, L., Wang, R. & Guo, Z. 2018 Discrete unified gas kinetic scheme for all Knudsen number flows. III. Binary gas mixtures of Maxwell molecules. Phys. Rev. E 97 (5), 053306.10.1103/PhysRevE.97.053306CrossRefGoogle ScholarPubMed