Hostname: page-component-5b777bbd6c-f9nfp Total loading time: 0 Render date: 2025-06-20T02:08:30.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Motion of a rigid sphere penetrating a deep pool

Published online by Cambridge University Press:  28 May 2025

Prasanna Kumar Billa ,
Tejaswi Josyula ,
Cameron Tropea Open the ORCID record for Cameron Tropea [Opens in a new window]  and
Pallab Sinha Mahapatra Open the ORCID record for Pallab Sinha Mahapatra [Opens in a new window]
Prasanna Kumar Billa
Affiliation:
Multiscale Multiphysics Group (MMG), Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
Tejaswi Josyula
Affiliation:
Multiscale Multiphysics Group (MMG), Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India FLOW, Department of Engineering Mechanics, KTH Royal Institute of Technology Stockholm, Stockholm, 11428, Sweden
Cameron Tropea*
Affiliation:
Multiscale Multiphysics Group (MMG), Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India Institute for Fluid Mechanics and Aerodynamics, Technical University of Darmstadt, Darmstadt 64287, Germany
Pallab Sinha Mahapatra*
Affiliation:
Multiscale Multiphysics Group (MMG), Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
*
Corresponding authors: Pallab Sinha Mahapatra, pallab@iitm.ac.in; Cameron Tropea, tropea@sla.tu-darmstadt.de
Corresponding authors: Pallab Sinha Mahapatra, pallab@iitm.ac.in; Cameron Tropea, tropea@sla.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

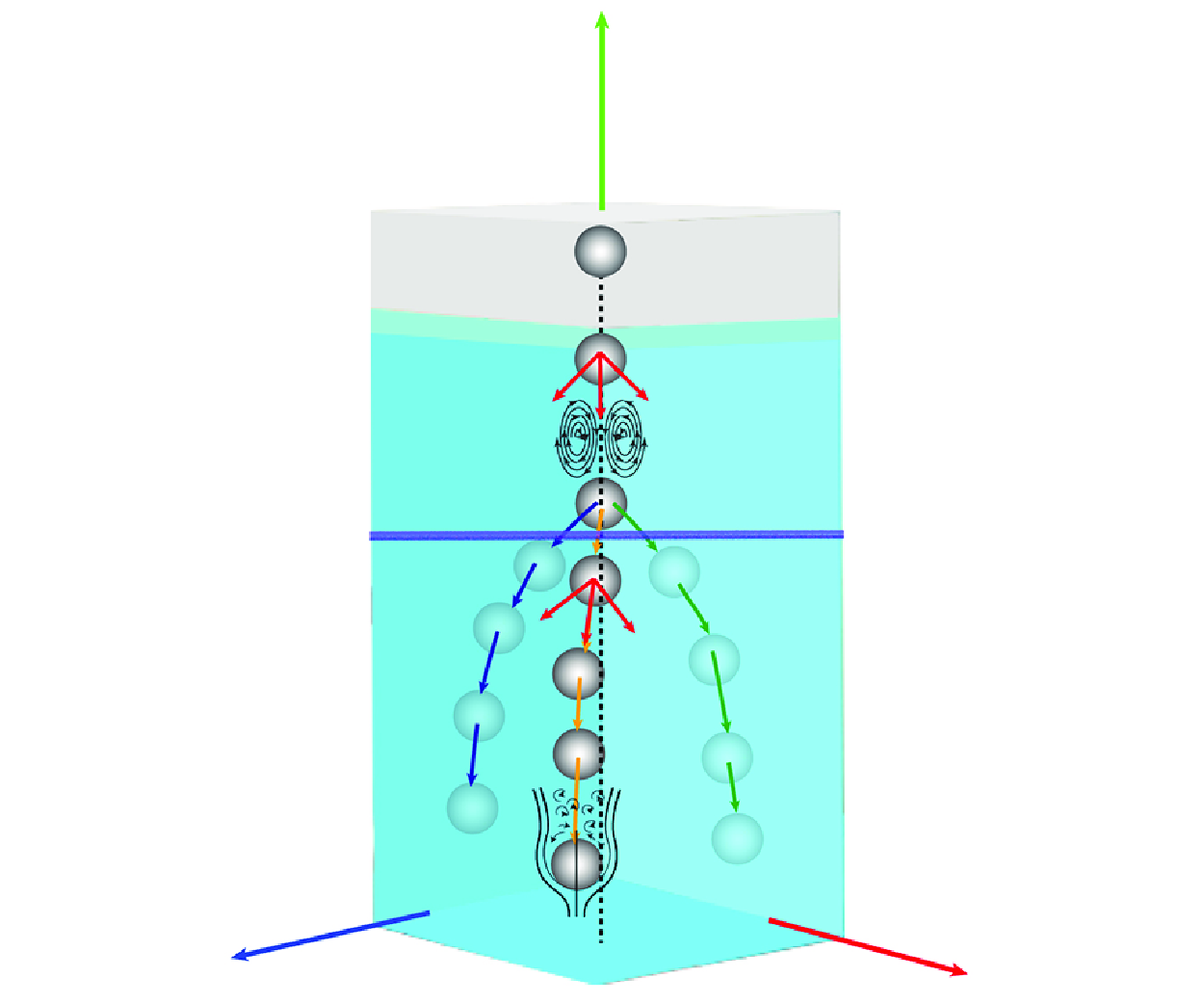
In this study, we experimentally examine the behaviour of a free-falling rigid sphere penetrating a quiescent liquid pool. Observations of the sphere trajectory in time are made using two orthogonally placed high-speed cameras, yielding the velocity and acceleration vectors through repeated differentiation of the time-resolved trajectories. The novelty of this study is twofold. On the one hand, a methodology is introduced by which the instantaneous forces acting on the sphere can be derived by tracking the sphere trajectory. To do this, we work in a natural coordinate system aligned with the pathline of the sphere. In particular, the instantaneous lift and drag forces can be separately estimated. On the other hand, the results reveal that when decelerating, the sphere experiences a very high drag force compared with steady flow. This is attributed to an upstream shift of the mean boundary-layer separation. The sphere also experiences significant lift force fluctuations, attributed to unsteady and asymmetric wake fluctuations. The trajectories can be reduced to three stages, common in duration for all initial Reynolds numbers and density ratios when expressed in dimensionless time. In addition, the sphere velocity and deceleration magnitude for different initial parameters exhibit a high degree of uniformity when expressed in dimensionless form. This offers prediction capability of how far a sphere penetrates in time and the forces acting on it.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Boundary Layers: Boundary layer separation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1012 , 10 June 2025 , A5
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abraham, J., Gorman, J., Reseghetti, F., Sparrow, E., Stark, J. & Shepard, T. 2014 Modeling and numerical simulation of the forces acting on a sphere during early-water entry. Ocean Engng 76, 1–9.10.1016/j.oceaneng.2013.11.015CrossRefGoogle Scholar
Achenbach, E. 1974 Vortex shedding from spheres. J. Fluid Mech. 62 (2), 209–221.10.1017/S0022112074000644CrossRefGoogle Scholar
Aristoff, J.M. & Bush, J.W.M. 2009 Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78.10.1017/S0022112008004382CrossRefGoogle Scholar
Aristoff, J.M., Truscott, T.T., Techet, A.H. & Bush, J.W.M. 2010 The water entry of decelerating spheres. Phys. Fluids 22 (3), 1–8.10.1063/1.3309454CrossRefGoogle Scholar
Billa, P.K., Josyula, T., Tropea, C. & Mahapatra, P.S. 2024 Supplementary material to the publication motion of a rigid sphere entering and penetrating a deep pool. J. Fluid Mech. https://tudatalib.ulb.tu-darmstadt.de/handle/tudatalib/4180.2 Google Scholar
Christiansen, E.B. & Barker, D.H. 1965 The effect of shape and density on the free settling of particles at high Reynolds numbers. AIChE J. 11 (1), 145–151.10.1002/aic.690110130CrossRefGoogle Scholar
Constantinescu, G. & Squires, K. 2004 Numerical investigations of flow over a sphere in the subcritical and supercritical regimes. Phys. Fluids 16 (5), 1449–1466.10.1063/1.1688325CrossRefGoogle Scholar
Crowe, C.T., Schwarzkopf, J.D., Sommerfeld, M. & Tsuji, Y. 2011 Multiphase Flows with Droplets and Particles. CRC Press LLC.10.1201/b11103CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2011 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44 (1), 97–121.10.1146/annurev-fluid-120710-101250CrossRefGoogle Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20 (5), 051702.10.1063/1.2909609CrossRefGoogle Scholar
Faltinsen, O. 1990 Sea Loads On Ships and Offshore Structures. The Press Syndicate of the University of Cambridge.Google Scholar
Gregorio, E., Balaras, E. & Leftwich, M.C. 2023 Air cavity deformation by single jointed diver model entry bodies. Exp. Fluids 64 (11), 168.10.1007/s00348-023-03712-wCrossRefGoogle Scholar
Guo, J. 2011 Motion of spheres falling through fluids. J. Hydraul. Res. 49 (1), 32–41.10.1080/00221686.2010.538572CrossRefGoogle Scholar
Hadžić, I., Bakić, V., Perić, M., Šajn, V. & Kosel, F. 2002 Experimental and numerical studies of flow around sphere at sub-critical Reynolds number. In Engineering Turbulence Modelling and Experiments, vol. 5, pp. 667–676. Elsevier.10.1016/B978-008044114-6/50064-8CrossRefGoogle Scholar
Horowitz, M. & Williamson, C.H.K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.10.1017/S0022112009993934CrossRefGoogle Scholar
Howison, S.D., Ockendon, J.R. & Oliver, J.M. 2002 Deep-and shallow-water slamming at small and zero deadrise angles. J. Engng Maths 42 (3/4), 373–388.10.1023/A:1016177401868CrossRefGoogle Scholar
Kuwabara, G., Chiba, S. & Kono, K. 1983 Anomalous motion of a sphere falling through water. J. Phys. Soc. Japan 52 (10), 3373–3381.10.1143/JPSJ.52.3373CrossRefGoogle Scholar
Liu, F., Liu, P., Qu, Q., Lin, Li, Hu, T. & Agarwal, R.K. 2018 Numerical study of flow physics and drag of spheres in unsteady motion. In 2018 Fluid Dynamics Conference, pp. 3082.Google Scholar
Mansoor, M.M., Marston, J.O., Vakarelski, I.U. & Thoroddsen, S.T. 2014 Water entry without surface seal: extended cavity formation. J. Fluid Mech. 743, 295–326.10.1017/jfm.2014.35CrossRefGoogle Scholar
Mansoor, M.M., Vakarelski, I.U., Marston, J.O., Truscott, T.T. & Thoroddsen, S.T. 2017 Stable–streamlined and helical cavities following the impact of Leidenfrost spheres. J. Fluid Mech. 823, 716–754.10.1017/jfm.2017.337CrossRefGoogle Scholar
Marchildon, E.K. & Gauvin, W.H. 1979 Effects of acceleration, deceleration and particle shape on single‐particle drag coefficients in still air. AIChE J. 25 (6), 938–948.10.1002/aic.690250604CrossRefGoogle Scholar
May, A. 1951 Effect of surface condition of a sphere on its water-entry cavity. J. Appl. Phys. 22 (10), 1219–1222.10.1063/1.1699831CrossRefGoogle Scholar
May, A. 1975 Water Entry and the Cavity-Running Behavior of Missiles. US Government Printing Office.10.21236/ADA020429CrossRefGoogle Scholar
McHale, G., Shirtcliffe, N.J., Evans, C.R. & Newton, M.I. 2009 Terminal velocity and drag reduction measurements on superhydrophobic spheres. Appl. Phys. Lett. 94 (6), 064104.10.1063/1.3081420CrossRefGoogle Scholar
Nouri, R., Ganji, D.D. & Hatami, M. 2014 Unsteady sedimentation analysis of spherical particles in Newtonian fluid media using analytical methods. Propul. Power Res. 3 (2), 96–105.10.1016/j.jppr.2014.05.003CrossRefGoogle Scholar
Potvin, J., Peek, G. & Brocato, B. 2003 New model of decelerating bluff-body drag. J. Aircraft 40 (2), 370–377.10.2514/2.3103CrossRefGoogle Scholar
Richardson, E.G. 1948 The impact of a solid on a liquid surface. Proc. Phys. Soc. 61 (4), 352–367.10.1088/0959-5309/61/4/308CrossRefGoogle Scholar
Rubinow, S.I. & Keller, J.B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11 (3), 447–459.10.1017/S0022112061000640CrossRefGoogle Scholar
Saffman, P.G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.10.1017/S0022112065000824CrossRefGoogle Scholar
Scoggins, J.R. 1967 Sphere Behavior and the Measurement of Wind Profiles. National Aeronautics and Space Administration.Google Scholar
Shafrir, U. 1965 Horizontal Oscillations of Falling Spheres. University of California, Institute of Geophysics and Planetary Science.Google Scholar
Shi, P., Rzehak, R. 2019 Lift forces on solid spherical particles in unbounded flows. Chem. Engng Sci. 208, 115145.10.1016/j.ces.2019.08.003CrossRefGoogle Scholar
Speirs, N.B., Mansoor, M.M., Belden, J. & Truscott, T.T. 2019 Water entry of spheres with various contact angles. J. Fluid Mech. 862, 1–13.10.1017/jfm.2018.985CrossRefGoogle Scholar
Spurk, J. & Aksel, N. 2007 Fluid Mechanics. Springer Science & Business Media.Google Scholar
Tan, B.C.-W., Vlaskamp, J.H.A., Denissenko, P. & Thomas, P.J. 2016 Cavity formation in the wake of falling spheres submerging into a stratified two-layer system of immiscible liquids. J. Fluid Mech. 790, 33–56.10.1017/jfm.2016.10CrossRefGoogle Scholar
Taneda, S. 1978 Visual observations of the flow past a sphere at Reynolds numbers between $10^4$ and $10^6$ . J. Fluid Mech. 85 (1), 187–192.10.1017/S0022112078000580CrossRefGoogle Scholar
Temkin, S. & Mehta, H.K. 1982 Droplet drag in an accelerating and decelerating flow. J. Fluid Mech. 116, 297–313.10.1017/S0022112082000470CrossRefGoogle Scholar
Truscott, T.T., Epps, B.P. & Belden, J. 2014 Water entry of projectiles. Annu. Rev. Fluid Mech. 46 (1), 355–378.10.1146/annurev-fluid-011212-140753CrossRefGoogle Scholar
Truscott, T.T., Epps, B.P. & Techet, A.H. 2012 Unsteady forces on spheres during free-surface water entry. J. Fluid Mech. 704, 173–210.10.1017/jfm.2012.232CrossRefGoogle Scholar
Truscott, T.T. & Techet, A.H. 2009 A spin on cavity formation during water entry of hydrophobic and hydrophilic spheres. Phys. Fluids 21 (12), 1–4.10.1063/1.3272264CrossRefGoogle Scholar
Vakarelski, I.U., Marston, J.O., Chan, D.Y.C. & Thoroddsen, S.T. 2011 Drag reduction by leidenfrost vapor layers. Phys. Rev. Lett. 106 (21), 3–6.10.1103/PhysRevLett.106.214501CrossRefGoogle ScholarPubMed
Valladares, R.M., Goldstein, P., Stern, C. & Calles, A. 2003 Simulation of the motion of a sphere through a viscous fluid. Revista Mexicana de Fisica 49 (2), 166–174.Google Scholar
Velazquez, A. & Barrero-Gill, A. 2024 Simplified dynamics model of a sphere decelerating freely in a fluid. Phys. Fluids 36 (2), 023104.10.1063/5.0187705CrossRefGoogle Scholar
Veldhuis, C., Biesheuvel, A., Wijngaarden, L. & Lohse, D. 2005 Motion and wake structure of spherical particles. Nonlinearity 18 (1), C1–C8.10.1088/0951-7715/18/1/000CrossRefGoogle Scholar
Von Karman, T. 1929 The Impact On Seaplane Floats during Landing. National Advisory Committee on Aeronautics.Google Scholar
Worthington, A.M. 1883 On impact with a liquid surface. Proc. R. Soc. Lond. A 34 (220-223), 217–230.Google Scholar
Yun, G., Kim, D. & Choi, H. 2006 Vortical structures behind a sphere at subcritical Reynolds numbers. Phys. Fluids 18 (1), 015102.10.1063/1.2166454CrossRefGoogle Scholar
Zhao, R. & Faltinsen, O. 1993 Water entry of two-dimensional bodies. J. Fluid Mech. 246, 593–612.10.1017/S002211209300028XCrossRefGoogle Scholar
Zhu, C. & Fan, L.S. 1998 Multiphase flow: gas/solid. In The Handbook of Fluid Dynamics. CRC Press LLC.Google Scholar