1. Introduction
Sound or pressure wave propagation is of importance to the field of fluid mechanics and has been the subject of several studies over the past decades. Einstein (Reference Einstein1920) and Clarke & McChesney (Reference Clarke and McChesney1964) observed that sound waves propagating through an initial equilibrium mixture, which is perturbed into a dissociated state by the wave itself, always results in the attenuation of the wave. On the contrary, Clarke (Reference Clarke1973, Reference Clarke1974) and Toong et al. (Reference Toong1965) have demonstrated that, for combustion and flame problems in which sound waves are propagated through an already chemically reactive mixture in non-equilibrium, the disturbance is amplified. The same conclusion was drawn by Srinivasan & Vincenti (Reference Srinivasan and Vincenti1975) for a medium maintained in non-equilibrium by an external energy source and by Bauer & Bass (Reference Bauer and Bass1973) in the case of vibrational and radiation non-equilibrium. The scenario in which the background medium is initially in equilibrium and then perturbed into non-equilibrium is representative of hypersonic flight, where exothermic reactions caused by the flow passing through a shock wave can lead to the attenuation of sound waves through various mechanisms.
The identification of the nonlinear chemicalacoustic coupling of the chemical kinetic processes with the sound waves is of relevance since it may cause problems for the choice and definition of speed to be used in a chemically reacting flow computation (Barbante, Magin & Reference Barbante2004). In fact, while the speed of sound is unequivocally defined when the disturbance propagates at a period much longer or shorter than the finite chemistry’s characteristic time, respectively referred to as frozen and equilibrium conditions, its non-equilibrium definition remains ambiguous. Clarke & McChesney (Reference Clarke and McChesney1976) recognised that when the period of the disturbances is of the same order as the characteristic chemistry time, an intermediate propagation speed is expected as illustrated in figure 1.
To address the need for a single, unequivocal, macroscopic and heuristic measure of non-equilibrium, this paper aims to define the speed of sound under the effect of thermochemical non-equilibrium conditions due to both the effect of chemical reactions including dissociation and ionisation as well as the vibrational relaxation of molecules representative of hypersonic flight.
1.1. Absorption of sound in air
The attenuation of acoustic waves in gases results from different processes that transfer the energy of the wave into other forms. These processes can be reduced to two basic mechanisms (Bass et al. Reference Bass, Sutherland, Piercy and Evans1984): the first one is the classical absorption due to viscosity, diffusion and thermal conduction. Given the frequency at which the wave propagates
![]() $f$
, the pressure
$f$
, the pressure
![]() $p$
, specific heat ratio
$p$
, specific heat ratio
![]() $\gamma$
, speed of sound
$\gamma$
, speed of sound
![]() $c$
, specific heat capacity at constant pressure
$c$
, specific heat capacity at constant pressure
![]() $c_p$
and coefficients of viscosity
$c_p$
and coefficients of viscosity
![]() $\nu$
and thermal conductivity
$\nu$
and thermal conductivity
![]() $\lambda$
, the classical absorption coefficient
$\lambda$
, the classical absorption coefficient
![]() $\alpha _c$
may be evaluated with sufficient accuracy using (1.1) (Herzfeld & Litovitz Reference Herzfeld and Litovitz2013)
$\alpha _c$
may be evaluated with sufficient accuracy using (1.1) (Herzfeld & Litovitz Reference Herzfeld and Litovitz2013)
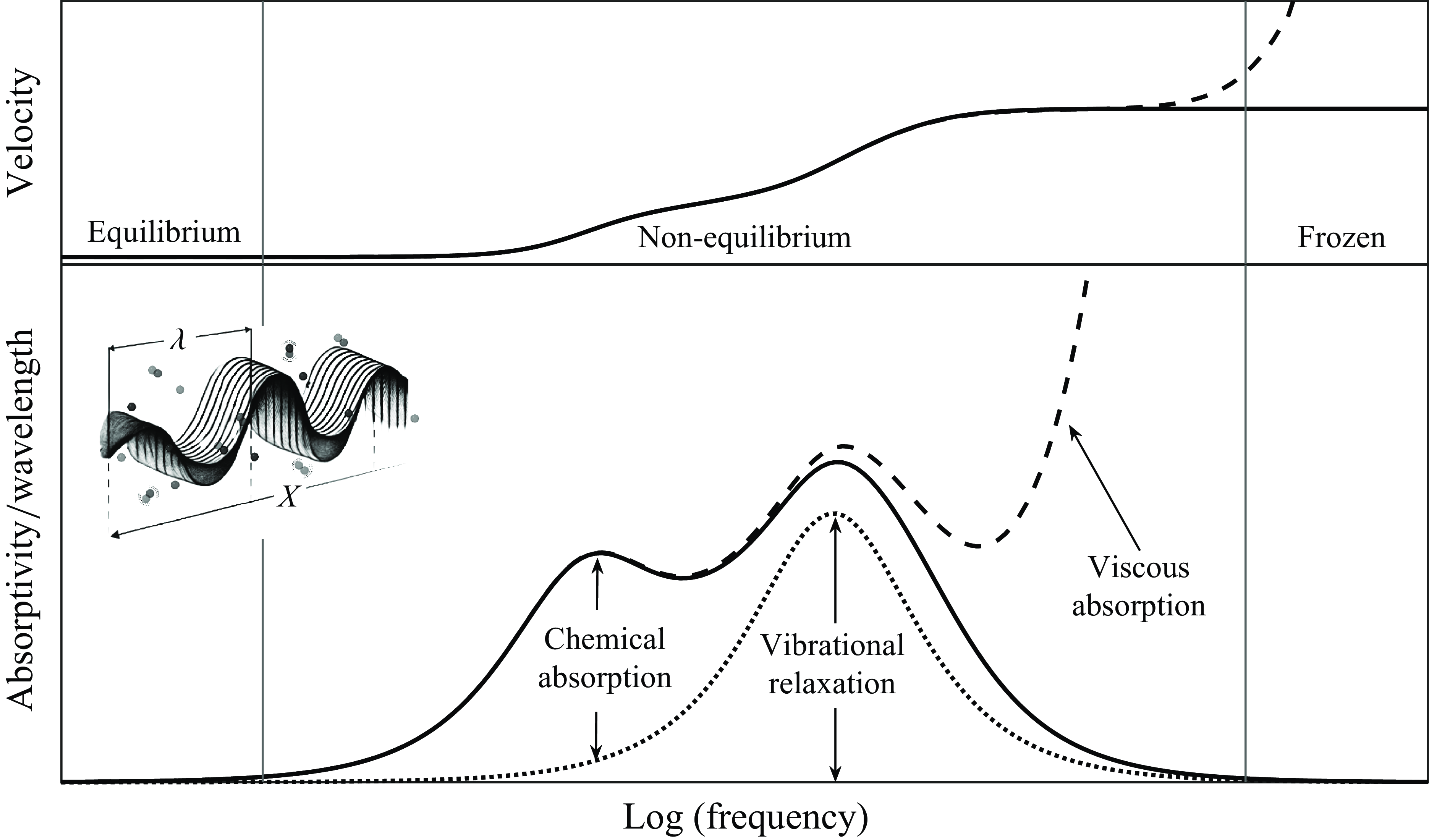
Figure 1. Dependence of sound absorption and velocity on frequency for chemically active fluid.
The second mechanism is due to the internal structure of the molecules and is caused by the effect of the chemical reactions coupled with the vibrational and rotational relaxation of polyatomic gases (Bass et al. Reference Bass, Sutherland, Piercy and Evans1984). The phenomenon, as discussed by Bass (Reference Bass1976), is caused by the impingement of an adiabatic sound wave onto the gas segment causing a temperature rise, prompting the gas molecules to adjust their excitation states to maintain a Boltzmann distribution. However, as this can only occur through collisions, a finite time is needed to respond to the temperature change. Consequently, provided that the sound-wave period is comparable to or shorter than the time needed to establish a new distribution of excited molecules, a phase lag damping the acoustic signal arises.
The increased degree of acoustic absorption due to molecular relaxation, which is not captured by classical theory, was first measured by Mandelshtam & Leontovich (Reference Mandelshtam and Leontovich1937) and later by Tisza (Reference Tisza1942). This prompted the introduction of the bulk viscosity coefficient in classical theory as an additional mechanism to characterise the redistribution of energy within the internal degrees of freedom of the gas. Numerical studies have highlighted that the ratio of bulk to shear viscosity coefficients can be significant (Cramer Reference Cramer2012), although considerable uncertainties remain for polyatomic gases (Kustova et al. Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023). Furthermore, the inclusion of bulk viscosity in non-equilibrium fluid-dynamics simulations can affect shock wave structure and compressible flow dynamics, especially in the presence of large velocity divergence. At the same time, overestimating the bulk viscosity coefficient may introduce numerical artefacts (Kustova et al. Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023). The utilisation of the effective internal energy relaxation time is therefore identified as the most robust numerical strategy.
While the classical absorption has been extensively characterised across an extensive range of frequencies and thermodynamic conditions for different fluids (Boyer Reference Boyer1952; Greenspan Reference Greenspan1956; Bass et al. Reference Bass, Sutherland, Piercy and Evans1984; Hüttig & Hiller Reference Hüttig and Hiller1989; Ejakov et al. Reference Ejakov, Phillips, Dain, Lueptow and Visser2003; Sutherland & Bass Reference Sutherland and Bass2004), scarcer experimental data are available for the absorption of the speed of sound in plasma air due to finite-rate chemistry. In fact, most studies retrieved focus on the determination of the different energy modes relaxation in gases: Tempest & Parbrook (Reference Tempest and Parbrook1957) measured the absorption of sound waves in nitrogen, oxygen and dry air for frequencies up to 3 MHz at normal temperature and pressure conditions. Greenspan (Reference Greenspan1959) conducted radio-frequency measurements under similar conditions and reduced pressure levels but only focused on the rotational relaxation of nitrogen, oxygen and air to increase the range to 11 MHz, which was later extended to 20 MHz by Bond, Chiang & Fortunko (Reference Bond, Chiang and Fortunko1992). The dependency on temperature was addressed by Bass & Keeton (Reference Bass and Keeton1975), but only up to a maximum value of 689 K, meaning that no dissociation would have occurred. More recently, Sun et al. (Reference Sun, Cui, Li, Lin and Su2023) have measured the dispersion of nitrogen ultrasonic waves at low temperatures and pressures.
The only experimental study retrieved from the literature that covers temperatures high enough for chemical reactions to occur is the one conducted by Carnevale et al. (Reference Carnevale, Larson, Lynnworth, Carey, Panaro and Marshall1967b ) at frequencies of 1–1.5 MHz for standard pressure conditions and temperature levels varying between 300 K and approximately 12 000 K in nitrogen. The results revealed that the absorption at high temperatures may increase by one order of magnitude, underscoring the significant changes in the speed of sound in the presence of chemical non-equilibrium. As depicted in figure 1, while the viscous absorption may be dominant in the range of ultrasonic frequencies, the non-equilibrium region is governed by the chemical absorption.
Recognising the significance of non-equilibrium processes, recent numerical efforts have been devoted to studying acoustic wave propagation at high temperatures. Arima, Ruggeri & Sugiyama (Reference Arima, Ruggeri and Sugiyama2017) utilised rational extended thermodynamics of rarefied polyatomic gases to evaluate attenuation coefficients under strong non-equilibrium conditions, treating the effect of rotational and vibrational relaxation separately. Kremer et al. (Reference Kremer, Kunova, Kustova and Oblapenko2018) examined the impact of state-to-state vibrational kinetics on diatomic gases in non-equilibrium conditions, utilising the generalised Chapman–Enskog formalism to compute transport properties. The findings indicated that vibrational excitation has a weak influence on sound properties when starting from an initial Boltzmann distribution and that a thermal equilibrium model would be adequate for such scenarios. The validity of various continuum models for attenuation coefficients in non-equilibrium polyatomic gases was evaluated by Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023), who demonstrated that two-temperature dispersion relations show excellent agreement with experimental data. Additionally, the study revealed that diffusion plays an insignificant role at low to moderate frequencies in multi-component mixtures, with relaxation processes dominating under these conditions. While the continuum models do not capture deviations from the Boltzmann distribution, Hanford et al. (Reference Hanford, O’Connor, Anderson and Long2008) demonstrated that the differences between the classical and quantum vibration models are minimal at elevated temperatures, suggesting that the former can serve as a good approximation for non-equilibrium vibrational energy exchange.
To model the post-shock evolution of a sound wave passing through a high-enthalpy chemically reacting plasma, where both relaxation of the thermal vibrational modes and finite-rate chemical kinetics occur simultaneously, a computational generalised eigenvalue model is proposed in this paper. By analysing the thermodynamic conditions expected in the hypersonic regime, the utilisation of acoustic properties – such as speed of sound and sound absorption – is advocated for in-flight measurements and on-ground facilities including plasma flow facilities and shock tubes (Collen et al. Reference Collen2021) as metrics of non-equilibrium.
2. Methodology
The governing equations for a chemically reacting one-dimensional flow incorporating vibrational relaxation are presented in vector conservative form (Lee Reference Lee1984; Gnoffo Reference Gnoffo1989)
The vector of conserved variables
![]() $\boldsymbol{{U}}$
, the inviscid flux vector
$\boldsymbol{{U}}$
, the inviscid flux vector
![]() $\boldsymbol{{F}}$
, the vector of viscous and diffusive contributions
$\boldsymbol{{F}}$
, the vector of viscous and diffusive contributions
![]() $\boldsymbol{{G}}$
and the vector of source terms for the production rates
$\boldsymbol{{G}}$
and the vector of source terms for the production rates
![]() $\boldsymbol{{W}}$
are expressed in Cartesian coordinates in (2.2)
$\boldsymbol{{W}}$
are expressed in Cartesian coordinates in (2.2)
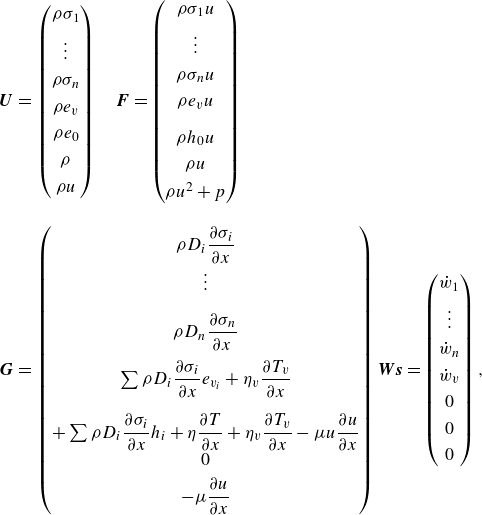 \begin{eqnarray} \boldsymbol{{U}} &=& \begin{pmatrix} \rho \sigma _1\\[4pt] \vdots \\[4pt] \rho \sigma _{n} \\[4pt] \rho e_v \\[4pt] \rho e_0 \\[4pt] \rho \\[4pt] \rho u \end{pmatrix} \quad \boldsymbol{{F}}= \begin{pmatrix} \rho \sigma _1 u\\[4pt] \vdots \\[4pt] \rho \sigma _{n} u \\[4pt] \rho e_v u \\[10pt] \rho h_0 u\\[4pt] \rho u \\[4pt] \rho u^2 +p \end{pmatrix} \nonumber\\[10pt] \boldsymbol{{G}} &=& \begin{pmatrix} \rho D_i \displaystyle\frac {\partial \sigma _i}{\partial x}\\[4pt] \vdots \\[10pt] \rho D_n \displaystyle\frac {\partial \sigma _n}{\partial x} \\[10pt] \sum \rho D_i \displaystyle\frac {\partial \sigma _i}{\partial x}e_{v_i} +\eta _{v} \displaystyle\frac {\partial T_v}{\partial x} \\[14pt] +\sum \rho D_i \displaystyle\frac {\partial \sigma _i}{\partial x} h_{i} + \eta \displaystyle\frac {\partial T}{\partial x} +\eta _{v} \displaystyle\frac {\partial T_v}{\partial x} - \mu u \displaystyle\frac {\partial u}{\partial x}\\[4pt] 0\\[4pt] -\mu \displaystyle\frac {\partial u}{\partial x} \end{pmatrix} \boldsymbol{{Ws}} = \begin{pmatrix} \dot {w}_1\\[4pt] \vdots \\[4pt] \dot {w}_n \\[4pt] \dot {w}_v \\[4pt] 0 \\[4pt] 0 \\[4pt] 0 \end{pmatrix}, \end{eqnarray}
\begin{eqnarray} \boldsymbol{{U}} &=& \begin{pmatrix} \rho \sigma _1\\[4pt] \vdots \\[4pt] \rho \sigma _{n} \\[4pt] \rho e_v \\[4pt] \rho e_0 \\[4pt] \rho \\[4pt] \rho u \end{pmatrix} \quad \boldsymbol{{F}}= \begin{pmatrix} \rho \sigma _1 u\\[4pt] \vdots \\[4pt] \rho \sigma _{n} u \\[4pt] \rho e_v u \\[10pt] \rho h_0 u\\[4pt] \rho u \\[4pt] \rho u^2 +p \end{pmatrix} \nonumber\\[10pt] \boldsymbol{{G}} &=& \begin{pmatrix} \rho D_i \displaystyle\frac {\partial \sigma _i}{\partial x}\\[4pt] \vdots \\[10pt] \rho D_n \displaystyle\frac {\partial \sigma _n}{\partial x} \\[10pt] \sum \rho D_i \displaystyle\frac {\partial \sigma _i}{\partial x}e_{v_i} +\eta _{v} \displaystyle\frac {\partial T_v}{\partial x} \\[14pt] +\sum \rho D_i \displaystyle\frac {\partial \sigma _i}{\partial x} h_{i} + \eta \displaystyle\frac {\partial T}{\partial x} +\eta _{v} \displaystyle\frac {\partial T_v}{\partial x} - \mu u \displaystyle\frac {\partial u}{\partial x}\\[4pt] 0\\[4pt] -\mu \displaystyle\frac {\partial u}{\partial x} \end{pmatrix} \boldsymbol{{Ws}} = \begin{pmatrix} \dot {w}_1\\[4pt] \vdots \\[4pt] \dot {w}_n \\[4pt] \dot {w}_v \\[4pt] 0 \\[4pt] 0 \\[4pt] 0 \end{pmatrix}, \end{eqnarray}
where
![]() $\rho$
represents the density of the gas mixture,
$\rho$
represents the density of the gas mixture,
![]() $u$
the velocity,
$u$
the velocity,
![]() $p$
the pressure,
$p$
the pressure,
![]() $e_0$
the total specific energy,
$e_0$
the total specific energy,
![]() $h_0$
the total specific enthalpy,
$h_0$
the total specific enthalpy,
![]() $e_v$
the specific vibrational energy,
$e_v$
the specific vibrational energy,
![]() $T$
the rotational–translational temperature,
$T$
the rotational–translational temperature,
![]() $T_v$
the vibrational temperature,
$T_v$
the vibrational temperature,
![]() $\sigma _i$
the individual mole-mass ratio,
$\sigma _i$
the individual mole-mass ratio,
![]() $\dot {w}_i$
the associated mass production and destruction for each chemical species and, finally, the source term of the electro-vibrational equation
$\dot {w}_i$
the associated mass production and destruction for each chemical species and, finally, the source term of the electro-vibrational equation
![]() $\dot {w}_v$
. The transport properties due to diffusive–viscous effects are determined from Chapman–Enskog theory as presented by Hirschfelder, Curtiss & Bird (Reference Hirschfelder, Curtiss and Bird1964). The multi-diffusion fluxes are computed as given by Sutton & Gnoffo (Reference Sutton and Gnoffo1998), with
$\dot {w}_v$
. The transport properties due to diffusive–viscous effects are determined from Chapman–Enskog theory as presented by Hirschfelder, Curtiss & Bird (Reference Hirschfelder, Curtiss and Bird1964). The multi-diffusion fluxes are computed as given by Sutton & Gnoffo (Reference Sutton and Gnoffo1998), with
![]() $D_i$
being the diffusion coefficient,
$D_i$
being the diffusion coefficient,
![]() $\mu$
the mixture viscosity and
$\mu$
the mixture viscosity and
![]() $\eta$
the thermal conductivity for translational–rotational energy of heavy particles, while
$\eta$
the thermal conductivity for translational–rotational energy of heavy particles, while
![]() $\eta _v$
is the vibrational thermal conductivity due to collisions between molecules and all particles as given by Gupta et al. (Reference Gupta, Yos, Thompson and Lee1990). In the case of an inviscid, non-conducting and non-diffusive flow, vector
$\eta _v$
is the vibrational thermal conductivity due to collisions between molecules and all particles as given by Gupta et al. (Reference Gupta, Yos, Thompson and Lee1990). In the case of an inviscid, non-conducting and non-diffusive flow, vector
![]() $\boldsymbol{{G}}$
can be neglected to yield the reactive form of the Euler equations.
$\boldsymbol{{G}}$
can be neglected to yield the reactive form of the Euler equations.
2.1. Thermodynamic model
According to the model proposed by Park (Reference Park1987, Reference Park1988), it is assumed that the partitioning between the discrete internal energy modes of the individual species can be characterised by two temperatures. Specifically, the translational mode of the heavy particles is treated as being fully equilibrated with the rotational mode of molecules such that both can be represented by a singular temperature
![]() $T$
(Lee Reference Lee1984). At the same time, the distribution of vibrational, electronic and electron translational energies is described by the vibrational temperature
$T$
(Lee Reference Lee1984). At the same time, the distribution of vibrational, electronic and electron translational energies is described by the vibrational temperature
![]() $T_v$
(Park Reference Park1987; Gnoffo Reference Gnoffo1989). The specific heats and enthalpies of the gas species in question are determined at thermal equilibrium using McBride’s (Reference McBride2002) polynomial expressions and then extended to thermal non-equilibrium conditions by assuming full excitation of the translational–rotational energy modes (Gnoffo Reference Gnoffo1989).
$T_v$
(Park Reference Park1987; Gnoffo Reference Gnoffo1989). The specific heats and enthalpies of the gas species in question are determined at thermal equilibrium using McBride’s (Reference McBride2002) polynomial expressions and then extended to thermal non-equilibrium conditions by assuming full excitation of the translational–rotational energy modes (Gnoffo Reference Gnoffo1989).
The partitioning of the energy modes is of great importance to distinguish between the specific heat ratio due to translational–rotational contribution
![]() $\bar {\gamma }$
(Grossman & Cinnella Reference Grossman and Cinnella1988), which equals the frozen specif heat ratio for fully excited translational–rotational states, and the equilibrium ratio of specific heats
$\bar {\gamma }$
(Grossman & Cinnella Reference Grossman and Cinnella1988), which equals the frozen specif heat ratio for fully excited translational–rotational states, and the equilibrium ratio of specific heats
![]() $\gamma _{{eq}}$
(Anderson Reference Anderson1989). These quantities are convenient to define the frozen speed of sound
$\gamma _{{eq}}$
(Anderson Reference Anderson1989). These quantities are convenient to define the frozen speed of sound
![]() $c_{{frz}}$
in (2.3) and its equilibrium equivalent
$c_{{frz}}$
in (2.3) and its equilibrium equivalent
![]() $c_{{eq}}$
in (2.4) by constraining the entropy
$c_{{eq}}$
in (2.4) by constraining the entropy
![]() $s$
and chemical composition
$s$
and chemical composition
![]() $\sigma$
(Clarke & McChesney Reference Clarke and McChesney1976). As noted by Chu (Reference Chu1957), these two speeds typically differ in a chemically reacting gas mixture
$\sigma$
(Clarke & McChesney Reference Clarke and McChesney1976). As noted by Chu (Reference Chu1957), these two speeds typically differ in a chemically reacting gas mixture
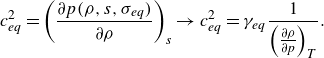 \begin{equation} c_{{eq}}^2 = \left (\frac {\partial p (\rho, s, \sigma _{{eq}})}{\partial \rho } \right )_{s} \rightarrow c_{{eq}}^2=\gamma _{{eq}} \frac {1}{\left ( \frac {\partial \rho }{\partial p} \right )_T} .\end{equation}
\begin{equation} c_{{eq}}^2 = \left (\frac {\partial p (\rho, s, \sigma _{{eq}})}{\partial \rho } \right )_{s} \rightarrow c_{{eq}}^2=\gamma _{{eq}} \frac {1}{\left ( \frac {\partial \rho }{\partial p} \right )_T} .\end{equation}
The equilibrium thermodynamic composition of high-enthalpy gas mixtures is evaluated using the in-house Oxford chemical equilibrium analysis (OCEAN) code, developed by The University of Oxford Hypersonics Group and validated by Clarke et al. (Reference Clarke, Brody, Steer, McGilvray and Di Mare2024a
). For air, a 11-species gas mixture is adopted (e
![]() $^-$
, N
$^-$
, N
![]() $^+$
, N
$^+$
, N
![]() $_2^+$
, O
$_2^+$
, O
![]() $^+$
, O
$^+$
, O
![]() $_2^+$
, NO
$_2^+$
, NO
![]() $^+$
, NO, N, O, N
$^+$
, NO, N, O, N
![]() $_2$
and O
$_2$
and O
![]() $_2$
).
$_2$
).
2.2. Chemistry model
The stoichiometric relations between the reactants and products of a multi-component gas, consisting of
![]() $n$
chemical species and
$n$
chemical species and
![]() $r \in nr$
number of reactions, are presented in a generic form in (2.5). The stoichiometric coefficients of the reactants and products for each species are denoted by
$r \in nr$
number of reactions, are presented in a generic form in (2.5). The stoichiometric coefficients of the reactants and products for each species are denoted by
![]() $\alpha _{i,r}$
and
$\alpha _{i,r}$
and
![]() $\beta _{i, r}$
, respectively. The chemical species in the fluid are represented by
$\beta _{i, r}$
, respectively. The chemical species in the fluid are represented by
![]() $X_i$
, while the forward and backward reactant rate coefficients for the
$X_i$
, while the forward and backward reactant rate coefficients for the
![]() $r_{th}$
reaction are given by
$r_{th}$
reaction are given by
![]() $k_{f,r}$
and
$k_{f,r}$
and
![]() $k_{b,r}$
, respectively (Gupta et al. Reference Gupta, Yos, Thompson and Lee1990)
$k_{b,r}$
, respectively (Gupta et al. Reference Gupta, Yos, Thompson and Lee1990)
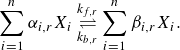 \begin{equation} \sum _{i=1}^{n} \alpha _{i, r} X_i \underset {k_{b, r}}{\stackrel {k_{f, r}}{\rightleftharpoons }} \sum _{i=1}^{n} \beta _{i, r} X_i. \end{equation}
\begin{equation} \sum _{i=1}^{n} \alpha _{i, r} X_i \underset {k_{b, r}}{\stackrel {k_{f, r}}{\rightleftharpoons }} \sum _{i=1}^{n} \beta _{i, r} X_i. \end{equation}
The production and destruction of the chemical species in
![]() $\boldsymbol{{W}}$
due to finite-rate chemical reactions may be defined in terms of molar concentration
$\boldsymbol{{W}}$
due to finite-rate chemical reactions may be defined in terms of molar concentration
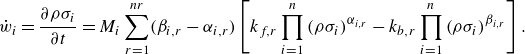 \begin{equation} \dot {w}_i=\frac {\partial {\rho \sigma _i}}{\partial t}=M_i\sum _{r=1}^{nr}(\beta _{i,r}-\alpha _{i,r}) \left [k_{f, r} \prod _{i=1}^n\left ( \rho \sigma _i \right )^{\alpha _{i, r}}-k_{b, r} \prod _{i=1}^n\left (\rho \sigma _i \right )^{\beta _{i,r}}\right ] .\end{equation}
\begin{equation} \dot {w}_i=\frac {\partial {\rho \sigma _i}}{\partial t}=M_i\sum _{r=1}^{nr}(\beta _{i,r}-\alpha _{i,r}) \left [k_{f, r} \prod _{i=1}^n\left ( \rho \sigma _i \right )^{\alpha _{i, r}}-k_{b, r} \prod _{i=1}^n\left (\rho \sigma _i \right )^{\beta _{i,r}}\right ] .\end{equation}
To account for the influence of thermal non-equilibrium on the reaction rates, the forward reaction rate coefficients are determined using the modified Arrhenius form as a function of the effective temperature
![]() $T_{d}$
defined by Park (Reference Park1989) as the geometric mean of the translational–rotational and electron–vibrational temperatures (
$T_{d}$
defined by Park (Reference Park1989) as the geometric mean of the translational–rotational and electron–vibrational temperatures (
![]() $T_{d}=\sqrt {T T_v}$
). Conversely, the backward reaction rates are maintained as being a function only of the translational temperature
$T_{d}=\sqrt {T T_v}$
). Conversely, the backward reaction rates are maintained as being a function only of the translational temperature
![]() $T$
(Gupta et al. Reference Gupta, Yos, Thompson and Lee1990). For air, the reactions in table 1 and the corresponding rates taken from Park (Reference Park1993) are adopted. In the case of argon, the reaction rate coefficient of the ionisation process due to electron–atom collisions is taken from Petschek & Byron (Reference Petschek and Byron1957); Ahtye (Reference Ahtye1968) as detailed in Appendix A.3.
$T$
(Gupta et al. Reference Gupta, Yos, Thompson and Lee1990). For air, the reactions in table 1 and the corresponding rates taken from Park (Reference Park1993) are adopted. In the case of argon, the reaction rate coefficient of the ionisation process due to electron–atom collisions is taken from Petschek & Byron (Reference Petschek and Byron1957); Ahtye (Reference Ahtye1968) as detailed in Appendix A.3.
The vibration energy source term in (2.1) can be decomposed as shown in (2.7). The specific vibrational energy change for diatomic molecules at the rate
![]() $\dot {w}_i$
is denoted by
$\dot {w}_i$
is denoted by
![]() $\hat {D}_s$
. Preferential dissociation and recombination in the higher vibrational states are modelled by assuming that
$\hat {D}_s$
. Preferential dissociation and recombination in the higher vibrational states are modelled by assuming that
![]() $\hat {D}_s$
is a fraction
$\hat {D}_s$
is a fraction
![]() $\hat {c}_1$
of the dissociation energy per unit mass (Gnoffo Reference Gnoffo1989). A value of
$\hat {c}_1$
of the dissociation energy per unit mass (Gnoffo Reference Gnoffo1989). A value of
![]() $\hat {c}_1=0.3$
is chosen as indicated by Sharma, Huo & Park (Reference Sharma, Huo and Park1992). The electron energy loss due to ionisation is represented by the product of the molar ionisation rate
$\hat {c}_1=0.3$
is chosen as indicated by Sharma, Huo & Park (Reference Sharma, Huo and Park1992). The electron energy loss due to ionisation is represented by the product of the molar ionisation rate
![]() $\dot {n}_{e,s}$
and the first ionisation energy
$\dot {n}_{e,s}$
and the first ionisation energy
![]() $\hat {I}_s$
. The energy exchange between translational-rotational modes and electro-vibrational modes follows Landau–Teller’s model (Landau Reference Landau1936) and uses relaxation times from Millikan and White’s correlation (Millikan & White Reference Millikan and White1963), with Park’s correction (Park Reference Park1985) for temperatures above 8000 K. Further details are provided in Appendix A.4. Additionally, the work done by the electric field due to the electron pressure gradient
$\hat {I}_s$
. The energy exchange between translational-rotational modes and electro-vibrational modes follows Landau–Teller’s model (Landau Reference Landau1936) and uses relaxation times from Millikan and White’s correlation (Millikan & White Reference Millikan and White1963), with Park’s correction (Park Reference Park1985) for temperatures above 8000 K. Further details are provided in Appendix A.4. Additionally, the work done by the electric field due to the electron pressure gradient
![]() $p_e \nabla u$
is included (Gnoffo Reference Gnoffo1989)
$p_e \nabla u$
is included (Gnoffo Reference Gnoffo1989)
2.3. Small perturbation analysis
To study the dynamics of small-amplitude waves propagating in a chemically reactive mixture, it is assumed that the perturbations of macroscopic fields have small amplitudes. It follows that the state variables only slightly deviate from equilibrium. The linearisation of the governing equations around an equilibrium state
![]() $\boldsymbol{{q}}$
is thus appropriate to describe the perturbations induced on the hydrodynamic field (Ramos, Ribeiro & Soares Reference Ramos, Ribeiro and Soares2018). The adoption of primitive variables is here reported to describe the state variables
$\boldsymbol{{q}}$
is thus appropriate to describe the perturbations induced on the hydrodynamic field (Ramos, Ribeiro & Soares Reference Ramos, Ribeiro and Soares2018). The adoption of primitive variables is here reported to describe the state variables
![]() $\boldsymbol{{q}}$
.
$\boldsymbol{{q}}$
.
Given a disturbance with angular frequency
![]() $\omega$
and wavenumber
$\omega$
and wavenumber
![]() $\nu$
described by a harmonic wave of type
$\nu$
described by a harmonic wave of type
the linearised conservation equations in (2.1) are written as
For a non-conductive and inviscid flow,
![]() $\boldsymbol{{G}}$
can be neglected such that the linearised equations are expressed as in (2.10). This takes the form of a generalised eigenvalue problem of type
$\boldsymbol{{G}}$
can be neglected such that the linearised equations are expressed as in (2.10). This takes the form of a generalised eigenvalue problem of type
![]() $\boldsymbol{A}(\omega ) \boldsymbol{{\hat {q}}}=\nu \boldsymbol{B} \boldsymbol{{\hat {q}}}$
, (Damköhler Reference Damköhler1950) where the right eigenvectors are the perturbations
$\boldsymbol{A}(\omega ) \boldsymbol{{\hat {q}}}=\nu \boldsymbol{B} \boldsymbol{{\hat {q}}}$
, (Damköhler Reference Damköhler1950) where the right eigenvectors are the perturbations
![]() $\boldsymbol{{\hat {q}}}$
. Given a finite frequency value
$\boldsymbol{{\hat {q}}}$
. Given a finite frequency value
![]() $\omega$
, the associated wavenumber
$\omega$
, the associated wavenumber
![]() $\nu$
can therefore be calculated
$\nu$
can therefore be calculated
While the frequency
![]() $\omega$
is always real, the wavenumber
$\omega$
is always real, the wavenumber
![]() $\nu$
is in general complex and can be separated into its real and imaginary components as
$\nu$
is in general complex and can be separated into its real and imaginary components as
![]() $\nu =\nu _r+\nu _i$
. The absorption coefficient
$\nu =\nu _r+\nu _i$
. The absorption coefficient
![]() $\alpha$
and instantaneous phase velocity
$\alpha$
and instantaneous phase velocity
![]() $v_p$
are defined as follows:
$v_p$
are defined as follows:
The diagonal matrix of eigenvalues
![]() $\nu$
that are a solution to the generalised eigenvalue problem in (2.10) is defined in (2.12), where
$\nu$
that are a solution to the generalised eigenvalue problem in (2.10) is defined in (2.12), where
![]() $\lambda _1,\ldots \lambda _n$
are the eigenvalue components due to the presence of chemical reactions. The first two eigenvalues that appear are due to the propagation of a sound wave and are equivalent to the eigenvalues
$\lambda _1,\ldots \lambda _n$
are the eigenvalue components due to the presence of chemical reactions. The first two eigenvalues that appear are due to the propagation of a sound wave and are equivalent to the eigenvalues
![]() $u\pm c$
in the Euler equations, while the remaining ones correspond to
$u\pm c$
in the Euler equations, while the remaining ones correspond to
![]() $u$
. For a vanishing velocity
$u$
. For a vanishing velocity
![]() $(u=0)$
, it is clear that the local speed
$(u=0)$
, it is clear that the local speed
![]() $c$
of sound can be derived from the first two eigenvalues by relating them to the phase velocity (
$c$
of sound can be derived from the first two eigenvalues by relating them to the phase velocity (
![]() $c=\frac {\omega }{\nu _r}$
)
$c=\frac {\omega }{\nu _r}$
)
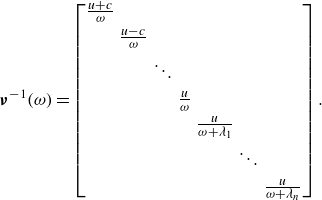 \begin{equation} {{\boldsymbol{\nu }^{-1}(\omega )}}= \begin{bmatrix} \frac {u+c}{\omega } & & & & \\[3pt] & \frac {u-c}{\omega }& & & \\[3pt] & & \ddots & & \\[3pt] & & & \frac {u}{\omega } \\[3pt] & & & & \frac {u}{\omega + \lambda _1} \\[3pt] & & & & & \ddots \\[3pt] & & & & & & \frac {u}{\omega + \lambda _n} \end{bmatrix} .\end{equation}
\begin{equation} {{\boldsymbol{\nu }^{-1}(\omega )}}= \begin{bmatrix} \frac {u+c}{\omega } & & & & \\[3pt] & \frac {u-c}{\omega }& & & \\[3pt] & & \ddots & & \\[3pt] & & & \frac {u}{\omega } \\[3pt] & & & & \frac {u}{\omega + \lambda _1} \\[3pt] & & & & & \ddots \\[3pt] & & & & & & \frac {u}{\omega + \lambda _n} \end{bmatrix} .\end{equation}
When the flow may not be assumed to be inviscid and non-conductive the term
![]() $\boldsymbol{{G}}$
must be retained. Equation (2.9) is equivalent to a quadratic eigenvalue problem of type
$\boldsymbol{{G}}$
must be retained. Equation (2.9) is equivalent to a quadratic eigenvalue problem of type
![]() $(\boldsymbol{{D}} \nu ^2 + \boldsymbol{{B}} \nu + \boldsymbol{{A}}(\omega )) \boldsymbol{{\hat {q}}}=0$
. The exact solution is obtained via linearisation as discussed in Appendix A.5.
$(\boldsymbol{{D}} \nu ^2 + \boldsymbol{{B}} \nu + \boldsymbol{{A}}(\omega )) \boldsymbol{{\hat {q}}}=0$
. The exact solution is obtained via linearisation as discussed in Appendix A.5.
3. Results and discussion
3.1. Sound attenuation
To validate the methodology outlined in the previous section, the absorption of the speed of sound is investigated at different thermodynamic conditions for various gases. Given that according to classical theory the total sound absorption is equivalent to the sum of the individual contributions, these may be verified independently (Carnevale et al. Reference Carnevale, Carey and Larson1967a
). First, the viscousdiffusive contributions are isolated by computing the absorption coefficient of sound waves travelling through an argon mixture at ambient conditions. Since the monoatomic gas mixture can experience no vibrational relaxation, the only mechanisms responsible for sound absorption are those of diffusion, conduction and viscosity, which are completely accounted for by classical theory (Markham, Beyer & Lindsay Reference Markham, Beyer and Lindsay1951). The numerical results predicted by the eigenvalue model are shown in figure 2 against the experimental measurements by Greenspan (Reference Greenspan1956) and Meyer & Sessler (Reference Meyer and Sessler1957). A reasonable agreement with the dispersion curve obtained in the present work and the experimental measurements is observed. Frequency independence in the
![]() ${\alpha }/{\omega }$
ratio is correctly predicted in the limit of
${\alpha }/{\omega }$
ratio is correctly predicted in the limit of
![]() $\omega \gt \gt p/\eta$
, and the slope in accordance with the experimental data at
$\omega \gt \gt p/\eta$
, and the slope in accordance with the experimental data at
![]() $\omega \lt \lt p/\eta$
is identified.
$\omega \lt \lt p/\eta$
is identified.
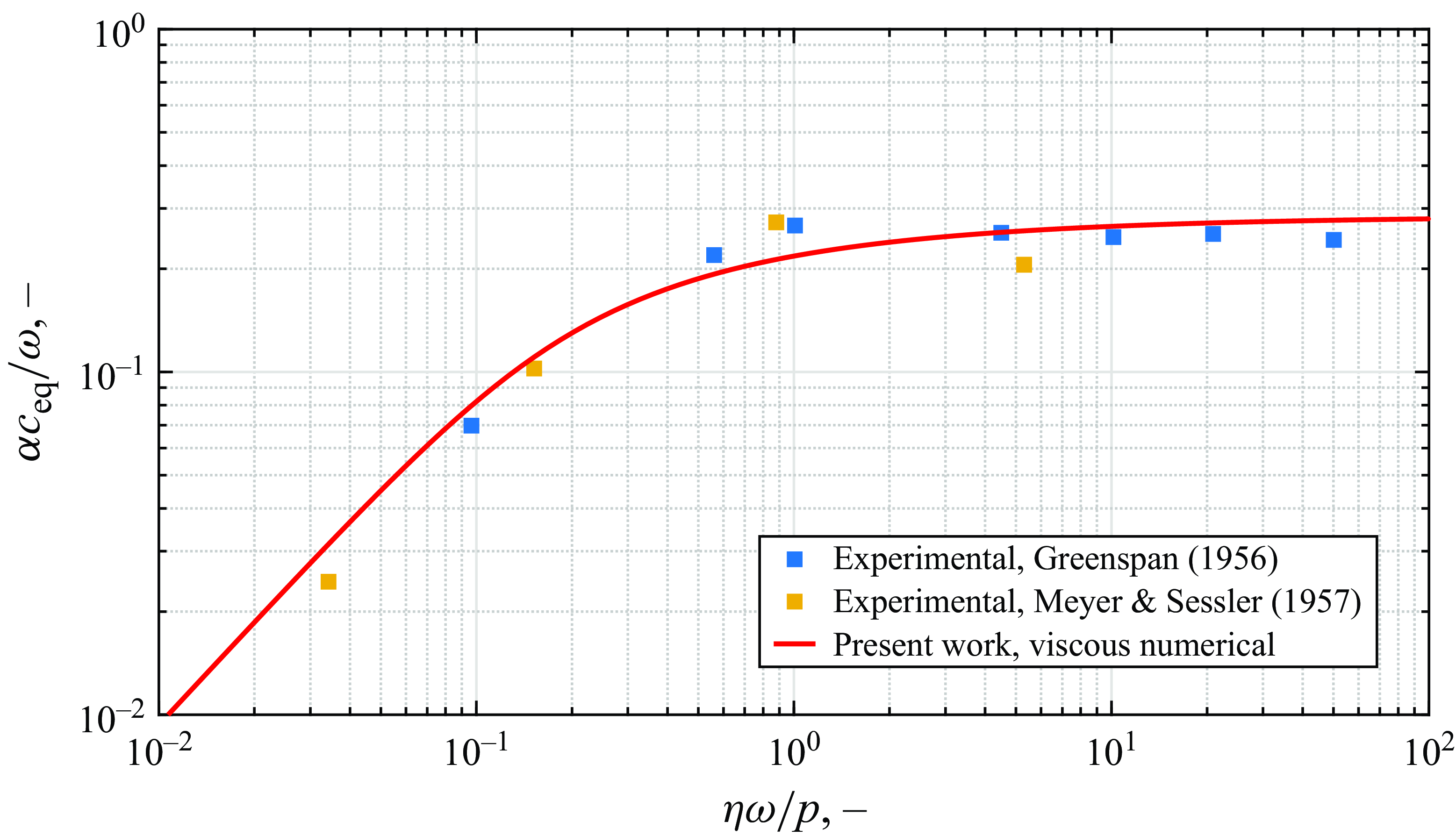
Figure 2. Normalied sound absorption in argon at 1 atm and 300 K.
To include the effects of vibrational relaxation in addition to viscosity, the dimensionless attenuation coefficient per wavelength for a single-component gas is compared with the experimental data presented by Ejakov et al. (Reference Ejakov, Phillips, Dain, Lueptow and Visser2003) for air at ambient conditions, as shown in figure 3(a). Scatter in the data is noted due to different transducers being used, and the presence of negative attenuation is considered an anomaly (Zuckerwar & Griffin Reference Zuckerwar and Griffin1980; Ejakov et al. Reference Ejakov, Phillips, Dain, Lueptow and Visser2003). The predictions from the empirical model developed by Bass et al. (Reference Bass, Sutherland, Piercy and Evans1984) based on acoustic attenuation in air due to classical attenuation and attenuation from relaxation and vibrational modes are also included in comparison with the current work, yielding a maximum percentage error of 9.6 %. The increase in
![]() $\alpha /\nu$
at higher frequencies agrees well with both sets of results.
$\alpha /\nu$
at higher frequencies agrees well with both sets of results.
A further validation case is presented in figure 3(b) for methane CH
![]() $_4$
at 1 atm and a temperature of 571.3 K, in comparison with the numerical results of the present work with the experimental results of Ejakov et al. (Reference Ejakov, Phillips, Dain, Lueptow and Visser2003) and numerical data by Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023). The classical Stokes–Kirchhoff formula used by the latter shows reasonable agreement with the present work both in terms of magnitude and increasing trend, yielding a mean percentage error of 6.8 % over the available range of frequencies. As noted by Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023), minor deviations are noted for
$_4$
at 1 atm and a temperature of 571.3 K, in comparison with the numerical results of the present work with the experimental results of Ejakov et al. (Reference Ejakov, Phillips, Dain, Lueptow and Visser2003) and numerical data by Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023). The classical Stokes–Kirchhoff formula used by the latter shows reasonable agreement with the present work both in terms of magnitude and increasing trend, yielding a mean percentage error of 6.8 % over the available range of frequencies. As noted by Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023), minor deviations are noted for
![]() $\omega /p \gt 30$
$\omega /p \gt 30$
![]() $\rm Hz/Pa$
due to the continuum limit assumption being approached between the results of Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023) and the measurements of Ejakov et al. (Reference Ejakov, Phillips, Dain, Lueptow and Visser2003). The present model accurately captures the experimental data points and the location of the maximum attenuation coefficient, highlighting the validity of the present methodology.
$\rm Hz/Pa$
due to the continuum limit assumption being approached between the results of Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023) and the measurements of Ejakov et al. (Reference Ejakov, Phillips, Dain, Lueptow and Visser2003). The present model accurately captures the experimental data points and the location of the maximum attenuation coefficient, highlighting the validity of the present methodology.

Figure 3. Dimensionless attenuation coefficient as a function of
![]() $\omega /p$
in polyatomic gases.
$\omega /p$
in polyatomic gases.
Having established the validity of the present model for absorption due to viscousdiffusive and relaxation mechanisms, further validation is presented for multi-component reactive gas mixtures subject to chemical reactions under a broader range of temperatures. The results presented for the remainder of this work assume a thermochemical equilibrium state unless otherwise specified. The equilibrium compositions obtained from OCEAN in air are plotted and verified in Appendix A.2. The normalised measurements recorded by Carnevale et al. (Reference Carnevale, Larson, Lynnworth, Carey, Panaro and Marshall1967b
) in nitrogen at a temperature range between 300 K and approximately 12 000 K via ultrasonic pulses (Carnevale et al. Reference Carnevale, Carey and Larson1967a
) are plotted in figure 4 along with the associated results obtained from the resolution of the eigenvalue problem in (2.9) for thermodynamic equilibrium and chemical non-equilibrium conditions. It is noted that the pressure and frequency (
![]() $f= {\omega }/{2\pi }$
) terms are included in the normalisation of the absorptivity in a similar form to (1.1). This confers the advantage that the normalised coefficient remains constant when the ultrasonic angular frequency is substantially lower than the relaxation frequency of a particular loss mechanism. As a result, when the normalised absorptivity tends to zero for an internal mode, the classical absorption due to thermal conduction and viscosity is still finite (Carnevale et al. Reference Carnevale, Larson, Lynnworth, Carey, Panaro and Marshall1967b
).
$f= {\omega }/{2\pi }$
) terms are included in the normalisation of the absorptivity in a similar form to (1.1). This confers the advantage that the normalised coefficient remains constant when the ultrasonic angular frequency is substantially lower than the relaxation frequency of a particular loss mechanism. As a result, when the normalised absorptivity tends to zero for an internal mode, the classical absorption due to thermal conduction and viscosity is still finite (Carnevale et al. Reference Carnevale, Larson, Lynnworth, Carey, Panaro and Marshall1967b
).
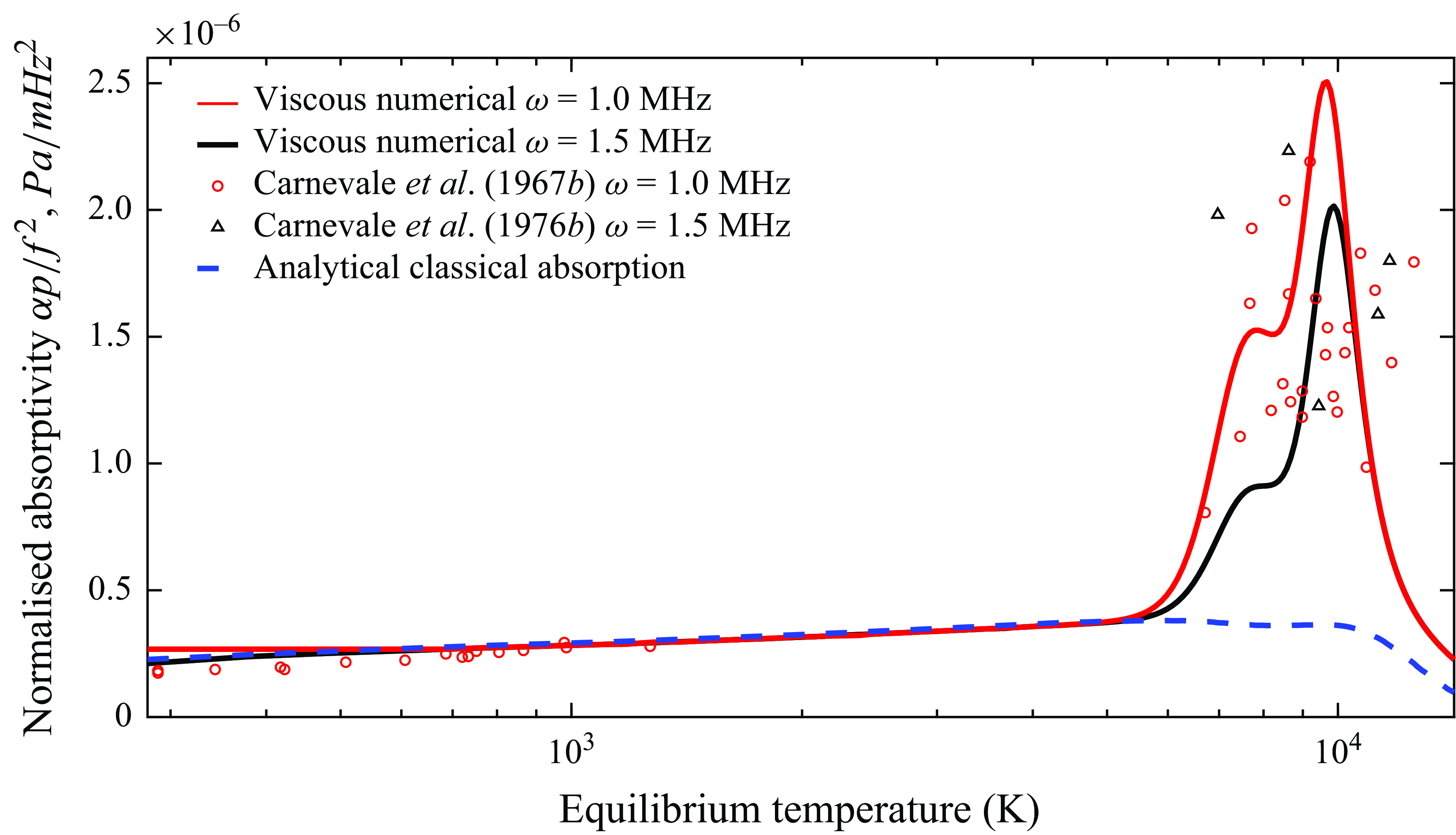
Figure 4. Normalised sound absorption for nitrogen
![]() $(\mathrm{N}, \mathrm{N}_2, \mathrm{N}^+, \mathrm{N}_2^+, \mathrm{e}^-)$
at 1 atm.
$(\mathrm{N}, \mathrm{N}_2, \mathrm{N}^+, \mathrm{N}_2^+, \mathrm{e}^-)$
at 1 atm.
The acoustic absorption results are clearly separated into two temperature regions; the first one from 300to 1300 K is dominated by the transport properties of the gas and the relaxation mechanisms between the internal energy modes (Carnevale et al. Reference Carnevale, Larson, Lynnworth, Carey, Panaro and Marshall1967a
). This region is independent of the perturbation frequency and is well characterised by the classic absorption theory through (1.1). The excellent agreement with classical absorption theory confirms that the viscous, diffusive and conductive processes are adequately captured by the method presented in this paper. Slight differences are present below 1000 K due to the rotational degrees of freedom which are assumed to be fully excited in the model proposed, and not accounted for by the classical absorption. The vibrational degrees of freedom are expected to be frozen out at such frequencies and low temperatures. Conversely, at temperatures beyond 5000 K, the experimental data at
![]() $\omega = 1-1.5$
MHz show a drastic increase in sound absorption with further temperature increases. The marked discrepancy between the classical absorption model and the experimental measurements at such temperatures unveils the physical presence of additional absorption mechanisms. On the other hand, the reactive model proposed in this work successfully captures the sudden increase in absorptivity. While the experimental data do not provide sufficient confidence to discern the effect of different frequencies at high temperatures, they do confirm that the effect of excited electronic states, dissociation and ionisation are mechanisms responsible for sound absorption. The peak absorption observed at temperatures greater than 9000 K are dominated by chemical absorption since the equilibrium base flow is almost fully dissociated, with
$\omega = 1-1.5$
MHz show a drastic increase in sound absorption with further temperature increases. The marked discrepancy between the classical absorption model and the experimental measurements at such temperatures unveils the physical presence of additional absorption mechanisms. On the other hand, the reactive model proposed in this work successfully captures the sudden increase in absorptivity. While the experimental data do not provide sufficient confidence to discern the effect of different frequencies at high temperatures, they do confirm that the effect of excited electronic states, dissociation and ionisation are mechanisms responsible for sound absorption. The peak absorption observed at temperatures greater than 9000 K are dominated by chemical absorption since the equilibrium base flow is almost fully dissociated, with
![]() $N$
making up 96 % of the total composition by molar fractions, meaning that the effect of vibrational relaxation is minor. The higher peak is caused by the increasing significance of the electron-impact ionisation reaction with atomic nitrogen that increases with temperature. On the contrary, the lower peak is due to the interplay of ionisation of both atomic and molecular nitrogen, competing with the dissociation of the remaining molecules of nitrogen. It is noted that while the numerical simulations were performed using an initial equilibrium thermodynamic composition, it is plausible that the high-temperature measurements in the high-pressure direct-current arc plasma were subject to a non-negligible degree of non-equilibrium.
$N$
making up 96 % of the total composition by molar fractions, meaning that the effect of vibrational relaxation is minor. The higher peak is caused by the increasing significance of the electron-impact ionisation reaction with atomic nitrogen that increases with temperature. On the contrary, the lower peak is due to the interplay of ionisation of both atomic and molecular nitrogen, competing with the dissociation of the remaining molecules of nitrogen. It is noted that while the numerical simulations were performed using an initial equilibrium thermodynamic composition, it is plausible that the high-temperature measurements in the high-pressure direct-current arc plasma were subject to a non-negligible degree of non-equilibrium.
The validity of the model is further established by comparison with experimental data of sound absorption in pure argon, as shown in figure 5. Different to the nitrogen data, only a single frequency of 2 MHz is reported by Carnevale et al. (Reference Carnevale, Larson, Lynnworth, Carey, Panaro and Marshall1967b
). In agreement with the previous discussion, the normalised absorptivity at relatively low temperatures (T
![]() $\lt$
11 000 K) is correctly captured by classical absorption theory. Above 11 000 K an anomalous increase in absorption is measured which is not predicted by the diffusive and viscous phenomena, and must be the result of chemical ionisation since no vibrational relaxation can occur, as correctly captured by the model that matches the increasing trend in experimental absorption.
$\lt$
11 000 K) is correctly captured by classical absorption theory. Above 11 000 K an anomalous increase in absorption is measured which is not predicted by the diffusive and viscous phenomena, and must be the result of chemical ionisation since no vibrational relaxation can occur, as correctly captured by the model that matches the increasing trend in experimental absorption.
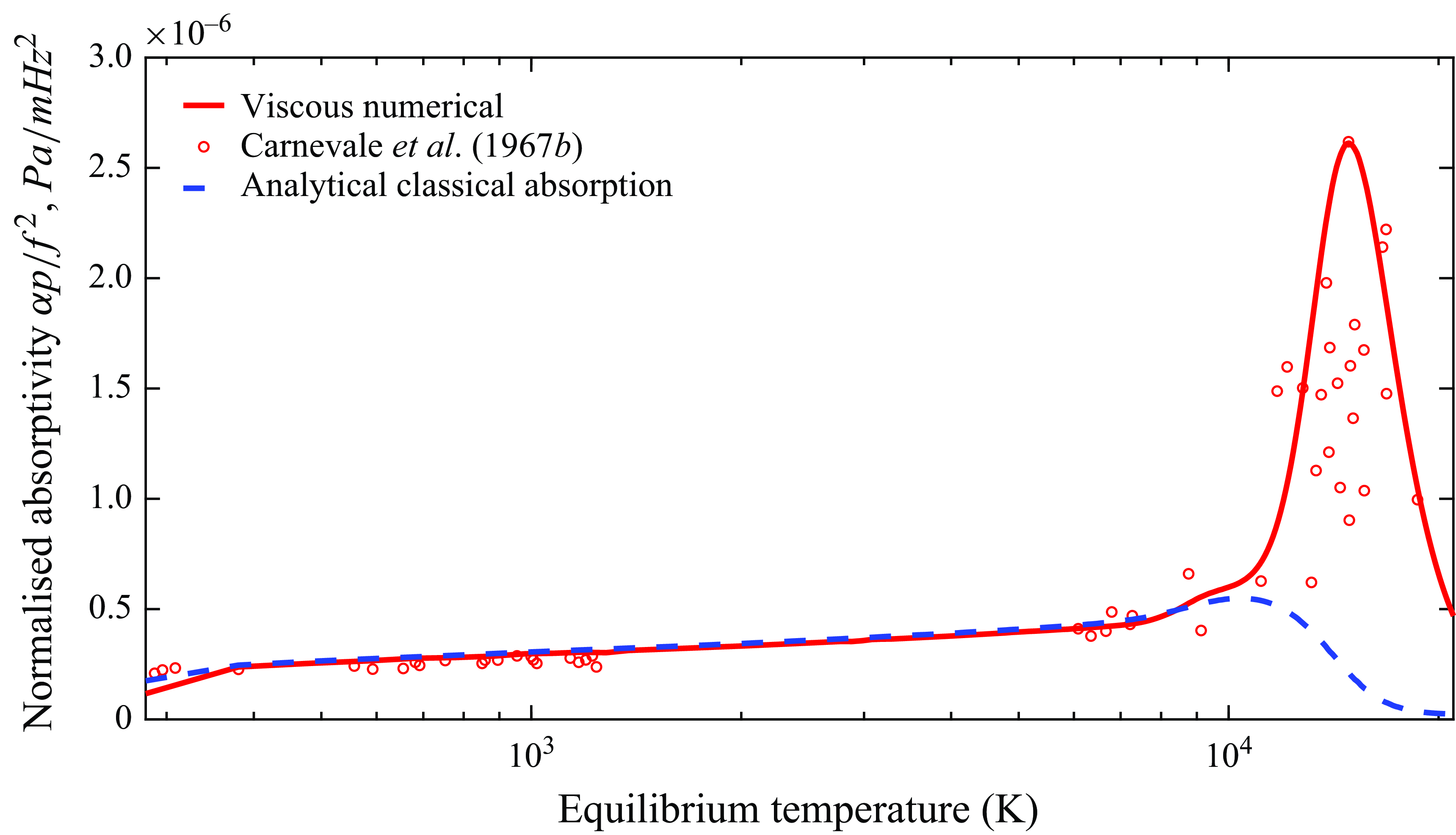
Figure 5. Normalised sound absorption for argon
![]() $(\mathrm{Ar}, \mathrm{Ar}^+, \mathrm{e}^-)$
at 2 MHz and 1 atm.
$(\mathrm{Ar}, \mathrm{Ar}^+, \mathrm{e}^-)$
at 2 MHz and 1 atm.
The dominating mechanisms responsible for the sound absorption in nitrogen
![]() $(\mathrm{N}, \mathrm{N}_2, \mathrm{N}^+, \mathrm{N}_2^+, \mathrm{e}^-)$
at a temperature of 9000 K and a pressure of 1 atm are plotted in figure 6(a). The relative contributions to the absorption per wavelength reveal that the viscous contribution becomes dominant at high frequencies but is less than the chemical contribution at low frequencies, in accordance with figure 1. The departure from the inviscid solution at high frequencies is also captured by the experimental data points, normalised by the numerical wavenumbers at the closest temperature, although the two available frequencies only provide a limited comparison with the presented results. Within the chemical contributions, the dominant reactions for the specific thermochemical state are electron-impact ionisation, associative ionisation due to nitrogennitrogen collisions and molecular dissociation due to molecular nitrogen collisions. The latter is responsible for the second peak, whereas the first two reactions cause the first peak within the frequency range of vibrational relaxation. Depending on the the frequency region of vibrational relaxation and the relaxation frequencies of the expected reactions, the absorption due to chemical effects results from a combination of the individual reactions. The same figure is shown in figure 6(b) for argon at 14 700 K, corresponding to the point of maximum sound absorption. A similar qualitative trend to the nitrogen case is observed for both viscous and inviscid absorptivity. Nevertheless, given the presence of only one responsible mechanism for the observed behaviour, namely the ionisation of argon, only one peak is noted in the ultrasonic region as indicated in the figure.
$(\mathrm{N}, \mathrm{N}_2, \mathrm{N}^+, \mathrm{N}_2^+, \mathrm{e}^-)$
at a temperature of 9000 K and a pressure of 1 atm are plotted in figure 6(a). The relative contributions to the absorption per wavelength reveal that the viscous contribution becomes dominant at high frequencies but is less than the chemical contribution at low frequencies, in accordance with figure 1. The departure from the inviscid solution at high frequencies is also captured by the experimental data points, normalised by the numerical wavenumbers at the closest temperature, although the two available frequencies only provide a limited comparison with the presented results. Within the chemical contributions, the dominant reactions for the specific thermochemical state are electron-impact ionisation, associative ionisation due to nitrogennitrogen collisions and molecular dissociation due to molecular nitrogen collisions. The latter is responsible for the second peak, whereas the first two reactions cause the first peak within the frequency range of vibrational relaxation. Depending on the the frequency region of vibrational relaxation and the relaxation frequencies of the expected reactions, the absorption due to chemical effects results from a combination of the individual reactions. The same figure is shown in figure 6(b) for argon at 14 700 K, corresponding to the point of maximum sound absorption. A similar qualitative trend to the nitrogen case is observed for both viscous and inviscid absorptivity. Nevertheless, given the presence of only one responsible mechanism for the observed behaviour, namely the ionisation of argon, only one peak is noted in the ultrasonic region as indicated in the figure.
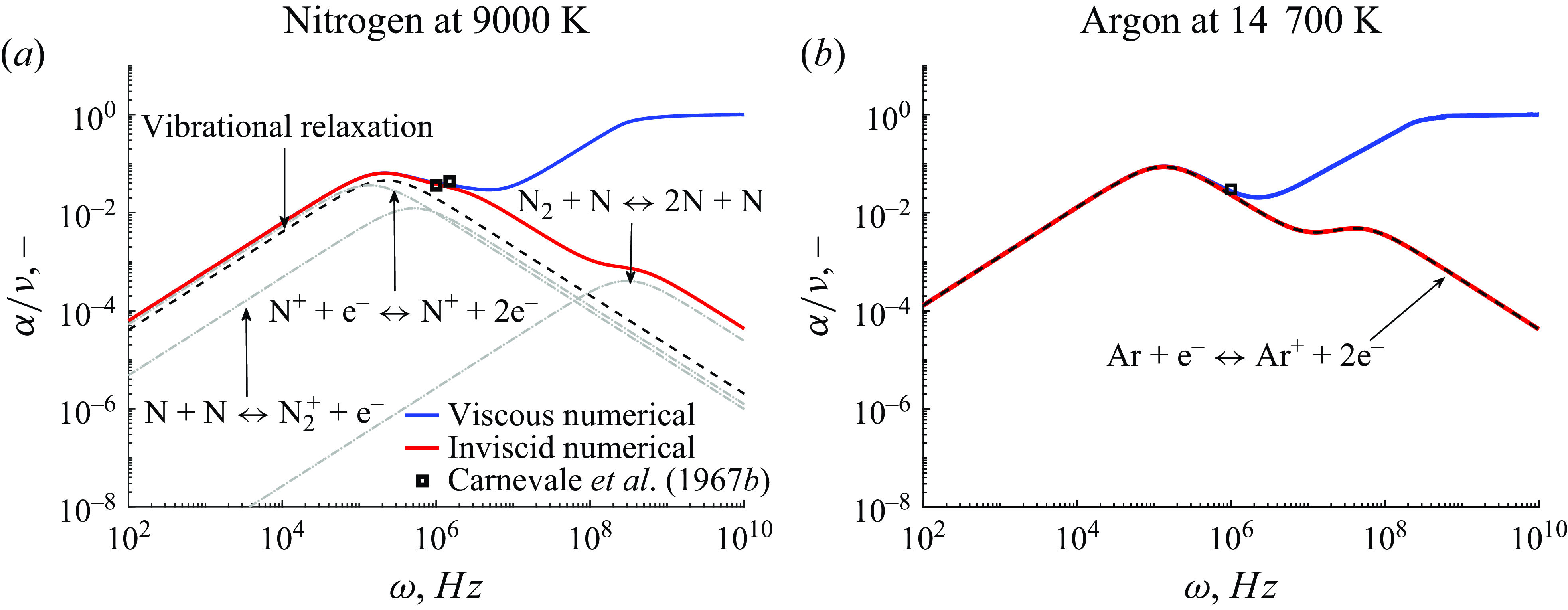
Figure 6. Absorption per wavelength against frequency at 1 atm.
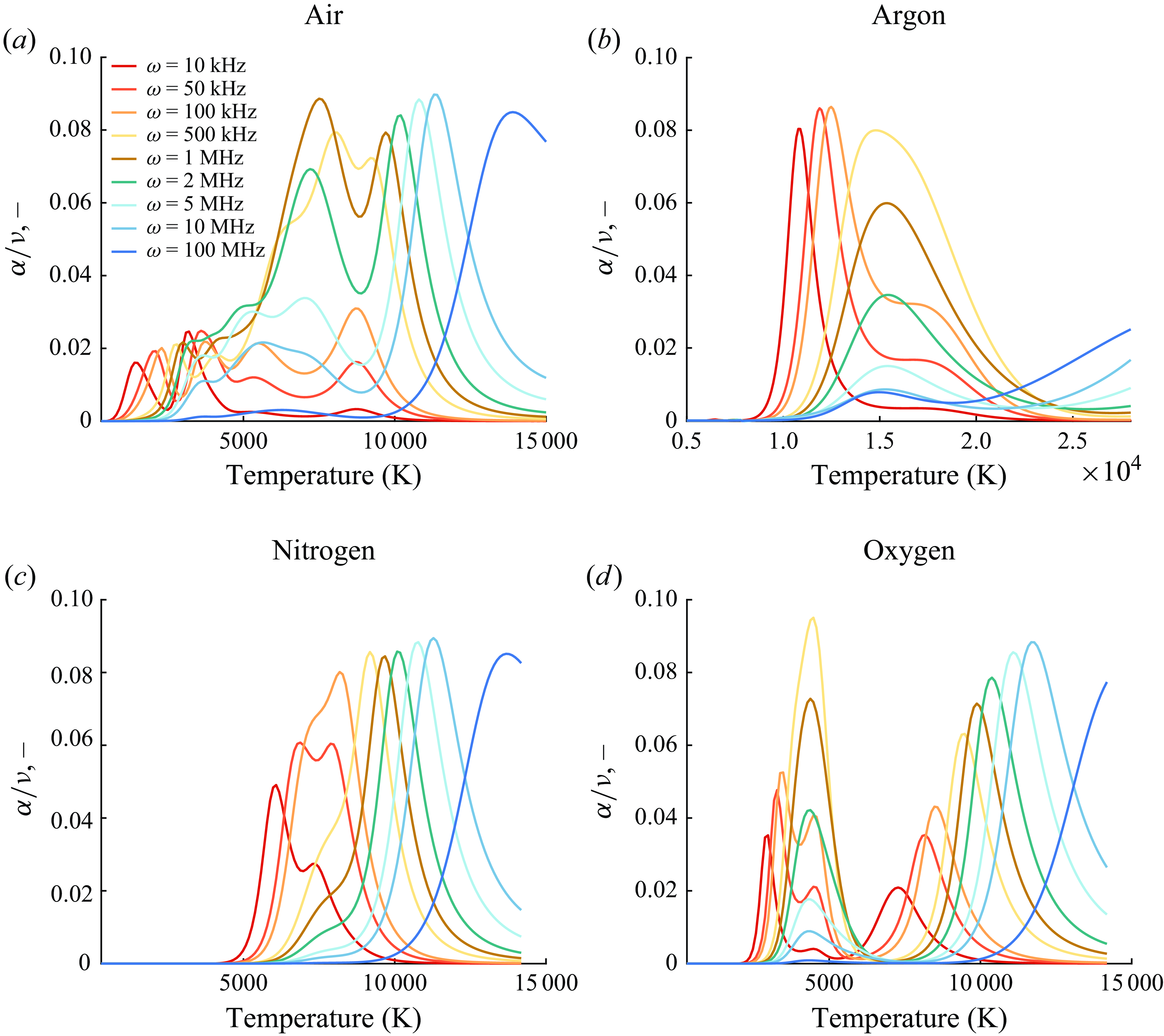
Figure 7. Inviscid normalised sound absorption for varying
![]() $\omega$
at 1 atm.
$\omega$
at 1 atm.
The normalised absorption coefficient for sound waves travelling in air, nitrogen, oxygen
![]() $(\mathrm{O}, \mathrm{O}_2, \mathrm{O}^+, \mathrm{O}_2^+, \mathrm{e}^-)$
and argon (
$(\mathrm{O}, \mathrm{O}_2, \mathrm{O}^+, \mathrm{O}_2^+, \mathrm{e}^-)$
and argon (
![]() $\mathrm{Ar}, \mathrm{Ar}^+, \mathrm{e}^-$
) is plotted in figure 7 for varying frequencies and temperatures using the inviscid model starting from initial equilibrium compositions. The cumulative effects of finite-rate chemical kinetics and vibrational relaxations are visible in the peaks and their distribution, as different reactions have different relaxation frequencies and are active under varying temperature conditions. The curves provided can be used to determine the required absorptivity throughout the frequency domain of interest due to molecular relaxation and chemical phenomena. The absorption solely due to chemical reactions is provided in figure 22. It follows that the difference between these two figures would yield the isolated absorption due to molecular relaxation. The results for argon are only characterised by ionisation since no vibrational relaxation occurs. Inspection of these figures for air, nitrogen and oxygen reveals that low-temperature absorption is only caused by vibrational relaxation, with peak frequencies shifting as a function of temperature. At elevated temperatures, the combined effect of the two absorption mechanisms overlaps and results in an increased normalised attenuation. For air and its constituents, no vibrational relaxation is obtained at sufficiently high temperatures since, for sufficiently high frequencies, chemical absorption is responsible for most of the absorption. For instance, while the curves at 100 MHz are generated by the ionisation reactions in the inviscid solution, the viscous–diffusive absorption mechanism is expected to prevail, as discussed in the next sections.
$\mathrm{Ar}, \mathrm{Ar}^+, \mathrm{e}^-$
) is plotted in figure 7 for varying frequencies and temperatures using the inviscid model starting from initial equilibrium compositions. The cumulative effects of finite-rate chemical kinetics and vibrational relaxations are visible in the peaks and their distribution, as different reactions have different relaxation frequencies and are active under varying temperature conditions. The curves provided can be used to determine the required absorptivity throughout the frequency domain of interest due to molecular relaxation and chemical phenomena. The absorption solely due to chemical reactions is provided in figure 22. It follows that the difference between these two figures would yield the isolated absorption due to molecular relaxation. The results for argon are only characterised by ionisation since no vibrational relaxation occurs. Inspection of these figures for air, nitrogen and oxygen reveals that low-temperature absorption is only caused by vibrational relaxation, with peak frequencies shifting as a function of temperature. At elevated temperatures, the combined effect of the two absorption mechanisms overlaps and results in an increased normalised attenuation. For air and its constituents, no vibrational relaxation is obtained at sufficiently high temperatures since, for sufficiently high frequencies, chemical absorption is responsible for most of the absorption. For instance, while the curves at 100 MHz are generated by the ionisation reactions in the inviscid solution, the viscous–diffusive absorption mechanism is expected to prevail, as discussed in the next sections.
3.2. Speed of sound in reactive medium
The speed of sound in air arising from the eigenvalues in the presence of reactive terms as shown in (2.12) is investigated around the equilibrium conditions at the typical temperature ranges required for activation of different classes of physicochemical phenomena (Anderson Reference Anderson1989; Park Reference Park1989). First, the results from the inviscid model are discussed such that the effect of vibrational relaxation and chemical reactions is investigated independently of viscous–diffusive effects. Whilst maintaining the pressure fixed at atmospheric conditions, the chosen temperature values are representative of typical hypersonic conditions experienced during re-entry from Mars missions at 12 000 K, from the Moon at 9000 K and low-Earth orbits at 6000 K (Putnam et al. Reference Putnam, Braun, Rohrschneider and Dec2007).
To verify the consistency of the solution to the eigenvalue problem proposed, the low- and high-frequency solutions are first investigated. As outlined in figure 1, the equilibrium speed of sound
![]() $c=c_{{eq}}$
is attained in the limit of
$c=c_{{eq}}$
is attained in the limit of
![]() $\omega \rightarrow 0$
, whereas frozen conditions are predicted at
$\omega \rightarrow 0$
, whereas frozen conditions are predicted at
![]() $\omega \rightarrow \infty$
for which
$\omega \rightarrow \infty$
for which
![]() $c=c_{{frz}}$
. While the former may be evaluated analytically using (2.3), the equilibrium speed of sound is computed using both OCEAN and the independent chemical equilibrium and applications (CEA) program developed by Gordon & McBride (Reference Gordon and McBride1994). The comparison with the eigenvalue solution, plotted in figure 8, shows excellent agreement amongst all methods, confirming the accuracy of the numerical eigenvalues at low and high frequencies for both air and argon.
$c=c_{{frz}}$
. While the former may be evaluated analytically using (2.3), the equilibrium speed of sound is computed using both OCEAN and the independent chemical equilibrium and applications (CEA) program developed by Gordon & McBride (Reference Gordon and McBride1994). The comparison with the eigenvalue solution, plotted in figure 8, shows excellent agreement amongst all methods, confirming the accuracy of the numerical eigenvalues at low and high frequencies for both air and argon.
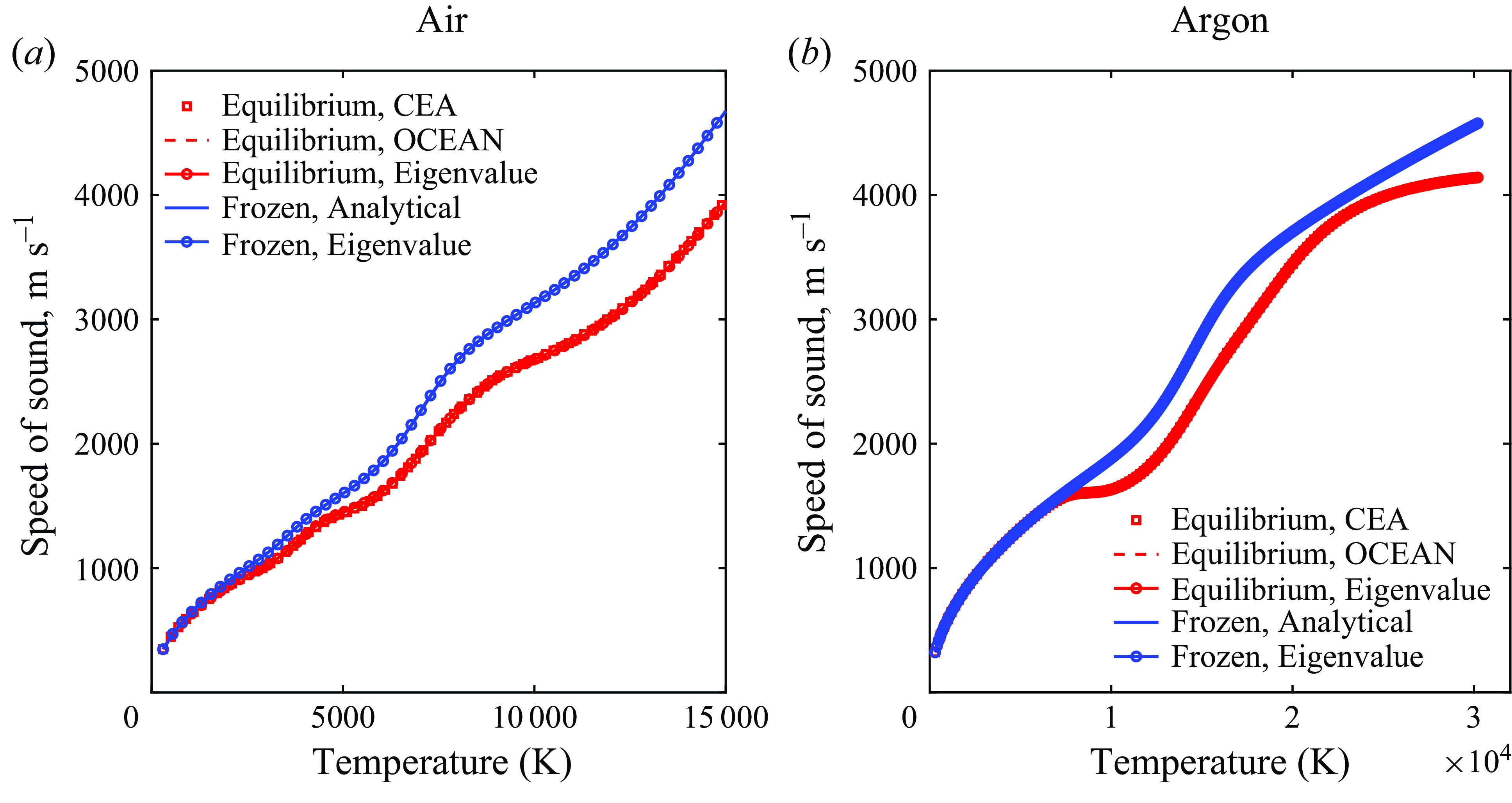
Figure 8. Comparison of frozen and equilibrium speed of sound at 1 atm.
Having determined the correct equilibrium and frozen speed of sound, the solution to the eigenvalue problem at finite frequencies is shown in figure 9, which unveils the behaviour of the propagation speed as the frequency of the disturbance inducing the chemical reactions increases. The results show that, at room temperature, when air is not reactive, the propagation speed varies slightly as a result of vibrational relaxation. As the temperature is increased, the activation energy for given classes of chemical reactions is reached. At approximately 2500 K, the effect of dissociation of
![]() $\mathrm{O}_2$
and exchange reactions of NO becomes noticeable in the ultrasonic regime as a nonlinear continuous increase of the speed of sound from the frozen value.
$\mathrm{O}_2$
and exchange reactions of NO becomes noticeable in the ultrasonic regime as a nonlinear continuous increase of the speed of sound from the frozen value.
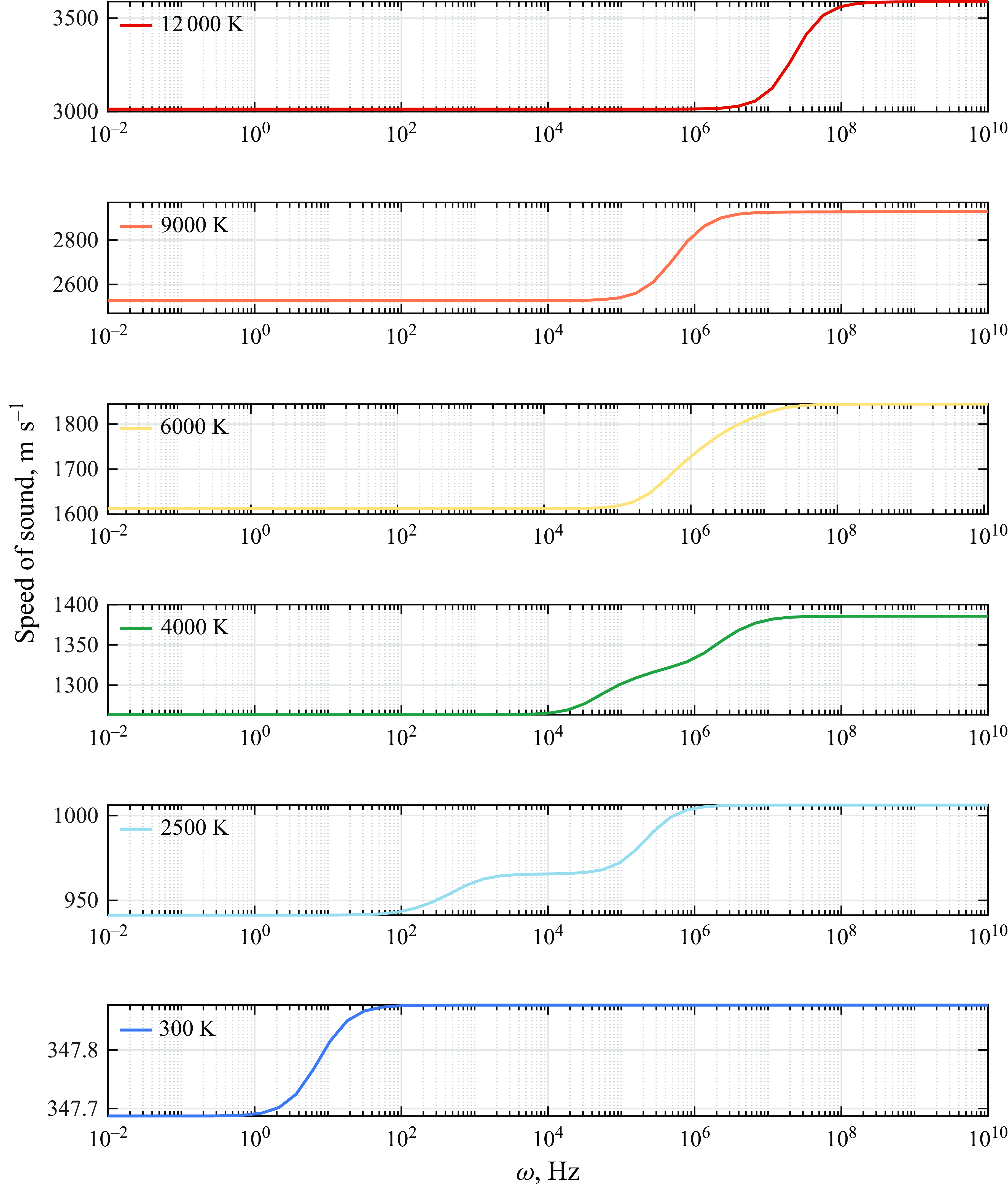
Figure 9. Speed of sound in air as a function of
![]() $\omega$
at different equilibrium temperatures and 1 atm.
$\omega$
at different equilibrium temperatures and 1 atm.
As the frequency is increased, the propagation speed is displaced from its frozen value due to chemical relaxation such that it enters the non-equilibrium regime, where the time scale of the reactions is comparable to that of the disturbance period. As the frequency is increased even further into the ultrasonic region for a temperature of 2500 K, the propagation speed reaches its equilibrium condition. While the transitional frequency from frozen to non-equilibrium and from non-equilibrium to equilibrium conditions varies with temperature, the same qualitative behaviour is observed in figure 9 at 4000 and 6000 K, where further dissociation and exchange reactions of N
![]() $_2$
and NO occur, and 9000–12 000 K where ionisation is predicted (Anderson Reference Anderson1989).
$_2$
and NO occur, and 9000–12 000 K where ionisation is predicted (Anderson Reference Anderson1989).
In order to identify the individual mechanisms responsible for the finite variations observed in the speed of sound, the absorption of sound is plotted in figure 10 for the individual processes. The dominating chemical reactions, indicated by dashed lines, are also annotated. It is found that peak absorption frequency due to vibrational relaxation increases with temperature. The same is true for chemical absorption, which, however, peaks at lower frequencies than vibrational relaxation for temperatures up to 4000 K. Some initial overlapping between the two contributions is seen around 6000 and 9000 K, with ionising reactions occurring at greater frequencies than vibrational relaxation at 12 000 K. The cumulative effect of these processes is clearly responsible for the profile seen in figure 9.
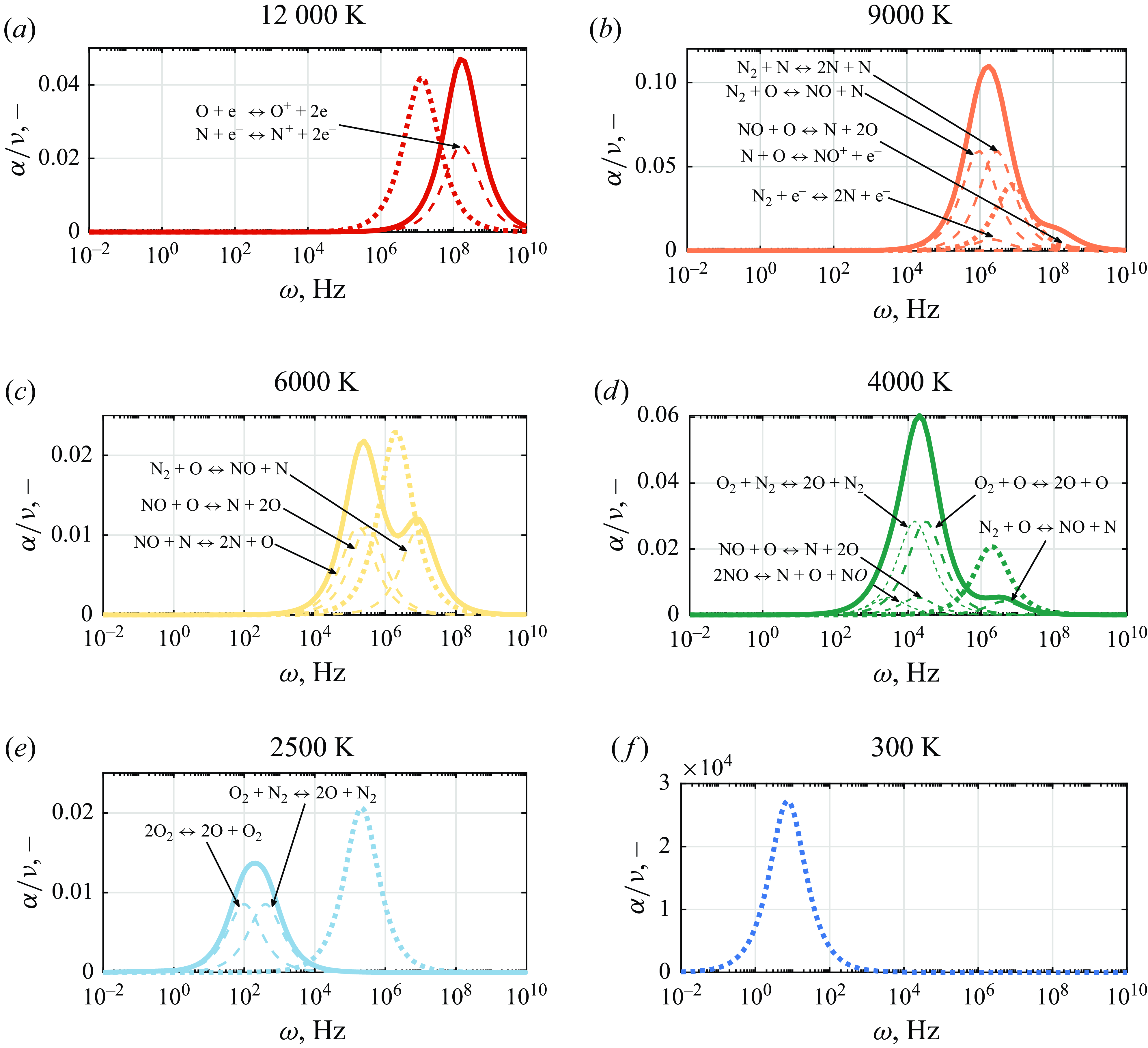
Figure 10. Chemical and vibrational relaxation contributions to normalised attenuation coefficient at different temperatures at 1 atm —, cumulative chemical; - - -, individual reaction; ……, vibrational relaxation.
The influence of equilibrium pressure is particularly significant in hypersonic flows, as it can vary across several orders of magnitude depending on flight conditions or on-ground testing environments. To capture this variability, equilibrium pressure levels ranging from atmospheric levels down to
![]() $10$
Pa are investigated in figure 11. At 300 K, in the absence of finite-rate chemistry, the results at different pressures collapse onto the same curve for the
$10$
Pa are investigated in figure 11. At 300 K, in the absence of finite-rate chemistry, the results at different pressures collapse onto the same curve for the
![]() $\omega /p$
dependency. The frozen speed of sound and its corresponding equilibrium values are independent of pressures given the absence of reactions. However, the finite increase of approximately 0.05 % in speed of sound from frozen to equilibrium, driven by vibrational relaxation, is shifted to lower activation frequencies as pressure decreases. This shift, which is not observable when the frequency is normalised by the pressure at 300 K, occurs because vibrational relaxation is governed by collision frequency, with the characteristic relaxation time – during which molecular vibrations equilibrate with translational modes – being inversely proportional to pressure (Park Reference Park1989). Consequently, at lower pressures, the transition from frozen to equilibrium sound speeds occurs at lower frequencies, reflecting slower energy exchange between vibrational and translational modes due to reduced collision rates.
$\omega /p$
dependency. The frozen speed of sound and its corresponding equilibrium values are independent of pressures given the absence of reactions. However, the finite increase of approximately 0.05 % in speed of sound from frozen to equilibrium, driven by vibrational relaxation, is shifted to lower activation frequencies as pressure decreases. This shift, which is not observable when the frequency is normalised by the pressure at 300 K, occurs because vibrational relaxation is governed by collision frequency, with the characteristic relaxation time – during which molecular vibrations equilibrate with translational modes – being inversely proportional to pressure (Park Reference Park1989). Consequently, at lower pressures, the transition from frozen to equilibrium sound speeds occurs at lower frequencies, reflecting slower energy exchange between vibrational and translational modes due to reduced collision rates.
A separate discussion is required to address the effect of equilibrium pressure on sound-wave propagation through a reactive medium. Figure 11(b) illustrates the sound speed and dimensionless attenuation coefficient at 6000 K. It is evident that normalising the frequency by pressure does not collapse the data onto a single curve. Instead, a much more intricate variation is observed, reflecting the complex interplay of physical and chemical processes. At lower pressures, slower collision dynamics results in longer relaxation time scales, and reaction rates are also significantly reduced at different magnitudes. These effects, combined with the involvement of multiple reaction mechanisms, lead to a nonlinear trend where the peak absorption shifts towards lower
![]() $\omega /p$
values as pressure decreases. This shift occurs because chemical processes, such as dissociation, absorb energy from the acoustic waves, causing the absorption peaks to move to lower frequencies due to slower relaxation at low pressures. However, the magnitude of the absorption peaks increases with pressure around 1 kPa, after which a drop in absorption is observed. The pattern arises from the competing time scales of nitric oxide dissociation and exchange reactions. Furthermore, both the equilibrium and frozen sound speeds exhibit a nonlinear dependence on pressure. This behaviour is influenced by the combined effects of changes in the specific heat ratio and density, which are themselves functions of the thermodynamic state and the chemical composition of the medium. Referring to figure 10, it is possible to infer that the variations in pressure increase the relative distance between the peak frequency due to vibrational relaxation and that of chemical absorption. This results in a more pronounced two-peak variation in speed of sound.
$\omega /p$
values as pressure decreases. This shift occurs because chemical processes, such as dissociation, absorb energy from the acoustic waves, causing the absorption peaks to move to lower frequencies due to slower relaxation at low pressures. However, the magnitude of the absorption peaks increases with pressure around 1 kPa, after which a drop in absorption is observed. The pattern arises from the competing time scales of nitric oxide dissociation and exchange reactions. Furthermore, both the equilibrium and frozen sound speeds exhibit a nonlinear dependence on pressure. This behaviour is influenced by the combined effects of changes in the specific heat ratio and density, which are themselves functions of the thermodynamic state and the chemical composition of the medium. Referring to figure 10, it is possible to infer that the variations in pressure increase the relative distance between the peak frequency due to vibrational relaxation and that of chemical absorption. This results in a more pronounced two-peak variation in speed of sound.
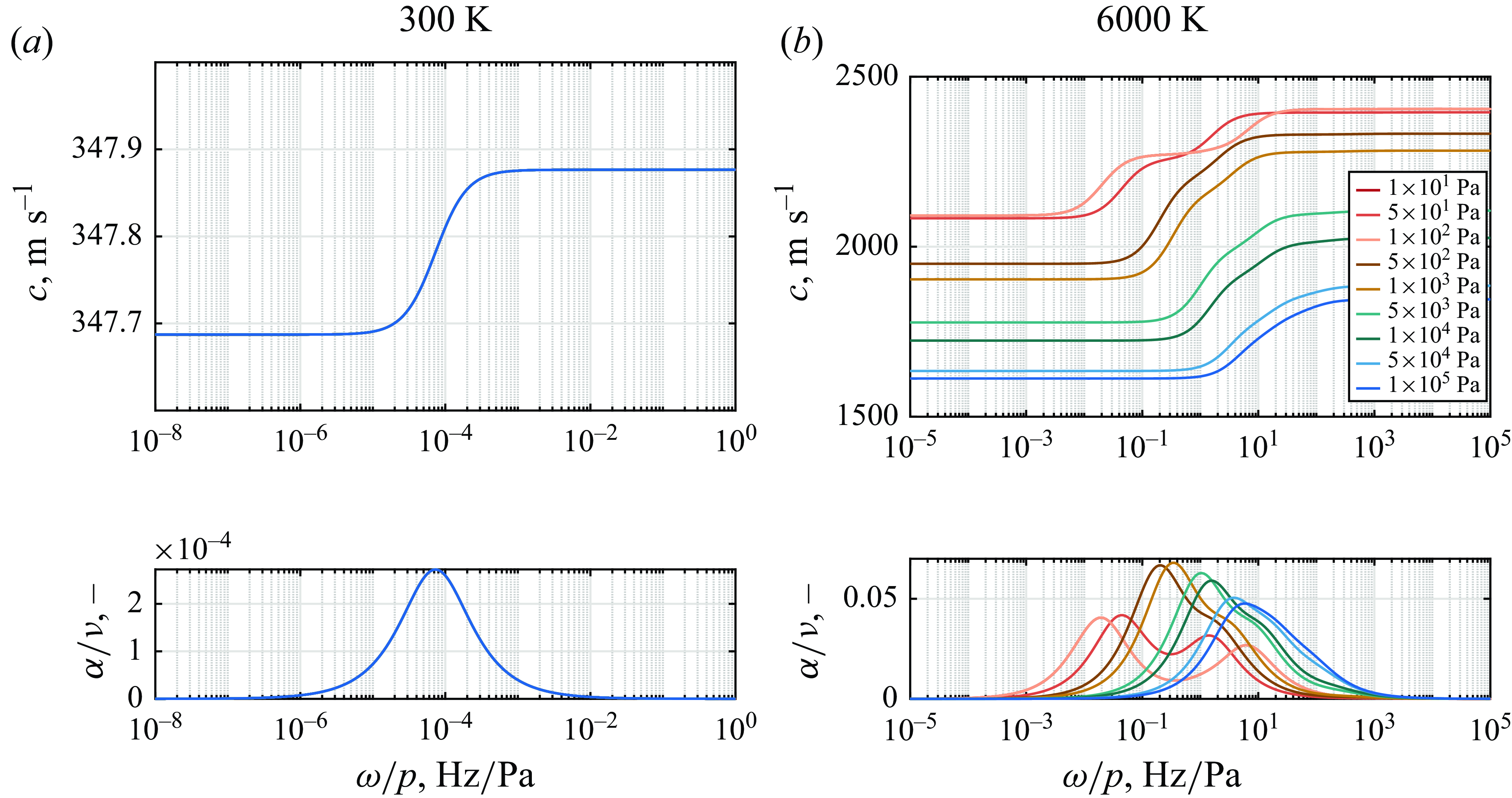
Figure 11. Effect of pressure on speed of sound in air mixture and dimensionless attenuation coefficient as a function of
![]() $\omega /p$
.
$\omega /p$
.
These results unequivocally define the speed of sound in non-equilibrium media, which is of profound significance for high-temperature flows as they not only readily enable the visualisation of non-equilibrium and its transition to the extreme ends of the spectrum, namely the frozen and equilibrium conditions, but they open up to the viable utilisation of the speed of sound as a macroscopic measure of non-equilibrium, provided that the thermodynamic state and composition of the gas are known. Following the same reasoning, the same conclusion can be drawn concerning the absorption coefficient of the speed of sound in figure 4 to be used as a macroscopic measure. Reference plots for the propagation of the speed of sound at a finite frequency are provided in figure 20 for argon and figure 21 for pure nitrogen and oxygen mixtures.
The right eigenvectors
![]() $\boldsymbol{\hat {q}}$
, which represent the perturbations in the state variables, may offer valuable insight into the dynamics of the chemical reactions. By projecting
$\boldsymbol{\hat {q}}$
, which represent the perturbations in the state variables, may offer valuable insight into the dynamics of the chemical reactions. By projecting
![]() $\boldsymbol{\hat {q}}$
onto the active chemical reactions
$\boldsymbol{\hat {q}}$
onto the active chemical reactions
![]() $\hat {R}_s$
and normalising the result by the perturbed velocity term, the amplitude
$\hat {R}_s$
and normalising the result by the perturbed velocity term, the amplitude
![]() $|\hat {R}_s|$
and phase
$|\hat {R}_s|$
and phase
![]() $\langle {\hat {R}}_s$
of the normalised perturbations can be obtained to visualise the activation and relaxation frequencies of the air mixture, as shown in figure 12 for 4000 K at 1 atm.
$\langle {\hat {R}}_s$
of the normalised perturbations can be obtained to visualise the activation and relaxation frequencies of the air mixture, as shown in figure 12 for 4000 K at 1 atm.

Figure 12. Amplitude and phase of normalised perturbations in chemical reactions at 4000 K and 1 atm.
The interplay of oxygen dissociation and nitric oxide exchange reactions at 4000 K leads to the creation of atomic oxygen and molecular nitrogen at lower frequencies associated with the consumption of nitric oxide and molecular oxygen, to then produce nitric oxide and atomic nitrogen at the expense of atomic oxygen and molecular nitrogen in the ultrasonic region. This is noted by the dominating amplitude of the dissociation of molecular oxygen into atomic oxygen by collision with nitrogen molecules and pre-existing atomic oxygen particles. As more atomic oxygen is produced, the dissociation of nitric oxide is observed to increase, leading to the creation of molecular oxygen and atomic nitrogen. Conversely, as the NO exchange reactions are activated, the interactions with molecular nitrogen cause an increase in nitric oxide and atomic nitrogen at higher frequencies. The direction of the driving mechanisms is also visible from the phase angle. The two oxygen dissociation processes are in phase, indicating that they both propagate along the same direction and are synchronised, while this is not the case for the NO exchange reactions. The positive increase in phase angles shows that the reactions are damping the sound wave. The initial negative trend in the exchange reaction involving molecular nitrogen, on the contrary, reveals an initial excitation of the sound wave which then turns into a damping mode. The combination of the reactive mechanisms under different temperatures and frequencies is evidently responsible for the peaks in the speed of sound seen in figure 8. In addition to the definition of the non-equilibrium region, the current model also allows the identification of the specific reactions responsible for such non-equilibrium and the associated composition variations.
The results presented in this section have thus far been concerned with the inviscid model, therefore addressing the effect of vibrational relaxation and chemical reactions typical of shock layers. However, in boundary layers and shear layers, the effect of viscosity should not be disregarded. The viscous model is therefore implemented, with the dissipative effects expected to be dominating at high frequencies (Liebermann Reference Liebermann1949; Herzfeld & Litovitz Reference Herzfeld and Litovitz2013). To ensure that viscous phenomena are correctly captured by the proposed method, the simple case of sound waves propagating in an argon mixture under ambient conditions is investigated. Given the low temperature, no ionisation of argon occurs. Thus, only the effect of viscosity is observed. The numerical results presented in figure 13 for the normalised variation in speed of sound show good agreement with the experimental results obtained by Boyer (Reference Boyer1952) and Greenspan (Reference Greenspan1956), as well as the analytical expression utilised by Huetz-Aubert & Huetz (Reference Huetz-Aubert and Huetz1959). The differences between the numerical and experimental data are particularly relevant at higher values of
![]() $\omega /p$
, as noted by Huetz-Aubert & Huetz (Reference Huetz-Aubert and Huetz1959), given that the continuum assumption limit is being reached. This is in agreement with the collision frequencies calculated using kinetic theory in figure 18, which indicate a limit of approximately
$\omega /p$
, as noted by Huetz-Aubert & Huetz (Reference Huetz-Aubert and Huetz1959), given that the continuum assumption limit is being reached. This is in agreement with the collision frequencies calculated using kinetic theory in figure 18, which indicate a limit of approximately
![]() $2.7 \times 10^4$
$2.7 \times 10^4$
![]() $\rm Hz/Pa$
for the conditions considered.
$\rm Hz/Pa$
for the conditions considered.
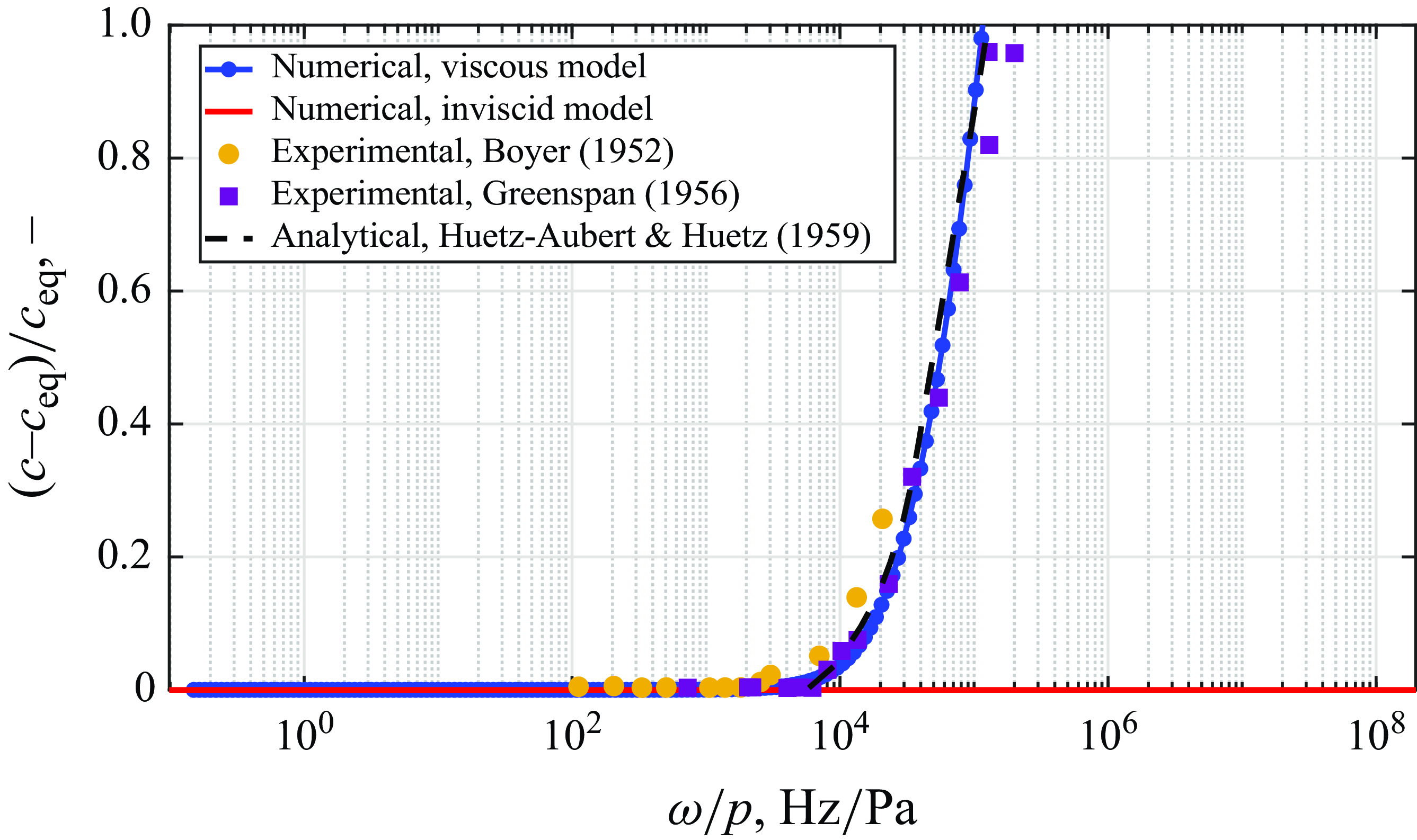
Figure 13. Validation of viscous effects on sound velocity in argon mixture at 300 K and 1 atm.
The thermodynamic state used to generate figure 13 is compared with a higher temperature of 9000 K such that partial ionisation of argon has occurred, as shown in figure 14(a)–(b). At 300 K, the inviscid solution shows no variations in the speed of sound with frequency and associated absorption coefficient of zero. On the contrary, the viscous model captures the finite variation in wave propagation speed, therefore confirming that the only phenomenon responsible for the attenuation is due to the viscous terms. The effect of ionisation is present at 9000 K, as visible at frequencies of the order of
![]() $ 10^2\lt \omega /p \lt 10^3$
$ 10^2\lt \omega /p \lt 10^3$
![]() $\rm Hz/Pa$
. The viscous and inviscid solutions start to diverge at frequencies higher than
$\rm Hz/Pa$
. The viscous and inviscid solutions start to diverge at frequencies higher than
![]() $\omega /p \sim 10^4$
$\omega /p \sim 10^4$
![]() $\rm Hz/Pa$
, where the viscous phenomena prevail. The normalised attenuation coefficient is also seen to rapidly increase until a value of unity is attained.
$\rm Hz/Pa$
, where the viscous phenomena prevail. The normalised attenuation coefficient is also seen to rapidly increase until a value of unity is attained.
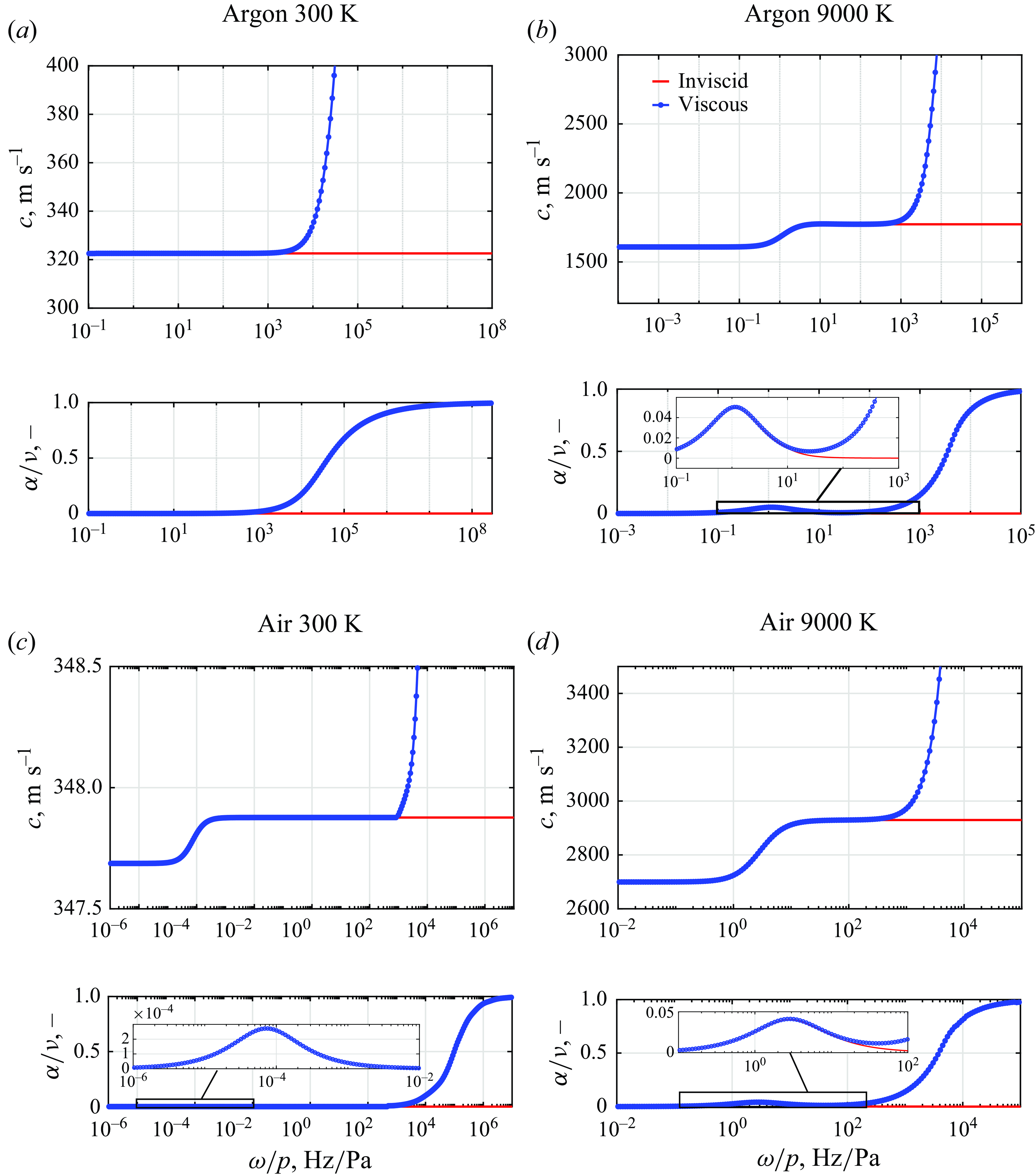
Figure 14. Viscous–diffusive effect on sound propagation as a function of
![]() $\omega /p$
at 1 atm —, inviscid model; -
$\omega /p$
at 1 atm —, inviscid model; -
![]() $\circ$
-
$\circ$
-
![]() $\circ$
-
$\circ$
-
![]() $\circ$
viscous model.
$\circ$
viscous model.
Similar trends are observed in the numerical results for air at 300 K and 9000 K in figures 14(c) and 14(d), respectively. Unlike the argon mixture, the effect of vibrational relaxation is present. This is particularly evident at 300 K, where absorption due to vibrational relaxation peaks at
![]() $\omega /p \approx 10^{-4}$
Hz/Pa. On the contrary, viscous effects only become significant above
$\omega /p \approx 10^{-4}$
Hz/Pa. On the contrary, viscous effects only become significant above
![]() $\omega /p = 1-3\times 10^1$
$\omega /p = 1-3\times 10^1$
![]() $\rm Hz/Pa$
for all considered temperatures. Below this threshold the difference between the viscous and inviscid model is negligible. The insignificant contribution of viscosity at low frequencies was previously inferred by Tsien & Schamberg (Reference Tsien and Schamberg1946) as a justification for employing the adiabatic propagation speed in a non-reactive medium. The frequency range of departure from the inviscid model identified in the present work is in agreement with the discussion presented by Chang & Uhlenbeck (Reference Chang and Uhlenbeck1948), who argues that the viscous effects are appreciable only when
$\rm Hz/Pa$
for all considered temperatures. Below this threshold the difference between the viscous and inviscid model is negligible. The insignificant contribution of viscosity at low frequencies was previously inferred by Tsien & Schamberg (Reference Tsien and Schamberg1946) as a justification for employing the adiabatic propagation speed in a non-reactive medium. The frequency range of departure from the inviscid model identified in the present work is in agreement with the discussion presented by Chang & Uhlenbeck (Reference Chang and Uhlenbeck1948), who argues that the viscous effects are appreciable only when
![]() $(f/p)^2 \sim 10^3$
$(f/p)^2 \sim 10^3$
![]() $\rm Hz/Pa$
based on the elastic spheres model.
$\rm Hz/Pa$
based on the elastic spheres model.
The results show that the diffusive–viscous effects may not be neglected at high frequencies, as the speed of sound continues to increase indefinitely with the square root of
![]() $\omega$
and
$\omega$
and
![]() $\alpha =\nu$
. The numerical results are in agreement with the classical theory published by Herzfeld & Litovitz (Reference Herzfeld and Litovitz2013). The speed of sound is generally observed to vary only in regions where the wave period is comparable to the reaction rate and relaxation times, reflecting non-equilibrium effects. Outside these regions, the speed of sound appears independent of frequency in both the low- and high-frequency limits. However, at high frequencies, this independence holds only in the absence of viscous dissipation. It must be specified that, in the current implementation of the transport properties, the diffusive fluxes due to pressure gradient and due to external force such as the influence of an electric field, as modelled by Hirschfelder et al. (Reference Hirschfelder, Curtiss and Bird1964), are not included. While these would provide a further contribution to the absorption mechanism due to diffusion (Chapman & Livens Reference Chapman and Livens1921), particularly at high temperatures with the increased degree of ionisation, Evans, Bass & Sutherland (Reference Evans, Bass and Sutherland1972) have demonstrated that diffusion losses contribute onlyto 0.3 % of classical theory and that viscosity and heat conduction are the predominant phenomena. A similar conclusion was also reached by Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023) who showed that the role of mass diffusion and thermal diffusion is negligible for multi-component mixtures. The computation of transport properties for highly ionised gases is, however, still an active area of research and would require additional effort for temperatures greater than
$\alpha =\nu$
. The numerical results are in agreement with the classical theory published by Herzfeld & Litovitz (Reference Herzfeld and Litovitz2013). The speed of sound is generally observed to vary only in regions where the wave period is comparable to the reaction rate and relaxation times, reflecting non-equilibrium effects. Outside these regions, the speed of sound appears independent of frequency in both the low- and high-frequency limits. However, at high frequencies, this independence holds only in the absence of viscous dissipation. It must be specified that, in the current implementation of the transport properties, the diffusive fluxes due to pressure gradient and due to external force such as the influence of an electric field, as modelled by Hirschfelder et al. (Reference Hirschfelder, Curtiss and Bird1964), are not included. While these would provide a further contribution to the absorption mechanism due to diffusion (Chapman & Livens Reference Chapman and Livens1921), particularly at high temperatures with the increased degree of ionisation, Evans, Bass & Sutherland (Reference Evans, Bass and Sutherland1972) have demonstrated that diffusion losses contribute onlyto 0.3 % of classical theory and that viscosity and heat conduction are the predominant phenomena. A similar conclusion was also reached by Kustova et al. (Reference Kustova, Mekhonoshina, Bechina, Lagutin and Voroshilova2023) who showed that the role of mass diffusion and thermal diffusion is negligible for multi-component mixtures. The computation of transport properties for highly ionised gases is, however, still an active area of research and would require additional effort for temperatures greater than
![]() $2\times 10^4$
K in air (Istomin & Oblapenko Reference Istomin and Oblapenko2018).
$2\times 10^4$
K in air (Istomin & Oblapenko Reference Istomin and Oblapenko2018).
Moreover, at such high frequencies, further difficulties arise from the validity of the continuum model implemented. In fact, for the frequencies where the viscous–diffusive phenomena prevail, the wavelength of sound approaches the magnitude of the mean free path. The Navier–Stokes equations adopted in the present work are no longer valid, and higher-order corrections to the Enskog solution of the Boltzmann equation are needed Hirschfelder et al. (Reference Hirschfelder, Curtiss and Bird1964). Corrections to the absorption coefficient at such short wavelength have been proposed by Primakoff (Reference Primakoff1942) and Tsien & Schamberg (Reference Tsien and Schamberg1946) and applied by Chang & Uhlenbeck (Reference Chang and Uhlenbeck1948), but are often impractical.
3.3. Thermochemical non-equilibrium regime
Having established the importance of the reaction mechanisms in the definition of the speed of sound and its absorption coefficient at high temperatures, the frequency range of activity for each major class of reactions is shown in figure 15. While the figure does not indicate the reactions’ intensity or their relative importance, it does show that the ultrasonic region is of the highest relevance to determining the chemical non-equilibrium effects along with the type of reactions that should be modelled for air mixtures and argon. The cumulative contributions of the reactions shown result in the sound absorption presented in figure 22, where the only mechanism included is chemical absorption, and illustrate the dissipative pathways of sound waves at different frequencies and temperatures.
Figure 15. Range of activity of chemical reactions in air and argon at 1 bar.
The numerical results discussed so far were computed for gas mixtures in initial states of thermochemical equilibrium. The results unequivocally showed that the high-frequency velocity of a sound wave propagating in a medium under thermodynamic equilibrium is always greater than its low-frequency equilibrium equivalent. However, a different sound absorption mechanism occurs in media with thermodynamic non-equilibrium, which may be physically representative of laser media, glow-discharge plasma and reactive media (Molevich & Oraevsky Reference Molevich and Oraevsky1988). In fact, in the presence of an external energy source, such as radiation (DePlomb Reference DePlomb1971), or external electric and magnetic fields that generate additional energy dissipation channels, the electron temperature may be significantly greater than that of the gas and a non-Maxwellian distribution may be reached by the excited population states (Aleksandrov et al. Reference Aleksandrov, Konchakov, Napartovich and Starostin1989). Experimental measurements in non-equilibrium molecular plasma conducted by Shields (Reference Shields1987), Ruppel & Shields (Reference Ruppel and Shields1990) and Galechyan & Mkrtchyan (Reference Galechyan and Mkrtchyan2002) have shown that in the presence of such thermodynamic non-equilibrium, the phenomenon referred to as Rayleigh instability of sound leads to the amplification of sound waves.
This instability was analysed by Bauer & Bass (Reference Bauer and Bass1973) and Shields (Reference Shields1984) for sound waves propagating in vibrationally excited media with acoustic losses arising from molecular relaxation. Their work identified a gain mechanism in metastable gases with overpopulated vibrational states. Bauer & Bass (Reference Bauer and Bass1973) postulated that excessive energy transfer to vibrational modes necessitates increased de-excitation to the ground state to achieve steady state. The instability manifests when the energy required for translational mode excitation is fully supplied by vibrational relaxation, thereby positively sustaining the non-equilibrium condition.
Although the current methodology does not resolve individual kinetic vibrational states, the two-temperature model may be adapted such that the excited states are characterised by the vibrational temperature
![]() $T_v$
and the ground state by the translational–rotational temperature
$T_v$
and the ground state by the translational–rotational temperature
![]() $T$
. Vibrational excitation is induced by setting
$T$
. Vibrational excitation is induced by setting
![]() $T_v\gt T$
. This framework was adopted by Kogan & Molevich (Reference Kogan and Molevich1986), Molevich & Oraevsky (Reference Molevich and Oraevsky1988), Molevich (Reference Molevich2003) and Makaryan & Molevich (Reference Makaryan and Molevich2006) to yield the dispersion relation in (3.1) for a medium with constant pressure and volume undergoing relaxation with characteristic time
$T_v\gt T$
. This framework was adopted by Kogan & Molevich (Reference Kogan and Molevich1986), Molevich & Oraevsky (Reference Molevich and Oraevsky1988), Molevich (Reference Molevich2003) and Makaryan & Molevich (Reference Makaryan and Molevich2006) to yield the dispersion relation in (3.1) for a medium with constant pressure and volume undergoing relaxation with characteristic time
![]() $\tau _v$
. The complex specific heats at constant pressure
$\tau _v$
. The complex specific heats at constant pressure
![]() $c_p(\omega )$
and volume
$c_p(\omega )$
and volume
![]() $c_v(\omega )$
depend on low-frequency and high-frequency asymptotes – defined respectively by subscript
$c_v(\omega )$
depend on low-frequency and high-frequency asymptotes – defined respectively by subscript
![]() $0$
(
$0$
(
![]() $c_{v_0},c_{p_0}$
) and
$c_{v_0},c_{p_0}$
) and
![]() $\infty$
(
$\infty$
(
![]() $c_{v_\infty },c_{p_\infty }$
) – which are related to the complex specific heat ratio
$c_{v_\infty },c_{p_\infty }$
) – which are related to the complex specific heat ratio
![]() $\gamma (\omega )=\gamma _r(\omega ) +j \gamma _i(\omega )$
. Under thermal equilibrium,
$\gamma (\omega )=\gamma _r(\omega ) +j \gamma _i(\omega )$
. Under thermal equilibrium,
![]() $\gamma _0=\gamma _{{eq}}$
,
$\gamma _0=\gamma _{{eq}}$
,
![]() $c_0=c_{{eq}}$
and
$c_0=c_{{eq}}$
and
![]() $\gamma _{\infty }=\gamma _{{frz}}=\tilde {\gamma }$
,
$\gamma _{\infty }=\gamma _{{frz}}=\tilde {\gamma }$
,
![]() $c_\infty =c_{{frz}}$
, as defined in (2.4)–(2.3)
$c_\infty =c_{{frz}}$
, as defined in (2.4)–(2.3)
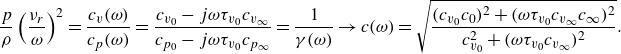 \begin{equation} \frac {p }{\rho } \left ( \frac {\nu _r}{\omega }\right )^2 =\frac {c_{v}(\omega )}{c_{p}(\omega )}=\frac {c_{v_0}-j\omega \tau _{v_0}c_{v_\infty }}{c_{p_0}-j\omega \tau _{v_0}c_{p_\infty }}=\frac {1}{\gamma (\omega )} \rightarrow c(\omega )=\sqrt {\frac {(c_{v_0}c_0)^2+(\omega \tau _{v_0}c_{v_\infty }c_\infty )^2}{c_{v_0}^2+(\omega \tau _{v_0}c_{v_\infty })^2}} .\end{equation}
\begin{equation} \frac {p }{\rho } \left ( \frac {\nu _r}{\omega }\right )^2 =\frac {c_{v}(\omega )}{c_{p}(\omega )}=\frac {c_{v_0}-j\omega \tau _{v_0}c_{v_\infty }}{c_{p_0}-j\omega \tau _{v_0}c_{p_\infty }}=\frac {1}{\gamma (\omega )} \rightarrow c(\omega )=\sqrt {\frac {(c_{v_0}c_0)^2+(\omega \tau _{v_0}c_{v_\infty }c_\infty )^2}{c_{v_0}^2+(\omega \tau _{v_0}c_{v_\infty })^2}} .\end{equation}
This dispersion relation, however, does not account for the effect of finite-rate kinetics, despite experimental studies by Abouseif, Toong & Converti (Reference Abouseif, Toong and Converti1979) demonstrating substantial sound amplification in non-equilibrium exothermic reactive flows. Linearised analytical models incorporated chemical and relaxation effects (Nakoryakov & Borisov Reference Nakoryakov and Borisov1976; Molevich Reference Molevich2003) or isolated chemical processes (Molevich Reference Molevich2004), but were limited to single-step reactions due to mathematical generalisation complexity. The present work expands upon these studies by relaxing the assumption of constant pressure and volume, and by investigating coupled molecular relaxation and chemical kinetics in a multi-component air mixture subjected to the complete set of reactions provided in table 1. For direct comparison with (3.1) in case of pure molecular relaxation, the gas mixture relaxation time is computed as
![]() $\tau _v={\sum _{s=mol} \sigma _s}/{\sum _{s=mol} \sigma _s \lt \tau _s\gt }$
(Gnoffo Reference Gnoffo1989) from Landau–Teller’s model in (2.7).
$\tau _v={\sum _{s=mol} \sigma _s}/{\sum _{s=mol} \sigma _s \lt \tau _s\gt }$
(Gnoffo Reference Gnoffo1989) from Landau–Teller’s model in (2.7).
Figure 16. Dependence of sound speed relation
![]() $c_{0}^2/c_{\infty}^2$
on thermal non-equilibrium degree
$c_{0}^2/c_{\infty}^2$
on thermal non-equilibrium degree
![]() $T_v/T$
for air mixture at 1 atm —, vibrational relaxation; -
$T_v/T$
for air mixture at 1 atm —, vibrational relaxation; -
![]() $\circ$
-
$\circ$
-
![]() $\circ$
-
$\circ$
-
![]() $\circ$
, vibrational relaxation with chemistry.
$\circ$
, vibrational relaxation with chemistry.
Numerical results for the low-to-high-frequency sound speed ratio
![]() $c_0/c_\infty$
obtained using the proposed eigenvalue method are presented in figure 16 over varying degrees of thermal non-equilibrium
$c_0/c_\infty$
obtained using the proposed eigenvalue method are presented in figure 16 over varying degrees of thermal non-equilibrium
![]() $T_v/T$
. The inviscid model is adopted in order for the high-frequency asymptote of the dispersion equation to be finite such that (2.3) can be used. The effect of viscosity along with thermal damping are hereby neglected. The dashed line at
$T_v/T$
. The inviscid model is adopted in order for the high-frequency asymptote of the dispersion equation to be finite such that (2.3) can be used. The effect of viscosity along with thermal damping are hereby neglected. The dashed line at
![]() $(c_0/c_\infty )^2=1$
is used to demarcate the regime of sound amplification
$(c_0/c_\infty )^2=1$
is used to demarcate the regime of sound amplification
![]() $(c_0\gt c_\infty )$
. In the absence of finite-rate chemistry, vibrational relaxation solely governs sound attenuation. In thermal equilibrium, the high-frequency speed of sound propagates with a frozen velocity with respect to both chemical equilibrium and vibration excitation
$(c_0\gt c_\infty )$
. In the absence of finite-rate chemistry, vibrational relaxation solely governs sound attenuation. In thermal equilibrium, the high-frequency speed of sound propagates with a frozen velocity with respect to both chemical equilibrium and vibration excitation
![]() $c_\infty =c_0$
. For low levels of vibrational excitations
$c_\infty =c_0$
. For low levels of vibrational excitations
![]() $(T_v \sim T)$
, values of
$(T_v \sim T)$
, values of
![]() $c_0/c_\infty \approx 0.92$
are obtained for all temperatures considered, showing consistent behaviour with the stable wave propagation in thermodynamic equilibrium. Amplification emerges at critical
$c_0/c_\infty \approx 0.92$
are obtained for all temperatures considered, showing consistent behaviour with the stable wave propagation in thermodynamic equilibrium. Amplification emerges at critical
![]() $T_v/T$
values dependent on translational temperature
$T_v/T$
values dependent on translational temperature
![]() $T$
, aligning with the criterion
$T$
, aligning with the criterion
![]() $(T_v/T)\gt 1+ (c_{v_\infty }-{\partial ln\tau _{v}}/{\partial ln T} )^{-1}$
derived by Kogan & Molevich (Reference Kogan and Molevich1986). This reflects the competing effects between
$(T_v/T)\gt 1+ (c_{v_\infty }-{\partial ln\tau _{v}}/{\partial ln T} )^{-1}$
derived by Kogan & Molevich (Reference Kogan and Molevich1986). This reflects the competing effects between
![]() $c_{v_\infty }(T)$
and the weakening temperature dependence of
$c_{v_\infty }(T)$
and the weakening temperature dependence of
![]() $\tau _v$
where
$\tau _v$
where
![]() $\partial ln \tau _v / \partial ln T\lt 0$
in air. As the vibrational temperature is increased, more energy is supplied to the translational mode directly from the release of vibrational energy (Bauer & Bass Reference Bauer and Bass1973). This causes a positive feedback between the sound perturbation and the non-equilibrium heat source responsible for the overexcited populations that leads to increasing amplification of the wave speed (i.e.
$\partial ln \tau _v / \partial ln T\lt 0$
in air. As the vibrational temperature is increased, more energy is supplied to the translational mode directly from the release of vibrational energy (Bauer & Bass Reference Bauer and Bass1973). This causes a positive feedback between the sound perturbation and the non-equilibrium heat source responsible for the overexcited populations that leads to increasing amplification of the wave speed (i.e.
![]() $c_{\textrm {0}}\gt c_{\mathrm{\infty }}$
) with increasing degrees of thermal non-equilibrium
$c_{\textrm {0}}\gt c_{\mathrm{\infty }}$
) with increasing degrees of thermal non-equilibrium
![]() $T_v/T$
(Dunaevskii et al. Reference Dunaevskii, Zhdanok, Napartovich and Starostin1988). An alternative amplification mechanism for weakly ionised flows was proposed by Aleksandrov et al. (Reference Aleksandrov, Konchakov, Napartovich and Starostin1989) as being the result of friction between hotter electrons and colder neutral particles. In the case of air, this would only become relevant for
$T_v/T$
(Dunaevskii et al. Reference Dunaevskii, Zhdanok, Napartovich and Starostin1988). An alternative amplification mechanism for weakly ionised flows was proposed by Aleksandrov et al. (Reference Aleksandrov, Konchakov, Napartovich and Starostin1989) as being the result of friction between hotter electrons and colder neutral particles. In the case of air, this would only become relevant for
![]() $T \geq 9000 \, K$
given the activation threshold of ionising reactions.
$T \geq 9000 \, K$
given the activation threshold of ionising reactions.
In proximity to the acoustic instability the gas exhibits increased stiffness, with small temperature increments causing large increases in
![]() $c_{0}$
(Molevich Reference Molevich2004). The resonance-like behaviour in figure 16 is caused by a greater heat release from the non-equilibrium degrees of freedom in the wave maxima than minima (Molevich, Klimov & Makaryan Reference Molevich, Klimov and Makaryan2005). Beyond peak instability, long-wavelength propagation ceases (
$c_{0}$
(Molevich Reference Molevich2004). The resonance-like behaviour in figure 16 is caused by a greater heat release from the non-equilibrium degrees of freedom in the wave maxima than minima (Molevich, Klimov & Makaryan Reference Molevich, Klimov and Makaryan2005). Beyond peak instability, long-wavelength propagation ceases (
![]() $ c_0 \rightarrow 0$
), leading to aperiodic perturbations as density variations do not generate any pressure variations. Similarly to the thermodynamic non-equilibrium ratio for first amplification, the critical
$ c_0 \rightarrow 0$
), leading to aperiodic perturbations as density variations do not generate any pressure variations. Similarly to the thermodynamic non-equilibrium ratio for first amplification, the critical
![]() $ T_v/T$
values for
$ T_v/T$
values for
![]() $c_0\rightarrow \infty$
vary nonlinearly with
$c_0\rightarrow \infty$
vary nonlinearly with
![]() $ T$
. The critical value observed is
$ T$
. The critical value observed is
![]() $ T_v/T \approx 2.05\!-\!2.10$
for
$ T_v/T \approx 2.05\!-\!2.10$
for
![]() $ T = 2500, 6000 \, \text{K}$
, but shifts to
$ T = 2500, 6000 \, \text{K}$
, but shifts to
![]() $ T_v/T \approx 2.75$
at
$ T_v/T \approx 2.75$
at
![]() $ T = 4000 \, \text{K}$
.
$ T = 4000 \, \text{K}$
.
Incorporating chemical reactions amplifies temperature dependence. At low levels of vibrational excitation
![]() $ T_v \sim T$
,
$ T_v \sim T$
,
![]() $ c_0$
decreases, reducing
$ c_0$
decreases, reducing
![]() $ (c_0/c_\infty )^2$
. For
$ (c_0/c_\infty )^2$
. For
![]() $ T = 2500, 4000 \, \text{K}$
, where O
$ T = 2500, 4000 \, \text{K}$
, where O
![]() $_2$
dissociation and NO formation dominate, chemical processes delay amplification onset to higher
$_2$
dissociation and NO formation dominate, chemical processes delay amplification onset to higher
![]() $ T_v/T$
. At
$ T_v/T$
. At
![]() $ T = 6000 \, \text{K}$
, where the dissociation of N
$ T = 6000 \, \text{K}$
, where the dissociation of N
![]() $_2$
prevails, instability occurs at lower
$_2$
prevails, instability occurs at lower
![]() $ T_v/T$
but exhibits accelerated growth. The interplay of chemistry and relaxation is further examined in figure 17 for
$ T_v/T$
but exhibits accelerated growth. The interplay of chemistry and relaxation is further examined in figure 17 for
![]() $ T_v/T = 2$
and
$ T_v/T = 2$
and
![]() $ T = 4000 \, \text{K}$
. Both processes amplify low-frequency sound speeds relative to high frequencies, with relaxation contributing
$ T = 4000 \, \text{K}$
. Both processes amplify low-frequency sound speeds relative to high frequencies, with relaxation contributing
![]() $\sim$
80 % of the total effect. The negative attenuation coefficient
$\sim$
80 % of the total effect. The negative attenuation coefficient
![]() $ \alpha /\nu$
confirms the amplification of the sound waves caused both by molecular relaxation and chemical reactions. Equation (3.1) accurately describes single-relaxation processes due to vibrational excitation, given the agreement with the numerical results for molecular relaxation. While no analytical model was presented in this work for coupled chemistry–relaxation systems, their effects may be combined in parallel as independent contributions (Landau & Lifshitz Reference Landau and Lifshitz2013).
$ \alpha /\nu$
confirms the amplification of the sound waves caused both by molecular relaxation and chemical reactions. Equation (3.1) accurately describes single-relaxation processes due to vibrational excitation, given the agreement with the numerical results for molecular relaxation. While no analytical model was presented in this work for coupled chemistry–relaxation systems, their effects may be combined in parallel as independent contributions (Landau & Lifshitz Reference Landau and Lifshitz2013).
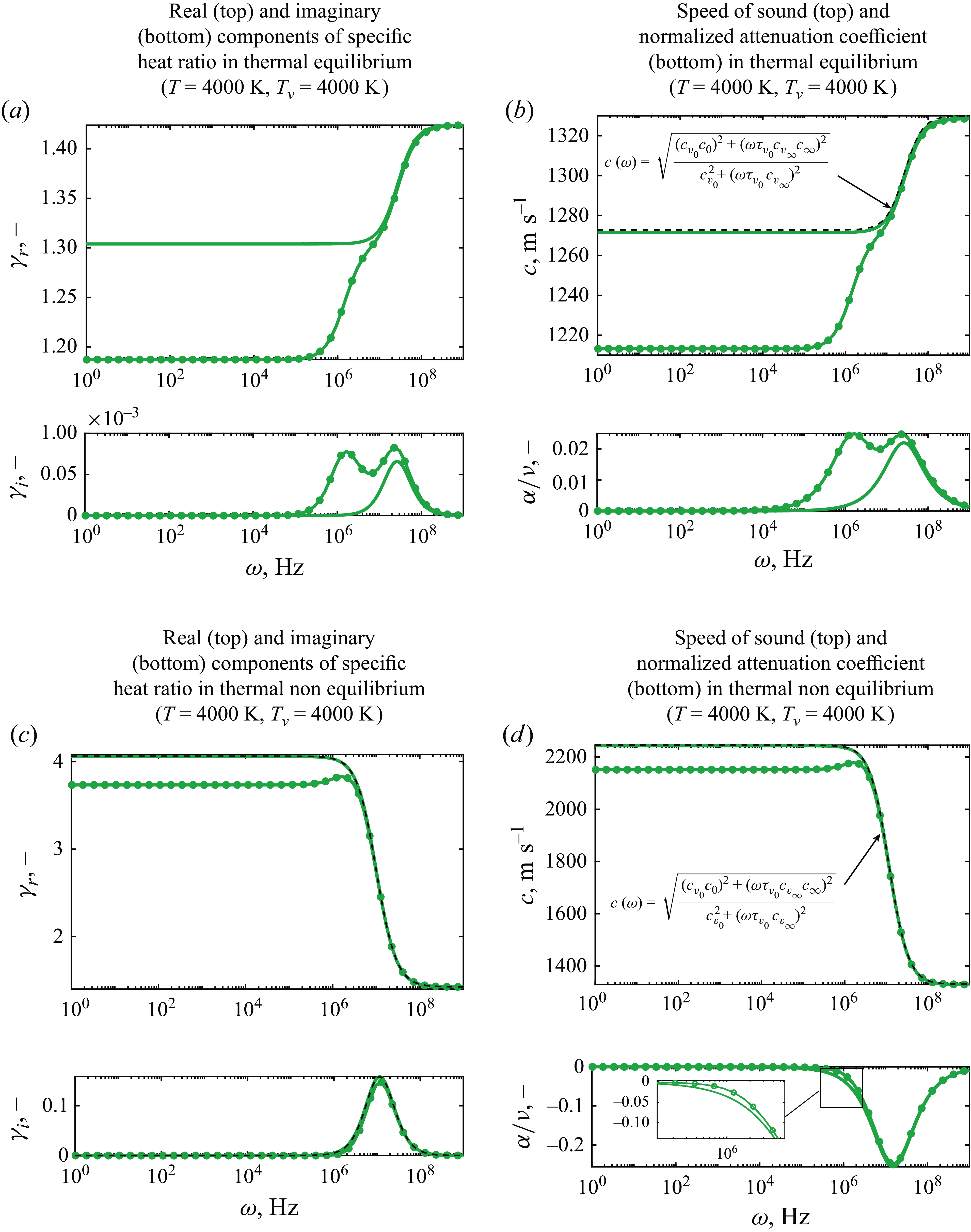
Figure 17. Sound properties in inviscid thermodynamic non-equilibrium in air at 1 atm and varying translational temperatures
![]() $T$
. —, vibrational relaxation; -
$T$
. —, vibrational relaxation; -
![]() $\circ$
-
$\circ$
-
![]() $\circ$
-
$\circ$
-
![]() $\circ$
, vibrational relaxation with chemistry - - -, analytical expression for vibrational relaxation.
$\circ$
, vibrational relaxation with chemistry - - -, analytical expression for vibrational relaxation.
The real component of the specific heat ratio
![]() $\gamma (\omega )$
under thermal equilibrium in figure 17 exhibits a transition from a low-frequency asymptote (
$\gamma (\omega )$
under thermal equilibrium in figure 17 exhibits a transition from a low-frequency asymptote (
![]() $\gamma _r (\omega \rightarrow 0)\approx 1.2$
), where vibrational modes are fully relaxed and contribute to the specific heat, to a high-frequency asymptote (
$\gamma _r (\omega \rightarrow 0)\approx 1.2$
), where vibrational modes are fully relaxed and contribute to the specific heat, to a high-frequency asymptote (
![]() $\gamma _r(\omega \rightarrow \infty ) \approx 1.4$
), where vibrational modes freeze out and only translational–rotational contributions remain. When finite-rate chemistry is neglected, dissociation and recombination processes do not contribute to internal energy storage at low frequencies, resulting in an intermediate
$\gamma _r(\omega \rightarrow \infty ) \approx 1.4$
), where vibrational modes freeze out and only translational–rotational contributions remain. When finite-rate chemistry is neglected, dissociation and recombination processes do not contribute to internal energy storage at low frequencies, resulting in an intermediate
![]() $\gamma _r (\omega \rightarrow 0)\approx 1.3$
. The imaginary component
$\gamma _r (\omega \rightarrow 0)\approx 1.3$
. The imaginary component
![]() $\gamma _i (\omega )$
peaks at the characteristic vibrational relaxation frequency
$\gamma _i (\omega )$
peaks at the characteristic vibrational relaxation frequency
![]() ${1}/{\tau _{v_0}}= {1}/{4.88\times 10^{-8}}=2.05\times 10^7\,\rm Hz$
, corresponding to the frequency of maximum energy dissipation via vibrational relaxation. Maximum acoustic attenuation occurs at this frequency. Beyond this peak, attenuation diminishes as vibrational modes do not keep up with the acoustic oscillation. A second peak is clearly visible due to finite-rate kinetics occurring at a separate frequency characterised by the prevailing chemical time scales. These trends are mirrored in the frequency-dependent speed of sound
${1}/{\tau _{v_0}}= {1}/{4.88\times 10^{-8}}=2.05\times 10^7\,\rm Hz$
, corresponding to the frequency of maximum energy dissipation via vibrational relaxation. Maximum acoustic attenuation occurs at this frequency. Beyond this peak, attenuation diminishes as vibrational modes do not keep up with the acoustic oscillation. A second peak is clearly visible due to finite-rate kinetics occurring at a separate frequency characterised by the prevailing chemical time scales. These trends are mirrored in the frequency-dependent speed of sound
![]() $c(\omega )\propto \sqrt {\gamma (\omega )}$
.
$c(\omega )\propto \sqrt {\gamma (\omega )}$
.
When the vibrational modes are overpopulated, the low-frequency specific heat ratio rises significantly (
![]() $(\gamma _r (\omega \rightarrow 0) \approx 4)$
as more internal energy is stored in vibrational states, while the high-frequency value remains unaffected. The relaxation peak in
$(\gamma _r (\omega \rightarrow 0) \approx 4)$
as more internal energy is stored in vibrational states, while the high-frequency value remains unaffected. The relaxation peak in
![]() $\gamma _i(\omega )$
broadens and shifts compared with the equilibrium case, while finite-rate kinetic effects superimpose with vibrational relaxation as their characteristic frequencies are brought closer. Notably, the low-frequency case exceeds its high-frequency counterpart
$\gamma _i(\omega )$
broadens and shifts compared with the equilibrium case, while finite-rate kinetic effects superimpose with vibrational relaxation as their characteristic frequencies are brought closer. Notably, the low-frequency case exceeds its high-frequency counterpart
![]() $\gamma _r(\omega \rightarrow 0)\gt \gamma _r(\omega \rightarrow \infty )$
, contrasting with the equilibrium behaviour.
$\gamma _r(\omega \rightarrow 0)\gt \gamma _r(\omega \rightarrow \infty )$
, contrasting with the equilibrium behaviour.
Whilst of great scientific interest, the numerical model and results presented in this work yield a relevant significance for several engineering applications. Sound dispersion, and the associated variation in frozen and equilibrium speeds, in non-equilibrium gases may alter the aerodynamic drag and lift coefficients. Vincenti (Reference Vincenti1959) and Clarke & McChesney (Reference Clarke and McChesney1976) have demonstrated that the drag force in a thermochemical non-equilibrium medium lies within the range defined by the wave drag in non-dissipative gases at the frozen and equilibrium Mach numbers, respectively.
Moreover, the acoustic absorption mechanisms investigated in these sections are of interest for high-speed facilities, particularly at Mach numbers greater than 2.5 where acoustic disturbances are likely to dominate the disturbance environment (Laufer Reference Laufer1961). The very same absorption phenomenon presented in this work, as a result of vibrational excitation and relaxation, has been experimentally shown by Fujii & Hornung (Reference Fujii and Hornung2001, Reference Fujii and Hornung2003), Leyva et al. (Reference Leyva, Laurence, Beierholm, Hornung, Wagnild and Candler2009) and Jewell et al. (Reference Jewell, Wagnild, Leyva, Candler and Shepherd2013) to delay laminar to turbulent transition. This was attributed to the damping of the second Mack mode measured by Hornung et al. (Reference Hornung, Adam, Germain, Fujii and Rasheed2002), an inviscid mechanism caused primarily by acoustic wave disturbances trapped within the boundary layer at hypervelocities (Leyva et al. Reference Leyva, Laurence, Beierholm, Hornung, Wagnild and Candler2009). The phenomenon is particularly important for blunt geometries exposed to high temperatures, where significant thermochemical processes may alter the flow. The computational study by Elliott et al. (Reference Elliott, Greendyke, Jewell and Komives2019) showed the importance of being able to model these mechanisms, demonstrating that a reduction in disturbance amplitude could be attained within a boundary layer by increasing the concentration of
![]() $\mathrm{CO}_2$
. The first experimental measurements on the influence of vibrational non-equilibrium on acoustic disturbances with different helium and carbon dioxide compositions have recently been obtained by Gillespie & Laurence (Reference Gillespie and Laurence2024), showing decreasing trends for increased amounts of carbon dioxide. The presence of negative attenuation modelled in this work would further contribute to lowering the critical Reynolds number on flow transition (Molevich Reference Molevich1999), thereby allowing for enhanced boundary-layer stability control.
$\mathrm{CO}_2$
. The first experimental measurements on the influence of vibrational non-equilibrium on acoustic disturbances with different helium and carbon dioxide compositions have recently been obtained by Gillespie & Laurence (Reference Gillespie and Laurence2024), showing decreasing trends for increased amounts of carbon dioxide. The presence of negative attenuation modelled in this work would further contribute to lowering the critical Reynolds number on flow transition (Molevich Reference Molevich1999), thereby allowing for enhanced boundary-layer stability control.
The effect of negative attenuation coefficient has also been found to be significant by Makaryan & Molevich (Reference Makaryan and Molevich2006) for predicting the structure of shock waves. Under nominal conditions with a positive attenuation, the shock results in a compression from the frozen to equilibrium states. However, in the case of negative attenuation for a thermally non-equilibrium gas, the fast compression in the frozen state is followed by a gradual expansion to equilibrium. This means that a greater degree of amplification leads to a more diffusive shock wave, subject to expansion (Makaryan & Molevich Reference Makaryan and Molevich2006). In addition, sound-wave amplification can prove insightful in assessing weak shock wave instabilities. As discussed by Landau & Lifshitz (Reference Landau and Lifshitz2013), shock waves may become unstable when the speed of sound behind the shock front exceeds the velocity of the shock wave relative to the gas behind it. While in an equilibrium medium the weak shock wave has a diffused front, Makaryan & Molevich (Reference Makaryan and Molevich2006) have shown that negative attenuation may lead to the destabilisation of weak shock waves, leading to its disintegration into a sequence of steady-state pulses. Other types of acoustic shock instabilities are well documented in the literature, such as the D’yakovKontorovich instability, which leads to the generation of entropy and rotational perturbations downstream of the shock, along with the emission of constant-amplitude sonic waves (Huete & Vera Reference Huete and Vera2019). These phenomena could be further understood through the study of sound absorption. This is the case for the theoretical study by Molevich (Reference Molevich2001), which suggests that the interaction between vortex and temperature waves in an acoustically active gas medium grows due to energy transfer from unstable acoustic modes. While this effect is limited by the shock discontinuity in a dissipative medium, it is found to increase sharply in the presence of negative attenuation, with no threshold in the spectral region of scattering. It is therefore clear that the study of sound propagation, particularly in reactive thermochemical non-equilibrium media, has significant implications for the fields of gas dynamics and hypersonics.
4. Conclusion
This paper formulates a generalised eigenvalue problem based on the governing equations of a reactive, viscous, diffusive and conductive one-dimensional flow, whose solution defines the structure of sound waves. The adoption of Park’s two-temperature model (Park Reference Park1993) with 11 species for air and associated chemical kinetics provide insight into the space and time evolution of flow mixtures representative of hypersonic conditions. The three major conclusions drawn from this paper are summarised as follows:
-
(i) Sound absorption significantly increases in the presence of chemical reactions and vibrational relaxation. Classical absorption theory is insufficient to characterise the ultrasonic regime in high-temperature high-enthalpy flows.
-
(ii) It is well established that the propagation of sound waves is a dispersive phenomenon dependent on the frequency and intensity of the specific perturbation mechanism. The proposed methodology advances a unified framework integrating thermochemical non-equilibrium mechanisms representative of high-speed partially ionised and dissociated plasma flows – encompassing viscous–diffusive transport, vibrational energy relaxation and finite-rate chemical kinetics. In the absence of viscosity, the model predicts that the speed of sound is in equilibrium in the low-frequency limit and frozen conditions at high frequencies. The intermediate speed of sound in non-equilibrium conditions in the ultrasonic regime can be defined provided the thermodynamic state of the gas, its composition and the relaxation processes involved. When viscous effects are considered, the speed of sound exhibits a frequency-squared dependence in its high-frequency limit, aligning with classical theory. Building on the extensive literature on negative sound attenuation, the model captures the coupled effects of molecular excitation and chemical reactions in a thermodynamically non-equilibrium medium, demonstrating its ability to reproduce the gain mechanism responsible for sound-wave amplification using detailed chemical kinetics for a multi-component gas mixture.
-
(iii) The utilisation of acoustic properties – namely the sound speed and sound-wave absorption – as an experimental diagnostic technique is advocated to measure the degree of non-equilibrium in a plasma flow and its local reactive properties. This would, however, require reliable reaction rates for the reaction sets considered and accurate knowledge of the thermodynamic state and composition of the gas.

Figure 18. Collision frequency normalised by pressure for varying equilibrium pressure and temperature conditions.
The computational results presented in air, nitrogen, oxygen and argon under thermochemical non-equilibrium conditions provide relevant references to experimentally measure local acoustic flow properties in both impulsive shock tubes and on-ground plasma facilities.
The study of sound propagation in high-speed flows has both fundamental scientific significance and substantial engineering applications, particularly for high-speed flows. Sound absorption mechanisms may significantly impact the aerodynamic performance of hypersonic and re-entry vehicles through multiple processes, namely viscous–diffusive absorption, molecular relaxation and chemical absorption. These mechanisms have also been found to reduce the critical Reynolds number associated with laminar–turbulent transition, which subsequently affects vehicle heat transfer rates and enables enhanced flow control by attenuation of acoustic disturbances. Furthermore, sound absorption processes influence shock waves’ structure and their stability. The presence of thermochemical non-equilibrium in high-temperature flows introduces negative attenuation effects, revealing promising avenues for future research into mostly unexplored phenomena.
Acknowledgements.
The authors acknowledge the Oxford-Ashton Memorial Graduate Scholarship.
Declaration of interests.
The authors report no conflict of interest.
Appendix A.
A.1 Continuum kinetic theory
The reactive Euler and Navier–Stokes equations adopted in the present work are valid for a continuum gas. The continuum method requires that the wavelength of sound does not approach the mean free path, or that the sound-wave frequency
![]() $f$
is much greater than the collision frequency
$f$
is much greater than the collision frequency
![]() $f_c$
of the flow particles (i.e.
$f_c$
of the flow particles (i.e.
![]() $f_c \lt \lt f$
). The collision frequency
$f_c \lt \lt f$
). The collision frequency
![]() $f_c$
is computed using (A1) based on the definition given by Anderson (Reference Anderson1989), where
$f_c$
is computed using (A1) based on the definition given by Anderson (Reference Anderson1989), where
![]() $n$
is the gas number density,
$n$
is the gas number density,
![]() $d$
is the particle diameter,
$d$
is the particle diameter,
![]() $v_c$
is the average thermal speed and
$v_c$
is the average thermal speed and
![]() $k_b$
is the Boltzmann constant
$k_b$
is the Boltzmann constant
Table 1. Reaction rate coefficients for air from Park (Reference Park1993).
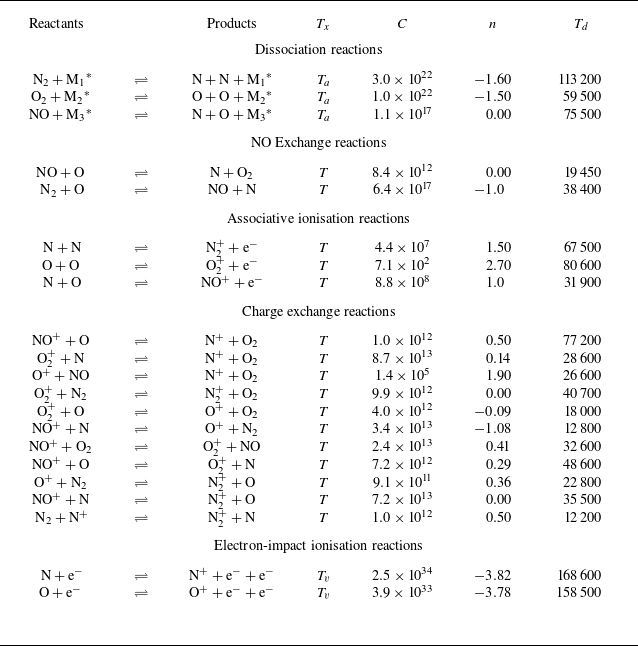
![]() $^*$
Third-body efficiencies are provided in Table 2
$^*$
Third-body efficiencies are provided in Table 2
For the air, oxygen, nitrogen and argon mixtures, the hard-sphere model used by Park (Reference Park1993) is implemented to determine the collision cross-sectional area. The resulting collision frequency profiles normalised by the pressure
![]() $f_c/p$
are plotted in figure 18. It is noted that the effect of different pressure conditions collapses onto the same curve in the absence of chemical reactions. The onset of dissociation and ionisation results into varying profiles due to the equilibrium composition changing the mass
$f_c/p$
are plotted in figure 18. It is noted that the effect of different pressure conditions collapses onto the same curve in the absence of chemical reactions. The onset of dissociation and ionisation results into varying profiles due to the equilibrium composition changing the mass
![]() $m$
of the mixture.
$m$
of the mixture.
A.2 Chemical equilibrium composition
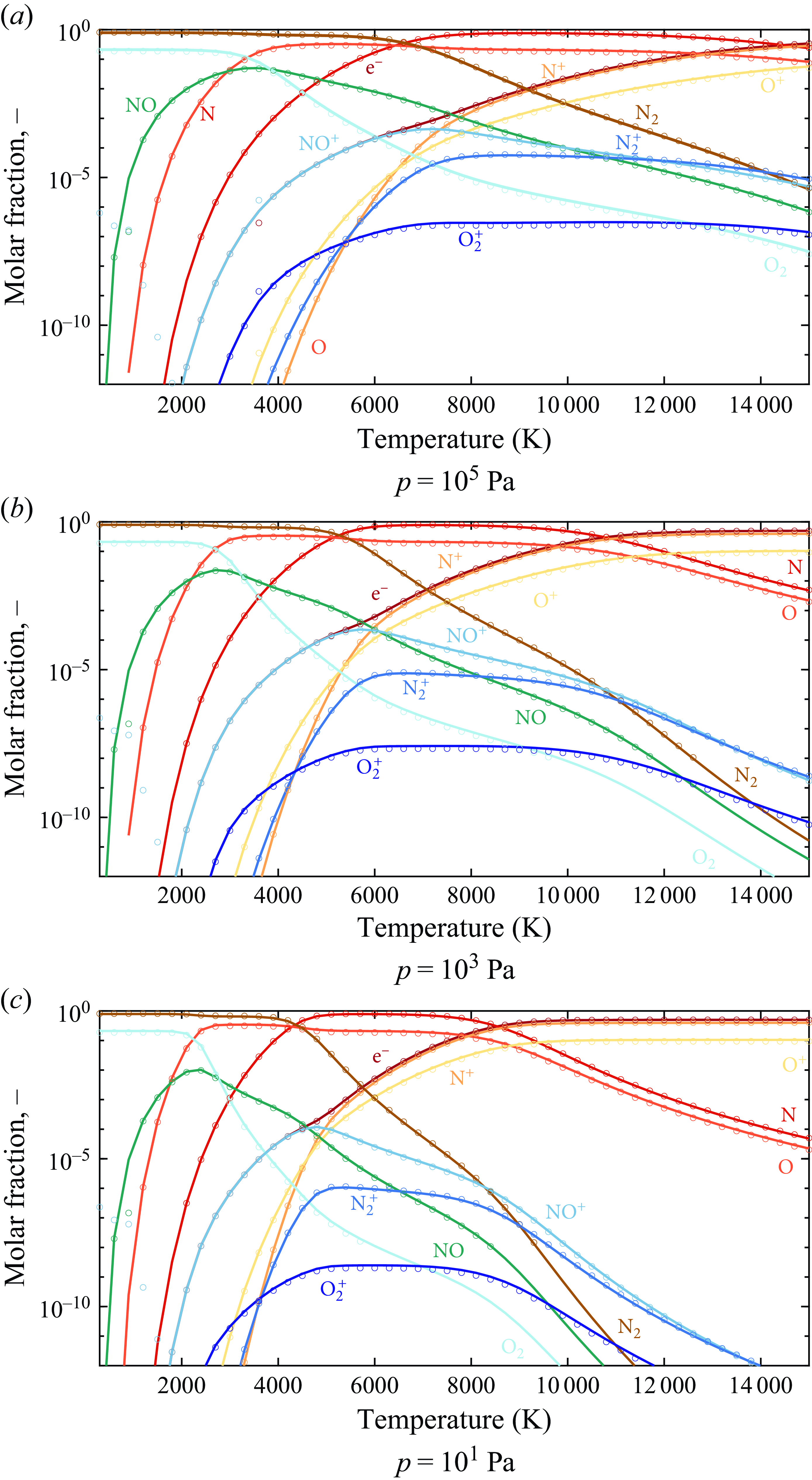
Figure 19. Equilibrium composition in air mixture for different temperatures and pressures —, OCEAN;
![]() $\circ$
$\circ$
![]() $\circ$
$\circ$
![]() $\circ$
CEA.
$\circ$
CEA.
A.3 Chemical reactions
The forward reaction rate coefficients are calculated according to (A2), where the values for the controlling temperature
![]() $T_x$
, pre-exponential power factor
$T_x$
, pre-exponential power factor
![]() $C$
and exponent
$C$
and exponent
![]() $n$
are provided in table 1 for air (Park Reference Park1993). The backwards reaction rates are computed using the equilibrium constant which is derived from the minimisation of Gibbs free energy
$n$
are provided in table 1 for air (Park Reference Park1993). The backwards reaction rates are computed using the equilibrium constant which is derived from the minimisation of Gibbs free energy
Table 2. Third-body
![]() $M$
efficiencies calculated from Park (Reference Park1993).
$M$
efficiencies calculated from Park (Reference Park1993).
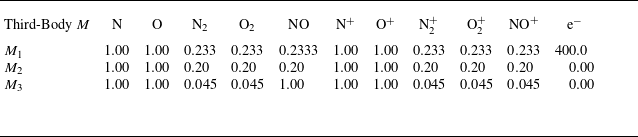
The following ionisation reaction is modelled for pure argon according to Petschek & Byron (Reference Petschek and Byron1957) and Nelson, Park & Whiting (Reference Nelson, Park and Whiting1991), where the reaction rate is taken from Ahtye (Reference Ahtye1968) with an excitation energy of 134 000 K
Further considerations on global ionisation rates and collisional radiative models for argon are discussed by Annaloro et al. (Reference Annaloro, Morel, Bultel and Omaly2012) and Han et al. (Reference Han, Wu, Chen, Qi, Wang, Li, Zhang and Cao2022).
A.4 Energy relaxation
To model translational-vibrational relaxation times, (A4) is implemented based on the approach by Millikan & White (Reference Millikan and White1963)
where
![]() $A_{ij}$
and
$A_{ij}$
and
![]() $b_{ij}$
are given for each interacting pair
$b_{ij}$
are given for each interacting pair
![]() $ij$
as
$ij$
as
with
![]() $\upsilon$
representing the reduced molecular mass between the two species of interest and
$\upsilon$
representing the reduced molecular mass between the two species of interest and
![]() $\theta _i$
the characteristic temperature of the dissociating species. The values used for the latter have been computed by Clarke et al. (Reference Clarke, Glenn, Varley, Luca and McGilvray2024b
) using harmonic vibrational frequencies as provided in table 3. Further detail on the relaxation times can be found in Clarke et al. (Reference Clarke, Glenn, Varley, Luca and McGilvray2024a
). For temperatures above 8000 K in air, Park (Reference Park1985) correction is used as shown in (A6) where
$\theta _i$
the characteristic temperature of the dissociating species. The values used for the latter have been computed by Clarke et al. (Reference Clarke, Glenn, Varley, Luca and McGilvray2024b
) using harmonic vibrational frequencies as provided in table 3. Further detail on the relaxation times can be found in Clarke et al. (Reference Clarke, Glenn, Varley, Luca and McGilvray2024a
). For temperatures above 8000 K in air, Park (Reference Park1985) correction is used as shown in (A6) where
![]() $\bar {c}_s$
is the thermal speed,
$\bar {c}_s$
is the thermal speed,
![]() $n_s$
the number density and
$n_s$
the number density and
![]() $\sigma _v$
the effective cross-section for vibrational relaxation. The form of
$\sigma _v$
the effective cross-section for vibrational relaxation. The form of
![]() $\sigma _v$
is also given in (A6) according to Park (Reference Park1993)
$\sigma _v$
is also given in (A6) according to Park (Reference Park1993)
The electron–neutral cross-sections from Gnoffo (Reference Gnoffo1989) are utilised in conjunction with the Appleton & Bray (Reference Appleton and Bray1964) correlation to estimate the relaxation time between the translational and electronic energy modes. The utilisation of this relaxation model in conjunction with Park’s correction was deemed suitable by Kim, Kang & Park (Reference Kim, Kang and Park2020) for the range of temperatures investigated in this work.
Table 3. Characteristic temperatures (K) of molecular species for the Millikan–White approximations (Clarke et al. Reference Clarke, Glenn, Varley, Luca and McGilvray2024b ).

A.5 Quadratic eigenvalue problem
The quadratic eigenvalue problem in (2.9) takes the form of
![]() $(\boldsymbol{{D}} \nu ^2 + \boldsymbol{{B}} \nu + \boldsymbol{{A}}(\omega )) \boldsymbol{{\hat {q}}}=0$
. The exact solution to this problem can be found by linearisation as shown below
$(\boldsymbol{{D}} \nu ^2 + \boldsymbol{{B}} \nu + \boldsymbol{{A}}(\omega )) \boldsymbol{{\hat {q}}}=0$
. The exact solution to this problem can be found by linearisation as shown below
The exact solution may be obtained via linearisation as in (A7). However, when the viscous–diffusive terms are much smaller than the reactive and advective contributions, the solution may be determined using a perturbation analysis from the zeroth-order inviscid solution. The quadratic term in Equation 2.1) is expressed as a small disturbance
![]() $\epsilon$
$\epsilon$
Both the eigenvalues and eigenvectors are expanded in series of
![]() $\epsilon$
for small values of the perturbations. The apex
$\epsilon$
for small values of the perturbations. The apex
![]() $l$
refers to the column of the eigenvector and associated eigenvalue whereas the indices indicate the order of the expansion. The subscript
$l$
refers to the column of the eigenvector and associated eigenvalue whereas the indices indicate the order of the expansion. The subscript
![]() $j$
refers to the row element
$j$
refers to the row element
By substitution of the expanded eigenvalues and eigenvectors into the governing equations, the zeroth-order solution
![]() $\epsilon ^0$
of (A11) is readily found analogously to the inviscid eigenvalue problem. The first-order
$\epsilon ^0$
of (A11) is readily found analogously to the inviscid eigenvalue problem. The first-order
![]() $\epsilon ^1$
approximation is similarly given in (A12)
$\epsilon ^1$
approximation is similarly given in (A12)
The solution to (A12) is found by mapping the first-order eigenvectors
![]() $\hat {q}^{l,1}$
as a linear combination of zeroth-order terms with coefficients
$\hat {q}^{l,1}$
as a linear combination of zeroth-order terms with coefficients
![]() $\alpha _m^l$
(i.e.
$\alpha _m^l$
(i.e.
![]() $ \hat {q}_j^{l,1}=\alpha _m^{l,1} \hat {q}_j^{m,0}$
). The definition of the zeroth-order eigenvalue is employed, for which
$ \hat {q}_j^{l,1}=\alpha _m^{l,1} \hat {q}_j^{m,0}$
). The definition of the zeroth-order eigenvalue is employed, for which
![]() $ ( \nu ^{l,0} B_{ij} + C_{ij} ) \hat {q}_j^{l,0}=0$
, such that when
$ ( \nu ^{l,0} B_{ij} + C_{ij} ) \hat {q}_j^{l,0}=0$
, such that when
![]() $m=l$
column
$m=l$
column
![]() $h$
in the
$h$
in the
![]() $t$
matrix is overwritten to yield a system of linear equations
$t$
matrix is overwritten to yield a system of linear equations
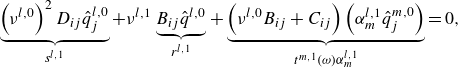 \begin{equation} \underbrace {\left(\nu ^{l,0}\right)^2 D_{ij} \hat {q}_j^{l,0}}_{s^{l,1}} + \nu ^{l,1} \underbrace {B_{ij} \hat {q}^{l,0}}_{r^{l,1}} +\underbrace {\left(\nu ^{l,0} B_{ij}+C_{ij}\right) {\left(\alpha _m^{l,1} \hat {q}_j^{m,0}\right)}}_{t^{m,1}(\omega ) \alpha _m^{l,1}}=0, \end{equation}
\begin{equation} \underbrace {\left(\nu ^{l,0}\right)^2 D_{ij} \hat {q}_j^{l,0}}_{s^{l,1}} + \nu ^{l,1} \underbrace {B_{ij} \hat {q}^{l,0}}_{r^{l,1}} +\underbrace {\left(\nu ^{l,0} B_{ij}+C_{ij}\right) {\left(\alpha _m^{l,1} \hat {q}_j^{m,0}\right)}}_{t^{m,1}(\omega ) \alpha _m^{l,1}}=0, \end{equation}
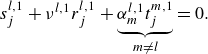 \begin{equation} s_j^{l,1}+\nu ^{l,1} r_j^{l,1} + \underbrace {\alpha _m^{l,1} t_j^{m,1}}_{m \neq l}=0 .\end{equation}
\begin{equation} s_j^{l,1}+\nu ^{l,1} r_j^{l,1} + \underbrace {\alpha _m^{l,1} t_j^{m,1}}_{m \neq l}=0 .\end{equation}
The second-order expansion term
![]() $\epsilon ^2$
is found in a similar manner as shown below, for a mapping of the second-order eigenvectors given by
$\epsilon ^2$
is found in a similar manner as shown below, for a mapping of the second-order eigenvectors given by
![]() $\hat {q}_j^{l,2}=\alpha _m^{l,2} \hat {q}_j^{m,0}$
$\hat {q}_j^{l,2}=\alpha _m^{l,2} \hat {q}_j^{m,0}$
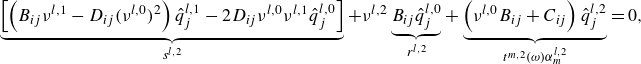 \begin{equation} \underbrace {\left [ \left (B_{ij} \nu ^{l,1}- D_{ij} (\nu ^{l,0})^2 \right ) \hat {q}_j^{l,1} - 2 D_{ij} \nu ^{l,0} \nu ^{l,1} \hat {q}_j^{l,0} \right ]}_{s^{l,2}} + \nu ^{l,2} \underbrace {B_{ij} \hat {q}_j^{l,0}}_{r^{l,2}}+ \underbrace {\left (\nu ^{l,0}B_{ij} + C_{ij} \right ) \hat {q}_j^{l,2}}_{t^{m,2}(\omega )\alpha _m^{l,2}}=0, \end{equation}
\begin{equation} \underbrace {\left [ \left (B_{ij} \nu ^{l,1}- D_{ij} (\nu ^{l,0})^2 \right ) \hat {q}_j^{l,1} - 2 D_{ij} \nu ^{l,0} \nu ^{l,1} \hat {q}_j^{l,0} \right ]}_{s^{l,2}} + \nu ^{l,2} \underbrace {B_{ij} \hat {q}_j^{l,0}}_{r^{l,2}}+ \underbrace {\left (\nu ^{l,0}B_{ij} + C_{ij} \right ) \hat {q}_j^{l,2}}_{t^{m,2}(\omega )\alpha _m^{l,2}}=0, \end{equation}
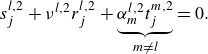 \begin{equation} s_j^{l,2}+\nu ^{l,2} r_j^{l,2} + \underbrace {\alpha _m^{l,2} t_j^{m,2}}_{m \neq l}=0 .\end{equation}
\begin{equation} s_j^{l,2}+\nu ^{l,2} r_j^{l,2} + \underbrace {\alpha _m^{l,2} t_j^{m,2}}_{m \neq l}=0 .\end{equation}
A.6 Supplementary numerical results of acoustic properties
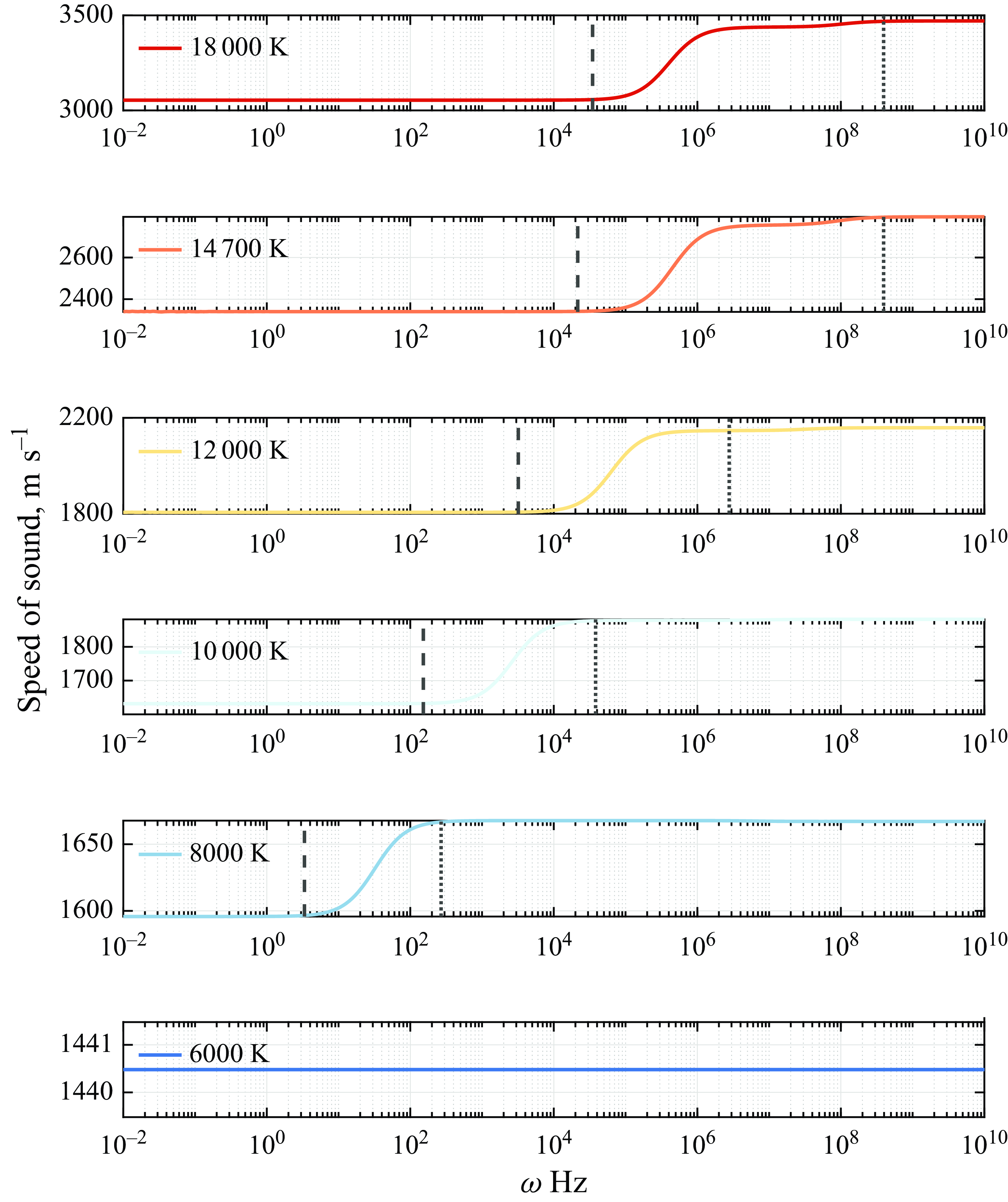
Figure 20. Speed of sound in argon as a function of frequency at different temperatures - - - - -, frozen to non-equilibrium;
![]() $\cdots$
$\cdots$
![]() $\cdots$
, non-equilibrium to equilibrium.
$\cdots$
, non-equilibrium to equilibrium.

Figure 21. Non-equilibrium speed of sound: - - - - -, nitrogen;
![]() $\cdots$
$\cdots$
![]() $\cdots$
, oxygen.
$\cdots$
, oxygen.
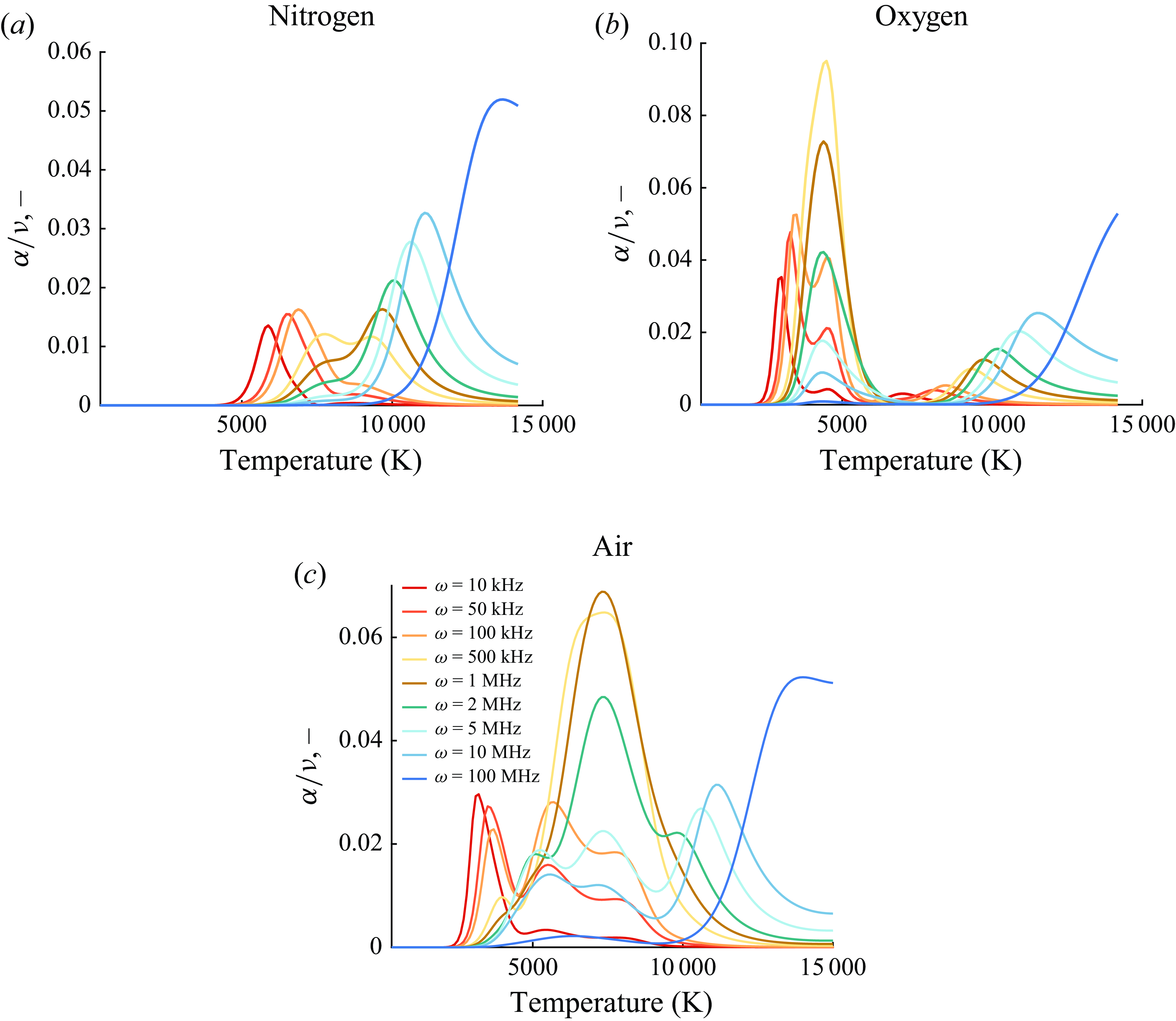
Figure 22. Inviscid normalised sound absorption due only to chemical reactions for varying
![]() $\omega$
at 1 atm.
$\omega$
at 1 atm.
























































