The stability of stratified horizontal flows of carbon dioxide at supercritical pressures

Abstract

Fluids at supercritical pressures exhibit large variations in density near the pseudo-critical line, such that buoyancy plays a crucial role in their fluid dynamics. Here, we experimentally investigate heat transfer and turbulence in horizontal hydrodynamically developed channel flows of carbon dioxide at $88.5$ bar and $32.6\,^{\circ }\rm C$, heated at either the top or bottom surface to induce a strong vertical density gradient. In order to visualise the flow and evaluate its heat transfer, shadowgraphy is used concurrently with surface temperature measurements. With moderate heating, the flow is found to strongly stratify for both heating configurations, with bulk Richardson numbers $Ri$ reaching up to 100. When the carbon dioxide is heated from the bottom upwards, the resulting unstably stratified flow is found to be dominated by the increasingly prevalent secondary motion of thermal plumes, enhancing vertical mixing and progressively improving heat transfer compared with a neutrally buoyant setting. Conversely, stable stratification, induced by heating from the top, suppresses the vertical motion, leading to deteriorated heat transfer that becomes invariant to the Reynolds number. The optical results provide novel insights into the complex dynamics of the directionally dependent heat transfer in the near-pseudo-critical region. These insights contribute to the reliable design of heat exchangers with highly property-variant fluids, which are critical for the decarbonisation of power and industrial heat. However, the results also highlight the need for further progress in the development of experimental techniques to generate reliable reference data for a broader range of non-ideal supercritical conditions.

1. Introduction

Beyond the vapour–liquid critical point, a fluid no longer undergoes a discrete phase transition from liquid to gas when it is heated. Instead, at supercritical pressure, fluids undergo a boiling-like process in which they remain in a continuous phase. During this pseudo-boiling process, fluids exhibit considerable nonlinear variations of thermodynamic properties. The thermodynamic gradients are particularly large near the pseudo-critical temperature $T_{{pc}}$ , defined at the temperature where the specific isobaric heat capacity has its maximum along a supercritical isobar (Banuti 2015). The location of the pseudo-critical (p-c) line that spans all p-c temperatures is indicated in figure 1. Several novel energy conversion systems are currently being designed to operate with fluids at supercritical pressures, as they can yield higher conversion efficiencies and compacter designs (Brunner 2010). Therewith, supercritical energy systems are promising solutions for the generation of power from non-fossil heat sources, for compact district heating systems and for the generation of high-temperature industrial heat. However, as a result of the large thermophysical variations in these systems, the flows within them differ considerably from those in their counterparts with subcritical single-phase fluids.

At a supercritical pressure, the fluid dynamics of heated or cooled fluids is often strongly affected by buoyancy. In this complex thermodynamic region, moderate heating rates can already induce significant variations in density that lead to sharp, local flow accelerations or mixed convection when buoyancy becomes significant. Therefore, heat transfer in engineering applications, which operate with supercritical fluids, often depends on the direction of gravity. These effects can be significant, as noted in the review on heat transfer at supercritical pressure by Wang et al. (2023a ). In their work, a comparison of the empirical heat transfer rates of various experimental facilities showed that heat transfer rates can either increase or decrease (depending on the direction of the heat transfer) by up to an order of magnitude with respect to a neutrally buoyant setting. This effect is most notably prevalent in horizontal flows with vertical gradients of density, in which turbulence can be either enhanced or suppressed by buoyancy. In such settings, in particular with fluids in proximity of the p-c region, it is essential to understand how buoyancy modulates the flow and turbulence to accurately capture and predict trends in heat transfer.

So far, mixed convection has been studied extensively (Pirozzoli et al. 2017; Zonta & Soldati 2018; Caulfield 2021) for fluids that follow the Oberbeck–Boussinesq (OB) approximation (Oberbeck 1879; Boussinesq 1897). Contrary to a fluid at a supercritical pressure, the density of OB fluids is assumed to vary only moderately and linearly with temperature. Therefore, large temperature differences or large length scales are required to induce strong stratifications in the conventional single-phase fluids that are accurately described with the OB approximation (Zonta & Soldati 2018).

The unstable stratification of a horizontal flow of an OB fluid, in which a lighter layer is formed below a denser bulk flow, is characterised by ejections of warmer fluid away from the heated wall, and the concurrent sweeping of colder fluid in the opposite direction (Garai, Kleissl & Sarkar 2014). However, unlike in purely convective flows, the ejected plumes form roll vortices towards the bulk of the channel in the direction of the forced convection (Garai et al. 2014; Scagliarini, Gylfason & Toschi 2014; Pirozzoli et al. 2017). In the direct numerical simulations (DNS) of Garai et al. (2014), the wide roll vortices are seen to align after one another in the streamwise direction. Furthermore, the DNS of both Zonta & Soldati (2014) and Li, Luo & Fan (2017) have shown that the intensity of the near-wall turbulence and the mixing efficiency increase when roller ejection and sweep processes are incited in a previously neutrally buoyant channel flow. Here, the improvements in mixing efficiency are diminished as the relative strength of the forced convection is increased (Zonta & Soldati 2014). Moreover, the concurrent processes in which rollers are ejected from and swept towards the bottom surface become the dominant mechanism of wall-normal heat transfer in mixed convective flows (Garai et al. 2014; Blass et al. 2020). As such, the wall–fluid heat transfer of flows with buoyant plumes differs from – and far exceeds – the heat transfer of neutrally buoyant forced convection.

Distinctly different behaviour is observed and simulated in stably stratified flows of OB fluids, in which a lower-density layer is formed on top of a denser bulk flow. Here, fluid parcels of a certain density are preferentially redistributed along the vertical density gradient that is imposed on the flow (Lienhard & Van Atta 1990). If the gradient is sharp enough, the potential energy required to stir fluid parcels away from their preferential vertical positions is not met (García-Villalba & Del Alamo 2011). As a result, overturns and vertical thermal structures are elongated and eventually aligned with the direction of the flow (Williams et al. 2017; Smith, Caulfield & Taylor 2021; Zonta, Sichani & Soldati 2022). The resulting restriction of vertical momentum transfer has been noted to greatly reduce turbulent mixing and near-wall heat transfer (Ohya, Neff & Meroney 1997; García-Villalba & Del Alamo 2011; Williams et al. 2017), in both numerical studies and experiments. Often, the distinction is made between weak and strong stratification, following the findings of Gage & Reid (1968). In the weak limit, turbulence is sustained close to the wall where shear overcomes buoyancy (Zonta et al. 2022), as the latter preferentially acts on larger scales of vertical motion (Lienhard V & Van Atta 1990; Zonta & Soldati 2018). In the case of strong stratification, a global turbulent state cannot be sustained (Nieuwstadt 2005; Zonta & Soldati 2018). The flow is said to become intermittent, with regions of complete turbulence suppression. For higher values of the Reynolds number $\textit {Re}$ the formed laminar patches are more confined to the top wall, instead of spanning the entire domain, according to the results of Deusebio, Caulfield & Taylor (2015).

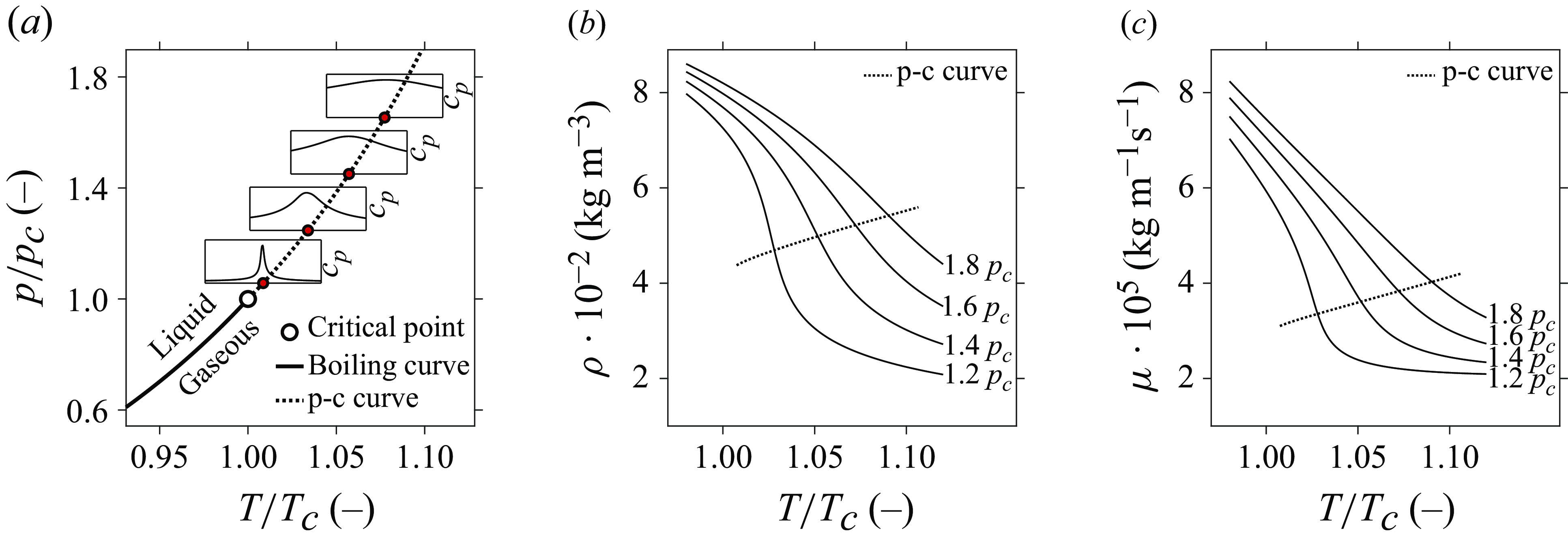
Figure 1. Thermodynamic properties of carbon dioxide at supercritical pressures, for which the critical temperature and pressure are at $T_{{c}}=31.0\,^{\circ}\rm C$ and $p_{{c}}=73.8$ bar, respectively. Panel (a) shows normalised profiles of the isobaric heat capacity $c_{{p}}$ along several isobars, the pressure of which is indicated in red. The pseudo-critical (p-c) curve is defined at the local maxima of $c_{{p}}$ along an isobar (Banuti 2015). Distributions of density $\rho$ and viscosity $\mu$ near the p-c line are shown for several supercritical pressures in (b) and (c), respectively.

Unfortunately, the amount of work that consider the stratification of fluids with thermodynamic gradients beyond the limits of the OB approximation has so far remained limited. However, it is with such fluids, most notably so for fluids at a supercritical pressure, that strong stratifications most readily prevail in practical applications. The influence of buoyancy on the flow of a fluid at a supercritical pressure have been studied in the context of vertical pipe flows (Bae, Yoo & Choi 2005; Nemati et al. 2015) and for vertical annular flows (Peeters et al. 2016). Additionally, Valori et al. (2019) have optically explored a purely convective flow of supercritical carbon dioxide. The effect of buoyancy on a horizontal supercritical flow has first been considered by Chu & Laurien (2016). In their work, Chu & Laurien (2016) have numerically (DNS) investigated the non-axisymmetric temperature profiles in heated horizontal pipe flows previously found in experimental investigations of pipe surface temperatures (Adebiyi & Hall 1976; Yu et al. 2013; Tian et al. 2021; Cheng, Wang & Xu 2024). Here, the overall deterioration in heat transfer with respect to a neutrally buoyant flow (Theologou et al. 2022; Cheng et al. 2024) was attributed to the accumulation of a light, warmer layer at the top of the horizontal pipe (Chu & Laurien 2016). Furthermore, the thermal stratification of the flow of a supercritical fluid through a heat exchanger channel has been touched upon in the DNS of Wang et al. (2023b ). Here, the initially turbulent flow was predicted to laminarise along the imposed density gradient, subsequently deteriorating its wall-normal heat transfer. A first experimental investigation of horizontal buoyancy-affected flows of supercritical $\text{CO}_2$ was presented by Whitaker et al. (2024). Here, side-view schlieren imaging was used to study the flow within a heated microchannel. In their work, the optical signal was greatly affected by the direction of the heat transfer. Nevertheless, only a moderate difference between the heat transfer of the bottom-up heated surface and the top-down heated surface was measured for their operating conditions. Therewith, the effects of strong stratifications on the heat transfer of continuous, mixed convective flows at supercritical pressures remain experimentally unexplored.

The current study experimentally investigates horizontal flows of carbon dioxide at supercritical pressure in which buoyancy is non-negligible, or even becomes dominant. More specifically, initially hydrodynamically developed steady horizontal channel flows are considered, subject to one-sided heating such that vertical gradients of density are induced. The large, non-ideal variations in thermodynamic properties of the heated carbon dioxide mean that the OB approximation does not apply, and that significant buoyant contributions can be induced at the moderate heating rates that are attainable in laboratory-scale experiments. As such, the modulation of turbulence in both stably and unstably stratified channel flows can be addressed in the current work.

To visualise the stratifications of carbon dioxide at supercritical pressure, the surface temperature measurements are complemented with optical diagnostics in this work. The optical tools exploit variations in refractive index in the working fluid to visualise the thermally inhomogeneous turbulent carbon dioxide. Contrary to the investigations of wall temperature, the resolution of these optical measurements is not limited in time by the thermal inertia of the system, or in space by the finite physical size of probes and probe wells. Therewith, the current optical methods can partially fill the knowledge gap left by the incompatibility of high-frequency hot-wires with non-ideal media (Vukoslavčević et al. 2005). As such, the qualitative visualisations are used to explain trends in the wall temperature data by revealing highly intermittent local flow patterns previously unexplored in experiments with fluids at supercritical pressures.

A description of the experimental facility and the (optical) measurement tools is given in § 2. An overview of the considered cases and the corresponding thermodynamic parameter space is presented in § 3. In § 4, the applicability of the optical diagnostics is first evaluated by considering the unheated base flow. Thereafter, visualisations of heated channel flows in both stably and unstably stratified configurations are presented and discussed. Furthermore, surface temperature data are presented for both configurations. Finally, a summary of the most important conclusions is presented in § 5. At the end of this document, supplementary information on the used optical filters is given in Appendix A.

2. Methodology

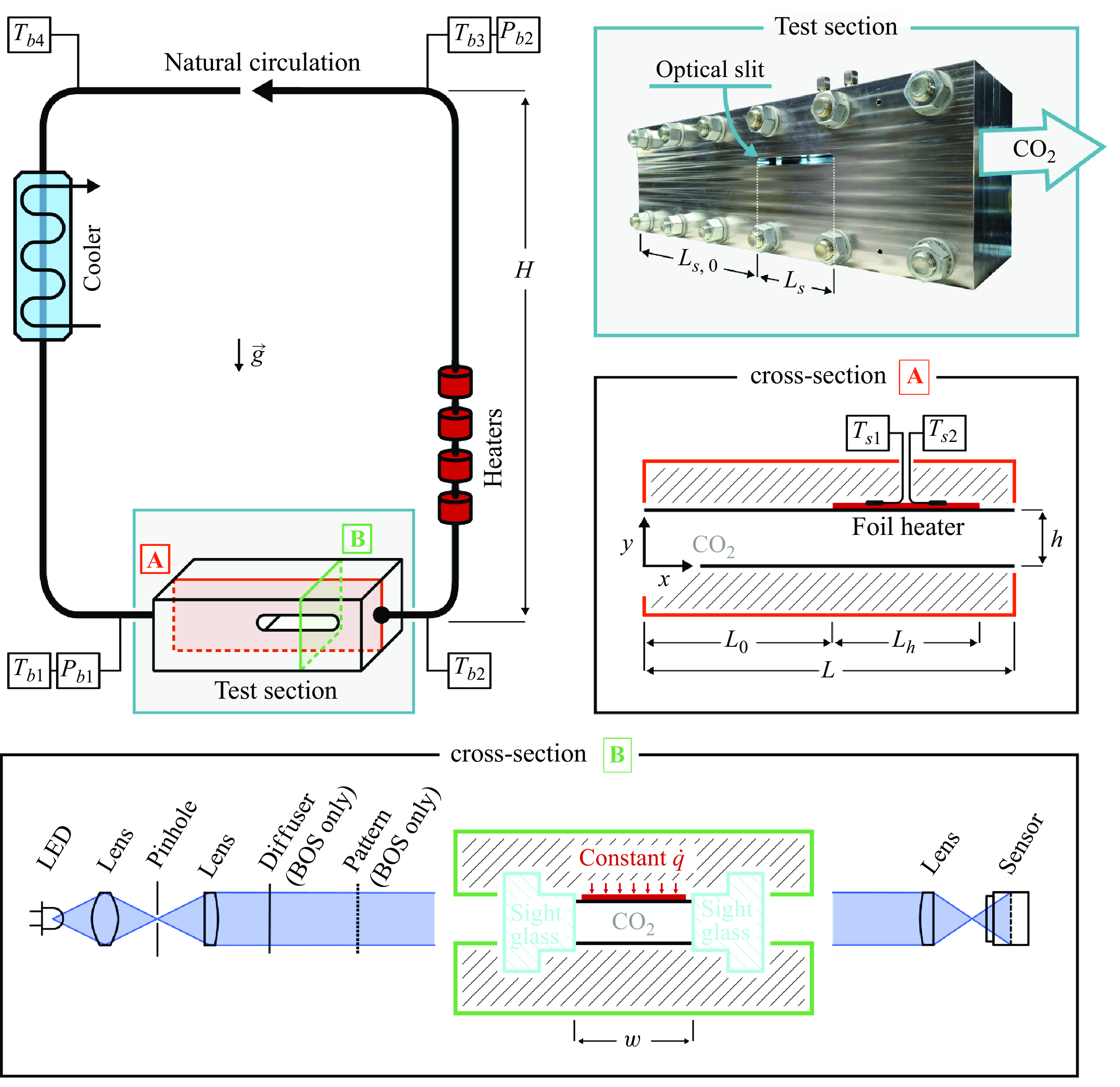
Figure 2. Schematic of the current experimental facility, in which carbon dioxide at supercritical pressures is naturally circulated to a test section that is bi-laterally optically accessible. An image of the test section is outlined in blue. In the image, any usually present thermal insulation (30 mm polyethylene foam) has been removed. A schematic of lateral cross-section A is outlined in orange. In order to change the direction of the heating with respect to the schematic, the test section is inverted. The current optical configuration is shown alongside green-outlined cross-section B, which also indicates the additional components used for the background-oriented schlieren (BOS) measurements. Any symbols in the figure are explained in the main text, and in table 1.

2.1. Experimental facility

In this work, the stratification of a non-ideal fluid is studied experimentally in a novel test facility that provides optical access to a continuous flow of carbon dioxide at supercritical pressures. The experimental facility is shown schematically in figure 2 and an overview of the geometric parameters is given in table 1.

Table 1. Description of the experimental facility. The table gives the values of the parameters indicated in figure 2.

2.1.1. Natural circulation

A steady, continuous flow of carbon dioxide is generated using natural circulation. The current natural circulation loop (NCL) is shown schematically in the top-left corner of figure 2. In the NCL, the nonlinear gradients in density of the $\text{CO}_2$ are exploited to generate a differential buoyant force over the vertical legs of the NCL, therewith inducing a natural circulation. Contrary to most forced convective systems, NCLs do not require pumps that contain lubricants that may contaminate the working fluid and therefore limit its optical accessibility. Furthermore, the inherent induction of mechanical noise, and the intrinsic presence of leakages of mechanical propulsion are avoided. Additionally, the NCL allows for the test section pressure, its inlet bulk temperature, the imposed mass flow rate and the foil heating rate to be individually varied. A detailed description of the NCL and its steady-state performance is given by Draskic, Bugeat & Pecnik (2024).

2.1.2. Test section

A high-pressure stainless steel test section lies at the core of the experimental facility. As shown in the top left of figure 2, the test section is part of the bottom horizontal section of the NCL. An image of the apparatus, outlined in blue, is shown in the top right of figure 2. The test section provides bi-lateral optical access to a rectangular channel through tempered obround borosilicate visors, as shown in cross-section B in figure 2. Cross-section A shows the side view of the rectangular channel between two gradual round-to-rectangular reducers. The reducers serve to connect the channel to the round pipe connections of the experimental facility. The top surface of the rectangular channel is heated after a length $L_0$ . In order to apply heat from the opposite, bottom surface, the test section is flipped in its entirety. However, in the flipped, bottom-up heating configuration the origin of the considered coordinate system remains on the bottom surface of the test section, consistent with cross-section A of figure 2. The heating is provided by a self-adhesive 40 W polyimide foil resistance heater that spans the full width of the channel. In order to avoid a forward facing step of the surface, the foil heater is bonded to the rear side of a removable surface plate that spans the full top surface, as indicated using the top black line in cross-section A of figure 2. The surface plate, a 0.8 mm thick polished aluminium surface mirror, is oriented towards the carbon dioxide with its polished side. The rear-side surface temperature of the foil heater is measured using two K-type thermocouple probes, mounted in the lateral middle of the channel at different streamwise locations, as indicated with $T_{{s}1}$ and $T_{{s}2}$ in cross-section A of figure 2. The thermocouple probes are embedded in a small cavity behind the aluminium plate, and therefore do not directly capture the near-wall temperature of the carbon dioxide. Instead, sensors $T_{{s1}}$ and $T_{{s2}}$ reflect the thermal response of the heater itself. Given the high thermal resistance between the cavity and the surroundings, nearly all of the heat imposed by the heaters is expected to be transferred to the working fluid.

2.1.3. Instrumentation

To continuously monitor the facility, it is equipped with a series of sensors that are indicated throughout figure 2. To measure bulk temperatures throughout the NCL, Pt100 thermometers are radially inserted into the flow. These resistance thermometers, labelled $T_{{b}1}$ – $T_{{b}4}$ in figure 2, have a nominal accuracy of $\pm 0.1^\circ C$ . Absolute pressure measurements $P_{{b}1}$ and $P_{{b}2}$ are taken using welded STS ATM.1st sensors, with a nominal uncertainty of $\pm 0.16$ bar or $0.1\,\%$ . Thermocouples $T_{{s}1}$ and $T_{{s}2}$ yield measurements of the foil heater surface temperature with a nominal uncertainty of $\pm 0.5\,^\circ\rm{C}$ . The thermocouples are calibrated, and their readings are adjusted once, during a neutrally buoyant flow condition, to match those of the resistance sensor $T_{{b}1}$ in situ. The steady-state mass flow rate $\dot {m}$ is deducted from the heating rate $\dot {Q}_{{imp}}$ imposed by the vertically placed heaters in figure 2 and the increase in enthalpy $\mathcal{H}$ across the heater, evaluated over the vertical leg of the NCL, i.e.

(2.1) \begin{equation} \dot {m}=\frac {\dot {Q}_{{imp}}}{\mathcal{H}(T_{{b}3},P_{{b}2})-\mathcal{H}(T_{{b}2},P_{{b}1})}. \end{equation}

The value of $\mathcal{H}$ , or any other thermophysical quantity, is interpolated from a table generated using the REFPROP database (Lemmon et al. 2018) for given values of $T$ and $p$ . As found in the experiments of Draskic et al. (2024), the mass flow rate estimated by (2.1) is in close agreement with the readings of a Coriolis mass flow meter when the system is at a steady state, when the pressure drop over the horizontal sections of the NCL is limited at moderate bulk velocities, and when the loop is insulated with a 40 mm layer of mineral wool to minimise heat losses. As these conditions are met in the current experiments, the Coriolis mass flow meter is removed to avoid any unnecessary disturbances to the flow, and equation (2.1) is used to determine the mass flow rate within the NCL.

The uncertainty of all results shown in this work is evaluated by assuming the independence of the respective quantities measured by the sensors in the system. As a result, the standard deviation of any considered quantity is evaluated from the standard deviations of sensor data used to determine the considered quantity. For instance, the standard deviation $\sigma _{\mathcal{H}}$ for $\mathcal{H}(T,P)$ is obtained using

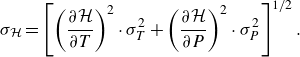(2.2) \begin{equation} \sigma _{\mathcal{H}}=\left [\left (\frac {\partial \mathcal{H}}{\partial T}\right )^2\cdot \sigma _{{T}}^2+\left (\frac {\partial \mathcal{H}}{\partial P}\right )^2\cdot \sigma _{{P}}^2\right ]^{1/2}. \end{equation}

Here, $\sigma _T$ and $\sigma _P$ denote the standard deviations of process measurements $T$ and $P$ , respectively.

2.2. Optical methodology

2.2.1. Shadowgraphy

A parallel-light shadowgraphy configuration is used to yield shadowgrams, as is shown schematically in cross-section B of figure 2. The object plane for the shadowgraphy is at the right channel surface in the figure. The brightness of the resulting shadowgram varies proportionally to the second spatial derivative of the path-integrated refractive index field (Settles 2001; Merzkirch 2012). As the refractive index is proportional to the fluid density (Michels & Hamers 1937), variations in density of the carbon dioxide can be recorded. In the current setting, the shadowgrams outline the boundaries of depth-integrated thermal structures with consecutive maxima and minima in image brightness. In order to increase the sensitivity of the shadowgrams, to reduce the distortion of shadows and to reduce geometric blur with respect to non-parallel light shadowgraphy (Settles 2001), the light source (a monochromatic blue LED with a nominal wavelength of 455 nm) is collimated in the current optical set-up. As imperfections in the sight glass surfaces can be perceived in these collimated-light shadowgrams, a spatial digital image filter is applied to the images shown in this work to highlight only the thermal structures of interest. The filter is further elaborated on in Appendix A.

A Pixelink PL-D755MU-T CMOS camera (2448 $\times$ 2048 pixels, monochromatic) is used to record images. The exposure time of the sensor is maintained at 20 $\unicode{x03BC}$ s for all shadowgrams. The contrast of the recorded images is stretched to cover the full brightness range. Both the image sensor and the light collimator are traversed in the streamwise direction using synchronised linear traversing stages on either side of the test section to visualise the $\text{CO}_2$ at any position along the optical slit.

2.2.2. Shadow image velocimetry

A comparison of consecutive shadowgrams can reveal flow patterns within a compressible flow. When the currently studied flow is both turbulent and refractive, it is naturally seeded by eddies that travel at the local convective speed of the flow. As such, the correlation of consecutive shadowgrams enables seedless velocity measurements of the flow (Jonassen, Settles & Tronosky 2006; Hargather et al. 2011; Settles & Hargather 2017). In order for the pseudo-tracers to be distinguishable in consecutive images, thermal gradients should be sparsely distributed along the optical axis, and the diffusive time scale of the flow should far exceed its advective time scale. The applicability of shadow image velocimetry to turbulent flows of carbon dioxide at supercritical pressure in particular was previously demonstrated by Okamoto et al. (2003). Whereas particle image velocimetry (PIV) can yield near-planar velocities, the integrating property of shadowgraphy yields measurements of eddy motion across the full width of the test section when using shadow image velocimetry. Much like planar PIV, shadow image velocimetry only yields displacements in directions perpendicular to the optical axis. In the current work, a fast-Fourier-transform-based cross-correlation algorithm is used to yield displacements between consecutive shadowgrams. An interrogation window size of 128 $\times$ 128 pixels with 80 $\,\%$ overlap is used to capture a sufficient number of property-variant structures in each correlation window (Jonassen et al. 2006). The qualitative descriptions of the shadowgram pair displacements in this work are supported by an additional assessment of the image correlation profiles themselves, as elaborated on in Appendix B.

2.2.3. Background oriented schlieren

The magnitude of the vertical refractive index gradients across the test section can be evaluated by considering the deformation of a known pattern by the highly property-variant $\text{CO}_2$ . In the current background oriented schlieren (BOS) configuration, an in-focus background pattern is placed on the left side of the test section in cross-section B of figure 2. Here, a computer-generated and known dot pattern printed on a transparent plastic sheet is placed along the optical axis. By placing diffusing glass before the background pattern, the incoming light is decollimated. At the expense of the global image brightness, the diffuse light is found to produce a more homogeneously illuminated and globally sharp image when refractive index gradients are present in the test section channel. When a diffuser is used, the sensor exposure time is increased to 150 $\unicode{x03BC}$ s to provide sufficient illumination. Using the image correlation method previously used for shadow image velocimetry in this work, the apparent deformation $(\Delta x(x,y),\Delta y(x,y))$ of the background pattern in the image plane caused by gradients in refractive index in the test section can be measured. By assuming small deflection angles, the unidirectional, vertical deformation of the background pattern and the presence of a schlieren object that is homogeneous across the full width of the channel, the path-integrated spatial refractive index gradient $\partial n/\partial y$ can be expressed as

(2.3) \begin{equation} \frac {\partial n}{\partial y}=\frac {n_0 \Delta y}{MZ_{{D}}w}, \end{equation}

(Schröder et al. 2009; Raffel 2015). Here, $n_0$ is the reference refractive index of the carbon dioxide when it is homogeneous in density. Furthermore, $M$ is the magnification of the optical system, and $Z_{{D}}$ is the distance from the middle of the channel to the background pattern, and $w$ is the width of the flow channel. Unfortunately, large density gradients are present throughout the limited field of view of the current set-up, and the exact magnitude of the path-integrated density is unknown within the imaged volume. As such, no appropriate set of boundary conditions can be posed for the calculation of a line-of-sight-integrated density field for the current configuration (Venkatakrishnan & Meier 2004). Nevertheless, the current BOS approach can be used for a relative comparison of density gradients in the channel, and for the evaluation of the applicability of particle-based optical diagnostics with the studied fluid.

2.3. Experimental procedure

As carbon dioxide dilates strongly for the conditions and flow rates of the current study, all data are gathered by following a measurement procedure that aims to minimise thermal gradients within the test section block itself. The test section is initially at the ambient temperature. In order to increase its temperature to the desired value, a large mass flow rate of carbon dioxide at the appropriate temperature is forced through the thermally insulated test section for several hours. Over time, the measured temperature drop over the test section $(T_{{b1}}-T_{{b2}})$ reduces, as the temperature of the test section converges towards a steady state. When changing the inlet condition to reach different operating conditions, the procedure to reach steady state is repeated.

When the test section temperature reaches a value sufficiently close to the desired test section inlet temperature, therewith at a value of $(T_{{b1}}-T_{{b2}})$ within the nominal accuracy of $T_{{b1}}$ and $T_{{b2}}$ , a measurement cycle is commenced. At a constant mass flow rate, the imposed foil heating rate is gradually increased in a stepwise manner. In order to maintain a constant pressure and mass flow rate $\dot {m}$ , the applied heating rate to drive the NCL is gradually decreased. The acquisition of images and loop sensor data is started some time $t_{{w}}$ after imposing each step in heating power. In the current work, $t_{{w}}=120$ s. After the completion of all heating steps, the mass flow rate is changed, and the above process is repeated.

3. Cases and parameter space

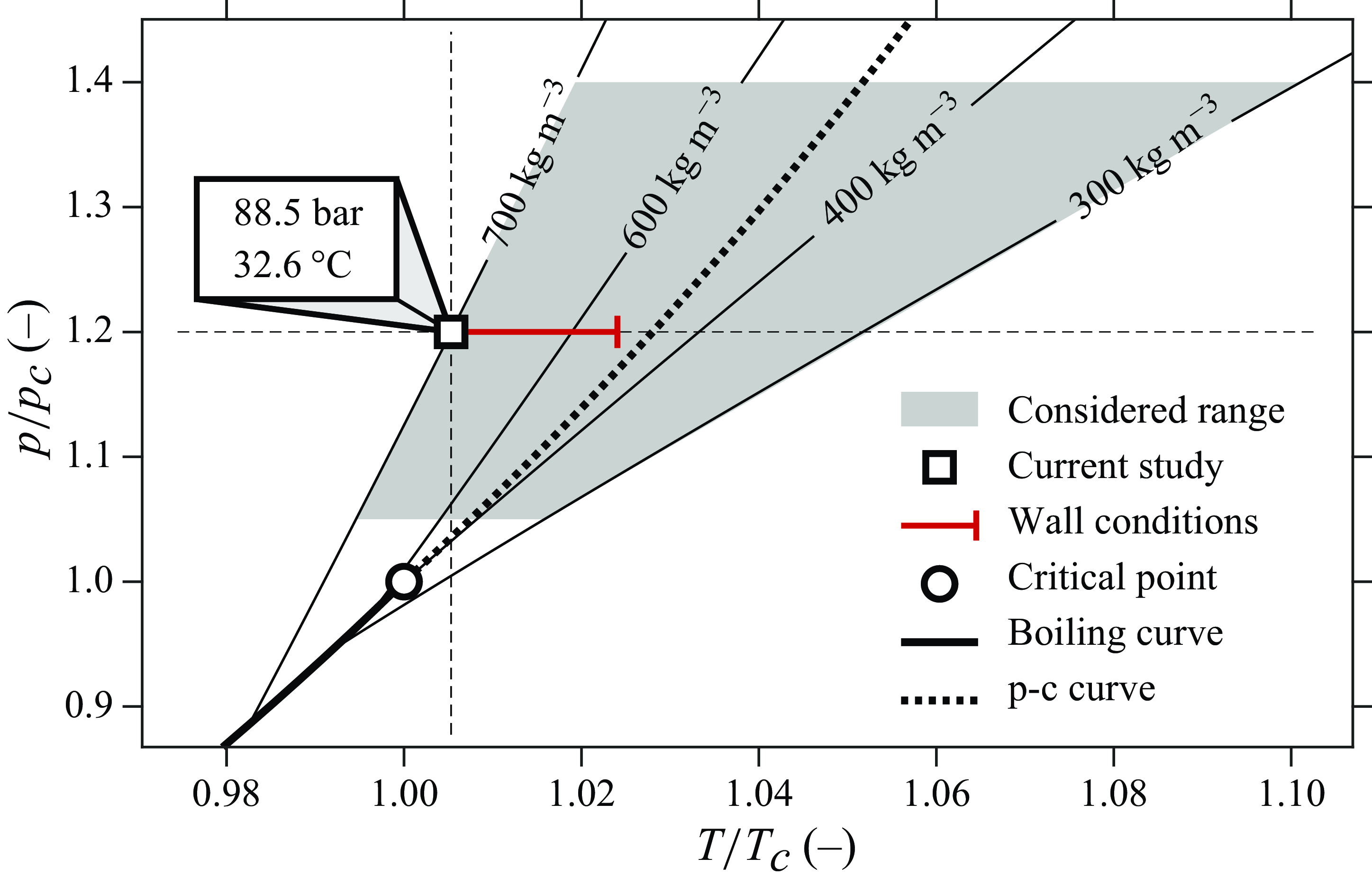
Figure 3. Range of thermodynamic conditions of carbon dioxide at the test section inlet for the current study. Any presented results are evaluated at a nominal density and a nominal pressure of $\rho =700\text{ kg m}^{-3}$ and $p=1.2$ $p_{{c}}$ , respectively. Here, $p_{{c}}$ is the critical pressure.

3.1. Thermodynamic conditions

All presented results are recorded at the same thermodynamic conditions at the test section inlet, whereas the imposed heating rates and the applied mass flow rates are varied throughout this work. The nominal thermodynamic state of the test section inlet ( $T_{{b}1}$ and $P_{{b}1}$ in figure 2) of the current study is indicated in figure 3. The full thermodynamic range that was initially explored is indicated in grey in figure 3.

Within the considered thermodynamic range, channel inlet conditions that are liquid-like provide the most distinguishable shadowgrams. Therefore, such conditions are chosen as the initial state for the current experiments. On the contrary, images of near-p-c and gas-like neutrally buoyant carbon dioxide reveal the intermittent presence of blurry, irregular, downward moving structures. Whereas downward plumes are similarly perceived when the $\text{CO}_2$ is denser, they are less prevalent, their presence is more sporadic and their outlines remain sharp in a shadowgram. These secondary flows are likely the result of the moderate cooling of the carbon dioxide by the ambient air, either through the insulated walls of the test section, or via the less insulated optical visors. Within the considered domain, the temperature of the carbon dioxide at the test section inlet exceeds the ambient temperature. On the right side of the p-c curve in figure 3, the driving temperature difference with the surroundings is relatively large. Furthermore, the cooling of the gas-like medium brings about sharp changes in refractive index in the steep, nonlinear near-p-c region. To the left of the p-c curve, both the driving temperature of the cooling by the ambient and the thermodynamic gradients induced by the cooling are significantly lower. Therewith, the moderately colder structures in the flow do not sufficiently distort the light through the channel to blur the resulting image in the liquid-like region of the considered thermodynamic parameter range.

Additionally, the large near-p-c gradients in density that are induced when the liquid-like carbon dioxide is heated, mean that strong stratifications can be reached with the attainable experimental heating rates. The range of measured surface temperatures $T_{{s}1}$ and $T_{{s}2}$ is indicated using the red horizontally bounded line in figure 3. For the presented results, the p-c curve is not crossed in the near-wall region.

Figure 4. Instantaneous shadowgrams of bottom-heated channel flows of carbon dioxide at the thermodynamic conditions indicated in figure 3. The relevant nominal Reynolds numbers ${\textit {Re}}_{Dh}$ and the nominal imposed heating rates $\dot {q}$ are displayed on the vertical and the horizontal axes, respectively. The cases, e.g. R2 : bh1, are labelled by an indicator of the nominal Reynolds number (R) and an indicator of the applied heating ( $\textbf {n}$ or $\textbf {bh}$ ). Here, $\textbf {n}$ represents an unheated flow, whereas $\textbf {bh}$ implies that bottom-upward heating is applied. In all cases, the flow is from left to right. Supplementary movie 2 (available at https://doi.org/10.1017/jfm.2025.10162) provides the dynamic evolution of the current figure in time by showing 300 consecutive shadowgrams.

Figure 5. Instantaneous shadowgrams of top-heated channel flows of carbon dioxide at the thermodynamic conditions indicated in figure 3. The relevant nominal Reynolds numbers ${\textit {Re}}_{Dh}$ and the nominal imposed heating rates $\dot {q}$ are displayed on the vertical and the horizontal axes, respectively, and the cases, e.g. R6 : th1, are labelled by an indicator of the nominal Reynolds number (R) and an indicator of the applied heating ( $\textbf {n}$ or $\textbf {th}$ ). Here, $\textbf {n}$ represents an unheated flow, whereas $\textbf {th}$ implies that top-downward heating is applied. In all cases, the flow is from left to right. Supplementary movie 2 (available at https://doi.org/10.1017/jfm.2025.10162) provides the dynamic evolution of the current figure in time by showing 300 consecutive shadowgrams.

3.2. Case overview

An overview of the cases considered in this work is given in figures 4 and 5. Both figures show instantaneous shadowgrams of carbon dioxide at supercritical pressure. In figure 5, the carbon dioxide is heated in the top-down configuration shown in orange outlined cross-section A of figure 2. For the cases shown in figure 4, the test section is inverted and the bottom surface of the test section channel is heated. In both figures, the inlet mass flow rate $\dot {m}$ and the foil heating rate $\dot {q}$ are varied to yield twenty cases with varying hydraulic Reynolds numbers $Re_{Dh}$ and bulk Richardson numbers $Ri$ respectively, where

(3.1) \begin{equation} Re_{Dh}=\frac {\rho _{{b1}} U_{{imp}}D_{{h}}}{\mu _{{b1}}}, \: \: \: Ri=\frac {\rho _{{b1}}-\rho _{{w}}}{\rho _{{b1}}}\cdot \frac {gh}{U_{{imp}}^2}. \end{equation}

Here, g is the gravitational acceleration. The inlet density $\rho _{{b1}}$ and the inlet viscosity $\mu _{{b1}}$ are evaluated at the temperature and pressure of sensors $T_{{b1}}$ and $P_{{b1}}$ of figure 2, respectively. Thereafter, $\rho _{{b1}}$ is used to evaluate the imposed bulk velocity $U_{{imp}}$ , with

(3.2) \begin{equation} U_{{imp}}= \frac {\dot {m}}{\rho _{{b1}}A_{{cs}}}. \end{equation}

Here, the test section cross-sectional flow area is defined as $A_{{cs}}=hw$ . The bulk Richardson number is evaluated using wall density $\rho _{{w}}$ . Under the assumption of constant test section pressure, $\rho _{{w}}$ is evaluated at $P_{{b1}}$ and the mean wall temperature $T_{{w}}$ , where

(3.3) \begin{equation} T_{{w}}=\frac {1}{2}\left (T_{{s1}}+T_{{s2}}\right ). \end{equation}

The corresponding values of $Ri$ for the non-neutrally buoyant cases shown in figures 4 and 5 are given in table 2. The complete range of $Ri$ obtained with the available surface heating power is presented in figure 6. As the hydraulic Reynolds number $Re_{Dh}$ is increased, the attained value of $Ri$ decreases. Furthermore, at a constant heating rate, the measured value of $Ri$ is consistently higher for the top-down heated configuration than it is for bottom-up heating.

Table 2. Values of $Ri$ for the non-neutrally buoyant snapshots shown in figures 4 and 5. The cases, e.g. R1 : bh1, are labelled by an indicator of the nominal Reynolds number (R) and an indicator of the applied heating ( $\textbf {bh}$ or $\textbf {th}$ ). Here, $\textbf {bh}$ represents a flow to which bottom-upward heating is applied, whereas $\textbf {th}$ indicates that top-downward heating is applied. The data are shown with intervals of $\pm 2\sigma$ .

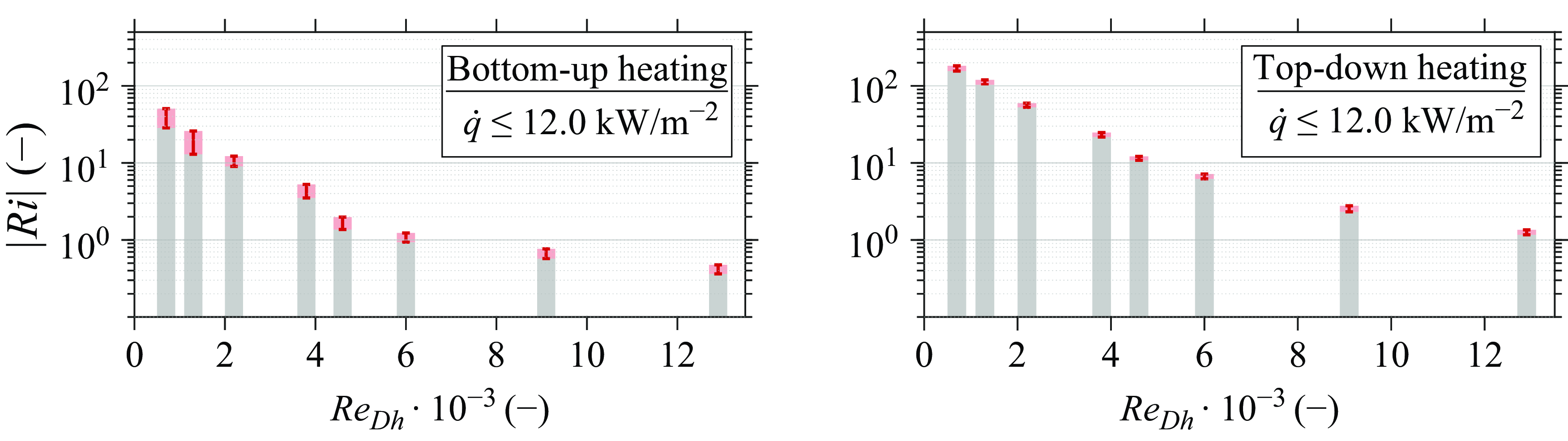
Figure 6. Range of $Ri$ considered in this work for the nominal Reynolds numbers $Re_{{Dh}}$ indicated in figures 4 and 5. The carbon dioxide is heated in the unstably stratified configuration on the left, whereas a stably stratified configuration is considered for the data on the right. The error bars correspond to $\pm 2\sigma _{Ri}$ of the time series with the largest value of $Ri$ .

4. Results

4.1. Characterisation of unheated base flow

For the conditions considered in this work, structures that are naturally present in the channel can be perceived in the shadowgrams and persist throughout consecutive frames. Due to turbulent mixing and the thermal heterogeneity of the fluid, the density of the operating fluid changes locally. Consequently, the refractive index also changes. The variation in the (second derivative of the) refractive index in the carbon dioxide throughout the channel is then registered by the shadowgraphy. In the shadowgrams, the variations manifest as fluctuations in the image brightness. These structures have a finite lifetime while being advected by the flow; they appear then as ‘thermal tracers’ that visualise the fluid motion. Provided that these structures remain to exist over at least one imaging frame pair, they can be considered as (nearly) passive tracers in the fluid that can be used to measure the fluid motion, as in conventional PIV (Adrian & Westerweel 2011). In some of the current results, the fluctuations maintain a consistent shape throughout consecutive frames, indicating that their time scale of mixing exceeds the interval between consecutive recordings. Therefore, their motions can be distinguished. The axial evolution of the fluctuations is shown in figure 7. Here, the shadowgrams shown in the leftmost columns of figures 4 and 5 are considered, in which the $\text{CO}_2$ is neutrally buoyant. In figure 7, the parameter $b$ describes the achieved image width for the current frame rates. The optical signal of the shadowgraphy is shown over time at the red horizontal line of the snapshot that is indicated in figure 7(a). The resulting space–time graphs show the passage of thermal structures in the form of angled streaks of constant brightness. The nominal angle of the streaks in the space–time graphs is indicated by green dashed lines for each case. Given that no structures are perceived over time along the red curve for case R1 : n, a nominal angle cannot be inferred from the graph. As the imposed Reynolds number is increased for the other cases, the observed structures pass the red line in a shorter time span, and the angle of the streaks with the horizontal axis decreases. Evidently, a velocity-like quantity can be deducted from the streak angles of passing thermal structures in the current representation.

Figure 7. Space–time (b) representation of the optical signal at the horizontal line that is indicated in the instantaneous shadowgram shown in (a). The value of ${\textit {Re}}_{Dh}$ is progressively increased by increasing the mass flow rate for the cases shown in (b).

In order to determine whether the movement of the image brightness fluctuations corresponds to the movement of the fluid, the correlated velocity of the fluctuations $U_{C}$ is measured and subsequently compared with the velocity imposed by the NCL $U_{{imp}}$ . In order to measure $U_{C}$ , consecutive shadowgrams are correlated to yield the instantaneous displacements of the distinctly shaped image brightness fluctuations in all directions perpendicular to the optical axis. Here, the total image height is assumed to correspond to $h$ . Furthermore, the averaged image is assumed to correspond linearly to the object plane when the $\text{CO}_2$ remains unheated. As such, the means of image-plane displacements $\Delta x$ and $\Delta y$ can be divided by the optical magnification $M$ to yield the physical displacements within the test section. Therewith, $U_{C}$ can be approximated using

(4.1) \begin{equation} U_{C}=\frac {\Delta x}{M\Delta t}, \end{equation}

where $\Delta t$ is equal to the period between consecutive frames. However, when the carbon dioxide is heated, the averaged image deforms as a result of large local gradients in refractive index. Therefore, the imaged displacements no longer linearly correspond to the physical displacements as $M$ is no longer constant throughout the image, and an accurate average value of $U_{C}$ can no longer be directly deducted. As such, only image-plane displacements are reported for the cases with heating.

The correlated velocity of the refractive structures corresponds conditionally to the imposed velocity of the system. Figure 8 shows a comparison of the correlated velocities of the structures in the shadowgrams with the velocities of the natural circulation for unheated flows. In figure 8(a), the correlated mean $x$ -direction velocity $U_{C}$ (deducted from 2999 frame pairs) is compared with $U_{{imp}}$ . The magnitude of the mean reconstructed velocity $\bar {U}_{C}$ corresponds to the actual bulk velocity $U_{{imp}}$ for sufficiently large Reynolds numbers, i.e. $Re_{Dh}\geqslant 3\times 10^{3}$ .

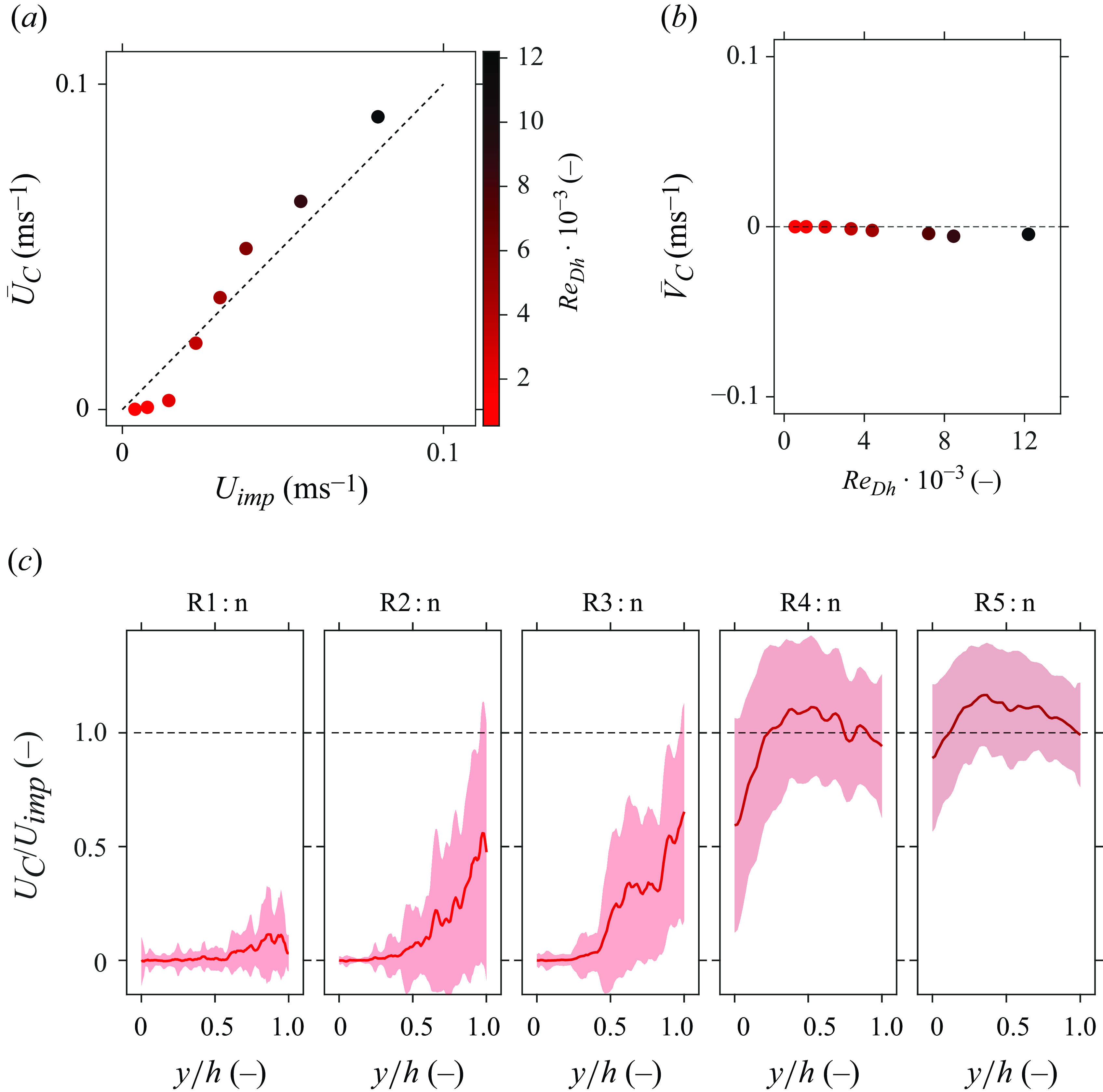
Figure 8. Comparison of the correlated velocity with the imposed velocity. Panel (a) shows the correlated mean velocity $\bar {U}_{C}$ with respect to the measured velocity. Panel (b) shows the mean value of the vertical component $\bar {V}_{C}$ . A comparison of several instantaneous profiles of $U_{C}$ with the measured bulk velocity is shown in (c). The data in (a) and (b) are shown with error bars of $\pm 2\sigma /\sqrt {N}$ , where $N$ is the number of frame pairs. The data in (c) contain error bars of $\pm \sigma$ .

As shown in the two rightmost plots of figure 8(c), a mean velocity profile of $U_{C}$ is reconstructed in which the centre-line velocity exceeds the correlated velocity near the channel walls. Furthermore, as expected for a hydrodynamically developed flow, the centre-line velocity exceeds the bulk velocity of the channel. As such, the imaged structures are assumed to travel at the local velocity of the flow. Hence, the fluctuations in image brightness can serve as ‘pseudo-tracers’ of the flow field when it is turbulent for the current thermodynamic conditions. However, the integrating property of shadowgraphy means that variations of refractive index at any lateral location in the channel are imaged. As a result, the resulting instantaneous displacement fields do not directly correspond to instantaneous, planar flow fields. Instead, the movement of all refractive structures throughout the channel is superimposed. Therefore, as the streamwise velocity of the pseudo-tracers varies laterally, their image velocimetry is characterised by relatively large fluctuations.

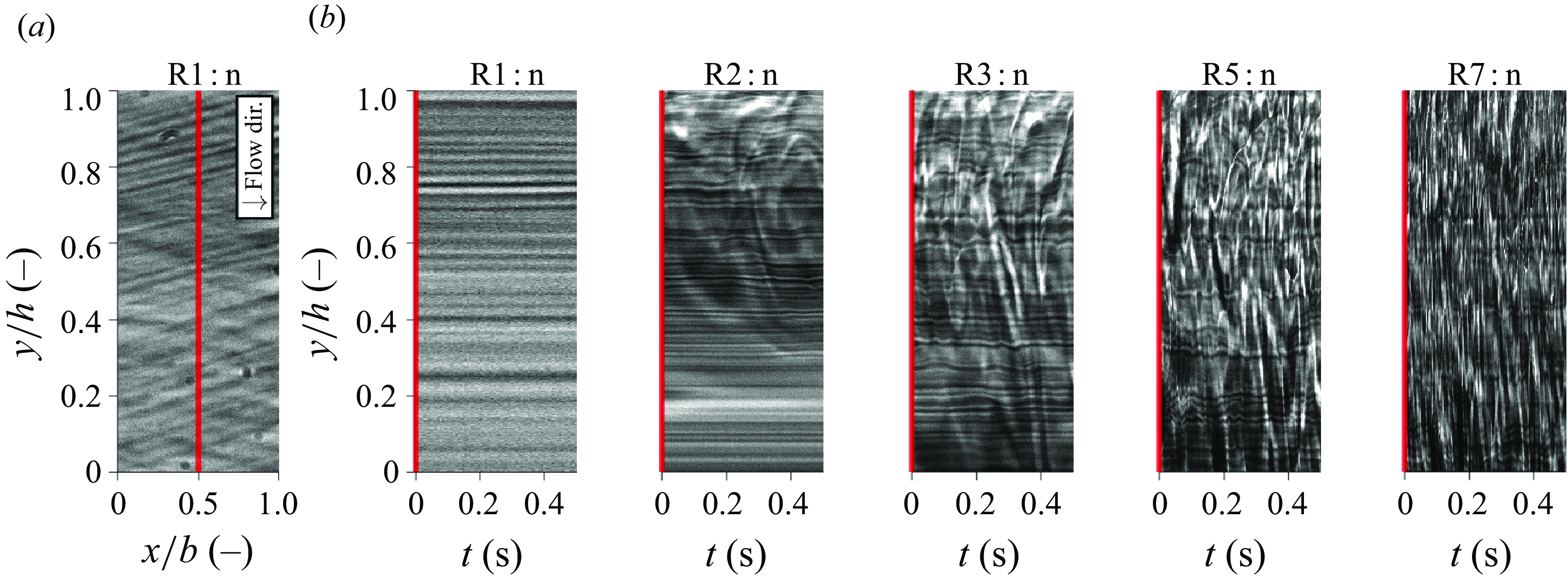
Figure 9. Space–time (b) representation of the optical signal at the vertical line that is indicated in the instantaneous shadowgrams shown in (a). The value of ${\textit {Re}}_{Dh}$ is progressively increased by increasing the mass flow rate for the cases shown in (b).

At low velocities the structures may decorrelate, yielding no contribution to the displacement correlation, and therewith biasing the result to lower displacements. Figure 8(c) shows this under-reconstruction of the bulk velocity in detail. In the figure, a range of reconstructed mean profiles of $U_{C}$ is presented, normalised with $U_{{imp}}$ . The NCL velocity $U_{{imp}}$ is increasingly under-captured for $Re_{Dh}\leqslant 3\times 10^3$ , most notably so near the bottom channel surface. Figure 9 elucidates the cause of this inadequate characterisation of the channel bulk velocity. Here, figure 9(b) shows the optical data captured over time along the vertical red line in figure 9(a). In the figure, strong fluctuations in image brightness are shown throughout the channel for large Reynolds number cases R5 : n and R7 : n, indicative of the passage of pseudo-tracers. As the Reynolds number is decreased, the flow becomes more sparsely ‘seeded.’ Initially, for R3 : n and R2 : n, fluctuations of the optical signal only persist in the region confined to the upper wall. In these cases the channel flow is likely thermally stratified, in which a separate layer that is lighter and more turbulent is formed on top of a denser, laminar layer. In figure 9(b), the latter is characterised by an optical signal that is predominantly constant in brightness over time. Whereas this quiescent region is confined to the bottom wall for cases R3 : n and R2 : n, it spans the full channel height for case R1 : n. As such, the channel flow in case R1 : n is assumed to be entirely laminar. As the laminar layer is largely homogeneous in density, its shadowgraphy will not portray the passage of thermal structures. As a result, the correlation of consecutive images underestimates the actual motion of the fluid. Therefore, only where sufficient turbulent mixing is present in cases R2 : n and R3 : n, near the top boundary of the channel, a velocity in the order of magnitude of $U_{C}$ is captured in figure 8(c). As the flow is sufficiently mixed such that no stratified layers appear throughout the channel for cases R4 : n and beyond, a more appropriate mean flow field is captured throughout the channel.

Lastly, the characterisation of the mean flow field shows a moderately negative mean $y$ -direction velocity $\bar {V}_{C}$ for the larger values of $Re_{Dh}$ within the considered range. Here, the downward motion of sporadic cold plumes within the channel is captured by the image velocimetry. The downdraughts, likely caused by the slight cooling of the $\text{CO}_2$ by the ambient in the vicinity of the visors, have previously been discussed.

The visualisation of the flow field using thermal turbulence as tracers has revealed a mean streamwise flow field characterised by features similar to those of hydrodynamically developed flows with subcritical fluids. However, the large uncertainty of the current method, and its inability to reconstruct a flow field when the flow is in a thermally homogeneous laminar flow state, makes its applicability limited. As such, the complete characterisation of instantaneous, planar flow fields at supercritical and thermally heterogeneous conditions requires additional and yet to be developed experimental techniques. Nevertheless, the shadowgrams and the velocimetry thereof can reveal instantaneous fluid motion and flow patterns (or the lack thereof) across the channel at high spatial and temporal frequencies when there is sufficient turbulent mixing in the property-variant working fluid. As such, shadowgrams reveal the transient, local phenomena underlying the greatly atypical heat transfer correlations reported in open experimental literature. Therefore, shadowgraphy is used to study the modulation of the channel flow by thermal stratification from here onwards.

4.2. Unstable stratification

Figure 10. Spacetime (b) representation of the optical signal at the vertical line that is indicated in the instantaneous shadowgram shown in (a). The bottom-up heating rate is progressively increased for the consecutive cases shown in (b).

When the rectangular channel is heated in the bottom-upward configuration, the perceived flow field within it is characterised by increased, mostly vertical movement. Currently, the cases shown in figure 4 are considered. Figure 10 shows the evolution of the shadowgraphy signal of the vertical red line indicated in figure 10(a) in figure 10(b). Here, the initially quiescent flow of case R1 : n is disturbed by movement induced by the unstably stratified $\text{CO}_2$ , and images of fluctuating brightness follow. Initially, for R1 : bh1, the upward motion in the shadowgrams is predominantly confined to the near-wall region at the bottom of the channel. As warm, lighter plumes rise towards the top of the channel when buoyancy is moderate, they are advected by the bulk flow in the streamwise direction. For this process, the angle of a streak of constant brightness with respect to the vertical axis increases over time in a space–time graph. The process of plume advection by the mean flow is more clearly shown in figure 11. Here, the channel is imaged in the period after which the heating state is instantaneously changed from R1 : n to R1 : bh5. For R1 : bh5, a heat flux of $\dot {q}=12.0\text{ kWm}^{-2}$ is applied. Mushroom-like plumes arise from the bottom of the channel in figures 11(a) and 11(b), as part of a wide, turbulent front. The plumes at the top of the front are overturned in the streamwise direction of the flow as they near the top of the domain in figure 11(d–f). As such, they form rollers that are ordered one after another in the streamwise direction of the flow, similar to those simulated by Garai et al. (2014) and Pirozzoli et al. (2017) for mixed unstable convection in ideal fluids. For the conditions in case R1 : bh1, the rollers are exclusively confined to the bottom two thirds of the channel.

Figure 11. Series of shadowgrams that show the evolution of the flow after an instantaneous step in bottom-upwards heating from cases R1 : n to R1 : bh5. For R1 : bh5, a heat flux of $\dot {q}=12.0\text{ kWm}^{-2}$ is applied. At time $t_0$ , the heating is commenced.

As the heating rate is increased from R1 : bh1 to R1 : bh2, the thermal structures originating from the heated bottom wall sporadically reach the top surface of the channel. The movement of these updrafts is characterised by straight lines of constant brightness at an angle with the vertical axis in figure 10(b). As the heating rate is further increased for cases R1 : bh3 and R1 : bh4, the relative number of plumes that traverse the channel in its entirety increases, and the image is eventually dominated entirely by the presence of these upward moving structures. Whereas shadowgraphy yields images of mostly constant brightness (see figure 10 a) when no heating is applied, instantaneous shadowgrams show a chaotic superposition of many plumes for cases R1 : bh3 and R1 : bh4, as shown in figure 11(f). In this buoyancy-dominated limit, the natural convection dominates the shadowgraphy, and the natural flow rates far exceeds the forced convection. Instead, the flow much resembles purely natural convection.

Figure 12 shows the reconstruction of the $x$ -component of the velocity for cases R1–R3 for a selection of heating rates. As explained in Appendix B, the flow field is reconstructed more accurately as the plumes act as traceable structures in the shadowgrams at moderate heating rates, e.g. bh1 and bh2. Conversely, in the limit of dominant natural convection at bh3 and beyond in the current experiments, the uncertainty in deducing image-pair displacements increases due to the rapid decorrelation of the superimposed thermal structures. Initially, a near-zero magnitude flow velocity is reconstructed for a large fraction of the channel for neutrally buoyant case n in figure 12(a). Here, the mean downstream flow imposed by the NCL is not captured by the shadow image velocimetry as it lacks contrast due to the absence of any fluctuations in intensity. As heating is applied the bottom surface, the channel flow is characterised by increasingly strong secondary flows. At first, for case bh1, moderate counter flow can be observed near the heated bottom surface. Eventually, for cases bh2 and beyond, a positive flow rate in the downstream direction is perceived near the opposite wall. Here, thermal plumes that reach the top of the channel act effectively as tracers of fluid motion, yielding a non-zero displacement field throughout the domain. As can be seen in figure 12(c–e), the two near-wall regions show velocities of opposite signs. Here, the significant dilation of the carbon dioxide has led to the formation of a cell in which the fluid recirculates continuously, with a cell width much larger than the current field of view.

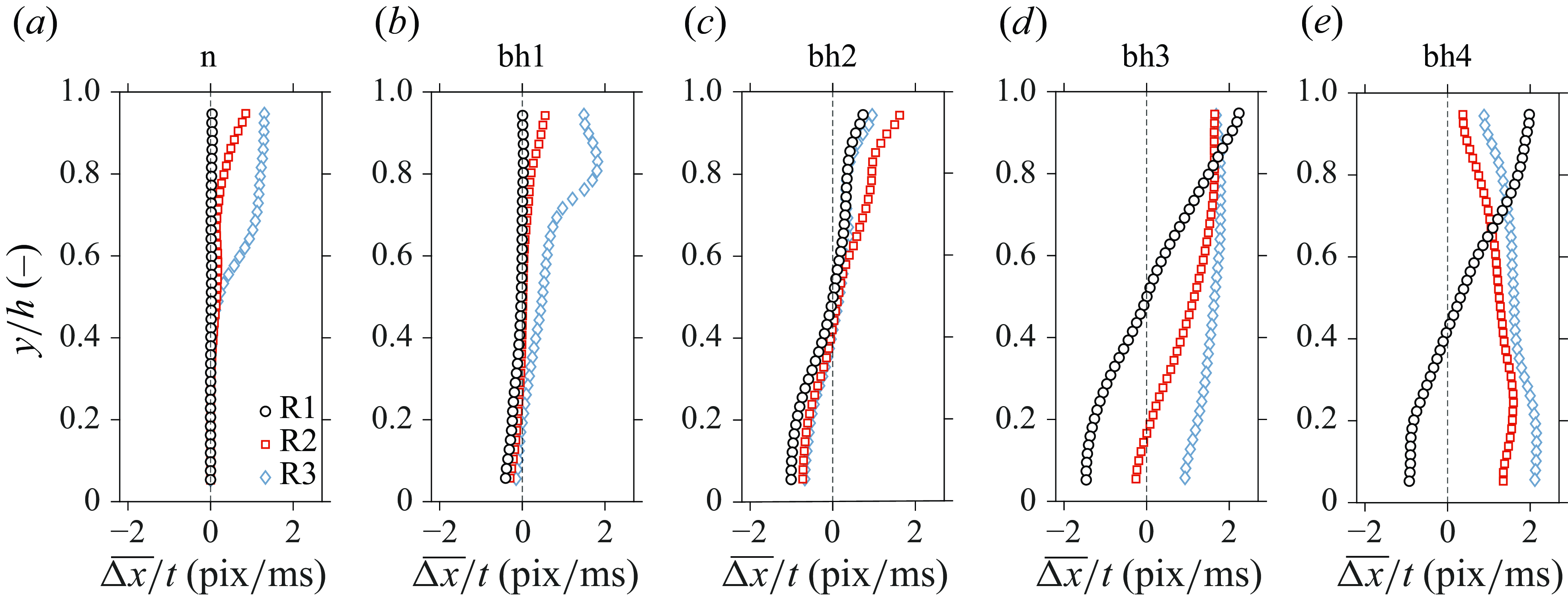
Figure 12. Mean perceived horizontal displacement rates $\overline {\Delta x}/t$ for cases R1–R3, with progressively increased bottom-up heating rates in the consecutive panels.

Figure 13. Mean perceived vertical displacements $\overline {\Delta y}/t$ for cases R1–R3, with progressively increased bottom-up heating rates in the consecutive panels.

In the unstably stratified configuration, the velocity of the upward plumes depends on the applied heating rate. The mean displacement rates of the plume motion is shown in figure 13. For cases bh1 and bh2, moderate and positive non-zero motion is only observed in the vicinity of the heated wall, in which plumes are perceived in the shadowgrams. The vertical velocity of the plumes increases as the heating rate is increased from bh1 to bh2. As the heating rate is further increased to case bh3, finite upward motion is seen throughout the channel. Here, the thermal plumes traverse the test section channel at a larger velocity than for cases bh1 and bh2. As the number of plumes that are produced increases further, the uncertainty in the deduction of their mean velocity also increases. Eventually, for case bh4, the upward displacement rates of a similar magnitude as the maximum $x$ -direction displacement rates for R1 and R2, as can be deducted from a comparison between figures 12(e) and 13(e). Importantly, the results of figure 13 do not necessarily imply that a net upward flow is present in the channel. Instead, figure 13 shows the motion of refractive structures somewhere within the channel.

4.3. Stable stratification

4.3.1. Turbulence attenuation

A process in which fluctuations and vertical movement are diminished follows from the top-down heating of the highly property-variant fluid for the cases in figure 5. Therewith, the flow of carbon dioxide is modulated in a distinctly dissimilar manner than for bottom-up heating. The sharp contrast between the response of flows subject to either stratification type can be highlighted by considering several points at different vertical positions within the channel. Figure 14 shows the normalised shadowgram intensity of the points over time. Initially, cases R2 : n and R5 : n are considered in figures 14(a) and 14(b), respectively. Here, the fluid in the channel remains unheated. Whereas the variability in the signal of case R2 : n is larger in its lighter top layer than in its denser bulk, its brightness (and therefore its density) is relatively homogeneous in time. After 9.3 s, a heating rate $\dot {q}$ with a magnitude of $12.0$ kWm $^{-2}$ is applied to the channel surface in the bottom-upwards configuration in figure 14(a). Some time after the heating has started, the unstably stratified density interface that is formed near the heated wall breaks down. A plume-laden front rises to the top of the channel follows, as is shown in figure 11. Eventually, the signal is saturated with frequent passages of rising plumes, evidenced by a large variability in image brightness over time.

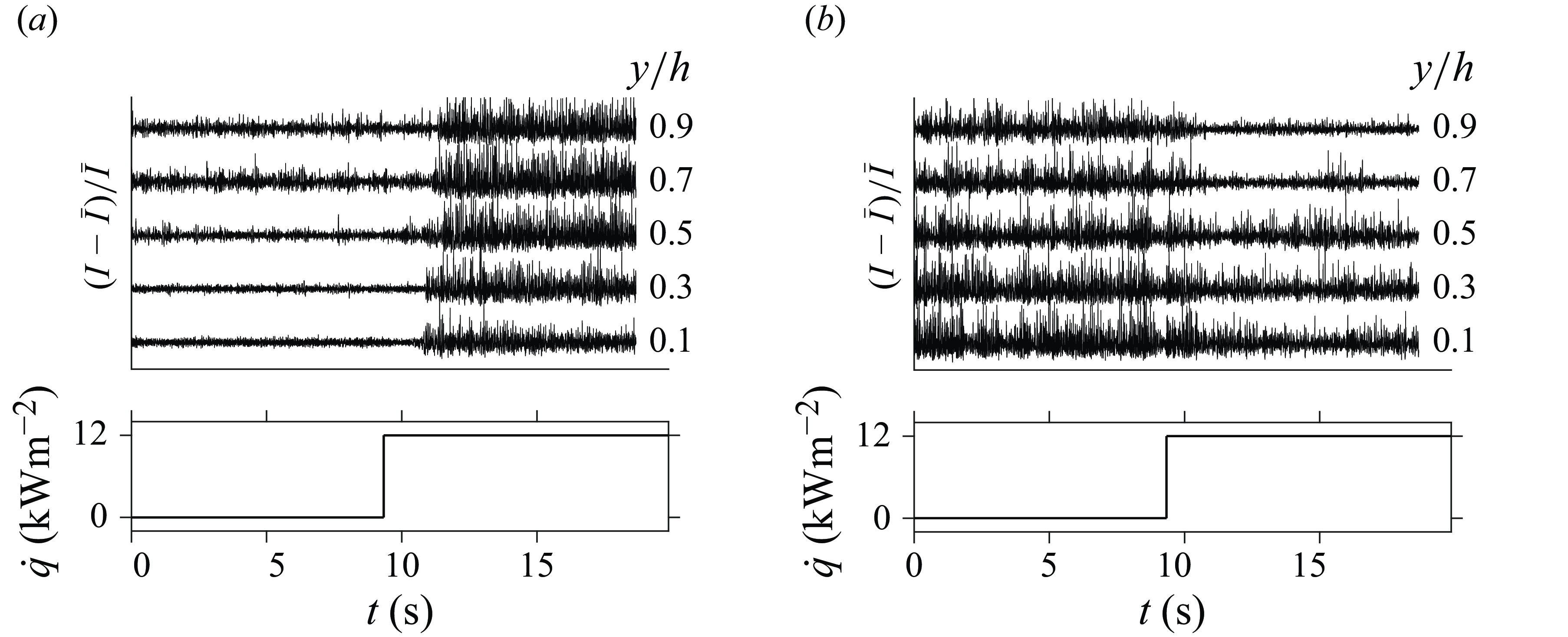
Figure 14. Image brightness $I$ over time. In (a) the carbon dioxide is heated from the bottom upwards from an initial state R2 : n. In (b) the carbon dioxide is heated from the top downwards from an initial state R5 : n.

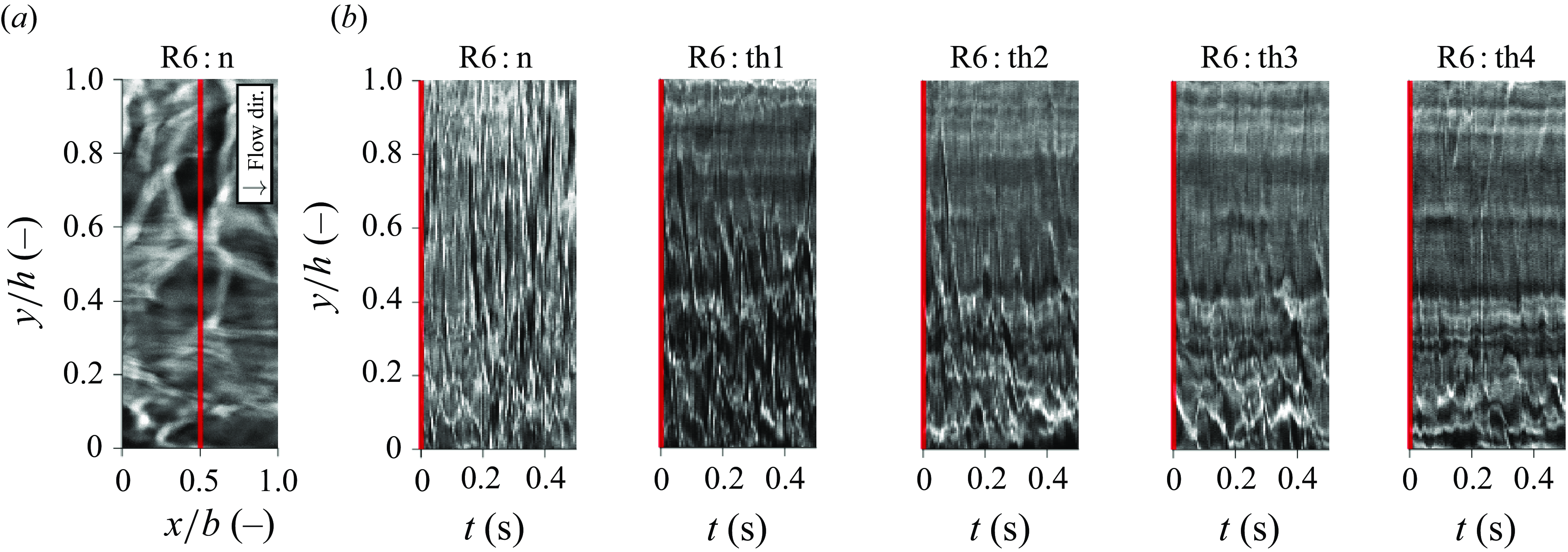
Figure 15. Space–time (b) representation of the optical signal at the vertical line that is indicated in the instantaneous shadowgram shown in (a). The top-down heating rate is progressively increased for the consecutive cases shown in (b).

Shadowgrams of case R5 : n, in which a larger mass flow rate is applied through the test section, are characterised by the intermittent passage of shadowgraph structures in an unheated setting. As the passage of refractive structures corresponds to consecutive maxima and minima in image brightness, the variability of the signal far exceeds that of case R2 : n. Similarly, a heating rate $\dot {q}$ with a magnitude of $12.0 \text{ kWm}^{-2}$ is applied to the channel surface in the top-down configuration after 9.3 s. Consequently, the variation in shadowgraphy signal in the region near the heated wall decreases significantly. Here, a region that is mostly homogeneous in brightness (and hence density) is formed. The layer is characterised by a near-complete suppression of fluctuations, with the occasional passage of a single refractive streak at moderate heating rates. Given its apparent homogeneity in density in both space and time, the flow of CO $_2$ within the homogeneous layer is considered to have relaminarised. The emergence of a homogeneous layer can also be observed in figure 15(b), in which the signal along the red, vertical line in figure 15(a) is shown over time. Here, the top-down heating rate is incrementally increased from R6 : n to R6 : th4. As the heating rate is increased, the non-fluctuating region expands away from the heated wall to cover a greater fraction of the channel height. As can be deducted from figure 5, the thickness of the layer furthermore depends on the imposed Reynolds number. There, the homogeneous layer becomes more limited in size as the Reynolds number is increased.

When the top surface of the flow is heated, the shape of the refractive structures in the shadowgrams changes. The orientation of the structures in the channel flow under unstable stratification for the cases shown in figure 5 is considered in figure 16. The boundaries of the refractive structures for the instantaneous shadowgram shown in figure 16(a) are presented in figure 16(b). An edge detection algorithm, similar to the one described by Lefauve & Couchman (2024), is used to detect the structure boundaries in the shadowgrams. Thereafter, the angle of all edges with the x-axis $\theta (x,y)$ is evaluated. The normalised value of $\bar {\theta }$ , averaged over 300 images, is presented in figure 16(c). When unheated, the flow contains structures of any shape and orientation, exhibiting gradients in density in any direction. Then, the value of $\bar {\theta }$ approaches $\pi /2$ . After heating is applied, the imaged streaks are found to re-orient within the channel. Structures that represent a constant density that initially span a finite vertical height are increasingly stretched in the streamwise direction. As a result, $\bar {\theta }$ reduces. As such, the fraction of the height of a channel spanned by a structure of constant density decreases. In the near-wall layer, vertically oriented streaks disappear altogether, revealing an axially homogeneous density field. Here, the originally irregular density field is assumed to be redistributed in the channel as the flow is heated.

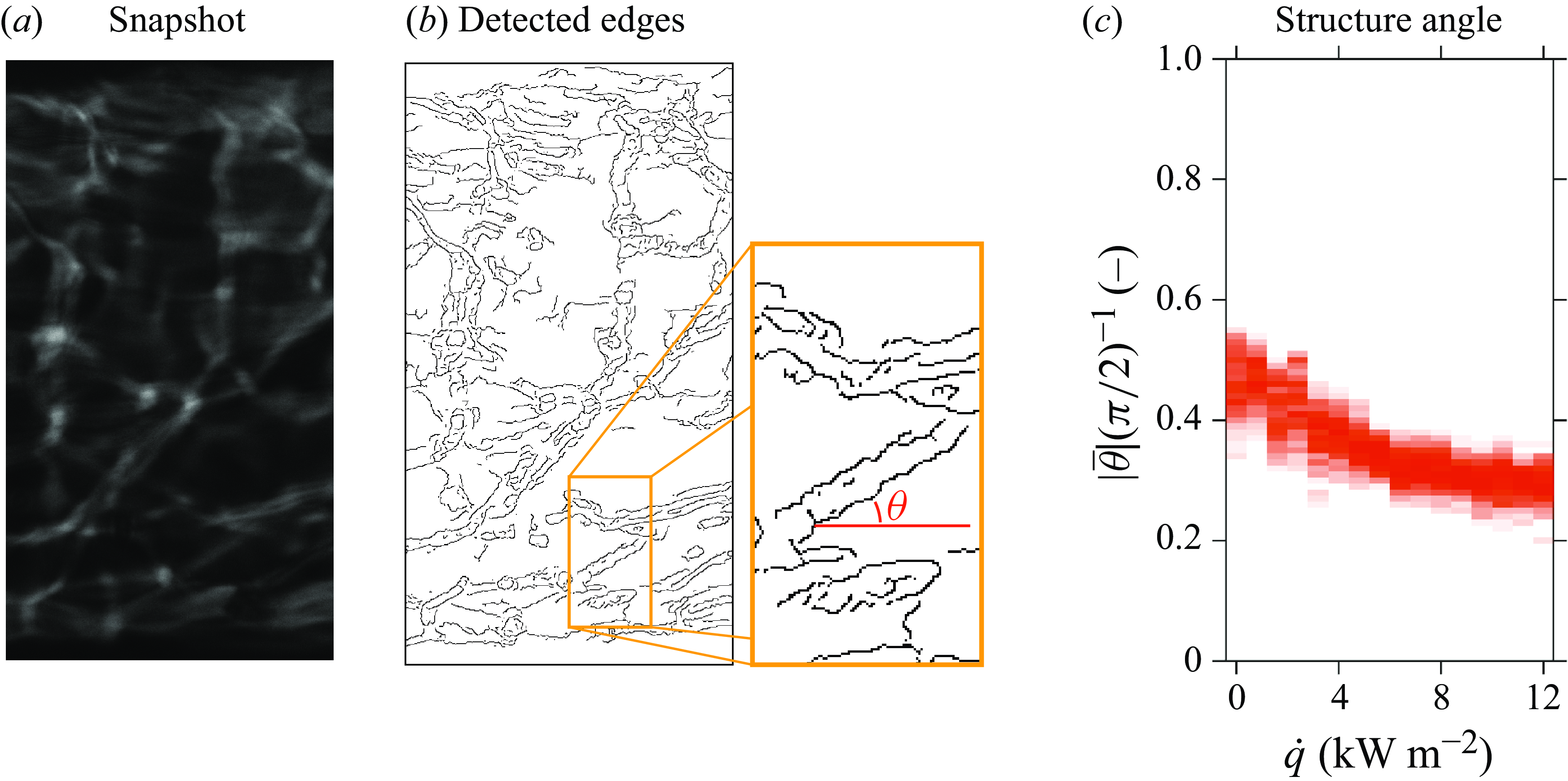
Figure 16. Thermal structure orientation as a function of the applied top-down heating rate. The edges (b) within any instantaneous shadowgraph (a) are detected as per Lefauve & Couchman (2024), and their local angle $\theta$ with the x-axis is evaluated. In (c), the mean absolute angles $|\bar {\theta }|$ of 300 snapshots are superimposed for each increment in $\dot {q}$ for case R7.

Figure 17. The displaced state of an in-focus pattern that is imaged through carbon dioxide at supercritical pressure is shown for various top-down heating rates for case R1 in (a). The original pattern is shown in black. The mean, interpolated local displacement for each point is used to shift the black pattern, yielding the pattern shown in red. Profiles of the path-integrated vertical gradients in refractive index are shown in (b). The data in (b) are shown with error bars of $\pm 2\sigma$ .

Figure 17 reveals that the initial density field is redistributed along a mean density gradient, imposed by the top-down heating. For the purpose of highlighting such mean gradients in refractive index, the BOS configuration indicated in cross-section B of figure 2 is considered. In figure 17, the deformation of a background pattern by the refractive $\text{CO}_2$ is considered. Only under stable stratification do the fluctuations in the optical signal attenuate sufficiently to get a clear BOS image. The considered reference pattern, shown in black in figure 17(a), is printed onto a transparent sheet and placed behind the $\text{CO}_2$ . As the carbon dioxide is heated, the pattern’s image deforms. The deformed images for cases R1: n, R1: th2 and R1: th4 are shown in red in figure 17(a). Here, the black pattern is shifted with the correlated deformation displacements at any point, yielding the deformed pattern shown in red. In neutrally buoyant case R1 : n, the imaged pattern remains in a predominantly undeformed state. As heating is applied to the top of the channel in cases R1: th2 and R1: th4, the dot pattern in the top half of the channel is stretched by variations in the refractive index. Here, the background pattern is deformed to a greater extent when the applied heating rate is increased. Figure 17(b) shows the vertical gradients in path-integrated refractive index that are deducted from the dot pattern displacements. Here, $n_0=1.17, M=0.5$ and $Z_{{D}}=8.9\cdot 10^{-2}$ m. The magnitude of the refractive index gradients are found to increase as greater heating rates are applied to the channel flow. Furthermore, the gradients are the largest in the near-wall region for all considered cases. The presence of a strong vertical gradient in $\bar {n}$ suggests the existence of an equivalent gradient in $\text{CO}_2$ density $\bar {\rho }$ in the current top-down heated configuration. Given the positive values of $\partial \bar {n}/\partial y$ in figure 17(b), the density of the carbon dioxide increases away from the heated wall. The imposed vertical gradient in $\bar {\rho }$ imposes a buoyant force on the fluid in the channel. As discussed by García-Villalba & Del Alamo (2011), fluid parcels of a certain density are pushed towards a preferential vertical position along the constant gradient.

Figure 18. Maximum instantaneous vertical displacements in the negative $y$ -direction for cases R4–R6, with progressively increased top-down heating rates in the consecutive panels.

If the buoyant force exceeds the inertial forces of a fluid parcel, its vertical movement is diminished once it is at its preferential position. This is true for an increasingly large density range and for an increasingly large portion of the channel as the imposed density gradient becomes sharper when the heating rate is increased. As a result, vertical motion is increasingly diminished in the near-wall region when heating is applied, as also shown in figure 18. In the figure, the largest instantaneous downward shadow displacements within the considered measurement interval are shown for cases R4–R6. Initially, for unheated case n, the flow is characterised by the sporadic vertical movement of eddies with a variable density. As moderate heating is applied for th1 and th2, vertical motion in the near-wall region is suppressed along the vertical density gradient. The region within which the vertical motion of turbulent eddies is suppressed grows as the heating rate is increased towards case th3. Eventually, most vertical motion is suppressed in case th4. The suppression of vertical motion is supported by the vertical thinning of the averaged correlation profiles, as shown in figure 23 of Appendix B.

4.3.2. Implications for PIV

The large deformation of the background pattern reveals limitations to the further characterisation of the flow at a near-p-c state beyond the spatial resolution that the current thermal tracers allow for. In particular, the large image distortions affect the applicability of PIV, where a correlation of the displacements of tracer particles is used to re-construct a flow field. The images of carbon dioxide at the current near-p-c conditions are characterised by large deformations both when the $\text{CO}_2$ is heated locally, and when refractive structures that correlate with the fluid motion are present in an unheated turbulent flow. Furthermore, the gradients of these deformations can be particularly large for heated turbulent flows, leading to image blur. Additionally, total internal reflections across stratified layers can lead to the local compression of the object in the image plane, obscuring its features. As a result, the apparent displacements of the particles may not correspond to their actual displacements. This is most prevalent as the tracers move across density gradients within the flow. The current back-projected error in determining the particle positions within the channel can be of the order of 100 $\unicode{x03BC} \text{m}$ . Therewith, it can exceed the particle diameters of the tracers (Valori et al. 2019; Michelis et al. 2024) that are relatively small to reduce slip velocities with the property-variant working fluid. As such, PIV systems may prove to be particularly difficult to calibrate when a flow displays large local variations in thermodynamic properties.

Figure 19. Wall temperature (a) and deducted wall density data (b) for a selection of cases with different nominal Reynolds numbers from figures 4 and 5. Bottom-up (bh) heating data points are shown with black-outlined markers, whereas top-down (th) heating data points are shown with homogenous markers. The data are shown with error bars of $\pm 2\sigma$ .

4.4. Overall heat transfer

4.4.1. Thermal response data

Measurements of the surface temperature of the heated walls serve to provide a quantitative context to the optical results presented in this work. Figure 19(a) shows the mean increase in heater temperature $T_{{w}}$ with respect to the constant bulk temperature $T_{{b}}$ for a selection of cases of either configuration. When the $\text{CO}_2$ is unstably stratified, the increase in surface temperature remains within 1.5 $^{\circ } \textrm{C}$ for the shown parameter range. Furthermore, the measured step in wall temperature decreases as the imposed heat flux is increased. Therefore, the heat transfer rate is expected to progressively improve as greater heating rates are imposed. Initially, a qualitatively similar trend is observed when the top surface of the channel is heated. However, beyond a threshold heat flux, a near-linear increase in wall temperatures (indicative of a predominantly constant heat transfer coefficient) is found for increasing heating rates. This threshold heat flux decreases with decreasing Reynolds numbers. Beyond $\dot {q}=4\text{ kWm}^{-2}$ , the near-wall temperatures of the two heating configurations start to significantly differ for any of the considered Reynolds numbers. Eventually, for the largest heating rate considered in this work, the increase in surface temperature of the stable stratification exceeds the unstable stratification’s temperature increase by twofold. As such, heat is removed much more effectively from the heated wall in the unstably stratified setting than it is in a stably stratified configuration for the current experimental conditions of supercritical pressure CO $_2$ .

Figure 19(b) shows the relative expansion of the carbon dioxide in the vicinity of the heated wall, as deducted from the wall temperature data of figure 19(a). In accordance with the wall temperature data, the heating-induced density change is significantly larger for stable stratification than it is for unstable stratification. As such, the degree of stratification (expressed by the Richardson number) is greater when the stratification is stable than when it is unstable under equivalent heating, as previously noted in figure 6. The relative difference in dilation even exceeds the relative difference in surface temperature increase, as can be deducted from the increasingly superlinear trend in density variation during stable stratification. Here, the carbon dioxide exhibits increasingly large variations in density as it is heated towards the nonlinear p-c curve from the liquid-like test section inlet conditions.

4.4.2. Characterisation of heat transfer

The analysis of the current experimental heat transfer data reveals trends that are in qualitative agreement with findings from the open literature, and with the optical data presented in this work. When sub-p-c CO $_2$ is heated, its heat transfer changes through changes in the near-wall heat capacity, viscosity, thermal conduction and density (Hall, Jackson & Watson 1967; Yoo 2013). To understand the current experimental results, we first focus on the influence of variations in the former three thermophysical properties, which dominate when buoyancy effects are negligible at moderate heating rates in forced convection (Jackson 1979). As the fluid is heated towards the p-c curve at a set bulk Reynolds number, its near-wall viscosity and thermal conductivity decrease. These reductions lead to a decrease in the skin friction coefficient and wall-normal conduction, worsening the convective heat transfer (Nemati et al. 2015). However, this effect is overshadowed (Jackson 1979; Licht, Anderson & Corradini 2008; Nemati et al. 2015) by the stronger increase in near-wall heat capacity, $c_{{p}}$ , as is illustrated in figure 1, resulting in an overall enhancement of heat transfer (Yamagata et al. 1972; Jackson 1979; Licht et al. 2008). The rise in near-wall heat capacity limits the temperature increase of the near-wall CO $_2$ at a constant heat flux, reducing the temperature difference between the bulk and the near-wall region (Licht et al. 2008). Consequently, the apparent convective heat transfer coefficient and the Nusselt number increase (Jackson 1979; Licht et al. 2008). The heat transfer of the initially liquid-like carbon dioxide continues to improve until the near-wall temperature reaches the p-c curve, where $c_{{p}}$ peaks.

Variations in near-wall density affect the behaviour of fluids at supercritical pressures in two distinct ways. The strong expansion of the fluid upon heating can accelerate the near-wall flow, depending on both the direction of the fluid flow and the direction of the heat transfer (Nemati et al. 2015; Wahl et al. 2022). This modulation of shear rates increases skin friction, thereby enhancing the overall heat transfer rate. In the current experiment, such acceleration is expected only in the top-down heating configuration. There, stable stratification counteracts the vertical transport of the lighter, hotter fluid throughout the channel, accelerating the near-wall layer of fluid at the top (Jackson 2013; Chu & Laurien 2016). However, limitations of the current ‘shadow velocimetry’ prevent reliable measurements of this acceleration when the homogeneous layer forms under stable stratification. Therefore, the remainder of the present discussion on the measured heat transfer instead only considers the consequences of the modulation of the flow by buoyancy when sufficiently large variation in density is induced (Jackson 2013). These buoyant effects either aid or oppose the heat transfer enhancement by the increasing magnitude of $c_{{p}}$ , depending on the heat transfer configuration.

To highlight the influence of buoyancy on the measured heat transfer, the mean Nusselt number $Nu_{{w}}$ is shown as a function of the Richardson number $Ri$ in figure 20, for a selection of cases of either configuration. There

(4.2) \begin{equation} Nu_{{w}}=\alpha \cdot \frac {h}{\lambda _{{w}}}=\frac {\dot {q}}{T_{{w}}-T_{{b}}}\cdot \frac {h}{\lambda _{{w}}}, \end{equation}

with $\alpha$ as the convective heat transfer coefficient, evaluated in experiment using the imposed heat flux $\dot {q}$ and the temperature difference over the channel. Moreover, $\lambda _{{w}}$ is the near-wall thermal conductivity, evaluated at $T_{{w}}$ and $P_{{b}1}$ . When buoyancy is non-dominant, at $Ri\lesssim 0.1$ , the empirical heat transfer coefficients of the two considered heat transfer orientations are of a similar magnitude. However, as buoyancy becomes non-negligible for larger heating rates, the values for $Nu_{{w}}$ diverge.

When the carbon dioxide is heated from the bottom upwards at the current thermodynamic conditions, both buoyancy effects and an increase in specific heat act to enhance its heat transfer, increasing $Nu_{{w}}$ with respect to its neutrally buoyant value. The shadowgrams of unstably stratified $\text{CO}_2$ (shown in figure 4) are characterised by the strong secondary flows that are elaborated on in figures 10–13. In the limit of small Reynolds numbers, plume motion is observed to form recirculation cells that locally counteract the imposed forced convection. For any $Re_{Dh}$ , the expansion of $\text{CO}_2$ causes motion in the wall-normal direction, in which parcels of lighter fluid are locally lifted towards the denser bulk flow. Here, hotter fluid is continuously carried away from the heated wall, replacing it with a denser and colder fluid that is recirculated. Therewith, the mean near-wall fluid temperature decreases with respect to an equivalent neutrally buoyant setting, leading to the sub-linear increase of $(T_{{w}}-T_{{b}})$ in figure 19(a). Furthermore, the vertical plume motion increases the wall-normal momentum transport in the channel. Consequently, the vertical energy transport also increases with respect to purely forced convection, as characterised by the enhancement of $Nu_{w}$ in figure 20. However, this effect diminishes as the relative inertial contributions increase. Therefore, $Nu_{{w}}$ decreases with increasing $Re_{{Dh}}$ at a set heating rate. Contrary to a previous empirical investigation of purely bottom-upwards heated micro-channels of $\text{CO}_2$ with $Ri\lessapprox 1$ by Whitaker et al. (2024), the relative enhancement of the heat transfer progressively increases as buoyant forces become increasingly dominant at larger $Ri$ within the current parameter range. A progressive improvement of the heat transfer with increasing degrees of unstable stratification is, however, in accordance with the current optical data. Here, the spatial density of the plumes and their lift velocities are found to both increase at greater heating rates, increasing the vertical momentum transfer in the channel. As such, the progressive enhancement of the heat transfer as buoyancy becomes more dominant with increasing degrees of unstable stratification in figure 20 is expected from the increasingly prevalent motion of the thermal plumes.

Figure 20. Nusselt number (main figure) and heat transfer coefficient data (top right corner) for a selection of cases from figures 4 and 5, as a function of the deducted value for $Ri$ . Bottom-up (bh) heating data points are shown with black-outlined markers, whereas top-down (th) heating data points are shown with homogenous markers. The data are shown with error bars of $\pm 2\sigma$ .

When the carbon dioxide is heated in the top-down configuration, the buoyancy caused by decreasing near-wall density opposes the heat transfer enhancement induced by the variation in near-wall heat capacity. At low $Ri$ , the effects of a variable $c_{{p}}$ dominate, improving the heat transfer as $\dot {q}$ is increased. Eventually, as buoyancy becomes more dominant for larger $Ri$ , the heat transfer deteriorates, yielding a maximum in $Nu_{{w}}$ that resembles the results of Yamagata et al. (1972) and Bae, Kim & Kang (2010). This deterioration of the heat transfer by buoyancy is supported by the current optical results. In the shadowgrams, the imposed density gradient of figure 17 is found to counteract vertical movement as the carbon dioxide is heated at the top surface of the channel, as is elaborated in figures 15 and 18. The resulting flow is characterised by the suppression of intermittent, irregular motion. Here, the mixing of distinct layers with different densities is counteracted. As such, the lighter fluid that is formed at the heated top wall remains predominantly in the near-wall region. As a result, the overall near-wall temperature increases. Therewith, the wall-normal heat transfer rate deteriorates in comparison with a neutrally buoyant flow, in which the wall-normal movement of warmer eddies removes hot fluid from the heated wall. Notably, at large values of $Ri$ , the values of $Nu_{{w}}$ for the current results coincide, as is shown in figure 20. Here, $Nu_{{w}}$ attains an asymptotic value, irrespective of the imposed Reynolds number. For these conditions, $Nu_{{w}}$ can be described using

(4.3) \begin{equation} Nu_{{w}}=\frac {120}{Ri^{\frac {1}{3}}}+185, \end{equation}

as indicated with the black, dashed line in figure 20. Contrary to the progressive enhancement of the heat transfer under unstable stratification, $Nu_{{w}}$ only moderately decreases as a function of $Ri$ when the heat transfer deteriorates. This moderate dependence on $Ri$ is in qualitative agreement with the shadowgraphy, as the intermittency of the optical signal shows minimal changes upon the initial suppression of fluctuations by the thermal stratifications. Then, only a change in the height of the homogenised layer follows from a further increase in $Ri$ .

To highlight the non-ideality of the current heat transfer, we plot the Nusselt number as a function of the Richardson number in the inset of figure 20. There, the Nusselt number is expressed in terms of the Richardson number, which is re-defined as a function of $(T_{{w}}-T_{{b}})$ and $\beta _{{b}}$ , with

(4.4) \begin{equation} Ri = \frac {\beta _{{b}}\left (T_{{w}}-T_{{b}}\right )gh}{U_{{imp}}^2}, \end{equation}

where $\beta _{{b}}$ is the volumetric expansivity, evaluated at $T_{{b}1}$ and $P_{{b}1}$ . By substituting $(T_{{w}}-T_{{b}})$ into a Nusselt number that is evaluated at the bulk conditions, with

(4.5) \begin{equation} Nu = \frac {\dot {q}}{\left (T_{{w}}-T_{{b}}\right )}\frac {h}{\lambda _{{b}}}, \end{equation}

where $Nu$ can be expressed as a function of $Ri$ , namely

(4.6) \begin{equation} Nu = \dot {q}\cdot \frac {\rho _{{b}}^2\beta _{{b}}}{\mu _{{b}}^2\lambda _{{b}}}\cdot \frac {gh^2D_{{h}}^2}{Re_{{Dh}}^2}\cdot \frac {1}{Ri}. \end{equation}

Equation (4.6) enables a comparison of $Nu$ for several fluids at similar operating parameters corresponding to the current experiments. The respective curves in the inset are plotted using the thermophysical properties of air and water at atmospheric conditions (at 20 $^{\circ }$ C) and of CO $_2$ at the current experimental conditions, all for a heat flux of $\dot {q}=\dot {q}_{{max}}=12\,\textrm{kWm}^{-2}$ . The experimental data (indicated using markers in the inset) for both stably and unstably stratification coincide with the curves of $Nu$ for CO $_2$ at the current conditions. The results reveal a striking contrast: for a heat transfer configuration with a given Nusselt number, the Richardson numbers for CO $_2$ exceed those of air and water by several orders of magnitude. This confirms that buoyancy effects, which are negligible in typical subcritical single-phase systems, readily dominate heat transfer at supercritical pressures.

The significant non-ideality of the observed heat transfer strongly affects the performance of near-p-c heat exchangers in energy conversion systems at supercritical pressures. As buoyancy readily dominates at their operating conditions, the resulting heat transfer deviates strongly from equivalent but neutrally buoyant systems. As a result, the direction of the applied heat transfer strongly affects the behaviour within heat exchangers that operate in the vicinity of the p-c curve. Within the current parameter range, a significant difference between the heat transfer rates of purely top-heated and purely bottom-heated flow of carbon dioxide at supercritical pressure is observed. This difference is most notable for the larger heating rates in this work, for which the bottom-up heat transfer coefficient exceeds the top-down heat transfer coefficient by nearly a full order of magnitude, as shown in figure 20. However, in the flow channels of plate heat exchangers or a printed circuit heat Exchanger, heat is generally exchanged in multiple directions. As such, the heat transfer enhancement near the bottom wall and the heat transfer deterioration near the top wall compete when the flow is heated. If the heating rate for both surfaces is equal, much like in the current work, the degree of stratification is greater in the region near the top wall. Therefore, the lower-density layer near the top wall would likely not be fully disrupted by the upward movement of plumes created at the bottom wall. Therewith, the behaviour within the heat exchanger would be qualitatively similar to a pipe flow to which a constant heat flux is applied (Chu & Laurien 2016). Therefore, the equivalent heat transfer coefficient of the heat exchanger channel is expected to lie between the deteriorated and enhanced values of the one-sided heating configurations that are considered in this work.

5. Conclusions

In this work, the modulation of the turbulence and the stability of a continuous flow of a supercritical fluid by non-negligible buoyancy is investigated. Such flows are for instance prevalent in novel energy conversion systems that operate at supercritical pressures, which have gained particular recent interest for their potential to sustainably produce power and industrial heat. Within the heat exchangers of these energy systems in particular, non-negligible buoyancy may lead to highly non-ideal and configuration-dependent heat transfer.

The current experimental facility employs the natural circulation of carbon dioxide that is passed through an optically accessible test section. To study the hydrodynamically developed flows of carbon dioxide at supercritical pressures within the test section, shadowgraphy is used in parallel with surface temperature measurements. The shadowgraphy is used to visualise a side-view, path-integrated flow field. When the temperature of the $\text{CO}_2$ is sufficiently heterogeneous, thermal structures within the flow can be distinguished in the shadowgrams. As the structures are observed to move with the flow, they are considered to act as thermal flow tracers. As such, a correlation of their displacements yields velocity components in the directions perpendicular to the optical axis. It is validated that the mean streamwise displacements of these pseudo-tracers correspond to the expected mean flow velocity inside the test section, provided that the $\text{CO}_2$ is sufficiently turbulent (i.e. $Re_{{Dh}}\gtrsim 3\cdot 10^3$ ) and neutrally buoyant. However, the shadow image velocimetry is characterised by relatively large uncertainties, as the method depends on the local occurrence of density fluctuations (leading to variations in refractive index) of the flow, and the finite coherence of these structures in time. Furthermore, additional, rigorous calibration is necessary to translate the shadow displacements to physical velocities when large global refractive index gradients are present in the channel under heating conditions. Nevertheless, the shadowgrams can distinguish flow movement patterns within the channel unique to either stratification type when the $\text{CO}_2$ is heated either from the bottom or from the top of the test section. As such, the shadowgraphy serves to reveal the highly transient behaviour behind the non-ideal, and thermally inert heat transfer results in the existing open literature to date.

The rectangular flow channel is heated unidirectionally in either vertical direction to impose a density gradient on the carbon dioxide within it. The $\text{CO}_2$ , initially at 88.5 bar and 32.6 $^{\circ } C$ , is heated towards the p-c curve. As the carbon dioxide displays sharp variations in thermodynamic properties in the vicinity of this curve, strong stratifications are observed for remarkably moderate heating rates. Achieving a comparable degree of stratification in subcritical single-phase fluids would require significantly larger length scales and heating rates. Consequently, these strong stratifications lead to the modulation of the initially neutrally buoyant base flow, as is shown in figures 4 and 5. Depending on the stratification type, the variability in the flow is either enhanced or suppressed.

When the channel is heated from the bottom upwards, the flow is characterised by increasingly strong secondary movement. Here, light plumes are seen to intermittently depart from the heated surface, limiting its increase in temperature. Both the wall-normal velocity and the spatial density of these plumes are found to increase as the applied heating rate is increased. As these effects enhance the energy exchange with the heated wall, they further support the heat transfer enhancement by the increase in near-wall heat capacity of the supercritical working fluid. As a result, the Nusselt number is found to progressively increase with respect to the neutrally buoyant case for all considered Reynolds numbers.

On the contrary, when only the top surface of the flow channel is heated buoyancy acts against the heat transfer enhancement by the varying specific heat capacity. Consequently, the heat transfer deteriorates at large heating rates when buoyancy becomes more significant. This deterioration in heat transfer coincides with the suppression of oscillations in the optical signal by the stable density gradient imposed by the heating. This imposes a restriction in vertical motion and mixing across the density gradient that limits the wall-normal motion of hot $\text{CO}_2$ from the heated surface, therewith reducing its heat transfer coefficient.

The present work emphasises the necessity for the further investigation of buoyancy modulated turbulence and heat transfer in the near-p-c region beyond the current experimental conditions. Whereas the current results provide novel empirical insights in strong one-directional stratifications, the interplay of the opposing stratification remains unknown in the context of channel flows. Therefore, in order to properly describe the flow of supercritical carbon dioxide within horizontal heat exchanger channels, two-sided heating should also be considered. Furthermore, the current experimental framework can be extended to study the influence of non-negligible buoyancy in physical configurations beyond the current one. Therewith, vertical flows of highly property-variant fluids, where buoyancy also has a pronounced effect, can also be considered.

By improving the used optical diagnostics, they can serve as references for the improvement of hydrodynamic and heat transfer models. A further increase in the spatial resolution in of the shadow velocimetry in particular can for instance be achieved with the local, in situ generation of thermal tracers. As an additional consequence, the flow can also be visualised when thermal tracers are not naturally present in the supercritical carbon dioxide. Furthermore, by controlling the ambient temperature of the test section, the current framework could be extended to obtain discernible optical data for a greater thermodynamic range at supercritical pressures.