Hostname: page-component-5b777bbd6c-2c8nx Total loading time: 0 Render date: 2025-06-19T12:19:43.400Z Has data issue: false hasContentIssue false
  • English
  • Français

A unified framework for mean temperature analysis in compressible turbulent channel flows

Published online by Cambridge University Press:  28 May 2025

Xuke Zhu ,
Peng Zhang ,
Xiaoshuo Yang ,
Yongchao Ji  and
Zhenhua Xia Open the ORCID record for Zhenhua Xia [Opens in a new window]
Xuke Zhu
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems and Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, PR China
Peng Zhang
Affiliation:
College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, PR China
Xiaoshuo Yang
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems and Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, PR China
Yongchao Ji
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems and Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, PR China
Zhenhua Xia*
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems and Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, PR China
*
Corresponding author: Zhenhua Xia, xiazh1006@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

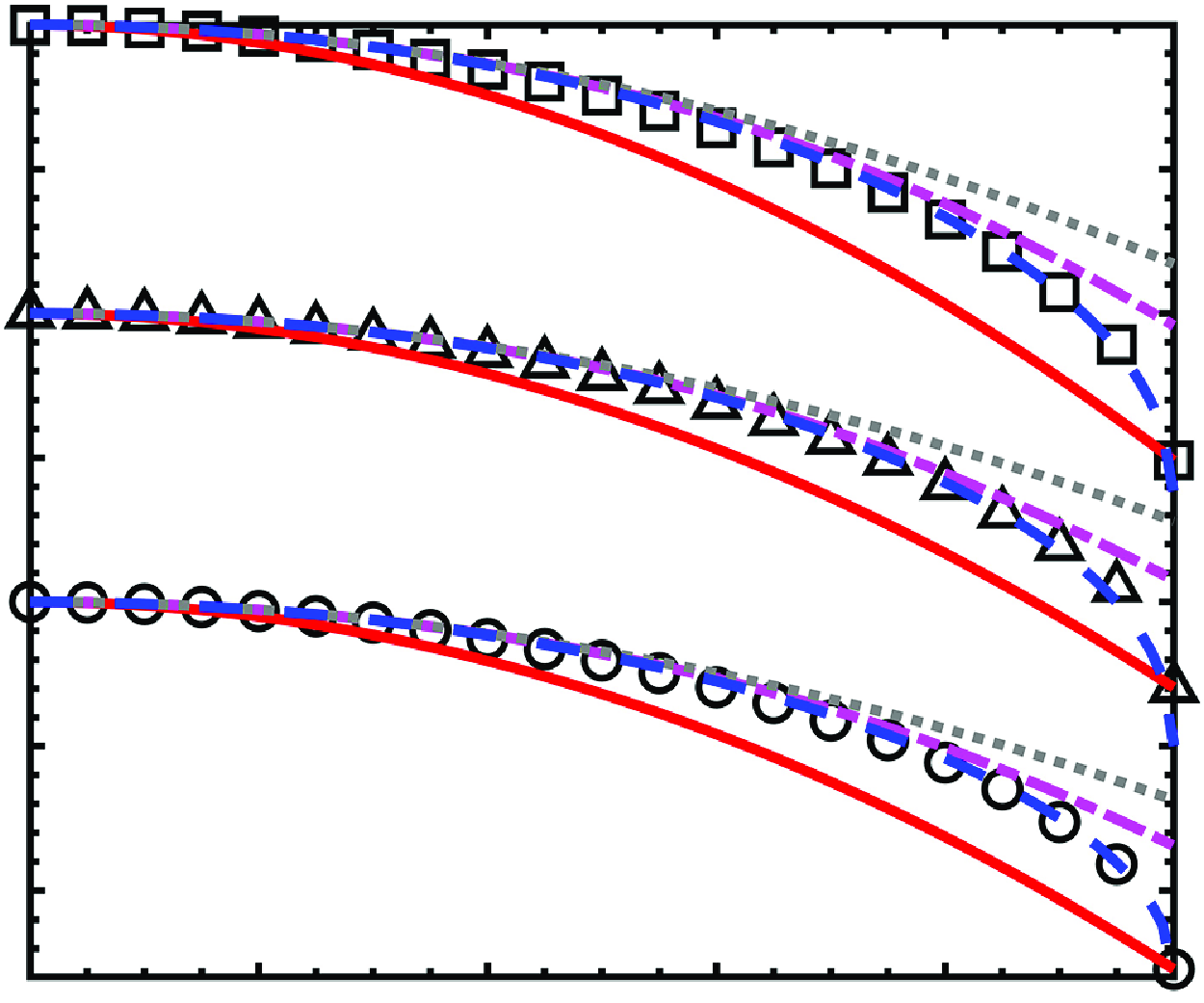
We present a unified framework derived from the total heat flux equation, enabling the direct formulation of the relationship between mean temperature and velocity fields, as well as the development of mean temperature scalings in compressible turbulent channel flows. The proposed mean temperature–velocity relationship, combined with a simple damping function model for the mixed Prandtl number, demonstrates high efficacy in channels with both symmetric and asymmetric thermal boundary conditions across a range of Mach and Reynolds numbers. In contrast, the state-of-the-art generalised Reynolds analogy (GRA) relation (Zhang et al., 2014, J. Fluid Mech., vol. 739, pp. 392–420) is shown to be insufficient for asymmetric cases due to mismatched boundary conditions at the effective boundary layer edge. By introducing a mean temperature decomposition, we clarify that while the GRA relation effectively characterises the component associated with turbulence production and viscous dissipation, it fails to account for the contribution arising from non-zero edge total heat flux. Furthermore, we rigorously derive mean temperature transformations compatible with arbitrary velocity scalings for the first time. These findings provide some physical insights into the mean momentum and heat transport in compressible wall-bounded turbulence, and may be helpful for developing near-wall models.

JFM classification

Turbulent Flows: Compressible turbulence Turbulent Flows: Turbulence theory
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 1012 , 10 June 2025 , R2
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abe, H. & Antonia, R.A. 2019 Mean temperature calculations in a turbulent channel flow for air and mercury. Intl J. Heat Mass Transfer 132, 1152–1165.10.1016/j.ijheatmasstransfer.2018.11.100CrossRefGoogle Scholar
Busemann, A. 1931 Handbuch der Experimentalphysik, vol. 4. Geest und Portig.Google Scholar
Chen, P.E.S., Huang, G.P., Shi, Y.P., Yang, X.I.A. & Lv, Y. 2022 a A unified temperature transformation for high-Mach-number flows above adiabatic and isothermal walls. J.Fluid Mech. 951, A38.10.1017/jfm.2022.860CrossRefGoogle Scholar
Chen, P.E.S., Lv, Y., Xu, H.H.H.A., Shi, Y.P. & Yang, X.I.A. 2022 b LES wall modeling for heat transfer at high speeds. Phys. Rev. Fluids 7 (1), 014608.10.1103/PhysRevFluids.7.014608CrossRefGoogle Scholar
Chen, X.L., Gan, J.P. & Fu, L. 2024 An improved Baldwin–Lomax algebraic wall model for high-speed canonical turbulent boundary layers using established scalings. J.Fluid Mech. 987, A7.10.1017/jfm.2024.383CrossRefGoogle Scholar
Chen, X.L., Gan, J.P. & Fu, L. 2025 The mean temperature–velocity relation and a new temperature wall model for compressible laminar and turbulent flows. J.Fluid Mech. 1009, A39.10.1017/jfm.2025.312CrossRefGoogle Scholar
Cheng, C., Chen, X.L., Zhu, W.K., Shyy, W. & Fu, L. 2024 Progress in physical modeling of compressible wall-bounded turbulent flows. Acta Mech. Sin. 40 (1), 323663.10.1007/s10409-024-23663-xCrossRefGoogle Scholar
Cheng, C. & Fu, L. 2024 a Mean temperature scalings in compressible wall turbulence. Phys. Rev. Fluids 9 (5), 054610.10.1103/PhysRevFluids.9.054610CrossRefGoogle Scholar
Cheng, C. & Fu, L. 2024 b A Reynolds analogy model for compressible wall turbulence. J.Fluid Mech. 999, A20.10.1017/jfm.2024.981CrossRefGoogle Scholar
Crocco, L. 1932 Sulla trasmissione del calore da una lamina piana a un fluido scorrente ad alta velocita. L’Aerotecnica 12, 181–197.Google Scholar
Duan, L. & Martin, M.P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part 4. Effect of high enthalpy. J.Fluid Mech. 684, 25–59.10.1017/jfm.2011.252CrossRefGoogle Scholar
Gatski, T.B. & Bonnet, J.-P. 2013 Compressibility, Turbulence and High Speed Flow. Academic Press.Google Scholar
Griffin, K.P., Fu, L. & Moin, P. 2021 Velocity transformation for compressible wall-bounded turbulent flows with and without heat transfer. Proc. Natl Acad. Sci. USA 118 (34), e2111144118.10.1073/pnas.2111144118CrossRefGoogle ScholarPubMed
Griffin, K.P., Fu, L. & Moin, P. 2023 Near-wall model for compressible turbulent boundary layers based on an inverse velocity transformation. J. Fluid Mech. 970, A36.10.1017/jfm.2023.627CrossRefGoogle Scholar
Hasan, A.M., Larsson, J., Pirozzoli, S. & Pecnik, R. 2023 Incorporating intrinsic compressibility effects in velocity transformations for wall-bounded turbulent flows. Phys. Rev. Fluids 8 (11), L112601.10.1103/PhysRevFluids.8.L112601CrossRefGoogle Scholar
Hendrickson, T.R., Subbareddy, P. & Candler, G.V. 2022 Improving eddy viscosity based turbulence models for high speed, cold wall flows. In AIAA SCITECH. 2022 Forum. AIAA.10.2514/6.2022-0589CrossRefGoogle Scholar
Hendrickson, T.R., Subbareddy, P., Candler, G.V. & Macdonald, R.L. 2023 Applying compressible transformations to wall modeled LES of cold wall flat plate boundary layers, AIAA SCITECH. 2023 Forum.. AIAA.10.2514/6.2023-2635CrossRefGoogle Scholar
Huang, P.G., Bradshaw, P. & Coakley, T.J. 1993 Skin friction and velocity profile family for compressible turbulentboundary layers. AIAA J. 31 (9), 1600–1604.10.2514/3.11820CrossRefGoogle Scholar
Huang, P.G., Bradshaw, P. & Coakley, T.J. 1994 Turbulence models for compressible boundary layers. AIAA J. 32 (4), 735–740.10.2514/3.12046CrossRefGoogle Scholar
Huang, P.G. & Coleman, G.N. 1994 Van Driest transformation and compressible wall-bounded flows. AIAA J. 32 (10), 2110–2113.10.2514/3.12259CrossRefGoogle Scholar
Huang, P.G., Coleman, G.N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.10.1017/S0022112095004599CrossRefGoogle Scholar
Huang, P.G., Coleman, G.N., Spalart, P.R. & Yang, X.I.A. 2023 Velocity and temperature scalings leading to compressible laws of the wall. J. Fluid Mech. 977, A49.10.1017/jfm.2023.1013CrossRefGoogle Scholar
Lluesma-Rodríguez, F., Hoyas, S. & Perez-Quiles, M.J. 2018 Influence of the computational domain on DNS of turbulent heat transfer up to $Re_\tau = 2000$ for $Pr = 0.71$ . Intl J. Heat Mass Transfer 122, 983–992.10.1016/j.ijheatmasstransfer.2018.02.047CrossRefGoogle Scholar
Lusher, D.J. & Coleman, G.N. 2022 Numerical study of compressible wall-bounded turbulence – the effect of thermal wall conditions on the turbulent Prandtl number in the low-supersonic regime. Intl J. Comput. Fluid Dyn. 36 (9), 797–815.10.1080/10618562.2023.2189247CrossRefGoogle Scholar
Modesti, D. & Pirozzoli, S. 2024 Friction and heat transfer in forced air convection with variable physical properties. J. Fluid Mech. 1001, A27.10.1017/jfm.2024.1098CrossRefGoogle Scholar
Patel, A., Boersma, B.J. & Pecnik, R. 2017 Scalar statistics in variable property turbulent channel flows. Phys. Rev. Fluids 2 (8), 084604.10.1103/PhysRevFluids.2.084604CrossRefGoogle Scholar
Smits, A.J. & Dussauge, J.P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer Science & Business Media.Google Scholar
Song, Y.B., Zhang, P. & Xia, Z.H. 2023 Predicting mean profiles in compressible turbulent channel and pipe flows. Phys. Rev. Fluids 8 (3), 034604.10.1103/PhysRevFluids.8.034604CrossRefGoogle Scholar
Trettel, A. & Larsson, J. 2016 Mean velocity scaling for compressible wall turbulence with heat transfer. Phys. Fluids 28 (2), 026102.10.1063/1.4942022CrossRefGoogle Scholar
Van Driest, E.R. 1951 Turbulent boundary layer in compressible fluids. J. Aeronaut. Sci. 18 (3), 145–160.10.2514/8.1895CrossRefGoogle Scholar
Walz, A. 1969 Boundary Layers of Flow and Temperature. MIT Press.Google Scholar
Yao, J. & Hussain, F. 2020 Turbulence statistics and coherent structures in compressible channel flow. Phys. Rev. Fluids 5 (8), 084603.10.1103/PhysRevFluids.5.084603CrossRefGoogle Scholar
Yu, M., Dong, S.W., Yuan, X.X. & Xu, C.X. 2024 Statistics and dynamics of coherent structures in compressible wall-bounded turbulence. Sci. China Phys. Mech. Astron. 67 (12), 124701.10.1007/s11433-024-2481-8CrossRefGoogle Scholar
Zhang, P., Song, Y.B. & Xia, Z.H. 2023 Compressibility effect in compressible turbulent channel flows (in Chinese). Sci. Sin. Phys. Mech. Astron. 53 (4), 244711.Google Scholar
Zhang, P., Song, Y.B. & Xia, Z.H. 2024 Direct numerical simulations of compressible turbulent channel flows with asymmetric thermal walls. J. Fluid Mech. 984, A37.10.1017/jfm.2024.226CrossRefGoogle Scholar
Zhang, P. & Xia, Z.H. 2020 Contribution of viscous stress work to wall heat flux in compressible turbulent channel flows. Phys. Rev. E 102 (4), 043107.10.1103/PhysRevE.102.043107CrossRefGoogle ScholarPubMed
Zhang, Y.S., Bi, W.T., Hussain, F. & She, Z.S. 2014 A generalized Reynolds analogy for compressible wall-bounded turbulent flows. J. Fluid Mech. 739, 392–420.10.1017/jfm.2013.620CrossRefGoogle Scholar
Zhu, X.K., Song, Y.B., Yang, X.S. & Xia, Z.H. 2024 Velocity transformation for compressible wall-bounded turbulence – an approach through the mixing length hypothesis. Sci. China Phys. Mech. Astron. 67 (9), 294711.10.1007/s11433-024-2420-5CrossRefGoogle Scholar