1. Introduction
We study the dynamics of a discretized Landau–de Gennes energy functional for ![]() $3 \times 3$ Q-tensors in the regime of small intersite coupling, the “anticontinuous limit” regime. Of special interest are static configurations, their stability, and their relation to equilibria of discrete Oseen–Frank energy functionals that involve a director field. The two discretized functionals are defined in finite graphs and we consider one-elastic-constant models [Reference Assanto and Karpierz1, Reference Gartland14, Reference Majumdar and Zarnescu21, Reference Peccianti and Assanto28, Reference Ravnik and Žumer32].
$3 \times 3$ Q-tensors in the regime of small intersite coupling, the “anticontinuous limit” regime. Of special interest are static configurations, their stability, and their relation to equilibria of discrete Oseen–Frank energy functionals that involve a director field. The two discretized functionals are defined in finite graphs and we consider one-elastic-constant models [Reference Assanto and Karpierz1, Reference Gartland14, Reference Majumdar and Zarnescu21, Reference Peccianti and Assanto28, Reference Ravnik and Žumer32].
The Oseen–Frank and Landau–de Gennes continuum theories are commonly used models for nematic liquid crystals [Reference De Gennes and Prost9, Reference Frank13]. The Landau–de Gennes theory can be thought of as a generalization of the Oseen–Frank theory that includes biaxiality, spatial variations of the order parameter, and more general singular-like structures [Reference De Gennes and Prost9, Reference Ravnik and Žumer32]. Our study is partially motivated by results of Majumdar and Zarnescu [Reference Majumdar and Zarnescu21] for 3−dimensional domains and ![]() $3\times 3$ Q-tensors showing that, as the coupling constant vanishes, the minimizers of the Landau–de Gennes energy converge to Oseen–Frank minimizers. The convergence is in
$3\times 3$ Q-tensors showing that, as the coupling constant vanishes, the minimizers of the Landau–de Gennes energy converge to Oseen–Frank minimizers. The convergence is in ![]() $ W^{1,2}(D)$,
$ W^{1,2}(D)$, ![]() $D \subset \textbf{R}^3$ the domain, and is uniform away from the vicinity of singularities of the Oseen–Frank minimizers.
$D \subset \textbf{R}^3$ the domain, and is uniform away from the vicinity of singularities of the Oseen–Frank minimizers.
In [Reference Panayotaros25] vanishing coupling constant equilibria were studied in a simpler discrete and finite setting using a combination of implicit function theorem and symmetry arguments. Similar ideas were used in proofs of existence of small intersite “breather solutions” of discrete nonlinear Schrödinger (DNLS) equations [Reference Panayotaros and Pelinovsky27, Reference Pelinovsky, Kevrekidis and Frantzeskakis29, Reference Pelinovsky, Kevrekidis and Frantzeskakis30]. The strategy originates in [Reference Aubry and Daeron2, Reference MacKay and Aubry19] and has also been applied to equilibria of discrete nonlinear parabolic equations [Reference Caputo, Cruz and Panayotaros7]. In [Reference Panayotaros25] the liquid crystal problem is also simplified by considering ![]() $2 \times 2$ Q-tensors. The generalization of the discrete theory to the
$2 \times 2$ Q-tensors. The generalization of the discrete theory to the ![]() $3\times3$ Q-tensor case requires a more systematic use of the symmetries of the decoupled problem [Reference Panayotaros26], i.e. some theory of Lie group actions, see e.g. [Reference Michor23]. The computations used in the proof also imply that the gradient flow of the discrete Landau–de Gennes energy has a normally hyperbolic attractor, a manifold that is parametrized by the uniaxial Q-tensors and is diffeomorphic to a product of projective planes [Reference Panayotaros25, Reference Panayotaros26]. The theory is likely relevant to other multicomponent parabolic systems with onsite nonlinearities that are invariant under Lie group actions.
$3\times3$ Q-tensor case requires a more systematic use of the symmetries of the decoupled problem [Reference Panayotaros26], i.e. some theory of Lie group actions, see e.g. [Reference Michor23]. The computations used in the proof also imply that the gradient flow of the discrete Landau–de Gennes energy has a normally hyperbolic attractor, a manifold that is parametrized by the uniaxial Q-tensors and is diffeomorphic to a product of projective planes [Reference Panayotaros25, Reference Panayotaros26]. The theory is likely relevant to other multicomponent parabolic systems with onsite nonlinearities that are invariant under Lie group actions.
The first part of the paper states and shows necessary and sufficient conditions for the continuation of equilibria of the decoupled Landau–de Gennes discrete theory in lattices and graphs without boundary, see Propositions 2.3, 2.4. The results are based on the reduction to equations on submanifolds parametrized by uniaxial Q-tensors, see Lemma 3.11. The reduction step is shown as in the case with boundary [Reference Panayotaros26]. In the case without boundary the reduced equation has an additional equivariance under the diagonal adjoint action of SO(3) on products of projective planes, see Lemma 3.12, and equilibria belong to submanifolds. In Proposition 3.13, we classify the isotropy subgroups of this action, this is a first step towards classifying these manifolds. Generically, the isotropy subgroup is trivial, however nontrivial finite subgroups are also possible.
In the second part of the paper, we show results from numerical integrations of the gradient flow of the Landau–de Gennes functional in open and periodic chains, these are the simplest geometries where we expect to see multiple attracting equilibria related to the topology of the domain and the target space (projective plane). Integrating the gradient flow we see a rapid approach to configurations where the Q-tensor is near uniaxial at all sites and then a much slower evolution to the equilibrium. These observations are consistent with the existence of the normally hyperbolic attractor parametrized by the uniaxial Q-tensors. The time scale of the slower evolution is several orders of magnitude longer than the fast scale. This slow scale is generally seen to increase with the size of the lattice. In the periodic chain we see evidence for two attracting equilibria, corresponding to spatial configurations that are discrete analogues of curves that belong to the two homotopy classes of the projective plane. In open chains we typically see convergence to an equilibrium where the Q-tensor at the interior sites interpolates between the Q-tensors at the two boundary points. Additional stable equilibria are also possible, and we show an example of boundary conditions leading to two attracting equilibria of opposite helicity. The discrete Landau–de Gennes system and more general parabolic systems with a similar structure can exhibit other dynamical behaviours such as propagating fronts, see e.g. [Reference Caputo, Cruz and Panayotaros7], these can be examined in future work.
The paper is organized as follows. In section 2, we define the discrete Landau–de Gennes and Oseen–Frank functionals and state the main results on continuation of equilibria and normally hyperbolic invariant manifolds of the decoupled system. In section 3, we review the geometry of critical sets of the decoupled Landau–de Gennes system and prove the results of the paper. In section 4, we present the numerical results on the Landau–de Gennes gradient flow in the interval and the circle. Possible extensions are discussed in section 5.
2. Discrete Landau–de Gennes system and anticontinuous limit
To define discrete Landau–de Gennes systems we first recall the continuous version. The Landau–de Gennes theory for nematic liquid crystals describes the orientational state of the liquid crystal by the “Q − tensor”, a q × q symmetric traceless real matrix-valued function defined on the domain ![]() $D \subset \mathbb{R}^d $ of the liquid crystal. Typically q = d. In this work, we are interested in the case q = 3. In the numerical examples below we consider q = 3 in discretized d = 1 domains.
$D \subset \mathbb{R}^d $ of the liquid crystal. Typically q = d. In this work, we are interested in the case q = 3. In the numerical examples below we consider q = 3 in discretized d = 1 domains.
Static configurations in D are obtained by extremizing the Landau–de Gennes energy functional
 \begin{equation}
\mathcal{F}_{LG}(Q) = \int_{D} \left( \frac{L}{2} |\nabla Q|^2 + f_B(Q) \right),
\end{equation}
\begin{equation}
\mathcal{F}_{LG}(Q) = \int_{D} \left( \frac{L}{2} |\nabla Q|^2 + f_B(Q) \right),
\end{equation} where  $ |\nabla Q|^2 = \sum_{i,j = 1}^q \sum_{k = 1}^{d} (\partial_{x_k} Q_{i,j} )^2 $, and
$ |\nabla Q|^2 = \sum_{i,j = 1}^q \sum_{k = 1}^{d} (\partial_{x_k} Q_{i,j} )^2 $, and
 \begin{equation}
f_B(Q) = - \frac{a^2}{2} \hbox{tr}(Q^2) - \frac{b^2}{3} \hbox{tr}(Q^3) + \frac{c^2}{4} (\hbox{tr}(Q^2))^2.
\end{equation}
\begin{equation}
f_B(Q) = - \frac{a^2}{2} \hbox{tr}(Q^2) - \frac{b^2}{3} \hbox{tr}(Q^3) + \frac{c^2}{4} (\hbox{tr}(Q^2))^2.
\end{equation} L, a 2, b 2, c 2 are positive constants that describe the material and its state. The Dirichlet problem is obtained by varying over configurations with fixed boundary values of Q at ![]() $\partial D$.
$\partial D$.
A simpler model for nematic liquid crystals is the Oseen–Frank theory, where the orientation of the liquid crystal is described by the “director field”, a unit vector field ![]() $ \textbf{n} \in \mathbb{R}^q$ on the domain
$ \textbf{n} \in \mathbb{R}^q$ on the domain ![]() $D \subset \mathbb{R}^d$. Static configurations are obtained by extremizing the Oseen–Frank energy functional
$D \subset \mathbb{R}^d$. Static configurations are obtained by extremizing the Oseen–Frank energy functional
 \begin{equation}
\mathcal{F}_{OF}(Q) = \frac{1}{2} \int_{D} |\nabla \textbf{n}|^2,
\end{equation}
\begin{equation}
\mathcal{F}_{OF}(Q) = \frac{1}{2} \int_{D} |\nabla \textbf{n}|^2,
\end{equation} where  $|\nabla \textbf{n}|^2 = \sum_{k = 1}^{d} \sum_{i = 1}^q ( \partial_{x_k} \textbf{n}_i )^2 $. The Dirichlet problem is obtained by varying over configurations with fixed boundary values of n at
$|\nabla \textbf{n}|^2 = \sum_{k = 1}^{d} \sum_{i = 1}^q ( \partial_{x_k} \textbf{n}_i )^2 $. The Dirichlet problem is obtained by varying over configurations with fixed boundary values of n at ![]() $\partial D$.
$\partial D$.
In this study, we are also interested in discrete versions of the theory in domains D without boundary, e.g. tori, spheres, etc., with possible modification of the quadratic part of the energy for nonflat geometries. Suitable gradient flows of ![]() $-\mathcal{F}_{LG}$,
$-\mathcal{F}_{LG}$, ![]() $- \mathcal{F}_{OF}$ describe the dynamics of approach to equilibria.
$- \mathcal{F}_{OF}$ describe the dynamics of approach to equilibria.
Discrete versions of the above systems are used in numerical computation with finite difference methods [Reference Davis and Gartland8, Reference Mkaddem and Gartland24, Reference Ravnik and Žumer32]. Energy functionals (2.1), (2.3) are widely studied special cases of more general (and realistic) Landau–de Gennes and Oseen–Frank functionals that include three elastic parameters, see e.g. [Reference Assanto and Karpierz1, Reference Gartland14, Reference Majumdar20, Reference Peccianti and Assanto28, Reference Ravnik and Žumer32].
The Oseen–Frank energy (2.3) can be formally obtained from the Landau–de Gennes energy (2.1) by using the “uniaxial approximation” Ansatz, see e.g. [Reference Martinez-Gonzalez, Li, Sadati, Zhou, Zhang, Nealey and de Pablo22, Reference Ravnik and Žumer32]. The results of the paper extend [Reference Panayotaros25, Reference Panayotaros26] and give a mathematical interpretation of this approximation in the limit of vanishing coupling L for both the static and dynamic problems of finite discretized versions.
In the discrete version of the Landau–de Gennes theory Q is a function on a discrete set ![]() $\overline G$ that has the structure of a finite graph, i.e. a pair
$\overline G$ that has the structure of a finite graph, i.e. a pair ![]() $({\overline G},c)$ defined by a nonempty finite discrete set
$({\overline G},c)$ defined by a nonempty finite discrete set ![]() $\overline G$ and a function
$\overline G$ and a function ![]() $c :{\overline G} \times {\overline G} \rightarrow \{0,1\}$ satisfying
$c :{\overline G} \times {\overline G} \rightarrow \{0,1\}$ satisfying ![]() $c(n,n) = 0$,
$c(n,n) = 0$, ![]() $\forall n \in {\overline G}$, and
$\forall n \in {\overline G}$, and ![]() $c(n,m) = c(m,n)$,
$c(n,m) = c(m,n)$, ![]() $\forall n$,
$\forall n$, ![]() $m \in {\overline G}$. The function c is the connectivity matrix of the graph, i.e.
$m \in {\overline G}$. The function c is the connectivity matrix of the graph, i.e. ![]() $c(n,m) = 1$ represents sites n, m that are connected by an edge.
$c(n,m) = 1$ represents sites n, m that are connected by an edge.
We further consider a set ![]() ${\partial G} \subset {\overline G}$, and let
${\partial G} \subset {\overline G}$, and let ![]() $G = {\overline G}\setminus {\partial G}$. We assume that G is connected. We will consider two versions of the discrete theory: (i)
$G = {\overline G}\setminus {\partial G}$. We assume that G is connected. We will consider two versions of the discrete theory: (i) ![]() $\partial G$ is empty and the discretized functional is defined on functions on
$\partial G$ is empty and the discretized functional is defined on functions on ![]() $\overline G$, and (ii)
$\overline G$, and (ii) ![]() $\partial G$ is nonempty and the discretized functional is defined on functions on G. In the second case, the values at
$\partial G$ is nonempty and the discretized functional is defined on functions on G. In the second case, the values at ![]() $\partial G$ are fixed and play the role of the boundary values.
$\partial G$ are fixed and play the role of the boundary values.
In applications to numerical solution of the Landau–de Gennes system in domains ![]() $D \subset \mathbb{R}^d$, G and
$D \subset \mathbb{R}^d$, G and ![]() $\partial G$ are discrete analogues of D and
$\partial G$ are discrete analogues of D and ![]() $\partial D$ respectively. The use of graphs allows for more variety, e.g. lattices that discretize manifolds and branched manifolds. The notion of a boundary in the discrete problem is also more general, the boundary can be any subset of
$\partial D$ respectively. The use of graphs allows for more variety, e.g. lattices that discretize manifolds and branched manifolds. The notion of a boundary in the discrete problem is also more general, the boundary can be any subset of ![]() $\overline G$ where we fix Q.
$\overline G$ where we fix Q.
Let  $\hbox{Sym}^q_0$ denote the set of symmetric traceless q × q real matrices. The set
$\hbox{Sym}^q_0$ denote the set of symmetric traceless q × q real matrices. The set  $\hbox{Sym}^q_0 $ is a real linear space of dimension
$\hbox{Sym}^q_0 $ is a real linear space of dimension ![]() $d_q = {q(q-1)}/{2} - 1$. Also, given
$d_q = {q(q-1)}/{2} - 1$. Also, given ![]() $A \subset {\overline G}$ we let X(A) denote the set of functions
$A \subset {\overline G}$ we let X(A) denote the set of functions  $f: A \rightarrow \hbox{Sym}^q_0$. Given A 1, A 2 disjoint subsets of
$f: A \rightarrow \hbox{Sym}^q_0$. Given A 1, A 2 disjoint subsets of ![]() $\overline G$ such that
$\overline G$ such that ![]() $A_1 \cup A_2 = {\overline G}$ we have
$A_1 \cup A_2 = {\overline G}$ we have ![]() $X({\overline G}) = X(A_1) \times X(A_2)$, and we may write
$X({\overline G}) = X(A_1) \times X(A_2)$, and we may write ![]() ${\overline Q} \in X({\overline G})$ as
${\overline Q} \in X({\overline G})$ as ![]() ${\overline Q} = [Q_1,Q_2]$ with
${\overline Q} = [Q_1,Q_2]$ with ![]() $Q_j \in X(A_j)$.
$Q_j \in X(A_j)$.
The first discrete version of ![]() $\mathcal{F}_{LG}$ we consider has the form
$\mathcal{F}_{LG}$ we consider has the form
with ![]() $\overline{\mathcal{F}}_2$,
$\overline{\mathcal{F}}_2$, ![]() $\overline{\mathcal{F}}_4: X({\overline G}) \rightarrow \mathbb{R}$ defined by
$\overline{\mathcal{F}}_4: X({\overline G}) \rightarrow \mathbb{R}$ defined by
 \begin{equation}
\overline{\mathcal{F}}_2 ({\overline Q}) = \frac{1}{4} \sum_{n,m \in {\overline G}} c(n,m) |{\overline Q}(n) - {\overline Q}(m)|^2, \quad
\overline{\mathcal{F}}_4 ({\overline Q}) = \sum_{n \in {\overline G}} f_B({\overline Q}(n)),
\end{equation}
\begin{equation}
\overline{\mathcal{F}}_2 ({\overline Q}) = \frac{1}{4} \sum_{n,m \in {\overline G}} c(n,m) |{\overline Q}(n) - {\overline Q}(m)|^2, \quad
\overline{\mathcal{F}}_4 ({\overline Q}) = \sum_{n \in {\overline G}} f_B({\overline Q}(n)),
\end{equation} with  $ |M|^2 = \sum_{i,j = 1}^q M_{i,j}^2$ and fB as in (2.2).
$ |M|^2 = \sum_{i,j = 1}^q M_{i,j}^2$ and fB as in (2.2).
The define the discrete analogue of equations with Dirichlet boundary data, we consider a nonempty ![]() ${\partial G} \subset {\overline G}$, and choose a function
${\partial G} \subset {\overline G}$, and choose a function  $Q_b:{\partial D} \rightarrow \hbox{Sym}^q_0$. Let
$Q_b:{\partial D} \rightarrow \hbox{Sym}^q_0$. Let ![]() $G = {\overline G}\setminus {\partial G}$. We have
$G = {\overline G}\setminus {\partial G}$. We have ![]() $X({\overline G}) = X(G) \times X({\partial G})$. Then the second discretized version of
$X({\overline G}) = X(G) \times X({\partial G})$. Then the second discretized version of ![]() $\mathcal{F}_{LG}$ will have the form
$\mathcal{F}_{LG}$ will have the form
with ![]() $ \mathcal{F}_2$,
$ \mathcal{F}_2$, ![]() $ \mathcal{F}_4: X(G) \rightarrow \mathbb{R}$ defined by
$ \mathcal{F}_4: X(G) \rightarrow \mathbb{R}$ defined by
with ![]() $ \overline{\mathcal{F}}_2$,
$ \overline{\mathcal{F}}_2$, ![]() $ \overline{\mathcal{F}}_4$ as in (2.5). The function Qb represents the boundary data.
$ \overline{\mathcal{F}}_4$ as in (2.5). The function Qb represents the boundary data.
The discretization of the quadratic part of the energy of (2.1) by ![]() $\overline{\mathcal{F}}_2$ is indicative of more general discrete quadratic energies, e.g. with c symmetric and positive. The theory below extends to such generalizations.
$\overline{\mathcal{F}}_2$ is indicative of more general discrete quadratic energies, e.g. with c symmetric and positive. The theory below extends to such generalizations.
We identify ![]() $X({\overline A})$, A = G or
$X({\overline A})$, A = G or ![]() $\overline G$, with
$\overline G$, with  $(\hbox{Sym}^q_0)^{|A|} \subset (\hbox{Mat}(q))^{|{A}|}$. The trace inner product
$(\hbox{Sym}^q_0)^{|A|} \subset (\hbox{Mat}(q))^{|{A}|}$. The trace inner product ![]() $\langle R(k),S(k)\rangle = \sum_{k \in {A}} \hbox{tr}(R(k)S^T(k))$, R(k),
$\langle R(k),S(k)\rangle = \sum_{k \in {A}} \hbox{tr}(R(k)S^T(k))$, R(k), ![]() $S(k) \in \hbox{Mat}(q)$,
$S(k) \in \hbox{Mat}(q)$, ![]() $k\in {A}$, induces a metric topology and a Riemannian metric on
$k\in {A}$, induces a metric topology and a Riemannian metric on ![]() $(\hbox{Mat}(q))^{|{A}|}$, and
$(\hbox{Mat}(q))^{|{A}|}$, and  $(\hbox{Sym}_0^q)^{|{A}|}$ in a standard way. The functionals of (2.4)-(2.5), (2.7) are real analytic in
$(\hbox{Sym}_0^q)^{|{A}|}$ in a standard way. The functionals of (2.4)-(2.5), (2.7) are real analytic in ![]() $X({\overline G})$, X(G), respectively.
$X({\overline G})$, X(G), respectively.
The gradient flow of ![]() $-\overline{\mathcal{F}}$ in the phase space
$-\overline{\mathcal{F}}$ in the phase space ![]() $X({\overline G})$ with the trace inner product is the system
$X({\overline G})$ with the trace inner product is the system  $ {\dot {\overline Q}} = - \nabla \overline{\mathcal{F}}({\overline Q})$. Equilibria are critical points of
$ {\dot {\overline Q}} = - \nabla \overline{\mathcal{F}}({\overline Q})$. Equilibria are critical points of ![]() $\overline{\mathcal{F}}$ in
$\overline{\mathcal{F}}$ in ![]() $X({\overline G})$. The gradient flow of
$X({\overline G})$. The gradient flow of ![]() $\cal F$ is the system
$\cal F$ is the system ![]() $ {\dot Q} = - \nabla_Q \mathcal{F}(Q;Q_b)$. Equilibria are critical points of
$ {\dot Q} = - \nabla_Q \mathcal{F}(Q;Q_b)$. Equilibria are critical points of ![]() $\mathcal{F}$ in X(G).
$\mathcal{F}$ in X(G).
We consider the problem of continuation of L = 0 equilibria in the discrete setting. To state the results, we first classify the equilibria of the L = 0 system. At L = 0 the equations for the critical points of ![]() $\overline{\mathcal{F}}$,
$\overline{\mathcal{F}}$, ![]() $\cal F$ at different sites decouple and it suffices to study solutions of the dq equations
$\cal F$ at different sites decouple and it suffices to study solutions of the dq equations ![]() $D f_B (Q) = 0$,
$D f_B (Q) = 0$,  $Q \in \hbox{Sym}^q_0$.
$Q \in \hbox{Sym}^q_0$.
The critical points for cases q = 2, 3 are well known [Reference Forrest, Wang and Zhou12, Reference Majumdar20, Reference Majumdar and Zarnescu21]. In the case q = 3, ![]() $d_q = 5$, the following [Reference Panayotaros26] summarizes the result.
$d_q = 5$, the following [Reference Panayotaros26] summarizes the result.
Proposition 2.1. The solutions of ![]() $D f_B = 0 $ consist of the origin (Q = 0), and the sets
$D f_B = 0 $ consist of the origin (Q = 0), and the sets
 \begin{equation}
\Sigma^3_+ := \{Q \in \hbox{Sym}^3_0:
Q = Q_+({\hat \nu}) := - 3 x_+ ( {\hat \nu} \otimes {\hat \nu} - \frac{1}{3} I), {\hat \nu} \in S^2 \},
\end{equation}
\begin{equation}
\Sigma^3_+ := \{Q \in \hbox{Sym}^3_0:
Q = Q_+({\hat \nu}) := - 3 x_+ ( {\hat \nu} \otimes {\hat \nu} - \frac{1}{3} I), {\hat \nu} \in S^2 \},
\end{equation} \begin{equation}
\Sigma^3_- := \{Q \in \hbox{Sym}^3_0:
Q = Q_-({\hat \nu}) = - 3 x_- ( {\hat \nu} \otimes {\hat \nu} - \frac{1}{3} I), {\hat \nu} \in S^2 \},
\end{equation}
\begin{equation}
\Sigma^3_- := \{Q \in \hbox{Sym}^3_0:
Q = Q_-({\hat \nu}) = - 3 x_- ( {\hat \nu} \otimes {\hat \nu} - \frac{1}{3} I), {\hat \nu} \in S^2 \},
\end{equation} with ![]() $x_+$,
$x_+$, ![]() $x_-$ positive and negative roots of
$x_-$ positive and negative roots of ![]() $- a^2 + 6 c^2 x^2 + b^2 x = 0$ respectively, I the
$- a^2 + 6 c^2 x^2 + b^2 x = 0$ respectively, I the ![]() $3\times 3$ identity,
$3\times 3$ identity, ![]() $S^2 \subset \mathbb{R}^3$ the unit sphere. Expressions (2.8), (2.9) define embeddings of the projective plane
$S^2 \subset \mathbb{R}^3$ the unit sphere. Expressions (2.8), (2.9) define embeddings of the projective plane ![]() $\mathbb{R}\mathrm{P}^2$ into
$\mathbb{R}\mathrm{P}^2$ into  $\hbox{Sym}^3_0$, i.e. the sets
$\hbox{Sym}^3_0$, i.e. the sets ![]() $\Sigma^3_\pm$ are submanifolds of
$\Sigma^3_\pm$ are submanifolds of  $\hbox{Sym}^3_0$ and are diffeomorphic to
$\hbox{Sym}^3_0$ and are diffeomorphic to ![]() $\mathbb{R}\mathrm{P}^2$. Furthermore, the infimum of fB in
$\mathbb{R}\mathrm{P}^2$. Furthermore, the infimum of fB in  $\hbox{Sym}^3_0$ is attained at
$\hbox{Sym}^3_0$ is attained at ![]() $\Sigma^3_-$, and
$\Sigma^3_-$, and ![]() $\nabla^2 f_B$ at
$\nabla^2 f_B$ at ![]() $\Sigma_-^3$ has two null and three positive eigenvalues. The origin is a local maximum of fB and is nondegenerate, while
$\Sigma_-^3$ has two null and three positive eigenvalues. The origin is a local maximum of fB and is nondegenerate, while ![]() $\nabla^2 f_B$ at
$\nabla^2 f_B$ at ![]() $\Sigma_+^3$ has null, negative and positive eigenvalues.
$\Sigma_+^3$ has null, negative and positive eigenvalues.
The set of critical points of ![]() $ \overline{\mathcal{F}}_4$ is the set of maps
$ \overline{\mathcal{F}}_4$ is the set of maps  $\Phi: {\overline G} \rightarrow 0 \cup \Sigma_-^3 \cup \Sigma_+^3 \subset
\hbox{Sym}^3_0$ and consists of a finite collection of maximal connected subsets of
$\Phi: {\overline G} \rightarrow 0 \cup \Sigma_-^3 \cup \Sigma_+^3 \subset
\hbox{Sym}^3_0$ and consists of a finite collection of maximal connected subsets of ![]() $X({\overline G})$. The maximal connected sets of nontrivial critical points of
$X({\overline G})$. The maximal connected sets of nontrivial critical points of ![]() $\mathcal{F}_4$ are labelled by pairs of disjoint subsets
$\mathcal{F}_4$ are labelled by pairs of disjoint subsets ![]() $U_+$,
$U_+$, ![]() $U_-$ of
$U_-$ of ![]() $\overline G$ with nonempty union. Given any such pair, let
$\overline G$ with nonempty union. Given any such pair, let ![]() $\mathcal{C}_0(\overline{\mathcal{F}}_4; {U}_+,{U}_-)$ denote the set of maps
$\mathcal{C}_0(\overline{\mathcal{F}}_4; {U}_+,{U}_-)$ denote the set of maps  $\Phi:{\overline G} \rightarrow \hbox{Sym}^3_0$ with the property that if
$\Phi:{\overline G} \rightarrow \hbox{Sym}^3_0$ with the property that if ![]() ${U}_j \neq \emptyset$,
${U}_j \neq \emptyset$, ![]() $j \in \{+,-\}$, then
$j \in \{+,-\}$, then  $ \Phi(n) \in \Sigma^3_j$,
$ \Phi(n) \in \Sigma^3_j$, ![]() $\forall n \in {U}_j$, and
$\forall n \in {U}_j$, and ![]() $ \Phi(n) = 0$, for all n in the complement of
$ \Phi(n) = 0$, for all n in the complement of ![]() $ {U} = {U}_+\cup {U}_-$ in
$ {U} = {U}_+\cup {U}_-$ in ![]() $\overline G$. Then
$\overline G$. Then ![]() $\mathcal{C}_0(\overline{\mathcal{F}}_4; {U}_+,{U}_-) = (\Sigma_+^3)^{|{U}_+|} \times (\Sigma_-^3)^{|{U}_-|}$ is a maximal connected set of critical points of
$\mathcal{C}_0(\overline{\mathcal{F}}_4; {U}_+,{U}_-) = (\Sigma_+^3)^{|{U}_+|} \times (\Sigma_-^3)^{|{U}_-|}$ is a maximal connected set of critical points of ![]() $\overline{\mathcal{F}}_4$ that is diffeomorphic to
$\overline{\mathcal{F}}_4$ that is diffeomorphic to ![]() $(\mathbb{R}\mathrm{P}^2)^{|{U}|}$, see Lemma 3.10 of [Reference Panayotaros26]. These considerations give a complete list of the manifolds of critical points of
$(\mathbb{R}\mathrm{P}^2)^{|{U}|}$, see Lemma 3.10 of [Reference Panayotaros26]. These considerations give a complete list of the manifolds of critical points of ![]() $ \overline{\mathcal{F}}_4$.
$ \overline{\mathcal{F}}_4$.
Similarly, the set of critical points of ![]() $ \mathcal{F}_4$ is the set of maps
$ \mathcal{F}_4$ is the set of maps  $\Phi: G \rightarrow 0 \cup \Sigma_-^3 \cup \Sigma_+^3 \subset
\hbox{Sym}^3_0$ and consists of a finite collection of maximal connected subsets of X(G). The maximal connected sets of nontrivial critical points of
$\Phi: G \rightarrow 0 \cup \Sigma_-^3 \cup \Sigma_+^3 \subset
\hbox{Sym}^3_0$ and consists of a finite collection of maximal connected subsets of X(G). The maximal connected sets of nontrivial critical points of ![]() $\mathcal{F}_4$ are labelled by pairs of disjoint subsets
$\mathcal{F}_4$ are labelled by pairs of disjoint subsets ![]() $U_+$,
$U_+$, ![]() $U_-$ of G with nonempty union. Given any such pair we let
$U_-$ of G with nonempty union. Given any such pair we let ![]() $\mathcal{C}_0(\mathcal{F},U_+,U_-)$ denote the set of maps
$\mathcal{C}_0(\mathcal{F},U_+,U_-)$ denote the set of maps  $\Phi:G \rightarrow \hbox{Sym}^3_0$ with the property that if
$\Phi:G \rightarrow \hbox{Sym}^3_0$ with the property that if ![]() $U_j \neq \emptyset$,
$U_j \neq \emptyset$, ![]() $j \in \{+,-\}$, then
$j \in \{+,-\}$, then  $ \Phi(n) \in \Sigma^3_j$,
$ \Phi(n) \in \Sigma^3_j$, ![]() $\forall n \in U_j$, and
$\forall n \in U_j$, and ![]() $ \Phi(n) = 0$, for all n in the complement of
$ \Phi(n) = 0$, for all n in the complement of ![]() $ U = U_+\cup U_-$ in G. Then
$ U = U_+\cup U_-$ in G. Then ![]() $\mathcal{C}_0(\mathcal{F}_4; U_+,U_-) = (\Sigma_+^3)^{|U_+|} \times (\Sigma_-^3)^{|U_-|}$ is a maximal connected set of critical points of
$\mathcal{C}_0(\mathcal{F}_4; U_+,U_-) = (\Sigma_+^3)^{|U_+|} \times (\Sigma_-^3)^{|U_-|}$ is a maximal connected set of critical points of ![]() $\mathcal{F}_4$ that is diffeomorphic to
$\mathcal{F}_4$ that is diffeomorphic to ![]() $(\mathbb{R}\mathrm{P}^2)^{|U|}$. These considerations give a complete list of the manifolds of critical points of
$(\mathbb{R}\mathrm{P}^2)^{|U|}$. These considerations give a complete list of the manifolds of critical points of ![]() $\mathcal{F}_4$, see also [Reference Panayotaros26].
$\mathcal{F}_4$, see also [Reference Panayotaros26].
The main question is which of the L = 0 equilibria can be continued to solutions of the L > 0 problem. We present below necessary and sufficient conditions.
The new results of the paper concern the case without boundary.
Lemma 2.2. Let q = 3, then for ![]() $|L|$ sufficiently small every nontrivial critical point of
$|L|$ sufficiently small every nontrivial critical point of ![]() $ \overline{\mathcal{F}}$ belongs to a maximal compact embedded manifold of critical points of
$ \overline{\mathcal{F}}$ belongs to a maximal compact embedded manifold of critical points of ![]() $ \overline{\mathcal{F}}$.
$ \overline{\mathcal{F}}$.
Thus critical points are not isolated. A manifold M of critical points of ![]() $\overline{\mathcal{F}} $ is nondegenerate if for every
$\overline{\mathcal{F}} $ is nondegenerate if for every ![]() $Q \in M$,
$Q \in M$, ![]() $\nabla^2 \overline{\mathcal{F}}(Q)$ has a nullspace of dimension
$\nabla^2 \overline{\mathcal{F}}(Q)$ has a nullspace of dimension ![]() $\hbox{dim}(M)$. The manifolds that can occur as maximal sets of critical points of
$\hbox{dim}(M)$. The manifolds that can occur as maximal sets of critical points of ![]() $ \overline{\mathcal{F}}$ are classified in section 3.
$ \overline{\mathcal{F}}$ are classified in section 3.
We first state a necessary condition satisfied by a one-parameter family Q(L) of critical points of ![]() $\overline{\mathcal{F}}$.
$\overline{\mathcal{F}}$.
Proposition 2.3. Let q = 3. Suppose there exists an ![]() $\epsilon_0 \gt 0$ such that
$\epsilon_0 \gt 0$ such that  $Q(L) \in \hbox{Sym}^q_0$ is a critical point of
$Q(L) \in \hbox{Sym}^q_0$ is a critical point of ![]() $\overline{\mathcal{F}} = L \overline{\mathcal{F}}_2 + \overline{\mathcal{F}}_4$, for every
$\overline{\mathcal{F}} = L \overline{\mathcal{F}}_2 + \overline{\mathcal{F}}_4$, for every ![]() $L \in [0, \epsilon_0]$. Assume also that Q(L) is C 1 in
$L \in [0, \epsilon_0]$. Assume also that Q(L) is C 1 in ![]() $[0,\epsilon_0]$ and that there exist disjoint subsets
$[0,\epsilon_0]$ and that there exist disjoint subsets ![]() ${U}_+$,
${U}_+$, ![]() ${U}_-$ of
${U}_-$ of ![]() ${\overline G}$,
${\overline G}$, ![]() ${U}_+ \cup {U}_- \neq \emptyset$, such that
${U}_+ \cup {U}_- \neq \emptyset$, such that ![]() $Q(0) \in \mathcal{C}_0({\overline {F}_4}, {U}_+,{U}_-)$. Then Q(0) is a critical point of
$Q(0) \in \mathcal{C}_0({\overline {F}_4}, {U}_+,{U}_-)$. Then Q(0) is a critical point of ![]() $ \overline{\mathcal{F}}_2 $, restricted to
$ \overline{\mathcal{F}}_2 $, restricted to ![]() $\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$.
$\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$.
Thus the continued branches must be critical points of the quadratic functional ![]() $ \overline{\mathcal{F}}_2 $, restricted to
$ \overline{\mathcal{F}}_2 $, restricted to ![]() $\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$. The equation for these restricted critical points will be referred to as the reduced (or bifurcation equation) at L = 0. The following is a sufficient condition for continuation of critical points of the L = 0 problem.
$\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$. The equation for these restricted critical points will be referred to as the reduced (or bifurcation equation) at L = 0. The following is a sufficient condition for continuation of critical points of the L = 0 problem.
Proposition 2.4. Let q = 3. Let U 1, U 2 disjoint subsets of ![]() ${\overline G}$ with nonempty union. Suppose that
${\overline G}$ with nonempty union. Suppose that ![]() $\mathcal{M}_0$ is a nondegenerate embedded manifold of critical points of
$\mathcal{M}_0$ is a nondegenerate embedded manifold of critical points of ![]() $ \overline{\mathcal{F}}_2 $, restricted to
$ \overline{\mathcal{F}}_2 $, restricted to ![]() $\mathcal{C}_0(\overline{\mathcal{F}}_4,U_1,U_2)$. Then there exists
$\mathcal{C}_0(\overline{\mathcal{F}}_4,U_1,U_2)$. Then there exists ![]() $\epsilon_0 \gt 0$ and a unique real analytic one-parameter family
$\epsilon_0 \gt 0$ and a unique real analytic one-parameter family ![]() $\mathcal{M}(L)$,
$\mathcal{M}(L)$, ![]() $|L| \lt \epsilon_0 $, of embedded manifolds of critical points of
$|L| \lt \epsilon_0 $, of embedded manifolds of critical points of ![]() $\overline{\mathcal{F}} = L \overline{\mathcal{F}}_2 + \overline{\mathcal{F}}_4$ that also satisfies
$\overline{\mathcal{F}} = L \overline{\mathcal{F}}_2 + \overline{\mathcal{F}}_4$ that also satisfies ![]() $ \mathcal{M}(0) = \mathcal{M}_0$.
$ \mathcal{M}(0) = \mathcal{M}_0$.
Analogous necessary and sufficient conditions for the discrete problem with boundaries were shown in [Reference Panayotaros26]. We include them below for completeness, also the numerical examples below consider geometries of both types.
Proposition 2.5. Let q = 3. Let  $Q_b: {\partial G} \rightarrow \hbox{Sym}^q_0$. Suppose there exists an
$Q_b: {\partial G} \rightarrow \hbox{Sym}^q_0$. Suppose there exists an ![]() $\epsilon_0 \gt 0$ such that
$\epsilon_0 \gt 0$ such that  $Q(L) \in \hbox{Sym}^q_0$ is a critical point of
$Q(L) \in \hbox{Sym}^q_0$ is a critical point of ![]() $\mathcal{F} = L \mathcal{F}_2(Q;Q_b) + \mathcal{F}_4(Q;Q_b)$, for every
$\mathcal{F} = L \mathcal{F}_2(Q;Q_b) + \mathcal{F}_4(Q;Q_b)$, for every ![]() $L \in [0, \epsilon_0]$. Assume also that Q(L) is C 1 in
$L \in [0, \epsilon_0]$. Assume also that Q(L) is C 1 in ![]() $[0,\epsilon_0] $ and that there exist disjoint subsets U 1, U 2 of G,
$[0,\epsilon_0] $ and that there exist disjoint subsets U 1, U 2 of G, ![]() $U_1 \cup U_2 \neq \emptyset$, such that
$U_1 \cup U_2 \neq \emptyset$, such that ![]() $Q(0) \in \mathcal{C}_0( \mathcal{F}_4,U_1,U_2)$. Then Q(0) is a critical point of
$Q(0) \in \mathcal{C}_0( \mathcal{F}_4,U_1,U_2)$. Then Q(0) is a critical point of ![]() $\mathcal{F}_2$ restricted to
$\mathcal{F}_2$ restricted to ![]() $ \mathcal{C}_0( \mathcal{ F}_4,U_1,U_2)$
$ \mathcal{C}_0( \mathcal{ F}_4,U_1,U_2)$
Proposition 2.6. Let q = 3. Let U 1, U 2 be disjoint subsets of G with nonempty union. Also let  $Q_b: {\partial G} \rightarrow \hbox{Sym}^q_0$. Suppose that ψ 0 is a nondegenerate critical point of
$Q_b: {\partial G} \rightarrow \hbox{Sym}^q_0$. Suppose that ψ 0 is a nondegenerate critical point of ![]() $ \mathcal{F}_2(\cdot;Q_b)$, restricted to
$ \mathcal{F}_2(\cdot;Q_b)$, restricted to ![]() $\mathcal{C}_0(\mathcal{F}_4,U_1,U_2)$. Then there exists
$\mathcal{C}_0(\mathcal{F}_4,U_1,U_2)$. Then there exists ![]() $\epsilon_0 \gt 0$ and a unique real analytic one-parameter family Q(L),
$\epsilon_0 \gt 0$ and a unique real analytic one-parameter family Q(L), ![]() $|L| \lt \epsilon_0 $ of critical points of
$|L| \lt \epsilon_0 $ of critical points of ![]() $\mathcal{F}(\cdot;Q_b) = L \mathcal{F}_2(\cdot;Q_b) + \mathcal{F}_4(\cdot;Q_b)$ that also satisfies
$\mathcal{F}(\cdot;Q_b) = L \mathcal{F}_2(\cdot;Q_b) + \mathcal{F}_4(\cdot;Q_b)$ that also satisfies ![]() $ Q(0) = \psi_0$.
$ Q(0) = \psi_0$.
The difference between the results for graphs with and without boundary is due to symmetry. In graphs without boundary ![]() $ \overline{\mathcal{F}}_2$,
$ \overline{\mathcal{F}}_2$, ![]() $ \overline{\mathcal{F}}_4$ and
$ \overline{\mathcal{F}}_4$ and ![]() $ \overline{\mathcal{F}}$ are invariant under an action of SO(3) on
$ \overline{\mathcal{F}}$ are invariant under an action of SO(3) on ![]() $X(\overline G)$ we describe in the next section. In graphs with boundary
$X(\overline G)$ we describe in the next section. In graphs with boundary ![]() $\mathcal{F}_2$, and
$\mathcal{F}_2$, and ![]() $\cal F$ do not have this symmetry because of terms that couple sites in the “interior” G and the “boundary”
$\cal F$ do not have this symmetry because of terms that couple sites in the “interior” G and the “boundary” ![]() $\partial G$ where the data is fixed. A consequence is that critical points of
$\partial G$ where the data is fixed. A consequence is that critical points of ![]() $\cal F$ can be isolated, while nontrivial critical points of
$\cal F$ can be isolated, while nontrivial critical points of ![]() $ \overline{\mathcal{F}}$ belong to manifolds obtained by the diagonal adjoint action of SO(3) on any critical point. This action is a generalization of rotations of the directions defining the projective plane, see section 2, Definition 3.9, and can be applied at all sites, see section 3.
$ \overline{\mathcal{F}}$ belong to manifolds obtained by the diagonal adjoint action of SO(3) on any critical point. This action is a generalization of rotations of the directions defining the projective plane, see section 2, Definition 3.9, and can be applied at all sites, see section 3.
The proofs of Propositions 2.3, 2.4 are similar to their analogues for the case with boundary Propositions 2.5, 2.6 in [Reference Panayotaros26]. The main step is Lemma 3.11 on the reduction of the equation for equilibria to an equation on a product of product of projective planes. We summarize the proofs in the next section. The modifications due to the additional global SO(3) symmetry are minor. The main additional property is the equivariance of the reduced equation under the diagonal adjoint action of SO(3) on products of projective planes, see Lemma 3.12. The isotropy subgroups of this action are classified in Proposition 3.13, this result leads to a list of possible manifolds of critical points, see e.g. [Reference Kolář, Michor and Slovák16].
The most interesting critical points are local and global minima of ![]() $ \overline{\mathcal{F}}_4$ and
$ \overline{\mathcal{F}}_4$ and ![]() $\mathcal{F}_4$. Minima correspond to the cases
$\mathcal{F}_4$. Minima correspond to the cases ![]() $U_- = {\overline G}$ for
$U_- = {\overline G}$ for ![]() $ \overline{\mathcal{F}}_4$, and
$ \overline{\mathcal{F}}_4$, and ![]() $U_- = G$ for
$U_- = G$ for ![]() $\mathcal{F}_4$. The corresponding bifurcation equation for these cases is the equation for critical points of discrete generalized Oseen–Frank functionals.
$\mathcal{F}_4$. The corresponding bifurcation equation for these cases is the equation for critical points of discrete generalized Oseen–Frank functionals.
Proposition 2.7. Let q = 3. (i) Let ![]() $U_- = {\overline G}$,
$U_- = {\overline G}$, ![]() $U_+ = \emptyset$. Then critical points of the function
$U_+ = \emptyset$. Then critical points of the function ![]() $ \overline{\mathcal{F}}_2$, restricted to
$ \overline{\mathcal{F}}_2$, restricted to ![]() $\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$, can be mapped bijectively to critical points of a discrete generalized Oseen–Frank functional
$\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$, can be mapped bijectively to critical points of a discrete generalized Oseen–Frank functional  $\overline{\mathcal{F}}_{2_r}:( \mathbb{R}\mathrm{P}^2)^{|\overline G| }
\rightarrow \mathbb{R}$ that is also invariant an action of SO(3). (ii) Let
$\overline{\mathcal{F}}_{2_r}:( \mathbb{R}\mathrm{P}^2)^{|\overline G| }
\rightarrow \mathbb{R}$ that is also invariant an action of SO(3). (ii) Let ![]() $U_- = G$,
$U_- = G$, ![]() $U_+ = \emptyset$, and consider a Qb with values in
$U_+ = \emptyset$, and consider a Qb with values in ![]() $\Sigma^2_-$. Then critical points of the function
$\Sigma^2_-$. Then critical points of the function ![]() $ \mathcal{F}_2$, restricted to
$ \mathcal{F}_2$, restricted to ![]() $\mathcal{C}_0(\mathcal{F}_4,U_+,U_-)$, can be mapped bijectively to critical points of a discrete generalized Oseen–Frank functional
$\mathcal{C}_0(\mathcal{F}_4,U_+,U_-)$, can be mapped bijectively to critical points of a discrete generalized Oseen–Frank functional ![]() $ \mathcal{F}_{2_r}:(\mathbb{R}\mathrm{P}^2)^{|G|} \rightarrow
\mathbb{R}$.
$ \mathcal{F}_{2_r}:(\mathbb{R}\mathrm{P}^2)^{|G|} \rightarrow
\mathbb{R}$.
The generalized discrete Oseen–Frank functional ![]() $\overline{\mathcal{F}}_{2_r}$ of the proposition is given in section 3, see [Reference Panayotaros26] for
$\overline{\mathcal{F}}_{2_r}$ of the proposition is given in section 3, see [Reference Panayotaros26] for ![]() $\mathcal{F}_{2,r}$.
$\mathcal{F}_{2,r}$.
A corollary of the nondegeneracy of the critical points of fB, Lemma 3.5, is the existence of normally hyperbolic invariant sets in the gradient flow of the Landau–de Gennes energy. The statement uses the terminology of [Reference Eldering10].
Proposition 2.8. Let q = 3. Let ![]() $r \geq 1$. (i) Let
$r \geq 1$. (i) Let ![]() $U_+, U_{-} $ be disjoint subsets of
$U_+, U_{-} $ be disjoint subsets of ![]() $\overline G$ with nonempty union. Then the set
$\overline G$ with nonempty union. Then the set ![]() $\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+, U_-)$ is
$\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+, U_-)$ is ![]() $r-$normally hyperbolic under the flow of
$r-$normally hyperbolic under the flow of ![]() $ - \nabla \overline{\mathcal{F}}_4$. Also, every point of
$ - \nabla \overline{\mathcal{F}}_4$. Also, every point of ![]() $\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$ has
$\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$ has ![]() $5 |U^c| + 2 |U_+|$ unstable directions, and
$5 |U^c| + 2 |U_+|$ unstable directions, and ![]() $3 |U_-| + |U_+|$ stable directions, Uc the complement of
$3 |U_-| + |U_+|$ stable directions, Uc the complement of ![]() $U_+ \cup U_-$ in
$U_+ \cup U_-$ in ![]() $\overline G$. (ii) Let
$\overline G$. (ii) Let  $Q_b:\partial G \rightarrow \hbox{Sym}^q_0$. Let
$Q_b:\partial G \rightarrow \hbox{Sym}^q_0$. Let ![]() $U_+, U_- $ be disjoint subsets of G with nonempty union. Then the set
$U_+, U_- $ be disjoint subsets of G with nonempty union. Then the set ![]() $\mathcal{C}_0(\mathcal{F}_4,U_+,U_-)$ is
$\mathcal{C}_0(\mathcal{F}_4,U_+,U_-)$ is ![]() $r-$normally hyperbolic under the flow of
$r-$normally hyperbolic under the flow of  $ - \nabla_Q \overline{\mathcal{F}}_4(Q;Q_b)$. Also, every point of
$ - \nabla_Q \overline{\mathcal{F}}_4(Q;Q_b)$. Also, every point of ![]() $ \mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$ has
$ \mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$ has ![]() $5 |U^c| + 2 |U_+|$ unstable directions, and
$5 |U^c| + 2 |U_+|$ unstable directions, and ![]() $3 |U_-| + |U_+|$ stable directions, Uc the complement of
$3 |U_-| + |U_+|$ stable directions, Uc the complement of ![]() $U_+ \cup U_-$ in G.
$U_+ \cup U_-$ in G.
By the theory of normal hyperbolicity [Reference Bates, Lu and Zheng3, Reference Berger and Bounemoura4, Reference Eldering10, Reference Fenichel11, Reference Hirsch, Pugh and Shub15] all the invariant sets ![]() $\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$ and
$\mathcal{C}_0( \overline{\mathcal{F}}_4,U_+,U_-)$ and ![]() $\mathcal{C}_0(\mathcal{F}_4,U_+,U_-)$ of the L = 0 gradient flow of
$\mathcal{C}_0(\mathcal{F}_4,U_+,U_-)$ of the L = 0 gradient flow of ![]() $\overline{\mathcal{F}}$,
$\overline{\mathcal{F}}$, ![]() $\cal F$ respectively persist for
$\cal F$ respectively persist for ![]() $|L|$ sufficiently small and conserve their normal contraction and expansion properties.
$|L|$ sufficiently small and conserve their normal contraction and expansion properties.
The numerical study in section 4 is motivated primarily by Proposition 2.8. In the case ![]() $U = U_-$,
$U = U_-$, ![]() $U^c = \emptyset$, the expected L ≠ 0 invariant sets attract orbits in their vicinity. We expect that for L > 0 and sufficiently small, trajectories of the gradient flows should approach the attracting invariant manifold that is parametrized by the uniaxial Q-tensors of
$U^c = \emptyset$, the expected L ≠ 0 invariant sets attract orbits in their vicinity. We expect that for L > 0 and sufficiently small, trajectories of the gradient flows should approach the attracting invariant manifold that is parametrized by the uniaxial Q-tensors of ![]() $(\Sigma^3_-)^{|U|}$,
$(\Sigma^3_-)^{|U|}$, ![]() $U = \overline G$ or G. The numerical observations are consistent with this scenario. We see that the Q-tensor first becomes nearly uniaxial at all sites and then slowly converges to an equilibrium. The slow realignment of the director fields over this longer time scale is interpreted as motion on the invariant manifold.
$U = \overline G$ or G. The numerical observations are consistent with this scenario. We see that the Q-tensor first becomes nearly uniaxial at all sites and then slowly converges to an equilibrium. The slow realignment of the director fields over this longer time scale is interpreted as motion on the invariant manifold.
The theory of the equilibria presented is a generalization of the theory developed for “breather solutions” of the discrete nonlinear Schrödinger equation [Reference Pelinovsky, Kevrekidis and Frantzeskakis29–Reference Penati, Sansottera, Paleari, Koukouloyannis and Kevrekidis31, Reference Sansottera, Danesi, Penati and Paleari33]. These solutions are periodic orbits of a Hamiltonian system. In the present problem the gradient structure of the dynamics allows us to approximate attracting equilibria by integrating the evolution equations. We see in section 4 that convergence is generally slow. Other tools to compute these equilibria may be used in future work, the literature on the numerical continuation and bifurcations of such solutions in is extensive.
3. Reduced equation and continuation of solutions
In this section, we prove the theoretical results of the paper and introduce notation used in the numerical study of section 4. In subsection 3.1 we review the geometry of the critical sets of fB and the geometrical constructions used in the proofs of the main results and in section 4. The proofs are presented in subsection 3.2.
In subsection 3.1, we use the symmetry of the onsite energy fB under rotations to analyse the geometry of its critical sets and their neighbourhood, see Definition 1 for a precise description of this symmetry. A main idea is that, due to the symmetry of the nontrivial critical sets ![]() $\Sigma^3_\pm$ of fB, computations involving derivatives of fB can be performed at any point of
$\Sigma^3_\pm$ of fB, computations involving derivatives of fB can be performed at any point of ![]() $\Sigma^3_\pm$, see Lemmas 3.2, 3.3. This point is chosen to simplify the computations. This idea is implemented more effectively by a suitable choice of coordinates for the linear space
$\Sigma^3_\pm$, see Lemmas 3.2, 3.3. This point is chosen to simplify the computations. This idea is implemented more effectively by a suitable choice of coordinates for the linear space  $\hbox{Sym}^3_0$, see Lemma 3.4. The nondegeneracy of the sets
$\hbox{Sym}^3_0$, see Lemma 3.4. The nondegeneracy of the sets ![]() $\Sigma^3_\pm$ is summarized in Lemma 3.5. The remaining part of subsection 3.1 uses the symmetry to define a special system of coordinates for tubular neighbourhoods of the nontrivial critical sets
$\Sigma^3_\pm$ is summarized in Lemma 3.5. The remaining part of subsection 3.1 uses the symmetry to define a special system of coordinates for tubular neighbourhoods of the nontrivial critical sets ![]() $\Sigma^3_\pm$ of fB, see Remarks 3.7, 3.8 and Lemma 3.9 for their properties.
$\Sigma^3_\pm$ of fB, see Remarks 3.7, 3.8 and Lemma 3.9 for their properties.
In subsection 3.2, we use this construction to define analogous systems of coordinates for tubular neighbourhoods of the anticontinuous limit critical sets of ![]() $\cal F$. We use the fact that these sets are products of the
$\cal F$. We use the fact that these sets are products of the ![]() $\Sigma^3_\pm$. The use of these coordinates greatly simplifies the computations needed to show key Lemma 3.11 on the reduced equations, and its consequences, Propositions 2.3, 2.4. The same computation is also the main step to show Propositions 2.7, 2.8. In the case without boundary the reduced energy has an additional global symmetry, see Lemma 3.12. This implies the possibility of manifolds of critical points of the reduced equations, Proposition 3.13 leads to their classification.
$\Sigma^3_\pm$. The use of these coordinates greatly simplifies the computations needed to show key Lemma 3.11 on the reduced equations, and its consequences, Propositions 2.3, 2.4. The same computation is also the main step to show Propositions 2.7, 2.8. In the case without boundary the reduced energy has an additional global symmetry, see Lemma 3.12. This implies the possibility of manifolds of critical points of the reduced equations, Proposition 3.13 leads to their classification.
3.1. Critical sets of the onsite energy fB and their geometry
We review the polar coordinate system for ![]() $3\times3$ Q-tensors and the classification of the critical points of fB, summarized in Lemma 3.1. We also review an alternative system of coordinates that is used to describe the neighbourhood of the critical sets of fB. The construction uses the invariance of fB under the adjoint action of the rotation group, see Definition 1.
$3\times3$ Q-tensors and the classification of the critical points of fB, summarized in Lemma 3.1. We also review an alternative system of coordinates that is used to describe the neighbourhood of the critical sets of fB. The construction uses the invariance of fB under the adjoint action of the rotation group, see Definition 1.
For any  $Q \in \hbox{Sym}^3_0 $ we have the spectral decomposition
$Q \in \hbox{Sym}^3_0 $ we have the spectral decomposition
with ![]() $\lambda_1 \geq \lambda_2 \geq \lambda_3$ the eigenvalues of Q, and
$\lambda_1 \geq \lambda_2 \geq \lambda_3$ the eigenvalues of Q, and ![]() ${\hat n}$,
${\hat n}$, ![]() ${\hat m}$,
${\hat m}$, ![]() ${\hat p} \in \mathbb{R}^3$ the corresponding orthonormal system of eigenvectors. In the case
${\hat p} \in \mathbb{R}^3$ the corresponding orthonormal system of eigenvectors. In the case ![]() $\lambda_1 \gt \lambda_2 \gt \lambda_1$ the vectors
$\lambda_1 \gt \lambda_2 \gt \lambda_1$ the vectors ![]() $\hat n$,
$\hat n$, ![]() $\hat m$,
$\hat m$, ![]() $\hat p$ are determined uniquely up to signs.
$\hat p$ are determined uniquely up to signs.
Since Q is traceless, we have ![]() $\lambda_3 = - \lambda_1 - \lambda_2$ and we see that
$\lambda_3 = - \lambda_1 - \lambda_2$ and we see that
 \begin{equation}
Q = s ( {\hat n} \otimes {\hat n} - \frac{1}{3} I) + r ( {\hat m} \otimes {\hat m} - \frac{1}{3} I),
\end{equation}
\begin{equation}
Q = s ( {\hat n} \otimes {\hat n} - \frac{1}{3} I) + r ( {\hat m} \otimes {\hat m} - \frac{1}{3} I),
\end{equation}where
and I is the ![]() $3 \times 3$ identity matrix.
$3 \times 3$ identity matrix.
We examine the range of values the λ 1, λ 2, assuming ![]() $\lambda_1 \geq \lambda_2 \geq \lambda_3$. The case
$\lambda_1 \geq \lambda_2 \geq \lambda_3$. The case ![]() $\lambda_1 = 0 $ implies
$\lambda_1 = 0 $ implies ![]() $\lambda_2 = \lambda_3 = 0$, and corresponds to Q = 0.
$\lambda_2 = \lambda_3 = 0$, and corresponds to Q = 0.
If ![]() $\lambda_1 \neq 0$ the trace condition implies
$\lambda_1 \neq 0$ the trace condition implies ![]() $\lambda_1 \gt 0 $ and
$\lambda_1 \gt 0 $ and ![]() $\lambda_3 \lt 0$. Considering any
$\lambda_3 \lt 0$. Considering any ![]() $\lambda_1 \gt 0$, the values of λ 2 belong to two intervals: region I where
$\lambda_1 \gt 0$, the values of λ 2 belong to two intervals: region I where ![]() $\lambda_1 \geq \lambda_2 \geq 0 \gt \lambda_3 $, and region II where
$\lambda_1 \geq \lambda_2 \geq 0 \gt \lambda_3 $, and region II where ![]() $\lambda_1 \gt 0 \gt \lambda_2 \geq \lambda_3 $.
$\lambda_1 \gt 0 \gt \lambda_2 \geq \lambda_3 $.
In region I, we have ![]() $\lambda_2 \in [0, \lambda_1]$, and by (3.3),
$\lambda_2 \in [0, \lambda_1]$, and by (3.3), ![]() $r \in [s/2,s]$, with
$r \in [s/2,s]$, with ![]() $s \in [2 \lambda_1, 3 \lambda_1]$.
$s \in [2 \lambda_1, 3 \lambda_1]$.
In region II, we have ![]() $\lambda_2 \in [- \lambda_1/2, 0)$, and by (3.3),
$\lambda_2 \in [- \lambda_1/2, 0)$, and by (3.3), ![]() $r \in [0, s/2)$,
$r \in [0, s/2)$, ![]() $s \in [3/2 \lambda_1, 2 \lambda_1)$.
$s \in [3/2 \lambda_1, 2 \lambda_1)$.
The boundaries of regions I, and II intersect at ![]() $\lambda_2 = 0$. The second (upper) boundary of interval I,
$\lambda_2 = 0$. The second (upper) boundary of interval I, ![]() $\lambda_2 = \lambda_1$, corresponds to
$\lambda_2 = \lambda_1$, corresponds to ![]() $r = s = 3 \lambda_1$. In that case, by (3.2) we have
$r = s = 3 \lambda_1$. In that case, by (3.2) we have
 \begin{equation}
Q = - s ( {\hat p} \otimes {\hat p} - \frac{1}{3} I) = - 3 \lambda_1 ( {\hat p} \otimes {\hat p} - \frac{1}{3} I).
\end{equation}
\begin{equation}
Q = - s ( {\hat p} \otimes {\hat p} - \frac{1}{3} I) = - 3 \lambda_1 ( {\hat p} \otimes {\hat p} - \frac{1}{3} I).
\end{equation} The second (lower) boundary of interval II,  $\lambda_2 = - \frac{1}{2} \lambda_1 = \lambda_3$, corresponds to r = 0,
$\lambda_2 = - \frac{1}{2} \lambda_1 = \lambda_3$, corresponds to r = 0,  $s = \frac{3}{2} \lambda_1 = - 3 \lambda_2$. Then
$s = \frac{3}{2} \lambda_1 = - 3 \lambda_2$. Then
 \begin{equation}
Q = s ( {\hat n} \otimes {\hat n} - \frac{1}{3} I) = - 3 \lambda_2 ( {\hat n} \otimes {\hat n} - \frac{1}{3} I).
\end{equation}
\begin{equation}
Q = s ( {\hat n} \otimes {\hat n} - \frac{1}{3} I) = - 3 \lambda_2 ( {\hat n} \otimes {\hat n} - \frac{1}{3} I).
\end{equation}Recall that Q is termed uniaxial if it has two equal nonzero eigenvalues, and isotropic if Q = 0. Otherwise Q is biaxial. The uniaxial Q-tensors correspond to the boundary of the union of regions I and II.
Lemma 3.1. Let ![]() $x_+$,
$x_+$, ![]() $x_-$ denote the positive and negative roots of
$x_-$ denote the positive and negative roots of
respectively. Then the critical points of fB consist of the sets defined by
(i) ![]() $\lambda_1 = \lambda_2 = 0$, where Q = 0,
$\lambda_1 = \lambda_2 = 0$, where Q = 0,
(ii) ![]() $\lambda_1 \gt 0$ with
$\lambda_1 \gt 0$ with ![]() $r = s = 3 \lambda_1 \gt 0$ (upper boundary of region I), where
$r = s = 3 \lambda_1 \gt 0$ (upper boundary of region I), where
 \begin{equation}
Q = - 3 x_+ ( {\hat p} \otimes {\hat p} - \frac{1}{3} I), \quad {\hat p} \in S^2 \subset \mathbb{R}^3,
\end{equation}
\begin{equation}
Q = - 3 x_+ ( {\hat p} \otimes {\hat p} - \frac{1}{3} I), \quad {\hat p} \in S^2 \subset \mathbb{R}^3,
\end{equation} (iii) ![]() $\lambda_1 \gt 0$ with r = 0,
$\lambda_1 \gt 0$ with r = 0,  $s = \frac{3}{2} \lambda_1$ (lower boundary of region II), where
$s = \frac{3}{2} \lambda_1$ (lower boundary of region II), where
 \begin{equation}
Q = - 3 x_- ( {\hat n} \otimes {\hat n} - \frac{1}{3} I), \quad {\hat n} \in S^2 \subset \mathbb{R}^3.
\end{equation}
\begin{equation}
Q = - 3 x_- ( {\hat n} \otimes {\hat n} - \frac{1}{3} I), \quad {\hat n} \in S^2 \subset \mathbb{R}^3.
\end{equation} The infimum of fB is attained at the set (iii), denoted by ![]() $\Sigma^3_-$. The set (ii) is denoted by
$\Sigma^3_-$. The set (ii) is denoted by ![]() $\Sigma^3_+$ and is not a set of local extrema of fB. The results are summarized by Proposition 2.1, see [Reference Majumdar20, Reference Majumdar and Zarnescu21, Reference Panayotaros26] for details.
$\Sigma^3_+$ and is not a set of local extrema of fB. The results are summarized by Proposition 2.1, see [Reference Majumdar20, Reference Majumdar and Zarnescu21, Reference Panayotaros26] for details.
In the polar representation the value of r quantifies the deviation from the set of uniaxial tensors ![]() $\Sigma^3_\pm$. However, the polar representation is singular at the critical points of fB, and we need alternative systems of coordinates for the neighbourhood of the sets
$\Sigma^3_\pm$. However, the polar representation is singular at the critical points of fB, and we need alternative systems of coordinates for the neighbourhood of the sets ![]() $\Sigma^3_\pm$. The system of coordinates we define below is motivated by the symmetries of fB. We recall the following.
$\Sigma^3_\pm$. The system of coordinates we define below is motivated by the symmetries of fB. We recall the following.
Definition 1. Given ![]() $A \in SO(3)$, we define
$A \in SO(3)$, we define ![]() $\Psi_A $ on the set
$\Psi_A $ on the set ![]() $\hbox{Mat}(3)$ of real
$\hbox{Mat}(3)$ of real ![]() $3 \times 3 $ matrices by
$3 \times 3 $ matrices by
Also define ![]() $\Psi:SO(3) \times \hbox{Mat}(3) \rightarrow \hbox{Mat}(3)$ by
$\Psi:SO(3) \times \hbox{Mat}(3) \rightarrow \hbox{Mat}(3)$ by ![]() $\Psi(A,Q) = \Psi_A(Q)$.
$\Psi(A,Q) = \Psi_A(Q)$.
Lemma 3.2. Let ![]() $A \in SO(3)$, then
$A \in SO(3)$, then ![]() $\Psi_A: \hbox{Mat}(3) \rightarrow \hbox{Mat}(3)$ is an invertible linear transformation that preserves
$\Psi_A: \hbox{Mat}(3) \rightarrow \hbox{Mat}(3)$ is an invertible linear transformation that preserves  $ \hbox{Sym}^3_0 $. Furthermore
$ \hbox{Sym}^3_0 $. Furthermore  $f_B:\hbox{Sym}^3_0 \rightarrow \mathbb{R}$ is invariant under
$f_B:\hbox{Sym}^3_0 \rightarrow \mathbb{R}$ is invariant under ![]() $\Psi_A$.
$\Psi_A$.
The restrictions of the ![]() $\Psi_A$,
$\Psi_A$, ![]() $A \in SO(3)$, to
$A \in SO(3)$, to  $\hbox{Sym}^3_0$, and Ψ to
$\hbox{Sym}^3_0$, and Ψ to  $ SO(3) \times \hbox{Sym}^3_0$ are denoted by
$ SO(3) \times \hbox{Sym}^3_0$ are denoted by ![]() $\Psi_A$, Ψ, respectively.
$\Psi_A$, Ψ, respectively.
By Lemma 3.2 the maps ![]() $\Psi_A$,
$\Psi_A$, ![]() $A \in SO(3)$, in
$A \in SO(3)$, in ![]() $\hbox{Mat}(3)$,
$\hbox{Mat}(3)$,  $ \hbox{Sym}^3_0 $ can be represented by matrix multiplication in
$ \hbox{Sym}^3_0 $ can be represented by matrix multiplication in ![]() $\mathbb{R}^9$,
$\mathbb{R}^9$, ![]() $\mathbb{R}^5$, respectively. The matrices depend on the choice of basis in
$\mathbb{R}^5$, respectively. The matrices depend on the choice of basis in ![]() $\hbox{Mat}(3)$,
$\hbox{Mat}(3)$,  $\hbox{Sym}^3_0$, respectively.
$\hbox{Sym}^3_0$, respectively.
Consider a basis  $\{{\hat W}_j\}_{j = 1}^5$ in
$\{{\hat W}_j\}_{j = 1}^5$ in  $\hbox{Sym}^3_0$, with
$\hbox{Sym}^3_0$, with  $Q = \sum_{j=1}^5 w_j {\hat W}_j$,
$Q = \sum_{j=1}^5 w_j {\hat W}_j$,  $\forall Q \in \hbox{Sym}^3_0$, and the isomorphism
$\forall Q \in \hbox{Sym}^3_0$, and the isomorphism  ${\overline{\beta}}^w(Q) = w := [w_1, \ldots, w_5]^T \in \mathbb{R}^5$. Then the matrix representation of
${\overline{\beta}}^w(Q) = w := [w_1, \ldots, w_5]^T \in \mathbb{R}^5$. Then the matrix representation of ![]() $\Psi_A$,
$\Psi_A$, ![]() $A \in SO(3)$, in this basis is the unique matrix
$A \in SO(3)$, in this basis is the unique matrix ![]() $T^w_A$ satisfying
$T^w_A$ satisfying  $T^w_A({\overline{\beta}}^w(Q)) = {\overline{\beta}}^w( \Psi_A(Q))$.
$T^w_A({\overline{\beta}}^w(Q)) = {\overline{\beta}}^w( \Psi_A(Q))$. ![]() $T^w_A$ has inverse
$T^w_A$ has inverse ![]() $T^w_{A^{-1}}$,
$T^w_{A^{-1}}$, ![]() $\forall A \in SO(3)$. Also define
$\forall A \in SO(3)$. Also define ![]() $T^w:SO(3) \times \mathbb{R}^5 \rightarrow \mathbb{R}^5$ by
$T^w:SO(3) \times \mathbb{R}^5 \rightarrow \mathbb{R}^5$ by ![]() $ T^w(A,q) = T^w_Aq$.
$ T^w(A,q) = T^w_Aq$.
The application of the actions Ψ, Tw to the analysis of the critical sets of fB is based on the following observations, see [Reference Panayotaros26] for more details.
Lemma 3.3. The sets ![]() $\Sigma^3_\pm$ are invariant under Ψ, moreover the orbit of any point of
$\Sigma^3_\pm$ are invariant under Ψ, moreover the orbit of any point of ![]() $\Sigma^3_\pm$ under Ψ is
$\Sigma^3_\pm$ under Ψ is ![]() $\Sigma^3_\pm$. Also, let
$\Sigma^3_\pm$. Also, let  ${\overline{\beta}}^w:\hbox{Sym}^3_0 \rightarrow \mathbb{R}^5$ be an isomorphism, then the sets
${\overline{\beta}}^w:\hbox{Sym}^3_0 \rightarrow \mathbb{R}^5$ be an isomorphism, then the sets  ${\overline{\beta}}^w(\Sigma^3_\pm)$ are invariant under Tw, moreover the orbit of any point of
${\overline{\beta}}^w(\Sigma^3_\pm)$ are invariant under Tw, moreover the orbit of any point of  ${\overline{\beta}}^w (\Sigma^3_\pm)$ under Tw is
${\overline{\beta}}^w (\Sigma^3_\pm)$ under Tw is  ${\overline{\beta}}^w(\Sigma^3_\pm)$.
${\overline{\beta}}^w(\Sigma^3_\pm)$.
The lemma is used to simplify computations in the neighbourhood of the sets  ${\overline{\beta}}^w(\Sigma^3_\pm)$. In particular, we can compute quantities of interest related to the derivative of fB at a single point and use the properties of Tw to extend the result to all points of
${\overline{\beta}}^w(\Sigma^3_\pm)$. In particular, we can compute quantities of interest related to the derivative of fB at a single point and use the properties of Tw to extend the result to all points of  ${\overline{\beta}}^w(\Sigma^3_\pm)$.
${\overline{\beta}}^w(\Sigma^3_\pm)$.
To implement this idea it is also convenient to define bases of ![]() $\hbox{Mat}(3)$ that lead to a representation of the
$\hbox{Mat}(3)$ that lead to a representation of the ![]() $\Psi_A$,
$\Psi_A$, ![]() $A\in SO(3)$, and Ψ, restricted to
$A\in SO(3)$, and Ψ, restricted to  $\hbox{Sym}^3_0$, by rotation matrices. This construction allows us to understand the local geometry of the critical sets of fB by computations at a single point. This point is chosen below to further simplify the computations.
$\hbox{Sym}^3_0$, by rotation matrices. This construction allows us to understand the local geometry of the critical sets of fB by computations at a single point. This point is chosen below to further simplify the computations.
Consider first the standard basis of ![]() $\hbox{Mat}(3) $ of matrices
$\hbox{Mat}(3) $ of matrices  ${\hat Q}_{i,j}$ with
${\hat Q}_{i,j}$ with ![]() $i,j$th entry unity and all other entries zero. We let
$i,j$th entry unity and all other entries zero. We let  ${\hat Z}_k = {\hat Q}_{i,j}$, where the enumeration
${\hat Z}_k = {\hat Q}_{i,j}$, where the enumeration ![]() $k(i,j)$ is defined by
$k(i,j)$ is defined by
 \begin{equation}
Q = \left[
\begin{array}{ccc}
z_1 & z_2 & z_3 \\
z_4 & z_5 & z_6 \\
z_7 & z_8 & z_9
\end{array}
\right], \quad Q = \sum_{k=1}^9 z_k {\hat Z}_k.
\end{equation}
\begin{equation}
Q = \left[
\begin{array}{ccc}
z_1 & z_2 & z_3 \\
z_4 & z_5 & z_6 \\
z_7 & z_8 & z_9
\end{array}
\right], \quad Q = \sum_{k=1}^9 z_k {\hat Z}_k.
\end{equation} We define the inner product ![]() $\langle \cdot,\cdot \rangle$ in
$\langle \cdot,\cdot \rangle$ in ![]() $\hbox{Mat(3)}$ by
$\hbox{Mat(3)}$ by  $\langle R,S\rangle = \hbox{tr} (R S^T) = \sum_{k = 1}^9 r_k s_k$,
$\langle R,S\rangle = \hbox{tr} (R S^T) = \sum_{k = 1}^9 r_k s_k$,  $ R = \sum_{k=1}^9 r_k {\hat Z}_k$,
$ R = \sum_{k=1}^9 r_k {\hat Z}_k$,  $ S = \sum_{k=1}^9 s_k {\hat Z}_k$. The corresponding norm is denoted by
$ S = \sum_{k=1}^9 s_k {\hat Z}_k$. The corresponding norm is denoted by ![]() $||\cdot||$.
$||\cdot||$.
The isomorphism ![]() $\beta^z: \hbox{Mat}(3) \rightarrow \mathbb{R}^9$ defined by
$\beta^z: \hbox{Mat}(3) \rightarrow \mathbb{R}^9$ defined by ![]() $\beta^z(Q) = z := [z_1, \ldots, z_9]^T$,
$\beta^z(Q) = z := [z_1, \ldots, z_9]^T$,  $Q = \sum_{k=1}^9 z_k {\hat Z}_k$, is an isometry between
$Q = \sum_{k=1}^9 z_k {\hat Z}_k$, is an isometry between ![]() $\hbox{Mat}(3) $ with
$\hbox{Mat}(3) $ with ![]() $|| \cdot ||$, and
$|| \cdot ||$, and ![]() $\mathbb{R}^9$ with the Euclidean norm. The map
$\mathbb{R}^9$ with the Euclidean norm. The map ![]() $\Psi_A$,
$\Psi_A$, ![]() $A \in SO(3)$, is represented by multiplication by the matrix
$A \in SO(3)$, is represented by multiplication by the matrix ![]() $[\Psi_A]^z$, that is
$[\Psi_A]^z$, that is ![]() $\beta^z(\Psi_A(Q)) = [\Psi_A]^z \beta^z(Q)$,
$\beta^z(\Psi_A(Q)) = [\Psi_A]^z \beta^z(Q)$, ![]() $\forall Q \in \hbox{Mat}(3)$. Then
$\forall Q \in \hbox{Mat}(3)$. Then ![]() $[\Psi_A]^z$ is orthogonal in
$[\Psi_A]^z$ is orthogonal in ![]() $\mathbb{R}^9$ with the Euclidean norm,
$\mathbb{R}^9$ with the Euclidean norm, ![]() $\forall A \in SO(3)$, see [Reference Panayotaros26].
$\forall A \in SO(3)$, see [Reference Panayotaros26].
Consider a new basis  $\{{\hat Y}_j \}_{j = 1}^9$ of
$\{{\hat Y}_j \}_{j = 1}^9$ of ![]() $\hbox{Mat}(3)$, let
$\hbox{Mat}(3)$, let  $Q = \sum_{k=1}^9 y_k {\hat Y}_k$,
$Q = \sum_{k=1}^9 y_k {\hat Y}_k$, ![]() $\forall Q \in \hbox{Mat}(3)$, and define the isomorphism
$\forall Q \in \hbox{Mat}(3)$, and define the isomorphism ![]() $\beta^y: \hbox{Mat}(3) \rightarrow \mathbb{R}^9$ by
$\beta^y: \hbox{Mat}(3) \rightarrow \mathbb{R}^9$ by ![]() $\beta^y(Q) = y := [y_1,\ldots,y_9]^T$. Assume that (i):
$\beta^y(Q) = y := [y_1,\ldots,y_9]^T$. Assume that (i):  ${\hat Y}_i = \sum_{j = 1}^9 M_{i,j} {\hat Z}_j$, with M an orthogonal matrix with respect to the Euclidean inner product on
${\hat Y}_i = \sum_{j = 1}^9 M_{i,j} {\hat Z}_j$, with M an orthogonal matrix with respect to the Euclidean inner product on ![]() $\mathbb{R}^9$, and (ii):
$\mathbb{R}^9$, and (ii):  $Q \in \hbox{Sym}^3_0$ if and only if
$Q \in \hbox{Sym}^3_0$ if and only if ![]() $(\beta^y(Q))_i = 0$, for
$(\beta^y(Q))_i = 0$, for ![]() $i \in \cal I$,
$i \in \cal I$, ![]() $\mathcal{I} \subset \{1, \ldots, 9\}$,
$\mathcal{I} \subset \{1, \ldots, 9\}$, ![]() $| \mathcal{I } | = 4$.
$| \mathcal{I } | = 4$.
Denote the matrix representation of ![]() $\Psi_A$ in the basis
$\Psi_A$ in the basis  $\{{\hat Y}_j \}_{j = 1}^9$ by
$\{{\hat Y}_j \}_{j = 1}^9$ by ![]() $[\Psi_A]^y$. Let the matrix TA that represents the restriction of
$[\Psi_A]^y$. Let the matrix TA that represents the restriction of ![]() $\Psi_A$ to
$\Psi_A$ to  $\hbox{Sym}^3_0$ in the basis
$\hbox{Sym}^3_0$ in the basis  $\{{\hat Y}_j \}_{j \in \mathcal{J}}$,
$\{{\hat Y}_j \}_{j \in \mathcal{J}}$, ![]() $\mathcal{J} = \{1, \ldots,9\}\setminus\mathcal{I}$. We can show the following, see [Reference Panayotaros26].
$\mathcal{J} = \{1, \ldots,9\}\setminus\mathcal{I}$. We can show the following, see [Reference Panayotaros26].
Lemma 3.4. Multiplication by TA, ![]() $A \in SO(3)$, is an isometry in
$A \in SO(3)$, is an isometry in ![]() $\mathbb{R}^5$ with the Euclidean norm.
$\mathbb{R}^5$ with the Euclidean norm.
An example of a basis  $\{{\hat Y}_j \}_{j = 1}^9$ satisfying (i), (ii) is defined by
$\{{\hat Y}_j \}_{j = 1}^9$ satisfying (i), (ii) is defined by
 \begin{equation}
y_{2} = \frac{1}{\sqrt{2}} ( z_2 + z_4), \quad
y_{4} = \frac{1}{\sqrt{2}} ( z_2 - z_4),
\end{equation}
\begin{equation}
y_{2} = \frac{1}{\sqrt{2}} ( z_2 + z_4), \quad
y_{4} = \frac{1}{\sqrt{2}} ( z_2 - z_4),
\end{equation} \begin{equation}
y_{3} = \frac{1}{\sqrt{2}} ( z_3 + z_7), \quad
y_{7} = \frac{1}{\sqrt{2}} ( z_3 - z_7),
\end{equation}
\begin{equation}
y_{3} = \frac{1}{\sqrt{2}} ( z_3 + z_7), \quad
y_{7} = \frac{1}{\sqrt{2}} ( z_3 - z_7),
\end{equation} \begin{equation}
y_{6} = \frac{1}{\sqrt{2}} ( z_6 + z_8), \quad
y_{8} = \frac{1}{\sqrt{2}} ( z_6 - z_8),
\end{equation}
\begin{equation}
y_{6} = \frac{1}{\sqrt{2}} ( z_6 + z_8), \quad
y_{8} = \frac{1}{\sqrt{2}} ( z_6 - z_8),
\end{equation} \begin{equation}
y_{9} = \frac{1}{\sqrt{3}}( z_1 + z_5 + z_9), \quad
y_{1} = \frac{1}{\sqrt{2}}( z_1 - z_5 ), \quad
y_{5} = \frac{1}{\sqrt{6}} ( z_1 + z_5 - 2 z_9 ).
\end{equation}
\begin{equation}
y_{9} = \frac{1}{\sqrt{3}}( z_1 + z_5 + z_9), \quad
y_{1} = \frac{1}{\sqrt{2}}( z_1 - z_5 ), \quad
y_{5} = \frac{1}{\sqrt{6}} ( z_1 + z_5 - 2 z_9 ).
\end{equation} Thus  $Q \in \hbox{Sym}^3_0$ is equivalent to
$Q \in \hbox{Sym}^3_0$ is equivalent to
i.e. ![]() $\mathcal{J} = \{1, 2, 3, 5, 6 \}$.
$\mathcal{J} = \{1, 2, 3, 5, 6 \}$.
The onsite energy fB of (2.2) in terms of yj, ![]() $j \in \cal J$, is then computed from
$j \in \cal J$, is then computed from
 \begin{equation}
\hbox{tr}(Q^2) = y_1^2 + y_2^2 + y_3^2 + y_5^2 + y_6^2,
\end{equation}
\begin{equation}
\hbox{tr}(Q^2) = y_1^2 + y_2^2 + y_3^2 + y_5^2 + y_6^2,
\end{equation} \begin{equation}
\hbox{tr}(Q^3) = \frac{3}{\sqrt{6}} y_2^2 y_5 + \frac{3}{\sqrt{2}} y_2 y_3 y_6
+ \frac{3}{2\sqrt{2}} (y_3^2 y_1 - y_6^2 y_1 ) - \frac{3}{2\sqrt{6}} (y_3^2 y_5 + y_6^2 y_5)
- \frac{1}{\sqrt{6}} y^3_5 + \frac{3}{\sqrt{6}} y_1^2 y_5.
\end{equation}
\begin{equation}
\hbox{tr}(Q^3) = \frac{3}{\sqrt{6}} y_2^2 y_5 + \frac{3}{\sqrt{2}} y_2 y_3 y_6
+ \frac{3}{2\sqrt{2}} (y_3^2 y_1 - y_6^2 y_1 ) - \frac{3}{2\sqrt{6}} (y_3^2 y_5 + y_6^2 y_5)
- \frac{1}{\sqrt{6}} y^3_5 + \frac{3}{\sqrt{6}} y_1^2 y_5.
\end{equation} The critical sets ![]() $\Sigma^\pm$ of fB can be also parametrized by polar coordinates. Using
$\Sigma^\pm$ of fB can be also parametrized by polar coordinates. Using
for unit vectors in ![]() $\mathbb{R}^3$,
$\mathbb{R}^3$, ![]() $\hat n \in S^2\setminus\{{\hat e}_1,-{\hat e}_1\} $, the corresponding Q-tensors are
$\hat n \in S^2\setminus\{{\hat e}_1,-{\hat e}_1\} $, the corresponding Q-tensors are
 \begin{equation}
Q_\pm({\hat n}(\theta,\phi)) = - 3 x_\pm \left[
\begin{array}{ccc}
\sin^2 \theta \cos^2 \phi - \frac{1}{3} & \frac{1}{2} \sin^2 \theta \sin 2 \phi & \frac{1}{2} \sin 2 \theta \cos \phi \\
\frac{1}{2} \sin^2 \theta \sin 2 \phi & \sin^2 \theta \sin^2\phi - \frac{1}{3} & \frac{1}{2} \sin 2\theta \sin \phi \\
\frac{1}{2} \sin 2 \theta \cos \phi & \frac{1}{2} \sin 2\theta \sin \phi & \cos^2 \theta - \frac{1}{3}
\end{array}
\right],
\end{equation}
\begin{equation}
Q_\pm({\hat n}(\theta,\phi)) = - 3 x_\pm \left[
\begin{array}{ccc}
\sin^2 \theta \cos^2 \phi - \frac{1}{3} & \frac{1}{2} \sin^2 \theta \sin 2 \phi & \frac{1}{2} \sin 2 \theta \cos \phi \\
\frac{1}{2} \sin^2 \theta \sin 2 \phi & \sin^2 \theta \sin^2\phi - \frac{1}{3} & \frac{1}{2} \sin 2\theta \sin \phi \\
\frac{1}{2} \sin 2 \theta \cos \phi & \frac{1}{2} \sin 2\theta \sin \phi & \cos^2 \theta - \frac{1}{3}
\end{array}
\right],
\end{equation} see (2.8), (2.9). By (3.10) and (3.11)-(3.14) their coordinates in the variables yj, ![]() $j \in \cal J$, are
$j \in \cal J$, are
 \begin{equation*}
\nonumber
y_1^\pm = - \frac{3 x_\pm}{\sqrt{2}} \sin^2 \theta (\cos^2 \phi - \sin^2 \phi), \quad
y_2^\pm = - \frac{3 x_\pm}{\sqrt{2}}\sin^2 \theta \sin 2 \phi, \quad y_3^\pm = - \frac{3 x_\pm}{\sqrt{2}}\sin 2 \theta \cos \phi,
\end{equation*}
\begin{equation*}
\nonumber
y_1^\pm = - \frac{3 x_\pm}{\sqrt{2}} \sin^2 \theta (\cos^2 \phi - \sin^2 \phi), \quad
y_2^\pm = - \frac{3 x_\pm}{\sqrt{2}}\sin^2 \theta \sin 2 \phi, \quad y_3^\pm = - \frac{3 x_\pm}{\sqrt{2}}\sin 2 \theta \cos \phi,
\end{equation*} \begin{equation}
y_5^\pm = - \frac{3 x_\pm}{\sqrt{6}}(\sin^2 \theta - 2 \cos^2 \theta), \quad
y_6^\pm = - \frac{3 x_\pm}{\sqrt{2}}\sin 2 \theta \sin \phi.
\end{equation}
\begin{equation}
y_5^\pm = - \frac{3 x_\pm}{\sqrt{6}}(\sin^2 \theta - 2 \cos^2 \theta), \quad
y_6^\pm = - \frac{3 x_\pm}{\sqrt{2}}\sin 2 \theta \sin \phi.
\end{equation} These expressions can be used to produce local coordinates for ![]() $\mathbb{R}\mathrm{P}^2$ and to describe its embedding to
$\mathbb{R}\mathrm{P}^2$ and to describe its embedding to  $\hbox{Sym}^3_0$, details are given below.
$\hbox{Sym}^3_0$, details are given below.
In the remaining part of this subsection, we construct coordinates for a tubular neighbourhood of the critical sets ![]() $\Sigma^3_\pm$ of fB. The results and notation are used in the proofs of subsection 3.2. The construction uses the spectral decomposition of
$\Sigma^3_\pm$ of fB. The results and notation are used in the proofs of subsection 3.2. The construction uses the spectral decomposition of ![]() $\nabla^2 f_B$.
$\nabla^2 f_B$.
Let  $ Q \in \hbox{Sym}^3_0$, then
$ Q \in \hbox{Sym}^3_0$, then  $ Q = \sum_{k=1}^5 w_j {\hat W}_j$, with
$ Q = \sum_{k=1}^5 w_j {\hat W}_j$, with
Define  ${\overline{\beta}}^w: \hbox{Sym}^3_0 \rightarrow \mathbb{R}^5$ by
${\overline{\beta}}^w: \hbox{Sym}^3_0 \rightarrow \mathbb{R}^5$ by  ${\overline{\beta}}^w(Q) = w :=[w_1, \ldots, w_5]^T$. The maps
${\overline{\beta}}^w(Q) = w :=[w_1, \ldots, w_5]^T$. The maps ![]() $\Psi_A$ are represented by multiplication by the matrix
$\Psi_A$ are represented by multiplication by the matrix ![]() $T^w_A$, and
$T^w_A$, and  $(T^w_A)_{i,j} = \langle [\Psi_A]^y {\hat W}_j , {\hat W}_i \rangle $, i,
$(T^w_A)_{i,j} = \langle [\Psi_A]^y {\hat W}_j , {\hat W}_i \rangle $, i, ![]() $j = 1, \ldots, 5$, i.e.
$j = 1, \ldots, 5$, i.e. ![]() $T^w_A$ coincides with TA, assuming the enumeration of
$T^w_A$ coincides with TA, assuming the enumeration of ![]() $\cal J$ in (3.20). The trace inner product
$\cal J$ in (3.20). The trace inner product ![]() $\langle \cdot, \cdot \rangle $ in
$\langle \cdot, \cdot \rangle $ in  $\hbox{Sym}^3_0$ is given by
$\hbox{Sym}^3_0$ is given by  $\langle w, w' \rangle = \sum_{i=1}^5 w_i w'_i = \sum_{j \in \mathcal{J}}^5 y_j y'_j $. Lemma 3.4 implies that multiplication by
$\langle w, w' \rangle = \sum_{i=1}^5 w_i w'_i = \sum_{j \in \mathcal{J}}^5 y_j y'_j $. Lemma 3.4 implies that multiplication by ![]() $T^w_A$ is an isometry,
$T^w_A$ is an isometry, ![]() $\forall A \in SO(3)$.
$\forall A \in SO(3)$.
The application of the rotations ![]() $\Psi_A$, and their representation by orthogonal matrices to the analysis of the critical points of fB is a consequence of the following observations.
$\Psi_A$, and their representation by orthogonal matrices to the analysis of the critical points of fB is a consequence of the following observations.
Let ![]() $\mathcal{L} = f_B \circ {\overline \gamma}^w: \mathbb{R}^5 \rightarrow \mathbb{R}$,
$\mathcal{L} = f_B \circ {\overline \gamma}^w: \mathbb{R}^5 \rightarrow \mathbb{R}$,  ${\overline \gamma}^w = ({\overline{\beta}}^w)^{-1}$, and
${\overline \gamma}^w = ({\overline{\beta}}^w)^{-1}$, and ![]() $h:\mathbb{R}^5 \rightarrow \mathbb{R}^5$ defined by
$h:\mathbb{R}^5 \rightarrow \mathbb{R}^5$ defined by ![]() $h(q) = T^w_Aq$,
$h(q) = T^w_Aq$, ![]() $A \in SO(3)$. We have that q a critical point of
$A \in SO(3)$. We have that q a critical point of ![]() $\cal L$ implies that h(q) is also a critical point of
$\cal L$ implies that h(q) is also a critical point of ![]() $\cal L$, moreover the Hessians of at q, h(q) are related by
$\cal L$, moreover the Hessians of at q, h(q) are related by
Thus to check that ![]() $\Sigma^3_\pm$ are critical sets, it suffices to check that DfB vanishes at any point of
$\Sigma^3_\pm$ are critical sets, it suffices to check that DfB vanishes at any point of ![]() $\Sigma^3_\pm$. Also, since the Hessians of
$\Sigma^3_\pm$. Also, since the Hessians of ![]() $\cal L$ at Q,
$\cal L$ at Q, ![]() $Q'= \Psi_A(Q) \in \Sigma^3_\pm$,
$Q'= \Psi_A(Q) \in \Sigma^3_\pm$, ![]() $A \in SO(3)$, are related by (3.21) the spectrum of the Hessian is then same at all points of the two nontrivial critical sets of
$A \in SO(3)$, are related by (3.21) the spectrum of the Hessian is then same at all points of the two nontrivial critical sets of ![]() $\cal L$. Also, the fact that
$\cal L$. Also, the fact that ![]() $T^w_A$ is an isometry implies that if v an eigenvector of
$T^w_A$ is an isometry implies that if v an eigenvector of ![]() $(\nabla^2 \mathcal{L})(q) $ then
$(\nabla^2 \mathcal{L})(q) $ then ![]() $Dh(q) v$ an eigenvector of
$Dh(q) v$ an eigenvector of ![]() $(\nabla^2 \mathcal{L})(h(q)) $, corresponding to the same eigenvalue. The computation of the spectral data of
$(\nabla^2 \mathcal{L})(h(q)) $, corresponding to the same eigenvalue. The computation of the spectral data of ![]() $\nabla^2 \mathcal{L}$ is summarized by the following.
$\nabla^2 \mathcal{L}$ is summarized by the following.
Lemma 3.5. The origin is a nondegenerate critical point of fB in  $\hbox{Sym}^3_0$ and is a local maximum. The two sets of nontrivial critical points of fB in
$\hbox{Sym}^3_0$ and is a local maximum. The two sets of nontrivial critical points of fB in  $\hbox{Sym}^3_0$ are given by the uniaxial Q-tensors of (3.7), (3.8) and are nondegenerate. The Hessian at the points of (3.8) has two zero eigenvalues and three positive eigenvalues, while the Hessian at the points of (3.7) has two zero eigenvalues, two negative eigenvalues and one positive eigenvalue. The normal subspace is spanned by the eigenvector
$\hbox{Sym}^3_0$ are given by the uniaxial Q-tensors of (3.7), (3.8) and are nondegenerate. The Hessian at the points of (3.8) has two zero eigenvalues and three positive eigenvalues, while the Hessian at the points of (3.7) has two zero eigenvalues, two negative eigenvalues and one positive eigenvalue. The normal subspace is spanned by the eigenvector ![]() $[\sqrt{3},0,0,1,0]^T $ that corresponds to the eigenvalue
$[\sqrt{3},0,0,1,0]^T $ that corresponds to the eigenvalue ![]() $ b^2 x_\pm + 12 c^2 x_\pm^2$ and is colinear to the solution
$ b^2 x_\pm + 12 c^2 x_\pm^2$ and is colinear to the solution ![]() $y^\beta(Q_\pm)$ of (3.22), and the two-dimensional eigenspace corresponding to the double eigenvalue
$y^\beta(Q_\pm)$ of (3.22), and the two-dimensional eigenspace corresponding to the double eigenvalue ![]() $- 3 b^2 x_\pm$.
$- 3 b^2 x_\pm$.
The proof follows from computations of the Q-tensors (3.7), (3.8) obtained from ![]() ${\hat p} = {\hat n} = {\hat e}_1 := [1,0,0]^T $ respectively, see [Reference Panayotaros26]. By (3.17), (3.11)-(3.14) these critical points are
${\hat p} = {\hat n} = {\hat e}_1 := [1,0,0]^T $ respectively, see [Reference Panayotaros26]. By (3.17), (3.11)-(3.14) these critical points are
 \begin{equation}
y_1 = - \frac{3}{\sqrt{2}} x_\pm, \quad y_5 = - \frac{3}{\sqrt{6}} x_\pm, \quad y_2 = y_3 = y_6 = 0.
\end{equation}
\begin{equation}
y_1 = - \frac{3}{\sqrt{2}} x_\pm, \quad y_5 = - \frac{3}{\sqrt{6}} x_\pm, \quad y_2 = y_3 = y_6 = 0.
\end{equation} The Hessian of ![]() $\mathcal{L} = f_B \circ {\overline \gamma}^w$ at this point is simplified and its eigenvalues and eigenvectors are computed explicitly.
$\mathcal{L} = f_B \circ {\overline \gamma}^w$ at this point is simplified and its eigenvalues and eigenvectors are computed explicitly.
We use the information of Lemma 3.5 to describe the sets ![]() $\Sigma^3_\pm $ as the image of embeddings of the projective plane to
$\Sigma^3_\pm $ as the image of embeddings of the projective plane to  $\hbox{Sym}^3_0$, and to construct a normal sets of coordinates in the neighbourhood of the
$\hbox{Sym}^3_0$, and to construct a normal sets of coordinates in the neighbourhood of the ![]() $\Sigma^3_\pm$.
$\Sigma^3_\pm$.
The projective plane ![]() $\mathbb{R}\mathrm{P}^2$ is the set of points of the 2-sphere S 2 with antipodal points identified, i.e. pairs
$\mathbb{R}\mathrm{P}^2$ is the set of points of the 2-sphere S 2 with antipodal points identified, i.e. pairs ![]() $\{n,-n\}$,
$\{n,-n\}$, ![]() $n \in S^2$, with
$n \in S^2$, with ![]() $\{n,-n\} = \{n',-n'\}$, n,
$\{n,-n\} = \{n',-n'\}$, n, ![]() $n' \in S^2$, if and only if
$n' \in S^2$, if and only if ![]() $n = n'$ or −nʹ. Equivalently,
$n = n'$ or −nʹ. Equivalently, ![]() $\mathbb{R}\mathrm{P}^2$ is the set of projectors
$\mathbb{R}\mathrm{P}^2$ is the set of projectors ![]() $ {\hat \nu} \otimes {\hat \nu}$,
$ {\hat \nu} \otimes {\hat \nu}$, ![]() ${\hat \nu} \in S^2$, see e.g. [Reference Lee17], p.18, for the topology in each description.
${\hat \nu} \in S^2$, see e.g. [Reference Lee17], p.18, for the topology in each description.
Consider the maps  $Q_\pm:S^2 \rightarrow \hbox{Sym}_0^3 \subset \hbox{Mat}(3)$ defined in (2.8), (2.9). We have
$Q_\pm:S^2 \rightarrow \hbox{Sym}_0^3 \subset \hbox{Mat}(3)$ defined in (2.8), (2.9). We have ![]() $Q_\pm(-{\hat \nu}) = Q_\pm({\hat \nu})$. Define
$Q_\pm(-{\hat \nu}) = Q_\pm({\hat \nu})$. Define  ${\tilde Q}_\pm:\mathbb{R}\mathrm{P}^2 \rightarrow \hbox{Sym}_0^3$ by
${\tilde Q}_\pm:\mathbb{R}\mathrm{P}^2 \rightarrow \hbox{Sym}_0^3$ by ![]() ${\tilde Q}_\pm(\{{\hat n}, -{\hat n} \}) := Q_\pm({\hat n})$, and let
${\tilde Q}_\pm(\{{\hat n}, -{\hat n} \}) := Q_\pm({\hat n})$, and let
 \begin{equation}
{\Gamma}_\pm := {\overline{\beta}}^y \circ Q_\pm:S^2 \rightarrow \mathbb{R}^5, \quad
{\tilde \Gamma}_\pm := {\overline{\beta}}^y \circ {\tilde Q}_\pm:\mathbb{R}\mathrm{P}^2 \rightarrow \mathbb{R}^5.
\end{equation}
\begin{equation}
{\Gamma}_\pm := {\overline{\beta}}^y \circ Q_\pm:S^2 \rightarrow \mathbb{R}^5, \quad
{\tilde \Gamma}_\pm := {\overline{\beta}}^y \circ {\tilde Q}_\pm:\mathbb{R}\mathrm{P}^2 \rightarrow \mathbb{R}^5.
\end{equation} Then ![]() $\Sigma^3_\pm = {\tilde Q}_\pm(\mathbb{R}\mathrm{P}^2)$.
$\Sigma^3_\pm = {\tilde Q}_\pm(\mathbb{R}\mathrm{P}^2)$.
To study these maps locally we define a chart in a neighbourhood ![]() $\boldsymbol{\cal{U}}$ of
$\boldsymbol{\cal{U}}$ of ![]() $ {\hat e}_1 \in S^2$ and its antipodal points, and compose with rotations to cover
$ {\hat e}_1 \in S^2$ and its antipodal points, and compose with rotations to cover ![]() $\mathbb{R}\mathrm{P}^2$. We further use this idea to construct tangential and normal coordinates for points in the neighbourhood of the critical sets
$\mathbb{R}\mathrm{P}^2$. We further use this idea to construct tangential and normal coordinates for points in the neighbourhood of the critical sets  $\Sigma^3_\pm \subset \hbox{Sym}^3_0$: we first construct normal coordinates for points in
$\Sigma^3_\pm \subset \hbox{Sym}^3_0$: we first construct normal coordinates for points in ![]() $\boldsymbol{\cal{U}}$ and then apply the matrices representing rotations to translate the normal basis vectors to all other critical points. Furthermore, our choice of tangential and normal coordinates for the neighbourhood of
$\boldsymbol{\cal{U}}$ and then apply the matrices representing rotations to translate the normal basis vectors to all other critical points. Furthermore, our choice of tangential and normal coordinates for the neighbourhood of ![]() $\boldsymbol{\cal{U}}$ makes the Hessian of fB diagonal at all points of the critical sets. This simplifies the computations of the next section.
$\boldsymbol{\cal{U}}$ makes the Hessian of fB diagonal at all points of the critical sets. This simplifies the computations of the next section.
Let ![]() $\boldsymbol{\cal{U}}$ be the set of unit vectors
$\boldsymbol{\cal{U}}$ be the set of unit vectors
where
Choose Δ small enough so that ![]() $\boldsymbol{\cal{U}}$ does not contain antipodal points. The set
$\boldsymbol{\cal{U}}$ does not contain antipodal points. The set ![]() $\boldsymbol{\cal{U}}$ is an open neighbourhood of
$\boldsymbol{\cal{U}}$ is an open neighbourhood of ![]() ${\hat e}_1 = [1, 0 , 0]^T \in S^2$. The inverse
${\hat e}_1 = [1, 0 , 0]^T \in S^2$. The inverse ![]() $\psi_1 := {\hat n}^{-1}$ of
$\psi_1 := {\hat n}^{-1}$ of ![]() $ {\hat n}:B \rightarrow \mathcal{U} $ is a coordinate chart for
$ {\hat n}:B \rightarrow \mathcal{U} $ is a coordinate chart for ![]() $\mathcal{U} \in S^2$. Given a pair of antipodal points
$\mathcal{U} \in S^2$. Given a pair of antipodal points ![]() $\{m, -m\}$, with m or
$\{m, -m\}$, with m or ![]() $-m \in \mathcal{ U}$, we identify the unique point that belongs to
$-m \in \mathcal{ U}$, we identify the unique point that belongs to ![]() $\boldsymbol{\cal{U}}$ and map it to B via ψ 1. This defines a function (chart) from
$\boldsymbol{\cal{U}}$ and map it to B via ψ 1. This defines a function (chart) from ![]() $ \tilde{\mathcal{U} } = \{\mathcal{U},-\mathcal{U}\}$ that we denote by
$ \tilde{\mathcal{U} } = \{\mathcal{U},-\mathcal{U}\}$ that we denote by ![]() ${\tilde \psi}_1 $.
${\tilde \psi}_1 $.
We generate charts around other points of S 2 and ![]() $\mathbb{R}\mathrm{P}^2$ using rotations of
$\mathbb{R}\mathrm{P}^2$ using rotations of ![]() $\boldsymbol{\cal{U}}$,
$\boldsymbol{\cal{U}}$, ![]() $\tilde{\mathcal{U}}$.
$\tilde{\mathcal{U}}$.
Letting ![]() $\hat \nu \in S^2$, we let
$\hat \nu \in S^2$, we let ![]() $H^\pm(\nu)$ denote the open hemisphere of unit vectors
$H^\pm(\nu)$ denote the open hemisphere of unit vectors ![]() $\hat \mu $ satisfying
$\hat \mu $ satisfying ![]() ${\hat \mu} \cdot {\hat \nu} \gt rless 0$. Consider a collection
${\hat \mu} \cdot {\hat \nu} \gt rless 0$. Consider a collection ![]() $\{A_p\}_{p \in \mathcal{K}}$ of matrices
$\{A_p\}_{p \in \mathcal{K}}$ of matrices ![]() $A_p \in SO(3)$,
$A_p \in SO(3)$, ![]() $\forall p \in \mathcal{K}$, where
$\forall p \in \mathcal{K}$, where ![]() $\mathcal{K} \subset \mathbb{N}$ is an index set with the properties
$\mathcal{K} \subset \mathbb{N}$ is an index set with the properties ![]() $1 \in \mathcal{K}$,
$1 \in \mathcal{K}$, ![]() $A_1 = I$, the identity matrix, and that the sets
$A_1 = I$, the identity matrix, and that the sets ![]() $ \{A_p \mathcal{U}, - A_p \mathcal{U} \}$,
$ \{A_p \mathcal{U}, - A_p \mathcal{U} \}$, ![]() $p \in \mathcal{K}$, form a cover of of
$p \in \mathcal{K}$, form a cover of of ![]() $\mathbb{R}\mathrm{P}^2$. The set
$\mathbb{R}\mathrm{P}^2$. The set ![]() $\cal K$ can be assumed finite by compactness. We use the notation
$\cal K$ can be assumed finite by compactness. We use the notation ![]() $\mathcal{U}_p = A_p \mathcal{U}$.
$\mathcal{U}_p = A_p \mathcal{U}$.
Given ![]() $p \in \mathcal{K}$, and the rotation matrix Ap, define
$p \in \mathcal{K}$, and the rotation matrix Ap, define ![]() $ {\hat n}_p: B \rightarrow \mathcal{U}_p$ by
$ {\hat n}_p: B \rightarrow \mathcal{U}_p$ by ![]() ${\hat n}_p = A_p {\hat n} $, and let
${\hat n}_p = A_p {\hat n} $, and let  $\psi_p = {\hat n}^{-1}_p:\mathcal{U}_p \rightarrow B$. ψp is a coordinate chart on
$\psi_p = {\hat n}^{-1}_p:\mathcal{U}_p \rightarrow B$. ψp is a coordinate chart on ![]() $\mathcal{U}_p \subset S^2$. The
$\mathcal{U}_p \subset S^2$. The ![]() ${\hat n}_p$ are real analytic and injective in B, therefore the ψp are also real analytic in
${\hat n}_p$ are real analytic and injective in B, therefore the ψp are also real analytic in ![]() $\mathcal{U}_p$,
$\mathcal{U}_p$, ![]() $\forall p \in \mathcal{K}$. Given the set
$\forall p \in \mathcal{K}$. Given the set  $\tilde{\mathcal{U}}_p = \{\mathcal{U}_p, - \mathcal{U}_p\}$ define the chart
$\tilde{\mathcal{U}}_p = \{\mathcal{U}_p, - \mathcal{U}_p\}$ define the chart  ${\tilde \psi}_p:\tilde{\mathcal{U}}_p \rightarrow B$ by letting
${\tilde \psi}_p:\tilde{\mathcal{U}}_p \rightarrow B$ by letting 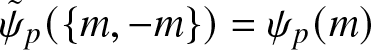 ${\tilde \psi}_p(\{m,-m\}) = \psi_p(m)$ if
${\tilde \psi}_p(\{m,-m\}) = \psi_p(m)$ if ![]() $m \in H^+({A}_p {\hat e}_1)$, and
$m \in H^+({A}_p {\hat e}_1)$, and  ${\tilde \psi}_p(\{m,-m\}) = \psi_p(-m)$ if
${\tilde \psi}_p(\{m,-m\}) = \psi_p(-m)$ if ![]() $-m \in H^+({A}_p {\hat e}_1)$. Given
$-m \in H^+({A}_p {\hat e}_1)$. Given  $m \in \tilde{\mathcal{U}}_p$,
$m \in \tilde{\mathcal{U}}_p$, ![]() $p \in \mathcal{K}$, we use the notation
$p \in \mathcal{K}$, we use the notation  $(\theta_p, \phi_p) = (\theta_p(m), \phi_p(m)) = ({\tilde \psi}_{p,1}(m),{\tilde \psi}_{p,2}(m)) =
({\tilde \psi}_{p,1},{\tilde \psi}_{p,2})$ for the two components of the chart
$(\theta_p, \phi_p) = (\theta_p(m), \phi_p(m)) = ({\tilde \psi}_{p,1}(m),{\tilde \psi}_{p,2}(m)) =
({\tilde \psi}_{p,1},{\tilde \psi}_{p,2})$ for the two components of the chart ![]() ${\tilde \psi}_p$, i.e. we use the same symbol for the charts and the variables. For p = 1 we have
${\tilde \psi}_p$, i.e. we use the same symbol for the charts and the variables. For p = 1 we have ![]() $(\theta_1, \phi_1) = (\theta,\phi)$.
$(\theta_1, \phi_1) = (\theta,\phi)$.
To see the transition functions consider ![]() $\tilde{\mathcal{U}}_p $,
$\tilde{\mathcal{U}}_p $,  $\tilde{\mathcal{U}}_p' \subset \mathbb{R}\mathrm{P}^2$, p,
$\tilde{\mathcal{U}}_p' \subset \mathbb{R}\mathrm{P}^2$, p, ![]() $p' \in \mathcal{K}$ with nonempty intersection. Then either
$p' \in \mathcal{K}$ with nonempty intersection. Then either ![]() $\mathcal{U}_p \cap \mathcal{U}_{p'} \neq \emptyset$ or
$\mathcal{U}_p \cap \mathcal{U}_{p'} \neq \emptyset$ or ![]() $\mathcal{U}_p \cap (-\mathcal{ U}_{p'}) \neq \emptyset$ (and not both). Let
$\mathcal{U}_p \cap (-\mathcal{ U}_{p'}) \neq \emptyset$ (and not both). Let ![]() $\mathcal{V}_{p'}$ be the element of the pair
$\mathcal{V}_{p'}$ be the element of the pair ![]() $\mathcal{U}_{p'}$,
$\mathcal{U}_{p'}$, ![]() $-\mathcal{U}_{p'}$ that intersects
$-\mathcal{U}_{p'}$ that intersects ![]() $\mathcal{U}_p$. Then
$\mathcal{U}_p$. Then  $\mathcal{V}_p = A'_{p'} \mathcal{U}$, for some
$\mathcal{V}_p = A'_{p'} \mathcal{U}$, for some  $A'_{p'} \in SO(3)$, and
$A'_{p'} \in SO(3)$, and
 \begin{equation}
{\hat n}(\theta_{p'},\phi_{p'}) = (A'_{p'})^{-1} A_{p} {\hat n}(\theta_{p},\phi_{p}).
\end{equation}
\begin{equation}
{\hat n}(\theta_{p'},\phi_{p'}) = (A'_{p'})^{-1} A_{p} {\hat n}(\theta_{p},\phi_{p}).
\end{equation} The transition function  ${\tilde \psi}_{p'} \circ {\tilde \psi}^{-1}_p:
{\tilde \psi}_p( \tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'} ) \rightarrow
{\tilde \psi}_{p'}(\tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'}) $ is the map from
${\tilde \psi}_{p'} \circ {\tilde \psi}^{-1}_p:
{\tilde \psi}_p( \tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'} ) \rightarrow
{\tilde \psi}_{p'}(\tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'}) $ is the map from  $ (\theta_{p},\phi_{p}) \in {\tilde \psi}_{p}(\tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'}) \subset B$ to the unique
$ (\theta_{p},\phi_{p}) \in {\tilde \psi}_{p}(\tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'}) \subset B$ to the unique  $(\theta_{p'},\phi_{p'}) \in {\tilde \psi}_{p'}(\tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'}) \subset B$ satisfying (3.26). Real analyticity of the transition function follows from the fact that the right hand side of (3.26), and
$(\theta_{p'},\phi_{p'}) \in {\tilde \psi}_{p'}(\tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'}) \subset B$ satisfying (3.26). Real analyticity of the transition function follows from the fact that the right hand side of (3.26), and ![]() ${\hat n}^{-1}$ are real analytic.
${\hat n}^{-1}$ are real analytic.
Remark 3.6. By (3.24) we have ![]() $ {\hat n}(\theta, \phi) = A_\phi A_\theta {\hat e}_1$, and
$ {\hat n}(\theta, \phi) = A_\phi A_\theta {\hat e}_1$, and ![]() $\mathcal{U} $ is the set of
$\mathcal{U} $ is the set of ![]() $A {\hat e}_1$,
$A {\hat e}_1$, ![]() $ A = A_\phi A_\theta$, where
$ A = A_\phi A_\theta$, where ![]() $(\theta, \phi) \in B$,
$(\theta, \phi) \in B$,
 \begin{equation}
A_\phi = \left[
\begin{array}{ccc}
\cos \phi & - \sin \phi & 0 \\
\sin \phi & \cos \phi & 0 \\
0 & 0 & 1
\end{array}
\right], \quad
A_\theta =
\left[
\begin{array}{ccc}
\sin \theta & 0 & - \cos \theta \\
0 & 1 & 0 \\
\cos \theta & 0 & \sin \theta
\end{array}
\right].
\end{equation}
\begin{equation}
A_\phi = \left[
\begin{array}{ccc}
\cos \phi & - \sin \phi & 0 \\
\sin \phi & \cos \phi & 0 \\
0 & 0 & 1
\end{array}
\right], \quad
A_\theta =
\left[
\begin{array}{ccc}
\sin \theta & 0 & - \cos \theta \\
0 & 1 & 0 \\
\cos \theta & 0 & \sin \theta
\end{array}
\right].
\end{equation} Part of the statement of Proposition 2.1 is that the ![]() ${\tilde \Gamma}_\pm$ are embeddings, see [Reference Panayotaros26]. We can then define tubular neighbourhoods of their image
${\tilde \Gamma}_\pm$ are embeddings, see [Reference Panayotaros26]. We can then define tubular neighbourhoods of their image  ${\overline{\beta}}^y (\Sigma_\pm^3)$ using the atlas
${\overline{\beta}}^y (\Sigma_\pm^3)$ using the atlas  $\{\tilde{\mathcal{U}}_p, {\tilde \psi}_p \}_{p \in \mathcal{K}} $ for the component along the
$\{\tilde{\mathcal{U}}_p, {\tilde \psi}_p \}_{p \in \mathcal{K}} $ for the component along the  ${\overline\beta}^y (\Sigma_\pm^3)$, and coordinates along normal directions, see [Reference Lee17], ch. 3, [Reference Burns and Gidea6], section 6.2.
${\overline\beta}^y (\Sigma_\pm^3)$, and coordinates along normal directions, see [Reference Lee17], ch. 3, [Reference Burns and Gidea6], section 6.2.
In particular, given any ![]() $p \in \mathcal{K}$, and the open set
$p \in \mathcal{K}$, and the open set  $\tilde{\mathcal{U}}_p \in \mathbb{R}\mathrm{P}^2$, there exists an open neighbourhood of
$\tilde{\mathcal{U}}_p \in \mathbb{R}\mathrm{P}^2$, there exists an open neighbourhood of  ${\tilde \Gamma}_\pm(\tilde{\mathcal{U}}_p)$ in
${\tilde \Gamma}_\pm(\tilde{\mathcal{U}}_p)$ in ![]() $\mathbb{R}^5$ that consists of points
$\mathbb{R}^5$ that consists of points
 \begin{equation}
y^\pm({\tilde \psi}_p,r_p) = {\tilde \Gamma}_\pm(\theta_p,\phi_p) + \sum_{j = 1}^3 r_{p,j} {\hat N}^\pm_{p,j}(\theta_p,\phi_p),
\quad {\tilde \psi}_p = (\theta_p,\phi_p) \in B,
\quad r \in I_\delta^3,
\end{equation}
\begin{equation}
y^\pm({\tilde \psi}_p,r_p) = {\tilde \Gamma}_\pm(\theta_p,\phi_p) + \sum_{j = 1}^3 r_{p,j} {\hat N}^\pm_{p,j}(\theta_p,\phi_p),
\quad {\tilde \psi}_p = (\theta_p,\phi_p) \in B,
\quad r \in I_\delta^3,
\end{equation} ![]() $I_\delta = (-\delta,\delta)$, δ > 0,
$I_\delta = (-\delta,\delta)$, δ > 0,  ${\tilde \psi}_p = (\theta_p,\phi_p)$,
${\tilde \psi}_p = (\theta_p,\phi_p)$, ![]() $r_p = (r_{p,1}, r_{p,2}, r_{p,3})$, B as in (3.25), (3.24), where the
$r_p = (r_{p,1}, r_{p,2}, r_{p,3})$, B as in (3.25), (3.24), where the  ${\hat N}_{p,j}^\pm:\tilde{\mathcal{U}}_p \rightarrow S^5$,
${\hat N}_{p,j}^\pm:\tilde{\mathcal{U}}_p \rightarrow S^5$, ![]() $j = 1, 2, 3$ are smooth unit vector fields that are normal to
$j = 1, 2, 3$ are smooth unit vector fields that are normal to  $\tilde \Gamma_\pm( \tilde{\mathcal{U}}_p)$ with respect to the Euclidean inner product in
$\tilde \Gamma_\pm( \tilde{\mathcal{U}}_p)$ with respect to the Euclidean inner product in ![]() $\mathbb{R}^5$.
$\mathbb{R}^5$.
The local normal vector fields  ${\hat N}^\pm_{p,j}$ of (3.28) are not unique. We choose normal vectors that are eigenvectors of
${\hat N}^\pm_{p,j}$ of (3.28) are not unique. We choose normal vectors that are eigenvectors of ![]() $\nabla^2 f_B$, see Lemma 3.9 below. This choice simplifies the proof of Lemma 3.11 in the next section, see [Reference Panayotaros26] for details.
$\nabla^2 f_B$, see Lemma 3.9 below. This choice simplifies the proof of Lemma 3.11 in the next section, see [Reference Panayotaros26] for details.
Define first local normal vector fields  ${N}^\pm_{1,j}:{\mathcal{U}} \rightarrow S^5$, j = 1, 2, 3: let
${N}^\pm_{1,j}:{\mathcal{U}} \rightarrow S^5$, j = 1, 2, 3: let  ${N}^\pm_1 (\pi/2,0) = ||\Gamma_\pm( {\hat e}_1)||^{-1} \Gamma_\pm( {\hat e}_1)$, and choose two unit vectors
${N}^\pm_1 (\pi/2,0) = ||\Gamma_\pm( {\hat e}_1)||^{-1} \Gamma_\pm( {\hat e}_1)$, and choose two unit vectors  ${N}^\pm_j (\pi/2,0) $, j = 2, 3, so that
${N}^\pm_j (\pi/2,0) $, j = 2, 3, so that  ${N}^\pm_j (\pi/2,0) $, j = 1, 2, 3 form a orthonormal basis of the orthogonal complement of the tangent space of
${N}^\pm_j (\pi/2,0) $, j = 1, 2, 3 form a orthonormal basis of the orthogonal complement of the tangent space of ![]() ${\Gamma}_\pm( \mathcal{U}_p)$ at at
${\Gamma}_\pm( \mathcal{U}_p)$ at at ![]() $\Gamma_\pm({\hat e}_1)$. (The choice of the
$\Gamma_\pm({\hat e}_1)$. (The choice of the  ${N}^\pm_j (\pi/2,0) $, j = 2, 3 is not unique.) Also let
${N}^\pm_j (\pi/2,0) $, j = 2, 3 is not unique.) Also let
 \begin{equation}
{N}^\pm_{1,j}(\theta,\phi) = T_{A_\theta A_\phi} {N}^\pm_j (\pi/2,0), \quad j = 1,2,3, \quad (\theta,\phi) \in B.
\end{equation}
\begin{equation}
{N}^\pm_{1,j}(\theta,\phi) = T_{A_\theta A_\phi} {N}^\pm_j (\pi/2,0), \quad j = 1,2,3, \quad (\theta,\phi) \in B.
\end{equation} We then define the  ${\hat N}^\pm_{p,j}:\tilde{\mathcal{U}}_p \rightarrow S^5$ by
${\hat N}^\pm_{p,j}:\tilde{\mathcal{U}}_p \rightarrow S^5$ by
 \begin{equation}
{\hat N}^\pm_{p,j} (\{\psi_p, - \psi_p \}) = T_{A_p} {N}^\pm_{1,j}({\psi}_1), \quad
\quad {\tilde \psi}_1 \in B, \quad j = 1, 2, 3,
\quad p \in \mathcal{K}.
\end{equation}
\begin{equation}
{\hat N}^\pm_{p,j} (\{\psi_p, - \psi_p \}) = T_{A_p} {N}^\pm_{1,j}({\psi}_1), \quad
\quad {\tilde \psi}_1 \in B, \quad j = 1, 2, 3,
\quad p \in \mathcal{K}.
\end{equation} By Lemma 3.5, and Remark 3.6 the  ${\hat N}^\pm_j(p,m)$ are real analytic vector fields and form an orthonormal set of eigenvectors of
${\hat N}^\pm_j(p,m)$ are real analytic vector fields and form an orthonormal set of eigenvectors of ![]() $\nabla^2 f_B$ at
$\nabla^2 f_B$ at  $m \in \tilde{\mathcal{U}}_p$ corresponding to
$m \in \tilde{\mathcal{U}}_p$ corresponding to ![]() $\lambda^\pm_j$,
$\lambda^\pm_j$, ![]() $j = 1, 2, 3$, respectively, for all
$j = 1, 2, 3$, respectively, for all  $m \in \tilde{\mathcal{U}}_p$,
$m \in \tilde{\mathcal{U}}_p$, ![]() $p \in \mathcal{K}$.
$p \in \mathcal{K}$.
Recall that the matrices TA, ![]() $A \in SO(3)$, represent rotations in the basis y and leave the image of
$A \in SO(3)$, represent rotations in the basis y and leave the image of  $ {\overline{\beta}}^y (\hbox{Sym}^3_0) $ invariant. The following show that the particular choice of normal coordinates for
$ {\overline{\beta}}^y (\hbox{Sym}^3_0) $ invariant. The following show that the particular choice of normal coordinates for ![]() $\boldsymbol{\cal{U}}$, and its extension to the whole critical set by rotations makes the Hessian of fB diagonal everywhere in the critical set.
$\boldsymbol{\cal{U}}$, and its extension to the whole critical set by rotations makes the Hessian of fB diagonal everywhere in the critical set.
Remark 3.7. Let  $\Omega^\pm_p = ({\tilde \psi}_p,r^\pm_{p}) \in B \times I_\delta^3$, where B, Iδ are defined in (3.25)-(3.24), and (3.28) respectively. Then (3.28)-(3.29) imply
$\Omega^\pm_p = ({\tilde \psi}_p,r^\pm_{p}) \in B \times I_\delta^3$, where B, Iδ are defined in (3.25)-(3.24), and (3.28) respectively. Then (3.28)-(3.29) imply
 \begin{equation}
D_{\Omega_p} y^\pm {(\tilde \psi}_p,0) = [
t^\pm_{\theta_p}, t^\pm_{\phi_p}, {\hat N}^\pm_{p,1}, {\hat N}^\pm_{p,2}, {\hat N}^\pm_{p,3}]({\tilde \psi}_p,0),
\end{equation}
\begin{equation}
D_{\Omega_p} y^\pm {(\tilde \psi}_p,0) = [
t^\pm_{\theta_p}, t^\pm_{\phi_p}, {\hat N}^\pm_{p,1}, {\hat N}^\pm_{p,2}, {\hat N}^\pm_{p,3}]({\tilde \psi}_p,0),
\end{equation} where  $ t^\pm_{\theta_p}({\tilde \psi}_p,0)$,
$ t^\pm_{\theta_p}({\tilde \psi}_p,0)$,  $t^\pm_{\phi_p}({\tilde \psi}_p,0)$ are tangent to the critical set at
$t^\pm_{\phi_p}({\tilde \psi}_p,0)$ are tangent to the critical set at  $({\tilde \psi}_p,0)$, and the
$({\tilde \psi}_p,0)$, and the  ${\hat N}^\pm_j({\tilde \psi}_p,0)$ are normal to the critical set at
${\hat N}^\pm_j({\tilde \psi}_p,0)$ are normal to the critical set at  $({\tilde \psi}_p,0)$. Thus
$({\tilde \psi}_p,0)$. Thus  $ D_{\Omega_p} y^\pm {(\tilde \psi}_p,0) $ is invertible and it follows that the map defined by (3.28) is an analytic diffeomorphism from
$ D_{\Omega_p} y^\pm {(\tilde \psi}_p,0) $ is invertible and it follows that the map defined by (3.28) is an analytic diffeomorphism from  $B \times I_\delta^3$ to an open subset of
$B \times I_\delta^3$ to an open subset of ![]() $\mathbb{R}^5$ that intersects
$\mathbb{R}^5$ that intersects  ${\tilde \Gamma}(\tilde{\mathcal{U}}_p)$.
${\tilde \Gamma}(\tilde{\mathcal{U}}_p)$.
Remark 3.8. By (3.28), the linearity of TA, and (3.30)-(3.29), the transition function between components rp, ![]() $r_{p'}$ for any neighbuorhood of
$r_{p'}$ for any neighbuorhood of  $ \tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'} \neq \emptyset$ is the identity,
$ \tilde{\mathcal{U}}_p \cap \tilde{\mathcal{U}}_{p'} \neq \emptyset$ is the identity, ![]() $\forall p, p' \in \mathcal{K}$. It similarly follows that the angular component of
$\forall p, p' \in \mathcal{K}$. It similarly follows that the angular component of  $ T_A y^\pm(\tilde \psi_p,r_p) $,
$ T_A y^\pm(\tilde \psi_p,r_p) $,  $r_p \in I_\delta^3$, depends only on
$r_p \in I_\delta^3$, depends only on ![]() $\tilde \psi_p $. Also, the radial component of
$\tilde \psi_p $. Also, the radial component of  $ T_A y^\pm(\tilde \psi_p,r_p) $,
$ T_A y^\pm(\tilde \psi_p,r_p) $,  $r_p \in I_\delta^3$, is rp.
$r_p \in I_\delta^3$, is rp.
Lemma 3.9. Let  $m \in \tilde{\mathcal{U}}_p \subset \mathbb{R}\mathrm{P}^2$,
$m \in \tilde{\mathcal{U}}_p \subset \mathbb{R}\mathrm{P}^2$, ![]() $p \in \mathcal{K}$. Define the coordinates
$p \in \mathcal{K}$. Define the coordinates  $\Omega^\pm_p = ({\tilde \psi}_p,r^\pm_{p}) \in B \times I_\delta^3$, by (3.28) in the neighbuorhoods
$\Omega^\pm_p = ({\tilde \psi}_p,r^\pm_{p}) \in B \times I_\delta^3$, by (3.28) in the neighbuorhoods  $y^\pm(B \times I_\delta^3)$ of
$y^\pm(B \times I_\delta^3)$ of ![]() ${\tilde \Gamma}_\pm(m)$, and let
${\tilde \Gamma}_\pm(m)$, and let  ${\tilde f}_B(\Omega_p^\pm) = f_B(y^\pm(\Omega_p^\pm))$. Then, (i)
${\tilde f}_B(\Omega_p^\pm) = f_B(y^\pm(\Omega_p^\pm))$. Then, (i)  $\nabla^2_{\Omega_p^\pm} {\tilde f_B}{(\tilde \psi}_p,0)$ is diagonal with
$\nabla^2_{\Omega_p^\pm} {\tilde f_B}{(\tilde \psi}_p,0)$ is diagonal with
 \begin{equation}
\frac{\partial^2 {\tilde f}_B}{\partial {\tilde \psi}^2_{p,j}}({\tilde \psi}_p,0) = 0, \quad j = 1, 2; \quad
\frac{\partial^2 {\tilde f}_B}{\partial r^{\pm 2}_{p,j}}({\tilde \psi}_p,0) = \lambda^\pm_j, \quad j = 1, 2, 3,
\end{equation}
\begin{equation}
\frac{\partial^2 {\tilde f}_B}{\partial {\tilde \psi}^2_{p,j}}({\tilde \psi}_p,0) = 0, \quad j = 1, 2; \quad
\frac{\partial^2 {\tilde f}_B}{\partial r^{\pm 2}_{p,j}}({\tilde \psi}_p,0) = \lambda^\pm_j, \quad j = 1, 2, 3,
\end{equation}  $\forall {\tilde \psi}_p \in B$. Also, (ii)
$\forall {\tilde \psi}_p \in B$. Also, (ii)  $ \frac{\partial {\tilde f}_B}{\partial {\tilde \psi}_{p,j}}(\Omega_p^\pm ) = 0$,
$ \frac{\partial {\tilde f}_B}{\partial {\tilde \psi}_{p,j}}(\Omega_p^\pm ) = 0$, ![]() $j = 1, 2$,
$j = 1, 2$,  $\forall
\Omega_p^\pm \in B \times I_\delta^3$.
$\forall
\Omega_p^\pm \in B \times I_\delta^3$.
3.2. Reduced equation and continuation of solutions
In this section, we outline the proofs of Propositions 2.3, 2.4, and 2.8. The main step is Lemma 3.11 below on the equivalence of the equation for critical points of ![]() $\overline{\mathcal{F}}$ for small
$\overline{\mathcal{F}}$ for small ![]() $|L|$ to a reduced equation for the “angular variables” parametrizing the L = 0 critical set. In the case
$|L|$ to a reduced equation for the “angular variables” parametrizing the L = 0 critical set. In the case ![]() $U_- = \overline{G}$ the bifurcation equation is a discrete version of the equation for Oseen–Frank equilibria.
$U_- = \overline{G}$ the bifurcation equation is a discrete version of the equation for Oseen–Frank equilibria.
To set up Lemma 3.11, we parametrize a neighbourhood of the critical sets ![]() $\mathcal{C}_0(\overline{\mathcal{F}_4},U_+,U_-)$ of
$\mathcal{C}_0(\overline{\mathcal{F}_4},U_+,U_-)$ of ![]() $\overline{\mathcal{F}}_4$ in
$\overline{\mathcal{F}}_4$ in ![]() $X({\overline{G}})$. We let
$X({\overline{G}})$. We let ![]() $U = U_+ \cup U_-$, and
$U = U_+ \cup U_-$, and ![]() $U^c = G\setminus U$. U is assumed nonempty.
$U^c = G\setminus U$. U is assumed nonempty.
The set ![]() $X({\overline{G}})$ is a product of the linear spaces
$X({\overline{G}})$ is a product of the linear spaces  $\hbox{Sym}^3_0$, and we use the coordinates yj (and wj) of the previous section at each site:
$\hbox{Sym}^3_0$, and we use the coordinates yj (and wj) of the previous section at each site:  $Q(k) \in \hbox{Sym}_0^3$,
$Q(k) \in \hbox{Sym}_0^3$, ![]() $k \in U \cup U^c$, is written as
$k \in U \cup U^c$, is written as  $ Q(k) = \sum_{k \in U \cup U^c} \sum_{j \in \mathcal{J}} y_{k,j} {\hat Y}_j =
\sum_{k \in U\cup U^c} \sum_{i = 1}^5 w_{k,i} {\hat W}_i $, see (3.20). This defines an isomorphism (or chart)
$ Q(k) = \sum_{k \in U \cup U^c} \sum_{j \in \mathcal{J}} y_{k,j} {\hat Y}_j =
\sum_{k \in U\cup U^c} \sum_{i = 1}^5 w_{k,i} {\hat W}_i $, see (3.20). This defines an isomorphism (or chart)  $\overline{\mathcal{B}}^w: (\hbox{Sym}_0^3)^{|U|+|U^c| }
\rightarrow \mathbb{R}^{5( |U| +|U^c|)}$, where
$\overline{\mathcal{B}}^w: (\hbox{Sym}_0^3)^{|U|+|U^c| }
\rightarrow \mathbb{R}^{5( |U| +|U^c|)}$, where  $(\overline{\mathcal{B}}^w(Q))(k) = w(k) := [w_{k,1}, \ldots, w_{k,5}]^T$. (An alternative notation is
$(\overline{\mathcal{B}}^w(Q))(k) = w(k) := [w_{k,1}, \ldots, w_{k,5}]^T$. (An alternative notation is ![]() $\overline{\mathcal{B}}^y$.) The Riemannian metric on
$\overline{\mathcal{B}}^y$.) The Riemannian metric on ![]() $\mathbb{R}^{5( |U| +|U^c|)}$ is the one induced by the standard Euclidean inner product, as in subsection 3.2. This metric is invariant under multiplication by the
$\mathbb{R}^{5( |U| +|U^c|)}$ is the one induced by the standard Euclidean inner product, as in subsection 3.2. This metric is invariant under multiplication by the ![]() $5 \times 5$ matrices
$5 \times 5$ matrices ![]() $T_{A_k}$,
$T_{A_k}$, ![]() $A_k \in SO(3)$, applied (independently) at each site
$A_k \in SO(3)$, applied (independently) at each site ![]() $k \in U \cup U^c$.
$k \in U \cup U^c$.
Also, the ![]() $\mathcal{C}_0(\overline{\mathcal{F}_4},U_+,U_-)$ of
$\mathcal{C}_0(\overline{\mathcal{F}_4},U_+,U_-)$ of ![]() $\overline{\mathcal{F}}_4$ in
$\overline{\mathcal{F}}_4$ in ![]() $X({\overline{G}})$ are products of projective planes, and their neighbourhood can be described using products of the coordinate systems of the previous section at the sites of U. The tangential directions at each site of U parametrize the critical sets.
$X({\overline{G}})$ are products of projective planes, and their neighbourhood can be described using products of the coordinate systems of the previous section at the sites of U. The tangential directions at each site of U parametrize the critical sets.
Lemma 3.10. Let ![]() $U_+$,
$U_+$, ![]() $U_-$ be disjoint subsets of
$U_-$ be disjoint subsets of ![]() $\overline G$ with nonzero union. Then the critical set
$\overline G$ with nonzero union. Then the critical set ![]() $\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$ of
$\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$ of ![]() $\overline{\mathcal{F}}_4$ is an embedded submanifold of
$\overline{\mathcal{F}}_4$ is an embedded submanifold of ![]() $X({\overline G})$ and is diffeomorphic to
$X({\overline G})$ and is diffeomorphic to ![]() $(\mathbb{R}\mathrm{P}^2)^{|U|}$.
$(\mathbb{R}\mathrm{P}^2)^{|U|}$.
The proof follows by defining a map ![]() $\boldsymbol{\tilde{\Gamma}}:(\mathbb{R}\mathrm{P}^2)^{|U|} \rightarrow X({\overline G})$ that is an embedding and an immersion, see [Reference Panayotaros26]. Consider first the case where
$\boldsymbol{\tilde{\Gamma}}:(\mathbb{R}\mathrm{P}^2)^{|U|} \rightarrow X({\overline G})$ that is an embedding and an immersion, see [Reference Panayotaros26]. Consider first the case where ![]() $U_+$,
$U_+$, ![]() $U_-$, Uc are nonempty. We let
$U_-$, Uc are nonempty. We let
by
 \begin{equation}
\boldsymbol{\tilde{\Gamma}}_k(m_+,m_-) =
\begin{cases}
{\tilde \Gamma}_-(m_{+,k}), & k \in U_+, \\
{\tilde \Gamma}_+(m_{-,k}), & k \in U_-, \\
0, & k \in U^c,
\end{cases}
\end{equation}
\begin{equation}
\boldsymbol{\tilde{\Gamma}}_k(m_+,m_-) =
\begin{cases}
{\tilde \Gamma}_-(m_{+,k}), & k \in U_+, \\
{\tilde \Gamma}_+(m_{-,k}), & k \in U_-, \\
0, & k \in U^c,
\end{cases}
\end{equation} where ![]() $m_\pm = \{m_{\pm,k}\}_{k \in U_\pm}$, and
$m_\pm = \{m_{\pm,k}\}_{k \in U_\pm}$, and ![]() ${\tilde \Gamma_\pm}$ is as in (3.23). In the case where one of
${\tilde \Gamma_\pm}$ is as in (3.23). In the case where one of ![]() $U_+$,
$U_+$, ![]() $U_-$, Uc is empty we delete the corresponding line from (3.34).
$U_-$, Uc is empty we delete the corresponding line from (3.34).
Assume that ![]() $U_+$,
$U_+$, ![]() $U_-$, Uc are nonempty. We then define a tubular neighbourhood
$U_-$, Uc are nonempty. We then define a tubular neighbourhood ![]() $\cal T$ of the sets
$\cal T$ of the sets ![]() $ \boldsymbol{\tilde{\Gamma}}(\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-))$ in
$ \boldsymbol{\tilde{\Gamma}}(\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-))$ in ![]() $\mathbb{R}^{5|G|}$ as the union over
$\mathbb{R}^{5|G|}$ as the union over ![]() $\textbf{p} \in \mathcal{K}^{|U|}$ of the images of the maps
$\textbf{p} \in \mathcal{K}^{|U|}$ of the images of the maps  $\textbf{y}_\textbf{p}: \tilde{\mathcal{U}}_\textbf{p} \times I_\delta^{3|U|} \times I_\delta^{5 |U^c|} \rightarrow \mathbb{R}^{5(|U|+|U^c|)}$ with components
$\textbf{y}_\textbf{p}: \tilde{\mathcal{U}}_\textbf{p} \times I_\delta^{3|U|} \times I_\delta^{5 |U^c|} \rightarrow \mathbb{R}^{5(|U|+|U^c|)}$ with components
 \begin{equation}
\textbf{y}_{k,\textbf{p}}({\tilde \psi}_\textbf{p},r_\textbf{p},q_\textbf{p}) =
\begin{cases}
{\tilde \Gamma}_+({\tilde \psi}_{p_k}) + \sum_{i = 1}^3 r_{p_k, i} {\hat N}^+_{p_k, i}({\tilde \psi}_{p_k}), & k \in U_+, \\
{\tilde \Gamma}_-({\tilde \psi}_{p_k}) + \sum_{i = 1}^3 r_{p_k, i} {\hat N}^-_{p_k, i}({\tilde \psi}_{p_k}), & k \in U_-, \\
q_{p_k}, & k \in U^c,
\end{cases}
\end{equation}
\begin{equation}
\textbf{y}_{k,\textbf{p}}({\tilde \psi}_\textbf{p},r_\textbf{p},q_\textbf{p}) =
\begin{cases}
{\tilde \Gamma}_+({\tilde \psi}_{p_k}) + \sum_{i = 1}^3 r_{p_k, i} {\hat N}^+_{p_k, i}({\tilde \psi}_{p_k}), & k \in U_+, \\
{\tilde \Gamma}_-({\tilde \psi}_{p_k}) + \sum_{i = 1}^3 r_{p_k, i} {\hat N}^-_{p_k, i}({\tilde \psi}_{p_k}), & k \in U_-, \\
q_{p_k}, & k \in U^c,
\end{cases}
\end{equation} with δ > 0, ![]() $ r_{p_k,i} \in I_\delta$, for all
$ r_{p_k,i} \in I_\delta$, for all ![]() $k \in U$,
$k \in U$, ![]() $p_k \in \mathcal{K}$,
$p_k \in \mathcal{K}$, ![]() $i = 1, 2, 3$, and
$i = 1, 2, 3$, and  $q_{p_k} \in I_\delta^5$, for all
$q_{p_k} \in I_\delta^5$, for all ![]() $k \in U^c$. The
$k \in U^c$. The  ${\hat N}^\pm_{p_k,i}({\tilde \psi}_{p_j})$,
${\hat N}^\pm_{p_k,i}({\tilde \psi}_{p_j})$,  ${\tilde \psi}_{p_k} \in \tilde{\mathcal{U}}_{p_k}$,
${\tilde \psi}_{p_k} \in \tilde{\mathcal{U}}_{p_k}$, ![]() $p_k \in \mathcal{K}$,
$p_k \in \mathcal{K}$, ![]() $k \in U$, are the normal vectors defined in the previous section. They are therefore eigenvectors of the Hessian of fB with respect to the variables w(k) at
$k \in U$, are the normal vectors defined in the previous section. They are therefore eigenvectors of the Hessian of fB with respect to the variables w(k) at  $ {\tilde f}_\pm({\tilde \psi}_{p_k})$, for all
$ {\tilde f}_\pm({\tilde \psi}_{p_k})$, for all ![]() $k \in U$. By Remark 3.8 the transition function between
$k \in U$. By Remark 3.8 the transition function between ![]() $r_{p_k}$,
$r_{p_k}$, ![]() $r_{p'_k}$ is the identity, for any pk,
$r_{p'_k}$ is the identity, for any pk, ![]() $p'_k \in \mathcal{K}$ with
$p'_k \in \mathcal{K}$ with  $\tilde{\mathcal{U}_{p_k}} \cap \tilde{\mathcal{U}}_{p'_k} \neq \emptyset$. Also
$\tilde{\mathcal{U}_{p_k}} \cap \tilde{\mathcal{U}}_{p'_k} \neq \emptyset$. Also  $q_{p_k} = \{q_{p_k,i}\}_{i=1}^5 = \{w_{k,i}\}_{i=1}^5 $, i.e. “cartesian coordinates” wi, see (3.20), at each site of Uc. Transition functions for these components are the identity.
$q_{p_k} = \{q_{p_k,i}\}_{i=1}^5 = \{w_{k,i}\}_{i=1}^5 $, i.e. “cartesian coordinates” wi, see (3.20), at each site of Uc. Transition functions for these components are the identity.
By Remark 3.7, expressions (3.35) with δ > 0 sufficiently small define implicitly local coordinates for ![]() $\cal T$, in particular,
$\cal T$, in particular, ![]() $\cal T$ is a union of neighbourhoods of
$\cal T$ is a union of neighbourhoods of  $\boldsymbol{\tilde{\Gamma}}(\tilde{\mathcal{U}}_\textbf{p})$, where we have the “polar-cartesian” coordinates
$\boldsymbol{\tilde{\Gamma}}(\tilde{\mathcal{U}}_\textbf{p})$, where we have the “polar-cartesian” coordinates
 \begin{equation}
{\tilde \psi}_{p_k} \in \tilde{\mathcal{U}}_{p_k}, \quad r_{p_k} \in I_\delta^3, \quad k \in U, \quad p_k \in \mathcal{K},
\end{equation}
\begin{equation}
{\tilde \psi}_{p_k} \in \tilde{\mathcal{U}}_{p_k}, \quad r_{p_k} \in I_\delta^3, \quad k \in U, \quad p_k \in \mathcal{K},
\end{equation} \begin{equation}
q_{p_k} \in I_\delta^5, \quad k \in U^c.
\end{equation}
\begin{equation}
q_{p_k} \in I_\delta^5, \quad k \in U^c.
\end{equation} In the case where one of Uj is empty, we delete the first (![]() $j = +$) or second (
$j = +$) or second (![]() $j=-$) line of (3.35), and (3.36). In the case where Uc is empty we delete the last line of (3.35), and (3.37).
$j=-$) line of (3.35), and (3.36). In the case where Uc is empty we delete the last line of (3.35), and (3.37).
We consider critical points of ![]() $\overline{\mathcal{F}}$ in the neighbourhood
$\overline{\mathcal{F}}$ in the neighbourhood ![]() $\cal T $ of the L = 0 nontrivial critical sets.
$\cal T $ of the L = 0 nontrivial critical sets.
Consider first the case where Uc is nonempty. We let
 \begin{align}
g_{\textbf{p},i}(k) & = \frac{\partial \overline{\mathcal{F}} }{\partial {{\tilde \psi}_{{p}_k,i}} }, \quad i = 1,2, \quad k \in U,
\end{align}
\begin{align}
g_{\textbf{p},i}(k) & = \frac{\partial \overline{\mathcal{F}} }{\partial {{\tilde \psi}_{{p}_k,i}} }, \quad i = 1,2, \quad k \in U,
\end{align} \begin{align}
h_{\textbf{p},i}(k) & = \frac{\partial \overline{\mathcal{F}}}{\partial r_{{p}_{k},i}} , \quad i = 1,2,3, \quad k \in U,
\end{align}
\begin{align}
h_{\textbf{p},i}(k) & = \frac{\partial \overline{\mathcal{F}}}{\partial r_{{p}_{k},i}} , \quad i = 1,2,3, \quad k \in U,
\end{align} \begin{align}
w_{\textbf{p},i}(k) & = \frac{\partial \overline{\mathcal{F}} }{\partial q_{{p}_{k}, i} }, \quad \quad i = 1,\ldots,5, \quad k \in U^c.
\end{align}
\begin{align}
w_{\textbf{p},i}(k) & = \frac{\partial \overline{\mathcal{F}} }{\partial q_{{p}_{k}, i} }, \quad \quad i = 1,\ldots,5, \quad k \in U^c.
\end{align} These are the components of the derivative ![]() $D \overline{\mathcal{F}}$ in local coordinates
$D \overline{\mathcal{F}}$ in local coordinates ![]() $ {\tilde \psi}_\textbf{p}$,
$ {\tilde \psi}_\textbf{p}$, ![]() $r_\textbf{p}$,
$r_\textbf{p}$, ![]() $q_\textbf{p}$,
$q_\textbf{p}$, ![]() $\textbf{p} \in \mathcal{K}^{|U|}$.
$\textbf{p} \in \mathcal{K}^{|U|}$.
Denoting the corresponding vectors by ![]() $g_\textbf{p} \in \mathbb{R}^{2|U|}$,
$g_\textbf{p} \in \mathbb{R}^{2|U|}$, ![]() $h_\textbf{p} \in \mathbb{R}^{3|U|}$,
$h_\textbf{p} \in \mathbb{R}^{3|U|}$,  $ w_\textbf{p} \in \mathbb{R}^{5|U^c|}$, and letting
$ w_\textbf{p} \in \mathbb{R}^{5|U^c|}$, and letting  $ z_\textbf{p} = [r_\textbf{p},q_\textbf{p}] \in I_\delta^{3|U|} \times {I_\delta}^{5|U^c|}$, we also define
$ z_\textbf{p} = [r_\textbf{p},q_\textbf{p}] \in I_\delta^{3|U|} \times {I_\delta}^{5|U^c|}$, we also define
 \begin{equation}
F_{{\tilde \psi}_\textbf{p }}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = g_\textbf{p}({\tilde \psi}_\textbf{p},z_\textbf{p},L), \quad
F_{z_\textbf{p}}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = [h_\textbf{p}({\tilde \psi}_\textbf{p},z_\textbf{p},L), w_\textbf{p}({\tilde \psi}_\textbf{p},z_\textbf{p},L)].
\end{equation}
\begin{equation}
F_{{\tilde \psi}_\textbf{p }}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = g_\textbf{p}({\tilde \psi}_\textbf{p},z_\textbf{p},L), \quad
F_{z_\textbf{p}}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = [h_\textbf{p}({\tilde \psi}_\textbf{p},z_\textbf{p},L), w_\textbf{p}({\tilde \psi}_\textbf{p},z_\textbf{p},L)].
\end{equation} Then critical points of ![]() $\overline{\mathcal{F}}$ in the vicinity of
$\overline{\mathcal{F}}$ in the vicinity of  $\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)\cap \tilde{\mathcal{U}}_\textbf{p}$ are solutions of
$\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)\cap \tilde{\mathcal{U}}_\textbf{p}$ are solutions of
 \begin{equation}
F_{\psi_\textbf{p}}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = 0, \quad
F_{z_\textbf{p}}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = 0.
\end{equation}
\begin{equation}
F_{\psi_\textbf{p}}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = 0, \quad
F_{z_\textbf{p}}({\tilde \psi}_\textbf{p},z_\textbf{p},L) = 0.
\end{equation} This follows from the fact that the polar-cartesian coordinate system is nonsingular in the neighbourhood of the sets  $\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-) \cap \tilde{\mathcal{U}}_\textbf{p}$.
$\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-) \cap \tilde{\mathcal{U}}_\textbf{p}$.
The notation above also applies to the case where one of U 1 or U 2 is empty. In the case where Uc is empty, the ![]() $q_\textbf{p}$, and
$q_\textbf{p}$, and ![]() $w_\textbf{p}$ are not defined, and (3.40) is deleted. Also we use (3.41), (3.42) with
$w_\textbf{p}$ are not defined, and (3.40) is deleted. Also we use (3.41), (3.42) with  $ z_\textbf{p} = r_\textbf{p } \in I_\delta^{3|U|}$.
$ z_\textbf{p} = r_\textbf{p } \in I_\delta^{3|U|}$.
Lemma 3.11. Let ![]() $\overline{\mathcal{F}} = L \overline{\mathcal{F}}_2 + \overline{\mathcal{F}}_4$ be defined in a tubular neighbuorhood
$\overline{\mathcal{F}} = L \overline{\mathcal{F}}_2 + \overline{\mathcal{F}}_4$ be defined in a tubular neighbuorhood ![]() $\cal T$ of
$\cal T$ of ![]() $\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$ as above. (i) There exists
$\mathcal{C}_0(\overline{\mathcal{F}}_4,U_+,U_-)$ as above. (i) There exists ![]() $L_0 \gt 0$ such that for every
$L_0 \gt 0$ such that for every ![]() $\textbf{p} \in \mathcal{K}^{|U|}$,
$\textbf{p} \in \mathcal{K}^{|U|}$,  ${\tilde \psi}_\textbf{p } \in \tilde{\mathcal{ U}}_\textbf{p}$, and
${\tilde \psi}_\textbf{p } \in \tilde{\mathcal{ U}}_\textbf{p}$, and ![]() $L \in (-L_0,L_0)$ there exists a unique
$L \in (-L_0,L_0)$ there exists a unique  $\zeta_\textbf{p}({\tilde \psi}_\textbf{p}, L) \in I_\delta^{3 |U|} \times I_\delta^{5|U^c|}$ satisfying
$\zeta_\textbf{p}({\tilde \psi}_\textbf{p}, L) \in I_\delta^{3 |U|} \times I_\delta^{5|U^c|}$ satisfying
 \begin{equation}
F_{z_\textbf{p}}({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L) = 0,
\end{equation}
\begin{equation}
F_{z_\textbf{p}}({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L) = 0,
\end{equation} and ![]() $\zeta_\textbf{p}({\tilde \psi}_\textbf{p},0) = z_{\textbf{p},0} = [0,0]$. The solution
$\zeta_\textbf{p}({\tilde \psi}_\textbf{p},0) = z_{\textbf{p},0} = [0,0]$. The solution ![]() $\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L)$ is real analytic in
$\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L)$ is real analytic in ![]() ${\tilde \psi}_\textbf{p}$,
${\tilde \psi}_\textbf{p}$,  $\forall {\tilde \psi}_\textbf{p} \in \tilde{\mathcal{U}}_\textbf{p}$, and in L,
$\forall {\tilde \psi}_\textbf{p} \in \tilde{\mathcal{U}}_\textbf{p}$, and in L, ![]() $\forall L \in (-L_0,L_0)$. (ii) For
$\forall L \in (-L_0,L_0)$. (ii) For ![]() $L \in (-L_0,L_0)$, solutions of the first equation of (3.42) are of the form
$L \in (-L_0,L_0)$, solutions of the first equation of (3.42) are of the form ![]() ${\tilde \psi}_\textbf{p} = \chi$,
${\tilde \psi}_\textbf{p} = \chi$, ![]() $ z_\textbf{p} = \zeta_\textbf{p}(\chi)$, with
$ z_\textbf{p} = \zeta_\textbf{p}(\chi)$, with ![]() $\zeta_\textbf{p}(\cdot)$ as in (i), and χ solutions of the equation
$\zeta_\textbf{p}(\cdot)$ as in (i), and χ solutions of the equation
 \begin{equation}
\mathbf{g}_{\mathbf{p}}(\chi,L) = 0, \quad \chi \in \tilde{\mathcal{U}}_\textbf{p},
\end{equation}
\begin{equation}
\mathbf{g}_{\mathbf{p}}(\chi,L) = 0, \quad \chi \in \tilde{\mathcal{U}}_\textbf{p},
\end{equation}where
 \begin{equation}
\mathbf{g}_{\mathbf{p}}({\tilde \psi}_\textbf{p},L) = D_{{\tilde \psi}_\textbf{p}} {\mathcal{G} }({\tilde \psi}_\textbf{p},L), \quad
{\mathcal{G}}( {\tilde \psi}_\textbf{p},L ) := \overline{\mathcal{F}}({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L),
\end{equation}
\begin{equation}
\mathbf{g}_{\mathbf{p}}({\tilde \psi}_\textbf{p},L) = D_{{\tilde \psi}_\textbf{p}} {\mathcal{G} }({\tilde \psi}_\textbf{p},L), \quad
{\mathcal{G}}( {\tilde \psi}_\textbf{p},L ) := \overline{\mathcal{F}}({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L),
\end{equation}  $\forall {\tilde \psi}_\textbf{p} \in \tilde{\mathcal{U}}_\textbf{p}$, i.e.
$\forall {\tilde \psi}_\textbf{p} \in \tilde{\mathcal{U}}_\textbf{p}$, i.e. ![]() ${\mathcal{G}}$ is the restriction of
${\mathcal{G}}$ is the restriction of ![]() $\overline{\mathcal{F}}$ to the graph of
$\overline{\mathcal{F}}$ to the graph of ![]() $\zeta_\textbf{p}$,
$\zeta_\textbf{p}$,  $ \forall {\tilde \psi}_\textbf{p} \in \tilde{\mathcal{U}}_\textbf{p} $,
$ \forall {\tilde \psi}_\textbf{p} \in \tilde{\mathcal{U}}_\textbf{p} $, ![]() $\textbf{p} \in \mathcal{K}^{|U|}$. (iii) Let
$\textbf{p} \in \mathcal{K}^{|U|}$. (iii) Let ![]() $L \in (-L_0,L_0)$, then (i), (ii) define ζ,
$L \in (-L_0,L_0)$, then (i), (ii) define ζ, ![]() $\bf g$,
$\bf g$, ![]() ${\mathcal{G}}$ globally on
${\mathcal{G}}$ globally on ![]() $\mathcal{M} = (\mathbb{R}\mathrm{P}^2)^{|U|}$ by
$\mathcal{M} = (\mathbb{R}\mathrm{P}^2)^{|U|}$ by ![]() $ \zeta|_{\mathcal{U}_\textbf{p}} = \zeta_\textbf{p}$,
$ \zeta|_{\mathcal{U}_\textbf{p}} = \zeta_\textbf{p}$, ![]() $\textbf{g}|_{\mathcal{U}_\textbf{p}} = \textbf{g}_\textbf{p}$,
$\textbf{g}|_{\mathcal{U}_\textbf{p}} = \textbf{g}_\textbf{p}$, ![]() ${\mathcal{G}}|_{\mathcal{U}_\textbf{p}} = {\mathcal{G}}_\textbf{p}$, for all
${\mathcal{G}}|_{\mathcal{U}_\textbf{p}} = {\mathcal{G}}_\textbf{p}$, for all ![]() $\textbf{p} \in \mathcal{K}^{|U|} $.
$\textbf{p} \in \mathcal{K}^{|U|} $.
Lemma 3.11 reduces the problem of finding equilibria of the Landau–de Gennes system for L sufficiently near the origin to that of finding critical points of ![]() $\cal G$ on
$\cal G$ on ![]() $(\mathbb{R}\mathrm{P}^2)^{|U|}$. The proof is based on the implicit function theorem [Reference Buffoni and Tolland5] and is omitted as it is exactly as in the case with boundary, see Lemma 4.2, [Reference Panayotaros26]. The system of coordinates defined above using the symmetry of fB makes the computation of the derivative straightforward.
$(\mathbb{R}\mathrm{P}^2)^{|U|}$. The proof is based on the implicit function theorem [Reference Buffoni and Tolland5] and is omitted as it is exactly as in the case with boundary, see Lemma 4.2, [Reference Panayotaros26]. The system of coordinates defined above using the symmetry of fB makes the computation of the derivative straightforward.
A consequence of Lemma 3.11 is that given a solution  $\chi \in \tilde{\mathcal{U}}_\textbf{p}$ of the reduced equation, the components
$\chi \in \tilde{\mathcal{U}}_\textbf{p}$ of the reduced equation, the components ![]() $r_\textbf{p}$,
$r_\textbf{p}$, ![]() $q_\textbf{p}$ of the equilibrium are given by
$q_\textbf{p}$ of the equilibrium are given by ![]() $\zeta_\textbf{p}(\chi,L)$. Necessary continuation conditions are obtained by the reduced equation at L = 0.
$\zeta_\textbf{p}(\chi,L)$. Necessary continuation conditions are obtained by the reduced equation at L = 0.
Proof of Proposition 2.3
By Lemma 3.11, for L sufficiently near 0 it is sufficient to study solutions of the reduced equation (3.45)
 \begin{equation*} \textbf{g}_\textbf{p}({\tilde \psi}_\textbf{p},L) =
D_{{\tilde \psi}_\textbf{p}} \overline{\mathcal{F}} ({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L)
=
D_1 \overline{\mathcal{F}}({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L) = 0,
\end{equation*}
\begin{equation*} \textbf{g}_\textbf{p}({\tilde \psi}_\textbf{p},L) =
D_{{\tilde \psi}_\textbf{p}} \overline{\mathcal{F}} ({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L)
=
D_1 \overline{\mathcal{F}}({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},L),L) = 0,
\end{equation*} for some ![]() $\textbf{p} \in \mathcal{K}^{|U|}$. The functions
$\textbf{p} \in \mathcal{K}^{|U|}$. The functions ![]() $\zeta_\textbf{p}$ and
$\zeta_\textbf{p}$ and ![]() $\overline{\mathcal{F}}$ are real analytic and we can expand
$\overline{\mathcal{F}}$ are real analytic and we can expand ![]() $\textbf{g}_\textbf{p} $ in powers of L as
$\textbf{g}_\textbf{p} $ in powers of L as
 \begin{equation}
\textbf{g}_\textbf{p}(\psi,L) =
\sum_{k=1}^{\infty} L^k \textbf{g}_{\textbf{p}, k}(\psi),
\quad |L| \lt L_0.
\end{equation}
\begin{equation}
\textbf{g}_\textbf{p}(\psi,L) =
\sum_{k=1}^{\infty} L^k \textbf{g}_{\textbf{p}, k}(\psi),
\quad |L| \lt L_0.
\end{equation} Moreover ![]() $D_1 \overline{\mathcal{F}}_4$ vanishes identically by Lemma 3.9 (ii). The lowest order term in (3.46) is then
$D_1 \overline{\mathcal{F}}_4$ vanishes identically by Lemma 3.9 (ii). The lowest order term in (3.46) is then
 \begin{equation}
\textbf{g}_{\textbf{p}, 1} ({\tilde \psi}_\textbf{p}) =
D_{{\tilde \psi}_\textbf{p}} \overline{\mathcal{F}}_2 ({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},0)) =
D_{\tilde \psi_\textbf{p}} \overline{\mathcal{F}}_2 ({\tilde \psi}_\textbf{p},0).
\end{equation}
\begin{equation}
\textbf{g}_{\textbf{p}, 1} ({\tilde \psi}_\textbf{p}) =
D_{{\tilde \psi}_\textbf{p}} \overline{\mathcal{F}}_2 ({\tilde \psi}_\textbf{p},\zeta_\textbf{p}({\tilde \psi}_\textbf{p},0)) =
D_{\tilde \psi_\textbf{p}} \overline{\mathcal{F}}_2 ({\tilde \psi}_\textbf{p},0).
\end{equation} By the hypothesis of Proposition 2.3, and Lemma 3.11, we have a branch ![]() ${\tilde \Theta}(L)$,
${\tilde \Theta}(L)$, ![]() $L \in[0,\epsilon_0)$,
$L \in[0,\epsilon_0)$, ![]() $\epsilon_0 \leq L_0$, of solutions of
$\epsilon_0 \leq L_0$, of solutions of  $ \textbf{g}_\textbf{p}({\tilde \Theta}(L) ,L) = 0 $, and therefore
$ \textbf{g}_\textbf{p}({\tilde \Theta}(L) ,L) = 0 $, and therefore
 \begin{equation}
L^{-1} \textbf{g}_\textbf{p}({\tilde \Theta}(L) ,L) = 0, \quad \forall L \in (0, \epsilon_0).
\end{equation}
\begin{equation}
L^{-1} \textbf{g}_\textbf{p}({\tilde \Theta}(L) ,L) = 0, \quad \forall L \in (0, \epsilon_0).
\end{equation} Taking the limit ![]() $L \rightarrow 0^+$, and using (3.46), (3.47), we have that
$L \rightarrow 0^+$, and using (3.46), (3.47), we have that ![]() $\Theta = {\tilde \Theta}(0)$ satisfies
$\Theta = {\tilde \Theta}(0)$ satisfies
 \begin{equation}
\textbf{g}_{\textbf{p}, 1} (\Theta) =
D_{{\tilde \psi}_\textbf{p}} \overline{\mathcal{F}}_2 (\Theta, 0) = 0,
\end{equation}
\begin{equation}
\textbf{g}_{\textbf{p}, 1} (\Theta) =
D_{{\tilde \psi}_\textbf{p}} \overline{\mathcal{F}}_2 (\Theta, 0) = 0,
\end{equation}as stated.
The main feature of the continuation problem for graphs without boundary is that the reduced equations for ![]() $\overline{\mathcal{F}}$ have a global SO(3) symmetry. This implies that solutions of the reduced equations are in general not isolated points.
$\overline{\mathcal{F}}$ have a global SO(3) symmetry. This implies that solutions of the reduced equations are in general not isolated points.
To see how the continuation argument is modified, fix ![]() $A \in SO(3)$ and define
$A \in SO(3)$ and define  $\Psi_A^d: (\hbox{Sym}_0^3)^{|\overline G|} \rightarrow (\hbox{Sym}_0^3)^{|\overline G | } $ by
$\Psi_A^d: (\hbox{Sym}_0^3)^{|\overline G|} \rightarrow (\hbox{Sym}_0^3)^{|\overline G | } $ by
 \begin{equation}
\Psi_A^d ({\overline Q})(m) = \Psi_A ({\overline Q}(m)), \quad m \in {\overline G}.
\end{equation}
\begin{equation}
\Psi_A^d ({\overline Q})(m) = \Psi_A ({\overline Q}(m)), \quad m \in {\overline G}.
\end{equation} By (2.6) and Lemmas 3.2, 3.4 ![]() $\overline{\mathcal{F}}$ is invariant under
$\overline{\mathcal{F}}$ is invariant under ![]() $\Psi_A^d$, for all
$\Psi_A^d$, for all ![]() $ A \in SO(3)$ and L real.
$ A \in SO(3)$ and L real.
Also define  $T_A^d: \mathbb{R}^{5|\overline G|} \rightarrow \mathbb{R}^{5|\overline G|}$ by
$T_A^d: \mathbb{R}^{5|\overline G|} \rightarrow \mathbb{R}^{5|\overline G|}$ by
 \begin{equation}
(T_A^d y)(m) = T_A y (m), \quad m \in {\overline G}.
\end{equation}
\begin{equation}
(T_A^d y)(m) = T_A y (m), \quad m \in {\overline G}.
\end{equation} The manifold ![]() $\cal M$ is invariant under
$\cal M$ is invariant under ![]() $T_A^d$,
$T_A^d$, ![]() $\forall A \in SO(3)$. Also define
$\forall A \in SO(3)$. Also define  $T^d:SO(3)\times \mathbb{R}^{5|\overline G|} \rightarrow \mathbb{R}^{5|\overline G|}$ by
$T^d:SO(3)\times \mathbb{R}^{5|\overline G|} \rightarrow \mathbb{R}^{5|\overline G|}$ by ![]() $T^d(A,y) = T^dy$. We use the polar-cartesian coordinates above in the neighbuorhood of
$T^d(A,y) = T^dy$. We use the polar-cartesian coordinates above in the neighbuorhood of ![]() $\mathcal{M} \subset \mathbb{R}^{5|\overline G|} $, and denote the angular, and polar components of
$\mathcal{M} \subset \mathbb{R}^{5|\overline G|} $, and denote the angular, and polar components of ![]() $ T_A^d $ in the neighbuorhood of some
$ T_A^d $ in the neighbuorhood of some ![]() $\tilde{\mathcal{U}}_\textbf{p}$ by
$\tilde{\mathcal{U}}_\textbf{p}$ by  $\mathcal{ R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p})$,
$\mathcal{ R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p})$,  $Z^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p})$ respectively. By Remark 3.8,
$Z^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p})$ respectively. By Remark 3.8,  $\mathcal{R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p})$ coincides with the restriction of
$\mathcal{R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p})$ coincides with the restriction of ![]() $T^d_A$ to
$T^d_A$ to ![]() $\cal M$, and depends only on the angular part. We thus write
$\cal M$, and depends only on the angular part. We thus write  $\mathcal{R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p}) = \mathcal{ R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p})$. Also let
$\mathcal{R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p}, z_\textbf{p}) = \mathcal{ R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p})$. Also let  $\mathcal{R}_A^d$ denote the restriction of
$\mathcal{R}_A^d$ denote the restriction of ![]() $T^d_A$ to
$T^d_A$ to ![]() $\cal M$, and denote the corresponding action of SO(3) on
$\cal M$, and denote the corresponding action of SO(3) on ![]() $\cal M$ by
$\cal M$ by ![]() $\mathcal{R}^d$.
$\mathcal{R}^d$.
Lemma 3.12. Consider the functions ζ, g, and ![]() $\mathcal{G}$ of Lemma 3.11, with
$\mathcal{G}$ of Lemma 3.11, with ![]() $|L| \lt L_0$. Then (i) ζ is equivariant under
$|L| \lt L_0$. Then (i) ζ is equivariant under  $\mathcal{R}_A^d$, see (3.52),
$\mathcal{R}_A^d$, see (3.52), ![]() $\forall A \in SO(3)$, (ii)
$\forall A \in SO(3)$, (ii) ![]() $ \mathcal{G}$ is invariant under
$ \mathcal{G}$ is invariant under  $\mathcal{R}_A^d$,
$\mathcal{R}_A^d$, ![]() $\forall A \in SO(3)$, and (iii) critical points of
$\forall A \in SO(3)$, and (iii) critical points of ![]() $ \mathcal{G}$ belong to compact embedded submanifolds of
$ \mathcal{G}$ belong to compact embedded submanifolds of ![]() $ \mathcal{M} \approx (\mathbb{R}\mathrm{P}^2)^{|U|}$.
$ \mathcal{M} \approx (\mathbb{R}\mathrm{P}^2)^{|U|}$.
Proof. To see (i) fix ![]() $L \in (-\epsilon_0,\epsilon_0)$ and let
$L \in (-\epsilon_0,\epsilon_0)$ and let ![]() $ \zeta_\textbf{p}({\tilde \psi}_\textbf{p}) = \zeta_\textbf{p}({\tilde \psi}_\textbf{p},L) $,
$ \zeta_\textbf{p}({\tilde \psi}_\textbf{p}) = \zeta_\textbf{p}({\tilde \psi}_\textbf{p},L) $, ![]() $\textbf{p} \in \mathcal{K}^{|U|}$. Assume first that A is such that
$\textbf{p} \in \mathcal{K}^{|U|}$. Assume first that A is such that ![]() $T_A^d$ maps a critical point
$T_A^d$ maps a critical point  $m \in \tilde{\mathcal{U}}_\textbf{p}$ to a point in the same domain. It suffices to show the local version of equivariance, namely
$m \in \tilde{\mathcal{U}}_\textbf{p}$ to a point in the same domain. It suffices to show the local version of equivariance, namely
 \begin{equation}
Z^d_{A,\textbf{p}}( {\tilde \psi}_\textbf{p}, \zeta_\textbf{p}( {\tilde \psi}_\textbf{p})) =
\zeta_\textbf{p}( \mathcal{R}^d_{A,\textbf{p}}( {\tilde \psi}_\textbf{p}) ).
\end{equation}
\begin{equation}
Z^d_{A,\textbf{p}}( {\tilde \psi}_\textbf{p}, \zeta_\textbf{p}( {\tilde \psi}_\textbf{p})) =
\zeta_\textbf{p}( \mathcal{R}^d_{A,\textbf{p}}( {\tilde \psi}_\textbf{p}) ).
\end{equation} Note that  $z = \zeta( \mathcal{R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p} ) ) $ is a solution of (3.43). Invariance of
$z = \zeta( \mathcal{R}^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p} ) ) $ is a solution of (3.43). Invariance of ![]() $ \overline{\mathcal{F}}$ under
$ \overline{\mathcal{F}}$ under  $\mathcal{R}_A^d$ implies that the image of a critical point of
$\mathcal{R}_A^d$ implies that the image of a critical point of ![]() $ \overline{\mathcal{F}}$ under
$ \overline{\mathcal{F}}$ under  $\mathcal{R}_A^d$ is also a critical point of
$\mathcal{R}_A^d$ is also a critical point of ![]() $\overline{\mathcal{F}} $, therefore
$\overline{\mathcal{F}} $, therefore  $z = Z^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p})$ also satisfies (3.43). By Lemma 3.11 the solution of (3.43) is unique and the two sides of (3.52) must coincide. In the case of arbitrary
$z = Z^d_{A,\textbf{p}}({\tilde \psi}_\textbf{p})$ also satisfies (3.43). By Lemma 3.11 the solution of (3.43) is unique and the two sides of (3.52) must coincide. In the case of arbitrary ![]() $A \in SO(3)$ we write A as a finite product of elements of SO(3) satisfying the above assumption.
$A \in SO(3)$ we write A as a finite product of elements of SO(3) satisfying the above assumption.
To show (ii) we similarly work with compositions of ![]() $T_A^d$, restricted to
$T_A^d$, restricted to ![]() $\cal M$, that map a subset of
$\cal M$, that map a subset of ![]() $\tilde{\mathcal{U}}_\textbf{p}$ to a subset of
$\tilde{\mathcal{U}}_\textbf{p}$ to a subset of ![]() $\tilde{\mathcal{U}}_\textbf{p}$. We have
$\tilde{\mathcal{U}}_\textbf{p}$. We have
 \begin{equation*}\tilde{\mathcal{G} } ( \mathcal{R}^d_A ( {\tilde \psi}_\textbf{p} ) )=
\overline{\mathcal{F} } (\mathcal{R}^d_A({\tilde \psi}_\textbf{p} ), \zeta_\textbf{p} ( \mathcal{ R}_A^d ({\tilde \psi}_\textbf{p} ) ) =
\overline{\mathcal{F}} (\mathcal{R}^d_A({\tilde \psi}_\textbf{p} ), Z^d_\textbf{p} (\psi_\textbf{p}, \zeta_\textbf{p} ({\tilde \psi}_\textbf{p})) =
\overline{\mathcal{F} } ( {\tilde \psi}_\textbf{p}, \zeta_\textbf{p} ({\tilde \psi}_\textbf{p} ) ), \end{equation*}
\begin{equation*}\tilde{\mathcal{G} } ( \mathcal{R}^d_A ( {\tilde \psi}_\textbf{p} ) )=
\overline{\mathcal{F} } (\mathcal{R}^d_A({\tilde \psi}_\textbf{p} ), \zeta_\textbf{p} ( \mathcal{ R}_A^d ({\tilde \psi}_\textbf{p} ) ) =
\overline{\mathcal{F}} (\mathcal{R}^d_A({\tilde \psi}_\textbf{p} ), Z^d_\textbf{p} (\psi_\textbf{p}, \zeta_\textbf{p} ({\tilde \psi}_\textbf{p})) =
\overline{\mathcal{F} } ( {\tilde \psi}_\textbf{p}, \zeta_\textbf{p} ({\tilde \psi}_\textbf{p} ) ), \end{equation*} using (i) and the invariance of ![]() $ \overline{\mathcal{F}}$ under
$ \overline{\mathcal{F}}$ under ![]() $T_A^d$. Thus
$T_A^d$. Thus  ${\mathcal{G} } ( \mathcal{R}^d_A ({\tilde \psi}_\textbf{p}) )= {\mathcal{G}} ( {\tilde \psi}_\textbf{p}) $.
${\mathcal{G} } ( \mathcal{R}^d_A ({\tilde \psi}_\textbf{p}) )= {\mathcal{G}} ( {\tilde \psi}_\textbf{p}) $.
To see (iii), we use a similar strategy using local coordinates in ![]() $ (\mathbb{R}\mathrm{P}^2)^{|U|}$ and a standard argument to see that the critical points
$ (\mathbb{R}\mathrm{P}^2)^{|U|}$ and a standard argument to see that the critical points ![]() $\tilde{\mathcal{G}}$ are mapped to critical points under
$\tilde{\mathcal{G}}$ are mapped to critical points under  $\mathcal{R}_A^d$ Furthermore
$\mathcal{R}_A^d$ Furthermore  $\mathcal{R}_A^d$ is a smooth
$\mathcal{R}_A^d$ is a smooth ![]() $SO(3)-$action on
$SO(3)-$action on ![]() $\mathcal{M} \approx (\mathbb{R}\mathrm{P}^2)^{|U|}$. Since SO(3) is compact, the orbit of every point
$\mathcal{M} \approx (\mathbb{R}\mathrm{P}^2)^{|U|}$. Since SO(3) is compact, the orbit of every point ![]() $x \in \mathcal{M}$ under this action is a compact embedded submanifold
$x \in \mathcal{M}$ under this action is a compact embedded submanifold ![]() $\mathcal{O}_{SO(3)} (x)$ of
$\mathcal{O}_{SO(3)} (x)$ of ![]() $\cal M$, see [Reference Lee18].
$\cal M$, see [Reference Lee18].
Proof of Lemma 2.2
Let ![]() $L_0 \gt 0$ be as in Lemma 3.11. Critical sets of
$L_0 \gt 0$ be as in Lemma 3.11. Critical sets of ![]() $\overline{\mathcal{F}}$,
$\overline{\mathcal{F}}$, ![]() $|L| \lt L_0$, are graphs of critical points of
$|L| \lt L_0$, are graphs of critical points of ![]() $ \mathcal{G}$ under the map ζ of Lemma 3.11. This map embedds
$ \mathcal{G}$ under the map ζ of Lemma 3.11. This map embedds ![]() $ (\mathbb{R}\mathrm{P}^2)^{|U|}$ to
$ (\mathbb{R}\mathrm{P}^2)^{|U|}$ to ![]() $\mathbb{R}^{5|\overline G|}$. Its restriction to critical sets of
$\mathbb{R}^{5|\overline G|}$. Its restriction to critical sets of ![]() $\cal G$ are also embeddings and are critical sets of
$\cal G$ are also embeddings and are critical sets of ![]() $\cal G$. By Lemma 3.11, all critical set of
$\cal G$. By Lemma 3.11, all critical set of ![]() $\cal G$,
$\cal G$, ![]() $|L| \lt L_0$, are of that form.
$|L| \lt L_0$, are of that form.
Proof of Proposition 2.4
s By Lemma 3.11, to find critical points of ![]() $\overline{\mathcal{F}}$,
$\overline{\mathcal{F}}$, ![]() $|L| \lt L_0$, it suffices to find critical points of the functional
$|L| \lt L_0$, it suffices to find critical points of the functional ![]() $ \mathcal{E}({\tilde \psi},L) = \overline{\mathcal{F}}_2 ({\tilde \psi}, \zeta(\tilde \psi, L))$,
$ \mathcal{E}({\tilde \psi},L) = \overline{\mathcal{F}}_2 ({\tilde \psi}, \zeta(\tilde \psi, L))$, ![]() $ |L | \lt L_0$,
$ |L | \lt L_0$, ![]() ${\tilde \psi} \in (\mathbb{R}\mathrm{P}^2)^{|U|}$. The statement follows from the assumption by using normal coordinates around each manifold of critical points and the implicit function theorem argument of Lemma 3.11.
${\tilde \psi} \in (\mathbb{R}\mathrm{P}^2)^{|U|}$. The statement follows from the assumption by using normal coordinates around each manifold of critical points and the implicit function theorem argument of Lemma 3.11.
The manifolds of critical points of the reduced energy ![]() $ \mathcal{G}$ on
$ \mathcal{G}$ on ![]() $\mathcal{M} \approx (\mathbb{R}\mathrm{P}^2)^{d}$ can be classified by classifying the topology of orbits of the diagonal action
$\mathcal{M} \approx (\mathbb{R}\mathrm{P}^2)^{d}$ can be classified by classifying the topology of orbits of the diagonal action ![]() $\mathcal{R}^d$ of SO(3) on
$\mathcal{R}^d$ of SO(3) on ![]() $\mathcal{M} $, i.e. Td of (3.51), restricted to
$\mathcal{M} $, i.e. Td of (3.51), restricted to ![]() $\cal M$. The basic fact from the theory of Lie group actions is that the orbit
$\cal M$. The basic fact from the theory of Lie group actions is that the orbit ![]() $\mathcal{O}(x)$ of
$\mathcal{O}(x)$ of ![]() $x \in \mathcal{M}$ under the action of SO(3) is the manifold
$x \in \mathcal{M}$ under the action of SO(3) is the manifold ![]() $SO(3)/SO(3)_x$, where
$SO(3)/SO(3)_x$, where ![]() $SO(3)_x$ is the isotropy subgroup of x under the action, see the theorem of section 5.15 of [Reference Kolář, Michor and Slovák16]. In what follows we classify the isotropy subgroups.
$SO(3)_x$ is the isotropy subgroup of x under the action, see the theorem of section 5.15 of [Reference Kolář, Michor and Slovák16]. In what follows we classify the isotropy subgroups.
By the definition of the action, the isotropy subgroup ![]() $SO(3)_x$ under
$SO(3)_x$ under ![]() $\mathcal{R}^d$ is the set of all
$\mathcal{R}^d$ is the set of all ![]() $R \in SO(3)$ satisfying
$R \in SO(3)$ satisfying
The set of such matrices is a subgroup of SO(3).
By (3.53) The action only affects the directions of the Q-tensors on ![]() $\Sigma_\pm$, thus a configuration on
$\Sigma_\pm$, thus a configuration on ![]() $\boldsymbol{\cal{M}}$ is determined by the directions
$\boldsymbol{\cal{M}}$ is determined by the directions ![]() $\{{\hat n}_j, - {\hat n}_j\}$, where j is either in
$\{{\hat n}_j, - {\hat n}_j\}$, where j is either in ![]() $U_-$ or
$U_-$ or ![]() $U_+$. Denote by
$U_+$. Denote by ![]() $\mathcal{V}(x)$,
$\mathcal{V}(x)$, ![]() $x = \in (x_1, \ldots, x_{d}) \in (\mathbb{R}\mathrm{P}^2)^d$, the set distinct points of
$x = \in (x_1, \ldots, x_{d}) \in (\mathbb{R}\mathrm{P}^2)^d$, the set distinct points of ![]() $\mathbb{R}\mathrm{P}^2$ in
$\mathbb{R}\mathrm{P}^2$ in ![]() $\{x_1, \ldots, x_{d}\}$. Let
$\{x_1, \ldots, x_{d}\}$. Let ![]() ${\tilde d}(x)$ denote the number of values of
${\tilde d}(x)$ denote the number of values of ![]() $x \in (\mathbb{R}\mathrm{P}^2)^d$. Clearly
$x \in (\mathbb{R}\mathrm{P}^2)^d$. Clearly ![]() $ 1 \leq {\tilde d}(x) \leq d$,
$ 1 \leq {\tilde d}(x) \leq d$, ![]() $\forall x \in (\mathbb{R}\mathrm{P}^2)^d$. By (3.53) the isotropy subgroup of x depends on
$\forall x \in (\mathbb{R}\mathrm{P}^2)^d$. By (3.53) the isotropy subgroup of x depends on ![]() $\mathcal{V}(x)$. For l,
$\mathcal{V}(x)$. For l, ![]() $l'\in \mathcal{V}(x)$ we use expressions
$l'\in \mathcal{V}(x)$ we use expressions ![]() $l \perp l'$,
$l \perp l'$, ![]() $l^\perp$, etc., to denote orthogonality, orthogonal complement, etc., of directions in
$l^\perp$, etc., to denote orthogonality, orthogonal complement, etc., of directions in ![]() $\mathbb{R}^3$ with respect to the Euclidean inner product.
$\mathbb{R}^3$ with respect to the Euclidean inner product.
In the case ![]() ${\tilde d}(x) = 1$ we have
${\tilde d}(x) = 1$ we have  $\mathcal{O}_{SO(3)} (x) \approx \mathbb{R}\mathrm{P}^2$ by Lemma 3.3. The isotropy subgroup below for that case describes the projective plane as a quotient of SO(3) by the isotropy subgroup of points in the diagonal of
$\mathcal{O}_{SO(3)} (x) \approx \mathbb{R}\mathrm{P}^2$ by Lemma 3.3. The isotropy subgroup below for that case describes the projective plane as a quotient of SO(3) by the isotropy subgroup of points in the diagonal of ![]() $\cal M$. The case where
$\cal M$. The case where ![]() $U_\pm = {\overline G}$,
$U_\pm = {\overline G}$, ![]() $U_\mp = \emptyset$ and
$U_\mp = \emptyset$ and ![]() ${\tilde d} = 1$ corresponds to the constant critical points of
${\tilde d} = 1$ corresponds to the constant critical points of ![]() $\overline{\mathcal{F}}$. For abelian group actions on products the orbits of points in the diagonal are diffeomorphic to all orbits. This is not necessarily the case for nonabelian group actions.
$\overline{\mathcal{F}}$. For abelian group actions on products the orbits of points in the diagonal are diffeomorphic to all orbits. This is not necessarily the case for nonabelian group actions.
Let
 \begin{equation}
R_\phi = \left[
\begin{array}{ccc}
\cos \phi & - \sin \phi & 0 \\
\sin \phi & \cos \phi & 0 \\
0 & 0 & 1
\end{array}
\right], \quad
A_- =
\left[
\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right].
\end{equation}
\begin{equation}
R_\phi = \left[
\begin{array}{ccc}
\cos \phi & - \sin \phi & 0 \\
\sin \phi & \cos \phi & 0 \\
0 & 0 & 1
\end{array}
\right], \quad
A_- =
\left[
\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right].
\end{equation} Note that ![]() $(A_-)^{-1} = A_-$,
$(A_-)^{-1} = A_-$,  $R_\phi^{-1} = R_{- \phi}$,
$R_\phi^{-1} = R_{- \phi}$, ![]() $(A_- R_\phi)^{-1} = R_{-\phi} A_- $, for all
$(A_- R_\phi)^{-1} = R_{-\phi} A_- $, for all ![]() $\phi \in [0,2 \pi)$ also the matrices
$\phi \in [0,2 \pi)$ also the matrices ![]() $A_-$, Rπ,
$A_-$, Rπ, ![]() $A_- R_\pi$ describe rotations by π around the vectors
$A_- R_\pi$ describe rotations by π around the vectors ![]() ${\hat e_1}$,
${\hat e_1}$, ![]() ${\hat e}_3$,
${\hat e}_3$, ![]() ${\hat e}_2$ respectively, and
${\hat e}_2$ respectively, and ![]() $\{I, A_-, R_\pi, A_- R_\pi \}$,
$\{I, A_-, R_\pi, A_- R_\pi \}$, ![]() $I = R_0$, form an abelian group that contains the subgroups
$I = R_0$, form an abelian group that contains the subgroups ![]() $\{I, A_-\}$,
$\{I, A_-\}$, ![]() $\{I, R_\pi\}$,
$\{I, R_\pi\}$, ![]() $\{I, A_- R_\pi \}$, and the trivial group
$\{I, A_- R_\pi \}$, and the trivial group ![]() $\{I \}$.
$\{I \}$.
Let ![]() $\mathcal{S}_1$,
$\mathcal{S}_1$, ![]() $\mathcal{S}_2$ be subgroups of SO(3). We say that
$\mathcal{S}_2$ be subgroups of SO(3). We say that ![]() $\mathcal{S}_1$,
$\mathcal{S}_1$, ![]() $\mathcal{S}_2$ are isomorphic (under conjugacy) and we write
$\mathcal{S}_2$ are isomorphic (under conjugacy) and we write ![]() $\mathcal{S}_1 \sim \mathcal{S}_2$ if there exists an
$\mathcal{S}_1 \sim \mathcal{S}_2$ if there exists an ![]() $ {A} \in SO(3)$ such that the map
$ {A} \in SO(3)$ such that the map ![]() $ad_A: \mathcal{S}_1 \rightarrow \mathcal{S}_2$, defined by
$ad_A: \mathcal{S}_1 \rightarrow \mathcal{S}_2$, defined by ![]() $ad_A(g_1) = A^{-1}g_1 {A}$,
$ad_A(g_1) = A^{-1}g_1 {A}$, ![]() $g_1 \in \mathcal{S}_1$, is a group isomorphism. Note that the isotropy subgroups of x,
$g_1 \in \mathcal{S}_1$, is a group isomorphism. Note that the isotropy subgroups of x, ![]() $y \in (\mathbb{R}\mathrm{P}^2)^d$ with
$y \in (\mathbb{R}\mathrm{P}^2)^d$ with ![]() $ x_j = {A} y_j $,
$ x_j = {A} y_j $, ![]() $A \in SO(3)$,
$A \in SO(3)$, ![]() $j = 1, \ldots, d$, are isomorphic since by (3.53),
$j = 1, \ldots, d$, are isomorphic since by (3.53), ![]() $R \in SO(3)_x$ if and only if
$R \in SO(3)_x$ if and only if ![]() ${A}^{-1} R {A} \in SO(3)_y$.
${A}^{-1} R {A} \in SO(3)_y$.
Proposition 3.13. Let ![]() $ x \in \boldsymbol{\cal{M}}$, then the isotropy group
$ x \in \boldsymbol{\cal{M}}$, then the isotropy group ![]() $SO(3)_x$ under
$SO(3)_x$ under ![]() $ \mathcal{R}^d $ is as follows.
$ \mathcal{R}^d $ is as follows.
(i) If ![]() $ {\tilde d}(x) = 1$ then
$ {\tilde d}(x) = 1$ then ![]() $ SO(3)_x $ is isomorphic to the set
$ SO(3)_x $ is isomorphic to the set ![]() $ \mathcal{S}_r$ of all Rϕ,
$ \mathcal{S}_r$ of all Rϕ, ![]() $R_\phi A_-$,
$R_\phi A_-$, ![]() $A_- R_\phi$,
$A_- R_\phi$, ![]() $\phi \in [0,2\pi)$.
$\phi \in [0,2\pi)$.
(ii) Let ![]() ${\tilde d}(x) = 2$ and
${\tilde d}(x) = 2$ and ![]() $\boldsymbol{\mathcal{V}}(x) = \{l_1,l_2\}$ If (α)
$\boldsymbol{\mathcal{V}}(x) = \{l_1,l_2\}$ If (α) ![]() $l_1 \not\perp l_2$ then
$l_1 \not\perp l_2$ then ![]() $SO(3)_x$ is isomorphic to the set
$SO(3)_x$ is isomorphic to the set ![]() $\{I, R_{\pi} A_- \}$. If (β)
$\{I, R_{\pi} A_- \}$. If (β) ![]() $l_1 \perp l_2$ then
$l_1 \perp l_2$ then ![]() $ SO(3)_x $ is isomorphic to the set
$ SO(3)_x $ is isomorphic to the set ![]() $\{I, A_-, R_{\pi}, R_{\pi} A_- \}$.
$\{I, A_-, R_{\pi}, R_{\pi} A_- \}$.
(iii) Let ![]() ${\tilde d}= 3 $. If the elements of
${\tilde d}= 3 $. If the elements of ![]() $\boldsymbol{\mathcal{V}}(x)$ lie on the same plane then
$\boldsymbol{\mathcal{V}}(x)$ lie on the same plane then ![]() $SO(3)_x$ is isomorphic to the set
$SO(3)_x$ is isomorphic to the set ![]() $\{I, R_{\pi} A_- \}$. If the elements
$\{I, R_{\pi} A_- \}$. If the elements ![]() ${l_1,l_2,l_3}$
${l_1,l_2,l_3}$ ![]() $\mathcal{V}(x)$ are linearly independent we have four subcases: (α)
$\mathcal{V}(x)$ are linearly independent we have four subcases: (α) ![]() $l_i \not\perp l_j$,
$l_i \not\perp l_j$, ![]() $\forall i, j \in \{1,2,3\}$, then
$\forall i, j \in \{1,2,3\}$, then ![]() $SO(3)_x$ is
$SO(3)_x$ is ![]() $\{I \}$; (β)
$\{I \}$; (β) ![]() $l_1 \perp l_2 $ with
$l_1 \perp l_2 $ with ![]() $l_3 \not\perp l_1$ and
$l_3 \not\perp l_1$ and ![]() $l_3 \not\perp l_2$ (up to renumbering), then
$l_3 \not\perp l_2$ (up to renumbering), then ![]() $SO(3)_x$ is
$SO(3)_x$ is ![]() $\{I \}$; (γ) l 2,
$\{I \}$; (γ) l 2, ![]() $l_3 \in l_1^\perp$ and
$l_3 \in l_1^\perp$ and ![]() $l_2 \not\perp l_3$ (up to renumbering), then
$l_2 \not\perp l_3$ (up to renumbering), then ![]() $SO(3)_x$ is isomorphic to the set
$SO(3)_x$ is isomorphic to the set ![]() $\{I, R_{\pi} \}$; (δ)
$\{I, R_{\pi} \}$; (δ) ![]() $l_i \perp l_j$,
$l_i \perp l_j$, ![]() $\forall i, j \in \{1,2,3\}$,
$\forall i, j \in \{1,2,3\}$, ![]() $SO(3)_x$ is isomorphic to the set
$SO(3)_x$ is isomorphic to the set ![]() $\{I, A_-, R_{\pi}, R_\pi A_- \}$.
$\{I, A_-, R_{\pi}, R_\pi A_- \}$.
(iv) Let ![]() ${\tilde d} \geq 4$. If all the elements of
${\tilde d} \geq 4$. If all the elements of ![]() $\mathcal{V}(x)$ lie on the same plane then
$\mathcal{V}(x)$ lie on the same plane then ![]() $SO(3)_x$ is isomorphic to the set
$SO(3)_x$ is isomorphic to the set ![]() $\{I, R_{\pi} A_- \}$. If the elements of
$\{I, R_{\pi} A_- \}$. If the elements of ![]() $\mathcal{V}(x)$ are not on the same plane and there is no pair of
$\mathcal{V}(x)$ are not on the same plane and there is no pair of ![]() $l_1, l_2 \in \mathcal{V}(x)$ satisfying
$l_1, l_2 \in \mathcal{V}(x)$ satisfying ![]() $l_1 \perp l_2$, then
$l_1 \perp l_2$, then ![]() $SO(3)_x$ is
$SO(3)_x$ is ![]() $\{I \}$. If there exists a pair of vectors
$\{I \}$. If there exists a pair of vectors ![]() $l_1, l_2 \in \mathcal{V}(x)$ satisfying
$l_1, l_2 \in \mathcal{V}(x)$ satisfying ![]() $l_1 \perp l_2$ and either
$l_1 \perp l_2$ and either ![]() $\mathcal{V}\setminus \{l_1\} \in l_2^\perp$ or
$\mathcal{V}\setminus \{l_1\} \in l_2^\perp$ or ![]() $\mathcal{V}\setminus \{l_2\} \in l_1^\perp$ then
$\mathcal{V}\setminus \{l_2\} \in l_1^\perp$ then ![]() $SO(3)_x$ is isomorphic to
$SO(3)_x$ is isomorphic to ![]() $\{I, R_\pi\}$, otherwise
$\{I, R_\pi\}$, otherwise ![]() $SO(3)_x$ is
$SO(3)_x$ is ![]() $\{I\}$.
$\{I\}$.
Proof. Note that the isotropy subgroups of x, ![]() $y \in (\mathbb{R}\mathrm{P}^2)^d$ with
$y \in (\mathbb{R}\mathrm{P}^2)^d$ with ![]() $ x_j = {\tilde R} y_j $,
$ x_j = {\tilde R} y_j $, ![]() $\tilde R \in SO(3)$,
$\tilde R \in SO(3)$, ![]() $j = 1, \ldots, d$, are isomorphic since by (3.53)
$j = 1, \ldots, d$, are isomorphic since by (3.53) ![]() $R \in SO(3)_x$ if and only if
$R \in SO(3)_x$ if and only if  ${\tilde R}^{-1} R {\tilde R} \in SO(3)_y$. To compute
${\tilde R}^{-1} R {\tilde R} \in SO(3)_y$. To compute ![]() $SO(3)_x$ up to isomorphism we may rotate the elements of
$SO(3)_x$ up to isomorphism we may rotate the elements of ![]() $\mathcal{V}(x)$ to some standard configurations.
$\mathcal{V}(x)$ to some standard configurations.
(i) The line ![]() $l \in \cal V(x)$ can be rotated to the direction of
$l \in \cal V(x)$ can be rotated to the direction of ![]() ${\hat e}_3$ by two rotation matrices R 1, R 2. Solutions of (3.53) with
${\hat e}_3$ by two rotation matrices R 1, R 2. Solutions of (3.53) with ![]() ${\hat n} = {\hat e}_3$ are rotation matrices whose third column is
${\hat n} = {\hat e}_3$ are rotation matrices whose third column is ![]() $\pm {\hat e}_3$. In the case where the third column is
$\pm {\hat e}_3$. In the case where the third column is ![]() ${\hat e}_3$, the solutions are the matrices Rϕ,
${\hat e}_3$, the solutions are the matrices Rϕ, ![]() $\phi \in [0,2 \pi)$. In the case where the third column is
$\phi \in [0,2 \pi)$. In the case where the third column is ![]() $- {\hat e}_3$, the first
$- {\hat e}_3$, the first ![]() $2 \times 2$ block is a rotation matrix with determinant −1. The resulting rotation matrices are of the form
$2 \times 2$ block is a rotation matrix with determinant −1. The resulting rotation matrices are of the form ![]() $R_\phi A_-$,
$R_\phi A_-$, ![]() $A_- R_\phi$,
$A_- R_\phi$, ![]() $\phi \in [0,2 \pi)$.
$\phi \in [0,2 \pi)$.
(ii) Let ![]() $\mathcal{V}(x) = \{l_1, l_2 \}$. Rotate l 1 to the direction of
$\mathcal{V}(x) = \{l_1, l_2 \}$. Rotate l 1 to the direction of ![]() ${\hat e}_3$, then rotate around the axis of
${\hat e}_3$, then rotate around the axis of ![]() ${\hat e}_3$ to obtain the directions of two noncolinear vectors
${\hat e}_3$ to obtain the directions of two noncolinear vectors ![]() ${\hat e_3}$,
${\hat e_3}$, ![]() ${\tilde n}_2$ on the plane
${\tilde n}_2$ on the plane ![]() $\hbox{span}\{{\hat e}_3, {\hat e}_1\}$. If
$\hbox{span}\{{\hat e}_3, {\hat e}_1\}$. If ![]() ${\tilde n}_2 \neq \pm {\hat e}_1$, case (α), then (3.53) with
${\tilde n}_2 \neq \pm {\hat e}_1$, case (α), then (3.53) with ![]() ${\hat n} = {\tilde n}_2$ has solutions R = I,
${\hat n} = {\tilde n}_2$ has solutions R = I, ![]() $R_\pi A_- = A_- R_\pi = (R_\pi A_-)^{-1}$. These matrices also leave the axis of
$R_\pi A_- = A_- R_\pi = (R_\pi A_-)^{-1}$. These matrices also leave the axis of ![]() $\hat e_3$ invariant. If
$\hat e_3$ invariant. If ![]() ${\tilde n}_2 = \pm {\hat e}_1$, case (β), then (3.53) with
${\tilde n}_2 = \pm {\hat e}_1$, case (β), then (3.53) with ![]() ${\hat n} = {\tilde n}_2$ has solutions R = I,
${\hat n} = {\tilde n}_2$ has solutions R = I, ![]() $A_-$, Rπ,
$A_-$, Rπ, ![]() $R_\pi A_-$. These matrices also leave the directions of
$R_\pi A_-$. These matrices also leave the directions of ![]() ${\hat e}_j$,
${\hat e}_j$, ![]() $j = 1, 2, 3 $, invariant.
$j = 1, 2, 3 $, invariant.
(iii) Let ![]() $\mathcal{V}(x) = \{l_1, l_2, l_3\}$. We apply a rotation to transform the first two directions to the directions of the vectors
$\mathcal{V}(x) = \{l_1, l_2, l_3\}$. We apply a rotation to transform the first two directions to the directions of the vectors ![]() ${\hat e_3}$,
${\hat e_3}$, ![]() ${\tilde n}_2$ on the plane
${\tilde n}_2$ on the plane ![]() $\hbox{span}\{{\hat e}_3, {\hat e}_1\}$ as in (ii). We also obtain a third direction along a vector
$\hbox{span}\{{\hat e}_3, {\hat e}_1\}$ as in (ii). We also obtain a third direction along a vector ![]() ${\tilde n_3}$.
${\tilde n_3}$.
If the three directions of ![]() $\mathcal{V}(x)$ are on the same plane then
$\mathcal{V}(x)$ are on the same plane then ![]() ${\tilde n}_3 \in \hbox{span}\{{\hat e}_3, {\tilde n}_2 \}$, and we have case (α) of (ii) for two of the directions. The third direction belongs to the same plane, and we have the isotropy subgroup of (ii) (α).
${\tilde n}_3 \in \hbox{span}\{{\hat e}_3, {\tilde n}_2 \}$, and we have case (α) of (ii) for two of the directions. The third direction belongs to the same plane, and we have the isotropy subgroup of (ii) (α).
In the case where ![]() $\{l_1, l_2, l_3\}$ are linearly independent, subcase (α), we have
$\{l_1, l_2, l_3\}$ are linearly independent, subcase (α), we have ![]() ${\tilde n_3} \not\in \hbox{span} \{{\hat e}_3, {\hat e}_1\}$, and
${\tilde n_3} \not\in \hbox{span} \{{\hat e}_3, {\hat e}_1\}$, and ![]() ${\tilde n}_3 \not\perp {\hat e}_3$, then
${\tilde n}_3 \not\perp {\hat e}_3$, then ![]() ${\tilde n}_3 = [x_1,x_2,x_3]$, with
${\tilde n}_3 = [x_1,x_2,x_3]$, with ![]() $x_2, x_3 \neq 0$. Also the isotropy subgroup is a subset of that of (ii), case (α) since
$x_2, x_3 \neq 0$. Also the isotropy subgroup is a subset of that of (ii), case (α) since ![]() $ {\hat e}_3 \not\perp {\tilde n}_2$. The equation
$ {\hat e}_3 \not\perp {\tilde n}_2$. The equation ![]() $ R_\pi A_- {\tilde n}_3 = \pm {\tilde n}_3 $ implies
$ R_\pi A_- {\tilde n}_3 = \pm {\tilde n}_3 $ implies ![]() $x_2 = x_2$,
$x_2 = x_2$, ![]() $-x_3 = x_3$ or
$-x_3 = x_3$ or ![]() $x_2 = -x_2$,
$x_2 = -x_2$, ![]() $x_3 = x_3$, and there are no solutions with both x 2, x 3 nonvanishing.
$x_3 = x_3$, and there are no solutions with both x 2, x 3 nonvanishing.
In subcase (β) we may assume that ![]() $l_1 \perp l_2$, and
$l_1 \perp l_2$, and ![]() ${\tilde n}_2 = {\hat e}_1$. Then l 3 is mapped to
${\tilde n}_2 = {\hat e}_1$. Then l 3 is mapped to ![]() ${\tilde n}_3 = [x_1,x_2,x_3]$, with x 1,
${\tilde n}_3 = [x_1,x_2,x_3]$, with x 1, ![]() $x_2, x_3 \neq 0$ by the assumptions. The isotropy subgroup is a subset of the set of (ii), case (β) since
$x_2, x_3 \neq 0$ by the assumptions. The isotropy subgroup is a subset of the set of (ii), case (β) since ![]() $l_1 \perp l_2$. By the argument of subcase (iii) (α) the direction of
$l_1 \perp l_2$. By the argument of subcase (iii) (α) the direction of ![]() ${\tilde n}_3$ is not invariant under
${\tilde n}_3$ is not invariant under ![]() $A_-$, Rπ,
$A_-$, Rπ, ![]() $A_- R_\pi$, they all leave one component invariant and change the sign of the other two, and we cannot have solutions with all components nonzero.
$A_- R_\pi$, they all leave one component invariant and change the sign of the other two, and we cannot have solutions with all components nonzero.
In subcase (γ), the transformed vectors satisfy ![]() ${\tilde n}_2 = {\hat e}_1$,
${\tilde n}_2 = {\hat e}_1$, ![]() ${\tilde n}_3 \in {\hat e}_3$,
${\tilde n}_3 \in {\hat e}_3$, ![]() $ {\tilde n}_2 \not\perp {\tilde n}_3$. Moreover
$ {\tilde n}_2 \not\perp {\tilde n}_3$. Moreover ![]() ${\tilde n}_3 = [x_1,x_2,0]$ with x 1,
${\tilde n}_3 = [x_1,x_2,0]$ with x 1, ![]() $x_2 \neq 0$. The isotropy subgroup is a subset of the group of (ii), case (β). The direction of
$x_2 \neq 0$. The isotropy subgroup is a subset of the group of (ii), case (β). The direction of ![]() ${\tilde n}_3$ is invariant under Rπ, but not under
${\tilde n}_3$ is invariant under Rπ, but not under ![]() $A_-$ or
$A_-$ or ![]() $A_- R_\pi$, thus
$A_- R_\pi$, thus ![]() $SO(3)_x$ is isomorphic to
$SO(3)_x$ is isomorphic to ![]() $\{I, R_\pi \}$.
$\{I, R_\pi \}$.
In the subcase (δ) the transformed directions are ![]() ${\hat e}_j$,
${\hat e}_j$, ![]() $j = 1, 2, 3$, and we have the isotropy group of (ii), case (β) since the additional direction of
$j = 1, 2, 3$, and we have the isotropy group of (ii), case (β) since the additional direction of ![]() ${\hat e}_3$ is also invariant under its transformations. The above cover all possible
${\hat e}_3$ is also invariant under its transformations. The above cover all possible ![]() $\mathcal{V}(x)$ with three elements.
$\mathcal{V}(x)$ with three elements.
(iv) In the case where all directions of ![]() $\mathcal{V}(x)$ are on the same plane, we use the argument of (iii) to bring all directions to the plane of
$\mathcal{V}(x)$ are on the same plane, we use the argument of (iii) to bring all directions to the plane of ![]() ${\hat e}_3$,
${\hat e}_3$, ![]() ${\hat e}_1$. The isotropy subgroup is the same as the the one obtained for the
${\hat e}_1$. The isotropy subgroup is the same as the the one obtained for the ![]() ${\tilde d} = 3$ coplanar case as the extra directions are also invariant under the
${\tilde d} = 3$ coplanar case as the extra directions are also invariant under the ![]() $T_- R_\pi$.
$T_- R_\pi$.
If the directions of ![]() $\mathcal{V}(x)$ are not on the same plane we distinguish the cases where the none or at least one pair of orthogonal directions. In the first case we have three directions as in (iii), subcase (α) and the isotropy subgroup is trivial.
$\mathcal{V}(x)$ are not on the same plane we distinguish the cases where the none or at least one pair of orthogonal directions. In the first case we have three directions as in (iii), subcase (α) and the isotropy subgroup is trivial.
In the second case consider a pair of ![]() $l_1 \perp l_2 \in \mathcal{V}(x)$. We first consider the subcase where all other vectors are in
$l_1 \perp l_2 \in \mathcal{V}(x)$. We first consider the subcase where all other vectors are in ![]() $l_j^\perp$,
$l_j^\perp$, ![]() $j \in \{1, 2 \}$. Then we transform lj to
$j \in \{1, 2 \}$. Then we transform lj to ![]() ${\hat e}_3$ and see that we have at least two other transformed vectors in
${\hat e}_3$ and see that we have at least two other transformed vectors in ![]() ${\hat e}^\perp$ that are as in (ii), subcase (γ). These directions are invariant under
${\hat e}^\perp$ that are as in (ii), subcase (γ). These directions are invariant under ![]() $A_- R_\pi$, and so are all other vectors in
$A_- R_\pi$, and so are all other vectors in ![]() ${\hat e}^\perp$. Thus the isotropy subspace is
${\hat e}^\perp$. Thus the isotropy subspace is ![]() $\{I, A_- R_\pi\}$. If on the contrary, there is at least one direction not in either
$\{I, A_- R_\pi\}$. If on the contrary, there is at least one direction not in either ![]() $l_1^\perp$ or
$l_1^\perp$ or ![]() $l_2^\perp$, we have three directions satisfying the assumptions of (ii), subcase
$l_2^\perp$, we have three directions satisfying the assumptions of (ii), subcase ![]() $(\beta)$, and the isotropy subgroup is trivial. The above cover all possible
$(\beta)$, and the isotropy subgroup is trivial. The above cover all possible ![]() $\mathcal{V}(x)$ with at least four elements.
$\mathcal{V}(x)$ with at least four elements.
Since the vectors ![]() ${\hat e}_j$ can be transformed to each other by a rotation the groups
${\hat e}_j$ can be transformed to each other by a rotation the groups ![]() $\{I, A_-\}$,
$\{I, A_-\}$, ![]() $\{I, R_\pi\}$,
$\{I, R_\pi\}$, ![]() $\{I, A_- R_\pi \}$ are isomorphic. Thus the isotropy subgroups found are, up to isomorphism, the set
$\{I, A_- R_\pi \}$ are isomorphic. Thus the isotropy subgroups found are, up to isomorphism, the set ![]() $\mathcal{S}_r$ of (i), the abelian group of two elements
$\mathcal{S}_r$ of (i), the abelian group of two elements ![]() $\{I, R_\pi\}$, the abelian group
$\{I, R_\pi\}$, the abelian group ![]() $\{I, A_-, R_\pi, A_-\}$, and the trivial subgroup
$\{I, A_-, R_\pi, A_-\}$, and the trivial subgroup ![]() $\{I\}$.
$\{I\}$.
Proposition 2.7 on the connection between the reduced functionals appearing in the bifurcation equation and discretized Oseen–Frank functionals for the case without boundary follows from the computation of [Reference Panayotaros26] for the case with boundary.
The main observation is that equation (3.49) for critical points of ![]() $\overline{\mathcal{F}}_2$, see (2.5), restricted to
$\overline{\mathcal{F}}_2$, see (2.5), restricted to ![]() $C^0 = \mathcal{C}^0(\overline{\mathcal{F}_4}, U_1,U_2)$ with
$C^0 = \mathcal{C}^0(\overline{\mathcal{F}_4}, U_1,U_2)$ with ![]() $U_1 = {\overline G}$,
$U_1 = {\overline G}$, ![]() $U_2 = \emptyset$ are critical points over configurations where the Q(m) have
$U_2 = \emptyset$ are critical points over configurations where the Q(m) have ![]() $i, j$th entry
$i, j$th entry
 \begin{equation}
{\overline Q}_{i,j}(m) = - 3 x_- \big( {\hat n}_i(m) {\hat n}_j(m) - \frac{1}{3} \delta_{i,j} \big), \quad {\hat n}(m) \in S^2,
\end{equation}
\begin{equation}
{\overline Q}_{i,j}(m) = - 3 x_- \big( {\hat n}_i(m) {\hat n}_j(m) - \frac{1}{3} \delta_{i,j} \big), \quad {\hat n}(m) \in S^2,
\end{equation} for all ![]() $m \in {\overline G}$. Denoting
$m \in {\overline G}$. Denoting ![]() $\overline{\mathcal{F}}_2$ restricted to C 0 by
$\overline{\mathcal{F}}_2$ restricted to C 0 by ![]() $\overline{\mathcal{F}}_{2,r}$ and using (2.5) we have
$\overline{\mathcal{F}}_{2,r}$ and using (2.5) we have
 \begin{equation}
\overline{\mathcal{F}}_{2,r}({\hat n}) = - \frac{3 x_- }{2} \sum_{k,m \in {\overline G}} c(k,m)
\big( 2 - 2 ( {\hat n}(k) \cdot {\hat n}(m) )^2 \big), \quad {\hat n}:{\overline G} \rightarrow S^2,
\end{equation}
\begin{equation}
\overline{\mathcal{F}}_{2,r}({\hat n}) = - \frac{3 x_- }{2} \sum_{k,m \in {\overline G}} c(k,m)
\big( 2 - 2 ( {\hat n}(k) \cdot {\hat n}(m) )^2 \big), \quad {\hat n}:{\overline G} \rightarrow S^2,
\end{equation} with · the standard inner product in ![]() $\mathbb{R}^3$. Thus
$\mathbb{R}^3$. Thus ![]() $\overline{\mathcal{F}}_{2,r}$ does not depend on the signs of the
$\overline{\mathcal{F}}_{2,r}$ does not depend on the signs of the ![]() ${\hat n}(m)$,
${\hat n}(m)$, ![]() $m \in {\overline G}$, and is well-defined as a functional on maps from
$m \in {\overline G}$, and is well-defined as a functional on maps from ![]() $\overline G$ to
$\overline G$ to ![]() $\mathbb{R}\mathrm{P}^2$.
$\mathbb{R}\mathrm{P}^2$.
In contrast, the Oseen–Frank functional ![]() $\mathcal{F}_{OF} $ of (2.3) can be discretized by
$\mathcal{F}_{OF} $ of (2.3) can be discretized by
 \begin{align}
\overline{\mathcal{F}}_{OF} ({\overline{\textbf{n}}}) & := \frac{1}{2} \sum_{k,m \in {\overline G}} c(k,m)
|{\overline{\textbf{n}}}(k) - {\overline{\textbf{n}}}(m)|^2 \nonumber\\& = \frac{1}{2} \sum_{k,m \in {\overline G}} c(n,m) \big(2 - 2 ({\overline{\textbf{n}}}(k) \cdot {\overline{\textbf{n}}}(m) ) \big),
\quad
{\overline{\textbf{n}}}:{\overline G}\rightarrow {S^2}.
\end{align}
\begin{align}
\overline{\mathcal{F}}_{OF} ({\overline{\textbf{n}}}) & := \frac{1}{2} \sum_{k,m \in {\overline G}} c(k,m)
|{\overline{\textbf{n}}}(k) - {\overline{\textbf{n}}}(m)|^2 \nonumber\\& = \frac{1}{2} \sum_{k,m \in {\overline G}} c(n,m) \big(2 - 2 ({\overline{\textbf{n}}}(k) \cdot {\overline{\textbf{n}}}(m) ) \big),
\quad
{\overline{\textbf{n}}}:{\overline G}\rightarrow {S^2}.
\end{align} This functional is not invariant under arbitrary changes of sign of ![]() $\overline {\bf{n}}$ at the different sites, see discussion in [Reference Panayotaros26] comparing (3.56), (3.57).
$\overline {\bf{n}}$ at the different sites, see discussion in [Reference Panayotaros26] comparing (3.56), (3.57).
The proof of Proposition 2.8 for the case without boundary is as in the case without boundary in [Reference Panayotaros26] and is omitted.
4. Numerical integration of the gradient flow
We present results obtained by numerical integration of the gradient of the Landau–de Gennes energy in some simple geometries. We are interested in the regime of small L > 0, with ![]() $U_- = \overline G$ (case without boundary) and
$U_- = \overline G$ (case without boundary) and ![]() $U_- = G$ (case with boundary). The first effect sought is convergence to equilibria that are near-uniaxial. We also compare the time scales of approach to a near-uniaxial state and convergence to an equilibrium. A second effect we examine is the possibility of multiple attracting equilibria in the periodic chain.
$U_- = G$ (case with boundary). The first effect sought is convergence to equilibria that are near-uniaxial. We also compare the time scales of approach to a near-uniaxial state and convergence to an equilibrium. A second effect we examine is the possibility of multiple attracting equilibria in the periodic chain.
4.1. Discrete geometries: boundary and initial conditions
For a set G of N sites, the Q-tensor Q(k) at site ![]() $k \in \{1, \ldots, N\}$ is described by its components
$k \in \{1, \ldots, N\}$ is described by its components ![]() $y_j(k)$,
$y_j(k)$, ![]() $j \in \{1, \ldots, 5\}$, defined in section 3. The gradient equations
$j \in \{1, \ldots, 5\}$, defined in section 3. The gradient equations
![]() $\mathcal{G}(Q) = \mathcal{F}_{LG}(Q)$ (case without boundary),
$\mathcal{G}(Q) = \mathcal{F}_{LG}(Q)$ (case without boundary), ![]() $ \mathcal{G}(Q) = \overline{\mathcal{F}}_{LG}(Q;Q_b)$ (case with boundary),
$ \mathcal{G}(Q) = \overline{\mathcal{F}}_{LG}(Q;Q_b)$ (case with boundary), ![]() $\nabla = \nabla_Q$, have the general form
$\nabla = \nabla_Q$, have the general form
 \begin{equation}
{\dot y}_j(k) = - L (\Delta y_j)(k) -
\frac{\partial f_B(Q(k))}{\partial y_j(k) }, \quad j \in \{1, \ldots, 5\},
\quad k \in \{1, \ldots, N\}.
\end{equation}
\begin{equation}
{\dot y}_j(k) = - L (\Delta y_j)(k) -
\frac{\partial f_B(Q(k))}{\partial y_j(k) }, \quad j \in \{1, \ldots, 5\},
\quad k \in \{1, \ldots, N\}.
\end{equation}The second term is the gradient of the onsite energy
 \begin{equation}
f_B(Q(k)) = - \frac{a^2}{2} \hbox{tr}(Q(k)^2) -
\frac{b^2}{3} \hbox{tr}(Q(k)^3) + \frac{c^2}{4} (\hbox{tr}(Q(k)^2))^2,
\end{equation}
\begin{equation}
f_B(Q(k)) = - \frac{a^2}{2} \hbox{tr}(Q(k)^2) -
\frac{b^2}{3} \hbox{tr}(Q(k)^3) + \frac{c^2}{4} (\hbox{tr}(Q(k)^2))^2,
\end{equation} \begin{align*}
\hbox{tr}(Q^3(k)) & =
\frac{3}{\sqrt{6}} y_2(k)^2 y_5(k) +
\frac{3}{\sqrt{2}} y_2(k) y_3(k) y_6(k)
+ \frac{3}{2\sqrt{2}} (y_3(k)^2 y_1(k) - y_6(k)^2 y_1(k) )\\
& \quad -
\frac{3}{2\sqrt{6}} (y_3(k)^2 y_5(k) + y_6(k)^2 y_5(k))
- \frac{1}{\sqrt{6}} y_5(k)^3 + \frac{3}{\sqrt{6}} y_1(k)^2 y(k)_5,
\end{align*}
\begin{align*}
\hbox{tr}(Q^3(k)) & =
\frac{3}{\sqrt{6}} y_2(k)^2 y_5(k) +
\frac{3}{\sqrt{2}} y_2(k) y_3(k) y_6(k)
+ \frac{3}{2\sqrt{2}} (y_3(k)^2 y_1(k) - y_6(k)^2 y_1(k) )\\
& \quad -
\frac{3}{2\sqrt{6}} (y_3(k)^2 y_5(k) + y_6(k)^2 y_5(k))
- \frac{1}{\sqrt{6}} y_5(k)^3 + \frac{3}{\sqrt{6}} y_1(k)^2 y(k)_5,
\end{align*} for all ![]() $k \in \{1, \ldots, N \}$, and has the same form at all interior sites.
$k \in \{1, \ldots, N \}$, and has the same form at all interior sites.
The first term ![]() $ (\Delta y_j)(k)$ at site k is the linear coupling to other sites and contains the information about the geometry of the set G.
$ (\Delta y_j)(k)$ at site k is the linear coupling to other sites and contains the information about the geometry of the set G.
Geometry A. Chain with two boundary points. In the case of a chain with nearest-neighbour interactions and boundary values yL, ![]() $y_R \in \mathbb{R}^5$, e.g. setting
$y_R \in \mathbb{R}^5$, e.g. setting ![]() $y(0) = y_L$,
$y(0) = y_L$, ![]() $y(N+1) = y_R$, we have
$y(N+1) = y_R$, we have
with  $y_L = \{y_{L,j} \}_{j=1}^5$,
$y_L = \{y_{L,j} \}_{j=1}^5$,  $y_R = \{y_{R,j} \}_{j=1}^5$, for all
$y_R = \{y_{R,j} \}_{j=1}^5$, for all ![]() $ j \in \{1, \ldots, 5\}$.
$ j \in \{1, \ldots, 5\}$.
Geometry B. Closed chain. In the case of a chain with nearest-neighbour interactions and periodic boundary conditions
for all ![]() $ j \in \{1, \ldots, 5\}$.
$ j \in \{1, \ldots, 5\}$.
We integrate numerically the equations for the two systems with initial conditions that are not uniaxial.
Geometry A. In the case of the open chain, we choose uniaxial boundary conditions QL, QR
 \begin{equation}
Q_j = - 3 x_- \left ({\hat n}(j) \otimes {\hat n}(j) - \frac{1}{3}I \right), \quad j = L, R,
\end{equation}
\begin{equation}
Q_j = - 3 x_- \left ({\hat n}(j) \otimes {\hat n}(j) - \frac{1}{3}I \right), \quad j = L, R,
\end{equation} ![]() $x_-$ the negative solution of
$x_-$ the negative solution of ![]() $-a^2 + 6c^2 x + b^2x^2 = 0$.
$-a^2 + 6c^2 x + b^2x^2 = 0$.
We use the values ![]() $ b^2 = \sqrt{6}$,
$ b^2 = \sqrt{6}$,  $a^2 = \frac{1}{2}$,
$a^2 = \frac{1}{2}$,  $c^2 = \frac{2}{3}$, then
$c^2 = \frac{2}{3}$, then  $x_- = \frac{1}{\sqrt{6}}$.
$x_- = \frac{1}{\sqrt{6}}$.
The unit vectors ![]() ${\hat n}(L)$,
${\hat n}(L)$, ![]() ${\hat n}(R)$ are at an angle. The corresponding Q-tensors are obtained from the polar representation (3.24) of the vectors
${\hat n}(R)$ are at an angle. The corresponding Q-tensors are obtained from the polar representation (3.24) of the vectors ![]() ${\hat n}(L)$,
${\hat n}(L)$, ![]() ${\hat n}(R)$, via (3.18).
${\hat n}(R)$, via (3.18).
The corresponding vectors yL, yR are obtained via (3.11)-(3.14), i.e. the respective QL, QR are as in (3.10) The initial condition at the interior points is chosen to be
 \begin{equation}
y(k) = \frac{k}{N+1} (y_R - y_L), \quad k = 1, \ldots, N.
\end{equation}
\begin{equation}
y(k) = \frac{k}{N+1} (y_R - y_L), \quad k = 1, \ldots, N.
\end{equation}The interior values interpolate linearly between the boundary values, and are not generally uniaxial. In cases of boundary conditions expected to lead to more than one attracting equilibria, we use small perturbations of (4.9) that may lead to different asymptotic states.
Geometry B. In the closed chain we use uniaxial initial conditions of the form
 \begin{equation*} Q(k) = s(k) \left( {\hat n}(k) \otimes {\hat n}(k) - \frac{1}{3}I \right), \quad k \in \{1, \ldots, N\}, \end{equation*}
\begin{equation*} Q(k) = s(k) \left( {\hat n}(k) \otimes {\hat n}(k) - \frac{1}{3}I \right), \quad k \in \{1, \ldots, N\}, \end{equation*} with different choices of the functions s, ![]() $\hat n$. The choice
$\hat n$. The choice ![]() $s = -3 x_-$ at all sites,
$s = -3 x_-$ at all sites, ![]() $x_-$ the negative solution of
$x_-$ the negative solution of ![]() $-a^2 + 6c^2 x + b^2x^2 = 0$, corresponds to an initial condition of uniaxial tensors on the manifold of minima of fB.
$-a^2 + 6c^2 x + b^2x^2 = 0$, corresponds to an initial condition of uniaxial tensors on the manifold of minima of fB.
We use the values ![]() $ b^2 = \sqrt{6}$,
$ b^2 = \sqrt{6}$,  $a^2 = \frac{1}{2}$,
$a^2 = \frac{1}{2}$,  $c^2 = \frac{2}{3}$, then
$c^2 = \frac{2}{3}$, then  $x_- = \frac{1}{\sqrt{6}}$.
$x_- = \frac{1}{\sqrt{6}}$.
Also, we consider
for σ smooth 1−periodic functions that oscillate around the value ![]() $-3 x_-$, and
$-3 x_-$, and
where ![]() ${\hat \nu}: [0,1] \rightarrow S^2$ are smooth parameterized curves.
${\hat \nu}: [0,1] \rightarrow S^2$ are smooth parameterized curves.
We are interested in two classes of curves ![]() $\hat \nu$, corresponding to initial conditions expected to converge to states that are discrete analogues of the two homotopy classes of
$\hat \nu$, corresponding to initial conditions expected to converge to states that are discrete analogues of the two homotopy classes of ![]() $\mathbb{R}\mathrm{P}^2$.
$\mathbb{R}\mathrm{P}^2$.
First, we consider closed curves that are continuous deformations of curves whose image is a subset of an open hemisphere, see e.g. Figure 1(a). The corresponding initial conditions are expected to converge to discrete analogues of homotopicaly trivial curves on ![]() $\mathbb{R}\mathrm{P}^2$, i.e. curves that can be continuously deformed to point.
$\mathbb{R}\mathrm{P}^2$, i.e. curves that can be continuously deformed to point.
Also, we consider curves that are continuous deformations of curves that join any two antipodal points of S 2, see e.g. Figure 1(b). The corresponding initial conditions are expected to converge to discrete analogues of homotopicaly nontrivial curves on ![]() $\mathbb{R}\mathrm{P}^2$, i.e. curves that cannot be continuously deformed to a point.
$\mathbb{R}\mathrm{P}^2$, i.e. curves that cannot be continuously deformed to a point.

Figure 1. Examples of closed curves of the two homotopy classes of ![]() $\mathbb{R}\mathrm{P}^2$, visualization using the 2−sphere. When antipodal points are identified, (a) depicts a homotopicaly trivial curve on the projective plane, while (b) depicts a homotopicaly non-trivial curve on the projective plane.
$\mathbb{R}\mathrm{P}^2$, visualization using the 2−sphere. When antipodal points are identified, (a) depicts a homotopicaly trivial curve on the projective plane, while (b) depicts a homotopicaly non-trivial curve on the projective plane.
An example of an initial condition expected to converge to a configuration that is a discrete analogue of a homotopicaly trivial curve in ![]() $\mathbb{R}\mathrm{P}^2$ is
$\mathbb{R}\mathrm{P}^2$ is
 \begin{equation}
\phi(k) = \frac{\pi}{2} + \frac{1}{5} \cos \frac{2 (k-1) \pi}{N}, \quad
\theta(k) = \frac{\pi}{2} + \frac{1}{5} \sin \frac{2 (k-1) \pi}{N}, \quad
s(k) = \frac{3}{\sqrt{6}};
\end{equation}
\begin{equation}
\phi(k) = \frac{\pi}{2} + \frac{1}{5} \cos \frac{2 (k-1) \pi}{N}, \quad
\theta(k) = \frac{\pi}{2} + \frac{1}{5} \sin \frac{2 (k-1) \pi}{N}, \quad
s(k) = \frac{3}{\sqrt{6}};
\end{equation} ![]() $ k =1, \ldots, N$. The corresponding Q(k), and y(k) are obtained via (3.18), (3.11)-(3.14), (3.10). Figure 1(a) depicts the vectors
$ k =1, \ldots, N$. The corresponding Q(k), and y(k) are obtained via (3.18), (3.11)-(3.14), (3.10). Figure 1(a) depicts the vectors ![]() $\hat n$ of the curve defined by (4.10). This is an homotopicaly trivial curve on the projective plane since it is continuously contractible to a point.
$\hat n$ of the curve defined by (4.10). This is an homotopicaly trivial curve on the projective plane since it is continuously contractible to a point.
Examples of initial conditions that are expected to converge to discrete analogues of homotopicaly nontrivial curves in ![]() $\mathbb{R}\mathrm{P}^2$ are
$\mathbb{R}\mathrm{P}^2$ are
 \begin{equation}
\phi(k) = \frac{(k - 1)\pi}{N}, \quad \theta(k) = \frac{\pi}{2}, \quad
s(k) = \frac{3}{\sqrt{6}};
\end{equation}
\begin{equation}
\phi(k) = \frac{(k - 1)\pi}{N}, \quad \theta(k) = \frac{\pi}{2}, \quad
s(k) = \frac{3}{\sqrt{6}};
\end{equation} \begin{equation}
\phi(k) = \frac{(k - 1) \pi}{N}, \quad
\theta(k) = \frac{\pi}{2} + \frac{1}{5}\sin \frac{2 \pi(k-1) }{N}, \quad
s(k) = - \frac{3}{\sqrt{6}}+ \frac{1}{5} \sin \frac{2 \pi (k-1)}{N};
\end{equation}
\begin{equation}
\phi(k) = \frac{(k - 1) \pi}{N}, \quad
\theta(k) = \frac{\pi}{2} + \frac{1}{5}\sin \frac{2 \pi(k-1) }{N}, \quad
s(k) = - \frac{3}{\sqrt{6}}+ \frac{1}{5} \sin \frac{2 \pi (k-1)}{N};
\end{equation} ![]() $ k =1, \ldots, N$. The corresponding Q(k), and y(k) are obtained via (3.18), (3.11)-(3.14), (3.10). Figure 1(b) depicts the vectors
$ k =1, \ldots, N$. The corresponding Q(k), and y(k) are obtained via (3.18), (3.11)-(3.14), (3.10). Figure 1(b) depicts the vectors ![]() $\hat n$ of the curve defined in (4.11). The first discretizes a curve on the 2−sphere that connects antipodal points and cannot be continuously contracted to a point. In (4.12) we add a deformation, and vary the radius s.
$\hat n$ of the curve defined in (4.11). The first discretizes a curve on the 2−sphere that connects antipodal points and cannot be continuously contracted to a point. In (4.12) we add a deformation, and vary the radius s.
To verify the approach to near uniaxial Q-tensors at all sites k of ![]() $\overline G$ or G, we obtain Q(k) at each time t from the numerically computed y(k) at time t using the inverse of the linear transformation defined by (3.11)-(3.14), and (3.10). We further compute the eigenvalues and eigenvectors of Q(k) used in the polar representation (3.2) of Q(k), and the quantities
$\overline G$ or G, we obtain Q(k) at each time t from the numerically computed y(k) at time t using the inverse of the linear transformation defined by (3.11)-(3.14), and (3.10). We further compute the eigenvalues and eigenvectors of Q(k) used in the polar representation (3.2) of Q(k), and the quantities
where ![]() $\lambda_1(k) \geq \lambda_2(k) \geq \lambda_3(k) $ are the eigenvalues of Q(k) at each time. The normalized eigenvector that corresponds to
$\lambda_1(k) \geq \lambda_2(k) \geq \lambda_3(k) $ are the eigenvalues of Q(k) at each time. The normalized eigenvector that corresponds to ![]() $\lambda_1(k)$ is denoted by
$\lambda_1(k)$ is denoted by ![]() $\bf n$, and the notation
$\bf n$, and the notation
for its components. The dependence on time is not explicit in this notation. The eigenvalues should satisfy strict inequalities in the vicinity of ![]() $\Sigma^3_-$.
$\Sigma^3_-$.
4.2. Numerical observations: summary
The main observations after several integrations of the gradient flow (4.1) are the following:
(i) All initial conditions for geometries A, and B lead to trajectories for which the Q-tensor becomes near-uniaxial after a few time units, with s, r converging to values in the vicinity of ![]() $s = -3 x_-$, r = 0. The velocity of approach to near-uniaxial states is not seen to depend significantly on the number of sites N.
$s = -3 x_-$, r = 0. The velocity of approach to near-uniaxial states is not seen to depend significantly on the number of sites N.
(ii) All initial conditions for geometries A, and B lead to an equilibrium configuration. This occurs at a time scale that is much longer than the time scale of approach to near-uniaxial Q-tensors. The time to approach the equilibrium depends on the number of sites N and the initial condition.
(iii) In the case of the closed chain, geometry B, we see two attracting asymptotic states, the constant state, and a state that connects two antipodal points that lie on a plane. The constant state is homotopicaly trivial and is the global minimum of the energy. The second state is a discretization of a homotopicaly non-trivial curve, similar to Figure 1(b). Multiple (at least two) stable equilibria are also observed for geometry A with some special boundary conditions. These equilibria are discrete analogues of non-homotopic curves on the projective plane and may occur under more general boundary conditions.
In what follows we describe in more detail some of numerical experiments with geometries A and B. The results below are typical a larger set of experiments performed.
4.3. Geometry A: open chain
We consider the evolution of the open chain system of (4.1) with boundary conditions yL, yR as in (4.8), and ![]() $\hat n$ as in (3.24) with
$\hat n$ as in (3.24) with ![]() $\theta = \pi/2$, ϕ = 0, and
$\theta = \pi/2$, ϕ = 0, and ![]() $\theta = \pi/2 - 0.5$, ϕ = 0.5 respectively. Also
$\theta = \pi/2 - 0.5$, ϕ = 0.5 respectively. Also ![]() $x_-= - 1/\sqrt{6}$. The initial condition is obtained from (4.9).
$x_-= - 1/\sqrt{6}$. The initial condition is obtained from (4.9).
The rapid approach to a near uniaxial Q-tensor is seen over a range of coupling constants ![]() $0.01 \leq L \leq 0.2$. Table 1 shows results using N = 65, and L = 0.01. The value of rmax at t = 0 indicates the departure from uniaxiality at the interior sites. The time scale of approach to near-axisymmetric tensors indicated of a few units is typical of what we saw in all numerical experiments with geometries A and B and
$0.01 \leq L \leq 0.2$. Table 1 shows results using N = 65, and L = 0.01. The value of rmax at t = 0 indicates the departure from uniaxiality at the interior sites. The time scale of approach to near-axisymmetric tensors indicated of a few units is typical of what we saw in all numerical experiments with geometries A and B and ![]() $30 \leq N \leq 85$. The parameter s similarly approaches the value s ≈ 1.22 at all sites, as expected from
$30 \leq N \leq 85$. The parameter s similarly approaches the value s ≈ 1.22 at all sites, as expected from  $s=-3 x_-=\frac{3}{\sqrt{6}} \approx 1.2247$ for the radius of the critical manifold of fB.
$s=-3 x_-=\frac{3}{\sqrt{6}} \approx 1.2247$ for the radius of the critical manifold of fB.
Table 1. rmax, ![]() $s_{\max}$ at time t for an open chain of N = 65 sites, L = 0.001.
$s_{\max}$ at time t for an open chain of N = 65 sites, L = 0.001. ![]() $r_{\max}$,
$r_{\max}$, ![]() $s_{\max}$ are numbers that satisfy
$s_{\max}$ are numbers that satisfy ![]() $ |r(k)| \leq r_{max}$,
$ |r(k)| \leq r_{max}$, ![]() $s(k)\geq s_{max}$ for all
$s(k)\geq s_{max}$ for all ![]() $k \in \{1, \ldots, N \}$ at time t, see (4.13). Geometry A, boundary conditions (4.8),
$k \in \{1, \ldots, N \}$ at time t, see (4.13). Geometry A, boundary conditions (4.8), ![]() ${\hat n}(L)$,
${\hat n}(L)$, ![]() ${\hat n}(R)$ as in (3.24) with
${\hat n}(R)$ as in (3.24) with ![]() $\theta = \pi/2$, ϕ = 0, and
$\theta = \pi/2$, ϕ = 0, and ![]() $\theta = \pi/2 - 0.5$, ϕ = 0.5 respectively; initial condition as in (4.9). Parameter values
$\theta = \pi/2 - 0.5$, ϕ = 0.5 respectively; initial condition as in (4.9). Parameter values ![]() $ b^2 = \sqrt{6}$,
$ b^2 = \sqrt{6}$,  $a^2 = \frac{1}{2}$,
$a^2 = \frac{1}{2}$,  $c^2 = \frac{2}{3}$,
$c^2 = \frac{2}{3}$,  $x_- = - \frac{1}{\sqrt{6}}$
$x_- = - \frac{1}{\sqrt{6}}$

In Figure 2, we consider the same initial and boundary conditions with L = 0.01 and three values of N = 30, 65, 80. The initial conditions are obtained from the boundary values and (4.9). The plots show that the parameter s reaches the same approximate asymptotic value s ≈ 1.22 indicating that the Q-tensor is uniaxial. The dependence of the asymptotic values of s on the site is not significant. The time taken to reach the near-uniaxial state is t ≈ 5 for the three chains considered.

Figure 2. s v.s. t for open chains with N = 30, 65, 80, L = 0.01, see (4.13) for definition of s. Geometry A, boundary conditions (4.8), ![]() ${\hat n}(L)$,
${\hat n}(L)$, ![]() ${\hat n}(R)$ as in (3.24) with
${\hat n}(R)$ as in (3.24) with ![]() $\theta = \pi/2$, ϕ = 0, and
$\theta = \pi/2$, ϕ = 0, and ![]() $\theta = \pi/2 - 0.5$, ϕ = 0.5 respectively; initial condition as in (4.9). Parameter values
$\theta = \pi/2 - 0.5$, ϕ = 0.5 respectively; initial condition as in (4.9). Parameter values ![]() $ b^2 = \sqrt{6}$,
$ b^2 = \sqrt{6}$,  $a^2 = \frac{1}{2}$,
$a^2 = \frac{1}{2}$,  $c^2 = \frac{2}{3}$,
$c^2 = \frac{2}{3}$,  $x_- = - \frac{1}{\sqrt{6}}$. (a) Evolution of s, site k = 17, N = 30. (b) Evolution of s, site k = 28, N = 30. (c) Evolution of s, site k = 36, N = 65. (d) Evolution of s, site k = 36, N = 65 open chain,site 58, n=65. (e) Evolution of s, site k = 36, N = 80. (f) Evolution of s, site k = 68, N = 80.
$x_- = - \frac{1}{\sqrt{6}}$. (a) Evolution of s, site k = 17, N = 30. (b) Evolution of s, site k = 28, N = 30. (c) Evolution of s, site k = 36, N = 65. (d) Evolution of s, site k = 36, N = 65 open chain,site 58, n=65. (e) Evolution of s, site k = 36, N = 80. (f) Evolution of s, site k = 68, N = 80.
The approach to equilibrium in these experiments is indicated in Figure 3 where we show the evolution of the first component ![]() $\hat n_1(k)$ of the normalized eigenvector of the largest eigenvalue of Q(k) at some representative sites
$\hat n_1(k)$ of the normalized eigenvector of the largest eigenvalue of Q(k) at some representative sites ![]() $ k \in \{1, \ldots, N\}$. In all the plots we see an initial rapid increase or decrease in the value of n 1 followed by a slow approach to the asymptotic value. For the case of N = 30, we show the behaviour at sites k = 17 and k = 28. The value of n 1 differs slightly between the two: at site 17, the asymptotic values is
$ k \in \{1, \ldots, N\}$. In all the plots we see an initial rapid increase or decrease in the value of n 1 followed by a slow approach to the asymptotic value. For the case of N = 30, we show the behaviour at sites k = 17 and k = 28. The value of n 1 differs slightly between the two: at site 17, the asymptotic values is ![]() $ n_1 \approx 0.9289$, while at site 28, the asymptotic
$ n_1 \approx 0.9289$, while at site 28, the asymptotic ![]() $ n_1 \approx 0.810 $. The different values reflect the spatial pattern of the equilibrium state, and its dependence on the boundary condition. Similar time evolution patterns are observed for systems with N = 65 and N = 80 sites, see Figure 3. Figure 4 shows the spatial asymptotic spatial configurations for the N = 30, 65, 80 chains.
$ n_1 \approx 0.810 $. The different values reflect the spatial pattern of the equilibrium state, and its dependence on the boundary condition. Similar time evolution patterns are observed for systems with N = 65 and N = 80 sites, see Figure 3. Figure 4 shows the spatial asymptotic spatial configurations for the N = 30, 65, 80 chains.

Figure 3. n 1 v.s. t for open chains of N = 30, 65, 80 sites, L = 0.01, see (4.14) for definition of n 1. Geometry A, boundary and initial conditions, and parameter values as in Figure 2. (a) Evolution of n 1, site k = 17, N = 30. (b) Evolution of n 1, site k = 28, N = 30. (c) Evolution of n 1, site k = 36, N = 65 site 36, N = 65. (d) Evolution of n 1, site k = 58, N = 65. (e) Evolution of n 1, site k = 36, N = 80. (f) Evolution of n 1, site k = 68, N = 80.
Figure 5 shows the evolution from initial condition
 \begin{equation}
y(k) =- \frac{k}{N+1} (y_R - y_L), \quad k = 1, \ldots, N.
\end{equation}
\begin{equation}
y(k) =- \frac{k}{N+1} (y_R - y_L), \quad k = 1, \ldots, N.
\end{equation}
Figure 5. n 1 v.s. t for open chains of N = 30, 65, 80 sites, L = 0.01, see definition of n 1 in (4.13). Geometry A, boundary conditions and parameter values as in Figures 2, 3. Initial conditions are obtained from (4.15), different from those of Figures 2, 3. (a) Evolution of n 1, site k = 17, N = 30. (b) Evolution of n 1, site k = 28, N = 30. (c) Evolution of n 1, site k = 36, N = 65. (d) Evolution of n 1, site k = 58, N = 65. (e) Evolution of n 1, site k = 36, N = 80. (f) Evolution of n 1, site k = 68, N = 80.
This configuration is expected to be further from the equilibrium, and the time to the reach the asymptotic values of the ![]() $\hat n (k)$ is longer than the time of Figure 3. The time scale is however comparable.
$\hat n (k)$ is longer than the time of Figure 3. The time scale is however comparable.
Figures 3, 5 indicate that the approach to equilibrium is achieved at a much slower rate, e.g. a time scale of ![]() $ t \approx 10^5$. Moreover the time to equilibrium increases with the number of sites.
$ t \approx 10^5$. Moreover the time to equilibrium increases with the number of sites.
We also see examples of boundary conditions that lead to at least two stable equilibria. An example is shown in Figure 6 where we see two different equilibrium states for uniaxial boundary conditions of the form (3.19) with ![]() $\phi_L = 0$,
$\phi_L = 0$, ![]() $\theta_L = \pi/2$;
$\theta_L = \pi/2$; ![]() $\phi_R = \pi/2$,
$\phi_R = \pi/2$, ![]() $\theta_R = \pi/2$, i.e. the directors at the two ends are perpendicular. We may expect the existence of equilibria where the interior directions interpolate between the two perpendicular directions at the two edges by rotating in opposite directions. To see these two equilibria we use initial conditions are two different small perturbations of (4.9).
$\theta_R = \pi/2$, i.e. the directors at the two ends are perpendicular. We may expect the existence of equilibria where the interior directions interpolate between the two perpendicular directions at the two edges by rotating in opposite directions. To see these two equilibria we use initial conditions are two different small perturbations of (4.9).

Figure 6. Evidence for bistability for a uniaxial boundary condition where the directions at the two boundary points are perpendicular, open chain geometry A, N = 65 sites. Boundary conditions for (a), (b) given by Q-tensor of (3.19), with ![]() $\textstyle\phi_L=\;\mathrm\pi/2$,
$\textstyle\phi_L=\;\mathrm\pi/2$, ![]() $\textstyle\theta_L=\mathrm\pi/2$;
$\textstyle\theta_L=\mathrm\pi/2$; ![]() $\phi_{R\;}=0$,
$\phi_{R\;}=0$, ![]() $\theta_R=\mathrm\pi/2$ for left and right boundaries respectively. Initial conditions for (a), (b) two are different perturbations of (4.9) at the leftmost interior site k = 1. Figures (a), (b) show the corresponding vector n at t = 100000. In both cases lies on on the same plane at all sites and we show values (in radians) of direction angles at sites k
$\theta_R=\mathrm\pi/2$ for left and right boundaries respectively. Initial conditions for (a), (b) two are different perturbations of (4.9) at the leftmost interior site k = 1. Figures (a), (b) show the corresponding vector n at t = 100000. In both cases lies on on the same plane at all sites and we show values (in radians) of direction angles at sites k ![]() $\textstyle=\;1,\;32,\;65$. The angle difference at k = 32 is 1.47, close to
$\textstyle=\;1,\;32,\;65$. The angle difference at k = 32 is 1.47, close to ![]() $\pi/2\approx1.57$, thus the configurations of (a), (b) are different, and have opposite helicity.
$\pi/2\approx1.57$, thus the configurations of (a), (b) are different, and have opposite helicity.
In the asymptotic state shown in Figure 6(a) we used initial condition (4.9), perturbed by adding 0.1 to all ![]() $y_i(k)$,
$y_i(k)$, ![]() $i = 1, \ldots, 6$, at site k = 1. We show the vector
$i = 1, \ldots, 6$, at site k = 1. We show the vector ![]() $\bf n$ at the interior sites
$\bf n$ at the interior sites ![]() $k = 1, \ldots N$, N = 65, at time
$k = 1, \ldots N$, N = 65, at time ![]() $t = 100,000$. The vector
$t = 100,000$. The vector ![]() $\bf n$ at different sites is on the same plane, and we indicate the angles ϕ at sites
$\bf n$ at different sites is on the same plane, and we indicate the angles ϕ at sites ![]() $1,\ 32$, and 65 (0.02, 0.72 and 1.55 respectively in radians). (The angle θ is approximately
$1,\ 32$, and 65 (0.02, 0.72 and 1.55 respectively in radians). (The angle θ is approximately ![]() $\pi/2$ in all the sites.) In the asymptotic state shown in Figure 6(b), we used initial condition (4.9), perturbed by adding −0.07 to all
$\pi/2$ in all the sites.) In the asymptotic state shown in Figure 6(b), we used initial condition (4.9), perturbed by adding −0.07 to all ![]() $y_i(k=65)$,
$y_i(k=65)$, ![]() $i = 1, \ldots, 6$ at site k = 65. We show the vector
$i = 1, \ldots, 6$ at site k = 65. We show the vector ![]() $\bf n$ at the interior sites
$\bf n$ at the interior sites ![]() $k = 1, \ldots N$, N = 65, at time
$k = 1, \ldots N$, N = 65, at time ![]() $t = 100,000$. Again, the vector
$t = 100,000$. Again, the vector ![]() $\bf n$ at different sites is on the same plane, and we indicate the angles ϕ angles sites
$\bf n$ at different sites is on the same plane, and we indicate the angles ϕ angles sites ![]() $1,\ 32$, and 65 (1.55, 0.86, 0.02, respectively, in radians). We see that the two configurations are different, e.g. the angle difference at k = 32 is 1.47, close to
$1,\ 32$, and 65 (1.55, 0.86, 0.02, respectively, in radians). We see that the two configurations are different, e.g. the angle difference at k = 32 is 1.47, close to ![]() $\pi/2 \approx 1.57$. Each configuration also exhibits different helicity as the direction rotates in opposite directions as we move from the left to the right end of the chain. which are
$\pi/2 \approx 1.57$. Each configuration also exhibits different helicity as the direction rotates in opposite directions as we move from the left to the right end of the chain. which are
The above solutions are discrete analogues of curves γ 1, γ 2 on the unit sphere S 2 that connect each of the unit vectors m, −m to a third unit vector p, ![]() $\textbf{p} \perp \textbf{m}$ and also belong to the plane of
$\textbf{p} \perp \textbf{m}$ and also belong to the plane of ![]() $\bf m$,
$\bf m$, ![]() $\bf p$. The two curves define curves
$\bf p$. The two curves define curves ![]() ${\tilde \gamma}_1$,
${\tilde \gamma}_1$, ![]() ${\tilde \gamma}_2$ on
${\tilde \gamma}_2$ on ![]() $\mathbb{R}\mathrm{P}^2$ that are not homotopic since a homotopy of
$\mathbb{R}\mathrm{P}^2$ that are not homotopic since a homotopy of ![]() ${\tilde \gamma}_1$ to
${\tilde \gamma}_1$ to ![]() ${\tilde \gamma}_2$ would produce a homotopy of the homotopicaly nontrivial closed curve
${\tilde \gamma}_2$ would produce a homotopy of the homotopicaly nontrivial closed curve ![]() $\tilde \gamma$ obtained from concatenating γ 1 and γ 2 and projecting to
$\tilde \gamma$ obtained from concatenating γ 1 and γ 2 and projecting to ![]() $\mathbb{R}\mathrm{P}^2$ to the homotopicaly trivial curve from
$\mathbb{R}\mathrm{P}^2$ to the homotopicaly trivial curve from ![]() $\{\textbf{m}, -\textbf{m} \}$ to
$\{\textbf{m}, -\textbf{m} \}$ to ![]() $\{\textbf{p}, -\textbf{p} \}$ and then back to
$\{\textbf{p}, -\textbf{p} \}$ and then back to ![]() $\{\textbf{m}, -\textbf{m} \}$. Thus the two solutions seen are discretizations of two non-homotopic curves on
$\{\textbf{m}, -\textbf{m} \}$. Thus the two solutions seen are discretizations of two non-homotopic curves on ![]() $\mathbb{R}\mathrm{P}^2$.
$\mathbb{R}\mathrm{P}^2$.
Analogous curves γ 1, γ 2 on S 2 can be obtained by connecting unit vectors ![]() $\bf m$ and −m to a third unit vector
$\bf m$ and −m to a third unit vector ![]() $\bf p$ that is not perpendicular to
$\bf p$ that is not perpendicular to ![]() $\bf m$. The two curves are again chosen to lie to the plane of
$\bf m$. The two curves are again chosen to lie to the plane of ![]() $\bf m$,
$\bf m$, ![]() $\bf p$, and similarly define curves
$\bf p$, and similarly define curves ![]() ${\tilde \gamma}_1$,
${\tilde \gamma}_1$, ![]() ${\tilde \gamma}_2$ on
${\tilde \gamma}_2$ on ![]() $\mathbb{R}\mathrm{P}^2$ that are not homotopic. The curves γ 1, γ 2 would now have different lengths. Their discretized analogues would interpolate between different endpoint angles, and are expected to have different energies and basins of attraction.
$\mathbb{R}\mathrm{P}^2$ that are not homotopic. The curves γ 1, γ 2 would now have different lengths. Their discretized analogues would interpolate between different endpoint angles, and are expected to have different energies and basins of attraction.
4.4. Geometry B: homotopicaly trivial and nontrivial equilibria
In periodic chains we observe that the gradient system has at least two attracting equilibria, corresponding to the two homotopy classes of the projective plane. In all integrations we see a fast approach to near-uniaxial Q-tensors, and a slower approach to the equilibria. The fast and slow time scales are comparable to those seen in the open chain examples.
An example of convergence to the homotopicaly trivial constant state is shown in Figure 7, where we see the evolution of ![]() $\hat n_2(k)$ for some sites k. Components
$\hat n_2(k)$ for some sites k. Components ![]() $n_1(k)$,
$n_1(k)$, ![]() $n_3(k)$ tend to 0 in all the sites k. We use L = 0.01, N = 30, 65, 80, and the initial condition (4.10). Figure 7 shows the evolution of n 2. The asymptotic state is constant. The initial and asymptotic states are shown in Figure 8. Figure 7 shows that the time of convergence increases with the size of the chain N. The convergence to the equilibrium is comparable but faster than the convergence to the equilibrium of Figure 3 for the open chain.
$n_3(k)$ tend to 0 in all the sites k. We use L = 0.01, N = 30, 65, 80, and the initial condition (4.10). Figure 7 shows the evolution of n 2. The asymptotic state is constant. The initial and asymptotic states are shown in Figure 8. Figure 7 shows that the time of convergence increases with the size of the chain N. The convergence to the equilibrium is comparable but faster than the convergence to the equilibrium of Figure 3 for the open chain.

Figure 7. n 2 v.s. t for periodic chains with N = 30, 65, 80 sites, L = 0.01, definition of n 2 in (4.14). Geometry B, initial condition of (4.10) discretizes homotopicaly trivial curve on projective plane. Parameter values ![]() $ b^2 = \sqrt{6}$,
$ b^2 = \sqrt{6}$,  $a^2 = \frac{1}{2}$,
$a^2 = \frac{1}{2}$,  $c^2 = \frac{2}{3}$,
$c^2 = \frac{2}{3}$,  $x_- = - \frac{1}{\sqrt{6}}$. (a) Evolution of n 2, k = 17, N = 30. (b) Evolution of n 2, site k = 28, N = 30. (c) Evolution of n 2, site K = 36, N = 65. (d) Evolution of n 2, site k = 58, N = 65. (e) Evolution of n 2, site k = 36, N = 80. (f) Evolution of n 2, site k = 68, N = 80
$x_- = - \frac{1}{\sqrt{6}}$. (a) Evolution of n 2, k = 17, N = 30. (b) Evolution of n 2, site k = 28, N = 30. (c) Evolution of n 2, site K = 36, N = 65. (d) Evolution of n 2, site k = 58, N = 65. (e) Evolution of n 2, site k = 36, N = 80. (f) Evolution of n 2, site k = 68, N = 80

Figure 8. Normalized vectors ![]() $\textbf{n}(k)$,
$\textbf{n}(k)$, ![]() $k = 1, \ldots N$, N = 65, at two different times for homotopicaly trivial configuration, experiment of Figure 7, N = 65, see (4.14). (a) Initial configuration of vectors
$k = 1, \ldots N$, N = 65, at two different times for homotopicaly trivial configuration, experiment of Figure 7, N = 65, see (4.14). (a) Initial configuration of vectors ![]() $\textbf{n}(k)$, as in (4.10). (b) Numerical asymptotic configuration of vectors
$\textbf{n}(k)$, as in (4.10). (b) Numerical asymptotic configuration of vectors ![]() $\textbf{n}(k)$ (t = 200000). The vectors are visualized on the 2−sphere, (a), (b) use different perspectives.
$\textbf{n}(k)$ (t = 200000). The vectors are visualized on the 2−sphere, (a), (b) use different perspectives.
The homotopicaly trivial equilibrium is the state where the Q-tensor is uniaxial and takes the same value at all sites. This state corresponds to the global minimum of the energy since it minimizes both parts of the Landau–de Gennes energy.
We have also seen convergence to a discrete analogue of a homotopically non-trivial state. In Figures 9, 10 we show results from integration with the initial condition of (4.12), using L = 0.01 and chain sizes N = 30, 65, 80. The convergence to near-uniaxial tensors occurs rapidly as in the previous cases and is not shown. Figure 9 shows the slower convergence of n 1 at two sites for ![]() $N=30, 65, 80$. Figure 10 shows the evolution of the vectors
$N=30, 65, 80$. Figure 10 shows the evolution of the vectors ![]() $\hat n$ after their rapid approach to projective plane defined by
$\hat n$ after their rapid approach to projective plane defined by ![]() $s=-3x_-$, r = 0. The time scale is comparable to that of the previous examples. The main observation is that the vectors
$s=-3x_-$, r = 0. The time scale is comparable to that of the previous examples. The main observation is that the vectors ![]() $\hat n(k)$ belong to a plane, for all
$\hat n(k)$ belong to a plane, for all ![]() $k \in \{1, \ldots, N\}$. This state is stable. The system may have additional equilibria corresponding to nontrivial homotopy classes of the circle. The existence and stability of additional equilibria will be examined elsewhere.
$k \in \{1, \ldots, N\}$. This state is stable. The system may have additional equilibria corresponding to nontrivial homotopy classes of the circle. The existence and stability of additional equilibria will be examined elsewhere.

Figure 9. n 1 v.s. t for periodic chains with N = 30, 65, 80 sites, L = 0.01. Initial condition of (4.12) discretizes homotopicaly non-trivial curve on projective plane. Parameter values ![]() $ b^2 = \sqrt{6}$,
$ b^2 = \sqrt{6}$,  $a^2 = \frac{1}{2}$,
$a^2 = \frac{1}{2}$,  $c^2 = \frac{2}{3}$,
$c^2 = \frac{2}{3}$,  $x_- = - \frac{1}{\sqrt{6}}$. (a) Evolution of n 1, site k = 17, N = 30. (b) Evolution of n 1, site k = 28, N = 30. (c) Evolution of n 1, site k = 36, N = 65. (d) Evolution of n 1, site k = 58, N = 65. (e) Evolution of n 1, site k = 36, N = 80. (f) Evolution of n 1, site k = 68, N = 80.
$x_- = - \frac{1}{\sqrt{6}}$. (a) Evolution of n 1, site k = 17, N = 30. (b) Evolution of n 1, site k = 28, N = 30. (c) Evolution of n 1, site k = 36, N = 65. (d) Evolution of n 1, site k = 58, N = 65. (e) Evolution of n 1, site k = 36, N = 80. (f) Evolution of n 1, site k = 68, N = 80.

Figure 10. Normalized vectors ![]() $\textbf{n}(k)$,
$\textbf{n}(k)$, ![]() $k = 1, \ldots N$, N = 65, at two different times for homotopicaly non-trivial configuration, experiment of Figure 9, N = 65, initial configuration as in (4.12). (a) Configuration of vectors
$k = 1, \ldots N$, N = 65, at two different times for homotopicaly non-trivial configuration, experiment of Figure 9, N = 65, initial configuration as in (4.12). (a) Configuration of vectors ![]() $\textbf{n}(k)$ at t = 1000. (b) Numerical asymptotic configuration of vectors
$\textbf{n}(k)$ at t = 1000. (b) Numerical asymptotic configuration of vectors ![]() $\textbf{n}(k)$ (t = 200000).
$\textbf{n}(k)$ (t = 200000).
5. Discussion
We have considered a discrete version of the Landau–de Gennes theory in graphs and lattices without boundary in the regime of small intersite coupling L. The main theoretical results are necessary and sufficient conditions for continuation of equilibria of the decoupled system and the presence equivariance of the reduced or bifurcation equations. The proof uses the strategy of [Reference Panayotaros26] that also implies the existence of a normally hyperbolic invariant manifold of the gradient flow of the Landau–de Gennes that is parametrized by the uniaxial Q-tensors. The theory makes use of the symmetry of the on-site energy under rotations, this structure and related results should be relevant to more general discrete parabolic multicomponent systems with symmetries under Lie group actions.
We also report results from numerical integration of the Landau–de Gennes gradient flow for two simple one-dimensional geometries, an open chain, and a periodic chain. We observe rapid approach to a near-uniaxial state, and a slower convergence to the equilibrium. The fast scale is independent of the size of the chain while the slow scale increases with the size of the chain. In closed chains we see at least two stable equilibria that are discrete analogues of the two homotopy classes of the projective plane. We also see bistability in the open chain, under boundary conditions of perpendicular directors at the two endpoints.
The equilibria seen here are uniaxial Q-tensors with directions that lie on the same plane at all sites. Connections with the theory for ![]() $2 \times 2$ Q-tensors [Reference Panayotaros25] should be examined further. We expect additional equilibria of periodic and open chains that correspond to homotopy classes of S 1 with higher rotation number. These solutions are expected from the theory of discrete vortices in the discrete Schrödinger equation [Reference Pelinovsky, Kevrekidis and Frantzeskakis29]. Their stability in the
$2 \times 2$ Q-tensors [Reference Panayotaros25] should be examined further. We expect additional equilibria of periodic and open chains that correspond to homotopy classes of S 1 with higher rotation number. These solutions are expected from the theory of discrete vortices in the discrete Schrödinger equation [Reference Pelinovsky, Kevrekidis and Frantzeskakis29]. Their stability in the ![]() $2\times 2$ and
$2\times 2$ and ![]() $3 \times 3$ Q-tensor theories could be studied further. Further work will address similar effects in more general one-dimensional geometries, e.g. discrete analogues of some graphs, where we may see some discrete analogues of dislocations. One of our future goals is to examine higher dimensional geometries and domains such as the disc on the plane. Also of interest are phenomena of front propagation in discrete Landau–de Gennes equation and related parabolic systems, see e.g. [Reference Caputo, Cruz and Panayotaros7]. In the Landau–de Gennes system these are fronts connecting the isotropic and nematic states, where Q = 0, and
$3 \times 3$ Q-tensor theories could be studied further. Further work will address similar effects in more general one-dimensional geometries, e.g. discrete analogues of some graphs, where we may see some discrete analogues of dislocations. One of our future goals is to examine higher dimensional geometries and domains such as the disc on the plane. Also of interest are phenomena of front propagation in discrete Landau–de Gennes equation and related parabolic systems, see e.g. [Reference Caputo, Cruz and Panayotaros7]. In the Landau–de Gennes system these are fronts connecting the isotropic and nematic states, where Q = 0, and ![]() $Q \in \Sigma^3_-$, respectively. The nematic region is expected to expand since the isotropic state is unstable.
$Q \in \Sigma^3_-$, respectively. The nematic region is expected to expand since the isotropic state is unstable.
As mentioned in section 2, the discrete theory is relevant to numerical simulations of continuous models and experimental studies. The calibration of the parameters of the discrete model is discussed in [Reference Davis and Gartland8, Reference Martinez-Gonzalez, Li, Sadati, Zhou, Zhang, Nealey and de Pablo22, Reference Ravnik and Žumer32]. One of the main observable consequences of the theory is the geometrical shape of the nematic field, detected optically. Qualitative features such as dislocations and their positions seen in two-dimensional simulations are therefore observable. The present study indicates multistabilty in simple geometries that can also be detected optically. A possible quantitative result is the time to reach the equilibrium, and its dependence on the coupling constant, boundary conditions, and the size of the domain.
Data availability statement
All numerical can be made available upon request.
Acknowledgments
We acknowledge helpful discussions with Adrian Reyes and Carlos Garcia Azpeitia.
Author contributions
Conceptualization: P.P.; G.R.V. Methodology: P.P.; G.R.V. Formal Analysis: P.P.; G.R.V. Software: P.P.; G.R.V. Visualization: G.R.V. Writing – original draft: P.P; G.R.V. Writing – review & editing: P.P.; G.R.V. All authors approved the final submitted draft.
Funding statement
This research was supported by grants DGAPA-UNAM PAPIIT IG100522, and IN103725, SECIHTI CF-2023-I-65, and SECHITI Estancias Posdoctorales por México.
Competing interests
None.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.






























































