Nonlinear modulation of arbitrary intense electromagnetic waves in magnetized electron–positron plasmas with temperature

Abstract

A theoretical framework has been established to investigate the modulational instability of electromagnetic waves in magnetized electron–positron plasmas. The framework is capable of analyzing electromagnetic waves of any intensity and plasmas at any temperature. A fully relativistic hydrodynamic model, incorporating relativistic velocities and thermal effects, is used to describe the relativistic dynamics of particles in plasmas. Under the weakly magnetized approximation, a modified nonlinear Schrödinger equation, governing the dynamics of the envelope of electromagnetic waves in plasmas, is obtained. The growth rate of the modulational instability is then given both theoretically and numerically. By analyzing the dependence of the growth rate on some key physical parameters, the coupled interplay of relativistic effects, ponderomotive forces, thermal effects and magnetic fields on electromagnetic waves can be clarified. The findings demonstrate that specific combinations of physical parameters can significantly enhance modulational instability, providing a theoretical basis for controlling the propagation of electromagnetic waves in plasmas. This framework has broad applicability to most current laser–plasma experiments and high-energy radiation phenomena from stellar surfaces.

1. Introduction

Magnetized electron–positron (EP) plasmas widely exist in many high-energy astrophysical environments, such as accretion disks (Filho 2009), pulsar magnetospheres (Sturrock 1971; Luo & Ji 2012), black holes (Putten & Maurice 1999; Laurent & Titarchuk 2018) and so on. In the pulsar magnetosphere, pair plasma is generated through a cascade process of EP pair production, and becomes highly magnetized due to the super-strong magnetic field of the pulsar. Additionally, EP plasmas form near black hole horizons during gamma-ray flares emitted by stellar-mass black holes. Therefore, these environments serve as natural laboratories for studying interactions between electromagnetic waves and magnetized EP plasmas.

In recent years, with the rapid development of laser technology, both experimental and theoretical studies have pointed out that an EP plasma can also be generated under laboratory conditions (Sarri et al. 2015). In 1997, Burke et al. (1997) reported the first laboratory production of positrons by colliding a 46.6 GeV electron beam with a terawatt laser pulse at 527 nm wavelength. Ridgers et al. (2012) numerically simulated the pair-production process in which a laser with an intensity of $4\times 10^{23} \textrm{W}\, \textrm{cm}^{-2}$ strikes an aluminum target, producing an EP plasma with the maximum density of $10^{26}\,\textrm{cm}^{-3}$ . Used the ASTRA-GEMINI laser system (the peak intensity of the laser is $3\times 10^{19} \textrm{W}\, \textrm{cm}^{-2}$ ), Sarri et al. (2015) achieved an EP plasma density of $10^{16}\,\textrm{cm}^{-3}$ . Li et al. (2017) proposed an all-optical scheme for ultra-bright gamma-ray emission and dense positron production with lasers at an intensity of $10^{22-23}\textrm{W}\, \textrm{cm}^{-2}$ , in which a positron beam with a density of $2.5\times 10^{22}\, \textrm{cm}^{-3}$ was achieved. Gong et al. (2020) investigated the momentum spectrum and number density of created EP pairs in frequency-modulated laser fields. These studies provide a window for investigating laboratory astrophysics at laser facilities.

If there exists a magnetic field, we will achieve a magnetized EP plasma in the laboratory. The magnetic source may be an external magnetic field, such as in magnetic confinement fusion experiments where a strong magnetic field is applied to the plasma, or may be a self-generated magnetic field arising from laser–plasma interactions (Lehner 2000; Najmudin et al. 2001; Tatarakis et al. 2002; Abudurexiti, Okada & Ishikawa 2009). Self-generated magnetic fields can also be generated by a laser-induced plasma in the process of inertial confinement fusion implosion (Srinivasan, Dimonte & Tang 2012; Walsh et al. 2017; Sadler et al. 2022).

In the previously mentioned high-energy astrophysical environments and intense laser–plasma systems, plasmas typically possess well-defined temperatures. For example, the order of magnitude of the plasma temperature in the pulsar magnetosphere is reported to be $10^6\,\textrm{K}$ (Helfand, Chanan & Novick 1980; Timokhin & Harding 2019). This kind of plasma is referred to as a cold or warm plasma, in which the thermal energy of a particle is much smaller than its rest energy, that is $k_{\textrm{B}}T_{j}\ll m_{\!j}c^2$ , with $k_{\textrm{B}}$ being the Boltzmann constant, the subindex $j$ denoting the species of the particles in the plasma, $T_{j}$ being the temperature of the $j$ type of particle, $m_{\!j}$ being the rest mass of the $j$ type of particle, $c$ being the speed of light in vacuum. An electron temperature in the laser channel was found to be several MeV, which is given by the two-dimensional particle-in-cell (PIC) simulations of the laser channeling in millimeter-scale underdense plasmas for fast ignition (Li et al. 2008). A peak plasma temperature as high as 40 MeV was achieved in laser-driven ion acceleration processes, studied via PIC simulations (Weng et al. 2016). Such plasmas are termed relativistic hot plasmas due to the condition $k_{\textrm{B}}T_{j}\gg m_{\!j}c^2$ .

In this paper, we focus on the modulational instability (MI) of intense electromagnetic waves in a magnetized EP plasma, which is one of the fundamental phenomena in the nonlinear interaction between electromagnetic waves and plasmas (Shukla, Marklund & Eliasson 2004; Sprangle, Hafizi & Peñano 2020). Nonlinear development of the MI plays a key role in many nonlinear processes, such as envelope solitons, envelope shocks, freak waves and self-focusing of electromagnetic waves (Jha et al. 2006; Lehmann, Laedke & Spatschek 2008; Abedi-Varaki & Jafari 2017; Roozehdar Mogaddam et al. 2018; Das, Chandra & Ghosh 2020; Cheng et al. 2023). Spurred by the significance of MI in electromagnetic waves, researchers have extensively studied this phenomenon under different kinds of physical conditions over the past few decades (Shukla & Bharuthram 1987; Chen, Liu & Li, 2011; Sprangle, Esarey & Hafizi 1997; Rozina et al. 2016; Luo & Wang 2020). Some studies have specifically addressed MI in magnetized plasmas. For instance, the MI of laser pulses in transversely magnetized underdense plasmas is investigated by Jha et al. (2005), analyzing magnetic field effects. The MI of the right-hand elliptically polarized laser pulses in cold magnetized EP plasmas is explored by Chen et al. (2011). While the MI of circularly polarized electromagnetic waves and the formation of the solitary waves in hot magnetized EP plasmas are studied by Asenjo et al. (2012). The MI of intense lasers in hot magnetized EP plasmas in the quasi-neutral limit is examined by Sepehri Javan (2012), discussing the dependences of the MI on the plasma temperature and external magnetic fields. Sobacchi et al. (2021) investigated self-modulation of fast radio bursts in pulsars, analyzing instabilities developing for arbitrary directions of the perturbation wave vector. However, these researchers primarily focus on the propagation of electromagnetic waves with normalized amplitude $a_0\lt 1$ (corresponding to laser intensities $I\lt 10^{18}\textrm{W}/\textrm{cm}^2$ ) in low-temperature plasmas where $k_{\textrm{B}}T_{j}\lt m_{\!j}c^2$ . To date, the MI of electromagnetic waves with arbitrary intensity in relativistic hot plasmas is rarely discussed. This paper addresses this gap by studying MI across intensities ranging from weakly relativistic ( $a_0\ll 1$ ) to ultra-relativistic ( $a_0\gg 1$ ) regimes in magnetized EP plasmas. For this purpose, we employ a fully relativistic fluid model (Asenjo et al. 2009), incorporating a temperature-dependent function to characterize plasma thermal effects.

The paper is structured as follows. In § 2, a nonlinear wave equation is obtained under the weak magnetization approximation, which characterizes the amplitude evolution of electromagnetic waves in magnetized EP plasmas. In § 3, the growth rate of MI is derived. In § 4, through numerical analysis in both low-temperature and high-temperature regimes, we examined the dependence of the MI growth rate on some key physical parameters. Furthermore MI characteristics of $\gamma$ -rays emitted by a pulsar are investigated. Finally, the principal findings are summarized in § 5.

2. Nonlinear wave equations

In the following, the propagation of an electromagnetic wave in a magnetized EP plasma is investigated. The plasma system maintains local equilibrium with charge neutrality, expressed as $n_{e0}=n_{\!p0}$ , where $n_{e0}$ and $n_{\!p0}$ are unperturbed densities of electrons and positrons in the laboratory frame. A circularly polarized electromagnetic wave is considered to propagate along the external magnetic field ${\boldsymbol{B}}_0=B_0\hat {{\boldsymbol{e}}}_{z}$ . The corresponding vector potential $\boldsymbol{A}$ of the laser can be expressed as

(2.1) \begin{equation} {\boldsymbol{A}}=\tfrac{1}{2}A(z,t)(\hat {{\boldsymbol{e}}}_{\!x}+{i}\sigma \hat {{\boldsymbol{e}}}_{\!y})\exp [{i}(k_0z-\omega _0 t)]+c.c., \end{equation}

where $\omega _0$ is the frequency of the wave, $k_0$ is the wavenumber, $\sigma = +1$ (−1) denotes the right-hand (left-hand) circularly polarized wave and $A(z,t)$ is the slowly varying amplitude satisfying the condition

(2.2) \begin{equation} \left |\frac {1}{\omega _0}\frac {\partial A}{\partial t}\right |\ll |A|. \end{equation}

From the Maxwell equations and using

(2.3) \begin{equation} {\boldsymbol{E}}=-\frac {1}{c}\frac {\partial {\boldsymbol{A}}}{\partial t}-\nabla \phi , {\boldsymbol{B}}=\nabla \times {\boldsymbol{A}}+{\boldsymbol{B}}_0, \end{equation}

we can obtain the wave equation

(2.4) \begin{equation} \frac {1}{c^2}\frac {\partial ^2{\boldsymbol{A}}}{\partial t^2}-\nabla ^2{\boldsymbol{A}} =\frac {4\pi }{c}{\boldsymbol{J}}, \end{equation}

where ${\boldsymbol{J}}=\sum _{j}-\eta _{j}en_{\!j}{\boldsymbol{p}}_{\!j}/(\gamma _{j}m)$ is the current density of the pair plasma, $e$ is the charge of an electron or a positron, $j=e, p$ denote the electron and positron, respectively, $\eta _{e}=1$ and $\eta _{p}=-1$ are charge polarity indicators, $m$ is the rest mass of an electron or a positron and $n_{\!j}$ , ${\boldsymbol{p}}_{\!j}$ and $\gamma _{j}=[1+p_{j}^2/(m^2c^2)]^{1/2}$ are the number density, momentum and Lorentz factor of $j$ sort of particles, respectively.

The relativistic fluid momentum equation for the $j$ type of plasma particle can be represented as (Asenjo et al. 2012)

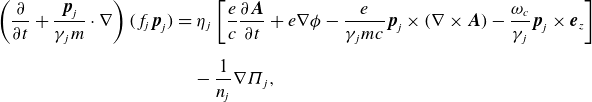(2.5) \begin{align} \left (\frac {\partial }{\partial t}+\frac {{\boldsymbol{p}}_{\!j}}{\gamma _{j} m}\cdot \nabla \right ) (f_{\!j}{\boldsymbol{p}}_{\!j}) & =\eta _{j} \left [\frac {e}{c}\frac {\partial {\boldsymbol{A}}}{\partial t}+e\nabla \phi -\frac {e}{\gamma _{j}mc}{\boldsymbol{p}}_{\!j}\times (\nabla \times {\boldsymbol{A}}) -\frac {\omega _{c}}{\gamma _{j}}{\boldsymbol{p}}_{\!j}\times {\boldsymbol{e}}_{z}\right ]\nonumber\\[5pt]& \quad -\frac {1}{n_{\!j}}\nabla \unicode{x1D6F1} _{j}, \end{align}

where the pressure of particles $\unicode{x1D6F1} _{j}=n_{\!j}k_{\textrm{B}}T_{j}$ for an ideal gas, $\omega _{c}=eB_0/(mc)$ is the electron cyclotron frequency, and $\phi$ is the scalar potential satisfying Poisson’s equation

(2.6) \begin{equation} \nabla ^2\phi =4\pi e(n_{e}-n_{p}). \end{equation}

In the equation (2.5), $f_{\!j}$ is a function of temperature. It can be expressed as $f_{\!j}=K_{3}(mc^2/k_{\textrm{B}}T_{j})/K_{2}(mc^2/k_{\textrm{B}}T_{j})$ , assuming that the plasma system follows a relativistic Maxwell–Jüttner distribution, where $K_{3}(x)$ and $K_{2}(x)$ are modified Bessel functions of order 3 and 2 (Asenjo et al. 2012; Banerjee, Dutta & Misra 2020). The function can be approximated by $f_{\!j}\approx 1+5k_{\textrm{B}}T_{j}/(2\, \mathrm{mc}^{2})$ in the low-temperature limit $k_{\textrm{B}}T_{j}\ll mc^2$ , while $f_{\!j}\approx 4k_{\textrm{B}}T_{j}/(mc^2)$ in the high-temperature limit $k_{\textrm{B}}T_{j}\gg mc^2$ .

By substituting equation (2.1) into (2.5), we can obtain the momentum of plasma particles from the high-frequency response of moving particles to the incident wave

(2.7) \begin{equation} {\boldsymbol{p}}_{\!j}=\eta _{j}\frac {mc{\boldsymbol{a}}}{f_{\!j}-\eta _{j}\frac {\sigma \mu }{\gamma _{j}}}, \end{equation}

where $\mu =\omega _{c}/\omega _0$ is the normalized cyclotron frequency, and ${\boldsymbol{a}}=e{\boldsymbol{A}}/(mc^2)$ is the normalized vector potential.

Substituting the expression (2.7) into $\gamma _{j}=[1+p_{j}^2/(m^2c^2)]^{1/2}$ , we can derive

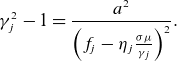(2.8) \begin{eqnarray} \gamma _{j}^2-1=\frac {a^2}{\left(f_{\!j}-\eta _{j}\frac {\sigma \mu }{\gamma _{j}}\right)^2}. \end{eqnarray}

For weakly magnetized plasmas, the condition $\mu \ll f_{\!j}\gamma _{j}$ holds. In this limit, the right-hand side of the (2.8) can be expanded as a power series in $\mu$ . Retaining terms to first order in $\mu$ , the equation for the Lorentz factors simplifies to

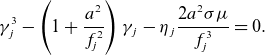(2.9) \begin{eqnarray} \gamma _{j}^3-\left (1+\frac {a^2}{f_{\!j}^2}\right )\gamma _{j}-\eta _{j}\frac {2a^2\sigma \mu }{f_{\!j}^3}=0 . \end{eqnarray}

Thus the approximate solutions for the Lorentz factors of each fluid can be expressed as

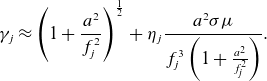(2.10) \begin{eqnarray} \gamma _{j}\approx \left (1+\frac {a^2}{f_{\!j}^2}\right )^\frac {1}{2}+\eta _{j}\frac {a^2\sigma \mu }{f_{\!j}^3\left(1+\frac {a^2}{f_{\!j}^2}\right)}. \end{eqnarray}

From equation (2.5), we can also obtain the equation that the plasma density perturbation satisfies

(2.11) \begin{eqnarray} k_{\textrm{B}}T_{j}\nabla \ln n_{\!j}=\nabla \left (\eta _{j} e\phi -\varphi _{pj}\right ), \end{eqnarray}

where $\varphi _{pj}$ is the relativistic ponderomotive potential, expressed as

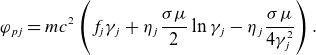(2.12) \begin{eqnarray} \varphi _{pj}=mc^2\left (f_{\!j}\gamma _{j}+\eta _{j}\frac {\sigma \mu }{2}\ln \gamma _{j} -\eta _{j}\frac {\sigma \mu }{4\gamma _{j}^2}\right ). \end{eqnarray}

In the absence of an external magnetic field, the ponderomotive potential reduces to the standard expression in a cold plasma $\varphi _{pj}=mc^2\gamma _{j}$ . By integrating equation (2.11), and assuming the plasma being unperturbed at infinity, i.e. using the boundary conditions $n_{e,p}=n_{e0,p0}$ , $\phi \rightarrow 0$ and $\gamma \rightarrow 1$ at $|z|\rightarrow \infty$ , we can obtain the number densities of electrons and positrons

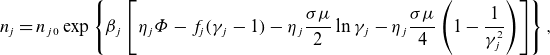(2.13) \begin{align} n_{\!j}=n_{j0}\exp \left \{\beta _{j}\left [\eta _{j}\unicode{x1D6F7} -f_{\!j}(\gamma _{j}-1)-\eta _{j}\frac {\sigma \mu }{2}\ln \gamma _{j} -\eta _{j}\frac {\sigma \mu }{4}\left (1-\frac {1}{\gamma _{j}^2}\right )\right ]\right \},\nonumber\\ \end{align}

where $\unicode{x1D6F7} =e\phi /(mc^2)$ , $\beta _{j}=mc^2/(k_{\textrm{B}}T_{j})$ .

Substituting (2.13) into the quasi-neutrality condition $n_{e}-n_{p}-n_{i0}=0$ , we obtain

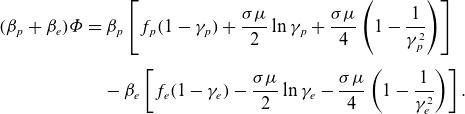(2.14) \begin{align} (\beta _{p}+\beta _{e})\unicode{x1D6F7} & = \beta _{p}\left [f_{p}(1-\gamma _{p})+\frac {\sigma \mu }{2}\ln \gamma _{p}+\frac {\sigma \mu }{4}\left(1-\frac {1}{\gamma _{p}^2}\right)\right ]\nonumber \\[5pt]& \quad -\beta _{e}\left [f_{e}(1-\gamma _{e})-\frac {\sigma \mu }{2}\ln \gamma _{e}-\frac {\sigma \mu }{4}\left(1-\frac {1}{\gamma _{e}^2}\right)\right ]. \end{align}

Substituting the expression of $\unicode{x1D6F7}$ into (2.13), and assuming the plasma to be in thermal equilibrium, i.e. $f_{e}=f_{p}=f$ , the number density of the j-particle can be rewritten as

(2.15) \begin{equation} n_{\!j}=n_{j0}\exp \{\beta \xi (\gamma _{e},\gamma _{p})\} , \end{equation}

where $\beta =2\beta _{e}\beta _{p}/(\beta _{p}+\beta _{e})$ is the temperature parameter, the function

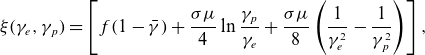(2.16) \begin{eqnarray} \xi (\gamma _{e},\gamma _{p})=\left [f(1-\bar {\gamma })+\frac {\sigma \mu }{4}\ln \frac {\gamma _{p}}{\gamma _{e}}+\frac {\sigma \mu }{8} \left (\frac {1}{\gamma _{e}^2}-\frac {1}{\gamma _{p}^2}\right )\right ], \end{eqnarray}

and $\bar {\gamma }=(\gamma _{e}+\gamma _{p})/2$ .

Substituting the vector potential $\boldsymbol{A}$ and current density $\boldsymbol{J}$ into (2.4) yields the electromagnetic-wave envelope equation

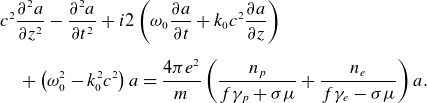(2.17) \begin{align} & c^2\frac {\partial ^2 a}{\partial z^2}-\frac {\partial ^2 a}{\partial t^2}+{i}2\left (\omega _0\frac {\partial a}{\partial t}+k_0c^2\frac {\partial a}{\partial z}\right )\nonumber\\[5pt]& \quad +\left(\omega _0^2-k_0^2c^2\right)a =\frac {4\pi e^2}{m}\left (\frac {n_{p}}{f\gamma _{p}+\sigma \mu }+\frac {n_{e}}{f\gamma _{e}-\sigma \mu }\right )a. \end{align}

Linearizing equation (2.17), we can get the nonlinear dispersion relation of the wave

(2.18) \begin{eqnarray} \omega _0^2-k_0^2c^2=Q_{L}\omega _{pe}^2 , \end{eqnarray}

where $\omega _{pe}=(4\pi e^2n_{e0}/m)^{1/2}$ is the plasma frequency in the laboratory frame, and

(2.19) \begin{eqnarray} Q_{L}=\left (\frac {1}{f+\sigma \mu }+\frac {1}{f-\sigma \mu }\right ). \end{eqnarray}

The dispersion relationship can also be expressed in a more common form

(2.20) \begin{eqnarray} \omega _0^2-k_0^2c^2=\frac {2f\omega _0^2\omega _{pe}^2}{f^2\omega _0^2-\omega _{c}^2}. \end{eqnarray}

For $f=1$ , the dispersion relation for a cold plasma is recovered. Let $k_0=0$ , the cutoff frequency of the electromagnetic wave in the magnetized pair plasma can be obtained as

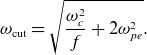(2.21) \begin{eqnarray} \omega _{\mathrm{cut}}=\sqrt {\frac {\omega _{c}^2}{f}+2\omega _{pe}^2}. \end{eqnarray}

Obviously, the cutoff frequency of waves decreases with the increasing of the plasma temperature in the hot plasmas.

Substituting equations (2.15) and (2.18) into equation (2.17), leads to

(2.22) \begin{eqnarray} \frac {1}{2}\left (c^2\frac {\partial ^2a}{\partial z^2}-\frac {\partial ^2a}{\partial t^2}\right ) +{i}\left (\omega _0\frac {\partial a}{\partial t}+k_0c^2\frac {\partial a}{\partial z}\right ) +D_{NL}\omega _{pe}^2a=0, \end{eqnarray}

where $D_{NL}=\{Q_{L}-Q \exp [\beta \xi (\gamma _{e},\gamma _{p})]\}/2$ and

(2.23) \begin{eqnarray} Q=\left (\frac {1}{f\gamma _{p}+\sigma \mu }+\frac {1}{f\gamma _{e}-\sigma \mu }\right ) .\end{eqnarray}

Introducing the dimensionless variables $\tau =\omega _{pe}^2t/\omega _0$ , $\tilde {z}=\omega _{pe}z/c+u_{g}\tau$ , $u_{g}=(\omega _0/\omega _{pe})v_{g}/c$ , where $v_{g}=kc^2/\omega _0$ is the group velocity of the wave, we write (2.22) as

(2.24) \begin{eqnarray} \frac {1}{2}\frac {\partial ^2a}{\partial \tilde {z}^2}+i\frac {\partial a}{\partial \tau }+D_{NL}a=0, \end{eqnarray}

where the slowly varying envelope approximation is used. Equation (2.24) is the modified nonlinear Schrödinger equation governing the dynamics of the envelope of an electromagnetic wave in magnetized EP plasmas.

The theoretical framework is derived under the weakly magnetized approximation, requiring the magnetic field strength to satisfy $\omega _{c}\ll f_{\!j}\gamma _{j}\omega _0$ . This condition remains broadly applicable to most contemporary laser–plasma experiments and high-energy radiation processes on stellar surfaces.

For instance, in experiments utilizing magnetic fields of the order of $10^{4}-10^{5}$ G, such as those in magnetic confinement fusion research, the weak magnetization condition is trivially met. Modern solid-state and conventional electromagnets can generate fields up to $10^{6}$ G (Sims et al. 2008), corresponding to electron cyclotron frequencies of $\omega _{c}\sim 10^{13}\, \textrm{s}^{-1}$ . To satisfy $\omega _{c}\ll f_{\!j}\gamma _{j}\omega _0$ in such systems, laser wavelengths below 10 $\mu \textrm{m}$ ( $\omega _0\gt 10^{14}\,\textrm{s}^{-1}$ ) are typically sufficient. In scenarios involving stronger fields, such as inertial confinement fusion experiments with $10^{6}-10^{7}$ G fields ( $\omega _{c}\sim 10^{13}-10^{14}\, \textrm{s}^{-1}$ ), near-infrared lasers (e.g. Nd lasers at 1.06 $\mu \textrm{m}$ , $\omega _0=1.8\times 10^{15}\, \textrm{s}^{-1}$ ) still comply with the approximation. This robustness extends to ultra-intense laser–plasma interactions generating several kilo-tesla fields (Knauer et al. 2010; Fujioka et al. 2013), where $\omega _{c}\sim 10^{15}\, \textrm{s}^{-1}$ . Here, even mid-infrared lasers (3–10 $\mu \textrm{m}$ ) remain viable due to the relativistic and thermal effects ( $f_{\!j}\gamma _{j}\gg 1$ ). Recently, some studies have proposed laser-driven schemes to generate ultra-strong magnetic fields of the order of $10^8$ G (corresponding to $\omega _{c}\sim 10^{15}\, \textrm{s}^{-1}$ ) (Wilson et al. 2021; Shi et al. 2023). For such fields, in cold and weakly relativistic plasmas ( $f_{\!j}\gamma _{j}\approx 1$ ), the laser frequency must far exceed $10^{15}\, \textrm{s}^{-1}$ . If ultraviolet or X-ray lasers ( $\omega _0\geq 10^{16}\, \textrm{s}^{-1}$ ) are used, the model remains applicable. While relativistic hot plasmas ( $f_{\!j}\gamma _{j}\gg 1$ ) significantly relax this constraint. The weak magnetization condition still holds even for laser frequencies below $10^{15}\, \textrm{s}^{-1}$ .

This framework also accommodates astrophysical environments like pulsar surfaces, where typical magnetic fields reach $10^{12}$ G ( $\omega _{c}\sim 10^{19}\,\textrm{s}^{-1}$ ). For such systems, the weak magnetization condition demands radiation frequencies exceeding $10^{19}\, \textrm{s}^{-1}$ , naturally aligning with X-ray or $\gamma$ -ray emission processes.

3. Modulational instability

The MI of electromagnetic waves can be analyzed using a common method introduced in references (Shukla & Bharuthram 1987; Shukla et al. 2004). Assume that

(3.1) \begin{eqnarray} a=(a_0+a_1)e^{{i}\delta \tau }, \end{eqnarray}

where $a_0$ is a real constant, $a_1(\ll a_0)$ denotes the small perturbation amplitude and $\delta$ represents the nonlinear frequency shift. Substituting (3.1) into (2.24), and linearizing the resulting equation with respect to $a_1$ , we obtain the nonlinear frequency shift at the lowest order

(3.2) \begin{eqnarray} \delta =D_{NL}(|a|=a_0), \end{eqnarray}

where $D_{NL}(|a|=a_0)=[Q_{L}-Q_0 e^{\beta \xi (\gamma _{e0},\gamma _{\!p0})}]/2$ , $Q_0=1/(f\gamma _{\!p0}+\sigma \mu )+1/(f\gamma _{e0}-\sigma \mu )$ and $\gamma _{j0}=\gamma _{j}(|a|=a_0)$ .

By analyzing the first-order terms in the derived equation, we obtain an equation governing the perturbation amplitude

(3.3) \begin{eqnarray} \frac {1}{2}\frac {\partial ^2a_1}{\partial \tilde {z}^2} +i\frac {\partial a_1}{\partial \tau } +\unicode{x1D6EC} a_0^2(a_1+a_1^\ast )=0, \end{eqnarray}

where

(3.4) \begin{align} \unicode{x1D6EC} =\frac {1}{4}\exp [\beta \xi (\gamma _{e0},\gamma _{\!p0})]\left [\frac {f\unicode{x1D6E4} _{p}}{(f\gamma _{\!p0}+\sigma \mu )^2} +\frac {f\unicode{x1D6E4} _{e}}{(f\gamma _{e0}-\sigma \mu )^2}-\beta Q_0(s_{e}\unicode{x1D6E4} _{e}+s_{p}\unicode{x1D6E4} _{p})\right ], \end{align}

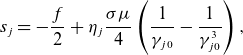(3.5) \begin{eqnarray} s_{j}=-\frac {f}{2}+\eta _{j}\frac {\sigma \mu }{4}\left (\frac {1}{\gamma _{j0}}-\frac {1}{\gamma _{j0}^3}\right ), \end{eqnarray}

and

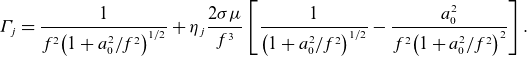(3.6) \begin{eqnarray} \unicode{x1D6E4} _{j}=\frac {1}{f^2\big(1+a_0^2/f^2\big)^{1/2}}+\eta _{j}\frac {2\sigma \mu }{f^3}\left [\frac {1}{\big(1+a_0^2/f^2\big)^{1/2}}-\frac {a_0^2}{f^2\big(1+a_0^2/f^2\big)^{2}}\right ]. \end{eqnarray}

Inserting $a_1=X+\textrm{i}Y$ into (3.3) yields

(3.7) \begin{eqnarray} \frac {1}{2}\frac {\partial ^2X}{\partial \tilde {z}^2} -\frac {\partial Y}{\partial \tau } +2\unicode{x1D6EC} a_0^2X=0 ,\end{eqnarray}

and

(3.8) \begin{eqnarray} \frac {1}{2}\frac {\partial ^2Y}{\partial \tilde {z}^2} +\frac {\partial X}{\partial \tau }=0. \end{eqnarray}

For the real part $X$ and imaginary part $Y$ of $a_1$ , we consider the following oscillation forms: $X=\tilde {X}\exp ({i}K\tilde {z}-{i}\Omega \tau )$ and $Y=\tilde {Y}\exp ({i}K\tilde {z}-{i}\Omega \tau )$ , where $\tilde {X}$ and $\tilde {Y}$ are the real amplitudes, $K$ is the modulation wavenumber normalized by $\omega _{pe}/c$ and $\Omega$ is the modulation frequency normalized by $\omega _{pe}^2/\omega _0$ . The nonlinear dispersion relation of MI is obtained as

(3.9) \begin{eqnarray} \Omega ^2=-\frac {K^2}{2}\left [2\unicode{x1D6EC} a_0^2-\frac {K^2}{2}\right ], \end{eqnarray}

from which we can extract the MI growth rate $\unicode{x1D6E4} =-{i}\Omega$ as follows:

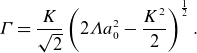(3.10) \begin{eqnarray} \unicode{x1D6E4} =\frac {K}{\sqrt {2}} \left (2\unicode{x1D6EC} a_0^2-\frac {K^2}{2}\right )^{\frac {1}{2}}. \end{eqnarray}

We can see that the result degenerates to the growth rate formula of Shukla et al. (Shukla et al. 2004), for the cold non-magnetized pair plasmas.

When $K=(2\unicode{x1D6EC} )^{1/2}a_0$ that is the modulation wavenumber of the fastest-growing mode, the growth rate of MI has a maximum

(3.11) \begin{eqnarray} \unicode{x1D6E4}_{\mathrm{max}}=\unicode{x1D6EC} a_0^2. \end{eqnarray}

As can be seen from the previous derivation process, the MI of the electromagnetic field in the magnetized plasmas is closely related to the coupling effect of the ponderomotive force, thermal pressure, relativistic effect and magnetic field.

4. Numerical results and discussions

In this section, we numerically analyze factors influencing the growth rate of MI, with a focus on two plasma regimes: the low-temperature limit ( $\beta _{j}\gg 1$ ) and high-temperature limit ( $\beta _{j}\ll 1$ ). Owing to the symmetry of the EP plasma, the modes of the circularly polarized electromagnetic waves do not affect its MI. Therefore, we set $\sigma =1$ in the numerical calculations presented below.

4.1. Numerical analysis

4.1.1. In the low-temperature limit

For the case of the low-temperature limit, $k_{\textrm{B}}T_{j}\ll mc^2\approx 510$ keV ( $\beta _{j}\gg 1$ ). The dependence of the maximum growth rate of MI ( $\unicode{x1D6E4}_{\mathrm{max}}$ ) on the amplitude of electromagnetic wave $a_0$ is shown in figure 1, where the particle temperatures $k_{\textrm{B}}T_{e,p}$ are 0.1, 1 and 10 keV, respectively. It can be seen that, initially, the maximum growth rate gradually increases with an increase in the amplitude of electromagnetic wave for a fixed particle temperature. When the amplitude of the electromagnetic wave increases to a critical value (threshold), the maximum growth rate reaches its peak (maximum value), and then begins to decrease. This behavior can be attributed to the competition between the ponderomotive force of the electromagnetic wave and relativistic effects. As the intensity of the electromagnetic wave increases, the ponderomotive force also increases, causing more particles to be pushed out of their original regions and thereby enhancing the disturbance acting on the electromagnetic wave. However, when the amplitude of the electromagnetic wave increases further, the mass of the particle becomes larger, and the relativistic effect gradually takes over. This makes it increasingly difficult for the ponderomotive force to displace the particles.

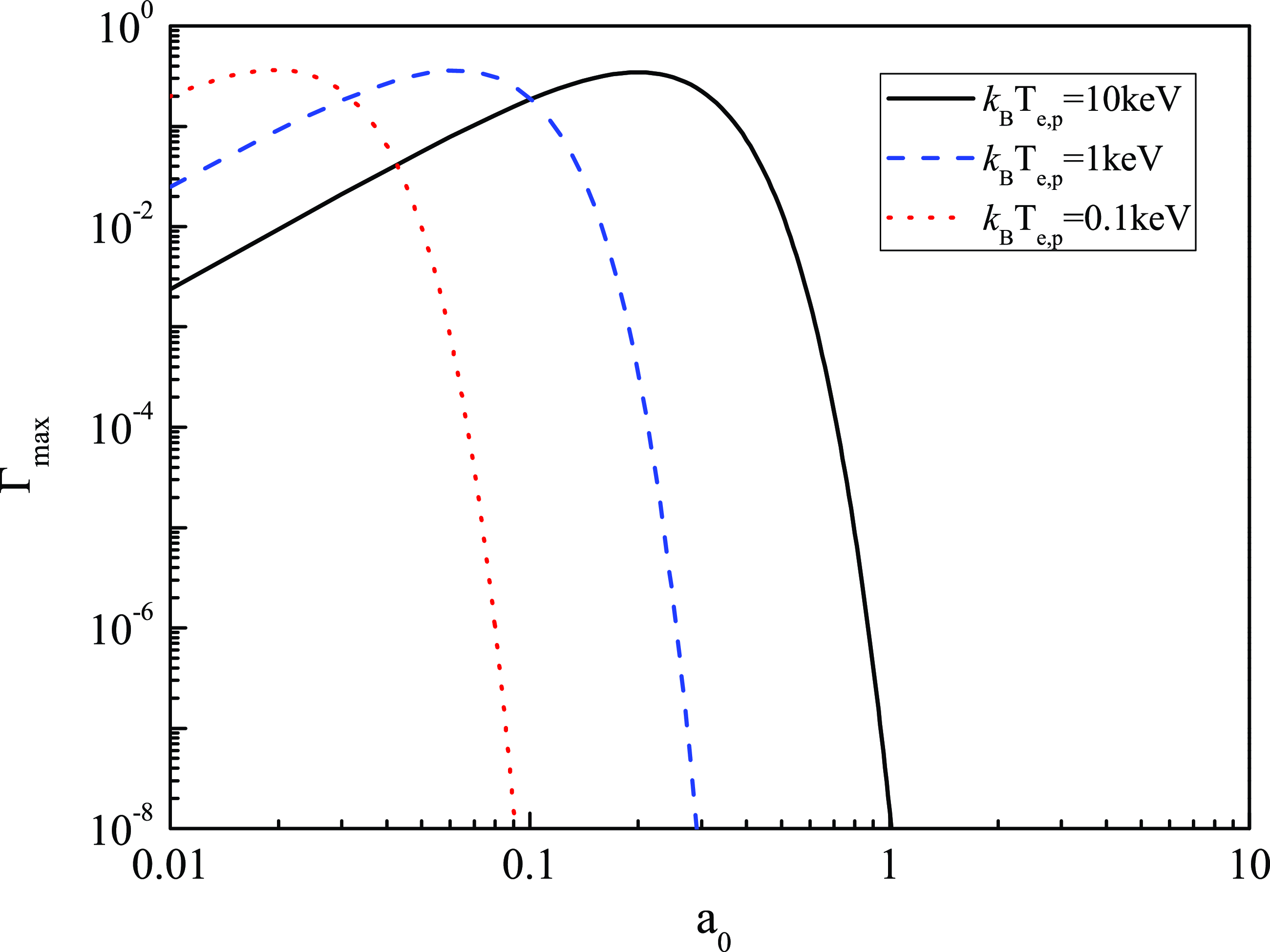
Figure 1. The variations of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the electromagnetic-wave amplitude $a_0$ for different particle temperatures $k_{\textrm{B}}T_{e,p}$ in the low-temperature limit, with fixed parameter $\mu =0.1$ .

The maximum growth rate $\unicode{x1D6E4}_{\mathrm{max}}$ as a function of the particle temperature $k_{\textrm{B}}T_{e,p}$ for different amplitudes of electromagnetic wave $a_0=0.01, 0.1, 0.5$ is shown in figure 2. For a fixed amplitude $a_0$ , with the increase of temperature, the function $\unicode{x1D6E4}_{\mathrm{max}}$ initially increases and then decreases. As the temperature rises, the thermal pressure increases significantly. It should be noted that the ponderomotive force also increases, as indicated by the exponential term $\exp \{\beta \xi (\gamma _{e0},\gamma _{\!p0})\}$ in the expression of $\unicode{x1D6E4}_{\mathrm{max}}$ . At low temperatures, the ponderomotive force exceeds the thermal pressure and dominates, leading to an enhancement of MI. The growth rate reaches its maximum when these two forces balance each other. However, as the temperature continues to increases, the thermal pressure becomes dominant, resulting in a suppression of MI.

In order to give the law of the growth rate of MI with the amplitude of electromagnetic waves $a_0$ and particle temperature $k_{\textrm{B}}T_{e,p}$ more clearly, we plot the results in figure 3. Figure 3(a) presents a three-dimensional plot of the maximum growth rate $\unicode{x1D6E4}_{\mathrm{max}}$ versus $a_0$ and $k_{\textrm{B}}T_{e,p}$ under low-temperature conditions, where $a_0$ ranges from 0.01 to 10, and $k_{\textrm{B}}T_{e,p}$ spans 0.1 to 50 keV. Figure 3(b) displays the MI phase diagram in the $a_0$ - $k_{\textrm{B}}T_{e,p}$ parameter space. These figures clearly reveal the combinations of physical parameters associated with higher instability, providing insights for controlling electromagnetic-wave propagation in plasmas.

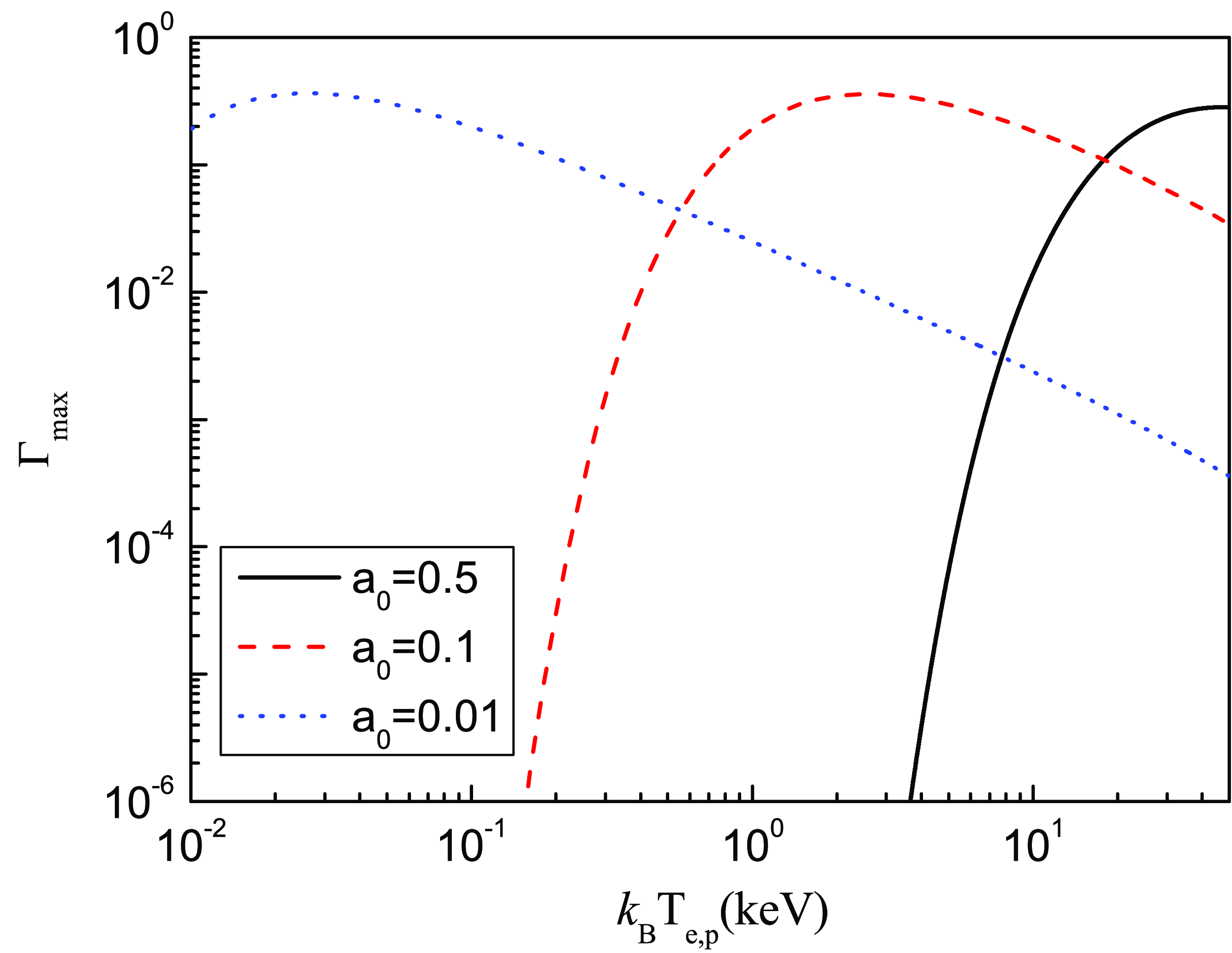
Figure 2. The variations of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the particle temperature $k_{\textrm{B}}T_{e,p}$ in the low-temperature limit for different electromagnetic-wave amplitudes $a_0$ , with fixed parameter $\mu =0.1$ .

Figure 3. Low-temperature limit ( $\mu =0.1$ ): (a) dependence of $\unicode{x1D6E4}_{\mathrm{max}}$ on $a_0$ and $k_{\textrm{B}}T_{e,p}$ , (b) phase diagram of MI in the $a_0$ - $k_{\textrm{B}}T_{e,p}$ plane.

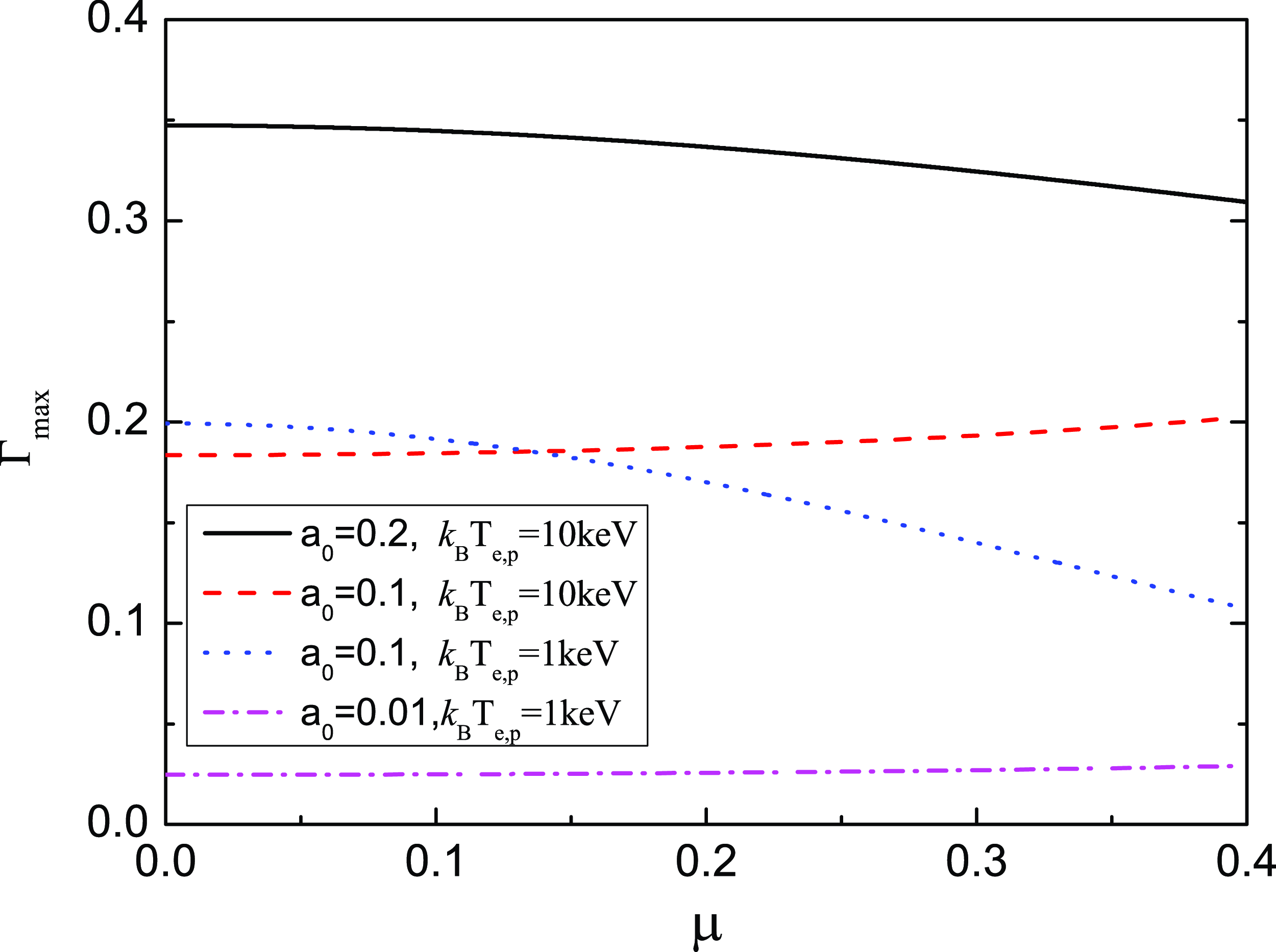
Figure 4. The variations of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the magnetic parameter $\mu$ for different electromagnetic-wave amplitudes $a_0$ and particle temperatures $k_{\textrm{B}}T_{e,p}$ in low-temperature limit.

Figure 4 depicts the dependence of the maximum growth rate $\unicode{x1D6E4}_{\mathrm{max}}$ on the magnetic parameter $\mu$ under low-temperature conditions. The dependence of the growth rate on the magnetic field is governed by the electromagnetic-wave intensity $a_0$ and plasma temperature $k_{\textrm{B}}T_{e,p}$ . For example, at $a_0 = 0.1$ and $k_{\textrm{B}}T_{e,p} = 1$ keV, $\unicode{x1D6E4}_{\mathrm{max}}$ exhibits a monotonic decrease with increasing magnetic field. Conversely, at $a_0 = 0.1$ and $k_{\textrm{B}}T_{e,p} = 10$ keV, $\unicode{x1D6E4}_{\mathrm{max}}$ increases gradually with the increasing of the magnetic field. Furthermore, for fixed temperatures ( $k_{\textrm{B}}T_{e,p} = 1$ or 10 keV), at low intensities ( $a_0 = 0.01$ or 0.1), enhancing the magnetic field elevates $\unicode{x1D6E4}_{\mathrm{max}}$ , while at high intensities ( $a_0 = 0.1$ or 0.2), the trend reverses. These observations align with the predictions in Sepehri Javan (2012), which focused on weakly relativistic and low-temperature regimes.

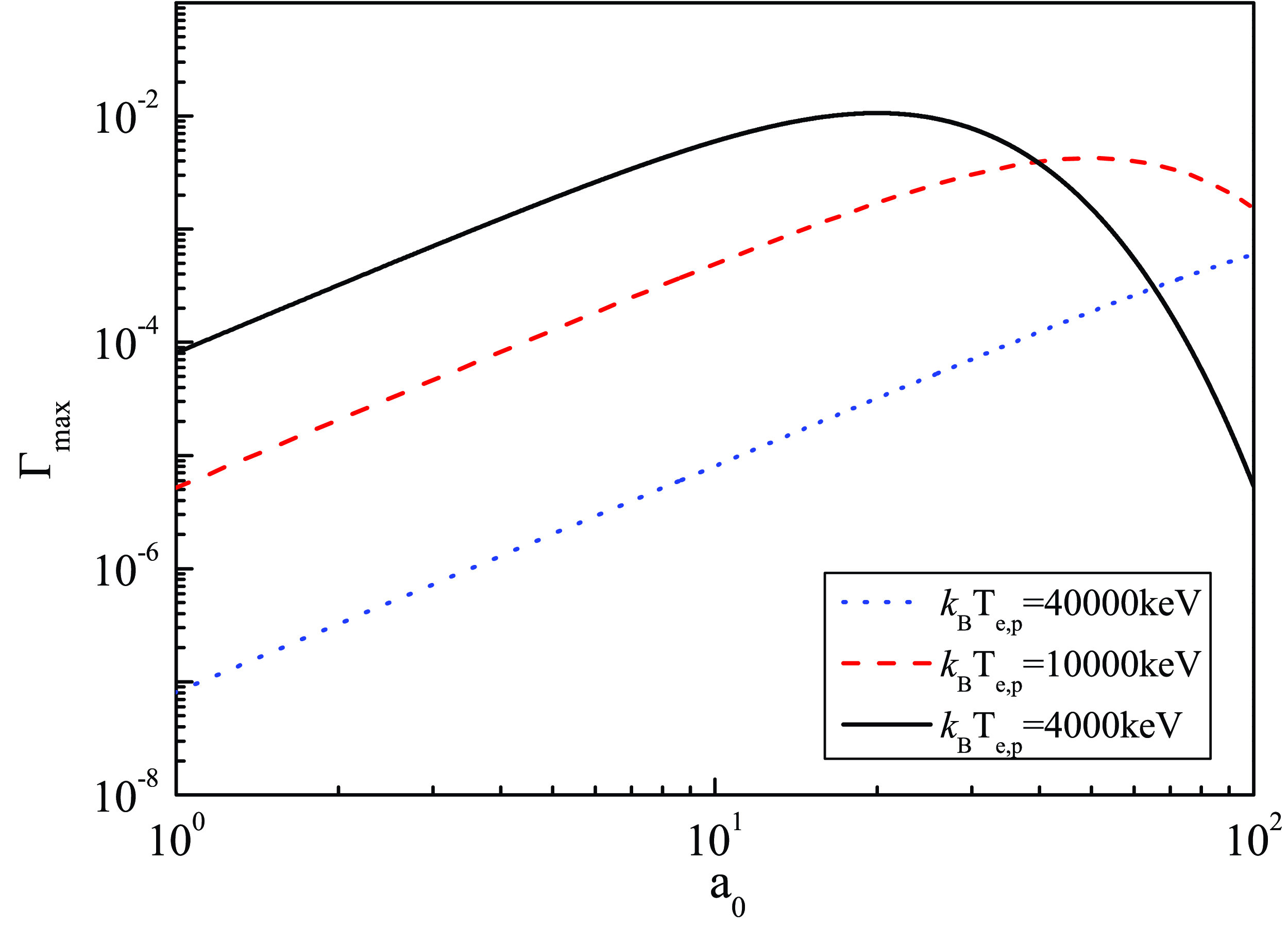
Figure 5. The variations of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the electromagnetic-wave amplitude $a_0$ for different particle temperatures $k_{\textrm{B}}T_{e,p}$ in the high-temperature limit, with fixed parameter $\mu =0.1$ .

4.1.2. In the high-temperature limit

Figures 5–8 demonstrate the growth rate of MI versus the amplitude of electromagnetic waves $a_0$ , particle temperatures $k_{\textrm{B}}T_{e,p}$ and magnetic field strength in the high-temperature limit $k_{\textrm{B}}T_{j}\gg mc^2\approx 510$ keV ( $\beta _{j}\ll 1$ ). A comparison between figures 1 and 5 reveals that the growth rate of MI increases firstly and then decreases with rising $a_0$ , while the value of $a_0$ corresponding to the maximum value of the curve becomes larger.

Figure 6 shows the behavior of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the particle temperatures, where relativistic-temperature plasma exhibits stronger modulation efficiency on high-intensity electromagnetic waves. The corresponding three-dimensional plot and the phase diagram in the $a_0$ - $k_{\textrm{B}}T_{e,p}$ plane are given in figure 7, where $a_0$ ranges from 0.1 to 100, and $k_{\textrm{B}}T_{e,p}$ ranges from 5 to 50 MeV. The analysis reveals a suppression of MI growth rate for low-intensity waves ( $a_0\lt 1$ ) in relativistic hot plasmas, whereas high-intensity waves ( $a_0\gt 1$ ) experience enhanced modulation.

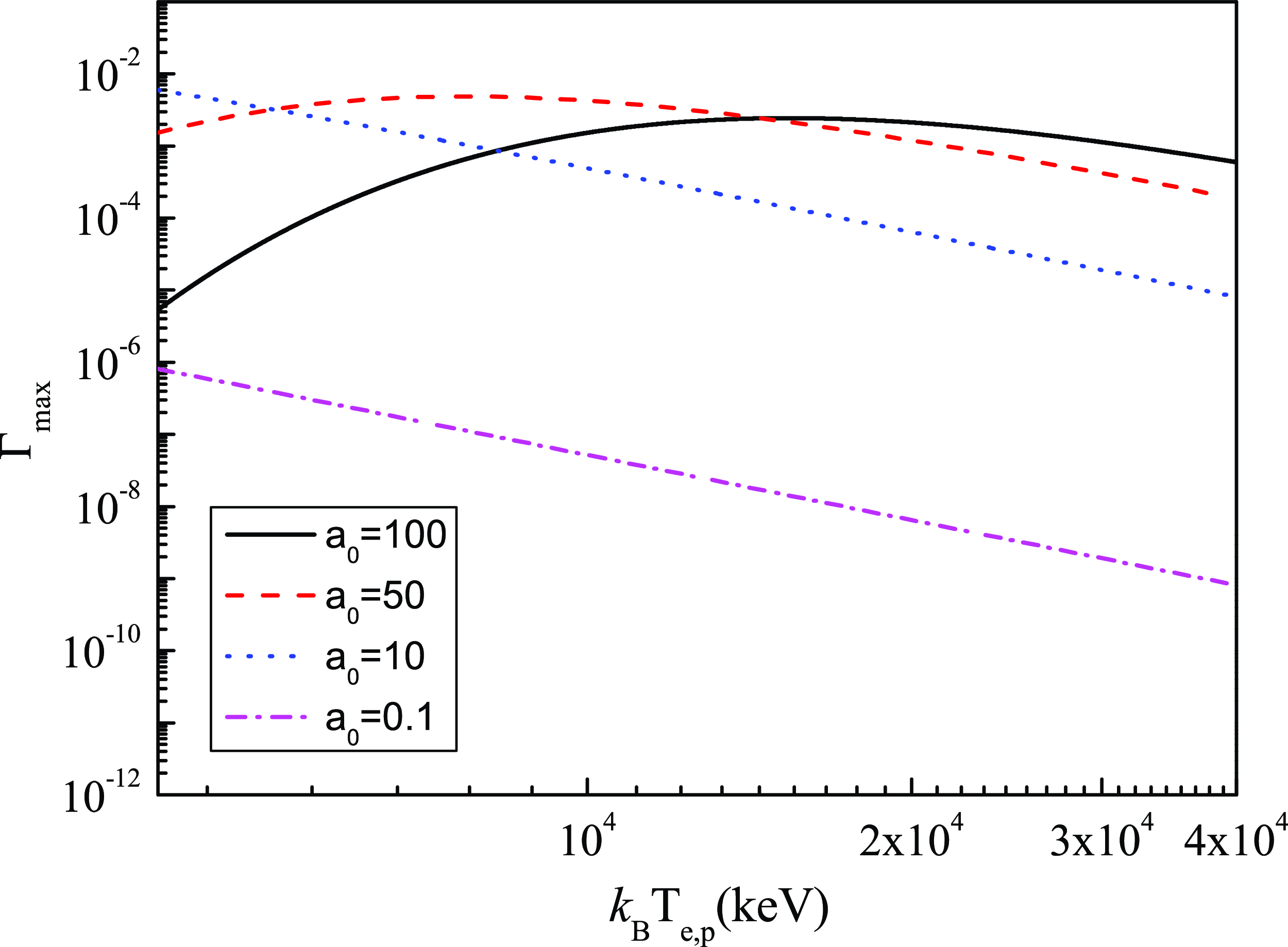
Figure 6. The variations of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the particle temperature $k_{\textrm{B}}T_{e,p}$ in the low-temperature limit for the different electromagnetic-wave amplitudes $a_0$ , with fixed parameter $\mu =0.1$ .

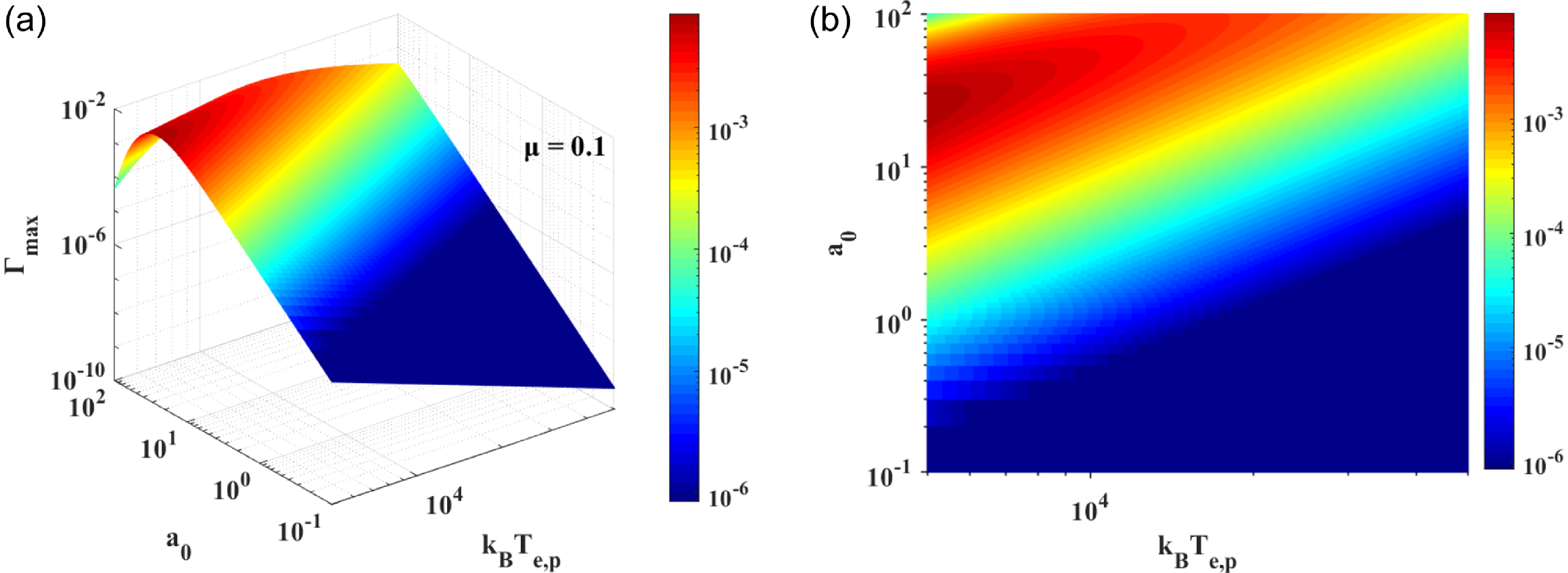
Figure 7. High-temperature limit ( $\mu =0.1$ ): (a) dependence of $\unicode{x1D6E4}_{\mathrm{max}}$ on $a_0$ and $k_{\textrm{B}}T_{e,p}$ , (b) phase diagram of MI in the $a_0$ - $k_{\textrm{B}}T_{e,p}$ plane.

The dependence of the function $\unicode{x1D6E4}_{\mathrm{max}}$ on the magnetic parameter $\mu$ in the limit of high temperature is shown in figure 8. The figure demonstrates that variations in magnetic field strength exhibit negligible influence on the MI of the electromagnetic wave under high-temperature plasma conditions. For example, at $a_0=40$ and $k_{\textrm{B}}T_{e,p}=4000$ keV, $\unicode{x1D6E4}_{\mathrm{max}}$ decreases marginally from $3.80955\times 10^{-3}$ to $3.80885\times 10^{-3}$ as the parameter $\mu$ increases from 0 to 0.4, corresponding to a relative reduction of 0.018 %.

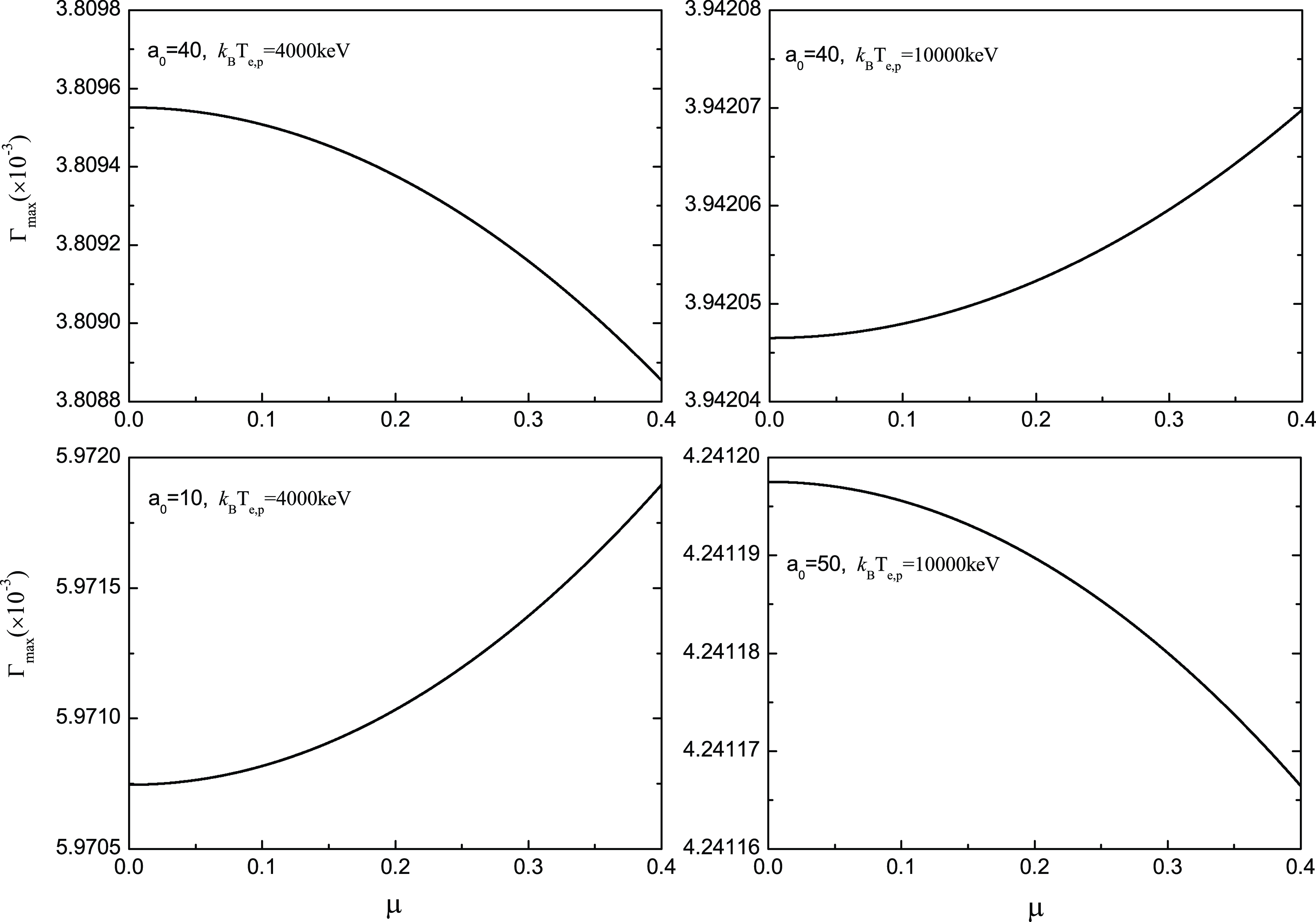
Figure 8. The variation of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the magnetic parameter $\mu$ for different amplitudes of electromagnetic waves $a_0$ and particle temperatures $k_{\textrm{B}}T_{e,p}$ in the high-temperature limit.

4.2. Examples: MI of high-energy radiation in pulsar

In the following, we investigate the MI of the $\gamma$ -ray radiation emitted from the pulsar as it propagates through the magnetized pair plasmas. Here, we consider a typical pulsar with an intense intrinsic magnetic fields $B_{\textrm{s}}\approx 10^{12}$ G at the pulsar surface, a rotation period $P_\ast \approx 1$ s and a radius $R_\ast \approx 10$ km. In the polar cap regions, the pair plasma (with the density $n_0\approx 10^{14}-10^{16}\,\textrm{cm}^{-3}$ (Daugherty & Harding 1982)), is produced via cascade processes of EP pairs, from which high-energy radiation is emitted. The pair plasma typically forms behind a thin layer termed the ‘pair formation front’, located at an altitude $h\approx 10^{4}\,\textrm{cm}$ from the star’s surface. After generation, the plasma moves outward at high velocity, and may propagate to altitudes of up to $100R_\ast$ .

The plasma temperature in the pulsar magnetosphere is reported to be $10^6$ K (Helfand et al. 1980), corresponding to $k_{\textrm{B}}T_{e,p}=0.1$ keV. The amplitude of the electric field $E_0$ (in the laboratory frame) produced by the high-energy radiation can be estimated from the luminosity of pulsars as

(4.1) \begin{eqnarray} L=\int {\boldsymbol{S}}\cdot {\rm d}\sigma \simeq \frac {cE_0^2}{4\pi }A_{\textrm{s}}, \end{eqnarray}

where $\boldsymbol{S}$ is the Poynting vector describing the electromagnetic (EM) energy flux, and $A_{\textrm{s}}$ is the transverse area though which the energy flux flows. Therefore we have

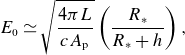(4.2) \begin{eqnarray} E_0\simeq \sqrt {\frac {4\pi L}{cA_{\textrm{p}}}}\left(\frac {R_{\ast }}{R_{\ast }+h}\right), \end{eqnarray}

where $A_{\textrm{p}}$ is the polar cap area (with radius $r_{\textrm{p}}=10^4P_\ast ^{-1/2}\,\textrm{cm}$ ), and $h$ is the altitude from the stellar surface. In polar gap models, high-energy emissions originate at lower altitudes $h\approx 10^{-2}R_\ast =10^4$ cm (Ruderman & Sutherland 1975; Hibschman 2002). Strong radiation in the bands of $\gamma$ -rays with luminosity $L_{\gamma }\approx 10^{33}-10^{36}\textrm{erg/s}$ has been observed from a few pulsars (Ulmer 1994). Therefore, the amplitude of the electric field $E_0\approx 10^7-10^9 \textrm{esu}$ for $\gamma$ -rays is estimated. Correspondingly, the normalized vector potential is $a_0=eE_0/(m_ec\omega _0)\approx 10^{-6}-10^{-4}$ for $\gamma$ -rays with $\omega _0\approx 10^{20}\, \textrm{s}^{-1}$ .

The local magnetic field follows the dipolar approximation

(4.3) \begin{equation} B_0\simeq B_{\textrm{s}}\left(\frac {R_\ast }{R_\ast +h}\right)^{3}. \end{equation}

Figure 9 shows the dependence of $\unicode{x1D6E4}_{\mathrm{max}}$ on altitude $h$ for $a_0=10^{-4}$ and $n_0\approx 10^{16}\,\mathrm{cm}^{-3}$ (corresponding to $\omega _{pe}=5.64\times 10^{12}\,\textrm{s}^{-1}$ ), as $\gamma$ -rays propagate from $h\approx 10^{4}\textrm{}$ to $h\approx 10^{7}\, \textrm{cm}$ . The curve showed a trend of decreasing firstly and then increasing, which is caused by changes in the strength of the magnetic field and the amplitude of the electromagnetic wave.

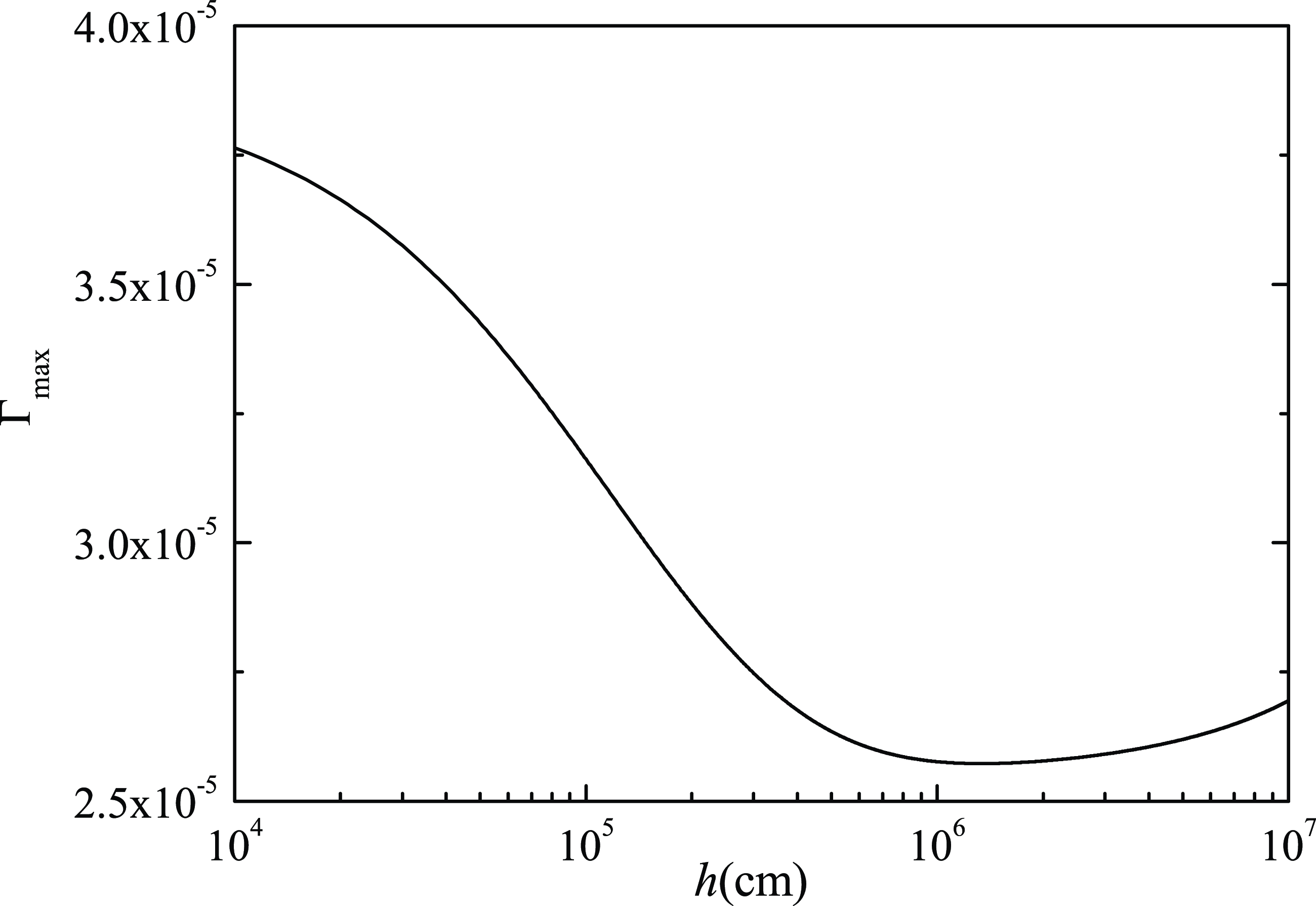
Figure 9. The variation of the function $\unicode{x1D6E4}_{\mathrm{max}}$ with the altitude $h$ for $a_0=10^{-4}$ and $n_0\approx 10^{16}\,\textrm{cm}^{-3}$ .

Using the dimensional growth rate $\unicode{x1D6E4}'_{\mathrm{max}}=\unicode{x1D6E4}_{\mathrm{max}}\omega _{pe}^2/\omega _0$ , the amplitude of electromagnetic radiations being modulated can be written as

(4.4) \begin{equation} a=a_0\exp \left (\int _0^t\unicode{x1D6E4}'_{\mathrm{max}}\textrm{d} t\right ). \end{equation}

The relative amplitude increase $[(a-a_0)/a_0]\,\%$ with the altitude $h$ is shown in figure 10. It shows that the amplitude of the electromagnetic radiation increases by $2.81\,\%$ , when it travels from $10^{4}\textrm{}$ to $10^{7}\, \textrm{cm}$ in the magnetosphere of the pair plasma.

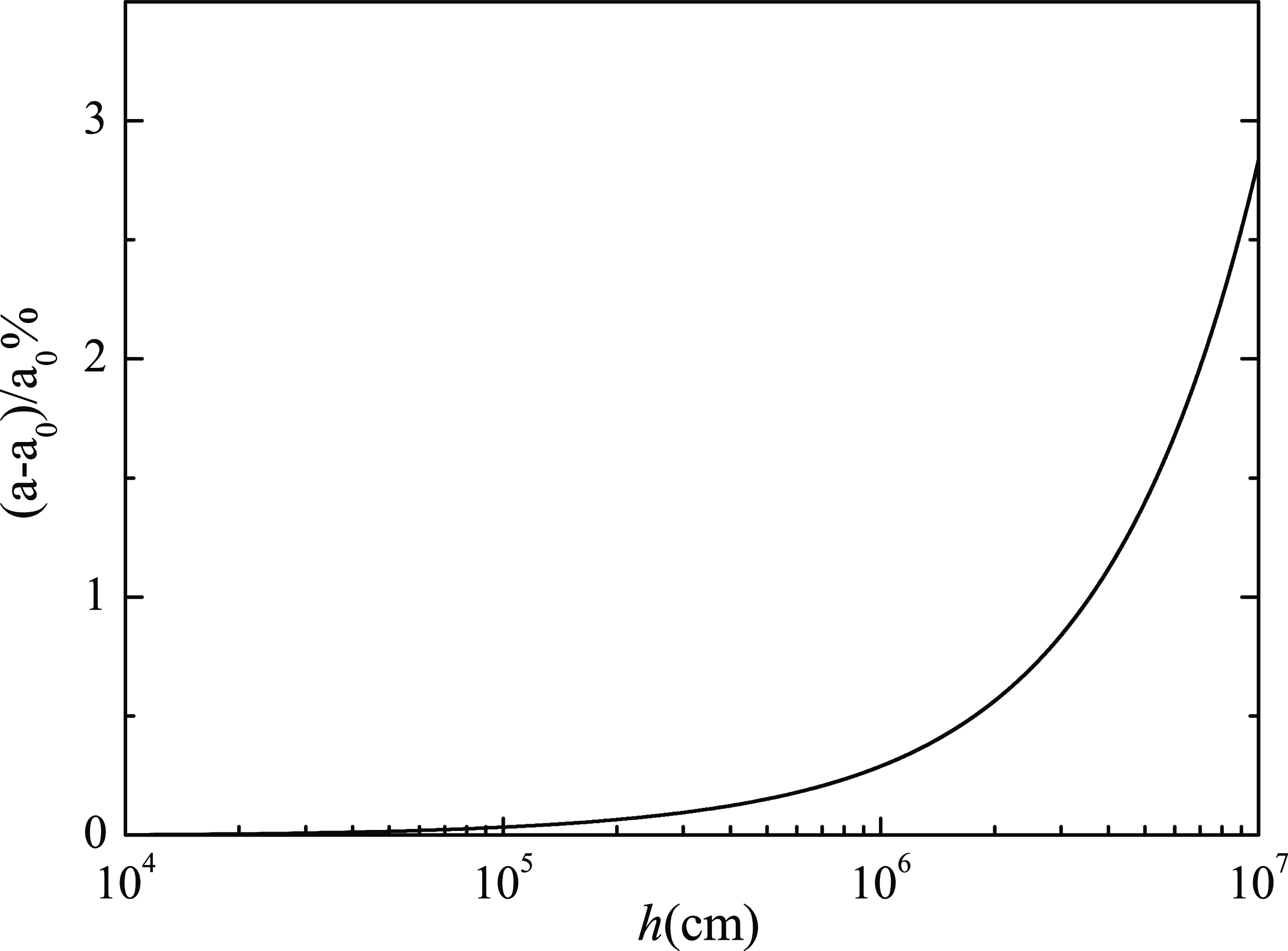
Figure 10. The relative amplitude increase $[(a-a_0)/a_0]\,\%$ with the altitude $h$ for $a_0=10^{-4}$ .

5. Summary and conclusion

In this work, the MI of an electromagnetic wave propagating along an external magnetic field in an EP plasma is investigated. The normalized amplitude of electromagnetic waves $a_0$ considered in this work ranges from 0.01 to 100, covering regimes from weakly relativistic to ultra-relativistic. A fully relativistic fluid model for particles is used, in which a temperature-dependent function $f_{\!j}=K_{3}(mc^2/k_{\textrm{B}}T_{j})/K_{2}(mc^2/k_{\textrm{B}}T_{j})$ is included to account for thermal effects. In the regime of weakly magnetized plasmas, we derive a modified nonlinear Schrödinger equation that describes the evolution of the envelope of an electromagnetic wave in magnetized EP plasmas. The dispersion relation and the growth rate of MI are studied theoretically and numerically. The variation of the MI growth rate with the wave amplitude $a_0$ , particle temperature $k_{\textrm{B}}T_{e,p}$ and magnetic field strength is analyzed in detail for two limiting cases: the low-temperature limit ( $k_{\textrm{B}}T_{j}\ll mc^2$ ) and the high-temperature limit ( $k_{\textrm{B}}T_{j}\gg mc^2$ ).

Due to the coupled multi-parameter effects, the MI exhibits a non-monotonic dependence on the individual parameters. From the numerical analysis, we draw the following conclusions:

1. i. When the plasma temperature and magnetic field intensity are fixed, the growth rate of MI increases first and then decreases with increasing wave amplitude.

2. ii. When the wave amplitude and magnetic field intensity are fixed, the growth rate of MI also demonstrates a non-monotonic trend, initially increasing then decreasing with rising plasma temperature.

3. iii. At fixed plasma temperature, the growth rate of MI increases with external magnetic field strength for low-intensity waves but decreases for high-intensity waves.

4. iv. At fixed wave amplitude, the MI growth rate decreases with increasing magnetic field strength for lower plasma temperatures, whereas it increases for higher temperatures. It should be pointed out that the magnetic field-induced variation in growth rate becomes negligible in the high-temperature limit.

We apply the theoretical results obtained in this paper to analyze the MI of gamma rays emitted from the pulsar surface. The result shows that the amplitude of the radiation increases by $2.81\,\%$ when propagating from $10^{4}\textrm{}$ to $10^{7}\, \textrm{cm}$ in the magnetosphere of the pulsar. This study enhances our understanding of the nonlinear dynamics in electromagnetic radiation propagating through magnetized pair plasmas on pulsar surfaces, and provides insights into intense laser–plasma interactions in magnetized hot pair plasmas.