1 Introduction
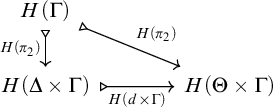
Gabriel–Ulmer duality [Reference Gabriel and Ulmer16] is a contravariant biequivalence
between the
![]() $2$
-category
$2$
-category
![]() ${\mathsf {FL}}$
of small finite-limit categories, and the
${\mathsf {FL}}$
of small finite-limit categories, and the
![]() $2$
-category
$2$
-category
![]() $\mathsf {LFP}$
of locally finitely presentable categories, i.e., locally small cocomplete categories admitting a dense set of compact (a.k.a. finitely presentable) objects. The duality assigns to every small finite-limit category
$\mathsf {LFP}$
of locally finitely presentable categories, i.e., locally small cocomplete categories admitting a dense set of compact (a.k.a. finitely presentable) objects. The duality assigns to every small finite-limit category
![]() $\mathcal {C}$
the category
$\mathcal {C}$
the category
![]() ${\mathsf {FL}}(\mathcal {C},\mathsf {Set})$
of finite-limit preserving functors to
${\mathsf {FL}}(\mathcal {C},\mathsf {Set})$
of finite-limit preserving functors to
![]() $\mathsf {Set}$
, and conversely it associates to every locally finitely presentable
$\mathsf {Set}$
, and conversely it associates to every locally finitely presentable
![]() $\mathfrak {X}$
the category
$\mathfrak {X}$
the category
![]() $\mathsf {LFP}(\mathfrak {X},\mathsf {Set})$
of finitary right adjoints to
$\mathsf {LFP}(\mathfrak {X},\mathsf {Set})$
of finitary right adjoints to
![]() $\mathsf {Set}$
, which is equivalent to the opposite of the full subcategory
$\mathsf {Set}$
, which is equivalent to the opposite of the full subcategory
![]() $\mathsf {comp}(\mathfrak {X})\subseteq \mathfrak {X}$
of compact objectsFootnote
1
.
$\mathsf {comp}(\mathfrak {X})\subseteq \mathfrak {X}$
of compact objectsFootnote
1
.
We view Gabriel–Ulmer duality as a theory-model duality: small finite-limit categories
![]() $\mathcal {C}$
are viewed as theories (which we call “finite-limit theories”), and—in the spirit of Lawverian functorial semantics [Reference Lawvere27]—the functor category
$\mathcal {C}$
are viewed as theories (which we call “finite-limit theories”), and—in the spirit of Lawverian functorial semantics [Reference Lawvere27]—the functor category
![]() ${\mathsf {FL}}(\mathcal {C},\mathsf {Set})$
is viewed as the category of models of the finite-limit theory
${\mathsf {FL}}(\mathcal {C},\mathsf {Set})$
is viewed as the category of models of the finite-limit theory
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
It is well known that finite-limit theories are equally expressive as various syntactically defined classes of theories, including
-
(1) Freyd’s essentially algebraic theories [Reference Freyd15], which permit a controlled form of partiality,
-
(2) Cartmell’s generalized algebraic theories (GATs) [Reference Cartmell12, Reference Cartmell13], which extend algebra by “dependent sorts,
-
(3) Johnstone’s cartesian theories [Reference Johnstone25, Definition D1.3.4], which permit a limited form of existential quantification, and
-
(4) Palmgren–Vickers’ Partial Horn theories [Reference Palmgren and Vickers34], which are based on a calculus of first order logic with partial terms and also admit relation symbols,
in the sense that for any theory
![]() $\mathbb {T}$
from one of these classes, the category
$\mathbb {T}$
from one of these classes, the category
![]() $\mathbb {T}\text {-}\mathsf {Mod}$
of models is locally finitely presentable, and conversely for every locally finitely presentable category
$\mathbb {T}\text {-}\mathsf {Mod}$
of models is locally finitely presentable, and conversely for every locally finitely presentable category
![]() $\mathfrak {X}$
there exists a theory from that class whose category of models is equivalent to
$\mathfrak {X}$
there exists a theory from that class whose category of models is equivalent to
![]() $\mathfrak {X}$
. While from a certain perspective this means that the classes (1)–(4) of theories are all equivalent to finite-limit theories, the syntactic representations of theories contain additional information that is not reflected in the categories of models, nor in the finite-limit theories. This “abstracting away” of syntactic details is typically viewed as a strength of the categorical/functorial approach, and indeed in mathematical practice we no more want to distinguish between the classical axiomatization of groups and Higman–Neumann’s axiomatization in terms of one operation and one equation [Reference Higman and Neumann20], than we want to distinguish between the symmetric group
$\mathfrak {X}$
. While from a certain perspective this means that the classes (1)–(4) of theories are all equivalent to finite-limit theories, the syntactic representations of theories contain additional information that is not reflected in the categories of models, nor in the finite-limit theories. This “abstracting away” of syntactic details is typically viewed as a strength of the categorical/functorial approach, and indeed in mathematical practice we no more want to distinguish between the classical axiomatization of groups and Higman–Neumann’s axiomatization in terms of one operation and one equation [Reference Higman and Neumann20], than we want to distinguish between the symmetric group
![]() $S_3$
and the dihedral group
$S_3$
and the dihedral group
![]() $D_3$
.
$D_3$
.
However, it turns out that in the case of GATs, the theories contain additional information that is not reflected in the corresponding finite-limit category, but nevertheless goes beyond mere syntactic details. This information is related to the structure of sort dependency in the theories, and we show here that it is reflected by certain weak factorization systems on the l.f.p. categories of models. For example, the
![]() $2$
-sorted theory of graphs
$2$
-sorted theory of graphs
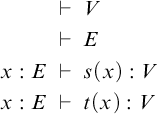 $$ \begin{align*} & \;\vdash\; V \\ & \;\vdash\; E \\ x : E & \;\vdash\; s(x):V \\ x : E & \;\vdash\; t(x):V \end{align*} $$
$$ \begin{align*} & \;\vdash\; V \\ & \;\vdash\; E \\ x : E & \;\vdash\; s(x):V \\ x : E & \;\vdash\; t(x):V \end{align*} $$
with sorts V and E and source and target operations s and t, has the same category of models as the dependently sorted theory
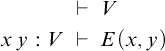 $$ \begin{align*} & \;\vdash\; V \\ x\, y : V & \;\vdash\; E(x,y) \end{align*} $$
$$ \begin{align*} & \;\vdash\; V \\ x\, y : V & \;\vdash\; E(x,y) \end{align*} $$
with a base sort V of vertices and a dependent sort E of edges (and no operations). But the syntactic categories of the theories are different, and this is reflected by different weak factorization systems on the categories of models: in the first case, the w.f.s. is cofibrantly generated by the initial inclusions
![]() $\varnothing \hookrightarrow (\bullet )$
and
$\varnothing \hookrightarrow (\bullet )$
and
![]() $\varnothing \hookrightarrow (\bullet {\to }\bullet )$
of the free graphs on one vertex and one edge, respectively, whereas in the second case the w.f.s. is generated by the inclusions
$\varnothing \hookrightarrow (\bullet {\to }\bullet )$
of the free graphs on one vertex and one edge, respectively, whereas in the second case the w.f.s. is generated by the inclusions
![]() $\varnothing \hookrightarrow (\bullet )$
and
$\varnothing \hookrightarrow (\bullet )$
and
![]() $(\bullet {\phantom {{\to }}}\bullet )\hookrightarrow (\bullet {\to }\bullet )$
. The non-trivial domain of the second generator reflects the dependency of the sort of edges on the sort of vertices.
$(\bullet {\phantom {{\to }}}\bullet )\hookrightarrow (\bullet {\to }\bullet )$
. The non-trivial domain of the second generator reflects the dependency of the sort of edges on the sort of vertices.
Concretely, the present work gives in Theorem 6.19 a duality
of
![]() $2$
-categories which extends Gabriel–Ulmer duality by incorporating this additional structure. On the right we have the
$2$
-categories which extends Gabriel–Ulmer duality by incorporating this additional structure. On the right we have the
![]() $2$
-category of clan-algebraic categories, which are locally finitely presentable categories equipped with a well-behaved kind of weak factorization system (Definition 6.1), while on the left we have a
$2$
-category of clan-algebraic categories, which are locally finitely presentable categories equipped with a well-behaved kind of weak factorization system (Definition 6.1), while on the left we have a
![]() $2$
-category of Cauchy-complete clans (Definition 2.1). These are categorical representations of GATs which can be viewed as a non-strict variant of Cartmell’s contextual categories (Definition 10.2), and are given by small categories equipped with a class of “display maps” representing type families, admitting certain (but not all) finite limits.
$2$
-category of Cauchy-complete clans (Definition 2.1). These are categorical representations of GATs which can be viewed as a non-strict variant of Cartmell’s contextual categories (Definition 10.2), and are given by small categories equipped with a class of “display maps” representing type families, admitting certain (but not all) finite limits.
Besides extending Gabriel–Ulmer duality, the duality (1.1) recovers Adámek–Rosický–Vitale’s duality between algebraic theories and algebraic categories [Reference Adámek, Rosický and Vitale3, Theorem 9.15] as a special case, and the latter duality was in fact inspirational for the present work. See Remark 6.20(a).
1.1 Structure of the paper
§2 introduces clans (Definition 2.1), the category of models of a clan
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
(Definition 2.6), and the extension–full weak factorization system on models (Definition 2.10).
$\mathcal {T}\!\text {-}\mathsf {Mod}$
(Definition 2.6), and the extension–full weak factorization system on models (Definition 2.10).
§3 gives a characterization of
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
as a kind of cocompletion of
$\mathcal {T}\!\text {-}\mathsf {Mod}$
as a kind of cocompletion of
![]() $\mathcal {T}^{\mathsf {op}}$
(Theorem 3.3), and uses this to give presentations of slice categories
$\mathcal {T}^{\mathsf {op}}$
(Theorem 3.3), and uses this to give presentations of slice categories
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/A$
, and of coslice categories
$\mathcal {T}\!\text {-}\mathsf {Mod}/A$
, and of coslice categories
![]() $H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
under representable models, as categories of models of derived clans (Propositions 3.5 and 3.6).
$H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
under representable models, as categories of models of derived clans (Propositions 3.5 and 3.6).
§4 introduces in Definition 4.1 the auxiliary notion of
![]() $(\mathsf {E},\mathsf {F})$
-category (a l.f.p. category with a w.f.s.
$(\mathsf {E},\mathsf {F})$
-category (a l.f.p. category with a w.f.s.
![]() $(\mathsf {E},\mathsf {F})$
), and shows that the mapping
$(\mathsf {E},\mathsf {F})$
), and shows that the mapping
![]() $\mathcal {T}\mapsto \mathcal {T}\!\text {-}\mathsf {Mod}$
gives rise to a contravariant
$\mathcal {T}\mapsto \mathcal {T}\!\text {-}\mathsf {Mod}$
gives rise to a contravariant
![]() $2$
-functor from clans to
$2$
-functor from clans to
![]() $(\mathsf {E},\mathsf {F})$
-categories which admits a left biadjoint (Proposition 4.6).
$(\mathsf {E},\mathsf {F})$
-categories which admits a left biadjoint (Proposition 4.6).
§5 shows that this biadjunction is idempotent, and that its fixed points in clans are precisely the Cauchy complete clans (Definition 5.1). For this we use the notion of flat model (Definition 5.3), and the fat small object argument, a Corollary of which we state in Corollary 5.5, but whose systematic treatment we defer to Appendix 11. Lemma 5.7 is an argument about compact objects in coslice categories which was not found in the literature.
§6 characterizes the fixed points of the biadjunction among
![]() $(\mathsf {E},\mathsf {F})$
-categories as clan-algebraic categories, which are
$(\mathsf {E},\mathsf {F})$
-categories as clan-algebraic categories, which are
![]() $(\mathsf {E},\mathsf {F})$
-categories satisfying a density and an exactness condition (Definition 6.1). The characterization is given by Theorems 6.2 and 6.18, where the proof of the latter requires a quite lot of machinery including a Reedy-like resolution argument. As a consequence, we obtain our main result in Theorem 6.19. As an application, §6.1 gives additional clan-algebraic w.f.s.s on the example
$(\mathsf {E},\mathsf {F})$
-categories satisfying a density and an exactness condition (Definition 6.1). The characterization is given by Theorems 6.2 and 6.18, where the proof of the latter requires a quite lot of machinery including a Reedy-like resolution argument. As a consequence, we obtain our main result in Theorem 6.19. As an application, §6.1 gives additional clan-algebraic w.f.s.s on the example
![]() $\mathsf {Cat}$
, which by the duality result correspond to additional clan-representations of
$\mathsf {Cat}$
, which by the duality result correspond to additional clan-representations of
![]() $\mathsf {Cat}$
.
$\mathsf {Cat}$
.
§7 contains a common counterexample to two natural questions about clan-algebraic w.f.s.s, and §8 discusses
![]() $\infty $
-models of clans in higher types.
$\infty $
-models of clans in higher types.
Appendix 9 contains basic facts about locally finitely presentable categories, weak factorization systems, and Quillen’s small-object argument, and Appendix 10 is an informal introduction to Cartmell’s generalized algebraic theories.
Finally, Appendix 11 contains a careful development of the fat small object argument for clans. The fat small object is a variant of Quillen’s small object argument due to Makkai, Rosický, and Vokrinek [Reference Makkai, Rosicky and Vokrinek33] (based on ideas by Lurie), which allows a more fine grained analysis of the process of saturating a class of maps. We use it to show that
![]() $0$
-extensions are flat (Corollary 11.9), which is needed in Sections 5 and 6.
$0$
-extensions are flat (Corollary 11.9), which is needed in Sections 5 and 6.
2 Clans
Definition 2.1. A clan is a small category
![]() $\mathcal {T}$
with a distinguished class
$\mathcal {T}$
with a distinguished class
![]() $\mathcal {T}_\dagger $
of arrows called display maps, such that:
$\mathcal {T}_\dagger $
of arrows called display maps, such that:
-
(i) Pullbacks of display maps along arbitrary maps exist and are display maps, i.e., if
 is a display map and
is a display map and
 $s:\Delta \to \Gamma $
is arbitrary, then there exists a pullback square (2.1)
$s:\Delta \to \Gamma $
is arbitrary, then there exists a pullback square (2.1)
where q is a display map.
-
(ii) Isomorphisms and compositions of display maps are display maps.
-
(iii)
 $\mathcal {T}$
has a terminal object, and terminal projections are display maps.
$\mathcal {T}$
has a terminal object, and terminal projections are display maps.
A clan morphism is a functor between clans which preserves display maps, pullbacks of display maps, and the terminal object. We write
![]() $\mathsf {Clan}$
for the
$\mathsf {Clan}$
for the
![]() $2$
-category of clans, clan-morphisms, and natural transformations.
$2$
-category of clans, clan-morphisms, and natural transformations.
Remarks 2.2.
-
(a) Definition 2.1 (apart from the smallness condition), and the term “display map”, were introduced by Taylor in his thesis [Reference Taylor41, §4.3.2], the explicit link to Cartmell’s work was made in his textbook [Reference Taylor42, Chapter VIII]. The name “clan” is due to Joyal [Reference Joyal26, Definition 1.1.1].
-
(b) Following Cartmell, we use the arrow symbol
 for display maps.
for display maps. -
(c) We have defined clans to be small by default, since this fits with our point of view of clans as theories, and makes the duality theory work.
However, it is also reasonable to consider non-small, “semantic” clans, and we will mention them occasionally (e.g., in Example 2.3(c) below), using the term large clan in this case.
Examples 2.3.
-
(a) Small finite-limit categories can be viewed as clans where all morphisms are display maps. We call such clans finite-limit clans.
-
(b) Small finite-product categories can be viewed as clans where the display maps are the morphisms that are (isomorphic to) product projections. We call such clans finite-product clans.
-
(c)
 $\mathsf {Kan}$
is the large clan whose underlying category is the full subcategory of the category
$\mathsf {Kan}$
is the large clan whose underlying category is the full subcategory of the category
 $[\Delta ^{\mathsf {op}},\mathsf {Set}]$
of simplicial sets on Kan complexes, and whose display maps are the Kan fibrations.
$[\Delta ^{\mathsf {op}},\mathsf {Set}]$
of simplicial sets on Kan complexes, and whose display maps are the Kan fibrations. -
(d) The syntactic category of every generalized algebraic theory in the sense of Cartmell [Reference Cartmell12, Reference Cartmell13] is a clan. This is explained in §10, and we discuss the example of the clan for categories in greater detail in §2.2 below.
Since it seems to lead to a more readable exposition, we introduce explicit notation and terminology for the dual notion.
Definition 2.4. A coclan is a small category
![]() $\mathcal {C}$
with a distinguished class
$\mathcal {C}$
with a distinguished class
![]() $\mathcal {C}_\dagger $
of arrows called codisplay maps satisfying the dual axioms of clans. The
$\mathcal {C}_\dagger $
of arrows called codisplay maps satisfying the dual axioms of clans. The
![]() $2$
-category
$2$
-category
![]() $\mathsf {CoClan}$
of coclans is defined dually to that of clans, i.e.,
$\mathsf {CoClan}$
of coclans is defined dually to that of clans, i.e.,
for coclans
![]() $\mathcal {C},\mathcal {D}$
. We use the arrow symbol
$\mathcal {C},\mathcal {D}$
. We use the arrow symbol ![]() for co-display maps.
for co-display maps.
Remark 2.5. Coclans appear under the name cofibration categories in [Reference Henry19, Definition 2.1.5]. This is however in conflict with Baues’ notion of cofibration category, which also includes a notion of weak equivalence [Reference Baues6, Section I.1]. See also Remark 2.11(d) below.
2.1 Models
Definition 2.6. A model of a clan
![]() $\mathcal {T}$
is a functor
$\mathcal {T}$
is a functor
![]() $A:\mathcal {T}\to \mathsf {Set}$
which preserves the terminal object and pullbacks of display maps. We write
$A:\mathcal {T}\to \mathsf {Set}$
which preserves the terminal object and pullbacks of display maps. We write
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
for the category of models of
$\mathcal {T}\!\text {-}\mathsf {Mod}$
for the category of models of
![]() $\mathcal {T}$
, viewed as a full subcategory of the functor category
$\mathcal {T}$
, viewed as a full subcategory of the functor category
![]() $[\mathcal {T},\mathsf {Set}]$
.
$[\mathcal {T},\mathsf {Set}]$
.
Remark 2.7. In other words, a model of a clan
![]() $\mathcal {T}$
is a clan morphism into the large clan with underlying category
$\mathcal {T}$
is a clan morphism into the large clan with underlying category
![]() $\mathsf {Set}$
set and the maximal (i.e., finite-limit) clan structure.
$\mathsf {Set}$
set and the maximal (i.e., finite-limit) clan structure.
In the spirit of functorial semantics, it is possible to consider models of clans in other categories than sets, and even in other (typically large) clans. However, the duality theory presented here is about models in
![]() $\mathsf {Set}$
and we don’t consider any other kind (apart from some speculations about
$\mathsf {Set}$
and we don’t consider any other kind (apart from some speculations about
![]() $\infty $
-categorical models in §8).
$\infty $
-categorical models in §8).
Examples 2.8.
-
(a) If
 $\mathcal {C}$
is a finite-limit clan (Example 2.3(a)) then
$\mathcal {C}$
is a finite-limit clan (Example 2.3(a)) then
 $\mathsf {Mod}(\mathcal {C})$
coincides with the category
$\mathsf {Mod}(\mathcal {C})$
coincides with the category
 ${\mathsf {FL}}(\mathcal {C},\mathsf {Set})$
of finite-limit preserving functors into
${\mathsf {FL}}(\mathcal {C},\mathsf {Set})$
of finite-limit preserving functors into
 $\mathsf {Set}$
, which we also view as category of models of
$\mathsf {Set}$
, which we also view as category of models of
 $\mathcal {C}$
qua finite-limit theory. This means that it makes sense to view finite-limit theories as a special case of clans.
$\mathcal {C}$
qua finite-limit theory. This means that it makes sense to view finite-limit theories as a special case of clans. -
(b) If
 $\mathcal {C}$
is a finite-product clan, then
$\mathcal {C}$
is a finite-product clan, then
 $\mathsf {Mod}(\mathcal {C})$
is the category
$\mathsf {Mod}(\mathcal {C})$
is the category
 ${\mathsf {FP}}(\mathcal {C},\mathsf {Set})$
of finite-product preserving functors into
${\mathsf {FP}}(\mathcal {C},\mathsf {Set})$
of finite-product preserving functors into
 $\mathsf {Set}$
.
$\mathsf {Set}$
.In Adámek, Rosický and Vitale’s textbook [Reference Adámek, Rosický and Vitale3, Definition 1.1], small finite-product categories are called algebraic theories, and models of algebraic theories are defined to be finite-product preserving functors into
 $\mathsf {Set}$
. Thus, we recover their notions as a special case, i.e., finite-product clans correspond to algebraic theories, and models correspond to algebras. To emphasize the analogy to the finite-limit case, we refer to algebraic theories also as finite-product theories.
$\mathsf {Set}$
. Thus, we recover their notions as a special case, i.e., finite-product clans correspond to algebraic theories, and models correspond to algebras. To emphasize the analogy to the finite-limit case, we refer to algebraic theories also as finite-product theories. -
(c) If
 $\mathbb {T}$
is a GAT, then the category of models of its syntactic category
$\mathbb {T}$
is a GAT, then the category of models of its syntactic category
 $\mathcal {C}[\mathbb {T}]$
(with the clan structure described in §10.1) is equivalent to the models of
$\mathcal {C}[\mathbb {T}]$
(with the clan structure described in §10.1) is equivalent to the models of
 $\mathbb {T}$
, which Cartmell definesFootnote
2
to be the category
$\mathbb {T}$
, which Cartmell definesFootnote
2
to be the category
 $\mathsf {ConFunc}(\mathcal {C}[\mathbb {T}],\mathsf {Fam})$
of contextual functors and natural transformations into the contextual category
$\mathsf {ConFunc}(\mathcal {C}[\mathbb {T}],\mathsf {Fam})$
of contextual functors and natural transformations into the contextual category
 $\mathsf {Fam}$
of iterated families of sets.
$\mathsf {Fam}$
of iterated families of sets.
The following remarks discuss some categorical properties of the category
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
of models of a clan, establishing in particular that it is locally finitely presentable. We refer to §9 for the relevant definitions.
$\mathcal {T}\!\text {-}\mathsf {Mod}$
of models of a clan, establishing in particular that it is locally finitely presentable. We refer to §9 for the relevant definitions.
Remarks 2.9.
-
(a) As a category of models of a finite-limit sketch,
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
is reflective (and therefore closed under arbitrary limits) in
$\mathcal {T}\!\text {-}\mathsf {Mod}$
is reflective (and therefore closed under arbitrary limits) in
 $[\mathcal {T},\mathsf {Set}]$
, and moreover it is closed under filtered colimits [Reference Adámek and Rosicky2, Section 1.C]. In particular,
$[\mathcal {T},\mathsf {Set}]$
, and moreover it is closed under filtered colimits [Reference Adámek and Rosicky2, Section 1.C]. In particular,
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
is locally finitely presentable.
$\mathcal {T}\!\text {-}\mathsf {Mod}$
is locally finitely presentable. -
(b) The representable functors
 $\mathcal {T}(\Gamma ,-):\mathcal {T}\to \mathsf {Set}$
are models of
$\mathcal {T}(\Gamma ,-):\mathcal {T}\to \mathsf {Set}$
are models of
 $\mathcal {T}$
for all
$\mathcal {T}$
for all
 $\Gamma \in \mathcal {T}$
, thus the Yoneda embedding
$\Gamma \in \mathcal {T}$
, thus the Yoneda embedding  lifts along the inclusion
lifts along the inclusion
 $\mathcal {T}\!\text {-}\mathsf {Mod}\hookrightarrow [\mathcal {T},\mathsf {Set}]$
to a fully faithful functor
$\mathcal {T}\!\text {-}\mathsf {Mod}\hookrightarrow [\mathcal {T},\mathsf {Set}]$
to a fully faithful functor
 $H:\mathcal {T}^{\mathsf {op}}\to \mathcal {T}\!\text {-}\mathsf {Mod}$
.
$H:\mathcal {T}^{\mathsf {op}}\to \mathcal {T}\!\text {-}\mathsf {Mod}$
. 
-
(c) For
 $\Gamma \in \mathcal {T}$
, the representable functor
$\Gamma \in \mathcal {T}$
, the representable functor  $$ \begin{align*} \mathcal{T}\!\text{-}\mathsf{Mod}(H(\Gamma),-):\mathcal{T}\!\text{-}\mathsf{Mod}\to\mathsf{Set} \end{align*} $$
$$ \begin{align*} \mathcal{T}\!\text{-}\mathsf{Mod}(H(\Gamma),-):\mathcal{T}\!\text{-}\mathsf{Mod}\to\mathsf{Set} \end{align*} $$
is isomorphic to the evaluation functor
 $A\mapsto A(\Gamma )$
, hence it preserves filtered colimits as those are computed in
$A\mapsto A(\Gamma )$
, hence it preserves filtered colimits as those are computed in
 $[\mathcal {T},\mathsf {Set}]$
and therefore pointwise. This means that
$[\mathcal {T},\mathsf {Set}]$
and therefore pointwise. This means that
 $H(\Gamma )$
is compact
Footnote
3
in
$H(\Gamma )$
is compact
Footnote
3
in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
.
$\mathcal {T}\!\text {-}\mathsf {Mod}$
.
2.2 The clan for categories
§10.1 describes how the syntactic category
![]() $\mathcal {C}[\mathbb {T}]$
of every GAT
$\mathcal {C}[\mathbb {T}]$
of every GAT
![]() $\mathbb {T}$
can be viewed as a clan. The present section elaborates this for the specific case of the GAT
$\mathbb {T}$
can be viewed as a clan. The present section elaborates this for the specific case of the GAT
![]() $\mathbb {T}_{\mathsf {Cat}}$
of categories (10.1). We will use this clan and variations as a running example throughout the article.
$\mathbb {T}_{\mathsf {Cat}}$
of categories (10.1). We will use this clan and variations as a running example throughout the article.
Recall from Definition 10.1 that the objects of
![]() $\mathcal {T}_{\mathsf {Cat}}:=\mathcal {C}[\mathbb {T}_{\mathsf {Cat}}]$
are equivalence classes of contexts, and the arrows are equivalence classes of substitutions. By inspection of the axioms we see that sorts in
$\mathcal {T}_{\mathsf {Cat}}:=\mathcal {C}[\mathbb {T}_{\mathsf {Cat}}]$
are equivalence classes of contexts, and the arrows are equivalence classes of substitutions. By inspection of the axioms we see that sorts in
![]() $\mathbb {T}_{\mathsf {Cat}}$
cannot depend on non-variable terms, since the only non-constant sort symbol is
$\mathbb {T}_{\mathsf {Cat}}$
cannot depend on non-variable terms, since the only non-constant sort symbol is
![]() $x\,y:O\vdash A(x,y)$
and there are no function symbols of type O. This means that up to reordering, all contexts are of the form
$x\,y:O\vdash A(x,y)$
and there are no function symbols of type O. This means that up to reordering, all contexts are of the form
where
![]() $n,k\geq 0$
(such that
$n,k\geq 0$
(such that
![]() $n> 0$
whenever
$n> 0$
whenever
![]() $k>0$
) and
$k>0$
) and
![]() $1\leq s_l,t_l\leq n$
for
$1\leq s_l,t_l\leq n$
for
![]() $1\leq l\leq k$
; declaring first a list of object variables and then a list of arrow variables, each depending on a pair of the object variables. Given another context
$1\leq l\leq k$
; declaring first a list of object variables and then a list of arrow variables, each depending on a pair of the object variables. Given another context
![]() $(u_1\dots u_m,v_1 \dots v_h)$
, a substitution
$(u_1\dots u_m,v_1 \dots v_h)$
, a substitution
is a tuple
![]() $\sigma = (u_{i_1}\dots u_{i_n},f_1\dots f_k)$
where
$\sigma = (u_{i_1}\dots u_{i_n},f_1\dots f_k)$
where
![]() $1\leq i_1,\dots ,i_n\leq m$
and the
$1\leq i_1,\dots ,i_n\leq m$
and the
![]() $f_l$
are terms
$f_l$
are terms
Some reflection shows that
![]() $\mathcal {C}[\mathbb {T}_{\mathsf {Cat}}]$
is dual to the full subcategory of
$\mathcal {C}[\mathbb {T}_{\mathsf {Cat}}]$
is dual to the full subcategory of
![]() $\mathsf {Cat}$
on free categories on finite graphs: the data of a context (2.2) is that of finite sets
$\mathsf {Cat}$
on free categories on finite graphs: the data of a context (2.2) is that of finite sets
![]() $V=\{x_1,\dots ,x_n\}$
,
$V=\{x_1,\dots ,x_n\}$
,
![]() $E=\{y_1,\dots ,y_k\}$
of vertices and edges, and source and target functions
$E=\{y_1,\dots ,y_k\}$
of vertices and edges, and source and target functions
![]() $s,t:E\to V$
, and a substitution
$s,t:E\to V$
, and a substitution
![]() $\sigma $
as above consists of a mapping from
$\sigma $
as above consists of a mapping from
![]() $\{x_1,\dots ,x_n\}$
to
$\{x_1,\dots ,x_n\}$
to
![]() $\{u_1,\dots ,u_m\}$
and a mapping from
$\{u_1,\dots ,u_m\}$
and a mapping from
![]() $\{y_1,\dots ,y_k\}$
to suitable paths in the graph represented by the domain. This is not surprising, since every clan embeds contravariantly into its category of models by Remark 2.9(b). Finally, the display maps in
$\{y_1,\dots ,y_k\}$
to suitable paths in the graph represented by the domain. This is not surprising, since every clan embeds contravariantly into its category of models by Remark 2.9(b). Finally, the display maps in
![]() $\mathcal {T}_{\mathsf {Cat}}$
, which syntactically correspond to projections “from longer contexts to shorter ones”, correspond to functors
$\mathcal {T}_{\mathsf {Cat}}$
, which syntactically correspond to projections “from longer contexts to shorter ones”, correspond to functors
![]() $G^*\hookrightarrow H^*$
between free categories induced by inclusions (i.e., monomorphisms)
$G^*\hookrightarrow H^*$
between free categories induced by inclusions (i.e., monomorphisms)
![]() $G\hookrightarrow H$
of finite graphs in the dual presentation.
$G\hookrightarrow H$
of finite graphs in the dual presentation.
2.3 The weak factorization system on models
Next we introduce the extension–full weak factorization system on the category of models of a clan. We refer to §9 for basic facts about lifting properties and weak factorization systems (w.f.s.s) as well as pointers to the literature.
Definition 2.10. Let
![]() $\mathcal {T}$
be a clan.
$\mathcal {T}$
be a clan.
-
(i) We call a map
 $f:A\to B$
in
$f:A\to B$
in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
full, if it has the right lifting property (r.l.p., see Definition 9.4(i)) w.r.t. all maps
$\mathcal {T}\!\text {-}\mathsf {Mod}$
full, if it has the right lifting property (r.l.p., see Definition 9.4(i)) w.r.t. all maps
 $H(p)$
for p a display map.
$H(p)$
for p a display map. -
(ii) We call
 $f:A\to B$
an extension, if it has the left lifting property (l.l.p.) w.r.t. all full maps.
$f:A\to B$
an extension, if it has the left lifting property (l.l.p.) w.r.t. all full maps. -
(iii) We call
 $A\in \mathcal {T}\!\text {-}\mathsf {Mod}$
a
$A\in \mathcal {T}\!\text {-}\mathsf {Mod}$
a
 $0$
-extension, if
$0$
-extension, if
 $0\to A$
is an extension.
$0\to A$
is an extension.
Remarks 2.11.
-
(a) We use the arrow symbols “
 ” for extensions (just as for codisplay maps), and “
” for extensions (just as for codisplay maps), and “
 $\twoheadrightarrow $
” for full maps. We write
$\twoheadrightarrow $
” for full maps. We write
 $\mathsf {E}$
and
$\mathsf {E}$
and
 $\mathsf {F}$
for the classes of extensions and full maps in
$\mathsf {F}$
for the classes of extensions and full maps in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
, respectively. By the small object argument (Theorem 9.5), extensions and full maps form a weak factorization system
$\mathcal {T}\!\text {-}\mathsf {Mod}$
, respectively. By the small object argument (Theorem 9.5), extensions and full maps form a weak factorization system
 $(\mathsf {E},\mathsf {F})$
.
$(\mathsf {E},\mathsf {F})$
. -
(b) A map
 $f:A\to B$
in
$f:A\to B$
in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
is full if and only if the naturality square
$\mathcal {T}\!\text {-}\mathsf {Mod}$
is full if and only if the naturality square 
is a weak pullback Footnote 4 in
 $\mathsf {Set}$
for all display maps
$\mathsf {Set}$
for all display maps  . Setting
. Setting
 $\Gamma =1$
we see that full maps are pointwise surjective and therefore regular epimorphisms (the pointwise kernel pair
$\Gamma =1$
we see that full maps are pointwise surjective and therefore regular epimorphisms (the pointwise kernel pair
 $p,q: R\to A$
of f is in
$p,q: R\to A$
of f is in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
since
$\mathcal {T}\!\text {-}\mathsf {Mod}$
since
 $\mathcal {T}\!\text {-}\mathsf {Mod}\hookrightarrow [\mathcal {T},\mathsf {Set}]$
creates limits, and pointwise surjective maps are coequalizers of their kernel pairs in
$\mathcal {T}\!\text {-}\mathsf {Mod}\hookrightarrow [\mathcal {T},\mathsf {Set}]$
creates limits, and pointwise surjective maps are coequalizers of their kernel pairs in
 $[\mathcal {T},\mathsf {Set}]$
, hence all the more so in
$[\mathcal {T},\mathsf {Set}]$
, hence all the more so in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
).
$\mathcal {T}\!\text {-}\mathsf {Mod}$
). -
(c) For every display map
 in
in
 $\mathcal {T}$
, the arrow
$\mathcal {T}$
, the arrow  is an extension—these are precisely the generators of the w.f.s. In particular, all representable models
is an extension—these are precisely the generators of the w.f.s. In particular, all representable models
 $H(\Gamma )$
are
$H(\Gamma )$
are
 $0$
-extensions, since all terminal projections
$0$
-extensions, since all terminal projections  are display maps in
are display maps in
 $\mathcal {T}$
.
$\mathcal {T}$
. -
(d) The same w.f.s. was already defined by Simon Henry in [Reference Henry19, Definition 2.4.2], using the terminology of “cofibration categories” mentioned in Remark 2.5. There, extensions are called cofibrations, and full maps trivial fibrations. We have not used this homotopical terminology here since we don’t want to think about full maps as being “trivial” in any way.
Examples 2.12.
-
(a) If
 $\mathcal {T}$
is a finite-product clan, then
$\mathcal {T}$
is a finite-product clan, then
 $(\mathsf {E},\mathsf {F})$
is cofibrantly generated by initial injections
$(\mathsf {E},\mathsf {F})$
is cofibrantly generated by initial injections  , since for every display map
, since for every display map  the generator
the generator
 $H(p)$
is a pushout
$H(p)$
is a pushout 
in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
of an initial inclusion, and left classes of w.f.s.s are closed under pushout. It follows that the full maps are precisely the pointwise surjective maps, which in this case also coincide with the regular epis, since finite-product preserving functors are closed under image factorization in
$\mathcal {T}\!\text {-}\mathsf {Mod}$
of an initial inclusion, and left classes of w.f.s.s are closed under pushout. It follows that the full maps are precisely the pointwise surjective maps, which in this case also coincide with the regular epis, since finite-product preserving functors are closed under image factorization in
 $[\mathcal {T},\mathsf {Set}]$
(and thus every non-surjective arrow factors through a strict subobject). Thus, the
$[\mathcal {T},\mathsf {Set}]$
(and thus every non-surjective arrow factors through a strict subobject). Thus, the
 $0$
-extensions are precisely the regular-projective objects in the finite-product case, which also play a central role in [Reference Adámek, Rosický and Vitale3].
$0$
-extensions are precisely the regular-projective objects in the finite-product case, which also play a central role in [Reference Adámek, Rosický and Vitale3]. -
(b) If
 $\mathcal {T}$
is a finite-limit clan then all naturality squares of full maps
$\mathcal {T}$
is a finite-limit clan then all naturality squares of full maps
 $f:A\twoheadrightarrow B$
are weak pullbacks, including the naturality squares
$f:A\twoheadrightarrow B$
are weak pullbacks, including the naturality squares 
of diagonals
 $\Gamma \to \Gamma \times \Gamma $
. From this it follows easily that
$\Gamma \to \Gamma \times \Gamma $
. From this it follows easily that
 $f_\Gamma $
is injective, and since we have shown that it is surjective above, we conclude that only isomorphisms are full in the finite-limit case.
$f_\Gamma $
is injective, and since we have shown that it is surjective above, we conclude that only isomorphisms are full in the finite-limit case. -
(c) The w.f.s. on
 $\mathsf {Cat}$
induced by the presentation
$\mathsf {Cat}$
induced by the presentation
 $\mathsf {Cat}=\mathcal {T}_{\mathsf {Cat}}\text {-}\mathsf {Mod}$
(see §2.2) has as full maps functors
$\mathsf {Cat}=\mathcal {T}_{\mathsf {Cat}}\text {-}\mathsf {Mod}$
(see §2.2) has as full maps functors
 $F:\mathbb {C}\to \mathbb {D}$
which have the r.l.p. w.r.t. all functors
$F:\mathbb {C}\to \mathbb {D}$
which have the r.l.p. w.r.t. all functors
 $G^*\hookrightarrow H^*$
for inclusions
$G^*\hookrightarrow H^*$
for inclusions
 $G\hookrightarrow H$
of finite graphs. It is not difficult to see that these are precisely the functors which are full in the classical sense and moreover surjective on objects, and that the w.f.s. is already generated by the functors
$G\hookrightarrow H$
of finite graphs. It is not difficult to see that these are precisely the functors which are full in the classical sense and moreover surjective on objects, and that the w.f.s. is already generated by the functors
 $(0\hookrightarrow 1)$
and
$(0\hookrightarrow 1)$
and  , where
, where
 $2$
is the discrete category with two objects and
$2$
is the discrete category with two objects and  is the interval category.
is the interval category.
3 Comodels and the universal property of
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
$\mathcal {T}\!\text {-}\mathsf {Mod}$
3.1 Nerve–realization adjunctions
We recall basic facts about nerve–realization adjunctions, to establish notation and conventions. Recall that for small
![]() $\mathbb {C}$
the presheaf category
$\mathbb {C}$
the presheaf category
![]() $\widehat {\mathbb {C}}=[\mathbb {C}^{\mathsf {op}},\mathsf {Set}]$
is the small-colimit completion of
$\widehat {\mathbb {C}}=[\mathbb {C}^{\mathsf {op}},\mathsf {Set}]$
is the small-colimit completion of
![]() $\mathbb {C}$
, in the sense that for every cocomplete category
$\mathbb {C}$
, in the sense that for every cocomplete category
![]() $\mathfrak {X}$
, precomposition with the Yoneda embedding
$\mathfrak {X}$
, precomposition with the Yoneda embedding ![]() induces an equivalence
induces an equivalence
between the categories of cocontinuous functors
![]() $\widehat {\mathbb {C}}\to \mathfrak {X}$
, and of functors
$\widehat {\mathbb {C}}\to \mathfrak {X}$
, and of functors
![]() $\mathbb {C}\to \mathfrak {X}$
. Specifically, the cocontinuous functor
$\mathbb {C}\to \mathfrak {X}$
. Specifically, the cocontinuous functor
![]() $F_\otimes :\widehat {\mathbb {C}}\to \mathfrak {X}$
corresponding to
$F_\otimes :\widehat {\mathbb {C}}\to \mathfrak {X}$
corresponding to
![]() $F:\mathbb {C}\to \mathfrak {X}$
is the left Kan extension of F along
$F:\mathbb {C}\to \mathfrak {X}$
is the left Kan extension of F along ![]() , whose value at
, whose value at
![]() $A\in \widehat {\mathbb {C}}$
admits alternative representations
$A\in \widehat {\mathbb {C}}$
admits alternative representations
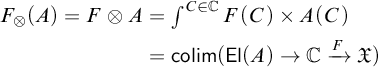 $$ \begin{align*} F_\otimes(A)=F\otimes A&=\textstyle\int^{C\in\mathbb{C}}F(C)\times A(C) \\&=\mathsf{colim}(\mathsf{El}(A)\to\mathbb{C}\xrightarrow{F}\mathfrak{X}) \end{align*} $$
$$ \begin{align*} F_\otimes(A)=F\otimes A&=\textstyle\int^{C\in\mathbb{C}}F(C)\times A(C) \\&=\mathsf{colim}(\mathsf{El}(A)\to\mathbb{C}\xrightarrow{F}\mathfrak{X}) \end{align*} $$
as a coend and as a colimit indexed by the category
![]() $\mathsf {El}(A)$
of elements of A. If
$\mathsf {El}(A)$
of elements of A. If
![]() $\mathfrak {X}$
is locally small then
$\mathfrak {X}$
is locally small then
![]() $F_\otimes $
has a right adjoint
$F_\otimes $
has a right adjoint
![]() $F_N:\mathfrak {X}\to \widehat {\mathbb {C}}$
given by
$F_N:\mathfrak {X}\to \widehat {\mathbb {C}}$
given by
![]() $F_N(X)=\mathfrak {X}(F(-),X)$
. We call
$F_N(X)=\mathfrak {X}(F(-),X)$
. We call
![]() $F_N$
and
$F_N$
and
![]() $F_\otimes $
the nerve and realization functors of F, respectively, and
$F_\otimes $
the nerve and realization functors of F, respectively, and
![]() $F_\otimes \dashv F_N$
the nerve–realization adjunction of F.
$F_\otimes \dashv F_N$
the nerve–realization adjunction of F.
3.2 Comodels and the universal property of
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
$\mathcal {T}\!\text {-}\mathsf {Mod}$
The universal property of
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
is an equivalence between cocontinuous functors out of
$\mathcal {T}\!\text {-}\mathsf {Mod}$
is an equivalence between cocontinuous functors out of
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
and coclan morphisms out of
$\mathcal {T}\!\text {-}\mathsf {Mod}$
and coclan morphisms out of
![]() $\mathcal {T}^{\mathsf {op}}$
. Following a suggestion by Mathieu Anel, we refer to the latter as comodels of the clan. We will only use this term for coclan morphisms with cocomplete codomain.
$\mathcal {T}^{\mathsf {op}}$
. Following a suggestion by Mathieu Anel, we refer to the latter as comodels of the clan. We will only use this term for coclan morphisms with cocomplete codomain.
Definition 3.1. A comodel of a clan
![]() $\mathcal {T}$
in a cocomplete category
$\mathcal {T}$
in a cocomplete category
![]() $\mathfrak {X}$
is a functor
$\mathfrak {X}$
is a functor
![]() $F:\mathcal {T}^{\mathsf {op}}\to \mathfrak {X}$
which sends
$F:\mathcal {T}^{\mathsf {op}}\to \mathfrak {X}$
which sends
![]() $1$
to
$1$
to
![]() $0$
, and display-pullbacks to pushouts. We write
$0$
, and display-pullbacks to pushouts. We write
![]() $\mathcal {T}\!\text {-}\mathsf {CoMod}(\mathfrak {X})$
for the category of comodels of
$\mathcal {T}\!\text {-}\mathsf {CoMod}(\mathfrak {X})$
for the category of comodels of
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\mathfrak {X}$
, as a full subcategory of the functor category.
$\mathfrak {X}$
, as a full subcategory of the functor category.
Remark 3.2. In other words, a comodel of
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\mathfrak {X}$
is a coclan morphism from
$\mathfrak {X}$
is a coclan morphism from
![]() $\mathcal {T}^{\mathsf {op}}$
to the large coclan with underlying category
$\mathcal {T}^{\mathsf {op}}$
to the large coclan with underlying category
![]() $\mathfrak {X}$
and the maximal coclan structure.
$\mathfrak {X}$
and the maximal coclan structure.
Theorem 3.3 (The universal property of
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
).
$\mathcal {T}\!\text {-}\mathsf {Mod}$
).
Let
![]() $\mathcal {T}$
be a clan.
$\mathcal {T}$
be a clan.
-
(i) The functor
 $H:\mathcal {T}^{\mathsf {op}}\to \mathcal {T}\!\text {-}\mathsf {Mod}$
from Remark 2.9(b) is a comodel.
$H:\mathcal {T}^{\mathsf {op}}\to \mathcal {T}\!\text {-}\mathsf {Mod}$
from Remark 2.9(b) is a comodel. -
(ii) For every cocomplete
 $\mathfrak {X}$
and comodel
$\mathfrak {X}$
and comodel
 $F:\mathcal {T}^{\mathsf {op}}\to \mathfrak {X}$
, the restriction of
$F:\mathcal {T}^{\mathsf {op}}\to \mathfrak {X}$
, the restriction of
 $F_\otimes :[\mathcal {T},\mathsf {Set}]\to \mathfrak {X}$
to
$F_\otimes :[\mathcal {T},\mathsf {Set}]\to \mathfrak {X}$
to
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
is cocontinuous. Thus, precomposition with H gives rise to an equivalence (3.2)
$\mathcal {T}\!\text {-}\mathsf {Mod}$
is cocontinuous. Thus, precomposition with H gives rise to an equivalence (3.2) $$ \begin{align} \mathsf{CoCont}(\mathcal{T}\!\text{-}\mathsf{Mod},\mathfrak{X})\stackrel{\simeq}{\longrightarrow}\mathcal{T}\!\text{-}\mathsf{CoMod}(\mathfrak{X}) \end{align} $$
$$ \begin{align} \mathsf{CoCont}(\mathcal{T}\!\text{-}\mathsf{Mod},\mathfrak{X})\stackrel{\simeq}{\longrightarrow}\mathcal{T}\!\text{-}\mathsf{CoMod}(\mathfrak{X}) \end{align} $$
between categories of continuous functors and of comodels.
-
(iii) If
 $F:\mathcal {T}^{\mathsf {op}}\to \mathfrak {X}$
is a comodel and
$F:\mathcal {T}^{\mathsf {op}}\to \mathfrak {X}$
is a comodel and
 $\mathfrak {X}$
is locally small, then the nerve functor
$\mathfrak {X}$
is locally small, then the nerve functor
 $F_N:\mathfrak {X}\to [\mathcal {T},\mathsf {Set}]$
factors through the inclusion
$F_N:\mathfrak {X}\to [\mathcal {T},\mathsf {Set}]$
factors through the inclusion
 $\mathcal {T}\!\text {-}\mathsf {Mod}\hookrightarrow [\mathcal {T},\mathsf {Set}]$
, giving rise to a restricted nerve realization adjunction
$\mathcal {T}\!\text {-}\mathsf {Mod}\hookrightarrow [\mathcal {T},\mathsf {Set}]$
, giving rise to a restricted nerve realization adjunction
 $F_\otimes :\mathcal {T}\!\text {-}\mathsf {Mod}\leftrightarrows \mathfrak {X}:F_N$
.
$F_\otimes :\mathcal {T}\!\text {-}\mathsf {Mod}\leftrightarrows \mathfrak {X}:F_N$
. 
Proof. Analogous statements to (i) and (ii) hold more generally for arbitrary small realizedFootnote 5 limit sketches. As Brandenburg points out on MathOverflowFootnote 6 , the earliest reference for this seems to be [Reference Pultr37, Theorem 2.5]. See also [Reference Brandenburg10] which gives a careful account of an even more general statement for non-small sketches.
For claim (iii), it’s easy to see that for
![]() $X\in \mathfrak {X}$
, the functor
$X\in \mathfrak {X}$
, the functor
![]() $F_N(X)=\mathfrak {X}(F(-),X)$
is a model since F is a comodel.
$F_N(X)=\mathfrak {X}(F(-),X)$
is a model since F is a comodel.
3.3 Slicing and coslicing
As an application of Theorem 3.3, this subsection gives statements about clan presentations of slice categories
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/A$
of categories of models (Proposition 3.6), and of coslice categories
$\mathcal {T}\!\text {-}\mathsf {Mod}/A$
of categories of models (Proposition 3.6), and of coslice categories
![]() $H(A)/\mathcal {T}\!\text {-}\mathsf {Mod}$
under representable models (Proposition 3.5).
$H(A)/\mathcal {T}\!\text {-}\mathsf {Mod}$
under representable models (Proposition 3.5).
Definition 3.4. For
![]() $\mathcal {T}$
a clan and
$\mathcal {T}$
a clan and
![]() $\Gamma \in \mathcal {T}$
, we write
$\Gamma \in \mathcal {T}$
, we write
![]() $\mathcal {T}_\Gamma $
for the full subcategory of
$\mathcal {T}_\Gamma $
for the full subcategory of
![]() $\mathcal {T}\!/\Gamma $
on display maps. Then
$\mathcal {T}\!/\Gamma $
on display maps. Then
![]() $\mathcal {T}_\Gamma $
is a clan where an arrow in
$\mathcal {T}_\Gamma $
is a clan where an arrow in
![]() $\mathcal {T}_\Gamma $
is a display map if its underlying map is one in
$\mathcal {T}_\Gamma $
is a display map if its underlying map is one in
![]() $\mathcal {T}$
. Compare [Reference Joyal26, Proposition 1.1.6].
$\mathcal {T}$
. Compare [Reference Joyal26, Proposition 1.1.6].
Proposition 3.5. Let
![]() $\Gamma $
be an object of a clan
$\Gamma $
be an object of a clan
![]() $\mathcal {T}$
. Then the functor
$\mathcal {T}$
. Then the functor
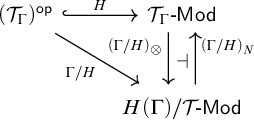
which sends ![]() to
to ![]() is a comodel. Moreover, its restricted nerve–realization adjunction (in the sense of Theorem 3.3(iii))
is a comodel. Moreover, its restricted nerve–realization adjunction (in the sense of Theorem 3.3(iii))
is an equivalence and identifies the extension–full w.f.s. on
![]() $\mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
with the coslice w.f.s. on
$\mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
with the coslice w.f.s. on
![]() $H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
.
$H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
.
Proof. It is easy to see that
![]() $\Gamma /H$
is a comodel. For the second claim, since arrows
$\Gamma /H$
is a comodel. For the second claim, since arrows
![]() $H(\Gamma )\to A$
correspond to elements of
$H(\Gamma )\to A$
correspond to elements of
![]() $A(\Gamma )$
, we can identify the coslice category
$A(\Gamma )$
, we can identify the coslice category
![]() $H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
with the category of “
$H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
with the category of “
![]() $\Gamma $
-pointed models of
$\Gamma $
-pointed models of
![]() $\mathcal {T}$
”, i.e., pairs
$\mathcal {T}$
”, i.e., pairs
![]() $(A,x)$
of a model A and an element
$(A,x)$
of a model A and an element
![]() $x\in A(\Gamma )$
, and morphisms preserving chosen elements.
$x\in A(\Gamma )$
, and morphisms preserving chosen elements.
Under this identification, we first verify that the functor
![]() $(\Gamma /H)_N$
is given by
$(\Gamma /H)_N$
is given by
and then that it is an equivalence with inverse
![]() $\Phi :\mathcal {T}_\Gamma \text {-}\mathsf {Mod}\to H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
given by
$\Phi :\mathcal {T}_\Gamma \text {-}\mathsf {Mod}\to H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
given by
where
![]() $\star $
is the unique element of
$\star $
is the unique element of
![]() $B(\mathrm {id}_\Gamma )$
and
$B(\mathrm {id}_\Gamma )$
and
![]() $\delta :\Gamma \to \Gamma \times \Gamma $
is the diagonal map viewed as global element of
$\delta :\Gamma \to \Gamma \times \Gamma $
is the diagonal map viewed as global element of ![]() in
in
![]() $\mathcal {T}_\Gamma $
. Thus,
$\mathcal {T}_\Gamma $
. Thus,
![]() $(\Gamma /H)_\otimes =\Phi $
.
$(\Gamma /H)_\otimes =\Phi $
.
Finally we note that the w.f.s. on
![]() $H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
is cofibrantly generated by commutative triangles
$H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
is cofibrantly generated by commutative triangles
for display maps ![]() [Reference Hirschhorn21, Theorem 2.7]. On the other hand, since
[Reference Hirschhorn21, Theorem 2.7]. On the other hand, since
![]() $(\Gamma /H)_\otimes \circ H = \Gamma /H$
(see (3.4)), the functor
$(\Gamma /H)_\otimes \circ H = \Gamma /H$
(see (3.4)), the functor
![]() $(\Gamma /H)_\otimes $
sends the generators of the extension–full w.f.s. on
$(\Gamma /H)_\otimes $
sends the generators of the extension–full w.f.s. on
![]() $\mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
to triangles
$\mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
to triangles
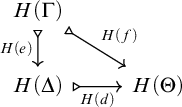
for arbitrary display maps
![]() $d,e,f$
in
$d,e,f$
in
![]() $\mathcal {T}$
. Now the triangles of shape (3.6) contain the triangles of shape (3.5), but are contained in their saturation, which is the left class of the coslice w.f.s. Thus, the two w.f.s.s are equal.
$\mathcal {T}$
. Now the triangles of shape (3.6) contain the triangles of shape (3.5), but are contained in their saturation, which is the left class of the coslice w.f.s. Thus, the two w.f.s.s are equal.
Proposition 3.6. Let A be a model of a clan
![]() $\mathcal {T}$
. Then the projection functor
$\mathcal {T}$
. Then the projection functor
![]() $\mathsf {El}(A)\to \mathcal {T}^{\mathsf {op}}$
creates a coclan structure on
$\mathsf {El}(A)\to \mathcal {T}^{\mathsf {op}}$
creates a coclan structure on
![]() $\mathsf {El}(A)$
, i.e.,
$\mathsf {El}(A)$
, i.e.,
![]() $\mathsf {El}(A)$
is a coclan with codisplay maps those arrows that are mapped to display maps in
$\mathsf {El}(A)$
is a coclan with codisplay maps those arrows that are mapped to display maps in
![]() $\mathcal {T}$
. Moreover, the canonical functor
$\mathcal {T}$
. Moreover, the canonical functor
is a comodel, and its restricted nerve–realization adjunction
is an equivalence which identifies the extension–full w.f.s. on
![]() $\mathsf {El}(A)^{\mathsf {op}}\text {-}\mathsf {Mod}$
and the slice w.f.s. on
$\mathsf {El}(A)^{\mathsf {op}}\text {-}\mathsf {Mod}$
and the slice w.f.s. on
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/A$
.
$\mathcal {T}\!\text {-}\mathsf {Mod}/A$
.
Proof. The verification that
![]() $\mathsf {El}(A)^{\mathsf {op}}$
is a clan and
$\mathsf {El}(A)^{\mathsf {op}}$
is a clan and
![]() $H/A$
is a coclan morphism is straightforward. The equivalence is a restriction of the well-known equivalence
$H/A$
is a coclan morphism is straightforward. The equivalence is a restriction of the well-known equivalence
![]() $\widehat {\mathcal {T}^{\mathsf {op}}}/A\simeq \widehat {\mathcal {T}^{\mathsf {op}}/A}$
. The w.f.s.s coincide since—again by
$\widehat {\mathcal {T}^{\mathsf {op}}}/A\simeq \widehat {\mathcal {T}^{\mathsf {op}}/A}$
. The w.f.s.s coincide since—again by
![]() $(H/A)_\otimes \circ H=H/A$
—the functor
$(H/A)_\otimes \circ H=H/A$
—the functor
![]() $(H/A)_\otimes $
sends the generators of the w.f.s. on
$(H/A)_\otimes $
sends the generators of the w.f.s. on
![]() $\mathsf {El}(A)^{\mathsf {op}}\text {-}\mathsf {Mod}$
to commutative triangles
$\mathsf {El}(A)^{\mathsf {op}}\text {-}\mathsf {Mod}$
to commutative triangles
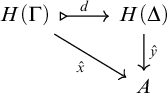
in
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/A$
, where
$\mathcal {T}\!\text {-}\mathsf {Mod}/A$
, where ![]() is a display map in
is a display map in
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $x\in A(\Gamma )$
and
$x\in A(\Gamma )$
and
![]() $y\in A(\Delta )$
are elements with
$y\in A(\Delta )$
are elements with
![]() $d\cdot y = x$
. By [Reference Hirschhorn21, Theorem 1.5], these form a set of generators for the slice w.f.s. on
$d\cdot y = x$
. By [Reference Hirschhorn21, Theorem 1.5], these form a set of generators for the slice w.f.s. on
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/A$
.
$\mathcal {T}\!\text {-}\mathsf {Mod}/A$
.
4
 $(\mathsf {E},\mathsf {F})$
-categories and the biadjunction
$(\mathsf {E},\mathsf {F})$
-categories and the biadjunction
Definition 4.1. An
![]() $(\mathsf {E},\mathsf {F})$
-category is a l.f.p. category
$(\mathsf {E},\mathsf {F})$
-category is a l.f.p. category ![]() with a w.f.s.
with a w.f.s.
![]() $(\mathsf {E},\mathsf {F})$
whose maps we call extensions and full maps. A morphism of
$(\mathsf {E},\mathsf {F})$
whose maps we call extensions and full maps. A morphism of
![]() $(\mathsf {E},\mathsf {F})$
-categories is a functor
$(\mathsf {E},\mathsf {F})$
-categories is a functor ![]() preserving small limits, filtered colimits, and full maps. We write
preserving small limits, filtered colimits, and full maps. We write
![]() $\mathsf {EFCat}$
for the
$\mathsf {EFCat}$
for the
![]() $2$
-category of
$2$
-category of
![]() $(\mathsf {E},\mathsf {F})$
-categories, morphisms of
$(\mathsf {E},\mathsf {F})$
-categories, morphisms of
![]() $(\mathsf {E},\mathsf {F})$
-categories, and natural transformations.
$(\mathsf {E},\mathsf {F})$
-categories, and natural transformations.
Lemma 4.2. If ![]() is a morphism of
is a morphism of
![]() $(\mathsf {E},\mathsf {F})$
-categories, then it has a left adjoint
$(\mathsf {E},\mathsf {F})$
-categories, then it has a left adjoint ![]() which preserves compact objects and extensions. Conversely, if
which preserves compact objects and extensions. Conversely, if ![]() is a cocontinuous functor preserving compact objects and extensions, then it has a right adjoint
is a cocontinuous functor preserving compact objects and extensions, then it has a right adjoint ![]() which is a morphism of
which is a morphism of
![]() $(\mathsf {E},\mathsf {F})$
-categories. Writing
$(\mathsf {E},\mathsf {F})$
-categories. Writing ![]() for the category of cocontinuous functors
for the category of cocontinuous functors ![]() preserving extensions and compact objects, we thus have
preserving extensions and compact objects, we thus have ![]() .
.
Proof. That morphisms of
![]() $(\mathsf {E},\mathsf {F})$
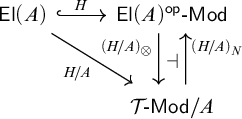
-categories have left adjoints follows from the adjoint functor theorem for presentable categories [Reference Adámek and Rosicky2, Theorem 1.66], and conversely the special adjoint functor theorem [Reference Lane31, Section V-8] implies that cocontinuous functors between l.f.p. categories have right adjoints. It follows from standard arguments that the left adjoint preserves compact objects iff the right adjoint preserves filtered colimits, and that the left adjoint preserves extensions iff the right adjoint preserves full maps.
$(\mathsf {E},\mathsf {F})$
-categories have left adjoints follows from the adjoint functor theorem for presentable categories [Reference Adámek and Rosicky2, Theorem 1.66], and conversely the special adjoint functor theorem [Reference Lane31, Section V-8] implies that cocontinuous functors between l.f.p. categories have right adjoints. It follows from standard arguments that the left adjoint preserves compact objects iff the right adjoint preserves filtered colimits, and that the left adjoint preserves extensions iff the right adjoint preserves full maps.
Lemma 4.3. For any morphism
![]() $F:\mathcal {S}\to \mathcal {T}$
of clans, the precomposition functor
$F:\mathcal {S}\to \mathcal {T}$
of clans, the precomposition functor
is a morphism of
![]() $(\mathsf {E},\mathsf {F})$
-categories. Thus the assignment
$(\mathsf {E},\mathsf {F})$
-categories. Thus the assignment
![]() $\mathcal {T}\mapsto \mathcal {T}\!\text {-}\mathsf {Mod}$
extends to a
$\mathcal {T}\mapsto \mathcal {T}\!\text {-}\mathsf {Mod}$
extends to a
![]() $2$
-functor
$2$
-functor
from clans to
![]() $(\mathsf {E},\mathsf {F})$
-categories.
$(\mathsf {E},\mathsf {F})$
-categories.
Proof. The preservation of small limits and filtered colimits is obvious since they are computed pointwise (Remark 2.9(a)). To show that
![]() $(-\circ F)$
preserves full maps, let
$(-\circ F)$
preserves full maps, let
![]() $f:A\to B$
be full in
$f:A\to B$
be full in
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
. It is sufficient to show that the
$\mathcal {T}\!\text {-}\mathsf {Mod}$
. It is sufficient to show that the
![]() $(f\circ F)$
-naturality squares are weak pullbacks at all display maps
$(f\circ F)$
-naturality squares are weak pullbacks at all display maps
![]() $p:$
in
$p:$
in
![]() $\mathcal {S}\text {-}\mathsf {Mod}$
. But the
$\mathcal {S}\text {-}\mathsf {Mod}$
. But the
![]() $(f\circ F)$
-naturality square at p is the same as the f-naturality square at
$(f\circ F)$
-naturality square at p is the same as the f-naturality square at
![]() $F(p)$
so the claim follows since f is full and F preserves display maps.
$F(p)$
so the claim follows since f is full and F preserves display maps.
Definition 4.4. Given an
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() , write
, write ![]() for the full subcategory on compact
for the full subcategory on compact
![]() $0$
-extensions.
$0$
-extensions.
Lemma 4.5.
![]() is a coclan with extensions as codisplay maps.
is a coclan with extensions as codisplay maps.
Proposition 4.6. The assignment ![]() extends to a pseudofunctor
extends to a pseudofunctor
which is left biadjoint to
![]() $(-)\text {-}\mathsf {Mod}:\mathsf {Clan}^{\mathsf {op}}\to \mathsf {EFCat}$
.
$(-)\text {-}\mathsf {Mod}:\mathsf {Clan}^{\mathsf {op}}\to \mathsf {EFCat}$
.
Proof. We show that for every
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() , the
, the
![]() $2$
-functor
$2$
-functor
is birepresented by ![]() . Given a clan
. Given a clan
![]() $\mathcal {T}$
it is easy to see that the equivalence
$\mathcal {T}$
it is easy to see that the equivalence
from Theorem 3.3 restricts to an equivalence
Taking opposite categories on both sides we get
as required.
Remark 4.7. From the construction of the natural equivalence (4.1) we can extract explicit descriptions of the components
of the unit
![]() $\Theta $
and the counit E of the biadjunction
$\Theta $
and the counit E of the biadjunction
at an
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() and a clan
and a clan
![]() $\mathcal {T}$
, respectively. Specifically,
$\mathcal {T}$
, respectively. Specifically, ![]() is the nerve of the inclusion
is the nerve of the inclusion ![]() (which is obviously a comodel), and
(which is obviously a comodel), and
![]() $E_{\mathcal {T}}$
is
$E_{\mathcal {T}}$
is
![]() $(-)^{\mathsf {op}}$
of the evident corestriction of
$(-)^{\mathsf {op}}$
of the evident corestriction of
![]() $H:\mathcal {T}^{\mathsf {op}}\to \mathcal {T}\!\text {-}\mathsf {Mod}$
.
$H:\mathcal {T}^{\mathsf {op}}\to \mathcal {T}\!\text {-}\mathsf {Mod}$
.
In §5 and §6 we show that the biadjunction (4.2) is idempotent (in the sense that the associated monad and comonad are), and characterize the fixed points on both sides (Theorems 5.9 and 6.18).
5 Cauchy complete clans and the fat small object argument
Definition 5.1. A clan
![]() $\mathcal {T}$
is called Cauchy complete if its underlying category is Cauchy complete (i.e., idempotents split), and retracts of display maps are display maps.
$\mathcal {T}$
is called Cauchy complete if its underlying category is Cauchy complete (i.e., idempotents split), and retracts of display maps are display maps.
Examples 5.2.
-
(a) Finite-limit clans are always Cauchy complete, since finite-limit categories are and all arrows are display maps in finite-limit clans.
-
(b) A finite-product clan is Cauchy complete if and only if idempotents split in the underlying finite-product category, which may or may not be the case for the presentation of a single-sorted algebraic theory
 $\mathbb {T}$
as Lawvere theory (i.e., the opposite of the full subcategory of
$\mathbb {T}$
as Lawvere theory (i.e., the opposite of the full subcategory of
 $\mathsf {Mod}(\mathbb {T})$
on finitely generated free models). For example the Lawvere theory of abelian groups is Cauchy complete since all finitely presented projective abelian groups are free, whereas the Lawvere theory of distributive lattices is not Cauchy complete. A non-free retract of a finitely generated free distributive lattice may be obtained by starting with a section–retraction pair
$\mathsf {Mod}(\mathbb {T})$
on finitely generated free models). For example the Lawvere theory of abelian groups is Cauchy complete since all finitely presented projective abelian groups are free, whereas the Lawvere theory of distributive lattices is not Cauchy complete. A non-free retract of a finitely generated free distributive lattice may be obtained by starting with a section–retraction pair
 $s:\{0 < 1 < 2\}\leftrightarrows \{0<1\}^2:r$
in posets, and then taking the distributive lattice of upper sets on both sides, i.e., applying the functor
$s:\{0 < 1 < 2\}\leftrightarrows \{0<1\}^2:r$
in posets, and then taking the distributive lattice of upper sets on both sides, i.e., applying the functor
 $\mathsf {Pos}(-,\{0<1\}):\mathsf {Pos}^{\mathsf {op}}\to \mathsf {DLat}$
. Then
$\mathsf {Pos}(-,\{0<1\}):\mathsf {Pos}^{\mathsf {op}}\to \mathsf {DLat}$
. Then
 $\mathsf {Pos}(\{0<1\}^2,\{0 < 1\})$
is the free distributive lattice on
$\mathsf {Pos}(\{0<1\}^2,\{0 < 1\})$
is the free distributive lattice on
 $2$
generators, but
$2$
generators, but
 $\mathsf {Pos}(\{0<1<1\},\{0<1\})$
is not free.
$\mathsf {Pos}(\{0<1<1\},\{0<1\})$
is not free.Further details on the question of Cauchy-completeness of finite-limit theories, including a discussion of how the classical theory of Morita equivalence of rings fits into the picture, can be found in [Reference Adámek, Rosický and Vitale3, Sections 8, 15].
-
(c) The clan
 $\mathcal {T}_{\mathsf {Cat}}$
of categories is Cauchy complete. To see this assume that G is a finite graph and that
$\mathcal {T}_{\mathsf {Cat}}$
of categories is Cauchy complete. To see this assume that G is a finite graph and that
 $\mathbb {D}$
is a retract of the free category
$\mathbb {D}$
is a retract of the free category
 $G^*$
on G. Then we know that
$G^*$
on G. Then we know that
 $\mathbb {D}$
is a compact
$\mathbb {D}$
is a compact
 $0$
-extension and we have to show that
$0$
-extension and we have to show that
 $\mathbb {D}$
is free on a finite graph. Call an arrow f in
$\mathbb {D}$
is free on a finite graph. Call an arrow f in
 $\mathbb {D}$
irreducible if it is not an identity and in any decomposition
$\mathbb {D}$
irreducible if it is not an identity and in any decomposition
 $f = gh$
, either g or h is an identity. Since the factors of every non-trivial decomposition have shorter length in
$f = gh$
, either g or h is an identity. Since the factors of every non-trivial decomposition have shorter length in
 $G^*$
, every arrow in
$G^*$
, every arrow in
 $\mathbb {D}$
admits a decomposition into irreducible factors. Let H be the graph of irreducible arrows in
$\mathbb {D}$
admits a decomposition into irreducible factors. Let H be the graph of irreducible arrows in
 $\mathbb {D}$
, and let
$\mathbb {D}$
, and let
 $F:H^*\to \mathbb {D}$
be the canonical functor. Then F is full since all arrows in D are composites of irreducibles, and it admits a section
$F:H^*\to \mathbb {D}$
be the canonical functor. Then F is full since all arrows in D are composites of irreducibles, and it admits a section
 $K:\mathbb {D}\to H^*$
since
$K:\mathbb {D}\to H^*$
since
 $\mathbb {D}$
is a
$\mathbb {D}$
is a
 $0$
-extension. As a section, K sends arrows in
$0$
-extension. As a section, K sends arrows in
 $\mathbb {D}$
to decompositions into irreducibles, thus it sends irreducible arrows to themselves. It follows that
$\mathbb {D}$
to decompositions into irreducibles, thus it sends irreducible arrows to themselves. It follows that
 $K(F(j))=j$
for generators j in H, and from this we can deduce that
$K(F(j))=j$
for generators j in H, and from this we can deduce that
 $K\circ F=\mathrm {id}_{H^*}$
. Thus,
$K\circ F=\mathrm {id}_{H^*}$
. Thus,
 $\mathbb {D}\cong H^*$
. Finiteness of H follows from compactness.
$\mathbb {D}\cong H^*$
. Finiteness of H follows from compactness.This argument is an adaption of a similar argument for monoids [Reference Head18].
-
(d) For every
 $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category  , the clan
, the clan  (Definition 4.4) is Cauchy complete, since compact objects and extensions are closed under retracts.
(Definition 4.4) is Cauchy complete, since compact objects and extensions are closed under retracts.
By Example 5.2(d), Cauchy completeness is a necessary condition for the counit
![]() $E_{\mathcal {T}}:\mathcal {T}\to \mathfrak C(\mathcal {T}\!\text {-}\mathsf {Mod})^{\mathsf {op}}$
of the biadjunction (4.2) to be an equivalence. We will show that it is also sufficient, but for this we need the notion of flat model, and the fat small object argument.
$E_{\mathcal {T}}:\mathcal {T}\to \mathfrak C(\mathcal {T}\!\text {-}\mathsf {Mod})^{\mathsf {op}}$
of the biadjunction (4.2) to be an equivalence. We will show that it is also sufficient, but for this we need the notion of flat model, and the fat small object argument.
Recall that for small
![]() $\mathbb {C}$
, a functor
$\mathbb {C}$
, a functor
![]() $F:\mathbb {C}\to \mathsf {Set}$
is called flat if
$F:\mathbb {C}\to \mathsf {Set}$
is called flat if
![]() $\mathsf {El}(F)$
is filtered, or equivalently if
$\mathsf {El}(F)$
is filtered, or equivalently if
![]() $F_\otimes :[\mathbb {C}^{\mathsf {op}},\mathsf {Set}]\to \mathsf {Set}$
preserves finite limits [Reference Borceux8, Definition 6.3.1 and Proposition 6.3.8]. From the second characterization it follows that flat functors preserve all finite limits that exist in
$F_\otimes :[\mathbb {C}^{\mathsf {op}},\mathsf {Set}]\to \mathsf {Set}$
preserves finite limits [Reference Borceux8, Definition 6.3.1 and Proposition 6.3.8]. From the second characterization it follows that flat functors preserve all finite limits that exist in
![]() $\mathbb {C}$
, thus for the case of a clan
$\mathbb {C}$
, thus for the case of a clan
![]() $\mathcal {T}$
, flat functors
$\mathcal {T}$
, flat functors
![]() $F:\mathcal {T}\to \mathsf {Set}$
are always models. We refer to them as flat models.
$F:\mathcal {T}\to \mathsf {Set}$
are always models. We refer to them as flat models.
Definition 5.3. A model
![]() $A:\mathcal {T}\to \mathsf {Set}$
of a clan
$A:\mathcal {T}\to \mathsf {Set}$
of a clan
![]() $\mathcal {T}$
is called flat, if
$\mathcal {T}$
is called flat, if
![]() $\mathsf {El}(F)$
is filtered.
$\mathsf {El}(F)$
is filtered.
Lemma 5.4. A
![]() $\mathcal {T}$
-model A is flat iff it is a filtered colimit of representable models.
$\mathcal {T}$
-model A is flat iff it is a filtered colimit of representable models.
Proof. We always have
![]() $A=\mathsf {colim}(\mathsf {El}(A)\to \mathcal {T}^{\mathsf {op}}\xrightarrow {H}\mathcal {T}\!\text {-}\mathsf {Mod})$
, thus if A is flat then it is a filtered colimit of representable models. The other direction follows since representable models are flat, and flat functors are closed under filtered colimits in
$A=\mathsf {colim}(\mathsf {El}(A)\to \mathcal {T}^{\mathsf {op}}\xrightarrow {H}\mathcal {T}\!\text {-}\mathsf {Mod})$
, thus if A is flat then it is a filtered colimit of representable models. The other direction follows since representable models are flat, and flat functors are closed under filtered colimits in
![]() $[\mathcal {T},\mathsf {Set}]$
[Reference Borceux8, Proposition 6.3.6].
$[\mathcal {T},\mathsf {Set}]$
[Reference Borceux8, Proposition 6.3.6].
Corollary 5.5. For any clan
![]() $\mathcal {T}$
, the
$\mathcal {T}$
, the
![]() $0$
-extensions in
$0$
-extensions in
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
are flat.
$\mathcal {T}\!\text {-}\mathsf {Mod}$
are flat.
Proof. This follows from the fat small object argument and can be seen as a special case of [Reference Makkai, Rosicky and Vokrinek33, Corollary 5.1], but we give a direct proof in Appendix 11 (Corollary 11.9).
Definition 5.6. Let
![]() $\mathfrak {X}$
be a cocomplete locally small category.
$\mathfrak {X}$
be a cocomplete locally small category.
-
(i) We say that an arrow
 $f:A\to B$
is orthogonal to a small diagram
$f:A\to B$
is orthogonal to a small diagram
 $D:\mathbb {J}\to \mathfrak {X}$
, and write
$D:\mathbb {J}\to \mathfrak {X}$
, and write
 $f\perp D$
, if the following square is a pullback in
$f\perp D$
, if the following square is a pullback in
 $\mathsf {Set}$
.
$\mathsf {Set}$
. 
-
(ii) We call f compact if it is orthogonal to all small filtered diagrams.
Lemma 5.7. Let
![]() $\mathfrak {X}$
be a locally small cocomplete category.
$\mathfrak {X}$
be a locally small cocomplete category.
-
(i) An object
 $A\in \mathfrak {X}$
is compact in the usual sense that
$A\in \mathfrak {X}$
is compact in the usual sense that
 $\mathfrak {X}(A,-)$
preserves filtered colimits, if and only if the arrow
$\mathfrak {X}(A,-)$
preserves filtered colimits, if and only if the arrow
 $0\to A$
is compact in the sense of Definition 5.6.
$0\to A$
is compact in the sense of Definition 5.6. -
(ii) If the arrow g in a commutative triangle
 is compact, then f is compact if and only if h is compact. In other words, compact arrow are closed under composition and have the right cancellation property.
is compact, then f is compact if and only if h is compact. In other words, compact arrow are closed under composition and have the right cancellation property. -
(iii) If
 $f:A\to B$
is compact as an arrow in
$f:A\to B$
is compact as an arrow in
 $\mathfrak {X}$
, then it is compact as an object in
$\mathfrak {X}$
, then it is compact as an object in
 $A/\mathfrak {X}$
.
$A/\mathfrak {X}$
. -
(iv) If
 $h:B\to C$
is an arrow between compact objects in
$h:B\to C$
is an arrow between compact objects in
 $\mathfrak {X}$
, then h is compact as an object in
$\mathfrak {X}$
, then h is compact as an object in
 $B/\mathfrak {X}$
.
$B/\mathfrak {X}$
.
Proof. (i) is obvious, and (ii) follows from the pullback lemma.
For (iii) assume that f is compact as an arrow in
![]() $\mathfrak {X}$
and consider a filtered diagram in
$\mathfrak {X}$
and consider a filtered diagram in
![]() $A/\mathfrak {X}$
, given by a filtered diagram
$A/\mathfrak {X}$
, given by a filtered diagram
![]() $D:\mathbb {I}\to \mathfrak {X}$
and a cocone
$D:\mathbb {I}\to \mathfrak {X}$
and a cocone
![]() $\gamma =(\gamma _i:A\to D_i)_{i\in \mathbb {I}}$
. Note that since the forgetful functor
$\gamma =(\gamma _i:A\to D_i)_{i\in \mathbb {I}}$
. Note that since the forgetful functor
![]() $A/\mathfrak {X}\to \mathfrak {X}$
creates connected colimits, we have
$A/\mathfrak {X}\to \mathfrak {X}$
creates connected colimits, we have
![]() $\mathsf {colim}(\gamma ):A\to \mathsf {colim}(D)$
. Also because
$\mathsf {colim}(\gamma ):A\to \mathsf {colim}(D)$
. Also because
![]() $\mathbb {I}$
is connected, all
$\mathbb {I}$
is connected, all
![]() $\gamma _i$
are in the same equivalence class in
$\gamma _i$
are in the same equivalence class in
![]() $\mathsf {colim}_{i\in \mathbb {I}}\mathfrak {X}(A,D_i)$
, which we denote by
$\mathsf {colim}_{i\in \mathbb {I}}\mathfrak {X}(A,D_i)$
, which we denote by
![]() $\overline {\gamma }:1\to \mathsf {colim}_{i\in \mathbb {I}}\mathfrak {X}(A,D_i)$
. We have to show that the canonical map
$\overline {\gamma }:1\to \mathsf {colim}_{i\in \mathbb {I}}\mathfrak {X}(A,D_i)$
. We have to show that the canonical map
is a bijection. This follows because this function can be presented by a pullback in ![]() as in the following diagram.
as in the following diagram.

The front square is a pullback since the back one is by compactness of f as an arrow, and since the side ones are pullbacks by construction. Thus the gray horizontal arrow is a bijection since
![]() $1\to 1$
is.
$1\to 1$
is.
Finally, claim (iv) now follows directly from (i), (ii), and (iii).
Remark 5.8. One can show the implication of Lemma 5.7(iii) is actually an equivalence, i.e.,
![]() $f:A\to B$
is compact as an arrow if and only if it is so as an object of the coslice category, but the other direction is more awkward to write down and we don’t need it.
$f:A\to B$
is compact as an arrow if and only if it is so as an object of the coslice category, but the other direction is more awkward to write down and we don’t need it.
Theorem 5.9. If
![]() $\mathcal {T}$
is a Cauchy complete clan, then
$\mathcal {T}$
is a Cauchy complete clan, then
![]() $E_{\mathcal {T}}:\mathcal {T}\to \mathfrak C(\mathcal {T}\!\text {-}\mathsf {Mod})^{\mathsf {op}}$
is an equivalence of clans.
$E_{\mathcal {T}}:\mathcal {T}\to \mathfrak C(\mathcal {T}\!\text {-}\mathsf {Mod})^{\mathsf {op}}$
is an equivalence of clans.
Proof. Let
![]() $C\in \mathcal {T}\!\text {-}\mathsf {Mod}$
be a compact
$C\in \mathcal {T}\!\text {-}\mathsf {Mod}$
be a compact
![]() $0$
-extension. Then by Corollary 5.5, C is a filtered colimit of representable models, and since C is compact the identity
$0$
-extension. Then by Corollary 5.5, C is a filtered colimit of representable models, and since C is compact the identity
![]() $\mathrm {id}_C$
factors through one of the colimit inclusions, whence C is a retract of a representable model. By Cauchy completeness, C is thus itself representable, i.e., we have an equivalence of categories.
$\mathrm {id}_C$
factors through one of the colimit inclusions, whence C is a retract of a representable model. By Cauchy completeness, C is thus itself representable, i.e., we have an equivalence of categories.
It remains to show that
![]() $E_{\mathcal {T}}$
reflects extensions to display maps. Assume
$E_{\mathcal {T}}$
reflects extensions to display maps. Assume
![]() $f:\Delta \to \Gamma $
in
$f:\Delta \to \Gamma $
in
![]() $\mathcal {T}$
such that
$\mathcal {T}$
such that
![]() $H(f): H(\Gamma )\to H(\Delta )$
is an extension. Then
$H(f): H(\Gamma )\to H(\Delta )$
is an extension. Then
![]() $H(f)$
is compact in
$H(f)$
is compact in
![]() $H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
by Lemma 5.7(iv) and
$H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}$
by Lemma 5.7(iv) and
![]() $H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}\simeq \mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
by Proposition 3.5. This means that the object corresponding to
$H(\Gamma )/\mathcal {T}\!\text {-}\mathsf {Mod}\simeq \mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
by Proposition 3.5. This means that the object corresponding to
![]() $H(f)$
in
$H(f)$
in
![]() $\mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
is a compact
$\mathcal {T}_\Gamma \text {-}\mathsf {Mod}$
is a compact
![]() $0$
-extension, and thus it is isomorphic to a representable model
$0$
-extension, and thus it is isomorphic to a representable model
![]() $\mathcal {T}_\Gamma (d,-)$
for a display map
$\mathcal {T}_\Gamma (d,-)$
for a display map ![]() by the argument in the first part of the proof. This means that f is isomorphic to d over
by the argument in the first part of the proof. This means that f is isomorphic to d over
![]() $\Gamma $
, and therefore a display map.
$\Gamma $
, and therefore a display map.
The preceding proposition together with Example 5.2(d) shows that the pseudomonad on
![]() $\mathsf {Clan}$
induced by the biadjunction (4.2) is idempotent: applying the pseudomonad once produces a Cauchy complete clan, and applying it again gives something equivalent. By general facts about (bi)adjunctions, the induced pseudomonad on
$\mathsf {Clan}$
induced by the biadjunction (4.2) is idempotent: applying the pseudomonad once produces a Cauchy complete clan, and applying it again gives something equivalent. By general facts about (bi)adjunctions, the induced pseudomonad on
![]() $\mathsf {EFCat}$
is also idempotent. In the next section we characterize its fixed points as being clan-algebraic categories.
$\mathsf {EFCat}$
is also idempotent. In the next section we characterize its fixed points as being clan-algebraic categories.
6 Clan-algebraic categories
Definition 6.1. An
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() is called clan-algebraic if
is called clan-algebraic if
-
(D) the inclusion
 is dense,
is dense, -
(CG) the w.f.s.
 $(\mathsf {E},\mathsf {F})$
is cofibrantly generated by
$(\mathsf {E},\mathsf {F})$
is cofibrantly generated by  , and
, and -
(FQ) equivalence relations
 $\langle p,q\rangle :R\rightarrowtail A\times A$
in
$\langle p,q\rangle :R\rightarrowtail A\times A$
in  with full components
with full components
 $p,q$
are effective, and have full coequalizers.
$p,q$
are effective, and have full coequalizers.
A clan-algebraic weak factorization system is a w.f.s. on a l.f.p. category ![]() making
making ![]() into a clan-algebraic category.
into a clan-algebraic category.
Theorem 6.2. The category
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
is clan-algebraic for every clan
$\mathcal {T}\!\text {-}\mathsf {Mod}$
is clan-algebraic for every clan
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Proof. Conditions (D) and (CG) are straightforward. For for (FQ) let
![]() $\langle p,q\rangle : R\rightarrowtail A\times A$
be an equivalence relation with full components. This means that we have an equivalence relation
$\langle p,q\rangle : R\rightarrowtail A\times A$
be an equivalence relation with full components. This means that we have an equivalence relation
![]() $\sim $
on each
$\sim $
on each
![]() $A(\Gamma )$
, such that
$A(\Gamma )$
, such that
-
• for all arrows
 $s : \Delta \to \Gamma $
, the function
$s : \Delta \to \Gamma $
, the function
 $A(s) = s\cdot (-) : A(\Delta )\to A(\Gamma )$
preserves this relation, and
$A(s) = s\cdot (-) : A(\Delta )\to A(\Gamma )$
preserves this relation, and -
• for every display map
 and all
and all
 $a,b\in A(\Gamma )$
and
$a,b\in A(\Gamma )$
and
 $c\in A(\Gamma ^+)$
such that
$c\in A(\Gamma ^+)$
such that
 $a\sim b$
and
$a\sim b$
and
 $p\cdot c = a$
, there exists a
$p\cdot c = a$
, there exists a
 $d\in A(\Gamma ^+)$
with
$d\in A(\Gamma ^+)$
with
 $c\sim d$
and
$c\sim d$
and
 $p\cdot d=b$
.
$p\cdot d=b$
.
We show first that the pointwise quotient
![]() $A/R$
is a model. Clearly
$A/R$
is a model. Clearly
![]() $(A/R)(1)=1$
, and it remains to show that given a pullback
$(A/R)(1)=1$
, and it remains to show that given a pullback
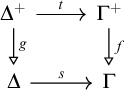
with f and g display maps, and elements
![]() $a\in A(\Delta )$
,
$a\in A(\Delta )$
,
![]() $b\in A(\Gamma ^+)$
with
$b\in A(\Gamma ^+)$
with
![]() $s\cdot a\sim f\cdot b$
, there exists a unique-up-to-
$s\cdot a\sim f\cdot b$
, there exists a unique-up-to-
![]() $\sim $
element
$\sim $
element
![]() $c\in A(\Delta ^+)$
with
$c\in A(\Delta ^+)$
with
![]() $g\cdot c\sim a$
and
$g\cdot c\sim a$
and
![]() $t\cdot c\sim b$
. Since f is a display map, there exists a
$t\cdot c\sim b$
. Since f is a display map, there exists a
![]() $b'$
with
$b'$
with
![]() $b\sim b'$
and
$b\sim b'$
and
![]() $v\cdot b'=s\cdot a$
, and since A is a model there exists therefore a c with
$v\cdot b'=s\cdot a$
, and since A is a model there exists therefore a c with
![]() $q\cdot c = a$
and
$q\cdot c = a$
and
![]() $t\cdot c = b'$
. For uniqueness assume that
$t\cdot c = b'$
. For uniqueness assume that
![]() $c,c'\in A(\Delta ^+)$
with
$c,c'\in A(\Delta ^+)$
with
![]() $q\cdot c\sim q\cdot c'$
and
$q\cdot c\sim q\cdot c'$
and
![]() $t\cdot c\sim t\cdot c'$
. Then
$t\cdot c\sim t\cdot c'$
. Then
![]() $c\sim c'$
follows from the fact that R is a model. This shows that
$c\sim c'$
follows from the fact that R is a model. This shows that
![]() $A/R$
is a model, and also that the quotient is effective, since the kernel pair is computed pointwise. The fact that
$A/R$
is a model, and also that the quotient is effective, since the kernel pair is computed pointwise. The fact that
![]() $A\to A/R$
is full is similarly easy to see.
$A\to A/R$
is full is similarly easy to see.
The following counterexample shows that conditions (D) and (CG) alone are not sufficient to characterize categories
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
.
$\mathcal {T}\!\text {-}\mathsf {Mod}$
.
Example 6.3. Let
![]() $\mathsf {Inj}$
be the full subcategory of
$\mathsf {Inj}$
be the full subcategory of ![]() on injections, and let
on injections, and let
![]() $(\mathsf {E},\mathsf {F})$
be the w.f.s. generated by
$(\mathsf {E},\mathsf {F})$
be the w.f.s. generated by ![]() and
and ![]() . Then
. Then
![]() $(\mathsf {E},\mathsf {F})$
satisfies (D) and (CG), and
$(\mathsf {E},\mathsf {F})$
satisfies (D) and (CG), and
![]() $\mathsf {F}$
consists precisely of the pointwise surjective maps, in particular it contains all split epis. However, the equivalence relation on
$\mathsf {F}$
consists precisely of the pointwise surjective maps, in particular it contains all split epis. However, the equivalence relation on
![]() $\mathrm {id}_2$
which is discrete on the domain and codiscrete on the codomain is not effective.
$\mathrm {id}_2$
which is discrete on the domain and codiscrete on the codomain is not effective.
The following is a restatement of Remark 2.11(b) for clan-algebraic categories.
Lemma 6.4. Full maps in clan-algebraic categories are regular epimorphisms.
Proof. Given a full map in a clan-algebraic category ![]() , the lifting property against
, the lifting property against
![]() $0$
-extensions implies that
$0$
-extensions implies that ![]() is componentwise surjective in
is componentwise surjective in ![]() , and therefore the coequalizer of its kernel pair. Since left adjoints preserve regular epis, we deduce that
, and therefore the coequalizer of its kernel pair. Since left adjoints preserve regular epis, we deduce that
![]() $J_\otimes (J_N(f))$
is regular epic in
$J_\otimes (J_N(f))$
is regular epic in ![]() and the claim follows since
and the claim follows since
![]() $J_\otimes \circ J_N\cong \mathrm {id}$
by (D).
$J_\otimes \circ J_N\cong \mathrm {id}$
by (D).
Remark 6.5. Observe that we only used property (D) in the proof, no exactness.
Lemma 6.6. The class
![]() $\mathsf {F}$
of full maps in a clan-algebraic category
$\mathsf {F}$
of full maps in a clan-algebraic category ![]() has the right cancellation property, i.e., we have
has the right cancellation property, i.e., we have
![]() $g\in \mathsf {F}$
whenever
$g\in \mathsf {F}$
whenever
![]() $gf\in \mathsf {F}$
and
$gf\in \mathsf {F}$
and
![]() $f\in \mathsf {F}$
for composable pairs
$f\in \mathsf {F}$
for composable pairs
![]() $f:A\to B$
,
$f:A\to B$
,
![]() $g:B\to C$
.
$g:B\to C$
.
Proof. By (CG) it suffices to show that g has the r.l.p. w.r.t. extensions ![]() between compact
between compact
![]() $0$
-extensions
$0$
-extensions
![]() $I,J$
. Let
$I,J$
. Let
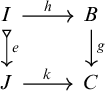
be a filling problem. Since I is a
![]() $0$
-extension and f is full, there exists a map
$0$
-extension and f is full, there exists a map
![]() $h':I\to A$
with
$h':I\to A$
with
![]() $fh'=h$
. We obtain a new filling problem
$fh'=h$
. We obtain a new filling problem
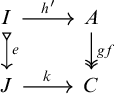
which can be filled by a map
![]() $m:J\to A$
since
$m:J\to A$
since
![]() $gf$
is full. Then
$gf$
is full. Then
![]() $m'=fm$
is a filler for the original problem (the upper triangle commutes since
$m'=fm$
is a filler for the original problem (the upper triangle commutes since
![]() $m'e=fme= fh'=h$
).
$m'e=fme= fh'=h$
).
Lemma 6.7. Let ![]() be a clan-algebraic category, let
be a clan-algebraic category, let
![]() $f:A\to B$
be an arrow in
$f:A\to B$
be an arrow in ![]() with componentwise full kernel pair
with componentwise full kernel pair
![]() $p,q:R\twoheadrightarrow A$
, and let
$p,q:R\twoheadrightarrow A$
, and let
![]() $e:A\twoheadrightarrow C$
be the coequalizer of p and q. Then the unique
$e:A\twoheadrightarrow C$
be the coequalizer of p and q. Then the unique
![]() $m:C\to B$
with
$m:C\to B$
with
![]() $me=f$
is monic.
$me=f$
is monic.
Proof. By (D) it is sufficient to test monicity of m on maps out of compact
![]() $0$
-extensions E. Let
$0$
-extensions E. Let
![]() $h,k:E\to C$
such that
$h,k:E\to C$
such that
![]() $mh = mk$
. Since e is full by (FQ), there exist
$mh = mk$
. Since e is full by (FQ), there exist
![]() $h',k':E\to A$
with
$h',k':E\to A$
with
![]() $eh'=h$
and
$eh'=h$
and
![]() $ek'=k$
. In particular we have
$ek'=k$
. In particular we have
![]() $fh'=fk'$
and therefore there is a unique
$fh'=fk'$
and therefore there is a unique
![]() $u:E\to R$
with
$u:E\to R$
with
![]() $pu=h'$
and
$pu=h'$
and
![]() $qu=k'$
. Thus we can argue
$qu=k'$
. Thus we can argue
which shows that m is monic.
Lemma 6.8. If ![]() is flat then
is flat then
![]() $A\to J_N(J_\otimes (A))$
is an isomorphism. Thus,
$A\to J_N(J_\otimes (A))$
is an isomorphism. Thus,
![]() $J_\otimes $
restricted to flat models is fully faithful.
$J_\otimes $
restricted to flat models is fully faithful.
Proof. For the fist claim we have
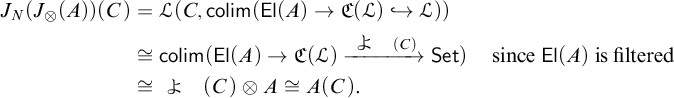
The second claim follows since for flat B, the mapping
can be decomposed as
Lemma 6.9. The following are equivalent for a cone
![]() $\phi :\Delta C\to D$
on a diagram
$\phi :\Delta C\to D$
on a diagram ![]() in an
in an
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() .
.
-
(i) Given an extension
 $e:A\to B$
, an arrow
$e:A\to B$
, an arrow
 $h:A\to C$
, and a cone
$h:A\to C$
, and a cone
 $\kappa :\Delta B\to D$
such that
$\kappa :\Delta B\to D$
such that
 $\phi _j h=\kappa _j e$
for all
$\phi _j h=\kappa _j e$
for all
 $j\in \mathbb {J}$
, there exists
$j\in \mathbb {J}$
, there exists
 $l:B\to C$
such that
$l:B\to C$
such that
 $le=h$
and
$le=h$
and
 $\phi _jl=\kappa _j$
for all
$\phi _jl=\kappa _j$
for all
 $j\in \mathbb {J}$
.
$j\in \mathbb {J}$
. 
-
(ii) The mediating arrow
 $:C\to \operatorname *{{\mathsf {lim}}}(D)$
is full.
$:C\to \operatorname *{{\mathsf {lim}}}(D)$
is full.
Proof. The data of
![]() $e,h,\kappa $
is equivalent to e, h, and
$e,h,\kappa $
is equivalent to e, h, and
![]() $k:B\to \operatorname *{{\mathsf {lim}}}(D)$
such that
$k:B\to \operatorname *{{\mathsf {lim}}}(D)$
such that
commutes, and
![]() $l:B\to C$
fills the latter square iff it fills all the squares with the
$l:B\to C$
fills the latter square iff it fills all the squares with the
![]() $D_j$
.
$D_j$
.
Definition 6.10. A cone
![]() $\phi $
satisfying the conditions of the lemma is called jointly full.
$\phi $
satisfying the conditions of the lemma is called jointly full.
Remark 6.11. The interest of this is that it allows us to talk about full “covers” of limits without actually computing the limits, which is useful when talking about cones and diagrams in the full subcategory of a clan-algebraic category on
![]() $0$
-extensions, which does not admit limits.
$0$
-extensions, which does not admit limits.
Definition 6.12. A nice diagram in an
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() is a
is a
![]() $2$
-truncated semi-simplicial diagram
$2$
-truncated semi-simplicial diagram
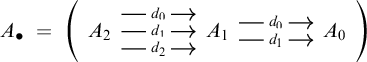
where
-
(i)
 $A_0$
,
$A_0$
,
 $A_1$
, and
$A_1$
, and
 $A_2$
are
$A_2$
are
 $0$
-extensions,
$0$
-extensions, -
(ii) the maps
 $d_0,d_1:A_1\to A_0$
are full,
$d_0,d_1:A_1\to A_0$
are full, -
(iii) in the commutative square
 the span constitutes a jointly full cone over the cospan,
the span constitutes a jointly full cone over the cospan, -
(iv) there exists a “symmetry” map
 making the triangles commute, and
making the triangles commute, and -
(v) there exists a
 $0$
-extension
$0$
-extension
 $\tilde A$
and full maps
$\tilde A$
and full maps
 $f,g:\tilde A\twoheadrightarrow A_1$
constituting a jointly full cone over the diagram
$f,g:\tilde A\twoheadrightarrow A_1$
constituting a jointly full cone over the diagram 
Lemma 6.13. If
![]() $A_\bullet $
is a nice diagram in a clan-algebraic category
$A_\bullet $
is a nice diagram in a clan-algebraic category ![]() , the pairing
, the pairing
![]() $\langle d_0,d_1\rangle :A_1\to A_0\times A_0$
factors as
$\langle d_0,d_1\rangle :A_1\to A_0\times A_0$
factors as
![]() $A_1\xrightarrow {f}R\xrightarrow {\langle r_0,r_1\rangle }A_0\times A_0$
, where f is full and
$A_1\xrightarrow {f}R\xrightarrow {\langle r_0,r_1\rangle }A_0\times A_0$
, where f is full and
![]() $r=\langle r_0,r_1\rangle $
is monic and a componentwise full equivalence relation.
$r=\langle r_0,r_1\rangle $
is monic and a componentwise full equivalence relation.
Proof. Condition (v) of the preceding definition gives us the following diagram
i.e., S is the kernel of
![]() $\langle d_0,d_1\rangle $
with projections
$\langle d_0,d_1\rangle $
with projections
![]() $p,q$
,
$p,q$
,
![]() $\tilde A$
is a
$\tilde A$
is a
![]() $0$
-extension, and
$0$
-extension, and
![]() $f,g,h$
are full. By right cancellation we deduce that p and q are full, and the existence of the factorization follows from Lemma 6.7. Fullness of
$f,g,h$
are full. By right cancellation we deduce that p and q are full, and the existence of the factorization follows from Lemma 6.7. Fullness of
![]() $r_0,r_1$
follows again from right cancellation because f,
$r_0,r_1$
follows again from right cancellation because f,
![]() $d_0$
, and
$d_0$
, and
![]() $d_1$
are full.
$d_1$
are full.
It remains to show that r is an equivalence relation. This is easy: condition 4 gives symmetry, and condition 3 gives transitivity, and reflexivity follows from the fact that
![]() $r_0$
admits a section as a full map into a
$r_0$
admits a section as a full map into a
![]() $0$
-extension, together with symmetry (we internalize the argument that if in a symmetric and transitive relation everything is related to something, then it is reflexive.)
$0$
-extension, together with symmetry (we internalize the argument that if in a symmetric and transitive relation everything is related to something, then it is reflexive.)
Definition 6.14. A
![]() $0$
-extension replacement of an object A in an
$0$
-extension replacement of an object A in an
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() is a full map
is a full map
![]() $f:\overline A\twoheadrightarrow A$
from a
$f:\overline A\twoheadrightarrow A$
from a
![]() $0$
-extension
$0$
-extension
![]() $\overline A$
to A.
$\overline A$
to A.
![]() $0$
-extension replacements can always be obtained as
$0$
-extension replacements can always be obtained as
![]() $(\mathsf {E},\mathsf {F})$
-factorizations of
$(\mathsf {E},\mathsf {F})$
-factorizations of
![]() $0\to A$
.
$0\to A$
.
Lemma 6.15. For every object A in an
![]() $(\mathsf {E},\mathsf {F})$
-category
$(\mathsf {E},\mathsf {F})$
-category ![]() there exists a nice diagram
there exists a nice diagram
![]() $A_\bullet $
with colimit A.
$A_\bullet $
with colimit A.
Proof.
![]() $A_0$
is constructed as a
$A_0$
is constructed as a
![]() $0$
-extension replacement
$0$
-extension replacement
![]() $f: A_0\twoheadrightarrow A$
of A. Similarly,
$f: A_0\twoheadrightarrow A$
of A. Similarly,
![]() $A_1$
is given by a
$A_1$
is given by a
![]() $0$
-extension replacement
$0$
-extension replacement
![]() $f_1:A_1\twoheadrightarrow A_0\times _AA_0$
of
$f_1:A_1\twoheadrightarrow A_0\times _AA_0$
of
![]() $A_0\times _AA_0$
, and
$A_0\times _AA_0$
, and
![]() $A_2$
is a
$A_2$
is a
![]() $0$
-extension replacement
$0$
-extension replacement
![]() $f_2:A_2\twoheadrightarrow P$
of the pullback
$f_2:A_2\twoheadrightarrow P$
of the pullback
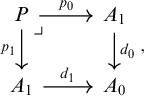
with
![]() $d_0,d_1,d_2:A_2\to A_1$
given by
$d_0,d_1,d_2:A_2\to A_1$
given by
![]() $d_0=p_0\circ f$
,
$d_0=p_0\circ f$
,
![]() $d_2=p_1\circ f$
, and
$d_2=p_1\circ f$
, and
![]() $d_1$
a lifting of
$d_1$
a lifting of
![]() $\langle d_0\circ d_0,d_1\circ d_2\rangle $
along
$\langle d_0\circ d_0,d_1\circ d_2\rangle $
along
![]() $f_1$
. The map
$f_1$
. The map
![]() $\sigma $
is constructed as a lifting of the symmetry of
$\sigma $
is constructed as a lifting of the symmetry of
![]() $A_0\times _AA_0$
along
$A_0\times _AA_0$
along
![]() $f_1$
. The object
$f_1$
. The object
![]() $\tilde A$
is a
$\tilde A$
is a
![]() $0$
-extension replacement of the kernel of
$0$
-extension replacement of the kernel of
![]() $f_1$
.
$f_1$
.
Lemma 6.16. For any clan-algebraic category ![]() , the realization functor
, the realization functor
![]() $J_\otimes $
preserves jointly full cones in flat models, and nice diagrams.
$J_\otimes $
preserves jointly full cones in flat models, and nice diagrams.
Proof. The first claim follows since
![]() $J_\otimes $
is fully faithful on
$J_\otimes $
is fully faithful on
![]() $0$
-extensions by Lemma 6.8 and in both sides the weak factorization system determined by the same generators. Thus there’s a one-to-one correspondence between lifting problems. The second claim follows since
$0$
-extensions by Lemma 6.8 and in both sides the weak factorization system determined by the same generators. Thus there’s a one-to-one correspondence between lifting problems. The second claim follows since
![]() $J_\otimes $
preserves
$J_\otimes $
preserves
![]() $0$
-extensions and
$0$
-extensions and
![]() $0$
-extensions are flat by the fat small object argument.
$0$
-extensions are flat by the fat small object argument.
Lemma 6.17. For any clan-algebraic category ![]() , the functor
, the functor ![]() preserves quotients of nice diagrams.
preserves quotients of nice diagrams.
Proof. Given a nice diagram
![]() $A_\bullet $
in
$A_\bullet $
in ![]() , its colimit is the coequalizer of
, its colimit is the coequalizer of
![]() $d_0,d_1:A_1\to A_0$
. By Lemma 6.13,
$d_0,d_1:A_1\to A_0$
. By Lemma 6.13,
![]() $\langle d_0,d_1\rangle $
factors as
$\langle d_0,d_1\rangle $
factors as
![]() $\langle r_0,r_1\rangle \circ f$
with f full and
$\langle r_0,r_1\rangle \circ f$
with f full and
![]() $r=\langle r_0,r_1\rangle $
an equivalence relation. The pairs
$r=\langle r_0,r_1\rangle $
an equivalence relation. The pairs
![]() $d_0,d_1$
and
$d_0,d_1$
and
![]() $r_0,r_1$
have the same coequalizer (since f is epic), and
$r_0,r_1$
have the same coequalizer (since f is epic), and
![]() $J_N$
preserves the coequalizer of
$J_N$
preserves the coequalizer of
![]() $r_0,r_1$
since it preserves full maps and kernel pairs. Finally, the coequalizer of
$r_0,r_1$
since it preserves full maps and kernel pairs. Finally, the coequalizer of
![]() $J_N(r_0),J_N(r_1)$
is also the coequalizer of
$J_N(r_0),J_N(r_1)$
is also the coequalizer of
![]() $J_N(d_0),J_N(d_1)$
since
$J_N(d_0),J_N(d_1)$
since
![]() $J_N(f)$
is full and therefore epic.
$J_N(f)$
is full and therefore epic.
Theorem 6.18. If ![]() is clan-algebraic, then
is clan-algebraic, then ![]() is an equivalence.
is an equivalence.
Proof. By density,
![]() $J_N$
is fully faithful. It remains to verify that it is essentially surjective, and to this end we show that the unit map
$J_N$
is fully faithful. It remains to verify that it is essentially surjective, and to this end we show that the unit map
![]() $\eta _A:A\to J_N(J_\otimes (A))$
is an isomorphism for all
$\eta _A:A\to J_N(J_\otimes (A))$
is an isomorphism for all ![]() . Let
. Let
![]() $A_\bullet $
be a nice diagram with colimit A. We have:
$A_\bullet $
be a nice diagram with colimit A. We have:
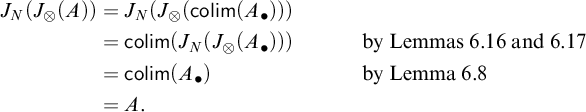 $$ \begin{align*} J_N(J_\otimes(A)) &= J_N(J_\otimes(\mathsf{colim}(A_\bullet)))\\ &=\mathsf{colim}(J_N(J_\otimes(A_\bullet)))&&\text{by Lemmas 6.16 and 6.17}\\ &=\mathsf{colim}(A_\bullet) &&\text{by Lemma 6.8}\\ &=A.\\[-24pt] \end{align*} $$
$$ \begin{align*} J_N(J_\otimes(A)) &= J_N(J_\otimes(\mathsf{colim}(A_\bullet)))\\ &=\mathsf{colim}(J_N(J_\otimes(A_\bullet)))&&\text{by Lemmas 6.16 and 6.17}\\ &=\mathsf{colim}(A_\bullet) &&\text{by Lemma 6.8}\\ &=A.\\[-24pt] \end{align*} $$
We are now ready to prove our main theorem.
Theorem 6.19. The contravariant biadjunction between clans and
![]() $(\mathsf {E},\mathsf {F})$
-categories from Proposition 4.6 restricts to a contravariant biequivalence between Cauchy-complete clans and clan-algebraic categories.
$(\mathsf {E},\mathsf {F})$
-categories from Proposition 4.6 restricts to a contravariant biequivalence between Cauchy-complete clans and clan-algebraic categories.

Proof. By Theorem 5.9 the biadjunction is idempotent, and its fixed points in
![]() $\mathsf {Clan}$
are Cauchy-complete clans. By Theorems 6.2 and 6.18, the fixed points in
$\mathsf {Clan}$
are Cauchy-complete clans. By Theorems 6.2 and 6.18, the fixed points in
![]() $\mathsf {EFCat}$
are precisely the clan-algebraic categories.
$\mathsf {EFCat}$
are precisely the clan-algebraic categories.
Remarks 6.20.
-
(a) The characterization of
 $(\mathsf {E},\mathsf {F})$
-categories of the form
$(\mathsf {E},\mathsf {F})$
-categories of the form
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
in terms of conditions (D), (CG), and (FQ) generalizes, and is in fact inspired by, Adámek–Rosický–Vitale’s characterization of algebraic categories (i.e., categories of models of algebraic theories) as Barr-exact cocomplete locally small categories with a strong generator of compact regular projectives [Reference Adámek, Rosický and Vitale3, Corollary 18.4]Footnote
7
. In particular, if
$\mathcal {T}\!\text {-}\mathsf {Mod}$
in terms of conditions (D), (CG), and (FQ) generalizes, and is in fact inspired by, Adámek–Rosický–Vitale’s characterization of algebraic categories (i.e., categories of models of algebraic theories) as Barr-exact cocomplete locally small categories with a strong generator of compact regular projectives [Reference Adámek, Rosický and Vitale3, Corollary 18.4]Footnote
7
. In particular, if
 $\mathcal {T}$
is a finite-product clan then the regular projectives in
$\mathcal {T}$
is a finite-product clan then the regular projectives in
 $\mathcal {T}\!\text {-}\mathsf {Mod}$
are precisely the
$\mathcal {T}\!\text {-}\mathsf {Mod}$
are precisely the
 $0$
-extensions, thus the strong generation requirement corresponds to (D) (which we have elected to state in terms of density). The Barr-exactness requirement refines to the existence of full coequalizers of componentwise full equivalence relations in the clanic case. The fullness requirements are void in the finite-product case, since coequalizers as well as split epimorphisms are always regular epimorphisms.
$0$
-extensions, thus the strong generation requirement corresponds to (D) (which we have elected to state in terms of density). The Barr-exactness requirement refines to the existence of full coequalizers of componentwise full equivalence relations in the clanic case. The fullness requirements are void in the finite-product case, since coequalizers as well as split epimorphisms are always regular epimorphisms. -
(b) As emphasized by the referee, Definition 6.12 of “nice diagrams” resembles Carboni–Vitale’s definition of pseudo-equivalence relations [Reference Carboni and Vitale11, Definition 6]. Indeed, the resolution by nice diagrams given in Lemma 6.15 reduces to pseudo-equivalence relations in projective objects in the case of finite-product clans, which are related to the fact that algebraic categories are ex/wlex-completions in the sense of Carboni and Vitale. An analogous presentation of clan-algebraic categories as a completion of categories of
 $0$
-extensions (suitably axiomatized) is subject of future work.
$0$
-extensions (suitably axiomatized) is subject of future work.
6.1 Clan-algebraic weak factorization systems on
 $\mathsf {Cat}$
$\mathsf {Cat}$
The characterization of
![]() $(\mathsf {E},\mathsf {F})$
-categories of models of clans as clan-algebraic categories allows to exhibit new clans by defining suitable w.f.s.s on l.f.p. categories. In this subsection we demonstrate this by defining three more clan-algebraic w.f.s.s on
$(\mathsf {E},\mathsf {F})$
-categories of models of clans as clan-algebraic categories allows to exhibit new clans by defining suitable w.f.s.s on l.f.p. categories. In this subsection we demonstrate this by defining three more clan-algebraic w.f.s.s on
![]() $\mathsf {Cat}$
.
$\mathsf {Cat}$
.
We start with the clan-algebraic w.f.s. from Example 2.12(c), corresponding to the “standard” clan-presentation
![]() $\mathcal {T}_{\mathsf {Cat}}$
from §2.2. We observed that this w.f.s. is cofibrantly generated by the functors
$\mathcal {T}_{\mathsf {Cat}}$
from §2.2. We observed that this w.f.s. is cofibrantly generated by the functors
![]() $0\hookrightarrow 1$
and
$0\hookrightarrow 1$
and ![]() . Our strategy to define new clan-algebraic w.f.s.s is to add additional generators. If we make sure that the domain and codomain of these are compact
. Our strategy to define new clan-algebraic w.f.s.s is to add additional generators. If we make sure that the domain and codomain of these are compact
![]() $0$
-extensions, we only have to verify condition (FQ) when verifying that the new w.f.s. is still clan-algebraic. The additional generators we consider are the arrows
$0$
-extensions, we only have to verify condition (FQ) when verifying that the new w.f.s. is still clan-algebraic. The additional generators we consider are the arrows ![]() and
and
![]() $2\to 1$
, where
$2\to 1$
, where
![]() $\mathbb {P}$
is the “parallel pair category”
$\mathbb {P}$
is the “parallel pair category”
![]() $\bullet \rightrightarrows \bullet $
. By adding either one or both of the additional generators we obtain three additional w.f.s.s
$\bullet \rightrightarrows \bullet $
. By adding either one or both of the additional generators we obtain three additional w.f.s.s
![]() $(\mathsf {E}_{\mathsf {O}},\mathsf {F}_{\mathsf {O}})$
,
$(\mathsf {E}_{\mathsf {O}},\mathsf {F}_{\mathsf {O}})$
,
![]() $(\mathsf {E}_{\mathsf {A}},\mathsf {F}_{\mathsf {A}})$
, and
$(\mathsf {E}_{\mathsf {A}},\mathsf {F}_{\mathsf {A}})$
, and
![]() $(\mathsf {E}_{\mathsf {OA}},\mathsf {F}_{\mathsf {OA}})$
, where:
$(\mathsf {E}_{\mathsf {OA}},\mathsf {F}_{\mathsf {OA}})$
, where:
We have already observed that
![]() $\mathsf {F}$
consists of the functors that are full and surjective on objects, and it is easy to see that
$\mathsf {F}$
consists of the functors that are full and surjective on objects, and it is easy to see that
![]() $\mathsf {F}_{\mathsf {O}}$
contains only those functors which are full and bijective on objects, whereas
$\mathsf {F}_{\mathsf {O}}$
contains only those functors which are full and bijective on objects, whereas
![]() $\mathsf {F}_{\mathsf {A}}$
consists of functors which are fully faithful and surjective on objects. Finally,
$\mathsf {F}_{\mathsf {A}}$
consists of functors which are fully faithful and surjective on objects. Finally,
![]() $\mathsf {F}_{\mathsf {OA}}$
only contains functors which are fully faithful and bijective on objects, i.e., isomorphisms of categories.
$\mathsf {F}_{\mathsf {OA}}$
only contains functors which are fully faithful and bijective on objects, i.e., isomorphisms of categories.
To convince ourselves that the new w.f.s.s are indeed clan-algebraic we only have to verify that for every equivalence relation
![]() $\langle p,q\rangle :\mathbb {R}\to \mathbb {A}\times \mathbb {A}$
in
$\langle p,q\rangle :\mathbb {R}\to \mathbb {A}\times \mathbb {A}$
in
![]() $\mathsf {Cat}$
, the coequalizer is in either of
$\mathsf {Cat}$
, the coequalizer is in either of
![]() $\mathsf {F}_{\mathsf {O}},\mathsf {F}_{\mathsf {A}},\mathsf {F}_{\mathsf {OA}}$
whenever p and q are, since effectivity has already been established for equivalence relations with components in
$\mathsf {F}_{\mathsf {O}},\mathsf {F}_{\mathsf {A}},\mathsf {F}_{\mathsf {OA}}$
whenever p and q are, since effectivity has already been established for equivalence relations with components in
![]() $\mathsf {F}$
. This is not difficult to see for
$\mathsf {F}$
. This is not difficult to see for
![]() $\mathsf {F}_{\mathsf {O}}$
and
$\mathsf {F}_{\mathsf {O}}$
and
![]() $\mathsf {F}_{\mathsf {A}}$
, and trivial for
$\mathsf {F}_{\mathsf {A}}$
, and trivial for
![]() $\mathsf {F}_{\mathsf {OA}}$
.
$\mathsf {F}_{\mathsf {OA}}$
.
The coclans corresponding to the new w.f.s.s are:
-
•
 $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}^{\mathsf {op}}= \{\text {categories free on finite graphs}\}$
, with functors
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}^{\mathsf {op}}= \{\text {categories free on finite graphs}\}$
, with functors
 $G^*\to H^*$
arising from faithful graph morphisms as codisplay maps,
$G^*\to H^*$
arising from faithful graph morphisms as codisplay maps, -
•
 $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}^{\mathsf {op}} = \{\text {finitely presented categories}\}$
, with injective-on-objects functors as codisplay maps, and
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}^{\mathsf {op}} = \{\text {finitely presented categories}\}$
, with injective-on-objects functors as codisplay maps, and -
•
 $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}^{\mathsf {op}} = \{\text {finitely presented categories}\}$
, with arbitrary functors as codisplay maps.
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}^{\mathsf {op}} = \{\text {finitely presented categories}\}$
, with arbitrary functors as codisplay maps.
We note the clan
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
is simply the finite-limit theory of categories. One may ask whether the clans
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
is simply the finite-limit theory of categories. One may ask whether the clans
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
,
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
,
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
, and
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
, and
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
admit simple syntactic presentations by GATs, and indeed they do. To obtain such a presentation e.g., for
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
admit simple syntactic presentations by GATs, and indeed they do. To obtain such a presentation e.g., for
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
, we have to modify the GAT
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
, we have to modify the GAT
![]() $\mathbb {T}_{\mathsf {Cat}}$
in such a way that the syntactic category stays the same, but acquires additional display maps, such as the diagonal
$\mathbb {T}_{\mathsf {Cat}}$
in such a way that the syntactic category stays the same, but acquires additional display maps, such as the diagonal
![]() $(x:O)\to (x\,y:O)$
corresponding to the new generator
$(x:O)\to (x\,y:O)$
corresponding to the new generator
![]() $2\to 1$
. Display maps in the syntactic category of a GAT are always of the form
$2\to 1$
. Display maps in the syntactic category of a GAT are always of the form
![]() $p\circ i$
where p is a projection omitting a finite number of variables and i is an isomorphism (Proposition 10.3), so to turn
$p\circ i$
where p is a projection omitting a finite number of variables and i is an isomorphism (Proposition 10.3), so to turn
![]() $(x:O)\to (x\,y:O)$
into a display map we have to make
$(x:O)\to (x\,y:O)$
into a display map we have to make
![]() $(x:O)$
isomorphic to an extension of
$(x:O)$
isomorphic to an extension of
![]() $(x\,y:O)$
. To achieve this we postulate a new type family
$(x\,y:O)$
. To achieve this we postulate a new type family
![]() $x\,y:O\vdash E_O(x,y)$
and add axioms forcing the projection
$x\,y:O\vdash E_O(x,y)$
and add axioms forcing the projection
![]() $(x\,y:A\,,\, z:E_O(x,y))\to (x:A)$
to become an isomorphism:
$(x\,y:A\,,\, z:E_O(x,y))\to (x:A)$
to become an isomorphism:
 $$ \begin{align} \begin{aligned} x\,y:O & \;\vdash\; E_O(x,y) \\ x:O & \;\vdash\; r_O(x):E_O(x,x) \\ x\,y:O\,,\,p:E_O(x,y) & \;\vdash\; x=y \\ x:O\,,\,p:E_O(x,x) & \;\vdash\; r_O(x)=p. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} x\,y:O & \;\vdash\; E_O(x,y) \\ x:O & \;\vdash\; r_O(x):E_O(x,x) \\ x\,y:O\,,\,p:E_O(x,y) & \;\vdash\; x=y \\ x:O\,,\,p:E_O(x,x) & \;\vdash\; r_O(x)=p. \end{aligned} \end{align} $$
The function symbol
![]() $r_O$
gives a section for the projection, and the two last axioms force the retract to be an isomorphism. We recognize at once that these axioms make
$r_O$
gives a section for the projection, and the two last axioms force the retract to be an isomorphism. We recognize at once that these axioms make
![]() $E_O$
an extensional identity type of O [Reference Hofmann23, Section 3.2]: the term
$E_O$
an extensional identity type of O [Reference Hofmann23, Section 3.2]: the term
![]() $r_O$
is reflexivity, and the third and fourth rule give equality reflection and uniqueness of identity proofs. We write
$r_O$
is reflexivity, and the third and fourth rule give equality reflection and uniqueness of identity proofs. We write
![]() $\mathbb {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
for the extension of the GAT
$\mathbb {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
for the extension of the GAT
![]() $\mathbb {T}_{\mathsf {Cat}}$
by the axioms (6.1), and
$\mathbb {T}_{\mathsf {Cat}}$
by the axioms (6.1), and
![]() $\mathsf {Cat}_{_{\mathsf {O}}}$
for the corresponding clan-algebraic category.
$\mathsf {Cat}_{_{\mathsf {O}}}$
for the corresponding clan-algebraic category.
Similarly, we obtain a GAT-representation
![]() $\mathbb {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
of the clan
$\mathbb {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
of the clan
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
by augmenting
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
by augmenting
![]() $\mathbb {T}_{\mathsf {Cat}}$
by a type family
$\mathbb {T}_{\mathsf {Cat}}$
by a type family
![]() $E_A$
with the following rules:
$E_A$
with the following rules:
 $$ \begin{align} \begin{aligned} x\,y:O\,,\,f\,g:A(x,y) &\;\vdash\; E_A(f,g) \\ x\,y:O\,,\,f:A(x,y) &\;\vdash\; r_A(f):E_A(f,f) \\ x\,y:O\,,\,f\,g:A(x,y)\,,\,p:E_A(f,g) &\;\vdash\; f=g \\ x\,y:O\,,\,f:A(x,y)\,,\,p:E_A(f,f) &\;\vdash\; r_A(f)=p. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} x\,y:O\,,\,f\,g:A(x,y) &\;\vdash\; E_A(f,g) \\ x\,y:O\,,\,f:A(x,y) &\;\vdash\; r_A(f):E_A(f,f) \\ x\,y:O\,,\,f\,g:A(x,y)\,,\,p:E_A(f,g) &\;\vdash\; f=g \\ x\,y:O\,,\,f:A(x,y)\,,\,p:E_A(f,f) &\;\vdash\; r_A(f)=p. \end{aligned} \end{align} $$
Adding both sets of axioms (6.1) and (6.2) to
![]() $\mathbb {T}_{\mathsf {Cat}}$
yields a GAT for the clan
$\mathbb {T}_{\mathsf {Cat}}$
yields a GAT for the clan
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
, i.e., the finite-limit theory of categories.
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
, i.e., the finite-limit theory of categories.
Remark 6.21. As pointed out by the referee, an enriched version of the
![]() $(\mathsf {E}_{\mathsf {A}},\mathsf {F}_{\mathsf {A}})$
-instance of the exactness condition (FQ) appears under the name ff-exactness in Bourke and Garner’s [Reference Bourke and Garner9]. Further investigation may be needed.
$(\mathsf {E}_{\mathsf {A}},\mathsf {F}_{\mathsf {A}})$
-instance of the exactness condition (FQ) appears under the name ff-exactness in Bourke and Garner’s [Reference Bourke and Garner9]. Further investigation may be needed.
7 A counterexample
This section gives a common counterexample to two related natural questions about the extension–full w.f.s. on a clan-algebraic category ![]() :
:
-
(1) Does every compact object admit a full map from a compact
 $0$
-extension?
$0$
-extension? -
(2) Does the weak factorization system always restrict to compact
 $0$
-extensions?
$0$
-extensions?
The counterexample to both question is given by the category of models of the following GAT with infinitely many sorts and operations:
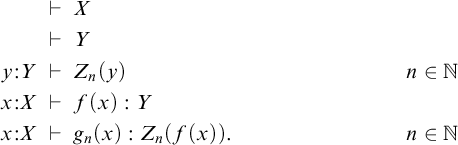 $$ \begin{align*} &\;\vdash\; X\\ &\;\vdash\; Y\\ y{:}Y&\;\vdash\; Z_n(y)&n\in\mathbb{N}\\ x{:}X&\;\vdash\; f(x):Y\\ x{:}X&\;\vdash\; g_n(x):Z_n(f(x)).{\qquad}&n\in\mathbb{N} \end{align*} $$
$$ \begin{align*} &\;\vdash\; X\\ &\;\vdash\; Y\\ y{:}Y&\;\vdash\; Z_n(y)&n\in\mathbb{N}\\ x{:}X&\;\vdash\; f(x):Y\\ x{:}X&\;\vdash\; g_n(x):Z_n(f(x)).{\qquad}&n\in\mathbb{N} \end{align*} $$
Its category of models is equivalent to the set-valued functors on the posetal category
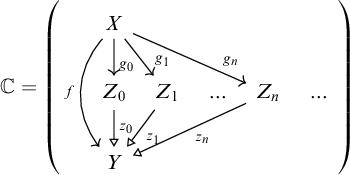
and the w.f.s. on
![]() $[\mathbb {C},\mathsf {Set}]$
is generated by the arrows
$[\mathbb {C},\mathsf {Set}]$
is generated by the arrows ![]() ,
, ![]() , and
, and ![]() for
for
![]() $n\in \mathbb {N}$
, reflecting the idea that models
$n\in \mathbb {N}$
, reflecting the idea that models
![]() $A:\mathbb {C}\to \mathsf {Set}$
can be built up by successively adding elements to
$A:\mathbb {C}\to \mathsf {Set}$
can be built up by successively adding elements to
![]() $A(X)$
or
$A(X)$
or
![]() $A(Y)$
, and to
$A(Y)$
, and to
![]() $A(Z_n)$
over a given element x of
$A(Z_n)$
over a given element x of
![]() $A(Y)$
, as in the following pushouts.
$A(Y)$
, as in the following pushouts.
The following lemma gives explicit descriptions of the w.f.s. and the compact objects in
![]() $[\mathbb {C},\mathsf {Set}]$
.
$[\mathbb {C},\mathsf {Set}]$
.
Lemma 7.1. Let
![]() $f:A\to B$
in
$f:A\to B$
in
![]() $[\mathbb {C},\mathsf {Set}]$
.
$[\mathbb {C},\mathsf {Set}]$
.
-
(i) f is full if and only if it is componentwise surjective and the naturality squares for
 $z_n$
are weak pullbacks for all
$z_n$
are weak pullbacks for all
 $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
. -
(ii) f is an extension if an only if
 $f_X:A(X)\to B(X)$
is injective, and the squares
$f_X:A(X)\to B(X)$
is injective, and the squares 
are quasi-pushouts, in the sense that the gap maps
 $A(Y)+_{A(X)}B(X)\to B(Y)$
and
$A(Y)+_{A(X)}B(X)\to B(Y)$
and
 $A(Z_n)+_{A(X)}B(X)\to B(Z_n)$
are injective. (This implies that the components
$A(Z_n)+_{A(X)}B(X)\to B(Z_n)$
are injective. (This implies that the components
 $f_{Y}$
and
$f_{Y}$
and
 $f_{Z_n}$
are also injective).
$f_{Z_n}$
are also injective). -
(iii) A is a
 $0$
-extension if an only if
$0$
-extension if an only if
 $A(f)$
and all
$A(f)$
and all
 $A(g_n)$
are injective.
$A(g_n)$
are injective. -
(iv) A is compact if an only if (a) it is componentwise finite, and (b)
 $A({f_n}):A(X)\to A(Z_n)$
is a bijection for all but finitely many
$A({f_n}):A(X)\to A(Z_n)$
is a bijection for all but finitely many
 $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Using this lemma, we can give negative answers to the two question at the beginning of the section.
Proposition 7.2.
-
(i) The object P in the pushout

is compact, but does not admit a full map from a compact
 $0$
-extension.
$0$
-extension. -
(ii) The map
 does not admit an extension–full factorization through a compact object.
does not admit an extension–full factorization through a compact object.
Proof. For the first claim, P is compact as a finite colimit of representables. Let
![]() $f:E\twoheadrightarrow P$
be a full map with E a
$f:E\twoheadrightarrow P$
be a full map with E a
![]() $0$
-extension. For each
$0$
-extension. For each
![]() $n\in \mathbb {N}$
we get a diagram
$n\in \mathbb {N}$
we get a diagram
where
![]() $E(f)$
and
$E(f)$
and
![]() $E(g_n)$
are injective because E is a
$E(g_n)$
are injective because E is a
![]() $0$
-extension, and the components of f are surjective and the
$0$
-extension, and the components of f are surjective and the
![]() $z_n$
-naturality square is a weak pullback since because f is full. In particular
$z_n$
-naturality square is a weak pullback since because f is full. In particular
![]() $E(Y)$
is inhabited and the fibers of
$E(Y)$
is inhabited and the fibers of
![]() $E(z_n)$
have at least two elements. Since the fibers of
$E(z_n)$
have at least two elements. Since the fibers of
![]() $E(f)$
have at most one element, this means that
$E(f)$
have at most one element, this means that
![]() $E(g_n)$
can’t be surjective for any n, and it follows from Lemma 7.1(iv) that E is not compact.
$E(g_n)$
can’t be surjective for any n, and it follows from Lemma 7.1(iv) that E is not compact.
For the second claim consider an extension ![]() such that
such that ![]() is full. Then
is full. Then
![]() $A(Y)$
is inhabited, all
$A(Y)$
is inhabited, all
![]() $A(Z_n)\to A(Y)$
are surjective, and
$A(Z_n)\to A(Y)$
are surjective, and
![]() $1+A(X)\to A(Y)$
is injective. From this we can again deduce that none of the
$1+A(X)\to A(Y)$
is injective. From this we can again deduce that none of the
![]() $A(g_n)$
are surjective and thus A is not compact.
$A(g_n)$
are surjective and thus A is not compact.
8 Models in higher types
One practical use of having inequivalent clans with equivalent categories of
![]() $\mathsf {Set}$
-models is that they can have inequivalent
$\mathsf {Set}$
-models is that they can have inequivalent
![]() $\infty $
-categories of models in the
$\infty $
-categories of models in the
![]() $\infty $
-category
$\infty $
-category ![]() of homotopy types (a.k.a. “spaces”). We leave this issue for future work and content ourselves here with outlining some main ideas.
of homotopy types (a.k.a. “spaces”). We leave this issue for future work and content ourselves here with outlining some main ideas.
Reasoning informally, in the following we identify sets with discrete (
![]() $0$
-truncated) homotopy types, and
$0$
-truncated) homotopy types, and
![]() $1$
-categories with
$1$
-categories with
![]() $\infty $
-categories all of whose
$\infty $
-categories all of whose
![]() $\hom $
-types are
$\hom $
-types are
![]() $0$
-truncated. Given a clan
$0$
-truncated. Given a clan
![]() $\mathcal {T}$
it then makes sense to define an
$\mathcal {T}$
it then makes sense to define an
![]() $\infty $
-model to be an
$\infty $
-model to be an
![]() $\infty $
-functor
$\infty $
-functor ![]() into spaces which preserves the terminal object and pullbacks of display maps in the suitable
into spaces which preserves the terminal object and pullbacks of display maps in the suitable
![]() $\infty $
-categorical sense, and to write
$\infty $
-categorical sense, and to write ![]() for the
for the
![]() $\infty $
-category of models, as a full
$\infty $
-category of models, as a full
![]() $\infty $
-subcategory of the functor-
$\infty $
-subcategory of the functor-
![]() $\infty $
-category
$\infty $
-category ![]() .
.
The first observation is that for
![]() $\mathcal {T}$
a finite-limit clan, the
$\mathcal {T}$
a finite-limit clan, the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}_\infty $
of
$\mathcal {T}\!\text {-}\mathsf {Mod}_\infty $
of
![]() $\infty $
-models is in fact equivalent to (the
$\infty $
-models is in fact equivalent to (the
![]() $\infty $
-category corresponding to) the
$\infty $
-category corresponding to) the
![]() $1$
-category
$1$
-category
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
of
$\mathcal {T}\!\text {-}\mathsf {Mod}$
of
![]() $1$
-models! This is because finite
$1$
-models! This is because finite
![]() $\infty $
-limit preserving
$\infty $
-limit preserving
![]() $\infty $
-functors preserve truncation levels, and thus every finite
$\infty $
-functors preserve truncation levels, and thus every finite
![]() $\infty $
-limit preserving
$\infty $
-limit preserving ![]() must factor through the inclusion of
must factor through the inclusion of ![]() , since all objects of
, since all objects of
![]() $1$
-categories are (representably)
$1$
-categories are (representably)
![]() $0$
-truncated.
$0$
-truncated.
For finite-product clans, on the other hand, there is no such restriction. The
![]() $\infty $
-models of the finite-product clan
$\infty $
-models of the finite-product clan
![]() $\mathcal {C}_{\mathsf {Mon}}$
of monoids, for example, are the models of the associative
$\mathcal {C}_{\mathsf {Mon}}$
of monoids, for example, are the models of the associative
![]() $\infty $
-operad [Reference Lurie30, Section 4.11], whereas the
$\infty $
-operad [Reference Lurie30, Section 4.11], whereas the
![]() $\infty $
-models of the finite-product theory of abelian groups are related to the Dold–Kan correspondence. Variants of this phenomenon are discussed under the name “animation” in [Reference Cesnavicius and Scholze14]; Rosický’s [Reference Rosický40] contains an earlier account.
$\infty $
-models of the finite-product theory of abelian groups are related to the Dold–Kan correspondence. Variants of this phenomenon are discussed under the name “animation” in [Reference Cesnavicius and Scholze14]; Rosický’s [Reference Rosický40] contains an earlier account.
Now the nice thing about clans is that they admit finer graduations of “levels of strictness”. Among the clans
![]() $\mathcal {T}$
,
$\mathcal {T}$
,
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
,
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
,
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
, and
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
, and
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
from §6.1, for example, we know that the
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
from §6.1, for example, we know that the
![]() $\infty $
-models of the finite-limit clan
$\infty $
-models of the finite-limit clan
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
are precisely the strict
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {OA}}}}$
are precisely the strict
![]() $1$
-categories. The presence of the extensional identity type on O in
$1$
-categories. The presence of the extensional identity type on O in
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
behaves like a kind of “partial finite-limit completion”, and has the effect that the sort O is interpreted by a
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
behaves like a kind of “partial finite-limit completion”, and has the effect that the sort O is interpreted by a
![]() $0$
-type in every model
$0$
-type in every model ![]() , whereas the presence of extensional identities on A in
, whereas the presence of extensional identities on A in
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
has the effect that the projection
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
has the effect that the projection
![]() $(x\,y:O\,,\,f:A(x,y))\to (x\,y:O)$
is mapped to a function with
$(x\,y:O\,,\,f:A(x,y))\to (x\,y:O)$
is mapped to a function with
![]() $0$
-truncated fibers by every
$0$
-truncated fibers by every
![]() $\infty $
-model
$\infty $
-model ![]() . This means that
. This means that
![]() $\infty $
-models of
$\infty $
-models of
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
are pre-categories in the sense of Homotopy Type Theory [43, Definition 9.1.1], whereas
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {A}}}}$
are pre-categories in the sense of Homotopy Type Theory [43, Definition 9.1.1], whereas
![]() $\infty $
-models of
$\infty $
-models of
![]() $\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
seem to correspond to Segal-categories [Reference Hirschowitz and Simpson22, Section 2], [Reference Bergner7, Section 5]. Finally, the clan
$\mathcal {T}_{\mathsf {Cat}_{_{\mathsf {O}}}}$
seem to correspond to Segal-categories [Reference Hirschowitz and Simpson22, Section 2], [Reference Bergner7, Section 5]. Finally, the clan
![]() $\mathcal {T}_{\mathsf {Cat}}$
does not impose any truncation conditions, which makes its
$\mathcal {T}_{\mathsf {Cat}}$
does not impose any truncation conditions, which makes its
![]() $\infty $
-models resemble Segal spaces (not necessarily complete), in the sense of [Reference Rezk38, Section 4].
$\infty $
-models resemble Segal spaces (not necessarily complete), in the sense of [Reference Rezk38, Section 4].
Remark 8.1. Notably absent from the list of higher algebraic structures represented by the variants of
![]() $\mathcal {T}_{\mathsf {Cat}}$
are univalent
$\mathcal {T}_{\mathsf {Cat}}$
are univalent
![]() $\infty $
-categories. In fact, the requirement on a clan
$\infty $
-categories. In fact, the requirement on a clan
![]() $\mathcal {T}$
that
$\mathcal {T}$
that
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}_\infty \simeq \infty \text {-}\mathsf {Cat}$
is incompatible with the requirement that
$\mathcal {T}\!\text {-}\mathsf {Mod}_\infty \simeq \infty \text {-}\mathsf {Cat}$
is incompatible with the requirement that
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}\simeq \mathsf {Cat}$
, since
$\mathcal {T}\!\text {-}\mathsf {Mod}\simeq \mathsf {Cat}$
, since
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
is the full subcategory of
$\mathcal {T}\!\text {-}\mathsf {Mod}$
is the full subcategory of
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}_\infty $
on
$\mathcal {T}\!\text {-}\mathsf {Mod}_\infty $
on
![]() $0$
-truncated objects, and the only
$0$
-truncated objects, and the only
![]() $0$
-truncated univalent
$0$
-truncated univalent
![]() $1$
-categories are the rigid ones, i.e., those whose with only trivial automorphisms. It seems unlikely to the author that
$1$
-categories are the rigid ones, i.e., those whose with only trivial automorphisms. It seems unlikely to the author that
![]() $\infty \text {-}\mathsf {Cat}$
can be described by a “
$\infty \text {-}\mathsf {Cat}$
can be described by a “
![]() $1$
-clan”. See [Reference Ahrens, North, Shulman and Tsementzis4, Reference Ahrens, North, Shulman and Tsementzis5] for recent work addressing this univalence issue, using techniques building on Makkai’s First order logic with dependent sorts (FOLDS) [Reference Makkai32]. Another recent work connecting Cartmell’s GATs and Makkai’s FOLDS is Chaitanya Leena Subramaniam’s thesis [Reference Subramaniam28].
$1$
-clan”. See [Reference Ahrens, North, Shulman and Tsementzis4, Reference Ahrens, North, Shulman and Tsementzis5] for recent work addressing this univalence issue, using techniques building on Makkai’s First order logic with dependent sorts (FOLDS) [Reference Makkai32]. Another recent work connecting Cartmell’s GATs and Makkai’s FOLDS is Chaitanya Leena Subramaniam’s thesis [Reference Subramaniam28].
9 Appendix. Locally finitely presentable categories, weak factorization systems, and Quillen’s small object argument
This appendix recalls basic definitions and facts about the concepts mentioned in the title.
Definition 9.1. A category
![]() $\mathcal {C}$
is called filtered, if every diagram
$\mathcal {C}$
is called filtered, if every diagram
![]() $D:\mathbb {J}\to \mathcal {C}$
with finite domain admits a cocone. A filtered colimit is a colimit of a diagram indexed by a filtered category.
$D:\mathbb {J}\to \mathcal {C}$
with finite domain admits a cocone. A filtered colimit is a colimit of a diagram indexed by a filtered category.
Definition 9.2. Let
![]() $\mathfrak {X}$
be a cocomplete locally small category.
$\mathfrak {X}$
be a cocomplete locally small category.
-
(i) An object
 $C\in \mathfrak {X}$
is called compact, if the covariant representable functor
$C\in \mathfrak {X}$
is called compact, if the covariant representable functor  $$ \begin{align*} \mathfrak{X}(C,-):\mathfrak{X}\to\mathsf{Set} \end{align*} $$
$$ \begin{align*} \mathfrak{X}(C,-):\mathfrak{X}\to\mathsf{Set} \end{align*} $$
preserves small filtered colimits.
-
(ii)
 $\mathfrak {X}$
is called locally finitely presentable (l.f.p.) if it admits a small dense family of compact objects, i.e., a family
$\mathfrak {X}$
is called locally finitely presentable (l.f.p.) if it admits a small dense family of compact objects, i.e., a family
 $(C_i)_{i\in I}$
of compact objects indexed by a small set I, such that the nerve functor
$(C_i)_{i\in I}$
of compact objects indexed by a small set I, such that the nerve functor  $$ \begin{align*} J_N:\mathfrak{X}\to\widehat{\mathbb{C}} \end{align*} $$
$$ \begin{align*} J_N:\mathfrak{X}\to\widehat{\mathbb{C}} \end{align*} $$
of the inclusion
 $J:\mathbb {C}\hookrightarrow \mathfrak {X}$
of the full subcategory on the
$J:\mathbb {C}\hookrightarrow \mathfrak {X}$
of the full subcategory on the
 $(C_i)_{i\in I}$
is fully faithful.
$(C_i)_{i\in I}$
is fully faithful.
Remarks 9.3.
-
(a) Compact objects are also known as finitely presentable objects, e.g., in [Reference Gabriel and Ulmer16, Reference Adámek and Rosicky2]. We adopted the term compact from [Reference Lurie29, Definition A.1.1.1] since it is more concise, and in particular since compact
 $0$
-extension sounds less awkward than finitely presented
$0$
-extension sounds less awkward than finitely presented
 $0$
-extension. Moreover I think the fact that objects of algebraic categories (such as groups, rings, modules …) are compact if and only if they admit a presentation by finitely many generators and relations is an important theorem, which is difficult to state if one uses the same terminology for the syntactic and the categorical notion.
$0$
-extension. Moreover I think the fact that objects of algebraic categories (such as groups, rings, modules …) are compact if and only if they admit a presentation by finitely many generators and relations is an important theorem, which is difficult to state if one uses the same terminology for the syntactic and the categorical notion. -
(b) The density condition in the definition is equivalent to saying that the family
 $(C_i)_{{i\in I}}$
is a strong generator, in the sense that the canonical arrow
$(C_i)_{{i\in I}}$
is a strong generator, in the sense that the canonical arrow  $$ \begin{align*} \coprod_{i\in I,f:C_i\to A}\!\!\!C_i\to A \end{align*} $$
$$ \begin{align*} \coprod_{i\in I,f:C_i\to A}\!\!\!C_i\to A \end{align*} $$
is an extremal epimorphism for all
 $A\in \mathfrak {X}$
. We stated the definition in terms of density here, since nerve functors play a central role in this work, contrary to strong generation.
$A\in \mathfrak {X}$
. We stated the definition in terms of density here, since nerve functors play a central role in this work, contrary to strong generation. -
(c) The notion of l.f.p. category is a special case of the notion of locally
 $\alpha $
-presentable category for a regular cardinal
$\alpha $
-presentable category for a regular cardinal
 $\alpha $
[Reference Gabriel and Ulmer16, Reference Adámek and Rosicky2]. In this work, only the case
$\alpha $
[Reference Gabriel and Ulmer16, Reference Adámek and Rosicky2]. In this work, only the case
 $\alpha =\omega $
plays a role.
$\alpha =\omega $
plays a role.
Definition 9.4. Let
![]() $\mathcal {C}$
be a category.
$\mathcal {C}$
be a category.
-
(i) Given two arrows
 $f:A\to B$
,
$f:A\to B$
,
 $g:X\to Y$
in
$g:X\to Y$
in
 $\mathcal {C}$
, we say that f has the left lifting property (l.l.p.) w.r.t. g (or equivalently that g has the right lifting property (r.l.p.) w.r.t. f), and write
$\mathcal {C}$
, we say that f has the left lifting property (l.l.p.) w.r.t. g (or equivalently that g has the right lifting property (r.l.p.) w.r.t. f), and write
 $f\pitchfork g$
, if in each commutative square
$f\pitchfork g$
, if in each commutative square 
there exists a diagonal arrow h making the two triangles commute.
-
(ii) Given a class
 $\mathsf {E}\subseteq {\mathsf {mor}(\mathcal {C})}$
of arrows in
$\mathsf {E}\subseteq {\mathsf {mor}(\mathcal {C})}$
of arrows in
 $\mathcal {C}$
, we define:
$\mathcal {C}$
, we define:  $$ \begin{align*} {}^\pitchfork\mathsf{E}&=\{f\in\mathsf{mor}(\mathcal{C})\mathrel| {\forall g\in\mathsf{E}\,.\, f\pitchfork g}\}\\ \mathsf{E}^\pitchfork&=\{g\in\mathsf{mor}(\mathcal{C})\mathrel| {\forall f\in\mathsf{E}\,.\, f\pitchfork g}\}. \end{align*} $$
$$ \begin{align*} {}^\pitchfork\mathsf{E}&=\{f\in\mathsf{mor}(\mathcal{C})\mathrel| {\forall g\in\mathsf{E}\,.\, f\pitchfork g}\}\\ \mathsf{E}^\pitchfork&=\{g\in\mathsf{mor}(\mathcal{C})\mathrel| {\forall f\in\mathsf{E}\,.\, f\pitchfork g}\}. \end{align*} $$
-
(iii) A weak factorization system (w.f.s.) on
 $\mathcal {C}$
is a pair
$\mathcal {C}$
is a pair
 $\mathcal {L},\mathcal {R}\subseteq \mathsf {mor}(\mathcal {C})$
of classes of morphisms such that
$\mathcal {L},\mathcal {R}\subseteq \mathsf {mor}(\mathcal {C})$
of classes of morphisms such that
 $\mathcal {L}^\pitchfork = \mathcal {R}$
,
$\mathcal {L}^\pitchfork = \mathcal {R}$
,
 $\mathcal {R}^\pitchfork = \mathcal {L}$
, and every
$\mathcal {R}^\pitchfork = \mathcal {L}$
, and every
 $f:A\to B$
in
$f:A\to B$
in
 $\mathcal {C}$
admits a factorization
$\mathcal {C}$
admits a factorization
 $f=r\circ l$
with
$f=r\circ l$
with
 $l\in \mathcal {L}$
and
$l\in \mathcal {L}$
and
 $r\in \mathcal {R}$
.
$r\in \mathcal {R}$
.
We call
![]() $\mathcal {L}$
the left class, and
$\mathcal {L}$
the left class, and
![]() $\mathcal {R}$
the right class of the w.f.s. One can show that left classes of w.f.s.s contain all isomorphisms, and are closed under composition and pushouts, i.e., if
$\mathcal {R}$
the right class of the w.f.s. One can show that left classes of w.f.s.s contain all isomorphisms, and are closed under composition and pushouts, i.e., if
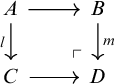
is a pushout in
![]() $\mathcal {C}$
and is a left map, then so is m. Dually, right maps are closed under (isomorphisms, composition, and) pullbacks. With this, we have the prerequisites to state Quillen’s small object argument.
$\mathcal {C}$
and is a left map, then so is m. Dually, right maps are closed under (isomorphisms, composition, and) pullbacks. With this, we have the prerequisites to state Quillen’s small object argument.
Theorem 9.5 (Small object argument for l.f.p. categories).
Let
![]() $\mathsf {E}\subseteq \mathsf {mor}(\mathfrak {X})$
be a small set of morphisms in a l.f.p. category. Then
$\mathsf {E}\subseteq \mathsf {mor}(\mathfrak {X})$
be a small set of morphisms in a l.f.p. category. Then
![]() $({}^\pitchfork (\mathsf {E}^\pitchfork ),\mathsf {E}^\pitchfork )$
is a w.f.s. on
$({}^\pitchfork (\mathsf {E}^\pitchfork ),\mathsf {E}^\pitchfork )$
is a w.f.s. on
![]() $\mathfrak {X}$
.
$\mathfrak {X}$
.
Proof. Hovey [Reference Hovey24, Theorem 2.1.14] and Riehl [Reference Riehl39, Theorem 12.2.2] prove stronger statements in a more general setting.
10 Appendix. Generalized algebraic theories
Cartmell’s generalized algebraic theories extend the notion of algebraic theory (which can be ‘single sorted’, such as the theories of groups or rings, or ‘many sorted’, such as the theories of reflexive graphs, chain complexes of abelian groups, or modules over a non-fixed base ring) by introducing dependent sorts (a.k.a. dependent ‘types’), which represent families of sets and can be used e.g., to axiomatize the notion of a (small) category
![]() $\mathbb {C}$
as a structure with a set
$\mathbb {C}$
as a structure with a set
![]() $\mathbb {C}_0$
of objects, and a family
$\mathbb {C}_0$
of objects, and a family
![]() $(\mathbb {C}(A,B))_{A,B\in \mathbb {C}_0}$
of
$(\mathbb {C}(A,B))_{A,B\in \mathbb {C}_0}$
of
![]() $\hom $
-sets (see (10.1) below).
$\hom $
-sets (see (10.1) below).
Compared to ordinary algebraic theories, whose specification in terms of sorts, operations, and equations is fairly straightforward, the syntactic description of generalized algebraic theories is complicated by the fact that the domains of definition of operations and dependent sorts, and the codomains of operations, may themselves be compound expressions involving previously declared operations and sorts, whose well-formedness has to be ensured and may even depend on the equations of the theory. This means that we have to state the declarations of sorts and of operations, and the equations (which we collectively refer to as axioms of the theory) in an ordered way, where the later axioms have to be well-formed on the basis of the earlier axioms. This looks as follows in the case of the generalized algebraic theory
![]() $\mathbb {T}_{\mathsf {Cat}}$
of categories:
$\mathbb {T}_{\mathsf {Cat}}$
of categories:
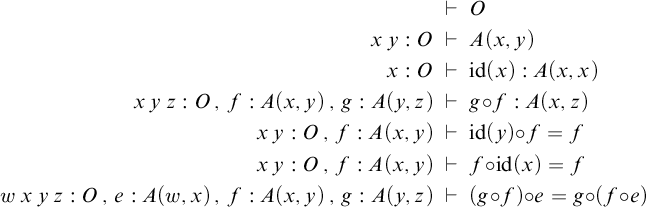
Each line contains one axiom, the first two declaring the sort O of objects and the dependent sort
![]() $A(x,y)$
of arrows, the third and the fourth declaring the identity and composition operations, and the last three stating the identity and associativity axioms.
$A(x,y)$
of arrows, the third and the fourth declaring the identity and composition operations, and the last three stating the identity and associativity axioms.
Each axiom is of the form
![]() $\Gamma \vdash \mathcal {J}$
, where the
$\Gamma \vdash \mathcal {J}$
, where the
![]() $\mathcal {J}$
on the right of the ‘turnstile’ symbol ‘
$\mathcal {J}$
on the right of the ‘turnstile’ symbol ‘
![]() $\vdash $
’ is the actual declaration or equation, and the part
$\vdash $
’ is the actual declaration or equation, and the part
![]() $\Gamma $
on the left—called ‘context’—specifies the sorts of the variables occurring in
$\Gamma $
on the left—called ‘context’—specifies the sorts of the variables occurring in
![]() $\mathcal {J}$
. Note that the ordering of these ‘variable declarations’ is not arbitrary, since the sorts of variables may themselves contain variables which have to be declared further left in the context. An example is the context
$\mathcal {J}$
. Note that the ordering of these ‘variable declarations’ is not arbitrary, since the sorts of variables may themselves contain variables which have to be declared further left in the context. An example is the context
![]() $(x\,y\,z:O \,,\, f:A(x,y)\,,\, g:A(y,z))$
of the composition operation, where the sorts of the ‘arrow’ variables
$(x\,y\,z:O \,,\, f:A(x,y)\,,\, g:A(y,z))$
of the composition operation, where the sorts of the ‘arrow’ variables
![]() $f,g$
depend on the ‘object’ variables
$f,g$
depend on the ‘object’ variables
![]() $x,y,z$
. See Figure 1 for another example generalized algebraic theory: the generalized algebraic theory of rings graded over monoids.
$x,y,z$
. See Figure 1 for another example generalized algebraic theory: the generalized algebraic theory of rings graded over monoids.
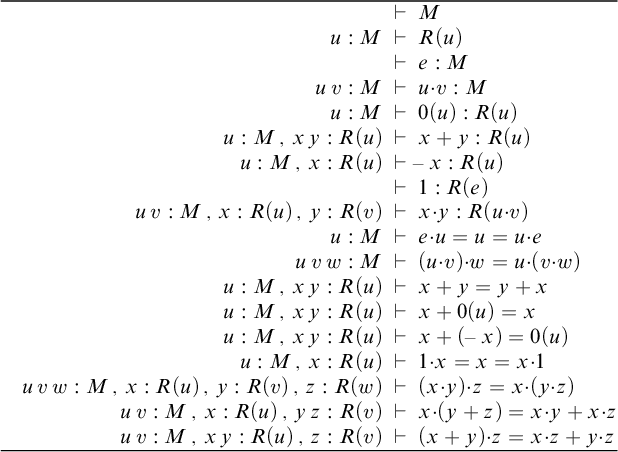
Figure 1 The generalized algebraic theory of monoid-graded rings
The dependent structure of contexts and the well-formedness requirement of axioms on the basis of other axioms makes the formulation of a general notion of generalized algebraic theory somewhat subtle and technical. We refer to [Reference Cartmell12, Reference Cartmell13] for the authoritative account and to [Reference Pitts36, Section 6] and [Reference Garner17, Section 2] for rigorous and concise summaries. The good news is that to understand specific examples of GATs, these technicalities may safely be ignored: all we have to know is that for every generalized algebraic theory
![]() $\mathbb {T}$
there is a notion of ‘derivable judgment’ which includes the axioms and is closed under various rules expressing that the set of derivable judgments is closed under operations like substitutions and weakening, and that equality is reflexive, symmetric, and transitive.
$\mathbb {T}$
there is a notion of ‘derivable judgment’ which includes the axioms and is closed under various rules expressing that the set of derivable judgments is closed under operations like substitutions and weakening, and that equality is reflexive, symmetric, and transitive.
Besides the forms of judgments
 $$ \begin{align*} \Gamma&\vdash S &&\text{`}S \text{ is a sort in context } \Gamma\text{'}\\ \Gamma&\vdash t:S &&\text{`}t \text{ is term of sort } S \text{ in context } \Gamma\text{'}\\ \Gamma&\vdash s=t:S &&\text{`}s \text{ and } t \text{ are equal terms in context } \Gamma\text{'} \end{align*} $$
$$ \begin{align*} \Gamma&\vdash S &&\text{`}S \text{ is a sort in context } \Gamma\text{'}\\ \Gamma&\vdash t:S &&\text{`}t \text{ is term of sort } S \text{ in context } \Gamma\text{'}\\ \Gamma&\vdash s=t:S &&\text{`}s \text{ and } t \text{ are equal terms in context } \Gamma\text{'} \end{align*} $$
that we have already encountered, we consider the following additional forms of judgments:
 $$ \begin{align*} \Gamma&\vdash S = T &&\text{`}S \text{ and } T \text{ are equal sorts in context } \Gamma\text{'}\\ \Gamma&\vdash &&\text{`}\Gamma \text{ is a context'}\\ \Gamma=\Delta&\vdash &&\text{`}\Gamma \text{ and } \Delta \text{ are equal contexts'}\\ \Gamma&\vdash \sigma:\Delta &&\text{`}\sigma \text{ is a substitution from } \Gamma \text{ to } \Delta'\\ \Gamma&\vdash \sigma=\tau:\Delta &&\text{`}\sigma \text{ and } \tau \text{ are equal substitutions from } \Gamma \text{ to } \Delta\text{'} \end{align*} $$
$$ \begin{align*} \Gamma&\vdash S = T &&\text{`}S \text{ and } T \text{ are equal sorts in context } \Gamma\text{'}\\ \Gamma&\vdash &&\text{`}\Gamma \text{ is a context'}\\ \Gamma=\Delta&\vdash &&\text{`}\Gamma \text{ and } \Delta \text{ are equal contexts'}\\ \Gamma&\vdash \sigma:\Delta &&\text{`}\sigma \text{ is a substitution from } \Gamma \text{ to } \Delta'\\ \Gamma&\vdash \sigma=\tau:\Delta &&\text{`}\sigma \text{ and } \tau \text{ are equal substitutions from } \Gamma \text{ to } \Delta\text{'} \end{align*} $$
The last two of these introduce a novel kind of expression called substitution: a substitution
![]() $\Gamma \vdash \sigma :\Delta $
is a list of terms that is suitable to be simultaneously substituted for the variables in a judgment in context
$\Gamma \vdash \sigma :\Delta $
is a list of terms that is suitable to be simultaneously substituted for the variables in a judgment in context
![]() $\Delta $
(in particular
$\Delta $
(in particular
![]() $\sigma $
and
$\sigma $
and
![]() $\Delta $
must have the same length), to produce a new judgment in context
$\Delta $
must have the same length), to produce a new judgment in context
![]() $\Gamma $
, as expressed by the following substitution rule.
$\Gamma $
, as expressed by the following substitution rule.
Here,
![]() $\mathcal {J}[\sigma ]$
is the result of simultaneous substitution of the terms in
$\mathcal {J}[\sigma ]$
is the result of simultaneous substitution of the terms in
![]() $\sigma $
for the variables in
$\sigma $
for the variables in
![]() $\mathcal {J}$
, replacing each occurrence of the ith variable declared in
$\mathcal {J}$
, replacing each occurrence of the ith variable declared in
![]() $\Delta $
with the ith term in
$\Delta $
with the ith term in
![]() $\sigma $
. This operation of simultaneous substitution also appears in the derivation rules for substitutions themselves, which we present in the following table together with the rules for the formation of well-formed contexts:
$\sigma $
. This operation of simultaneous substitution also appears in the derivation rules for substitutions themselves, which we present in the following table together with the rules for the formation of well-formed contexts:
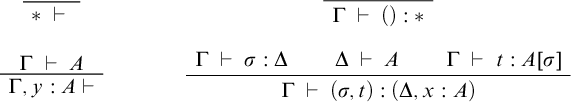
The two rules in the first line say respectively that the empty context
![]() $\varnothing $
is a context, and that for any context
$\varnothing $
is a context, and that for any context
![]() $\Gamma $
, the empty substitution
$\Gamma $
, the empty substitution
![]() $()$
is a substitution to the empty context. The first rule in the second line is known as context extension, since it says that we can extend any context by a well-formed sort in this context (here y has to be a ‘fresh’ variable, i.e., a variable not appearing in
$()$
is a substitution to the empty context. The first rule in the second line is known as context extension, since it says that we can extend any context by a well-formed sort in this context (here y has to be a ‘fresh’ variable, i.e., a variable not appearing in
![]() $\Gamma $
). The last rule says that a substitution to an extended context is a pair of a substitution into the original context and a term whose sort is a substitution instance of the extending sort—it wouldn’t make sense to ask for t to be of sort A since A is only well-formed in context
$\Gamma $
). The last rule says that a substitution to an extended context is a pair of a substitution into the original context and a term whose sort is a substitution instance of the extending sort—it wouldn’t make sense to ask for t to be of sort A since A is only well-formed in context
![]() $\Delta $
, and we want something in context
$\Delta $
, and we want something in context
![]() $\Gamma $
.
$\Gamma $
.
10.1 The syntactic category of a generalized algebraic theory
Definition 10.1. The syntactic category
![]() $\mathcal {C}[\mathbb {T}]$
of a generalized algebraic theory
$\mathcal {C}[\mathbb {T}]$
of a generalized algebraic theory
![]() $\mathbb {T}$
is given as follows.
$\mathbb {T}$
is given as follows.
-
• The objects are the contexts of
 $\Gamma $
modulo derivable equality, i.e., contexts
$\Gamma $
modulo derivable equality, i.e., contexts
 $\Gamma $
and
$\Gamma $
and
 $\Delta $
are identified if the judgment
$\Delta $
are identified if the judgment
 $\Gamma =\Delta \vdash $
is derivable.
$\Gamma =\Delta \vdash $
is derivable. -
• Similarly, morphisms
 $[\Gamma ]\to [\Delta ]$
from the equivalence class of
$[\Gamma ]\to [\Delta ]$
from the equivalence class of
 $\Gamma $
to the equivalence class of
$\Gamma $
to the equivalence class of
 $\Delta $
are substitutions
$\Delta $
are substitutions
 $\Gamma \vdash \sigma :\Delta $
modulo derivable equality. (The closure conditions on the set of derivable judgments ensure independence of representatives, e.g., that
$\Gamma \vdash \sigma :\Delta $
modulo derivable equality. (The closure conditions on the set of derivable judgments ensure independence of representatives, e.g., that
 $\Gamma '\vdash \sigma :\Delta '$
whenever
$\Gamma '\vdash \sigma :\Delta '$
whenever
 $\Gamma \vdash \sigma :\Delta $
and
$\Gamma \vdash \sigma :\Delta $
and
 $\Gamma =\Gamma '\vdash $
and
$\Gamma =\Gamma '\vdash $
and
 $\Delta =\Delta '\vdash $
.)
$\Delta =\Delta '\vdash $
.) -
• Composition is given by substitution of representatives, and identities are given by lists of variables:
-
–
 $[\Delta \vdash \tau :\Theta ]\circ [\Gamma \vdash \sigma :\Delta ] =[\Gamma \;\vdash \;\tau [\sigma ]:\Theta ]$
$[\Delta \vdash \tau :\Theta ]\circ [\Gamma \vdash \sigma :\Delta ] =[\Gamma \;\vdash \;\tau [\sigma ]:\Theta ]$
-
–
 $\mathrm {id}_\Gamma =(\Gamma \vdash (\vec x):\Gamma )$
where
$\mathrm {id}_\Gamma =(\Gamma \vdash (\vec x):\Gamma )$
where
 $\vec x$
is the list of variables declared in
$\vec x$
is the list of variables declared in
 $\Gamma $
.
$\Gamma $
.
-
The syntactic category
![]() $\mathcal {C}[\mathbb {T}]$
of a GAT
$\mathcal {C}[\mathbb {T}]$
of a GAT
![]() $\mathbb {T}$
has the structure of a contextual category:
$\mathbb {T}$
has the structure of a contextual category:
Definition 10.2. A contextual category consists of
-
(1) a small category
 $\mathcal {C}$
with a grading function
$\mathcal {C}$
with a grading function
 $\deg :\mathcal {C}_0\to \mathbb {N}$
on its objects, and
$\deg :\mathcal {C}_0\to \mathbb {N}$
on its objects, and -
(2) a presheaf
 $\mathsf {Ty}:\mathcal {C}^{\mathsf {op}}\to \mathsf {Set}$
, together with
$\mathsf {Ty}:\mathcal {C}^{\mathsf {op}}\to \mathsf {Set}$
, together with-
• an object
 $\Gamma .A$
and an arrow
$\Gamma .A$
and an arrow
 $p_A:\Gamma .A\to \Gamma $
for each
$p_A:\Gamma .A\to \Gamma $
for each
 $\Gamma \in \mathcal {C}$
and
$\Gamma \in \mathcal {C}$
and
 $A\in \mathsf {Ty}(\Gamma )$
, and
$A\in \mathsf {Ty}(\Gamma )$
, and -
• an arrow
 $\sigma .A:\Delta .A\sigma \to \Gamma .A$
for each
$\sigma .A:\Delta .A\sigma \to \Gamma .A$
for each
 $\Gamma \in \mathcal {C}$
,
$\Gamma \in \mathcal {C}$
,
 $A\in \mathsf {Ty}(\Gamma )$
, and
$A\in \mathsf {Ty}(\Gamma )$
, and
 $\sigma :\Delta \to \Gamma $
,
$\sigma :\Delta \to \Gamma $
,
-
such that:
-
(i) The square
 is a pullback for all
is a pullback for all
 $A\in \mathsf {Ty}(\Gamma )$
and
$A\in \mathsf {Ty}(\Gamma )$
and
 $\sigma :\Delta \to \Gamma $
.
$\sigma :\Delta \to \Gamma $
. -
(ii) The mappings
 $(\Gamma ,A)\mapsto \Gamma .A$
and
$(\Gamma ,A)\mapsto \Gamma .A$
and
 $(\sigma ,A)\mapsto \sigma .A$
constitute a functor
$(\sigma ,A)\mapsto \sigma .A$
constitute a functor
 $\mathsf {El}(\mathsf {Ty})\to \mathcal {C}$
.
$\mathsf {El}(\mathsf {Ty})\to \mathcal {C}$
. -
(iii) We have
 $\deg (\Gamma .A)=\deg (\Gamma )+1$
for all
$\deg (\Gamma .A)=\deg (\Gamma )+1$
for all
 $\Gamma \in \mathcal {C}$
and
$\Gamma \in \mathcal {C}$
and
 $A\in \mathsf {Ty}(\Gamma )$
.
$A\in \mathsf {Ty}(\Gamma )$
. -
(iv) There is a unique object
 $\ast $
of degree
$\ast $
of degree
 $0$
, and
$0$
, and
 $\ast $
is terminal.
$\ast $
is terminal. -
(v) For all
 $\Gamma $
with
$\Gamma $
with
 $\deg (\Gamma )>0$
there is a unique
$\deg (\Gamma )>0$
there is a unique
 $(\Gamma _0,A)\in \mathsf {El}(\mathsf {Ty})$
with
$(\Gamma _0,A)\in \mathsf {El}(\mathsf {Ty})$
with
 $\Gamma =\Gamma _0.A$
.
$\Gamma =\Gamma _0.A$
.
In the case of the syntactic category
![]() $\mathcal {C}[\mathbb {T}]$
of a GAT
$\mathcal {C}[\mathbb {T}]$
of a GAT
![]() $\mathbb {T}$
, the grading assigns to each context its length, and
$\mathbb {T}$
, the grading assigns to each context its length, and
![]() $\mathsf {Ty}(\Gamma )$
is the set of ‘types in context
$\mathsf {Ty}(\Gamma )$
is the set of ‘types in context
![]() $\Gamma $
’, i.e., equivalence classes of type expressions A such that
$\Gamma $
’, i.e., equivalence classes of type expressions A such that
![]() $\Gamma \vdash A$
is derivable, modulo the equivalence relation of derivable equality. The presheaf action is given by substitution. Given a type
$\Gamma \vdash A$
is derivable, modulo the equivalence relation of derivable equality. The presheaf action is given by substitution. Given a type
![]() $A\in \mathsf {Ty}(\Gamma )$
, the extended context
$A\in \mathsf {Ty}(\Gamma )$
, the extended context
![]() $\Gamma .A$
is given by
$\Gamma .A$
is given by
![]() $\Gamma ,y{:}A$
obtained via the context formation rule in (10.2), and
$\Gamma ,y{:}A$
obtained via the context formation rule in (10.2), and
![]() $p_A$
is the substitution
$p_A$
is the substitution
where
![]() $\vec x$
is the list of variables declared in
$\vec x$
is the list of variables declared in
![]() $\Gamma $
. For
$\Gamma $
. For
![]() $\sigma :\Gamma \to \Delta $
and
$\sigma :\Gamma \to \Delta $
and
![]() $A\in \mathsf {Ty}(\Delta )$
, the substitution
$A\in \mathsf {Ty}(\Delta )$
, the substitution
![]() $\sigma .A$
is given by
$\sigma .A$
is given by
Then the fact that the square in Definition 10.2 10.2 is a pullback follows from the substitution formation rule in (10.2) together with the equality rules for substitutions that can be found in the cited references.
The following describes the relationship between contextual categories and clans.
Proposition 10.3. Every contextual category
![]() $\mathcal {C}$
admits a clan structure where the display maps are the composites
$\mathcal {C}$
admits a clan structure where the display maps are the composites
![]() $p_{A_1}\circ \dots \circ p_{A_n}\circ i$
of a finite sequence of projections and an isomorphism.
$p_{A_1}\circ \dots \circ p_{A_n}\circ i$
of a finite sequence of projections and an isomorphism.
11 Appendix. The fat small object argument for clans
11.1 Colimit decomposition formula and pushouts of sieves
This subsection discusses two results that are needed in the proof of the fat small object argument.
Theorem 11.1 (Colimit decomposition formula (CDF)).
Let
![]() $\mathbb {C}:\mathbb {J}\to \mathsf {Cat}$
be a small diagram in the
$\mathbb {C}:\mathbb {J}\to \mathsf {Cat}$
be a small diagram in the
![]() $1$
-category of small categories, and let
$1$
-category of small categories, and let
![]() $D:\mathsf {colim}(\mathbb {C})\to \mathfrak {X}$
be a diagram in a category
$D:\mathsf {colim}(\mathbb {C})\to \mathfrak {X}$
be a diagram in a category
![]() $\mathfrak {X}$
such that
$\mathfrak {X}$
such that
-
(i) for all
 $j\in \mathbb {J}$
, the colimit
$j\in \mathbb {J}$
, the colimit
 $\mathsf {colim}_{c\in \mathbb {C}_j} D_{\sigma _jc}=\mathsf {colim}(\mathbb {C}_j\xrightarrow {\sigma _j}\mathsf {colim}(\mathbb {C})\stackrel {D}\to \mathfrak {X})$
exists, and
$\mathsf {colim}_{c\in \mathbb {C}_j} D_{\sigma _jc}=\mathsf {colim}(\mathbb {C}_j\xrightarrow {\sigma _j}\mathsf {colim}(\mathbb {C})\stackrel {D}\to \mathfrak {X})$
exists, and -
(ii) the iterated colimit
 $\mathsf {colim}_{j\in \mathbb {J}}\mathsf {colim}_{c\in \mathbb {C}_j} D_{\sigma _jc}$
exists.
$\mathsf {colim}_{j\in \mathbb {J}}\mathsf {colim}_{c\in \mathbb {C}_j} D_{\sigma _jc}$
exists.
Then
![]() $\mathsf {colim}_{j\in \mathbb {J}}\mathsf {colim}_{c\in \mathbb {C}_j} D_{\sigma _jc}$
is a colimit of D.
$\mathsf {colim}_{j\in \mathbb {J}}\mathsf {colim}_{c\in \mathbb {C}_j} D_{\sigma _jc}$
is a colimit of D.
Proof. Peschke and Tholen [Reference Peschke and Tholen35] give three proofs of this under the additional assumption that
![]() $\mathfrak {X}$
is cocomplete. The third proof (§5.3, ‘via Fubini’) easily generalizes to the situation where only the necessary colimits are assumed to exist. We sketch a simplified argument here. Let
$\mathfrak {X}$
is cocomplete. The third proof (§5.3, ‘via Fubini’) easily generalizes to the situation where only the necessary colimits are assumed to exist. We sketch a simplified argument here. Let
![]() ${\textstyle \int }\mathbb {C}$
be the covariant Grothendieck construction of
${\textstyle \int }\mathbb {C}$
be the covariant Grothendieck construction of
![]() $\mathbb {C}$
, whose projection
$\mathbb {C}$
, whose projection
![]() ${\textstyle \int }\mathbb {C}\to \mathbb {J}$
is a split opfibration. Then
${\textstyle \int }\mathbb {C}\to \mathbb {J}$
is a split opfibration. Then
![]() $\mathsf {colim}(\mathbb {C})$
is the ‘joint coidentifier’ of the splitting, i.e., there is a functor
$\mathsf {colim}(\mathbb {C})$
is the ‘joint coidentifier’ of the splitting, i.e., there is a functor
![]() $E:{\textstyle \int }\mathbb {C}\to \mathsf {colim}(\mathbb {C})$
such that for every category
$E:{\textstyle \int }\mathbb {C}\to \mathsf {colim}(\mathbb {C})$
such that for every category
![]() $\mathfrak {X}$
, the precomposition functor
$\mathfrak {X}$
, the precomposition functor
restricts to an isomorphism between the functor category
![]() $[\mathsf {colim}(\mathbb {C}),\mathfrak {X}]$
and the full subcategory of
$[\mathsf {colim}(\mathbb {C}),\mathfrak {X}]$
and the full subcategory of
![]() $[{\textstyle \int } \mathbb {C},\mathfrak {X}]$
on functors which send the arrows of the splitting to identities. In particular,
$[{\textstyle \int } \mathbb {C},\mathfrak {X}]$
on functors which send the arrows of the splitting to identities. In particular,
![]() $(-\circ E)$
is fully faithful and thus it induces an isomorphism
$(-\circ E)$
is fully faithful and thus it induces an isomorphism
of co-presheaves of cocones for every diagram
![]() $D:\mathsf {colim}(\mathbb {C})\to \mathfrak {X}$
. In other words, E is final, which is the crucial point of the argument, and for which Peschke and Tholen give a lengthier proof in [Reference Peschke and Tholen35, Theorem 5.8].
$D:\mathsf {colim}(\mathbb {C})\to \mathfrak {X}$
. In other words, E is final, which is the crucial point of the argument, and for which Peschke and Tholen give a lengthier proof in [Reference Peschke and Tholen35, Theorem 5.8].
Finality of E implies that D has a colimit if and only if
![]() $D\circ E$
has a colimit, and the existence of the latter follows if successive left Kan extensions along the composite
$D\circ E$
has a colimit, and the existence of the latter follows if successive left Kan extensions along the composite
![]() ${\textstyle \int } \mathbb {C}\to \mathbb {J} \to 1$
exist. The first of these can be computed as fiberwise colimit since
${\textstyle \int } \mathbb {C}\to \mathbb {J} \to 1$
exist. The first of these can be computed as fiberwise colimit since
![]() ${\textstyle \int }\mathbb {C}\to \mathbb {J}$
is a split cofibration [Reference Peschke and Tholen35, Theorem 4.6], which yields the inner term in the double colimit in the proposition.
${\textstyle \int }\mathbb {C}\to \mathbb {J}$
is a split cofibration [Reference Peschke and Tholen35, Theorem 4.6], which yields the inner term in the double colimit in the proposition.
In the following we use the CDF specifically for pushouts of sieve inclusions of posets. Recall that a sieve (a.k.a. downset or lower set) in a poset P is a subset
![]() $U\subseteq P$
satisfying
$U\subseteq P$
satisfying
for all
![]() $x,y\in P$
. A monotone map
$x,y\in P$
. A monotone map
![]() $f:P\to Q$
is called a sieve inclusion if it is order-reflecting and its image
$f:P\to Q$
is called a sieve inclusion if it is order-reflecting and its image
![]() $\mathsf {im}(f)=f[P]$
is a sieve in Q. The proof of the following lemma is straightforward, but we state it explicitly since it will play a central role.
$\mathsf {im}(f)=f[P]$
is a sieve in Q. The proof of the following lemma is straightforward, but we state it explicitly since it will play a central role.
Lemma 11.2.
-
(i) If
 $f:P\to Q$
and
$f:P\to Q$
and
 $g:P\to R$
are sieve inclusions of posets, a pushout of f and g in the
$g:P\to R$
are sieve inclusions of posets, a pushout of f and g in the
 $1$
-category
$1$
-category
 $\mathsf {Cat}$
of small categories is given by
$\mathsf {Cat}$
of small categories is given by 
where
 $Q+_{P}R$
is the set-theoretic pushout, ordered by
$Q+_{P}R$
is the set-theoretic pushout, ordered by  $$\begin{align*}\begin{array}{l@{\quad}l}\sigma_1(x)\leq \sigma_1(y) &\text{iff }\; x\leq y\\ \sigma_1(x)\leq \sigma_2(y) &\text{iff }\; \exists z\,.\, x=f(z)\wedge g(z)\leq y \\ \sigma_2(x)\leq \sigma_2(y) &\text{iff }\; x\leq y\\ \sigma_2(x)\leq \sigma_1(y) &\text{iff }\; \exists z\,.\, x=g(z)\wedge f(z)\leq y. \end{array}\end{align*}$$
$$\begin{align*}\begin{array}{l@{\quad}l}\sigma_1(x)\leq \sigma_1(y) &\text{iff }\; x\leq y\\ \sigma_1(x)\leq \sigma_2(y) &\text{iff }\; \exists z\,.\, x=f(z)\wedge g(z)\leq y \\ \sigma_2(x)\leq \sigma_2(y) &\text{iff }\; x\leq y\\ \sigma_2(x)\leq \sigma_1(y) &\text{iff }\; \exists z\,.\, x=g(z)\wedge f(z)\leq y. \end{array}\end{align*}$$
In particular, the maps
 $\sigma _1$
and
$\sigma _1$
and
 $\sigma _2$
are also sieve inclusions.
$\sigma _2$
are also sieve inclusions. -
(ii) If U and V are sieves in a poset P then the square

is a pushout in
 $\mathsf {Cat}$
, where the sieves are equipped with the induced ordering.
$\mathsf {Cat}$
, where the sieves are equipped with the induced ordering.
11.2 The fat small object argument
Throughout this subsection let
![]() $\mathcal {C}$
be a coclan.
$\mathcal {C}$
be a coclan.
We start by establishing some notation. Given a poset P and an element
![]() $x\in P$
, we write
$x\in P$
, we write
![]() ${P}_{\leq x} = \{y\in P\mathrel | y\leq x\}$
for the principal sieve generated by x, and
${P}_{\leq x} = \{y\in P\mathrel | y\leq x\}$
for the principal sieve generated by x, and
![]() ${P}_{< x} = \{y\in P\mathrel | y< x\}$
for its subset on elements that are strictly smaller than x. If x is a maximal element of P, we write
${P}_{< x} = \{y\in P\mathrel | y< x\}$
for its subset on elements that are strictly smaller than x. If x is a maximal element of P, we write
![]() $P{\setminus } x$
for the sub-poset obtained by removing x. Given a diagram
$P{\setminus } x$
for the sub-poset obtained by removing x. Given a diagram
![]() $D:P\to \mathcal {C}$
, we write
$D:P\to \mathcal {C}$
, we write
![]() ${D}_{\leq x}$
,
${D}_{\leq x}$
,
![]() ${D}_{<x}$
, and
${D}_{<x}$
, and
![]() $D{\setminus } x$
for the restrictions of D to
$D{\setminus } x$
for the restrictions of D to
![]() ${P}_{\leq x}$
,
${P}_{\leq x}$
,
![]() ${P}_{<x}$
, and
${P}_{<x}$
, and
![]() $P{\setminus } x$
, respectively. More generally we write
$P{\setminus } x$
, respectively. More generally we write
![]() $D_U$
for the restriction of D to arbitrary sieves
$D_U$
for the restriction of D to arbitrary sieves
![]() $U\subseteq P$
.
$U\subseteq P$
.
Note that we have
![]() ${P}_{\leq x} = {P}_{<x} \star 1$
, where
${P}_{\leq x} = {P}_{<x} \star 1$
, where
![]() $\star $
is the join or ordinal sum, thus diagrams
$\star $
is the join or ordinal sum, thus diagrams
![]() $D : {P}_{\leq x}\to \mathcal {C}$
are in correspondence with cocones on
$D : {P}_{\leq x}\to \mathcal {C}$
are in correspondence with cocones on
![]() ${D}_{<x}$
with vertex
${D}_{<x}$
with vertex
![]() $D_x$
, and with arrows
$D_x$
, and with arrows
![]() $\mathsf {colim}({D}_{<x})\to D_x$
whenever the colimit exists.
$\mathsf {colim}({D}_{<x})\to D_x$
whenever the colimit exists.
Definition 11.3. A finite
![]() $\mathcal {C}$
-complex is a pair
$\mathcal {C}$
-complex is a pair
![]() ${(P,D)}$
of a finite poset P and a diagram
${(P,D)}$
of a finite poset P and a diagram
![]() $D:P\to \mathcal {C}$
, such that:
$D:P\to \mathcal {C}$
, such that:
-
(i)
 $\mathsf {colim}({D}_{<x})$
exists for all
$\mathsf {colim}({D}_{<x})$
exists for all
 $x\in P$
, and the induced
$x\in P$
, and the induced
 $\alpha _x : \mathsf {colim}(D_{<x}) \to D_x$
is codisplay.
$\alpha _x : \mathsf {colim}(D_{<x}) \to D_x$
is codisplay. -
(ii) For
 $x,y\in P$
we have
$x,y\in P$
we have
 $x=y$
whenever
$x=y$
whenever
 $P_{<x}=P_{<y}$
,
$P_{<x}=P_{<y}$
,
 $D_x=D_y$
, and
$D_x=D_y$
, and
 $\alpha _x=\alpha _y$
.
$\alpha _x=\alpha _y$
.
An inclusion of finite
![]() $\mathcal {C}$
-complexes
$\mathcal {C}$
-complexes
![]() $f:{(P,D)}\to {(Q,E)}$
is a sieve inclusion
$f:{(P,D)}\to {(Q,E)}$
is a sieve inclusion
![]() $f:P\to Q$
such that
$f:P\to Q$
such that
![]() $D=E\circ f$
. We write
$D=E\circ f$
. We write
![]() $\mathsf {FC}(\mathcal {C})$
for the category of finite
$\mathsf {FC}(\mathcal {C})$
for the category of finite
![]() $\mathcal {C}$
-complexes and inclusions.
$\mathcal {C}$
-complexes and inclusions.
Remark 11.4. We view a finite
![]() $\mathcal {C}$
-complex as a construction of an object by a finite (though not necessarily linearly ordered) number of ‘cell attachments’, represented by the codisplay maps
$\mathcal {C}$
-complex as a construction of an object by a finite (though not necessarily linearly ordered) number of ‘cell attachments’, represented by the codisplay maps ![]() . Condition (ii) should be read as saying that ‘every cell can only be attached once at the same stage’. This is needed in Lemma 11.7 to show that
. Condition (ii) should be read as saying that ‘every cell can only be attached once at the same stage’. This is needed in Lemma 11.7 to show that
![]() $\mathsf {FC}(\mathcal {C})$
is a preorder.
$\mathsf {FC}(\mathcal {C})$
is a preorder.
Lemma 11.5.
-
(i) The colimit
 $\mathsf {colim}(D)$
exists for every finite
$\mathsf {colim}(D)$
exists for every finite
 $\mathcal {C}$
-complex
$\mathcal {C}$
-complex
 ${(P,D)}$
.
${(P,D)}$
. -
(ii) The induced functor
(11.1) $$ \begin{align} \mathsf{Colim} : \mathsf{FC}(\mathcal{C})\to\mathcal{C} \end{align} $$
$$ \begin{align} \mathsf{Colim} : \mathsf{FC}(\mathcal{C})\to\mathcal{C} \end{align} $$
sends inclusions of finite
 $\mathcal {C}$
-complexes to codisplay maps.
$\mathcal {C}$
-complexes to codisplay maps.
Proof. The first claim is shown by induction on
![]() $\vert P\vert $
. For empty P the statement is true since coclans have initial objects. For
$\vert P\vert $
. For empty P the statement is true since coclans have initial objects. For
![]() $\vert P\vert =n+1$
assume that
$\vert P\vert =n+1$
assume that
![]() $x\in P$
is a maximal element. Then the square
$x\in P$
is a maximal element. Then the square
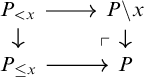
is a pushout in
![]() $\mathsf {Cat}$
by Lemma 11.2, which by the colimit decomposition formula 11.1 means that the pushout of the span
$\mathsf {Cat}$
by Lemma 11.2, which by the colimit decomposition formula 11.1 means that the pushout of the span
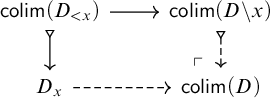
—which exists since the left arrow is a codisplay map by 11.3(i)—is a colimit of D in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
For the second claim let
![]() $f:(E,Q)\to (D,P)$
be an inclusion of finite
$f:(E,Q)\to (D,P)$
be an inclusion of finite
![]() $\mathcal {C}$
-complexes. Since every inclusion of finite
$\mathcal {C}$
-complexes. Since every inclusion of finite
![]() $\mathcal {C}$
-complexes can be decomposed into ‘atomic’ inclusions with
$\mathcal {C}$
-complexes can be decomposed into ‘atomic’ inclusions with
![]() $\vert P{\setminus } f[Q]\vert =1$
, we may assume without loss of generality that
$\vert P{\setminus } f[Q]\vert =1$
, we may assume without loss of generality that
![]() $Q=P{\setminus } x$
for some maximal
$Q=P{\setminus } x$
for some maximal
![]() $x\in P$
. Then the image of f under
$x\in P$
. Then the image of f under
![]() $\mathsf {Colim}$
is the right dashed arrow in (11.2), which is codisplay since codisplay maps are stable under pushout.
$\mathsf {Colim}$
is the right dashed arrow in (11.2), which is codisplay since codisplay maps are stable under pushout.
Remark 11.6. Lemma 11.5 implies that the assumption ‘
![]() $\mathsf {colim}({D}_{<x})$
exists’ in Definition 11.3(i) is redundant, since the colimits in question are colimits of finite subcomplexes.
$\mathsf {colim}({D}_{<x})$
exists’ in Definition 11.3(i) is redundant, since the colimits in question are colimits of finite subcomplexes.
Lemma 11.7. The category
![]() $\mathsf {FC}(\mathcal {C})$
is an essentially small preorder with finite joins.
$\mathsf {FC}(\mathcal {C})$
is an essentially small preorder with finite joins.
Proof.
![]() $\mathsf {FC}(\mathcal {C})$
is essentially small as a collection of finite diagrams in a small category. To see that it is a preorder let
$\mathsf {FC}(\mathcal {C})$
is essentially small as a collection of finite diagrams in a small category. To see that it is a preorder let
![]() $f,g:{(P,D)}\to {(Q,E)}$
be inclusions of finite
$f,g:{(P,D)}\to {(Q,E)}$
be inclusions of finite
![]() $\mathcal {C}$
-complexes. We show that
$\mathcal {C}$
-complexes. We show that
![]() $f(x) = g(x)$
by well-founded induction on
$f(x) = g(x)$
by well-founded induction on
![]() $x\in P$
. Let
$x\in P$
. Let
![]() $x\in P$
and assume that
$x\in P$
and assume that
![]() $f(y)=g(y)$
for all
$f(y)=g(y)$
for all
![]() $y<x$
. Then since f and g are sieve inclusions we have
$y<x$
. Then since f and g are sieve inclusions we have
![]() ${Q}_{<{f(x)}} = {Q}_{<{g(x)}}$
and since
${Q}_{<{f(x)}} = {Q}_{<{g(x)}}$
and since
![]() $E\,f=D=E\,g$
we have the equalities
$E\,f=D=E\,g$
we have the equalities
of cocones, whence
![]() $f(x)=g(x)$
by Definition 11.3(ii).
$f(x)=g(x)$
by Definition 11.3(ii).
It remains to show that
![]() $\mathsf {FC}(\mathcal {C})$
has finite suprema. The empty complex is clearly initial. We show that a supremum of
$\mathsf {FC}(\mathcal {C})$
has finite suprema. The empty complex is clearly initial. We show that a supremum of
![]() ${(P,D)}$
and
${(P,D)}$
and
![]() ${(Q,E)}$
exists by induction on
${(Q,E)}$
exists by induction on
![]() $\vert P\vert $
. The empty case is trivial, so assume that P is inhabited and let x be a maximal element. Let
$\vert P\vert $
. The empty case is trivial, so assume that P is inhabited and let x be a maximal element. Let
![]() $(R,F)$
be a supremum of
$(R,F)$
be a supremum of
![]() $(P{\setminus } x, D{\setminus } x)$
and
$(P{\setminus } x, D{\setminus } x)$
and
![]() ${(Q,E)}$
, with inclusion maps
${(Q,E)}$
, with inclusion maps
![]() $f:(P{\setminus } x, D{\setminus } x)\to (R,F)$
and
$f:(P{\setminus } x, D{\setminus } x)\to (R,F)$
and
![]() $g:{(Q,E)}\longrightarrow (R,F)$
. If there exists a
$g:{(Q,E)}\longrightarrow (R,F)$
. If there exists a
![]() $y\in R$
such that
$y\in R$
such that
![]() ${R}_{<y} = f[{P}_{<x}]$
and
${R}_{<y} = f[{P}_{<x}]$
and
![]() $\left (D_z\to D_x\right )_{z<x} = \left (R_{f(z)}\to R_y\right )_{z<x}$
then ‘the cell-attachment corresponding to x is already contained in
$\left (D_z\to D_x\right )_{z<x} = \left (R_{f(z)}\to R_y\right )_{z<x}$
then ‘the cell-attachment corresponding to x is already contained in
![]() $(R,F)$
’, i.e., f extends to an inclusion
$(R,F)$
’, i.e., f extends to an inclusion
![]() $f':{(P,D)}\to (R,F)$
of finite complexes with
$f':{(P,D)}\to (R,F)$
of finite complexes with
![]() $f'(x)=y$
, whence
$f'(x)=y$
, whence
![]() $(R,F)$
is a supremum of
$(R,F)$
is a supremum of
![]() ${(P,D)}$
and
${(P,D)}$
and
![]() ${(Q,E)}$
.
${(Q,E)}$
.
If no such y exists then a supremum of
![]() ${(P,D)}$
and
${(P,D)}$
and
![]() $(R,F)$
is given by
$(R,F)$
is given by
![]() $(P+_{P{\setminus } x}R,[D,F])$
, as in the pushout diagram
$(P+_{P{\setminus } x}R,[D,F])$
, as in the pushout diagram
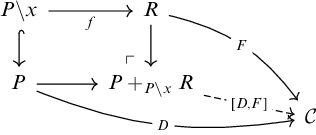
constructed as in Lemma 11.2.
Theorem 11.8. The object
![]() $\textstyle C = \mathsf {colim}_{{(P,D)}\in \mathsf {FC}(\mathcal {C})}H(\mathsf {colim}(D))$
is a
$\textstyle C = \mathsf {colim}_{{(P,D)}\in \mathsf {FC}(\mathcal {C})}H(\mathsf {colim}(D))$
is a
![]() $0$
-extension in
$0$
-extension in
![]() $\mathcal {C}^{\mathsf {op}}\!\text {-}\mathsf {Alg}$
and
$\mathcal {C}^{\mathsf {op}}\!\text {-}\mathsf {Alg}$
and
![]() $C\to 1$
is full.
$C\to 1$
is full.
Proof. To see that
![]() $C\to 1$
is full, let
$C\to 1$
is full, let ![]() be codisplay in
be codisplay in
![]() $\mathcal {C}$
and let
$\mathcal {C}$
and let
![]() $f:H(I)\to C$
. Since
$f:H(I)\to C$
. Since
![]() $\mathsf {FC}(\mathcal {C})$
is filtered and
$\mathsf {FC}(\mathcal {C})$
is filtered and
![]() $H(I)$
is compact, f factors through a colimit inclusion as
$H(I)$
is compact, f factors through a colimit inclusion as
for some finite complex
![]() ${(P,D)}$
. We form the pushout
${(P,D)}$
. We form the pushout
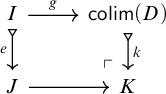
and extend the finite complex
![]() ${(P,D)}$
to
${(P,D)}$
to
![]() $(P\star 1,D\star k)$
where
$(P\star 1,D\star k)$
where
![]() $P\star 1$
is the join of P and
$P\star 1$
is the join of P and
![]() $1$
, and
$1$
, and
![]() $D\star k:P\star 1 \to \mathcal {C}$
is the diagram extending D with the cell-attachment
$D\star k:P\star 1 \to \mathcal {C}$
is the diagram extending D with the cell-attachment ![]() . Then
. Then
![]() $K=\mathsf {colim}(D\star k)$
and k is the image of the inclusion
$K=\mathsf {colim}(D\star k)$
and k is the image of the inclusion
![]() ${(P,D)}\hookrightarrow (P\star 1,D\star k)$
of finite complexes under the colimit functor (11.1), thus we obtain an extension of f along
${(P,D)}\hookrightarrow (P\star 1,D\star k)$
of finite complexes under the colimit functor (11.1), thus we obtain an extension of f along
![]() $H(e)$
as in the following diagram.
$H(e)$
as in the following diagram.
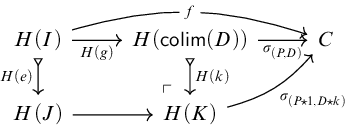
To see that C is a
![]() $0$
-extension, consider a full map
$0$
-extension, consider a full map
![]() $f:Y\twoheadrightarrow X$
in
$f:Y\twoheadrightarrow X$
in
![]() $\mathcal {C}^{\mathsf {op}}\!\text {-}\mathsf {Alg}$
and an arrow
$\mathcal {C}^{\mathsf {op}}\!\text {-}\mathsf {Alg}$
and an arrow
![]() $h:C\to X$
. To show that h lifts along f we construct a lift of the cocone
$h:C\to X$
. To show that h lifts along f we construct a lift of the cocone
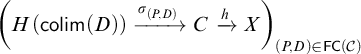 $$ \begin{align*} \left(H(\mathsf{colim}(D))\xrightarrow{\sigma_{(P,D)}}C\xrightarrow{h}X\right)_{{(P,D)}\in\mathsf{FC}(\mathcal{C})} \end{align*} $$
$$ \begin{align*} \left(H(\mathsf{colim}(D))\xrightarrow{\sigma_{(P,D)}}C\xrightarrow{h}X\right)_{{(P,D)}\in\mathsf{FC}(\mathcal{C})} \end{align*} $$
by induction over the preorder
![]() $\mathsf {FC}(\mathcal {C})$
which is well-founded since every finite
$\mathsf {FC}(\mathcal {C})$
which is well-founded since every finite
![]() $\mathcal {C}$
-complex has only finitely many subcomplexes. Given a finite complex
$\mathcal {C}$
-complex has only finitely many subcomplexes. Given a finite complex
![]() $(D,P)$
it is sufficient to exhibit a lift
$(D,P)$
it is sufficient to exhibit a lift
![]() $\kappa _{(P,D)}:H(\mathsf {colim} (D))\to Y$
satisfying
$\kappa _{(P,D)}:H(\mathsf {colim} (D))\to Y$
satisfying
where we may assume that the
![]() $\kappa _{(Q,E)}$
satisfy the analogous equations by induction hypothesis. We distinguish two cases:
$\kappa _{(Q,E)}$
satisfy the analogous equations by induction hypothesis. We distinguish two cases:
1. If P has a greatest element x then we can take
![]() $\kappa _{(P,D)}$
to be a lift in the square
$\kappa _{(P,D)}$
to be a lift in the square
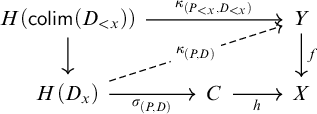
whose left side is an extension by Lemma 11.5 and whose right side is full by assumption. Then (11.3) holds by construction, and (11.4) holds for all subcomplexes since it holds for the largest strict subcomplex
![]() $({P}_{<x},{D}_{<x})\to {(P,D)}$
.
$({P}_{<x},{D}_{<x})\to {(P,D)}$
.
2. If P doesn’t have a greatest element we can write
![]() $P=U\cup V$
as union of two strict sub-sieves, whence we have pushouts
$P=U\cup V$
as union of two strict sub-sieves, whence we have pushouts
by Lemma 11.2 and the CDF. This means that condition (11.4) forces us to define
![]() $\kappa _{(P,D)}$
to be the unique arrow fitting into
$\kappa _{(P,D)}$
to be the unique arrow fitting into
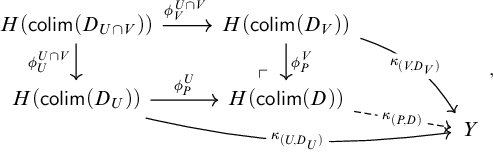
where for the remainder of the proof we write
![]() $\phi ^X_W:H(\mathsf {colim}(D_X))\to H(\mathsf {colim}(D_W))$
for the canonical arrows induced by successive sieve inclusions
$\phi ^X_W:H(\mathsf {colim}(D_X))\to H(\mathsf {colim}(D_W))$
for the canonical arrows induced by successive sieve inclusions
![]() $X\subseteq W\subseteq P$
. Using the fact that the
$X\subseteq W\subseteq P$
. Using the fact that the
![]() $\phi ^U_P$
and
$\phi ^U_P$
and
![]() $\phi ^V_P$
are jointly epic it is easy to see that the
$\phi ^V_P$
are jointly epic it is easy to see that the
![]() $\kappa _{(P,D)}$
defined in this way satisfies condition (11.3), and it remains to show that (11.4) is satisfied for arbitrary sieves
$\kappa _{(P,D)}$
defined in this way satisfies condition (11.3), and it remains to show that (11.4) is satisfied for arbitrary sieves
![]() $W\subseteq P$
, i.e.,
$W\subseteq P$
, i.e.,
![]() $\kappa _{(P,D)}\circ \phi ^W_P = \kappa _{(W,D_W)}:H(\mathsf {colim}(D_W))\to Y$
. Since
$\kappa _{(P,D)}\circ \phi ^W_P = \kappa _{(W,D_W)}:H(\mathsf {colim}(D_W))\to Y$
. Since
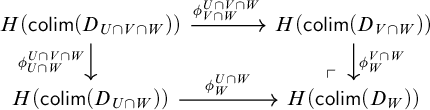
is a pushout it is enough to verify this equation after precomposing with
![]() $\phi ^{U\cap W}_W$
and
$\phi ^{U\cap W}_W$
and
![]() $\phi ^{V\cap W}_W$
. We have
$\phi ^{V\cap W}_W$
. We have
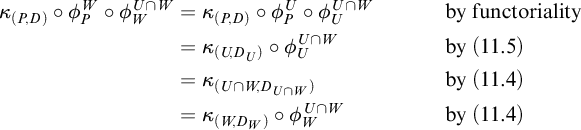 $$ \begin{align*} \kappa_{(P,D)}\circ\phi^W_P\circ\phi^{U\cap W}_W &=\kappa_{(P,D)}\circ\phi^U_P\circ\phi^{U\cap W}_U &&\text{by functoriality}\\ &=\kappa_{(U,D_U)}\circ\phi^{U\cap W}_U &&\text{by (11.5)}\\ &= \kappa_{(U\cap W,D_{U\cap W})} && \text{by (11.4)}\\ &=\kappa_{(W,D_W)}\circ\phi^{U\cap W}_W&& \text{by (11.4)} \end{align*} $$
$$ \begin{align*} \kappa_{(P,D)}\circ\phi^W_P\circ\phi^{U\cap W}_W &=\kappa_{(P,D)}\circ\phi^U_P\circ\phi^{U\cap W}_U &&\text{by functoriality}\\ &=\kappa_{(U,D_U)}\circ\phi^{U\cap W}_U &&\text{by (11.5)}\\ &= \kappa_{(U\cap W,D_{U\cap W})} && \text{by (11.4)}\\ &=\kappa_{(W,D_W)}\circ\phi^{U\cap W}_W&& \text{by (11.4)} \end{align*} $$
and the case with
![]() $\phi ^{V\cap W}_W$
is analogous.
$\phi ^{V\cap W}_W$
is analogous.
Corollary 11.9. For any clan
![]() $\mathcal {T}$
, the
$\mathcal {T}$
, the
![]() $0$
-extensions in
$0$
-extensions in
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
are flat.
$\mathcal {T}\!\text {-}\mathsf {Mod}$
are flat.
Proof. Let
![]() $E\in \mathcal {T}\!\text {-}\mathsf {Mod}$
be a
$E\in \mathcal {T}\!\text {-}\mathsf {Mod}$
be a
![]() $0$
-extension. By applying Theorem 11.8 in
$0$
-extension. By applying Theorem 11.8 in
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/E$
(using Proposition 3.6), we obtain a full map
$\mathcal {T}\!\text {-}\mathsf {Mod}/E$
(using Proposition 3.6), we obtain a full map
![]() $f:F\twoheadrightarrow E$
where F is a
$f:F\twoheadrightarrow E$
where F is a
![]() $0$
-extension and f is a filtered colimit of arrows
$0$
-extension and f is a filtered colimit of arrows
![]() $H(\Gamma )\to E$
in
$H(\Gamma )\to E$
in
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/A$
. Since
$\mathcal {T}\!\text {-}\mathsf {Mod}/A$
. Since
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}/A\to \mathcal {T}\!\text {-}\mathsf {Mod}$
creates colimits this means that F is a filtered colimit of representable models in
$\mathcal {T}\!\text {-}\mathsf {Mod}/A\to \mathcal {T}\!\text {-}\mathsf {Mod}$
creates colimits this means that F is a filtered colimit of representable models in
![]() $\mathcal {T}\!\text {-}\mathsf {Mod}$
, and therefore flat (Lemma 5.4). Since f is a full map into a
$\mathcal {T}\!\text {-}\mathsf {Mod}$
, and therefore flat (Lemma 5.4). Since f is a full map into a
![]() $0$
-extension it has a section, thus E is a retract of F and therefore flat as well.
$0$
-extension it has a section, thus E is a retract of F and therefore flat as well.
Acknowledgments
Thanks to Steve Awodey, Andrew Swan, Fernando Larrain, and especially to Mathieu Anel for many discussions on the topic of this paper. Thanks to Reid Barton for telling me about the fat small object argument. Thanks to Benjamin Steinberg for locating the reference [Reference Head18] for me after I asked about it on MathOverflowFootnote 8 . Thanks to Kian Cho for feedback on the manuscript and catching many typos.
Funding
This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-20-1-0305, and the Army Research Office under award number W911NF-21-1-0121.












 is compact, then f is compact if and only if h is compact. In other words, compact arrow are closed under composition and have the right cancellation property.
is compact, then f is compact if and only if h is compact. In other words, compact arrow are closed under composition and have the right cancellation property.
 the span constitutes a jointly full cone over the cospan,
the span constitutes a jointly full cone over the cospan, making the triangles commute, and
making the triangles commute, and




 is a pullback for all
is a pullback for all 



