Hostname: page-component-5b777bbd6c-6lqsf Total loading time: 0 Render date: 2025-06-19T19:58:03.719Z Has data issue: false hasContentIssue false
  • English
  • Français

On Σ11 equivalence relations with Borel classes of bounded rank1

Published online by Cambridge University Press:  12 March 2014

Ramez L. Sami
Ramez L. Sami*
Affiliation:
Cairo University, Cairo, Egypt
*
U.E.R. de Mathématique, Université Paris VII, Paris, France
Get access Rights & Permissions [Opens in a new window]

Abstract

In Baire space 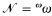we define a sequence of equivalence relations ‹Ev ∣ v < 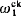, each Ev being 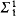with classes in 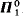+ v + 1 and such that (i) Ev does not have perfectly many classes, and (ii) 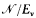is countable iff 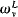< ω1. This construction can be extended cofinally in 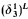. A new proof is given of a theorem of Hausdorff on partitions of R into ω1 many 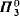sets.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 4 , December 1984 , pp. 1273 - 1283
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

1

The main results of this paper were presented at the Sixth International Congress of Logic, Methodology and the Philosophy of Science (Hannover, 1979).

References

REFERENCES

[1]Burgess, J. P., Equivalences generated by families of Borel sets, Proceedings of the American Mathematical Society, vol. 69 (1978), pp. 323–326.CrossRefGoogle Scholar
[2]Fremlin, D. H. and Shelah, S., On partitions of the real line, Israel Journal of Mathematics, vol. 32 (1979), pp. 299–304.CrossRefGoogle Scholar
[3]Friedman, H., Higher set theory and mathematical practice, Annals of Mathematical Logic, vol. 2 (1971), pp. 325–357.CrossRefGoogle Scholar
[4]Grzegorczyk, A., Mostowski, A. and Ryll-Nardzewski, C., Definability of sets in models of axiomatic theories. Bulletin de l'Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 9 (1961), pp. 163–167.Google Scholar
[5]Hausdorff, F., Summen von ℵ1, Mengen, Fundamenta Mathematical vol. 26 (1936), pp. 241–255.CrossRefGoogle Scholar
[6]Louveau, A., Ensembles analytiques et boréliens dans les espaces produits, Astérisque, vol. 78, Société Mathématique de France, Paris, 1981.Google Scholar
[7]Martin, D. A., Borel determinacy, Annals of Mathematics, ser. 2, vol. 102 (1975), pp. 363–371.CrossRefGoogle Scholar
[8]Morley, M., The number of countable models, this Journal, vol. 35 (1970), pp. 14–18.Google Scholar
[9]Moschovakis, Y. N., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[10]Scott, D., Invariant Borel sets, Fundamenta Mathematicae, vol. 56 (1964) pp. 117–128.CrossRefGoogle Scholar
[11]Simpson, S. and Weitkamp, G., High and low Kleene degrees of coanalytic sets, this Journal, vol. 48 (1983), pp. 356–368.Google Scholar
[12]Stern, J., Suites transfinies d'ensembles boréliens, Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. Série A, vol. 289 (1979), pp. 527–529.Google Scholar
[13]Stern, J., Effective partitions of the real line into Borel sets of bounded rank, Annals of Mathematical Logic, vol. 18 (1980), pp. 29–60.CrossRefGoogle Scholar
[14]Stern, J., On Lusin's restricted continuum problem, Annals of Mathematics (to appear).Google Scholar
[15]Stern, J., Analytic equivalence relations and coanalytic gamesPatras Logic Symposion (Metakides, G., editor), North-Holland, Amsterdam, 1982, pp. 239–260.CrossRefGoogle Scholar