Hostname: page-component-5b777bbd6c-gcwzt Total loading time: 0 Render date: 2025-06-25T07:51:13.892Z Has data issue: false hasContentIssue false
  • English
  • Français

HALL CLASSES OF GROUPS WITH A LOCALLY FINITE OBSTRUCTION

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  24 July 2023

F. DE GIOVANNI Open the ORCID record for F. DE GIOVANNI [Opens in a new window] ,
M. TROMBETTI Open the ORCID record for M. TROMBETTI [Opens in a new window]  and
B. A. F. WEHRFRITZ
F. DE GIOVANNI*
Affiliation:
Dipartimento di Matematica e Appl., Università di Napoli Federico II, Napoli, Italy
M. TROMBETTI
Affiliation:
Dipartimento di Matematica e Appl., Università di Napoli Federico II, Napoli, Italy e-mail: marco.trombetti@unina.it
B. A. F. WEHRFRITZ
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, London, UK e-mail: b.a.f.wehrfritz@qmul.ac.uk
*
e-mail: degiovan@unina.it
Get access Rights & Permissions [Opens in a new window]

Abstract

A well-known theorem of Philip Hall states that if a group G has a nilpotent normal subgroup N such that 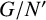$G/N'$ is nilpotent, then G itself is nilpotent. We say that a group class 𝔛 is a Hall class if it contains every group G admitting a nilpotent normal subgroup N such that 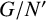$G/N'$ belongs to 𝔛. Hall classes have been considered by several authors, such as Plotkin [‘Some properties of automorphisms of nilpotent groups’, Soviet Math. Dokl. 2 (1961), 471–474] and Robinson [‘A property of the lower central series of a group’, Math. Z. 107 (1968), 225–231]. A further detailed study of Hall classes is performed by us in another paper [‘Hall classes of groups’, to appear] and we also investigate the behaviour of the class of finite-by-𝔜 groups for a given Hall class 𝔜 [‘Hall classes in linear groups’, to appear]. The aim of this paper is to prove that for most natural choices of the Hall class 𝔜, also the classes 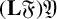$(\mathbf{L}\mathfrak{F})\mathfrak{Y}$ and 𝔅𝔜 are Hall classes, where L𝔉 is the class of locally finite groups and 𝔅 is the class of locally finite groups of finite exponent.

Keywords

Hall classnilpotent grouplocally finite group

MSC classification

Primary: 20F18: Nilpotent groups
Secondary: 20F19: Generalizations of solvable and nilpotent groups 20F50: Periodic groups; locally finite groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 117 , Issue 1 , August 2024 , pp. 16 - 43
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Benjamin Martin

References

Amberg, B., Franciosi, S. and de Giovanni, F., ‘Groups with an $\mathrm{FC}$ -nilpotent triple factorization’, Ric. Mat. 36 (1987), 103–114.Google Scholar
Casolo, C., Groups with all Subgroups Subnormal (AGTA Lost Monographs, Adiuvare, Rome, 2022).Google Scholar
De Falco, M., de Giovanni, F., Musella, C. and Sysak, Y. P., ‘On the upper central series of infinite groups’, Proc. Amer. Math. Soc. 139 (2011), 385–389.10.1090/S0002-9939-2010-10625-1CrossRefGoogle Scholar
de Giovanni, F. and Trombetti, M., ‘Infinite minimal non-hypercyclic groups’, J. Algebra Appl. 14 (2015), 1550143, 15 pages.10.1142/S0219498815501431CrossRefGoogle Scholar
de Giovanni, F., Trombetti, M. and Wehrfritz, B. A. F., ‘Linear groups whose proper subgroups are close to being nilpotent’, Comm. Algebra 49 (2021), 3020–3033.10.1080/00927872.2021.1887206CrossRefGoogle Scholar
de Giovanni, F., Trombetti, M. and Wehrfritz, B. A. F., ‘Subnormality in linear groups’, J. Pure Appl. Algebra 227 (2023), 107185, 16 pages.10.1016/j.jpaa.2022.107185CrossRefGoogle Scholar
de Giovanni, F., Trombetti, M. and Wehrfritz, B. A. F., ‘Hall classes of groups’, to appear.Google Scholar
de Giovanni, F., Trombetti, M. and Wehrfritz, B. A. F., ‘Hall classes in linear groups’, to appear.Google Scholar
Endimioni, G. and Traustason, G., ‘On torsion-by-nilpotent groups’, J. Algebra 241 (2001), 669–676.10.1006/jabr.2001.8772CrossRefGoogle Scholar
Franciosi, S. and de Giovanni, F., ‘Groups with many supersoluble subgroups’, Ric. Mat. 40 (1991), 321–333.Google Scholar
Hall, P., ‘Some sufficient conditions for a group to be nilpotent’, Illinois J. Math. 2 (1958), 787–801.10.1215/ijm/1255448649CrossRefGoogle Scholar
Mann, A., ‘The exponents of central factor and commutator groups’, J. Group Theory 10 (2007), 435–436.10.1515/JGT.2007.035CrossRefGoogle Scholar
McLain, D. H., ‘Remarks on the upper central series of a group’, Proc. Glasg. Math. Assoc. 3 (1956), 38–44.10.1017/S2040618500033414CrossRefGoogle Scholar
Ol’shanskiĭ, A. Y. Geometry of Defining Relations in Groups (Kluwer, Dordrecht, 1989).Google Scholar
Plotkin, B. I., ‘Some properties of automorphisms of nilpotent groups’, Soviet Math. Dokl. 2 (1961), 471–474.Google Scholar
Robinson, D. J. S., ‘A property of the lower central series of a group’, Math. Z. 107 (1968), 225–231.10.1007/BF01110261CrossRefGoogle Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).10.1007/978-3-662-07241-7CrossRefGoogle Scholar
Shumyatsky, P., ‘On extensions of groups of finite exponent’, Glasg. Math. J. 45 (2003), 535–538.10.1017/S0017089503001435CrossRefGoogle Scholar
Wehrfritz, B. A. F., ‘Supersoluble and locally supersoluble linear groups’, J. Algebra 17 (1971), 41–58.10.1016/0021-8693(71)90041-XCrossRefGoogle Scholar
Wehrfritz, B. A. F., Infinite Linear Groups (Springer, Berlin, 1973).10.1007/978-3-642-87081-1CrossRefGoogle Scholar
Wehrfritz, B. A. F., Group and Ring Theoretic Properties of Polycyclic Groups (Springer, London, 2009).10.1007/978-1-84882-941-1CrossRefGoogle Scholar
Wehrfritz, B. A. F., ‘Rank–Engel conditions on linear groups’, Rend. Circ. Mat. Palermo (2) 70 (2021), 45–56.10.1007/s12215-020-00485-7CrossRefGoogle Scholar