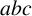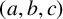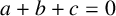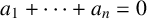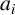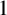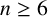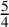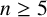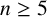IMPROVED LOWER BOUNDS FOR STRONG n-CONJECTURES

Abstract

The well-known $abc$-conjecture concerns triples $(a,b,c)$ of nonzero integers that are coprime and satisfy ${a+b+c=0}$. The strong n-conjecture is a generalisation to n summands where integer solutions of the equation ${a_1 + \cdots + a_n = 0}$ are considered such that the $a_i$ are pairwise coprime and satisfy a certain subsum condition. Ramaekers studied a variant of this conjecture with a slightly different set of conditions. He conjectured that in this setting the limit superior of the so-called qualities of the admissible solutions equals $1$ for any n. In this paper, we follow results of Konyagin and Browkin. We restrict to a smaller, and thus more demanding, set of solutions, and improve the known lower bounds on the limit superior: for ${n \geq 6}$ we achieve a lower bound of $\frac 54$; for odd $n \geq 5$ we even achieve $\frac 53$. In particular, Ramaekers’ conjecture is false for every ${n \ge 5}$.

1 Introduction

The $abc$ -conjecture [5, 6, 11] is a well-known open problem in mathematics. It postulates that there is no constant $q> 1$ such that there exist infinitely many triples $(a,b,c)$ of coprime and nonzero integers with $a+b+c=0$ and such that the ‘quality’ of $(a,b,c)$ exceeds q.

More precisely, the radical $\mathrm {rad}(n)$ of a nonzero integer n is defined as the largest square-free positive divisor of n. Now let $(a,b,c) \in \mathbb {Z}^3$ be such that ${a,b,c \ne 0}$ . Then the quality of $(a,b,c)$ is defined as

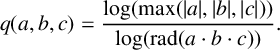$$ \begin{align*} q(a,b,c) = \frac{\log(\max(|a|,|b|,|c|))}{\log(\mathrm{rad}(a \cdot b \cdot c))}. \end{align*} $$

For example, given the triple ${(8192,-8181,-11) = (2^{13},-3^4 \cdot 101, -11)}$ , its entries are pairwise coprime, their largest square-free positive divisor is $6666 = 2 \cdot 3 \cdot 11 \cdot 101$ , and its quality is $\log (8192)/\!\log (6666) \approx 1.0234$ , seemingly supporting the claim of the $abc$ -conjecture.

The conjecture itself has been rather well studied but is still unresolved. However, on the way towards partial solutions, various variants of the original problem were formulated and conjectures about the achievable qualities in these cases were made. While Vojta [9, 10] has studied a very general statement that implies the $abc$ -conjecture, a more immediate generalisation is the n-conjecture first studied by Browkin and Brzeziński [2].

The topic of this paper is not this n-conjecture but two variants, respectively, introduced by Browkin [1], building on work of Konyagin, and Ramaekers [8]; both used the term ‘strong n-conjectures’ for their versions. Before we can state these conjectures, we first need to generalise the above definition of quality from triples to n-tuples.

Definition 1.1. For ${a = (a_1,\ldots ,a_n) \in \mathbb {Z}^n}$ , with $a_i\neq 0$ for $1 \leq i \leq n$ , we write

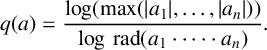$$ \begin{align*}q(a) = \frac{\log(\max(|a_1|,\ldots,|a_n|))}{\log\,\mathrm{rad}(a_1 \cdot \cdots \cdot a_n)}. \end{align*} $$

Then for a sequence $A = \{a^{(1)}, a^{(2)},\ldots \} \subseteq \mathbb {Z}^n$ of n-tuples as above, let the quality of A be defined as

$$ \begin{align*} Q_A = \limsup_{k \rightarrow \infty} q(a^{(k)}). \end{align*} $$

Different strong n-conjectures concern the qualities of different sets A of n-tuples of integers; it is not hard to see that q and therefore $Q_A$ cannot take values less than $1$ for any A.

We can now state the strong n-conjectures mentioned above. We first recall the n-conjecture and how it relates to the $abc$ -conjecture.

Conjecture 1.2 (n-conjecture; Browkin and Brzeziński [2]).

Let ${n \geq 3}$ and let ${A(n) \subseteq \mathbb {Z}^n}$ be the set of n-tuples $(a_1,\ldots ,a_n)$ such that

1. (i) $a_1+\cdots +a_n=0$ ,

2. (ii) there are no ${b_1,\ldots ,b_n \in \{0,1\}}$ and $i,j$ with ${1\leq i,j\leq n}$ such that ${b_i=0}$ and ${b_j=1}$ and ${\sum _{k=1}^n b_k \cdot a_k = 0}$ ,

3. (iii) $\mathrm {gcd}(a_1,\ldots ,a_n) = 1$ .

Then $Q_{A(n)}=2n-5$ for every n.

In the following we informally refer to condition (ii), as well as to analogous statements introduced below, as the subsum condition. Note that in the case $n=3$ this condition excludes only finitely many triples and is therefore irrelevant for the value of $Q_{A(3)}$ ; this implies that the statement ‘ $Q_{A(3)}=1$ ’ is equivalent to the $abc$ -conjecture. For larger n, we have the following relationship.

Theorem 1.3 (Browkin and Brzeziński [2]).

If the $abc$ -conjecture is false then the n-conjecture is false for every $n \geq 4$ .

One half of the n-conjecture is known: Browkin and Brzeziński [2, Theorem 1] proved for ${n \ge 3}$ that $Q_{A(n)} \ge 2n - 5$ . This statement is not hard to prove; we come back to it in Remark 4.1 at the end of this paper.

Different conjectures arise when considering different sets A and one of the main goals of this paper is to clarify the relation between these different conjectures and to try to unify the picture.

Browkin [1] introduced the following conjecture he referred to as the ‘strong n-conjecture’. It is obtained from the n-conjecture by requiring that the entries in each n-tuple are pairwise coprime and removing the subsum condition.

Conjecture 1.4 (Browkin [1]).

Let $n \geq 3$ and let $B(n)$ be the set of n-tuples ${(a_1,\ldots ,a_n)\in \mathbb {Z}^n}$ such that

1. (i) $a_1+\cdots +a_n=0$ ,

2. (ii) $\mathrm {gcd}(a_i,a_j) = 1$ for all $i,\ j$ with ${1 \leq i < j \leq n}$ .

Then $Q_{B(n)}<\infty $ for every n.

The statement ‘ $Q_{B(3)}=1$ ’ is a reformulation of the $abc$ -conjecture.

Remark 1.5.

1. (1) If $Q_{A(4)} \leq 3$ , then ${Q_{B(3)} = 1}$ . Indeed, assume that there are infinitely many counterexamples $(a,b,c)$ to the $abc$ -conjecture of quality at least q with ${q>1}$ . Then $Q_{A(4)} \geq 3q$ is witnessed by the quadruples

   $$ \begin{align*}(a^3,b^3,c^3,-3abc).\end{align*} $$

2. (2) Similarly, ${Q_{A(5)} \leq 5}$ implies that ${Q_{B(3)} = 1}$ via quintuples of the form

   $$ \begin{align*}(a^5,b^5,c^5,-5abc^3,5a^2b^2c).\end{align*} $$

3. (3) More generally, if ${Q_{A(n)} \leq 2n-5}$ for some ${n \geq 4}$ , since the reverse inequality is known as mentioned above, it would follow that the n-conjecture is true for this particular n. As a consequence, in view of Theorem 1.3, the $abc$ -conjecture would be true as well in this case.

Konyagin established the following result about Conjecture 1.4.

Theorem 1.6 (Konyagin; see Browkin [1]).

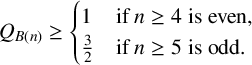$$ \begin{align*}Q_{B(n)} \geq \begin{cases} 1 & \text{if } n \geq 4 \text{ is even,}\\ \frac32 & \text{if } n \geq 5 \text{ is odd.}\\ \end{cases}\end{align*} $$

For completeness we mention that Konyagin’s result can also be derived from an example given by Darmon and Granville [4, item (d) on page 542] by choosing ${t = 2^k}$ ; they cite correspondence with Noam D. Elkies as the source.

Another variant of the n-conjecture that we study is as follows.

Remark 1.7. We point out that there is a typo when Browkin states Konyagin’s result; where we say ‘ $n \geq 5$ ’ he says ‘ $n \geq 3$ ’. But then Theorem 1.6 would already disprove the $abc$ -conjecture. Indeed, Konyagin’s proof only works for odd $n \geq 5$ .

Conjecture 1.8 (Ramaekers [8]).

Let $n \geq 3$ and let $R(n)$ be the set of n-tuples ${(a_1,\ldots ,a_n)\in \mathbb {Z}^n}$ such that

1. (i) $a_1+\cdots +a_n=0$ ,

2. (ii) there are no ${b_1,\ldots ,b_n \in \{0,1\}}$ and $i,j$ with ${1\leq i,j\leq n}$ such that ${b_i=0}$ and ${b_j=1}$ and ${\sum _{k=1}^n b_k \cdot a_k = 0}$ ,

3. (iii) ${\mathrm {gcd}(a_i,a_j) = 1}$ for $i,j$ with ${1 \leq i < j \leq n}$ .

Then $Q_{R(n)}=1$ for every n.

Note that Ramaekers’ conjecture maintains the subsum condition from the original n-conjecture, unlike Browkin’s. Darmon and Granville [4, end of Section 5.2] also mention this statement as the ‘generalised $abc$ -conjecture’, but only conjecturing $Q_{R(n)} < \infty $ and not clarifying whether they require pairwise or setwise coprimeness.

Except for $(1,-1,0)$ and its reorderings, all triples in $B(3)$ are also in $R(3)$ ; thus the $abc$ -conjecture is equivalent to the claim that ${Q_{R(3)} = 1}$ as well. Ramaekers computed numerous example elements of $R(3)$ , $R(4)$ and $R(5)$ of quality larger than $1$ . Here, the examples in $R(4)$ exhibited a tendency to be of smaller quality than those in $R(3)$ , which could make one suspect that disproving the claim ‘ $Q_{R(4)} = 1$ ’ might be even harder than disproving the $abc$ -conjecture. We are, however, unaware of any known implications between the cases $n=3$ and $n=4$ ; for larger n, though, we see below that $Q_{R(n)}> 1$ .

As $R(n)$ is a strictly smaller set than $B(n)$ , a priori $Q_{R(n)}$ could be smaller than $Q_{B(n)}$ . Thus, we cannot directly deduce anything about $Q_{R(n)}$ from Theorem 1.6; indeed, for odd $n \geq 7$ , Konyagin’s proof of Theorem 1.6 uses n-tuples that are in $B(n)\setminus R(n)$ .

In this paper we introduce two new restrictions, namely a stronger subsum condition on the one hand, and the set of forbidden factors F on the other hand. We will work with the following definition, which is purposely designed for proving lower bounds on $Q_{R(n)}$ ; see Fact 1.12 below.

Definition 1.9. Let $n \geq 3$ and let ${F \subseteq \mathbb {N}}$ be a finite set, where ${\min F \geq 3}$ if $F\neq \emptyset $ . We let $U(F,n)$ contain all ${(a_1,\ldots ,a_n)\in \mathbb {Z}^n}$ satisfying the following conditions:

1. (i) $a_1+\cdots +a_n=0$ ;

2. (ii) there are no $b_1,\ldots ,b_n \in \{-1,0,1\}$ and $i,j$ with $1\leq i,j\leq n$ such that $b_i=0$ and $b_j=1$ and $\sum _{k=1}^n b_k \cdot a_k = 0$ ;

3. (iii) $\mathrm {gcd}(a_i,a_j) = 1$ for $i,j$ with $1 \leq i < j \leq n$ ;

4. (iv) none of the numbers $a_1,\ldots ,a_n$ is a multiple of any number in F.

Remark 1.10.

1. (1) If F is empty then condition (iv) is vacuously satisfied by every n-tuple.

2. (2) If ${2 \in F}$ and n is odd, then ${U(F,n) = \emptyset }$ since the sum of an odd number of odd integers cannot be $0$ . For the case where n is even, note that by condition (iii) at most one of the $a_i$ can be even; but then by condition (i) no $a_i$ can be even. Thus the assumption $2\in F$ is unnecessary in this case, and can be omitted. In summary, we do not consider the case $2\in F$ .

3. (3) Using condition (iii), it is again easy to see that the claim ‘ ${Q_{U(\emptyset ,3)} = 1}$ ’ is equivalent to the $abc$ -conjecture.

We are interested in questions of the following type.

Question 1.11. Fixing different choices of F and n, what are valid lower bounds on $Q_{U(F,n)}$ ?

While Browkin and Brzeziński opted to only allow coefficients $b_j\in \{0,1\}$ in the subsum condition in Conjecture 1.2, our new condition (ii) above is more demanding as it allows negative coefficients as well. Thus the quality lower bounds we establish below are proven for a smaller set of n-tuples and will therefore also hold for the conjectures stated above. More precisely stated, the following relationships between the different strong n-conjectures are immediate.

Fact 1.12. For every ${n \in \mathbb {N}}$ and any F as above we have ${Q_{U(F, n)} \leq Q_{A(n)}}$ as well as ${Q_{U(F, n)} \leq Q_{R(n)} \leq Q_{B(n)}}$ .

This means in particular that, by fixing the right parameters, our new definition provides a framework that can be used to prove lower bounds on both Browkin’s and Ramaekers’ versions of the problem.

In the remainder of this paper, we prove lower bounds for $Q_{U(F,n)}$ for suitable parameters F and n. First, we improve Konyagin’s construction cited above to obtain the following stronger version of his result.

Theorem 1.13. Let F be such that $2,5,10 \notin F$ . Then ${Q_{U(F,n)} \geq \frac 53}$ for each odd ${n \geq 5}$ . In particular, ${Q_{U(\emptyset ,n)} \geq \frac 53}$ for these n.

In particular, Ramaekers’ conjecture is wrong for odd ${n \geq 5}$ . Even integers are covered by our second main result, which holds for arbitrary ${n \ge 6}$ and arbitrary finite F.

Theorem 1.14. Let $n \geq 6$ and let F be an arbitrary finite set. Then

$$ \begin{align*}Q_{U(F,n)} \geq \tfrac54.\end{align*} $$

In particular, $Q_{R(n)} \geq \frac 54$ for each ${n \geq 6}$ .

We stress that these results disprove Ramaekers’ conjecture for any ${n \geq 5}$ .

Finally, we conclude with a brief discussion of n-tuples $(a_1, \ldots , a_n)$ that are coprime but not necessarily pairwise coprime, with a particular focus on Conjecture 1.2 of Browkin and Brzeziński.

2 The case of odd $n \geq 5$

As a warm-up and an illustration of Konyagin’s technique, we first give a proof of a weaker version of Theorem 1.13 for $n=5$ . In the process we slightly modify the construction that he used to prove Theorem 2.1, so as to obtain a bound on $Q_{U(\emptyset ,5)}$ in place of $Q_{B(5)}$ .

Theorem 2.1. ${Q_{U(\emptyset ,5)} \geq \frac 32}$ .

Proof. Fix any integer $k \geq 1$ and let

$$ \begin{align*}{a = (6^{2^k}+1)^3},\quad {b = -(6^{2^k}-1)^3},\quad {c = -6 \cdot (6^{2^k})^2}, \quad d = -31, \quad e = 29.\end{align*} $$

Then $\log (a) \geq 3 \cdot 2^k \cdot \log (6)$ holds, while $\mathrm {rad}(a \cdot b \cdot c \cdot d \cdot e)$ is a factor of $(6^{2^k}+1) \cdot (6^{2^k}-1) \cdot 6 \cdot 31 \cdot 29$ , so that its logarithm must be bounded by $2 \cdot 2^k \cdot \log (6) + \ell $ for some constant $\ell $ . Thus,

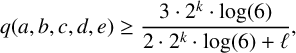$$ \begin{align*} q(a,b,c,d,e) \geq \frac{3 \cdot 2^k \cdot \log(6)}{2 \cdot 2^k \cdot \log(6) + \ell}, \end{align*} $$

which converges to $\frac 32$ for $k \rightarrow \infty $ .

We claim that for every $k\geq 1$ , if $a,b,c,d,e$ are chosen as above, then they are pairwise coprime. If we write $s = 6^{2^k}$ , then a, b and c are of the forms $(s+1)^3$ , $-(s-1)^3$ and $-6s^2$ , respectively. Trivially, $s-1$ and s are coprime, and the same holds for s and $s+1$ . As $2$ and $3$ are the only factors of s, neither of them can be a factor of $s-1$ or $s+1$ , and thus $(s+1)^3$ and $6s^2$ , as well as $(s-1)^3$ and $6s^2$ , are coprime. As $s-1$ and $s+1$ are both odd, they cannot have $2$ as a common factor, and thus $s-1$ and $s+1$ must be coprime; consequently, $(s-1)^3$ and $(s+1)^3$ are coprime. To complete the argument, consider the sequence $(6^{2^k})_{k \geq 1}$ ; if we can show that, modulo $29$ and modulo $31$ , none of its elements equals $-1$ , $0$ , or $1$ , then none of $s-1$ , s or $s+1$ can be a multiple of $29$ or $31$ , implying that each of $a,b,c$ is coprime with both $d=29$ and $e=31$ . We proceed by repeated squaring; first we obtain

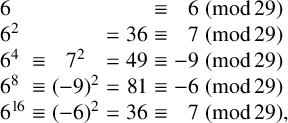$$ \begin{align*}\begin{array}{l@{\;}c@{\;}c@{\;}c@{\;}r@{\;}c@{\;}r@{\;}l} 6&&&&&\equiv & 6 & \pmod{\,29} \\ 6^2 &&& = & 36 & \equiv & 7 & \pmod{\,29} \\ 6^4 & \equiv & 7^2 & = & 49 & \equiv & -9 & \pmod{\,29} \\ 6^8 & \equiv & (-9)^2 & = & 81 & \equiv & -6 & \pmod{\,29} \\ 6^{16} & \equiv & (-6)^2 & = & 36 & \equiv & 7 & \pmod{\,29}, \end{array}\end{align*} $$

and so on. Similarly, modulo $31$ , we obtain the sequence $6$ , $5$ , $-6$ , $5$ , and so on. Thus, $a,b,c,d,e$ are pairwise coprime, establishing condition (iii) of Definition 1.9.

Condition (i) is immediate. For condition (ii), assume that there exist nontrivial subsums equalling $0$ and fix one. Clearly, no combination of only the elements c, d and e exists that sums to $0$ . Thus at least one of a or b must occur in our subsum. But if ${\pm (s+1)^3}$ is part of the subsum, so must ${\mp (s-1)^3}$ , as otherwise there would be no hope of the subsum equalling $0$ . Also, the signs of these two numbers must clearly be opposite; assume without loss of generality that they are chosen in such a way that the sum of these two elements is positive, that is, that it equals $6 \cdot s^2+2$ . Then $-6s^2$ must also be part of the subsum in order to have any hope of achieving a subsum equalling $0$ . But $ {(s+1)^3 - (s-1)^3 -6s^2 = 2}$ , and thus the only way to achieve a sum of $0$ in this case is by also including $29$ and $-31$ . Thus all five of $a,b,c,d,e$ are required in a subsum for it to equal $0$ ; this contradicts our assumption that our subsum was a nontrivial example.

Finally, condition (iv) of Definition 1.9 is vacuous as ${F = \emptyset }$ .

To obtain the stronger Theorem 1.13 stated in the introduction, we use a proof that is similar to the previous one, except that we employ a degree $5$ polynomial instead of a degree $3$ one to obtain a better bound. We begin by proving an auxiliary result.

Lemma 2.2. Let $u,m \in \mathbb Z$ with ${u < 0 < m}$ and ${m \geq \max (2,|u|)}$ , write

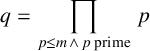$$ \begin{align*} q=\prod_{p \leq m \,\wedge\, p \text{ prime}} \, p \end{align*} $$

and let ${F = \{3,4,\ldots ,m\}}$ . Then there are a natural number ${v> 0}$ and an odd integer ${w \leq 0}$ with ${u=v+w}$ such that

• • ${q < v \le |w| \leq (m+1) \cdot q}$ ,

• • ${\mathrm {gcd}(v,w)=1}$ , and

• • no element of F divides v or w.

Proof. Let q be as in the statement. We run the following algorithm.

1. (1) Let $v = u+1+q$ and $w=-q-1$ .

2. (2) For all prime numbers $3 \leq p \leq m$ ,

3. (3) while p divides one of v or w,

4. (4) let $v = v+q/p$ and $w = w-q/p$ .

5. (5) If $4$ divides v then let $v = v+q$ and $w = w-q$ .

Note that the sum $v+w=u$ and the fact that w is odd are invariants during the execution of this algorithm. Further note that ${q < v}$ and ${|w| \leq (m+1) \cdot q}$ are immediate by construction.

During the ‘for’ loop over p, since $q/p$ is not a multiple of p, only one of v, $v+q/p$ and $v+q/p+q/p$ can be a multiple of p. The same applies to w, $w-q/p$ , and $w-q/p-q/p$ . Thus, for each p, the instruction inside the ‘while’ loop will be executed $0$ , $1$ or $2$ times, and afterwards neither v nor w will be divisible by p.

We claim that, once established, this property is preserved throughout the rest of the algorithm. Indeed, consider some prime $p' \neq p$ which was handled in a previous iteration of the ‘while’ loop, and assume that at the beginning of the iteration for p we have that neither v nor w is divisible by $p'$ . Since $q/p$ is a multiple of $p'$ , we have $v \equiv v + q/p {\;(\textrm {mod}\;p')}$ and $w \equiv w - q/p {\;(\textrm {mod}\;p')}$ ; thus the property is preserved by the action taken at line (4). For similar reasons, the property also is preserved during the final execution of (5). This proves the claim, and it follows that after the algorithm terminates, v and w are not divisible by any odd prime less than or equal to m.

Assume that v is divisible by $4$ before the execution of line (5). Then, since q is not divisible by $4$ , $v+q$ is an even number not divisible by $4$ . Thus, in any case, after the execution of line (5), v is not divisible by $4$ . Since w was odd, it is still odd after the execution of line (5); in particular, it is not divisible by $4$ .

Overall we have established that, when the algorithm terminates, none of the numbers $3,4,\ldots ,m$ divide v or w.

To see that v and w are coprime, first note that $2$ cannot be a common prime factor since w is odd. By construction, any odd common prime factor p of v and w must be larger than m. But any such p also is a prime factor of $u=v+w$ , which is impossible as $u \leq m$ .

Finally, since ${v + w = u}$ and ${u < 0}$ it is obvious that ${v \le |w|}$ .

With this established, we are ready to prove the first main result of this paper. We point out that it is closely related to an observation of Ramaekers [8, Section 4.4]; he gives credit for the idea of using polynomial identities to the previously mentioned examples of Darmon and Granville [4] and Elkies. For these, the condition that the $a_i$ have to be pairwise coprime is dropped; see Remark 4.1.

Theorem 1.12 (restated).

Let F be such that $2,5,10 \notin F$ . Then ${Q_{U(F,n)} \geq \frac 53}$ for each odd ${n \geq 5}$ . In particular, ${Q_{U(\emptyset ,n)} \geq \frac 53}$ for these n.

Proof. We will construct infinitely many n-tuples $(a_1,\ldots ,a_n)$ where

• • $a_1=(x-1)^5$ ,

• • $a_2=10(x^2+1)^2$ ,

• • $a_3=-(x+1)^5$ .

We will then show that there exist choices for $a_4,\ldots ,a_n$ that only depend on n and such that there are infinitely many x such that these n-tuples satisfy the conditions posited by Definition 1.9. We begin by letting

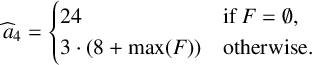$$ \begin{align*}\widehat{a}_4 = \begin{cases} 24 & \text{if } F = \emptyset,\\ 3 \cdot (8+\max(F)) & \text{otherwise.} \end{cases}\end{align*} $$

For ${i = 4,5,\ldots ,n-2}$ we proceed inductively by letting each $a_i$ be any prime number larger than $\widehat {a}_i$ and by letting each ${\widehat {a}_{i+1} = 3 \cdot a_i}$ .

Next, we let $a_{n-1}$ and $a_n$ be the numbers v and w provided by Lemma 2.2 when applied with parameters

• • ${u = -(8+a_4+a_5+\cdots +a_{n-2})}$ ,

• • ${m = \widehat {a}_{n-2}}$ ;

in particular, ${a_{n-1}> 0}$ . Finally, let ${\widehat {a}_n = 3 \cdot (|a_{n-1}|+|a_n|)}$ .

Note that ${(x-1)^5 + 10(x^2+1)^2 -(x+1)^5 = 8}$ holds independently of the choice of x; thus by choice of u we have ${a_1+a_2+\cdots +a_n = 0}$ . Recall that n is odd by assumption. As ${a_4+a_5+\cdots +a_{n-2}}$ is composed of an even number of all odd summands, u must be even. Therefore, $a_{n-1}$ and $a_n$ must have the same parity; however, by Lemma 2.2 they cannot both be even. Thus it follows that all of ${a_4,a_5,\ldots ,a_n}$ are odd; moreover, they are pairwise coprime by construction.

Set ${y = \widehat {a}_n!}$ and consider the equation

(2-1) $$ \begin{align} y^2 \cdot s^2 - (y^2+1) \cdot t^2 = -1. \end{align} $$

As there is an initial solution ${(s, t) = (1,1)}$ and as ${y^2 \cdot (y^2+1)}$ is positive and not a square, it follows that equation (2-1) has infinitely many integer solutions (see, for instance, Bundschuh [3, Subsection 4.3.7, page 198]). Fix any solution $(s,t)$ of equation (2-1) and let ${x = y \cdot s}$ .

Thus x is a multiple of each element of F and of each of ${a_4,a_5,\ldots ,a_n}$ ; and therefore ${x-1}$ , ${x+1}$ and ${x^2+1}$ are each coprime with any of these numbers. Furthermore, each of $2$ , $5$ and $10$ is coprime with each of ${a_4,a_5,\ldots ,a_n}$ ; as a result ${10 (x^2+1)^2}$ is coprime with these numbers as well. As x is even, ${(x-1)^5}$ and ${(x+1)^5}$ are coprime and ${(x^2+1)}$ is coprime with ${x^2-1}$ , and thus with ${x-1}$ and ${x+1}$ as well. As $10$ divides x, the numbers ${x-1}$ , ${x+1}$ and ${x^2+1}$ are coprime with $10$ . Also, no element of F divides any of ${a_1,\ldots ,a_n}$ .

In summary, conditions (i), (iii) and (iv) in Definition 1.9 are satisfied. Now assume there exists a nontrivial zero subsum, that is, that there are ${b_1, \ldots , b_n}$ such that ${b_1 \cdot a_1 + \cdots + b_n \cdot a_n}=0$ and such that not all $b_i$ equal $0$ . We distinguish two cases.

If $b_1,b_2,b_3$ are not all equal, then $(b_1, b_2, b_3)$ or $(-b_1, -b_2, -b_3)$ must equal one of

$$ \begin{align*} \begin{array}{ccccc} (1,0,0), & (0,1,0), & (0,0,1), & (1,0,1), & (1,0,-1), \\ (1,1,0), & (1,-1,0), & (1,-1,1), & (1,1,-1), & (1,-1,-1). \end{array} \end{align*} $$

Recalling that x is a multiple of y, it is easy to verify that in each of these cases we have $|b_1 \cdot a_1 + b_2 \cdot a_2 + b_3 \cdot a_3|>y$ . But then, since their absolute values are too small compared with ${y = \widehat {a}_n!}$ , no combination of the remaining $a_i$ with ${i \geq 4}$ is possible that would lead to a zero subsum.

In the other case, if $b_1=b_2=b_3$ , then their sum is $-8$ , $0$ or $+8$ . We distinguish all three possible cases concerning the value of $b_n$ .

• • If $b_n=0$ , then the subsum is empty. This is because in the sequence

  $$ \begin{align*}|a_1+a_2+a_3|,|a_4|,|a_5|,\ldots,|a_{n-1}|\end{align*} $$
  each entry is at least $3$ times larger than the previous one; thus the only way of obtaining a zero subsum in this case is when ${b_k=0}$ for all ${1\leq k \leq n}$ .

• • If $b_n=1$ , then $b_k=1$ for all ${1\leq k \leq n}$ . Assume that for some choice of $(b_k)_{1\leq k \leq n}$ with ${b_n=1}$ we have ${\sum _{k=1}^n b_k \cdot a_k = 0}$ . Since we also have ${\sum _{k=1}^n a_k = 0}$ it follows that

  $$ \begin{align*}\begin{array}{c@{\;}l} &\displaystyle\sum_{k=1}^n a_k - \displaystyle\sum_{k=1}^n b_k \cdot a_k \\[0.5em] &\quad = (1-b_1) \cdot (a_1+a_2+a_3)+\displaystyle\sum_{k=4}^{n-1} (1-b_k) \cdot a_k\\[0.5em] &\quad= 0, \end{array} \end{align*} $$
  where $1-b_k \in \{0,1,2\}$ for $k \in \{1,4,5,\ldots , n-1\}$ . For the same reason as in the previous item, the only choice of $(1-b_k)_{k \in \{1,4,5,\ldots , n-1\}}$ that makes this equality true is $1-b_k =0 $ (thus $b_k =1 $ ) for all $k \in \{1,4,5,\ldots , n-1\}$ .

• • If $b_n=-1$ , then $b_k=-1$ for all $1\leq k \leq n$ , by a symmetric argument.

In summary, the subsum condition (ii) in Definition 1.9 is satisfied as well.

It remains to estimate the qualities of the constructed n-tuples. Note that the terms y and $y^2+1$ as well as the terms $a_4,\ldots ,a_n$ are constant, and that by equation (2-1) the term ${a_2 = 10 (x^2+1)^2 = 10 (y^2+1)^2 \cdot t^4}$ only contributes a factor $t \in O(x)$ to the radical. Thus we have $\mathrm {rad}(a_1 \cdot \cdots \cdot a_n) \in {O(x^3)}$ .

On the other hand, $\max (|a_1|,\ldots ,|a_n|) = |a_3| = |x+1|^5$ , and so there is a constant C such that we have

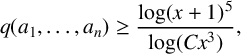$$ \begin{align*} q(a_1,\ldots,a_n) \geq \frac{\log(x+1)^5}{\log(Cx^3)}, \end{align*} $$

and therefore

$$ \begin{align*} Q_{U(F,n)} \geq \lim_{x \rightarrow \infty} q(a_1,\ldots,a_n) \geq \lim_{x \rightarrow \infty} \frac{\log(x^5)}{\log(x^3) + \log(C)} = \frac53. \end{align*} $$

This completes the proof.

The above result only holds for F not containing $2$ , $5$ or $10$ . If we do allow $5$ or $10$ in F, we can still obtain the following weaker lower bound by considering polynomials whose degrees depend on F.

Theorem 2.3. Let F be a finite set with $\min (F) \geq 3$ . Then ${Q_{U(F,5)}> 1}$ .

Proof. As before, we may assume ${F=\{3,4,\ldots ,m\}}$ for some m. Let ${s = h!-1}$ for ${h> 9m}$ and keep h and s constant during the remainder of the construction. Let ${x = k!}$ for some ${k>s}$ ; as in the previous construction, we demonstrate that for sufficiently large k all required properties are satisfied. Then by letting k go to infinity we obtain infinitely many examples that together witness the desired lower bound for $Q_{U(F,5)}$ .

We consider the following numbers; here, the choice of $a_1$ , $a_2$ , $a_3$ and $a_4+a_5$ follows Ramaekers [8, Section 4.4] but we then additionally split $a_4+a_5$ into two summands:

• • $a_1 = (x+1)^s$ ,

• • $a_2 = -(x-1)^s$ ,

• • $a_3 = -2s \cdot (x^2+(s-2)/3)^{(s-1)/2}$ ,

• • $a_4 = -(a_1+a_2+a_3+y)$ for some fixed odd ${y>s}$ that we choose below,

• • $a_5 = y$ .

Note that, as a polynomial in x, we have that $a_1+a_2$ is of degree $s-1$ and even, that is, of the form $c_0 + c_2x^2+ c_4x^4 + c_6x^6+\cdots $ . Similarly, note that $a_1+a_2+a_3$ is an even polynomial in x of degree $s-5$ . Finally, note that, when dividing an even polynomial by a polynomial of the form $x^2+c$ , for some $c \in \mathbb Z$ , the remainder is an integer not depending on x; if we write $z_0$ , $z_1$ and $z_2$ for the remainders of $a_1+a_2+a_3$ modulo $x^2$ , modulo $x^2-1$ and modulo $x^2+(s-2)/3$ , respectively, then the following auxiliary statement holds.

Lemma 2.4. We have that $6$ divides $z_0$ and that there exists an integer y such that

• • none of y, $y+z_0$ , $y+z_1$ and $y+z_2$ has a prime factor q where

  $$ \begin{align*}5 \leq q \leq (2s)^s+|z_0|+|z_1|+|z_2|,\end{align*} $$

• • neither y nor $y+z_0$ is divisible by $2$ or $3$ .

Proof. We achieve this by a method similar to that in the proof of Lemma 2.2.

Let ${b = (2s)^s+|z_0|+|z_1|+|z_2|}$ , ${r = \prod _{q \leq b \,\wedge \, q \text { prime}}}$ and proceed as follows.

1. (1) Let $y=1$ .

2. (2) For all primes q with ${5 \leq q \leq b}$ ,

3. (3) replace y by $\min (M \cap N)$ where

   $$ \begin{align*}\begin{array}{l@{\;}c@{\;}l} \quad\quad M & = & \{y+i\cdot r/q\colon\; 0 \leq i \leq 4\}, \\ \quad\quad N & = & \{y'\colon\; q \nmid y' \wedge q \nmid (y'+z_0) \wedge q \nmid (y'+z_1) \wedge q\nmid (y'+z_2)\}. \end{array}\end{align*} $$

Note that q does not divide $r/q$ , and thus, for each

$$ \begin{align*}z \in \{y',y'+z_0,y'+z_1,y'+z_2\},\end{align*} $$

at most one among ${z,z+r/q,\ldots ,z+4 \cdot r/q}$ can be a multiple of q. Thus, by the pigeonhole principle, the choice of y in (3) is always possible.

That the final y emerging from this process has the first of the two stipulated properties then follows from an argument analogous to that used in the proof of Lemma 2.2.

To argue that y and ${y + z_0}$ have the second property, we first prove that $z_0$ is divisible by $6$ . An easy calculation shows that ${z_0=2-2s \cdot ((s-2)/3)^{(s-1)/2}}$ , an even number. To see that ${z_0 \equiv 0 {\;(\textrm {mod}\;3)}}$ , it is enough to show that

$$ \begin{align*} 2s \cdot ((s-2)/3)^{(s-1)/2} \equiv 2 {\;(\textrm{mod}\;3)}.\end{align*} $$

To that end, note that, as ${h! \equiv 0 {\;(\textrm {mod}\;4)}}$ , we have that ${s-1=h!-2 \equiv 2 {\;(\textrm {mod}\;4)}}$ , and thus that $(s-1)/2$ is odd. Recall that ${s = h!-1}$ , thus ${s \equiv 8 {\;(\textrm {mod}\;9)}}$ . Now ${s-2 \equiv 6 {\;(\textrm {mod}\;9)}}$ and ${(s-2)/3 \equiv 2 {\;(\textrm {mod}\;3)}}$ . Moreover, ${2s \equiv 2 \cdot 2 \equiv 1 {\;(\textrm {mod}\;3)}}$ . Therefore, $2s \cdot ((s-2)/3)^{(s-1)/2} \equiv 2 {\;(\textrm {mod}\;3)}$ and thus ${z_0 \equiv 0 {\;(\textrm {mod}\;6)}}$ .

To complete the proof of the lemma, note that after executing (1), ${y + z_0 \equiv y \equiv 1 {\;(\textrm {mod}\;6)}}$ . As all terms $r/q$ appearing in the algorithm are multiples of $6$ , this last property is invariant during the algorithm’s execution, and the final y and ${y+z_0}$ are not divisible by $2$ or $3$ .

To continue with the proof of Theorem 2.3, fix an integer y as provided by Lemma 2.4; note that y does not depend on x, a fact which will prove crucial in our closing arguments below. We verify conditions (i)–(iv) stipulated by Definition 1.9. Condition (i) is trivially satisfied by choice.

By construction, x is a multiple of $3$ while neither s nor $(s-2)/3$ is a multiple of $3$ by the arguments given in the proof of Lemma 2.4; thus, $3$ does not divide $a_3=-2s \cdot (x^2+(s-2)/3)^{(s-1)/2}$ . We further claim that $a_3$ is not divisible by $4$ either; this is because x is even, s is odd, and $(s-2)/3$ is easily seen to be odd by construction. Now let ${q> 3}$ be a prime factor of any element of F. By construction, q divides x but neither s nor ${(s-2)/3}$ . It follows that none of ${x+1}$ , ${x-1}$ and ${x^2-(s-2)/3}$ is a multiple of q. By Lemma 2.4 neither y nor ${y+z_0}$ is divisible by q. Thus none of ${a_1,a_2,a_3,a_4,a_5}$ is a multiple of any element of F and thus condition (iv) is satisfied.

Clearly, the fact that x is even implies that $a_1$ and $a_2$ are coprime by construction. Observe that ${(x^2+(s-2)/3) - (x^2-1) = (s+1)/3 = h!/3}$ ; this implies that if $x+1$ or $x-1$ has a common factor q with $a_3$ , then q must divide either $2s$ or ${(s+1)/3}$ . By construction, any such q also divides x, which implies $q=1$ . In summary, we have that $a_1$ , $a_2$ and $a_3$ are pairwise coprime.

For sufficiently large k we have

(2-2) $$ \begin{align} k \geq 2s+|y|+|z_0+y|+|z_1+y|+|z_2+y|; \end{align} $$

from now we assume that such a k was chosen. Then a prime factor q of any of the summands in this inequality is also a factor of ${x = k!}$ , and therefore not of $x-1$ or $x+1$ . By Lemma 2.4, no prime factor q of y, ${z_0+y}$ , ${z_1+y}$ , or ${z_2+y}$ divides $2s$ or $(s-2)/3$ either. Altogether we obtain that no such q is a factor of $a_1$ , $a_2$ or $a_3$ , and therefore all three must be coprime with $a_5$ .

Next suppose that there exists a prime q dividing both $a_3$ and $a_4$ . As $a_4$ is odd, this would mean that either q divides s or q divides ${x^2+(s-2)/3}$ . In the first case, q would divide ${x = k!}$ since ${k> s}$ . Therefore, ${a_1 + a_2 + a_3 \equiv z_0 {\;(\textrm {mod}\;q)}}$ and thus $a_4$ would be congruent to ${-(z_0 + y)}$ modulo q. Since q divides $a_4$ by assumption (and as we have already seen that $a_3$ is not divisible by 3), this would contradict the choice of y in Lemma 2.4. So suppose that q divides ${x^2+(s-2)/3}$ . Since ${a_4 \equiv -(z_2+y) \pmod {\,x^2+(s-2)/3}}$ it would follow that q is a prime factor of ${z_2 + y}$ . In view of (2-2) this would imply that q divides ${x = k!}$ . But then q would also divide $(s-2)/3$ , which, together with the fact that q divides ${y + z_2}$ , would again imply ${q \le 3}$ . Since q divides the odd $a_4$ and also $a_3$ , which is not divisible by $3$ , this is impossible.

If a prime q divides one of $a_1$ or $a_2$ then q must also divide ${x^2-1}$ . However,

$$ \begin{align*}a_4 \equiv -(z_1+y)\ \pmod{\,x^2-1};\end{align*} $$

thus if q divided $a_4$ then it would also divide ${z_1+y}$ . For k large enough so that (2-2) holds, it would follow that q divides ${x = k!}$ , yielding a contradiction.

Finally, we prove that $a_4$ and $a_5$ are coprime. First note that by (2-2) every prime factor of $a_5$ is a factor of x and, as ${a_4 \equiv 2s \cdot ((s-2)/3)^{(s-1)/2} {\;(\textrm {mod}\;x)}}$ , any common prime factor of $a_4$ and $a_5$ must be a factor of ${2s \cdot ((s-2)/3)^{(s-1)/2}}$ . But as we argued above, no prime factor of ${y = a_5}$ divides ${2s}$ or ${(s-2)/3}$ . Thus $a_4$ and $a_5$ are coprime. In summary, condition (iii) is satisfied.

To see that condition (ii) is satisfied for all sufficiently large k, consider $a_1$ , $a_2$ , $a_3$ and $a_4$ as polynomials in $x= k!$ . In order for a subset of these numbers or their negations to sum to $0$ all terms depending on x need to be eliminated. To achieve this, if one of $a_1$ or $a_2$ is present in a subsum, that is, if its coefficient is in $\{-1,1\}$ , the other clearly needs to be present using the same coefficient as well. First assume that they are both present; then their sum is of degree ${s-1}$ ; thus $a_3$ would be needed in the subsum as well with a suitable coefficient taken from $\{-1,1\}$ . Regardless of the choice of coefficients, the polynomials $a_1$ , $a_2$ and $a_3$ cannot be combined in such a way as to produce a polynomial that is of degree less than $s-5$ ; which implies that $a_4$ is also needed. Finally, as $a_1+a_2+a_3+a_4=-y$ by definition, we also require $a_5$ in the subsum to make it equal $0$ . A similar argument applies if neither $a_1$ nor $a_2$ is present in a subsum. We conclude that no nontrivial subsum can equal $0$ .

We complete the proof by estimating the quality of $(a_1,\ldots ,a_5)$ . We have that

$$ \begin{align*}\mathrm{rad}(a_1 \cdot \cdots \cdot a_5) \in y \cdot O((x^2-1) \cdot (x^2+(s-2)/3) \cdot x^{s-5});\end{align*} $$

that is, using that y is independent of x, there exists a polynomial in x of degree ${s-1}$ upper-bounding $\mathrm {rad}(a_1 \cdot \cdots \cdot a_5)$ .

Thus there is a constant C such that for large enough k we have

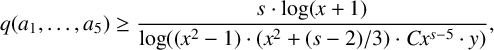$$ \begin{align*} q(a_1,\ldots,a_5) \geq \frac{s \cdot \log(x+1)}{\log((x^2-1) \cdot (x^2+(s-2)/3) \cdot C x^{s-5} \cdot y)}, \end{align*} $$

and therefore, recalling that ${x = k!}$ ,

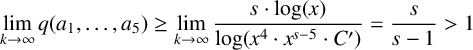$$ \begin{align*} \lim_{k \rightarrow \infty} q(a_1,\ldots,a_5) \geq \lim_{k \rightarrow \infty} \frac{s \cdot \log(x)}{\log(x^4 \cdot x^{s-5} \cdot C')} = \frac{s}{s-1}> 1 \end{align*} $$

for some constant $C'$ . We conclude that ${Q_{U(F,5)}> 1}$ .

Note that the value of s in the proof depends on ${m = \max (F)}$ and therefore we cannot provide a fixed lower bound ${q> 1}$ that works for any set F.

3 The case of arbitrary ${n \ge 6}$

The results obtained in the previous section concerned only odd $n \geq 5$ . Here, we prove our next main result, which holds true for general $n \geq 6$ and, in particular, refutes Ramaekers’ conjecture for these n.

Theorem 1.13 (restated).

Let $n \geq 6$ and let F be an arbitrary finite set. Then

$$ \begin{align*}Q_{U(F,n)} \geq \tfrac54.\end{align*} $$

Proof. As enlarging F only makes the statement harder to prove, we can assume that $F = \{3,4,\ldots ,\ell \}$ for some $\ell \geq 11$ . Let $s = \ell !$ , fix a ${t> 101}$ , and let ${y = s \cdot t}$ .

Lemma 3.1. In the above setting,

$$ \begin{align*}\mathrm{gcd}(y+1, 10y -1) = \mathrm{gcd}(y-1, 10y -1) = \mathrm{gcd}(y+1, 10y + 1) = 1.\\[-35pt]\end{align*} $$

Proof. Suppose that a prime p divides ${y+1}$ . Then ${y \equiv -1\ (\mathrm {mod}{\,p})}$ and therefore ${10y - 1\equiv -11\ (\mathrm {mod}{\,p})}$ . Then for ${p \ne 11}$ we clearly have ${p \nmid \mathrm {gcd}(y+1, 10y -1)}$ . On the other hand, since ${\ell \geq 11}$ , we have that ${y = \ell ! \cdot t \equiv 0\ (\mathrm {mod}{\,11})}$ , and thus $11$ is not a divisor of ${y+1}$ either.

Analogously, if p divides ${y-1}$ then ${y \equiv 1\ (\mathrm {mod}{\,p})}$ and thus ${10y - 1 \equiv 9\ (\mathrm {mod}{\,p})}$ . Since ${p = 3}$ is a divisor of ${s = \ell !}$ , we can conclude that ${\mathrm {gcd}(y-1, 10y - 1) = 1}$ .

Finally, if p divides ${y+1}$ then ${10 y + 1 \equiv -9\ (\mathrm {mod}{\,p})}$ . Again, ${p = 3}$ is excluded by the choices made above, and thus ${\mathrm {gcd}(y+1, 10y + 1) = 1}$ .

Note that there are infinitely many positive integers $h_1$ such that

$$ \begin{align*}{(y+1)^{h_1} \equiv 1 {\;(\textrm{mod}\;10y -1)}}\end{align*} $$

as it suffices to choose $h_1$ as any multiple of the order of the coset of ${y+1}$ in the multiplicative group of the ring of residue classes modulo ${10y - 1}$ . Analogously, there exist infinitely many integers $h_2$ such that

$$ \begin{align*}{(y+1)^{h_2} \equiv 1 {\;(\textrm{mod}\;10y +1)}}.\end{align*} $$

Fixing some such $h_1$ and $h_2$ , and letting h be any integer greater than or equal to $\max (h_1, h_2)$ , we have both

$$ \begin{align*}(y+1)^{h!} \equiv 1 {\;(\textrm{mod}\;10y -1)} \quad \text{and} \quad (y+1)^{h!} \equiv 1 {\;(\textrm{mod}\;10y +1)}.\end{align*} $$

Later we let h go to infinity, but for the moment we give an analysis that holds true independently of the exact value of h as long as it is sufficiently large.

So let $x=(y+1)^{h!}$ . First note that since y is even, x is odd by definition. Secondly, it is clear that ${\mathrm {gcd}(x,y)=1}$ and, in particular, that

(3-1) $$ \begin{align} \text{there is no } m \in {F \cup \{2\}} \text{ that divides } x. \end{align} $$

• • We choose the first four entries of the n-tuple $(a_1,\ldots ,a_n)$ as

  $$ \begin{align*} a_1 &= (x+y)^5,\\ a_2 &= -(x-y)^5,\\ a_3 &= -(10 y - 1) \cdot x^4,\\ a_4 &= -(x^2+10y^3)^2. \end{align*} $$

Of course we have not fixed h yet, so that the exact value of x is undetermined, and the same is consequently true for ${a_1,a_2,a_3, a_4}$ . However, we can already observe that

(3-2) $$ \begin{align} a_1+a_2+a_3+a_4 = 2y^5 - 100 y^6 \end{align} $$

and therefore that $a_1+a_2+a_3+a_4$ is independent of x. We continue with the definition of $a_7,a_8,\ldots ,a_n$ in a way that does not depend on x, either.

• • Let $a_7,a_8,\ldots ,a_n$ be negative odd prime numbers such that ${|a_7|> 200 y^6}$ and such that ${|a_{k+1}|> 2 \cdot |a_{k}|}$ for ${k=7,8,\ldots ,n-1}$ . Then, using (3-2),

  $$ \begin{align*}|a_7|> 2 \cdot |a_1 + a_2 + a_3 + a_4|.\end{align*} $$

Finally, we need to fix the remaining two elements $a_5$ and $a_6$ ; by the preceding choices and arguments the following definition is again independent of x.

• • Let ${u = a_1+a_2+a_3+a_4+(\sum _{k=7}^{n} a_k)}$ and let $m=-4u$ . By the previous choices, it is easy to see that u must be a negative number. So it is possible to apply Lemma 2.2 to u and m and let $a_5$ and $a_6$ be the numbers $-v$ and $-w$ with $u=v+w$ as provided by that lemma.

We will show in a moment that, for every large enough h, the conditions in Definition 1.9 are met by $(a_1,\ldots ,a_n)$ . We claim that this then implies that ${Q(F,n) \geq \frac 54}$ ; to see that, note that $\mathrm {rad}(a_1 \cdot \cdots \cdot a_n)$ will be a divisor of

$$ \begin{align*} (x+y) \cdot (x-y) \cdot (10y-1)\cdot (y+1) \cdot (x^2+10y^3) \cdot a_5 \cdot \cdots \cdot a_n.\end{align*} $$

Letting h go to infinity does not affect $a_5, a_6, \ldots , a_n$ at all. Inside $a_1, a_2, a_3, a_4$ , only x grows with h while all other terms remain constant. Thus, $\mathrm {rad}(a_1 \cdot \cdots \cdot a_n)$ is bounded from above by a polynomial in x of degree at most $4$ , while due to the choice of $a_1$ we have that $\max (|a_1|,\ldots ,|a_n|)$ is bounded from below by a polynomial in x of degree $5$ . Therefore, ${Q_{U(F,n)} \geq \frac 54}$ .

It remains to show that, for all h large enough, the four conditions in Definition 1.9 are met by $(a_1,\ldots ,a_n)$ . That condition (i) holds is immediate by the choice of $a_5$ and $a_6$ .

If p is an arbitrary prime factor of y then, since ${x \equiv 1 {\;(\textrm {mod}\;p)}}$ by definition, it follows that each of $a_1$ , $a_2$ , $a_3$ and $a_4$ is congruent to $\pm 1$ modulo p. It follows that none of $a_1$ , $a_2$ , $a_3$ , $a_4$ is divisible by any element of F; and since the same is true for each of $a_5,a_6,\ldots ,a_n$ by construction, condition (iv) is satisfied.

Next, we establish condition (iii) in several intermediate steps.

• • $a_1$ and $a_2$ are coprime. Note that any common prime divisor of $a_1$ and $a_2$ must also be a factor of $2y$ , as it must divide ${x+y}$ and ${x-y}$ and thus their difference. Note that y is even by construction, so that y has the same prime divisors as $2y$ . Thus, any common prime divisor of $a_1$ and $a_2$ must also divide y and, consequently, x. But we already know that ${\mathrm {gcd}(x,y)=1}$ .

• • $a_3$ is coprime with both $a_1$ and $a_2$ . The factor x of $a_3$ is coprime with $x+y$ and $x-y$ , as x is coprime with y. Furthermore,

  $$ \begin{align*} x=(y+1)^{h!} \equiv 1\ (\mathrm{mod}{\,10 y -1})\end{align*} $$
  by the choice of h, and thus
  $$ \begin{align*}\begin{array}{r@{\;}c@{\;}r@{}c} x+y & \equiv & 1+y &\ \pmod{\,10 y -1}, \\ x-y & \equiv & 1-y &\ \pmod{\,10 y -1}. \end{array} \end{align*} $$
  By Lemma 3.1, ${10 y -1}$ is coprime with both ${1+y}$ and ${1-y}$ . Therefore, $a_3$ is coprime with $a_1$ and $a_2$ .

• • $a_3$ and $a_4$ are coprime. We establish this by showing that $a_4$ is coprime with both factors of $a_3$ . First, to determine $\mathrm {gcd}(10 y -1,a_4)$ , note that $x \equiv 1 {\;(\textrm {mod}\;10 y-1)}$ and that

  (3-3) $$ \begin{align} 100 y^2 - 1 = (10 y -1) \cdot (10 y+1) \equiv 0 {\;(\textrm{mod}\;10 y -1)}.\end{align} $$
  This implies $y^2+1 \equiv 101 y^2 {\;(\textrm {mod}\;10 y-1)}$ and thus
  
  As $101$ is prime and ${10 y-1>101}$ , they have no common factor. Moreover, in view of (3-3), any common factor of $y^2$ with $10 y-1$ would also have to be a factor of $1$ ; as a result, $\mathrm {gcd}(10 y -1,a_4)=1$ . Secondly, we must determine
  $$ \begin{align*} \mathrm{gcd}(x, a_4)=\mathrm{gcd}(x,x^2 + 10 y^3) = \mathrm{gcd}(x, 10y^3).\end{align*} $$
  But by (3-1), no divisor of y nor any element of ${F \cup \{2\}}$ divides x. Therefore, ${\mathrm {gcd}(x, a_4)=1}$ .

• • $a_4$ is coprime with both $a_1$ and $a_2$ . Clearly, $a_1 \cdot a_2$ is a power of

  $$ \begin{align*} (x+y)(x-y)=x^2-y^2 \end{align*} $$
  while $a_4$ is a (negated) power of $x^2+10 y^3$ . Any common prime factor p of $a_4$ with either $a_1$ or $a_2$ would therefore have to be a factor of the difference between these two expressions, that is, of ${10 y^3+y^2 = y^2 \cdot (10y+1)}$ . Such a p divides one of ${x+y}$ or ${x-y}$ ; thus, it cannot be a factor of y, because otherwise it would divide x, contradicting the coprimeness of x and y. Thus, such a p would have to be a prime factor of ${10y+1}$ .

  Recall that x was chosen such that ${x \equiv 1 {\;(\textrm {mod}\;10y+1)}}$ ; thus we would have ${x \equiv 1 {\;(\textrm {mod}\;p)}}$ . Since p divides one of ${x+y}$ or ${x-y}$ , it would also be a prime factor of either

  $$ \begin{align*} (10y+1) - 10\cdot (x+y) = -10x + 1 \equiv -9 {\;(\textrm{mod}\;p)}\end{align*} $$
  or
  $$ \begin{align*} (10y+1) + 10\cdot (x-y)= 10x + 1 \equiv 11 {\;(\textrm{mod}\;p)}.\end{align*} $$
  This could only be true if $p\in \{3,11\}$ , which is impossible since both $3$ and $11$ divide y and thus cannot divide $10y+1$ . In conclusion, $a_4$ is coprime with both $a_1$ and $a_2$ .

• • Each of $a_1,a_2,a_3$ is coprime with each of $a_5,a_6,\ldots ,a_n$ . Note that $a_5$ and $a_6$ do not depend on x by construction. For sufficiently large h any prime factor of $a_5$ and $a_6$ is at most h. Observe that for any prime p with ${p \leq h}$ we have that $p-1$ divides $h!$ , and thus, by Fermat’s little theorem,

  $$ \begin{align*}{x=(y+1)^{h!} \equiv 1 {\;(\textrm{mod}\;p)}}.\end{align*} $$
  This holds, in particular, for any prime p dividing $a_5$ or $a_6$ and, if h is large enough, for all primes ${p\in \{a_7,a_8,\ldots ,a_n\}}$ ; thus any such p is coprime with x. Moreover, we have
  $$ \begin{align*} x + y & \equiv 1 + y {\;(\textrm{mod}\;p)}, \\ x -y & \equiv 1 - y {\;(\textrm{mod}\;p)} \end{align*} $$
  for these primes p. Since for such a p we also have ${p> 200y^6 > y \pm 1}$ by construction, it follows that p is coprime with $x+y$ and $x-y$ as well. As we trivially have $p \nmid (10 y-1)$ , we can conclude that p does not divide any of ${a_1,a_2,a_3}$ .

• • $a_4$ is coprime with each of $a_5, a_6,\ldots , a_n$ . For the same reasons as in the previous item, we only need to consider potential prime factors p between ${200 y^6}$ and h. For such p, we again have that $x \equiv 1 {\;(\textrm {mod}\;p)}$ . Then

  $$ \begin{align*}x^2+10y^3 \equiv 1+10y^3 \not\equiv 0 {\;(\textrm{mod}\;p)},\end{align*} $$
  which implies that p does not divide $a_4$ .

• • $a_5,a_6,\ldots ,a_n$ are pairwise coprime. Firstly, since they are pairwise distinct primes, $a_7,a_8,\ldots ,a_n$ are trivially pairwise coprime. Secondly, recall how $a_5$ and $a_6$ were defined using Lemma 2.2 in such a way as to ensure that $a_5$ and $a_6$ are coprime with each other. Finally, Lemma 2.2 also guarantees that no primes less than m divide $a_5$ or $a_6$ ; and as ${m = -4u}$ is larger than any of $|a_i|$ for ${7 \leq i \leq n}$ by the choice of u, we have, in particular, that both of $a_5$ and $a_6$ are coprime with each of ${a_7,a_8,\ldots ,a_n}$ .

It remains to establish subsum condition (ii) for $(a_1,\ldots ,a_n)$ . Assume that we have fixed $b_1,\ldots ,b_n \in \{-1,0,+1\}$ such that $\sum _{k=1}^n b_k \cdot a_k = 0$ . We proceed via a series of claims.

• • It must be true that $b_1=b_2=b_3=b_4$ . Recall that $a_5,a_6,\ldots ,a_n$ do not depend on x. Since $x = (y+1)^{h!}$ , this implies for h large enough that ${x> |a_5|+|a_6|+\cdots +|a_n|}$ . Thus, if for some choice of $(b_1,b_2,b_3,b_4)$ we have that $|\!\sum_{k=1}^4 b_k \cdot a_k|> x$ , then no choice of $(b_5,b_6,\ldots ,b_n)$ can lead to ${\sum _{k=1}^n b_k \cdot a_k = 0}$ . We will argue that this must be the case unless we have $b_1=b_2=b_3=b_4$ .

  So let us inspect all possible choices of $(b_1,b_2,b_3,b_4)$ . We first exclude some trivial cases. Firstly, if only one of $b_1,b_2,b_3,b_4$ is nonzero, then $|\!\sum_{k=1}^4 b_k \cdot a_k|> x$ . Secondly, we can omit choices of $(b_1,b_2,b_3,b_4)$ where the summands ${b_k \cdot a_k}$ are all positive or all negative. Finally, to further reduce the numbers of cases to consider, we assume without loss of generality that $b_i=1$ when $\{1 \leq i \leq 4\}$ is the smallest index such that $\{b_i \neq 0\}$ ; the case $b_i=-1$ is symmetric. Then the following cases not satisfying $b_1=b_2=b_3=b_4$ remain:

  1. – $a_1+a_2+ b_3 \cdot a_3 +b_4 \cdot a_4$ where $(b_3,b_4)\neq (1,1)$ ,

  2. – $a_1-a_2+ b_3 \cdot a_3 +b_4 \cdot a_4$ where ${b_3, b_4 \in \{-1,0,+1\}}$ ,

  3. – $a_1+b_3 \cdot a_3 + b_4 \cdot a_4$ where ${b_3, b_4 \in \{-1,0,+1\}}$ ,

  4. – $a_2+b_3 \cdot a_3+b_4 \cdot a_4$ where ${b_3, b_4 \in \{-1,0,+1\}}$ ,

  5. – $a_3+b_4 \cdot a_4$ where ${b_4 \in \{-1,0,+1\}}$ ,

  and the absolute values of all of these expressions are easily seen to be lower-bounded by x.

With the preceding claim established, we can from now on treat $a_1+a_2+a_3+a_4$ as a single number that can either be included in a subsum with positive or negative sign, or not.

• • It must be true that $b_5=b_6$ . Note that by the choice of $a_5$ and $a_6$ and by the properties ensured by Lemma 2.2 we have that $a_5>0$ and $a_6<0$ and that

  $$ \begin{align*} \begin{array}{r@{\;}c@{\;}l} |a_5|, a_6 &>&\left|a_1+a_2+a_3+a_4\phantom{|} + \displaystyle\sum_{k=7}^{n} \phantom{|}a_k\right|\\[0.8em] &=& \phantom{|} |a_1+a_2+a_3+a_4|+\displaystyle\sum_{k=7}^{n} |a_k|; \end{array} \end{align*} $$
  here the equality uses the fact that $a_1+a_2+a_3+a_4$ is negative by (3-2) while $a_7,a_8\ldots ,a_n$ are negative by choice. As a consequence, in any subsum equalling zero, $a_5$ and $a_6$ must either not occur at all or occur in such a way that they partly cancel each other out additively. This is only possible when ${b_5=b_6}$ .

Again, from now on we treat $a_5+a_6$ as a single number that may be part of a subsum or not. To complete the proof we distinguish all three possible cases concerning the value of ${b_5=b_6}$ .

• • If $b_5=b_6=0$ , then the subsum is empty. This is because in the sequence

  $$ \begin{align*}|a_1+a_2+a_3+a_4|,|a_7|,|a_8|,\ldots,|a_n|\end{align*} $$
  each entry is more than twice larger than the previous one; thus the only way of obtaining a zero subsum in this case is when ${b_k=0}$ for all ${1\leq k \leq n}$ .

• • If $b_5=b_6=1$ , then $b_k=1$ for all ${1\leq k \leq n}$ . Assume that for some choice of $(b_k)_{1\leq k \leq n}$ with ${b_5=b_6=1}$ we have ${\sum _{k=1}^n b_k \cdot a_k = 0}$ . Since we also have ${\sum _{k=1}^n a_k = 0}$ it follows that

  $$ \begin{align*}\begin{array}{c@{\;}l} &\displaystyle\sum_{k=1}^n a_k - \displaystyle\sum_{k=1}^n b_k \cdot a_k \\[0.5em] &\quad= (1-b_1) \cdot (a_1+a_2+a_3+a_4)+\displaystyle\sum_{k=7}^n (1-b_k) \cdot a_k\\[0.5em] &\quad= 0, \end{array} \end{align*} $$
  where $1-b_k \in \{0,1,2\}$ for $k \in \{1,7,8,\ldots , n\}$ . For the same reason as in the previous item, the only choice of $(1-b_k)_{k \in \{1,7,8,\ldots , n\}}$ that makes this equality true is $1-b_k =0 $ (thus $b_k =1 $ ) for all $k \in \{1,7,8,\ldots , n\}$ .

• • If $b_5=b_6=-1$ , then $b_k=-1$ for all $1\leq k \leq n$ , by a symmetric argument.

Thus condition (ii) holds, completing the proof.

4 Closing remarks

In the preceding sections we established new lower bounds for strong variants of the n-conjecture. In that context, we always exclusively considered n-tuples of pairwise coprime integers. To conclude the paper, we make some closing remarks about instances that are not necessarily pairwise coprime.

Remark 4.1. If we allow common factors in n-tuples, we could, for example, consider the set of quadruples of the form

$$ \begin{align*}{((2^h+1)^3,-2^{3h},-3 \cdot 2^h \cdot(2^h+1),-1)}\end{align*} $$

for ${h \in \mathbb N}$ . Note that we still have ${\mathrm {gcd}(a_1, a_2, a_3, a_4) = 1}$ , but that arbitrarily large common divisors occur between pairs of these numbers; for instance, $2^h$ divides both $a_2$ and $a_3$ . It is not too difficult to see that these quadruples belong to the set $A(4)$ from Conjecture 1.2. The limit superior of the qualities of these quadruples is $3$ ; that is, under these relaxed conditions, it is possible to achieve considerably larger qualities than in the preceding sections.

This is in accordance with Conjecture 1.2 and the previously known result of Browkin and Brzeziński [2, Theorem 1] that ${Q_{A(n)} \ge 2n -5}$ for every ${n \ge 3}$ . The proof of this fact starts from the geometric sum equation

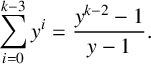$$ \begin{align*} \sum_{i=0}^{k-3} y^i = \frac{y^{k-2} - 1}{y-1}.\end{align*} $$

Multiplying both sides of the equation by ${x := y-1}$ we obtain

$$ \begin{align*} y^{k-2} - xy^{k-3} - xy^{k-4} - \cdots - x - 1 = 0. \end{align*} $$

It is easy to see that conditions (i) and (iii) from Conjecture 1.2 are satisfied. Using a clever choice of k and ${x = y-1}$ , Browkin and Brzeziński were able to obtain a sequence of n-tuples summing to $0$ such that each single n-tuple satisfies the subsum condition and such that the sequence of corresponding qualities has an accumulation point greater than or equal to ${2n-5}$ .

The previous comments concern the case where we allow unbounded common divisors between the elements of the solution n-tuples. This can be thought of as the opposite extreme of the situation studied in the main parts of this paper where we only considered n-tuples whose entries were required to be pairwise coprime. In between these two extremes, we could also study a case where finitely many (that is, bounded) common divisors are permitted. We conclude the paper by giving an example of an intermediate result that can be obtained for this setting.

Lemma 4.2. There is a finite set E such that there exists a sequence $(a^{(h)})$ of quintuples $(a_1, a_2,a_3,a_4,a_5)$ of integers such that:

1. (i) $a_1+\cdots +a_5=0$ ;

2. (ii) there are no $b_1,\ldots ,b_5 \in \{-1,0,1\}$ and $i,j$ with $1\leq i,j\leq 5$ such that $b_i=0$ and $b_j=1$ and $\sum _{k=1}^5 b_k \cdot a_k = 0$ ;

3. (iii) ${\mathrm {gcd}(a_i,a_j) \in E}$ for any ${1 \le i < j \le 5}$ ;

4. (iv) ${\mathrm {gcd}(a_1, \ldots , a_5) = 1}$ ; and

5. (v) ${\limsup _{h \rightarrow \infty } q(a^{(h)}) \geq \frac 95}$ .

Proof. Let x be ${\ell ^h-1}$ for some $h\in \mathbb {N}$ and some fixed odd prime number $\ell $ . Fix

$$ \begin{align*} a_1 &= 189(x+1)^9, \\ a_2 &= -189(x-1)^9,\\ a_3 &= -42(3x^2+7)^4,\\ a_4 &= 16(63x^2+79)^2,\\ a_5 &= 608. \end{align*} $$

The greatest common divisor of $a_1$ and $a_2$ is $189$ .

We claim that $\mathrm {gcd}({a_1 \cdot a_2},a_3)$ divides $1890$ . To see this, first note that, on the one hand, the least common multiple of $189$ and $42$ is $378$ . On the other hand, if a prime p divides both ${x^2-1}$ and ${3x^2 + 7}$ , then ${x^2 \equiv 1\ (\mathrm {mod}{\,p})}$ and therefore ${3x^2 + 7 \equiv 10\ (\mathrm {mod}{\,p})}$ ; thus, since p divides ${3x^2 + 7}$ by assumption, we may conclude that p is a factor of $10$ . Note that 1890 is the least common multiple of $378$ and $10$ .

In an analogous way, we can argue that $\mathrm {gcd}({a_1 \cdot a_2},a_4)$ is a factor of $214\,704$ and that $\mathrm {gcd}(a_3, a_4)$ is a factor of $5712$ . Note that $\mathrm{gcd}(a_5,a_i)$ for any $i \neq 5$ is a factor of $608$ . Then, letting

$$ \begin{align*}E = \{r\colon r \text{ divides one of } 608, 1890, 5712, 214704\},\end{align*} $$

we have that all common divisors of the entries of $(a_1,\ldots ,a_5)$ are contained in E. We also note that ${\mathrm {gcd}(a_1, \ldots , a_5)}$ divides ${\mathrm {gcd}(\mathrm {gcd}(a_1, a_2), a_5) = 1}$ .

An easy calculation shows that (i) is satisfied. To see that condition (ii) holds, argue as in the proof of Theorem 2.3.

By definition, $x+1$ is a power of $\ell $ . Thus, ${\mathrm {rad}(a_1 \cdot a_2 \cdot a_3 \cdot a_4 \cdot a_5)}$ is a factor of

$$ \begin{align*}189 \cdot 42 \cdot 16 \cdot 608 \cdot \ell \cdot (x-1) \cdot (3x^2+7) \cdot (63x^2+79).\end{align*} $$

As this is a polynomial of degree $5$ , whereas $a_1$ is a polynomial of degree $9$ , we conclude that ${\limsup _{h \rightarrow \infty } q(a^{(h)}) \geq \frac 95}$ .

Similarly, Pomerance [7, p. 362] describes a family of 4-tuples ${a^{(h)} = (a_1, a_2, a_3, a_4)}$ such that ${\mathrm{gcd}(a_i, a_j) \in \{1,2\}}$ for all $i$ and $j$ ; for this family, the limit superior of the qualities $q(a^{(h)})$ is greater than or equal to $\frac{5}{3}$ .