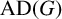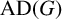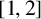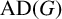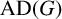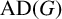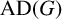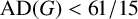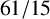1 Introduction
1.1 Background context
Given a finite group G, the algebra of complex-valued functions on G (equipped with the pointwise product) only depends on the cardinality of G and does not detect the group structure. However, there is a canonical submultiplicative norm on this algebra, the Fourier norm, such that the resulting normed algebra
![]() $\operatorname {A}(G)$
characterizes the starting group G up to isomorphism. (More precisely: given finite groups G and H, there is an isometric algebra isomorphism between
$\operatorname {A}(G)$
characterizes the starting group G up to isomorphism. (More precisely: given finite groups G and H, there is an isometric algebra isomorphism between
![]() $\operatorname {A}(G)$
and
$\operatorname {A}(G)$
and
![]() $\operatorname {A}(H)$
if and only if G and H are isomorphic groups; this is a special case of a result of Walter [Reference Walter14].)
$\operatorname {A}(H)$
if and only if G and H are isomorphic groups; this is a special case of a result of Walter [Reference Walter14].)
By identifying a subset of G with its indicator function, one can speak of the Fourier norm of a subset of G. Calculating Fourier norms of arbitrary subsets is hard (see [Reference Sanders12] for a systematic approach), but there is one case where an exact calculation is possible and gives interesting answers. Consider the set
![]() $\{ (g,g^{-1})\colon g\in G\}$
. The Fourier norm of this subset of
$\{ (g,g^{-1})\colon g\in G\}$
. The Fourier norm of this subset of
![]() $G\times G$
, denoted by
$G\times G$
, denoted by
![]() $\operatorname { {AD}}(G)$
in this paper, is the Fourier anti-diagonal constant mentioned in the title. It was recently shown by the author [Reference Choi3, Theorem 1.4] that we have the following explicit formula for
$\operatorname { {AD}}(G)$
in this paper, is the Fourier anti-diagonal constant mentioned in the title. It was recently shown by the author [Reference Choi3, Theorem 1.4] that we have the following explicit formula for
![]() $\operatorname { {AD}}(G)$
:
$\operatorname { {AD}}(G)$
:
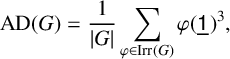 $$ \begin{align} \operatorname{{AD}}(G) = \frac{1}{{\lvert G \rvert}}\sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^3, \end{align} $$
$$ \begin{align} \operatorname{{AD}}(G) = \frac{1}{{\lvert G \rvert}}\sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^3, \end{align} $$
where
![]() $\operatorname { {Irr}}(G)$
is the set of irreducible complex characters of G and
$\operatorname { {Irr}}(G)$
is the set of irreducible complex characters of G and
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
is the degree of
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
is the degree of
![]() $\varphi $
.
$\varphi $
.
Equation (1-1) implies that
![]() $\operatorname { {AD}}(G\times H)=\operatorname { {AD}}(G)\operatorname { {AD}}(H)$
and that
$\operatorname { {AD}}(G\times H)=\operatorname { {AD}}(G)\operatorname { {AD}}(H)$
and that
![]() $\operatorname { {AD}}$
is invariant under isoclinism. Additionally,
$\operatorname { {AD}}$
is invariant under isoclinism. Additionally,
![]() $\operatorname { {AD}}(H)\leq \operatorname { {AD}}(G)$
whenever
$\operatorname { {AD}}(H)\leq \operatorname { {AD}}(G)$
whenever
![]() $H\leq G$
(see Proposition 3.5 below). These hereditary properties suggest that
$H\leq G$
(see Proposition 3.5 below). These hereditary properties suggest that
![]() $\operatorname { {AD}}(G)$
, viewed as a numerical invariant of G, deserves further study. Furthermore, the sum on the right-hand side of (1-1) already arose in earlier work of Johnson [Reference Johnson8] on Fourier algebras of compact groups. The results in [Reference Johnson8, Section 4] provide an attractive application of the character theory of finite groups to obtain new (counter-)examples in functional analysis. (For a fuller discussion, see [Reference Choi3, Section 1].)
$\operatorname { {AD}}(G)$
, viewed as a numerical invariant of G, deserves further study. Furthermore, the sum on the right-hand side of (1-1) already arose in earlier work of Johnson [Reference Johnson8] on Fourier algebras of compact groups. The results in [Reference Johnson8, Section 4] provide an attractive application of the character theory of finite groups to obtain new (counter-)examples in functional analysis. (For a fuller discussion, see [Reference Choi3, Section 1].)
The following observations, taken from [Reference Johnson8, Proposition 4.3], are easy consequences of (1-1):
-
• if G is abelian, then
 $\operatorname { {AD}}(G)=1$
;
$\operatorname { {AD}}(G)=1$
; -
• if G is nonabelian, then
 $\operatorname { {AD}}(G)\geq \tfrac 32$
.
$\operatorname { {AD}}(G)\geq \tfrac 32$
.
Since
![]() $\operatorname { {AD}}(G^n) = \operatorname { {AD}}(G)^n$
, this shows that
$\operatorname { {AD}}(G^n) = \operatorname { {AD}}(G)^n$
, this shows that
![]() $\operatorname { {AD}}(G)$
can take arbitrarily large values. However, to the author’s knowledge, nothing further has been done to study the possible values of
$\operatorname { {AD}}(G)$
can take arbitrarily large values. However, to the author’s knowledge, nothing further has been done to study the possible values of
![]() $\operatorname { {AD}}(G)$
as G ranges over all nonabelian finite groups. The purpose of the present paper is to make a start on filling this gap.
$\operatorname { {AD}}(G)$
as G ranges over all nonabelian finite groups. The purpose of the present paper is to make a start on filling this gap.
1.2 Our main new results
The following result has probably been noticed independently by many readers of Johnson’s paper, although it is not stated explicitly there. (A proof is given in Section 2 for the sake of completeness.)
Proposition 1.1 (Implicitly folklore).
Let G be a finite group and suppose that
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})\leq 2$
for all
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})\leq 2$
for all
![]() $\varphi \in \operatorname { {Irr}}(G)$
. Then,
$\varphi \in \operatorname { {Irr}}(G)$
. Then,
![]() $\operatorname { {AD}}(G) \in \{ 2- n^{-1} \colon n\in \mathbb N\}$
.
$\operatorname { {AD}}(G) \in \{ 2- n^{-1} \colon n\in \mathbb N\}$
.
Moreover, every number in
![]() $\{2-n^{-1} \colon n\in \mathbb N\}$
is realized as the
$\{2-n^{-1} \colon n\in \mathbb N\}$
is realized as the
![]() $\operatorname { {AD}}$
-constant of some (nonunique) finite group: this can be seen by considering cyclic groups and dihedral groups. Our first main result is that these are the only values of
$\operatorname { {AD}}$
-constant of some (nonunique) finite group: this can be seen by considering cyclic groups and dihedral groups. Our first main result is that these are the only values of
![]() $\operatorname { {AD}}$
attained by finite groups in the interval
$\operatorname { {AD}}$
attained by finite groups in the interval
![]() $[1,2]$
. To be precise, we state the following theorem.
$[1,2]$
. To be precise, we state the following theorem.
Theorem 1.2 (Possible values of
 $\operatorname { {AD}}(G)$
in
$\operatorname { {AD}}(G)$
in
 $[1,2]$
).
$[1,2]$
).
Let G be a finite group and suppose that
![]() $\operatorname { {AD}}(G)\leq 2$
. Then,
$\operatorname { {AD}}(G)\leq 2$
. Then,
![]() $\operatorname { {AD}}(G) \in \{2 -n^{-1} \colon n\in \mathbb N\}$
.
$\operatorname { {AD}}(G) \in \{2 -n^{-1} \colon n\in \mathbb N\}$
.
Corollary 1.3. The set
![]() $\{\operatorname { {AD}}(G) \colon G\ \mathrm{a}\ \mathrm{finite}\ \mathrm{group}\}$
is not a closed subset of
$\{\operatorname { {AD}}(G) \colon G\ \mathrm{a}\ \mathrm{finite}\ \mathrm{group}\}$
is not a closed subset of
![]() $[1,\infty )$
.
$[1,\infty )$
.
Theorem 1.2 is an immediate consequence of combining Proposition 1.1 with the following lower bound for
![]() $\operatorname { {AD}}(G)$
, which appears to be new.
$\operatorname { {AD}}(G)$
, which appears to be new.
Proposition 1.4. Let G be a finite group. If there exists
![]() $\varphi \in \operatorname { {Irr}}(G)$
with
$\varphi \in \operatorname { {Irr}}(G)$
with
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})\geq 3$
, then
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})\geq 3$
, then
![]() $\operatorname { {AD}}(G)\geq 2+ {\lvert G' \rvert }^{-1}$
.
$\operatorname { {AD}}(G)\geq 2+ {\lvert G' \rvert }^{-1}$
.
The proof of Proposition 1.4 requires some basic character theory, but nothing harder than Frobenius reciprocity. Perhaps surprisingly, while we do need character theory for finite groups, we do not rely on any structure theory (we do not even need the Sylow theorems). In contrast, our other main result requires the classification of finite simple groups with characters of small degree.
Theorem 1.5 (A threshold ensuring solvability).
Let G be a finite group. If
![]() $\operatorname { {AD}}(G) < {61}/{15}$
, then G is solvable.
$\operatorname { {AD}}(G) < {61}/{15}$
, then G is solvable.
A direct calculation shows that
![]() $\operatorname { {AD}}(A_5)= {61}/{15}$
and so, in this sense, Theorem 1.5 is sharp. Particular properties of
$\operatorname { {AD}}(A_5)= {61}/{15}$
and so, in this sense, Theorem 1.5 is sharp. Particular properties of
![]() $A_5$
, such as its subgroup structure and its Schur multiplier, play an important role in the proof of Theorem 1.5, since we need to analyse perfect groups that quotient onto
$A_5$
, such as its subgroup structure and its Schur multiplier, play an important role in the proof of Theorem 1.5, since we need to analyse perfect groups that quotient onto
![]() $A_5$
.
$A_5$
.
One difficulty in proving Theorem 1.5 is that
![]() $\operatorname { {AD}}$
is not monotone (in either direction) with respect to taking quotients, and so knowing that a group H quotients onto
$\operatorname { {AD}}$
is not monotone (in either direction) with respect to taking quotients, and so knowing that a group H quotients onto
![]() $A_5$
does not immediately imply that
$A_5$
does not immediately imply that
![]() $\operatorname { {AD}}(H)\geq \operatorname { {AD}}(A_5)$
. Instead, we require a detour through the commuting probability
$\operatorname { {AD}}(H)\geq \operatorname { {AD}}(A_5)$
. Instead, we require a detour through the commuting probability
![]() $\operatorname { {cp}}(G)$
(see the start of Section 5 for its definition). Our strategy is inspired by an argument of Tong-Viet in [Reference Tong-Viet13] and, indeed, the main work needed to prove Theorem 1.5 lies in establishing the following stronger version of [Reference Tong-Viet13, Lemma 2.4].
$\operatorname { {cp}}(G)$
(see the start of Section 5 for its definition). Our strategy is inspired by an argument of Tong-Viet in [Reference Tong-Viet13] and, indeed, the main work needed to prove Theorem 1.5 lies in establishing the following stronger version of [Reference Tong-Viet13, Lemma 2.4].
Proposition 1.6. Let H be a finite nontrivial perfect group satisfying
![]() $\operatorname { {cp}}(H)> {1}/{20}$
. Then,
$\operatorname { {cp}}(H)> {1}/{20}$
. Then,
![]() $H\cong A_5$
or
$H\cong A_5$
or
![]() $H\cong \mathrm {SL}(2,5)$
.
$H\cong \mathrm {SL}(2,5)$
.
1.3 Outline of this paper
After some preliminary results in Section 2, the proof of Proposition 1.4 is given in Section 3. Since the paper is intended for a general audience, we spell things out in more detail than specialists in group theory would require. In Section 4.1, we calculate the values of
![]() $\operatorname { {AD}}(G)$
for some particular families of groups, some of which are related to calculations in earlier sections; and in Section 4.2, we present some partial results on the general theme that ‘small values’ of
$\operatorname { {AD}}(G)$
for some particular families of groups, some of which are related to calculations in earlier sections; and in Section 4.2, we present some partial results on the general theme that ‘small values’ of
![]() $\operatorname { {AD}}(G)$
imply that G is close to abelian in some sense. Section 5 is dedicated to the proof of Proposition 1.6 and Theorem 1.5; this is the only part of the paper that makes use of the theory of the
$\operatorname { {AD}}(G)$
imply that G is close to abelian in some sense. Section 5 is dedicated to the proof of Proposition 1.6 and Theorem 1.5; this is the only part of the paper that makes use of the theory of the
![]() $\operatorname { {cp}}$
invariant. In the appendix, we collect some proofs of results that are used in the main body of the paper; these results are special cases or weaker versions of known results, but we take the opportunity to provide some extra details and give more elementary arguments.
$\operatorname { {cp}}$
invariant. In the appendix, we collect some proofs of results that are used in the main body of the paper; these results are special cases or weaker versions of known results, but we take the opportunity to provide some extra details and give more elementary arguments.
We finish this introduction by establishing some conventions and fixing notation. To reduce unnecessary repetition, we adopt the following convention: henceforth, all groups are assumed to be finite unless explicitly stated otherwise. The identity element of a group G is denoted by
![]() $\mathord {\underline {\mathsf {1}}_{}}$
, or
$\mathord {\underline {\mathsf {1}}_{}}$
, or
![]() $\mathord {\underline {\mathsf {1}}_{G}}$
if we wish to avoid ambiguity, and the derived subgroup of G (also known as its commutator subgroup) is denoted by
$\mathord {\underline {\mathsf {1}}_{G}}$
if we wish to avoid ambiguity, and the derived subgroup of G (also known as its commutator subgroup) is denoted by
![]() $G'$
.
$G'$
.
Throughout this article, all representations and characters are taken over the complex field. The basic representation theory and character theory that we need can be found in several introductory texts, such as [Reference James and Liebeck7]. We denote the degree of a character
![]() $\varphi $
by
$\varphi $
by
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
; note that this is equal to the dimension of any representation whose trace is
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
; note that this is equal to the dimension of any representation whose trace is
![]() $\varphi $
.
$\varphi $
.
The set of irreducible characters of G is denoted by
![]() $\operatorname { {Irr}}(G)$
and we write
$\operatorname { {Irr}}(G)$
and we write
![]() $\operatorname { {cd}}(G)$
for the set
$\operatorname { {cd}}(G)$
for the set
![]() $\{ {\varphi }(\mathord {\underline {\mathsf {1}}_{}}) \colon \varphi \in \operatorname { {Irr}}(G)\}$
(note that here, we are not counting the multiplicities of the irreducible character degrees). We write
$\{ {\varphi }(\mathord {\underline {\mathsf {1}}_{}}) \colon \varphi \in \operatorname { {Irr}}(G)\}$
(note that here, we are not counting the multiplicities of the irreducible character degrees). We write
![]() $\operatorname { {Irr}}_n(G)$
for the set of all
$\operatorname { {Irr}}_n(G)$
for the set of all
![]() $\varphi \in \operatorname { {Irr}}(G)$
that have degree n. If G is nonabelian, we define
$\varphi \in \operatorname { {Irr}}(G)$
that have degree n. If G is nonabelian, we define
For any G (possibly abelian), we define
Finally, given a group G, we equip
![]() $\mathbb C^G$
with the following inner product:
$\mathbb C^G$
with the following inner product:
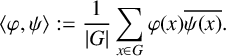 $$ \begin{align*} {\langle {\varphi}, {\psi}\rangle} := \frac{1}{{\lvert G \rvert}} \sum_{x\in G} \varphi(x)\overline{\psi(x)} . \end{align*} $$
$$ \begin{align*} {\langle {\varphi}, {\psi}\rangle} := \frac{1}{{\lvert G \rvert}} \sum_{x\in G} \varphi(x)\overline{\psi(x)} . \end{align*} $$
If
![]() $\psi $
is a character of G, then it is irreducible if and only if
$\psi $
is a character of G, then it is irreducible if and only if
![]() ${\langle {\psi }, {\psi }\rangle }=1$
[Reference James and Liebeck7, Theorem 14.20].
${\langle {\psi }, {\psi }\rangle }=1$
[Reference James and Liebeck7, Theorem 14.20].
2 Some easy lower bounds on
 $\textbf {AD}$
$\textbf {AD}$
We start by giving a proof of Proposition 1.1, since it also serves as a prototype for later arguments. No novelty is claimed.
Proof of Proposition 1.1.
Since
![]() $\operatorname { {cd}}(G)\subseteq \{1,2\}$
,
$\operatorname { {cd}}(G)\subseteq \{1,2\}$
,
On the other hand, basic character theory tells us that
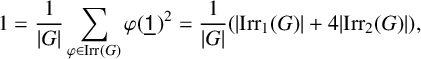 $$ \begin{align*} 1 = \frac{1}{{\lvert G \rvert}} \sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 = \frac{1}{{\lvert G \rvert}} ( {\lvert \operatorname{{Irr}}_1(G) \rvert} + 4 {\lvert \operatorname{{Irr}}_2(G) \rvert} ), \end{align*} $$
$$ \begin{align*} 1 = \frac{1}{{\lvert G \rvert}} \sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 = \frac{1}{{\lvert G \rvert}} ( {\lvert \operatorname{{Irr}}_1(G) \rvert} + 4 {\lvert \operatorname{{Irr}}_2(G) \rvert} ), \end{align*} $$
and therefore
![]() $\operatorname { {AD}}(G)-2 = - {\lvert \operatorname { {Irr}}_1(G) \rvert }\, {\lvert G \rvert }^{-1} $
.
$\operatorname { {AD}}(G)-2 = - {\lvert \operatorname { {Irr}}_1(G) \rvert }\, {\lvert G \rvert }^{-1} $
.
It is also standard (see for example [Reference James and Liebeck7, Theorem 17.11]) that, since
![]() $\operatorname { {Irr}}_1(G)$
can be identified with the (Pontrjagin) dual of the abelian group
$\operatorname { {Irr}}_1(G)$
can be identified with the (Pontrjagin) dual of the abelian group
![]() $G/G'$
, we have
$G/G'$
, we have
![]() ${\lvert \operatorname { {Irr}}_1(G) \rvert } ={\lvert G:G' \rvert }$
. Hence,
${\lvert \operatorname { {Irr}}_1(G) \rvert } ={\lvert G:G' \rvert }$
. Hence,
![]() $\operatorname { {AD}}(G) = 2 - {\lvert G' \rvert }^{-1}$
and since
$\operatorname { {AD}}(G) = 2 - {\lvert G' \rvert }^{-1}$
and since
![]() ${\lvert G' \rvert }\in \mathbb N$
, the result follows.
${\lvert G' \rvert }\in \mathbb N$
, the result follows.
Example 2.1 (Dihedral groups).
Let G be a dihedral group of order
![]() $2k$
, so that
$2k$
, so that
![]() $\operatorname { {cd}}(G)=\{1,2\}$
. If k is odd, then
$\operatorname { {cd}}(G)=\{1,2\}$
. If k is odd, then
![]() ${\lvert G' \rvert }=k$
, and if k is even, then
${\lvert G' \rvert }=k$
, and if k is even, then
![]() ${\lvert G' \rvert }={k}/{2}$
. By repeating the calculation in the proof of Proposition 1.1, we see that
${\lvert G' \rvert }={k}/{2}$
. By repeating the calculation in the proof of Proposition 1.1, we see that
![]() $\operatorname { {AD}}(G)=2-({1}/{k})$
when k is odd and
$\operatorname { {AD}}(G)=2-({1}/{k})$
when k is odd and
![]() $\operatorname { {AD}}(G)=2-({2}/{k})$
when k is even.
$\operatorname { {AD}}(G)=2-({2}/{k})$
when k is even.
For general nonabelian G, the proof of Proposition 1.1 still suggests a way to proceed. Informally, since
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})^3 \geq \operatorname { {mindeg}}(G){\varphi }(\mathord {\underline {\mathsf {1}}_{}})^2$
for all
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})^3 \geq \operatorname { {mindeg}}(G){\varphi }(\mathord {\underline {\mathsf {1}}_{}})^2$
for all
![]() $\varphi \in \operatorname { {Irr}}(G)\setminus \operatorname { {Irr}}_1(G)$
, we can add a correction factor to
$\varphi \in \operatorname { {Irr}}(G)\setminus \operatorname { {Irr}}_1(G)$
, we can add a correction factor to
![]() $\operatorname { {AD}}(G)$
to obtain something bounded below by
$\operatorname { {AD}}(G)$
to obtain something bounded below by
![]() $\operatorname { {mindeg}}(G)$
, and the size of the correction factor is controlled by the size of
$\operatorname { {mindeg}}(G)$
, and the size of the correction factor is controlled by the size of
![]() ${\lvert G' \rvert }$
. Making this precise leads us to the following lemma, which provides a convenient tool for dealing with ‘generic’ cases.
${\lvert G' \rvert }$
. Making this precise leads us to the following lemma, which provides a convenient tool for dealing with ‘generic’ cases.
Lemma 2.2 (An all-purpose lower bound).
Let G be nonabelian, and let
![]() $m,n\in \mathbb N$
satisfy
$m,n\in \mathbb N$
satisfy
![]() $\operatorname { {mindeg}}(G)\geq m$
and
$\operatorname { {mindeg}}(G)\geq m$
and
![]() ${\lvert G' \rvert }\geq n$
. Then,
${\lvert G' \rvert }\geq n$
. Then,
Proof. Since
![]() $\operatorname { {Irr}}_j(G)$
is empty whenever
$\operatorname { {Irr}}_j(G)$
is empty whenever
![]() $2\leq j\leq m-1$
,
$2\leq j\leq m-1$
,
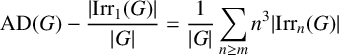 $$ \begin{align*} \operatorname{{AD}}(G) - \frac{{\lvert \operatorname{{Irr}}_1(G) \rvert}}{{\lvert G \rvert}} = \frac{1}{{\lvert G \rvert}}\sum_{n\geq m} n^3 {\lvert \operatorname{{Irr}}_n(G) \rvert} \end{align*} $$
$$ \begin{align*} \operatorname{{AD}}(G) - \frac{{\lvert \operatorname{{Irr}}_1(G) \rvert}}{{\lvert G \rvert}} = \frac{1}{{\lvert G \rvert}}\sum_{n\geq m} n^3 {\lvert \operatorname{{Irr}}_n(G) \rvert} \end{align*} $$
and
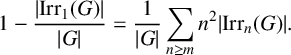 $$ \begin{align*} 1 - \frac{{\lvert \operatorname{{Irr}}_1(G) \rvert}}{{\lvert G \rvert}} = \frac{1}{{\lvert G \rvert}}\sum_{n\geq m} n^2 {\lvert \operatorname{{Irr}}_n(G) \rvert}. \end{align*} $$
$$ \begin{align*} 1 - \frac{{\lvert \operatorname{{Irr}}_1(G) \rvert}}{{\lvert G \rvert}} = \frac{1}{{\lvert G \rvert}}\sum_{n\geq m} n^2 {\lvert \operatorname{{Irr}}_n(G) \rvert}. \end{align*} $$
Hence,
As in the proof of Proposition 1.1,
![]() ${\lvert \operatorname { {Irr}}_1(G) \rvert } = {\lvert G:G' \rvert }$
. Hence,
${\lvert \operatorname { {Irr}}_1(G) \rvert } = {\lvert G:G' \rvert }$
. Hence,
![]() ${\lvert \operatorname { {Irr}}_1(G) \rvert } {\lvert G \rvert }^{-1} \leq n^{-1}$
. Plugging this into the previous inequality gives
${\lvert \operatorname { {Irr}}_1(G) \rvert } {\lvert G \rvert }^{-1} \leq n^{-1}$
. Plugging this into the previous inequality gives
which completes the proof.
Corollary 2.3 (A sharper form of [Reference Johnson8, Proposition 4.3]).
Let G be nonabelian. Then, either
![]() $\operatorname { {AD}}(G) \geq \tfrac 53$
, or
$\operatorname { {AD}}(G) \geq \tfrac 53$
, or
![]() $\operatorname { {cd}}(G)=\{1,2\}$
and
$\operatorname { {cd}}(G)=\{1,2\}$
and
![]() ${\lvert G' \rvert }=2$
; in the latter case,
${\lvert G' \rvert }=2$
; in the latter case,
![]() $\operatorname { {AD}}(G)=\tfrac 32$
.
$\operatorname { {AD}}(G)=\tfrac 32$
.
Proof. Note that
![]() $\operatorname { {mindeg}}(G)\geq 2 {\iff} G \text { is nonabelian} {\iff} {\lvert G' \rvert }\geq 2$
. Therefore, if either
$\operatorname { {mindeg}}(G)\geq 2 {\iff} G \text { is nonabelian} {\iff} {\lvert G' \rvert }\geq 2$
. Therefore, if either
![]() $\operatorname { {mindeg}}(G)\geq 3$
or
$\operatorname { {mindeg}}(G)\geq 3$
or
![]() ${\lvert G' \rvert }\geq 3$
, applying Lemma 2.2 with
${\lvert G' \rvert }\geq 3$
, applying Lemma 2.2 with
![]() $(m,n)=(3,2)$
and
$(m,n)=(3,2)$
and
![]() $(m,n)=(2,3)$
yields
$(m,n)=(2,3)$
yields
![]() $\operatorname { {AD}}(G)\geq \tfrac 53$
. Otherwise, we must have
$\operatorname { {AD}}(G)\geq \tfrac 53$
. Otherwise, we must have
![]() $\operatorname { {cd}}(G)=\{1,2\}$
and
$\operatorname { {cd}}(G)=\{1,2\}$
and
![]() ${\lvert G' \rvert }=2$
, and following the steps in the proof of Lemma 2.2 yields
${\lvert G' \rvert }=2$
, and following the steps in the proof of Lemma 2.2 yields
![]() $\operatorname { {AD}}(G)=\tfrac 32$
.
$\operatorname { {AD}}(G)=\tfrac 32$
.
Remark 2.4. In [Reference Choi3], the present author studied a generalization of
![]() $\operatorname { {AD}}(G)$
to the setting of virtually abelian groups, and showed that
$\operatorname { {AD}}(G)$
to the setting of virtually abelian groups, and showed that
![]() $\operatorname { {AD}}(G)=\tfrac 32$
if and only if
$\operatorname { {AD}}(G)=\tfrac 32$
if and only if
![]() ${\lvert G:Z(G) \rvert }=4$
. The proof goes via a version of Corollary 2.3, but substantial work is required since G may be infinite. It is therefore worth noting that when G is finite, there is a much simpler proof of this equivalence; details are given in Appendix A.1.
${\lvert G:Z(G) \rvert }=4$
. The proof goes via a version of Corollary 2.3, but substantial work is required since G may be infinite. It is therefore worth noting that when G is finite, there is a much simpler proof of this equivalence; details are given in Appendix A.1.
We saw in the proof of Corollary 2.3 that if
![]() $\operatorname { {AD}}(G)> \tfrac 32$
, then either
$\operatorname { {AD}}(G)> \tfrac 32$
, then either
![]() $\operatorname { {mindeg}}(G)\geq 3$
or
$\operatorname { {mindeg}}(G)\geq 3$
or
![]() ${\lvert G' \rvert }\geq 3$
. The example of
${\lvert G' \rvert }\geq 3$
. The example of
![]() $S_3$
shows that we can have
$S_3$
shows that we can have
![]() $\operatorname { {mindeg}}(G)=2$
and
$\operatorname { {mindeg}}(G)=2$
and
![]() ${\lvert G' \rvert }=3$
. In contrast, the next result shows that we can never have
${\lvert G' \rvert }=3$
. In contrast, the next result shows that we can never have
![]() $\operatorname { {mindeg}}(G)=3$
and
$\operatorname { {mindeg}}(G)=3$
and
![]() ${\lvert G' \rvert }=2$
.
${\lvert G' \rvert }=2$
.
Lemma 2.5. Let G be a group with
![]() ${\lvert G' \rvert }=2$
. If
${\lvert G' \rvert }=2$
. If
![]() $\varphi \in \operatorname { {Irr}}(G)$
and
$\varphi \in \operatorname { {Irr}}(G)$
and
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})>1$
, then
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})>1$
, then
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
is even.
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
is even.
Lemma 2.5 follows from more precise results of Miller, stated in [Reference Miller11, Section 1]. His presentation is rather terse and uses the finiteness of G in an essential way. We provide a direct proof of Lemma 2.5 in Appendix A.2, which also works for (irreducible, finite-dimensional, unitary) representations of infinite groups.
Proposition 2.6. Let G be nonabelian. If
![]() $2\notin \operatorname { {cd}}(G)$
, then
$2\notin \operatorname { {cd}}(G)$
, then
![]() $\operatorname { {AD}}(G)\geq \tfrac 73$
.
$\operatorname { {AD}}(G)\geq \tfrac 73$
.
Proof. We split into two cases. If
![]() ${\lvert G' \rvert }\geq 3$
, then using Lemma 2.2 with
${\lvert G' \rvert }\geq 3$
, then using Lemma 2.2 with
![]() $m=2$
and
$m=2$
and
![]() $n=3$
gives
$n=3$
gives
![]() $\operatorname { {AD}}(G)\geq \tfrac 73$
. If
$\operatorname { {AD}}(G)\geq \tfrac 73$
. If
![]() ${\lvert G' \rvert }=2$
, then
${\lvert G' \rvert }=2$
, then
![]() $3\notin \operatorname { {cd}}(G)$
by Lemma 2.5 and so
$3\notin \operatorname { {cd}}(G)$
by Lemma 2.5 and so
![]() $\operatorname { {mindeg}}(G)\geq 4$
; using Lemma 2.2 with
$\operatorname { {mindeg}}(G)\geq 4$
; using Lemma 2.2 with
![]() $m=4$
and
$m=4$
and
![]() $n=2$
gives
$n=2$
gives
![]() $\operatorname { {AD}}(G) \geq \tfrac 52> \tfrac 73$
.
$\operatorname { {AD}}(G) \geq \tfrac 52> \tfrac 73$
.
In both cases of the proof, the lower bounds are sharp; see Example 4.1 below for details.
3 The proof of Proposition 1.4
For a finite set X and a function
![]() $f:X\to \mathbb C$
, we write
$f:X\to \mathbb C$
, we write
![]() $\operatorname { {supp}}(f)$
for the support of f, that is, the set
$\operatorname { {supp}}(f)$
for the support of f, that is, the set
![]() $\{x\in X \colon f(x)\neq 0\}$
.
$\{x\in X \colon f(x)\neq 0\}$
.
Lemma 3.1 (The ‘
 ${\mathcal L}$
-orbit method’ for lower bounds).
${\mathcal L}$
-orbit method’ for lower bounds).
Let
![]() $\varphi \in \operatorname { {Irr}}(G)$
and let
$\varphi \in \operatorname { {Irr}}(G)$
and let
![]() $n={\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
. Let K be the normal subgroup of G generated by
$n={\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
. Let K be the normal subgroup of G generated by
![]() $\operatorname { {supp}}(\varphi )$
. Then,
$\operatorname { {supp}}(\varphi )$
. Then,
Proof. To simplify notation, let
![]() ${\mathcal L}=\operatorname { {Irr}}_1(G)$
. Then,
${\mathcal L}=\operatorname { {Irr}}_1(G)$
. Then,
![]() ${\mathcal L}$
is a group with respect to the pointwise product, and multiplication of characters defines a group action
${\mathcal L}$
is a group with respect to the pointwise product, and multiplication of characters defines a group action
![]() ${\mathcal L}\times \operatorname { {Irr}}_n(G)\to \operatorname { {Irr}}_n(G)$
for each n. The
${\mathcal L}\times \operatorname { {Irr}}_n(G)\to \operatorname { {Irr}}_n(G)$
for each n. The
![]() ${\mathcal L}$
-orbit of
${\mathcal L}$
-orbit of
![]() $\varphi $
is a subset of
$\varphi $
is a subset of
![]() $\operatorname { {Irr}}_n(G)$
and it has size
$\operatorname { {Irr}}_n(G)$
and it has size
![]() ${\lvert {\mathcal L} \rvert }\, {\lvert \operatorname { {Stab}}_{{\mathcal L}}(\varphi ) \rvert }^{-1}$
.
${\lvert {\mathcal L} \rvert }\, {\lvert \operatorname { {Stab}}_{{\mathcal L}}(\varphi ) \rvert }^{-1}$
.
Let
![]() ${\mathbb T}$
denote the set of complex numbers of unit modulus, viewed as a group with respect to multiplication. Observe that each
${\mathbb T}$
denote the set of complex numbers of unit modulus, viewed as a group with respect to multiplication. Observe that each
![]() $\gamma \in {\mathcal L}$
is
$\gamma \in {\mathcal L}$
is
![]() ${\mathbb T}$
-valued and that
${\mathbb T}$
-valued and that
which is the set of group homomorphisms
![]() $G\to {\mathbb T}$
that factor through
$G\to {\mathbb T}$
that factor through
![]() $G\to G/K$
. Therefore, writing A for the abelianization of
$G\to G/K$
. Therefore, writing A for the abelianization of
![]() $G/K$
,
$G/K$
,
and so the
![]() ${\mathcal L}$
-orbit of
${\mathcal L}$
-orbit of
![]() $\varphi $
has at least
$\varphi $
has at least
![]() ${\lvert {\mathcal L} \rvert }\,{\lvert G:K \rvert }^{-1}$
elements. The result now follows.
${\lvert {\mathcal L} \rvert }\,{\lvert G:K \rvert }^{-1}$
elements. The result now follows.
Corollary 3.2. Let
![]() $n\in \mathbb N$
. If
$n\in \mathbb N$
. If
![]() $\operatorname { {Irr}}_n(G)$
is nonempty, then
$\operatorname { {Irr}}_n(G)$
is nonempty, then
![]() ${\lvert \operatorname { {Irr}}_n(G) \rvert }\geq n^{-2}\,{\lvert \operatorname { {Irr}}_1(G) \rvert }$
.
${\lvert \operatorname { {Irr}}_n(G) \rvert }\geq n^{-2}\,{\lvert \operatorname { {Irr}}_1(G) \rvert }$
.
Proof. Pick some
![]() $\varphi \in \operatorname { {Irr}}_n(G)$
and let K be the normal subgroup of G generated by
$\varphi \in \operatorname { {Irr}}_n(G)$
and let K be the normal subgroup of G generated by
![]() $\operatorname { {supp}}(\varphi )$
. Since
$\operatorname { {supp}}(\varphi )$
. Since
![]() $\varphi $
is irreducible,
$\varphi $
is irreducible,
![]() ${\langle {\varphi }, {\varphi }\rangle }=1$
. Therefore, since
${\langle {\varphi }, {\varphi }\rangle }=1$
. Therefore, since
![]() ${\lvert \varphi (x) \rvert } \leq {\varphi }(\mathord {\underline {\mathsf {1}}_{}})=n$
for all
${\lvert \varphi (x) \rvert } \leq {\varphi }(\mathord {\underline {\mathsf {1}}_{}})=n$
for all
![]() $x\in G$
,
$x\in G$
,
Hence,
![]() ${\lvert G:K \rvert } \leq {\lvert G \rvert }\, {\lvert \operatorname { {supp}}(\varphi ) \rvert }^{-1} \leq n^2$
. Applying Lemma 3.1, the result follows.
${\lvert G:K \rvert } \leq {\lvert G \rvert }\, {\lvert \operatorname { {supp}}(\varphi ) \rvert }^{-1} \leq n^2$
. Applying Lemma 3.1, the result follows.
Remark 3.3. Although the estimates in the proof of Lemma 3.1 are potentially wasteful, the resulting lower bound in Corollary 3.2 is sharp. For if G is an extraspecial group of order
![]() $2^{2k+1}$
, it has exactly
$2^{2k+1}$
, it has exactly
![]() $2^{2k}$
characters of degree
$2^{2k}$
characters of degree
![]() $1$
and a single irreducible character of degree
$1$
and a single irreducible character of degree
![]() $2^k$
. However, it is important later that in certain situations, we can do significantly better (Lemma 3.10 below).
$2^k$
. However, it is important later that in certain situations, we can do significantly better (Lemma 3.10 below).
Proposition 3.4. If G is nonabelian, then
![]() $\operatorname { {AD}}(G) \geq 2+ (\operatorname { {maxdeg}}(G)-3){\lvert G' \rvert }^{-1}$
.
$\operatorname { {AD}}(G) \geq 2+ (\operatorname { {maxdeg}}(G)-3){\lvert G' \rvert }^{-1}$
.
Proof. Let
![]() $d=\operatorname { {maxdeg}}(G)$
. Since
$d=\operatorname { {maxdeg}}(G)$
. Since
![]() ${\lvert G \rvert } =\sum _{n=1}^d n^2 {\lvert \operatorname { {Irr}}_n(G) \rvert }$
,
${\lvert G \rvert } =\sum _{n=1}^d n^2 {\lvert \operatorname { {Irr}}_n(G) \rvert }$
,
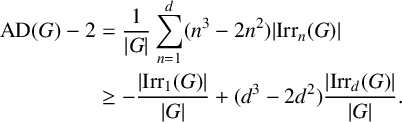 $$ \begin{align*} \begin{aligned} \operatorname{{AD}}(G) -2 &= \frac{1}{{\lvert G \rvert}}\sum_{n=1}^d (n^3-2n^2) {\lvert \operatorname{{Irr}}_n(G) \rvert} \\ & \geq -\frac{ {\lvert \operatorname{{Irr}}_1(G) \rvert} }{{\lvert G \rvert}} + (d^3-2d^2) \frac{{\lvert \operatorname{{Irr}}_d(G) \rvert} }{{\lvert G \rvert}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \operatorname{{AD}}(G) -2 &= \frac{1}{{\lvert G \rvert}}\sum_{n=1}^d (n^3-2n^2) {\lvert \operatorname{{Irr}}_n(G) \rvert} \\ & \geq -\frac{ {\lvert \operatorname{{Irr}}_1(G) \rvert} }{{\lvert G \rvert}} + (d^3-2d^2) \frac{{\lvert \operatorname{{Irr}}_d(G) \rvert} }{{\lvert G \rvert}}. \end{aligned} \end{align*} $$
Since
![]() $\operatorname { {Irr}}_d(G)$
is nonempty, applying Corollary 3.2 gives the desired inequality.
$\operatorname { {Irr}}_d(G)$
is nonempty, applying Corollary 3.2 gives the desired inequality.
The rest of this section deals with cases where
![]() $\operatorname { {cd}}(G)=\{1,2,3\}$
. We require a property of
$\operatorname { {cd}}(G)=\{1,2,3\}$
. We require a property of
![]() $\operatorname { {AD}}$
that is not obvious from the definition, but which seems to be crucial to understanding its behaviour.
$\operatorname { {AD}}$
that is not obvious from the definition, but which seems to be crucial to understanding its behaviour.
Proposition 3.5 (Johnson).
![]() $\operatorname { {AD}}$
is monotone with respect to subgroup inclusion. That is, if
$\operatorname { {AD}}$
is monotone with respect to subgroup inclusion. That is, if
![]() $H\leq G$
, then
$H\leq G$
, then
![]() $\operatorname { {AD}}(H)\leq \operatorname { {AD}}(G)$
.
$\operatorname { {AD}}(H)\leq \operatorname { {AD}}(G)$
.
Remark 3.6. Proposition 3.5 follows from results in [Reference Johnson8, Section 4] concerning ‘amenability constants’ of Fourier algebras, or from the general theory in [Reference Choi3, Section 2]. One can give a direct proof, based on considering the induction of characters from H to G: see the author’s MathOverflow question [Reference Choi4] and the comments and answers. It is quite possible that a direct proof along these lines was already known to Johnson.
Proposition 3.7. Let G be a group such that
![]() $\operatorname { {AD}}(G)< \tfrac 73$
and let
$\operatorname { {AD}}(G)< \tfrac 73$
and let
![]() $H\leq G$
. If
$H\leq G$
. If
![]() ${\lvert G:H \rvert }=2$
and
${\lvert G:H \rvert }=2$
and
![]() $\operatorname { {cd}}(G)=\{1,2,3\}$
, then
$\operatorname { {cd}}(G)=\{1,2,3\}$
, then
![]() $\operatorname { {cd}}(H)=\{1,2,3\}$
.
$\operatorname { {cd}}(H)=\{1,2,3\}$
.
The proof of Proposition 3.7 requires some general facts, which we state in a separate lemma for convenience.
Lemma 3.8 (Character degrees of subgroups of index
 $2$
).
$2$
).
Let
![]() $H\leq G$
with
$H\leq G$
with
![]() ${\lvert G:H \rvert }=2$
. Then,
${\lvert G:H \rvert }=2$
. Then,
![]() $\operatorname { {maxdeg}}(H)\leq \operatorname { {maxdeg}}(G)$
and
$\operatorname { {maxdeg}}(H)\leq \operatorname { {maxdeg}}(G)$
and
![]() $\operatorname { {cd}}(G)\subseteq \operatorname { {cd}}(H)\cup 2\operatorname { {cd}}(H)$
.
$\operatorname { {cd}}(G)\subseteq \operatorname { {cd}}(H)\cup 2\operatorname { {cd}}(H)$
.
Both parts of the lemma are standard results. For completeness, we quickly sketch their proofs.
Proof. Given
![]() $\psi \in \operatorname { {Irr}}(H)$
, let
$\psi \in \operatorname { {Irr}}(H)$
, let
![]() $\varphi \in \operatorname { {Irr}}(G)$
be one of the irreducible summands of
$\varphi \in \operatorname { {Irr}}(G)$
be one of the irreducible summands of
![]() ${\operatorname {Ind}\nolimits }^G_H\psi $
. By Frobenius reciprocity,
${\operatorname {Ind}\nolimits }^G_H\psi $
. By Frobenius reciprocity,
![]() $\psi $
is contained in
$\psi $
is contained in
![]() ${\varphi \rvert }_{H}$
, so
${\varphi \rvert }_{H}$
, so
![]() ${\psi }(\mathord {\underline {\mathsf {1}}_{}})\leq {{\varphi \rvert }_{H}}(\mathord {\underline {\mathsf {1}}_{}})={\varphi }(\mathord {\underline {\mathsf {1}}_{}})\leq \operatorname { {maxdeg}}(G)$
. This proves the first claim.
${\psi }(\mathord {\underline {\mathsf {1}}_{}})\leq {{\varphi \rvert }_{H}}(\mathord {\underline {\mathsf {1}}_{}})={\varphi }(\mathord {\underline {\mathsf {1}}_{}})\leq \operatorname { {maxdeg}}(G)$
. This proves the first claim.
For the second claim, let
![]() $\varphi \in \operatorname { {Irr}}(G)$
. If
$\varphi \in \operatorname { {Irr}}(G)$
. If
![]() ${\varphi \rvert }_{H}$
is irreducible, then
${\varphi \rvert }_{H}$
is irreducible, then
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})\in \operatorname { {cd}}(H)$
. If not, then it follows from Clifford theory (or direct arguments using Frobenius reciprocity) that
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})\in \operatorname { {cd}}(H)$
. If not, then it follows from Clifford theory (or direct arguments using Frobenius reciprocity) that
![]() ${\varphi \rvert }_{H}$
splits as the sum of two irreducible characters, say
${\varphi \rvert }_{H}$
splits as the sum of two irreducible characters, say
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
, which satisfy
$\beta _2$
, which satisfy
![]() $\varphi ={\operatorname {Ind}\nolimits }^G_H\beta _1={\operatorname {Ind}\nolimits }^G_H\beta _2$
. In particular,
$\varphi ={\operatorname {Ind}\nolimits }^G_H\beta _1={\operatorname {Ind}\nolimits }^G_H\beta _2$
. In particular,
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})=2{\beta _1}(\mathord {\underline {\mathsf {1}}_{}})\in 2\operatorname { {cd}}(H)$
.
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})=2{\beta _1}(\mathord {\underline {\mathsf {1}}_{}})\in 2\operatorname { {cd}}(H)$
.
Proof of Proposition 3.7.
By monotonicity of
![]() $\operatorname { {AD}}$
(Proposition 3.5),
$\operatorname { {AD}}$
(Proposition 3.5),
![]() $\operatorname { {AD}}(H)\leq \operatorname { {AD}}(G)< \tfrac 73$
. Hence, by Lemma 3.8,
$\operatorname { {AD}}(H)\leq \operatorname { {AD}}(G)< \tfrac 73$
. Hence, by Lemma 3.8,
![]() $\operatorname { {maxdeg}}(H)\leq 3$
and
$\operatorname { {maxdeg}}(H)\leq 3$
and
![]() $3\in \operatorname { {cd}}(H)$
. Since H is nonabelian and
$3\in \operatorname { {cd}}(H)$
. Since H is nonabelian and
![]() $\operatorname { {AD}}(H)< \tfrac 73$
, the contrapositive of Proposition 2.6 implies that
$\operatorname { {AD}}(H)< \tfrac 73$
, the contrapositive of Proposition 2.6 implies that
![]() $2\in \operatorname { {cd}}(H)$
.
$2\in \operatorname { {cd}}(H)$
.
We now observe that two-dimensional irreducible representations of G can be used to produce three-dimensional representations with useful properties. In what follows,
![]() $\varepsilon $
denotes the constant function
$\varepsilon $
denotes the constant function
![]() $1$
, regarded as the trivial representation of the group.
$1$
, regarded as the trivial representation of the group.
Lemma 3.9. Let
![]() $\pi $
be a two-dimensional irreducible representation of G and let
$\pi $
be a two-dimensional irreducible representation of G and let
![]() $\pi ^\ast $
denote its contragredient.
$\pi ^\ast $
denote its contragredient.
-
(i) The representation
 $\varepsilon $
occurs in
$\varepsilon $
occurs in
 $\pi \otimes \pi ^\ast $
with multiplicity
$\pi \otimes \pi ^\ast $
with multiplicity
 $1$
.
$1$
. -
(ii) Let
 $\rho $
be the summand in
$\rho $
be the summand in
 $\pi \otimes \pi ^\ast $
complementary to
$\pi \otimes \pi ^\ast $
complementary to
 $\varepsilon $
. Suppose that
$\varepsilon $
. Suppose that
 $\rho $
is reducible. Then, G has a subgroup of index
$\rho $
is reducible. Then, G has a subgroup of index
 $2$
.
$2$
.
This is surely not a new observation, but since we are unaware of a precise reference, a full proof is given below.
Proof. Part (i) follows from Schur’s lemma. (Alternatively, let
![]() $\psi =\operatorname { {Tr}}\pi $
; then the multiplicity of
$\psi =\operatorname { {Tr}}\pi $
; then the multiplicity of
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $\pi \otimes \pi ^\ast $
is equal to
$\pi \otimes \pi ^\ast $
is equal to
![]() ${\langle {\psi \overline {\psi }}, {\varepsilon }\rangle } = {\lvert G \rvert }^{-1} \sum _{x\in G} \psi (x)\overline {\psi (x)} = 1$
.)
${\langle {\psi \overline {\psi }}, {\varepsilon }\rangle } = {\lvert G \rvert }^{-1} \sum _{x\in G} \psi (x)\overline {\psi (x)} = 1$
.)
For part (ii), let
![]() $\varphi =\operatorname { {Tr}}\rho $
; by part (i),
$\varphi =\operatorname { {Tr}}\rho $
; by part (i),
![]() $\varphi $
is real-valued and
$\varphi $
is real-valued and
![]() ${\langle {\varphi }, {\varepsilon }\rangle }=0$
. We claim that there exists a real-valued character on G of degree
${\langle {\varphi }, {\varepsilon }\rangle }=0$
. We claim that there exists a real-valued character on G of degree
![]() $1$
occurring as a summand of
$1$
occurring as a summand of
![]() $\varphi $
. Assuming such a character exists, it may be viewed as a group homomorphism
$\varphi $
. Assuming such a character exists, it may be viewed as a group homomorphism
![]() $\sigma :G\to \{\pm 1\}$
. Since
$\sigma :G\to \{\pm 1\}$
. Since
![]() $\varepsilon $
is not a summand of
$\varepsilon $
is not a summand of
![]() $\varphi $
, we know that
$\varphi $
, we know that
![]() $\sigma \neq \varepsilon $
and so
$\sigma \neq \varepsilon $
and so
![]() $\ker \sigma $
has index
$\ker \sigma $
has index
![]() $2$
in G, as required.
$2$
in G, as required.
To prove the claim, note that since
![]() $\varphi $
has degree
$\varphi $
has degree
![]() $3$
and is reducible, its decomposition into irreducible characters includes at least one
$3$
and is reducible, its decomposition into irreducible characters includes at least one
![]() $\gamma \in \operatorname { {Irr}}_1(G)$
. If
$\gamma \in \operatorname { {Irr}}_1(G)$
. If
![]() $\gamma $
is real-valued, we are done. If not, then
$\gamma $
is real-valued, we are done. If not, then
![]() $\overline {\gamma }\neq \gamma $
and
$\overline {\gamma }\neq \gamma $
and
![]() ${\langle {\varphi }, {\overline {\gamma }}\rangle }= \overline {{\langle {\varphi }, {\gamma }\rangle }}\geq 1$
. Hence,
${\langle {\varphi }, {\overline {\gamma }}\rangle }= \overline {{\langle {\varphi }, {\gamma }\rangle }}\geq 1$
. Hence,
![]() $\gamma $
and
$\gamma $
and
![]() $\overline {\gamma }$
occur in
$\overline {\gamma }$
occur in
![]() $\varphi $
with multiplicity
$\varphi $
with multiplicity
![]() $1$
, and
$1$
, and
![]() $\varphi =\gamma +\overline {\gamma }+\sigma $
, where
$\varphi =\gamma +\overline {\gamma }+\sigma $
, where
![]() $\sigma \in \operatorname { {Irr}}_1(G)$
is real-valued.
$\sigma \in \operatorname { {Irr}}_1(G)$
is real-valued.
If G has no subgroups of index
![]() $2$
and
$2$
and
![]() $2\in \operatorname { {cd}}(G)$
, then by Lemma 3.9, for each
$2\in \operatorname { {cd}}(G)$
, then by Lemma 3.9, for each
![]() $\psi \in \operatorname { {Irr}}_2(G)$
, the character
$\psi \in \operatorname { {Irr}}_2(G)$
, the character
![]() $\beta :=\psi \overline {\psi }-\varepsilon $
must be irreducible; and because
$\beta :=\psi \overline {\psi }-\varepsilon $
must be irreducible; and because
![]() $\beta $
is a ‘small perturbation’ of a nonnegative character, we can obtain improved lower bounds on
$\beta $
is a ‘small perturbation’ of a nonnegative character, we can obtain improved lower bounds on
![]() ${\lvert \operatorname { {supp}}(\beta ) \rvert }$
, allowing us to apply Lemma 3.1 more effectively. It turns out that the relevant estimates have nothing to do with group structure, so we present them as a separate lemma.
${\lvert \operatorname { {supp}}(\beta ) \rvert }$
, allowing us to apply Lemma 3.1 more effectively. It turns out that the relevant estimates have nothing to do with group structure, so we present them as a separate lemma.
Lemma 3.10. Let X be a finite nonempty set and let
![]() $d\geq 1$
. Suppose that
$d\geq 1$
. Suppose that
![]() $f:X\to [-1,d]$
has mean
$f:X\to [-1,d]$
has mean
![]() $0$
and variance
$0$
and variance
![]() $1$
, that is,
$1$
, that is,
Then,
![]() ${\lvert \operatorname { {supp}}(f) \rvert }\geq d^{-1}{\lvert X \rvert }$
.
${\lvert \operatorname { {supp}}(f) \rvert }\geq d^{-1}{\lvert X \rvert }$
.
Proof. Fix some ‘threshold value’
![]() $c \in [0,d]$
, to be determined later, and partition
$c \in [0,d]$
, to be determined later, and partition
![]() $\operatorname { {supp}}(f)$
as
$\operatorname { {supp}}(f)$
as
![]() $N\cup P \cup R$
where:
$N\cup P \cup R$
where:
-
•
 $N := \{ x\in X \colon -1\leq f(x) < 0 \}$
;
$N := \{ x\in X \colon -1\leq f(x) < 0 \}$
; -
•
 $P := \{ x\in X \colon 0 < f(x) \leq c \}$
;
$P := \{ x\in X \colon 0 < f(x) \leq c \}$
; -
•
 $R := \{ x\in X \colon c < f \leq d \}$
.
$R := \{ x\in X \colon c < f \leq d \}$
.
Then, since
![]() $\sum _{x\in \operatorname { {supp}}(f)} f(x)^2 ={\lvert X \rvert }$
,
$\sum _{x\in \operatorname { {supp}}(f)} f(x)^2 ={\lvert X \rvert }$
,
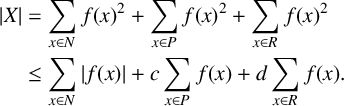 $$\begin{align} {\lvert X \rvert} & = \sum_{x\in N} f(x)^2 + \sum_{x\in P} f(x)^2 + \sum_{x\in R} f(x)^2 \nonumber\\ & \leq \sum_{x\in N} {\lvert f(x) \rvert} + c \sum_{x\in P} f(x) + d \sum_{x\in R} f(x) . \end{align} $$
$$\begin{align} {\lvert X \rvert} & = \sum_{x\in N} f(x)^2 + \sum_{x\in P} f(x)^2 + \sum_{x\in R} f(x)^2 \nonumber\\ & \leq \sum_{x\in N} {\lvert f(x) \rvert} + c \sum_{x\in P} f(x) + d \sum_{x\in R} f(x) . \end{align} $$
On the other hand, since
![]() $\sum _{x\in \operatorname { {supp}}(f)} f(x)=0$
,
$\sum _{x\in \operatorname { {supp}}(f)} f(x)=0$
,
and substituting this into (*) yields
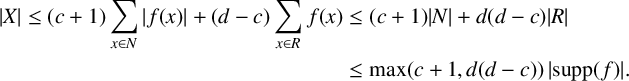 $$ \begin{align*} \begin{aligned} {\lvert X \rvert} \leq (c+1) \sum_{x\in N} {\lvert f(x) \rvert} + (d-c) \sum_{x\in R} f(x) & \leq (c+1) {\lvert N \rvert} + d(d-c) {\lvert R \rvert} \\ & \leq \max(c+1, d(d-c))\, {\lvert \operatorname{{supp}}(f) \rvert}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\lvert X \rvert} \leq (c+1) \sum_{x\in N} {\lvert f(x) \rvert} + (d-c) \sum_{x\in R} f(x) & \leq (c+1) {\lvert N \rvert} + d(d-c) {\lvert R \rvert} \\ & \leq \max(c+1, d(d-c))\, {\lvert \operatorname{{supp}}(f) \rvert}. \end{aligned} \end{align*} $$
Taking
![]() $c=d-1$
gives
$c=d-1$
gives
![]() ${\lvert X \rvert }\leq d{\lvert \operatorname { {supp}}(f) \rvert }$
as required.
${\lvert X \rvert }\leq d{\lvert \operatorname { {supp}}(f) \rvert }$
as required.
Proposition 3.11. Suppose that G has no subgroups of index
![]() $2$
, but has an irreducible representation of degree
$2$
, but has an irreducible representation of degree
![]() $2$
. Then,
$2$
. Then,
![]() ${\lvert \operatorname { {Irr}}_3(G) \rvert }\geq \tfrac 13{\lvert \operatorname { {Irr}}_1(G) \rvert }$
.
${\lvert \operatorname { {Irr}}_3(G) \rvert }\geq \tfrac 13{\lvert \operatorname { {Irr}}_1(G) \rvert }$
.
Proof. Let
![]() $\psi \in \operatorname { {Irr}}_2(G)$
and let
$\psi \in \operatorname { {Irr}}_2(G)$
and let
![]() $\beta =\psi \overline {\psi }-\varepsilon $
. We observe that:
$\beta =\psi \overline {\psi }-\varepsilon $
. We observe that:
-
•
 $\beta $
takes values in
$\beta $
takes values in
 $[-1,3]$
, since
$[-1,3]$
, since
 $0\leq {\lvert \psi (x) \rvert }^2\leq 4$
for all
$0\leq {\lvert \psi (x) \rvert }^2\leq 4$
for all
 $x\in G$
;
$x\in G$
; -
•
 ${\langle {\beta }, {\varepsilon }\rangle }=0$
, by Lemma 3.9(i);
${\langle {\beta }, {\varepsilon }\rangle }=0$
, by Lemma 3.9(i); -
•
 ${\langle {\beta }, {\beta }\rangle }=1$
, since
${\langle {\beta }, {\beta }\rangle }=1$
, since
 $\beta $
is irreducible by Lemma 3.9(ii).
$\beta $
is irreducible by Lemma 3.9(ii).
Hence, by Lemma 3.10,
![]() ${\lvert \operatorname { {supp}}(\beta ) \rvert }\geq \tfrac 13{\lvert G \rvert }$
, and applying Lemma 3.1 completes the proof.
${\lvert \operatorname { {supp}}(\beta ) \rvert }\geq \tfrac 13{\lvert G \rvert }$
, and applying Lemma 3.1 completes the proof.
Remark 3.12. In general, the bound in Proposition 3.11 cannot be improved. To see this, take
![]() $G=\mathrm {SL}(2,3)$
. Then,
$G=\mathrm {SL}(2,3)$
. Then,
![]() $\operatorname { {cd}}(G)=\{1,2,3\}$
and
$\operatorname { {cd}}(G)=\{1,2,3\}$
and
![]() ${\lvert \operatorname { {Irr}}_1(G) \rvert }=3 = 3{\lvert \operatorname { {Irr}}_3(G) \rvert }$
, while
${\lvert \operatorname { {Irr}}_1(G) \rvert }=3 = 3{\lvert \operatorname { {Irr}}_3(G) \rvert }$
, while
![]() ${\lvert G:G' \rvert }=3$
(so that G cannot quotient onto the two-element group).
${\lvert G:G' \rvert }=3$
(so that G cannot quotient onto the two-element group).
Proof of Proposition 1.4.
Let G be a group with
![]() $\operatorname { {maxdeg}}(G)\geq 3$
. If
$\operatorname { {maxdeg}}(G)\geq 3$
. If
![]() $\operatorname { {maxdeg}}(G)\geq 4$
, then
$\operatorname { {maxdeg}}(G)\geq 4$
, then
![]() $\operatorname { {AD}}(G)\geq 2 + {\lvert G' \rvert }^{-1}$
by Proposition 3.4. So we assume henceforth that
$\operatorname { {AD}}(G)\geq 2 + {\lvert G' \rvert }^{-1}$
by Proposition 3.4. So we assume henceforth that
![]() $\operatorname { {maxdeg}}(G)=3$
. Note that this implies
$\operatorname { {maxdeg}}(G)=3$
. Note that this implies
![]() ${\lvert G' \rvert }\geq 3$
, by Lemma 2.5. Moreover, if
${\lvert G' \rvert }\geq 3$
, by Lemma 2.5. Moreover, if
![]() $\operatorname { {cd}}(G)=\{1,3\}$
, then by Proposition 2.6,
$\operatorname { {cd}}(G)=\{1,3\}$
, then by Proposition 2.6,
![]() $\operatorname { {AD}}(G) \geq \tfrac 73 \geq 2+ {\lvert G' \rvert }^{-1}$
.
$\operatorname { {AD}}(G) \geq \tfrac 73 \geq 2+ {\lvert G' \rvert }^{-1}$
.
It only remains to deal with the cases where
![]() $\operatorname { {cd}}(G)=\{1,2,3\}$
. If
$\operatorname { {cd}}(G)=\{1,2,3\}$
. If
![]() $\operatorname { {AD}}(G)\geq \tfrac 73$
, then we are done, as before. So we may assume that
$\operatorname { {AD}}(G)\geq \tfrac 73$
, then we are done, as before. So we may assume that
![]() $\operatorname { {cd}}(G)=\{1,2,3\}$
and
$\operatorname { {cd}}(G)=\{1,2,3\}$
and
![]() $\operatorname { {AD}}(G)< \tfrac 73$
. Put
$\operatorname { {AD}}(G)< \tfrac 73$
. Put
![]() $H_0=G$
and apply the following recursive procedure: if
$H_0=G$
and apply the following recursive procedure: if
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $H_{n-1}$
has a subgroup of index
$H_{n-1}$
has a subgroup of index
![]() $2$
, choose
$2$
, choose
![]() $H_n$
to be such a subgroup; otherwise, stop. Note that at each stage, Proposition 3.7 ensures that
$H_n$
to be such a subgroup; otherwise, stop. Note that at each stage, Proposition 3.7 ensures that
![]() $\operatorname { {cd}}(H_n)=\{1,2,3\}$
.
$\operatorname { {cd}}(H_n)=\{1,2,3\}$
.
Since G is finite, this procedure must terminate; let H be the last subgroup in this sequence. Since
![]() $\operatorname { {cd}}(H)=\{1,2,3\}$
,
$\operatorname { {cd}}(H)=\{1,2,3\}$
,
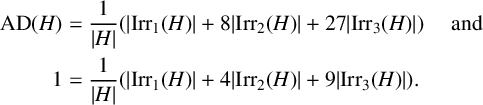 $$ \begin{align*} \begin{aligned} \operatorname{{AD}}(H) & = \frac{1}{{\lvert H \rvert}} ( {\lvert \operatorname{{Irr}}_1(H) \rvert} + 8 {\lvert \operatorname{{Irr}}_2(H) \rvert} + 27 {\lvert \operatorname{{Irr}}_3(H) \rvert} )\quad \text{ and} \\ 1 & = \frac{1}{{\lvert H \rvert}} ( {\lvert \operatorname{{Irr}}_1(H) \rvert} + 4 {\lvert \operatorname{{Irr}}_2(H) \rvert} + 9 {\lvert \operatorname{{Irr}}_3(H) \rvert} ). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \operatorname{{AD}}(H) & = \frac{1}{{\lvert H \rvert}} ( {\lvert \operatorname{{Irr}}_1(H) \rvert} + 8 {\lvert \operatorname{{Irr}}_2(H) \rvert} + 27 {\lvert \operatorname{{Irr}}_3(H) \rvert} )\quad \text{ and} \\ 1 & = \frac{1}{{\lvert H \rvert}} ( {\lvert \operatorname{{Irr}}_1(H) \rvert} + 4 {\lvert \operatorname{{Irr}}_2(H) \rvert} + 9 {\lvert \operatorname{{Irr}}_3(H) \rvert} ). \end{aligned} \end{align*} $$
Hence,
![]() $\operatorname { {AD}}(H) = 2-{\lvert H \rvert }^{-1} {\lvert \operatorname { {Irr}}_1(H) \rvert } + 9 {\lvert H \rvert }^{-1} {\lvert \operatorname { {Irr}}_3(H) \rvert }$
. Since H has no subgroups of index
$\operatorname { {AD}}(H) = 2-{\lvert H \rvert }^{-1} {\lvert \operatorname { {Irr}}_1(H) \rvert } + 9 {\lvert H \rvert }^{-1} {\lvert \operatorname { {Irr}}_3(H) \rvert }$
. Since H has no subgroups of index
![]() $2$
, it satisfies the hypotheses of Proposition 3.11, and so
$2$
, it satisfies the hypotheses of Proposition 3.11, and so
As
![]() $\operatorname { {AD}}(G)\geq \operatorname { {AD}}(H)$
(Proposition 3.5) and
$\operatorname { {AD}}(G)\geq \operatorname { {AD}}(H)$
(Proposition 3.5) and
![]() ${\lvert G' \rvert }\geq {\lvert H' \rvert }$
, we conclude that
${\lvert G' \rvert }\geq {\lvert H' \rvert }$
, we conclude that
![]() $\operatorname { {AD}}(G) \geq 2 + 2{\lvert G' \rvert }^{-1}$
, which completes the proof of Proposition 1.4.
$\operatorname { {AD}}(G) \geq 2 + 2{\lvert G' \rvert }^{-1}$
, which completes the proof of Proposition 1.4.
4 Further examples and implications of small values
4.1 Values of
 $\textbf {AD}$
for particular groups
$\textbf {AD}$
for particular groups
We present three families of groups with rather different properties (nilpotent, solvable with trivial centre and quasi-simple), where one obtains rather simple formulae for the
![]() $\operatorname { {AD}}$
-constants in each family. In each case, the ratio
$\operatorname { {AD}}$
-constants in each family. In each case, the ratio
![]() $\operatorname { {AD}}(G) \operatorname { {maxdeg}}(G)^{-1}$
converges to
$\operatorname { {AD}}(G) \operatorname { {maxdeg}}(G)^{-1}$
converges to
![]() $1$
as
$1$
as
![]() ${\lvert G \rvert }\to \infty $
.
${\lvert G \rvert }\to \infty $
.
Example 4.1 (Extraspecial p-groups).
Let p be a prime and let
![]() $n\in \mathbb N$
. If G is an extraspecial p-group of order
$n\in \mathbb N$
. If G is an extraspecial p-group of order
![]() $p^{2n+1}$
, then the degrees of its irreducible characters and their multiplicities are well documented. Namely, G has exactly
$p^{2n+1}$
, then the degrees of its irreducible characters and their multiplicities are well documented. Namely, G has exactly
![]() $p^{2n}$
characters of degree
$p^{2n}$
characters of degree
![]() $1$
and exactly
$1$
and exactly
![]() $p-1$
irreducible characters of degree
$p-1$
irreducible characters of degree
![]() $p^n$
. Hence,
$p^n$
. Hence,
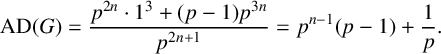 $$ \begin{align*} \operatorname{{AD}}(G)= \frac{p^{2n}\cdot 1^3 + (p-1)p^{3n}}{p^{2n+1}} = p^{n-1}(p-1) + \frac{1}{p}. \end{align*} $$
$$ \begin{align*} \operatorname{{AD}}(G)= \frac{p^{2n}\cdot 1^3 + (p-1)p^{3n}}{p^{2n+1}} = p^{n-1}(p-1) + \frac{1}{p}. \end{align*} $$
We note two particular cases, relevant to Proposition 2.6. If
![]() $p=2$
and
$p=2$
and
![]() $n=2$
, then
$n=2$
, then
![]() $\operatorname { {cd}}(G)=\{1,4\}$
and
$\operatorname { {cd}}(G)=\{1,4\}$
and
![]() $\operatorname { {AD}}(G)=\tfrac 52$
. If
$\operatorname { {AD}}(G)=\tfrac 52$
. If
![]() $p=3$
and
$p=3$
and
![]() $n=1$
, then
$n=1$
, then
![]() $\operatorname { {cd}}(G)=\{1,3\}$
and
$\operatorname { {cd}}(G)=\{1,3\}$
and
![]() $\operatorname { {AD}}(G)=\tfrac 73$
.
$\operatorname { {AD}}(G)=\tfrac 73$
.
Example 4.2 (Affine groups of finite fields).
For q a prime power
![]() $\geq 3$
, let
$\geq 3$
, let
![]() ${\mathbb F}_q$
denote the finite field with q elements and consider the natural semidirect product
${\mathbb F}_q$
denote the finite field with q elements and consider the natural semidirect product
![]() ${\mathbb F}_q\rtimes {\mathbb F}_q^\times $
(sometimes referred to as the affine group or ‘
${\mathbb F}_q\rtimes {\mathbb F}_q^\times $
(sometimes referred to as the affine group or ‘
![]() $ax+b$
group’ of
$ax+b$
group’ of
![]() ${\mathbb F}_q$
). This group has exactly
${\mathbb F}_q$
). This group has exactly
![]() $q-1$
characters of degree
$q-1$
characters of degree
![]() $1$
and a single irreducible character of degree
$1$
and a single irreducible character of degree
![]() $q-1$
. Hence,
$q-1$
. Hence,
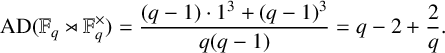 $$ \begin{align*} \operatorname{{AD}}({\mathbb F}_q\rtimes{\mathbb F}_q^\times) = \frac{(q-1)\cdot 1^3 + (q-1)^3}{q(q-1)} = q- 2+ \frac{2}{q}. \end{align*} $$
$$ \begin{align*} \operatorname{{AD}}({\mathbb F}_q\rtimes{\mathbb F}_q^\times) = \frac{(q-1)\cdot 1^3 + (q-1)^3}{q(q-1)} = q- 2+ \frac{2}{q}. \end{align*} $$
Note that when
![]() $q=3$
, this group is isomorphic to the dihedral group of order
$q=3$
, this group is isomorphic to the dihedral group of order
![]() $6$
, and its
$6$
, and its
![]() $\operatorname { {AD}}$
-constant is
$\operatorname { {AD}}$
-constant is
![]() $\tfrac 53$
; this matches the calculation in Example 2.1.
$\tfrac 53$
; this matches the calculation in Example 2.1.
Example 4.3 (Special linear groups of degree
 $2$
).
$2$
).
Let q be a prime power and let
![]() $\mathrm {SL}(2,q)$
denote the special linear group of degree
$\mathrm {SL}(2,q)$
denote the special linear group of degree
![]() $2$
over the finite field with q elements; this has order
$2$
over the finite field with q elements; this has order
![]() $q^3-q$
.
$q^3-q$
.
For q even, put
![]() $q=2r$
; then
$q=2r$
; then
![]() $\operatorname { {Irr}}(\mathrm {SL}(2,q))$
is the union of four pairwise disjoint sets
$\operatorname { {Irr}}(\mathrm {SL}(2,q))$
is the union of four pairwise disjoint sets
![]() $X_1$
,
$X_1$
,
![]() $X_{q-1}$
,
$X_{q-1}$
,
![]() $X_q$
and
$X_q$
and
![]() $X_{q+1}$
, where each member of
$X_{q+1}$
, where each member of
![]() $X_j$
has degree j, and
$X_j$
has degree j, and
For q odd, put
![]() $q=2r+1$
; then
$q=2r+1$
; then
![]() $\operatorname { {Irr}}(\mathrm {SL}(2,q))$
is the union of six pairwise disjoint sets
$\operatorname { {Irr}}(\mathrm {SL}(2,q))$
is the union of six pairwise disjoint sets
![]() $X_1$
,
$X_1$
,
![]() $X_r$
,
$X_r$
,
![]() $X_{r+1}$
,
$X_{r+1}$
,
![]() $X_q$
and
$X_q$
and
![]() $X_{q+1}$
, where each member of
$X_{q+1}$
, where each member of
![]() $X_j$
has degree j, and
$X_j$
has degree j, and
By brute-force calculation, we eventually obtain
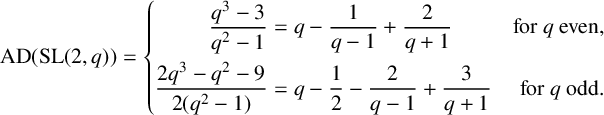 $$ \begin{align*} \operatorname{{AD}}(\mathrm{SL}(2,q)) = \left\{ \begin{aligned} \dfrac{q^3-3}{q^2-1} &= q - \dfrac{1}{q-1} + \dfrac{2}{q+1} & \text{for }q\text{ even,} \\ \dfrac{2q^3-q^2-9}{2(q^2-1)} &= q - \dfrac{1}{2} - \dfrac{2}{q-1} + \dfrac{3}{q+1}&\text{for }q\text{ odd.} \end{aligned}\right. \end{align*} $$
$$ \begin{align*} \operatorname{{AD}}(\mathrm{SL}(2,q)) = \left\{ \begin{aligned} \dfrac{q^3-3}{q^2-1} &= q - \dfrac{1}{q-1} + \dfrac{2}{q+1} & \text{for }q\text{ even,} \\ \dfrac{2q^3-q^2-9}{2(q^2-1)} &= q - \dfrac{1}{2} - \dfrac{2}{q-1} + \dfrac{3}{q+1}&\text{for }q\text{ odd.} \end{aligned}\right. \end{align*} $$
The next set of examples was suggested to the author by P. Levy.
Example 4.4 (Finite subgroups of
 $\mathrm {SO}(3)$
and
$\mathrm {SO}(3)$
and
 $\mathrm {SU}(2)$
).
$\mathrm {SU}(2)$
).
We ignore the cyclic groups and dihedral groups, and their double covers inside
![]() $\mathrm {SU}(2)$
, since these are covered by previous results. So there are only three new examples to consider. In the following list, when we refer to the ‘character degrees’ of a group H, we mean ‘the degrees of its irreducible characters, listed with multiplicity’.
$\mathrm {SU}(2)$
, since these are covered by previous results. So there are only three new examples to consider. In the following list, when we refer to the ‘character degrees’ of a group H, we mean ‘the degrees of its irreducible characters, listed with multiplicity’.
-
(a) The alternating group
 $A_4$
has character degrees
$A_4$
has character degrees
 $1,1,1,3$
. Its double cover is the binary tetrahedral group
$1,1,1,3$
. Its double cover is the binary tetrahedral group
 $2T\cong \mathrm {SL}(2,3)$
, whose character degrees are
$2T\cong \mathrm {SL}(2,3)$
, whose character degrees are
 $1, 1, 1, 2, 2, 2, 3$
. Thus,
$1, 1, 1, 2, 2, 2, 3$
. Thus,  $$ \begin{align*} \operatorname{{AD}}(A_4)= \tfrac{30}{12} = \tfrac{5}{2} \quad\text{and}\quad \operatorname{{AD}}(2T)= \tfrac{54}{24} =\tfrac{9}{4} < \operatorname{{AD}}(A_4). \end{align*} $$
$$ \begin{align*} \operatorname{{AD}}(A_4)= \tfrac{30}{12} = \tfrac{5}{2} \quad\text{and}\quad \operatorname{{AD}}(2T)= \tfrac{54}{24} =\tfrac{9}{4} < \operatorname{{AD}}(A_4). \end{align*} $$
-
(b) The symmetric group
 $S_4$
has character degrees
$S_4$
has character degrees
 $1,1,2,3,3$
. Its double cover is the binary octahedral group
$1,1,2,3,3$
. Its double cover is the binary octahedral group
 $2O$
, whose character degrees are
$2O$
, whose character degrees are
 $1, 1, 2, 2, 2, 3, 3, 4$
. Thus,
$1, 1, 2, 2, 2, 3, 3, 4$
. Thus,  $$ \begin{align*} \operatorname{{AD}}(S_4) = \tfrac{64}{24} = \tfrac{8}{3} \quad\text{and}\quad \operatorname{{AD}}(2O) = \tfrac{144}{48} = 3> \operatorname{{AD}}(S_4). \end{align*} $$
$$ \begin{align*} \operatorname{{AD}}(S_4) = \tfrac{64}{24} = \tfrac{8}{3} \quad\text{and}\quad \operatorname{{AD}}(2O) = \tfrac{144}{48} = 3> \operatorname{{AD}}(S_4). \end{align*} $$
-
(c) The alternating group
 $A_5$
has character degrees
$A_5$
has character degrees
 $1, 3, 3, 4, 5$
. Its double cover is the binary icosahedral group
$1, 3, 3, 4, 5$
. Its double cover is the binary icosahedral group
 $2I\cong \mathrm {SL}(2,5)$
, whose character degrees are
$2I\cong \mathrm {SL}(2,5)$
, whose character degrees are
 $1, 2, 2, 3, 3, 4, 4, 5, 6$
. Thus,
$1, 2, 2, 3, 3, 4, 4, 5, 6$
. Thus,  $$ \begin{align*} \operatorname{{AD}}(A_5) = \tfrac{244}{60} = \tfrac{61}{15} \quad\text{and}\quad \operatorname{{AD}}(2I) = \tfrac{540}{120} = \tfrac{9}{2}> \operatorname{{AD}}(A_5). \end{align*} $$
$$ \begin{align*} \operatorname{{AD}}(A_5) = \tfrac{244}{60} = \tfrac{61}{15} \quad\text{and}\quad \operatorname{{AD}}(2I) = \tfrac{540}{120} = \tfrac{9}{2}> \operatorname{{AD}}(A_5). \end{align*} $$
Remark 4.5. It is already known that although
![]() $\operatorname { {AD}}$
cannot increase when passing to subgroups, it can increase when passing to a quotient. For instance, in a ‘note added in proof’ in [Reference Lau, Loy and Willis10], it is observed that the Schur cover of
$\operatorname { {AD}}$
cannot increase when passing to subgroups, it can increase when passing to a quotient. For instance, in a ‘note added in proof’ in [Reference Lau, Loy and Willis10], it is observed that the Schur cover of
![]() $A_6$
has an
$A_6$
has an
![]() $\operatorname { {AD}}$
-constant strictly smaller than that of the triple cover of
$\operatorname { {AD}}$
-constant strictly smaller than that of the triple cover of
![]() $A_6$
. However, Example 4.4(a) shows that there exists a much smaller example.
$A_6$
. However, Example 4.4(a) shows that there exists a much smaller example.
4.2 Structural consequences for G of upper bounds on
 $\textbf {AD}$
$\textbf {AD}$
Proposition 4.6 (A cheap lower bound for p-groups).
Let p be a prime. If G is a nonabelian p-group, then
![]() $\operatorname { {AD}}(G) \geq p - 1 + {1}/{p}$
. Equality is attained by an extraspecial p-group of order
$\operatorname { {AD}}(G) \geq p - 1 + {1}/{p}$
. Equality is attained by an extraspecial p-group of order
![]() $p^3$
.
$p^3$
.
Proof. Since G is a p-group, both
![]() $\operatorname { {mindeg}}(G)$
and
$\operatorname { {mindeg}}(G)$
and
![]() ${\lvert G' \rvert }$
are powers of p. Therefore, both are
${\lvert G' \rvert }$
are powers of p. Therefore, both are
![]() $\geq p$
, since G is nonabelian. The rest follows from Lemma 2.2 and the calculation in Example 4.1.
$\geq p$
, since G is nonabelian. The rest follows from Lemma 2.2 and the calculation in Example 4.1.
A similar idea can be used to control (sub)groups of odd order whose
![]() $\operatorname { {AD}}$
-constants are small. The next result is a slightly stronger version of an observation by G. Robinson (personal communication).
$\operatorname { {AD}}$
-constants are small. The next result is a slightly stronger version of an observation by G. Robinson (personal communication).
Lemma 4.7. If
![]() $\operatorname { {AD}}(G)< \tfrac 73$
, then every odd order subgroup of G is abelian.
$\operatorname { {AD}}(G)< \tfrac 73$
, then every odd order subgroup of G is abelian.
Proof. We prove the contrapositive. Suppose that G has a nonabelian subgroup H that has odd order. Since
![]() ${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
divides
${\varphi }(\mathord {\underline {\mathsf {1}}_{}})$
divides
![]() ${\lvert H \rvert }$
for each
${\lvert H \rvert }$
for each
![]() $\varphi \in \operatorname { {Irr}}(H)$
, we have
$\varphi \in \operatorname { {Irr}}(H)$
, we have
![]() $\operatorname { {mindeg}}(H)\geq 3$
; since
$\operatorname { {mindeg}}(H)\geq 3$
; since
![]() ${\lvert H' \rvert }$
divides
${\lvert H' \rvert }$
divides
![]() ${\lvert H \rvert }$
, we have
${\lvert H \rvert }$
, we have
![]() ${\lvert H' \rvert }\geq 3$
. Therefore, by monotonicity (Proposition 3.5) and Lemma 2.2,
${\lvert H' \rvert }\geq 3$
. Therefore, by monotonicity (Proposition 3.5) and Lemma 2.2,
as required.
Corollary 4.8. If G is nilpotent and
![]() $\operatorname { {AD}}(G)< \tfrac 73$
, then G is the product of a
$\operatorname { {AD}}(G)< \tfrac 73$
, then G is the product of a
![]() $2$
-group and an abelian group of odd order.
$2$
-group and an abelian group of odd order.
Proof. If p is an odd prime, then by Lemma 4.7, each p-Sylow subgroup of G is abelian. However, since G is finite and nilpotent, it factorizes as the direct product of its Sylow subgroups.
Remark 4.9. We can show by relatively elementary arguments that
![]() $\operatorname { {AD}}(G)> 4$
whenever G is nonabelian and simple; since
$\operatorname { {AD}}(G)> 4$
whenever G is nonabelian and simple; since
![]() $\operatorname { {AD}}(A_5)={61}/{15}$
, this is already quite close to the optimal result. Although we obtain a stronger result in Section 5, we include the proof of the weaker result here as an illustration of our earlier method.
$\operatorname { {AD}}(A_5)={61}/{15}$
, this is already quite close to the optimal result. Although we obtain a stronger result in Section 5, we include the proof of the weaker result here as an illustration of our earlier method.
The main idea is similar to the proof of Lemma 2.2. Let
![]() $m=\operatorname { {mindeg}}(G)$
. Since m divides
$m=\operatorname { {mindeg}}(G)$
. Since m divides
![]() ${\lvert G \rvert }=\sum _{\varphi \in \operatorname { {Irr}}(G)} {\varphi }(\mathord {\underline {\mathsf {1}}_{}})^2$
and since
${\lvert G \rvert }=\sum _{\varphi \in \operatorname { {Irr}}(G)} {\varphi }(\mathord {\underline {\mathsf {1}}_{}})^2$
and since
![]() ${\lvert \operatorname { {Irr}}_1(G) \rvert }=1$
,
${\lvert \operatorname { {Irr}}_1(G) \rvert }=1$
,
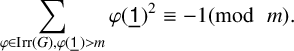 $$ \begin{align*} \sum_{\varphi \in\operatorname{{Irr}}(G), {\varphi}(\mathord{\underline{\mathsf{1}}_{}})>m} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 \equiv -1 (\mod\ m). \end{align*} $$
$$ \begin{align*} \sum_{\varphi \in\operatorname{{Irr}}(G), {\varphi}(\mathord{\underline{\mathsf{1}}_{}})>m} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 \equiv -1 (\mod\ m). \end{align*} $$
Hence, there is at least one
![]() $\sigma \in \operatorname { {Irr}}(G)$
with
$\sigma \in \operatorname { {Irr}}(G)$
with
![]() ${\sigma }(\mathord {\underline {\mathsf {1}}_{}})\geq m+1$
. Therefore,
${\sigma }(\mathord {\underline {\mathsf {1}}_{}})\geq m+1$
. Therefore,
 $$ \begin{align*} \begin{aligned} \operatorname{{AD}}(G)- m & = \sum_{\varphi\in\operatorname{{Irr}}(G)} \frac{ ({\varphi}(\mathord{\underline{\mathsf{1}}_{}})-m) {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 }{ {\lvert G \rvert} } \\ & \geq - \frac{m-1}{{\lvert G \rvert}} + \frac{({\sigma}(\mathord{\underline{\mathsf{1}}_{}})-m){\sigma}(\mathord{\underline{\mathsf{1}}_{}})^2}{{\lvert G \rvert}} \geq - \frac{m-1}{{\lvert G \rvert}} + \frac{(m+1)^2}{{\lvert G \rvert}}> 0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \operatorname{{AD}}(G)- m & = \sum_{\varphi\in\operatorname{{Irr}}(G)} \frac{ ({\varphi}(\mathord{\underline{\mathsf{1}}_{}})-m) {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 }{ {\lvert G \rvert} } \\ & \geq - \frac{m-1}{{\lvert G \rvert}} + \frac{({\sigma}(\mathord{\underline{\mathsf{1}}_{}})-m){\sigma}(\mathord{\underline{\mathsf{1}}_{}})^2}{{\lvert G \rvert}} \geq - \frac{m-1}{{\lvert G \rvert}} + \frac{(m+1)^2}{{\lvert G \rvert}}> 0. \end{aligned} \end{align*} $$
If
![]() $m\geq 4$
, this immediately gives
$m\geq 4$
, this immediately gives
![]() $\operatorname { {AD}}(G)>4$
. So, it only remains to deal with cases where
$\operatorname { {AD}}(G)>4$
. So, it only remains to deal with cases where
![]() $m=3$
. The finite simple subgroups of
$m=3$
. The finite simple subgroups of
![]() $\mathrm {PGL}(3,\mathbb C)$
were determined by Blichfeldt in [Reference Blichfeldt2] and, using his classification, one can show that the only simple groups with
$\mathrm {PGL}(3,\mathbb C)$
were determined by Blichfeldt in [Reference Blichfeldt2] and, using his classification, one can show that the only simple groups with
![]() $m=3$
are
$m=3$
are
![]() $A_5$
and
$A_5$
and
![]() $\mathrm {PSL}(2,7)$
(some further explanation is given in Appendix A.3). We see in Example 4.4(c) that
$\mathrm {PSL}(2,7)$
(some further explanation is given in Appendix A.3). We see in Example 4.4(c) that
![]() $\operatorname { {AD}}(A_5)={61}/{15}> 4$
, and since
$\operatorname { {AD}}(A_5)={61}/{15}> 4$
, and since
![]() $\mathrm {PSL}(2,7)$
has character degrees
$\mathrm {PSL}(2,7)$
has character degrees
![]() $1,3,3,6,7,8$
, we find that
$1,3,3,6,7,8$
, we find that
![]() $\operatorname { {AD}}(\mathrm {PSL}(2,7))={563}/{84}> 6$
.
$\operatorname { {AD}}(\mathrm {PSL}(2,7))={563}/{84}> 6$
.
5 A sharp lower bound on
 $\textbf {AD}$
for nonsolvable groups
$\textbf {AD}$
for nonsolvable groups
Our aim in this section is to prove Theorem 1.5: if G is nonsolvable, then
![]() $\operatorname { {AD}}(G) \geq {61}/{15}$
. One difficulty, if we rely on our existing tools, is that although
$\operatorname { {AD}}(G) \geq {61}/{15}$
. One difficulty, if we rely on our existing tools, is that although
![]() $\operatorname { {AD}}$
behaves well with respect to taking subgroups, it does not behave well with respect to taking quotients (see Remark 4.5).
$\operatorname { {AD}}$
behaves well with respect to taking subgroups, it does not behave well with respect to taking quotients (see Remark 4.5).
Instead, our proof is inspired by techniques used in [Reference Tong-Viet13] to prove an analogous ‘threshold’ result for the quantity
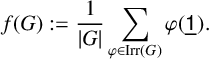 $$ \begin{align*} f(G) := \frac{1}{{\lvert G \rvert}} \sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}}). \end{align*} $$
$$ \begin{align*} f(G) := \frac{1}{{\lvert G \rvert}} \sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}}). \end{align*} $$
The key in [Reference Tong-Viet13] is to exploit the inequality
![]() $f(G)^2\leq \operatorname { {cp}}(G)$
, where the commuting probability
$f(G)^2\leq \operatorname { {cp}}(G)$
, where the commuting probability
![]() $\operatorname { {cp}}(G)$
is equal to
$\operatorname { {cp}}(G)$
is equal to
![]() ${\lvert G \rvert }^{-1} {\lvert \operatorname { {Irr}}(G) \rvert }$
. (Strictly speaking, this is not the original definition of
${\lvert G \rvert }^{-1} {\lvert \operatorname { {Irr}}(G) \rvert }$
. (Strictly speaking, this is not the original definition of
![]() $\operatorname { {cp}}$
, but its equivalence with the original definition is well known.) The inequality relating f with
$\operatorname { {cp}}$
, but its equivalence with the original definition is well known.) The inequality relating f with
![]() $\operatorname { {cp}}$
is immediate from the Cauchy–Schwarz inequality; in our setting, we can use Hölder’s inequality to obtain an analogous relationship between
$\operatorname { {cp}}$
is immediate from the Cauchy–Schwarz inequality; in our setting, we can use Hölder’s inequality to obtain an analogous relationship between
![]() $\operatorname { {AD}}$
and
$\operatorname { {AD}}$
and
![]() $\operatorname { {cp}}$
, but in the opposite direction.
$\operatorname { {cp}}$
, but in the opposite direction.
Proposition 5.1. For every G, we have
![]() $1\leq \operatorname { {AD}}(G)^2 \operatorname { {cp}}(G)$
. Equality is strict if G is nonabelian.
$1\leq \operatorname { {AD}}(G)^2 \operatorname { {cp}}(G)$
. Equality is strict if G is nonabelian.
Proof. Applying Hölder’s inequality with conjugate exponents
![]() $\tfrac 32$
and
$\tfrac 32$
and
![]() $3$
gives
$3$
gives
 $$ \begin{align*} {\lvert G \rvert} = \sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2\cdot 1 \leq \bigg(\sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^3 \bigg)^{{2}/{3}} \bigg( \sum_{\varphi\in\operatorname{{Irr}}(G)} 1^3\bigg)^{{1}/{3}}, \end{align*} $$
$$ \begin{align*} {\lvert G \rvert} = \sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2\cdot 1 \leq \bigg(\sum_{\varphi\in\operatorname{{Irr}}(G)} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^3 \bigg)^{{2}/{3}} \bigg( \sum_{\varphi\in\operatorname{{Irr}}(G)} 1^3\bigg)^{{1}/{3}}, \end{align*} $$
and the inequality is strict unless every
![]() $\varphi \in \operatorname { {Irr}}(G)$
has the same degree, that is, unless G is abelian. The result now follows by dividing both sides by
$\varphi \in \operatorname { {Irr}}(G)$
has the same degree, that is, unless G is abelian. The result now follows by dividing both sides by
![]() ${\lvert G \rvert }$
and then cubing.
${\lvert G \rvert }$
and then cubing.
Remark 5.2. The invariant
![]() $\operatorname { {cp}}$
has been intensively studied and, in particular, it is shown in [Reference Guralnick and Robinson6, Theorem 11] that if
$\operatorname { {cp}}$
has been intensively studied and, in particular, it is shown in [Reference Guralnick and Robinson6, Theorem 11] that if
![]() ${1}/{12}> \operatorname { {cp}}(G) >{3}/{40}$
, then G is solvable. Although this result itself is not strong enough to imply Theorem 1.5, the ideas in its proof can be seen (refracted through the prism of [Reference Tong-Viet13]) in what follows.
${1}/{12}> \operatorname { {cp}}(G) >{3}/{40}$
, then G is solvable. Although this result itself is not strong enough to imply Theorem 1.5, the ideas in its proof can be seen (refracted through the prism of [Reference Tong-Viet13]) in what follows.
The key advantage of working with
![]() $\operatorname { {cp}}$
, compared with either f or
$\operatorname { {cp}}$
, compared with either f or
![]() $\operatorname { {AD}}$
, is that it behaves well with respect to both taking subgroups and taking quotients. In particular, we make crucial use of the following result.
$\operatorname { {AD}}$
, is that it behaves well with respect to both taking subgroups and taking quotients. In particular, we make crucial use of the following result.
Lemma 5.3 (Gallagher, [Reference Gallagher5]).
Suppose that
![]() $N\unlhd G$
. Then,
$N\unlhd G$
. Then,
It was observed by Dixon that the largest value of
![]() $\operatorname { {cp}}$
on simple nonabelian groups is attained at
$\operatorname { {cp}}$
on simple nonabelian groups is attained at
![]() $A_5$
. We need some information about the second largest value attained by
$A_5$
. We need some information about the second largest value attained by
![]() $\operatorname { {cp}}$
on this class of groups. The following is a slightly stronger version of [Reference Tong-Viet13, Lemma 2.3].
$\operatorname { {cp}}$
on this class of groups. The following is a slightly stronger version of [Reference Tong-Viet13, Lemma 2.3].
Lemma 5.4. There exists
![]() ${1}/{28} \leq \delta _0 \leq {1}/{20}$
with the following property: if S is a finite nonabelian simple group and
${1}/{28} \leq \delta _0 \leq {1}/{20}$
with the following property: if S is a finite nonabelian simple group and
![]() $\operatorname { {cp}}(S)> \delta _0$
, then
$\operatorname { {cp}}(S)> \delta _0$
, then
![]() $S\cong A_5$
(and
$S\cong A_5$
(and
![]() $\operatorname { {cp}}(S)={1}/{12}$
).
$\operatorname { {cp}}(S)={1}/{12}$
).
By consulting the classification of finite simple groups (CFSG) and considering the minimal degrees of nontrivial irreducible characters, it can be shown that one can take
![]() $\delta _0={1}/{28}$
. (This is best possible since
$\delta _0={1}/{28}$
. (This is best possible since
![]() $\operatorname { {cp}}(\mathrm {PSL}(2,7))={1}/{28}$
.) We can show without resorting to the full CFSG that
$\operatorname { {cp}}(\mathrm {PSL}(2,7))={1}/{28}$
.) We can show without resorting to the full CFSG that
![]() $\delta _0 = {1}/{20}$
works. Details are given in Appendix A.3: our approach invokes parts of the classification of finite subgroups of
$\delta _0 = {1}/{20}$
works. Details are given in Appendix A.3: our approach invokes parts of the classification of finite subgroups of
![]() $\mathrm {PGL}(3,\mathbb C)$
and
$\mathrm {PGL}(3,\mathbb C)$
and
![]() $\mathrm {PGL}(4,\mathbb C)$
, given by Blichfeldt in the 1900s [Reference Blichfeldt1, Reference Blichfeldt2].
$\mathrm {PGL}(4,\mathbb C)$
, given by Blichfeldt in the 1900s [Reference Blichfeldt1, Reference Blichfeldt2].
The following lemma is presumably standard knowledge, but it seems quicker to give an explanation than to look up a reference.
Lemma 5.5. Let H be a perfect group.
-
(a) If W is a solvable group and
 $\theta :H\to W$
is a homomorphism, then
$\theta :H\to W$
is a homomorphism, then
 $\theta (H)=\{\mathord {\underline {\mathsf {1}}_{W}}\}$
.
$\theta (H)=\{\mathord {\underline {\mathsf {1}}_{W}}\}$
. -
(b) If X is any set on which H acts, then each H-orbit in X either has size
 $1$
or size
$1$
or size
 $\geq 5$
.
$\geq 5$
.
Proof. Part (a) follows by induction on the derived series of W. For part (b), observe that an H-orbit of size n defines a homomorphism
![]() $\alpha :H \to S_n$
whose image acts transitively on the original orbit. If
$\alpha :H \to S_n$
whose image acts transitively on the original orbit. If
![]() $n\leq 4$
, then
$n\leq 4$
, then
![]() $S_n$
is solvable and so
$S_n$
is solvable and so
![]() $\alpha (H)$
is trivial by part (a); this is only possible if
$\alpha (H)$
is trivial by part (a); this is only possible if
![]() $n=1$
.
$n=1$
.
We now turn to the proof that the only perfect groups with commuting probability greater than
![]() ${1}/{20}$
are
${1}/{20}$
are
![]() $A_5$
and
$A_5$
and
![]() $\mathrm {SL}(2,5)$
(Proposition 1.6). Our argument is patterned on the proof of [Reference Tong-Viet13, Lemma 2.4], but since we need better bounds than those in Tong-Viet’s paper, we take the opportunity to make some simplifications and give a more streamlined approach.
$\mathrm {SL}(2,5)$
(Proposition 1.6). Our argument is patterned on the proof of [Reference Tong-Viet13, Lemma 2.4], but since we need better bounds than those in Tong-Viet’s paper, we take the opportunity to make some simplifications and give a more streamlined approach.
Proof of Proposition 1.6.
Let S be the quotient of H by any maximal proper normal subgroup. Then, S is simple (by maximality), nontrivial (by properness) and nonabelian (since H is perfect). By Lemma 5.3,
![]() $\operatorname { {cp}}(S)\geq \operatorname { {cp}}(H)> {1}/{20}$
, so by Lemma 5.4,
$\operatorname { {cp}}(S)\geq \operatorname { {cp}}(H)> {1}/{20}$
, so by Lemma 5.4,
![]() $S\cong A_5$
.
$S\cong A_5$
.
Thus, we have a surjective homomorphism
![]() $H \to A_5$
, with kernel N, say. If N is trivial, there is nothing to prove; so henceforth, we assume
$H \to A_5$
, with kernel N, say. If N is trivial, there is nothing to prove; so henceforth, we assume
![]() ${\lvert N \rvert }\geq 2$
and aim to prove that
${\lvert N \rvert }\geq 2$
and aim to prove that
![]() $H\cong \mathrm {SL}(2,5)$
.
$H\cong \mathrm {SL}(2,5)$
.
By definition, H is an extension of
![]() $A_5$
by the group N. Suppose that we can show it is a central extension; then, since H is perfect, it must be a quotient of the Schur cover of
$A_5$
by the group N. Suppose that we can show it is a central extension; then, since H is perfect, it must be a quotient of the Schur cover of
![]() $A_5$
, which is isomorphic to
$A_5$
, which is isomorphic to
![]() $\mathrm {SL}(2,5)$
. Since
$\mathrm {SL}(2,5)$
. Since
![]() ${\lvert \mathrm {SL}(2,5) \rvert }=2{\lvert A_5 \rvert }\leq {\lvert H \rvert }$
, the quotient map from
${\lvert \mathrm {SL}(2,5) \rvert }=2{\lvert A_5 \rvert }\leq {\lvert H \rvert }$
, the quotient map from
![]() $\mathrm {SL}(2,5)$
onto H must be injective, and we are done.
$\mathrm {SL}(2,5)$
onto H must be injective, and we are done.
Therefore, it suffices to prove that
![]() $N\subseteq Z(H)$
. Let
$N\subseteq Z(H)$
. Let
![]() $k_H(N)$
denote the number of H-conjugacy classes contained in N. As in the proof of [Reference Tong-Viet13, Lemma 2.4], we have the inequality
$k_H(N)$
denote the number of H-conjugacy classes contained in N. As in the proof of [Reference Tong-Viet13, Lemma 2.4], we have the inequality
(We briefly sketch how this works. If M is any finite group and
![]() $N\unlhd M$
, then [Reference Guralnick and Robinson6, Lemma 1(iii)], which is actually proved in [Reference Kovács and Robinson9, Remark A2’], tells us that
$N\unlhd M$
, then [Reference Guralnick and Robinson6, Lemma 1(iii)], which is actually proved in [Reference Kovács and Robinson9, Remark A2’], tells us that
We then apply this inequality with
![]() $M=H$
, noting that
$M=H$
, noting that
![]() ${\lvert H:N \rvert }=60$
, and appeal to the fact that each subgroup of
${\lvert H:N \rvert }=60$
, and appeal to the fact that each subgroup of
![]() $A_5$
has at most five distinct irreducible characters.)
$A_5$
has at most five distinct irreducible characters.)
Since
![]() $\operatorname { {cp}}(H)>{1}/{20}$
, it follows from (5-1) that
$\operatorname { {cp}}(H)>{1}/{20}$
, it follows from (5-1) that
![]() $k_H(N)> \tfrac 35{\lvert N \rvert }$
. By definition
$k_H(N)> \tfrac 35{\lvert N \rvert }$
. By definition
![]() $k_H(N)$
counts the number of orbits for the conjugation action of H on N. By Lemma 5.5, the size of each nonsingleton orbit is at least
$k_H(N)$
counts the number of orbits for the conjugation action of H on N. By Lemma 5.5, the size of each nonsingleton orbit is at least
![]() $5$
. Therefore, if F denotes the set of fixed points of the action,
$5$
. Therefore, if F denotes the set of fixed points of the action,
and combining this with the previous lower bound on
![]() $k_H(N)$
gives
$k_H(N)$
gives
Now observe that
![]() $F=Z(H)\cap N$
. So by the previous inequality,
$F=Z(H)\cap N$
. So by the previous inequality,
![]() ${\lvert N:Z(H)\cap N \rvert }<2$
, which is only possible if
${\lvert N:Z(H)\cap N \rvert }<2$
, which is only possible if
![]() $Z(H)\cap N =N$
, and this completes the proof.
$Z(H)\cap N =N$
, and this completes the proof.
We can now show that on the class of finite perfect groups, the
![]() $\operatorname { {AD}}$
-constant is minimized at
$\operatorname { {AD}}$
-constant is minimized at
![]() $A_5$
. In fact, a more precise statement can be made.
$A_5$
. In fact, a more precise statement can be made.
Corollary 5.6. Let H be a nontrivial perfect group which satisfies
![]() $\operatorname { {AD}}(H)\leq 2\sqrt {5} \approxeq 4.47$
. Then,
$\operatorname { {AD}}(H)\leq 2\sqrt {5} \approxeq 4.47$
. Then,
![]() $H\cong A_5$
and
$H\cong A_5$
and
![]() $\operatorname { {AD}}(H)={61}/{15}\approxeq 4.07$
.
$\operatorname { {AD}}(H)={61}/{15}\approxeq 4.07$
.
Proof. By Proposition 5.1,
![]() $\operatorname { {cp}}(H)> \operatorname { {AD}}(H)^{-2} \geq {1}/{20}$
. Hence, by Proposition 1.6, H is isomorphic to either
$\operatorname { {cp}}(H)> \operatorname { {AD}}(H)^{-2} \geq {1}/{20}$
. Hence, by Proposition 1.6, H is isomorphic to either
![]() $A_5$
or
$A_5$
or
![]() $\mathrm {SL}(2,5)$
. However, the second possibility is excluded, since we saw in Example 4.4(c) that
$\mathrm {SL}(2,5)$
. However, the second possibility is excluded, since we saw in Example 4.4(c) that
![]() $\operatorname { {AD}}(\mathrm {SL}(2,5))=\tfrac 92> 2\sqrt {5}$
.
$\operatorname { {AD}}(\mathrm {SL}(2,5))=\tfrac 92> 2\sqrt {5}$
.
Proof of Theorem 1.5.
Since G is not solvable, its derived series stabilizes at some subgroup
![]() $H\leq G$
that is perfect and nontrivial. By monotonicity,
$H\leq G$
that is perfect and nontrivial. By monotonicity,
![]() $\operatorname { {AD}}(G)\geq \operatorname { {AD}}(H)$
; and by Corollary 5.6, we have
$\operatorname { {AD}}(G)\geq \operatorname { {AD}}(H)$
; and by Corollary 5.6, we have
![]() $\operatorname { {AD}}(H) \geq \min (2\sqrt {5}, {61}/{15})={61}/{15}$
.
$\operatorname { {AD}}(H) \geq \min (2\sqrt {5}, {61}/{15})={61}/{15}$
.
Acknowledgements
The results presented here are part of a wider programme to understand the amenability constants of Fourier algebras of locally compact groups, some of which were presented at the 2022 meeting of the Canadian Abstract Harmonic Analysis Symposium. I would like to thank the organizers and participants of that meeting for their interest; particular thanks are due to Brian Forrest and John Sawatzky. Closer to home, thanks are due to Paul Levy for several helpful conversations. I also thank Geoff Robinson for his interest in the topic of this paper at an earlier stage and for various messages of encouragement. The paper has also benefited from a close reading by an anonymous referee, whose suggestions have improved the clarity and consistency of the presentation in several places. Finally, I would like to acknowledge the work of the contributors and maintainers of the GroupPropsWiki, and all those on MathOverflow who have been willing to share ideas and expertise with a Bear of Very Little Brain.
Appendix Easier proofs of some known results
A.1 Finite groups with two character degrees and derived subgroup of order
 $2$
$2$
The groups described in the title are, by Corollary 2.3, those finite nonabelian groups where
![]() $\operatorname { {AD}}$
attains its minimum value. In this section, we give a quick proof that these groups are precisely those in which the centre has index
$\operatorname { {AD}}$
attains its minimum value. In this section, we give a quick proof that these groups are precisely those in which the centre has index
![]() $4$
.
$4$
.
Let G be a finite group with
![]() $\operatorname { {cd}}(G)=\{1,2\}$
and
$\operatorname { {cd}}(G)=\{1,2\}$
and
![]() ${\lvert G' \rvert }=2$
. We have
${\lvert G' \rvert }=2$
. We have
![]() $\operatorname { {Irr}}(G)=\operatorname { {Irr}}_1(G)\cup \operatorname { {Irr}}_2(G)$
; let
$\operatorname { {Irr}}(G)=\operatorname { {Irr}}_1(G)\cup \operatorname { {Irr}}_2(G)$
; let
![]() $l={\lvert \operatorname { {Irr}}_1(G) \rvert }$
and
$l={\lvert \operatorname { {Irr}}_1(G) \rvert }$
and
![]() $m={\lvert \operatorname { {Irr}}_2(G) \rvert }$
. Also, since every conjugacy class injects into
$m={\lvert \operatorname { {Irr}}_2(G) \rvert }$
. Also, since every conjugacy class injects into
![]() $G'$
and
$G'$
and
![]() ${\lvert G' \rvert }=2$
, each conjugacy class in G has size
${\lvert G' \rvert }=2$
, each conjugacy class in G has size
![]() $1$
or
$1$
or
![]() $2$
. Let
$2$
. Let
![]() $s={\lvert Z(G) \rvert }$
and let n be the number of conjugacy classes of size
$s={\lvert Z(G) \rvert }$
and let n be the number of conjugacy classes of size
![]() $2$
.
$2$
.
Note that
![]() ${\lvert G \rvert }=\sum _{\varphi \in \operatorname { {Irr}}(G)}{\varphi }(\mathord {\underline {\mathsf {1}}_{}})^2 =l+4m$
. Since
${\lvert G \rvert }=\sum _{\varphi \in \operatorname { {Irr}}(G)}{\varphi }(\mathord {\underline {\mathsf {1}}_{}})^2 =l+4m$
. Since
![]() ${\lvert G' \rvert }=2$
, we have
${\lvert G' \rvert }=2$
, we have
![]() ${\lvert G \rvert }=2l$
, and so
${\lvert G \rvert }=2l$
, and so
![]() $l=4m$
. Moreover,
$l=4m$
. Moreover,
![]() ${\lvert G \rvert }= s+2n$
, while
${\lvert G \rvert }= s+2n$
, while
![]() $s+n=l+m$
since the character table is square. Therefore,
$s+n=l+m$
since the character table is square. Therefore,
Solving for s and n yields
![]() $s=2m$
and
$s=2m$
and
![]() $n=3m$
. In particular, we conclude that
$n=3m$
. In particular, we conclude that
Conversely, suppose that
![]() ${\lvert G:Z(G) \rvert }=4$
. The argument that follows is essentially the same as in [Reference Choi3], but we include the details for the sake of completeness.
${\lvert G:Z(G) \rvert }=4$
. The argument that follows is essentially the same as in [Reference Choi3], but we include the details for the sake of completeness.
Note that
![]() $G/Z(G)$
cannot be cyclic (otherwise, by lifting the generator, we would find that G is abelian) and hence it is isomorphic to
$G/Z(G)$
cannot be cyclic (otherwise, by lifting the generator, we would find that G is abelian) and hence it is isomorphic to
![]() $C_2\times C_2$
. Pick two generators for
$C_2\times C_2$
. Pick two generators for
![]() $G/Z(G)$
and lift them to
$G/Z(G)$
and lift them to
![]() $x,y\in G$
. Then,
$x,y\in G$
. Then,
![]() $x^2$
,
$x^2$
,
![]() $y^2$
and
$y^2$
and
![]() $[x,y]$
all belong to
$[x,y]$
all belong to
![]() $Z(G)$
. Since
$Z(G)$
. Since
![]() $G= Z(G) \cup xZ(G) \cup yZ(G) \cup xy Z(G)$
, a short case-by-case analysis shows that every commutator in G equals either
$G= Z(G) \cup xZ(G) \cup yZ(G) \cup xy Z(G)$
, a short case-by-case analysis shows that every commutator in G equals either
![]() $\mathord {\underline {\mathsf {1}}_{}}$
or
$\mathord {\underline {\mathsf {1}}_{}}$
or
![]() $[x,y]$
. In particular,
$[x,y]$
. In particular,
![]() ${\lvert G' \rvert }=2$
.
${\lvert G' \rvert }=2$
.
Moreover,
![]() $A=Z(G)\cup x Z(G)$
is an abelian subgroup of G with index
$A=Z(G)\cup x Z(G)$
is an abelian subgroup of G with index
![]() $2$
. Hence, as shown in the proof of Lemma 3.8,
$2$
. Hence, as shown in the proof of Lemma 3.8,
![]() $\operatorname { {cd}}(G)\subseteq \{1,2\}$
. Since G is nonabelian, this inclusion of sets is an equality.
$\operatorname { {cd}}(G)\subseteq \{1,2\}$
. Since G is nonabelian, this inclusion of sets is an equality.
A.2 A self-contained proof of Lemma 2.5
We give a proof of Lemma 2.5, which works even for infinite groups. Thus, for this subsection only, we let G be a not-necessarily-finite group and we suppose that
![]() ${\lvert G' \rvert }=2$
.
${\lvert G' \rvert }=2$
.
Let
![]() $\pi $
be a finite-dimensional, unitary, irreducible representation of G with dimension
$\pi $
be a finite-dimensional, unitary, irreducible representation of G with dimension
![]() $d\geq 2$
. (When G is finite, every irreducible representation of G is automatically finite-dimensional and is equivalent to a unitary representation.) Our aim is to show that d is even.
$d\geq 2$
. (When G is finite, every irreducible representation of G is automatically finite-dimensional and is equivalent to a unitary representation.) Our aim is to show that d is even.
Lemma A.1. Let
![]() $G'=\{\mathord {\underline {\mathsf {1}}_{}},z\}$
. Then,
$G'=\{\mathord {\underline {\mathsf {1}}_{}},z\}$
. Then,
![]() $z\in Z(G)$
.
$z\in Z(G)$
.
Proof. If
![]() $\alpha \in \operatorname {Aut}(G)$
, then
$\alpha \in \operatorname {Aut}(G)$
, then
![]() $\alpha (G')=G'$
and
$\alpha (G')=G'$
and
![]() $\alpha '(\mathord {\underline {\mathsf {1}}_{}})=\mathord {\underline {\mathsf {1}}_{}}$
, and hence
$\alpha '(\mathord {\underline {\mathsf {1}}_{}})=\mathord {\underline {\mathsf {1}}_{}}$
, and hence
![]() $\alpha (z)=z$
. Now take
$\alpha (z)=z$
. Now take
![]() $\alpha $
to be an arbitrary inner automorphism of G.
$\alpha $
to be an arbitrary inner automorphism of G.
Lemma A.2. Let
![]() $g\in G$
. Then,
$g\in G$
. Then,
![]() $g^2\in Z(G)$
.
$g^2\in Z(G)$
.
Proof. Let
![]() $g,x\in G$
. Then,
$g,x\in G$
. Then,
![]() $gxg^{-1}=[g,x]x$
. Since
$gxg^{-1}=[g,x]x$
. Since
![]() $[g,x]$
is central (by Lemma A.1) and
$[g,x]$
is central (by Lemma A.1) and
![]() $[g,x]^2=\mathord {\underline {\mathsf {1}}_{}}$
,
$[g,x]^2=\mathord {\underline {\mathsf {1}}_{}}$
,
Thus,
![]() $g^2$
is central.
$g^2$
is central.
Proof that d is even.
Recall that every nontrivial commutator in G is equal to z. Since
![]() $\pi $
is irreducible and
$\pi $
is irreducible and
![]() $d\geq 2$
,
$d\geq 2$
,
![]() $\pi (G)$
is not abelian, and hence
$\pi (G)$
is not abelian, and hence
![]() $\pi (z)\neq I_\pi $
. By Lemma A.1 and Schur’s lemma,
$\pi (z)\neq I_\pi $
. By Lemma A.1 and Schur’s lemma,
![]() $\pi (z)$
is a scalar multiple of
$\pi (z)$
is a scalar multiple of
![]() $I_\pi $
; since
$I_\pi $
; since
![]() $z^2=\mathord {\underline {\mathsf {1}}_{}}$
, it follows that
$z^2=\mathord {\underline {\mathsf {1}}_{}}$
, it follows that
![]() $\pi (z)=-I_\pi $
.
$\pi (z)=-I_\pi $
.
Since G is nonabelian, there exist
![]() $x,y\in G$
that do not commute. Since
$x,y\in G$
that do not commute. Since
![]() $xyx^{-1}=zy$
, we have
$xyx^{-1}=zy$
, we have
![]() $\pi (x)\pi (y)\pi (x)^{-1}=-\pi (y)$
. However, by Lemma A.2 and Schur’s lemma,
$\pi (x)\pi (y)\pi (x)^{-1}=-\pi (y)$
. However, by Lemma A.2 and Schur’s lemma,
![]() $\pi (y^2)$
is a scalar multiple of
$\pi (y^2)$
is a scalar multiple of
![]() $I_\pi $
. Pick
$I_\pi $
. Pick
![]() $\lambda \in {\mathbb T}$
such that
$\lambda \in {\mathbb T}$
such that
![]() $\pi (y)^2=\lambda ^2 I_\pi $
; then
$\pi (y)^2=\lambda ^2 I_\pi $
; then
![]() $U:=\lambda ^{-1}\pi (y)$
is an involution in
$U:=\lambda ^{-1}\pi (y)$
is an involution in
![]() $\operatorname {Lin}(H_\pi )$
and U is conjugate to
$\operatorname {Lin}(H_\pi )$
and U is conjugate to
![]() $-U$
.
$-U$
.
Since U is an involution, it has exactly d eigenvalues counted with multiplicity, and these eigenvalues belong to
![]() $\{-1,1\}$
; moreover, since U is conjugate to
$\{-1,1\}$
; moreover, since U is conjugate to
![]() $-U$
, the eigenvalues
$-U$
, the eigenvalues
![]() $-1$
and
$-1$
and
![]() $1$
must occur with equal multiplicity, m say. Thus,
$1$
must occur with equal multiplicity, m say. Thus,
![]() $d=2m$
. (Alternatively, observe that
$d=2m$
. (Alternatively, observe that
![]() $\tfrac 12(I_d+U)$
is an idempotent that has trace equal to
$\tfrac 12(I_d+U)$
is an idempotent that has trace equal to
![]() ${d}/{2}$
, which again forces d to be even.)
${d}/{2}$
, which again forces d to be even.)
A.3 A proof of Lemma 5.4 with
 $\delta _0= 1/20$
$\delta _0= 1/20$
We follow the general strategy seen in the proofs of [Reference Tong-Viet13, Lemma 2.3] and [Reference Guralnick and Robinson6, Theorem 11]. Suppose that S is simple and nonabelian. Writing m for
![]() $\operatorname { {mindeg}}(S)$
,
$\operatorname { {mindeg}}(S)$
,
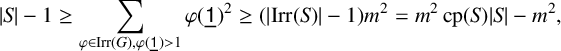 $$ \begin{align*} {\lvert S \rvert} -1 \geq \sum_{\varphi\in\operatorname{{Irr}}(G), {\varphi}(\mathord{\underline{\mathsf{1}}_{}})>1} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 \geq ({\lvert \operatorname{{Irr}}(S) \rvert}-1)m^2 = m^2\operatorname{{cp}}(S){\lvert S \rvert}- m^2, \end{align*} $$
$$ \begin{align*} {\lvert S \rvert} -1 \geq \sum_{\varphi\in\operatorname{{Irr}}(G), {\varphi}(\mathord{\underline{\mathsf{1}}_{}})>1} {\varphi}(\mathord{\underline{\mathsf{1}}_{}})^2 \geq ({\lvert \operatorname{{Irr}}(S) \rvert}-1)m^2 = m^2\operatorname{{cp}}(S){\lvert S \rvert}- m^2, \end{align*} $$
and rearranging gives
![]() $m^2-1 \geq (m^2\operatorname { {cp}}(S)-1) {\lvert S \rvert }$
. If we are given an explicit
$m^2-1 \geq (m^2\operatorname { {cp}}(S)-1) {\lvert S \rvert }$
. If we are given an explicit
![]() $\delta _0>0$
such that
$\delta _0>0$
such that
![]() $\operatorname { {cp}}(S)>\delta _0$
, it follows that
$\operatorname { {cp}}(S)>\delta _0$
, it follows that
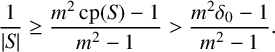 $$ \begin{align} \frac{1}{{\lvert S \rvert}} \geq \frac{m^2\operatorname{{cp}}(S)-1}{m^2-1}> \frac{m^2\delta_0-1}{m^2-1}. \end{align} $$
$$ \begin{align} \frac{1}{{\lvert S \rvert}} \geq \frac{m^2\operatorname{{cp}}(S)-1}{m^2-1}> \frac{m^2\delta_0-1}{m^2-1}. \end{align} $$
Provided that
![]() $m^2\delta _0> 1$
, the inequality (A.1) gives an explicit upper bound on
$m^2\delta _0> 1$
, the inequality (A.1) gives an explicit upper bound on
![]() ${\lvert S \rvert }$
.
${\lvert S \rvert }$
.
Thus, in cases where m is sufficiently large, S belongs to some small list of known examples and, in each case, we can see by inspection that m is actually small (giving a contradiction). Separate ad hoc arguments are then needed to deal with the cases where m is ‘small’.
In [Reference Tong-Viet13, Lemma 2.3], this strategy is used with
![]() $\delta _0 = {16}/{225}$
and so the easy part of the argument works for all
$\delta _0 = {16}/{225}$
and so the easy part of the argument works for all
![]() $m\geq 4$
; the only remaining cases are those with
$m\geq 4$
; the only remaining cases are those with
![]() $m=3$
, and these are covered by the following result.
$m=3$
, and these are covered by the following result.
Theorem A.3 (Blichfeldt, implicitly).
Let S be a finite simple group with an irreducible representation of degree
![]() $3$
. Then,
$3$
. Then,
![]() $S\cong A_5$
or
$S\cong A_5$
or
![]() $S\cong \mathrm {PSL}(2,7)$
.
$S\cong \mathrm {PSL}(2,7)$
.
Inspecting the proof of [Reference Tong-Viet13, Lemma 2.3], the ‘threshold value’ stated there can be improved from
![]() ${16}/{225}$
to
${16}/{225}$
to
![]() ${1}/{15}$
, provided that we know the simple groups of order
${1}/{15}$
, provided that we know the simple groups of order
![]() $\leq 225$
. However, the methods in that paper cannot reach
$\leq 225$
. However, the methods in that paper cannot reach
![]() ${1}/{16}$
(since we require
${1}/{16}$
(since we require
![]() $m^2\delta _0>1$
), and for our eventual application to Proposition 1.6, we require
$m^2\delta _0>1$
), and for our eventual application to Proposition 1.6, we require
![]() $\delta _0\leq {1}/{20}$
. We therefore need the following additional result.
$\delta _0\leq {1}/{20}$
. We therefore need the following additional result.
Theorem A.4 (Blichfeldt, implicitly).
Let S be a finite simple group with an irreducible representation of degree
![]() $4$
. Then,
$4$
. Then,
![]() $S\cong A_5$
.
$S\cong A_5$
.
For the reader who wishes to consult the original papers, we provide some details of how the theorems stated above are derived from the results stated in [Reference Blichfeldt1, Reference Blichfeldt2].
Proofs of Theorem A.3 and A.4.
Let
![]() $d\in \{3,4\}$
and let S be a finite simple group with an irreducible representation of degree d. Then, the image of S under this representation can be identified with a finite subgroup
$d\in \{3,4\}$
and let S be a finite simple group with an irreducible representation of degree d. Then, the image of S under this representation can be identified with a finite subgroup
![]() $\widetilde {S}\leq SU(d)$
that acts irreducibly on
$\widetilde {S}\leq SU(d)$
that acts irreducibly on
![]() $\mathbb C^d$
. Let
$\mathbb C^d$
. Let
![]() $S_0$
be the image of
$S_0$
be the image of
![]() $\widetilde {S}$
in
$\widetilde {S}$
in
![]() $\mathrm {PGL}_d(\mathbb C)$
. Of course,
$\mathrm {PGL}_d(\mathbb C)$
. Of course,
![]() $S\cong \widetilde {S}\cong S_0$
.
$S\cong \widetilde {S}\cong S_0$
.
In the language of [Reference Blichfeldt2, page 553] and [Reference Blichfeldt1, page 205],
![]() $S_0$
is primitive: this follows from the fact that simple groups cannot act nontrivially on sets of size
$S_0$
is primitive: this follows from the fact that simple groups cannot act nontrivially on sets of size
![]() $\leq 4$
, see Lemma 5.5.
$\leq 4$
, see Lemma 5.5.
The case
![]() $d=3$
. The primitive simple finite subgroups of
$d=3$
. The primitive simple finite subgroups of
![]() $\mathrm {PGL}_3(\mathbb C)$
are determined up to isomorphism in [Reference Blichfeldt2, Section 24] (relying on previous work of Maschke): any such subgroup must be isomorphic to
$\mathrm {PGL}_3(\mathbb C)$
are determined up to isomorphism in [Reference Blichfeldt2, Section 24] (relying on previous work of Maschke): any such subgroup must be isomorphic to
![]() $A_5$
,
$A_5$
,
![]() $\mathrm {PSL}(2,7)$
or
$\mathrm {PSL}(2,7)$
or
![]() $A_6$
. Moreover, it is observed that in the last case,
$A_6$
. Moreover, it is observed that in the last case,
![]() $A_6$
cannot be lifted from
$A_6$
cannot be lifted from
![]() $\mathrm {PGL}_3(\mathbb C)$
up to
$\mathrm {PGL}_3(\mathbb C)$
up to
![]() $\mathrm {GL}_3(\mathbb C)$
; thus
$\mathrm {GL}_3(\mathbb C)$
; thus
![]() $\widetilde {S}$
must be isomorphic to either
$\widetilde {S}$
must be isomorphic to either
![]() $A_5$
or
$A_5$
or
![]() $\mathrm {PSL}(2,7)$
, and this completes the proof of Theorem A.3.
$\mathrm {PSL}(2,7)$
, and this completes the proof of Theorem A.3.
The case
![]() $d=4$
. The primitive simple finite subgroups of
$d=4$
. The primitive simple finite subgroups of
![]() $\mathrm {PGL}_4(\mathbb C)$
are determined up to isomorphism in [Reference Blichfeldt1, Section III]; the list appears as items
$\mathrm {PGL}_4(\mathbb C)$
are determined up to isomorphism in [Reference Blichfeldt1, Section III]; the list appears as items
![]() $22^\circ $
–
$22^\circ $
–
![]() $27^\circ $
on pages 225–226 of that paper, and consists (in modern notation) of
$27^\circ $
on pages 225–226 of that paper, and consists (in modern notation) of
![]() $A_5$
,
$A_5$
,
![]() $A_6$
,
$A_6$
,
![]() $A_7$
,
$A_7$
,
![]() $\mathrm {PSL}(2,7)$
and
$\mathrm {PSL}(2,7)$
and
![]() $\mathrm {PSp}(4,3)$
. Blichfeldt does not state for which of these
$\mathrm {PSp}(4,3)$
. Blichfeldt does not state for which of these
![]() $S_0$
the corresponding ‘lift’ in
$S_0$
the corresponding ‘lift’ in
![]() $\mathrm {GL}(4,\mathbb C)$
is simple, but if we invoke known character tables for these groups, then we see that the only possibility for
$\mathrm {GL}(4,\mathbb C)$
is simple, but if we invoke known character tables for these groups, then we see that the only possibility for
![]() $\widetilde {S}$
is
$\widetilde {S}$
is
![]() $A_5$
(none of the others have irreducible representations of degree
$A_5$
(none of the others have irreducible representations of degree
![]() $4$
), and this completes the proof of Theorem A.4.
$4$
), and this completes the proof of Theorem A.4.
Proof of Lemma 5.4 with
 $\delta _0={1}/{20}$
.
$\delta _0={1}/{20}$
.
Let S be nonabelian and simple, and let
![]() $m=\operatorname { {mindeg}}(S)$
. Suppose that
$m=\operatorname { {mindeg}}(S)$
. Suppose that
![]() $\operatorname { {cp}}(S)>{1}/{20}$
. We start by showing that this forces
$\operatorname { {cp}}(S)>{1}/{20}$
. We start by showing that this forces
![]() $m\leq 4$
. For, if
$m\leq 4$
. For, if
![]() $m\geq 5$
, taking
$m\geq 5$
, taking
![]() $\delta _0={1}/{20}$
in (A.1) gives
$\delta _0={1}/{20}$
in (A.1) gives
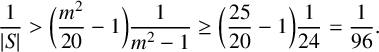 $$ \begin{align*} \frac{1}{{\lvert S \rvert}}> \bigg(\frac{m^2}{20}-1 \bigg) \frac{1}{m^2-1} \geq \bigg(\frac{25}{20}-1\bigg)\frac{1}{24} = \frac{1}{96}. \end{align*} $$
$$ \begin{align*} \frac{1}{{\lvert S \rvert}}> \bigg(\frac{m^2}{20}-1 \bigg) \frac{1}{m^2-1} \geq \bigg(\frac{25}{20}-1\bigg)\frac{1}{24} = \frac{1}{96}. \end{align*} $$
However, up to isomorphism, the only nonabelian simple group of order
![]() $< 96$
is
$< 96$
is
![]() $A_5$
, which we know has
$A_5$
, which we know has
![]() $m=3$
, and this gives a contradiction.
$m=3$
, and this gives a contradiction.
Therefore,
![]() $m\in \{2,3,4\}$
. It is well documented that finite simple groups have no irreducible representations of degree
$m\in \{2,3,4\}$
. It is well documented that finite simple groups have no irreducible representations of degree
![]() $2$
(see for example [Reference James and Liebeck7, Corollary 22.13] for an elementary proof), and it follows from Theorem A.4 that
$2$
(see for example [Reference James and Liebeck7, Corollary 22.13] for an elementary proof), and it follows from Theorem A.4 that
![]() $m\neq 4$
. The only remaining possibility is that
$m\neq 4$
. The only remaining possibility is that
![]() $m=3$
. By Theorem A.3, this implies that
$m=3$
. By Theorem A.3, this implies that
![]() $S\cong A_5$
or
$S\cong A_5$
or
![]() $S\cong \mathrm {PSL}(2,7)$
; and since
$S\cong \mathrm {PSL}(2,7)$
; and since
![]() $\operatorname { {cp}}(\mathrm {PSL}(2,7)) = {1}/{28} < {1}/{20}$
, the second case is ruled out. We conclude that
$\operatorname { {cp}}(\mathrm {PSL}(2,7)) = {1}/{28} < {1}/{20}$
, the second case is ruled out. We conclude that
![]() $S\cong A_5$
, as required.
$S\cong A_5$
, as required.