Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-31T01:51:56.652Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPACTNESS AND STRUCTURE OF ZERO-STATES FOR UNORIENTED AVILES–GIGA FUNCTIONALS

Part of: Variational principles of physics Elliptic equations and systems Equilibrium (steady-state) problems Manifolds Hyperbolic equations and systems Partial differential equations

Published online by Cambridge University Press:  10 March 2023

M. Goldman ,
B. Merlet Open the ORCID record for B. Merlet [Opens in a new window] ,
M. Pegon  and
S. Serfaty
M. Goldman
Affiliation:
Université de Paris and Sorbonne Université, CNRS, LJLL, F-75005 Paris, France (michael.goldman@u-paris.fr)
B. Merlet*
Affiliation:
Univ. Lille, CNRS, UMR 8524, Inria - Laboratoire Paul Painlevé, F-59000 Lille
M. Pegon
Affiliation:
Univ. Lille, CNRS, UMR 8524, Inria - Laboratoire Paul Painlevé, F-59000 Lille (marc.pegon@univ-lille.fr)
S. Serfaty
Affiliation:
Courant Institute of Mathematical Sciences, 251 Mercer St., New York NY 10012, USA (serfaty@cims.nyu.edu)
*
benoit.merlet@univ-lille.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by some models of pattern formation involving an unoriented director field in the plane, we study a family of unoriented counterparts to the Aviles–Giga functional. We introduce a nonlinear 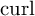$\operatorname {\mathrm {curl}}$ operator for such unoriented vector fields as well as a family of even entropies which we call ‘trigonometric entropies’. Using these tools, we show two main theorems which parallel some results in the literature on the classical Aviles–Giga energy. The first is a compactness result for sequences of configurations with uniformly bounded energies. The second is a complete characterization of zero-states, that is, the limit configurations when the energies go to 0. These are Lipschitz continuous away from a locally finite set of points, near which they form either a vortex pattern or a disclination with degree 1/2. The proof is based on a combination of regularity theory together with techniques coming from the study of the Ginzburg–Landau energy. Our methods provide alternative proofs in the classical Aviles–Giga context.

MSC classification

Primary: 49Q20: Variational problems in a geometric measure-theoretic setting
Secondary: 35B36: Pattern formation 35B65: Smoothness and regularity of solutions 35J60: Nonlinear elliptic equations 35L65: Conservation laws 49S05: Variational principles of physics (should also be assigned at least one other classification number in section 49) 74G65: Energy minimization

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 2 , March 2024 , pp. 941 - 982
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ambrosio, L., De Lellis, C. and Mantegazza, C., ‘Line energies for gradient vector fields in the plane’, Calc. Var. Partial Differential Equations 9(4) (1999), 327–255.CrossRefGoogle Scholar
Ambrosio, L., Fusco, N. and Pallara, D.. Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs (The Clarendon Press, Oxford University Press, New York, 2000).CrossRefGoogle Scholar
Aviles, P. and Giga, Y., ‘A mathematical problem related to the physical theory of liquid crystal configurations’, in Miniconference on Geometry and Partial Differential Equations, 2 (Canberra, 1986), Proc. Centre Math. Anal. Austral. Nat. Univ., vol. 12 (Austral. Nat. Univ., Canberra, 1987), 1–16.Google Scholar
Aviles, P. and Giga, Y., ‘The distance function and defect energy’, Proc. Roy. Soc. Edinburgh Sect. A 126(5) (1996), 923–938.CrossRefGoogle Scholar
Ambrosio, L., Kirchheim, B., Lecumberry, M. and Rivière, T., ‘On the rectifiability of defect measures arising in a micromagnetics model’, in Nonlinear Problems in Mathematical Physics and Related Topics, II, Int. Math. Ser. vol. 2 (Kluwer/Plenum, New York, 2002), 29–60.Google Scholar
Alicandro, R. and Ponsiglione, M., ‘Ginzburg–Landau functionals and renormalized energy: A revised $\varGamma$ -convergence approach’, J. Funct. Anal. 266(8) (2014), 4890–4907.CrossRefGoogle Scholar
Alouges, F., Rivière, T. and Serfaty, S., ‘Néel and cross-tie wall energies for planar micromagnetic configurations’, ESAIM Control Optim. Calc. Var. 8 (2002), 31–68. A tribute to J. L. Lions.CrossRefGoogle Scholar
Bethuel, F., Brezis, H. and Hélein, F., Ginzburg–Landau Vortices, Progress in Nonlinear Differential Equations and their Applications, 13 (Birkhäuser Boston, Inc., Boston, MA, 1994).CrossRefGoogle Scholar
Brezis, H., Mironescu, P. and Ponce, A. C., ‘ ${W}^{1,1}$ -maps with values into ${S}^1$ ’, in Geometric Analysis of PDE and Several Complex Variables, Contemp. Math., vol. 368 (Amer. Math. Soc., Providence, RI, 2005), 69–100.CrossRefGoogle Scholar
Conti, S. and De Lellis, C., ‘Sharp upper bounds for a variational problem with singular perturbation’, Math. Ann. 338(1) (2007), 119–146.CrossRefGoogle Scholar
Demengel, F., ‘Une caractérisation des applications de ${W}^{1,p}\left({B}^N,{S}^1\right)$ qui peuvent être approchées par des fonctions régulières’, C. R. Acad. Sci. Paris Sér. I Math. 310(7) (1990), 553–557.Google Scholar
Dávila, J. and Ignat, R., ‘Lifting of BV functions with values in ${S}^1$ ’, C. R. Math. Acad. Sci. Paris 337(3) (2003), 159–164.CrossRefGoogle Scholar
DeSimone, A., Kohn, R. V., Müller, S., Otto, F. and Schäfer, R., ‘Two-dimensional modelling of soft ferromagnetic films’, R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 457(2016) (2001), 2983–2991.CrossRefGoogle Scholar
DeSimone, A., Kohn, R. V., Müller, S. and Otto, Felix. A compactness result in the gradient theory of phase transitions. Proc. Roy. Soc. Edinburgh Sect. A, 131(4):833–844, 2001.CrossRefGoogle Scholar
Desimone, A., Kohn, R. V., Müller, S. and Otto, F., ‘A reduced theory for thin-film micromagnetics’, Comm. Pure Appl. Math. 55(11) (2002), 1408–1460.CrossRefGoogle Scholar
DeSimone, A., Kohn, R. V., Müller, S. and Otto, F., ‘Recent analytical developments in micromagnetics’, in The Science of Hysteresis, Vol. 2 (Elsevier Academic Press, 2005), 269–381.Google Scholar
De Lellis, C. and Ignat, R., ‘A regularizing property of the $2D$ -eikonal equation’, Comm. Partial Differential Equations 40(8) (2015), 1543–1557.CrossRefGoogle Scholar
De Lellis, C. and Otto, F., ‘Structure of entropy solutions to the eikonal equation’, J. Eur. Math. Soc. (JEMS) 5(2) (2003) 107–145.Google Scholar
Ercolani, N., Indik, R. A., Newell, A. C. and Passot, T., ‘Global description of patterns far from onset: A case study’, Physica D: Nonlinear Phenomena 184(1–4) (2003), 127–140.CrossRefGoogle Scholar
Ercolani, N. and Venkataramani, S. C., ‘A variational theory for point defects in patterns’, J. Nonlinear Sci. 19(3) (2009), 267–300.CrossRefGoogle Scholar
Ghiraldin, F. and Lamy, X., ‘Optimal Besov differentiability for entropy solutions of the eikonal equation’, Comm. Pure Appl. Math. 73(2) (2020), 317–349.CrossRefGoogle Scholar
Goldman, M., Merlet, B. and Millot, V., ‘A Ginzburg–Landau model with topologically induced free discontinuities’, Ann. Inst. Fourier (Grenoble) 70(6) (2020), 2583–2675.CrossRefGoogle Scholar
Ignat, R., ‘Two-dimensional unit-length vector fields of vanishing divergence’, J. Funct. Anal. 262(8) (2012), 3465–3494.CrossRefGoogle Scholar
Ignat, R. and Lamy, X., ‘Lifting of ${\mathbb{RP}}^{d-1}$ -valued maps in $\mathrm{BV}$ . Applications to uniaxial $Q$ -tensors. With an appendix on an intrinsic BV-energy for manifold-valued maps’, Calc. Var. Partial Differential Equations 58(2) (2019), paper no. 68.Google Scholar
Ignat, R. and Merlet, B., ‘Lower bound for the energy of Bloch walls in micromagnetics’, Arch. Ration. Mech. Anal. 199(2) (2011), 369–406.CrossRefGoogle Scholar
Ignat, R. and Merlet, B., ‘Entropy method for line-energies’, Calc. Var. Partial Differential Equations 44(3–4) (2012), 375–418.CrossRefGoogle Scholar
Jin, W. M. and Kohn, R. V., ‘Singular perturbation and the energy of folds’, J. Nonlinear Sci. 10(3) (2000), 355–390.CrossRefGoogle Scholar
Jabin, P.-E., Otto, F. and Perthame, B., ‘Line-energy Ginzburg–Landau models: Zero-energy states’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 1(1) (2002), 187–202.Google Scholar
Jabin, P.-E. and Perthame, B., ‘Compactness in Ginzburg–Landau energy by kinetic averaging’, Comm. Pure Appl. Math. 54(9) (2001), 1096–1109.CrossRefGoogle Scholar
Lamy, X., Lorent, A. and Peng, G., ‘Rigidity of a non-elliptic differential inclusion related to the Aviles–Giga conjecture’, Arch. Ration. Mech. Anal. 238(1) (2020), 383–413.CrossRefGoogle Scholar
Lorent, A., ‘A quantitative characterisation of functions with low Aviles Giga energy on convex domains’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 13(1) (2014), 1–66.Google Scholar
Lorent, A. and Peng, G., ‘Regularity of the eikonal equation with two vanishing entropies’, Ann. Inst. H. Poincaré Anal. Non Linéaire 35(2) (2018), 481–516.CrossRefGoogle Scholar
Lorent, A. and Peng, G., ‘Factorization for entropy production of the eikonal equation and regularity’ (2021). arXiv:2104.01467.Google Scholar
Marconi, E., ‘Rectifiability of entropy defect measures in a micromagnetics model’, Adv. Calc. Var. 16(1) (2023), 233–257.CrossRefGoogle Scholar
Marconi, E., ‘Characterization of minimizers of Aviles–Giga functionals in special domains’, Arch. Ration. Mech. Anal. 242(2) (2021), 1289–1316.CrossRefGoogle Scholar
Merlet, B., ‘Two remarks on liftings of maps with values into ${S}^1$ ’, C. R. Math. Acad. Sci. Paris 343(7) (2006), 467–472.CrossRefGoogle Scholar
Merlet, B. and Serfaty, S., In preparation.Google Scholar
Müller, S., ‘Variational models for microstructure and phase transitions’, in Calculus of Variations and Geometric Evolution Problems (Cetraro, 1996), Lecture Notes in Math., vol. 1713 (Springer, Berlin, 1999), 85–210.CrossRefGoogle Scholar
Murat, F., ‘Compacité par compensation’, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 5(3) (1978), 489–507, 1978.Google Scholar
Murat, F., ‘L’injection du cône positif de ${H}^{-1}$ dans ${W}^{-1,q}$ est compacte pour tout $q<2$ ’, J. Math. Pures Appl. (9) 60(3) (1981), 309–322.Google Scholar
Poliakovsky, A., ‘Upper bounds for singular perturbation problems involving gradient fields’, J. Eur. Math. Soc. (JEMS) 9(1) (2007), 1–43.CrossRefGoogle Scholar
Rivière, T. and Serfaty, S., ‘Limiting domain wall energy for a problem related to micromagnetics’, Comm. Pure Appl. Math. 54(3) (2001), 294–338.3.0.CO;2-S>CrossRefGoogle Scholar
Sandier, E. and Serfaty, S., Vortices in the Magnetic Ginzburg–Landau Model, Progress in Nonlinear Differential Equations and their Applications, vol. 70 (Birkhäuser Boston, Inc., Boston, MA, 2007).CrossRefGoogle Scholar
Tartar, L., ‘Compensated compactness and applications to partial differential equations’, in Nonlinear Analysis and Mechanics: Heriot–Watt Symposium, Vol. IV, Res. Notes in Math., vol. 39 (Pitman, Boston, MA, 1979), 136–212.Google Scholar
Šverák, V., ‘On Tartar’s conjecture’, Ann. Inst. H. Poincaré Anal. Non Linéaire 10(4) (1993), 405–412.CrossRefGoogle Scholar
Zhang, C., Acharya, A., Newell, A. C. and Venkataramani, S. C. ‘Computing with non-orientable defects: Nematics, smectics and natural patterns’, Physica D: Nonlinear Phenomena 417 (2021), 132828.CrossRefGoogle Scholar