Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T16:36:42.559Z Has data issue: false hasContentIssue false
  • English
  • Français

DERIVED NON-ARCHIMEDEAN ANALYTIC HILBERT SPACE

Part of: Algebraic geometry: Foundations Arithmetic problems. Diophantine geometry Special categories Categories and geometry

Published online by Cambridge University Press:  26 August 2020

Jorge António Open the ORCID record for Jorge António [Opens in a new window]  and
Mauro Porta
Jorge António
Affiliation:
Institut de Mathématiques de Toulouse, 118 Rue de Narbonne, 31400 Toulouse, France (jorge_tiago.ferrera_antonio@math.univ-toulouse.fr)
Mauro Porta
Affiliation:
Institut de Recherche Mathématique Avancée, 7 Rue René Descartes,67000 Strasbourg, France (porta@math.unistra.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this short paper, we combine the representability theorem introduced in [Porta and Yu, Representability theorem in derived analytic geometry, preprint, 2017, arXiv:1704.01683; Porta and Yu, Derived Hom spaces in rigid analytic geometry, preprint, 2018, arXiv:1801.07730] with the theory of derived formal models introduced in [António, 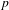$p$-adic derived formal geometry and derived Raynaud localization theorem, preprint, 2018, arXiv:1805.03302] to prove the existence representability of the derived Hilbert space 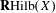$\mathbf{R}\text{Hilb}(X)$ for a separated 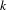$k$-analytic space 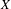$X$. Such representability results rely on a localization theorem stating that if 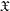$\mathfrak{X}$ is a quasi-compact and quasi-separated formal scheme, then the 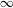$\infty$-category 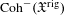$\text{Coh}^{-}(\mathfrak{X}^{\text{rig}})$ of almost perfect complexes over the generic fiber can be realized as a Verdier quotient of the 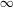$\infty$-category 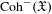$\text{Coh}^{-}(\mathfrak{X})$. Along the way, we prove several results concerning the 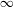$\infty$-categories of formal models for almost perfect modules on derived 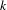$k$-analytic spaces.

Keywords

derived geometryrigid geometryHilbert schemeformal modelsderived generic fiber

MSC classification

Primary: 14G22: Rigid analytic geometry
Secondary: 14A20: Generalizations (algebraic spaces, stacks) 18B25: Topoi 18F99: None of the above, but in this section

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 1 , January 2022 , pp. 335 - 366
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

António, J., Moduli of $p$ -adic representations of a profinite group, preprint, 2017, arXiv:1709.04275.Google Scholar
António, J., $p$ -adic derived formal geometry and derived Raynaud localization theorem, preprint, 2018, arXiv:1805.03302.Google Scholar
António, J., Moduli of $\ell$ -adic pro-étale local systems for smooth non-proper schemes, preprint, 2019, arXiv:1904.08001.Google Scholar
Bosch, S., Lectures on Formal and Rigid Geometry, Lecture Notes in Mathematics, (Springer International Publishing, 2014). ISBN: 978-3-319-04416-3; 978-3-319-04417-0.CrossRefGoogle Scholar
Bosch, S. and Lütkebohmert, W., Formal and rigid geometry. II. Flattening techniques, Math. Ann. 296(3) (1993), 403–429.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Formal and rigid geometry. IV. The reduced fibre theorem, Invent. Math. 119(2) (1995), 361–398.CrossRefGoogle Scholar
Conrad, B. and Gabber, O., Spreading-out for rigid-analytic families, preprint, 2016.Google Scholar
Hennion, B., Porta, M. and Vezzosi, G., Formal gluing along non-linear flags, preprint, 2016, arXiv:1607.04503.Google Scholar
Lurie, J., Spectral algebraic geometry, available at http://www.math.harvard.edu/∼lurie/papers/SAG-rootfile.pdf, 2018.Google Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, Volume 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
Lurie, J., DAG IX: Closed immersions, preprint, 2011.Google Scholar
Lurie, J., DAG V: Structured spaces, preprint, 2011.Google Scholar
Lurie, J., DAG VII: Spectral schemes, preprint, 2011.Google Scholar
Porta, M. and Yu, T. Y., Derived non-archimedean analytic spaces, preprint, 2016, arXiv:1601.00859. To appear in Selecta Mathematica:MR 3782411.Google Scholar
Porta, M. and Yu, T. Y., Higher analytic stacks and GAGA theorems, Adv. Math. 302 (2016), 351–409.CrossRefGoogle Scholar
Porta, M. and Yu., T. Y., Representability theorem in derived analytic geometry, preprint, 2017, arXiv:1704.01683. To appear in J. Eur. Math. Soc.Google Scholar
Porta, M. and Yu, T. Y., Derived Hom spaces in rigid analytic geometry, preprint, 2018, arXiv:1801.07730.Google Scholar