Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T03:46:17.692Z Has data issue: false hasContentIssue false
  • English
  • Français

MOMENTS AND HYBRID SUBCONVEXITY FOR SYMMETRIC-SQUARE L-FUNCTIONS

Part of: Discontinuous groups and automorphic forms Zeta and $L$-functions: analytic theory Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  06 December 2021

Rizwanur Khan Open the ORCID record for Rizwanur Khan [Opens in a new window]  and
Matthew P. Young
Rizwanur Khan*
Affiliation:
Department of Mathematics, University of Mississippi, University, MS 38677
Matthew P. Young
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843-3368 (myoung@math.tamu.edu)
*
rrkhan@olemiss.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish sharp bounds for the second moment of symmetric-square L-functions attached to Hecke Maass cusp forms 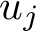$u_j$ with spectral parameter 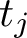$t_j$, where the second moment is a sum over 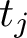$t_j$ in a short interval. At the central point 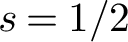$s=1/2$ of the L-function, our interval is smaller than previous known results. More specifically, for 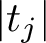$\left \lvert t_j\right \rvert $ of size T, our interval is of size 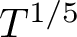$T^{1/5}$, whereas the previous best was 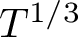$T^{1/3}$, from work of Lam. A little higher up on the critical line, our second moment yields a subconvexity bound for the symmetric-square L-function. More specifically, we get subconvexity at 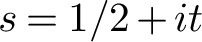$s=1/2+it$ provided 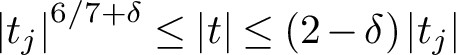$\left \lvert t_j\right \rvert ^{6/7+\delta }\le \lvert t\rvert \le (2-\delta )\left \lvert t_j\right \rvert $ for any fixed 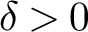$\delta>0$. Since 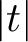$\lvert t\rvert $ can be taken significantly smaller than 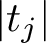$\left \lvert t_j\right \rvert $, this may be viewed as an approximation to the notorious subconvexity problem for the symmetric-square L-function in the spectral aspect at 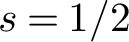$s=1/2$.

Keywords

L-functionssymmetric-squaremomentssubconvexityMaass formsquantum unique ergodicity

MSC classification

Primary: 11M41: Other Dirichlet series and zeta functions 11F12: Automorphic forms, one variable
Secondary: 58J51: Relations between spectral theory and ergodic theory, e.g. quantum unique ergodicity

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 5 , September 2023 , pp. 2029 - 2073
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Balkanova, O., The first moment of Maass form symmetric square $L$ -functions, Ramanujan J. 55(2) (2021), 761—781.CrossRefGoogle Scholar
Balkanova, O. and Frolenkov, D., The mean value of symmetric square $L$ -functions, Algebra Number Theory 12(1) (2018), 35–59.CrossRefGoogle Scholar
Blomer, V., On the central value of symmetric square L-functions, Math. Z. 260(4) (2008), 755–777.CrossRefGoogle Scholar
Blomer, V., Sums of Hecke eigenvalues over values of quadratic polynomials, Int. Math. Res. Not. IMRN 2008(16) (2008) 1–29.CrossRefGoogle Scholar
Blomer, V. and Buttcane, J., On the subconvexity problem for L-functions on $\mathrm{GL}(3)$ , Ann. Sci. Éc. Norm. Supér. (4) 53(6) (2020), 1441–1500.CrossRefGoogle Scholar
Blomer, V. and Harcos, G., Hybrid bounds for twisted L-functions, J. Reine Angew. Math. 621 (2008), 53–79.Google Scholar
Blomer, V., Humphries, P., Khan, R. and Milinovich, M., Motohashi’s fourth moment identity for non-archimedean test functions and applications, Compos. Math. 156(5) (2020), 1004–1038.CrossRefGoogle Scholar
Blomer, V., Khan, R. and Young, M., Distribution of mass of holomorphic cusp forms, Duke Math. J. 162(14) (2013), 2609–2644.10.1215/00127094-2380967CrossRefGoogle Scholar
Bourgain, J., Decoupling, exponential sums and the Riemann zeta function, J. Amer. Math. Soc. 30(1) (2017), 205–224.CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, 7th ed. (Elsevier/Academic Press, Amsterdam, 2007). Translation edited by Jeffrey, A. and Zwillinger, D..Google Scholar
Harcos, G. and Michel, P., The subconvexity problem for Rankin-Selberg L-functions and equidistribution of Heegner points, II, Invent. Math. 163(3) (2006), 581–655.CrossRefGoogle Scholar
Heath-Brown, D. R., A mean value estimate for real character sums, Acta Arith. 72(3) (1995), 235–275.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Iwaniec, H. and Michel, P., The second moment of the symmetric square L-functions, Ann. Acad. Sci. Fenn. Math. 26(2) (2001), 465–482.Google Scholar
Iwaniec, H. and Sarnak, P., Perspectives on the analytic theory of L-functions, Geom. Funct. Anal. Special Volume Part II 2000, 705–741.Google Scholar
Jung, J., Quantitative quantum ergodicity and the nodal domains of Hecke-Maass cusp forms, Comm. Math. Phys. 348(2) (2016), 603–653.CrossRefGoogle Scholar
Jutila, M. and Motohashi, Y., Uniform bound for Hecke L-functions, Acta Math. 195 (2005), 61–115.CrossRefGoogle Scholar
Khan, R., Non-vanishing of the symmetric square L-function at the central point, Proc. Lond. Math. Soc. (3) 100(3) (2010), 736–762.CrossRefGoogle Scholar
Khan, R. and Das, S., The third moment of symmetric square L-functions, Q. J. Math. 69(3) (2018), 1063–1087.Google Scholar
Kıral, E., Petrow, I. and Young, M., Oscillatory integrals with uniformity in parameters, J. Théor. Nombres Bordeaux 31(1) (2019), 145–159.CrossRefGoogle Scholar
Kumar, S., Mallesham, K. and Singh, S. K., ‘Sub-convexity bound for $\mathrm{GL}(3)\times \mathrm{GL}(2)$ L-functions: $\mathrm{GL}(3)$ -spectral aspect’, Preprint, 2020, arXiv:2006.07819.Google Scholar
Lam, J. W. C., The second moment of the central values of the symmetric square L-functions, Ramanujan J. 38(1) (2015), 129–145.CrossRefGoogle Scholar
Li, X., Bounds for $\mathrm{GL}(3)\times \mathrm{GL}(2)$ L-functions and $\mathrm{GL}(3)$ L-functions, Ann. of Math. (2) 173(1) (2011), 301–336.CrossRefGoogle Scholar
Lindenstrauss, E., Invariant measures and arithmetic quantum unique ergodicity, Ann. of Math. (2) 163(1) (2006), 165–219.CrossRefGoogle Scholar
Michel, P. and Venkatesh, A., The subconvexity problem for $G{L}_2$ , Publ. Math. Inst. Hautes Études Sci. 111 (2010), 171–271.CrossRefGoogle Scholar
Munshi, R., The circle method and bounds for L-functions—III: t-aspect subconvexity for $\mathrm{GL}(3)$ L-functions, J. Amer. Math. Soc. 28(4) (2015), 913–938.CrossRefGoogle Scholar
Munshi, R., The circle method and bounds for L-functions—IV: Subconvexity for twists of $\mathrm{GL}(3)$ L-functions, Ann. of Math. (2) 182(2) (2015), 617–672.CrossRefGoogle Scholar
Nelson, P. D., Bounds for twisted symmetric square $L$ -functions via half-integral weight periods, Forum Math. Sigma 8(e44) (2020), 21 pp.10.1017/fms.2020.33CrossRefGoogle Scholar
Petrow, I. and Young, M. P., The Weyl bound for Dirichlet L-functions of cube-free conductor, Ann. of Math. (2) 192(2) (2020), 437–486.CrossRefGoogle Scholar
Sharma, P., ‘Subconvexity for $\mathrm{GL}(3)\times \mathrm{GL}(2)\ L$ -functions in $\mathrm{GL}(3)$ spectral aspect, Preprint, 2020, arXiv:2010.10153.Google Scholar
Soudry, D., On Langlands functoriality from classical groups to $G{L}_n$ , Astérisque 298 (2005), 335–390.Google Scholar
Soundararajan, K., Invariant measures and arithmetic quantum unique ergodicity, Ann. of Math. (2) 172(3) (2010), 1529–1538.CrossRefGoogle Scholar
Watson, T. C., Rankin Triple Products and Quantum Chaos , Ph.D. thesis, Princeton University, 2002.Google Scholar