1. Problem, conjecture and results
In a recent paper [Reference Gan, Gross and PrasadGGP23], a twisted version of the Gan–Gross–Prasad (GGP) conjecture was formulated in the context of skew-Hermitian spaces and their associated unitary groups over local and global fields. Some evidence was provided in [Reference Gan, Gross and PrasadGGP23] for the local twisted conjecture, such as in low rank situations and for unitary principal series representations. The purpose of this paper is to provide further affirmative evidence by establishing the local conjecture for a family of tempered L-packets of unitary groups using the technique of theta correspondence. Let us recall the setup and conjecture of [Reference Gan, Gross and PrasadGGP23] in greater precision and formulate our main result.
1.1. Biquadratic extension
Let F be a non-Archimedean local field of characteristic
![]() $0$
and
$0$
and
![]() $E \neq K$
two distinct quadratic field extensions of F. Let
$E \neq K$
two distinct quadratic field extensions of F. Let
![]() $L=E \otimes _F K$
so that L is a biquadratic extension of F. We thus have the picture:
$L=E \otimes _F K$
so that L is a biquadratic extension of F. We thus have the picture:
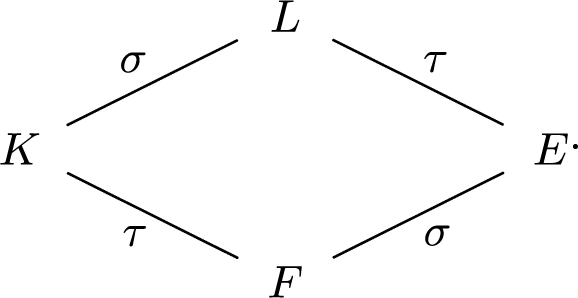
In particular, we have set:
We also fix a nontrivial additive character
![]() $\psi _F$
of F and set
$\psi _F$
of F and set
![]() $\psi _K=\psi _F\circ \operatorname {Tr}_{K/F}$
. In this paper, when we talk about Weil representations or theta correspondence, we always use the additive character
$\psi _K=\psi _F\circ \operatorname {Tr}_{K/F}$
. In this paper, when we talk about Weil representations or theta correspondence, we always use the additive character
![]() $\psi _F$
or
$\psi _F$
or
![]() $\psi _K$
(see Section 2.1).
$\psi _K$
(see Section 2.1).
1.2. Skew-Hermitian spaces
Let V be an n-dimensional skew-Hermitian space over E. There are exactly two such spaces, which are distinguished by their sign
where
![]() $\mathrm {disc} V=(-1)^{n(n-1)/2}\cdot \det V$
, and
$\mathrm {disc} V=(-1)^{n(n-1)/2}\cdot \det V$
, and
![]() $\delta $
is a fixed trace zero element in
$\delta $
is a fixed trace zero element in
![]() $E^\times $
. As observed in [Reference Gan, Gross and PrasadGGP23, Lem. 8.1], the scalar extension
$E^\times $
. As observed in [Reference Gan, Gross and PrasadGGP23, Lem. 8.1], the scalar extension
![]() $V_K = V \otimes _F K$
is a distinguished split skew-Hermitian space over L whose isomorphism class is independent of the choice of V. In particular, if we continue to use the trace zero element
$V_K = V \otimes _F K$
is a distinguished split skew-Hermitian space over L whose isomorphism class is independent of the choice of V. In particular, if we continue to use the trace zero element
![]() $\delta \in L^\times $
to define the sign of
$\delta \in L^\times $
to define the sign of
![]() $V_K$
, then we always have
$V_K$
, then we always have
![]() $\epsilon (V_K)=+1$
.
$\epsilon (V_K)=+1$
.
1.3. Twisted GGP problem
We come now to the restriction problem to be studied. For the skew-Hermitian space V over E, we have the Weil representation
![]() $\omega _{V,\mu }$
, where
$\omega _{V,\mu }$
, where
![]() $\mu $
is a conjugate-symplectic character of
$\mu $
is a conjugate-symplectic character of
![]() $E^\times $
. Then we are interested in determining
$E^\times $
. Then we are interested in determining
Here is the main local conjecture for the twisted GGP problem:
Conjecture 1.1.
-
(1) For each
 $\pi \in \operatorname {Irr}\left (\operatorname {U}(V_K)\right )$
,
$\pi \in \operatorname {Irr}\left (\operatorname {U}(V_K)\right )$
,
 $m_{V}(\pi ,\mu ) \leq 1$
.
$m_{V}(\pi ,\mu ) \leq 1$
. -
(2) Let M be a generic L-parameter of
 $\operatorname {U}(V_K)$
with associated L-packet
$\operatorname {U}(V_K)$
with associated L-packet
 $\Pi _M$
. Then where the first sum runs over the two skew-Hermitian spaces over E of dimension n, and the second runs over the L-packet
$\Pi _M$
. Then where the first sum runs over the two skew-Hermitian spaces over E of dimension n, and the second runs over the L-packet $$\begin{align*}\sum_V \sum_{\pi\in\Pi_M} m_{V}(\pi,\mu) =1, \end{align*}$$
$$\begin{align*}\sum_V \sum_{\pi\in\Pi_M} m_{V}(\pi,\mu) =1, \end{align*}$$
 $\Pi _M$
.
$\Pi _M$
.
-
(3) The unique
 $V_0$
which has nonzero contribution to the sum in
$V_0$
which has nonzero contribution to the sum in
 $(2)$
is characterized by where
$(2)$
is characterized by where $$\begin{align*}\epsilon(V_0)=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}(M)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n-1)/2}, \end{align*}$$
$$\begin{align*}\epsilon(V_0)=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}(M)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n-1)/2}, \end{align*}$$
 $\delta$
is the fixed trace zero element in
$\delta$
is the fixed trace zero element in
 $E^\times$
(used in the definition of
$E^\times$
(used in the definition of
 $\epsilon (V_0)$
), and
$\epsilon (V_0)$
), and
 $\psi _{E,\delta }=\psi _F(\operatorname {Tr}_{E/F}(\delta \cdot ~))$
.
$\psi _{E,\delta }=\psi _F(\operatorname {Tr}_{E/F}(\delta \cdot ~))$
.
-
(4) The unique
 $\pi \in \Pi _M$
which has nonzero contribution to the sum in
$\pi \in \Pi _M$
which has nonzero contribution to the sum in
 $(2)$
corresponds via local Langlands correspondence (LLC) (with respect to the Whittaker datum of
$(2)$
corresponds via local Langlands correspondence (LLC) (with respect to the Whittaker datum of
 $\operatorname {U}(V_K)$
associated to
$\operatorname {U}(V_K)$
associated to
 $\psi _K$
) to the character of local component group
$\psi _K$
) to the character of local component group
 $A_M=\prod _{i\in I}\mathbb {Z}/2\mathbb {Z}\cdot a_i$
given by where
$A_M=\prod _{i\in I}\mathbb {Z}/2\mathbb {Z}\cdot a_i$
given by where $$ \begin{align*}\eta(a_i) &= \epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_i \otimes (M/M_i)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\\ &= \epsilon\left(\frac{1}{2}, [\operatorname{As}(M_i)+\operatorname{As}(M)+\operatorname{As}(M/M_i)]\cdot\mu^{-1}, \psi_{E,\delta}\right), \end{align*} $$
$$ \begin{align*}\eta(a_i) &= \epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_i \otimes (M/M_i)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\\ &= \epsilon\left(\frac{1}{2}, [\operatorname{As}(M_i)+\operatorname{As}(M)+\operatorname{As}(M/M_i)]\cdot\mu^{-1}, \psi_{E,\delta}\right), \end{align*} $$
 $M_i$
is the irreducible constituent of M corresponding to
$M_i$
is the irreducible constituent of M corresponding to
 $a_i\in A_M$
.
$a_i\in A_M$
.
We remark that [Reference Gan, Gross and PrasadGGP23] also formulated a conjecture in the case
![]() $E = K$
and showed that, in this case, the conjecture can be reduced to the case of discrete series representations of
$E = K$
and showed that, in this case, the conjecture can be reduced to the case of discrete series representations of
![]() $\operatorname {U}(V_K) \simeq \operatorname {GL}(V)$
. However, we do not deal with the case
$\operatorname {U}(V_K) \simeq \operatorname {GL}(V)$
. However, we do not deal with the case
![]() $E = K$
in this paper.
$E = K$
in this paper.
In [Reference Gan, Gross and PrasadGGP23, Sect. 9 & 10], the three authors have proved that:
1.4. Main result
Our main result is the following theorem.
Theorem 1.3. Let M be a tempered L-parameter for
![]() $\operatorname {U}(V_K)$
of the form
$\operatorname {U}(V_K)$
of the form
with each
![]() $M_i$
one-dimensional and conjugate self-dual of parity
$M_i$
one-dimensional and conjugate self-dual of parity
![]() $(-1)^{n-1}$
. Then Conjecture 1.1 holds for M.
$(-1)^{n-1}$
. Then Conjecture 1.1 holds for M.
The parity condition on each
![]() $M_i$
is equivalent to requiring that the L-parameter M is of good parity. Note that, though these tempered L-parameters M are maximally reducible and hence not the most general in the p-adic case, they are the ones whose L-packets are of maximal size. Hence, in some sense, they provide the most stringent test for Conjecture 1.1.
$M_i$
is equivalent to requiring that the L-parameter M is of good parity. Note that, though these tempered L-parameters M are maximally reducible and hence not the most general in the p-adic case, they are the ones whose L-packets are of maximal size. Hence, in some sense, they provide the most stringent test for Conjecture 1.1.
Recall that by properties of the LLC, tempered L-packets can be constructed using irreducible parabolic induction from good parity L-packets. An immediate corollary of our result (combining with [Reference Gan, Gross and PrasadGGP23, Thm. 10.1]) is that we may complete Theorem 1.2(2) above:
Corollary 1.4. Conjecture 1.1 holds for the tempered L-packets consisting of the constituents of unitary principal series representations.
1.5. Idea of proof
The main tool for the proof of Theorem 1.3 is the theta correspondence. Using theta correspondence, we shall effectively show that Theorem 1.3 for the case
![]() $\dim V = n+1$
can be reduced to the case for
$\dim V = n+1$
can be reduced to the case for
![]() $\dim V = n$
. In this way, for the type of tempered L-parameters M considered in Theorem 1.3, we may use theta correspondence to successively strip off the irreducible summands
$\dim V = n$
. In this way, for the type of tempered L-parameters M considered in Theorem 1.3, we may use theta correspondence to successively strip off the irreducible summands
![]() $M_i$
one at a time and reduce the conjecture for such M’s to the case when
$M_i$
one at a time and reduce the conjecture for such M’s to the case when
![]() $\dim V = 1$
. In fact, since the conjecture has been shown for
$\dim V = 1$
. In fact, since the conjecture has been shown for
![]() $\dim V \leq 2$
, we could have formulated a slightly more general main result. We content ourselves with just the following corollary:
$\dim V \leq 2$
, we could have formulated a slightly more general main result. We content ourselves with just the following corollary:
Corollary 1.5. Conjecture 1.1 holds for all endoscopic tempered L-packets of
![]() $\operatorname {U}(V_K)$
when
$\operatorname {U}(V_K)$
when
![]() $\dim V = 3$
.
$\dim V = 3$
.
This is because all endoscopic tempered L-packets of
![]() $\operatorname {U}_3$
can be constructed by theta lifting from tempered L-packets of
$\operatorname {U}_3$
can be constructed by theta lifting from tempered L-packets of
![]() $\operatorname {U}_2$
.
$\operatorname {U}_2$
.
The rest of the paper is devoted to the proof of Theorem 1.3. In §2, we study a local theta lift of a Weil representation of a unitary group to the edge of the stable range. The main point here is to show that the resulting big theta lift is irreducible. Then in §3, we show how the conjecture in dimension
![]() $n+1$
can be reduced to that in dimension n by invoking two seesaw arguments. In the proofs, we have made use of the so-called Adams’ conjecture, which describes the theta correspondence in terms of (conjectural) A-packets. But our result is not conditional on the construction of A-packets; we refer the readers to Remark 2.2 for details.
$n+1$
can be reduced to that in dimension n by invoking two seesaw arguments. In the proofs, we have made use of the so-called Adams’ conjecture, which describes the theta correspondence in terms of (conjectural) A-packets. But our result is not conditional on the construction of A-packets; we refer the readers to Remark 2.2 for details.
2. Weil representations
In this section, we examine the Weil representation
![]() $\omega _{V,\mu }$
and investigate its behavior under the theta correspondence.
$\omega _{V,\mu }$
and investigate its behavior under the theta correspondence.
2.1. Local theta correspondence
We first recall the basic setup of the local theta correspondence. Let
![]() $F\subset E$
be a quadratic extension of non-Archimedean local fields, V an skew-Hermitian space of dimension n and W an Hermitian space of dimension m. We shall use the symbol
$F\subset E$
be a quadratic extension of non-Archimedean local fields, V an skew-Hermitian space of dimension n and W an Hermitian space of dimension m. We shall use the symbol
![]() $\mathcal {H}$
(resp.
$\mathcal {H}$
(resp.
![]() $\mathcal {H}'$
) to denote the skew-Hermitian (resp. Hermitian) hyperbolic plane.
$\mathcal {H}'$
) to denote the skew-Hermitian (resp. Hermitian) hyperbolic plane.
To consider the theta correspondence for the reductive dual pair
![]() $\operatorname {U}(V)\times \operatorname {U}(W)$
, one requires some additional data:
$\operatorname {U}(V)\times \operatorname {U}(W)$
, one requires some additional data:
-
• a nontrivial additive character
 $\psi _F$
of F;
$\psi _F$
of F; -
• a pair of characters
 $\chi _V$
and
$\chi _V$
and
 $\chi _W$
of
$\chi _W$
of
 $E^\times $
such that
$E^\times $
such that  $$ \begin{align*} \chi_V\big|_{F^\times}=\omega_{E/F}^{\dim V}\quad\textit{and}\quad\chi_W\big|_{F^\times}=\omega_{E/F}^{\dim W}. \end{align*} $$
$$ \begin{align*} \chi_V\big|_{F^\times}=\omega_{E/F}^{\dim V}\quad\textit{and}\quad\chi_W\big|_{F^\times}=\omega_{E/F}^{\dim W}. \end{align*} $$
To elaborate, the tensor product
![]() $V\otimes W$
has a natural symplectic form, which induces a natural map
$V\otimes W$
has a natural symplectic form, which induces a natural map
One has the metaplectic
![]() $S^1$
-cover
$S^1$
-cover
![]() $\operatorname {Mp}(V\otimes W)$
of
$\operatorname {Mp}(V\otimes W)$
of
![]() $\operatorname {Sp}(V\otimes W)$
, and the character
$\operatorname {Sp}(V\otimes W)$
, and the character
![]() $\psi _F$
determines a Weil representation
$\psi _F$
determines a Weil representation
![]() $\omega _{\psi _F}$
of
$\omega _{\psi _F}$
of
![]() $\operatorname {Mp}(V\otimes W)$
. The datum
$\operatorname {Mp}(V\otimes W)$
. The datum
![]() $(\psi _F,\chi _V,\chi _W)$
then allows one to specify a splitting of the metaplectic cover over
$(\psi _F,\chi _V,\chi _W)$
then allows one to specify a splitting of the metaplectic cover over
![]() $\operatorname {U}(V)\times \operatorname {U}(W)$
following [Reference KudlaKud94]. Hence, we have a Weil representation
$\operatorname {U}(V)\times \operatorname {U}(W)$
following [Reference KudlaKud94]. Hence, we have a Weil representation
![]() $\omega =\omega _{V,W}$
of
$\omega =\omega _{V,W}$
of
![]() $\operatorname {U}(V)\times \operatorname {U}(W)$
.
$\operatorname {U}(V)\times \operatorname {U}(W)$
.
As explicated in [Reference KudlaKud94] and [Reference Harris, Kudla and SweetHKS96], the splitting over
![]() $\operatorname {U}(V)$
is determined by
$\operatorname {U}(V)$
is determined by
![]() $(\psi _F,\chi _W)$
, whereas that of
$(\psi _F,\chi _W)$
, whereas that of
![]() $\operatorname {U}(W)$
by
$\operatorname {U}(W)$
by
![]() $(\psi _F,\chi _V)$
. In particular, taking W such that
$(\psi _F,\chi _V)$
. In particular, taking W such that
![]() $\dim W=1$
and
$\dim W=1$
and
![]() $\chi _W=\mu $
a conjugate symplectic character of
$\chi _W=\mu $
a conjugate symplectic character of
![]() $E^\times $
, one gets a splitting over
$E^\times $
, one gets a splitting over
![]() $\operatorname {U}(V)$
associated to
$\operatorname {U}(V)$
associated to
![]() $(\psi _F,\mu )$
, and thus a Weil representation
$(\psi _F,\mu )$
, and thus a Weil representation
![]() $\omega _{V,\mu }$
of
$\omega _{V,\mu }$
of
![]() $\operatorname {U}(V)$
, which is the one appearing in the main conjecture.
$\operatorname {U}(V)$
, which is the one appearing in the main conjecture.
Given an irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {U}(V)$
, the maximal
$\operatorname {U}(V)$
, the maximal
![]() $\pi $
-isotypic quotient of
$\pi $
-isotypic quotient of
![]() $\omega $
is of the form
$\omega $
is of the form
for some smooth representation
![]() $\Theta (\pi )$
of
$\Theta (\pi )$
of
![]() $\operatorname {U}(W)$
of finite length. By the Howe duality [Reference WaldspurgerWal90] [Reference Gan and TakedaGT16a] [Reference Gan and TakedaGT16b], we have:
$\operatorname {U}(W)$
of finite length. By the Howe duality [Reference WaldspurgerWal90] [Reference Gan and TakedaGT16a] [Reference Gan and TakedaGT16b], we have:
-
• The maximal semisimple quotient
 $\theta (\pi )$
of
$\theta (\pi )$
of
 $\Theta (\pi )$
is irreducible if
$\Theta (\pi )$
is irreducible if
 $\Theta (\pi )$
is nonzero;
$\Theta (\pi )$
is nonzero; -
• If
 $\pi _1\not \simeq \pi _2$
are two nonisomorphic irreducible smooth representations of
$\pi _1\not \simeq \pi _2$
are two nonisomorphic irreducible smooth representations of
 $\operatorname {U}(V)$
such that both
$\operatorname {U}(V)$
such that both
 $\theta (\pi _1)$
and
$\theta (\pi _1)$
and
 $\theta (\pi _2)$
are nonzero, then
$\theta (\pi _2)$
are nonzero, then
 $\theta (\pi _1)\not \simeq \theta (\pi _2)$
.
$\theta (\pi _1)\not \simeq \theta (\pi _2)$
.
2.2. A refinement of Adams’ conjecture
Next, we give a description of the theta correspondence in terms of A-parameters. We fix a nontrivial additive character
![]() $\psi _F$
once and for all. Assume that
$\psi _F$
once and for all. Assume that
Fix a pair of splitting characters
![]() $(\chi _V,\chi _W)$
, and consider the theta correspondence between
$(\chi _V,\chi _W)$
, and consider the theta correspondence between
![]() $\operatorname {U}(V) \times \operatorname {U}(W)$
with respect to it.
$\operatorname {U}(V) \times \operatorname {U}(W)$
with respect to it.
Let
![]() $\Psi $
be a local A-parameter of
$\Psi $
be a local A-parameter of
![]() $\operatorname {U}(V)$
. If we write it as a sum of irreducible subrepresentations
$\operatorname {U}(V)$
. If we write it as a sum of irreducible subrepresentations
we say that
![]() $\Psi $
is of good parity if
$\Psi $
is of good parity if
![]() $\rho _i S_{a_i} \boxtimes S_{b_i}$
is conjugate self-dual of parity
$\rho _i S_{a_i} \boxtimes S_{b_i}$
is conjugate self-dual of parity
![]() $(-1)^{n-1}$
for all i. Here, we are following Atobe–Gan’s notation [Reference Atobe and GanAG17] on irreducible representations of the Weil–Deligne group
$(-1)^{n-1}$
for all i. Here, we are following Atobe–Gan’s notation [Reference Atobe and GanAG17] on irreducible representations of the Weil–Deligne group
![]() $WD_E=W_E\times \operatorname {SL}_2(\mathbb C)$
; we omit the tensor symbol between
$WD_E=W_E\times \operatorname {SL}_2(\mathbb C)$
; we omit the tensor symbol between
![]() $\rho _i$
and
$\rho _i$
and
![]() $S_{a_i}$
to distinguish finite-dimensional representations of the Weil–Deligne
$S_{a_i}$
to distinguish finite-dimensional representations of the Weil–Deligne
![]() $\operatorname {SL}_2(\mathbb C)$
and the Arthur
$\operatorname {SL}_2(\mathbb C)$
and the Arthur
![]() $\operatorname {SL}_2(\mathbb C)$
.
$\operatorname {SL}_2(\mathbb C)$
.
Theorem 2.1.
-
(1) Assume that
 $\Psi $
is of good parity and Let
$\Psi $
is of good parity and Let $$\begin{align*}m-n \geq \max_i \left\{b_i-a_i+1~\big|~\rho_i\simeq\chi_W\right\}. \end{align*}$$
$$\begin{align*}m-n \geq \max_i \left\{b_i-a_i+1~\big|~\rho_i\simeq\chi_W\right\}. \end{align*}$$
 $\pi $
be an irreducible unitary representation in the local A-packet
$\pi $
be an irreducible unitary representation in the local A-packet
 $\Pi _\Psi (\operatorname {U}(V))$
. Then the theta lift
$\Pi _\Psi (\operatorname {U}(V))$
. Then the theta lift
 $\theta (\pi )$
of
$\theta (\pi )$
of
 $\pi $
to
$\pi $
to
 $\operatorname {U}(W)$
lies in the local A-packet
$\operatorname {U}(W)$
lies in the local A-packet
 $\Pi _{\theta (\Psi )}(\operatorname {U}(W))$
if it is nonzero, where
$\Pi _{\theta (\Psi )}(\operatorname {U}(W))$
if it is nonzero, where  $$\begin{align*}\theta(\Psi)=\Psi\chi_W^{-1}\chi_V+\chi_V\boxtimes S_{m-n}. \end{align*}$$
$$\begin{align*}\theta(\Psi)=\Psi\chi_W^{-1}\chi_V+\chi_V\boxtimes S_{m-n}. \end{align*}$$
-
(2) Moreover, if we further assume that
then $$\begin{align*}m-n> \max_i \left\{b_i+a_i-1~\big|~\rho_i\simeq\chi_W\right\}, \end{align*}$$
$$\begin{align*}m-n> \max_i \left\{b_i+a_i-1~\big|~\rho_i\simeq\chi_W\right\}, \end{align*}$$
 $\theta (\pi )$
must be nonzero for any
$\theta (\pi )$
must be nonzero for any
 $\pi \in \Pi _\Psi (\operatorname {U}(V))$
.
$\pi \in \Pi _\Psi (\operatorname {U}(V))$
.
Proof. This is [Reference MœglinMœg11, Thm. 5.2].
Remark 2.2.
-
(1) There is a caveat here: Mœglin’s result [Reference MœglinMœg11, Thm. 5.2] is for the symplectic-orthogonal dual pair. If one assumes Mœglin’s explicit construction of A-packets for unitary groups (both quasi-split and nonquasi-split), then Mœglin’s proof of [Reference MœglinMœg11, Thm. 5.2] should also work for unitary dual pairs.
-
(2) In later proofs of our main result, we will only use A-packets of unitary groups in some special cases; those A-packets are the Zelevinsky–Aubert dual of some tempered L-packets. Since the LLC for unitary groups has been fully established (see [Reference MokMok15, Reference Kaletha, Minguez, Shin and WhiteKMSW14, Reference Mœglin and RenardMR18, Reference Chen and ZouCZ21a]), all the properties of those A-packets that we need can be easily checked using the properties of the LLC and the Zelevinsky–Aubert duality. Hence, our main result in this paper is not conditional on the construction of A-packets for unitary groups.
Recall that for each local A-parameter
![]() $\Psi $
, the local A-packet
$\Psi $
, the local A-packet
![]() $\Pi _\Psi (\operatorname {U}(V))$
is also equipped with a map (depending on the choice of the additive character
$\Pi _\Psi (\operatorname {U}(V))$
is also equipped with a map (depending on the choice of the additive character
![]() $\psi _F$
)
$\psi _F$
)
where
![]() $A_\Psi $
is the component group associated to
$A_\Psi $
is the component group associated to
![]() $\Psi $
. For example, if
$\Psi $
. For example, if
![]() $\Psi $
is a local A-parameter of good parity as above, then
$\Psi $
is a local A-parameter of good parity as above, then
is a free
![]() $\mathbb {Z}/2\mathbb {Z}$
-module with a canonical basis
$\mathbb {Z}/2\mathbb {Z}$
-module with a canonical basis
![]() $\{a_j\}_j$
, where j runs over a representative set of inequivalent subrepresentations of
$\{a_j\}_j$
, where j runs over a representative set of inequivalent subrepresentations of
![]() $\Psi $
.
$\Psi $
.
Theorem 2.3. In the context of Theorem 2.1(1), let
![]() $\pi \in \Pi _\Psi (\operatorname {U}(V))$
and
$\pi \in \Pi _\Psi (\operatorname {U}(V))$
and
![]() $\eta $
the character of
$\eta $
the character of
![]() $A_\Psi $
associated to
$A_\Psi $
associated to
![]() $\pi $
. If the theta lift
$\pi $
. If the theta lift
![]() $\theta (\pi )$
is nonzero, then it corresponds to the character
$\theta (\pi )$
is nonzero, then it corresponds to the character
![]() $\theta (\eta )$
of
$\theta (\eta )$
of
![]() $A_{\theta (\Psi )}$
, where
$A_{\theta (\Psi )}$
, where
![]() $\theta (\eta )$
can be uniquely determined as follows:
$\theta (\eta )$
can be uniquely determined as follows:
-
• if n and m are of different parity, then
 $$\begin{align*}\theta(\eta)~\Big|_{A_\Psi} =\eta; \end{align*}$$
$$\begin{align*}\theta(\eta)~\Big|_{A_\Psi} =\eta; \end{align*}$$
-
• if n and m are of the same parity, then
where $$\begin{align*}\theta(\eta)(a_j)/\eta(a_j)=\epsilon \left(\frac{1}{2}, \Psi_j\chi_W^{-1}, \psi_{E,\delta}\right), \end{align*}$$
$$\begin{align*}\theta(\eta)(a_j)/\eta(a_j)=\epsilon \left(\frac{1}{2}, \Psi_j\chi_W^{-1}, \psi_{E,\delta}\right), \end{align*}$$
 $a_j\in A_\Psi $
is the basis element corresponding to the irreducible summand
$a_j\in A_\Psi $
is the basis element corresponding to the irreducible summand
 $\Psi _j$
of
$\Psi _j$
of
 $\Psi $
.
$\Psi $
.
Here, we regard
![]() $A_\Psi $
as a subgroup of
$A_\Psi $
as a subgroup of
![]() $A_{\theta (\Psi )}$
via the canonical injection
$A_{\theta (\Psi )}$
via the canonical injection
![]() $A_{\Psi }\hookrightarrow A_{\theta (\Psi )}$
sending each basis element
$A_{\Psi }\hookrightarrow A_{\theta (\Psi )}$
sending each basis element
![]() $a_j\in A_\Psi $
corresponding to
$a_j\in A_\Psi $
corresponding to
![]() $\Psi _j\subset \Psi $
to the basis element
$\Psi _j\subset \Psi $
to the basis element
![]() $a^{\prime }_j\in A_{\theta (\Psi )}$
corresponding to
$a^{\prime }_j\in A_{\theta (\Psi )}$
corresponding to
![]() $\Psi _j\chi _W^{-1}\chi _V\subset \theta (\Psi )$
.
$\Psi _j\chi _W^{-1}\chi _V\subset \theta (\Psi )$
.
Proof. This can be proved as in [Reference AtobeAto18, Sect. 7.4]. See also [Reference Chen and ZouCZ21b, Cor. 7.4].
2.3. A result of Atobe
The following lemma, which is essentially due to Atobe, is useful to us in the later proofs. Let
![]() $\nu $
be the normalized absolute value of
$\nu $
be the normalized absolute value of
![]() $E^\times $
.
$E^\times $
.
Lemma 2.4. Let
![]() $G_0=\operatorname {U}(V_0)$
be the unitary group associated to some Hermitian (or skew-Hermitian) space
$G_0=\operatorname {U}(V_0)$
be the unitary group associated to some Hermitian (or skew-Hermitian) space
![]() $V_0$
, and
$V_0$
, and
![]() $\Psi _0$
an A-parameter of
$\Psi _0$
an A-parameter of
![]() $G_0$
. Suppose that
$G_0$
. Suppose that
![]() $\Psi _0$
is of good parity, multiplicity free and trivial on the Weil–Deligne
$\Psi _0$
is of good parity, multiplicity free and trivial on the Weil–Deligne
![]() $\operatorname {SL}_2(\mathbb C)$
. Let
$\operatorname {SL}_2(\mathbb C)$
. Let
![]() $\rho $
be an irreducible representation of
$\rho $
be an irreducible representation of
![]() $W_E$
and
$W_E$
and
![]() $x\in \frac {1}{2}\mathbb {Z}$
positive such that
$x\in \frac {1}{2}\mathbb {Z}$
positive such that
Then for any
![]() $\pi _0\in \Pi _{\Psi _0}(G_0)$
, we have a nonsplit exact sequence:
$\pi _0\in \Pi _{\Psi _0}(G_0)$
, we have a nonsplit exact sequence:
where
![]() $\pi $
is the unique irreducible subrepresentation and
$\pi $
is the unique irreducible subrepresentation and
![]() $\pi '$
is the unique irreducible quotient of
$\pi '$
is the unique irreducible quotient of
![]() $\rho \nu ^{-x}\rtimes \pi _0$
. In particular, the length of the induced representation
$\rho \nu ^{-x}\rtimes \pi _0$
. In particular, the length of the induced representation
![]() $\rho \nu ^{-x}\rtimes \pi _0$
is
$\rho \nu ^{-x}\rtimes \pi _0$
is
![]() $2$
.
$2$
.
Proof. Let
![]() $\phi _0=\widehat {\Psi _0}$
be the Aubert dual of
$\phi _0=\widehat {\Psi _0}$
be the Aubert dual of
![]() $\psi _0$
, namely the L-parameter of
$\psi _0$
, namely the L-parameter of
![]() $G_0$
obtained from
$G_0$
obtained from
![]() $\Psi _0$
by exchanging the Weil–Deligne
$\Psi _0$
by exchanging the Weil–Deligne
![]() $\operatorname {SL}_2(\mathbb C)$
and the Arthur
$\operatorname {SL}_2(\mathbb C)$
and the Arthur
![]() $\operatorname {SL}_2(\mathbb C)$
. By our assumption,
$\operatorname {SL}_2(\mathbb C)$
. By our assumption,
![]() $\phi _0$
is a discrete L-parameter. Then apply [Reference AtobeAto20, Lem. 5.1] to
$\phi _0$
is a discrete L-parameter. Then apply [Reference AtobeAto20, Lem. 5.1] to
![]() ${\widehat {\pi _0}\in \Pi _{\phi _0}(G_0)}$
.
${\widehat {\pi _0}\in \Pi _{\phi _0}(G_0)}$
.
Remark 2.5. Although Atobe only considered split odd orthogonal groups and symplectic groups in [Reference AtobeAto20], his Lemma 5.1 is true for unitary groups as well. Indeed the three ingredients used in his proof of orthogonal/symplectic groups are: Mœglin’s construction of tempered L-packets, Tadić’s formula and a lemma of Gan–Ichino [Reference Gan and IchinoGI16, Lem. A.6]. Since all of these three ingredients are also valid for unitary groups, his proof also works for unitary groups with very minor modifications.
2.4. Some local A-packets
Now, we use the Adams’ conjecture to describe Weil representations. Let
![]() $E^1$
be the subgroup of
$E^1$
be the subgroup of
![]() $E^\times $
consists of norm
$E^\times $
consists of norm
![]() $1$
elements. Let
$1$
elements. Let
![]() $\chi _0$
be a character of
$\chi _0$
be a character of
![]() $E^1$
and
$E^1$
and
![]() $\chi $
the character of
$\chi $
the character of
![]() $E^\times $
obtained from
$E^\times $
obtained from
![]() $\chi _0$
by base change; we may regard
$\chi _0$
by base change; we may regard
![]() $\chi $
as the L-parameter of the unitary group
$\chi $
as the L-parameter of the unitary group
![]() $E^1$
corresponding to
$E^1$
corresponding to
![]() $\chi _0$
. We denote by
$\chi _0$
. We denote by
![]() $\omega _{V,\mu }[\chi ]$
the maximal subrepresentation of
$\omega _{V,\mu }[\chi ]$
the maximal subrepresentation of
![]() $\omega _{V,\mu }$
such that the center of
$\omega _{V,\mu }$
such that the center of
![]() $\operatorname {U}(V)$
acts by
$\operatorname {U}(V)$
acts by
![]() $\chi _0$
. When
$\chi _0$
. When
![]() $n=1$
, the representation
$n=1$
, the representation
![]() $\omega _{V,\mu }[\chi ]$
has been studied by [Reference MoenMoe87] and [Reference RogawskiRog92]. So we shall concentrate on the case
$\omega _{V,\mu }[\chi ]$
has been studied by [Reference MoenMoe87] and [Reference RogawskiRog92]. So we shall concentrate on the case
![]() $n \geq 2$
.
$n \geq 2$
.
Lemma 2.6.
-
(1) If
 $n=2$
and
$n=2$
and
 $\chi =\mu ^2$
, then the representation
$\chi =\mu ^2$
, then the representation
 $\omega _{V,\mu }[\chi ]$
is nonzero only when the space V is of sign
$\omega _{V,\mu }[\chi ]$
is nonzero only when the space V is of sign
 $+1$
, in which case
$+1$
, in which case
 $\omega _{V,\mu }[\chi ]$
is the generic member (with respect to the generic datum defined by
$\omega _{V,\mu }[\chi ]$
is the generic member (with respect to the generic datum defined by
 $\psi _F$
) in the L-packet
$\psi _F$
) in the L-packet
 $\Pi _\phi (\operatorname {U}(V))$
, where
$\Pi _\phi (\operatorname {U}(V))$
, where  $$\begin{align*}\phi=\mu+\mu. \end{align*}$$
$$\begin{align*}\phi=\mu+\mu. \end{align*}$$
-
(2) For any
 $n=\dim V\geq 2$
, excluding the special case above, the representation
$n=\dim V\geq 2$
, excluding the special case above, the representation
 $\omega _{V,\mu }[\chi ]$
is nonzero, irreducible and unitary. It lies in the A-packet
$\omega _{V,\mu }[\chi ]$
is nonzero, irreducible and unitary. It lies in the A-packet
 $\Pi _{\Psi }(\operatorname {U}(V))$
, where The character
$\Pi _{\Psi }(\operatorname {U}(V))$
, where The character $$\begin{align*}\Psi=\chi\cdot\mu^{-n+1}+\mu\boxtimes S_{n-1}. \end{align*}$$
$$\begin{align*}\Psi=\chi\cdot\mu^{-n+1}+\mu\boxtimes S_{n-1}. \end{align*}$$
 $\eta \in \operatorname {Irr} A_\Psi $
associated to
$\eta \in \operatorname {Irr} A_\Psi $
associated to
 $\omega _{V,\mu }[\chi ]$
is Here,
$\omega _{V,\mu }[\chi ]$
is Here, $$\begin{align*}\eta:(e_1, e_{n-1})\longmapsto \begin{cases} (1,\epsilon(V)) \quad &\textit{if }n\ \textit{is even,}\\ \\ \Big(\epsilon\left(\frac{1}{2},\chi\mu^{-n},\psi_{E,\delta}\right)\,,\,\epsilon(V)\epsilon\left(\frac{1}{2},\chi\mu^{-n},\psi_{E,\delta}\right)\Big) \quad &\textit{if }n\ \textit{is odd.} \end{cases} \end{align*}$$
$$\begin{align*}\eta:(e_1, e_{n-1})\longmapsto \begin{cases} (1,\epsilon(V)) \quad &\textit{if }n\ \textit{is even,}\\ \\ \Big(\epsilon\left(\frac{1}{2},\chi\mu^{-n},\psi_{E,\delta}\right)\,,\,\epsilon(V)\epsilon\left(\frac{1}{2},\chi\mu^{-n},\psi_{E,\delta}\right)\Big) \quad &\textit{if }n\ \textit{is odd.} \end{cases} \end{align*}$$
 $e_1$
and
$e_1$
and
 $e_{n-1}$
are the basis elements of
$e_{n-1}$
are the basis elements of
 $A_{\Psi }$
corresponding to
$A_{\Psi }$
corresponding to
 $\chi \cdot \mu ^{-n+1}$
and
$\chi \cdot \mu ^{-n+1}$
and
 $\mu \boxtimes S_{n-1}$
, respectively.
$\mu \boxtimes S_{n-1}$
, respectively.
Proof. Let
![]() $L_1$
be the one-dimensional Hermitian space associated to
$L_1$
be the one-dimensional Hermitian space associated to
![]() $1\in F^\times $
. Let
$1\in F^\times $
. Let
![]() $\chi _V$
be a character of
$\chi _V$
be a character of
![]() $E^\times $
such that
$E^\times $
such that
![]() $\chi _V~\big |_{F^\times }=\omega _{E/F}^n$
and
$\chi _V~\big |_{F^\times }=\omega _{E/F}^n$
and
![]() $\Omega _{L_1,V}$
the Weil representation associated to
$\Omega _{L_1,V}$
the Weil representation associated to
![]() $\operatorname {U}(L_1)\times \operatorname {U}(V)$
with respect to the splitting character
$\operatorname {U}(L_1)\times \operatorname {U}(V)$
with respect to the splitting character
![]() $(\mu ,\chi _V)$
. Then we have
$(\mu ,\chi _V)$
. Then we have
Hence,
![]() $\omega _{V,\mu }[\chi ]$
can be regarded as the theta lift of the character
$\omega _{V,\mu }[\chi ]$
can be regarded as the theta lift of the character
![]() $\chi \mu ^{-n}\chi _V$
. Thus, our first assertion follows from Theorem 2.1, and the second follows from Theorem 2.3.
$\chi \mu ^{-n}\chi _V$
. Thus, our first assertion follows from Theorem 2.1, and the second follows from Theorem 2.3.
2.5. Irreducibility of big theta lifts
Finally, we investigate the irreducibility of the big theta lift of
![]() $\omega _{V,\mu }[\chi ]$
. We shall work in a slightly more general setting.
$\omega _{V,\mu }[\chi ]$
. We shall work in a slightly more general setting.
We retain the notations of Section 2.2. From now on, we assume that m is even and
![]() $m\geq \max \{2n-2,n\}$
. Let
$m\geq \max \{2n-2,n\}$
. Let
be a local A-parameter of
![]() $\operatorname {U}(V)$
, where
$\operatorname {U}(V)$
, where
![]() $\delta $
and
$\delta $
and
![]() $\mu $
are conjugate self-dual characters of parity
$\mu $
are conjugate self-dual characters of parity
![]() $(-1)^{n-1}$
and
$(-1)^{n-1}$
and
![]() $-1$
, respectively. Our goal is to show the following.
$-1$
, respectively. Our goal is to show the following.
Theorem 2.7. For any
![]() $\pi \in \Pi _\Psi (\operatorname {U}(V))$
, the big theta lift
$\pi \in \Pi _\Psi (\operatorname {U}(V))$
, the big theta lift
![]() $\Theta (\pi )$
to
$\Theta (\pi )$
to
![]() $\operatorname {U}(W)$
is irreducible if it is nonzero. Moreover, we have
$\operatorname {U}(W)$
is irreducible if it is nonzero. Moreover, we have
for all
![]() $i>0$
. Here,
$i>0$
. Here,
![]() $\Omega $
is the Weil representation associated to
$\Omega $
is the Weil representation associated to
![]() $\operatorname {U}(V)\times \operatorname {U}(W)$
, and the subscript ‘
$\operatorname {U}(V)\times \operatorname {U}(W)$
, and the subscript ‘
![]() $sm$
’ stands for taking the
$sm$
’ stands for taking the
![]() $\operatorname {U}(W)$
-smooth vectors.
$\operatorname {U}(W)$
-smooth vectors.
Remark 2.8. Although in this theorem we do not assert the nonvanishing of
![]() $\Theta (\pi )$
, in the range we are considering (i.e.,
$\Theta (\pi )$
, in the range we are considering (i.e.,
![]() $m\geq 2n-2$
and
$m\geq 2n-2$
and
![]() $n\geq 2$
), we are almost always in the situation of Theorem 2.1(2), except for the following low rank cases:
$n\geq 2$
), we are almost always in the situation of Theorem 2.1(2), except for the following low rank cases:
-
•
 $n=2$
and
$n=2$
and
 $m=2$
(this case will not be used in the proof of our main theorem);
$m=2$
(this case will not be used in the proof of our main theorem); -
•
 $n=3$
,
$n=3$
,
 $m=4$
and
$m=4$
and
 $\delta =\chi _W$
.
$\delta =\chi _W$
.
We shall prove this theorem by induction on the dimension of V. Let
![]() $x_n=-n/2+1$
. According to Mœglin [Reference MœglinMœg06, Sect. 2.4], we know that:
$x_n=-n/2+1$
. According to Mœglin [Reference MœglinMœg06, Sect. 2.4], we know that:
Lemma 2.9. Assume that
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $\pi \in \Pi _\Psi (\operatorname {U}(V))$
. If
$\pi \in \Pi _\Psi (\operatorname {U}(V))$
. If
![]() $\pi $
is not supercuspidal, then there exists a unique
$\pi $
is not supercuspidal, then there exists a unique
![]() $\pi _0\in \Pi _{\Psi _0}(\operatorname {U}(V_0))$
such that
$\pi _0\in \Pi _{\Psi _0}(\operatorname {U}(V_0))$
such that
Here,
and
![]() $V_0$
is a subspace of V such that
$V_0$
is a subspace of V such that
![]() $V\simeq V_0 \oplus \mathcal {H}$
.
$V\simeq V_0 \oplus \mathcal {H}$
.
Using this fact, we now do the induction step.
Proposition 2.10. In the context of Lemma 2.9, assume that
Let
![]() $W_0$
be a subspace of W such that
$W_0$
be a subspace of W such that
![]() $W\simeq W_0 \oplus \mathcal {H}'$
. Consider the theta correspondence of
$W\simeq W_0 \oplus \mathcal {H}'$
. Consider the theta correspondence of
![]() $\operatorname {U}(V_0)\times \operatorname {U}(W_0)$
(with respect to the same splitting characters). Then if Theorem 2.7 holds for
$\operatorname {U}(V_0)\times \operatorname {U}(W_0)$
(with respect to the same splitting characters). Then if Theorem 2.7 holds for
![]() $\pi _0$
, it also holds for
$\pi _0$
, it also holds for
![]() $\pi $
.
$\pi $
.
Remark 2.11. In the setting of Theorem 2.7, we have assumed that
![]() $m\geq 2n-2$
. Note that the dimensions of
$m\geq 2n-2$
. Note that the dimensions of
![]() $V_0$
and
$V_0$
and
![]() $W_0$
also satisfy this inequality. Hence, it makes sense to talk about Theorem 2.7 for
$W_0$
also satisfy this inequality. Hence, it makes sense to talk about Theorem 2.7 for
![]() $\pi _0$
.
$\pi _0$
.
Proof of Proposition 2.10
Let P be the standard parabolic subgroup of
![]() $\operatorname {U}(V)$
with Levi component
$\operatorname {U}(V)$
with Levi component
![]() $\operatorname {GL}_1\times \operatorname {U}(V_0)$
. For
$\operatorname {GL}_1\times \operatorname {U}(V_0)$
. For
![]() $i\geq 0$
, by the (derived version of) Frobenius reciprocity, we have
$i\geq 0$
, by the (derived version of) Frobenius reciprocity, we have
where
![]() $R_P$
is the normalized Jacquet module along P. To compute the right-hand side of above, one can appeal to the Kudla’s filtration. There is a two-step filtration on
$R_P$
is the normalized Jacquet module along P. To compute the right-hand side of above, one can appeal to the Kudla’s filtration. There is a two-step filtration on
![]() $R_P\Omega $
:
$R_P\Omega $
:
whose successive quotient
![]() $J^a=R^a/R^{a+1}$
can be described as follows:
$J^a=R^a/R^{a+1}$
can be described as follows:
and
Here:
-
•
 $\Omega _0$
is the Weil representation associated to
$\Omega _0$
is the Weil representation associated to
 $\operatorname {U}(V_0)\times \operatorname {U}(W)$
;
$\operatorname {U}(V_0)\times \operatorname {U}(W)$
; -
• Q is a maximal parabolic subgroup of
 $\operatorname {U}(W)$
stabilizing an isotropic line of W; the Levi subgroup of Q is isomorphic to
$\operatorname {U}(W)$
stabilizing an isotropic line of W; the Levi subgroup of Q is isomorphic to
 $\operatorname {GL}_1\times \operatorname {U}(W_0)$
;
$\operatorname {GL}_1\times \operatorname {U}(W_0)$
; -
•
 $\mathcal {S}(E^\times )$
is the space of Schwartz functions on
$\mathcal {S}(E^\times )$
is the space of Schwartz functions on
 $E^\times $
, equipped with the natural action of two copies of
$E^\times $
, equipped with the natural action of two copies of
 $\operatorname {GL}_1$
(twisted by the splitting characters);
$\operatorname {GL}_1$
(twisted by the splitting characters); -
•
 $\Omega _{00}$
is the Weil representation associated to
$\Omega _{00}$
is the Weil representation associated to
 $\operatorname {U}(V_0)\times \operatorname {U}(W_0)$
.
$\operatorname {U}(V_0)\times \operatorname {U}(W_0)$
.
Applying the functor
![]() $\operatorname {Hom}_{\operatorname {GL}_1\times \operatorname {U}(V_0)}(\cdot ,\mu \nu ^{x_n}\boxtimes \pi _0)$
to the short exact sequence
$\operatorname {Hom}_{\operatorname {GL}_1\times \operatorname {U}(V_0)}(\cdot ,\mu \nu ^{x_n}\boxtimes \pi _0)$
to the short exact sequence
we get a long exact sequence
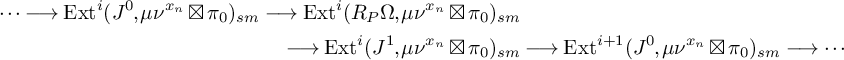 $$ \begin{align*} \cdots\longrightarrow \operatorname{Ext}^i(J^0,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \longrightarrow \operatorname{Ext}^i(R_P\Omega &,\mu\nu^{x_n}\boxtimes\pi_0)_{sm}\\ \longrightarrow \operatorname{Ext}^i(J^1 &,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \longrightarrow \operatorname{Ext}^{i+1}(J^0,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \longrightarrow\cdots \end{align*} $$
$$ \begin{align*} \cdots\longrightarrow \operatorname{Ext}^i(J^0,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \longrightarrow \operatorname{Ext}^i(R_P\Omega &,\mu\nu^{x_n}\boxtimes\pi_0)_{sm}\\ \longrightarrow \operatorname{Ext}^i(J^1 &,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \longrightarrow \operatorname{Ext}^{i+1}(J^0,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \longrightarrow\cdots \end{align*} $$
Here, for the exactness of taking
![]() $\operatorname {U}(W)$
-smooth vectors, one may refer to [Reference Adams, Prasad and SavinAPS17, Lem. 5.14, Lem. 7.4]. Since by our assumptions
$\operatorname {U}(W)$
-smooth vectors, one may refer to [Reference Adams, Prasad and SavinAPS17, Lem. 5.14, Lem. 7.4]. Since by our assumptions
![]() ${x_n} \ne \frac {m-n+1}{2}$
, we know that
${x_n} \ne \frac {m-n+1}{2}$
, we know that
for all
![]() $i\geq 0$
. This implies that
$i\geq 0$
. This implies that
 $$ \begin{align*} \operatorname{Ext}^i(R_P\Omega,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \simeq & \operatorname{Ext}^i(J^1,\mu\nu^{x_n}\boxtimes\pi_0)_{sm}\\ =&\left(\mu'\right)^c\nu^{x_n}\rtimes \operatorname{Ext}^i(\Omega_{00},\pi_0)_{sm}, \end{align*} $$
$$ \begin{align*} \operatorname{Ext}^i(R_P\Omega,\mu\nu^{x_n}\boxtimes\pi_0)_{sm} \simeq & \operatorname{Ext}^i(J^1,\mu\nu^{x_n}\boxtimes\pi_0)_{sm}\\ =&\left(\mu'\right)^c\nu^{x_n}\rtimes \operatorname{Ext}^i(\Omega_{00},\pi_0)_{sm}, \end{align*} $$
where
![]() $\mu '=\mu \chi _W^{-1}\chi _V$
. Here, in the last equality, we have made use of (an
$\mu '=\mu \chi _W^{-1}\chi _V$
. Here, in the last equality, we have made use of (an
![]() $\operatorname {Ext}$
-version of) [Reference Adams, Prasad and SavinAPS17, Lem. 2.6] and the Künneth formula [Reference Adams, Prasad and SavinAPS17, Lem. 3.3]. In particular, we get
$\operatorname {Ext}$
-version of) [Reference Adams, Prasad and SavinAPS17, Lem. 2.6] and the Künneth formula [Reference Adams, Prasad and SavinAPS17, Lem. 3.3]. In particular, we get
and
by our induction hypothesis. Similarly, we also have
![]() $-{x_n} \ne \frac {m-n+1}{2}$
. The same argument gives that
$-{x_n} \ne \frac {m-n+1}{2}$
. The same argument gives that
Now, note that Lemma 2.4 asserts that
![]() $\mu \nu ^{x_n}\rtimes \pi _0$
is of length
$\mu \nu ^{x_n}\rtimes \pi _0$
is of length
![]() $2$
. Let
$2$
. Let
![]() $\pi '$
be the unique irreducible quotient of
$\pi '$
be the unique irreducible quotient of
![]() $\mu \nu ^{x_n}\rtimes \pi _0$
, the sequence
$\mu \nu ^{x_n}\rtimes \pi _0$
, the sequence
is exact. Applying the functor
![]() $\operatorname {Hom}_{\operatorname {U}(V)}(\Omega ,\cdot )$
to this short exact sequence and taking
$\operatorname {Hom}_{\operatorname {U}(V)}(\Omega ,\cdot )$
to this short exact sequence and taking
![]() $\operatorname {U}(W)$
-smooth vectors, we get
$\operatorname {U}(W)$
-smooth vectors, we get
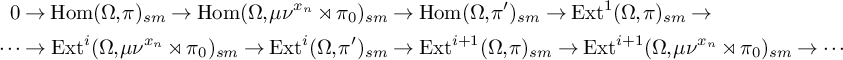 $$ \begin{align} 0\rightarrow \operatorname{Hom}(\Omega,\pi)_{sm}\rightarrow \operatorname{Hom}(\Omega,\mu\nu^{x_n}\rtimes\pi_0)_{sm}&\rightarrow \operatorname{Hom}(\Omega,\pi')_{sm}\rightarrow \operatorname{Ext}^1(\Omega,\pi)_{sm} \rightarrow \nonumber\\ \cdots\rightarrow\operatorname{Ext}^i(\Omega,\mu\nu^{x_n}\rtimes\pi_0)_{sm}\rightarrow\operatorname{Ext}^i(\Omega,\pi')_{sm}&\rightarrow\operatorname{Ext}^{i+1}(\Omega,\pi)_{sm}\rightarrow\operatorname{Ext}^{i+1}(\Omega,\mu\nu^{x_n}\rtimes\pi_0)_{sm}\rightarrow\cdots \end{align} $$
$$ \begin{align} 0\rightarrow \operatorname{Hom}(\Omega,\pi)_{sm}\rightarrow \operatorname{Hom}(\Omega,\mu\nu^{x_n}\rtimes\pi_0)_{sm}&\rightarrow \operatorname{Hom}(\Omega,\pi')_{sm}\rightarrow \operatorname{Ext}^1(\Omega,\pi)_{sm} \rightarrow \nonumber\\ \cdots\rightarrow\operatorname{Ext}^i(\Omega,\mu\nu^{x_n}\rtimes\pi_0)_{sm}\rightarrow\operatorname{Ext}^i(\Omega,\pi')_{sm}&\rightarrow\operatorname{Ext}^{i+1}(\Omega,\pi)_{sm}\rightarrow\operatorname{Ext}^{i+1}(\Omega,\mu\nu^{x_n}\rtimes\pi_0)_{sm}\rightarrow\cdots \end{align} $$
It follows from Equation (♠) that
Dually, apply both the contragredient and MVW-involution (see [Reference Mœglin, Vignéras and WaldspurgerMVW, Chap. 4.II.1]) to
![]() ${\mu \nu ^{x_n}\rtimes \pi _0}$
, we get a dualized short exact sequence
${\mu \nu ^{x_n}\rtimes \pi _0}$
, we get a dualized short exact sequence
Similar to the argument above, this short exact sequence leads to a long exact sequence
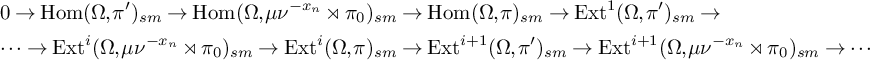 $$ \begin{align} 0\rightarrow \operatorname{Hom}(\Omega,\pi')_{sm}\rightarrow \operatorname{Hom}(\Omega,\mu\nu^{-x_n}\rtimes\pi_0)_{sm}&\rightarrow \operatorname{Hom}(\Omega,\pi)_{sm}\rightarrow \operatorname{Ext}^1(\Omega,\pi')_{sm} \rightarrow \nonumber\\ \cdots\rightarrow\operatorname{Ext}^i(\Omega,\mu\nu^{-x_n}\rtimes\pi_0)_{sm}\rightarrow\operatorname{Ext}^i(\Omega,\pi)_{sm}&\rightarrow\operatorname{Ext}^{i+1}(\Omega,\pi')_{sm}\rightarrow\operatorname{Ext}^{i+1}(\Omega,\mu\nu^{-x_n}\rtimes\pi_0)_{sm}\rightarrow\cdots \end{align} $$
$$ \begin{align} 0\rightarrow \operatorname{Hom}(\Omega,\pi')_{sm}\rightarrow \operatorname{Hom}(\Omega,\mu\nu^{-x_n}\rtimes\pi_0)_{sm}&\rightarrow \operatorname{Hom}(\Omega,\pi)_{sm}\rightarrow \operatorname{Ext}^1(\Omega,\pi')_{sm} \rightarrow \nonumber\\ \cdots\rightarrow\operatorname{Ext}^i(\Omega,\mu\nu^{-x_n}\rtimes\pi_0)_{sm}\rightarrow\operatorname{Ext}^i(\Omega,\pi)_{sm}&\rightarrow\operatorname{Ext}^{i+1}(\Omega,\pi')_{sm}\rightarrow\operatorname{Ext}^{i+1}(\Omega,\mu\nu^{-x_n}\rtimes\pi_0)_{sm}\rightarrow\cdots \end{align} $$
which combining with Equation (♣) similarly implies that
Playing ‘Ping-Pong’, one can see that
![]() $\operatorname {Ext}^i(\Omega ,\pi )$
is periodic:
$\operatorname {Ext}^i(\Omega ,\pi )$
is periodic:
Since the higher extensions vanish when the degree is sufficiently large [Reference BernsteinBer92, Pg. 98, Sect. 4.2], these groups
![]() $\operatorname {Ext}^i(\Omega ,\pi )_{sm}$
must vanish for all
$\operatorname {Ext}^i(\Omega ,\pi )_{sm}$
must vanish for all
![]() $i>0$
with no other choice. The same reason also gives the vanishing of higher extensions of
$i>0$
with no other choice. The same reason also gives the vanishing of higher extensions of
![]() $\pi '$
.
$\pi '$
.
Suppose that
![]() $\Theta (\pi )\ne 0$
. It remains to show that
$\Theta (\pi )\ne 0$
. It remains to show that
![]() $\Theta (\pi )$
is irreducible. Thanks to the vanishing of higher extensions, we deduce from the long exact sequence (♡) that
$\Theta (\pi )$
is irreducible. Thanks to the vanishing of higher extensions, we deduce from the long exact sequence (♡) that
is exact. In particular,
![]() $\Theta (\pi _0)$
must be nonzero, hence irreducible by our induction hypothesis. It then follows from Theorem 2.1 that
$\Theta (\pi _0)$
must be nonzero, hence irreducible by our induction hypothesis. It then follows from Theorem 2.1 that
![]() $\Theta (\pi _0)$
lies in
$\Theta (\pi _0)$
lies in
![]() $\Pi _{\theta (\Psi _0)}(\operatorname {U}(W_0))$
, where
$\Pi _{\theta (\Psi _0)}(\operatorname {U}(W_0))$
, where
Now, we claim that the induced representation
![]() $\left (\mu '\right )^c\nu ^{x_n}\rtimes \Theta (\pi _0)^\vee $
is of length
$\left (\mu '\right )^c\nu ^{x_n}\rtimes \Theta (\pi _0)^\vee $
is of length
![]() $2$
, and the two subquotients are nonisomorphic. Indeed, if
$2$
, and the two subquotients are nonisomorphic. Indeed, if
![]() $m-n=1$
and
$m-n=1$
and
![]() $\delta =\chi _W$
, one can easily check this by hand. Otherwise, note that:
$\delta =\chi _W$
, one can easily check this by hand. Otherwise, note that:
-
•
 $\theta (\Psi _0)$
is of good parity, multiplicity free and trivial on the Weil–Deligne
$\theta (\Psi _0)$
is of good parity, multiplicity free and trivial on the Weil–Deligne
 $\operatorname {SL}_2(\mathbb C)$
;
$\operatorname {SL}_2(\mathbb C)$
; -
•
 $\mu '\boxtimes S_{-2x_n-1}\subset \theta (\Psi _0)$
but
$\mu '\boxtimes S_{-2x_n-1}\subset \theta (\Psi _0)$
but
 $\mu '\boxtimes S_{-2x_n+1}\not \subset \theta (\Psi _0)$
.
$\mu '\boxtimes S_{-2x_n+1}\not \subset \theta (\Psi _0)$
.
In short, we are again in a situation such that we can appeal to Lemma 2.4, from which our claim follows. Therefore, it suffices to check that
![]() $\Theta (\pi ') \ne 0$
. We shall argue by contradiction to show this. Suppose on the contrary that
$\Theta (\pi ') \ne 0$
. We shall argue by contradiction to show this. Suppose on the contrary that
![]() $\Theta (\pi ') = 0$
. Then on the one hand, we have
$\Theta (\pi ') = 0$
. Then on the one hand, we have
which implies that
![]() $\left (\mu '\right )^c\nu ^{x_n}\rtimes \Theta (\pi _0)^\vee $
has socle
$\left (\mu '\right )^c\nu ^{x_n}\rtimes \Theta (\pi _0)^\vee $
has socle
![]() $\theta (\pi )^\vee $
. On the other hand, we also deduce from the long exact sequence (♢) that
$\theta (\pi )^\vee $
. On the other hand, we also deduce from the long exact sequence (♢) that
is exact. Since we had assumed that
![]() $\Theta (\pi ') = 0$
, this exact sequence implies that
$\Theta (\pi ') = 0$
, this exact sequence implies that
Applying both the contragredient and the MVW-involution, we get
which implies that
![]() $\left (\mu '\right )^c\nu ^{x_n}\rtimes \Theta (\pi _0)^\vee $
also has cosocle
$\left (\mu '\right )^c\nu ^{x_n}\rtimes \Theta (\pi _0)^\vee $
also has cosocle
![]() $\theta (\pi )^\vee $
. This contradicts our claim. Thus,
$\theta (\pi )^\vee $
. This contradicts our claim. Thus,
![]() $\Theta (\pi ') \ne 0$
as desired.
$\Theta (\pi ') \ne 0$
as desired.
Now, we can prove our goal.
Proof of Theorem 2.7
By using the previous proposition, we can reduce Theorem 2.7 to the case that
![]() $\pi $
is supercuspidal or to the case that
$\pi $
is supercuspidal or to the case that
![]() $n=0$
. In the supercuspidal case:
$n=0$
. In the supercuspidal case:
-
• it is well known that the big theta lift of a supercuspidal representation is irreducible;
-
• all higher extensions vanish since supercuspidal representations of a unitary group are compact.
In the case that
![]() $n=0$
,
$n=0$
,
![]() $\operatorname {U}(V)$
is trivial and the Weil representation is simply a character of
$\operatorname {U}(V)$
is trivial and the Weil representation is simply a character of
![]() $\operatorname {U}(W)$
. Hence, Theorem 2.7 holds.
$\operatorname {U}(W)$
. Hence, Theorem 2.7 holds.
3. Proof of the main result
In this section, we shall prove the main result: Theorem 1.3. We first note:
Lemma 3.1. Assume that Conjecture 1.1 holds for a tempered L-parameter M. Then for any conjugate orthogonal character
![]() $\mathcal {X}$
of
$\mathcal {X}$
of
![]() $L^\times $
, Conjecture 1.1 also holds for the L-parameter
$L^\times $
, Conjecture 1.1 also holds for the L-parameter
![]() $M\cdot \mathcal {X}$
.
$M\cdot \mathcal {X}$
.
Proof. To see this, one simply notes that
where
![]() ${\mathcal {X}_0}$
is the character of
${\mathcal {X}_0}$
is the character of
![]() $L^1$
whose base change to
$L^1$
whose base change to
![]() $L^\times $
is
$L^\times $
is
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Let
![]() $n \geq 2$
be an integer, and V an
$n \geq 2$
be an integer, and V an
![]() $(n+1)$
-dimensional skew-Hermitian space over E. We shall start with an L-parameter of the form
$(n+1)$
-dimensional skew-Hermitian space over E. We shall start with an L-parameter of the form
where
![]() $M_1$
is a conjugate self-dual character of parity
$M_1$
is a conjugate self-dual character of parity
![]() $(-1)^n$
.
$(-1)^n$
.
3.1. Two seesaw diagrams: uniqueness
If there is an irreducible tempered representation
![]() $\Pi $
in the L-packet
$\Pi $
in the L-packet
![]() $\Pi _M$
corresponding to
$\Pi _M$
corresponding to
![]() $\eta \in \operatorname {Irr} A_M$
such that
$\eta \in \operatorname {Irr} A_M$
such that
we would like to lift
![]() $\Pi $
to some unitary group of n-variables to obtain some information. Let
$\Pi $
to some unitary group of n-variables to obtain some information. Let
![]() $\{a_i\}_{i=1}^r$
be a canonical basis of
$\{a_i\}_{i=1}^r$
be a canonical basis of
![]() $A_M$
, where each
$A_M$
, where each
![]() $a_i$
corresponds to some irreducible subrepresentation
$a_i$
corresponds to some irreducible subrepresentation
![]() $M_i$
of M (so
$M_i$
of M (so
![]() $a_1$
corresponds to
$a_1$
corresponds to
![]() $M_1$
). We set
$M_1$
). We set
![]() $\epsilon =\eta (a_1)$
and W the unique n-dimensional Hermitian space over L of sign
$\epsilon =\eta (a_1)$
and W the unique n-dimensional Hermitian space over L of sign
![]() $\epsilon $
. Let
$\epsilon $
. Let
![]() $\left (\mathcal {X}_V,\mathcal {X}_W\right )$
be a pair of characters of
$\left (\mathcal {X}_V,\mathcal {X}_W\right )$
be a pair of characters of
![]() $L^\times $
such that
$L^\times $
such that
Then one can consider the theta correspondence between
![]() $\operatorname {U}(V_K)\times \operatorname {U}(W)$
with respect to the splitting character
$\operatorname {U}(V_K)\times \operatorname {U}(W)$
with respect to the splitting character
![]() $\left (\mathcal {X}_V,\mathcal {X}_W\right )$
. By [Reference Gan and IchinoGI16, Sect. 4.6(P2)], one knows that there is an irreducible tempered representation
$\left (\mathcal {X}_V,\mathcal {X}_W\right )$
. By [Reference Gan and IchinoGI16, Sect. 4.6(P2)], one knows that there is an irreducible tempered representation
![]() $\Sigma $
of
$\Sigma $
of
![]() $\operatorname {U}(W)$
such that
$\operatorname {U}(W)$
such that
is the big theta lift of
![]() $\Sigma $
. Indeed, one knows that
$\Sigma $
. Indeed, one knows that
![]() $\Sigma $
has the L-parameter
$\Sigma $
has the L-parameter
and corresponds to the character
![]() $\theta (\eta ) = \eta ~\big |_{A_{\theta (M)}}$
. Consider the following seesaw diagram:
$\theta (\eta ) = \eta ~\big |_{A_{\theta (M)}}$
. Consider the following seesaw diagram:
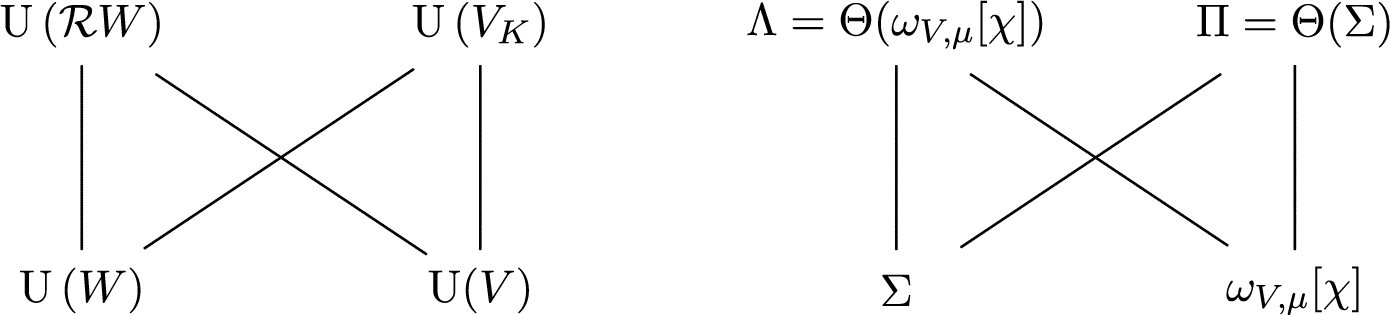
where:
-
•
 $\mathcal {R} W$
is the restriction of scalar of W to E;
$\mathcal {R} W$
is the restriction of scalar of W to E; -
• the theta correspondence between
 $\operatorname {U}(V_K)\times \operatorname {U}(W)$
is with respect to some splitting characters
$\operatorname {U}(V_K)\times \operatorname {U}(W)$
is with respect to some splitting characters
 $(\mathcal {X}_V,\mathcal {X}_W)$
;
$(\mathcal {X}_V,\mathcal {X}_W)$
; -
• the theta correspondence between
 $\operatorname {U}(V)\times \operatorname {U}\left (\mathcal {R} W\right )$
is with respect to some splitting characters
$\operatorname {U}(V)\times \operatorname {U}\left (\mathcal {R} W\right )$
is with respect to some splitting characters
 $(\chi _V,\chi _W)$
;
$(\chi _V,\chi _W)$
; -
• to make use of this seesaw diagram, we choose these splitting characters so that:
 $$\begin{align*}\mathcal{X}_V=\chi_V\circ\operatorname{Nm}_{L/E} \quad \textit{and} \quad \chi_W=\mathcal{X}_W~\big|_{E^\times}; \end{align*}$$
$$\begin{align*}\mathcal{X}_V=\chi_V\circ\operatorname{Nm}_{L/E} \quad \textit{and} \quad \chi_W=\mathcal{X}_W~\big|_{E^\times}; \end{align*}$$
-
•
 $\chi $
is the L-parameter of the central character of the restriction of
$\chi $
is the L-parameter of the central character of the restriction of
 $\Pi $
to
$\Pi $
to
 $\operatorname {U}(V)$
, that is,
$\operatorname {U}(V)$
, that is,  $$\begin{align*}\chi=\det(M)~\big|_{E^\times}. \end{align*}$$
$$\begin{align*}\chi=\det(M)~\big|_{E^\times}. \end{align*}$$
Then by the seesaw identity, we get
In particular,
![]() $\Lambda $
is nonzero. By Lemma 2.6, Theorem 2.1 and Theorem 2.7, we know that:
$\Lambda $
is nonzero. By Lemma 2.6, Theorem 2.1 and Theorem 2.7, we know that:
-
•
 $\omega _{V,\mu }[\chi ]$
lies in the A-packet
$\omega _{V,\mu }[\chi ]$
lies in the A-packet
 $\Pi _{\Psi _{M,\mu }}(\operatorname {U}(V))$
, where
$\Pi _{\Psi _{M,\mu }}(\operatorname {U}(V))$
, where  $$\begin{align*}\Psi_{M,\mu}=\chi\cdot\mu^{-n}+\mu\boxtimes S_n; \end{align*}$$
$$\begin{align*}\Psi_{M,\mu}=\chi\cdot\mu^{-n}+\mu\boxtimes S_n; \end{align*}$$
-
•
 $\Lambda $
is an irreducible unitary representation lies in the A-packet
$\Lambda $
is an irreducible unitary representation lies in the A-packet
 $\Pi _{\theta (\Psi _{M,\mu })}\left (\operatorname {U}\left (\mathcal {R} W\right )\right )$
, where
$\Pi _{\theta (\Psi _{M,\mu })}\left (\operatorname {U}\left (\mathcal {R} W\right )\right )$
, where  $$ \begin{align*} \theta\left(\Psi_{M,\mu}\right) &= \Psi_{M,\mu}\cdot\chi_W^{-1}\chi_V+\chi_V\boxtimes S_{n-1} \\ &= \chi\cdot\mu^{-n}\cdot\chi_W^{-1}\chi_V + \chi_V\boxtimes S_{n-1} + \mu\cdot\chi_W^{-1}\chi_V\boxtimes S_n. \end{align*} $$
$$ \begin{align*} \theta\left(\Psi_{M,\mu}\right) &= \Psi_{M,\mu}\cdot\chi_W^{-1}\chi_V+\chi_V\boxtimes S_{n-1} \\ &= \chi\cdot\mu^{-n}\cdot\chi_W^{-1}\chi_V + \chi_V\boxtimes S_{n-1} + \mu\cdot\chi_W^{-1}\chi_V\boxtimes S_n. \end{align*} $$
To compute the right-hand side of equality (✠.1), we shall use another seesaw diagram:
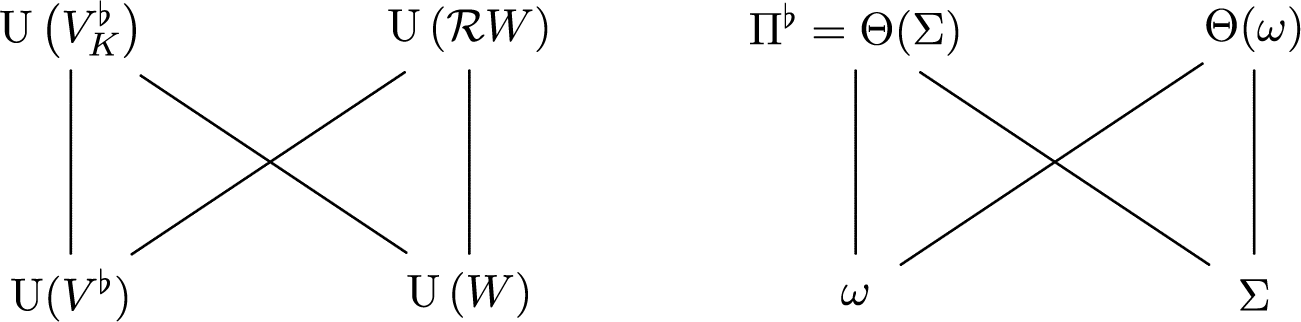
where:
-
•
 $V^\flat $
is an n-dimensional skew-Hermitian space over E which will be suitably chosen later, and
$V^\flat $
is an n-dimensional skew-Hermitian space over E which will be suitably chosen later, and
 $V^\flat _K$
is its scalar extension to L;
$V^\flat _K$
is its scalar extension to L; -
• the theta correspondence between
 $\operatorname {U}(V^\flat )\times \operatorname {U}\left (\mathcal {R} W\right )$
is with respect to some splitting characters
$\operatorname {U}(V^\flat )\times \operatorname {U}\left (\mathcal {R} W\right )$
is with respect to some splitting characters
 $(\chi _{V^\flat },\chi ^{\prime }_W)$
;
$(\chi _{V^\flat },\chi ^{\prime }_W)$
; -
• the theta correspondence between
 $\operatorname {U}(V^\flat _K)\times \operatorname {U}(W)$
is with respect to some splitting characters
$\operatorname {U}(V^\flat _K)\times \operatorname {U}(W)$
is with respect to some splitting characters
 $(\mathcal {X}_{V^\flat },\mathcal {X}^{\prime }_W)$
;
$(\mathcal {X}_{V^\flat },\mathcal {X}^{\prime }_W)$
; -
• to make use of this seesaw diagram, we choose these splitting characters so that:
 $$\begin{align*}\mathcal{X}_{V^\flat}=\chi_{V^\flat}\circ\operatorname{Nm}_{L/E} \quad \textit{and} \quad \chi^{\prime}_W=\mathcal{X}^{\prime}_W~\big|_{E^\times}; \end{align*}$$
$$\begin{align*}\mathcal{X}_{V^\flat}=\chi_{V^\flat}\circ\operatorname{Nm}_{L/E} \quad \textit{and} \quad \chi^{\prime}_W=\mathcal{X}^{\prime}_W~\big|_{E^\times}; \end{align*}$$
-
•
 $\omega $
is some irreducible unitary representation of
$\omega $
is some irreducible unitary representation of
 $\operatorname {U}(V^\flat )$
which will also be suitably chosen later.
$\operatorname {U}(V^\flat )$
which will also be suitably chosen later.
We would like to choose these data appropriately such that
![]() $\omega $
is the theta lift of certain character of
$\omega $
is the theta lift of certain character of
![]() $\operatorname {U}_1$
, and
$\operatorname {U}_1$
, and
![]() $\Lambda =\Theta (\omega )$
. To make this possible, we need to pick up these splitting characters very carefully. Let
$\Lambda =\Theta (\omega )$
. To make this possible, we need to pick up these splitting characters very carefully. Let
where
![]() $\Upsilon $
is a conjugate orthogonal character of
$\Upsilon $
is a conjugate orthogonal character of
![]() $L^\times $
so that
$L^\times $
so that
It is not hard to see that such
![]() $\Upsilon $
exists. Then again by Theorem 2.1 one can see that
$\Upsilon $
exists. Then again by Theorem 2.1 one can see that
![]() $\omega $
(if exists) lies in the A-packet
$\omega $
(if exists) lies in the A-packet
![]() $\Pi _{\Psi ^\flat }(\operatorname {U}(V^\flat ))$
, where
$\Pi _{\Psi ^\flat }(\operatorname {U}(V^\flat ))$
, where
Indeed, we have:
Proposition 3.2. Let
![]() $V^\flat $
be the n-dimensional skew-Hermitian space of sign
$V^\flat $
be the n-dimensional skew-Hermitian space of sign
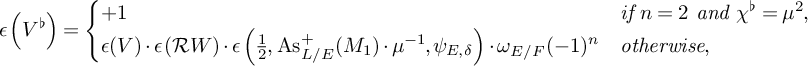 $$ \begin{align} \epsilon\left(V^\flat\right)=\begin{cases} +1 \quad & \textit{if }n=2 \textit{ and }\chi^\flat=\mu^2, \\ \epsilon(V)\cdot\epsilon\left(\mathcal{R} W\right)\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{E/F}(-1)^n \quad & \textit{otherwise}, \end{cases} \end{align} $$
$$ \begin{align} \epsilon\left(V^\flat\right)=\begin{cases} +1 \quad & \textit{if }n=2 \textit{ and }\chi^\flat=\mu^2, \\ \epsilon(V)\cdot\epsilon\left(\mathcal{R} W\right)\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{E/F}(-1)^n \quad & \textit{otherwise}, \end{cases} \end{align} $$
and
Then
![]() $\Lambda $
is the (big) theta lift of
$\Lambda $
is the (big) theta lift of
![]() $\omega $
to
$\omega $
to
![]() $\operatorname {U}(\mathcal {R} W)$
, that is,
$\operatorname {U}(\mathcal {R} W)$
, that is,
![]() $\Lambda =\Theta (\omega )$
.
$\Lambda =\Theta (\omega )$
.
Proof. We first check the special case that
![]() $n=2$
and
$n=2$
and
![]() $\chi ^\flat =\mu ^2$
. So
$\chi ^\flat =\mu ^2$
. So
and
where
![]() $\chi _0$
is the character of
$\chi _0$
is the character of
![]() $E^1$
whose base change to
$E^1$
whose base change to
![]() $E^\times $
is
$E^\times $
is
![]() $\mu \cdot \chi _W^{-1}\chi _V$
. By the induction principle, one knows that the theta correspondence between
$\mu \cdot \chi _W^{-1}\chi _V$
. By the induction principle, one knows that the theta correspondence between
![]() $\operatorname {U}(V^\flat )\times \operatorname {U}(\mathcal {R} W)$
defines a bijection
$\operatorname {U}(V^\flat )\times \operatorname {U}(\mathcal {R} W)$
defines a bijection
where
![]() $\phi =\mu +\mu $
is an L-parameter of
$\phi =\mu +\mu $
is an L-parameter of
![]() $\operatorname {U}(V^\flat )$
. Hence,
$\operatorname {U}(V^\flat )$
. Hence,
![]() $\Lambda $
is the (big) theta lift of some
$\Lambda $
is the (big) theta lift of some
![]() $\omega \in \Pi _\phi (\operatorname {U}(V^\flat ))$
. To check that
$\omega \in \Pi _\phi (\operatorname {U}(V^\flat ))$
. To check that
![]() $\omega =\omega _{V^\flat ,\mu }[\chi ^\flat ]$
, one can compute the character
$\omega =\omega _{V^\flat ,\mu }[\chi ^\flat ]$
, one can compute the character
![]() $\eta ^\flat \in \operatorname {Irr} A_\phi $
associated to
$\eta ^\flat \in \operatorname {Irr} A_\phi $
associated to
![]() $\omega $
. Recall that
$\omega $
. Recall that
![]() $\Lambda $
is also the theta lift of
$\Lambda $
is also the theta lift of
![]() $\omega _{V,\mu }[\chi ]$
. If we denote by
$\omega _{V,\mu }[\chi ]$
. If we denote by
![]() $\eta \in \operatorname {Irr} A_{\Psi _{M,\mu }}$
and
$\eta \in \operatorname {Irr} A_{\Psi _{M,\mu }}$
and
![]() $\theta (\eta )\in \operatorname {Irr} A_{\theta (\Psi _{M,\mu })}$
the character associated to
$\theta (\eta )\in \operatorname {Irr} A_{\theta (\Psi _{M,\mu })}$
the character associated to
![]() $\omega _{V,\mu }[\chi ]$
and
$\omega _{V,\mu }[\chi ]$
and
![]() $\Lambda $
, respectively, then by Lemma 2.6 and Theorem 2.3, we have
$\Lambda $
, respectively, then by Lemma 2.6 and Theorem 2.3, we have
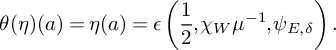 $$ \begin{align*} \theta(\eta)(a)&=\eta(a)=\epsilon\left(\frac{1}{2},\chi_W\mu^{-1},\psi_{E,\delta}\right). \end{align*} $$
$$ \begin{align*} \theta(\eta)(a)&=\eta(a)=\epsilon\left(\frac{1}{2},\chi_W\mu^{-1},\psi_{E,\delta}\right). \end{align*} $$
Here,
![]() $a\in A_{\theta (\Psi _{M,\mu })}$
is the basis element corresponding to
$a\in A_{\theta (\Psi _{M,\mu })}$
is the basis element corresponding to
![]() $\chi _V$
, and we regard
$\chi _V$
, and we regard
![]() $A_\phi $
and
$A_\phi $
and
![]() $A_{\Psi _{M,\mu }}$
as subgroups of
$A_{\Psi _{M,\mu }}$
as subgroups of
![]() $A_{\theta (\Psi _{M,\mu })}$
. Apply Theorem 2.3 again, we get
$A_{\theta (\Psi _{M,\mu })}$
. Apply Theorem 2.3 again, we get
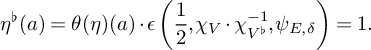 $$ \begin{align*} \eta^\flat(a)&=\theta(\eta)(a)\cdot\epsilon\left(\frac{1}{2},\chi_V\cdot\chi_{V^\flat}^{-1},\psi_{E,\delta}\right)=1. \end{align*} $$
$$ \begin{align*} \eta^\flat(a)&=\theta(\eta)(a)\cdot\epsilon\left(\frac{1}{2},\chi_V\cdot\chi_{V^\flat}^{-1},\psi_{E,\delta}\right)=1. \end{align*} $$
This implies that
![]() $\omega =\omega _{V^\flat ,\mu }[\chi ^\flat ]$
.
$\omega =\omega _{V^\flat ,\mu }[\chi ^\flat ]$
.
Now, excluding the special case above, we prove the general case. It would be convenient to consider the cases of odd and even n separately. In the following, we check the case of odd n in full details.
Let
![]() $e_1$
,
$e_1$
,
![]() $e_{n-1}$
and
$e_{n-1}$
and
![]() $e_{n}$
be the basis elements of
$e_{n}$
be the basis elements of
![]() $A_{\theta \left (\Psi _{M,\mu }\right )}$
corresponding to
$A_{\theta \left (\Psi _{M,\mu }\right )}$
corresponding to
![]() $\chi \cdot \mu ^{-n}\cdot \chi _W^{-1}\chi _V$
,
$\chi \cdot \mu ^{-n}\cdot \chi _W^{-1}\chi _V$
,
![]() $\chi _V\boxtimes S_{n-1}$
and
$\chi _V\boxtimes S_{n-1}$
and
![]() $\mu \cdot \chi _W^{-1}\chi _V\boxtimes S_n$
, respectively. Then:
$\mu \cdot \chi _W^{-1}\chi _V\boxtimes S_n$
, respectively. Then:
-
•
 $A_{\Psi _{M,\mu }}$
can be regarded as the subgroup of
$A_{\Psi _{M,\mu }}$
can be regarded as the subgroup of
 $A_{\theta \left (\Psi _{M,\mu }\right )}$
generated by
$A_{\theta \left (\Psi _{M,\mu }\right )}$
generated by
 $e_1$
and
$e_1$
and
 $e_n$
;
$e_n$
; -
•
 $A_{\Psi ^\flat }$
can be regarded as the subgroup of
$A_{\Psi ^\flat }$
can be regarded as the subgroup of
 $A_{\theta \left (\Psi _{M,\mu }\right )}$
generated by
$A_{\theta \left (\Psi _{M,\mu }\right )}$
generated by
 $e_1$
and
$e_1$
and
 $e_{n-1}$
.
$e_{n-1}$
.
Recall that
![]() $\omega _{V,\mu }[\chi ]\in \Pi _{\Psi _{M,\mu }}(\operatorname {U}(V))$
corresponds to the character
$\omega _{V,\mu }[\chi ]\in \Pi _{\Psi _{M,\mu }}(\operatorname {U}(V))$
corresponds to the character
![]() $\nu _{n+1}$
of
$\nu _{n+1}$
of
![]() $A_{\Psi _{M,\mu }}$
such that
$A_{\Psi _{M,\mu }}$
such that
Then by Theorem 2.3,
![]() $\Lambda =\Theta \left (\omega _{V,\mu }[\chi ]\right )$
corresponds to the character
$\Lambda =\Theta \left (\omega _{V,\mu }[\chi ]\right )$
corresponds to the character
![]() $\nu $
of
$\nu $
of
![]() $A_{\theta \left (\Psi _{M,\mu }\right )}$
such that
$A_{\theta \left (\Psi _{M,\mu }\right )}$
such that
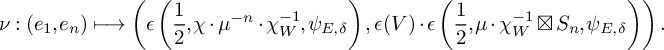 $$\begin{align*}\nu: (e_1,e_n)\longmapsto \left(\epsilon\left(\frac{1}{2},\chi\cdot\mu^{-n}\cdot\chi_W^{-1},\psi_{E,\delta}\right),\, \epsilon(V)\cdot\epsilon\left(\frac{1}{2},\mu\cdot\chi_W^{-1}\boxtimes S_n, \psi_{E,\delta}\right)\right). \end{align*}$$
$$\begin{align*}\nu: (e_1,e_n)\longmapsto \left(\epsilon\left(\frac{1}{2},\chi\cdot\mu^{-n}\cdot\chi_W^{-1},\psi_{E,\delta}\right),\, \epsilon(V)\cdot\epsilon\left(\frac{1}{2},\mu\cdot\chi_W^{-1}\boxtimes S_n, \psi_{E,\delta}\right)\right). \end{align*}$$
The evaluation of
![]() $\nu $
at
$\nu $
at
![]() $e_{n-1}$
can be determined by its evaluation at
$e_{n-1}$
can be determined by its evaluation at
![]() $(e_1,e_n)$
and the sign of
$(e_1,e_n)$
and the sign of
![]() $\mathcal {R} W$
. To be more precise,
$\mathcal {R} W$
. To be more precise,
![]() $\nu $
takes
$\nu $
takes
![]() $e_{n-1}$
to
$e_{n-1}$
to
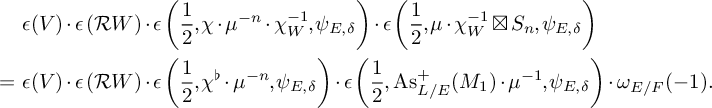 $$ \begin{align*} &\epsilon(V)\cdot\epsilon\left(\mathcal{R} W\right)\cdot\epsilon\left(\frac{1}{2},\chi\cdot\mu^{-n}\cdot\chi_W^{-1},\psi_{E,\delta}\right)\cdot\epsilon\left(\frac{1}{2},\mu\cdot\chi_W^{-1}\boxtimes S_n, \psi_{E,\delta}\right) \\ =\ &\epsilon(V)\cdot\epsilon\left(\mathcal{R} W\right)\cdot\epsilon\left(\frac{1}{2},\chi^\flat\cdot\mu^{-n},\psi_{E,\delta}\right)\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{E/F}(-1). \end{align*} $$
$$ \begin{align*} &\epsilon(V)\cdot\epsilon\left(\mathcal{R} W\right)\cdot\epsilon\left(\frac{1}{2},\chi\cdot\mu^{-n}\cdot\chi_W^{-1},\psi_{E,\delta}\right)\cdot\epsilon\left(\frac{1}{2},\mu\cdot\chi_W^{-1}\boxtimes S_n, \psi_{E,\delta}\right) \\ =\ &\epsilon(V)\cdot\epsilon\left(\mathcal{R} W\right)\cdot\epsilon\left(\frac{1}{2},\chi^\flat\cdot\mu^{-n},\psi_{E,\delta}\right)\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{E/F}(-1). \end{align*} $$
Hence, if we let
![]() $V^\flat $
be the n-dimensional skew-Hermitian space as in Equation (†), then again by Theorem 2.3, one can check that:
$V^\flat $
be the n-dimensional skew-Hermitian space as in Equation (†), then again by Theorem 2.3, one can check that:
-
•
 $\omega _{V^\flat ,\mu }[\chi ^\flat ]\in \Pi _{\Psi ^\flat }(\operatorname {U}(V^\flat ))$
corresponding to the character
$\omega _{V^\flat ,\mu }[\chi ^\flat ]\in \Pi _{\Psi ^\flat }(\operatorname {U}(V^\flat ))$
corresponding to the character
 $\nu _{n}$
of
$\nu _{n}$
of
 $A_{\Psi ^\flat }$
such that
$A_{\Psi ^\flat }$
such that  $$\begin{align*}\nu_{n}: (e_1, e_{n-1})\longmapsto \left(\epsilon\left(\frac{1}{2},\chi^\flat\cdot\mu^{-n},\psi_{E,\delta}\right),\, \epsilon\left(V^\flat\right)\cdot\epsilon\left(\frac{1}{2},\chi^\flat\cdot\mu^{-n},\psi_{E,\delta}\right)\right); \end{align*}$$
$$\begin{align*}\nu_{n}: (e_1, e_{n-1})\longmapsto \left(\epsilon\left(\frac{1}{2},\chi^\flat\cdot\mu^{-n},\psi_{E,\delta}\right),\, \epsilon\left(V^\flat\right)\cdot\epsilon\left(\frac{1}{2},\chi^\flat\cdot\mu^{-n},\psi_{E,\delta}\right)\right); \end{align*}$$
-
• the theta lift of
 $\omega _{V^\flat ,\mu }[\chi ^\flat ]$
to
$\omega _{V^\flat ,\mu }[\chi ^\flat ]$
to
 $\operatorname {U}(\mathcal {R} W)$
is nonzero and exactly equal to
$\operatorname {U}(\mathcal {R} W)$
is nonzero and exactly equal to
 $\Lambda $
.
$\Lambda $
.
These complete the proof of the case when n is odd.
Similarly, when n is even,
![]() $\omega _{V,\mu }[\chi ]\in \Pi _{\Psi _{M,\mu }}(\operatorname {U}(V))$
corresponds to
$\omega _{V,\mu }[\chi ]\in \Pi _{\Psi _{M,\mu }}(\operatorname {U}(V))$
corresponds to
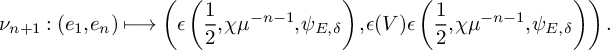 $$\begin{align*}\nu_{n+1}: (e_1,e_n) \longmapsto \left(\epsilon\left(\frac{1}{2},\chi\mu^{-n-1},\psi_{E,\delta}\right),\epsilon(V)\epsilon\left(\frac{1}{2},\chi\mu^{-n-1},\psi_{E,\delta}\right)\right). \end{align*}$$
$$\begin{align*}\nu_{n+1}: (e_1,e_n) \longmapsto \left(\epsilon\left(\frac{1}{2},\chi\mu^{-n-1},\psi_{E,\delta}\right),\epsilon(V)\epsilon\left(\frac{1}{2},\chi\mu^{-n-1},\psi_{E,\delta}\right)\right). \end{align*}$$
By Theorem 2.3,
![]() $\Lambda $
corresponds to
$\Lambda $
corresponds to
![]() $\nu \in \operatorname {Irr} A_{\theta \left (\Psi _{M,\mu }\right )}$
such that
$\nu \in \operatorname {Irr} A_{\theta \left (\Psi _{M,\mu }\right )}$
such that
![]() $\nu ~\big |_{A_{\Psi _{M,\mu }}}=\nu _{n+1}$
, so
$\nu ~\big |_{A_{\Psi _{M,\mu }}}=\nu _{n+1}$
, so
Then again one can appeal to Theorem 2.3 to show that the theta lift of
![]() $\omega _{V^\flat ,\mu }[\chi ^\flat ]$
is exactly
$\omega _{V^\flat ,\mu }[\chi ^\flat ]$
is exactly
![]() $\Lambda $
.
$\Lambda $
.
With this proposition in hand, we get
is nonzero. In particular,
![]() $\Pi ^\flat $
is nonzero. By [Reference Gan and IchinoGI16, Sect. 4.4(P1)], we know that:
$\Pi ^\flat $
is nonzero. By [Reference Gan and IchinoGI16, Sect. 4.4(P1)], we know that:
-
• The sign of the Hermitian space W is given by
where $$\begin{align*}\epsilon(W)=\epsilon\left(\frac{1}{2}, M_0\cdot {^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right), \end{align*}$$
$$\begin{align*}\epsilon(W)=\epsilon\left(\frac{1}{2}, M_0\cdot {^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right), \end{align*}$$
 $\psi _{L,\delta }=\psi _F\left (\operatorname {Tr}_{L/F}(\delta \cdot ~)\right )$
.
$\psi _{L,\delta }=\psi _F\left (\operatorname {Tr}_{L/F}(\delta \cdot ~)\right )$
.
-
•
 $\Pi ^\flat $
is an irreducible tempered representation has L-parameter
$\Pi ^\flat $
is an irreducible tempered representation has L-parameter
 $M^\flat =M^{\prime }_0$
and corresponds to
$M^\flat =M^{\prime }_0$
and corresponds to
 $\eta ^\flat $
, where and
$\eta ^\flat $
, where and $$\begin{align*}M^{\prime}_0=M_0\cdot {^{\tau}M_{1}}\cdot M_{1}^{-1}\cdot\Upsilon\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \end{align*}$$
for all
$$\begin{align*}M^{\prime}_0=M_0\cdot {^{\tau}M_{1}}\cdot M_{1}^{-1}\cdot\Upsilon\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \end{align*}$$
for all $$\begin{align*}\eta^\flat(a_i)/\eta(a_i) = \epsilon\left(\frac{1}{2}, M_i\cdot{^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right) \end{align*}$$
$$\begin{align*}\eta^\flat(a_i)/\eta(a_i) = \epsilon\left(\frac{1}{2}, M_i\cdot{^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right) \end{align*}$$
 $i\geq 2$
.
$i\geq 2$
.
Also note that
Substitute these into Equation (†), we get
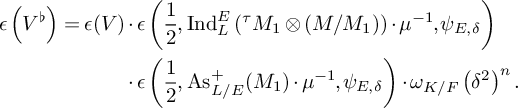 $$ \begin{align}\epsilon\left(V^\flat\right)=\epsilon(V)&\cdot\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_{1} \otimes (M/M_{1})\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\nonumber\\&\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^n. \end{align} $$
$$ \begin{align}\epsilon\left(V^\flat\right)=\epsilon(V)&\cdot\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_{1} \otimes (M/M_{1})\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\nonumber\\&\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^n. \end{align} $$
Now, if we assume that Conjecture 1.1 holds for the L-parameter
![]() $M^\flat $
, then it follows that:
$M^\flat $
, then it follows that:
-
(1) The multiplicity
 $m_{V}(\Pi ,\mu )=1$
.
$m_{V}(\Pi ,\mu )=1$
. -
(2) V is the unique
 $(n+1)$
-dimensional Hermitian space over E predicted by the formula in Conjecture 1.1(3). Indeed, note that for any semisimple representation N and any character
$(n+1)$
-dimensional Hermitian space over E predicted by the formula in Conjecture 1.1(3). Indeed, note that for any semisimple representation N and any character
 $\mathcal {X}$
of
$\mathcal {X}$
of
 $WD_L$
, we have Combining this with Conjecture 1.1(3) for
$WD_L$
, we have Combining this with Conjecture 1.1(3) for $$\begin{align*}\operatorname{As}^+(N\cdot\mathcal{X})=\operatorname{As}^+(N)\cdot\left(\mathcal{X}~\Big|_{E^\times}\right). \end{align*}$$
$$\begin{align*}\operatorname{As}^+(N\cdot\mathcal{X})=\operatorname{As}^+(N)\cdot\left(\mathcal{X}~\Big|_{E^\times}\right). \end{align*}$$
 $M^\flat $
, we know that Then applying the equality (††), we get
$M^\flat $
, we know that Then applying the equality (††), we get $$ \begin{align*} \epsilon\left(V^\flat\right)&=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}\left(M^\flat\right)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n-1)/2}\\ &=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}\left(M_0\right)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n-1)/2}. \end{align*} $$
$$ \begin{align*} \epsilon\left(V^\flat\right)&=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}\left(M^\flat\right)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n-1)/2}\\ &=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}\left(M_0\right)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n-1)/2}. \end{align*} $$
 $$ \begin{align*}\epsilon(V)&=\epsilon\left(V^\flat\right)\cdot\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_{1} \otimes (M/M_{1})\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\\&\qquad\qquad\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^n\\ &=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}(M)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n+1)/2}. \end{align*} $$
$$ \begin{align*}\epsilon(V)&=\epsilon\left(V^\flat\right)\cdot\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_{1} \otimes (M/M_{1})\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\\&\qquad\qquad\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^n\\ &=\epsilon\left(\frac{1}{2}, \operatorname{As}^+_{L/E}(M)\otimes\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{K/F}\left(\delta^2\right)^{n(n+1)/2}. \end{align*} $$
-
(3)
 $\Pi $
is the unique member in
$\Pi $
is the unique member in
 $\Pi _{M}$
predicted by the formula in Conjecture 1.1(4). Similar to (2), it follows from Conjecture 1.1(4) that for all
$\Pi _{M}$
predicted by the formula in Conjecture 1.1(4). Similar to (2), it follows from Conjecture 1.1(4) that for all $$ \begin{align*}\eta^\flat(a_i) &= \epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_i \otimes (M_0/M_i)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\\ &= \epsilon\left(\frac{1}{2}, {^{\tau}M_i} \otimes (M_0/M_i)\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \psi_{L,\delta}\right) \end{align*} $$
$$ \begin{align*}\eta^\flat(a_i) &= \epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_i \otimes (M_0/M_i)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right)\\ &= \epsilon\left(\frac{1}{2}, {^{\tau}M_i} \otimes (M_0/M_i)\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \psi_{L,\delta}\right) \end{align*} $$
 $i\geq 2$
. Hence, for all
$i\geq 2$
. Hence, for all $$ \begin{align*} \eta(a_i)&=\eta^\flat(a_i)\cdot\epsilon\left(\frac{1}{2}, M_i\cdot{^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right)\\ &=\epsilon\left(\frac{1}{2}, {^{\tau}M_i} \otimes (M/M_i)\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right)\\ &=\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_i \otimes (M/M_i)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right) \end{align*} $$
$$ \begin{align*} \eta(a_i)&=\eta^\flat(a_i)\cdot\epsilon\left(\frac{1}{2}, M_i\cdot{^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right)\\ &=\epsilon\left(\frac{1}{2}, {^{\tau}M_i} \otimes (M/M_i)\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right)\\ &=\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_i \otimes (M/M_i)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right) \end{align*} $$
 $i\geq 2$
. On the other hand, recall that
$i\geq 2$
. On the other hand, recall that
 $\eta (a_1)=\epsilon (W)$
. This implies the desired equality
$\eta (a_1)=\epsilon (W)$
. This implies the desired equality  $$ \begin{align*}\eta(a_1)&=\epsilon\left(\frac{1}{2}, M_0\cdot {^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right) \\ &=\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_1 \otimes (M/M_1)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right). \end{align*} $$
$$ \begin{align*}\eta(a_1)&=\epsilon\left(\frac{1}{2}, M_0\cdot {^{\tau}M_{1}}\cdot\mu^{-1}\circ\operatorname{Nm}_{L/E}, \,\psi_{L,\delta}\right) \\ &=\epsilon \left(\frac{1}{2}, \operatorname{Ind}_L^E\left(^{\tau}M_1 \otimes (M/M_1)\right)\cdot\mu^{-1}, \psi_{E,\delta}\right). \end{align*} $$
The computation above shows that there is at most one
![]() $\Pi $
in the L-packet
$\Pi $
in the L-packet
![]() $\Pi _M$
such that
$\Pi _M$
such that
![]() $m_V(\Pi ,\mu )\ne 0$
.
$m_V(\Pi ,\mu )\ne 0$
.
3.2. Reversing two seesaw diagrams: existence
Conversely, still under the assumption that Conjecture 1.1 holds for the L-parameter
![]() $M^\flat $
, we can produce an irreducible tempered representation
$M^\flat $
, we can produce an irreducible tempered representation
![]() $\Pi '\in \Pi _M$
such that
$\Pi '\in \Pi _M$
such that
for some
![]() $(n+1)$
-dimensional skew-Hermitian space
$(n+1)$
-dimensional skew-Hermitian space
![]() $V'$
, from the unique irreducible tempered representation
$V'$
, from the unique irreducible tempered representation
![]() $\Pi ^\flat \in \Pi _{M^\flat }$
such that
$\Pi ^\flat \in \Pi _{M^\flat }$
such that
We do it by applying the two seesaw diagrams reversely as follows. First, consider an analog of the seesaw diagram (♮.2) (using the same splitting characters):
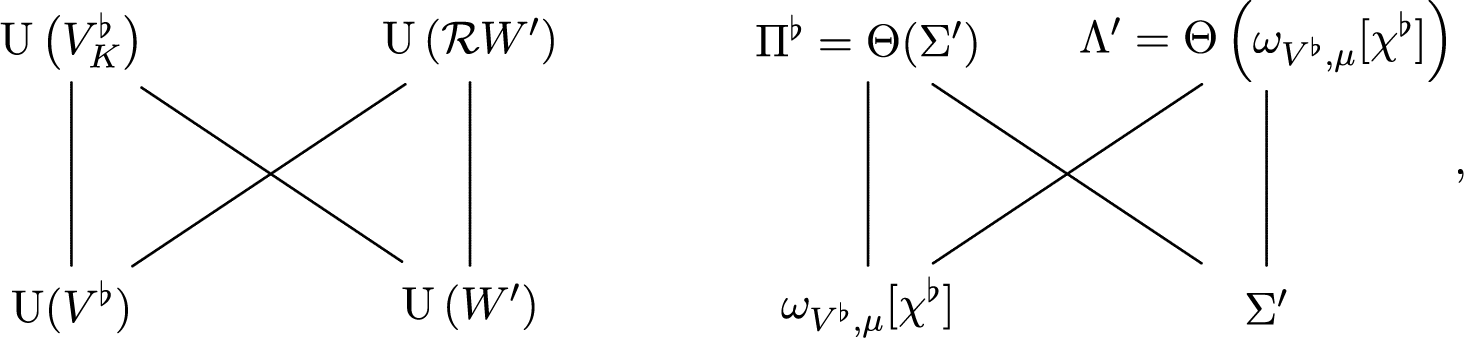
where
![]() $W'$
is the unique n-dimensional Hermitian space over L chosen by the theta dichotomy [Reference Gan and IchinoGI16, Sect. 4.4(P1)]; that is, the theta lift
$W'$
is the unique n-dimensional Hermitian space over L chosen by the theta dichotomy [Reference Gan and IchinoGI16, Sect. 4.4(P1)]; that is, the theta lift
![]() $\Sigma '$
of
$\Sigma '$
of
![]() $\Pi ^\flat $
to
$\Pi ^\flat $
to
![]() $\operatorname {U}(W')$
is nonzero. Symmetrically,
$\operatorname {U}(W')$
is nonzero. Symmetrically,
![]() $\Pi ^\flat =\Theta \left (\Sigma '\right )$
is the big theta lift of
$\Pi ^\flat =\Theta \left (\Sigma '\right )$
is the big theta lift of
![]() $\Sigma '$
. By the seesaw identity, we have
$\Sigma '$
. By the seesaw identity, we have
In particular,
![]() $\Lambda '$
is nonzero. It then follows from Theorem 2.1 and Theorem 2.3 that
$\Lambda '$
is nonzero. It then follows from Theorem 2.1 and Theorem 2.3 that
![]() $\Lambda '$
is an irreducible unitary representation lies in the A-packet
$\Lambda '$
is an irreducible unitary representation lies in the A-packet
![]() $\Pi _{\theta (\Psi _{M,\mu })}\left (\operatorname {U}\left (\mathcal {R} W'\right )\right )$
, where
$\Pi _{\theta (\Psi _{M,\mu })}\left (\operatorname {U}\left (\mathcal {R} W'\right )\right )$
, where
Next, we shall use an analog of the seesaw diagram (♮.1). The following is an analog of the key Proposition 3.2.
Proposition 3.3. Let
![]() $V'$
be the
$V'$
be the
![]() $(n+1)$
-dimensional skew-Hermitian space of sign
$(n+1)$
-dimensional skew-Hermitian space of sign
 $$ \begin{align} \epsilon\left(V^\prime\right)= \epsilon\left(V^\flat\right)\cdot\epsilon\left(\mathcal{R} W'\right)\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{E/F}(-1)^n \end{align} $$
$$ \begin{align} \epsilon\left(V^\prime\right)= \epsilon\left(V^\flat\right)\cdot\epsilon\left(\mathcal{R} W'\right)\cdot\epsilon\left(\frac{1}{2},\operatorname{As}^+_{L/E}(M_{1})\cdot\mu^{-1}, \psi_{E,\delta}\right)\cdot\omega_{E/F}(-1)^n \end{align} $$
and
Then
![]() $\Lambda '$
is the (big) theta lift of
$\Lambda '$
is the (big) theta lift of
![]() $\omega '$
to
$\omega '$
to
![]() $\operatorname {U}(\mathcal {R} W')$
, that is,
$\operatorname {U}(\mathcal {R} W')$
, that is,
![]() $\Lambda '=\Theta (\omega ')$
. Here, we are using the same splitting characters as described in Equation (♮.1).
$\Lambda '=\Theta (\omega ')$
. Here, we are using the same splitting characters as described in Equation (♮.1).
Proof. We first check the special case that
![]() $n=2$
and
$n=2$
and
![]() $\chi ^\flat =\mu ^2$
. So
$\chi ^\flat =\mu ^2$
. So
and
Let
![]() $V"$
and
$V"$
and
![]() $\mathcal {R} W"$
be the companion spaces of
$\mathcal {R} W"$
be the companion spaces of
![]() $V'$
and
$V'$
and
![]() $\mathcal {R} W'$
respectively. Consider the following map given by the theta correspondence:
$\mathcal {R} W'$
respectively. Consider the following map given by the theta correspondence:
where
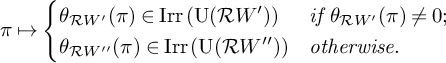 $$ \begin{align*} \pi\mapsto\begin{cases} \theta_{\mathcal{R} W'}(\pi)\in\operatorname{Irr}\left(\operatorname{U}(\mathcal{R} W')\right) \quad &\textit{if } \theta_{\mathcal{R} W'}(\pi)\ne 0;\\ \theta_{\mathcal{R} W"}(\pi)\in\operatorname{Irr}\left(\operatorname{U}(\mathcal{R} W")\right) \quad &\textit{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \pi\mapsto\begin{cases} \theta_{\mathcal{R} W'}(\pi)\in\operatorname{Irr}\left(\operatorname{U}(\mathcal{R} W')\right) \quad &\textit{if } \theta_{\mathcal{R} W'}(\pi)\ne 0;\\ \theta_{\mathcal{R} W"}(\pi)\in\operatorname{Irr}\left(\operatorname{U}(\mathcal{R} W")\right) \quad &\textit{otherwise}. \end{cases} \end{align*} $$
This map is well defined by the theta dichotomy. Using Theorem 2.1, One can easily check by hand that this map restricts to a bijection
Hence,
![]() $\Lambda '$
is the (big) theta lift of some
$\Lambda '$
is the (big) theta lift of some
To check that
![]() $\omega '=\omega _{V',\mu }[\chi ]$
, one can use Theorem 2.3 and Lemma 2.6 to compute the character
$\omega '=\omega _{V',\mu }[\chi ]$
, one can use Theorem 2.3 and Lemma 2.6 to compute the character
![]() $\eta '\in \operatorname {Irr} A_{\Psi _{M,\mu }}$
associated to
$\eta '\in \operatorname {Irr} A_{\Psi _{M,\mu }}$
associated to
![]() $\omega '$
. We omit the details.
$\omega '$
. We omit the details.
Excluding the special case above, the theta correspondence between
![]() $\operatorname {U}(V')\times \operatorname {U}(\mathcal {R} W')$
is in the situation of Theorem 2.1(2). It follows that the theta lift
$\operatorname {U}(V')\times \operatorname {U}(\mathcal {R} W')$
is in the situation of Theorem 2.1(2). It follows that the theta lift
![]() $\Theta (\omega _{V',\mu }[\chi ])$
to
$\Theta (\omega _{V',\mu }[\chi ])$
to
![]() $\operatorname {U}(\mathcal {R} W')$
is nonvanishing. So the proof of the general case comes down to a computation of the labellings similar to the proof of Proposition 3.2. We shall not repeat the tedious computation here.
$\operatorname {U}(\mathcal {R} W')$
is nonvanishing. So the proof of the general case comes down to a computation of the labellings similar to the proof of Proposition 3.2. We shall not repeat the tedious computation here.
Now, we can consider the following seesaw diagram, with respect to the same splitting characters as described in Equation (♮.1):
Again by the seesaw identity, we have
is nonzero. In particular,
![]() $\Pi '$
is nonzero. By [Reference Gan and IchinoGI16, Sect. 4.6(P2)], we know that
$\Pi '$
is nonzero. By [Reference Gan and IchinoGI16, Sect. 4.6(P2)], we know that
![]() $\Pi '$
is an irreducible tempered representation of
$\Pi '$
is an irreducible tempered representation of
![]() $\operatorname {U}(V^{\prime }_K)$
lies in the L-packet
$\operatorname {U}(V^{\prime }_K)$
lies in the L-packet
![]() $\Pi _M$
. The construction above shows the existence of
$\Pi _M$
. The construction above shows the existence of
![]() $\Pi '\in \Pi _M$
such that
$\Pi '\in \Pi _M$
such that
![]() $m_{V'}(\Pi ',\mu )\ne 0$
.
$m_{V'}(\Pi ',\mu )\ne 0$
.
3.3. Conclusion
In summary, we have shown that:
Proposition 3.4. Let
![]() $V_0$
be an n-dimensional Hermitian space over E and
$V_0$
be an n-dimensional Hermitian space over E and
![]() $M^{\prime }_0$
a tempered L-parameter for the unitary group
$M^{\prime }_0$
a tempered L-parameter for the unitary group
![]() $\operatorname {U}(V_{0,K})$
. Assume that Conjecture 1.1 holds for the L-parameter
$\operatorname {U}(V_{0,K})$
. Assume that Conjecture 1.1 holds for the L-parameter
![]() $M^{\prime }_0$
. Then it also holds for the L-parameter of the form
$M^{\prime }_0$
. Then it also holds for the L-parameter of the form
where
![]() $\mathcal {X}$
is any conjugate symplectic character of
$\mathcal {X}$
is any conjugate symplectic character of
![]() $L^\times $
, and
$L^\times $
, and
![]() $M_1$
is any conjugate self-dual character of
$M_1$
is any conjugate self-dual character of
![]() $L^\times $
of parity
$L^\times $
of parity
![]() $(-1)^n$
.
$(-1)^n$
.
Proof. As we have explicated above, given such an L-parameter M, one can construct an L-parameter
![]() $M^\flat $
of
$M^\flat $
of
![]() $\operatorname {U}(V_{0,K})$
. As long as Conjecture 1.1 holds for the L-parameter
$\operatorname {U}(V_{0,K})$
. As long as Conjecture 1.1 holds for the L-parameter
![]() $M^\flat $
, it also holds for M. On the other hand, from the construction of
$M^\flat $
, it also holds for M. On the other hand, from the construction of
![]() $M^\flat $
, one can see that
$M^\flat $
, one can see that
for some conjugate orthogonal character
![]() $\mathcal {Y}$
of
$\mathcal {Y}$
of
![]() $L^\times $
. Thus, by Lemma 3.1, Conjecture 1.1 holds for
$L^\times $
. Thus, by Lemma 3.1, Conjecture 1.1 holds for
![]() $M^\flat $
.
$M^\flat $
.
Now, we can prove the main result of this paper.
Proof of Theorem 1.3
Simply note that if M is a summation of conjugate self-dual characters as described in Theorem 1.3, then so is
![]() $M^\flat $
.
$M^\flat $
.
The reader may notice the similarity of our setup with the paper [Reference XueXue23] of Hang Xue, in which he showed the Bessel case of the local GGP conjecture for unitary groups over
![]() $\mathbb {R}$
. There, he worked also with L-parameters M of the same form as those in Theorem 1.3. Indeed, we are partly inspired by his results to consider these M’s. However, the inductive argument in our proof is different from that in [Reference XueXue23] (not to mention that the setting of our result is different).
$\mathbb {R}$
. There, he worked also with L-parameters M of the same form as those in Theorem 1.3. Indeed, we are partly inspired by his results to consider these M’s. However, the inductive argument in our proof is different from that in [Reference XueXue23] (not to mention that the setting of our result is different).
We end up this paper with a remark on the global conjecture [Reference Gan, Gross and PrasadGGP23, Conj. 11.1]. One can expect to prove the global conjecture for the near equivalence class
with each
![]() $M_i$
conjugate self-dual automorphic character of
$M_i$
conjugate self-dual automorphic character of
![]() $\operatorname {GL}_1$
of parity
$\operatorname {GL}_1$
of parity
![]() $(-1)^{n-1}$
by using the same argument. Instead of the Adams’ conjecture used in this paper, one will need to show an analog of the Siegel–Weil formula in the global case so that one can compare the theta integrals of
$(-1)^{n-1}$
by using the same argument. Instead of the Adams’ conjecture used in this paper, one will need to show an analog of the Siegel–Weil formula in the global case so that one can compare the theta integrals of
![]() $\omega _{V,\mu }$
and
$\omega _{V,\mu }$
and
![]() $\omega _{V^\flat ,\mu }$
. More precisely, let
$\omega _{V^\flat ,\mu }$
. More precisely, let
![]() $\Omega _{V}$
and
$\Omega _{V}$
and
![]() $\Omega _{V^\flat }$
be the Weil representation associated to
$\Omega _{V^\flat }$
be the Weil representation associated to
![]() $\operatorname {U}(V)\times \operatorname {U}(\mathcal {R} W)$
and
$\operatorname {U}(V)\times \operatorname {U}(\mathcal {R} W)$
and
![]() $\operatorname {U}(V^\flat )\times \operatorname {U}(\mathcal {R} W)$
, respectively, one needs to compare
$\operatorname {U}(V^\flat )\times \operatorname {U}(\mathcal {R} W)$
, respectively, one needs to compare
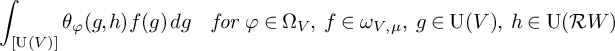 $$\begin{align*}\int_{[\operatorname{U}(V)]}\theta_\varphi(g,h)f(g)\,dg \quad \textit{for }\varphi\in\Omega_V,\ f\in\omega_{V,\mu},\ g\in\operatorname{U}(V),\ h\in\operatorname{U}(\mathcal{R} W) \end{align*}$$
$$\begin{align*}\int_{[\operatorname{U}(V)]}\theta_\varphi(g,h)f(g)\,dg \quad \textit{for }\varphi\in\Omega_V,\ f\in\omega_{V,\mu},\ g\in\operatorname{U}(V),\ h\in\operatorname{U}(\mathcal{R} W) \end{align*}$$
and
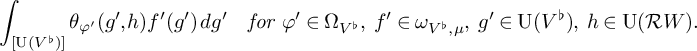 $$\begin{align*}\int_{[\operatorname{U}(V^\flat)]}\theta_{\varphi'}(g',h)f'(g')\,dg' \quad \textit{for }\varphi'\in\Omega_{V^\flat},\ f'\in\omega_{V^\flat,\mu},\ g'\in\operatorname{U}(V^\flat),\ h\in\operatorname{U}(\mathcal{R} W). \end{align*}$$
$$\begin{align*}\int_{[\operatorname{U}(V^\flat)]}\theta_{\varphi'}(g',h)f'(g')\,dg' \quad \textit{for }\varphi'\in\Omega_{V^\flat},\ f'\in\omega_{V^\flat,\mu},\ g'\in\operatorname{U}(V^\flat),\ h\in\operatorname{U}(\mathcal{R} W). \end{align*}$$
Unfortunately, these theta integrals diverge in general. So one has to properly regularize these theta integrals first. Once a global analog of Proposition 3.2 has been established, the remaining parts should go over smoothly.
Acknowledgements
Both authors were supported by a Singapore government MOE Tier One grant R-146-000-320-114 during the course of this work. The work was completed when the second author visited the Erwin Schrodinger Institute (ESI) in Vienna in April 2022; he thanks the ESI for excellent working conditions and inspiring atmosphere. The authors thank Petar Bakić, Marcela Hanzer and Jialiang Zou for helpful discussion and comments.
Competing interests
The authors have no competing interest to declare.















