Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T06:04:39.606Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Schur product of H-matrices and non-negative matrices, and related inequalities

Published online by Cambridge University Press:  24 October 2008

M. S. Lynn
M. S. Lynn
Affiliation:
Mathematics Division, National Physical Laboratory
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction. Let ℛn denote the set of all n × n matrices with real elements, and let 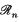denote the subset of ℛn consisting of all real, n × n, symmetric positive-definite matrices. We shall use the notation 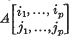to denote that minor of the matrix A = (aij) ∈ ℛn which is the determinant of the matrix

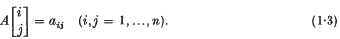
The Schur Product (Schur (14)) of two matrices A, B ∈ ℛn is denned by

where A = (aij), B = (bij), C = (cij) and

Let ϕ be the mapping of ℛn into the real line defined by

for all A ∈ ℛn, where, as in the sequel, .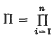

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 60 , Issue 3 , July 1964 , pp. 425 - 431
Copyright
Copyright © Cambridge Philosophical Society 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1) Bachmann, P. Die Arithmetik der Quadratischen Formen (1925).Google Scholar
(2) Beckenbach, E. F. An inequality for definite Hermitian determinants. Bull. American Math. Soc. 35 (1929), 325–329.CrossRefGoogle Scholar
(3) Collatz, L. Einschliessungssatz für die characteristischen Zahlen von Matrizen. Math. Z. 48 (1942), 221–226.CrossRefGoogle Scholar
(4) Fischer, E. Über den Hadamard'schen Determinantensatz. Archiv. Math. Physik (3), 13 (1908), 32–40.Google Scholar
(5) Frisch, M. R. Sur le théorème des déterminants de M. Hadamard. C.R. Acad. Sci., Paris, 185 (1927), 1244–1245.Google Scholar
(6) Gantmacher, F. R. The theory of matrices. Vol. II (Chelsea, New York, 1959).Google Scholar
(7) Gantmacher, F. R. and Krein, M. G. Oscillation matrices and kernels and small vibrations of dynamical systems (2nd ed., Gostekhizdat, Moscow, 1950). German translation in preparation.Google Scholar
(8) Mirsky, L. An introduction to linear algebra (Oxford University Press, 1955).Google Scholar
(9) Oppenheim, A. Inequalities connected with definite Hermitian forms. J. London Math. Soc. 5 (1930), 114–119.CrossRefGoogle Scholar
(10) Ostrowski, A. Über die Determinanten mit überwiegender Hauptdiagonale. Comment. Math. Helv. 10 (1937), 69–96.CrossRefGoogle Scholar
(11) Ostrowski, A. Note on bounds for some determinants. Duke Math. J. 22 (1955), 95–102.CrossRefGoogle Scholar
(12) Ostrowski, A. Determinanten mit überwiegender Hauptdiagonale und die absolute Konvergenz von Iterationsprozessen. Comment. Math. Helv. 30 (1956), 175–210.CrossRefGoogle Scholar
(13) Ostrowski, A. On some metrical properties of operator matrices and matrices partitioned into blocks. J. Math. Anal. Appl. 2 (1961), 161–209.CrossRefGoogle Scholar
(14) Schur, I. Bemerkungen zur Theorie der beschränkten Bilinearformen mit unendlichen vielen Veranderliehen. J. Reine Angew. Math. 140 (1911), 1–28.CrossRefGoogle Scholar
(15) Wielandt, H. Unzerlegbare, nicht negative Matrizen. Math. Z. 52 (1950), 642–648.CrossRefGoogle Scholar