Hostname: page-component-784d4fb959-wvrvt Total loading time: 0 Render date: 2025-07-15T23:24:45.900Z Has data issue: false hasContentIssue false
  • English
  • Français

Rings of Frobenius operators

Published online by Cambridge University Press:  24 April 2014

MORDECHAI KATZMAN ,
KARL SCHWEDE ,
ANURAG K. SINGH  and
WENLIANG ZHANG
MORDECHAI KATZMAN
Affiliation:
Department of Pure Mathematics, University of Sheffield, Hicks Building, Sheffield, S3 7RH. e-mail: M.Katzman@sheffield.ac.uk
KARL SCHWEDE
Affiliation:
Department of Mathematics, The Pennsylvania State University, University Park, PA 16802, U.S.A. e-mail: schwede@math.psu.edu
ANURAG K. SINGH
Affiliation:
Department of Mathematics, University of Utah, 155 S 1400 E, Salt Lake City, UT 84112, U.S.A. e-mail: singh@math.utah.edu
WENLIANG ZHANG
Affiliation:
Department of Mathematics, University of Nebraska, Lincoln, NE 68505, U.S.A. e-mail: wzhang15@unl.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let R be a local ring of prime characteristic. We study the ring of Frobenius operators 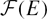${\mathcal F}(E)$, where E is the injective hull of the residue field of R. In particular, we examine the finite generation of 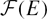${\mathcal F}(E)$ over its degree zero component 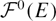${\mathcal F}^0(E)$, and show that 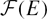${\mathcal F}(E)$ need not be finitely generated when R is a determinantal ring; nonetheless, we obtain concrete descriptions of 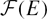${\mathcal F}(E)$ in good generality that we use, for example, to prove the discreteness of F-jumping numbers for arbitrary ideals in determinantal rings.

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 157 , Issue 1 , July 2014 , pp. 151 - 167
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[ABZ]Montaner, J. Àlvarez, Boix, A. F. and Zarzuela, S.Frobenius and Cartier algebras of Stanley–Reisner rings. J. Algebra. 358 (2012), 162–177.CrossRefGoogle Scholar
[An]Anderson, G. W.An elementary approach to L-functions mod p. J. Number Theory. 80 (2000), 291–303.CrossRefGoogle Scholar
[Bl1]Blickle, M. The intersection homology D-module in finite characteristic. Ph.D. thesis. University of Michigan (2001), arXiv:math/0110244 [math.AG].Google Scholar
[Bl2]Blickle, M.Test ideals via algebras of p −e-linear maps. J. Algebraic Geom. 22 (2013), 49–83.CrossRefGoogle Scholar
[BV]Bruns, W. and Vetter, U.Determinantal rings. Lecture Notes in Math. 1327 (Springer-Verlag, Berlin, 1988).Google Scholar
[Ei]Eisenbud, D.The geometry of syzygies. Graduate Texts in Math. 229 (Springer-Verlag, New York, 2005).Google Scholar
[Fe]Fedder, R.F-purity and rational singularity. Trans. Amer. Math. Soc. 278 (1983), 461–480.Google Scholar
[GW]Goto, S. and Watanabe, K.-i.On graded rings I. J. Math. Soc. Japan. 30 (1978), 179–213.CrossRefGoogle Scholar
[ILL+]Iyengar, S. B., Leuschke, G. J., Leykin, A., Miller, C., Miller, E., Singh, A. K. and Walther, U.Twenty-four hours of local cohomology. Grad. Stud. Math. 87 (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar
[Ka]Katzman, M.A non-finitely generated algebra of Frobenius maps. Proc. Amer. Math. Soc. 138 (2010), 2381–2383.CrossRefGoogle Scholar
[KZ]Katzman, M. and Zhang, W. Castelnuovo–Mumford regularity and the discreteness of F-jumping coefficients in graded rings. Trans. Amer. Math. Soc., to appear, arXiv:1110.2093 [math.AC].Google Scholar
[LS]Lyubeznik, G. and Smith, K. E.On the commutation of the test ideal with localization and completion. Trans. Amer. Math. Soc. 353 (2001), 3149–3180.CrossRefGoogle Scholar
[Sc]Schwede, K.Test ideals in non-${\mathbb Q}$-Gorenstein rings. Trans. Amer. Math. Soc. 363 (2011), 5925–5941.CrossRefGoogle Scholar
[SV]Smith, K. E. and Van den Bergh, M.Simplicity of rings of differential operators in prime characteristic. Proc. London Math. Soc. (3). 75 (1997), 32–62.CrossRefGoogle Scholar
[TT]Takagi, S. and Takahashi, R.D-modules over rings with finite F-representation type. Math. Res. Lett. 15 (2008), 563–581.CrossRefGoogle Scholar