Hostname: page-component-6bb9c88b65-9rk55 Total loading time: 0 Render date: 2025-07-27T02:48:41.354Z Has data issue: false hasContentIssue false
  • English
  • Français

Some qualitative properties of solutions of a generalised diffusion equation

Published online by Cambridge University Press:  24 October 2008

C. Atkinson  and
J. E. Bouillet
C. Atkinson
Affiliation:
Imperial College, London and Universidad National de Salta, Argentina
J. E. Bouillet
Affiliation:
Imperial College, London and Universidad National de Salta, Argentina
Get access Rights & Permissions [Opens in a new window]

Extract

Atkinson and Peletier (2,3) have considered similarity solutions of the differential equation

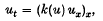
where the function k(s) is defined, real and continuous for s ≥ 0 and k(s) > 0 if s > 0 (in (2) k(0) = 0 is also assumed). In particular they look for similarity solutions of the form u(x, t) = f(η) where η = x(t+l)−½ with boundary conditions f(0) = A and 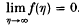. They show that if k(s) satisfies the condition

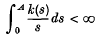
then for any A > 0 there is a unique similarity solution which is non-negative and has compact support in [0, ∞). They also show in (2) that

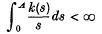
is a necessary condition for the solution to have compact support. In (3) they prove existence of similarity solutions when

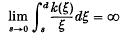
and show that in this case the similarity solution has the property that f(η) > 0 for all η > 0.

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 3 , November 1979 , pp. 495 - 510
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

(1)Atkinson, C. and Jones, C. W.Similarity solutions in some non-linear diffusion problems and in boundary layer flow of a pseudo-plastic fluid. Quart. J. Mech. Appl. Math. 27 (1974), 193–211.CrossRefGoogle Scholar
(2)Atkinson, F. V. and Peletier, L. A.Similarity profiles of flows through porous media. Arch. Rational Mech. Anal. 42 (1971), 369–379.CrossRefGoogle Scholar
(3)Atkinson, F. V. and Peletier, L. A., Similarity solutions of the non-linear diffusion equation. Arch. Rational Mech. Anal. 54 (1974), 373–391.CrossRefGoogle Scholar
(4)Bouillet, J. E.On similarity solutions of the equation of diffusion in one dimension. Trabajos de Matematica 15 (1977). Inst. Argentino de Matematica, Conicet.Google Scholar
(5)Brezis, H.On some degenerate non-linear parabolic equations. Proc. Symp. Pure Math. 18 (1970), 28–38, A.M.S.CrossRefGoogle Scholar
(6)Dunford, N. and Schwartz, J. T.Linear Operators, vol. 1, p. 459 (New York, Interscience Publishers, 1958).Google Scholar
(7)Philip, J. R.n-diffusion. Austral. Phys. 14 (1961), 1–13.CrossRefGoogle Scholar