Contents
Research Article
Meromorphic Functions with Large Sets of Julia Points
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-6
-
- Article
-
- You have access
- Export citation
Boundary Isomorphism between Dirichlet Finite Solutions of Δu = Pu and Harmonic Functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 7-20
-
- Article
-
- You have access
- Export citation
Dedekind Sums for a Fuchsian Group, I
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 21-47
-
- Article
-
- You have access
- Export citation
On Meromorphic Mappings into Taut Complex Analytic Spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 49-65
-
- Article
-
- You have access
- Export citation
Order Comparisons on Canonical Isomorphisms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 67-87
-
- Article
-
- You have access
- Export citation
Stochastic Integrals in Abstruct Wiener Space II: Regularity Properties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 89-116
-
- Article
-
- You have access
- Export citation
Noyaux Réguliers et Noyaux Singuliers
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 117-148
-
- Article
-
- You have access
- Export citation
Sur le Principe de Domination Pour les Noyaux de Convolution
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 149-173
-
- Article
-
- You have access
- Export citation
Characterization of Relative Domination Principle
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 175-184
-
- Article
-
- You have access
- Export citation
Operators on Tensor Products of ℒ1, ℒ2 and ℒ∞ Spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-198
-
- Article
-
- You have access
- Export citation
Holomorphic Mappings into Projective Space with Lacunary Hyperplanes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 199-216
-
- Article
-
- You have access
- Export citation
On the Grobal Dimension of Ore-Extensions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 217-225
-
- Article
-
- You have access
- Export citation
A Note on Gorenstein Rings of Embedding Codimension Three
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 227-232
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 50 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 50 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

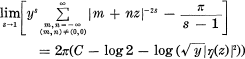
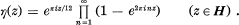
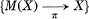 of
of 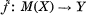 such that
such that 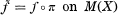 except some nowhere dense complex analytic set, where Sg(
except some nowhere dense complex analytic set, where Sg(