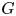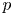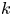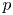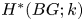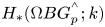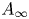Massey products in the homology of the loop space of a p-completed classifying space: finite groups with cyclic Sylow p-subgroups

Abstract

Let $G$ be a finite group with cyclic Sylow $p$-subgroups, and let $k$ be a field of characteristic $p$. Then $H^{*}(BG;k)$ and $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)$ are $A_\infty$ algebras whose structure we determine up to quasi-isomorphism.

1. Introduction

The general context is that we have a finite group $G$, and a field $k$ of characteristic $p$. We are interested in the differential graded cochain algebra $C^{*}(BG;k)$ and the differential graded algebra $C_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$ of chains on the loop space: these two are Koszul dual to each other, and the Eilenberg–Moore and Rothenberg–Steenrod spectral sequences relate the cohomology ring $H^{*}(BG;k)$ to the homology ring $H_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$, see § 5. Of course if $G$ is a $p$-group, $BG$ is $p$-complete so $\Omega (BG{{}^{{}^{\wedge }}_p})\simeq G$, but, in general, $H_*(\Omega (BG{{}^{{}^{\wedge }}_p}); k)$ is infinite dimensional. Henceforth, we will omit the brackets from $\Omega (BG{{}^{{}^{\wedge }}_p})$.

We consider a simple case where the two rings are not formal, but we can identify the $A_{\infty }$ structures precisely (see § 3 for a brief summary on $A_{\infty }$-algebras). From now on, we suppose specifically that $G$ is a finite group with cyclic Sylow $p$-subgroup $P$, and let $BG$ be its classifying space. Then the inclusion of the Sylow $p$-normaliser $N_G(P) \to G$ and the quotient map $N_G(P) \to N_G(P)/O_{p'}N_G(P)$ induce mod $p$ cohomology equivalences

\[ B(N_G(P)/O_{p'}N_G(P)) \leftarrow BN_G(P) \to BG, \]

see Swan [15] or Theorem II.6.8 of Adem and Milgram [1]. Hence, after $p$-completion, we have homotopy equivalences

\[ B(N_G(P)/O_{p'}N_G(P)){{}^{{}^{{\wedge}}}_p} \xleftarrow{\ \sim\ } BN_G(P){{}^{{}^{{\wedge}}}_p} \xrightarrow{\ \sim \ } BG{{}^{{}^{{\wedge}}}_p}, \]

see Lemma I.5.5 of Bousfield and Kan [3]. Here, $O_{p'}N_G(P)$ denotes the largest normal $p'$-subgroup of $N_G(P)$. Thus, $N_G(P)/O_{p'}N_G(P)$ is a semidirect product $\mathbb {Z}/p^{n}\rtimes \mathbb {Z}/q$, where $q$ is a divisor of $p-1$, and $\mathbb {Z}/q$ acts faithfully as a group of automorphisms of $\mathbb {Z}/p^{n}$. In particular, the isomorphism type of $N_G(P)/O_{p'}N_G(P)$ only depends on $|P|=p^{n}$ and the inertial index $q=|N_G(P):C_G(P)|$, and therefore so does the homotopy type of $BG{{}^{{}^{\wedge }}_p}$. Our main theorem determines the multiplication maps $m_i$ in the $A_\infty$ structure on $H^{*}(BG;k)$ and $H_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$ arising from $C^{*}(BG;k)$ and $C_*(\Omega (BG{{}^{{}^{\wedge }}_p}); k)$ respectively. We will suppose from now on that $p^{n}>2,\, q>1$ since the case of a $p$-group is well understood.

The starting point is the cohomology ring

\[ H^{*}(BG; k)=H^{*}(B\mathbb{Z}/p^{n}; k)^{\mathbb{Z}/q}=k[x]\otimes \Lambda(t) \mbox{ with }|x|={-}2q,\quad |t|={-}2q+1. \]

There is a preferred generator $t_1\in H^{1}(B\mathbb {Z}/p^{n};k)=\mathrm {Hom}(\mathbb {Z}/p^{n},\,k)$ and we take $x_1\in H^{2}(B\mathbb {Z}/p^{n};k)$ to be the $n$th Bockstein of $t_1$. Now take $x=x_1^{q},\, t=x_1^{q-1}t_1$.

Before stating our result, we should be clear about grading and signs.

Remark 1.1 We will be discussing both homology and cohomology, so we should be explicit that everything is graded homologically, so that differentials always lower degree. Explicitly, the degree of an element of $H^{i}(G;k)$ is $-i$.

Remark 1.2 Sign conventions for Massey products and $A_{\infty }$ algebras mean that a specific sign will enter repeatedly in our statements, so for brevity, we write

\[ \epsilon (s)=({-}1)^{s(s-1)/2}= \begin{cases} +1 & s\equiv 0, 1 \mod 4\\ -1 & s\equiv 2, 3 \mod 4\\ \end{cases}. \]

Theorem 1.3 Let $G$ be a finite group with cyclic Sylow $p$-subgroup $P$ of order $p^{n}$ and inertial index $q$ so that

\[ H^{*}(BG;k) =k[x]\otimes \Lambda(t) \mbox{ with } |x|={-}2q,\quad |t|={-}2q+1\quad \mbox{and}\quad \beta_nt=x \]

Up to quasi-isomorphism, the $A_\infty$ structure on $H^{*}(BG;k)$ is determined by

\[ m_{p^{n}}(t,\ldots,t)=\epsilon (p^{n}) x^{h} \]

where $h=p^{n}-(p^{n}-1)/q$. This implies

\[ m_{p^{n}}(x^{j_1}t,\ldots,x^{j_{p^{n}}}t)=\epsilon (p^{n}) x^{h+j_1+\cdots+j_{p^{n}}} \]

for all $j_1,\, \ldots ,\, j_{p^{n}}\geq 0$. All $m_i$ for $i>2$ on all other $i$-tuples of monomials give zero.

If $q>1$ and $p^{n}\ne 3$ then

\[ H_*(\Omega BG{{}^{{}^{{\wedge}}}_p};k) = k[\tau] \otimes \Lambda(\xi)\quad \mbox{where}\ |\tau|=2q-2,\quad |\xi|=2q-1. \]

Up to quasi-isomorphism, the $A_\infty$ structure is determined by

\[ m_h(\xi,\ldots,\xi )=\epsilon (h) \tau^{p^{n}}. \]

This implies

\[ m_h(\tau^{j_1}\xi,\ldots,\tau^{j_h}\xi)=\epsilon (h) \tau^{p^{n}+j_1+\cdots+j_h} \]

for all $j_1,\, \ldots ,\, j_{p^{n}}\geq 0$. All $m_i$ for $i>2$ on all other $i$-tuples of monomials give zero.

If $q>1$ and $p^{n}=3$ then $q=2$ and

\[ H_*(\Omega BG{{}^{{}^{{\wedge}}}_p};k) = k[\tau,\xi]/(\xi^{2}+\tau^{3}), \]

and all $m_i$ are zero for $i>2$.

2. The group algebra and its cohomology

We assume from now on, without loss of generality, that $G$ has a normal cyclic Sylow $p$-subgroup $P=C_G(P)$, with inertial index $q=|G:P|$. We shall assume that $q>1$, which then forces $p$ to be odd. For notation, let

\[ G=\langle g,s\mid g^{p^{n}}=1, s^{q}=1, sgs^{{-}1}=g^{\gamma}\rangle\cong \mathbb{Z}/p^{n}\rtimes\mathbb{Z}/q, \]

where $\gamma$ is a primitive $q$th root of unity modulo $p^{n}$. Let $P=\langle g\rangle$ and $H=\langle s\rangle$ as subgroups of $G$.

In this section, we introduce a grading on $kG$. This comes from the fact that the radical filtration of $kG$ is isomorphic to its associated graded in this case. This is a somewhat rare phenomenon, but when it happens, it induces an extra grading on mod $p$ cohomology of $BG$ and homology of $\Omega BG{{}^{{}^{\wedge }}_p}$, that we can exploit to good effect.

Let $k$ be a field of characteristic $p$. The action of $H$ on $kP$ by conjugation preserves the radical series, and since $|H|$ is not divisible by $p$, there are invariant complements. Thus, we may choose an element $U\in J(kP)$ such that $U$ spans an $H$-invariant complement of $J^{2}(kP)$ in $J(kP)$. It can be checked that

\[ U = \sum_{\substack{1\leqslant j \leqslant p^{n}-1, \\j^{p}\equiv j\pmod{p}}} g^{j}/j \]

is such an element, and that $sUs^{-1}=\gamma U$. This gives us the following presentation for $kG$:

\[ kG = k\langle s,U \mid U^{p^{n}}=0, s^{q}=1, sU = \gamma Us \rangle. \]

We shall regard $kG$ as a $\mathbb {Z}[{1}/{q}]$-graded algebra with $|s|=0$ and $|U|=1/q$. Then the bar resolution is doubly graded, and taking homomorphisms into $k$, the cochains $C^{*}(BG;k)$ inherit a double grading. The differential decreases the homological grading and preserves the internal grading. Thus, the cohomology $H^{*}(G,\,k)=H^{*}(BG;k)$ is doubly graded:

\[ H^{*}(BG;k) = k[x] \otimes \Lambda(t) \]

where $|x|=(-2q,\,-p^{n})$, $|t|=(-2q+1,\,-h)$, and $h=p^{n}-(p^{n}-1)/q$. Here, the first degree is homological, the second internal. The Massey product $\langle t,\,t,\,\ldots ,\,t\rangle$ ($p^{n}$ repetitions) is equal to $-x^{h}$. This may easily be determined by restriction to $P$, where it is well known that the $p^{n}$-fold Massey product of the degree one exterior generator is a non-zero degree two element. The usual convention is to make the constant $-1$, because this Massey product is minus the $n$th Bockstein of $t$ [10, Theorem 19].

3. $A_\infty$-algebras

An $A_{\infty }$-algebra over a field is a $\mathbb {Z}$-graded vector space $A$ with graded maps $m_n: A^{\otimes n}\rightarrow A$ of degree $n-2$ for $n\geq 1$ satisfying

\[ \sum_{r+s+t=n}({-}1)^{r+st}m_{r+1+t}(id^{{\otimes} r}\otimes m_s \otimes id^{{\otimes} t})=0 \]

for $n\geq 1$. The map $m_1$ is therefore a differential, and the map $m_2$ induces a product on $H_*(A)$.

A theorem of Kadeishvili [7] (see also Keller [8, 9] or Merkulov [13]) may be stated as follows. Suppose that we are given a differential graded algebra $A$, over a field $k$. Let $Z^{*}(A)$ be the cocycles, $B^{*}(A)$ be the coboundaries, and $H^{*}(A)=Z^{*}(A)/B^{*}(A)$. Choose a vector space splitting $f_1\colon H^{*}(A) \to Z^{*}(A) \subseteq A$ of the quotient. Then this gives by an inductive procedure an $A_\infty$ structure on $H^{*}(A)$ so that the map $f_1$ is the degree one part of a quasi-isomorphism of $A_\infty$-algebras.

If $A$ happens to carry auxiliary gradings respected by the product structure and preserved by the differential, then it is easy to check from the inductive procedure that the maps in the construction may be chosen so that they also respect these gradings. It then follows that the structure maps $m_i$ of the $A_\infty$ structure on $H^{*}(A)$ also respect these gradings.

Let us apply this to $H^{*}(BG;k)$. We examine the elements $m_i(t,\,\ldots ,\,t)$. By definition, we have $m_1(t)=0$ and $m_2(t,\,t)=0$. The degree of $m_i(t,\,\ldots ,\,t)$ is $i$ times the degree of $t$, increased in the homological direction by $i-2$. This gives

\[ |m_i(t,\ldots,t)| = i({-}2q+1,h)+(i-2,0) =({-}2iq+2i-2,ih). \]

The homological degree is even, so if $m_i(t,\, \ldots ,\, t)$ is non-zero then it is a multiple of a power of $x$. Comparing degrees, if $m_i(t,\,\ldots ,\,t)$ is a non-zero multiple of $x^{\alpha }$ then we have

\[ 2iq-2i+2=2\alpha q,\quad ih = \alpha p^{n}. \]

Eliminating $\alpha$, we obtain $(iq-i+1)p^{n}=ihq$. Substituting $h=p^{n}-(p^{n}-1)/q$, this gives $i=p^{n}$. Finally, since the Massey product of $p^{n}$ copies of $t$ is equal to $-x^{h}$, it follows that $m_{p^{n}}(t,\,\ldots ,\,t)=\epsilon (p^{n}) x^{h}$, where the sign is as defined in Remark 1.2 ([11, Theorem 3.1], corrected in [4, Theorem 3.2]). Thus, we have

\[ m_i(t,\ldots,t) = \begin{cases} \epsilon (p^{n}) x^{h} & i=p^{n} \\ 0 & \text{otherwise.} \end{cases} \]

We shall elaborate on this argument in a more general context in the next section, where we shall see that the rest of the $A_\infty$ structure is also determined in a similar way.

4. $A_\infty$ structures on a polynomial tensor exterior algebra

In this section, we shall examine the following general situation. Our goal is to establish that there are only two possible $A_\infty$ structures satisfying Hypothesis 4.1, and that the Koszul dual also satisfies the same hypothesis with the roles of $a$ and $b$, and of $h$ and $\ell$ reversed.

Hypothesis 4.1 $A$ is a $\mathbb {Z}\times \mathbb {Z}$-graded $A_\infty$-algebra over a field $k$, where the operators $m_i$ have degree $(i-2,\,0)$, satisfying

1. (1) $m_1=0$, so that $m_2$ is strictly associative,

2. (2) ignoring the $m_i$ with $i>2$, the algebra $A$ is $k[x] \otimes \Lambda (t)$ where $|x|=(-2a,\,-\ell )$ and $|t|=(-2b-1,\,-h)$, and

3. (3) $ha-\ell b = 1$.

Remarks 4.2

1. (i) The $A_\infty$-algebra $H^{*}(BG;k)$ of the last section satisfies this hypothesis, with $a=q$, $b=q-1$, $h=p^{n}-(p^{n}-1)/q$, $\ell =p^{n}$.

2. (ii) By comparing degrees, if we have $m_\ell (t,\,\ldots ,\,t)=\epsilon (\ell ) x^{h}$ then

$(2b+1)\ell + 2-\ell = 2ah$ and so $ha-\ell b = 1$. This explains the role of part (3) of the hypothesis. The consequence is, of course, that $a$ and $b$ are coprime, and so are $h$ and $\ell$.

Lemma 4.3 If $m_i(t,\,\ldots ,\,t)$ is non-zero, then $i=\ell > 2$ and $m_\ell (t,\,\ldots ,\,t)$ is a multiple of $x^{h}$.

Proof. The argument is the same as in the last section. The degree of $m_i(t,\,\ldots ,\,t)$ is $i|t| +(i- 2,\,0) = (-2ib - 2,\, -ih)$. Since the homological degree is even, if $m_i(t,\,\ldots ,\,t)$ is non-zero then it is a multiple of some power of $x$, say $x^{\alpha }$. Then we have

\[ 2ib+2 = 2\alpha a,\qquad ih = \alpha\ell. \]

Eliminating $\alpha$ gives $(ib+1)\ell =iha$, and so using $ha-\ell b =1$ we have $i=\ell$. Substituting back gives $\alpha = h$.

Elaborating on this argument gives the entire $A_\infty$ structure. If $m_\ell (t,\,\ldots ,\,t)$ is non-zero, then by rescaling the variables $t$ and $x$ if necessary we can assume that $m_\ell (t,\,\ldots ,\,t)=\epsilon (\ell ) x^{h}$ (note that we can even do this without extending the field, since $\ell$ and $h$ are coprime).

Proposition 4.4 If $m_\ell (t,\,\ldots ,\,t)=0$ then all $m_i$ are zero for $i>2$. If $m_\ell (t,\,\ldots ,\,t)= \epsilon (\ell ) x^{h}$ then $m_\ell (x^{j_1}t,\,\ldots ,\,x^{j_\ell }t)= \epsilon (\ell )x^{h+j_1+\cdots +j_\ell }$, and all $m_i$ for $i>2$ on all other $i$-tuples of monomials give zero.

Proof. All monomials live in different degrees, so we do not need to consider linear combinations of monomials. Suppose that $m_i(x^{j_1}t^{\varepsilon _1},\,\ldots ,\,x^{j_i}t^{\varepsilon _i})$ is some constant multiple of $x^{j}t^{\varepsilon }$, where each of $\varepsilon _1,\,\ldots ,\,\varepsilon _i,\,\varepsilon$ is either zero or one. Then comparing degrees, we have

\[ (j_1+\cdots+j_i)|x| + (\varepsilon_1+\cdots+\varepsilon_i)|t| + (i-2,0) = j|x| + \varepsilon|t|. \]

Setting

\[ \alpha=j_1+\cdots+j_i-j,\quad \beta = \varepsilon_1+\cdots+\varepsilon_i-\varepsilon \]

we have $\beta \leqslant i$, and

\[ \alpha({-}2a,-\ell) + \beta({-}2b-1,-h) + (i-2,0) = 0. \]

Thus

\[ 2\alpha a + 2\beta b + \beta + 2 - i = 0, \quad \alpha \ell +\beta h = 0. \]

Eliminating $\alpha$, we obtain

\[{-}2\beta ha + 2\beta \ell b + \beta \ell + 2 \ell - i \ell = 0. \]

Since $ha-\ell b=1$, this gives $\beta = \ell (i-2) /(\ell -2)$. Combining this with $\beta \leqslant i$ gives $i\leqslant \ell$. If $i<\ell$ then $\beta$ is not divisible by $\ell$, and so $\alpha \ell + \beta h = 0$ cannot hold. So we have $\beta =i=\ell$, $\varepsilon _1=\dots =\varepsilon _\ell =1$, $\varepsilon =0$, $\alpha =-h$, and $j=h+j_1+\cdots +j_\ell$. Finally, the identities satisfied by the $m_i$ for an $A_\infty$ structure show that all the constant multiples have to be the same, hence all equal to zero or after rescaling, all equal to $\epsilon (\ell )$.

Theorem 4.5 Under Hypothesis 4.1, if $\ell > 2$ then there are two possible $A_\infty$ structures on $A$. There is the formal one, where $m_i$ is equal to zero for $i>2$, and the non-formal one, where after replacing $x$ and $t$ by suitable multiples, the only non-zero $m_i$ with $i>2$ is $m_\ell$, and the only non-zero values on monomials are given by

\[ m_\ell(x^{j_1}t,\ldots,x^{j_\ell}t)=\epsilon(\ell)x^{h+j_1+\cdots+j_\ell}. \]

Proof. This follows from Lemma 4.3 and Proposition 4.4.

Theorem 4.6 Let $G=\mathbb {Z}/p^{n} \rtimes \mathbb {Z}/q$ as above, and $k$ a field of characteristic $p$. Then the $A_\infty$ structure on $H^{*}(G,\,k)$ given by Kadeishvili's theorem may be taken to be the non-formal possibility named in the above theorem, with $a=q$, $b=q-1$, $h=p^{n}-(p^{n}-1)/q$, $\ell =p^{n}$.

Proof. Since we have $m_{p^{n}}(t,\,\ldots ,\,t)=\epsilon (p^{n}) x^{h}$, the formal possibility does not hold.

Remark 4.7 Dag Madsen's thesis [12] has an appendix in which the $A_\infty$ structure is computed for the cohomology of a truncated polynomial ring, reaching similar conclusions by more direct methods. A similar computation appears in Examples 7.1.5 and 7.2.4 of the book by Witherspoon [16].

5. Loops on $BG{{}^{{}^{\wedge }}_p}$

In general, for a finite group $G$, the classifying space $BG$ is $p$-good, see Proposition VII.5.1 of Bousfield and Kan [3]. So its $p$-completion $BG{{}^{{}^{\wedge }}_p}$ is $p$-complete. This space and its loop space have been the subject of considerable study, beginning with the work of Cohen and Levi [5]. We have $H^{*}(BG{{}^{{}^{\wedge }}_p};k)\cong H^{*}(BG;k)=H^{*}(G,\,k)$ and $\pi _1(BG{{}^{{}^{\wedge }}_p})=G/O^{p}(G)$, the largest $p$-quotient of $G$. In our case, $G=\mathbb {Z}/p^{n}\rtimes \mathbb {Z}/q$ with $q>1$, we have $G=O^{p}(G)$ and so $BG{{}^{{}^{\wedge }}_p}$ is simply connected. So the Eilenberg–Moore spectral sequence converges to the homology of its loop space:

\[ \mathsf{Ext}^{*,*}_{H^{*}(BG;k)}(k,k) \cong \mathsf{Cotor}^{*,*}_{H_*(BG;k)}(k,k) \Rightarrow H_*(\Omega BG{{}^{{}^{{\wedge}}}_p};k) \]

(Eilenberg–Moore [6], Smith [14]). The internal grading on $C^{*}(BG;k)$ gives this spectral sequence a third grading that is preserved by the differentials, and $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)$ is again doubly graded. Since $H^{*}(G,\,k)=k[x] \otimes \Lambda (t)$ with $|x|=(-2q,\,-p^{n})$ and $|t|=(-2q+1,\,-h)$, it follows that the $E^{2}$ page of this spectral sequence is $k[\tau ] \otimes \Lambda (\xi )$ where $|\xi |=(-1,\,2q,\,p^{n})$ and $|\tau |=(-1,\,2q-1,\,h)$ (recall $h=p^{n}-(p^{n}-1)/q$). Provided that we are not in the case $h=2$, which only happens if $p^{n}=3$, ungrading $E^{\infty }$ gives

\[ H_*(\Omega BG{{}^{{}^{{\wedge}}}_p};k) = k[\tau] \otimes \Lambda(\xi) \]

with $|\tau |=(2q-2,\,h)$ and $|\xi |=(2q-1,\,p^{n})$.

In the exceptional case $h=2$, $p^{n}=3$, we have $q=2$, and the group $G$ is the symmetric group $\Sigma _3$ of degree three. An explicit computation (for example by squeezed resolutions [2]) gives

\[ H_*(\Omega (B\Sigma_3){}^{{}^{{\wedge}}}_3;k) = k[\tau,\xi]/(\xi^{2}+\tau^{3}) \]

with $|\tau |=(2,\,2)$ and $|\xi |=(3,\,3)$, and the two gradings collapse to a single grading.

Applying Theorem 4.5, and using the fact that either formal case is Koszul dual to the other, we have the following.

Theorem 5.1 Suppose that $p^{n}\ne 3$. Then the $A_\infty$ structure on $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)=k[\tau ]\otimes \Lambda (\xi )$ is given by

\[ m_h(\tau^{j_1}\xi,\ldots,\tau^{j_h}\xi)=\epsilon (h) \tau^{p^{n}+j_1+\cdots+j_h}, \]

and for $i>2$, all $m_i$ on all other $i$-tuples of monomials give zero.

Again using [11] corrected in [4], we may reinterpret this in terms of Massey products.

Corollary 5.2 In $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)$, the Massey products $\langle \xi ,\,\ldots ,\,\xi \rangle$ ($i$ times) vanish for $0< i< h$, and give $-\tau ^{p^{n}}$ for $i=h$.

Note that the exceptional case $p^{n}=3$ also fits the corollary, if we interpret a $2$-fold Massey product as an ordinary product.