Hostname: page-component-5b777bbd6c-gcwzt Total loading time: 0 Render date: 2025-06-24T14:49:09.049Z Has data issue: false hasContentIssue false
  • English
  • Français

Moishezon manifolds with no nef and big classes

Part of: Automorphic functions Compact analytic spaces Complex spaces with a group of automorphisms

Published online by Cambridge University Press:  26 November 2024

Jia Jia Open the ORCID record for Jia Jia [Opens in a new window]  and
Sheng Meng
Jia Jia*
Affiliation:
Department of Mathematics, National University of Singapore, Singapore, Republic of Singapore Yau Mathematical Sciences Center, Jingzhai, Tsinghua University, Beijing, China
Sheng Meng
Affiliation:
School of Mathematical Sciences, Shanghai Key Laboratory of PMMP, East China Normal University, Shanghai, People’s Republic of China Korea Institute For Advanced Study, Seoul, Republic of Korea
*
Corresponding author: Jia Jia, email: jia_jia@u.nus.edu; mathjiajia@tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a compact complex manifold X has no non-trivial nef 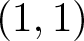$(1,1)$-classes if there is a non-biholomorphic bimeromorphic map 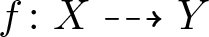$f\colon X\dashrightarrow Y$, which is an isomorphism in codimension 1 to a compact Kähler manifold Y with 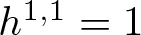$h^{1,1}=1$. In particular, there exist infinitely many isomorphic classes of smooth compact Moishezon threefolds with no nef and big 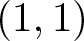$(1,1)$-classes. This contradicts a recent paper (Strongly Jordan property and free actions of non-abelian free groups, Proc. Edinb. Math. Soc., 65(3) (2022), 736–746).

Keywords

Moishezon spaceFujiki’s class 𝒞nef and big

MSC classification

Primary: 32J27: Compact Kähler manifolds
Secondary: 32M05: Complex Lie groups, automorphism groups acting on complex spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 198 - 204
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Clemens, H., Homological equivalence, modulo algebraic equivalence, is not finitely generated, Inst, Hautes Études Sci. Publ. Math. 58 (1983), 19–38.CrossRefGoogle Scholar
Demailly, J.-P. and Păun, M., Numerical characterization of the Kähler cone of a compact Kähler manifold, Ann. Math. (2) 159(3) (2004), 1247–1274.CrossRefGoogle Scholar
Fujiki, A., On automorphism groups of compact Kähler manifolds, Invent. Math. 44(3) (1978), 225–258.CrossRefGoogle Scholar
Fujiki, A., A theorem on bimeromorphic maps of Kähler manifolds and its applications, Publ. Res. Inst. Math. Sci. 17(2) (1981), 735–754.CrossRefGoogle Scholar
Fujiki, A., and Nakano, S., Supplement to ‘On the inverse of monoidal transformation’, Publ. Res. Inst. Math. Sci. 7(3) (1971/72), 637–644.CrossRefGoogle Scholar
Golota, A., Jordan property for groups of bimeromorphic automorphisms of compact Kähler threefolds, arXiv:2112.02673, 2021.Google Scholar
Grauert, H. and Remmert, R., Zur theorie der modifikationen. I. Stetige und eigentliche modifikationen komplexer räume, Math. Ann. 129 (1955), 274–296.CrossRefGoogle Scholar
Grauert, H. and Remmert, R., Coherent analytic sheaves, Grundlehren der Mathematischen Wissenschaften, Volume 265 (Springer, Berlin, 1984).CrossRefGoogle Scholar
Höring, A. and Peternell, T., Minimal models for Kähler threefolds, Invent. Math. 203(1) (2016), 217–264.CrossRefGoogle Scholar
Hartshorne, R., Graduate texts in mathematics, Volume 52 (Springer, New York, 1977).Google Scholar
Hironaka, H., Flattening theorem in complex-analytic geometry, Amer. J. Math. 97(2) (1975), 503–547.CrossRefGoogle Scholar
Huybrechts, D., The Kähler cone of a compact hyperkähler manifold, Math. Ann. 326(3) (2003), 499–513.CrossRefGoogle Scholar
Jia, J. and Meng, S., Equivariant Kähler model for Fujiki’s class, J. Geom. Anal, 34(349) (2024).CrossRefGoogle Scholar
Katz, S., On the finiteness of rational curves on quintic threefolds, Comp. Math. 60 (1986), 151–162.Google Scholar
Kim, J., Strongly Jordan property and free actions of non-abelian free groups, Proc. Edinb. Math. Soc. 65(3) (2022), 736–746, doi:10.1017/S0013091522000311.CrossRefGoogle Scholar
Mondal, P., Algebraicity of normal analytic compactifications of $\mathbb{C}^2$ with one irreducible curve at infinity, Algebra Number Theory 10(8) (2016), 1641–1682.CrossRefGoogle Scholar
Nakamura, I., Moishezon threefolds homeomorphic to $\mathbb{P}^3$, J. Math. Soc. Japan 39(3) (1987), 521–535.CrossRefGoogle Scholar
Nakayama, N., A variant of Shokurov’s criterion of toric surface, Algebraic varieties and automorphism groups, Adv. Stud. Pure Math. 75 (2017), 287–392.CrossRefGoogle Scholar
Oguiso, K., Two remarks on Calabi-Yau Moishezon threefolds, J. Reine Angew. Math. 452 (1994), 153–161.Google Scholar
Rao, S., Yang, S. and Yang, X., Dolbeault cohomologies of blowing up complex manifolds, J. Math. Pures Appl. (9) 130 (2019), 68–92.CrossRefGoogle Scholar
Schröer, S., On non-projective normal surfaces, Manuscripta Math. 100(3) (1999), 317–321.Google Scholar
Varouchas, J., Kähler spaces and proper open morphisms, Math. Ann. 283(1) (1989), 13–52.CrossRefGoogle Scholar
Wang, J., On the Iitaka conjecture $C_{n,m}$ for Kähler fibre spaces, Ann. Fac. Sci. Toulouse Math. (6) 30(4) (2021), 813–897.CrossRefGoogle Scholar