Hostname: page-component-5b777bbd6c-6lqsf Total loading time: 0 Render date: 2025-06-18T22:25:39.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Property $(\diamond)$ for Ore extensions of small Krull dimension

Part of: Chain conditions, growth conditions, and other forms of finiteness Modules, bimodules and ideals Rings and algebras arising under various constructions

Published online by Cambridge University Press:  21 May 2025

Ken Brown Open the ORCID record for Ken Brown [Opens in a new window] ,
Paula A. A. B. Carvalho Open the ORCID record for Paula A. A. B. Carvalho [Opens in a new window]  and
Jerzy Matczuk Open the ORCID record for Jerzy Matczuk [Opens in a new window]
Ken Brown
Affiliation:
School of Mathematics and Statistics, University of Glasgow, Glasgow, Scotland, United Kingdom
Paula A. A. B. Carvalho
Affiliation:
CMUP, Departamento de Matemática, Faculdade de Ciências, Universidade do Porto, Porto, Portugal
Jerzy Matczuk*
Affiliation:
Institute of Mathematics, University of Warsaw, Warsaw, Poland
*
Corresponding author: Jerzy Matczuk, email: jmatczuk@mimuw.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is a continuation of a project to determine which skew polynomial algebras 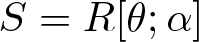$S = R[\theta; \alpha]$ satisfy property $(\diamond)$, namely that the injective hull of every simple S-module is locally Artinian, where k is a field, R is a commutative Noetherian k-algebra and α is a k-algebra automorphism of R. Earlier work (which we review) and further analysis done here lead us to focus on the case where S is a primitive domain and R has Krull dimension 1 and contains an uncountable field. Then we show first that if 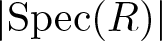$|\mathrm{Spec}(R)|$ is infinite then S does not satisfy $(\diamond)$. Secondly, we show that when 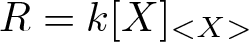$R = k[X]_{ \lt X \gt }$ and 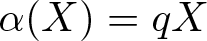$\alpha (X) = qX$ where 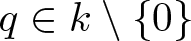$q \in k \setminus \{0\}$ is not a root of unity then S does not satisfy $(\diamond)$. This is in complete contrast to our earlier result that, when 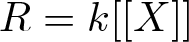$R = k[[X]]$ and α is an arbitrary k-algebra automorphism of infinite order, S satisfies $(\diamond)$. A number of open questions are stated.

Keywords

injective moduleNoetherian ringsimple moduleskew polynomial ring

MSC classification

Primary: 16D50: Injective modules, self-injective rings
Secondary: 16P40: Noetherian rings and modules 16S35: Twisted and skew group rings, crossed products
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bavula, V. and Van Oystaeyen, F., The simple modules of certain generalized crossed products, J. Algebra 194(2): (1997), 521–566.10.1006/jabr.1997.7038CrossRefGoogle Scholar
Brown, K. A. and Goodearl, K. R., Lectures on algebraic quantum groups. Volume CRM Barcelona of Advanced Courses in Mathematics (Birkhäuser Verlag, Basel, 2002).Google Scholar
Brown, K., Carvalho, P. A. A. B. and Matczuk, J., Simple modules and their essential extensions for skew polynomial rings, Math. Z. 291(3–4): (2019), 877–903.10.1007/s00209-018-2128-8CrossRefGoogle Scholar
Brown, K., Carvalho, P. A. A. B. and Matczuk, J., Critical and injective modules over skew polynomial rings, J. Pure Appl. Algebra 227(11): (2023), 26.10.1016/j.jpaa.2023.107441CrossRefGoogle Scholar
Carvalho, P. A. A. B., Lomp, C. and Pusat-Yilmaz, D., Injective modules over down-up algebras, Glasg. Math. J. 52(A): (2010), 53–59.10.1017/S0017089510000261CrossRefGoogle Scholar
Damiano, R. F. and Shapiro, J., Twisted polynomial rings satisfying a polynomial identity, J. Algebra 92(1): (1985), 116–127.10.1016/0021-8693(85)90148-6CrossRefGoogle Scholar
Goodearl, K. R. and Schofield, A. H., Non-Artinian essential extensions of simple modules, Proc. Amer. Math. Soc. 97(2): (1986), 233–236.10.1090/S0002-9939-1986-0835871-0CrossRefGoogle Scholar
Irving, R. S., Prime ideals of Ore extensions over commutative rings, J. Algebra 56(2): (1979), 315–342.10.1016/0021-8693(79)90341-7CrossRefGoogle Scholar
Leroy, A. and Matczuk, J., Primitivity of skew polynomial and skew Laurent polynomial rings, Comm. Algebra 24(7): (1996), 2271–2284.10.1080/00927879608825699CrossRefGoogle Scholar
Matlis, E., Injective modules over Noetherian rings, Pacific J. Math. 8 (3): (1958), 511–528.10.2140/pjm.1958.8.511CrossRefGoogle Scholar
Musson, I. M., Finitely generated, non-Artinian monolithic modules, Contemp. Math. 562 (2012), 211–220.10.1090/conm/562/11138CrossRefGoogle Scholar
Rosenberg, A. and Zelinsky, D., Finiteness of the injective hull, Math. Z. 70 (1958/59), 372–380.10.1007/BF01558598CrossRefGoogle Scholar
Sharp, R. Y. and Vámos, P., Baire’s category theorem and prime avoidance in complete local rings, Arch. Math. (Basel) 44(3): (1985), 243–248.10.1007/BF01237858CrossRefGoogle Scholar