Cartesian closed varieties II: links to algebra and self-similarity

Abstract

This article is the second in a series investigating cartesian closed varieties. In first of these, we showed that every non-degenerate finitary cartesian variety is a variety of sets equipped with an action by a Boolean algebra B and a monoid M which interact to form what we call a matched pair 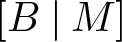${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$. In this article, we show that such pairs 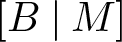${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$ are equivalent to Boolean restriction monoids and also to ample source-étale topological categories; these are generalizations of the Boolean inverse monoids and ample étale topological groupoids used to encode self-similar structures such as Cuntz and Cuntz–Krieger 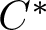$C^\ast$-algebras, Leavitt path algebras, and the 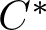$C^\ast$-algebras associated with self-similar group actions. We explain and illustrate these links and begin the programme of understanding how topological and algebraic properties of such groupoids can be understood from the logical perspective of the associated varieties.

1. Introduction

This article is a continuation of the investigations of [16] into cartesian closed varieties—that is, varieties of single-sorted, possibly infinitary algebras which, seen as categories, are cartesian closed. One of the main results of op. cit. was that the category of non-degenerate, finitary, cartesian closed varieties is equivalent to the category of non-degenerate matched pairs of algebras ${\left[\smash{{B} \mathbin{\mid}{M}}\right]}$. Here, a matched pair of algebras comprises a Boolean algebra B and a monoid M which act on each other in a way first described in [23]; one way to say it is that M acts on B via continuous endomorphisms of its associated Stone space, while B acts on M so as to make it into a sheaf of continuous functions on B. When M acts faithfully on B, the structure generalizes that of a pseudogroup [13] of automorphisms, where the generalization is that M is a monoid of not-necessarily-invertible functions.

This description points to a connection between our matched pairs of algebras and the study of self-similar structures in non-commutative algebra, operator algebra, and semigroup theory. Following the pioneering work of Renault [39] and, later, Steinberg [43], a key idea in this area has been that analytic and algebraic objects such as the Cuntz $C^\ast$-algebra or the Leavitt algebras can be constructed from certain kinds of topological groupoids known as ample groupoids; these are groupoids whose space of objects C ₀ is a Stone (= totally disconnected compact Hausdorff) space and which are source-étale, meaning that the source map $s \colon C_1 \rightarrow C_0$ is a local homeomorphism. In [33], Lawson showed that such groupoids correspond under ‘non-commutative Stone duality’ to Boolean inverse monoids, which are abstract monoids of partial isomorphisms equipped with extra structure allowing them to be represented on the inverse monoid of partial homeomorphisms of a Stone space.

The first main result of this article shows that the two-sorted notion of matched pair of algebras ${\left[\smash{{B} \mathbin{\mid}{M}}\right]}$ corresponds to a single-sorted notion which generalizes that of a Boolean inverse monoid, namely, that of a Boolean restriction monoid [11] or a modal restriction semigroup with preferential union [24]; this is an abstract monoid of partial functions equipped with extra structure allowing it to be represented on the monoid of partial endomorphisms of a Stone space. Thus, in §3, we prove (theorems 3.5 and 3.11):

Theorem 1.1 The category of (Grothendieck) matched pairs of algebras is equivalent to the category of (Grothendieck) Boolean restriction monoids.

We should explain the modifier ‘Grothendieck’. The matched pairs of algebras ${\left[\smash{{B} \mathbin{\mid}{M}}\right]}$ described above corresponds to finitary cartesian closed varieties. However, there are also what we have termed Grothendieck matched pairs ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$ which correspond to possibly infinitary cartesian closed varieties. In these, our Boolean algebra B comes equipped with a collection ${\mathcal J}$ of ‘well-behaved’ infinite partitions, encoding the operations of infinite arity. Correspondingly, there is a notion of Grothendieck Boolean restriction monoid involving partial functions which can be patched together over possibly infinite partitions from such a collection ${\mathcal J}$; these, then, are the two sides of the extended correspondence above.

Now, as shown in [10], Boolean restriction monoids correspond under an extended non-commutative Stone duality to what might be termed ample topological categories—namely, source-étale topological categories with a Stone space of objects. Thus, our matched pairs ${\left[\smash{{B} \mathbin{\mid}{M}}\right]}$ present, among other things, the ample topological groupoids of interest to operator algebraists. (In the Grothendieck case, a little more care is necessary; for here, the analogue of the Boolean prime ideal lemma may fail to hold, i.e., $B_{\mathcal J}$ may fail to have enough points, so there may be no faithful representation by a topological category; nonetheless, in the spirit of [40], we do always obtain a zero-dimensional localic category.)

The preceding observations indicate a potentially interesting new research direction. A particularly fruitful line of enquiry in recent years has involved relating analytic properties of the $C^\ast$-algebras generated by ample groupoids and algebraic properties of the corresponding algebras (‘Steinberg algebras’) over a ring. The new direction would seek to further relate these to syntactic and semantic properties of the variety associated with a given ample groupoid. (At present, there is rather little to the analytic or algebraic side that matches up with the varieties associated with ample topological categories, but some recent progress has been made in [12].)

The second and third main results of this article can be seen as first steps in this new direction. We begin by re-addressing a question considered by Johnstone in [25]: when is a variety a topos? As we recall in §4, a topos is a finitely complete cartesian closed category with a subobject classifier, and so we can equally well phrase the question as: when is a cartesian closed variety a topos? In [25], Johnstone gives a rather delicate syntactic description, but using our now-richer understanding of cartesian closed varieties, we can simplify this drastically. We will show (theorem 4.7):

Theorem 1.2 The cartesian closed variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$-sets is a topos just when, for any $b \neq 0 \in B$, there exists some $m \in M$ such that $m^\ast b = 1$; or equivalently, just when the associated topological or localic category is minimal.

Here, $m^\ast b$ is the action of m on b—which from the spatial perspective is obtained by taking the inverse image of the clopen set b along the continuous endomorphism m. Rather than prove the above theorem directly, we approach it via a new proof of one of the main results of [26]. Theorem 1.2 of op. cit. shows that every cartesian closed variety arises as the ‘two-valued collapse’ of an essentially unique topos ${\mathcal E}$, where the ‘two-valued collapse’ is obtained by restricting to those objects whose support is either 0 or 1. In [26], the topos ${\mathcal E}$ whose collapse is a given cartesian closed variety is found via a tour de force construction which leaves its nature rather mysterious. Our results allow us to give a concrete presentation of ${\mathcal E}$ as a topos of sheaves on the (Grothendieck) matched pair of algebras which classifies our variety. Once we have this (in proposition 4.5), theorem 4.7 follows easily.

The third main result of this article describes the semantic and syntactic properties of a variety which corresponds to its associated topological or localic category actually being a groupoid, and as such in the more traditional purview of operator algebra. These properties of a variety can be motivated by the case of M-sets, for which the obvious ‘groupoidal’ condition is that the monoid M should in fact be a group. This syntactic condition on M corresponds to a semantic one: the monoid M is a group precisely when the forgetful functor from M-sets to sets preserves the cartesian closed structure. It turns out that exactly the same semantic condition characterizes the groupoidality of the associated category for an arbitrary ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$; this is our theorem 5.3, which shows, among other things, that:

Theorem 1.3 The associated localic category of a Grothendieck matched pair ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$ is a groupoid if, and only if, the forgetful functor from ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$-sets to $B_{{\mathcal J}}$-sets preserves the cartesian closed structure.

Corresponding to this semantic condition, we provide a syntactic condition on ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$ which is slightly complex but is very natural in terms of the associated Boolean restriction monoid, where it becomes precisely the condition that this should be generated by its Boolean inverse monoid of partial isomorphisms.

The final contribution made by this article is not in further results, but in further examples, which describe explicitly the cartesian closed varieties which give rise to some of the better-known ample topological groupoids studied in operator algebra. In particular, we show (§6.1) that the Cuntz groupoid $\mathfrak{O}_2$, whose $C^\ast$-algebra is the Cuntz $C^\ast$-algebra ${\mathcal O}_2$, is the associated groupoid of the cartesian closed variety—in fact a topos—of Jónsson–Tarski algebras, that is, sets X endowed with an isomorphism $X \cong X \times X$. This result has an obvious generalization, replacing 2 by any finite cardinal n, but in fact, since we have the notion of Grothendieck Boolean algebra available, we can consider (§6.2) an infinitary generalization which replaces 2 by an arbitrary set A, and considers the topos of sets endowed with an isomorphism $X \rightarrow X^A$. As a further generalization of this, we describe (§7) a topos which encodes the topological groupoid associated with a self-similar group action in the sense of [37, 38]. For our final substantive example (§8), we describe following [17, 35] a cartesian closed variety which encodes the graph groupoid associated with any directed graph by the machinery of [30].

We should note that here we have only really scratched the surface of the links with operator algebra. For example, the varieties just described can be extended to ones which encode the topological groupoids associated with higher rank graphs [29]; self-similar actions of groupoids on graphs [31]; or graphs of groups [6]. Moreover, it seems there may be low-hanging fruit towards a general structure theory of matched pairs ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$; for example, both the self-similar group examples studied here and also the examples involving higher-rank graphs should arise as instances of a Zappa-Szép product or distributive law between matched pairs ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M}}\right]}$ and $\left[\smash{{C_{\mathcal{ K}}} \mathbin{\mid}{N} }\right]$. In a similar spirit, we could enquire after a general notion of correspondence between two matched pairs, and a Cuntz–Pimsner construction for building new matched pairs out of such a correspondence: but all of this must await future work.

2. Background

2.1. B-sets and $B_{{\mathcal J}}$-sets

In this preliminary section, we gather together background from [16] that will be needed for the further developments of this article. We begin by recalling the notion of an ‘action’ of a Boolean algebra on a set, due to [4].

Definition 2.1. B-sets

Let $B = (B, \wedge, \vee, 0, 1, ({\mathord{\text{--}}})^{\prime})$ be a non-degenerate Boolean algebra (i.e., $0 \neq 1$). A B-set is a set X with an operation $B \times X \times X \rightarrow X$, written $(b,x,y) \mapsto b(x,y)$, satisfying the axioms

(2.1)\begin{equation} \begin{aligned} b(x,x) &= x \qquad b(b(x,y),z) = b(x,z) \qquad b(x,b(y,z)) = b(x,z)\\ 1(x,y) &= x \qquad b^{\prime}(x,y) = b(y,x) \qquad (b \wedge c)(x,y) = b(c(x,y),y)\rlap{.} \end{aligned} \end{equation}

One way to think of a B-set is as a set of ‘random variables’ varying over the (logical) state space B; then the element $b(x,y)$ can be interpreted as the random variable $\mathsf{if}\ b\ \mathsf{then}\ x\ \mathsf{else}\ y$. Another interpretation is that elements of a B-set X are objects with ‘parts’ indexed by the elements of B; then $b(x,y)$ is the result of restricting x to its b-part and y to its $b^{\prime}$-part, and glueing the results back together again. One readily recognizes this as part of the structure of a sheaf on the Boolean algebra B—more precisely, the structure borne by the set of global sections of such a sheaf. Not every sheaf on B has a global section; but for one which does, every section can be extended to a global section, so that the B-sets are equally those sheaves on B which are either empty or have at least one global section.

Now, the notion of B-set is a finitary one, and this may be inconvenient in a Boolean algebra which admits infinite partitions; one may wish to ‘logically condition’ on the elements of such an infinite partition, but none of the finitary B-set operations allow for this. This can be rectified with a more refined kind of action by a Boolean algebra that is equipped with a suitable collection of ‘well-behaved’ infinite joins:

Definition 2.2. Partition

Let B be a Boolean algebra and $b \in B$. A partition of b is a subset $P \subseteq B \setminus \{0\}$ such that $\bigvee P = b$, and $c \wedge d = 0$ whenever $c \neq d \in P$. An extended partition of b is a subset $P \subseteq B$ (possibly containing 0) satisfying the same conditions. If P is an extended partition of b, then we write $P^- = P \setminus \{0\}$ for the corresponding partition. We say merely ‘partition’ to mean ‘partition of 1’.

Definition 2.3. Zero-dimensional topology, Grothendieck Boolean algebra

A zero-dimensional topology on a Boolean algebra B is a collection ${\mathcal J}$ of partitions of B which contains every finite partition, and satisfies:

1. (i) If $P \in {\mathcal J}$, and $Q_b \in {\mathcal J}$ for each $b \in P$, then $P(Q) = \{b \wedge c : b \in P, c \in Q_b\}^- \in {\mathcal J}$;

2. (ii) If $P \in {\mathcal J}$ and $\alpha \colon P \rightarrow I$ is a surjective map, then each join $\bigvee \alpha^{-1}(i)$ exists and $\alpha_!(P) = \{\textstyle\bigvee \alpha^{-1}(i) : i \in I\} \in {\mathcal J}$.

A Grothendieck Boolean algebra $B_{{\mathcal J}}$ is a Boolean algebra B with a zero-dimensional topology ${\mathcal J}$. A homomorphism of Grothendieck Boolean algebras $f \colon B_{{\mathcal J}} \rightarrow C_{\mathcal{ K}}$ is a Boolean homomorphism $f \colon B \rightarrow C$ such that $P \in {\mathcal J}$ implies $f(P)^- \in {\mathcal{ K}}$. If $B_{{\mathcal J}}$ is a Grothendieck Boolean algebra and $b \in B$, then we write ${\mathcal J}_b$ for the set of partitions of b characterized by:

\begin{equation*} P \in {\mathcal J}_b \iff P \cup \{b^{\prime}\} \in {\mathcal J} \iff P \subseteq Q \in {\mathcal J} \mathrm{and } \bigvee P = b\rlap{.} \end{equation*}

Given a Grothendieck Boolean algebra, we can now define a variety of (infinitary) algebras which allows for infinite conditioning over its privileged partitions.

Definition 2.4. $B_{{\mathcal J}}$-sets

Let $B_{{\mathcal J}}$ be a non-degenerate Grothendieck Boolean algebra. A $B_{{\mathcal J}}$-set is a B-set X equipped with a function $P \colon X^P \rightarrow X$ for each infinite $P \in {\mathcal J}$, satisfying:

(2.2)\begin{equation} P(\lambda b\cdot\, x) = x\ \ \ \ \ P(\lambda b\cdot\, b(x_b, y_b)) = P(\lambda b\cdot\, x_b)\ \ \ \ \ b(P(x), x_b) = x_b \forall b \in P. \end{equation}

In this definition, and henceforth, we use the following notational conventions:

Notation 2.5.

Given sets I and J we write J^I for the set of functions from I to J. If $u \in J^I$, we write u_i for the value of the function u at $i \in I$; on the other hand, given a family of elements $(t_i \in J : i \in I)$, we write $\lambda i\cdot\, t_i$ for the corresponding element of J^I. We may identify a natural number n with the set $\{1, \dots, n\} \subseteq \mathbb{N}$.

It turns out [16, proposition 3.9] that an operation P on a B-set X satisfying the axioms (2.2) is unique if it exists, and that any homomorphism of B-sets $f \colon X \rightarrow Y$ will preserve it. Thus, the category of $B_{{\mathcal J}}$-sets and homomorphisms is a full subcategory of the category of B-sets. Moreover, any non-degenerate Boolean algebra B has a least zero-dimensional topology given by the collection of all finite partitions of B, and in this case, $B_{\mathcal J}$-sets are just B-sets; as such, we may without loss of generality work exclusively with $B_{{\mathcal J}}$-sets in what follows.

As explained in [16], $B_{{\mathcal J}}$-set structure on a set X can also be described in terms of a family of equivalence relations $\equiv_b$ which we read as ‘$\mathsf{if}\ b\ \mathsf{then}\ x = y$’ or as ‘x and y have the same restriction to b’. The following result combines propositions 3.2, 3.10, and 3.11 and lemma 3.12 of op. cit.

Proposition 2.6. Let $B_{{\mathcal J}}$ be a non-degenerate Grothendieck Boolean algebra. Any $B_{{\mathcal J}}$-set structure on a set X induces equivalence relations $\equiv_b$ (for $b \in B$) given by:

\begin{equation*} x \equiv_b y \quad \quad \iff \quad \quad b(x,y) = y\rlap{.} \end{equation*}

These equivalence relations satisfy the following axioms:

1. (i) If $x \equiv_b y$ and $c \leqslant b$ then $x \equiv_c y$;

2. (ii) $x \equiv_1 y$ if and only if x = y, and $x \equiv_0 y$ always;

3. (iii) For any $P \in {\mathcal J}_b$, if $x \equiv_{c} y$ for all $c \in P$, then $x \equiv_{b} y$;

4. (iv) For any $P \in {\mathcal J}$ and $x \in X^P$, there is $z \in X$ such that $z \equiv_b x_b$ for all $b \in P$.

Any family of equivalence relations $(\mathord{\equiv_b} : b \in B)$ satisfying (i)–(iv) arises in this way from a unique $B_{{\mathcal J}}$-set structure on X whose operations are characterized by the fact that $b(x,y) \equiv_b x$ and $b(x,y) \equiv_{b^{\prime}} y$ for all $b \in B$ and $x,y \in X$; and that $P(x) \equiv_b x_b$ for all $P \in {\mathcal J}$, $x \in X^P$ and $b \in P$. Such a $B_{{\mathcal J}}$-set structure is equally well-determined by equivalence relations $\equiv_b$ satisfying (i) and:

1. (ii)’ For any $P \in {\mathcal J}$ and $x \in X^P$, there is a unique $z \in X$ with $z \equiv_{b} x_b$ for all $b \in P$.

Under the above correspondences, a function $X \rightarrow Y$ between $B_{{\mathcal J}}$-sets is a homomorphism just when it preserves each $\equiv_b$.

Remark 2.7. The conditions (i)–(iii) imply that, for all elements $x,y$ in a $B_{{\mathcal J}}$-set X, the set $[[x=y]]=\{b\in B:x \equiv_{\textit{by}}\}$ is an ideal of the Boolean algebra B, and in fact a ${\mathcal J}$-closed ideal—meaning that $b \in {{\unicode{x27E6}{{x}=y}{}\unicode{x27E7}}}$ whenever $P \subseteq {\unicode{x27E6}{{x}=y}{}\unicode{x27E7}}$ for some $P \in {\mathcal J}_b$.

2.2. Matched pairs of algebras ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$ and ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$

We now describe the algebraic structure which [16] identifies as encoding precisely the non-degenerate cartesian closed varieties. In the finitary case, this structure was already considered in [23, §4], in a related, though different, context.

Definition 2.8. Matched pair of algebras

A non-degenerate Grothendieck matched pair of algebras ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ comprises a non-degenerate Grothendieck Boolean algebra $B_{{\mathcal J}}$; a monoid M; $B_{{\mathcal J}}$-set structure on M, written as $b, m, n \mapsto b(m,n)$; and left M-set structure on B, written as $m, b \mapsto m^\ast b$. We require that M acts on $B_{{\mathcal J}}$ by Grothendieck Boolean homomorphisms, and that the following axioms hold:

• • $b(m,n)p = b(mp,np)$;

• • $m(b(n,p)) = (m^\ast b)(mn,mp)$; and

• • $b(m,n)^\ast(c) = b(m^\ast c, n^\ast c)$,

for all $m,n,p \in M$ and $b,c \in B$. Here, in the final axiom, we view B itself as a B-set under the operation of conditioned disjunction $b(c,d) = (b \wedge c) \vee (b^{\prime} \wedge d)$. These axioms are equivalently the conditions that:

• • $m \equiv_b n \implies mp \equiv_b np$;

• • $n \equiv_b p \implies mn \equiv_{m^\ast b} mp$;

• • $m \equiv_b n \implies m^\ast c \equiv_b n^\ast c$, i.e., $b \wedge m^\ast c = b \wedge n^\ast c$.

When ${\mathcal J}$ is the topology of finite partitions, we can drop the ${\mathcal J}$ and the modifier ‘Grothendieck’ and speak simply of a matched pair of algebras ${\left[\smash{{B} \mathbin{\mid}{M } }\right]}$.

A homomorphism $\left[\smash{{\varphi} \mathbin{\mid}{f} }\right] \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M } }\right]} \rightarrow \left[\smash{{B^{\prime}_{{\mathcal J}^{\prime}}} \mathbin{\mid}{M^{\prime} } }\right]$ of Grothendieck matched pairs of algebras comprises a Grothendieck Boolean homomorphism $\varphi \colon B_{{\mathcal J}} \rightarrow B^{\prime}_{{\mathcal J}^{\prime}}$ and a monoid homomorphism $f \colon M \rightarrow M^{\prime}$ such that, for all $m,n \in M$ and $b \in B$:

(2.3)\begin{equation} \varphi(b)(f(m),f(n)) = f(b(m,n)) \ \ \ \mathrm{and} \ \ \ f(m)^\ast(\varphi(b)) = \varphi(m^\ast b)\rlap{,} \end{equation}

or equivalently, such that

(2.4)\begin{equation} \ \ \quad m \equiv_b n \implies f(m) \equiv_{\varphi(b)} f(n) \qquad \mathrm{and} \qquad f(m)^\ast(\varphi(b)) = \varphi(m^\ast b)\text{.} \end{equation}

The cartesian closed variety which corresponds to the Grothendieck matched pair of algebras ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ can be described explicitly as the variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets:

Definition 2.9. Variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M } }\right]}$-sets

Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M } }\right]}$ be a non-degenerate matched pair of algebras. A ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set is a set X endowed with $B_{{\mathcal J}}$-set structure and M-set structure, such that in addition we have:

(2.5)\begin{equation} b(m,n) \cdot x = b(m \cdot x, n \cdot x) \qquad \mathrm{and} \qquad m \cdot b(x,y) = (m^\ast b)(m \cdot x, m \cdot y) \end{equation}

for all $b\in B$, $m,n \in M$ and $x,y \in X$; or equivalently, such that:

(2.6)\begin{equation} m \equiv_b n \implies m \cdot x \equiv_b n \cdot x \qquad \mathrm{and} \qquad x \equiv_b y \implies m \cdot x \equiv_{m^\ast b} m \cdot y\rlap{.} \end{equation}

A homomorphism of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets is a function which preserves both $B_{{\mathcal J}}$-set and M-set structure. We write ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ for the variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M } }\right]}$-sets. In the finitary case, we speak of ‘${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$-sets’ and the (finitary) variety ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$.

The fact that ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M } }\right]}$-sets are indeed a cartesian closed variety was verified in [16, proposition 7.11], which we recall as:

Proposition 2.10. For any non-degenerate Grothendieck Boolean matched pair ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$, the category ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ is cartesian closed.

Proof. Given ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets Y and Z, the function space Z^Y is the set of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set homomorphisms $f \colon M \times Y \rightarrow Z$. We make this into an M-set under the action

\begin{equation*} (m \cdot f)(n,y) = f(nm, y)\rlap{,} \end{equation*}

and into a $B_{{\mathcal J}}$-set via the equivalence relations:

\begin{equation*} f \equiv_b g \qquad \iff \qquad f(m,y) \equiv_{m^\ast b} g(m,y)\ \ \text{ for all}\, m,y \in M \times Y. \end{equation*}

The evaluation homomorphism $\mathrm{ev} \colon Z^Y \times Y \rightarrow Z$ is given by $\mathrm{ev}(f, y) = f(1, y)$; and given a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set homomorphism $f \colon X \times Y \rightarrow Z$, its transpose $\bar f \colon X \rightarrow Z^Y$ is given by $\bar f(x)(m, y) = f(mx, y)$.

Conversely, if we are presented with a cartesian closed variety ${\mathcal {C}}$, then we can reconstruct the ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ for which ${\mathcal {C}} \cong {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ using [16, proposition 7.12], which we restate (slightly less generally) here as:

Proposition 2.11. Let ${\mathcal {C}}$ be a non-degenerate cartesian closed variety, and let $X \in {\mathcal {C}}$ be the free algebra on one generator. Then ${\mathcal {C}} \cong {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$, where

1. (a) The monoid M is ${\mathcal {C}}(X,X)$, with unit $\mathrm{id}_X$ and product given by composition in diagrammatic order, i.e., mn is m followed by n;

2. (b) Writing 1 for the one-element algebra, and $\iota_\top, \iota_\bot \colon 1 \rightarrow 1+1$ for the two coproduct injections, the Boolean algebra B is ${\mathcal {C}}(X,1 + 1)$ with operations

   \begin{gather*} \smash{1 = X \xrightarrow{!} 1 \xrightarrow{\iota_\top} 1+1 \qquad \qquad b^{\prime} = X \xrightarrow{b} 1 + 1 \xrightarrow{{\langle{\iota_2, \iota_1}\rangle}} 1+1}\\ \mathrm{and} \quad \smash{b \wedge c = X \xrightarrow{(b,c)} (1 + 1) \times (1 + 1) \xrightarrow{\wedge} 1+1} \end{gather*}

   where $\wedge \colon (1+1) \times (1+1) \rightarrow 1+1$ satisfies $\wedge \circ (\iota_i \times \iota_j) = \iota_{i \wedge j}$ for $i,j \in \{\top, \bot\}$;

3. (c) The zero-dimensional coverage ${\mathcal J}$ on B has $P \subseteq B$ is in ${\mathcal J}$ just when there exists a map $f \colon X \rightarrow P \cdot 1$ with ${\langle{\delta_{bc}}\rangle}_{b \in B} \circ f = c$ for all $c \in P$, where here $\delta_{bc} \colon 1 \rightarrow 1+1$ is given by $\delta_{bc} = \iota_{\top}$ when b = c and $\delta_{bc} = \iota_\bot$ otherwise;

4. (d) M acts on B via precomposition;

5. (e) B acts on M via:

   \begin{equation*} \smash{(b, m, n) \mapsto X \xrightarrow{(b, \mathrm{id})} (1+1) \times X \xrightarrow{\cong} X + X \xrightarrow{{\langle{m,n}\rangle}} X\rlap{.}} \end{equation*}

The isomorphism ${\mathcal {C}} \cong {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ sends $Y \in {\mathcal {C}}$ to the set ${\mathcal {C}}(X,Y)$, made into a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set via the action of M by precomposition, and the action of B by

\begin{equation*} \smash{(b, x, y) \mapsto X \xrightarrow{(b, \mathrm{id})} (1+1) \times X \xrightarrow{\cong} X + X \xrightarrow{{\langle{x,y}\rangle}} Y\rlap{.}} \end{equation*}

Finally, by [16, remark 7.9], the free ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set on a given set of generators X can be described in terms of the notion of B-valued distribution:

Definition 2.12. Let $B_{{\mathcal J}}$ be a non-degenerate Grothendieck Boolean algebra. A $B_{{\mathcal J}}$-valued distribution on a set I is a function $\omega \colon I \rightarrow B$ whose restriction to $\mathrm{supp}(\omega) = \{i \in I : \omega(i) \neq 0\}$ is an injection onto a partition in ${\mathcal J}$. We write $T_{B_{{\mathcal J}}}(I)$ for the set of $B_{{\mathcal J}}$-valued distributions on I.

Now the free ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set on a set X is given by the product of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets $M \times T_{B_{{\mathcal J}}} X$. Here, M is seen as a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set via its canonical structures of $B_{{\mathcal J}}$- and M-set, while $T_{B_{{\mathcal J}}}(X)$ is seen as a $B_{{\mathcal J}}$-set via

\begin{equation*} \omega \equiv_b \gamma \qquad \iff \qquad b \wedge \omega(x) = b \wedge \gamma(x)\ \ \text{ for all } x \in X \end{equation*}

and as an M-set via $n \cdot (m, \omega) = (nm, n^\ast \circ \omega)$. The function $\eta \colon X \rightarrow M \times T_{B_{{\mathcal J}}}(X)$ exhibiting $M \times T_{B_{{\mathcal J}}}(X)$ as free on X is given by $x \mapsto (1, \pi_x)$.

3. Matched pairs as Boolean restriction monoids

In this section, we prove our first main result, identifying (Grothendieck) matched pairs of algebras with (Grothendieck) Boolean restriction monoids. We begin by recalling the notion of restriction monoid. These appear in the semigroup literature under the name ‘left weakly E-ample semigroups’ [14], with the below axiomatization first appearing in [22]; the name ‘restriction monoid’ is now standard, with the nomenclature coming from [9]. See [20] for a historical overview.

Definition 3.1. Restriction monoid

A (left) restriction monoid is a monoid S endowed with a unary operation $s \mapsto {s}^{+}$ (called restriction), satisfying the axioms

\begin{equation*} {s}^{+} s = s \qquad {({s}^{+}t)}^{+} = {s}^{+} {t}^{+} \qquad {s}^{+} {t}^{+} = {t}^{+} {s}^{+} \qquad \mathrm{and} \qquad s {t}^{+} = {(st)}^{+}s \rlap{.} \end{equation*}

A homomorphism of restriction monoids is a monoid homomorphism φ which also preserves restriction, i.e., $\varphi(s^+) = \varphi(s)^+$.

Some basic examples of a restriction monoid are the monoid of partial endofunctions of a set X, or the partial continuous endofunctions of a space X. In both cases, the restriction of a partial map $f \colon X \rightharpoonup X$ is the idempotent partial function ${f}^{+} \colon X \rightharpoonup X$ with ${f}^{+}(x) = x$ if x is defined and ${f}^{+}(x)$ undefined otherwise. In general, each element $s^+$ in a restriction monoid S is idempotent, and an element b is of the form $s^+$ if, and only if, $b^+ = b$; we write E(S) for the set of all $s^+$ and call them restriction idempotents. On the other hand, we call $s \in S$ total if ${s}^{+} = 1$. Total maps are easily seen to constitute a submonoid $\mathrm{Tot}(S)$ of S.

There is a partial order $\leqslant$ on any restriction monoid S defined by $s \leqslant t$ iff ${s}^{+} t = s$, expressing that s is the restriction of t to a smaller domain of definition. When ordered by $\leqslant$, the set of restriction idempotents E(S) becomes a meet-semilattice, with top element 1 and binary meet $b \wedge c = bc$. Of course, $b, c \in E(S)$ are disjoint if bc = 0; more generally, we say that $s,t \in S$ are disjoint if ${s}^{+} {t}^{+} = 0$.

The above axioms have various consequences; one of the more important is the fact that $(s\,t^+)^+ = (st)^+$, which can be derived as follows.

\begin{equation*} (s\,t^+)^+ = ((st)^+s)^+ = (st)^+ s^+ = s^+ (st)^+ = (s^+st)^+ = (st)^+. \end{equation*}

Definition 3.2. Boolean restriction monoid [11]

A Boolean restriction monoid is a restriction monoid S in which:

• • $(E(S), \leqslant)$ admits a negation $({\mathord{\text{--}}})^{\prime}$ making it into a Boolean algebra;

• • The least element 0 of E(S) is also a least element of S;

• • Every pair of disjoint elements $s,t \in S$ has a join $s \vee t$ with respect to $\leqslant$;

• • We have $s0 = 0$ and $s(t \vee u) = st \vee su$ for all $s, t,u \in S$ with $t,u$ disjoint.

As explained in [8, proposition 2.14], these conditions imply moreover that:

• • $0 s = 0$ and $(s \vee t)u = su \vee tu$ for all $s,t,u \in S$ with $t,u$ disjoint;

• • $0^+ = 0$ and ${(s \vee t)}^{+} = {s}^{+} \vee {t}^{+}$.

A homomorphism of Boolean restriction monoids is a restriction monoid homomorphism $S \rightarrow T$ which also preserves the least element 0 and joins of disjoint elements, or equivalently, by [10, lemma 2.10], which restricts to a Boolean homomorphism $E(S) \rightarrow E(T)$.

Boolean restriction monoids are the same thing as the modal restriction semigroups with preferential union of [24]. We now wish to show, further, that non-degenerate Boolean restriction monoids are coextensive with non-degenerate matched pairs of algebras. In our arguments, we will freely use basic consequences of the restriction monoid axioms as found, for example, in [9, lemma 2.1]. In one direction, we have:

Proposition 3.3. Let S be a non-degenerate Boolean restriction monoid (i.e., $0\neq 1$ in S). The Boolean algebra $B = (E(S), \leqslant)$ and the monoid $M = \mathrm{Tot}(S)$ constitute a non-degenerate matched pair of algebras $S^\downarrow = {\left[\smash{{B} \mathbin{\mid}{M} }\right]}$, where B becomes an M-set by taking $m^\ast b = (mb)^+$, and M becomes a $B_{{\mathcal J}}$-set by taking $m \equiv_b n \iff bm = bn$.

Proof. For axiom (i), if $c \leqslant b$, then cb = c and so bm = bn implies $cm=cbm=cbn=cn$, i.e., $m \equiv_b n$ implies $m \equiv_c n$. For axiom (ii), we have $m \equiv_{\top} n$ just when $1m = 1n$, i.e., when m = n. For (iii), if $m \equiv_b n$ and $m \equiv_c n$, then $(b \vee c)m = bm \vee cm = bn \vee cn = (b \vee c)n$ so that $m \equiv_{b \vee c} n$. Finally, for (iv), if $m,n \in M$ and $b \in B$, then the element $bm \vee b^{\prime}n$ is clearly total and satisfies $b(bm \vee b^{\prime}n) = bbm \vee bb^{\prime}n = bm \vee 0 n = bm$ and similarly $b^{\prime}(bm \vee b^{\prime}n) = b^{\prime}n$, whence $b(m,n) = bm \vee b^{\prime}m$ satisfies $b(m,n) \equiv_b m$ and $b(m,n) \equiv_{b^{\prime}} n$ as desired.

We next check that $m \mapsto m^\ast$ is an action by Boolean homomorphisms. Firstly:

\begin{equation*} 1^\ast b= {(1b)}^{+} = {b}^{+} = b \qquad \mathrm{and} \qquad m^\ast n^\ast b = {(m {(nb)}^{+})}^{+} = {(mnb)}^{+} = (mn)^\ast b\rlap{.} \end{equation*}

Next, we have $m^\ast(1) = {(m1)}^{+} = {m}^{+} = 1$ since m is assumed total, and

\begin{equation*} m^\ast(b \wedge c) = {(mbc)}^{+} = {(m {b}^{+} c)}^{+} = {({(mb)}^{+} mc)}^{+} = {(mb)}^{+}{(mc)}^{+} = (m^\ast b) \wedge (m^\ast c)\rlap{.} \end{equation*}

Furthermore, since $m^\ast(b) \wedge m^\ast(b^{\prime}) = m^\ast(b \wedge b^{\prime}) = m^\ast(0) = {(m0)}^{+} = 0$ and

\begin{equation*} m^\ast(b) \vee m^\ast(b^{\prime}) = {(mb)}^{+} \vee {(mb^{\prime})}^{+} = {(m(b \vee b^{\prime}))}^{+} = {m}^{+} = 1 \end{equation*}

we have $m^\ast b^{\prime} = (m^\ast b)^{\prime}$ so that $m^\ast$ is a Boolean homomorphism. It remains to check the three axioms for a matched pair of algebras. Axiom (i) is the trivial fact that bm = bn implies bmp = bnp. Axiom (ii) is the calculation

\begin{equation*} bn = bp \quad \implies \quad (m^\ast b)mn = {(mb)}^{+}mn = mbn = mbp = {(mb)}^{+}mp = (m^\ast b)mp\rlap{,} \end{equation*}

and, finally, axiom (iii) is:

\begin{equation*} bm = bn \quad \implies \quad b \wedge m^\ast c = b{(mc)}^{+} = {(bmc)}^{+} = {(bnc)}^{+} = b {(nc)}^{+} = b \wedge n^\ast c\text{.} \end{equation*}

In the converse direction, we have the following construction, which also appears, in a more general context, in unpublished work of Stokes [44].

Proposition 3.4. For any non-degenerate matched pair of algebras ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$, there is a non-degenerate Boolean restriction monoid S with $S^\downarrow \cong {\left[\smash{{B} \mathbin{\mid}{M} }\right]}$.

Proof. We define $S = \{(b,m) : b \in B, m \in M / \mathord{\equiv_b}\}$, whose elements we write more suggestively as $\left.{m}\right|_{b }$. We claim this is a Boolean restriction monoid on taking $1 = \left.{1}\right|_{1}$, ${(\left.{m}\right|_{b})}^{+} = \left.{1}\right|_{b}$ and $\left.{m}\right|_{b} \left.{n}\right|_{c} = \left.{mn}\right|_{b \wedge m^\ast c}$. First, the multiplication $\left.{m}\right|_{b} \left.{n}\right|_{c}$ is well-defined, as if $m \equiv_b m^{\prime}$ and $n \equiv_{c} n^{\prime}$, then $m^\ast c \equiv_{b} (m^{\prime})^\ast c$, i.e., $b \wedge m^\ast c = b \wedge (m^{\prime})^\ast c$; moreover, we have $mn \equiv_b mn^{\prime}$ and $mn^{\prime} \equiv_{m^\ast c} mn^{\prime}$, whence $mn \equiv_{b \wedge m^\ast c} m^{\prime}n^{\prime}$. So $\left.{mn}\right|_{b \wedge m^\ast c} = \left.{m^{\prime}n^{\prime}}\right|_{b \wedge (m^{\prime})^\ast c}$ as required.

We now check the monoid axioms for S, noting the equality $\left.{1}\right|_{b} \left.{n}\right|_{c} = \left.{n}\right|_{b \wedge c}$, which we will use repeatedly. For the unit axioms, $\left.{1}\right|_{1} \left.{m}\right|_{b} = \left.{m}\right|_{1 \wedge b} = \left.{m}\right|_{b}$ and $\left.{m}\right|_{b} \left.{1}\right|_{1} = \left.{m}\right|_{b \wedge m^\ast 1} = \left.{m}\right|_{b}$. For associativity,

\begin{align*} (\left.{m}\right|_{b} \left.{n}\right|_{c})\left.{p}\right|_{d} &= \left.{mn}\right|_{b \wedge m^\ast c} \left.{p}\right|_{d} = \left.{mnp}\right|_{b \wedge m^\ast c \wedge (mn)^\ast d} = \left.{mnp}\right|_{b \wedge m^\ast c \wedge m^\ast n^\ast d} \\ &= \left.{mnp}\right|_{b \wedge m^\ast(c \wedge n\ast d)} = \left.{m}\right|_{b} \left.{np}\right|_{c \wedge n^\ast d} = \left.{m}\right|_{b} (\left.{n}\right|_{c} \left.{p}\right|_{d})\rlap{.} \end{align*}

The following calculations now establish the four restriction monoid axioms:

\begin{align*} {\left.{m}\right|_{b}\!}^{+}\left.{m}\right|_{b} &= \left.{1}\right|_{b} \left.{m}\right|_{b} = \left.{m}\right|_{b \wedge b} = \left.{m}\right|_{b}\\ \smash{{\smash{({\left.{m}\right|_{b}\!}^{+}\!\left.{n}\right|_{c})}}^{+}} &= {(\left.{1}\right|_{b}\! \left.{n}\right|_{ } c)}^{+} = {\left.{n}\right|_{b \wedge c}\!}^{+} = \left.{1}\right|_{b \wedge c} = \left.{1}\right|_{b} \!\left.{1}\right|_{c} = {\left.{n}\right|_{c}\!}^{+}{\left.{m}\right|_{b}\!}^{+}\\ {\left.{m}\right|_{b}\!}^{+}{\left.{n}\right|_{c}\!}^{+} &= \left.{1}\right|_{b} \left.{1}\right|_{c} = \left.{1}\right|_{b \wedge c} = \left.{1}\right|_{c \wedge b} = \left.{1}\right|_{c} \left.{1}\right|_{b} = {\left.{n}\right|_{c}\!}^{+}{\left.{m}\right|_{b}\!}^{+}\\ \left.{m}\right|_{b}{\left.{n}\right|_{c}\!}^{+} &= \left.{m}\right|_{b} \left.{1}\right|_{c} = \left.{m}\right|_{b \wedge m^\ast c} = \left.{1}\right|_{b \wedge m^\ast c}\left.{m}\right|_{b} = {\left.{mn}\right|_{b \wedge m^\ast c}\!}^{+} \left.{m}\right|_{b} = {(\left.{m}\right|_{b}\! \left.{n}\right|_{c})}^{+}\left.{m}\right|_{b}\text{.} \end{align*}

So S is a restriction monoid, wherein $E(S) = \{\left.{1}\right|_{b} : b\in B\}$, and $\left.{m}\right|_{b} \leqslant \left.{n}\right|_{c}$ just when $b \leqslant c$ and $m \equiv_b n$. In particular, the map $B \rightarrow E(S)$ sending b to $\left.{1}\right|_{b}$ is an isomorphism of partially ordered sets, and so E(S) is a Boolean algebra. Moreover, the least element $\left.{1}\right|_{0}$ of E(S) is a least element of S, as $1 \equiv_0 m$ is always true.

We next show that any pair $s = \left.{m}\right|_{b}$ and $t= \left.{n}\right|_{c} \in S$ which are disjoint (i.e., $b \wedge c = 0$) have a join with respect to $\leqslant$. We claim $u = \left.{b(m,n)}\right|_{b \vee c}$ is suitable. Indeed, as $b \leqslant b \vee c$ and $m \equiv_b b(m,n)$, we have $s \leqslant u$; while as $c \leqslant b \vee c$ and $n \equiv_{c} b(m,n)$ (since $c \leqslant b^{\prime}$) we also have $t \leqslant u$. Now let $v = \left.{p}\right|_{d}$ and suppose $s,t \leqslant v$. Then $b,c \leqslant d$ and so $b \vee c \leqslant d$; moreover, $m \equiv_b p$ and $n \equiv_c p$ and so also $b(m,n) \equiv_b p$ and $b(m,n) \equiv_c p$. Thus $b(m,n) \equiv_{b \vee c} p$ and so $u \leqslant v$ as required.

Finally, we show joins are stable under left multiplication. For the nullary case, we have $\left.{m}\right|_{b} \left.{1}\right|_{0} = \left.{m}\right|_{b \wedge m^\ast 0} = \left.{m}\right|_{0} = \left.{1}\right|_{0}$. For binary joins, given $s = \left.{m}\right|_{b}$ and $t = \left.{n}\right|_{c}$ and $u = \left.{p}\right|_{ } d$ with $c, d$ disjoint, we necessarily have $st \vee su \leqslant s(t \vee u)$, since $st \leqslant s(t \vee u)$ and $su \leqslant s(t \vee u)$; so it suffices to show $(st \vee su)^+ = (s(t \vee u))^+$. But:

\begin{align*} (st \vee su)^+ &= (\left.{mn}\right|_{b \wedge m^\ast c}\vee \left.{mp}\right|_{b \wedge m^\ast d})^+ = \left.{1}\right|_{(b \wedge m^\ast c) \vee (b \wedge m^\ast d)}\\ \text{while} \ \ (s(t \vee u))^+ &= (s(t \vee u)^+)^+ = (\left.{m}\right|_{b} \left.{1}\right|_{c \vee d})^+ = \left.{1}\right|_{b \wedge m^\ast(c \vee d)} \end{align*}

which are the same since $m^\ast$ is a Boolean homomorphism.

This proves S is a Boolean restriction monoid. Now we already saw that $b \mapsto \left.{1}\right|_{b}$ is an isomorphism of Boolean algebras $B \rightarrow E(S)$, and the map $m \mapsto \left.{m}\right|_{1}$ is likewise a monoid isomorphism $M \rightarrow \mathrm{Tot}(S)$. To see that these maps constitute an isomorphism of matched pairs of algebras ${\left[\smash{{B} \mathbin{\mid}{M} }\right]} \rightarrow S^\downarrow$, we must check the two axioms in (2.3). On the one hand, for all $(b,m,n) \in B \times M \times M$, we have

\begin{equation*} \left.{1}\right|_{b}(\left.{m}\right|_{1}, \left.{n}\right|_{1}) = \left.{1}\right|_{b} \left.{m}\right|_{1} \vee \left.{1}\right|_{b^{\prime}} \left.{n}\right|_{1} = \left.{m}\right|_{b} \vee \left.{n}\right|_{b^{\prime}} = \left.{b(m,n)}\right|_{{b \vee b^{\prime}}} = \left.{b(m,n)}\right|_{1} \end{equation*}

which gives the first axiom in (2.3). On the other hand, for all $(m,b) \in M \times B$, $(\left.{m}\right|_{1})^\ast (\left.{1}\right|_{b}) = {(\left.{m}\right|_{1} \left.{1}\right|_{b})}^{+} = {\left.{m}\right|_{{m^\ast b}}}^{+} = \left.{1}\right|_{m^\ast b}$ giving the second axiom in (2.3).

We now show that the two processes just described underlie a functorial equivalence. Let us write $\mathrm{br}\mathrm{\mathcal Mon}$ for the category of Boolean restriction monoids and their homomorphisms, and $[\smash{{\mathrm{\mathcal B {\mathcal A} lg}}|\mathrm{\mathcal Mon}}]$ for the category of matched pairs of algebras.

Theorem 3.5 The assignment $S \mapsto S^\downarrow$ of proposition 3.3 is the action on objects of an equivalence of $({\mathord{\text{--}}})^\downarrow \colon \mathrm{br}\mathrm{\mathcal Mon} \rightarrow \left[\smash{{\mathrm{\mathcal B {\mathcal A} lg}} \mathbin{\mid}{ } }\right] {\mathrm{\mathcal Mon}}$ categories which on morphisms sends $\varphi \colon S \rightarrow T \left[\smash{{\left.{\varphi}\right|_{E(S)}} \mathbin{\mid}{} }\right]{\left.{\varphi}\right|_{\mathrm{Tot}(S)}}$ to $\colon S^\downarrow \rightarrow T^\downarrow$.

Recall here that a functor $F \colon {\mathcal A} \rightarrow {\mathcal B}$ is an equivalence just when it is both full and faithful, and also essentially surjective on objects, meaning that each $B \in {\mathcal B}$ is isomorphic to F(A) for some $A \in {\mathcal A}$.

Proof. Any homomorphism $\varphi \colon S \rightarrow T$ of Boolean restriction monoids preserves restriction idempotents and total maps and has restriction to $E(S) \rightarrow E(T)$ a Boolean homomorphism; moreover, these restrictions easily satisfy the two axioms of (2.4). So $({\mathord{\text{--}}})^\downarrow$ is well-defined on morphisms, is clearly functorial, and is essentially surjective by proposition 3.4. It remains to show it is full and faithful. Given a Boolean restriction monoid S and $s \in S$, we write

(3.1)\begin{equation} s^- = ({s}^{+})^{\prime} \qquad \mathrm{and} \qquad \check s = s \vee s^-\rlap{.} \end{equation}

Clearly s and $s^-$ are disjoint, so that this join exists; moreover, $\check s$ is total and so $s = {s}^{+} \check s$ expresses s as a product of a restriction idempotent and a total element.

In particular, this implies fidelity of $({\mathord{\text{--}}})^\downarrow$: for if $\varphi, \psi \colon S \rightarrow S^{\prime}$ act in the same way on restriction idempotents and total elements, then they act the same on each $s = s^+ \check s$ and so are equal. To show fullness, let S and S ^ʹ be Boolean restriction monoids and $\left[\smash{{\varphi} \mathbin{\mid}{f} }\right] \colon {\left[\smash{{B} \mathbin{\mid}{M} }\right]} \rightarrow \left[\smash{{B^{\prime}} \mathbin{\mid}{M^{\prime}} }\right]$ a homomorphism of the associated matched pairs. By (2.4), this is to say that for all $b \in B$ and $m,n \in M$:

(3.2)\begin{equation} bm = bn \implies \varphi(b) f(m) = \varphi(b) f(n) \quad \mathrm{and} \quad {(f(m)\varphi(b))}^{+} = \varphi({(mb)}^{+})\rlap{.} \end{equation}

We claim that $\psi \colon S \rightarrow S^{\prime}$ defined by $\psi(s) = \varphi({s}^{+})f(\check s)$ is a homomorphism of Boolean restriction monoids with $\psi^\downarrow = \left[\smash{{\varphi} \mathbin{\mid}{f} }\right]$. The latter claim follows easily since for $b \in E(S)$, we have $(b^+, \check b) = (b,1)$ and for $m \in \mathrm{Tot}(S)$ we have $(m^+, \check m) = (1,m)$. As for showing ψ is indeed a homomorphism of Boolean restriction monoids, it is clear that it preserves 1, and it preserves restriction since

\begin{equation*} {\psi(s)}^{+} = {(\varphi({s}^{+})f(\check s))}^{+} = {\varphi({s}^{+})}^{+}{f(\check s)}^{+} = \varphi({s}^{+}) = \psi({s}^{+})\rlap{.} \end{equation*}

To see that it preserves the monoid operation, we first calculate that:

\begin{equation*} {s}^{+} {(\check s {t}^{+})}^{+} = {s}^{+} {(\check s t)}^{+} = {s}^{+} {(s t)}^{+} \vee {s}^{+} {(s^- t)}^{+} = {(st)}^{+} \vee 0 = {(st)}^{+} \end{equation*}

using that $(st^+)^+ = (st)^+$; definition of $\check s$ and distributivity of joins; and the fact that ${(st)}^{+} \leqslant {s}^{+}$ and ${(s^- t)}^{+} \leqslant s^-$. Thus

\begin{align*} \psi(s)\psi(t) &= \varphi({s}^{+})f(\check s)\varphi({t}^{+})f(\check t) & \text{definition}\\ &= \smash{\varphi({s}^{+}){(f(\check s)\varphi({t}^{+}))}^{+}f(\check s)f(\check t)} & \text{fourth restriction axiom}\\ &= \smash{\varphi({s}^{+})\varphi({(\check s {t}^{+})}^{+})f(\check s)f(\check t)}& \text{right equality in (3.2)}\\ &= \smash{\varphi({s}^{+} {(\check s {t}^{+})}^{+})f(\check s\check t)} & \varphi, f\, \text{homomorphisms}\\ &= \smash{\varphi({(st)}^{+})f(\check s\check t)} & \text{preceding calculation}\\ &= \smash{\varphi({(st)}^{+})f(\check{st}) = \psi(st)} & \text{left implication in (3.2)} \end{align*}

where to apply (3.2) in the last line, we use that $s \leqslant \check s$ and $t \leqslant \check t$, whence $st \leqslant \check s \check t$ and so ${(st)}^{+} \check s \check t = st = {(st)}^{+} \check{st}$. Finally, since ψ restricts to φ on E(S), this restriction is a Boolean homomorphism, whence ψ is a homomorphism of Boolean restriction monoids as required.

As explained in the introduction, under the generalized non-commutative Stone duality of [10], Boolean restriction monoids correspond to source-étale topological categories with Stone space of objects. We do not recount the correspondence in detail here but simply apply it to describe explicitly the topological category associated with a matched pair of algebras.

Definition 3.6. Classifying topological category

Let ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$ be a matched pair of algebras. The classifying topological category $\mathbb{C}_{{\left[\smash{{B} \mathbin{\mid}{M} }\right]}}$ has:

• • Space of objects the Stone space of B, i.e., the set of all ultrafilters on B under the topology with basic (cl)open sets $[b] = \{{\mathcal U} \in C_0 : b \in {\mathcal U}\}$ for $b \in B$;

• • Space of arrows given by the set of all pairs $({\mathcal U} \in C_0, m \in M / \equiv_{\mathcal U}$), where $m \equiv_{\mathcal U} n$ just when $m \equiv_b n$ for some $b \in {\mathcal U}$, under the topology whose basic open sets are $\left[\smash{{b} \mathbin{\mid}{} }\right]m = \{({\mathcal U}, m) \in C_1 : b \in {\mathcal U}\}$ for any $b \in B$ and $m \in M$;

• • The source and target of $({\mathcal U}, m)$ given by ${\mathcal U}$ and

  \begin{align*}m_! {\mathcal U} := \{b \in B : m^\ast b \in {\mathcal U}\};\end{align*}

• • The identity on ${\mathcal U}$ given by $({\mathcal U}, 1) \colon {\mathcal U} \rightarrow {\mathcal U}$;

• • The composition of $({\mathcal U}, m) \colon {\mathcal U} \rightarrow m_! {\mathcal U}$ and $(m_! {\mathcal U}, n) \colon m_! {\mathcal U} \rightarrow n_! m_! {\mathcal U} = (mn)_! {\mathcal U}$ given by $({\mathcal U}, mn) \colon {\mathcal U} \rightarrow (mn)_! {\mathcal U}$.

When the action of M on B is faithful, we may under Stone duality identify elements $m \in M$ with continuous endomorphisms of the Stone space of B; whereupon the morphisms of $\mathbb{C}_{{\left[\smash{{B} \mathbin{\mid}{M} }\right]}}$ from W to W ^ʹ can equally well be described as germs at W of continuous functions in M which map W to W ^ʹ.

One might expect homomorphisms of matched pairs of algebras to induce functors between the classifying topological categories, but this is not so; rather, as in [10], they induce cofunctors [1, 18], which are equally the algebraic morphisms of [7].

Definition 3.7. Cofunctor

A cofunctor $F \colon \mathbb{C} \rightsquigarrow \mathbb{D}$ between categories comprises a mapping on objects $\mathrm{ob}(\mathbb{D}) \rightarrow \mathrm{ob}(\mathbb{C})$, written $d \mapsto Fd$, and a mapping which associates to each $d \in \mathrm{ob}(\mathbb{D})$ and arrow $f \colon Fd \rightarrow c$ of $\mathbb{C}$ an object $f_* d$ of $\mathbb{D}$ with $F(f_* d) = c$ and an arrow $F_d(f) \colon d \rightarrow f_* d$, subject to the axioms that $F_d(1_{Fd}) = 1_d$ and $F_{f_* d}(g) \circ F_d(f) = F_d(gf)$ (note that these imply in particular that $(1_{Fd})_* d = d$ and $g_* f_* d = (gf)_* d$). If $\mathbb{C}$ and $\mathbb{D}$ are topological categories, then a topological cofunctor is a cofunctor for which $d \mapsto Fd$ is continuous $\mathrm{ob}(\mathbb{D}) \rightarrow \mathrm{ob}(\mathbb{C})$ and $(d, f) \mapsto F_d(f)$ is continuous $\mathrm{mor}(\mathbb{C}) \times_{\mathrm{ob}(\mathbb{C})} \mathrm{ob}(\mathbb{D}) \rightarrow \mathrm{mor}(\mathbb{D})$.

Definition 3.8. Classifying cofunctor

Let $\left[\smash{{\varphi} \mathbin{\mid}{f} }\right] \colon {\left[\smash{{B} \mathbin{\mid}{M} }\right]} \rightarrow \left[\smash{{C} \mathbin{\mid}{N} }\right]$ be a homomorphism of matched pairs of algebras. The classifying cofunctor $\mathbb{C}_{{\left[\smash{{B} \mathbin{\mid}{M} }\right]}} \rightarrow \mathbb{C}_{\left[\smash{{C} \mathbin{\mid}{N } }\right]}$ is given as follows:

• • On objects it takes ${\mathcal U} \in \mathbb{C}_{\left[\smash{{C} \mathbin{\mid}{N } }\right]}$ to $\varphi^\ast({\mathcal U}) = \{b \in B : \varphi(b) \in {\mathcal U}\} \in \mathbb{C}_{{\left[\smash{{B} \mathbin{\mid}{M} }\right]}}$;

• • On maps it takes an object ${\mathcal U} \in \mathbb{C}_{\left[\smash{{C} \mathbin{\mid}{N } }\right]}$ and map $(\varphi^\ast {\mathcal U}, m) \colon \varphi^\ast {\mathcal U} \rightarrow m_! \varphi^\ast {\mathcal U}$ in $\mathbb{C}_{{\left[\smash{{B} \mathbin{\mid}{M} }\right]}}$ to the object $f(m)_! {\mathcal U}$ and map $({\mathcal U}, f(m)) \colon {\mathcal U} \rightarrow f(m)_! {\mathcal U}$ in $\mathbb{C}_{\left[\smash{{C} \mathbin{\mid}{N } }\right]}$. Note this is well-defined by the left-hand axiom in (2.6) and satisfies $\varphi^\ast f(m)_! {\mathcal U} = m_! \varphi^\ast {\mathcal U}$ by the right-hand one.

Combining theorem 3.5 with [10, Theorem 5.17], we thus see that the operation which assigns to the variety of ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$-sets the topological category $\mathbb{C}_{{\left[\smash{{B} \mathbin{\mid}{M} }\right]}}$ induces an equivalence between the category of non-degenerate finitary cartesian closed varieties and the category of non-empty ample topological groupoids and cofunctors.

We now describe the infinitary generalizations of the above.

Definition 3.9. Grothendieck Boolean restriction monoid

Let S be a Boolean restriction monoid and ${\mathcal J}$ a zero-dimensional topology on E(S). We say that $A \subseteq S$ is admissible if its elements are pairwise-disjoint, and the set $A^+ = \{a^+ : a \in A\}^-$ is contained in a partition in ${\mathcal J}$. We say that ${\mathcal J}$ makes S into a Grothendieck Boolean restriction monoid $S_{\mathcal J}$ if any admissible subset $A \subseteq S$ admits a join with respect to $\leqslant$, and whenever $A \subseteq S$ is admissible and $s \in S$, $sA = \{sa : a \in A\}$ is also admissible and $\bigvee sA = s (\bigvee A)$.

Proposition 3.10. Let S be a Boolean restriction monoid with $S^\downarrow= {\left[\smash{{B} \mathbin{\mid}{M} }\right]}$. A zero-dimensional topology ${\mathcal J}$ on B makes S a Grothendieck Boolean restriction monoid $S_{\mathcal J}$ just when it makes ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$ a Grothendieck matched pair of algebras ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$.

Proof. Suppose first $S_{\mathcal J}$ is a Grothendieck Boolean restriction monoid. We begin by proving that $m^\ast \colon B_{{\mathcal J}} \rightarrow B_{{\mathcal J}}$ for each $m \in M$. Indeed, any $P \in {\mathcal J}$ is admissible as a subset of S, and so mP is also admissible; which says that $\{(mb)^+ : b \in P\}^- = \{m^\ast b : b \in P\}^-$ is in ${\mathcal J}$, i.e., $m^\ast \colon B_{{\mathcal J}} \rightarrow B_{{\mathcal J}}$ as desired. We now prove that M is a $B_{{\mathcal J}}$-set. Given $P \in {\mathcal J}$ and $x \in M^P$, note that the family $A = \{bx_b : b \in P\}$ is admissible; write z for its join and observe that for all $b \in P$ we have $bA^- = \{bx_b\}$ since bc = 0 whenever $b \neq c \in P$. Thus $bz = \bigvee bA = bx_b$, i.e., $z \equiv_b x_b$ for all $b \in P$. Moreover, if $z^{\prime} \in M$ also satisfied $z^{\prime} \equiv_b x_b$ for all $b \in P$, i.e., $bz^{\prime} = bx_b$, then necessarily $bx_b \leqslant z^{\prime}$ for all b, whence $z = \bigvee A \leqslant z^{\prime}$; but since both z and z ^ʹ are total, we must have $z = z^{\prime}$ as required.

Suppose conversely that ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ is a Grothendieck matched pair, and let $A \subseteq S$ be admissible. So the set $A^+ = \{a^+ : a \in A\}^-$ is contained in a partition $P \in {\mathcal J}$; thus, since M is a $B_{{\mathcal J}}$-set, we can consider the unique element $z \in M$ such that

\begin{equation*} z \equiv_{a^+} \check a \;\text{for}\, a \in A \qquad \mathrm{and} \qquad z \equiv_{b} 1\; \text{for}\, b \in P \setminus A\ , \end{equation*}

where, as in (3.1), we write $\check a = a \vee (a^+)^{\prime}$. Since $A^+ \subseteq P$, the join $d = \bigvee_{a \in A} a^+$ exists, and so we have the element $dz \in S$. Now $a^+dz = a^+z = a^+ \check a = a$ for all $a \in A$, i.e., $a \leqslant dz$ for all $a \in A$; while if $a \leqslant u$ for all $a \in A$, i.e., $a^+ u = a$, then $a^+ z = a^+ \check a = a = a^+ u$, i.e., $z \equiv_{a^+} u$ for all $a \in A$, whence $z \equiv_d u$ by proposition 2.6 (iii), i.e., $dz = du = (dz)^+u$, i.e., $dz \leqslant u$. So dz is the join of A.

We now show stability of joins under left multiplication. Given $A \subseteq S$ admissible and $s \in S$, we may write $b = s^+$ and $m = \check s$ so that s = bm. It is easy to see that, if $A^+ \subseteq P \in {\mathcal J}$, then $\{(sa)^+ : a \in A\}^- \subseteq b \wedge m^\ast P \in {\mathcal J}$, so that sA is also admissible. Now necessarily $\bigvee sA \leqslant s (\bigvee A)$, and so it suffices to show their restrictions are the same. But we have

\begin{align*} \textstyle (s (\bigvee A))^+ &= \textstyle(s (\bigvee A)^+)^+ = (s (\bigvee A^+))^+ = b(m (\bigvee A^+))^+ = b \cdot m^\ast(\bigvee A^+)\\ &= \textstyle b \cdot \bigvee m^\ast(A^+) = b \cdot \bigvee_{a \in A} (ma)^+ = \bigvee_{a} b(ma)^+ = \bigvee_{a} (sa)^+ = (\bigvee sA)^+ \end{align*}

as desired, where in going from the first to the second line we use the (easy) fact that any Grothendieck Boolean algebra homomorphism preserves admissible joins.

A homomorphism of Grothendieck Boolean restriction monoids $\varphi \colon S_{\mathcal J} \rightarrow T_{\mathcal{ K}}$ is a Boolean restriction homomorphism which also preserves admissible families and joins of admissible families. By a similar argument to before, φ is a Grothendieck Boolean restriction homomorphism if and only if it is a restriction monoid homomorphism and its action on restriction idempotents is a Grothendieck Boolean homomorphism $E(S)_{\mathcal J} \rightarrow E(T)_{\mathcal{ K}}$. Writing $\mathrm{gbr}\mathrm{\mathcal Mon}$ for the category of Grothendieck Boolean restriction monoids and their homomorphisms, it follows that:

Theorem 3.11 The equivalence of categories $({\mathord{\text{--}}})^\downarrow \colon \mathrm{br}\mathrm{\mathcal Mon} \rightarrow \left[\smash{{\mathrm{\mathcal B {\mathcal A} lg}} \mathbin{\mid}{ } }\right] {\mathrm{\mathcal Mon}}$ extends to an equivalence of categories $({\mathord{\text{--}}})^\downarrow \colon \mathrm{gbr}\mathrm{\mathcal Mon} \rightarrow \left[\smash{{\mathrm{gr}\mathrm{\mathcal {\mathcal B} {\mathcal A} lg}} \mathbin{\mid}{ } }\right] {\mathrm{\mathcal Mon}}$ with action on objects $S_{\mathcal J} \mapsto {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$.

In the infinitary case, the further correspondence with topological categories breaks down; the reason is that a Grothendieck Boolean restriction monoid need not satisfy a ‘${\mathcal J}$-closed ideal lemma’ analogous to the Boolean prime ideal lemma. Instead, in the spirit of [40], we get a correspondence with certain localic categories: namely, those whose object-space is strongly zero-dimensional and whose source projection is a local homeomorphism. Again, we give the construction, which we extract from the presentation of [10, §5.3], but none of the further details.

Definition 3.12. Classifying localic category

Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. The classifying localic category $\mathbb{C}$ has:

• • Locale of objects C ₀ given by $\mathrm{Idl}_{\mathcal J}(B)$;

• • Locale of arrows C ₁ given by the $B_{{\mathcal J}}$-set homomorphisms $M \rightarrow \mathrm{Idl}_{\mathcal J}(B)$ ordered pointwise; here $\mathrm{Idl}_{\mathcal J}(B)$ is a $B_{{\mathcal J}}$-set via $I \equiv_b J$ when $I \cap \mathop{\downarrow} b = J \cap \mathop{\downarrow} b$;

• • The source map $s \colon C_1 \rightarrow C_0$ is given by $s^\ast(I) = \lambda m.\, I$;

• • The target map $t \colon C_1 \rightarrow C_0$ is given by $t^\ast(I) = \lambda m\cdot\, m^\ast I$, where $m^\ast I$ is the ${\mathcal J}$-closed ideal generated by the elements $m^\ast b$ for $b \in I$;

• • The identity map $i \colon C_0 \rightarrow C_1$ is given by $i^\ast(f) = f(1)$.

• • The composition map $m \colon C_1 \times_{C_0} C_1 \rightarrow C_1$ is given by $m^\ast(f) = \lambda m, n.\, f(mn)$. Here, we identify $C_1 \times_{C_0} C_1$ with the locale of all functions $f \colon M \times M \rightarrow \mathrm{Idl}_{\mathcal J}(B)$ for which each $f({\mathord{\text{--}}}, n)$ is a $B_{{\mathcal J}}$-set homomorphism $M \rightarrow \mathrm{Idl}_{\mathcal J}(B)$ and each $f(m, {\mathord{\text{--}}})$ is a $B_{{\mathcal J}}$-set homomorphism $M \rightarrow m^\ast\mathrm{Idl}_{\mathcal J}(B)$.

Like before, we can also associate a localic cofunctor to each homomorphism of Grothendieck matched pairs of algebras and in this way obtain an equivalence between the category of non-degenerate cartesian closed varieties and the category of non-empty ample localic categories and cofunctors.

4. When is a variety a topos?

In this section, we prove the second main result of the article, which gives a syntactic characterization of when a given cartesian closed variety is a topos, and shows that this condition can be re-expressed in terms of the minimality of the classifying topological or localic category. Recall that a topos is a cartesian closed category ${\mathcal {C}}$ which has all pullbacks and a subobject classifier: that is, an object Ω endowed with a map $\top \colon 1 \rightarrowtail \Omega$ with the property that, for any monomorphism $m \colon Y \rightarrowtail X$ in ${\mathcal {C}}$, there is a unique ‘classifying map’ $\chi_m \colon X \rightarrow \Omega$ for which the following square is apullback:

As explained in the introduction, the question posed in the title of this section was answered by Johnstone in [25], yielding a slightly delicate syntactic characterization theorem (theorem 3.1 of op. cit.). Of course, a non-degenerate variety which is a topos is in particular cartesian closed, and so, as we know now, must be a variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets. It is therefore natural to ask whether Johnstone’s conditions in [25] can be transformed in light of this knowledge into a condition on a Grothendieck matched pair ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ which ensures that ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ not just cartesian closed, but a topos. The answer is yes: we will show ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ is a topos precisely when:

(4.2)\begin{equation} \text{For all } b \in B \setminus \{0\} \text{, there exists } m \in M \;\text{with } m^\ast b = 1\rlap{.} \end{equation}

While it would be possible to prove this result directly, it is scarcely any extra effort to do something more general. In [26], Johnstone shows that any non-degenerate cartesian closed variety ${\mathcal V}$ has an associated topos ${\mathcal E}$, which is uniquely characterized by the fact that ${\mathcal V}$ can be re-found as its two-valued collapse. This implies that a non-degenerate cartesian closed variety ${\mathcal V}$ is itself a topos just when its associated topos ${\mathcal E}$ is two-valued, i.e., equal to its two-valued collapse. Here, the notion of ‘two-valued collapse’ is given by:

Definition 4.1. Two-valued collapse

Let ${\mathcal E}$ be a cartesian closed category. The two-valued collapse ${\mathcal E}_{\mathrm{tv}}$ is the full subcategory of ${\mathcal E}$ whose objects X are either well-supported—meaning that the unique map $X \rightarrow 1$ is epimorphic—or initial.

For a given cartesian closed variety ${\mathcal V}$, finding the topos which collapses to it is done by theorem 6.1 of op. cit., which is quite delicate; but armed with the knowledge that ${\mathcal V} \cong {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$, we are able to give a simpler construction of the associated topos¹, from which the characterization (4.2) above will follow straightforwardly.

Definition 4.2. Category of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaves

Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. A ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-presheaf X comprises sets X(b) for all $b \in B \setminus \{0\}$, together with:

• • For all $c \in B$ and $m \in M$ with $m^\ast c \neq 0$, a function $m \cdot ({\mathord{\text{--}}}) \colon X(c) \rightarrow X(m^\ast c)$;

• • For all $b,c \in B$ with $b \wedge c \neq 0$, a function $b \wedge ({\mathord{\text{--}}}) \colon X(c) \rightarrow X(b \wedge c)$;

such that for all $x \in X(c)$ and all suitable $a,b \in B$ and $m,n \in M$ we have:

1. (i) $c \wedge x = x$ and $(a \wedge b) \wedge x = a \wedge (b \wedge x)$;

2. (ii) $1 \cdot x = x$ and $(mn) \cdot x = m \cdot (n \cdot x)$;

3. (iii) $m \cdot (b \wedge x) = (m^\ast b) \wedge (m \cdot x)$; and

4. (iv) If $m \equiv_b n$ then $b \wedge (m \cdot x) = b \wedge (n \cdot x)$.

Such a presheaf is a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaf if for each $P \in {\mathcal J}_c$ and family $x \in \prod_{b \in P}X(b)$, there is given an element $P(x) \in X(c)$, and these elements satisfy:

(4.3)\begin{equation} b \wedge P(x) = x_b \text{ for all } x \in \textstyle\prod_{b \in P}X(b) \ \text{ and } P(\lambda b.\, b \wedge x) = x \text{ for all } x \in X(c)\text{.} \end{equation}

A homomorphism of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-presheaves is a family of functions ${f_c \colon X(c) \rightarrow Y(c)}$ that preserve each $m \cdot ({\mathord{\text{--}}})$ and $b \wedge ({\mathord{\text{--}}})$; between sheaves, such an f will necessarily also preserve each $P({\mathord{\text{--}}})$. We write ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ for the category of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaves.

Proposition 4.3. For any Grothendieck matched pair of algebras ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$, the category ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ is both a many-sorted variety and a (Grothendieck) topos.

Proof. The only axiom for a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaf which is not obviously equational is the condition that if $m \equiv_b n$ then $b \wedge (m \cdot x) = b \wedge (n \cdot x)$; however, this can be re-expressed as the condition that $b \wedge (m \cdot x) = b \wedge (b(m,n) \cdot x)$ for all $m,n \in M$, $b \in B$ and $x \in X(c)$. Thus, ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ is a many-sorted variety. To see that it is a Grothendieck topos, it suffices to exhibit it as equivalent to the category of sheaves on a suitable site [28, §C2]. So consider the category ${\mathcal {C}}$ in which:

• • Objects are elements of $B \setminus \{0\}$;

• • Morphisms $b \rightarrow c$ are elements $m \in M / \equiv_b$ for which $b \leqslant m^\ast c$; this is well-posed, as if $m \equiv_b n$ then $b \wedge m^\ast c = b \wedge n^\ast c$, so $b \leqslant m^\ast c$ if and only if $b \leqslant n^\ast c$;

• • The identity on b is $1 \colon b \rightarrow b$;

• • The composition of $m \colon b \rightarrow c$ and $n \colon c \rightarrow d$ is $mn \colon b \rightarrow d$. This is well-posed, as if $m \equiv_{b} m^{\prime}$ and $n \equiv_c n^{\prime}$ then $mn \equiv_b m^{\prime}n \equiv_b m^{\prime}n^{\prime}$, using $b \leqslant (m^{\prime})^\ast(c)$ for the second equality; and clearly $b \leqslant m^\ast c$ and $c \leqslant n^\ast d$ imply $b \leqslant (mn)^\ast d$.

Given a family of sets X(b), the ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-presheaf structures thereon are now in bijection with the ${\mathcal {C}}$-presheaf structures; indeed, from the former we obtain the latter by defining $X(m \colon b \rightarrow c)$ as $b \wedge (m \cdot {\mathord{\text{--}}})$, while from the latter we obtain the former by defining $m \cdot ({\mathord{\text{--}}})$ and $c \wedge ({\mathord{\text{--}}})$ as $X(m \colon m^\ast b \rightarrow b)$ and $X(1 \colon c \wedge b \rightarrow b)$. Under this correspondence, axioms (i)–(iii) correspond to functoriality in ${\mathcal {C}}$, while axiom (iv) corresponds to the equivalence relation on the homs of ${\mathcal {C}}$.

Now consider the Grothendieck coverage J on the category ${\mathcal {C}}$ for which the covers of $c \in {\mathcal {C}}$ are the families $(1 \colon b \rightarrow c)_{b \in P}$ for each $P \in {\mathcal J}_c$. This is indeed a coverage: for given the above cover of c and a map $m \colon d \rightarrow c$ in ${\mathcal {C}}$, since $m^\ast$ is a Grothendieck Boolean algebra homomorphism we have $m^\ast P \in {\mathcal J}_{m^\ast c}$ and so by axiom (i) for a Grothendieck Boolean algebra that $d \wedge m^\ast P = \{d \wedge m^\ast b : b \in P\}^-$ is in ${\mathcal J}_{d}$; and for each $1 \colon d \wedge m^\ast b \rightarrow d$ in the corresponding cover, the composite $m \colon d \wedge m^\ast b \rightarrow c$ factors through $1 \colon b \rightarrow c$ via $m \colon d \wedge m^\ast b \rightarrow b$.

Now given a ${\mathcal {C}}$-presheaf X, a matching family for the cover $(1 \colon b \rightarrow c)_{b \in P}$ is, by disjointness of P, simply a family $x \in \prod_{b \in P} X(b)$, and the sheaf axiom for this cover asserts that there is a unique $P(x) \in X(c)$ whose image under $X(1 \colon b \rightarrow c)$ is x_b for all $b \in P$. But in terms of the corresponding ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-presheaf, this asserts exactly the existence of elements P(x) satisfying (4.3). So $({\mathcal {C}}, J)$-sheaves correspond bijectively with ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaves; since clearly the homomorphisms match up under this correspondence, ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv} \cong \mathrm{\mathcal Sh}({\mathcal {C}}, J)$ is a Grothendieck topos.

We will now show that, if ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ is a Grothendieck matched pair of algebras, then the topos ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ has ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ as its two-valued collapse. The key point is how we embed ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ into ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$. To motivate this, note that what a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set lacks relative to a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaf are the actions $b \wedge ({\mathord{\text{--}}})$, so it makes sense to adjoin these ‘formally’. To this end, if X is a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set, let us suggestively write elements of the quotient $X/\!\!\equiv_b$ as $b \wedge x$; so $b \wedge x = b \wedge y$ just when $x \equiv_b y$. Using this notation, we now have:

Proposition 4.4. For any ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set X, there is a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaf $B \wedge X$ with

\begin{equation*} (B \wedge X)(b)\, = \,\mathord{X / \mathord{\equiv_b}}\, =\, \{b \wedge x : x \in X\}\rlap{,} \end{equation*}

and operations $b \wedge ({\mathord{\text{--}}}) \colon X(c) \rightarrow X(b \wedge c)$ and $m \cdot ({\mathord{\text{--}}}) \colon X(c) \rightarrow X(m^\ast c)$ given by

\begin{equation*} b \wedge (c \wedge x) = (b \wedge c) \wedge x \qquad \mathrm{and} \qquad m \cdot (c \wedge x) = (m^\ast c) \wedge (m \cdot x)\rlap{.} \end{equation*}

Proof. The ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-presheaf operations are well-defined by proposition 2.6 (i) and the second $B_{{\mathcal J}}$-set axiom in (2.5); they trivially satisfy axiom (i) for a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-presheaf and satisfy axioms (ii) and (iii) since M acts on B via Boolean homomorphisms. As for axiom (iv), if $m \equiv_b n$ then $b \wedge (m \cdot (c \wedge x)) = (b \wedge m^\ast c) \wedge (m \cdot x) = (b \wedge n^\ast c) \wedge (n \cdot x) = b \wedge (m \cdot (c \wedge x))$ where the first and last equalities just unfold definitions, and the middle equality follows from $m \equiv_b n$, since this condition implies that $b \wedge m^\ast c = b \wedge n^\ast c$ and $m \cdot x \equiv_b n \cdot x$.

It remains to show $B \wedge X$ is in fact a sheaf. If X is empty then this is trivial; otherwise, choose an arbitrary element $u \in X$ and now for any $P \in {\mathcal J}_c$ and family $x \in \prod_{b \in P}X(b)$, define $P(x) = c \wedge z$, where $z \in X$ is unique such that

\begin{equation*} z \equiv_b x_b\,\text{for all}\, b \in P \quad \mathrm{and} \quad z \equiv_{c^{\prime}} u\rlap{.} \end{equation*}

Now $b \wedge P(x) = b \wedge z = b \wedge x_b$ for each $c \in P$, giving the first axiom in (4.3); furthermore, for any $x \in X(c)$, we have $P(\lambda b.\, b \wedge x) = c \wedge z$ where z is unique such that $z \equiv_b x$ for all $b \in P$ and $z \equiv_{c^{\prime}} u$. By proposition 2.6 (iii), we conclude that $z \equiv_c x$, i.e., $P(\lambda b.\, b \wedge x) = x$, which is the second axiom of (4.3).

Proposition 4.5. Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a non-degenerate Grothendieck matched pair. The assignment $X \mapsto B \wedge X$ is the action on objects of a full and faithful functor

(4.4)\begin{equation} B \wedge ({\mathord{\text{--}}}) \colon {{\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}}\text-\mathrm{\mathcal Set} \rightarrow {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv} \end{equation}

which exhibits ${{\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}}\text-\mathrm{\mathcal Set}$ as equivalent to the two-valued collapse of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$.

Proof. Each ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set homomorphism $f \colon X \rightarrow Y$ induces a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaf homomorphism $B \wedge f \colon B \wedge X \rightarrow B \wedge Y$ which sends $b \wedge x$ to $b \wedge f(x)$; this is well-defined since $x \equiv_b y$ implies $f(x) \equiv_b f(y)$, clearly preserves the B-actions, and preserves the M-actions because f does so. Functoriality is obvious, and so we have a functor (4.4), which is faithful since we can recover f from $B \wedge f$ via its action on total elements, i.e., those in $(B \wedge X)(1) = X$. For fullness, suppose $g \colon B \wedge X \rightarrow B \wedge Y$ is a homomorphism, with action $f \colon X \rightarrow Y$ on total elements. Since $g(b \wedge x) = g(b \wedge (1 \wedge x)) = b \wedge g(1 \wedge x) = b \wedge f(x)$, we will have $g = B \wedge f$ so long as f is a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set homomorphism. It clearly preserves M-actions; while if $x \equiv_b y$ in X then $b \wedge x = b \wedge y$, so $b \wedge f(x) = b \wedge f(y)$, i.e., $f(x) \equiv_b f(y)$ as required.

To complete the proof, it remains to show that a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaf is in the essential image of (4.4) just when it is either empty or well-supported. Since the terminal object of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ has $1(b) = 1$ for all $b \in B \setminus \{0\}$, a sheaf Y is well-supported just when each Y(b) is non-empty which by virtue of the B-action happens just when Y(1) is non-empty. Clearly, then, each $B \wedge X$ is either empty or well-supported according as X is empty or non-empty.

Suppose conversely that $Y \in {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ has $Y(1) \neq \emptyset$. Note that this implies that each $b \wedge ({\mathord{\text{--}}}) \colon Y(1) \rightarrow Y(b)$ is surjective. For indeed, let us choose some $u \in Y(1)$; then for any $y \in Y(b)$, the sheaf condition gives a unique $z \in Y(1)$ with $b \wedge z = y$ and $b^{\prime} \wedge z = b^{\prime} \wedge u$—so, in particular, y is in the image of $b \wedge ({\mathord{\text{--}}})$.

We now show that $X = Y(1)$ is a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set and that $B \wedge X \cong Y$. Clearly, X is an M-set via the operations $m \cdot ({\mathord{\text{--}}})$ of Y; as for the $B_{{\mathcal J}}$-set structure, define $x \equiv_b y$ just when $b \wedge x = b \wedge y \in Y(b)$ (and $x \equiv_0 y$ always). Easily, the $\equiv_b$‘s are equivalence relations satisfying axiom (i) of proposition 2.6; however, they also satisfy axiom (ii)$^{\prime}$ therein. Indeed, for any $P \in {\mathcal J}$ and $x \in X^P$, we have the element $z = P(\lambda b\cdot\, b \wedge x_b) \in X$ which by the left equation of (4.3) satisfies $b \wedge z = b \wedge x_b$, i.e., $z \equiv_b x_b$, for all $b \in P$. But if $z^{\prime} \in X$ also satisfied $z^{\prime} \equiv_b x_b$ for all $b \in P$, then we would have $z^{\prime} = P(\lambda b\cdot\, b \wedge z^{\prime}) = P(\lambda b\cdot\, b \wedge x_b) = z$ by the right equation of (4.3); so z is unique such that $z \equiv_b x_b$ for all $b \in P$, as required. This proves that $X = Y(1)$ is a $B_{{\mathcal J}}$-set, and it remains to check the ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set axioms (2.6). But if $m \equiv_b n$ and $x \in X$ then $b \wedge (m \cdot x) = b \wedge (n \cdot x)$ in Y(b) by axiom (iv) for a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-presheaf, i.e., $m \cdot x \equiv_b n \cdot x$; while if $x \equiv_b y$ in X, i.e., $b \wedge x = b \wedge y$ in Y(b), then $m^\ast b \wedge m \cdot x = m \cdot (b \wedge x) = m \cdot (b \wedge y) = m^\ast b \wedge m \cdot y$, i.e., $m \cdot x \equiv_{m^\ast b} m \cdot y$.

So X is a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set. Now, since $x \equiv_b y$ in $X=Y(1)$ just when $b \wedge x = b \wedge y$ in Y(b), we can identify $(B \wedge X)(b) = X/\!\!\equiv_b$ with the image of the map $b \wedge ({\mathord{\text{--}}}) \colon Y(1) \rightarrow Y(b)$. But, as noted above, this map is surjective, and so we have isomorphisms $(B \wedge X)(b) \cong Y(b)$ for each $b \in B \setminus \{0\}$. It is not hard to see that the presheaf structures match under these isomorphisms, so $B \wedge X \cong Y$ as desired.

We can now give our promised characterizations of when ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ is a topos. As mentioned above, one form of our characterization will involve a condition of minimality on the classifying category; the relevant notion here is the following one, which extends the standard terminology for topological groupoids (for which a sieve is typically called an ‘invariant subset’).

Definition 4.6. Minimality

An open sieve on a topological category $\mathbb{C}$ is an open subset of $\mathrm{ob}(\mathbb{C})$ which contains the source s(f) of any arrow of $\mathbb{C}$ whenever it contains its target t(f). Correspondingly, an open sieve on a localic category $\mathbb{C}$ is an element $u \in \mathrm{ob}(\mathbb{C})$ such that $t^\ast(u) \leqslant s^\ast(u)$ in C ₁. A topological (resp., localic) category is minimal if its only open sieves are $\emptyset$ and $\mathrm{ob}(\mathbb{C})$ (resp., 0 and 1).

Theorem 4.7 Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. The following are equivalent:

1. (i) For all $b \in B \setminus \{0\}$, there exists $m \in M$ with $m^\ast b = 1$;

2. (ii) The topos ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ is two-valued;

3. (iii) $B \wedge ({\mathord{\text{--}}}) \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ is an equivalence of categories;

4. (iv) ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ is a topos;

5. (v) The classifying (topological or localic) category of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ is minimal.

Proof. We first show (i) $\Rightarrow$ (ii). ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ is two-valued if any subobject U of the terminal sheaf 1 is either empty or equal to 1. But if any U(b) is non-empty then on choosing m as in (i), we see that U(1) is also non-empty: so U is well-supported and so must equal 1. Now (ii) $\Rightarrow$ (iii) follows since $B \wedge ({\mathord{\text{--}}})$ exhibits ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ as equivalent to the two-valued collapse of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$, and (iii) $\Rightarrow$ (iv) is trivial as ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ is a topos. We now prove (iv) $\Rightarrow$ (i). Given $b \in B \setminus \{0\}$, consider the following diagram in ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$, where $\varphi \colon M \rightarrow B$ is the homomorphism $m \mapsto m^\ast b$, the bottom maps pick out $0,1 \in B$, and both squares are pullbacks:

The two pullback objects are given by

\begin{equation*} \varphi^{-1}(0) = \{m \in M : m^\ast b = 0\} \qquad \mathrm{and} \qquad \varphi^{-1}(1) = \{m \in M : m^\ast b = 1\} \end{equation*}

and so to prove (i) we must show $\varphi^{-1}(1)$ is non-empty. The maps on the bottom row are jointly epimorphic, since $0,1$ generate B as a $B_{{\mathcal J}}$-set; thus, as jointly epimorphic families are pullback-stable in a topos, the maps on the top row must also be jointly epimorphic. So if $\varphi^{-1}(1)$ were empty, $\varphi^{-1}(0) \rightarrowtail M$ would be an epimorphic monomorphism in a topos, and hence invertible. But then $1 \in \varphi^{-1}(0)$, i.e., $b = 1^\ast b = 0$, contradicting $b \in B \setminus \{0\}$. So $\varphi^{-1}(1)$ is non-empty as required.

To complete the proof, we show that (i) is equivalent to (v). It suffices to consider the localic classifying category, since in the finitary case, the classifying localic category is spatial, and the minimality of the localic category and the corresponding topological category come to the same thing. We first prove the following claim: given $b \neq 0 \in B$, the ${\mathcal J}$-closed ideal $M^\ast b \subseteq B$ generated by the elements $\{m^\ast b : m \in M\}$ is all of B if and only if there exists $m \in M$ with $m^\ast b = 1$. Since $M^\ast b=B$ just when $1 \in M^\ast b$, the ‘if’ direction is trivial. For the converse, to say $1 \in M^\ast b$ is to say that there exists $\{c_i : i \in I\} \in {\mathcal J}$ and $(n_i \in M : i \in I)$ such that $c_i \leqslant n_i^\ast(b)$ for each $i \in I$. Taking $m \in M$ unique such that $m \equiv_{c_i} n_i$ for each i, we have $m^\ast b = \textstyle\bigvee_{i} c_i \wedge n_i^\ast(b) = \bigvee_i c_i = 1$ as desired.

We now prove (i) $\Leftrightarrow$ (v). An open sieve of the classifying localic groupoid $\mathbb{C}_{{\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}}$ is, by definition, an ideal $I \in \mathrm{Idl}_{\mathcal J}(B)$ such that $t^\ast(I) \leqslant s^\ast(I) \colon M \rightarrow \mathrm{Idl}_{\mathcal J}(B)$, i.e., such that $m^\ast I \subseteq I$ for all $m \in M$. Clearly, any ideal of the form $M^\ast b$ is an open sieve; conversely, if I is an open sieve and $b \in B$ then $M^\ast b \subseteq I$, so that we can write I as a union of open sieves $I = \bigcup_{b \in I} M^\ast b$. By these observations, to ask that the only open sieves of $\mathbb{C}$ are $\{0\}$ and B is equally well to ask that every sieve of the form $M^\ast b$ is either $\{0\}$ or B. Of course, $M^\ast b = \{0\}$ only when b = 0, and so $\mathbb{C}$ is minimal just when $M^\ast b = B$ for all b ≠ 0, which, by the claim proved above, is to say that for all b ≠ 0 there exists $m \in M$ with $m^\ast b = 1$.

5. The groupoidal case

In this section, we describe semantic and syntactic conditions on a cartesian closed variety which are equivalent to its classifying topological or localic category being a groupoid. To motivate this, we consider the category of left M-sets for a monoid M; this is a cartesian closed variety whose classifying topological category is M itself, seen as a one-object discrete topological category, and clearly this is a groupoid just when M is a group.

This syntactic condition can be recast in terms of the cartesian closed structure of the category of M-sets. In general, this is given by the usual formula for internal homs in a presheaf category, so that Z^Y is the set of M-set maps $M \times Y \rightarrow Z$, with the M-set structure $(m \cdot f)(n,y) = f(nm,y)$. However, when M is a group, we have an alternative, simpler presentation; we may take $Z^Y = \mathrm{\mathcal Set}(Y,Z)$ with the M-set structure given by conjugation:

(5.1)\begin{equation} (m \cdot f)(y) = m \cdot f(m^{-1} \cdot y)\rlap{.} \end{equation}

Thus, when M is a group, the function-spaces in $M\text-\mathrm{\mathcal Set}$ are lifts of the function-spaces of $\mathrm{\mathcal Set}$. A more precise way of saying this is that the forgetful functor $U \colon M\text-\mathrm{\mathcal Set} \rightarrow \mathrm{\mathcal Set}$ is cartesian closed:

Definition 5.1. Let ${\mathcal {C}}$ and ${\mathcal D}$ be cartesian closed categories. A finite-product-preserving functor $U \colon {\mathcal {C}} \rightarrow {\mathcal D}$ is cartesian closed if, for all $Y,Z \in {\mathcal {C}}$, the map $U(Z^Y) \rightarrow UZ^{UY}$ in ${\mathcal D}$ found as the transpose of the following map is invertible:

\begin{equation*} U(Z^Y) \times UY \xrightarrow{\cong} U(Z^Y \times Y) \xrightarrow{U(\mathrm{ev})} UY\rlap{.} \end{equation*}

It is therefore natural to conjecture that, for a general (Grothendieck) matched pair ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$, the classifying topological or localic category $\mathbb{C}_{{\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}}$ should be a groupoid precisely when the internal homs in ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ are computed as in $B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$; that is, just when the forgetful functor $U \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$ is cartesian closed. The main result of this section will show that this is the case. Before stating it, we need to say what it means for a Grothendieck Boolean restriction monoid $S_{\mathcal J}$ to be ‘generated by partial isomorphisms’:

Definition 5.2. Partial isomorphism, étale Grothendieck Boolean restriction monoid

An element s of a Grothendieck Boolean restriction monoid $S_{\mathcal J}$ is a partial isomorphism if there exists a—necessarily unique—$t \in S$ with $st = s^+$ and $ts = t^+$. We call $S_{\mathcal J}$ étale if each $s \in S_{\mathcal J}$ is an admissible join of partial isomorphisms.

Theorem 5.3 Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. The following are equivalent:

1. (i) The forgetful functor $U \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$ is cartesian closed;

2. (ii) The following condition holds:

   (5.2)\begin{equation} \begin{gathered} \text{For all } m \in M \text{, there exists } \{b_i : i \in I\} \in {\mathcal J} \text{and families } (n_i \in M : i \in I) \\[-3pt] \text{and } (c_i \in B : i \in I) \text{with } b_i \leqslant m^\ast c_i \text{, } mn_i \equiv_{b_i} 1 \text{and } n_i m \equiv_{c_i} 1 \text{for all }i\text{.} \end{gathered} \end{equation}

3. (iii) The associated Grothendieck Boolean restriction monoid $S_{\mathcal J}$ is étale;

4. (iv) The classifying (topological or localic) category of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ is a groupoid.

Remark 5.4. A Grothendieck topos is called an étendue when it is equivalent to the category of equivariant sheaves on an étale localic groupoid, and it is natural to ask for which ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ the topos ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ is an étendue. Since ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ can be presented as the topos of equivariant sheaves on the associated localic or topological category, we see that for any ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ to which theorem 5.3 applies, the topos ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Shv}$ will be an étendue. However, this sufficient condition is not necessary; for example, the topos $\mathbb{N}\text-\mathrm{\mathcal Set}$ is an étendue but does not satisfy theorem 5.3. We leave it to further work to characterize exactly which matched pairs ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ give rise to étendue.

Leaving aside the equivalence of (i) and (ii), we can dispatch the remaining parts of the proof of theorem 5.3 rather quickly:

Proof. (iii) $\Leftrightarrow$ (iv) is a consequence of [10, theorem 6.3]. To see (ii) $\Leftrightarrow$ (iii), note first that in (5.2), on replacing each c_i by $c_i \wedge n_i^\ast b_i$, we may without loss of generality assume that we also have $c_i \leqslant n_i^\ast b_i$ for each i. Considering now (iii), if $s \leqslant t \in S_{{\mathcal J}}$ and t is a partial isomorphism, then so is s; whence $S_{{\mathcal J}}$ will be étale as soon as every total element $\left.{m}\right|_{1}$ is an admissible join of partial isomorphisms. This is equally to say that, for each $m \in M$, there is some $\{b_i : i \in I\} \in {\mathcal J}$ for which each $\left.{m}\right|_{{b_i}}$ has a partial inverse $\left.{n_i}\right|_{{c_i}}$, i.e., $\left.{m}\right|_{{b_i}} \left.{n_i}\right|_{{c_i}} = \left.{1}\right|_{{b_i}}$ and $\left.{n_i}\right|_{{c_i}} \left.{m}\right|_{{b_i}} = \left.{1}\right|_{{c_i}}$. This says that:

\begin{equation*} b_i \leqslant m^\ast c_i \qquad mn_i \equiv_{b_i} 1 \qquad c_i \leqslant n_i^\ast b_i \qquad \mathrm{and} \qquad n_i m \equiv_{c_i} 1 \end{equation*}

for each i, which are precisely the conditions of (5.2) augmented by the additional inequalities $c_i \leqslant n_i^\ast b_i$ which we justified above.

This leaves only the proof (i) $\Leftrightarrow$ (ii); this will rest on the fact, explained in [27, proposition 1.5.8], that an adjunction $U \colon {\mathcal D} \leftrightarrows {\mathcal {C}} \colon F$ between cartesian closed categories has U cartesian closed just when the canonical (‘Frobenius’) maps $F(B \times UA) \rightarrow FB \times A$ are invertible. To exploit this, we must to describe the functor $M \otimes_B ({\mathord{\text{--}}}) \colon B_{{\mathcal J}}\text-\mathrm{\mathcal Set} \rightarrow {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ which is left adjoint to $U \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$.

As a first approximation, we could try taking $M \otimes_B X = M \times X$ with the free M-action $m \cdot (n, x) = (mn, x)$. Of course, this is an M-set; but how would we define $B_{{\mathcal J}}$-set structure? Well, since the unit map $X \rightarrow M \times X$ sending $x \mapsto (1,x)$ should be a $B_{{\mathcal J}}$-set homomorphism, $x_1 \equiv_b x_2$ should imply $(1, x_1) \equiv_b (1,x_1)$, but also, since $m \cdot (1,x_i) = (m,x_i)$, that $(m,x_1) \equiv_{m^\ast b} (m, x_2)$. Since, as in remark 2.7, the set ${\unicode{x27E6}{{(m, x_1)}{ = y}{(m, x_2)}}{}\unicode{x27E7}}$ should be a ${\mathcal J}$-closed ideal of B, this suggests taking it to be the closed ideal generated by the elements $m^\ast b$ where $x_1 \equiv_b x_2$, as follows:

Definition 5.5. Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. For any $m \in M$, any $B_{{\mathcal J}}$-set X, and any $x,y \in X$, write $m^\ast {\unicode{x27E6}{{x}=y}\unicode{x27E7}} \subseteq B$ for the ${\mathcal J}$-closed ideal generated by $\{m^\ast b : x \equiv_{by}\}$, and write $x \equiv^m_b y$ to mean that $b \in m^\ast {\unicode{x27E6}{{x}=y}{}\unicode{x27E7}}$.

Remark 5.6. By axiom (i) for a zero-dimensional topology, the ${\mathcal J}$-closed ideal generated by a set $S \subseteq B$ is composed of all $b \in B$ such that $P \subseteq \mathop{\downarrow} S$ for some $P \in {\mathcal J}_b$. It follows that $x \equiv^m_b y$ just when there exists $\{b_i : i \in I\} \in {\mathcal J}_b$ and a family $(c_i \in B : i \in I)$ with $b_i \leqslant m^\ast c_i$ and $x \equiv_{c_i} y$ for each i. However, in what follows, we will avoid using this concrete description of $\equiv^m_b$ until the very last moment—namely, in the proof of (ii) $\Leftrightarrow$ (iii) in proposition 5.10.

The following lemma records the basic properties of the relations $\equiv^m_b$. Its proof is a straightforward exercise in locale theory but we include it for self-containedness.

Lemma 5.7. Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras and X a $B_{{\mathcal J}}$-set. The relations $\equiv_b^m$ are equivalence relations and satisfy the following conditions:

1. (i) If $x \equiv_{b} y$ then $x \equiv^m_{m^\ast b} y$;

2. (ii) If $x \equiv^m_{b} y$ and $c \leqslant b$ then $x \equiv^m_{c} y$;

3. (iii) If $P \in {\mathcal J}_b$ and $x \equiv^m_{c} y$ for all $c \in P$, then $x \equiv^m_{b} y$;

4. (iv) If $x \equiv^m_{b} y$ then $x \equiv^{nm}_{n^\ast b} y$ for any $n \in M$;

5. (v) If X is a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set and $x \equiv^m_{b} y$ then $m \cdot x \equiv_b m \cdot y$;

6. (vi) If $m \equiv_b n$ then $\equiv^m_{c}$ and $\equiv^n_{c}$ coincide for all $c \leqslant b$.

Proof. $\equiv_b^m$ is reflexive and symmetric since $m^\ast {\unicode{x27E6}{{x}{ = y}x}{}\unicode{x27E7}} = m^\ast B = B$ and $m^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}} = m^\ast {\unicode{x27E6}{{y}{ = y}x}{}\unicode{x27E7}}$. For transitivity, we proceed in stages:

1. (a) If $x\equiv_b y$ and $y \equiv_c z$, then $x \equiv_{b \wedge c} z$ and so $m^\ast(b \wedge c) = m^\ast b \wedge m^\ast c \in m^\ast {\unicode{x27E6}{{x}{ = y}z}{}\unicode{x27E7}}$;

2. (b) If $x \equiv_b y$, we may consider the ${\mathcal J}$-closed ideal $I = \{d \in B : m^\ast b \wedge d \in m^\ast {\unicode{x27E6}{{x}{ = y}z}{}\unicode{x27E7}}\}$. By (a), each $m^\ast c$ with $y \equiv_c z$ is in I and so $m^\ast {\unicode{x27E6}{{y}{ = y}z}{}\unicode{x27E7}} \subseteq I$.

3. (c) Consider the ${\mathcal J}$-closed ideal $J = \{e \in B : e \wedge d \in m^\ast {\unicode{x27E6}{{x}{ = y}z}{}\unicode{x27E7}} \,\forall d \in m^\ast {\unicode{x27E6}{{y}{ = y}z}{}\unicode{x27E7}}\}$. By (b), J contains $m^\ast b$ whenever $x \equiv_b y$ and so $m^\ast {\unicode{x27E6}{{x}{ = y}y\!}{ }\unicode{x27E7}} \subseteq J$.

But (c) says that $x \equiv^m_b y$ and $y \equiv^m_c z$ imply $x \equiv^m_{b \wedge c} z$, whence each $\equiv^m_b$ is transitive.

Now, conditions (i)–(iii) simply say that each $m^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}$ is a closed ideal. For (iv), note that $\{b : n^\ast b \in (nm)^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}\}$ is a closed ${\mathcal J}$-ideal which contains the set $\{m^\ast b : x \equiv_b y\}$ and so contains $m^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}$. (v) follows similarly starting from the ${\mathcal J}$-closed ideal $\{b : m \cdot x \equiv_b m \cdot y\}$. Finally, for (vi), it suffices by symmetry to show that $(c \in m^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}} \text{and } c \leqslant b)$ implies $c \in n^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}$; or equivalently, that $c \in m^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}$ implies $b \wedge c \in n^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}$. But we observe that the ${\mathcal J}$-closed ideal $K = \{d \in B : b \wedge d \in n^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}\}$ contains $m^\ast c$ whenever $x \equiv_c y$, since $m \equiv_b n$ implies $b \wedge m^\ast c = b \wedge n^\ast c \leqslant n^\ast c \in n^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}}$; whence $m^\ast {\unicode{x27E6}{{x}{ = y}y}{}\unicode{x27E7}} \subseteq K$ as desired.

The discussion above now suggests taking $M \otimes_B X$ to be M × X with the free M-action and the $B_{{\mathcal J}}$-set equalities $(m,x) \equiv_b (n,y)$ iff $m \equiv_b n$ and $x \equiv^m_b y$ (equivalently, $x \equiv^n_b y$ by part (vi) of the previous lemma). One immediate problem is that $\equiv_1$ with this definition need not be the identity; so we had better quotient out by it. That is, we refine our first guess by taking $M \otimes_B X = \{(m, x) : m \in M, x \in X / \equiv^m_1\}$ under the M-action and $B_{{\mathcal J}}$-set equalities described above. If we work this through, we get all of the necessary axioms for a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set except for the condition that, for any partition $P \in {\mathcal J}$ and family of elements $(m_b, x_b)$ indexed by $b \in P$, there should be an element (n, z) with $(n,z)\equiv_b (m_b, x_b)$ for all $b \in B$. In the first component, there is no problem: we use the $B_{{\mathcal J}}$-set structure of M. However, in the second component, we must formally adjoin the missing elements, while accounting for the ones which do already exist; and we can do so by replacing X by the $B_{{\mathcal J}}$-set of distributions $T_{B_{{\mathcal J}}} X$ and quotienting appropriately. This motivates:

Proposition 5.8. Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. The forgetful functor $U \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$ has a left adjoint $M \otimes_B ({\mathord{\text{--}}})$, whose value $M \otimes_B X$ at a $B_{{\mathcal J}}$-set X is given by the quotient of the free ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set $M \times T_{B_{{\mathcal J}}} X$ by the ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set congruence ∼ for which

\begin{equation*} (m, \omega) \sim (n, \gamma) \quad \iff \quad m = n\,\, \mathrm{and }\,\, x \equiv^m_{\omega(x) \wedge \gamma(y)} y\,\, \mathrm{for\,all}\,\, x, y \in X. \end{equation*}

Proof. We first show ∼ is an equivalence relation. Symmetry is clear. For reflexivity, if $x \neq y \in X$ then $\omega(x) \wedge \omega(y) = 0$ and so $x \equiv^m_{\omega(x) \wedge \omega(y)} y$ is always true. For transitivity, suppose $(m, \omega) \sim (m, \gamma) \sim (m, \delta)$. We must show $(m, \omega) \sim (m, \delta)$, i.e., $x \equiv^m_{\omega(x) \wedge \delta(z)} z$ for all $x,z \in X$. Now $\{\omega(x) \wedge \gamma(x) \wedge \delta(z) : y \in Y\}^-$ is in ${\mathcal J}_{\omega(x) \wedge \delta(z)}$ so by lemma 5.7 (iii) it suffices to check $x \equiv^m_{\omega(x) \wedge \gamma(y) \vee \delta(z)} z$ which follows from $x \equiv^m_{\omega(x) \wedge \gamma(y)} y$ (as $(m, \omega) \sim (m, \gamma)$) and $y \equiv^m_{\gamma(y) \wedge \delta(z)} z$ (as $(m, \gamma) \sim (m, \delta)$).

We now show ∼ is a congruence. For the M-set structure, if $(m, \omega) \sim (m, \delta)$, i.e., $x \equiv^m_{\omega(x) \wedge \gamma(y)} y$ for all $x,y \in X$, then $x \equiv^{nm}_{n^\ast \omega(x) \wedge n^\ast \gamma(y)} y$ by lemma 5.7 (iv), whence $(nm, n^\ast \circ \omega) \sim (nm, n^\ast \circ \gamma)$. For the $B_{{\mathcal J}}$-set structure, let $P \in {\mathcal J}$ and suppose $(m_b, \omega_b) \sim (m_b, \gamma_b)$ for all $b \in B$, i.e.,

(5.3)\begin{equation} x \equiv^{m_b}_{\omega_b(x) \wedge \gamma_b(y)} y \;\text{for all } x,y \in X\rlap{.} \end{equation}

We must show that $(P(m), P(\omega)) \sim (P(m), P(\gamma))$, i.e., that

\begin{equation*} x \equiv^{P(m)}_{\bigvee_{b} (b \wedge \omega_b(x) \wedge \gamma_b(y))} y\; \text{for all } x,y \in X\rlap{.} \end{equation*}

For this, it suffices by lemma 5.7 (iii) to show $x \equiv^{P(m)}_{b \wedge \omega_b(x) \wedge \gamma_b(y)} y$ for all $x,y \in X$ and $b \in P$; but since $P(m) \equiv_b m_b$, this is equally by lemma 5.7 (vi) to show that $x \equiv^{m_b}_{b \wedge \omega_b(x) \wedge \gamma_b(y)} y$ for all $x,y \in X$ and $b \in P$; which follows from (5.3) via lemma 5.7 (ii). So ∼ is a congruence and we can form the ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set $M \otimes_B X = (M \times T_{B_{{\mathcal J}}} X) / \sim$. We now show that the composite map

(5.4)\begin{equation} \eta := X \xrightarrow{\ \ \ } M \times T_{B_{{\mathcal J}}}X \xrightarrow{\ q \ } M \otimes_B X \end{equation}

exhibits $M \otimes_B X$ as the free ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set on the $B_{{\mathcal J}}$-set X; here, the first part is the free morphism $X \rightarrow M \times T_{B_{{\mathcal J}}} X$ sending $x \mapsto (1, \pi_x)$, and the second part is the quotient map for ∼.

First of all, this map is a $B_{{\mathcal J}}$-set homomorphism, since if $x,y \in X$ and $b \in B$, then $(1, \pi_{b(x,y)}) \sim (1, b(\pi_{x}, \pi_{y}))$ in $M \times T_{B_{{\mathcal J}}}X$; for indeed, the only non-trivial cases for ∼ are that $b(x,y) \equiv^1_{1 \wedge b} x$ and $b(x,y) \equiv^1_{1 \wedge b^{\prime}} y$, which simply says that $b(x,y) \equiv_b x$ and $b(x,y) \equiv_{b^{\prime}} y$, which is so by definition of $b(x,y)$.

Moreover, if $f \colon X \rightarrow Y$ is a $B_{{\mathcal J}}$-set homomorphism, then we have a unique extension along η to a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set homomorphism $\bar f \colon M \times T_{B_{{\mathcal J}}} X \rightarrow Y$. To complete the proof, it suffices to show this extension factors through q. So suppose $(m, \omega) \sim (m, \gamma)$ in $M \times T_{B_{{\mathcal J}}} X$. We have that $\bar f(m, \omega) \equiv_{\omega(x)} m \cdot f(x)$ and $\bar f(m, \gamma) \equiv_{\gamma(y)} m \cdot y(x)$ for all $x,y \in X$; and since $x \equiv^m_{\omega(x) \wedge \gamma(y)} y$, we have $m \cdot f(x) \equiv_{\omega(x) \wedge \gamma(y)} m \cdot f(y)$ by lemma 5.7 (v). Thus $\bar f(m, \omega) \equiv_{\omega(x) \wedge \gamma(y)} m \cdot f(x) \equiv_{\omega(x) \wedge \gamma(y)} m \cdot f(y) \equiv_{\omega(x) \wedge \gamma(y)} \bar f(m, \gamma)$, and joining over x and y gives $\bar f(m, \omega) = \bar f(m, \gamma)$ as desired.

We are now in a position to analyse when the forgetful functor $U \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$ is cartesian closed. Spelling it out, we see that the condition in definition 5.1 is equivalent to asking that, for all ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets X, Y, the function

\begin{align*} {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}(M \times X,Y) &\rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}(X, Y) & f & \mapsto f(1, {\mathord{\text{--}}}) \end{align*}

is invertible. Thus, U is cartesian closed just if, whenever $X,Y$ are ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets, each $B_{{\mathcal J}}$-set map $g \colon X \rightarrow Y$ extends uniquely to a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set map $M \times X \rightarrow Y$ along the $B_{{\mathcal J}}$-set homomorphism $\gamma \colon X \rightarrow M \times X$ sending x to $(1,x)$; in other words, if γ exhibits M × X as the free ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set on the $B_{{\mathcal J}}$-set UX. However, since we already know that the $B_{{\mathcal J}}$-set homomorphism $\eta \colon X \rightarrow M \otimes_B X$ of (5.4) exhibits $M \otimes_B X$ as the free ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set on UX, this is equally to say that the unique extension $M \otimes_B X \rightarrow M \times X$ of γ to a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set homomorphism, as described in the proof of proposition 5.8, is invertible. We record this as:

Lemma 5.9. Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. The forgetful functor $U \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$ is cartesian closed if, and only if, for each ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set X, the function:

(5.5)\begin{equation} \begin{aligned} \theta_X \colon M \otimes_B X &\rightarrow M \times X \\ (m, \omega) &\mapsto (m, \varepsilon_m(\omega)) \end{aligned} \end{equation}

is invertible, where $\varepsilon_m(\omega)$ is characterized by $\varepsilon_m(\omega) \equiv_{\omega(x)} m \cdot x$ for all $x \in \mathrm{supp}(\omega)$.

We are now in a position to complete the proof of theorem 5.3 by showing:

Proposition 5.10. Let ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ be a Grothendieck matched pair of algebras. The following are equivalent:

1. (i) The forgetful functor $U \colon {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set} \rightarrow B_{{\mathcal J}}\text-\mathrm{\mathcal Set}$ is cartesian closed;

2. (ii) For all $m \in M$, there exists $\{b_i : i \in I\} \in {\mathcal J}$ and a family $(n_i \in M : i \in I)$ with $mn_i \equiv_{b_i} 1$ and $n_i m \equiv^m_{b_i} 1$ for all i;

3. (iii) For all $m \in M$, there exists $\{b_i : i \in I\} \in {\mathcal J}$ and families $(n_i \in M : i \in I)$ and $(c_i \in B : i \in I)$ with $b_i \leqslant m^\ast c_i$, $mn_i \equiv_{b_i} 1$ and $n_i m \equiv_{c_i} 1$ for all i.

Proof. We first prove (i) $\Rightarrow$ (ii). So suppose U is cartesian closed; we begin by showing that for any ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set X, any $x,y \in X$ and any $b \in B$, we have

(5.6)\begin{equation} x \equiv^m_b y \iff m \cdot x \equiv_b m \cdot y\rlap{.} \end{equation}

Indeed, since θ_X is an isomorphism by lemma 5.9, we have $\theta_X(m, \pi_x) \equiv_b \theta_X(m, \pi_{y})$ in M × X just when $(m, \pi_x) \equiv_b (m, \pi_{y})$ in $M \otimes_B X$. Since $\theta_X(m, \pi_x) = (m,m \cdot x)$ and similarly for y, this is equally to say that $m \cdot x \equiv_b m \cdot y$ just when $(m, b(\pi_x, \pi_{y})) \sim (m, \pi_{y})$ in $M \times T_{B_{{\mathcal J}}}X$, which by definition of ∼ says exactly that $x \equiv^m_b y$.

Now, since U is cartesian closed, (5.5) is in particular invertible when X = M. Thus for each $m \in M$, the element $(m,1)$ is in the image of θ_M, and so there exists a distribution $\omega \colon M \rightarrow B$ such that $\varepsilon_m(\omega) = 1$, i.e., such that $1 \equiv_{\omega(n)} mn$ for all $n \in \mathrm{supp}(\omega)$. Writing $\{b_i : i \in I\}$ for the partition $(im \omega)^-$ and $n_i \in M$ for the elements with $\omega(n_i) = b_i$, we thus have $\{b_i : i \in I\} \in {\mathcal J}$ and a family $(n_i \in M : i \in I)$ such that $mn_i \equiv_{b_i} 1$ for all i. It follows that $mn_i m \equiv_{b_i} m$ for all i, and so by (5.6) that $n_i m \equiv^m_{b_i} 1$ for all $i \in I$. This gives (ii).

We now show (ii) $\Rightarrow$ (i). We again begin by proving (5.6) for any ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set X. The rightward implication is lemma 5.7 (v). As for the leftward one, suppose $m \cdot x \equiv_b m \cdot y$. By (ii), we find $\{b_i\} \in {\mathcal J}$ and $(n_i \in M : i \in I)$ such that $mn_i \equiv_{b_i} 1$ and $n_im \equiv^m_{b_i} 1$ for each i. Now the ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set axioms for X and lemma 5.7 (i) say that $m \cdot x \equiv_b m \cdot y \implies n_im \cdot x \equiv_{n_i^\ast b} n_im \cdot y \implies n_im \cdot x \equiv^m_{m^\ast n_i^\ast b} n_im \cdot y$ for each i; and since $mn_i \equiv_{b_i} 1$, we have $b_i \wedge m^\ast n_i^\ast b = b_i \wedge b$, and so for each i we have $n_i m \cdot x \equiv^m_{b \wedge b_i} n_i m \cdot y$. Now, since ${\unicode{x27E6}{{n_i m}{ = y}1}{}\unicode{x27E7}} \leqslant {\unicode{x27E6}{{n_i m \cdot x}{ = y}x}{}\unicode{x27E7}}{}$ by the ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set axioms for X, also $m^\ast{\unicode{x27E6}{{n_i m}{ = y}1}{}\unicode{x27E7}} \leqslant m^\ast{\unicode{x27E6}{{n_i m \cdot x}{ = y}x}{}\unicode{x27E7}}$, whence $n_i m \equiv^m_{b_i} 1$ implies $n_i m \cdot x \equiv^m_{b_i} x$. Putting this together, we have $x\equiv^m_{b \wedge b_i} n_i m \cdot x \equiv^m_{b \wedge b_i} n_i m \cdot y \equiv^m_{b \wedge b_i} y$ for each i, whence $x \equiv^m_b y$ by lemma 5.7 (iii).

We immediately conclude that each (5.5) is injective: for indeed, if $\theta_X(m, \omega) = \theta_M(n, \gamma)$, then m = n and $\varepsilon_m(\omega) = \varepsilon_m(\gamma)$, which says that $m \cdot x \equiv_{\omega(x) \wedge \gamma(y)} m \cdot y$ for each $x,y \in X$. By (5.6), this is equivalent to $x \equiv^m_{\omega(x) \wedge \gamma(y)} y$ for all $x,y \in X$—which is to say that $(m, \omega) = (n, \gamma)$ in $M \otimes_B X$. Finally, to show surjectivity of θ_X, consider $(m,x) \in M \times X$, let $\{b_i\} \in {\mathcal J}$ and $(n_i \in M)$ be as in (ii) for m, and let $\omega \colon X \rightarrow B$ be the distribution with $\omega(y) = \bigvee_{y = n_i \cdot x} b_i$. We claim $\theta_X(m, \omega) = (m,x)$; for which we must show that $x \equiv_{\omega(y)} m \cdot y$ for all $y \in X$. This is equally to show $x \equiv_{b_i} m n_i \cdot x$ for all $x \in X$, which is so since $mn_i \equiv_{b_i} 1$ for each i.

Finally, we prove (ii) $\Leftrightarrow$ (iii). Given $m \in M$ and the associated data $\{b_i\}$, $(c_i)$ and $(n_i)$ in (iii), we have by lemma 5.7 (i) and (ii) that $n_i m \equiv_{c_i} 1 \implies n_i m \equiv^m_{m^\ast c_i} 1 \implies n_i m \equiv^m_{b_i} 1$ for each i: which gives the data needed for (ii). Conversely, given the data $\{b_i\}$ and $(n_i)$ as in (ii), since $n_i m \equiv^m_{b_i} 1$ for each i we have by remark 5.6 partitions $\{b_{ij} : j \in J_i\} \in {\mathcal J}_{b_i}$ and elements $(c_{ij} : i \in I, j \in J_i)$ such that $b_{ij} \leqslant m^\ast c_{ij} $ and $n_i m \equiv_{c_{ij}} 1$ for each $i \in I$ and $j \in J_i$. Thus taking the partition $\{b_{ij} : i \in I, j \in J_i\} \in {\mathcal J}$, the elements $(n_{ij} = n_i \in M : i \in I, j \in J_i)$ and the elements $(c_{ij} \in B : i \in I, j \in J_i)$ we obtain the required witnesses for (iii).

Of course, when the equivalent conditions of theorem 5.3 are satisfied, the function-space Z^Y in ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ is given by the $B_{{\mathcal J}}$-set of $B_{{\mathcal J}}$-set homomorphisms $Y \rightarrow Z$, with a suitable M-set structure. From the above proof, we can extract a direct description of this structure. Given $f \in Z^Y$ a $B_{{\mathcal J}}$-set homomorphism and $m \in M$ with associated data $\{b_i\} \in {\mathcal J}$, $(c_i)$ and $(n_i)$ as above, the element $m \cdot f \in Z^Y$ is characterized by

(5.7)\begin{equation} (m \cdot f)(y) \equiv_{b_i} m \cdot f(n_i \cdot y) \quad \text{for all } i \in I\rlap{;} \end{equation}

this is the natural generalization of (5.1) above.

6. Jónsson–Tarski toposes

We conclude this article by discussing a range of examples of cartesian closed varieties whose classifying categories are the kinds of ample topological groupoids that are of interest to operator algebraists. In this section, we describe cartesian closed varieties (in fact toposes) which correspond to the Cuntz groupoids of [39], whose corresponding $C^\ast$-algebras are Cuntz $C^\ast$-algebras and whose corresponding R-algebras are Leavitt algebras.

6.1. The Jónsson–Tarski topos

We begin with the simplest non-trivial case involving a binary alphabet $\{\ell, r\}$, for which the appropriate variety will be the so-called Jónsson–Tarski topos. A Jónsson–Tarski algebra [21] is a set X endowed with functions $\ell, r \colon X \rightarrow X$—which we write as left actions $x \mapsto \ell \cdot x$ and $x \mapsto r \cdot x$—and a function $m \colon X \times X \rightarrow X$ satisfying the axioms

(6.1)\begin{equation} m(\ell \cdot x,r \cdot x) = x \qquad \ell \cdot m(x,y) = x \quad \mathrm{and} \quad r \cdot m(x,y) = y\rlap{.} \end{equation}

These say that the functions $x \mapsto (\ell \cdot x,r \cdot x)$ and $x,y \mapsto m(x,y)$ are inverse; so a Jónsson–Tarski algebra is equally well a set X with an isomorphism $X \cong X \times X$.

The concrete category ${\mathcal J}{\mathcal T}$ of Jónsson–Tarski algebras is a non-degenerate finitary variety, but also, as observed by Freyd, a topos; indeed, as explained in [25, example 1.3], it can be presented as the topos of sheaves on the free monoid $A^\ast$—where A denotes the two-letter alphabet $\{\ell, r\}$—for the topology generated by the covering family $\{\ell, r\}$. In particular, ${\mathcal J}{\mathcal T}$ is cartesian closed and so via proposition 2.11 can be presented as a category of ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$-sets.

When we calculate B and M, it will turn out that, on the one hand, B is the Boolean algebra of clopen sets of Cantor space C which, because of our conventions, it will be best to think of as the set $\{\ell, r\}^{-\omega}$ of words $W = \cdots a_2 a_1 a_0$ in $\ell,r$ which extend infinitely to the left. On the other hand, M will be the monoid of those (continuous) endomorphisms $\varphi \colon C \rightarrow C$ which are specified by finite words $u_1, \dots, u_k, v_1, \dots, v_k \in A^{\ast}$ via the formula:

(6.2)\begin{equation} \left. \begin{aligned} \varphi(Wu_1) &= Wv_1 \\ & \ \ \vdots \\ \varphi(Wu_k) &= Wv_k \end{aligned} \ \right\} \quad \text{for all } W \in A^{-\omega}\rlap{;} \end{equation}

i.e., φ maps the clopen set $[u_i]$ of words starting with u_i affinely to the clopen set $[v_i]$. (Although our infinite words extend to the left, we still think of them as starting with their rightmost segments $a_n \cdots a_0$.) The invertible elements of this monoid comprise Thompson’s group V, and so it is no surprise that M is already known as a monoid generalization of V; in the nomenclature of [5], it is the ‘Thompson–Higman total function monoid $\mathit{tot}M_{2,1}$’.

Now, by proposition 2.11, we can compute M and B as ${\mathcal J}{\mathcal T}(F1,F1)$ and ${\mathcal J}{\mathcal T}(F1, 1+1)$, where $F1$ is the free Jónsson–Tarski algebra on one generator. The obvious way to find these would be via a universal-algebraic description of $F1$ and $1+1$; this was the approach of Higman in [19], who used it to show that $\mathrm{Aut}(F1,F1) \cong V$. However, [5] follows a combinatorially smoother approach due to [42], which describes V and its monoid generalizations in terms of certain morphisms between ideals of the monoid $A^\ast$. As we now show, there is a direct derivation of this perspective which exploits the nature of ${\mathcal J}{\mathcal T}$ as a topos of sheaves on $A^\ast$. Again, due to our conventions it will be best if we work with left, rather than right, $A^\ast$-sets; this is harmless due to the anti-homomorphism $A^\ast \rightarrow A^\ast$ which reverses each word.

Thus ${\mathcal J}{\mathcal T}$ is relatedto the category of left $A^\ast$-sets by adjunctions:

where $(A^\ast\text-\mathrm{\mathcal Set})_{\mathrm{sep}}$ is the category of separated left $A^\ast$-sets for the Grothendieck topology on $A^\ast$; concretely, X is separated if x = y whenever $\ell \cdot x = \ell \cdot y$ and $r \cdot x = r \cdot y$. The free separated $A^\ast$-set $L_1(X)$ on an $A^\ast$-set X is $X/\!\!\sim$, where ∼ is the smallest equivalence relation that relates x and y whenever $\ell \cdot x = \ell \cdot y$ and $r \cdot x = r \cdot y$. As for the left-hand adjunction in (6.3), we may by [45, theorems 43.6 and 45.8] see L ₂ as the functor which formally inverts the class of dense inclusions for the Grothendieck topology on $A^\ast$, which we can make explicit as follows:

Definition 6.1. Let X be a left $A^\ast$-set and $U \leqslant X$ a sub-$A^\ast$-set. We say:

• • U is closed in X (written $U \leqslant_c X$) if $\ell \cdot x \in U, r \cdot x \in U \implies x \in U$;

• • U is dense in X (written $U \leqslant_d X$) if the closure of U in X is X.

Here, the closure of U in X is, of course, the smallest closed $U^{\prime} \leqslant X$ which contains U; and it is not hard to see that it can be described explicitly as:

(6.4)\begin{equation} U^{\prime} = \{\,x \in X : \mathrm{there\,exists}\,n \in \mathbb{N}\,\, \mathrm{with }\,\, w \cdot x \in U\,\mathrm{for\,all}\,\, w \in A^n\,\}\rlap{.} \end{equation}

Now, since the class of dense inclusions in $(A^\ast\text-\mathrm{\mathcal Set})_\mathrm{sep}$ is closed under composition and under inverse image along any $A^\ast$-set homomorphism, the result of formally inverting them can be described via a category of fractions [15]. This is to say that ${\mathcal J}{\mathcal T}$ is equivalent to the category ${\mathcal J}{\mathcal T}^{\prime}$ wherein:

• • Objects are separated left $A^\ast$-sets;

• • Morphisms $X \rightarrow Y$ are ∼-equivalence classes of dense partial $A^\ast$-set maps, i.e., pairs $(U \leqslant_d X, f \colon U \rightarrow Y)$ where f is an $A^\ast$-set homomorphism. Here, $(U, f) \sim (V, g)$ when they have a lower bound in the inclusion ordering $\sqsubseteq$, i.e., the ordering with $(U^{\prime},f^{\prime}) \sqsubseteq (U,f)$ when $U^{\prime} \leqslant U$ and $f^{\prime} = \left.{f}\right|_{U^{\prime}}$;

• • The composite of $(U,f) \colon X \rightarrow Y$ and $(V,g) \colon Y \rightarrow Z$ is their composite as partial maps, namely, $(f^{-1}(V), \lambda x.\,gfx) \colon X \rightarrow Z$; and

• • The identity on X is $(X, 1_X)$,

In fact, we can simplify the description of ${\mathcal J}{\mathcal T}^{\prime}$ further, due to the following result; this is really a general argument about dense and closed monomorphisms with respect to a Grothendieck topology, but we give a concrete proof for our situation.

Lemma 6.2. Each equivalence-class of morphisms $X \rightarrow Y$ in ${\mathcal J}{\mathcal T}^{\prime}$ has a $\sqsubseteq$-largest representative. These representatives are precisely those (U, f) for which the graph $\{(x, fx) : x \in U\}$ of f is closed in X × Y.

Proof. Given a dense partial map $(U,f) \colon X \rightarrow Y$, let $G \leqslant X \times Y$ be the graph of f and $G^{\prime} \leqslant_c X \times Y$ its closure. We claim that G ^ʹ is in turn the graph of a function, i.e., that if $\{(x,y), (x,y^{\prime})\} \subseteq G^{\prime}$, then $y = y^{\prime}$. From (6.4), if $(x,y) \in G^{\prime}$, then there is some n so that $(w \cdot x, w \cdot y) \in G$ for every $w \in A^n$. We get a corresponding n for $(x,y^{\prime})$ and so on taking the larger of the two we may assume that $(w \cdot x, w \cdot y)$ and $(w \cdot x, w \cdot y^{\prime})$ are in G for all $w \in A^n$. But then, as G is the graph of a function, $w \cdot y = w \cdot y^{\prime}$ for all $w \in A^n$, whence $y = y^{\prime}$ by separatedness of Y.

So taking $U^{\prime} = \{x \in X : (x,y) \in G^{\prime}\}$ we see that G ^ʹ is the graph of a $A^\ast$-set homomorphism $f^{\prime} \colon U^{\prime} \rightarrow Y$; and since $U \leqslant U^{\prime} \leqslant X$ and $U \leqslant_d X$, also $U^{\prime} \leqslant_d X$, so that $(U^{\prime},f^{\prime})$ is a dense partial map, which, since clearly $(U, f) \sqsubseteq (U^{\prime}, f^{\prime})$, is equivalent to (U, f). Finally, note that if $(U,f) \sqsubseteq (V,g) \colon X \rightarrow Y$, then $U \leqslant_d V$ and so the graph of f is dense in the graph of g; as such, they have the same closures, so that $(U^{\prime}, f^{\prime}) = (V^{\prime}, g^{\prime})$. Thus, the assignment $(U,f) \mapsto (U^{\prime},f^{\prime})$ picks out a $\sqsubseteq$-maximal representative of each equivalence class.

Combining this with our preceding observations, we arrive at:

Lemma 6.3. The category ${\mathcal J}{\mathcal T}$ is equivalent to the category ${\mathcal J}{\mathcal T}^{\prime}$ wherein:

• • Objects are separated left $A^\ast$-sets;

• • Morphisms $X \rightarrow Y$ are dense partial maps $(U,f) \colon X \rightarrow Y$ which are maximal, in the sense that the graph of f is closed in X × Y;

• • The composite of (U, f) and (V, g) is the maximal extension of $(f^{-1}(V), \lambda x.\,gfx)$;

• • The identity on X is $(X, 1_X)$, via an equivalence which identifies $L_2 \colon (A^\ast\text-\mathrm{\mathcal Set})_\mathrm{sep} \rightarrow {\mathcal J}{\mathcal T}$ with the identity-on-objects functor $(A^\ast\text-\mathrm{\mathcal Set})_{\mathrm{sep}} \rightarrow {\mathcal J}{\mathcal T}^{\prime}$ sending $f \colon X \rightarrow Y$ to $(X,f) \colon X \rightarrow Y$.

Now, $F1 \in {\mathcal J}{\mathcal T}$ is the image under $L_2L_1$ of the free left $A^\ast$-set on one generator which is, of course, $A^\ast$ itself. Since $A^\ast$ is left-cancellable, it is separated as a left $A^\ast$-set, and so $L_1(A^\ast) = A^\ast$; whence, by the preceding lemma, we can identify $F1 \in {\mathcal J}{\mathcal T}$ with $A^\ast \in {\mathcal J}{\mathcal T}^{\prime}$, and so identify the monoid $M = {\mathcal J}{\mathcal T}(F1,F1)$ with ${\mathcal J}{\mathcal T}^{\prime}(A^\ast, A^\ast)$, the monoid of maximal dense partial left $A^\ast$-set maps $A^\ast \rightarrow A^\ast$.

To relate this to [5], let us note that a left ideal (i.e., sub-$A^\ast$-set) $I \leqslant A^\ast$ is dense just when its closure I ^ʹ contains the empty word, which, by (6.4), happens just when $A^n \subseteq I$ for some $n \in \mathbb{N}$. This is easily equivalent to I being cofinite, i.e., $A^\ast \setminus I$ being finite, but also, as explained in [42], to I being finitely generated and essential, meaning that it intersects every non-trivial left ideal of $A^\ast$. Thus, $M = {\mathcal J}{\mathcal T}^{\prime}(A^\ast, A^\ast)$ is the monoid of pairs (I, f), where $I \leqslant A^\ast$ is a finitely generated essential left ideal and $f \colon I \rightarrow A^\ast$ is a maximal $A^\ast$-set map, with the monoid product given by partial map composition followed by maximal extension. Modulo our conventions (left, not right, actions; product in M given by composition in diagrammatic, not applicative, order), this is the definition of $\mathit{tot}M_{2,1}$ in [5].

To further relate this description of M to the presentation in (6.2), note that any ideal $I \leqslant A^\ast$ is generated by the (finite) set of those words $u_1, \dots, u_k \in I$ which have no proper initial segment in I (where, again, ‘initial’ means ‘rightmost’); we call these words the basis of I and write $I = {\langle{u_1, \dots, u_k}\rangle}$. Now given $(I,f) \colon A^\ast \rightarrow A^\ast$ in M, on taking the basis $\{u_i\}$ of I and associated elements $v_i = f(u_i)$, we obtain data for a function $\varphi \colon C \rightarrow C$ as in (6.2). Density of I ensures this φ is total; while maximality of f ensures each such φ is represented by a unique (I, f).

We now describe the Boolean algebra $B = {\mathcal J}{\mathcal T}(F1, 1+1)$. Since $1+1 \in {\mathcal J}{\mathcal T}$ is the image under L ₂ of the separated $A^\ast$-set $\{\top, \bot\}$ with the trivial $A^\ast$-action, we can describe B as ${\mathcal J}{\mathcal T}^{\prime}(A^\ast, \{\top, \bot\})$, that is, as the set of maximal dense partial maps $(I,f) \colon A^\ast \rightarrow \{\top, \bot\}$. For such a map, the inverse images $I_\top = f^{-1}(\top)$ and $I_\bot = f^{-1}(\bot)$ are sub-ideals of I which partition it and which, by maximality of f, must be closed in $A^\ast$. Furthermore, if $I = {\langle{G}\rangle}$, then $I_\top = {\langle{G \cap I_\top}\rangle}$ and $I_\bot = {\langle{G \cap I_\bot}\rangle}$; in particular, they are finitely generated. Of course, we can re-find I from $I_\bot$ and $I_\top$ as their (disjoint) union, whence ${\mathcal J}{\mathcal T}^{\prime}(A^\ast, \{\top, \bot\})$ is isomorphic to the set of pairs of finitely generated closed ideals $I_\top, I_\bot \leqslant_c A^\ast$ which are complementary, meaning that $I_\top \cap I_\bot = \emptyset$ and $I_\top \cup I_\bot$ is dense in $A^\ast$.

In fact, any finitely generated closed ideal I has a unique finitely generated closed complement I ^ʹ; indeed, if $I = {\langle{G}\rangle}$ and n is the length of the longest word in G, then I ^ʹ is the closed ideal generated by $\{w \in A^n : w \notin I\}$. Thus, we can identify B with the Boolean algebra of finitely generated closed left ideals of $A^\ast$, which in turn can be identified with the Boolean algebra of clopen sets of Cantor space A ^−ω, where $I \leqslant_c A^\ast$ corresponds to the clopen set of words with an initial segment in I; note closedness ensures each clopen set is represented by a unique I.

To complete the description of ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$, we must give the actions of B and M on each other; using the structure of ${\mathcal J}{\mathcal T}^{\prime}$, it is not hard to show that these are given as follows. If $m = (I,f)$ and $n = (J,g)$ are in M, and $b = (K \leqslant_c A^\ast)$ is in B, then

• • $m^\ast b \in B$ is the closure of $f^{-1}(K) \leqslant I \leqslant A^\ast$.

• • $b(m,n) \in M$ is the maximal extension of $(K \cap I + K^{\prime} \cap J, {\langle{{\left.{f}\right|_{K\cap I}}, {\left.{g}\right|_{K^{\prime} \cap J}}}\rangle})$.

Equally, if we view elements of M as continuous endomorphisms φ of Cantor space, and elements of B as clopens U of Cantor space, then the M-action on B is given by $\varphi, U \mapsto \varphi^{-1}(U)$, while the B-action on M is given by $U, \varphi, \psi \mapsto {\langle{\left.{\varphi}\right|_{U}, \left.{\psi}\right|_{U^c}}\rangle}$.

Let us also indicate how each Jónsson–Tarski algebra X becomes a ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$-set. First note that, viewing such an X as a left $A^\ast$-set, the maximal extension $(I^{\prime},f^{\prime})$ of a dense partial map $(I \leqslant_d A^\ast, f \colon I \rightarrow X)$ is a total map, i.e, $I^{\prime} = A^\ast$; for indeed, if not, then on choosing a word w of maximal length in $A^\ast \setminus I^{\prime}$, we would have $(\ell w, x)$ and (rw, y) in the graph of f ^ʹ but then by closedness would have $(w, m(x,y))$ also in the graph, a contradiction. Thus, for the B-set structure on X, given $x,y \in X$ and $b = (J \leqslant_c A^\ast)$ in B, we take $b(x,y)$ to be the element classified by the maximal extension of the dense partial map

\begin{equation*} J + J^{\prime} \xrightarrow{\text{inclusion}} A^\ast + A^\ast \xrightarrow{{\langle{x,y}\rangle}} X\rlap{;} \end{equation*}

while given $m = (I, f)$ in M and $x \in X$, we take $m \cdot x$ as the element classified by the maximal extension of the dense partial map $x \circ f \colon I \rightarrow A^\ast \rightarrow X$.

Finally, we remark on some of the other perspectives on ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$. The associated Boolean restriction monoid S is the Thompson–Higman partial function monoid $M_{2,1}$ of [5], whose elements are maximal partial maps $(I, f) \colon A^\ast \rightarrow A^\ast$ defined on an arbitrary finitely generated ideal. If we consider the following elements of S:

\begin{equation*} \ell = (A^\ast, ({\mathord{\text{--}}}) \cdot \ell) \quad r = (A^\ast, ({\mathord{\text{--}}}) \cdot r) \quad \ell^\ast = (A^\ast\ell, \partial) \quad r^\ast = (A^\ast r, \partial) \end{equation*}

where $\partial$ is the function which deletes the last element of a non-empty word, then S can equally be described as the free Boolean restriction monoid generated by $\ell, r, \ell^\ast, r^\ast$ subject to the axioms

(6.5)\begin{equation} \ell \ell^\ast = rr^\ast = 1 \qquad \ell r^\ast = r \ell^\ast = 0 \quad \mathrm{and} \quad \ell^\ast \ell \vee r^\ast r = 1\rlap{.} \end{equation}

(These may look backwards to those familiar with the Cuntz $C^\ast$-algebra, but recall st means ‘first s then t’.) If for a word $a_1 \cdots a_k \in A^\ast$, we write $(a_1 \cdots a_k)^\ast = a_k^\ast \cdots a_1^\ast$, then these equations allow every $s \in S$ to be written as $s = u_1^\ast v_1 \vee \cdots \vee u_k^\ast v_k$ where the u_i’s and v_i’s are in $A^\ast$ with the u_i’s the basis of an ideal I; composition is then given by juxtaposition and reduction using the axioms (6.5). Note each such element $s = u_1^\ast v_1 \vee \cdots \vee u_k^\ast v_k$ corresponds to a partial endomorphism $C \rightharpoonup C$ defined as in (6.2), so that S can equally be identified with the Boolean restriction monoid of all such partial endomorphisms of C.

Eq. (6.5) also implies that each generator of S is a partial isomorphism; whence S is étale (cf. [34, proposition 5.1]) and so generated by its Boolean inverse monoid of partial isomorphisms. This Boolean inverse monoid is the ‘Thompson–Higman inverse monoid’ $\mathit{Inv}_{2,1}$ of [5], or equally, the Cuntz inverse monoid of [34]. This last identification implies, in turn, that the classifying topological category of ${\left[\smash{{B} \mathbin{\mid}{M} }\right]}$ is the well-known Cuntz groupoid $\mathfrak{O}_2$ of [39, definition III.2.1], whose Stone space of objects is Cantor space and whose morphisms $W \rightarrow W^{\prime}$ are integers i such that $W_{n} = W^{\prime}_{n+i}$ for all sufficiently large n. We can also see this directly; indeed, since B comprises the clopen subsets of Cantor space C, the classifying topological category must have space of objects C; and since M comprises all continuous maps $C \rightarrow C$ of the form (6.2), the arrows $W \rightarrow W^{\prime}$ must be germs at W of those maps (6.2) for which $\varphi(W) = W^{\prime}$. This is a well-known alternative description of $\mathfrak{O}_2$.

Now, since ${\mathcal J}{\mathcal T}$ is a topos, we recover the fact that the Cuntz groupoid $\mathfrak{O}_2$ is minimal. On the other hand, since $\mathfrak{O}_2$ is a groupoid and not just a category, the theory of Jónsson–Tarski algebras is groupoidal—which also follows from the fact that the Boolean restriction monoid S is étale. In particular, this yields a simple description of the cartesian closed structure of ${\mathcal J}{\mathcal T}$. Given $Y,Z \in {\mathcal J}{\mathcal T}$, their function-space Z^Y comprises the B-set homomorphisms $Y \rightarrow Z$, i.e., the set

\begin{equation*} Z^Y = \{f \colon Y \rightarrow Z \mid w \cdot y = w \cdot y^{\prime} \implies w \cdot f(y) = w \cdot f(y^{\prime})\ \ \text{ for all } w \in A^\ast\}\rlap{,} \end{equation*}

under an algebra structure which we can read off from (5.7) as being:

\begin{equation*} (\ell \cdot f)(y) = \ell \cdot f(m(y,y)) \quad \mathrm{and} \quad (r \cdot f)(y) = r \cdot f(m(y,y))\rlap{,} \end{equation*}

with inverse $m \colon Z^Y \times Z^Y \rightarrow Z^Y$ given by $m(g,h)(y) = m(g(\ell \cdot y), h(r \cdot y))$. The correspondence between algebra maps $X \times Y \rightarrow Z$ and ones $X \rightarrow Z^Y$ is now given by the usual exponential transpose of functions.

6.2. The infinite Jónsson–Tarski topos

As noted in [41, example 2], we may generalize the notion of Jónsson–Tarski algebra to involve a set X endowed with an isomorphism $X \rightarrow X^A$ for any fixed set A. The resulting concrete category ${\mathcal J}{\mathcal T}_A$ is still a non-degenerate variety and may still be described as a topos of sheaves, now on the free monoid $A^\ast$ for the topology generated by the cover $\{a : a \in A\}$.

This generalization is unproblematic when A is finite, and this case was already studied by Higman, Scott, and Birget [5, 19, 42]. When A is infinite, things are more interesting, not least because ${\mathcal J}{\mathcal T}_A$ is then a non-finitary variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets. With this being said, much of the work we did above carries over. We can define dense and closed inclusions mutatis mutandis as before, and we still find M as the monoid of maximal dense partial maps $A^\ast \rightarrow A^\ast$. The main difference is in the characterization of the dense ideals. When A is finite, these correspond to finite A-ary branching trees, where a given tree τ corresponds to the ideal generated by the addresses of its leaves. In the infinite case, they correspond to well-founded A-ary branching trees; these are potentially infinite but have no infinite path starting at the root. The following lemma translates this into ideal-theoretic language.

Lemma 6.4. An ideal $I \leqslant A^\ast$ is dense if, and only if, each infinite word $\cdots w_2 w_1 w_0 \in A^{-\omega}$ has an initial segment in I.

Proof. The closure of the ideal I may be computed transfinitely: we take $I_0 = I$, take $I_{\alpha + 1} = \{w \in A^\ast : aw \in I_\alpha \text{for all } a \in A\}$ and at limit stages take $I_{\gamma} = \bigcup_{\alpha \lt \gamma} I_\alpha$. By Hartog’s lemma, this transfinite sequence stabilizes at some λ and now $I_\lambda = I^{\prime}$.

Suppose first that $I^{\prime} = I_\lambda = A^\ast$ and let $W \in A^{-\omega}$. Writing $\left.{W}\right|_n$ for the initial segment of W of length n, we define $\alpha_n = \mathrm{min}\{\gamma \leqslant \lambda : \left.{W}\right|_n \in I_\gamma\}$; note this is the minimum of a non-empty set of ordinals, since the empty word ϵ is in I_λ. Now if $\alpha_n \gt 0$ then by the construction of the transfinite sequence we must have $\alpha_{n+1} \lt \alpha_n$; thus, by well-foundedness we must have $\alpha_n = 0$ for some n, i.e., $\left.{W}\right|_n \in I$. Conversely, suppose every infinite word W has an initial segment in I; we show that $\epsilon \in I_\lambda$. Indeed, suppose not. Since $I_\lambda = I_{\lambda+1}$, for every $w \notin I_\lambda$, there must exist some $a \in A$ for which $aw \notin I_\lambda$. Starting from ϵ and making countably many dependent choices, we thus obtain a sequence of words $\epsilon, w_0, w_1w_0, w_2w_1w_0, \dots$ and so an infinite sequence $W = \cdots w_2w_1w_0$ with no initial segment in I_λ and so certainly no initial segment in I—which is a contradiction.

The characterization of B is likewise slightly different. Again, we can identify its elements with complementary pairs of closed ideals of $A^\ast$, but the characterization of such pairs is more delicate. One should think of them as well-founded A-ary trees whose leaves have been labelled with 0 or 1; the addresses of the 0- and 1-labelled leaves of such a tree then constitute the ideals in the complemented pair. This leads to the following characterization of the complemented closed ideals:

Lemma 6.5. A closed ideal $I \leqslant_c A^\ast$ has a complement if, and only if, for every infinite word $W \in A^{-\omega}$ there is a finite initial segment w of W for which either $A^\ast w \leqslant I$ or $A^\ast w \cap I = \emptyset$.

Proof. If I has a complement I ^ʹ then $I+I^{\prime}$ is dense, whence for any $W \in A^{-\omega}$ there is a finite initial segment w with $w \in I+I^{\prime}$. If $w \in I$ then $A^\ast w \leqslant I$; while if $w \in I^{\prime}$ then $A^\ast w \cap I = \emptyset$. Suppose conversely that I satisfies the stated condition; then we define $I^{\prime} = \{w \in A^\ast \mid A^\ast w \cap I = \emptyset\}$. It is easy to see that I ^ʹ is a closed ideal which is obviously disjoint from I. Moreover, $I+I^{\prime}$ is dense: for if W is any infinite word, then there is an initial segment w for which either $A^\ast w \leqslant I$, whence $w \in I \leqslant I+I^{\prime}$, or $A^\ast w \cap I = \emptyset$, whence $w \in I^{\prime} \leqslant I+I^{\prime}$.

Now B is the Boolean algebra of these complemented closed ideals, and the actions of B and M on each other are much as before. The extra ingredient is the zero-dimensional topology on B; and it is not hard to see that a disjoint family of complemented closed ideals $(I_x : x \in X)$ is in ${\mathcal J}$ just when every infinite word $W \in A^{-\omega}$ has an initial segment in (exactly) one of the I_x’s.

The motivating topological perspective also generalizes to the infinitary case. This may come as a surprise: after all, according to what we said earlier, in the Grothendieck case we should only expect a localic perspective. However, in this example there are enough ${\mathcal J}$-closed ideals to separate elements of B (this is essentially the force of the last two lemmas), so that $B_{{\mathcal J}}$ can be identified with the Grothendieck Boolean algebra of clopen sets of the space of ${\mathcal J}$-prime filters on B—which is the (non-compact) prodiscrete space A ^−ω. With this identification made, we may now view M as the monoid of continuous functions $A^{-\omega} \rightarrow A^{-\omega}$ of the form (6.2) but now for a possibly infinite family of pairs $(u_i, v_i)$.

It follows from the above that the classifying localic category of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ is in fact spatial and, like before, a groupoid; it is the obvious generalization of $\mathfrak{O}_2$, with space of objects A ^−ω and morphisms defined just as before. On the other hand, the associated Grothendieck Boolean restriction monoid $S_{\mathcal J}$ is generated by elements a and $a^\ast$ for each $a \in A$, subject to the axioms

(6.6)\begin{equation} aa^\ast = 1\,\text{for all } a \in A\text{,} \quad ab^\ast = 0\,\text{for all } a \neq b \in A \quad \mathrm{and} \quad \textstyle\bigvee_{a \in A} a^\ast a = 1\rlap{,} \end{equation}

and, much as before, elements of $S_{\mathcal J}$ correspond to the partial continuous maps $A^{-\omega} \rightharpoonup A^{-\omega}$ of the form (6.2).

7. Nekrashevych toposes

Our next example draws on the material of [37, 38]; the idea is to extend the monoids M studied in the previous two sections to monoids of endomorphisms $\varphi \colon A^{-\omega} \rightarrow A^{-\omega}$ which can be written in the form

(7.1)\begin{equation} \varphi(Wu_i) = W^{\prime}v_i \qquad \text{with} \qquad W^{\prime} = p_i(W)\rlap{,} \end{equation}

where each p_i lies in a monoid of ‘well-behaved’ endomorphisms of A ^−ω.

Definition 7.1. Self-similar monoid

Let P be a monoid of continuous functions $A^{-\omega} \rightarrow A^{-\omega}$. We say that P is self-similar if for every $p \in P$ and $a \in A$ there exists $b \in A$ and $q \in P$ such that $p(Wa) = q(W)b$ for all $W \in A^{-\omega}$.

In [37, 38], the ‘well-behaved’ endomorphisms are always invertible, whereupon we speak of self-similar groups, but the invertibility has no bearing on constructing a cartesian closed variety, and so we develop the more general case here.

If we name the b and q in the above definition as $p \star a$ and $\left.{p}\right|_{a}$, then we can finitistically encode the action of elements of P on infinite words via what a computer scientist would call a Mealy machine, an algebraist would call a matched pair of monoids [36], and a category theorist would call a distributive law [3]:

Definition 7.2. Self-similar monoid action

Let P be a monoid. A self-similar action of P on a set A is a function

\begin{align*} \delta \colon A \times P &\rightarrow P \times A & (a,p) &\mapsto (\left.{p}\right|_{a}, a \star p) \rlap{,} \end{align*}

satisfying the axioms:

• • $a \star 1 = a$ and $a \star (pq) = (a \star p) \star q$ (i.e., $\star$ is a monoid action on A); and

• • $\left.{1}\right|_{a} = 1$ and $\left.{(pq)}\right|_{a} = \left.{p}\right|_{a} \left.{q}\right|_{a \star p}$.

A self-similar action of P on A induces one on $A^\ast$, where:

(7.2)\begin{equation} \begin{aligned} \left.{p}\right|_{a_n \cdots a_1} &= \left.{\smash{(\cdots (\left.{\smash{(\left.{p}\right|_{a_1})}}\right|_{a_{2}}) \cdots)}}\right|_{a_n} \\ \text{and } (a_n \cdots a_1) \star p &= (a_n \star \left.{p}\right|_{a_{n-1} \cdots a_1}) \cdots (a_3 \star \left.{p}\right|_{a_2a_1})(a_2 \star \left.{p}\right|_{a_1})(a_1 \star p)\rlap{;} \end{aligned} \end{equation}

and we say δ is a faithful self-similar action if the action $\star$ of P on $A^\ast$ is faithful.

If $\delta \colon A \times P \rightarrow P \times A$ is a self-similar action, then the action of P on $A^\ast$ determines a continuous action of P on A ^−ω, given by:

\begin{equation*} p(\cdots a_3 a_2 a_1) \qquad = \qquad \cdots( a_3 \star \left.{p}\right|_{a_2a_1})(a_2 \star \left.{p}\right|_{a_1})(a_1 \star p) \rlap{;} \end{equation*}

and if δ is a faithful self-similar action, then this action on A ^−ω is again faithful, so that we can identify P with a self-similar monoid of continuous endomorphisms $A^{-\omega} \rightarrow A^{-\omega}$. Thus, self-similar submonoids of $\mathrm{End}(A^{-\omega}, A^{-\omega})$ amount to the same thing as faithful self-similar monoid actions on A.

We now construct a cartesian closed variety from any self-similar monoid action.

Definition 7.3. Nekrashevych algebras

Given a self-similar action of a monoid P on A and a left P-set X, we define a left P-set structure on X^A via $(p \cdot \varphi)(a) = \left.{p}\right|_{a} \cdot \varphi(a \star p)$. A Nekrashevych δ-algebra is a left P-set X endowed with an P-set isomorphism $X \cong X^A$. We write ${\mathcal N}_\delta$ for the variety of Nekrashevych δ-algebras.

Like before, ${\mathcal N}_\delta$ is cartesian closed by virtue of being a topos of sheaves on a monoid. The monoid in question we write as $P \bowtie_\delta A^\ast$, the Zappa–Szép product of P and $A^\ast$ over δ; its underlying set is $P \times A^\ast$, its unit element is $(1, \epsilon)$, and its multiplication is given using the self-similar action (7.2) of P on $A^\ast$ by $(p,u) (q,v) = (p (\left.{q}\right|_u), (u \star p)v)$. (In fact, the monoids arising in this way from self-similar group actions have an abstract characterization due to Perrot; see [32] for the details.)

$P \bowtie_\delta A^\ast$ has an obvious presentation: the generators are $(1,a)$ for $a \in A$ together with $(p,\epsilon)$ for $p \in P$, and the axioms are $1 = (1,\epsilon)$, $(p,\epsilon)(q,\epsilon) = (pq,\epsilon)$, and $(1,a)(p,\epsilon) = (\left.{p}\right|_{a}, \epsilon)(1,a \star p)$. Thus, a left $P \bowtie_\delta A^\ast$-set structure on X is the same thing as a left P-set structure and a left $A^\ast$-set structure such that $a \cdot (p \cdot x) = \left.{p}\right|_{a} \cdot ((a \star p) \cdot x)$ for all $x \in X$, $p \in P$ and $a \in A$, but this is precisely to say that the family of maps $a \cdot ({\mathord{\text{--}}}) \colon X \rightarrow X$ assemble to give a left P-set map $X \rightarrow X^A$, where X^A is given the P-set structure from definition 7.3. It follows as in [25, example 1.3] that ${\mathcal N}_\delta$ can be presented as the topos of sheaves on $P \bowtie_\delta A^\ast$ for the topology generated by the covering family $\{(1,a) : a \in A\}$.

We can now follow through the argument of the preceding sections to obtain a presentation of the matched pair ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ for which ${\mathcal N}_\delta \cong {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$. A subtle point that requires some additional work is the following:

Proposition 7.4. Let $\delta \colon A \times P \rightarrow P \times A$ be a self-similar action of P on A. If δ is a faithful action, then $P \bowtie_\delta A^\ast$ is separated as a left $P \bowtie_\delta A^\ast$-set.

Proof. Let $(p,u), (q,v) \in M_0$ and suppose that $(1,a) \cdot (p,u) = (1,a) \cdot (q,v)$ for all $a \in A$; we must show that $(p,u) = (q,v)$. The hypothesis says that $(\left.{p}\right|_{a}, (a \star p)u) = (\left.{q}\right|_{a}, (a \star q)v)$ for all $a \in A$; clearly, then, u = v. On the other hand, we have $a \star p = a \star q$ and $\left.{p}\right|_{a} = \left.{q}\right|_{a}$ for all $a \in A$, which implies that p and q have the same actions on $A^\ast$. By fidelity of δ we conclude that p = q as desired.

So when δ is faithful, we can describe M like before as the monoid of maximal dense partial $P \bowtie_\delta A^\ast$-set maps $P \bowtie_\delta A^\ast \rightarrow P \bowtie_\delta A^\ast$. Here, although the ideal structure of $P \bowtie_\delta A^\ast$ is now more complex, the dense ideals are no harder; they are exactly the ideals of the form P × I where $I \leqslant_d A^\ast$. Likewise, the complemented closed ideals of M ₀ are those of the form P × I for I a complemented closed ideal of $A^\ast$; and so we find that:

• • M is the monoid of all maximal partial maps $(P \times I, f) \colon P \bowtie_\delta A^\ast \rightarrow P \bowtie_\delta A^\ast$ where $I \leqslant_d A^\ast$, under the monoid operation given by partial map composition followed by maximal extension;

• • $B_{\mathcal J}$ is the Grothendieck Boolean algebra of complemented closed ideals of $A^\ast$;

• • M and $B_{\mathcal J}$ act on each other like before, after identifying each complemented closed ideal $I \leqslant A^\ast$ with the corresponding ideal $P \times I \leqslant P \bowtie_\delta A^\ast$.

Since $B_{{\mathcal J}}$ is the same Grothendieck Boolean algebra as before, the topological perspective on these data again involves seeing M as a monoid of continuous endomorphisms of the space A ^−ω. This time, given $(P \times I, f) \colon P \bowtie_\delta A^\ast \rightarrow P \bowtie_\delta A^\ast$ in M with $I = {\langle{u_i}\rangle}$, the elements $\{u_i\}$ and $(p_i, v_i) = f(1, u_i)$ provide the data as in (7.1) for the corresponding continuous endomorphism of A ^−ω; note that fidelity of δ ensures that distinct elements of M encode distinct endomorphisms of A ^−ω. It follows that the classifying topological category of ${\mathcal N}_\delta$ has space of objects A ^−ω, and as morphisms $W \rightarrow W^{\prime}$, germs at W of functions (7.1) with $\varphi(W) = W^{\prime}$. When P is a group and A is finite, this is exactly the topological category $\mathfrak{O}_G$ described in [38, §5.2].

Finally, let us consider the associated Grothendieck Boolean restriction monoid $S_{\mathcal J}$ of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$; this is generated by elements $a,a^\ast$ as in (6.6) but now augmented by total elements p for each $p \in P$, which multiply as in p and additionally satisfy $ap = (\left.{p}\right|_{a})(a \star p)$. From this and $p = \bigvee_{a \in A} a^\ast a p$, we deduce the left equality in:

(7.3)\begin{equation} p = \bigvee_{a \in A} a^\ast \left.{p}\right|_{a} (a \star p) \qquad \qquad pb^\ast = \bigvee_{a \star p = b} a^\ast \left.{p}\right|_{a} \end{equation}

which on multiplying by $b^\ast$ yields the equality to the right. Using this, we can rewrite any element of $S_{\mathcal J}$ in the form $\bigvee_i u_i^\ast p_i v_i$ where $\{u_i\}$ is the basis of a complemented ideal; and much as before, each such element represents a partial function $A^{-\omega} \rightarrow A^{-\omega}$ via the formula (7.1).

Now, because we are considering self-similar monoid actions, rather than group actions, it need not be the case that the cartesian closed variety ${\mathcal N}_\delta$ is groupoidal. As we would hope, this is certainly the case when we do start from a group, but prima facie there could be further examples beyond this. Part (b) of the following result appears to indicate that this is so; however, part (c) shows that this apparent extra generality is in fact spurious: a theory of Nekrashevych algebras is groupoidal just when it is the theory of δ-algebras for some self-similar group action.

Proposition 7.5. For a faithful self-similar action δ, the following are equivalent:

1. (a) The theory of Nekrashevych δ-algebras is groupoidal;

2. (b) For each $p \in P$, there is a dense ideal $I \leqslant A^\ast$ with $\left.{p}\right|_w$ invertible for all $w \in I$;

3. (c) The forgetful functor ${\mathcal N}_\delta \rightarrow {\mathcal N}_{\delta^{\prime}}$ is an isomorphism, where $\delta^{\prime} \colon A \times G \rightarrow G \times A$ is the restriction of δ to the group G of invertible elements of P.

Note the restriction in (c) is well-posed, since if $p \in P$ is invertible, then each $\left.{p}\right|_{a}$ is also invertible with inverse $\left.{\smash{p^{-1}}}\right|_{a \star p}$.

Proof. We first show (b) $\Rightarrow$ (a). The theory of Nekrashevych δ-algebras will be groupoidal just when the associated $S_{\mathcal J}$ is étale; since each generator $a,a^\ast$ is already a partial isomorphism, this will be the case just when each $p \in S_{\mathcal J}$ is an admissible join of partial isomorphisms. So assuming (b), we have for each p a dense ideal I with $\left.{p}\right|_w$ invertible for all $w \in I$. Thus for each $w \in I$, the map $w^\ast w p$ has partial inverse $(w \star p)^\ast (\left.{p}\right|_w)^{-1} w$, since $(w \star p)^\ast (\left.{p}\right|_w)^{-1} w w^\ast w p = (w \star p)^\ast (\left.{p}\right|_w)^{-1} \left.{p}\right|_w (w \star p) = (w \star p)^\ast (w \star p) = (w \star p)^+$ and $w^\ast w p (w \star p)^\ast (\left.{p}\right|_w)^{-1} w = w^\ast \left.{p}\right|_w (w \star p) (w \star p)^\ast (\left.{p}\right|_w)^{-1} w = w^\ast \left.{p}\right|_w (\left.{p}\right|_w)^{-1} w = w^\ast w = w^+$. So if $I = {\langle{u_i}\rangle}$ then the expression $\bigvee_i u_i^\ast u_i p$ expresses p as an admissible join of partial isomorphisms.

Now, towards proving (a) $\Rightarrow$ (b), let $p \in P$ and suppose that for some $w \in A^\ast$, the map $w^\ast wp$ has a partial inverse q. We can write $q = \bigvee_i u_i^\ast q_i v_i$ and by using the left equation of (7.3) where necessary we can assume each v_i is at least as long as w. Now, we calculate that

\begin{equation*} q w^\ast wp = \bigvee_i u_i^\ast q_i v_i w^\ast wp = \bigvee_{\substack{i \text{s.t.} \\ v_i \in {\langle{w}\rangle}}} u_i^\ast q_i v_ip = \bigvee_{\substack{i \text{s.t.} \\ v_i \in {\langle{w}\rangle}}} u_i^\ast q_i \left.{p}\right|_{v_i} (v_i \star p)\rlap{;} \end{equation*}

but since this must equal $q^+ = \bigvee_i u_i^\ast u_i$, we must have for all i that $v_i \in {\langle{w}\rangle}$, that $q_i \left.{p}\right|_{v_i} = 1$ and that $u_i = v_i \star p$. Now using the right equation in (7.3), we have:

\begin{equation*} w^\ast wpq = \bigvee_i w^\ast wp u_i^\ast q_i v_i = \bigvee_i \bigvee_{a \star p = u_i} w^\ast w a^\ast \left.{p}\right|_{a} q_i v_i\rlap{.} \end{equation*}

This join must equal $w^\ast w$; but since in particular $v_i \star p = u_i$, the join includes the terms $w^\ast wv_i^\ast \left.{p}\right|_{v_i}q_i v_i = v_i^\ast \left.{p}\right|_{v_i}q_i v_i$, which must thus be restriction idempotents: and this is only possible if $\left.{p}\right|_{v_i} q_i = 1$; but since already $q_i \left.{p}\right|_{v_i} = 1$ we see that $\left.{p}\right|_{v_i}$ has inverse q_i. Now any other a with $a \star p = u_i$ must satisfy $\left.{p}\right|_{a} q_i = 1$ and so $\left.{p}\right|_{a} = \left.{p}\right|_{v_i}$. Since also $a \star p = u_i = v_i \star p$ we have $a = v_i$ by fidelity of the action. Thus, the join displayed above is equal to $\bigvee_i w^\ast w v_i^\ast \left.{p}\right|_{v_i} q_i v_i = \bigvee_i w^\ast w v_i^\ast v_i = \bigvee_i v_i^\ast v_i$; since it also equals $w^\ast w$, the ideal J_w generated by the v_i’s must be dense in ${\langle{w}\rangle}$.

Now, suppose as in (a) that every $p \in P$ is a join of partial isomorphisms $p = \bigvee_i u_i^\ast u_i p$; then we have ideals $J_{u_i} \leqslant_d {\langle{u_i}\rangle}$ for each i such that $\left.{p}\right|_v$ is invertible for all $v \in J_{u_i}$. So taking $I = \sum_i J_{u_i}$, we have $I = \sum_i J_{u_i} \leqslant_d \sum_i {\langle{u_i}\rangle} \leqslant_d M_0$ and $\left.{p}\right|_w$ invertible for all $w \in I$, which gives (b).

Next, for (c) $\Rightarrow$ (a), note that the theory of Nekrashevych $\delta^{\prime}$-algebras trivially satisfies (b), and so is groupoidal, whence also the isomorphic theory of Nekrashevych δ-algebras. Finally, to prove (b) $\Rightarrow$ (c), it suffices to show that the map of Grothendieck Boolean restriction monoids $S^{\delta^{\prime}} \rightarrow S^\delta$ induced by the inclusion $G \subseteq P$ is invertible. It is injective since both $S^{\delta^{\prime}}$ and S ^δ are submonoids of the monoid of partial continuous endofunctions of A ^−ω; for surjectivity, we need only show that each $p \in P$ is in its image. But letting $I = {\langle{u_i}\rangle}$ be a dense ideal as in (b), and using the left equation in (7.3), we can write $p = \bigvee_{i} u_i^\ast \left.{p}\right|_{u_i} (p \star u_i)$; since each $\left.{p}\right|_{u_i}$ lies in G, this provides the desired expression.

8. Cuntz–Krieger toposes

The Cuntz $C^\ast$-algebra on alphabet A can be generalized to the Cuntz–Krieger $C^\ast$-algebra on a directed graph ${\mathbb{A}}$ [30]; the way in which the former becomes a special case of the latter is by considering the graph with a single vertex and A self-loops. Correspondingly, the notion of Leavitt algebra has a generalization to the notion of Leavitt path algebra, and both of these generalizations in fact come from a generalization of the Cuntz topological groupoid on A to the ‘path groupoid’ on ${\mathbb{A}}$. In this final section, we explain how this generalization plays out from the perspective of cartesian closed varieties.

The situation this time is subtly different. We will again describe a topos which is a variety, but now it will be a many-sorted variety, with one sort for each vertex of ${\mathbb{A}}$. The corresponding variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets will not be the topos we started from, but rather its two-valued collapse in the sense of §4; indeed, by virtue of proposition 4.5, the topos we started from will instead be the category of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sheaves (definition 4.2). The missing result we need is the following:

Proposition 8.1. Let ${\mathcal {C}}$ be a many-sorted variety which is also a non-degenerate topos, and let $X \in {\mathcal {C}}$ be the free algebra on one generator of each sort. Then ${\mathcal {C}}_{\mathrm{tv}}$ is equivalent to a single-sorted cartesian closed variety ${\mathcal V}$, with X corresponding under this equivalence to the free ${\mathcal V}$-algebra on one generator. Thus ${\mathcal {C}}_\mathrm{tv} \simeq {\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}\text-\mathrm{\mathcal Set}$ where ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ is defined from X as in proposition 2.11.

Proof. Since ${\mathcal {C}}$ is a non-degenerate topos, its initial object is strict, so the theory which presents it as a variety has no constants. Hence, by [2], ${\mathcal {C}} = {\mathcal E}_\mathrm{tv}$ is equivalent to a variety when equipped with the functor ${\mathcal {C}} \rightarrow \mathrm{\mathcal Set}$ sending a model $(M(s) : s \in S)$ to $\prod_{s \in S}M(s)$. But this functor is just ${\mathcal {C}}(X, {\mathord{\text{--}}})$, and as in [26], ${\mathcal {C}}_{\mathrm{tv}}$ is cartesian closed since ${\mathcal {C}}$ is so.

8.1. Presheaf toposes

Before considering groupoids associated with directed graphs, as a kind of warm-up exercise we start with a simpler case of proposition 8.1 wherein ${\mathcal {C}}$ is a presheaf category.

Given our ongoing conventions, it will be most convenient to look at a covariant presheaf category $[{\mathbb{A}}, \mathrm{\mathcal Set}]$. We call objects $X \in [{\mathbb{A}}, \mathrm{\mathcal Set}]$ left ${\mathbb{A}}$-sets and present them as a family of sets X_a indexed by the objects of ${\mathbb{A}}$, together with reindexing operators $f \cdot ({\mathord{\text{--}}}) \colon X_a \rightarrow X_b$ for every morphism $f \colon a \rightarrow b$ of ${\mathbb{A}}$, satisfying the usual associativity and unitality axioms. The cartesian closed variety $[{\mathbb{A}}, \mathrm{\mathcal Set}]_{\mathrm{tv}}$ to which this collapses is the variety of left ${\mathbb{A}}$-sets for which either all X_a’s are empty or all X_a’s are non-empty. An explicit theory presenting this variety was given in [26, example 8.7]; our objective is to present it as a variety of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-sets.

Now, $[{\mathbb{A}}, \mathrm{\mathcal Set}]$ is a variety with set of sorts $\mathrm{ob}({\mathbb{A}})$, and the free object on one generator of each sort is the ${\mathbb{A}}$-set, which will denote simply by ${\mathbb{A}}$, for which ${\mathbb{A}}_a$ is the set of all morphisms of ${\mathbb{A}}$ with codomain a, and for which $f \cdot ({\mathord{\text{--}}}) \colon {\mathbb{A}}_a \rightarrow {\mathbb{A}}_b$ is given by postcomposition. Now by proposition 8.1, the monoid M and Boolean algebra B can be found as $[{\mathbb{A}}, \mathrm{\mathcal Set}]({\mathbb{A}}, {\mathbb{A}})$ and $[{\mathbb{A}}, \mathrm{\mathcal Set}]({\mathbb{A}},1+1)$ respectively.

On the one hand, a map ${\mathbb{A}} \rightarrow {\mathbb{A}}$ in $[{\mathbb{A}}, \mathrm{\mathcal Set}]$ is by freeness determined uniquely by elements $f_a \in {\mathbb{A}}_a$ for each $a \in {\mathbb{A}}$; thus, an element $f \in M$ comprises a family of objects $(f^\ast a)_{a \in \mathrm{ob}({\mathbb{A}})}$ and a family of arrows $(f_a \colon f^\ast a \rightarrow a)_{a \in \mathrm{ob}({\mathbb{A}})}$ of ${\mathbb{A}}$. It is now easy to see that the unit of M is $(1_a \colon a \rightarrow a)_{a \in A}$, while the product of f and g is characterized by $(f \cdot g)_a = f_a \circ g_{f^\ast{a}} \colon g^\ast f^\ast a \rightarrow f^\ast a \rightarrow a$. In the nomenclature of [1, chapter I.5], M is the monoid of admissible sections of ${\mathbb{A}}$.

On the other hand, the ${\mathbb{A}}$-set $1+1$ has $(1+1)_a = \{\top, \bot\}$ for all objects a, whence an ${\mathbb{A}}$-set map ${\mathbb{A}} \rightarrow 1+1$ amounts to a function $\mathrm{ob}({\mathbb{A}}) \rightarrow \{\top, \bot\}$. It follows easily that B is the power-set Boolean algebra ${\mathcal P}(\mathrm{ob}({\mathbb{A}}))$, and that, in the infinite case, the zero-dimensional topology ${\mathcal J}$ comprises all partitions of ${\mathcal P}(\mathrm{ob}({\mathbb{A}}))$. Similar straightforward calculations now show that:

• • $f\in M$ acts on $U \in B$ to yield $f^\ast(U) = \{a \in \mathrm{ob}({\mathbb{A}}) : f^\ast a \in U\} \in B$.

• • $U \in B$ acts on $f,g \in M$ to yield the $U(f,g) \in M$ with $U(f,g)_a = f_a$ for $a \in U$ and $U(f,g)_a = g_a$ for $a \notin U$.

Now, if $X \in [{\mathbb{A}}, \mathrm{\mathcal Set}]_\mathrm{tv}$ then the set $\tilde X = [{\mathbb{A}}, \mathrm{\mathcal Set}]({\mathbb{A}},X) = \prod_{a \in A} X_a$ becomes a ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$-set as in proposition 2.11; explicitly, if $x,y \in \tilde{X}$, $f \in M$ and $U \in B$, then:

• • $f \cdot x \in \tilde{X}$ is given by $(f \cdot x)_a = f_a \cdot x_{f^\ast a}$;

• • $U(x,y) \in \tilde{X}$ is given by $U(x,y)_a = x_a$ for $a \in U$ and $U(x,y)_a = y_a$ for $a \notin U$.

We are once again in the situation where there are enough ${\mathcal J}$-closed ideals in $B_{{\mathcal J}}$ to separate elements, so that there is a topological, rather than localic, perspective on ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$. Indeed, $B_{{\mathcal J}}$ is the Grothendieck Boolean algebra of clopen sets of the discrete space $\mathrm{ob}({\mathbb{A}})$, and under this correspondence, the action of $f \in M$ on B is given by inverse image under the function $a \mapsto f^\ast a$. It follows from this that the classifying localic category of ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ is again spatial and is simply the discrete topological category ${\mathbb{A}}$. Of course, this topological category is a groupoid just when ${\mathbb{A}}$ is a groupoid, and so this characterizes when the cartesian closed variety $[{\mathbb{A}}, \mathrm{\mathcal Set}]_\mathrm{tv}$ is groupoidal. On the other hand, ${\mathbb{A}}$ is minimal, so that $[{\mathbb{A}}, \mathrm{\mathcal Set}]_\mathrm{tv} = [{\mathbb{A}}, \mathrm{\mathcal Set}]$ is a topos, just when every object of ${\mathbb{A}}$ admits an arrow to every other object of ${\mathbb{A}}$; which is to say that ${\mathbb{A}}$ is strongly connected in the sense of [26, example 8.7].

8.2. Cuntz–Krieger toposes

We now describe the cartesian closed varieties which correspond to Cuntz–Krieger $C^\ast$-algebras associated with directed graphs. As explained, these varieties will be obtained from many-sorted varieties which are (Grothendieck) toposes. These toposes were introduced by Leinster [35], with the connection to operator algebra being made explicit in [17, §5].

Definition 8.2. Let ${\mathbb{A}}$ be a directed graph, that is, a pair of sets $A_1, A_0$ together with source and target functions $s, t \colon A_1 \rightrightarrows A_0$. As usual, we write $e \colon v \rightarrow v^{\prime}$ to indicate that $e \in A_1$ with $s(e) = v$ and $t(e) = v^{\prime}$, and we will also make use of the sets $s^{-1}(v)$ of all edges in ${\mathbb{A}}$ with a given fixed source v. Now a Cuntz–Krieger ${\mathbb{A}}$-algebra is a family of sets $(X_v : v \in A_0)$ together with, for each $v \in A_0$, a specified isomorphism between X_v and the set

\begin{equation*} \prod_{e \in s^{-1}(v)} X_{t(e)} = \prod_{e \colon v \rightarrow v^{\prime}} X_{v^{\prime}}\rlap{.} \end{equation*}

We write ${\mathcal {C}}{\mathcal{ K}}_{{\mathbb{A}}}$ for the many-sorted variety of Cuntz–Krieger ${\mathbb{A}}$-algebras.

As shown in [17, 35], ${\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}}$ is a topos. To see this, we first define ${\mathbb{A}}^\ast$ to be the free category on the graph ${\mathbb{A}}$, whose objects are vertices of ${\mathbb{A}}$, and whose morphisms $v \rightarrow w$ are finite paths of edges from v to w, i.e.:

\begin{equation*} {\mathbb{A}}(v,w) = \{\,e_n \cdots e_1 \mid s(e_1) = v, t(e_{i}) = s(e_{i+1}), t(e_n) = w\,\}\rlap{,} \end{equation*}

where by convention ${\mathbb{A}}(v,v)$ also contains the empty path ϵ_v from v to v. Now a left ${\mathbb{A}}^\ast$-set X is the same as a family of sets $(X_v : v \in A_0)$ together with functions $e \cdot ({\mathord{\text{--}}}) \colon X_v \rightarrow X_{v^{\prime}}$ for each edge $e \colon v \rightarrow v^{\prime}$ of ${\mathbb{A}}$. We can endow ${\mathbb{A}}^\ast$ with a topology by requiring that, for each object v, the family $(e \colon v \rightarrow v^{\prime} \mid e \in s^{-1}(v))$ is a cover of v (note that, since we are taking covariant presheaves, a covering family is a family of morphisms with common domain, rather than common codomain). Now as explained in [17], a left ${\mathbb{A}}^\ast$-set X will satisfy the sheaf condition for this topology just when, for each vertex v, the map $X_v \rightarrow \prod_{e \in s^{-1}(v)} X_{t(e)}$ induced by the functions $e \cdot ({\mathord{\text{--}}}) \colon X_v \rightarrow X_{v^{\prime}}$ is an isomorphism. Thus ${\mathcal {C}}{\mathcal{ K}}_{{\mathbb{A}}} \simeq \mathrm{\mathcal Sh}({\mathbb{A}}^\ast)$ as claimed.

In the single-sorted case, we described ${\mathcal J}{\mathcal T}_A$ in terms of a localization of the category of separated left $A^\ast$-sets. We can proceed in exactly the same way here. Unfolding the definitions yields:

Definition 8.3. Given a left ${\mathbb{A}}^\ast$-set X and a sub-left-${\mathbb{A}}^\ast$-set $Y \leqslant X$:

• • X is separated if $x,y \in X_v$ are equal whenever $e \cdot x = e \cdot y$ for all $e \in s^{-1}(v)$.

• • $Y \leqslant X$ is closed if any $x \in X_v$ with $e \cdot x \in Y_{t(e)}$ for all $e \in s^{-1}(v)$ is in Y_v.

• • $Y \leqslant X$ is dense if the closure of Y in X is X.

With these definitions in place, we can now identify the Cuntz–Krieger topos ${\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}}$, just like before, with the category ${\mathcal {C}}{\mathcal{ K}}^{\prime}_{\mathbb{A}}$ of maximal dense partial maps between separated left ${\mathbb{A}}^\ast$-sets, with composition given by partial map composition followed by maximal extension. We now use this to describe the matched pair ${\left[\smash{{B_{{\mathcal J}}} \mathbin{\mid}{M} }\right]}$ which presents the cartesian closed variety $({\mathcal {C}}{\mathcal{ K}}_{{\mathbb{A}}})_{\mathrm{tv}}$.

First, as we saw in the preceding section, the free left ${\mathbb{A}}^\ast$-set on one generator of each sort is ${\mathbb{A}}^\ast$ acting on itself by composition: thus, $({\mathbb{A}}^\ast)_v$ is the set of all finite ${\mathbb{A}}$-paths $e_n e_{n-1} \cdots e_1$ ending at the vertex v, and the function $({\mathbb{A}}^\ast)_v \rightarrow ({\mathbb{A}}^\ast)_{v^{\prime}}$ induced by an edge $e \colon v \rightarrow v^{\prime}$ simply appends e to the end of the path: $e \cdot (e_n \cdots e_1) = ee_n \cdots e_1$. Clearly, ${\mathbb{A}}^\ast$ is separated as an ${\mathbb{A}}^\ast$-set, and so the monoid M is equally well the monoid ${\mathcal {C}}{\mathcal{ K}}^{\prime}({\mathbb{A}}^\ast,{\mathbb{A}}^\ast)$ of all maximal dense partial left ${\mathbb{A}}^\ast$-set maps ${\mathbb{A}}^\ast \rightarrow {\mathbb{A}}^\ast$. Now, a sub-${\mathbb{A}}^\ast$-set $I \leqslant {\mathbb{A}}^\ast$ is an ideal of ${\mathbb{A}}^\ast$: that is, a collection $I \subseteq \mathrm{mor}({\mathbb{A}}^\ast)$ of morphisms of ${\mathbb{A}}^\ast$ which is closed under postcomposition, and as before, we can be more explicit about the dense ideals. Intuitively, these are given by a family $(\tau_a : a \in A_0)$ of well-founded trees, where:

• • Each vertex of each tree is labelled by a vertex of ${\mathbb{A}}$;

• • The child edges of a v-labelled vertex are labelled bijectively by edges $e \in s^{-1}(v)$, with the far end of the e-labelled edge being a t(e)-labelled vertex; and

• • The root of each τ_a is labelled by a.

Such a family of trees can, as before, be specified by listing the addresses of its leaves, where the ‘address’ of a leaf is now the path of edges to the leaf from the root. These addresses generate an ideal of ${\mathbb{A}}^\ast$, and well-foundedness assures that the ideals so arising should be the dense ones. Said algebraically, this becomes the following generalization of lemma 6.4; the proof is, mutatis mutandis, the same.

Lemma 8.4. An ideal $I \leqslant {\mathbb{A}}^\ast$ is dense if, and only if, each infinite path of edges $\cdots e_3 e_2 e_1$ has a finite initial segment $e_n \cdots e_1$ in I.

Similarly, we can characterize the Boolean algebra $B = {\mathcal {C}}{\mathcal{ K}}^{\prime}({\mathbb{A}}^\ast, 1+1)$ as comprising all complemented closed ideals of ${\mathbb{A}}^\ast$, for which we have the following recognition result generalizing lemma 6.5. Here, we write in the obvious manner ${\mathbb{A}}^\ast w$ for the ideal generated by a finite path w.

Lemma 8.5. A closed ideal $I \leqslant_c {\mathbb{A}}^\ast$ has a complement if, and only if, for every infinite path of edges $\cdots e_3 e_2 e_1$ of ${\mathbb{A}}$ there is a finite initial segment $w = e_n \cdots e_1$ of W for which either ${\mathbb{A}}^\ast w \leqslant I$ or ${\mathbb{A}}^\ast w \cap I = \emptyset$.

With these results in place, the description of the zero-dimensional topology on B and the actions of M and B on each other goes through mutatis mutandis as before. Once again, there are enough ${\mathcal J}$-closed ideals to separate elements of B, and so there is a legitimate topological perspective on these data. Indeed, $B_{\mathcal J}$ in this case is the Grothendieck Boolean algebra of clopen sets of the infinite path space ${\mathbb{A}}^{-\omega}$, whose elements are infinite paths $\cdots e_2 e_1 e_0$ in ${\mathbb{A}}$ starting at any vertex of ${\mathbb{A}}$, and whose topology is generated by the basic clopen sets $[e_n \cdots e_1]$ of all paths which have $e_n \cdots e_1$ as an initial segment.

We can now use this to describe the continuous map $\varphi \colon {\mathbb{A}}^{-\omega} \rightarrow {\mathbb{A}}^{-\omega}$ induced by a maximal dense partial map $(I,f) \colon {\mathbb{A}}^\ast \rightarrow {\mathbb{A}}^\ast$. First, we can like before find a basis $\{p_i\}$ of minimal-length paths for the dense ideal I. Suppose that each p_i is a path from u_i to v_i; then $q_i = f(p_i)$ is some other path with target v_i and source, say, w_i. One way to visualize this is in terms of the family of well-founded trees $(\tau_a : a \in A_0)$ associated with the dense ideal I; the maximal-length directed paths from the root are labelled by the basis elements p_i, and we can imagine the v_i-labelled leaf at the end of each of these paths as having the path q_i, which also ends at v_i, attached to it. Now the set of pairs of paths $\{(p_i, q_i)\}$ completely specify (I, f)’s action on infinite paths as being the function $\varphi \colon {\mathbb{A}}^{-\omega} \rightarrow {\mathbb{A}}^{-\omega}$ given by:

(8.1)\begin{equation} \varphi(W^{\prime}p_i) = W^{\prime}q_i \qquad \text{for all}\,\, W^{\prime} \in {\mathbb{A}}^{-\omega}\, \text{starting at}\, t(p_i). \end{equation}

From this description, it follows that the classifying topological category of $({\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}})_{\mathrm{tv}}$ is the category whose space of objects is ${\mathbb{A}}^{-\omega}$, and whose morphisms $W \rightarrow W^{\prime}$ are germs at W of continuous functions of the form (8.1) with $\varphi(W) = W^{\prime}$. It is not hard to identify such germs with integers i such that $W_n = W^{\prime}_{i+n}$ for sufficiently large n, so that the classifying topological category is the well-known path groupoid $P({\mathbb{A}})$ of ${\mathbb{A}}$ [30].

Of course, we conclude from this that the theory of Cuntz–Krieger ${\mathbb{A}}$-algebras is groupoidal. On the other hand, it is not necessarily the case that $({\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}})_\mathrm{tv}$ is a topos. This will be so just when, in fact, $({\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}})_\mathrm{tv} = {\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}}$, or equivalently, just when the path groupoid is minimal, the condition for which is well-known in the literature. We sketch another proof of this fact which exploits our ideal-theoretic perspective.

Definition 8.6. Let ${\mathbb{A}}$ be a directed graph. A vertex v of ${\mathbb{A}}$ is cofinal if for any infinite path $\cdots v_2 \xleftarrow{e_2} v_1 \xleftarrow{e_1} v_1 \xleftarrow{e_0} v_0$ in ${\mathbb{A}}$ there is some k for which there exists a finite path from v to v_k.

Proposition 8.7. For any directed graph ${\mathbb{A}}$, the following are equivalent:

1. (a) The cartesian closed variety $({\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}})_\mathrm{tv}$ is a topos (and thus equal to ${\mathcal {C}}{\mathcal{ K}}_{\mathbb{A}}$);

2. (b) Every vertex of ${\mathbb{A}}$ is cofinal.

Proof. We first prove (a) $\Rightarrow$ (b). Given a vertex v of ${\mathbb{A}}$, consider $b \in B$ given by the closed complemented ideal ${\mathbb{A}}^\ast v \leqslant {\mathbb{A}}^\ast$ of all paths starting at the vertex v. Since (a) holds, by theorem 4.7, there must exist $m \in M$ with $m^\ast b = 1$, i.e., there is a maximal dense partial map $(I,f) \colon {\mathbb{A}}^\ast \rightarrow {\mathbb{A}}^\ast$ with $f^{-1}({\mathbb{A}}^\ast v)$ dense in ${\mathbb{A}}^\ast$. Thus, for any infinite path $\cdots v_2 \xleftarrow{e_2} v_1 \xleftarrow{e_1} v_1 \xleftarrow{e_0} v_0$, there is some k for which $e_k \cdots e_0 \in f^{-1}({\mathbb{A}}^\ast v)$. But this says that $f(e_k \cdots e_0)$ is a path starting at v and ending, like $e_k \cdots e_0$, at v_k, which shows that v is cofinal in ${\mathbb{A}}$.

Conversely, suppose every vertex is cofinal in ${\mathbb{A}}$, and let $b \neq 0 \in B$; we must find some $m \in M$ with $m^\ast b = 1$. Now b is a non-empty closed ideal $I \leqslant_c {\mathbb{A}}^\ast$; so let p be any path in it and let $u = t(p)$. Consider the set

\begin{equation*} J = \{q \in {\mathbb{A}}^\ast(v,w) \mid {\mathbb{A}}^\ast(u,w)\; \text{is non-empty}\} \subseteq \mathrm{mor}({\mathbb{A}}^\ast)\rlap{.} \end{equation*}

This is clearly an ideal, and because u is cofinal it is dense in ${\mathbb{A}}^\ast$. Letting $\{q_i\} \subseteq J$ be the basis of minimal paths, we can now define an ${\mathbb{A}}^\ast$-set map $f \colon J \rightarrow {\mathbb{A}}^\ast$ by taking $f(q_i) = r_i \cdot p$, where r_i is any path in ${\mathbb{A}}^\ast(u,t(q_i))$. If we let $m = (J,f) \in M$, then $m^\ast(b) = f^{-1}(I)$ contains $f^{-1}({\mathbb{A}}^\ast p)$, which is clearly all of the dense ideal $J \leqslant {\mathbb{A}}^\ast$; whence $m^\ast b = 1$ as desired.