Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T14:52:01.339Z Has data issue: false hasContentIssue false
  • English
  • Français

Partitions with parts separated by parity: conjugation, congruences and the mock theta functions

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  30 November 2023

Shishuo Fu  and
Dazhao Tang Open the ORCID record for Dazhao Tang [Opens in a new window]
Shishuo Fu
Affiliation:
College of Mathematics and Statistics, Chongqing University, Huxi Campus, Chongqing 401331, People's Republic of China (fsshuo@cqu.edu.cn)
Dazhao Tang*
Affiliation:
School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, People's Republic of China (dazhaotang@sina.com)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

Noting a curious link between Andrews’ even-odd crank and the Stanley rank, we adopt a combinatorial approach building on the map of conjugation and continue the study of integer partitions with parts separated by parity. Our motivation is twofold. Firstly, we derive results for certain restricted partitions with even parts below odd parts. These include a Franklin-type involution proving a parametrized identity that generalizes Andrews’ bivariate generating function, and two families of Andrews–Beck type congruences. Secondly, we introduce several new subsets of partitions that are stable (i.e. invariant under conjugation) and explore their connections with three third-order mock theta functions $\omega (q)$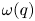, $\nu (q)$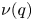, and $\psi ^{(3)}(q)$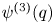, introduced by Ramanujan and Watson.

Keywords

partitionsconjugationAndrews–Beck type congruencesmock theta functionsparity

MSC classification

Primary: 11P81: Elementary theory of partitions
Secondary: 11P83: Partitions; congruences and congruential restrictions 05A17: Partitions of integers 05A15: Exact enumeration problems, generating functions

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 155 , Issue 3 , June 2025 , pp. 954 - 974
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrews, G. E.. The Theory of Partitions (New York: Addison-Wesley Pub. Co., 1976). Reissued, Cambridge University Press, New York, 1998.Google Scholar
Andrews, G. E.. On a partition function of Richard Stanley. Electron. J. Combin. 11 (2004), R1.CrossRefGoogle Scholar
Andrews, G. E.. Partitions, Durfee symbols, and the Atkin–Garvan moments of ranks. Invent. Math. 169 (2007), 37–73.CrossRefGoogle Scholar
Andrews, G. E.. Integer partitions with even parts below odd parts and the mock theta functions. Ann. Comb. 22 (2018), 433–445.CrossRefGoogle Scholar
Andrews, G. E.. Partitions with parts separated by parity. Ann. Comb. 23 (2019), 241–248.CrossRefGoogle Scholar
Andrews, G. E.. The Ramanujan–Dyson identities and George Beck's congruence conjectures. Int. J. Num. Theory 17 (2021), 239–249.CrossRefGoogle Scholar
Andrews, G. E., Dixit, A. and Yee, A. J.. Partitions associated with the Ramanujan/Watson mock theta functions $\omega (q)$, $\nu (q)$ and $\phi (q)$. Res. Num. Theory 1 (2015), 19.CrossRefGoogle Scholar
Andrews, G. E., Passary, D., Sellers, J. A. and Yee, A. J.. Congruences related to the Ramanujan/Watson mock theta functions $\omega (q)$ and $\nu (q)$. Ramanujan J. 43 (2017), 347–357.CrossRefGoogle Scholar
Berkovich, A. and Garvan, F. G.. Dissecting the Stanley partition function. J. Combin. Theory Ser. A. 112 (2005), 277–291.CrossRefGoogle Scholar
Berkovich, A. and Garvan, F. G.. On the Andrews–Stanley refinement of Ramanujan's partition congruence modulo $5$ and generalizations. Trans. Am. Math. Soc. 358 (2005), 703–726.CrossRefGoogle Scholar
Bruinier, J. and Ono, K.. Identities and congruences for the coefficients of Ramanujan's $\omega (q)$. Ramanujan J. 23 (2010), 151–157.CrossRefGoogle Scholar
Chan, S. H., Mao, R. and Osburn, R.. Variations of Andrews–Beck type congruences. J. Math. Anal. Appl. 495 (2021), 124771.CrossRefGoogle Scholar
Chen, R. and Garvan, F. G.. A proof of the mod 4 unimodal sequence conjectures and related mock theta functions. Adv. Math. 398 (2022), 108235.CrossRefGoogle Scholar
Chern, S., Weighted partition rank and crank moments. I. Andrews–Beck type congruences, in Proceedings of the Conference in Honor of Bruce Berndt (2023), in press.Google Scholar
Chern, S.. Weighted partition rank and crank moments II. Odd-order moments. Ramanujan J. 57 (2022), 471–485.CrossRefGoogle Scholar
Chern, S.. Weighted partition rank and crank moments. III. A list of Andrews–Beck type congruences modulo $5$, $7$, $11$ and $13$. Int. J. Number Theory 18 (2022), 141–163.CrossRefGoogle Scholar
Corteel, S. and Lovejoy, J.. Overpartitions. Trans. Am. Math. Soc. 356 (2004), 1623–1635.CrossRefGoogle Scholar
Du, J. Q. D. and Tang, D.. Proofs of two conjectural Andrews–Beck type congruences due to Lin, Peng and Toh. Int. J. Number Theory 19 (2023), 1387–1404.CrossRefGoogle Scholar
Du, J. Q. D. and Tang, D., Andrews–Beck type congruences for $k$-colored partitions, preprint.Google Scholar
Dyson, F. J.. Some guesses in the theory of partitions. Eureka 8 (1944), 10–15.Google Scholar
Fu, S.. Combinatorial proofs and refinements of three partition theorems of Andrews. Ramanujan J. 60 (2023), 847–860.CrossRefGoogle Scholar
Fu, S. and Tang, D.. Partitions with fixed largest hook length. Ramanujan J. 45 (2018), 375–390.CrossRefGoogle Scholar
Garthwaite, S. and Penniston, D.. $p$-adic properties of Maass forms arising from theta series. Math. Res. Lett. 15 (2008), 459–470.CrossRefGoogle Scholar
Garvan, F., Kim, D. and Stanton, D.. Cranks and $t$-cores. Invent. Math. 101 (1990), 1–17.CrossRefGoogle Scholar
Hirschhorn, M. D.. Ramanujan's partition congruences. Discrete Math. 131 (1994), 351–355.CrossRefGoogle Scholar
Hirschhorn, M. D., The Power of $q$. A personal journey. Developments in Mathematics, Vol. 49 (Cham: Springer, 2017).CrossRefGoogle Scholar
Jin, L., Liu, E. H. and Xia, E. X. W.. Proofs of some conjectures of Chan–Mao–Osburn on Beck's partition statistics. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 116 (2022), 135.CrossRefGoogle Scholar
Keith, W. J. and Nath, R.. Partitions with prescribed hooksets. J. Comb. Number Theory 3 (2011), 39–50.Google Scholar
Kim, B.. Group actions on partitions. Electron. J. Combin. 24 (2017), 3.58.CrossRefGoogle Scholar
Kim, E.. Andrews–Beck type congruences for overpartitions. Electron. J. Combin. 29 (2022), 1.37.CrossRefGoogle Scholar
Lin, B. L. S., Peng, L. and Toh, P.. Weighted generalized crank moments for $k$-colored partitions and Andrews–Beck type congruences. Discrete Math. 344 (2021), 112450.CrossRefGoogle Scholar
Lin, Z., Xiong, H. and Yan, S. H. F.. Combinatorics of integer partitions with prescribed perimeter. J. Combin. Theory Ser. A 197 (2023), 105747.CrossRefGoogle Scholar
Mao, R.. On total number parts functions associated to ranks of overpartitions. J. Math. Anal. Appl. 506 (2022), 125715.CrossRefGoogle Scholar
Mao, R.. On the total number of parts functions associated with ranks of partitions modulo 5 and 7. Ramanujan J. 58 (2022), 1201–1243.CrossRefGoogle Scholar
Mao, R.. Congruences for Andrews–Beck partition statistics modulo powers of primes. Adv. Appl. Math. 146 (2023), 102488.CrossRefGoogle Scholar
Passary, D., Studies of partition functions with conditions on parts and parity, Thesis (Ph.D.), The Pennsylvania State University. 2019. p. 84.Google Scholar
Ray, C. and Barman, R.. On Andrews’ integer partitions with even parts below odd parts. J. Number Theory 215 (2020), 321–338.CrossRefGoogle Scholar
Sagan, B. E., The Symmetric Group: Representations, Combinatorial Algorithms, and Symmetric Functions, 2nd ed., Grad. Texts in Math., Vol. 203 (New York, Springer-Verlag: 2001).CrossRefGoogle Scholar
Stanley, R. P.. Some remarks on sign-balanced and maj-balanced posets. Adv. Appl. Math. 34 (2005), 880–902.CrossRefGoogle Scholar
Wang, L.. Parity of coefficients of mock theta functions. J. Number Theory 229 (2021), 53–99.CrossRefGoogle Scholar
Watson, G. N.. The final problem: an account of the mock theta functions. J. London Math. Soc. 11 (1936), 55–80.CrossRefGoogle Scholar
Yao, O. X. M.. Proof of a Lin–Peng–Toh's conjecture on an Andrews–Beck type congruence. Discrete Math. 345 (2022), 112672.CrossRefGoogle Scholar