Hostname: page-component-5b777bbd6c-cp4x8 Total loading time: 0 Render date: 2025-06-19T18:19:57.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Truncated Jacobi triple product series II: Li, Lin, and Wang’s nonnegativity conjecture

Published online by Cambridge University Press:  19 June 2025

Shane Chern  and
Chun Wang
Shane Chern
Affiliation:
Fakultät für Mathematik, Universität Wien, Oskar-Morgenstern-Platz 1, Wien 1090, Austria (chenxiaohang92@gmail.com)
Chun Wang
Affiliation:
Department of Mathematics, Shanghai Normal University, Shanghai 200234, P.R. China (wangchun@shnu.edu.cn) (corresponding author)
Get access Rights & Permissions [Opens in a new window]

Abstract

The investigation of truncated theta series was popularized by Andrews and Merca. In this article, we establish an explicit expression with nonnegative coefficients for the bivariate truncated Jacobi triple product series: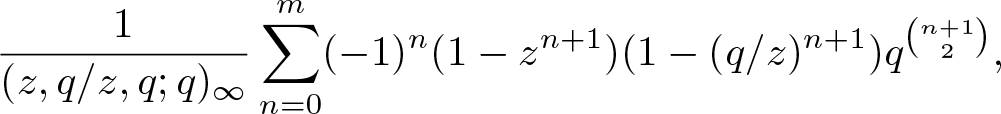

\begin{equation*}\frac{1}{(z,q/z,q;q)_\infty}\sum_{n=0}^{m}(-1)^n(1-z^{n+1})(1-(q/z)^{n+1})q^{\binom{n+1}{2}},\end{equation*}

which can be regarded as a companion to Wang and Yee’s truncation of the triple product identity. As applications, our result confirms a conjecture of Li, Lin, and Wang and implies a family of linear inequalities for a bi-parametric partition function. We also work on another truncated triple product series arising from the work of Xia, Yee, and Zhao and derive similar nonnegativity results and linear inequalities.

Keywords

Bailey pairJacobi triple product identitylinear inequalities for partition functionsnonnegativitytruncated theta series11P8411F2705A2033D90
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrews, G. E.. q-Series: Their development and application in analysis, number theory, combinatorics, physics, and computer algebra (American Mathematical Society, Providence, RI, 1986).Google Scholar
Andrews, G. E.. Bailey chains and generalized Lambert series. I. Four identities of Ramanujan. Illinois J. Math. 36 (1992), 251–274.10.1215/ijm/1255987533CrossRefGoogle Scholar
Andrews, G. E.. The theory of partitions (Cambridge University Press, Cambridge, 1998).Google Scholar
Andrews, G. E. and Merca, M.. The truncated pentagonal number theorem. J. Combin. Theory Ser. A 119 (2012), 1639–1643.10.1016/j.jcta.2012.05.001CrossRefGoogle Scholar
Andrews, G. E. and Merca, M.. Truncated theta series and a problem of Guo and Zeng. J. Combin. Theory Ser. A 154 (2018), 610–619.10.1016/j.jcta.2017.10.003CrossRefGoogle Scholar
Berkovich, A. and Garvan, F. G.. Some observations on Dyson’s new symmetries of partitions. J. Combin. Theory Ser. A 100 (2002), 61–93.10.1006/jcta.2002.3281CrossRefGoogle Scholar
Corteel, S. and Lovejoy, J.. Overpartitions. Trans. Amer. Math. Soc. 356 (2004), 1623–1635.10.1090/S0002-9947-03-03328-2CrossRefGoogle Scholar
Fine, N. J.. Basic hypergeometric series and applications (American Mathematical Society, Providence, RI, 1988).10.1090/surv/027CrossRefGoogle Scholar
Gasper, G. and Rahman, M.. Basic hypergeometric series. 2nd edn (Cambridge University Press, Cambridge, 2004).10.1017/CBO9780511526251CrossRefGoogle Scholar
Guo, V. J. W. and Zeng, J.. Two truncated identities of Gauss. J. Combin. Theory Ser. A 120 (2013), 700–707.10.1016/j.jcta.2012.12.004CrossRefGoogle Scholar
Li, X., Lin, B. L. S. and Wang, A. Y. Z.. Strong truncated Jacobi triple product series. Submitted.Google Scholar
Mao, R.. Proofs of two conjectures on truncated series. J. Combin. Theory Ser. A 130 (2015), 15–25.10.1016/j.jcta.2014.10.004CrossRefGoogle Scholar
Wang, C. and Yee, A. J.. Truncated Jacobi triple product series. J. Combin. Theory Ser. A 166 (2019), 382–392.10.1016/j.jcta.2019.03.003CrossRefGoogle Scholar
Xia, E. X. W., Yee, A. J. and Zhao, X.. New truncated theorems for three classical theta function identities. European J. Combin. 101 (2022), .10.1016/j.ejc.2021.103470CrossRefGoogle Scholar
Yee, A. J.. A truncated Jacobi triple product theorem. J. Combin. Theory Ser. A 130 (2015), 1–14.10.1016/j.jcta.2014.10.005CrossRefGoogle Scholar