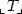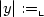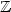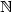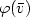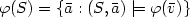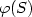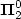Refine listing
Actions for selected content:
A nonstandard spirit among computer scientists:a tribute to Serge Grigorieff at the occasion of his 60th birthday
Volume
42 -
Issue 1
-
January 2008
Contents
Introduction
Preface
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 1-4
-
- Article
- Export citation
Research Article
Tree inclusion problems
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 5-20
-
- Article
- Export citation
About the domino problem in the hyperbolic plane from an algorithmicpoint of view
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 21-36
-
- Article
- Export citation
Exemples de classes d'automates cellulaires
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 37-53
-
- Article
- Export citation
An intrinsically non minimal-time Minsky-like 6-states solution to the Firing Squad synchronization problem
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 55-68
-
- Article
- Export citation
A complete characterization of primitive recursive intensionalbehaviours
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 69-82
-
- Article
- Export citation
When is the orbit algebra of a groupan integral domain ? Proof of a conjecture of P.J. Cameron
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 83-103
-
- Article
- Export citation
Arithmetization of the field of realswith exponentiation extended abstract
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 105-119
-
- Article
- Export citation
Deciding whether a relation defined inPresburger logiccan be defined in weaker logics
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 121-135
-
- Article
- Export citation
Weakly maximal decidable structures
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 137-145
-
- Article
- Export citation
Computing the jth solutionof a first-order query
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 147-164
-
- Article
- Export citation
Learning discrete categorial grammars from structures
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 165-182
-
- Article
- Export citation
On the continuity setof an Omega rational function
-
- Published online by Cambridge University Press:
- 18 January 2008, pp. 183-196
-
- Article
- Export citation