Hostname: page-component-784d4fb959-mvngg Total loading time: 0 Render date: 2025-07-14T14:55:57.414Z Has data issue: false hasContentIssue false
  • English
  • Français

SELF-REFERENCE IN ARITHMETIC II

Published online by Cambridge University Press:  07 October 2014

VOLKER HALBACH  and
ALBERT VISSER
VOLKER HALBACH*
Affiliation:
Oxford University
ALBERT VISSER*
Affiliation:
Utrecht University
*
*NEW COLLEGE OXFORD, OX1 3BN, ENGLAND E-mail: volker.halbach@new.ox.ac.uk
†PHILOSOPHY, FACULTY OF HUMANITIES UTRECHT UNIVERSITY JANSKERHOF 13 3512 BL UTRECHT, THE NETHERLANDS E-mail: albert.visser@phil.uu.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

In this sequel to Self-reference in arithmetic I we continue our discussion of the question: What does it mean for a sentence of arithmetic to ascribe to itself a property? We investigate how the properties of the supposedly self-referential sentences depend on the chosen coding, the formulae expressing the properties and the way a fixed point for the expressing formulae are obtained. In this second part we look at some further examples. In particular, we study sentences apparently expressing their Rosser-provability, their own 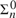${\rm{\Sigma }}_n^0$-truth or their own 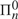${\rm{\Pi }}_n^0$-truth. Finally we offer an assessment of the results of both papers.

Information

Type
Research Article
Information
The Review of Symbolic Logic , Volume 7 , Issue 4 , December 2014 , pp. 692 - 712
Copyright
Copyright © Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

BIBLIOGRAPHY

Burgess, J. P. (1986, September). The truth is never simple. Journal of Symbolic Logic, 51, 663–81.CrossRefGoogle Scholar
Feferman, S. (1960). Arithmetization of metamathematics in a general setting. Fundamenta Mathematicae, 49, 35–91.Google Scholar
Guaspari, D., & Solovay, R. M. (1979). Rosser sentences. Annals of Mathematical Logic, 16, 81–99.Google Scholar
Hájek, P., & Pudlák, P. (1993). Metamathematics of First-Order Arithmetic. Perspectives in Mathematical Logic, Vol. 3. Berlin: Springer.CrossRefGoogle Scholar
Halbach, V. (1994). A system of complete and consistent truth. Notre Dame Journal of Formal Logic, 35, 311–327.Google Scholar
Heck, R. (2007). Self-reference and the languages of arithmetic. Philosophia Mathematica, 15, 1–29.CrossRefGoogle Scholar
Kaye, R. (1991). Models of Peano Arithmetic. Oxford Logic Guides. Oxford: Oxford University Press.CrossRefGoogle Scholar
Kreisel, G. (1953). On a problem of Henkin’s. Indagationes Mathematicae, 15, 405–406.Google Scholar
Kreisel, G., & Lévy, A. (1968). Reflection principles and their use for establishing the complexity of axiomatic systems. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 14, 97–142.CrossRefGoogle Scholar
Kurahashi, T. (2014). Henkin sentences and local reflection principles for Rosser provability. To appear.Google Scholar
Ono, H. (1987). Reflection principles in fragments of Peano arithmetic. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 33, 317–333.CrossRefGoogle Scholar
Shavrukov, V. Y. (1994). A smart child of Peano’s. Notre Dame Journal of Formal Logic, 35, 161–185.Google Scholar
Visser, A. (1989). Peano’s smart children: A provability logical study of systems with built-in consistency. Notre Dame Journal of Formal Logic, 30, 161–196.Google Scholar
Visser, A. (2004). Semantics and the liar paradox. In Gabbay, D., & Guenthner, F., editors. Handbook of Philosophical Logic (second ed.), Vol. 11, Heidelberg: Springer, 149–240.Google Scholar
van Fraassen, B. C. (1970). Inference and self-reference. Synthese, 21, 425–438.Google Scholar
von Bülow, C. (2008). A remark on equivalent Rosser sentences. Annals of Pure and Applied Logic, 151, 62–67.Google Scholar
Voorbraak, F. (1989). A simplification of the completeness proofs for Guaspari and Solovay’s R. Notre Dame Journal of Formal Logic, 31, 44–63.Google Scholar