FreeCHR – An Algebraic Framework for Constraint Handling Rules Embeddings

Abstract

We introduce the framework FreeCHR which formalizes the embedding of Constraint Handling Rules (CHR) into a host language, using the concept of initial algebra semantics from category theory. We hereby establish a high-level implementation scheme for CHR as well as a common formalization for both theory and practice. We propose a lifting of the syntax of CHR via an endofunctor in the category Set and a lifting of the very abstract operational semantics of CHR into FreeCHR, using the free algebra, generated by the endofunctor. We give proofs for soundness and completeness with its original definition. We also propose a first abstract execution algorithm and prove correctness with the operational semantics. Finally, we show the practicability of our approach by giving two possible implementations of this algorithm in Haskell and Python. Under consideration in Theory and Practice of Logic Programming.

1 Introduction

Constraint Handling Rules (CHR) is a rule-based programing language that is designed to be embedded into a general-purpose language. Having a CHR implementation available enables software developers to solve problems in a declarative and elegant manner. Aside from the obvious task of implementing constraint solvers (Frühwirth (2006); De Koninck et al. (2006)), it has been used, for example, to solve scheduling problems (Abdennadher and Marte (2000)) implement concurrent and multi-agent systems (Thielscher (2002, 2005); Lam and Sulzmann (2006, 2007)). In general, CHR is ideally suited for any problem that involves the transformation of collections of data, as programs consist of a set of rewriting rules, hiding away the process of finding suitable candidates for rule application. Hereby, we get a purely declarative representation of the algorithm without the otherwise necessary boilerplate code.

The literature on CHR as a formalism consists of a rich body of theoretical work concerning CHR, including a rigorous formalization of its declarative and operational semantics (Frühwirth (2009); Sneyers et al. (2010); Frühwirth (2015)), relations to other rule-based formalisms (e.g., Betz (2007) and Gall and Frühwirth (2018)) and results on properties like confluence (Christiansen and Kirkeby (2015)).

Implementations of CHR exist for a number of languages, such as Prolog (Schrijvers and Demoen (2004)), C (Wuille et al. (2007)), C++ (Barichard (2024)), Haskell (Lam and Sulzmann (2007); Chin et al. (2003)), JavaScript (Nogatz et al. (2018)) and Java (Abdennadher et al. (2002); Van Weert et al. (2005); Ivanović (2013); Wibiral (2022)).

While the implementations adhere to the formally defined operational semantics, they are not direct implementations of a common formal model. Therefore, the two aspects of CHR (formalism and programing language) are not strictly connected with each other and there is hence no strict guarantee that the results on the formalism CHR are applicable on the programing language CHR. Although, such a strict connection is probably not entirely achievable (unless we define and use everything inside a proof assistant like Coq or Agda), it is desirable to have both formal definition and implementation as closely linked as possible. Additionally, to being able to directly benefit from theoretical results, implementors of CHR embeddings and users of the CHR language can also use the formally defined properties to define more profound tests for their software.

Another apparent issue within the CHR ecosystem is that many of the implementations of CHR are currently unmaintained. Although some of them are mere toy implementations, others might have been of practical use. One example is JCHR (Van Weert et al. (2005)) which would be a useful tool if it was kept on par with the development of Java, especially with modern build tools like Gradle. Having a unified formal model from which every implementation is derived could ease contributing to implementations of CHR as it provides a strict documentation and description of the system a priori. Also, different projects might even be merged which would prevent confusion due to multiple competing, yet very similar implementations, as it can be observed in the miniKanren ecosystem (e.g., there exist about 20 implementations of miniKanren dialects only for Haskell ² ).

A third major issue is that many implementations, like the aforementioned JCHR or CCHR (Wuille et al. (2007)), are implemented as external EDSL, this is, they rely on a separate compiler which translates CHR code into code of the host language. This makes it significantly less convenient to use and hence also less likely to be adopted into the standard distribution of the host language. This is somewhat demonstrated by the K.U.Leuven CHR system which is implemented as a library in Prolog and distributed as a standard package with SWI-Prolog, ³ or by the library core.logic ⁴ which implements miniKanren for the LISP dialect Clojure.

To solve the three issues stated above, we introduce the framework FreeCHR which formalizes the embedding of CHR, using initial algebra semantics. This common concept in functional programing is used to inductively define languages and their semantics (Hudak (1998); Johann and Ghani (2007)). FreeCHR provides both a guideline and high-level architecture to implement and maintain CHR implementations across host languages and a strong connection between the practical and formal aspects of CHR. To our knowledge, the presented execution algorithm and its implementations, although simple, will be the first implementations of CHR for which there are formal proofs of correctness. Also, by FreeCHR-instances being internal embeddings, we get basic tooling like syntax highlighting and type-checking for free (Fowler and Parsons (2011)) and are able to implement CHR as a library, without the need for any external tooling like source-to-source compilers.

Ultimately, the framework shall serve a fourfold purpose by providing

• • a general guideline on how to implement a CHR system in modern high-level languages,

• • a guideline for future maintenance of FreeCHR instances,

• • a common framework for both formal considerations and practical implementations

• • and a framework for the definition and verification of general criteria of correctness.

In this work, we will give first formal definitions of FreeCHR, upon which we will build our future work. Section 2 will provide the necessary background and intuitions. Section 3 introduces the syntax and semantics of Constraint Handling Rules and generalizes them to non-Herbrand domains. Section 4 introduces the framework FreeCHR. Section 4.1 lifts the syntax of CHR programs to a Set-endofunctor and introduces the free algebra, generated by that functor, Section 4.2 lifts the very abstract operational semantics $\omega _a$ of CHR to the very abstract operational semantics $\omega ^{\star }_a$ of FreeCHR and Section 4.3 proves soundness and completeness of $\omega ^{\star }_a$ with respect to $\omega _a$ .

Section 5 introduces a simple execution algorithm for a formal instance with very abstact operational semantics and proves their correctness. This is the second main contribution of this paper, as it gives an example use of a proven correct guideline to implement FreeCHR.

This is finally demonstrated with the two case studies in Section 6. The section provides two implementations of the defined instance in Haskell and Python. The languages were chosen, as they can be considered to be on the opposite sides of a static-dynamic spectrum of programing languages. They will hence give a good intuition of how the host language flavors FreeCHR.

Finally, Section 7 discusses the limitations of FreeCHR as presented in this paper, Section 8 discusses related work, Section 9 will give an overview over planned and ongoing future work and Section 10 concludes the paper.

2 Preliminaries

2.1 Endofunctors and F-algebras

In this section, we want to introduce endofunctors and $F$ -algebras. Both concepts are taken from category theory and will be introduced as instances in the category of sets Set.

We do not assume any previous knowledge of category theory, but to readers more interested in the topic in general we recommend Milewski (2019) as introductory literature.

2.1.1 Basic definitions

The disjoint union of two sets $A$ and $B$

\begin{align*} A \sqcup B = \left \{l_A(a) \mid a \in A\right \} \cup \left \{l_B(b) \mid b \in B\right \} \end{align*}

is the union of both sets with additional labels $l_A$ and $l_B$ added to the elements to keep track of the origin set of each element. We will also use the labels $l_A$ and $l_B$ as injection functions $l_A : A \rightarrow A \sqcup B$ and $l_B : B \rightarrow A \sqcup B$ which construct elements of $A \sqcup B$ from elements of $A$ or $B$ , respectively.

For two functions $f : A \rightarrow C$ and $g : B \rightarrow C$ , the function

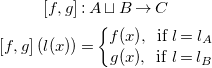\begin{align*} \left [f,g\right ] &: A \sqcup B \rightarrow C\\ \left [f,g\right ](l(x)) &=\left \{\begin{matrix}f(x), & & \mbox{if}\ l = l_A \\ g(x), & & \mbox{if}\ l = l_B \\ \end{matrix}\right . \end{align*}

is called a case analysis function of the disjoint union $A \sqcup B$ . It can be understood as a formal analog to a case-of expression. Furthermore, we define two functions

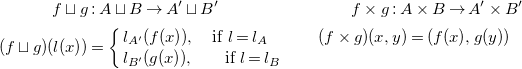\begin{align*} f \sqcup g &: A \sqcup B \rightarrow A' \sqcup B'\qquad \qquad\qquad\qquad f \times g : A \times B \rightarrow A' \times B'\\ (f \sqcup g)(l(x)) &= \left \{ \begin{array}{l} l_{A'}(f(x)),\quad \mbox{if}\ l = l_A \quad \quad \quad (f \times g)(x,y) = (f(x), g(y))\\ l_{B'}(g(x)),\,\,\,\,\quad \mbox{if}\ l = l_B \end{array} \right . \end{align*}

which lift two functions $f : A \rightarrow A'$ and $g : B \rightarrow B'$ to the disjoint union and the Cartesian product, respectively.

2.1.2 Endofunctors

A Set-endofunctor ⁵ $F$ maps all sets $A$ to sets $F A$ and all functions $f : A \rightarrow B$ to functions $F f : F A \rightarrow F B$ , such that $F \mathbf{id}_A = \mathbf{id}_{F A}$ and $F (g \circ f) = F g \circ F f$ , where $\mathbf{id}_X(x) = x$ is the identity function on a set $X$ . ⁶ A signature $\Sigma = \left \{\sigma _1/a_1,\ldots ,\sigma _n/a_n\right \}$ , where $\sigma _i$ are operators and $a_i$ their arity, generates a functor

\begin{align*} F_{\Sigma } X = \bigsqcup _{\sigma /a\in \Sigma } X^{a} && F_{\Sigma } f = \bigsqcup _{\sigma /a\in \Sigma } f^{a} \end{align*}

with $X^0 = \unicode[times]{x1D7D9}$ and $f^0 = \mathbf{id}_{\unicode[times]{x1D7D9}}$ , where $\unicode[times]{x1D7D9}$ is a singleton set. Such a functor $F_{\Sigma }$ models flat (this is, not nested) terms over the signature $\Sigma$ .

Example 1. The signature

\begin{align*} \Gamma = \left \{\mathbf{0}/0, \oplus /2, \mathbf{1}/0, \otimes /2\right \} \end{align*}

models two constants $\mathbf{0}$ and $\mathbf{1}$ , as well as two binary operators $\oplus$ and $\otimes$ . It generates the functor

\begin{align*} F_{\Gamma } X &= \unicode[times]{x1D7D9} \sqcup X \times X \sqcup \unicode[times]{x1D7D9} \sqcup X \times X\\ F_{\Gamma } f &= \mathbf{id}_{\unicode[times]{x1D7D9}} \sqcup f \times f \sqcup \mathbf{id}_{\unicode[times]{x1D7D9}} \sqcup f \times f \end{align*}

2.1.3 $F$ -algebras

Since an endofunctor $F$ defines the syntax of terms, an evaluation function $\alpha : F A \rightarrow A$ defines the semantics of terms. We call such a function $\alpha$ , together with its carrier $A$ , an $F$ -algebra $(A, \alpha )$ .

If there are two $F$ -algebras $\left (A, \alpha \right )$ and $\left (B, \beta \right )$ and a function $h : A \rightarrow B$ , we call $h$ an $F$ -algebra homomorphism if and only if $h \circ \alpha = \beta \circ F h$ , that is $h$ preserves the structure of $\left (A, \alpha \right )$ in $\left (B, \beta \right )$ when mapping $A$ to $B$ . In this case, we also write $h : \left (A,\alpha \right ) \rightarrow \left (B, \beta \right )$ .

A special $F$ -algebra is the free $F$ -algebra $F^{\star } = (\mu F, \mathbf{in}_F)$ , for which there is a homomorphism ${(\!| \alpha |\!)} : F^{\star } \rightarrow \left (A, \alpha \right )$ for any other algebra $\left (A, \alpha \right )$ . We call those homomorphisms $(\!| \alpha |\!)$ $F$ -catamorphisms. The functions $(\!| \alpha |\!)$ encapsulate structured recursion on values in $\mu F$ with the semantics defined by the function $\alpha$ which is itself only defined on flat terms. The carrier of $F^{\star }$ , with $\mu F = F \mu F$ , is the set of inductively defined values in the shape defined by $F$ . The function $\mathbf{in}_F : F \mu F \rightarrow \mu F$ inductively constructs the values in $\mu F$ .

Example 2. The initial $F_{\Gamma }$ -algebra

\begin{align*} \left (\mu F_{\Gamma }, \left [\mathbf{0}, \oplus , \mathbf{1}, \otimes \right ]\right ) \end{align*}

can be used to construct the nested expressions like $\mathbf{1} \oplus (\mathbf{1} \otimes \mathbf{0})$ of $\mu F_{\Gamma }$ . The $F_\Gamma$ algebras

\begin{align*} \left(\unicode[times]{x1D7DA}, \left [{\mathit{false}}, {\vee }, {\mathit{true}}, {\wedge }\right ]\right ) && \left (\mathbb{N}_0, \left [0, +, 1, \cdot \right ]\right ) \end{align*}

give to $F_{\Gamma }$ the semantics of Boolean and arithmetic expressions, respectively. Using the catamorphism ${(\!| \!\left [{\mathit{false}}, {\vee }, {\mathit{true}}, {\wedge }\right ]\! |\!)} : \mu F_{\Gamma } \rightarrow \unicode[times]{x1D7DA}$ , we can evaluate the expression from above as

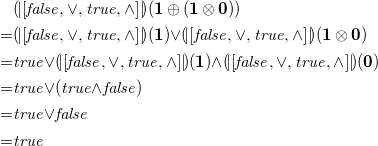\begin{align*} &{(\!| \!\left [{\mathit{false}}, {\vee }, {\mathit{true}}, {\wedge }\right ]\! |\!)}(\mathbf{1} \oplus (\mathbf{1} \otimes \mathbf{0}))\\ = &{(\!| \!\left [{\mathit{false}}, {\vee }, {\mathit{true}}, {\wedge }\right ]\! |\!)}(\mathbf{1}) {\vee } {(\!| \!\left [{\mathit{false}}, {\vee }, {\mathit{true}}, {\wedge }\right ]\! |\!)}(\mathbf{1} \otimes \mathbf{0})\\ = &{\mathit{true}} {\vee } {(\!| \!\left [{\mathit{false}}, {\vee }, {\mathit{true}}, {\wedge }\right ]\! |\!)}(\mathbf{1}) {\wedge } {(\!| \!\left [{\mathit{false}}, {\vee }, {\mathit{true}}, {\wedge }\right ]\! |\!)}(\mathbf{0})\\ = &{\mathit{true}} {\vee } ({\mathit{true}} {\wedge } {\mathit{false}})\\ = &{\mathit{true}} {\vee } {\mathit{false}}\\ = &{\mathit{true}} \end{align*}

Analogously, if we use ${(\!| \!\left [0, +, 1, \cdot \right ]\! |\!)} : \mu F_{\Gamma } \rightarrow \mathbb{N}_0$ , we get

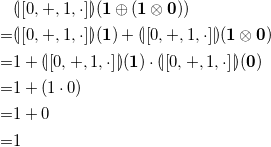\begin{align*} &{(\!| \!\left [0, +, 1, \cdot \right ]\! |\!)}(\mathbf{1} \oplus (\mathbf{1} \otimes \mathbf{0}))\\ = &{(\!| \!\left [0, +, 1, \cdot \right ]\! |\!)}(\mathbf{1}) + {(\!| \!\left [0, +, 1, \cdot \right ]\! |\!)}(\mathbf{1} \otimes \mathbf{0})\\ = &1 + {(\!| \!\left [0, +, 1, \cdot \right ]\! |\!)}(\mathbf{1}) \cdot {(\!| \!\left [0, +, 1, \cdot \right ]\! |\!)}(\mathbf{0})\\ = &1 + (1 \cdot 0)\\ = &1 + 0\\ = &1 \end{align*}

Technically, the constants $\mathbf{0}$ , $\mathbf{1}$ , $\mathrm{false}$ , $\mathrm{true}$ , $0$ and $1$ are supposed to be functions from the singleton set $\unicode[times]{x1D7D9}$ to the respective carrier. Since $\unicode[times]{x1D7D9}$ only has one element, there is essentially no difference between such a function and the constant itself. We will hence use the constant directly.

2.2 Labeled transition systems

In this section, we will lay out our definition and notation of labeled transition systems and notions of soundness and completeness.

Definition 1 (Labeled transition system). A labeled transition system (LTS) is a structure $\langle S, A, R \rangle$ , where $S$ is the set of states called the domain of the system, $A$ is a set of labels and $R \in S \times A \times S$ a ternary transition relation.

For an LTS $\omega = \langle S, A, \mapsto \rangle$ , we write , if $(s, a, s') \in (\mapsto )$ and for . Also, we will write if there is an $a \in A$ , such that , for $n \geq 0$ .

Definition 2 ( $\theta$ -Soundness). Given two labeled transition systems $\omega = \langle S, A, \mapsto \rangle$ and $\omega ' = \langle S, A', \hookrightarrow \rangle$ . For function $\theta : A \rightarrow A'$ , we call $\omega$ $\theta$ -sound with respect to $\omega '$ if and only if

for all $s, s' \in S$ and $a \in A$ ⁷ .

$\theta$ -soundness means that any transition defined by $\omega$ is also defined by $\omega '$ , when mapping labels with $\theta$ . This is typically used to verify a more constrained system ( $\omega$ ) against a more general one ( $\omega '$ ).

Dually, there exists a concept of completeness.

Definition 3 ( $\theta$ -Completeness). Given two labeled transition systems $\omega = \langle S, A, \mapsto \rangle$ and $\omega ' = \def\luminalatbreak{} \langle S, A', \hookrightarrow \rangle$ . For a function $\theta : A \rightarrow A'$ , we call $\omega$ $\theta$ -complete with respect to $\omega '$ if and only if

for all $s, s' \in S$ and $a \in A$ .

$\theta$ -completeness means that $\omega$ defines all transitions that are defined by $\omega '$ , but using only the mapped labels of $\omega$ .

We will also need a slightly relaxed notion of soundness.

Definition 4 ( $\theta$ -Soudness up to repeated transition). Given two labeled transition systems $\omega = \langle S, A, \mapsto \rangle$ and $\omega ' = \langle S, A', \hookrightarrow \rangle$ . For a function $\theta : A \rightarrow A'$ , we call $\omega$ $\theta$ -sound up to repeated transition with respect to $\omega '$ if and only if

for all $s, s' \in S$ , $a \in A$ and $l \geq 0$ .

This definition says that an LTS is also $\theta$ -sound with respect to another if we can accomplish a transition in one LTS with zero or more transitions in the other.

3 CHR over non-Herbrand domains

The first implementations of CHR were embedded into the logical programing language Prolog, where terms like are not evaluated, as is the case in most other programing languages, but interpreted as themselves. This is called the Herbrand interpretation of terms. Since we want to embed CHR in any programing language, we need to generalize the language to non-Herbrand interpretations of terms. We will formalize this, using initial algebra semantics.

3.1 Host language

We first define a data type in the host language. A data type determines the syntax and semantics of terms via a functor $\Lambda _T$ and an algebra $\tau _T$ . The fixed point $\mu \Lambda _T$ contains terms that are inductively defined via $\Lambda _T$ and the catamorphism $(\!| \tau _T |\!)$ evaluates those terms to values of $T$ .

Definition 5 (Data types). A data type is a triple $\langle T, \Lambda _{T}, \tau _T\rangle$ , where $T$ is a set, $\Lambda _T$ a functor and $\left (T, \tau _T\right )$ a $\Lambda _T$ -algebra.

We write $t \equiv _{T} t'$ for $t \in \mu \Lambda _T$ and $t' \in T$ if and only if ${(\!| \tau _T |\!)}(t) = t'$ .

Example 3 (Boolean data type). The signature

\begin{align*} \Sigma _{\unicode[times]{x1D7DA}} =& \left \{(n \leq m)/0 \mid n,m\in \mathbb{N}_0\right \} \cup \left \{(n \lt m)/0 \mid n,m\in \mathbb{N}_0\right \} \cup \left \{{\wedge }/2, {\mathit{true}}/0, {\mathit{false}}/0\right \} \end{align*}

defines Boolean terms ⁸ . $\Sigma _{\unicode[times]{x1D7DA}}$ generates the functor

\begin{align*} \Lambda _{\unicode[times]{x1D7DA}} X =&\ \mathbb{N}_0 \times \mathbb{N}_0 \sqcup \ \mathbb{N}_0 \times \mathbb{N}_0 \sqcup \ X \times X \sqcup \unicode[times]{x1D7D9} \sqcup \unicode[times]{x1D7D9} \end{align*}

the fixed point, $\mu \Lambda _{\unicode[times]{x1D7DA}}$ , of which is the set of valid nested Boolean terms like $\left (0 \lt 4 {\wedge } 4 \leq 6\right )$ . Let $\langle \unicode[times]{x1D7DA}, \Lambda _{\unicode[times]{x1D7DA}}, \tau _{\unicode[times]{x1D7DA}} \rangle$ , with $\unicode[times]{x1D7DA} = \left \{{\mathit{true}}, {\mathit{false}}\right \}$ , be a data type. If we assume $\tau _{\unicode[times]{x1D7DA}}$ to implement the usual semantics for Boolean terms and comparisons, $\left (0 \lt 4 {\wedge } 4 \leq 6\right )$ will evaluate as

\begin{align*} {(\!| \tau _{\unicode[times]{x1D7DA}} |\!)}(0 \lt 4 \,{\wedge }\, 4 \leq 6) = {(\!| \tau _{\unicode[times]{x1D7DA}} |\!)}(0 \lt 4) {\wedge } {(\!| \tau _{\unicode[times]{x1D7DA}} |\!)}(4 \leq 6) = {\mathit{true}}\, {\wedge }\, {\mathit{true}} = {\mathit{true}} \end{align*}

For a set $T$ , both $\Lambda _T$ and $\tau _T$ are determined by the host language which is captured by the next definition.

Definition 6 (Host environment). A mapping

\begin{align*} \mathcal{L} T = \langle T, \Lambda _T, \tau _T \rangle \end{align*}

where $\langle T, \Lambda _T, \tau _T \rangle$ is a data type, is called a host environment.

A host environment is implied by the host language (and by the program, the CHR program is part of) and assigns to a set $T$ a data type, effectively determining syntax and semantics of terms that evaluate to values of $T$ .

3.2 Embedding CHR

With the formalization of our host environment, we can define the syntax and semantics of CHR.

Definition 7 (CHR programs). CHR programs are sets of multiset-rewriting rules of the form

\begin{align*} &N\ @\ K\ \setminus \ R\ \Longleftrightarrow \ G\ |\ B \end{align*}

For a set $C$ , called the domain of the program, for which there is a data type $\mathcal{L} C = \langle C, \Lambda _C, \tau _C \rangle$ , $K, R \in {\mathtt {list}} C$ are called the kept and removed head, respectively. The backslash ( $\setminus$ ) is used to separate the kept and removed part of the head. Either $K$ or $R$ must be non-empty. If either head part is empty, the separator is omitted as well.

${\mathtt {list}} X = \bigcup _{i\in \mathbb{N}_0} X^i$ maps a set $X$ to the set of lists over X, with $X^0 = {\varepsilon }$ being the empty sequence, and functions $f : A \rightarrow B$ to functions

\begin{align*} {\mathtt {list}} f \left (a_1, \ldots , a_n\right ) = \left (f(a_1), \ldots , f(a_n)\right ) \end{align*}

The optional $G \in \mu \Lambda _{\unicode[times]{x1D7DA}}$ is called the guard. If $G$ is omitted, we assume $G \equiv _{\unicode[times]{x1D7DA}} {\mathit{true}}$ and omit the pipe ( $|$ ) which separates the guard from the body as well. $B \in {\mathtt {mset}}\mu \Lambda _C$ is called the body. The functor $\mathtt {mset}$ maps sets $X$ to the set of multisets over $X$ and functions $f : X \rightarrow Y$ to functions

\begin{align*} {\mathtt {mset}} f \left (\left \{a_1, a_2, \ldots \right \}\right ) = \left \{f(a_1), f(a_2), \ldots \right \} \end{align*}

$N$ is an optional name for the rule, which is generally used for debugging and tracing. The $@$ symbol is used to separate the name of the rule from the rule itself. It is also omitted if the rule is not given a name.

The members of the kept and removed head are matched against values of the domain $C$ . The guard $G$ is a term that can be evaluated to a Boolean value. The body $B$ is a multiset over terms which can be evaluated to values of $C$ . This includes any call of functions or operators which evaluate to Boolean, or values of $C$ , respectively.

In literature, rules with an empty kept head are called simplification rules and rules with an empty removed head propagation rules. Rules which have both a removed and kept head are called simpagation rules.

Definition7 corresponds to the positive range-restricted ground segment of CHR which is commonly used as the target for embeddings of other (rule-based) formalisms (e.g., colored Petri nets as by Betz (2007)) into CHR (Frühwirth, 2009, Chapter 6.2). Positive means that the body of the rule contains only user constraints (this is, values from $C$ ) which guarantees that computations do not fail. Range-restricted means that instantiating all variables of the head ( $K$ and $R$ ) will ground the whole rule. This also maintains the groundness of the segment of CHR which requires that the input and output of a program are ground. $\mathbf{PRG}_{C}$ denotes the set of all such programs over a domain $C$ .

Example 4 (Euclidean algorithm). The program $\textrm {GCD}=\left \{\mathit{zero}, \mathit{subtract}\right \}$ ⁹

\begin{align*} \mathit{zero}\ &@\ 0\ \Leftrightarrow \ \emptyset \\ \mathit{subtract}\ &@\ N\ \setminus \ M\ \Leftrightarrow \ 0 \lt N {\wedge } 0 \lt M {\wedge } N \leq M\ |\ M-N \end{align*}

computes the greatest common divisor of a collection of natural numbers. The first rule removes all zeros from the collection. For any pair of numbers $N$ and $M$ greater $0$ and $N \leq M$ , the second rule replaces $M$ by $M-N$ . Note that we omitted the kept head and guard of the $zero$ rule.

Definition 8 ( $C$ -instances of rules). For a positive range-restricted rule

\begin{align*} R\ @\ k_1,\ldots ,k_n\ \setminus \ r_{1},\ldots ,r_{m}\ \Leftrightarrow \ G\ |\ B \end{align*}

with universally quantified variables $v_1,\ldots ,v_l$ , and a data type $\mathcal{L} C = \langle C, \Lambda _{C}, \tau _{C} \rangle$ , we call the set

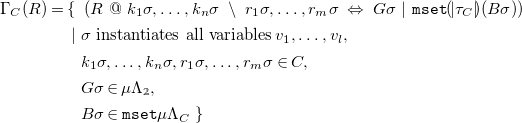\begin{align*} \Gamma _{C}(R) = \{\ &\left (R\ @\ k_1\sigma ,\ldots ,k_n\sigma \ \setminus \ r_{1}\sigma ,\ldots ,r_{m}\sigma \ \Leftrightarrow \ G\sigma \ |\ {\mathtt {mset}}{(\!| \tau _{C} |\!)}(B\sigma ) \right ) \\ \mid \ &\sigma \ \mbox{instantiates all variables}\, v_1, \ldots , v_l,\\ \ &k_1\sigma ,\ldots ,k_n\sigma , r_1\sigma ,\ldots ,r_m\sigma \in C,\\ \ &G \sigma \in \mu \Lambda _{\unicode[times]{x1D7DA}},\\ \ &B \sigma \in {\mathtt {mset}}\mu \Lambda _C\ \} \end{align*}

the $C$ -grounding of $R$ . Analogously, for a set $\mathcal{R}$ of rules, $\Gamma _C(\mathcal{R}) = \bigcup _{R \in \mathcal{R}} \Gamma _C(R)$ is the $C$ -grounding of $\mathcal{R}$ . An element $r' \in \Gamma _{C}(R)$ (or $\Gamma _C(\mathcal{R})$ respectively) is called a $C$ -instance of a rule $R \in \mathcal{R}$ .

A C-instance (or grounding) is obtained, by instantiating all variables and evaluating the then ground terms in the body of the rule, using the $\Lambda _C$ -catamorphism $(\!| \tau _C |\!)$ . The functor $\mathtt {mset}$ is used to lift $(\!| \tau _C |\!)$ into the multiset.

Example 5. Given a body $\left \{M - N\right \}$ and a substitution $\sigma = \left \{N \mapsto 4, M \mapsto 6\right \}$ , the body is instantiated like

\begin{align*} {\mathtt {mset}}{(\!| \tau _C |\!)}(\left \{M-N\right \}\sigma ) = {\mathtt {mset}}{(\!| \tau _C |\!)}(\left \{6-4\right \}) = \left \{{(\!| \tau _C |\!)}(6-4)\right \} = \left \{2\right \} \end{align*}

With Example5, we can also easily see that if we use a data type $\mathcal{L}\mu \Lambda _C = \langle \mu \Lambda _C, \Lambda _C, \mathbf{in}_{\Lambda _C} \rangle$ we get the Herbrand interpretation of terms over $C$ . Hence, for instance, an expression $\left (3+4\right ) \in \mu \Lambda _{\mathbb{N}_0}$ is evaluated to itself, as it is the case in Prolog.

Example 6 ( $C$ -instances). If we instantiate the rule

\begin{align*} subtract\ &@\ N\ \setminus \ M\ \Leftrightarrow \ 0 \lt N {\wedge } 0 \lt M {\wedge } N \leq M\ |\ M-N \end{align*}

with $\sigma _1 = \left \{N \mapsto 4, M \mapsto 6\right \}$ and $\sigma _2 = \left \{N \mapsto 0,M \mapsto 6\right \}$ , respectively, we get the $\mathbb{N}_0$ -instances

\begin{align*} (subtract) \sigma _1 = subtract\ &@\ 4\ \setminus \ 6\ \Leftrightarrow \ 0 \lt 4 {\wedge } 0 \lt 6 {\wedge } 4 \leq 6\ |\ 2\\ (subtract) \sigma _2 = subtract\ &@\ 0\ \setminus \ 6\ \Leftrightarrow \ 0 \lt 0 {\wedge } 0 \lt 6 {\wedge } 0 \leq 6\ |\ 6 \end{align*}

Both instances are elements of the $\mathbb{N}_0$ -grounding $\Gamma _{\mathbb{N}_0}\left (\textrm {GCD}\right )$ of the program in Example  4 .

Classically, the guard $G$ contains constraints which are defined with respect to a constraint theory $\mathcal{CT}$ . We typically write $\mathcal{CT} \models G$ ¹⁰ to denote that the guard is satisfiable with respect to $\mathcal{CT}$ and $\mathcal{CT} \models {\neg } G$ otherwise. Since in our case $G \in \mu \Lambda _{\unicode[times]{x1D7DA}}$ , $\mathcal{CT}$ is essentially $\tau _{\unicode[times]{x1D7DA}}$ , as it determines the semantics of Boolean terms. We thus write

\begin{align*} \tau _{\unicode[times]{x1D7DA}} \models G \Longleftrightarrow G \equiv _{\unicode[times]{x1D7DA}} {\mathit{true}} && \tau _{\unicode[times]{x1D7DA}} \models {\neg } G \Longleftrightarrow G \equiv _{\unicode[times]{x1D7DA}} {\mathit{false}} \end{align*}

Note that we always need a data type $\mathcal{L} \unicode[times]{x1D7DA}$ . In Prolog, for instance, $\unicode[times]{x1D7DA}$ corresponds to the set , representing successful or failed computations, respectively.

Finally, the operational semantics of CHR is defined as a state transition system where the states are multisets ¹¹ over the elements of $C$ .

Definition 9 (Very abstract operational semantics of CHR). The very abstract operational semantics of CHR programs over a domain $C$ is given by the labeled transition system

\begin{align*} \omega _a = \langle {\mathtt {mset}} C, {\mathbf{PRG}_{C}}, \mapsto \rangle \end{align*}

where the transition relation $\left (\mapsto \right )$ is defined by the inference rules in Figure 1 .

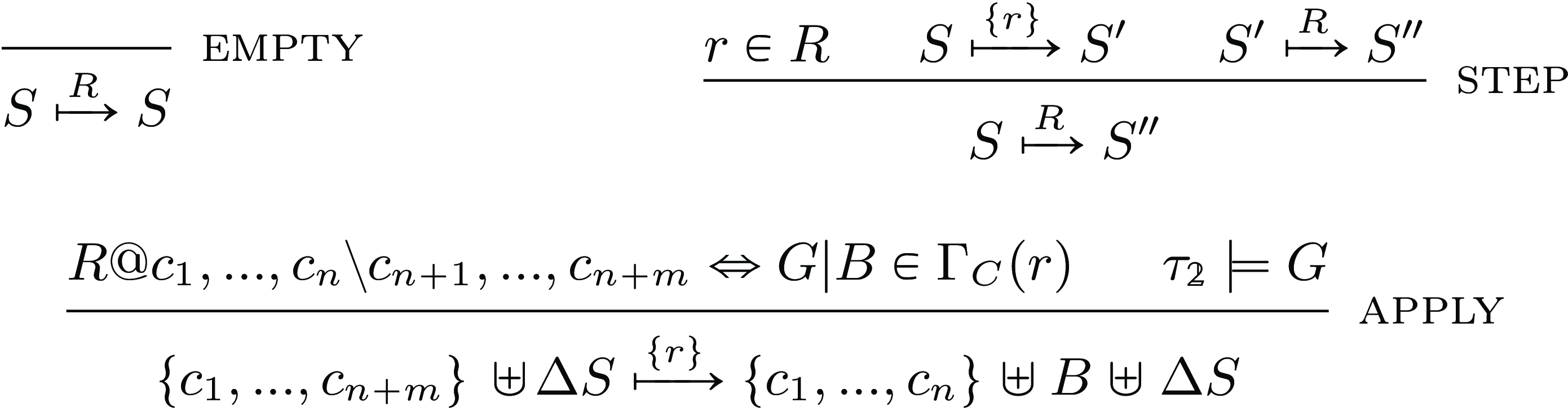
Fig. 1. Very abstract operational semantics for ground and pure CHR.

Rules are applied until no more are applicable to the state, this is, we have reached a final state.

Example 7 ( $\omega _a$ -transitions). Intuitively, both

\begin{align*} \tau _{\unicode[times]{x1D7DA}} \models 0 \lt 4 {\wedge } 0 \lt 6 {\wedge } 4 \leq 6 && \mbox{and} && \tau _{\unicode[times]{x1D7DA}} \models {\neg } (0 \lt 0 {\wedge } 0 \lt 6 {\wedge } 0 \leq 6) \end{align*}

hold. Hence, we can prove the transition , but not .

The following example shows the execution of the Euclidean algorithm as a final example of the operational semantics of CHR.

Example 8 (Euclidean algorithm (cont.)). The rules of GCD are applied until exhaustion, leaving only the greatest common divisor of all numbers of the input. For an input $\left \{4,6\right \}$ , the program will perform a sequence

of transformations.

4 FreeCHR

The main idea of FreeCHR is to model the syntax of CHR programs as a functor ${{\mbox{CHR}}}_C$ . We then use the free ${{\mbox{CHR}}}_C$ -algebra to define the operational semantics of FreeCHR.

4.1 Syntax

We first present the fundamental definition of our work which allows us to model CHR-programs over a domain $C$ .

Definition 10 (Syntax of FreeCHR programs). The functor ¹²

\begin{align*} {{\mbox{CHR}}}_C D =\ &{\mathtt {list}} \unicode[times]{x1D7DA}^C \times {\mathtt {list}} \unicode[times]{x1D7DA}^C \times \unicode[times]{x1D7DA}^{{\mathtt {list}} C} \times ({\mathtt {mset}} C)^{{\mathtt {list}} C} \sqcup D \times D\\ {{\mbox{CHR}}}_C f =\ &\mathbf{id} \sqcup f \times f \end{align*}

describes the syntax of FreeCHR programs.

The set ${\mathtt {list}}\unicode[times]{x1D7DA}^C \times {\mathtt {list}}\unicode[times]{x1D7DA}^C \times \unicode[times]{x1D7DA}^{{\mathtt {list}} C} \times ({\mathtt {mset}} C)^{{\mathtt {list}} C}$ is the set of single rules. The kept and removed head of a rule are sequences of functions in ${\mathtt {list}} \unicode[times]{x1D7DA}^C$ which map elements of $C$ to Booleans, effectively checking individual values for applicability of the rule. The guard of the rule is a function in $\unicode[times]{x1D7DA}^{{\mathtt {list}} C}$ and maps sequences of elements in $C$ to Booleans, checking all matched values in the context of each other. Finally, the body of the rule is a function in $({\mathtt {mset}} C)^{{\mathtt {list}} C}$ and maps the matched values to a multiset of newly generated values.

The set $D \times D$ represents the composition of FreeCHR programs by an execution strategy, allowing the construction of more complex programs from, ultimately, single rules.

By the structure of ${{\mbox{CHR}}}_C$ , a ${{\mbox{CHR}}}_C$ -algebra with carrier $D$ is defined by two functions

\begin{align*} \rho :\ {\mathtt {list}} \unicode[times]{x1D7DA}^C \times {\mathtt {list}} \unicode[times]{x1D7DA}^C \times \unicode[times]{x1D7DA}^{{\mathtt {list}} C} \times ({\mathtt {mset}} C)^{{\mathtt {list}} C} \longrightarrow D && \nu :\ D \times D \rightarrow D \end{align*}

as $(D, \left [\rho , \nu \right ])$ . The free ${{\mbox{CHR}}}_C$ -algebra ${\mbox{CHR}^{\star }_{C}}$ provides us with an inductively defined representation of programs which we will later use to lift the very abstract operational semantics $\omega _a$ .

Lemma 1 (Free ${{\mbox{CHR}}}_C$ -algebra). With

\begin{align*} \mu {{\mbox{CHR}}}_C = {\mathtt {list}} \unicode[times]{x1D7DA}^C \times {\mathtt {list}} \unicode[times]{x1D7DA}^C \times \unicode[times]{x1D7DA}^{{\mathtt {list}} C} \times ({\mathtt {mset}} C)^{{\mathtt {list}} C} \sqcup \mu {{\mbox{CHR}}}_C \times \mu {{\mbox{CHR}}}_C \end{align*}

and labels/injections

\begin{align*} rule &: {\mathtt {list}} \unicode[times]{x1D7DA}^C \times {\mathtt {list}} \unicode[times]{x1D7DA}^C \times \unicode[times]{x1D7DA}^{{\mathtt {list}} C} \times ({\mathtt {mset}} C)^{{\mathtt {list}} C} \longrightarrow \mu {{\mbox{CHR}}}_C \\ \odot &: \mu {{\mbox{CHR}}}_C \times \mu {{\mbox{CHR}}}_C \longrightarrow \mu {{\mbox{CHR}}}_C \end{align*}

${{\mbox{CHR}}}^{\star }_C = (\mu {{\mbox{CHR}}}_C, \left [rule, \odot \right ])$ is the free ${{\mbox{CHR}}}_C$ -algebra.

Proof. We show that ${{\mbox{CHR}}}^{\star }_C = (\mu {{\mbox{CHR}}}_C, \left [rule, \odot \right ])$ is the free ${{\mbox{CHR}}}_C$ -algebra, by constructing the ${{\mbox{CHR}}}_C$ -catamorphism

\begin{align*} {(\!| \!\left [\rho ,\nu \right ]\! |\!)} : \mu {{\mbox{CHR}}}_C \longrightarrow \left (A, \left [\rho , \nu \right ]\right ) \end{align*}

for any ${{\mbox{CHR}}}_C$ -algebra $\left (A, \left [\rho , \nu \right ]\right )$ . By definition of the free ${{\mbox{CHR}}}_C$ -algebra,

(1) \begin{align} {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(\left [rule, \odot \right ](p)) = \left [\rho , \nu \right ](({{\mbox{CHR}}}_C {(\!| \!\left [\rho ,\nu \right ]\! |\!)})(p)) \end{align}

needs to be true for any $p \in \mu {{\mbox{CHR}}}_C$ .

Case 1 ( $p = rule(k, r, g, b)$ ).

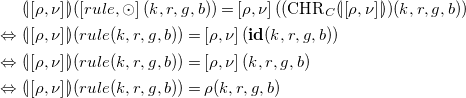\begin{align*} &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(\left [rule, \odot \right ](k,r,g,b)) = \left [\rho , \nu \right ](({{\mbox{CHR}}}_C {(\!| \!\left [\rho ,\nu \right ]\! |\!)})(k,r,g,b)) \\ \Leftrightarrow &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(rule(k,r,g,b)) = \left [\rho , \nu \right ](\mathbf{id}(k,r,g,b)) \\ \Leftrightarrow &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(rule(k,r,g,b)) = \left [\rho , \nu \right ](k,r,g,b) \\ \Leftrightarrow &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(rule(k,r,g,b)) = \rho (k,r,g,b) \\ \end{align*}

Case 2 ( $p = p_1 \odot p_2$ ).

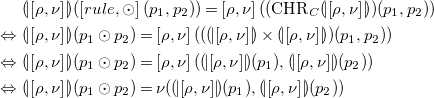\begin{align*} &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(\left [rule, \odot \right ](p_1, p_2)) = \left [\rho , \nu \right ](({{\mbox{CHR}}}_C {(\!| \!\left [\rho ,\nu \right ]\! |\!)})(p_1, p_2)) \\ \Leftrightarrow &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(p_1 \odot p_2) = \left [\rho , \nu \right ](({(\!| \!\left [\rho ,\nu \right ]\! |\!)} \times {(\!| \!\left [\rho ,\nu \right ]\! |\!)})(p_1, p_2)) \\ \Leftrightarrow &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(p_1 \odot p_2) = \left [\rho , \nu \right ]({(\!| \!\left [\rho ,\nu \right ]\! |\!)}(p_1), {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(p_2)) \\ \Leftrightarrow &\ {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(p_1 \odot p_2) = \nu ({(\!| \!\left [\rho ,\nu \right ]\! |\!)}(p_1), {(\!| \!\left [\rho ,\nu \right ]\! |\!)}(p_2)) \\ \end{align*}

Therefore, (1) holds if and only if

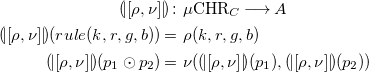\begin{align*} {(\!| \!\left [\rho , \nu \right ]\! |\!)} :&\ \mu {{\mbox{CHR}}}_C \longrightarrow A\\ {(\!| \!\left [\rho , \nu \right ]\! |\!)}(rule(k,r,g,b)) =&\ \rho (k,r,g,b)\\ {(\!| \!\left [\rho , \nu \right ]\! |\!)}(p_1 \odot p_2) =&\ \nu ({(\!| \!\left [\rho , \nu \right ]\! |\!)}(p_1), {(\!| \!\left [\rho , \nu \right ]\! |\!)}(p_2)) \end{align*}

for all ${{\mbox{CHR}}}_C$ -algebras $\left (A, \left [\rho , \nu \right ]\right )$ . Hence, there is a unique homomorphism

\begin{align*} {(\!| \!\left [\rho , \nu \right ]\! |\!)} : {{\mbox{CHR}}}^{\star }_C \rightarrow (A, \left [\rho , \nu \right ]) \end{align*}

for any ${{\mbox{CHR}}}_C$ -algebra $\left (A, \left [\rho , \nu \right ]\right )$ , making ${{\mbox{CHR}}}^{\star }_C$ the free ${{\mbox{CHR}}}_C$ -algebra.

The free ${{\mbox{CHR}}}_C$ -algebra corresponds to the definition of abstract syntax trees of programs, while the catamorphism $(\!| \alpha |\!)$ corresponds to an interpretation that preserves the semantics of $\alpha$ .

We can easily see that $\odot$ is associative up to isomorphism. ¹³ We thus will not explicitly write parentheses and generally use chained expressions like $p_1 \odot \ldots \odot p_l$ for some $l \in \mathbb{N}$ .

Example 9 (Euclidean algorithm (cont.)). The program $\mathit{gcd} = \mathit{zero} \odot \mathit{subtract}$ with

\begin{align*} \mathit{zero} &= rule({\varepsilon }, (\lambda n. n = 0), (\lambda n. {\mathit{true}}), (\lambda n. \emptyset )) \\ \mathit{subtract} &= rule((\lambda n. 0 \lt n), (\lambda m. 0 \lt m), (\lambda n\ m. n \leq m), (\lambda n\ m. \left \{m-n\right \})) \end{align*}

implements the euclidean algorithm, as defined in Example 4 . $\lambda$ -abstractions are used for ad-hoc definitions of functions.

4.2 Operational semantics

We now lift the very abstract operational semantics $\omega _a$ of CHR to the very abstract operational semantics $\omega ^{\star }_a$ of FreeCHR. We assume that our programs are defined over a domain $C$ , where there is a data type $\mathcal{L} C = \langle C, \Lambda _C, \tau _C \rangle$ . Like $\omega _a$ , $\omega ^{\star }_a$ is defined as a labeled transition system, where states are multisets over elements of $C$ .

Definition 11 (Very abstract operational semantics $\omega ^{\star }_a$ ). The very abstract operational semantics of FreeCHR is defined as the labeled transition system

\begin{align*} {\omega ^{\star }_a} = \langle {\mathtt {mset}} C, \mu {{\mbox{CHR}}}_C, \mapsto \rangle \end{align*}

where the transition relation $\left (\mapsto \right )$ is defined by the inference rules in Figure 2 .

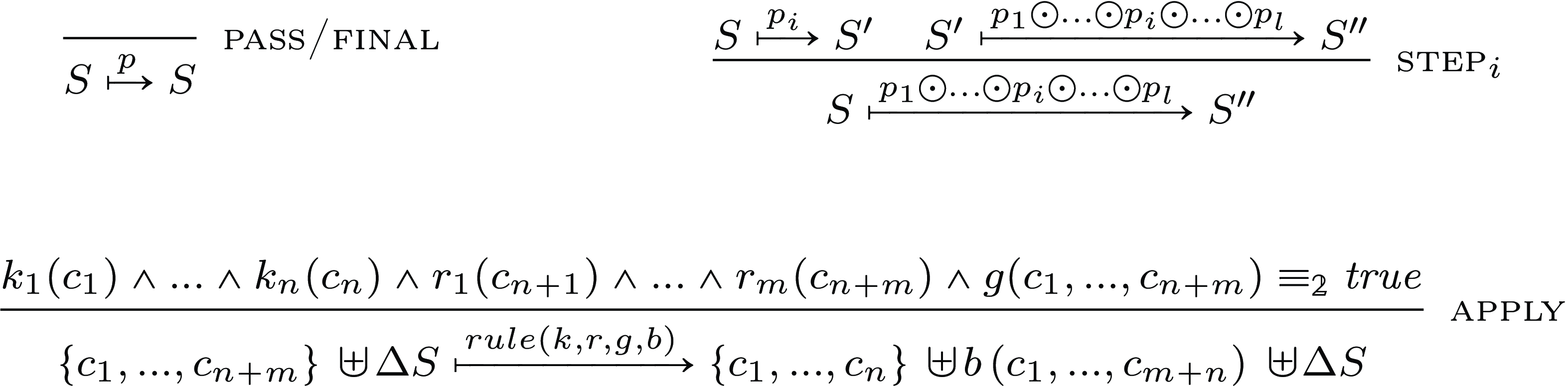
Fig. 2. Very abstract operational semantics of freeCHR.

The rule pass/final states that a program is always allowed to do nothing to a state. step $_i$ states that we can derive a transition from $S$ to $S''$ , if we can transition from $S$ to $S'$ with the $i$ -th program in the composition $p_1 \odot \ldots \odot p_l$ (for $1 \leq i \leq l$ ) and from $S'$ to $S''$ with the whole composition. The idea is that, without loss of generality $p_i$ is a rule that is applied to the current state, whereafter execution is continued. apply is the translation of the original apply-rule of $\omega _a$ . $k_i$ and $r_j$ denote the $i$ -th and $j$ -th elements of the sequences $k$ and $r$ .

We want to demonstrate the very abstract operational semantics of FreeCHR on a small example.

Example 10 (Euclidean algorithm (cont.)). Given the program gcd of Example 9 and the initial state $\left \{12, 9\right \}$ , we can prove the derivation

as follows. We first use the ${\textit{STEP}}$ transition to apply the subtract rule to the initial state.

and prove that this transition is valid

We repeat this process for the transitions , and . At this point, we have to apply the zero rule to remove the $0$ and use the ${\textit{PASS/FINAL}}$ transition to prove the empty transition .

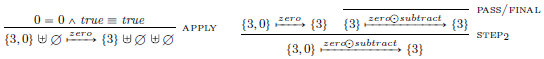
With this done, we have fully proven the derivation.

4.3 Soundness and completeness of $\omega ^{\star }_a$

To prove the soundness and completeness of $\omega ^{\star }_a$ with respect to $\omega _a$ , we first need to embed FreeCHR into the positive range-restricted ground segment of CHR. This is a common approach to relate rule-based formalisms to CHR (Frühwirth, 2009, Chapter 6).

Definition 12 (Embedding FreeCHR into CHR). Let

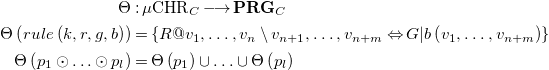\begin{align*} {\Theta } &: \mu {{\mbox{CHR}}}_C \longrightarrow {\mathbf{PRG}_{C}}\\ {\Theta }\left (rule\left (k, r, g, b\right )\right ) &= \left \{R@v_1, \ldots , v_n \setminus v_{n+1}, \ldots , v_{n+m} \Leftrightarrow G | b\left (v_1, \ldots , v_{n+m}\right ) \right \} \\ {\Theta }\left (p_1 \odot \ldots \odot p_l\right ) &= {\Theta }\left (p_1\right ) \cup \ldots \cup {\Theta }\left (p_l\right ) \end{align*}

be the function embedding FreeCHR programs into the positive range-restricted ground segment of CHR, with universally quantified variables $v_1$ ,…, $v_{n+m}$ , $R$ a uniquely generated rule name and

\begin{align*} G = k_1\left (v_1\right ) {\wedge } \ldots {\wedge } r_m\left (v_{n+m}\right ) {\wedge } g\left (v_1, \ldots , v_{n+m}\right ) \end{align*}

Example 11. If we apply the embedding $\Theta$ to the program $gcd$ (including the evaluation of function applications ¹⁴ ), we get the program

\begin{align*} zero\ &@\ {\varepsilon }\ \setminus \ n\ \Leftrightarrow \ n = 0 {\wedge } {\mathit{true}}\ |\ \emptyset \\ subtract\ &@\ n\ \setminus \ m\ \Leftrightarrow \ 0 \lt n {\wedge } 0 \lt m {\wedge } n \leq m\ |\ m - n \end{align*}

with universally quantified variables $n$ and $m$ . The program corresponds to the head-normalization (Duck (2005)) of the program in Example 4 .

We now prove $\Theta$ -soundness of $\omega ^{\star }_a$ with respect to $\omega _a$ , this is, if we can prove a derivation under $\omega ^{\star }_a$ for a program $p$ , we can prove it under $\omega _a$ for ${\Theta }(p)$ .

Theorem 1 ( $\Theta$ -Soundness of $\omega ^{\star }_a$ ). $\omega ^{\star }_a$ is $\Theta$ -sound with respect to $\omega _a$ , this is, for $S, S' \in {\mathtt {mset}}\, C$ and $p \in \mu {{\mbox{CHR}}}_C$ ,

Proof. We prove soundness by induction over the inference rules of $\omega ^{\star }_a$ .

Induction Base Case (pass/final). Follows directly from empty.

Induction Base Case (apply). Given a proof

with $r = rule(\left (k_1, \ldots , k_n\right ), \left (r_1, \ldots , r_m\right ), g, b)$ and

\begin{align*} G = k_1\left (t_1\right ) {\wedge } \ldots {\wedge } k_n\left (t_n\right ) {\wedge } r_1\left (t_{n+1}\right ) {\wedge } \ldots {\wedge } r_m\left (t_{n+m}\right ) {\wedge } g\left (t_1, \ldots , t_{n+m}\right ) \end{align*}

there is a $C$ -instance

\begin{align*} R\ @\ c_1, \ldots , c_n\ \setminus \ c_{n+1}, \ldots , c_{n+m}\ \Leftrightarrow \ G\ |\ b(c_1, \ldots , c_{n+m}) \in \Gamma _C({\Theta }(p)) \end{align*}

such that $\tau _{\unicode[times]{x1D7DA}} \models G$ . By Definition 12 we know that $\left \{p'\right \} = {\Theta }\left (p\right )$ . We can thus prove by

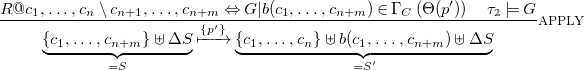
Induction Step (step $_i$ )

Given a proof

with $p = p_1 \odot \ldots \odot p_i \odot \ldots \odot p_l$ , for $1 \leq i \leq l$ , we assume

(2)

(3)

as induction hypotheses.

Since we can, without loss of generality, assume that $p_i = {\mathit{rule}}(\ldots )$ , we know from Definition12 that $\left \{p'\right \} = {\Theta }(p_i) \subseteq {\Theta }(p)$ . By induction hypothesis (2) we know from that . By induction hypothesis (3) we know from that . We can thus prove by

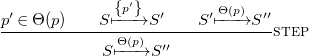
We established that we can prove any derivation we can prove with a program $p$ under $\omega ^{\star }_a$ , with a program ${\Theta }(p)$ under $\omega _a$ . We also want to prove $\Theta$ -completeness, this is, we can prove any derivation with a program ${\Theta }(p)$ under $\omega _a$ with a program $p$ under $\omega ^{\star }_a$ .

Theorem 2 ( $\Theta$ -completeness of $\omega ^{\star }_a$ ). $\omega ^{\star }_a$ is $\Theta$ -complete with respect to $\omega _a$ , this is, for $S, S' \in {\mathtt {mset}} C$ and $p \in \mu {{\mbox{CHR}}}_C$ ,

Proof. We prove $\Theta$ -completeness by induction over the inference rules of $\omega _a$

Induction Base Case (empty). Follows directly from pass/final

Induction Base Case (apply). Given a proof

By definition of $\omega _a$ , we know that ${\Theta }(p) = \left \{p'\right \}$ . Therefore, $p = rule(k, r, g, b)$ , and hence $G = k_1(c_1) {\wedge } \ldots {\wedge } r_m(c_{n+m}) {\wedge } g(c_1,\ldots ,c_{n+m})$ and $B = b(c_1,\ldots ,c_{n+m})$ . From $\tau _{\unicode[times]{x1D7DA}} \models G$ follows $G \equiv _{\unicode[times]{x1D7DA}} {\mathit{true}}$ . We can thus construct a proof

Induction Step (step). Given a proof

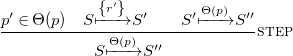
By Definition12, we know from $r' \in {\Theta }(p)$ that for $p = p_1 \odot \ldots \odot p_i \odot \ldots \odot p_l$ (with $l \geq 1$ ) there is a $p_i$ such that $\left \{p'\right \} = {\Theta }(p_i)$ . We hence assume as induction hypotheses that

(4)

(5)

From and induction hypothesis (4) follows $S {\stackrel {p_i}{\mapsto }} S'$ . From and induction hypothesis (5) follows . We can hence construct the proof

With Theorem1 and Theorem2, we have established that, up to $\Theta$ , FreeCHR is as expressive as CHR. Analogously to classical CHR, we are now able to define more refined operational semantics for FreeCHR and prove their soundness with respect to $\omega ^{\star }_a$ , which is ongoing future work.

5 An instance with very abstract operational semantics

In this section, we want to present a simple execution algorithm and prove its adherence to $\omega ^{\star }_a$ by using the inductive nature of our definition of syntax and semantics of FreeCHR. This will serve both as a first, albeit simple, guideline for implementations, as well as a case study on how a FreeCHR execution algorithm can be defined and verified.

5.1 Instances

Since the operational semantics define the execution of FreeCHR programs as a state transition system, an obvious way to implement FreeCHR is by mapping programs to functions mapping one state to its successor.

Definition 13 (FreeCHR instance). An instance of FreeCHR is a ${{\mbox{CHR}}}_C$ -algebra

\begin{align*} \left (({\mathtt {mset}} C)^{{\mathtt {mset}} C}, \left [\mathtt {rule}, \mathtt {compose}\right ] \right ) \end{align*}

with

\begin{align*} \mathtt {rule} &: {\mathtt {list}} \unicode[times]{x1D7DA}^C \times {\mathtt {list}} \unicode[times]{x1D7DA}^C \times \unicode[times]{x1D7DA}^{{\mathtt {list}} C} \times \left ({\mathtt {mset}} C\right )^{{\mathtt {list}} C} \longrightarrow ({\mathtt {mset}} C)^{{\mathtt {mset}} C}\\ \mathtt {compose} &: ({\mathtt {mset}} C)^{{\mathtt {mset}} C} \times ({\mathtt {mset}} C)^{{\mathtt {mset}} C} \longrightarrow ({\mathtt {mset}} C)^{{\mathtt {mset}} C} \end{align*}

A FreeCHR instance hence needs to define the two functions $\mathtt {rule}$ and $\mathtt {compose}$ which implement the execution of programs and hence the operational semantics of the program. $\mathtt {compose}$ implements the application of a single rule to a state if it is possible. $\mathtt {compose}$ implements the execution strategy of, fundamentally, a sequence of rules to a state. Both are only concerned with single execution steps. We hence also need the function

\begin{align*} \mathtt {run} : ({\mathtt {mset}} C)^{{\mathtt {mset}} C} \longrightarrow ({\mathtt {mset}} C)^{{\mathtt {mset}} C} \end{align*}

which maps a function performing singular steps to a function applying this function until a final state is reached. In CHR this generally means, until no rules are applicable to the state.

Since an instance practically also defines operational semantics it makes sense to directly associate it with an LTS as well.

Definition 14 (LTS of a FreeCHR instance). Let

\begin{align*} I = \left (({\mathtt {mset}} C)^{{\mathtt {mset}} C}, \left [\rho , \nu \right ]\right ) \end{align*}

$I$ implies an LTS

\begin{align*} \mathit{cr} I = \langle {\mathtt {mset}} C, L, \mapsto \rangle \end{align*}

where the labels $L$ are recursively defined as

\begin{align*} L =& \left \{\rho (k, r, g, b) \mid k, r \in {\mathtt {list}} (\unicode[times]{x1D7DA}^C), g \in \unicode[times]{x1D7DA}^{{\mathtt {list}} C}, b \in ({\mathtt {mset}} C)^{{\mathtt {list}} C}\right \} \cup \left \{\nu (f, g) \mid f, g \in L \right \} \end{align*}

and the transition relation as

With this, we can easily verify an instance against operational semantics, using the concepts from Section 2.2. We will do so from the perspective of the operational semantics, instead of from the perspective of the implementation. To verify, that an instance only performs valid transitions, we hence prove $\Theta$ -completeness

Consequentially, to prove that the implementation can perform all valid transitions, we prove $\Theta$ -soundness up to repeated transition

We need the relaxation ”up to repeated transition” since the instances, and hence their respective LTS, are only defined for singular steps.

5.2 Execution algorithm

The algorithm presented in this section implements the operations required for a FreeCHR instance as non-deterministic imperative pseudo-code. The $\mathit{rule}$ function is implemented by ${rule}$ , $\odot$ by $\rm{compose}$ , in Algorithm1.

Definition 15 (Pure CHR-programs in Set (cont.)). Algorithm 1 shows the abstract implementation of a ${{\mbox{CHR}}}_C$ -algebra

\begin{align*} {\mathbf{Exec}^{}_{a}} = \left (({\mathtt {mset}} C)^{{\mathtt {mset}} C}, \left [{rule}, \rm{compose}\right ]\right ) \end{align*}

Algorithm 1 Implementation of Exec

The function rule first checks whether there is a matching $\left \{c_1, \ldots , c_{n+m}\right \} \subseteq S$ , such that head constraints ${\mathtt {kept}}_i$ applied to $c_i$ and ${\mathtt {removed}}_j$ applied to $c_{n+j}$ evaluate to $\mathit{true}$ , as well as the guard, applied to all constraints of the matching (l. 2). If such a subset exists, the constraints $c_{n+j}$ with $1 \leq j \leq m$ are removed and the multiset resulting from applying the body to the matching will be added to $S$ (l. 3). The function compose checks if there is a $p\in \left \{p_1,\ldots ,p_l\right \}$ with $p(S) \neq S$ (l. 10). If this is the case, $p$ is applied to $S$ (l. 11). If in either function the respective check does not succeed, $S$ is returned unmodified (l. 5 and 13, respectively). The execution strategy implemented by compose is to non-deterministically select an applicable program and apply it to the state.

Note, that we will freely use currying on the last argument of either function, for instance, $\rm{rule}(k,r,g,b)$ is a function from ${\mathtt {mset}} C$ to ${\mathtt {mset}} C$ , and ${rule}(k,r,g,b,S)$ evaluates to an $S' \in {\mathtt {mset}} C$ . Also, $\rm{compose}$ will accept an arbitrary number of subprograms (but always an input state).

Finally, we need to implement the $run$ function.

Definition 16 (Pure CHR-programs in Set (cont.)). Algorithm 2 implements application until exhaustion for FreeCHR programs defined using Algorithm 1 .

Algorithm 2 Implementation of run

$\rm{run}(f,S)$ applies the function $f$ to the argument state $S$ repeatedly. After each iteration, it is compared to the last state. As soon as both are equal it is assumed that no more rules could be applied. Then, the state is returned as the final state.

Note, that this algorithm would also terminate if a propagation rule with an empty body is applied. As such rules are nonsensical, we will ignore this case.

5.3 Correctness

We will now prove the correctness of $\mathbf{Exec}^{}_{a}$ . With ${\mathbf{exec}^{}_{a}} = \left [{rule},\rm{compose}\right ]$ , let

\begin{align*} {(\!| {\mathbf{exec}^{}_{a}} |\!)} :\ &{{\mbox{CHR}^{\star }_{C}}} \rightarrow {\mathbf{Exec}^{}_{a}} \end{align*}

be the ${{\mbox{CHR}}}_C$ -catamorphism to $\mathbf{Exec}^{}_{a}$ , this is, the interpretation of programs in $\mu {{\mbox{CHR}}}_C$ that respects the semantics of Algorithm1.

Theorem 3. The very abstract operational semantics $\omega ^{\star }_a$ is $(\!| {\mathbf{exec}^{}_{a}} |\!)$ -complete with respect to $\mathbf{Exec}^{}_{a}$ (Algorithm 1 ), this is,

Proof. To prove the theorem, we will first discern two basic cases.

Case 3 ( $S = S'$ ). This case is trivial by rule ${\textit{PASS/FINAL}}$ .

Case 4 ( $S \neq S'$ ). We prove this case via induction over the structure of $p \in {{\mbox{CHR}}}_C$ .

Induction Base Case ( $p = {\mathit{rule}}(k, r, g, b)$ ). The transition

implies that

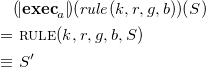\begin{align*} &{(\!| {\mathbf{exec}^{}_{a}} |\!)}({\mathit{rule}}(k, r, g, b))(S)\\ =&\ {{rule}}(k, r, g, b, S)\\ \equiv &\ S' \end{align*}

From Algorithm 1 follows that the condition in line 2 must be true, since there were changes to the state. This implies that there is a subset $\left \{c_1, \ldots , c_{n+m}\right \} \subseteq S$ for which

\begin{align*} k_1(c_1) \wedge \ldots \wedge k_n(c_n) \wedge r_1(c_{n+1}) \wedge \ldots \wedge r_m(c_{n+m}) \wedge g(c_1,\ldots ,c_{n+m}) \equiv _{\unicode[times]{x1D7DA}} {\mathit{true}} \end{align*}

Hence

\begin{align*} S &= \left \{c_1, \ldots , c_{n+m}\right \} \uplus \Delta S \end{align*}

and

From this, we can construct a proof

Induction Step ( $p = p_1 \odot \ldots \odot p_n$ ).

As the induction hypothesis, we assume

The transition

implies that

\begin{align*} {(\!| {\mathbf{exec}^{}_{a}} |\!)}(p_1 \odot \ldots \odot p_n)(S) = \rm{compose} (p_1, \ldots ,p_n, S) \equiv _{{\mathtt {mset}} C} S' \end{align*}

From Algorithm 1 , especially line 10, we know that there must hence be a $p_i$ with $1 \leq i \leq n$ such that ${(\!| {\mathbf{exec}^{}_{a}} |\!)}(p_i)(S) \equiv _{{\mathtt {mset}} C} S'$ , or in terms of the transition relation

By induction hypothesis, we then have a proof for . We can thus construct a proof

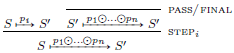
Theorem 4. The very abstract operational semantics $\omega ^{\star }_a$ is $(\!| {\mathbf{exec}^{}_{a}} |\!)$ -sound up to repeated transition with respect to $\mathbf{Exec}^{}_{a}$ (Algorithm 1 ), this is,

Proof. We prove the theorem by induction over the inference rules of $\omega ^{\star }_a$ .

Induction Base Case (pass/final). Trivial, since is always true for zero transition steps

Induction Base Case (apply). Given a proof

We want to show that

or respectively

\begin{align*} &{(\!| {\mathbf{exec}^{}_{a}} |\!)}({\mathit{rule}}(k, r, g, b))(\left \{c_1,\ldots ,c_{n+m}\right \} \uplus \Delta S)\\ =&\ {rule}(k, r, g, b, \left \{c_1,\ldots ,c_{n+m}\right \} \uplus \Delta S) \\ =& \left \{c_1,\ldots ,c_n\right \} \uplus b\left (c_1, \ldots , c_{n+m}\right ) \uplus \Delta S \end{align*}

Since by assumption the condition in line 2 will be $\mathit{true}$ . From line 3 we then know that

which can be simplified to $\left \{c_1,\ldots ,c_n\right \} \uplus b\left (c_1, \ldots , c_{n+m}\right ) \uplus \Delta S$ .

Induction Step (step $_i$ )

Given a proof

\begin{align*} \frac {S {\stackrel {p_i}{\mapsto }} S'\quad S' {\stackrel {p_1 \odot \ldots \odot p_l}{\mapsto }} S''}{S {\stackrel {p_1 \odot \ldots \odot p_l}{\mapsto }} S''}\rm{step}_i \end{align*}

with $1 \leq i \leq l$ . We assume

(6)

(7)

as induction hypotheses. We want to show that

From the premises of the given proof we can infer and by induction hypotheses (6) and (7), respectively. By the definition of compose we know that, since ${(\!| {\mathbf{exec}^{}_{a}} |\!)}(p_i)(S) \equiv S'$ , $S'$ is also a possible outcome of ${(\!| {\mathbf{exec}^{}_{a}} |\!)}(p_1 \odot \ldots \odot p_l)(S)$ . From , we can hence assume . Therefrom follows directly.

With Theorem3 and Theorem4 we established that Algorithm1 correctly implements the very abstract operational semantics $\omega ^{\star }_a$ . The theorems also imply that $\mathbf{Exec}^{}_{a}$ is an equivalent representation of $\omega ^{\star }_a$ .

6 Implementation case studies

We now present two implementations that are based on the execution algorithm described in Section 5 as case studies. The source code of the implementations is also available on GitHub. ¹⁵

The purpose of this section is twofold: first, we show how the abstract execution algorithm can be used as a guide to implement FreeCHR. Second, we show how the chosen host language flavors the implementation of FreeCHR both in the back end, as well as in the front end.

The presented implementations have two limitations to be noted: first, they solve any source of non-determinism in the original algorithm. Whenever the original algorithm chooses an element from a (multi) set, the implementations will sequentially search for them. Especially is the state, in both implementations, a list instead of a multiset. Also, the rules of a program will be traversed sequentially to find an applicable one. It is, though, easy to see that they will only perform transitions Algorithm1 would perform as well. They are, in other words, concretizations of $\mathbf{Exec}^{}_{a}$ .

Second, as they are based on the very abstract operational semantics, they do not yet account for trivial non-termination due to repeated application of propagation rules (this is, rules with an empty removed head) (Frühwirth (2009)). Hence, a program with such rules will not terminate if any of them is at some point applicable. This problem is solved with the abstract operational semantics by recording a propagation history. It saves applied constraints (by a unique identifier) as well as the rule applied to them. If a propagation rule is to be applied, it is first checked if the combination was already executed. If this is the case, the rule will not fire again.

The consequence for the presented implementations is that they only work on a subset of CHR/FreeCHR without propagation rules.

6.1 Host languages

To sufficiently demonstrate how FreeCHR can be implemented in different programing languages and how the respective host language flavors the implementation, we chose two programing languages of very different paradigms: Haskell and Python.

Haskell is a statically typed functional programing language with a powerful type system. Python is a dynamically typed imperative language with plenty of practical applications.

One might consider both languages to be on the opposite of a static-dynamic/functional-imperative spectrum as well. They will hence serve well for this case study, as most languages are featurewise somewhere in between. Languages like Java or C# successively adopt functional features but stay imperative in their core. They also have a static type system like Haskell, but not as powerful and strict. Languages like Kotlin move further towards the functional end of the spectrum but still inherit many characteristics from Java. On the other hand, the whole LISP family of programing languages is functional but dynamically typed.

6.2 Execution algorithm

We will now give a detailed overview of the implementations, connect them to the abstract algorithm and compare them to each other.

6.2.1 Carrier

We first want to discuss the implementation of the carrier of the implemented ${{\mbox{CHR}}}_C$ -algebra.

In Haskell, the carrier is explicitly defined as the type shown in Figure 3. The type is essentially equal to functions of type which is the Haskell representation of the set $({\mathtt {mset}} C)^{{\mathtt {mset}} C}$ . As mentioned above, we will use lists instead of multisets. This eliminates one source of non-determinism.

Wrapping the functions by defining a new type allows the implementation of type class instances (which is used for compose) and to discern programs that are ”in construction” from such that were already passed to

The Python implementation directly models functions mapping lists to lists. Since Python is (by default) dynamically typed, there are no constraints on the type of the elements of the lists. This, on the one hand, gives more freedom to the user of the FreeCHR instance since it is easier to define rules on different types of constraints. This is also possible when using Haskell, but needs additional work like defining and matching on a sum type. On the other hand, in Python, one should always explicitly check if the constraints have the correct type in the head of the rule.

For example, the program in Figure 4b allows values of any type in its state and will apply the rules only if integers are encountered. Not checking the type of constraints beforehand is a serious source of runtime errors. If a rule of the gcd program is applied to something other than two integers, the comparison operations (l. 3 and 6) in the guard or the subtraction (l. 7) in the body will raise an exception. Such errors are impossible in the Haskell version in Figure 4a since the input type needs to be some sort of integer (; see l. 1) which guarantees support for comparison () and subtraction (). ¹⁶

Fig. 3. Wrapped solver function type.

Fig. 4. Greatest common divisor.

6.2.2 ${\textit{RULE}}$

The implementations of rule can be seen in Figure 5. First, either function lazily computes the sequence of possible matchings (l. 5 in Figure 5a and l. 3–5 in Figure 5b). This is done using the match functions which are shown in Figure 6. Both generate a lazy sequence of all permutations of the state that have the same length as the head of the rule (l. 3–4 and l. 3, respectively) and select those for which the conjunction of the elementwise application (done by ) of the elements of the head evaluates to true, this is, those for which $k_1(c_1) {\wedge } \ldots {\wedge } k_n(c_n) {\wedge } r_1(c_{n+1}) {\wedge } \ldots {\wedge } r_m(c_{n+m}) \equiv _{\unicode[times]{x1D7DA}} {\mathit{true}}$ , for a head $\left [k_1, \ldots , k_{n}, r_1, \ldots , r_{m}\right ]$ and a permutation $\left [c_1, \ldots , c_{n+m}\right ]$ of the state. Then, both implementations of rule take the first of those sequences for which the guard $g$ holds, this is, $g(c_1,\ldots ,c_{n+m}) \equiv _{\unicode[times]{x1D7DA}} {\mathit{true}}$ . In total, this corresponds to l. 2 in Algorithm1. If such a matching is found, the new state is computed and returned as in l. 3 (l. 7 and 8–11). In the Python implementation, an explicit copy of the state is created to not modify the original state. If no matching is found, the state is returned unchanged (l. 8 and 6–7).

Note that both variants explicitly create and return a function after getting the rule elements passed. The implementations of compose (Figure 7) work in the same way.

Also, the Python implementation makes heavy use of the spread operator (* before function arguments) (l. 4 and 11). In consequence, we can write the guard and body of a rule as functions that accept as many arguments as the head has patterns. In Haskell, guard and body accept a list as their single argument (compare lines 6 and 7 in either implementation in Figure 4).

An issue specific to Python can be seen in Figure 8b. Python does only allow expressions in lambda functions. If any function of a rule needs to use statements, it must be defined separately.

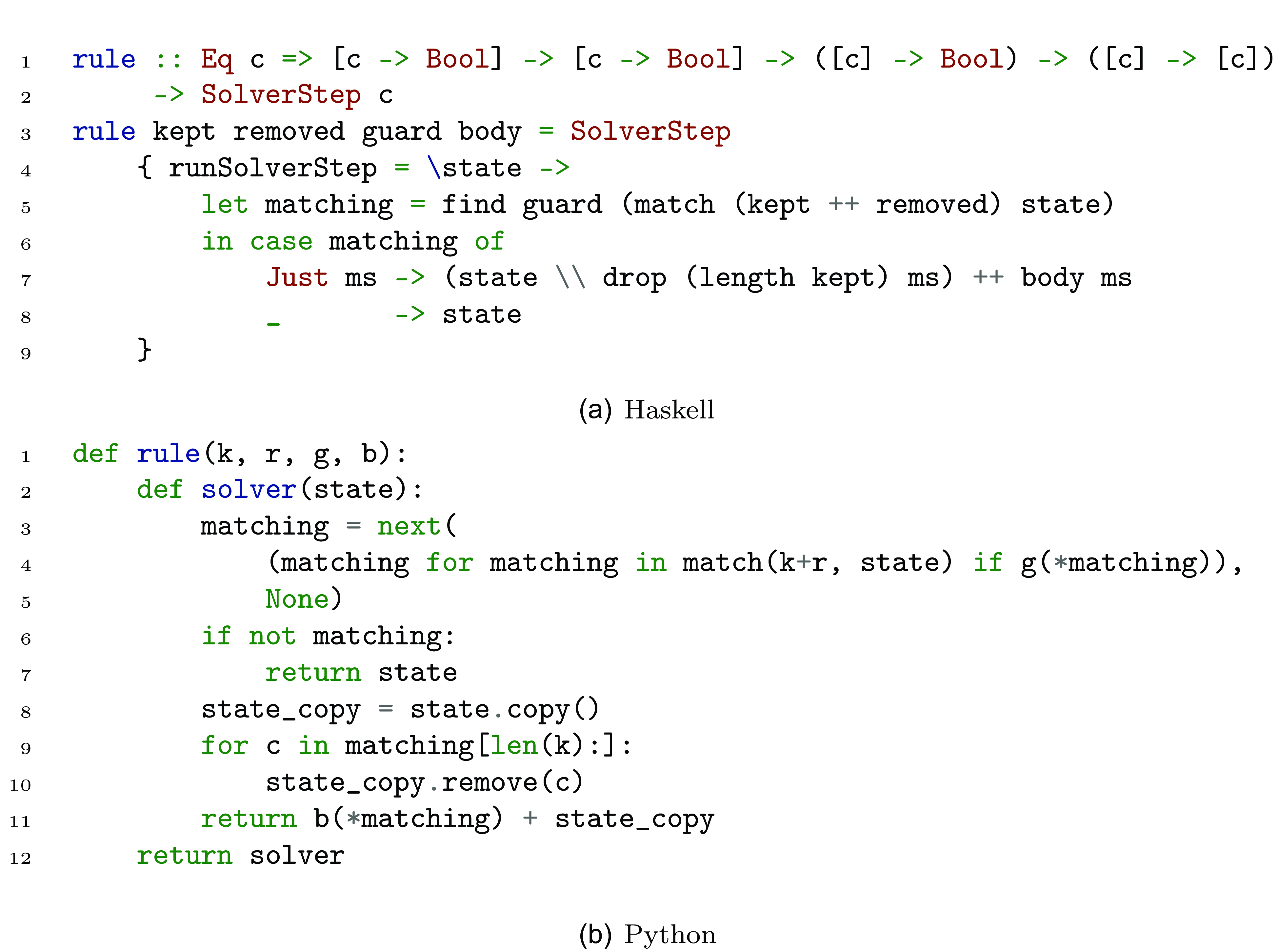
Fig. 5. Implementations of rule.

Fig. 6. Lazy matching.

6.2.3 ${\textit{COMPOSE}}$

Figure 7 shows the implementations of compose. Figure 7a implements the algorithm as the binary operator () of the type class. First, the left subprogram will be applied to the state (l. 5). If this has no effect, the second subprogram is applied (l. 7). Otherwise, the result of the first application which must have altered the state, is returned (l. 8). One can easily see that the implementation is associative, as required by . In nested expressions like , the algorithm will always perform a depth-first search, beginning from the leftmost subprogram, effectively traversing the program from left to right.

The same is true for the Python variant in Figure 7b. Here, we loop through the subprograms, passed to the function compose (l. 4–7) until a program alters the state (l. 6 & 7). Finally, result is returned which is either the input state (see l. 3) if the program made it through the loop without finding an applicable subprogram, or the first result of an effective application (see l. 5).

Contrary to the Haskell variant, compose is implemented as a variadic function by use of the spread operator in Python. The consequence for the user can be seen in Figure 4, where we use ( ) to compose the rules (l. 4) in Haskell and compose in Python.

Fig. 7. Implementations of compose.

6.2.4 ${\textit{RUN}}$

Figure 9 shows the implementations of run. The implementation in Figure 9a first applies the passed program to the query (also called the initial state) (l. 6). If this has no effect, the state is returned (l. 3). Otherwise, is recursively called with the new state (l. 4), repeatedly applying the program until exhaustion.

The algorithm in Figure 9b accomplishes the same by the loop in lines 5 to 9, which is interrupted if the state remains unchanged after applying the program (l. 6 & 7).

Fig. 8. Implementation of all_diff constraint.

Again, the use of the spread operator in Python causes a minor difference in usage. While in Haskell, we need to pass a list to , in Python run it is a variadic function. Hence, to calculate the greatest common divisor of $6$ , $9$ and $12$ , we call in Haskell and in Python and get in both cases [3] as the result.

6.3 Side effects

A major difference between the two presented implementations is the handling of side effects. Python allows for arbitrary side effects like I/O, assigning variables or raising exceptions, as can be seen in Figure 8b. Although this is also possible in Haskell (see Figure 8a), it is highly discouraged by the language. The programs raise an error if they encounter the same value in the query twice. Although the implementations allow it, this behavior is not defined by the operational semantics and domain of future work.

Fig. 9. Implementations of run.

7 Limitations

We want to briefly discuss the current limitations of FreeCHR as it is presented in this paper.

The very abstract operational semantics $\omega _a$ for CHR is meant as a tool for formal reasoning and an abstract baseline. It does not describe the behavior of an actual implementation, since it is heavily non-deterministic. As discussed above, it does also not account for trivial non-termination due to repeated application of a propagation rule on the same constraints. Since the very abstract operational semantics for FreeCHR $\omega ^{\star }_a$ is a direct translation of $\omega _a$ , it inherits these issues.

The presented implementations are hence only defined on programs without propagation rules as they would inevitably get stuck on the repeated application of such a rule. This issue is solved by the refined operational semantics $\omega _r$ as presented by Duck et al. (2004). Translating $\omega _r$ to FreeCHR is currently ongoing work. For now, the implementations hence only serve as a proof of concept of the applicability of our framework and are not meant for actual use. ¹⁷ We therefore did also not concern ourselves with applying any optimization techniques and do hence not yet expect any reasonable performance.

The approach presented herein is strictly to be understood as the formal foundation upon which we will build our future work, as it connects our framework to the original definition of CHR on the most fundamental level.

8 Related work

8.1 Constraint handling rules

8.1.1 Embeddings

The first approach to embed CHR into a host language was via source-to-source transformation. Holzbaur and Frühwirth (2000) and Schrijvers and Demoen (2004), for example, translate CHR via Prolog’s macro system. Similarily, Abdennadher et al. (2002) and Van Weert et al. (2005) use a precompiler to translate CHR programs into Java, Wuille et al. (2007) into C, Nogatz et al. (2018) into Javascript, and Barichard (2024) into C++.

Van Weert et al. (2008) introduces compilation schemes for imperative languages, upon which, for example, Nogatz et al. (2018) builds. The work of van Weert (2010) also provides compilation schemes for imperative languages, but optimizes the matching process by performing it lazily. The algorithms do not first compute a full matching and check it against the patterns and the guard but collect it sequentially.

The inherent disadvantage of an approach using source-to-source compilation is the need for a precompiler in the build chain if the host language does not have a sufficiently expressive macro system like Prolog or LISP. It comes with the cost of more sources of errors and an additional dependency that is often rather tedious to fulfill. Hanus (2015) approaches this problem by extending the Curry compiler to be able to compile CHR code. The obvious problem with this approach is that it is in most cases not viable to extend the compiler of the host language.

A relatively new approach by Ivanović (2013) was to implement CHR as an internal language in Java. This has a major advantage: CHR can now simply be imported as a library, similarly as if implemented by a macro system like by Schrijvers and Demoen (2004). Wibiral (2022) further builds upon this idea and introduces the idea of explicitly composing CHR programs of singular rules by an abstract and modular execution strategy and describing rules through anonymous functions. This was our main inspiration and FreeCHR aims to improve and generalize this idea for arbitrary languages.

8.1.2 Operational semantics

Duck et al. (2004) first formalized the behavior of existing implementations which were mostly derived from but not exactly true to existing formal definitions of operational semantics. The techniques used in the implementations were also generalized and improved upon by Van Weert et al. (2008) and van Weert (2010). Duck (2005) standardized call-based semantics for CHR, especially in logical programing languages.

8.2 Algebraic language embeddings

The idea of algebraic embeddings of a domain specific language (DSL) into a host language was first introduced by Hudak (1998). The style in which the languages are embedded was later called tagless, as it does not use an algebraic data type, to construct an abstract syntax tree (see, e.g., Carette et al. (2007)). The tags are the constructors of the data type which defines the syntax of the language. Instead, the embedding directly defines the functions which implement the semantics of the language. This is, defining the free $F$ -algebra versus defining the concrete $F$ -algebras, for a functor $F$ which defines the syntax of the language. The advantage of embedding a DSL in this way is that it does not rely on external build tools, but can instead be easily implemented and used as a library. It also enables the use of any features the host language offers, without any additional work. With an external code-to-code compiler, it would be necessary to re-implement at least the syntax of any desired host language features.

Hofer et al. (2008) and Hofer and Ostermann (2010) then extended this idea by using type families in order to provide more flexibility concerning the semantics of the language.

8.3 Logic and constraint based languages and formalisms

CHR was initially designed as a tool to implement constraint solvers for user-defined constraints. Hence, its domain intersects with those of Answer Set Programming (ASP) and Constraint Logic Programming (CLP). However, on the one hand, CHR can rather be understood as a tool in combination with ASP or especially CLP, as it provides an efficient language to implement solvers, than as an alternative approach. On the other hand, CHR has already exceeded its original purpose and developed more towards a general purpose language.

Another relevant logic based language is miniKanren (see Byrd (2009)). miniKanren is a family of EDSLs for relational and logic programing. There exists a myriad of implementations for plenty of different host languages as well as formal descriptions of operational semantics (see e.g., Rozplokhas et al. (2020)). The miniKanren language family, though, seems to suffer from similar issues as traditional Constraint Handling Rules does. As there is no unified embedding scheme, there is an inherent disconnect between any implementation and the formally defined semantics. Applying an approach similar to ours might be beneficial to the miniKanren project as well, especially as it generally is implemented in a way similar to the methods described by Hudak (1998) or Carette et al. (2007).

9 Future work

With this foundational introduction of FreeCHR in place, our future work will focus on three main aspects.

First, since the execution algorithm presented here is only of limited practical use, we plan to introduce an algorithm that implements the refined operational semantics $\omega _r$ of CHR. The $\omega _r$ semantics of CHR is the basis for most existing implementations. Since we already have the very abstract operational semantics as a baseline, we can use it as a basic anchor to verify any execution algorithm. The algorithm we intend to formalize is already implemented in Haskell ¹⁸ and Python. ¹⁹

Second, we currently work on translating the refined operational semantics and verifying them against $\omega ^{\star }_a$ , as well as the aforementioned execution algorithm. This will provide a base for theory concerning practically relevant aspects of FreeCHR.

We plan to verify both the execution algorithm implementing $\omega _r^{\star }$ and $\omega _r^{\star }$ itself by showing that they are valid concretization of $\omega ^{\star }_a$ .

Finally, we plan to tackle the issue of side effects that we encountered in the case study in Section 6. This can be done by generalizing the functor ${{\mbox{CHR}}}_C$ to use monads to encapsulate arbitrary side effects (see Jones and Wadler (1993)). This was already done in implementations in Haskell but is not yet formalized. This is an important aspect, as it further formalizes practical aspects of everyday programing.

10 Conclusion

In this paper, we introduced the framework FreeCHR that formalizes the embedding of CHR, using initial algebra semantics. We provided the fundamental definition of our framework which models the syntax of CHR programs over a domain $C$ as a Set-endofunctor ${{\mbox{CHR}}}_C$ . We defined the very abstract operational semantics $\omega ^{\star }_a$ , using the free ${{\mbox{CHR}}}_C$ -algebra ${\mbox{CHR}^{\star }_{C}}$ and proved soundness and completeness with respect to the original very abstract operational semantics $\omega _a$ of CHR. We also provided a first abstract instance $\mathbf{Exec}^{}_{a}$ of FreeCHR, proved its correctness with respect to to $\omega ^{\star }_a$ and discussed deterministic implementations of the algorithms in Haskell and Python.

Hereby, we established FreeCHR as a valid representation of the original definition of CHR and a usable framework for the implementation of the embedded language in a wide range of host languages.

Moreover, are the presented execution algorithm and the implementations of it, although very simple, to our knowledge the first implementations of CHR for which there is an actual prove of correctness with respect to to a formal definition of their operational semantics.