1. Introduction
This paper is about a duality between semiframes (an algebraic structure) and semitopologies (a topological one). We will define semiframes, study their duality with semitopologies and also motivate and define relevant well-behavedness conditions on semitopologies and investigate how these conditions dualise to algebraic conditions on semiframes.
Both semitopologies and semiframes are relatively recent developments, arising from a novel application of topological ideas to study decentralised computing systems. So while this paper is about pure mathematics, and it can be read as mathematics for its own sake, it would be nice to understand the motivation for why we looked at these structures in the first place.
1.1 The challenge of decentralised systems
Consider a computing system whose operation is distributed over many collaborating participants, like a blockchain. At a high level, how can we design algorithms that participants can run such that the overall system will act coherently in some appropriate sense?
We could just assume a central controller: a dictator participant. In this case, ‘collaborating’ just means doing as the dictator instructs, and ‘truth’ just means whatever the dictator says.
This is indeed how many distributed systems actually work, but it introduces tradeoffs of latency, scalability, availability and trust, which may or may not be acceptable depending on the use case. Do we trust the dictator? What if it crashes or gets hacked? What if the network is slow? What if it is just busy? Sometimes, we need participants to be able, to a greater or lesser extent, to collaborate independently of central control.
This is the topic of decentralised systems, which are distributed systems that do not adopt a central controller. Decentralised systems are hard to design and implement because control itself is spread out,Footnote 1 but often this is the only architecture that is practical at scale and speed.
While blockchains are an example of decentralised systems,Footnote 2 these design issues arise repeatedly: for example, if we want to manage a system of drones, or satellites, or low-power devices. An ant colony is an interesting example of a (semi-)decentralised system in nature: while a queen ant exists, she does not dictate every action of every ant; for much of the time, individual ants work autonomously, yet they still manage to do so coherently and for the good of the colony. The human brain is another important example of a decentralised system. These systems are all inherently decentralised: they maintain some clear notion of global coherence (e.g., there is an identifiable thing called ‘an ant colony’ or ‘my sense of self’) all while their parts collaborate to perform significant actions independently of any explicit central control.
This leads us to consider the concept of what in Gabbay (Reference Gabbay2024, Reference Gabbay2025) is called an actionable coalition: a set of participants in a decentralised system with sufficient resources to act (if the participants in the coalition choose to do so), without the involvement – that is, without the help, the permission or even the knowledge – of any other participants.Footnote 3
Let us return to our ant colony and consider a column of foraging ants: what are the actionable coalitions here, where the ants’ task is to bring food back to the colony? When the column discovers some food, a relevant notion of actionable coalition is any collection of ants with the physical strength to heave the food back to the hive. Note that the ants do not need anybody to organise them into a group or to tell them what to do: they swarm over the food until some group of them manage to move the food – aha, an actionable coalition has assembled and agreed on their action! – and then that coalition gets on with heaving while the rest of the ants move on.
When we describe an actionable coalition as ‘a group of participants with the resources to act’, note that – this being a decentralised system – the action concerns just participants in that coalition and not the entire set of participants. Contrast with, for example, a national voting system, which is distributed but still centralised in the sense that the winning candidate wins for everybody, not just for the people who voted for that candidate.Footnote 4
A union of actionable coalitions is an actionable coalition.Footnote
5
This makes the set of all actionable coalitions look a bit like a topology, except that an intersection of actionable coalitions need not be actionable (just because sets
![]() $S$
and
$S$
and
![]() $S'$
are each collectively strong enough to act does not mean that
$S'$
are each collectively strong enough to act does not mean that
![]() $S\cap S'$
is; e.g.,
$S\cap S'$
is; e.g.,
![]() $S\cap S'$
may consist of just a single ant).
$S\cap S'$
may consist of just a single ant).
This brings us to a mathematical abstraction: point-set semitopology, which generalises point-set topology by removing the condition that intersections of open sets are necessarily open.
1.2 Point-set semitopologies
Notation 1.2.1.
Suppose
![]() $\mathsf{P}$
is a set. Write
$\mathsf{P}$
is a set. Write
![]() $\textit{pow}(\mathsf{P})$
for the powerset of
$\textit{pow}(\mathsf{P})$
for the powerset of
![]() $\mathsf{P}$
(the set of subsets of
$\mathsf{P}$
(the set of subsets of
![]() $\mathsf{P}$
).
$\mathsf{P}$
).
Definition 1.2.2. A semitopological space, or semitopology for short, consists of a pair
![]() $(\mathsf{P}, \mathsf{Open}(\mathsf{P}))$
of a (possibly empty) set
$(\mathsf{P}, \mathsf{Open}(\mathsf{P}))$
of a (possibly empty) set
![]() $\mathsf{P}$
of points and a set
$\mathsf{P}$
of points and a set
![]() $\mathsf{Open}(\mathsf{P})\subseteq \textit{pow}(\mathsf{P})$
of open sets, such that:
$\mathsf{Open}(\mathsf{P})\subseteq \textit{pow}(\mathsf{P})$
of open sets, such that:
-
(1)
 $\varnothing \in \mathsf{Open}(\mathsf{P})$
and
$\varnothing \in \mathsf{Open}(\mathsf{P})$
and
 $\mathsf{P}\in \mathsf{Open}(\mathsf{P})$
.
$\mathsf{P}\in \mathsf{Open}(\mathsf{P})$
. -
(2) If
 $X\subseteq \mathsf{Open}(\mathsf{P})$
then
$X\subseteq \mathsf{Open}(\mathsf{P})$
then
 $\bigcup X\in \mathsf{Open}(\mathsf{P})$
.Footnote
6
$\bigcup X\in \mathsf{Open}(\mathsf{P})$
.Footnote
6
We may write
![]() $\mathsf{Open}(\mathsf{P})$
just as
$\mathsf{Open}(\mathsf{P})$
just as
![]() $\mathsf{Open}$
, if
$\mathsf{Open}$
, if
![]() $\mathsf{P}$
is irrelevant or understood, and we may write
$\mathsf{P}$
is irrelevant or understood, and we may write
![]() $\mathsf{Open}_{\neq \varnothing }$
for the set of nonempty open sets.
$\mathsf{Open}_{\neq \varnothing }$
for the set of nonempty open sets.
Remark 1.2.3 (Justification for semitopologies). A classic text, Vickers (Reference Vickers1989) justifies topology as follows:
-
(1) Logically, open sets model affirmations:Footnote 7 an open set
 $O$
corresponds to an affirmation (of
$O$
corresponds to an affirmation (of
 $O$
) (Vickers, Reference Vickers1989, p. 10).
$O$
) (Vickers, Reference Vickers1989, p. 10). -
(2) Computationally, open sets model semidecidable properties. See the first page of the preface in Vickers (Reference Vickers1989).
We can justify semitopologies in a similar style as follows:
-
(1) Logically, open sets model actionable affirmations: an open set
 $O$
corresponds to an outcome that is agreed on and can be actioned within
$O$
corresponds to an outcome that is agreed on and can be actioned within
 $O$
.
$O$
. -
(2) Computationally, open sets model actionable outcomes.
So the distinction between topology and semitopology is this: topology is about things that can be positively said, whereas semitopology is about things that can be positively done.
Identifying actionable coalitions as a topological concept is new, but as is often the case for key concepts, with hindsight we can see them everywhere. The notion corresponds to that of a quorum in the classic distributed systems literature (Lamport, Reference Lamport1998). Social choice theorists have a similar notion called a winning coalition (Riker, Reference Riker1962, Item 5, p. 40). In blockchains, the XRP Ledger (Schwartz et al., Reference Schwartz, Youngs and Britto2014) and the Stellar network (Lokhava et al., Reference Lokhava, Losa, Mazières, Hoare, Barry, Gafni, Jove, Malinowsky and McCaleb2019) have explicit notions of actionable coalition, in the sense that a participant must specify information about their desired actionable coalitions when they sign up to the system. In Ethereum and other proof-of-stake blockchains, an actionable coalition is (roughly speaking) any group of participants with more than half of the voting power of the system.
1.3 Well-behavedness conditions on semitopologies
It turns out that we can understand a surprising amount about a decentralised system just by analysing its actionable coalitions; that is, by viewing it as a semitopology. And when we do, the most relevant and interesting semitopologies turn out to be ill-behaved from the usual topological viewpoint, because they are almost never Hausdorff; indeed, the most well-behaved semitopologies satisfy an anti-Hausdorff property of being intertwined, such that all of their open set intersect.
This is because if all actionable coalitions intersect, then any two actions that are taken must be compatible, in the sense that there must exist at least one participant who was able to take both actions. This implies a practically useful form of coherence for the overall system: while it is not the case that participants must act in synchrony (since that would not be decentralised), any actions that are taken must be compatible on some nonempty overlap; we make this formal in Theorem3.2.3 and Corollary 3.2.4. In practice, it turns out that this property is often enough to derive important coherence properties for the overall system.
Notions of transitive open set (topen) and regular point become central to the theory, where topens are sets of pairwise intertwined participants (all their open neighbourhoods intersect), and points are called ‘regular’ when they have a topen neighbourhood. Briefly and in a nutshell: ‘good’ semitopologies have lots of regular points, and the best ones consist entirely of regular points.
The question we should ask then is: what are semitopologies, and what are well-behavedness properties like having topens and being regular?
One answer is that things are what the definitions define them to be – for example, semitopologies are Definition 1.2.2 – but the reader may know that we can use algebra to give better answers. In particular, looking at Definition 1.2.2 it might appear that semitopologies are just complete join-semilattices in sets. Well, this is not quite true, as we shall see.
1.4 Semiframes: the algebraic dual to semitopologies
There is a well-known recipe for understanding sets-based structures: we dualise them. That is, we decide what the morphisms should be (answer: continuous functions), we build a dual category of semiframes, and we study that.
It will turn out that a semiframe is a compatible complete semilattice. What ‘compatibility’ means is given in Definition 7.3.1, and it has to do with an algebraic abstraction of the nonempty intersection of open sets. What we can observe here is that the devil will be in the details (as always): the definition ‘compatible complete semilattice’ is not immediately obvious, and the proofs require work, and the duals to the well-behavedness conditions on semitopologies translate to algebraic structure in the world of semiframes.
Studying the dualities between semitopologies and semiframes, and how well-behavedness properties on points translate (or do not translate!) to their algebraic duals, is the topic of the paper.
Remark 1.4.1 (Semitopologies are compatible complete join-semilattices in sets). Something interesting will happen when we dualise semitopologies: we will find ourselves obliged to introduce the notion of a compatibility relation
![]() $\ast$
(Definition 7.2.1). This arises naturally twice:
$\ast$
(Definition 7.2.1). This arises naturally twice:
-
• as a key technicality in our duality result, and also
-
• as an algebraic analogue of the intertwinedness property
 $\between$
which we need to express well-behavedness properties such as regularity (Section 4).
$\between$
which we need to express well-behavedness properties such as regularity (Section 4).
It is interesting that
![]() $\ast$
/
$\ast$
/
![]() $\between$
appears for two reasons that, on the face of things, have quite distinct origins: algebraically in the duality and as a pragmatically motivated well-behavedness condition on sets.
$\between$
appears for two reasons that, on the face of things, have quite distinct origins: algebraically in the duality and as a pragmatically motivated well-behavedness condition on sets.
So a message of our study of duality is to corroborate that intertwinedness is both mathematically fundamental and practically useful, and that (as noted above) semitopologies are not just complete join semilattices in sets, but something a bit richer, namely compatible complete join-semilattices in sets.
1.5 Map of the paper
-
(1) Section 1 is the Introduction. You Are Here.
-
(2) In Section 2, we show how continuity corresponds to local agreement (Definition 1.2.2 and Lemma 2.2.4).
-
(3) In Section 3, we discuss transitive sets, topens and intertwined points. These are all anti-separation well-behavedness properties; for example, transitive and topen sets are guaranteed to be in agreement, in a sense made precise in Theorem3.2.3 and Corollary 3.2.4.
-
(4) In Section 4, we classify points in more detail, introducing notions of regular, weakly regular, and quasiregular points (Definition 4.1.4).Footnote 8
Regular points are points contained in a topen set, and as per Theorem3.2.3, they display good behaviour.
-
(5) In Section 5, we characterise regularity as regular = weakly regular + unconflicted: see Theorem5.3.4.
-
(6) In Section 6, we characterise regularity as regular = quasiregular + hypertransitive: see Theorem6.3.3.
This completes our treatment of point-set semitopologies, and next we dualise, as follows:
-
(7) In Section 7, we introduce semiframes. These are the algebraic version of semitopologies, and they are to semitopologies as frames are to topologies.
We discover that semiframes are not just join-semilattices; semiframes are compatible semilattices, which include a compatibility relation
 $\ast$
to abstract the property of set intersection
$\ast$
to abstract the property of set intersection
 $\between$
(see Remark 1.4.1).
$\between$
(see Remark 1.4.1). -
(8) In Section 8, we introduce semifilters. These play a similar role as filters do in topologies, except that semifilters have a compatibility condition instead of closure under finite meets. We develop the notion of abstract points (completely prime semifilters) and show how to build a semitopology out of the abstract points of a semiframe.
-
(9) In Section 9, we introduce sober semitopologies and spatial semiframes. The reader familiar with categorical duality may be familiar with these conditions, though some details are significantly different from the topological case (see, for instance, the discussion in Section 9.3.2).
-
(10) In Section 10, we consider the duality between suitable categories of (sober) semitopologies and (spatial) semiframes.
-
(11) In Section 11, we dualise the well-behavedness conditions from Section 3 to algebraic versions. The correspondence is good (Proposition 11.6.2) but also imperfect in some interesting ways (Remark 11.8.11).
-
(12) In Section 12, we conclude and discuss related and future work.
1.6 Comments on the context of this research
Remark 1.6.1 (Algebraic topology
![]() $\neq$
semitopology and semiframes). Algebraic topology has been applied to the solvability of distributed-computing tasks in computational models (e.g., the impossibility of
$\neq$
semitopology and semiframes). Algebraic topology has been applied to the solvability of distributed-computing tasks in computational models (e.g., the impossibility of
![]() $k$
-set consensus and the Asynchronous Computability Theorem (Herlihy and Shavit, Reference Herlihy and Shavit1993; Borowsky and Gafni, Reference Borowsky and Gafni1993; Saks and Zaharoglou, Reference Saks and Zaharoglou2000); see Herlihy et al. (Reference Herlihy, Kozlov and Rajsbaum2013) for a survey).
$k$
-set consensus and the Asynchronous Computability Theorem (Herlihy and Shavit, Reference Herlihy and Shavit1993; Borowsky and Gafni, Reference Borowsky and Gafni1993; Saks and Zaharoglou, Reference Saks and Zaharoglou2000); see Herlihy et al. (Reference Herlihy, Kozlov and Rajsbaum2013) for a survey).
This paper is not that! Algebra and topology are versatile tools: this paper is algebraic and topological, but in different senses and to different ends.
Remark 1.6.2 (Where the interesting properties are). Topology often studies spaces with strong separability properties between points, like Hausdorff separability. For our applications, the well-behavedness properties of semitopologies and corresponding properties in semiframes centre on clusters of points that cannot be separated.
For example, we state and discuss an ‘anti-Hausdorff’ anti-separation property which we call being intertwined (see Definition 3.5.1 and Remark 3.5.7). Within an intertwined set, continuity implies agreement in a particularly strong sense (see Corollary 3.5.6). This leads us to study classes of semitopologies and semiframes with various anti-separation well-behavedness conditions; see most notably regularity (Sections 4 and 11).
Remark 1.6.3. As the reader may know, frames and locales are the same thing: the category of locales is just the categorical opposite of the category of frames. So every time we write ‘semiframe’, the reader can safely read ‘semilocale'; these are two names for essentially the same structure up to reversing arrows.
The literature on frames and locales is huge, as indeed is the literature on topology. Classic texts are Johnstone (Reference Johnstone1986) and Mac Lane and Moerdijk (Reference Mac Lane and Moerdijk1992). More recent and very readable presentations are in Picado and Pultr (Reference Picado and Pultr2012, Reference Picado and Pultr2021). This literature is a rich source of ideas for things to do with semiframes, with respect to which we cannot possibly be comprehensive in this single paper: there are many things of interest that we simply have not done yet, or perhaps have not even (yet) realised could be done, and this is a feature, not a bug, since it reflects a wide scope for possible future research.
A partial list of possible future work is in Section 12.3; and lists of properties and non-properties of semiframes/semitopologies versus frames/topologies are in Sections 8.2.1, 8.2.2, 9.3.2 and 12.1.
Remark 1.6.4. This paper expands on selected material from a technical monograph by Gabbay (Reference Gabbay2024), and it continues where a journal paper on point-set topologies by Gabbay (Reference Gabbay2025) left off.
For this document to be meaningful and self-contained, we include some material on point-set semitopologies – just as a treatment of frames would define point-set topologies. The material has been organised, edited and streamlined specifically to provide a direct route to semiframes and their duality.
Our goal for this paper is to offer an accessible, dedicated and self-contained journal exposition on what is currently understood about semiframes and their relation to point-set semitopologies, in the context of current developments in decentralised systems.
Remark 1.6.5 (Who should read this paper?). This work is aimed at the advanced researcher interested in a new kind of point-free topology, albeit one that is grounded in the practical needs of modern decentralised systems, and at the advanced practitioner interested in seeing what they may already be doing in a new (and more abstract) mathematical light.
I hope this paper will stimulate interest in compatible complete join-semilattices and related structures as an elegant abstraction of decentralised systems.
2. Semitopology
2.1 Definition and examples
2.1.1 Semitopologies are not topologies
Recall from Definition 1.2.2 the definition of a semitopology. As a set structure, a semitopology on
![]() $\mathsf{P}$
is like a topology on
$\mathsf{P}$
is like a topology on
![]() $\mathsf{P}$
, but without the condition that the intersection of two open sets be an open set. This gives semitopologies their own distinct character, and we can see this before we have even developed much of the theory, as we discuss in Remark 2.1.1 and Lemma 2.1.2:
$\mathsf{P}$
, but without the condition that the intersection of two open sets be an open set. This gives semitopologies their own distinct character, and we can see this before we have even developed much of the theory, as we discuss in Remark 2.1.1 and Lemma 2.1.2:
Remark 2.1.1. Every semitopology
![]() $(\mathsf{P},\mathsf{Open})$
gives rise to a topology just by closing opens under intersections. But semitopologies are far more than just subbases for a corresponding topology:
$(\mathsf{P},\mathsf{Open})$
gives rise to a topology just by closing opens under intersections. But semitopologies are far more than just subbases for a corresponding topology:
-
(1) Completing a semitopology to a topology by closing under intersections loses information.
For example, the ‘many’, ‘all-but-one’ and ‘more-than-one’ semitopologies in Example 2.1.4 express three distinct notions of quorum, yet all three yield the discrete semitopology (Definition 2.1.3) if we close under intersections and
 $\mathsf{P}$
is infinite. See also the overview in Section 12.1.
$\mathsf{P}$
is infinite. See also the overview in Section 12.1. -
(2) We are explicitly interested in situations where intersections of open sets need not be open, due to our motivating interpretation of open sets as actionable coalitions (as discussed in Section 1).
Much of the difference in flavour between topologies and semitopologies comes down to this:
Lemma 2.1.2.
-
(1) In topologies, if a point
 $p$
has a minimal open neighbourhood, then it is least (= unique minimal).
$p$
has a minimal open neighbourhood, then it is least (= unique minimal).
-
(2) In semitopologies, a point may have multiple distinct minimal open neighbourhoods.
Proof.
To see that in a topology every minimal open neighbourhood is least, just note that if
![]() $p\in A$
and
$p\in A$
and
![]() $p\in B$
, then
$p\in B$
, then
![]() $p\in A\cap B$
. So if
$p\in A\cap B$
. So if
![]() $A$
and
$A$
and
![]() $B$
are two minimal open neighbourhoods, then
$B$
are two minimal open neighbourhoods, then
![]() $A\cap B$
is contained in both and, by minimality, is equal to both.
$A\cap B$
is contained in both and, by minimality, is equal to both.

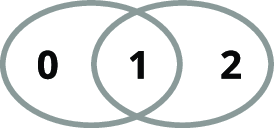
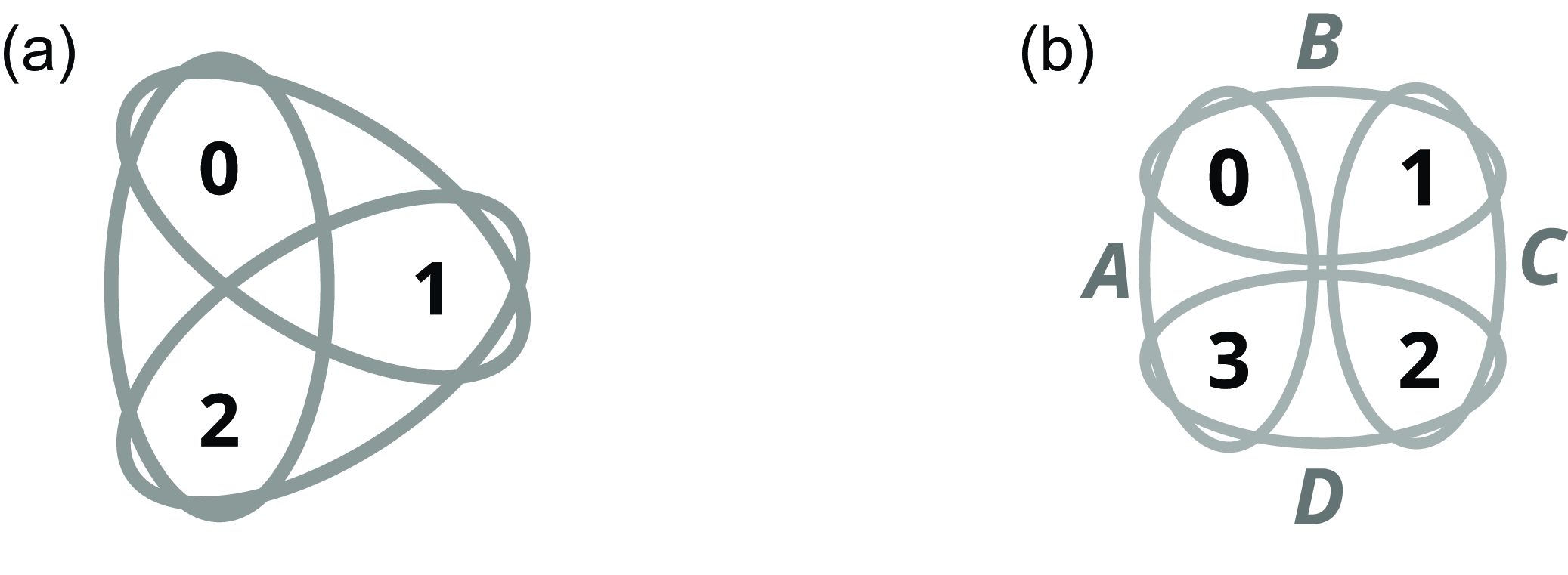
Figure 1. An example of a point with two minimal open neighbourhoods (Lemma 2.1.2).
To see that in a semitopology a minimal open neighbourhood need not be least, it suffices to provide an example. Consider
![]() $(\mathsf{P},\mathsf{Open})$
defined as follows, as illustrated in Figure 1:
$(\mathsf{P},\mathsf{Open})$
defined as follows, as illustrated in Figure 1:
-
•
 $\mathsf{P}=\{0,1,2\}$
$\mathsf{P}=\{0,1,2\}$
-
•
 $\mathsf{Open} = \bigl \{ \varnothing ,\ \{0,1\},\ \{1,2\},\ \{0,1,2\} \bigr \}$
$\mathsf{Open} = \bigl \{ \varnothing ,\ \{0,1\},\ \{1,2\},\ \{0,1,2\} \bigr \}$
Note that
![]() $1$
has two minimal open neighbourhoods:
$1$
has two minimal open neighbourhoods:
![]() $\{0,1\}$
and
$\{0,1\}$
and
![]() $\{1,2\}$
.
$\{1,2\}$
.
2.1.2 Examples
As standard, we can make any set
![]() $\mathsf{Val}$
into a semitopology (indeed, it is also a topology) just by letting open sets be the powerset:
$\mathsf{Val}$
into a semitopology (indeed, it is also a topology) just by letting open sets be the powerset:
Definition 2.1.3.
-
(1) Call
 $(\mathsf{P},\textit{pow}(\mathsf{P}))$
the discrete semitopology on
$(\mathsf{P},\textit{pow}(\mathsf{P}))$
the discrete semitopology on
 $\mathsf{P}$
.
$\mathsf{P}$
.We may call a set with the discrete semitopology a semitopology of values, and when we do, we will usually call it
 $\mathsf{Val}$
. We may identify
$\mathsf{Val}$
. We may identify
 $\mathsf{Val}$
-the-set and
$\mathsf{Val}$
-the-set and
 $\mathsf{Val}$
-the-discrete-semitopology; meaning will always be clear.
$\mathsf{Val}$
-the-discrete-semitopology; meaning will always be clear. -
(2) When
 $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
 $\mathsf{Val}$
is a semitopology of values, we may call a function
$\mathsf{Val}$
is a semitopology of values, we may call a function
 $f:\mathsf{P}\to \mathsf{Val}$
a value assignment.
$f:\mathsf{P}\to \mathsf{Val}$
a value assignment.Note that a value just assigns values to points, and in particular, we do not assume a priori that it is continuous, where continuity is defined just as for topologies (see Definition 2.2.1).
Example 2.1.4. We consider further examples of semitopologies:
-
(1) Every topology is also a semitopology; intersections of open sets are allowed to be open in a semitopology; they are just not constrained to be open. In particular, the discrete topology is also a discrete semitopology (Definition 2.1.3(1)).
-
(2) The initial semitopology
 $(\varnothing ,\{\varnothing \})$
and the final semitopology
$(\varnothing ,\{\varnothing \})$
and the final semitopology
 $(\{\ast \},\{\varnothing ,\{\ast \}\})$
are semitopologies.
$(\{\ast \},\{\varnothing ,\{\ast \}\})$
are semitopologies. -
(3) An important discrete semitopological space is
We may silently treat \begin{equation*} \mathbb B=\{\bot ,\top \} \quad \text{with the discrete semitopology}\quad \mathsf{Open}(\mathbb B)=\{\varnothing , \{\bot \},\{\top \},\{\bot ,\top \}\}. \end{equation*}
\begin{equation*} \mathbb B=\{\bot ,\top \} \quad \text{with the discrete semitopology}\quad \mathsf{Open}(\mathbb B)=\{\varnothing , \{\bot \},\{\top \},\{\bot ,\top \}\}. \end{equation*}
 $\mathbb B$
as a (discrete) semitopological space henceforth.
$\mathbb B$
as a (discrete) semitopological space henceforth.
-
(4) Take
 $\mathsf{P}$
to be any nonempty set. Let the trivial semitopology (this is also a topology) on
$\mathsf{P}$
to be any nonempty set. Let the trivial semitopology (this is also a topology) on
 $\mathsf{P}$
haveSo (as usual) there are only two open sets: the one containing nothing and the one containing every point.Footnote 9
$\mathsf{P}$
haveSo (as usual) there are only two open sets: the one containing nothing and the one containing every point.Footnote 9 \begin{equation*} \mathsf{Open} =\{\varnothing , \mathsf{P}\}. \end{equation*}
\begin{equation*} \mathsf{Open} =\{\varnothing , \mathsf{P}\}. \end{equation*}
The only nonempty open is
 $\mathsf{P}$
itself, reflecting a notion of actionable coalition that requires unanimous agreement.
$\mathsf{P}$
itself, reflecting a notion of actionable coalition that requires unanimous agreement. -
(5) Suppose
 $\mathsf{P}$
is a set and
$\mathsf{P}$
is a set and
 $\mathscr F\subseteq \textit{pow}(\mathsf{P})$
is nonempty and up-closed (so if
$\mathscr F\subseteq \textit{pow}(\mathsf{P})$
is nonempty and up-closed (so if
 $P\in \mathscr F$
and
$P\in \mathscr F$
and
 $P\subseteq P'\subseteq \mathsf{P}$
then
$P\subseteq P'\subseteq \mathsf{P}$
then
 $P'\in \mathscr F$
, then
$P'\in \mathscr F$
, then
 $(\mathsf{P},\mathscr F)$
is a semitopology. This is not necessarily a topology, because we do not insist that
$(\mathsf{P},\mathscr F)$
is a semitopology. This is not necessarily a topology, because we do not insist that
 $\mathscr F$
is a filter (i.e., is closed under intersections).
$\mathscr F$
is a filter (i.e., is closed under intersections).We give four sub-examples for different choices of
 $\mathscr P\subseteq \textit{pow}(\mathsf{P})$
:
$\mathscr P\subseteq \textit{pow}(\mathsf{P})$
:-
a. Take
 $\mathsf{P}$
to be any finite nonempty set. Let the supermajority semitopology haveSo
$\mathsf{P}$
to be any finite nonempty set. Let the supermajority semitopology haveSo \begin{equation*} \mathsf{Open} =\{\varnothing \}\cup \{O\subseteq \mathsf{P} \mid \textit{cardinality}(O)\geq \frac {2}{3}*\textit{cardinality}(\mathsf{P})\}. \end{equation*}
\begin{equation*} \mathsf{Open} =\{\varnothing \}\cup \{O\subseteq \mathsf{P} \mid \textit{cardinality}(O)\geq \frac {2}{3}*\textit{cardinality}(\mathsf{P})\}. \end{equation*}
 $O$
is open when it contains at least two-thirds of the points.
$O$
is open when it contains at least two-thirds of the points.
Two-thirds is a typical threshold used for making progress in consensus algorithms.
-
b. Take
 $\mathsf{P}$
to be any nonempty set. Let the many semitopology haveFor example, if
$\mathsf{P}$
to be any nonempty set. Let the many semitopology haveFor example, if \begin{equation*} \mathsf{Open} = \{\varnothing \}\cup \{O\subseteq \mathsf{P} \mid \textit{cardinality}(O)=\textit{cardinality}(\mathsf{P})\} . \end{equation*}
\begin{equation*} \mathsf{Open} = \{\varnothing \}\cup \{O\subseteq \mathsf{P} \mid \textit{cardinality}(O)=\textit{cardinality}(\mathsf{P})\} . \end{equation*}
 $\mathsf{P}=\mathbb N$
then open sets include
$\mathsf{P}=\mathbb N$
then open sets include
 $\textit{evens}=\{2*n \mid n\in \mathbb N\}$
and
$\textit{evens}=\{2*n \mid n\in \mathbb N\}$
and
 $\textit{odds}=\{2*n{+} 1 \mid n\in \mathbb N\}$
.
$\textit{odds}=\{2*n{+} 1 \mid n\in \mathbb N\}$
.
Its notion of open set captures an idea that an actionable coalition is a set that may not be all of
 $\mathsf{P}$
, but does at least biject with it.
$\mathsf{P}$
, but does at least biject with it. -
c. Take
 $\mathsf{P}$
to be any nonempty set. Let the all-but-one semitopology haveThis semitopology is not a topology.
$\mathsf{P}$
to be any nonempty set. Let the all-but-one semitopology haveThis semitopology is not a topology. \begin{equation*} \mathsf{Open} = \{\varnothing ,\ \mathsf{P}\}\cup \{\mathsf{P}\setminus \{p\}\mid p\in \mathsf{P}\} . \end{equation*}
\begin{equation*} \mathsf{Open} = \{\varnothing ,\ \mathsf{P}\}\cup \{\mathsf{P}\setminus \{p\}\mid p\in \mathsf{P}\} . \end{equation*}
The notion of actionable coalition here is that there may be at most one objector (but not two).
-
d. Take
 $\mathsf{P}$
to be any set with cardinality at least
$\mathsf{P}$
to be any set with cardinality at least
 $2$
. Let the more-than-one semitopology haveThis semitopology is not a topology.
$2$
. Let the more-than-one semitopology haveThis semitopology is not a topology. \begin{equation*} \mathsf{Open} = \{\varnothing \}\cup \{O\subseteq \mathsf{P} \mid \textit{cardinality}(O) \geq 2\} . \end{equation*}
\begin{equation*} \mathsf{Open} = \{\varnothing \}\cup \{O\subseteq \mathsf{P} \mid \textit{cardinality}(O) \geq 2\} . \end{equation*}
This notion of actionable coalition reflects a security principle in banking and accounting (and elsewhere) of separation of duties, that functional responsibilities be separated such that at least two people are required to complete an action – so that errors (or worse) cannot be made without being discovered by another person.
-
-
(6) Take
 $\mathsf{P}=\mathbb R$
(the set of real numbers) and let open sets be generated by intervals of the form
$\mathsf{P}=\mathbb R$
(the set of real numbers) and let open sets be generated by intervals of the form
 $[0,r)$
or
$[0,r)$
or
 $(- r,0]$
for any strictly positive real number
$(- r,0]$
for any strictly positive real number
 $r\gt 0$
.
$r\gt 0$
.This semitopology is not a topology, since (e.g.,)
 $(1,0]$
and
$(1,0]$
and
 $[0,1)$
are open, but their intersection
$[0,1)$
are open, but their intersection
 $\{0\}$
is not open.
$\{0\}$
is not open. -
(7) Naor and Wool (Reference Naor and Wool1994) discuss a notion of quorum system, defined as any collection of pairwise intersecting sets. Quorum systems are key to the theory and practical implementation of consensus algorithms.
Every quorum system gives rise naturally to the least semitopology that contains it, just by closing under arbitrary unions.
To give one specific example of a quorum system from Naor and Wool (Reference Naor and Wool1994), consider
 $n\times n$
grid of cells with quorums being sets consisting of any full row and a full column; note that any two quorums must intersect in at least two points. We obtain a semitopology just by closing under arbitrary unions.
$n\times n$
grid of cells with quorums being sets consisting of any full row and a full column; note that any two quorums must intersect in at least two points. We obtain a semitopology just by closing under arbitrary unions.
2.2 Continuity and its interpretation as agreement
Definition 2.2.1. We import standard topological notions of inverse image and continuity:
-
(1) Suppose
 $\mathsf{P}$
and
$\mathsf{P}$
and
 $\mathsf{P}'$
are any sets and
$\mathsf{P}'$
are any sets and
 $f:\mathsf{P}\to \mathsf{P}'$
is a function. Suppose
$f:\mathsf{P}\to \mathsf{P}'$
is a function. Suppose
 $O'\subseteq \mathsf{P}'$
. Then write
$O'\subseteq \mathsf{P}'$
. Then write
 $f^{\text{-}1}(O')$
for the inverse image or preimage of
$f^{\text{-}1}(O')$
for the inverse image or preimage of
 $O'$
, defined by
$O'$
, defined by \begin{equation*} f^{\text{-}1}(O')=\{p{\in }\mathsf{P} \mid f(p)\in O'\} . \end{equation*}
\begin{equation*} f^{\text{-}1}(O')=\{p{\in }\mathsf{P} \mid f(p)\in O'\} . \end{equation*}
-
(2) Suppose
 $(\mathsf{P},\mathsf{Open})$
and
$(\mathsf{P},\mathsf{Open})$
and
 $(\mathsf{P}',\mathsf{Open}')$
are semitopological spaces (Definition 1.2.2). Call a function
$(\mathsf{P}',\mathsf{Open}')$
are semitopological spaces (Definition 1.2.2). Call a function
 $f:\mathsf{P}\to \mathsf{P}'$
continuous when the inverse image of an open set is open. In symbols:
$f:\mathsf{P}\to \mathsf{P}'$
continuous when the inverse image of an open set is open. In symbols: \begin{equation*} \forall O'\in \mathsf{Open}'. f^{\text{-}1}(O')\in \mathsf{Open} . \end{equation*}
\begin{equation*} \forall O'\in \mathsf{Open}'. f^{\text{-}1}(O')\in \mathsf{Open} . \end{equation*}
-
(3) Call a function
 $f:\mathsf{P}\to \mathsf{P}'$
continuous at
$f:\mathsf{P}\to \mathsf{P}'$
continuous at
 $p\in \mathsf{P}$
whenIn words:
$p\in \mathsf{P}$
whenIn words: \begin{equation*} \forall O'{\in }\mathsf{Open}'.f(p)\in O'\Longrightarrow \exists O_{p,O'}{\in }\mathsf{Open}.p\in O_{p,O'}\land O_{p,O'}\subseteq f^{\text{-}1}(O') . \end{equation*}
\begin{equation*} \forall O'{\in }\mathsf{Open}'.f(p)\in O'\Longrightarrow \exists O_{p,O'}{\in }\mathsf{Open}.p\in O_{p,O'}\land O_{p,O'}\subseteq f^{\text{-}1}(O') . \end{equation*}
 $f$
is continuous at
$f$
is continuous at
 $p$
when the inverse image of every open neighbourhood of
$p$
when the inverse image of every open neighbourhood of
 $f(p)$
contains an open neighbourhood of
$f(p)$
contains an open neighbourhood of
 $p$
.
$p$
.
-
(4) Call a function
 $f:\mathsf{P}\to \mathsf{P}'$
continuous on
$f:\mathsf{P}\to \mathsf{P}'$
continuous on
 $P\subseteq \mathsf{P}$
when
$P\subseteq \mathsf{P}$
when
 $f$
is continuous at every
$f$
is continuous at every
 $p\in P$
.
$p\in P$
.
Lemma 2.2.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
and
$(\mathsf{P},\mathsf{Open})$
and
![]() $(\mathsf{P}',\mathsf{Open}')$
are semitopological spaces (Definition 1.2.2) and suppose
$(\mathsf{P}',\mathsf{Open}')$
are semitopological spaces (Definition 1.2.2) and suppose
![]() $f:\mathsf{P}\to \mathsf{P}'$
is a function. Then the following are equivalent:
$f:\mathsf{P}\to \mathsf{P}'$
is a function. Then the following are equivalent:
Proof.
The top-down implication is immediate, taking
![]() $O=f^{\text{-}1}(O')$
.
$O=f^{\text{-}1}(O')$
.
For the bottom-up implication, given
![]() $p$
and an open neighbourhood
$p$
and an open neighbourhood
![]() $O'\ni f(p)$
, we write
$O'\ni f(p)$
, we write
Above,
![]() $O_{p,O'}$
is the open neighbourhood of
$O_{p,O'}$
is the open neighbourhood of
![]() $p$
in the preimage of
$p$
in the preimage of
![]() $O'$
, which we know exists by Definition 2.2.1(3).
$O'$
, which we know exists by Definition 2.2.1(3).
It is routine to check that
![]() $O= f^{\text{-}1}(O')$
, and since this is a union of open sets, it is open.
$O= f^{\text{-}1}(O')$
, and since this is a union of open sets, it is open.
Definition 2.2.3. Suppose that:
-
•
 $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and -
•
 $\mathsf{Val}$
is a semitopology of values (Definition 2.1.3(1)) and
$\mathsf{Val}$
is a semitopology of values (Definition 2.1.3(1)) and -
•
 $f:\mathsf{P}\to \mathsf{Val}$
is a value assignment (Definition 2.1.3(2); an assignment of a value to each element in
$f:\mathsf{P}\to \mathsf{Val}$
is a value assignment (Definition 2.1.3(2); an assignment of a value to each element in
 $\mathsf{P}$
).
$\mathsf{P}$
).
Then:
-
(1) Call
 $f$
locally constant at
$f$
locally constant at
 $p\in \mathsf{P}$
when there exists
$p\in \mathsf{P}$
when there exists
 $p\in O_p\in \mathsf{Open}$
such thatSo
$p\in O_p\in \mathsf{Open}$
such thatSo \begin{equation*} \forall p'{\in }O_p.f(p)=f(p'). \end{equation*}
\begin{equation*} \forall p'{\in }O_p.f(p)=f(p'). \end{equation*}
 $f$
is locally constant at
$f$
is locally constant at
 $p$
when it is constant on some open neighbourhood
$p$
when it is constant on some open neighbourhood
 $O_p$
of
$O_p$
of
 $p$
.
$p$
.
-
(2) Call
 $f$
locally constant when it is locally constant at every
$f$
locally constant when it is locally constant at every
 $p\in \mathsf{P}$
.
$p\in \mathsf{P}$
.
Lemma 2.2.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $\mathsf{Val}$
is a semitopology of values and
$\mathsf{Val}$
is a semitopology of values and
![]() $f:\mathsf{P}\to \mathsf{Val}$
is a value assignment. Then the following are equivalent:
$f:\mathsf{P}\to \mathsf{Val}$
is a value assignment. Then the following are equivalent:
Proof. This is just by pushing around definitions, but we spell it out:
-
• Suppose
 $f$
is continuous, consider
$f$
is continuous, consider
 $p\in \mathsf{P}$
and write
$p\in \mathsf{P}$
and write
 $v=f(p)$
. By our assumptions, we know that
$v=f(p)$
. By our assumptions, we know that
 $f^{\text{-}1}(v)$
is open, and
$f^{\text{-}1}(v)$
is open, and
 $p\in f^{\text{-}1}(v)$
. This is an open neighbourhood
$p\in f^{\text{-}1}(v)$
. This is an open neighbourhood
 $O_p$
on which
$O_p$
on which
 $f$
is constant, so we are done.
$f$
is constant, so we are done. -
• Suppose
 $f$
is locally constant, consider
$f$
is locally constant, consider
 $p\in \mathsf{P}$
, and write
$p\in \mathsf{P}$
, and write
 $v=f(p)$
. By assumption we can find
$v=f(p)$
. By assumption we can find
 $p\in O_p\in \mathsf{Open}$
on which
$p\in O_p\in \mathsf{Open}$
on which
 $f$
is constant, so that
$f$
is constant, so that
 $O_p\subseteq f^{\text{-}1}(v)$
.
$O_p\subseteq f^{\text{-}1}(v)$
.
2.3 Neighbourhoods of a point
Definition 2.3.1 is standard from topology, and Lemma 2.3.2 is a (standard) characterisation of openness, which will be useful later:
Definition 2.3.1. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
and
$p\in \mathsf{P}$
and
![]() $O\in \mathsf{Open}$
. Then:
$O\in \mathsf{Open}$
. Then:
-
(1) Call
 $O$
an open neighbourhood of
$O$
an open neighbourhood of
 $p$
when
$p$
when
 $p\in O$
.
$p\in O$
. -
(2) Define
 $\textit{nbhd}(p)\subseteq \mathsf{Open}$
the neighbourhood system of
$\textit{nbhd}(p)\subseteq \mathsf{Open}$
the neighbourhood system of
 $p$
by
$p$
by \begin{equation*} \textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in \mathsf{Open}\} . \end{equation*}
\begin{equation*} \textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in \mathsf{Open}\} . \end{equation*}
Lemma 2.3.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology, and suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology, and suppose
![]() $P\subseteq \mathsf{P}$
is any set of points. Then the following are equivalent:
$P\subseteq \mathsf{P}$
is any set of points. Then the following are equivalent:
-
•
 $P\in \mathsf{Open}$
.
$P\in \mathsf{Open}$
. -
• Every point
 $p$
in
$p$
in
 $P$
has an open neighbourhood in
$P$
has an open neighbourhood in
 $P$
.
$P$
.
In symbols we can write:
Proof.
If
![]() $P$
is open, then
$P$
is open, then
![]() $P$
itself is an open neighbourhood for every point that it contains.
$P$
itself is an open neighbourhood for every point that it contains.
Conversely, if every
![]() $p\in P$
contains some open neighbourhood
$p\in P$
contains some open neighbourhood
![]() $p\in O_p \subseteq P$
, then
$p\in O_p \subseteq P$
, then
![]() $P=\bigcup \{O_p\mid p\in P\}$
, and this is open by condition 2 of Definition 1.2.2.
$P=\bigcup \{O_p\mid p\in P\}$
, and this is open by condition 2 of Definition 1.2.2.
Remark 2.3.3. An initial inspiration for modelling collaborative action using semitopologies came from noting that the standard topological property described above in Lemma 2.3.2 corresponds to the quorum sharing property in (Losa et al., Reference Losa, Gafni, Mazières and Suomela2019, Property 1); the connection to topological ideas had not been noticed in Losa et al. (Reference Losa, Gafni, Mazières and Suomela2019).
3. Transitive Sets & Topens
3.1 Some background on set intersection
Some notation will be convenient:
Notation 3.1.1.
Suppose
![]() $X$
,
$X$
,
![]() $Y$
and
$Y$
and
![]() $Z$
are sets.
$Z$
are sets.
-
(1) Write
When \begin{equation*} X\between Y \quad \text{when}\quad X\cap Y\neq \varnothing . \end{equation*}
\begin{equation*} X\between Y \quad \text{when}\quad X\cap Y\neq \varnothing . \end{equation*}
 $X\between Y$
holds, then we say (as standard) that
$X\between Y$
holds, then we say (as standard) that
 $X$
and
$X$
and
 $Y$
intersect
.
$Y$
intersect
.
-
(2) We may chain the
 $\between$
notation, writing, for example,
$\between$
notation, writing, for example,
 \begin{equation*} X\between Y\between Z \quad \text{for}\quad X\between Y\ \land \ Y\between Z \end{equation*}
\begin{equation*} X\between Y\between Z \quad \text{for}\quad X\between Y\ \land \ Y\between Z \end{equation*}
-
(3) We may write
 for
for
 $\neg (X\between Y)$
, thus
$\neg (X\between Y)$
, thus
 when
when
 $X\cap Y=\varnothing$
.
$X\cap Y=\varnothing$
.
Remark 3.1.2. Note on design in Notation 3.1.1: It is uncontroversial that if
![]() $X\neq \varnothing$
and
$X\neq \varnothing$
and
![]() $Y\neq \varnothing$
, then
$Y\neq \varnothing$
, then
![]() $X\between Y$
should hold precisely when
$X\between Y$
should hold precisely when
![]() $X\cap Y\neq \varnothing$
– but there is an edge case! What truth value should
$X\cap Y\neq \varnothing$
– but there is an edge case! What truth value should
![]() $X\between Y$
return when
$X\between Y$
return when
![]() $X$
or
$X$
or
![]() $Y$
is empty?
$Y$
is empty?
-
(1) It might be nice if
 $X\subseteq Y$
would imply
$X\subseteq Y$
would imply
 $X\between Y$
. This argues for setting
$X\between Y$
. This argues for setting \begin{equation*} (X=\varnothing \lor Y=\varnothing )\Longrightarrow X\between Y . \end{equation*}
\begin{equation*} (X=\varnothing \lor Y=\varnothing )\Longrightarrow X\between Y . \end{equation*}
-
(2) It might be nice if
 $X\between Y$
were monotone on both arguments (i.e., if
$X\between Y$
were monotone on both arguments (i.e., if
 $X\between Y$
and
$X\between Y$
and
 $X\subseteq X'$
, then
$X\subseteq X'$
, then
 $X'\between Y$
). This argues for setting
$X'\between Y$
). This argues for setting
-
(3) It might be nice if
 $X\between X$
always – after all, should a set not intersect itself? – and this argues for settingeven if we also set
$X\between X$
always – after all, should a set not intersect itself? – and this argues for settingeven if we also set \begin{equation*} \varnothing \between \varnothing , \end{equation*}
\begin{equation*} \varnothing \between \varnothing , \end{equation*}
 for nonempty
for nonempty
 $Y$
.
$Y$
.
All three choices are defensible, and they are consistent with the following nice property:
We choose the second – if
![]() $X$
or
$X$
or
![]() $Y$
is empty then
$Y$
is empty then  – because it gives the simplest definition that
– because it gives the simplest definition that
![]() $X\between Y$
precisely when
$X\between Y$
precisely when
![]() $X\cap Y\neq \varnothing$
.
$X\cap Y\neq \varnothing$
.
We list some elementary properties of
![]() $\between$
from Notation 3.1.1(1):
$\between$
from Notation 3.1.1(1):
Lemma 3.1.3.
-
(1)
 $X\between X$
if and only if
$X\between X$
if and only if
 $X\neq \varnothing$
.
$X\neq \varnothing$
. -
(2)
 $X\between Y$
if and only if
$X\between Y$
if and only if
 $Y\between X$
.
$Y\between X$
. -
(3)
 $X\between (Y\cup Z)$
if and only if
$X\between (Y\cup Z)$
if and only if
 $(X\between Y) \lor (X\between Z)$
.
$(X\between Y) \lor (X\between Z)$
. -
(4) If
 $X\subseteq X'$
and
$X\subseteq X'$
and
 $X\neq \varnothing$
then
$X\neq \varnothing$
then
 $X\between X'$
.
$X\between X'$
. -
(5) Suppose
 $X\between Y$
. Then
$X\between Y$
. Then
 $X\subseteq X'$
implies
$X\subseteq X'$
implies
 $X'\between Y$
, and
$X'\between Y$
, and
 $Y\subseteq Y'$
implies
$Y\subseteq Y'$
implies
 $X\between Y'$
.
$X\between Y'$
. -
(6) If
 $X\between Y$
then
$X\between Y$
then
 $X\neq \varnothing$
and
$X\neq \varnothing$
and
 $Y\neq \varnothing$
.
$Y\neq \varnothing$
.
Proof. By facts of set intersection.
3.2 Transitive open sets and value assignments
Remark 3.2.1 (Taking stock of topens). Transitive sets are of interest because values of continuous functions are strongly correlated on them. This is Theorem 3.2.3, especially part 2 of Theorem 3.2.3.
A transitive open set – a topen – is even more important, because an open set corresponds in our semitopological model to a quorum (a collection of participants that can make progress), so a transitive open set is a collection of participants that can make progress and are guaranteed to do so in consensus, where algorithms succeed.
For this and other reasons, we very much care about finding topens and understanding when points are associated with topen sets (e.g., by having topen neighbourhoods). As we develop the maths, this will then lead us on to consider various regularity properties (Definition 4.1.4). But first, we start with transitive sets and topens:
Definition 3.2.2. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Suppose
![]() $T\subseteq \mathsf{P}$
is any set of points.
$T\subseteq \mathsf{P}$
is any set of points.
-
(1) Call
 $T$
transitive when
$T$
transitive when \begin{equation*} \forall O,O'{\in }\mathsf{Open}. O\between T \between O' \Longrightarrow O\between O'. \end{equation*}
\begin{equation*} \forall O,O'{\in }\mathsf{Open}. O\between T \between O' \Longrightarrow O\between O'. \end{equation*}
-
(2) Call
 $T$
topen when
$T$
topen when
 $T$
is nonempty transitive and open.Footnote
10
$T$
is nonempty transitive and open.Footnote
10
We may write
 \begin{equation*} \mathsf{Topen}=\{ T\in \mathsf{Open}_{\neq \varnothing } \mid T\text{ is transitive}\} . \end{equation*}
\begin{equation*} \mathsf{Topen}=\{ T\in \mathsf{Open}_{\neq \varnothing } \mid T\text{ is transitive}\} . \end{equation*}
-
(3) Call
 $S$
a maximal topen when
$S$
a maximal topen when
 $S$
is a topen that is not a subset of any strictly larger topen.Footnote
11
$S$
is a topen that is not a subset of any strictly larger topen.Footnote
11
Theorem3.2.3 clarifies why transitivity is interesting: continuous value assignments are constant – if we think of points as participants, ‘constant function’ here means ‘in agreement’ – across transitive sets.
Theorem 3.2.3. Suppose that:
-
•
 $(\mathsf{P},\mathsf{Open})$
is a semitopology.
$(\mathsf{P},\mathsf{Open})$
is a semitopology.
-
•
 $\mathsf{Val}$
is a semitopology of values (a nonempty set with the discrete semitopology; see Definition 2.1.3(1)).
$\mathsf{Val}$
is a semitopology of values (a nonempty set with the discrete semitopology; see Definition 2.1.3(1)).
-
•
 $f:\mathsf{P}\to \mathsf{Val}$
is a value assignment (Definition 2.1.3(2)).
$f:\mathsf{P}\to \mathsf{Val}$
is a value assignment (Definition 2.1.3(2)).
-
•
 $T\subseteq \mathsf{P}$
is a transitive set (Definition 3.2.2) – in particular this will hold if
$T\subseteq \mathsf{P}$
is a transitive set (Definition 3.2.2) – in particular this will hold if
 $T$
is topen – and
$T$
is topen – and
 $p,p'\in T$
.
$p,p'\in T$
.
Then:
-
(1) If
 $f$
is continuous at
$f$
is continuous at
 $p$
and
$p$
and
 $p'$
then
$p'$
then
 $f(p)=f(p')$
.
$f(p)=f(p')$
. -
(2) As a corollary, if
 $f$
is continuous on
$f$
is continuous on
 $T$
, then
$T$
, then
 $f$
is constant on
$f$
is constant on
 $T$
.
$T$
.
In words we can say:
Continuous value assignments are constant across transitive sets.
Proof.
Part 2 follows from part 1 since if
![]() $f(p)=f(p')$
for any
$f(p)=f(p')$
for any
![]() $p,p'\in T$
, then by definition
$p,p'\in T$
, then by definition
![]() $f$
is constant on
$f$
is constant on
![]() $T$
. So we now just need to prove part 1 of this result.
$T$
. So we now just need to prove part 1 of this result.
Consider
![]() $p,p'\in T$
. By continuity on
$p,p'\in T$
. By continuity on
![]() $T$
, there exist open neighbourhoods
$T$
, there exist open neighbourhoods
![]() $p\in O\subseteq f^{\text{-}1}(f(p))$
and
$p\in O\subseteq f^{\text{-}1}(f(p))$
and
![]() $p'\in O'\subseteq f^{\text{-}1}(f(p'))$
. By construction
$p'\in O'\subseteq f^{\text{-}1}(f(p'))$
. By construction
![]() $O\between T \between O'$
(because
$O\between T \between O'$
(because
![]() $p\in O\cap T$
and
$p\in O\cap T$
and
![]() $p'\in T\cap O'$
). By transitivity of
$p'\in T\cap O'$
). By transitivity of
![]() $T$
, it follows that
$T$
, it follows that
![]() $O\between O'$
. Thus, there exists
$O\between O'$
. Thus, there exists
![]() $p''\in O\cap O'$
, and by construction
$p''\in O\cap O'$
, and by construction
![]() $f(p) = f(p'') = f(p')$
.
$f(p) = f(p'') = f(p')$
.
Corollary 3.2.4 is an easy and useful consequence of Theorem3.2.3:
Corollary 3.2.4. Suppose that:
-
•
 $(\mathsf{P},\mathsf{Open})$
is a semitopology.
$(\mathsf{P},\mathsf{Open})$
is a semitopology.
-
•
 $f:\mathsf{P}\to \mathsf{Val}$
is a value assignment to some set of values
$f:\mathsf{P}\to \mathsf{Val}$
is a value assignment to some set of values
 $\mathsf{Val}$
(Definition 2.1.3).
$\mathsf{Val}$
(Definition 2.1.3).
-
•
 $f$
is continuous on topen sets
$f$
is continuous on topen sets
 $T, T'\in \mathsf{Topen}$
.
$T, T'\in \mathsf{Topen}$
.
Then
Proof.
By Theorem3.2.3,
![]() $f$
is constant on
$f$
is constant on
![]() $T$
and
$T$
and
![]() $T'$
. We assumed that
$T'$
. We assumed that
![]() $T$
and
$T$
and
![]() $T'$
intersect, and the result follows.
$T'$
intersect, and the result follows.
A converse to Theorem3.2.3 also holds:
Proposition 3.2.5. Suppose that:
-
•
 $(\mathsf{P},\mathsf{Open})$
is a semitopology.
$(\mathsf{P},\mathsf{Open})$
is a semitopology.
-
•
 $\mathsf{Val}$
is a semitopology of values with at least two elements (to exclude a degenerate case where no functions exist, or they exist but there is only one because there is only one value to map to).
$\mathsf{Val}$
is a semitopology of values with at least two elements (to exclude a degenerate case where no functions exist, or they exist but there is only one because there is only one value to map to).
-
•
 $T\subseteq \mathsf{P}$
is any set.
$T\subseteq \mathsf{P}$
is any set.
Then
-
• if for every
 $p,p'\in T$
and every value assignment
$p,p'\in T$
and every value assignment
 $f:\mathsf{P}\to \mathsf{Val}$
,
$f:\mathsf{P}\to \mathsf{Val}$
,
 $f$
continuous at
$f$
continuous at
 $p$
and
$p$
and
 $p'$
implies
$p'$
implies
 $f(p)=f(p')$
,
$f(p)=f(p')$
, -
• then
 $T$
is transitive.
$T$
is transitive.
Proof.
We prove the contrapositive. Suppose
![]() $T$
is not transitive, so there exist
$T$
is not transitive, so there exist
![]() $O,O'\in \mathsf{Open}$
such that
$O,O'\in \mathsf{Open}$
such that
![]() $O\between T\between O'$
and yet
$O\between T\between O'$
and yet
![]() $O\cap O'=\varnothing$
. We choose two distinct values
$O\cap O'=\varnothing$
. We choose two distinct values
![]() $v\neq v'\in \mathsf{Val}$
and define
$v\neq v'\in \mathsf{Val}$
and define
![]() $f$
to map any point in
$f$
to map any point in
![]() $O$
to
$O$
to
![]() $v$
and any point in
$v$
and any point in
![]() $\mathsf{P}\setminus O$
to
$\mathsf{P}\setminus O$
to
![]() $v'$
.
$v'$
.
Choose some
![]() $p\in O$
and
$p\in O$
and
![]() $p'\in O'$
. It does not matter which, and some such
$p'\in O'$
. It does not matter which, and some such
![]() $p$
and
$p$
and
![]() $p'$
exist, because
$p'$
exist, because
![]() $O$
and
$O$
and
![]() $O'$
are nonempty by Lemma 3.1.3(6), since
$O'$
are nonempty by Lemma 3.1.3(6), since
![]() $O\between T$
and
$O\between T$
and
![]() $O'\between T$
).
$O'\between T$
).
We note that
![]() $f(p)=v$
and
$f(p)=v$
and
![]() $f(p')=v'$
and
$f(p')=v'$
and
![]() $f$
is continuous at
$f$
is continuous at
![]() $p\in O$
and
$p\in O$
and
![]() $p'\in O'\subseteq \mathsf{P}\setminus O$
, yet
$p'\in O'\subseteq \mathsf{P}\setminus O$
, yet
![]() $f(p)\neq f(p')$
.
$f(p)\neq f(p')$
.
We can sum up what Theorem3.2.3 and Proposition 3.2.5 mean as follows:
Remark 3.2.6. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology, and
$(\mathsf{P},\mathsf{Open})$
is a semitopology, and
![]() $\mathsf{Val}$
is a semitopology of values with at least two elements. Say that a value assignment
$\mathsf{Val}$
is a semitopology of values with at least two elements. Say that a value assignment
![]() $f:\mathsf{P}\to \mathsf{Val}$
splits a set
$f:\mathsf{P}\to \mathsf{Val}$
splits a set
![]() $T\subseteq \mathsf{P}$
when there exist
$T\subseteq \mathsf{P}$
when there exist
![]() $p,p'\in T$
such that
$p,p'\in T$
such that
![]() $f$
is continuous at
$f$
is continuous at
![]() $p$
and
$p$
and
![]() $p'$
and
$p'$
and
![]() $f(p)\neq f(p')$
. Then Theorem 3.2.3 and Proposition 3.2.5 together say in words that:
$f(p)\neq f(p')$
. Then Theorem 3.2.3 and Proposition 3.2.5 together say in words that:
![]() $T\subseteq \mathsf{P}$
is transitive if and only if it cannot be split by a value assignment that is continuous on
$T\subseteq \mathsf{P}$
is transitive if and only if it cannot be split by a value assignment that is continuous on
![]() $T$
.
$T$
.
Intuitively, transitive sets characterise areas of guaranteed agreement.
3.3 Examples and discussion of transitive sets and topens
We may routinely order sets by subset inclusion, including open sets, topens, closed sets, and so on, and we may talk about maximal, minimal, greatest and least elements. We include the (standard) definition for reference:
Notation 3.3.1.
Suppose
![]() $(\mathsf{P},\leq )$
is a poset. Then:
$(\mathsf{P},\leq )$
is a poset. Then:
-
(1) Call
 $p\in \mathsf{P}$
maximal
when
$p\in \mathsf{P}$
maximal
when
 $\forall p'.p{\leq }p'\Longrightarrow p'=p$
and
minimal
when
$\forall p'.p{\leq }p'\Longrightarrow p'=p$
and
minimal
when
 $\forall p'.p'{\leq }p\Longrightarrow p'=p$
.
$\forall p'.p'{\leq }p\Longrightarrow p'=p$
. -
(2) Call
 $p\in \mathsf{P}$
greatest
when
$p\in \mathsf{P}$
greatest
when
 $\forall p.p'\leq p$
and
least
when
$\forall p.p'\leq p$
and
least
when
 $\forall p'.p\leq p'$
.
$\forall p'.p\leq p'$
.
Example 3.3.2 (Examples of transitive sets).
-
(1)
 $\{p\}$
is transitive, for any single point
$\{p\}$
is transitive, for any single point
 $p\in \mathsf{P}$
.
$p\in \mathsf{P}$
.
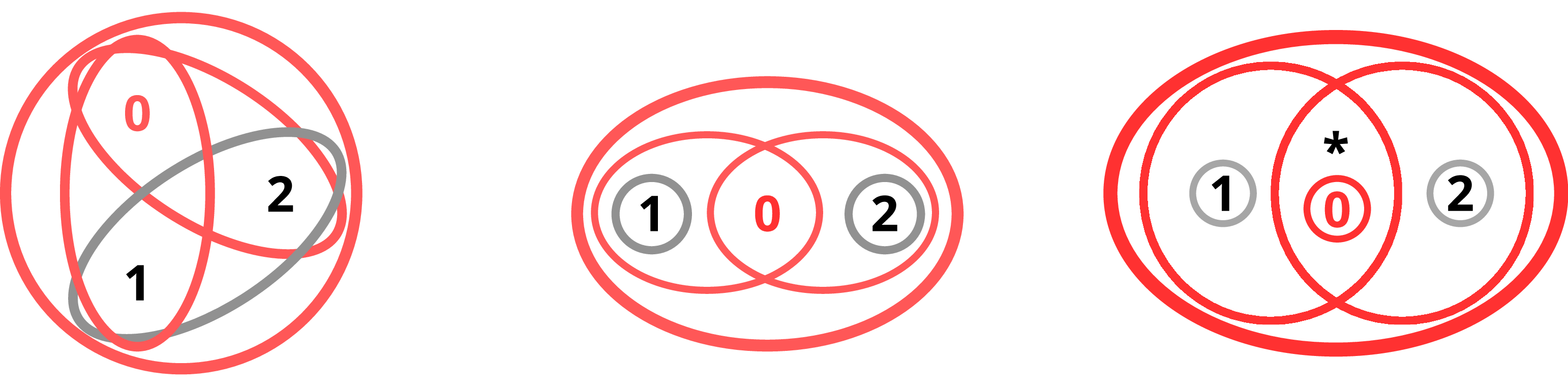
Figure 2. Examples of topens (Example 3.3.3).
-
(2) The empty set
 $\varnothing$
is (trivially) transitive. It is not topen because we insist in Definition 3.2.2(2) that topens are nonempty.
$\varnothing$
is (trivially) transitive. It is not topen because we insist in Definition 3.2.2(2) that topens are nonempty. -
(3) Call a set
 $P\subseteq \mathsf{P}$
topologically indistinguishable when (using Notation 3.1.1) for every open set
$P\subseteq \mathsf{P}$
topologically indistinguishable when (using Notation 3.1.1) for every open set
 $O$
,It is easy to check that if
$O$
,It is easy to check that if \begin{equation*} P\between O\Longleftrightarrow P\subseteq O . \end{equation*}
\begin{equation*} P\between O\Longleftrightarrow P\subseteq O . \end{equation*}
 $P$
is topologically indistinguishable, then it is transitive.
$P$
is topologically indistinguishable, then it is transitive.
Example 3.3.3 (Examples of topens).
-
(1) Take
 $\mathsf{P}=\{0, 1, 2\}$
, with open sets
$\mathsf{P}=\{0, 1, 2\}$
, with open sets
 $\varnothing$
,
$\varnothing$
,
 $\mathsf{P}$
,
$\mathsf{P}$
,
 $\{0\}$
and
$\{0\}$
and
 $\{2\}$
. This has two maximal topens
$\{2\}$
. This has two maximal topens
 $\{0\}$
and
$\{0\}$
and
 $\{2\}$
as illustrated in Figure 2 (top-left diagram).
$\{2\}$
as illustrated in Figure 2 (top-left diagram). -
(2) Take
 $\mathsf{P}=\{0, 1, 2\}$
, with open sets
$\mathsf{P}=\{0, 1, 2\}$
, with open sets
 $\varnothing$
,
$\varnothing$
,
 $\mathsf{P}$
,
$\mathsf{P}$
,
 $\{0\}$
,
$\{0\}$
,
 $\{0, 1\}$
,
$\{0, 1\}$
,
 $\{2\}$
,
$\{2\}$
,
 $\{1,2\}$
and
$\{1,2\}$
and
 $\{0,2\}$
. This has two maximal topens
$\{0,2\}$
. This has two maximal topens
 $\{0\}$
and
$\{0\}$
and
 $\{2\}$
, as illustrated in Figure 2 (top-right diagram).
$\{2\}$
, as illustrated in Figure 2 (top-right diagram). -
(3) Take
 $\mathsf{P}=\{0,1,2,3,4\}$
, with open sets generated by
$\mathsf{P}=\{0,1,2,3,4\}$
, with open sets generated by
 $\{0, 1\}$
,
$\{0, 1\}$
,
 $\{1\}$
,
$\{1\}$
,
 $\{3\}$
and
$\{3\}$
and
 $\{3,4\}$
. This has two maximal topens
$\{3,4\}$
. This has two maximal topens
 $\{0,1\}$
and
$\{0,1\}$
and
 $\{3,4\}$
, as illustrated in Figure 2 (lower-left diagram).
$\{3,4\}$
, as illustrated in Figure 2 (lower-left diagram). -
(4) Take
 $\mathsf{P}=\{0,1,2,\ast \}$
, with open sets generated by
$\mathsf{P}=\{0,1,2,\ast \}$
, with open sets generated by
 $\{0\}$
,
$\{0\}$
,
 $\{1\}$
,
$\{1\}$
,
 $\{2\}$
,
$\{2\}$
,
 $\{0, 1,\ast \}$
and
$\{0, 1,\ast \}$
and
 $\{1,2,\ast \}$
. This has three maximal topens
$\{1,2,\ast \}$
. This has three maximal topens
 $\{0\}$
,
$\{0\}$
,
 $\{1\}$
and
$\{1\}$
and
 $\{2\}$
, as illustrated in Figure 2 (lower-right diagram).
$\{2\}$
, as illustrated in Figure 2 (lower-right diagram). -
(5) Take the all-but-one semitopology from Example 2.1.4(5c) on
 $\mathbb N$
: so
$\mathbb N$
: so
 $\mathsf{P}=\mathbb N$
with opens
$\mathsf{P}=\mathbb N$
with opens
 $\varnothing$
,
$\varnothing$
,
 $\mathbb N$
and
$\mathbb N$
and
 $\mathbb N\setminus \{x\}$
for every
$\mathbb N\setminus \{x\}$
for every
 $x\in \mathbb N$
. This has a single maximal topen
$x\in \mathbb N$
. This has a single maximal topen
 $\mathbb N$
.
$\mathbb N$
. -
(6) The semitopology in Figure 3 has no topen sets at all (
 $\varnothing$
is transitive and open, but by definition in Definition 3.2.2(2) topens have to be nonempty).
$\varnothing$
is transitive and open, but by definition in Definition 3.2.2(2) topens have to be nonempty).
Here and elsewhere, we might omit open sets that are unions of open sets that are illustrated. For example, we explicitly draw the universal open set in the left-hand diagrams above, but not in the right-hand and bottom diagrams above. Meaning is clear, and we get cleaner diagrams.
3.4 Closure properties of transitive sets and topens
Remark 3.4.1. Transitive sets have some nice closure properties which we treat in this subsection – here, we mean ‘closure’ in the sense of “the set of transitive sets is closed under various operations”, and not in the topological sense of ‘closed sets’. Topens – nonempty transitive open sets – have even better closure properties, which emanate from the requirement in Lemma 3.4.3 that at least one of the transitive sets
![]() $T$
or
$T$
or
![]() $T'$
is open.
$T'$
is open.
Lemma 3.4.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $T\subseteq \mathsf{P}$
. Then:
$T\subseteq \mathsf{P}$
. Then:
-
(1) If
 $T$
is transitive and
$T$
is transitive and
 $T'\subseteq T$
, then
$T'\subseteq T$
, then
 $T'$
is transitive.
$T'$
is transitive.
-
(2) If
 $T$
is topen and
$T$
is topen and
 $\varnothing \neq T'\subseteq T$
is nonempty and open, then
$\varnothing \neq T'\subseteq T$
is nonempty and open, then
 $T'$
is topen.
$T'$
is topen.
Proof.
-
(1) By Definition 3.2.2, it suffices to consider open sets
 $O$
and
$O$
and
 $O'$
such that
$O'$
such that
 $O\between T'\between O'$
and prove that
$O\between T'\between O'$
and prove that
 $O\between O'$
. But this is simple: by Lemma 3.1.3(5)
$O\between O'$
. But this is simple: by Lemma 3.1.3(5)
 $O\between T\between O'$
, so
$O\between T\between O'$
, so
 $O\between O'$
follows by transitivity of
$O\between O'$
follows by transitivity of
 $T$
.
$T$
. -
(2) Direct from part 1 of this result and Definition 3.2.2(2).
Lemma 3.4.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $T,T'\subseteq \mathsf{P}$
are transitive, and suppose that at least one of
$T,T'\subseteq \mathsf{P}$
are transitive, and suppose that at least one of
![]() $T$
and
$T$
and
![]() $T'$
is open. Then
$T'$
is open. Then
Proof.
We simplify using Definition 3.2.2 and our assumption that one of
![]() $T$
and
$T$
and
![]() $T'$
is open. We consider the case that
$T'$
is open. We consider the case that
![]() $T'$
is open:
$T'$
is open:
The argument for when
![]() $T$
is open is precisely similar.
$T$
is open is precisely similar.
Proposition 3.4.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then if
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then if
![]() $\mathscr T$
is a set of pairwise intersecting topens, then
$\mathscr T$
is a set of pairwise intersecting topens, then
![]() $\bigcup \mathscr T$
is topen.
$\bigcup \mathscr T$
is topen.
Proof.
![]() $\bigcup \mathscr T$
is open by Definition 1.2.2(2). Also, if
$\bigcup \mathscr T$
is open by Definition 1.2.2(2). Also, if
![]() $O\between \bigcup \mathscr T\ \between O'$
then there exist
$O\between \bigcup \mathscr T\ \between O'$
then there exist
![]() $T,T'\in \mathscr T$
such that
$T,T'\in \mathscr T$
such that
![]() $O\between T$
and
$O\between T$
and
![]() $T'\between O'$
. We assumed
$T'\between O'$
. We assumed
![]() $T\between T'$
, so by Lemma 3.4.3 (since
$T\between T'$
, so by Lemma 3.4.3 (since
![]() $T$
and
$T$
and
![]() $T'$
are open) we have
$T'$
are open) we have
![]() $O\between O'$
as required.
$O\between O'$
as required.
Corollary 3.4.5.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then every topen
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then every topen
![]() $T$
is contained in a unique maximal topen.
$T$
is contained in a unique maximal topen.
Proof.
Consider
![]() $\mathscr T\ = \{T\cup T' \mid T'\text{ topen}\land T\between T'\}$
. By Proposition 3.4.4, this is a set of topens. By construction, they all contain
$\mathscr T\ = \{T\cup T' \mid T'\text{ topen}\land T\between T'\}$
. By Proposition 3.4.4, this is a set of topens. By construction, they all contain
![]() $T$
, so by our assumption that
$T$
, so by our assumption that
![]() $T\neq \varnothing$
, they pairwise intersect, and by Proposition 3.4.4 again
$T\neq \varnothing$
, they pairwise intersect, and by Proposition 3.4.4 again
![]() $\bigcup \mathscr T$
is topen. It is easy to check that this is the unique maximal topen that contains
$\bigcup \mathscr T$
is topen. It is easy to check that this is the unique maximal topen that contains
![]() $T$
.
$T$
.
3.5 Intertwined points
3.5.1 The basic definition
Definition 3.5.1. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p,p'\in \mathsf{P}$
.
$p,p'\in \mathsf{P}$
.
-
(1) Call
 $p$
and
$p$
and
 $p'$
intertwined when
$p'$
intertwined when
 $\{p,p'\}$
is transitive. Unpacking Definition 3.2.2, this means:By a mild abuse of notation, write
$\{p,p'\}$
is transitive. Unpacking Definition 3.2.2, this means:By a mild abuse of notation, write \begin{equation*} \forall O,O'{\in }\mathsf{Open}. (p\in O\land p'\in O') \Longrightarrow O\between O' . \end{equation*}
\begin{equation*} \forall O,O'{\in }\mathsf{Open}. (p\in O\land p'\in O') \Longrightarrow O\between O' . \end{equation*}
 \begin{equation*} p\mathrel {\between } p' \quad \text{when}\quad \text{$p$ and $p'$ are intertwined}. \end{equation*}
\begin{equation*} p\mathrel {\between } p' \quad \text{when}\quad \text{$p$ and $p'$ are intertwined}. \end{equation*}
-
(2) Define
 $p_{\between }$
(read ‘intertwined of
$p_{\between }$
(read ‘intertwined of
 $p$
’) to be the set of points intertwined with
$p$
’) to be the set of points intertwined with
 $p$
. In symbols:
$p$
. In symbols: \begin{equation*} p_{\between }=\{p'\in \mathsf{P} \mid p\mathrel {\between } p'\} . \end{equation*}
\begin{equation*} p_{\between }=\{p'\in \mathsf{P} \mid p\mathrel {\between } p'\} . \end{equation*}
Example 3.5.2. We return to the examples in Example 3.3.3. There we note that:
-
(1)
 $1_{\between }=\{0,1,2\}$
and
$1_{\between }=\{0,1,2\}$
and
 $0_{\between }=\{0,1\}$
and
$0_{\between }=\{0,1\}$
and
 $2_{\between }=\{1,2\}$
.
$2_{\between }=\{1,2\}$
. -
(2)
 $1_{\between }=\{1\}$
and
$1_{\between }=\{1\}$
and
 $0_{\between }=\{0\}$
and
$0_{\between }=\{0\}$
and
 $2_{\between }=\{2\}$
.
$2_{\between }=\{2\}$
. -
(3)
 $x_{\between }=\mathsf{P}$
for every
$x_{\between }=\mathsf{P}$
for every
 $x$
.
$x$
.
Lemma 3.5.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the ‘is intertwined’ relation
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the ‘is intertwined’ relation
![]() $\between$
is not necessarily transitive. That is,
$\between$
is not necessarily transitive. That is,
![]() $p\mathrel {\between } p'\mathrel {\between } p''$
does not necessarily imply
$p\mathrel {\between } p'\mathrel {\between } p''$
does not necessarily imply
![]() $p\mathrel {\between } p''$
.
$p\mathrel {\between } p''$
.
Proof.
It suffices to provide a counterexample. The semitopology from Example 3.3.3(1) (illustrated in Figure 2, top-left diagram) will do. So take
![]() $\mathsf{P}=\{0,1,2\}$
and
$\mathsf{P}=\{0,1,2\}$
and
![]() $\mathsf{Open}=\{\varnothing ,\mathsf{P},\{0\},\{2\}\}$
. Then
$\mathsf{Open}=\{\varnothing ,\mathsf{P},\{0\},\{2\}\}$
. Then
3.5.2 Pointwise characterisation of transitive sets
Lemma 3.5.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $T\subseteq \mathsf{P}$
. Then the following are equivalent:
$T\subseteq \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $T$
is transitive.
$T$
is transitive.
-
(2)
 $p\mathrel {\between } p'$
(meaning by Definition 3.5.1 that
$p\mathrel {\between } p'$
(meaning by Definition 3.5.1 that
 $\{p,p'\}$
is transitive) for every
$\{p,p'\}$
is transitive) for every
 $p,p'\in T$
.
$p,p'\in T$
.
Proof.
Suppose
![]() $T$
is transitive. Then by Lemma 3.4.2(1),
$T$
is transitive. Then by Lemma 3.4.2(1),
![]() $\{p,p'\}$
is transitive for every
$\{p,p'\}$
is transitive for every
![]() $p,p'\in T$
.
$p,p'\in T$
.
Suppose
![]() $\{p,p'\}$
is transitive for every
$\{p,p'\}$
is transitive for every
![]() $p,p'\in T$
. Consider open sets
$p,p'\in T$
. Consider open sets
![]() $O$
and
$O$
and
![]() $O'$
such that
$O'$
such that
![]() $O\between T\between O'$
. Choose
$O\between T\between O'$
. Choose
![]() $p\in O\cap T$
and
$p\in O\cap T$
and
![]() $p'\in O\cap T'$
. By construction
$p'\in O\cap T'$
. By construction
![]() $\{p,p'\}\subseteq T$
so, this is transitive. It follows that
$\{p,p'\}\subseteq T$
so, this is transitive. It follows that
![]() $O\between O'$
as required.
$O\between O'$
as required.
Theorem 3.5.5.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $T\subseteq \mathsf{P}$
. Then the following are equivalent:
$T\subseteq \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $T$
is topen.
$T$
is topen.
-
(2)
 $T\in \mathsf{Open}_{\neq \varnothing }$
and
$T\in \mathsf{Open}_{\neq \varnothing }$
and
 $\forall p,p'{\in }T.p\mathrel {\between } p'$
.
$\forall p,p'{\in }T.p\mathrel {\between } p'$
.
In words we can say:
A topen is a nonempty open set of intertwined points.
Proof.
By Definition 3.2.2(2),
![]() $T$
is topen when it is nonempty, open and transitive. By Lemma 3.5.4, this last condition is equivalent to
$T$
is topen when it is nonempty, open and transitive. By Lemma 3.5.4, this last condition is equivalent to
![]() $p\mathrel {\between } p'$
for every
$p\mathrel {\between } p'$
for every
![]() $p,p'\in T$
.
$p,p'\in T$
.
A value assignment is constant on a pair of intertwined points, where it is continuous:
Corollary 3.5.6.
Suppose
![]() $\mathsf{Val}$
is a semitopology of values and
$\mathsf{Val}$
is a semitopology of values and
![]() $f:\mathsf{P}\to \mathsf{Val}$
is a value assignment (Definition 2.1.3) and
$f:\mathsf{P}\to \mathsf{Val}$
is a value assignment (Definition 2.1.3) and
![]() $p,p'\in \mathsf{P}$
and
$p,p'\in \mathsf{P}$
and
![]() $p\between p'$
. Then if
$p\between p'$
. Then if
![]() $f$
continuous at
$f$
continuous at
![]() $p$
and
$p$
and
![]() $p'$
then
$p'$
then
![]() $f(p)=f(p')$
.
$f(p)=f(p')$
.
Remark 3.5.7 (Intertwined as ‘non-Hausdorff’). Recall that we call a topological space
![]() $(\mathsf{P},\mathsf{Open})$
Hausdorff (or
$(\mathsf{P},\mathsf{Open})$
Hausdorff (or
![]() $T_2$
) when any two points can be separated by pairwise disjoint open sets. Using the
$T_2$
) when any two points can be separated by pairwise disjoint open sets. Using the
![]() $\between$
symbol from Notation 3.1.1, we rephrase the Hausdorff condition as
$\between$
symbol from Notation 3.1.1, we rephrase the Hausdorff condition as
we can simplify to
and thus we simplify the Hausdorff condition just to
Note how distinct
![]() $p$
and
$p$
and
![]() $p'$
being intertwined is the opposite of being Hausdorff:
$p'$
being intertwined is the opposite of being Hausdorff:
![]() $p\mathrel {\between } p'$
when
$p\mathrel {\between } p'$
when
![]() $p'\in p_{\between }$
, and they cannot be separated by pairwise disjoint open sets. Thus the assertion
$p'\in p_{\between }$
, and they cannot be separated by pairwise disjoint open sets. Thus the assertion
![]() $p\mathrel {\between } p'$
in Theorem 3.5.5 is a negation of the Hausdorff property:
$p\mathrel {\between } p'$
in Theorem 3.5.5 is a negation of the Hausdorff property:
![]() $ \exists p.p_{\between }\neq \{p\} .$
$ \exists p.p_{\between }\neq \{p\} .$
4. Interiors, Communities & Regular Points
4.1 Community of a (regular) point
Definition 4.1.1 is standard:
Definition 4.1.1 (Open interior). Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $P\subseteq \mathsf{P}$
. Define
$P\subseteq \mathsf{P}$
. Define
![]() $\textit{interior}(P)$
the (open) interior of
$\textit{interior}(P)$
the (open) interior of
![]() $P$
by
$P$
by
Lemma 4.1.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $P\subseteq \mathsf{P}$
. Then the
$P\subseteq \mathsf{P}$
. Then the
![]() $\textit{interior}(P)$
from Definition 4.1.1 is the greatest open subset of
$\textit{interior}(P)$
from Definition 4.1.1 is the greatest open subset of
![]() $P$
.
$P$
.
Proof. Routine by the construction in Definition 4.1.1 and closure of open sets under unions (Definition 1.2.2(2)).
Corollary 4.1.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $P,P'\subseteq \mathsf{P}$
. Then if
$P,P'\subseteq \mathsf{P}$
. Then if
![]() $P\subseteq P'$
then
$P\subseteq P'$
then
![]() $\textit{interior}(P)\subseteq \textit{interior}(P')$
.
$\textit{interior}(P)\subseteq \textit{interior}(P')$
.
Proof. Routine using Lemma 4.1.2.
Definition 4.1.4 (Community of a point and regularity). Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then:
$p\in \mathsf{P}$
. Then:
-
(1) Define
 $\textit{K}(p)$
the community of
$\textit{K}(p)$
the community of
 $p$
byThe community of
$p$
byThe community of \begin{equation*} \textit{K}(p)=\textit{interior}(p_{\between }) . \end{equation*}
\begin{equation*} \textit{K}(p)=\textit{interior}(p_{\between }) . \end{equation*}
 $p$
is always an open set by Lemma 4.1.2.
$p$
is always an open set by Lemma 4.1.2.
-
(2) Extend
 $\textit{K}$
to subsets
$\textit{K}$
to subsets
 $P\subseteq \mathsf{P}$
by taking a sets union:
$P\subseteq \mathsf{P}$
by taking a sets union: \begin{equation*} \textit{K}(P) = \bigcup \{\textit{K}(p) \mid p\in P\} . \end{equation*}
\begin{equation*} \textit{K}(P) = \bigcup \{\textit{K}(p) \mid p\in P\} . \end{equation*}
-
(3) Call
 $p$
a regular point when its community is a topen neighbourhood of
$p$
a regular point when its community is a topen neighbourhood of
 $p$
. In symbols:
$p$
. In symbols: \begin{equation*} p\text{ is regular}\quad \text{when}\quad p\in \textit{K}(p)\in \mathsf{Topen} . \end{equation*}
\begin{equation*} p\text{ is regular}\quad \text{when}\quad p\in \textit{K}(p)\in \mathsf{Topen} . \end{equation*}
-
(4) Call
 $p$
a weakly regular point when its community is an open (but not necessarily topen) neighbourhood of
$p$
a weakly regular point when its community is an open (but not necessarily topen) neighbourhood of
 $p$
. In symbols:
$p$
. In symbols: \begin{equation*} p\text{ is weakly regular}\quad \text{when}\quad p\in \textit{K}(p)\in \mathsf{Open} . \end{equation*}
\begin{equation*} p\text{ is weakly regular}\quad \text{when}\quad p\in \textit{K}(p)\in \mathsf{Open} . \end{equation*}
-
(5) Call
 $p$
a quasiregular point when its community is nonempty. In symbols:
$p$
a quasiregular point when its community is nonempty. In symbols: \begin{equation*} p\text{ is quasiregular}\quad \text{when}\quad \varnothing \neq \textit{K}(p)\in \mathsf{Open} . \end{equation*}
\begin{equation*} p\text{ is quasiregular}\quad \text{when}\quad \varnothing \neq \textit{K}(p)\in \mathsf{Open} . \end{equation*}
-
(6) If
 $p$
is not regular, then we may call it an irregular point or just say that it is not regular.
$p$
is not regular, then we may call it an irregular point or just say that it is not regular. -
(7) If
 $P\subseteq \mathsf{P}$
and every
$P\subseteq \mathsf{P}$
and every
 $p\in P$
is regular/weakly regular/quasiregular/irregular then we may call
$p\in P$
is regular/weakly regular/quasiregular/irregular then we may call
 $P$
a regular/weakly regular/quasiregular/irregular set, respectively (see also Definition 5.3.1(2)).
$P$
a regular/weakly regular/quasiregular/irregular set, respectively (see also Definition 5.3.1(2)).
Remark 4.1.5. The notion of a regular point in Definition 4.1.4 is a key well-behavedness property. Let’s remember why it matters:
A topen set is a transitive open set. We care about transitivity because it implies agreement, as per Theorem 3.2.3 (continuous value assignments are constant on transitive sets). We care about being open because we understand this as ‘being actionable’. Thus, a regular point is interesting because it is a participant in a topen and thus is capable of safely making progress in algorithms we write on top of the underlying semitopology. For convenient reference, the semiframe characterisation of regularity is in Section 11.5.
Lemma 4.1.6 gives an initial overview of the relationships between the properties in Definition 4.1.4. A more detailed treatment follows, which repeats these main points and expands on them and puts them in a detailed context.
Lemma 4.1.6.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then:
$p\in \mathsf{P}$
. Then:
-
(1) If
 $p$
is regular, then
$p$
is regular, then
 $p$
is weakly regular.
$p$
is weakly regular.
-
(2) If
 $p$
is weakly regular, then
$p$
is weakly regular, then
 $p$
is quasiregular.
$p$
is quasiregular.
-
(3) The converse implications need not hold.
-
(4) Furthermore, it is possible for a point
 $p$
to not be quasiregular.
$p$
to not be quasiregular.
Proof. We consider each part in turn:
-
(1) If
 $p$
is regular, then by Definition 4.1.4(3)
$p$
is regular, then by Definition 4.1.4(3)
 $p\in \textit{K}(p)\in \mathsf{Topen}$
, so certainly
$p\in \textit{K}(p)\in \mathsf{Topen}$
, so certainly
 $p\in \textit{K}(p)$
and by Definition 4.1.4(4)
$p\in \textit{K}(p)$
and by Definition 4.1.4(4)
 $p$
is weakly regular.
$p$
is weakly regular. -
(2) If
 $p$
is weakly regular, then by Definition 4.1.4(4)
$p$
is weakly regular, then by Definition 4.1.4(4)
 $p\in \textit{K}(p)\in \mathsf{Open}$
, so certainly
$p\in \textit{K}(p)\in \mathsf{Open}$
, so certainly
 $\textit{K}(p)\neq \varnothing$
, and by Definition 4.1.4(5),
$\textit{K}(p)\neq \varnothing$
, and by Definition 4.1.4(5),
 $p$
is quasiregular.
$p$
is quasiregular. -
(3) To see that the converse implications need not hold, note that:
-
– Point
 $1$
in Example 4.1.7(2) (illustrated in Figure 2, top-left diagram) is weakly regular (
$1$
in Example 4.1.7(2) (illustrated in Figure 2, top-left diagram) is weakly regular (
 $\textit{K}(1)=\{0,1,2\}$
) but not regular (
$\textit{K}(1)=\{0,1,2\}$
) but not regular (
 $\textit{K}(1)$
is open but not topen).
$\textit{K}(1)$
is open but not topen). -
– Point
 $\ast$
in Example 4.1.7(3) (illustrated in Figure 2, lower-right diagram) is quasiregular (
$\ast$
in Example 4.1.7(3) (illustrated in Figure 2, lower-right diagram) is quasiregular (
 $\textit{K}(\ast )=\{1\}$
is nonempty but does not contain
$\textit{K}(\ast )=\{1\}$
is nonempty but does not contain
 $\ast$
).
$\ast$
).
-
-
(4) To see that
 $p$
may not even be quasiregular, take
$p$
may not even be quasiregular, take
 $\mathsf{P}=\mathbb R$
(real numbers), with its usual topology (which is also a semitopology). Then
$\mathsf{P}=\mathbb R$
(real numbers), with its usual topology (which is also a semitopology). Then
 $x_{\between }=\{x\}$
and
$x_{\between }=\{x\}$
and
 $\textit{K}(x)=\varnothing$
for every
$\textit{K}(x)=\varnothing$
for every
 $x\in \mathbb R$
.
$x\in \mathbb R$
.
Example 4.1.7.
-
(1) In Figure 2 (bottom diagram),
 $0$
,
$0$
,
 $1$
and
$1$
and
 $2$
are three intertwined points, and the entire space
$2$
are three intertwined points, and the entire space
 $\{0,1,2\}$
consists of a single topen set. It follows that
$\{0,1,2\}$
consists of a single topen set. It follows that
 $0$
,
$0$
,
 $1$
and
$1$
and
 $2$
are all regular, and their community is
$2$
are all regular, and their community is
 $\{0,1,2\}$
.
$\{0,1,2\}$
. -
(2) In Figure 2 (top-left diagram),
 $0$
and
$0$
and
 $2$
are regular, and
$2$
are regular, and
 $1$
is weakly regular but not regular (
$1$
is weakly regular but not regular (
 $1\in \textit{K}(1)=\{0,1,2\}$
but
$1\in \textit{K}(1)=\{0,1,2\}$
but
 $\{0,1,2\}$
is not topen).
$\{0,1,2\}$
is not topen). -
(3) In Figure 2 (lower-right diagram),
 $0$
,
$0$
,
 $1$
and
$1$
and
 $2$
are regular, and
$2$
are regular, and
 $\ast$
is quasiregular (
$\ast$
is quasiregular (
 $\textit{K}(\ast )=\{1\}$
).
$\textit{K}(\ast )=\{1\}$
). -
(4) In Figure 2 (top-right diagram),
 $0$
and
$0$
and
 $2$
are regular, and
$2$
are regular, and
 $1$
is neither regular, weakly regular, nor quasiregular (
$1$
is neither regular, weakly regular, nor quasiregular (
 $\textit{K}(1)=\varnothing$
).
$\textit{K}(1)=\varnothing$
). -
(5) In a semitopology of values
 $(\mathsf{Val},\textit{pow}(\mathsf{Val}))$
(Definition 2.1.3), every value
$(\mathsf{Val},\textit{pow}(\mathsf{Val}))$
(Definition 2.1.3), every value
 $v\in \mathsf{Val}$
is regular, weakly regular and unconflicted.
$v\in \mathsf{Val}$
is regular, weakly regular and unconflicted. -
(6) In
 $\mathbb R$
with its usual topology (which is also a semitopology), every point is unconflicted because the topology is Hausdorff, and by Equation (1) in Remark 3.5.7, this means precisely that
$\mathbb R$
with its usual topology (which is also a semitopology), every point is unconflicted because the topology is Hausdorff, and by Equation (1) in Remark 3.5.7, this means precisely that
 $p_{\between }=\{p\}$
, so
$p_{\between }=\{p\}$
, so
 $p$
is intertwined just with itself. Furthermore,
$p$
is intertwined just with itself. Furthermore,
 $p$
is not (quasi/weakly) regular, because
$p$
is not (quasi/weakly) regular, because
 $\textit{K}(p)=\textit{interior}(p_{\between })=\varnothing$
.
$\textit{K}(p)=\textit{interior}(p_{\between })=\varnothing$
.
4.2 Further exploration of (quasi-/weak) regularity and topen sets
Remark 4.2.1. Recall three common separation axioms from topology:
-
(1)
 $T_0$
: if
$T_0$
: if
 $p_1\neq p_2$
, then there exists some
$p_1\neq p_2$
, then there exists some
 $O\in \mathsf{Open}$
such that
$O\in \mathsf{Open}$
such that
 $(p_1\in O)\mathbin {\mathsf{\small xor}} (p_2\in O)$
, where
$(p_1\in O)\mathbin {\mathsf{\small xor}} (p_2\in O)$
, where
 $\mathbin {\mathsf{\small xor}}$
denotes exclusive or.
$\mathbin {\mathsf{\small xor}}$
denotes exclusive or. -
(2)
 $T_1$
: if
$T_1$
: if
 $p_1\neq p_2$
, then there exist
$p_1\neq p_2$
, then there exist
 $O_1,O_2\in \mathsf{Open}$
such that
$O_1,O_2\in \mathsf{Open}$
such that
 $p_i\in O_j \Longleftrightarrow i=j$
for
$p_i\in O_j \Longleftrightarrow i=j$
for
 $i,j\in \{1,2\}$
.
$i,j\in \{1,2\}$
. -
(3)
 $T_2$
, or the Hausdorff condition: if
$T_2$
, or the Hausdorff condition: if
 $p_1\neq p_2$
, then there exist
$p_1\neq p_2$
, then there exist
 $O_1,O_2\in \mathsf{Open}$
such that
$O_1,O_2\in \mathsf{Open}$
such that
 $p_i\in O_j \Longleftrightarrow i=j$
for
$p_i\in O_j \Longleftrightarrow i=j$
for
 $i,j\in \{1,2\}$
, and
$i,j\in \{1,2\}$
, and
 $O_1\cap O_2=\varnothing$
. Cf. the discussion in Remark 3.5.7.
$O_1\cap O_2=\varnothing$
. Cf. the discussion in Remark 3.5.7.
Even the weakest of the well-behavedness properties for semitopologies that we consider in Definition 4.1.4 – quasiregularity – is in some sense strongly opposed to the space being Hausdorff/
![]() $T_2$
(though not to being
$T_2$
(though not to being
![]() $T_1$
), as Lemma 4.2.2 makes formal.
$T_1$
), as Lemma 4.2.2 makes formal.
Lemma 4.2.2.
-
(1) Every quasiregular Hausdorff semitopology is discrete.
In more detail: if
 $(\mathsf{P},\mathsf{Open})$
is a semitopology that is quasiregular (Definition 4.1.4(5)) and Hausdorff (Equation (
1
) in Remark 3.5.7), then
$(\mathsf{P},\mathsf{Open})$
is a semitopology that is quasiregular (Definition 4.1.4(5)) and Hausdorff (Equation (
1
) in Remark 3.5.7), then
 $\mathsf{Open}=\textit{pow}(\mathsf{P})$
.
$\mathsf{Open}=\textit{pow}(\mathsf{P})$
. -
(2) There exists a (quasi)regular
 $T_1$
semitopology that is not discrete.
$T_1$
semitopology that is not discrete.
Proof. We consider each part in turn:
-
(1) By the Hausdorff property,
 $p_{\between }=\{p\}$
. By the quasiregularity property,
$p_{\between }=\{p\}$
. By the quasiregularity property,
 $\textit{K}(p)\neq \varnothing$
. It follows that
$\textit{K}(p)\neq \varnothing$
. It follows that
 $\textit{K}(p)=\{p\}$
. But by construction in Definition 4.1.4(1),
$\textit{K}(p)=\{p\}$
. But by construction in Definition 4.1.4(1),
 $\textit{K}(p)$
is an open interior. Thus
$\textit{K}(p)$
is an open interior. Thus
 $\{p\}\in \mathsf{Open}$
. The result follows.
$\{p\}\in \mathsf{Open}$
. The result follows. -
(2) It suffices to provide an example. We use the bottom semitopology in Figure 2. Thus
 $\mathsf{P}=\{0,1,2\}$
and
$\mathsf{P}=\{0,1,2\}$
and
 $\mathsf{Open}$
is generated by
$\mathsf{Open}$
is generated by
 $\{0,1\}$
,
$\{0,1\}$
,
 $\{1,2\}$
and
$\{1,2\}$
and
 $\{2,0\}$
. The reader can check that this is regular (since all three points are intertwined) and
$\{2,0\}$
. The reader can check that this is regular (since all three points are intertwined) and
 $T_1$
.
$T_1$
.
So what is
![]() $\textit{K}(p)$
? We start by characterising
$\textit{K}(p)$
? We start by characterising
![]() $\textit{K}(p)$
as the greatest topen neighbourhood of
$\textit{K}(p)$
as the greatest topen neighbourhood of
![]() $p$
, if this exists:
$p$
, if this exists:
Lemma 4.2.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology, and recall from Definition 4.1.4(3) that
$(\mathsf{P},\mathsf{Open})$
is a semitopology, and recall from Definition 4.1.4(3) that
![]() $p$
is regular when
$p$
is regular when
![]() $\textit{K}(p)$
is a topen neighbourhood of
$\textit{K}(p)$
is a topen neighbourhood of
![]() $p$
.
$p$
.
-
(1) If
 $\textit{K}(p)$
is a topen neighbourhood of
$\textit{K}(p)$
is a topen neighbourhood of
 $p$
(i.e., if
$p$
(i.e., if
 $p$
is regular), then
$p$
is regular), then
 $\textit{K}(p)$
is a maximal topen.
$\textit{K}(p)$
is a maximal topen.
-
(2) If
 $p\in T\in \mathsf{Topen}$
is a maximal topen neighbourhood of
$p\in T\in \mathsf{Topen}$
is a maximal topen neighbourhood of
 $p$
then
$p$
then
 $T=\textit{K}(p)$
.
$T=\textit{K}(p)$
.
Proof.
-
(1) Since
 $p$
is regular, by definition,
$p$
is regular, by definition,
 $\textit{K}(p)$
is topen and is a neighbourhood of
$\textit{K}(p)$
is topen and is a neighbourhood of
 $p$
. It remains to show that
$p$
. It remains to show that
 $\textit{K}(p)$
is a maximal topen.
$\textit{K}(p)$
is a maximal topen.Suppose
 $T$
is a topen neighbourhood of
$T$
is a topen neighbourhood of
 $p$
; we wish to prove
$p$
; we wish to prove
 $T\subseteq \textit{K}(p)=\textit{interior}(p_{\between })$
. Since
$T\subseteq \textit{K}(p)=\textit{interior}(p_{\between })$
. Since
 $T$
is open, it would suffice to show that
$T$
is open, it would suffice to show that
 $T\subseteq p_{\between }$
. By Theorem3.5.5,
$T\subseteq p_{\between }$
. By Theorem3.5.5,
 $p\mathrel {\between } p'$
for every
$p\mathrel {\between } p'$
for every
 $p'\in T$
, and it follows immediately that
$p'\in T$
, and it follows immediately that
 $T\subseteq p_{\between }$
.
$T\subseteq p_{\between }$
. -
(2) Suppose
 $T$
is a maximal topen neighbourhood of
$T$
is a maximal topen neighbourhood of
 $p$
.
$p$
.First, note that
 $T$
is open, and by Theorem3.5.5
$T$
is open, and by Theorem3.5.5
 $T\subseteq p_{\between }$
, so
$T\subseteq p_{\between }$
, so
 $T\subseteq \textit{K}(p)$
.
$T\subseteq \textit{K}(p)$
.Now consider any open
 $O\subseteq p_{\between }$
. Note that
$O\subseteq p_{\between }$
. Note that
 $T\cup O$
is an open subset of
$T\cup O$
is an open subset of
 $p_{\between }$
, so by Theorem3.5.5
$p_{\between }$
, so by Theorem3.5.5
 $T\cup O$
is topen, and by maximality
$T\cup O$
is topen, and by maximality
 $T\cup O\subseteq T$
and thus
$T\cup O\subseteq T$
and thus
 $O\subseteq T$
. It follows that
$O\subseteq T$
. It follows that
 $\textit{K}(p)\subseteq T$
.
$\textit{K}(p)\subseteq T$
.
Remark 4.2.4. We can use Lemma 4.2.3 to characterise regularity in five equivalent ways: see Theorem 4.2.5 and Corollary 4.2.6.
Theorem 4.2.5.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following are equivalent:
$p\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $p$
is regular, or in full:
$p$
is regular, or in full:
 $p\in \textit{K}(p)\in \mathsf{Topen}$
.
$p\in \textit{K}(p)\in \mathsf{Topen}$
. -
(2)
 $\textit{K}(p)$
is the greatest topen neighbourhood of
$\textit{K}(p)$
is the greatest topen neighbourhood of
 $p$
.
$p$
. -
(3)
 $\textit{K}(p)$
is a maximal topen neighbourhood of
$\textit{K}(p)$
is a maximal topen neighbourhood of
 $p$
.
$p$
. -
(4)
 $p$
has a maximal topen neighbourhood.
$p$
has a maximal topen neighbourhood.
-
(5)
 $p$
has some topen neighbourhood.
$p$
has some topen neighbourhood.
Proof. We prove a cycle of implications:
-
(1) If
 $\textit{K}(p)$
is a topen neighbourhood of
$\textit{K}(p)$
is a topen neighbourhood of
 $p$
, then it is maximal by Lemma 4.2.3(1). Furthermore, this maximal topen neighbourhood of
$p$
, then it is maximal by Lemma 4.2.3(1). Furthermore, this maximal topen neighbourhood of
 $p$
is necessarily the greatest, since if we have two maximal topen neighbourhoods of
$p$
is necessarily the greatest, since if we have two maximal topen neighbourhoods of
 $p$
, then their union is a larger topen neighbourhood of
$p$
, then their union is a larger topen neighbourhood of
 $p$
by Proposition 3.4.4.
$p$
by Proposition 3.4.4. -
(2) If
 $p_{\between }$
is the greatest topen neighbourhood of
$p_{\between }$
is the greatest topen neighbourhood of
 $p$
, then certainly it is maximal.
$p$
, then certainly it is maximal. -
(3) If
 $p_{\between }$
is a maximal topen neighbourhood of
$p_{\between }$
is a maximal topen neighbourhood of
 $p$
, then certainly
$p$
, then certainly
 $p$
has a maximal topen neighbourhood.
$p$
has a maximal topen neighbourhood. -
(4) If
 $p$
has a maximal topen neighbourhood then certainly
$p$
has a maximal topen neighbourhood then certainly
 $p$
has a topen neighbourhood.
$p$
has a topen neighbourhood. -
(5) Suppose
 $p$
has a topen neighbourhood
$p$
has a topen neighbourhood
 $T$
. By Corollary 3.4.5 we may assume without loss of generality that
$T$
. By Corollary 3.4.5 we may assume without loss of generality that
 $T$
is a maximal topen. We use Lemma 4.2.3(2).
$T$
is a maximal topen. We use Lemma 4.2.3(2).
Corollary 4.2.6.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following are equivalent:
$p\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $p$
is regular.
$p$
is regular.
-
(2)
 $p$
is weakly regular and
$p$
is weakly regular and
 $\textit{K}(p)=\textit{K}(p')$
for every
$\textit{K}(p)=\textit{K}(p')$
for every
 $p'\in \textit{K}(p)$
.
$p'\in \textit{K}(p)$
.
It might be useful to look at Example 3.3.3(2) and Figure
2
(top-right diagram). In that example the point
![]() $1$
is not regular, and its community
$1$
is not regular, and its community
![]() $\{0,1,2\}$
is not a community for
$\{0,1,2\}$
is not a community for
![]() $0$
or
$0$
or
![]() $2$
.
$2$
.
Proof. We prove two implications, using Theorem4.2.5:
-
• Suppose
 $p$
is regular. By Lemma 4.1.6(1),
$p$
is regular. By Lemma 4.1.6(1),
 $p$
is weakly regular. Now consider
$p$
is weakly regular. Now consider
 $p'\in \textit{K}(p)$
. By Theorem4.2.5,
$p'\in \textit{K}(p)$
. By Theorem4.2.5,
 $\textit{K}(p)$
is topen, so it is a topen neighbourhood of
$\textit{K}(p)$
is topen, so it is a topen neighbourhood of
 $p'$
. By Theorem4.2.5,
$p'$
. By Theorem4.2.5,
 $\textit{K}(p')$
is a greatest topen neighbourhood of
$\textit{K}(p')$
is a greatest topen neighbourhood of
 $p'$
. But by Theorem4.2.5,
$p'$
. But by Theorem4.2.5,
 $\textit{K}(p)$
is also a greatest topen neighbourhood of
$\textit{K}(p)$
is also a greatest topen neighbourhood of
 $p$
, and
$p$
, and
 $\textit{K}(p)\between \textit{K}(p')$
since they both contain
$\textit{K}(p)\between \textit{K}(p')$
since they both contain
 $p'$
. By Proposition 3.4.4 and maximality, they are equal.
$p'$
. By Proposition 3.4.4 and maximality, they are equal. -
• Suppose
 $p$
is weakly regular and suppose
$p$
is weakly regular and suppose
 $\textit{K}(p)=\textit{K}(p')$
for every
$\textit{K}(p)=\textit{K}(p')$
for every
 $p'\in \textit{K}(p)$
, and consider
$p'\in \textit{K}(p)$
, and consider
 $p',p''\in \textit{K}(p)$
. Then
$p',p''\in \textit{K}(p)$
. Then
 $p'\mathrel {\between } p''$
holds, since
$p'\mathrel {\between } p''$
holds, since
 $p''\in \textit{K}(p')=\textit{K}(p)$
. By Theorem3.5.5,
$p''\in \textit{K}(p')=\textit{K}(p)$
. By Theorem3.5.5,
 $\textit{K}(p)$
is topen, and by weak regularity,
$\textit{K}(p)$
is topen, and by weak regularity,
 $p\in \textit{K}(p)$
, so by Theorem4.2.5,
$p\in \textit{K}(p)$
, so by Theorem4.2.5,
 $p$
is regular as required.
$p$
is regular as required.
Corollary 4.2.7.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p,p'\in \mathsf{P}$
. Then if
$p,p'\in \mathsf{P}$
. Then if
![]() $p$
is regular and
$p$
is regular and
![]() $p'\in \textit{K}(p)$
, then
$p'\in \textit{K}(p)$
, then
![]() $p'$
is regular and has the same community.
$p'$
is regular and has the same community.
4.3 Intersection and partition properties of regular spaces
Proposition 4.3.1 is useful for consensus in practice. Suppose we are at a regular point
![]() $q$
and we have reached consensus with some topen neighbourhood
$q$
and we have reached consensus with some topen neighbourhood
![]() $O\ni q$
. Suppose further that our topen neighbourhood
$O\ni q$
. Suppose further that our topen neighbourhood
![]() $O$
intersects with the maximal topen neighbourhood
$O$
intersects with the maximal topen neighbourhood
![]() $\textit{K}(p)$
of some other regular point
$\textit{K}(p)$
of some other regular point
![]() $p$
. Then Proposition 4.3.1 tells us that we were inside
$p$
. Then Proposition 4.3.1 tells us that we were inside
![]() $\textit{K}(p)$
all along.
$\textit{K}(p)$
all along.
Proposition 4.3.1.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
is regular and
$p\in \mathsf{P}$
is regular and
![]() $O\in \mathsf{Topen}$
is topen. Then
$O\in \mathsf{Topen}$
is topen. Then
Proof. The right-to-left implication is immediate from Notation 3.1.1(1), given that topens are nonempty by Definition 3.2.2(2).
For the left-to-right implication, suppose
![]() $O\between \textit{K}(p)$
. By Theorem4.2.5,
$O\between \textit{K}(p)$
. By Theorem4.2.5,
![]() $\textit{K}(p)$
is a maximal topen, and by Proposition 3.4.4,
$\textit{K}(p)$
is a maximal topen, and by Proposition 3.4.4,
![]() $O\cup \textit{K}(p)$
is topen. Then
$O\cup \textit{K}(p)$
is topen. Then
![]() $O\subseteq \textit{K}(p)$
follows by maximality.
$O\subseteq \textit{K}(p)$
follows by maximality.
Proposition 4.3.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology, and suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology, and suppose
![]() $p,p'\in \mathsf{P}$
are regular. Then
$p,p'\in \mathsf{P}$
are regular. Then
Proof. We prove two implications.
-
• Suppose there exists
 $p''\in \textit{K}(p)\cap \textit{K}(p')$
. By Corollary 4.2.7 (
$p''\in \textit{K}(p)\cap \textit{K}(p')$
. By Corollary 4.2.7 (
 $p''$
is regular and)
$p''$
is regular and)
 $\textit{K}(p)=\textit{K}(p'')=\textit{K}(p')$
.
$\textit{K}(p)=\textit{K}(p'')=\textit{K}(p')$
. -
• Suppose
 $\textit{K}(p)=\textit{K}(p')$
. By assumption
$\textit{K}(p)=\textit{K}(p')$
. By assumption
 $p\in \textit{K}(p)$
, so
$p\in \textit{K}(p)$
, so
 $p\in \textit{K}(p')$
. Thus
$p\in \textit{K}(p')$
. Thus
 $p\in \textit{K}(p)\cap \textit{K}(p')$
.
$p\in \textit{K}(p)\cap \textit{K}(p')$
.
Corollary 4.3.3 is a simple characterisation of regular semitopological spaces:
Corollary 4.3.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the following are equivalent:
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the following are equivalent:
-
(1)
 $(\mathsf{P},\mathsf{Open})$
is regular.
$(\mathsf{P},\mathsf{Open})$
is regular.
-
(2)
 $\mathsf{P}$
partitions into topen sets: there exists some set of topen sets
$\mathsf{P}$
partitions into topen sets: there exists some set of topen sets
 $\mathscr T$
such that
$\mathscr T$
such that
 for every
for every
 $T,T'\in \mathscr T$
and
$T,T'\in \mathscr T$
and
 $\mathsf{P}=\bigcup \mathscr T$
.
$\mathsf{P}=\bigcup \mathscr T$
. -
(3) Every
 $X\subseteq \mathsf{P}$
has a cover of topen sets: there exists some set of topen sets
$X\subseteq \mathsf{P}$
has a cover of topen sets: there exists some set of topen sets
 $\mathscr T$
such that
$\mathscr T$
such that
 $X\subseteq \bigcup \mathscr T$
.
$X\subseteq \bigcup \mathscr T$
.
Proof. The proof is routine from the machinery that we already have. We prove equivalence of parts 1 and 2:
-
(1) Suppose
 $(\mathsf{P},\mathsf{Open})$
is regular, meaning by Definition 4.1.4(7 and 3) that
$(\mathsf{P},\mathsf{Open})$
is regular, meaning by Definition 4.1.4(7 and 3) that
 $p\in \textit{K}(p)\in \mathsf{Topen}$
for every
$p\in \textit{K}(p)\in \mathsf{Topen}$
for every
 $p\in \mathsf{P}$
. We set
$p\in \mathsf{P}$
. We set
 $\mathscr T\ =\{\textit{K}(p) \mid p\in \mathsf{P}\}$
. By assumption, this covers
$\mathscr T\ =\{\textit{K}(p) \mid p\in \mathsf{P}\}$
. By assumption, this covers
 $\mathsf{P}$
in topens, and by Proposition 4.3.2, the cover is a partition.
$\mathsf{P}$
in topens, and by Proposition 4.3.2, the cover is a partition. -
(2) Suppose
 $\mathscr T$
is a topen partition of
$\mathscr T$
is a topen partition of
 $\mathsf{P}$
. By definition for every point
$\mathsf{P}$
. By definition for every point
 $p$
there exists
$p$
there exists
 $T\in \mathscr T$
such that
$T\in \mathscr T$
such that
 $p\in T$
and so
$p\in T$
and so
 $p$
has a topen neighbourhood. By Theorem4.2.5(5 and 1),
$p$
has a topen neighbourhood. By Theorem4.2.5(5 and 1),
 $p$
is regular.
$p$
is regular.
We prove equivalence of parts 2 and 1:
-
(1) Suppose
 $\mathscr T$
is a topen partition of
$\mathscr T$
is a topen partition of
 $\mathsf{P}$
, and suppose
$\mathsf{P}$
, and suppose
 $X\subseteq \mathscr P$
. Then trivially
$X\subseteq \mathscr P$
. Then trivially
 $X\subseteq \bigcup \mathscr T$
.
$X\subseteq \bigcup \mathscr T$
. -
(2) Suppose every
 $X\subseteq \mathsf{P}$
has a cover of topen sets. Then
$X\subseteq \mathsf{P}$
has a cover of topen sets. Then
 $\mathsf{P}$
has a cover of topen sets; write it
$\mathsf{P}$
has a cover of topen sets; write it
 $\mathscr T$
. By Corollary 3.4.5, we may assume without loss of generality that
$\mathscr T$
. By Corollary 3.4.5, we may assume without loss of generality that
 $\mathscr T$
is a partition, and we are done.
$\mathscr T$
is a partition, and we are done.
Notation 4.3.4.
Call a semitopology
![]() $(\mathsf{P},\mathsf{Open})$
singular
when it contains a single maximal topen subset.
$(\mathsf{P},\mathsf{Open})$
singular
when it contains a single maximal topen subset.
Remark 4.3.5. The moral we take from the results and examples above (and those to follow) is that the world we are entering has rather different well-behavedness criteria than those familiar from the study of typical Hausdorff topologies like
![]() $\mathbb R$
:
$\mathbb R$
:
-
(1) ‘Bad’ spaces are spaces that are not regular.
 $\mathbb R$
with its usual topology (which is also a semitopology) is an example of a ‘bad’ semitopology; it is not even quasiregular.
$\mathbb R$
with its usual topology (which is also a semitopology) is an example of a ‘bad’ semitopology; it is not even quasiregular. -
(2) ‘Good’ spaces are spaces that are regular.
The supermajority and all-but-one semitopologies from Example 2.1.4(5a and 5c) are typical examples of ‘good’ semitopologies; both are singular regular spaces.
-
(3) Corollary 4.3.3 shows that the ‘good’ spaces are just the (disjoint, possibly infinite) unions of singular regular spaces.
So to sum this up: modulo disjoint unions, the study of consensus behaviour is the study of semitopological spaces that consist of a single topen set of points that are all intertwined with one another.
5. Regular = Weakly Regular + Unconflicted
5.1 Closed sets
In Section 5.1, we check that some familiar properties of closures carry over from topologies to semitopologies. There are no technical surprises, but this in itself is a mathematical result that needs to be checked. Then, we will use this to study the relation between closures and sets of intertwined points.
Definition 5.1.1. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology, and suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology, and suppose
![]() $p\in \mathsf{P}$
and
$p\in \mathsf{P}$
and
![]() $P\subseteq \mathsf{P}$
. Then:
$P\subseteq \mathsf{P}$
. Then:
-
(1) Define
 $|P|\subseteq \mathsf{P}$
to be the closure of
$|P|\subseteq \mathsf{P}$
to be the closure of
 $P$
to be the set of points
$P$
to be the set of points
 $p$
such that every open neighbourhood of
$p$
such that every open neighbourhood of
 $p$
intersects
$p$
intersects
 $P$
. In symbols using Notation 3.1.1:
$P$
. In symbols using Notation 3.1.1: \begin{equation*} |P| = \{ p'\in \mathsf{P} \mid \forall O{\in }\mathsf{Open}. p'\in O \Longrightarrow P\between O\} . \end{equation*}
\begin{equation*} |P| = \{ p'\in \mathsf{P} \mid \forall O{\in }\mathsf{Open}. p'\in O \Longrightarrow P\between O\} . \end{equation*}
-
(2) As is standard, we may write
 $|p|$
for
$|p|$
for
 $|\{p\}|$
. Unpacking definitions for reference:
$|\{p\}|$
. Unpacking definitions for reference: \begin{equation*} |p| = \{ p'\in \mathsf{P} \mid \forall O{\in }\mathsf{Open}. p'\in O \Longrightarrow p\in O\} . \end{equation*}
\begin{equation*} |p| = \{ p'\in \mathsf{P} \mid \forall O{\in }\mathsf{Open}. p'\in O \Longrightarrow p\in O\} . \end{equation*}
Lemma 5.1.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
![]() $P,P'\subseteq \mathsf{P}$
. Then taking the closure of a set is:
$P,P'\subseteq \mathsf{P}$
. Then taking the closure of a set is:
-
(1) Monotone: If
 $P\subseteq P'$
then
$P\subseteq P'$
then
 $|P|\subseteq |P'|$
.
$|P|\subseteq |P'|$
. -
(2) Increasing:
 $P\subseteq |P|$
.
$P\subseteq |P|$
. -
(3) Idempotent:
 $|P|=||P||$
.
$|P|=||P||$
.
Proof. By routine calculations from Definition 5.1.1.
Lemma 5.1.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $P\subseteq \mathsf{P}$
and
$P\subseteq \mathsf{P}$
and
![]() $O\in \mathsf{Open}$
. Then
$O\in \mathsf{Open}$
. Then
Proof.
Suppose
![]() $P\between O$
. Then
$P\between O$
. Then
![]() $|P|\between O$
using Lemma 5.1.2(2).
$|P|\between O$
using Lemma 5.1.2(2).
Suppose
![]() $|P|\between O$
. Pick
$|P|\between O$
. Pick
![]() $p\in |P|\cap O$
. By construction of
$p\in |P|\cap O$
. By construction of
![]() $|P|$
in Definition 5.1.1,
$|P|$
in Definition 5.1.1,
![]() $p\in O\Longrightarrow P\between O$
. It follows that
$p\in O\Longrightarrow P\between O$
. It follows that
![]() $P\between O$
as required.
$P\between O$
as required.
Definition 5.1.4. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
![]() $C\subseteq \mathsf{P}$
.
$C\subseteq \mathsf{P}$
.
-
(1) Call
 $C$
a closed set when
$C$
a closed set when
 $C=|C|$
.
$C=|C|$
. -
(2) Call
 $C$
a clopen set when
$C$
a clopen set when
 $C$
is closed and open.
$C$
is closed and open. -
(3) Write
 $\mathsf{Closed}$
for the set of closed sets (as we wrote
$\mathsf{Closed}$
for the set of closed sets (as we wrote
 $\mathsf{Open}$
for the open sets; the ambient semitopology will always be clear or understood).
$\mathsf{Open}$
for the open sets; the ambient semitopology will always be clear or understood).
Lemma 5.1.5.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
![]() $P\subseteq \mathsf{P}$
. Then
$P\subseteq \mathsf{P}$
. Then
![]() $|P|$
is closed and contains
$|P|$
is closed and contains
![]() $P$
. In symbols:
$P$
. In symbols:
Example 5.1.6.
-
(1) Take
 $\mathsf{P}=\{0,1\}$
and
$\mathsf{P}=\{0,1\}$
and
 $\mathsf{Open}=\{\varnothing , \{0\}, \{0,1\}\}$
. Then the reader can verify that:
$\mathsf{Open}=\{\varnothing , \{0\}, \{0,1\}\}$
. Then the reader can verify that:-
–
 $\{0\}$
is open.
$\{0\}$
is open. -
– The closure of
 $\{1\}$
is
$\{1\}$
is
 $\{1\}$
, and
$\{1\}$
, and
 $\{1\}$
is closed.
$\{1\}$
is closed. -
– The closure of
 $\{0\}$
is
$\{0\}$
is
 $\{0,1\}$
.
$\{0,1\}$
. -
–
 $\varnothing$
and
$\varnothing$
and
 $\{0,1\}$
are the only clopen sets.
$\{0,1\}$
are the only clopen sets.
-
-
(2) Now take
 $\mathsf{P}=\{0,1\}$
and
$\mathsf{P}=\{0,1\}$
and
 $\mathsf{Open}=\{\varnothing , \{0\}, \{1\}, \{0,1\}\}$
.Footnote
12
Then the reader can verify that:
$\mathsf{Open}=\{\varnothing , \{0\}, \{1\}, \{0,1\}\}$
.Footnote
12
Then the reader can verify that:-
– Every set is clopen.
-
– The closure of every set is itself.
-
Remark 5.1.7. There are two standard definitions for when a set is closed: when it is equal to its closure (as per Definition 5.1.4(1)) and when it is the complement of an open set. In topology these are equivalent. We do need to check that the same holds in semitopology, but as it turns out, the proof is routine:
Lemma 5.1.8.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then:
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then:
Proof.
-
(1) Suppose
 $p\in \mathsf{P}\setminus C$
. Since
$p\in \mathsf{P}\setminus C$
. Since
 $C=|C|$
, we have
$C=|C|$
, we have
 $p\in \mathsf{P}\setminus |C|$
. Unpacking Definition 5.1.1, this means precisely that there exists
$p\in \mathsf{P}\setminus |C|$
. Unpacking Definition 5.1.1, this means precisely that there exists
 $O_p\in \mathsf{Open}$
with
$O_p\in \mathsf{Open}$
with  . We use Lemma 2.3.2.
. We use Lemma 2.3.2. -
(2) Suppose
 $O\in \mathsf{Open}$
. Combining Lemma 2.3.2 with Definition 5.1.1, it follows that
$O\in \mathsf{Open}$
. Combining Lemma 2.3.2 with Definition 5.1.1, it follows that  so that
so that
 $|\mathsf{P}\setminus O|\subseteq \mathsf{P}\setminus O$
. Furthermore, by Lemma 5.1.2(2),
$|\mathsf{P}\setminus O|\subseteq \mathsf{P}\setminus O$
. Furthermore, by Lemma 5.1.2(2),
 $\mathsf{P}\setminus O\subseteq |\mathsf{P}\setminus O|$
.
$\mathsf{P}\setminus O\subseteq |\mathsf{P}\setminus O|$
.
The usual duality between forming closures and interiors remains valid in semitopologies:
Lemma 5.1.9.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $O\in \mathsf{Open}$
and
$O\in \mathsf{Open}$
and
![]() $C\in \mathsf{Closed}$
. Then:
$C\in \mathsf{Closed}$
. Then:
-
(1)
 $O\subseteq \textit{interior}(|O|)$
. The inclusion may be strict.
$O\subseteq \textit{interior}(|O|)$
. The inclusion may be strict.
-
(2)
 $|\textit{interior}(C)|\subseteq C$
. The inclusion may be strict.
$|\textit{interior}(C)|\subseteq C$
. The inclusion may be strict.
-
(3)
 $\textit{interior}(\mathsf{P}\setminus O)=\mathsf{P}\setminus |O|$
.
$\textit{interior}(\mathsf{P}\setminus O)=\mathsf{P}\setminus |O|$
. -
(4)
 $|\mathsf{P}\setminus C|=\mathsf{P}\setminus \textit{interior}(C)$
.
$|\mathsf{P}\setminus C|=\mathsf{P}\setminus \textit{interior}(C)$
.
Proof. The reasoning is just as for topologies, but we spell out the details:
-
(1) By Lemma 5.1.2(2),
 $O\subseteq |O|$
. By Corollary 4.1.3,
$O\subseteq |O|$
. By Corollary 4.1.3,
 $\textit{interior}(O)\subseteq \textit{interior}(|O|)$
. By Lemma 4.1.2,
$\textit{interior}(O)\subseteq \textit{interior}(|O|)$
. By Lemma 4.1.2,
 $O=\textit{interior}(O)$
, so we are done.
$O=\textit{interior}(O)$
, so we are done.For an example of the strict inclusion, consider
 $\mathbb R$
with the usual topology (which is also a semitopology) and take
$\mathbb R$
with the usual topology (which is also a semitopology) and take
 $O=(0,1)\cup (1,2)$
. Then
$O=(0,1)\cup (1,2)$
. Then
 $O\subsetneq \textit{interior}(|O|)=(0,2)$
.
$O\subsetneq \textit{interior}(|O|)=(0,2)$
. -
(2) By Lemma 4.1.2,
 $\textit{interior}(C)\subseteq C$
. By Lemma 5.1.2(1),
$\textit{interior}(C)\subseteq C$
. By Lemma 5.1.2(1),
 $|\textit{interior}(C)|\subseteq |C|$
. By Definition 5.1.4(1), (since we assumed
$|\textit{interior}(C)|\subseteq |C|$
. By Definition 5.1.4(1), (since we assumed
 $C\in \mathsf{Closed}$
)
$C\in \mathsf{Closed}$
)
 $|C|=C$
, so we are done.
$|C|=C$
, so we are done.For an example of the strict inclusion, consider
 $\mathbb R$
with the usual topology and take
$\mathbb R$
with the usual topology and take
 $C=\{0\}$
. Then
$C=\{0\}$
. Then
 $|\textit{interior}(C)|=\varnothing \subsetneq C$
.
$|\textit{interior}(C)|=\varnothing \subsetneq C$
. -
(3) Consider some
 $p'\in \mathsf{P}$
. By Definition 4.1.1,
$p'\in \mathsf{P}$
. By Definition 4.1.1,
 $p'\in \textit{interior}(\mathsf{P}\setminus O)$
when there exists some
$p'\in \textit{interior}(\mathsf{P}\setminus O)$
when there exists some
 $O'\in \mathsf{Open}$
such that
$O'\in \mathsf{Open}$
such that  . By definition in Definition 5.1.1(1), this happens precisely when
. By definition in Definition 5.1.1(1), this happens precisely when
 $p'\notin |O|$
.
$p'\notin |O|$
. -
(4) By Definition 5.1.1(1),
 $p'\notin |\mathsf{P}\setminus C|$
precisely when there exists some
$p'\notin |\mathsf{P}\setminus C|$
precisely when there exists some
 $O'\in \mathsf{Open}$
such that
$O'\in \mathsf{Open}$
such that  . By facts of sets, this means precisely that
. By facts of sets, this means precisely that
 $p'\in O'\subseteq C$
. By Definition 4.1.1, this means precisely that
$p'\in O'\subseteq C$
. By Definition 4.1.1, this means precisely that
 $p'\in \textit{interior}(C)$
.
$p'\in \textit{interior}(C)$
.
5.2 Closed neighbourhoods and intertwined points
Definition 5.2.1. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. We generalise Definition 2.3.1 as follows:
$(\mathsf{P},\mathsf{Open})$
is a semitopology. We generalise Definition 2.3.1 as follows:
-
(1) Call
 $P\subseteq \mathsf{P}$
a neighbourhood when it contains an open set (i.e., when
$P\subseteq \mathsf{P}$
a neighbourhood when it contains an open set (i.e., when
 $\textit{interior}(P)\neq \varnothing$
), and call
$\textit{interior}(P)\neq \varnothing$
), and call
 $P$
a neighbourhood of
$P$
a neighbourhood of
 $p$
when
$p$
when
 $p\in \mathsf{P}$
and
$p\in \mathsf{P}$
and
 $P$
contains an open neighbourhood of
$P$
contains an open neighbourhood of
 $p$
(i.e., when
$p$
(i.e., when
 $p\in \textit{interior}(P)$
). In particular:
$p\in \textit{interior}(P)$
). In particular: -
(2)
 $C\subseteq \mathsf{P}$
is a closed neighbourhood of
$C\subseteq \mathsf{P}$
is a closed neighbourhood of
 $p\in \mathsf{P}$
when
$p\in \mathsf{P}$
when
 $C$
is closed and
$C$
is closed and
 $p\in \textit{interior}(C)$
.
$p\in \textit{interior}(C)$
. -
(3)
 $C\subseteq \mathsf{P}$
is a closed neighbourhood when
$C\subseteq \mathsf{P}$
is a closed neighbourhood when
 $C$
is closed and
$C$
is closed and
 $\textit{interior}(C)\neq \varnothing$
.
$\textit{interior}(C)\neq \varnothing$
.
Remark 5.2.2.
-
(1) If
 $C$
is a closed neighbourhood of
$C$
is a closed neighbourhood of
 $p$
in the sense of Definition 5.2.1(2), then
$p$
in the sense of Definition 5.2.1(2), then
 $C$
is a closed neighbourhood in the sense of Definition 5.2.1(3), just because if
$C$
is a closed neighbourhood in the sense of Definition 5.2.1(3), just because if
 $p\in \textit{interior}(C)$
, then
$p\in \textit{interior}(C)$
, then
 $\textit{interior}(C)\neq \varnothing$
.
$\textit{interior}(C)\neq \varnothing$
. -
(2)
 $p\in C$
is not enough for
$p\in C$
is not enough for
 $C$
to be a closed neighbourhood of
$C$
to be a closed neighbourhood of
 $p$
; we require the stronger condition
$p$
; we require the stronger condition
 $p\in \textit{interior}(C)$
. For instance, consider the Sierpiński space
is a topology and so also a semitopology (cf. Remark 12.3.2), and consider
$p\in \textit{interior}(C)$
. For instance, consider the Sierpiński space
is a topology and so also a semitopology (cf. Remark 12.3.2), and consider \begin{equation*} \textit{Sk}=(\{0,1\},\ \{\varnothing ,\{1\},\{0,1\}\}) . \end{equation*}
\begin{equation*} \textit{Sk}=(\{0,1\},\ \{\varnothing ,\{1\},\{0,1\}\}) . \end{equation*}
 $p=0$
and
$p=0$
and
 $C=\{0\}$
. Then
$C=\{0\}$
. Then
 $p\in C$
but
$p\in C$
but
 $p\not \in \textit{interior}(C)=\varnothing$
, so that
$p\not \in \textit{interior}(C)=\varnothing$
, so that
 $C$
is not a closed neighbourhood of
$C$
is not a closed neighbourhood of
 $p$
.
$p$
.
Remark 5.2.3. Recall the definitions of
![]() $p_{\between }$
and
$p_{\between }$
and
![]() $|p|$
:
$|p|$
:
-
• The set
 $|p|$
is the closure of
$|p|$
is the closure of
 $p$
.
$p$
.By Definition 5.1.1, this is the set of
 $p'$
such that every open neighbourhood
$p'$
such that every open neighbourhood
 $O'\ni p'$
intersects with
$O'\ni p'$
intersects with
 $\{p\}$
.
$\{p\}$
. -
• The set
 $p_{\between }$
is the set of points intertwined with
$p_{\between }$
is the set of points intertwined with
 $p$
.
$p$
.By Definition 3.5.1(2), this is the set of
 $p'$
such that every open neighbourhood
$p'$
such that every open neighbourhood
 $O'\ni p'$
intersects with every open neighbourhood
$O'\ni p'$
intersects with every open neighbourhood
 $O \ni p$
.
$O \ni p$
.
Lemma 5.2.4 rephrases Remark 5.2.3 more precisely by looking at it through set complements. We will use it in Lemma 11.4.4(2):
Lemma 5.2.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then:
$p\in \mathsf{P}$
. Then:
-
(1)
 $\mathsf{P}\setminus |p| = \bigcup \{O\in \mathsf{Open} \mid p\notin O\}\in \mathsf{Open}$
.
$\mathsf{P}\setminus |p| = \bigcup \{O\in \mathsf{Open} \mid p\notin O\}\in \mathsf{Open}$
. -
(2)
.
-
(3)
 $\mathsf{P}\setminus p_{\between } = \bigcup \{O\in \mathsf{Open} \mid p\notin |O|\}\in \mathsf{Open}$
.
$\mathsf{P}\setminus p_{\between } = \bigcup \{O\in \mathsf{Open} \mid p\notin |O|\}\in \mathsf{Open}$
.
In words, we can say that
![]() $\mathsf{P}\!\setminus\!|p|$
is the union of the open sets such that
$\mathsf{P}\!\setminus\!|p|$
is the union of the open sets such that
![]() $p$
avoids them, and
$p$
avoids them, and
![]() $\mathsf{P}\setminus p_{\between }$
is the union of the open sets such that
$\mathsf{P}\setminus p_{\between }$
is the union of the open sets such that
![]() $p$
avoids their closures.
$p$
avoids their closures.
Proof.
Remark 5.2.5. We can relate Lemma 5.2.4 to a concept from topology. Following standard terminology ((Bourbaki, Reference Bourbaki1998, Definition 2, p. 69) or (Engelking, Reference Engelking1989, p. 52)), a cluster point
![]() $p\in \mathsf{P}$
of
$p\in \mathsf{P}$
of
![]() $\mathscr O\subseteq \mathsf{Open}$
is one such that every open neighbourhood of
$\mathscr O\subseteq \mathsf{Open}$
is one such that every open neighbourhood of
![]() $p$
intersects every
$p$
intersects every
![]() $O\in \mathscr O$
. Then Lemma 5.2.4(2) identifies
$O\in \mathscr O$
. Then Lemma 5.2.4(2) identifies
![]() $p_{\between }$
as the set of cluster points of
$p_{\between }$
as the set of cluster points of
![]() $\textit{nbhd}(p)\subseteq \mathsf{Open}$
from Definition 2.3.1.
$\textit{nbhd}(p)\subseteq \mathsf{Open}$
from Definition 2.3.1.
5.3 Regular = weakly regular + unconflicted
In Lemma 3.5.3, we asked whether the ‘is intertwined with’ relation
![]() $\mathrel {\between }$
from Definition 3.5.1(1) is transitive – answer: not necessarily.
$\mathrel {\between }$
from Definition 3.5.1(1) is transitive – answer: not necessarily.
Transitivity of
![]() $\mathrel {\between }$
is a natural condition. We now have enough machinery to study it in more detail, and this will help us gain a deeper understanding of the properties of not-necessarily-regular points.
$\mathrel {\between }$
is a natural condition. We now have enough machinery to study it in more detail, and this will help us gain a deeper understanding of the properties of not-necessarily-regular points.
Definition 5.3.1. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology.
$(\mathsf{P},\mathsf{Open})$
is a semitopology.
-
(1) Call a point
 $p$
conflicted when there exist
$p$
conflicted when there exist
 $p'$
and
$p'$
and
 $p''$
such that
$p''$
such that
 $p'\mathrel {\between } p$
and
$p'\mathrel {\between } p$
and
 $p\mathrel {\between } p''$
yet
$p\mathrel {\between } p''$
yet
 $\neg (p'\mathrel {\between } p'')$
.
$\neg (p'\mathrel {\between } p'')$
. -
(2) If
 $p'\mathrel {\between } p\mathrel {\between } p''$
implies
$p'\mathrel {\between } p\mathrel {\between } p''$
implies
 $p'\mathrel {\between } p''$
always, then call
$p'\mathrel {\between } p''$
always, then call
 $p$
unconflicted.
$p$
unconflicted. -
(3) Continuing Definition 4.1.4(7), if
 $P\subseteq \mathsf{P}$
and every
$P\subseteq \mathsf{P}$
and every
 $p\in P$
is conflicted/unconflicted, then we may call
$p\in P$
is conflicted/unconflicted, then we may call
 $P$
conflicted/unconflicted, respectively.
$P$
conflicted/unconflicted, respectively.
Example 5.3.2. We consider some examples:
-
(1) In Figure 2, in the top-left diagram,
 $0$
and
$0$
and
 $2$
are unconflicted and intertwined with themselves, and
$2$
are unconflicted and intertwined with themselves, and
 $1$
is conflicted (being intertwined with
$1$
is conflicted (being intertwined with
 $0$
,
$0$
,
 $1$
, and
$1$
, and
 $2$
).
$2$
).If the reader wants to know what a conflicted point looks like, it looks like
 $1$
.
$1$
. -
(2) In Figure 2, in the top-right diagram,
 $0$
and
$0$
and
 $2$
are unconflicted and intertwined with themselves, and
$2$
are unconflicted and intertwined with themselves, and
 $1$
is conflicted (being intertwined with
$1$
is conflicted (being intertwined with
 $0$
,
$0$
,
 $1$
, and
$1$
, and
 $2$
).
$2$
). -
(3) In Figure 2, in the lower-left diagram,
 $0$
and
$0$
and
 $1$
are unconflicted and intertwined with themselves, and
$1$
are unconflicted and intertwined with themselves, and
 $3$
and
$3$
and
 $4$
are unconflicted and intertwined with themselves, and
$4$
are unconflicted and intertwined with themselves, and
 $2$
is conflicted (being intertwined with
$2$
is conflicted (being intertwined with
 $0$
,
$0$
,
 $1$
,
$1$
,
 $2$
,
$2$
,
 $3$
, and
$3$
, and
 $4$
).
$4$
). -
(4) In Figure 2, in the lower-right diagram, all points are unconflicted, and
 $0$
and
$0$
and
 $2$
are intertwined just with themselves, and
$2$
are intertwined just with themselves, and
 $1$
and
$1$
and
 $\ast$
are intertwined with one another.
$\ast$
are intertwined with one another. -
(5) In Figure 3, all points are unconflicted and intertwined only with themselves. (This semitopology is useful for counterexamples, and we will use it again.)
Proposition 5.3.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then:
$p\in \mathsf{P}$
. Then:
-
(1) If
 $p$
is regular, then it is unconflicted.
$p$
is regular, then it is unconflicted.
Equivalently by the contrapositive: if
 $p$
is conflicted, then it is not regular.
$p$
is conflicted, then it is not regular.
-
(2)
 $p$
may be unconflicted and neither quasi-regular, weakly regular, nor regular.
$p$
may be unconflicted and neither quasi-regular, weakly regular, nor regular.
Proof. We consider each part in turn:
-
(1) So consider
 $q\mathrel {\between } p \mathrel {\between } q'$
. We must show that
$q\mathrel {\between } p \mathrel {\between } q'$
. We must show that
 $q\mathrel {\between } q'$
, so consider open neighbourhoods
$q\mathrel {\between } q'$
, so consider open neighbourhoods
 $Q\ni q$
and
$Q\ni q$
and
 $Q'\ni q'$
. By assumption
$Q'\ni q'$
. By assumption
 $p$
is regular, so unpacking Definition 4.1.4(3)
$p$
is regular, so unpacking Definition 4.1.4(3)
 $\textit{K}(p)$
is a topen (transitive and open) neighbourhood of
$\textit{K}(p)$
is a topen (transitive and open) neighbourhood of
 $p$
. By assumption
$p$
. By assumption
 $Q\between \textit{K}(p)\between Q'$
, and by transitivity of
$Q\between \textit{K}(p)\between Q'$
, and by transitivity of
 $\textit{K}(p)$
(Definition 3.2.2(1)) we have
$\textit{K}(p)$
(Definition 3.2.2(1)) we have
 $Q\between Q'$
as required.
$Q\between Q'$
as required. -
(2) Consider the semitopology illustrated in Figure 3. Note that the point
 $0$
is not conflicted (because it is not intertwined with any other point), but it is also neither quasiregular, weakly regular, nor regular, because its community is the empty set.
$0$
is not conflicted (because it is not intertwined with any other point), but it is also neither quasiregular, weakly regular, nor regular, because its community is the empty set.
We can combine Proposition 5.3.3 with a previous result, Lemma 4.1.6, to get a precise and attractive relation between being
-
• unconflicted (Definition 5.3.1),
as follows:
Theorem 5.3.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following are equivalent:
$p\in \mathsf{P}$
. Then the following are equivalent:
-
•
 $p$
is regular.
$p$
is regular.
-
•
 $p$
is weakly regular and unconflicted.
$p$
is weakly regular and unconflicted.
More succinctly we can write: regular = weakly regular + unconflicted. Footnote 13
Proof. We prove two implications:
-
• If
 $p$
is regular, then it is weakly regular by Lemma 4.1.6 and unconflicted by Proposition 5.3.3(1).
$p$
is regular, then it is weakly regular by Lemma 4.1.6 and unconflicted by Proposition 5.3.3(1). -
• Suppose
 $p$
is weakly regular and unconflicted. By Definition 4.1.4(4),
$p$
is weakly regular and unconflicted. By Definition 4.1.4(4),
 $p\in \textit{K}(p)$
, and by Lemma 3.5.4, it would suffice to show that
$p\in \textit{K}(p)$
, and by Lemma 3.5.4, it would suffice to show that
 $q\mathrel {\between } q'$
for any
$q\mathrel {\between } q'$
for any
 $q,q'\in \textit{K}(p)$
. So consider
$q,q'\in \textit{K}(p)$
. So consider
 $q,q'\in \textit{K}(p)$
. Now by Definition 4.1.4(1)
$q,q'\in \textit{K}(p)$
. Now by Definition 4.1.4(1)
 $\textit{K}(p)=\textit{interior}(p_{\between })$
so in particular
$\textit{K}(p)=\textit{interior}(p_{\between })$
so in particular
 $q,q'\in p_{\between }$
. Thus
$q,q'\in p_{\between }$
. Thus
 $q\mathrel {\between } p\mathrel {\between } q'$
, and since
$q\mathrel {\between } p\mathrel {\between } q'$
, and since
 $p$
is unconflicted
$p$
is unconflicted
 $q\mathrel {\between } q'$
as required.
$q\mathrel {\between } q'$
as required.
6. Regular = Quasiregular + Hypertransitive
6.1 Regular open/closed sets
We recall some simple results:
Definition 6.1.1. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Recall some standard terminology from topology (Willard, Reference Willard1970, Exercise 3D, p. 29):
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Recall some standard terminology from topology (Willard, Reference Willard1970, Exercise 3D, p. 29):
-
(1) We call an open set
 $O\in \mathsf{Open}$
a regular open set when
$O\in \mathsf{Open}$
a regular open set when
 $O=\textit{interior}(|O|)$
.
$O=\textit{interior}(|O|)$
. -
(2) We call a closed set
 $C\in \mathsf{Closed}$
a regular closed set when
$C\in \mathsf{Closed}$
a regular closed set when
 $C=|\textit{interior}(C)|$
.
$C=|\textit{interior}(C)|$
. -
(3) Write
 $\mathsf{Open}_{\textit{reg}}$
and
$\mathsf{Open}_{\textit{reg}}$
and
 $\mathsf{Closed}_{\textit{reg}}$
for the sets of regular open and regular closed sets, respectively.
$\mathsf{Closed}_{\textit{reg}}$
for the sets of regular open and regular closed sets, respectively.
Lemma 6.1.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $O\in \mathsf{Open}$
and
$O\in \mathsf{Open}$
and
![]() $C\in \mathsf{Closed}$
. Then:
$C\in \mathsf{Closed}$
. Then:
-
(1)
 $|O| = |\textit{interior}(|O|)|$
.
$|O| = |\textit{interior}(|O|)|$
. -
(2)
 $\textit{interior}(C)=\textit{interior}(|\textit{interior}(C)|)$
.
$\textit{interior}(C)=\textit{interior}(|\textit{interior}(C)|)$
.
The terminology ‘regular open/closed set’ is from the topological literature. It is not directly related to the terminology ‘regular point’ from Definition 4.1.4(3), which comes from semitopologies. However, it turns out that a mathematical connection does exist between these two notions:
Corollary 6.1.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $O\in \mathsf{Open}$
and
$O\in \mathsf{Open}$
and
![]() $C\in \mathsf{Closed}$
. Then:
$C\in \mathsf{Closed}$
. Then:
-
(1)
 $\textit{interior}(C)$
is a regular open set.
$\textit{interior}(C)$
is a regular open set.
-
(2)
 $|O|$
is a regular closed set.
$|O|$
is a regular closed set.
An elementary observation about open sets will be useful:
Lemma 6.1.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $O,O'\in \mathsf{Open}$
. Then the following are equivalent:
$O,O'\in \mathsf{Open}$
. Then the following are equivalent:
-
(1)
 $O\between O'$
.
$O\between O'$
. -
(2)
 $O\between \textit{interior}(|O'|)$
.
$O\between \textit{interior}(|O'|)$
. -
(3)
 $\textit{interior}(|O|)\between \textit{interior}(|O'|)$
.
$\textit{interior}(|O|)\between \textit{interior}(|O'|)$
.
Proof. First we prove the equivalence of parts 1 and 2:
-
(1) Suppose
 $O\between O'$
. By Lemma 5.1.9(1),
$O\between O'$
. By Lemma 5.1.9(1),
 $O\between \textit{interior}(|O'|)$
.
$O\between \textit{interior}(|O'|)$
. -
(2) Suppose there is some
 $p\in O\cap \textit{interior}(|O'|)$
. Then
$p\in O\cap \textit{interior}(|O'|)$
. Then
 $O$
is an open neighbourhood of
$O$
is an open neighbourhood of
 $p$
and
$p$
and
 $p\in |O'|$
, so by Definition 5.1.1(1),
$p\in |O'|$
, so by Definition 5.1.1(1),
 $O\between O'$
as required.Footnote
14
$O\between O'$
as required.Footnote
14
Equivalence of parts 1 and 3 then follows easily by two applications of the equivalence of parts 1 and 2.
Remark 6.1.5. Lemma 6.1.4 is true in topologies as well, but it is not prominent in the literature. Two standard reference works (Willard Reference Willard1970; Engelking Reference Engelking1989 do not seem to mention it. It appears as Equation (10) in Theorem 1.37 of Koppelberg (Reference Koppelberg1989) and as a lemma in
![]() $\pi$
-base
$\pi$
-base
![]() $\pi$
-Base (thanks to the mathematics StackExchange community for the pointers). Interestingly, this result is as true in topologies as it is in semitopologies, but somehow, it matters more in the latter than the former.
$\pi$
-Base (thanks to the mathematics StackExchange community for the pointers). Interestingly, this result is as true in topologies as it is in semitopologies, but somehow, it matters more in the latter than the former.
6.2 Hypertransitivity
We are now ready to define hypertransitivity.
Notation 6.2.1.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $O'\in \mathsf{Open}$
and
$O'\in \mathsf{Open}$
and
![]() $\mathscr O\subseteq \mathsf{Open}$
.
$\mathscr O\subseteq \mathsf{Open}$
.
-
(1) Write
 $O'\between \mathscr O$
, or equivalently
$O'\between \mathscr O$
, or equivalently
 $\mathscr O\between O'$
, when
$\mathscr O\between O'$
, when
 $O'\between O$
for every
$O'\between O$
for every
 $O\in \mathscr O$
. In symbols:
$O\in \mathscr O$
. In symbols:
 \begin{equation*} O'\between \mathscr O \quad \text{when}\quad \forall O{\in }\mathscr O.O'\between O . \end{equation*}
\begin{equation*} O'\between \mathscr O \quad \text{when}\quad \forall O{\in }\mathscr O.O'\between O . \end{equation*}
-
(2) As a special case of part 1 above, taking
 $\mathscr O=\textit{nbhd}(p)$
(Definition 2.3.1), if
$\mathscr O=\textit{nbhd}(p)$
(Definition 2.3.1), if
 $p\in \mathsf{P}$
, then write
$p\in \mathsf{P}$
, then write
 $O'\between \textit{nbhd}(p)$
, or equivalently
$O'\between \textit{nbhd}(p)$
, or equivalently
 $\textit{nbhd}(p)\between O'$
, when
$\textit{nbhd}(p)\between O'$
, when
 $O'\between O$
for every
$O'\between O$
for every
 $O\in \mathsf{Open}$
such that
$O\in \mathsf{Open}$
such that
 $p\in O$
.
$p\in O$
.
Lemma 6.2.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
and
$p\in \mathsf{P}$
and
![]() $O'\in \mathsf{Open}$
. Then
$O'\in \mathsf{Open}$
. Then
Definition 6.2.3. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Call
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Call
![]() $p\in \mathsf{P}$
a hypertransitive point when for every
$p\in \mathsf{P}$
a hypertransitive point when for every
![]() $O',O''\in \mathsf{Open}$
,
$O',O''\in \mathsf{Open}$
,
Call
![]() $(\mathsf{P},\mathsf{Open})$
a hypertransitive semitopology when every
$(\mathsf{P},\mathsf{Open})$
a hypertransitive semitopology when every
![]() $p\in \mathsf{P}$
is hypertransitive.
$p\in \mathsf{P}$
is hypertransitive.
Lemma 6.2.4 notes some equivalent formulations of hypertransitivity:
Lemma 6.2.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following are equivalent:
$p\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $p$
is hypertransitive.
$p$
is hypertransitive.
-
(2) For every pair of open sets
 $O',O''\in \mathsf{Open}$
,
$O',O''\in \mathsf{Open}$
,
 $p\in |O'|\cap |O''|$
implies
$p\in |O'|\cap |O''|$
implies
 $O'\between O''$
.
$O'\between O''$
. -
(3) For every pair of regular open sets
 $O',O''\in \mathsf{Open}_{\textit{reg}}$
,
$O',O''\in \mathsf{Open}_{\textit{reg}}$
,
 $p\in |O'|\cap |O''|$
implies
$p\in |O'|\cap |O''|$
implies
 $O'\between O''$
.
$O'\between O''$
.
Proof. For the equivalence of parts 1 and 2, we reason as follows:
-
• Suppose
 $p$
is hypertransitive, and suppose
$p$
is hypertransitive, and suppose
 $p\in |O'|$
and
$p\in |O'|$
and
 $p\in |O''|$
. By Lemma 6.2.2 it follows that
$p\in |O''|$
. By Lemma 6.2.2 it follows that
 $O'\between \textit{nbhd}(p)\between O''$
. By hypertransitivity,
$O'\between \textit{nbhd}(p)\between O''$
. By hypertransitivity,
 $O'\between O''$
as required.
$O'\between O''$
as required. -
• Suppose for every
 $O,O'\in \mathsf{Open}$
,
$O,O'\in \mathsf{Open}$
,
 $p\in |O|\cap |O'|$
implies
$p\in |O|\cap |O'|$
implies
 $O'\between O''$
, and suppose
$O'\between O''$
, and suppose
 $O'\between \textit{nbhd}(p)\between O''$
. By Lemma 6.2.2
$O'\between \textit{nbhd}(p)\between O''$
. By Lemma 6.2.2
 $p\in |O|\cap |O'|$
and therefore
$p\in |O|\cap |O'|$
and therefore
 $O'\between O''$
.
$O'\between O''$
.
For the equivalence of parts 2 and 3, we reason as follows:
-
• Part 2 implies part 3 follows since every open regular set is also an open set.
-
• To show part 3 implies part 2, suppose for every pair of regular opens
 $O',O''\in \mathsf{Open}_{\textit{reg}}$
,
$O',O''\in \mathsf{Open}_{\textit{reg}}$
,
 $p\in |O'|\cap |O''|$
implies
$p\in |O'|\cap |O''|$
implies
 $O'\between O''$
, and suppose
$O'\between O''$
, and suppose
 $O',O''\in \mathsf{Open}$
are two open sets that are not necessarily regular, and suppose
$O',O''\in \mathsf{Open}$
are two open sets that are not necessarily regular, and suppose
 $p\in |O'|\cap |O''|$
. We must show that
$p\in |O'|\cap |O''|$
. We must show that
 $O'\between O''$
.
$O'\between O''$
.Write
 $P'=\textit{interior}(|O'|)$
and
$P'=\textit{interior}(|O'|)$
and
 $P''=\textit{interior}(|O''|)$
and note by Corollary 6.1.3 and Lemma 5.1.5 that
$P''=\textit{interior}(|O''|)$
and note by Corollary 6.1.3 and Lemma 5.1.5 that
 $P'$
and
$P'$
and
 $P''$
are regular open sets and
$P''$
are regular open sets and
 $|P'|=|O'|$
and
$|P'|=|O'|$
and
 $|P''|=|O''|$
. Then
$|P''|=|O''|$
. Then
 $|P'|\between |P''|$
, so
$|P'|\between |P''|$
, so
 $P'\between P''$
, and
$P'\between P''$
, and
 $O'\between O''$
follows from Lemma 6.1.4.
$O'\between O''$
follows from Lemma 6.1.4.
6.3 Regular = quasiregular + hypertransitive
Lemma 6.3.1.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then:
$p\in \mathsf{P}$
. Then:
-
(1) If
 $p$
is regular, then it is hypertransitive.
$p$
is regular, then it is hypertransitive.
-
(2) If
 $p$
is hypertransitive, then it is unconflicted.
$p$
is hypertransitive, then it is unconflicted.
-
(3) The reverse implication need not hold: it is possible for
 $p$
to be unconflicted but not hypertransitive.
$p$
to be unconflicted but not hypertransitive.
-
(4) It is possible for
 $p$
to be hypertransitive (and unconflicted), but not quasiregular (and thus not weakly regular or regular).
$p$
to be hypertransitive (and unconflicted), but not quasiregular (and thus not weakly regular or regular).
Proof. We consider each part:
-
(1) Suppose
 $p$
is regular and
$p$
is regular and
 $O,O'\in \mathsf{Open}$
and
$O,O'\in \mathsf{Open}$
and
 $O\between \textit{nbhd}(p)\between O'$
. By Definition 4.1.4(3) (since
$O\between \textit{nbhd}(p)\between O'$
. By Definition 4.1.4(3) (since
 $p$
is regular),
$p$
is regular),
 $\textit{K}(p)$
is a topen (= open and transitive) neighbourhood of
$\textit{K}(p)$
is a topen (= open and transitive) neighbourhood of
 $p$
. Therefore, by transitivity,
$p$
. Therefore, by transitivity,
 $O\between O'$
as required.
$O\between O'$
as required. -
(2) Suppose
 $p$
is hypertransitive, and suppose
$p$
is hypertransitive, and suppose
 $p',p''\in \mathsf{P}$
and
$p',p''\in \mathsf{P}$
and
 $p'\mathrel {\between } p\mathrel {\between } p''$
. Now consider
$p'\mathrel {\between } p\mathrel {\between } p''$
. Now consider
 $p'\in O'\in \mathsf{Open}$
and
$p'\in O'\in \mathsf{Open}$
and
 $p''\in O''\in \mathsf{Open}$
. By our intertwinedness assumptions we have that
$p''\in O''\in \mathsf{Open}$
. By our intertwinedness assumptions we have that
 $O'\between \textit{nbhd}(p)\between O''$
. But
$O'\between \textit{nbhd}(p)\between O''$
. But
 $p$
is hypertransitive, so
$p$
is hypertransitive, so
 $O'\between O''$
as required.
$O'\between O''$
as required. -
(3) It suffices to provide a counterexample. Consider the bottom right semitopology in Figure 2, and take
 $p=\ast$
and
$p=\ast$
and
 $O'=\{1\}$
and
$O'=\{1\}$
and
 $O''=\{0,2\}$
. Note that:
$O''=\{0,2\}$
. Note that:-
–
 $\ast$
is unconflicted, since it is intertwined only with itself and
$\ast$
is unconflicted, since it is intertwined only with itself and
 $1$
.
$1$
. -
–
 $O'$
and
$O'$
and
 $O'$
intersect every open neighbourhood of
$O'$
intersect every open neighbourhood of
 $\ast$
, but
$\ast$
, but  , so
, so
 $\ast$
is not hypertransitive.
$\ast$
is not hypertransitive.
-
-
(4) It suffices to provide an example. Consider the semitopology illustrated in Figure 2, top-right diagram; so
 $\mathsf{P}=\{0,1,2\}$
and
$\mathsf{P}=\{0,1,2\}$
and
 $\mathsf{Open}=\{\varnothing ,\{0\},\{2\},\{1,2\},\{0,1\},\{0,1,2\}\}$
. The reader can check that
$\mathsf{Open}=\{\varnothing ,\{0\},\{2\},\{1,2\},\{0,1\},\{0,1,2\}\}$
. The reader can check that
 $p=1$
is hypertransitive, but
$p=1$
is hypertransitive, but
 $1_{\between }=\{1\}$
and
$1_{\between }=\{1\}$
and
 $\textit{K}(1)=\varnothing$
so
$\textit{K}(1)=\varnothing$
so
 $p$
is not quasiregular.
$p$
is not quasiregular.
(Yet) another characterisation of being quasiregular will be helpful:
Lemma 6.3.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following conditions are equivalent:
$p\in \mathsf{P}$
. Then the following conditions are equivalent:
Proof. Equivalence of parts 2 and 3 is immediate from Lemma 6.2.2.
For equivalence of parts 1 and 2, we prove two implications:
-
• Suppose
 $p$
is quasiregular, meaning by Definition 4.1.4(5) that
$p$
is quasiregular, meaning by Definition 4.1.4(5) that
 $\textit{K}(p)\neq \varnothing$
. Pick some
$\textit{K}(p)\neq \varnothing$
. Pick some
 $p'\in \textit{K}(p)$
(it does not matter which). It follows by construction in Definitions 3.5.1(2) and 4.1.4(1) and Lemma 4.1.2 that
$p'\in \textit{K}(p)$
(it does not matter which). It follows by construction in Definitions 3.5.1(2) and 4.1.4(1) and Lemma 4.1.2 that
 $p'\mathrel {\between } p$
, so that
$p'\mathrel {\between } p$
, so that
 $p'\in \textit{K}(p)$
. Using Definition 3.5.1(1), it follows that
$p'\in \textit{K}(p)$
. Using Definition 3.5.1(1), it follows that
 $\textit{K}(p)\between O$
for every
$\textit{K}(p)\between O$
for every
 $O\in \textit{nbhd}(p)$
, as required.
$O\in \textit{nbhd}(p)$
, as required. -
• Suppose
 $\textit{K}(p)\between \textit{nbhd}(p)$
. Then in particular
$\textit{K}(p)\between \textit{nbhd}(p)$
. Then in particular
 $\textit{K}(p)\between \mathsf{P}$
(because
$\textit{K}(p)\between \mathsf{P}$
(because
 $p\in \mathsf{P}\in \mathsf{Open}$
), and by Notation 3.1.1(1) it follows that
$p\in \mathsf{P}\in \mathsf{Open}$
), and by Notation 3.1.1(1) it follows that
 $\textit{K}(p)\neq \varnothing$
.
$\textit{K}(p)\neq \varnothing$
.
Compare and contrast Theorem6.3.3 with Theorem5.3.4:
Theorem 6.3.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following are equivalent:
$p\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $p$
is regular.
$p$
is regular.
-
(2)
 $p$
is quasiregular and hypertransitive.
$p$
is quasiregular and hypertransitive.
Proof. We consider two implications:
-
• Suppose
 $p$
is regular.
$p$
is regular.
Then
 $p$
is quasiregular by Lemma 4.1.6(1 and 2) and hypertransitive by Lemma 6.3.1(1).
$p$
is quasiregular by Lemma 4.1.6(1 and 2) and hypertransitive by Lemma 6.3.1(1). -
• Suppose
 $p$
is quasiregular and hypertransitive.
$p$
is quasiregular and hypertransitive.
By Lemma 6.3.1(2),
 $p$
is unconflicted. If we can prove that
$p$
is unconflicted. If we can prove that
 $p$
is weakly regular (meaning by Definition 4.1.4(4) that
$p$
is weakly regular (meaning by Definition 4.1.4(4) that
 $p\in \textit{K}(p)$
), then by Theorem5.3.4 it would follow that
$p\in \textit{K}(p)$
), then by Theorem5.3.4 it would follow that
 $p$
is regular as required. Thus, it would suffice to show that
$p$
is regular as required. Thus, it would suffice to show that
 $p\in \textit{K}(p)$
, thus that there is an open neighbourhood of points with which
$p\in \textit{K}(p)$
, thus that there is an open neighbourhood of points with which
 $p$
is intertwined.
$p$
is intertwined.Write
 $O''=\textit{interior}(\mathsf{P}\setminus \textit{K}(p))$
. We have two subcases to consider:
$O''=\textit{interior}(\mathsf{P}\setminus \textit{K}(p))$
. We have two subcases to consider:-
– Suppose
 $\textit{nbhd}(p)\between O''$
.
$\textit{nbhd}(p)\between O''$
.By Lemma 6.3.2 (since
 $p$
is quasiregular) we have that
$p$
is quasiregular) we have that
 $\textit{K}(p)\between \textit{nbhd}(p)$
. Thus
$\textit{K}(p)\between \textit{nbhd}(p)$
. Thus
 $\textit{K}(p)\between \textit{nbhd}(p)\between O''$
, and by hypertransitivity of
$\textit{K}(p)\between \textit{nbhd}(p)\between O''$
, and by hypertransitivity of
 $p$
it follows that
$p$
it follows that
 $\textit{K}(p)\between O''$
. But this contradicts the construction of
$\textit{K}(p)\between O''$
. But this contradicts the construction of
 $O''$
as being a subset of
$O''$
as being a subset of
 $\mathsf{P}\setminus \textit{K}(p)$
, so this case is impossible.
$\mathsf{P}\setminus \textit{K}(p)$
, so this case is impossible. -
– Suppose
 . Then there exists some
. Then there exists some
 $O\in \textit{nbhd}(p)$
such that
$O\in \textit{nbhd}(p)$
such that  , and it follows that
, and it follows that
 $O\subseteq \textit{K}(p)$
so that
$O\subseteq \textit{K}(p)$
so that
 $p\in \textit{K}(p)$
as required.
$p\in \textit{K}(p)$
as required.
Thus,
 $p$
is weakly regular, as required.
$p$
is weakly regular, as required. -
Remark 6.3.4. Recall from Definition 4.1.4(3) the notion of a regular point, which in the theory of semitopologies is a canonical well-behavedness property because it ensures that the point is part of a community of other regular points, all in a single maximal intertwined actionable coalition (i.e., open set). We have obtained two nice characterisations of regularity:
-
(1) Regular = weakly regular + unconflicted, by Theorem 5.3.4.
-
(2) Regular = quasiregular + hypertransitive, by Theorem 6.3.3.
We are now ready to dualise everything – including semitopologies, regularity, weak regularity, quasiregularity, and being unconflicted and hypertransitive – and thus we will investigate the algebraic structures which correspond to the set structures above:
7. Semiframes: Compatible Complete Semilattices
7.1 Complete join-semilattices and morphisms between them
We recall some (mostly standard) definitions and facts:
Definition 7.1.1.
-
(1) A poset
 $(\mathsf{X},\leq )$
is a set
$(\mathsf{X},\leq )$
is a set
 $\mathsf{X}$
of elements and a relation
$\mathsf{X}$
of elements and a relation
 ${\leq }\subseteq \mathsf{X}\times \mathsf{X}$
that is transitive, reflexive, and antisymmetric.
${\leq }\subseteq \mathsf{X}\times \mathsf{X}$
that is transitive, reflexive, and antisymmetric. -
(2) A poset
 $(\mathsf{X},\leq )$
is a complete join-semilattice when every
$(\mathsf{X},\leq )$
is a complete join-semilattice when every
 $X\subseteq \mathsf{X}$
(
$X\subseteq \mathsf{X}$
(
 $X$
may be empty or equal to all of
$X$
may be empty or equal to all of
 $\mathsf{X}$
) has a least upper bound – or join –
$\mathsf{X}$
) has a least upper bound – or join –
 $\bigvee X\in \mathsf{X}$
.
$\bigvee X\in \mathsf{X}$
.All the semilattices we consider will be join (rather than meet) semilattices, so we may omit the word ‘join’ and just call this a complete semilattice henceforth.
-
(3) If
 $(\mathsf{X},\leq )$
is a complete semilattice, then we may writeBy the least upper bound property,
$(\mathsf{X},\leq )$
is a complete semilattice, then we may writeBy the least upper bound property, \begin{equation*} {\boldsymbol \bot }_{\mathsf{X}}=\bigvee \varnothing . \end{equation*}
\begin{equation*} {\boldsymbol \bot }_{\mathsf{X}}=\bigvee \varnothing . \end{equation*}
 ${\boldsymbol \bot }_{\mathsf{X}}\leq x$
for every
${\boldsymbol \bot }_{\mathsf{X}}\leq x$
for every
 $x\in \mathsf{X}$
.
$x\in \mathsf{X}$
.
-
(4) If
 $(\mathsf{X},\leq )$
is a complete semilattice, then we may writeBy the least upper bound property,
$(\mathsf{X},\leq )$
is a complete semilattice, then we may writeBy the least upper bound property, \begin{equation*} {\boldsymbol \top }_{\mathsf{X}}=\bigvee \mathsf{X}. \end{equation*}
\begin{equation*} {\boldsymbol \top }_{\mathsf{X}}=\bigvee \mathsf{X}. \end{equation*}
 $x\leq {\boldsymbol \top }_{\mathsf{X}}$
for every
$x\leq {\boldsymbol \top }_{\mathsf{X}}$
for every
 $x\in \mathsf{X}$
.
$x\in \mathsf{X}$
.
Definition 7.1.2. Suppose
![]() $(\mathsf{X}',\leq ')$
and
$(\mathsf{X}',\leq ')$
and
![]() $(\mathsf{X},\leq )$
are complete join-semilattices. Define a morphism
$(\mathsf{X},\leq )$
are complete join-semilattices. Define a morphism
![]() $g:(\mathsf{X}',\leq ')\to (\mathsf{X},\leq )$
to be a function
$g:(\mathsf{X}',\leq ')\to (\mathsf{X},\leq )$
to be a function
![]() $\mathsf{X}'\to \mathsf{X}$
that commutes with joins and sends
$\mathsf{X}'\to \mathsf{X}$
that commutes with joins and sends
![]() ${\boldsymbol \top }_{\mathsf{X}'}$
to
${\boldsymbol \top }_{\mathsf{X}'}$
to
![]() ${\boldsymbol \top }_{\mathsf{X}}$
. That is:
${\boldsymbol \top }_{\mathsf{X}}$
. That is:
-
(1) If
 $X'\subseteq \mathsf{X}'$
, then
$X'\subseteq \mathsf{X}'$
, then
 $g(\bigvee X')=\bigvee _{x'{\in }\mathsf{X}'}g(x')$
.
$g(\bigvee X')=\bigvee _{x'{\in }\mathsf{X}'}g(x')$
. -
(2)
 $g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
.
$g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
.
Remark 7.1.3. In Definition 7.1.1(2), we insist that
![]() $g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
; that is, we want our notion of morphism to preserve the top element.
$g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
; that is, we want our notion of morphism to preserve the top element.
This does not follow from Definition 7.1.1(1), because
![]() $g$
need not be surjective onto
$g$
need not be surjective onto
![]() $\mathsf{X}$
, so we need to add this as a separate condition. Contrast with
$\mathsf{X}$
, so we need to add this as a separate condition. Contrast with
![]() $g({\boldsymbol \bot }_{\mathsf{X}})={\boldsymbol \bot }_{\mathsf{X}'}$
, which does follow from Definition 7.1.1(1), because
$g({\boldsymbol \bot }_{\mathsf{X}})={\boldsymbol \bot }_{\mathsf{X}'}$
, which does follow from Definition 7.1.1(1), because
![]() ${\boldsymbol \bot }_{\mathsf{X}}$
is the least upper bound of
${\boldsymbol \bot }_{\mathsf{X}}$
is the least upper bound of
![]() $\varnothing$
.
$\varnothing$
.
We want
![]() $g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
because our intended model is that
$g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
because our intended model is that
![]() $(\mathsf{X},\leq )=(\mathsf{Open},\subseteq )$
is the semilattice of open sets of a semitopology
$(\mathsf{X},\leq )=(\mathsf{Open},\subseteq )$
is the semilattice of open sets of a semitopology
![]() $(\mathsf{P},\mathsf{Open})$
, and similarly for
$(\mathsf{P},\mathsf{Open})$
, and similarly for
![]() $(\mathsf{X}',\leq ')$
, and
$(\mathsf{X}',\leq ')$
, and
![]() $g$
is equal to
$g$
is equal to
![]() $f^{\text{-}1}$
where
$f^{\text{-}1}$
where
![]() $f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
is a continuous function.
$f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
is a continuous function.
We recall a standard result:
Lemma 7.1.4.
Suppose
![]() $(\mathsf{X},\leq )$
is a complete join-semilattice. Then:
$(\mathsf{X},\leq )$
is a complete join-semilattice. Then:
-
(1) If
 $x_1,x_2\in \mathsf{X}$
, then
$x_1,x_2\in \mathsf{X}$
, then
 $x_1\leq x_2$
if and only if
$x_1\leq x_2$
if and only if
 $x_1{\boldsymbol \vee } x_2 = x_2$
.
$x_1{\boldsymbol \vee } x_2 = x_2$
. -
(2) If
 $f:(\mathsf{X},\leq )\to (\mathsf{X}',\leq ')$
is a semilattice morphism (Definition 7.1.2), then
$f:(\mathsf{X},\leq )\to (\mathsf{X}',\leq ')$
is a semilattice morphism (Definition 7.1.2), then
 $f$
is a
monotone morphism
: if
$f$
is a
monotone morphism
: if
 $x_1\leq x_2$
, then
$x_1\leq x_2$
, then
 $f(x_1)\leq f(x_2)$
, for every
$f(x_1)\leq f(x_2)$
, for every
 $x_1,x_2\in \mathsf{X}$
.
$x_1,x_2\in \mathsf{X}$
.
Proof. We consider each part in turn:
-
(1) Suppose
 $x_1\leq x_2$
. By the definition of a least upper bound, this means precisely that
$x_1\leq x_2$
. By the definition of a least upper bound, this means precisely that
 $x_2$
is a least upper bound for
$x_2$
is a least upper bound for
 $\{x_1,x_2\}$
. It follows that
$\{x_1,x_2\}$
. It follows that
 $x_1{\boldsymbol \vee } x_2=x_2$
. The converse implication follows just by reversing this reasoning.
$x_1{\boldsymbol \vee } x_2=x_2$
. The converse implication follows just by reversing this reasoning. -
(2) Suppose
 $x_1\leq x_2$
. By part 1 of this result
$x_1\leq x_2$
. By part 1 of this result
 $x_1{\boldsymbol \vee } x_2=x_2$
, so
$x_1{\boldsymbol \vee } x_2=x_2$
, so
 $f(x_1{\boldsymbol \vee } x_2)=f(x_2)$
. By Definition 7.1.2,
$f(x_1{\boldsymbol \vee } x_2)=f(x_2)$
. By Definition 7.1.2,
 $f(x_1){\boldsymbol \vee } f(x_2)=f(x_2)$
. By part 1 of this result,
$f(x_1){\boldsymbol \vee } f(x_2)=f(x_2)$
. By part 1 of this result,
 $f(x_1)\leq f(x_2)$
.
$f(x_1)\leq f(x_2)$
.
Remark 7.1.5. As the reader may know, frames and locales are the same thing: the category of locales is just the categorical opposite of the category of frames. So every time we write ‘semiframe’, the reader can safely read ‘semilocale'; these are two names for essentially the same structure up to reversing arrows. The literature on frames and locales is huge: the interested reader can consult two classic texts (Johnstone, Reference Johnstone1986; Mac Lane and Moerdijk, Reference Mac Lane and Moerdijk1992); more recent (and very readable) presentations include Picado and Pultr (Reference Picado and Pultr2012, Reference Picado and Pultr2021).
7.2 The compatibility relation
Definition 7.2.1 is a simple idea, but so far as we are aware, it is novel:
Definition 7.2.1. Suppose
![]() $(\mathsf{X},\leq )$
is a complete semilattice. A compatibility relation
$(\mathsf{X},\leq )$
is a complete semilattice. A compatibility relation
![]() ${\ast }\subseteq \mathsf{X}\times \mathsf{X}$
is a relation on
${\ast }\subseteq \mathsf{X}\times \mathsf{X}$
is a relation on
![]() $\mathsf{X}$
such that:
$\mathsf{X}$
such that:
-
(1)
 $\ast$
is symmetric, so if
$\ast$
is symmetric, so if
 $x,x'\in \mathsf{X}$
then
$x,x'\in \mathsf{X}$
then \begin{equation*} x\ast x' \quad \textit{if and only if}\quad x'\ast x. \end{equation*}
\begin{equation*} x\ast x' \quad \textit{if and only if}\quad x'\ast x. \end{equation*}
-
(2)
 $\ast$
is a properly reflexive relation,Footnote
15
by which we meanNote that it will follow from the axioms of a compatibility relation that
$\ast$
is a properly reflexive relation,Footnote
15
by which we meanNote that it will follow from the axioms of a compatibility relation that \begin{equation*} \forall x\in \mathsf{X}{\setminus }\{{\boldsymbol \bot }_{\mathsf{X}}\}. x\ast x . \end{equation*}
\begin{equation*} \forall x\in \mathsf{X}{\setminus }\{{\boldsymbol \bot }_{\mathsf{X}}\}. x\ast x . \end{equation*}
 $x\ast x\Longleftrightarrow x\neq {\boldsymbol \bot }_{\mathsf{X}}$
; see Lemma 7.3.7(2).
$x\ast x\Longleftrightarrow x\neq {\boldsymbol \bot }_{\mathsf{X}}$
; see Lemma 7.3.7(2).
-
(3)
 $\ast$
satisfies a distributive law, that if
$\ast$
satisfies a distributive law, that if
 $x\in \mathsf{X}$
and
$x\in \mathsf{X}$
and
 $X'\subseteq \mathsf{X}$
then
$X'\subseteq \mathsf{X}$
then \begin{equation*} x\ast \bigvee X' \Longleftrightarrow \exists x'{\in }X'. x\ast x' . \end{equation*}
\begin{equation*} x\ast \bigvee X' \Longleftrightarrow \exists x'{\in }X'. x\ast x' . \end{equation*}
Thus, we can say:
a compatibility relation
![]() ${\ast }\subseteq \mathsf{X}\times \mathsf{X}$
is a symmetric properly reflexive completely distributive relation on
${\ast }\subseteq \mathsf{X}\times \mathsf{X}$
is a symmetric properly reflexive completely distributive relation on
![]() $\mathsf{X}$
.
$\mathsf{X}$
.
When
![]() $x\ast x'$
holds, we may call
$x\ast x'$
holds, we may call
![]() $x$
and
$x$
and
![]() $x'$
compatible elements.
$x'$
compatible elements.
Remark 7.2.2. The compatibility relation
![]() $\ast$
is what it is, but we take a moment to discuss some intuitions, and to put it in the context of some natural generalisations:
$\ast$
is what it is, but we take a moment to discuss some intuitions, and to put it in the context of some natural generalisations:
-
(1) We can think of
 $\ast$
as an abstract intersection.
$\ast$
as an abstract intersection.It lets us observe whether
 $x$
and
$x$
and
 $x'$
intersect – but without having to explicitly represent this intersection as a meet
$x'$
intersect – but without having to explicitly represent this intersection as a meet
 $x{\boldsymbol \wedge } x'$
in the semilattice itself.
$x{\boldsymbol \wedge } x'$
in the semilattice itself.We call
 $\ast$
a compatibility relation following an intuition of
$\ast$
a compatibility relation following an intuition of
 $x,x'\in \mathsf{X}$
as observations, and
$x,x'\in \mathsf{X}$
as observations, and
 $x\ast x'$
holds when there is some possible world at which it is possible to observe
$x\ast x'$
holds when there is some possible world at which it is possible to observe
 $x$
and
$x$
and
 $x'$
together. More on this in Example 7.3.3.
$x'$
together. More on this in Example 7.3.3. -
(2) We can think of
 $\ast$
as a generalised intersection; so our notion of semiframe in Definition 7.3.1 is an instance of a frame with a generalised meet.
$\ast$
as a generalised intersection; so our notion of semiframe in Definition 7.3.1 is an instance of a frame with a generalised meet.We will concentrate on the case where
 $x \ast x'$
measures whether
$x \ast x'$
measures whether
 $x$
and
$x$
and
 $x'$
intersect, but there are other possibilities. Here are some natural ways to proceed:
$x'$
intersect, but there are other possibilities. Here are some natural ways to proceed:-
a.
 $(\mathsf{X},\leq )$
is a complete join-semilattice and
$(\mathsf{X},\leq )$
is a complete join-semilattice and
 ${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathsf{X}$
is any commutative distributive map. For concreteness, we can set
${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathsf{X}$
is any commutative distributive map. For concreteness, we can set
 $x\ast x' \in \{{\boldsymbol \bot }_{\mathsf{X}},{\boldsymbol \top }_{\mathsf{X}}\}\subseteq \mathsf{X}$
.
$x\ast x' \in \{{\boldsymbol \bot }_{\mathsf{X}},{\boldsymbol \top }_{\mathsf{X}}\}\subseteq \mathsf{X}$
. -
b.
 $(\mathsf{X},\leq )$
is a complete join-semilattice and
$(\mathsf{X},\leq )$
is a complete join-semilattice and
 ${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathbb N$
is any commutative distributive map. We think of
${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathbb N$
is any commutative distributive map. We think of
 $x\ast x'$
as returning the size of the intersection of
$x\ast x'$
as returning the size of the intersection of
 $x$
and
$x$
and
 $x'$
.
$x'$
. -
c. Any complete join-semilattice
 $(\mathsf{X},\leq )$
is of course a (generalised) semiframe by taking
$(\mathsf{X},\leq )$
is of course a (generalised) semiframe by taking
 $x\ast x' = \bigvee \{x'' \mid x''\leq x,\ x''\leq x'\}$
.
$x\ast x' = \bigvee \{x'' \mid x''\leq x,\ x''\leq x'\}$
. -
d. We can generalise further, in more than one direction. We would take
 $(\mathsf{X},\leq )$
and
$(\mathsf{X},\leq )$
and
 $(\mathsf{X}',\leq ')$
to be complete join-semilattices and
$(\mathsf{X}',\leq ')$
to be complete join-semilattices and
 ${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathsf{X}'$
to be any commutative distributive map (which generalises the above). We could also take
${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathsf{X}'$
to be any commutative distributive map (which generalises the above). We could also take
 $\mathsf{X}$
to be a cocomplete symmetric monoidal category (Mac Lane, Reference Mac Lane1971, Section VII): a category with all colimits and with a (symmetric) monoid action
$\mathsf{X}$
to be a cocomplete symmetric monoidal category (Mac Lane, Reference Mac Lane1971, Section VII): a category with all colimits and with a (symmetric) monoid action
 $\ast$
that distributes over (commutes with) colimits.
$\ast$
that distributes over (commutes with) colimits. -
e. The compatibility relation
 $\ast$
is binary: as noted in part 1 of this Remark, it abstracts two open sets having a nonempty open intersection.
$\ast$
is binary: as noted in part 1 of this Remark, it abstracts two open sets having a nonempty open intersection.However, the literature on distributed systems is rich in well-behavedness conditions based on intersections of sets: for example, ones corresponding to nonempty ternary intersections between open sets, and on intersections between open and closed sets, and on other types of intersections. These are not thought of in the literature in topological/algebraic terms – that way of looking at things is a contribution of this paper and the recent Gabbay (Reference Gabbay2025) – but they could be.
This suggests that
 $\ast$
may be a (canonical simplest) representative of a design space of ‘nonempty
$\ast$
may be a (canonical simplest) representative of a design space of ‘nonempty
 $n$
-ary intersection’ operators, which remains to be explored.
$n$
-ary intersection’ operators, which remains to be explored.
-
More details, with some references, are in Remark 12.3.6.
Lemma 7.2.3.
Suppose
![]() $(\mathsf{X},\leq )$
is a complete semilattice and suppose
$(\mathsf{X},\leq )$
is a complete semilattice and suppose
![]() ${\ast }\subseteq \mathsf{X}\times \mathsf{X}$
is a compatibility relation on
${\ast }\subseteq \mathsf{X}\times \mathsf{X}$
is a compatibility relation on
![]() $\mathsf{X}$
. Then:
$\mathsf{X}$
. Then:
-
(1)
 $\ast$
is monotone on both arguments.
$\ast$
is monotone on both arguments.
That is: if
 $x_1\ast x_2$
and
$x_1\ast x_2$
and
 $x_1\leq x_1'$
and
$x_1\leq x_1'$
and
 $x_2\leq x_2'$
, then
$x_2\leq x_2'$
, then
 $x_1'\ast x_2'$
.
$x_1'\ast x_2'$
. -
(2) If
 $x_1,x_2\in \mathsf{X}$
have a non-
$x_1,x_2\in \mathsf{X}$
have a non-
 $\boldsymbol \bot$
lower bound
$\boldsymbol \bot$
lower bound
 ${\boldsymbol \bot }_{\mathsf{X}}\lneq x\leq x_1,x_2$
, then
${\boldsymbol \bot }_{\mathsf{X}}\lneq x\leq x_1,x_2$
, then
 $x_1\ast x_2$
.
$x_1\ast x_2$
.In words we can write:
 $\ast$
reflects non-
$\ast$
reflects non-
 $\boldsymbol \bot$
lower bounds.
$\boldsymbol \bot$
lower bounds.
-
(3) The converse implication to part 2 need not hold: it may be that
 $x_1\ast x_2$
(
$x_1\ast x_2$
(
 $x_1$
and
$x_1$
and
 $x_2$
are compatible) but the greatest lower bound of
$x_2$
are compatible) but the greatest lower bound of
 $\{x_1,x_2\}$
is
$\{x_1,x_2\}$
is
 $\boldsymbol \bot$
.
$\boldsymbol \bot$
.
Proof. We consider each part in turn:
-
(1) We argue much as for Lemma 7.1.4(1). Suppose
 $x_1\ast x_2$
and
$x_1\ast x_2$
and
 $x_1\leq x_1'$
and
$x_1\leq x_1'$
and
 $x_2\leq x_2'$
. By Lemma 7.1.4
$x_2\leq x_2'$
. By Lemma 7.1.4
 $x_1{\boldsymbol \vee } x_1'=x_1'$
and
$x_1{\boldsymbol \vee } x_1'=x_1'$
and
 $x_2{\boldsymbol \vee } x_2'=x_2'$
. It follows using distributivity and commutativity (Definition 7.2.1(3 and 1)) that
$x_2{\boldsymbol \vee } x_2'=x_2'$
. It follows using distributivity and commutativity (Definition 7.2.1(3 and 1)) that
 $x_1\ast x_2$
implies that
$x_1\ast x_2$
implies that
 $(x_1{\boldsymbol \vee } x_1')\ast (x_2\ast x_2')$
, and thus that
$(x_1{\boldsymbol \vee } x_1')\ast (x_2\ast x_2')$
, and thus that
 $x_1'\ast x_2'$
as required.
$x_1'\ast x_2'$
as required. -
(2) Suppose
 ${\boldsymbol \bot }_{\mathsf{X}}\neq x \leq x_1,x_2$
, so
${\boldsymbol \bot }_{\mathsf{X}}\neq x \leq x_1,x_2$
, so
 $x$
is a non-
$x$
is a non-
 ${\boldsymbol \bot }_{\mathsf{X}}$
lower bound. By assumption
${\boldsymbol \bot }_{\mathsf{X}}$
lower bound. By assumption
 $\ast$
is properly reflexive (Definition 7.2.1(2)) so (since
$\ast$
is properly reflexive (Definition 7.2.1(2)) so (since
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
)
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
)
 $x\ast x$
. By part 1 of this result it follows that
$x\ast x$
. By part 1 of this result it follows that
 $x_1\ast x_2$
as required.
$x_1\ast x_2$
as required. -
(3) It suffices to provide a counterexample. Define
 $(\mathsf{X},\leq ,\ast )$
by:
$(\mathsf{X},\leq ,\ast )$
by:-
–
 $\mathsf{X} = \{{\boldsymbol \bot },0,1,{\boldsymbol \top }\}$
.
$\mathsf{X} = \{{\boldsymbol \bot },0,1,{\boldsymbol \top }\}$
. -
–
 ${\boldsymbol \bot }\leq 0,1 \leq {\boldsymbol \top }$
and
${\boldsymbol \bot }\leq 0,1 \leq {\boldsymbol \top }$
and
 $\neg (0\leq 1)$
and
$\neg (0\leq 1)$
and
 $\neg (1\leq 0)$
.
$\neg (1\leq 0)$
. -
–
 $x\ast x'$
for every
$x\ast x'$
for every
 ${\boldsymbol \bot }\neq x,x'\in \mathsf{X}$
.
${\boldsymbol \bot }\neq x,x'\in \mathsf{X}$
.
We note that
 $0\ast 1$
but the greatest lower bound of
$0\ast 1$
but the greatest lower bound of
 $\{0,1\}$
is
$\{0,1\}$
is
 $\boldsymbol \bot$
. We will revisit a slightly more elaborate version of this counterexample in Figure 5.
$\boldsymbol \bot$
. We will revisit a slightly more elaborate version of this counterexample in Figure 5. -
7.3 The definition of a semiframe
Definition 7.3.1. A semiframe is a tuple
![]() $(\mathsf{X},\leq ,\ast )$
such that
$(\mathsf{X},\leq ,\ast )$
such that
-
(1)
 $(\mathsf{X},\leq )$
is a complete semilattice (Definition 7.1.1), and
$(\mathsf{X},\leq )$
is a complete semilattice (Definition 7.1.1), and -
(2)
 $\ast$
is a compatibility relation on it (Definition 7.2.1).
$\ast$
is a compatibility relation on it (Definition 7.2.1).
Slightly abusing terminology, we can say that
semiframe = compatible complete semilattice.
Semiframes are new, so far as we know, but they are a natural idea. We consider some elementary ways to generate examples, starting with arguably the simplest possible instance:
Example 7.3.2 (The empty semiframe). Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe.
$(\mathsf{X},\leq ,\ast )$
is a semiframe.
-
(1) If
 $\mathsf{X}$
is a singleton set, so that
$\mathsf{X}$
is a singleton set, so that
 $\mathsf{X}=\{\bullet \}$
for some element
$\mathsf{X}=\{\bullet \}$
for some element
 $\bullet$
, then we call
$\bullet$
, then we call
 $(\mathsf{X},\leq ,\ast )$
the empty semiframe or singleton semiframe.
$(\mathsf{X},\leq ,\ast )$
the empty semiframe or singleton semiframe.Then necessarily
 $\bullet ={\boldsymbol \bot }_{\mathsf{X}}={\boldsymbol \top }_{\mathsf{X}}$
and
$\bullet ={\boldsymbol \bot }_{\mathsf{X}}={\boldsymbol \top }_{\mathsf{X}}$
and
 $\bullet \leq \bullet$
and
$\bullet \leq \bullet$
and
 $\neg (\bullet \ast \bullet )$
.
$\neg (\bullet \ast \bullet )$
. -
(2) If
 $\mathsf{X}$
has more than one element then we call
$\mathsf{X}$
has more than one element then we call
 $(\mathsf{X},\leq ,\ast )$
a nonempty semiframe. Then necessarily
$(\mathsf{X},\leq ,\ast )$
a nonempty semiframe. Then necessarily
 ${\boldsymbol \bot }_{\mathsf{X}}\neq {\boldsymbol \top }_{\mathsf{X}}$
.
${\boldsymbol \bot }_{\mathsf{X}}\neq {\boldsymbol \top }_{\mathsf{X}}$
.
Thus,
![]() $(\mathsf{X},\leq ,\ast )$
is nonempty if and only if
$(\mathsf{X},\leq ,\ast )$
is nonempty if and only if
![]() ${\boldsymbol \bot }_{\mathsf{X}}\neq {\boldsymbol \top }_{\mathsf{X}}$
. We call a singleton semiframe empty, because this corresponds to the semiframe of open sets of the empty topology, which has no points and one open set,
${\boldsymbol \bot }_{\mathsf{X}}\neq {\boldsymbol \top }_{\mathsf{X}}$
. We call a singleton semiframe empty, because this corresponds to the semiframe of open sets of the empty topology, which has no points and one open set,
![]() $\varnothing$
.
$\varnothing$
.
Example 7.3.3 continues Remark 7.2.2:
Example 7.3.3.
-
(1) Suppose
 $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the reader can check that the semiframe of open sets
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the reader can check that the semiframe of open sets
 $(\mathsf{P},\subseteq ,\between )$
is a semiframe. We will study this example in detail; see Definition 7.3.4 and Lemma 7.3.5.
$(\mathsf{P},\subseteq ,\between )$
is a semiframe. We will study this example in detail; see Definition 7.3.4 and Lemma 7.3.5. -
(2) Suppose
 $(\mathsf{X},\leq ,{\boldsymbol \bot },{\boldsymbol \top })$
is a frame (a complete lattice such that meets distribute over arbitrary joins). Then
$(\mathsf{X},\leq ,{\boldsymbol \bot },{\boldsymbol \top })$
is a frame (a complete lattice such that meets distribute over arbitrary joins). Then
 $(\mathsf{X},\leq ,\ast )$
is a semiframe, where
$(\mathsf{X},\leq ,\ast )$
is a semiframe, where
 $x\ast x'$
when
$x\ast x'$
when
 $x{\boldsymbol \wedge } x'\neq {\boldsymbol \bot }$
.Footnote
16
$x{\boldsymbol \wedge } x'\neq {\boldsymbol \bot }$
.Footnote
16
-
(3) Take
 $\mathsf{X}=\{{\boldsymbol \bot },0,1,{\boldsymbol \top }\}$
with
$\mathsf{X}=\{{\boldsymbol \bot },0,1,{\boldsymbol \top }\}$
with
 ${\boldsymbol \bot }\leq 0\leq {\boldsymbol \top }$
and
${\boldsymbol \bot }\leq 0\leq {\boldsymbol \top }$
and
 ${\boldsymbol \bot }\leq 1\leq {\boldsymbol \top }$
(so
${\boldsymbol \bot }\leq 1\leq {\boldsymbol \top }$
(so
 $0$
and
$0$
and
 $1$
are incomparable). There are two possible semiframe structures on this, characterised by choosing
$1$
are incomparable). There are two possible semiframe structures on this, characterised by choosing
 $0\ast 1$
or
$0\ast 1$
or
 $\neg (0\ast 1)$
.
$\neg (0\ast 1)$
. -
(4) See also the semiframes used in Lemmas 8.2.7.
Definition 7.3.4 is just an example of semiframes for now, though we will see much more of it later:
Definition 7.3.4 (Semitopology
![]() $\to$
semiframe). Suppose
$\to$
semiframe). Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Define the semiframe of open sets
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Define the semiframe of open sets
![]() $\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
(cf. Example 7.3.3(1)) by:
$\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
(cf. Example 7.3.3(1)) by:
-
(1)
 $\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
has elements open sets
$\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
has elements open sets
 $O\in \mathsf{Open}$
.
$O\in \mathsf{Open}$
. -
(2)
 $\leq$
is subset inclusion.
$\leq$
is subset inclusion. -
(3)
 $\ast$
is
$\ast$
is
 $\between$
(set intersection).
$\between$
(set intersection).
We may write
Lemma 7.3.5.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then
![]() $(\mathsf{Open},\subseteq ,\between )$
is indeed a semiframe.
$(\mathsf{Open},\subseteq ,\between )$
is indeed a semiframe.
Proof.
As per Definition 7.3.1 we must show that
![]() $\mathsf{Open}$
is a complete semilattice (Definition 7.1.1) and
$\mathsf{Open}$
is a complete semilattice (Definition 7.1.1) and
![]() $\between$
is a compatibility relation (Definition 7.2.1) – symmetric, properly reflexive, and distributive and satisfies a distributive law that if
$\between$
is a compatibility relation (Definition 7.2.1) – symmetric, properly reflexive, and distributive and satisfies a distributive law that if
![]() $O\between \bigcup \mathscr O'$
then
$O\between \bigcup \mathscr O'$
then
![]() $O\between O'$
for some
$O\between O'$
for some
![]() $O'\in \mathscr O'$
. These are all facts of sets.
$O'\in \mathscr O'$
. These are all facts of sets.
Remark 7.3.6. Definition 7.3.4 and Lemma 7.3.5 are the start of our development. Once we have built more machinery, we will have a pair of translations:
-
• Definition 7.3.4 and Lemma 7.3.5 go from semitopologies to semiframes.
-
• Definition 8.4.3 and Lemma 8.4.4 go from semiframes to semitopologies.
These translations are part of a dual pair of functors between categories of semitopologies and semiframes, as described in Definitions 10.1.1 and 10.2.1 and Proposition 10.3.7.
Semitopologies are (relatively) concrete: we have concrete points and open sets that are sets of points. Semiframes are more abstract: we have a join-complete semilattice, and a compatibility relation. The duality we are about to build will show how these two worlds interact and reflect each other.
We conclude with a simple technical lemma:
Lemma 7.3.7.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe (a complete semilattice with a compatibility relation) and
$(\mathsf{X},\leq ,\ast )$
is a semiframe (a complete semilattice with a compatibility relation) and
![]() $x\in \mathsf{X}$
. Then:
$x\in \mathsf{X}$
. Then:
-
(1)
 $\neg (x\ast {\boldsymbol \bot }_{\mathsf{X}})$
and in particular
$\neg (x\ast {\boldsymbol \bot }_{\mathsf{X}})$
and in particular
 $\neg ({\boldsymbol \bot }_{\mathsf{X}}\ast {\boldsymbol \bot }_{\mathsf{X}})$
.
$\neg ({\boldsymbol \bot }_{\mathsf{X}}\ast {\boldsymbol \bot }_{\mathsf{X}})$
. -
(2)
 $x\ast x$
if and only if
$x\ast x$
if and only if
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
.
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
. -
(3)
 $x\ast {\boldsymbol \top }_{\mathsf{X}}$
if and only if
$x\ast {\boldsymbol \top }_{\mathsf{X}}$
if and only if
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
.
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
. -
(4)
 ${\boldsymbol \top }_{\mathsf{X}}\ast {\boldsymbol \top }_{\mathsf{X}}$
holds precisely if
${\boldsymbol \top }_{\mathsf{X}}\ast {\boldsymbol \top }_{\mathsf{X}}$
holds precisely if
 $\mathsf{X}$
is nonempty (Example 7.3.2).
$\mathsf{X}$
is nonempty (Example 7.3.2).
Proof. We consider each part in turn:
-
(1) Recall from Definition 7.1.1(3) that
 ${\boldsymbol \bot }_{\mathsf{X}}=\bigvee \varnothing$
. By distributivity (Definition 7.2.1(3))
${\boldsymbol \bot }_{\mathsf{X}}=\bigvee \varnothing$
. By distributivity (Definition 7.2.1(3)) \begin{equation*} x\ast {\boldsymbol \bot }_{\mathsf{X}}\Longleftrightarrow \exists x'\in \varnothing .x\ast x' \Longleftrightarrow \bot . \end{equation*}
\begin{equation*} x\ast {\boldsymbol \bot }_{\mathsf{X}}\Longleftrightarrow \exists x'\in \varnothing .x\ast x' \Longleftrightarrow \bot . \end{equation*}
-
(2) We just combine part 1 of this result with Definition 7.2.1(2).
-
(3) Suppose
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
. Then
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
. Then
 ${\boldsymbol \bot }_{\mathsf{X}}\lneq x\leq x\leq {\boldsymbol \top }_{\mathsf{X}}$
, and by Lemma 7.2.3(2)
${\boldsymbol \bot }_{\mathsf{X}}\lneq x\leq x\leq {\boldsymbol \top }_{\mathsf{X}}$
, and by Lemma 7.2.3(2)
 $x\ast {\boldsymbol \top }_{\mathsf{X}}$
.
$x\ast {\boldsymbol \top }_{\mathsf{X}}$
.Suppose
 $x={\boldsymbol \bot }_{\mathsf{X}}$
. Then
$x={\boldsymbol \bot }_{\mathsf{X}}$
. Then
 $\neg (x\ast {\boldsymbol \top }_{\mathsf{X}})$
by combining commutativity of
$\neg (x\ast {\boldsymbol \top }_{\mathsf{X}})$
by combining commutativity of
 $\ast$
(Definition 7.2.1(1)) with part 1 of this result.
$\ast$
(Definition 7.2.1(1)) with part 1 of this result. -
(4) If
 $\mathsf{X}$
is nonempty then by Example 7.3.2
$\mathsf{X}$
is nonempty then by Example 7.3.2
 ${\boldsymbol \bot }_{\mathsf{X}}\neq {\boldsymbol \top }_{\mathsf{X}}$
and so
${\boldsymbol \bot }_{\mathsf{X}}\neq {\boldsymbol \top }_{\mathsf{X}}$
and so
 ${\boldsymbol \top }_{\mathsf{X}}\ast {\boldsymbol \top }_{\mathsf{X}}$
holds by part 2 of this result. However, in the degenerate case that
${\boldsymbol \top }_{\mathsf{X}}\ast {\boldsymbol \top }_{\mathsf{X}}$
holds by part 2 of this result. However, in the degenerate case that
 $\mathsf{X}$
has one element then
$\mathsf{X}$
has one element then
 ${\boldsymbol \top }_{\mathsf{X}}={\boldsymbol \bot }_{\mathsf{X}}$
and
${\boldsymbol \top }_{\mathsf{X}}={\boldsymbol \bot }_{\mathsf{X}}$
and
 ${\boldsymbol \top }_{\mathsf{X}}\ast {\boldsymbol \top }_{\mathsf{X}}$
does not hold.
${\boldsymbol \top }_{\mathsf{X}}\ast {\boldsymbol \top }_{\mathsf{X}}$
does not hold.
Remark 7.3.8. Recall from (Davey and Priestley, Reference Davey and Priestley2002, Definition 5.22, p. 128) that if
![]() $\mathsf{X}$
is a lattice, then the pseudocomplement to
$\mathsf{X}$
is a lattice, then the pseudocomplement to
![]() $x\in \mathsf{X}$
is
$x\in \mathsf{X}$
is
![]() $x^*=\bigvee \{x'\in \mathsf{X}\mid x'\wedge x={\boldsymbol \bot }\}$
. A semiframe
$x^*=\bigvee \{x'\in \mathsf{X}\mid x'\wedge x={\boldsymbol \bot }\}$
. A semiframe
![]() $(\mathsf{X},\leq ,\ast )$
naturally supports a notion of pseudocomplement for
$(\mathsf{X},\leq ,\ast )$
naturally supports a notion of pseudocomplement for
![]() $x\in \mathsf{X}$
, given by
$x\in \mathsf{X}$
, given by
It is easy to prove that
![]() $\neg (x^c\ast x)$
, arguing by contradiction: if
$\neg (x^c\ast x)$
, arguing by contradiction: if
![]() $x^c\ast x$
then
$x^c\ast x$
then
![]() $\bigvee \{x'\mid \neg (x'\ast x)\}\ast x$
, and by distributivity (Definition 7.2.1(3)) there exists
$\bigvee \{x'\mid \neg (x'\ast x)\}\ast x$
, and by distributivity (Definition 7.2.1(3)) there exists
![]() $x'\in \mathsf{X}$
such that
$x'\in \mathsf{X}$
such that
![]() $x'\ast x$
and
$x'\ast x$
and
![]() $\neg (x'\ast x)$
, a contradiction.
$\neg (x'\ast x)$
, a contradiction.
Note that it may be that
![]() $(x^c)^c\lneq x$
. For example, in the semiframe illustrated in Figure 5,
$(x^c)^c\lneq x$
. For example, in the semiframe illustrated in Figure 5,
![]() $0^c=\bigvee \{1,2,3\}={\boldsymbol \top }$
and
$0^c=\bigvee \{1,2,3\}={\boldsymbol \top }$
and
![]() $(0^c)^c={\boldsymbol \bot }\lneq 0$
(this behaviour will be familiar to the reader who has seen, e.g.,, double negation in intuitionistic logic).
$(0^c)^c={\boldsymbol \bot }\lneq 0$
(this behaviour will be familiar to the reader who has seen, e.g.,, double negation in intuitionistic logic).
![]() $x^c$
and related constructions will be useful later, in Definition 11.4.2 and Lemma 11.4.4.
$x^c$
and related constructions will be useful later, in Definition 11.4.2 and Lemma 11.4.4.
8. Semifilters & Abstract Points
8.1 The basic definition, and discussion
Definition 8.1.1. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
$(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
![]() $F\subseteq \mathsf{X}$
. Then:
$F\subseteq \mathsf{X}$
. Then:
-
(1) Call
 $F$
prime when for every
$F$
prime when for every
 $x,x'\in \mathsf{X}$
,
$x,x'\in \mathsf{X}$
, \begin{equation*} x{\boldsymbol \vee } x'\in F \quad \textit{implies}\quad x\in F\lor x'\in F . \end{equation*}
\begin{equation*} x{\boldsymbol \vee } x'\in F \quad \textit{implies}\quad x\in F\lor x'\in F . \end{equation*}
-
(2) Call
 $F$
completely prime when for every (possibly empty)
$F$
completely prime when for every (possibly empty)
 $X\subseteq \mathsf{X}$
,(This condition is used in Lemma 8.3.2, which is needed for Lemma 8.4.2.)
$X\subseteq \mathsf{X}$
,(This condition is used in Lemma 8.3.2, which is needed for Lemma 8.4.2.) \begin{equation*} \bigvee X\in F \quad \textit{implies}\quad \exists x{\in }X.x\in F. \end{equation*}
\begin{equation*} \bigvee X\in F \quad \textit{implies}\quad \exists x{\in }X.x\in F. \end{equation*}
-
(3) Call
 $F$
up-closed when
$F$
up-closed when
 $x\in F$
and
$x\in F$
and
 $x\leq x'$
implies
$x\leq x'$
implies
 $x'\in F$
.
$x'\in F$
. -
(4) Call
 $F$
compatible when its elements are pairwise compatible, by which we mean that
$F$
compatible when its elements are pairwise compatible, by which we mean that
 $x\ast x'$
for every
$x\ast x'$
for every
 $x, x'\in F$
.
$x, x'\in F$
. -
(5) A semifilter is a nonempty, up-closed, compatible subset
 $F\subseteq \mathsf{X}$
.
$F\subseteq \mathsf{X}$
. -
(6) Call
 $F\subseteq \mathsf{X}$
a maximal semifilter when it is a semifilter and is contained in no strictly greater semifilter.
$F\subseteq \mathsf{X}$
a maximal semifilter when it is a semifilter and is contained in no strictly greater semifilter. -
(7) An abstract point is a completely prime semifilter.
-
(8) Write
for the set of abstract points of \begin{equation*} \mathsf{Points}(\mathsf{X},\leq ,\ast ) \end{equation*}
\begin{equation*} \mathsf{Points}(\mathsf{X},\leq ,\ast ) \end{equation*}
 $(\mathsf{X},\leq ,\ast )$
.
$(\mathsf{X},\leq ,\ast )$
.
Notation 8.1.2.
We will generally write
![]() $F\subseteq \mathsf{X}$
for a subset of
$F\subseteq \mathsf{X}$
for a subset of
![]() $\mathsf{X}$
that is intended to be a semifilter, or for which in most cases of interest
$\mathsf{X}$
that is intended to be a semifilter, or for which in most cases of interest
![]() $F$
is a semifilter. We will generally write
$F$
is a semifilter. We will generally write
![]() $P\subseteq \mathsf{X}$
when the subset is intended to be an abstract point, or when in most cases of interest
$P\subseteq \mathsf{X}$
when the subset is intended to be an abstract point, or when in most cases of interest
![]() $P$
is an abstract point.
$P$
is an abstract point.
Remark 8.1.3. Note on design: The notion of semifilter from Definition 8.1.1 is, obviously, based on the standard notion of filter (Johnstone, Reference Johnstone1986, I.2.2, p. 12). We just replace the closure under binary meets condition
‘if
![]() $x,x'\in F$
then
$x,x'\in F$
then
![]() $x{\boldsymbol \wedge } x'\in F$
’
$x{\boldsymbol \wedge } x'\in F$
’
with a weaker compatibility condition
‘if
![]() $x,x'\in F$
then
$x,x'\in F$
then
![]() $x\ast x'$
’.
$x\ast x'$
’.
This is in keeping with our move from frames to semiframes, which weakens from
![]() $\boldsymbol \wedge$
to the compatibility relation
$\boldsymbol \wedge$
to the compatibility relation
![]() $\ast$
.
$\ast$
.
Note that a semifilter or abstract point need not be directed:
-
(1) Consider
 $\textit{nbhd}(0)$
in the (semiframes of open sets of the) semitopologies in the left-hand and middle examples in Figure 4. In both cases,
$\textit{nbhd}(0)$
in the (semiframes of open sets of the) semitopologies in the left-hand and middle examples in Figure 4. In both cases,
 $\{0,1\},\{0,2\}\in \textit{nbhd}(0)$
but
$\{0,1\},\{0,2\}\in \textit{nbhd}(0)$
but
 $\{0\}\notin \textit{nbhd}(0)$
because
$\{0\}\notin \textit{nbhd}(0)$
because
 $\{0\}$
is not an open set.
$\{0\}$
is not an open set. -
(2) Consider
 $\{0,1,2\}$
with the discrete semitopology (so every set is open). Then the set of all two- or three-element subsets
$\{0,1,2\}$
with the discrete semitopology (so every set is open). Then the set of all two- or three-element subsets
 $\{\{0,1\},\{1,2\},\{2,0\},\{0,1,2\}\}$
is a semifilter, but it is not closed under set intersections because it does not contain
$\{\{0,1\},\{1,2\},\{2,0\},\{0,1,2\}\}$
is a semifilter, but it is not closed under set intersections because it does not contain
 $\{0\}$
,
$\{0\}$
,
 $\{1\}$
, or
$\{1\}$
, or
 $\{2\}$
.
$\{2\}$
.
This second example is particularly interesting. As the reader may know, the intuition of a filter in topology is a set of approximations. But this example is clearly not approximating anything – after all, we are in the discrete semitopology and there is no need to approximate anything since we can just take a singleton set! This suggests that a better intuition for semiframe is a set of collaborations; in this case, of
![]() $0$
with
$0$
with
![]() $1$
,
$1$
,
![]() $1$
with
$1$
with
![]() $2$
, and
$2$
, and
![]() $2$
with
$2$
with
![]() $0$
.
$0$
.
Thus in particular, the standard result in frames that a proper finite filterFootnote
17
has a non-
![]() $\boldsymbol \bot$
least element (obtained as the finite meet of all the elements in the filter), does not hold for semifilters in semiframes. See also Remark 8.1.6 and Proposition 8.2.8(1).
$\boldsymbol \bot$
least element (obtained as the finite meet of all the elements in the filter), does not hold for semifilters in semiframes. See also Remark 8.1.6 and Proposition 8.2.8(1).
Example 8.1.4. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. We recall some (standard) facts about abstract points, which carry over from topologies and frames:
$(\mathsf{X},\leq ,\ast )$
is a semiframe. We recall some (standard) facts about abstract points, which carry over from topologies and frames:
-
(1) Suppose
 $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
 $(\mathsf{X},\leq ,\ast )=(\mathsf{Open},\subseteq ,\between )$
. By Lemma 7.3.5,
$(\mathsf{X},\leq ,\ast )=(\mathsf{Open},\subseteq ,\between )$
. By Lemma 7.3.5,
 $(\mathsf{X},\leq ,\ast )$
is a semiframe.
$(\mathsf{X},\leq ,\ast )$
is a semiframe.If
 $p\in \mathsf{P}$
thenfrom Definition 2.3.1 is an abstract point: see Proposition 9.2.2. Intuitively,
$p\in \mathsf{P}$
thenfrom Definition 2.3.1 is an abstract point: see Proposition 9.2.2. Intuitively, \begin{equation*} \textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\} \end{equation*}
\begin{equation*} \textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\} \end{equation*}
 $\textit{nbhd}(p)$
abstractly represents
$\textit{nbhd}(p)$
abstractly represents
 $p$
as the set of all of its open approximations in
$p$
as the set of all of its open approximations in
 $\mathsf{Open}$
.
$\mathsf{Open}$
.
-
(2) Suppose
 $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then
 $(\mathsf{Open},\subseteq ,\between )$
could contain an abstract point that is not the neighbourhood semifilter
$(\mathsf{Open},\subseteq ,\between )$
could contain an abstract point that is not the neighbourhood semifilter
 $\textit{nbhd}(p)$
of a point
$\textit{nbhd}(p)$
of a point
 $p\in \mathsf{P}$
.
$p\in \mathsf{P}$
.Set
 $\mathsf{X}=\{\mathbb Q\}\cup \{(\pi \text{-} q,\pi {+} q)\subseteq \mathbb Q \mid q\in \mathbb Q_{\geq 0}\}$
(the set of all symmetric open intervals around
$\mathsf{X}=\{\mathbb Q\}\cup \{(\pi \text{-} q,\pi {+} q)\subseteq \mathbb Q \mid q\in \mathbb Q_{\geq 0}\}$
(the set of all symmetric open intervals around
 $\pi$
in the rational numbers
$\pi$
in the rational numbers
 $\mathbb Q$
), and set
$\mathbb Q$
), and set
 ${\leq }={\subseteq }$
and
${\leq }={\subseteq }$
and
 ${\ast }={\between }$
.
${\ast }={\between }$
.Set
 $P=\mathsf{X}\setminus \{\varnothing \}$
to be the set of all nonempty symmetric open intervals around
$P=\mathsf{X}\setminus \{\varnothing \}$
to be the set of all nonempty symmetric open intervals around
 $\pi$
. Note that
$\pi$
. Note that
 $\pi \notin \mathbb Q$
, but
$\pi \notin \mathbb Q$
, but
 $P$
is a set of open sets ‘approximating’
$P$
is a set of open sets ‘approximating’
 $\pi$
.
$\pi$
. -
(3) We mention one more (standard) example. Consider
 $\mathbb N$
with the final segment semitopology such that opens are either
$\mathbb N$
with the final segment semitopology such that opens are either
 $\varnothing$
or sets
$\varnothing$
or sets
 $n_\geq = \{n'\in \mathbb N \mid n'\geq n\}$
. Then
$n_\geq = \{n'\in \mathbb N \mid n'\geq n\}$
. Then
 $\{n_\geq \mid n\in \mathbb N\}$
is an abstract point. Intuitively, this approximates a point at infinity, which we can understand as
$\{n_\geq \mid n\in \mathbb N\}$
is an abstract point. Intuitively, this approximates a point at infinity, which we can understand as
 $\omega$
.
$\omega$
.
Lemma 8.1.5.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
$(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
![]() $F\subseteq \mathsf{X}$
is compatible. Then
$F\subseteq \mathsf{X}$
is compatible. Then
![]() ${\boldsymbol \bot }_{\mathsf{X}}\notin F$
.
${\boldsymbol \bot }_{\mathsf{X}}\notin F$
.
Remark 8.1.6. We continue Remark 8.1.3.
As the reader may know, a semiframe still has greatest lower bounds, because we can build them as
![]() $x{\boldsymbol \wedge } x' = \bigvee \{x'' \mid x''\leq x,\ x''\leq x'\}$
. It is just that this greatest lower bound may be unhelpful. To see why, consider again the examples in Figure 4. In the left-hand and middle examples in Figure 4, the greatest lower bound of
$x{\boldsymbol \wedge } x' = \bigvee \{x'' \mid x''\leq x,\ x''\leq x'\}$
. It is just that this greatest lower bound may be unhelpful. To see why, consider again the examples in Figure 4. In the left-hand and middle examples in Figure 4, the greatest lower bound of
![]() $\{0,1\}$
and
$\{0,1\}$
and
![]() $\{0,2\}$
exists in the semiframe of open sets: but it is
$\{0,2\}$
exists in the semiframe of open sets: but it is
![]() $\varnothing$
the empty set in the left-hand and middle example, not
$\varnothing$
the empty set in the left-hand and middle example, not
![]() $\{0\}$
. In the right-hand example, the greatest lower bound of
$\{0\}$
. In the right-hand example, the greatest lower bound of
![]() $\{0,\ast ,1\}$
and
$\{0,\ast ,1\}$
and
![]() $\{0,\ast ,2\}$
is
$\{0,\ast ,2\}$
is
![]() $\{0\}$
, not
$\{0\}$
, not
![]() $\{0,\ast \}$
.
$\{0,\ast \}$
.
So the reader could ask whether perhaps we should add the following weakened meet-closure condition to the definition of semifilters (and thus to abstract points):
If
![]() $x, x'\in F$
and
$x, x'\in F$
and
![]() $x{\boldsymbol \wedge } x'\neq {\boldsymbol \bot }$
then
$x{\boldsymbol \wedge } x'\neq {\boldsymbol \bot }$
then
![]() $x{\boldsymbol \wedge } x'\in F$
.
$x{\boldsymbol \wedge } x'\in F$
.
Intuitively, this insists that semifilters are closed under non-
![]() $\boldsymbol \bot$
greatest lower bounds. However, there are two problems with this:
$\boldsymbol \bot$
greatest lower bounds. However, there are two problems with this:
-
• It would break our categorical duality proof in the construction of
 $g^\circ$
in Lemma 10.3.3; see the discussion in Remark 10.3.4. This technical difficulty may be superable, but …
$g^\circ$
in Lemma 10.3.3; see the discussion in Remark 10.3.4. This technical difficulty may be superable, but … -
• …the condition is probably not what we want anyway. It would mean that the set of open neighbourhoods of
 $\ast$
in the right-hand example of Figure 4, would not be a semifilter, because it contains
$\ast$
in the right-hand example of Figure 4, would not be a semifilter, because it contains
 $\{0,\ast ,1\}$
and
$\{0,\ast ,1\}$
and
 $\{0,\ast ,2\}$
but not its (non-
$\{0,\ast ,2\}$
but not its (non-
 $\varnothing$
) greatest lower bound
$\varnothing$
) greatest lower bound
 $\{0\}$
.
$\{0\}$
.
8.2 Properties of semifilters
8.2.1 Things that are familiar from filters
Lemma 8.2.1.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then:
$F\subseteq \mathsf{X}$
is a semifilter. Then:
-
(1)
 ${\boldsymbol \top }_{\mathsf{X}}\in F$
.
${\boldsymbol \top }_{\mathsf{X}}\in F$
. -
(2)
 ${\boldsymbol \bot }_{\mathsf{X}}\notin F$
.
${\boldsymbol \bot }_{\mathsf{X}}\notin F$
.
Proof. We consider each part in turn:
-
(1) By nonemptiness (Definition 8.1.1(7))
 $F$
is nonempty, so there exists some
$F$
is nonempty, so there exists some
 $x\in F$
. By definition
$x\in F$
. By definition
 $x\leq {\boldsymbol \top }_{\mathsf{X}}$
. By up-closure (Definition 8.1.1(3))
$x\leq {\boldsymbol \top }_{\mathsf{X}}$
. By up-closure (Definition 8.1.1(3))
 ${\boldsymbol \top }_{\mathsf{X}}\in F$
follows.
${\boldsymbol \top }_{\mathsf{X}}\in F$
follows. -
(2) By assumption in Definition 8.1.1(4) elements in
 $F$
are pairwise compatible (so
$F$
are pairwise compatible (so
 $x\ast x$
for every
$x\ast x$
for every
 $x\in F$
). We use Lemma 8.1.5.
$x\in F$
). We use Lemma 8.1.5.
Lemma 8.2.2.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. It is possible for a semifilter
$(\mathsf{X},\leq ,\ast )$
is a semiframe. It is possible for a semifilter
![]() $F\subseteq \mathsf{X}$
to be completely prime but not maximal.
$F\subseteq \mathsf{X}$
to be completely prime but not maximal.
Proof.
We give a standard example (which also works for frames and filters). Take
![]() $\mathsf{P}=\{0,1\}$
and
$\mathsf{P}=\{0,1\}$
and
![]() $\mathsf{Open}=\{\varnothing , \{0\}, \{0,1\}\}$
. Then
$\mathsf{Open}=\{\varnothing , \{0\}, \{0,1\}\}$
. Then
![]() $P'=\{\{0,1\}\}$
is an abstract point, but it is not a maximal semifilter (it is not even a maximal abstract point) since
$P'=\{\{0,1\}\}$
is an abstract point, but it is not a maximal semifilter (it is not even a maximal abstract point) since
![]() $P'$
is contained in the strictly larger semifilter
$P'$
is contained in the strictly larger semifilter
![]() $\{\{0\},\{0,1\}\}$
(which is itself also a strictly larger abstract point).
$\{\{0\},\{0,1\}\}$
(which is itself also a strictly larger abstract point).
Lemma 8.2.3.
If
![]() $(\mathsf{X},\leq ,\ast )$
is a finite semiframe (meaning that
$(\mathsf{X},\leq ,\ast )$
is a finite semiframe (meaning that
![]() $\mathsf{X}$
is finite) then the properties of
$\mathsf{X}$
is finite) then the properties of
coincide.
Proof.
This is almost trivial, except that if
![]() $X=\varnothing$
in the condition for being completely prime then we get that
$X=\varnothing$
in the condition for being completely prime then we get that
![]() ${\boldsymbol \bot }_{\mathsf{X}}\notin P$
– but we know that anyway from Lemma 8.2.1(2), from the compatibility condition on semifilters.
${\boldsymbol \bot }_{\mathsf{X}}\notin P$
– but we know that anyway from Lemma 8.2.1(2), from the compatibility condition on semifilters.
Lemma 8.2.4.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then:
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then:
-
(1) The union of an ascending chain of semifilters in
 $\mathsf{X}$
, is a semifilter in
$\mathsf{X}$
, is a semifilter in
 $\mathsf{X}$
.
$\mathsf{X}$
. -
(2) As a corollary, every semifilter
 $F\subseteq \mathsf{X}$
is contained in some maximal semifilter
$F\subseteq \mathsf{X}$
is contained in some maximal semifilter
 $F'\subseteq \mathsf{X}$
(assuming Zorn’s lemma).
$F'\subseteq \mathsf{X}$
(assuming Zorn’s lemma).
Proof. We consider each part in turn:
Remark 8.2.5.
-
(1) Lemma 8.2.1(2) has a small twist to it. In the theory of filters, it does not follow from the property of being nonempty, up-closed, and closed under finite meets, that
 ${\boldsymbol \bot }_{\mathsf{X}}\notin F$
; this must be added as a distinct condition if required.
${\boldsymbol \bot }_{\mathsf{X}}\notin F$
; this must be added as a distinct condition if required.In contrast, we see in the proof of Lemma 8.2.1(2) that for semifilters,
 ${\boldsymbol \bot }_{\mathsf{X}}\notin F$
follows from the compatibility condition.
${\boldsymbol \bot }_{\mathsf{X}}\notin F$
follows from the compatibility condition. -
(2) Lemma 8.2.3 matters in particular to us here, because we are particularly interested in abstracting the behaviours of finite semitopologies, because our original motivation for looking at both of these structures comes from looking at real networks, which are finite.Footnote 18
8.2.2 Things that are different from filters
Remark 8.2.6. Obviously, by definition semifilters are necessarily compatible but not necessarily closed under meets. But aside from this fact, we have so far seen semiframes and semifilters behave more-or-less like frames and filters, modulo small details like that mentioned in Remark 8.2.5(1).
But there are also differences, as we will now briefly explore. In the theory of (finite) frames, the following facts hold:
-
(1) Every proper filter
 $F$
has a greatest lower bound
$F$
has a greatest lower bound
 $x$
, and
$x$
, and
 $F=x^\leq =\{x'\mid x\leq x'\}$
.
$F=x^\leq =\{x'\mid x\leq x'\}$
.Just take
 $x=\bigwedge F$
the meet of all of its (finitely many) elements. This is not
$x=\bigwedge F$
the meet of all of its (finitely many) elements. This is not
 $\boldsymbol \bot$
, by the filter’s finite intersection property.
$\boldsymbol \bot$
, by the filter’s finite intersection property. -
(2) Every proper filter can be extended to a maximal filter.Footnote 19
Just extend using Zorn’s lemma (as in Lemma 8.2.4).
-
(3) Every maximal filter is completely prime.
It is a fact of finite frames that a maximal filter is prime,Footnote 20 and since we assume the frame is finite, it is also completely prime.
-
(4) Every non-
 $\boldsymbol \bot$
element
$\boldsymbol \bot$
element
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
in a finite frame is contained in some abstract point.
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
in a finite frame is contained in some abstract point.Just form
 $\{x'\mid x\leq x'\}$
, observe it is a filter, form a maximal filter above it, and we get an abstract point.
$\{x'\mid x\leq x'\}$
, observe it is a filter, form a maximal filter above it, and we get an abstract point. -
(5) As a corollary, if the frame is nonempty (so
 ${\boldsymbol \bot }\neq {\boldsymbol \top }$
; see Example 7.3.2) then it has at least one abstract point.
${\boldsymbol \bot }\neq {\boldsymbol \top }$
; see Example 7.3.2) then it has at least one abstract point.
In Lemma 8.2.7 and Proposition 8.2.8 we consider some corresponding non-properties of (finite) semiframes.
Lemma 8.2.7.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. It is possible for
$(\mathsf{X},\leq ,\ast )$
is a semiframe. It is possible for
![]() $\mathsf{Points}(\mathsf{X},\leq ,\ast )$
to be empty, even if
$\mathsf{Points}(\mathsf{X},\leq ,\ast )$
to be empty, even if
![]() $(\mathsf{X},\leq ,\ast )$
is nonempty (Example 7.3.2(2)). This is possible even if
$(\mathsf{X},\leq ,\ast )$
is nonempty (Example 7.3.2(2)). This is possible even if
![]() $\mathsf{X}$
is finite, and even if
$\mathsf{X}$
is finite, and even if
![]() $\mathsf{X}$
is infinite.
$\mathsf{X}$
is infinite.
Proof. It suffices to provide an example. We define a semiframe as below, and as illustrated in Figure 5:
-
•
 $\mathsf{X}=\{{\boldsymbol \bot },0,1,2,3,{\boldsymbol \top }\}$
.
$\mathsf{X}=\{{\boldsymbol \bot },0,1,2,3,{\boldsymbol \top }\}$
. -
• Let
 $x\leq x'$
when
$x\leq x'$
when
 $x=x'$
or
$x=x'$
or
 $x={\boldsymbol \bot }$
or
$x={\boldsymbol \bot }$
or
 $x'={\boldsymbol \top }$
.
$x'={\boldsymbol \top }$
. -
• Let
 $x\ast x'$
when
$x\ast x'$
when
 $x{\boldsymbol \wedge } x'\neq {\boldsymbol \bot }$
.Footnote
21
$x{\boldsymbol \wedge } x'\neq {\boldsymbol \bot }$
.Footnote
21
Then
![]() $(\mathsf{X},\leq ,\ast )$
has no abstract points.
$(\mathsf{X},\leq ,\ast )$
has no abstract points.
For suppose
![]() $P$
is one such. By Lemma 8.2.1
$P$
is one such. By Lemma 8.2.1
![]() ${\boldsymbol \top }\in P$
. Note that
${\boldsymbol \top }\in P$
. Note that
![]() ${\boldsymbol \top }=0{\boldsymbol \vee } 1=2{\boldsymbol \vee } 3$
. By assumption
${\boldsymbol \top }=0{\boldsymbol \vee } 1=2{\boldsymbol \vee } 3$
. By assumption
![]() $P$
is completely prime, we know that
$P$
is completely prime, we know that
![]() $0\in P \lor 1\in P$
, and also
$0\in P \lor 1\in P$
, and also
![]() $2\in P\lor 3\in P$
. But this is impossible because
$2\in P\lor 3\in P$
. But this is impossible because
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $2$
, and
$2$
, and
![]() $3$
are not compatible.
$3$
are not compatible.
For the infinite case, we just increase the width of the semiframe by taking
![]() $\mathsf{X}=\{{\boldsymbol \bot }\}\cup \mathbb N\cup \{{\boldsymbol \top }\}$
.
$\mathsf{X}=\{{\boldsymbol \bot }\}\cup \mathbb N\cup \{{\boldsymbol \top }\}$
.
Proposition 8.2.8.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then:
$F\subseteq \mathsf{X}$
is a semifilter. Then:
-
(1) It is not necessarily the case that
 $F$
has a non-
$F$
has a non-
 $\boldsymbol \bot$
greatest lower bound (even if
$\boldsymbol \bot$
greatest lower bound (even if
 $\mathsf{X}$
is finite).
$\mathsf{X}$
is finite).
-
(2) Every semifilter can be extended to a maximal semifilter, but …
-
(3) …this maximal semifilter is not necessarily prime (even if
 $\mathsf{X}$
is finite).
$\mathsf{X}$
is finite).
-
(4) There may exist a non-
 $\boldsymbol \bot$
element
$\boldsymbol \bot$
element
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
that is contained in no abstract point.
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
that is contained in no abstract point.
Proof. We consider each part in turn:
-
(1) Consider
 $(\textit{pow}(\{0,1,2\}),\subseteq ,\between )$
and takeThe greatest lower bound of
$(\textit{pow}(\{0,1,2\}),\subseteq ,\between )$
and takeThe greatest lower bound of \begin{equation*} F = \{\{0,1\},\ \{1,2\},\ \{0,2\},\ \{0,1,2\}\} . \end{equation*}
\begin{equation*} F = \{\{0,1\},\ \{1,2\},\ \{0,2\},\ \{0,1,2\}\} . \end{equation*}
 $F$
is
$F$
is
 $\varnothing$
.
$\varnothing$
.
-
(2) This is Lemma 8.2.4.
-
(3)
 $F$
from part 1 of this result is maximal, and it cannot be extended to a point
$F$
from part 1 of this result is maximal, and it cannot be extended to a point
 $P\supseteq F$
.
$P\supseteq F$
.Figure 5 gives another counterexample, and in a rather interesting way: the semitopology has four maximal semifilters
 $\{i,{\boldsymbol \top }\}$
for
$\{i,{\boldsymbol \top }\}$
for
 $i\in \{0,1,2,3\}$
, but by Lemma 8.2.7 it has no prime semifilters at all.Footnote
22
$i\in \{0,1,2,3\}$
, but by Lemma 8.2.7 it has no prime semifilters at all.Footnote
22
-
(4) We just take
 $x=0\in \mathsf{X}$
from the example in Lemma 8.2.7 (see Figure 5). Since this semiframe has no abstract points at all, there is no abstract point that contains
$x=0\in \mathsf{X}$
from the example in Lemma 8.2.7 (see Figure 5). Since this semiframe has no abstract points at all, there is no abstract point that contains
 $x$
.
$x$
.
Remark 8.2.9. For now, we will just read Proposition 8.2.8 as a caution not to assume that semiframes and semifilters behave like frames and filters. Sometimes they do, and sometimes they don’t; we have to check.

Figure 5. A semiframe with no abstract points (Lemma 8.2.7).
We now proceed to build our categorical duality, culminating with Theorem 10.4.2. Once that machinery is constructed, we will continue our study of the fine structure of semifilters in Section 11.
8.3 Sets of abstract points
Definition 8.3.1. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and recall
$(\mathsf{X},\leq ,\ast )$
is a semiframe and recall
![]() $\mathsf{Points}(\mathsf{X},\leq ,\ast )$
from Definition 8.1.1(7). Define a map
$\mathsf{Points}(\mathsf{X},\leq ,\ast )$
from Definition 8.1.1(7). Define a map
![]() $\textit{Op}:\mathsf{X}\to \textit{pow}(\mathsf{Points}(\mathsf{X},\leq ,\ast ))$
by
$\textit{Op}:\mathsf{X}\to \textit{pow}(\mathsf{Points}(\mathsf{X},\leq ,\ast ))$
by
Lemma 8.3.2.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $X\subseteq \mathsf{X}$
. Then
$X\subseteq \mathsf{X}$
. Then
In words: we can say that
![]() $\textit{Op}$
commutes with joins, and that
$\textit{Op}$
commutes with joins, and that
![]() $\textit{Op}$
commutes with taking least upper bounds.
$\textit{Op}$
commutes with taking least upper bounds.
Proof.
Suppose
![]() $P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. We reason as follows:
$P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. We reason as follows:

Proposition 8.3.3.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $x,x'\in \mathsf{X}$
. Then:
$x,x'\in \mathsf{X}$
. Then:
-
(1) If
 $x\leq x'$
then
$x\leq x'$
then
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
.
$\textit{Op}(x)\subseteq \textit{Op}(x')$
. -
(2) If
 $\textit{Op}(x)\between \textit{Op}(x')$
then
$\textit{Op}(x)\between \textit{Op}(x')$
then
 $x\ast x'$
.
$x\ast x'$
. -
(3)
 $\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
and
$\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
and
 $\textit{Op}({\boldsymbol \bot }_{\mathsf{X}})=\varnothing$
.
$\textit{Op}({\boldsymbol \bot }_{\mathsf{X}})=\varnothing$
. -
(4)
 $\textit{Op}(\bigvee X)=\bigcup _{x\in X}\textit{Op}(x)$
for
$\textit{Op}(\bigvee X)=\bigcup _{x\in X}\textit{Op}(x)$
for
 $X\subseteq \mathsf{X}$
.
$X\subseteq \mathsf{X}$
.
Proof. We consider each part in turn:
-
(1) We prove that
 $x\leq x'$
implies
$x\leq x'$
implies
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
.
$\textit{Op}(x)\subseteq \textit{Op}(x')$
.Suppose
 $x\leq x'$
, and consider some abstract point
$x\leq x'$
, and consider some abstract point
 $P\in \textit{Op}(x)$
. By Definition 8.3.1
$P\in \textit{Op}(x)$
. By Definition 8.3.1
 $x\in P$
, and by up-closure of
$x\in P$
, and by up-closure of
 $P$
(Definition 8.1.1(3))
$P$
(Definition 8.1.1(3))
 $x'\in P$
, so by Definition 8.3.1
$x'\in P$
, so by Definition 8.3.1
 $P\in \textit{Op}(x')$
.
$P\in \textit{Op}(x')$
.
 $P$
was arbitrary, and it follows that
$P$
was arbitrary, and it follows that
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
.
$\textit{Op}(x)\subseteq \textit{Op}(x')$
. -
(2) We prove that
 $\textit{Op}(x)\between \textit{Op}(x')$
implies
$\textit{Op}(x)\between \textit{Op}(x')$
implies
 $x\ast x'$
.
$x\ast x'$
.Suppose there exists an abstract point
 $P\in \textit{Op}(x)\cap \textit{Op}(x')$
. By Definition 8.3.1
$P\in \textit{Op}(x)\cap \textit{Op}(x')$
. By Definition 8.3.1
 $x,x'\in P$
, and by compatibility of
$x,x'\in P$
, and by compatibility of
 $P$
(Definition 8.1.1(4))
$P$
(Definition 8.1.1(4))
 $x\ast x'$
.
$x\ast x'$
. -
(3) Unpacking Definition 8.3.1, it suffices to show that
 ${\boldsymbol \top }_{\mathsf{X}}\in P$
and
${\boldsymbol \top }_{\mathsf{X}}\in P$
and
 ${\boldsymbol \bot }_{\mathsf{X}}\notin P$
, for every abstract point
${\boldsymbol \bot }_{\mathsf{X}}\notin P$
, for every abstract point
 $P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. This is from Lemma 8.2.1(1).
$P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. This is from Lemma 8.2.1(1). -
(4) This is just Lemma 8.3.2.
Remark 8.3.4. Proposition 8.3.3 carries a clear suggestion that
![]() $(\{\textit{Op}(x) \mid x\in \mathsf{X}\},\subseteq ,\between )$
is trying, in some sense, to be an isomorphic copy of
$(\{\textit{Op}(x) \mid x\in \mathsf{X}\},\subseteq ,\between )$
is trying, in some sense, to be an isomorphic copy of
![]() $(\mathsf{X},\leq ,\ast )$
. Lemma 8.3.5 notes that it may not quite manage this, because there may not be enough points (indeed, there may not be any abstract points at all). This will (just as for topologies and frames) lead us to the notion of a spatial semiframe in Definition 9.1.2 and Proposition 9.1.4.
$(\mathsf{X},\leq ,\ast )$
. Lemma 8.3.5 notes that it may not quite manage this, because there may not be enough points (indeed, there may not be any abstract points at all). This will (just as for topologies and frames) lead us to the notion of a spatial semiframe in Definition 9.1.2 and Proposition 9.1.4.
Lemma 8.3.5. The converse implications in Proposition 8.3.3(1 and 2) need not hold. That is:
-
(1) There exists a semiframe
 $(\mathsf{X},\leq ,\ast )$
and
$(\mathsf{X},\leq ,\ast )$
and
 $x,x'\in \mathsf{X}$
such that
$x,x'\in \mathsf{X}$
such that
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
yet
$\textit{Op}(x)\subseteq \textit{Op}(x')$
yet
 $x\not \leq x'$
.
$x\not \leq x'$
. -
(2) There exists a semiframe
 $(\mathsf{X},\leq ,\ast )$
and
$(\mathsf{X},\leq ,\ast )$
and
 $x,x'\in \mathsf{X}$
such that
$x,x'\in \mathsf{X}$
such that
 $x\ast x'$
yet
$x\ast x'$
yet 
8.4 The semitopology of abstract points
Recall from Definition 8.1.1(7) that an abstract point in a semiframe
![]() $(\mathsf{X},\leq ,\ast )$
is a nonempty up-closed compatible completely prime subset of
$(\mathsf{X},\leq ,\ast )$
is a nonempty up-closed compatible completely prime subset of
![]() $\mathsf{X}$
, and recall from Definition 8.3.1 that
$\mathsf{X}$
, and recall from Definition 8.3.1 that
or in words:
![]() $\textit{Op}(x)$
is the set of abstract points that contain
$\textit{Op}(x)$
is the set of abstract points that contain
![]() $x$
.
$x$
.
Definition 8.4.1. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then define
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then define
![]() $\mathsf{Op}(\mathsf{X},\leq ,\ast )$
by
$\mathsf{Op}(\mathsf{X},\leq ,\ast )$
by
Lemma 8.4.2.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then:
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then:
-
(1)
 $\mathsf{Op}(\mathsf{X},\leq ,\ast )$
from Definition 8.4.1 is closed under arbitrary sets union.
$\mathsf{Op}(\mathsf{X},\leq ,\ast )$
from Definition 8.4.1 is closed under arbitrary sets union.
-
(2) As a corollary,
 $(\mathsf{Op}(\mathsf{X},\leq ,\ast ),\subseteq )$
(in words:
$(\mathsf{Op}(\mathsf{X},\leq ,\ast ),\subseteq )$
(in words:
 $\mathsf{Op}(\mathsf{X},\leq ,\ast )$
ordered by subset inclusion) is a complete join-semilattice.
$\mathsf{Op}(\mathsf{X},\leq ,\ast )$
ordered by subset inclusion) is a complete join-semilattice.
Proof.
Part 1 is just Lemma 8.3.2. The corollary part 2 is just a fact, since
![]() $\mathsf{Op}(\mathsf{X},\leq ,\ast )\subseteq \textit{pow}(\mathsf{Points}(\mathsf{X},\leq ,\ast ))$
, and sets union is the join (least upper bound) in the powerset lattice.
$\mathsf{Op}(\mathsf{X},\leq ,\ast )\subseteq \textit{pow}(\mathsf{Points}(\mathsf{X},\leq ,\ast ))$
, and sets union is the join (least upper bound) in the powerset lattice.
Recall from Definition 7.3.4 and Lemma 7.3.5 that we showed how to go from a semitopology
![]() $(\mathsf{P},\mathsf{Open})$
to a semiframe
$(\mathsf{P},\mathsf{Open})$
to a semiframe
![]() $(\mathsf{Open},\subseteq ,\between )$
. We now show how to go in the other direction:
$(\mathsf{Open},\subseteq ,\between )$
. We now show how to go in the other direction:
Definition 8.4.3 (Semiframe
![]() $\to$
semitopology). Suppose
$\to$
semitopology). Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Define the semitopology of abstract points
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Define the semitopology of abstract points
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
by
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
by
Unpacking this a little:
-
(1) The set of points of
 $\mathsf{St}(\mathsf{X},\leq ,\ast )$
is the set of abstract points
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
is the set of abstract points
 $\mathsf{Points}(\mathsf{X},\leq ,\ast )$
from Definition 8.1.1(7) – namely, the completely prime nonempty up-closed compatible subsets of
$\mathsf{Points}(\mathsf{X},\leq ,\ast )$
from Definition 8.1.1(7) – namely, the completely prime nonempty up-closed compatible subsets of
 $\mathsf{X}$
.Footnote
23
$\mathsf{X}$
.Footnote
23
-
(2) Open sets
 $\mathsf{Opens}(\mathsf{X},\leq ,\ast )$
are the
$\mathsf{Opens}(\mathsf{X},\leq ,\ast )$
are the
 $\textit{Op}(x)$
from Definition 8.3.1:
$\textit{Op}(x)$
from Definition 8.3.1: \begin{equation*} \textit{Op}(x)=\{P\in \mathsf{Points}(\mathsf{X},\leq ,\ast ) \mid x\in P\} . \end{equation*}
\begin{equation*} \textit{Op}(x)=\{P\in \mathsf{Points}(\mathsf{X},\leq ,\ast ) \mid x\in P\} . \end{equation*}
Lemma 8.4.4.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
from Definition 8.4.3 is indeed a semitopology.
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
from Definition 8.4.3 is indeed a semitopology.
Proof.
From conditions 1 and 2 of Definition 1.2.2, we need to check that
![]() $\mathsf{Op}(\mathsf{X},\leq ,\ast )$
contains
$\mathsf{Op}(\mathsf{X},\leq ,\ast )$
contains
![]() $\varnothing$
and
$\varnothing$
and
![]() $\mathsf{Points}(\mathsf{X},\leq ,\ast )$
and is closed under arbitrary unions. This is from Proposition 8.3.3(3 and 4).
$\mathsf{Points}(\mathsf{X},\leq ,\ast )$
and is closed under arbitrary unions. This is from Proposition 8.3.3(3 and 4).
Recall from Definitions 8.4.3 and 7.3.4 that
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a semitopology, and
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a semitopology, and
![]() $\mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a semiframe each of whose elements is the set of abstract points of
$\mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a semiframe each of whose elements is the set of abstract points of
![]() $(\mathsf{X},\leq ,\ast )$
that contain some
$(\mathsf{X},\leq ,\ast )$
that contain some
![]() $x\in \mathsf{X}$
:
$x\in \mathsf{X}$
:
Lemma 8.4.5.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
![]() $\textit{Op}:(\mathsf{X},\leq ,\ast ) \to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
is surjective.
$\textit{Op}:(\mathsf{X},\leq ,\ast ) \to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
is surjective.
We conclude with Definition 8.4.6 and Proposition 8.4.7, which are standard properties of the construction in Definition 8.4.3.
Definition 8.4.6. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p,p'\in \mathsf{P}$
. Define
$p,p'\in \mathsf{P}$
. Define
![]() $p\mathrel {\mathring {=}} p'$
by
$p\mathrel {\mathring {=}} p'$
by
We recall some standard terminology from topology:
-
(1) Call
 $p$
and
$p$
and
 $p'$
topologically indistinguishable when
$p'$
topologically indistinguishable when
 $p\mathrel {\mathring {=}} p'$
.
$p\mathrel {\mathring {=}} p'$
. -
(2) Call
 $p$
and
$p$
and
 $p'$
topologically distinguishable when
$p'$
topologically distinguishable when
 $\neg (p\mathrel {\mathring {=}} p')$
(so there exists some
$\neg (p\mathrel {\mathring {=}} p')$
(so there exists some
 $O\in \mathsf{Open}$
such that
$O\in \mathsf{Open}$
such that
 $p\in O\land p'\notin O$
or
$p\in O\land p'\notin O$
or
 $p\notin O\land p'\in O$
).
$p\notin O\land p'\in O$
). -
(3) Call
 $(\mathsf{P},\mathsf{Open})$
a
$(\mathsf{P},\mathsf{Open})$
a
 $T_0$
space when points are topologically indistinguishable precisely when they are equal, or in symbols:
$T_0$
space when points are topologically indistinguishable precisely when they are equal, or in symbols:
 $\doteq$
$\doteq$
 $=$
$=$
 $=$
.
$=$
.
Proposition 8.4.7.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
(Definition 8.4.3) is a
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
(Definition 8.4.3) is a
![]() $T_0$
space.
$T_0$
space.
Proof.
Suppose
![]() $P,P'\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. Unpacking Definition 8.1.1(7), this means that
$P,P'\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. Unpacking Definition 8.1.1(7), this means that
![]() $P$
and
$P$
and
![]() $P'$
are completely prime nonempty up-closed compatible subsets of
$P'$
are completely prime nonempty up-closed compatible subsets of
![]() $\mathsf{X}$
.
$\mathsf{X}$
.
It is immediate that
![]() $P=P'$
implies
$P=P'$
implies
![]() $P\doteq P'$
.
$P\doteq P'$
.
Now suppose
![]() $P\doteq P'$
in
$P\doteq P'$
in
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
; to prove
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
; to prove
![]() $P=P'$
it would suffice to show that
$P=P'$
it would suffice to show that
![]() $x\in P \Longleftrightarrow x\in P'$
, for arbitrary
$x\in P \Longleftrightarrow x\in P'$
, for arbitrary
![]() $x\in \mathsf{X}$
. By Definition 8.4.3(2), every open set in
$x\in \mathsf{X}$
. By Definition 8.4.3(2), every open set in
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
has the form
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
has the form
![]() $\textit{Op}(x)$
for some
$\textit{Op}(x)$
for some
![]() $x\in \mathsf{X}$
. We reason as follows:
$x\in \mathsf{X}$
. We reason as follows:

Since
![]() $x$
was arbitrary and
$x$
was arbitrary and
![]() $P,P'\subseteq \mathsf{Open}$
, it follows that
$P,P'\subseteq \mathsf{Open}$
, it follows that
![]() $P=P'$
as required.
$P=P'$
as required.
9. Spatial Semiframes & Sober Semitopologies
9.1 Definition of spatial semiframes
Remark 9.1.1. We continue Remark 8.3.4. We saw in Example 8.1.4(2&3) that there may be more abstract points than there are concrete points, and in Remark 8.3.4 that there may also be fewer.
In the theory of frames, the condition of being spatial means that the abstract points and concrete points correspond. We imitate this terminology for a corresponding definition on semiframes:
Definition 9.1.2 (Spatial semiframe). Call a semiframe
![]() $(\mathsf{X},\leq ,\ast )$
spatial when:
$(\mathsf{X},\leq ,\ast )$
spatial when:
-
(1)
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
implies
$\textit{Op}(x)\subseteq \textit{Op}(x')$
implies
 $x\leq x'$
, for every
$x\leq x'$
, for every
 $x,x'\in \mathsf{X}$
.
$x,x'\in \mathsf{X}$
. -
(2)
 $x\ast x'$
implies
$x\ast x'$
implies
 $\textit{Op}(x)\between \textit{Op}(x')$
, for every
$\textit{Op}(x)\between \textit{Op}(x')$
, for every
 $x,x'\in \mathsf{X}$
.
$x,x'\in \mathsf{X}$
.
Remark 9.1.3. Not every semiframe is spatial, just as not every frame is spatial. Lemma 8.2.7 gives an example of a semiframe that is not spatial because it has no points at all, as illustrated in Figure 5.
We check that the conditions in Definition 9.1.2 correctly strengthen the implications in Proposition 8.3.3 to become logical equivalences:
Proposition 9.1.4.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a spatial semiframe and
$(\mathsf{X},\leq ,\ast )$
is a spatial semiframe and
![]() $x,x'\in \mathsf{X}$
. Then:
$x,x'\in \mathsf{X}$
. Then:
-
(1)
 $x\leq x'$
if and only if
$x\leq x'$
if and only if
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
.
$\textit{Op}(x)\subseteq \textit{Op}(x')$
. -
(2)
 $x\ast x'$
if and only if
$x\ast x'$
if and only if
 $\textit{Op}(x)\between \textit{Op}(x')$
.
$\textit{Op}(x)\between \textit{Op}(x')$
. -
(3)
 $x= x'$
if and only if
$x= x'$
if and only if
 $\textit{Op}(x)=\textit{Op}(x')$
.
$\textit{Op}(x)=\textit{Op}(x')$
. -
(4)
 $\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
and
$\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
and
 $\textit{Op}({\boldsymbol \bot }_{\mathsf{X}})=\varnothing$
.
$\textit{Op}({\boldsymbol \bot }_{\mathsf{X}})=\varnothing$
. -
(5)
 $\textit{Op}(\bigvee X)=\bigcup _{x\in X}\textit{Op}(x)$
for
$\textit{Op}(\bigvee X)=\bigcup _{x\in X}\textit{Op}(x)$
for
 $X\subseteq \mathsf{X}$
.
$X\subseteq \mathsf{X}$
.
Proof. We consider each part in turn:
-
(1) We prove that
 $x\leq x'$
if and only if
$x\leq x'$
if and only if
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
.
$\textit{Op}(x)\subseteq \textit{Op}(x')$
.The right-to-left implication is direct from Definition 9.1.2(1). The left-to-right implication is Proposition 8.3.3(1).
-
(2) We prove that
 $x\ast x'$
if and only if
$x\ast x'$
if and only if
 $\textit{Op}(x)\between \textit{Op}(x')$
.
$\textit{Op}(x)\between \textit{Op}(x')$
.The left-to-right implication is direct from Definition 9.1.2(2). The right-to-left implication is Proposition 8.3.3(2).
-
(3) We prove that
 $x= x'$
if and only if
$x= x'$
if and only if
 $\textit{Op}(x)= \textit{Op}(x')$
.
$\textit{Op}(x)= \textit{Op}(x')$
.If
 $x=x'$
then
$x=x'$
then
 $\textit{Op}(x)=\textit{Op}(x')$
is immediate. If
$\textit{Op}(x)=\textit{Op}(x')$
is immediate. If
 $\textit{Op}(x)=\textit{Op}(x')$
then
$\textit{Op}(x)=\textit{Op}(x')$
then
 $\textit{Op}(x)\subseteq \textit{Op}(x')$
and
$\textit{Op}(x)\subseteq \textit{Op}(x')$
and
 $\textit{Op}(x')\subseteq \textit{Op}(x)$
. By part 1 of this result (or direct from Definition 9.1.2(1))
$\textit{Op}(x')\subseteq \textit{Op}(x)$
. By part 1 of this result (or direct from Definition 9.1.2(1))
 $x\leq x'$
and
$x\leq x'$
and
 $x'\leq x$
. By antisymmetry of
$x'\leq x$
. By antisymmetry of
 $\leq$
it follows that
$\leq$
it follows that
 $x=x'$
.
$x=x'$
. -
(5) This is just Lemma 8.3.2.
Definition 9.1.5 will be useful in a moment:Footnote 24
Definition 9.1.5. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
and
$(\mathsf{X},\leq ,\ast )$
and
![]() $(\mathsf{X}',\leq ',\ast ')$
are semiframes. Then an isomorphism between them is a function
$(\mathsf{X}',\leq ',\ast ')$
are semiframes. Then an isomorphism between them is a function
![]() $g:\mathsf{X}\to \mathsf{X}'$
such that:
$g:\mathsf{X}\to \mathsf{X}'$
such that:
-
(1)
 $g$
is a bijection between
$g$
is a bijection between
 $\mathsf{X}$
and
$\mathsf{X}$
and
 $\mathsf{X}'$
.
$\mathsf{X}'$
. -
(2)
 $x_1\leq x_2$
if and only if
$x_1\leq x_2$
if and only if
 $g(x_1)\leq g(x_2)$
.
$g(x_1)\leq g(x_2)$
. -
(3)
 $x_1\ast x_2$
if and only if
$x_1\ast x_2$
if and only if
 $g(x_1)\ast g(x_2)$
.
$g(x_1)\ast g(x_2)$
.
Lemma 9.1.6.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
and
$(\mathsf{X},\leq ,\ast )$
and
![]() $(\mathsf{X}',\leq ',\ast ')$
are semiframes and
$(\mathsf{X}',\leq ',\ast ')$
are semiframes and
![]() $g:\mathsf{X}\to \mathsf{X}'$
is an isomorphism between them. Then
$g:\mathsf{X}\to \mathsf{X}'$
is an isomorphism between them. Then
![]() $g({\boldsymbol \bot }_{\mathsf{X}})=g({\boldsymbol \bot }_{\mathsf{X}'})$
and
$g({\boldsymbol \bot }_{\mathsf{X}})=g({\boldsymbol \bot }_{\mathsf{X}'})$
and
![]() $g({\boldsymbol \top }_{\mathsf{X}})={\boldsymbol \top }_{\mathsf{X}'}$
.
$g({\boldsymbol \top }_{\mathsf{X}})={\boldsymbol \top }_{\mathsf{X}'}$
.
Proof.
By construction
![]() ${\boldsymbol \bot }_{\mathsf{X}}\leq x$
for every
${\boldsymbol \bot }_{\mathsf{X}}\leq x$
for every
![]() $x\in \mathsf{X}$
. It follows from Definition 9.1.5(2) that
$x\in \mathsf{X}$
. It follows from Definition 9.1.5(2) that
![]() $g({\boldsymbol \bot }_{\mathsf{X}})\leq g(x)$
for every
$g({\boldsymbol \bot }_{\mathsf{X}})\leq g(x)$
for every
![]() $x\in \mathsf{X}$
; but
$x\in \mathsf{X}$
; but
![]() $g$
is a bijection, so
$g$
is a bijection, so
![]() $g({\boldsymbol \bot }_{\mathsf{X}})\leq x'$
for every
$g({\boldsymbol \bot }_{\mathsf{X}})\leq x'$
for every
![]() $x'\in \mathsf{X}'$
. It follows that
$x'\in \mathsf{X}'$
. It follows that
![]() $g({\boldsymbol \bot }_{\mathsf{X}})={\boldsymbol \bot }_{\mathsf{X}'}$
.
$g({\boldsymbol \bot }_{\mathsf{X}})={\boldsymbol \bot }_{\mathsf{X}'}$
.
By similar reasoning we conclude that
![]() $g({\boldsymbol \top }_{\mathsf{X}})={\boldsymbol \top }_{\mathsf{X}'}$
.
$g({\boldsymbol \top }_{\mathsf{X}})={\boldsymbol \top }_{\mathsf{X}'}$
.
Remark 9.1.7. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and recall from Definition 8.4.1 that
$(\mathsf{X},\leq ,\ast )$
is a semiframe and recall from Definition 8.4.1 that
![]() $\mathsf{Op}(\mathsf{X},\leq ,\ast )=\{\textit{Op}(x) \mid x\in \mathsf{X}\}$
. Then the intuitive content of Proposition 9.1.4 is that a semiframe
$\mathsf{Op}(\mathsf{X},\leq ,\ast )=\{\textit{Op}(x) \mid x\in \mathsf{X}\}$
. Then the intuitive content of Proposition 9.1.4 is that a semiframe
![]() $(\mathsf{X},\leq ,\ast )$
is spatial when
$(\mathsf{X},\leq ,\ast )$
is spatial when
![]() $(\mathsf{X},\leq ,\ast )$
is isomorphic (in the sense made formal by Definition 9.1.5) to
$(\mathsf{X},\leq ,\ast )$
is isomorphic (in the sense made formal by Definition 9.1.5) to
![]() $(\mathsf{Op}(\mathsf{X},\leq ,\ast ),\subseteq ,\between )$
.
$(\mathsf{Op}(\mathsf{X},\leq ,\ast ),\subseteq ,\between )$
.
And, because
![]() $\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
we can write a slogan:
$\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
we can write a slogan:
A semiframe is spatial when it is (up to isomorphism) generated by its abstract points.
We will go on to prove in Proposition 9.2.5 that every semitopology generates a spatial semiframe – and in Theorem 10.4.2 we will tighten and extend the slogan above to a full categorical duality.
9.2 The neighbourhood semifilter
 $\textit{nbhd}(p)$
$\textit{nbhd}(p)$
9.2.1 The definition and basic lemma
Recall from Definition 2.3.1 that we define
![]() $\textit{nbhd}(p)=\{O\in \mathsf{Open}\mid p\in O\}$
.
$\textit{nbhd}(p)=\{O\in \mathsf{Open}\mid p\in O\}$
.
Remark 9.2.1. If
![]() $(\mathsf{P},\mathsf{Open})$
is a topology, then
$(\mathsf{P},\mathsf{Open})$
is a topology, then
![]() $\textit{nbhd}(p)$
is a filter (a nonempty up-closed down-directed set) and is often called the neighbourhood filter of
$\textit{nbhd}(p)$
is a filter (a nonempty up-closed down-directed set) and is often called the neighbourhood filter of
![]() $p$
.
$p$
.
We are working with semitopologies, so
![]() $\mathsf{Open}$
is not necessarily closed under intersections, and
$\mathsf{Open}$
is not necessarily closed under intersections, and
![]() $\textit{nbhd}(p)$
is not necessarily a filter (it is still a compatible set, because every
$\textit{nbhd}(p)$
is not necessarily a filter (it is still a compatible set, because every
![]() $O\in \textit{nbhd}(p)$
contains
$O\in \textit{nbhd}(p)$
contains
![]() $p$
). Figure 4 illustrates examples of this: for example in the left-hand example
$p$
). Figure 4 illustrates examples of this: for example in the left-hand example
![]() $\{0,1\},\{0,2\}\in \textit{nbhd}(0)$
but
$\{0,1\},\{0,2\}\in \textit{nbhd}(0)$
but
![]() $\{0\}\not \in \textit{nbhd}(0)$
(because this is not an open set).
$\{0\}\not \in \textit{nbhd}(0)$
(because this is not an open set).
Recall from Definition 2.3.1 that
![]() $\textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\}$
.
$\textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\}$
.
Proposition 9.2.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
and
$p\in \mathsf{P}$
and
![]() $O\in \mathsf{Open}$
. Then:
$O\in \mathsf{Open}$
. Then:
-
(1)
 $\textit{nbhd}(p)$
(Definition 2.3.1) is an abstract point (a completely prime semifilter) in the semiframe
$\textit{nbhd}(p)$
(Definition 2.3.1) is an abstract point (a completely prime semifilter) in the semiframe
 $\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
(Definition 7.3.4). In symbols:
$\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
(Definition 7.3.4). In symbols:
 \begin{equation*} \textit{nbhd}:\mathsf{P}\to \mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open})) . \end{equation*}
\begin{equation*} \textit{nbhd}:\mathsf{P}\to \mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open})) . \end{equation*}
-
(2) The following are equivalent:
 \begin{equation*} \textit{nbhd}(p)\in \textit{Op}(O) \quad \Longleftrightarrow \quad O\in \textit{nbhd}(p) \quad \Longleftrightarrow \quad p\in O. \end{equation*}
\begin{equation*} \textit{nbhd}(p)\in \textit{Op}(O) \quad \Longleftrightarrow \quad O\in \textit{nbhd}(p) \quad \Longleftrightarrow \quad p\in O. \end{equation*}
-
(3) We have an equality:
 \begin{equation*} \textit{nbhd}^{\text{-}1}(\textit{Op}(O))=O. \end{equation*}
\begin{equation*} \textit{nbhd}^{\text{-}1}(\textit{Op}(O))=O. \end{equation*}
Proof. We consider each part in turn:
-
(1) From Definition 8.1.1(7), we must check that
 $\textit{nbhd}(p)$
is a nonempty, completely prime, up-closed, and compatible subset of
$\textit{nbhd}(p)$
is a nonempty, completely prime, up-closed, and compatible subset of
 $\mathsf{Open}$
when considered as a semiframe as per Definition 7.3.4. All properties are by facts of sets; we give brief details:
$\mathsf{Open}$
when considered as a semiframe as per Definition 7.3.4. All properties are by facts of sets; we give brief details:-
–
 $\textit{nbhd}(p)$
is nonempty because
$\textit{nbhd}(p)$
is nonempty because
 $p\in \mathsf{P}\in \mathsf{Open}$
.
$p\in \mathsf{P}\in \mathsf{Open}$
. -
–
 $\textit{nbhd}(p)$
is completely prime because it is a fact of sets that if
$\textit{nbhd}(p)$
is completely prime because it is a fact of sets that if
 $P\subseteq \mathsf{Open}$
and
$P\subseteq \mathsf{Open}$
and
 $p\in \bigcup P$
then
$p\in \bigcup P$
then
 $p\in O$
for some
$p\in O$
for some
 $O\in P$
.
$O\in P$
. -
–
 $\textit{nbhd}(p)$
is up-closed because it is a fact of sets that if
$\textit{nbhd}(p)$
is up-closed because it is a fact of sets that if
 $p\in O$
and
$p\in O$
and
 $O\subseteq O'$
then
$O\subseteq O'$
then
 $p\in O'$
.
$p\in O'$
. -
–
 $\textit{nbhd}(p)$
is compatible because if
$\textit{nbhd}(p)$
is compatible because if
 $p\in O$
and
$p\in O$
and
 $p\in O'$
then
$p\in O'$
then
 $O\between O'$
.
$O\between O'$
.
-
-
(2) By Definition 8.3.1,
 $\textit{Op}(O)$
is precisely the set of abstract points
$\textit{Op}(O)$
is precisely the set of abstract points
 $P$
that contain
$P$
that contain
 $O$
, and by part 1 of this result
$O$
, and by part 1 of this result
 $\textit{nbhd}(p)$
is one of those points. By Definition 2.3.1,
$\textit{nbhd}(p)$
is one of those points. By Definition 2.3.1,
 $\textit{nbhd}(p)$
is precisely the set of open sets that contain
$\textit{nbhd}(p)$
is precisely the set of open sets that contain
 $p$
. The equivalence follows.
$p$
. The equivalence follows. -
(3) We reason as follows:
 \begin{equation*} \begin{array}[b]{r@{\ }l@{\quad }l} p\in \textit{nbhd}^{\text{-}1}(\textit{Op}(O)) \Longleftrightarrow & \textit{nbhd}(p)\in \textit{Op}(O) &\text{Fact of function inverse} \\ \Longleftrightarrow & p\in O &\text{Part 2 of this result} \end{array} \end{equation*}
\begin{equation*} \begin{array}[b]{r@{\ }l@{\quad }l} p\in \textit{nbhd}^{\text{-}1}(\textit{Op}(O)) \Longleftrightarrow & \textit{nbhd}(p)\in \textit{Op}(O) &\text{Fact of function inverse} \\ \Longleftrightarrow & p\in O &\text{Part 2 of this result} \end{array} \end{equation*}
Corollary 9.2.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $O,O'\in \mathsf{Open}$
. Then:
$O,O'\in \mathsf{Open}$
. Then:
-
(1)
 $\textit{Op}(O)\subseteq \textit{Op}(O')$
if and only if
$\textit{Op}(O)\subseteq \textit{Op}(O')$
if and only if
 $O\subseteq O'$
.
$O\subseteq O'$
. -
(2)
 $\textit{Op}(O)\between \textit{Op}(O')$
if and only if
$\textit{Op}(O)\between \textit{Op}(O')$
if and only if
 $O\between O'$
.
$O\between O'$
. -
(3) As a corollary,
 $\textit{nbhd}^{\text{-}1}(\varnothing )=\varnothing$
and
$\textit{nbhd}^{\text{-}1}(\varnothing )=\varnothing$
and
 $\textit{nbhd}^{\text{-}1}(\mathsf{Points}(\mathsf{Open},\subseteq ,\between ))=\mathsf{P}$
; that is
$\textit{nbhd}^{\text{-}1}(\mathsf{Points}(\mathsf{Open},\subseteq ,\between ))=\mathsf{P}$
; that is
 $\textit{nbhd}^{\text{-}1}$
maps the bottom/top element to the bottom/top element.
$\textit{nbhd}^{\text{-}1}$
maps the bottom/top element to the bottom/top element.
Proof. We consider each part in turn:
-
(1) If
 $\textit{Op}(O)\subseteq \textit{Op}(O')$
then
$\textit{Op}(O)\subseteq \textit{Op}(O')$
then
 $\textit{nbhd}^{\text{-}1}(\textit{Op}(O))\subseteq \textit{nbhd}^{\text{-}1}(\textit{Op}(O'))$
by facts of inverse images, and
$\textit{nbhd}^{\text{-}1}(\textit{Op}(O))\subseteq \textit{nbhd}^{\text{-}1}(\textit{Op}(O'))$
by facts of inverse images, and
 $O\subseteq O'$
follows by Proposition 9.2.2(3).
$O\subseteq O'$
follows by Proposition 9.2.2(3).If
 $O\subseteq O'$
then
$O\subseteq O'$
then
 $\textit{Op}(O)\subseteq \textit{Op}(O')$
by Proposition 8.3.3(1).
$\textit{Op}(O)\subseteq \textit{Op}(O')$
by Proposition 8.3.3(1). -
(2) If
 $O\between O'$
then there exists some point
$O\between O'$
then there exists some point
 $p\in \mathsf{P}$
with
$p\in \mathsf{P}$
with
 $p\in O\cap O'$
. By Proposition 9.2.2(1)
$p\in O\cap O'$
. By Proposition 9.2.2(1)
 $\textit{nbhd}(p)$
is an abstract point, and by Proposition 9.2.2(2)
$\textit{nbhd}(p)$
is an abstract point, and by Proposition 9.2.2(2)
 $\textit{nbhd}(p)\in \textit{Op}(O)\cap \textit{Op}(O')$
; thus
$\textit{nbhd}(p)\in \textit{Op}(O)\cap \textit{Op}(O')$
; thus
 $\textit{Op}(O)\between \textit{Op}(O')$
.
$\textit{Op}(O)\between \textit{Op}(O')$
.If
 $\textit{Op}(O)\between \textit{Op}(O')$
then
$\textit{Op}(O)\between \textit{Op}(O')$
then
 $O\between O'$
by Proposition 8.3.3(2).
$O\between O'$
by Proposition 8.3.3(2). -
(3) Routine from Proposition 8.3.3(3) (or from Lemma 9.1.6).
9.2.2 Application to semiframes of open sets
Proposition 9.2.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then:
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then:
-
(1)
 $\textit{nbhd}^{\text{-}1}$
bijects open sets of
$\textit{nbhd}^{\text{-}1}$
bijects open sets of
 $\mathsf{St}(\mathsf{Open},\subseteq ,\between )$
(as defined in Definition 8.4.3(2)), with open sets of
$\mathsf{St}(\mathsf{Open},\subseteq ,\between )$
(as defined in Definition 8.4.3(2)), with open sets of
 $(\mathsf{P},\mathsf{Open})$
, taking
$(\mathsf{P},\mathsf{Open})$
, taking
 $\textit{Op}(O)$
to
$\textit{Op}(O)$
to
 $O$
.
$O$
. -
(2)
 $\textit{nbhd}^{\text{-}1}$
is an isomorphism between the semiframe of open sets of
$\textit{nbhd}^{\text{-}1}$
is an isomorphism between the semiframe of open sets of
 $\mathsf{St}(\mathsf{Open},\subseteq ,\between )$
, and the semiframe of open sets of
$\mathsf{St}(\mathsf{Open},\subseteq ,\between )$
, and the semiframe of open sets of
 $(\mathsf{P},\mathsf{Open})$
(Definition 9.1.5).
$(\mathsf{P},\mathsf{Open})$
(Definition 9.1.5).
Proof. We consider each part in turn:
-
(1) Unpacking Definition 8.4.3(2), an open set in
 $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
has the form
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
has the form
 $\textit{Op}(O)$
for some
$\textit{Op}(O)$
for some
 $O\in \mathsf{Open}$
. By Proposition 9.2.2(3)
$O\in \mathsf{Open}$
. By Proposition 9.2.2(3)
 $\textit{nbhd}^{\text{-}1}(\textit{Op}(O))=O$
, and so
$\textit{nbhd}^{\text{-}1}(\textit{Op}(O))=O$
, and so
 $\textit{nbhd}^{\text{-}1}$
is surjective and injective.
$\textit{nbhd}^{\text{-}1}$
is surjective and injective. -
(2) Unpacking Definition 9.1.5 it suffices to check that:
-
–
 $\textit{nbhd}^{\text{-}1}$
is a bijection, and maps
$\textit{nbhd}^{\text{-}1}$
is a bijection, and maps
 $\textit{Op}(O)$
to
$\textit{Op}(O)$
to
 $O$
.
$O$
. -
–
 $\textit{Op}(O)\subseteq \textit{Op}(O')$
if and only if
$\textit{Op}(O)\subseteq \textit{Op}(O')$
if and only if
 $O\subseteq O'$
.
$O\subseteq O'$
. -
–
 $\textit{Op}(O)\between \textit{Op}(O')$
if and only if
$\textit{Op}(O)\between \textit{Op}(O')$
if and only if
 $O\between O'$
.
$O\between O'$
.
The first condition is part 1 of this result; the second and third are from Corollary 9.2.3.
-
Proposition 9.2.5.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the semiframe
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the semiframe
![]() $\mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between )$
from Definition 7.3.4 is spatial.
$\mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between )$
from Definition 7.3.4 is spatial.
9.2.3 Application to characterise
 $T_0$
spaces
$T_0$
spaces
Lemma 9.2.6.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p,p'\in \mathsf{P}$
. Then the following are equivalent:
$p,p'\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $\textit{nbhd}(p)=\textit{nbhd}(p')$
(cf. also Lemma 11.7.1)
$\textit{nbhd}(p)=\textit{nbhd}(p')$
(cf. also Lemma 11.7.1)
-
(2)
 $\forall O{\in }\mathsf{Open}.p\in O\Longleftrightarrow p\in O'$
$\forall O{\in }\mathsf{Open}.p\in O\Longleftrightarrow p\in O'$
-
(3)
 $p\mathrel {\mathring {=}} p'$
(Definition 8.4.6
:
$p\mathrel {\mathring {=}} p'$
(Definition 8.4.6
:
 $p$
and
$p$
and
 $p'$
are topologically indistinguishable in
$p'$
are topologically indistinguishable in
 $(\mathsf{P},\mathsf{Open})$
).
$(\mathsf{P},\mathsf{Open})$
).
-
(4)
 $\textit{nbhd}(p)\mathrel {\mathring {=}} \textit{nbhd}(p')$
(
$\textit{nbhd}(p)\mathrel {\mathring {=}} \textit{nbhd}(p')$
(
 $\textit{nbhd}(p)$
and
$\textit{nbhd}(p)$
and
 $\textit{nbhd}(p')$
are topologically indistinguishable as – by Proposition 9.2.2(1) – abstract points in
$\textit{nbhd}(p')$
are topologically indistinguishable as – by Proposition 9.2.2(1) – abstract points in
 $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
).
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
).
Proof. Equivalence of parts 1 and 2 is direct from Definition 2.3.1. Equivalence of parts 2 and 3 is just Definition 8.4.6(1). Equivalence of parts 4 and 1 is from Proposition 8.4.7.
Corollary 9.2.7.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the following are equivalent:
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the following are equivalent:
Proof.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is
$(\mathsf{P},\mathsf{Open})$
is
![]() $T_0$
, and suppose
$T_0$
, and suppose
![]() $\textit{nbhd}(p)=\textit{nbhd}(p')$
. By Lemma 9.2.6(1 and 3)
$\textit{nbhd}(p)=\textit{nbhd}(p')$
. By Lemma 9.2.6(1 and 3)
![]() $p\mathrel {\mathring {=}} p'$
. By Definition 8.4.6(2)
$p\mathrel {\mathring {=}} p'$
. By Definition 8.4.6(2)
![]() $p=p'$
. Since
$p=p'$
. Since
![]() $p$
and
$p$
and
![]() $p'$
were arbitrary,
$p'$
were arbitrary,
![]() $\textit{nbhd}$
is injective.
$\textit{nbhd}$
is injective.
Suppose
![]() $\textit{nbhd}$
is injective. Reversing the reasoning of the previous paragraph, we deduce that
$\textit{nbhd}$
is injective. Reversing the reasoning of the previous paragraph, we deduce that
![]() $(\mathsf{P},\mathsf{Open})$
is
$(\mathsf{P},\mathsf{Open})$
is
![]() $T_0$
.
$T_0$
.
9.3 Sober semitopologies
Recall from Proposition 9.2.5 that if we go from a semitopology
![]() $(\mathsf{P},\mathsf{Open})$
to a semiframe
$(\mathsf{P},\mathsf{Open})$
to a semiframe
![]() $(\mathsf{Open},\subseteq ,\between )$
, then the result is not just any old semiframe – it is a spatial one.
$(\mathsf{Open},\subseteq ,\between )$
, then the result is not just any old semiframe – it is a spatial one.
We now investigate what happens when we go from a semiframe to a semitopology using Definition 8.4.3.
9.3.1 The definition and a key result
Definition 9.3.1. Call a semitopology
![]() $(\mathsf{P},\mathsf{Open})$
sober when every abstract point
$(\mathsf{P},\mathsf{Open})$
sober when every abstract point
![]() $P$
of
$P$
of
![]() $\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
– that is every completely prime nonempty up-closed compatible set of open sets – is equal to the neighbourhood semifilter
$\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
– that is every completely prime nonempty up-closed compatible set of open sets – is equal to the neighbourhood semifilter
![]() $\textit{nbhd}(p)$
of some unique
$\textit{nbhd}(p)$
of some unique
![]() $p\in \mathsf{P}$
.
$p\in \mathsf{P}$
.
Equivalently,
![]() $(\mathsf{P},\mathsf{Open})$
is sober when
$(\mathsf{P},\mathsf{Open})$
is sober when
![]() $\textit{nbhd}:\mathsf{P}\to \mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
(Definition 8.1.1(7)) is a bijection.
$\textit{nbhd}:\mathsf{P}\to \mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
(Definition 8.1.1(7)) is a bijection.
Remark 9.3.2. A bijection is a map that is injective and a surjective. We noted in Corollary 9.2.7 that a space is
![]() $T_0$
when
$T_0$
when
![]() $\textit{nbhd}$
is injective. So the sobriety condition can be thought of as having two parts:
$\textit{nbhd}$
is injective. So the sobriety condition can be thought of as having two parts:
-
•
 $\textit{nbhd}$
is injective and the space is
$\textit{nbhd}$
is injective and the space is
 $T_0$
, so it intuitively contains no ‘unnecessary’ duplicates of points;
$T_0$
, so it intuitively contains no ‘unnecessary’ duplicates of points; -
•
 $\textit{nbhd}$
is surjective, so the space contains ‘enough’ points that there is (precisely) one concrete point for every abstract point.Footnote
25
$\textit{nbhd}$
is surjective, so the space contains ‘enough’ points that there is (precisely) one concrete point for every abstract point.Footnote
25
We start with a very simple example of sober semitopologies:
Lemma 9.3.3.
Suppose
![]() $\mathsf{P}$
is any set. Then the discrete semitopology
$\mathsf{P}$
is any set. Then the discrete semitopology
![]() $(\mathsf{P},\textit{pow}(\mathsf{Open}))$
is sober.
$(\mathsf{P},\textit{pow}(\mathsf{Open}))$
is sober.
Proof.
Consider an abstract point
![]() $P\subseteq \mathsf{Open}$
(completely prime nonempty up-closed and compatible, as per Definition 8.1.1(7)). Then
$P\subseteq \mathsf{Open}$
(completely prime nonempty up-closed and compatible, as per Definition 8.1.1(7)). Then
![]() $\mathsf{P}\in P$
and
$\mathsf{P}\in P$
and
![]() $\mathsf{P}=\bigvee \{\{p\}\mid p\in \mathsf{P}\}$
. Since
$\mathsf{P}=\bigvee \{\{p\}\mid p\in \mathsf{P}\}$
. Since
![]() $P$
is completely prime,
$P$
is completely prime,
![]() $\{p\}\in P$
for some
$\{p\}\in P$
for some
![]() $p\in \mathsf{P}$
. It follows easily that
$p\in \mathsf{P}$
. It follows easily that
![]() $P=\textit{nbhd}(p)$
.
$P=\textit{nbhd}(p)$
.
Example 9.3.4. We give some more examples of sober and non-sober semitopologies.
-
(1) Take
 $\mathsf{P}=\{0,1\}$
and
$\mathsf{P}=\{0,1\}$
and
 $\mathsf{Open}=\{\varnothing ,\{0,1\}\}$
. This has one abstract point
$\mathsf{Open}=\{\varnothing ,\{0,1\}\}$
. This has one abstract point
 $P=\{\{0,1\}\}$
but two concrete points
$P=\{\{0,1\}\}$
but two concrete points
 $0$
and
$0$
and
 $1$
. It is therefore not sober.
$1$
. It is therefore not sober. -
(2) Take
 $\mathsf{P}=\{0,1\}$
and
$\mathsf{P}=\{0,1\}$
and
 $\mathsf{Open}=\{\varnothing ,\{1\},\{0,1\}\}$
. This has two abstract pointscorresponding to two concrete points
$\mathsf{Open}=\{\varnothing ,\{1\},\{0,1\}\}$
. This has two abstract pointscorresponding to two concrete points \begin{equation*} \{\{1\},\{0,1\}\} \quad \textit{and}\quad \{\{0,1\}\} \end{equation*}
\begin{equation*} \{\{1\},\{0,1\}\} \quad \textit{and}\quad \{\{0,1\}\} \end{equation*}
 $0$
and
$0$
and
 $1$
. It is sober.
$1$
. It is sober.
-
(3) Take
 $\mathsf{P}=\mathbb N$
with the final topology; so
$\mathsf{P}=\mathbb N$
with the final topology; so
 $O\in \mathsf{Open}$
when
$O\in \mathsf{Open}$
when
 $O=\varnothing$
or
$O=\varnothing$
or
 $O=n_\geq$
for some
$O=n_\geq$
for some
 $n\in \mathbb N$
, where
$n\in \mathbb N$
, where
 $n_\geq = \{n'\in \mathbb N \mid n'\geq n\}$
. Take
$n_\geq = \{n'\in \mathbb N \mid n'\geq n\}$
. Take
 $P=\{n_\geq \mid n\in \mathbb N\}$
. The reader can check that this is an abstract point (up-closed, completely prime, compatible); however
$P=\{n_\geq \mid n\in \mathbb N\}$
. The reader can check that this is an abstract point (up-closed, completely prime, compatible); however
 $P$
is not the neighbourhood semifilter of any
$P$
is not the neighbourhood semifilter of any
 $n\in \mathbb N$
. Thus this space is not sober.
$n\in \mathbb N$
. Thus this space is not sober. -
(4)
 $\mathbb R$
with its usual topology (which is also a semitopology) is sober.
$\mathbb R$
with its usual topology (which is also a semitopology) is sober.This is a known result for topologies, but Remark 8.1.3 (and also the later Remark 9.3.11) caution us that we cannot take this for granted, so we sketch the proof.
Suppose
 $P$
is an abstract point; we wish to exhibit a unique
$P$
is an abstract point; we wish to exhibit a unique
 $p\in \mathbb R$
such that
$p\in \mathbb R$
such that
 $P=\textit{nbhd}(p)$
.
$P=\textit{nbhd}(p)$
.We cover
 $\mathbb R$
with open intervals of radius
$\mathbb R$
with open intervals of radius
 $1$
by writing
$1$
by writing
 $\mathbb R=\bigcup \{(r\text{-} 0.5,r{+} 0.5) \mid r\in \mathbb R\}$
, and we use the completely prime property to find (at least one) such open interval that is in
$\mathbb R=\bigcup \{(r\text{-} 0.5,r{+} 0.5) \mid r\in \mathbb R\}$
, and we use the completely prime property to find (at least one) such open interval that is in
 $P$
; write it
$P$
; write it
 $O_1\in P$
. We then cover
$O_1\in P$
. We then cover
 $O_1$
with open intervals of radius at most
$O_1$
with open intervals of radius at most
 $1/2$
by writing
$1/2$
by writing
 $O_1=\bigcup \{O_1\cap (r\text{-} 0.25,r{+} 0.25)\mid r\in O_1\}$
, and we iterate to obtain a sequence
$O_1=\bigcup \{O_1\cap (r\text{-} 0.25,r{+} 0.25)\mid r\in O_1\}$
, and we iterate to obtain a sequence
 $(O_i\mid i\in \mathbb N)\subseteq P$
. This converges to some unique
$(O_i\mid i\in \mathbb N)\subseteq P$
. This converges to some unique
 $p\in \mathbb R$
. We check that
$p\in \mathbb R$
. We check that
 $P=\textit{nbhd}(p)$
:
$P=\textit{nbhd}(p)$
:-
– Suppose
 $O\in \mathsf{Open}$
is such that
$O\in \mathsf{Open}$
is such that
 $p\in O$
. Because
$p\in O$
. Because
 $p\in O$
, there exists some
$p\in O$
, there exists some
 $\epsilon$
such that
$\epsilon$
such that
 $(p\text{-}\epsilon ,p{+}\epsilon )\subseteq O$
. It follows that for
$(p\text{-}\epsilon ,p{+}\epsilon )\subseteq O$
. It follows that for
 $i\gt 1/\epsilon$
we have
$i\gt 1/\epsilon$
we have
 $O_i\subseteq O$
and thus
$O_i\subseteq O$
and thus
 $O\in P$
by up-closedness.
$O\in P$
by up-closedness. -
– Suppose
 $O'\in \mathsf{Open}$
is such that
$O'\in \mathsf{Open}$
is such that
 $p\notin O'$
. For a sufficiently large
$p\notin O'$
. For a sufficiently large
 $i$
we have
$i$
we have  , so by compatibility it follows that
, so by compatibility it follows that
 $O'\notin P$
.
$O'\notin P$
.
-
-
(5)
 $\mathbb Q$
is sober. The argument is much as for
$\mathbb Q$
is sober. The argument is much as for
 $\mathbb R$
above. We have to work just a little harder because the
$\mathbb R$
above. We have to work just a little harder because the
 $p$
we obtain need not be rational, but the arguments on open intervals remain valid.
$p$
we obtain need not be rational, but the arguments on open intervals remain valid.
Proposition 9.3.5.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
from Definition 8.4.3 is a sober semitopology.
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
from Definition 8.4.3 is a sober semitopology.
Proof.
We know from Lemma 8.4.4 that
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a semitopology. The issue is whether it is sober; thus by Definition 9.3.1 we wish to exhibit every abstract point
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a semitopology. The issue is whether it is sober; thus by Definition 9.3.1 we wish to exhibit every abstract point
![]() $P$
of
$P$
of
![]() $\mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
as a neighbourhood semifilter
$\mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
as a neighbourhood semifilter
![]() $\textit{nbhd}(p)$
for some unique abstract point
$\textit{nbhd}(p)$
for some unique abstract point
![]() $p$
of
$p$
of
![]() $(\mathsf{X},\leq ,\ast )$
. The calculations to do so are routine, but we give details.
$(\mathsf{X},\leq ,\ast )$
. The calculations to do so are routine, but we give details.
Fix some abstract point
![]() $P$
of
$P$
of
![]() $\mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
. By Definition 8.1.1(7),
$\mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
. By Definition 8.1.1(7),
![]() $P$
is a completely prime nonempty up-closed set of intersecting open sets in the semitopology
$P$
is a completely prime nonempty up-closed set of intersecting open sets in the semitopology
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
, and by Definition 8.4.3(2) each open set in
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
, and by Definition 8.4.3(2) each open set in
![]() $\mathsf{St}(\mathsf{X},\leq ,\ast )$
has the form
$\mathsf{St}(\mathsf{X},\leq ,\ast )$
has the form
![]() $\textit{Op}(x)=\{p\in \mathsf{Points}(\mathsf{X},\leq ,\ast ) \mid x\in p\}$
for some
$\textit{Op}(x)=\{p\in \mathsf{Points}(\mathsf{X},\leq ,\ast ) \mid x\in p\}$
for some
![]() $x\in \mathsf{X}$
.
$x\in \mathsf{X}$
.
We define
![]() $p\subseteq \mathsf{X}$
as follows:
$p\subseteq \mathsf{X}$
as follows:
By construction we have that
![]() $x\in p$
if and only if
$x\in p$
if and only if
![]() $\textit{Op}(x)\in P$
, and so
$\textit{Op}(x)\in P$
, and so

Now
![]() $P$
is completely prime, nonempty, up-closed, and compatible and it follows by elementary calculations using Proposition 9.1.4 that
$P$
is completely prime, nonempty, up-closed, and compatible and it follows by elementary calculations using Proposition 9.1.4 that
![]() $p$
is also completely prime, nonempty, up-closed, and compatible – so
$p$
is also completely prime, nonempty, up-closed, and compatible – so
![]() $p$
is an abstract point of
$p$
is an abstract point of
![]() $(\mathsf{X},\leq ,\ast )$
.
$(\mathsf{X},\leq ,\ast )$
.
So we have that
To prove uniqueness of
![]() $p$
, suppose
$p$
, suppose
![]() $p'$
is any other abstract point such that
$p'$
is any other abstract point such that
![]() $P=\textit{nbhd}(p')$
. We follow the definitions:
$P=\textit{nbhd}(p')$
. We follow the definitions:
![]() $\textit{Op}(x)\in \textit{nbhd}(p') \Longleftrightarrow \textit{Op}(x)\in \textit{nbhd}(p)$
, and thus by Definition 2.3.1
$\textit{Op}(x)\in \textit{nbhd}(p') \Longleftrightarrow \textit{Op}(x)\in \textit{nbhd}(p)$
, and thus by Definition 2.3.1
![]() $p'\in \textit{Op}(x) \Longleftrightarrow p\in \textit{Op}(x)$
, and thus by Definition 8.3.1
$p'\in \textit{Op}(x) \Longleftrightarrow p\in \textit{Op}(x)$
, and thus by Definition 8.3.1
![]() $x\in p'\Longleftrightarrow x\in p$
, and thus
$x\in p'\Longleftrightarrow x\in p$
, and thus
![]() $p'=p$
.
$p'=p$
.
9.3.2 Sober topologies contrasted with sober semitopologies
We will need Notation 9.3.6 for Remark 9.3.7:
Notation 9.3.6. Call a closed set irreducible when it cannot be written as the union of two proper closed subsets.
Remark 9.3.7. Topology has a wealth of separation actions. Three of them are:
![]() $T_0$
(distinct points have distinct neighbourhood (semi)filters);
$T_0$
(distinct points have distinct neighbourhood (semi)filters);
![]() $T_1$
(distinct points have distinct open neighbourhoods); and
$T_1$
(distinct points have distinct open neighbourhoods); and
![]() $T_2$
, also known as the Hausdorff condition (distinct points have disjoint open neighbourhoods) – see Remark 4.2.1 for formal statements. For topologies, the following is known of sobriety:
$T_2$
, also known as the Hausdorff condition (distinct points have disjoint open neighbourhoods) – see Remark 4.2.1 for formal statements. For topologies, the following is known of sobriety:
-
(1) Every finite
 $T_0$
(and thus every finite
$T_0$
(and thus every finite
 $T_1$
) topological space is sober.
$T_1$
) topological space is sober. -
(2) Every
 $T_2$
/Hausdorff space (including infinite ones) is sober (Mac Lane and Moerdijk, Reference Mac Lane and Moerdijk1992, p. 475, Theorem 3).
$T_2$
/Hausdorff space (including infinite ones) is sober (Mac Lane and Moerdijk, Reference Mac Lane and Moerdijk1992, p. 475, Theorem 3). -
(3) A topological space is sober if and only if every nonempty irreducible closed set is the closure of a unique point (Mac Lane and Moerdijk, Reference Mac Lane and Moerdijk1992, p. 475).
The situation for semitopologies is different, as we explore in the rest of this Subsection.
Lemma 9.3.8.
-
(1) It is not necessarily the case that a finite
 $T_0$
semitopology (or even a finite
$T_0$
semitopology (or even a finite
 $T_1$
semitopology) is sober (Definition 9.3.1).
$T_1$
semitopology) is sober (Definition 9.3.1).
-
(2) It is not necessarily the case that if every nonempty irreducible closed set is the closure of a unique point, then a semitopology is sober.
These non-implications hold even if the semitopology is regular (so
![]() $p\in \textit{K}(p)\in \mathsf{Topen}$
for every
$p\in \textit{K}(p)\in \mathsf{Topen}$
for every
![]() $p$
; see Definition 4.1.4(3)).
$p$
; see Definition 4.1.4(3)).
Proof. We provide a semitopology that is a counterexample for both parts.
Consider the left-hand semitopology illustrated in Figure 6, so that:
-
•
 $\mathsf{P}=\{0,1,2\}$
, and
$\mathsf{P}=\{0,1,2\}$
, and -
•
 $\mathsf{Open}=\{\varnothing ,\{0,1\},\{1,2\},\{0,2\},\{0,1,2\}\}$
.
$\mathsf{Open}=\{\varnothing ,\{0,1\},\{1,2\},\{0,2\},\{0,1,2\}\}$
.
We note that:
-
•
 $(\mathsf{P},\mathsf{Open})$
is
$(\mathsf{P},\mathsf{Open})$
is
 $T_0$
and
$T_0$
and
 $T_1$
.
$T_1$
. -
•
 $(\mathsf{P},\mathsf{Open})$
is regular because all points are intertwined, so that
$(\mathsf{P},\mathsf{Open})$
is regular because all points are intertwined, so that
 $\textit{K}(p)=\mathsf{P}$
for every
$\textit{K}(p)=\mathsf{P}$
for every
 $p\in \mathsf{P}$
.
$p\in \mathsf{P}$
. -
• The nonempty irreducible closed sets are
 $\{0\}$
(which is the complement of
$\{0\}$
(which is the complement of
 $\{1,2\}$
),
$\{1,2\}$
),
 $\{1\}$
, and
$\{1\}$
, and
 $\{2\}$
. Since these are singleton sets, they are certainly the closures of unique points.
$\{2\}$
. Since these are singleton sets, they are certainly the closures of unique points.
So
![]() $(\mathsf{P},\mathsf{Open})$
is
$(\mathsf{P},\mathsf{Open})$
is
![]() $T_0$
, regular, and irreducible closed sets are the closures of unique points.
$T_0$
, regular, and irreducible closed sets are the closures of unique points.
We take as our semifilter
![]() $P=\mathsf{Open}\setminus \{\varnothing \}$
. The reader can check that
$P=\mathsf{Open}\setminus \{\varnothing \}$
. The reader can check that
![]() $P$
is completely prime (Definition 8.1.1(2)), nonempty, up-closed, and compatible (
$P$
is completely prime (Definition 8.1.1(2)), nonempty, up-closed, and compatible (
![]() $P$
is also the greatest semifilter); but,
$P$
is also the greatest semifilter); but,
![]() $P$
is not the neighbourhood semifilter of
$P$
is not the neighbourhood semifilter of
![]() $0$
,
$0$
,
![]() $1$
, or
$1$
, or
![]() $2$
in
$2$
in
![]() $\mathsf{P}$
. Thus,
$\mathsf{P}$
. Thus,
![]() $(\mathsf{P},\mathsf{Open})$
is not sober.
$(\mathsf{P},\mathsf{Open})$
is not sober.
Remark 9.3.9. The counterexample used in Lemma 9.3.8 generalises, as follows: the reader can check that the all-but-one semitopology from Example 2.1.4(3) on three or more points (so open sets are generated by
![]() $\mathsf{P}\setminus \{p\}$
for every
$\mathsf{P}\setminus \{p\}$
for every
![]() $p\in \mathsf{P}$
) has similar behaviour.
$p\in \mathsf{P}$
) has similar behaviour.
In topology, every Hausdorff space is sober. In semitopologies, this implication does not hold, and in a rather strong sense:
Lemma 9.3.10.
-
(1) It is not necessarily the case that if a semitopology is Hausdorff, then it is sober.
-
(2) Every quasiregular Hausdorff semitopology is (discrete and therefore) sober.
Proof. We consider each part in turn:
-
(1) It suffices to give a counterexample. Consider the right-hand semitopology illustrated in Figure 6 (which we also used, for different purposes, in Figure 3), so that:
-
–
 $\mathsf{P}=\{0,1,2,3\}$
, and
$\mathsf{P}=\{0,1,2,3\}$
, and -
–
 $\mathsf{Open}$
is generated by
$\mathsf{Open}$
is generated by
 $X=\{\{3,0\},\{0,1\},\{1,2\},\{2,3\}\}$
.
$X=\{\{3,0\},\{0,1\},\{1,2\},\{2,3\}\}$
.
This is Hausdorff, but it is not sober: the reader can check that the up-closure
 $\{3,0\}^\leq \subseteq \mathsf{Open}$
is nonempty, up-closed, compatible, and completely prime, but it is not the neighbourhood filter of any
$\{3,0\}^\leq \subseteq \mathsf{Open}$
is nonempty, up-closed, compatible, and completely prime, but it is not the neighbourhood filter of any
 $p\in \mathsf{P}$
.
$p\in \mathsf{P}$
. -
-
(2) From Lemmas 4.2.2 (quasiregular Hausdorff is discrete) and 9.3.3 (discrete is sober).
Remark 9.3.11. A bit more discussion of Lemma 9.3.10.
-
(1) The space used in the counterexample for part 1 is Hausdorff,
 $T_1$
, and unconflicted (Definition 5.3.1(2)). It is not quasiregular (Definition 4.1.4(5)) because the community of every point is empty; see Proposition 5.3.3.
$T_1$
, and unconflicted (Definition 5.3.1(2)). It is not quasiregular (Definition 4.1.4(5)) because the community of every point is empty; see Proposition 5.3.3. -
(2) The implication holds if we add quasiregularity as a condition: every quasiregular Hausdorff space is sober. But, this holds for very bad reasons, because by Lemma 4.2.2 every quasiregular Hausdorff space is discrete.
-
(3) Thus, the non-implication discussed in Lemma 9.3.10 is informative and tells us something interesting about semitopological sobriety. Semitopological sobriety is not just a weak form of topological sobriety, and it has its own distinct personality.
Remark 9.3.12. We can inject the examples illustrated in Figure 6 (used in Lemmas 9.3.8 and 9.3.10) into soberified versions of the spaces that are sober and have an isomorphic lattice of open sets, as illustrated in Figure 7:
-
(1) The left-hand semitopology has abstract points (completely prime semifilters; see Definition 8.1.1(2)) generated as the
 $\subseteq$
-up-closures of the following sets:
$\subseteq$
-up-closures of the following sets:
 $\{A\}$
,
$\{A\}$
,
 $\{B\}$
,
$\{B\}$
,
 $\{C\}$
,
$\{C\}$
,
 $\{A,B\}$
,
$\{A,B\}$
,
 $\{B,C\}$
,
$\{B,C\}$
,
 $\{C,A\}$
, and
$\{C,A\}$
, and
 $\{A,B,C\}$
. Of these,
$\{A,B,C\}$
. Of these,
 $\{A,B\}^\subseteq =\textit{nbhd}(0)$
,
$\{A,B\}^\subseteq =\textit{nbhd}(0)$
,
 $\{B,C\}^\subseteq =\textit{nbhd}(1)$
, and
$\{B,C\}^\subseteq =\textit{nbhd}(1)$
, and
 $\{C,A\}^\subseteq =\textit{nbhd}(2)$
. The other completely prime semifilters are not generated as the neighbourhood semifilters of any point in the original space, so we add points as illustrated using
$\{C,A\}^\subseteq =\textit{nbhd}(2)$
. The other completely prime semifilters are not generated as the neighbourhood semifilters of any point in the original space, so we add points as illustrated using
 $\bullet$
in the left-hand diagram in Figure 7. This semitopology is sober, and has the same semiframe of open sets.
$\bullet$
in the left-hand diagram in Figure 7. This semitopology is sober, and has the same semiframe of open sets. -
(2) For the right-hand example, we again add a
 $\bullet$
point for every abstract point in the original space that is not already the neighbourhood semifilter of a point in the original space. These abstract points are generated as the
$\bullet$
point for every abstract point in the original space that is not already the neighbourhood semifilter of a point in the original space. These abstract points are generated as the
 $\subseteq$
-up-closures of
$\subseteq$
-up-closures of
 $\{A\}$
,
$\{A\}$
,
 $\{B\}$
,
$\{B\}$
,
 $\{C\}$
, and
$\{C\}$
, and
 $\{D\}$
. There is no need to add a
$\{D\}$
. There is no need to add a
 $\bullet$
for the abstract point generated as the
$\bullet$
for the abstract point generated as the
 $\subseteq$
-up-closure of
$\subseteq$
-up-closure of
 $\{A,B\}$
, because
$\{A,B\}$
, because
 $\{A,B\}^\subseteq =\textit{nbhd}(0)$
. Similarly
$\{A,B\}^\subseteq =\textit{nbhd}(0)$
. Similarly
 $\{B,C\}^\subseteq =\textit{nbhd}(1)$
,
$\{B,C\}^\subseteq =\textit{nbhd}(1)$
,
 $\{C,D\}^\subseteq =\textit{nbhd}(2)$
, and
$\{C,D\}^\subseteq =\textit{nbhd}(2)$
, and
 $\{D,A\}^\subseteq =\textit{nbhd}(3)$
. Note that
$\{D,A\}^\subseteq =\textit{nbhd}(3)$
. Note that
 $\{A,B,C\}$
does not generate an abstract point because it is not compatible:
$\{A,B,C\}$
does not generate an abstract point because it is not compatible:  . Similarly for
. Similarly for
 $\{B,C,D\}$
,
$\{B,C,D\}$
,
 $\{C,D,A\}$
,
$\{C,D,A\}$
,
 $\{D,A,C\}$
, and
$\{D,A,C\}$
, and
 $\{A,B,C,D\}$
.
$\{A,B,C,D\}$
.
These soberified spaces are instances of a general construction described in Theorem 10.1.4. And, continuing the observation made in Remark 9.3.11, note that neither of these spaces, with their extra points, are Hausdorff.
10. Four Categories & Functors Between Them
10.1 The categories SemiTop/Sober of semitopologies/sober semitopologies
Definition 10.1.1.
-
(1) Suppose
 $(\mathsf{P},\mathsf{Open})$
and
$(\mathsf{P},\mathsf{Open})$
and
 $(\mathsf{P}',\mathsf{Open}')$
are semitopologies and
$(\mathsf{P}',\mathsf{Open}')$
are semitopologies and
 $f:\mathsf{P}\to \mathsf{P}'$
is any function. Then call
$f:\mathsf{P}\to \mathsf{P}'$
is any function. Then call
 $f$
a morphism of semitopologies when
$f$
a morphism of semitopologies when
 $f$
is continuous, by which we mean (as standard) that
$f$
is continuous, by which we mean (as standard) that \begin{equation*} O'\in \mathsf{Open}' \quad \text{implies}\quad f^{\text{-}1}(O')\in \mathsf{Open} . \end{equation*}
\begin{equation*} O'\in \mathsf{Open}' \quad \text{implies}\quad f^{\text{-}1}(O')\in \mathsf{Open} . \end{equation*}
-
(2) Define
 $\mathsf{SemiTop}$
the category of semitopologies such that:
$\mathsf{SemiTop}$
the category of semitopologies such that:-
– objects are semitopologies, and
-
– arrows are morphisms of semitopologies (continuous maps on points).Footnote 26
-
-
(3) Write
 $\mathsf{Sober}$
for the category of sober semitopologies and continuous functions between them. By construction,
$\mathsf{Sober}$
for the category of sober semitopologies and continuous functions between them. By construction,
 $\mathsf{Sober}$
is the full subcategory of
$\mathsf{Sober}$
is the full subcategory of
 $\mathsf{SemiTop}$
, on its sober semitopologies.
$\mathsf{SemiTop}$
, on its sober semitopologies.
Remark 10.1.2. For convenience reading Theorem 10.1.4 we recall some facts:
-
(1) The semiframe
from Definition 7.3.4 has elements open sets \begin{equation*} \mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between ) \end{equation*}
\begin{equation*} \mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between ) \end{equation*}
 $O\in \mathsf{Open}$
, preordered by subset inclusion and with a compatibility relation given by set intersection.
$O\in \mathsf{Open}$
, preordered by subset inclusion and with a compatibility relation given by set intersection.
It is spatial, by Proposition 9.2.5.
-
(2) An abstract point
 $P$
in
$P$
in
 $\mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
is a completely prime nonempty up-closed compatible subset of
$\mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
is a completely prime nonempty up-closed compatible subset of
 $\mathsf{Open}$
.
$\mathsf{Open}$
. -
(3)
 $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
is by Definition 8.4.3 a semitopology such that:
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
is by Definition 8.4.3 a semitopology such that:-
a. Its set of points is
 $\mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
; the set of abstract points in
$\mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
; the set of abstract points in
 $\mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between )$
, the semilattice of open sets of
$\mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between )$
, the semilattice of open sets of
 $(\mathsf{P},\mathsf{Open})$
, and
$(\mathsf{P},\mathsf{Open})$
, and -
b. Its open sets are given by the
 $\textit{Op}(O)$
, for
$\textit{Op}(O)$
, for
 $O\in \mathsf{Open}$
.
$O\in \mathsf{Open}$
.
It is sober, by Proposition 9.3.5.
-
Continuing Remark 10.1.2, a notation will be useful:
Notation 10.1.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then define
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then define
We may use
![]() $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
and
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
and
![]() $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
interchangeably, depending on whether we want to emphasise “this is a sober semitopology obtained from
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
interchangeably, depending on whether we want to emphasise “this is a sober semitopology obtained from
![]() $(\mathsf{P},\mathsf{Open})$
” or “this is
$(\mathsf{P},\mathsf{Open})$
” or “this is
![]() $\mathsf{St}$
acting on
$\mathsf{St}$
acting on
![]() $\mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between )$
”.
$\mathsf{Fr}(\mathsf{P},\mathsf{Open})=(\mathsf{Open},\subseteq ,\between )$
”.
Theorem 10.1.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then
-
(1)
 $\textit{nbhd}:\mathsf{P}\to \mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
is a morphism of semitopologies from
$\textit{nbhd}:\mathsf{P}\to \mathsf{Points}(\mathsf{Fr}(\mathsf{P},\mathsf{Open}))$
is a morphism of semitopologies from
 $(\mathsf{P},\mathsf{Open})$
to
$(\mathsf{P},\mathsf{Open})$
to
 $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})=\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})=\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
-
(2) taking
 $(\mathsf{P},\mathsf{Open})$
to a sober semitopology
$(\mathsf{P},\mathsf{Open})$
to a sober semitopology
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
, such that
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
, such that
-
(3)
 $\textit{nbhd}^{\text{-}1}$
induces a bijection on open sets by mapping
$\textit{nbhd}^{\text{-}1}$
induces a bijection on open sets by mapping
 $\textit{Op}(O)$
to
$\textit{Op}(O)$
to
 $O$
, and furthermore this is an isomorphism of the semiframes of open sets, in the sense of Definition 9.1.5
.
$O$
, and furthermore this is an isomorphism of the semiframes of open sets, in the sense of Definition 9.1.5
.
Proof. We consider each part in turn:
-
(1) Following Definition 10.1.1 we must show that
 $\textit{nbhd}$
is continuous (inverse images of open sets are open) from
$\textit{nbhd}$
is continuous (inverse images of open sets are open) from
 $(\mathsf{P},\mathsf{Open})$
to
$(\mathsf{P},\mathsf{Open})$
to
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
. So following Definition 8.4.3(2), consider
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
. So following Definition 8.4.3(2), consider
 $\textit{Op}(O)\in \mathsf{Open}(\mathsf{Soberify}(\mathsf{P},\mathsf{Open}))$
. By Proposition 9.2.2(3)
$\textit{Op}(O)\in \mathsf{Open}(\mathsf{Soberify}(\mathsf{P},\mathsf{Open}))$
. By Proposition 9.2.2(3) \begin{equation*} \textit{nbhd}^{\text{-}1}(\textit{Op}(O))=O\in \mathsf{Open}. \end{equation*}
\begin{equation*} \textit{nbhd}^{\text{-}1}(\textit{Op}(O))=O\in \mathsf{Open}. \end{equation*}
Continuity follows.
-
(2)
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is sober by Proposition 9.3.5.
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is sober by Proposition 9.3.5. -
(3) This is Proposition 9.2.4.
Remark 10.1.5. We can summarise Theorem 10.1.4 as follows:
-
(1) By construction, the kernel of the
 $\textit{nbhd}$
function (the relation determined by which points it maps to equal elements) is topological indistinguishability
$\textit{nbhd}$
function (the relation determined by which points it maps to equal elements) is topological indistinguishability
 $\doteq$
.
$\doteq$
. -
(2) We can think of
 $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
as being obtained from
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
as being obtained from
 $(\mathsf{P},\mathsf{Open})$
by
$(\mathsf{P},\mathsf{Open})$
by-
a. quotienting topologically equivalent points to obtain a
 $T_0$
space, and then
$T_0$
space, and then -
b. adding extra points to make it sober.
See also the discussion in Remark 9.3.2 about what it means to have ‘enough’ points.
-
-
(3) This is done without affecting the semiframe of open sets (up to isomorphism), with the semiframe bijection given by
 $\textit{nbhd}^{\text{-}1}$
.
$\textit{nbhd}^{\text{-}1}$
.
In this sense, we can view
![]() $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
as a soberification of
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
as a soberification of
![]() $(\mathsf{P},\mathsf{Open})$
.
$(\mathsf{P},\mathsf{Open})$
.
10.2 The categories SemiFrame/Spatial of semiframes/spatial semiframes
Definition 10.2.1.
-
(1) Suppose
 $(\mathsf{X},\leq ,\ast )$
and
$(\mathsf{X},\leq ,\ast )$
and
 $(\mathsf{X}',\leq ',\ast ')$
are semiframes (Definition 7.3.1) and
$(\mathsf{X}',\leq ',\ast ')$
are semiframes (Definition 7.3.1) and
 $g:\mathsf{X}\to \mathsf{X}'$
is any function. Then call
$g:\mathsf{X}\to \mathsf{X}'$
is any function. Then call
 $g$
a morphism of semiframes when:
$g$
a morphism of semiframes when:-
a.
 $g$
is a morphism of complete semilattices (Definition 7.1.2).
$g$
is a morphism of complete semilattices (Definition 7.1.2). -
b.
 $g$
is compatible, by which we mean that
$g$
is compatible, by which we mean that
 $g(x')\ast g(x'')$
implies
$g(x')\ast g(x'')$
implies
 $x'\ast x''$
for every
$x'\ast x''$
for every
 $x',x''\in \mathsf{X}'$
.
$x',x''\in \mathsf{X}'$
.
-
-
(2) We define
 $\mathsf{SemiFrame}$
the category of semiframes such that:
$\mathsf{SemiFrame}$
the category of semiframes such that:-
– objects are semiframes, and
-
– arrows are morphisms of semiframes.
-
-
(3) Write
 $\mathsf{Spatial}$
for the category of spatial semiframes and semiframe morphisms between them. By construction,
$\mathsf{Spatial}$
for the category of spatial semiframes and semiframe morphisms between them. By construction,
 $\mathsf{Spatial}$
is the full subcategory of
$\mathsf{Spatial}$
is the full subcategory of
 $\mathsf{SemiFrame}$
, on its spatial semiframes (Definition 9.1.2).
$\mathsf{SemiFrame}$
, on its spatial semiframes (Definition 9.1.2).
Lemma 10.2.2.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then
![]() $\textit{Op}:(\mathsf{X},\leq ,\ast )\to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a morphism of semiframes and is surjective on underlying sets.
$\textit{Op}:(\mathsf{X},\leq ,\ast )\to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
is a morphism of semiframes and is surjective on underlying sets.
Proof. Following Definition 10.2.1(1) we must show that
-
•
 $\textit{Op}$
is a semilattice morphism (Definition 7.1.2) – commutes with joins and maps
$\textit{Op}$
is a semilattice morphism (Definition 7.1.2) – commutes with joins and maps
 ${\boldsymbol \top }_{\mathsf{X}}$
to
${\boldsymbol \top }_{\mathsf{X}}$
to
 $\mathsf{Points}(\mathsf{X},\leq ,\ast )$
) – and
$\mathsf{Points}(\mathsf{X},\leq ,\ast )$
) – and -
• is compatible with the compatibility relation
 $\ast$
, and
$\ast$
, and -
• we must show that
 $\textit{Op}$
is surjective.
$\textit{Op}$
is surjective.
We consider each property in turn:
-
•
 $\textit{Op}$
is a semilattice morphism.
$\textit{Op}$
is a semilattice morphism.
 $\textit{Op}(\bigvee X)=\bigvee _{x\in X} \textit{Op}(x)$
by Lemma 8.3.2, and
$\textit{Op}(\bigvee X)=\bigvee _{x\in X} \textit{Op}(x)$
by Lemma 8.3.2, and
 $\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
by Proposition 8.3.3(3).
$\textit{Op}({\boldsymbol \top }_{\mathsf{X}})=\mathsf{Points}(\mathsf{X},\leq ,\ast )$
by Proposition 8.3.3(3). -
•
 $\textit{Op}$
is compatible with
$\textit{Op}$
is compatible with
 $\ast$
.
$\ast$
.Unpacking Definition 10.2.1(2), we must show that
 $\textit{Op}(x)\between \textit{Op}(x')$
implies
$\textit{Op}(x)\between \textit{Op}(x')$
implies
 $x\ast x'$
. We use Proposition 8.3.3(2).
$x\ast x'$
. We use Proposition 8.3.3(2). -
•
 $\textit{Op}$
is surjective … by Lemma 8.4.5.
$\textit{Op}$
is surjective … by Lemma 8.4.5.
10.3 Functoriality of the maps
Definition 10.3.1. Suppose
![]() $g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast )\in \mathsf{SemiFrame}$
. Define a mapping
$g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast )\in \mathsf{SemiFrame}$
. Define a mapping
![]() $g^\circ :\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
by
$g^\circ :\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
by
Remark 10.3.2. We will show that
![]() $g^\circ$
from Definition 10.3.1 is an arrow in
$g^\circ$
from Definition 10.3.1 is an arrow in
![]() $\mathsf{SemiTop}$
. We will need to prove the following:
$\mathsf{SemiTop}$
. We will need to prove the following:
-
• If
 $P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
then
$P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
then
 $g^\circ (P)\in \mathsf{Points}(\mathsf{X}',\leq ',\ast ')$
.
$g^\circ (P)\in \mathsf{Points}(\mathsf{X}',\leq ',\ast ')$
. -
•
 $g^\circ$
is a morphism of semitopologies.
$g^\circ$
is a morphism of semitopologies.
Lemma 10.3.3 (
![]() $g^\circ$
well-defined). Suppose
$g^\circ$
well-defined). Suppose
![]() $g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
and suppose
$g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
and suppose
![]() $P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. Then
$P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
. Then
![]() $g^\circ (P)$
from Definition 10.3.1 is indeed in
$g^\circ (P)$
from Definition 10.3.1 is indeed in
![]() $\mathsf{Points}(\mathsf{X}',\leq ',\ast ')$
– and thus
$\mathsf{Points}(\mathsf{X}',\leq ',\ast ')$
– and thus
![]() $g^\circ$
is well-defined function from
$g^\circ$
is well-defined function from
![]() $\mathsf{Points}(\mathsf{X},\leq ,\ast )$
to
$\mathsf{Points}(\mathsf{X},\leq ,\ast )$
to
![]() $\mathsf{Points}(\mathsf{X}',\leq ',\ast ')$
.
$\mathsf{Points}(\mathsf{X}',\leq ',\ast ')$
.
Proof. For brevity write
We must check that
![]() $P'$
is a completely prime nonempty up-closed compatible subset of
$P'$
is a completely prime nonempty up-closed compatible subset of
![]() $\mathsf{X}'$
. We consider each property in turn:
$\mathsf{X}'$
. We consider each property in turn:
-
(1)
 $P'$
is completely prime.
$P'$
is completely prime.
Consider some
 $X'\subseteq P'$
and suppose
$X'\subseteq P'$
and suppose
 $g(\bigvee X')\in P$
. By Definition 10.2.1(1)
$g(\bigvee X')\in P$
. By Definition 10.2.1(1)
 $g$
is a semilattice homomorphism, so by Definition 7.1.1(2)
$g$
is a semilattice homomorphism, so by Definition 7.1.1(2)
 $g(\bigvee X')=\bigvee _{x'\in X'}g(x')$
. Thus
$g(\bigvee X')=\bigvee _{x'\in X'}g(x')$
. Thus
 $\bigvee _{x'\in X'} g(x')\in P$
. By assumption
$\bigvee _{x'\in X'} g(x')\in P$
. By assumption
 $P$
is completely prime, so
$P$
is completely prime, so
 $g(x')\in P$
for some
$g(x')\in P$
for some
 $x'\in X'$
. Thus
$x'\in X'$
. Thus
 $x'\in P'$
for that
$x'\in P'$
for that
 $x'$
. Since
$x'$
. Since
 $X'$
was arbitrary, it follows that
$X'$
was arbitrary, it follows that
 $P'$
is completely prime.
$P'$
is completely prime. -
(2)
 $P'$
is nonempty.
$P'$
is nonempty.
By assumption
 $g$
is an arrow in
$g$
is an arrow in
 $\mathsf{SemiFrame}$
(i.e. a semiframe morphism) and unpacking Definition 10.2.1(1) it follows that it is a semilattice homomorphism. In particular by Definition 7.1.1(2)
$\mathsf{SemiFrame}$
(i.e. a semiframe morphism) and unpacking Definition 10.2.1(1) it follows that it is a semilattice homomorphism. In particular by Definition 7.1.1(2)
 $g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
, and by Lemma 8.2.1(1)
$g({\boldsymbol \top }_{\mathsf{X}'})={\boldsymbol \top }_{\mathsf{X}}$
, and by Lemma 8.2.1(1)
 ${\boldsymbol \top }_{\mathsf{X}}\in P$
. Thus
${\boldsymbol \top }_{\mathsf{X}}\in P$
. Thus
 ${\boldsymbol \top }_{\mathsf{X}'}\in P'$
, so
${\boldsymbol \top }_{\mathsf{X}'}\in P'$
, so
 $P'$
is nonempty.
$P'$
is nonempty. -
(3)
 $P'$
is up-closed.
$P'$
is up-closed.
Suppose
 $x'\in P'$
and
$x'\in P'$
and
 $x'\leq x''$
. By construction
$x'\leq x''$
. By construction
 $g(x')\in P$
. By Lemma 7.1.4 (because
$g(x')\in P$
. By Lemma 7.1.4 (because
 $g$
is a semilattice morphism by Definition 10.2.1(1))
$g$
is a semilattice morphism by Definition 10.2.1(1))
 $g$
is monotone, so
$g$
is monotone, so
 $g(x')\leq g(x'')$
. By assumption in Definition 8.1.1(3)
$g(x')\leq g(x'')$
. By assumption in Definition 8.1.1(3)
 $P$
is up-closed, so that
$P$
is up-closed, so that
 $g(x'')\in P$
and thus
$g(x'')\in P$
and thus
 $x''\in P'$
as required.
$x''\in P'$
as required. -
(4)
 $P'$
is compatible.
$P'$
is compatible.
Suppose
 $x',x''\in P'$
. Thus
$x',x''\in P'$
. Thus
 $g(x'),g(x'')\in P$
. By assumption in Definition 8.1.1(4)
$g(x'),g(x'')\in P$
. By assumption in Definition 8.1.1(4)
 $P$
is compatible, so
$P$
is compatible, so
 $g(x')\ast g(x'')$
. By compatibility of
$g(x')\ast g(x'')$
. By compatibility of
 $g$
(Definition 10.2.1(2)) it follows that
$g$
(Definition 10.2.1(2)) it follows that
 $x'\ast x''$
. Thus
$x'\ast x''$
. Thus
 $P'$
is compatible.
$P'$
is compatible.
Remark 10.3.4. Note on design: If we want to impose further conditions on being an abstract point (such as those discussed in Remark 8.1.6) then Lemma 10.3.3 would need to be extended to show that these further conditions are preserved by the
![]() $g^\circ$
operation, so that for
$g^\circ$
operation, so that for
![]() $P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
an abstract point in
$P\in \mathsf{Points}(\mathsf{X},\leq ,\ast )$
an abstract point in
![]() $(\mathsf{X},\leq ,\ast )$
,
$(\mathsf{X},\leq ,\ast )$
,
![]() $g^\circ (P)=\{x'\in \mathsf{X}'\mid g(x')\in P\}$
is an abstract point in
$g^\circ (P)=\{x'\in \mathsf{X}'\mid g(x')\in P\}$
is an abstract point in
![]() $(\mathsf{X}',\leq ',\ast ')$
.
$(\mathsf{X}',\leq ',\ast ')$
.
For example: consider what would happen if we add the extra condition on semifilters from Remark 8.1.6. Then the
![]() $P'$
defined in the proof of Lemma 10.3.3 above might not be closed under this additional condition (it will be if
$P'$
defined in the proof of Lemma 10.3.3 above might not be closed under this additional condition (it will be if
![]() $g$
is surjective). This could be mended by closing
$g$
is surjective). This could be mended by closing
![]() $P'$
under greatest lower bounds that are not
$P'$
under greatest lower bounds that are not
![]() $\boldsymbol \bot$
, but that in turn might compromise the property of being completely prime. These comments are not a proof that the problems would be insuperable; but they suggest that complexity would be added. For now, we prefer to keep things simple!
$\boldsymbol \bot$
, but that in turn might compromise the property of being completely prime. These comments are not a proof that the problems would be insuperable; but they suggest that complexity would be added. For now, we prefer to keep things simple!
Lemma 10.3.5.
Suppose
![]() $g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
, and suppose
$g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
, and suppose
![]() $x'\in \mathsf{X}'$
. Then
$x'\in \mathsf{X}'$
. Then
Proof.
Consider an abstract point
![]() $P\in \mathsf{Point}(\mathsf{Gr}(\mathsf{X}',\leq ',\ast '))$
. We just chase definitions:
$P\in \mathsf{Point}(\mathsf{Gr}(\mathsf{X}',\leq ',\ast '))$
. We just chase definitions:

The choice of
![]() $P$
was arbitrary, so
$P$
was arbitrary, so
![]() $(g^\circ )^{\text{-}1}(\textit{Op}(x'))=\textit{Op}(g(x'))$
as required.
$(g^\circ )^{\text{-}1}(\textit{Op}(x'))=\textit{Op}(g(x'))$
as required.
Lemma 10.3.6 (
![]() $g^\circ$
continuous). Suppose
$g^\circ$
continuous). Suppose
![]() $g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
. Then
$g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
. Then
![]() $g^\circ :\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
is continuous:
$g^\circ :\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
is continuous:
for every
![]() $\mathscr O'\in \mathsf{Open}(\mathsf{St}(\mathsf{X}',\leq ',\ast '))$
.
$\mathscr O'\in \mathsf{Open}(\mathsf{St}(\mathsf{X}',\leq ',\ast '))$
.
Proof.
By Definition 8.4.3,
![]() $\mathscr O'=\textit{Op}(x')$
for some
$\mathscr O'=\textit{Op}(x')$
for some
![]() $x'\in \mathsf{X}'$
. By Lemma 10.3.5
$x'\in \mathsf{X}'$
. By Lemma 10.3.5
![]() $(g^\circ )^{\text{-}1}(\textit{Op}(x'))=\textit{Op}(g(x'))$
. By Definition 8.4.3(2)
$(g^\circ )^{\text{-}1}(\textit{Op}(x'))=\textit{Op}(g(x'))$
. By Definition 8.4.3(2)
![]() $\textit{Op}(g(x'))\in \mathsf{Open}(\mathsf{St}(\mathsf{X},\leq ,\ast ))$
.
$\textit{Op}(g(x'))\in \mathsf{Open}(\mathsf{St}(\mathsf{X},\leq ,\ast ))$
.
Proposition 10.3.7 (Functoriality).
-
(1) Suppose
 $f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}') \in \mathsf{SemiTop}$
(so
$f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}') \in \mathsf{SemiTop}$
(so
 $f$
is a continuous map on underlying points).
$f$
is a continuous map on underlying points).
Then
 $f^{\text{-}1}$
is an arrow
$f^{\text{-}1}$
is an arrow
 $\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')\to \mathsf{Fr}(\mathsf{P},\mathsf{Open})$
in
$\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')\to \mathsf{Fr}(\mathsf{P},\mathsf{Open})$
in
 $\mathsf{SemiFrame}$
.
$\mathsf{SemiFrame}$
. -
(2) Suppose
 $g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
.
$g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast ) \in \mathsf{SemiFrame}$
.Then
 $g^\circ$
from Definition 10.3.1 is an arrow
$g^\circ$
from Definition 10.3.1 is an arrow
 $\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
in
$\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
in
 $\mathsf{SemiTop}$
.
$\mathsf{SemiTop}$
. -
(3) The assignments
 $f\mapsto f^{\text{-}1}$
and
$f\mapsto f^{\text{-}1}$
and
 $g\mapsto g^\circ$
are
functorial
– they map identity maps to identity maps, and commute with function composition.
$g\mapsto g^\circ$
are
functorial
– they map identity maps to identity maps, and commute with function composition.
Proof. We consider each part in turn:
-
(1) Following Definition 10.2.1, we must check that
 $f^{\text{-}1}$
is a morphism of semiframes. We just unpack what this means and see that the required properties are just facts of taking inverse images:
$f^{\text{-}1}$
is a morphism of semiframes. We just unpack what this means and see that the required properties are just facts of taking inverse images:-
–
 $f^{\text{-}1}$
commutes with joins, that is with
$f^{\text{-}1}$
commutes with joins, that is with
 $\bigcup$
.
$\bigcup$
.This is a fact of inverse images.
-
–
 $f^{\text{-}1}$
maps
$f^{\text{-}1}$
maps
 ${\boldsymbol \top }_{\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')}=\mathsf{P}'$
to
${\boldsymbol \top }_{\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')}=\mathsf{P}'$
to
 ${\boldsymbol \top }_{\mathsf{Fr}(\mathsf{P},\mathsf{Open})}=\mathsf{P}$
.
${\boldsymbol \top }_{\mathsf{Fr}(\mathsf{P},\mathsf{Open})}=\mathsf{P}$
.This is a fact of inverse images.
-
–
 $f^{\text{-}1}$
is compatible, meaning that
$f^{\text{-}1}$
is compatible, meaning that
 $f^{\text{-}1}(O')\between f^{\text{-}1}(O'')$
implies
$f^{\text{-}1}(O')\between f^{\text{-}1}(O'')$
implies
 $O'\between O''$
.
$O'\between O''$
.This is a fact of inverse images.
-
-
(2) We must check that
 $g^\circ$
is continuous. This is Lemma 10.3.6.
$g^\circ$
is continuous. This is Lemma 10.3.6. -
(3) Checking functoriality is routine, but we sketch the reasoning anyway:
-
– Consider the identity function
 $\textit{id}$
on some semitopology
$\textit{id}$
on some semitopology
 $(\mathsf{P},\mathsf{Open})$
. Then
$(\mathsf{P},\mathsf{Open})$
. Then
 $\textit{id}^{\text{-}1}$
should be the identity function on
$\textit{id}^{\text{-}1}$
should be the identity function on
 $(\mathsf{Open},\subseteq ,\between )$
. It is.
$(\mathsf{Open},\subseteq ,\between )$
. It is. -
– Consider
 $f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
and
$f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
and
 $f':(\mathsf{P}',\mathsf{Open}')\to (\mathsf{P}'',\mathsf{Open}'')$
. Then
$f':(\mathsf{P}',\mathsf{Open}')\to (\mathsf{P}'',\mathsf{Open}'')$
. Then
 $(f'\circ f)^{\text{-}1}$
should be equal to
$(f'\circ f)^{\text{-}1}$
should be equal to
 $f^{\text{-}1}\circ (f')^{\text{-}1}$
. It is.
$f^{\text{-}1}\circ (f')^{\text{-}1}$
. It is. -
– Consider the identity function
 $\textit{id}$
on
$\textit{id}$
on
 $(\mathsf{X},\leq ,\ast )$
. Then
$(\mathsf{X},\leq ,\ast )$
. Then
 $\textit{id}^\circ$
should be the identity function on
$\textit{id}^\circ$
should be the identity function on
 $\mathsf{Points}(\mathsf{X},\leq ,\ast )$
. We look at Definition 10.3.1 and see that this amounts to checking that
$\mathsf{Points}(\mathsf{X},\leq ,\ast )$
. We look at Definition 10.3.1 and see that this amounts to checking that
 $P=\{x\in \mathsf{X} \mid \textit{id}(x)\in P\}$
. It is.
$P=\{x\in \mathsf{X} \mid \textit{id}(x)\in P\}$
. It is. -
– Consider
 $g:(\mathsf{X},\leq ,\ast )\to (\mathsf{X}',\leq ',\ast ')$
and
$g:(\mathsf{X},\leq ,\ast )\to (\mathsf{X}',\leq ',\ast ')$
and
 $g':(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X}'',\leq '',\ast '')$
and consider some
$g':(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X}'',\leq '',\ast '')$
and consider some
 $P''\in \mathsf{Points}(\mathsf{X}'',\leq '',\ast '')$
. Then
$P''\in \mathsf{Points}(\mathsf{X}'',\leq '',\ast '')$
. Then
 $(g'\circ g)^\circ (P'')$
should be equal to
$(g'\circ g)^\circ (P'')$
should be equal to
 $(g^\circ \circ (g')^\circ )(P'')$
. We look at Definition 10.3.1 and see that this amounts to checking that
$(g^\circ \circ (g')^\circ )(P'')$
. We look at Definition 10.3.1 and see that this amounts to checking that
 $\{x\in \mathsf{X} \mid g'(g(x))\in P''\}=\{x\in \mathsf{X} \mid g(x)\in P'\}$
where
$\{x\in \mathsf{X} \mid g'(g(x))\in P''\}=\{x\in \mathsf{X} \mid g(x)\in P'\}$
where
 $P'=\{x'\in \mathsf{X}' \mid g'(x')\in P''\}$
. Unpacking these definitions, we see that the equality does indeed hold.
$P'=\{x'\in \mathsf{X}' \mid g'(x')\in P''\}$
. Unpacking these definitions, we see that the equality does indeed hold.
-
10.4 Sober semitopologies are dual to spatial semiframes
Remark 10.4.1. A categorical duality between two categories
![]() $\mathbb C$
and
$\mathbb C$
and
![]() $\mathbb D$
is a categorical equivalence between
$\mathbb D$
is a categorical equivalence between
![]() $\mathbb C$
and
$\mathbb C$
and
![]() $\mathbb D^{op}$
. See (Mac Lane, Reference Mac Lane1971, IV.4) or (Riehl, Reference Riehl2016, Section 1.5 & Exercise 4.2.i).Footnote
27
It suffices to provide an adjoint pair of functors whose unit and counit are natural isomorphisms.Footnote
28
$\mathbb D^{op}$
. See (Mac Lane, Reference Mac Lane1971, IV.4) or (Riehl, Reference Riehl2016, Section 1.5 & Exercise 4.2.i).Footnote
27
It suffices to provide an adjoint pair of functors whose unit and counit are natural isomorphisms.Footnote
28
There are many duality results in the literature. The duality between topologies and frames is described (e.g.,) in Mac Lane and Moerdijk (Reference Mac Lane and Moerdijk1992, p. 479, Corollary 4). A duality between distributive lattices and coherent spaces is in Johnstone (Reference Johnstone1986, p. 66). There is the classic duality by Stone between Boolean algebras and compact Hausdorff spaces with a basis of clopen sets (Stone (Reference Stone1936); Johnstone (Reference Johnstone1986). An encyclopedic treatment is in Caramello (Reference Caramello2011), with a rather good overview in Example 2.9 on p. 17.
Theorem 10.4.2 states a duality result between
![]() $\mathsf{Sober}$
and
$\mathsf{Sober}$
and
![]() $\mathsf{Spatial}$
, thus appending another item to this extensive canon.
$\mathsf{Spatial}$
, thus appending another item to this extensive canon.
It also constructively moves us forward in studying semitopologies, because it gives us an algebraic treatment of semitopologies, and a formal framework for studying morphisms between semitopologies. For instance: taking morphisms to be continuous functions is sensible not just because this is also how things work for topologies, but also because this is what is categorically dual to the
![]() ${\leq }/{\ast }$
-homomorphisms between semiframes (Definition 10.2.1). And of course, if we become interested in different notions of semitopology morphism (a flavour of these is in Remark 12.3.1) then the algebraic framework gives us a distinct mathematical light with which to inspect and evaluate them.
${\leq }/{\ast }$
-homomorphisms between semiframes (Definition 10.2.1). And of course, if we become interested in different notions of semitopology morphism (a flavour of these is in Remark 12.3.1) then the algebraic framework gives us a distinct mathematical light with which to inspect and evaluate them.
Theorem 10.4.2.
The maps
![]() $\mathsf{St}$
(Definition 8.4.3) and
$\mathsf{St}$
(Definition 8.4.3) and
![]() $\mathsf{Fr}$
(Definition 7.3.4), with actions on arrows as described in Proposition 10.3.7
, form a categorical duality between the categories
$\mathsf{Fr}$
(Definition 7.3.4), with actions on arrows as described in Proposition 10.3.7
, form a categorical duality between the categories
Proof. There are various things to check:
-
• Proposition 9.3.5 shows that
 $\mathsf{St}$
maps spatial semiframes to sober semitopologies.
$\mathsf{St}$
maps spatial semiframes to sober semitopologies. -
• Proposition 9.2.5 shows that
 $\mathsf{Fr}$
maps sober semitopologies to spatial semiframes.
$\mathsf{Fr}$
maps sober semitopologies to spatial semiframes. -
• By Proposition 10.3.7 the maps
 $f\mapsto f^{\text{-}1}$
(inverse image) and
$f\mapsto f^{\text{-}1}$
(inverse image) and
 $g\mapsto g^\circ$
(Definition 10.3.1) are functorial.
$g\mapsto g^\circ$
(Definition 10.3.1) are functorial. -
• The equivalence morphisms are given by the bijections
 $\textit{Op}$
and
$\textit{Op}$
and
 $\textit{nbhd}$
:
$\textit{nbhd}$
:-
–
 $\textit{Op}$
is from Definition 8.3.1. By Lemma 10.2.2
$\textit{Op}$
is from Definition 8.3.1. By Lemma 10.2.2
 $\textit{Op}$
is a morphism
$\textit{Op}$
is a morphism
 $(\mathsf{X},\leq ,\ast )\to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
in
$(\mathsf{X},\leq ,\ast )\to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
in
 $\mathsf{Spatial}$
that is surjective on underlying sets. Injectivity is from Proposition 9.1.4(3).
$\mathsf{Spatial}$
that is surjective on underlying sets. Injectivity is from Proposition 9.1.4(3). -
–
 $\textit{nbhd}$
is from Definition 2.3.1. By Theorem10.1.4
$\textit{nbhd}$
is from Definition 2.3.1. By Theorem10.1.4
 $\textit{nbhd}$
is a morphism
$\textit{nbhd}$
is a morphism
 $(\mathsf{P},\mathsf{Open})\to \mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
in
$(\mathsf{P},\mathsf{Open})\to \mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
in
 $\mathsf{Sober}$
. It is a bijection on underlying sets by the sobriety condition in Definition 9.3.1.
$\mathsf{Sober}$
. It is a bijection on underlying sets by the sobriety condition in Definition 9.3.1.
-
Finally, we must check naturality of
![]() $\textit{Op}$
and
$\textit{Op}$
and
![]() $\textit{nbhd}$
, which means (as standard) checking commutativity of the following diagrams:
$\textit{nbhd}$
, which means (as standard) checking commutativity of the following diagrams:

We proceed as follows:
-
• Suppose
 $g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast )$
in
$g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast )$
in
 $\mathsf{Spatial}$
, so that
$\mathsf{Spatial}$
, so that
 $g^\circ :\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
in
$g^\circ :\mathsf{St}(\mathsf{X},\leq ,\ast )\to \mathsf{St}(\mathsf{X}',\leq ',\ast ')$
in
 $\mathsf{Sober}$
and
$\mathsf{Sober}$
and
 $(g^\circ )^{\text{-}1}:\mathsf{Fr}\,\mathsf{St}(\mathsf{X}',\leq ',\ast ')\to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
in
$(g^\circ )^{\text{-}1}:\mathsf{Fr}\,\mathsf{St}(\mathsf{X}',\leq ',\ast ')\to \mathsf{Fr}\,\mathsf{St}(\mathsf{X},\leq ,\ast )$
in
 $\mathsf{Spatial}$
. To prove naturality we must check thatfor every
$\mathsf{Spatial}$
. To prove naturality we must check thatfor every \begin{equation*} (g^\circ )^{\text{-}1}(\textit{Op}(x)) = \textit{Op}(g(x)) \end{equation*}
\begin{equation*} (g^\circ )^{\text{-}1}(\textit{Op}(x)) = \textit{Op}(g(x)) \end{equation*}
 $x\in \mathsf{X}$
. This is just Lemma 10.3.5.
$x\in \mathsf{X}$
. This is just Lemma 10.3.5.
-
• Suppose
 $f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
in
$f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
in
 $\mathsf{SemiTop}$
, so that
$\mathsf{SemiTop}$
, so that
 $f^{\text{-}1}:\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')\to \mathsf{Fr}(\mathsf{P},\mathsf{Open})$
in
$f^{\text{-}1}:\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')\to \mathsf{Fr}(\mathsf{P},\mathsf{Open})$
in
 $\mathsf{Spatial}$
and
$\mathsf{Spatial}$
and
 $(f^{\text{-}1})^\circ :\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})\to \mathsf{St}\,\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')$
in
$(f^{\text{-}1})^\circ :\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})\to \mathsf{St}\,\mathsf{Fr}(\mathsf{P}',\mathsf{Open}')$
in
 $\mathsf{SemiTop}$
. To prove naturality we must check thatWe just chase definitions, for an open set
$\mathsf{SemiTop}$
. To prove naturality we must check thatWe just chase definitions, for an open set \begin{equation*} (f^{\text{-}1})^\circ (\textit{nbhd}(p)) = \textit{nbhd}(f(p)) . \end{equation*}
\begin{equation*} (f^{\text{-}1})^\circ (\textit{nbhd}(p)) = \textit{nbhd}(f(p)) . \end{equation*}
 $O'\in \mathsf{Open}'$
:
$O'\in \mathsf{Open}'$
:
Remark 10.4.3. We review the background to Theorem 10.4.2:
-
(1) A semitopology
 $(\mathsf{P},\mathsf{Open})$
is a set of points
$(\mathsf{P},\mathsf{Open})$
is a set of points
 $\mathsf{P}$
and a set of open sets
$\mathsf{P}$
and a set of open sets
 $\mathsf{Open}\subseteq \textit{pow}(\mathsf{P})$
that contains
$\mathsf{Open}\subseteq \textit{pow}(\mathsf{P})$
that contains
 $\mathsf{P}$
and is closed under arbitrary (possibly empty) unions (Definition 1.2.2).
$\mathsf{P}$
and is closed under arbitrary (possibly empty) unions (Definition 1.2.2). -
(2) A morphism between semitopologies is a continuous function, just as for topologies (Definition 10.1.1(1)).
-
(3) A semiframe
 $(\mathsf{X},\leq ,\ast )$
is a complete join-semilattice
$(\mathsf{X},\leq ,\ast )$
is a complete join-semilattice
 $(\mathsf{X},\leq )$
with a properly reflexive distributive compatibility relation
$(\mathsf{X},\leq )$
with a properly reflexive distributive compatibility relation
 $\ast$
(Definition 7.3.1).
$\ast$
(Definition 7.3.1). -
(4) A morphism between semiframes is a morphism of complete join-semilattices with
 $\boldsymbol \top$
that is compatible with the compatibility relation (Definition 10.2.1(1)).
$\boldsymbol \top$
that is compatible with the compatibility relation (Definition 10.2.1(1)). -
(5) An abstract point of a semitopology
 $(\mathsf{P},\mathsf{Open})$
is a completely prime nonempty up-closed compatible subset
$(\mathsf{P},\mathsf{Open})$
is a completely prime nonempty up-closed compatible subset
 $P\subseteq \mathsf{Open}$
(Definition 8.1.1(7)).
$P\subseteq \mathsf{Open}$
(Definition 8.1.1(7)). -
(6) A semitopology is sober when the neighbourhood semifilter map
 $p\in \mathsf{P}\mapsto \textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\}$
is injective and surjective between the points of
$p\in \mathsf{P}\mapsto \textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\}$
is injective and surjective between the points of
 $\mathsf{P}$
and the abstract points of
$\mathsf{P}$
and the abstract points of
 $\mathsf{P}$
(Definition 9.3.1).
$\mathsf{P}$
(Definition 9.3.1). -
(7) By Theorem 10.1.4, and as discussed in Remark 10.1.5, every (possibly non-sober) semitopology
 $(\mathsf{P},\mathsf{Open})$
maps into its soberification
$(\mathsf{P},\mathsf{Open})$
maps into its soberification
 $\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
, which has an isomorphic semiframe of open sets. So even if our semitopology
$\mathsf{St}\,\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
, which has an isomorphic semiframe of open sets. So even if our semitopology
 $(\mathsf{P},\mathsf{Open})$
is not sober, there is a standard recipe to make it so.
$(\mathsf{P},\mathsf{Open})$
is not sober, there is a standard recipe to make it so. -
(8) A semiframe is spatial when
 $x\in \mathsf{X} \mapsto \textit{Op}(x)=\{P\in \mathsf{Point} \mid x\in P\}$
respects
$x\in \mathsf{X} \mapsto \textit{Op}(x)=\{P\in \mathsf{Point} \mid x\in P\}$
respects
 $\leq$
and
$\leq$
and
 $\ast$
in senses make formal in Definition 9.1.2 and Proposition 9.1.4.
$\ast$
in senses make formal in Definition 9.1.2 and Proposition 9.1.4. -
(9) Sober semitopologies and continuous functions between them, and spatial semiframes and semiframe morphisms between them, are categorically dual (Theorem 10.4.2).
Remark 10.4.4. Note what Theorem 10.4.2 does not do: it does not give a duality between all semitopologies and all semiframes; it gives a duality between sober semitopologies and spatial semiframes. This in itself is nothing new – the topological duality is just the same – but what is interesting is that our motivation for studying semitopologies comes from practical network systems. These tend to be (finite) non-sober semitopologies – non-sober, because a guarantee of sobriety cannot be enforced, and anyway it is precisely the point of the exercise to achieve coordination, without explicitly requiring every possible constellation of cooperating agents to be explicitly represented by a point.
It is true that by Theorem 10.1.4 every non-sober
![]() $T_0$
semitopology can be embedded into a sober one without affecting the semiframe of open sets, but this makes the system to which it corresponds larger, by adding points. Thus the duality in Theorem 10.4.2 is a mathematical statement, but not necessarily a practical one – and this is as expected, because we knew that this is an abstract result.
$T_0$
semitopology can be embedded into a sober one without affecting the semiframe of open sets, but this makes the system to which it corresponds larger, by adding points. Thus the duality in Theorem 10.4.2 is a mathematical statement, but not necessarily a practical one – and this is as expected, because we knew that this is an abstract result.
![]() $\textit{nbhd}$
maps a point to a set of (open) sets; and
$\textit{nbhd}$
maps a point to a set of (open) sets; and
![]() $\textit{Op}$
maps an (open) set of points to a set of sets of (open) sets. Of course these might not be computationally optimal.
$\textit{Op}$
maps an (open) set of points to a set of sets of (open) sets. Of course these might not be computationally optimal.
11. Well-Behavedness Conditions, Dually
We now study how properties of semifilters and abstract points correspond to the well-behavedness properties which we found useful in studying semitopologies – for example topens, regularity, and being unconflicted (Definitions 3.2.2, 4.1.4 and 5.3.1).
11.1 (Maximal) semifilters and transitive elements
Remark 11.1.1 (Semifilters are not filters). We know that semifilters do not necessarily behave like filters. For instance:
-
(1) It is possible for a finite semifilter to have more than one minimal element, because the closure under binary meets condition of filters is replaced by a weaker compatibility condition (see also Remarks 8.1.3 and 8.1.6).
-
(2) There are more semifilters than proper filters – even if the underlying space is a topology. For example, the discrete semitopology on
 $\{0,1,2\}$
(whose open sets are all subsets of the space) is a topology. Every proper filter in this space is a semifilter, but it also has a semifilter
$\{0,1,2\}$
(whose open sets are all subsets of the space) is a topology. Every proper filter in this space is a semifilter, but it also has a semifilter
 $\bigl \{\{0,1\},\{1,2\},\{2,0\},\{0,1,2\}\bigr \}$
(see the top-left diagram in Figure 6) and this is not a filter.
$\bigl \{\{0,1\},\{1,2\},\{2,0\},\{0,1,2\}\bigr \}$
(see the top-left diagram in Figure 6) and this is not a filter.
More on this in Section 8.2.2.
In summary: semifilters are different and we cannot necessarily take their behaviour for granted without checking it. We now examine them in more detail.
We start with some easy definitions and results:
Notation 11.1.2.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $X,Y\subseteq \mathsf{X}$
and
$X,Y\subseteq \mathsf{X}$
and
![]() $x\in \mathsf{X}$
. Then we generalise
$x\in \mathsf{X}$
. Then we generalise
![]() $x\ast y$
to
$x\ast y$
to
![]() $x\ast Y$
,
$x\ast Y$
,
![]() $X\ast y$
, and
$X\ast y$
, and
![]() $X\ast Y$
as follows:
$X\ast Y$
as follows:
-
(1) Write
 $x\ast Y$
for
$x\ast Y$
for
 $\forall y{\in }Y.x\ast y$
.
$\forall y{\in }Y.x\ast y$
. -
(2) Write
 $X\ast y$
for
$X\ast y$
for
 $\forall x{\in }X.x\ast y$
.
$\forall x{\in }X.x\ast y$
. -
(3) Write
 $X\ast Y$
for
$X\ast Y$
for
 $\forall x{\in }X.\forall y{\in }Y.x\ast y$
.
$\forall x{\in }X.\forall y{\in }Y.x\ast y$
.
We read
![]() $x\ast Y$
as ‘
$x\ast Y$
as ‘
![]() $x$
is
compatible
with
$x$
is
compatible
with
![]() $Y$
’, and similarly for
$Y$
’, and similarly for
![]() $X\ast y$
and
$X\ast y$
and
![]() $X\ast Y$
.
$X\ast Y$
.
Remark 11.1.3. We will see later on in Lemma 11.7.1 that
![]() $X\ast X'$
generalises
$X\ast X'$
generalises
![]() $p\mathrel {\between } p'$
, in the sense that if
$p\mathrel {\between } p'$
, in the sense that if
![]() $X=\textit{nbhd}(p)$
and
$X=\textit{nbhd}(p)$
and
![]() $X'=\textit{nbhd}(p')$
, then
$X'=\textit{nbhd}(p')$
, then
![]() $p\mathrel {\between } p'$
if and only if
$p\mathrel {\between } p'$
if and only if
![]() $\textit{nbhd}(p)\ast \textit{nbhd}(p')$
.
$\textit{nbhd}(p)\ast \textit{nbhd}(p')$
.
Lemma 11.1.4 (Characterisation of maximal semifilters). Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then the following conditions are equivalent:
$F\subseteq \mathsf{X}$
is a semifilter. Then the following conditions are equivalent:
-
(1)
 $F$
is maximal.
$F$
is maximal.
-
(2) For every
 $x\in \mathsf{X}$
,
$x\in \mathsf{X}$
,
 $x\ast F$
if and only if
$x\ast F$
if and only if
 $x\in F$
.
$x\in F$
.
Proof. We prove two implications:
-
• Suppose
 $F$
is a maximal semifilter.
$F$
is a maximal semifilter.
Suppose
 $x\in F$
. Then
$x\in F$
. Then
 $x\ast F$
is immediate from Notation 11.1.2(1) and semifilter compatibility (Definition 8.1.1(4)).
$x\ast F$
is immediate from Notation 11.1.2(1) and semifilter compatibility (Definition 8.1.1(4)).Suppose
 $x\ast F$
; thus by Notation 11.1.2(1)
$x\ast F$
; thus by Notation 11.1.2(1)
 $x$
is compatible with (every element of)
$x$
is compatible with (every element of)
 $F$
. We note that the
$F$
. We note that the
 $\leq$
-up-closure of
$\leq$
-up-closure of
 $\{x\}\cup F$
is a semifilter (nonempty, up-closed, compatible). By maximality,
$\{x\}\cup F$
is a semifilter (nonempty, up-closed, compatible). By maximality,
 $x\in F$
.
$x\in F$
. -
• Suppose
 $x\ast F$
if and only if
$x\ast F$
if and only if
 $x\in F$
, for every
$x\in F$
, for every
 $x\in \mathsf{X}$
.
$x\in \mathsf{X}$
.Suppose
 $F'$
is a semifilter and
$F'$
is a semifilter and
 $F\subseteq F'$
. Consider
$F\subseteq F'$
. Consider
 $x'\in F'$
. Then
$x'\in F'$
. Then
 $x\ast F$
by compatibility of
$x\ast F$
by compatibility of
 $F'$
, and so
$F'$
, and so
 $x\in F$
. Thus,
$x\in F$
. Thus,
 $F'\subseteq F$
.
$F'\subseteq F$
.
Definition 11.1.5. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $x\in \mathsf{X}$
. Call
$x\in \mathsf{X}$
. Call
![]() $x$
transitive when:
$x$
transitive when:
-
(1)
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
.
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
. -
(2)
 $x'\ast x\ast x''$
implies
$x'\ast x\ast x''$
implies
 $x'\ast x''$
, for every
$x'\ast x''$
, for every
 $x',x''\in \mathsf{X}$
.
$x',x''\in \mathsf{X}$
.
‘Being topen’ in semitopologies (Definition 3.2.2(2)) corresponds to ‘being transitive’ in semiframes (Definition 11.1.5):
Lemma 11.1.6 (Characterisation of topen sets). Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $O\in \mathsf{Open}$
. Then the following are equivalent:
$O\in \mathsf{Open}$
. Then the following are equivalent:
-
(1)
 $O$
is topen in
$O$
is topen in
 $(\mathsf{P},\mathsf{Open})$
in the sense of Definition 3.2.2(2).
$(\mathsf{P},\mathsf{Open})$
in the sense of Definition 3.2.2(2).
-
(2)
 $O$
is transitive in
$O$
is transitive in
 $(\mathsf{Open},\subseteq ,\between )$
in the sense of Definition 11.1.5
.Footnote
29
$(\mathsf{Open},\subseteq ,\between )$
in the sense of Definition 11.1.5
.Footnote
29
Proof.
We unpack the definitions and note that the condition for being topen – being a nonempty open set that is transitive for
![]() $\between$
– is identical to the condition for being transitive in
$\between$
– is identical to the condition for being transitive in
![]() $(\mathsf{Open},\subseteq ,\between )$
– being a non-
$(\mathsf{Open},\subseteq ,\between )$
– being a non-
![]() ${\boldsymbol \bot }_{\mathsf{Open}}$
element that is transitive for
${\boldsymbol \bot }_{\mathsf{Open}}$
element that is transitive for
![]() ${\ast }={\between }$
.
${\ast }={\between }$
.
11.2 The compatibility system
 $x^\ast$
$x^\ast$
Definition 11.2.1. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $x\in \mathsf{X}$
. Then define
$x\in \mathsf{X}$
. Then define
![]() $x^\ast$
the compatibility system of
$x^\ast$
the compatibility system of
![]() $x$
by
$x$
by
Lemma 11.2.2.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $X\subseteq \mathsf{X}$
. Then
$X\subseteq \mathsf{X}$
. Then
![]() $(\bigvee X)^\ast = \bigcup _{x{\in }X} x^\ast$
.
$(\bigvee X)^\ast = \bigcup _{x{\in }X} x^\ast$
.
Proof. We just follow the definitions:

Lemma 11.2.3.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $x\in \mathsf{X}$
is transitive. Then the following are equivalent for every
$x\in \mathsf{X}$
is transitive. Then the following are equivalent for every
![]() $y\in \mathsf{X}$
:
$y\in \mathsf{X}$
:
Proof. We prove a cycle of implications:
-
• Suppose
 $y\ast x$
. Then
$y\ast x$
. Then
 $y\in x^\ast$
is direct from Definition 11.2.1.
$y\in x^\ast$
is direct from Definition 11.2.1. -
• Suppose
 $y\in x^\ast$
. Then
$y\in x^\ast$
. Then
 $y\ast x^\ast$
– meaning by Notation 11.1.2(1) that
$y\ast x^\ast$
– meaning by Notation 11.1.2(1) that
 $y\ast x'$
for every
$y\ast x'$
for every
 $x'\in x^\ast$
– follows by transitivity of
$x'\in x^\ast$
– follows by transitivity of
 $x$
.
$x$
. -
• Suppose
 $y\ast x^\ast$
. By proper reflexivity of
$y\ast x^\ast$
. By proper reflexivity of
 $\ast$
(Definition 7.2.1(2); since
$\ast$
(Definition 7.2.1(2); since
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
)
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
)
 $x\in x^\ast$
, and
$x\in x^\ast$
, and
 $y\ast x$
follows.
$y\ast x$
follows.
Proposition 11.2.4.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
$(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
![]() ${\boldsymbol \bot }_{\mathsf{X}}\neq x\in \mathsf{X}$
. Then the following are equivalent:
${\boldsymbol \bot }_{\mathsf{X}}\neq x\in \mathsf{X}$
. Then the following are equivalent:
-
(1)
 $x$
is transitive.
$x$
is transitive.
-
(2)
 $x^\ast$
is a completely prime semifilter (i.e. an abstract point).
$x^\ast$
is a completely prime semifilter (i.e. an abstract point).
-
(3)
 $x^\ast$
is a semifilter.
$x^\ast$
is a semifilter.
-
(4)
 $x^\ast$
is compatible.
$x^\ast$
is compatible.
-
(5)
 $x^\ast$
is a maximal semifilter.
$x^\ast$
is a maximal semifilter.
Proof. We first prove a cycle of implications between parts 1–4:
-
(1) Suppose
 $x$
is transitive. We need to check that
$x$
is transitive. We need to check that
 $x^\ast$
is nonempty, up-closed, compatible, and completely prime. We consider each property in turn:
$x^\ast$
is nonempty, up-closed, compatible, and completely prime. We consider each property in turn:-
–
 $x\ast x$
by proper reflexivity of
$x\ast x$
by proper reflexivity of
 $\ast$
(Definition 7.2.1(2); since
$\ast$
(Definition 7.2.1(2); since
 $x\neq {\boldsymbol \bot }_{\mathsf{X}}$
), so
$x\neq {\boldsymbol \bot }_{\mathsf{X}}$
), so
 $x\in x^\ast$
.
$x\in x^\ast$
. -
– It follows from monotonicity of
 $\ast$
(Lemma 7.2.3(1)) that if
$\ast$
(Lemma 7.2.3(1)) that if
 $x'\leq x''$
and
$x'\leq x''$
and
 $x\ast x'$
then
$x\ast x'$
then
 $x\ast x''$
.
$x\ast x''$
. -
– Suppose
 $x'\ast x\ast x''$
. By transitivity of
$x'\ast x\ast x''$
. By transitivity of
 $x$
(Definition 11.1.5),
$x$
(Definition 11.1.5),
 $x'\ast x''$
.
$x'\ast x''$
. -
– Suppose
 $x\ast \bigvee X'$
; then by distributivity of
$x\ast \bigvee X'$
; then by distributivity of
 $\ast$
(Definition 7.2.1(3))
$\ast$
(Definition 7.2.1(3))
 $x\ast x'$
for some
$x\ast x'$
for some
 $x'\in X'$
.
$x'\in X'$
.
-
-
(2) If
 $x^\ast$
is a completely prime semifilter, then it is certainly a semifilter.
$x^\ast$
is a completely prime semifilter, then it is certainly a semifilter. -
(3) If
 $x^\ast$
is a semifilter, then it is compatible (Definition 8.1.1(5 and 4).
$x^\ast$
is a semifilter, then it is compatible (Definition 8.1.1(5 and 4). -
(4) Suppose
 $x^\ast$
is compatible (Definition 8.1.1(4)) and suppose
$x^\ast$
is compatible (Definition 8.1.1(4)) and suppose
 $x'\ast x\ast x''$
. By Lemma 11.2.3
$x'\ast x\ast x''$
. By Lemma 11.2.3
 $x',x''\in x^\ast$
, and by compatibility of
$x',x''\in x^\ast$
, and by compatibility of
 $x^\ast$
we have
$x^\ast$
we have
 $x'\ast x''$
. Thus,
$x'\ast x''$
. Thus,
 $x$
is transitive.
$x$
is transitive.
To conclude, we prove two implications between parts 4 and 5:
11.3 The compatibility system
 $F^\ast$
$F^\ast$
11.3.1 Basic definitions and results
Definition 11.3.1. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
$(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
![]() $F\subseteq \mathsf{X}$
(
$F\subseteq \mathsf{X}$
(
![]() $F$
may be a semifilter, but the definition does not depend on this). Define
$F$
may be a semifilter, but the definition does not depend on this). Define
![]() $F^\ast$
the compatibility system of
$F^\ast$
the compatibility system of
![]() $F$
by
$F$
by
Unpacking Notation 11.1.2(1), and combining with Definition 11.2.1, we can write:
Lemma 11.3.2 presents one easy and useful example of Definition 11.3.1:
Lemma 11.3.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
$(\mathsf{P},\mathsf{Open})$
is a semitopology and suppose
![]() $p\in \mathsf{P}$
and
$p\in \mathsf{P}$
and
![]() $O'\in \mathsf{Open}$
. Then:
$O'\in \mathsf{Open}$
. Then:

Lemma 11.3.3.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
. Then
$F\subseteq \mathsf{X}$
. Then
![]() $F^\ast$
is up-closed.
$F^\ast$
is up-closed.
Lemma 11.3.4.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then:
$F\subseteq \mathsf{X}$
is a semifilter. Then:
-
(1) If
 $x\in F$
then
$x\in F$
then
 $F \subseteq x^\ast$
.
$F \subseteq x^\ast$
. -
(2) As a corollary,
 $F\subseteq F^\ast$
.
$F\subseteq F^\ast$
.
Proof.
Suppose
![]() $x\in F$
. By compatibility of
$x\in F$
. By compatibility of
![]() $F$
(Definition 8.1.1(4)),
$F$
(Definition 8.1.1(4)),
![]() $x'\ast x$
for every
$x'\ast x$
for every
![]() $x'\in F$
. It follows from Definition 11.2.1 that
$x'\in F$
. It follows from Definition 11.2.1 that
![]() $F\subseteq x^\ast$
. The corollary is immediate from Definition 11.3.1.
$F\subseteq x^\ast$
. The corollary is immediate from Definition 11.3.1.
We can use Lemma 11.3.4 and Definition 11.3.1 to give a more succinct rendering of Lemma 11.1.4:
Corollary 11.3.5.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then the following are equivalent:
$F\subseteq \mathsf{X}$
is a semifilter. Then the following are equivalent:
-
(1)
 $F$
is maximal.
$F$
is maximal.
-
(2)
 $F^\ast =F$
.
$F^\ast =F$
. -
(3)
 $F^\ast \subseteq F$
.
$F^\ast \subseteq F$
.
11.3.2 Strong compatibility: when
 $F^\ast$
is a semifilter
$F^\ast$
is a semifilter
Proposition 11.2.4 relates good properties of
![]() $x$
(transitivity) to good properties of its compatibility system
$x$
(transitivity) to good properties of its compatibility system
![]() $x^\ast$
(e.g. being compatible). It will be helpful to ask similar questions of
$x^\ast$
(e.g. being compatible). It will be helpful to ask similar questions of
![]() $F^\ast$
. What good properties are of interest for
$F^\ast$
. What good properties are of interest for
![]() $F^\ast$
, and what conditions can we impose on
$F^\ast$
, and what conditions can we impose on
![]() $F$
to guarantee them?
$F$
to guarantee them?
Definition 11.3.6. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe. Then:
$(\mathsf{X},\leq ,\ast )$
is a semiframe. Then:
-
(1) Call
 $F\subseteq \mathsf{X}$
strongly compatible when
$F\subseteq \mathsf{X}$
strongly compatible when
 $F^\ast$
is nonempty and compatible.
$F^\ast$
is nonempty and compatible. -
(2) Call
 $(\mathsf{X},\leq ,\ast )$
strongly compatible when every abstract point (completely prime semifilter)
$(\mathsf{X},\leq ,\ast )$
strongly compatible when every abstract point (completely prime semifilter)
 $P\subseteq \mathsf{X}$
is strongly compatible.
$P\subseteq \mathsf{X}$
is strongly compatible.
Remark 11.3.7. For the reader’s convenience we unpack Definition 11.3.6.
-
(1) By Definition 8.1.1(4),
 $F^\ast$
is compatible when
$F^\ast$
is compatible when
 $x\ast x'$
for every
$x\ast x'$
for every
 $x,x'\in F^\ast$
. Combining this with Definition 11.3.1 and Notation 11.1.2,
$x,x'\in F^\ast$
. Combining this with Definition 11.3.1 and Notation 11.1.2,
 $F^\ast$
is compatible when
$F^\ast$
is compatible when
 $x\ast F\ast x'$
implies
$x\ast F\ast x'$
implies
 $x\ast x'$
, for every
$x\ast x'$
, for every
 $x,x'\in \mathsf{X}$
. Thus,
$x,x'\in \mathsf{X}$
. Thus,
 $F$
is strongly compatible when
$F$
is strongly compatible when \begin{equation*} \forall x,x'{\in }\mathsf{X}.\ x\ast F\ast x' \Longrightarrow x\ast x'. \end{equation*}
\begin{equation*} \forall x,x'{\in }\mathsf{X}.\ x\ast F\ast x' \Longrightarrow x\ast x'. \end{equation*}
-
(2)
 $(\mathsf{X},\leq ,\ast )$
is strongly compatible when every abstract point
$(\mathsf{X},\leq ,\ast )$
is strongly compatible when every abstract point
 $P\in \mathsf{Point}(\mathsf{X},\leq ,\ast )$
is strongly compatible in the sense just given above.
$P\in \mathsf{Point}(\mathsf{X},\leq ,\ast )$
is strongly compatible in the sense just given above.
Lemma 11.3.8.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Recall from Definition 7.3.4(3) and Lemma 7.3.5 that
$p\in \mathsf{P}$
. Recall from Definition 7.3.4(3) and Lemma 7.3.5 that
![]() $(\mathsf{Open},\subseteq ,\between )$
is a semiframe. Then the following are equivalent:
$(\mathsf{Open},\subseteq ,\between )$
is a semiframe. Then the following are equivalent:
Proof.
Remark 11.3.7 notes that the condition in Definition 6.2.3 is precisely the condition for
![]() $\textit{nbhd}(p)$
to be strongly compatible.
$\textit{nbhd}(p)$
to be strongly compatible.
Remark 11.3.9. Given Lemma 11.3.8, the reader might ask why we do not just call a strongly compatible semifilter ‘hypertransitive’.
There is a case for doing so, but caution is required: strong compatibility of semiframes is not quite the same thing as hypertransitivity of points. Every point
![]() $p$
generates a semifilter
$p$
generates a semifilter
![]() $\textit{nbhd}(p)$
, but there may be more semifilters than there are points, and this makes the strong compatibility condition subtly different from the hypertransitivity condition. We shall see the effects of this in Lemma 11.5.3(2), and in Theorem 11.5.4 (see Remark 11.5.5 for a brief discussion), and then again in Definition 11.8.8 where we define a notion of strongly compatible semitopology (essentially: all of its semifilters are strongly compatible), which is not the same thing as the space being hypertransitive (essentially: all of its points are hypertransitive).
$\textit{nbhd}(p)$
, but there may be more semifilters than there are points, and this makes the strong compatibility condition subtly different from the hypertransitivity condition. We shall see the effects of this in Lemma 11.5.3(2), and in Theorem 11.5.4 (see Remark 11.5.5 for a brief discussion), and then again in Definition 11.8.8 where we define a notion of strongly compatible semitopology (essentially: all of its semifilters are strongly compatible), which is not the same thing as the space being hypertransitive (essentially: all of its points are hypertransitive).
Therefore, we maintain a terminological distinction: points are hypertransitive, semiframes are strongly compatible. The notions are related, but not quite the same thing.
Lemma 11.3.10.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
$(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
![]() $F\subseteq \mathsf{X}$
is nonempty. Then the following are equivalent:
$F\subseteq \mathsf{X}$
is nonempty. Then the following are equivalent:
-
(1)
 $F^\ast$
is a semifilter.
$F^\ast$
is a semifilter.
-
(2)
 $F^\ast$
is compatible.
$F^\ast$
is compatible.
-
(3)
 $F$
is strongly compatible.
$F$
is strongly compatible.
Proof. Equivalence of parts 2 and 3 is just Definition 11.3.6. For equivalence of parts 1 and 2 we prove two implications:
Lemma 11.3.11.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
$(\mathsf{X},\leq ,\ast )$
is a semiframe and suppose
![]() $F\subseteq \mathsf{X}$
. Then it is not necessarily the case that
$F\subseteq \mathsf{X}$
. Then it is not necessarily the case that
![]() $F^\ast$
is a semifilter.
$F^\ast$
is a semifilter.
This non-implication holds even in strong well-behavedness conditions: that
![]() $(\mathsf{X},\leq ,\ast )$
is spatial and
$(\mathsf{X},\leq ,\ast )$
is spatial and
![]() $F$
is an abstract point (a completely prime semifilter).
$F$
is an abstract point (a completely prime semifilter).
Proof.
It suffices to provide a counterexample. Let
![]() $(\mathsf{P},\mathsf{Open})=(\{0,1,2\},\{\varnothing ,\{0\},\{2\},\mathsf{P}\})$
, as illustrated in the top-left semitopology in Figure 2. Take
$(\mathsf{P},\mathsf{Open})=(\{0,1,2\},\{\varnothing ,\{0\},\{2\},\mathsf{P}\})$
, as illustrated in the top-left semitopology in Figure 2. Take
![]() $(\mathsf{X},\leq ,\ast )=(\mathsf{Open},\subseteq ,\between )$
(which is spatial by Proposition 9.2.5) and set
$(\mathsf{X},\leq ,\ast )=(\mathsf{Open},\subseteq ,\between )$
(which is spatial by Proposition 9.2.5) and set
![]() $F=\textit{nbhd}(1)=\{0,1,2\}$
. Then
$F=\textit{nbhd}(1)=\{0,1,2\}$
. Then
![]() $\textit{nbhd}(1)^\ast =\{\{0\},\{2\},\{0,1,2\}\}$
, and this is not compatible because
$\textit{nbhd}(1)^\ast =\{\{0\},\{2\},\{0,1,2\}\}$
, and this is not compatible because  .Footnote
30
.Footnote
30
Remark 11.3.12. Lemma 11.3.11 gives an example of a semifilter
![]() $F$
that is not strongly compatible (i.e. such that
$F$
that is not strongly compatible (i.e. such that
![]() $F^\ast$
is not a semifilter). Note that in this example both the space and
$F^\ast$
is not a semifilter). Note that in this example both the space and
![]() $F$
are well-behaved. This raises the question of finding sufficient (though perhaps not necessary) criteria for strong compatibility. We conclude with Proposition 11.3.13 which provides one such criterion; it will be useful later in Lemma 11.5.3 and Theorem 11.8.10.
$F$
are well-behaved. This raises the question of finding sufficient (though perhaps not necessary) criteria for strong compatibility. We conclude with Proposition 11.3.13 which provides one such criterion; it will be useful later in Lemma 11.5.3 and Theorem 11.8.10.
Proposition 11.3.13 bears a family resemblance to Theorem4.2.5 (if a point has a topen neighbourhood then it is regular):
Proposition 11.3.13.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then:
$F\subseteq \mathsf{X}$
is a semifilter. Then:
-
(1) If
 $F$
contains a transitive element then
$F$
contains a transitive element then
 $F$
is strongly compatible.
$F$
is strongly compatible.
-
(2) The converse implication need not hold: it may be that
 $F$
is strongly compatible yet
$F$
is strongly compatible yet
 $F$
contains no transitive element.
$F$
contains no transitive element.
Proof. We consider each part in turn:
-
(1) Suppose
 $x\in F$
is transitive. By Lemma 11.3.10 it would suffice to show that
$x\in F$
is transitive. By Lemma 11.3.10 it would suffice to show that
 $F^\ast$
is compatible (Definition 8.1.1(4)). So consider
$F^\ast$
is compatible (Definition 8.1.1(4)). So consider
 $y\ast F\ast y'$
. Then
$y\ast F\ast y'$
. Then
 $y\ast x\ast y'$
and by transitivity
$y\ast x\ast y'$
and by transitivity
 $y\ast y'$
. Thus
$y\ast y'$
. Thus
 $F^\ast$
is compatible.
$F^\ast$
is compatible. -
(2) It suffices to provide a counterexample. We take, as illustrated in Figure 8,
-
–
 $\mathsf{P}=\{\text{-} 2,\text{-} 1,0,1,2\}$
and
$\mathsf{P}=\{\text{-} 2,\text{-} 1,0,1,2\}$
and
Figure 8. Strongly compatible filter that contains no transitive element.
-
– we let
 $\mathsf{Open}$
be generated by
$\mathsf{Open}$
be generated by
 $\{i,i{+} 1\}$
for
$\{i,i{+} 1\}$
for
 $\text{-} 2\leq i\leq 1$
(unordered pairs of adjacent numbers).
$\text{-} 2\leq i\leq 1$
(unordered pairs of adjacent numbers).
Write
 $A=\{\text{-} 1,0\}$
and
$A=\{\text{-} 1,0\}$
and
 $B=\{0,1\}$
and let
$B=\{0,1\}$
and let
 $F$
be the up-closure of
$F$
be the up-closure of
 $\{A,B\}$
. Note that
$\{A,B\}$
. Note that
 $A$
and
$A$
and
 $B$
are not transitive (i.e. not topen). The reader can check that
$B$
are not transitive (i.e. not topen). The reader can check that
 $F^\ast =F$
(e.g.
$F^\ast =F$
(e.g.
 $\{1,2\}\notin F^\ast$
because
$\{1,2\}\notin F^\ast$
because  , but
, but
 $F$
contains no transitive element.
$F$
contains no transitive element. -
11.4 Semiframe characterisation of community
Remark 11.4.1. We saw the notion of
![]() $\textit{K}(p)$
the community of a point in Definition 4.1.4(1). In this Subsection we construct an analogue to it in semiframes. We will give two characterisations: one in Definition 11.4.5, and another in Proposition 11.4.7.
$\textit{K}(p)$
the community of a point in Definition 4.1.4(1). In this Subsection we construct an analogue to it in semiframes. We will give two characterisations: one in Definition 11.4.5, and another in Proposition 11.4.7.
We will mostly be interested in Definition 11.4.2 when
![]() $F$
is a semifilter, but the definition does not require this:
$F$
is a semifilter, but the definition does not require this:
Definition 11.4.2. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
and
$F\subseteq \mathsf{X}$
and
![]() $x\in \mathsf{X}$
. Then define
$x\in \mathsf{X}$
. Then define
![]() $F^c\in \mathsf{X}$
,
$F^c\in \mathsf{X}$
,
![]() $F^{\ast c}\in \mathsf{X}$
, and
$F^{\ast c}\in \mathsf{X}$
, and
![]() $x^{\ast c}\in \mathsf{X}$
by
$x^{\ast c}\in \mathsf{X}$
by
Remark 11.4.3. We unpack the definitions of
![]() $F^{\ast c}$
and
$F^{\ast c}$
and
![]() $x^{\ast c}$
:
$x^{\ast c}$
:

Lemma 11.4.4 will be useful, and gives some intuition for
![]() $(\text{-})^c$
and
$(\text{-})^c$
and
![]() $(\text{-})^{\ast c}$
by unpacking their concrete meaning in the special case of a semiframe of open sets of a semitopology:
$(\text{-})^{\ast c}$
by unpacking their concrete meaning in the special case of a semiframe of open sets of a semitopology:
Lemma 11.4.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
and
$p\in \mathsf{P}$
and
![]() $O\in \mathsf{Open}$
. Then:
$O\in \mathsf{Open}$
. Then:
-
(1)
 $\textit{nbhd}(p)^c=\mathsf{P}\setminus |p|$
.
$\textit{nbhd}(p)^c=\mathsf{P}\setminus |p|$
. -
(2)
 $\textit{nbhd}(p)^{\ast c}=\mathsf{P}\setminus p_{\between }$
.
$\textit{nbhd}(p)^{\ast c}=\mathsf{P}\setminus p_{\between }$
. -
(3)
 $O^{\ast c}=\mathsf{P}\setminus |O|=\textit{interior}(\mathsf{P}\setminus O)$
.
$O^{\ast c}=\mathsf{P}\setminus |O|=\textit{interior}(\mathsf{P}\setminus O)$
.
Proof. We consider each part in turn:
-
(1) It is a fact of Definition 5.1.1 that
 $\mathsf{P}\setminus |p|=\bigcup \{O'\in \mathsf{Open} \mid p\notin O'\}$
. By Proposition 9.2.2(2)
$\mathsf{P}\setminus |p|=\bigcup \{O'\in \mathsf{Open} \mid p\notin O'\}$
. By Proposition 9.2.2(2)
 $p\notin O'$
if and only if
$p\notin O'$
if and only if
 $O'\notin \textit{nbhd}(p)$
.
$O'\notin \textit{nbhd}(p)$
. -
(2) It is a fact of Definition 3.5.1, which is spelled out in Lemma 5.2.4(2), that

 . By Lemma 11.3.2
. By Lemma 11.3.2  precisely when
precisely when
 $O'\notin \textit{nbhd}(p)^\ast$
.
$O'\notin \textit{nbhd}(p)^\ast$
. -
(3) By Definitions 11.4.2 and 11.3.1 we have

The result then follows by routine reasoning on closures (Definition 5.1.1).
Definition 11.4.5. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
. Then define
$F\subseteq \mathsf{X}$
. Then define
![]() $\textit{k}(F)\in \mathsf{X}$
the abstract community of
$\textit{k}(F)\in \mathsf{X}$
the abstract community of
![]() $F$
by
$F$
by
(For a more direct characterisation, see Proposition 11.4.7.)
Proposition 11.4.6.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then
$p\in \mathsf{P}$
. Then
In words: the abstract community of the abstract point
![]() $\textit{nbhd}(p)$
in
$\textit{nbhd}(p)$
in
![]() $(\mathsf{Open},\subseteq ,\between )$
, is identical to the community of
$(\mathsf{Open},\subseteq ,\between )$
, is identical to the community of
![]() $p$
.
$p$
.
Proof. We reason as follows:

We can also give a more direct characterisation of the abstract community from Definition 11.4.5:
Proposition 11.4.7.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
. Then
$F\subseteq \mathsf{X}$
. Then
and
![]() $\textit{k}(F)$
is the greatest element in
$\textit{k}(F)$
is the greatest element in
![]() $\mathsf{X}$
such that
$\mathsf{X}$
such that
![]() $\textit{k}(F)^\ast \subseteq F^\ast$
.
$\textit{k}(F)^\ast \subseteq F^\ast$
.
Proof. We follow the definitions:

To see that
![]() $\textit{k}(F)$
is the greatest element such that
$\textit{k}(F)$
is the greatest element such that
![]() $\textit{k}(F)^\ast \subseteq F^\ast$
, we note from Lemma 11.2.2 that
$\textit{k}(F)^\ast \subseteq F^\ast$
, we note from Lemma 11.2.2 that
11.5 Semiframe characterisation of regularity
We now have enough to generalise the notions of quasiregularity, weak regularity, and regularity from semitopologies (Definition 4.1.4 parts 5, 4, and 3) to semiframes:
Definition 11.5.1. Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter.
$F\subseteq \mathsf{X}$
is a semifilter.
-
(1) Call
 $F$
quasiregular when
$F$
quasiregular when
 $\textit{k}(F)\neq {\boldsymbol \bot }_{\mathsf{X}}$
.
$\textit{k}(F)\neq {\boldsymbol \bot }_{\mathsf{X}}$
.Thus, there exists some
 $x\in \mathsf{X}$
such that
$x\in \mathsf{X}$
such that
 $x^\ast \subseteq F^\ast$
.
$x^\ast \subseteq F^\ast$
. -
(2) Call
 $F$
weakly regular when
$F$
weakly regular when
 $\textit{k}(F)\in F$
.
$\textit{k}(F)\in F$
. -
(3) Call
 $F$
regular when
$F$
regular when
 $\textit{k}(F)\in F$
and
$\textit{k}(F)\in F$
and
 $\textit{k}(F)$
is transitive.
$\textit{k}(F)$
is transitive.
Lemma 11.5.2 does for semiframes what Lemma 4.1.6 does for semitopologies:
Lemma 11.5.2.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then:
$F\subseteq \mathsf{X}$
is a semifilter. Then:
-
(1) If
 $F$
is regular then it is weakly regular.
$F$
is regular then it is weakly regular.
-
(2) If
 $F$
is weakly regular then it is quasiregular.
$F$
is weakly regular then it is quasiregular.
(The converse implications need not hold, and it is possible for
![]() $F$
to not be quasiregular: it is convenient to defer the proofs to Corollary 11.6.3.)
$F$
to not be quasiregular: it is convenient to defer the proofs to Corollary 11.6.3.)
Proof.
The proofs are easy: If
![]() $\textit{k}(F)\in F$
and
$\textit{k}(F)\in F$
and
![]() $\textit{k}(F)$
is transitive, then certainly
$\textit{k}(F)$
is transitive, then certainly
![]() $\textit{k}(F)\in F$
. If
$\textit{k}(F)\in F$
. If
![]() $\textit{k}(F)\in F$
then by Lemma 8.2.1(2)
$\textit{k}(F)\in F$
then by Lemma 8.2.1(2)
![]() $\textit{k}(F)\neq {\boldsymbol \bot }_{\mathsf{X}}$
.
$\textit{k}(F)\neq {\boldsymbol \bot }_{\mathsf{X}}$
.
Lemma 11.5.3.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then:
$F\subseteq \mathsf{X}$
is a semifilter. Then:
-
(1) If
 $F$
is quasiregular and strongly compatible then
$F$
is quasiregular and strongly compatible then
 $\textit{k}(F)$
is transitive.
$\textit{k}(F)$
is transitive.
-
(2) The converse implication need not hold: it is possible for
 $F$
to be quasiregular and
$F$
to be quasiregular and
 $\textit{k}(F)$
to be transitive, yet
$\textit{k}(F)$
to be transitive, yet
 $F$
is not strongly compatible.
$F$
is not strongly compatible.
-
(3) If
 $F$
is weakly regular and
$F$
is weakly regular and
 $\textit{k}(F)$
is transitive then
$\textit{k}(F)$
is transitive then
 $F$
is strongly compatible.
$F$
is strongly compatible.
-
(4) If
 $F$
is weakly regular, then
$F$
is weakly regular, then
 $\textit{k}(F)$
is transitive if and only if
$\textit{k}(F)$
is transitive if and only if
 $F$
is strongly compatible.
$F$
is strongly compatible.
Proof. We consider each part in turn:
-
(1) Suppose
 $F$
is quasiregular and strongly compatible.
$F$
is quasiregular and strongly compatible.By quasiregularity
 ${\boldsymbol \bot }_{\mathsf{X}}\neq \textit{k}(F)$
. By Proposition 11.4.7
${\boldsymbol \bot }_{\mathsf{X}}\neq \textit{k}(F)$
. By Proposition 11.4.7
 $\textit{k}(F)^\ast \subseteq F^\ast$
. By strong compatibility
$\textit{k}(F)^\ast \subseteq F^\ast$
. By strong compatibility
 $F^\ast$
is a semifilter and so in particular
$F^\ast$
is a semifilter and so in particular
 $F^\ast$
is compatible. It follows from Proposition 11.2.4(1 and 4) that
$F^\ast$
is compatible. It follows from Proposition 11.2.4(1 and 4) that
 $\textit{k}(F)$
is transitive, as required.
$\textit{k}(F)$
is transitive, as required. -
(2) It suffices to provide a counterexample. Let
 $(\mathbb R,\mathsf{Open})$
be the real numbers with their usual topology, and let
$(\mathbb R,\mathsf{Open})$
be the real numbers with their usual topology, and let
 $(\mathbb R,\mathsf{Open}')$
be the topology generated by
$(\mathbb R,\mathsf{Open}')$
be the topology generated by
 $\mathsf{Open}\cup \{\{0\}\}$
– in words: we add
$\mathsf{Open}\cup \{\{0\}\}$
– in words: we add
 $\{0\}$
as an open set.
$\{0\}$
as an open set.Let
 $F$
be the semifilter of all
$F$
be the semifilter of all
 $\mathsf{Open}$
-open neighbourhoods of
$\mathsf{Open}$
-open neighbourhoods of
 $0$
.
$0$
.
 $F^\ast$
is the set of
$F^\ast$
is the set of
 $\mathsf{Open}'$
-open sets that intersect every
$\mathsf{Open}'$
-open sets that intersect every
 $\mathsf{Open}$
-open neighbourhood of
$\mathsf{Open}$
-open neighbourhood of
 $0$
. This is not compatible, because it contains
$0$
. This is not compatible, because it contains
 $(0,)$
(the set of numbers strictly less than
$(0,)$
(the set of numbers strictly less than
 $0$
) and
$0$
) and
 $(,0)$
(the set of numbers strictly greater than
$(,0)$
(the set of numbers strictly greater than
 $0$
), and these do not intersect. Using Proposition 11.4.7, we calculate that
$0$
), and these do not intersect. Using Proposition 11.4.7, we calculate that
 $\textit{k}(F)=\{0\}$
; this is transitive because it is a singleton set.
$\textit{k}(F)=\{0\}$
; this is transitive because it is a singleton set.So
 $F$
is quasiregular,
$F$
is quasiregular,
 $\textit{k}(F)$
is transitive, yet
$\textit{k}(F)$
is transitive, yet
 $F$
is not strongly compatible.
$F$
is not strongly compatible. -
(3) Suppose
 $\textit{k}(F)$
is transitive and suppose
$\textit{k}(F)$
is transitive and suppose
 $F$
is weakly regular, so
$F$
is weakly regular, so
 $\textit{k}(F)\in F$
. By Proposition 11.3.13
$\textit{k}(F)\in F$
. By Proposition 11.3.13
 $F$
is strongly compatible.
$F$
is strongly compatible. -
(4) From parts 1 and 3 of this result, noting from Lemma 11.5.2 that if
 $F$
is weakly regular then it is quasiregular.
$F$
is weakly regular then it is quasiregular.
Theorem 11.5.4.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then
$F\subseteq \mathsf{X}$
is a semifilter. Then
![]() $F$
is regular if and only if
$F$
is regular if and only if
![]() $F$
is weakly regular and strongly compatible. We can write this succinctly as follows:
$F$
is weakly regular and strongly compatible. We can write this succinctly as follows:
Regular = weakly regular + strongly compatible.
(Compare this slogan with the version for semitopologies in Theorem 5.3.4 .)
Proof.
Suppose
![]() $F$
is weakly regular and strongly compatible. By Lemma 11.5.3(4)
$F$
is weakly regular and strongly compatible. By Lemma 11.5.3(4)
![]() $\textit{k}(F)$
is transitive, and by Definition 11.5.1(3)
$\textit{k}(F)$
is transitive, and by Definition 11.5.1(3)
![]() $F$
is regular.
$F$
is regular.
For the converse implication we just reverse the reasoning above.
Remark 11.5.5. In Theorem 6.3.3 we characterised regularity of points in terms of quasiregularity and being hypertransitive. In view of Lemma 11.3.8 we might expect Theorem 11.5.4 to read ‘regular = quasiregular + strongly compatible’. But this is false, as per the discussion in Remark 11.3.9 and the counterexample in Lemma 11.5.3(2). Thus, the semiframes results are subtly different from those governing point-set semitopologies.
11.6 Semiframe characterisation of (quasi/weak)regularity
The direct translation in Definition 11.5.1 of parts 5, 4, and 3 of Definition 4.1.4, along with the machinery we have now built, makes Lemma 11.6.1 easy to prove:
Lemma 11.6.1.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Recall from Definition 2.3.1 and Proposition 9.2.2(1) that
$p\in \mathsf{P}$
. Recall from Definition 2.3.1 and Proposition 9.2.2(1) that
![]() $\textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\}$
is a (completely prime) semifilter. Then:
$\textit{nbhd}(p)=\{O\in \mathsf{Open} \mid p\in O\}$
is a (completely prime) semifilter. Then:
-
(1)
 $p$
is quasiregular in the sense of Definition 4.1.4(5) if and only if
$p$
is quasiregular in the sense of Definition 4.1.4(5) if and only if
 $\textit{nbhd}(p)$
is quasiregular in the sense of Definition 11.5.1(1).
$\textit{nbhd}(p)$
is quasiregular in the sense of Definition 11.5.1(1).
-
(2)
 $p$
is weakly regular in the sense of Definition 4.1.4(4) if and only if
$p$
is weakly regular in the sense of Definition 4.1.4(4) if and only if
 $\textit{nbhd}(p)$
is weakly regular in the sense of Definition 11.5.1(2).
$\textit{nbhd}(p)$
is weakly regular in the sense of Definition 11.5.1(2).
-
(3)
 $p$
is regular in the sense of Definition 4.1.4(3) if and only if
$p$
is regular in the sense of Definition 4.1.4(3) if and only if
 $\textit{nbhd}(p)$
is regular in the sense of Definition 11.5.1(3).
$\textit{nbhd}(p)$
is regular in the sense of Definition 11.5.1(3).
Proof. We consider each part in turn:
-
(1) Suppose
 $p$
is quasiregular. By Definition 4.1.4(5)
$p$
is quasiregular. By Definition 4.1.4(5)
 $\textit{K}(p)\neq \varnothing$
. By Proposition 11.4.6
$\textit{K}(p)\neq \varnothing$
. By Proposition 11.4.6
 $\textit{k}\textit{nbhd}(p))\neq \varnothing ={\boldsymbol \bot }_{\mathsf{Open}}$
. By Definition 11.5.1(1)
$\textit{k}\textit{nbhd}(p))\neq \varnothing ={\boldsymbol \bot }_{\mathsf{Open}}$
. By Definition 11.5.1(1)
 $\textit{nbhd}(p)$
is quasiregular.
$\textit{nbhd}(p)$
is quasiregular.The reverse implication follows just reversing the reasoning above.
-
(2) Suppose
 $p$
is weakly regular. By Definition 4.1.4(4)
$p$
is weakly regular. By Definition 4.1.4(4)
 $p\in \textit{K}(p)$
. By Definition 2.3.1
$p\in \textit{K}(p)$
. By Definition 2.3.1
 $\textit{K}(p)\in \textit{nbhd}(p)$
. By Proposition 11.4.6
$\textit{K}(p)\in \textit{nbhd}(p)$
. By Proposition 11.4.6
 $\textit{k}\textit{nbhd}(p))\in \textit{nbhd}(p)$
as required.
$\textit{k}\textit{nbhd}(p))\in \textit{nbhd}(p)$
as required.The reverse implication follows just reversing the reasoning above.
-
(3) Suppose
 $p$
is regular. By Definition 4.1.4(3)
$p$
is regular. By Definition 4.1.4(3)
 $p\in \textit{K}(p)\in \mathsf{Topen}$
. By Definition 2.3.1 and Proposition 11.4.6
$p\in \textit{K}(p)\in \mathsf{Topen}$
. By Definition 2.3.1 and Proposition 11.4.6
 $\textit{k}\textit{nbhd}(p))\in \textit{nbhd}(p)$
. By Proposition 11.4.6 and Lemma 11.1.6
$\textit{k}\textit{nbhd}(p))\in \textit{nbhd}(p)$
. By Proposition 11.4.6 and Lemma 11.1.6
 $\textit{k}\textit{nbhd}(p))$
is transitive.
$\textit{k}\textit{nbhd}(p))$
is transitive.The reverse implication follows just reversing the reasoning above.
Proposition 11.6.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then
$p\in \mathsf{P}$
. Then
Proof. We consider just the case of regularity; quasiregularity and weak regularity are no different.
Suppose
![]() $p$
is regular. By Definition 4.1.4(3)
$p$
is regular. By Definition 4.1.4(3)
![]() $p\in \textit{K}(p)\in \mathsf{Topen}$
. It follows from Lemma 11.1.6 that
$p\in \textit{K}(p)\in \mathsf{Topen}$
. It follows from Lemma 11.1.6 that
![]() $\textit{K}(p)$
is transitive in
$\textit{K}(p)$
is transitive in
![]() $(\mathsf{Open},\subseteq ,\between )$
, and from Proposition 9.2.2(2) that
$(\mathsf{Open},\subseteq ,\between )$
, and from Proposition 9.2.2(2) that
![]() $\textit{K}(p)\in \textit{nbhd}(p)$
. It follows from Proposition 11.4.6 that
$\textit{K}(p)\in \textit{nbhd}(p)$
. It follows from Proposition 11.4.6 that
![]() $\textit{nbhd}(p)$
is regular in the sense of Definition 11.5.1(3).
$\textit{nbhd}(p)$
is regular in the sense of Definition 11.5.1(3).
Corollary 11.6.3.
Suppose
![]() $(\mathsf{X},\leq ,\ast )$
is a semiframe and
$(\mathsf{X},\leq ,\ast )$
is a semiframe and
![]() $F\subseteq \mathsf{X}$
is a semifilter. Then the converse implications in Lemma 11.5.2 need not hold:
$F\subseteq \mathsf{X}$
is a semifilter. Then the converse implications in Lemma 11.5.2 need not hold:
![]() $F$
may be quasiregular but not regular, and it may be weakly regular but not regular, and it may not even be quasiregular.
$F$
may be quasiregular but not regular, and it may be weakly regular but not regular, and it may not even be quasiregular.
11.7 Characterisation of being intertwined
This Subsection continues Remark 11.1.3.
The notion of points being intertwined from Definition 3.5.1(1) generalises in semiframes to the notion of semifilters being compatible:
Lemma 11.7.1.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p,p'\in \mathsf{P}$
. Then
$p,p'\in \mathsf{P}$
. Then
For clarity and precision we unpack this. The following are equivalent:
-
(1)
 $p\mathrel {\between } p'$
in the semitopology
$p\mathrel {\between } p'$
in the semitopology
 $(\mathsf{P},\mathsf{Open})$
(Definition 3.5.1(1)).
$(\mathsf{P},\mathsf{Open})$
(Definition 3.5.1(1)).
In words: the point
 $p$
is intertwined with the point
$p$
is intertwined with the point
 $p'$
.
$p'$
. -
(2)
 $\textit{nbhd}(p)\ast \textit{nbhd}(p')$
in the semiframe
$\textit{nbhd}(p)\ast \textit{nbhd}(p')$
in the semiframe
 $(\mathsf{Open},\subseteq ,\between )$
(Notation 11.1.2(3)).
$(\mathsf{Open},\subseteq ,\between )$
(Notation 11.1.2(3)).
In words: the abstract point
 $\textit{nbhd}(p)$
is compatible with the abstract point
$\textit{nbhd}(p)$
is compatible with the abstract point
 $\textit{nbhd}(p')$
.
$\textit{nbhd}(p')$
. -
(3)
 $\textit{nbhd}(p)\mathrel {\between }\textit{nbhd}(p')$
in the semitopology
$\textit{nbhd}(p)\mathrel {\between }\textit{nbhd}(p')$
in the semitopology
 $\mathsf{St}(\mathsf{Open},\subseteq ,\between )$
(Definition 3.5.1(1)). In words: the point
$\mathsf{St}(\mathsf{Open},\subseteq ,\between )$
(Definition 3.5.1(1)). In words: the point
 $\textit{nbhd}(p)$
is intertwined with the point
$\textit{nbhd}(p)$
is intertwined with the point
 $\textit{nbhd}(p')$
.
$\textit{nbhd}(p')$
.
Proof. We unpack definitions:
-
• By Definition 3.5.1(1)
 $p\mathrel {\between } p'$
when for every pair of open neighbourhoods
$p\mathrel {\between } p'$
when for every pair of open neighbourhoods
 $p\in O$
and
$p\in O$
and
 $p'\in O'$
we have
$p'\in O'$
we have
 $O\between O'$
.
$O\between O'$
. -
• By Notation 11.1.2(3)
 $\textit{nbhd}(p)\ast \textit{nbhd}(p')$
when for every
$\textit{nbhd}(p)\ast \textit{nbhd}(p')$
when for every
 $O\in \textit{nbhd}(p)$
and
$O\in \textit{nbhd}(p)$
and
 $O'\in \textit{nbhd}(p')$
we have
$O'\in \textit{nbhd}(p')$
we have
 $O\ast O'$
.
$O\ast O'$
.By Proposition 9.2.2(2) we can simplify this to:
 $p\in O$
and
$p\in O$
and
 $p'\in O'$
implies
$p'\in O'$
implies
 $O\ast O'$
.
$O\ast O'$
. -
• By Definition 3.5.1(1) and Theorem10.1.4,
 $\textit{nbhd}(p)\mathrel {\between } \textit{nbhd}(p')$
when: for every pair of open neighbourhoods
$\textit{nbhd}(p)\mathrel {\between } \textit{nbhd}(p')$
when: for every pair of open neighbourhoods
 $\textit{nbhd}(p)\in \textit{Op}(O)$
and
$\textit{nbhd}(p)\in \textit{Op}(O)$
and
 $\textit{nbhd}(p')\in \textit{Op}(O')$
we have
$\textit{nbhd}(p')\in \textit{Op}(O')$
we have
 $\textit{Op}(O)\between \textit{Op}(O')$
.
$\textit{Op}(O)\between \textit{Op}(O')$
.By Proposition 9.2.2(2) we can simplify this to:
 $p\in O$
and
$p\in O$
and
 $p'\in O'$
implies
$p'\in O'$
implies
 $\textit{Op}(O)\between \textit{Op}(O')$
.
$\textit{Op}(O)\between \textit{Op}(O')$
.By Proposition 8.3.3(2) we can simplify this further to:
 $p\in O$
and
$p\in O$
and
 $p'\in O'$
implies
$p'\in O'$
implies
 $O\ast O'$
.
$O\ast O'$
.
But by definition, the compatibility relation
![]() $\ast$
of
$\ast$
of
![]() $(\mathsf{Open},\subseteq ,\between )$
is
$(\mathsf{Open},\subseteq ,\between )$
is
![]() $\between$
, so
$\between$
, so
![]() $O\ast O'$
and
$O\ast O'$
and
![]() $O\between O'$
are the same assertion. The equivalences follow.
$O\between O'$
are the same assertion. The equivalences follow.
The property of being intertwined is preserved and reflected when we use
![]() $\textit{nbhd}$
to map to the soberified space:
$\textit{nbhd}$
to map to the soberified space:
Corollary 11.7.2.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p,p'\in \mathsf{P}$
. Then
$p,p'\in \mathsf{P}$
. Then
![]() $p\mathrel {\between } p'$
in
$p\mathrel {\between } p'$
in
![]() $(\mathsf{P},\mathsf{Open})$
if and only if
$(\mathsf{P},\mathsf{Open})$
if and only if
![]() $\textit{nbhd}(p)\mathrel {\between }\textit{nbhd}(p')$
in
$\textit{nbhd}(p)\mathrel {\between }\textit{nbhd}(p')$
in
![]() $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
.
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
.
Proposition 11.7.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then:
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then:
-
(1) It may be that
 $(\mathsf{P},\mathsf{Open})$
is unconflicted (meaning that it contains no conflicted points), but the semitopology
$(\mathsf{P},\mathsf{Open})$
is unconflicted (meaning that it contains no conflicted points), but the semitopology
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
contains a conflicted point.
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
contains a conflicted point.
-
(2) It may further be that
 $(\mathsf{P},\mathsf{Open})$
is unconflicted and
$(\mathsf{P},\mathsf{Open})$
is unconflicted and
 $p\in \mathsf{P}$
is such that
$p\in \mathsf{P}$
is such that
 $\textit{nbhd}(p)$
is conflicted in the semitopology
$\textit{nbhd}(p)$
is conflicted in the semitopology
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
.
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
.
We can summarise the two assertions above as follows:
-
(1) Soberifying a space might introduce a conflicted point, even if none was originally present.
-
(2) Soberifying a space can make a point that was unconflicted, into a point that is conflicted. Footnote 31
Proof. It suffices to provide counterexamples.
-
(1) Consider the right-hand semitopology in Figure 6; this is unconflicted because every point is intertwined only with itself. The soberification of this space is illustrated in the right-hand semitopology in Figure 7. Each of the extra points is intertwined with the two numbered points next to it; for example the extra point in the open set
 $A$
– write it
$A$
– write it
 $\bullet _A$
(in-between
$\bullet _A$
(in-between
 $3$
and
$3$
and
 $0$
) – is intertwined with
$0$
) – is intertwined with
 $0$
and
$0$
and
 $3$
; so
$3$
; so
 $3\mathrel {\between } \bullet _A\mathrel {\between } 0$
. However, the reader can check that
$3\mathrel {\between } \bullet _A\mathrel {\between } 0$
. However, the reader can check that  . Thus,
. Thus,
 $\bullet _A$
is conflicted.
$\bullet _A$
is conflicted. -
(2) We define
 $(\mathsf{P},\mathsf{Open})$
by:
$(\mathsf{P},\mathsf{Open})$
by:-
–
 $\mathsf{P} = (\text{-} 1,1)$
(real numbers between
$\mathsf{P} = (\text{-} 1,1)$
(real numbers between
 $\text{-} 1$
and
$\text{-} 1$
and
 $1$
exclusive).
$1$
exclusive). -
–
 $\mathsf{Open}$
is generated by:
$\mathsf{Open}$
is generated by:-
– All open intervals that do not contain
 $0$
; so this is open intervals
$0$
; so this is open intervals
 $(r_1,r_2)$
where
$(r_1,r_2)$
where
 $\text{-} 1\leq r_1\lt r_2\leq 0$
or
$\text{-} 1\leq r_1\lt r_2\leq 0$
or
 $0\leq r_1\lt r_2\leq 1$
.
$0\leq r_1\lt r_2\leq 1$
. -
– All of the open intervals
 $(\text{-} 1/n,1/n)$
, for
$(\text{-} 1/n,1/n)$
, for
 $n\geq 2$
.
$n\geq 2$
.
-
The reader can check that:
-
– Points in this semitopology are intertwined only with themselves.
-
– The soberification includes four additional points, corresponding to completely prime semifilters
 $\text{-} 1/0$
generated by
$\text{-} 1/0$
generated by
 $\{(\text{-} 1/n,0) \mid n\geq 2\}$
and
$\{(\text{-} 1/n,0) \mid n\geq 2\}$
and
 ${+} 1/0$
generated by
${+} 1/0$
generated by
 $\{(0,1/n) \mid n\geq 2\}$
, and to the endpoints
$\{(0,1/n) \mid n\geq 2\}$
, and to the endpoints
 $\text{-} 1$
and
$\text{-} 1$
and
 $i{+} 1$
.
$i{+} 1$
. -
–
 $\text{-} 1/0$
and
$\text{-} 1/0$
and
 ${+} 1/0$
are intertwined with
${+} 1/0$
are intertwined with
 $0$
, but are not intertwined with one another.
$0$
, but are not intertwined with one another.
Thus,
 $0$
is conflicted in
$0$
is conflicted in
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
but not in
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
but not in
 $(\mathsf{P},\mathsf{Open})$
.
$(\mathsf{P},\mathsf{Open})$
. -
Remark 11.7.4. Proposition 11.7.3 may seem surprising in view of Corollary 11.7.2, but the key observation is that the soberified space may add points to the original space. These points can add conflicting behaviour that is ‘hidden’ in the completely prime semifilters of the original space.
Thus, Proposition 11.7.3 shows that the property of ‘being unconflicted’ cannot be characterised purely in terms of the semiframe of open sets – if it could be, then soberification would make no difference, by Theorem 10.1.4(3).
There is nothing wrong with that, except that we are interested in well-behavedness conditions on semiframes. We can now look for some other condition – but one having to do purely with open sets – that might play a similar role in the theory of (weak/quasi)regularity of semiframes, as being unconflicted does in theory of (weak/quasi)regularity of semitopologies.
We already saw a candidate for this in Theorem 11.5.4: strong compatibility. We examine this next.
11.8 Strong compatibility in semitopologies
Remark 11.8.1. Note that:
-
(1) Theorem 11.5.4 characterises ‘regular’ for semiframes as ‘weakly regular + strongly compatible’.
-
(2) Theorem 5.3.4 characterises ‘regular’ for semitopologies as ‘weakly regular + unconflicted’.
We know from results like Lemma 11.6.1 and Corollary 11.7.2 that there are accurate correspondences between notions of regularity in semiframes and semitopologies. This is by design, for example in Definition 11.5.1; we designed the semiframe definitions so that semiframe regularity and semitopological regularity would match up closely.
Yet there are differences too, since Theorem 11.5.4 uses strong compatibility, and Theorem 5.3.4 uses being unconflicted. What is the difference here, and why does it arise?
One answer is given by Proposition 11.7.3, which illustrates that the condition of ‘unconflicted’ (which comes from semitopologies) does not sit comfortably with the ‘pointless’ semiframe definitions. This raises the question of how strong compatibility (which comes from semiframes) translates into the context of semitopologies; and how this relates to being (un)conflicted?
We look into this now; see Remark 11.8.11 for a summary.
We can translate the notion of strongly compatible filter (Definition 11.3.6(1)) to semitopologies in the natural way, just applying it to the neighbourhood semifilter
![]() $\textit{nbhd}(p)$
of a point (Definition 2.3.1):
$\textit{nbhd}(p)$
of a point (Definition 2.3.1):
Definition 11.8.2. Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then call
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then call
![]() $p\in \mathsf{P}$
strongly compatible when the (by Example 8.1.4(1)) abstract point
$p\in \mathsf{P}$
strongly compatible when the (by Example 8.1.4(1)) abstract point
![]() $\textit{nbhd}(p)$
is strongly compatible (Definition 11.3.6) as a semifilter in
$\textit{nbhd}(p)$
is strongly compatible (Definition 11.3.6) as a semifilter in
![]() $(\mathsf{Open},\subseteq ,\between )$
.
$(\mathsf{Open},\subseteq ,\between )$
.
We unpack what Definition 11.8.2 means concretely:
Lemma 11.8.3.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following are equivalent:
$p\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $p$
is hypertransitive (Definition 6.2.3).
$p$
is hypertransitive (Definition 6.2.3).
-
(2)
 $\textit{nbhd}(p)$
is strongly compatible.
$\textit{nbhd}(p)$
is strongly compatible.
-
(3)
 $\textit{nbhd}(p)^\ast$
is compatible.
$\textit{nbhd}(p)^\ast$
is compatible.
-
(4) For every
 $O',O''\in \mathsf{Open}$
, if
$O',O''\in \mathsf{Open}$
, if
 $O'\ast \textit{nbhd}(p)\ast O''$
then
$O'\ast \textit{nbhd}(p)\ast O''$
then
 $O'\between O''$
.
$O'\between O''$
.
(Above,
![]() $O'\ast \textit{nbhd}(p)$
follows Notation 11.1.2(1) and means that
$O'\ast \textit{nbhd}(p)$
follows Notation 11.1.2(1) and means that
![]() $O'\between O$
for every
$O'\between O$
for every
![]() $p\in O\in \mathsf{Open}$
, and similarly for
$p\in O\in \mathsf{Open}$
, and similarly for
![]() $\textit{nbhd}(p)\ast O''$
.)
$\textit{nbhd}(p)\ast O''$
.)
Proof.
Equivalence of parts 1 and 2 is just Lemma 11.3.8. Equivalence of parts 2 and 3 is Definition 11.3.6(1). For the equivalence of parts 3 and 4, we just unpack what it means for
![]() $\textit{nbhd}(p)^\ast$
to be compatible (see Remark 11.3.7).
$\textit{nbhd}(p)^\ast$
to be compatible (see Remark 11.3.7).
‘
![]() $p\in \mathsf{P}$
is strongly compatible’ is a strictly stronger condition than ‘
$p\in \mathsf{P}$
is strongly compatible’ is a strictly stronger condition than ‘
![]() $p\in \mathsf{P}$
is unconflicted’:
$p\in \mathsf{P}$
is unconflicted’:
Lemma 11.8.4.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then:
$p\in \mathsf{P}$
. Then:
-
(1) If
 $p$
is strongly compatible then it is unconflicted.
$p$
is strongly compatible then it is unconflicted.
-
(2) If
 $p$
is conflicted then:
$p$
is conflicted then:
 $p$
is not strongly compatible,
$p$
is not strongly compatible,
 $\textit{nbhd}(p)$
is not strongly compatible, and
$\textit{nbhd}(p)$
is not strongly compatible, and
 $\textit{nbhd}(p)^\ast$
is not compatible.
$\textit{nbhd}(p)^\ast$
is not compatible.
-
(3) The reverse implication need not hold, even if
 $(\mathsf{P},\mathsf{Open})$
is sober:
Footnote
32
it is possible for
$(\mathsf{P},\mathsf{Open})$
is sober:
Footnote
32
it is possible for
 $p$
to be unconflicted but not strongly compatible.
$p$
to be unconflicted but not strongly compatible.
Proof. We consider each part in turn:
-
(1) Suppose
 $p$
is strongly compatible and suppose
$p$
is strongly compatible and suppose
 $p'\mathrel {\between } p\mathrel {\between } p''$
; we must show that
$p'\mathrel {\between } p\mathrel {\between } p''$
; we must show that
 $p'\mathrel {\between } p''$
. Consider open neighbourhoods
$p'\mathrel {\between } p''$
. Consider open neighbourhoods
 $p'\in O'$
and
$p'\in O'$
and
 $p''\in O''$
. By assumption
$p''\in O''$
. By assumption
 $p'\mathrel {\between } p$
and so by Lemma 11.7.1(1 and 2)
$p'\mathrel {\between } p$
and so by Lemma 11.7.1(1 and 2)
 $\textit{nbhd}(p')\ast \textit{nbhd}(p)$
. Since
$\textit{nbhd}(p')\ast \textit{nbhd}(p)$
. Since
 $O'\in \textit{nbhd}(p')$
, it follows that
$O'\in \textit{nbhd}(p')$
, it follows that
 $O'\ast \textit{nbhd}(p)$
, and similarly it follows that
$O'\ast \textit{nbhd}(p)$
, and similarly it follows that
 $\textit{nbhd}(p)\ast O''$
. Then by strong compatibility,
$\textit{nbhd}(p)\ast O''$
. Then by strong compatibility,
 $O'\between O''$
as required.
$O'\between O''$
as required. -
(2) We take the contrapositive of part 1 of this result, and use Lemma 11.8.3.
-
(3) It suffices to provide a counterexample. Consider the bottom right semitopology in Figure 2, and take
 $p=\ast$
and
$p=\ast$
and
 $O'=\{1\}$
and
$O'=\{1\}$
and
 $O''=\{0,2\}$
. Note that:
$O''=\{0,2\}$
. Note that:-
–
 $\ast$
is unconflicted, since it is intertwined only with itself and
$\ast$
is unconflicted, since it is intertwined only with itself and
 $1$
.
$1$
. -
–
 $O'$
and
$O'$
and
 $O'$
intersect every open neighbourhood of
$O'$
intersect every open neighbourhood of
 $\ast$
, but
$\ast$
, but  , so
, so
 $\ast$
is not strongly compatible.
$\ast$
is not strongly compatible.
This space is sober: the only completely prime filters are the neighbourhood semifilters of
 $\ast$
,
$\ast$
,
 $0$
,
$0$
,
 $1$
, and
$1$
, and
 $2$
.
$2$
. -
Example 11.8.5. Continuing Lemma 11.8.4(3), it is possible for a point to be strongly compatible (Definition 11.8.2) but not regular, or even quasiregular (Definition 4.1.4(3, 5)). Consider the right-hand semitopology illustrated in Figure 6 and take
![]() $p=0$
. The reader can check that
$p=0$
. The reader can check that
![]() $p$
is strongly compatible, but it is not quasiregular (i.e.
$p$
is strongly compatible, but it is not quasiregular (i.e.
![]() $\textit{K}(p)=\varnothing$
) and thus also not regular.
$\textit{K}(p)=\varnothing$
) and thus also not regular.
Lemma 11.8.6 shows that the situation outlined in Proposition 11.7.3(2) cannot arise if we work with a strongly compatible point instead of an unconflicted one …
Lemma 11.8.6.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p,p'\in \mathsf{P}$
. Then the following are equivalent:
$p,p'\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $p$
is hypertransitive in
$p$
is hypertransitive in
 $(\mathsf{P},\mathsf{Open})$
.
$(\mathsf{P},\mathsf{Open})$
. -
(2)
 $\textit{nbhd}(p)$
is hypertransitive in
$\textit{nbhd}(p)$
is hypertransitive in
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
(Notation 10.1.3).
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
(Notation 10.1.3).
Proof.
Note that from Lemma 11.8.3,
![]() $p$
is hypertransitive in
$p$
is hypertransitive in
![]() $(\mathsf{P},\mathsf{Open})$
when
$(\mathsf{P},\mathsf{Open})$
when
for every
![]() $O',O''\in \mathsf{Open}$
. Also, from Definition 8.4.3(2) and Lemma 11.8.3,
$O',O''\in \mathsf{Open}$
. Also, from Definition 8.4.3(2) and Lemma 11.8.3,
![]() $\textit{nbhd}(p)$
is hypertransitive in
$\textit{nbhd}(p)$
is hypertransitive in
![]() $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
when
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
when
for every
![]() $\textit{Op}(O'),\textit{Op}(O'')\in \mathsf{Opens}(\mathsf{Soberify}(\mathsf{P},\mathsf{Open}))$
.
$\textit{Op}(O'),\textit{Op}(O'')\in \mathsf{Opens}(\mathsf{Soberify}(\mathsf{P},\mathsf{Open}))$
.
Now by Proposition 9.2.2(2),
![]() $\textit{nbhd}(p)\in \textit{Op}(O)$
if and only if
$\textit{nbhd}(p)\in \textit{Op}(O)$
if and only if
![]() $p\in O$
, and by Corollary 9.2.3
$p\in O$
, and by Corollary 9.2.3
![]() $\textit{Op}(O')\between \textit{Op}(O)$
if and only if
$\textit{Op}(O')\between \textit{Op}(O)$
if and only if
![]() $O'\between O$
, and
$O'\between O$
, and
![]() $\textit{Op}(O)\between \textit{Op}(O'')$
if and only if
$\textit{Op}(O)\between \textit{Op}(O'')$
if and only if
![]() $O\between O''$
. The result follows.
$O\between O''$
. The result follows.
… but, the situation outlined in Proposition 11.7.3(1) can arise, indeed we use the same counterexample:
Lemma 11.8.7.
It may be that every point in
![]() $(\mathsf{P},\mathsf{Open})$
is hypertransitive, yet
$(\mathsf{P},\mathsf{Open})$
is hypertransitive, yet
![]() $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
contains a point that is not hypertransitive.
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
contains a point that is not hypertransitive.
Proof.
The same counterexample as used in Proposition 11.7.3(1) illustrates a space
![]() $(\mathsf{P},\mathsf{Open})$
such that every point in
$(\mathsf{P},\mathsf{Open})$
such that every point in
![]() $(\mathsf{P},\mathsf{Open})$
is hypertransitive, but
$(\mathsf{P},\mathsf{Open})$
is hypertransitive, but
![]() $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
contains a point that is not hypertransitive. We note that
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
contains a point that is not hypertransitive. We note that
![]() $\bullet _A$
(the extra point in-between
$\bullet _A$
(the extra point in-between
![]() $3$
and
$3$
and
![]() $0$
) is not hypertransitive, because both
$0$
) is not hypertransitive, because both
![]() $B$
and
$B$
and
![]() $D$
intersect with every open neighbourhood of
$D$
intersect with every open neighbourhood of
![]() $\bullet _A$
, but
$\bullet _A$
, but
![]() $B$
does not intersect with
$B$
does not intersect with
![]() $D$
.
$D$
.
The development above suggests that we define:
Definition 11.8.8. Call a semitopology
![]() $(\mathsf{P},\mathsf{Open})$
strongly compatible when
$(\mathsf{P},\mathsf{Open})$
strongly compatible when
![]() $(\mathsf{Open},\subseteq ,\between )$
is strongly compatible in the sense of Definition 11.3.6(2).
$(\mathsf{Open},\subseteq ,\between )$
is strongly compatible in the sense of Definition 11.3.6(2).
The proof of Proposition 11.8.9 is then very easy:
Proposition 11.8.9.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the following are equivalent:
$(\mathsf{P},\mathsf{Open})$
is a semitopology. Then the following are equivalent:
-
(1)
 $(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.8.8
.
$(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.8.8
. -
(2)
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.8.8
.
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.8.8
. -
(3)
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.3.6(2).
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.3.6(2).
-
(4)
 $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is hypertransitive in the sense of Definition 6.2.3
.
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is hypertransitive in the sense of Definition 6.2.3
.
Proof.
We unpack Definition 11.8.8 and note that strong compatibility of
![]() $(\mathsf{P},\mathsf{Open})$
is expressed purely as a property of its semiframe of open sets
$(\mathsf{P},\mathsf{Open})$
is expressed purely as a property of its semiframe of open sets
![]() $(\mathsf{Open},\subseteq ,\between )$
. By Theorem10.1.4(3), the semiframe of open sets of
$(\mathsf{Open},\subseteq ,\between )$
. By Theorem10.1.4(3), the semiframe of open sets of
![]() $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is isomorphic to
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
is isomorphic to
![]() $(\mathsf{Open},\subseteq ,\between )$
, via
$(\mathsf{Open},\subseteq ,\between )$
, via
![]() $\textit{nbhd}^{\text{-}1}$
. Equivalence of parts 1 and 2 follows.
$\textit{nbhd}^{\text{-}1}$
. Equivalence of parts 1 and 2 follows.
By Notation 10.1.3 and Remark 10.1.2(3), the points of
![]() $\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
are just abstract points of
$\mathsf{Soberify}(\mathsf{P},\mathsf{Open})$
are just abstract points of
![]() $(\mathsf{Open},\subseteq ,\between )$
. Equivalence of parts 2 and 3 follows.
$(\mathsf{Open},\subseteq ,\between )$
. Equivalence of parts 2 and 3 follows.
Equivalence of part 4 with the other parts follows using Lemmas 11.8.3 and 11.8.6.
Recall from Definition 4.1.4(7) that
![]() $(\mathsf{P},\mathsf{Open})$
being (weakly) regular means that every point in
$(\mathsf{P},\mathsf{Open})$
being (weakly) regular means that every point in
![]() $(\mathsf{P},\mathsf{Open})$
is (weakly) regular. Recall from Definition 11.8.8 that
$(\mathsf{P},\mathsf{Open})$
is (weakly) regular. Recall from Definition 11.8.8 that
![]() $(\mathsf{P},\mathsf{Open})$
being strongly compatible means that
$(\mathsf{P},\mathsf{Open})$
being strongly compatible means that
![]() $(\mathsf{Open},\subseteq ,\between )=\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.3.6(2). We can now prove an analogue of Theorems5.3.4 and 11.5.4:
$(\mathsf{Open},\subseteq ,\between )=\mathsf{Fr}(\mathsf{P},\mathsf{Open})$
is strongly compatible in the sense of Definition 11.3.6(2). We can now prove an analogue of Theorems5.3.4 and 11.5.4:
Theorem 11.8.10.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is a semitopology and
$(\mathsf{P},\mathsf{Open})$
is a semitopology and
![]() $p\in \mathsf{P}$
. Then the following are equivalent:
$p\in \mathsf{P}$
. Then the following are equivalent:
-
(1)
 $(\mathsf{P},\mathsf{Open})$
is regular.
$(\mathsf{P},\mathsf{Open})$
is regular.
-
(2)
 $(\mathsf{P},\mathsf{Open})$
is weakly regular and strongly compatible.
$(\mathsf{P},\mathsf{Open})$
is weakly regular and strongly compatible.
Proof.
Suppose
![]() $(\mathsf{P},\mathsf{Open})$
is regular, meaning that every
$(\mathsf{P},\mathsf{Open})$
is regular, meaning that every
![]() $p\in \mathsf{P}$
is regular.
$p\in \mathsf{P}$
is regular.
By Theorems5.3.4 and 6.3.3 every
![]() $p\in \mathsf{P}$
is weakly regular and hypertransitive. (So by Lemma 11.8.3 every
$p\in \mathsf{P}$
is weakly regular and hypertransitive. (So by Lemma 11.8.3 every
![]() $\textit{nbhd}(p)$
is strongly compatible, and by Lemma 11.8.6 also hypertransitive.) The definition of weak regularity for a space in Definition 4.1.4(7) is pointwise, so it follows immediately that
$\textit{nbhd}(p)$
is strongly compatible, and by Lemma 11.8.6 also hypertransitive.) The definition of weak regularity for a space in Definition 4.1.4(7) is pointwise, so it follows immediately that
![]() $(\mathsf{P},\mathsf{Open})$
is weakly regular.
$(\mathsf{P},\mathsf{Open})$
is weakly regular.
But, the definition of strong compatibility for a space in Definition 11.8.8 is on its semiframe of open sets, which may include abstract points not only of the form
![]() $\textit{nbhd}(p)$
. It therefore does not follow immediately that
$\textit{nbhd}(p)$
. It therefore does not follow immediately that
![]() $(\mathsf{P},\mathsf{Open})$
is strongly compatible; Lemma 11.8.7 contains a counterexample.
$(\mathsf{P},\mathsf{Open})$
is strongly compatible; Lemma 11.8.7 contains a counterexample.
We can still prove that
![]() $(\mathsf{P},\mathsf{Open})$
is strongly compatible – but we need to do a bit more work.
$(\mathsf{P},\mathsf{Open})$
is strongly compatible – but we need to do a bit more work.
Unpacking Definition 11.8.8, we must show that
![]() $(\mathsf{Open},\subseteq ,\between )$
is strongly compatible. Unpacking Definition 11.3.6(2), we must show that every abstract point in
$(\mathsf{Open},\subseteq ,\between )$
is strongly compatible. Unpacking Definition 11.3.6(2), we must show that every abstract point in
![]() $(\mathsf{Open},\subseteq ,\between )$
is strongly compatible.
$(\mathsf{Open},\subseteq ,\between )$
is strongly compatible.
So consider an abstract point
![]() $P\subseteq \mathsf{Open}$
. By Corollary 4.3.3
$P\subseteq \mathsf{Open}$
. By Corollary 4.3.3
![]() $\mathsf{P}$
has a topen partition
$\mathsf{P}$
has a topen partition
![]() $\mathscr T$
, which means that: every
$\mathscr T$
, which means that: every
![]() $T\in \mathscr T$
is topen; the elements of
$T\in \mathscr T$
is topen; the elements of
![]() $\mathscr T$
are disjoint; and
$\mathscr T$
are disjoint; and
![]() $\bigcup \mathscr T=\mathsf{P}$
.
$\bigcup \mathscr T=\mathsf{P}$
.
Now
![]() $\bigcup \mathscr T\ =\mathsf{P}\in T$
by Definition 8.1.1(7) and Lemma 8.2.1(1), so by Definition 8.1.1(2) there exists at least one (and in fact precisely one)
$\bigcup \mathscr T\ =\mathsf{P}\in T$
by Definition 8.1.1(7) and Lemma 8.2.1(1), so by Definition 8.1.1(2) there exists at least one (and in fact precisely one)
![]() $T\in \mathscr T$
such that
$T\in \mathscr T$
such that
![]() $T\in P$
. Now
$T\in P$
. Now
![]() $T$
is a transitive element in
$T$
is a transitive element in
![]() $\mathsf{Open}$
, so by Proposition 11.3.13
$\mathsf{Open}$
, so by Proposition 11.3.13
![]() $P\subseteq \mathsf{Open}$
is strongly compatible as required.
$P\subseteq \mathsf{Open}$
is strongly compatible as required.
Remark 11.8.11. We summarise what we have seen:
-
(1) The notions of (quasi/weak)regularity match up nicely between a semitopology, and its semiframe soberification (Proposition 11.6.2).
-
(2) We saw in Proposition 11.7.3 that the notions of (un)conflicted point and unconflicted space from Definition 5.3.1(2) are not robust under forming soberification (Notation 10.1.3). From the point of view of a pointless methodology in semitopologies – in which we seek to understand a semitopology
 $(\mathsf{P},\mathsf{Open})$
starting from its semiframe structure
$(\mathsf{P},\mathsf{Open})$
starting from its semiframe structure
 $(\mathsf{Open},\subseteq ,\between )$
– this is a defect.
$(\mathsf{Open},\subseteq ,\between )$
– this is a defect. -
(3) A pointwise notion of strong compatibility exists; by Lemma 11.8.3 it is actually hypertransitivity from Definition 6.2.3. This is preserved pointwise by soberification (Lemma 11.8.6), but soberification can still introduce extra points, and it turns out that the property of a space being pointwise hypertransitive is still not robust under soberification because the extra points need not necessarily be hypertransitive; see Lemma 11.8.7.
-
(4) This motivates the notion of a strongly compatible semitopology from Definition 11.8.8; and then Proposition 11.8.9 becomes easy.
Our larger point (no pun intended) is that the Definition and its corresponding Proposition are natural, and also that the other design decisions are less natural, as noted above.
Perhaps somewhat unexpectedly, ‘regular = weakly regular + strongly compatible’ then works pointwise and for the entire space; see Theorem 11.8.10. Thus Definition 11.8.8 has good properties and is natural from a pointless/semiframe/open sets perspective.
12. Conclusions and Related and Future Work
12.1 Topology versus semitopology
We briefly compare and contrast topology/frames and semitopology/semiframes. This list is not exhaustive but we hope it will give a feel for how the two differ:
-
(1) Topology: We are typically interested in spaces with separation axioms.Footnote 33
Semitopology: We are interested in guaranteeing agreement between participants of a distributed system, and this is all about anti-separation properties of their actionable coalitions. Semifilters have a compatibility condition (Definition 8.1.1(4)); and regularity, being intertwined, and being unconflicted or strongly compatible are anti-separation properties (see Definitions 3.5.1, 4.1.4, 5.3.1, and 11.3.6, and Remark 3.5.7).Footnote 34
-
(2) Topology: If a minimal open neighbourhood of a point exists then it is least, because we can intersect two minimal neighbourhoods to get a smaller one which by minimality is equal to both. A finite filter has a least element.
Semitopology: A point may have multiple minimal open neighbourhoods – examples are very easy to generate, see for example the top-right example in Figure 2. A finite semifilter need not have a least element (see Remark 8.1.6).
-
(3) Topology: Every finite
 $T_0$
topology is sober. A topology is sober if and only if every nonempty irreducible closed set is the closure of a unique point.
$T_0$
topology is sober. A topology is sober if and only if every nonempty irreducible closed set is the closure of a unique point.Semitopology: Neither property holds. See Lemma 9.3.8.
-
(4) Semitopological questions such as ‘is this a topen set’ or ‘are these two points intertwined’ or ‘does this point have a topen neighbourhood’ – and many other definitions in this paper, such as our taxonomy of points into regular, weakly regular, quasiregular, conflicted, and strongly compatible are novel and/or play a larger role in the theory than they typically do in topology.
12.2 Related work
Dualities
We discussed duality results in detail in Remark 10.4.1. The reader may know that there are a many such results, starting with Stone’s classic duality between Boolean algebras and compact Hausdorff spaces with a basis of clopen sets (Stone, Reference Stone1936; Johnstone, Reference Johnstone1986). The duality between frames and topologies is described in Mac Lane and Moerdijk (Reference Mac Lane and Moerdijk1992, p. 479, Corollary 4). See also the encyclopaedic treatment in Caramello (Reference Caramello2011), with an overview in Example 2.9 on page 17. Our duality between semiframes and semitopologies fits into this canon.
Union sets, closure spaces, and minimal structures
There is a thread of research into union-closed families; these are subsets of a finite powerset closed under unions, so that a union-closed families is precisely just a finite semitopology. The motivation is to study the combinatorics of finite subsemilattices of a powerset. Some progress has been made in this Poonen (Reference Poonen1992); the canonical reference for the relevant combinatorial conjectures is the ‘problem session’ on page 525 (conjectures 1.9, 1.9′, and 1.9′′) of Rival (Reference Rival1985). See also recent progress in a conjecture about union-closed families.Footnote 35 There is no direct connection to semitopologies, and certainly no consideration of duality results. Perhaps the duality in this paper may be of some interest in that community.
A closure space is a subset of a powerset that is closed under intersections (Erné, Reference Erné2009, p.173). Up to taking sets complements, a closure space is a semitopology, and likewise a finite closure space is, up to taking sets complements, a union-closed family. The motivation for closure spaces is to study closure operations in a topology-flavoured style, so closure spaces (unlike union-closed sets) share a topological flavour with semitopologies. However the applications are completely different, and algebra reveals how the underlying structures are also mathematically distinct, as is made clear by a lattice-based presentation of closure spaces and morphisms (Erné, Reference Erné2009, Section 2.4), which uses a structure of ‘based lattices’ (essentially: lattices plus a generating basis): this differs from semitopologies with their semiframe presentation as compatible complete semilattices.Footnote 36
A minimal structure on a set
![]() $X$
is a subset of
$X$
is a subset of
![]() $\textit{pow}(X)$
that contains
$\textit{pow}(X)$
that contains
![]() $\varnothing$
and
$\varnothing$
and
![]() $X$
. Thus a semitopology is a minimal structure that is also closed under arbitrary unions. There is a thread of research into minimal structures, studying how notions familiar from topology (such as continuity) fare in weak (minimal) settings (Popa and Noiri, Reference Popa and Noiri2001) and how this changes as axioms (such as closure under unions) are added or removed. An accessible discussion is in Száz (Reference Száz2007), and see the brief but comprehensive references in Remark 3.7 of that paper. Of course our focus is on properties of semitopologies which are not considered in that literature; but we share an observation with minimal structures that it is useful to study topology-like constructs, in the absence of closure under intersections.
$X$
. Thus a semitopology is a minimal structure that is also closed under arbitrary unions. There is a thread of research into minimal structures, studying how notions familiar from topology (such as continuity) fare in weak (minimal) settings (Popa and Noiri, Reference Popa and Noiri2001) and how this changes as axioms (such as closure under unions) are added or removed. An accessible discussion is in Száz (Reference Száz2007), and see the brief but comprehensive references in Remark 3.7 of that paper. Of course our focus is on properties of semitopologies which are not considered in that literature; but we share an observation with minimal structures that it is useful to study topology-like constructs, in the absence of closure under intersections.
Algebraic topology as applied to distributed computing tasks
The reader may know that solvability results about distributed computing tasks have been obtained from algebraic topology, starting with the impossibility of
![]() $k$
-set consensus and the Asynchronous Computability Theorem (Herlihy and Shavit, Reference Herlihy and Shavit1993; Borowsky and Gafni, Reference Borowsky and Gafni1993; Saks and Zaharoglou, Reference Saks and Zaharoglou2000) in 1993. See Herlihy et al. (Reference Herlihy, Kozlov and Rajsbaum2013) for numerous such results.
$k$
-set consensus and the Asynchronous Computability Theorem (Herlihy and Shavit, Reference Herlihy and Shavit1993; Borowsky and Gafni, Reference Borowsky and Gafni1993; Saks and Zaharoglou, Reference Saks and Zaharoglou2000) in 1993. See Herlihy et al. (Reference Herlihy, Kozlov and Rajsbaum2013) for numerous such results.
The basic observation is that states of a distributed algorithm form a simplicial complex, called its protocol complex, and topological properties of this complex, like connectivity, are constrained by the underlying communication and fault model. These topological properties in turn can determine what tasks are solvable. For example: every algorithm in the wait-free model with atomic read-write registers has a connected protocol complex, and because the consensus task’s output complex is disconnected, consensus in this model is not solvable (Herlihy et al., Reference Herlihy, Kozlov and Rajsbaum2013, Chapter 4).
This paper is also topological, but in a different way: we use (semi)topologies to study consensus in and of itself, rather than the solvability of consensus or other tasks in particular computation models. Put another way: the papers cited above use topology to study the solvability of distributed tasks, but this paper shows how the very idea of ‘distribution’ can be viewed as having a semitopological foundation.
Of course we can imagine that these might be combined – that in future work we may find interesting and useful things to say about the topologies of distributed algorithms when viewed as algorithms on and in a semitopology.
Fail-prone systems and quorum systems
Given a set of processes
![]() $\mathsf{P}$
, a fail-prone system (Malkhi and Reiter, Reference Malkhi and Reiter1998) (or adversary structure (Hirt and Maurer, Reference Hirt and Maurer2000)) is a set of fail-prone sets
$\mathsf{P}$
, a fail-prone system (Malkhi and Reiter, Reference Malkhi and Reiter1998) (or adversary structure (Hirt and Maurer, Reference Hirt and Maurer2000)) is a set of fail-prone sets
![]() $\mathscr{F}=\{F_1,\ldots ,F_n\}$
where, for every
$\mathscr{F}=\{F_1,\ldots ,F_n\}$
where, for every
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $F_i\subseteq \mathsf{P}$
.
$F_i\subseteq \mathsf{P}$
.
![]() $\mathscr{F}$
denotes the assumptions that the set of processes that will fail (potentially maliciously) is a subset of one of the fail-prone sets. A dissemination quorum system for
$\mathscr{F}$
denotes the assumptions that the set of processes that will fail (potentially maliciously) is a subset of one of the fail-prone sets. A dissemination quorum system for
![]() $\mathscr{F}$
is a set
$\mathscr{F}$
is a set
![]() $\{Q_1,\ldots , Q_m\}$
of quorums where, for every
$\{Q_1,\ldots , Q_m\}$
of quorums where, for every
![]() $1\leq i\leq m$
,
$1\leq i\leq m$
,
![]() $Q_i\subseteq \mathsf{P}$
, and such that
$Q_i\subseteq \mathsf{P}$
, and such that
-
• for every two quorums
 $Q$
and
$Q$
and
 $Q'$
and for every fail-prone set
$Q'$
and for every fail-prone set
 $F$
,
$F$
,
 $\left (Q\cap Q'\right )\setminus F\neq \emptyset$
and
$\left (Q\cap Q'\right )\setminus F\neq \emptyset$
and -
• for every fail-prone set
 $F$
, there exists a quorum disjoint from
$F$
, there exists a quorum disjoint from
 $F$
.
$F$
.
Several distributed algorithms, such as Bracha Broadcast (Bracha, Reference Bracha1987) and PBFT Castro and Liskov, Reference Castro and Liskov2002), rely on a quorum system for a fail-prone system
![]() $\mathscr{F}$
in order to solve problems such as reliable broadcast and consensus assuming (at least) that the assumptions denoted by
$\mathscr{F}$
in order to solve problems such as reliable broadcast and consensus assuming (at least) that the assumptions denoted by
![]() $\mathscr{F}$
are satisfied.
$\mathscr{F}$
are satisfied.
Several recent works generalise the fail-prone system model to heterogeneous systems. Under the failure assumptions of a traditional fail-prone system, Bezerra et al. (Reference Bezerra, Kuznetsov, Koroleva, Koulali and Mezini2022) study reliable broadcast when participants each have their own set of quorums. Asymmetric Fail-Prone Systems (Alpos et al., Reference Alpos, Cachin, Tackmann and Zanolini2024) generalise fail-prone systems to allow participants to make different failure assumption and have different quorums. In Permissionless Fail-Prone Systems (Cachin et al., Reference Cachin, Losa, Zanolini, Hillel, Palmieri and Rivière2023), participants not only make assumptions about failures, but also make assumptions about the assumptions of other processes; the resulting structure seems closely related to witness semitopologies, but the exact relationship still needs to be elucidated.
Federated Byzantine Agreement Systems (Mazières, Reference Mazières2015) are an instance of semitopologies. García-Pérez and Gotsman (Reference García-Pérez and Gotsman2018) rigorously prove the correctness of broadcast abstractions in Stellar’s Federated Byzantine Agreement model and investigate the model’s relationship to dissemination quorum systems. The Personal Byzantine Quorum System model (Losa et al., Reference Losa, Gafni, Mazières and Suomela2019) is an abstraction of Stellar’s Federated Byzantine Agreement System model and accounts for the existence of disjoint consensus clusters (in the terminology of the paper) which can each stay in agreement internally but may disagree between each other. Consensus clusters are closely related to the notion of topen in Definition 3.2.2(2).
Sheff et al., study heterogeneous consensus in a model called Learner Graphs (Sheff et al., Reference Sheff, Wang, Renesse, Myers, Bramas, Oshman and Romano2021) and propose a consensus algorithm called Heterogeneous Paxos.
Cobalt, the Stellar Consensus Protocol, Heterogeneous Paxos, and the Ripple Consensus Algorithm (Schwartz et al., Reference Schwartz, Youngs and Britto2014; Mazières, Reference Mazières2015; MacBrough, Reference MacBrough2018; Sheff et al., Reference Sheff, Wang, Renesse, Myers, Bramas, Oshman and Romano2021) are consensus algorithms that rely on heterogeneous quorums or variants thereof. The Stellar network (Lokhava et al., Reference Lokhava, Losa, Mazières, Hoare, Barry, Gafni, Jove, Malinowsky and McCaleb2019) and the XRP Ledger (Schwartz et al., Reference Schwartz, Youngs and Britto2014) are two global payment networks that use heterogeneous quorums to achieve consensus among an open set of participants; the Stellar network is an instance of a witness semitopology.
The literature on fail-prone systems and quorum systems is most interested in synchronisation algorithms for distributed systems and has been less concerned with their deeper mathematical structure. Some work by the second author and others (Losa et al., Reference Losa, Gafni, Mazières and Suomela2019) gets as far as proving an analogue to Proposition 3.4.4 (though we think it is fair to say that the presentation in this paper is simpler and clearer), but it fails to notice the connection with topology and the subsequent results which we present in this paper, and there is no consideration of algebra as used in this paper.
(Semi)lattices with extra structure
I am not aware of semiframes having been studied in the literature, but they are in excellent company, in the sense that things have been studied that are structurally similar. We mention two examples to give a flavour of this extensive literature:
-
(1) A quantale is a complete lattice
 $(\mathsf Q,\bigvee )$
with an associative multiplication operation
$(\mathsf Q,\bigvee )$
with an associative multiplication operation
 $\ast : (\mathsf{Q} \times \mathsf{Q}) \to \mathsf{Q}$
that distributes over
$\ast : (\mathsf{Q} \times \mathsf{Q}) \to \mathsf{Q}$
that distributes over
 $\bigvee$
in both arguments (Rosenthal, Reference Rosenthal1990). A commutative quantale whose multiplication is restricted to map to either the top or bottom element in
$\bigvee$
in both arguments (Rosenthal, Reference Rosenthal1990). A commutative quantale whose multiplication is restricted to map to either the top or bottom element in
 $\mathsf Q$
is close being a semiframe.Footnote
37
For reference, a pleasingly simple representation result for quantales is given in Brown and Gurr (Reference Brown and Gurr1993).
$\mathsf Q$
is close being a semiframe.Footnote
37
For reference, a pleasingly simple representation result for quantales is given in Brown and Gurr (Reference Brown and Gurr1993). -
(2) An overlap algebra is a complete Heyting algebra
 $\mathsf{X}$
with an overlap relation
$\mathsf{X}$
with an overlap relation
 ${\rlap {$\gt $}\,{\lt }}\subseteq \mathsf{X}\times \mathsf{X}$
whose intuition is that
${\rlap {$\gt $}\,{\lt }}\subseteq \mathsf{X}\times \mathsf{X}$
whose intuition is that
 $x{\rlap {$\gt $}\,{\lt }} y$
when
$x{\rlap {$\gt $}\,{\lt }} y$
when
 $x{\boldsymbol \wedge } y$
is inhabited. The motivation for this comes from constructive logic, in which
$x{\boldsymbol \wedge } y$
is inhabited. The motivation for this comes from constructive logic, in which
 $\exists p.(p\in x\land p\in y)$
is a different and stronger statement than
$\exists p.(p\in x\land p\in y)$
is a different and stronger statement than
 $\neg \forall p.\neg (p\in x\land p\in y)$
. Accordingly, overlap algebras are described as ‘a constructive look at Boolean algebras’ (Ciraulo and Contente, Reference Ciraulo and Contente2020). Overlap algebras are not semiframes, but they share an idea with semiframes in making a structural distinction between ‘intersect’ and ‘have a non-empty join’.
$\neg \forall p.\neg (p\in x\land p\in y)$
. Accordingly, overlap algebras are described as ‘a constructive look at Boolean algebras’ (Ciraulo and Contente, Reference Ciraulo and Contente2020). Overlap algebras are not semiframes, but they share an idea with semiframes in making a structural distinction between ‘intersect’ and ‘have a non-empty join’.
12.3 Future work
The list of future work below is not exhaustive, of course. If this list inspires, through some omission that is obvious to the reader, a new idea, then that is best of all: finding good questions is the first and arguably most important step in research.
Remark 12.3.1 (Other notions of morphism). In Definition 10.1.1(1) we take a morphism of semitopologies
![]() $f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
to be a continuous function
$f:(\mathsf{P},\mathsf{Open})\to (\mathsf{P}',\mathsf{Open}')$
to be a continuous function
![]() $f:\mathsf{P}\to \mathsf{P}'$
. Correspondingly, in Definition 10.2.1(1) we take a morphism of semiframes
$f:\mathsf{P}\to \mathsf{P}'$
. Correspondingly, in Definition 10.2.1(1) we take a morphism of semiframes
![]() $g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast )$
to be a compatible morphism of complete semilattices.
$g:(\mathsf{X}',\leq ',\ast ')\to (\mathsf{X},\leq ,\ast )$
to be a compatible morphism of complete semilattices.
The reader may be familiar with conditions on maps between topologies other than continuity, such as being open (
![]() $f$
maps open sets to open sets) and closed (
$f$
maps open sets to open sets) and closed (
![]() $f$
maps closed sets to closed sets). These also make sense in semitopologies.
$f$
maps closed sets to closed sets). These also make sense in semitopologies.
A further natural design space in the semitopological case is to include conditions on set intersections and strict inclusions. We briefly list some conditions that we could impose on
![]() $f:\mathsf{P}\to \mathsf{P}'$
:
$f:\mathsf{P}\to \mathsf{P}'$
:
-
(1) If
 $O\between O'$
then
$O\between O'$
then
 $f^{\text{-}1}(O)\between f^{\text{-}1}(O')$
(it is automatic that if
$f^{\text{-}1}(O)\between f^{\text{-}1}(O')$
(it is automatic that if
 $f^{\text{-}1}(O)\between f^{\text{-}1}(O')$
then
$f^{\text{-}1}(O)\between f^{\text{-}1}(O')$
then
 $O\between O'$
, but the reverse implication is a distinct condition).
$O\between O'$
, but the reverse implication is a distinct condition). -
(2) If
 $O\subsetneq O'$
then
$O\subsetneq O'$
then
 $f^{\text{-}1}(O)\subsetneq f^{\text{-}1}(O')$
.
$f^{\text{-}1}(O)\subsetneq f^{\text{-}1}(O')$
. -
(3)
 $O\between O'$
implies
$O\between O'$
implies
 $f^{\text{-}1}(O)\subseteq f^{\text{-}1}(O')$
implies
$f^{\text{-}1}(O)\subseteq f^{\text{-}1}(O')$
implies
 $O\subseteq O'$
, or an equivalent contrapositive:
$O\subseteq O'$
, or an equivalent contrapositive:
 $O\between O'$
implies
$O\between O'$
implies
 $O\not \subseteq O'$
implies
$O\not \subseteq O'$
implies
 $f^{\text{-}1}(O)\not \subseteq f^{\text{-}1}(O')$
.Footnote
38
$f^{\text{-}1}(O)\not \subseteq f^{\text{-}1}(O')$
.Footnote
38
Remark 12.3.2 (Representations). The Sierpiński space
![]() $\textit{Sk}=(\mathsf{P},\mathsf{Open})$
sets
$\textit{Sk}=(\mathsf{P},\mathsf{Open})$
sets
![]() $\mathsf{P}=\{0,1\}$
and
$\mathsf{P}=\{0,1\}$
and
![]() $\mathsf{Open}=\{\varnothing ,\{1\},\{0,1\}\}$
. This is both a topology and a semitopology, and it is a classifying space for open sets, in the sense that
$\mathsf{Open}=\{\varnothing ,\{1\},\{0,1\}\}$
. This is both a topology and a semitopology, and it is a classifying space for open sets, in the sense that
![]() $\textit{Hom}(\text{-},\textit{Sk}):\mathsf{SemiTop}\to \mathsf{Set}$
is naturally isomorphic to
$\textit{Hom}(\text{-},\textit{Sk}):\mathsf{SemiTop}\to \mathsf{Set}$
is naturally isomorphic to
![]() $\textit{Opns}:\mathsf{SemiTop}\to \mathsf{Set}$
which maps
$\textit{Opns}:\mathsf{SemiTop}\to \mathsf{Set}$
which maps
![]() $(\mathsf{P},\mathsf{Open})$
to
$(\mathsf{P},\mathsf{Open})$
to
![]() $\mathsf{Open}$
.
$\mathsf{Open}$
.
![]() $\textit{Sk}$
does not classify semitopologies, because semiframes suggest that we should view the set of open sets
$\textit{Sk}$
does not classify semitopologies, because semiframes suggest that we should view the set of open sets
![]() $\mathsf{Open}$
of a semitopology as a semiframe structure, having a subset inclusion (of course) and also a generalised intersection
$\mathsf{Open}$
of a semitopology as a semiframe structure, having a subset inclusion (of course) and also a generalised intersection
![]() $\between$
. A likely classifying space for this is the the top-left example in Figure 2, such that
$\between$
. A likely classifying space for this is the the top-left example in Figure 2, such that
-
•
 $\mathsf{P}=\{0,1,2\}$
and
$\mathsf{P}=\{0,1,2\}$
and -
•
 $\mathsf{Open}=\{\varnothing ,\{0\},\{2\},\{0,2\},\{0,1,2\}\}$
.
$\mathsf{Open}=\{\varnothing ,\{0\},\{2\},\{0,2\},\{0,1,2\}\}$
.
With
![]() $\textit{Sk}$
in mind, this space looks like two copies of
$\textit{Sk}$
in mind, this space looks like two copies of
![]() $\textit{Sk}$
glued end-to-end – that is like two open sets – where the
$\textit{Sk}$
glued end-to-end – that is like two open sets – where the
![]() $1\in \mathsf{P}$
represents where they might intersect. Call this space
$1\in \mathsf{P}$
represents where they might intersect. Call this space
![]() $\textbf{3}$
.
$\textbf{3}$
.
![]() $\textbf{3}$
suggests that a logic for semiframes might be naturally three-valued, with values
$\textbf{3}$
suggests that a logic for semiframes might be naturally three-valued, with values
![]() $\textbf{t}$
,
$\textbf{t}$
,
![]() $\textbf{f}$
, and also
$\textbf{f}$
, and also
![]() $\textbf{b}$
for ‘is in the intersection’, and that the spaces
$\textbf{b}$
for ‘is in the intersection’, and that the spaces
![]() $\textit{Hom}(\text{-},\textbf{3})$
of continuous mappings to
$\textit{Hom}(\text{-},\textbf{3})$
of continuous mappings to
![]() $\textbf{3}$
might play a useful role. This might also have some impact on suitable notions of exponential space (see Remark 12.3.3). Current research (Gabbay and Zanolini, Reference Gabbay and Zanolini2025) considers applying three-valued modal logics based on semitopologies to reason explicitly about decentralised algorithms, like Paxos (Lamport, Reference Lamport2001).
$\textbf{3}$
might play a useful role. This might also have some impact on suitable notions of exponential space (see Remark 12.3.3). Current research (Gabbay and Zanolini, Reference Gabbay and Zanolini2025) considers applying three-valued modal logics based on semitopologies to reason explicitly about decentralised algorithms, like Paxos (Lamport, Reference Lamport2001).
Remark 12.3.3 (Exponential spaces). It remains to check whether the category
![]() $\mathsf{SemiFrame}$
of semiframes is closed (Mac Lane, Reference Mac Lane1971, p. 180, Section VII.7), or Cartesian.Footnote
39
$\mathsf{SemiFrame}$
of semiframes is closed (Mac Lane, Reference Mac Lane1971, p. 180, Section VII.7), or Cartesian.Footnote
39
It remains to look into the Vietoris (also called the exponential) semitopologies (Engelking, Reference Engelking1989, Exercise 2.7.20, p. 120), though in view of Remark 12.3.2 it is also an open question what the most suitable notion of exponential would be – we speculate that exponentials over
![]() $\mathbf{3}$
would be suitable.
$\mathbf{3}$
would be suitable.
More generally, it remains to study functors of the from
![]() $\textit{Hom}(\text{-},B)$
and
$\textit{Hom}(\text{-},B)$
and
![]() $\textit{Hom}(A,\text{-})$
, for different values of
$\textit{Hom}(A,\text{-})$
, for different values of
![]() $A$
and
$A$
and
![]() $B$
.
$B$
.
Remark 12.3.4 (Finiteness and compactness). The relation of semitopologies to finiteness is interesting. On the one hand, our motivating examples – distributed networks – are finite because they exist in the real world. On the other hand, in distributed networks, precisely because they are distributed, participants may not be able to depend on an exhaustive search of the full network being practical (or even permitted – this could be interpreted as a waste of resources or even as hostile or dangerous).
This requires mathematical models and algorithms that make sense on at least countably infinitely many points.Footnote 40
In fact, arguably even ‘countably large’ is not quite right. The natural cardinality for semitopologies may be uncountable, since network latency means that we cannot even enumerate the network: no matter how carefully we count, we could always in principle discover new participants who have joined in the past (but we just had not heard of them yet).
This motivates future work in which we consider algebraic conditions on a semiframe
![]() $(\mathsf{X},\leq ,\ast )$
that mimic some of the properties of open sets of finite semitopologies (without necessarily insisting on finiteness itself). For instance:
$(\mathsf{X},\leq ,\ast )$
that mimic some of the properties of open sets of finite semitopologies (without necessarily insisting on finiteness itself). For instance:
-
(1) We could insist that a
 $\leq$
-descending chain of non-
$\leq$
-descending chain of non-
 ${\boldsymbol \bot }_{\mathsf{X}}$
elements in
${\boldsymbol \bot }_{\mathsf{X}}$
elements in
 $\mathsf{X}$
have a non-
$\mathsf{X}$
have a non-
 ${\boldsymbol \bot }_{\mathsf{X}}$
greatest lower bound in
${\boldsymbol \bot }_{\mathsf{X}}$
greatest lower bound in
 $\mathsf{X}$
.
$\mathsf{X}$
. -
(2) We could insist that a
 $\leq$
-descending chain of elements strictly
$\leq$
-descending chain of elements strictly
 $\leq$
-greater than some
$\leq$
-greater than some
 $x\in \mathsf{X}$
have a greatest lower bound that is strictly
$x\in \mathsf{X}$
have a greatest lower bound that is strictly
 $\leq$
-greater than
$\leq$
-greater than
 $x$
.
$x$
. -
(3) We could insist that if
 $(x_i\mid i\geq 0)$
and
$(x_i\mid i\geq 0)$
and
 $(y_i\mid i\geq 0)$
are two
$(y_i\mid i\geq 0)$
are two
 $\leq$
-descending chains of elements, and
$\leq$
-descending chains of elements, and
 $x_i\ast y_i$
for every
$x_i\ast y_i$
for every
 $i\geq 0$
– in words:
$i\geq 0$
– in words:
 $x_i$
is compatible with
$x_i$
is compatible with
 $y_i$
– then the greatest lower bounds of the two chains are compatible.
$y_i$
– then the greatest lower bounds of the two chains are compatible.
The reader may notice how these conditions are reminiscent of compactness conditions from topology: for example a metric space is compact if and only if every descending chain of open sets has a nonempty intersection. This is no coincidence, since one of the uses of compactness in topology is precisely to recover some of the characteristics of finite topologies.
Considering semiframes (and indeed semitopologies) with compactness/finiteness flavoured conditions, is future work.
Remark 12.3.5 (Computational/logical behaviour). The original motivation for semiframes comes from semitopologies, which are motivated by blockchains and other decentralised systems, which are often real software artefacts that do real computation. It might therefore be useful to think about ‘computable’ semiframes, whatever this should mean. Gabbay (Reference Gabbay2024) considers witness semitopologies as a model of computably tractable semitopologies (being a witness semitopology is a concrete condition on sets), and we propose an algebraic abstraction of these as (strongly) chain-complete semitopologies; a semitopology is (strongly) chain-complete when any infinite descending chain of (nonempty) open sets has a (nonempty) open intersection. we argue that being chain-complete is an appropriate generalisation of the familiar Alexandrov condition on topologies.
This observation, along with Remark 12.3.4, suggests that it would be interesting to look at semiframes with additional conditions having to do with limits of possibly infinite descending chains.
Remark 12.3.6 (Generalising
![]() $\ast$
). In Remark 7.2.2 we mentioned that we can think of semitopologies not as ‘topologies without intersections’ so much as ‘topologies with a generalised intersection’. In this paper we have studied a relation called
$\ast$
). In Remark 7.2.2 we mentioned that we can think of semitopologies not as ‘topologies without intersections’ so much as ‘topologies with a generalised intersection’. In this paper we have studied a relation called
![]() $\between$
(for point-set semitopologies) and
$\between$
(for point-set semitopologies) and
![]() $\ast$
(for semiframes), which intuitively measure whether two elements intersect. But really, this is just a notion of generalised meet, which suggests:
$\ast$
(for semiframes), which intuitively measure whether two elements intersect. But really, this is just a notion of generalised meet, which suggests:
-
• We would take
 $(\mathsf{X},\leq )$
and
$(\mathsf{X},\leq )$
and
 $(\mathsf{X}',\leq ')$
to be complete join-semilattices and the generalised meet
$(\mathsf{X}',\leq ')$
to be complete join-semilattices and the generalised meet
 ${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathsf{X}'$
is any commutative distributive map.
${\ast } : (\mathsf{X}\times \mathsf{X})\to \mathsf{X}'$
is any commutative distributive map. -
• We could generalise in a different direction and consider (e.g.,) cocomplete symmetric monoidal categories:
 $\ast$
becomes the (symmetric) monoid action.
$\ast$
becomes the (symmetric) monoid action. -
• We could generalise from binary intersections to
 $n$
-ary intersections. This generalisation deserves its own brief discussion:
$n$
-ary intersections. This generalisation deserves its own brief discussion:
The literature on decentralised systems is rich in intersection conditions. A
![]() $Q^2$
property from (Damgård et al., Reference Damgård, Desmedt, Fitzi, Nielsen and Kurosawa2007, Theorem 1) asserts (in semitopological language) that all pairs of nonempty open set intersect – but there is more, for example, a
$Q^2$
property from (Damgård et al., Reference Damgård, Desmedt, Fitzi, Nielsen and Kurosawa2007, Theorem 1) asserts (in semitopological language) that all pairs of nonempty open set intersect – but there is more, for example, a
![]() $Q^3$
property (Alpos et al., Reference Alpos, Cachin, Tackmann and Zanolini2024, Definition 2) asserts that all triples of nonempty open set intersect. Other unpublished work considers situations where up to five nonempty open sets should intersect. From the point of view of this paper, it suggests a sequence of
$Q^3$
property (Alpos et al., Reference Alpos, Cachin, Tackmann and Zanolini2024, Definition 2) asserts that all triples of nonempty open set intersect. Other unpublished work considers situations where up to five nonempty open sets should intersect. From the point of view of this paper, it suggests a sequence of
![]() $n$
-ary generalisations of
$n$
-ary generalisations of
![]() $\between$
and
$\between$
and
![]() $\ast$
.
$\ast$
.
Furthermore, a
![]() $B^3$
condition (Damgård et al., Reference Damgård, Desmedt, Fitzi, Nielsen and Kurosawa2007, Theorem 2) (Alpos et al., Reference Alpos, Cachin, Tackmann and Zanolini2024, Definition 5), considers a situation of even greater generality (and worse behaviour!), where open neighbourhoods are local to points in the sense that if
$B^3$
condition (Damgård et al., Reference Damgård, Desmedt, Fitzi, Nielsen and Kurosawa2007, Theorem 2) (Alpos et al., Reference Alpos, Cachin, Tackmann and Zanolini2024, Definition 5), considers a situation of even greater generality (and worse behaviour!), where open neighbourhoods are local to points in the sense that if
![]() $O\in \textit{nbhd}(p)$
and
$O\in \textit{nbhd}(p)$
and
![]() $p'\in O$
then it does not necessarily follow that
$p'\in O$
then it does not necessarily follow that
![]() $O\in \textit{nbhd}(p')$
. This suggests ‘heterogeneous’ generalisations of semitopology and semiframe whose mathematical behaviour is at time of writing unexplored.
$O\in \textit{nbhd}(p')$
. This suggests ‘heterogeneous’ generalisations of semitopology and semiframe whose mathematical behaviour is at time of writing unexplored.
Remark 12.3.7 (Homotopy and convergence). We have not looked in any detail at notions of path and convergence in semitopologies and semiframes. Preliminary considerations suggest that, in the finite case, a path converging to a point can be identified with a minimal open set containing that point. In the topological case this is trivial, since minimal open sets are least; in the semitopological case it is not, since there may be many minimal open sets (Lemma 2.1.2). Thus, even in a semitopology with no ‘holes’, it can be possible to approach a single point from multiple directions. Developing this part of the theory is future work.
Remark 12.3.8 (Constructive mathematics). We have not considered what semiframes would look like in a constructive setting. Much of the interest in frames and locales (vs. point-set topologies) comes from working in a constructive setting; for example, in the topos of sheaves over a base space, locales give a good fibrewise topology of bundles. To what extent similar structures might be built using semiframes, or what other structures might emerge instead, are currently entirely open questions.
Remark 12.3.9 (Semiframes, logic and analysis of real systems). A natural application of semiframes is to help build logics for consensus, and in particular logics for consensus algorithms (like Paxos Lamport (Reference Lamport2001)). A declarative approach to specifying consensus algorithms, based on the semitopological ideas in this paper, is current research recently submitted for publication (Gabbay and Zanolini, Reference Gabbay and Zanolini2025). In separate work current at the time of writing, these techniques have helped find errors in a real consensus algorithm; details are to be published in due course.
That work illustrates how the ideas in this paper can be made actionable to analyse properties of real consensus algorithms.
12.4 Final comments
Innovation in decentralised systems design is currently very active, and in particular there is much work on notions of consensus and quorum (García-Pérez and Gotsman, Reference García-Pérez and Gotsman2018; Lokhava et al., Reference Lokhava, Losa, Mazières, Hoare, Barry, Gafni, Jove, Malinowsky and McCaleb2019; Losa et al., Reference Losa, Gafni, Mazières and Suomela2019; Sheff et al., Reference Sheff, Wang, Renesse, Myers, Bramas, Oshman and Romano2021; Bezerra et al., Reference Bezerra, Kuznetsov, Koroleva, Koulali and Mezini2022; Florian et al., Reference Florian, Henningsen, Ndolo and Scheuermann2022; Cachin et al., Reference Cachin, Losa, Zanolini, Hillel, Palmieri and Rivière2023; Li et al., Reference Li, Chan, Lesani and Oshman2023; Li and Lesani, Reference Li and Lesani2023; Alpos et al., Reference Alpos, Cachin, Tackmann and Zanolini2024), and many new systems (Schwartz et al., Reference Schwartz, Youngs and Britto2014; Mazières, Reference Mazières2015; MacBrough, Reference MacBrough2018; Sheff et al., Reference Sheff, Wang, Renesse, Myers, Bramas, Oshman and Romano2021) (and this is just a sample of an active literature). This explosion of practical design is also an explosion of suggestions to the theory community, of new structures to consider. One way to do this is to apply a classic technique which has been usefully applied many times before: topologise, then dualise.
Of course, practitioners are also invited to learn more topology and algebra and consider phrasing some aspects of their systems in these terms.Footnote 41 If there is one thing holding back practical progress in decentralised algorithm design, it is that it is exceptionally hard. If (semi)topology, algebra, and logic can help, then that will be a useful contribution.
Acknowledgements
I dedicate this paper to the memory of Phil Scott: colleague, mentor, gentleman, friend, and inspiration to us all. I am extremely grateful to the anonymous referees for feedback on this work. Thanks to Giuliano Losa and the Stellar Development Foundation for their generous support and funding in pursuing this research.


 for
for 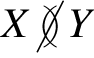 when
when 
 for nonempty
for nonempty 
 for every
for every  . We use Lemma
. We use Lemma  so that
so that  . By definition in Definition
. By definition in Definition  . By facts of sets, this means precisely that
. By facts of sets, this means precisely that 


 , so
, so  . Then there exists some
. Then there exists some  , and it follows that
, and it follows that 

 .
.
 , so by compatibility it follows that
, so by compatibility it follows that 

 . Similarly for
. Similarly for 

 , but
, but 
 . By Lemma
. By Lemma  precisely when
precisely when 
 . Thus,
. Thus,  , so
, so