Psychometric Model Framework for Multiple Response Items

Abstract

Multiple response (MR) items—such as multiple true-false, multiple-select, and select-N items—are increasingly used in assessments to identify partial knowledge and differentiate latent abilities more accurately. Allowing multiple selections, MR items provide richer information and reduce guessing effects compared to single-answer multiple-choice items. However, traditional scoring methods (e.g., Dichotomous, Ripkey, Partial scoring) compress response combination (RC) data, losing valuable information and ignoring issues like local dependence and incompatibility across item types. To address these challenges, we introduce a novel psychometric model framework: the Multiple Response Model with Inter-option Local Dependencies (MRM-LD), and its simplified version, the Multiple Response Model (MRM). These models preserve RC data across MR item types, offering a more comprehensive understanding for MR assessment. Parameters for MRM-LD and MRM were estimated using Markov chain Monte Carlo algorithms in Stan and R. Empirical data from an eighth-grade physics test showed that MRM-LD and MRM outperform Graded Response Model and Nominal Response Model combined with three scoring methods, by retaining more test information, improving reliability and validity, and providing more detailed analysis of item characteristics. Simulation studies confirmed the proposed models perform robustly under various conditions, including small samples and few items, demonstrating their applicability across diverse testing scenarios.

1 Introduction

Multiple-choice items have been a mainstay of educational and psychological assessments for nearly a century (Gierl et al., 2017). While single-answer multiple-choice (SAMC) items gained early popularity due to their simplicity and efficiency, they possess inherent limitations in assessing partial knowledge. The all-or-nothing response format of SAMC items is not conducive to partial credit (Bush, 2001; Cronbach, 1941), restricting researchers’ insights into a student’s reasoning. It is difficult to determine whether respondents have partially narrowed down the options or fundamentally lack understanding (Mobalegh & Barati, 2012; Parker et al., 2012).

To overcome these limitations, innovative item formats like multiple response (MR) items have been developed to capture more nuanced data on respondents’ knowledge. MR items allow respondents to select multiple options, providing richer, more detailed data (Betts et al., 2022; Duncan & Milton, 1978). The raw response data collected from MR items, known as response combinations (RCs), are also referred to as response patterns or multiple responses (Betts et al., 2022; Muntean & Betts, 2015). These RCs are defined as the data generated from various combinations of the selected options. They provide a more accurate differentiation of respondents’ latent abilities by capturing partial knowledge (Hsu et al., 1984; Pomplun & Omar, 1997). These advantages have led to the widespread incorporation of MR items into various assessments, including the Programme for International Student Assessment (PISA), Trends in International Mathematics and Science Study (TIMSS), International English Language Testing System (IELTS), and Graduate Record Examinations (GRE) (Emmerich et al., 1991; Rustanto et al., 2023; Suvorov & Li, 2023).

Despite these benefits, MR items present several analytical challenges. Current analysis approaches based on scoring methods often overlook subtle ability differences indicated by distinct RCs when they lead to identical scores, and they also disregard the information provided by different options. Existing Item Response Theory (IRT) models often struggle to handle the complexity of MR data. These IRT models typically rely on modeling compressed scores (see Section 3), which can lead to a potential loss of valuable information. Furthermore, the diverse range of MR item formats (see Section 2), each with its unique sets of RCs, complicates straightforward comparison and analysis (Schmidt et al., 2022). Finally, local dependencies among options are a common but frequently overlooked feature of MR items (Albanese & Sabers, 1988; Bauer et al., 2011; Frisbie & Druva, 1986; Smith et al., 2022). Particularly, neglecting such local dependence may result in biased estimates of both item parameters and respondent abilities, as well as an overestimation of test reliability (Pomplun & Omar, 1997; Sireci et al., 1991; DeMars, 2006).

This study introduces a novel psychometric model framework designed to leverage the richness of RC data in MR items. The model overcomes the restrictive nature of traditional scoring methods and the limitations of existing IRT approaches by directly modeling RC data, accounting for local dependencies within items, and accommodating diverse MR item formats. This approach aims to provide more accurate estimates of respondents’ latent abilities and enable a more comprehensive analysis of item characteristics.

The remainder of this paper is organized as follows. Section 2 introduces three common MR item formats and highlights their similarities and differences. Section 3 outlines three scoring methods for MR items and illustrates the impact of different MR item types and scoring methods on the collected data and resulting scores using an example. Section 4 proposes a novel Multiple Response Model (MRM) framework and describes its Bayesian parameter estimation. An empirical study is presented in Section 5, where we administered an MR test based on middle school physics concepts related to light phenomena, demonstrating the advantages of the proposed method in analyzing MR items. Section 6 presents four simulation studies designed to evaluate the parameter estimation performance and robustness of the proposed and traditional models across a wide range of test scenarios. Finally, Section 7 concludes with remarks and a discussion of limitations and future research directions. Important abbreviations employed in this paper are listed in Appendix Table A1.

2 Types of multiple response items

Based on their instructions and the resultant RCs, MR items can be classified into three primary types: multiple true-false (MTF) items, conventional multiple-select (CMS) items, and select-N items. Each MR item encompasses O options, and contingent upon the item type, these options can be merged to generate X possible RCs.

Multiple true-false items: MTF items present multiple options within a single item, each requiring a true or false judgment (Cronbach, 1939). Typically containing four to six options, MTF items allow any number of correct options. Figure 1 shows an MTF item from the PISA 2012 mathematics test sample (OECD, 2013), which includes four options. Respondents mark each option as either true or false, resulting in $X={2}^O=16$ possible RCs. The correct answer to this item is that all four options are false. MTF items allow for the possibility that all options are selected as incorrect. Hubbard et al. (2017) noted that MTF items require students to evaluate each option independently rather than simply recognizing a correct answer from a list, which can encourage deeper learning strategies akin to those promoted by free-response questions, making MTF items a valuable alternative to SAMC items.

Figure 1 An MTF example item from the PISA 2012 mathematics assessment.

Conventional multiple-select items: CMS items, also referred to as select-all-that-apply items, require respondents to select all correct options while leaving incorrect ones unmarked, making them the most prevalent MR format (Schmidt et al., 2021). In contrast to MTF items, CMS items typically exclude the all-zero RC offering $X={2}^O-1$ possible RCs. For example, Figure 2 shows a National Council Licensure Examination for Registered Nurses (NCLEX-RN) practice sample item. This CMS item presenting six options requires respondents to identify only the correct options, resulting in ${2}^6-1=63$ possible RCs. CMS is structurally similar to SAMC, but the allowance of multiple selections expands the response space (Muckle et al., 2011), and it is less prone to “acquiescence bias” (the tendency to agree) than MTF items (Cronbach, 1941).

Figure 2 A CMS example item from the NCLEX-RN practice test.

Select-N items: Also known as pick-N items, they are a variant of CMS items where respondents are informed of the exact number of correct options ( $T$ ) to select (Bauer et al., 2011; Schmidt et al., 2022; Schmittlein, 1984). Figure 3 presents a select-N item of the 2024 Taiwan General Scholastic Ability Test (GSAT), with five options and three correct answers, and respondents must select precisely three options, yielding $X={C}_O^T={C}_5^3=10$ possible RCs. This structure simplifies the response process and helps lower the cognitive load on respondents as the number of options increases.

Figure 3 A Select-N example item from the GSAT 2024.

3 Scoring methods for multiple response items

MR items inherently generate significantly more RCs than SAMC items, which substantially increases the complexity of scoring. Consequently, researchers have identified over 40 distinct scoring methods for MR items (Kanzow et al., 2023; Schmidt et al., 2021, 2022). These diverse methods primarily aim to compress RC data into either dichotomous or polytomous scores, which are then utilized for calculating overall test scores or estimating latent abilities. This article introduces three commonly used scoring methods that represent distinct points on a spectrum of scoring stringency: from strict, to moderate, to lenient.

Dichotomous scoring (DS): This method serves as a representative of the strictest scoring approach. It is the most demanding scoring method, where respondents receive full credit (typically designated as “1”) only if they answer all options correctly. If any option is incorrect, no points are awarded (Kolstad et al., 1983; Lahner et al., 2018). This “all-or-nothing” approach completely disregards partial knowledge. As the number of options per item increases, the scoring becomes even more demanding. While simple to implement and commonly used, this method overlooks partial understanding and its stringency escalates with the increase in item options.

Ripkey scoring (RS): Representing a moderate, or middle-ground, approach, this scoring method is commonly applied to CMS and select-N items (Ripkey et al., 1996). Each correct selection is awarded $\frac{1}{T}$ point, and incorrect selections are not penalized. However, a crucial caveat is that if the number of options selected exceeds the number of correct answers, the score for that item is zero. Unlike DS, RS allows for partial credit but introduces a penalty for over-selection, thus balancing the recognition of partial knowledge with a demand for response precision.

Partial scoring (PS): This method is representative of the most lenient approach and allows for the greatest number of distinct score levels. Also known as the MTF method or true/false testlet, PS is a commonly employed method for MTF and CMS items, awarding $\frac{1}{O}$ for each correct response. It is more forgiving than the other methods because it does not penalize incorrect answers. However, this leniency can incentivize random guessing, as respondents face no penalty for over-selecting options.

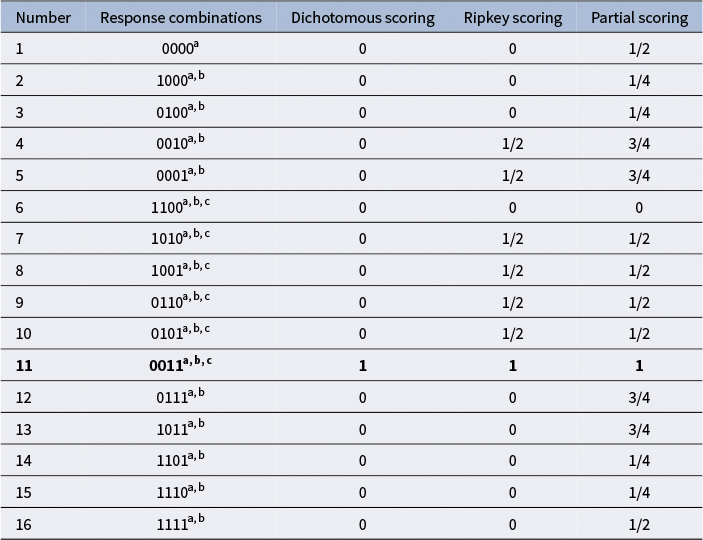
To illustrate the impact of item type and scoring method on scoring outcomes, consider a four-option MR item with options C and D as correct. Table 1 presents the valid RCs and their corresponding scores under DS, RS, and PS. For MTF, 1/0 denotes true/false; for CMS and select-N, it denotes selected/not selected. For example, the RC_[0,0,0,1] means only option D is endorsed, which yields a score of 0 under DS, 1/2 under RS, and 3/4 under PS. After compression, this item produces two distinct score levels under DS, three under RS, and five under PS (with select-N typically yielding three under PS). These compressed scores can then be analyzed with standard dichotomous or polytomous IRT models.

Table 1 Response combinations and corresponding scores for MR items (four-option item).

Note: The total score of this item is assumed to be 1. Multiple true-false includes all response combinations, denoted as a; conventional multiple-select excludes the response combination where no options are selected, denoted as b; and select-N includes only response combinations where the number of selected options matches the number of correct options, denoted as c. The response combination shown in bold represents the fully correct response.

4 Multiple response model framework

For SAMC items, option-level IRT models, such as the nominal response model (NRM; Bock, 1997) and the 3PL nested logit model (Suh & Bolt, 2010), have been established to provide superior performance over simple dichotomous scoring (Kim, 2006; Thissen & Cai, 2010). In contrast, option-level methods for MR items remain underdeveloped. Traditional score-based approaches typically compress RCs into dichotomous or polychotomous scores, thereby discarding information on option-specific effects (Verbić, 2012). Furthermore, existing optimized modeling strategies face significant limitations. First, treating each option as an independent dichotomous item fails to account for local dependence within an item and proves unsuitable for constrained formats such as select-N (Dudley, 2006). Second, the approach of collapsing dependent options into unordered categories for analysis with the NRM requires prior identification of dependencies, obscures individual option effects, and leads to parameter proliferation as the number of options increases (Smith et al., 2022). To address these problems, this paper introduces the MRM and the MRM with Inter-option Local Dependencies (MRM-LD), specifically developed to directly estimate the probabilities of all possible RCs for an item. Without substantially increasing model complexity, these models both account for the unique contribution of each option to item responses and quantify the local dependencies among options within an item, thereby better preserving the information provided by RC data.

4.1 The multiple response model

The MRM is grounded in the divide-by-total model family (Bolt et al., 2001; Thissen & Steinberg, 1986), which calculates the response probability of an RC based on the ratio of exponential terms, while being specifically tailored to accommodate RC data from various subtypes of MR items. To formalize the MRM, we define a design matrix ${\boldsymbol{Z}}_j$ that represents all possible RCs for item $j$ . Each element ${Z}_{jxo}$ indicates the status of option $o$ in RC $x$ : for MTF items, ${Z}_{jxo}=1$ means option $o$ is endorsed as true, and ${Z}_{jxo}=0$ as false; for CMS and select-N items, ${Z}_{jxo}=1$ means option $o$ is selected, and ${Z}_{jxo}=0$ otherwise. 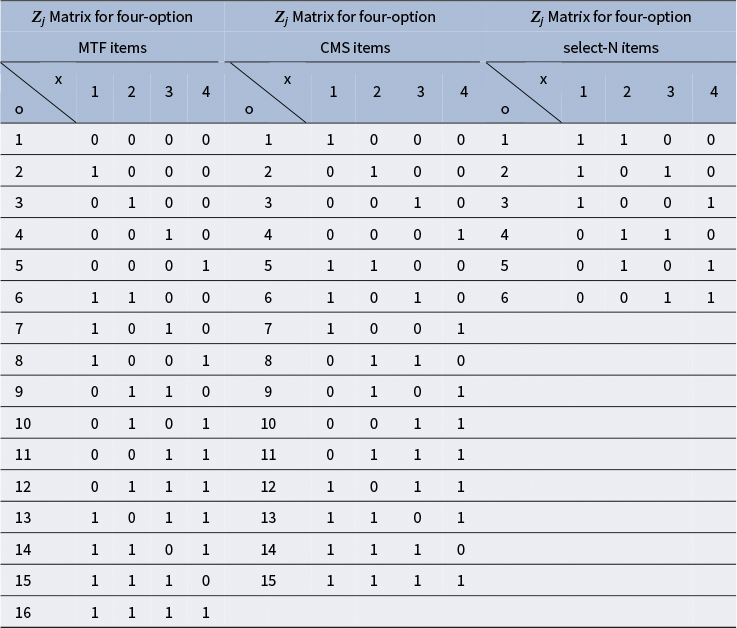The structure of ${\boldsymbol{Z}}_j$ varies across item types due to differing constraints on permissible RCs. Table 2 presents the ${\boldsymbol{Z}}_j$ matrices for four-option MTF, CMS, and select-N items with two correct options, which accommodate 16, 15, and 6 unique RCs, respectively. For example, RC_[1,1,0,0] corresponds to endorsing the first two options as true in an MTF item (Table 2) or selecting the first two options in CMS and select-N items (Table 2).

Table 2 ${\boldsymbol{Z}}_j$ Matrix for four-option MTF items, ${\boldsymbol{Z}}_j$ matrix for four-option CMS items, and ${\boldsymbol{Z}}_j$ Matrix for four-option MR items across different types.

The MRM defines the probability of choosing a specific RC as the ratio of the attractiveness of that RC to the sum of the attractiveness values across all ${X}_j$ possible RCs. The probability that respondent $i$ , with latent ability ${\theta}_i$ , selects RC $x$ for item $j$ is given by the Response Combination Probability Function (RCPF):

(1) $$\begin{align}P\left({Y}_{ij}=x|{\theta}_i,{\boldsymbol{a}}_j,{\boldsymbol{d}}_j\right)=\frac{\mathit{\exp}\left({h}_{ij x}\right)}{\sum \limits_{m=1}^{X_j}\mathit{\exp}\left({h}_{ij m}\right)}\end{align}$$

where the term ${h}_{ijx}$ represents the total attractiveness of RC $x$ . This total attractiveness is modeled as a linear combination of the attractiveness of its constituent options:

(2) $$\begin{align}{h}_{ijx}=\sum \limits_{O=1}^{O_j}{Z}_{jxo}{h}_{ijo}^{\prime }\end{align}$$

Here, the binary element ${Z}_{jxo}$ from the design matrix acts as a selector, determining which options contribute to the attractiveness of RC $x$ . The attractiveness of each individual option, ${h}_{ijo}^{\prime }$ , is in turn modeled as a linear function of the respondent’s latent ability:

(3) $$\begin{align}{h}_{ijo}^{\prime }={a}_{jo}{\theta}_i+{d}_{jo}\end{align}$$

By substituting Formulas (2) and (3) into Formula (1), the full RCPF expression for the MRM is obtained:

(4) $$\begin{align}P\left({Y}_{ij}=x|{\theta}_i,{\boldsymbol{a}}_j,{\boldsymbol{d}}_j\right)=\frac{\mathit{\exp}\left(\sum \limits_{o=1}^{O_j}{Z}_{jxo}\left({a}_{jo}{\theta}_i+{d}_{jo}\right)\right)}{\sum \limits_{m=1}^{X_j}\mathit{\exp}\left(\sum \limits_{o=1}^{O_j}{Z}_{jmo}\left({a}_{jo}{\theta}_i+{d}_{jo}\right)\right)}\end{align}$$

In this model, ${a}_{jo}$ is the slope parameter for option $o$ of item $j$ . A positive ${a}_{jo}$ indicates a correct option, as its attractiveness increases with higher levels of ${\theta}_i$ . Conversely, a negative ${a}_{jo}$ signifies an incorrect option, whose attractiveness decreases as ${\theta}_i$ increases. The parameter ${d}_{jo}$ is the intercept parameter, representing the baseline attractiveness of option $o$ when ${\theta}_i=0$ .

A specific consideration for model identifiability arises with select-N items. In this format, every valid RC consists of exactly T selected options. This structural constraint leads to a potential identifiability issue because if a constant value were added to the attractiveness of every individual option, the total attractiveness of every valid RC would increase by an identical amount, leaving the choice probabilities unchanged. This makes a unique parameter solution impossible without further constraints. Therefore, to ensure model identifiability for select-N items, we impose the sum-to-zero constraints: $\sum _{o=1}^{O_j}{a}_{jo}=0\kern0.1em$ and $\sum _{o=1}^{O_j}{d}_{jo}=0\kern0.1em$ . Consequently, one MTF or CMS item requires the estimation of ${O}_j$ slope and ${O}_j$ intercept parameters ( $2{O}_j$ total), whereas select-N items require ${O}_j-1$ slope and ${O}_j-1$ intercept parameters ( $2\left({O}_j-1\right)$ total).

4.2 Incorporating local dependencies between options

In the MRM, the attractiveness of options is primarily determined by the respondent’s latent ability ${\theta}_i$ . However, beyond this latent ability, local dependencies can naturally exist among options within the same item in MR items (Pomplun & Omar, 1997; Verbić, 2012). These dependencies are not related to the respondent’s ability but rather reflect specific interactions between the respondent and the item, arising from the common stimulus of the item stem and knowledge within the item (Beiting-Parrish et al., 2021). Motivated by the IRT testlet models (Li et al., 2006, 2010; Wang et al., 2002; Kang et al., 2022), we propose an extension to the MRM, termed the MRM-LD. The MRM-LD integrates these local dependencies by adding a term that represents person–item interactions into the definition of option attractiveness. This additional term accounts for specific abilities (Li, 2017) that may influence the respondent’s choice, separate from their general latent ability. The updated definition of attractiveness in the MRM-LD is shown in Formula (5), and the corresponding RCPF is provided in Formula (6):

(5) $$\begin{align}{h}_{ij o}^{\prime }={a}_{jo}{\theta}_i+{d}_{jo}+{W}_{jo}{a}_j^{\ast }{\gamma}_{ij}\end{align}$$

(6) $$\begin{align}P\left({Y}_{ij}=x|{\theta}_i,{\boldsymbol{a}}_j,{\boldsymbol{d}}_j,{a}_j^{\ast },{\gamma}_{ij}\right)=\frac{\exp \left(\sum \limits_{o=1}^{O_j}\kern0.20em {Z}_{jxo}\left({a}_{jo}{\theta}_i+{d}_{jo}+{W}_{jo}{a}_j^{\ast }{\gamma}_{ij}\right)\right)}{\sum \limits_{m=1}^{X_j}\kern0.20em \exp \left(\sum \limits_{o=1}^{O_j}\kern0.20em {Z}_{jmo}\left({a}_{jo}{\theta}_i+{d}_{jo}+{W}_{jo}{a}_j^{\ast }{\gamma}_{ij}\right)\right)}\end{align}$$

Both ${\gamma}_{ij}$ and ${\theta}_i$ are assumed to follow a standard normal distribution, i.e., $N\left(0,1\right)$ . Specifically, ${\gamma}_{ij}$ represents the respondent’s item-specific ability, reflecting a unique interaction between respondent $i$ and item $j$ . Parameter ${a}_j^{\ast }$ quantifies the magnitude of local dependence within item $j$ and is constrained to interval $\left(0,+\infty \right]$ . Indicator ${W}_{jo}$ determines the direction of this local dependence: it is set to 1 for correct options and to −1 for incorrect options. This ensures that the effect of local dependence ${\gamma}_{ij}$ on option attractiveness depends on both its sign and option correctness: when ${\gamma}_{ij}>0$ , correct options become more attractive and incorrect options less attractive, while when ${\gamma}_{ij}<0$ , the pattern reverses. It is important to note that for select-N items where only one correct answer is selected ( $T=1$ ) or only one incorrect answer is excluded ( $T={O}_j-1$ ), the response structure takes the form of SAMC items in which selecting one option automatically excludes all others. Since the SAMC format itself enforces mutual exclusivity among response categories, local dependencies are inherent to this structure and do not require additional local dependence parameters. By setting ${a}_j^{\ast }=0$ , the MRM-LD simplifies to the standard MRM. Furthermore, for these SAMC items (i.e., $T=1$ or ${O}_j-1$ ), the MRM is equivalent to the NRM.

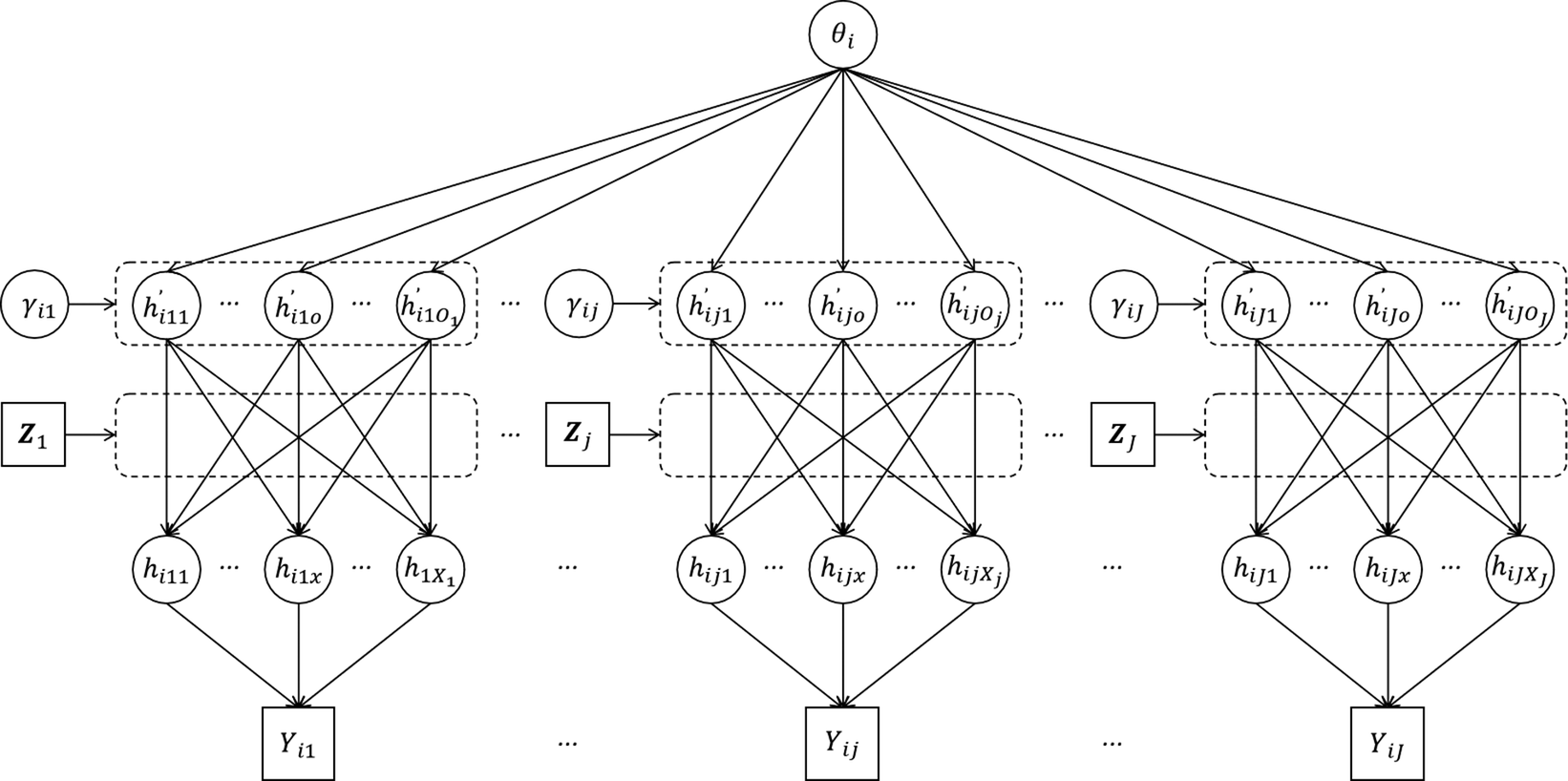
Figure 4 illustrates the architecture of the MRM-LD. The model’s core principle is that a respondent’s latent ability, ${\theta}_i$ , primarily determines the attractiveness ( ${h}_{ijo}^{\prime }$ ) of each individual option. For higher-ability respondents, correct options have higher attractiveness values and incorrect options have lower attractiveness values. Building upon this, the respondent’s item-specific ability, represented by ${\gamma}_{ij}$ , introduces a local dependence effect that further modulates the attractiveness of each option. Finally, the design matrix ${\boldsymbol{Z}}_j$ is used to aggregate this individual option attractiveness into the overall attractiveness ( ${h}_{ijx}$ ) for each possible RC. This overall attractiveness, in turn, determines the probability distribution over all possible RCs. The observed response is represented by ${Y}_{ij}$ , which indexes the RC selected by the respondent.

Figure 4 The MRM-LD model structure diagram.

4.3 Bayesian parameter estimation

In this study, both the MRM and MRM-LD models were developed using Stan (Carpenter et al., 2017) and then compiled and fitted in R through the cmdstanr package (Gabry et al., 2024). Stan is a probabilistic programming language that utilizes the No-U-Turn Sampler (NUTS) algorithm within the Hamiltonian Monte Carlo (HMC) framework (Hoffman & Gelman, 2014). Following previous research settings (Kim & Bolt, 2007; Luo & Jiao, 2018; Natesan et al., 2016), the prior distributions of the model parameters and responses are set as follows: ${\theta}_i\sim \mathrm{Normal}\left(0,1\right)$ , ${a}_{jo}\sim \mathrm{Normal}\left(0,2\right)$ , ${d}_{jo}\sim \mathrm{Normal}\left(0,2\right)$ , ${\gamma}_{ij}\sim \mathrm{Normal}\left(0,1\right)$ , ${a}_j^{\ast}\sim \mathrm{Lognormal}\left(0,2\right)$ , ${Y}_{ij}\sim \mathrm{Categorical}\left(P\left({Y}_{ij}=x|{\theta}_i,{\boldsymbol{a}}_j,{\boldsymbol{d}}_j,{a}_j^{\ast },{\gamma}_{ij}\right)\right)$ . For select-N items, the following constraints apply: $\sum _{o=1}^{O_j}\kern0.1em {a}_{jo}=0,\sum _{o=1}^{O_j}\kern0.1em {d}_{jo}=0$ .

Thus, the likelihood function for the MRM-LD can be expressed as:

(7) $$\begin{align}L\left(\boldsymbol{Y}\mid \boldsymbol{\theta}, \boldsymbol{a},\boldsymbol{d},{\boldsymbol{a}}^{\ast},\boldsymbol{\gamma} \right)=\prod \limits_{i=1}^N\kern0.1em \prod \limits_{j=1}^J\kern0.1em \frac{\exp \left(\sum \limits_{o=1}^{O_j}\kern0.20em {Z}_{j,{Y}_{ij},o}\left({a}_{jo}{\theta}_i+{d}_{jo}+{W}_{jo}{a}_j^{\ast }{\gamma}_{ij}\right)\right)}{\sum \limits_{m=1}^{X_j}\kern0.20em \exp \left(\sum \limits_{o=1}^{O_j}\kern0.20em {Z}_{jmo}\left({a}_{jo}{\theta}_i+{d}_{jo}+{W}_{jo}{a}_j^{\ast }{\gamma}_{ij}\right)\right)}\end{align}$$

${Z}_{j,{Y}_{ij},o}$ specifically refers to the element in ${\boldsymbol{Z}}_j$ matrix corresponding to this observed response index ${Y}_{ij}$ . Its value indicates whether option $o$ was selected (1) or not selected (0) within the specific RC indexed by ${Y}_{ij}$ . The joint posterior probability of the parameters in the MRM-LD can be expressed as:

(8) $$\begin{align}P\left(\boldsymbol{\theta}, \boldsymbol{a},\boldsymbol{d},{\boldsymbol{a}}^{\ast },\boldsymbol{\gamma} \mid \mathrm{data}\right)\propto L\left(\mathrm{data}\mid \boldsymbol{\theta}, \boldsymbol{a},\boldsymbol{d},{\boldsymbol{a}}^{\ast },\boldsymbol{\gamma} \right)\times P\left(\boldsymbol{\theta} \right)\times P\left(\boldsymbol{a}\right)\times P\left(\boldsymbol{d}\right)\times P\left({\boldsymbol{a}}^{\ast}\right)\times P\left(\boldsymbol{\gamma} \right)\end{align}$$

5 Empirical study

The primary objective of this study is to validate the advantages and practical applicability of the new models in comparison to traditional scoring methods through empirical data analysis, while also offering practical recommendations for theirs implementation. Additionally, this study compares the test performance of three MR item formats—CMS, MTF, and select-N—using the new models to provide empirical evidence for their relative psychometric properties.

5.1 Design

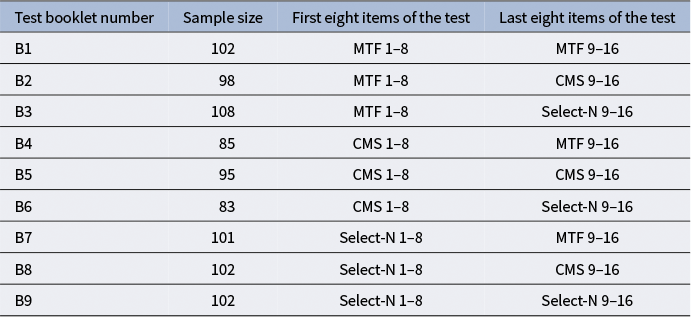
In this study, a set of 16 MR items were developed, each with five options, based on the “Light Phenomena” chapter of eighth-grade physics in Chinese. These items and their options were sourced from the item bank website (https://zujuan.xkw.com) and reviewed by two experienced junior high school physics teachers. Three versions of each item were created: MTF, CMS, and select-N, by modifying the wording of the instructions. Among the 16 items, one item has one correct option, seven items have two correct options, six items have three correct options, and two items have four correct options. The 16 items were divided into two parts, the first eight items and the last eight items, and combined into nine test booklets with different item format pairings (see Table 3). This design ensured anchor item consistency across different item formats; for instance, in test booklets B1, B2, and B3, the first half contains MTF items, making the second half of the booklets comparable. This resulted in nine anchor item combinations. This approach allows the model to estimate parameters that are comparable across items (Betts et al., 2022; Ricker & von Davier, 2007).

Table 3 Empirical study test booklet design.

Note: B1–B9 represent nine test booklets with different combinations of item formats across two halves of the test.

A computerized test was administered to 937 students from 19 classes in the eight grade of a junior high school in China, under the supervision of their teachers. Each student was randomly assigned one of the nine test booklets. Before the test, each student was asked to report their score category (seven ordinal levels: 1 for below 39, 2 for 40–49, 3 for 50–59, 4 for 60–69, 5 for 70–79, 6 for 80–89, and 7 for 90–100) based on their performance in the midterm physics examination, which was administered within one month prior to this test. This information was utilized as a criterion for validation. Since this was a low-stakes test, to prevent estimation bias due to lack of student effort, subjective effort scores on a 10-point (i.e., 1 means least effort and 10 means most effort) item were collected after the test (OECD, 2023). Students who scored 4 or below on the effort scale were excluded, resulting in a final sample size of 876. On average, each item was answered 292 times (SD = 13.3).

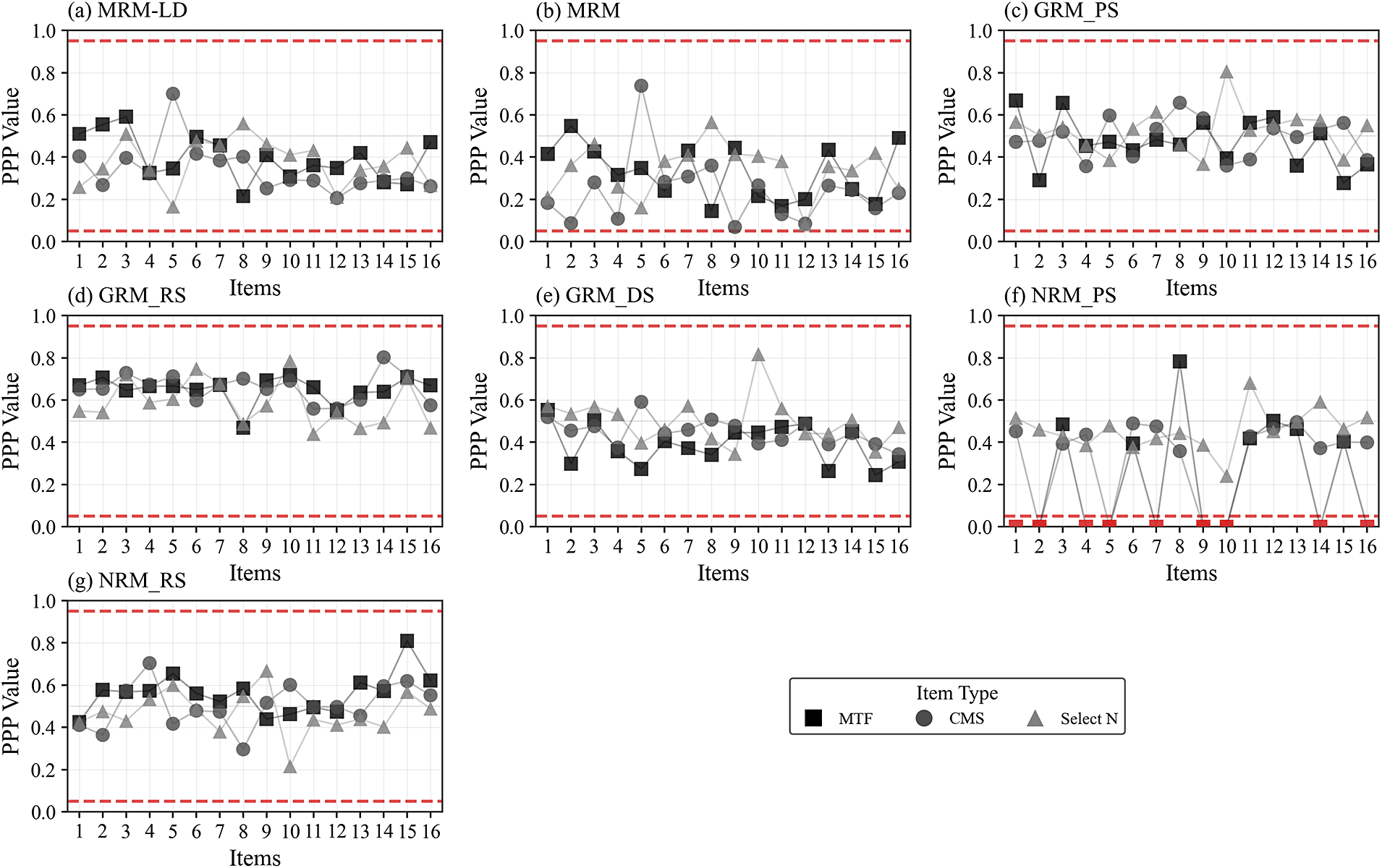
Figure 5 Posterior predictive model checks for each model across different MR item types.

Note: Red dashed horizontal lines mark the threshold boundaries at PPP = 0.05 and PPP = 0.95. Red points indicate PPP values outside the 0.05–0.95 acceptable range.

The data were fitted using the new models, MRM and MRM-LD, as well as traditional polytomous models, Graded Response Model (GRM, Samejima, 1968) and NRM. MRM and MRM-LD models were applied to RC data. In contrast, GRM and NRM utilized three distinct types of response data: PS, RS, and DS, forming models such as GRM_PS, NRM_PS, etc. When using DS data, GRM and NRM are mathematically equivalent; therefore, only the performance of GRM_DS is reported. All models were estimated using Stan with two parallel Markov Chain Monte Carlo (MCMC) chains, each with 1,000 samples. To ensure the stability of the sampling, the first 500 samples were discarded. To ensure fair comparisons across models and to align the latent ability in the same direction as the score, the initial value of ${\theta}_i$ for all models was set to the z-score of the total test score under DS, with all other parameters left to be randomly initialized by prior distributions. The convergence of model parameters was evaluated using the potential scale reduction factor (PSRF; Brooks & Gelman, 1998). A PSRF value below 1.1 was considered indicating sufficient convergence. In this study, the PSRF of all model parameters was below 1.1, indicating convergence and good mixing of the posterior distribution. All parameter estimates are presented in Supplementary Tables S1–S7.

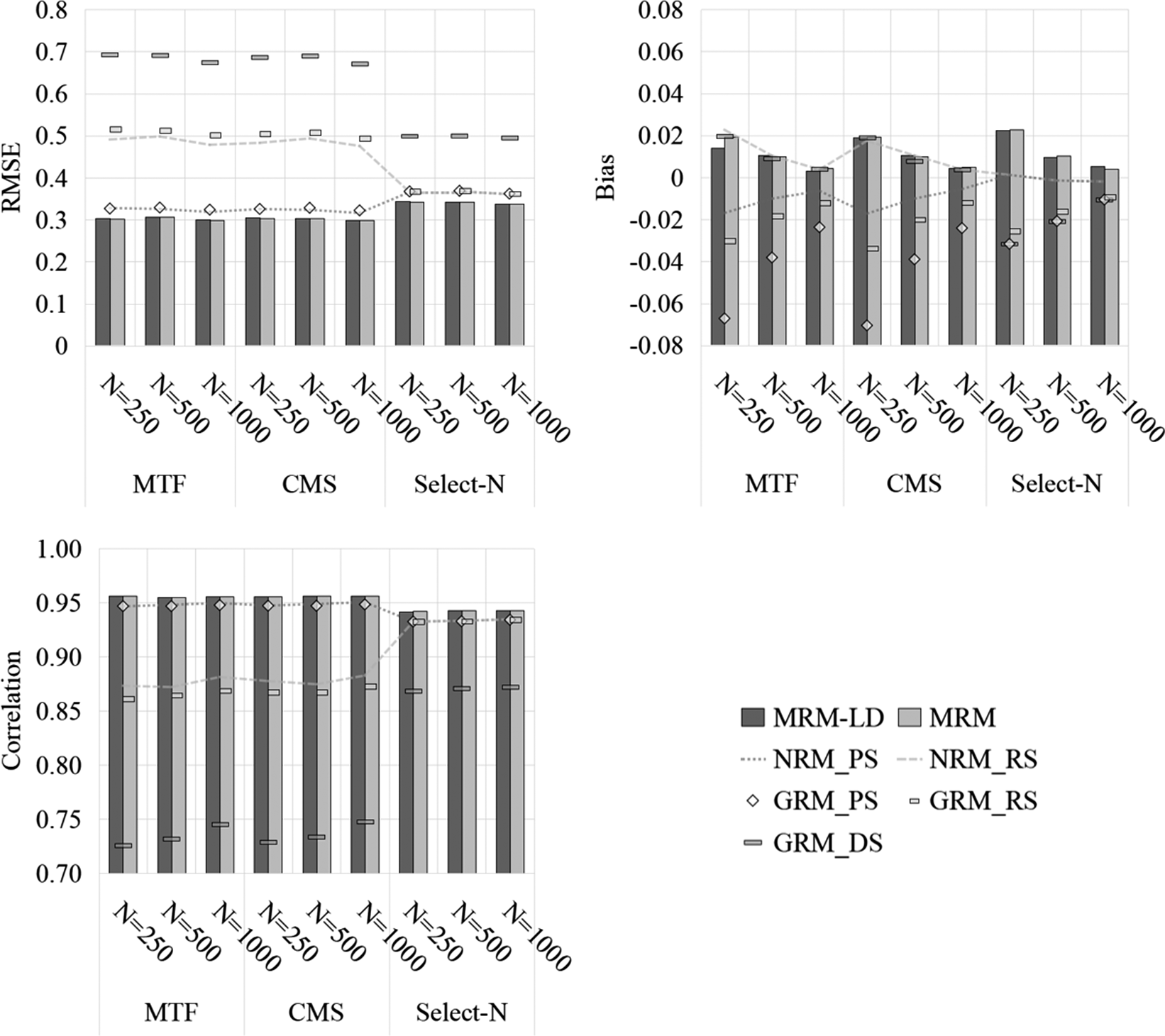
To evaluate model performance, we first assessed absolute fit using Posterior Predictive p-values (PPP) (Gelman et al., 1996; Sinharay, 2005). Relative fit was then compared using the Widely Applicable Information Criterion (WAIC) and Leave-One-Out Cross-Validation (LOO) (Vehtari et al., 2015). In addition, we also evaluated measurement precision via marginal IRT reliability (Green et al., 1984; Zu & Kyllonen, 2020) and compared test information functions, extending the calculation for MRM and MRM-LD against the GRM and NRM (Lima Passos et al., 2007; Ostini & Nering, 2006). Finally, criterion-related validity was examined using Spearman’s rank-order correlation with preliminary physics exam grades. The corresponding computational details for these metrics are presented in Appendix B.

5.2 Empirical study results

5.2.1 Absolute fit

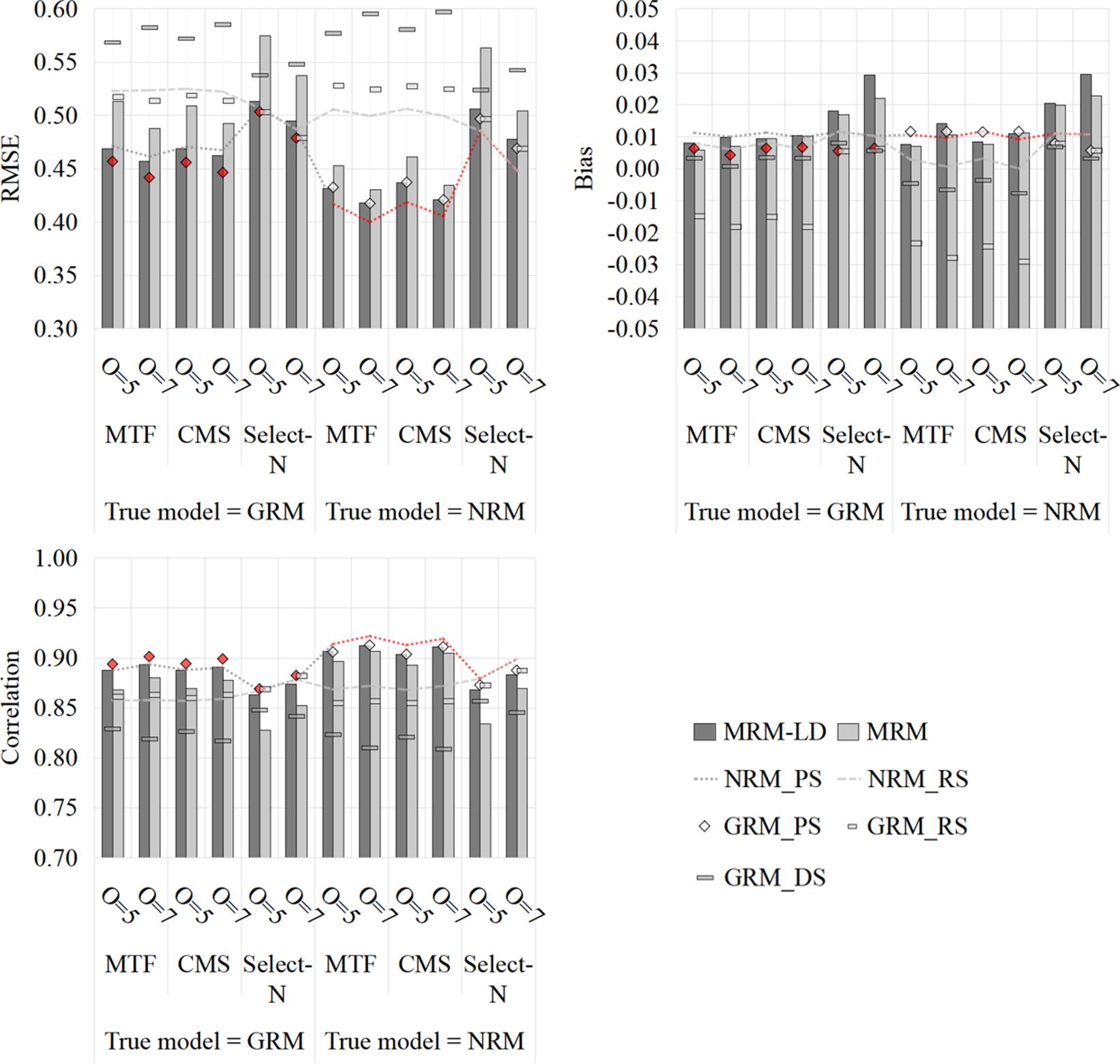
Figure 5 presents the PPP indices for the new models, the MRM-LD and MRM, fitted to the RC data of MR items, as well as for the GRM and NRM fitted to PS, RS, and DS data. The upper and lower red dashed lines in Figure 5 represent the limits of 0.95 and 0.05, respectively. It can be observed that except for the NRM fitted to PS data, where some MTF and CMS items exhibit misfit with PPP values less than 0.05, all other models show no significant discrepancies between model predictions and the data across the MTF, CMS, and select-N items.

5.2.2 Relative fit

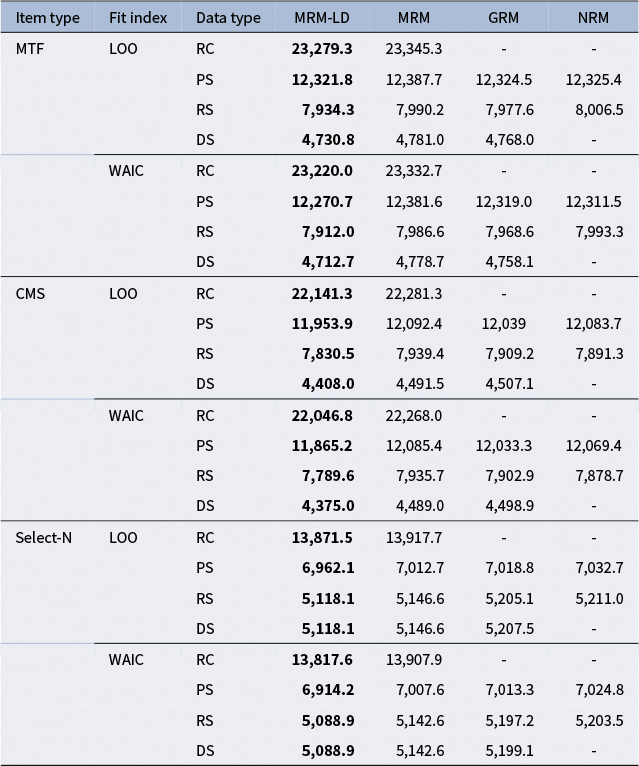
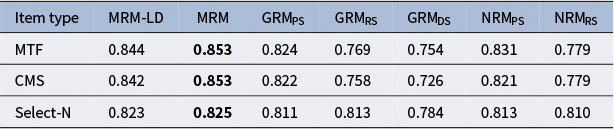
Table 4 presents the WAIC and LOO results for the four models across different MR item types. Lower WAIC and LOO values indicate superior model fit. Primarily, across all scenarios, the MRM-LD consistently outperforms the MRM, suggesting that incorporating the local dependence structure in the MRM-LD is crucial for improving the model fit when analyzing MR data. Furthermore, across all data types, the MRM-LD demonstrates the best performance according to both LOO and WAIC values. When compared with the GRM and the NRM, the MRM-LD shows superior performance at all data types. While the GRM and the NRM perform similarly, the GRM slightly outperforms the NRM in most cases.

Table 4 Results of relative fit indices.

Note: RC, PS, RS, and DS represent four data types: response combinations, partial scoring, Ripkey scoring, and dichotomous scoring, respectively. Boldface indicates the best-fitting model.

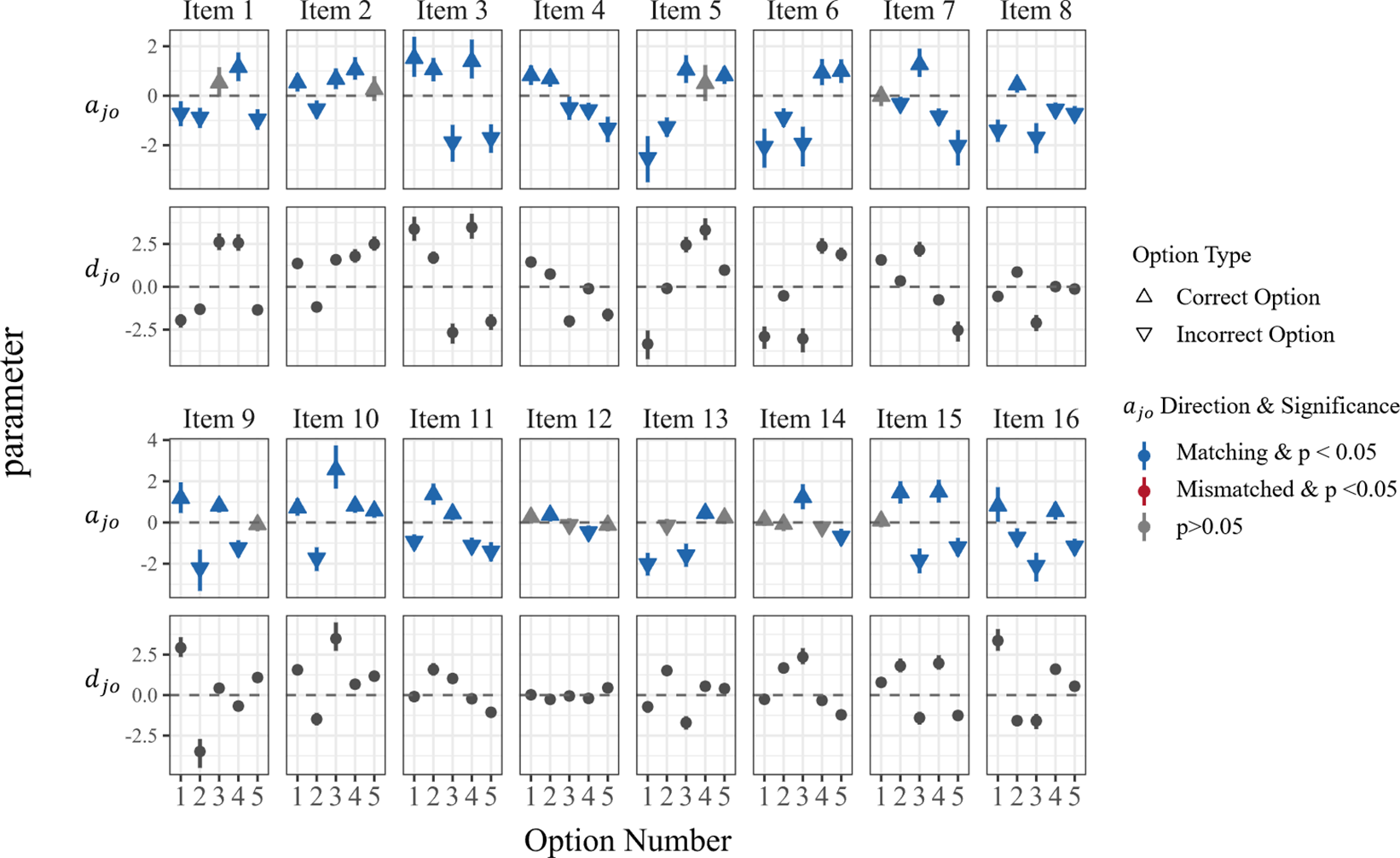
Figure 6 Item parameter distributions ( ${a}_{jo}$ and ${d}_{jo}$ ) of the MRM-LD for CMS items.

5.2.3 Item parameters

The fit indices consistently demonstrate that the MRM-LD is the optimal model for analyzing this real dataset. Given this finding, our subsequent analysis centers on the item parameters estimated by the MRM-LD model. These parameters are detailed in Supplementary Table S1.

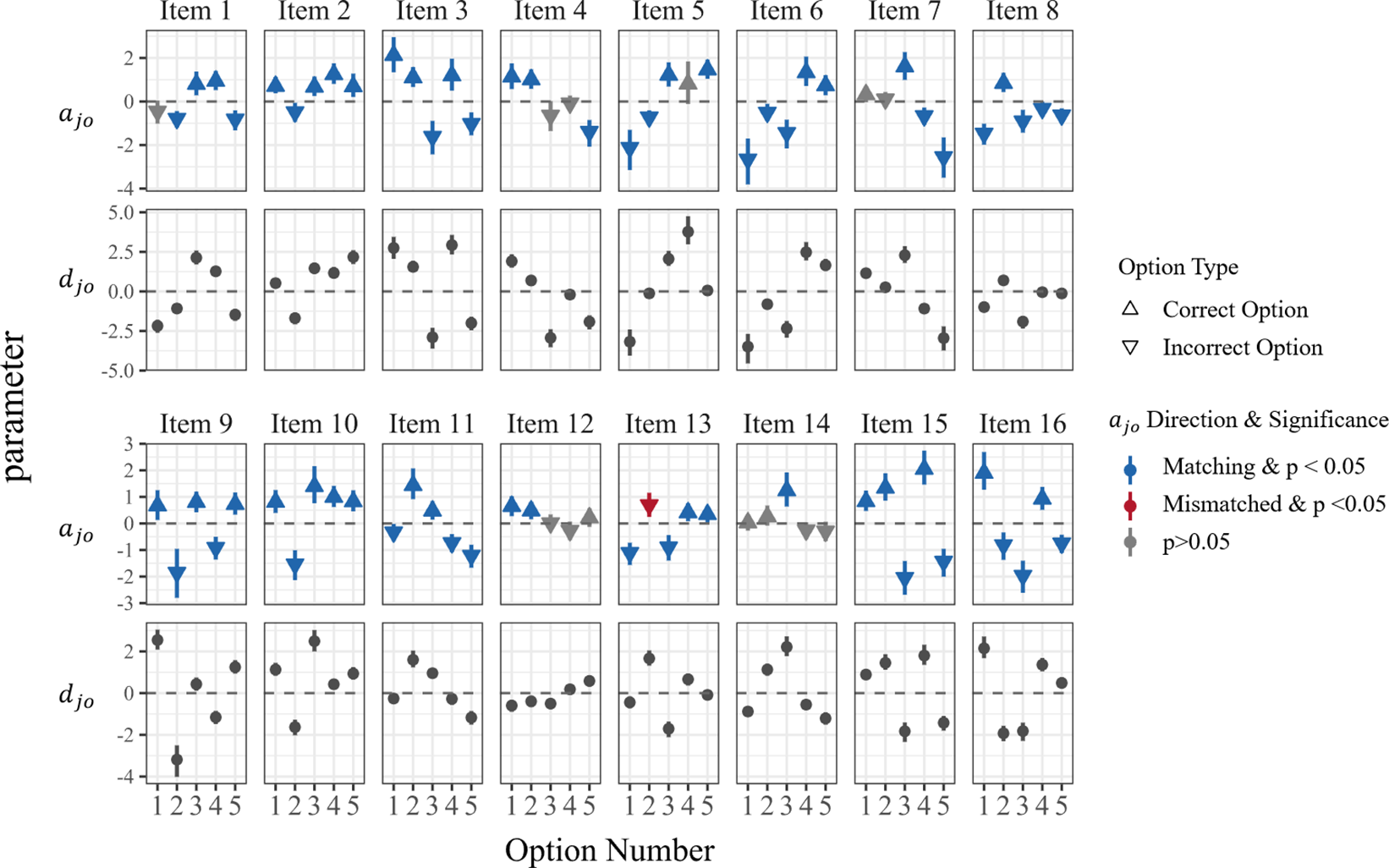
Taking CMS items as an example, Figure 6 illustrates the distributions of the estimated slope ( ${a}_{jo}$ ) and intercept ( ${d}_{jo}$ ) parameters from the MRM-LD. Appendix A includes Figures A1 and A2, which present similar distributions for MTF and select-N items, respectively.

At the option level, the sign and statistical significance of ${a}_{jo}$ parameter in relation to the predefined answer key ( ${W}_{jo}$ ) can reveal potential directional inconsistencies. When option $o$ for item $j$ is designated as correct ( ${W}_{jo}=1$ , indicated by an upward triangle in Figure 6), the expected ${a}_{jo}$ parameter should be positive. Conversely, if it is designated as incorrect ( ${W}_{jo}=-1$ , indicated by a downward triangle in Figure 6), the expected ${a}_{jo}$ should be negative. A significant ${a}_{jo}$ parameter whose sign is consistent with the designated answer (i.e., matches the expected direction) is marked in blue. A significant ${a}_{jo}$ parameter whose sign contradicts the intended direction (marked in red) indicates a discrepancy with the specified answer. Options with non-significant ${a}_{jo}$ parameters (marked in gray) are considered ambiguous or low-discriminating, suggesting areas for further item optimization.

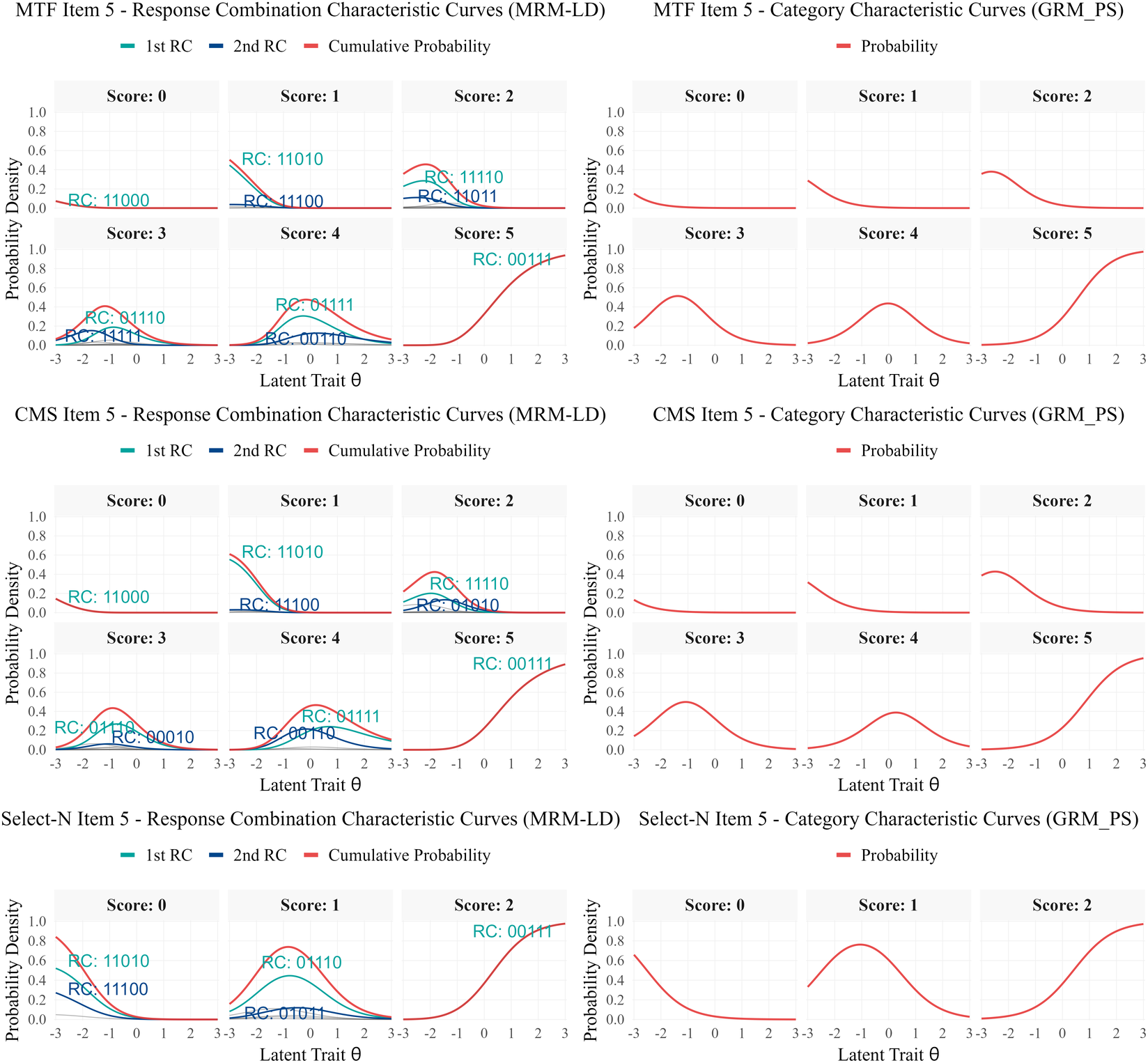
Figure 7 Item characteristic curves of the MRM-LD and GRM_PS for MTF, CMS and select-N item (item 5).

Note: Scores calculated using Partial Scoring method (1 point per correctly judged option). For each score level, 1st RC and 2nd RC indicate the most and second-most probable response combinations. Cumulative Probability shows the total probability of all RCs with that score. For MRM-LD, RC probabilities are calculated conditional on ${\gamma}_{ij} = 0$ .

Using CMS items as an example, we observe that the vast majority of options (83.75%) align with the theoretically expected direction of the ${a}_{jo}$ parameter with $p<.05$ (i.e., the 95% credible interval of estimates does not include zero). This indicates that for most options, the estimated ${a}_{jo}$ parameters are statistically significant and consistent with the intended direction based on the predefined answer key. A smaller proportion (15%) show non-significant ${a}_{jo}$ values, indicating potential ambiguity issues in these options. However, a notable contradiction emerged for the second option of item 13. Specifically, ${a}_{13,2}$ was estimated at 0.69 ( $p<.05$ ). According to the original item design, the fully correct RC was specified as RC_[0,0,0,1,1], meaning option 2 (corresponding to the second position in the vector) was intended to be an incorrect option. Yet, the empirical results indicate that option 2 exhibits a significant positive attraction. This suggests that as a respondent’s latent ability ( ${\theta}_i$ ) increases, the probability of selecting this option also increases, which is contrary to the item’s design intention. This specific item will be further analyzed in detail in the next section.

5.2.4 Response combination characteristic curve

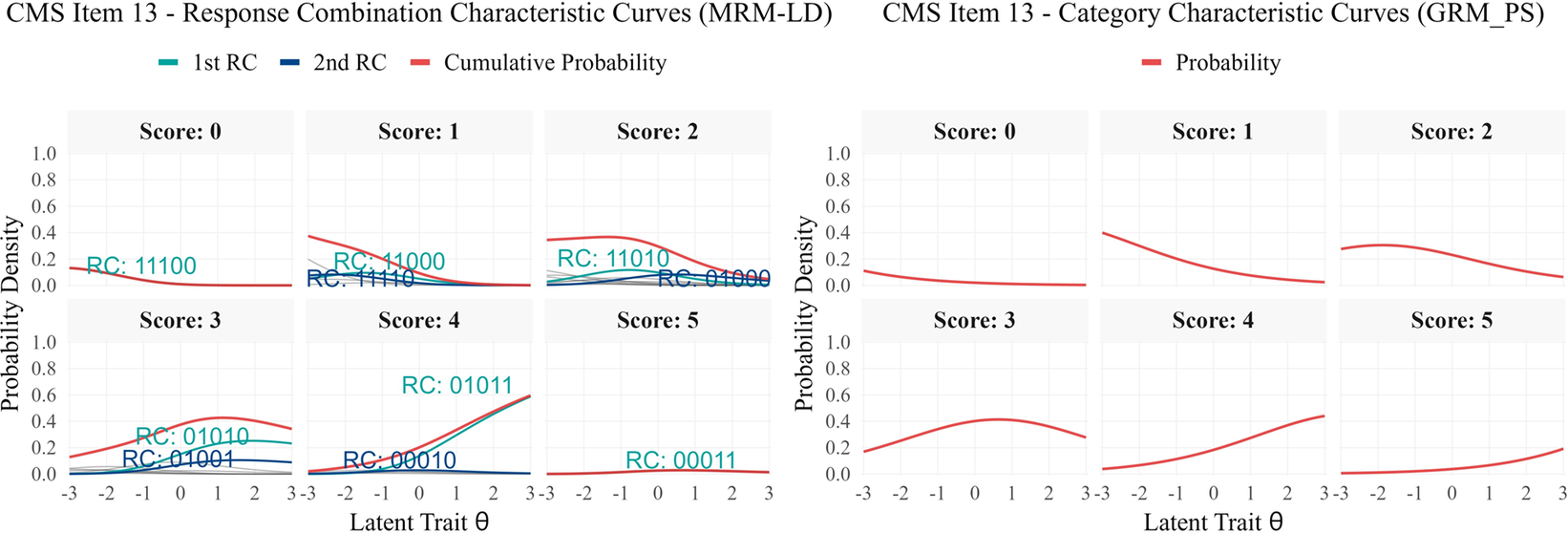
Based on Formula (6), response combination characteristic curves (RCCCs) depict how the probability of each RC varies with latent ability, offering a fine-grained view beyond score categories. Figure 7 compares the RCCCs from the MRM-LD with category characteristic curves from GRM_PS for item 5 across MTF, CMS, and select-N formats. In the MTF format, dominant RCs “migrate” as ability increases: respondents typically transition from easier RCs, through intermediate ones (e.g., RC_[1,1,0,1,0] → RC_[1,1,1,1,0]), ultimately to the fully correct RC_[0,0,1,1,1]. This progression reveals an implicit difficulty ordering among RCs. Notably, RCCCs demonstrate that among RCs sharing the same score, different RCs dominate at different ability levels. For example, among RCs with a score of 3, RC_[1,1,1,1,1] dominates at lower abilities, whereas RC_[0,1,1,1,0] dominates at higher abilities. A similar pattern is observed for CMS items, whereas the select-N format, by design, involves fewer RCs and score levels due to its structure. Although the MRM-LD and GRM_PS can produce similar probabilities at the score level, only the MRM-LD captures and resolves respondents’ behavior at the detailed RC level.

The potential issue of unexpected direction with option 2 of item 13, as previously noted, is further elucidated by the RCCC analysis. Figure 8 shows that the fully correct RC_[0,0,0,1,1] remains below 5% across the ability range, while the partially correct RC_[0,1,0,1,1] increases with ability and becomes dominant among high-ability respondents. A closer examination of the item stem and option content clarifies this pattern. The item asks respondents to identify correct statements regarding plane mirror imaging. Option 2 states: “Conducting multiple experiments to obtain multiple sets of data is to reduce errors.” This wording is subtly misleading. While repeating measurements to “reduce error” is appropriate when estimating a fixed quantity, it is less applicable when verifying a general law such as plane mirror imaging; in the latter context, multiple trials primarily serve to increase the reliability of conclusions. High-ability students appear to overgeneralize the “repetition reduces error” principle, leading them to select option 2.

Figure 8 Item characteristic curves of the MRM-LD and GRM_PS for CMS item type (item 13).

Note: Scores calculated using Partial Scoring method (1 point per correctly judged option). For each score level, 1st RC and 2nd RC indicate the most and second-most probable response combinations. Cumulative Probability shows the total probability of all RCs with that score. For MRM-LD, RC probabilities are calculated conditional on ${\gamma}_{ij} = 0$ .

Figure 9 The distribution of the estimate local dependence parameters ${a}_j^{\ast }$ with 95% CIs for the MRM-LD.

5.2.5 Inter-option local dependence

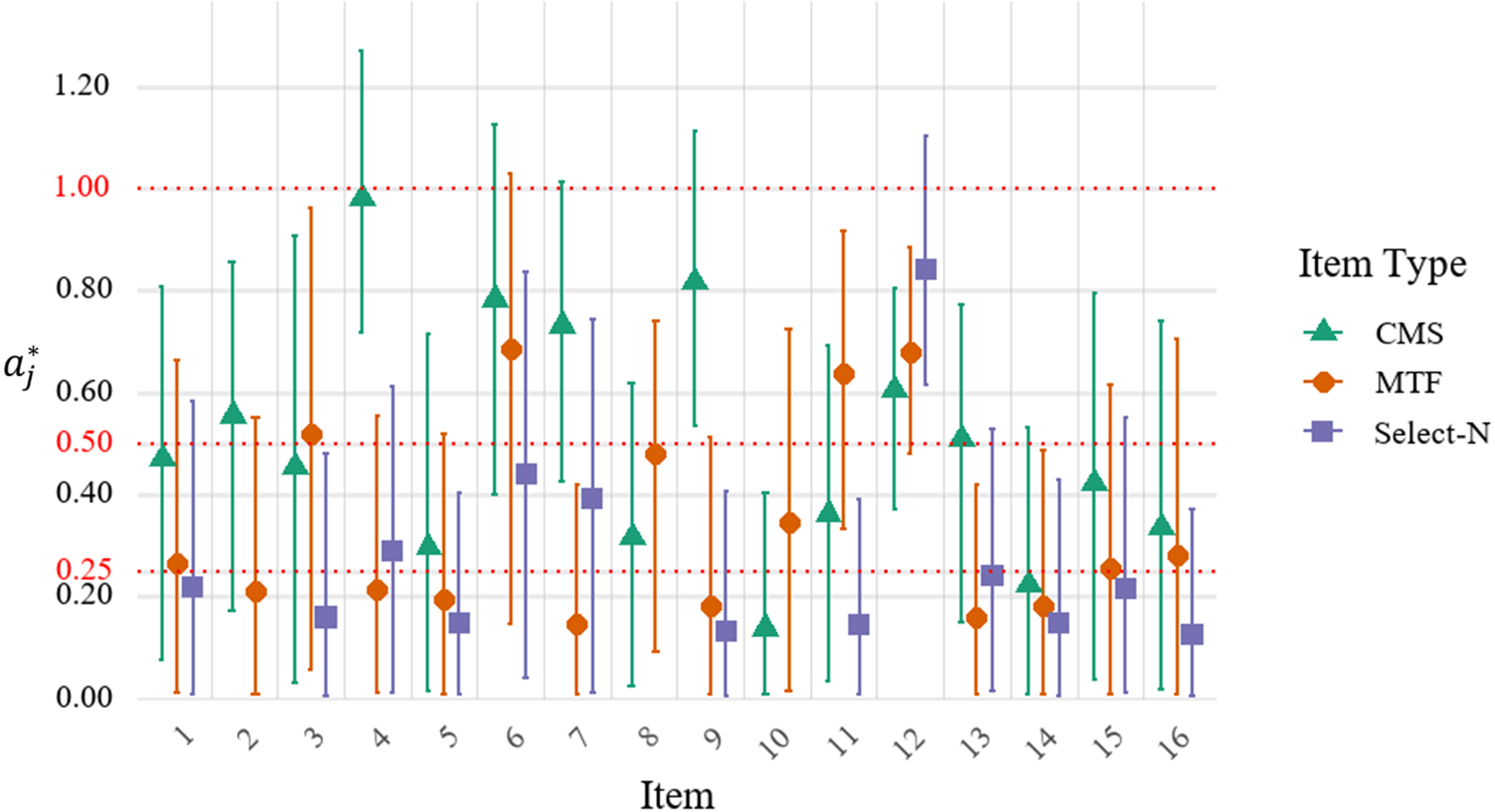
Figure 9 displays the estimated mean local dependence parameters ( ${a}_j^{\ast }$ ) and their 95% confidence intervals by the MRM-LD. Values exceeding 0.5, which typically represent a non-negligible or moderate level of local dependence (Kang et al., 2022; Wainer et al., 2007; Wang & Wilson, 2005), were found in MTF items 3, 6, 11, 12; CMS items 2, 4, 6, 7, 9, 12, 13; and select-N item 12. This widespread local dependence explains the better model fit of the MRM-LD over the standard MRM. It implies that responding to these items requires secondary skills beyond the main ability construct. For example, item 12 requires specific calculations for multiple mirror reflections. A student knowing the formula can solve for several options at once, creating strong dependence among them.

5.2.6 IRT reliability

Table 5 presents the IRT reliability for each model across three item types. The results indicate that both the MRM-LD and MRM yield superior IRT reliability compared to the three traditional methods. Furthermore, while the IRT reliability for MTF and CMS item types showed negligible differences, both were slightly superior to the select-N item type. Overall, the latent ability estimates ${\theta}_i$ derived from the MRM-LD and MRM are more reliable and exhibit lower measurement error compared to those obtained from traditional methods. Notably, the IRT reliability of the MRM was found to be higher than that of the MRM-LD. This finding aligns with previous research on local dependence modeling (Bradlow, 1999; Li et al., 2010; Lucke, 2005; Marais, 2012), which has demonstrated that unaccounted-for dependence can lead to an overestimation of ability measurement precision.

Table 5 IRT reliability of different models across item types.

Note: Boldface indicates the best model.

5.2.7 Criterion-related validity

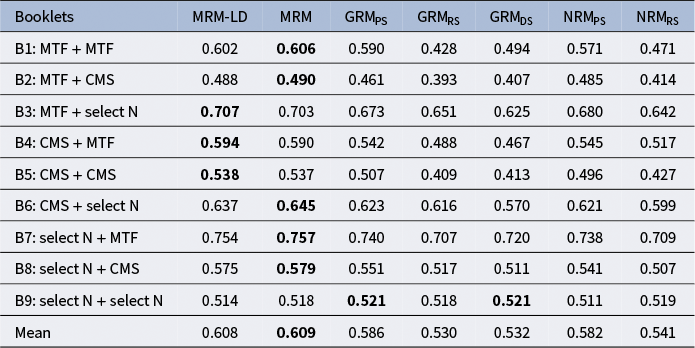
Table 6 presents the criterion-related validity of the four models across nine test booklets and different data types. The results reveal that both MRM and MRM-LD consistently achieve comparable criterion-related validities. Notably, the latent ability estimates from MRM-LD and MRM exhibit a stronger correlation with prior physics test scores across most test booklets, compared to those derived from the GRM and NRM (which are based on three traditional scoring methods).

Table 6 Criterion-related validity across nine booklets.

Note: Boldface indicates the best model. All correlation coefficients in the table are significant at the p < 0.001 level.

5.2.8 Information curve

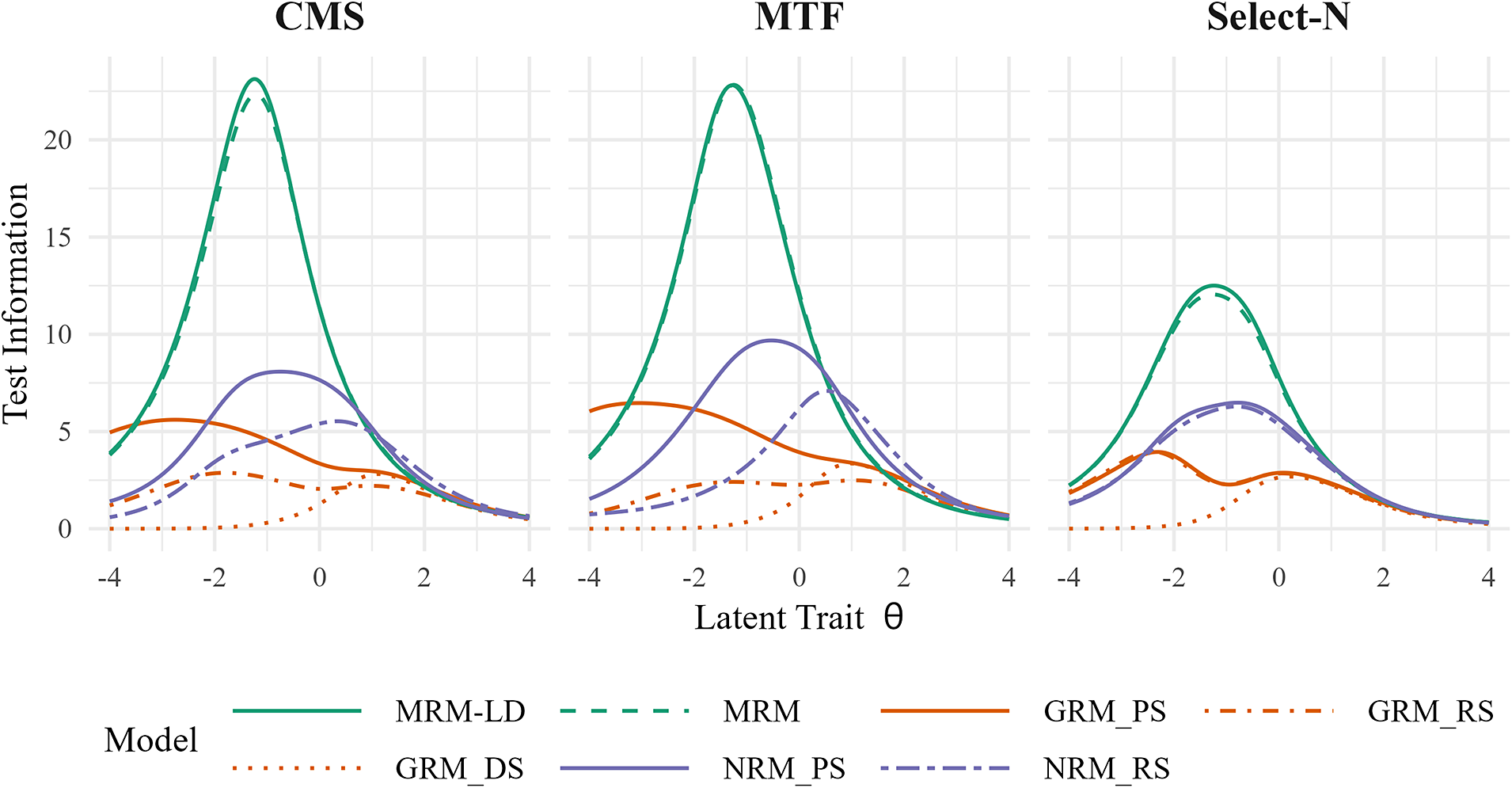
Figure 10 illustrates the test information yielded by the four models at different data types across the three MR item types. It is evident that the MRM-LD and the MRM display similar test information curves. For MTF and CMS items, the two new models provide substantially greater information than other models within the ability range of −3 to 0 (i.e., from low to moderate ability), with their peaks occurring at an ability level of approximately −1. Within the ability range of 1 to 3, the information they provide is on par with other models. However, for select-N items, the test information provided is relatively lower compared to the information volume offered by MTF and CMS items. The comparison of different scoring methods yields results consistent with previous research: PS retains the most test information, followed by RS and then DS (Betts et al., 2022; Muckle et al., 2011). This study further employed RC data modeling within the MRM framework to optimize response utilization by unlocking the potential information in uncompressed RC data that distinguishes respondents’ abilities. This approach significantly enhances test information and improves the reliability of the test.

Figure 10 Test information curves for each model across different item types.

Note: Information curves for MRM-LD are conditional on ${\gamma}_{ij} = 0$ .

6 Simulation studies

6.1 Simulation study 1

6.1.1 Design

This study systematically evaluates parameter estimation accuracy through Monte Carlo simulations under conditions mirroring the empirical study. The simulation replicates key elements: 16 five-option MR items with three structures (MTF, CMS, select-N), nine test booklets, sample size N = 876, and an average of 292 responses per item.

Based on MRM-LD parameter estimates (Supplementary Table S1), which demonstrated optimal fit in the empirical study, response probability vectors were calculated using Formula (6). Simulated RC data were generated via categorical distribution: ${Y}_{ij}\sim \mathrm{Categorical}\left(P\left({Y}_{ij}=x|{\theta}_i,{\boldsymbol{a}}_j,{\boldsymbol{d}}_j,{a}_j^{\ast },{\gamma}_{ij}\right)\right)$ , and then converted using PS, RS, and DS scoring methods. Both RC and converted datasets were analyzed using MRM, MRM-LD, GRM, and NRM models, following identical empirical settings (i.e., prior distributions, MCMC iterations, convergence criteria). Across 30 replications, all models converged with PSRF <1.1.

6.1.2 Evaluation metrics

The accuracy of parameter estimation is evaluated using bias and root mean square error (RMSE) indices: $\mathrm{Bias}\left(\phi \right)=\frac{1}{R}\sum _{r=1}^R\kern0.1em \left(\hat{\phi}^{(r)}-\phi \right)$ and $\mathrm{RMSE}\left(\phi \right)=\sqrt{\frac{1}{R}\sum _{r=1}^R\kern0.20em {\left(\hat{\phi}^{(r)}-\phi \right)}^2}$ , where $\phi$ represents the true parameter value and $\hat{\phi}^{(r)}$ is the estimated value obtained from the $r$ -th replication. These two indices were computed for the estimated values of ${a}_{jo}$ , ${d}_{jo}$ , ${a}_j^{\ast }$ , and ${\theta}_i$ . Subsequently, the mean values of these indices across all relevant parameters were reported. In addition to these, for person parameters, the Pearson correlation coefficient between the true and estimated latent abilities is also calculated: $r=\frac{\sum _{i=1}^N\kern0.20em \sum _{r=1}^R\kern0.20em \left({\phi}_i-\overline{\phi}\right)\left(\hat{\phi}_i^{(r)}-\overline{\hat{\phi }}\right)}{\sqrt{\sum _{i=1}^N\kern0.20em \sum _{r=1}^R\kern0.20em {\left({\phi}_i-\overline{\phi}\right)}^2}\cdotp \sqrt{\sum _{i=1}^N\kern0.20em \sum _{r=1}^R\kern0.20em {\left(\hat{\phi}_i^{(r)}-\overline{\hat{\phi }}\right)}^2}}$ .

6.1.3 Simulation study 1 results

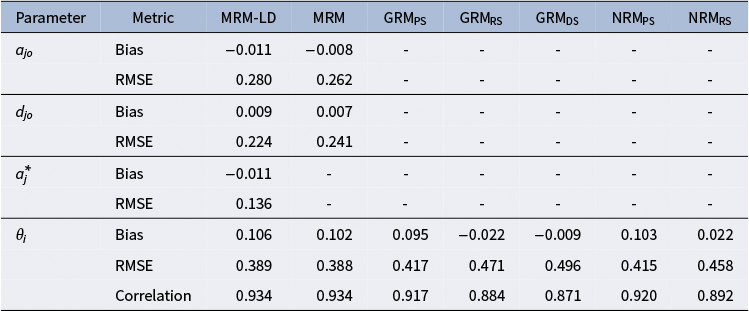
The Monte Carlo simulation results based on empirical data (see Table 7) are summarized as follows. For item parameter estimation within the MRM framework, both the MRM-LD and MRM showed absolute biases below 0.011 for ${a}_{jo}$ and ${d}_{jo}$ , with RMSE values not exceeding 0.280 and 0.224, respectively. Furthermore, the MRM-LD exhibited high estimation accuracy for ${a}_j^{\ast }$ (RMSE = 0.136), confirming its capability to accurately recover local dependence structures. For ${\theta}_i$ parameter, both MRM and MRM-LD substantially outperformed all competing models, achieving RMSE values between 0.388 and 0.389 and correlations with true ability of 0.934. Compared to the GRM_PS (correlation = 0.917, RMSE = 0.417) and NRM_PS (correlation = 0.884, RMSE = 0.458), both of which are based on PS data, the MRM and MRM-LD, fitted using raw RC data, improved correlation by 1.7%–5.0% and reduced RMSE by 6.9%–15.3%. When compared to models based on DS or RS data (e.g., GRM_DS with RMSE = 0.496, correlation = 0.871; GRM_RS with RMSE = 0.471, correlation = 0.892), the MRM and MRM-LD achieved RMSE reductions of 17.6%–21.6% and correlation increases of 4.2%–6.3%.

Table 7 Parameter estimation accuracy of each model in the simulation study 1.

Overall, the simulation validation based on empirical data confirms that the test booklet structure, number of items, and sample size configuration within the empirical research framework are highly feasible. The MRM and MRM-LD demonstrated robust parameter recovery performance. These findings further support the conclusions drawn from the empirical study.

6.2 Simulation study 2

6.2.1 Design

This study extends beyond the single setting of simulation study 1 by using Monte Carlo simulations to evaluate MRM-LD and MRM under broader data conditions, examining parameter estimation accuracy across testing scenarios and potential differences among MR item types.

A four-factor experimental design included: (1) item type: MTF, CMS, select-N; (2) test length: $J=5,10,15$ ; (3) options per item: $O=5,7$ ; (4) sample size: $N=250,500,1000$ ; and (5) fitted models: MRM-LD, MRM, GRM_PS, GRM_RS, GRM_DS, NRM_PS, and NRM_RS, yielding $3\times 3\times 2\times 3\times 7=378$ conditions. The number of correct options per item was configured proportionally for each test length. For J = 5, the configurations included items with 1, 2, 3 (×2), and four correct options for O = 5, and 2, 3, 4 (×2), and five correct options for O = 7. These patterns were scaled accordingly for J = 10 and J = 15.

Based on previous research (Kang et al., 2022; Natesan et al., 2016) and empirical findings, parameters were set as: ${\theta}_i\sim \mathrm{Norm}\left(0,1\right)$ , ${\gamma}_{ij}\sim \mathrm{Norm}\left(0,1\right)$ , ${d}_{jo}\sim \mathrm{Norm}\left(0,1\right)$ , and ${a}_{jo}\sim \mathrm{Lognormal}\left(0,0.5\right)$ for ${W}_{jo}=1$ or $-\mathrm{Lognormal}\left(0,0.5\right)$ for ${W}_{jo}=-1$ . Local dependence parameters ${a}_j^{\ast }$ were set to small (0.25), medium (0.5), and large (1) effects (Kang et al., 2022). The number of items at each effect level (small, medium, large) was (1, 2, 2) for J = 5, (3, 3, 4) for J = 10, and (5, 5, 5) for J = 15. Responses ${Y}_{ij}$ were generated from a categorical distribution based on probabilities from Formula (6), with all other settings consistent with simulation study 1.

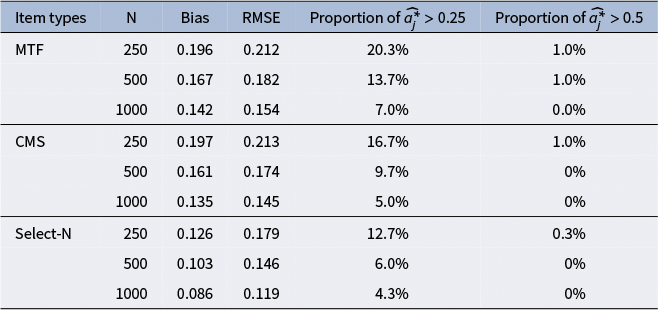
6.2.2 Simulation study 2 results

Supplementary Tables S8 and S9 indicate that both MRM-LD and MRM yielded unbiased (near-zero bias) estimates for the ${a}_{jo}$ and ${d}_{jo}$ parameters. For ${a}_{jo}$ , the MRM performed slightly better, with a mean RMSE of 0.193 (range: 0.118–0.307), compared to 0.205 (range: 0.124–0.327) for MRM-LD. Conversely, for ${d}_{jo}$ , the MRM-LD was slightly more accurate, showing a mean RMSE of 0.147 (range: 0.093–0.260) versus 0.158 (range: 0.105–0.268) for MRM. Sample size was the most significant factor: increasing it from 250 to 1000 reduced RMSE for both parameters by more than 50%. Item type also mattered, as MTF and CMS items yielded higher and comparable accuracy (e.g., the RMSEs of ${d}_{jo}$ for MRM-LD ranged from 0.093 to 0.200 for MTF and from 0.093 to 0.199 for CMS, respectively), outperforming select-N items (e.g., the RMSEs of ${d}_{jo}$ for MRM-LD ranged from 0.100 to 0.260). Increasing the number of options improved parameter recovery only for select-N items, whereas the number of items had no significant effect on the estimation of ${a}_{jo}$ or ${d}_{jo}$ .

Supplementary Table S10 confirms that MRM-LD provided unbiased estimates for the local dependence parameter ${a}_j^{\ast }$ , demonstrating good recovery performance (mean RMSE was 0.147, with a range of 0.093 to 0.260). Similar to the other parameters, increasing the sample size from 250 to 1000 reduced the RMSE by approximately 50%. A larger number of items also led to a slight improvement in the accuracy of ${a}_j^{\ast }$ , with MTF and CMS items showing slightly superior recovery than select-N items.

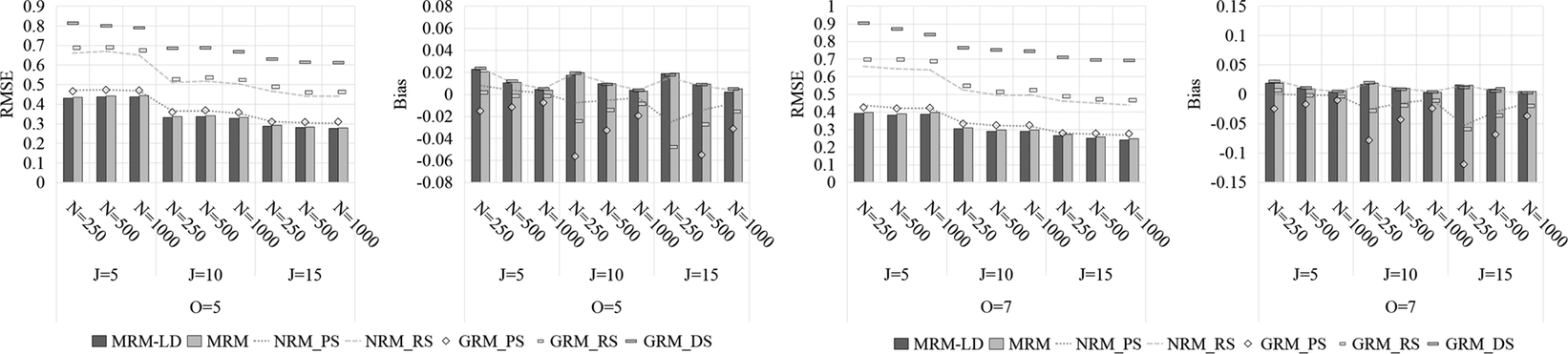
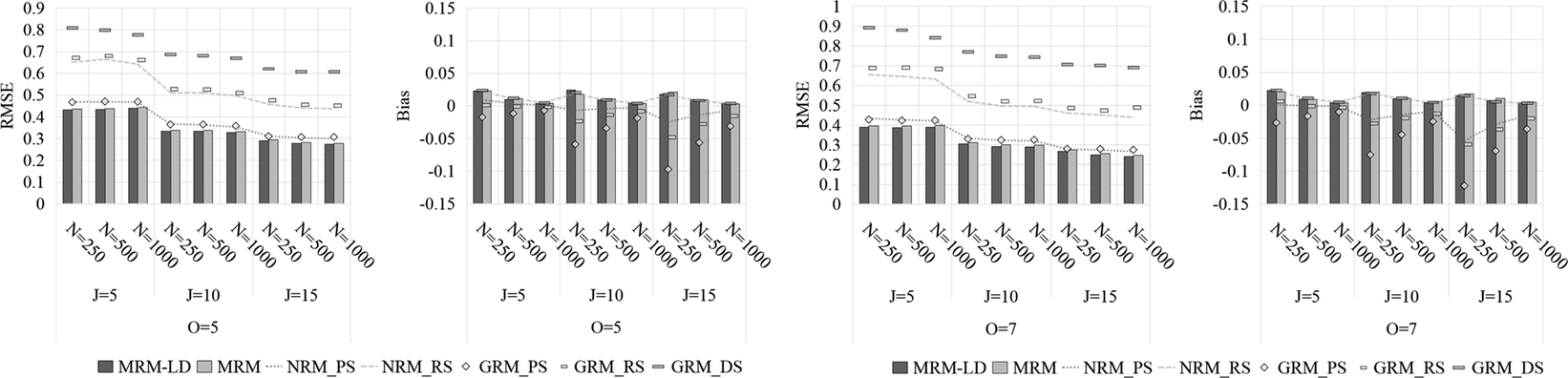
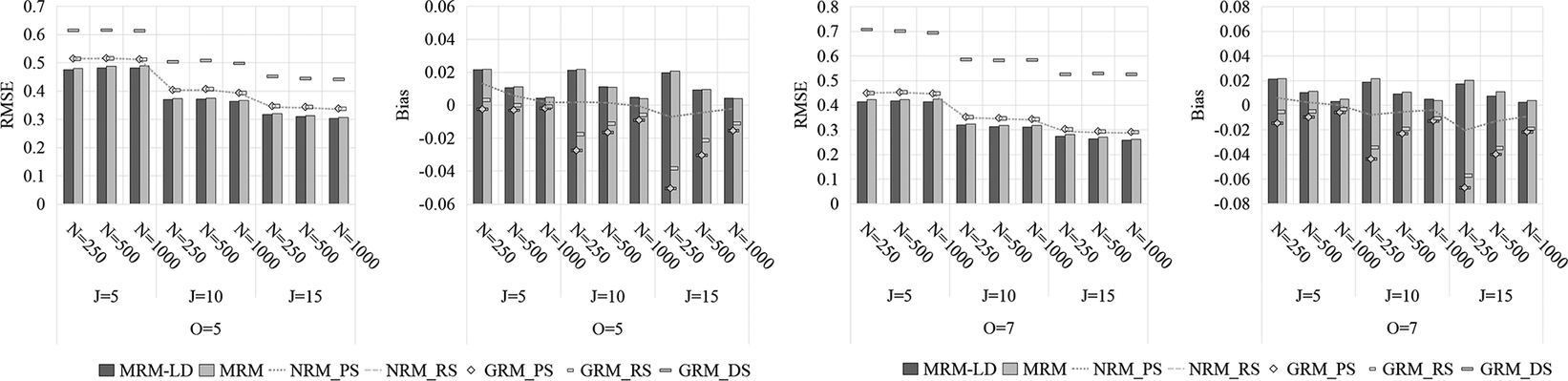
As shown in Figures 11–13, the MRM-LD consistently achieved the highest estimation accuracy for person parameter ${\theta}_i$ , closely followed by MRM. The overall ranking of accuracy was MRM-LD > MRM > GRM_PS/NRM_PS > GRM_RS/NRM_RS > GRM_DS. The MRM-LD reduced RMSE by 4.4%—12.2% compared to GRM_PS/NRM_PS; 5.8%—50.8% compared to GRM_RS/NRM_RS; and 21.4%—65.1% compared to GRM_DS. This pattern was corroborated by Pearson correlation results (see Supplementary Tables S11 and S12), where MRM-LD showed the highest values (0.901–0.972), followed by MRM (0.875–0.971). In contrast, GRM_RS (0.716–0.959) and NRM_RS (0.751–0.960) showed substantially lower correlations, while GRM_DS had the lowest (0.345–0.900). In terms of item types, MTF and CMS items yielded slightly higher accuracy than select-N items. Estimation accuracy also improved with longer tests and a greater number of options. Although sample size minimally affected RMSE but did reduce bias. Notably, even with limited test length (e.g., J = 5), both MRM-LD and MRM maintained high accuracy (RMSE <0.5) and strong correlations (>0.88).

Figure 11 Estimation accuracy of person parameter ${\theta}_i$ by various models in MTF tests.

Figure 12 Estimation accuracy of person parameter ${\theta}_i$ by various models in CMS tests.

Figure 13 Estimation accuracy of person parameter ${\theta}_i$ by various models in select-N tests.

Taking the MTF condition with J = 10, O = 5, and N = 500 as an example, the scatterplots of true versus estimated ${\theta}_i$ in Figure 14 provide visual confirmation of these findings. GRM_RS showed greater dispersion at high ability levels, while GRM_DS failed to differentiate among low-ability respondents. Although GRM_PS improved performance compared with GRM_RS and GRM_DS, the MRM and MRM-LD consistently exhibited the highest accuracy, minimizing estimation error and yielding the strongest correlations between estimated and true ${\theta}_i$ parameters.

Figure 14 Scatter plots of the true and estimated values of ${\theta}_i$ for the condition: MTF, J = 10, O = 5, and N = 500.

6.3 Simulation study 3

6.3.1 Design

This study aimed to investigate the performance of MRM-LD and MRM relative to traditional models under data-generating processes that assume no local dependence. Specifically, we investigated whether MRM-LD can maintain unbiased parameter estimation and correctly identify the absence of local dependence.

Building on the findings from simulation study 2 regarding the significant impact of sample size and MR item type on the estimation of ${a}_j^{\ast }$ , a three-factor experimental design was employed in this study. The factors included: (1) item type: MTF, CMS, select-N; (2) sample size: $N=250,500,1000$ ; and (3) fitted models: MRM-LD, MRM, GRM_PS, GRM_RS, GRM_DS, NRM_PS, and NRM_RS. This design yielded a total of 63 experimental conditions. The test length ( $J=10$ ) and number of options ( $O=5$ ) were fixed. The true value of the local dependence parameter ${a}_j^{\ast }$ was set to 0, making the MRM the true data-generating model. All other settings were consistent with those used in simulation study 1.

6.3.2 Simulation study 3 results

Supplementary Tables S13 and S14 show the recovery of parameters ${a}_{jo}$ and ${d}_{jo}$ when data were generated by the MRM. Both MRM-LD and MRM exhibited negligible bias, confirming that MRM-LD remains unbiased even without true local dependence. Mean RMSE values were highly comparable between the two models. For ${a}_{jo}$ , MRM-LD recorded 0.197 versus 0.193 for MRM. For ${d}_{jo}$ , MRM-LD showed 0.131 compared to 0.132 for MRM. These results indicate that estimating the additional local dependence parameter in MRM-LD did not lead to any notable loss of accuracy. Consistent with the findings of simulation study 2, MTF and CMS items exhibited better parameter recovery than select-N items.

Table 8 details the estimation accuracy of the local dependence parameter ${a}_j^{\ast }$ for MRM-LD when its true value was zero. Across all conditions, a positive bias was observed (ranging from 0.086 to 0.197), indicating a slight tendency to overestimate. This bias decreased progressively as the sample size increased. Similarly, RMSE values decreased with larger samples, with select-N items showing consistently lower RMSEs (0.119–0.179) than MTF (0.154–0.212) and CMS items (0.145–0.213).

Table 8 Estimation accuracy of the local dependence parameter ${a}_j^{\ast }$ for the MRM-LD in simulation study 3.

To evaluate the practical impact of these estimations, we calculated the proportion of estimated ${a}_j^{\ast }$ values exceeding 0.25 (indicating minor false positives) and 0.50 (indicating substantial false positives), based on criteria from previous research (Glas et al., 2000; Ravand, 2015; Wang & Wilson, 2005; Wang et al., 2002). At a sample size of 250, the false positive rates were 20.3% for MTF, 16.7% for CMS, and 12.7% for select-N items at the 0.25 threshold, while the rates at the 0.50 threshold were 1.0%, 1.0%, and 0.3%, respectively. When the sample size increased to 1000, the false positive rates at the 0.25 threshold decreased to 7.0% for MTF items, 5.0% for CMS items, and 4.3% for select-N items, and no false positives at the 0.50 threshold occurred occurred for any item type. Item type influenced susceptibility to false positive detection, with MTF items being most susceptible, CMS items performing better, and select-N items demonstrating the best control over false positive rates.

Figure 15 shows that MRM-LD and MRM consistently provided superior ${\theta}_i$ estimation, with the smallest RMSEs (0.298–0.343) and highest correlations (0.942–0.956) compared with GRM and NRM. The difference between MRM and MRM-LD was negligible (i.e., $\Delta$ RMSE < 0.001), highlighting the MRM-LD’s robustness even when true local dependence was absent.

Figure 15 Estimation accuracy of person parameter ${\theta}_i$ by various models in simulation study 3.

6.4 Simulation study 4

6.4.1 Design

To evaluate the robustness of MRM and its sensitivity to model misspecification, simulation study 4 examined scenarios where the data-generating process deviated from MR assumptions. Specifically, GRM_PS and NRM_PS, non-MR frameworks using only score information, were employed as data-generating models.

A four-factor experimental design was employed, comprising the following factors: (1) item type: MTF, CMS, select-N; (2) number of options: $O=5$ , $O=7$ ; (3) data-generating model: GRM_PS, NRM_PS; and (4) fitted Model: MRM-LD, MRM, GRM_PS, GRM_RS, GRM_DS, NRM_PS, NRM_RS. This resulted in a total of 84 data conditions, with test length fixed at J = 10 and sample size at N = 500.

For conditions where GRM_PS served as the data-generating model, item slope parameters ( ${a}_j$ ) were drawn from a uniform(0.5, 2) distribution, and intercept parameters ( ${d}_{jk}$ ) were sampled from a standard normal distribution (Kang et al., 2022; Nye et al., 2020). For NRM_PS, item category slope parameters ( ${a}_{jk}$ ) were drawn from a standard normal distribution with the order constraint ${a}_{j1}<{a}_{j2}<\cdots <{a}_{j\left({K}_j-1\right)}$ , and intercept parameters ( ${d}_{jk}$ ) were sampled from a standard normal distribution (García-Pérez, 2018). RC data were generated in three steps. First, item score probabilities were calculated for each respondent under the GRM or NRM with different scoring methods. Second, for each score level, these probabilities were randomly distributed among all possible RCs corresponding to that score. Third, for subsequent GRM and NRM analyses, the resulting RC data were re-aggregated into score-based formats using PS, RS, and DS scoring methods. All other experimental settings remained consistent with those used in the previous simulation studies.

6.4.2 Simulation study 4 results

Figure 16 presents the estimation accuracy of person parameters ${\theta}_i$ across various models in simulation study 4, which assessed the performance of MRM-LD and MRM under model misspecification. When data were generated by GRM_PS, the MRM-LD demonstrated notable robustness, with only a 3.0% increase in mean RMSE and a 0.8% decrease in correlation relative to the true model. In contrast, the standard MRM exhibited considerably greater sensitivity to misspecification, exhibiting a 12% rise in RMSE and a 3.1% reduction in correlation. A similar pattern was observed when NRM_PS served as the data-generating model. Compared to the true model, MRM-LD incurred only a 4.6% increase in RMSE and a 1.1% decline in correlation, whereas the standard MRM showed more pronounced deterioration, with a 9.3% rise in RMSE and a 2.7% drop in correlation.

Figure 16 Estimation accuracy of person parameter ${\theta}_i$ by various models in simulation study 4.

Note: True models are highlighted in red.

Across both generating scenarios, MRM-LD consistently exhibited stronger robustness to model misspecification than the standard MRM. Specifically, the RMSE increase for MRM-LD was only 30–42% of that for the standard MRM, and its correlation loss was approximately one-third as large. These results suggest that the standard MRM, which does not explicitly model within-item local dependence, is more adversely affected by deviations from its underlying assumptions than MRM-LD.

7 Discussion

This study introduced a psychometric model framework that integrates multiple MR item types, such as MTF, CMS, and Select-N, into a unified structure capable of analyzing RC data without losing information through data compression. Within this framework, we developed the MRM-LD and MRM and applied an MCMC algorithm for parameter estimation. Through empirical and simulation studies, we demonstrated that the proposed models outperform traditional scoring methods and existing analytical approaches by improving parameter estimation accuracy and providing more granular insights into respondents’ responses and item characteristics.

7.1 Importance of modeling response combination data in multiple response items

Our empirical study revealed that the MRM-LD model achieved the best fit, higher criterion validity, and greater test information compared to traditional models. Even under simulation conditions with small sample sizes and limited items, MRM-LD and MRM accurately recovered parameters, underscoring their practical applicability in real testing environments. Building upon RC data, the RCCCs enable a more granular representation of item characteristics and illuminate the more nuanced relationship between respondents’ latent abilities and the responses as reflected by the RCs. Furthermore, RCCCs reveal the ranking of option difficulty, which can inform more effective score improvement strategies by guiding respondents to progressively master the knowledge embodied in the options, moving from easier to more difficult ones (Smith & Bendjilali, 2022). Beyond item-score based modeling approaches, the MRM framework, by modeling option parameters, facilitates a deeper analysis of option-level quality. Specifically, the sign and significance of the ${a}_{jo}$ parameter can assist test developers in more effectively evaluating item quality, identifying ambiguous options, and correcting potentially mis-keyed options (Zu & Kyllonen, 2020).

Compared to using raw RC data, modeling methods that rely on item scores may introduce potential issues. While models using PS data are second only to the MRM and MRM-LD in terms of ability estimation accuracy, their application still faces challenges. Specifically, when employing the PS method, the compression of scores into multiple categories can lead to the absence of certain score categories, particularly for lower score levels (e.g., 0 or 1). This results in insufficient information for polytomous IRT models, especially the NRM, to accurately estimate intercept and slope parameters for each score category, thereby leading to deviations in data fit. Although these data can be handled by collapsing categories, this approach is not only inflexible but also loses the effective representation of lower-level data (Van Dusen & Nissen, 2020), especially when dealing with small sample sizes and limited items (Battauz, 2020).

While scoring raw RC using RS and DS can reduce complexity and enhance parameter estimation efficiency, it significantly compromises the accuracy of parameter estimates. Empirical study showed that using GRM and NRM with RS and DS data resulted in lower reliability and criterion-related validity for person parameter estimates. Consistent with previous research (Schmidt et al., 2021, 2022), simulations further indicated that RS and DS distort the linear relationship between true ability and estimated values, with DS particularly failing to differentiate low-ability respondents as the number of options increases.

7.2 Practical recommendations for choosing multiple response item types

Our comparisons among MTF, CMS, and select-N item types revealed that MTF and CMS items exhibit similar psychometric properties. In empirical data, the test information functions for both item types, estimated using the MRM-LD and MRM, were nearly identical. Simulation studies supported these findings, showing consistent parameter estimation performance for both types. This similarity suggests that MTF and CMS items can be used interchangeably to some extent. The primary difference lies in the fact that CMS items do not permit a “none selected” response, although in practice, respondents may avoid such responses in MTF items, especially when there are many options.

Nevertheless, select-N items demonstrated relatively poorer performance in both empirical and simulation studies, though still within acceptable ranges. In simulations, a select-N test with five items and five options achieved a correlation of approximately 0.9 between estimated and true person parameters using the MRM-LD. The results of parameter recovery for seven-option select-N items were comparable to those of five-option MTF and CMS items. In the present study, MRM-LD, MRM, GRM, and NRM consistently showed that select-N items yielded lower information and less accurate parameter estimations compared to their MTF and CMS format. However, select-N items required the shortest response times, an advantage in time-constrained contexts. The trade-off between response efficiency and information was not examined in this study but warrants future investigation. A potential underlying reason for this observed diminished performance is the reduced number of possible RCs inherent in the select-N format. This reduction constrains the potential response space, thereby leading to a less fine-grained discrimination of person abilities (Guo et al., 2016; Samejima, 1968).

7.3 Insights from the local dependence of multiple response items

In empirical study, the local dependence parameter ${a}_{jo}^{\ast }$ derived from the MRM-LD revealed significant local dependencies across many items in the dataset. This finding can explain why the standard MRM sometimes exhibited PPP values close to 0.05 for certain items. The standard MRM fails to capture these within-item random effects. Furthermore, simulation study 4 demonstrated that MRM-LD exhibits greater robustness compared to MRM when the data-generating models were GRM and NRM, respectively. Beyond statistical performance, the local dependence parameters provide additional analytical scope for analyzing MR items. Test developers and researchers can leverage the analysis of highly locally dependent items to identify additional knowledge components involved. By combining this with the slope parameters of the item options, they can ascertain whether the item truly measures the intended knowledge or if it primarily assesses knowledge from other dimensions (Xie, 2001).

In empirical study, the ${a}_{jo}^{\ast }$ parameters from MRM-LD showed that CMS items exhibited stronger local dependence characteristics. This dependence might be influenced by test taking strategies, where respondents focus more on the logical relationships between options to select the most appropriate combination. Consequently, this strategic approach by respondents often leads to larger local dependence parameters for CMS compared to MTF items. Conversely, the discrete response format of MTF items suggests that respondents respond options independently, potentially leading to less influence from test taking strategies and cues (Kreiter & Frisbie, 1989), thereby exhibiting weaker local dependence. In contrast to MTF and CMS, the empirical results indicated that the select-N format yielded lower local dependence, although no significant difference was found when compared to MTF. A potential explanation for this observation lies in the “select exactly T” rule inherent in the select-N format. This rule restricts the response space, preventing other invalid RCs from occurring. For instance, in a select-2 item, once a respondent chooses two options, they are precluded from selecting any further options, thereby limiting how local dependence can influence choices for other options. Another specific case concerns the select-N versions of SAMC items (e.g., empirical items 2, 8, 10). Since their correct answers require the selection of either only one option or four options, these items are functionally equivalent to a SAMC format. Consequently, the MRM-LD model reduces to an NRM for these items, negating the need to estimate additional local dependence parameters.

However, it is crucial to temper these findings with a note of caution. Results from simulation study 3 indicated that when the data-generating model was the standard MRM, which implies the absence of local dependence, the MRM-LD exhibited a slight tendency to falsely detect local dependence. This tendency was particularly evident at smaller sample sizes (i.e., N = 250 and N = 500). Therefore, when sample sizes are limited, the interpretation of small estimated local dependence parameters (e.g. $\widehat{a_j^{\ast }}<0.25$ ) requires careful consideration.

7.4 Potential model compatibility issues with the MRM and MRM-LD

Despite the successful implementation of parameter estimation for both MRM-LD and MRM in this study, and the validation of the new models’ accuracy through simulation and empirical studies, the proposed framework still faces several computational challenges. For instance, when fitting empirical data, the computational cost of the new models significantly increases. On an AMD 9950X CPU, with two MCMC chains running in parallel, the MRM-LD required 34 minutes and MRM took 22 minutes, in contrast to GRM_PS, which only needed 11.5 minutes.

Moreover, the current research primarily focused on three typical MR item formats with fewer than 10 options. However, technology-enhanced innovative MR items (e.g., highlighting and drag-and-drop items, Kang et al., 2022) often involve more options, posing more complex modeling challenges. When the number of options in an MR item exceeds 10, the number of possible RCs can reach thousands or even tens of thousands (e.g., a 12-option MTF item corresponds to ${2}^{12}=4096$ RCs), leading to computational difficulties in the categorical distribution sampling process. The current MCMC-based Bayesian estimation method faces efficiency bottlenecks due to the exponential increase in computational complexity. To address this, future research should develop more efficient parameter estimation strategies, such as replacing MCMC algorithms with more efficient alternatives like the EM algorithm or variational inference (Natesan et al., 2016), to meet the time requirements for parameter estimation in practical assessments.

Beyond that, not all possible RCs in the ${\boldsymbol{Z}}_j$ matrix are consistently observed in real test scenarios, especially when sample sizes are small and the number of options is large. This situation warrants further investigation. Although the MRM and MRM-LD define parameters at the option level rather than the RC level, their parameter identifiability can still be compromised under certain conditions. One such condition occurs when a particular option is consistently either selected or unselected across all observed RCs. In this case, the parameter for that option cannot be identified, and it is necessary to remove the corresponding column from ${\boldsymbol{Z}}_j$ matrix. Another scenario arises when options within an RC are highly collinear, such as when option 1 and option 2 are always co-selected or co-rejected). This collinearity prevents the models from correctly separating options’ unique contributions and potentially rendering the models non-identifiable. Consequently, the MRM and MRM-LD may not be suitable for type K multiple-choice items (Albanese, 1982, 1993), where the number of possible RCs is very limited and collinearity among options is a common issue. In such cases, one potential solution is to retain only one corresponding column in the ${\boldsymbol{Z}}_j$ matrix.

Additionally, existing models, based on the ${\boldsymbol{Z}}_j$ matrix, strictly constrain the combination rules for RCs (e.g., forcing a specific number of options to be selected in select-N items). While such violations were not observed in the computerized administration of our empirical study, they are a concern in actual assessments, especially paper-and-pencil tests, where respondents may violate these constraints (e.g., selecting too many, too few, or invalid combinations). For instance, if a respondent mistakenly selects three options in a select-2 item, the model cannot effectively process such data due to its lack of definition for anomalous RCs, leading to unattainable parameter estimates. One potential approach is to treat anomalous RCs as missing data. However, when the proportion of anomalous RCs is high, this might reflect a systematic behavior. In such cases, anomalous RCs could be modeled as response styles (Albanese, 1993; Brassil & Couch, 2019; Henninger & Meiser, 2020), characterizing the psychological attributes underlying these aberrant responses.

Furthermore, the directional constraint on local dependence in the MRM-LD model, where correct options ${W}_{jo}=1$ and incorrect options ${W}_{jo}=-1$ , may pose adaptability issues in non-cognitive assessment contexts. For example, in attitude surveys or value assessments (Golubovich et al., 2017; Kunz & Fuchs, 2019; Smyth et al., 2006), item options do not have clear “correct” or “incorrect” distinctions, making it difficult to predefine the direction of local dependence. This limitation might weaken the MRM-LD’s applicability to non-cognitive tests. Future research could explore relaxing this structural constraint on the direction of local dependence to broaden the model’s applicability.