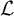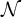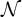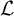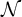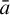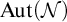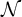1 Introduction
The past decade has seen the development of the study of invariant random structures. This field was kindled by the work of Petrov and Vershik [Reference Petrov and Vershik13] on exchangeable random triangle-free graphs. A fundamental result in this area is due to Ackerman, Freer, and Patel [Reference Ackerman, Freer and Patel5] who prove that, for a given countable
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() ${\mathcal {M}}$
, the existence of an invariant random structure almost surely isomorphic to
${\mathcal {M}}$
, the existence of an invariant random structure almost surely isomorphic to
![]() ${\mathcal {M}}$
is equivalent to
${\mathcal {M}}$
is equivalent to
![]() ${\mathcal {M}}$
satisfying a combinatorial property known as no-algebraicity.
${\mathcal {M}}$
satisfying a combinatorial property known as no-algebraicity.
Recall that for any first order language
![]() $\mathcal {L}$
which contains countably many relation and function symbols, the collection
$\mathcal {L}$
which contains countably many relation and function symbols, the collection
![]() $\mathrm {Str}({\mathcal {L}},{\mathbb {N}})$
of all
$\mathrm {Str}({\mathcal {L}},{\mathbb {N}})$
of all
![]() $\mathcal {L}$
-structures whose domain is the natural numbers
$\mathcal {L}$
-structures whose domain is the natural numbers
![]() $\mathbb {N}$
can be endowed with a natural Polish topology (see Section 2.1). For every structure
$\mathbb {N}$
can be endowed with a natural Polish topology (see Section 2.1). For every structure
![]() $\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
, the isomorphism class
$\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
, the isomorphism class
![]() $[\mathcal {N}]_{\mathrm {iso}}$
of
$[\mathcal {N}]_{\mathrm {iso}}$
of
![]() $\mathcal {N}$
is the set:
$\mathcal {N}$
is the set:
These classes can be identified with the orbits under the logic action
![]() $\mathrm {Sym}(\mathbb {N})\curvearrowright \mathrm {Str}(\mathcal {L},\mathbb {N})$
of the Polish group
$\mathrm {Sym}(\mathbb {N})\curvearrowright \mathrm {Str}(\mathcal {L},\mathbb {N})$
of the Polish group
![]() $\mathrm {Sym}(\mathbb {N})$
of all permutations of
$\mathrm {Sym}(\mathbb {N})$
of all permutations of
![]() $\mathbb {N}$
on
$\mathbb {N}$
on
![]() $\mathrm {Str}(\mathcal {L},\mathbb {N})$
(see Section 2.2).
$\mathrm {Str}(\mathcal {L},\mathbb {N})$
(see Section 2.2).
A random structure is just a Borel probability measure on
![]() $\mathrm {Str}({\mathcal {L}},{\mathbb {N}})$
. A random structure is said to be invariant if it is invariant under the logic action. In [Reference Ackerman, Freer and Patel5] it was shown that the existence of an invariant random structure supported on
$\mathrm {Str}({\mathcal {L}},{\mathbb {N}})$
. A random structure is said to be invariant if it is invariant under the logic action. In [Reference Ackerman, Freer and Patel5] it was shown that the existence of an invariant random structure supported on
![]() $[\mathcal {N}]_{\mathrm {iso}}$
is equivalent to
$[\mathcal {N}]_{\mathrm {iso}}$
is equivalent to
![]() $\mathcal {N}$
having no-algebraicity: for any tuple
$\mathcal {N}$
having no-algebraicity: for any tuple
![]() $\bar a$
,
$\bar a$
,
![]() $\mathrm {acl}(\bar {a},\mathcal {N})=\bar {a,}$
where
$\mathrm {acl}(\bar {a},\mathcal {N})=\bar {a,}$
where
![]() $\mathrm {acl}(\bar {a},\mathcal {N})$
refers to the points of
$\mathrm {acl}(\bar {a},\mathcal {N})$
refers to the points of
![]() $\mathcal {N}$
whose orbit is finite under the pointwise stabilizer of
$\mathcal {N}$
whose orbit is finite under the pointwise stabilizer of
![]() $\bar {a}$
(see Section 2.1). This result was followed by an extensive study of invariant random structures [Reference Ackerman1–Reference Ackerman, Freer, Kwiatkowska and Patel3, Reference Hodges8] and invariant random expansions [Reference Kechris10].
$\bar {a}$
(see Section 2.1). This result was followed by an extensive study of invariant random structures [Reference Ackerman1–Reference Ackerman, Freer, Kwiatkowska and Patel3, Reference Hodges8] and invariant random expansions [Reference Kechris10].
In the present article we study a generalization of invariant random structures: quasi-invariant random structures. Let
![]() $G\curvearrowright X$
be a Borel action of a Polish group on a standard Borel space and recall that a probability measure
$G\curvearrowright X$
be a Borel action of a Polish group on a standard Borel space and recall that a probability measure
![]() $\mu $
on X is G-quasi-invariant, if for every Borel
$\mu $
on X is G-quasi-invariant, if for every Borel
![]() $B\subseteq X$
and every
$B\subseteq X$
and every
![]() $g\in G$
we have that
$g\in G$
we have that
![]() $\mu (B)=0 \iff \mu (g\cdot B)=0$
. The class of
$\mu (B)=0 \iff \mu (g\cdot B)=0$
. The class of
![]() $S_\infty $
-quasi-invariant measures have been studied by Nessonov in [Reference Nessonov11].
$S_\infty $
-quasi-invariant measures have been studied by Nessonov in [Reference Nessonov11].
We call a countable structure
![]() $\mathcal {N}$
quasi-invariantly random if there exists a
$\mathcal {N}$
quasi-invariantly random if there exists a
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure
![]() $\mu $
on
$\mu $
on
![]() $\mathrm {Str}(\mathcal {L},\mathbb {N})$
with
$\mathrm {Str}(\mathcal {L},\mathbb {N})$
with
![]() $\mu ([\mathcal {N}]_{\mathrm {iso}})=1$
. The main result of this article is the following characterization of quasi-invariantly random structures in terms of the algebraic closure operator, similar in spirit to the main result of [Reference Ackerman, Freer and Patel5].
$\mu ([\mathcal {N}]_{\mathrm {iso}})=1$
. The main result of this article is the following characterization of quasi-invariantly random structures in terms of the algebraic closure operator, similar in spirit to the main result of [Reference Ackerman, Freer and Patel5].
Definition 1. We say that
![]() $\mathcal {N}$
is highly algebraic if for every finite
$\mathcal {N}$
is highly algebraic if for every finite
![]() ${F\subseteq \mathrm {dom}(\mathcal {N})}$
there exists a tuple
${F\subseteq \mathrm {dom}(\mathcal {N})}$
there exists a tuple
![]() $\bar {a}=(a_0,\ldots ,a_{n-1})$
in
$\bar {a}=(a_0,\ldots ,a_{n-1})$
in
![]() $\mathrm {dom}(\mathcal {N})$
so that
$\mathrm {dom}(\mathcal {N})$
so that
![]() $\mathrm {acl}(\bar {a},\mathcal {N})\not \subseteq F\cup \{a_0,\ldots ,a_{n-1}\}$
.
$\mathrm {acl}(\bar {a},\mathcal {N})\not \subseteq F\cup \{a_0,\ldots ,a_{n-1}\}$
.
Theorem 2. A countable structure is quasi-invariantly random if and only if it is not highly algebraic.
Notice that, when
![]() $\mathcal {L}$
contains symbols of arbitrarily large arity, the action of
$\mathcal {L}$
contains symbols of arbitrarily large arity, the action of
![]() $\mathrm {Sym}({\mathbb {N}})$
on
$\mathrm {Sym}({\mathbb {N}})$
on
![]() $\mathrm {Str}({\mathcal {L}},{\mathbb {N}})$
is universal (see [Reference Becker and Kechris6] section 2.7). Hence, up to embedding, Theorem 2 describes all
$\mathrm {Str}({\mathcal {L}},{\mathbb {N}})$
is universal (see [Reference Becker and Kechris6] section 2.7). Hence, up to embedding, Theorem 2 describes all
![]() $\mathrm {Sym}({\mathbb {N}})$
-quasi-invariant actions that admit an orbit of full measure. We also observe that
$\mathrm {Sym}({\mathbb {N}})$
-quasi-invariant actions that admit an orbit of full measure. We also observe that
![]() $\mathcal {N}$
is not highly algebraic if and only if
$\mathcal {N}$
is not highly algebraic if and only if
![]() $\mathrm {acl}(\emptyset ,\mathcal {N})$
is finite and, for all
$\mathrm {acl}(\emptyset ,\mathcal {N})$
is finite and, for all
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\mathrm {dom}(\mathcal {N})$
, we have
$\mathrm {dom}(\mathcal {N})$
, we have
![]() $\mathrm {acl}(\bar {a},\mathcal {N})\subseteq \mathrm {acl}(\emptyset ,\mathcal {N})\cup \{a_0,\ldots ,a_{n-1}\}$
. This simply follows from the
$\mathrm {acl}(\bar {a},\mathcal {N})\subseteq \mathrm {acl}(\emptyset ,\mathcal {N})\cup \{a_0,\ldots ,a_{n-1}\}$
. This simply follows from the
![]() $\mathrm {Aut}(\mathcal {N})$
-invariance of the union of all sets of the form
$\mathrm {Aut}(\mathcal {N})$
-invariance of the union of all sets of the form
![]() $\mathrm {acl}(\bar {a},\mathcal {N})\setminus \{a_0,\ldots ,a_{n-1}\}$
.
$\mathrm {acl}(\bar {a},\mathcal {N})\setminus \{a_0,\ldots ,a_{n-1}\}$
.
Finally, recall that to every quasi-invariant measure
![]() $\mu $
on a Borel G-space X one can use the Radon–Nikodym derivatives to associate with
$\mu $
on a Borel G-space X one can use the Radon–Nikodym derivatives to associate with
![]() $\mu $
a measurable cocycle
$\mu $
a measurable cocycle
![]() $c_{\mu }\colon G\times X \to \mathbb {R}$
. The following comes as a byproduct of our proof.
$c_{\mu }\colon G\times X \to \mathbb {R}$
. The following comes as a byproduct of our proof.
Theorem 3. If the structure
![]() $\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
is not highly algebraic, then
$\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
is not highly algebraic, then
![]() $[\mathcal {N}]_{\mathrm {iso}}$
is the support of a
$[\mathcal {N}]_{\mathrm {iso}}$
is the support of a
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure
![]() $\mu $
whose cocycle
$\mu $
whose cocycle
![]() $c_{\mu }$
induces a continuous map
$c_{\mu }$
induces a continuous map
![]() $c_{\mu }(-,\mathcal {N})\colon \mathrm {Sym}(\mathbb {N}) \to \mathbb {R}$
for each
$c_{\mu }(-,\mathcal {N})\colon \mathrm {Sym}(\mathbb {N}) \to \mathbb {R}$
for each
![]() $\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
.
$\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
.
1.1 Outline and sketch of proofs
Section 2 covers the essential definitions and results we need in the proofs. Section 3 is concerned with showing that highly algebraic structures are not quasi-invariantly random; the proof consists of constructing continuum many disjoint translates of any compact subset of the orbit of the structure. Section 4 shows the forward direction of Theorem 2. Here we use invariant measures from [Reference Ackerman, Freer and Patel5] to construct quasi-invariant measures concentrated on the orbit of a given a structure that is not highly algebraic. Section 5 collects some useful examples of
![]() $\mathcal {L}$
-structures in relation to high algebraicity.
$\mathcal {L}$
-structures in relation to high algebraicity.
2 Background
2.1 Countable
 $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
We follow the usual conventions from model theory (see, e.g., [Reference Jahel and Joseph9] for more details). A countable language
![]() $\mathcal {L}$
is a collection of function symbols and relation symbols. Each symbol has a prespecified arity. An
$\mathcal {L}$
is a collection of function symbols and relation symbols. Each symbol has a prespecified arity. An
![]() ${\mathcal {L}}$
-structure
${\mathcal {L}}$
-structure
![]() $\mathcal {M}$
is a set M together with an interpretation of
$\mathcal {M}$
is a set M together with an interpretation of
![]() ${\mathcal {L}}$
, i.e., for each relation symbol
${\mathcal {L}}$
, i.e., for each relation symbol
![]() $R\in {\mathcal {L}}$
of arity
$R\in {\mathcal {L}}$
of arity
![]() $n(R)\in \mathbb {{N}}$
, a subset
$n(R)\in \mathbb {{N}}$
, a subset
![]() $R^{\mathcal {M}}$
of
$R^{\mathcal {M}}$
of
![]() $M^n$
and for each function symbol
$M^n$
and for each function symbol
![]() $f\in {\mathcal {L}}$
of arity
$f\in {\mathcal {L}}$
of arity
![]() $n(f)\in \mathbb {N}$
, a map
$n(f)\in \mathbb {N}$
, a map
![]() $f^{\mathcal {M}}\colon M^n \to M$
. Given such
$f^{\mathcal {M}}\colon M^n \to M$
. Given such
![]() $\mathcal {L}$
and some countable set N, let
$\mathcal {L}$
and some countable set N, let
![]() $\mathrm {Str}(\mathcal {L},N)$
be the space of all
$\mathrm {Str}(\mathcal {L},N)$
be the space of all
![]() $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
![]() $\mathcal {N}$
with
$\mathcal {N}$
with
![]() $\mathrm {dom}(\mathcal {N})=N$
. As usual, we identify
$\mathrm {dom}(\mathcal {N})=N$
. As usual, we identify
![]() $\mathrm {Str}(\mathcal {L},N)$
with the Polish space
$\mathrm {Str}(\mathcal {L},N)$
with the Polish space
 $$\begin{align*}\big(\prod_{R \in \mathcal{L}} 2^{\overbrace{N\times\cdots \times N}^{n(R)}} \big)\times \big(\prod_{f \in \mathcal{L}} N^{{\overbrace{N\times\cdots \times N}^{n(f)}}} \big), \end{align*}$$
$$\begin{align*}\big(\prod_{R \in \mathcal{L}} 2^{\overbrace{N\times\cdots \times N}^{n(R)}} \big)\times \big(\prod_{f \in \mathcal{L}} N^{{\overbrace{N\times\cdots \times N}^{n(f)}}} \big), \end{align*}$$
where the products are taken over all relation and function symbols in
![]() $\mathcal {L}$
, respectively.
$\mathcal {L}$
, respectively.
Whenever the domain N is fixed, we will denote by
![]() $a,b,c,\ldots $
the elements of N and by
$a,b,c,\ldots $
the elements of N and by
![]() $\bar {a},\bar {b}, \bar {c}\ldots $
tuples in N. By a tuple we mean any finite map
$\bar {a},\bar {b}, \bar {c}\ldots $
tuples in N. By a tuple we mean any finite map
![]() $\bar {a} \colon n\to N,$
where
$\bar {a} \colon n\to N,$
where
![]() $n=\{0,\ldots ,n-1\}$
. Such tuple has length n and we often denote it by
$n=\{0,\ldots ,n-1\}$
. Such tuple has length n and we often denote it by
![]() $(a_0,\ldots ,a_{n-1})$
. and we denote by
$(a_0,\ldots ,a_{n-1})$
. and we denote by
![]() $\{\bar {a}\}$
the associated set
$\{\bar {a}\}$
the associated set
![]() $\{a_0,\ldots ,a_{n-1}\}$
of its elements. We denote by
$\{a_0,\ldots ,a_{n-1}\}$
of its elements. We denote by
![]() $\bar {a}\bar {b}$
the concatenation
$\bar {a}\bar {b}$
the concatenation
![]() $(a_0,\ldots ,a_{n-1},b_0,\ldots ,b_{m-1})$
of the tuples
$(a_0,\ldots ,a_{n-1},b_0,\ldots ,b_{m-1})$
of the tuples
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
.
$\bar {b}$
.
Let
![]() $\mathcal {N}$
be an
$\mathcal {N}$
be an
![]() $\mathcal {L}$
-structure with
$\mathcal {L}$
-structure with
![]() $\mathrm {dom}(\mathcal {N})=N$
and let
$\mathrm {dom}(\mathcal {N})=N$
and let
![]() $\bar {a}$
in N. The quantifier-free type
$\bar {a}$
in N. The quantifier-free type
![]() $\mathrm {qft}(\bar {a},\mathcal {N})$
of
$\mathrm {qft}(\bar {a},\mathcal {N})$
of
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\mathcal {N}$
is the collection of all quantifier-free
$\mathcal {N}$
is the collection of all quantifier-free
![]() $\mathcal {L}$
-formulas
$\mathcal {L}$
-formulas
![]() $\varphi (\bar {x})$
with
$\varphi (\bar {x})$
with
![]() $\mathcal {N}\models \varphi (\bar {a})$
. We say that
$\mathcal {N}\models \varphi (\bar {a})$
. We say that
![]() $\mathcal {N}$
is ultrahomogeneous if
$\mathcal {N}$
is ultrahomogeneous if
![]() $\mathrm {qft}(\bar {a},\mathcal {N})= \mathrm {qft}(\bar {b},\mathcal {N})$
holds if and only if there exists some
$\mathrm {qft}(\bar {a},\mathcal {N})= \mathrm {qft}(\bar {b},\mathcal {N})$
holds if and only if there exists some
![]() $g\in \mathrm {Aut}(\mathcal {N})$
with
$g\in \mathrm {Aut}(\mathcal {N})$
with
![]() $g\bar {a}=\bar {b}$
. A relation
$g\bar {a}=\bar {b}$
. A relation
![]() $R\in \mathcal {L}$
captures
$R\in \mathcal {L}$
captures
![]() $\mathrm {qft}(\bar {a},\mathcal {N})$
if for every
$\mathrm {qft}(\bar {a},\mathcal {N})$
if for every
![]() $\bar {b}$
in N we have that
$\bar {b}$
in N we have that
![]() $\mathcal {N}\models R(\bar {b})$
if and only if
$\mathcal {N}\models R(\bar {b})$
if and only if
![]() $\mathrm {qft}(\bar {a},\mathcal {N})= \mathrm {qft}(\bar {b},\mathcal {N})$
.
$\mathrm {qft}(\bar {a},\mathcal {N})= \mathrm {qft}(\bar {b},\mathcal {N})$
.
Finally, we say that
![]() $\mathcal {N}$
is R-ultrahomogeneous if it is ultrahomogeneous and for every
$\mathcal {N}$
is R-ultrahomogeneous if it is ultrahomogeneous and for every
![]() $\bar {a}$
in N we have that
$\bar {a}$
in N we have that
![]() $\mathrm {qft}(\bar {a},\mathcal {N})$
is captured by some relation R in
$\mathrm {qft}(\bar {a},\mathcal {N})$
is captured by some relation R in
![]() $\mathcal {L}$
. Let
$\mathcal {L}$
. Let
be the pointwise stabilizer of
![]() $\bar {a}$
. The algebraic closure of
$\bar {a}$
. The algebraic closure of
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\mathcal {N}$
is the set
$\mathcal {N}$
is the set
The following standard fact is going to be used later on.
Lemma 4. For every countable
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
there exists a countable
$\mathcal {N}$
there exists a countable
![]() $\mathcal {L}'\supseteq \mathcal {L}$
and some R-ultrahomogeneous
$\mathcal {L}'\supseteq \mathcal {L}$
and some R-ultrahomogeneous
![]() $\mathcal {L}'$
-structure
$\mathcal {L}'$
-structure
![]() $\mathcal {N}'$
whose
$\mathcal {N}'$
whose
![]() $\mathcal {L}$
-reduct
$\mathcal {L}$
-reduct
![]() $\mathcal {N}'\upharpoonright \mathcal {L}$
is
$\mathcal {N}'\upharpoonright \mathcal {L}$
is
![]() $\mathcal {N}$
and for all
$\mathcal {N}$
and for all
![]() $\bar {a}$
we have
$\bar {a}$
we have
In particular,
![]() $\mathrm {acl}(\bar {a},\mathcal {N})=\mathrm {acl}(\bar {a},\mathcal {N}')$
holds, for all
$\mathrm {acl}(\bar {a},\mathcal {N})=\mathrm {acl}(\bar {a},\mathcal {N}')$
holds, for all
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\mathrm {dom}(\mathcal {N})$
.
$\mathrm {dom}(\mathcal {N})$
.
Proof. This follows from the usual “orbit completion” argument which can be found in [Reference Jahel and Joseph9, Theorem 4.1.4] or [Reference Becker and Kechris6, Section 1.5]. In short, for every
![]() $n\in 1,2,\ldots $
, and for every orbit
$n\in 1,2,\ldots $
, and for every orbit
![]() $O\subseteq \mathrm {dom}(\mathcal {N})^n$
in the diagonal action
$O\subseteq \mathrm {dom}(\mathcal {N})^n$
in the diagonal action
![]() $g\cdot (a_0,\ldots ,a_{n-1})= (g\cdot a_0,\ldots ,g\cdot a_{n-1})$
of
$g\cdot (a_0,\ldots ,a_{n-1})= (g\cdot a_0,\ldots ,g\cdot a_{n-1})$
of
![]() $\mathrm {Aut}(\mathcal {N})$
on
$\mathrm {Aut}(\mathcal {N})$
on
![]() $\mathrm {dom}(\mathcal {N})^n$
, we introduce a n-ary relation symbol
$\mathrm {dom}(\mathcal {N})^n$
, we introduce a n-ary relation symbol
![]() $R^{n,O}$
and we set
$R^{n,O}$
and we set
![]() $\mathcal {N}'\models R^{n,O}(\bar {a})$
if and only if
$\mathcal {N}'\models R^{n,O}(\bar {a})$
if and only if
![]() $\bar {a}\in O$
.
$\bar {a}\in O$
.
2.2 Logic action
Let
![]() $\mathrm {Sym}(N)$
be the Polish group of all bijections
$\mathrm {Sym}(N)$
be the Polish group of all bijections
![]() $g\colon N\to N$
. The group operation is the operation of composition
$g\colon N\to N$
. The group operation is the operation of composition
![]() $(g\cdot h)(n)=g(h(n))$
and the topology is that of pointwise convergence. The logic action is the continuous action
$(g\cdot h)(n)=g(h(n))$
and the topology is that of pointwise convergence. The logic action is the continuous action
![]() $\mathrm {Sym}(N)\curvearrowright \mathrm {Str}(\mathcal {L},N)$
given by the push-forward operation:
$\mathrm {Sym}(N)\curvearrowright \mathrm {Str}(\mathcal {L},N)$
given by the push-forward operation:
 $$ \begin{align*} &(g,\mathcal{M})\mapsto g_* \mathcal{M}, \text{where}\\ &g_*\mathcal{M}\models R(a_0,\ldots,a_{n-1}) \iff \mathcal{M}\models R(g^{-1}(a_0),\ldots,g^{-1}(a_{n-1})), \text{ and}\\ &g_*\mathcal{M}\models \big(b=f(a_0,\ldots,a_{n-1}) \big)\iff \mathcal{M}\models \big(g^{-1}(b) =f(g^{-1}(a_0),\ldots,g^{-1}(a_{n-1}))\big). \end{align*} $$
$$ \begin{align*} &(g,\mathcal{M})\mapsto g_* \mathcal{M}, \text{where}\\ &g_*\mathcal{M}\models R(a_0,\ldots,a_{n-1}) \iff \mathcal{M}\models R(g^{-1}(a_0),\ldots,g^{-1}(a_{n-1})), \text{ and}\\ &g_*\mathcal{M}\models \big(b=f(a_0,\ldots,a_{n-1}) \big)\iff \mathcal{M}\models \big(g^{-1}(b) =f(g^{-1}(a_0),\ldots,g^{-1}(a_{n-1}))\big). \end{align*} $$
3 Highly algebraic structures are not quasi-invariantly random
We fix some
![]() $\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
and we assume throughout this section that
$\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
and we assume throughout this section that
![]() $\mathcal {N}$
is highly algebraic and R-ultrahomogeneous. We also set
$\mathcal {N}$
is highly algebraic and R-ultrahomogeneous. We also set
![]() $X:=[\mathcal {N}]_{\mathrm {iso}}$
to be the isomorphism class of
$X:=[\mathcal {N}]_{\mathrm {iso}}$
to be the isomorphism class of
![]() $\mathcal {N}$
in
$\mathcal {N}$
in
![]() $\mathrm {Str}(\mathcal {L},\mathbb {N})$
. Notice that the ultrahomogeneity of
$\mathrm {Str}(\mathcal {L},\mathbb {N})$
. Notice that the ultrahomogeneity of
![]() $\mathcal {N}$
implies that X is a
$\mathcal {N}$
implies that X is a
![]() $G_{\delta }$
subset of
$G_{\delta }$
subset of
![]() $\mathrm {Str}(\mathcal {L},\mathbb {N})$
and hence a Polish space. The main goal of this section is to prove the following.
$\mathrm {Str}(\mathcal {L},\mathbb {N})$
and hence a Polish space. The main goal of this section is to prove the following.
Lemma 5. If
![]() $K\subseteq X$
is compact, then there is a family
$K\subseteq X$
is compact, then there is a family
![]() $(g_{\alpha }\colon \alpha \in 2^{\mathbb {N}})$
of permutations
$(g_{\alpha }\colon \alpha \in 2^{\mathbb {N}})$
of permutations
![]() $g_{\alpha }\in \mathrm {Sym}(\mathbb {N})$
so that for all
$g_{\alpha }\in \mathrm {Sym}(\mathbb {N})$
so that for all
![]() $\alpha ,\beta \in 2^{\mathbb {N}}$
with
$\alpha ,\beta \in 2^{\mathbb {N}}$
with
![]() $\alpha \neq \beta $
we have that
$\alpha \neq \beta $
we have that
![]() $g_{\alpha } K \cap g_{\beta } K =\emptyset $
.
$g_{\alpha } K \cap g_{\beta } K =\emptyset $
.
This lemma directly implies one of the directions of Theorem 2.
Proof of
 $(\Rightarrow )$
direction of Theorem 2 from Lemma 5.
$(\Rightarrow )$
direction of Theorem 2 from Lemma 5.
Let
![]() $\mathcal {N}^*\in \mathrm {Str}(\mathcal {L}^*,\mathbb {N})$
be some highly algebraic structure and assume towards a contradiction that there exists a
$\mathcal {N}^*\in \mathrm {Str}(\mathcal {L}^*,\mathbb {N})$
be some highly algebraic structure and assume towards a contradiction that there exists a
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure
![]() $\mu $
on
$\mu $
on
![]() $\mathrm {Str}(\mathcal {L}^*,\mathbb {N})$
so that
$\mathrm {Str}(\mathcal {L}^*,\mathbb {N})$
so that
![]() ${\mu ([\mathcal {N}^*]_{\mathrm {iso}})=1}$
. Let
${\mu ([\mathcal {N}^*]_{\mathrm {iso}})=1}$
. Let
![]() $\mathcal {L}:=(\mathcal {L}^*)'$
and
$\mathcal {L}:=(\mathcal {L}^*)'$
and
![]() $\mathcal {N}:=(\mathcal {N}^*)'$
be the language and the structure provided by Lemma 4 and set
$\mathcal {N}:=(\mathcal {N}^*)'$
be the language and the structure provided by Lemma 4 and set
![]() $X:=[\mathcal {N}]_{\mathrm {iso}}$
.
$X:=[\mathcal {N}]_{\mathrm {iso}}$
.
Consider now the map
![]() $\pi \colon X \to \mathrm {Str}(\mathcal {L},\mathbb {N})$
, which implements the
$\pi \colon X \to \mathrm {Str}(\mathcal {L},\mathbb {N})$
, which implements the
![]() $\mathcal {L}$
-reduct
$\mathcal {L}$
-reduct
![]() ${\mathcal {M}\mapsto \mathcal {M}\upharpoonright \mathcal {L}}$
. Then
${\mathcal {M}\mapsto \mathcal {M}\upharpoonright \mathcal {L}}$
. Then
![]() $\pi $
is clearly a
$\pi $
is clearly a
![]() $\mathrm {Sym}(\mathbb {N})$
-equivariant Borel isomorphism and hence we can transfer
$\mathrm {Sym}(\mathbb {N})$
-equivariant Borel isomorphism and hence we can transfer
![]() $\mu $
to a
$\mu $
to a
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure on X by pushing it forward via
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure on X by pushing it forward via
![]() $\pi ^{-1}$
. Since
$\pi ^{-1}$
. Since
![]() $\mathcal {N}$
is ultrahomogeneous, we have that X is a Polish space, and Lemma 5 applies. But probability measures on Polish spaces are regular and hence, there exists a compact
$\mathcal {N}$
is ultrahomogeneous, we have that X is a Polish space, and Lemma 5 applies. But probability measures on Polish spaces are regular and hence, there exists a compact
![]() $K\subseteq X$
so that
$K\subseteq X$
so that
![]() $\mu (K)>0$
. By quasi-invariance of
$\mu (K)>0$
. By quasi-invariance of
![]() $\mu $
we have that
$\mu $
we have that
![]() $\mu (g_{\alpha }K)>0$
, for all
$\mu (g_{\alpha }K)>0$
, for all
![]() $\alpha \in 2^{\mathbb {N}}$
, where
$\alpha \in 2^{\mathbb {N}}$
, where
![]() $(g_{\alpha }\colon \alpha \in 2^{\mathbb {N}})$
is as in Lemma 5. Hence there is some
$(g_{\alpha }\colon \alpha \in 2^{\mathbb {N}})$
is as in Lemma 5. Hence there is some
![]() $\varepsilon>0$
so that
$\varepsilon>0$
so that
![]() $\{\alpha \in 2^{\mathbb {N}}\colon \mu (g_\alpha K)>\varepsilon \}$
is uncountable. But since
$\{\alpha \in 2^{\mathbb {N}}\colon \mu (g_\alpha K)>\varepsilon \}$
is uncountable. But since
![]() $g_{\alpha } K \cap g_{\beta } K =\emptyset $
when
$g_{\alpha } K \cap g_{\beta } K =\emptyset $
when
![]() $\alpha \neq \beta $
,
$\alpha \neq \beta $
,
![]() $\sigma $
-additivity of
$\sigma $
-additivity of
![]() $\mu $
contradicts that
$\mu $
contradicts that
![]() $\mu $
is a probability measure.
$\mu $
is a probability measure.
The proof of Lemma 5 occupies the rest of this section. Interestingly, there are two distinct ways for a structure
![]() $\mathcal {N}$
to exhibit high algebraicity. Each way contributes to the proof of Lemma 5 through a different argument. In Lemma 9 below we establish this dichotomy-in-behaviour, before we conclude with the proof of Lemma 5.
$\mathcal {N}$
to exhibit high algebraicity. Each way contributes to the proof of Lemma 5 through a different argument. In Lemma 9 below we establish this dichotomy-in-behaviour, before we conclude with the proof of Lemma 5.
3.1 Highly algebraic structures
Below we will make extensive use of the Neumann’s lemma [Reference Neumann12, Lemma 2.3]. Rephrased as in [Reference Cameron7, Theorem 6.2], it states the following.
Lemma 6 (Neumann).
Let H be a group acting on a countable set
![]() $\Omega $
with no finite orbit. Let
$\Omega $
with no finite orbit. Let
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
be finite subsets of
$\Delta $
be finite subsets of
![]() $\Omega $
, then there is
$\Omega $
, then there is
![]() $h\in H$
such that
$h\in H$
such that
![]() $h\cdot \Gamma \cap \Delta = \varnothing .$
$h\cdot \Gamma \cap \Delta = \varnothing .$
Lemma 7. For any
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
, the following statements are equivalent:
$\mathcal {M}$
, the following statements are equivalent:
-
(1)
 $\mathcal {M}$
is highly algebraic;
$\mathcal {M}$
is highly algebraic; -
(2) for all
 $\bar {c}$
there exist
$\bar {c}$
there exist
 $\bar {a}$
, b so that
$\bar {a}$
, b so that
 $\{\bar {a}\}, \{b\}, \{\bar {c}\}$
are pairwise disjoint and
$\{\bar {a}\}, \{b\}, \{\bar {c}\}$
are pairwise disjoint and
 $b\in \mathrm {acl}(\bar {a}\bar {c},\mathcal {M})$
;
$b\in \mathrm {acl}(\bar {a}\bar {c},\mathcal {M})$
; -
(3) for all
 $\bar {c}$
there exist
$\bar {c}$
there exist
 $\bar {a}$
, b so that
$\bar {a}$
, b so that
 $\{\bar {a}\}, \{b\}, \{\bar {c}\}$
are pairwise disjoint and
$\{\bar {a}\}, \{b\}, \{\bar {c}\}$
are pairwise disjoint and
 $b\in \mathrm {acl}(\bar {a},\mathcal {M})$
.
$b\in \mathrm {acl}(\bar {a},\mathcal {M})$
.
Proof. It is straightforward to see the equivalence between (1) and (2). It is also clear that (3) implies (2). We prove that (2) implies (3) as well. Assume (2) holds and let
![]() $\bar {c}$
be given.
$\bar {c}$
be given.
We may assume that
![]() $\mathrm {acl}(\emptyset ,\mathcal {M})$
is finite since, otherwise, (3) would follow by simply setting
$\mathrm {acl}(\emptyset ,\mathcal {M})$
is finite since, otherwise, (3) would follow by simply setting
![]() $\bar {a}:=\emptyset $
. Let now
$\bar {a}:=\emptyset $
. Let now
![]() $\bar {e}$
be a finite tuple enumerating
$\bar {e}$
be a finite tuple enumerating
![]() $\mathrm {acl}(\emptyset ,\mathcal {M})$
. By (2), and by shrinking
$\mathrm {acl}(\emptyset ,\mathcal {M})$
. By (2), and by shrinking
![]() $\bar {c}$
if necessary, we get
$\bar {c}$
if necessary, we get
![]() $\bar {a}, b$
so that
$\bar {a}, b$
so that
![]() $\{\bar {a}\}, \{b\}, \{\bar {c}\}, \{\bar {e}\}$
are pairwise disjoint and
$\{\bar {a}\}, \{b\}, \{\bar {c}\}, \{\bar {e}\}$
are pairwise disjoint and
![]() $b\in \mathrm {acl}(\bar {a}\bar {c}\bar {e})$
.
$b\in \mathrm {acl}(\bar {a}\bar {c}\bar {e})$
.
Claim 8. There exists
![]() $g\in \mathrm {Aut}(\mathcal {M})_{\bar {e}}$
so that the tuple
$g\in \mathrm {Aut}(\mathcal {M})_{\bar {e}}$
so that the tuple
![]() $g(\bar {a}b\bar {c})$
is disjoint from
$g(\bar {a}b\bar {c})$
is disjoint from
![]() $\bar {c}\bar {e}$
.
$\bar {c}\bar {e}$
.
Proof of Claim.
Every
![]() $d\in \mathrm {dom}(\mathcal {M})\setminus \{\bar {e}\}$
has an infinite orbit under
$d\in \mathrm {dom}(\mathcal {M})\setminus \{\bar {e}\}$
has an infinite orbit under
![]() $\mathrm {Aut}(\mathcal {M})_{\bar {e}}$
. Indeed, since
$\mathrm {Aut}(\mathcal {M})_{\bar {e}}$
. Indeed, since
![]() $\bar {e}$
enumerates
$\bar {e}$
enumerates
![]() $\mathrm {acl}(\emptyset ,\mathcal {M})$
, there exist
$\mathrm {acl}(\emptyset ,\mathcal {M})$
, there exist
![]() $h_1,\ldots ,h_k \in \mathrm {Aut}(\mathcal {M})$
so that every
$h_1,\ldots ,h_k \in \mathrm {Aut}(\mathcal {M})$
so that every
![]() $g\in \mathrm {Aut}(\mathcal {M})$
is of the form
$g\in \mathrm {Aut}(\mathcal {M})$
is of the form
![]() $g=h_ih$
for some
$g=h_ih$
for some
![]() $h\in \mathrm {Aut}(\mathcal {M})_{\bar {e}}$
and
$h\in \mathrm {Aut}(\mathcal {M})_{\bar {e}}$
and
![]() $i\leq k$
. Hence, if the set
$i\leq k$
. Hence, if the set
![]() $E=\{gd \colon g\in \mathrm {Aut}(\mathcal {M})_{\bar {e}} \}$
was finite, then so would be the set
$E=\{gd \colon g\in \mathrm {Aut}(\mathcal {M})_{\bar {e}} \}$
was finite, then so would be the set
![]() $\{gd \colon g\in \mathrm {Aut}(\mathcal {M})\}=\bigcup _i h_iE$
. Since
$\{gd \colon g\in \mathrm {Aut}(\mathcal {M})\}=\bigcup _i h_iE$
. Since
![]() $\{\bar {a}b\bar {c}\}\subseteq \mathrm {dom}(\mathcal {M})\setminus \{\bar {e}\}$
, by Lemma 6 there exists a g as in the statement of the claim.
$\{\bar {a}b\bar {c}\}\subseteq \mathrm {dom}(\mathcal {M})\setminus \{\bar {e}\}$
, by Lemma 6 there exists a g as in the statement of the claim.
Fix g as in the claim and set
![]() $\bar {a}':=g(\bar {a}\bar {c})$
and
$\bar {a}':=g(\bar {a}\bar {c})$
and
![]() $b':=g(b)$
. By the claim, and since
$b':=g(b)$
. By the claim, and since
![]() $\{\bar {a}\}, \{b\},$
and
$\{\bar {a}\}, \{b\},$
and
![]() $\{\bar {c}\}$
were pairwise disjoint, so are
$\{\bar {c}\}$
were pairwise disjoint, so are
![]() $\{\bar {a}'\}, \{b'\}$
, and
$\{\bar {a}'\}, \{b'\}$
, and
![]() $\{\bar {c}\}$
. But then we have that
$\{\bar {c}\}$
. But then we have that
where the last implication follows from the fact that
![]() $\bar {e}\in \mathrm {acl}(\emptyset ,\mathcal {N})$
, by an argument similar to the one in the previous claim.
$\bar {e}\in \mathrm {acl}(\emptyset ,\mathcal {N})$
, by an argument similar to the one in the previous claim.
Using the above reformulation (3) of high algebraicity, we get the following dichotomy. See Examples 20 and 21 for simple examples of structures on each side of the dichotomy.
Lemma 9. If
![]() $\mathcal {N}$
is highly algebraic, then for every finite tuple
$\mathcal {N}$
is highly algebraic, then for every finite tuple
![]() $\bar {c}$
there exist
$\bar {c}$
there exist
![]() $\bar {a}$
and b in
$\bar {a}$
and b in
![]() $\mathrm {dom}(\mathcal {N})$
so that the sets
$\mathrm {dom}(\mathcal {N})$
so that the sets
![]() $\{\bar {a}\}$
,
$\{\bar {a}\}$
,
![]() $\{b\}$
, and
$\{b\}$
, and
![]() $\{\bar {c}\}$
are pairwise disjoint and one of following holds:
$\{\bar {c}\}$
are pairwise disjoint and one of following holds:
-
(1)
 $\{\bar {a}\}=\{a\}$
is a singleton and both
$\{\bar {a}\}=\{a\}$
is a singleton and both
 $b\in \mathrm {acl}(a,\mathcal {N})$
and
$b\in \mathrm {acl}(a,\mathcal {N})$
and
 $a\in \mathrm {acl}(b,\mathcal {N})$
hold; or
$a\in \mathrm {acl}(b,\mathcal {N})$
hold; or -
(2)
 $b\in \mathrm {acl}(\bar {a},\mathcal {N})$
and there exists an infinite sequence
$b\in \mathrm {acl}(\bar {a},\mathcal {N})$
and there exists an infinite sequence
 $(\bar {a}^i\colon i\in \mathbb {N})$
of pairwise disjoint tuples so that for every
$(\bar {a}^i\colon i\in \mathbb {N})$
of pairwise disjoint tuples so that for every
 $i\in \mathbb {N}$
we have that
$i\in \mathbb {N}$
we have that
 $\mathrm {qft}(\bar {a}^ib,\mathcal {N})=\mathrm {qft}(\bar {a}b,\mathcal {N})$
.
$\mathrm {qft}(\bar {a}^ib,\mathcal {N})=\mathrm {qft}(\bar {a}b,\mathcal {N})$
.
Proof. By Lemma 7(3) there exist
![]() $\bar {a}$
and b in
$\bar {a}$
and b in
![]() $\mathrm {dom}(\mathcal {N})$
so that the sets
$\mathrm {dom}(\mathcal {N})$
so that the sets
![]() $\{\bar {a}\}$
,
$\{\bar {a}\}$
,
![]() $\{b\}$
, and
$\{b\}$
, and
![]() $\{\bar {c}\}$
are pairwise disjoint and
$\{\bar {c}\}$
are pairwise disjoint and
![]() $b\in \mathrm {acl}(\bar {a},\mathcal {N})$
. Assume that there is no such
$b\in \mathrm {acl}(\bar {a},\mathcal {N})$
. Assume that there is no such
![]() $\bar {a}$
and b satisfies (2) above. Choose
$\bar {a}$
and b satisfies (2) above. Choose
![]() $\bar {a}$
and b as in Lemma 7(3) so that
$\bar {a}$
and b as in Lemma 7(3) so that
![]() $\bar {a}$
is of minimum possible size. Since by assumption
$\bar {a}$
is of minimum possible size. Since by assumption
![]() $\bar {a}$
, b do not satisfy (2) we have that
$\bar {a}$
, b do not satisfy (2) we have that
![]() $\bar {a}\neq \emptyset $
.
$\bar {a}\neq \emptyset $
.
Let now a be any entry of
![]() $\bar {a}$
so that
$\bar {a}$
so that
![]() $a\in \mathrm {acl}(b,\mathcal {N})$
. Such entry exists since, otherwise, by Lemma 6 we would have that (2) holds for this
$a\in \mathrm {acl}(b,\mathcal {N})$
. Such entry exists since, otherwise, by Lemma 6 we would have that (2) holds for this
![]() $\bar {a}$
and b. But since
$\bar {a}$
and b. But since
![]() $\{b\}$
is a singleton for which there is
$\{b\}$
is a singleton for which there is
![]() $a\in \mathrm {acl}(b,\mathcal {N})$
, the minimality assumption on the length of
$a\in \mathrm {acl}(b,\mathcal {N})$
, the minimality assumption on the length of
![]() $\bar {a}$
above implies that
$\bar {a}$
above implies that
![]() $\{\bar {a}\}=\{a\}$
and hence (1) above follows.
$\{\bar {a}\}=\{a\}$
and hence (1) above follows.
3.2 Proof of Lemma 5
We may now conclude the proof of Lemma 5 which, in turn, establishes the
![]() $(\Rightarrow )$
direction of Theorem 2. Recall that throughout this section we assume that the structure
$(\Rightarrow )$
direction of Theorem 2. Recall that throughout this section we assume that the structure
![]() $\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
is highly algebraic and R-ultrahomogeneous.
$\mathcal {N}\in \mathrm {Str}(\mathcal {L},\mathbb {N})$
is highly algebraic and R-ultrahomogeneous.
Proof of Lemma 5.
Let
![]() $K\subseteq X$
be compact.
$K\subseteq X$
be compact.
For every
![]() $s\in 2^{<\mathbb {N}}$
we will define a natural number
$s\in 2^{<\mathbb {N}}$
we will define a natural number
![]() $\ell _s$
and some permutation
$\ell _s$
and some permutation
![]() $\gamma _s$
of the finite set
$\gamma _s$
of the finite set
![]() $\ell _s=\{0,1,\ldots ,\ell _s-1\}$
so that for all
$\ell _s=\{0,1,\ldots ,\ell _s-1\}$
so that for all
![]() $s\in 2^{<\mathbb {N}}$
we have that:
$s\in 2^{<\mathbb {N}}$
we have that:
-
(i)
 $\ell _{\emptyset }=0$
and
$\ell _{\emptyset }=0$
and
 $\gamma _{\emptyset }$
is the empty permutation;
$\gamma _{\emptyset }$
is the empty permutation; -
(ii)
 $\ell _{s^{\frown }0}= \ell _{s^{\frown }1}$
and
$\ell _{s^{\frown }0}= \ell _{s^{\frown }1}$
and
 $\ell _{s^{\frown }0},\ell _{s^{\frown }1}> \ell _s$
, as well as
$\ell _{s^{\frown }0},\ell _{s^{\frown }1}> \ell _s$
, as well as
 $\gamma _{s^{\frown }0}\upharpoonright \ell _s=\gamma _s$
and
$\gamma _{s^{\frown }0}\upharpoonright \ell _s=\gamma _s$
and
 $\gamma _{s^{\frown }1}\upharpoonright \ell _s=\gamma _s$
;
$\gamma _{s^{\frown }1}\upharpoonright \ell _s=\gamma _s$
; -
(iii)
 $g_0K\cap g_1 K=\emptyset $
, for all
$g_0K\cap g_1 K=\emptyset $
, for all
 $g_0,g_1\in \mathrm {Sym}(\mathbb {N})$
with
$g_0,g_1\in \mathrm {Sym}(\mathbb {N})$
with
 $g_0\upharpoonright \ell _{s^{\frown }0}=\gamma _{s^{\frown }0}$
and
$g_0\upharpoonright \ell _{s^{\frown }0}=\gamma _{s^{\frown }0}$
and
 $g_1\upharpoonright \ell _{s^{\frown }1}=\gamma _{s^{\frown }1}$
.
$g_1\upharpoonright \ell _{s^{\frown }1}=\gamma _{s^{\frown }1}$
.
Granted
![]() $(\gamma _s\colon s\in 2^{<\mathbb {N}})$
as above, we define the desired family
$(\gamma _s\colon s\in 2^{<\mathbb {N}})$
as above, we define the desired family
![]() $(g_{\alpha }\colon \alpha \in 2^{\mathbb {N}})$
by setting
$(g_{\alpha }\colon \alpha \in 2^{\mathbb {N}})$
by setting
Then, (ii) implies that
![]() $g_{\alpha }\in \mathrm {Sym}(\mathbb {N})$
and (iii) implies that
$g_{\alpha }\in \mathrm {Sym}(\mathbb {N})$
and (iii) implies that
![]() $g_{\alpha } K \cap g_{\beta } K =\emptyset $
, whenever
$g_{\alpha } K \cap g_{\beta } K =\emptyset $
, whenever
![]() $\alpha \neq \beta $
.
$\alpha \neq \beta $
.
We proceed now to the definition of
![]() $\ell _s,\gamma _s$
by induction on s. Assume that
$\ell _s,\gamma _s$
by induction on s. Assume that
![]() $\ell _s, \gamma _s$
have been defined. We define
$\ell _s, \gamma _s$
have been defined. We define
![]() $\ell _{s^{\frown }0},\ell _{s^{\frown }1}$
and
$\ell _{s^{\frown }0},\ell _{s^{\frown }1}$
and
![]() $ \gamma _{s^{\frown }0}, \gamma _{s^{\frown }1}$
using the following construction.
$ \gamma _{s^{\frown }0}, \gamma _{s^{\frown }1}$
using the following construction.
Claim 10. There exists a finite family
![]() $\{S_i\colon i\in I\}$
of
$\{S_i\colon i\in I\}$
of
![]() $\ell _s$
-ary relations
$\ell _s$
-ary relations
![]() $S_i$
so that:
$S_i$
so that:
-
(I) for every
 $\mathcal {M}\in K$
there is
$\mathcal {M}\in K$
there is
 $i\in I$
so that
$i\in I$
so that
 $\mathcal {M}\models S_i(0,1,\ldots ,\ell _s-1)$
;
$\mathcal {M}\models S_i(0,1,\ldots ,\ell _s-1)$
; -
(II) for every
 $\ell _s$
-ary tuple
$\ell _s$
-ary tuple
 $\bar {e}$
with
$\bar {e}$
with
 $\mathcal {N}\models S_i(\bar {e})$
we have that
$\mathcal {N}\models S_i(\bar {e})$
we have that
 $S_i$
captures
$S_i$
captures
 $\bar {e}$
in
$\bar {e}$
in
 $\mathcal {N}$
.
$\mathcal {N}$
.
Proof of Claim.
This follows from compactness of K since
![]() $\mathcal {N}$
is R-ultrahomogeneous.
$\mathcal {N}$
is R-ultrahomogeneous.
For each
![]() $i\in I$
let
$i\in I$
let
![]() $\bar {c}^i$
be a tuple in
$\bar {c}^i$
be a tuple in
![]() $\mathbb {N}$
so that
$\mathbb {N}$
so that
![]() $\mathcal {N}\models S_i(\bar {c}^i)$
and let
$\mathcal {N}\models S_i(\bar {c}^i)$
and let
![]() $\bar {c}$
be the union of all these tuples. Apply Lemma 9 for this
$\bar {c}$
be the union of all these tuples. Apply Lemma 9 for this
![]() $\bar {c}$
to get
$\bar {c}$
to get
![]() $\bar {a}$
, b so that
$\bar {a}$
, b so that
![]() $\{\bar {a}\}, \{b\}, \{\bar {c}\}$
are pairwise disjoint and for which either (1) or (2) of Lemma 9 holds. Since
$\{\bar {a}\}, \{b\}, \{\bar {c}\}$
are pairwise disjoint and for which either (1) or (2) of Lemma 9 holds. Since
![]() $\mathcal {N}$
is R-ultrahomogeneous, we may pick relations
$\mathcal {N}$
is R-ultrahomogeneous, we may pick relations
![]() $P,Q,R\in \mathcal {L}$
, so that: P captures
$P,Q,R\in \mathcal {L}$
, so that: P captures
![]() $\mathrm {qft}(\bar {a},\mathcal {N})$
; Q captures
$\mathrm {qft}(\bar {a},\mathcal {N})$
; Q captures
![]() $\mathrm {qft}(b,\mathcal {N})$
; and R captures
$\mathrm {qft}(b,\mathcal {N})$
; and R captures
![]() $\mathrm {qft}(\bar {a}b,\mathcal {N})$
. Below we will abuse notation and use the letters
$\mathrm {qft}(\bar {a}b,\mathcal {N})$
. Below we will abuse notation and use the letters
![]() $\bar {a}$
and b for potentially new tuples which satisfy P and Q, respectively, in any structure
$\bar {a}$
and b for potentially new tuples which satisfy P and Q, respectively, in any structure
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
.
$\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
.
We define
![]() $\ell _{s^{\frown }0}, \ell _{s^{\frown }1},\gamma _{s^{\frown }0},\gamma _{s^{\frown }1}$
by considering separately cases (1) and (2) of Lemma 9.
$\ell _{s^{\frown }0}, \ell _{s^{\frown }1},\gamma _{s^{\frown }0},\gamma _{s^{\frown }1}$
by considering separately cases (1) and (2) of Lemma 9.
Case (1). Assume that Lemma 9(1) holds for
![]() $\bar {a}, b$
,
$\bar {a}, b$
,
![]() $\bar {c}$
. In particular, we have that both
$\bar {c}$
. In particular, we have that both
![]() $P,Q$
are unary relations and R is a binary relation.
$P,Q$
are unary relations and R is a binary relation.
Claim 11. There exists
![]() $\ell{\kern-1pt}>{\kern-1pt}\ell _s$
and some set
$\ell{\kern-1pt}>{\kern-1pt}\ell _s$
and some set
![]() $Z{\kern-1pt}\subseteq{\kern-1pt} \mathbb {N}\setminus \{0,\ldots ,\ell -1\}$
with
$Z{\kern-1pt}\subseteq{\kern-1pt} \mathbb {N}\setminus \{0,\ldots ,\ell -1\}$
with
![]() $|Z|{\kern-1pt}={\kern-1pt}\ell {\kern-1pt}-{\kern-1pt}\ell _s$
, so that for every
$|Z|{\kern-1pt}={\kern-1pt}\ell {\kern-1pt}-{\kern-1pt}\ell _s$
, so that for every
![]() $\mathcal {M}\in K$
we have that:
$\mathcal {M}\in K$
we have that:
-
(a) there exist
 $a,b\in \{\ell _s,\ldots ,\ell -1\}$
so that
$a,b\in \{\ell _s,\ldots ,\ell -1\}$
so that
 $\mathcal {M}\models R(a,b)$
;
$\mathcal {M}\models R(a,b)$
; -
(b) for every two
 $p,q\in Z$
we have that
$p,q\in Z$
we have that
 $\mathcal {M}\not \models R(p,q)$
.
$\mathcal {M}\not \models R(p,q)$
.
Proof of Claim.
By the choice of R and
![]() $S_i$
, for every
$S_i$
, for every
![]() $i\in I$
we have that
$i\in I$
we have that
Hence, by Claim 10, for every
![]() $\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
there exists a least number
$\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
there exists a least number
![]() $n(\mathcal {M})\geq \ell _s$
so that
$n(\mathcal {M})\geq \ell _s$
so that
![]() $\mathcal {M}\models R(a,b)$
for some
$\mathcal {M}\models R(a,b)$
for some
![]() $a,b$
with
$a,b$
with
![]() $\ell _s\leq a,b <n(\mathcal {M})$
. Since
$\ell _s\leq a,b <n(\mathcal {M})$
. Since
![]() $\mathcal {M}\mapsto n(\mathcal {M})$
is a continuous map, by compactness of K we can find
$\mathcal {M}\mapsto n(\mathcal {M})$
is a continuous map, by compactness of K we can find
![]() $\ell :=\sup _K n(\mathcal {M})$
satisfying property (a) above.
$\ell :=\sup _K n(\mathcal {M})$
satisfying property (a) above.
We next build Z inductively, adding one point at a time, as follows. Assume that some fragment Y of Z has been defined so that for all
![]() $\mathcal {M}\in K$
property (b) above holds for Y in place of Z. By compactness of K and the fact that for each
$\mathcal {M}\in K$
property (b) above holds for Y in place of Z. By compactness of K and the fact that for each
![]() $\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
, and every fixed
$\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
, and every fixed
![]() $p,q\in \mathbb {N}$
, there exist at most finitely many solutions to the formulas
$p,q\in \mathbb {N}$
, there exist at most finitely many solutions to the formulas
![]() $\varphi (y) \equiv R(p,y)$
and
$\varphi (y) \equiv R(p,y)$
and
![]() $\psi (x) \equiv R(x,q)$
, we may find
$\psi (x) \equiv R(x,q)$
, we may find
![]() $\ell '> \max (Y), \ell $
, so that for every
$\ell '> \max (Y), \ell $
, so that for every
![]() $\mathcal {M}\in K$
we have that:
$\mathcal {M}\in K$
we have that:
-
(i) for every
 $p\in Y$
and every
$p\in Y$
and every
 $q\geq \ell '$
we have that
$q\geq \ell '$
we have that
 $\mathcal {M}\not \models R(p,q)$
;
$\mathcal {M}\not \models R(p,q)$
; -
(ii) for every
 $q\in Y$
and every
$q\in Y$
and every
 $p\geq \ell '$
we have that
$p\geq \ell '$
we have that
 $\mathcal {M}\not \models R(p,q)$
.
$\mathcal {M}\not \models R(p,q)$
.
It follows that property (b) above holds for
![]() $Y':=Y\cup \{\ell '\}$
in place of Z. Since
$Y':=Y\cup \{\ell '\}$
in place of Z. Since
![]() $|Y'|>|Y|$
, by repeating this process enough times we define Z, with
$|Y'|>|Y|$
, by repeating this process enough times we define Z, with
![]() $|Z|=\ell \setminus \ell _s$
, satisfying (b) above.
$|Z|=\ell \setminus \ell _s$
, satisfying (b) above.
Let now
![]() $\ell $
and Z as in the last claim and set
$\ell $
and Z as in the last claim and set
![]() $\ell _{s^{\frown }0}, \ell _{s^{\frown }1}:=\max (Z)+1$
. Let
$\ell _{s^{\frown }0}, \ell _{s^{\frown }1}:=\max (Z)+1$
. Let
![]() $\gamma _{s^{\frown }0}$
be the permutation on the set
$\gamma _{s^{\frown }0}$
be the permutation on the set
![]() $\ell _{s^{\frown }0}$
, with
$\ell _{s^{\frown }0}$
, with
![]() $\gamma _{s^{\frown }0}\upharpoonright \ell _s= \gamma _{s}$
, which is identity on
$\gamma _{s^{\frown }0}\upharpoonright \ell _s= \gamma _{s}$
, which is identity on
![]() $\ell _{s^{\frown }0}\setminus \ell _s$
. Let also
$\ell _{s^{\frown }0}\setminus \ell _s$
. Let also
![]() $\gamma _{s^{\frown }1}$
be any permutation on the set
$\gamma _{s^{\frown }1}$
be any permutation on the set
![]() $\ell _{s^{\frown }1}$
, with
$\ell _{s^{\frown }1}$
, with
![]() $\gamma _{s^{\frown }1}\upharpoonright \ell _s= \gamma _{s}$
, which induces a bijection between the sets
$\gamma _{s^{\frown }1}\upharpoonright \ell _s= \gamma _{s}$
, which induces a bijection between the sets
![]() $\ell \setminus \ell _s$
and Z. We are left to show that (iii) above holds.
$\ell \setminus \ell _s$
and Z. We are left to show that (iii) above holds.
Indeed, let
![]() $g_0,g_1\in \mathrm {Sym}(\mathbb {N})$
with
$g_0,g_1\in \mathrm {Sym}(\mathbb {N})$
with
![]() $g_0\upharpoonright \ell _{s^{\frown }0}=\gamma _{s^{\frown }0}$
and
$g_0\upharpoonright \ell _{s^{\frown }0}=\gamma _{s^{\frown }0}$
and
![]() $g_1\upharpoonright \ell _{s^{\frown }1}=\gamma _{s^{\frown }1}$
and assume towards a contradiction that
$g_1\upharpoonright \ell _{s^{\frown }1}=\gamma _{s^{\frown }1}$
and assume towards a contradiction that
![]() $g_0K\cap g_1 K\neq \emptyset $
. Set
$g_0K\cap g_1 K\neq \emptyset $
. Set
![]() $g:=g^{-1}_1g_0$
and fix some
$g:=g^{-1}_1g_0$
and fix some
![]() $\mathcal {M}\in K$
so that
$\mathcal {M}\in K$
so that
![]() $g_*\mathcal {M}\in K$
. Since
$g_*\mathcal {M}\in K$
. Since
![]() $\mathcal {M}\in K$
, by (a) above we get
$\mathcal {M}\in K$
, by (a) above we get
![]() $a,b<\ell $
so that
$a,b<\ell $
so that
![]() $\mathcal {M}\models R(a,b)$
. Hence,
$\mathcal {M}\models R(a,b)$
. Hence,
![]() $g_*\mathcal {M}\models R(ga,gb)$
. But since
$g_*\mathcal {M}\models R(ga,gb)$
. But since
![]() $g_*\mathcal {M}\in K$
, by (b) above and the fact that
$g_*\mathcal {M}\in K$
, by (b) above and the fact that
![]() $ga, gb \in Z$
we have
$ga, gb \in Z$
we have
![]() $g_*\mathcal {M}\not \models R(ga,gb)$
; a contradiction. If follows that
$g_*\mathcal {M}\not \models R(ga,gb)$
; a contradiction. If follows that
![]() $g_0K\cap g_1 K=\emptyset $
as desired.
$g_0K\cap g_1 K=\emptyset $
as desired.
Case (2). Assume that Lemma 9(2) holds for
![]() $\bar {a}, b$
, and
$\bar {a}, b$
, and
![]() $\bar {c}$
.
$\bar {c}$
.
Claim 12. There exist
![]() $\ell ,\ell ',\ell "\in \mathbb {N}$
with
$\ell ,\ell ',\ell "\in \mathbb {N}$
with
![]() $\ell ">\ell '>\ell >\ell _s$
so that for all
$\ell ">\ell '>\ell >\ell _s$
so that for all
![]() $\mathcal {M}\in K$
we have:
$\mathcal {M}\in K$
we have:
-
(a) there exists
 $b\in \mathbb {N}$
, with
$b\in \mathbb {N}$
, with
 $\ell _s \leq b<\ell $
, so that
$\ell _s \leq b<\ell $
, so that
 $\mathcal {M}\models Q(\bar {b})$
;
$\mathcal {M}\models Q(\bar {b})$
; -
(b) for all
 $b<\ell $
with
$b<\ell $
with
 $\mathcal {M}\models Q(\bar {b})$
, there is
$\mathcal {M}\models Q(\bar {b})$
, there is
 $\bar {a}$
in
$\bar {a}$
in
 $\ell '\setminus \ell $
so that
$\ell '\setminus \ell $
so that
 $\mathcal {M}\models R(\bar {a},b)$
;
$\mathcal {M}\models R(\bar {a},b)$
; -
(c) for all
 $\bar {a}$
in
$\bar {a}$
in
 $\ell '\setminus \ell $
with
$\ell '\setminus \ell $
with
 $\mathcal {M}\models P(\bar {a})$
, there exists no
$\mathcal {M}\models P(\bar {a})$
, there exists no
 $b\geq \ell "$
so that
$b\geq \ell "$
so that
 $\mathcal {M}\models R(\bar {a},b)$
.
$\mathcal {M}\models R(\bar {a},b)$
.
Proof of Claim.
By compactness of K we can find some
![]() $\ell>\ell _s$
so that for all
$\ell>\ell _s$
so that for all
![]() $\mathcal {M}\in K$
property (a) holds. Since each
$\mathcal {M}\in K$
property (a) holds. Since each
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
is R-ultrahomogeneous and
$\mathcal {M}\simeq _{\mathrm {iso}}\mathcal {N}$
is R-ultrahomogeneous and
![]() $P,Q,R$
capture the pertinent quantifier-free types, for any
$P,Q,R$
capture the pertinent quantifier-free types, for any
![]() $\mathcal {M}\in K$
and any fixed
$\mathcal {M}\in K$
and any fixed
![]() $b\in \mathbb {N}$
with
$b\in \mathbb {N}$
with
![]() $\mathcal {M}\models Q(b)$
there exists
$\mathcal {M}\models Q(b)$
there exists
![]() $\bar {a}$
so that
$\bar {a}$
so that
![]() $\mathcal {M}\models R(\bar {a},b)$
. In fact, since we are under the assumption that Lemma 9(2) holds, for every
$\mathcal {M}\models R(\bar {a},b)$
. In fact, since we are under the assumption that Lemma 9(2) holds, for every
![]() $\mathcal {M}\in K$
we can always find such
$\mathcal {M}\in K$
we can always find such
![]() $\bar {a}$
outside of
$\bar {a}$
outside of
![]() $\{0,1,\ldots ,\ell -1\}$
. Hence by a second application of compactness of K we may find some
$\{0,1,\ldots ,\ell -1\}$
. Hence by a second application of compactness of K we may find some
![]() $\ell '>\ell $
so that property (b) holds as well. By a third and final application of compactness of K, and since for each
$\ell '>\ell $
so that property (b) holds as well. By a third and final application of compactness of K, and since for each
![]() $\mathcal {M}\in K$
and every
$\mathcal {M}\in K$
and every
![]() $\bar {a}\in \mathbb {N}$
there are only finitely many solutions to the formula
$\bar {a}\in \mathbb {N}$
there are only finitely many solutions to the formula
![]() $\varphi (y) \equiv R(\bar {a},y)\wedge P(\bar {a})$
, we may find
$\varphi (y) \equiv R(\bar {a},y)\wedge P(\bar {a})$
, we may find
![]() $\ell ">\ell '$
for which property (c) holds.
$\ell ">\ell '$
for which property (c) holds.
Let now
![]() $\ell ,\ell ',\ell "$
as in the above claim and set
$\ell ,\ell ',\ell "$
as in the above claim and set
![]() $\ell _{s^{\frown }0}, \ell _{s^{\frown }1}:=\ell "+\ell $
.
$\ell _{s^{\frown }0}, \ell _{s^{\frown }1}:=\ell "+\ell $
.
Let
![]() $\gamma _{s^{\frown }0}$
be the permutation on the set
$\gamma _{s^{\frown }0}$
be the permutation on the set
![]() $\ell _{s^{\frown }0}$
, with
$\ell _{s^{\frown }0}$
, with
![]() $\gamma _{s^{\frown }0}\upharpoonright \ell _s= \gamma _{s}$
, which is identity on
$\gamma _{s^{\frown }0}\upharpoonright \ell _s= \gamma _{s}$
, which is identity on
![]() $\ell _{s^{\frown }0}\setminus \ell _s$
. Let also
$\ell _{s^{\frown }0}\setminus \ell _s$
. Let also
![]() $\gamma _{s^{\frown }1}$
be any permutation on the set
$\gamma _{s^{\frown }1}$
be any permutation on the set
![]() $\ell _{s^{\frown }1}$
, with
$\ell _{s^{\frown }1}$
, with
![]() $\gamma _{s^{\frown }1}\upharpoonright \ell _s= \gamma _{s}$
, which fixes every
$\gamma _{s^{\frown }1}\upharpoonright \ell _s= \gamma _{s}$
, which fixes every
![]() $k\in \{\ell ,\ldots ,\ell "-1\}$
, but which exchanges k and
$k\in \{\ell ,\ldots ,\ell "-1\}$
, but which exchanges k and
![]() $k+\ell "$
, for all k with
$k+\ell "$
, for all k with
![]() $\ell _s\leq k <\ell $
. We are left to show that (iii) above holds.
$\ell _s\leq k <\ell $
. We are left to show that (iii) above holds.
Let
![]() $g_0,g_1\in \mathrm {Sym}(\mathbb {N})$
with
$g_0,g_1\in \mathrm {Sym}(\mathbb {N})$
with
![]() $g_0\upharpoonright \ell _{s^{\frown }0}=\gamma _{s^{\frown }0}$
and
$g_0\upharpoonright \ell _{s^{\frown }0}=\gamma _{s^{\frown }0}$
and
![]() $g_1\upharpoonright \ell _{s^{\frown }1}=\gamma _{s^{\frown }1}$
and assume towards a contradiction that
$g_1\upharpoonright \ell _{s^{\frown }1}=\gamma _{s^{\frown }1}$
and assume towards a contradiction that
![]() $g_0K\cap g_1 K\neq \emptyset $
. Set
$g_0K\cap g_1 K\neq \emptyset $
. Set
![]() $g:=g^{-1}_1g_0$
and fix some
$g:=g^{-1}_1g_0$
and fix some
![]() $\mathcal {M}\in K$
so that
$\mathcal {M}\in K$
so that
![]() $g_*\mathcal {M}\in K$
. Since
$g_*\mathcal {M}\in K$
. Since
![]() $\mathcal {M}\in K$
, by (a) and (b) above we get b in
$\mathcal {M}\in K$
, by (a) and (b) above we get b in
![]() $\ell \setminus \ell _s$
and
$\ell \setminus \ell _s$
and
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\ell '\setminus \ell $
so that
$\ell '\setminus \ell $
so that
![]() $\mathcal {M}\models R(\bar {a},b)$
. Hence,
$\mathcal {M}\models R(\bar {a},b)$
. Hence,
![]() $g_*\mathcal {M}\models R(g\bar {a},gb)$
, and since g fixes
$g_*\mathcal {M}\models R(g\bar {a},gb)$
, and since g fixes
![]() $\bar {a}$
we have that
$\bar {a}$
we have that
![]() $g_*\mathcal {M}\models R(\bar {a},gb)$
. But then, by applying (c) to
$g_*\mathcal {M}\models R(\bar {a},gb)$
. But then, by applying (c) to
![]() $g_*\mathcal {M}\in K$
, we get a contradiction with the fact that
$g_*\mathcal {M}\in K$
, we get a contradiction with the fact that
![]() $gb\geq \ell "$
.
$gb\geq \ell "$
.
4 Structures which are not highly algebraic are quasi-invariantly random
The following is the main result of this section.
Theorem 13. Let
![]() $\mathcal {M}$
be a
$\mathcal {M}$
be a
![]() $\mathcal {L}$
-structure such that there is a finite
$\mathcal {L}$
-structure such that there is a finite
![]() $B\subset {\mathbb {N}}$
satisfying for all
$B\subset {\mathbb {N}}$
satisfying for all
![]() $\bar {a}\in {\mathbb {N}}$
,
$\bar {a}\in {\mathbb {N}}$
,
![]() $\mathrm {acl}(\bar {a},\mathcal {M})\subseteq \{\bar {a}\}\cup B$
. Then there is a
$\mathrm {acl}(\bar {a},\mathcal {M})\subseteq \{\bar {a}\}\cup B$
. Then there is a
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure on
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariant probability measure on
![]() $\mathrm {Str}(\mathcal {L},{\mathbb {N}})$
concentrated on structures isomorphic to
$\mathrm {Str}(\mathcal {L},{\mathbb {N}})$
concentrated on structures isomorphic to
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. We may assume without loss of generality that
![]() $\mathcal {L}$
only contains relation symbols. Indeed, if
$\mathcal {L}$
only contains relation symbols. Indeed, if
![]() $\mathcal {L}$
contained function symbols, then we can always move a the language
$\mathcal {L}$
contained function symbols, then we can always move a the language
![]() ${\mathcal {L}}'$
which contains all relational symbol of
${\mathcal {L}}'$
which contains all relational symbol of
![]() ${\mathcal {L}}$
; and for each
${\mathcal {L}}$
; and for each
![]() $f\in {\mathcal {L}}$
function symbol of arity r,
$f\in {\mathcal {L}}$
function symbol of arity r,
![]() ${\mathcal {L}}'$
contains a relation symbol
${\mathcal {L}}'$
contains a relation symbol
![]() $R_f$
of arity
$R_f$
of arity
![]() $r+1$
. Similarly, from
$r+1$
. Similarly, from
![]() $\mathcal {M}$
, move to the
$\mathcal {M}$
, move to the
![]() ${\mathcal {L}}'$
-structure
${\mathcal {L}}'$
-structure
![]() $\mathcal {M}'$
, with:
$\mathcal {M}'$
, with:
![]() $\mathrm {dom}(\mathcal {M})={\mathbb {N}}=\mathrm {dom}(\mathcal {M}')$
; relations from
$\mathrm {dom}(\mathcal {M})={\mathbb {N}}=\mathrm {dom}(\mathcal {M}')$
; relations from
![]() $\mathcal {L}$
are interpreted as in
$\mathcal {L}$
are interpreted as in
![]() $\mathcal {M}$
; and for each function symbol f from
$\mathcal {M}$
; and for each function symbol f from
![]() $\mathcal {L}$
, set
$\mathcal {L}$
, set
![]() $R_f^{\mathcal {M}'}(\bar x, a) \Leftrightarrow f^{\mathcal {M}}(\bar x) =a$
. Notice that
$R_f^{\mathcal {M}'}(\bar x, a) \Leftrightarrow f^{\mathcal {M}}(\bar x) =a$
. Notice that
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {M}'$
have the same automorphism group (as permutation groups). In particular,
$\mathcal {M}'$
have the same automorphism group (as permutation groups). In particular,
![]() $\mathcal {M}'$
is highly algebraic iff
$\mathcal {M}'$
is highly algebraic iff
![]() $\mathcal {M}$
is highly algebraic. Moreover this construction induces an
$\mathcal {M}$
is highly algebraic. Moreover this construction induces an
![]() $S_{\infty }$
-equivariant Borel isomorphism between
$S_{\infty }$
-equivariant Borel isomorphism between
![]() $[\mathcal {M}]_{\mathrm {iso}}\subseteq \mathrm {Str}(\mathcal {L},{\mathbb {N}})$
and
$[\mathcal {M}]_{\mathrm {iso}}\subseteq \mathrm {Str}(\mathcal {L},{\mathbb {N}})$
and
![]() $[\mathcal {M}']_{\mathrm {iso}}\subseteq \mathrm {Str}(\mathcal {L}',{\mathbb {N}})$
, the existence of a quasi-invariant probability measure on
$[\mathcal {M}']_{\mathrm {iso}}\subseteq \mathrm {Str}(\mathcal {L}',{\mathbb {N}})$
, the existence of a quasi-invariant probability measure on
![]() $[\mathcal {M}']_{\mathrm {iso}}$
implies the same for
$[\mathcal {M}']_{\mathrm {iso}}$
implies the same for
![]() $[\mathcal {M}]_{\mathrm {iso}}$
.
$[\mathcal {M}]_{\mathrm {iso}}$
.
Let now B as in the statement of Theorem 13 (for instance we can take B to be the algebraic closure of the empty set). We view the set B as enumerated by
![]() $\bar {b}=(b_0,\ldots ,b_{l-1})\in {\mathbb {N}}^{\ell }$
, with
$\bar {b}=(b_0,\ldots ,b_{l-1})\in {\mathbb {N}}^{\ell }$
, with
![]() $|B|=\ell $
, and we fix some new “atom”
$|B|=\ell $
, and we fix some new “atom”
![]() $z\notin {\mathbb {N}}$
.
$z\notin {\mathbb {N}}$
.
For each
![]() $\bar {c}\in \mathbb {N}^{\ell }$
we consider a new language
$\bar {c}\in \mathbb {N}^{\ell }$
we consider a new language
![]() $\mathcal {L}_{\bar {c}}$
. This language contains, for each
$\mathcal {L}_{\bar {c}}$
. This language contains, for each
![]() $R\in \mathcal {L}$
of arity n and each
$R\in \mathcal {L}$
of arity n and each
![]() $f\colon \{0,\ldots ,n-1\}\to \{\bar {c}\}\cup \{z\}$
, a symbol
$f\colon \{0,\ldots ,n-1\}\to \{\bar {c}\}\cup \{z\}$
, a symbol
![]() $R^{\bar {c}}_f$
of arity
$R^{\bar {c}}_f$
of arity
![]() $|f^{-1}(z)|$
. In addition, given any tuple
$|f^{-1}(z)|$
. In addition, given any tuple
![]() $\bar {a}\in ({\mathbb {N}}\setminus \{\bar {c}\})^k$
and any map
$\bar {a}\in ({\mathbb {N}}\setminus \{\bar {c}\})^k$
and any map
![]() $f\colon \{0,\ldots , n-1\}\to \{\bar {c}\}\cup \{z\}$
such that
$f\colon \{0,\ldots , n-1\}\to \{\bar {c}\}\cup \{z\}$
such that
![]() $|f^{-1}(z)|=k$
, we define
$|f^{-1}(z)|=k$
, we define
![]() $\bar {a}_f\in {\mathbb {N}}^{n}$
, as the unique tuple such that:
$\bar {a}_f\in {\mathbb {N}}^{n}$
, as the unique tuple such that:
-
i) for each
 $i\in n$
, with
$i\in n$
, with
 $f(i)\in \{\bar {c}\}$
, the i-th coordinate of
$f(i)\in \{\bar {c}\}$
, the i-th coordinate of
 $\bar {a}_f$
is
$\bar {a}_f$
is
 $f(i)$
;
$f(i)$
; -
ii) removing all entries of
 $\bar {a}_f$
that are in
$\bar {a}_f$
that are in
 $\{\bar {c}\}$
gives
$\{\bar {c}\}$
gives
 $\bar {a}$
.
$\bar {a}$
.
For any
![]() $\mathcal {N}\in \mathrm {Str}(\mathcal {L},{\mathbb {N}})$
and any fixed
$\mathcal {N}\in \mathrm {Str}(\mathcal {L},{\mathbb {N}})$
and any fixed
![]() $\bar {c}\in \mathbb {N}^{\ell }$
, we define
$\bar {c}\in \mathbb {N}^{\ell }$
, we define
![]() $\mathcal {N}_{\bar {c}}\in \mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}}\setminus \{\bar {c}\})$
by setting
$\mathcal {N}_{\bar {c}}\in \mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}}\setminus \{\bar {c}\})$
by setting
for every
![]() $R^{\bar {c}}_f\in \mathcal {L}_{\bar {c}}$
. Notice that there is a natural isomorphism of the permutation groups
$R^{\bar {c}}_f\in \mathcal {L}_{\bar {c}}$
. Notice that there is a natural isomorphism of the permutation groups
![]() $\mathrm {Aut}(\mathcal {N}_{\bar {c}})$
and
$\mathrm {Aut}(\mathcal {N}_{\bar {c}})$
and
![]() $\mathrm {Aut}(\mathcal {N})_{\bar {c}}$
, defined by extending each
$\mathrm {Aut}(\mathcal {N})_{\bar {c}}$
, defined by extending each
![]() $g\in \mathrm {Aut}(\mathcal {N}_{\bar {c}})$
to the identity on
$g\in \mathrm {Aut}(\mathcal {N}_{\bar {c}})$
to the identity on
![]() $\{\bar {c}\}$
.
$\{\bar {c}\}$
.
Claim 14. The
![]() $\mathcal {L}_{\bar {b}}$
-structure
$\mathcal {L}_{\bar {b}}$
-structure
![]() $\mathcal {M}_{\bar {b}}$
has no algebraicity.
$\mathcal {M}_{\bar {b}}$
has no algebraicity.
Proof of Claim.
Assume that
![]() $d\in {\mathbb {N}}\setminus \{\bar {b}\}$
has finite orbit under
$d\in {\mathbb {N}}\setminus \{\bar {b}\}$
has finite orbit under
![]() $\mathrm {Aut}(\mathcal {M}_{\bar {b}})_{\bar {a}}$
. Then d also has finite orbit under
$\mathrm {Aut}(\mathcal {M}_{\bar {b}})_{\bar {a}}$
. Then d also has finite orbit under
![]() $\mathrm {Aut}(\mathcal {M})_{\bar {a}\bar {b}}$
, since
$\mathrm {Aut}(\mathcal {M})_{\bar {a}\bar {b}}$
, since
![]() $\mathrm {Aut}(\mathcal {M}_{\bar {b}})_{\bar {a}}$
and
$\mathrm {Aut}(\mathcal {M}_{\bar {b}})_{\bar {a}}$
and
![]() $\mathrm {Aut}(\mathcal {M})_{\bar {a}\bar {b}}$
are the same permutation groups on
$\mathrm {Aut}(\mathcal {M})_{\bar {a}\bar {b}}$
are the same permutation groups on
![]() ${\mathbb {N}} \setminus \{\bar {b}\}$
. Therefore d must be in
${\mathbb {N}} \setminus \{\bar {b}\}$
. Therefore d must be in
![]() $\{\bar {a}\}\cup \{\bar {b}\}$
. Since
$\{\bar {a}\}\cup \{\bar {b}\}$
. Since
![]() $d\not \in \{\bar {b}\}$
, we have
$d\not \in \{\bar {b}\}$
, we have
![]() $d\in \{\bar {a}\}$
.
$d\in \{\bar {a}\}$
.
Let now W be the collection of all pairs
![]() $(\bar {c},\mathcal {N})$
, where
$(\bar {c},\mathcal {N})$
, where
![]() $\bar {c}\in {\mathbb {N}}^{\ell }$
and
$\bar {c}\in {\mathbb {N}}^{\ell }$
and
![]() $\mathcal {N}\in \mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}} \setminus \{\bar {c}\})$
. We define an analog of the logic action of
$\mathcal {N}\in \mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}} \setminus \{\bar {c}\})$
. We define an analog of the logic action of
![]() $\mathrm {Sym}({\mathbb {N}})$
on W as follows: for
$\mathrm {Sym}({\mathbb {N}})$
on W as follows: for
![]() $g\in \mathrm {Sym}({\mathbb {N}})$
and
$g\in \mathrm {Sym}({\mathbb {N}})$
and
![]() $(\bar {c},\mathcal {N})\in W$
we set
$(\bar {c},\mathcal {N})\in W$
we set
![]() $g\cdot (\bar {c},\mathcal {N}):=(g(\bar {c}),g_*\mathcal {N})$
, where
$g\cdot (\bar {c},\mathcal {N}):=(g(\bar {c}),g_*\mathcal {N})$
, where
![]() $g_*\mathcal {N}\in \mathrm {Str}(\mathcal {L}_{g(\bar {c})},{\mathbb {N}}\setminus \{ g(\bar {c})\})$
is defined by naturally extending the formulas from Section 2.2. That is, by setting, for all
$g_*\mathcal {N}\in \mathrm {Str}(\mathcal {L}_{g(\bar {c})},{\mathbb {N}}\setminus \{ g(\bar {c})\})$
is defined by naturally extending the formulas from Section 2.2. That is, by setting, for all
![]() $R^{\bar {c}}_f\in \mathcal {L}_{\bar {c}}$
,
$R^{\bar {c}}_f\in \mathcal {L}_{\bar {c}}$
,
Let Y be the
![]() $\mathrm {Sym}({\mathbb {N}})$
-orbit of
$\mathrm {Sym}({\mathbb {N}})$
-orbit of
![]() $(\bar {b},\mathcal {M}_{\bar {b}})$
in W and consider the map
$(\bar {b},\mathcal {M}_{\bar {b}})$
in W and consider the map
![]() $\beta \colon Y \to \mathrm {Str}(\mathcal {L},{\mathbb {N}})$
which is defined as follows: for all
$\beta \colon Y \to \mathrm {Str}(\mathcal {L},{\mathbb {N}})$
which is defined as follows: for all
![]() $(\bar {c},\mathcal {N})\in Y$
and
$(\bar {c},\mathcal {N})\in Y$
and
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() ${\beta (\bar {c},\mathcal {N})}\models R(\bar {a})$
holds if and only if
${\beta (\bar {c},\mathcal {N})}\models R(\bar {a})$
holds if and only if
![]() ${\mathcal {N}}\models R^{\bar {c}}_{f}(\bar {e})$
holds, for the unique
${\mathcal {N}}\models R^{\bar {c}}_{f}(\bar {e})$
holds, for the unique
![]() $f\colon n \to \{\bar {c}\}\cup \{z\}$
and
$f\colon n \to \{\bar {c}\}\cup \{z\}$
and
![]() $\bar {e}\in ({\mathbb {N}} \setminus \{\bar {c}\})^k$
such that
$\bar {e}\in ({\mathbb {N}} \setminus \{\bar {c}\})^k$
such that
![]() $\bar {e}_f=\bar {a}$
.
$\bar {e}_f=\bar {a}$
.
Claim 15.
![]() $\beta $
is
$\beta $
is
![]() $S_\infty $
-equivariant.
$S_\infty $
-equivariant.
Proof of Claim.
Let
![]() $g\in \mathrm {Sym}({\mathbb {N}})$
and
$g\in \mathrm {Sym}({\mathbb {N}})$
and
![]() $(\bar {c},\mathcal {N})\in Y$
, we need to prove that
$(\bar {c},\mathcal {N})\in Y$
, we need to prove that
To see this, let
![]() $R\in \mathcal L$
and
$R\in \mathcal L$
and
![]() $\bar {a}$
in
$\bar {a}$
in
![]() $\mathbb {N}$
. We have:
$\mathbb {N}$
. We have:
 $$ \begin{align*} \beta(g (\bar{c}), g_{*}\mathcal{N}) \models R(\bar{a})\!\!\! \quad \Leftrightarrow \kern-1.5pt\quad & \!\!{g_{*}\mathcal{N}} \models R^{g(\bar{c})}_{f}(\bar{e}), \text{for the unique }f\colon n\to \{g(\bar{c})\}\cup \{z\}\\& \!\!\text{and } \bar{e}\in ({\mathbb{N}} \setminus \{g (\bar{c})\})^k\text{ such that }\bar{e}_f=\bar{a}.\\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!{\mathcal{N}} {\kern-1pt}\models{\kern-1pt} R^{\bar{c}}_{g^{-1}\circ f}(g^{-1}(\bar{e})), \text{for the unique }{\kern-1pt}f{\kern-1pt}\colon{\kern-1pt} n{\kern-1pt}\to{\kern-1pt} \{g(\bar{c})\}{\kern-1pt}\cup{\kern-1pt} \{\kern-0.2pt z\kern-0.2pt \}\\& \!\!\text{and } \bar{e}\in ({\mathbb{N}} \setminus \{g (\bar{c})\})^k\text{ such that }\bar{e}_f=\bar{a}.\\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!{\mathcal{N}}\models R^{\bar{c}}_{h}(\bar{d}), \text{for the unique }h\colon n\to \{\bar{c}\}\cup \{z\}\\& \!\!\text{and } \bar{d}\in ({\mathbb{N}} \setminus \{\bar{c}\})^k\text{ such that }g(\bar{d}_h)=\bar{a}, \\& \!\!\text{namely, for } h:=g^{-1}\circ f \text{ and } \bar{d}:=g^{-1}(\bar{e}). \\\quad \Leftrightarrow\kern-1.5pt \quad & \!\!{\mathcal{N}}\models R^{\bar{c}}_{f}(\bar{e}), \text{for the unique } f \colon n\to \{\bar{c}\}\cup \{z\}\\& \!\!\text{and } \bar{e}\in ({\mathbb{N}} \setminus \{\bar{c}\})^k\text{ such that } \bar{e}_f=g^{-1}(\bar{a}). \\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!\beta(\bar{c},\mathcal{N}) \models R(g^{-1}(\bar{a})).\\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!{g_* \beta(\bar{c},\mathcal{N})}\models R(\bar{a}). \end{align*} $$
$$ \begin{align*} \beta(g (\bar{c}), g_{*}\mathcal{N}) \models R(\bar{a})\!\!\! \quad \Leftrightarrow \kern-1.5pt\quad & \!\!{g_{*}\mathcal{N}} \models R^{g(\bar{c})}_{f}(\bar{e}), \text{for the unique }f\colon n\to \{g(\bar{c})\}\cup \{z\}\\& \!\!\text{and } \bar{e}\in ({\mathbb{N}} \setminus \{g (\bar{c})\})^k\text{ such that }\bar{e}_f=\bar{a}.\\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!{\mathcal{N}} {\kern-1pt}\models{\kern-1pt} R^{\bar{c}}_{g^{-1}\circ f}(g^{-1}(\bar{e})), \text{for the unique }{\kern-1pt}f{\kern-1pt}\colon{\kern-1pt} n{\kern-1pt}\to{\kern-1pt} \{g(\bar{c})\}{\kern-1pt}\cup{\kern-1pt} \{\kern-0.2pt z\kern-0.2pt \}\\& \!\!\text{and } \bar{e}\in ({\mathbb{N}} \setminus \{g (\bar{c})\})^k\text{ such that }\bar{e}_f=\bar{a}.\\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!{\mathcal{N}}\models R^{\bar{c}}_{h}(\bar{d}), \text{for the unique }h\colon n\to \{\bar{c}\}\cup \{z\}\\& \!\!\text{and } \bar{d}\in ({\mathbb{N}} \setminus \{\bar{c}\})^k\text{ such that }g(\bar{d}_h)=\bar{a}, \\& \!\!\text{namely, for } h:=g^{-1}\circ f \text{ and } \bar{d}:=g^{-1}(\bar{e}). \\\quad \Leftrightarrow\kern-1.5pt \quad & \!\!{\mathcal{N}}\models R^{\bar{c}}_{f}(\bar{e}), \text{for the unique } f \colon n\to \{\bar{c}\}\cup \{z\}\\& \!\!\text{and } \bar{e}\in ({\mathbb{N}} \setminus \{\bar{c}\})^k\text{ such that } \bar{e}_f=g^{-1}(\bar{a}). \\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!\beta(\bar{c},\mathcal{N}) \models R(g^{-1}(\bar{a})).\\\quad \Leftrightarrow \kern-1.5pt\quad & \!\!{g_* \beta(\bar{c},\mathcal{N})}\models R(\bar{a}). \end{align*} $$
Claim 16.
![]() $\beta (Y)= [\mathcal {M}]_{\mathrm {iso.}}$
$\beta (Y)= [\mathcal {M}]_{\mathrm {iso.}}$
Proof. This follows from the previous claim, since
![]() $\mathcal {M}=\beta (\mathcal {M}_{\bar {b}},\bar {b})$
.
$\mathcal {M}=\beta (\mathcal {M}_{\bar {b}},\bar {b})$
.
Claim 17.
Y is a standard Borel space and
![]() $\beta $
is a Borel map.
$\beta $
is a Borel map.
Proof. Notice first that W is a Polish space as it is the countable disjoint union of the Polish spaces
![]() $\mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}}\setminus \{\bar {c}\})$
, where the union ranges over all
$\mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}}\setminus \{\bar {c}\})$
, where the union ranges over all
![]() $\bar {c}\in {\mathbb {N}}^\ell $
. Since Y is a single orbit of the continuous action of
$\bar {c}\in {\mathbb {N}}^\ell $
. Since Y is a single orbit of the continuous action of
![]() $\mathrm {Sym}({\mathbb {N}})$
on W we have that Y is a Borel subset of W, and hence, a standard Borel space. It is straightforward to check that the map
$\mathrm {Sym}({\mathbb {N}})$
on W we have that Y is a Borel subset of W, and hence, a standard Borel space. It is straightforward to check that the map
![]() $\beta $
is, in fact, continuous, as whether
$\beta $
is, in fact, continuous, as whether
![]() ${\beta (\bar {c},\mathcal {N})}\models R(\bar {a})$
holds depends only on whether
${\beta (\bar {c},\mathcal {N})}\models R(\bar {a})$
holds depends only on whether
![]() ${\mathcal {N}}\models R^{\bar {c}}_{f}(\bar {e})$
holds, for a single relation
${\mathcal {N}}\models R^{\bar {c}}_{f}(\bar {e})$
holds, for a single relation
![]() $R^{\bar {c}}_{f}$
and a single tuple
$R^{\bar {c}}_{f}$
and a single tuple
![]() $\bar {e}$
.
$\bar {e}$
.
Claim 18. There is a measure
![]() $\lambda $
on Y that is
$\lambda $
on Y that is
![]() $\mathrm {Sym}({\mathbb {N}})$
-quasi-invariant.
$\mathrm {Sym}({\mathbb {N}})$
-quasi-invariant.
Proof. First, using [Reference Ackerman, Freer and Patel5, Theorem 1.1] and Claim 14, we may fix some
![]() $\mathrm {Sym}({\mathbb {N}}\setminus \{\bar {b}\})$
-invariant measure
$\mathrm {Sym}({\mathbb {N}}\setminus \{\bar {b}\})$
-invariant measure
![]() $\mu _{\bar {b}}$
on
$\mu _{\bar {b}}$
on
![]() $\mathrm {Str}(\mathcal {L}_{\bar b},{\mathbb {N}} \setminus \{\bar {b}\})$
, which concentrates on the orbit of
$\mathrm {Str}(\mathcal {L}_{\bar b},{\mathbb {N}} \setminus \{\bar {b}\})$
, which concentrates on the orbit of
![]() $\mathcal {M}_{\bar {b}}$
. We now define a measure on
$\mathcal {M}_{\bar {b}}$
. We now define a measure on
![]() $\mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}} \setminus \{\bar {c}\})$
by taking any element g of
$\mathrm {Str}(\mathcal {L}_{\bar {c}},{\mathbb {N}} \setminus \{\bar {c}\})$
by taking any element g of
![]() $\mathrm {Sym}({\mathbb {N}})$
sending
$\mathrm {Sym}({\mathbb {N}})$
sending
![]() $\bar b$
to
$\bar b$
to
![]() $\bar c$
and setting
$\bar c$
and setting
![]() $\mu _{\bar {c}}=g_*\mu _{\bar b}$
. The obtained measure is
$\mu _{\bar {c}}=g_*\mu _{\bar b}$
. The obtained measure is
![]() $\mathrm {Sym}({\mathbb {N}}\setminus \{\bar {c}\})$
-invariant and does not depend on the choice of g by
$\mathrm {Sym}({\mathbb {N}}\setminus \{\bar {c}\})$
-invariant and does not depend on the choice of g by
![]() $\mathrm {Sym}({\mathbb {N}}\setminus \{\bar {b}\} )$
-invariance of
$\mathrm {Sym}({\mathbb {N}}\setminus \{\bar {b}\} )$
-invariance of
![]() $\mu _{\bar b}$
. Denote by
$\mu _{\bar b}$
. Denote by
![]() $\delta _{\bar c}$
the measure on
$\delta _{\bar c}$
the measure on
![]() ${\mathbb {N}}^\ell $
such that for
${\mathbb {N}}^\ell $
such that for
![]() $A\subseteq {\mathbb {N}}^\ell $
,
$A\subseteq {\mathbb {N}}^\ell $
,
![]() $\delta _{\bar {c}}(A)=1$
if
$\delta _{\bar {c}}(A)=1$
if
![]() $\bar {c}\in A$
and
$\bar {c}\in A$
and
![]() $0$
otherwise. Now take any fully supported measure
$0$
otherwise. Now take any fully supported measure
![]() $\nu $
on the countable set
$\nu $
on the countable set
![]() ${\mathbb {N}}^\ell $
and integrate
${\mathbb {N}}^\ell $
and integrate
![]() $\delta _{\bar c} \otimes \mu _{\bar c}$
along
$\delta _{\bar c} \otimes \mu _{\bar c}$
along
![]() $\nu $
, since
$\nu $
, since
![]() ${\mathbb {N}}^{\ell }$
is countable this is always well-defined. We denote by
${\mathbb {N}}^{\ell }$
is countable this is always well-defined. We denote by
![]() $\lambda $
the obtained measure on Y, as for every
$\lambda $
the obtained measure on Y, as for every
![]() $\bar c$
,
$\bar c$
,
![]() $\delta _{\bar c} \otimes \mu _{\bar c}$
is a measure on Y.
$\delta _{\bar c} \otimes \mu _{\bar c}$
is a measure on Y.
To see that
![]() $\lambda $
is
$\lambda $
is
![]() $\mathrm {Sym}({\mathbb {N}})$
-quasi-invariant, let
$\mathrm {Sym}({\mathbb {N}})$
-quasi-invariant, let
![]() $A\subseteq Y$
with
$A\subseteq Y$
with
![]() $\lambda (A)>0$
, and pick
$\lambda (A)>0$
, and pick
![]() $\bar {d}\in {\mathbb {N}}^\ell $
with
$\bar {d}\in {\mathbb {N}}^\ell $
with
This implies that
Let now
![]() $g\in \mathrm {Sym}({\mathbb {N}})$
and notice that, by the definition
$g\in \mathrm {Sym}({\mathbb {N}})$
and notice that, by the definition
![]() $\mu _{\bar {c}}$
, we have
$\mu _{\bar {c}}$
, we have
![]() $\mu _{g(\bar {d})}=g_*\mu _{\bar {d}}$
. Hence,
$\mu _{g(\bar {d})}=g_*\mu _{\bar {d}}$
. Hence,
Since
![]() $\nu $
is fully supported, we have that
$\nu $
is fully supported, we have that
![]() $\lambda (g(A))\geq \lambda \big ( \{(\bar {c},\mathcal {N})\in g(A) \colon \bar {c}= g(\bar {d}) \} \big )>0$
.
$\lambda (g(A))\geq \lambda \big ( \{(\bar {c},\mathcal {N})\in g(A) \colon \bar {c}= g(\bar {d}) \} \big )>0$
.
To conclude with the proof of Theorem 13, we simply push forward
![]() $\lambda $
via
$\lambda $
via
![]() $\beta $
. By Claims 16 and 17 we have an
$\beta $
. By Claims 16 and 17 we have an
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariant measure on
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariant measure on
![]() $[\mathcal {M}]_{\mathrm {iso}}$
which can be normalized to a probability measure without losing
$[\mathcal {M}]_{\mathrm {iso}}$
which can be normalized to a probability measure without losing
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariance.
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariance.
We would like to thanks the anonymous referee for suggesting the following alternative argument for establishing Theorem 13, which is based on [Reference Ackerman, Freer, Nesetril and Patel4, Proposition 6.14].
Remark 19. Recall from the discussion in the introduction, following Theorem 2, that the set B in the statement of Theorem 13 can be taken to be the algebraic closure
![]() $\mathrm {acl}(\emptyset ,\mathcal {M})$
of the empty set. Let
$\mathrm {acl}(\emptyset ,\mathcal {M})$
of the empty set. Let
![]() $\mathcal {L}':=\mathcal {L}\cup \{U\}$
, where U is a new unary predicate and set
$\mathcal {L}':=\mathcal {L}\cup \{U\}$
, where U is a new unary predicate and set
![]() $\mathcal {M}'\in \mathrm {Str}(\mathcal {L}',\mathbb {N})$
be the expansion of
$\mathcal {M}'\in \mathrm {Str}(\mathcal {L}',\mathbb {N})$
be the expansion of
![]() $\mathcal {M}$
, where U holds only for the elements of B. For each
$\mathcal {M}$
, where U holds only for the elements of B. For each
![]() $F\subseteq \mathbb {N}$
with
$F\subseteq \mathbb {N}$
with
![]() $|F|=|B|$
, let
$|F|=|B|$
, let
![]() $\mathcal {N}_F$
be the
$\mathcal {N}_F$
be the
![]() $\{U\}$
-structure on
$\{U\}$
-structure on
![]() $\mathbb {N}$
, where U holds exactly on F. By [Reference Ackerman, Freer, Nesetril and Patel4, Proposition 6.14], for each such F we obtain an
$\mathbb {N}$
, where U holds exactly on F. By [Reference Ackerman, Freer, Nesetril and Patel4, Proposition 6.14], for each such F we obtain an
![]() $\mathrm {Aut}(\mathcal {N}_F)$
-invariant probability measure
$\mathrm {Aut}(\mathcal {N}_F)$
-invariant probability measure
![]() $\mu _F$
on
$\mu _F$
on
![]() $\mathrm {Str}(\mathcal {L}',\mathbb {N})$
which is supported on the set of those
$\mathrm {Str}(\mathcal {L}',\mathbb {N})$
which is supported on the set of those
![]() $\mathcal {L}'$
-structures which are isomorphic to
$\mathcal {L}'$
-structures which are isomorphic to
![]() $\mathcal {M}'$
and whose
$\mathcal {M}'$
and whose
![]() $\{U\}$
-reduct is
$\{U\}$
-reduct is
![]() $\mathcal {N}_F$
. Then, the desired
$\mathcal {N}_F$
. Then, the desired
![]() $\mathrm {Sym}(\mathbb {N})$
-quasi-invariant measure
$\mathrm {Sym}(\mathbb {N})$
-quasi-invariant measure
![]() $\lambda $
on
$\lambda $
on
![]() $[\mathcal {M}]_{\mathrm {iso}}$
is just the
$[\mathcal {M}]_{\mathrm {iso}}$
is just the
![]() $\nu $
-mixture of the
$\nu $
-mixture of the
![]() $\mu _F$
-measures, where
$\mu _F$
-measures, where
![]() $\nu $
is any probability measure on the set of
$\nu $
is any probability measure on the set of
![]() $|B|$
-sized subsets of natural numbers with full support.
$|B|$
-sized subsets of natural numbers with full support.
5 Examples
We start by providing two examples of simple, highly algebraic structures. Each example realizes the respective side of the dichotomy that we established in Lemma 9.
Example 20. Let
![]() $\mathcal {L}:=\{R\}$
, where R is a binary relation, and let
$\mathcal {L}:=\{R\}$
, where R is a binary relation, and let
![]() $\mathcal {N}$
be a graph that comprises of the disjoint union of countably infinite many edges. For example, set
$\mathcal {N}$
be a graph that comprises of the disjoint union of countably infinite many edges. For example, set
![]() $\mathcal {N}=(\mathbb {N},R^{\mathcal {N}})$
, where for all
$\mathcal {N}=(\mathbb {N},R^{\mathcal {N}})$
, where for all
![]() $n,m\in \mathbb {N}$
we have that
$n,m\in \mathbb {N}$
we have that
![]() $(n,m)\in R^{\mathcal {N}}$
if and only if there is
$(n,m)\in R^{\mathcal {N}}$
if and only if there is
![]() $k\in \mathbb {N}$
so that
$k\in \mathbb {N}$
so that
![]() $\{n,m\}=\{2k,2k+1\}$
. Clearly
$\{n,m\}=\{2k,2k+1\}$
. Clearly
![]() $\mathcal {N}$
is highly algebraic and satisfies (1) of Lemma 9.
$\mathcal {N}$
is highly algebraic and satisfies (1) of Lemma 9.
Example 21. Let
![]() $\mathcal {L}:=\{R\}$
, where R is a binary relation, and let
$\mathcal {L}:=\{R\}$
, where R is a binary relation, and let
![]() $\mathcal {N}$
be a graph that comprises of the disjoint union of countably many copies of a bipartite graph whose one part is countably infinite and the other is a singleton. For example, set
$\mathcal {N}$
be a graph that comprises of the disjoint union of countably many copies of a bipartite graph whose one part is countably infinite and the other is a singleton. For example, set
![]() $\mathcal {N}=(\mathbb {N}^2,R^{\mathcal {N}})$
, where
$\mathcal {N}=(\mathbb {N}^2,R^{\mathcal {N}})$
, where
![]() $\big ((n_0,n_1),(m_0,m_1)\big )\in R^{\mathcal {N}}$
if and only if
$\big ((n_0,n_1),(m_0,m_1)\big )\in R^{\mathcal {N}}$
if and only if
![]() $m_0=n_0$
and either of the following two hold:
$m_0=n_0$
and either of the following two hold:
![]() $n_1=0$
and
$n_1=0$
and
![]() $m_1>0$
; or
$m_1>0$
; or
![]() $m_1=0$
and
$m_1=0$
and
![]() $n_1>0$
. Clearly
$n_1>0$
. Clearly
![]() $\mathcal {N}$
is highly algebraic and (its R-homogeneous expansion from Lemma 4) satisfies (2) of Lemma 9.
$\mathcal {N}$
is highly algebraic and (its R-homogeneous expansion from Lemma 4) satisfies (2) of Lemma 9.
We close with some examples of structures which have algebraicity but are not highly algebraic. In view of [Reference Ackerman, Freer and Patel5] and Theorem 2, these are quasi-invariantly random structures which are not invariantly random.
Example 22 (Finite inclusions).
Let
![]() $\mathcal {N}$
be any ultrahomogeneous structure without algebraicity and let F be a finite substructure of it. Then the structure
$\mathcal {N}$
be any ultrahomogeneous structure without algebraicity and let F be a finite substructure of it. Then the structure
![]() $(\mathcal {N},U_F)$
, which endows
$(\mathcal {N},U_F)$
, which endows
![]() $\mathcal {N}$
with a unary predicate interpreted on F, is not highly algebraic and hence, by Theorem 2, is quasi-invariantly random.
$\mathcal {N}$
with a unary predicate interpreted on F, is not highly algebraic and hence, by Theorem 2, is quasi-invariantly random.
Example 23 (Generic finite quotients).
Let
![]() $\mathcal {N}$
be any ultrahomogeneous structure without algebraicity and let
$\mathcal {N}$
be any ultrahomogeneous structure without algebraicity and let
![]() $\pi \colon \mathrm {dom}(N)\to B$
be a generic function with B being a finite set. Consider the structure
$\pi \colon \mathrm {dom}(N)\to B$
be a generic function with B being a finite set. Consider the structure
![]() $\mathcal {N}_{B}$
given by setting
$\mathcal {N}_{B}$
given by setting
![]() $\mathrm {dom}(\mathcal {N}_{B}):=\mathrm {dom}(\mathcal {N})\cup B$
and adding the map
$\mathrm {dom}(\mathcal {N}_{B}):=\mathrm {dom}(\mathcal {N})\cup B$
and adding the map
![]() $\pi $
, on top of the existing on
$\pi $
, on top of the existing on
![]() $\mathcal {N}$
, as the interpretation of a new function symbol. It follows that
$\mathcal {N}$
, as the interpretation of a new function symbol. It follows that
![]() $\mathcal {N}_B$
is not highly algebraic and hence, by Theorem 2, quasi-invariantly random.
$\mathcal {N}_B$
is not highly algebraic and hence, by Theorem 2, quasi-invariantly random.
Acknowledgments
We would like to thank the anonymous reviewer for their comments and remarks, in particular suggesting an alternative proof of Theorem 13.
Funding statement
This research was supported by the NSF Grants DMS-2154160 and DMS-2154258. C.J. was partially supported by DFG (Project FinHom, Grant 467967530).