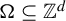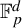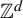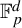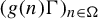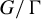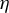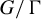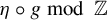Equidistribution for nilsequences along spheres over finite fields

Abstract

In this paper, we prove a quantitative equidistribution theorem for polynomial sequences in a nilmanifold, where the average is taken along spheres instead of cubes. To be more precise, let $\Omega \subseteq \mathbb {Z}^{d}$ be the preimage of a sphere $\mathbb {F}_{p}^{d}$ under the natural embedding from $\mathbb {Z}^{d}$ to $\mathbb {F}_{p}^{d}$. We show that if a rational polynomial sequence $(g(n)\Gamma )_{n\in \Omega }$ is not equidistributed on a nilmanifold $G/\Gamma $, then there exists a non-trivial horizontal character $\eta $ of $G/\Gamma $ such that $\eta \circ g \,\mod \mathbb {Z}$ vanishes on $\Omega $.

1 Introduction

Nilmanifolds and nilsequences have been studied extensively in the last decade. They play a fundamental role in combinatorial number theory, ergodic theory, additive combinatorics, and higher order Fourier analysis (see for example [3, 4, 7–9]). We begin with recalling some standard terminologies in this area.

Definition 1.1. (Filtered group)

Let G be a group. An $\mathbb {N}$ -filtration on G is a collection $G_{\mathbb {N}}=(G_{i})_{i\in \mathbb {N}}$ of subgroups of G indexed by $\mathbb {N}$ such that the following holds:

1. (i) for all $i,j\in \mathbb {N}$ with $i\leq j$ , we have that $G_{i}\supseteq G_{j}$ ;

2. (ii) for all $i,j\in \mathbb {N}$ , we have $[G_{i},G_{j}]\subseteq G_{i+j}$ .

For $s\in \mathbb {N}$ , we say that G is an ( $\mathbb {N}$ -filtered) nilpotent group of degree at most s (or of degree $\leq s$ ) with respect to some $\mathbb {N}$ -filtration $(G_{i})_{i\in \mathbb {N}}$ if $G_{i}$ is trivial whenever $i>s$ .

Definition 1.2. (Nilmanifold)

Let $\Gamma $ be a discrete and cocompact subgroup of a connected, simply connected nilpotent Lie group G with filtration $G_{\mathbb {N}}=(G_{i})_{i\in \mathbb {N}}$ such that ${\Gamma _{i}:=\Gamma \cap G_{i}}$ is a cocompact subgroup of $G_{i}$ for all $i\in \mathbb {N}$ . Then, we say that $G/\Gamma $ is an ( $\mathbb {N}$ -filtered) nilmanifold, and we use $(G/\Gamma )_{\mathbb {N}}$ to denote the collection $(G_{i}/\Gamma _{i})_{i\in \mathbb {N}}$ (which is called the $\mathbb {N}$ -filtration of $G/\Gamma $ ). We say that $G/\Gamma $ has degree $\leq s$ with respect to $(G/\Gamma )_{\mathbb {N}}$ if G has degree $\leq s$ with respect to $G_{\mathbb {N}}$ .

Definition 1.3. (Polynomial sequences)

Let $d,\in \mathbb {N}_{+}$ and G be a connected simply connected nilpotent Lie group and $(G_{i})_{i\in \mathbb {N}}$ be an $\mathbb {N}$ -filtration of G. Denote $\Delta _{h}g(n):= g(n+h)g(n)^{-1}$ for all $n, h\in G$ . A map $g\colon \mathbb {Z}^{d}\!\to G$ is an ( $\mathbb {N}$ -filtered) polynomial sequence if

$$ \begin{align*} \Delta_{h_{m}}\cdots \Delta_{h_{1}} g(n)\in G_{m} \end{align*} $$

for all $m\in \mathbb {N}$ and $n,h_{1},\ldots ,h_{m}\in \mathbb {Z}^{d}$ . The set of all $\mathbb {N}$ -filtered polynomial sequences is denoted by $\text {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ .

A fundamental question in higher order Fourier analysis is to study the equidistribution property of polynomial sequences. Let $\Omega $ be a non-empty subset of $\mathbb {Z}^{d}$ and $G/\Gamma $ be an $\mathbb {N}$ -filtered nilmanifold. A sequence $a\colon \Omega \to G/\Gamma $ is $\delta $ -equidistributed on $G/\Gamma $ if for all Lipschitz function $F\colon G/\Gamma \to \mathbb {C}$ (with respect to the metric $d_{G/\Gamma }$ to be defined in §3), we have that

$$ \begin{align*} \limsup_{N\to\infty}\bigg\vert\frac{1}{\vert \Omega\cap [N]^{d}\vert}\sum_{n\in\Omega\cap [N]^{d}}F(a(n))-\int_{G/\Gamma}F\,dm_{G/\Gamma}\bigg\vert\!\leq \delta\Vert F\Vert_{\mathrm{Lip}}, \end{align*} $$

where $m_{G/\Gamma }$ is the Haar measure of $G/\Gamma $ and the Lipschitz norm is defined as

$$ \begin{align*} \Vert F\Vert_{\mathrm{Lip}}:=\sup_{x\in G/\Gamma}\vert F(x)\vert+\sup_{x,y\in G/\Gamma, x\neq y}\frac{\vert F(x)-F(y)\vert}{d_{G/\Gamma}(x,y)}. \end{align*} $$

It is known that the equidistribution property of polynomial sequences is connected to the horizontal characters of $G/\Gamma $ , that is, group homomorphisms $\eta \colon G\to \mathbb {R}$ with $\eta (\Gamma )\subseteq \mathbb {Z}$ . It was proved by Green and Tao [5, 6] that for any $\delta>0$ and any polynomial sequence $g\in \text {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ , either $(g(n)\Gamma )_{n\in \mathbb {Z}^{d}}$ is $\delta $ -equidistributed on $G/\Gamma $ or there exists a non-trivial horizontal character $\eta $ of $G/\Gamma $ whose complexity is comparable with the complexity of $G/\Gamma $ (we will define complexity formally in §3) such that $\eta \circ g$ is a slowly varying function. This is a quantitative generalization of a result of Leibman [12].

It is natural to ask about the equidistribution property of polynomial sequences where the average is taken over some algebraic curves $\Omega \subseteq \mathbb {Z}^{d}$ . In this paper, we initiate the study in this direction by showing a quantitative equidistribution property for sequences of the form $(g(n)\Gamma )_{n\in \Omega }$ , where $\Omega $ is the preimage of a sphere over a finite field $\mathbb {F}_{p}^{d}$ under the natural embedding from $\mathbb {Z}^{d}$ to $\mathbb {F}_{p}^{d}$ (see [11, 14] for the study of related averages). The following is the main result of this paper (we refer the readers to §3 for definitions).

Theorem 1.4. (Equidistribution for polynomial sequence along spheres)

Let $0{\kern-1pt}<{\kern-1pt}\delta {\kern-1pt}<{\kern-1pt}1/2, C>0, d\in \mathbb {N}_{+},s\in \mathbb {N}$ with $d\geq s+13$ , and $p\gg _{C,d} \delta ^{-O_{C,d}(1)}$ be a prime. Denote $\Omega =\{n\in \mathbb {Z}^{d}\colon n\cdot n\equiv r\,\mod p\mathbb {Z}\}$ for some $r\in \mathbb {Z}$ (where $n\cdot n$ is the dot product of n and itself). Let $G/\Gamma $ be an s-step $\mathbb {N}$ -filtered nilmanifold of complexity at most C and $g\in \mathrm {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ be a rational polynomial sequence. Then, either $(g(n)\Gamma )_{n\in \Omega }$ is $\delta $ -equidistributed on $G/\Gamma $ or there exists a non-trivial horizontal character $\eta $ of complexity at most $O_{\delta ,d}(1)$ such that $\eta \circ g \,\mod \mathbb {Z}$ is a constant on $\Omega $ .

In fact, we will prove a stronger version of Theorem 1.4, which is Theorem 5.1 in this paper.

Remark 1.5. Note that in Theorem 1.4, it is not possible to require $\eta \circ g\,\mod \mathbb {Z}$ to be constant on the entire space $\mathbb {Z}^{d}$ . For example, let $G/\Gamma =\mathbb {R}/\mathbb {Z}$ , $g(n)=(n\cdot n)/p$ for all $n\in \mathbb {Z}^{d}$ . Since $g(n)\equiv r/p \,\mod \mathbb {Z}$ for all $n\in \Omega $ , it is not hard to see that $(g(n)\Gamma )_{n\in \Omega }$ is not $\delta $ -equidistributed on $G/\Gamma $ . However, since any non-trivial horizontal character of $G/\Gamma $ is of the form $\eta (x):=kx$ for some $k\in \mathbb {Z}\backslash \{0\}$ , we have that $\eta \circ g(n) \,\mod \mathbb {Z}=k(n\cdot n)/p \,\mod \mathbb {Z}$ cannot be constant on $\mathbb {Z}$ (but is constant on $\Omega $ ).

While our proof of Theorem 1.4 follows a framework similar to [5], they have many significant differences. The first is that to run the Green–Tao argument [5] in the spherical setting, we need to use a special property of hyperspheres called the inheriting principle, which says that many properties of hyperspheres are preserved under taking intersections (see §4 for a more precise statement). The second difference is that while in [5], one can easily obtain information of the ‘leading coefficients’ of the polynomial sequence g by applying the Cauchy–Schwarz inequality and induction hypothesis (at least when G is abelian), in our setting, only partial information can be obtained. This reduces the problem to solving some polynomial equations of the form (5.4). While the solution to (5.4) was immediate in the setting of [5], in our case, this is a difficulty question and it takes the bulk of the paper (§§6 and 7) to answer this question. We refer the readers to §5 for details.

It is natural to ask if a quantitative version of Theorem 1.4 holds for general (not necessarily rational) polynomial sequences. Nevertheless, the rational equidistribution theorem already has many applications in combinatorics and number theory. For example, as an immediate consequence of Theorem 1.4, we have the following immediate corollary for exponential sums along spheres, which is of independent interest in number theory.

Corollary 1.6. (Weyl’s equidistribution theorem along spheres over finite field)

Let $0<\delta <1/2, d\in \mathbb {N}_{+},s\in \mathbb {N}$ with $d\geq s+13$ and p be a prime. Let $g\colon \mathbb {Z}^{d}\to \mathbb {Z}$ be an integer valued polynomial of degree s. Denote $\Omega =\{n\in \mathbb {F}_{p}^{d}\colon n\cdot n=r\}$ for some $r\in \mathbb {F}_{p}$ . If $p\gg _{d} \delta ^{-O_{d}(1)}$ , then either

$$ \begin{align*} \bigg\vert\frac{1}{\vert\Omega\vert}\sum_{n\in\Omega}\exp(g\circ\tau(n)/p)\bigg\vert<\delta \end{align*} $$

or $g\circ \tau (n)/p \,\mod \mathbb {Z}$ is a constant on $\Omega $ , where $\tau \colon \mathbb {F}_{p}\to \{0,\ldots ,p-1\}$ is the natural bijective embedding. (By Corollary 7.3, we may further conclude that $g(n)=(n\cdot n -\tau (r))g_{1}(n)+pg_{2}(n)$ for some integer valued polynomials $g_{1}$ and $g_{2}$ .)

It is also worth noting that Theorem 1.4 is also the first step towards the geometric Ramsey conjecture over the finite fields. We refer the readers to [15–18] for details.

Motivated by [1, 5, 6], it is natural to ask whether Theorem 1.4 implies a factorization theorem, that is, whether one can decompose g as the product of a constant $\epsilon $ , a polynomial sequence $g'$ being equidistributed on a subnilmanifold of $G/\Gamma $ , and a polynomial sequence $\gamma $ having strong periodic properties. An affirmative answer to this question will be provided in the forthcoming paper [18]. For example, the following is a special case of [18, Theorem 1.4] (see §3 for definitions).

Theorem 1.7. Let $d\in \mathbb {N}_{+},s\in \mathbb {N}$ with $d\gg _{s} 1$ , $C>0$ , $\mathcal {F}\colon \mathbb {R}_{+}\to \mathbb {R}_{+}$ be a non-decreasing function with $\mathcal {F}(n)\geq n$ , and $p\gg _{C,d,\mathcal {F}} 1$ be a prime. Denote $\Omega {\kern1pt}={\kern1pt}\{n{\kern1pt}\in{\kern1pt} \mathbb {Z}^{d}\colon n\cdot n\equiv r\,\mod p\mathbb {Z}\}$ for some $r\in \mathbb {Z}$ . Let $G/\Gamma $ be an s-step $\mathbb {N}$ -filtered nilmanifold of complexity at most C and let $g\in \mathrm { poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ be a rational polynomial sequence on $\Omega $ . There exist some $C\leq C'\leq O_{C,d,\mathcal {F}}(1)$ , a proper subgroup $G'$ of G which is $C'$ -rational relative to $\mathcal {X}$ , and a factorization

$$ \begin{align*} g(n)=\epsilon g'(n)\gamma(n) \quad\text{for all } n\in \mathbb{Z}^{d} \end{align*} $$

such that $\epsilon \in G$ is of complexity $O_{C'}(1)$ , $g'\in \mathrm {poly}(\mathbb {Z}^{d}\to G^{\prime }_{\mathbb {N}})$ is rational, and $(g'(n)\Gamma )_{n\in \Omega }$ is $\mathcal {F}(C')^{-1}$ -totally equidistributed on $G'/\Gamma '$ , where $\Gamma ':=G'\cap \Gamma $ , and that $\gamma \in \mathrm {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ is such that $\gamma (n+rm)^{-1}\gamma (n)\in \Gamma $ for all $m,n\in \mathbb {Z}^{d}$ with $n,n+rm\in \Omega $ for some $r\leq O_{C,d,s}(C')$ .

1.1 Organization of the paper

We first provide the background material for polynomials, nilmanifolds, and quadratic forms in §§2, 3, and 4, respectively. Then, in §5, we state the main equidistribution result of the paper (that is, Theorem 5.1, which is a generalization of Theorem 1.4) and explain the outline of its proof. We also explain in §5 the main challenges in adapting the Green–Tao approach to the quadratic setting.

Sections 6, 7, and 9 are devoted to the proof of Theorem 5.1. In §6, we provide the solutions to some relevant algebraic equations for polynomials over $\mathbb {F}_{p}$ . Among other results, we solve a polynomial equation of the form (6.25), which plays a central role in the proof of Theorem 1.4 for p-periodic polynomial sequences. Then, in §7, we extend the results in §6 to polynomials in $\mathbb {Q}$ . Finally, in §9, we combine the results from §§6 and 7 with the approach of Green and Tao [5, 6] to complete the proof of Theorem 5.1.

1.2 Definitions and notation

Convention 1.8. Throughout this paper, we use $\tau \colon \mathbb {F}_{p}\to \{0,\ldots ,p-1\}$ to denote the natural bijective embedding, and use $\iota $ to denote the map from $\mathbb {Z}$ (or $\mathbb {Z}_{K}$ for any K divisible by p) to $\mathbb {F}_{p}$ given by $\iota (n):=\tau ^{-1}(n \,\mod p\mathbb {Z})$ . We also use $\tau $ to denote the map from $\mathbb {F}_{p}^{k}$ to $\mathbb {Z}^{k}$ (or $\mathbb {Z}_{K}^{k}$ ) given by $\tau (x_{1},\ldots ,x_{k}):=(\tau (x_{1}),\ldots ,\tau (x_{k}))$ , and $\iota $ to denote the map from $\mathbb {Z}^{k}$ (or $\mathbb {Z}_{K}^{k}$ ) to $\mathbb {F}_{p}^{k}$ given by $\iota (x_{1},\ldots ,x_{k}):=(\iota (x_{1}),\ldots , \iota (x_{k}))$ . When there is no confusion, we will not state the domain and range of $\tau $ and $\iota $ explicitly.

We may also extend the domain of $\iota $ to all the rational numbers of the form $x/y$ with $(x,y)=1, x\in \mathbb {Z}, y\in \mathbb {Z}\backslash p\mathbb {Z}$ by setting $\iota (x/y):=\iota (xy^{\ast })$ , where $y^{\ast }$ is any integer with $yy^{\ast }\equiv 1 \,\mod {p}\mathbb {Z}$ .

Below is the notation we use in this paper.

• • Let $\mathbb {N},\mathbb {N}_{+},\mathbb {Z},\mathbb {Q},\mathbb {R},\mathbb {R}_{+},\mathbb {C}$ denote the set of non-negative integers, positive integers, integers, rational numbers, real numbers, positive real numbers, and complex numbers, respectively. Denote $\mathbb {T}:=\mathbb {R}/\mathbb {Z}$ . Let $\mathbb {F}_{p}$ denote the finite field with p elements. Let $\mathbb {Z}_{K}$ denote the cyclic group with K elements, and let ${1}/{K}\mathbb {Z},\mathbb {Z}/K$ denote the set of numbers of the from $n/K$ for some $n\in \mathbb {Z}$ .

• • Throughout this paper, d is a fixed positive integer and p is a prime number.

• • Throughout this paper, unless otherwise stated, all vectors are assumed to be horizontal (row) vectors.

• • Let $\mathcal {C}$ be a collection of parameters and $A,B,c\in \mathbb {R}$ . We write $A\gg _{\mathcal {C}} B$ or $A=O_{\mathcal {C}}(B)$ if $\vert A\vert \geq K\vert B\vert $ for some $K>0$ depending only on the parameters in $\mathcal {C}$ . In the above definitions, we allow the set $\mathcal {C}$ to be empty. In this case, K will be a universal constant.

• • Let $[N]$ denote the set $\{0,\ldots ,N-1\}$ .

• • We use $\mathbf {0}$ to denote the zero vector in $\mathbb {F}_{p}^{k}$ or $\mathbb {R}^{k}$ , where the underlying space will be clear from the context.

• • For $i=(i_{1},\ldots ,i_{k})\in \mathbb {Z}^{k}$ , denote $\vert i\vert :=\vert i_{1}\vert +\cdots +\vert i_{k}\vert $ . For ${n=(n_{1},\ldots ,n_{k})\in \mathbb {Z}^{k}}$ and $i=(i_{1},\ldots ,i_{k})\in \mathbb {N}^{k}$ , denote $n^{i}:=n_{1}^{i_{1}}\cdots n_{k}^{i_{k}}$ and $i!:=i_{1}!\cdots i_{k}!$ . For $n=(n_{1},\ldots ,n_{k})\in \mathbb {N}^{k}$ and $i=(i_{1},\ldots ,i_{k})\in \mathbb {N}^{k}$ , denote $\binom {n}{i}:=\binom {n_{1}}{i_{1}}\cdots \binom {n_{k}}{i_{k}}$ .

• • For any set F, let $F[x_{1},\ldots ,x_{k}]$ denote the set of all polynomials in the variables $x_{1},\ldots ,x_{k}$ whose coefficients are from F.

• • For $x\in \mathbb {R}$ , let $\lfloor x\rfloor $ denote the largest integer that is not larger than x and $\lceil x\rceil $ denote the smallest integer that is not smaller than x. Denote $\{x\}:=x-\lfloor x\rfloor $ .

• • Let X be a finite set and $f\colon X\to \mathbb {C}$ be a function. Denote $\mathbb {E}_{x\in X}f(x):={1}/{\vert X\vert }\sum _{x\in X}f(x)$ , the average of f on X.

• • We say that a set $\Omega \subseteq \mathbb {Z}^{k}$ is Q-periodic if $\Omega =\Omega +Q\mathbb {Z}^{k}$ .

• • If $\Omega \subseteq \mathbb {Z}^{k}$ is a Q-periodic set and $f\colon \mathbb {Z}^{k}\to \mathbb {C}$ is such that $f(n)=f(n+Qm)$ for all $m,n\in \mathbb {Z}^{k}$ with $n,n+Qm\in \Omega $ , then we denote $\mathbb {E}_{x\in \Omega }f(x):=\mathbb {E}_{x\in \Omega \cap [Q]^{k}}f(x)$ .

• • For $F=\mathbb {Z}^{k}$ or $\mathbb {F}_{p}^{k}$ and $x=(x_{1},\ldots ,x_{k}), y=(y_{1},\ldots ,y_{k})\in F$ , let $x\cdot y\in \mathbb {Z}$ or $\mathbb {F}_{p}$ denote the dot product given by $x\cdot y:=x_{1}y_{1}+\cdots +x_{k}y_{k}.$

• • Let $\exp \colon \mathbb {R}\to \mathbb {C}$ denote the function $\exp (x):=e^{2\pi i x}$ .

• • If G is a connected, simply connected Lie group, then we use $\log G$ to denote its Lie algebra. Let $\exp \colon \log G\to G$ be the exponential map and $\log \colon G\to \log G$ be the logarithm map. For $t\in \mathbb {R}$ and $g\in G$ , denote $g^{t}:=\exp (t\log g)$ .

• • If $f\colon H\to G$ is a function from an abelian group $H=(H,+)$ to some group $(G,\cdot )$ , denote $\Delta _{h} f(n):=f(n+h)\cdot f(n)^{-1}$ for all $n,h\in H$ .

• • We write affine subspaces of $\mathbb {F}_{p}^{d}$ as $V+c$ , where V is a subspace of $\mathbb {F}_{p}^{d}$ passing through $\mathbf {0}$ , and $c\in \mathbb {F}_{p}^{d}$ .

Let $D,D'\in \mathbb {N}_{+}$ and $C>0$ . Here are some basic notions of complexities.

• • Real and complex numbers: a number $r\in \mathbb {R}$ is of complexity at most C if $r=a/b$ for some $a,b\in \mathbb {Z}$ with $-C\leq a,b\leq C$ . If $r\notin \mathbb {Q}$ , then we say that the complexity of r is infinity. A complex number is of complexity at most C if both its real and imaginary parts are of complexity at most C.

• • Vectors and matrices: a vector or matrix is of complexity at most C if all of its entries are of complexity at most C.

• • Subspaces: a subspace of $\mathbb {R}^{D}$ is of complexity at most C if it is the null space of a matrix of complexity at most C.

• • Linear transformations: let $L\colon \mathbb {C}^{D}\to \mathbb {C}^{D'}$ be a linear transformation. Then, L is associated with a $D\times D'$ matrix A in $\mathbb {C}$ . We say that L is of complexity at most C if A is of complexity at most C.

• • Lipschitz functions: a Lipschitz function is of complexity at most C if its Lipschitz norm is at most C.

2 Background material for polynomials

Definition 2.1. (Polynomials in finite field)

Let $\text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}^{d'}_{p})$ be the collection of all functions $f\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ of the form

(2.1) $$ \begin{align} f(n_{1},\ldots,n_{d})=\sum_{0\leq a_{1},\ldots,a_{d}\leq p-1, a_{i}\in\mathbb{N}}C_{a_{1},\ldots,a_{d}}n^{a_{1}}_{1}\cdots n^{a_{d-1}}_{d} \end{align} $$

for some $C_{a_{1},\ldots ,a_{d}}\in \mathbb {F}_{p}^{d'}$ . Let $f\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}^{d'}_{p})$ be a function which is not constant zero. The degree of f (denoted as $\deg (f)$ ) is the largest $r\in \mathbb {N}$ such that $C_{a_{1},\ldots ,a_{d}}\neq \mathbf {0}$ for some $a_{1}+\cdots +a_{d}=r$ . We say that f is homogeneous of degree r if $C_{a_{1},\ldots ,a_{d}}\neq \mathbf {0}$ implies that $a_{1}+\cdots +a_{d}=r$ . We say that f is a linear transformation if f is homogeneous of degree 1.

Convention 2.2. For convenience, the degree of the constant zero function is allowed to take any integer value. For example, 0 can be regarded as a homogeneous polynomial of degree 10, as a linear transformation, or as a polynomial of degree -1. Here, we also adopt the convention that the only polynomial of negative degree is 0.

Definition 2.3. For any $R'\subseteq R\subseteq \mathbb {R}$ and $\Omega \subseteq \mathbb {Z}^{d}$ , let $\text {poly}(\mathbb {Z}^{d}\to R)$ be the collection of all polynomials in $\mathbb {Z}^{d}$ taking values in R, and $\text {poly}(\Omega \to R\vert R')$ be the set of all ${f\in \text {poly}(\mathbb {Z}^{d}\to R)}$ such that $f(n)\in R'$ for all $n\in \Omega $ .

The following lemma is straightforward.

Lemma 2.4. Let $d\in \mathbb {N}_{+}$ , p be a prime, and $f\in \mathrm {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ be an integer valued polynomial of degree smaller than p. There exist integer valued polynomial ${f_{1}\in \mathrm {poly}(\mathbb {Z}^{d}\to \mathbb {Z})}$ and integer coefficient polynomial $f_{2}\in \mathrm {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ , both having degrees at most $\deg (f)$ such that $({1}/{p})f=f_{1}+({1}/{p})f_{2}$ .

Proof. Denote $s:=\deg (f)<p$ . By the multivariate polynomial interpolation, we may write

$$ \begin{align*}f(n)=\sum_{i\in\mathbb{N}^{d},\vert i\vert\leq s}\frac{a_{i}}{Q}n^{i}\end{align*} $$

for some $a_{i}\in \mathbb {Z}$ and $Q\in \mathbb {Z}, p\nmid Q$ (in fact, one can set $Q=(\deg (f)!)^{d}$ ). Let $Q^{\ast }\in \mathbb {Z}$ be such that $Q^{\ast }Q\equiv 1 \,\mod p\mathbb {Z}$ and set

$$ \begin{align*}f_{2}(n):=\sum_{i\in\mathbb{N}^{d},\vert i\vert\leq s}Q^{\ast}a_{i}n^{i}.\end{align*} $$

Then, $f_{2}$ is an integer coefficient polynomial of degree at most s. Note that for all $n\in \mathbb {Z}^{d}$ ,

$$ \begin{align*} \frac{1}{p}(f(n)-f_{2}(n))=\sum_{i\in\mathbb{N}^{d},\vert i\vert\leq s}\frac{a_{i}}{Q}\frac{1-Q^{\ast}Q}{p}n^{i}, \end{align*} $$

the left-hand side of which belongs to $\mathbb {Z}/p$ and the right-hand side of which belongs to $\mathbb {Z}/Q$ . So, $f_{1}(n):=({1}/{p})(f(n)-f_{2}(n))$ takes values in $(\mathbb {Z}/Q)\cap (\mathbb {Z}/p)=\mathbb {Z}$ .

There is a natural correspondence between polynomials taking values in $\mathbb {F}_{p}$ and polynomials taking values in $\mathbb {Z}/p$ . Let $F\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d'})$ and $f\in \text {poly}(\mathbb {Z}^{d}\to (\mathbb {Z}/p)^{d'})$ be polynomials of degree at most s for some $s<p$ . If $F=\iota \circ (pf)\circ \tau $ , then we say that F is induced by f and f is a lifting of F. (Note that since $pf\circ \tau $ takes values in $\mathbb {Z}^{d'}$ , the coefficients of $pf\circ \tau $ belong to $\mathbb {Z}^{d'}/s!$ , and thus $\iota \circ pf\circ \tau $ is well defined by Convention 1.8.) We say that f is a regular lifting of F if, in addition, f has the same degree as F and f has $\{0,({1}/{p}),\ldots ,{(p-1)}/{p}\}$ -coefficients.

We provide some basic properties of lifting for later uses. Their proofs are simple and so we omit them.

Lemma 2.5. (Basic properties of lifting)

Let $d,d',d"\in \mathbb {N}_{+}$ and $p>\max \{d,d',d"\}$ be a prime.

1. (i) Every $f\in \mathrm{poly}(\mathbb {Z}^{d}\to (\mathbb {Z}/p)^{d'})$ of degree less than p induces $\iota \circ (pf)\circ \tau $ , which is a polynomial of degree at most $\deg (f)$ . Moreover, if f is homogeneous, then so is $\iota \circ (pf)\circ \tau $ .

2. (ii) Every $F\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}^{d'}_{p})$ of degree less than p admits a regular lifting. Moreover, if F is homogeneous, we may further require the lifting to be homogeneous.

3. (iii) If $f\in \mathrm {poly}(\mathbb {Z}^{d}\to (\mathbb {Z}/p)^{d'})$ is a lifting of some $F\in \mathrm { poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d'})$ with both f and F having degrees at most $p-1$ , then for any $f'\in \mathrm { poly}(\mathbb {Z}^{d}\to (\mathbb {Z}/p)^{d'})$ of degree less than p, $f'$ is a lifting of F if and only if $f-f'$ is integer valued.

4. (iv) If $f,f'\in \mathrm {poly}(\mathbb {Z}^{d}\to (\mathbb {Z}/p)^{d'})$ are liftings of $F, F'\in \mathrm { poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d'})$ , respectively, with all of $f,f',F$ , and $F'$ having degrees at most $(p-1)/2$ , then $f+f'$ is a lifting of $F+F'$ and $pff'$ is a lifting of $FF'$ .

5. (v) If $f\in \mathrm {poly}(\mathbb {Z}^{d}\to (\mathbb {Z}/p)^{d'})$ is a lifting of some $F\in \mathrm { poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d'})$ with both f and F having degrees at most $\sqrt {p}$ , and $f\in \mathrm { poly}(\mathbb {Z}^{d'}\to (\mathbb {Z}/p)^{d"})$ is a lifting of some $F\in \mathrm { poly}(\mathbb {F}_{p}^{d'}\to \mathbb {F}_{p}^{d"})$ with both f and F having degrees less than $\sqrt {p}$ , then $f'\circ (pf)$ is a lifting of $F'\circ F$ .

6. (vi) If $f\in \mathrm {poly}(\mathbb {Z}^{d}\to (\mathbb {Z}/p)^{d'})$ is a lifting of some $F\in \mathrm { poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d'})$ with both f and F having degrees less than p, then $\tau \circ F\equiv (pf)\circ \tau \,\mod \mathbb {Z}^{d'}$ .

3 Background material for nilmanifolds

3.1 Nilmanifolds, filtrations, and polynomial sequences

We start with some basic definitions on nilmanifolds. Let G be a group and $g,h\in G$ . Denote $[g,h]:=g^{-1}h^{-1}gh$ . For subgroups $H,H'$ of G, let $[H,H']$ denote the group generated by $[h,h']$ for all $h\in H$ and $h'\in H'$ .

Definition 3.1. (Filtered group)

Let G be a group. An $\mathbb {N}$ -filtration on G is a collection $G_{\mathbb {N}}=(G_{i})_{i\in \mathbb {N}}$ of subgroups of G indexed by $\mathbb {N}$ with $G_{0}=G$ such that the following hold:

1. (i) for all $i,j\in \mathbb {N}$ with $i\leq j$ , we have that $G_{i}\supseteq G_{j}$ ;

2. (ii) for all $i,j\in \mathbb {N}$ , we have $[G_{i},G_{j}]\subseteq G_{i+j}$ .

For $s\in \mathbb {N}$ , we say that G is an ( $\mathbb {N}$ -filtered) nilpotent group of degree at most s (or of degree $\leq s$ ) with respect to some $\mathbb {N}$ -filtration $(G_{i})_{i\in \mathbb {N}}$ if $G_{i}$ is trivial whenever $i>s$ .

Example 3.2. The lower central series of a group G is the $\mathbb {N}$ -filtration $(G^{i})_{i\in \mathbb {N}}$ given by $G^{0}:=G$ and $G^{i+1}=[G^{i},G]$ for all $i\in \mathbb {N}$ . We say that G is a nilpotent group of step (or degree) at most s (with respect to the lower central series) if $G^{i}$ is trivial for all $i\geq s+1$ .

Definition 3.3. (Nilmanifold)

Let $\Gamma $ be a discrete and cocompact subgroup of a connected, simply connected nilpotent Lie group G with filtration $G_{\mathbb {N}}=(G_{i})_{i\in \mathbb {N}}$ such that ${\Gamma _{i}:=\Gamma \cap G_{i}}$ is a cocompact subgroup of $G_{i}$ for all $i\in \mathbb {N}$ . (In some papers, such $\Gamma _{i}$ is called a rational subgroup of G.) Then, we say that $G/\Gamma $ is an ( $\mathbb {N}$ -filtered) nilmanifold and we use $(G/\Gamma )_{\mathbb {N}}$ to denote the collection $(G_{i}/\Gamma _{i})_{i\in \mathbb {N}}$ (which is called the $\mathbb {N}$ -filtration of $G/\Gamma $ ). We say that $G/\Gamma $ has degree $\leq s$ with respect to $(G/\Gamma )_{\mathbb {N}}$ if G has degree $\leq s$ with respect to $G_{\mathbb {N}}$ . (Unlike the convention in literature, for our convenience, we do not require $G_{0}=G$ to be the same as $G_{1}$ .)

We also need to define some special types of nilmanifolds.

Definition 3.4. (Sub-nilmanifold)

Let $G/\Gamma $ be an $\mathbb {N}$ -filtered nilmanifold of degree $\leq s$ with filtration $G_{\mathbb {N}}$ and H be a rational subgroup of G. Then, $H/(H\cap \Gamma )$ is also an $\mathbb {N}$ -filtered nilmanifold of degree $\leq s$ with the filtration $H_{\mathbb {N}}$ given by $H_{i}:=G_{i}\cap H$ for all $i\in \mathbb {N}$ (see [8, Example 6.14]). We say that $H/(H\cap \Gamma )$ is a sub-nilmanifold of $G/\Gamma $ , $H_{\mathbb {N}}$ (or $(H/(H\cap \Gamma ))_{\mathbb {N}}$ ) is the filtration induced by $G_{\mathbb {N}}$ (or $(G/\Gamma )_{\mathbb {N}}$ ).

Definition 3.5. (Quotient nilmanifold)

Let $G/\Gamma $ be an $\mathbb {N}$ -filtered nilmanifold of degree $\leq s$ with filtration $G_{\mathbb {N}}$ and H be a normal subgroup of G. Then, $(G/H)/(\Gamma /(\Gamma \cap H))$ is also an $\mathbb {N}$ -filtered nilmanifold of most $\leq s$ with the filtration $(G/H)_{\mathbb {N}}$ given by $(G/H)_{i}:=G_{i}/(H\cap G_{i})$ for all $i\in \mathbb {N}$ . We say that $(G/H)/(\Gamma /(\Gamma \cap H))$ is the quotient nilmanifold of $G/\Gamma $ by H and that $(G/H)_{\mathbb {N}}$ is the filtration induced by $G_{\mathbb {N}}$ .

Definition 3.6. (Product nilmanifold)

Let $G/\Gamma $ and $G'/\Gamma '$ be $\mathbb {N}$ -filtered nilmanifolds of degree $\leq s$ with filtration $G_{\mathbb {N}}$ and $G^{\prime }_{\mathbb {N}}$ . Then, $(G\times G')/(\Gamma \times \Gamma ')$ is also an $\mathbb {N}$ -filtered nilmanifold of most $\subseteq J$ with the filtration $((G\times G')/(\Gamma \times \Gamma '))_{\mathbb {N}}$ given by $((G\times G')/ (\Gamma \times \Gamma '))_{i}:=(G_{i}\times G^{\prime }_{i})/(\Gamma _{i}\times \Gamma ^{\prime }_{i})$ for all $i\in \mathbb {N}$ . We say that $(G\times G')/(\Gamma \times \Gamma ')$ is the product nilmanifold of $G/\Gamma $ and $G'/\Gamma '$ , and that $((G\times G')/(\Gamma \times \Gamma '))_{\mathbb {N}}$ is the filtration induced by $G_{\mathbb {N}}$ and $G^{\prime }_{\mathbb {N}}$ .

We remark that although we used the same terminology ‘induce’ in Definitions 3.4, 3.5, and 3.6, this will not cause any confusion in the paper as the meaning of ‘induce’ will be clear from the context.

Definition 3.7. (Filtered homomorphism)

An ( $\mathbb {N}$ -filtered) homomorphism $\phi \colon G/\Gamma \to G'/\Gamma '$ between two $\mathbb {N}$ -filtered nilmanifolds is a group homomorphism $\phi \colon G\to G'$ which maps $\Gamma $ to $\Gamma '$ and maps $G_{i}$ to $G^{\prime }_{i}$ for all $i\in \mathbb {N}$ .

Every nilmanifold has an explicit algebraic description by using the Mal’cev basis.

Definition 3.8. (Mal’cev basis)

Let $s\in \mathbb {N}_{+}$ , $G/\Gamma $ be a nilmanifold of step at most s with the $\mathbb {N}$ -filtration $(G_{i})_{i\in \mathbb {N}}$ . Let $\dim (G)=m$ and $\dim (G_{i})=m_{i}$ for all $0\leq i\leq s$ . A basis $\mathcal {X}:=\{X_{1},\ldots ,X_{m}\}$ for the Lie algebra $\log G$ of G (over $\mathbb {R}$ ) is a Mal’cev basis for $G/\Gamma $ adapted to the filtration $G_{\mathbb {N}}$ if:

• • for all $0\leq j\leq m-1$ , $\log H_{j}:=\text {Span}_{\mathbb {R}}\{\xi _{j+1},\ldots ,\xi _{m}\}$ is a Lie algebra ideal of $\log G$ and so $H_{j}:=\exp (\log H_{j})$ is a normal Lie subgroup of $G;$

• • $G_{i}=H_{m-m_{i}}$ for all $0\leq i\leq s$ ;

• • the map $\psi ^{-1}\colon \mathbb {R}^{m}\to G$ given by

  $$ \begin{align*} \psi^{-1}(t_{1},\ldots,t_{m})=\exp(t_{1}X_{1})\cdots\exp(t_{m}X_{m}) \end{align*} $$
  is a bijection;

• • $\Gamma =\psi ^{-1}(\mathbb {Z}^{m})$ .

We call $\psi $ the Mal’cev coordinate map with respect to the Mal’cev basis $\mathcal {X}$ . If ${g=\psi ^{-1}(t_{1},\ldots ,t_{m})}$ , we say that $(t_{1},\ldots ,t_{m})$ are the Mal’cev coordinates of g with respect to $\mathcal {X}$ .

We say that the Mal’cev basis $\mathcal {X}$ is C-rational (or of complexity at most C) if all the structure constants $c_{i,j,k}$ in the relations

$$ \begin{align*}[X_{i},X_{j}]=\sum_{k}c_{i,j,k}X_{k}\end{align*} $$

are rational with complexity at most C.

By [5, Lemma A.14], for any $h\in G$ , there is a unique way to write h as $h=\{h\}[h]$ such that $\psi (\{h\})\in [0,1)^{m}$ and $[h]\in \Gamma $ . We adopt this notation throughout this paper.

It is known that for every filtration $G_{\bullet }$ which is rational for $\Gamma $ , there exists a Mal’cev basis adapted to it. See for example the discussion after [5, Definition 2.1].

We use the following quantities to describe the complexities of the objects defined above.

Definition 3.9. (Notions of complexities for nilmanifolds)

Let $G/\Gamma $ be a nilmanifold with an $\mathbb {N}$ -filtration $G_{\mathbb {N}}$ and a Mal’cev basis $\mathcal {X}=\{X_{1},\ldots ,X_{D}\}$ adapted to it. We say that $G/\Gamma $ is of complexity at most C if the Mal’cev basis $\mathcal {X}$ is C-rational and $\dim (G)\leq C$ .

An element $g\in G$ is of complexity at most C (with respect to the Mal’cev coordinate map $\psi \colon G/\Gamma \to \mathbb {R}^{m}$ ) if $\psi (g)\in [-C,C]^{m}$ .

Let $G'/\Gamma '$ be a nilmanifold endowed with the Mal’cev basis $\mathcal {X}'=\{X^{\prime }_{1},\ldots ,X^{\prime }_{D'}\}$ , respectively. Let $\phi \colon G/\Gamma \to G'/\Gamma '$ be a filtered homomorphism. We say that $\phi $ is of complexity at most C if the map $X_{i}\to \sum _{j}a_{i,j}X^{\prime }_{j}$ induced by $\phi $ is such that all $a_{i,j}$ are of complexity at most C.

Let $G'\subseteq G$ be a closed connected subgroup. We say that $G'$ is C-rational (or of complexity at most C) relative to $\mathcal {X}$ if the Lie algebra $\log G$ has a basis consisting of linear combinations $\sum _{i}a_{i}X_{i}$ such that $a_{i}$ are rational numbers of complexity at most C.

Convention 3.10. In the rest of the paper, all nilmanifolds are assumed to have a fixed filtration, Mal’cev basis, and a smooth Riemannian metric induced by the Mal’cev basis. Therefore, we will simply say that a nilmanifold, Lipschitz function, sub-nilmanifold, etc. are of complexity C without mentioning the reference filtration and Mal’cev basis.

Definition 3.11. (Polynomial sequences)

Let $k\in \mathbb {N}_{+}$ and G be a connected simply connected nilpotent Lie group. Let $(G_{i})_{i\in \mathbb {N}}$ be an $\mathbb {N}$ -filtration of G. A map $g\colon \mathbb {Z}^{k}\to G$ is an ( $\mathbb {N}$ -filtered) polynomial sequence if

$$ \begin{align*}\Delta_{h_{m}}\cdots \Delta_{h_{1}} g(n)\in G_{m}\end{align*} $$

for all $m\in \mathbb {N}$ and $n,h_{1},\ldots ,h_{m}\in \mathbb {Z}^{k}$ . (Recall that $\Delta _{h}g(n):=g(n+h)g(n)^{-1}$ for all $n, h\in H$ .)

The set of all $\mathbb {N}$ -filtered polynomial sequences is denoted by $\text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ .

By [8, Corollary B.4], $\text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ is a group with respect to the pointwise multiplicative operation. We refer the readers to [8, Appendix B] for more properties for polynomial sequences.

3.2 Different notions of polynomial sequences

We start with some conventional definitions for polynomial sequences.

Definition 3.12. (Null, rational, and periodic polynomial sequences)

Let $k\in \mathbb {N}_{+}$ , $G/\Gamma $ be a nilmanifold, $n_{\ast }\in \mathbb {Z}^{k}$ , and $g\in \text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ . We say that g is:

• • null if $g(n)\in \Gamma $ for all $n\in \mathbb {Z}^{k}$ ;

• • rational with base point $n_{\ast }$ if $g(Qn+n_{\ast })\in \Gamma $ for all $n\in \mathbb {Z}^{k}$ for some $Q\in \mathbb {N}_{+}$ , in which case, we also say that g is Q-rational with base point $n_{\ast }$ . We simply say that g is rational or Q-rational when $n_{\ast }=\mathbf {0}$ ;

• • periodic if $g(n+Qm)^{-1}g(n)\in \Gamma $ for all $m,n\in \mathbb {Z}^{k}$ for some $Q\in \mathbb {N}_{+}$ , in which case, we also say that g is Q-periodic.

We refer the readers to [5, Appendix A] for properties of rational/periodic polynomial sequences.

In this paper, since we will work with polynomial sequences which are null, rational, or periodic on certain subsets of $\mathbb {Z}^{k}$ , we introduce the following notation.

Definition 3.13. (Null, rational, and periodic polynomial sequences on subsets of $\mathbb {Z}^{k}$ )

Let $k,Q\in \mathbb {N}_{+}$ , $G/\Gamma $ be an $\mathbb {N}$ -filtered nilmanifold, $\Omega $ be a subset of $\mathbb {Z}^{k}$ , and $n_{\ast }\in \Omega $ .

• • We use $\text {poly}(\Omega \to G_{\mathbb {N}}\vert \Gamma )$ to denote the set of all $g\in \text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ that is null on $\Omega $ , meaning that $g(n)\in \Gamma $ for all $n\in \Omega $ .

• • We use $\text {poly}_{\approx Q,n_{\ast }}(\Omega \to G_{\mathbb {N}}\vert \Gamma )$ to denote the set of all $g\in \text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ that is Q-rational on $\Omega $ with base point $n_{\ast }$ meaning that $g(n_{\ast }+Qm)\in \Gamma $ for all $m\in \mathbb {Z}^{k}$ with $n_{\ast }+Qm\in \Omega $ .

• • We use $\text {poly}_{Q}(\Omega \to G_{\mathbb {N}}\vert \Gamma )$ to denote the set of all $g\in \text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ that is Q-periodic on $\Omega $ , meaning that $g(n+Qm)^{-1}g(n)\in \Gamma $ for all $m,n\in \mathbb {Z}^{k}$ with $n,n+Qm\in \Omega $ .

We informally say that a polynomial sequence is partially null if it is null on a subset of (instead of the entire) $\mathbb {Z}^{k}$ . We adopt similar conventions to rational and periodic sequences.

Example 3.14. The set $\text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}}\vert \Gamma )$ is simply the set of all $\Gamma $ -valued (that is, null) polynomials. In other words, $\text {poly}(\mathbb {Z}^{k}\to \Gamma _{\mathbb {N}})=\text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}}\vert \Gamma )$ . The set $\text {poly}_{\approx Q,\mathbf {0}}(\mathbb {Z}^{k}\to G_{\mathbb {N}}\vert \Gamma )$ is the set of Q-rational polynomial sequences in ${\text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})}$ . The set $\text {poly}_{Q}(\mathbb {Z}^{k}\to G_{\mathbb {N}}\vert \Gamma )$ is the set of Q-periodic polynomial sequences in ${\text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})}$ .

Example 3.15. Let $(\mathbb {R}/\mathbb {Z})_{\mathbb {N}}$ be the nilmanifold with the filtration given by $G_{0}=\cdots =G_{s}=\mathbb {R}$ and $G_{i}=\{\mathrm{id}_{G}\}$ for $i>s$ . Then, $\text {poly}(\Omega \to \mathbb {R}_{\mathbb {N}}\vert \mathbb {Z})$ is the collection of all polynomials in $\text {poly}(\Omega \to \mathbb {R}\vert \mathbb {Z})$ (see in Definition 2.3) of degree at most s.

Example 3.16. By [8, Corollary B.4], it is not hard to see that $\text {poly}(\Omega \to G_{\mathbb {N}}\vert \Gamma )$ and $\text {poly}_{\approx Q,n_{\ast }}(\mathbb {Z}^{k}\to G_{\mathbb {N}}\vert \Gamma )$ are groups. However, we caution the readers that $\text {poly}_{Q}(\mathbb {Z}^{k}\to G_{\mathbb {N}}\vert \Gamma )$ is not necessarily a group. Let $k=1$ and $G=(\mathbb {R}^{3},\ast )$ be the Heisenberg group with the group action given by

$$ \begin{align*} (x,y,z)\ast(x',y',z'):=(x+x',y+y',z+z'+xy') \end{align*} $$

with the lower central series as its $\mathbb {N}$ -filtration, meaning that $G_{0}=G_{1}=G$ , $G_{2}=\{0\}\times \{0\}\times \mathbb {R}$ , and $G_{s}=\{\mathbf {0}\}$ for $s\geq 3$ . Indeed, let $d=k=1$ , $\Gamma =\mathbb {Z}^{3}$ , $g_{1},g_{2}\in \Gamma $ , and ${f_{i}(n)=g_{i}^{n/Q}}$ for all $n\in \mathbb {Z}$ and $i=1,2$ . Then, $f_{1},f_{2}\in \text {poly}_{Q}(\mathbb {Z}\to G_{\mathbb {N}}\vert \Gamma )$ . However,

$$ \begin{align*} & f_{2}(n+Q)^{-1}f_{1}(n+Q)^{-1}f_{1}(n)f_{2}(n)\\ & \quad=g_{2}^{-1-({n}/{Q})}g_{1}^{-1}g_{2}^{{n}/{Q}}=g_{2}^{-1}[g_{2}^{{n}/{Q}},g_{1}]g_{1}^{-1}=[g_{2},g_{1}]^{{n}/{Q}}g_{2}^{-1}g_{1}^{-1}. \end{align*} $$

In general, $[g_{2},g_{1}]^{{n}/{Q}}$ does not always belong to $\Gamma $ if we choose $g_{1}$ and $g_{2}$ properly. This means that $f_{1}f_{2}$ does not need to belong to $\text {poly}_{p}(\mathbb {Z}\to G_{\mathbb {N}}\vert \Gamma )$ .

The next proposition shows that partially Q-rational sequences are also partially $O_{k,s}(Q^{O_{k,s}(1)})$ -periodic, the later characterization of which is typically more useful in applications.

Proposition 3.17. Let $k,Q,s\in \mathbb {N}_{+}$ , $p\gg _{k,Q,s} 1$ be a prime, $\Omega \subseteq \mathbb {Z}^{k}$ be a non-empty p-periodic set, $n_{\ast }\in \Omega $ , $G/\Gamma $ be a nilmanifold of step at most s and complexity at most Q, and $g\in \mathrm {poly}_{\approx Q,n_{\ast }}(\Omega \to G_{\mathbb {N}}\vert \Gamma )$ . Then, there exists $Q'\in \mathbb {N}_{+}$ with $Q'\ll _{k,s} Q^{O_{k,s}(1)}$ such that g belongs to $\mathrm {poly}_{Q'}(\Omega \to G_{\mathbb {N}}\vert \Gamma )$ .

To prove Proposition 3.17, we need the following result.

Proposition 3.18. Let $k,s\in \mathbb {N}_{+}$ , $\delta>0$ , and $P\in \mathrm {poly}(\mathbb {Z}^{k}\to \mathbb {Q})$ be a rational polynomial of degree at most s. Suppose that P is K-periodic for some $K\in \mathbb {N}_{+}$ and suppose that there exists a subset W of $[K]^{k}$ of cardinality at least $\delta K^{k}$ such that $P(W)\subseteq \mathbb {Z}$ . Then, the coefficients of P belong to $\mathbb {Z}/r$ for some $r\in \mathbb {N}_{+}$ with $r\ll _{k,s}\delta ^{-O_{k,s}(1)}$ .

Proof. Let $F\colon \mathbb {T}\to [0,1]$ be a Lipschitz function supported on $(-\delta /10,\delta /10)$ with $F(0)=1$ and with Lipschitz norm at most $100\delta ^{-1}$ . Then, $\mathbb {E}_{n\in \mathbb {Z}^{k}} F(P(n) \,\mod \mathbb {Z})\geq \delta $ and $\int _{\mathbb {T}}F\,dm\leq \delta /2$ (where m is the Lebesgue measure on $\mathbb {T}$ ). So,

$$ \begin{align*} \frac{\vert\mathbb{E}_{n\in\mathbb{Z}^{k}} F(P(n) \,\mod \mathbb{Z})-\int_{\mathbb{T}}F\,dm\vert}{\Vert F\Vert_{\mathrm{Lip}}}\geq \delta^{2}/200 \end{align*} $$

and thus, the sequence $(P(n) \,\mod \mathbb {Z})_{n\in \mathbb {Z}^{k}}$ is not $\delta ^{2}/200$ -equidistributed in $\mathbb {T}$ . By [5, Theorem 8.6], there exist $k\in \mathbb {Z}\backslash \{0\}$ with $0<\vert k\vert \ll _{k,s}\delta ^{-O_{k,s}(1)}$ and $a\in \mathbb {R}$ such that $kP(n)\equiv a\,\mod \mathbb {Z}$ for all $n\in \mathbb {Z}^{k}$ . Since W is non-empty, we may take $a=0$ . So, by interpolation, the coefficients of P belong to $\mathbb {Z}/r$ for some $r\in \mathbb {N}_{+}$ with $r\ll _{k,s}\delta ^{-O_{k,s}(1)}$ .

Proof of Proposition 3.17

Let $\psi =(\psi _{1},\ldots ,\psi _{m})\colon G\to \mathbb {R}^{m}$ be the Mal’cev coordinate map. Then, each $\psi _{i}(g(n))$ is a rational polynomial of degree at most s. For convenience, denote $f_{i}:=\psi _{i}\circ g$ . Since $p\gg _{Q} 1$ , for any $x\in \Omega $ , there exists $v_{x},u_{x}\in \mathbb {Z}^{k}$ such that ${n_{\ast }+Qv_{x}+pu_{x}=x}$ . Then, for all $y\in \mathbb {Z}^{k}$ , we have that $n_{\ast }+Qv_{x}+pQy=n_{\ast }+Q(v_{x}+py)\in \Omega $ and thus, $f_{i}(n_{\ast }+Qv_{x}+pQy)\in \mathbb {Z}$ . By interpolation, all the coefficients of the polynomial $f_{i}(n_{\ast }+Qv_{x}+pQ\cdot )$ belong to $\mathbb {Z}/(s!)^{k}$ and thus, all the coefficients of the polynomial $f_{i}(n_{\ast }+Qv_{x}+p\cdot )$ belong to $\mathbb {Z}/Q^{s}(s!)^{k}$ . So, we have that

(3.1) $$ \begin{align} \begin{aligned} f_{i}(x)\in\mathbb{Z}/Q^{s}(s!)^{k} \quad\text{for all } x\in\Omega. \end{aligned} \end{align} $$

For $h=(h_{1},\ldots ,h_{m}), h'=(h^{\prime }_{1},\ldots ,h^{\prime }_{m})\in \mathbb {R}^{m}$ , and $1\leq i\leq m$ , by [5, Lemma A.3], we may write $\psi _{i}(\psi ^{-1}(h)\psi ^{-1}(h'))$ as a polynomial of degree $O_{k,s}(1)$ with coefficients in $\mathbb {Z}/q_{1}$ for some $q_{1}\ll _{k,s} Q^{O_{k,s}(1)}$ , and this polynomial depends only on the first i variables of h and $h'$ . Since $\psi _{i}(\psi ^{-1}(h)\psi ^{-1}(h))=\mathbf {0}$ , we may write $\psi _{i}(\psi ^{-1}(h)\psi ^{-1}(h'))=\psi _{i}(\psi ^{-1}(h)\psi ^{-1}(h'))-\psi _{i}(\psi ^{-1}(h)\psi ^{-1}(h))$ as $\sum _{i'=1}^{i}(h_{i'}-h^{\prime }_{i'})P_{i,i'}(h,h')$ for some polynomials $P_{i,i'}$ of degree $O_{k,s}(1)$ with coefficients in $\mathbb {Z}/q_{1}$ for some $q_{1}\in \mathbb {N}_{+}$ with ${q_{1}\ll _{k,s} Q^{O_{k,s}(1)}}$ . Therefore, we have that

(3.2) $$ \begin{align} \begin{aligned} \psi_{i}(g(n'+qn)^{-1}g(n'))=\sum_{i'=1}^{i}(f_{i'}(n'+qn)-f_{i'}(n'))P_{i,i'}(\mathbf{f}(n'+qn),\mathbf{f}(n')) \end{aligned} \end{align} $$

for all $n,n'\in \mathbb {Z}^{k}$ and $q\in \mathbb {N}_{+}$ , where $\mathbf {f}(n):=(f_{1}(n),\ldots ,f_{i}(n))$ .

Since g is Q-rational with base point $n_{\ast }$ on $\Omega $ , we have that $f_{i}(n_{\ast }+Qn)\in \mathbb {Z}$ whenever $n_{\ast }+Qn\in \Omega $ . Since $\Omega $ is p-periodic, we have that $f_{i}(n_{\ast }+pQn)\in \mathbb {Z}$ for all $n\in \mathbb {Z}^{k}$ since $\Omega $ is p-periodic.

Since $f_{i}$ is rational, it is also $Q'$ -periodic for some $Q'\in \mathbb {N}$ . We may assume without loss of generality that $pQ\vert Q'$ . Note that the set W of $m\in [Q']^{k}$ for which $f_{i}(m)\in \mathbb {Z}$ contains vectors of the form $m=n_{\ast }+pQn$ for any $n\in \mathbb {Z}^{k}$ with $n_{\ast }+pQn\in [Q']^{k}$ . So, the density of W in $[Q']^{k}$ is at least $(pQ)^{-k}$ . So, by Proposition 3.18, the coefficients of the polynomial $f_{i}(n_{\ast }+pQ\cdot )$ belong to $\mathbb {Z}/rp^{O_{k,s}(1)}$ for some $r\ll _{k,s} Q^{O_{k,s}(1)}$ . So, by interpolation, all the coefficients of the polynomial $f_{i}$ belong to $\mathbb {Z}/Q^{s}rp^{O_{k,s}(1)}$ .

Moreover, for any $x,y\in \mathbb {Z}^{k}$ and $Q'\in \mathbb {N}_{+}$ , since all the coefficients of the polynomial $f_{i}$ belong to $\mathbb {Z}/Q^{s}rp^{O_{k,s}(1)}$ , we have that $f_{i}(x+Q'Q^{s}ry)-f_{i}(x)\in Q'\mathbb {Z}/p^{O_{k,s}(1)}$ . If, in addition, $x,x+Q'Q^{s}ry\in \Omega $ , then it follows from (3.1) that

$$ \begin{align*}f_{i}(x+Q'Q^{s}ry)-f_{i}(x)\in (\mathbb{Z}/Q^{s}(s!)^{k})\cap(Q'\mathbb{Z}/p^{O_{k,s}(1)})=Q'\mathbb{Z},\end{align*} $$

where the last equality follows from the fact that p is a prime with $p\gg _{k,Q,s} 1$ . Therefore, it follows from (3.2) that there exists some $Q'\in \mathbb {N}_{+}$ with $Q'\ll _{k,s} Q^{O_{k,s}(1)}$ such that $\psi _{i}(g(n'+Q'Q^{s}rn)^{-1}g(n'))\in \mathbb {Z}$ for all $n,n'\in \mathbb {Z}^{k}$ with $n',n'+Q'Q^{s}rn\in \Omega $ . This means that g is $Q'Q^{s}r$ -periodic on $\Omega $ . This completes the proof.

Since $\mathbb {Z}^{k}$ is p-periodic, as a consequence of Proposition 3.17, we recover [5, Lemma A.12].

Corollary 3.19. [5, Lemma A.12]

Let $k,s\in \mathbb {N}_{+}$ and $G/\Gamma $ be a nilmanifold of step at most s. Then, every rational polynomial sequence in $\mathrm {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ is periodic.

3.3 Type-I horizontal torus and character

Horizontal torus and character are important notions which characterize the equidistribution properties of nilsequences. In the literature, there are at least three different types of horizontal torus and character. In this paper, as well as the series of work [15–17], we refer to them as type-I, type-II, and type-III. In this paper, we use the type-I horizontal torus and character defined next. (We will define the type-II horizontal torus and character in [16], and the type-III horizontal torus and character in [17].)

Definition 3.20. (Type-I horizontal torus and character)

Let $G/\Gamma $ be a nilmanifold endowed with a Mal’cev basis $\mathcal {X}$ . The type-I horizontal torus of $G/\Gamma $ is $G/[G,G]\Gamma $ . A type-I horizontal character is a continuous homomorphism $\eta \colon G\to \mathbb {R}$ such that ${\eta (\Gamma )\subseteq \mathbb {Z}}$ . When written in the coordinates relative to $\mathcal {X}$ , we may write $\eta (g)=k\cdot \psi (g)$ for some unique $k=(k_{1},\ldots ,k_{m})\in \mathbb {Z}^{m}$ , where $\psi \colon G\to \mathbb {R}^{m}$ is the coordinate map with respect to the Mal’cev basis $\mathcal {X}$ . We call the quantity $\Vert \eta \Vert :=\vert k\vert =\vert k_{1}\vert +\cdots +\vert k_{m}\vert $ the complexity of $\eta $ (with respect to $\mathcal {X}$ ).

It is not hard to see that any type-I horizontal character mod $\mathbb {Z}$ vanishes on $[G,G]\Gamma $ and thus descends to a continuous homomorphism between the type-I horizontal torus $G/[G,G]\Gamma $ and $\mathbb {R}/\mathbb {Z}$ . Moreover, $\eta \,\mod \mathbb {Z}$ is a well-defined map from $G/\Gamma $ to $\mathbb {R}/\mathbb {Z}$ .

Type-I horizontal torus and character are used to characterize whether a nilsequence is equidistributed on a nilmanifold [5, 12]. We provide some properties for later use. The proof of the following lemma is similar to that of [5, Lemma 6.7], [8, Lemma B.9], and [1, Lemma 2.8]. We omit the details.

Lemma 3.21. Let $k\in \mathbb {N}_{+}$ , $s\in \mathbb {N}$ , and G be an $\mathbb {N}$ -filtered group of degree at most s. A function $g\colon \mathbb {Z}^{k}\to G$ belongs to $\mathrm { poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ if and only if for all $i\in \mathbb {N}^{k}$ with $\vert i\vert \leq s$ , there exists $X_{i}\in \log (G_{\vert i\vert })$ such that

$$ \begin{align*} g(n)=\prod_{i\in\mathbb{N}^{k}, \vert i\vert\leq s}\exp\bigg(\binom{n}{i}X_{i}\bigg). \end{align*} $$

Moreover, if $g\in \mathrm {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ , then the choice of $X_{i}$ is unique.

Furthermore, if $G'$ is a subgroup of G and g takes values in $G'$ , then $X_{i}\in \log (G')$ for all $i\in \mathbb {N}^{k}$ .

An equivalent way of saying that a function $g\colon \mathbb {Z}^{k}\to G$ belongs to $\text {poly}(\mathbb {Z}^{k}\to G_{\mathbb {N}})$ is that

(3.3) $$ \begin{align} g(n)=\prod_{i\in\mathbb{N}^{k}, \vert i\vert\leq s}g_{i}^{\binom{n}{i}} \end{align} $$

for some $g_{i}\in G_{\vert i\vert }$ (with any fixed order in $\mathbb {N}^{k}$ ). We call $g_{i}$ the (ith) type-I Taylor coefficient of g, and (3.3) the type-I Taylor expansion of g.

3.4 Vertical torus and character

The vertical torus is an important concept that allows us to do Fourier decompositions on nilmanifolds.

Definition 3.22. (Vertical torus and character)

Let $s\in \mathbb {N}$ , $G/\Gamma $ be a nilmanifold with an $\mathbb {N}$ -filtration $(G_{i})_{i\in \mathbb {N}}$ of degree $\leq s$ with a Mal’cev basis $\mathcal {X}$ adapted to it. Then, $G_{s}$ lies in the center of G. The vertical torus of $G/\Gamma $ is the set $G_{s}/(\Gamma \cap G_{s})$ , which is a connected compact abelian Lip group isomorphic to $\mathbb {T}^{\dim (G_{s})}$ . A vertical character of $G/\Gamma $ (with respect to the filtration $(G_{i})_{i\in \mathbb {N}}$ ) is a continuous homomorphism $\xi \colon G_{s}\to \mathbb {R}$ such that $\xi (\Gamma \cap G_{s})\subseteq \mathbb {Z}$ (in particular, $\xi $ descends to a continuous homomorphism from the vertical torus $G_{s}/(\Gamma \cap G_{s})$ to $\mathbb {T}$ ). Let $\psi \colon G\to \mathbb {R}^{m}$ be the Mal’cev coordinate map and denote $m_{s}=\dim (G_{s})$ . Then, there exists $k\in \mathbb {Z}^{m_{s}}$ such that $\xi (g_{s})=(\mathbf {0},k)\cdot \psi (g_{s})$ for all $g_{s}\in G_{s}$ (note that the first $\dim (G)-m_{s}$ coordinates of $\psi (g_{s})$ are all zero). We call the quantity $\Vert \xi \Vert :=\vert k\vert $ the complexity of $\xi $ (with respect to $\mathcal {X}$ ).

The following lemma is useful in the study of equidistribution properties on nilmanifolds.

Lemma 3.23. Let $\Omega $ be a non-empty subset of $\mathbb {Z}^{d}$ and $G/\Gamma $ be a nilmanifold with an $\mathbb {N}$ -filtration $G_{\mathbb {N}}$ of degree s. Let $m_{s}=\dim (G_{s})$ and $0<\delta <1/2$ . If a sequence $a\colon \Omega \to G/\Gamma $ is not $\delta $ -equidistributed on $G/\Gamma $ , then there exists a Lipschitz function $F\in \mathrm {Lip}(G/\Gamma \to \mathbb {C})$ with a vertical character of complexity at most $O_{m_{s}}(\delta ^{-O_{m_{s}}(1)})$ such that

$$ \begin{align*} \limsup_{N\to\infty}\bigg\vert\mathbb{E}_{n\in \Omega\cap [N]^{d}}F(a(n))-\int_{G/\Gamma} F\,dm_{G/\Gamma}\bigg\vert\gg_{m_{s}} \delta^{O_{m_{s}}(1)}\Vert F\Vert_{\mathrm{Lip}}, \end{align*} $$

where $m_{G/\Gamma }$ is the Haar measure of $G/\Gamma $ .

The proof of Lemma 3.23 is a straightforward extension of [5, Lemma 3.7], we omit the details.

4 Background materials for quadratic forms

4.1 Basic properties for quadratic forms

Definition 4.1. (Quadratic forms on $\mathbb {F}_{p}^{d}$ )

We say that a function $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ is a quadratic form if

$$ \begin{align*}M(n)=(nA)\cdot n+n\cdot u+v\end{align*} $$

for some $d\times d$ symmetric matrix A in $\mathbb {F}_{p}$ , some $u\in \mathbb {F}_{p}^{d}$ , and some $v\in \mathbb {F}_{p}$ . We say that A is the matrix associated to M. (Sometimes in the literature, a quadratic form is defined to be a map $B\colon \mathbb {F}_{p}^{d}\times \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d}$ with $B(x,y)=(xA)\cdot y$ for some symmetric matrix A. We define quadratic forms differently for the convenience of this paper.)

We say that M is pure if $u=\mathbf {0}$ . We say that M is homogeneous if $u=\mathbf {0}$ and $v=0$ . We say that M is non-degenerate if $\det (A)\neq 0$ .

A quadratic form in which we are particularly interested is the one induced by the dot product, namely $M(n):=n\cdot n$ , which is associated with the identity matrix.

Throughout this paper, we will crucially use the following philosophy.

Inheriting principle: the intersection of a hypersphere (that is, the set of zeros of a quadratic form) with a subspace or another hypersphere is a hypersphere inheriting properties of the original hypersphere.

One example of this principle is that the intersection inherits the rank of a quadratic form (Proposition 4.8). To make it precise, we need to define quadratic forms on affine subspaces of $\mathbb {F}_{p}^{d}$ . Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form. We use $\mathrm {rank}(M):=\mathrm {rank}(A)$ to denote the rank of M. The M being non-degenerate is equivalent of having rank equal to d. Let $V+c$ be an affine subspace of $\mathbb {F}_{p}^{d}$ of dimension r. There exists a (not necessarily unique) bijective linear transformation $\phi \colon \mathbb {F}_{p}^{r}\to V$ . We say that a function $M\colon V+c\to \mathbb {F}_{p}$ is a quadratic form if there exists a quadratic form $M'\colon \mathbb {F}_{p}^{r}\to \mathbb {F}_{p}$ and a bijective linear transformation $\phi \colon \mathbb {F}_{p}^{r}\to V$ such that $M(n)=M'(\phi ^{-1}(n-c))$ for all $n\in V+c$ (or equivalently, $M'(m)=M(\phi (m)+c)$ for all $m\in \mathbb {F}_{p}^{r}$ ). We define the rank $\mathrm {rank}(M\vert _{V+c})$ of M restricted to $V+c$ as the rank of $M'$ . Note that if ${M(n)=M'(\phi ^{-1}(n-c))=M"({\phi '}^{-1}(n-c))}$ for some quadratic forms $M',M"$ associated to the matrices $A',A"$ , then $A'=BA"{B}^{T}$ , where B is the unique $r\times r$ invertible matrix such that $\phi ^{-1}\circ \phi (m)=mB$ for all $m\in \mathbb {F}_{p}^{r}$ . So, $\mathrm {rank}(M\vert _{V+c})$ is independent of the choice of $M'$ and $\phi '$ .

The following is a straightforward property for quadratic forms, which we record for later use.

Lemma 4.2. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form associated with the matrix A, and $x,y,z\in \mathbb {F}_{p}^{d}$ . Suppose that $M(x)=M(x+y)=M(x+z)=0$ and that $p>2$ . Then, $M(x+y+z)=0$ if and only if $(yA)\cdot z=0$ .

Proof. The conclusion follows from the equality

$$ \begin{align*} M(x+y+z)-M(x+y)-M(x+z)+M(x)=2(yA)\cdot z. \\[-37pt] \end{align*} $$

The next lemma says that using translations and linear transformations, any quadratic form can be transformed into a ‘standard’ form.

Lemma 4.3. Let $d\in \mathbb {N}_{+}$ , $d'\in \mathbb {N}$ , and $p>2$ be a prime. For any quadratic form $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ of rank $d'$ , there exist $c,c',\unicode{x3bb} \in \mathbb {F}_{p}$ and $v\in \mathbb {F}_{p}^{d}$ with $c\neq 0$ and a $d\times d$ invertible matrix R in $\mathbb {F}_{p}$ such that writing $M'(n):=M(nR+v)$ , we have that

(4.1) $$ \begin{align} M'(n_{1},\ldots,n_{d})=cn^{2}_{1}+n_{2}^{2}+\cdots+n^{2}_{d'}+c'n_{d'+1}-\unicode{x3bb}. \end{align} $$

Moreover, if M is homogeneous, then we may further require $c'=\unicode{x3bb} =0$ in (4.1); if M is pure, then we may further require $v=\mathbf {0}$ ; if M is non-degenerate, then we may further require that $d'=d$ .

Remark 4.4. Throughout this paper, whenever we write a quadratic form $M'$ in the form (4.1), if $d'=d$ , then we consider the term $c'n_{d'+1}$ as non-existing.

Proof. Similar to the real valued quadratic forms, by a suitable substitution $n\mapsto nR$ for some upper triangular invertible matrix R and some $v\in \mathbb {F}_{p}^{d}$ , it suffices to consider the case when the matrix A associated to M is diagonal. Since $\mathrm {rank}(M)=d'$ , we may assume without loss of generality that the first $d'$ entry of the diagonal of A is non-zero. Let $c\in \{2,\ldots ,p-1\}$ be the smallest element such that $c\neq x^{2}$ for all $x\in \mathbb {F}_{p}$ (such an element obviously exists). Under a suitable change of variables $(n_{1},\ldots ,n_{d})\mapsto (c_{1}n_{1},\ldots ,c_{d'}n_{d'},n_{d'+1},\ldots ,n_{d})$ for some $c_{1},\ldots ,c_{d'}\in \mathbb {F}_{p}\backslash \{0\}$ and a change of the orders of $n_{1},\ldots ,n_{d'}$ , we may reduce the problem to the case when

$$ \begin{align*}M(n_{1},\ldots,n_{d})=n_{1}^{2}+\cdots+n_{k}^{2}+cn_{k+1}^{2}+\cdots+cn_{d'}^{2}+a_{1}n_{1}+\cdots+a_{d}n_{d}-\unicode{x3bb}\end{align*} $$

for some $0\leq k\leq d'$ , where k is the number of non-zero diagonal entries in A that are quadratic residues. By a suitable substitution $n\mapsto n+m$ for some $m\in \mathbb {F}_{p}^{d}$ , we may reduce the problem to the case when

$$ \begin{align*}M(n_{1},\ldots,n_{d})=n_{1}^{2}+\cdots+n_{k}^{2}+cn_{k+1}^{2}+\cdots+cn_{d'}^{2}+a_{d'+1}n_{d'+1}+\cdots+a_{d}n_{d}-\unicode{x3bb}.\end{align*} $$

By another change of variables, we may reduce the problem to the case when

$$ \begin{align*}M(n_{1},\ldots,n_{d})=n_{1}^{2}+\cdots+n_{k}^{2}+cn_{k+1}^{2}+\cdots+cn_{d'}^{2}+c'n_{d'+1}-\unicode{x3bb}.\end{align*} $$

By the minimality of c, we have that $a^{2}+1\equiv c \,\mod p\mathbb {Z}$ for some $1\leq a\leq p-1$ . If $k\leq d-2$ , then

$$ \begin{align*}cn_{k+1}^{2}+cn_{k+2}^{2}=(an_{k+1}+n_{k+2})^{2}+(n_{k+1}-an_{k+2})^{2}.\end{align*} $$

So, if $k+2\leq d'$ , then since $a^{2}+1\not \equiv 0 \,\mod p$ , under another change of variables, we may use another change of variables to replace $cn_{k+1}^{2}+cn_{k+2}^{2}$ by $n_{k+1}^{2}+n_{k+2}^{2}$ in the expression of M. Inductively, we are reduced to the case $k=d'-1$ or $d'$ . Therefore, (4.1) holds by switching the position of $n_{1}$ and $n_{d'}$ .

The ‘moreover’ part follows immediately through the proof.

4.2 M-isotropic subspaces

Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form associated with the matrix A and V be a subspace of $\mathbb {F}_{p}^{d}$ . Let $V^{\perp {M}}$ denote the set of $\{n\in \mathbb {F}_{p}^{d}\colon (mA)\cdot \text {n=0} \text { for all } m\in V\}$ .

Proposition 4.5. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form associated with the matrix A and V be a subspace of $\mathbb {F}_{p}^{d}$ .

1. (i) $V^{\perp {M}}$ is a subspace of $\mathbb {F}_{p}^{d}$ , and $V\subseteq (V^{\perp {M}})^{\perp {M}}$ . Moreover, $(V^{\perp {M}})^{\perp {M}}=V$ if M is non-degenerate.

2. (ii) Let $\phi \colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d}$ be a bijective linear transformation, $v\in \mathbb {F}_{p}^{d}$ , and $c\in \mathbb {F}_{p}$ . Let $M'\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be the quadratic form given by $M'(n):=M(\phi (n)+v)+c$ . We have that $\mathrm {rank}(M)=\mathrm {rank}(M')$ and $\phi (V^{\perp {M'}})=(\phi (V))^{\perp {M}}$ .

3. (iii) $\mathrm {rank}(M)$ is equal to $d-\dim ((\mathbb {F}_{p}^{d})^{\perp {M}})$ .

Proof. Part (i) is easy to check by definition and the symmetry of A. For part (ii), assume that $\phi (x)=xB$ for some $d\times d$ invertible matrix B, then $\mathrm {rank}(M)=\mathrm {rank}(A)=\mathrm { rank}(BAB^{T})=\mathrm {rank}(M\circ \phi )$ . So, $\mathrm {rank}(M)= \mathrm {rank}(M\circ \phi )=\mathrm {rank}(M(\phi (n)+v))$ since shifting by v does not affect the rank of a quadratic form. The part $\phi (V^{\perp {M'}})=(\phi (V))^{\perp {M}}$ is easy to check by definition.

We now prove part (iii). Let $r=\mathrm {rank}(M)$ . Then, $1\leq r\leq d$ . By Lemma 4.3, we may assume that $M(n)=M'(\phi (n)+v)$ for some bijective linear transformation $\phi \colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}^{d}$ , $v\in \mathbb {F}_{p}^{d}$ , $c,c',\unicode{x3bb} \in \mathbb {F}_{p}, c\neq 0$ , and some quadratic form $M'\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ of the form

$$ \begin{align*} M'(n_{1},\ldots,n_{d})=cn^{2}_{1}+n_{2}^{2}+\cdots+n^{2}_{r}+c'n_{r+1}-\unicode{x3bb}. \end{align*} $$

It is clear that $\mathrm {rank}(M')=d-\dim ((\mathbb {F}_{p}^{d})^{\perp {M'}})=r=\mathrm {rank}(M)$ . By part (iii), $(\mathbb {F}_{p}^{d})^{ \perp {M}}=\phi ^{-1}((\phi (\mathbb {F}_{p}^{d}))^{ \perp {M'}})=\phi ^{-1}((\mathbb {F}_{p}^{d})^{ \perp {M'}})$ . So, $\dim ((\mathbb {F}_{p}^{d})^{ \perp {M}})=\dim ((\mathbb {F}_{p}^{d})^{ \perp {M'}})$ and thus, $\mathrm {rank} (M)=d-\dim ((\mathbb {F}_{p}^{d})^{\perp {M}})$ .

For $n\in \mathbb {R}^{d}$ , the dot product induces the Euclidean norm $\vert n\vert ^{2}:=n\cdot n$ . However, in $\mathbb {F}_{p}^{d}$ , the dot product (as well as general quadratic forms) does not induce a norm in $\mathbb {F}_{p}^{d}$ , due to the existence of isotropic subspaces.

Definition 4.6. (M-isotropic subspaces)

Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form associated with the matrix A. A subspace V of $\mathbb {F}_{p}^{d}$ is M-isotropic if $V\cap V^{\perp {M}}\neq \{\mathbf {0}\}$ . We say that a tuple $(h_{1},\ldots ,h_{k})$ of vectors in $\mathbb {F}_{p}^{d}$ is M-isotropic if the span of $h_{1},\ldots ,h_{k}$ is an M-isotropic subspace. We say that a subspace or tuple of vectors is non- M-isotropic if it is not M-isotropic.

For example, if $M(n)=n\cdot n$ and $V=\text {span}_{\mathbb {F}_{11}}\{(1,1,3),(1,2,-1)\}$ , then $(1,1,3)\in V^{ \perp {M}}$ and so, V is M-isotropic. However, for $V'=\text {span}_{\mathbb {F}_{11}}\{(1,1,3),(1,1,1)\}$ , if $v\in V'\cap (V')^{ \perp {M}}$ , then since $v\in V$ , we may write $v=x(1,1,3)+y(1,1,1)$ for some $x,y\in \mathbb {F}_{11}$ . Since v is orthogonal to $(1,1,3)$ and $(1,1,1)$ , we have that $0x+5y= 5x+3y=0$ , which implies that $x=y=0$ . So, $V'$ is not M-isotropic.

Let $V=\text {span}_{\mathbb {F}_{p}}\{h_{1},\ldots ,h_{k}\}$ be a subspace of $\mathbb {F}_{p}^{d}$ and A be the matrix associated to M. Then, V is M-isotropic if and only if the determinant of the matrix $((h_{i}A)\cdot h_{j})_{1\leq i,j\leq k}$ is 0. To see this, suppose that $v\in V\cap V^{ \perp {M}}$ . Since $v\in V$ , we may write ${v=\sum _{i=1}^{k}x_{i}h_{i}}$ for some $x_{i}\in \mathbb {F}_{p}$ . Then, $v\in V\cap V^{ \perp {M}}\Leftrightarrow (vA)\cdot h_{j}=\sum _{i=1}^{k}x_{i}(h_{i}A)\cdot h_{j}=0$ for ${1\leq j\leq k}$ , the right-hand side of which is a $k\times k$ linear equation system whose coefficient matrix is $((h_{i}A)\cdot h_{j})_{1\leq i,j\leq k}$ .

The next lemma ensures the existence of non-M-isotropic subspaces.

Lemma 4.7. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a non-degenerate quadratic form. Then, for all ${0\leq k\leq \mathrm {rank}(M)}$ , there exists a non-M-isotropic subspace of $\mathbb {F}_{p}^{d}$ of dimension k.

Proof. Since $\{\mathbf {0}\}$ is non-M-isotropic, it suffices to consider the case $k\geq 1$ . Let ${d'=\mathrm {rank}(M)}$ . By Lemma 4.3, under a change of variables, it suffices to consider the case when the associated matrix A of M is a diagonal matrix whose diagonal can be written as $(a_{1},\ldots ,a_{d'},0,\ldots ,0)$ for some $a_{1},\ldots ,a_{d'}\neq 0$ . Let $e_{1},\ldots ,e_{d}$ denote the standard unit vectors. Clearly, for $1\leq k\leq d'$ , the matrix $((e_{i}A)\cdot e_{j})_{1\leq i,j\leq k}$ is the upper left $k\times k$ block of A, which is of determinant $a_{1}\cdot \cdots \cdot a_{k}\neq 0$ . This implies that $\text {span}_{\mathbb {F}_{p}}\{e_{1},\ldots ,e_{k}\}$ is a non-M-isotropic subspace of $\mathbb {F}_{p}^{d}$ of dimension k.

We summarize some basic properties of M-isotropic subspaces for later use.

Proposition 4.8. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form and V be a subspace of $\mathbb {F}_{p}^{d}$ of co-dimension r, and $c\in \mathbb {F}_{p}^{d}$ .

1. (i) We have $\dim (V\cap V^{\perp {M}})\leq \min \{d-\mathrm {rank}(M)+r,d-r\}$ .

2. (ii) The rank of $M\vert _{V+c}$ is equal to $d-r-\dim (V\cap V^{\perp {M}})$ (that is, $\dim (V)-\dim (V\cap V^{\perp {M}})$ ).

3. (iii) The rank of $M\vert _{V+c}$ is at most $d-r$ and at least $\mathrm {rank}(M)-2r$ .

4. (iv) $M\vert _{V+c}$ is non-degenerate (that is, $\mathrm {rank}(M\vert _{V+c})=d-r$ ) if and only if V is not an M-isotropic subspace.

Proof. Part (i). Let $v_{1},\ldots ,v_{d-r}$ be a basis of V. Let $B=\Big [\!\begin {smallmatrix} v_{1}\\ \cdots \\ v_{d-r} \end {smallmatrix}\!\Big ]$ . The dimension of $\dim (V^{\perp {M}})$ is equal to d minus the rank of the matrix $BA$ . Since $\mathrm { rank}(BA)\geq \mathrm {rank}(B)+\mathrm {rank}(A)-d=\mathrm {rank}(M)-r$ , we have that $\dim (V^{\perp {M}})\leq d-\mathrm {rank}(M)+r$ . So, part (i) holds because $\dim (V\cap V^{\perp {M}})\leq \min \{\dim (V),\dim (V^{\perp {M}})\}$ .

Part (ii). Let $\phi \colon \mathbb {F}_{p}^{d-r}\to V$ be a bijective linear transformation and denote ${M'(m):=M(\phi (m)+c)}$ . Then, the rank of $M\vert _{V+c}$ is equal to the rank of $M'$ . Assume that $\phi (m)=mB$ for some $(d-r)\times d$ matrix B of rank $d-r$ . Then, the matrix associated to $M'$ is $BAB^{T}$ . Note that for all $m\in \mathbb {F}_{p}^{r}$ ,

$$ \begin{align*} \begin{aligned} & m\in (\mathbb{F}_{p}^{r})^{ \perp{M'}} \Leftrightarrow ((mB)A)\cdot (nB)=0 \quad\text{for all } n\in\mathbb{F}_{p}^{r}\\ &\Leftrightarrow ((mB)A)\cdot v=0 \quad\text{for all } v\in V \Leftrightarrow mB\in V\cap V^{\perp{M}}. \end{aligned} \end{align*} $$

By Proposition 4.5,

$$ \begin{align*}\mathrm{rank}(M')=d-r-\dim(\mathbb{F}_{p}^{r})^{ \perp{M'}}=d-r-\dim(V\cap V^{\perp{M}}).\end{align*} $$

This proves part (ii).

Parts (iii) and (iv) follows directly from parts (i) and (ii).

An annoying issue when working with subspaces of $\mathbb {F}_{p}^{d}$ is that the restriction of a non-degenerate quadratic form M to an M-isotropic subspace V of $\mathbb {F}_{p}^{d}$ is not necessarily non-degenerate. Fortunately, due to Proposition 4.8(iii), the nullity of M does not increase too much when restricted to V, provided that the co-dimension of V is small. This is why Proposition 4.8 can be viewed as the inheriting principle for the ranks of quadratic forms.

The following is a consequence of Proposition 4.8, which will be used in [15].

Lemma 4.9. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a non-degenerate quadratic form, V be a subspace of $\mathbb {F}_{p}^{d}$ of dimension r, and $V'$ be a subspace of $\mathbb {F}_{p}^{d}$ of dimension $r'$ . Suppose that $\mathrm { rank}(M\vert _{V^{\perp {M}}})=d-r$ . Then, $\mathrm {rank}(M\vert _{(V+V')^{\perp {M}}})\geq d-r-2r'$ .

Proof. Since $V^{\perp {M}}$ is of co-dimension r, by Proposition 4.8(ii), $\mathrm {rank}(M\vert _{V^{\perp {M}}})=d-r$ implies that $\dim (V\cap V^{\perp {M}})=0$ . Since $\dim (V+V')\leq r+r'$ and M is non-degenerate, we have that $\dim ((V+V')^{\perp {M}})\geq d-r-r'$ . By Proposition 4.8(ii),

$$ \begin{align*} \begin{aligned} \mathrm{rank}(M\vert_{(V+V')^{\perp{M}}}) & \geq d-r-r'-\dim((V+V')\cap(V+V')^{\perp{M}}) \\&\geq d-r-r'-\dim((V+V')\cap V^{\perp{M}}). \end{aligned} \end{align*} $$

So, it remains to show that $\dim ((V+V')\cap V^{\perp {M}})\leq r'$ . It suffices to show that for any $v_{1},\ldots ,v_{r'+1}\in (V+V')\cap V^{\perp {M}}$ , these vectors are linearly dependent. Since $v_{1},\ldots ,v_{r'+1}\in V+V'$ , we may write $v_{i}=u_{i}+w_{i}$ for some $u_{i}\in V$ and $w_{i}\in V'$ for all $1\leq i\leq r'+1$ . Since $\dim (V')=r'$ , there exist $c_{1},\ldots ,c_{r'+1}$ not all equal to 0 such that $c_{1}w_{1}+\cdots +c_{r'+1}w_{r'+1}=\mathbf {0}$ . Therefore, we have that $c_{1}v_{1}+\cdots +c_{r'+1}v_{r'+1}=c_{1}u_{1}+\cdots +c_{r'+1}u_{r'+1}\in V$ . Since $c_{1}v_{1}+\cdots +c_{r'+1}v_{r'+1}\in V^{\perp {M}}$ and $V\cap V^{\perp {M}}=\{\mathbf {0}\}$ , we have that $c_{1}v_{1}+\cdots +c_{r'+1}v_{r'+1}=\mathbf {0}$ . This means that $\dim ((V+V')\cap V^{\perp {M}})\leq r'$ and we are done.

4.3 Counting the zeros of quadratic forms

For a polynomial $P\in \text {poly}(\mathbb {F}_{p}^{k}\to \mathbb {F}_{p})$ , let $V(P)$ denote the set of $n\in \mathbb {F}_{p}^{k}$ such that $P(n)=0$ . For a family of polynomials $\mathcal {J}=\{P_{1},\ldots ,P_{k}\}\subseteq \text {poly}(\mathbb {F}_{p}^{k}\to \mathbb {F}_{p})$ , denote $V(\mathcal {J}):=\bigcap _{i=1}^{k}V(P_{i})$ . The purpose of this section is to provide estimates on the cardinality of $V(\mathcal {J})$ for families of polynomials arising from quadratic forms.

We start with some basic estimates.

Lemma 4.10. (Schwartz–Zippel lemma)

Let $P\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ be of degree at most r. Then, $\vert V(P)\vert \leq O_{d,r}(p^{d-1})$ unless $P\equiv 0$ .

As an application of Lemma 4.10, we have the following lemma.

Lemma 4.11. Let $d,k\in \mathbb {N}_{+}$ , p be a prime, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a non-degenerate quadratic form.

1. (i) The number of tuples $(h_{1},\ldots ,h_{k})\in (\mathbb {F}_{p}^{d})^{k}$ such that $h_{1},\ldots ,h_{k}$ are linearly dependent is at most $kp^{(d+1)(k-1)}$ .

2. (ii) The number of M-isotropic tuples $(h_{1},\ldots ,h_{k})\in (\mathbb {F}_{p}^{d})^{k}$ is at most $O_{d,k}(p^{kd-1})$ .

Proof. Part (i). If $h_{1},\ldots ,h_{k}$ are linearly dependent, then there exists $1\leq i\leq k$ such that $h_{i}=\sum _{1\leq j\leq k, j\neq i}c_{j}h_{j}$ for some $c_{j}\in \mathbb {F}_{p}$ . For each j, there are p choices of $c_{j}$ and $p^{d}$ choices of $h_{j}$ . Since there are k choices of i, in total, there are at most $k\cdot (p\cdot p^{d})^{k-1}=kp^{(d+1)(k-1)}$ possibilities.

Part (ii). By the discussion after Definition 4.6, $h_{1},\ldots ,h_{k}$ are M-isotropic if and only if the determinant of the matrix $((h_{i}A)\cdot h_{j})_{1\leq i,j\leq k}$ is zero. Viewing this matrix as a non-constant polynomial in $h_{1},\ldots ,h_{k}$ , we get the conclusion from Lemma 4.10.

A very useful application of Lemma 4.11 is as follows. Whenever we have a collection X of k-tuples $(h_{1},\ldots ,h_{k})\in (\mathbb {F}_{p}^{d})^{k}$ of positive density $\delta>0$ , if the dimension d is sufficiently large compared with k, and if p is sufficiently large compared with $\delta ,d,k$ , then by passing to a subset of X, we may further require all the tuples in X to be linearly independent/non-M-isotropic with X still having a positive density.

The following lemma was proved in [10]. We provide its details for completeness.

Lemma 4.12. Let $d\in \mathbb {N}_{+}$ and p be a prime number. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form of rank r. Suppose that $r\geq 3$ . Then,

$$ \begin{align*} \vert V(M)\vert=p^{d-1}(1+O(p^{-{(r-2)}/{2}})), \end{align*} $$

and for all $\xi =(\xi _{1},\ldots ,\xi _{d})\in \mathbb {Z}^{d}$ , we have that

(4.2) $$ \begin{align} \begin{aligned} \mathbb{E}_{n\in V(M)}\exp\bigg(\frac{\xi}{p}\cdot n\bigg)=\mathbf{1}_{\xi=\mathbf{0}}+O(p^{-{(r-2)}/{2}}). \end{aligned} \end{align} $$

Here, we slightly abuse the notation in ${\xi }/{p}\cdot n$ by identifying $n\in \mathbb {F}_{p}^{d}$ with its embedding $\tau (n)\in \mathbb {Z}^{d}$ .

Proof. By Lemma 4.3, it is easy to see we only need to prove this lemma for the case when

$$ \begin{align*} M(n_{1},\ldots,n_{d})=a_{1}n^{2}_{1}+\cdots+a_{r}n^{2}_{r}+a_{r+1}n_{r+1}+\cdots+a_{d}n_{d}-\unicode{x3bb} \end{align*} $$

for some $a_{1},\ldots ,a_{r}\in \mathbb {F}_{p}\backslash \{0\}, a_{r+1},\ldots ,a_{d}\in \mathbb {F}_{p}$ and $\unicode{x3bb} \in \mathbb {F}_{p}$ . (Here, we do not need to use the full strength of Lemma 4.3.) Note that

$$ \begin{align*} \begin{aligned} &\sum_{n\in V(M)}\exp\bigg(\frac{\xi}{p}\cdot n\bigg)=\sum_{n\in \mathbb{F}_{p}^{d}}\mathbb{E}_{j\in\mathbb{F}_{p}}\exp\bigg(\frac{\xi}{p}\cdot n+\frac{j}{p}M(n)\bigg)\\&\quad=p^{d-1}\mathbf{1}_{\xi=\mathbf{0}}+\frac{1}{p}\sum_{j\in\mathbb{F}_{p}\backslash\{0\}}\exp(-j\unicode{x3bb})\sum_{n\in \mathbb{F}_{p}^{d}}\exp\bigg(\frac{\xi}{p}\cdot n+\frac{j}{p}\!\sum_{i=1}^{r}a_{i}n^{2}_{i}+\frac{j}{p}\sum_{i=r+1}^{d}a_{i}n_{i}\!\bigg). \end{aligned} \end{align*} $$

By a change of coordinate, we have that

$$ \begin{align*} &\bigg\vert\frac{1}{p}\sum_{j\in\mathbb{F}_{p}\backslash\{0\}}\exp(-j\unicode{x3bb})\sum_{n\in \mathbb{F}_{p}^{d}}\exp\bigg(\frac{\xi}{p}\cdot n+\frac{j}{p}\sum_{i=1}^{r}a_{i}n^{2}_{i}+\frac{j}{p}\sum_{i=r+1}^{d}a_{i}n_{i}\bigg)\bigg\vert\\ &\quad\leq \frac{1}{p}\sum_{j\in\mathbb{F}_{p}\backslash\{0\}}\bigg\vert\!\sum_{n\in \mathbb{F}_{p}^{d}}\exp\bigg(\frac{\xi}{p}\cdot n+\frac{j}{p}\sum_{i=1}^{r}a_{i}n^{2}_{i}+\frac{j}{p}\sum_{i=r+1}^{d}a_{i}n_{i}\bigg)\bigg\vert\\ &\quad=\frac{1}{p}\sum_{j\in\mathbb{F}_{p}\backslash\{0\}}\bigg\vert\!\sum_{n\in \mathbb{F}_{p}^{d}}\exp\bigg(\frac{j}{p}\sum_{i=1}^{r}a_{i}n^{2}_{i}+\frac{j}{p}\sum_{i=r+1}^{d}a_{i}n_{i}\bigg)\bigg\vert\\ &\quad=\frac{1}{p}\sum_{j\in\mathbb{F}_{p}\backslash\{0\}}\prod_{i=1}^{r}\bigg\vert\!\sum_{n\in \mathbb{F}_{p}}\exp(ja_{i}n^{2}/p)\bigg\vert\cdot\prod_{i=r+1}^{d}\bigg\vert\!\sum_{n\in \mathbb{F}_{p}}\exp(ja_{i}n/p)\bigg\vert\\ &\quad\leq \frac{1}{p}\sum_{j\in\mathbb{F}_{p}\backslash\{0\}}p^{d-r}\prod_{i=1}^{r}\bigg\vert\!\sum_{n\in \mathbb{F}_{p}}\exp(ja_{i}n^{2}/p)\bigg\vert. \end{align*} $$

Since

$$ \begin{align*} & \bigg\vert\!\sum_{n\in \mathbb{F}_{p}}\exp(ja_{i}n^{2}/p)\bigg\vert^{2}\\ & \quad=\bigg\vert\!\sum_{n,h\in \mathbb{F}_{p}}\exp(ja_{i}(2hn+h^{2})/p)\bigg\vert\leq \sum_{h\in\mathbb{F}_{p}}\bigg\vert\!\sum_{n\in\mathbb{F}_{p}}\exp(ja_{i}(2hn+h^{2})/p)\bigg\vert=p, \end{align*} $$

we have that

(4.3) $$ \begin{align} \begin{aligned} \sum_{n\in V(M)}\exp\bigg(\frac{\xi}{p}\cdot n\bigg)= p^{d-1}\mathbf{1}_{\xi=\mathbf{0}}+O(p^{d-({r}/{2})}). \end{aligned} \end{align} $$

Setting $\xi =\mathbf {0}$ , we have that $\vert V(M)\vert =p^{d-1}(1+O(p^{-{(r-2)}/{2}}))$ . Dividing both sides of (4.3) by $\vert V(M)\vert $ , we get (4.2).

We remark that while the argument of Lemma 4.12 works for all $r\in \mathbb {N}$ , the term $O(p^{-{(r-2)}/{2}})$ may be dominant if $r\leq 2$ . For example, if $M(n_{1},n_{2})=n_{1}^{2}+an_{2}^{2}$ for some $a\in \mathbb {F}_{p}$ such that $x^{2}\neq -a$ for all $x\in \mathbb {F}_{p}$ , then $V(M)$ is an empty set.

The following is an application of Lemma 4.12. We say that t is a quadratic residue of $\mathbb {F}_{p}$ if there exists $n\in \mathbb {F}_{p}$ such that $n^{2}=t$ . It is clear that if $p>2$ , then the number of quadratic residues of $\mathbb {F}_{p}$ is ${(p+1)}/{2}$ . We have the following lemma.

Lemma 4.13. Let $d,r\in \mathbb {N}_{+}$ , p be a prime number, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form of rank r. Then, the number of $n\in \mathbb {F}_{p}^{d}$ such that $M(n)$ is a quadratic residue is $\frac {1}{2}p^{d}(1+O(p^{-{(r-2)}/{2}}))$ if $r\geq 3$ , and $\frac {1}{2}p^{d}(1+O(p^{-(1/2)}))$ for $r=2$ .

Proof. Let $S=\{s_{1},\ldots ,s_{(p+1)/2}\}$ be the set of quadratic residues of $\mathbb {F}_{p}$ . We first consider the case $r\geq 3$ . By Lemma 4.12, the number of $n\in \mathbb {F}_{p}^{d}$ such that $M(n)\in S$ is

$$ \begin{align*} \sum_{i=1}^{(p+1)/2}\vert V(M-s_{i})\vert=\frac{p+1}{2}\cdot p^{d-1}(1+O(p^{-(r-2)/2}))=\frac{1}{2}p^{d}(1+O(p^{-(1/2)})). \end{align*} $$

We now consider the case $r=2$ . By [13, Theorem 5A on p. 52], the number of $n\in \mathbb {F}_{p}^{2}$ such that $M(n)=s_{i}$ is $p(1+O(p^{-1/2}))$ . So, the total number of $n\in \mathbb {F}_{p}^{d}$ such that $M(n)$ is a quadratic residue is $\frac {1}{2}p(p+1)(1+O(p^{-1/2}))$ . We are done.

In the rest of this section, we provide some generalizations of Lemma 4.12. These results can be interpreted as the inheriting principle for the size of hyperspheres. First of all, as an immediate corollary of Lemma 4.12, we have the following estimate on the intersection of $V(M)$ with an affine subspace of $\mathbb {F}_{p}^{d}$ .

Corollary 4.14. Let $d\in \mathbb {N}_{+},r\in \mathbb {N}$ , and p be a prime number. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form and $V+c$ be an affine subspace of $\mathbb {F}_{p}^{d}$ of co-dimension r. If either $\mathrm { rank}(M\vert _{V+c})\geq 3$ or $\mathrm {rank}(M)-2r\geq 3$ , then

$$ \begin{align*} \vert V(M)\cap (V+c)\vert=p^{d-r-1}(1+O(p^{-(1/2)})). \end{align*} $$

Proof. If $\mathrm {rank}(M)-2r\geq 3$ , then $\mathrm {rank}(M\vert _{V+c})\geq 3$ by Proposition 4.8(iii). So, in both cases, we have that $\mathrm {rank}(M\vert _{V+c})\geq 3$ . Let $\phi \colon \mathbb {F}_{p}^{d-r}\to V$ be a bijective linear transformation and denote $M'(m):=M(\phi (m)+c)$ for all $m\in \mathbb {F}_{p}^{d-r}$ . Then, $\mathrm {rank}(M')\geq 3$ . Note that $n\in V(M)\cap (V+c)$ if and only if $n=\phi (m)+c$ for some $m\in \mathbb {F}_{p}^{d-r}$ such that $M'(m)=0$ . So, the conclusion follows from Lemma 4.12.

The following sets are studied extensively in this paper.

Definition 4.15. Let $r\in \mathbb {N}_{+}$ , $h_{1},\ldots ,h_{r}\in \mathbb {F}_{p}^{d}$ , and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form. Denote

$$ \begin{align*}V(M)^{h_{1},\ldots,h_{r}}:=\bigcap_{i=1}^{r}V(M(\cdot+h_{i}))\cap V(M).\end{align*} $$

Lemma 4.12 can also be used to study the cardinality of $V(M)^{h_{1},\ldots ,h_{r}}$ .

Corollary 4.16. Let $d,r\in \mathbb {N}_{+}$ and p be a prime number. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a non-degenerate quadratic form and $h_{1},\ldots ,h_{r}$ be linearly independent vectors. If $d-2r\geq 3$ , then

$$ \begin{align*}\vert V(M)^{h_{1},\ldots,h_{r}}\!\vert=p^{d-r-1}(1+O(p^{-(1/2)})).\end{align*} $$

Proof. Since $h_{1},\ldots ,h_{r}$ are linearly independent and M is non-degenerate, it is not hard to see that $V(M)^{h_{1},\ldots ,h_{r}}$ is the intersection of $V(M)$ with an affine subspace $V+c$ of $\mathbb {F}_{p}^{d}$ of co-dimension r. The conclusion follows from Corollary 4.14.

We also need to study the following sets in this paper.

Definition 4.17. (Gowers set)

Let $\Omega $ be a subset of $\mathbb {F}_{p}^{d}$ and $s\in \mathbb {N}$ . Let $\Box _{s}(\Omega )$ denote the set of $(n,h_{1},\ldots ,h_{s})\in (\mathbb {F}_{p}^{d})^{s+1}$ such that $n+\epsilon _{1}h_{1}+\cdots +\epsilon _{s}h_{s}\in \Omega $ for all $(\epsilon _{1},\ldots ,\epsilon _{s})\in \{0,1\}^{s}$ . Here, we allow s to be 0, in which case, $\Box _{0}(\Omega )=\Omega $ . We say that $\Box _{s}(\Omega )$ is the sth Gowers set of $\Omega $ .

It is worth noting that the Gowers set will also be used for the study of the spherical Gowers norms in [16]. We have the following description for Gowers sets.

Lemma 4.18. Let $s\in \mathbb {N}$ , $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form associated with the matrix A, and $V+c$ be an affine subspace of $\mathbb {F}_{p}^{d}$ . For $n,h_{1},\ldots ,h_{s}\in \mathbb {F}_{p}^{d}$ , we have that $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M)\cap (V+c))$ if and only if:

• • $n\in V+c$ , $h_{1},\ldots ,h_{s}\in V$ ;

• • $n\in V(M)^{h_{1},\ldots ,h_{s}}$ ;

• • $(h_{i}A)\cdot h_{j}=0$ for all $1\leq i,j\leq s, i\neq j$ .

In particular, let $\phi \colon \mathbb {F}_{p}^{r}\to V$ be any bijective linear transformation, $M'(m):=M(\phi (m)+c)$ . We have that $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M)\cap (V+c))$ if and only if $(n,h_{1}, \ldots ,h_{s})=(\phi (n')+c,\phi (h^{\prime }_{1}),\ldots ,\phi (h^{\prime }_{s}))$ for some $(n',h^{\prime }_{1},\ldots ,h^{\prime }_{s})\in \Box _{s}(V(M'))$ .

Proof. If $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M)\cap (V+c))$ , then clearly, $n\in V(M)^{h_{1},\ldots ,h_{s}}$ . Since $n,n+h_{1},\ldots ,n+h_{s}\in V+c$ , we have that $h_{1},\ldots ,h_{s}\in V$ . Finally, the fact that $(h_{i}A)\cdot h_{j}{\kern-1pt}={\kern-1pt}0$ for all $1{\kern-1pt}\leq{\kern-1pt} i,j{\kern-1pt}\leq{\kern-1pt} s, i{\kern-1pt}\neq{\kern-1pt} j$ follows from the definition of $\Box _{s}(V(M){\kern-1pt}\cap{\kern-1pt} (V{\kern-1pt}+{\kern-1pt}c))$ and Lemma 4.2.

Conversely, if $n\in V+c$ , $h_{1},\ldots ,h_{s}\in V$ , then $n+\epsilon _{1}h_{1}+\cdots +\epsilon _{s}h_{s}\in V+c$ for all $\epsilon _{1},\ldots ,\epsilon _{s}\in \{0,1\}$ . Since $n\in V(M)^{h_{1},\ldots ,h_{s}}$ , we have that $M(n+\epsilon _{1}h_{1}+\cdots +\epsilon _{s}h_{s})=0$ whenever $\vert \epsilon \vert :=\epsilon _{1}+\cdots +\epsilon _{s}=0$ or 1. Suppose we have shown that $M(n+\epsilon _{1}h_{1}+\cdots +\epsilon _{s}h_{s})=0$ whenever $\vert \epsilon \vert :=\epsilon _{1}+\cdots +\epsilon _{s}\leq i$ for some $1\leq i\leq s-1$ , then it follows from Lemma 4.2 and the fact that $(h_{i}A)\cdot h_{j}=0$ for all $1\leq i,j\leq s, i\neq j$ that $M(n+\epsilon _{1}h_{1}+\cdots +\epsilon _{s}h_{s})=0$ whenever $\vert \epsilon \vert :=\epsilon _{1}+\cdots +\epsilon _{s}\leq i+1$ . In conclusion, we have that $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M)\cap (V+c))$ .

The proof of the ‘in particular’ part is left to the interested readers.

We summarize some basic properties of Gowers sets.

Proposition 4.19. (Some preliminary properties for Gowers sets)

Let $d\in \mathbb {N}_{+}, s\in \mathbb {N}$ and p be a prime. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form with $\mathrm {rank}(M)\geq s^{2}+s+3$ . Then:

1. (i) we have $\vert \Box _{s}(V(M))\vert =p^{(s+1)d-((s(s+1)/2)+1)}(1+O_{s}(p^{-1/2}))$ ;

2. (ii) for all but at most $s(s+1)p^{d+s-\mathrm {rank}(M)}$ many $h_{s}\in \mathbb {F}_{p}^{d}$ , the set of $(n,h_{1},\ldots , h_{s-1})\in (\mathbb {F}_{p}^{d})^{s}$ with $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ is at most $p^{ds-((s(s+1)/2)+1)}$ ;

3. (iii) if $s=1$ , then for any function $f\colon \Box _{1}(V(M))\to \mathbb {C}$ with norm bounded by 1, we have that

   $$ \begin{align*} \mathbb{E}_{(n,h)\in\Box_{1}(V(M))}f(n,h)=\mathbb{E}_{h\in\mathbb{F}_{p}^{d}}\mathbb{E}_{n\in V(M)^{h}}f(n,h)+O(p^{-1/2}). \end{align*} $$

It is worth mentioning that Proposition 4.19(iii) can be interpreted as Fubini’s theorem on $\Box _{1}(V(M))$ , which says the two-dimensional average of $(n,h)$ over $\Box _{1}(V(M))$ is approximately the same as the double average of n and h.

Proposition 4.19 can either be proved by direct computation plus the counting properties developed in §4, or it can be derived from a more general framework using [18, Example 5.4 and Theorem 5.11]. So, we only provide a sketch of the proof.

Sketch of the proof.

Clearly, part (i) holds for $s=0$ by Lemma 4.12. Suppose that part (i) holds for s and now we prove it for $s+1$ . By Lemma 4.18, $(n,h_{1},\ldots ,h_{s+1})\in \Box _{s+1}(V(M))$ if and only if $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ and $h_{s+1}$ belongs to the set

$$ \begin{align*}W(n,h_{1},\ldots,h_{s}):=\{m\in\mathbb{F}_{p}^{d}\colon M(n+m)=(h_{1}A)\cdot m=\cdots=(h_{s}A)\cdot m=0\}.\end{align*} $$

For most of the choices of $(n,h_{1},\ldots ,h_{s})$ , $W(n,h_{1},\ldots ,h_{s})$ is the intersection of a hypersphere with a hyperplane of codimension s, and so is of cardinality approximately $p^{d-s-1}$ by Corollary 4.14. So, by induction hypothesis,

$$ \begin{align*} &\vert \Box_{s+1}(V(M))\vert\approx \vert \Box_{s}(V(M))\vert\cdot p^{d-s-1}\approx p^{(s+1)d-((s(s+1)/2)+1)}\cdot p^{d-s-1}\\ & \quad =p^{(s+2)d-(({(s+1)(s+2)}/{2})+1)}. \end{align*} $$

For part (ii), using Lemma 4.18, one can show that $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ if and only if $(n,h_{1},\ldots ,h_{s-1})\in \Box _{s-1}(V(M))$ , $n\in V+c$ , and $h_{1},\ldots ,h_{s-1}\in V$ , where $V+c$ is the affine subspace of $\mathbb {F}_{p}^{d}$ consisting of all h with $M(h+h_{s})=M(h)$ , and V is the affine subspace of $\mathbb {F}_{p}^{d}$ consisting of all h with $(h_{s}A)\cdot h=0$ . This is equivalent of saying that $(n,h_{1},\ldots ,h_{s-1})\in \Box _{s-1}(V(M)\cap (V+c))$ . One can informally think of $V(M)\cap (V+c)$ as a hypersphere in a subspace of dimension $d-1$ (for most of $h_{s}$ ), and so the number of such $(n,h_{1},\ldots ,h_{s-1})$ by part (i) is approximately $p^{s(d-1)-(((s-1)s/2)+1)}=p^{sd-((s(s+1)/2)+1)}$ .

Part (iii) can be derived by combining parts (i) and (ii). We omit the details.

5 The main equidistribution theorem

With the help of the preparation in the previous sections, we are now ready to state the main result in this paper, which is a generalization of Theorem 1.4.

Theorem 5.1. (Equidistribution theorem on $V(M)$ )

Let $0{\kern-1pt}<{\kern-1pt}\delta {\kern-1pt}<{\kern-1pt}1/2, d,m{\kern-1pt}\in{\kern-1pt} \mathbb {N}_{+},s,r{\kern-1pt}\in{\kern-1pt} \mathbb {N}$ with $d\geq r$ , and p be a prime. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form and $V+c$ be an affine subspace of $\mathbb {F}_{p}^{d}$ of co-dimension r. Suppose that $\mathrm {rank}(M\vert _{V+c})\geq s+13$ . Let $G/\Gamma $ be an s-step $\mathbb {N}$ -filtered nilmanifold of dimension m, equipped with a ${1}/{\delta }$ -rational Mal’cev basis $\mathcal {X}$ , and let $g\in \mathrm { poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ be a rational polynomial sequence. If $p\gg _{d,m} \delta ^{-O_{d,m}(1)}$ and $(g(n)\Gamma )_{n\in \iota ^{-1}(V(M)\cap (V+c))}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then there exists a non-trivial type-I horizontal character $\eta $ with $0<\Vert \eta \Vert \ll _{d,m} \delta ^{-O_{d,m}(1)}$ (independent of $k,M$ , and p) such that $\eta \circ g \,\mod \mathbb {Z}$ is a constant on $\iota ^{-1}(V(M)\cap (V+c))$ . (It follows from Corollary 4.14 that $V(M)\cap (V+c)$ is non-empty since $d-r\geq s+13$ .)

To illustrate the idea for the proof of Theorem 5.1, we first present an outline of the proof of Corollary 1.6 (which is a special case of Theorem 5.1). Assume for simplicity that g is p-periodic. Suppose we have proven Corollary 1.6 for the case $s-1$ . Denote $\Omega =V(M)$ . Assume on the contrary that

(5.1) $$ \begin{align} \bigg\vert\frac{1}{\vert\Omega\vert}\sum_{n\in\Omega}\exp(g\circ\tau(n)/p)\bigg\vert>\delta. \end{align} $$

Taking squares on both sides and performing a change of variables, we have that

$$ \begin{align*} &\delta^{2}<\frac{1}{\vert\Omega\vert^{2}}\sum_{n,n+h\in\Omega}\exp((g\circ\tau(n+h)-g\circ\tau(n))/p)\\ & \quad =\frac{1}{\vert\Omega\vert^{2}}\sum_{h\in\mathbb{F}_{p}^{d}}\sum_{n\in \Omega\cap (\Omega-h)}\exp((g\circ\tau(n+h)-g\circ\tau(n))/p). \end{align*} $$

Since (by the inheriting principle) the sets $\Omega \cap (\Omega -h), h\in \mathbb {F}_{p}^{d}$ are hyperspheres whose cardinalities are comparable with each other for most of h, we have that

$$ \begin{align*} \frac{1}{p^{d}}\sum_{h\in\mathbb{F}_{p}^{d}}\bigg\vert\frac{1}{\vert\Omega\cap (\Omega-h)\vert}\sum_{n\in \Omega\cap (\Omega-h)}\exp((g\circ\tau(n+h)-g\circ\tau(n))/p)\bigg\vert\gg\delta^{2} \end{align*} $$

(this argument can be made precise by Proposition 4.19). By the pigeonhole principle, for ‘many’ $h\in \mathbb {F}_{p}^{d}$ , we have that

$$ \begin{align*} \bigg\vert\frac{1}{\vert\Omega\cap (\Omega-h)\vert}\sum_{n\in \Omega\cap (\Omega-h)}\exp((g\circ\tau(n+h)-g\circ\tau(n))/p)\bigg\vert\gg \delta^{2}. \end{align*} $$

Informally, one can view $\Omega \cap (\Omega -h)$ as a sphere whose dimension is lower than $\Omega $ by 1. So, we may then apply the induction hypothesis to the degree $(s-1)$ polynomial sequence $g\circ \tau (n+h)-g\circ \tau (n)$ to conclude that

(5.2) $$ \begin{align} (g\circ\tau(n+h)-g\circ\tau(n))/p \ \,\mod \mathbb{Z} \text{ is a constant on } \Omega\cap (\Omega-h)\quad \text{ for `many' } h\in \mathbb{F}_{p}^{d}. \end{align} $$

(For the case when g is a polynomial sequence on a nilmanifold, the conclusion becomes $(\eta _{h}\circ g\circ \tau (n+h)-\eta _{h}\circ g\circ \tau (n))/p \,\mod \mathbb {Z}$ is a constant on $\Omega \cap (\Omega -h)$ for ‘many’ $h\in \mathbb {F}_{p}^{d}$ for some horizontal character $\eta _{h}$ of low complexity. The dependence of $\eta _{h}$ on h can then be dropped by using the pigeonhole principle.)

For convenience, denote $Q:=\iota \circ pg\circ \tau $ , then $Q\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ is a polynomial of degree at most s. It then follows from (5.2) that

(5.3) $$ \begin{align} \Delta_{h_{2}}\Delta_{h_{1}}Q(n)=0 \quad\text{for `many'} (n,h_{1},h_{2})\in \Box_{2}(\Omega), \end{align} $$

where $\Box _{2}(\Omega )$ is the second Gowers set of $\Omega $ defined in Definition 4.17.

We have now reduced Corollary 1.6 to a problem of solving the polynomial equation (5.3). If $\Omega $ were the entire space $\mathbb {F}_{p}^{d}$ , then using some basic knowledge for polynomials, it is not hard to show that (5.3) would imply that Q is of degree at most $s-1$ , which would complete the proof of Corollary 1.6 by induction. When $\Omega $ is a sphere, the difficulty of the analysis of (5.3) increases significantly. Therefore, solving (5.3) (as well as its various generalizations) is a central topic in this paper and this is the main challenge in adapting the Green–Tao approach [5] to the quadratic case.

In Proposition 6.8, we show that (5.3) implies that Q can be written as $Q=MQ_{1}+Q_{2}$ for some $Q_{1},Q_{2}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (Q_{2})\leq 1$ . Then, (5.1) implies that

$$ \begin{align*} \bigg\vert\frac{1}{\vert\Omega\vert}\sum_{n\in\Omega}\exp\bigg(\frac{1}{p}\tau\circ Q(n)\bigg)\bigg\vert=\bigg\vert\frac{1}{\vert\Omega\vert}\sum_{n\in\Omega}\exp\bigg(\frac{1}{p}\tau\circ Q_{2}(n)\bigg)\bigg\vert>\delta. \end{align*} $$

Since $Q_{2}$ is linear, it forces $Q_{2}(n)/p \,\mod Z$ to be a constant and therefore, $Q(n)/p\,\mod \mathbb {Z}$ is a constant on $\Omega $ . This implies that $g\circ \tau (n)/p \,\mod \mathbb {Z}$ is a constant on $\Omega $ , completing the (outline of the) proof of Corollary 1.6.

To prove Theorem 5.1, a more general version of Corollary 1.6, following the idea of Green and Tao [5, 6], one can reduce the problem to solving the following generalized versions of (5.3) (see also (9.19)):

(5.4) $$ \begin{align} \Delta_{h_{3}}\Delta_{h_{2}}\Delta_{h_{1}}P(n)+\Delta_{h_{2}}\Delta_{h_{1}}Q(n)=0 \quad\text{for `many' } (n,h_{1},h_{2},h_{3})\in\Box_{3}(\Omega), \end{align} $$

where $Q\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ comes from the composition of g with some type-I horizontal character of $G/\Gamma $ (so $\deg (Q)\leq s$ ), and $P\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ is a polynomial of degree at most $s-1$ arising from the ‘nonlinear’ part of g.

The bulk of §6 is devoted to solving the following generalized version of (5.4) (see also (6.25)):

(5.5) $$ \begin{align} \Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P(n)+\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q(n)=0 \quad\text{for `many' } (n,h_{1},\ldots,h_{s})\in\Box_{s}(\Omega). \end{align} $$

(We study (5.5) for any $s\in \mathbb {N}$ not just for $s=3$ for the purpose of future research.) We provide a solution to (5.5) in Proposition 6.6. In the same section, we also prove some other properties for polynomial equations in $\text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ for later use.

One can then combine the solution to (5.4) together with the machinery of Green and Tao [5, 6] to prove Theorem 5.1 for the case when g is p-periodic. However, to deal with a partially p-periodic sequence g, we need to deal with the following even more general version of (5.5):

(5.6) $$ \begin{align} \Delta_{h_{s-1}}{\kern-1pt}\cdots\Delta_{h_{1}}P(n){\kern-1pt}+{\kern-1pt}\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q(n)\in\mathbb{Z} \quad\text{for `many' } (n,h_{1},\ldots,h_{s}){\kern-1pt}\in {\kern-1pt}\iota^{-1}(\Box_{s}(\Omega)), \end{align} $$

where $P,Q\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Q})$ are partially p-periodic polynomials on $\iota ^{-1}(\Omega )$ . The bulk of §7 is devoted to solving (5.6) (and we eventually solve (5.6) in Proposition 7.6). To solve (5.6), we develop an approach called the p-expansion trick, which allows us to lift the solutions to (5.6) from $\mathbb {Z}/p$ -valued polynomials to $\mathbb {Z}/p^{s}$ -valued polynomials. In the same section, we also use the same trick to extend other results in §6 to the partially p-periodic case. We remark that §§6 and 7 are the essential deviation of our approach from the work of Green and Tao [5].

Finally, in §9, we combine the algebraic preparations from §§6 and 7 with the approach of Green and Tao [5, 6] to complete the proof of Theorem 5.1. While the outline of this section is similar to the approach of Green and Tao [5], there are a couple of highly non-trivial challenges to overcome to adopt this method, including the treatment of (9.22), and Propositions 9.8 and 9.9.

6 Algebraic properties for quadratic forms in $\mathbb {F}_{p}$

6.1 Irreducible properties for quadratic forms

We begin with a dichotomy on the intersection of the sets of solutions of a polynomial and a quadratic form.

Lemma 6.1. Let $d\in \mathbb {N}_{+},s\in \mathbb {N}$ and p be a prime such that $p\gg _{d,s} 1$ . Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form of rank at least 3. For any $P\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most s, either $\vert V(P)\cap V(M)\vert \leq O_{d,s}(p^{d-2})$ or $V(M)\subseteq V(P)$ .

Proof. Denote $r=\mathrm {rank}(M)$ . We first assume that M and P are homogeneous. By Lemma 4.3, it suffices to consider the special case when

$$ \begin{align*}M(n)=c_{1}n^{2}_{1}+\cdots+c_{r}n_{r}^{2}\end{align*} $$

for some $c_{1},\ldots ,c_{r}\in \mathbb {F}_{p}\backslash \{0\}$ . Let $U:=V(P)\cap V(M)$ . By the pigeonhole principle, there exists $1\leq i\leq r$ such that the ith coordinate of at least $(\vert U\vert -p^{d-r})/r$ many $n\in U$ is non-zero. We may assume without loss of generality that $i=1$ . Write $n=(t,y)$ , where $t\in \mathbb {F}_{p}$ and $y\in \mathbb {F}_{p}^{d-1}$ . Since $\deg (P)=s\ll p$ , by the long division algorithm, we may write

(6.1) $$ \begin{align} P(t,y)=M(t,y)R(t,y)+N_{1}(y)t+N_{0}(y) \end{align} $$

for some $R\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p}), N_{1},N_{0}\in \text {poly}(\mathbb {F}_{p}^{d-1}\to \mathbb {F}_{p})$ such that the degrees of $R, N_{1}$ , and $N_{0}$ are at most $s-2$ , $s-1$ , and s, respectively. Then,

(6.2) $$ \begin{align} P(t,y)=M(t,y)=N_{1}(y)t+N_{0}(y)=0 \quad\text{for all } (t,y)\in U. \end{align} $$

Note that if $M(t,y)=N_{1}(y)t+N_{0}(y)=0$ , then we must have that $t=-N_{0}(y)/N_{1}(y)$ (provided that $N_{1}(y)\neq 0$ ). Substituting this expression back to $M(t,y)=0$ , we have that $\Delta (y)N_{1}(y)^{-2}=0$ , where

$$ \begin{align*}\Delta(y):=M(0,y)N_{1}(y)^{2}+c_{1}N^{2}_{0}(y).\end{align*} $$

So, $\Delta (y)$ is an important polynomial in the study of (6.2). We first assume that $\Delta (y)$ is not constant 0. Let $U'$ be the set of $(t,y)\in U$ such that $N_{1}(y)=0$ . Then, it follows from (6.2) that $N_{0}(y)=0$ and so $\Delta (y)=0$ . Since we assumed that $\Delta (y)$ is not constant 0 and $\deg (\Delta (y))\leq 2s$ , by Lemma 4.10, we have that $\vert U'\vert \leq O_{d,s}(p^{d-2})$ .

Suppose that $(t,y)\in U\backslash U'$ and $t\neq 0$ . Then, $M(t,y)=N_{1}(y)t+N_{0}(y)=0$ by (6.2). So, $t=-N_{0}(y)N_{1}(y)^{-1}$ and so, $M(0,y)=M(t,y)-c_{1}t^{2}=-c_{1}t^{2}=-c_{1}N^{2}_{0}(y)N_{1}(y)^{-2}$ , or equivalently, $\Delta (y)=0$ . Since $\Delta (y)$ is not constant 0, by Lemma 4.10, we have that $\vert (U\backslash U')\cap \{(t,y)\colon t\neq \mathbf {0}\}\vert \leq O_{d,s}(p^{d-2})$ . Since we assumed that $\vert U\cap \{(t,y)\colon t\neq \mathbf {0}\}\vert \geq {(\vert U\vert -p^{d-r})}/{r}$ , we deduce that $\vert U\vert \leq O_{d,s}(p^{d-2})$ since $r\geq 3$ .

We now consider the case that $\Delta (y)\equiv 0$ . Let W be the set of $y\in \mathbb {F}_{p}^{d-1}$ such that $-c_{1}M(0,y)$ is not a square residue in $\mathbb {F}_{p}$ . Since $\mathrm {rank}(M(0,\cdot ))\geq 2$ , by Lemma 4.13, $\vert W\vert =\frac {1}{2}p^{d-1}(1+O(p^{-1/2}))$ . Since $\Delta (y)\equiv 0$ for all $y\in W$ , we have that $N_{1}(y)=0$ . By Lemma 4.10, $\vert W\vert \leq O_{s}(p^{d-2})$ unless $N_{1}(y)\equiv 0$ . If $p\gg _{d,s} 1$ , then $\vert W\vert =\frac {1}{2}p^{d-1}(1+O(p^{-1/2}))\gg _{s}p^{d-2}$ and so we must have that $N_{1}(y)\equiv 0$ . Since $\Delta (y)\equiv 0$ , we also have that $N_{0}(y)\equiv 0$ . So, (6.1) implies that $P=MR$ , which implies that $V(M)\subseteq V(P)$ .

Finally, we consider the general case when M and P are not necessarily homogeneous. Then, there exist homogeneous polynomials $\tilde {M},\tilde {P}\colon \mathbb {F}_{p}^{d+1}\to \mathbb {F}_{p}$ of degrees at most 2 and s, respectively, such that $M=\tilde {M}(\cdot ,1)$ and $P=\tilde {P}(\cdot ,1)$ . Then, $\tilde {M}$ is a quadratic form of rank at least 3. By the previous case, either $\vert V(\tilde {P})\cap V(\tilde {M})\vert \leq O_{d,s}(p^{d-1})$ or ${V(\tilde {M})\subseteq V(\tilde {P})}$ . In the former case, since

(6.3) $$ \begin{align} \vert V(\tilde{P})\cap V(\tilde{M})\vert &\geq \sum_{i=1}^{p-1}\vert V(\tilde{P}(\cdot,i))\cap V(\tilde{M}(\cdot,i))\vert \nonumber\\ &=(p-1)\vert V(\tilde{P}(\cdot,1))\cap V(\tilde{M}(\cdot,1))\vert \text{(since } \tilde{P} \text{ and } \tilde{M} \text{ are homogeneous)}\nonumber\\ &=(p-1)\vert V(P)\cap V(M)\vert, \end{align} $$

we have that $\vert V(P)\cap V(M)\vert \leq O_{d,s}(p^{d-2})$ . In the latter case, we have that $V(\tilde {M}(\cdot ,1))\subseteq V(\tilde {P}(\cdot ,1))$ , which implies that $V(M)\subseteq V(P)$ .

Let $P\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a polynomial of degree s for some $s<p$ and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form associated with matrix A. For the purpose of [18], we need a concrete algorithm to divide P by M. If the upper left entry of the matrix A is non-zero (that is, M contains a non-trivial $n_{1}^{2}$ term), we divide P by M as follows: whenever P has a term of the form $n_{1}^{i_{1}}\cdots n_{d}^{i_{d}}$ with $i_{1}\geq 2$ , by subtracting a suitable multiple of M, we may convert this term to several terms of the form $n_{1}^{i^{\prime }_{1}}\cdots n_{d}^{i^{\prime }_{d}}$ with $i^{\prime }_{1}<i_{1}$ . This eventually leads to a decomposition of the form

(6.4) $$ \begin{align} P(n)=M(n)Q(n)+(n)_{1}R_{1}((n)_{2\sim d})+R_{0}((n)_{2\sim d}), \end{align} $$

where for $n\in \mathbb {F}_{p}^{d}$ , we use $(n)_{1}$ to denote the first coordinate of n and $(n)_{2\sim d}$ to denote the last $d-1$ coordinate of n. We call this decomposition the standard long division algorithm.

However, the above decomposition is non-valid if M does not have the $n_{1}^{2}$ term (one example is $M(n_{1},\ldots ,n_{d})=n_{1}n_{2}+n_{3}^{2}+\cdots +n_{d}^{2}$ ). In this case, one has to do a change of variables before applying the standard long algorithm. Let B be a $d\times d$ non-degenerate matrix such that the upper left entry of the matrix $BAB^{T}$ is non-zero. Then, we may use the standard long division algorithm to write

$$ \begin{align*}P(nB)=M(nB)Q(n)+n_{1}R_{1}(n_{2\sim d})+R_{0}(n_{2\sim d}).\end{align*} $$

So,

(6.5) $$ \begin{align} P(n)=M(n)Q(nB^{-1})+(nB^{-1})_{1}R_{1}((nB^{-1})_{2\sim d})+R_{0}((nB^{-1})_{2\sim d}), \end{align} $$

where for $n\in \mathbb {F}_{p}^{d}$ , we use $n_{1}$ to denote the first coordinate of n and $n_{2\sim d}$ to denote the last $d-1$ coordinates of n. We call this decomposition (6.5) of P the B-standard long division algorithm (in particular, the standard long division algorithm in (6.4) is the I-standard long division algorithm with I being the identity matrix).

An advantage of this algorithm is that all the coefficients of $Q,R_{1}$ , and $R_{0}$ can be written in the form $F/c_{1,1}^{s}$ with F being a polynomial function (dependent on B) with respect to the coefficients of P and M of degree at most s, where $c_{1,1}$ is the coefficient of the $n_{1}^{2}$ term of $M(nB)$ . This simple observation will be useful in [18].

We say that M divides P with respect to the B-standard long division algorithm if ${R_{1}=R_{0}=0}$ in the B-standard long division algorithm (6.5). We have the following Hilbert Nullstellensatz type result for $V(M)$ .

Proposition 6.2. (Hilbert Nullstellensatz for $V(M)$ )

Let $d\in \mathbb {N}_{+},s\in \mathbb {N}$ , $p\gg _{d,s} 1$ be a prime number, $P\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ be of degree at most s, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form of rank at least 3 associated with the matrix A. If $V(M)\subseteq V(P)$ , then for all $d\times d$ non-degenerate matrix B with the upper left entry of the matrix $BAB^{T}$ being non-zero, M divides P with respect to the B-standard long division algorithm. In particular, $P=MR$ for some $R\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most $s-2$ .

It is tempting to prove Proposition 6.2 by using Hilbert Nullstellensatz. Let $F_{i}(n_{1},\ldots ,n_{d}) :=n_{i}^{p}-n_{i}$ for all $1\leq i\leq d$ . By using Hilbert Nullstellensatz in the finite field (see [2]), if $V(M)\subseteq V(P)$ , then one can show that

$$ \begin{align*}P=MR+\sum_{i=1}^{d}F_{i}R_{i}\end{align*} $$

for some polynomials $R,R_{1},\ldots ,R_{d}$ . Unfortunately, this is not helpful for Proposition 6.2, since there is no restriction on the degree of R, and it is unclear how to remove the polynomials $R_{1},\ldots ,R_{d}$ . So, we have to prove Proposition 6.2 with a different method relying on the long division algorithm.

Proof of Proposition 6.2

Denote $r=\mathrm {rank}(M)$ . Under a change of variables, it suffices to show that for any $P\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most s and any quadratic form, $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ of rank at least 3 associated with the matrix A whose upper left entry is non-zero. If $V(M)\subseteq V(P)$ , then M divides P with respect to the standard long division algorithm.

We first assume that M and P are homogeneous. Write $n=(t,y)$ , where $t\in \mathbb {F}_{p}$ and $y\in \mathbb {F}_{p}^{d-1}$ . Since the coefficient of the $t^{2}$ term of $M(t,y)$ is non-zero, we may apply the standard long division algorithm to write

(6.6) $$ \begin{align} P(t,y)=M(t,y)R(t,y)+N_{1}(y)t+N_{0}(y) \end{align} $$

for some $R, N_{1},N_{0}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degrees at most $s-2,s-1$ , and s, respectively. Our goal is to show that $N_{0}, N_{1}\equiv 0$ . By Lemma 4.3 and a change of variables, it suffices to show that if (6.6) holds for

$$ \begin{align*}M(n)=c_{1}n^{2}_{1}+\cdots+c_{r}n_{r}^{2}\end{align*} $$

for some $c_{1},\ldots ,c_{r}\in \mathbb {F}_{p}\backslash \{0\}$ , and that $V(M)\subseteq V(P)$ , then $N_{0}, N_{1}\equiv 0$ .

Let

$$ \begin{align*}\Delta(y):=M(0,y)N_{1}(y)^{2}+c_{1}N^{2}_{0}(y).\end{align*} $$

If $\Delta (y)$ is not constant 0, then by the proof of Lemma 6.1, the number of $n\in \mathbb {F}_{p}^{d}$ such that $M(n)=P(n)=0$ is at most $O_{d,s}(p^{d-2})$ . However, since $V(M)\subseteq V(P)$ , by Lemma 4.12, the number of $n\in \mathbb {F}_{p}^{d}$ such that $M(n)=P(n)=0$ is $p^{d-1}(1+O(p^{-({r-2}/{2})}))$ , which is a contradiction.

So, we must have that $\Delta (y)\equiv 0$ . Following the proof of Lemma 6.1, we have that $N_{0}(y)=N_{0}(y)\equiv 0$ and so $P=MR$ . Since the degree of R is at most $s-2$ , we are done.

We now consider the general case when M and P are not necessarily homogeneous. Then, there exist homogeneous polynomials $\tilde {M},\tilde {P}\colon \mathbb {F}_{p}^{d+1}\to \mathbb {F}_{p}$ of degrees at most 2 and s, respectively, such that $M=\tilde {M}(\cdot ,1)$ and $P=\tilde {P}(\cdot ,1)$ . Since $\vert V(P)\cap V(M)\vert =\vert V(M)\vert =p^{d-1}(1+O(p^{-1/2}))$ by Lemma 4.12, it follows from (6.3) that $\vert V(\tilde {P})\cap V(\tilde {M})\vert =p^{d}(1+O(p^{-1/2}))$ . By Lemma 6.1, we have that $V(\tilde {M})\subseteq V(\tilde {P})$ . So, by the previous case, we have that $\tilde {M}$ divides $\tilde {P}$ with respect to the standard long division algorithm. Since the $n_{1}^{2}$ term of M is non-zero, it is not hard to see that M also divides P with respect the standard long division algorithm.

6.2 A special anti-derivative property

For a polynomial

$$ \begin{align*}Q(n_{1},\ldots,n_{d})=\sum_{0\leq a_{1},\ldots,a_{d}\leq p-1}C_{a_{1},\ldots,a_{d}}n_{1}^{a_{1}}\cdots n_{d}^{a_{d}},\end{align*} $$

denote the ith directional formal derivative of Q by

$$ \begin{align*}\partial_{i}Q(n_{1},\ldots,n_{d}):=\sum_{0\leq a_{1},\ldots,a_{d}\leq p-1}a_{i}C_{a_{1},\ldots,a_{d}}n_{1}^{a_{1}}\cdots n_{i}^{a_{i}-1}\cdots n_{d}^{a_{d}}.\end{align*} $$

In many scenarios (such as in (5.5)), we need to recover information on Q from the information on its derivatives $\partial _{1}Q,\ldots ,\partial _{d}Q$ . In particular, a question we need to understand is: what is a characterization of the property that Q is a constant in $V(M)$ in terms of $\partial _{1}Q,\ldots ,\partial _{d}Q$ ? If Q is constant zero in $V(M)$ , then by Proposition 6.2, we have that $Q=MQ'$ for some polynomial $Q'$ . Then, it is not hard to see that

$$ \begin{align*}(\partial_{j}M)(\partial_{i}Q)-(\partial_{i}M)(\partial_{j}Q)=M((\partial_{j}M)(\partial_{i}Q')-(\partial_{i}M)(\partial_{j}Q')),\end{align*} $$

that is, $\partial _{j}M\partial _{i}Q$ is equal to $\partial _{i}M\partial _{j}Q$ on $V(M)$ . We now show that the converse also holds.

Proposition 6.3. Let $d\in \mathbb {N}_{+},s\in \mathbb {N}$ with $d\geq 3$ , p be a prime, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form of rank at least 3. Let $Q\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ be a polynomial of degree at most s with $Q(\mathbf {0})=0$ such that

$$ \begin{align*}\partial_{1}M(n)\partial_{i}Q(n)=\partial_{i}M(n)\partial_{1}Q(n)\end{align*} $$

for all $1{\kern-1pt}\leq{\kern-1pt} i{\kern-1pt}\leq{\kern-1pt} d$ and $n{\kern-1pt}\in{\kern-1pt} V(M)$ . If $p{\kern-1pt}\gg _{d,s}{\kern-1pt} 1$ , then $Q{\kern-1pt}={\kern-1pt}MQ'$ for some ${Q'{\kern-1pt}\in{\kern-1pt} \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})}$ of degree at most $s-2$ .

To deduce Proposition 6.3, we consider its following variation.

Proposition 6.4. Let $d\in \mathbb {N}_{+},s\in \mathbb {N}$ with $d\geq 3$ , p be a prime, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form of rank at least 3. Let $H_{1},\ldots ,H_{d}\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ be polynomials of degree at most s such that

(6.7) $$ \begin{align} \partial_{i}M(n)H_{j}(n)=\partial_{j}M(n)H_{i}(n) \end{align} $$

for all $1\leq i,j\leq d$ and $n\in V(M)$ . If $p\gg _{d,s} 1$ , then there exist $G,F_{1},\ldots , F_{d}\in \mathrm { poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (G)\leq s-1$ and $\deg (F_{i})\leq s-2$ such that

$$ \begin{align*}H_{i}=(\partial_{i}M)G+MF_{i} \quad\text{for all } 1\leq i\leq d.\end{align*} $$

Proof of Proposition 6.3 assuming Proposition 6.4

Our strategy is to apply Proposition 6.4 repeatedly. For $\ell \geq 1$ , we say that Property $\ell $ holds if there exist $W,R_{1},\ldots , R_{d}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (W)\leq s-2, \deg (R_{i})\leq s-2\ell -1$ such that

(6.8) $$ \begin{align} \partial_{i}(Q-MW)=M^{\ell}R_{i} \end{align} $$

for all $1\leq i\leq d$ . Setting $N_{i}=\partial _{i}Q$ , it follows from Proposition 6.4 that there exist $F,R_{1},\ldots ,R_{d}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (F)\leq s-2, \deg (R_{i})\leq s-3$ such that

$$ \begin{align*} \partial_{i}Q=(\partial_{i}M)F+MR_{i}. \end{align*} $$

This implies that Property 1 holds since for all $1\leq i\leq d$ , we have that

$$ \begin{align*} \partial_{i}(Q-MF)=M(R_{i}-\partial_{i}F). \end{align*} $$

Now, suppose that Property- $\ell $ holds for some $1\leq \ell <p$ . Since $\deg (\partial _{i}Q')\leq p-1$ , for all $1\leq j\leq d$ , it follows from (6.8) that

(6.9) $$ \begin{align} \partial_{j}\partial_{i}(Q-MW)=\partial_{j}(M^{\ell-1}R_{i})=M^{\ell-2}((\ell-1)(\partial_{j}M)R_{i}+M\partial_{j}R_{i}). \end{align} $$

By symmetry,

(6.10) $$ \begin{align} \partial_{i}\partial_{j}(Q-MW)=M^{\ell-2}((\ell-1)(\partial_{i}M)R_{j}+M\partial_{i}R_{j}). \end{align} $$

Combining (6.9) and (6.10), we have that for all $1\leq i,j\leq d$ , there exists a polynomial $N_{i,j}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ such that

$$ \begin{align*} (\partial_{i}M)R_{j}-(\partial_{j}M)R_{i}=MN_{i,j}. \end{align*} $$

By Proposition 6.4, we may write

$$ \begin{align*}R_{i}=(\partial_{i}M)F'+MR^{\prime}_{i}\end{align*} $$

for some $F',R^{\prime }_{1},\ldots ,R^{\prime }_{d}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (F')\leq s-2\ell -2, \deg (R_{i})\leq s-2\ell -3$ . Substituting this back to (6.8), we have that

$$ \begin{align*} \partial_{i}(Q-M(W+F'))=M^{\ell+1}(R^{\prime}_{i}-\partial_{i} F') \end{align*} $$

for all $1\leq i\leq d$ . So Property $(\ell +1)$ holds.

So, we may inductively conclude that Property $\ell $ holds when $\ell =[(s+1)/2]$ , in which case, the polynomials $H_{i}$ in (6.8) are constant 0 and so all the formal derivatives of ${Q-MW}$ are zero for some polynomial W of degree at most $s-2$ . Since $Q(\mathbf {0})=0$ , we must have that $Q=MW$ and we are done.

The rest of the section is devoted to the proof of Proposition 6.4. We first provide an outline of the proof. For convenience, assume that $M(n)=n\cdot n$ . Assume first that (6.7) holds for all $n\in \mathbb {F}_{p}^{d}$ (not just for $n\in V(M)$ ). Then, (6.7) implies that $n_{i}H_{j}(n)$ is divisible by $n_{j}$ and so $H_{j}(n)$ is divisible by $n_{j}$ (by choosing $i\neq j$ ). So, we may write $H_{j}(n)=2n_{j}G_{j}(n)$ for some polynomial $G_{j}$ . Substituting this back to (6.7), we have that all of $G_{j}$ are equal to the same G. So, $H_{j}(n)=2n_{j}G(n)=\partial _{i}M(n)G(n)$ and we are done.

For the general case, our goal is to show that each $H_{i}$ can be written as the sum of a multiple of $\partial _{i}M(n)$ (or $n_{i}$ ) and a multiple of M.

Step 1: factorization over $n_{i}$ . By Proposition 6.2, for all $1\leq i,j\leq d$ , there exist some polynomial $N_{i,j}$ such that

(6.11) $$ \begin{align} n_{i}H_{j}(n)-n_{j}H_{i}(n)=M(n)N_{i,j}(n) \quad\text{for all } n\in \mathbb{F}_{p}^{d}. \end{align} $$

In this case, $n_{j}H_{i}(n)$ is no longer divisible by $n_{i}$ because of the appearance of the term $MN_{i,j}$ . However, if we decompose $N_{i,j}$ as

$$ \begin{align*}N_{i,j}(n)=n_{i}N_{1,i,j}(n)+n_{j}N_{2,i,j}(n)+n_{i}n_{j}N_{3,i,j}(n),\end{align*} $$

we can deduce from (6.11) that $n_{i}(H_{j}-MN_{1,i,j})$ is divisible by $n_{j}$ and thus $H_{j}-MN_{1,i,j}$ is divisible by $n_{j}$ . So, there exists some polynomial $G_{i,j}$ such that

(6.12) $$ \begin{align} H_{j}(n)=2n_{j}G_{i,j}(n)+M(n)N_{1,i,j}(n)= \partial_{j}M(n)G_{i,j}(n)+M(n)N_{1,i,j}(n). \end{align} $$

Step 2: removing the dependence of $N_{1,i,j}$ on i. Let $E_{i,j}$ denote the left-hand side of (6.11). Then, we have that $E_{i,j}+E_{j,i}=E_{i,j}+E_{j,k}+E_{k,i}=0$ . These symmetric properties provide extra information for $N_{i,j}$ , and one can use them to show that the polynomials $N_{1,i,j}$ and $G_{i,j}$ in (6.12) are independent of i. So,

(6.13) $$ \begin{align} H_{j}(n)=2n_{j}G_{j}(n)+M(n)N_{j}(n) \end{align} $$

for some polynomials $G_{j}$ and $N_{j}$ . See the proof for details of this step.

Step 3: removing the dependence on j. Our final step is to show that the polynomial $G_{j}$ in (6.13) can be chosen to be independent of j. Substituting (6.13) back to (6.11), we have that $n_{i}n_{j}(G_{i}-G_{j})$ is divisible by M, which implies that $G_{i}-G_{j}$ is divisible by M. We may then set $G_{i}=G_{j}$ for all $1\leq i,j\leq d$ by absorbing the error term in $M(n)N_{j}(n)$ .

We now provide the rigorous proof of Proposition 6.4.

Proof of Proposition 6.4

For convenience, write $n=(n_{1},\ldots ,n_{d})\in \mathbb {F}_{p}^{d}$ . By Lemma 4.3 and a change of variables, we may assume without loss of generality that

$$ \begin{align*}M(n)=cn_{1}^{2}+n_{2}^{2}+\cdots+n_{d'}^{2}+c'n_{d'+1}-\unicode{x3bb}\end{align*} $$

for some $3\leq d'\leq d$ , and $\unicode{x3bb} ,c,c'\in \mathbb {F}_{p}$ with $c\neq 0$ . Let A be the (diagonal) matrix associated to M with $a_{i}$ being the $(i,i)$ th entry of A. Then, $a_{1}{\kern-1pt}={\kern-1pt}c{\kern-1pt}\neq{\kern-1pt} 0$ , ${a_{2}{\kern-1pt}=\cdots ={\kern-1pt}a_{d'}=1}$ , and $a_{d'+1}=\cdots =a_{d}=0$ . First-time readers are advised to focus on the case when $M(n)=n\cdot n, c=1$ , and $d'=d$ , which already captures the most essential part of the proof.

Step 1: factorization over $\partial _{i}M$ . By assumption and Proposition 6.2, we have that for all $1\leq i,j\leq d$ , there exists a polynomial $N_{i,j}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ such that

(6.14) $$ \begin{align} (\partial_{i}M)H_{j}-(\partial_{j}M)H_{i}=MN_{i,j}. \end{align} $$

By Proposition 6.2, $\deg (N_{i,j})\leq s-1$ . For all $1\leq i,j\leq d', i\neq j$ , there exist unique polynomials $N_{1,i,j},N_{2,i,j},N_{3,i,j}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (N_{1,i,j}),\deg (N_{2,i,j})\leq s-2$ and $\deg (N_{3,i,j})\leq s-3$ such that

(6.15) $$ \begin{align} N_{i,j}=(\partial_{i}M)N_{1,i,j}+(\partial_{j}M)N_{2,i,j}+\tfrac{1}{2}(\partial_{i}M)(\partial_{j}M)N_{3,i,j}, \end{align} $$

where $N_{1,i,j}$ is independent of $n_{j}$ and $N_{2,i,j}$ is independent of $n_{i}$ . We could derive from this a conclusion in analogous to (6.12). However, this is unnecessary and thus, we now directly move to Step 2.

Step 2: removing the dependence of $N_{1,i,j}$ on i. We first use the property ${E_{i,j}{\kern-1pt}+{\kern-1pt}E_{j,i}{\kern-1pt}={\kern-1pt}0}$ to show some anti-symmetric properties on the indices i and j in $N_{1,i,j},N_{2,i,j}$ and $N_{3,i,j}$ (i.e., (6.18)). Since (6.14) implies that

(6.16) $$ \begin{align} a_{i}n_{i}H_{j}(n)-a_{j}n_{j}H_{i}(n)=M(n)N_{i,j}(n)/2 \end{align} $$

and thus

(6.17) $$ \begin{align} a_{j}n_{j}H_{i}(n)-a_{i}n_{i}H_{j}(n)=M(n)N_{j,i}(n)/2 \end{align} $$

by symmetry, it follows from (6.16) and (6.17) that $N_{i,j}+N_{j,i}=0$ . So,

$$ \begin{align*}n_{i}(N_{1,i,j}(n)+N_{2,j,i}(n))+n_{j}(N_{1,j,i}(n)+N_{2,i,j}(n))+n_{i}n_{j}(N_{3,i,j}(n)+N_{3,j,i}(n))=0.\end{align*} $$

Since $N_{1,i,j}+N_{2,j,i}$ is independent of $n_j$ and $N_{1,j,i}(n)+N_{2,i,j}(n)$ is independent of $n_i$ , we have that

(6.18) $$ \begin{align} N_{1,i,j}+N_{2,j,i}=N_{3,i,j}+N_{3,j,i}=0. \end{align} $$

Combining (6.15), (6.16), and (6.18), we have that

(6.19) $$ \begin{align} a_{i}n_{i}H_{j}(n)-a_{j}n_{j}H_{i}(n)=M(n)(n_{i}N_{1,i,j}(n)-n_{j}N_{1,j,i}(n)+n_{i}n_{j}N_{3,i,j}) \end{align} $$

for all distinct $1\leq i,j\leq d'$ .

Next, we use the property $E_{i,j}+E_{j,k}+E_{k,i}=0$ to show that $N_{1,i,j}$ is independent of i. For all $1\leq k\leq d', k\neq i,j$ , (6.19) implies that

(6.20) $$ \begin{align} & a_{i}n_{k}n_{i}H_{j}(n)-a_{j}n_{j}n_{k}H_{i}(n) =M(n)(n_{k}n_{i}N_{1,i,j}(n)-n_{j}n_{k}N_{1,j,i}(n)+n_{i}n_{j}n_{k}N_{3,i,j}). \end{align} $$

By symmetry,

(6.21) $$ \begin{align} & a_{j}n_{i}n_{j}H_{k}(n)-a_{k}n_{k}n_{i}H_{j}(n) =M(n)(n_{i}n_{j}N_{1,j,k}(n)-n_{k}n_{i}N_{1,k,j}(n)+n_{i}n_{j}n_{k}N_{3,j,k}) \end{align} $$

and

(6.22) $$ \begin{align} & a_{k}n_{j}n_{k}H_{i}(n)-a_{i}n_{i}n_{j}H_{k}(n) =M(n)(n_{j}n_{k}N_{1,k,i}(n)-n_{i}n_{j}N_{1,i,k}(n)+n_{i}n_{j}n_{k}N_{3,k,i}). \end{align} $$

To remove the term $N_{3,i,j}$ , we consider $(6.20)\times a_{k}+(6.21)\times a_{i}+(6.22)\times a_{j}$ and get

$$ \begin{align*}n_{k}n_{i}(a_{k}N_{1,i,j}-a_{i}N_{1,k,j})+n_{i}n_{j}(a_{i}N_{1,j,k}-a_{j}N_{1,i,k})+n_{j}n_{k}(a_{j}N_{1,k,i}-a_{k}N_{1,j,i})\end{align*} $$

is divisible by $n_{i}n_{j}n_{k}$ . In particular, $n_{k}n_{i}(a_{k}N_{1,i,j}(n)-a_{i}N_{1,k,j}(n))$ is divisible by $n_{j}$ . Since $N_{1,i,j}-N_{1,k,j}$ is independent from $n_{j}$ , we must have that $a_{k}N_{1,i,j}=a_{i}N_{1,k,j}$ for all distinct $1\leq i,j,k\leq d'$ . This implies that $N_{1,i,j}=a_{i}N_{j}$ for some $N_{j}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most $s-2$ for all $1\leq i\leq d', i\neq j$ . This completes the second step.

Step 3: removing the dependence on j. Let $H^{\prime }_{j}=H_{j}-MN_{j}$ . Substituting the conclusion that $N_{1,i,j}=a_{i}N_{j}$ back to (6.19), we have that for all $1\leq i,j\leq d',i\neq j$ ,

(6.23) $$ \begin{align} a_{i}n_{i}H^{\prime}_{j}(n)-a_{j}n_{j}H^{\prime}_{i}(n)=n_{i}n_{j}M(n)N_{3,i,j}. \end{align} $$

Setting $j=1$ and $i=2$ , (6.23) implies that

(6.24) $$ \begin{align} H^{\prime}_{1}(n)=2cn_{1}G(n)=\partial_{1}M(n)G(n) \end{align} $$

for some polynomial G of degree at most $s-1$ .

By (6.14) and (6.24), for all $1\leq j\leq d$ ,

$$ \begin{align*} \begin{aligned} (\partial_{1}M)H_{j}=MN_{1,j}+(\partial_{j}M)H_{1} =M(N_{1,j}+(\partial_{j}M)N_{1}) +(\partial_{j}M)(\partial_{1}M)G, \end{aligned} \end{align*} $$

which implies that

$$ \begin{align*} \begin{aligned} 2cn_{1}H^{\prime}_{j}(n)=M(n)(N_{1,j}(n)+\partial_{j}M(n)N_{1}(n)). \end{aligned} \end{align*} $$

It is not hard to see that $N_{1,j}(n)+\partial _{j}M(n)N_{1}(n)=2cn_{1}F_{j}(n)$ for some polynomial $F_{j}$ of degree at most $s-2$ . Therefore,

$$ \begin{align*} \begin{aligned} H_{j}-(\partial_{j}M)G=MF_{j}. \end{aligned} \end{align*} $$

We are done.

6.3 Solution to a special polynomial equation

In this section, we study the solutions to polynomial equations of the form

(6.25) $$ \begin{align} \Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P(n)+\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q(n)=0 \!\quad\text{for all/many } (n,h_{1},\ldots,h_{s})\in\Box_{s}(V(M)) \end{align} $$

for some quadratic form $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ , which will be used crucially later in the paper. We begin with a preparatory result.

Proposition 6.5. Let $\delta>0$ , $d,d',s\in \mathbb {N}$ with $d\geq d'\geq 4$ , $p\gg _{d,s} \delta ^{-O_{d,s}(1)}$ be a prime number, $P,Q\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ be polynomials of degrees at most s and $s+1$ , respectively, with $Q(\mathbf {0})=0$ , $c\in \mathbb {F}_{p}\backslash \{0\}$ , and $H\subseteq \mathbb {F}_{p}^{d}$ with $\vert H\vert>\delta p^{d}$ . Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a non-degenerate quadratic form given by

$$ \begin{align*}M(n_{1},\ldots,n_{d}):=cn^{2}_{1}+n^{2}_{2}+\cdots+n_{d'}^{2}.\end{align*} $$

Suppose that for all $n\in \mathbb {F}_{p}^{d}$ and $h=(h_{1},\ldots ,h_{d})\in H$ with $M(n)=(nA)\cdot h=0$ (where A is the matrix associated to M), we have that

(6.26) $$ \begin{align} P(n)+\sum_{i=1}^{d}h_{i}\partial_{i}Q(n)=0. \end{align} $$

Then, there exist $P',Q'\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degrees at most $s-2$ and $s-1$ , respectively, such that $P=MP'$ and $Q=MQ'$ .

We first explain why Proportion 6.5 is useful to study (6.25). For convenience, assume that $s=1$ , M is homogeneous, $\deg (P)=k$ , and $\deg (Q)=k+1$ . Intuitively, if (6.25) holds for all $(n,h)\in \Box _{1}(V(M))$ , then by the spirit of Hilbert Nullstenllensatz, we may expect to write $P(n)+\Delta _{h}Q(n)$ as a linear combination of $M(n)$ and $M(n+h)-M(n)$ . Considering h as a fixed vector, the leading terms of $P(n)+\Delta _{h}Q(n)$ must be a linear combination of the leading terms of $M(n)$ and $M(n+h)-M(n)$ . It is not hard to see that the leading terms of $P(n)+\Delta _{h}Q(n)$ are

(6.27) $$ \begin{align} P+h\cdot\nabla Q=P+\sum_{i=1}^{d}h_{i}\partial_{i}Q, \end{align} $$

where $h=(h_{1},\ldots ,h_{d})$ and $\nabla Q=(\partial _{1}Q,\ldots ,\partial _{d}Q)$ . However, the leading terms of $M(n)$ and $M(n+h)-M(n)$ are $M(n)$ and $(nA)\cdot h$ , respectively. Therefore, we have that (6.27) is zero if $M(n)=(nA)\cdot h=0$ . This is where Proposition 6.5 becomes useful.

We now explain the outline of the proof of Proposition 6.5. Fix $n\in \mathbb {F}_{p}^{d}$ . The lower bound $\vert H\vert>\delta p^{d}$ ensures that (6.26) holds for many h with $(nA)\cdot h=0$ . By linearity, we must have that (6.26) holds for all $h\in \mathbb {F}_{p}^{d}$ with $(nA)\cdot h=0$ . This will force $P(n)=0$ and $(\partial _{1}Q(n),\ldots ,\partial _{d}Q(n))$ to be parallel to $2nA=(\partial _{1}M(n),\ldots ,\partial _{d}M(n))$ . So, $\partial _{i}Q(n)/\partial _{i}M(n)$ is independent of the choice of i. If this is the case for many $n\in V(M)$ , then it follows from Lemma 6.1 and Proposition 6.3 that P and Q are divisible by M.

Proof of Proposition 6.5

Throughout the proof, all the constants will depend implicitly on d and s. Since $d'\geq 3$ , by Lemma 4.12, the set of $h\in \mathbb {F}_{p}^{d}$ with $M(h)=0$ is of cardinality $O_{d,s}(p^{d-1})$ . Passing to a subset if necessary, we may assume without loss of generality that $M(h)\neq 0$ for all $h\in H$ . Let A be the (diagonal) matrix associated to M and $a_{i}$ be the $(i,i)$ th entry of A. To carry out the strategy described above, our first task is to identify those $n\in V(M)$ for which there are many $h\in \mathbb {F}_{p}^{d}$ with $(nA)\cdot h=0$ . Denote

$$ \begin{align*}V_{h}:=\{n\in\mathbb{F}_{p}^{d}\colon (nA)\cdot h=0\}=(\text{span}_{\mathbb{F}_{p}}\{h\})^{\perp{M}}.\end{align*} $$

Note that for most of the choices of h, the set $V_{h}$ is of cardinality $\gg p^{d-2}$ . So, there are in total $\gg _{\delta } p^{2d-2}$ number of pairs of $(n,h)$ for which (6.26) holds. Since $V(M)$ is of cardinality $\gg p^{d-1}$ , on average, there are $\gg _{\delta } p^{d-1}$ many ‘good’ $n\in V(M)$ for which (6.26) holds for at least $\gg _{\delta } p^{d-1}$ many $h\in H$ . Our first goal is to identify those ‘good’ n (as well as those h for which (6.26) holds for the pair $(n,h)$ ).

Let Z be the set of $n\in \mathbb {F}_{p}^{d}$ with $nA=\mathbf {0}$ . Then, $\vert Z\vert =p^{d-d'}\leq p^{d-4}$ . We say that $(n,h)\in \mathbb {F}_{p}^{d}\times \mathbb {F}_{p}^{d}$ is a good pair if

$$ \begin{align*} (nA)\cdot h=M(n)=0,\quad n\in\mathbb{F}_{p}^{d}\backslash Z \quad\text{and}\quad h\in H. \end{align*} $$

For each $h\in H$ , $V_{h}$ is a subspace of $\mathbb {F}_{p}^{d}$ of co-dimension 1 and $V_{h}\cap (V_{h})^{ \perp {M}}=\{\mathbf {0}\}$ (since $M(h)\neq 0$ ). By Proposition 4.8, $\mathrm {rank}(M\vert _{V_{h}})\geq d'-1\geq 3$ . By Corollary 4.14 and the fact that $\vert Z\vert \leq p^{d-4}$ , there exist $p^{d-2}(1+O(p^{-1/2}))$ many $n\in \mathbb {F}_{p}^{d}$ such that $(n,h)$ is a good pair. So, there are in total at least $\delta p^{2d-2}(1+O(p^{-1/2}))$ many good pairs. However, for each $n\in \mathbb {F}_{p}^{d}\backslash Z$ with $M(n)=0$ , since $nA\neq \mathbf {0}$ , there exist $p^{d-1}$ many $h\in \mathbb {F}_{p}^{d}$ such that $(nA)\cdot h=0$ . By Lemma 6.1, the number of $n\in \mathbb {F}_{p}^{d}\backslash Z$ with $M(n)=0$ is $p^{d-1}(1+O(p^{-1/2}))$ . From this, it is easy to see that there exists a subset $X\subseteq \mathbb {F}_{p}^{d}\backslash Z$ with

$$ \begin{align*} \vert X\vert>\frac{\delta}{2}p^{d-1}(1+O(p^{-1/2})) \end{align*} $$

such that $M(n)=0$ for all $n\in X$ , and there exists a subset $H_{n}\subseteq H$ with

$$ \begin{align*} \vert H_{n}\vert>\frac{\delta}{2}p^{d-1}(1+O(p^{-1/2})) \end{align*} $$

such that $(n,h)$ is a good pair for all $h\in H_{n}$ .

Our next step is to show that for any $n\in X$ , (6.26) holds not only for $h\in H_{n}$ , but also for all $h\in V_{n}$ . To see this, we may view the left-hand side of (6.26) as the dot product $(P(n),\partial _{1}Q(n),\ldots ,\partial _{d}Q(n))\cdot (1,h)$ . If the dot product is zero for all $h\in H_{n}$ , then by linearity and the largeness of $H_{n}$ (this is where we need the lower bound $\vert H\vert>\delta p^{d}$ to ensure the largeness of $H_{n}$ ), $(P(n),\partial _{1}Q(n),\ldots ,\partial _{d}Q(n))$ is orthogonal to $W_{n}$ , the subspace of $\mathbb {F}_{p}^{d+1}$ spanned by $(1,h), h\in H_{n}$ .

We claim that $W_{n}=\mathbb {F}_{p}\times V_{n}$ . Clearly, $W_{n}\subseteq \mathbb {F}_{p}\times V_{n}$ , so it suffices to show that $W_{n}$ is of dimension d. Suppose in contrast that $W_{n}$ is of dimension at most $d-1$ . Let $v_{i}=(v_{i,0},\ldots ,v_{i,d})\in \mathbb {F}_{p}^{d+1}, 1\leq i\leq L$ be a basis of $W_{n}$ . If $(1,h)=a_{1}v_{1}+\cdots +a_{L}v_{L}$ , we must have that $a_{1}v_{i,0}+\cdots +a_{L}v_{L,0}=1$ . So, there are at most $p^{L-1}\leq p^{d-2}$ many $(1,h)$ belonging to $W_{n}$ , meaning that $\vert H_{n}\vert \leq p^{d-2}$ , which is a contradiction since ${\vert H_{n}\vert>(\delta /2)p^{d-1}(1+O(p^{-1/2}))}$ and $p\gg \delta ^{-O(1)}$ . So, $W_{n}=\mathbb {F}_{p}\times V_{n}$ . This proves the claim.

We are now ready to complete the proof of the proposition. Since $P(n)+\sum _{i=1}^{d}h_{i}Q_{i}(n)=0$ for all $n\in X$ and $h\in H_{n}$ , we have that

$$ \begin{align*}(P(n),Q_{1}(n),\ldots,Q_{d}(n))\cdot (1,h)=0\end{align*} $$

for all $h\in H_{n}$ . By linearity,

$$ \begin{align*} (P(n),Q_{1}(n),\ldots,Q_{d}(n))\cdot v=0 \end{align*} $$

for all $v\in W_{n}$ . Since by the claim $W_{n}=\mathbb {F}_{p}\times V_{n}$ , we have that $P(n)=0$ and that

$$ \begin{align*} (nA)\cdot h=0 \Rightarrow (Q_{1}(n),\ldots,Q_{d}(n))\cdot h=0 \end{align*} $$

for all $h{\kern-1pt}\in{\kern-1pt} \mathbb {F}_{p}^{d}$ and $n{\kern-1pt}\in{\kern-1pt} X$ . This implies that the vector $nA$ is parallel to $(Q_{1}(n),\ldots ,Q_{d}(n))$ , and so we may write $(Q_{1}(n),\ldots ,Q_{d}(n))=F(n)(nA)=(cn_{1}F(n),n_{2}F(n),\ldots , n_{d}F(n))$ for some $F(n)\in \mathbb {F}_{p}$ for all $n\in X$ . In other words, for all $1\leq i,j\leq d$ and $n\in X$ ,

$$ \begin{align*}\partial_{j}M(n)Q_{i}(n)=2c_{j}a_{j}Q_{i}(n)=2c_{j}c_{i}a_{j}a_{i}=\partial_{i}M(n)Q_{j}(n),\end{align*} $$

where $c_{1}=c$ and $c_{2}=\cdots =c_{d}=1$ .

Finally, since $\vert X\vert{\kern-1pt}>{\kern-1pt}{(\delta /2)}p^{d-1}(1{\kern-1pt}+{\kern-1pt}O(p^{-1/2}))$ , by Lemma 6.1, for all $n{\kern-1pt}\in{\kern-1pt} \mathbb {F}_{p}^{d}$ , ${M(n)=0}$ implies that $P(n)=0$ and $\partial _{j}M(n)Q_{i}(n)=\partial _{i}M(n)Q_{j}(n)$ for all $1\leq i,j\leq d$ . The conclusion then follows from Proposition 6.3.

We are now able provide a solution to (6.25).

Proposition 6.6. Let $d,s\in \mathbb {N}_{+}$ , $k\in \mathbb {N}$ , $\delta>0$ , $p\gg _{d,k} \delta ^{-O_{d,k}(1)}$ be a prime, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form. Let W be a subset of $\Box _{s}(V(M))$ such that either:

• • $W=\Box _{s}(V(M))$ and $\mathrm {rank}(M)\geq s+3$ ; or

• • $\vert W\vert \geq \delta \vert \Box _{s}(V(M))\vert $ and $\mathrm {rank}(M)\geq s^{2}+s+3$ .

Let $P,Q\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P)\leq k-1$ and $\deg (Q)\leq k$ be such that for all $(n,h_{1},\ldots ,h_{s})\in W$ , we have that

(6.28) $$ \begin{align} \begin{aligned} \Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P(n)+\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q(n)=0 \end{aligned} \end{align} $$

(where $\Delta _{h_{s-1}}\cdots \Delta _{h_{1}}P(n)$ is understood as $P(n)$ when $s=1$ ). Then,

$$ \begin{align*} P=MP_{1}+P_{2} \quad\text{and}\quad Q=MQ_{1}+Q_{2} \end{align*} $$

for some $P_{1},P_{2},Q_{1},Q_{2}\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P_{1})\leq k-3$ , $\deg (P_{2})\leq s-2$ , $\deg (Q_{1})\leq k-2$ , $\deg (Q_{2})\leq s-1$ .

Therefore, Proposition 6.6 provides solutions to (6.25) in two cases. The first case is when (6.25) holds for all $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ , the second case is when (6.25) holds for a dense subset of $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ (in the latter case, we need to impose a stronger lower bound for the dimension d).

We remark that Proposition 6.6 is trivial if $k\leq s-1$ . We briefly explain the outline of the proof. Assume for convenience that $W=\Box _{s}(V(M))$ . We prove it by induction.

Step 1. Fix $h_{s}\in \mathbb {F}_{p}^{d}$ and write $h=h_{s}$ for convenience. Note that

$$ \begin{align*}\Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P+\Delta_{h}\cdots\Delta_{h_{1}}Q=\Delta_{h_{s-1}}\cdots\Delta_{h_{1}}(P+\Delta_{h}Q)\end{align*} $$

and that $(n,h_{1},\ldots ,h_{s-1},h)\in \Box _{s}(V(M))\Leftrightarrow (n,h_{1},\ldots ,h_{s-1})\in \Box _{s-1}(V(M)^{h})$ . By the inheriting principle, we may informally think of $V(M)^{h}$ as a lower degree hypersphere (which is the set of zeros of a lower dimensional quadratic form $M_{h}$ and a subspace $V_{h}$ of $\mathbb {F}_{p}^{d}$ ) and apply the induction hypothesis to conclude that the restriction of $P_{h}+\Delta _{h}Q_{h}$ on $V_{h}$ can be written as $M_{h}R_{h}+R^{\prime }_{h}$ for some lower degree polynomial $R^{\prime }_{h}$ , where $P_{h}$ and $Q_{h}$ are the ‘restrictions’ of P and Q on $V_{h}$ (this can be made precise by (6.31)).

Step 2. For simplicity, assume that all of $M,P,Q$ are homogeneous. Then, $R^{\prime }_{h}$ vanishes and so the conclusion of Step 1 implies that $P(n)+\Delta _{h}Q(n)=0$ for all $n\in V(M)^{h}$ , that is, whenever $(n,h)\in \Box _{1}(V(M))$ . Since $P,Q$ are homogeneous, similar to (6.27), the degree $k-1$ terms of $P(n)+Q(n+h)-Q(n)$ are equal to

$$ \begin{align*}P+h\cdot\nabla Q=P+h_{s}\cdot\nabla Q=P+\sum_{i=1}^{d}h_{s,i}\partial_{i}Q,\end{align*} $$

where $h=h_{s}=(h_{s,1},\ldots ,h_{s,d})$ . Since (6.28) holds for all $(n,h_{1})\in \Box _{1}(V(M))$ , we may invoke Proposition 6.5 to the degree $k-1$ terms of the left-hand side of (6.28) to conclude that P and Q are divisible by M.

Proof of Proposition 6.6

Throughout the proof, we assume that $p\gg _{d,k} \delta ^{-O_{d,k}(1)}$ . Let A be the matrix associated with M and denote $d'=\mathrm {rank}(M)$ . By Lemmas 4.3 and 4.18, under a change of variables, it suffices to consider the case when A is a diagonal matrix with diagonal $(c,1,\ldots ,1,0,\ldots ,0)$ for some $c\in \mathbb {F}_{p}\backslash \{0\}$ , where there are $d-d'$ zeros on the diagonal.

To carry out Step 1 of the outline, it is convenient to work on the set $V(M)^{h}-h/2$ instead of $V(M)^{h}$ . So, we need some definitions to describe such a set (this will make the notation of the proof slightly different from that used in the outline). For $h\in \mathbb {F}_{p}^{d}$ , let

$$ \begin{align*} U_{h}:=V(M)^{h}-h/2=\{n\in\mathbb{F}_{p}^{d}\colon M(n+h/2)=M(n-h/2)\}. \end{align*} $$

Then, we may write $U_{h}=V_{h}+u_{h}$ for some $u_{h}\in \mathbb {F}_{p}^{d}$ , where

$$ \begin{align*} V_{h}:=\{n\in\mathbb{F}_{p}^{d}\colon (nA)\cdot h=0\}. \end{align*} $$

Let $L_{h}\colon \mathbb {F}_{p}^{d-1}\to V_{h}$ be any bijective linear transformation and denote

$$ \begin{align*} M_{h}(m):=M(L_{h}(m)+u_{h}-h/2). \end{align*} $$

By the definition of $U_{h}$ , we have that $M(L_{h}(m)+u_{h}-h/2)=M(L_{h}(m)+u_{h}+h/2)$ for all $m\in \mathbb {F}_{p}^{d-1}$ . From this, it is not hard to check that

(6.29) $$ \begin{align} &(m,m_{1},\ldots,m_{s-1})\in \Box_{s-1}(M_{h})\Leftrightarrow (L_{h}(m)\nonumber\\ & \quad+u_{h}-h/2,L_{h}(m_{1}),\ldots,L_{h}(m_{s-1}),h)\in \Box_{s}(M). \end{align} $$

So, the assumption and (6.29) imply that

(6.30) $$ \begin{align} \begin{aligned} \Delta_{m_{s-1}}\cdots\Delta_{m_{1}}(P_{h}(m)+Q_{h}(m))=0 \end{aligned} \end{align} $$

for all $(m,m_{1},\ldots ,m_{s-1})\in \Box _{s-1}(M_{h})$ with $(L_{h}(m)+u_{h}-h/2,L_{h}(m_{1}),\ldots , L_{h}(m_{s-1}),h)\in W$ , where

$$ \begin{align*} P_{h}:=P(L_{h}(\cdot)+u_{h}-h/2) \!\quad\text{and}\quad\! Q_{h}:=Q(L_{h}(\cdot){\kern-1pt}+{\kern-1pt}u_{h}{\kern-1pt}+{\kern-1pt}h/2){\kern-1pt}-{\kern-1pt}Q(L_{h}(\cdot)+u_{h}-h/2). \end{align*} $$

We remark that (6.30) is also valid when $s=1$ , in which case, (6.30) is understood as

(6.31) $$ \begin{align} P_{h}(m)+Q_{h}(m)=0. \end{align} $$

We introduce some further notation to describe the set of $(m,m_{1},\ldots ,m_{s-1})$ satisfying (6.29). For all $h\in \mathbb {F}_{p}^{d}$ , let $W_{h}$ be the set of $(n,h_{1},\ldots ,h_{s-1})\in (\mathbb {F}_{p}^{d})^{s}$ such that $(n,h_{1},\ldots ,h_{s-1},h)\in W$ (that is, we decompose W into fibers $W_{h}$ with respect to the last variable). We now parameterize $W_{h}$ using $m,m_{1},\ldots ,m_{s-1}$ . For all $h\in \mathbb {F}_{p}^{d}$ , let $W^{\prime }_{h}$ be the set of $(m,m_{1},\ldots ,m_{s-1})$ such that

$$ \begin{align*} (L_{h}(m)+u_{h}-h/2,L_{h}(m_{1}),\ldots,L_{h}(m_{s-1}))\in W_{h}. \end{align*} $$

Since $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ for all $(n,h_{1},\ldots ,h_{s-1})\in W_{h_{s}}$ , it follows from (6.29) that

(6.32) $$ \begin{align} W^{\prime}_{h}\subseteq \Box_{s-1}(V(M_{h})) \quad\text{and}\quad \vert W^{\prime}_{h}\vert=\vert W_{h}\vert \quad\text{for all } h\in \mathbb{F}_{p}^{d}. \end{align} $$

Therefore, we have that (6.30) holds for all $h\in \mathbb {F}_{p}^{d}$ and $(m,m_{1},\ldots ,m_{s-1})\in W^{\prime }_{h}$ .

Recall that Step 1 is to fix h and use the induction hypothesis or Proposition 6.2 on (6.30) to obtain a description for $P_{h}+Q_{h}$ . So, we need to choose h carefully so that the dimension of $V_{h}$ is $d-1$ , the rank of $M_{h}$ is $d'-1$ , and the set $W^{\prime }_{h}$ is large. Let Z be the set of $h\in \mathbb {F}_{p}^{d}$ such that $\dim (V_{h})\neq d-1$ or $\dim (V_{h}\cap V_{h}^{\perp {M}})\neq d-d'$ . Then, by Proposition 4.8(ii), for all $h\in \mathbb {F}_{p}^{d}\backslash Z$ , we have that $\mathrm {rank}(M_{h})=d'-1$ . We now show that Z is a small set.

Claim 1. We have that $\vert Z\vert \leq O_{d}(p^{d-1})$ .

Proof of Claim 1

Let $Z'$ be the set of $h\in \mathbb {F}_{p}^{d}$ such that either $(hA)\cdot h=0$ or at least one of the coordinates of h is 0. Since $\mathrm {rank}(A)=d'\geq 3$ , by Lemma 4.12, it is not hard to see that $\vert Z'\vert =O_{d}(p^{d-1})$ . Now, fix any $h=(h_{1},\ldots ,h_{d})\in \mathbb {F}_{p}^{d}\backslash Z'$ . Then, since $hA\neq \mathbf {0}$ , we have that $\dim (V_{h})=d-1$ . Note that

$$ \begin{align*}\{-h_{i}e_{1}+ch_{1}e_{i}\colon 2\leq i\leq d'\}\cup\{e_{j}\colon d'+1\leq j\leq d\}\end{align*} $$

is a basis of $V_{h}$ , where $e_{i}$ is the ith standard unit vector. From this, it is not hard to compute that

$$ \begin{align*} (h_{1},\ldots,h_{d'},0,\ldots,0), e_{d'+1},\ldots,e_{d} \end{align*} $$

is a basis of $(V_{h})^{\perp {M}}$ . Therefore, $\dim ((V_{h})^{\perp {M}})=d-d'+1$ . Finally, it is not hard to compute by induction that

$$ \begin{align*}\det\begin{bmatrix} -h_{2} & ch_{1} & & & \\ -h_{3} & & ch_{1} & & \\ \cdots & & & \cdots & \\ -h_{d'} & & & & ch_{1} \\ h_{1} & \cdots & \cdots & \cdots & h_{d'} \end{bmatrix}=(-1)^{d'+1}(ch_{1})^{d'-2}((hA)\cdot h)\neq 0.\end{align*} $$

This implies that $V_{h}+(V_{h})^{\perp {M}}=\mathbb {F}_{p}^{d}$ . So,

$$ \begin{align*} \dim(V_{h}\cap V_{h}^{\perp{M}})& = \dim(V_{h})+\dim(V_{h}^{\perp{M}})-\dim(V_{h}+(V_{h})^{\perp{M}})\\ & = (d-1)+(d-d'+1)-d=d-d'. \end{align*} $$

Therefore, $Z\subseteq Z'$ and thus, $\vert Z\vert \leq O_{d}(p^{d-1})$ . This proves Claim 1.

We still need to remove those h for which $\vert W^{\prime }_{h}\vert $ is small. This is done by the next claim.

Claim 2. There exists $W_{\ast }\subseteq \mathbb {F}_{p}^{d}$ of cardinality at least $\delta p^{d}/4$ such that for all $h\in W_{\ast }\backslash Z$ ,

(6.33) $$ \begin{align} \vert W^{\prime}_{h}\vert=\vert W_{h}\vert\geq O(\delta) \vert \Box_{s-1}(V(M_{h}))\vert. \end{align} $$

Proof of Claim 2

If $\vert W\vert \geq \delta \vert \Box _{s}(V(M))\vert $ and $\mathrm {rank}(M)\geq s^{2}+s+3$ , then by Proposition 4.19, we have that

$$ \begin{align*} \sum_{h\in\mathbb{F}_{p}^{d}}\vert W_{h}\vert=\vert W\vert>\delta\vert\Box_{s}(V(M))\vert=\delta p^{(s+1)d-(({s(s+1)}/2)+1)}(1+O_{s}(p^{-1/2})). \end{align*} $$

Moreover, for all but at most $s(s+1)p^{d+s-\mathrm {rank}(M)}$ many $h_{s}\in \mathbb {F}_{p}^{d}$ , we have that $\vert W_{h_{s}}\vert \leq p^{ds-((s(s+1)/2)+1)}$ . Also, the sum of $\vert W_{h_{s}}\vert $ over those at most $s(s+1)p^{d+s-d'}$ exceptionally $h_{s}\in \mathbb {F}_{p}^{d}$ is at most $s(s+1)p^{(s+1)d+s-d'}$ . It then follows from the pigeonhole principle that there exists $W_{\ast }\subseteq \mathbb {F}_{p}^{d}\backslash Z$ of cardinality at least $\delta p^{d}/4$ such that $\vert W_{h}\vert \geq \delta p^{ds-((s(s+1)/2)+1)}/4$ for all $h_{s}\in W_{\ast }$ . Since $\mathrm {rank}(M_{h})\geq (s-1)^{2}+(s-1)+3$ , by Proposition 4.19 and (6.32), we have that

$$ \begin{align*} \vert W^{\prime}_{h}\vert=\vert W_{h}\vert\geq\delta p^{ds-((s(s+1)/2)+1)}/4=\delta p^{(d-1)s-((s(s-1)/2)+1)}/4=O(\delta) \vert \Box_{s-1}(V(M_{h}))\vert \end{align*} $$

for all $h\in W_{\ast }\backslash Z$ .

However, if $W=\Box _{s}(V(M))$ and $\mathrm {rank}(M)\geq s+3$ , then for all $h\in \mathbb {F}_{p}^{d}\backslash Z$ , it follows from (6.29) that $ W^{\prime }_{h}=\Box _{s-1}(V(M_{h}))$ . This completes the proof of Claim 2.

Step 2 is summarized by the following claim.

Claim 3. Let $t\in \mathbb {N}$ . Suppose that for all $h\in W_{\ast }\backslash Z$ , we may write

(6.34) $$ \begin{align} P_{h}+Q_{h}=M_{h}R_{h}+R^{\prime}_{h} \end{align} $$

for some $R_{h},R^{\prime }_{h}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (R_{h})\leq k-3$ and $\deg (R^{\prime }_{h})\leq t-1$ . Then,

$$ \begin{align*}P=MP'+P" \quad\text{and}\quad Q=MQ'+Q" \end{align*} $$

for some $P',P",Q',Q"\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P')\leq k-3$ , $\deg (P")\leq t-1$ , $\deg (Q')\leq k-2$ , and $\deg (Q")\leq t$ .

We first show that Claim 3 implies the desired conclusion by following the two steps described in the outline. We prove by induction on s. If $s=1$ , then for all $h\in W_{\ast }\backslash Z$ , since $\mathrm {rank}(M_{h})\geq 3$ and (6.31) holds for all $(m,m_{1},\ldots ,m_{s-1})\in W^{\prime }_{h}$ , it follows from Proposition 6.2 that

$$ \begin{align*} P_{h}+Q_{h}=M_{h}R_{h} \end{align*} $$

for some $R_{h}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (R_{h})\leq k-3$ . By Claim 3 (setting $t=0$ ),

$$ \begin{align*}P=MP_{1} \quad\text{and}\quad Q=MQ_{1}+C\end{align*} $$

for some $C\in \mathbb {F}_{p}$ and $P_{1},Q_{1}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P_{1})\leq k-3$ , $\deg (Q_{1})\leq k-2$ .

Suppose we have proved Proposition 6.6 for $s-1$ for some $s\geq 2$ . We now prove it for s. For all $h\in W_{\ast }\backslash Z$ , since $\mathrm {rank}(M_{h})=\mathrm {rank}(M)-1$ , $\deg (P_{h}+\Delta _{h}Q_{h})\leq k-1$ , and since (6.30) holds for all $(m,m_{1},\ldots ,m_{s-1})\in W^{\prime }_{h}$ , by the induction hypothesis, we may write

$$ \begin{align*}P_{h}+Q_{h}=M_{h}R_{h}+R^{\prime}_{h}\end{align*} $$

for some $R_{h},R^{\prime }_{h}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (R_{h})\leq k-3$ and $\deg (R^{\prime }_{h})\leq s-2$ for all $h\in W_{\ast }\backslash Z$ . By Claim 3 (setting $t=s+1$ ),

$$ \begin{align*}P=MP'+P",\quad Q=MQ'+Q"\end{align*} $$

for some $P',P",Q',Q"\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P')\leq k-3$ , $\deg (P")\leq s-2$ , $\deg (Q')\leq k-2$ , and $\deg (Q")\leq s-1$ . This completes the induction step and we are done.

It remains to prove Claim 3.

Proof of Claim 3

The idea is to apply Proposition 6.5 to the leading terms of the polynomials. Unlike the special case discussed in the outline, here, the polynomials $M,P$ , and Q are not homogeneous. To overcome this difficulty, each time we apply Proposition 6.5 to the leading terms, we may factor out a multiple of M to lower the degrees of P and Q. Then, we apply Proposition 6.5 again to the leading terms of the new P and Q, until $k\leq s-1$ . So, we prove Claim 3 by induction on k.

If $\max \{\deg (P),\deg (Q)-1\}{\kern-1pt}\leq{\kern-1pt} s{\kern-1pt}-{\kern-1pt}1$ , then Claim 3 follows by setting $P{\kern-1pt}={\kern-1pt}P",Q{\kern-1pt}={\kern-1pt}Q"$ , and $P'{\kern-1pt}={\kern-1pt}Q'{\kern-1pt}={\kern-1pt}0$ . Assume now that Claim 3 holds when $\max \{\deg (P),\deg (Q)-1\}{\kern-1pt}\leq k'{\kern-1pt}-{\kern-1pt}1$ for some $s\leq k'\leq k-1$ and we prove that Claim 3 holds when $\max \{\deg (P), \deg (Q)-1\}\leq k'$ . Note that (6.34) implies that

(6.35) $$ \begin{align} &P(L_{h}(m)+u_{h}-h/2)+Q(L_{h}(m)+u_{h}+h/2)-Q(L_{h}(m)+u_{h}-h/2)\nonumber\\ & \quad =M(L_{h}(m)+u_{h}-h/2)R_{h}(m)+R^{\prime}_{h}(m) \end{align} $$

for all $h\in W_{\ast }\backslash Z$ . Since $\deg (R^{\prime }_{h})\leq k'-1$ , it is not hard to see that $\deg (R_{h})\leq k'-2$ . Let $\tilde {P},\tilde {Q},\tilde {M},\tilde {R}_{h}$ be the degree $k',k'+1,2,k'-2$ terms of $P,Q,M,R_{h}$ , respectively. Write $h=(h_{1},\ldots ,h_{d})$ . Comparing the degree $k'$ terms of (6.35) and noticing that the degree $k'$ terms of $Q(L_{h}(m)+u_{h}+h/2)-Q(L_{h}(m)+u_{h}-h/2)$ are $\sum _{i=1}^{d}h_{i}\partial _{i}\tilde {Q}(L_{h}(m))$ , we have that

$$ \begin{align*} \tilde{P}(L_{h}(m))+\sum_{i=1}^{d}h_{i}\partial_{i}\tilde{Q}(L_{h}(m))=\tilde{M}(L_{h}(m))\tilde{R}_{h}(m). \end{align*} $$

Therefore, for all $n\in \mathbb {F}_{p}^{d}$ and $h\in W_{\ast }\backslash Z$ with $(nA)\cdot h=M(n)=0$ , there exists $m\in \mathbb {F}_{p}^{d-1}$ with $L_{h}(m)=n$ and thus,

$$ \begin{align*} \tilde{P}(n)+\sum_{i=1}^{d}h_{i}\partial_{i}\tilde{Q}(n)=\tilde{M}(n)\tilde{R}_{h}(m)=0. \end{align*} $$

Since $\vert Z\vert \leq O_{d}(p^{d-1})$ by Claim 1, we have that $\vert W_{\ast }\backslash Z\vert \geq p^{d}/8$ . Since $\mathrm {rank}(M)\geq s+3\geq 4$ , by Proposition 6.5, we have that $\tilde {P}=\tilde {M}P'$ and $\tilde {Q}=\tilde {M}Q'$ for some $P',Q'\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P')\leq k'-2\leq k-3$ and $\deg (Q')\leq k'-1\leq k-2$ . Since $M-\tilde {M}$ is of degree at most 1, we may write

$$ \begin{align*}P=MP'+P",\quad Q=MQ'+Q"\end{align*} $$

for some $P",Q"\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P")\leq k'-1$ and $\deg (Q")\leq k'$ . Writing $P^{\prime \prime }_{h}:=P"(L_{h}(\cdot )+u_{h}-h/2)$ and $Q^{\prime \prime }_{h}:=Q"(L_{h}(\cdot )+u_{h}+h/2)-Q"(L_{h}(\cdot )+u_{h}-h/2)$ , it follows from (6.34) and the identity

$$ \begin{align*}M_{h}=M(L_{h}(\cdot)+u_{h}-h/2)=M(L_{h}(\cdot)+u_{h}+h/2)\end{align*} $$

that for all $h\in W_{\ast }\backslash Z$ , we may write

(6.36) $$ \begin{align} P^{\prime\prime}_{h}+Q^{\prime\prime}_{h}=M_{h}R^{\prime\prime}_{h}+R^{\prime\prime\prime}_{h} \end{align} $$

for some $R^{\prime \prime }_{h},R^{\prime \prime }_{h}\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (R^{\prime \prime }_{h})\leq k-3$ and $\deg (R^{\prime \prime \prime }_{h})\leq s-1$ . Since $\max \{\deg (P"),\deg (Q")-1\}\leq k'-1$ , by induction hypothesis, (6.36) implies that

$$ \begin{align*} P"=MP"'+P"",\quad Q"=MQ"'+Q"" \end{align*} $$

for some $P"',P"",Q"',Q""\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (P"')\leq k-3, \deg (P"")\leq s-1$ , $\deg (Q"')\leq k-2$ , and $\deg (Q"")\leq s$ . Then,

$$ \begin{align*} P=M(P'+P"')+P"" \quad\text{and}\quad Q=M(Q'+Q"')+Q"". \end{align*} $$

This completes the induction step and proves Claim 3.

This therefore completes the proof of Proposition 6.6.

6.4 Intrinsic definitions for polynomials on $V(M)$

Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form. Recall that we define a function $f\colon V(M)\to \mathbb {F}_{p}$ to be a polynomial if f is the restriction to $V(M)$ of some polynomial $f'\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ defined in $\mathbb {F}_{p}^{d}$ . It is natural to ask if there is an intrinsic way to define polynomials on $V(M)$ (that is, without looking at points outside $V(M)$ ). A natural way to do so is to use anti-derivative properties of polynomials. Let $g\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ . It is not hard to see that g is of degree at most $s-1$ if and only if $\Delta _{h_{s}}\cdots \Delta _{h_{1}}g(n)=0$ for all $n,h_{1},\ldots ,h_{s}\in \mathbb {F}_{p}^{d}$ . This observation provides us with a promising alternative way to define polynomials and leads to the following question.

Conjecture 6.7. (Intrinsic definition for polynomials)

Let $g\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a function, $d,s\in \mathbb {N}_{+}$ , and $p\gg _{d} 1$ be a prime. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form with $\mathrm {rank}(M)\gg _{s} 1$ . Then, the following are equivalent:

1. (i) $\Delta _{h_{s}}\cdots \Delta _{h_{1}}g(n)=0$ for all $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ ;

2. (ii) there exists a polynomial $g'\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most $s-1$ such that $g(n)=g'(n)$ for all $n\in V(M)$ .

If Conjecture 6.7 holds, then we may use part (i) of Conjecture 6.7 as an intrinsic definition for polynomials on $V(M)$ . In this paper, we were unable to prove Conjecture 6.7. Instead, we prove the following special case of Conjecture 6.7, which is good enough for the purpose of this paper.

Proposition 6.8. Let $d,s\in \mathbb {N}_{+}$ , $p\gg _{d} 1$ be a prime, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form associated with the matrix A of rank at least $s+3$ . Then, for any $g\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (g)\leq s$ , the following are equivalent:

1. (i) for all $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ , we have that $\Delta _{h_{s}}\cdots \Delta _{h_{1}}g(n)=0;$

2. (ii) we have

   $$ \begin{align*}g=Mg_{1}+g_{2}\end{align*} $$
   for some $g_{1},g_{2}\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (g_{1})\leq s-2$ , $\deg (g_{2})\leq s-1$ ;

3. (i) we have

   $$ \begin{align*}g(n)=((nA)\cdot n)g_{1}(n)+g_{2}(n)\end{align*} $$
   for some $g_{1},g_{2}\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (g_{1})\leq s-2$ , $\deg (g_{2})\leq s-1$ .

Proof. We first show that (ii) $\Rightarrow $ (i). For all $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M))$ , note that

$$ \begin{align*} \Delta_{h_{s}}\cdots\Delta_{h_{1}}g(n)=\Delta_{h_{s}}\cdots\Delta_{h_{1}}(M(n)g_{1}(n)). \end{align*} $$

Since $M(n+\epsilon _{1}h_{1}+\cdots +\epsilon _{s}h_{s})=0$ for all $\epsilon _{1},\ldots ,\epsilon _{s}\in \{0,1\}$ , we have $\Delta _{h_{s}}\cdots \Delta _{h_{1}} (M(n)g_{1}(n))=0$ and we are done.

The part (i) $\Rightarrow $ (ii) follows from Proposition 6.6 (by setting $k=s$ , $P\equiv 0$ , and $Q=g$ ). Finally, (ii) $\Leftrightarrow $ (iii), since the degree of the polynomial $M(n)-(nA)\cdot n$ is at most 1.

As a corollary of Proposition 6.8, we have the following.

Corollary 6.9. Let $d,k,s\in \mathbb {N}_{+}$ , $p\gg _{d} 1$ be a prime, and $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a non-degenerate quadratic form associated with the matrix A. Let $m_{1},\ldots ,m_{k}\in \mathbb {F}_{p}^{d}$ be linearly independent and non-M-isotropic vectors. If $d\geq k+s+3$ , then for any polynomial $g\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most s, the following are equivalent:

1. (i) for all $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M)^{m_{1},\ldots ,m_{k}})$ , we have that $\Delta _{h_{s}}\cdots \Delta _{h_{1}}g(n)=0$ ;

2. (ii) we have

   $$ \begin{align*} g(n)=M(n)g_{0}(n)+\sum_{i=1}^{k}(M(n+m_{i})-M(n))g_{i}(n)+g'(n) \end{align*} $$
   for some homogeneous $g_{0},\ldots ,g_{k}\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (g_{0})=s-2$ and $\deg (g_{1})=\cdots =\deg (g_{k})=s-1$ , and some $g'\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most $s-1$ (recall that $g_{0},\ldots ,g_{k}$ are allowed to be constant 0 by Convention 2.2);

3. (iii) we have

   $$ \begin{align*} g(n)=((nA)\cdot n)g_{0}(n)+\sum_{i=1}^{k}((nA)\cdot m_{i})g_{i}(n)+g'(n) \end{align*} $$
   for some homogeneous $g_{0},\ldots ,g_{k}\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (g_{0})=s-2$ and $\deg (g_{1})=\cdots =\deg (g_{k})=s-1$ , and some $g'\in \mathrm {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most $s-1$ .

Proof. Let V be the span of $m_{1},\ldots ,m_{k}$ . Since $m_{1},\ldots ,m_{k}$ are linearly independent and non-M-isotropic, and since A is invertible, we have that $V^{\perp {M}}$ is a subspace of $\mathbb {F}_{p}^{d}$ of dimension $d-k$ with $V\cap V^{\perp {M}}=\{\mathbf {0}\}$ . Let

$$ \begin{align*}W:=\{n\in\mathbb{F}_{p}^{d}\colon 2(nA)\cdot m_{i}+(m_{i}A)\cdot m_{i}=0, 1\leq i\leq k\}.\end{align*} $$

Since $m_{1},\ldots ,m_{k}$ are linearly independent and A is invertible, we may write ${W{\kern-1pt}={\kern-1pt}V^{\perp {M}}{\kern-1pt}+{\kern-1pt}w}$ for some $w\in \mathbb {F}_{p}^{d}$ .

Let $\phi \colon \mathbb {F}_{p}^{d-k}\to V^{\perp {M}}$ be any bijective linear transformation. Denote $M'(n'):=M(\phi (n')+w)$ and $g'(n'):=g(\phi (n')+w)$ for all $n'\in \mathbb {F}_{p}^{d-k}$ . By Proposition 4.8(ii), $M'$ is a non-degenerate quadratic form and thus, $\mathrm {rank}(M')=d-k\geq s+3$ . By Lemma 4.18, we have that $(n,h_{1},\ldots ,h_{s})\in \Box _{s}(V(M)^{m_{1},\ldots ,m_{k}})$ if and only if there exists $(n',h^{\prime }_{1},\ldots ,h^{\prime }_{s})\in \Box _{s}(V(M'))$ with $(n,h_{1},\ldots ,h_{s})=(\phi (n')+w,\phi (h^{\prime }_{1}),\ldots ,\phi (h^{\prime }_{s}))$ .

We may then apply Proposition 6.8 to the polynomial $g'$ and the quadratic form $M'$ , and then apply the change of variables $\phi $ to get to the conclusions. We leave the details to the interested readers.

6.5 A parallel matrix proposition

Let A and B be $\mathbb {F}_{p}$ -valued $d\times d$ matrices. If B is a multiple of A, then clearly $nB=\mathbf {0}$ implies that $nA=\mathbf {0}$ . It is natural to ask if the converse is true, namely, if for many $n\in \mathbb {F}_{p}^{d}$ , $nB=\mathbf {0}$ implies that $nA=\mathbf {0}$ , then is it true that B must be a multiple of A. The next proposition answers this question.

Proposition 6.10. Let $d\in \mathbb {N}_{+}$ , $\delta>0$ , $p\gg _{d}\delta ^{-O_{d}(1)}$ be a prime, and A be a $\mathbb {F}_{p}$ -valued $d\times d$ matrix of rank at least 3. Let B be an $\mathbb {F}_{p}$ -valued $d\times d$ matrix and $v\in \mathbb {F}_{p}^{d}$ . Let W be a subset of $\mathbb {F}_{p}^{d}$ of cardinality at least $\delta p^{d}$ . Suppose that for all $w\in W$ and $n\in \mathbb {F}_{p}^{d}$ with $(nA)\cdot w=0$ , we have that

$$ \begin{align*}(nB+v)\cdot w=0.\end{align*} $$

Then, $v=\mathbf {0}$ and $B=cA$ for some $c\in \mathbb {F}_{p}$ .

Proof. Throughout the proof, we assume that $p\gg _{d}\delta ^{-O_{d}(1)}$ . Since $\mathrm {rank}(A)\geq 1$ , the set of $w\in \mathbb {F}_{p}^{d}$ with $wA=\mathbf {0}$ is of cardinality at most $p^{d-1}$ . So, shrinking $\delta $ to $\delta /2$ if necessary, we may assume without loss of generality that $wA\neq \mathbf {0}$ for all $w\in W$ . Fix any $w\in W$ . Pick any $n\in \mathbb {F}_{p}^{d}$ with $(nA)\cdot w=0$ , then also $(2nA)\cdot w=0$ . By assumption, we have ${(nB+v)\cdot w=(2nB+v)\cdot w=0}$ , which implies that $v\cdot w=0$ . Moreover, we have $(nA)\cdot w=0\Rightarrow (nB)\cdot w=0$ , or equivalently, $(wA)\cdot n=0\Rightarrow (wB)\cdot n=0$ for all $n\in \mathbb {F}_{p}^{d}$ . So, $wA$ is parallel to $wB$ . Since $wA\neq \mathbf {0}$ , we have that $wB=c_{w}wA$ for some $c_{w}\in \mathbb {F}_{p}$ .

Since W is of cardinality at least $\delta p^{d}$ , by Lemma 4.11, there exist linearly independent $w_{1},\ldots ,w_{d}\in W$ . So, $v\cdot w_{i}=0$ for $1\leq i\leq d$ . This implies that $v=\mathbf {0}$ .

For $z\in \mathbb {F}_{p}^{d}$ , let $M_{z}(n):=(nA)\cdot (n+z)$ . Then,

(6.37) $$ \begin{align} \sum_{z\in\mathbb{F}_{p}^{d}}\vert V(M_{z})\cap W\vert & =\sum_{z\in\mathbb{F}_{p}^{d}}\vert\{w\in W\colon (wA)\cdot (w+z)=0\}\vert \nonumber\\ &=\sum_{w\in W}\vert\{z\in \mathbb{F}_{p}^{d}\colon (wA)\cdot (w+z)=0\}\vert. \end{align} $$

Since $wA\neq \mathbf {0}$ , we have $\vert \{z\in \mathbb {F}_{p}^{d}\colon (wA)\cdot (w+z)=0\}\vert =p^{d-1}$ . So, (6.37) is at least $\vert W\vert \cdot p^{d-1}\geq \delta p^{2d-1}$ . By the pigeonhole principle, there exists $z\in \mathbb {F}_{p}^{d}$ such that ${\vert V(M_{z})\cap W\vert \gg \delta p^{d-1}}$ .

Since $wB=c_{w}wA$ for some $c_{w}\in \mathbb {F}_{p}$ for all $w\in W$ , we have that

$$ \begin{align*}(wB)\cdot (w+z)=c_{w}(wA)\cdot (w+z)=0\end{align*} $$

for all $w\in V(M_{z})\cap W$ . Since $\vert V(M_{z})\cap W\vert \gg \delta p^{d-1}$ , by Lemma 6.1 and Proposition 6.2, we may write

$$ \begin{align*}(wB)\cdot (w+z)=r_{z}M_{z}(w)=r_{z}(wA)\cdot (w+z)\end{align*} $$

for some $r_{z}\in \mathbb {F}_{p}$ for all $w\in \mathbb {F}_{p}^{d}$ . Viewing both sides as polynomials in the variable w and comparing all of their degree 2 terms, we must have that $B=r_{z}A$ . We are done.

7 Algebraic properties for quadratic forms in $\mathbb {Z}/p$

In this section, we extend the results in §6 to $\mathbb {Q}$ -valued polynomials.

7.1 Quadratic forms in $\mathbb {Z}/p$

By using the correspondence between polynomials in $\mathbb {F}_{p}^{d}$ and in $\mathbb {Z}^{d}$ , we may lift all the definitions pertaining to quadratic forms in $\mathbb {F}_{p}^{d}$ to the $\mathbb {Z}^{d}$ setting in the natural way.

Definition 7.1. (Quadratic forms in $\mathbb {Z}^{d}$ )

We say that a function $M\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ is a quadratic form if

$$ \begin{align*}M(n)=\frac{1}{p}((nA)\cdot n+n\cdot u+v)\end{align*} $$

for some $d\times d$ symmetric matrix A in $\mathbb {Z}$ , some $u\in \mathbb {Z}^{d}$ , and some $v\in \mathbb {Z}$ . We say that A is the matrix associated to M.

It is more rigorous to name M as a p-quadratic form. However, since the quantity p is always clear in this paper, we simply call M to be a quadratic form for short. Whenever we define a quadratic form in this paper, we will write either $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ or $M\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ to specify the domain and range of M, so that the term quadratic form will not cause confusion.

By Lemma 2.5, any quadratic form $\tilde {M}\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ associated with the matrix $\tilde {A}$ induces a quadratic form $M:=\iota \circ (p\tilde {M})\circ \tau \colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ associated with the matrix $\iota (\tilde {A})$ . Conversely, any quadratic form $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ associated with the matrix A admits a regular lifting $\tilde {M}\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ , which is a quadratic form associated with the matrix $\tau (A)$ .

For a quadratic form $\tilde {M}\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ , we say that $\tilde {M}$ is pure/homogeneous/ p-non-degenerate if the quadratic form $M:=\iota \circ (p\tilde {M})\circ \tau $ induced by $\tilde {M}$ is pure/homogeneous/non-degenerate. The p-rank of $\tilde {M}$ , denoted by $\mathrm {rank}_{p}(\tilde {M})$ , is defined to be the rank of M.

We say that $h_{1},\ldots ,h_{k}\in \mathbb {Z}^{d}$ are p-linearly independent if for all $c_{1},\ldots ,c_{k}\in \mathbb {Z}/p$ , $c_{1}h_{1}+\cdots +c_{k}h_{k}\in \mathbb {Z}$ implies that $c_{1},\ldots ,c_{k}\in \mathbb {Z}$ , or equivalently, if $\iota (h_{1}),\ldots ,\iota (h_{k})$ are linearly independent.

We can also lift the definitions of sets of zeros and Gowers sets to the $\mathbb {Z}/p$ setting.

• • For a polynomial $P\in \text {poly}(\mathbb {Z}^{k}\to \mathbb {R})$ , let $V_{p}(P)$ denote the set of $n\in \mathbb {Z}^{k}$ such that $P(n+pm)\in \mathbb {Z}$ for all $m\in \mathbb {Z}^{k}$ .

• • For $h_{1},\ldots ,h_{t}\in \mathbb {Z}^{k}$ , let $V_{p}(P)^{h_{1},\ldots ,h_{t}}$ denote the set of $n\in \mathbb {Z}^{k}$ such that $P(n+pm), P(n+h_{1}+pm),\ldots ,P(n+h_{t}+pm)\in \mathbb {Z}$ for all $m\in \mathbb {Z}^{k}$ .

• • For $\Omega \subseteq \mathbb {Z}^{d}$ and $s\in \mathbb {N}$ , let $\Box _{p,s}(\Omega )$ denote the set of $(n,h_{1},\ldots ,h_{s})\in (\mathbb {Z}^{d})^{s+1}$ such that $n+\epsilon _{1}h_{1}+\cdots +\epsilon _{s}h_{s}\in \Omega +p\mathbb {Z}^{d}$ for all $\epsilon _{1},\ldots ,\epsilon _{s}\in \{0,1\}$ . We say that $\Box _{p,s}(\Omega )$ is the sth p-Gowers set of $\Omega $ .

The following lemma is straightforward.

Lemma 7.2. For any p-periodic set $\Omega \subseteq \mathbb {Z}^{k}$ (recall the definition in §1.2) and $K\in \mathbb {N}_{+}$ , we have that

$$ \begin{align*}\frac{1}{p^{k}}\vert \Omega \cap [p]^{k}\vert=\frac{1}{(pK)^{k}}\vert \Omega \cap [pK]^{k}\vert.\end{align*} $$

Using the connections between $\mathbb {F}_{p}$ -valued polynomials and $\mathbb {Z}/p$ -valued polynomials, one can easily extend many results in §6 to the $\mathbb {Z}/p$ -setting. The following is an example.

Corollary 7.3. (Lifting of Proposition 6.2)

Let $d\in \mathbb {N}_{+}$ , $s\in \mathbb {N}$ , $p\gg _{d,s} 1$ be a prime number, $P\in \mathrm {poly}(\mathbb {Z}^{d}\to \mathbb {Z}/p)$ be a polynomial of degree at most s, and ${M\colon \mathbb {Z}^{d}\to \mathbb {Z}/p}$ be a quadratic form of p-rank at least 3. Then, either $\vert V_{p}(M)\cap V_{p}(P)\cap [p]^{d}\vert \leq O_{d,s}(p^{d-2})$ or $V_{p}(M)\subseteq V_{p}(P)$ .

Moreover, if $V_{p}(M)\subseteq V_{p}(P)$ , then $P=MP_{1}+P_{0}$ for some $P_{0}\in \mathrm {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ of degree at most s, and some integer coefficient polynomial $P_{1}\in \mathrm { poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ of degree at most $s-2$ .

Proof. Let $M'\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be the quadratic form of rank at least 3 induced by M, $P'\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be the polynomial of degree at most s induced by P (whose existence is given by Lemma 2.5(i)). By Proposition 6.2, either $\vert V(M')\cap V(P')\vert \leq O_{d,s}(p^{d-2})$ or $V(M')\subseteq V(P')$ . By the definition of lifting, the form case implies that $\vert V_{p}(M)\cap V_{p}(P)\cap [p]^{d}\vert =\vert V(M')\cap V(P')\vert \leq O_{d,s}(p^{d-2})$ , and the later case implies that $V_{p}(M)\subseteq V_{p}(P)$ .

We now assume that $V_{p}(M)\subseteq V_{p}(P)$ . By the definition of lifting, we have that $V(M')\subseteq V(P')$ . By Proposition 6.2, $P'=M'Q'$ for some $Q'\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ of degree at most $s-2$ . Let $Q\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Z}/p)$ be a regular lifting of $Q'$ of degree at most $s-2$ (whose existence is given by Lemma 2.5(ii)). By Lemma 2.5(iv) and (v), $P-pMQ$ is a lifting of $P'-M'Q'\equiv 0$ . Then, by Lemma 2.5(iii), we have that $P-pMQ$ is integer valued and is of degree at most s. By Lemma 2.4, we may write $Q=pQ_{1}+Q_{2}$ for some $\mathbb {Z}$ -valued polynomial $Q_{1}$ and some integer coefficient polynomial $Q_{2}$ both having degrees at most $s-2$ . Then, $P=MQ_{2}+((P-pMQ)+pMQ_{1})$ with $(P-pMQ)+pMQ_{1}$ being an integer valued polynomial of degree at most s. We are done.

We remark that for factorization results, the $\mathbb {Z}/p$ setting differs from the $\mathbb {F}_{p}$ setting in the appearances of integer valued polynomials. For example, the factorization in Corollary 7.3 is of the form $P=MP_{1}+P_{0}$ , while the factorization in Proposition 6.2 is of the form $P=MP_{1}$ (where $P_{1}$ is the R in the statement of Proposition 6.2). This extra integer valued polynomial $P_{0}$ arises when passing from a factorization in the $\mathbb {F}_{p}$ setting to that in the $\mathbb {Z}/p$ setting. The same comment applies to all the results in this section.

The approach in the proof of Corollary 7.3 can be adapted to lift many other results from the $\mathbb {F}_{p}$ -setting to the $\mathbb {Z}/p$ -setting. Below are the liftings of some results from §6 that will be used in the future. We leave the proofs to the interested readers.

Corollary 7.4. (Lifting of a special case of Proposition 6.6)

Let $d,s\in \mathbb {N}_{+}$ , $k\in \mathbb {N}$ , $\delta>0$ , $p\gg _{d,k} \delta ^{-O_{d,k}(1)}$ be a prime, $M\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ be a quadratic form of p-rank at least $s^{2}+s+3$ , and W be a subset of $\Box _{p,s}(V(M))\cap ([p]^{d})^{s+1}$ of cardinality at least $\delta \vert \Box _{p,s}(V(M))\cap ([p]^{d})^{s+1}\vert $ . Let $P,Q\in \mathrm { poly}(\mathbb {Z}^{d}\to \mathbb {Z}/p)$ with $\deg (P)\leq k-1$ and $\deg (Q)\leq k$ . Suppose that for all $(n,h_{1},\ldots ,h_{s})\in W$ , we have that

$$ \begin{align*}\Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P(n)+\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q(n)\in\mathbb{Z},\end{align*} $$

(where $\Delta _{h_{s}}\cdots \Delta _{h_{2}}P(n)$ is understood as $P(n)$ when $s=1$ ). Then,

(7.1) $$ \begin{align} \begin{aligned} P=MP_{1}+P_{2}+P_{3} \quad\text{and}\quad Q=MQ_{1}+Q_{2}+Q_{3} \end{aligned} \end{align} $$

for some integer coefficient polynomials $P_{1}$ and $Q_{1}$ of degrees at most $k-3$ and $k-2$ , respectively, some integer valued polynomials $P_{2}$ and $Q_{2}$ of degrees at most $k-1$ and k, respectively, and some $\mathbb {Z}/p$ -valued polynomials $P_{3}$ and $Q_{3}$ of degrees at most $s-2$ and $s-1$ , respectively.

Corollary 7.5. (Lifting of Proposition 6.10)

Let $d\in \mathbb {N}_{+}$ , $\delta>0$ , $p\gg _{d} \delta ^{-O_{d}(1)}$ be a prime, and A be a $\mathbb {Z}$ -valued $d\times d$ matrix of p-rank at least 3. Let B be a $\mathbb {Z}$ -valued $d\times d$ matrix and $v\in \mathbb {Z}^{d}$ . Let W be a subset of $[p]^{d}$ of cardinality at least $\delta p^{d}$ . Suppose that for all $w\in W$ and $n\in \mathbb {Z}^{d}$ with $(nA)\cdot w\in p\mathbb {Z}$ , we have that

$$ \begin{align*}(nB+v)\cdot w\in p\mathbb{Z}.\end{align*} $$

Then, $v\in p\mathbb {Z}$ and $B=cA+pB_{0}$ for some $c\in \mathbb {Z}$ and some $d\times d$ integer valued matrix $B_{0}$ .

7.2 Passing from p-periodic polynomials to rational ones

In this section, we extend Corollary 7.4 from $\mathbb {Z}/p$ -valued polynomials to rational polynomials.

Proposition 7.6. Let $d,K,s\in \mathbb {N}_{+}$ , $k\in \mathbb {N}$ , $\delta>0$ , $p\gg _{d,k} \delta ^{-O_{d,k}(1)}$ be a prime, $M\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ be a quadratic form of p-rank at least $s^{2}+s+3$ , and W be a subset of $\Box _{p,s}(V(M))\cap ([p^{2}K]^{d})^{s+1}$ of cardinality at least $\delta \vert \Box _{p,s}(V(M))\cap ([p^{2}K]^{d})^{s+1}\vert $ . Let $P,Q\in \mathrm {poly}(\mathbb {Z}^{d}\to \mathbb {Q})$ with $\deg (P)\leq k-1$ and $\deg (Q)\leq k$ . Suppose that

(7.2) $$ \begin{align} \Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P(n){\kern-1pt}+{\kern-1pt}\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q(n)\in\mathbb{Z}\! \quad\text{for all } (n,h_{1},\ldots,h_{s}){\kern-1pt}\in{\kern-1pt} W{\kern-1pt}+{\kern-1pt}p^{2}K(\mathbb{Z}^{d})^{s+1} \end{align} $$

(where $\Delta _{h_{s}}\cdots \Delta _{h_{2}}P(n)$ is understood as $P(n)$ when $s=1$ ). Then,

$$ \begin{align*} qP=P_{1}+P_{2} \quad\text{and}\quad qQ=Q_{1}+Q_{2} \end{align*} $$

for some integer $q\in \mathbb {N}_{+}$ with $q\ll _{d,k} \delta ^{-O_{d,k}(1)}$ , some $P_{1},Q_{1}\in \mathrm {poly}(V_{p}(M)\to \mathbb {R}\vert \mathbb {Z})$ with $\deg (P_{1}){\kern-1pt}\leq{\kern-1pt} k{\kern-1pt}-{\kern-1pt}1$ , $\deg (Q_{1}){\kern-1pt}\leq{\kern-1pt} k$ , and some $P_{2},Q_{2}{\kern-1pt}\in{\kern-1pt} \mathrm { poly}(\mathbb {Z}^{d}{\kern-1pt}\to{\kern-1pt} \mathbb {Q})$ with ${\deg (P_{2}){\kern-1pt}\leq{\kern-1pt} s-2}$ , $\deg (Q_{2})\leq s-1$ .

In applications, K will be a large number. We also remark that all the constants in Proposition 7.6 are independent of s since the statement holds trivially when $s\geq k$ .

Let $f=P$ or Q. Our strategy is to decompose f as $qf=\sum _{i=0}^{k}({f_{i}}/{p^{i}})$ for some $k\in \mathbb {N}$ and $q\in \mathbb {Z}, p\nmid q$ , where each $f_{i}$ is a ‘good’ polynomial, meaning that it behaves very similarly to a $\mathbb {Z}/p$ -valued polynomial. One can then prove that periodicity conditions on f descend to similar conditions on $f_{k}$ , leading to the conclusion that ${f_{k}}/{p}$ is ‘good’. We may then absorb the term ${f_{k}}/{p^{k}}$ into ${(f_{k-1})}/{(p^{k-1})}$ and reduce k by 1. Inductively, we have $k=0$ , which implies that $qf$ itself is ‘good’. For future references, we refer to this approach as the p-expansion trick.

Proof of Proposition 7.6

Throughout the proof, we assume that $p\gg _{d,k} \delta ^{-O_{d,k}(1)}$ .

Step 1: setup for the induction. For convenience, denote ${d':=\mathrm {rank}_{p}(M)\geq s^{2}+s+3}$ . We assume that $s{\kern-1pt}\leq{\kern-1pt} k{\kern-1pt}+{\kern-1pt}1$ since otherwise, one can simply take $P{\kern-1pt}={\kern-1pt}P_{2}, Q{\kern-1pt}={\kern-1pt}Q_{2}, q{\kern-1pt}={\kern-1pt}1$ , and $P_{1}=Q_{1}=0$ . Since $P,Q$ take values in $\mathbb {Q}$ and are of degree at most k, by the multivariate polynomial interpolation, there exists $q\in \mathbb {N}, p\nmid q$ , and $t_{0}\in \mathbb {N}$ such that

$$ \begin{align*} qP=\sum_{j=0}^{t_{0}}\frac{P^{\prime}_{j}}{p^{j}} \quad \text{and} \quad qQ=\sum_{j=0}^{t_{0}}\frac{Q^{\prime}_{j}}{p^{j}} \end{align*} $$

for some integer coefficient polynomials $P^{\prime }_{j},Q^{\prime }_{j}\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ with $\deg (P^{\prime }_{j})\leq k-1$ and $\deg (Q^{\prime }_{j})\leq k$ . We say that a polynomial $f\colon \mathbb {Z}^{d}\to \mathbb {Z}$ is good if

$$ \begin{align*}f=\sum_{j=0}^{\lfloor \deg(f)/2\rfloor}M^{j}f_{j}\end{align*} $$

for some integer coefficient polynomial $f_{j}\colon \mathbb {Z}^{d}\to \mathbb {Z}$ of degree at most $\deg (f)-2j$ . A good polynomial not only takes integer values in $V_{p}(M)$ , but also admits a nice decomposition in terms of M. Clearly, $P^{\prime }_{0},\ldots ,P^{\prime }_{t_{0}},Q^{\prime }_{0},\ldots ,Q^{\prime }_{t_{0}}$ are good polynomials.

Let $t\in \mathbb {N}$ be the smallest integer such that we can write

$$ \begin{align*} q'P=\sum_{j=0}^{t}\frac{P^{\prime\prime}_{j}}{p^{j}}+P' \quad \text{and} \quad q'Q=\sum_{j=0}^{t}\frac{Q^{\prime\prime}_{j}}{p^{j}}+Q' \end{align*} $$

for some $q'\in \mathbb {N}, p\nmid q'$ , some good polynomials $P^{\prime \prime }_{j},Q^{\prime \prime }_{j}\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ with $\deg (P^{\prime \prime }_{j}){\kern-1pt}\leq{\kern-1pt} k{\kern-1pt}-{\kern-1pt}1$ , $\deg (Q^{\prime \prime }_{j}){\kern-1pt}\leq{\kern-1pt} k$ , and some $P',Q'{\kern-1pt}\in{\kern-1pt} \text {poly}(\mathbb {Z}^{d}\to \mathbb {Q})$ with ${\deg (P')\leq s-2}$ and $\deg (Q')\leq s-1$ . Obviously, such t exists and is at most $t_{0}$ . Our first goal is to show that $t=0$ .

Suppose in contrast that $t>0$ . We consider the last terms and write

$$ \begin{align*} P^{\prime\prime}_{t}=\sum_{j=0}^{\lfloor (k-1)/2\rfloor}M^{j}P_{j} \quad\text{and}\quad Q^{\prime\prime}_{t}=\sum_{j=0}^{\lfloor k/2\rfloor}M^{j}Q_{j} \end{align*} $$

for some integer coefficient polynomials $P_{j},Q_{j}\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ with $\deg (P_{j})\leq k-1-2j$ and $\deg (Q_{j})\leq k-2j$ . We say that a polynomial $g\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ is s-simple if

$$ \begin{align*} q'g=pg_{0}+pMg_{1}+g_{2} \end{align*} $$

for some $q'\in \mathbb {N}_{+}, q'\leq O_{k,s}(1)$ , some $g_{0}\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ with $\deg (g_{0})\leq \deg (g)$ , some integer coefficient polynomials $g_{1}\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Z})$ with $\deg (g_{0})\leq \deg (g)-2$ , and some $g_{2}\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Q})$ with $\deg (g_{2})\leq s-1$ . Roughly speaking, if g is s-simple, then ${Q=q'g/p}$ is a $\mathbb {Z}/p$ -valued polynomial that admits a decomposition similar to (7.1). If we can show that all of $P_{0},\ldots ,P_{\lfloor (k-1)/2\rfloor }$ are $(s-1)$ -simple and all of $Q_{0},\ldots ,Q_{\lfloor k/2\rfloor }$ are s-simple, then enlarging the constant $q'$ if necessary, we may absorb the term ${P^{\prime \prime }_{t}}/{p^{t}}$ into ${(P^{\prime \prime }_{t-1})}/{(p^{t-1})}+P'$ , and the term ${Q^{\prime \prime }_{t}}/{p^{t}}$ by ${(Q^{\prime \prime }_{t-1})}/{(p^{t-1})}+Q'$ , which contradicts the minimality of t.

In the rest of the proof, we say that g is simple instead of s-simple if the value of s is clear from the context. By induction, it then suffices to show that if all of $P_{i+1},\ldots ,P_{\lfloor k/2\rfloor }, Q_{i+1},\ldots ,Q_{\lfloor k/2\rfloor }$ are simple for some $0\leq i\leq \lfloor k/2\rfloor $ , then $P_{i}$ and $Q_{i}$ are also simple (for the special case $i=\lfloor k/2\rfloor $ , we show that $P_{i}$ and $Q_{i}$ are simple without induction hypothesis).

Since $P_{i+1},\ldots ,P_{\lfloor k/2\rfloor },Q_{i+1},\ldots ,Q_{\lfloor k/2\rfloor }$ are simple, enlarging the constant $q'$ and absorbing the term ${1}/{p^{t}}\sum _{j=i+1}^{\lfloor k/2\rfloor }M^{j}P_{j}$ into ${(P^{\prime \prime }_{t-1})}/{(p^{t-1})}+P'$ , and the term $({1}/{p^{t}})\sum _{j=i+1}^{\lfloor k/2\rfloor }M^{j}Q_{j}$ by ${(Q^{\prime \prime }_{t-1})}/{(p^{t-1})}+Q'$ if necessary, we may assume without loss of generality that

$$ \begin{align*} P^{\prime\prime}_{t}=\sum_{j=0}^{i}M^{j}P_{j} \quad\text{and}\quad Q^{\prime\prime}_{t}=\sum_{j=0}^{i}M^{j}Q_{j}. \end{align*} $$

Step 2: the isolation trick. We first provide an outline ti show that $P_{i},Q_{i}$ are simple. For simplicity, we assume for the moment that (7.2) holds for $(n,h_{1},\ldots ,h_{s})\in \Box _{p,s}(V(M))$ . By the construction of $P^{\prime \prime }_{t}$ and $Q^{\prime \prime }_{t}$ , and by multiplying (7.2) by $p^{t}$ , we have

(7.3) $$ \begin{align} \Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P^{\prime\prime}_{t}(n){\kern-1pt}+{\kern-1pt}\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q^{\prime\prime}_{t}(n){\kern-1pt}\in{\kern-1pt} p\mathbb{Z} \quad\text{for all } (n,h_{1},\ldots,h_{s}){\kern-1pt}\in{\kern-1pt}\Box_{p,s}(V(M)). \end{align} $$

If $i=0$ , then we may apply Corollary 7.4 directly to show that $P_{0}$ and $Q_{0}$ are simple. When $i>0$ , our strategy is to replace $(n,h_{1},\ldots ,h_{s})$ by $(n+pm_{0},h_{1}+pm_{1},\ldots ,h_{s}+pm_{s})$ and use the periodicity property of $P^{\prime \prime }_{t}$ and $Q^{\prime \prime }_{t}$ to isolate $P_{i}$ and $Q_{i}$ for different i (for convenience, we call this the isolation trick). To illustrate this, consider the case when $i=1$ , $s=1$ , and $M(n)={1}/{p}(n\cdot n)$ . Then, (7.3) implies that

(7.4) $$ \begin{align} & P_{0}(n+pm_{0})+(MP_{1})(n+pm_{0})+\Delta_{h_{1}+pm_{1}}Q_{0}(n+pm_{0})\nonumber\\ & \quad+\Delta_{h_{1}+pm_{1}}(MQ_{1})(n+pm_{0})\in p\mathbb{Z} \end{align} $$

for all $m_{0},m_{1}\in \mathbb {Z}^{d}.$ Since $M(n+pm)\equiv M(n)+2m\cdot n \,\mod p\mathbb {Z}$ and $R(n+pm)\equiv R(n)\,\mod p\mathbb {Z}$ for all integer coefficient polynomial R, one can show that the expression in (7.4) modulo $p\mathbb {Z}$ is equal to $P_{0}(n)+(MP_{1})(n)+\Delta _{h_{1}}Q_{0}(n)+\Delta _{h_{1}}(MQ_{1})(n)+2(m_{0}\cdot n)P_{1}(n)$ plus

$$ \begin{align*}2(n+h_{1})\cdot (m_{0}+m_{1})Q_{1}(n+h_{1})-2n\cdot m_{0}Q_{1}(n)+2n\cdot m_{0}P_{1}(n).\end{align*} $$

Since $m_{0}$ and $m_{1}$ are arbitrary, this implies that $Q_{1}(n+h_{1}), Q_{1}(n)-p_{1}(n)\in p\mathbb {Z}$ whenever $n,n+h_{1}\in V_{p}(M)$ and $n,n+h\neq \mathbf {0}$ , which implies that $P_{1}$ and $Q_{1}$ are simple.

We now carry out this trick to the general setting. To apply the isolation trick, we need to restrict ourself to the set of $(n,h_{1},\ldots ,h_{s})$ where there is sufficient freedom in choosing $m_{0},\ldots ,m_{s}$ . By the pigeonhole principle, there exists a subset $W_{0}$ of $\Box _{p,s}(V(M))\cap ([p]^{d})^{s+1}$ of cardinality at least $\delta \vert \Box _{p,s}(V(M))\cap ([p]^{d})^{s+1}\vert /2$ and for each $(n,h_{1},\ldots ,h_{s})\in W_{0}$ , a set $W_{0}(n,h_{1},\ldots ,h_{s})\subseteq ([pK]^{d})^{s+1}$ of cardinality at least $\delta (pK)^{d(s+1)}/2$ such that

$$ \begin{align*}(n+pm_{0},h_{1}+pm_{1},\ldots,h_{s}+pm_{s})\in W\end{align*} $$

for all $(n,h_{1},\ldots ,h_{s})\in W_{0}$ and $(m_{0},\ldots ,m_{s})\in W_{0}(n,h_{1},\ldots ,h_{s})$ . Now, fix any $(n,h_{1},\ldots ,h_{s})\in W_{0}$ and $(m_{0},\ldots ,m_{s})\in W_{0}(n,h_{1},\ldots ,h_{s})$ . We have

$$ \begin{align*}\Delta_{h_{s-1}+pm_{s-1}}\cdots \Delta_{h_{1}+pm_{1}}P(n)+\Delta_{h_{s}+pm_{s}}\cdots \Delta_{h_{1}+pm_{1}}Q(n)\in\mathbb{Z}\end{align*} $$

by assumption. So,

(7.5) $$ \begin{align} \begin{aligned} \Delta_{h_{s-1}+pm_{s-1}}\cdots \Delta_{h_{1}+pm_{1}}P^{\prime\prime}_{t}(n)+\Delta_{h_{s}+pm_{s}}\cdots \Delta_{h_{1}+pm_{1}}Q^{\prime\prime}_{t}(n)\in p\mathbb{Z}. \end{aligned} \end{align} $$

We now show that (7.5) in fact holds for all $m_{0},\ldots ,m_{s}$ (and thus, we are in good shape to use the isolation trick). Assume that

$$ \begin{align*} M(n)=\frac{1}{p}((nA)\cdot n+u\cdot n+v) \end{align*} $$

for some $d\times d$ symmetric integer coefficient matrix A, some $u\in \mathbb {Z}^{d}$ , and some $v\in \mathbb {Z}$ . Then, for all $m,n\in V_{p}(M)$ , we have

(7.6) $$ \begin{align} M(n+pm)\equiv M(n)+((2(nA)+u)\cdot m) \,\mod p\mathbb{Z}. \end{align} $$

For any $r\in \mathbb {N}_{+} \epsilon =(\epsilon _{1},\ldots ,\epsilon _{r})\in \{0,1\}^{r}$ and $a=(a_{1},\ldots ,a_{r})\in (\mathbb {Z}^{d})^{r}$ , denote

$$ \begin{align*}\epsilon\cdot a:=\epsilon_{1}a_{1}+\cdots+\epsilon_{r}a_{r}\in \mathbb{Z}^{d}.\end{align*} $$

Since $P_{j}$ and $Q_{j}$ have integer coefficients, it is not hard to see from (7.5) and (7.6) that for any $(n,h_{1},\ldots ,h_{s})\in W_{0}$ and $(m_{0},\ldots ,m_{s})\in W_{0}(n,h_{1},\ldots ,h_{s})$ , we have

(7.7) $$ \begin{align} & \frac{1}{p}\sum_{j=0}^{i}\sum_{\epsilon_{\ast}\in\{0,1\}^{s-1}}(-1)^{\vert\epsilon_{\ast}\vert}(M(n'+\epsilon_{\ast}\cdot h_{\ast}) \nonumber \\ & \qquad\qquad\qquad\qquad\qquad +(2(n'+\epsilon_{\ast}\cdot h_{\ast})A+u)\cdot (\epsilon_{\ast}\cdot m_{\ast}))^{j} P_{j}(n'+\epsilon_{\ast}\cdot h_{\ast}) \nonumber\\ &\quad+\frac{1}{p}\sum_{j=0}^{i}\sum_{\epsilon\in\{0,1\}^{s}}(-1)^{\vert\epsilon\vert}(M(n'+\epsilon\cdot h)\nonumber\\ & \qquad\qquad\qquad\qquad\qquad\quad +(2(n'+\epsilon\cdot h)A+u)\cdot (\epsilon\cdot m))^{j} Q_{j}(n'+\epsilon\cdot h)\in \mathbb{Z}, \end{align} $$

where $n'=n+pm_{0}$ , $h=(h_{1},\ldots ,h_{s})$ , $h_{\ast }=(h_{1},\ldots ,h_{s-1})$ , $m=(m_{1},\ldots ,m_{s})$ , and $m_{\ast }=(m_{1},\ldots ,m_{s-1})$ , and the terms $\epsilon _{\ast }, h_{\ast },m_{\ast }$ are regarded as non-existing if $s=1$ . Since $P_{i}$ and $Q_{i}$ have integer coefficients, the residue class mod $\mathbb {Z}$ of the left-hand side of (7.7) remains unchanged if we replace $m_{i}$ by $m_{i} \,\mod p\mathbb {Z}$ for $0\leq i\leq s$ . In other words, for fixed $(n,h_{1},\ldots ,h_{s})\in W_{0}$ , the left-hand side of (7.7) is a p-periodic polynomial in the variables $(m_{0},\ldots ,m_{s})$ . Since $W_{0}(n,h_{1},\ldots ,h_{s}) \,\mod p(\mathbb {Z}^{d})^{s+1}$ contains at least $\delta p^{d(s+1)}/2$ residue classes mod $p\mathbb {Z}$ , it follows from Lemma 4.10 that (7.7) (and thus (7.5)) holds for all $m_{0},\ldots ,m_{s}\in \mathbb {Z}^{d}$ and for all $(n,h_{1},\ldots ,h_{s})\in W_{0}$ (and thus, for all $(n,h_{1},\ldots ,h_{s})\in W_{0}+p(\mathbb {Z}^{d})^{s+1}$ ).

We now apply the isolation trick to (7.7) to deduce information on $P_{i}$ and $Q_{i}$ . We first consider the case when $2nA+u,h_{1}A,\ldots ,h_{s}A$ are p-linearly independent (this corresponds to the condition where $n,n+h\neq \mathbf {0}$ in the outlined example). It is not hard to see that for any $1\leq j\leq i$ and $c_{j}\in \mathbb {Z}^{d}$ , there exists $m_{j}\in \mathbb {Z}^{d}$ such that

$$ \begin{align*}(2nA+u)\cdot m_{j}, (h_{j'}A)\cdot m_{j}, (h_{i+j}A)\cdot m_{j}-c_{j}\in p\mathbb{Z}\end{align*} $$

for all $1\leq j'\leq s, j'\neq i+j$ . For $i+1\leq j\leq s$ , let $m_{j}=\mathbf {0}$ .

The generalization of the isolation trick to the case $i\geq 2$ requires a lot of computations, which is what we will do now. Then, for all $0\leq j\leq i$ and $\epsilon _{\ast }\in \{0,1\}^{s-1}$ , we have that

(7.8) $$ \begin{align} & (M(n+\epsilon_{\ast}\cdot h_{\ast})+(2(n+\epsilon_{\ast}\cdot h_{\ast})A+u)\cdot (\epsilon_{\ast}\cdot m_{\ast}))^{j}P_{j}(n+\epsilon_{\ast}\cdot h_{\ast})\nonumber\\ &\quad=(M(n+\epsilon_{\ast}\cdot h_{\ast})+(2(n+\epsilon'\cdot h'+\epsilon^{\prime\prime}_{\ast}\cdot h^{\prime\prime}_{\ast})A+u)\cdot (\epsilon'\cdot m'))^{j}P_{j}(n+\epsilon_{\ast}\cdot h_{\ast})\nonumber\\ &\quad \equiv\bigg(M(n+\epsilon_{\ast}\cdot h_{\ast})+2\sum_{\ell=1}^{i}\epsilon_{\ell}\epsilon_{i+\ell}c_{\ell}\bigg)^{j}P_{j}(n+\epsilon_{\ast}\cdot h_{\ast}) \,\mod p\mathbb{Z}, \end{align} $$

where $h':=(h_{1},\ldots ,h_{i})$ , $h^{\prime \prime }_{\ast }:=(h_{i+1},\ldots ,h_{s-1})$ , $\epsilon ':=(\epsilon _{1},\ldots ,\epsilon _{i})$ , and $\epsilon ^{\prime \prime }_{\ast }:=(\epsilon _{i+1}, \ldots ,\epsilon _{s-1})$ . Similarly, for all $0\leq j\leq i$ and $\epsilon \in \{0,1\}^{s}$ , we have that

(7.9) $$ \begin{align} &(M(n+\epsilon\cdot h)+(2(n+\epsilon\cdot h)A+u)\cdot (\epsilon\cdot m))^{j}Q_{j}(n+\epsilon\cdot h)\nonumber\\ &\quad\equiv\bigg(M(n+\epsilon\cdot h)+2\sum_{\ell=1}^{i}\epsilon_{\ell}\epsilon_{i+\ell}c_{\ell}\bigg)^{j}Q_{j}(n+\epsilon\cdot h) \,\mod p\mathbb{Z}. \end{align} $$

Combining (7.7), (7.8), and (7.9), we have that

(7.10) $$ \begin{align} &\sum_{j=0}^{i}\sum_{\epsilon_{\ast}\in\{0,1\}^{s-1}}(-1)^{\vert\epsilon_{\ast}\vert} \bigg(M(n+\epsilon_{\ast}\cdot h_{\ast})+2\sum_{\ell=1}^{i}\epsilon_{\ell}\epsilon_{i+\ell}c_{\ell}\bigg)^{j}P_{j}(n+\epsilon_{\ast}\cdot h_{\ast}) \nonumber\\ &\quad+\sum_{j=0}^{i}\sum_{\epsilon\in\{0,1\}^{s}}(-1)^{\vert\epsilon\vert} \bigg(M(n+\epsilon\cdot h)+2\sum_{\ell=1}^{i}\epsilon_{\ell}\epsilon_{i+\ell}c_{\ell}\bigg)^{j}Q_{j}(n+\epsilon\cdot h)\in p\mathbb{Z} \end{align} $$

for all $c_{1},\ldots ,c_{j}\in \mathbb {Z}^{d}$ . Viewing (7.10) as a polynomial of $c_{1},\ldots ,c_{i}$ and considering the coefficient of the term $c_{1}\cdot \cdots \cdot c_{i}$ , by interpolation, we have that

$$ \begin{align*} \begin{aligned} & q"\sum_{\epsilon^{\prime\prime\prime}_{\ast}\in\{0,1\}^{s-2i-1}}(-1)^{\vert\epsilon^{\prime\prime\prime}_{\ast}\vert} P_{i}(n+h_{1}+\cdots+h_{2i}+\epsilon^{\prime\prime\prime}_{\ast}\cdot h^{\prime\prime\prime}_{\ast})\\ & \quad +q"\sum_{\epsilon"'\in\{0,1\}^{s-2i}}(-1)^{\vert\epsilon"'\vert} Q_{i}(n+h_{1}+\cdots+h_{2i}+\epsilon"'\cdot h"')\in p\mathbb{Z} \end{aligned} \end{align*} $$

for some $q"\in \mathbb {N}_{+}, q"\leq O_{d,k}(1)$ , where $h"'=(h_{2i+1},\ldots ,h_{s}), h^{\prime \prime \prime }_{\ast }=(h_{2i+1},\ldots ,h_{s-1})$ , $\epsilon ^{\prime \prime \prime }_{\ast }=(\epsilon _{2i+1},\ldots ,\epsilon _{s-1})$ , and $\epsilon "'=(\epsilon _{2i+1},\ldots ,\epsilon _{s})$ , and the sum

$$ \begin{align*} \sum_{\epsilon\in\{0,1\}^{r}}(-1)^{\vert\epsilon\vert}a(n+\epsilon\cdot h) \end{align*} $$

is considered as $a(n)$ if $r=0$ , and as $0$ if $r<0$ . In conclusion, we have that

(7.11) $$ \begin{align} \begin{aligned} q"(\Delta_{h_{s-1}}\cdots\Delta_{h_{2i+1}}P_{i}(n')+\Delta_{h_{s}}\cdots\Delta_{h_{2i+1}}Q_{i}(n')) \in p\mathbb{Z} \end{aligned} \end{align} $$

with $n'=n+h_{1}+\cdots +h_{2i}$ for all $(n,h_{1},\ldots ,h_{s})\in W_{0}+p(\mathbb {Z}^{d})^{s+1}$ such that $2nA+u,h_{1}A,\ldots ,h_{s}A$ are p-linearly independent.

Step 3: imposing linear independent conditions. The problem is now reduced to a point where Corollary 7.4 is applicable, as long as $2nA+u,h_{1}A,\ldots ,h_{s}A$ are rarely p-linearly dependent. It is convenient to work in the $\mathbb {F}_{p}^{d}$ -setting in Step 3. Let $\tilde {M}\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be the non-degenerate quadratic form induced by M, and $W'$ be the set of $(n',h_{2i+1},\ldots ,h_{s})\in (\mathbb {F}_{p}^{d})^{s-2i+1}$ such that $n'=n+h_{1}+\cdots +h_{2i}$ for some $(n,h_{1},\ldots ,h_{s})\in \iota (W_{0})$ such that $2n\iota (A)+\iota (u),h_{1}\iota (A),\ldots ,h_{s}\iota (A)$ are linearly independent. Then, it is not hard to see that (7.11) holds for all $(n',h_{2i+1},\ldots ,h_{s})\in \iota ^{-1}(W')$ . If we can show that ${\vert W'\vert \geq \delta \vert \Box _{s-2i}(V(\tilde {M}))\vert /8}$ , then it follows from (7.11) and Corollary 7.4 that $P_{i}$ and $Q_{i}$ are simple.

We now estimate the cardinality of $W'$ . Since $d'\geq s^{2}+s+3$ , it follows from Proposition 4.19 that

(7.12) $$ \begin{align} \vert\Box_{j}(V(\tilde{M}))\vert=p^{(j+1)d-(({j(j+1)}/{2})+1)}(1+O_{j}(p^{-1/2})) \end{align} $$

for all $0\leq j\leq s$ . For convenience, denote $\mathbf {x}:=(n',h_{2i+1},\ldots ,h_{s})$ . We say that $\mathbf {x}$ is good if $2n'\iota (A)+\iota (u),h_{2i+1}\iota (A),\ldots ,h_{s}\iota (A)$ are linearly independent. Let $W^{\prime }_{\mathbf {x}}$ denote the set of $(h_{1},\ldots ,h_{2i})\in (\mathbb {F}_{p}^{d})^{2i}$ such that $(n'-h_{1}-\cdots -h_{2i},h_{1},\ldots ,h_{s})\in \iota (W)$ . Then,

(7.13) $$ \begin{align} \sum_{\mathbf{x}\in \Box_{s-2i}(V(\tilde{M}))}\vert W^{\prime}_{\mathbf{x}}\vert{\kern-1pt}={\kern-1pt}\vert W_{0}\vert\geq \delta \vert\Box_{s}(V(\tilde{M}))\vert/2{\kern-1pt}={\kern-1pt}\frac{1}{2}\delta p^{(s+1)d-(({s(s+1)}/{2})+1)}(1+O_{s}(p^{-1/2})). \end{align} $$

Therefore, informally speaking, by (7.12) and (7.13), on average, the cardinality of $W^{\prime }_{\mathbf {x}}$ is at least $\delta p^{2id-(2s-2i+1)i}/2$ .

Note that for good $\mathbf {x}$ , $(h_{1},\ldots ,h_{2i})\in W^{\prime }_{\mathbf {x}}$ only if $(n'-h_{1}-\cdots -h_{2i},h_{1},\ldots ,h_{s})\in \Box _{s}(V(\tilde {M}))$ . Using Lemma 4.18, this is equivalent of saying that:

• • $\tilde {M}(n')-\tilde {M}(n'-h_{j})=(2n'\iota (A)+\iota (u))\cdot h_{j}=0$ for all $1\leq j\leq 2i$ ;

• • $(h_{j}\iota (A))\cdot h_{j'}=0$ for all $1\leq j,j'\leq s$ with at least one of $j,j'$ belonging to $\{1,\ldots ,2i\}$ .

There are in total $(2s-2i+1)i\leq (s+1/2)^{2}/2$ independent equations above in total. Since $d\geq s^{2}+s+3$ , by repeatedly using Corollary 4.16 and the fact that $\mathbf {x}$ is good, it is not difficult to show that

(7.14) $$ \begin{align} \vert W^{\prime}_{\mathbf{x}}\vert\leq p^{2id-(2s-2i+1)i}(1+O_{s}(p^{-1/2})). \end{align} $$

We leave the proof of (7.14) to the interested readers. (Alternatively, (7.14) can also be deduced as a special case of [18, Theorem 5.11] (in the terminology introduced in [18], $W^{\prime }_{\mathbf {x}}$ is a subset of an $\tilde {M}$ -set of total co-dimension $(2s-2i+1)i$ ).)

Let $V:=\{n\iota (A)\colon n\in \mathbb {F}_{p}^{d}\}\subseteq \mathbb {F}_{p}^{d}$ . Then, V is a subspace of $\mathbb {F}_{p}^{d}$ of dimension $d'$ . Let $V'$ be the set of $m,m_{2i+1},\ldots ,m_{s}\in V$ such that $2m+\iota (u),m_{2i+1},\ldots ,m_{s}$ are linearly dependent. Similar to the proof of Lemma 4.11(i), it is not hard to see the ${\vert V'\vert \leq sp^{(d+1)(s-2i)}}$ . However, for each $m\in V$ , the number of $n\in \mathbb {F}_{p}^{d}$ such that ${n\iota (A)=m}$ is at most $p^{d-d'}$ . Therefore, the number of $\mathbf {x}\in (\mathbb {F}_{p}^{d})^{s-2i+1}$ which are not good is at most $p^{d-d'}\vert V'\vert \leq sp^{(s-2i+1)d+(s-2i)-d'}$ . So,

(7.15) $$ \begin{align} \sum_{\mathbf{x}\in (\mathbb{F}_{p}^{d})^{s-2i+1},\ \textbf{x} \text{ is not good}}\vert W^{\prime}_{\mathbf{x}}\vert\leq sp^{(s-2i+1)d+(s-2i)-d'}\cdot p^{2id}=sp^{(s+1)d+(s-2i)-d'}. \end{align} $$

Since $(s+1)d+(s-2i)-d'<(s+1)d-(({s(s+1)}/{2})+1)$ , it follows from (7.12), (7.13), (7.14), (7.15), and the pigeonhole principle that there exists a subset $W"\subseteq \Box _{s-2i} (V(\tilde {M}))$ of cardinality at least $\delta \vert \Box _{s-2i}(V(\tilde {M}))\vert /20$ such that $\vert W^{\prime }_{\mathbf {x}}\vert \geq \delta p^{2id-(2s-2i+1)i}/20$ for all $\mathbf {x}\in W"$ . In particular, $W^{\prime }_{\mathbf {x}}$ is non-empty for all $\mathbf {x}\in W"$ . Therefore, $W"$ is a subset of $W'$ and thus, $\vert W'\vert \geq \vert W"\vert \geq \delta \vert \Box _{s-2i}(V(\tilde {M}))\vert /20$ .

Step 4: reducing the complexity of the denominator. In conclusion, we have shown by induction that $t=0$ and, therefore, we may write

$$ \begin{align*}qP=P^{\prime}_{0}+P' \quad\text{and}\quad qQ=Q^{\prime}_{0}+Q'\end{align*} $$

for some good polynomials $P^{\prime }_{0},Q^{\prime }_{0}$ of degrees at most $k-1$ and k, respectively, and some $P',Q'\in \text {poly}(\mathbb {Z}^{d}\to \mathbb {Q})$ of with $\deg (P')\leq s-2$ and $\deg (Q')\leq s-1$ . Our final goal is to show that one can further require q to be small.

Let $q^{\ast }\in \mathbb {N}_{+}$ be such that $qq^{\ast }\equiv 1 \,\mod p^{k}\mathbb {Z}$ . Then, $P=({1-qq^{\ast }}/{q})P^{\prime }_{0}+q^{\ast }P^{\prime }_{0}+{1}/{q}P'$ . Denote $P_{0}:=(1-qq^{\ast })P^{\prime }_{0}$ . Since $P^{\prime }_{0}$ is good, we have that $P_{0}$ has coefficients in $\mathbb {Z}$ and that $\Delta _{h_{s-1}}\cdots \Delta _{h_{1}}(q^{\ast }P^{\prime }_{0})(n)\in \mathbb {Z}$ for all $(n,h_{1},\ldots ,h_{s})\in \Box _{p,s}(V(M))$ . Similarly, $Q_{0}:=(1-qq^{\ast })Q^{\prime }_{0}$ also has coefficients in $\mathbb {Z}$ , and $\Delta _{h_{s}}\cdots \Delta _{h_{1}}(q^{\ast }Q^{\prime }_{0})(n)\in \mathbb {Z}$ for all $(n,h_{1},\ldots ,h_{s})\in \Box _{p,s}(V(M))$ . So, we have that

(7.16) $$ \begin{align} \Delta_{h_{s-1}}\cdots\Delta_{h_{1}}P_{0}(n)+\Delta_{h_{s}}\cdots\Delta_{h_{1}}Q_{0}(n)\in q\mathbb{Z} \end{align} $$

for all $(n,h_{1},\ldots ,h_{s})\in W+([pK']^{d})^{s+1}$ , where for convenience, we denote $K':=pK$ .

Our strategy is to fix $(n,h_{1},\ldots ,h_{s})$ , apply (7.16) for $(n{\kern-1pt}+{\kern-1pt}pm_{0},h_{1}{\kern-1pt}+{\kern-1pt}pm_{1},\ldots , h_{s}{\kern-1pt}+{\kern-1pt}pm_{s})$ , and then apply Proposition 3.18 as a polynomial in the variables $m_{0},\ldots ,m_{s}$ . By the pigeonhole principle, there exists some $(n,h_{1},\ldots ,h_{s})\in \Box _{p,s}(V(M))\cap ([p]^{d})^{s+1}$ and a subset $J\subseteq ([K']^{d})^{s+1}$ of cardinality at least $\delta { K'}^{d(s+1)}$ such that $(n+pm_{0},h_{1}+pm_{1},\ldots ,h_{s}+pm_{s})\in W$ for all $(m_{0},\ldots ,m_{s})\in J$ . Write

$$ \begin{align*} & G(m_{0},m_{1},\ldots,m_{s}):=\Delta_{h_{s-1}+pm_{s-1}}\cdots\Delta_{h_{1}+pm_{1}}P_{0}(n+pm_{0})\\ & \quad+\Delta_{h_{s}+pm_{s}}\cdots\Delta_{h_{1}+pm_{1}}Q_{0}(n+pm_{0}). \end{align*} $$

Then, G is a rational polynomial of degree at most k. By assumption, $({1}/{q})G(\mathbf {m})\in \mathbb {Z}$ for all $\mathbf {m}\in J+([K']^{d})^{s+1}$ . So, by Proposition 3.18, there exists $r\in \mathbb {N}_{+}$ with $r\ll _{d,k,s} \delta ^{-O_{d,k,s}(1)}$ such that all the coefficients of $({1}/{q})G$ are in $\mathbb {Z}/r$ . Write

$$ \begin{align*} \begin{aligned} &G'(m_{0},m_{1},\ldots,m_{s}):=\frac{1}{q}G\bigg(\frac{1}{p}m_{0}-n,\frac{1}{p}m_{1}-h_{1},\ldots,\frac{1}{p}m_{s}-h_{s}\bigg)\\ &\quad=\Delta_{m_{s-1}}\cdots\Delta_{m_{1}}\bigg(\frac{1}{q}P_{0}\bigg)(m_{0})+\Delta_{m_{s}}\cdots\Delta_{m_{1}}\bigg(\frac{1}{q}Q_{0}\bigg)(m_{0}). \end{aligned} \end{align*} $$

Then, the coefficients of $G'$ are in $\mathbb {Z}/rp^{k}$ . However, since $P_{0}$ and $Q_{0}$ are integer coefficient polynomials, the coefficients of $G'$ are in $\mathbb {Z}/q$ and are thus in $(\mathbb {Z}/rp^{k})\cap (\mathbb {Z}/q)\subseteq \mathbb {Z}/r$ .

Now, assume that

$$ \begin{align*}\frac{1}{q}P_{0}(n):=\sum_{i\in\mathbb{N}^{d},\vert i\vert\leq k} a_{i}n^{i} \quad\text{and}\quad \frac{1}{q}Q_{0}(n):=\sum_{i\in\mathbb{N}^{d},\vert i\vert\leq k} b_{i}n^{i}\end{align*} $$

for some $a_{i},b_{i}{\kern-1pt}\in{\kern-1pt} \mathbb {Q}$ . Fix any $i{\kern-1pt}={\kern-1pt}(i_{1},\ldots ,i_{d}){\kern-1pt}\in{\kern-1pt} \mathbb {N}^{d}$ with $\vert i\vert {\kern-1pt}\geq{\kern-1pt} s{\kern-1pt}-{\kern-1pt}1$ . Let $(m_{1},\ldots ,m_{\vert i\vert +1})\in (\mathbb {Z}^{d})^{\vert i\vert }$ be any vector such that $m_{s}=\mathbf {0}$ and such that the number of $m_{i'}, 1\leq i'\leq \vert i\vert +1, i'\neq s$ which is equal to the jth standard unit vector is equal to $i_{j}$ for all $1\leq j\leq d$ . Then, it is not hard to see that

$$ \begin{align*}\Delta_{m_{\vert i\vert+1}}\cdots\Delta_{m_{s+1}}G'(\mathbf{0},m_{1},\ldots,m_{s})=i!a_{i}.\end{align*} $$

Since the coefficients of $G'$ are in $\mathbb {Z}/r$ , we have that $a_{i}\in \mathbb {Z}/r'$ for all $i\in \mathbb {N}^{d}$ with $\vert i\vert \geq s-1$ , where $r':=(k!)^{d}r$ .

Now, fix any $i=(i_{1},\ldots ,i_{d})\in \mathbb {N}^{d}$ with $\vert i\vert \geq s$ . Let $(m_{1},\ldots ,m_{\vert i\vert })\in (\mathbb {Z}^{d})^{\vert i\vert }$ be any vector such that the number of $m_{i'}, 1\leq i'\leq \vert i\vert $ which is equal to the jth standard unit vector is equal to $i_{j}$ for all $1\leq j\leq d$ . Then, it is not hard to see that

$$ \begin{align*} \Delta_{m_{\vert i\vert}}\cdots\Delta_{m_{s+1}}G'(\mathbf{0},m_{1},\ldots,m_{s})=i!b_{i}+(i-m_{s})!a_{i-m_{s}}. \end{align*} $$

Since the coefficients of $G'$ are in $\mathbb {Z}/r$ and since $a_{i-m_{s}}\in \mathbb {Z}/r'$ , we have that $b_{i}\in \mathbb {Z}/r'$ for all $i\in \mathbb {N}^{d}$ with $\vert i\vert \geq s$ . So, we may write $P_{0}$ as $({1}/{q})P_{0}=P_{1}+P_{2}$ for some polynomial $P_{1}$ with coefficients in $\mathbb {Z}/r'$ having at most the same degree as P and some $P_{2}$ of degree at most $s-2$ . So,

$$ \begin{align*} r'P=r'(q^{\ast}P^{\prime}_{0}+P_{1})+\bigg(r'P_{2}+\frac{1}{q}P'\bigg), \end{align*} $$

where $r'(q^{\ast }P^{\prime }_{0}+P_{1})$ take integer values in $V_{p}(M)$ . A similar decomposition apples to Q and so we are done.

8 An example for the Heisenberg group

Before proving Theorem 5.1, we use a sample case to illustrate the idea of the proof. The Heisenberg group is the set $G=\mathbb {R}^{3}$ with the group action given by

$$ \begin{align*} (a,b,c)\ast (a',b',c'):=(a+a',b+b',c+c'+ab') \quad\text{for all } a,b,c,a',b',c'\in\mathbb{R}. \end{align*} $$

This is a 2-step nilmanifold with respect to the lower central series $G_{\mathbb {N}}$ (that is, $G_{0}=G_{1}=G, G_{2}=\{0\}^{2}\times \mathbb {R}$ , and $G_{i}=\{(0,0,0)\}$ for all $i\geq 3$ ). Let $\Gamma =\mathbb {Z}^{3}$ . The Lie algebra of G has a Mal’cev basis $\mathcal {X}=\{X_{1},X_{2},X_{3}\}$ with the Mal’cev coordinate map $\psi ^{-1}\colon \mathbb {R}^{3}\to G$ given by

$$ \begin{align*}\psi^{-1}(t_{1},t_{2},t_{3}):=\exp(t_{1}X_{1})\exp(t_{2}X_{2})\exp(t_{3}X_{3})=(t_{1},t_{2},t_{1}t_{2}+t_{3}).\end{align*} $$

In this section, we provide an outline for the proof of the following simple case of Theorem 5.1 for linear polynomial sequences.

Proposition 8.1. Let $0<\delta <1/2, d\in \mathbb {N}_{+},s\in \mathbb {N}$ with $d\gg _{s} 1$ , and p be a prime. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be the quadratic form given by $M(n)=n\cdot n$ . Let $G_{\mathbb {N}}$ be the Heisenberg group with the lower central series filtration and $g\colon \mathbb {Z}^{d}\to G$ be of the form $g(n_{1},\ldots ,n_{d})=a_{1}^{n_{1}}\cdot \cdots \cdot a_{d}^{n_{d}}$ for some $a_{1},\ldots ,a_{d}\in G$ commuting with each other with $a_{i}^{p}\in \Gamma $ . If $p\gg _{\delta ,d} 1$ and $(g(n)\Gamma )_{n\in \iota ^{-1}(V(M))}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then there exists a non-trivial type-I horizontal character $\eta $ with $0<\Vert \eta \Vert \ll _{\delta , d} 1$ such that $\eta \circ g \,\mod \mathbb {Z}$ is a constant on $V_{p}(M)$ .

Sketch of the proof of Proposition 8.1.

Step 1: construction of a nilsequence in a joining system. By Lemma 3.23, if $(g(n)\Gamma )_{n\in \iota ^{-1}(V(M))}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then there exist $\xi \in \mathbb {Z}$ with ${\vert \xi \vert \ll \delta ^{-O(1)}}$ and a function $F\colon G/\Gamma \to \mathbb {C}$ with $\Vert F\Vert _{\mathrm { Lip}}\leq 1$ and vertical frequency $\xi $ such that

$$ \begin{align*} \begin{aligned} \bigg\vert\mathbb{E}_{n\in \iota^{-1}(V(M))}F(g(n)\Gamma)-\int_{G/\Gamma} F\,dm_{G/\Gamma}\bigg\vert\gg_{d} \delta^{O_{d}(1)}, \end{aligned} \end{align*} $$

where $m_{G/\Gamma }$ is the Haar measure of $G/\Gamma $ . If $\xi =0$ , then we may invoke the discussion in [5, after (7.1)] to reduce the problem to the 1-step case, which can be addressed by Lemma 9.6. So, from now on, we assume that $\xi \neq 0$ . Then, it follows that

$$ \begin{align*} \begin{aligned} \vert\mathbb{E}_{n\in \iota^{-1}(V(M))}F(g(n)\Gamma)\vert\gg_{d} \delta^{O_{d}(1)}. \end{aligned} \end{align*} $$

For $h=(h_{1},\ldots ,h_{d})\in \mathbb {Z}^{d}$ and $a=(a_{1},\ldots ,a_{d})\in G^{d}$ , denote $a^{h}:=a_{1}^{h_{1}}\cdot \cdots \cdot a_{d}^{h_{d}}$ . Denote

$$ \begin{align*}\tilde{F}_{h}(x,y):=F(\{a^{h}\}x)\overline{F}(y) \quad\text{for all } x,y\in G/\Gamma.\end{align*} $$

Using the (multi-dimensional version of) Green–Tao argument in [5, §5], we may generalize the outline of the proof of Corollary 1.6 described in §5 to non-abelian nilmanifolds and conclude that

$$ \begin{align*}\vert\mathbb{E}_{n\in \iota^{-1}(V(M)^{\iota(h)})}F^{\square}_{h}(\tilde{a}_{h}^{n}\Gamma^{\square})\vert\gg_{d} \delta^{O_{d}(1)},\end{align*} $$

where $G^{\square }:=\{(g,g')\in G^{2}\colon g^{-1}g'\in G_{2}\}$ , $\Gamma ^{\square }:=\{(g,g')\in \Gamma ^{2}\colon g^{-1}g'\in G_{2}\}$ , $F^{\square }_{h}$ is the restriction of $\tilde {F}_{h}$ on $G^{\square }$ , and

$$ \begin{align*}\tilde{a}_{h}^{n}:=(\{a^{h}\}^{-1}a_{1}^{n_{1}}\{a^{h}\},\ldots,\{a^{h}\}^{-1}a_{d}^{n_{d}}\{a^{h}\},a_{1}^{n_{1}},\ldots,a_{d}^{n_{d}}).\end{align*} $$

It is not hard to see that $\tilde {F}_{h}$ is invariant under $[G^{\square },G^{\square }]$ and, thus, one can use the tools for 1-step nilmanifold (such as Lemma 9.6) to conclude that there exists a non-trivial type-I horizontal character $\eta _{h}\colon G^{\square }\to \mathbb {R}$ with $0<\Vert \eta _{h}\Vert \ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $P_{h}(n):=\eta _{h}\circ \tilde {a}_{h}^{n} \,\mod \mathbb {Z}$ is a constant on $V_{p}(M)^{h}$ . By the pigeonhole principle, we may assume without loss of generality that $\eta _{h}$ equals the same $\eta $ for many h. Writing $P_{h}(n)=n\cdot (\eta \circ \tilde {a}_{h}^{1}):=n\cdot v_{h}\colon \mathbb {Z}^{d}\to \mathbb {R}$ for some $v_{h}\in \mathbb {Z}^{d}/p$ , we have that

(8.1) $$ \begin{align} P_{h} \,\, \mod \mathbb{Z} \text{ is a constant on } \iota^{-1}(V(M)^{\iota(h)})=\iota^{-1}(V(M)\cap \{n\in\mathbb{F}_{p}^{d}\colon 2n\cdot h+h\cdot h=0\}). \end{align} $$

Step 2: solving polynomial equations. For any linear polynomial $F\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ , if it vanishes on $V(M)$ , then it must vanish everywhere (this is because F is of the form $MR$ by Proposition 6.2, which forces $F=R\equiv 0$ by comparing the degrees of F and $MR$ ). Similarly, if a linear polynomial F vanishes on the intersection of $V(M)$ and the affine subspace $\{n\in \mathbb {F}_{p}^{d}\colon 2n\cdot h+h\cdot h=0\}$ , then the inheriting principle implies that F must vanish on this entire affine subspace. Translating this observation into the $\mathbb {Z}/p$ -setting, the linearity of $P_{h}$ and (8.1) implies that $P_{h} \,\mod \mathbb {Z}$ must be a constant on $\iota ^{-1}(\{n\in \mathbb {F}_{p}^{d}\colon 2n\cdot h+h\cdot h=0\})=\{n\in \mathbb {Z}^{d}\colon 2n\cdot h+h\cdot h\in p\mathbb {Z}\}$ ). This implies that the vector $v_{h}$ is parallel to $({1}/{p})h$ mod $\mathbb {Z}^{d}$ . Unlike in the case of [5], here, we cannot conclude that $v_{h}\in p\mathbb {Z}^{d}$ .

Step 3: analyzing the coefficients. Suppose that $\psi (a_{i})=(\gamma _{i,1},\gamma _{i,2},\ast )$ . Write ${\gamma _{i}:=(\gamma _{i,1},\gamma _{i,2})}$ and $\zeta _{i}:=(-\gamma _{i,2},\gamma _{i,1})$ . Following the Green–Tao argument in [5, §5], one can conclude that the ith coordinate of $v_{h}$ is equal to $k_{1}\cdot \gamma _{i}+k_{2}\zeta _{i}\cdot \{\sum _{i=1}^{d}h_{i}\gamma _{i}\}$ for some $k_{1}\in \mathbb {Z}^{2}$ and $k_{2}\in \mathbb {Z}$ of complexities $\ll _{d,m}\delta ^{-O_{d,m}(1)}$ which are not all zero (this is a multi-dimensional version of [5, equation before (5.7)]). Since $v_{h}$ is parallel to $({1}/{p})h$ mod $\mathbb {Z}^{d}$ , one can conclude that

(8.2) $$ \begin{align} & \bigg(k_{1}\cdot\gamma_{1}+k_{2}\zeta_{1}\cdot \bigg\{\sum_{i=1}^{d}h_{i}\gamma_{i}\bigg\},\ldots,k_{1}\cdot\gamma_{d} +k_{2}\zeta_{d}\cdot \bigg\{\sum_{i=1}^{d}h_{i}\gamma_{i}\bigg\}\bigg)\nonumber \\ &\quad -c_{h}h\in\mathbb{Z}^{d} \quad\text{for some } c_{h}\in\mathbb{Z}/p, \end{align} $$

whose general case is (9.26). The expression (8.2) differs from [6, Lemma 4.3] because of the appearance of the term $c_{h}h$ . However, its generalization (to be proved in Proposition 9.8) allows us to deduce that there exists $k\in \mathbb {Z}^{2}$ with $0<\vert k\vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $k\cdot \gamma _{i}\in \mathbb {Z}$ for all $1\leq i\leq d$ . Let $\eta '$ be the type-I horizontal character induced by k, then $\eta '\circ g \,\mod \mathbb {Z}$ is a constant on $\mathbb {Z}^{d}$ and thus on $V_{p}(M)$ .

Step 4: completion of the proof. The proof of Proposition 8.1 is already completed in Step 3. However, it is worth mentioning that for general polynomial sequences, due to the appearance of nonlinear terms, one still has to run an argument similar to [5, discussion after Claim 7.7] to complete the proof.

9 Proof of the main equidistribution theorem

9.1 Some preliminary reductions

We prove Theorem 5.1 in this section. We start with a technical lemma on the connections between subspaces of $\mathbb {F}_{p}^{d}$ and those of $\mathbb {Z}^{d}$ . Let $V+c$ be an affine subspace of $\mathbb {F}_{p}^{d}$ of dimension $d'$ and $L\colon \mathbb {F}_{p}^{d'}\to V$ be a bijective linear transformation. Let $\tilde {V}$ be the $\mathbb {Z}$ -span of $\tau (L(e_{1})),\ldots ,\tau (L(e_{d'}))$ and $\tilde {L}\colon \mathbb {Z}^{d'}\to \tilde {V}$ be the bijective linear transformation given by

$$ \begin{align*}\tilde{L}(n_{1},\ldots,n_{d'}):=n_{1}\tau(L(e_{1}))+\cdots+n_{d'}\tau(L(e_{d'})).\end{align*} $$

In other words, $\tilde {L}/p$ is the regular lifting of L. Then, it is clear that $\iota \circ \tilde {L}=L\circ \iota $ and $\tilde {L}\circ \tau \equiv \tau \circ L \,\mod p\mathbb {Z}^{d}$ .

Let B be a subset of $V+c$ . It is clear that there is a bijection between $L^{-1}(B-c)$ and B given by $z\mapsto L(z)+c$ . However, the map $z\mapsto \tilde {L}(z)+\tau (c)$ is not necessarily a bijection between $\iota ^{-1}(L^{-1}(B-c))$ and $\iota ^{-1}(B)$ . To connect the sets $\iota ^{-1}(L^{-1}(B-c))$ and $\iota ^{-1}(B)$ by $\tilde {L}$ , we define a map $\Phi _{L,c}\colon \mathbb {Z}^{d'}\times \mathbb {Z}^{d}\to \mathbb {Z}^{d}$ as

$$ \begin{align*}\Phi_{L,c}(z,w):=\tau(c)+\tilde{L}(z)+pw.\end{align*} $$

Lemma 9.1. For all $K,K'\in \mathbb {N}_{+}$ , the map $\Phi _{L,c} \,\mod pK\mathbb {Z}^{d}$ is a ${K'}^{d}$ -to-1 map between $(\iota ^{-1}(L^{-1}(B-c))\cap [pK']^{d'})\times [K]^{d}$ and $\iota ^{-1}(B)\cap [pK]^{d}$ .

Proof. For convenience, denote $\Phi :=\Phi _{L,c}$ . Let $(z,w)\in \iota ^{-1}(L^{-1}(B-c))\times \mathbb {Z}^{d}$ . Then,

$$ \begin{align*}\iota\circ\Phi(z,w)=\iota(\tau(c)+\tilde{L}(z)+pw)=c+\iota\circ\tilde{L}(z)=c+L\circ\iota(z)\in B.\end{align*} $$

So, the range of $\Phi \,\mod pK\mathbb {Z}^{d}$ is contained in $\iota ^{-1}(B)\cap [pK]^{d}$ .

Now, for all $n{\kern-1pt}\in{\kern-1pt} \iota ^{-1}(B)$ , we may pick some $z'{\kern-1pt}\in{\kern-1pt} L^{-1}(B-c)$ such that $\iota (n){\kern-1pt}={\kern-1pt}L(z')+c$ . Let $z=\tau (z')$ . Then, z belongs to $\iota ^{-1}(L^{-1}(B-c))\cap [p]^{d'}$ and

$$ \begin{align*}\tilde{L}(z)+\tau(c)=\tilde{L}\circ\tau(z')+\tau(c)\equiv \tau\circ L(z')+\tau(c)=\tau\circ\iota(n)\equiv n \,\mod p\mathbb{Z}^{d}.\end{align*} $$

So, there exists $w{\kern-1pt}\in{\kern-1pt} \mathbb {Z}^{d}$ such that $n{\kern-1pt}={\kern-1pt}\tilde {L}(z)+\tau (c){\kern-1pt}+{\kern-1pt}pw.$ Therefore, $\Phi (z, w \,\mod K\mathbb {Z}^{d})\equiv n \,\mod pk\mathbb {Z}^{d}$ . So, the map $\Phi \,\mod pK\mathbb {Z}^{d}$ is surjective.

Finally, for $(z,w), (z',w')\in (\iota ^{-1}(L^{-1}(B-c))\cap [pK']^{d'})\times [K]^{d}$ , we have that $\Phi (z,w)\equiv \Phi (z',w') \,\mod \!{pK}\mathbb {Z}^{d}$ if and only if $\tilde {L}(z-z')+p(w-w')\in pK\mathbb {Z}^{d}$ . If this is the case, then $\tilde {L}(z-z')\in p\mathbb {Z}^{d}$ and thus, $\mathbf {0}=\iota \circ \tilde {L}(z-z')=L\circ \iota (z-z')$ . Since L is injective, this implies that $\iota (z-z')=\mathbf {0}$ and thus, $z\equiv z' \,\mod p\mathbb {Z}^{d'}$ . Now, for any such $z-z'$ and any fixed w, there is a unique $w'\in [K]^{d}$ such that $({1}/{p})\tilde {L}(z-z')+(w-w')\in K\mathbb {Z}^{d}$ . Since for each $z\in \mathbb {Z}^{d'}$ , the number of $z'\in [pK']^{d}$ for which $z\equiv z' \,\mod p\mathbb {Z}^{d'}$ is equal to ${K'}^{d}$ . So, $\Phi \,\mod pK\mathbb {Z}^{d}$ is a ${K'}^{d}$ -to-1 map.

Before proving Theorem 5.1, we start with some simplifications. Suppose first that the conclusion holds for $V+c=\mathbb {F}_{p}^{d}$ . For the general case, let $L\colon \mathbb {F}_{p}^{d-r}\to V$ be a bijective linear transformation. Let $M'\colon \mathbb {F}_{p}^{d-r}\to \mathbb {F}_{p}$ be the quadratic map given by $M'(z):=M(L(z)+c)$ . Then, it is clear that $L^{-1}((V(M)\cap (V+c))-c)=V(M')$ .

Let $g\in \text {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ be rational. By Corollary 3.19, we may assume that g is $pK$ -periodic for some $K\in \mathbb {N}_{+}$ . Then, for any function $F\colon G/\Gamma \to \mathbb {C}$ , it follows from Lemma 9.1 (setting $B=V(M)\cap (V+c)$ and $K'=K$ ) that

$$ \begin{align*} &\mathbb{E}_{n\in \iota^{-1}(V(M)\cap(V+c))}F(g(n)\Gamma)=\mathbb{E}_{n\in \iota^{-1}(V(M)\cap(V+c))\cap [pK]^{d}}F(g(n)\Gamma)\\ &\quad=\mathbb{E}_{z\in \iota^{-1}(V(M'))\cap [pK]^{d-r}}\mathbb{E}_{w\in [K]^{d}}F(g(\tau(c)+\tilde{L}(z)+pw)\Gamma)\\ &\quad=\mathbb{E}_{(z,w)\in \iota^{-1}(V(M"))\cap [pK]^{2d-r}}F(g(\tau(c)+\tilde{L}(z)+pw)\Gamma), \end{align*} $$

where $M"\colon \mathbb {F}_{p}^{2d-r}\to \mathbb {F}_{p}$ is the quadratic form given by $M"(z,w):=M'(z)$ and $\tilde {L}/p$ is the regular lifting of L. It is clear that all of $M,M'$ , and $M"$ have the same rank, and that the map $(z,w)\mapsto g(\tau (c)+\tilde {L}(z)+pw)$ is rational. So, by assumption, if $(g(n)\Gamma )_{n\in \iota ^{-1}(V(M)\cap (V+c))}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then there exists a non-trivial type-I horizontal character $\eta $ with $0<\Vert \eta \Vert \ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $\eta \circ g(\tau (c)+ \tilde {L}(z)+pw) \,\mod \mathbb {Z}$ is a constant for all $z\in \iota ^{-1}(V(M'))$ and $w\in \mathbb {Z}^{d}$ . By Lemma 9.1, we have that $\eta \circ g(n) \,\mod \mathbb {Z}$ is a constant for all $n\in \iota ^{-1}(V(M)\cap (V+c))$ . So, in the rest of §9, we may make the following assumption.

Assumption 9.2. Assume $V+c=\mathbb {F}_{p}^{d}, r=0$ , and $\mathrm {rank}(M)\geq s+13$ .

Denote $d'=\mathrm {rank}(M)$ . Suppose that we have already proved Theorem 5.1 for all quadratic forms of the form

(9.1) $$ \begin{align} M_{c,c',\unicode{x3bb}}(n_{1},\ldots,n_{d}):=cn_{1}^{2}+n^{2}_{2}+\cdots+n_{d'}^{2}+c'n_{d'+1}-\unicode{x3bb} \end{align} $$

for some $c,c',\unicode{x3bb} \in \mathbb {F}_{p}, c\neq 0$ . Let M be an arbitrary quadratic form of rank $d'$ . By Lemma 4.3, there exist $c,c',\unicode{x3bb} \in \mathbb {F}_{p}$ and $v\in \mathbb {F}_{p}^{d}$ with $c\neq 0$ and a $d\times d$ invertible matrix R in $\mathbb {F}_{p}$ such that $M(n)=M_{c,c',\unicode{x3bb} }(nR+v)$ .

For convenience, denote $M':=M_{c,c',\unicode{x3bb} }$ . Then, $R(V(M)+vR^{-1})=V(M')$ . Let ${g\in \text {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})}$ be rational. By Corollary 3.19, we may assume that g is $pK$ -periodic for some $K\in \mathbb {N}_{+}$ . Then, for any function $F\colon G/\Gamma \to \mathbb {C}$ , it follows from Lemma 9.1 (setting $B=V(M)$ and $K'=K$ ) that

$$ \begin{align*} &\mathbb{E}_{n\in \iota^{-1}(V(M))}F(g(n)\Gamma)=\mathbb{E}_{n\in \iota^{-1}(V(M))\cap [pK]^{d}}F(g(n)\Gamma)\\ &\quad=\mathbb{E}_{z\in \iota^{-1}(V(M'))\cap [pK]^{d}}\mathbb{E}_{w\in [K]^{d}}F(g(\tau(-vR^{-1})+\tilde{R^{-1}}(z)+pw)\Gamma)\\ &\quad=\mathbb{E}_{(z,w)\in \iota^{-1}(V(M"))\cap [pK]^{2d}}F(g(\tau(-vR^{-1})+\tilde{R^{-1}}(z)+pw)\Gamma), \end{align*} $$

where $M"\colon \mathbb {F}_{p}^{2d}\to \mathbb {F}_{p}$ is the quadratic form given by $M"(z,w):=M'(z)$ and $\tilde {R^{-1}}/p$ is the regular lifting of $R^{-1}$ . It is clear that all of $M,M'$ , and $M"$ have the same rank, and that $M"$ is also of the form (9.1) (for the same $d'$ but with dimension increased from d to $2d$ ). Moreover, the map $(z,w)\mapsto g(\tau (-vR^{-1})+\tilde {R}^{-1}(z)+pw)$ is rational. So, by assumption, if $(g(n)\Gamma )_{n\in \iota ^{-1}(V(M))}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then there exists a non-trivial type-I horizontal character $\eta $ with $0<\Vert \eta \Vert \ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $\eta \circ g(\tau (-vR^{-1})+\tilde {R^{-1}}(z)+pw)\,\mod \mathbb {Z}$ is a constant for all $z\in \iota ^{-1}(V(M'))$ and ${w\in \mathbb {Z}^{d}}$ . By Lemma 9.1, we have that $\eta \circ g(n) \,\mod \mathbb {Z}$ is a constant for all $n\in \iota ^{-1}(V(M))$ . So, in the rest of §9, we may make the following assumption.

Assumption 9.3. Assume $M=M_{c,c',\unicode{x3bb} }$ is given by (9.1).

Let $\psi \colon G\to \mathbb {R}^{m}$ denote the Mal’cev coordinate map associated to $\mathcal {X}$ . Now, suppose that the conclusion holds under the additional assumption that $g(\mathbf {0})=\mathrm {id}_{G}$ , the identity element of G. For the general case, write $g(\mathbf {0})=\{g(\mathbf {0})\}[g(\mathbf {0})]$ . Let $g'(n):=\{g(\mathbf {0})\}^{-1}g(n)g(\mathbf {0})^{-1}\{g(\mathbf {0})\}$ . Then, $g'$ is rational by the Baker–Campbell–Hausdorff formula and $g(n)\Gamma =\{g(\mathbf {0})\}g'(n)\Gamma $ for all $n\in \mathbb {Z}^{d}$ . Since $\Vert F(\{g(\mathbf {0})\}\cdot )\Vert _{\mathrm {Lip}}\leq O(1)\Vert F\Vert _{\mathrm {Lip}}$ by [5, Lemma A.5], if $(g(n)\Gamma )_{n\in \iota ^{-1}(V(M))}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then $(g'(n)\Gamma )_{n\in \iota ^{-1}(V(M))}$ is not $O(\delta )$ -equidistributed on $G/\Gamma $ . Since $g'(\mathbf {0})=\mathrm {id}_{G}$ , by assumption, there exists a non-trivial type-I horizontal character $\eta $ with $0<\Vert \eta \Vert \ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that for all $n\in \iota ^{-1}(V(M))$ , $\eta \circ g'(n) \,\mod \mathbb {Z}$ is a constant, and thus, $\eta \circ g(n) \,\mod \mathbb {Z}$ is a constant. So, in the rest of §9, we may make the following assumption.

Assumption 9.4. Assume $g(\mathbf {0})=\mathrm {id}_{G}$ . As a result, we may further assume that $G=G_{0}=G_{1}$ .

Now, suppose that the conclusion holds under the additional assumption that $\psi (g(e_{i}))$ belongs to $[0,1)^{m}$ for all $1\leq i\leq d$ , where $e_{i}$ is the ith standard unit vector in $\mathbb {Z}^{d}$ . For the general case, write $g(e_{i})=\{g(e_{i})\}[g(e_{i})]$ and let $g'(n):=g(n)\prod _{i=1}^{d}[g(e_{i})]^{-n_{i}}$ . Then, $\psi (g'(e_{i}))\in [0,1)^{m}$ and $g'$ is rational by the Baker–Campbell–Hausdorff formula. Moreover, for any type-I horizontal character $\eta $ , since $\eta $ vanishes on $\Gamma $ , $\eta \circ g'$ differs from $\eta \circ g$ by a constant. This enables us to prove the general case of Theorem 5.1. So, in the rest of §9, we may make the following assumption.

Assumption 9.5. Assume $\psi (g(e_{i}))\in [0,1)^{m}$ for all $1\leq i\leq d$ .

It is helpful to introduce some further convention of notation. Throughout this section, we assume that $p\gg _{d,m}\delta ^{-O_{d,m}(1)}$ . Denote

$$ \begin{align*}M_{c}(n_{1},\ldots,n_{d})=cn_{1}^{2}+n^{2}_{2}+\cdots+n_{d'}^{2},\end{align*} $$

which is the degree two terms of M, and let $\tilde {M}\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ be a regular lifting of M and $\tilde {M}_{c}\colon \mathbb {Z}^{d}\to \mathbb {Z}/p$ be an homogeneous regular lifting of $M_{c}$ (whose existence is guaranteed by Lemma 2.5). Then, $M(n)=\iota \circ (p\tilde {M})\circ \tau (n)$ and $M_{c}(n)=\iota \circ (p\tilde {M}_{c})\circ \tau (n)$ for all ${n\in \mathbb {F}_{p}^{d}}$ . It is clear that $\iota ^{-1}(V(M))=V_{p}(\tilde {M})$ .

Let A be the $d\times d \mathbb {F}_{p}$ -valued matrix associated to M and $M_{c}$ . Then, $\tau (A)$ is the $d\times d$ integer valued matrix associated to $\tilde {M}$ and $\tilde {M}_{c}$ . With a slight abuse of notation, we identify the matrix A both as the $\mathbb {F}_{p}$ -valued matrix and as the $[p]$ -valued matrix $\tau (A)$ .

Let $(G/\Gamma )_{\mathbb {N}}$ be a nilmanifold with filtration $(G_{i})_{i\in \mathbb {N}}$ . Denote $m:=\dim (G)$ , ${m_{i}:=\dim (G_{i})}$ , $m_{ab}:=\dim (G)-\dim ([G,G])$ (the dimension of the Type-I horizontal torus of $(G/\Gamma )_{\mathbb {N}}$ ), $m_{\mathrm {lin}}:=m-m_{2}$ (the linear degree of $(G/\Gamma )_{\mathbb {N}}$ ), and $m_{\ast }:=m_{ab}-m_{\mathrm {lin}}$ (the nonlinear degree of $(G/\Gamma )_{\mathbb {N}}$ ).

9.2 The case $s=1$

We first prove Theorem 5.1 for the case $s=1$ (the case $s=0$ is trivial). We make use of the following corollary of Lemma 4.12.

Lemma 9.6. Let $d,K\in \mathbb {N}_{+}$ and p be a prime number. Let $\tilde {M}\colon \mathbb {Z}\to \mathbb {Z}/p$ be a quadratic form of p-rank r. Suppose that $r\geq 3$ . Then, for all $\xi =(\xi _{1},\ldots ,\xi _{d})\in \mathbb {Z}^{d}\backslash pK\mathbb {Z}^{d}$ , we have that

$$ \begin{align*} \begin{aligned} \mathbb{E}_{n\in V_{p}(\tilde{M})\cap [pK]^{d}}\exp\bigg(\frac{\xi}{pK}\cdot n\bigg)=O(p^{-(r-2)/{2}}). \end{aligned} \end{align*} $$

Proof. Note that

$$ \begin{align*} & \mathbb{E}_{n\in V_{p}(\tilde{M})\cap [pK]^{d}}\exp\bigg(\frac{\xi}{pK}\cdot n\bigg) =\mathbb{E}_{n\in V_{p}(\tilde{M})\cap [p]^{d}}\mathbb{E}_{m\in [K]^{d}}\exp\bigg(\frac{\xi}{pK}\cdot (n+pm)\bigg)\\ &\quad =\mathbb{E}_{n\in V_{p}(\tilde{M})\cap [p]^{d}}\mathbb{E}_{m\in [K]^{d}}\exp\bigg(\frac{\xi}{pK} \cdot n\bigg)\mathbb{E}_{m\in [K]^{d}}\exp\bigg(\frac{\xi}{K}\cdot m\bigg). \end{align*} $$

Since $\xi \in \mathbb {Z}^{d}$ , it is not hard to see that $\mathbb {E}_{m\in [K]^{d}}\exp ({\xi }/{K}\cdot m)=0$ unless $\xi =K\xi '$ for some $\xi '\in \mathbb {Z}^{d}$ , in which case,

$$ \begin{align*} \mathbb{E}_{n\in V_{p}(\tilde{M})\cap [pK]^{d}}\exp\bigg(\frac{\xi}{pK}\cdot n\bigg)=\mathbb{E}_{n\in V_{p}(\tilde{M})\cap [p]^{d}}\exp\bigg(\frac{\xi'}{p}\cdot n\bigg) \end{align*} $$

and thus, the conclusion follows from Lemma 4.12.

Since $s=1$ , we have $m_{\ast }=m$ and $G/\Gamma =\mathbb {R}^{m}/\mathbb {Z}^{m}=\mathbb {T}^{m}$ . We may write

$$ \begin{align*} g(n)=(b_{1}\cdot n,\ldots,b_{m}\cdot n)+(v_{1},\ldots,v_{m}) \end{align*} $$

for some $K\in \mathbb {N}_{+}$ , $b_{i}\in \mathbb {Z}^{d}/pK$ , and $v_{i}\in \mathbb {R}$ . Clearly, g is $pK$ -periodic. If $(g(n)\Gamma )_{n\in V_{p}(\tilde {M})\cap [pK]^{d}}$ is not $\delta $ -equidistributed, then by Lemma 3.23, there exists a vertical frequency $\xi =(\xi _{1},\ldots ,\xi _{m})\in \mathbb {Z}^{m}$ with $\vert \xi \vert \ll _{m} \delta ^{-O_{m}(1)}$ such that

(9.2) $$ \begin{align} \begin{aligned} \bigg\vert\mathbb{E}_{n\in V_{p}(\tilde{M})\cap[pK]^{d}}\exp(\xi\cdot g(n))-\int_{\mathbb{T}^{m}} \exp(\xi\cdot x)\,dm_{\mathbb{T}^{m}}(x)\bigg\vert\gg_{m} \delta^{O_{m}(1)}, \end{aligned} \end{align} $$

where $m_{\mathbb {T}^{m}}$ is the Haar measure on $\mathbb {T}^{m}$ . So, we have that $\xi \neq \mathbf {0}$ as otherwise, the left-hand side of (9.2) is zero. Thus,

$$ \begin{align*}\vert\mathbb{E}_{n\in V_{p}(\tilde{M})\cap[pK]^{d}}\exp(\xi\cdot g(n))\vert\gg_{m} \delta^{O_{m}(1)}.\end{align*} $$

Note that $\xi \cdot g(n)=(\xi B)\cdot n+\xi \cdot v$ , where B is the $\mathbb {Z}/pK$ -valued $m\times d$ matrix whose ith row is $b_{i}$ . If $\xi B\notin \mathbb {Z}^{d}$ , then since $\mathrm {rank}_{p}(M)\geq 3$ , Lemma 9.6 implies that

$$ \begin{align*}\vert\mathbb{E}_{n\in V_{p}(\tilde{M})\cap[pK]^{d}}\exp((\xi B)\cdot n)\vert=O(p^{-{(d-2)}/{2}}), \end{align*} $$

which is impossible if $p\gg _{m} \delta ^{-O_{m}(1)}$ . So, we must have that $\xi B\in \mathbb {Z}^{d}$ , which implies that $\xi \circ g \,\mod \mathbb {Z}$ is a constant. This finishes the proof.

9.3 Construction of a nilsequence in a joining system

We now assume that $s\geq 2$ (and thus, $d'\geq s+13$ ) and that Theorem 5.1 holds for smaller s (and any $m_{\ast }$ ), and for the same value of s and a smaller value of $m_{\ast }$ . The readers are advised to familiarize themselves with the machinery in [5, §8] before reading this section in detail. We follow the outline of the proof of Proposition 8.1 in §8. Following Step 1 in §8, we first run the argument of [5] to reduce the problem to a polynomial equation (9.18). By Corollary 3.19, we may assume that g is $pK$ -periodic for some $K\in \mathbb {N}_{+}$ . By Lemma 3.23, if $(g(n)\Gamma )_{n\in V_{p}(\tilde {M})\cap [pK]^{d}}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then there exist a vertical frequency $\xi \in \mathbb {Z}^{m_{s}}$ with $\Vert \xi \Vert \ll _{m} \delta ^{-O_{m}(1)}$ , and a function $F\colon G/\Gamma \to \mathbb {C}$ with $\Vert F\Vert _{\mathrm {Lip}}\leq 1$ and vertical frequency $\xi $ such that

(9.3) $$ \begin{align} \begin{aligned} \bigg\vert\mathbb{E}_{n\in V_{p}(\tilde{M})\cap[pK]^{d}}F(g(n)\Gamma)-\int_{G/\Gamma} F\,dm_{G/\Gamma}\bigg\vert\gg_{m} \delta^{O_{m}(1)}, \end{aligned} \end{align} $$

where $m_{G/\Gamma }$ is the Haar measure of $G/\Gamma $ . If $\xi =\mathbf {0}$ , then we may invoke the discussion in [5, after (7.1)] to reduce the problem to the $s-1$ degree case and then use the induction hypothesis to finish the proof. So, from now on, we assume that $\xi \neq \mathbf {0}$ .

Since F is of vertical frequency $\xi $ , (9.3) implies that

(9.4) $$ \begin{align} \begin{aligned} \vert\mathbb{E}_{n\in V_{p}(\tilde{M})\cap[pK]^{d}}F(g(n)\Gamma)\vert\gg_{m} \delta^{O_{m}(1)}. \end{aligned} \end{align} $$

By taking squares on both sides of (9.4), we have that

$$ \begin{align*} & \delta^{O_{m}(1)} \ll_{m} \mathbb{E}_{n,m\in V_{p}(\tilde{M})\cap[pK]^{d}}F(g(m)\Gamma)\overline{F}(g(n)\Gamma)\\ & \quad=\mathbb{E}_{(n,h)\in \Box_{p,1}(V_{p}(\tilde{M}))\cap[pK]^{2d}}F(g(n+h)\Gamma)\overline{F}(g(n)\Gamma), \end{align*} $$

where we used Lemma 7.2 and the fact that $\Box _{p,1}(V_{p}(\tilde {M}))$ is a p-periodic set. By Lemma 4.12, $\vert \Box _{p,1}(V_{p}(\tilde {M}))\cap [p]^{d}\vert =\vert V_{p}(\tilde {M})\cap [p]^{d}\vert ^{2}=p^{2d-2}(1+O(p^{-1/2}))$ . So, this implies that

(9.5) $$ \begin{align} \begin{aligned} \frac{1}{\vert V_{p}(\tilde{M})\cap[pK]^{d}\vert^{2}}\sum_{h\in V_{p}(\tilde{M})\cap[pK]^{d}}\sum_{n\in V_{p}(\tilde{M})^{h}\cap[pK]^{d}}F(g(n+h)\Gamma)\overline{F}(g(n)\Gamma) \gg_{m} \delta^{O_{m}(1)}. \end{aligned} \end{align} $$

Since $d\geq 5$ , it follows from Proposition 4.19 that

$$ \begin{align*}\mathbb{E}_{h\in [pK]^{d}}\vert\mathbb{E}_{n\in V_{p}(\tilde{M})^{h}\cap [pK]^{d}}F(g(n+h)\Gamma)\overline{F}(g(n)\Gamma)\vert\gg_{m} \delta^{O_{m}(1)}.\end{align*} $$

By the pigeonhole principle, there exists a subset $J_{1}$ of $[pK]^{d}$ of cardinality $\gg _{m}\delta ^{O_{m}(1)}(pK)^{d}$ such that

(9.6) $$ \begin{align} \begin{aligned} \vert\mathbb{E}_{n\in V_{p}(\tilde{M})^{h}\cap [pK]^{d}}F(g(n+h)\Gamma)\overline{F(g(n)\Gamma)}\vert\gg_{m} \delta^{O_{m}(1)} \end{aligned} \end{align} $$

for all $h\in J_{1}$ . Recall that A is the $d\times d \mathbb {Z}$ -valued matrix associated to M. Since $d'\geq 3$ , by Lemmas 4.12 and 7.2, passing to a subset if necessary, we may assume that

(9.7) $$ \begin{align} (hA)\cdot h, h_{1},\ldots,h_{d}\notin p\mathbb{Z} \quad\text{for all } h=(h_{1},\ldots,h_{d})\in J_{1}. \end{align} $$

It is helpful to view $V_{p}(\tilde {M})^{h}$ as the preimage of $\iota $ of the intersection of the hyperspheres $V(M)$ and $V(M(\cdot +h))$ . We will use the inheriting principle to apply the induction hypothesis on these sub-hyperspheres. Recall that $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ is the quadratic form induced by $\tilde {M}$ and $V_{p}(\tilde {M})^{h}=\iota ^{-1}(V(M)^{\iota (h)})$ . For $h\in J_{1}$ , note that $V(M)^{\iota (h)}=V(M)\cap U_{h}$ , where $U_{h}:=\{n\in \mathbb {F}_{p}^{d}\colon M(n+\iota (h))=M(n)\}$ . Then, we may write $U_{h}=V_{h}+u_{h}$ for some $u_{h}\in \mathbb {F}_{p}^{d}$ , where $V_{h}:=\{n\in \mathbb {F}_{p}^{d}\colon (nA)\cdot \iota (h)=0\}$ . It follows from (9.6) that $V_{h}$ is a subspace of $\mathbb {F}_{p}^{d}$ of co-dimension 1. Let $L_{h}\colon \mathbb {F}_{p}^{d-1}\to V_{h}$ be any bijective linear transformation, and let $M_{h}\colon \mathbb {F}_{p}^{d-1}\to \mathbb {F}_{p}$ be the quadratic form given by $M_{h}(z):=M(L_{h}(z)+u_{h})$ and let $\tilde {M}_{h}\colon \mathbb {Z}^{d-1}\to \mathbb {Z}/p$ be the quadratic form induced by $M_{h}$ . Since $(hA)\cdot h\notin p\mathbb {Z}$ , we have that

(9.8) $$ \begin{align} &\mathrm{rank}_{p}(\tilde{M}_{h})=\mathrm{rank}(M_{h})=\mathrm{rank}(M\vert_{\text{span}_{\mathbb{F}_{p}}\{\iota(h)\}^{ \perp{M}}})\nonumber \\ & \quad=\mathrm{rank}(M)-1\geq (s-1)+13 \quad\text{for all } h\in J_{1}. \end{align} $$

Let $\tilde {L}_{h}/p$ be the regular lifting of $L_{h}$ . Then,

(9.9) $$ \begin{align} (hA)\cdot \tilde{L}_{h}(z)\in p\mathbb{Z} \quad\text{for all } z\in \mathbb{Z}^{d-1}. \end{align} $$

Since $V(M)^{\iota (h)}=V(M)\cap (V_{h}+u_{h})$ , it is not hard to see that $L_{h}^{-1}(V(M)^{\iota (h)}-u_{h})=V(M_{h})$ and $V_{p}(\tilde {M}_{h})=\iota ^{-1}(V(M_{h}))$ . Since g is $pK$ -periodic, by (9.6) and Lemma 9.1 (setting $B=V(M)^{\iota (h)}$ and $K'=K$ ), the average

(9.10) $$ \begin{align} \vert\mathbb{E}_{(z,m)\in (V_{p}(\tilde{M}_{h})\cap [pK]^{d-1})\times [pK]^{d}}F(g(pm +\tilde{L}_{h}(z)+\tau(u_{h})+h)\Gamma)\overline{F(g(pm+\tilde{L}_{h}(z)+\tau(u_{h}))\Gamma)}\vert\\[-24pt]\nonumber \end{align} $$

is at least $\gg _{m} \delta ^{O_{m}(1)}$ for all $h\in J_{1}$ .

We decompose g as $g=g_{\text {nlin}}g_{\mathrm {lin}}$ , where

$$ \begin{align*}g_{\mathrm{lin}}(n_{1},\ldots,n_{d}):=g(e_{1})^{n_{1}}\cdots g(e_{d})^{n_{d}}\end{align*} $$

is the linear component of g and

$$ \begin{align*}g_{\text{nlin}}(n):=g(n)g_{\mathrm{lin}}(n)^{-1}\end{align*} $$

is the nonlinear component of g, where $e_{i}$ is the ith standard unit vector in $\mathbb {Z}^{d}$ . Since $g\in \text {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ , we have that $g_{\mathrm { lin}},g_{\text {nlin}}\in \text {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ by [8, Corollary B.4].

Note that $g_{\text {nlin}}(\mathbf {0})=g_{\text {nlin}}(e_{1})=\cdots =g_{\text {nlin}}(e_{d})=\mathrm {id}_{G}$ , and $g_{\text {nlin}}$ takes values in $G_{2}$ by the Baker–Campbell–Hausdorff formula. For all $h\in \mathbb {Z}^{d}$ , let $g_{h}\colon \mathbb {Z}^{d}\to G^{2}$ be the sequence

(9.11) $$ \begin{align} \begin{aligned} g_{h}(n):= (\{{g}_{\mathrm{lin}}(h)\}^{-1}{g}(n+h)[{g}_{\mathrm{lin}}(h)]^{-1},{g}(n)), \end{aligned} \end{align} $$

and $F_{h}\colon G^{2}/\Gamma ^{2}\to \mathbb {C}$ be the function

$$ \begin{align*} F_{h}(x,y):=F(\{{g}_{\mathrm{lin}}(h)\}x)\overline{F}(y). \end{align*} $$

Then, (9.10) implies that

(9.12) $$ \begin{align} \begin{aligned} \vert\mathbb{E}_{(z,m)\in (V_{p}(\tilde{M}_{h})\cap [pK]^{d-1})\times [pK]^{d}}F_{h}({g}_{h}(pm+\tilde{L}_{h}(z)+\tau(u_{h}))\Gamma^{2})\vert\gg_{m} \delta^{O_{m}(1)} \end{aligned} \end{align} $$

for all $h\in J_{1}$ .

For groups G and H with $H<G$ , denote

$$ \begin{align*}G\times_{H}G:=\{(g,h)\in G\times G\colon g^{-1}h\in H\}.\end{align*} $$

Note that $G\times _{H}G$ is a group as long as $[G,H]\subseteq H$ . It is not hard to check that ${g}_{h}$ takes values in $G^{\square }:=G\times _{G_{2}}G$ for all $h\in \mathbb {Z}^{d}$ (see the argument in [5, after (7.6)]). So (9.12) implies that

(9.13) $$ \begin{align} \begin{aligned} \vert\mathbb{E}_{(z,m)\in (V_{p}(\tilde{M}_{h})\cap [pK]^{d-1})\times [pK]^{d}}F^{\square}_{h}(g^{\square}_{h}(pm+\tilde{L}_{h}(z)+\tau(u_{h}))\Gamma^{\square})\vert\gg_{m} \delta^{O_{m}(1)} \end{aligned} \end{align} $$

for all $h\in J_{1}$ , where $F^{\square }_{h}$ , $g^{\square }_{h}$ , and $\Gamma ^{\square }$ are the restrictions of $F_{h}, {g}_{h}$ , and $\Gamma ^{2}$ to $G^{\square }$ , respectively. By repeating the argument in [5, after (7.7)], $F^{\square }_{h}$ is invariant under ${G^{\triangle }_{s}:=\{(g_{s},g_{s})\colon g_{s}\in G_{s}\}}$ . Thus, $F^{\square }_{h}$ induces a function $\overline {F_{h}^{\square }}$ on $\overline {G^{\square }}:=G^{\square }/G^{\triangle }_{s}$ . By (9.13), we have that

(9.14) $$ \begin{align} \begin{aligned} \vert\mathbb{E}_{(z,m)\in (V_{p}(\tilde{M}_{h})\cap [pK]^{d-1})\times [pK]^{d}}\overline{F^{\square}_{h}}(\overline{g^{\square}_{h}}(pm+\tilde{L}_{h}(z)+\tau(u_{h}))\overline{\Gamma^{\square}})\vert\gg_{m} \delta^{O_{m}(1)}, \end{aligned} \end{align} $$

where $\overline {\Gamma ^{\square }}:=\Gamma ^{\square }/(\Gamma ^{\square }\cap G_{k}^{\triangle })$ and $\overline {g^{\square }_{h}}$ is the projection of $g^{\square }_{h}$ to $\overline {G^{\square }}$ .

By [6, Proposition 4.2] and [5, Lemma 7.4], we have that:

• • the groups $G^{\square }$ and $\overline {G^{\square }}$ are connected, simply connected nilpotent Lie groups of degree $s-1$ with respect to the $\mathbb {N}$ -filtrations given by $(G^{\square })_{i}:=G_{i}\times _{G_{i+1}}G_{i}$ and $(\overline {G^{\square }})_{i}:=(G_{i}\times _{G_{i+1}}G_{i})/G^{\triangle }_{k}$ , respectively;

• • there exist $O_{m,s}(\delta ^{-O_{m,s}(1)})$ -rational Mal’cev basis $\mathcal {X}^{\square }$ for $G^{\square }/\Gamma ^{\square }$ , and $\overline {\mathcal {X}^{\square }}$ for $\overline {G^{\square }}/\overline {\Gamma ^{\square }}$ , adapted to the filtrations $(G^{\square })_{\mathbb {N}}$ and $(\overline {G^{\square }})_{\mathbb {N}}$ , respectively;

• • the Mal’cev coordinate map $\psi _{\mathcal {X}^{\square }}(x,x')$ of $\mathcal {X}^{\square }$ is a polynomial of degree $O_{m,s}(1)$ with rational coefficients of complexity $O_{m,s}(\delta ^{-O_{m,s}(1)})$ in the coordinates $\psi (x)$ and $\psi (x')$ ;

• • under the metrics induced by $\mathcal {X}^{\square }$ and $\overline {\mathcal {X}^{\square }}$ , we have that $\Vert F^{\square }_{h}\Vert _{\mathrm {Lip}}, \Vert \overline {F^{\square }_{h}}\Vert _{\mathrm {Lip}}\ll _{m,s}(\delta ^{-O_{m,s}(1)})$ ;

• • $g^{\square }_{h}$ belongs to $\text {poly}(\mathbb {Z}^{d}\to (G^{\square })_{\mathbb {N}})$ and $\overline {g^{\square }_{h}}$ belongs to $\text {poly}(\mathbb {Z}^{d}\to (\overline {G^{\square }})_{\mathbb {N}})$ .

Since g is rational and $pK$ -periodic, it is not hard to see that:

• • $g^{\square }_{h}$ and $\overline {g^{\square }_{h}}$ are rational and $pK$ -periodic.

Let $\tilde {M}^{\prime }_{h}\colon \mathbb {Z}^{2d-1}\to \mathbb {Z}/p$ be the quadratic form given by $\tilde {M}^{\prime }_{h}(z,m):=\tilde {M}_{h}(z)$ . It is clear from (9.8) that $\mathrm {rank}_{p}(\tilde {M}^{\prime }_{h})=\mathrm {rank}_{p}(\tilde {M}_{h})\geq (s-1)+13$ for all $h\in J_{1}$ . So, by (9.14) and the induction hypothesis, for all $h\in J_{1}$ , there exist a type-I horizontal character $\overline {\eta }_{h}\colon \overline {G^{\square }}\to \mathbb {R}$ with $0<\Vert \overline {\eta }_{h}\Vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ and a constant $a_{h}\in \mathbb {R}$ such that for all $m\in \mathbb {Z}^{d}$ and $z\in V_{p}(\tilde {M}_{h})$ ,

$$ \begin{align*}\overline{\eta}_{h}\circ \overline{g^{\square}_{h}}(pm+\tilde{L}_{h}(z)+\tau(u_{h}))\equiv a_{h} \,\mod \mathbb{Z}.\end{align*} $$

By the pigeonhole principle, there exists a subset $J_{2}$ of $J_{1}$ with $\vert J_{2}\vert \gg _{d,m}\delta ^{O_{d,m}(1)}(pK)^{d}$ such that $\overline {\eta }_{h}$ is equal to a same $\overline {\eta }$ for all $h\in J_{2}$ . Writing $\eta _{0}\colon G^{\square }\to \mathbb {R}$ to be the type-I horizontal character $\eta _{0}(x)=\overline {\eta }(\overline {x})$ , where $\overline {x}$ is the projection of x, we have that $\eta _{0}$ is a type-I horizontal character with $0<\Vert \eta _{0}\Vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ and that

(9.15) $$ \begin{align} \begin{aligned} \eta_{0}\circ g^{\square}_{h}(pm+\tilde{L}_{h}(z)+\tau(u_{h}))\equiv a_{h} \,\mod \mathbb{Z} \quad\text{for all } h\in J_{2}, m\in\mathbb{Z}^{d}, z\in V_{p}(\tilde{M}_{h}). \end{aligned} \end{align} $$

We apply Lemma 9.1 to simplify this condition. Denote $\Phi _{L_{h},u_{h}}(z,m):=pm+\tilde {L}_{h}(z)+\tau (u_{h})$ . Applying Lemma 9.1 with $d'=d-1, K'=1, V=V_{h}, c=u_{h}$ , and ${B{\kern-1pt}={\kern-1pt}V(M)^{\iota (h)}}$ , we have that $\Phi _{L_{h},u_{h}} \,\mod p\mathbb {Z}^{d}$ is a bijection between $\iota ^{-1}((L_{h}^{-1}(V(M)^{\iota (h)}-u_{h}))\cap [p]^{d-1})\times [K]^{d}$ and $\iota ^{-1}(V(M)^{\iota (h)})\cap [pK]^{d}$ , which is between $V_{p}(\tilde {M}_{h})\times [K]^{d}$ and $V_{p}(\tilde {M})^{h}\cap [pK]^{d}$ (recall the discussion between (9.9) and (9.10)). Since $g^{\square }_{h}$ is $pK$ -periodic, by (9.15),

(9.16) $$ \begin{align} \begin{aligned} \eta_{0}\circ g^{\square}_{h}(n)\equiv a_{h} \,\mod \mathbb{Z} \quad\text{for all } h\in J_{2}, n\in V_{p}(\tilde{M})^{h}. \end{aligned} \end{align} $$

Finally, since g is $pK$ -periodic, $(g^{\square }_{h+pKm})^{-1}g^{\square }_{h}$ take values in $\Gamma ^{2}$ for all $h\in J_{2}$ and ${m\in \mathbb {Z}^{d}}$ . So $ \eta _{0}\circ g^{\square }_{h}= \eta _{0}\circ g^{\square }_{h+pKm} \,\mod \mathbb {Z}$ . Therefore, we may upgrade (9.16) to conclude that

(9.17) $$ \begin{align} \begin{aligned} \eta_{0}\circ g^{\square}_{h}(n)\equiv a_{h} \,\mod \mathbb{Z} \quad\text{for all } h\in J_{2}+pK\mathbb{Z}^{d}, n\in V_{p}(\tilde{M})^{h} \end{aligned} \end{align} $$

for some constant $a_{h}$ .

Denote $\eta _{1}\colon G\to \mathbb {R}, \eta _{1}(g):=\eta _{0}(g,g)$ and $\eta _{2}\colon G_{2}\to \mathbb {R}, \eta _{2}(g)=\eta _{0}(g,\mathrm {id}_{G})$ , we have that $\eta _{0}(g',g)=\eta _{1}(g)+\eta _{2}(g'g^{-1})$ for all $(g',g)\in G^{\square }$ . Similar to [5, Lemma 7.5], $\eta _{1}$ is a type-I horizontal character on G, and $\eta _{2}$ is a type-I horizontal character on $G_{2}$ which annihilates $[G,G_{2}]$ . Moreover, $\Vert \eta _{1}\Vert ,\Vert \eta _{2}\Vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ .

Similar to the approach [6, between (4.8) and (4.10)] (along with some notation changes), one can compute that (we leave the details to the interested readers)

(9.18) $$ \begin{align} \begin{aligned} Q(n+h)-Q(n)+P(n)+\sigma(h)\cdot n-a_{h}\equiv 0 \,\mod \mathbb{Z} \end{aligned} \end{align} $$

for all $h\in J_{2}+pK\mathbb {Z}^{d}$ and $n\in V_{p}(\tilde {M})^{h}$ , where

$$ \begin{align*} \kern-28pt P(n):=\eta_{1}({g}(n)), \, Q(n):=\eta_{2}({g}_{\text{nlin}}(n)), \, \sigma(h):=\omega_{h}+h\Lambda, \end{align*} $$

$$ \begin{align*} \omega_{h}:=(\eta_{2}([{g}(e_{1}),\{{g}_{\mathrm{lin}}(h)\}]),\ldots,\eta_{2}([{g}(e_{d}),\{{g}_{\mathrm{ lin}}(h)\}]))\in\mathbb{R}^{d}, \end{align*} $$

and $\Lambda =(\unicode{x3bb} _{i,j})_{1\leq i,j\leq d}$ is the $d\times d$ matrix in $\mathbb {R}$ with $\unicode{x3bb} _{i,j}=\eta _{2}([{g}(e_{i}),{g}(e_{j})])$ if $i<j$ and $\unicode{x3bb} _{i,j}=0$ otherwise. Since g is rational, it is clear that all the entries of $\Lambda $ are in $\mathbb {Q}$ .

9.4 Solving polynomial equations

Following Step 2 in §8, we now solve (9.18). Note that (9.18) is more complicated than the equation in the Heisenberg case (8.1) due to the appearance of the nonlinear terms, and than [6, (4.10)] since (9.18) only holds on some hyperspheres. As a result, this step is the most challenging part in adapting the Green–Tao approach, which is also the reason why the efforts in §§6 and 7 are needed.

Since g is rational and is of step at most s, we have that P and Q are of degree at most s and take values in $\mathbb {Q}$ . Replacing n in (9.18) by $n, n+h_{2}, n+h_{3},n+h_{2}+h_{3}$ , respectively, replacing h in (9.18) by $h_{1}$ , and taking the second-order differences, we have that

(9.19) $$ \begin{align} \begin{aligned} \Delta_{h_{3}}\Delta_{h_{2}}\Delta_{h_{1}}Q(n)+\Delta_{h_{2}}\Delta_{h_{1}}P(n)\in\mathbb{Z} \end{aligned} \end{align} $$

for all $h_{3}\in J_{2}+pK\mathbb {Z}^{d}$ and $(n,h_{1},h_{2})\in \Box _{p,2}(V_{p}(\tilde {M})^{h_{3}})$ . By Proposition 4.19 (and a change of variables), it is not hard to compute that the number of $(n,h_{1},h_{2},h_{3})\in \Box _{p,3}(V_{p}(\tilde {M}))\cap ([pK]^{d})^{4}$ with $h_{3}\in J_{2}$ is $\gg _{d,m}\delta ^{-O_{d,m}(1)}\vert \Box _{p,3}(V_{p}(\tilde {M}))\cap ([pK]^{d})^{4}\vert $ . Since $d'\geq s+13\geq 3^{2}+3+3$ , it follows from (9.19) and Proposition 7.6 (if K is not divisible by p, then we may replace the set $J_{2}$ by $(J_{2}+pK\mathbb {Z}^{d})\cap [p^{2}K]^{d}$ to apply Proposition 7.6) that

(9.20) $$ \begin{align} Q=\frac{1}{q}Q_{1}+Q_{0} \quad\text{and} \quad P=\frac{1}{q}P_{1}+P_{0} \end{align} $$

for some $q\in \mathbb {N}_{+}$ with $q\ll _{d}\delta ^{-O_{d}(1)}$ , some polynomials $Q_{1},P_{1}\in \text {poly}(V_{p}(\tilde {M})\to \mathbb {R}\vert \mathbb {Z})$ with $\deg (Q_{1})\leq \deg (Q), \deg (P_{1})\leq \deg (P)$ , and some $Q_{0},P_{0}\colon \mathbb {Z}^{d}\to \mathbb {R}$ such that

(9.21) $$ \begin{align} Q_{0}(n)=(n\Omega)\cdot n+v\cdot n+v_{0} \quad\text{and}\quad P_{0}(n)=u\cdot n+u_{0} \end{align} $$

for some $v,u\in \mathbb {R}^{d}$ , $v_{0},u_{0}\in \mathbb {R}$ , and symmetric $d\times d \mathbb {Q}$ -valued matrix $\Omega $ . (If P and Q were $\mathbb {Z}/p$ -valued polynomials, then we could apply Corollary 7.4 instead of Proposition 7.6 and simplify the proof. However, this is not the case in general. This is the reason why we need to improve Corollary 7.4 to the more general version Proposition 7.6.)

9.5 Analyzing the low degree terms

Following Step 3 in §8, our next goal is to derive better descriptions for the lower degree polynomials $Q_{0}$ and $P_{0}$ by substituting (9.20) and (9.21) back to (9.18). For all $h\in J_{2}+pK\mathbb {Z}^{d}$ and $n\in V_{p}(\tilde {M})^{h}$ , it follows from (9.20) that

$$ \begin{align*}Q(n)-Q_{0}(n)\equiv Q(n+h)-Q_{0}(n+h)\equiv P(n)- P_{0}(n)\equiv 0 \ \,\mod \frac{1}{q}\mathbb{Z}. \end{align*} $$

So (9.18) implies that

(9.22) $$ \begin{align} \begin{aligned} t_{h}\cdot n\equiv b_{h} \,\mod \mathbb{Z} \quad\text{for all } h\in J_{2}+pK\mathbb{Z}^{d} \quad\text{and}\quad n\in V_{p}(\tilde{M})^{h} \end{aligned} \end{align} $$

for some $b_{h}\in \mathbb {R}$ , where

(9.23) $$ \begin{align} \begin{aligned} t_{h}:=q(2h\Omega+u+\sigma(h)). \end{aligned} \end{align} $$

Note that the conditions $n\in V_{p}(\tilde {M})^{h}$ remain unchanged if we replace n by $n+pn'$ for any $n'\in \mathbb {Z}^{d}$ . So, the condition $t_{h}\cdot n\equiv b_{h} \,\mod \mathbb {Z}$ is also unaffected if we change n to $n+pn'$ . Therefore, we must have that $t_{h}\in \mathbb {Z}^{d}/p, b_{h}\in \mathbb {Z}/p$ for all $h\in J_{2}+pK\mathbb {Z}^{d}$ .

This is another place where our approach deviates from that of [5] (in which case, one can easily conclude that $t_{h}\in \mathbb {Z}^{d}$ ). Recall that the $\iota $ -image of the set $V_{p}(\tilde {M})^{h}$ is the intersection of the hypersphere $V(M)$ and an affine subspace of co-dimension at most 1 which is orthogonal to $hA$ . Therefore, we may expect to deduce from (9.22) that the $\iota $ image of $t_{h}$ is parallel to $hA.$ To be more precise, we now show that

(9.24) $$ \begin{align} \begin{aligned} t_{h}-c_{h}(hA)\in\mathbb{Z}^{d} \quad\text{for some } c_{h}\in\mathbb{Z}/p \ \text{for all } h\in J_{2}+pK\mathbb{Z}^{d}. \end{aligned} \end{align} $$

Note that (9.22) implies that the $\iota (t_{h})$ is orthogonal to the $\iota (V_{p}(\tilde {M})^{h}-V_{p}(\tilde {M})^{h})$ . So, (9.24) follows if one can show that the span of $\iota (V_{p}(\tilde {M})^{h}-V_{p}(\tilde {M})^{h})$ is the orthogonal complement of $\iota (hA)$ . To do so, we fix $h\in J_{2}+pK\mathbb {Z}^{d}$ and identify $V_{p}(\tilde {M})^{h}$ by $V_{p}(\tilde {M}_{h})$ via the linear transformation $\tilde {L}_{h}$ . The desired spanning property can be restated as follows.

Claim. There exist $w_{0},\ldots ,w_{d-1}\in V_{p}(\tilde {M}_{h})$ such that $w_{1}-w_{0},\ldots ,w_{d-1}-w_{0}$ are p-linearly independent.

Proof of Claim

Recall that $M_{h}\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ is the quadratic form induced by $\tilde {M}_{h}$ and by (9.8) $\mathrm {rank}(M_{h})\geq 3$ . Translating everything in the $\mathbb {F}_{p}^{d}$ -setting, it suffices to show that there exist $v_{0},\ldots ,v_{d-1}\in V(M_{h})$ such that $v_{1}-v_{0},\ldots ,v_{d-1}-v_{0}$ are linearly independent. Fix any $v_{0}\in V(M_{h})$ (whose existence is given by Lemma 4.12). Suppose that for some $0\leq k\leq d-2$ , we have chosen $v_{1},\ldots ,v_{k}\in V(M_{h})$ such that $v_{1}-v_{0},\ldots ,v_{k}-v_{0}$ are linearly independent. If $k\leq d-3$ , then the number of $v\in \mathbb {F}_{p}^{d}$ with $v_{1}-v_{0},\ldots ,v_{k}-v_{0}, v-v_{0}$ being linearly dependent is at most $p^{k}\leq p^{d-3}$ , while ${\vert V(M_{h})\vert =p^{d-2}(1+O(p^{-1/2}))}$ . If $p\gg _{d} 1$ , then there exists $v_{k+1}\in V(M_{h})$ such that $v_{1}-v_{0},\ldots ,v_{k+1}-v_{0}$ are linearly independent. If $k=d-2$ , then let $Q(v)$ denote the determinant of the $(d-1)\times (d-1)$ matrix with $v_{1}-v_{0},\ldots ,v_{d-2}-v_{0}, v-v_{0}$ being the row vectors. Then, Q is a non-constant degree 1 polynomial in v. So, Q cannot be written in the form $Q=Q'M_{h}$ for some $Q'\in \text {poly}(\mathbb {F}_{p}^{d}\to \mathbb {F}_{p})$ with $\deg (Q')\leq \deg (Q)$ . By Proposition 6.2, there exists $v_{d-1}\in V(M_{h})\backslash V(Q)$ . So, $v_{1}-v_{0},\ldots ,v_{d-1}-v_{0}$ are linearly dependent. This completes the proof of the claim.

We now continue the proof of (9.24). Let $w_{0},\ldots ,w_{d-1}\in V_{p}(\tilde {M}_{h})$ be given by the claim. Then, for all $1\leq i\leq d-1$ , it follows from (9.22) that

$$ \begin{align*}t_{h}\cdot (\tilde{L}_{h}(w_{i}-w_{0}))=t_{h}\cdot ((\tilde{L}_{h}(w_{i})+u_{h})-(\tilde{L}_{h}(w_{0})+u_{h}))\equiv b_{h}-b_{h}=0 \,\mod\mathbb{Z}.\end{align*} $$

Since $w_{1}-w_{0},\ldots ,w_{d-1}-w_{0}$ are p-linearly independent, by linearity, there exists $q_{h}\in \mathbb {N}, p\nmid q_{h}$ such that $q_{h}t_{h}\cdot \tilde {L}_{h}(e_{i})\in \mathbb {Z}$ for all $1\leq i\leq d-1$ . Since $t_{h}\in \mathbb {Z}^{d}/p$ , we have

(9.25) $$ \begin{align} t_{h}\cdot \tilde{L}_{h}(e_{i})\in \frac{1}{q_{h}}\mathbb{Z}\cap \frac{1}{p}\mathbb{Z}=\mathbb{Z}. \end{align} $$

Recall that $h_{1}\notin p\mathbb {Z}$ since $h\in J_{2}+pK\mathbb {Z}^{d}$ . Since $t_{h}\in \mathbb {Z}^{d}/p$ , we may write ${t_{h}=c_{h}(hA)+(0,t^{\prime }_{h})}$ for some $c_{h}\in \mathbb {Z}/p$ and $t^{\prime }_{h}\in \mathbb {Z}^{d-1}/p$ . Since $(hA)\cdot \tilde {L}_{h}(e_{i})\in p\mathbb {Z}$ for all $1\leq i\leq d-1$ by (9.9), it follows from (9.25) that $t^{\prime }_{h}B\in \mathbb {Z}^{d-1}$ , where B is the $(d-1)\times (d-1)$ matrix whose column vectors are transposes of $\tilde {L}_{h}(e_{1}),\ldots ,\tilde {L}_{h}(e_{d-1})$ with the first coefficient removed.

If $\tilde {L}_{h}(e_{1}),\ldots , \tilde {L}_{h}(e_{d-1}),(1,0,\ldots ,0)$ are p-linearly dependent, then the fact that $(hA)\cdot \tilde {L}_{h}(e_{i})\in p\mathbb {Z}, 1\leq i\leq d-1$ implies that $(hA)\cdot \tilde {L}_{h}(1,0,\ldots ,0)=\tau (c)h_{1}\in p\mathbb {Z}$ , which is a contradiction. Therefore, $\tilde {L}_{h}(e_{1}),\ldots ,\tilde {L}_{h}(e_{d-1}),(1,0,\ldots ,0)$ are p-linearly independent and thus, $\det (B)\notin p\mathbb {Z}$ . So, $t^{\prime }_{h}\in ({1}/{q^{\prime }_{h}})\mathbb {Z}^{d-1}$ for some $q^{\prime }_{h}\in \mathbb {N}, p\nmid q^{\prime }_{h}$ . Since $t^{\prime }_{h}\in ({1}/{p})\mathbb {Z}^{d-1}$ , we have that $t^{\prime }_{h}\in \mathbb {Z}^{d-1}$ . This completes the proof of (9.24).

Next, we need to take a closer look at (9.24) by unpacking the definition of $\sigma (h)$ . Since the map $(b,c)\to \eta _{2}([b,c])$ is bilinear, the map $c\to \eta _{2}([g(e_{i}),c])$ is a homomorphism. So, there exists $\xi =(\xi _{1},\ldots ,\xi _{d})\in (\mathbb {R}^{m})^{d}$ such that

$$ \begin{align*}\eta_{2}([g(e_{i}),x])=\xi_{i}\cdot\psi(x) \,\mod \mathbb{Z}\end{align*} $$

for all $1\leq i\leq d$ and $x\in G$ . Similar to [5, discussion after (7.15)], all but the first $m_{\mathrm {lin}}$ coefficients of $\xi _{i}$ are non-zero, and $\vert \xi _{i}\vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ . Denote $\gamma _{i}:=\psi (g(e_{i}))$ and ${\gamma :=(\gamma _{1},\ldots ,\gamma _{d})\in (\mathbb {R}^{m})^{d}}$ . Since g is rational, it is clear that $\xi ,\gamma \in (\mathbb {Q}^{m})^{d}$ .

Denote $\gamma (h):=\sum _{j=1}^{d}\gamma _{j}h_{j}\in \mathbb {Q}^{m}$ . Let $\{\gamma (h)\}\in [0,1)^{m}$ be the coordinate-wise fractional part of $\gamma (h)$ . Then,

$$ \begin{align*}\sigma(h)=h\Lambda+\xi\ast \{\gamma(h)\},\end{align*} $$

where $\ast $ is the coordinate-wise product of vectors in $\mathbb {R}^{m}$ . So for all $h\in J_{2}+pK\mathbb {Z}^{d}$ , it follows from (9.23) and (9.24) that

(9.26) $$ \begin{align} q(hB+u+\xi\ast \{\gamma(h)\})-c_{h}(hA)\in\mathbb{Z}^{d} \quad\text{for some } c_{h}\in\mathbb{Z}/p, \end{align} $$

where $B:=2\Omega +\Lambda $ .

We need the following lemma to study (9.26).

Lemma 9.7. Let $d,m,N\in \mathbb {N}_{+}$ , p be a prime, $\delta>0, \beta ,\alpha _{1},\ldots ,\alpha _{d}\in \mathbb {R}$ , and $\xi ,\gamma _{0},\gamma _{1},\ldots ,\gamma _{d}\in \mathbb {Q}^{m}$ . Let V be a subset of $\{-N,\ldots ,N\}^{d}$ of cardinality at least $\delta (2N+1)^{d}$ such that

$$ \begin{align*} \beta+\sum_{i=1}^{d}\alpha_{i}h_{i}+\xi\cdot\bigg\{\gamma_{0}+\sum_{i=1}^{d}\gamma_{i}h_{i}\bigg\}\in \mathbb{Z} \end{align*} $$

for all $h=(h_{1},\ldots ,h_{d})\in V$ . If $N\gg _{\delta ,d,m,p}1$ (we caution the readers that N is dependent on p. However, this will not cause any trouble for the application of this lemma) then at least one of the following holds:

1. (i) there exists $r\in \mathbb {Z}$ with $0<r\ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $r\xi \in \mathbb {Z}^{m}$ ;

2. (ii) there exists $k{\kern-1pt}\in{\kern-1pt} \mathbb {Z}^{m}$ with $0<\vert k\vert {\kern-1pt}\ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $k\cdot \gamma _{i}\in \mathbb {Z}$ for all $1{\kern-1pt}\leq{\kern-1pt} i{\kern-1pt}\leq{\kern-1pt} d$ .

Proof. Lemma 9.7 generalizes [6, Lemma 4.3] in two aspects. The first is that Lemma 9.7 allows the appearance of the term $\gamma _{0}$ . The second is that we do not impose any bound for the complexity of $\xi $ . The strategy of the proof is to reduce the problem to the case when $\gamma _{0}$ is zero and $\xi $ is bounded in the unit box, and then apply [6, Lemma 4.3].

Since

(9.27) $$ \begin{align} \bigg\{\gamma_{0}\bigg\}+\bigg\{\sum_{i=1}^{d}\gamma_{i}h_{i}\bigg\}-\bigg\{\gamma_{0}+\sum_{i=1}^{d}\gamma_{i}h_{i}\bigg\} \end{align} $$

takes at most $2^{m}$ different values, passing to a subset of V if necessary, we may assume without loss of generality that (9.27) take the same value for all $h\in V$ . Absorbing constant terms into $\beta $ if necessary, we may assume without loss of generality that $\gamma _{0}=\mathbf {0}$ .

Since

$$ \begin{align*}a\{b\}=\{a\}\{b\}+\lfloor a\rfloor b-\lfloor a\rfloor\lfloor b\rfloor\end{align*} $$

for all $a,b\in \mathbb {R}$ , we have that

$$ \begin{align*} \beta+\sum_{i=1}^{d}\alpha_{i}h_{i}+\xi\cdot\bigg\{\sum_{i=1}^{d}\gamma_{i}h_{i}\bigg\}\equiv \beta+\sum_{i=1}^{d}(\alpha_{i}+\lfloor\xi\rfloor\cdot \gamma_{i})h_{i}+\{\xi\}\cdot\bigg\{\sum_{i=1}^{d}\gamma_{i}h_{i}\bigg\}\,\mod \mathbb{Z}. \end{align*} $$

So, it suffices to prove Lemma 9.7 for the case $\xi \in [0,1)^{m}$ . By [6, Lemma 4.3], either there exists $r{\kern-1pt}\in{\kern-1pt} \mathbb {Z}, 0{\kern-1pt}<{\kern-1pt}r\ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $\Vert r\xi _{i} \Vert _{\mathbb {R}/\mathbb {Z}}\ll _{d,m} \delta ^{-O_{d,m}(1)}/N$ for all $1{\kern-1pt}\leq{\kern-1pt} i{\kern-1pt}\leq{\kern-1pt} d$ (where $\xi =(\xi _{1},\ldots ,\xi _{m})$ ), or there exists $k\in \mathbb {Z}^{m}$ with $0<\vert k\vert \ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $\Vert k\cdot \gamma _{i}\Vert _{\mathbb {R}/\mathbb {Z}}\ll _{d,m} \delta ^{-O_{d,m}(1)}/N$ for all $1\leq i\leq d$ .

Since $\xi ,\gamma _{1},\ldots ,\gamma _{d}\in \mathbb {Q}^{m}$ , by choosing N to be sufficiently large depending on $\delta ,d,m$ , and p, we have that either $r\xi _{i}\in \mathbb {Z}$ for all $1\leq i\leq d$ or $k\cdot \gamma _{i}\in \mathbb {Z}$ for all $1\leq i\leq d$ .

With the help of Lemma 9.26, we may conclude from (9.26) the following proposition.

Proposition 9.8. We have that either there exists $r\in \mathbb {N}_{+}$ with $r\ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $r\xi \in (\mathbb {Z}^{m})^{d}$ , or there exists $k\in \mathbb {Z}^{m_{\mathrm {lin}}}\times \{0\}^{m-m_{\mathrm {lin}}}$ with $0<\vert k\vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $k\cdot \gamma _{i}\in \mathbb {Z}$ for all $1\leq i\leq d$ .

Proof. We remark that we cannot apply the Green–Tao approach (or Lemma 9.26) directly due to the appearance of the term $c_{h}(hA)$ in (9.26). To overcome this difficulty, we get rid of this term by multiplying both sides of (9.26) by vectors which are orthogonal to $hA$ .

Let $N\gg _{\delta ,d,m,p} 1$ be chosen later. For $w\in \mathbb {F}_{p}^{d}$ , let $V_{w}:=\{n\in \mathbb {F}_{p}^{d}\colon (nA)\cdot w=0\}$ and $Z_{w}=J_{2}\cap \iota ^{-1}(V_{w})$ . For $w'\in \iota ^{-1}(w)$ and $h\in Z_{w}+pK\mathbb {Z}^{d}$ , note that $(hA)\cdot w'\equiv \tau ((\iota (h)A)\cdot w)=0 \,\mod p\mathbb {Z}$ . Taking the dot product of both sides of (9.26) with $w'$ , we have that

(9.28) $$ \begin{align} hB\cdot qw'+u\cdot qw'+\bigg(\sum_{i=1}^{d}qw^{\prime}_{i}\xi_{i}\bigg)\cdot \{\gamma(h)\}\in\mathbb{Z} \end{align} $$

for all $w\in \mathbb {F}_{p}^{d}, w'\in \iota ^{-1}(w)$ and $h\in Z_{w}+pK\mathbb {Z}^{d}$ . To apply Lemma 9.7, we need to identify those w for which the set $Z_{w}$ is large.

Since

$$ \begin{align*}\sum_{w\in \mathbb{F}_{p}^{d}, wA\neq \mathbf{0}}\vert Z_{w}\vert\geq p^{d-1}\vert J_{2}\vert\gg_{d,m} \delta^{O_{d,m}(1)}p^{d-1}(pK)^{d},\end{align*} $$

$\vert Z_{w}\vert \leq (pK)^{d}$ , and

$$ \begin{align*}\vert\{w\in \mathbb{F}_{p}^{d}, wA\neq \mathbf{0}\}\vert\geq p^{d}-p^{d-d'}\geq p^{d}-p^{d-2},\end{align*} $$

by the pigeonhole principle, there exists a subset W of $\{w\in \mathbb {F}_{p}^{d}, wA\neq \mathbf {0}\}$ of cardinality $\gg _{d,m}\delta ^{O_{d,m}(1)} p^{d}$ such that $\vert Z_{w}\vert \gg _{d,m} \delta ^{O_{d,m}(1)} p^{d-1}K^{d}$ for all $w\in W$ .

To apply Lemma 9.7, we also need to rewrite (9.28) by identifying $V_{w}$ as $\mathbb {F}_{p}^{d-1}$ via linear transformations. Since $wA\neq \mathbf {0}$ , $V_{w}$ is a subspace of $\mathbb {F}_{p}^{d}$ of co-dimension 1. Let $L_{w}\colon \mathbb {F}_{p}^{d-1}\to V_{w}$ be any bijective linear transformation and let $\tilde {L}_{w}/p$ be the regular lifting of $L_{w}$ . Since all of $B,\xi _{i},\gamma $ are rational, there exists $K'\in \mathbb {N}_{+}$ such that for any ${h,h'\in \mathbb {Z}^{d}}$ , $\{\gamma (h)\}$ remains unchanged if we replace h by $h+pK'h'$ . By Lemma 9.1, the map $\Phi \colon \mathbb {Z}^{d-1}\times \mathbb {Z}^{d}\to \mathbb {Z}^{d}$ given by

$$ \begin{align*}\Phi(z,m):=\tilde{L}_{w}(z)+pm\end{align*} $$

mod $pK\mathbb {Z}^{d}$ is a ${K'}^{d-1}$ -to-1 map between $[pK']^{d-1}\times [K]^{d}$ and $\iota ^{-1}(V_{w})\cap [pK]^{d}$ . Since $\vert Z_{w}\vert =\vert \iota ^{-1}(V_{w})\cap J_{2}\vert \gg _{d,m} \delta ^{O_{d,m}(1)} p^{d-1}K^{d}$ , we have that $\vert \Phi ^{-1}(Z_{w})\cap ([pK']^{d-1}\times [K]^{d})\vert \gg _{d,m} \delta ^{O_{d,m}(1)} (pK')^{d-1}K^{d}$ . So, there exists some $m_{w}\in [K]^{d}$ such that the set

$$ \begin{align*}I_{w}:=\{z\in [pK']^{d-1}\colon \Phi(z,m_{w}) \in Z_{w}+pK\mathbb{Z}^{d}\}\end{align*} $$

is of cardinality $\gg _{d,m} \delta ^{O_{d,m}(1)} (pK')^{d-1}$ . So, it follows from (9.28) that

(9.29) $$ \begin{align} \tilde{L}_{w}(z)B\cdot qw'+u+(pm_{w}B)\cdot qw'+\bigg(\sum_{i=1}^{d}qw^{\prime}_{i}\xi_{i}\bigg)\cdot \{\gamma(\tilde{L}_{w}(z)+pm_{w})\}\in\mathbb{Z} \end{align} $$

for all $z\in I_{w}$ . By the choice of $K'$ , we have that (9.29) also holds for all $z\in I_{w}+pK'\mathbb {Z}^{d-1}$ .

We are now ready to apply Lemma 9.7. Note that

$$ \begin{align*} \begin{aligned} \liminf_{N\to\infty}\frac{\vert (I_{w}+pK'\mathbb{Z}^{d-1})\cap \{-N,\ldots,N\}^{d-1}\vert}{(2N+1)^{d-1}} =\frac{\vert I_{w}\vert}{(pK')^{d-1}}\gg_{d,m}\delta^{O_{d,m}(1)}. \end{aligned} \end{align*} $$

Recall that the last $m-m_{\mathrm {lin}}$ coefficients of $\xi _{i}$ are zero and so the last $m-m_{\mathrm {lin}}$ coefficients of $\xi _{i}$ and $\gamma _{i}$ does not affect the expression in (9.29). If $N\gg _{\delta ,d,m,p} 1$ , then we may apply Lemma 9.7 to (9.29) to conclude that either there exists $r_{w}\in \mathbb {Z}, 0<r_{w}\ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $r_{w}q\sum _{i=1}^{d}w^{\prime }_{i}\xi _{i}\in \mathbb {Z}^{m}$ for all $w'\in \iota ^{-1}(w)$ , or there exists $k_{w}\in \mathbb {Z}^{m_{\mathrm {lin}}}\times \{0\}^{m-m_{\mathrm {lin}}}$ , $0<\vert k_{w}\vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $k_{w}\cdot (\gamma \circ \tilde {L}_{w}(z))\in \mathbb {Z}$ for all $z\in \mathbb {Z}^{d-1}$ (or equivalently, $k_{w}\cdot \gamma (h)\in \mathbb {Z}$ for all $h\in V_{w}$ ).

By the pigeonhole principle, there exists a subset $W'$ of W of cardinality $\gg _{d,m}\delta ^{O_{d,m}(1)} p^{d}$ such that either there exists $r\in \mathbb {Z}$ with $0<r\ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $rq\sum _{i=1}^{d}w^{\prime }_{i}\xi _{i}\in \mathbb {Z}^{m}$ for all $w'\in \iota ^{-1}(W')$ , or there exists $k\in \mathbb {Z}^{m}$ with $0<\vert k\vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $k\cdot \gamma (h) \in \mathbb {Z}$ for all $h\in \tilde {V}_{w}:=\tilde {L}_{w}(\mathbb {Z}^{d-1})=\text {span}_{\mathbb {Z}}\{\tau (L_{w}(e_{1})),\ldots , \tau (L_{w}(e_{d-1}))\}$ .

If it is the former case, then since $\iota ^{-1}(W')=\tau (W')+p\mathbb {Z}^{d}$ , we must have that $rq\xi _{i}\in \mathbb {Z}^{m}/p$ for all $1\leq i\leq d$ . Since $p\gg _{d,m}\delta ^{-O_{d,m}(1)}$ , there exist $w_{1},\ldots ,w_{d}\in W'$ such that the determinant Q of the matrix $(w_{i,j})_{1\leq i,j\leq d}$ is not divisible by p, where ${w_{j}:=(w_{j,1},\ldots ,w_{j,d})}$ . Then, the fact that $rq\sum _{i=1}^{d}\tau (w_{j,i})\xi _{i}\in \mathbb {Z}^{m}$ for $1\leq j\leq d$ implies that $rq\xi _{i}\in \mathbb {Z}^{m}/Q$ . So, $rq\xi _{i}\in ({1}/{Q})\mathbb {Z}^{m}\cap ({1}/{p})\mathbb {Z}^{m}=\mathbb {Z}^{m}$ and thus, $rq\xi \in (\mathbb {Z}^{m})^{d}$ (recall that $q\ll _{d}\delta ^{-O_{d}(1)}$ ).

If it is the latter case, then it is clear that there exist two $w,w'\in W'$ such that $\tilde {V}_{w}\neq \tilde {V}_{w'}$ and that $\theta \cdot \gamma (h)\in \mathbb {Z}$ for all $h\in \tilde {V}_{w}\cup \tilde {V}_{w}$ . By linearity, $k\cdot \gamma (h)\in \mathbb {Z}$ for all $h\in \tilde {V}_{w}+\tilde {V}_{w'}$ . Since $\tilde {V}_{w}$ and $\tilde {V}_{w'}$ are distinct subspaces of $\mathbb {Z}^{d}$ of co-dimension 1 and $d\geq 2$ , we have that $\tilde {V}_{w}+\tilde {V}_{w'}=\mathbb {Z}^{d}$ . Equivalently, this means that $k\cdot \gamma _{i}\in \mathbb {Z}$ for all $1\leq i\leq d$ .

9.6 Completion of the proof

As is mentioned in Step 4 in §8, our final task is to use Proposition 9.8 to complete the proof of Theorem 5.1. Except for Proposition 9.9, the outline of the proof is similar to the argument in [5, after Claim 7.7 to the end of §7]. Suppose first that there exists $k\in \mathbb {Z}^{m_{\mathrm {lin}}}\times \{0\}^{m-m_{\mathrm {lin}}}$ with $0<\vert k\vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $k\cdot \gamma _{i}\in \mathbb {Z}$ for all $1\leq i\leq d$ . Consider the map $\eta \colon G\to \mathbb {R}/\mathbb {Z}$ defined by

$$ \begin{align*}\eta(x):=k\cdot \psi(x).\end{align*} $$

Then, $\eta $ is a type-I horizontal character and is of complexity at most $O_{d,m}(\delta ^{-O_{d,m}(1)})$ . Moreover, for all $n_{1},\ldots ,n_{d}\in \mathbb {Z}$ , we have that

$$ \begin{align*}\eta(g(n_{1},\ldots,n_{d}))=\eta(g(e_{1})^{n_{1}}\cdots g(e_{d})^{n_{d}})=\sum_{i=1}^{d}n_{i}k\cdot\gamma_{i}\equiv 0 \,\mod \mathbb{Z}.\end{align*} $$

This completes the proof of Theorem 5.1.

We now consider the case $r\xi \in (\mathbb {Z}^{m})^{d}$ for some $r\in \mathbb {N}_{+}$ with $r\ll _{d,m} \delta ^{-O_{d,m}(1)}$ . For $1\leq j\leq m$ , let $\alpha _{j}\colon G\to \mathbb {R}$ be given by $\alpha _{j}(x):=\eta _{2}([x,\exp (X_{j})])$ . Note that $\alpha _{j}$ is a type-I horizontal character, annihilates $G_{2}$ , and $\Vert \alpha _{j}\Vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ . If $\alpha _{j}$ is non-trivial for some $1\leq j\leq m$ , then for all $n_{1},\ldots ,n_{d}\in \mathbb {Z}$ , we have that

$$ \begin{align*}r\alpha_{j}\circ g(n_{1},\ldots,n_{d})=r\alpha_{j}(g(e_{1})^{n_{1}}\cdots g(e_{d})^{n_{d}})=\sum_{i=1}^{d}n_{i}r\xi_{i}\cdot\psi(X_{j})\equiv 0 \,\mod \mathbb{Z},\end{align*} $$

and we again prove Theorem 5.1.

Now, suppose that all of $\alpha _{j}$ are trivial. In this case, $\eta _{2}$ annihilates $[G,G]$ . So, we have that $\Lambda $ is the zero matrix and that $\xi $ is the zero vector. Therefore, $\sigma (h)=0$ . It follows from (9.24) that

(9.30) $$ \begin{align} t_{h}-c_{h}(hA)=q(2h\Omega+u)-c_{h}(hA)\in\mathbb{Z}^{d} \end{align} $$

for some $c_{h}\in \mathbb {Z}/p$ for all $h\in J_{2}+pK\mathbb {Z}^{d}$ . This implies that $t_{h}=q(2h\Omega +u)\in \mathbb {Z}^{d}/p$ for all $h\in J_{2}+pK\mathbb {Z}^{d}$ , which further implies that $q\Omega $ and $qu$ takes $\mathbb {Z}/p$ coefficients. So, for all $h\in J_{2}+pK\mathbb {Z}^{d}$ and $n\in \mathbb {Z}^{d}$ with $(nA)\cdot w\in p\mathbb {Z}^{d}$ , (9.30) implies that ${q(2h\Omega +u)\cdot n\in \mathbb {Z}.}$ Since $J_{2}$ contains $\gg _{d,m}\delta ^{O_{d,m}(1)}p^{d}$ residue classes mod $p\mathbb {Z}$ , it follows from Corollary 7.5 that $qu\in \mathbb {Z}$ and $2q\Omega =rA+B'$ for some $r\in \mathbb {Z}/p$ and matrix $B'$ with integer entries. It then follows from (9.20) and (9.21) that (replacing q by $2q$ if necessary)

(9.31) $$ \begin{align} \eta_{2}(g_{\text{nlin}}(n))=Q(n)=\frac{1}{q}Q_{2}(n)+T(n) \end{align} $$

for some $Q_{2}\in \text {poly}(V_{p}(\tilde {M})\to \mathbb {R}\vert \mathbb {Z})$ and some polynomial $T\colon \mathbb {Z}^{d}\to \mathbb {R}$ of degree at most 1.

If $\eta _{2}$ is trivial, then $Q\equiv 0$ and $\Omega $ can be taken to be the zero matrix. It follows from (9.30) that

$$ \begin{align*}qu-c_{h}(hA)\in\mathbb{Z}^{d}\end{align*} $$

for some $c_{h}\in \mathbb {Z}/p$ for all $h\in J_{2}$ . Note that if $qu\notin \mathbb {Z}^{d}$ , then the number of such h is at most $K^{d}\cdot p^{d+1-\mathrm {rank}_{p}(A)}\leq K^{d}p^{d-1}<\vert J_{2}\vert $ , which is a contradiction. So, we must have that $qu\in \mathbb {Z}^{d}$ . So, it follows from (9.20) that if $M(n)\in \mathbb {Z}$ , then

$$ \begin{align*}q\eta_{1}(g(n))=qP(n)=P_{1}(n)+(qu)\cdot n+qu_{0}\in \mathbb{Z}+qu_{0}.\end{align*} $$

Since $\eta _{0}(g',g)=\eta _{1}(g)+\eta _{2}(g'g^{-1})$ is non-trivial and $\eta _{2}$ is trivial, we have that $\eta _{1}$ is non-trivial. Since $q\ll _{d}\delta ^{-O_{d}(1)}$ , this completes the proof of Theorem 5.1 by setting ${\eta =q\eta _{1}}$ .

So, from now on, we assume that $\eta _{2}$ is not trivial. If $m_{\ast }=0$ , then $\eta _{2}$ vanishes on $G_{2}$ and so it is trivial, which is a contradiction. We now assume that $m_{\ast }\geq 1$ . Since $\eta _{2}$ annihilates $[G,G]$ , we may extend $\eta _{2}$ to a genuine type-I horizontal character $\tilde {\eta }_{2}$ on G in an arbitrary way such that $\tilde {\eta }_{2}\vert _{G_{2}}=\eta _{2}$ , and that the complexity of $\tilde {\eta }_{2}$ is comparable to $\eta _{2}$ . With a slight abuse of notation, we denote $\tilde {\eta }_{2}$ by $\eta _{2}$ as well and treat $\eta _{2}$ as a genuine type-I horizontal character on G. Suppose that $\eta _{2}\colon G\to \mathbb {R}$ is given by $\eta _{2}(x)=k\cdot \psi (x)$ for some $k=(k_{1},\ldots ,k_{m})\in \mathbb {Z}^{m}$ with $\vert k\vert \ll _{d,m}\delta ^{-O_{d,m}(1)}$ . Since $\eta _{2}$ annihilates $[G,G]$ , we have that $k_{i}=0$ for all $i>m_{ab}$ .

Denote $G^{\prime }_{0}=G^{\prime }_{1}=G$ and $G^{\prime }_{i}=G_{i}\cap \ker (\eta _{2})$ for $i\geq 2$ . By [5, Lemma 7.8], $G_{\mathbb {N}}'=(G^{\prime }_{i})_{i\in \mathbb {N}}$ is a filtration of G with degree at most s and nonlinearity degree $m^{\prime }_{\ast }\leq m_{\ast }-1$ . Each $G^{\prime }_{i}$ is closed, connected, and $O_{d,m}(\delta ^{-O_{d,m}(1)})$ -rational with respect to the Mal’cev basis $\mathcal {X}$ on $G/\Gamma $ adapted to $G_{\mathbb {N}}$ . We need a special factorization proposition.

Proposition 9.9. Fix any $n_{\ast }\in V_{p}(\tilde {M})$ . There exists $r\in \mathbb {N}_{+}$ with ${r\ll _{d,m}\delta ^{-O_{d,m}(1)}}$ such that we may write $g=g'\gamma $ for some rational $g'\in \mathrm {poly}(\mathbb {Z}^{d}\to G^{\prime }_{\mathbb {N}})$ and some ${\gamma \in \mathrm {poly}_{\approx r, n_{\ast }}(V_{p}(\tilde {M})\to G_{\mathbb {N}}\vert \Gamma )}$ .

We first complete the proof of Theorem 5.1 assuming Proposition 9.9. Let the notation be the same as Proposition 9.9. By Proposition 3.17, there exists $r'\in \mathbb {N}_{+}$ with $r'\ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $\gamma \in \text {poly}_{r'}(V_{p}(\tilde {M})\to G_{\mathbb {N}}\vert \Gamma )$ . For all $m\in [r']^{d}$ , there exists $\tilde {m}\in \mathbb {Z}^{d}$ with $\tilde {m}-m\in r'\mathbb {Z}^{d}$ and $\tilde {m}-n_{\ast }\in p\mathbb {Z}^{d}$ . Since $n_{\ast }\in V_{p}(\tilde {M})$ , we have $\tilde {m}\in V_{p}(\tilde {M})$ . Since $\gamma \in \text {poly}_{r'}(V_{p}(\tilde {M})\to G_{\mathbb {N}})$ , we have that

(9.32) $$ \begin{align} \gamma(\tilde{m})\Gamma=\gamma(r'n+m)\Gamma \quad\text{for all } n\in\mathbb{Z}^{d} \quad\text{with } r'n+m\in V_{p}(\tilde{M}). \end{align} $$

Denote

$$ \begin{align*}g^{\prime}_{m}(n):=\{\gamma(\tilde{m})\}^{-1}g'(r'n+m)\{\gamma(\tilde{m})\}.\end{align*} $$

Since $g'$ and $\gamma $ are rational, by Corollary 3.19, there exists $K'\in \mathbb {N}_{+}$ which is divisible by $pK$ such that $g'$ and $g^{\prime }_{m}, m\in [r']^{d}$ are all $K'$ -periodic. For $m\in \mathbb {Z}^{d}$ , let ${M_{m}\colon \mathbb {Z}^{d}\to \mathbb {Z}/p}$ be the quadratic map given by $\tilde {M}_{m}(n):=\tilde {M}(r'n+m)$ . Then, since $r\ll _{d,m}\delta ^{-O_{d,m}(1)}$ , $\tilde {M}_{m}$ and $\tilde {M}$ have the same p-rank. Note that for all $n\in V_{p}(\tilde {M}_{m})$ , we have that $r'n+m\in V_{p}(\tilde {M})$ . Then, it follows from (9.32) and (9.4) that

$$ \begin{align*} & \delta^{O_{d,m}(1)}\ll_{d,m} \vert\mathbb{E}_{n\in V_{p}(\tilde{M})\cap[pK]^{d}}F(g(n)\Gamma)\vert =\vert\mathbb{E}_{n\in V_{p}(\tilde{M})\cap[r'K']^{d}}F(g(n)\Gamma)\vert\\ &\quad=\vert\mathbb{E}_{m\in [r']^{d}}\mathbb{E}_{n\in V_{p}(\tilde{M}_{m})\cap [K']^{d}}F(g(r'n+m)\Gamma)\vert+O(p^{-1/2})\\ &\quad=\vert\mathbb{E}_{m\in [r']^{d}}\mathbb{E}_{n\in V_{p}(\tilde{M}_{m})\cap [K']^{d}}F(g'(r'n+m)\gamma(r'n+m)\Gamma)\vert+O(p^{-1/2})\\ &\quad=\vert\mathbb{E}_{m\in [r']^{d}}\mathbb{E}_{n\in V_{p}(\tilde{M}_{m})\cap [K']^{d}}F(g'(r'n+m)\gamma(\tilde{m})\Gamma)\vert+O(p^{-1/2})\\ &\quad=\vert\mathbb{E}_{m\in [r']^{d}}\mathbb{E}_{n\in V_{p}(\tilde{M}_{m})\cap [K']^{d}}F(\{\gamma(\tilde{m})\}g^{\prime}_{m}(n)\Gamma)\vert+O(p^{-1/2}). \end{align*} $$

So by the pigeonhole principle, there exists some $m\in [r']^{d}$ such that

$$ \begin{align*}\vert\mathbb{E}_{n\in V_{p}(\tilde{M}_{m})\cap [K']^{d}}F^{\prime}_{m}(g^{\prime}_{m}(n)\Gamma)\vert\gg_{d,m}\delta^{O_{d,m}(1)},\end{align*} $$

where $F^{\prime }_{m}:=F(\{\gamma (\tilde {m})\}\cdot )$ . By the construction of $K'$ , $g^{\prime }_{m}$ is a rational and $K'$ -periodic polynomial in $\text {poly}(\mathbb {Z}^{d}\to G^{\prime }_{\mathbb {N}})$ and $\Vert F'\Vert _{\mathrm {Lip}}=O(1)$ . We may now invoke the induction hypothesis to deduce that there exists a non-trivial type-I horizontal character $\eta $ of complexity at most $O_{d,m}(\delta ^{-O_{d,m}(1)})$ such that $\eta \circ g^{\prime }_{m}\,\mod \mathbb {Z}$ is a constant on $V_{p}(\tilde {M}_{m})$ . Since

$$ \begin{align*} & \eta\circ g^{\prime}_{m}(n)=\eta\circ g'(r'n+m)\\ & \quad=\eta\circ g(r'n+m)-\eta\circ \gamma(r'n+m)\equiv \eta\circ g(r'n+m)-\eta\circ \gamma(m)\,\mod \mathbb{Z} \end{align*} $$

for all $n\in V_{p}(\tilde {M}_{m})$ , we have that $\eta \circ g\,\mod \mathbb {Z}$ is a constant on $V_{p}(\tilde {M})$ . This finishes the proof of Theorem 5.1.

So, it remains to prove Proposition 9.9. Proposition 9.9 can be viewed as an analog of [5, Lemma 7.9], but its proof deviates significantly from [5, Lemma 7.9].

Proof of Proposition 9.9

Let $0\leq s'\leq s$ be the largest integer such that at least one of the entries $k_{m-m_{s'}+1},\ldots ,k_{m-m_{s'+1}}$ is non-zero (where we denote $m_{0}:=0$ ). Since $\eta _{2}$ is non-trivial, such an $s'$ always exists and $s'\geq 2$ . Denote $m':=m-m_{s'+1}$ . Then, we may write $k=(k',\mathbf {0})$ for some $k'\in \mathbb {Z}^{m'}$ .

Assume that

$$ \begin{align*}\psi(g(n))=\sum_{i\in\mathbb{N}^{d},0\leq\vert i\vert\leq s}w_{i}\binom{n}{i}\end{align*} $$

for some $w_{i}\in \{0\}^{m-m_{\vert i\vert }}\times \mathbb {R}^{m_{\vert i\vert }}$ . Since $Q(\mathbf {0})=Q(e_{i})=0$ , we may write

$$ \begin{align*}\psi(g_{\text{nlin}}(n))=\sum_{m\in\mathbb{N}^{d},2\leq \vert i\vert\leq s}t_{i}\binom{n}{i}\end{align*} $$

for some $t_{i}\in \{0\}^{m-m_{\vert i\vert }}\times \mathbb {R}^{m_{\vert i\vert }}$ . Write $w_{i}=(w^{\prime }_{i},w^{\prime \prime }_{i}), t_{i}=(t^{\prime }_{i},t^{\prime \prime }_{i})$ for some $t^{\prime }_{i},w^{\prime }_{i}\in \mathbb {R}^{m'}$ and $t^{\prime \prime }_{i},w^{\prime \prime }_{i}\in \mathbb {R}^{m-m'}$ . Since the first $m-m_{\vert i\vert }$ entries of $t_{i}$ are zero and the last $m_{s'+1}$ entries of k are zero, we have that $k\cdot t_{i}=0$ if $\vert i\vert \geq s'+1$ . By (9.31),

$$ \begin{align*} \frac{1}{q}Q_{2}(n)+T(n)=\eta_{2}(g_{\text{nlin}}(n))=\sum_{i\in\mathbb{N}^{d},2\leq \vert i\vert\leq s}(k\cdot t_{i})\binom{n}{i}=\sum_{i\in\mathbb{N}^{d},2\leq \vert i\vert\leq s'}(k'\cdot t^{\prime}_{i})\binom{n}{i}. \end{align*} $$

In particular, we have that $\deg (Q_{2})\leq s'$ .

Since k is of complexity $\ll _{d,m}\delta ^{-O_{d,m}(1)}$ , there exists $q'\in \mathbb {N}_{+}, q'\ll _{d,m}\delta ^{-O_{d,m}(1)}$ , and $u=(u_{1},\ldots ,u_{m})\in \mathbb {Z}^{m}$ whose only non-zero entries are $u_{m-m_{s'}+1},\ldots ,u_{m-m_{s'+1}}$ such that $k\cdot u=q'.$ Denote

$$ \begin{align*}\gamma(n):=\prod_{i=m-m_{s'}+1}^{m-m_{s'+1}}\exp\bigg(\frac{1}{qq'}u_{i}(Q_{2}(n)-Q_{2}(n_{\ast}))X_{i}\bigg).\end{align*} $$

Since $\deg (Q_{2})\leq s'$ , it follows from [8, Corollary B.4] that $\gamma \in \text {poly}(\mathbb {Z}^{d}\to (G_{2})_{\mathbb {N}})$ .

We now show that there exists $r\in \mathbb {N}_{+}$ with $r\ll _{d,m}\delta ^{-O_{d,m}(1)}$ such that $\gamma $ belongs to $\text {poly}_{\approx r, n_{\ast }}(V_{p}(\tilde {M})\to G_{\mathbb {N}}\vert \Gamma )$ and takes values in $G_{2}$ . In fact, it suffices to show that $Q_{2}(n_{\ast }+rn)-Q_{2}(n_{\ast })\in qq'\mathbb {Z}$ for all $n\in \mathbb {Z}^{d}$ with $n_{\ast }+rn\in V_{p}(\tilde {M})$ . By interpolation, all the coefficients of the polynomial $Q_{2}$ belongs to $\mathbb {Z}/p^{s'}q"$ for some $s'=O_{d,s}(1)$ and $q"\in \mathbb {N}_{+}$ with $q"\leq O_{d,s}(1)$ . So, for all $n\in \mathbb {Z}^{d}$ , we have that $Q_{2}(n_{\ast }+rn)-Q_{2}(n_{\ast })\in qq'\mathbb {Z}/p^{s'}$ , where $r:=qq'q"$ . However, if $n_{\ast }+rn, n_{\ast }\in V_{p}(\tilde {M})$ , then $Q_{2}(n_{\ast }+rn)-Q_{2}(n_{\ast })\in \mathbb {Z}$ . Since $qq'$ is not divisible by p, this implies that $Q_{2}(n_{\ast }+rn)-Q_{2}(n_{\ast })\in qq'\mathbb {Z}$ . So, $\gamma \in \text {poly}_{\approx r, n_{\ast }}(V_{p}(\tilde {M})\to G_{\mathbb {N}}\vert \Gamma )$ and takes values in $G_{2}$ .

Writing $h:=g\gamma ^{-1}$ , we have that $h\in \text {poly}(\mathbb {Z}^{d}\to (G_{2})_{\mathbb {N}}\vert (\Gamma \cap G_{2}))$ . Note that for all $n,h_{1},h_{2}\in \mathbb {Z}^{d}$ ,

(9.33) $$ \begin{align} & \Delta_{h_{2}}\Delta_{h_{1}}(\eta_{2}\circ g(n)) =\eta_{2}\circ(\Delta_{h_{2}}\Delta_{h_{1}}g)(n)=\eta_{2}\circ(\Delta_{h_{2}}\Delta_{h_{1}}g_{\text{nlin}})(n)\nonumber\\ &\quad =\Delta_{h_{2}}\Delta_{h_{1}}(\eta_{2}\circ g_{\text{nlin}})(n) =\Delta_{h_{2}}\Delta_{h_{1}}\bigg(\frac{1}{q}Q_{2}(n)+T(n)\bigg)=\Delta_{h_{2}}\Delta_{h_{1}}\bigg(\frac{1}{q}Q_{2}(n)\bigg). \end{align} $$

So, (9.33) implies that

(9.34) $$ \begin{align} \begin{aligned} &\quad \Delta_{h_{2}}\Delta_{h_{1}}(\eta_{2}\circ h(n)) =\Delta_{h_{2}}\Delta_{h_{1}}(\eta_{2}\circ g(n))-\Delta_{h_{2}}\Delta_{h_{1}}(\eta_{2}\circ \gamma(n)) =0. \end{aligned} \end{align} $$

Set $g':=g\gamma ^{-1}=g_{\text {nlin}}g_{\mathrm {lin}}\gamma ^{-1}$ . It is clear that $g'\in \text {poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ . Moreover, by (9.34),

$$ \begin{align*}\Delta_{h_{2}}\Delta_{h_{1}}(\eta_{2}\circ g')(n)=\eta_{2}(\Delta_{h_{2}}\Delta_{h_{1}}g'(n))=0\end{align*} $$

for all $n,h_{1},h_{2}\in \mathbb {Z}^{d}$ . So, it is not hard to see that $g'$ belongs to $\text {poly}(\mathbb {Z}^{d}\to G^{\prime }_{\mathbb {N}})$ . Finally, since $g'=g\gamma ^{-1}$ , it follows from the Baker–Campbell–Hausdorff formula that $g'$ is rational.

We end this paper with an immediate consequence of Theorem 5.1, which will be used in [16].

Corollary 9.10. Let $0<\delta <1/2, d,k,m\in \mathbb {N}_{+},s,r\in \mathbb {N}$ with $d\geq r$ , and $p\gg _{d,m} \delta ^{-O_{d,m}(1)}$ be a prime. Let $M\colon \mathbb {F}_{p}^{d}\to \mathbb {F}_{p}$ be a quadratic form and $V+c$ be an affine subspace of $\mathbb {F}_{p}^{d}$ of co-dimension r. Suppose that $\mathrm {rank}(M\vert _{V+c})\geq s+13$ . Let $G/\Gamma $ be an s-step $\mathbb {N}$ -filtered nilmanifold of dimension m, equipped with a ${1}/{\delta }$ -rational Mal’cev basis $\mathcal {X}$ , and that $g\in \mathrm { poly}(\mathbb {Z}^{d}\to G_{\mathbb {N}})$ be a rational polynomial sequence. Let $\gamma \in G$ be an element of complexity at most 1, and let $g'\in \mathrm {poly}(\mathbb {Z}^{d}\to G^{\prime }_{\mathbb {N}})$ be the map given by $g'(n):=\gamma ^{-1}g(n)\gamma $ for all $n\in \mathbb {Z}^{d}$ , where $G^{\prime }_{i}:=\gamma ^{-1} G_{i}\gamma $ for all $i\in \mathbb {N}$ . Denote $\Gamma ':=\gamma ^{-1}\Gamma \gamma $ . If $(g(n)\Gamma )_{n\in \iota ^{-1}(V(M)\cap (V+c))}$ is not $\delta $ -equidistributed on $G/\Gamma $ , then $(g'(n)\Gamma ')_{n\in \iota ^{-1}(V(M)\cap (V+c))}$ is not $C^{-1}\delta ^{C}$ -equidistributed on $G'/\Gamma '$ for some $C=C(d,m)\geq 1$ .

Proof. By Theorem 5.1, there exists a non-trivial type-I horizontal character $\eta $ with $0<\Vert \eta \Vert \ll _{d,m} \delta ^{-O_{d,m}(1)}$ such that $\eta \circ g'=\eta \circ g \,\mod \mathbb {Z}$ is a constant on $\iota ^{-1}(V(M)\cap (V+c))$ . By [5, Lemma A.13], $G'/\Gamma '$ is an s-step $\mathbb {N}$ -filtered nilmanifold of dimension m, equipped with a ${1}/({\delta ^{O(1)}})$ -rational Mal’cev basis. Since $\vert \mathbb {E}_{n\in \iota ^{-1}(V(M)\cap (V+c))}\exp (\eta (g'(n)))\vert =1$ , this implies that $(g'(n)\Gamma ')_{n\in \iota ^{-1}(V(M)\cap (V+c))}$ is not $C^{-1}\delta ^{C}$ -equidistributed on $G'/\Gamma '$ for some $C=C(d,m)\geq 1$ .