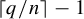1 Introduction
The goal of this work is two-fold. First, to extend the first-order perturbation theory for exact twist maps developed in [Reference Damasceno, Dias Carneiro and Ramírez-Ros17, Reference Pinto-de-Carvalho and Ramírez-Ros39, Reference Ramírez-Ros41] to a higher-order theory. Second, to apply that theory to the study of high-order persistence of resonant caustics in perturbed circular billiards. The second goal is strongly motivated by some of the numerical experiments discussed in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37].
The computational aspects of our analysis are greatly simplified when working with the Bialy–Mironov generating function for convex billiards discovered in [Reference Bialy4, Reference Bialy and Mironov7]. We were also inspired by [Reference Bialy and Tabachnikov10]. We know just a few practical high-order Melnikov theories for time-periodic perturbations of integrable continuous systems (ODEs)—see, for instance, [Reference Chen and Wang14, Reference Chen and Wang15]—but none for perturbations of integrable discrete systems (maps). In that sense, our theory is novel.
The fragility of resonant caustics is a key idea behind recent proofs of local versions of the Birkhoff conjecture (see below) and related results about the rigidity of the length spectrum of strictly convex domains [Reference Avila, De Simoi and Kaloshin1, Reference Hezari and Zelditch23–Reference Huang, Kaloshin and Sorrentino25, Reference Kaloshin and Sorrentino29, Reference Kaloshin and Sorrentino30]. See also the surveys [Reference Fierobe, Kaloshin and Sorrentino19, Reference Kaloshin and Sorrentino28]. Almost all these works describe the first-order persistence condition of resonant caustics contained in [Reference Ramírez-Ros41]. We hope that our new high-order persistence conditions will be equally useful.
A caustic is a curve such that any billiard trajectory, once tangent to the curve, stays tangent after every reflection. The robustness of a convex caustic is closely related to the arithmetic properties of its rotation number
![]() $\rho \in (0,1)$
, a number that measures the number of turns around the caustic per impact. Tangent lines to the caustic can be counterclockwise or clockwise oriented. We fix the counterclockwise orientation, so
$\rho \in (0,1)$
, a number that measures the number of turns around the caustic per impact. Tangent lines to the caustic can be counterclockwise or clockwise oriented. We fix the counterclockwise orientation, so
![]() $\rho \in (0,1/2]$
. Lazutkin [Reference Lazutkin33] showed that for any smooth strictly convex domain, there is a positive measure Cantor set
$\rho \in (0,1/2]$
. Lazutkin [Reference Lazutkin33] showed that for any smooth strictly convex domain, there is a positive measure Cantor set
![]() $\mathcal {R} \subset (0,1/2)$
of Diophantine rotation numbers that accumulates to
$\mathcal {R} \subset (0,1/2)$
of Diophantine rotation numbers that accumulates to
![]() $0$
such that there is a caustic for any rotation number
$0$
such that there is a caustic for any rotation number
![]() $\rho \in \mathcal {R}$
. These caustics persist under smooth deformations of the domain [Reference Popov40].
$\rho \in \mathcal {R}$
. These caustics persist under smooth deformations of the domain [Reference Popov40].
Let
![]() $\rho = p/q \in (0,1/2]$
be a rational rotation number such that
$\rho = p/q \in (0,1/2]$
be a rational rotation number such that
![]() $\gcd (p,q) = 1$
. A convex caustic is called
$\gcd (p,q) = 1$
. A convex caustic is called
![]() $p/q$
-resonant (or
$p/q$
-resonant (or
![]() $p/q$
-rational) when all its tangent trajectories form closed polygons with q sides that make p turns around the caustic. We say that q is the period of the caustic. Resonant caustics generically break up under perturbation. Recent results in [Reference Fierobe and Sorrentino20] confirm their fragility. Once
$p/q$
-rational) when all its tangent trajectories form closed polygons with q sides that make p turns around the caustic. We say that q is the period of the caustic. Resonant caustics generically break up under perturbation. Recent results in [Reference Fierobe and Sorrentino20] confirm their fragility. Once
![]() $q \ge 2$
is fixed, the space of convex domains with a resonant caustic of period q has infinite dimension and codimension [Reference Baryshnikov and Zharnitsky2]. The space of convex domains with at least one resonant caustic is dense in the space of all convex domains [Reference Kaloshin and Zhang31].
$q \ge 2$
is fixed, the space of convex domains with a resonant caustic of period q has infinite dimension and codimension [Reference Baryshnikov and Zharnitsky2]. The space of convex domains with at least one resonant caustic is dense in the space of all convex domains [Reference Kaloshin and Zhang31].
We shall not deal with the case
![]() $\rho = 1/2$
, since convex domains with
$\rho = 1/2$
, since convex domains with
![]() $1/2$
-resonant caustics are easily characterized as the constant width domains [Reference Gutkin22, Reference Knill32]. Centrally symmetric convex domains with a
$1/2$
-resonant caustics are easily characterized as the constant width domains [Reference Gutkin22, Reference Knill32]. Centrally symmetric convex domains with a
![]() $1/4$
-resonant caustic have also been completely characterized in terms of the Fourier coefficients of the square of the support function of the convex domain in [Reference Bialy and Tsodikovich11]. Some non-circular convex domains with a
$1/4$
-resonant caustic have also been completely characterized in terms of the Fourier coefficients of the square of the support function of the convex domain in [Reference Bialy and Tsodikovich11]. Some non-circular convex domains with a
![]() $1/3$
-resonant caustic were constructed in [Reference Innami26].
$1/3$
-resonant caustic were constructed in [Reference Innami26].
Circles and ellipses are the only known strictly convex smooth domains almost completely foliated by convex caustics. The centenary Birkhoff conjecture claims that they are the only ones [Reference Tabachnikov42]. Bialy [Reference Bialy3] proved the following weak version of this conjecture. If almost every billiard trajectory in a convex domain is tangent to a convex caustic, then the domain is a disk. A much stronger version of the Birkhoff conjecture for centrally symmetric
![]() $C^2$
-domains, based on the structure of the
$C^2$
-domains, based on the structure of the
![]() $1/4$
-resonant caustic, was recently established by Bialy and Mironov [Reference Bialy and Mironov8]. See also [Reference Bialy6, Reference Bialy and Tsodikovich11] for effective (that is, quantitative) versions on these two results. Near centrally symmetric domains were considered in [Reference Kaloshin, Koudjinan and Zhang27].
$1/4$
-resonant caustic, was recently established by Bialy and Mironov [Reference Bialy and Mironov8]. See also [Reference Bialy6, Reference Bialy and Tsodikovich11] for effective (that is, quantitative) versions on these two results. Near centrally symmetric domains were considered in [Reference Kaloshin, Koudjinan and Zhang27].
We are interested in two practical problems. First, to characterize the deformations of the circle that preserve a given resonant caustic. Second, to determine all resonant caustics that are preserved under a given deformation of the circle. In that regard, we recall that any
![]() $\mathbb {Z}_2$
-symmetric analytical deformation of a circle (with certain Fourier decaying rate) preserving both its
$\mathbb {Z}_2$
-symmetric analytical deformation of a circle (with certain Fourier decaying rate) preserving both its
![]() $1/2$
-resonant and
$1/2$
-resonant and
![]() $1/3$
-resonant caustics has to be an isometric transformation [Reference Zhang44].
$1/3$
-resonant caustics has to be an isometric transformation [Reference Zhang44].
In what follows, we introduce some notation and state our two main results.
Let
![]() $\Gamma _\epsilon $
be a deformation of the unit circle with smooth support function
$\Gamma _\epsilon $
be a deformation of the unit circle with smooth support function
where
![]() $\psi \in \mathbb {T} = \mathbb {R}/2\pi \mathbb {Z}$
is the normal angle and
$\psi \in \mathbb {T} = \mathbb {R}/2\pi \mathbb {Z}$
is the normal angle and
![]() $\epsilon \in [-\epsilon _0,\epsilon _0]$
is the perturbative parameter. We say that a resonant caustic of the unit circle
$\epsilon \in [-\epsilon _0,\epsilon _0]$
is the perturbative parameter. We say that a resonant caustic of the unit circle
![]() $\mathrm {O} (\epsilon ^m)$
-persists under
$\mathrm {O} (\epsilon ^m)$
-persists under
![]() $\Gamma _\epsilon $
when the billiard in
$\Gamma _\epsilon $
when the billiard in
![]() $\Gamma _\epsilon $
is
$\Gamma _\epsilon $
is
![]() $\mathrm {O} (\epsilon ^{m+1})$
-close to having that resonant caustic. See Definition 3.3 for more details.
$\mathrm {O} (\epsilon ^{m+1})$
-close to having that resonant caustic. See Definition 3.3 for more details.
Let
![]() $\nu _l:(0,1/2) \to \mathbb {R} \cup \{\infty \}$
, with
$\nu _l:(0,1/2) \to \mathbb {R} \cup \{\infty \}$
, with
![]() $l \in \mathbb {Z}$
and
$l \in \mathbb {Z}$
and
![]() $|l| \ge 2$
, be the sequence of functions given by
$|l| \ge 2$
, be the sequence of functions given by
 $$ \begin{align} \nu_l(\rho) = \nu_{-l}(\rho) = \begin{cases} \dfrac{\tan(l \pi \rho) - l \tan (\pi \rho)}{\tan (\pi \rho) \tan(l\pi \rho)} & \text{if }2 l \rho \not \in \mathbb{Z}, \\ 1/\tan(\pi \rho) & \text{if }2l \rho \in \mathbb{Z}\text{ but }l \rho \not \in \mathbb{Z}, \\ \infty & \text{if }l \rho \in \mathbb{Z}. \end{cases} \end{align} $$
$$ \begin{align} \nu_l(\rho) = \nu_{-l}(\rho) = \begin{cases} \dfrac{\tan(l \pi \rho) - l \tan (\pi \rho)}{\tan (\pi \rho) \tan(l\pi \rho)} & \text{if }2 l \rho \not \in \mathbb{Z}, \\ 1/\tan(\pi \rho) & \text{if }2l \rho \in \mathbb{Z}\text{ but }l \rho \not \in \mathbb{Z}, \\ \infty & \text{if }l \rho \in \mathbb{Z}. \end{cases} \end{align} $$
Once again, we realize that Gutkin’s equation
![]() $\tan (l\pi \rho ) = l \tan (\pi \rho )$
is ubiquitous in billiard problems. See [Reference Bialy4, Reference Bialy, Mironov and Shalom9, Reference Bialy and Tsodikovich12, Reference Gutkin22] for other examples. Cyr [Reference Cyr16] proved that
$\tan (l\pi \rho ) = l \tan (\pi \rho )$
is ubiquitous in billiard problems. See [Reference Bialy4, Reference Bialy, Mironov and Shalom9, Reference Bialy and Tsodikovich12, Reference Gutkin22] for other examples. Cyr [Reference Cyr16] proved that
![]() $\nu _l(\rho )$
has no rational roots
$\nu _l(\rho )$
has no rational roots
![]() $\rho = p/q \in (0,1/2)$
when
$\rho = p/q \in (0,1/2)$
when
![]() $|l| \ge 2$
. The case
$|l| \ge 2$
. The case
![]() $l \rho \in \mathbb {Z}$
never takes place in our computations. The singular value
$l \rho \in \mathbb {Z}$
never takes place in our computations. The singular value
![]() $\nu _l(\rho ) = \infty $
has been written just for definiteness. It is irrelevant.
$\nu _l(\rho ) = \infty $
has been written just for definiteness. It is irrelevant.
Fourier coefficients of
![]() $2\pi $
-periodic functions are denoted with a hat:
$2\pi $
-periodic functions are denoted with a hat:
![]() $a(t) = \sum _{l \in \mathbb {Z}} \hat {a}_l \mathit {e}^{\mskip 2mu{i}\mskip 1mu l t}$
. Given a
$a(t) = \sum _{l \in \mathbb {Z}} \hat {a}_l \mathit {e}^{\mskip 2mu{i}\mskip 1mu l t}$
. Given a
![]() $2\pi $
-periodic smooth function
$2\pi $
-periodic smooth function
![]() $a(t)$
and a subset
$a(t)$
and a subset
![]() $R \subset \mathbb {Z}$
, let
$R \subset \mathbb {Z}$
, let
![]() $\mu _R\{a(t)\} = \sum _{l \in R} \hat {a}_l \mathit {e}^{\mskip 2mu{i}\mskip 1mu l t}$
be the projection of
$\mu _R\{a(t)\} = \sum _{l \in R} \hat {a}_l \mathit {e}^{\mskip 2mu{i}\mskip 1mu l t}$
be the projection of
![]() $a(t)$
onto its R-harmonics. We only consider the cases
$a(t)$
onto its R-harmonics. We only consider the cases
![]() $R = q\mathbb {Z}$
or
$R = q\mathbb {Z}$
or
![]() $R = q\mathbb {Z}^\star $
with
$R = q\mathbb {Z}^\star $
with
![]() $\mathbb {Z}^\star = \mathbb {Z} \setminus \{ 0 \}$
.
$\mathbb {Z}^\star = \mathbb {Z} \setminus \{ 0 \}$
.
Theorem 1.1. Let
![]() $\rho = p/q \in (0,1/2)$
be any rational rotation number such that
$\rho = p/q \in (0,1/2)$
be any rational rotation number such that
![]() $\gcd (p,q) = 1$
. The high-order persistence of the
$\gcd (p,q) = 1$
. The high-order persistence of the
![]() $p/q$
-resonant caustic of the unit circle under the deformation with support function (1) can be determined as follows.
$p/q$
-resonant caustic of the unit circle under the deformation with support function (1) can be determined as follows.
-
(a) It
 $\mathrm {O} (\epsilon )$
-persists if and only if
$\mathrm {O} (\epsilon )$
-persists if and only if
 $\mu _{q\mathbb {Z}^\star } \{ h_1 \} = 0$
.
$\mu _{q\mathbb {Z}^\star } \{ h_1 \} = 0$
. -
(b) It
 $\mathrm {O} (\epsilon ^2)$
-persists if and only if it
$\mathrm {O} (\epsilon ^2)$
-persists if and only if it
 $\mathrm {O} (\epsilon )$
-persists and
$\mathrm {O} (\epsilon )$
-persists and
 $\mu _{q\mathbb {Z}^\star } \{ h_2 + \theta ^2_1/2 \} = 0$
, where
$\mu _{q\mathbb {Z}^\star } \{ h_2 + \theta ^2_1/2 \} = 0$
, where  $$ \begin{align*} \theta_1(t) = \sum_{l \not \in q\mathbb{Z} \cup \{-1,1\}} \nu_l(\rho) \hat{h}_{1,l} \ \mathit{e}^{\mskip2mu{i}\mskip1mu l t} \quad \text{if } h_1(\psi) = \sum_{l \in \mathbb{Z}} \hat{h}_{1,l} \ \mathit{e}^{\mskip2mu{i}\mskip1mu l \psi}. \end{align*} $$
$$ \begin{align*} \theta_1(t) = \sum_{l \not \in q\mathbb{Z} \cup \{-1,1\}} \nu_l(\rho) \hat{h}_{1,l} \ \mathit{e}^{\mskip2mu{i}\mskip1mu l t} \quad \text{if } h_1(\psi) = \sum_{l \in \mathbb{Z}} \hat{h}_{1,l} \ \mathit{e}^{\mskip2mu{i}\mskip1mu l \psi}. \end{align*} $$
-
(c) It
 $\mathrm {O} (\epsilon ^m)$
-persists for some
$\mathrm {O} (\epsilon ^m)$
-persists for some
 $m \ge 3$
if and only if it
$m \ge 3$
if and only if it
 $\mathrm {O} (\epsilon ^{m-1})$
-persists and
$\mathrm {O} (\epsilon ^{m-1})$
-persists and
 $\mu _{q\mathbb {Z}^\star } \{ h_m + \zeta _m \} = 0$
, where
$\mu _{q\mathbb {Z}^\star } \{ h_m + \zeta _m \} = 0$
, where
 $\zeta _m$
is a smooth
$\zeta _m$
is a smooth
 $2\pi $
-periodic function, only depending on
$2\pi $
-periodic function, only depending on
 $h_1,\ldots ,h_{m-1}$
, which can be explicitly computed from recurrences given in the paper.
$h_1,\ldots ,h_{m-1}$
, which can be explicitly computed from recurrences given in the paper.
The
![]() $\mathrm {O} (\epsilon )$
-persistence result in Theorem 1.1 is just a reformulation of the main theorem in [Reference Ramírez-Ros41]. Condition
$\mathrm {O} (\epsilon )$
-persistence result in Theorem 1.1 is just a reformulation of the main theorem in [Reference Ramírez-Ros41]. Condition
![]() $\mu _{q\mathbb {Z}^\star } \{ h_m + \zeta _m \} = 0$
is equivalent to
$\mu _{q\mathbb {Z}^\star } \{ h_m + \zeta _m \} = 0$
is equivalent to
![]() $\mu _{q\mathbb {Z}}\{ h^{\prime }_m + \zeta ^{\prime }_m\} = 0$
. In particular, condition
$\mu _{q\mathbb {Z}}\{ h^{\prime }_m + \zeta ^{\prime }_m\} = 0$
. In particular, condition
![]() $\mu _{q\mathbb {Z}^\star } \{ h_2 + \theta _1^2/2 \}$
is equivalent to
$\mu _{q\mathbb {Z}^\star } \{ h_2 + \theta _1^2/2 \}$
is equivalent to
![]() $\mu _{q\mathbb {Z}} \{ h^{\prime }_2 + \theta _1 \theta ^{\prime }_1 \} = 0$
.
$\mu _{q\mathbb {Z}} \{ h^{\prime }_2 + \theta _1 \theta ^{\prime }_1 \} = 0$
.
Let
![]() $T_n[\psi ]$
be the space of
$T_n[\psi ]$
be the space of
![]() $2\pi $
-periodic real trigonometric polynomials of degree
$2\pi $
-periodic real trigonometric polynomials of degree
![]() $\le n$
in
$\le n$
in
![]() $\psi $
.
$\psi $
.
Definition 1.2. We say that a deformation
![]() $\Gamma _\epsilon $
of the unit circle with support function (1) is polynomial of degree
$\Gamma _\epsilon $
of the unit circle with support function (1) is polynomial of degree
![]() $\le n$
when
$\le n$
when
and is centrally or anti-centrally symmetric when
![]() $h_\epsilon (\psi +\pi ) = h_\epsilon (\psi )$
or
$h_\epsilon (\psi +\pi ) = h_\epsilon (\psi )$
or
![]() $h_\epsilon (\psi +\pi ) = h_{-\epsilon }(\psi )$
.
$h_\epsilon (\psi +\pi ) = h_{-\epsilon }(\psi )$
.
Being centrally symmetric is a property of single curves. Being anti-centrally symmetric is a property of deformations.
Theorem 1.3. Let
![]() $\lceil x \rceil = \min \{ k \in \mathbb {Z}: k \ge x \}$
be the ceil function. If
$\lceil x \rceil = \min \{ k \in \mathbb {Z}: k \ge x \}$
be the ceil function. If
![]() $\rho = p/q \in (0,1/2)$
is a rational rotation number such that
$\rho = p/q \in (0,1/2)$
is a rational rotation number such that
![]() $\gcd (p,q) = 1$
and
$\gcd (p,q) = 1$
and
![]() $\Gamma _\epsilon $
is a polynomial deformation of the unit circle of degree
$\Gamma _\epsilon $
is a polynomial deformation of the unit circle of degree
![]() $\le n$
, then the
$\le n$
, then the
![]() $p/q$
-resonant caustic
$p/q$
-resonant caustic
![]() $\mathrm {O} (\epsilon ^{\chi -1})$
-persists under
$\mathrm {O} (\epsilon ^{\chi -1})$
-persists under
![]() $\Gamma _\epsilon $
, where
$\Gamma _\epsilon $
, where
 $$ \begin{align*} \chi = \chi(\Gamma_\epsilon,q) = \begin{cases} 1 + 2 \lceil (q-n)/2n \rceil & \text{for anti-centrally symmetric }\Gamma_\epsilon\text{ and odd }q, \\ 2\lceil q/2n \rceil & \text{for anti-centrally symmetric }\Gamma_\epsilon\text{ and even }q, \\ \lceil 2q/n \rceil & \text{for centrally symmetric }\Gamma_\epsilon\text{ and odd }q, \\ \lceil q/n \rceil & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \chi = \chi(\Gamma_\epsilon,q) = \begin{cases} 1 + 2 \lceil (q-n)/2n \rceil & \text{for anti-centrally symmetric }\Gamma_\epsilon\text{ and odd }q, \\ 2\lceil q/2n \rceil & \text{for anti-centrally symmetric }\Gamma_\epsilon\text{ and even }q, \\ \lceil 2q/n \rceil & \text{for centrally symmetric }\Gamma_\epsilon\text{ and odd }q, \\ \lceil q/n \rceil & \text{otherwise.} \end{cases} \end{align*} $$
The idea behind this theorem is quite simple. For non-symmetric deformations, it suffices to check that
![]() $\zeta _m(t) \in T_{nm}[t]$
for
$\zeta _m(t) \in T_{nm}[t]$
for
![]() $m = 1,\ldots ,\chi -1$
, where
$m = 1,\ldots ,\chi -1$
, where
![]() $\zeta _m(t)$
are the functions introduced in Theorem 1.1. Symmetric deformations require to check that, in addition, those polynomials
$\zeta _m(t)$
are the functions introduced in Theorem 1.1. Symmetric deformations require to check that, in addition, those polynomials
![]() $\zeta _m(t)$
are
$\zeta _m(t)$
are
![]() $\pi $
-periodic or
$\pi $
-periodic or
![]() $\pi $
-anti-periodic.
$\pi $
-anti-periodic.
Polynomial deformations of the unit circle of degree
![]() $\le n$
can be defined without mentioning support functions. For instance, we can define them in Cartesian coordinates
$\le n$
can be defined without mentioning support functions. For instance, we can define them in Cartesian coordinates
![]() $(x,y)$
as
$(x,y)$
as
for some smooth function
![]() $P(x,y;\epsilon )$
of the form
$P(x,y;\epsilon )$
of the form
![]() $P(x,y;\epsilon ) \asymp 1 + \sum _{k \ge 1} \epsilon ^k P_k(x,y)$
as
$P(x,y;\epsilon ) \asymp 1 + \sum _{k \ge 1} \epsilon ^k P_k(x,y)$
as
![]() $\epsilon \to 0$
with
$\epsilon \to 0$
with
![]() $P_k(x,y) \in \mathbb {R}_{kn}[x,y]$
for all
$P_k(x,y) \in \mathbb {R}_{kn}[x,y]$
for all
![]() $k \ge 1$
. Alternatively, we can also define them in polar coordinates
$k \ge 1$
. Alternatively, we can also define them in polar coordinates
![]() $(r,\phi )$
as
$(r,\phi )$
as
for some smooth polar function
![]() $r(\phi ;\epsilon )$
of the form
$r(\phi ;\epsilon )$
of the form
![]() $r(\phi ;\epsilon ) \asymp 1 + \sum _{k\ge 1} \epsilon ^k r_k(\phi )$
as
$r(\phi ;\epsilon ) \asymp 1 + \sum _{k\ge 1} \epsilon ^k r_k(\phi )$
as
![]() $\epsilon \to 0$
with
$\epsilon \to 0$
with
![]() $r_k(\phi ) \in T_{kn}[\phi ]$
for all
$r_k(\phi ) \in T_{kn}[\phi ]$
for all
![]() $k \ge 1$
. The Cartesian setting was considered in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37] with
$k \ge 1$
. The Cartesian setting was considered in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37] with
![]() $P(x,y;\epsilon ) = 1 - \epsilon y^n$
. The polar setting was considered in [Reference Ramírez-Ros41] with
$P(x,y;\epsilon ) = 1 - \epsilon y^n$
. The polar setting was considered in [Reference Ramírez-Ros41] with
![]() $r(\phi ;\epsilon ) = 1 +\epsilon r_1(\phi ) + \mathrm {O} (\epsilon ^2)$
and in [Reference Zhang44] with
$r(\phi ;\epsilon ) = 1 +\epsilon r_1(\phi ) + \mathrm {O} (\epsilon ^2)$
and in [Reference Zhang44] with
![]() $r(\phi ;\epsilon ) = 1 +\epsilon r_1(\phi ) + \epsilon ^2 r_2(\phi ) + \mathrm {O} (\epsilon ^3)$
. Any deformation of the unit circle expressed in Cartesian coordinates as (4) for some
$r(\phi ;\epsilon ) = 1 +\epsilon r_1(\phi ) + \epsilon ^2 r_2(\phi ) + \mathrm {O} (\epsilon ^3)$
. Any deformation of the unit circle expressed in Cartesian coordinates as (4) for some
![]() $P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
with
$P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
with
![]() $P_1(x,y) \in \mathbb {R}_n[x,y]$
is a polynomial deformation of degree
$P_1(x,y) \in \mathbb {R}_n[x,y]$
is a polynomial deformation of degree
![]() $\le n$
in the sense of Definition 1.2 with
$\le n$
in the sense of Definition 1.2 with
![]() $h_1(\psi ) = \tfrac 12 P_1(\cos \psi ,\sin \psi )$
. See Lemma 5.2. We are interested in such deformations because we want to understand the numerical experiments discussed in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37]. However, for brevity, we omit the corresponding proofs for deformations written in polar coordinates or in Cartesian coordinates with more than the first-order term
$h_1(\psi ) = \tfrac 12 P_1(\cos \psi ,\sin \psi )$
. See Lemma 5.2. We are interested in such deformations because we want to understand the numerical experiments discussed in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37]. However, for brevity, we omit the corresponding proofs for deformations written in polar coordinates or in Cartesian coordinates with more than the first-order term
![]() $\epsilon P_1(x,y)$
. Such proofs are just a slew of boring computations based on the Taylor, multinomial, and Lagrange inversion theorems. We only stress that
$\epsilon P_1(x,y)$
. Such proofs are just a slew of boring computations based on the Taylor, multinomial, and Lagrange inversion theorems. We only stress that
![]() $h_1(\psi ) = r_1(\psi )$
, which justifies that the
$h_1(\psi ) = r_1(\psi )$
, which justifies that the
![]() $\mathrm {O} (\epsilon )$
-persistence result in Theorem 1.1 is just a reformulation of the main theorem in [Reference Ramírez-Ros41].
$\mathrm {O} (\epsilon )$
-persistence result in Theorem 1.1 is just a reformulation of the main theorem in [Reference Ramírez-Ros41].
The map
![]() $q \mapsto \chi (\Gamma _\epsilon ,q)$
is unbounded for any polynomial deformation
$q \mapsto \chi (\Gamma _\epsilon ,q)$
is unbounded for any polynomial deformation
![]() $\Gamma _\epsilon $
of degree
$\Gamma _\epsilon $
of degree
![]() $\le n$
, since
$\le n$
, since
![]() $\chi (\Gamma _\epsilon ,q) \asymp 2q/n$
as odd
$\chi (\Gamma _\epsilon ,q) \asymp 2q/n$
as odd
![]() $q \to +\infty $
for centrally symmetric deformations, and
$q \to +\infty $
for centrally symmetric deformations, and
![]() $\chi (\Gamma _\epsilon ,q) \asymp q/n$
as
$\chi (\Gamma _\epsilon ,q) \asymp q/n$
as
![]() $q \to +\infty $
otherwise. The experiments described in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37, Numerical Result 5], which cover degrees
$q \to +\infty $
otherwise. The experiments described in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37, Numerical Result 5], which cover degrees
![]() $3\le n\le 8$
and periods
$3\le n\le 8$
and periods
![]() $3\le q \le 100$
, suggest that none of the
$3\le q \le 100$
, suggest that none of the
![]() $p/q$
-resonant caustics
$p/q$
-resonant caustics
![]() $\mathrm {O} (\epsilon ^\chi )$
-persists under monomial deformations (4) with
$\mathrm {O} (\epsilon ^\chi )$
-persists under monomial deformations (4) with
![]() $P(x,y;\epsilon ) = 1 - \epsilon y^n$
and
$P(x,y;\epsilon ) = 1 - \epsilon y^n$
and
![]() $n \ge 3$
. Its proof requires to check that
$n \ge 3$
. Its proof requires to check that
![]() $\mu _{q\mathbb {Z}^\ast }\{h_\chi + \zeta _\chi \} \neq 0$
, which is a challenge. If
$\mu _{q\mathbb {Z}^\ast }\{h_\chi + \zeta _\chi \} \neq 0$
, which is a challenge. If
![]() $\Gamma _\epsilon $
is a polynomial deformation of the unit circle of degree
$\Gamma _\epsilon $
is a polynomial deformation of the unit circle of degree
![]() $\le n$
such that
$\le n$
such that
![]() $\mu _{q\mathbb {Z}^\ast }\{h_\chi + \zeta _\chi \} \neq 0$
for all
$\mu _{q\mathbb {Z}^\ast }\{h_\chi + \zeta _\chi \} \neq 0$
for all
![]() $p/q \in (0,1/2)$
, then
$p/q \in (0,1/2)$
, then
![]() $\Gamma _\epsilon $
would break all resonant caustics in such a way that there would be breakups of any order, because the map
$\Gamma _\epsilon $
would break all resonant caustics in such a way that there would be breakups of any order, because the map
![]() $q \mapsto \chi (\Gamma _\epsilon ,q) \in \mathbb {N}$
is exhaustive.
$q \mapsto \chi (\Gamma _\epsilon ,q) \in \mathbb {N}$
is exhaustive.
The paper is organized as follows. Section 2 begins with a description of the Bialy–Mironov generating function and ends with a list of necessary conditions for the existence of smooth convex resonant caustics in smooth strictly convex domains. The general notion of high-order persistence of convex resonant caustics in deformed smooth convex domains is presented in §3 and applied to deformed circles in §4, where Theorem 1.1 is proved. The results about polynomial deformations of circles, including Theorem 1.3, are presented in §5. Finally, we discuss three open problems: the co-preservation of resonant caustics with different rotation numbers, the convergence of a procedure to correct the original deformation to preserve a chosen resonant caustic, and the asymptotic measure of some exponentially small phenomena as the period q grows. See §6. Several technical proofs have been relegated to the appendices.
2 Existence of smooth convex resonant caustics
To begin with, we introduce coordinates in the space of oriented lines, define the support function and the billiard map of a convex domain, and describe the Bialy–Mironov generating function following [Reference Bialy and Tabachnikov10]. We also recall the periodic version of the variational principle for twist maps following [Reference Meiss38]. Next, we combine all those elements to find necessary conditions for the existence of smooth convex resonant caustics in Theorem 2.3. This part is inspired by the computations in [Reference Bialy and Tabachnikov10, Theorem 2.2] and the Lagrangian approach to the existence of rotational invariant curves (RICs) of twist maps described in [Reference Kaloshin and Zhang31, Reference Levi and Moser34]. Finally, we discuss five simple examples: circles, ellipses, constant width curves, Gutkin billiard tables (also called constant angle curves), and centrally symmetric curves with
![]() $1/4$
-resonant caustics.
$1/4$
-resonant caustics.
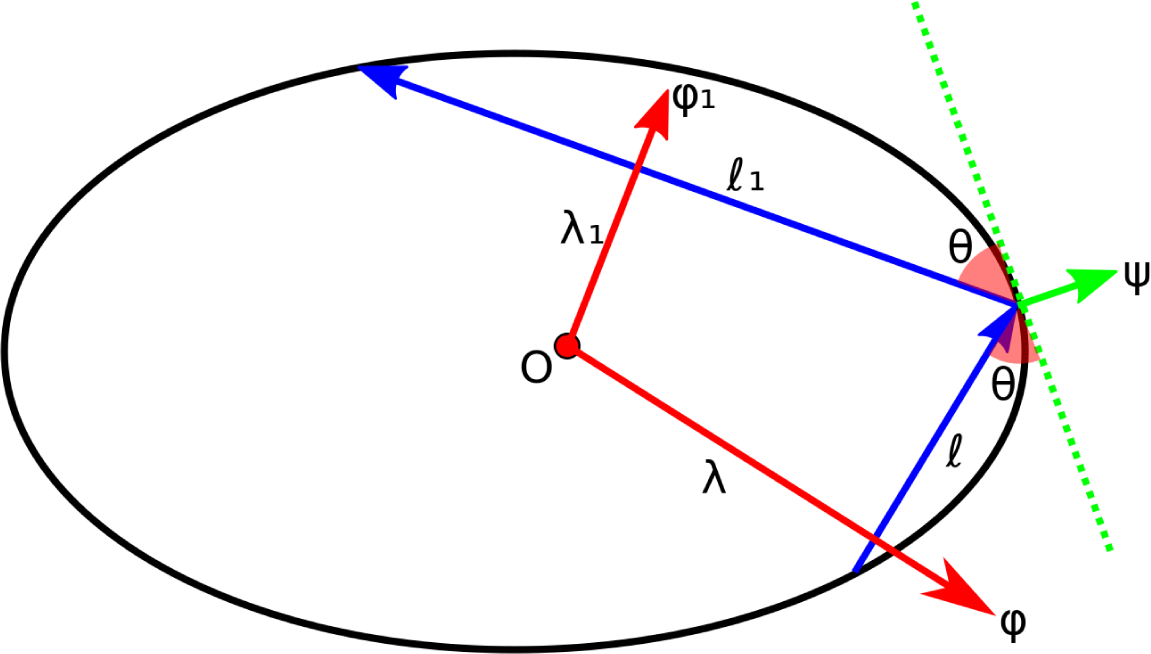
The billiard dynamics acts on the subset of oriented lines (rays) that intersect the boundary of the convex domain. An oriented line
![]() $\ell $
can be written as
$\ell $
can be written as
where
![]() $\varphi \in \mathbb {T} := \mathbb {R}/2\pi \mathbb {Z}$
is the direction of the right normal to the oriented line and
$\varphi \in \mathbb {T} := \mathbb {R}/2\pi \mathbb {Z}$
is the direction of the right normal to the oriented line and
![]() $\unicode{x3bb} \in \mathbb {R}$
is the signed distance to the origin. Thus,
$\unicode{x3bb} \in \mathbb {R}$
is the signed distance to the origin. Thus,
![]() $(\varphi ,\unicode{x3bb} ) \in \mathbb {A} := \mathbb {T} \times \mathbb {R}$
are coordinates in the space of oriented lines, which is topologically a cylinder.
$(\varphi ,\unicode{x3bb} ) \in \mathbb {A} := \mathbb {T} \times \mathbb {R}$
are coordinates in the space of oriented lines, which is topologically a cylinder.
Let
![]() $\Gamma $
be a smooth strictly convex closed curve of
$\Gamma $
be a smooth strictly convex closed curve of
![]() $\mathbb {R}^2$
. We fix its counterclockwise orientation and assume its interior contains the origin O, so there is a positive smooth
$\mathbb {R}^2$
. We fix its counterclockwise orientation and assume its interior contains the origin O, so there is a positive smooth
![]() $2\pi $
-periodic function
$2\pi $
-periodic function
![]() $h(\varphi )$
, called the support function of
$h(\varphi )$
, called the support function of
![]() $\Gamma $
, such that
$\Gamma $
, such that
![]() $\{ \unicode{x3bb} = h(\varphi ) \}$
and
$\{ \unicode{x3bb} = h(\varphi ) \}$
and
![]() $\{ \unicode{x3bb} = -h(\varphi +\pi ) \}$
are the 1-parameter families of oriented lines positively and negatively tangent to
$\{ \unicode{x3bb} = -h(\varphi +\pi ) \}$
are the 1-parameter families of oriented lines positively and negatively tangent to
![]() $\Gamma $
. Then,
$\Gamma $
. Then,
is a parameterization of
![]() $\Gamma $
, where
$\Gamma $
, where
![]() $\varphi \in \mathbb {T}$
is the counterclockwise angle between the positive x-axis and the outer normal to
$\varphi \in \mathbb {T}$
is the counterclockwise angle between the positive x-axis and the outer normal to
![]() $\Gamma $
at the point
$\Gamma $
at the point
![]() $z(\varphi )$
.
$z(\varphi )$
.
The space of the oriented lines that intersect the interior of
![]() $\Gamma $
is the open cylinder
$\Gamma $
is the open cylinder
and the billiard map
![]() $f: \mathbb {A}_\Gamma \to \mathbb {A}_\Gamma $
acts by the reflection law in
$f: \mathbb {A}_\Gamma \to \mathbb {A}_\Gamma $
acts by the reflection law in
![]() $\Gamma $
. That is,
$\Gamma $
. That is,
![]() $f(\varphi ,\unicode{x3bb} ) = (\varphi _1,\unicode{x3bb} _1)$
means that the oriented line
$f(\varphi ,\unicode{x3bb} ) = (\varphi _1,\unicode{x3bb} _1)$
means that the oriented line
![]() $\ell _1$
with coordinates
$\ell _1$
with coordinates
![]() $(\varphi _1,\unicode{x3bb} _1)$
is the reflection of the oriented line
$(\varphi _1,\unicode{x3bb} _1)$
is the reflection of the oriented line
![]() $\ell $
with coordinates
$\ell $
with coordinates
![]() $(\varphi ,\unicode{x3bb} )$
with respect to the tangent to
$(\varphi ,\unicode{x3bb} )$
with respect to the tangent to
![]() $\Gamma $
at the second intersection of
$\Gamma $
at the second intersection of
![]() $\ell $
with
$\ell $
with
![]() $\Gamma $
. See Figure 1. The shocking discovery by Bialy and Mironov was that the billiard map f is an exact twist map with generating function
$\Gamma $
. See Figure 1. The shocking discovery by Bialy and Mironov was that the billiard map f is an exact twist map with generating function
To be precise,
![]() $\unicode{x3bb} _1 \,\mathit {d} \varphi _1 - \unicode{x3bb} \,\mathit {d} \varphi = f^* (\unicode{x3bb} \,\mathit {d} \varphi ) - \unicode{x3bb} \,\mathit {d} \varphi = \,\mathit {d} S$
, so
$\unicode{x3bb} _1 \,\mathit {d} \varphi _1 - \unicode{x3bb} \,\mathit {d} \varphi = f^* (\unicode{x3bb} \,\mathit {d} \varphi ) - \unicode{x3bb} \,\mathit {d} \varphi = \,\mathit {d} S$
, so
 $$ \begin{align} f(\varphi,\unicode{x3bb}) = (\varphi_1,\unicode{x3bb}_1) \Leftrightarrow \begin{cases} \unicode{x3bb} = -\partial_1 S(\varphi,\varphi_1) = h(\psi) \cos \theta - h'(\psi) \sin \theta, \\ \unicode{x3bb}_1 = \partial_2 S(\varphi,\varphi_1) = h(\psi) \cos \theta + h'(\psi) \sin \theta, \end{cases} \end{align} $$
$$ \begin{align} f(\varphi,\unicode{x3bb}) = (\varphi_1,\unicode{x3bb}_1) \Leftrightarrow \begin{cases} \unicode{x3bb} = -\partial_1 S(\varphi,\varphi_1) = h(\psi) \cos \theta - h'(\psi) \sin \theta, \\ \unicode{x3bb}_1 = \partial_2 S(\varphi,\varphi_1) = h(\psi) \cos \theta + h'(\psi) \sin \theta, \end{cases} \end{align} $$
and f preserves the standard area form
![]() $\mathit {d} \varphi \wedge \,\mathit {d} \unicode{x3bb} $
. See, for instance, [Reference Bialy and Tabachnikov10, Proposition 2.1]. Here,
$\mathit {d} \varphi \wedge \,\mathit {d} \unicode{x3bb} $
. See, for instance, [Reference Bialy and Tabachnikov10, Proposition 2.1]. Here,
![]() $\partial _i S$
denotes the derivative with respect to the ith variable. The strict convexity of
$\partial _i S$
denotes the derivative with respect to the ith variable. The strict convexity of
![]() $\Gamma $
implies the twist condition:
$\Gamma $
implies the twist condition:
![]() $\partial _{12}S(\varphi ,\varphi _1) = \tfrac 12 \rho (\psi )\sin \theta> 0$
, where
$\partial _{12}S(\varphi ,\varphi _1) = \tfrac 12 \rho (\psi )\sin \theta> 0$
, where
![]() ${\rho (\psi ) = h"(\psi ) + h( \psi )}$
is the radius of curvature of
${\rho (\psi ) = h"(\psi ) + h( \psi )}$
is the radius of curvature of
![]() $\Gamma $
at the point
$\Gamma $
at the point
![]() $z(\psi )$
.
$z(\psi )$
.

Figure 1 The billiard map
![]() $f(\varphi ,\unicode{x3bb} ) = (\varphi _1,\unicode{x3bb} _1)$
, the normal angle
$f(\varphi ,\unicode{x3bb} ) = (\varphi _1,\unicode{x3bb} _1)$
, the normal angle
![]() $\psi = (\varphi _1 + \varphi )/2$
, and the incidence–reflection angle
$\psi = (\varphi _1 + \varphi )/2$
, and the incidence–reflection angle
![]() $\theta = (\varphi _1 - \varphi )/2$
.
$\theta = (\varphi _1 - \varphi )/2$
.
We say that
![]() $\psi \in \mathbb {T}$
and
$\psi \in \mathbb {T}$
and
![]() $\theta \in (0,\pi )$
are the normal angle and the angle of incidence/reflection at each impact point, whereas
$\theta \in (0,\pi )$
are the normal angle and the angle of incidence/reflection at each impact point, whereas
![]() $\varphi \in \mathbb {T}$
is the side angle. We consider
$\varphi \in \mathbb {T}$
is the side angle. We consider
![]() $S(\varphi ,\varphi _1)$
defined on the universal cover
$S(\varphi ,\varphi _1)$
defined on the universal cover
![]() $\{ (\varphi ,\varphi _1) \in \mathbb {R}^2 : \varphi < \varphi _1 < \varphi + 2\pi \}$
because
$\{ (\varphi ,\varphi _1) \in \mathbb {R}^2 : \varphi < \varphi _1 < \varphi + 2\pi \}$
because
![]() ${S(\varphi +2\pi ,\varphi _1+2\pi ) = S(\varphi ,\varphi _1)}$
.
${S(\varphi +2\pi ,\varphi _1+2\pi ) = S(\varphi ,\varphi _1)}$
.
Let us briefly recall the classical variational principle for exact twists maps. The interested reader can find more details in [Reference Meiss38, §V]. We will introduce several operators which are not standard in the variational approach, but they simplify computations and shorten formulas.
Given any sequence
![]() $\{a_j\}$
, we consider the shift, sum, difference, and q-average operators
$\{a_j\}$
, we consider the shift, sum, difference, and q-average operators
For simplicity, we omit the dependence of
![]() $\mu $
on q and we just say that
$\mu $
on q and we just say that
![]() $\mu $
is the average operator.
$\mu $
is the average operator.
Let
![]() $p/q \in (0,1)$
be a rational number with
$p/q \in (0,1)$
be a rational number with
![]() $\gcd (p,q) = 1$
. We call the elements of the space
$\gcd (p,q) = 1$
. We call the elements of the space
![]() $p/q$
-periodic sequences. We define the
$p/q$
-periodic sequences. We define the
![]() $p/q$
-periodic action
$p/q$
-periodic action
![]() $A: X \to \mathbb {R}$
as
$A: X \to \mathbb {R}$
as
 $$ \begin{align*} A\{ \varphi_j \} = \sum_{j=0}^{q-1} S(\varphi_j,\varphi_{j+1}) = 2 \sum_{j=0}^{q-1} h(\psi_j) \sin \theta_j, \end{align*} $$
$$ \begin{align*} A\{ \varphi_j \} = \sum_{j=0}^{q-1} S(\varphi_j,\varphi_{j+1}) = 2 \sum_{j=0}^{q-1} h(\psi_j) \sin \theta_j, \end{align*} $$
where
![]() $\psi _j = \sigma \{ \varphi _j \}/2$
and
$\psi _j = \sigma \{ \varphi _j \}/2$
and
![]() $\theta _j = \delta \{ \varphi _j \}/2$
. Periodicities
$\theta _j = \delta \{ \varphi _j \}/2$
. Periodicities
![]() $\varphi _{j+q} = \varphi _j + 2\pi p$
,
$\varphi _{j+q} = \varphi _j + 2\pi p$
,
![]() $\psi _{j+q} = \psi _j + 2\pi p$
, and
$\psi _{j+q} = \psi _j + 2\pi p$
, and
![]() $\theta _{j+q} = \theta _j$
imply that
$\theta _{j+q} = \theta _j$
imply that
![]() $\mu \{ S(\varphi _{j_0+j},\varphi _{j_0+j+1}) \} = 2\mu \{ h(\psi _{j_0+j}) \sin \theta _{j_0+j} \} = A\{ \varphi _j \}/q$
for all
$\mu \{ S(\varphi _{j_0+j},\varphi _{j_0+j+1}) \} = 2\mu \{ h(\psi _{j_0+j}) \sin \theta _{j_0+j} \} = A\{ \varphi _j \}/q$
for all
![]() $j_0 \in \mathbb {Z}$
. Critical points of the action, which we call
$j_0 \in \mathbb {Z}$
. Critical points of the action, which we call
![]() $p/q$
-periodic configurations, can be lifted to full
$p/q$
-periodic configurations, can be lifted to full
![]() $p/q$
-periodic orbits of the billiard map f by taking
$p/q$
-periodic orbits of the billiard map f by taking
![]() $\unicode{x3bb} _j = -\partial _1 S(\varphi _j,\varphi _{j+1}) = \partial _2 S(\varphi _{j-1},\varphi _j)$
. Thus, any
$\unicode{x3bb} _j = -\partial _1 S(\varphi _j,\varphi _{j+1}) = \partial _2 S(\varphi _{j-1},\varphi _j)$
. Thus, any
![]() $p/q$
-periodic configuration defines a
$p/q$
-periodic configuration defines a
![]() $p/q$
-periodic billiard trajectory inside
$p/q$
-periodic billiard trajectory inside
![]() $\Gamma $
with side angles
$\Gamma $
with side angles
![]() $\varphi _j$
, normal angles
$\varphi _j$
, normal angles
![]() $\psi _j = \sigma \{ \varphi _j \}/2$
, and incidence–reflection angles
$\psi _j = \sigma \{ \varphi _j \}/2$
, and incidence–reflection angles
![]() $\theta _j = \delta \{ \varphi _j \}/2$
.
$\theta _j = \delta \{ \varphi _j \}/2$
.
We characterize such configurations in the next proposition, where we also recall a formula for the length of their corresponding periodic billiard trajectories.
Proposition 2.1. A
![]() $p/q$
-periodic sequence
$p/q$
-periodic sequence
![]() $\{ \varphi _j \}$
is a
$\{ \varphi _j \}$
is a
![]() $p/q$
-periodic configuration if and only if
$p/q$
-periodic configuration if and only if
where
![]() $\psi _j = \sigma \{ \varphi _j \}/2$
and
$\psi _j = \sigma \{ \varphi _j \}/2$
and
![]() $\theta _j = \delta \{ \varphi _j \}/2$
, in which case,
$\theta _j = \delta \{ \varphi _j \}/2$
, in which case,
where L is the length of the
![]() $p/q$
-periodic configuration
$p/q$
-periodic configuration
![]() $\{ \varphi _j \}$
.
$\{ \varphi _j \}$
.
Proof. A
![]() $p/q$
-periodic sequence
$p/q$
-periodic sequence
![]() $\{ \varphi _j \}$
is a critical point of the action if and only if
$\{ \varphi _j \}$
is a critical point of the action if and only if
for all
![]() $j \in \mathbb {Z}$
. The first equality above follows from
$j \in \mathbb {Z}$
. The first equality above follows from
![]() $S(\varphi _j,\varphi _{j+1}) = 2 h(\psi _j) \sin \theta _j$
, and relations
$S(\varphi _j,\varphi _{j+1}) = 2 h(\psi _j) \sin \theta _j$
, and relations
![]() $\psi _j = \sigma \{ \varphi _j \}/2 = (\varphi _{j+1} + \varphi _j)/2$
and
$\psi _j = \sigma \{ \varphi _j \}/2 = (\varphi _{j+1} + \varphi _j)/2$
and
![]() $\theta _j = \delta \{ \varphi _j \}/2 = (\varphi _{j+1} - \varphi _j)/2$
.
$\theta _j = \delta \{ \varphi _j \}/2 = (\varphi _{j+1} - \varphi _j)/2$
.
Identities
![]() $2q \mu \big \{ h(\psi _j) \sin \theta _j \big \} = L$
and
$2q \mu \big \{ h(\psi _j) \sin \theta _j \big \} = L$
and
![]() $\mu \{ h'(\psi _j) \sin \theta _j \} = 0$
are proved in [Reference Bialy and Tabachnikov10, Theorem 2.2]. By q-periodicity of
$\mu \{ h'(\psi _j) \sin \theta _j \} = 0$
are proved in [Reference Bialy and Tabachnikov10, Theorem 2.2]. By q-periodicity of
![]() $\{\theta _j\}$
, we get
$\{\theta _j\}$
, we get
 $$ \begin{align*} \mu \{ \theta_j \} &= \frac{1}{q} \sum_{i=0}^{q-1} \theta_{j+i} = \frac{1}{q} \sum_{i=0}^{q-1} \frac{\theta_{j+i} + \theta_{j+i+1}}{2} = \frac{1}{q} \sum_{i=0}^{q-1} \frac{\psi_{j+i+1} - \psi_{j+i}}{2}\\& = \frac{\psi_{j+q} - \psi_j}{2q} = \frac{\pi p}{q}.\\[-41pt] \end{align*} $$
$$ \begin{align*} \mu \{ \theta_j \} &= \frac{1}{q} \sum_{i=0}^{q-1} \theta_{j+i} = \frac{1}{q} \sum_{i=0}^{q-1} \frac{\theta_{j+i} + \theta_{j+i+1}}{2} = \frac{1}{q} \sum_{i=0}^{q-1} \frac{\psi_{j+i+1} - \psi_{j+i}}{2}\\& = \frac{\psi_{j+q} - \psi_j}{2q} = \frac{\pi p}{q}.\\[-41pt] \end{align*} $$
We look for necessary conditions for the existence of convex resonant caustics inside
![]() $\Gamma $
. Tangent lines to such a caustic can be counterclockwise or clockwise oriented. We fix the counterclockwise orientation, so we assume that
$\Gamma $
. Tangent lines to such a caustic can be counterclockwise or clockwise oriented. We fix the counterclockwise orientation, so we assume that
![]() $p/q < 1/2$
from now on. Any
$p/q < 1/2$
from now on. Any
![]() $p/q$
-resonant convex caustic gives rise to a 1-parameter family of
$p/q$
-resonant convex caustic gives rise to a 1-parameter family of
![]() $p/q$
-periodic orbits of the billiard map. We want to parameterize this family using a dynamical parameter
$p/q$
-periodic orbits of the billiard map. We want to parameterize this family using a dynamical parameter
![]() $t \in \mathbb {R}$
in which the billiard map acts as the constant shift
$t \in \mathbb {R}$
in which the billiard map acts as the constant shift
![]() $t \mapsto t + \omega $
with angular frequency
$t \mapsto t + \omega $
with angular frequency
![]() $\omega = 2\pi p/q$
. The dynamical parameter is not unique. If
$\omega = 2\pi p/q$
. The dynamical parameter is not unique. If
![]() $a(t)$
is any smooth
$a(t)$
is any smooth
![]() $\omega $
-periodic function such that
$\omega $
-periodic function such that
![]() $1 + a'(t)> 0$
, then
$1 + a'(t)> 0$
, then
![]() $s = t + a(t)$
is another dynamical parameter.
$s = t + a(t)$
is another dynamical parameter.
Let us stress the three main differences between this setting, where we deal with functions of a continuous variable
![]() $t \in \mathbb {R}$
, and the previous setting, where we had sequences whose elements are labeled by a discrete index
$t \in \mathbb {R}$
, and the previous setting, where we had sequences whose elements are labeled by a discrete index
![]() $k \in \mathbb {Z}$
.
$k \in \mathbb {Z}$
.
First, we define the shift, sum, difference, and average operators as
and
![]() $\mu \{ a(t) \} = ({1}/{q}) \sum _{j=0}^{q-1} a(t + j \omega )$
. These operators diagonalize in the Fourier basis. Operator
$\mu \{ a(t) \} = ({1}/{q}) \sum _{j=0}^{q-1} a(t + j \omega )$
. These operators diagonalize in the Fourier basis. Operator
![]() $\mu $
is the projection onto the resonant
$\mu $
is the projection onto the resonant
![]() $q\mathbb {Z}$
-harmonics:
$q\mathbb {Z}$
-harmonics:
![]() $\mu = \mu _{q\mathbb {Z}}$
, but we omit the
$\mu = \mu _{q\mathbb {Z}}$
, but we omit the
![]() $q\mathbb {Z}$
subscript for simplicity. Both claims are proved in Appendix A.
$q\mathbb {Z}$
subscript for simplicity. Both claims are proved in Appendix A.
Second, we define the
![]() $p/q$
-periodic action of a side function
$p/q$
-periodic action of a side function
![]() $\varphi (t)$
as
$\varphi (t)$
as
where
![]() $\varphi (t)$
, the normal function
$\varphi (t)$
, the normal function
![]() $\psi (t)$
, and the incidence-reflection function
$\psi (t)$
, and the incidence-reflection function
![]() $\theta (t)$
are related by
$\theta (t)$
are related by
We ask functions
![]() $\varphi (t) - t$
,
$\varphi (t) - t$
,
![]() $\psi (t) - t$
, and
$\psi (t) - t$
, and
![]() $\theta (t)$
to be
$\theta (t)$
to be
![]() $2\pi $
-periodic, as a continuous analogue of the discrete periodicity conditions
$2\pi $
-periodic, as a continuous analogue of the discrete periodicity conditions
![]() $\varphi _{j+q} = \varphi _j + 2\pi p$
,
$\varphi _{j+q} = \varphi _j + 2\pi p$
,
![]() $\psi _{j+q} = \psi _j + 2\pi p$
, and
$\psi _{j+q} = \psi _j + 2\pi p$
, and
![]() ${\theta _{j+q} = \theta _j}$
. Hence, they are lifts of some functions
${\theta _{j+q} = \theta _j}$
. Hence, they are lifts of some functions
![]() $\varphi ,\psi : \mathbb {T} \to \mathbb {T}$
and
$\varphi ,\psi : \mathbb {T} \to \mathbb {T}$
and
![]() $\theta : \mathbb {T} \to \mathbb {R}$
. To simplify the exposition, we sometimes abuse the notation, and use the same symbol for an object and its lift. Other times, we denote lifts with a tilde. We also ask that
$\theta : \mathbb {T} \to \mathbb {R}$
. To simplify the exposition, we sometimes abuse the notation, and use the same symbol for an object and its lift. Other times, we denote lifts with a tilde. We also ask that
![]() $\varphi '(t)> 0$
, so that
$\varphi '(t)> 0$
, so that
![]() $\varphi :\mathbb {R} \to \mathbb {R}$
can be inverted.
$\varphi :\mathbb {R} \to \mathbb {R}$
can be inverted.
Third, condition
![]() $\sigma \{ h'(\psi _j) \sin \theta _j \} - \delta \{ h(\psi _j) \cos \theta _j \} = 0$
becomes the difference equation
$\sigma \{ h'(\psi _j) \sin \theta _j \} - \delta \{ h(\psi _j) \cos \theta _j \} = 0$
becomes the difference equation
Remark 2.2. Relations (6) are redundant, but we have listed all of them for future references. They can be used to determine all three functions
![]() $\varphi (t)$
,
$\varphi (t)$
,
![]() $\psi (t)$
, and
$\psi (t)$
, and
![]() $\theta (t)$
from any one of them. Usually, we will determine
$\theta (t)$
from any one of them. Usually, we will determine
![]() $\varphi (t)$
and
$\varphi (t)$
and
![]() $\psi (t)$
from
$\psi (t)$
from
![]() $\theta (t)$
. If
$\theta (t)$
. If
![]() $\theta (t)$
is a smooth
$\theta (t)$
is a smooth
![]() $2\pi $
-periodic function such that
$2\pi $
-periodic function such that
![]() $\mu \{ \theta \} = \omega /2$
, then there is a unique smooth
$\mu \{ \theta \} = \omega /2$
, then there is a unique smooth
![]() $2\pi $
-periodic function
$2\pi $
-periodic function
![]() $\varphi (t)-t$
such that
$\varphi (t)-t$
such that
![]() $\delta \{ \varphi \} = 2\theta $
and
$\delta \{ \varphi \} = 2\theta $
and
![]() $\mu \{ t - \varphi \} = \omega /2$
. See Lemma A.2 in Appendix A for a proof. Then,
$\mu \{ t - \varphi \} = \omega /2$
. See Lemma A.2 in Appendix A for a proof. Then,
![]() $\psi = \varphi + \theta $
implies that
$\psi = \varphi + \theta $
implies that
![]() $\psi = \sigma \{ \varphi \}/2$
and
$\psi = \sigma \{ \varphi \}/2$
and
![]() $\mu \{ \psi - t \} = 0$
.
$\mu \{ \psi - t \} = 0$
.
Theorem 2.3. Let
![]() $p/q \in (0,1/2)$
be any rational rotational number with
$p/q \in (0,1/2)$
be any rational rotational number with
![]() ${\gcd (p,q) = 1}$
. If there is a smooth convex
${\gcd (p,q) = 1}$
. If there is a smooth convex
![]() $p/q$
-resonant caustic inside
$p/q$
-resonant caustic inside
![]() $\Gamma $
, the following necessary conditions hold.
$\Gamma $
, the following necessary conditions hold.
-
(f) There are three smooth
 $2\pi $
-periodic functions
$2\pi $
-periodic functions
 $\varphi (t) - t$
,
$\varphi (t) - t$
,
 $\psi (t) - t$
, and
$\psi (t) - t$
, and
 $\theta (t)$
related by (6) that satisfy the difference equation (7). In addition,
$\theta (t)$
related by (6) that satisfy the difference equation (7). In addition,
 $\varphi '(t)> 0$
.
$\varphi '(t)> 0$
. -
(p) There is a smooth parameterization
 $c:\mathbb {T} \to \mathbb {A}_\Gamma $
such that
$c:\mathbb {T} \to \mathbb {A}_\Gamma $
such that
 $G = c(\mathbb {T})$
is a graph and
$G = c(\mathbb {T})$
is a graph and
 $f(c(t)) = c(t+\omega )$
.
$f(c(t)) = c(t+\omega )$
. -
(a) The
 $p/q$
-periodic action is constant on the side function:
$p/q$
-periodic action is constant on the side function:
 $A\{\varphi (t)\} = L$
, where L is the length of all
$A\{\varphi (t)\} = L$
, where L is the length of all
 $p/q$
-periodic billiard trajectories in
$p/q$
-periodic billiard trajectories in
 $\Gamma $
.
$\Gamma $
.
Proof. (f) Let
![]() $g(\varphi )$
be the smooth support function of the
$g(\varphi )$
be the smooth support function of the
![]() $p/q$
-resonant caustic. Set
$p/q$
-resonant caustic. Set
The caustic is inside
![]() $\Gamma $
, so
$\Gamma $
, so
![]() $G \subset \mathbb {A}_\Gamma $
. Clearly, G is f-invariant, so
$G \subset \mathbb {A}_\Gamma $
. Clearly, G is f-invariant, so
![]() $f|_G$
defines a smooth preserving orientation circle diffeomorphism
$f|_G$
defines a smooth preserving orientation circle diffeomorphism
![]() $r: \mathbb {T} \to \mathbb {T}$
such that
$r: \mathbb {T} \to \mathbb {T}$
such that
where
![]() $\tilde {f}:\tilde {\mathbb {A}}_\Gamma \to \tilde {\mathbb {A}}_\Gamma $
,
$\tilde {f}:\tilde {\mathbb {A}}_\Gamma \to \tilde {\mathbb {A}}_\Gamma $
,
![]() $\tilde {g}:\mathbb {R} \to \mathbb {R}$
, and
$\tilde {g}:\mathbb {R} \to \mathbb {R}$
, and
![]() $\tilde {r}:\mathbb {R} \to \mathbb {R}$
are the corresponding lifts. Identity
$\tilde {r}:\mathbb {R} \to \mathbb {R}$
are the corresponding lifts. Identity
![]() $\tilde {r}^q(\varphi ) = \varphi + q\omega $
is the key. It follows from the definition of
$\tilde {r}^q(\varphi ) = \varphi + q\omega $
is the key. It follows from the definition of
![]() $p/q$
-resonant caustic. It implies that
$p/q$
-resonant caustic. It implies that
![]() $\varphi \mapsto \tilde {r}(\varphi )$
becomes the constant shift
$\varphi \mapsto \tilde {r}(\varphi )$
becomes the constant shift
![]() $t \mapsto t +\omega $
in the smooth parameter
$t \mapsto t +\omega $
in the smooth parameter
 $$ \begin{align*} t = \tilde{s}(\varphi) := \frac{1}{q} \sum_{j=0}^{q-1} ( \tilde{r}^j(\varphi) - j \omega ). \end{align*} $$
$$ \begin{align*} t = \tilde{s}(\varphi) := \frac{1}{q} \sum_{j=0}^{q-1} ( \tilde{r}^j(\varphi) - j \omega ). \end{align*} $$
Inversion of
![]() $\tilde {s}(\varphi (t)) = t$
defines a smooth function such that
$\tilde {s}(\varphi (t)) = t$
defines a smooth function such that
![]() $\varphi '(t)> 0$
,
$\varphi '(t)> 0$
,
![]() $\varphi (t) - t$
is
$\varphi (t) - t$
is
![]() $2\pi $
-periodic, and any sequence
$2\pi $
-periodic, and any sequence
![]() $\{ \varphi (t + j\omega ) \}$
,
$\{ \varphi (t + j\omega ) \}$
,
![]() $t \in \mathbb {R}$
, is a
$t \in \mathbb {R}$
, is a
![]() $p/q$
-periodic configuration of f. Then, Proposition 2.1 implies that the normal function
$p/q$
-periodic configuration of f. Then, Proposition 2.1 implies that the normal function
![]() $\psi (t)$
and the incidence–reflection function
$\psi (t)$
and the incidence–reflection function
![]() $\theta (t)$
obtained from
$\theta (t)$
obtained from
![]() $\varphi (t)$
by relations (6) satisfy the difference equation (7).
$\varphi (t)$
by relations (6) satisfy the difference equation (7).
(p) We define
Since
![]() $\varphi (t) - t$
and
$\varphi (t) - t$
and
![]() $\unicode{x3bb} (t)$
are
$\unicode{x3bb} (t)$
are
![]() $2\pi $
-periodic, the map
$2\pi $
-periodic, the map
![]() $c = (\varphi ,\unicode{x3bb} ) : \mathbb {R} \to \mathbb {R}^2$
can be projected to a map from
$c = (\varphi ,\unicode{x3bb} ) : \mathbb {R} \to \mathbb {R}^2$
can be projected to a map from
![]() $\mathbb {T}$
to
$\mathbb {T}$
to
![]() $\mathbb {A}$
. Since
$\mathbb {A}$
. Since
![]() $g(\varphi )$
is the support function of the caustic, we get that
$g(\varphi )$
is the support function of the caustic, we get that
![]() $\unicode{x3bb} (t) = g(\varphi (t))$
and
$\unicode{x3bb} (t) = g(\varphi (t))$
and
![]() $c(\mathbb {T}) = G \subset \mathbb {A}_\Gamma $
. Condition
$c(\mathbb {T}) = G \subset \mathbb {A}_\Gamma $
. Condition
![]() $\varphi '(t)> 0$
implies that
$\varphi '(t)> 0$
implies that
![]() $c'(t) \neq (0,0)$
, so
$c'(t) \neq (0,0)$
, so
![]() $c:\mathbb {T} \to G$
is a parameterization. Implicit equations (5) imply
$c:\mathbb {T} \to G$
is a parameterization. Implicit equations (5) imply
![]() $f(c(t)) = c(t+\omega )$
.
$f(c(t)) = c(t+\omega )$
.
(a) The
![]() $p/q$
-periodic sequences
$p/q$
-periodic sequences
![]() $\{ \varphi (t + j\omega ) \}_{j \in \mathbb {Z}}$
form a
$\{ \varphi (t + j\omega ) \}_{j \in \mathbb {Z}}$
form a
![]() $1$
-parameter family of critical points of the
$1$
-parameter family of critical points of the
![]() $p/q$
-periodic action, with
$p/q$
-periodic action, with
![]() $t \in \mathbb {R}$
a smooth parameter. Therefore, the action is constant on this
$t \in \mathbb {R}$
a smooth parameter. Therefore, the action is constant on this
![]() $1$
-parameter family. That is, all periodic billiard trajectories tangent to the
$1$
-parameter family. That is, all periodic billiard trajectories tangent to the
![]() $p/q$
-resonant caustic have the same length.
$p/q$
-resonant caustic have the same length.
Remark 2.4. If these three necessary conditions hold, then
![]() $\mu \{ h' \circ \psi \cdot \sin \theta \} = 0$
. This relation follows by applying operator
$\mu \{ h' \circ \psi \cdot \sin \theta \} = 0$
. This relation follows by applying operator
![]() $\mu $
to (7), since
$\mu $
to (7), since
![]() $\mu \circ \sigma = 2\mu $
and
$\mu \circ \sigma = 2\mu $
and
![]() $\mu \circ \delta = 0$
on the space of smooth
$\mu \circ \delta = 0$
on the space of smooth
![]() $2\pi $
-periodic functions.
$2\pi $
-periodic functions.
To provide a first insight into the usefulness of condition (f) in Theorem 2.3, let us give some information about functions
![]() $\varphi (t)$
,
$\varphi (t)$
,
![]() $\psi (t)$
, and
$\psi (t)$
, and
![]() $\theta (t)$
in five examples.
$\theta (t)$
in five examples.
Example 2.5. The simplest example is the completely integrable circular billiard. If
![]() $\Gamma $
is a circle of radius one centered at the origin, then
$\Gamma $
is a circle of radius one centered at the origin, then
![]() $h(\psi ) \equiv 1$
, so
$h(\psi ) \equiv 1$
, so
![]() $\mathbb {A}_\Gamma = \mathbb {T} \times (-1,1)$
and the billiard map
$\mathbb {A}_\Gamma = \mathbb {T} \times (-1,1)$
and the billiard map
![]() $f:\mathbb {A}_\Gamma \to \mathbb {A}_\Gamma $
is given by
$f:\mathbb {A}_\Gamma \to \mathbb {A}_\Gamma $
is given by
![]() $f(\varphi ,\unicode{x3bb} ) = (\varphi + \varpi (\unicode{x3bb} ),\unicode{x3bb} )$
with
$f(\varphi ,\unicode{x3bb} ) = (\varphi + \varpi (\unicode{x3bb} ),\unicode{x3bb} )$
with
![]() $\varpi (\unicode{x3bb} ) = 2 \arccos \unicode{x3bb} $
. In particular, we can take
$\varpi (\unicode{x3bb} ) = 2 \arccos \unicode{x3bb} $
. In particular, we can take
![]() $\varphi (t) = t - \omega /2$
,
$\varphi (t) = t - \omega /2$
,
![]() $\psi (t) = t$
,
$\psi (t) = t$
,
![]() $\theta (t) \equiv \omega /2$
,
$\theta (t) \equiv \omega /2$
,
![]() $\omega = 2 \pi p/q$
, and
$\omega = 2 \pi p/q$
, and
![]() $L = 2 q \sin (\omega /2)$
for any
$L = 2 q \sin (\omega /2)$
for any
![]() $p/q \in (0,1/2)$
. Straightforward computations show that these functions satisfy condition (f).
$p/q \in (0,1/2)$
. Straightforward computations show that these functions satisfy condition (f).
Example 2.6. Elliptic billiards are integrable too, but their computations are harder. If
![]() $\Gamma $
is the ellipse
$\Gamma $
is the ellipse
![]() $\{ x^2/a^2 + y^2/b^2 = 1\}$
, then
$\{ x^2/a^2 + y^2/b^2 = 1\}$
, then
![]() $h(\psi ) = \sqrt {a^2 \cos ^2 \psi + b^2 \sin ^2 \psi }$
; see [Reference Bialy5, Lemma 1]. The explicit expression of
$h(\psi ) = \sqrt {a^2 \cos ^2 \psi + b^2 \sin ^2 \psi }$
; see [Reference Bialy5, Lemma 1]. The explicit expression of
![]() $\varphi (t)$
,
$\varphi (t)$
,
![]() $\psi (t)$
, and
$\psi (t)$
, and
![]() $\theta (t)$
as functions of a dynamical parameter t requires the use of elliptic functions whose modulus depends on the eccentricity of the ellipse and the rotation number
$\theta (t)$
as functions of a dynamical parameter t requires the use of elliptic functions whose modulus depends on the eccentricity of the ellipse and the rotation number
![]() $p/q$
of each resonant caustic. See [Reference Bialy5, Reference Damasceno, Dias Carneiro and Ramírez-Ros17, Reference Pinto-de-Carvalho and Ramírez-Ros39] for similar computations. We omit the details, since we only deal with deformations of circles in this work, but we stress that
$p/q$
of each resonant caustic. See [Reference Bialy5, Reference Damasceno, Dias Carneiro and Ramírez-Ros17, Reference Pinto-de-Carvalho and Ramírez-Ros39] for similar computations. We omit the details, since we only deal with deformations of circles in this work, but we stress that
![]() $\varphi '(t),\psi '(t) \not \equiv 1$
in elliptic billiards, unlike circular billiards.
$\varphi '(t),\psi '(t) \not \equiv 1$
in elliptic billiards, unlike circular billiards.
Example 2.7. Constant width curves are a classic example. Any such curve, other than a circle, has a non-smooth (with cusps) and non-convex
![]() $1/2$
-resonant caustic [Reference Knill32]. The curve
$1/2$
-resonant caustic [Reference Knill32]. The curve
![]() $\Gamma $
has constant width
$\Gamma $
has constant width
![]() $w> 0$
when
$w> 0$
when
![]() $h(\psi ) + h(\psi + \pi ) \equiv w$
, which implies that all
$h(\psi ) + h(\psi + \pi ) \equiv w$
, which implies that all
![]() $(2\mathbb {Z} \setminus \{0 \})$
-harmonics of
$(2\mathbb {Z} \setminus \{0 \})$
-harmonics of
![]() $h(\psi )$
vanish. In that case, we take
$h(\psi )$
vanish. In that case, we take
![]() $\varphi (t) = t - \omega /2$
,
$\varphi (t) = t - \omega /2$
,
![]() $\psi (t) = t$
,
$\psi (t) = t$
,
![]() $\theta (t) \equiv \omega /2$
,
$\theta (t) \equiv \omega /2$
,
![]() $\omega = \pi $
, and
$\omega = \pi $
, and
![]() $L = 2w$
for
$L = 2w$
for
![]() $p/q = 1/2$
. These functions satisfy condition (f) because
$p/q = 1/2$
. These functions satisfy condition (f) because
![]() $\sin \theta (t) \equiv 1$
,
$\sin \theta (t) \equiv 1$
,
![]() $\cos \theta (t) \equiv 0$
, and
$\cos \theta (t) \equiv 0$
, and
![]() $h'(\psi ) + h'(\psi +\pi ) \equiv 0$
.
$h'(\psi ) + h'(\psi +\pi ) \equiv 0$
.
Example 2.8.
Gutkin billiard tables [Reference Bialy4, Reference Gutkin22], also called constant angle curves, are another classic example. We claim that circles are the only convex billiard tables with a
![]() $p/q$
-resonant caustic, with
$p/q$
-resonant caustic, with
![]() $p/q \in (0,1/2)$
, whose incidence–reflection function
$p/q \in (0,1/2)$
, whose incidence–reflection function
![]() $\theta (t)$
is constant. In that case,
$\theta (t)$
is constant. In that case,
![]() $\theta (t) \equiv \omega /2$
with
$\theta (t) \equiv \omega /2$
with
![]() $\omega = 2\pi p/q$
, so
$\omega = 2\pi p/q$
, so
![]() $\varphi (t) = t - \omega /2$
and
$\varphi (t) = t - \omega /2$
and
![]() $\psi (t) = t$
are the functions determined from
$\psi (t) = t$
are the functions determined from
![]() $\theta (t)$
by relations (6). Therefore, the difference equation (7) becomes
$\theta (t)$
by relations (6). Therefore, the difference equation (7) becomes
If
![]() $h(t) = \sum _{l \in \mathbb {Z}} \hat {h}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
satisfies this equation, then
$h(t) = \sum _{l \in \mathbb {Z}} \hat {h}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
satisfies this equation, then
![]() $\hat {h}_l = 0$
for any index
$\hat {h}_l = 0$
for any index
![]() $l \in \mathbb {Z}$
such that
$l \in \mathbb {Z}$
such that
Cyr [Reference Cyr16] proved that given any integer
![]() $l \not \in \{-1,0,1\}$
, equation
$l \not \in \{-1,0,1\}$
, equation
![]() $\tan (l \pi p/q) = l \tan (\pi p /q)$
has no rational solution
$\tan (l \pi p/q) = l \tan (\pi p /q)$
has no rational solution
![]() $p/q \in (0,1/2)$
. This proves the claim, because circles are the only convex curves whose support function is a trigonometric polynomial of degree one.
$p/q \in (0,1/2)$
. This proves the claim, because circles are the only convex curves whose support function is a trigonometric polynomial of degree one.
Example 2.9. A smooth centrally symmetric convex curve
![]() $\Gamma $
with support function
$\Gamma $
with support function
![]() $h(\psi )$
has a convex
$h(\psi )$
has a convex
![]() $1/4$
-resonant caustic if and only if
$1/4$
-resonant caustic if and only if
This claim is proved in [Reference Bialy and Tsodikovich11, Proposition 3.1]. Along the proof, the authors check three facts. First, all such curves are centrally symmetric:
![]() $h(\psi + \pi ) = h(\psi )$
. Second, once one of such curves is fixed, there is a constant
$h(\psi + \pi ) = h(\psi )$
. Second, once one of such curves is fixed, there is a constant
![]() $R> 0$
such that
$R> 0$
such that
![]() $h^2(\psi ) + h^2(\psi + \pi /2) = R^2$
. Third, then we can take
$h^2(\psi ) + h^2(\psi + \pi /2) = R^2$
. Third, then we can take
![]() $\psi (t) = t$
and determine the incidence–reflection function
$\psi (t) = t$
and determine the incidence–reflection function
![]() $\theta (t)$
by means of
$\theta (t)$
by means of
Note that
![]() $\theta (t + \pi /2) = \pi /2 - \theta (t)$
and
$\theta (t + \pi /2) = \pi /2 - \theta (t)$
and
![]() $\psi (t + \pi /2) = \psi (t) + \pi /2$
. The last relation means that the tangent lines to
$\psi (t + \pi /2) = \psi (t) + \pi /2$
. The last relation means that the tangent lines to
![]() $\Gamma $
at the impacts of any
$\Gamma $
at the impacts of any
![]() $1/4$
-periodic trajectory form a rectangle. This fact plays a key role in the Bialy–Mironov proof of a strong version of the Birkhoff conjecture [Reference Bialy and Mironov8]. If we set
$1/4$
-periodic trajectory form a rectangle. This fact plays a key role in the Bialy–Mironov proof of a strong version of the Birkhoff conjecture [Reference Bialy and Mironov8]. If we set
![]() $\varphi = \psi - \theta $
and
$\varphi = \psi - \theta $
and
![]() $\omega = \pi /2$
, then functions
$\omega = \pi /2$
, then functions
![]() $\varphi (t)$
,
$\varphi (t)$
,
![]() $\psi (t)$
, and
$\psi (t)$
, and
![]() $\theta (t)$
satisfy condition (f).
$\theta (t)$
satisfy condition (f).
3 Persistence of smooth convex resonant caustics
Necessary conditions in Theorem 2.3 are not sufficient for the existence of smooth convex resonant caustics, see Example 2.7. However, if the envelope of the 1-parameter family of lines from
![]() $z(\psi (t))$
to
$z(\psi (t))$
to
![]() $z(\psi (t+\omega ))$
, where t is the dynamical parameter, is a smooth convex curve, then those conditions are sufficient too. That is the case when we consider small enough smooth deformations
$z(\psi (t+\omega ))$
, where t is the dynamical parameter, is a smooth convex curve, then those conditions are sufficient too. That is the case when we consider small enough smooth deformations
![]() $\Gamma _\epsilon = \Gamma _0 + \mathrm {O} (\epsilon )$
of a smooth strictly convex curve
$\Gamma _\epsilon = \Gamma _0 + \mathrm {O} (\epsilon )$
of a smooth strictly convex curve
![]() $\Gamma _0$
, not necessarily a circle, with a smooth strictly convex resonant caustic.
$\Gamma _0$
, not necessarily a circle, with a smooth strictly convex resonant caustic.
We consider that setting. To be precise, we assume the following hypothesis from here on.
-
(H) Let
 $p/q \in (0,1/2)$
be a rational rotational number such that
$p/q \in (0,1/2)$
be a rational rotational number such that
 $\gcd (p,q) = 1$
. Let
$\gcd (p,q) = 1$
. Let
 $\Gamma _0$
be a smooth strictly convex curve with support function
$\Gamma _0$
be a smooth strictly convex curve with support function
 $h_0(\varphi )$
. We assume that there is a smooth convex
$h_0(\varphi )$
. We assume that there is a smooth convex
 $p/q$
-resonant caustic with support function
$p/q$
-resonant caustic with support function
 $g_0(\varphi )$
inside
$g_0(\varphi )$
inside
 $\Gamma _0$
. We also assume that the origin is in the interior of the caustic, so
$\Gamma _0$
. We also assume that the origin is in the interior of the caustic, so
 $0 < g_0(\varphi ) < h_0(\varphi )$
. Let
$0 < g_0(\varphi ) < h_0(\varphi )$
. Let
 $\Gamma _\epsilon = \Gamma _0 + \mathrm {O} (\epsilon )$
, with
$\Gamma _\epsilon = \Gamma _0 + \mathrm {O} (\epsilon )$
, with
 $\epsilon \in [-\epsilon _0,\epsilon _0]$
, be a deformation of the unperturbed curve with smooth support function
$\epsilon \in [-\epsilon _0,\epsilon _0]$
, be a deformation of the unperturbed curve with smooth support function
 $h(\varphi ;\epsilon )$
. Let
$h(\varphi ;\epsilon )$
. Let
 $(\varphi _1,\unicode{x3bb} _1) = f_\epsilon (\varphi ,\unicode{x3bb} )$
,
$(\varphi _1,\unicode{x3bb} _1) = f_\epsilon (\varphi ,\unicode{x3bb} )$
,
 $S_\epsilon (\varphi ,\varphi _1) = 2 h(\psi ;\epsilon ) \sin \theta $
, and
$S_\epsilon (\varphi ,\varphi _1) = 2 h(\psi ;\epsilon ) \sin \theta $
, and
 $A_\epsilon \{\varphi \} = q \mu \{ S_\epsilon (\varphi ,\tau \{\varphi \}) \} = 2 q \mu \{ h \circ \psi \cdot \sin \theta \}$
be the perturbed billiard map in
$A_\epsilon \{\varphi \} = q \mu \{ S_\epsilon (\varphi ,\tau \{\varphi \}) \} = 2 q \mu \{ h \circ \psi \cdot \sin \theta \}$
be the perturbed billiard map in
 $\Gamma _\epsilon $
, the perturbed generating function, and the perturbed action, respectively.
$\Gamma _\epsilon $
, the perturbed generating function, and the perturbed action, respectively.
We need two parameters in that perturbed setting. The dynamical parameter t parameterizes the invariant objects. The perturbative parameter
![]() $\epsilon \in [-\epsilon _0,\epsilon _0]$
labels the ovals. Then, the shift, sum, difference, and average operators are applied to functions that depend on t and
$\epsilon \in [-\epsilon _0,\epsilon _0]$
labels the ovals. Then, the shift, sum, difference, and average operators are applied to functions that depend on t and
![]() $\epsilon $
, although they only act on t. For instance,
$\epsilon $
, although they only act on t. For instance,
![]() $\tau \{ a(t;\epsilon ) \} = a(t + \omega ;\epsilon )$
. We will denote the derivatives of the support function
$\tau \{ a(t;\epsilon ) \} = a(t + \omega ;\epsilon )$
. We will denote the derivatives of the support function
![]() $h(\psi ;\epsilon ) = h_\epsilon (\psi )$
as
$h(\psi ;\epsilon ) = h_\epsilon (\psi )$
as
![]() $h' = {\mathit {d} h}/{\mathit {d} \psi }$
and
$h' = {\mathit {d} h}/{\mathit {d} \psi }$
and
![]() $\dot {h} = {\mathit {d} h}/{\mathit {d} \epsilon }$
. Analogously, we will denote the derivatives of any function
$\dot {h} = {\mathit {d} h}/{\mathit {d} \epsilon }$
. Analogously, we will denote the derivatives of any function
![]() $a(t;\epsilon ) = a_\epsilon (t)$
as
$a(t;\epsilon ) = a_\epsilon (t)$
as
![]() $a' = {\mathit {d} a}/{\mathit {d} t}$
and
$a' = {\mathit {d} a}/{\mathit {d} t}$
and
![]() $\dot {a} = {\mathit {d} a}/{\mathit {d} \epsilon }$
.
$\dot {a} = {\mathit {d} a}/{\mathit {d} \epsilon }$
.
Next, we state an immediate extension of Theorem 2.3.
Corollary 3.1. If
![]() $0 < \epsilon _0 \ll 1$
, the unperturbed smooth convex resonant
$0 < \epsilon _0 \ll 1$
, the unperturbed smooth convex resonant
![]() $p/q$
-caustic persists under deformation
$p/q$
-caustic persists under deformation
![]() $\Gamma _\epsilon $
,
$\Gamma _\epsilon $
,
![]() $\epsilon \in [-\epsilon _0,\epsilon _0]$
, if and only if the following three conditions hold.
$\epsilon \in [-\epsilon _0,\epsilon _0]$
, if and only if the following three conditions hold.
-
(F) There are three smooth
 $2\pi $
-periodic functions
$2\pi $
-periodic functions
 $\varphi (t;\epsilon ) - t$
,
$\varphi (t;\epsilon ) - t$
,
 $\psi (t;\epsilon ) - t$
, and
$\psi (t;\epsilon ) - t$
, and
 $\theta (t;\epsilon )$
related by (6) that satisfy the difference equation (7). In addition,
$\theta (t;\epsilon )$
related by (6) that satisfy the difference equation (7). In addition,
 $\varphi '(t;\epsilon )> 0$
.
$\varphi '(t;\epsilon )> 0$
. -
(P) There are smooth parameterizations
 $c_\epsilon :\mathbb {T} \to \mathbb {A}_{\Gamma _\epsilon }$
such that
$c_\epsilon :\mathbb {T} \to \mathbb {A}_{\Gamma _\epsilon }$
such that
 $G_\epsilon = c_\epsilon (\mathbb {T})$
are graphs and
$G_\epsilon = c_\epsilon (\mathbb {T})$
are graphs and  $$ \begin{align*} f_\epsilon (c_\epsilon(t)) = c_\epsilon(t+\omega). \end{align*} $$
$$ \begin{align*} f_\epsilon (c_\epsilon(t)) = c_\epsilon(t+\omega). \end{align*} $$
-
(A) The
 $p/q$
-periodic action is constant on the side function:
$p/q$
-periodic action is constant on the side function:
 $A_\epsilon \{\varphi (t;\epsilon )\} = L(\epsilon )$
, where
$A_\epsilon \{\varphi (t;\epsilon )\} = L(\epsilon )$
, where
 $L(\epsilon )$
is the length of all
$L(\epsilon )$
is the length of all
 $p/q$
-periodic billiard trajectories in
$p/q$
-periodic billiard trajectories in
 $\Gamma _\epsilon $
for
$\Gamma _\epsilon $
for
 $\epsilon \in [-\epsilon _0,\epsilon _0]$
.
$\epsilon \in [-\epsilon _0,\epsilon _0]$
.
Remark 3.2. Similarly to Remark 2.4, if these necessary conditions hold, then
Only the last formula is new. Let us prove it. If we derive the first relation with respect to
![]() $\epsilon $
, use the summation by parts formula, and take advantage of (7), we get
$\epsilon $
, use the summation by parts formula, and take advantage of (7), we get
 $$ \begin{align*} \dot{L} &= 2q\mu \{ \dot{h} \circ \psi \cdot \sin \theta + h'\circ \psi \cdot \sin \theta \cdot \dot{\psi} + h \circ \psi \cdot \cos \theta \cdot \dot{\theta} \} \\ &= 2q\mu\{ \dot{h} \circ \psi \cdot \sin \theta \} + q\mu\{ h'\circ \psi \cdot \sin \theta \cdot \sigma\{ \dot{\varphi} \} + h \circ \psi \cdot \cos \theta \cdot \delta\{ \dot{\varphi} \} \} \\ &= 2q\mu\{ \dot{h} \circ \psi \cdot \sin \theta \} + q\mu\{ [ \sigma\{ h'\circ \psi \cdot \sin \theta \} - \delta\{ h\circ \psi \cdot \cos\theta \} ] \cdot \tau\{\dot{\varphi}\} \} \\ &= 2q\mu\{ \dot{h} \circ \psi \cdot \sin \theta \}. \end{align*} $$
$$ \begin{align*} \dot{L} &= 2q\mu \{ \dot{h} \circ \psi \cdot \sin \theta + h'\circ \psi \cdot \sin \theta \cdot \dot{\psi} + h \circ \psi \cdot \cos \theta \cdot \dot{\theta} \} \\ &= 2q\mu\{ \dot{h} \circ \psi \cdot \sin \theta \} + q\mu\{ h'\circ \psi \cdot \sin \theta \cdot \sigma\{ \dot{\varphi} \} + h \circ \psi \cdot \cos \theta \cdot \delta\{ \dot{\varphi} \} \} \\ &= 2q\mu\{ \dot{h} \circ \psi \cdot \sin \theta \} + q\mu\{ [ \sigma\{ h'\circ \psi \cdot \sin \theta \} - \delta\{ h\circ \psi \cdot \cos\theta \} ] \cdot \tau\{\dot{\varphi}\} \} \\ &= 2q\mu\{ \dot{h} \circ \psi \cdot \sin \theta \}. \end{align*} $$
We can normalize
![]() $\Gamma _\epsilon $
by a scaling in such a way that
$\Gamma _\epsilon $
by a scaling in such a way that
![]() $\dot {L} = 0$
, but we do not need it.
$\dot {L} = 0$
, but we do not need it.
Full persistence of resonant caustics is an extremely rare phenomenon, so we introduce the more common concept of
![]() $\mathrm {O} (\epsilon ^m)$
-persistence for some order
$\mathrm {O} (\epsilon ^m)$
-persistence for some order
![]() $m \in \mathbb {N} \cup \{ 0 \}$
.
$m \in \mathbb {N} \cup \{ 0 \}$
.
Definition 3.3. Let
![]() $m \in \mathbb {N} \cup \{ 0 \}$
. The unperturbed resonant
$m \in \mathbb {N} \cup \{ 0 \}$
. The unperturbed resonant
![]() $p/q$
-caustic
$p/q$
-caustic
![]() $\mathrm {O} (\epsilon ^m)$
-persists under deformation
$\mathrm {O} (\epsilon ^m)$
-persists under deformation
![]() $\Gamma _\epsilon $
if and only if the following three conditions hold.
$\Gamma _\epsilon $
if and only if the following three conditions hold.
-
(F) m There are smooth
 $2\pi $
-periodic functions
$2\pi $
-periodic functions
 $\varphi (t;\epsilon ) - t$
,
$\varphi (t;\epsilon ) - t$
,
 $\psi (t;\epsilon ) - t$
, and
$\psi (t;\epsilon ) - t$
, and
 $\theta (t;\epsilon )$
related by (6) such that
$\theta (t;\epsilon )$
related by (6) such that
 $\varphi '(t;\epsilon )> 0$
and (8)
$\varphi '(t;\epsilon )> 0$
and (8) $$ \begin{align} \sigma \{ h'\circ \psi \cdot \sin \theta \} - \delta \{ h\circ \psi \cdot \cos \theta \} = \mathrm{O}(\epsilon^{m+1}) \quad \text{as } \epsilon \to 0. \end{align} $$
$$ \begin{align} \sigma \{ h'\circ \psi \cdot \sin \theta \} - \delta \{ h\circ \psi \cdot \cos \theta \} = \mathrm{O}(\epsilon^{m+1}) \quad \text{as } \epsilon \to 0. \end{align} $$
-
(P) m There are smooth parameterizations
 $c_\epsilon :\mathbb {T} \to \mathbb {A}_{\Gamma _\epsilon }$
such that
$c_\epsilon :\mathbb {T} \to \mathbb {A}_{\Gamma _\epsilon }$
such that
 $G_\epsilon = c_\epsilon (\mathbb {T})$
are graphs and
$G_\epsilon = c_\epsilon (\mathbb {T})$
are graphs and  $$ \begin{align*} f_\epsilon \circ c_\epsilon - \tau\{ c_\epsilon \} = ( 0,\mathrm{O}(\epsilon^{m+1}) ) \quad \text{as } \epsilon \to 0. \end{align*} $$
$$ \begin{align*} f_\epsilon \circ c_\epsilon - \tau\{ c_\epsilon \} = ( 0,\mathrm{O}(\epsilon^{m+1}) ) \quad \text{as } \epsilon \to 0. \end{align*} $$
-
(A) m There is a ‘length’
 $L(\epsilon )> 0$
such that the side function
$L(\epsilon )> 0$
such that the side function
 $\varphi = \varphi (t;\epsilon )$
satisfies
$\varphi = \varphi (t;\epsilon )$
satisfies  $$ \begin{align*} A_\epsilon \{\varphi\} - L(\epsilon) = \mathrm{O}(\epsilon^{m+1}) \quad \text{as } \epsilon \to 0. \end{align*} $$
$$ \begin{align*} A_\epsilon \{\varphi\} - L(\epsilon) = \mathrm{O}(\epsilon^{m+1}) \quad \text{as } \epsilon \to 0. \end{align*} $$
If the resonant caustic
![]() $\mathrm {O} (\epsilon ^m)$
-persists, but not
$\mathrm {O} (\epsilon ^m)$
-persists, but not
![]() $\mathrm {O} (\epsilon ^{m+1})$
-persists, we say that deformation
$\mathrm {O} (\epsilon ^{m+1})$
-persists, we say that deformation
![]() $\Gamma _\epsilon $
$\Gamma _\epsilon $
![]() $\mathrm {O} (\epsilon ^{m+1})$
-breaks the caustic.
$\mathrm {O} (\epsilon ^{m+1})$
-breaks the caustic.
Since
![]() $\mathrm {O} (\epsilon ^m)$
-persistence is the main concept of this work, some comments are in order. If
$\mathrm {O} (\epsilon ^m)$
-persistence is the main concept of this work, some comments are in order. If
![]() $\varphi _0(t)$
,
$\varphi _0(t)$
,
![]() $\psi _0(t)$
, and
$\psi _0(t)$
, and
![]() $\theta _0(t)$
are the unperturbed side, normal, and incidence–reflection functions, then
$\theta _0(t)$
are the unperturbed side, normal, and incidence–reflection functions, then
since
![]() $h = h_0 + \mathrm {O} (\epsilon )$
. Therefore, the unperturbed caustic always
$h = h_0 + \mathrm {O} (\epsilon )$
. Therefore, the unperturbed caustic always
![]() $\mathrm {O} (\epsilon ^0)$
-persists. We do not need to check all three conditions (F)
$\mathrm {O} (\epsilon ^0)$
-persists. We do not need to check all three conditions (F)
![]() ${}_m$
, (P)
${}_m$
, (P)
![]() ${}_m$
, and (A)
${}_m$
, and (A)
![]() ${}_m$
, because there are logical dependencies among them. We prove in Proposition 3.4 that conditions (F)
${}_m$
, because there are logical dependencies among them. We prove in Proposition 3.4 that conditions (F)
![]() ${}_m$
and (P)
${}_m$
and (P)
![]() ${}_m$
are equivalent and both imply condition (A)
${}_m$
are equivalent and both imply condition (A)
![]() ${}_m$
. We will only check condition (F)
${}_m$
. We will only check condition (F)
![]() ${}_m$
in our computations. We have included the other conditions as part of our definition to present a broader view of the problem.
${}_m$
in our computations. We have included the other conditions as part of our definition to present a broader view of the problem.
The three conditions look similar, but they have different characteristics. On the one hand, conditions (F)
![]() ${}_m$
and (P)
${}_m$
and (P)
![]() ${}_m$
are stated in terms of a single iteration of the perturbed map
${}_m$
are stated in terms of a single iteration of the perturbed map
![]() $f_\epsilon $
. On the other hand, condition (A)
$f_\epsilon $
. On the other hand, condition (A)
![]() ${}_m$
requires to consider all the shifts
${}_m$
requires to consider all the shifts
Hence, conditions (F)
![]() ${}_m$
and (P)
${}_m$
and (P)
![]() ${}_m$
are easier to deal with from a computational point of view.
${}_m$
are easier to deal with from a computational point of view.
Condition (F)
![]() ${}_m$
means that there is a reparameterization
${}_m$
means that there is a reparameterization
![]() $\varphi _\epsilon (t) = \varphi (t;\epsilon )$
of the original angle
$\varphi _\epsilon (t) = \varphi (t;\epsilon )$
of the original angle
![]() $\varphi $
in terms of a new dynamical parameter t such that
$\varphi $
in terms of a new dynamical parameter t such that
Thus, condition (F)
![]() ${}_m$
is related to the Lagrangian formulation as a second-order difference equation of the invariance condition for (non-resonant and resonant) rotational curves of exact twist maps. It was inspired by ideas contained in [Reference Kaloshin and Zhang31, Reference Levi and Moser34]. Compare with [Reference Levi and Moser34, (3)] in the non-resonant setting and with [Reference Kaloshin and Zhang31, (1)] in the resonant setting. Finally, condition (A)
${}_m$
is related to the Lagrangian formulation as a second-order difference equation of the invariance condition for (non-resonant and resonant) rotational curves of exact twist maps. It was inspired by ideas contained in [Reference Kaloshin and Zhang31, Reference Levi and Moser34]. Compare with [Reference Levi and Moser34, (3)] in the non-resonant setting and with [Reference Kaloshin and Zhang31, (1)] in the resonant setting. Finally, condition (A)
![]() ${}_m$
follows the variational approach in [Reference Damasceno, Dias Carneiro and Ramírez-Ros17].
${}_m$
follows the variational approach in [Reference Damasceno, Dias Carneiro and Ramírez-Ros17].
Let us prove the logical dependencies among these
![]() $\mathrm {O} (\epsilon ^m)$
-persistence conditions and how the dominant terms in their
$\mathrm {O} (\epsilon ^m)$
-persistence conditions and how the dominant terms in their
![]() $\mathrm {O} (\epsilon ^{m+1})$
-errors are related.
$\mathrm {O} (\epsilon ^{m+1})$
-errors are related.
Proposition 3.4. Conditions
![]() $(\mathbf{F})_m$
and
$(\mathbf{F})_m$
and
![]() $(\mathbf{P})_m$
are equivalent and both imply condition
$(\mathbf{P})_m$
are equivalent and both imply condition
![]() $(\mathbf{A})_m$
. Let
$(\mathbf{A})_m$
. Let
![]() $\varphi _0(t) = \varphi (t;0)$
be the unperturbed side function. If the
$\varphi _0(t) = \varphi (t;0)$
be the unperturbed side function. If the
![]() $p/q$
-resonant caustic
$p/q$
-resonant caustic
![]() $\mathrm {O} (\epsilon ^m)$
-persists and we follow the notation introduced in Definition 3.3, then there is a smooth
$\mathrm {O} (\epsilon ^m)$
-persists and we follow the notation introduced in Definition 3.3, then there is a smooth
![]() $2\pi $
-periodic function
$2\pi $
-periodic function
![]() $\mathcal {E}_{m+1}(t)$
and a smooth
$\mathcal {E}_{m+1}(t)$
and a smooth
![]() $2\pi /q$
-periodic function
$2\pi /q$
-periodic function
![]() $\mathcal {L}_{m+1}(t)$
such that
$\mathcal {L}_{m+1}(t)$
such that
as
![]() $\epsilon \to 0$
. In addition,
$\epsilon \to 0$
. In addition,
![]() $\mu \{ \mathcal {E}_{m+1} \varphi ^{\prime }_0 \} = \mathcal {L}^{\prime }_{m+1}$
and
$\mu \{ \mathcal {E}_{m+1} \varphi ^{\prime }_0 \} = \mathcal {L}^{\prime }_{m+1}$
and
![]() $\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = 0$
.
$\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = 0$
.
Proof. First, we check that
![]() $(\mathbf{F})_m \Rightarrow (\mathbf{P})_m$
and
$(\mathbf{F})_m \Rightarrow (\mathbf{P})_m$
and
![]() $(\mathbf{A})_m$
,
$(\mathbf{A})_m$
,
![]() $\mathcal {L}^{\prime }_{m+1} = \mu \{ \mathcal {E}_{m+1} \varphi ^{\prime }_0 \}$
, and
$\mathcal {L}^{\prime }_{m+1} = \mu \{ \mathcal {E}_{m+1} \varphi ^{\prime }_0 \}$
, and
![]() $\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = 0$
.
$\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = 0$
.
Let
![]() $\varphi (t;\epsilon )$
,
$\varphi (t;\epsilon )$
,
![]() $\psi (t;\epsilon )$
, and
$\psi (t;\epsilon )$
, and
![]() $\theta (t;\epsilon )$
be the functions described in condition (F)
$\theta (t;\epsilon )$
be the functions described in condition (F)
![]() ${}_m$
and
${}_m$
and
![]() $\mathcal {E}_{m+1}(t)$
be the function determined by (9a). Set
$\mathcal {E}_{m+1}(t)$
be the function determined by (9a). Set
![]() $\varphi _1(t;\epsilon ) = \varphi (t+\omega ;\epsilon )$
, so
$\varphi _1(t;\epsilon ) = \varphi (t+\omega ;\epsilon )$
, so
![]() $\varphi _1 = \tau \{ \varphi \}$
. We consider the smooth
$\varphi _1 = \tau \{ \varphi \}$
. We consider the smooth
![]() $2\pi $
-periodic functions
$2\pi $
-periodic functions
![]() $\unicode{x3bb} (t;\epsilon )$
and
$\unicode{x3bb} (t;\epsilon )$
and
![]() $\unicode{x3bb} _1(t;\epsilon )$
given by
$\unicode{x3bb} _1(t;\epsilon )$
given by
Set
![]() $c_\epsilon (t) = \big ( \varphi (t;\epsilon ),\unicode{x3bb} (t;\epsilon ) \big )$
and
$c_\epsilon (t) = \big ( \varphi (t;\epsilon ),\unicode{x3bb} (t;\epsilon ) \big )$
and
![]() $d_\epsilon (t) = \big ( \varphi _1(t;\epsilon ),\unicode{x3bb} _1(t;\epsilon ) \big )$
. Implicit equations (5) imply that
$d_\epsilon (t) = \big ( \varphi _1(t;\epsilon ),\unicode{x3bb} _1(t;\epsilon ) \big )$
. Implicit equations (5) imply that
![]() $f \circ c_\epsilon = d_\epsilon $
. In addition,
$f \circ c_\epsilon = d_\epsilon $
. In addition,
![]() $\unicode{x3bb} _1 - \tau \{ \unicode{x3bb} \} = \sigma \{ h' \circ \psi \cdot \sin \theta \} - \delta \{ h \circ \psi \cdot \cos \theta \} = \epsilon ^{m+1} \tau \{ \mathcal {E}_{m+1} \} + \mathrm {O} (\epsilon ^{m+2})$
, which is equivalent to estimate (9b). This proves condition (P)
$\unicode{x3bb} _1 - \tau \{ \unicode{x3bb} \} = \sigma \{ h' \circ \psi \cdot \sin \theta \} - \delta \{ h \circ \psi \cdot \cos \theta \} = \epsilon ^{m+1} \tau \{ \mathcal {E}_{m+1} \} + \mathrm {O} (\epsilon ^{m+2})$
, which is equivalent to estimate (9b). This proves condition (P)
![]() ${}_m$
.
${}_m$
.
Set
![]() $\bar {\varphi }_j = \tau ^j \{ \varphi \}$
,
$\bar {\varphi }_j = \tau ^j \{ \varphi \}$
,
![]() $\bar {\psi }_j = \tau ^j \{ \psi \}$
and
$\bar {\psi }_j = \tau ^j \{ \psi \}$
and
![]() $\bar {\theta }_j = \tau ^j \{ \theta \}$
for all
$\bar {\theta }_j = \tau ^j \{ \theta \}$
for all
![]() $j \in \mathbb {Z}$
. Note that
$j \in \mathbb {Z}$
. Note that
![]() $\bar {\varphi }_{j+q}(t;\epsilon ) = \bar {\varphi }_j(t;\epsilon ) + 2\pi p$
,
$\bar {\varphi }_{j+q}(t;\epsilon ) = \bar {\varphi }_j(t;\epsilon ) + 2\pi p$
,
![]() $\bar {\psi }_{j+q}(t;\epsilon ) = \bar {\psi }_j(t;\epsilon ) + 2\pi p$
, and
$\bar {\psi }_{j+q}(t;\epsilon ) = \bar {\psi }_j(t;\epsilon ) + 2\pi p$
, and
![]() $\bar {\theta }_{j+q}(t;\epsilon ) = \bar {\theta }_j(t;\epsilon )$
. If we derive the expression that defines the action and we recall that
$\bar {\theta }_{j+q}(t;\epsilon ) = \bar {\theta }_j(t;\epsilon )$
. If we derive the expression that defines the action and we recall that
![]() $\varphi = \varphi _0 + \mathrm {O} (\epsilon )$
, then we obtain the estimate
$\varphi = \varphi _0 + \mathrm {O} (\epsilon )$
, then we obtain the estimate
 $$ \begin{align*} \frac{\mathit{d}}{\mathit{d} t}[ A_\epsilon \{ \varphi \} ] &= \sum_{j=0}^{q-1} [ \partial_1 S_\epsilon (\bar{\varphi}_j,\bar{\varphi}_{j+1}) \bar{\varphi}^{\prime}_j + \partial_2 S_\epsilon (\bar{\varphi}_j,\bar{\varphi}_{j+1}) \bar{\varphi}^{\prime}_{j+1} ] \\ &= \sum_{j=0}^{q-1} [ \partial_2 S_\epsilon (\bar{\varphi}_{j-1},\bar{\varphi}_j) + \partial_1 S_\epsilon (\bar{\varphi}_j,\bar{\varphi}_{j+1}) ]\bar{\varphi}^{\prime}_j \\ &= \sum_{j=0}^{q-1} [ \sigma \{ h'\circ \bar{\psi}_{j-1} \cdot \sin \bar{\theta}_{j-1} \} - \delta \{ h\circ \bar{\psi}_{j-1} \cdot \cos \bar{\theta}_{j-1} \} ] \bar{\varphi}^{\prime}_j \\ &= \epsilon^{m+1} \sum_{j=0}^{q-1} \tau^j\{ \mathcal{E}_{m+1} \varphi' \} + \mathrm{O}(\epsilon^{m+2}) \\ &= \epsilon^{m+1} q \mu\{ \mathcal{E}_{m+1} \varphi'\} + \mathrm{O}(\epsilon^{m+2}) \\ &= \epsilon^{m+1} q \mu\{ \mathcal{E}_{m+1} \varphi^{\prime}_0 \} + \mathrm{O}(\epsilon^{m+2}), \end{align*} $$
$$ \begin{align*} \frac{\mathit{d}}{\mathit{d} t}[ A_\epsilon \{ \varphi \} ] &= \sum_{j=0}^{q-1} [ \partial_1 S_\epsilon (\bar{\varphi}_j,\bar{\varphi}_{j+1}) \bar{\varphi}^{\prime}_j + \partial_2 S_\epsilon (\bar{\varphi}_j,\bar{\varphi}_{j+1}) \bar{\varphi}^{\prime}_{j+1} ] \\ &= \sum_{j=0}^{q-1} [ \partial_2 S_\epsilon (\bar{\varphi}_{j-1},\bar{\varphi}_j) + \partial_1 S_\epsilon (\bar{\varphi}_j,\bar{\varphi}_{j+1}) ]\bar{\varphi}^{\prime}_j \\ &= \sum_{j=0}^{q-1} [ \sigma \{ h'\circ \bar{\psi}_{j-1} \cdot \sin \bar{\theta}_{j-1} \} - \delta \{ h\circ \bar{\psi}_{j-1} \cdot \cos \bar{\theta}_{j-1} \} ] \bar{\varphi}^{\prime}_j \\ &= \epsilon^{m+1} \sum_{j=0}^{q-1} \tau^j\{ \mathcal{E}_{m+1} \varphi' \} + \mathrm{O}(\epsilon^{m+2}) \\ &= \epsilon^{m+1} q \mu\{ \mathcal{E}_{m+1} \varphi'\} + \mathrm{O}(\epsilon^{m+2}) \\ &= \epsilon^{m+1} q \mu\{ \mathcal{E}_{m+1} \varphi^{\prime}_0 \} + \mathrm{O}(\epsilon^{m+2}), \end{align*} $$
which, by integration, is equivalent to estimate (9c) for any smooth
![]() $2\pi /q$
-periodic function
$2\pi /q$
-periodic function
![]() $\mathcal {L}_{m+1}$
such that
$\mathcal {L}_{m+1}$
such that
![]() $\mathcal {L}^{\prime }_{m+1} = \mu \{ \mathcal {E}_{m+1} \varphi ^{\prime }_0 \}$
. This proves condition (A)
$\mathcal {L}^{\prime }_{m+1} = \mu \{ \mathcal {E}_{m+1} \varphi ^{\prime }_0 \}$
. This proves condition (A)
![]() ${}_m$
, and the relation between
${}_m$
, and the relation between
![]() $\mathcal {L}_{m+1}$
and
$\mathcal {L}_{m+1}$
and
![]() $\mathcal {E}_{m+1}$
. The operator
$\mathcal {E}_{m+1}$
. The operator
![]() $\mu $
is the projection onto the
$\mu $
is the projection onto the
![]() $q\mathbb {Z}$
-harmonics, so the zeroth harmonics of
$q\mathbb {Z}$
-harmonics, so the zeroth harmonics of
![]() $\mathcal {E}_{m+1} \varphi ^{\prime }_0$
and
$\mathcal {E}_{m+1} \varphi ^{\prime }_0$
and
![]() $\mathcal {L}^{\prime }_{m+1}$
coincide, so
$\mathcal {L}^{\prime }_{m+1}$
coincide, so
![]() $\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = \int _{\mathbb {T}} \mathcal {L}^{\prime }_{m+1} = 0$
.
$\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = \int _{\mathbb {T}} \mathcal {L}^{\prime }_{m+1} = 0$
.
Second, we check that (P)
![]() ${}_m \Rightarrow $
(F)
${}_m \Rightarrow $
(F)
![]() ${}_m$
. Let
${}_m$
. Let
![]() $c_\epsilon (t) = ( \varphi (t;\epsilon ),\unicode{x3bb} (t;\epsilon ) )$
be the parameterization described in condition (P)
$c_\epsilon (t) = ( \varphi (t;\epsilon ),\unicode{x3bb} (t;\epsilon ) )$
be the parameterization described in condition (P)
![]() ${}_m$
and
${}_m$
and
![]() $\mathcal {E}_{m+1}(t)$
be the error function given in (9b). Property
$\mathcal {E}_{m+1}(t)$
be the error function given in (9b). Property
![]() $\varphi '> 0$
holds because
$\varphi '> 0$
holds because
![]() $c_\epsilon : \mathbb {T} \to G_\epsilon \subset \mathbb {A}_{\Gamma _\epsilon }$
is a parameterization and
$c_\epsilon : \mathbb {T} \to G_\epsilon \subset \mathbb {A}_{\Gamma _\epsilon }$
is a parameterization and
![]() $G_\epsilon $
is a graph. Functions
$G_\epsilon $
is a graph. Functions
![]() $\varphi $
,
$\varphi $
,
![]() $\psi = \sigma \{\varphi \}/2$
, and
$\psi = \sigma \{\varphi \}/2$
, and
![]() $\theta = \delta \{ \varphi \}/2$
satisfy relations (6). Set
$\theta = \delta \{ \varphi \}/2$
satisfy relations (6). Set
![]() $( \varphi _1(t;\epsilon ),\unicode{x3bb} _1(t;\epsilon ) ) = f_\epsilon (c_\epsilon (t))$
. We deduce from implicit equations (5) that
$( \varphi _1(t;\epsilon ),\unicode{x3bb} _1(t;\epsilon ) ) = f_\epsilon (c_\epsilon (t))$
. We deduce from implicit equations (5) that
which is exactly estimate (9a). This proves condition (F)
![]() ${}_m$
.
${}_m$
.
Remark 3.5. We can prove that
![]() $\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = 0$
in another way. The flux of the exact twist map
$\int _{\mathbb {T}} \mathcal {E}_{m+1} \varphi ^{\prime }_0 = 0$
in another way. The flux of the exact twist map
![]() $f_\epsilon $
across the graph
$f_\epsilon $
across the graph
![]() $G_\epsilon = c_\epsilon (\mathbb {T})$
, which is a rotational curve, is zero [Reference Meiss38, §V]. This flux is
$G_\epsilon = c_\epsilon (\mathbb {T})$
, which is a rotational curve, is zero [Reference Meiss38, §V]. This flux is
 $$ \begin{align*} \int_{f_\epsilon(G_\epsilon)} \unicode{x3bb} \,\mathit{d} \varphi - \int_{G_\epsilon} \unicode{x3bb} \,\mathit{d} \varphi &= \int_{\mathbb{T}} (\unicode{x3bb}_1 \varphi^{\prime}_1 - \unicode{x3bb} \varphi') \\ &= \int_{\mathbb{T}} \delta \{ \unicode{x3bb} \varphi'\} + \epsilon^{m+1} \int_{\mathbb{T}} \tau\{ \mathcal{E}_{m+1} \varphi' \} + \mathrm{O}(\epsilon^{m+2}) \\ &= \epsilon^{m+1} \int_{\mathbb{T}} \mathcal{E}_{m+1} \varphi^{\prime}_0 + \mathrm{O}(\epsilon^{m+2}) \quad \text{as } \epsilon \to 0. \end{align*} $$
$$ \begin{align*} \int_{f_\epsilon(G_\epsilon)} \unicode{x3bb} \,\mathit{d} \varphi - \int_{G_\epsilon} \unicode{x3bb} \,\mathit{d} \varphi &= \int_{\mathbb{T}} (\unicode{x3bb}_1 \varphi^{\prime}_1 - \unicode{x3bb} \varphi') \\ &= \int_{\mathbb{T}} \delta \{ \unicode{x3bb} \varphi'\} + \epsilon^{m+1} \int_{\mathbb{T}} \tau\{ \mathcal{E}_{m+1} \varphi' \} + \mathrm{O}(\epsilon^{m+2}) \\ &= \epsilon^{m+1} \int_{\mathbb{T}} \mathcal{E}_{m+1} \varphi^{\prime}_0 + \mathrm{O}(\epsilon^{m+2}) \quad \text{as } \epsilon \to 0. \end{align*} $$
We have used that if
![]() $c_\epsilon (t) = ( \varphi (t;\epsilon ),\unicode{x3bb} (t;\epsilon ) )$
and
$c_\epsilon (t) = ( \varphi (t;\epsilon ),\unicode{x3bb} (t;\epsilon ) )$
and
![]() $(\varphi _1,\unicode{x3bb} _1) = f(\varphi ,\unicode{x3bb} )$
, then
$(\varphi _1,\unicode{x3bb} _1) = f(\varphi ,\unicode{x3bb} )$
, then
![]() $\varphi _1 = \tau \{ \varphi \}$
and
$\varphi _1 = \tau \{ \varphi \}$
and
![]() $\unicode{x3bb} _1 = \tau \{ \unicode{x3bb} \} + \epsilon ^{m+1} \tau \{ \mathcal {E}_{m+1} \} + \mathrm {O} (\epsilon ^{m+2})$
. We have also used that
$\unicode{x3bb} _1 = \tau \{ \unicode{x3bb} \} + \epsilon ^{m+1} \tau \{ \mathcal {E}_{m+1} \} + \mathrm {O} (\epsilon ^{m+2})$
. We have also used that
![]() $\varphi = \varphi _0 + \mathrm {O} (\epsilon )$
.
$\varphi = \varphi _0 + \mathrm {O} (\epsilon )$
.
Remark 3.6. Following [Reference Pinto-de-Carvalho and Ramírez-Ros39, Reference Ramírez-Ros41], we could also have considered a fourth condition defined in terms of
![]() $\varphi \in \mathbb {T}$
instead of
$\varphi \in \mathbb {T}$
instead of
![]() $t \in \mathbb {R}$
. However, such an approach forces us to deal with the power map
$t \in \mathbb {R}$
. However, such an approach forces us to deal with the power map
![]() $f^q_\epsilon $
, which is technically impractical. We have not pursued it. That discarded condition is the following.
$f^q_\epsilon $
, which is technically impractical. We have not pursued it. That discarded condition is the following.
-
(G) m There are smooth functions
 $g^\bullet _\epsilon ,g^\star _\epsilon :\mathbb {T} \to \mathbb {R}$
such that
$g^\bullet _\epsilon ,g^\star _\epsilon :\mathbb {T} \to \mathbb {R}$
such that
 $f^q_\epsilon (\varphi ,g^\bullet _\epsilon (\varphi )) = (\varphi ,g^\star _\epsilon (\varphi ))$
,
$f^q_\epsilon (\varphi ,g^\bullet _\epsilon (\varphi )) = (\varphi ,g^\star _\epsilon (\varphi ))$
,
 $g^\star _\epsilon , g^\bullet _\epsilon = g_0 + \mathrm {O} (\epsilon )$
, and
$g^\star _\epsilon , g^\bullet _\epsilon = g_0 + \mathrm {O} (\epsilon )$
, and
 $g^\star _\epsilon - g^\bullet _\epsilon = \mathrm {O} (\epsilon ^{m+1})$
as
$g^\star _\epsilon - g^\bullet _\epsilon = \mathrm {O} (\epsilon ^{m+1})$
as
 $\epsilon \to 0$
.
$\epsilon \to 0$
.
It means that
![]() $f^q_\epsilon $
projects
$f^q_\epsilon $
projects
![]() $G^\bullet _\epsilon = \mathrm {graph} (g^\bullet _\epsilon )$
onto
$G^\bullet _\epsilon = \mathrm {graph} (g^\bullet _\epsilon )$
onto
![]() $G^\star _\epsilon = \mathrm {graph} (g^\star _\epsilon )$
in the vertical direction. None of these two graphs have to coincide with
$G^\star _\epsilon = \mathrm {graph} (g^\star _\epsilon )$
in the vertical direction. None of these two graphs have to coincide with
![]() $G_\epsilon = c_\epsilon (\mathbb {T})$
, but all of them are
$G_\epsilon = c_\epsilon (\mathbb {T})$
, but all of them are
![]() $\mathrm {O} (\epsilon ^{m+1})$
-close. Conditions (F)
$\mathrm {O} (\epsilon ^{m+1})$
-close. Conditions (F)
![]() ${}_m$
or (P)
${}_m$
or (P)
![]() ${}_m$
imply condition (G)
${}_m$
imply condition (G)
![]() ${}_m$
. The proof of this implication is based on two ideas. First, we check that the restriction of the power map
${}_m$
. The proof of this implication is based on two ideas. First, we check that the restriction of the power map
![]() $f^q_\epsilon $
to the graph
$f^q_\epsilon $
to the graph
![]() $G_\epsilon $
is
$G_\epsilon $
is
![]() $\mathrm {O} (\epsilon ^{m+1})$
-close to the identity, although the error in the horizontal direction may be non-zero. Next, we use the twist condition to cancel the horizontal error, so we get the graphs
$\mathrm {O} (\epsilon ^{m+1})$
-close to the identity, although the error in the horizontal direction may be non-zero. Next, we use the twist condition to cancel the horizontal error, so we get the graphs
![]() $G^\bullet _\epsilon , G^\star _\epsilon = G_\epsilon + \mathrm {O} (\epsilon ^{m+1})$
. We omit the technical details since we do not need this result. In contrast, we do not know whether condition (G)
$G^\bullet _\epsilon , G^\star _\epsilon = G_\epsilon + \mathrm {O} (\epsilon ^{m+1})$
. We omit the technical details since we do not need this result. In contrast, we do not know whether condition (G)
![]() ${}_m$
implies conditions (F)
${}_m$
implies conditions (F)
![]() ${}_m$
and (P)
${}_m$
and (P)
![]() ${}_m$
, because it is not clear how to extract information about a single iterate of the perturbed map from information about the power map
${}_m$
, because it is not clear how to extract information about a single iterate of the perturbed map from information about the power map
![]() $f^q_\epsilon $
.
$f^q_\epsilon $
.
Definition 3.7. The
![]() $2\pi /q$
-periodic function
$2\pi /q$
-periodic function
![]() $\mathcal {L}_{m+1}(t)$
is the
$\mathcal {L}_{m+1}(t)$
is the
![]() $p/q$
-resonant potential of order
$p/q$
-resonant potential of order
![]() $m+1$
. The
$m+1$
. The
![]() $2\pi $
-periodic function
$2\pi $
-periodic function
![]() $\mathcal {E}_{m+1}(t)$
is the
$\mathcal {E}_{m+1}(t)$
is the
![]() $p/q$
-resonant error of order
$p/q$
-resonant error of order
![]() $m+1$
.
$m+1$
.
We will check in the next section that if the
![]() $p/q$
-resonant caustic
$p/q$
-resonant caustic
![]() $\mathrm {O} (\epsilon ^m)$
-persists under a deformation of the unit circle, then the Melnikov potential
$\mathrm {O} (\epsilon ^m)$
-persists under a deformation of the unit circle, then the Melnikov potential
![]() $\mathcal {L}_{m+1}(t)$
is uniquely determined from previously computed objects. See the second item in Proposition 4.2.
$\mathcal {L}_{m+1}(t)$
is uniquely determined from previously computed objects. See the second item in Proposition 4.2.
4 High-order persistence in deformed circles
Let us apply the previous high-order persistence theory to smooth deformations of circles. The main goal is to check that the smooth
![]() $2\pi $
-periodic coefficients of the Taylor expansions in powers of the perturbative parameter
$2\pi $
-periodic coefficients of the Taylor expansions in powers of the perturbative parameter
![]() $\epsilon $
of the perturbed side, normal, and incidence–reflection functions can be computed recursively order by order as long as some compatibility conditions hold. Such compatibility conditions have to do with the inversion of the difference operator
$\epsilon $
of the perturbed side, normal, and incidence–reflection functions can be computed recursively order by order as long as some compatibility conditions hold. Such compatibility conditions have to do with the inversion of the difference operator
![]() $\delta $
, so they boil down to the fact that certain smooth
$\delta $
, so they boil down to the fact that certain smooth
![]() $2\pi $
-periodic functions have no
$2\pi $
-periodic functions have no
![]() $q\mathbb {Z}$
-resonant harmonics. We look for a practical way to find the exact order at which a given resonant caustic is destroyed, so we write down explicit formulas for all recursive computations.
$q\mathbb {Z}$
-resonant harmonics. We look for a practical way to find the exact order at which a given resonant caustic is destroyed, so we write down explicit formulas for all recursive computations.
To begin with, we assume the following hypothesis from here on.
-
(H′) Let
 $p/q \in (0,1/2)$
be a rational rotational number such that
$p/q \in (0,1/2)$
be a rational rotational number such that
 $\gcd (p,q) = 1$
. Let
$\gcd (p,q) = 1$
. Let
 $\Gamma _0$
be the unit circle centered at the origin, see Example 2.5. The unperturbed side, normal, and incidence–reflection functions are
$\Gamma _0$
be the unit circle centered at the origin, see Example 2.5. The unperturbed side, normal, and incidence–reflection functions are  $$ \begin{align*} \varphi_0(t) = t - \omega/2, \quad \psi_0(t) = t, \quad \theta_0(t) = \omega/2, \quad \omega = 2\pi p/q. \end{align*} $$
$$ \begin{align*} \varphi_0(t) = t - \omega/2, \quad \psi_0(t) = t, \quad \theta_0(t) = \omega/2, \quad \omega = 2\pi p/q. \end{align*} $$
Let
 $\Gamma _\epsilon $
, with
$\Gamma _\epsilon $
, with
 $\epsilon \in [-\epsilon _0,\epsilon _0]$
, be a deformation of
$\epsilon \in [-\epsilon _0,\epsilon _0]$
, be a deformation of
 $\Gamma _0$
with smooth support function (1).
$\Gamma _0$
with smooth support function (1).
We look for some perturbed side, normal, and incidence–reflection functions
that satisfy condition (F)
![]() ${}_m$
for an order
${}_m$
for an order
![]() $m \in \mathbb {N} \cup \{0\}$
as high as possible.
$m \in \mathbb {N} \cup \{0\}$
as high as possible.
Notation 1. If
![]() $a(t;\epsilon ) \asymp \sum _{k \ge 0} a_k(t) \epsilon ^k$
as
$a(t;\epsilon ) \asymp \sum _{k \ge 0} a_k(t) \epsilon ^k$
as
![]() $\epsilon \to 0$
, then
$\epsilon \to 0$
, then
![]() $a_{\le m}(t;\epsilon ) = \sum _{k=0}^m a_k(t) \epsilon ^k$
. Symbol
$a_{\le m}(t;\epsilon ) = \sum _{k=0}^m a_k(t) \epsilon ^k$
. Symbol
![]() $a_{\le m}(t;\epsilon )$
may be used even when there are no coefficients
$a_{\le m}(t;\epsilon )$
may be used even when there are no coefficients
![]() $a_k(t)$
with
$a_k(t)$
with
![]() $k> m$
. Symbol
$k> m$
. Symbol
![]() $a_{<m}(t;\epsilon )$
has a similar meaning. An expression like
$a_{<m}(t;\epsilon )$
has a similar meaning. An expression like
![]() $\mathcal {C}_m = \mathcal {C}_m[{\kern-1.8pt}[ a_{\le m},b_{<m} ]{\kern-1.8pt}]$
means that
$\mathcal {C}_m = \mathcal {C}_m[{\kern-1.8pt}[ a_{\le m},b_{<m} ]{\kern-1.8pt}]$
means that
![]() $\mathcal {C}_m$
is a smooth
$\mathcal {C}_m$
is a smooth
![]() $2\pi $
-periodic function that can be written as a differential expression in some smooth
$2\pi $
-periodic function that can be written as a differential expression in some smooth
![]() $2\pi $
-periodic functions
$2\pi $
-periodic functions
![]() $a_k$
for
$a_k$
for
![]() $1 \le k \le m$
and
$1 \le k \le m$
and
![]() $b_k$
for
$b_k$
for
![]() $1 \le k < m$
. The term differential means that the derivatives of functions
$1 \le k < m$
. The term differential means that the derivatives of functions
![]() $a_k$
and
$a_k$
and
![]() $b_k$
can appear in those expressions.
$b_k$
can appear in those expressions.
The study of the approximate difference equation (8) requires to recursively compute the asymptotic expansions of
![]() $\mathcal {R} := h \circ \psi \cdot \cos \theta $
and
$\mathcal {R} := h \circ \psi \cdot \cos \theta $
and
![]() $\mathcal {Q} := h' \circ \psi \cdot \sin \theta $
as
$\mathcal {Q} := h' \circ \psi \cdot \sin \theta $
as
![]() $\epsilon \to 0$
.
$\epsilon \to 0$
.
Lemma 4.1. Set
![]() $c = \cos (\omega /2)$
and
$c = \cos (\omega /2)$
and
![]() $s = \sin (\omega /2)$
. The coefficients of the asymptotic expansions
$s = \sin (\omega /2)$
. The coefficients of the asymptotic expansions
have the form
 $$ \begin{align*} \mathcal{Q}_k &= \mathcal{Q}_k [{\kern-1.8pt}[ h^{\prime}_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] = s h^{\prime}_k + \tilde{\mathcal{Q}}_k [{\kern-1.8pt}[ h^{\prime}_{<k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}], \\\mathcal{R}_k &= \mathcal{R}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{\le k} ]{\kern-1.8pt}] = \tilde{\mathcal{R}}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] - s\theta_k. \end{align*} $$
$$ \begin{align*} \mathcal{Q}_k &= \mathcal{Q}_k [{\kern-1.8pt}[ h^{\prime}_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] = s h^{\prime}_k + \tilde{\mathcal{Q}}_k [{\kern-1.8pt}[ h^{\prime}_{<k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}], \\\mathcal{R}_k &= \mathcal{R}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{\le k} ]{\kern-1.8pt}] = \tilde{\mathcal{R}}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] - s\theta_k. \end{align*} $$
In addition,
![]() $\tilde {\mathcal {Q}}_1 = 0$
,
$\tilde {\mathcal {Q}}_1 = 0$
,
![]() $\tilde {\mathcal {R}}_1 = ch_1$
,
$\tilde {\mathcal {R}}_1 = ch_1$
,
![]() $\tilde {\mathcal {Q}}_2 = s h^{\prime \prime }_1 \psi _1 + c h^{\prime }_1 \theta _1$
, and
$\tilde {\mathcal {Q}}_2 = s h^{\prime \prime }_1 \psi _1 + c h^{\prime }_1 \theta _1$
, and
![]() $\tilde {\mathcal {R}}_2 = c h_2 + c h^{\prime }_1 \psi _1 - s h_1 \theta _1 - c \theta ^2_1/2$
.
$\tilde {\mathcal {R}}_2 = c h_2 + c h^{\prime }_1 \psi _1 - s h_1 \theta _1 - c \theta ^2_1/2$
.
The proof of Lemma 4.1 is postponed to Appendix B. The first coefficients are obtained from the explicit recurrences for
![]() $\tilde {\mathcal {Q}}_k$
and
$\tilde {\mathcal {Q}}_k$
and
![]() $\tilde {\mathcal {R}}_k$
given in Lemma B.4.
$\tilde {\mathcal {R}}_k$
given in Lemma B.4.
Once we know that
![]() $\mathcal {Q}_{< k}$
and
$\mathcal {Q}_{< k}$
and
![]() $\mathcal {R}_{< k}$
only depend on
$\mathcal {R}_{< k}$
only depend on
![]() $\psi _{<k}$
and
$\psi _{<k}$
and
![]() $\theta _{< k}$
, we deduce that if
$\theta _{< k}$
, we deduce that if
![]() $\varphi _{<k}(t;\epsilon )$
,
$\varphi _{<k}(t;\epsilon )$
,
![]() $\psi _{<k}(t;\epsilon )$
and
$\psi _{<k}(t;\epsilon )$
and
![]() $\theta _{<k}(t;\epsilon )$
satisfy condition (F)
$\theta _{<k}(t;\epsilon )$
satisfy condition (F)
![]() $_{k-1}$
, then
$_{k-1}$
, then
![]() $\varphi _{\le k}(t;\epsilon )$
,
$\varphi _{\le k}(t;\epsilon )$
,
![]() $\psi _{\le k}(t;\epsilon )$
and
$\psi _{\le k}(t;\epsilon )$
and
![]() $\theta _{\le k}(t;\epsilon )$
satisfy condition (F)
$\theta _{\le k}(t;\epsilon )$
satisfy condition (F)
![]() ${}_k$
provided coefficients
${}_k$
provided coefficients
![]() $\varphi _k(t)$
,
$\varphi _k(t)$
,
![]() $\psi _k(t)$
and
$\psi _k(t)$
and
![]() $\theta _k(t)$
are chosen in such a way that
$\theta _k(t)$
are chosen in such a way that
![]() $\sigma \{ \mathcal {Q}_k \} = \delta \{ \mathcal {R}_k \}$
. We prove below that these kth coefficients can be found if and only if
$\sigma \{ \mathcal {Q}_k \} = \delta \{ \mathcal {R}_k \}$
. We prove below that these kth coefficients can be found if and only if
![]() $\mathcal {Q}_k$
has no
$\mathcal {Q}_k$
has no
![]() $q\mathbb {Z}$
-resonant harmonics, in which case, all three kth coefficients are uniquely determined provided that they have no
$q\mathbb {Z}$
-resonant harmonics, in which case, all three kth coefficients are uniquely determined provided that they have no
![]() $q\mathbb {Z}$
-resonant harmonics either.
$q\mathbb {Z}$
-resonant harmonics either.
Proposition 4.2. Let
![]() $k \in \mathbb {N}$
be a fixed order. If the
$k \in \mathbb {N}$
be a fixed order. If the
![]() $p/q$
-resonant caustic
$p/q$
-resonant caustic
![]() $\mathrm {O} (\epsilon ^{k-1})$
- persists, then the following properties hold.
$\mathrm {O} (\epsilon ^{k-1})$
- persists, then the following properties hold.
-
(a)
 $\bar {\mathcal {Q}}_k := ({1}/{2\pi }) \int _{\mathbb {T}} \mathcal {Q}_k = 0$
.
$\bar {\mathcal {Q}}_k := ({1}/{2\pi }) \int _{\mathbb {T}} \mathcal {Q}_k = 0$
. -
(b) The
 $p/q$
-resonant Melnikov potential of order k is completely determined from previously computed objects:
$p/q$
-resonant Melnikov potential of order k is completely determined from previously computed objects:
 $\mathcal {L}_k = \mathcal {L}_k [{\kern-1.8pt}[ h_{\le k},\psi _{<k},\theta _{<k} ]{\kern-1.8pt}]$
.
$\mathcal {L}_k = \mathcal {L}_k [{\kern-1.8pt}[ h_{\le k},\psi _{<k},\theta _{<k} ]{\kern-1.8pt}]$
. -
(c) The
 $p/q$
-resonant caustic
$p/q$
-resonant caustic
 $\mathrm {O} (\epsilon ^k)$
-persists if and only if (11)in which case,
$\mathrm {O} (\epsilon ^k)$
-persists if and only if (11)in which case, $$ \begin{align} \mu\{ \mathcal{Q}_k \} = 0, \end{align} $$
$$ \begin{align} \mu\{ \mathcal{Q}_k \} = 0, \end{align} $$
 $\theta _k(t)$
is the unique smooth
$\theta _k(t)$
is the unique smooth
 $2\pi $
-periodic solution of (12)and then
$2\pi $
-periodic solution of (12)and then $$ \begin{align} s \delta\{ \theta_k \} = \delta\{ \tilde{\mathcal{R}}_k \} - \sigma\{ \mathcal{Q}_k \},\quad \mu\{ \theta_k \} = 0, \end{align} $$
$$ \begin{align} s \delta\{ \theta_k \} = \delta\{ \tilde{\mathcal{R}}_k \} - \sigma\{ \mathcal{Q}_k \},\quad \mu\{ \theta_k \} = 0, \end{align} $$
 $\varphi _k(t)$
and
$\varphi _k(t)$
and
 $\psi _k(t)$
are uniquely determined from
$\psi _k(t)$
are uniquely determined from
 $\theta _k(t)$
by (13)
$\theta _k(t)$
by (13) $$ \begin{align} \delta\{ \varphi_k \} = 2\theta_k, \quad \mu\{ \varphi_k\} = 0, \quad \psi_k = \varphi_k + \theta_k. \end{align} $$
$$ \begin{align} \delta\{ \varphi_k \} = 2\theta_k, \quad \mu\{ \varphi_k\} = 0, \quad \psi_k = \varphi_k + \theta_k. \end{align} $$
-
(d) If condition (11) fails, then it is satisfied for any support function
 $h^\star = h + \epsilon ^k \eta _k$
such that (14)so the
$h^\star = h + \epsilon ^k \eta _k$
such that (14)so the $$ \begin{align} \mu\{ s \eta^{\prime}_k + \mathcal{Q}_k \} = 0, \end{align} $$
$$ \begin{align} \mu\{ s \eta^{\prime}_k + \mathcal{Q}_k \} = 0, \end{align} $$
 $p/q$
-resonant caustic
$p/q$
-resonant caustic
 $\mathrm {O} (\epsilon ^k)$
-persists under a corrected deformation
$\mathrm {O} (\epsilon ^k)$
-persists under a corrected deformation
 $\Gamma ^\star _\epsilon = \Gamma _\epsilon + \mathrm {O} (\epsilon ^k)$
. We can choose the correction
$\Gamma ^\star _\epsilon = \Gamma _\epsilon + \mathrm {O} (\epsilon ^k)$
. We can choose the correction
 $\eta _k$
in such a way that it only contains
$\eta _k$
in such a way that it only contains
 $(q\mathbb {Z} \setminus \{0\})$
-harmonics.
$(q\mathbb {Z} \setminus \{0\})$
-harmonics.
Proof. We use several times along this proof that
![]() $\mu \circ \tau = \mu $
,
$\mu \circ \tau = \mu $
,
![]() $\mu \circ \sigma = 2\mu $
, and
$\mu \circ \sigma = 2\mu $
, and
![]() $\mu \circ \delta = 0$
on the space of smooth
$\mu \circ \delta = 0$
on the space of smooth
![]() $2\pi $
-periodic functions. We also use that if
$2\pi $
-periodic functions. We also use that if
![]() $b(t)$
is a smooth
$b(t)$
is a smooth
![]() $2\pi $
-periodic function,
$2\pi $
-periodic function,
![]() $\delta \{ a \} = b$
has a smooth
$\delta \{ a \} = b$
has a smooth
![]() $2\pi $
-periodic solution
$2\pi $
-periodic solution
![]() $a(t)$
if and only if
$a(t)$
if and only if
![]() $\mu \{ b \} = 0$
, in which case, the solution is unique under the additional condition
$\mu \{ b \} = 0$
, in which case, the solution is unique under the additional condition
![]() $\mu \{ a \} = 0$
. See Lemma A.2.
$\mu \{ a \} = 0$
. See Lemma A.2.
(a) The asymptotic expansions in Lemma 4.1 imply that
 $$ \begin{align*} \sigma \{ h'\circ \psi \cdot \sin \theta \} - \delta \{ h\circ \psi \cdot \cos \theta \} = \sum_{j = 1}^k ( \sigma\{ \mathcal{Q}_j \} - \delta\{ \mathcal{R}_j \} ) \epsilon^j + \mathrm{O}(\epsilon^{k+1}). \end{align*} $$
$$ \begin{align*} \sigma \{ h'\circ \psi \cdot \sin \theta \} - \delta \{ h\circ \psi \cdot \cos \theta \} = \sum_{j = 1}^k ( \sigma\{ \mathcal{Q}_j \} - \delta\{ \mathcal{R}_j \} ) \epsilon^j + \mathrm{O}(\epsilon^{k+1}). \end{align*} $$
The
![]() $\mathrm {O} (\epsilon ^{k-1})$
-persistence hypothesis means that
$\mathrm {O} (\epsilon ^{k-1})$
-persistence hypothesis means that
![]() $\sigma \{ \mathcal {Q}_j \} = \delta \{ \mathcal {R}_j \}$
for
$\sigma \{ \mathcal {Q}_j \} = \delta \{ \mathcal {R}_j \}$
for
![]() $j=1,\ldots , k-1$
. If
$j=1,\ldots , k-1$
. If
![]() $\mathcal {E}_k$
and
$\mathcal {E}_k$
and
![]() $\mathcal {L}_k$
are the
$\mathcal {L}_k$
are the
![]() $p/q$
-resonant error and potential of order k, respectively, then
$p/q$
-resonant error and potential of order k, respectively, then
![]() $\tau \{ \mathcal {E}_k \} = \sigma \{ \mathcal {Q}_k \} - \delta \{ \mathcal {R}_k \}$
and
$\tau \{ \mathcal {E}_k \} = \sigma \{ \mathcal {Q}_k \} - \delta \{ \mathcal {R}_k \}$
and
![]() $\mathcal {L}^{\prime }_k = \mu \{ \mathcal {E}_k \} = 2\mu \{ \mathcal {Q}_k \}$
, since
$\mathcal {L}^{\prime }_k = \mu \{ \mathcal {E}_k \} = 2\mu \{ \mathcal {Q}_k \}$
, since
![]() $\varphi ^{\prime }_0(t) = 1$
. Finally,
$\varphi ^{\prime }_0(t) = 1$
. Finally,
![]() $\bar {\mathcal {Q}}_k = ({1}/{2\pi }) \int _{\mathbb {T}} \mathcal {Q}_k = ({1}/{4\pi }) \int _{\mathbb {T}} \mathcal {E}_k = 0$
. (See the last claims in Proposition 3.4.)
$\bar {\mathcal {Q}}_k = ({1}/{2\pi }) \int _{\mathbb {T}} \mathcal {Q}_k = ({1}/{4\pi }) \int _{\mathbb {T}} \mathcal {E}_k = 0$
. (See the last claims in Proposition 3.4.)
(b) It is a direct consequence of properties
![]() $\mathcal {L}^{\prime }_k = 2\mu \{ \mathcal {Q}_k \}$
and
$\mathcal {L}^{\prime }_k = 2\mu \{ \mathcal {Q}_k \}$
and
![]() $\mathcal {Q}_k = \mathcal {Q}_k [{\kern-1.8pt}[ h^{\prime }_{\le k},\psi _{<k},\theta _{<k} ]{\kern-1.8pt}]$
.
$\mathcal {Q}_k = \mathcal {Q}_k [{\kern-1.8pt}[ h^{\prime }_{\le k},\psi _{<k},\theta _{<k} ]{\kern-1.8pt}]$
.
(c) Condition (11) is necessary:
![]() $\mathrm {O} (\epsilon ^k)$
-persistence means
$\mathrm {O} (\epsilon ^k)$
-persistence means
![]() $\sigma \{ \mathcal {Q}_k \} = \delta \{ \mathcal {R}_k \}$
, so
$\sigma \{ \mathcal {Q}_k \} = \delta \{ \mathcal {R}_k \}$
, so
![]() ${\mu \{ \mathcal {Q}_k \} = 0}$
. Condition (11) is sufficient: if
${\mu \{ \mathcal {Q}_k \} = 0}$
. Condition (11) is sufficient: if
![]() $\mu \{ \mathcal {Q}_k \} = 0$
, then
$\mu \{ \mathcal {Q}_k \} = 0$
, then
so (12) has a unique smooth
![]() $2\pi $
-periodic solution
$2\pi $
-periodic solution
![]() $\theta _k(t)$
. Then, we find
$\theta _k(t)$
. Then, we find
![]() $\varphi _k$
and
$\varphi _k$
and
![]() $\psi _k$
by means of relations (13). Finally, the
$\psi _k$
by means of relations (13). Finally, the
![]() $\mathrm {O} (\epsilon ^k)$
-terms of
$\mathrm {O} (\epsilon ^k)$
-terms of
![]() $\sigma \{ h'\circ \psi \cdot \sin \theta \}$
and
$\sigma \{ h'\circ \psi \cdot \sin \theta \}$
and
![]() $\delta \{ h\circ \psi \cdot \cos \theta \}$
are
$\delta \{ h\circ \psi \cdot \cos \theta \}$
are
![]() $\sigma \{ \mathcal {Q}_k \}$
and
$\sigma \{ \mathcal {Q}_k \}$
and
![]() $\delta \{ \tilde {\mathcal {R}}_k - s \theta _k \}$
, respectively. See Lemma 4.1. Both terms coincide when the first relation in (12) holds. Property
$\delta \{ \tilde {\mathcal {R}}_k - s \theta _k \}$
, respectively. See Lemma 4.1. Both terms coincide when the first relation in (12) holds. Property
![]() $\varphi '(t;\epsilon ) = 1 + \mathrm {O} (\epsilon )> 0$
holds for
$\varphi '(t;\epsilon ) = 1 + \mathrm {O} (\epsilon )> 0$
holds for
![]() $\epsilon \in [-\epsilon _0,\epsilon _0]$
if
$\epsilon \in [-\epsilon _0,\epsilon _0]$
if
![]() $0 < \epsilon _0 \ll 1$
. Relations (6) follow from condition
$0 < \epsilon _0 \ll 1$
. Relations (6) follow from condition
![]() $\mu \{ \theta _k \} = 0$
and relations (13), since
$\mu \{ \theta _k \} = 0$
and relations (13), since
![]() $\psi _k = \varphi _k + \theta _k$
implies that
$\psi _k = \varphi _k + \theta _k$
implies that
![]() $\mu \{ \psi _k \} = 0$
and
$\mu \{ \psi _k \} = 0$
and
![]() $\psi _k = \sigma \{ \varphi _k \}/2$
. This proves that condition (F)
$\psi _k = \sigma \{ \varphi _k \}/2$
. This proves that condition (F)
![]() ${}_k$
holds.
${}_k$
holds.
(d) We deduce from Lemma 4.1 that if
![]() $\mathcal {Q}^\star _k$
is the
$\mathcal {Q}^\star _k$
is the
![]() $\mathrm {O} (\epsilon ^k)$
-coefficient of
$\mathrm {O} (\epsilon ^k)$
-coefficient of
![]() $(h^\star )' \circ \psi _{<k} \cdot \sin \theta _{<k}$
, then
$(h^\star )' \circ \psi _{<k} \cdot \sin \theta _{<k}$
, then
![]() $\mathcal {Q}^\star _k = s \eta ^{\prime }_k + \mathcal {Q}_k$
. The existence of the correction
$\mathcal {Q}^\star _k = s \eta ^{\prime }_k + \mathcal {Q}_k$
. The existence of the correction
![]() $\eta _k$
follows from property
$\eta _k$
follows from property
![]() $\bar {\mathcal {Q}}_k = 0$
.
$\bar {\mathcal {Q}}_k = 0$
.
Finally, we prove Theorem 1.1 by recursively applying Proposition 4.2 for
![]() ${k=1},\ldots ,m$
.
${k=1},\ldots ,m$
.
Proof of Theorem 1.1
We denote the Fourier coefficients of smooth
![]() $2\pi $
-periodic functions with a hat, so we write
$2\pi $
-periodic functions with a hat, so we write
![]() $h_1(t) = \sum _{l \in \mathbb {Z}} \hat {h}_{1,l} \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
and
$h_1(t) = \sum _{l \in \mathbb {Z}} \hat {h}_{1,l} \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
and
![]() $\theta _1(t) = \sum _{l \in \mathbb {Z}} \hat {\theta }_{1,l} \mathit {e}^{\mskip 2mu{i}\mskip 1mu l t}$
.
$\theta _1(t) = \sum _{l \in \mathbb {Z}} \hat {\theta }_{1,l} \mathit {e}^{\mskip 2mu{i}\mskip 1mu l t}$
.
(a) We know that
![]() $\mathcal {Q}_1 = s h^{\prime }_1$
from Lemma 4.1. Hence, the necessary and sufficient condition (11) for
$\mathcal {Q}_1 = s h^{\prime }_1$
from Lemma 4.1. Hence, the necessary and sufficient condition (11) for
![]() $\mathrm {O} (\epsilon )$
-persistence becomes
$\mathrm {O} (\epsilon )$
-persistence becomes
![]() $\mu \{ h^{\prime }_1 \} = 0$
or, equivalently,
$\mu \{ h^{\prime }_1 \} = 0$
or, equivalently,
![]() $\mu _{q\mathbb {Z}^\star } \{ h_1 \} = 0$
.
$\mu _{q\mathbb {Z}^\star } \{ h_1 \} = 0$
.
(b) We know that
![]() $\mathcal {Q}_2 = s h^{\prime }_2 + \tilde {\mathcal {Q}}_2$
and
$\mathcal {Q}_2 = s h^{\prime }_2 + \tilde {\mathcal {Q}}_2$
and
![]() $\tilde {\mathcal {Q}}_2 = s h^{\prime \prime }_1 \psi _1 + c h^{\prime }_1 \theta _1$
from Lemma 4.1. Let us check that
$\tilde {\mathcal {Q}}_2 = s h^{\prime \prime }_1 \psi _1 + c h^{\prime }_1 \theta _1$
from Lemma 4.1. Let us check that
![]() $\mu \{ \tilde {\mathcal {Q}}_2 \} = s \mu \{ \theta _1 \theta ^{\prime }_1 \}$
. To do that, we need three properties.
$\mu \{ \tilde {\mathcal {Q}}_2 \} = s \mu \{ \theta _1 \theta ^{\prime }_1 \}$
. To do that, we need three properties.
First, once we know that the resonant caustic
![]() $\mathrm {O} (\epsilon )$
-persists, we determine the first-order coefficient
$\mathrm {O} (\epsilon )$
-persists, we determine the first-order coefficient
![]() $\theta _1(t)$
by solving (12) with
$\theta _1(t)$
by solving (12) with
![]() $k=1$
. That is,
$k=1$
. That is,
Second, we determine
![]() $\varphi _1(t)$
and
$\varphi _1(t)$
and
![]() $\psi _1(t)$
by solving (13) with
$\psi _1(t)$
by solving (13) with
![]() $k=1$
. In particular,
$k=1$
. In particular,
Third, we recall that if
![]() $a(t)$
and
$a(t)$
and
![]() $b(t)$
are
$b(t)$
are
![]() $2\pi $
-periodic functions, then
$2\pi $
-periodic functions, then
Next, we use these three properties to get the formula we are looking for:
 $$ \begin{align*} \mu\{ \tilde{\mathcal{Q}}_2 \} &= \mu\{ s h^{\prime\prime}_1 \psi_1 + c h^{\prime}_1 \theta_1 \} = \mu\{ s h^{\prime\prime}_1 \sigma\{ \varphi_1\} + c h^{\prime}_1 \delta\{ \varphi_1 \} \}/2 \\ &= \mu\{ [\sigma\{ s h^{\prime\prime}_1\} - \delta\{ c h^{\prime}_1\} ] \tau\{ \varphi_1 \} \}/2 = \mu\{ [\sigma\{ s h^{\prime}_1\} - \delta\{ c h_1\} ]' \tau\{ \varphi_1 \} \}/2 \\ &= -s \mu\{ \delta\{ \theta^{\prime}_1\} \tau\{\varphi_1 \} \}/2 = s \mu\{ \delta\{ \varphi_1\} \theta^{\prime}_1 \}/2 = s \mu\{ \theta_1 \theta^{\prime}_1 \}. \end{align*} $$
$$ \begin{align*} \mu\{ \tilde{\mathcal{Q}}_2 \} &= \mu\{ s h^{\prime\prime}_1 \psi_1 + c h^{\prime}_1 \theta_1 \} = \mu\{ s h^{\prime\prime}_1 \sigma\{ \varphi_1\} + c h^{\prime}_1 \delta\{ \varphi_1 \} \}/2 \\ &= \mu\{ [\sigma\{ s h^{\prime\prime}_1\} - \delta\{ c h^{\prime}_1\} ] \tau\{ \varphi_1 \} \}/2 = \mu\{ [\sigma\{ s h^{\prime}_1\} - \delta\{ c h_1\} ]' \tau\{ \varphi_1 \} \}/2 \\ &= -s \mu\{ \delta\{ \theta^{\prime}_1\} \tau\{\varphi_1 \} \}/2 = s \mu\{ \delta\{ \varphi_1\} \theta^{\prime}_1 \}/2 = s \mu\{ \theta_1 \theta^{\prime}_1 \}. \end{align*} $$
Thus, condition (11) for
![]() $\mathrm {O} (\epsilon ^2)$
-persistence becomes
$\mathrm {O} (\epsilon ^2)$
-persistence becomes
![]() $\mu \{ h^{\prime }_2 + \theta _1 \theta ^{\prime }_1 \} = 0$
or, equivalently,
$\mu \{ h^{\prime }_2 + \theta _1 \theta ^{\prime }_1 \} = 0$
or, equivalently,
Set
![]() $e^\pm _l = \mathit {e}^{\mskip 2mu {i}\mskip 1mu l \omega } \pm 1$
. The Fourier coefficients of the unique smooth
$e^\pm _l = \mathit {e}^{\mskip 2mu {i}\mskip 1mu l \omega } \pm 1$
. The Fourier coefficients of the unique smooth
![]() $2\pi $
-periodic solution of (15) are easily determined:
$2\pi $
-periodic solution of (15) are easily determined:
![]() $\hat {\theta }_{1,l} = 0$
for all
$\hat {\theta }_{1,l} = 0$
for all
![]() $l \in q\mathbb {Z}$
and
$l \in q\mathbb {Z}$
and
The right-hand side of this identity vanishes, and
![]() $\hat {\theta }_{1,l}$
too, when
$\hat {\theta }_{1,l}$
too, when
![]() $l = \pm 1$
. If
$l = \pm 1$
. If
![]() $l \not \in q\mathbb {Z} \cup \{-1,1\}$
, then
$l \not \in q\mathbb {Z} \cup \{-1,1\}$
, then
 $$ \begin{align*} \hat{\theta}_{1,l} = \bigg( \frac{c}{s} - \mskip2mu{i}\mskip1mu l \frac{e^+_l}{e^-_l} \bigg) \hat{h}_{1,l} = \begin{cases} \dfrac{\tan(l\omega/2) - l \tan(\omega/2)} {\tan(\omega/2) \tan(l\omega/2)} \hat{h}_{1,l} & \text{if }2l \not \in q\mathbb{Z}, \\[6pt] \dfrac{\hat{h}_{1,l}}{\tan(\omega/2)} & \text{if }2l \in q\mathbb{Z}. \end{cases} \end{align*} $$
$$ \begin{align*} \hat{\theta}_{1,l} = \bigg( \frac{c}{s} - \mskip2mu{i}\mskip1mu l \frac{e^+_l}{e^-_l} \bigg) \hat{h}_{1,l} = \begin{cases} \dfrac{\tan(l\omega/2) - l \tan(\omega/2)} {\tan(\omega/2) \tan(l\omega/2)} \hat{h}_{1,l} & \text{if }2l \not \in q\mathbb{Z}, \\[6pt] \dfrac{\hat{h}_{1,l}}{\tan(\omega/2)} & \text{if }2l \in q\mathbb{Z}. \end{cases} \end{align*} $$
We have used that
![]() $e^+_l = 0$
when
$e^+_l = 0$
when
![]() $2l \in q\mathbb {Z}$
and
$2l \in q\mathbb {Z}$
and
![]() $l \not \in q\mathbb {Z}$
, whereas
$l \not \in q\mathbb {Z}$
, whereas
![]() $e^-_l \neq 0$
for all
$e^-_l \neq 0$
for all
![]() $l \not \in q\mathbb {Z}$
. The formulas above are equivalent to the expression of
$l \not \in q\mathbb {Z}$
. The formulas above are equivalent to the expression of
![]() $\theta _1(t)$
given in Theorem 1.1.
$\theta _1(t)$
given in Theorem 1.1.
(c) We know from Lemma 4.1 that
![]() $\mathcal {Q}_m = s h^{\prime }_m + \tilde {\mathcal {Q}}_m$
, where
$\mathcal {Q}_m = s h^{\prime }_m + \tilde {\mathcal {Q}}_m$
, where
![]() $\tilde {\mathcal {Q}}_m$
is a smooth
$\tilde {\mathcal {Q}}_m$
is a smooth
![]() $2\pi $
-periodic function, only depending on
$2\pi $
-periodic function, only depending on
![]() $h_1,\ldots ,h_{m-1}$
—since approximations
$h_1,\ldots ,h_{m-1}$
—since approximations
![]() $\varphi _{<k}$
,
$\varphi _{<k}$
,
![]() $\psi _{<k}$
and
$\psi _{<k}$
and
![]() $\theta _{<k}$
are uniquely determined from
$\theta _{<k}$
are uniquely determined from
![]() $h_{<k}$
for any
$h_{<k}$
for any
![]() $k = 1, \ldots , m-1$
—that can be explicitly computed from recurrences given in Appendix B. We also know that
$k = 1, \ldots , m-1$
—that can be explicitly computed from recurrences given in Appendix B. We also know that
![]() $\int _{\mathbb {T}} \mathcal {Q}_m = 0$
and so
$\int _{\mathbb {T}} \mathcal {Q}_m = 0$
and so
![]() $\int _{\mathbb {T}} \tilde {\mathcal {Q}}_m = 0$
. This means that there is a smooth
$\int _{\mathbb {T}} \tilde {\mathcal {Q}}_m = 0$
. This means that there is a smooth
![]() $2\pi $
-periodic function
$2\pi $
-periodic function
![]() $\zeta _m$
such that
$\zeta _m$
such that
![]() $s \zeta ^{\prime }_m = \tilde {\mathcal {Q}}_m$
. Finally, the necessary and sufficient condition for
$s \zeta ^{\prime }_m = \tilde {\mathcal {Q}}_m$
. Finally, the necessary and sufficient condition for
![]() $\mathrm {O} (\epsilon ^m)$
-persistence becomes
$\mathrm {O} (\epsilon ^m)$
-persistence becomes
![]() $\mu \{ h^{\prime }_m + \zeta ^{\prime }_m \} = 0$
or, equivalently,
$\mu \{ h^{\prime }_m + \zeta ^{\prime }_m \} = 0$
or, equivalently,
![]() $\mu _{q\mathbb {Z}^\star } \{ h_m + \zeta _m \} = 0$
.
$\mu _{q\mathbb {Z}^\star } \{ h_m + \zeta _m \} = 0$
.
Functions
![]() $\zeta _m$
can be recursively computed from the formulas listed in Appendix B. For instance, we have already seen that
$\zeta _m$
can be recursively computed from the formulas listed in Appendix B. For instance, we have already seen that
![]() $\zeta _1 = 0$
and
$\zeta _1 = 0$
and
![]() $\zeta _2 = \theta ^2_1/2$
along the proof of Theorem 1.1. After some tedious computations by hand that we do not include here, we get that
$\zeta _2 = \theta ^2_1/2$
along the proof of Theorem 1.1. After some tedious computations by hand that we do not include here, we get that
which will allow us to analyze some
![]() $\mathrm {O} (\epsilon ^3)$
-persistence problems in the future. See §6. We stress that further expressions for
$\mathrm {O} (\epsilon ^3)$
-persistence problems in the future. See §6. We stress that further expressions for
![]() $\zeta _4,\zeta _5,\ldots $
can be obtained using a symbolic algebra system, but we have doubts about their practical usefulness.
$\zeta _4,\zeta _5,\ldots $
can be obtained using a symbolic algebra system, but we have doubts about their practical usefulness.
5 Polynomial deformations of the unit circle
We tackle two problems in this section, both related with polynomial deformations of the unit circle. First, to prove Theorem 1.3. Second, to prove that the support function (1) of any polynomial deformation (4) with
![]() $P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
and
$P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
and
![]() $P_1(x,y) \in \mathbb {R}_n[x,y]$
satisfies condition (3); see Lemma 5.2. This second result allows us to explain with Theorem 1.3 some of the numerical experiments about the polynomial deformations (4) with
$P_1(x,y) \in \mathbb {R}_n[x,y]$
satisfies condition (3); see Lemma 5.2. This second result allows us to explain with Theorem 1.3 some of the numerical experiments about the polynomial deformations (4) with
![]() $P(x,y;\epsilon ) = 1 - \epsilon y^n$
performed in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37], which was the original motivation of this work.
$P(x,y;\epsilon ) = 1 - \epsilon y^n$
performed in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37], which was the original motivation of this work.
To begin with, we check that, once the order
![]() $m \in \mathbb {N}$
and the degree
$m \in \mathbb {N}$
and the degree
![]() $n \ge 3$
are fixed, all resonant caustics of high enough period
$n \ge 3$
are fixed, all resonant caustics of high enough period
![]() $\mathrm {O} (\epsilon ^m)$
-persists under polynomial deformations of degree
$\mathrm {O} (\epsilon ^m)$
-persists under polynomial deformations of degree
![]() $\le n$
. We explicitly quantify how high this period q should be. Some resonant caustics become more persistent in the presence of symmetries.
$\le n$
. We explicitly quantify how high this period q should be. Some resonant caustics become more persistent in the presence of symmetries.
Theorem 5.1. Under the hypotheses of Theorem 1.3, the
![]() $p/q$
-resonant caustic
$p/q$
-resonant caustic
![]() $\mathrm {O} (\epsilon ^m)$
-persists if any of the following three conditions are met:
$\mathrm {O} (\epsilon ^m)$
-persists if any of the following three conditions are met:
-
(a)
 $q> nm$
;
$q> nm$
; -
(b)
 $\Gamma _\epsilon $
is centrally symmetric, q is odd, and
$\Gamma _\epsilon $
is centrally symmetric, q is odd, and
 $2q> nm$
; or
$2q> nm$
; or -
(c)
 $\Gamma _\epsilon $
is anti-centrally symmetric,
$\Gamma _\epsilon $
is anti-centrally symmetric,
 $q \neq m\ \mod 2$
,
$q \neq m\ \mod 2$
,
 $m \ge 2$
, and
$m \ge 2$
, and
 $q> n(m-1)$
.
$q> n(m-1)$
.
Lemma 5.2. Any deformation of the unit circle expressed in Cartesian coordinates as (4) for some
![]() $P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
with
$P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
with
![]() $P_1(x,y) \in \mathbb {R}_n[x,y]$
is a polynomial deformation of degree
$P_1(x,y) \in \mathbb {R}_n[x,y]$
is a polynomial deformation of degree
![]() $\le n$
in the sense of Definition 1.2. If
$\le n$
in the sense of Definition 1.2. If
![]() $P_1$
is even (respectively odd), then this deformation is centrally (respectively anti-centrally) symmetric.
$P_1$
is even (respectively odd), then this deformation is centrally (respectively anti-centrally) symmetric.
We have postponed the proofs of Theorem 5.1 and Lemma 5.2 to Appendix C, since they are technically similar. The main difficulty is to check that some recursively computed
![]() $2\pi $
-periodic trigonometric polynomials have degrees
$2\pi $
-periodic trigonometric polynomials have degrees
![]() $\le mn$
by induction on a recursive index
$\le mn$
by induction on a recursive index
![]() $m \ge 1$
.
$m \ge 1$
.
Theorem 1.3 is a direct consequence of Theorem 5.1.
Proof of Theorem 1.3
Let
![]() $\chi = \chi (\Gamma _\epsilon ,q) \in \mathbb {N}$
be the exponent defined in Theorem 1.3. Let
$\chi = \chi (\Gamma _\epsilon ,q) \in \mathbb {N}$
be the exponent defined in Theorem 1.3. Let
![]() $m = \chi - 1$
. We deduce from Theorem 5.1 that the
$m = \chi - 1$
. We deduce from Theorem 5.1 that the
![]() $p/q$
-resonant caustic
$p/q$
-resonant caustic
![]() $\mathrm {O} (\epsilon ^m)$
-persists because:
$\mathrm {O} (\epsilon ^m)$
-persists because:
-
• if
 $\Gamma _\epsilon $
is anti-centrally symmetric, then
$\Gamma _\epsilon $
is anti-centrally symmetric, then
 $nm < q$
or
$nm < q$
or
 $n(m-1) < q$
with
$n(m-1) < q$
with
 $m \neq q \mod 2$
and
$m \neq q \mod 2$
and
 $m \ge 2$
;
$m \ge 2$
; -
• if
 $\Gamma _\epsilon $
is centrally symmetric and q is odd, then
$\Gamma _\epsilon $
is centrally symmetric and q is odd, then
 $nm < 2q$
; and
$nm < 2q$
; and -
• otherwise,
 $nm < q$
.
$nm < q$
.
The experiments described in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37, Numerical Result 5] suggest that the
![]() $p/q$
-resonant caustic does not
$p/q$
-resonant caustic does not
![]() $\mathrm {O} (\epsilon ^\chi )$
-persist under the polynomial deformation (4) with
$\mathrm {O} (\epsilon ^\chi )$
-persist under the polynomial deformation (4) with
![]() $P(x,y;\epsilon ) = 1 - \epsilon y^n$
. To prove it, we should check that
$P(x,y;\epsilon ) = 1 - \epsilon y^n$
. To prove it, we should check that
![]() $h_\chi + \zeta _\chi $
has some non-zero
$h_\chi + \zeta _\chi $
has some non-zero
![]() $(q\mathbb {Z} \setminus \{0\})$
-harmonic.
$(q\mathbb {Z} \setminus \{0\})$
-harmonic.
6 Open problems
We describe three open problems that have arisen during the development of our high-order perturbation theory. We have not addressed them here. Each of them is a non-trivial research challenge. They are works in progress.
As a general principle, we claim that many billiard computations are greatly simplified when working with the Bialy–Mironov generating function, so its discovery opens the door to the resolution of many billiard problems that seemed almost intractable.
We also stress that both our high-order perturbation theory and our list of open problems can be extended to the setting of dual, symplectic, wire, pensive, and coin billiards, provided we deal with those billiards in deformed circles.
6.1 Co-preservation of resonant caustics
Tabachnikov asked whether there are convex domains, other than circles and ellipses, that possess resonant caustics with different rotation numbers. See [Reference Bolsinov, Matveev, Miranda and Tabachnikov13, Question 4.7]. Theorem 1.1 and Cyr’s result on Gutkin’s equation provide an excellent framework to study the co-preservation of resonant caustics under deformations of the unit circle. We mention two problems about such co-preservation.
First, we consider the co-preservation of caustics with different rotation numbers but equal periods. Let
![]() $q \neq 2, 3, 4, 6$
be a fixed period, so
$q \neq 2, 3, 4, 6$
be a fixed period, so
has several elements. If the deformation of the unit circle with support function (1) preserves all
![]() $p/q$
-resonant caustics with
$p/q$
-resonant caustics with
![]() $p \in \mathcal {P}_q$
, then none of the smooth
$p \in \mathcal {P}_q$
, then none of the smooth
![]() $2\pi $
-periodic functions
$2\pi $
-periodic functions
![]() $h_1$
and
$h_1$
and
![]() $h_2 + \big (\theta _1^{[p/q]}\big )^2/2$
with
$h_2 + \big (\theta _1^{[p/q]}\big )^2/2$
with
![]() $p \in \mathcal {P}_q$
have resonant
$p \in \mathcal {P}_q$
have resonant
![]() $(q\mathbb {Z} \setminus \{ 0 \})$
-harmonics, where
$(q\mathbb {Z} \setminus \{ 0 \})$
-harmonics, where
 $$ \begin{align*} \theta_1^{[p/q]}(t) = \sum_{l \not \in q\mathbb{Z} \cup \{-1,1\}} \hat{\theta}_{1,l}^{[p/q]} \mathit{e}^{\mskip2mu{i}\mskip1mu l t}, \quad \hat{\theta}_{1,l}^{[p/q]} = \nu_l(p/q) \hat{h}_{1,l} \end{align*} $$
$$ \begin{align*} \theta_1^{[p/q]}(t) = \sum_{l \not \in q\mathbb{Z} \cup \{-1,1\}} \hat{\theta}_{1,l}^{[p/q]} \mathit{e}^{\mskip2mu{i}\mskip1mu l t}, \quad \hat{\theta}_{1,l}^{[p/q]} = \nu_l(p/q) \hat{h}_{1,l} \end{align*} $$
for some functions
![]() $\nu _l:(0,1/2) \to \mathbb {R}$
defined in (2), which have no rational roots when
$\nu _l:(0,1/2) \to \mathbb {R}$
defined in (2), which have no rational roots when
![]() $|l| \ge 2$
. The above necessary conditions for
$|l| \ge 2$
. The above necessary conditions for
![]() $\mathrm {O} (\epsilon ^2)$
-persistence impose rather stringent restrictions on the first-order coefficient
$\mathrm {O} (\epsilon ^2)$
-persistence impose rather stringent restrictions on the first-order coefficient
![]() $h_1$
. We do not state any specific result because we have not yet found one satisfactory enough.
$h_1$
. We do not state any specific result because we have not yet found one satisfactory enough.
Second, we consider the co-preservation of caustics with rotation numbers
![]() $1/2$
and
$1/2$
and
![]() $1/q$
for some fixed period
$1/q$
for some fixed period
![]() $q \ge 3$
under deformations of the unit circle. The preservation of the
$q \ge 3$
under deformations of the unit circle. The preservation of the
![]() $1/2$
-resonant caustic implies that all
$1/2$
-resonant caustic implies that all
![]() $(2\mathbb {Z} \setminus \{0\})$
-harmonics of the support function (1) are zero, which greatly simplifies the problem. The case
$(2\mathbb {Z} \setminus \{0\})$
-harmonics of the support function (1) are zero, which greatly simplifies the problem. The case
![]() $q=3$
for centrally symmetric deformations was studied by J. Zhang [Reference Zhang44]. His method consists in a careful analysis of the obstructions for
$q=3$
for centrally symmetric deformations was studied by J. Zhang [Reference Zhang44]. His method consists in a careful analysis of the obstructions for
![]() $\mathrm {O} (\epsilon ^2)$
-persistence of the
$\mathrm {O} (\epsilon ^2)$
-persistence of the
![]() $1/3$
-resonant caustic. His computations are more involved than those outlined here because he uses the standard generating function for billiards (that is, the minus distance between consecutive impacts) and he considers deformations of the unit circle written in polar coordinates. We plan to extend Zhang’s results to some periods
$1/3$
-resonant caustic. His computations are more involved than those outlined here because he uses the standard generating function for billiards (that is, the minus distance between consecutive impacts) and he considers deformations of the unit circle written in polar coordinates. We plan to extend Zhang’s results to some periods
![]() $q>3$
, starting with periods
$q>3$
, starting with periods
![]() $q=4,5$
for which it is necessary to study the obstructions for
$q=4,5$
for which it is necessary to study the obstructions for
![]() $\mathrm {O} (\epsilon ^3)$
-persistence.
$\mathrm {O} (\epsilon ^3)$
-persistence.
6.2 A convergence problem
We recall that the function
![]() $\zeta _m$
in Theorem 1.1 only depends on
$\zeta _m$
in Theorem 1.1 only depends on
![]() $h_1,\ldots ,h_{m-1}$
. Hence, if the
$h_1,\ldots ,h_{m-1}$
. Hence, if the
![]() $p/q$
-resonant caustic
$p/q$
-resonant caustic
![]() $\mathrm {O} (\epsilon ^m)$
-persists, but not
$\mathrm {O} (\epsilon ^m)$
-persists, but not
![]() $\mathrm {O} (\epsilon ^{m+1})$
-persists, and we fix any higher order
$\mathrm {O} (\epsilon ^{m+1})$
-persists, and we fix any higher order
![]() $r> m$
, then there is a smooth
$r> m$
, then there is a smooth
![]() $2\pi $
-periodic function
$2\pi $
-periodic function
![]() $\eta ^{[r]}_\epsilon = \mathrm {O} (\epsilon ^{m+1})$
such that the resonant caustic
$\eta ^{[r]}_\epsilon = \mathrm {O} (\epsilon ^{m+1})$
such that the resonant caustic
![]() $\mathrm {O} (\epsilon ^r)$
-persists under the new deformation
$\mathrm {O} (\epsilon ^r)$
-persists under the new deformation
![]() $\Gamma ^{[r]}_\epsilon = \Gamma _\epsilon + \mathrm {O} (\epsilon ^{m+1})$
with support function
$\Gamma ^{[r]}_\epsilon = \Gamma _\epsilon + \mathrm {O} (\epsilon ^{m+1})$
with support function
![]() $h^{[r]}_\epsilon = h_\epsilon + \eta ^{[r]}_\epsilon $
. This function
$h^{[r]}_\epsilon = h_\epsilon + \eta ^{[r]}_\epsilon $
. This function
![]() $\eta ^{[r]}_\epsilon $
can also be recursively computed and only contains
$\eta ^{[r]}_\epsilon $
can also be recursively computed and only contains
![]() $(q\mathbb {Z} \setminus \{0\})$
-harmonics. See the last item in Proposition 4.2.
$(q\mathbb {Z} \setminus \{0\})$
-harmonics. See the last item in Proposition 4.2.
A natural question is the following. Does
![]() $h^{[\infty ]}_\epsilon := \lim _{r \to +\infty } h^{[r]}_\epsilon $
exist? That is, we look for a corrected support function
$h^{[\infty ]}_\epsilon := \lim _{r \to +\infty } h^{[r]}_\epsilon $
exist? That is, we look for a corrected support function
![]() $h^{[\infty ]}_\epsilon = h_\epsilon + \mathrm {O} (\epsilon ^{m+1})$
such that the
$h^{[\infty ]}_\epsilon = h_\epsilon + \mathrm {O} (\epsilon ^{m+1})$
such that the
![]() $p/q$
-resonant caustic persists at all orders under the deformation
$p/q$
-resonant caustic persists at all orders under the deformation
![]() $\Gamma ^{[\infty ]}_\epsilon $
with support function
$\Gamma ^{[\infty ]}_\epsilon $
with support function
![]() $h^{[\infty ]}_\epsilon $
. This problem is closely related to the density property established in [Reference Kaloshin and Zhang31].
$h^{[\infty ]}_\epsilon $
. This problem is closely related to the density property established in [Reference Kaloshin and Zhang31].
The first author, in collaboration with V. Kaloshin and K. Zhang, is working on a more ambitious version of this problem. Namely, once a rational rotation number
![]() $1/q$
is fixed, the goal is to construct a functional
$1/q$
is fixed, the goal is to construct a functional
such that: (1)
![]() $\mathcal {H}_A$
is a neighborhood of zero in a suitable space of
$\mathcal {H}_A$
is a neighborhood of zero in a suitable space of
![]() $2\pi $
-periodic functions with only A-harmonics; (2)
$2\pi $
-periodic functions with only A-harmonics; (2)
![]() $\mathcal {F}_{1/q}(0) = 0$
; (3)
$\mathcal {F}_{1/q}(0) = 0$
; (3)
![]() $\mathcal {F}_{1/q}$
is as regular as possible at
$\mathcal {F}_{1/q}$
is as regular as possible at
![]() $h = 0$
; and (4) the convex domain with support function
$h = 0$
; and (4) the convex domain with support function
![]() $1 + h + \mathcal {F}_{1/q}[h]$
has a
$1 + h + \mathcal {F}_{1/q}[h]$
has a
![]() $1/q$
-resonant caustic for any
$1/q$
-resonant caustic for any
![]() $h \in \mathcal {H}_{\mathbb {Z} \setminus q\mathbb {Z}}$
.
$h \in \mathcal {H}_{\mathbb {Z} \setminus q\mathbb {Z}}$
.
6.3 Exponentially small phenomena
Let
![]() $\Gamma _\epsilon $
be a polynomial deformation of the unit circle of degree
$\Gamma _\epsilon $
be a polynomial deformation of the unit circle of degree
![]() $\le n$
in the sense of Definition 1.2. Let
$\le n$
in the sense of Definition 1.2. Let
![]() $q \ge 3$
be a fixed period. Theorem 1.3 implies that the
$q \ge 3$
be a fixed period. Theorem 1.3 implies that the
![]() $p/q$
-resonant caustics
$p/q$
-resonant caustics
![]() $\mathrm {O} (\epsilon ^{\chi - 1})$
-persist under
$\mathrm {O} (\epsilon ^{\chi - 1})$
-persist under
![]() $\Gamma _\epsilon $
for all
$\Gamma _\epsilon $
for all
![]() $p \in \mathcal {P}_q$
, so there are perturbed normal functions
$p \in \mathcal {P}_q$
, so there are perturbed normal functions
![]() $\psi ^{[p/q]}_\epsilon (t)$
and perturbed incidence–reflection functions
$\psi ^{[p/q]}_\epsilon (t)$
and perturbed incidence–reflection functions
![]() $\theta ^{[p/q]}_\epsilon (t)$
such that the error
$\theta ^{[p/q]}_\epsilon (t)$
such that the error
is
![]() $\mathrm {O} (\epsilon ^\chi )$
as
$\mathrm {O} (\epsilon ^\chi )$
as
![]() $\epsilon \to 0$
. We recall that
$\epsilon \to 0$
. We recall that
![]() $\chi \asymp 2q/n$
as odd
$\chi \asymp 2q/n$
as odd
![]() $q \to +\infty $
for centrally symmetric deformations, and
$q \to +\infty $
for centrally symmetric deformations, and
![]() $\chi \asymp q/n$
as
$\chi \asymp q/n$
as
![]() $q \to +\infty $
otherwise. Let us focus on the second case, which is the generic one. It is natural to ask whether, in this generic case,
$q \to +\infty $
otherwise. Let us focus on the second case, which is the generic one. It is natural to ask whether, in this generic case,
as
![]() $q \to +\infty $
for fixed
$q \to +\infty $
for fixed
![]() $\epsilon \in [-\epsilon _0,\epsilon _0]$
. This is a hard problem. It was partially addressed in [Reference Martín, Tamarit-Sariol and Ramírez-Ros36], where the authors establish an exponentially small upper bound on the difference of lengths of
$\epsilon \in [-\epsilon _0,\epsilon _0]$
. This is a hard problem. It was partially addressed in [Reference Martín, Tamarit-Sariol and Ramírez-Ros36], where the authors establish an exponentially small upper bound on the difference of lengths of
![]() $1/q$
-periodic billiard trajectories in analytic strictly convex domains as
$1/q$
-periodic billiard trajectories in analytic strictly convex domains as
![]() $q \to +\infty $
. The numerical experiments described in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37] suggest that these upper bounds can be improved to exponentially small asymptotic formulas for some deformations. To be precise, we deduce from the computations about the polynomial deformations (4) with
$q \to +\infty $
. The numerical experiments described in [Reference Martín, Tamarit-Sariol and Ramírez-Ros37] suggest that these upper bounds can be improved to exponentially small asymptotic formulas for some deformations. To be precise, we deduce from the computations about the polynomial deformations (4) with
![]() $P(x,y;\epsilon ) = 1 - \epsilon y^n$
that there are constants
$P(x,y;\epsilon ) = 1 - \epsilon y^n$
that there are constants
![]() $\xi (\Gamma _\epsilon )$
with a finite limit as
$\xi (\Gamma _\epsilon )$
with a finite limit as
![]() $\epsilon \to 0$
such that the error
$\epsilon \to 0$
such that the error
![]() $\mathcal {E}^{[1/q]}_\epsilon (t)$
has ‘size’
$\mathcal {E}^{[1/q]}_\epsilon (t)$
has ‘size’
![]() $q^{-3} \mathit {e}^{-q [|\!\log \epsilon |/n)+ \xi (\Gamma _\epsilon )]}$
as
$q^{-3} \mathit {e}^{-q [|\!\log \epsilon |/n)+ \xi (\Gamma _\epsilon )]}$
as
![]() $q \to +\infty $
for any fixed
$q \to +\infty $
for any fixed
![]() $\epsilon \in [-\epsilon _0,\epsilon _0]$
.
$\epsilon \in [-\epsilon _0,\epsilon _0]$
.
This problem can be addressed by the direct approach used by Wang in [Reference Wang43] or the approach used by Kaloshin and Zhang in [Reference Kaloshin and Zhang31]. However, we feel that exponentially small asymptotic formulas can only be obtained with more refined techniques, like the extension of
![]() $\psi ^{[p/q]}_\epsilon (t)$
and
$\psi ^{[p/q]}_\epsilon (t)$
and
![]() $\theta ^{[p/q]}_\epsilon (t)$
to complex values of t, the analysis of their complex singularities, resurgence theory, and complex matching. See [Reference Delshams and Ramírez-Ros18, Reference Gelfreich21, Reference Martín, Sauzin and Seara35] for examples of how these refined techniques are applied in the setting of discrete systems (maps).
$\theta ^{[p/q]}_\epsilon (t)$
to complex values of t, the analysis of their complex singularities, resurgence theory, and complex matching. See [Reference Delshams and Ramírez-Ros18, Reference Gelfreich21, Reference Martín, Sauzin and Seara35] for examples of how these refined techniques are applied in the setting of discrete systems (maps).
Acknowledgments
C.E.K. gratefully acknowledges support from the European Research Council (ERC) through the Advanced Grant ‘SPERIG’ (#885 707). R.R.-R. was supported in part by the grant PID-2021-122954NB-100, which was funded by MCIN/AEI/10.13039/501100011033 and ‘ERDF: A way of making Europe’. R.R.-R. thanks Pau Martín and Tere Seara for many long and stimulating conversations on related problems. We are also indebted to the referee for suggestions that helped us to improve the exposition.
A Appendix. Shift, sum, difference, and average operators
Let
![]() $0 < p < q$
be integers such that
$0 < p < q$
be integers such that
![]() $\gcd (p,q) = 1$
. Set
$\gcd (p,q) = 1$
. Set
![]() $\omega = 2\pi p/q$
. The shift, sum, difference, and average operators act on smooth functions
$\omega = 2\pi p/q$
. The shift, sum, difference, and average operators act on smooth functions
![]() $a: \mathbb {T} \to \mathbb {R}$
as follows:
$a: \mathbb {T} \to \mathbb {R}$
as follows:
 $$ \begin{align*} \tau\{ a(t) \} &= a(t + \omega),\\\sigma\{ a(t) \} &= a(t + \omega) + a(t), \\\delta\{ a(t) \} &= a(t + \omega) - a(t), \\\mu \{ a(t) \} &= \frac{1}{q} \sum_{j=0}^{q-1} a(t + j \omega). \end{align*} $$
$$ \begin{align*} \tau\{ a(t) \} &= a(t + \omega),\\\sigma\{ a(t) \} &= a(t + \omega) + a(t), \\\delta\{ a(t) \} &= a(t + \omega) - a(t), \\\mu \{ a(t) \} &= \frac{1}{q} \sum_{j=0}^{q-1} a(t + j \omega). \end{align*} $$
They diagonalize in the Fourier basis and the average operator is the projection onto the resonant
![]() $q\mathbb {Z}$
-harmonics.
$q\mathbb {Z}$
-harmonics.
Lemma A.1. If
![]() $a(t) = \sum _{l\in \mathbb {Z}} \hat {a}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
is a smooth
$a(t) = \sum _{l\in \mathbb {Z}} \hat {a}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
is a smooth
![]() $2\pi $
-periodic function, then
$2\pi $
-periodic function, then
 $$ \begin{align*} \tau\{ a(t) \} &= \sum_{l \in \mathbb{Z}} \mathit{e}^{\mskip2mu{i}\mskip1mu l \omega} \hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t},\\ \sigma\{ a(t) \} &= \sum_{l \in \mathbb{Z}} (\mathit{e}^{\mskip2mu{i}\mskip1mu l \omega} + 1 )\hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t}, \\ \delta\{ a(t) \} &= \sum_{l \in \mathbb{Z}} (\mathit{e}^{\mskip2mu{i}\mskip1mu l \omega} - 1) \hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t}, \\ \mu \{ a(t) \} &= \sum_{l \in q\mathbb{Z}} \hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t}. \end{align*} $$
$$ \begin{align*} \tau\{ a(t) \} &= \sum_{l \in \mathbb{Z}} \mathit{e}^{\mskip2mu{i}\mskip1mu l \omega} \hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t},\\ \sigma\{ a(t) \} &= \sum_{l \in \mathbb{Z}} (\mathit{e}^{\mskip2mu{i}\mskip1mu l \omega} + 1 )\hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t}, \\ \delta\{ a(t) \} &= \sum_{l \in \mathbb{Z}} (\mathit{e}^{\mskip2mu{i}\mskip1mu l \omega} - 1) \hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t}, \\ \mu \{ a(t) \} &= \sum_{l \in q\mathbb{Z}} \hat{a}_l \mathit{e}^{\mskip2mu{i}\mskip1mu l t}. \end{align*} $$
Hence,
![]() $\mu \circ \tau = \mu \circ \mu = \mu $
,
$\mu \circ \tau = \mu \circ \mu = \mu $
,
![]() $\mu \circ \sigma = 2\mu $
, and
$\mu \circ \sigma = 2\mu $
, and
![]() $\mu \circ \delta = 0$
on the set of smooth
$\mu \circ \delta = 0$
on the set of smooth
![]() $2\pi $
-periodic functions.
$2\pi $
-periodic functions.
Proof. The average
![]() $({1}/{q})\sum _{j=0}^{q-1} \mathit {e}^{\mskip 2mu {i}\mskip 1mu j l \omega }$
is equal to one when
$({1}/{q})\sum _{j=0}^{q-1} \mathit {e}^{\mskip 2mu {i}\mskip 1mu j l \omega }$
is equal to one when
![]() $l \in q\mathbb {Z}$
, but it vanishes otherwise.
$l \in q\mathbb {Z}$
, but it vanishes otherwise.
We deduce from this lemma that persistence condition (11) holds if and only if all resonant
![]() $q\mathbb {Z}$
-harmonics of
$q\mathbb {Z}$
-harmonics of
![]() $\mathcal {Q}_k$
are equal to zero.
$\mathcal {Q}_k$
are equal to zero.
Next, we invert operator
![]() $\delta $
, which is the key point in solving (12) and (13).
$\delta $
, which is the key point in solving (12) and (13).
Lemma A.2. Let
![]() $b(t)$
be any smooth
$b(t)$
be any smooth
![]() $2\pi $
-periodic function. Equation
$2\pi $
-periodic function. Equation
has a smooth
![]() $2\pi $
-periodic solution
$2\pi $
-periodic solution
![]() $a(t)$
if and only if
$a(t)$
if and only if
![]() $\mu \{ b(t) \} = 0$
, in which case, the solution is unique once we fix its smooth
$\mu \{ b(t) \} = 0$
, in which case, the solution is unique once we fix its smooth
![]() $2\pi /q$
-periodic average
$2\pi /q$
-periodic average
![]() $\mu \{a(t)\}$
. Analogously, equation
$\mu \{a(t)\}$
. Analogously, equation
has a smooth
![]() $2\pi $
-periodic solution
$2\pi $
-periodic solution
![]() $\tilde {a}(t)$
if and only if
$\tilde {a}(t)$
if and only if
![]() $\mu \{ b(t) \} \equiv \omega $
, in which case, the solution is unique once we fix its smooth
$\mu \{ b(t) \} \equiv \omega $
, in which case, the solution is unique once we fix its smooth
![]() $2\pi /q$
-periodic average
$2\pi /q$
-periodic average
![]() $\mu \{\tilde {a}(t)\}$
.
$\mu \{\tilde {a}(t)\}$
.
Proof. If
![]() $a(t)$
is a
$a(t)$
is a
![]() $2\pi $
-periodic solution, then
$2\pi $
-periodic solution, then
 $$ \begin{align*} \mu \{ b(t) \} &= \mu \{ a(t + \omega) - a(t) \} = \frac{1}{q} \sum_{j=0}^{q-1} [a(t+(j+1)\omega) - a(t + j\omega) ]\\ &= \frac{a(t + q\omega) - a(t) }{q} = 0. \end{align*} $$
$$ \begin{align*} \mu \{ b(t) \} &= \mu \{ a(t + \omega) - a(t) \} = \frac{1}{q} \sum_{j=0}^{q-1} [a(t+(j+1)\omega) - a(t + j\omega) ]\\ &= \frac{a(t + q\omega) - a(t) }{q} = 0. \end{align*} $$
Conversely, if
![]() $\mu \{ b(t) \} = 0$
, then
$\mu \{ b(t) \} = 0$
, then
![]() $b(t) = \sum _{l \not \in q\mathbb {Z}} \hat {b}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
so that
$b(t) = \sum _{l \not \in q\mathbb {Z}} \hat {b}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
so that
defines the Fourier coefficients of the unique smooth
![]() $2\pi $
-periodic solution
$2\pi $
-periodic solution
![]() $a(t) = \sum _{l \not \in q\mathbb {Z}} \hat {a}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
such that
$a(t) = \sum _{l \not \in q\mathbb {Z}} \hat {a}_l \mathit {e}^{\mskip 2mu {i}\mskip 1mu l t}$
such that
![]() $\mu \{ a(t) \} = 0$
. Smoothness follows from the bounds
$\mu \{ a(t) \} = 0$
. Smoothness follows from the bounds
![]() $|\hat {a}|_l \le \nu |\hat {b}_l|$
for all
$|\hat {a}|_l \le \nu |\hat {b}_l|$
for all
![]() $l \not \in q \mathbb {Z}$
, where
$l \not \in q \mathbb {Z}$
, where
![]() $\nu = 1/|\mathit {e}^{\mskip 2mu {i}\mskip 1mu 2 \pi /q} -1|> 0$
. Since
$\nu = 1/|\mathit {e}^{\mskip 2mu {i}\mskip 1mu 2 \pi /q} -1|> 0$
. Since
![]() $\delta \circ \mu = 0$
, we deduce that the average
$\delta \circ \mu = 0$
, we deduce that the average
![]() $\mu \{ a(t) \}$
does not need to be zero, but can be determined freely.
$\mu \{ a(t) \}$
does not need to be zero, but can be determined freely.
If
![]() $a(t) = t + \tilde {a}(t)$
is a solution such that
$a(t) = t + \tilde {a}(t)$
is a solution such that
![]() $\tilde {a}(t)$
is
$\tilde {a}(t)$
is
![]() $2\pi $
-periodic, then
$2\pi $
-periodic, then
 $$ \begin{align*} \mu \{ b(t) \} = \frac{a(t + q\omega) - a(t) }{q} = \frac{ q\omega + \tilde{a}(t + q\omega) - \tilde{a}(t)}{q} = \omega. \end{align*} $$
$$ \begin{align*} \mu \{ b(t) \} = \frac{a(t + q\omega) - a(t) }{q} = \frac{ q\omega + \tilde{a}(t + q\omega) - \tilde{a}(t)}{q} = \omega. \end{align*} $$
The converse is obtained with the same argument as before.
B Appendix. Computation of some asymptotic expansions
Recall that
![]() $\omega = 2\pi p/q$
,
$\omega = 2\pi p/q$
,
![]() $c = \cos (\omega /2)$
, and
$c = \cos (\omega /2)$
, and
![]() $s = \sin (\omega /2)> 0$
, where
$s = \sin (\omega /2)> 0$
, where
![]() $p/q \in (0,1/2)$
is some rational number such that
$p/q \in (0,1/2)$
is some rational number such that
![]() $\gcd (p,q) = 1$
. Let us compute the asymptotic expansions of
$\gcd (p,q) = 1$
. Let us compute the asymptotic expansions of
from the asymptotic expansion (1) of the support function and the asymptotic expansions (10) of the side, normal, and incidence–reflection functions. We assume that all coefficients
![]() $h_k(\psi )$
,
$h_k(\psi )$
,
![]() $\varphi _k(t)$
,
$\varphi _k(t)$
,
![]() $\psi _k(t)$
, and
$\psi _k(t)$
, and
![]() $\theta _k(t)$
are smooth
$\theta _k(t)$
are smooth
![]() $2\pi $
-periodic functions.
$2\pi $
-periodic functions.
Lemma B.1. The coefficients of the asymptotic expansions
can be computed from the initial values
![]() $\mathcal {S}_0 = s$
and
$\mathcal {S}_0 = s$
and
![]() $\mathcal {C}_0 = c$
by means of the recurrences
$\mathcal {C}_0 = c$
by means of the recurrences
 $$ \begin{align} \mathcal{S}_k = c \theta_k + \frac{1}{k} \sum_{l=1}^{k-1} l \theta_l \mathcal{C}_{k-l}, \quad \mathcal{C}_k = -s \theta_k - \frac{1}{k} \sum_{l=1}^{k-1} l \theta_l \mathcal{S}_{k-l} \quad \text{for all } k \ge 1. \end{align} $$
$$ \begin{align} \mathcal{S}_k = c \theta_k + \frac{1}{k} \sum_{l=1}^{k-1} l \theta_l \mathcal{C}_{k-l}, \quad \mathcal{C}_k = -s \theta_k - \frac{1}{k} \sum_{l=1}^{k-1} l \theta_l \mathcal{S}_{k-l} \quad \text{for all } k \ge 1. \end{align} $$
In particular,
![]() $\mathcal {S}_k = \mathcal {S}_k [{\kern-1.8pt}[ \theta _{\le k} ]{\kern-1.8pt}] = c \theta _k + \tilde {\mathcal {S}}_k [{\kern-1.8pt}[ \theta _{< k} ]{\kern-1.8pt}]$
and
$\mathcal {S}_k = \mathcal {S}_k [{\kern-1.8pt}[ \theta _{\le k} ]{\kern-1.8pt}] = c \theta _k + \tilde {\mathcal {S}}_k [{\kern-1.8pt}[ \theta _{< k} ]{\kern-1.8pt}]$
and
![]() $\mathcal {C}_k = \mathcal {C}_k [{\kern-1.8pt}[ \theta _{\le k} ]{\kern-1.8pt}] = -s \theta _k + \tilde {\mathcal {C}}_k [{\kern-1.8pt}[ \theta _{< k} ]{\kern-1.8pt}]$
.
$\mathcal {C}_k = \mathcal {C}_k [{\kern-1.8pt}[ \theta _{\le k} ]{\kern-1.8pt}] = -s \theta _k + \tilde {\mathcal {C}}_k [{\kern-1.8pt}[ \theta _{< k} ]{\kern-1.8pt}]$
.
Proof. These recurrences are directly obtained from identities
Definition B.2. If
![]() ${\boldsymbol {\alpha }} = \{\alpha _1,\alpha _2,\ldots \}$
is a sequence of non-negative integers with a finite number of non-zero terms and
${\boldsymbol {\alpha }} = \{\alpha _1,\alpha _2,\ldots \}$
is a sequence of non-negative integers with a finite number of non-zero terms and
![]() ${\boldsymbol {\psi }} = \{\psi _1,\psi _2,\ldots \}$
is a sequence of smooth
${\boldsymbol {\psi }} = \{\psi _1,\psi _2,\ldots \}$
is a sequence of smooth
![]() $2\pi $
-periodic functions, then
$2\pi $
-periodic functions, then
Lemma B.3. The coefficients of the asymptotic expansion
are given by
![]() $\mathcal {H}_k = \mathcal {H}_k [{\kern-1.8pt}[ h_{\le k},\psi _{<k} ]{\kern-1.8pt}] = h_k + \tilde {\mathcal {H}}_k [{\kern-1.8pt}[ h_{<k},\psi _{<k} ]{\kern-1.8pt}]$
with
$\mathcal {H}_k = \mathcal {H}_k [{\kern-1.8pt}[ h_{\le k},\psi _{<k} ]{\kern-1.8pt}] = h_k + \tilde {\mathcal {H}}_k [{\kern-1.8pt}[ h_{<k},\psi _{<k} ]{\kern-1.8pt}]$
with
 $$ \begin{align} \tilde{\mathcal{H}}_k = \sum_{i=1}^{k-1} \sum_{j=1}^{k-i} \bigg(\sum_{|{\boldsymbol{\alpha}}| = j,\| {\boldsymbol{\alpha}} \| = k-i} \frac{{\boldsymbol{\psi}}^{\boldsymbol{\alpha}}}{{\boldsymbol{\alpha}} !} \bigg) h_i^{(j)} \quad \text{for all } k \ge 1. \end{align} $$
$$ \begin{align} \tilde{\mathcal{H}}_k = \sum_{i=1}^{k-1} \sum_{j=1}^{k-i} \bigg(\sum_{|{\boldsymbol{\alpha}}| = j,\| {\boldsymbol{\alpha}} \| = k-i} \frac{{\boldsymbol{\psi}}^{\boldsymbol{\alpha}}}{{\boldsymbol{\alpha}} !} \bigg) h_i^{(j)} \quad \text{for all } k \ge 1. \end{align} $$
Analogously,
![]() $h' \circ \psi \asymp \sum _{k \ge 1} \mathcal {H}_k[{\kern-1.8pt}[ h^{\prime }_{\le k},\psi _{<k} ]{\kern-1.8pt}] \epsilon ^k$
as
$h' \circ \psi \asymp \sum _{k \ge 1} \mathcal {H}_k[{\kern-1.8pt}[ h^{\prime }_{\le k},\psi _{<k} ]{\kern-1.8pt}] \epsilon ^k$
as
![]() $\epsilon \to 0$
.
$\epsilon \to 0$
.
Proof. Set
![]() $\Delta \psi := \psi - t \asymp \sum _{i \ge 1} \epsilon ^i \psi _i$
as
$\Delta \psi := \psi - t \asymp \sum _{i \ge 1} \epsilon ^i \psi _i$
as
![]() $\epsilon \to 0$
. Equation (B.2) is a direct consequence of the asymptotic expansions
$\epsilon \to 0$
. Equation (B.2) is a direct consequence of the asymptotic expansions
 $$ \begin{align*} h_i(t + \Delta \psi) \asymp \sum_{j \ge 0} \frac{(\Delta \psi)^j}{j!} h_i^{(j)},\quad \frac{(\Delta \psi)^j}{j!} \asymp \sum_{|{\boldsymbol{\alpha}}| = j} \frac{{\boldsymbol{\psi}}^{\boldsymbol{\alpha}}}{{\boldsymbol{\alpha}}!} \epsilon^{\| {\boldsymbol{\alpha}} \|} \end{align*} $$
$$ \begin{align*} h_i(t + \Delta \psi) \asymp \sum_{j \ge 0} \frac{(\Delta \psi)^j}{j!} h_i^{(j)},\quad \frac{(\Delta \psi)^j}{j!} \asymp \sum_{|{\boldsymbol{\alpha}}| = j} \frac{{\boldsymbol{\psi}}^{\boldsymbol{\alpha}}}{{\boldsymbol{\alpha}}!} \epsilon^{\| {\boldsymbol{\alpha}} \|} \end{align*} $$
as
![]() $\Delta \psi \to 0$
and
$\Delta \psi \to 0$
and
![]() $\epsilon \to 0$
, respectively. The first expansion is the Taylor theorem. The second expansion is the multinomial theorem.
$\epsilon \to 0$
, respectively. The first expansion is the Taylor theorem. The second expansion is the multinomial theorem.
On the one hand, if
![]() $| {\boldsymbol {\alpha }} | = j = 0$
and
$| {\boldsymbol {\alpha }} | = j = 0$
and
![]() $\| {\boldsymbol {\alpha }} \| = k-i$
, then
$\| {\boldsymbol {\alpha }} \| = k-i$
, then
![]() $i=k$
and
$i=k$
and
![]() ${\boldsymbol {\alpha }} = \{0,0,\ldots \}$
. On the other hand, if
${\boldsymbol {\alpha }} = \{0,0,\ldots \}$
. On the other hand, if
![]() $| {\boldsymbol {\alpha }} | = j \ge 1$
and
$| {\boldsymbol {\alpha }} | = j \ge 1$
and
![]() $\| {\boldsymbol {\alpha }} \| = k - i$
, then
$\| {\boldsymbol {\alpha }} \| = k - i$
, then
![]() $i \le k-1$
,
$i \le k-1$
,
![]() $j \le k - i$
, and
$j \le k - i$
, and
![]() $\alpha _l = 0$
for all
$\alpha _l = 0$
for all
![]() $l \ge k$
. This justifies that
$l \ge k$
. This justifies that
![]() $\mathcal {H}_k = \mathcal {H}_k [{\kern-1.8pt}[ h_{\le k},\psi _{<k} ]{\kern-1.8pt}] = h_k + \tilde {\mathcal {H}}_k [{\kern-1.8pt}[ h_{<k},\psi _{<k} ]{\kern-1.8pt}]$
.
$\mathcal {H}_k = \mathcal {H}_k [{\kern-1.8pt}[ h_{\le k},\psi _{<k} ]{\kern-1.8pt}] = h_k + \tilde {\mathcal {H}}_k [{\kern-1.8pt}[ h_{<k},\psi _{<k} ]{\kern-1.8pt}]$
.
The next result is a more informative version of Lemma 4.1, whose proof was pending.
Lemma B.4. The coefficients of the asymptotic expansions
are given by
 $$ \begin{align*} \mathcal{Q}_k &= \mathcal{Q}_k [{\kern-1.8pt}[ h^{\prime}_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] = s h^{\prime}_k + \tilde{\mathcal{Q}}_k [{\kern-1.8pt}[ h^{\prime}_{<k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}], \\ \tilde{\mathcal{Q}}_k &= s \tilde{\mathcal{H}}_k [{\kern-1.8pt}[ h^{\prime}_{<k},\psi_{<k} ]{\kern-1.8pt}] + \sum_{l=1}^{k-1} \mathcal{H}_l [{\kern-1.8pt}[ h^{\prime}_{\le l},\psi_{<l} ]{\kern-1.8pt}] \mathcal{S}_{k-l} [{\kern-1.8pt}[ \theta_{\le k-l} ]{\kern-1.8pt}], \\ \mathcal{R}_k &= \mathcal{R}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{\le k} ]{\kern-1.8pt}] = \tilde{\mathcal{R}}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] - s\theta_k, \\ \tilde{\mathcal{R}}_k &= c \mathcal{H}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k} ]{\kern-1.8pt}] + \tilde{\mathcal{C}}_k [{\kern-1.8pt}[ \theta_{<k} ]{\kern-1.8pt}] + \sum_{l=1}^{k-1} \mathcal{H}_l [{\kern-1.8pt}[ h_{\le l},\psi_{<l} ]{\kern-1.8pt}] \mathcal{C}_{k-l} [{\kern-1.8pt}[ \theta_{\le k-l} ]{\kern-1.8pt}]. \end{align*} $$
$$ \begin{align*} \mathcal{Q}_k &= \mathcal{Q}_k [{\kern-1.8pt}[ h^{\prime}_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] = s h^{\prime}_k + \tilde{\mathcal{Q}}_k [{\kern-1.8pt}[ h^{\prime}_{<k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}], \\ \tilde{\mathcal{Q}}_k &= s \tilde{\mathcal{H}}_k [{\kern-1.8pt}[ h^{\prime}_{<k},\psi_{<k} ]{\kern-1.8pt}] + \sum_{l=1}^{k-1} \mathcal{H}_l [{\kern-1.8pt}[ h^{\prime}_{\le l},\psi_{<l} ]{\kern-1.8pt}] \mathcal{S}_{k-l} [{\kern-1.8pt}[ \theta_{\le k-l} ]{\kern-1.8pt}], \\ \mathcal{R}_k &= \mathcal{R}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{\le k} ]{\kern-1.8pt}] = \tilde{\mathcal{R}}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k},\theta_{<k} ]{\kern-1.8pt}] - s\theta_k, \\ \tilde{\mathcal{R}}_k &= c \mathcal{H}_k [{\kern-1.8pt}[ h_{\le k},\psi_{<k} ]{\kern-1.8pt}] + \tilde{\mathcal{C}}_k [{\kern-1.8pt}[ \theta_{<k} ]{\kern-1.8pt}] + \sum_{l=1}^{k-1} \mathcal{H}_l [{\kern-1.8pt}[ h_{\le l},\psi_{<l} ]{\kern-1.8pt}] \mathcal{C}_{k-l} [{\kern-1.8pt}[ \theta_{\le k-l} ]{\kern-1.8pt}]. \end{align*} $$
Finally, we compute the asymptotic expansion of the support function of the deformation of the unit circle given by (4) in Cartesian coordinates. We assume that
![]() $P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
and
$P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
and
![]() $P_1(x,y) \in \mathbb {R}_n[x,y]$
.
$P_1(x,y) \in \mathbb {R}_n[x,y]$
.
Lemma B.5. If
![]() $P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
with
$P(x,y;\epsilon ) = 1 + \epsilon P_1(x,y)$
with
![]() $P_1(x,y) = \sum _{i,j \ge 0, i+j \le n} p_{ij} x^i y^j$
, then the coefficients of the asymptotic expansion (1) of the support function of the deformation (4) can be computed from recurrences
$P_1(x,y) = \sum _{i,j \ge 0, i+j \le n} p_{ij} x^i y^j$
, then the coefficients of the asymptotic expansion (1) of the support function of the deformation (4) can be computed from recurrences
where
 $$ \begin{align*}\mathcal{G}^\star_k &=2h_k + \tilde{\mathcal{G}}^\star_k =2h_k + 2 \sum_{|{\boldsymbol{\alpha}}| = 2, \| {\boldsymbol{\alpha}} \| = k}{\vphantom{\sum}\kern-16pt}^{\prime}\, \quad {\boldsymbol{h}}^{\boldsymbol{\alpha}}/{\boldsymbol{\alpha}}!, \\\tilde{\mathcal{G}}^\bullet_k &= 2 \sum_{|{\boldsymbol{\alpha}}| = 2, \| {\boldsymbol{\alpha}} \| = k}{\vphantom{\sum}\kern-16pt}^{\prime} \quad({\boldsymbol{h}}')^{\boldsymbol{\alpha}}/{\boldsymbol{\alpha}}!, \\\mathcal{G}^\diamond_k &= \sum_{i,j \ge 0, i+j \le n} p_{ij} \ i! \ j!\sum_{|{\boldsymbol{\alpha}}| = i, |{\boldsymbol{\beta}}| = j, \| {\boldsymbol{\alpha}} \| + \| {\boldsymbol{\beta}} \| = k}{\boldsymbol{x}}^{\boldsymbol{\alpha}} {\boldsymbol{y}}^{\boldsymbol{\beta}}/ {\boldsymbol{\alpha}}! {\boldsymbol{\beta}}!, \\{\boldsymbol{x}} &= \cos \psi \cdot {\boldsymbol{h}} - \sin \psi \cdot {\boldsymbol{h}}', \\{\boldsymbol{y}} &= \sin \psi \cdot {\boldsymbol{h}} + \cos \psi \cdot {\boldsymbol{h}}'. \end{align*} $$
$$ \begin{align*}\mathcal{G}^\star_k &=2h_k + \tilde{\mathcal{G}}^\star_k =2h_k + 2 \sum_{|{\boldsymbol{\alpha}}| = 2, \| {\boldsymbol{\alpha}} \| = k}{\vphantom{\sum}\kern-16pt}^{\prime}\, \quad {\boldsymbol{h}}^{\boldsymbol{\alpha}}/{\boldsymbol{\alpha}}!, \\\tilde{\mathcal{G}}^\bullet_k &= 2 \sum_{|{\boldsymbol{\alpha}}| = 2, \| {\boldsymbol{\alpha}} \| = k}{\vphantom{\sum}\kern-16pt}^{\prime} \quad({\boldsymbol{h}}')^{\boldsymbol{\alpha}}/{\boldsymbol{\alpha}}!, \\\mathcal{G}^\diamond_k &= \sum_{i,j \ge 0, i+j \le n} p_{ij} \ i! \ j!\sum_{|{\boldsymbol{\alpha}}| = i, |{\boldsymbol{\beta}}| = j, \| {\boldsymbol{\alpha}} \| + \| {\boldsymbol{\beta}} \| = k}{\boldsymbol{x}}^{\boldsymbol{\alpha}} {\boldsymbol{y}}^{\boldsymbol{\beta}}/ {\boldsymbol{\alpha}}! {\boldsymbol{\beta}}!, \\{\boldsymbol{x}} &= \cos \psi \cdot {\boldsymbol{h}} - \sin \psi \cdot {\boldsymbol{h}}', \\{\boldsymbol{y}} &= \sin \psi \cdot {\boldsymbol{h}} + \cos \psi \cdot {\boldsymbol{h}}'. \end{align*} $$
Here,
![]() ${\boldsymbol {\alpha }} = \{ \alpha _0, \alpha _1, \ldots \}$
,
${\boldsymbol {\alpha }} = \{ \alpha _0, \alpha _1, \ldots \}$
,
![]() ${\boldsymbol {\beta }} = \{ \beta _0, \beta _1, \ldots \}$
,
${\boldsymbol {\beta }} = \{ \beta _0, \beta _1, \ldots \}$
,
![]() ${\boldsymbol {h}} = \{1, h_1, h_2, \ldots \}$
, and
${\boldsymbol {h}} = \{1, h_1, h_2, \ldots \}$
, and
![]() ${\boldsymbol {h}}' = \{0, h^{\prime }_1, h^{\prime }_2,\ldots \}$
. Symbol
${\boldsymbol {h}}' = \{0, h^{\prime }_1, h^{\prime }_2,\ldots \}$
. Symbol
![]() $\sum ^{\prime }_{|{\boldsymbol {\alpha }}| = 2, \| {\boldsymbol {\alpha }} \| = k}$
means that we do not include the term with
$\sum ^{\prime }_{|{\boldsymbol {\alpha }}| = 2, \| {\boldsymbol {\alpha }} \| = k}$
means that we do not include the term with
![]() $\alpha _0 = 1$
and
$\alpha _0 = 1$
and
![]() $\alpha _k = 1$
.
$\alpha _k = 1$
.
Proof. We know that
![]() $z(\psi ;\epsilon ) = \big ( x(\psi ;\epsilon ), y(\psi ;\epsilon ) \big )$
, where
$z(\psi ;\epsilon ) = \big ( x(\psi ;\epsilon ), y(\psi ;\epsilon ) \big )$
, where
 $$ \begin{align*} x = x(\psi;\epsilon) &= \cos \psi \cdot h(\psi;\epsilon) - \sin \psi \cdot h'(\psi;\epsilon),\\ y = y(\psi;\epsilon) &= \sin \psi \cdot h(\psi;\epsilon) + \cos \psi \cdot h'(\psi;\epsilon), \end{align*} $$
$$ \begin{align*} x = x(\psi;\epsilon) &= \cos \psi \cdot h(\psi;\epsilon) - \sin \psi \cdot h'(\psi;\epsilon),\\ y = y(\psi;\epsilon) &= \sin \psi \cdot h(\psi;\epsilon) + \cos \psi \cdot h'(\psi;\epsilon), \end{align*} $$
is a normal parameterization of
![]() $\Gamma _\epsilon $
, so the support function satisfies the implicit equation
$\Gamma _\epsilon $
, so the support function satisfies the implicit equation
Therefore, recurrence (B.3) is a direct consequence of the asymptotic expansions
as
![]() $\epsilon \to 0$
, all of which follow from the multinomial theorem.
$\epsilon \to 0$
, all of which follow from the multinomial theorem.
C Appendix. Proofs of Theorem 5.1 and Lemma 5.2
There are two main tools for both proofs. First, the explicit formulas for the asymptotic coefficients
![]() $\mathcal {S}_k = c \theta _k + \tilde {\mathcal {S}}_k$
,
$\mathcal {S}_k = c \theta _k + \tilde {\mathcal {S}}_k$
,
![]() $\mathcal {C}_k = \tilde {\mathcal {C}}_k - s\theta _k$
,
$\mathcal {C}_k = \tilde {\mathcal {C}}_k - s\theta _k$
,
![]() $\mathcal {H}_k = h_k + \tilde {\mathcal {H}}_k$
,
$\mathcal {H}_k = h_k + \tilde {\mathcal {H}}_k$
,
![]() $\mathcal {R}_k = \tilde {\mathcal {R}}_k - s\theta _k$
,
$\mathcal {R}_k = \tilde {\mathcal {R}}_k - s\theta _k$
,
![]() $\mathcal {Q}_k$
,
$\mathcal {Q}_k$
,
![]() $\tilde {\mathcal {G}}^\star _k$
,
$\tilde {\mathcal {G}}^\star _k$
,
![]() $\tilde {\mathcal {G}}^\bullet _k$
, and
$\tilde {\mathcal {G}}^\bullet _k$
, and
![]() $\mathcal {G}^\diamond _k$
given in Appendix B. Second, the following elementary properties:
$\mathcal {G}^\diamond _k$
given in Appendix B. Second, the following elementary properties:
-
•
 $T_k[t]$
is a real vector space;
$T_k[t]$
is a real vector space; -
•
 $a(t) \in T_k[t], \ b(t) \in T_l[t] \Rightarrow a(t)b(t) \in T_{k+l}[t], \ a'(t) \in T_k[t]$
;
$a(t) \in T_k[t], \ b(t) \in T_l[t] \Rightarrow a(t)b(t) \in T_{k+l}[t], \ a'(t) \in T_k[t]$
; -
•
 ${\boldsymbol {\alpha }} = \{ \alpha _0,\alpha _1,\ldots \}$
and
${\boldsymbol {\alpha }} = \{ \alpha _0,\alpha _1,\ldots \}$
and
 ${\boldsymbol {a}} = \{ a_0,a_1,\ldots \}$
with
${\boldsymbol {a}} = \{ a_0,a_1,\ldots \}$
with
 $a_j(t) \in T_{nj}[t] \Rightarrow {\boldsymbol {a}}^{\boldsymbol {\alpha }}(t) \in T_{n \| {\boldsymbol {\alpha }} \|}[t]$
;
$a_j(t) \in T_{nj}[t] \Rightarrow {\boldsymbol {a}}^{\boldsymbol {\alpha }}(t) \in T_{n \| {\boldsymbol {\alpha }} \|}[t]$
; -
•
 $a(t) \in T_k[t] \Rightarrow \sigma \{a(t)\}, \delta \{ a(t) \}, \mu \{ a(t) \} \in T_k[t]$
; and
$a(t) \in T_k[t] \Rightarrow \sigma \{a(t)\}, \delta \{ a(t) \}, \mu \{ a(t) \} \in T_k[t]$
; and -
•
 $b(t) \in T_k[t], \ \mu \{ b(t) \} = 0 \Rightarrow \text { there exists } ! a(t) \in T_k[t]$
such that
$b(t) \in T_k[t], \ \mu \{ b(t) \} = 0 \Rightarrow \text { there exists } ! a(t) \in T_k[t]$
such that
 $\delta \{ a(t) \} = b(t)$
and
$\delta \{ a(t) \} = b(t)$
and
 $\mu \{ a(t) \} = 0$
.
$\mu \{ a(t) \} = 0$
.
We will use these properties without any explicit mention in what follows.
Lemma C.1. If condition (3) holds and
![]() $q> nm$
, then we can compute the
$q> nm$
, then we can compute the
![]() $\mathrm {O} (\epsilon ^m)$
- corrections
$\mathrm {O} (\epsilon ^m)$
- corrections
![]() $\theta _{\le m}(t;\epsilon )$
,
$\theta _{\le m}(t;\epsilon )$
,
![]() $\varphi _{\le m}(t;\epsilon )$
and
$\varphi _{\le m}(t;\epsilon )$
and
![]() $\psi _{\le m}(t;\epsilon )$
by solving the compatible equations (12) and (13) for
$\psi _{\le m}(t;\epsilon )$
by solving the compatible equations (12) and (13) for
![]() $k=1,\ldots ,m$
. Compatibility is guaranteed because all necessary and sufficient persistence conditions (11) hold for
$k=1,\ldots ,m$
. Compatibility is guaranteed because all necessary and sufficient persistence conditions (11) hold for
![]() $k=1,\ldots ,m$
.
$k=1,\ldots ,m$
.
Proof. It suffices to check that:
-
(i)
 $\mathcal {H}_k = h_k + \tilde {\mathcal {H}}_k \in T_{nk}[t]$
;
$\mathcal {H}_k = h_k + \tilde {\mathcal {H}}_k \in T_{nk}[t]$
; -
(ii)
 $\tilde {\mathcal {R}}_k,\mathcal {Q}_k \in T_{nk}[t]$
, so condition (11) holds because
$\tilde {\mathcal {R}}_k,\mathcal {Q}_k \in T_{nk}[t]$
, so condition (11) holds because
 $q> nm$
and
$q> nm$
and
 $\bar {\mathcal {Q}}_k = 0$
;
$\bar {\mathcal {Q}}_k = 0$
; -
(iii)
 $\theta _k, \varphi _k, \psi _k \in T_{nk}[t]$
; and
$\theta _k, \varphi _k, \psi _k \in T_{nk}[t]$
; and -
(iv)
 $\mathcal {S}_k, \mathcal {C}_k \in T_{nk}[t]$
;
$\mathcal {S}_k, \mathcal {C}_k \in T_{nk}[t]$
;
for
![]() $k=1,\ldots ,m$
. We prove it by induction over m.
$k=1,\ldots ,m$
. We prove it by induction over m.
The base case
![]() $m=1$
is trivial. Namely,
$m=1$
is trivial. Namely,
![]() $\mathcal {H}_1 = h_1 \in T_n[t]$
by condition (3),
$\mathcal {H}_1 = h_1 \in T_n[t]$
by condition (3),
![]() $\tilde {\mathcal {R}}_1 = ch_1 \in T_n[t]$
,
$\tilde {\mathcal {R}}_1 = ch_1 \in T_n[t]$
,
![]() $\mathcal {Q}_1 = sh^{\prime }_1 \in T_n[t]$
,
$\mathcal {Q}_1 = sh^{\prime }_1 \in T_n[t]$
,
![]() $\theta _1 \in T_n[t]$
is the unique solution of problem (15),
$\theta _1 \in T_n[t]$
is the unique solution of problem (15),
![]() $\varphi _1 \in T_n[t]$
is the unique solution of equation
$\varphi _1 \in T_n[t]$
is the unique solution of equation
![]() $\delta \{ \varphi _1 \} = 2\theta _1$
such that
$\delta \{ \varphi _1 \} = 2\theta _1$
such that
![]() $\mu \{ \varphi _1 \} = 0$
,
$\mu \{ \varphi _1 \} = 0$
,
![]() $\psi _1 = \varphi _1 + \theta _1 \in T_n[t]$
,
$\psi _1 = \varphi _1 + \theta _1 \in T_n[t]$
,
![]() $\mathcal {S}_1 = c \theta _1 \in T_n[t]$
, and
$\mathcal {S}_1 = c \theta _1 \in T_n[t]$
, and
![]() $\mathcal {C}_1 = -s \theta _1 \in T_n[t]$
.
$\mathcal {C}_1 = -s \theta _1 \in T_n[t]$
.
Next, let us assume that properties (i)–(iv) hold for
![]() $k=1,\ldots ,m-1$
. We need to prove that they also hold for
$k=1,\ldots ,m-1$
. We need to prove that they also hold for
![]() $k=m$
. Property (i) follows from (B.2) and condition (3). Property (ii) follows from the recurrences given in Lemma B.4. Then,
$k=m$
. Property (i) follows from (B.2) and condition (3). Property (ii) follows from the recurrences given in Lemma B.4. Then,
![]() $\theta _m \in T_{nm}[t]$
is the unique solution of equation
$\theta _m \in T_{nm}[t]$
is the unique solution of equation
![]() $s \delta \{ \theta _m \} = \delta \{ \tilde {\mathcal {R}}_m \} -\sigma \{ \mathcal {Q}_m \}$
such that
$s \delta \{ \theta _m \} = \delta \{ \tilde {\mathcal {R}}_m \} -\sigma \{ \mathcal {Q}_m \}$
such that
![]() $\mu \{ \theta _m \} = 0$
,
$\mu \{ \theta _m \} = 0$
,
![]() $\varphi _m \in T_{nm}[t]$
is the unique solution of equation
$\varphi _m \in T_{nm}[t]$
is the unique solution of equation
![]() $\delta \{ \varphi _m \} = 2\theta _m$
such that
$\delta \{ \varphi _m \} = 2\theta _m$
such that
![]() $\mu \{ \varphi _m \} = 0$
, and
$\mu \{ \varphi _m \} = 0$
, and
![]() $\psi _m = \varphi _m + \theta _m \in T_{nm}[t]$
. This proves property (iii). Property (iv) follows from recurrences (B.1).
$\psi _m = \varphi _m + \theta _m \in T_{nm}[t]$
. This proves property (iii). Property (iv) follows from recurrences (B.1).
Lemma C.2. If condition (3) holds,
![]() $\Gamma _\epsilon $
is centrally symmetric, q is odd, and
$\Gamma _\epsilon $
is centrally symmetric, q is odd, and
![]() $2q> nm$
, then we can compute all
$2q> nm$
, then we can compute all
![]() $\mathrm {O} (\epsilon ^m)$
-corrections too.
$\mathrm {O} (\epsilon ^m)$
-corrections too.
Proof. If
![]() $\Gamma _\epsilon $
is centrally symmetric, then its support function
$\Gamma _\epsilon $
is centrally symmetric, then its support function
![]() $h(\psi ;\epsilon )$
is
$h(\psi ;\epsilon )$
is
![]() $\pi $
-periodic in
$\pi $
-periodic in
![]() $\psi $
. In that case, it is not hard to prove by induction over m that items (i)–(iv) listed in the proof of the previous lemma are also
$\psi $
. In that case, it is not hard to prove by induction over m that items (i)–(iv) listed in the proof of the previous lemma are also
![]() $\pi $
-periodic for
$\pi $
-periodic for
![]() $k=1,\ldots ,m$
. In particular, if q is odd and
$k=1,\ldots ,m$
. In particular, if q is odd and
![]() $2q> nm$
, then persistence condition (11) holds because all resonant
$2q> nm$
, then persistence condition (11) holds because all resonant
![]() $q\mathbb {Z}$
-harmonics of the
$q\mathbb {Z}$
-harmonics of the
![]() $\pi $
-periodic trigonometric polynomial
$\pi $
-periodic trigonometric polynomial
![]() $\mathcal {Q}_k \in T_{nk}[t]$
are equal to zero for
$\mathcal {Q}_k \in T_{nk}[t]$
are equal to zero for
![]() $k=1,\ldots ,m$
.
$k=1,\ldots ,m$
.
Lemma C.3. If condition (3) holds,
![]() $\Gamma _\epsilon $
is anti-centrally symmetric,
$\Gamma _\epsilon $
is anti-centrally symmetric,
![]() $q \neq m\ \mod 2$
,
$q \neq m\ \mod 2$
,
![]() $m \ge 2$
, and
$m \ge 2$
, and
![]() $q> n(m-1)$
, then we can compute all
$q> n(m-1)$
, then we can compute all
![]() $\mathrm {O} (\epsilon ^m)$
-corrections too.
$\mathrm {O} (\epsilon ^m)$
-corrections too.
Proof. We already know from Lemma C.1 that we can compute the
![]() $\mathrm {O} (\epsilon ^{m-1})$
-corrections, since
$\mathrm {O} (\epsilon ^{m-1})$
-corrections, since
![]() $q> n(m-1)$
. Therefore, we only need to check that the last persistence condition
$q> n(m-1)$
. Therefore, we only need to check that the last persistence condition
holds. That is, we need to check that all resonant
![]() $q \mathbb {Z}$
-harmonics of
$q \mathbb {Z}$
-harmonics of
![]() $\mathcal {Q}_m$
are equal to zero.
$\mathcal {Q}_m$
are equal to zero.
If the perturbation
![]() $\Gamma _\epsilon $
is anti-centrally symmetric, then its support function satisfies that
$\Gamma _\epsilon $
is anti-centrally symmetric, then its support function satisfies that
![]() $h(\psi ;\epsilon ) = h(\psi +\pi ;-\epsilon )$
and its asymptotic coefficients satisfy that
$h(\psi ;\epsilon ) = h(\psi +\pi ;-\epsilon )$
and its asymptotic coefficients satisfy that
In that case, it is not hard to prove by induction over m that items (i)–(iv) listed in the proof of Lemma C.1 satisfy the same property. Namely, that they are
![]() $\pi $
-periodic and
$\pi $
-periodic and
![]() $\pi $
-antiperiodic functions for even and odd indexes k, respectively. In particular, if m is even (respectively odd), then
$\pi $
-antiperiodic functions for even and odd indexes k, respectively. In particular, if m is even (respectively odd), then
![]() $\mathcal {Q}_m$
only contains even (respectively odd) harmonics. Hence,
$\mathcal {Q}_m$
only contains even (respectively odd) harmonics. Hence,
![]() $\mathcal {Q}_m$
does not contain harmonics
$\mathcal {Q}_m$
does not contain harmonics
![]() $\mathit {e}^{\pm \mskip 2mu{i}\mskip 1mu q t}$
, because
$\mathit {e}^{\pm \mskip 2mu{i}\mskip 1mu q t}$
, because
![]() $q \neq m\ \mod 2$
, and it does not contain any harmonic
$q \neq m\ \mod 2$
, and it does not contain any harmonic
![]() $\mathit {e}^{\pm \mskip 2mu\mathrm {i}\mskip 1mu l q t}$
with
$\mathit {e}^{\pm \mskip 2mu\mathrm {i}\mskip 1mu l q t}$
with
![]() $l \ge 2$
either, because
$l \ge 2$
either, because
![]() $lq \ge 2q> 2n(m-1) \ge nm$
and
$lq \ge 2q> 2n(m-1) \ge nm$
and
![]() $\mathcal {Q}_m \in T_{nm}[t]$
. We have used that
$\mathcal {Q}_m \in T_{nm}[t]$
. We have used that
![]() $m \ge 2$
in the last inequality.
$m \ge 2$
in the last inequality.
Theorem 5.1 is a direct consequence of the previous three lemmas.
Proof of Lemma 5.2
We have to check that
![]() $\tilde {\mathcal {G}}^\star _k, \tilde {\mathcal {G}}^\bullet _k, \mathcal {G}^\diamond _{k-1}, h_k \in T_{nk}$
for all
$\tilde {\mathcal {G}}^\star _k, \tilde {\mathcal {G}}^\bullet _k, \mathcal {G}^\diamond _{k-1}, h_k \in T_{nk}$
for all
![]() $k \ge 1$
. We prove it by induction over k. The base case
$k \ge 1$
. We prove it by induction over k. The base case
![]() $k=1$
is trivial, because
$k=1$
is trivial, because
![]() $\tilde {\mathcal {G}}^\star _1 = 0$
,
$\tilde {\mathcal {G}}^\star _1 = 0$
,
![]() $\tilde {\mathcal {G}}^\bullet _1 = 0$
,
$\tilde {\mathcal {G}}^\bullet _1 = 0$
,
![]() $\mathcal {G}^\diamond _0 = P_1(\cos \psi ,\sin \psi )$
, and
$\mathcal {G}^\diamond _0 = P_1(\cos \psi ,\sin \psi )$
, and
![]() $h_1 = \tfrac 12 P_1(\cos \psi ,\sin \psi )$
. The induction step follows from the explicit formulas given in Lemma B.5 and the elementary properties listed at the beginning of this appendix. The claims about symmetries are trivial.
$h_1 = \tfrac 12 P_1(\cos \psi ,\sin \psi )$
. The induction step follows from the explicit formulas given in Lemma B.5 and the elementary properties listed at the beginning of this appendix. The claims about symmetries are trivial.