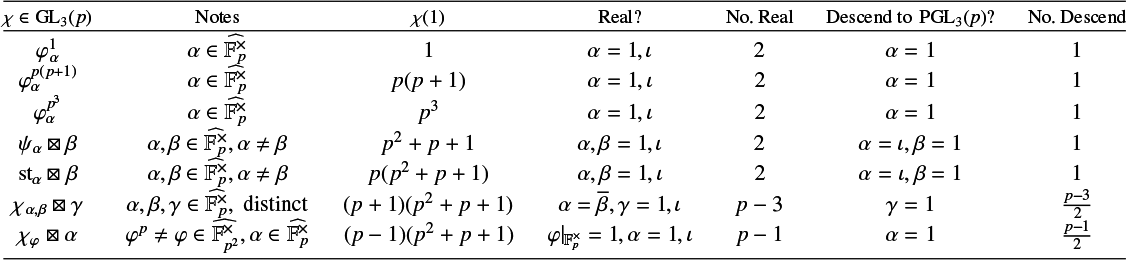1 Introduction
Let k be an algebraically closed field of characteristic
![]() $p> 0$
, let G be a finite group and let B be a block of
$p> 0$
, let G be a finite group and let B be a block of
![]() $kG$
. One way to encode the local structure of B is via a pair
$kG$
. One way to encode the local structure of B is via a pair
![]() $(\mathcal {F},\alpha )$
, where
$(\mathcal {F},\alpha )$
, where
![]() $\mathcal {F} = \mathcal {F}_S(B)$
is the fusion system of the block on the defect group S of B and
$\mathcal {F} = \mathcal {F}_S(B)$
is the fusion system of the block on the defect group S of B and
![]() $\alpha = (\alpha _{Q})_{Q \in \mathcal {F}^c}$
is a certain compatible family of
$\alpha = (\alpha _{Q})_{Q \in \mathcal {F}^c}$
is a certain compatible family of
![]() $2$
-cohomology classes of automorphism groups of centric subgroups of the fusion system. In this context, an Alperin weight is a projective simple module for the twisted group algebra
$2$
-cohomology classes of automorphism groups of centric subgroups of the fusion system. In this context, an Alperin weight is a projective simple module for the twisted group algebra
![]() $k_{\alpha }\operatorname {Out}_{\mathcal {F}}(Q)$
, and so the number
$k_{\alpha }\operatorname {Out}_{\mathcal {F}}(Q)$
, and so the number
![]() $\operatorname {\mathbf {w}}(B) = \operatorname {\mathbf {w}}(\mathcal {F},\alpha )$
of B-weights can be counted from the information in the pair.
$\operatorname {\mathbf {w}}(B) = \operatorname {\mathbf {w}}(\mathcal {F},\alpha )$
of B-weights can be counted from the information in the pair.
If
![]() $\mathcal {F}$
is a saturated fusion system on a finite p-group, there is nothing preventing one from fixing a compatible family
$\mathcal {F}$
is a saturated fusion system on a finite p-group, there is nothing preventing one from fixing a compatible family
![]() $\alpha $
and imagining
$\alpha $
and imagining
![]() $(\mathcal {F},\alpha )$
arose from a block in the above fashion, even if this is not actually the case. In [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19], we took this point of view. There, we defined two numbers
$(\mathcal {F},\alpha )$
arose from a block in the above fashion, even if this is not actually the case. In [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19], we took this point of view. There, we defined two numbers
![]() $\operatorname {\mathbf {k}}(\mathcal {F},\alpha )$
and
$\operatorname {\mathbf {k}}(\mathcal {F},\alpha )$
and
![]() $\operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
that are both stand-ins for the number of ‘ordinary irreducible characters’ of
$\operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
that are both stand-ins for the number of ‘ordinary irreducible characters’ of
![]() $(\mathcal {F},\alpha )$
. If
$(\mathcal {F},\alpha )$
. If
![]() $(\mathcal {F},\alpha )$
comes from a block B, then
$(\mathcal {F},\alpha )$
comes from a block B, then
![]() $\operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
is exactly the local side of the equality appearing in a certain ‘summed-up’ version of Robinson’s ordinary weight conjecture (SOWC), which is supposed to count the number of ordinary irreducible characters in B (see the paragraph preceding [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Conjecture 2.3]). However,
$\operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
is exactly the local side of the equality appearing in a certain ‘summed-up’ version of Robinson’s ordinary weight conjecture (SOWC), which is supposed to count the number of ordinary irreducible characters in B (see the paragraph preceding [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Conjecture 2.3]). However,
![]() $\operatorname {\mathbf {k}}(\mathcal {F},\alpha )$
is the local side of an equality that is an immediate consequence of Alperin’s weight conjecture (AWC) and which is supposed to count the same number. It was shown in [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19] that
$\operatorname {\mathbf {k}}(\mathcal {F},\alpha )$
is the local side of an equality that is an immediate consequence of Alperin’s weight conjecture (AWC) and which is supposed to count the same number. It was shown in [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19] that
![]() $\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) = \operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
for all pairs
$\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) = \operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
for all pairs
![]() $(\mathcal {F},\alpha )$
, possibly with
$(\mathcal {F},\alpha )$
, possibly with
![]() $\mathcal {F}$
an exotic fusion system, conditional on the validity of AWC for all blocks of finite group algebras. Indeed, our proof of this is a fusion-theoretic version of Robinson’s theorem that AWC holds for all blocks if and only if SOWC does.
$\mathcal {F}$
an exotic fusion system, conditional on the validity of AWC for all blocks of finite group algebras. Indeed, our proof of this is a fusion-theoretic version of Robinson’s theorem that AWC holds for all blocks if and only if SOWC does.
With Alperin’s and Robinson’s weight conjectures as a bridge from local to global, one can formulate purely local analogues of several of the local-to-global counting conjectures in block theory and there seems to be no reason why these should not hold also for exotic pairs. It was shown in [Reference Lynd and SemeraroLS23] that the exotic Benson–Solomon fusion systems at the prime
![]() $2$
have only the trivial compatible family, and some of the conjectures were verified for these systems in [Reference SemeraroSem23]. The recent paper [Reference Kessar, Semeraro, Serwene and TuvayKSST24] verifies six of the conjectures for fusion systems on a Sylow p-subgroup of
$2$
have only the trivial compatible family, and some of the conjectures were verified for these systems in [Reference SemeraroSem23]. The recent paper [Reference Kessar, Semeraro, Serwene and TuvayKSST24] verifies six of the conjectures for fusion systems on a Sylow p-subgroup of
![]() $\mathrm{G}_2(p)$
, a class which contains 27 exotic systems.
$\mathrm{G}_2(p)$
, a class which contains 27 exotic systems.
In this paper, we show that a nonconstrained saturated fusion system
![]() $\mathcal {F}$
on an extraspecial p-group S of order
$\mathcal {F}$
on an extraspecial p-group S of order
![]() $p^3$
and exponent p supports just the trivial compatible family (Theorem 4.4) and that many of the purely local counting conjectures hold for
$p^3$
and exponent p supports just the trivial compatible family (Theorem 4.4) and that many of the purely local counting conjectures hold for
![]() $\mathcal {F}$
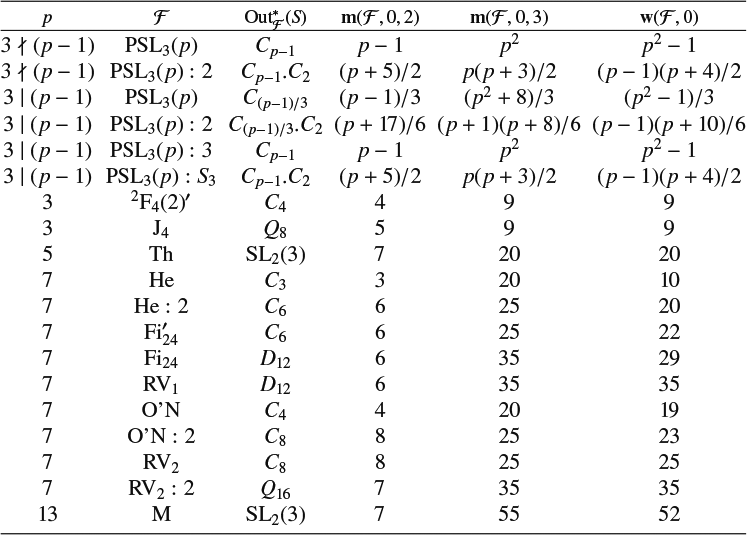
(for the list, see Conjecture 2.1). Along with the other fusion systems on extraspecial groups, like those coming from sporadic groups, we give counts of the above representation theoretic quantities (as well as others that take into account defects of characters) for the exotic Ruiz–Viruel fusion systems [Reference Ruiz and ViruelRV04]. For example, we show that
$\mathcal {F}$
(for the list, see Conjecture 2.1). Along with the other fusion systems on extraspecial groups, like those coming from sporadic groups, we give counts of the above representation theoretic quantities (as well as others that take into account defects of characters) for the exotic Ruiz–Viruel fusion systems [Reference Ruiz and ViruelRV04]. For example, we show that
![]() $\operatorname {\mathbf {m}}(\mathrm{RV}_1,0) = 41$
and
$\operatorname {\mathbf {m}}(\mathrm{RV}_1,0) = 41$
and
![]() $\operatorname {\mathbf {m}}(\mathrm{RV}_2,0) = 33$
, that is, that a
$\operatorname {\mathbf {m}}(\mathrm{RV}_2,0) = 33$
, that is, that a
![]() $7$
-block with a simple Ruiz–Viruel exotic fusion system at the prime
$7$
-block with a simple Ruiz–Viruel exotic fusion system at the prime
![]() $7$
would have
$7$
would have
![]() $41$
or
$41$
or
![]() $33$
ordinary irreducible characters, respectively, were such a block to exist (it does not [Reference Kessar and StancuKS08]). Furthemore, in Proposition 5.8, we combine our results with those of [Reference Narasaki and UnoNU09] to observe that Robinson’s ordinary weight conjecture (OWC) holds for the principal p-blocks of all almost simple groups G that realise a nonconstrained fusion system
$33$
ordinary irreducible characters, respectively, were such a block to exist (it does not [Reference Kessar and StancuKS08]). Furthemore, in Proposition 5.8, we combine our results with those of [Reference Narasaki and UnoNU09] to observe that Robinson’s ordinary weight conjecture (OWC) holds for the principal p-blocks of all almost simple groups G that realise a nonconstrained fusion system
![]() $\mathcal {F}$
on an extraspecial group of order
$\mathcal {F}$
on an extraspecial group of order
![]() $p^3$
and exponent p. In [Reference EatonEat04], Eaton shows that OWC is equivalent to the Dade projective conjecture in the sense that a minimal counterexample to one is a minimal counterexample to the other. This latter conjecture has previously been verified for principal p-blocks of some of the groups considered above (see, for example, [Reference AnAn98, Reference An, O’Brien and WilsonAOW03, Reference NarasakiNar07]) and in fact for all cases at the prime
$p^3$
and exponent p. In [Reference EatonEat04], Eaton shows that OWC is equivalent to the Dade projective conjecture in the sense that a minimal counterexample to one is a minimal counterexample to the other. This latter conjecture has previously been verified for principal p-blocks of some of the groups considered above (see, for example, [Reference AnAn98, Reference An, O’Brien and WilsonAOW03, Reference NarasakiNar07]) and in fact for all cases at the prime
![]() $3$
(see [Reference UsamiUsa01]).
$3$
(see [Reference UsamiUsa01]).
2 Some weight conjectures for fusion systems
We recall in this section just enough detail to state seven conjectures that we verify for nonconstrained fusion systems on extraspecial p-groups, and refer to [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19] and [Reference LinckelmannLin19a, Sections 8.13–8.15] for more details and additional motivation. For notation involving fusion systems, we follow [Reference Aschbacher, Kessar and OliverAKO11]. As before, we fix an algebraically closed field k of positive characteristic p. Let
![]() $\mathcal {F}$
be a saturated fusion system on a finite p-group S and
$\mathcal {F}$
be a saturated fusion system on a finite p-group S and
![]() $\mathcal {F}^c$
the set of
$\mathcal {F}^c$
the set of
![]() $\mathcal {F}$
-centric subgroups of S. Assume given a compatible family
$\mathcal {F}$
-centric subgroups of S. Assume given a compatible family
![]() $\alpha = (\alpha _Q)_{Q \in \mathcal {F}^c}$
of
$\alpha = (\alpha _Q)_{Q \in \mathcal {F}^c}$
of
![]() $2$
-cohomology classes,
$2$
-cohomology classes,
![]() $\alpha _Q \in H^2(\operatorname {Out}_{\mathcal {F}}(Q),k^\times )$
with coefficients in the multiplicative group of k; see [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Definition 4.1] or [Reference LinckelmannLin19a, Theorem 8.14.5]. If
$\alpha _Q \in H^2(\operatorname {Out}_{\mathcal {F}}(Q),k^\times )$
with coefficients in the multiplicative group of k; see [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Definition 4.1] or [Reference LinckelmannLin19a, Theorem 8.14.5]. If
![]() $\mathcal {F}$
is the fusion system of a block, there is a canonical compatible family of Külshammer–Puig classes of this form.
$\mathcal {F}$
is the fusion system of a block, there is a canonical compatible family of Külshammer–Puig classes of this form.
Denote by
![]() $k_{\alpha _Q}\operatorname {Out}_{\mathcal {F}}(Q)$
the twisted group algebra and define
$k_{\alpha _Q}\operatorname {Out}_{\mathcal {F}}(Q)$
the twisted group algebra and define
 $$ \begin{align*} \operatorname{\mathbf{w}}(\mathcal{F},\alpha) = \sum_{Q \in \mathcal{F}^c/\mathcal{F}} z(k_{\alpha_Q}\operatorname{Out}_{\mathcal{F}}(Q)), \end{align*} $$
$$ \begin{align*} \operatorname{\mathbf{w}}(\mathcal{F},\alpha) = \sum_{Q \in \mathcal{F}^c/\mathcal{F}} z(k_{\alpha_Q}\operatorname{Out}_{\mathcal{F}}(Q)), \end{align*} $$
where
![]() $z(-)$
denotes the number of isomorphism classes of projective simple modules for an algebra and the sum runs over a set of representatives for the
$z(-)$
denotes the number of isomorphism classes of projective simple modules for an algebra and the sum runs over a set of representatives for the
![]() $\mathcal {F}$
-conjugacy classes of centric subgroups Q. Thus,
$\mathcal {F}$
-conjugacy classes of centric subgroups Q. Thus,
![]() $\operatorname {\mathbf {w}}(\mathcal {F},\alpha )$
is the number of Alperin B-weights if
$\operatorname {\mathbf {w}}(\mathcal {F},\alpha )$
is the number of Alperin B-weights if
![]() $(\mathcal {F},\alpha )$
comes from a block B [Reference LinckelmannLin19a, Theorem 8.14.4], so B satisfies AWC just when
$(\mathcal {F},\alpha )$
comes from a block B [Reference LinckelmannLin19a, Theorem 8.14.4], so B satisfies AWC just when
![]() $\ell (B) = \operatorname {\mathbf {w}}(\mathcal {F},\alpha )$
.
$\ell (B) = \operatorname {\mathbf {w}}(\mathcal {F},\alpha )$
.
Set
 $$ \begin{align*} \operatorname{\mathbf{k}}(\mathcal{F},\alpha) = \sum_{x \in S/\mathcal{F}} \operatorname{\mathbf{w}}(C_{\mathcal{F}}(x),\alpha(x)), \end{align*} $$
$$ \begin{align*} \operatorname{\mathbf{k}}(\mathcal{F},\alpha) = \sum_{x \in S/\mathcal{F}} \operatorname{\mathbf{w}}(C_{\mathcal{F}}(x),\alpha(x)), \end{align*} $$
where
![]() $C_{\mathcal {F}}(x)$
is the centralizer subsystem,
$C_{\mathcal {F}}(x)$
is the centralizer subsystem,
![]() $\alpha (x)$
is the restriction of
$\alpha (x)$
is the restriction of
![]() $\alpha $
along the inclusion functor
$\alpha $
along the inclusion functor
![]() $C_{\mathcal {F}}(x)^c \to \mathcal {F}^c$
and the sum runs over fully centralized representatives for
$C_{\mathcal {F}}(x)^c \to \mathcal {F}^c$
and the sum runs over fully centralized representatives for
![]() $\mathcal {F}$
-conjugacy classes of elements. If
$\mathcal {F}$
-conjugacy classes of elements. If
![]() $(\mathcal {F},\alpha )$
comes from a block B, then using a lemma of Brauer about decomposing conjugacy classes by p-sections, the block satisfies AWC just when the number
$(\mathcal {F},\alpha )$
comes from a block B, then using a lemma of Brauer about decomposing conjugacy classes by p-sections, the block satisfies AWC just when the number
![]() $\mathbf {k}(B)$
of ordinary irreducible characters in B is
$\mathbf {k}(B)$
of ordinary irreducible characters in B is
![]() $\operatorname {\mathbf {k}}(\mathcal {F},\alpha )$
.
$\operatorname {\mathbf {k}}(\mathcal {F},\alpha )$
.
Finally, we define quantities motivated by OWC [Reference RobinsonRob96]. For a nonnegative integer d and a subgroup Q of S, write
![]() $\operatorname {Irr}_d(Q)$
for the ordinary characters
$\operatorname {Irr}_d(Q)$
for the ordinary characters
![]() $\mu $
of defect d, that is, such that the p-part of
$\mu $
of defect d, that is, such that the p-part of
![]() $|Q|/\mu (1)$
is
$|Q|/\mu (1)$
is
![]() $p^d$
. Let
$p^d$
. Let
![]() $\mathcal {N}_Q$
be the set of normal chains
$\mathcal {N}_Q$
be the set of normal chains
of p-subgroups in
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
, those such that
$\operatorname {Out}_{\mathcal {F}}(Q)$
, those such that
![]() $X_i$
is normal in
$X_i$
is normal in
![]() $X_n$
for each i and which begin with the trivial subgroup. The length of
$X_n$
for each i and which begin with the trivial subgroup. The length of
![]() $\sigma $
as displayed is n. The sets
$\sigma $
as displayed is n. The sets
![]() $\mathcal {N}_{\mathcal {Q}}$
and
$\mathcal {N}_{\mathcal {Q}}$
and
![]() $\operatorname {Irr}_K^d(Q)$
are
$\operatorname {Irr}_K^d(Q)$
are
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
-invariant, and we let
$\operatorname {Out}_{\mathcal {F}}(Q)$
-invariant, and we let
![]() $I(\sigma )$
and
$I(\sigma )$
and
![]() $I(\sigma , \mu )$
be the stabilizers in
$I(\sigma , \mu )$
be the stabilizers in
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
of
$\operatorname {Out}_{\mathcal {F}}(Q)$
of
![]() $\sigma $
and of the pair
$\sigma $
and of the pair
![]() $(\sigma ,\mu )$
, respectively.
$(\sigma ,\mu )$
, respectively.
For a pair
![]() $(\mathcal {F},\alpha )$
and
$(\mathcal {F},\alpha )$
and
![]() $d \geqslant 0$
, set
$d \geqslant 0$
, set
 $$ \begin{align*} w_{Q}(\mathcal{F},\alpha,d) = \sum_{\sigma \in \mathcal{N}_Q/\operatorname{Out}_{\mathcal{F}}(Q)} (-1)^{|\sigma|} \sum_{\mu \in \operatorname{Irr}_K^d(Q)/I(\sigma)} z(k_\alpha I(\sigma,\mu)) \end{align*} $$
$$ \begin{align*} w_{Q}(\mathcal{F},\alpha,d) = \sum_{\sigma \in \mathcal{N}_Q/\operatorname{Out}_{\mathcal{F}}(Q)} (-1)^{|\sigma|} \sum_{\mu \in \operatorname{Irr}_K^d(Q)/I(\sigma)} z(k_\alpha I(\sigma,\mu)) \end{align*} $$
and
 $$ \begin{align*} \operatorname{\mathbf{m}}(\mathcal{F},\alpha,d) = \sum_{Q \in \mathcal{F}^c/\mathcal{F}} w_Q(\mathcal{F},\alpha,d). \end{align*} $$
$$ \begin{align*} \operatorname{\mathbf{m}}(\mathcal{F},\alpha,d) = \sum_{Q \in \mathcal{F}^c/\mathcal{F}} w_Q(\mathcal{F},\alpha,d). \end{align*} $$
If
![]() $(\mathcal {F},\alpha )$
arises from a block B, then OWC is the statement that the number
$(\mathcal {F},\alpha )$
arises from a block B, then OWC is the statement that the number
![]() $\mathbf {k}_d(B)$
of ordinary characters of defect d is equal to
$\mathbf {k}_d(B)$
of ordinary characters of defect d is equal to
![]() $\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,d)$
.
$\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,d)$
.
We can now state the seven conjectures from [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19] that we verify for nonconstrained fusion systems on an extraspecial group.
Conjecture 2.1. Let
![]() $\mathcal {F}$
be a saturated fusion system on finite p-group S of order
$\mathcal {F}$
be a saturated fusion system on finite p-group S of order
![]() $p^e$
and let
$p^e$
and let
![]() $\alpha $
be a compatible family. Then:
$\alpha $
be a compatible family. Then:
-
(1)
 $\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) = \operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
;
$\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) = \operatorname {\mathbf {m}}(\mathcal {F},\alpha )$
; -
(2)
 $\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) \leqslant |S|$
;
$\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) \leqslant |S|$
; -
(3)
 $\operatorname {\mathbf {w}}(\mathcal {F},\alpha ) \leqslant p^s$
, where s is the sectional rank of S;
$\operatorname {\mathbf {w}}(\mathcal {F},\alpha ) \leqslant p^s$
, where s is the sectional rank of S; -
(4) for each positive integer d, we have
 $\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,d) \ge 0$
;
$\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,d) \ge 0$
; -
(5) if S is nonabelian, then
 $\operatorname {\mathbf {m}}(\mathcal {F}, \alpha , d) \ne 0$
for some
$\operatorname {\mathbf {m}}(\mathcal {F}, \alpha , d) \ne 0$
for some
 $d \ne e$
;
$d \ne e$
; -
(6) if S is nonabelian and
 $r> 0$
is the smallest positive integer such that S has a character of degree
$r> 0$
is the smallest positive integer such that S has a character of degree
 $p^r$
, then r is the smallest positive integer such that
$p^r$
, then r is the smallest positive integer such that
 $\operatorname {\mathbf {m}}(\mathcal {F}, \alpha , d-r) \ne 0$
;
$\operatorname {\mathbf {m}}(\mathcal {F}, \alpha , d-r) \ne 0$
; -
(7)
-
(a)
 $\operatorname {\mathbf {k}}(\mathcal {F}, \alpha )/\operatorname {\mathbf {m}}(\mathcal {F}, \alpha , e)$
is at most the number of conjugacy classes of
$\operatorname {\mathbf {k}}(\mathcal {F}, \alpha )/\operatorname {\mathbf {m}}(\mathcal {F}, \alpha , e)$
is at most the number of conjugacy classes of
 $[S,S]$
.
$[S,S]$
. -
(b)
 $\operatorname {\mathbf {k}}(\mathcal {F}, \alpha )/\operatorname {\mathbf {w}}(\mathcal {F}, \alpha )$
is at most the number of conjugacy classes of S.
$\operatorname {\mathbf {k}}(\mathcal {F}, \alpha )/\operatorname {\mathbf {w}}(\mathcal {F}, \alpha )$
is at most the number of conjugacy classes of S.
-
If
![]() $(\mathcal {F},\alpha )$
comes from a block B then Statement (1), respectively Statement (4), holds if AWC, respectively OWC, holds for B as well as for all of its Brauer correspondents. Moreover, each of the other statements in Conjecture 2.1 hold if and only if a known conjecture holds for the block B. Those conjectures are Statement (2) (the
$(\mathcal {F},\alpha )$
comes from a block B then Statement (1), respectively Statement (4), holds if AWC, respectively OWC, holds for B as well as for all of its Brauer correspondents. Moreover, each of the other statements in Conjecture 2.1 hold if and only if a known conjecture holds for the block B. Those conjectures are Statement (2) (the
![]() $\mathbf {k}(B)$
-conjecture), Statement (3) (the Malle–Robinson conjecture [Reference Malle and RobinsonMR17]), Statement (5) (Brauer’s height zero conjecture), Statement (6) (the Eaton–Moreto conjecture [Reference Eaton and MoretóEM14]) and Statement (7) (the Malle–Navarro conjecture [Reference Malle and NavarroMN06]).
$\mathbf {k}(B)$
-conjecture), Statement (3) (the Malle–Robinson conjecture [Reference Malle and RobinsonMR17]), Statement (5) (Brauer’s height zero conjecture), Statement (6) (the Eaton–Moreto conjecture [Reference Eaton and MoretóEM14]) and Statement (7) (the Malle–Navarro conjecture [Reference Malle and NavarroMN06]).
We conclude this section by showing that Statement (2) would follow as a consequence of Statement (7)(a).
Proposition 2.2. Let
![]() $\mathcal {F}$
be a saturated fusion system on a finite p-group S of order
$\mathcal {F}$
be a saturated fusion system on a finite p-group S of order
![]() $p^e$
and let
$p^e$
and let
![]() $\alpha $
be a compatible family. Then,
$\alpha $
be a compatible family. Then,
In particular, Conjecture 2.1(7)(a) implies Conjecture 2.1(2).
Proof. Since
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
is a
$\operatorname {Out}_{\mathcal {F}}(S)$
is a
![]() $p'$
-group,
$p'$
-group,
![]() $|\mathcal {N}_S|=1$
and we have
$|\mathcal {N}_S|=1$
and we have
 $$ \begin{align*}\operatorname{\mathbf{m}}(\mathcal{F},\alpha,e)=\sum_{\mu \in \operatorname{Irr}^e(S)/\operatorname{Out}_{\mathcal{F}}(S)} z(k_{\alpha_S}C_{\operatorname{Out}_{\mathcal{F}}(S)}(\mu)). \end{align*} $$
$$ \begin{align*}\operatorname{\mathbf{m}}(\mathcal{F},\alpha,e)=\sum_{\mu \in \operatorname{Irr}^e(S)/\operatorname{Out}_{\mathcal{F}}(S)} z(k_{\alpha_S}C_{\operatorname{Out}_{\mathcal{F}}(S)}(\mu)). \end{align*} $$
Let
![]() $\mathcal {F}_0 = N_{\mathcal {F}}(S)$
and let E be a complement to
$\mathcal {F}_0 = N_{\mathcal {F}}(S)$
and let E be a complement to
![]() $\operatorname {Inn} (S)$
in
$\operatorname {Inn} (S)$
in
![]() $\operatorname {Aut}_{\mathcal {F}}(S)$
. Then,
$\operatorname {Aut}_{\mathcal {F}}(S)$
. Then,
![]() $S \rtimes E $
is a model for
$S \rtimes E $
is a model for
![]() $\mathcal {F}_0$
. Moreover, there exists a central extension, say G, of
$\mathcal {F}_0$
. Moreover, there exists a central extension, say G, of
![]() $ S \rtimes E $
by a
$ S \rtimes E $
by a
![]() $p'$
-group and a block B of
$p'$
-group and a block B of
![]() $kG$
with fusion system
$kG$
with fusion system
![]() $\mathcal {F}_0$
and Külshammer–Puig cocycle at S equal to
$\mathcal {F}_0$
and Külshammer–Puig cocycle at S equal to
![]() $\alpha _S$
(see [AKO11, Proposition IV.5.35] and its proof). By [Reference RobinsonRob04, Theorem 2.5], the ordinary weight conjecture holds for B, that is, the number of maximal defect characters in B is
$\alpha _S$
(see [AKO11, Proposition IV.5.35] and its proof). By [Reference RobinsonRob04, Theorem 2.5], the ordinary weight conjecture holds for B, that is, the number of maximal defect characters in B is
 $$ \begin{align*} \sum_{\mu \in \operatorname{Irr}^e(S)/\operatorname{Out}_{\mathcal{F}_0}(S)} z(k_{\alpha_S}C_{\operatorname{Out}_{\mathcal{F}_0}(S)}(\mu)),\end{align*} $$
$$ \begin{align*} \sum_{\mu \in \operatorname{Irr}^e(S)/\operatorname{Out}_{\mathcal{F}_0}(S)} z(k_{\alpha_S}C_{\operatorname{Out}_{\mathcal{F}_0}(S)}(\mu)),\end{align*} $$
which is
![]() $\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e)$
since
$\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e)$
since
![]() $\operatorname {Out}_{\mathcal {F}_0}(S)=\operatorname {Out}_{\mathcal {F}}(S)$
. Thus, by [Reference KülshammerKül87, Theorem 1], the inequality
$\operatorname {Out}_{\mathcal {F}_0}(S)=\operatorname {Out}_{\mathcal {F}}(S)$
. Thus, by [Reference KülshammerKül87, Theorem 1], the inequality
![]() $\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e) \le |S:[S,S]|$
is a consequence of Brauer’s
$\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e) \le |S:[S,S]|$
is a consequence of Brauer’s
![]() $\operatorname {\mathbf {k}}(B)$
-conjecture for p-solvable groups, or equivalently the
$\operatorname {\mathbf {k}}(B)$
-conjecture for p-solvable groups, or equivalently the
![]() $k(GV)$
-conjecture (see [Reference NagaoNag62]). Since this latter statement is known by [Reference Gluck, Magaard, Riese and SchmidGMRS04], the result holds. Finally, if Conjecture 2.1(7)(a) holds, then
$k(GV)$
-conjecture (see [Reference NagaoNag62]). Since this latter statement is known by [Reference Gluck, Magaard, Riese and SchmidGMRS04], the result holds. Finally, if Conjecture 2.1(7)(a) holds, then
![]() $\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) \le |[S,S]^{cl}| \operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e) \le |[S,S]|\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e) \le |S|$
and so Conjecture 2.1(2) also holds.
$\operatorname {\mathbf {k}}(\mathcal {F},\alpha ) \le |[S,S]^{cl}| \operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e) \le |[S,S]|\operatorname {\mathbf {m}}(\mathcal {F},\alpha ,e) \le |S|$
and so Conjecture 2.1(2) also holds.
3 Fusion systems on an extraspecial group of order
 $p^3$
$p^3$
In this section, we recall the Ruiz–Viruel classification [Reference Ruiz and ViruelRV04] of the saturated fusion systems over an extraspecial group S of order
![]() $p^3$
and exponent p while setting up notation. There are three exotic fusion systems over S when
$p^3$
and exponent p while setting up notation. There are three exotic fusion systems over S when
![]() $p = 7$
.
$p = 7$
.
For the remainder of this section,
![]() $S \cong p_+^{1+2}$
denotes an extraspecial group of order
$S \cong p_+^{1+2}$
denotes an extraspecial group of order
![]() $p^3$
and exponent p. Fix the presentation
$p^3$
and exponent p. Fix the presentation
for S. Each element of S can then be written in the form
![]() $\textbf {a}^r\textbf {b}^s\textbf {c}^t$
for unique nonnegative integers
$\textbf {a}^r\textbf {b}^s\textbf {c}^t$
for unique nonnegative integers
![]() $0 \leqslant r,s,t \leqslant p-1$
. Let
$0 \leqslant r,s,t \leqslant p-1$
. Let
![]() $\varepsilon $
be a fixed primitive pth root of
$\varepsilon $
be a fixed primitive pth root of
![]() $1$
in
$1$
in
![]() $\mathbb {C}$
. We first list some basic information about S, along with general information about the associated saturated fusion systems on S.
$\mathbb {C}$
. We first list some basic information about S, along with general information about the associated saturated fusion systems on S.
Lemma 3.1. Let S be an extraspecial p-group of order
![]() $p^3$
and of exponent p, as given above.
$p^3$
and of exponent p, as given above.
-
(1) The map that sends
 $X:=(\begin {smallmatrix} x & y \\ z & w \end {smallmatrix} )$
to the class
$X:=(\begin {smallmatrix} x & y \\ z & w \end {smallmatrix} )$
to the class
 $[\varphi ] \in \operatorname {Out}(S)$
of the automorphism
$[\varphi ] \in \operatorname {Out}(S)$
of the automorphism
 $\varphi $
given by is an isomorphism from
$\varphi $
given by is an isomorphism from $$ \begin{align*}\textbf{a} \longmapsto \textbf{a}^x\textbf{b}^z, \hspace{4mm} \textbf{b} \longmapsto \textbf{a}^y\textbf{b}^w, \hspace{4mm} \textbf{c} \longmapsto \textbf{c}^{\det(X)}\end{align*} $$
$$ \begin{align*}\textbf{a} \longmapsto \textbf{a}^x\textbf{b}^z, \hspace{4mm} \textbf{b} \longmapsto \textbf{a}^y\textbf{b}^w, \hspace{4mm} \textbf{c} \longmapsto \textbf{c}^{\det(X)}\end{align*} $$
 $\operatorname {GL}_2(p)$
to
$\operatorname {GL}_2(p)$
to
 $\operatorname {Out}(S)$
.
$\operatorname {Out}(S)$
.
-
(2) A complete set of S-conjugacy class representatives of elements of S is given by
 $$ \begin{align*} \{\textbf{a}^i\textbf{b}^j \mid 0 \le i,j \le p-1 \} \cup \{\textbf{c}^k \mid 1 \le k \le p-1\}. \end{align*} $$
$$ \begin{align*} \{\textbf{a}^i\textbf{b}^j \mid 0 \le i,j \le p-1 \} \cup \{\textbf{c}^k \mid 1 \le k \le p-1\}. \end{align*} $$
-
(3)
 $\operatorname {Irr}(S)$
consists of
$\operatorname {Irr}(S)$
consists of
 $p^2$
linear characters
$p^2$
linear characters
 $\chi _{u,v}$
,
$\chi _{u,v}$
,
 $0 \le u,v \le p-1$
, and
$0 \le u,v \le p-1$
, and
 $p-1$
faithful characters
$p-1$
faithful characters
 $\varphi _u$
,
$\varphi _u$
,
 $1 \le u \le p-1$
, of degree p. The characters are given explicitly by
$1 \le u \le p-1$
, of degree p. The characters are given explicitly by  $$ \begin{align*} \chi_{u,v}(\textbf{a}^r\textbf{b}^s\textbf{c}^t):= \varepsilon^{ru+sv} \quad\text{and}\quad \varphi_u(\textbf{a}^r\textbf{b}^s\textbf{c}^t):= \begin{cases} p\varepsilon^{ut} & \mbox{if } r=s=0, \\ 0 & \mbox{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \chi_{u,v}(\textbf{a}^r\textbf{b}^s\textbf{c}^t):= \varepsilon^{ru+sv} \quad\text{and}\quad \varphi_u(\textbf{a}^r\textbf{b}^s\textbf{c}^t):= \begin{cases} p\varepsilon^{ut} & \mbox{if } r=s=0, \\ 0 & \mbox{otherwise.} \end{cases} \end{align*} $$
Proof. See [Reference Ruiz and ViruelRV04], for example, for parts (1) and (2). Part (3) is contained in [Reference GorensteinGor80, Theorem 5.5.4].
The elementary abelian subgroups of S of order
![]() $p^2$
are in one-to-one correspondence with the points of the projective line over
$p^2$
are in one-to-one correspondence with the points of the projective line over
![]() $\mathbb {F}_p$
; set
$\mathbb {F}_p$
; set
From [Reference Aschbacher, Kessar and OliverAKO11, Section III.6.2], we have the following description of the fusion systems on S.
Theorem 3.2. Let
![]() $\mathcal {F}$
be a saturated fusion system on S. Then,
$\mathcal {F}$
be a saturated fusion system on S. Then,
and the following hold:
-
(1)
 $\operatorname {Out}_{\mathcal {F}}(S)$
is a
$\operatorname {Out}_{\mathcal {F}}(S)$
is a
 $p'$
-group;
$p'$
-group; -
(2) for each i and
 $\alpha \in \operatorname {Aut}_{\mathcal {F}}(S)$
such that
$\alpha \in \operatorname {Aut}_{\mathcal {F}}(S)$
such that
 $\alpha (Q_i)=Q_i, \alpha |_{Q_i} \in \operatorname {Aut}_{\mathcal {F}}(Q_i)$
;
$\alpha (Q_i)=Q_i, \alpha |_{Q_i} \in \operatorname {Aut}_{\mathcal {F}}(Q_i)$
; -
(3) if
 $Q_i \in \mathcal {F}^r$
, then
$Q_i \in \mathcal {F}^r$
, then
 $\operatorname {SL}_2(p) \le \operatorname {Aut}_{\mathcal {F}}(Q_i) \le \operatorname {GL}_2(p)$
. If
$\operatorname {SL}_2(p) \le \operatorname {Aut}_{\mathcal {F}}(Q_i) \le \operatorname {GL}_2(p)$
. If
 $Q_i \notin \mathcal {F}^r$
, then
$Q_i \notin \mathcal {F}^r$
, then
 $\operatorname {Aut}_{\mathcal {F}}(Q_i)=\{\varphi |_{Q_i} \mid \varphi \in N_{\operatorname {Aut}_{\mathcal {F}}(S)}(Q_i)\}$
;
$\operatorname {Aut}_{\mathcal {F}}(Q_i)=\{\varphi |_{Q_i} \mid \varphi \in N_{\operatorname {Aut}_{\mathcal {F}}(S)}(Q_i)\}$
; -
(4) if
 $Q_i \in \mathcal {F}^r$
and
$Q_i \in \mathcal {F}^r$
and
 $\beta \in N_{\operatorname {Aut}_{\mathcal {F}}(Q_i)}(Z(S))$
, then
$\beta \in N_{\operatorname {Aut}_{\mathcal {F}}(Q_i)}(Z(S))$
, then
 $\beta $
extends to an element of
$\beta $
extends to an element of
 $\operatorname {Aut}_{\mathcal {F}}(S)$
.
$\operatorname {Aut}_{\mathcal {F}}(S)$
.
Conversely, any fusion system
![]() $\mathcal {F}$
over S for which Conditions (1)–(4) hold and for which each morphism is a composition of restrictions of
$\mathcal {F}$
over S for which Conditions (1)–(4) hold and for which each morphism is a composition of restrictions of
![]() $\mathcal {F}$
-automorphism of S and the
$\mathcal {F}$
-automorphism of S and the
![]() $Q_i$
is saturated. Moreover, in this case,
$Q_i$
is saturated. Moreover, in this case,
![]() $\mathcal {F}$
is constrained if and only if at most
$\mathcal {F}$
is constrained if and only if at most
![]() $1$
of the
$1$
of the
![]() $Q_i$
is centric and radical.
$Q_i$
is centric and radical.
When
![]() $\mathcal {F}$
is nonconstrained, the possibilities for
$\mathcal {F}$
is nonconstrained, the possibilities for
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
and
$\operatorname {Out}_{\mathcal {F}}(S)$
and
![]() $\operatorname {Out}_{\mathcal {F}}(Q_i)$
(and hence,
$\operatorname {Out}_{\mathcal {F}}(Q_i)$
(and hence,
![]() $\mathcal {F}$
) are given in [Reference Ruiz and ViruelRV04, Tables 1.1 and 1.2]. Apart from the p-fusion systems of
$\mathcal {F}$
) are given in [Reference Ruiz and ViruelRV04, Tables 1.1 and 1.2]. Apart from the p-fusion systems of
![]() $\operatorname {PSL}_3(p)$
,
$\operatorname {PSL}_3(p)$
,
![]() $p \ge 3$
and their almost simple extensions, there are thirteen exceptional fusion systems for
$p \ge 3$
and their almost simple extensions, there are thirteen exceptional fusion systems for
![]() $3 \le p \le 13$
, three of which are exotic.
$3 \le p \le 13$
, three of which are exotic.
4 Compatible families
The goal of this section is to show that there are no nonzero compatible families for the nonconstrained fusion systems over S. Recall that the Schur multiplier
![]() $M(G)$
of a finite group G is a finite abelian group, which may be defined as the second cohomology group
$M(G)$
of a finite group G is a finite abelian group, which may be defined as the second cohomology group
![]() $H^2(G,\mathbb {C}^\times )$
. In computing the Schur multiplier of various groups, we make use of its connection with stem extensions. A stem extension of a group G is a central extension
$H^2(G,\mathbb {C}^\times )$
. In computing the Schur multiplier of various groups, we make use of its connection with stem extensions. A stem extension of a group G is a central extension
![]() $1 \to Z \to \widehat {G} \xrightarrow {\pi } G \to 1$
such that
$1 \to Z \to \widehat {G} \xrightarrow {\pi } G \to 1$
such that
![]() $\ker (\pi ) \leqslant Z(\widehat {G}) \cap [\widehat {G},\widehat {G}]$
. We often identify
$\ker (\pi ) \leqslant Z(\widehat {G}) \cap [\widehat {G},\widehat {G}]$
. We often identify
![]() $\ker (\pi )$
with Z. If
$\ker (\pi )$
with Z. If
![]() $Z \cong M(G)$
in this situation, then the extension (or
$Z \cong M(G)$
in this situation, then the extension (or
![]() $\pi $
, or
$\pi $
, or
![]() $\widehat {G})$
is said to be a Schur covering of G. Given a central extension as above, there is an associated inflation-restriction exact sequence
$\widehat {G})$
is said to be a Schur covering of G. Given a central extension as above, there is an associated inflation-restriction exact sequence
in which three of the maps are given by inflation or restriction, and the fourth is the transgression map. This is defined by first choosing a cocycle
![]() $\alpha $
representing the class
$\alpha $
representing the class
![]() $[\alpha ] \in H^2(G,Z)$
of the extension. For any homomorphism
$[\alpha ] \in H^2(G,Z)$
of the extension. For any homomorphism
![]() $\varphi \in \operatorname {Hom}(Z,\mathbb {C}^\times )$
, post-composition with
$\varphi \in \operatorname {Hom}(Z,\mathbb {C}^\times )$
, post-composition with
![]() $\varphi $
yields a 2-cocycle with values in
$\varphi $
yields a 2-cocycle with values in
![]() $\mathbb {C}^\times $
, and then
$\mathbb {C}^\times $
, and then
![]() $\operatorname {tra}(\varphi )$
is defined as the class
$\operatorname {tra}(\varphi )$
is defined as the class
![]() $[\varphi \circ \alpha ] \in H^2(G, \mathbb {C}^\times )$
.
$[\varphi \circ \alpha ] \in H^2(G, \mathbb {C}^\times )$
.
The next lemma collects a number of general results regarding the Schur multiplier, which are used later in special cases. The first four parts are due to Schur. In parts (4) and (5), results of Schur and of Blackburn [Reference BlackburnBla72] are quoted, and require the following additional notation. Denote the abelianization of a group G by
![]() $G^{\operatorname {ab}}$
, and write
$G^{\operatorname {ab}}$
, and write
![]() $G^{\operatorname {ab}} \wedge G^{\operatorname {ab}}$
for the quotient of
$G^{\operatorname {ab}} \wedge G^{\operatorname {ab}}$
for the quotient of
![]() $G^{\operatorname {ab}} \otimes _{\mathbb {Z}} G^{\operatorname {ab}}$
by the subgroup generated by
$G^{\operatorname {ab}} \otimes _{\mathbb {Z}} G^{\operatorname {ab}}$
by the subgroup generated by
![]() $a \otimes b + b \otimes a$
as a and b range over
$a \otimes b + b \otimes a$
as a and b range over
![]() $G^{\operatorname {ab}}$
.
$G^{\operatorname {ab}}$
.
Lemma 4.1. The following hold for a finite group G.
-
(1) If
 $1 \to Z \to \widehat {G} \to G \to 1$
is a stem extension, then the transgression map
$1 \to Z \to \widehat {G} \to G \to 1$
is a stem extension, then the transgression map
 $\operatorname {tra}$
in (4-1) is injective and hence,
$\operatorname {tra}$
in (4-1) is injective and hence,
 $Z \cong \operatorname {Hom}(Z,\mathbb {C}^\times )$
is isomorphic to a subgroup of
$Z \cong \operatorname {Hom}(Z,\mathbb {C}^\times )$
is isomorphic to a subgroup of
 $M(G)$
.
$M(G)$
. -
(2) There exists a Schur covering
 $1 \to Z \to \widehat {G} \xrightarrow {\pi } G \to 1$
and, for any such covering, the associated transgression map is an isomorphism.
$1 \to Z \to \widehat {G} \xrightarrow {\pi } G \to 1$
and, for any such covering, the associated transgression map is an isomorphism. -
(3) If there exists a Schur covering as in Condition (2) such that
 $\pi \colon \pi ^{-1}(H) \to H$
is a stem extension of some subgroup H of G, then the restriction map
$\pi \colon \pi ^{-1}(H) \to H$
is a stem extension of some subgroup H of G, then the restriction map
 $M(G) \to M(H)$
is injective.
$M(G) \to M(H)$
is injective. -
(4) If
 $G = G_1 \times G_2$
is a direct product, then one has
$G = G_1 \times G_2$
is a direct product, then one has  $$ \begin{align*} M(G) \cong M(G_1) \times M(G_2) \times (G_1^{\operatorname{ab}} \otimes_{\mathbb{Z}} G_2^{\operatorname{ab}}). \end{align*} $$
$$ \begin{align*} M(G) \cong M(G_1) \times M(G_2) \times (G_1^{\operatorname{ab}} \otimes_{\mathbb{Z}} G_2^{\operatorname{ab}}). \end{align*} $$
-
(5) (Blackburn) Assume
 $G = K \wr H$
is a wreath product and write m for the number of involutions in H. Then,
$G = K \wr H$
is a wreath product and write m for the number of involutions in H. Then,
 $M(G)$
is isomorphic to the direct product of
$M(G)$
is isomorphic to the direct product of
 $M(H)$
,
$M(H)$
,
 $M(K)$
,
$M(K)$
,
 $\tfrac 12(|H|-m-1)$
copies of
$\tfrac 12(|H|-m-1)$
copies of
 $K^{\operatorname {ab}} \otimes K^{\operatorname {ab}}$
and m copies of
$K^{\operatorname {ab}} \otimes K^{\operatorname {ab}}$
and m copies of
 $K^{\operatorname {ab}} \wedge K^{\operatorname {ab}}$
.
$K^{\operatorname {ab}} \wedge K^{\operatorname {ab}}$
.
Proof. We refer to [Reference Curtis and ReinerCR90, Lemma 11.42] for part (1) and to [Reference Curtis and ReinerCR90, Theorem 11.43] for part (2). Assume the hypotheses of part (3) and set
![]() $\widehat {H} = \pi ^{-1}(H)$
. Choose a
$\widehat {H} = \pi ^{-1}(H)$
. Choose a
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
representing the class of the central extension
$\alpha $
representing the class of the central extension
![]() $1 \to Z \to \widehat {G} \to G \to 1$
. Then,
$1 \to Z \to \widehat {G} \to G \to 1$
. Then,
![]() $\alpha |_{H\times H}$
represents the class of the central extension
$\alpha |_{H\times H}$
represents the class of the central extension
![]() $1 \to Z \to \widehat {H} \to H \to 1$
, and the square
$1 \to Z \to \widehat {H} \to H \to 1$
, and the square

commutes. As
![]() $\operatorname {tra}_H$
is injective by part (1) and
$\operatorname {tra}_H$
is injective by part (1) and
![]() $\operatorname {tra}_G$
an isomorphism by part (2), part (3) follows. Finally, a proof of part (4) may be found in [Reference WiegoldWie71, Corollary 3] and part (5) is [Reference BlackburnBla72, Theorem 1]; see also [Reference KarpilovskyKar87, Theorems 2.2.10 and 6.3.3].
$\operatorname {tra}_G$
an isomorphism by part (2), part (3) follows. Finally, a proof of part (4) may be found in [Reference WiegoldWie71, Corollary 3] and part (5) is [Reference BlackburnBla72, Theorem 1]; see also [Reference KarpilovskyKar87, Theorems 2.2.10 and 6.3.3].
Whenever p is a prime, we write
![]() $M(G)_p$
for the p-primary part of
$M(G)_p$
for the p-primary part of
![]() $M(G)$
, and
$M(G)$
, and
![]() $M(G)_{p'}$
for the
$M(G)_{p'}$
for the
![]() $p'$
-primary part of
$p'$
-primary part of
![]() $M(G)$
. The following lemma collects some basic information about the various primary parts of the Schur multiplier.
$M(G)$
. The following lemma collects some basic information about the various primary parts of the Schur multiplier.
Lemma 4.2. Let G be a finite group, let p be a prime and let k be an algebraically closed field of characteristic p.
-
(1)
 $H^2(G,k^\times )$
is isomorphic to the
$H^2(G,k^\times )$
is isomorphic to the
 $p'$
-part
$p'$
-part
 $M(G)_{p'}$
of the Schur multiplier.
$M(G)_{p'}$
of the Schur multiplier. -
(2) If
 $H \leqslant G$
contains a Sylow p-subgroup of G, then the restriction map
$H \leqslant G$
contains a Sylow p-subgroup of G, then the restriction map
 $M(G)_p \to M(H)_p$
is injective.
$M(G)_p \to M(H)_p$
is injective. -
(3) If G has cyclic Sylow p-subgroups, then
 $M(G)_p = 1$
.
$M(G)_p = 1$
.
Proof. See [Reference KarpilovskyKar87, Proposition 2.1.14] for part (1). Part (2) is derived from the fact that restriction to H followed by transfer to G is multiplication by the index of H in G, which by assumption is prime to p. Then, part (3) follows from part (2) and the fact that the second cohomology group of a finite cyclic group with coefficients in a divisible group with trivial action is trivial, but see also [Reference Curtis and ReinerCR90, Proposition 11.46].
We now specialize to the following computations of Schur multipliers of specific finite groups that appear as subgroups of automorphism groups of centric radicals in certain nonconstrained saturated systems over S.
Lemma 4.3. The following hold.
-
(1) If p is any prime and G is a subgroup of
 $\operatorname {GL}_2(p)$
containing
$\operatorname {GL}_2(p)$
containing
 $\operatorname {SL}_2(p)$
, then
$\operatorname {SL}_2(p)$
, then
 ${M(G) = 1}$
.
${M(G) = 1}$
. -
(2) Let G be a
 $2$
-group of maximal class. Then,
$2$
-group of maximal class. Then,
 $M(G) \cong C_{2}$
if G is dihedral, while
$M(G) \cong C_{2}$
if G is dihedral, while
 $M(G) = 1$
if G is semidihedral or quaternion. If G is a dihedral
$M(G) = 1$
if G is semidihedral or quaternion. If G is a dihedral
 $2$
-group and V is any
$2$
-group and V is any
 $4$
-subgroup of G, then the restriction
$4$
-subgroup of G, then the restriction
 $M(G) \to M(V)$
is injective.
$M(G) \to M(V)$
is injective. -
(3) Let
 $G = C_n \wr C_2$
with
$G = C_n \wr C_2$
with
 $n \geqslant 2$
. Then,
$n \geqslant 2$
. Then,
 $M(G) \cong C_2$
if n is even and
$M(G) \cong C_2$
if n is even and
 $M(G) = 1$
if n is odd. If
$M(G) = 1$
if n is odd. If
 $J \leqslant G$
is the homocyclic subgroup of rank
$J \leqslant G$
is the homocyclic subgroup of rank
 $2$
and exponent n, then the restriction
$2$
and exponent n, then the restriction
 $M(G) \to M(J)$
is injective.
$M(G) \to M(J)$
is injective. -
(4) If
 $G = \operatorname {Out}_{\mathcal {F}}(S)$
for some fusion system
$G = \operatorname {Out}_{\mathcal {F}}(S)$
for some fusion system
 $\mathcal {F}$
over S appearing in [Reference Ruiz and ViruelRV04, Table 1.2], then
$\mathcal {F}$
over S appearing in [Reference Ruiz and ViruelRV04, Table 1.2], then
 $M(G)_{2'} = 1$
. Moreover, either
$M(G)_{2'} = 1$
. Moreover, either
 $M(G)_2 = 1$
, or
$M(G)_2 = 1$
, or
 $M(G)_2 \cong C_2$
and G is
$M(G)_2 \cong C_2$
and G is
 $D_8$
,
$D_8$
,
 $S_3 \times C_6$
,
$S_3 \times C_6$
,
 $C_6 \wr C_2$
,
$C_6 \wr C_2$
,
 $D_8 \times C_3$
, or
$D_8 \times C_3$
, or
 $D_{16} \times C_3$
.
$D_{16} \times C_3$
.
Proof. The fact that
![]() $\operatorname {SL}_2(p)$
has trivial multiplier for all primes p is standard: note that all Sylow r-subgroups of
$\operatorname {SL}_2(p)$
has trivial multiplier for all primes p is standard: note that all Sylow r-subgroups of
![]() $\operatorname {SL}_2(p)$
are cyclic, except when
$\operatorname {SL}_2(p)$
are cyclic, except when
![]() $p \geqslant 3$
and
$p \geqslant 3$
and
![]() $r = 2$
, in which case a Sylow r-subgroup is generalized quaternion. It follows that
$r = 2$
, in which case a Sylow r-subgroup is generalized quaternion. It follows that
![]() $M(G)_r = 1$
for all primes r by part (2) above and Lemma 4.2(2). Also,
$M(G)_r = 1$
for all primes r by part (2) above and Lemma 4.2(2). Also,
![]() $\operatorname {GL}_2(3)$
has trivial multiplier by part (2) and Lemma 4.2(2) since a Sylow
$\operatorname {GL}_2(3)$
has trivial multiplier by part (2) and Lemma 4.2(2) since a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\operatorname {GL}_2(3)$
is semidihedral. So, to finish the proof of part (1), we may assume that
$\operatorname {GL}_2(3)$
is semidihedral. So, to finish the proof of part (1), we may assume that
![]() $p \geqslant 5$
. Let G be a subgroup of
$p \geqslant 5$
. Let G be a subgroup of
![]() $\operatorname {GL}_2(p)$
containing
$\operatorname {GL}_2(p)$
containing
![]() $N = \operatorname {SL}_2(p)$
. Since
$N = \operatorname {SL}_2(p)$
. Since
![]() $p \geqslant 5$
, N is perfect. Fix a group
$p \geqslant 5$
, N is perfect. Fix a group
![]() $\widehat {G}$
having a central subgroup Z such that
$\widehat {G}$
having a central subgroup Z such that
![]() $\widehat {G}/Z \cong G$
. Identify
$\widehat {G}/Z \cong G$
. Identify
![]() $\widehat {G}/Z$
with G and let
$\widehat {G}/Z$
with G and let
![]() $\pi \colon \widehat {G} \to G$
be the canonical projection. We show that there is a complement to Z in
$\pi \colon \widehat {G} \to G$
be the canonical projection. We show that there is a complement to Z in
![]() $\widehat {G}$
. Let
$\widehat {G}$
. Let
![]() $\widehat {N}$
be the preimage of N under
$\widehat {N}$
be the preimage of N under
![]() $\pi $
. Then,
$\pi $
. Then,
![]() $\widehat {N}$
contains Z and splits over it, as
$\widehat {N}$
contains Z and splits over it, as
![]() $M(N) = 1$
. Fix any complement
$M(N) = 1$
. Fix any complement
![]() $N_0$
of Z in
$N_0$
of Z in
![]() $\widehat {N}$
, so that
$\widehat {N}$
, so that
![]() $\widehat {N} = N_0 \times Z$
. Then,
$\widehat {N} = N_0 \times Z$
. Then,
![]() $N_0 \cong \operatorname {SL}_2(p)$
. We claim that
$N_0 \cong \operatorname {SL}_2(p)$
. We claim that
![]() $N_0$
is normal in
$N_0$
is normal in
![]() $\widehat {G}$
; it is clear that
$\widehat {G}$
; it is clear that
![]() $N_0$
is normal in
$N_0$
is normal in
![]() $\widehat {N}$
. In general, conjugation by
$\widehat {N}$
. In general, conjugation by
![]() $g \in \widehat {G}$
sends an element
$g \in \widehat {G}$
sends an element
![]() $h \in N_0$
to
$h \in N_0$
to
![]() $h'\zeta _g(h)$
, where
$h'\zeta _g(h)$
, where
![]() $h' \in N_0$
and
$h' \in N_0$
and
![]() $\zeta _g(h) \in Z$
are uniquely determined. Also, since Z is central in
$\zeta _g(h) \in Z$
are uniquely determined. Also, since Z is central in
![]() $\widehat {G}$
, the assignment
$\widehat {G}$
, the assignment
![]() $h \mapsto \zeta _g(h)$
is a group homomorphism from
$h \mapsto \zeta _g(h)$
is a group homomorphism from
![]() $N_0$
to Z. Since
$N_0$
to Z. Since
![]() $N_0$
is perfect, it follows that
$N_0$
is perfect, it follows that
![]() $\zeta _g = 1$
for each
$\zeta _g = 1$
for each
![]() $g \in \widehat {G}$
, that is,
$g \in \widehat {G}$
, that is,
![]() $N_0$
is normal in
$N_0$
is normal in
![]() $\widehat {G}$
. Write quotients by
$\widehat {G}$
. Write quotients by
![]() $N_0$
with pluses. Now,
$N_0$
with pluses. Now,
![]() $\widehat {G}^+$
is a central extension of Z by
$\widehat {G}^+$
is a central extension of Z by
![]() $\widehat {G}/\widehat {N} \cong G/N$
, which is a cyclic
$\widehat {G}/\widehat {N} \cong G/N$
, which is a cyclic
![]() $p'$
-group. However, we have
$p'$
-group. However, we have
![]() $M(G/N) = 1$
by Lemma 4.2(3), applied with each prime divisor r of
$M(G/N) = 1$
by Lemma 4.2(3), applied with each prime divisor r of
![]() $|G/N|$
in the role of ‘p’ there. Thus, we may fix a complement
$|G/N|$
in the role of ‘p’ there. Thus, we may fix a complement
![]() $K^+$
of
$K^+$
of
![]() $Z^+$
in
$Z^+$
in
![]() $\widehat {G}^+$
and let K be the preimage of
$\widehat {G}^+$
and let K be the preimage of
![]() $K^+$
in
$K^+$
in
![]() $\widehat {G}$
. Then, K is a complement to Z in
$\widehat {G}$
. Then, K is a complement to Z in
![]() $\widehat {G}$
.
$\widehat {G}$
.
Part (2) is implied by Lemma 4.1 as follows. Let G be a
![]() $2$
-group of maximal class, so that G is dihedral, semidihedral or quaternion. Then,
$2$
-group of maximal class, so that G is dihedral, semidihedral or quaternion. Then,
![]() $M(G)$
is a
$M(G)$
is a
![]() $2$
-group. Let
$2$
-group. Let
![]() $\pi \colon \widehat {G} \to G$
be any Schur covering of G with
$\pi \colon \widehat {G} \to G$
be any Schur covering of G with
![]() $Z = \ker (\pi )$
. Then, since
$Z = \ker (\pi )$
. Then, since
![]() $Z \leqslant [\widehat {G}, \widehat {G}]$
, it follows that
$Z \leqslant [\widehat {G}, \widehat {G}]$
, it follows that
![]() $\widehat {G}^{\operatorname {ab}} \cong G^{\operatorname {ab}}$
is of order
$\widehat {G}^{\operatorname {ab}} \cong G^{\operatorname {ab}}$
is of order
![]() $4$
. By [Reference GorensteinGor80, Theorem 5.4.5],
$4$
. By [Reference GorensteinGor80, Theorem 5.4.5],
![]() $\widehat {G}$
is of maximal class, so
$\widehat {G}$
is of maximal class, so
![]() $Z(\widehat {G})$
is of order
$Z(\widehat {G})$
is of order
![]() $2$
. Then, either
$2$
. Then, either
![]() $M(G) = 1$
or
$M(G) = 1$
or
![]() $Z(\widehat {G}) = Z$
and
$Z(\widehat {G}) = Z$
and
![]() $M(G) = C_2$
. In the latter case, since
$M(G) = C_2$
. In the latter case, since
![]() $\widehat {G}$
is of maximal class, we have
$\widehat {G}$
is of maximal class, we have
![]() $\widehat {G}/Z \cong G$
is dihedral. Conversely, the dihedral group
$\widehat {G}/Z \cong G$
is dihedral. Conversely, the dihedral group
![]() $\widehat {G} = D_{2^{k+1}}$
provides a Schur covering
$\widehat {G} = D_{2^{k+1}}$
provides a Schur covering
![]() $\pi \colon \widehat {G} \to G$
of
$\pi \colon \widehat {G} \to G$
of
![]() $G = D_{2^{k}}$
. Fix a
$G = D_{2^{k}}$
. Fix a
![]() $4$
-subgroup V of G. Then, as
$4$
-subgroup V of G. Then, as
![]() $\pi ^{-1}(V)$
is dihedral of order
$\pi ^{-1}(V)$
is dihedral of order
![]() $8$
, we have that the restriction map
$8$
, we have that the restriction map
![]() $M(G) \to M(V)$
is injective by Lemma 4.1(3). This completes the proof of part (2).
$M(G) \to M(V)$
is injective by Lemma 4.1(3). This completes the proof of part (2).
To prove part (3), apply Lemma 4.1(5) with
![]() $K = C_n$
and
$K = C_n$
and
![]() $H = C_2$
. Hence,
$H = C_2$
. Hence,
![]() $m = 1$
there. By Lemma 4.2(3) and that result,
$m = 1$
there. By Lemma 4.2(3) and that result,
![]() $M(G) = K^{\operatorname {ab}} \wedge K^{\operatorname {ab}}$
. The multiplication map
$M(G) = K^{\operatorname {ab}} \wedge K^{\operatorname {ab}}$
. The multiplication map
![]() $C_n \otimes C_n \to C_n$
is an isomorphism, where
$C_n \otimes C_n \to C_n$
is an isomorphism, where
![]() $C_n$
is viewed as an additive group, and under that map,
$C_n$
is viewed as an additive group, and under that map,
![]() $a \otimes b + b \otimes a$
is sent to
$a \otimes b + b \otimes a$
is sent to
![]() $2ab$
. Hence,
$2ab$
. Hence,
![]() $M(G) \cong C_n/2C_n \cong C_2$
if n is even, and
$M(G) \cong C_n/2C_n \cong C_2$
if n is even, and
![]() $1$
if n is odd. To prove the claim about the restriction to J, we may by Lemma 4.2(2) assume that
$1$
if n is odd. To prove the claim about the restriction to J, we may by Lemma 4.2(2) assume that
![]() $n = 2^l$
for some l, and then it suffices by Lemma 4.1(3) to produce a double covering of G which restricts to a stem extension of J. To this end, the group
$n = 2^l$
for some l, and then it suffices by Lemma 4.1(3) to produce a double covering of G which restricts to a stem extension of J. To this end, the group
![]() $G = C_{2^l} \wr C_2$
has a presentation with generators x, y and t, and defining relations
$G = C_{2^l} \wr C_2$
has a presentation with generators x, y and t, and defining relations
![]() $x^{2^l} = y^{2^l} = t^2 = xyx^{-1}y^{-1} = 1$
and
$x^{2^l} = y^{2^l} = t^2 = xyx^{-1}y^{-1} = 1$
and
![]() $txt^{-1} = y$
. Consider the group
$txt^{-1} = y$
. Consider the group
![]() $\widehat {G}$
with generators
$\widehat {G}$
with generators
![]() $\textbf {x}, \mathbf {y}, \textbf {t}$
and defining relations
$\textbf {x}, \mathbf {y}, \textbf {t}$
and defining relations
![]() $\textbf {x}^{2^l} = \mathbf {y}^{2^l} = \textbf {t}^2 = 1$
,
$\textbf {x}^{2^l} = \mathbf {y}^{2^l} = \textbf {t}^2 = 1$
,
![]() $\textbf {t}\textbf {x}\textbf {t}^{-1} = \mathbf {y}$
and
$\textbf {t}\textbf {x}\textbf {t}^{-1} = \mathbf {y}$
and
![]() $\textbf {z} = [\textbf {x},\mathbf {y}]$
is of order
$\textbf {z} = [\textbf {x},\mathbf {y}]$
is of order
![]() $2$
and central. Thus,
$2$
and central. Thus,
![]() $\widehat {G}/\langle \textbf {x}^2,\mathbf {y}^2 \rangle \cong D_{16}$
and the obvious map
$\widehat {G}/\langle \textbf {x}^2,\mathbf {y}^2 \rangle \cong D_{16}$
and the obvious map
![]() $\pi \colon \widehat {G} \to G$
is the pullback of the Schur covering
$\pi \colon \widehat {G} \to G$
is the pullback of the Schur covering
![]() $D_{16} \to D_{8}$
. Let
$D_{16} \to D_{8}$
. Let
![]() $\mathbf {J}$
be the preimage of J in
$\mathbf {J}$
be the preimage of J in
![]() $\widehat {G}$
and set
$\widehat {G}$
and set
![]() $Z = \ker (\pi ) = \langle \textbf {z} \rangle $
. Then, by construction,
$Z = \ker (\pi ) = \langle \textbf {z} \rangle $
. Then, by construction,
![]() $Z \leqslant [\mathbf {J},\mathbf {J}] \cap Z(\mathbf {J})$
, so
$Z \leqslant [\mathbf {J},\mathbf {J}] \cap Z(\mathbf {J})$
, so
![]() $\pi \colon \mathbf {J} \to J$
is a stem extension of J. As noted above, this completes the proof of part (3).
$\pi \colon \mathbf {J} \to J$
is a stem extension of J. As noted above, this completes the proof of part (3).
We now prove part (4). When G is
![]() $D_8$
,
$D_8$
,
![]() $SD_{16}$
,
$SD_{16}$
,
![]() $C_6 \wr C_2$
,
$C_6 \wr C_2$
,
![]() $S_3 \times C_3$
,
$S_3 \times C_3$
,
![]() $S_3 \times C_6$
,
$S_3 \times C_6$
,
![]() $D_8 \times C_3$
,
$D_8 \times C_3$
,
![]() $D_{16} \times C_3$
or
$D_{16} \times C_3$
or
![]() $SD_{32} \times C_3$
, the claim follows from parts (1), (2), (3) and Lemma 4.1(4). It remains to consider the groups ‘
$SD_{32} \times C_3$
, the claim follows from parts (1), (2), (3) and Lemma 4.1(4). It remains to consider the groups ‘
![]() $4S_4$
’ and ‘
$4S_4$
’ and ‘
![]() $C_3 \times 4S_4$
’ in [Reference Ruiz and ViruelRV04, Table 1.2]. Note that
$C_3 \times 4S_4$
’ in [Reference Ruiz and ViruelRV04, Table 1.2]. Note that
![]() $4S_4$
as appears in [Reference Ruiz and ViruelRV04] is the normalizer G in
$4S_4$
as appears in [Reference Ruiz and ViruelRV04] is the normalizer G in
![]() $\operatorname {GL}_2(5)$
of a Sylow
$\operatorname {GL}_2(5)$
of a Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $Q \cong Q_8$
of
$Q \cong Q_8$
of
![]() $\operatorname {SL}_2(5)$
. The normalizer N in
$\operatorname {SL}_2(5)$
. The normalizer N in
![]() $\operatorname {SL}_2(5)$
of Q is the commutator subgroup of G, isomorphic to
$\operatorname {SL}_2(5)$
of Q is the commutator subgroup of G, isomorphic to
![]() $\operatorname {SL}_2(3)$
, and the quotient
$\operatorname {SL}_2(3)$
, and the quotient
![]() $G/N$
is cyclic of order
$G/N$
is cyclic of order
![]() $4$
. Thus,
$4$
. Thus,
![]() $G^{\operatorname {ab}}$
is cyclic of order
$G^{\operatorname {ab}}$
is cyclic of order
![]() $4$
. Therefore, it suffices to show that
$4$
. Therefore, it suffices to show that
![]() $M(G) = 1$
, for then by Lemma 4.1(4), we have
$M(G) = 1$
, for then by Lemma 4.1(4), we have
![]() $M(C_3 \times G) = 1$
. Since G has Sylow
$M(C_3 \times G) = 1$
. Since G has Sylow
![]() $3$
-subgroups of order
$3$
-subgroups of order
![]() $3$
, it follows from Lemma 4.2(3) that
$3$
, it follows from Lemma 4.2(3) that
![]() $M(G) = M_2(G)$
. Since
$M(G) = M_2(G)$
. Since
![]() $\operatorname {SL}_2(3) \cong Q \rtimes C_3$
is
$\operatorname {SL}_2(3) \cong Q \rtimes C_3$
is
![]() $2$
-perfect and
$2$
-perfect and
![]() $G/N$
is cyclic, the exact same argument as given in part (1) applies with Z a
$G/N$
is cyclic, the exact same argument as given in part (1) applies with Z a
![]() $2$
-group to show that
$2$
-group to show that
![]() $M(G)_2 = 1$
. This completes the proof of part (4) and the lemma.
$M(G)_2 = 1$
. This completes the proof of part (4) and the lemma.
Let now k be a fixed algebraically closed field of characteristic p and
![]() $\mathcal {F}$
a saturated fusion system on a finite p-group. Recall from [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Section 4] that by a compatible family for
$\mathcal {F}$
a saturated fusion system on a finite p-group. Recall from [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Section 4] that by a compatible family for
![]() $\mathcal {F}$
(of
$\mathcal {F}$
(of
![]() $2$
-cohomology classes with coefficients in
$2$
-cohomology classes with coefficients in
![]() $k^\times $
), we mean an element of
$k^\times $
), we mean an element of
![]() $\lim _{[S(\mathcal {F}^c)]} \mathcal {A}^2_{\mathcal {F}}$
, where
$\lim _{[S(\mathcal {F}^c)]} \mathcal {A}^2_{\mathcal {F}}$
, where
![]() $\mathcal {A}^2(\mathcal {F}) \colon [S(\mathcal {F}^c)] \to \mathrm {Ab}$
is the functor sending the
$\mathcal {A}^2(\mathcal {F}) \colon [S(\mathcal {F}^c)] \to \mathrm {Ab}$
is the functor sending the
![]() $\mathcal {F}$
-isomorphism class of a chain
$\mathcal {F}$
-isomorphism class of a chain
![]() $[\sigma ] = [Q_0 < \cdots < Q_m]$
of
$[\sigma ] = [Q_0 < \cdots < Q_m]$
of
![]() $\mathcal {F}$
-centric subgroups to the
$\mathcal {F}$
-centric subgroups to the
![]() $p'$
-part
$p'$
-part
![]() $M(\operatorname {Out}_{\mathcal {F}}(\sigma ))_{p'} = H^2(\operatorname {Out}_{\mathcal {F}}(\sigma ),k^\times )$
of the Schur multiplier of
$M(\operatorname {Out}_{\mathcal {F}}(\sigma ))_{p'} = H^2(\operatorname {Out}_{\mathcal {F}}(\sigma ),k^\times )$
of the Schur multiplier of
![]() $\operatorname {Out}_{\mathcal {F}}(\sigma )$
.
$\operatorname {Out}_{\mathcal {F}}(\sigma )$
.
Theorem 4.4. Let p be an odd prime, and let
![]() $\mathcal {F}$
be a nonconstrained saturated fusion system on an extraspecial p-group S of order
$\mathcal {F}$
be a nonconstrained saturated fusion system on an extraspecial p-group S of order
![]() $p^3$
and of exponent p. Then,
$p^3$
and of exponent p. Then,
![]() $\lim \mathcal {A}^2_{\mathcal {F}} = 0$
.
$\lim \mathcal {A}^2_{\mathcal {F}} = 0$
.
Proof. Consider the cochain complex
![]() $(C^*(\mathcal {A}_{\mathcal {F}}^2), \delta )$
computing the limits of
$(C^*(\mathcal {A}_{\mathcal {F}}^2), \delta )$
computing the limits of
![]() $\mathcal {A}_{\mathcal {F}}^2$
as in [Reference LinckelmannLin09]. By Lemma 4.3(1),
$\mathcal {A}_{\mathcal {F}}^2$
as in [Reference LinckelmannLin09]. By Lemma 4.3(1),
![]() $M(\operatorname {Out}_{\mathcal {F}}(Q))_{p'} = 1$
for all elementary abelian subgroups
$M(\operatorname {Out}_{\mathcal {F}}(Q))_{p'} = 1$
for all elementary abelian subgroups
![]() $Q \in \mathcal {F}^{cr}$
. Thus, the zeroth cochain group is
$Q \in \mathcal {F}^{cr}$
. Thus, the zeroth cochain group is
![]() $C^0(\mathcal {A}_{\mathcal {F}}^2) = M(\operatorname {Out}_{\mathcal {F}}(S))_{p'} = M(\operatorname {Out}_{\mathcal {F}}(S))$
and the coboundary map
$C^0(\mathcal {A}_{\mathcal {F}}^2) = M(\operatorname {Out}_{\mathcal {F}}(S))_{p'} = M(\operatorname {Out}_{\mathcal {F}}(S))$
and the coboundary map
 $$ \begin{align*} \delta^0 \colon M(\operatorname{Out}_{\mathcal{F}}(S)) \longrightarrow \bigoplus_{Q \in \mathcal{F}^{cr}, |Q| = p^2} M(\operatorname{Out}_{\mathcal{F}}([Q < S])) \end{align*} $$
$$ \begin{align*} \delta^0 \colon M(\operatorname{Out}_{\mathcal{F}}(S)) \longrightarrow \bigoplus_{Q \in \mathcal{F}^{cr}, |Q| = p^2} M(\operatorname{Out}_{\mathcal{F}}([Q < S])) \end{align*} $$
is the sum of the restriction maps
![]() $M(\operatorname {Out}_{\mathcal {F}}(S)) \to M(\operatorname {Out}_{\mathcal {F}}([Q<S]))$
. Thus, to complete the proof, it suffices to show that at least one of these restriction maps is injective.
$M(\operatorname {Out}_{\mathcal {F}}(S)) \to M(\operatorname {Out}_{\mathcal {F}}([Q<S]))$
. Thus, to complete the proof, it suffices to show that at least one of these restriction maps is injective.
We regard
![]() $\operatorname {Out}_{\mathcal {F}}(S) \leqslant \operatorname {GL}_2(p)$
as acting on
$\operatorname {Out}_{\mathcal {F}}(S) \leqslant \operatorname {GL}_2(p)$
as acting on
![]() $\{Q_i \mid 0 \leqslant i \leqslant p\}$
as it does on the projective line, and then
$\{Q_i \mid 0 \leqslant i \leqslant p\}$
as it does on the projective line, and then
![]() $\operatorname {Out}_{\mathcal {F}}([Q < S])$
is the stabilizer of the point Q. We go through the possibilities for
$\operatorname {Out}_{\mathcal {F}}([Q < S])$
is the stabilizer of the point Q. We go through the possibilities for
![]() $\mathcal {F}$
appearing in [RV04, Tables 1.1 and 1.2]. Consider first a fusion system
$\mathcal {F}$
appearing in [RV04, Tables 1.1 and 1.2]. Consider first a fusion system
![]() $\mathcal {F}$
over S occurring in Table 1.2. Then,
$\mathcal {F}$
over S occurring in Table 1.2. Then,
![]() $C^0(\mathcal {A}_{\mathcal {F}}^2) = 1$
unless
$C^0(\mathcal {A}_{\mathcal {F}}^2) = 1$
unless
![]() $G := \operatorname {Out}_{\mathcal {F}}(S)$
is listed in Lemma 4.3(4). By inspection of Table 1.2 for those cases, there is some
$G := \operatorname {Out}_{\mathcal {F}}(S)$
is listed in Lemma 4.3(4). By inspection of Table 1.2 for those cases, there is some
![]() $Q\in \mathcal {F}^{cr}$
with
$Q\in \mathcal {F}^{cr}$
with
![]() $|Q| = p^2$
that is stabilized by a
$|Q| = p^2$
that is stabilized by a
![]() $4$
-subgroup V of G. Let D be a Sylow
$4$
-subgroup V of G. Let D be a Sylow
![]() $2$
-subgroup of G containing V. Then, D is dihedral. As
$2$
-subgroup of G containing V. Then, D is dihedral. As
![]() $M(G) = M(G)_2$
by Lemma 4.3(4), the composite
$M(G) = M(G)_2$
by Lemma 4.3(4), the composite
![]() $M(G) \to M(D) \to M(V)$
is injective by Lemma 4.2(2) and the last sentence of Lemma 4.3(2), and hence,
$M(G) \to M(D) \to M(V)$
is injective by Lemma 4.2(2) and the last sentence of Lemma 4.3(2), and hence,
![]() $M(G) \to M(\operatorname {Out}_{\mathcal {F}}([Q < S]))$
is also injective.
$M(G) \to M(\operatorname {Out}_{\mathcal {F}}([Q < S]))$
is also injective.
Now, consider a nonconstrained fusion system appearing in Table 1.1. Then,
![]() $\mathcal {F}^{cr} = \{Q_0,Q_p\}$
and
$\mathcal {F}^{cr} = \{Q_0,Q_p\}$
and
![]() $G := \operatorname {Out}_{\mathcal {F}}(S)$
may be taken in the normalizer in
$G := \operatorname {Out}_{\mathcal {F}}(S)$
may be taken in the normalizer in
![]() $\mathrm{GL}_2(p)$
of the subgroup T of diagonal matrices, which stabilizes
$\mathrm{GL}_2(p)$
of the subgroup T of diagonal matrices, which stabilizes
![]() $Q_0$
and
$Q_0$
and
![]() $Q_p$
. Write
$Q_p$
. Write
![]() $G_0 = \operatorname {Out}_{\mathcal {F}}([Q_0<S])$
, for short. Then,
$G_0 = \operatorname {Out}_{\mathcal {F}}([Q_0<S])$
, for short. Then,
![]() $G_0 = G \cap T$
. Assume first that
$G_0 = G \cap T$
. Assume first that
![]() $r \neq p$
is an odd prime. If r divides
$r \neq p$
is an odd prime. If r divides
![]() $p+1$
, then a Sylow r-subgroup of
$p+1$
, then a Sylow r-subgroup of
![]() $\mathrm{GL}_2(p)$
is cyclic and hence,
$\mathrm{GL}_2(p)$
is cyclic and hence,
![]() $M(G)_r = 1$
by Lemma 4.2(3). Suppose r divides
$M(G)_r = 1$
by Lemma 4.2(3). Suppose r divides
![]() $p-1$
. Then, a Sylow r-subgroup of G is contained in T and so
$p-1$
. Then, a Sylow r-subgroup of G is contained in T and so
![]() $G_0$
contains a Sylow r-subgroup of G. Thus, the restriction
$G_0$
contains a Sylow r-subgroup of G. Thus, the restriction
![]() $M(G)_r \to M(G_0)_r$
is injective by Lemma 4.2(2). It remains to consider
$M(G)_r \to M(G_0)_r$
is injective by Lemma 4.2(2). It remains to consider
![]() $r = 2$
. Inspection of [Reference Ruiz and ViruelRV04, Table 1.1] shows that either a Sylow
$r = 2$
. Inspection of [Reference Ruiz and ViruelRV04, Table 1.1] shows that either a Sylow
![]() $2$
-subgroup of G stabilizes
$2$
-subgroup of G stabilizes
![]() $Q_0$
, in which case
$Q_0$
, in which case
![]() $M(G)_2 \to M(G_0)_2$
is injective by Lemma 4.2(2), or a Sylow
$M(G)_2 \to M(G_0)_2$
is injective by Lemma 4.2(2), or a Sylow
![]() $2$
-subgroup R of G is isomorphic to
$2$
-subgroup R of G is isomorphic to
![]() $C_{2^l} \wr C_2$
for some
$C_{2^l} \wr C_2$
for some
![]() $l \geqslant 1$
and
$l \geqslant 1$
and
![]() $R \cap G_0$
is the homocyclic subgroup of R of index
$R \cap G_0$
is the homocyclic subgroup of R of index
![]() $2$
. The restriction map
$2$
. The restriction map
![]() $M(G)_2 \to M(G_0)_2$
is injective in this latter case by Lemma 4.3(3).
$M(G)_2 \to M(G_0)_2$
is injective in this latter case by Lemma 4.3(3).
5 Verification of the conjectures
We now verify a number of the conjectures in Section 1 for a nonconstrained saturated fusion system
![]() $\mathcal {F}$
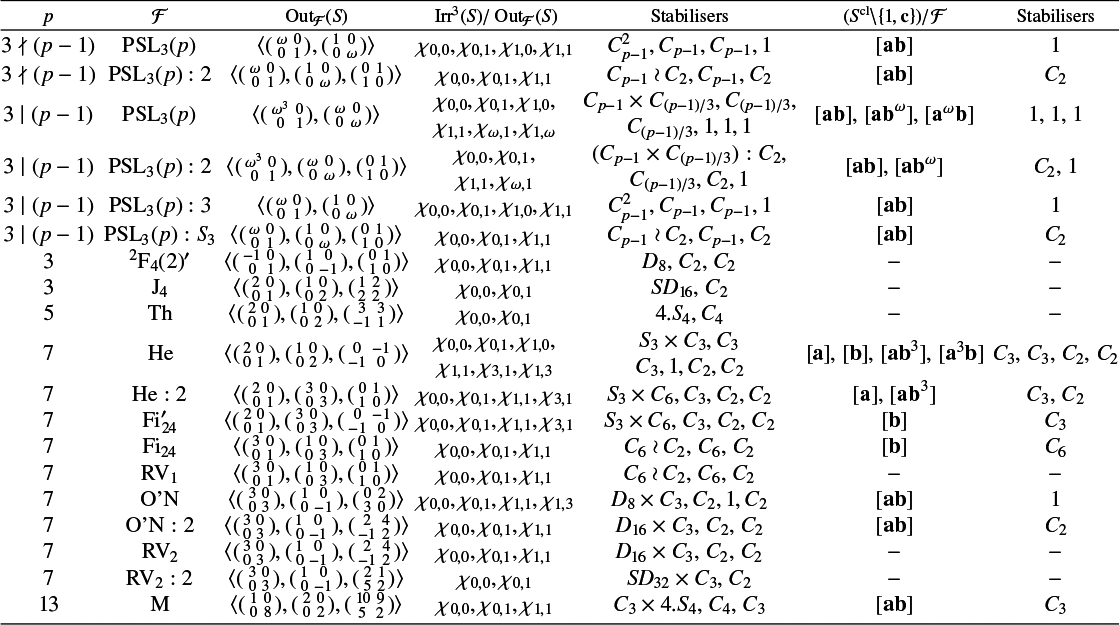
over S. In the 13 exceptional cases, complete proofs by hand could be written down, but since we have no reasonably general argument for the specific numerical computations, the conjectures are ultimately verified using computer calculations in Magma [Reference Bosma, Cannon and PlayoustBCP97].
$\mathcal {F}$
over S. In the 13 exceptional cases, complete proofs by hand could be written down, but since we have no reasonably general argument for the specific numerical computations, the conjectures are ultimately verified using computer calculations in Magma [Reference Bosma, Cannon and PlayoustBCP97].
First, we need the following well-known lemma.
Lemma 5.1. Let G be a finite group with normal subgroup N. Suppose that V is an inertial projective simple
![]() $kN$
-module and that
$kN$
-module and that
![]() $G/N$
is a cyclic
$G/N$
is a cyclic
![]() $p'$
-group. Then, G has exactly
$p'$
-group. Then, G has exactly
![]() $|G:N|$
projective simple modules lying over V. In particular, if q is a power of p and
$|G:N|$
projective simple modules lying over V. In particular, if q is a power of p and
![]() $N = \operatorname {SL}_n(q) \le G \le \operatorname {GL}_n(q)$
, then
$N = \operatorname {SL}_n(q) \le G \le \operatorname {GL}_n(q)$
, then
![]() $z(kG)=|G:\operatorname {SL}_n(q)|$
.
$z(kG)=|G:\operatorname {SL}_n(q)|$
.
Proof. Since
![]() $G/N$
is a cyclic group, we have that
$G/N$
is a cyclic group, we have that
![]() $H^2(G/N,k^\times )$
is trivial. Thus, the hypotheses of [Reference LinckelmannLin19b, Corollary 5.3.13] hold. By that result and its proof, we may fix a simple
$H^2(G/N,k^\times )$
is trivial. Thus, the hypotheses of [Reference LinckelmannLin19b, Corollary 5.3.13] hold. By that result and its proof, we may fix a simple
![]() $kG$
-module U with
$kG$
-module U with
![]() $\operatorname {Res}_N^G(U) \cong V$
, and then the collection of isomorphism classes of one-dimensional
$\operatorname {Res}_N^G(U) \cong V$
, and then the collection of isomorphism classes of one-dimensional
![]() $kG/N$
-modules is in one-to-one correspondence with the collection of simple
$kG/N$
-modules is in one-to-one correspondence with the collection of simple
![]() $kG$
-modules restricting to V via the map
$kG$
-modules restricting to V via the map
![]() $W \mapsto U \otimes _k W$
, where we regard W as a module for G by inflation. Also, the
$W \mapsto U \otimes _k W$
, where we regard W as a module for G by inflation. Also, the
![]() $U \otimes _k W$
are precisely the summands of the induced module
$U \otimes _k W$
are precisely the summands of the induced module
![]() $\operatorname {Ind}_N^G V$
and hence, are all projective. This completes the proof of the first statement.
$\operatorname {Ind}_N^G V$
and hence, are all projective. This completes the proof of the first statement.
In the special case of the last statement, by results of Steinberg (see [Reference HumphreysHum06, Theorems 3.7 and 8.3]),
![]() $N = \operatorname {SL}_n(p)$
has exactly one projective simple module, the Steinberg module, which is therefore inertial. Since
$N = \operatorname {SL}_n(p)$
has exactly one projective simple module, the Steinberg module, which is therefore inertial. Since
![]() $G/N$
is a cyclic
$G/N$
is a cyclic
![]() $p'$
-group in this case and since any projective
$p'$
-group in this case and since any projective
![]() $kG$
-module is projective also as a
$kG$
-module is projective also as a
![]() $kN$
-module, the last statement follows.
$kN$
-module, the last statement follows.
In a saturated fusion system
![]() $\mathcal {F}$
on S, Lemma 3.1(a) and Lemma 3.2(1) allow one to identify
$\mathcal {F}$
on S, Lemma 3.1(a) and Lemma 3.2(1) allow one to identify
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
with a subgroup of
$\operatorname {Out}_{\mathcal {F}}(S)$
with a subgroup of
![]() $\operatorname {GL}_2(p)$
of order prime to p. Relative to this setup, we identify elements of
$\operatorname {GL}_2(p)$
of order prime to p. Relative to this setup, we identify elements of
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
with matrices with respect to the basis
$\operatorname {Out}_{\mathcal {F}}(S)$
with matrices with respect to the basis
![]() $\{\textbf {a},\textbf {b}\}$
(or rather, the basis
$\{\textbf {a},\textbf {b}\}$
(or rather, the basis
![]() $\{\textbf {a} Z(S), \textbf {b} Z(S)\}$
of
$\{\textbf {a} Z(S), \textbf {b} Z(S)\}$
of
![]() $S^{\operatorname {ab}}$
). Write
$S^{\operatorname {ab}}$
). Write
![]() $\operatorname {Out}^*_{\mathcal {F}}(S)$
for those elements of
$\operatorname {Out}^*_{\mathcal {F}}(S)$
for those elements of
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
that have determinant
$\operatorname {Out}_{\mathcal {F}}(S)$
that have determinant
![]() $1$
. The next lemma gives a general calculation of the quantity
$1$
. The next lemma gives a general calculation of the quantity
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,d)$
.
$\operatorname {\mathbf {m}}(\mathcal {F},0,d)$
.
Lemma 5.2. Let
![]() $\mathcal {F}$
be a saturated fusion system on S. Then:
$\mathcal {F}$
be a saturated fusion system on S. Then:
-
(1)
 $\operatorname {\mathbf {m}}(\mathcal {F},0,0) = \operatorname {\mathbf {m}}(\mathcal {F},0,1) = 0$
;
$\operatorname {\mathbf {m}}(\mathcal {F},0,0) = \operatorname {\mathbf {m}}(\mathcal {F},0,1) = 0$
; -
(2)
 $\operatorname {\mathbf {m}}(\mathcal {F},0,2) = {(p-1)}/{l} \cdot |\!\operatorname {Out}_{\mathcal {F}}^*(S)^{\operatorname {cl}}|$
, where l denotes the index of
$\operatorname {\mathbf {m}}(\mathcal {F},0,2) = {(p-1)}/{l} \cdot |\!\operatorname {Out}_{\mathcal {F}}^*(S)^{\operatorname {cl}}|$
, where l denotes the index of
 $\operatorname {Out}_{\mathcal {F}}^*(S)$
in
$\operatorname {Out}_{\mathcal {F}}^*(S)$
in
 $\operatorname {Out}_{\mathcal {F}}(S)$
; and
$\operatorname {Out}_{\mathcal {F}}(S)$
; and -
(3)
 $\operatorname {\mathbf {m}}(\mathcal {F},0,3) = \sum _{\mu } z(kC_{\operatorname {Out}_{\mathcal {F}}(S)}(\mu ))$
, where
$\operatorname {\mathbf {m}}(\mathcal {F},0,3) = \sum _{\mu } z(kC_{\operatorname {Out}_{\mathcal {F}}(S)}(\mu ))$
, where
 $\mu $
runs over a set of representatives for the
$\mu $
runs over a set of representatives for the
 $\operatorname {Out}_{\mathcal {F}}(S)$
-orbits of linear characters of S and where
$\operatorname {Out}_{\mathcal {F}}(S)$
-orbits of linear characters of S and where
 $C_{\operatorname {Out}_{\mathcal {F}}(S)}(\mu )$
denotes the stabilizer of
$C_{\operatorname {Out}_{\mathcal {F}}(S)}(\mu )$
denotes the stabilizer of
 $\mu $
in
$\mu $
in
 $\operatorname {Out}_{\mathcal {F}}(S)$
.
$\operatorname {Out}_{\mathcal {F}}(S)$
.
Thus,
 $$ \begin{align*} \operatorname{\mathbf{m}}(\mathcal{F},0) = \frac{p-1}{l} \cdot |\!\operatorname{Out}^*_{\mathcal{F}}(S)^{\operatorname{cl}}| + \sum_{\mu \in \operatorname{Irr}^3(S)/\operatorname{Out}_{\mathcal{F}}(S)} z(kC_{\operatorname{Out}_{\mathcal{F}}(S)}(\mu)). \end{align*} $$
$$ \begin{align*} \operatorname{\mathbf{m}}(\mathcal{F},0) = \frac{p-1}{l} \cdot |\!\operatorname{Out}^*_{\mathcal{F}}(S)^{\operatorname{cl}}| + \sum_{\mu \in \operatorname{Irr}^3(S)/\operatorname{Out}_{\mathcal{F}}(S)} z(kC_{\operatorname{Out}_{\mathcal{F}}(S)}(\mu)). \end{align*} $$
Proof. Each character of
![]() $Q_i \cong C_p \times C_p$
is linear, so has defect
$Q_i \cong C_p \times C_p$
is linear, so has defect
![]() $2$
, while each character of S has defect
$2$
, while each character of S has defect
![]() $2$
or
$2$
or
![]() $3$
by Lemma 3.1(3). This shows part (1).
$3$
by Lemma 3.1(3). This shows part (1).
The quantity
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,2)$
is a sum over
$\operatorname {\mathbf {m}}(\mathcal {F},0,2)$
is a sum over
![]() $\mathcal {F}$
-conjugacy classes of centric radicals Q of the quantities
$\mathcal {F}$
-conjugacy classes of centric radicals Q of the quantities
![]() $\operatorname {\mathbf {w}}_Q(\mathcal {F},0,2)$
. Fix first a centric radical Q of order
$\operatorname {\mathbf {w}}_Q(\mathcal {F},0,2)$
. Fix first a centric radical Q of order
![]() $p^2$
. We claim
$p^2$
. We claim
![]() $\operatorname {\mathbf {w}}_{Q}(\mathcal {F},0,2) = 0$
. By Theorem 3.2,
$\operatorname {\mathbf {w}}_{Q}(\mathcal {F},0,2) = 0$
. By Theorem 3.2,
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
is a subgroup of
$\operatorname {Out}_{\mathcal {F}}(Q)$
is a subgroup of
![]() $\operatorname {GL}_2(p)$
containing
$\operatorname {GL}_2(p)$
containing
![]() $\operatorname {SL}_2(p)$
with index a, say. First, consider the trivial chain
$\operatorname {SL}_2(p)$
with index a, say. First, consider the trivial chain
![]() $\sigma = (\overline {Q}) \in \mathcal {N}_Q$
. Then,
$\sigma = (\overline {Q}) \in \mathcal {N}_Q$
. Then,
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
stabilizes
$\operatorname {Out}_{\mathcal {F}}(Q)$
stabilizes
![]() $\sigma $
. There are two orbits on characters, one nontrivial and one trivial. Given a nontrivial character
$\sigma $
. There are two orbits on characters, one nontrivial and one trivial. Given a nontrivial character
![]() $\mu $
, the stabilizer of
$\mu $
, the stabilizer of
![]() $\mu $
in
$\mu $
in
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
is a Frobenius group with normal subgroup of order p, and so has
$\operatorname {Out}_{\mathcal {F}}(Q)$
is a Frobenius group with normal subgroup of order p, and so has
![]() $0$
projective simple modules by [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Lemma 4.11]. Also, the trivial character has stabilizer
$0$
projective simple modules by [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Lemma 4.11]. Also, the trivial character has stabilizer
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
, which by Lemma 5.1 has a projective simple modules. Thus, the contribution to
$\operatorname {Out}_{\mathcal {F}}(Q)$
, which by Lemma 5.1 has a projective simple modules. Thus, the contribution to
![]() $\operatorname {\mathbf {w}}_Q(\mathcal {F},0,2)$
from the trivial chain is a. Next, let
$\operatorname {\mathbf {w}}_Q(\mathcal {F},0,2)$
from the trivial chain is a. Next, let
![]() $\sigma = (\overline {Q} < \overline {S}) \in \mathcal {N}_Q$
be the nontrivial chain. The stabilizer
$\sigma = (\overline {Q} < \overline {S}) \in \mathcal {N}_Q$
be the nontrivial chain. The stabilizer
![]() $I(\sigma )$
in
$I(\sigma )$
in
![]() $\operatorname {Out}_{\mathcal {F}}(Q)$
of
$\operatorname {Out}_{\mathcal {F}}(Q)$
of
![]() $\sigma $
has a normal subgroup
$\sigma $
has a normal subgroup
![]() $\overline {S}$
and the quotient by
$\overline {S}$
and the quotient by
![]() $\overline {S}$
is abelian of order
$\overline {S}$
is abelian of order
![]() $(p-1)a$
. Then,
$(p-1)a$
. Then,
![]() $I(\sigma )$
has one orbit of size
$I(\sigma )$
has one orbit of size
![]() $1$
containing the trivial character, and one of size
$1$
containing the trivial character, and one of size
![]() $p-1$
consisting of those characters with kernel
$p-1$
consisting of those characters with kernel
![]() $Z(S)$
. The respective stabilizers have
$Z(S)$
. The respective stabilizers have
![]() $\overline {S}$
as a normal subgroup, so the contribution from these orbits is
$\overline {S}$
as a normal subgroup, so the contribution from these orbits is
![]() $0$
, by [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Lemma 4.11]. The group
$0$
, by [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Lemma 4.11]. The group
![]() $\overline {S}$
acts regularly on the remaining points of
$\overline {S}$
acts regularly on the remaining points of
![]() $\mathbb {P}^1(Q)$
, and a subgroup in
$\mathbb {P}^1(Q)$
, and a subgroup in
![]() $I(\sigma ) \cap SL(Q)$
of order
$I(\sigma ) \cap SL(Q)$
of order
![]() $p-1$
acts regularly on the characters with kernel a given point. Thus, there is one further orbit with stabilizer of order a and this contributes
$p-1$
acts regularly on the characters with kernel a given point. Thus, there is one further orbit with stabilizer of order a and this contributes
![]() $-a$
to
$-a$
to
![]() $\operatorname {\mathbf {w}}_{Q}(\mathcal {F},0,2)$
. Hence,
$\operatorname {\mathbf {w}}_{Q}(\mathcal {F},0,2)$
. Hence,
![]() $\operatorname {\mathbf {w}}_Q(\mathcal {F},0,2) = a-a = 0$
, as claimed.
$\operatorname {\mathbf {w}}_Q(\mathcal {F},0,2) = a-a = 0$
, as claimed.
Lastly, consider
![]() $\operatorname {\mathbf {w}}_{S}(\mathcal {F},0,2)$
. Here, there is only the trivial chain with stabilizer
$\operatorname {\mathbf {w}}_{S}(\mathcal {F},0,2)$
. Here, there is only the trivial chain with stabilizer
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
. Note that
$\operatorname {Out}_{\mathcal {F}}(S)$
. Note that
![]() $\operatorname {Irr}^2(S)$
consists of the
$\operatorname {Irr}^2(S)$
consists of the
![]() $p-1$
faithful characters denoted
$p-1$
faithful characters denoted
![]() $\varphi _u$
in Lemma 3.1. Let l be the index of
$\varphi _u$
in Lemma 3.1. Let l be the index of
![]() $\operatorname {Out}^*_{\mathcal {F}}(S)$
in
$\operatorname {Out}^*_{\mathcal {F}}(S)$
in
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
. The action of
$\operatorname {Out}_{\mathcal {F}}(S)$
. The action of
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
on
$\operatorname {Out}_{\mathcal {F}}(S)$
on
![]() $\operatorname {Irr}^2(S)$
is the same as the action on
$\operatorname {Irr}^2(S)$
is the same as the action on
![]() $Z(S)^\#$
(nonidentity elements) and there,
$Z(S)^\#$
(nonidentity elements) and there,
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
acts semiregularly via the determinant map. So, there are
$\operatorname {Out}_{\mathcal {F}}(S)$
acts semiregularly via the determinant map. So, there are
![]() $(p-1)/l$
orbits, each of size l, and a representative for each orbit has stabilizer
$(p-1)/l$
orbits, each of size l, and a representative for each orbit has stabilizer
![]() $\operatorname {Out}^*_{\mathcal {F}}(S)$
. As
$\operatorname {Out}^*_{\mathcal {F}}(S)$
. As
![]() $\operatorname {Out}^*_{\mathcal {F}}(S)$
is a
$\operatorname {Out}^*_{\mathcal {F}}(S)$
is a
![]() $p'$
-group, we have
$p'$
-group, we have
![]() $z(k\operatorname {Out}^*_{\mathcal {F}}(S))$
is the number of simple
$z(k\operatorname {Out}^*_{\mathcal {F}}(S))$
is the number of simple
![]() $k\operatorname {Out}^*_{\mathcal {F}}(S)$
-modules, which is the number of conjugacy classes. This completes the proof of part (2).
$k\operatorname {Out}^*_{\mathcal {F}}(S)$
-modules, which is the number of conjugacy classes. This completes the proof of part (2).
In part (3), since
![]() $\operatorname {Irr}^3(Q_i)$
is empty, there is only one pair
$\operatorname {Irr}^3(Q_i)$
is empty, there is only one pair
![]() $(Q,\sigma )$
for which the innermost sum in
$(Q,\sigma )$
for which the innermost sum in
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
is nonzero, namely the pair
$\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
is nonzero, namely the pair
![]() $(S, 1)$
. We thus have
$(S, 1)$
. We thus have
![]() $I(\sigma ) = \operatorname {Out}_{\mathcal {F}}(S)$
for this pair. Thus,
$I(\sigma ) = \operatorname {Out}_{\mathcal {F}}(S)$
for this pair. Thus,
 $$ \begin{align*}\operatorname{\mathbf{m}}(\mathcal{F},0,3) = \sum_{\mu \in \operatorname{Irr}^3(S)/\operatorname{Out}_{\mathcal{F}}(S)} z(kC_{\operatorname{Out}_{\mathcal{F}}(S)}(\mu)),\end{align*} $$
$$ \begin{align*}\operatorname{\mathbf{m}}(\mathcal{F},0,3) = \sum_{\mu \in \operatorname{Irr}^3(S)/\operatorname{Out}_{\mathcal{F}}(S)} z(kC_{\operatorname{Out}_{\mathcal{F}}(S)}(\mu)),\end{align*} $$
which completes the proof of part (3). The last statement then follows from parts (1)–(3), since clearly
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,d) = 0$
for
$\operatorname {\mathbf {m}}(\mathcal {F},0,d) = 0$
for
![]() $d> 3$
.
$d> 3$
.
We now calculate
![]() $\operatorname {\mathbf {k}}(\mathcal {F},0)$
.
$\operatorname {\mathbf {k}}(\mathcal {F},0)$
.
Lemma 5.3. Let
![]() $\mathcal {F}$
be a saturated fusion system on S. Then,
$\mathcal {F}$
be a saturated fusion system on S. Then,
 $$ \begin{align*}\operatorname{\mathbf{k}}(\mathcal{F},0)=\operatorname{\mathbf{w}}(\mathcal{F},0)+\frac{p-1}{l} \cdot |\!\operatorname{Out}^*_{\mathcal{F}}(S)^{\operatorname{cl}}| +\sum_{([x] \in S^{\operatorname{cl}}\backslash \{1,\textbf{c}\})/\mathcal{F}} z(kC_{\operatorname{Out}_{\mathcal{F}}(S)}([x])).\end{align*} $$
$$ \begin{align*}\operatorname{\mathbf{k}}(\mathcal{F},0)=\operatorname{\mathbf{w}}(\mathcal{F},0)+\frac{p-1}{l} \cdot |\!\operatorname{Out}^*_{\mathcal{F}}(S)^{\operatorname{cl}}| +\sum_{([x] \in S^{\operatorname{cl}}\backslash \{1,\textbf{c}\})/\mathcal{F}} z(kC_{\operatorname{Out}_{\mathcal{F}}(S)}([x])).\end{align*} $$
Proof. By definition, we have
 $$ \begin{align*}\operatorname{\mathbf{k}}(\mathcal{F},0)= \operatorname{\mathbf{w}}(\mathcal{F},0)+\operatorname{\mathbf{w}}(C_{\mathcal{F}}(\textbf{c}),0)+ \sum_{[x] \in (S^{\operatorname{cl}}\backslash \{1,\textbf{c}\})/\mathcal{F}} \operatorname{\mathbf{w}}(C_{\mathcal{F}}(x),0),\end{align*} $$
$$ \begin{align*}\operatorname{\mathbf{k}}(\mathcal{F},0)= \operatorname{\mathbf{w}}(\mathcal{F},0)+\operatorname{\mathbf{w}}(C_{\mathcal{F}}(\textbf{c}),0)+ \sum_{[x] \in (S^{\operatorname{cl}}\backslash \{1,\textbf{c}\})/\mathcal{F}} \operatorname{\mathbf{w}}(C_{\mathcal{F}}(x),0),\end{align*} $$
where in the latter sum,
![]() $[x]$
runs over S-classes for which
$[x]$
runs over S-classes for which
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}$
-centralized. Let
$\mathcal {F}$
-centralized. Let
![]() $1 \neq x \in S$
be such that x is not
$1 \neq x \in S$
be such that x is not
![]() $\mathcal {F}$
-conjugate to
$\mathcal {F}$
-conjugate to
![]() $\textbf {c}$
and
$\textbf {c}$
and
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}$
-centralized. If
$\mathcal {F}$
-centralized. If
![]() $Q \le C_S(x)$
is a
$Q \le C_S(x)$
is a
![]() $C_{\mathcal {F}}(x)$
-centric radical, then
$C_{\mathcal {F}}(x)$
-centric radical, then
![]() $|Q|=p^2$
and
$|Q|=p^2$
and
![]() $x \in C_S(Q)=Q$
. Therefore,
$x \in C_S(Q)=Q$
. Therefore,
![]() $Q = \langle x, \textbf {c} \rangle $
and
$Q = \langle x, \textbf {c} \rangle $
and
![]() $\operatorname {Out}_{C_{\mathcal {F}}(x)}(Q)$
does not contain a copy of
$\operatorname {Out}_{C_{\mathcal {F}}(x)}(Q)$
does not contain a copy of
![]() $\operatorname {SL}_2(p)$
, which is a contradiction. We conclude that
$\operatorname {SL}_2(p)$
, which is a contradiction. We conclude that
![]() $C_S(x) \unlhd C_{\mathcal {F}}(x)$
and
$C_S(x) \unlhd C_{\mathcal {F}}(x)$
and
by [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19, Lemma 3.3]. We claim that
![]() $C_{\operatorname {Out}_{\mathcal {F}}(C_S(x))}([x]) \cong C_{\operatorname {Out}_{\mathcal {F}}(S)}([x])$
. Since
$C_{\operatorname {Out}_{\mathcal {F}}(C_S(x))}([x]) \cong C_{\operatorname {Out}_{\mathcal {F}}(S)}([x])$
. Since
![]() $\mathcal {F}$
is saturated, the restriction map
$\mathcal {F}$
is saturated, the restriction map
is surjective with kernel containing
![]() $C_{\operatorname {Inn}(S)}(x)$
as a Sylow p-subgroup. If A is a
$C_{\operatorname {Inn}(S)}(x)$
as a Sylow p-subgroup. If A is a
![]() $p'$
-subgroup of
$p'$
-subgroup of
![]() $\ker (\operatorname {res})$
, then A commutes with both
$\ker (\operatorname {res})$
, then A commutes with both
![]() $C_{\operatorname {Inn}(S)}(x) \cong \langle x \rangle $
and
$C_{\operatorname {Inn}(S)}(x) \cong \langle x \rangle $
and
![]() $C_S(C_{\operatorname {Inn}(S)}(x))$
. Hence, Thompson’s
$C_S(C_{\operatorname {Inn}(S)}(x))$
. Hence, Thompson’s
![]() $A \times B$
lemma [Reference GorensteinGor80, Theorem 5.3.4] implies that
$A \times B$
lemma [Reference GorensteinGor80, Theorem 5.3.4] implies that
![]() $A=1$
, and
$A=1$
, and
![]() $C_{\operatorname {Out}_{\mathcal {F}}(S)}([x]) \cong C_{\operatorname {Aut}_{\mathcal {F}}(S)}(x)/C_{\operatorname {Inn}(S)}(x) \cong C_{\operatorname {Out}_{\mathcal {F}}(C_S(x))}(x)$
as claimed.
$C_{\operatorname {Out}_{\mathcal {F}}(S)}([x]) \cong C_{\operatorname {Aut}_{\mathcal {F}}(S)}(x)/C_{\operatorname {Inn}(S)}(x) \cong C_{\operatorname {Out}_{\mathcal {F}}(C_S(x))}(x)$
as claimed.
Clearly,
![]() $S \unlhd C_{\mathcal {F}}(\textbf {c})$
and so
$S \unlhd C_{\mathcal {F}}(\textbf {c})$
and so
where l is as given in Lemma 5.2. This completes the proof.
Remark 5.4. From the classification in [Reference Ruiz and ViruelRV04], we see that for any nonconstrained fusion system
![]() $\mathcal {F}$
over S, one has
$\mathcal {F}$
over S, one has
![]() $l = p-1$
in Lemmas 5.2 and 5.3. Indeed, if
$l = p-1$
in Lemmas 5.2 and 5.3. Indeed, if
![]() $\mathcal {F}$
is nonconstrained, then
$\mathcal {F}$
is nonconstrained, then
![]() $Z(S) = ZJ(S)$
is not weakly
$Z(S) = ZJ(S)$
is not weakly
![]() $\mathcal {F}$
-closed and then a result of Glauberman then suggests that
$\mathcal {F}$
-closed and then a result of Glauberman then suggests that
![]() $\operatorname {Out}_{\mathcal {F}}(Z(S)) \cong C_{p-1}$
for any nonconstrained fusion system over S; see [Reference GlaubermanGla71, Theorem 14.14].
$\operatorname {Out}_{\mathcal {F}}(Z(S)) \cong C_{p-1}$
for any nonconstrained fusion system over S; see [Reference GlaubermanGla71, Theorem 14.14].
Lemma 5.5. Let
![]() $\omega $
be a generator of the multiplicative group
$\omega $
be a generator of the multiplicative group
![]() $\mathbb {F}_p^\times $
.
$\mathbb {F}_p^\times $
.
-
(1) The wreath product
 $ \langle (\begin {smallmatrix} \omega & 0 \\ 0 & 1 \end {smallmatrix} ), (\begin {smallmatrix} 1 & 0 \\ 0 & \omega \end {smallmatrix} ), (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix} )\rangle \cong C_{p-1} \wr C_2$
has
$ \langle (\begin {smallmatrix} \omega & 0 \\ 0 & 1 \end {smallmatrix} ), (\begin {smallmatrix} 1 & 0 \\ 0 & \omega \end {smallmatrix} ), (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix} )\rangle \cong C_{p-1} \wr C_2$
has
 $(p-1)(p+2)/2$
conjugacy classes.
$(p-1)(p+2)/2$
conjugacy classes. -
(2)
 $ \langle (\begin {smallmatrix} \omega & 0 \\ 0 & \omega ^{-1} \end {smallmatrix} ), (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix} ) \rangle \cong C_{p-1}.C_2$
has
$ \langle (\begin {smallmatrix} \omega & 0 \\ 0 & \omega ^{-1} \end {smallmatrix} ), (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix} ) \rangle \cong C_{p-1}.C_2$
has
 $(p+5)/2$
conjugacy classes.
$(p+5)/2$
conjugacy classes. -
(3) If
 $3 \mid p-1$
, then
$3 \mid p-1$
, then
 $\langle (\begin {smallmatrix} \omega ^3 & 0 \\ 0 & 1 \end {smallmatrix} ), (\begin {smallmatrix} \omega & 0 \\ 0 & \omega \end {smallmatrix} ), (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix} ) \rangle $
has
$\langle (\begin {smallmatrix} \omega ^3 & 0 \\ 0 & 1 \end {smallmatrix} ), (\begin {smallmatrix} \omega & 0 \\ 0 & \omega \end {smallmatrix} ), (\begin {smallmatrix} 0 & 1 \\ 1 & 0 \end {smallmatrix} ) \rangle $
has
 $(p-1)(p+8)/6$
conjugacy classes.
$(p-1)(p+8)/6$
conjugacy classes. -
(4) If
 $3 \mid p-1$
, then
$3 \mid p-1$
, then
 $\langle (\begin {smallmatrix} \omega ^3 & 0 \\ 0 & \omega ^{-3} \end {smallmatrix} ), (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix} ) \rangle $
has
$\langle (\begin {smallmatrix} \omega ^3 & 0 \\ 0 & \omega ^{-3} \end {smallmatrix} ), (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix} ) \rangle $
has
 $(p+17)/2$
conjugacy classes.
$(p+17)/2$
conjugacy classes.
Proof. If B denotes the base of the wreath product
![]() $G:=C_n \wr C_2$
, then
$G:=C_n \wr C_2$
, then
![]() $Z(G)$
is a cyclic subgroup of order n in B so
$Z(G)$
is a cyclic subgroup of order n in B so
![]() $B \backslash Z(G)$
is the union of
$B \backslash Z(G)$
is the union of
![]() $(n^2-n)/2$
classes. There are n classes of elements in G outside B, which yields
$(n^2-n)/2$
classes. There are n classes of elements in G outside B, which yields
![]() $n(n+3)/2$
classes altogether and part (1) holds. Next, if G denotes the group in part (2) and H is the cyclic subgroup of order
$n(n+3)/2$
classes altogether and part (1) holds. Next, if G denotes the group in part (2) and H is the cyclic subgroup of order
![]() $p-1$
, we see that, apart from
$p-1$
, we see that, apart from
![]() $Z(G)$
(of order
$Z(G)$
(of order
![]() $2$
), there are
$2$
), there are
![]() $(p-3)/2$
classes of elements in H. There are two classes of elements outside of H, which yields
$(p-3)/2$
classes of elements in H. There are two classes of elements outside of H, which yields
![]() $(p+5)/2$
classes altogether. A similar argument proves part (4). Finally, we prove part (3). Let G denote the group in question and set
$(p+5)/2$
classes altogether. A similar argument proves part (4). Finally, we prove part (3). Let G denote the group in question and set
![]() $B:=\langle (\begin {smallmatrix} \omega ^3 & 0 \\ 0 & 1 \end {smallmatrix} ), (\begin {smallmatrix} \omega & 0 \\ 0 & \omega \end {smallmatrix} ) \rangle $
. We see that
$B:=\langle (\begin {smallmatrix} \omega ^3 & 0 \\ 0 & 1 \end {smallmatrix} ), (\begin {smallmatrix} \omega & 0 \\ 0 & \omega \end {smallmatrix} ) \rangle $
. We see that
![]() $Z(G)$
has order
$Z(G)$
has order
![]() $p-1$
and so
$p-1$
and so
![]() $B \backslash Z(G)$
is the union of
$B \backslash Z(G)$
is the union of
![]() $(p-1)(p-4)/6$
classes. There are
$(p-1)(p-4)/6$
classes. There are
![]() $p-1$
classes of elements in G outside B and this yields
$p-1$
classes of elements in G outside B and this yields
![]() $(p-1)(p+8)/6$
classes altogether, as needed.
$(p-1)(p+8)/6$
classes altogether, as needed.
We now describe the computations of the quantities
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0)$
,
$\operatorname {\mathbf {m}}(\mathcal {F},0)$
,
![]() $\operatorname {\mathbf {w}}(\mathcal {F},0)$
and
$\operatorname {\mathbf {w}}(\mathcal {F},0)$
and
![]() $\operatorname {\mathbf {k}}(\mathcal {F},0)$
that were carried out in Magma [Reference Bosma, Cannon and PlayoustBCP97] and listed in Tables 2 and 3. The list of nonconstrained saturated fusion systems on S is given in Table 2, based on the list in [Reference Ruiz and ViruelRV04, Tables 1.1 and 1.2]. Generators for
$\operatorname {\mathbf {k}}(\mathcal {F},0)$
that were carried out in Magma [Reference Bosma, Cannon and PlayoustBCP97] and listed in Tables 2 and 3. The list of nonconstrained saturated fusion systems on S is given in Table 2, based on the list in [Reference Ruiz and ViruelRV04, Tables 1.1 and 1.2]. Generators for
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
are listed in the third column of Table 2 for the convenience of the reader: in each case, there is exactly one
$\operatorname {Out}_{\mathcal {F}}(S)$
are listed in the third column of Table 2 for the convenience of the reader: in each case, there is exactly one
![]() $\operatorname {Out}(S)$
-conjugacy class of subgroups isomorphic with
$\operatorname {Out}(S)$
-conjugacy class of subgroups isomorphic with
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
and a representative is chosen to contain as many diagonal matrices as possible. Then,
$\operatorname {Out}_{\mathcal {F}}(S)$
and a representative is chosen to contain as many diagonal matrices as possible. Then,
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
-orbit representatives and stabilizers for the actions on linear characters of S and S-conjugacy classes were computed and listed in columns four through seven, using the notation of Lemma 3.1. In each case,
$\operatorname {Out}_{\mathcal {F}}(S)$
-orbit representatives and stabilizers for the actions on linear characters of S and S-conjugacy classes were computed and listed in columns four through seven, using the notation of Lemma 3.1. In each case,
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
is computed using Lemma 5.2(3), by summing up the number of projective simple modules of the stabilizers listed in the fifth column of Table 2. Then,
$\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
is computed using Lemma 5.2(3), by summing up the number of projective simple modules of the stabilizers listed in the fifth column of Table 2. Then,
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
is listed in Table 3. The quantity
$\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
is listed in Table 3. The quantity
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,2)$
is computed using Lemmas 5.2(2) and 5.5, which computes the number of conjugacy classes of the various
$\operatorname {\mathbf {m}}(\mathcal {F},0,2)$
is computed using Lemmas 5.2(2) and 5.5, which computes the number of conjugacy classes of the various
![]() $\operatorname {Out}_{\mathcal {F}}^*(S)$
listed in Table 3. This completes the description of the computation of
$\operatorname {Out}_{\mathcal {F}}^*(S)$
listed in Table 3. This completes the description of the computation of
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0)$
as the sum of
$\operatorname {\mathbf {m}}(\mathcal {F},0)$
as the sum of
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,2)$
and
$\operatorname {\mathbf {m}}(\mathcal {F},0,2)$
and
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
. Then,
$\operatorname {\mathbf {m}}(\mathcal {F},0,3)$
. Then,
![]() $\operatorname {\mathbf {w}}(\mathcal {F},0)$
is calculated using the list of outer automorphism groups of centric radicals in [Reference Ruiz and ViruelRV04, Tables 1.1 and 1.2]. For example, we have denoted the three exotic fusion systems at the prime
$\operatorname {\mathbf {w}}(\mathcal {F},0)$
is calculated using the list of outer automorphism groups of centric radicals in [Reference Ruiz and ViruelRV04, Tables 1.1 and 1.2]. For example, we have denoted the three exotic fusion systems at the prime
![]() $7$
by
$7$
by
![]() $\operatorname {RV}_{1}$
,
$\operatorname {RV}_{1}$
,
![]() $\operatorname {RV}_2$
and
$\operatorname {RV}_2$
and
![]() $\operatorname {RV}_2:2$
in the tables, where
$\operatorname {RV}_2:2$
in the tables, where
![]() $\operatorname {Out}_{\operatorname {RV}_1}(S) \cong C_6 \wr C_2$
,
$\operatorname {Out}_{\operatorname {RV}_1}(S) \cong C_6 \wr C_2$
,
![]() $\operatorname {Out}_{\operatorname {RV}_2}(S) \cong D_{16} \times C_3$
and
$\operatorname {Out}_{\operatorname {RV}_2}(S) \cong D_{16} \times C_3$
and
![]() $\operatorname {Out}_{\operatorname {RV}_2:2}(S) \cong SD_{32} \times C_3$
. Note that
$\operatorname {Out}_{\operatorname {RV}_2:2}(S) \cong SD_{32} \times C_3$
. Note that
![]() $\operatorname {RV}_{2}:2$
contains
$\operatorname {RV}_{2}:2$
contains
![]() $\operatorname {RV}_2$
as a normal subsystem of index
$\operatorname {RV}_2$
as a normal subsystem of index
![]() $2$
. These systems have the following invariants:
$2$
. These systems have the following invariants:
-
•
 $\operatorname {\mathbf {m}}(\operatorname {RV}_1,0) = 41$
and
$\operatorname {\mathbf {m}}(\operatorname {RV}_1,0) = 41$
and
 $\operatorname {\mathbf {w}}(\operatorname {RV}_1,0) = 35$
;
$\operatorname {\mathbf {w}}(\operatorname {RV}_1,0) = 35$
; -
•
 $\operatorname {\mathbf {m}}(\operatorname {RV}_2,0) = 33$
and
$\operatorname {\mathbf {m}}(\operatorname {RV}_2,0) = 33$
and
 $\operatorname {\mathbf {w}}(\operatorname {RV}_2,0) = 25$
; and
$\operatorname {\mathbf {w}}(\operatorname {RV}_2,0) = 25$
; and -
•
 $\operatorname {\mathbf {m}}(\operatorname {RV}_2:2,0) = 42$
and
$\operatorname {\mathbf {m}}(\operatorname {RV}_2:2,0) = 42$
and
 $\operatorname {\mathbf {w}}(\operatorname {RV}_2:2,0) = 35$
.
$\operatorname {\mathbf {w}}(\operatorname {RV}_2:2,0) = 35$
.
Table 1 Real characters of
![]() $\operatorname {PGL}_3(p)$
.
$\operatorname {PGL}_3(p)$
.

Table 2
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
-orbits of
$\operatorname {Out}_{\mathcal {F}}(S)$
-orbits of
![]() $\operatorname {Irr}^3(S)$
,
$\operatorname {Irr}^3(S)$
,
![]() $\mathcal {F}$
-classes of
$\mathcal {F}$
-classes of
![]() $S^{\operatorname {cl}}$
and their
$S^{\operatorname {cl}}$
and their
![]() $\operatorname {Out}_{\mathcal {F}}(S)$
-stabilisers.
$\operatorname {Out}_{\mathcal {F}}(S)$
-stabilisers.

Table 3
![]() $\operatorname {\mathbf {w}}(\mathcal {F},0)$
and
$\operatorname {\mathbf {w}}(\mathcal {F},0)$
and
![]() $\operatorname {\mathbf {m}}(\mathcal {F},0,d)$
for
$\operatorname {\mathbf {m}}(\mathcal {F},0,d)$
for
![]() $d=2,3$
.
$d=2,3$
.

Finally,
![]() $\operatorname {\mathbf {k}}(\mathcal {F},0)$
is calculated using Lemma 5.3 by adding
$\operatorname {\mathbf {k}}(\mathcal {F},0)$
is calculated using Lemma 5.3 by adding
![]() $\operatorname {\mathbf {w}}(\mathcal {F},0)$
and
$\operatorname {\mathbf {w}}(\mathcal {F},0)$
and
![]() ${(p-1)}/{l}|\!\operatorname {Out}_{\mathcal {F}}^*(S)^{\operatorname {cl}}|$
to the sum of the number of projective simple modules of the stabilizers listed in the seventh column of Table 2.
${(p-1)}/{l}|\!\operatorname {Out}_{\mathcal {F}}^*(S)^{\operatorname {cl}}|$
to the sum of the number of projective simple modules of the stabilizers listed in the seventh column of Table 2.
Proposition 5.6. Let
![]() $\mathcal {F}$
be a nonconstrained saturated fusion system on S. Then, Conjectures 2.1(1)–(7) all hold for
$\mathcal {F}$
be a nonconstrained saturated fusion system on S. Then, Conjectures 2.1(1)–(7) all hold for
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Proof. This can be easily verified at this point using the tables.
Our final result, Proposition 5.8, is a verification of OWC for principal p-blocks of all almost simple groups that realise
![]() $\mathcal {F}$
. We require the following result concerning character degrees of extensions of
$\mathcal {F}$
. We require the following result concerning character degrees of extensions of
![]() $\operatorname {PSL}_3(p)$
.
$\operatorname {PSL}_3(p)$
.
Lemma 5.7. For
![]() $p \ge 3$
, the character degrees of
$p \ge 3$
, the character degrees of
![]() $\operatorname {PSL}_3(p)$
,
$\operatorname {PSL}_3(p)$
,
![]() $\operatorname {PGL}_3(p)$
,
$\operatorname {PGL}_3(p)$
,
![]() $\operatorname {PSL}_3(p):2$
and
$\operatorname {PSL}_3(p):2$
and
![]() $\operatorname {PGL}_3(p):2$
are listed in Table 4.
$\operatorname {PGL}_3(p):2$
are listed in Table 4.
Table 4 Counts of character degrees of G for
![]() $\operatorname {PSL}_3(p) \le G \le \operatorname {Aut}(\operatorname {PSL}_3(p))$
.
$\operatorname {PSL}_3(p) \le G \le \operatorname {Aut}(\operatorname {PSL}_3(p))$
.

Proof. The character degrees for
![]() $\operatorname {PSL}_3(p)$
are obtained using [Reference Simpson and FrameSF73, Table 2] and those for
$\operatorname {PSL}_3(p)$
are obtained using [Reference Simpson and FrameSF73, Table 2] and those for
![]() $\operatorname {PGL}_3(p)$
are given in [Reference SteinbergSte51, Table VIII]. This accounts for the degrees in columns
$\operatorname {PGL}_3(p)$
are given in [Reference SteinbergSte51, Table VIII]. This accounts for the degrees in columns
![]() $2,4,6$
of Table 4. The entries in columns
$2,4,6$
of Table 4. The entries in columns
![]() $3$
and
$3$
and
![]() $7$
are respectively computed from those of columns
$7$
are respectively computed from those of columns
![]() $2$
and
$2$
and
![]() $6$
in the following way. The group in columns
$6$
in the following way. The group in columns
![]() $2$
and
$2$
and
![]() $6$
is
$6$
is
![]() $\operatorname {PGL}_3(p) $
and the group in columns
$\operatorname {PGL}_3(p) $
and the group in columns
![]() $3$
and
$3$
and
![]() $7$
is
$7$
is
![]() $\operatorname {Aut}(\operatorname {PSL}_3(p))= \operatorname {PGL}_3(p) \langle \tau \rangle $
with
$\operatorname {Aut}(\operatorname {PSL}_3(p))= \operatorname {PGL}_3(p) \langle \tau \rangle $
with
![]() $\tau $
acting as the transpose inverse automorphism. Since every
$\tau $
acting as the transpose inverse automorphism. Since every
![]() $\operatorname {GL}_3(p)$
-conjugacy class is invariant under taking transposes, an irreducible character of
$\operatorname {GL}_3(p)$
-conjugacy class is invariant under taking transposes, an irreducible character of
![]() $\operatorname {PGL}_3(p) $
is
$\operatorname {PGL}_3(p) $
is
![]() $\tau $
-stable if and only if it is real-valued. Thus, by Clifford theory, if an irreducible character
$\tau $
-stable if and only if it is real-valued. Thus, by Clifford theory, if an irreducible character
![]() $\chi $
of
$\chi $
of
![]() $\operatorname {PGL}_3(p) $
is real, then it is covered by two characters of
$\operatorname {PGL}_3(p) $
is real, then it is covered by two characters of
![]() $\operatorname {Aut}(\operatorname {PSL}_3(p))$
of the same degree as
$\operatorname {Aut}(\operatorname {PSL}_3(p))$
of the same degree as
![]() $\chi $
and if
$\chi $
and if
![]() $\chi $
is not real, it is covered by a unique character of
$\chi $
is not real, it is covered by a unique character of
![]() $\operatorname {Aut}(\operatorname {PSL}_3(p))$
of degree twice that of
$\operatorname {Aut}(\operatorname {PSL}_3(p))$
of degree twice that of
![]() $\chi $
.
$\chi $
.
It thus suffices to determine the real characters of
![]() $\operatorname {PGL}_3(p)$
. By [Reference Fulton and HarrisFH91, Section 5.2], the characters of
$\operatorname {PGL}_3(p)$
. By [Reference Fulton and HarrisFH91, Section 5.2], the characters of
![]() $\operatorname {GL}_2(p)$
comprise:
$\operatorname {GL}_2(p)$
comprise:
-
•
 $p-1$
linear characters
$p-1$
linear characters
 $\psi _\alpha $
for
$\psi _\alpha $
for
 $\alpha \in \widehat {\mathbb {F}_p^\times } = \operatorname {Hom}(\mathbb {F}_p^\times , \mathbb {C}^\times )$
;
$\alpha \in \widehat {\mathbb {F}_p^\times } = \operatorname {Hom}(\mathbb {F}_p^\times , \mathbb {C}^\times )$
; -
•
 $p-1$
characters
$p-1$
characters
 $\operatorname {st}_\alpha $
of degree p for
$\operatorname {st}_\alpha $
of degree p for
 $\alpha \in \widehat {\mathbb {F}_p^\times }$
;
$\alpha \in \widehat {\mathbb {F}_p^\times }$
; -
•
 ${p-1 \choose 2}$
characters
${p-1 \choose 2}$
characters
 $\chi _{\alpha ,\beta }$
of degree
$\chi _{\alpha ,\beta }$
of degree
 $p+1$
for distinct
$p+1$
for distinct
 $\alpha , \beta \in \widehat {\mathbb {F}_p^\times }$
;
$\alpha , \beta \in \widehat {\mathbb {F}_p^\times }$
; -
•
 ${p \choose 2}$
characters
${p \choose 2}$
characters
 $\chi _\varphi $
of degree
$\chi _\varphi $
of degree
 $p-1$
for
$p-1$
for
 $\varphi \in \widehat {\mathbb {F}_{p^2}^\times }$
with
$\varphi \in \widehat {\mathbb {F}_{p^2}^\times }$
with
 $\varphi \neq \varphi ^p$
.
$\varphi \neq \varphi ^p$
.
For
![]() $\chi \in \operatorname {Irr}(\operatorname {GL}_2(p))$
and
$\chi \in \operatorname {Irr}(\operatorname {GL}_2(p))$
and
![]() $\psi \in \widehat {\mathbb {F}_p^\times }$
, let
$\psi \in \widehat {\mathbb {F}_p^\times }$
, let
![]() $\chi \boxtimes \psi $
denote the character of
$\chi \boxtimes \psi $
denote the character of
![]() $\operatorname {GL}_3(p)$
obtained via parabolic induction. Let
$\operatorname {GL}_3(p)$
obtained via parabolic induction. Let
![]() $\varphi ^1$
,
$\varphi ^1$
,
![]() $\varphi ^{p(p+1)}$
and
$\varphi ^{p(p+1)}$
and
![]() $\varphi ^{p^3}$
denote the unipotent characters of
$\varphi ^{p^3}$
denote the unipotent characters of
![]() $\operatorname {GL}_3(p)$
, and set
$\operatorname {GL}_3(p)$
, and set
![]() $\varphi ^{(-)}_\alpha :=\varphi ^{(-)} \otimes \alpha $
for
$\varphi ^{(-)}_\alpha :=\varphi ^{(-)} \otimes \alpha $
for
![]() $\alpha \in \widehat {\mathbb {F}_p^\times }$
. Further, let
$\alpha \in \widehat {\mathbb {F}_p^\times }$
. Further, let
![]() $\iota \in \widehat {\mathbb {F}_p^\times }$
be of order
$\iota \in \widehat {\mathbb {F}_p^\times }$
be of order
![]() $2$
. In terms of these descriptions, column
$2$
. In terms of these descriptions, column
![]() $4$
of Table 1 lists
$4$
of Table 1 lists
![]() $2p+6$
distinct real characters of
$2p+6$
distinct real characters of
![]() $\operatorname {GL}_3(p)$
and so these must account for all real characters by [Reference Gill and SinghGS11]. Those which descend to
$\operatorname {GL}_3(p)$
and so these must account for all real characters by [Reference Gill and SinghGS11]. Those which descend to
![]() $\operatorname {PGL}_3(p)$
are described in column 6. This explains the degrees listed in columns
$\operatorname {PGL}_3(p)$
are described in column 6. This explains the degrees listed in columns
![]() $3$
and
$3$
and
![]() $7$
of Table 4.
$7$
of Table 4.
The entries in column
![]() $5$
can be determined in the following fashion. Let
$5$
can be determined in the following fashion. Let
![]() ${N=\operatorname {PSL}_3(p)}$
, G be as in column
${N=\operatorname {PSL}_3(p)}$
, G be as in column
![]() $5$
and
$5$
and
![]() $G_1= \operatorname {PGL}_3(p)$
. Let
$G_1= \operatorname {PGL}_3(p)$
. Let
![]() $\chi \in \operatorname {Irr}(N)$
. By Clifford theory, we have the following.
$\chi \in \operatorname {Irr}(N)$
. By Clifford theory, we have the following.
-
• If
 $\chi $
is
$\chi $
is
 $G_1$
-stable and covered by a real character of
$G_1$
-stable and covered by a real character of
 $G_1$
, then
$G_1$
, then
 $\chi $
is G-stable (and hence extends to two characters of G).
$\chi $
is G-stable (and hence extends to two characters of G). -
• If
 $\chi $
is
$\chi $
is
 $G_1$
-stable but not covered by any real character of
$G_1$
-stable but not covered by any real character of
 $G_1$
, then
$G_1$
, then
 $\chi $
is not G-stable.
$\chi $
is not G-stable. -
• If
 $\chi $
is not
$\chi $
is not
 $G_1$
-stable but is covered by a real character of
$G_1$
-stable but is covered by a real character of
 $G_1$
, then one character in the
$G_1$
, then one character in the
 $G_1$
-orbit of
$G_1$
-orbit of
 $\chi $
is G-stable and the other two are permuted by G.
$\chi $
is G-stable and the other two are permuted by G. -
• If
 $\chi $
is not
$\chi $
is not
 $G_1$
-stable and is not covered by a real character of
$G_1$
-stable and is not covered by a real character of
 $G_1$
, then no character in the
$G_1$
, then no character in the
 $G_1 $
-orbit of
$G_1 $
-orbit of
 $\chi $
is G-stable.
$\chi $
is G-stable.
Which of the four cases applies can be determined from the information in [Reference Simpson and FrameSF73, Reference SteinbergSte51] and from Table 1.
Proposition 5.8. Let G be a finite almost simple group with extraspecial Sylow p-subgroups of order
![]() $p^3$
and nonconstrained fusion system at the odd prime p. The principal p-block of G satisfies Robinson’s ordinary weight conjecture.
$p^3$
and nonconstrained fusion system at the odd prime p. The principal p-block of G satisfies Robinson’s ordinary weight conjecture.
Proof. Let N be a finite simple group and
![]() $N \leqslant G \leqslant \operatorname {Aut}(N)$
. Fix a Sylow p-subgroup
$N \leqslant G \leqslant \operatorname {Aut}(N)$
. Fix a Sylow p-subgroup
![]() $S \cong p_+^{1+2}$
of G with p odd and set
$S \cong p_+^{1+2}$
of G with p odd and set
![]() $\mathcal {F} = \mathcal {F}_S(G)$
. If
$\mathcal {F} = \mathcal {F}_S(G)$
. If
![]() $|G/N|$
is divisible by p, then there can be at most one radical elementary abelian subgroup of order
$|G/N|$
is divisible by p, then there can be at most one radical elementary abelian subgroup of order
![]() $p^2$
and so
$p^2$
and so
![]() $\mathcal {F}$
is constrained. We may thus assume that
$\mathcal {F}$
is constrained. We may thus assume that
![]() $S \leqslant N$
. If
$S \leqslant N$
. If
![]() $ p=3 $
, then the result follows by comparing Table 3 with the table after [NU09, Proposition 63]. Now, suppose
$ p=3 $
, then the result follows by comparing Table 3 with the table after [NU09, Proposition 63]. Now, suppose
![]() $p\geqslant 5 $
. If N is sporadic, then by [Reference Ruiz and ViruelRV04, Remark 1.4], G is one of
$p\geqslant 5 $
. If N is sporadic, then by [Reference Ruiz and ViruelRV04, Remark 1.4], G is one of
![]() $\operatorname {Th}$
,
$\operatorname {Th}$
,
![]() $\operatorname {Ru} (p=5)$
,
$\operatorname {Ru} (p=5)$
,
![]() $\operatorname {He}$
,
$\operatorname {He}$
,
![]() $\operatorname {He}.2$
,
$\operatorname {He}.2$
,
![]() $\operatorname {Fi}^{\prime }_{24}$
,
$\operatorname {Fi}^{\prime }_{24}$
,
![]() $\operatorname {Fi}_{24}$
,
$\operatorname {Fi}_{24}$
,
![]() $\operatorname {O}'\operatorname {N}$
,
$\operatorname {O}'\operatorname {N}$
,
![]() $\operatorname {O}'\operatorname {N}.2 (p=7)$
,
$\operatorname {O}'\operatorname {N}.2 (p=7)$
,
![]() $\operatorname {M} (p=13)$
. Character degrees for these groups and their partition into blocks are recovered from GAP [GAP24] using the PrimeBlocks command and the result follows by comparison with Table 3. So, we may assume that N is not sporadic. By [Reference Narasaki and UnoNU09, Theorem 31], N is one of
$\operatorname {M} (p=13)$
. Character degrees for these groups and their partition into blocks are recovered from GAP [GAP24] using the PrimeBlocks command and the result follows by comparison with Table 3. So, we may assume that N is not sporadic. By [Reference Narasaki and UnoNU09, Theorem 31], N is one of
![]() $\operatorname {PSL}_3(p)$
or
$\operatorname {PSL}_3(p)$
or
![]() $\operatorname {PSU}_3(p)$
. The normalizer of a Sylow p-subgroup in
$\operatorname {PSU}_3(p)$
. The normalizer of a Sylow p-subgroup in
![]() $\operatorname {PSU}_3(p)$
is strongly p-embedded by [Reference Gorenstein, Lyons and SolomonGLS98, Theorem 7.6.2(a)] and so S is normal in
$\operatorname {PSU}_3(p)$
is strongly p-embedded by [Reference Gorenstein, Lyons and SolomonGLS98, Theorem 7.6.2(a)] and so S is normal in
![]() $\mathcal {F}_S(N)$
in this case. Thus, N is
$\mathcal {F}_S(N)$
in this case. Thus, N is
![]() $\operatorname {PSL}_3(p)$
(and this has a nonconstrained p-fusion system). By Lemma 5.7, the character degrees of G are listed in Table 4, and those for its principal p-block are obtained by excluding rows
$\operatorname {PSL}_3(p)$
(and this has a nonconstrained p-fusion system). By Lemma 5.7, the character degrees of G are listed in Table 4, and those for its principal p-block are obtained by excluding rows
![]() $6$
and
$6$
and
![]() $7$
from this list. Again, the result follows by comparing with Table 3.
$7$
from this list. Again, the result follows by comparing with Table 3.
Acknowledgements
We thank Robin Allen for help with the proof of Lemma 5.7 and Shigeo Koshitani for bringing the paper of Narasaki and Uno to our attention. Thanks also to the referee for their careful reading of the paper and for helpful comments. The third author thanks City St. George’s, University of London, and Peter Symonds at the University of Manchester for support and hospitality during research visits where some of the work on this paper took place.