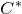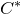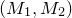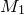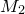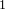1. Introduction
The main object of study in this paper is the space of tracial states, or traces, of a
![]() $C^*$
-algebra. The space of traces
$C^*$
-algebra. The space of traces
![]() $\mathrm{T}(A)$
of a unital and separable
$\mathrm{T}(A)$
of a unital and separable
![]() $C^*$
-algebra A is a metrizable Choquet simplex [Reference SakaiSak71, Theorem 3.1.18] (see also [Reference Blackadar and RørdamBR24, Theorem 1.1]), i.e., a compact convex set where every point is the barycenter of a unique Borel probability measure supported on its extreme points, in the sense that the set of extreme points is of measure 1. Conversely, any metrizable Choquet simplex can be realized as the trace simplex of a unital, separable (and moreover simple and AF)
$C^*$
-algebra A is a metrizable Choquet simplex [Reference SakaiSak71, Theorem 3.1.18] (see also [Reference Blackadar and RørdamBR24, Theorem 1.1]), i.e., a compact convex set where every point is the barycenter of a unique Borel probability measure supported on its extreme points, in the sense that the set of extreme points is of measure 1. Conversely, any metrizable Choquet simplex can be realized as the trace simplex of a unital, separable (and moreover simple and AF)
![]() $C^*$
-algebra, see [Reference GoodearlGoo77, Theorem 5.1] and [Reference BlackadarBla80, Theorem 3.10].
$C^*$
-algebra, see [Reference GoodearlGoo77, Theorem 5.1] and [Reference BlackadarBla80, Theorem 3.10].
The trace simplex has long been recognized as a useful invariant, playing a prominent role in the Elliott classification program for nuclear simple
![]() $C^*$
-algebras, see, e.g., [Reference RørdamRør02, Reference WinterWin18, Reference WhiteWhi23, Reference Carrión, Gabe, Schafhauser, Tikuisis and WhiteCGS+23]. When
$C^*$
-algebras, see, e.g., [Reference RørdamRør02, Reference WinterWin18, Reference WhiteWhi23, Reference Carrión, Gabe, Schafhauser, Tikuisis and WhiteCGS+23]. When
![]() $A=C^*G$
is the full group
$A=C^*G$
is the full group
![]() $C^*$
-algebra of a countable discrete group G, traces on A are in one-to-one correspondence with traces on G, i.e., positive definite, conjugation-invariant functions
$C^*$
-algebra of a countable discrete group G, traces on A are in one-to-one correspondence with traces on G, i.e., positive definite, conjugation-invariant functions
![]() $\varphi :G\rightarrow\mathbb C$
with
$\varphi :G\rightarrow\mathbb C$
with
![]() $\varphi(e)=1$
. Recently, the use of traces on groups has found exciting applications to dynamics, representation theory, operator algebras, and group stability; see, e.g., [Reference BekkaBek07, Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17, Reference PetersonPet14, Reference Hadwin and ShulmanHS18, Reference Boutonnet and HoudayerBH21, Reference Bader, Boutonnet, Houdayer and PetersonBBHP22, Reference Levit and VigdorovichLV24].
$\varphi(e)=1$
. Recently, the use of traces on groups has found exciting applications to dynamics, representation theory, operator algebras, and group stability; see, e.g., [Reference BekkaBek07, Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17, Reference PetersonPet14, Reference Hadwin and ShulmanHS18, Reference Boutonnet and HoudayerBH21, Reference Bader, Boutonnet, Houdayer and PetersonBBHP22, Reference Levit and VigdorovichLV24].
1.1 The trace simplex of free products
It is well known that the category of unital
![]() $C^*$
-algebras admits coproducts, implemented by the unital full free product construction, see, e.g., [Reference AvitzourAvi82, Reference Voiculescu, Dykema and NicaVDN92]. For the rest of this paper, the free product
$C^*$
-algebras admits coproducts, implemented by the unital full free product construction, see, e.g., [Reference AvitzourAvi82, Reference Voiculescu, Dykema and NicaVDN92]. For the rest of this paper, the free product
![]() $A=A_1*A_2$
of two unital
$A=A_1*A_2$
of two unital
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
will refer to their unital full free product. The main objective of this paper is to understand
$A_2$
will refer to their unital full free product. The main objective of this paper is to understand
![]() $\mathrm{T}(A)$
in terms of
$\mathrm{T}(A)$
in terms of
![]() $\text{T}(A_1)$
and
$\text{T}(A_1)$
and
![]() $\text{T}(A_2)$
. We note that another important invariant, the K-theory, has been much studied for free product
$\text{T}(A_2)$
. We note that another important invariant, the K-theory, has been much studied for free product
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A=A_1*A_2$
and shown to be completely determined by the K-theories of
$A=A_1*A_2$
and shown to be completely determined by the K-theories of
![]() $A_1$
and
$A_1$
and
![]() $A_2$
(see, e.g., [Reference CuntzCun82, Reference GermainGer97, Reference ThomsenTho03, Reference Fima and GermainFG20]). In contrast with the situation of general
$A_2$
(see, e.g., [Reference CuntzCun82, Reference GermainGer97, Reference ThomsenTho03, Reference Fima and GermainFG20]). In contrast with the situation of general
![]() $C^*$
-algebras where any prescribed Choquet simplex can arise as the trace simplex, we find that, under mild assumptions on
$C^*$
-algebras where any prescribed Choquet simplex can arise as the trace simplex, we find that, under mild assumptions on
![]() $\text{T}(A_1)$
and
$\text{T}(A_1)$
and
![]() $\text{T}(A_2)$
, the space of traces of A is always the same object: the Poulsen simplex. Strikingly, this implies that, unlike K-theory, the trace space of a free product
$\text{T}(A_2)$
, the space of traces of A is always the same object: the Poulsen simplex. Strikingly, this implies that, unlike K-theory, the trace space of a free product
![]() $A=A_1*A_2$
does not typically depend on the trace spaces of
$A=A_1*A_2$
does not typically depend on the trace spaces of
![]() $A_1$
and
$A_1$
and
![]() $A_2$
.
$A_2$
.
In our first main result we characterize exactly when the trace space of a free product
![]() $C^*$
-algebra is the Poulsen simplex. In [Reference PoulsenPou61], Poulsen was the first to construct a metrizable Choquet simplex whose extreme points are dense. It was shown in [Reference Lindenstrauss, Olsen and SternfeldLOS78] that there exists a unique non-trivial (i.e., neither empty nor a singleton) Poulsen simplex up to affine homeomorphisms, now called the Poulsen simplex. Moreover, the Poulsen simplex is universal in the sense that it admits every metrizable Choquet simplex as a closed face. Hereafter, any non-trivial metrizable Poulsen simplex will be referred to as the Poulsen simplex.
$C^*$
-algebra is the Poulsen simplex. In [Reference PoulsenPou61], Poulsen was the first to construct a metrizable Choquet simplex whose extreme points are dense. It was shown in [Reference Lindenstrauss, Olsen and SternfeldLOS78] that there exists a unique non-trivial (i.e., neither empty nor a singleton) Poulsen simplex up to affine homeomorphisms, now called the Poulsen simplex. Moreover, the Poulsen simplex is universal in the sense that it admits every metrizable Choquet simplex as a closed face. Hereafter, any non-trivial metrizable Poulsen simplex will be referred to as the Poulsen simplex.
Before stating our first main result, we also recall that the Gelfand–Naimark–Segal (GNS) construction associates, to any trace
![]() $\varphi$
on a unital
$\varphi$
on a unital
![]() $C^*$
-algebra A, a von Neumann algebra M with a faithful normal trace
$C^*$
-algebra A, a von Neumann algebra M with a faithful normal trace
![]() $\tau$
, together with a
$\tau$
, together with a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi :A\rightarrow M$
such that
$\pi :A\rightarrow M$
such that
![]() $\varphi=\tau\circ\pi$
and
$\varphi=\tau\circ\pi$
and
![]() $\pi(A)''=M$
. It is well known that
$\pi(A)''=M$
. It is well known that
![]() $\varphi$
is an extreme point of
$\varphi$
is an extreme point of
![]() $\mathrm{T}(A)$
if and only if M is a factor. We say that
$\mathrm{T}(A)$
if and only if M is a factor. We say that
![]() $\varphi$
is one-dimensional if M is one-dimensional, and similarly for finite or infinite dimensional M.
$\varphi$
is one-dimensional if M is one-dimensional, and similarly for finite or infinite dimensional M.
Theorem A. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $A_i$
be a unital, separable
$A_i$
be a unital, separable
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $\textit{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace. Let
$\textit{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace. Let
![]() $A=A_1*A_2$
be their free product. Then the following are equivalent.
$A=A_1*A_2$
be their free product. Then the following are equivalent.
-
(1) The space of traces
 $\textit{T}(A)$
is a Poulsen simplex.
$\textit{T}(A)$
is a Poulsen simplex. -
(2) If
 $A_1$
(respectively
$A_1$
(respectively
 $A_2$
) has an isolated extreme one-dimensional trace, then
$A_2$
) has an isolated extreme one-dimensional trace, then
 $A_2$
(respectively
$A_2$
(respectively
 $A_1$
) does not have an isolated extreme finite dimensional trace.
$A_1$
) does not have an isolated extreme finite dimensional trace. -
(3) The free product A does not have an isolated extreme finite-dimensional trace.
Moreover, if these equivalent conditions hold, then the set of extreme, infinite-dimensional traces is dense in
![]() $\textit{T}(A)$
.
$\textit{T}(A)$
.
The assumption in Theorem A that
![]() $\mathrm{T}(A_i)$
does not consist of a single one-dimensional trace is necessary. If, for example,
$\mathrm{T}(A_i)$
does not consist of a single one-dimensional trace is necessary. If, for example,
![]() $A_1$
has a unique trace that is one-dimensional, then the restriction map
$A_1$
has a unique trace that is one-dimensional, then the restriction map
![]() $\mathrm{T}(A)\ni \varphi\mapsto\varphi_{|A_2}\in\mathrm{T}(A_2)$
is an affine homeomorphism. But, as explained above,
$\mathrm{T}(A)\ni \varphi\mapsto\varphi_{|A_2}\in\mathrm{T}(A_2)$
is an affine homeomorphism. But, as explained above,
![]() $\mathrm{T}(A_2)$
can be any metrizable Choquet simplex. This assumption also implies that
$\mathrm{T}(A_2)$
can be any metrizable Choquet simplex. This assumption also implies that
![]() $\text{T}(A)$
is not a singleton. Theorem A therefore establishes the following lack of rigidity: a large family of
$\text{T}(A)$
is not a singleton. Theorem A therefore establishes the following lack of rigidity: a large family of
![]() $C^*$
-algebras, consisting of most free product
$C^*$
-algebras, consisting of most free product
![]() $C^*$
-algebras, all have the same trace simplex.
$C^*$
-algebras, all have the same trace simplex.
In [Reference Rørdam and MusatRM21], Rørdam and Musat studied the trace simplex of the free product of matrix algebras
![]() $\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C)$
. They showed that
$\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C)$
. They showed that
![]() $\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
parametrizes the so-called factorizable quantum channels
$\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
parametrizes the so-called factorizable quantum channels
![]() $\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)$
. Additionally, they proved that the Poulsen simplex is a face of
$\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)$
. Additionally, they proved that the Poulsen simplex is a face of
![]() $\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
and asked whether
$\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
and asked whether
![]() $\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
is the Poulsen simplex, for
$\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
is the Poulsen simplex, for
![]() $n\geq 3$
.
$n\geq 3$
.
Motivated by this question, Orovitz, Slutsky and Vigdorovich recently showed in [Reference OrovitzOSV25] that
![]() $\mathrm{T}(\mathbb{M}_n(\mathbb{C})\ast \mathbb{M}_n(\mathbb{C}))$
, for
$\mathrm{T}(\mathbb{M}_n(\mathbb{C})\ast \mathbb{M}_n(\mathbb{C}))$
, for
![]() $n\geq 4$
, and
$n\geq 4$
, and
![]() $\mathrm{T}(C^*\mathbb{F}_m)$
, for
$\mathrm{T}(C^*\mathbb{F}_m)$
, for
![]() $2\leq m\leq\infty$
, are the Poulsen simplex. However, their method does not extend to general free products, as it relies heavily on the structure of the matrix algebras (for which, moreover, the condition
$2\leq m\leq\infty$
, are the Poulsen simplex. However, their method does not extend to general free products, as it relies heavily on the structure of the matrix algebras (for which, moreover, the condition
![]() $n\geq 4$
is needed) and the free groups, respectively.
$n\geq 4$
is needed) and the free groups, respectively.
Theorem A significantly generalizes these results. Indeed, condition (2) from Theorem A is satisfied if one of the algebras admits no finite-dimensional trace. This condition is also satisfied if both algebras are finite-dimensional, but have no one-dimensional direct summands, allowing us to classify the free products of finite-dimensional
![]() $C^*$
-algebras whose trace simplex is the Poulsen simplex.
$C^*$
-algebras whose trace simplex is the Poulsen simplex.
Corollary B. Let
![]() $A=A_1*A_2$
be the free product of finite-dimensional
$A=A_1*A_2$
be the free product of finite-dimensional
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. Then
$A_2$
. Then
![]() $\mathrm{T}(A)$
is the Poulsen simplex if and only if
$\mathrm{T}(A)$
is the Poulsen simplex if and only if
![]() $A_1$
and
$A_1$
and
![]() $A_2$
have no one-dimensional direct summands.
$A_2$
have no one-dimensional direct summands.
In particular, Corollary B shows that
![]() $\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
is the Poulsen simplex, for every
$\text{T}(\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C))$
is the Poulsen simplex, for every
![]() $n\geq 2$
, thereby completely answering the question from [Reference Rørdam and MusatRM21] discussed above.
$n\geq 2$
, thereby completely answering the question from [Reference Rørdam and MusatRM21] discussed above.
Theorem A also yields a complete characterization of when the trace simplex of a free product of countable groups is the Poulsen simplex. Given a countable discrete group G, recall that the space of traces on G, which we denote by
![]() $\text{Tr}(G)$
, is naturally identified with
$\text{Tr}(G)$
, is naturally identified with
![]() $\text{T}(C^*G)$
. In this context, extreme traces are often called ‘characters’. Following [Reference OrovitzOSV25, Definition 7.1], we say that the group G has property (ET) if the trivial character
$\text{T}(C^*G)$
. In this context, extreme traces are often called ‘characters’. Following [Reference OrovitzOSV25, Definition 7.1], we say that the group G has property (ET) if the trivial character
![]() $1_G$
is isolated in the space of all characters of G.
$1_G$
is isolated in the space of all characters of G.
Corollary C. Let
![]() $G=G_1*G_2$
be the free product of non-trivial countable discrete groups
$G=G_1*G_2$
be the free product of non-trivial countable discrete groups
![]() $G_1$
and
$G_1$
and
![]() $G_2$
. Then the following are equivalent.
$G_2$
. Then the following are equivalent.
-
(1) The space of traces on G is the Poulsen simplex.
-
(2) The
 $G_i$
do not have property (ET), for some
$G_i$
do not have property (ET), for some
 $i\in\{1,2\}.$
$i\in\{1,2\}.$
-
(3) The group G does not have property (ET).
This result significantly generalizes [Reference OrovitzOSV25, Theorem 1.1]. Indeed, since property (ET) passes to quotient groups by [Reference OrovitzOSV25, Lemma 7.2] and countable infinite abelian groups do not have property (ET), Corollary group C*-algebrasC implies that
![]() $\text{Tr}(G_1*G_2)$
is the Poulsen simplex, for any non-trivial countable groups
$\text{Tr}(G_1*G_2)$
is the Poulsen simplex, for any non-trivial countable groups
![]() $G_1$
and
$G_1$
and
![]() $G_2$
such that
$G_2$
such that
![]() $G_1$
admits an infinite abelian quotient.
$G_1$
admits an infinite abelian quotient.
Note that countable groups with Kazhdan’s property (T) also satisfy property (ET). It is shown in [Reference Levit, Slutsky and VigdorovichLSV23] that the trace simplex of Kazhdan groups is, in fact, as far as possible from being a Poulsen simplex; it is a Bauer simplex, meaning that the set of extreme points is closed.
1.2 Approximation in the Wasserstein topology
To put our results from the previous subsection into a better perspective, let us point out that the proofs show much more than that the trace space of the
![]() $C^*$
-algebras in question is a Poulsen simplex. Recall that the trace space of a unital separable
$C^*$
-algebras in question is a Poulsen simplex. Recall that the trace space of a unital separable
![]() $C^*$
-algebra admits, in addition to the weak
$C^*$
-algebra admits, in addition to the weak
![]() $^*$
-topology, a second natural topology, the so-called Wasserstein topology introduced by Biane and Voiculescu in [Reference Biane and VoiculescuBV01].
$^*$
-topology, a second natural topology, the so-called Wasserstein topology introduced by Biane and Voiculescu in [Reference Biane and VoiculescuBV01].
Definition 1.1 (See [Reference Biane and VoiculescuBV01, Section 1.2]). Let A be a unital, separable
![]() $C^*$
-algebra, and
$C^*$
-algebra, and
![]() $(a_n)_{n=1}^\infty$
a norm dense sequence in the unit ball of A. For
$(a_n)_{n=1}^\infty$
a norm dense sequence in the unit ball of A. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\varphi_i\in\text{T}(A)$
,
$\varphi_i\in\text{T}(A)$
,
![]() $(M_i,\tau_i)$
be a tracial von Neumann algebra and
$(M_i,\tau_i)$
be a tracial von Neumann algebra and
![]() $\pi_i:A\rightarrow M_i$
be a unital
$\pi_i:A\rightarrow M_i$
be a unital
![]() $*$
-homomorphism such that
$*$
-homomorphism such that
![]() $\varphi_i=\tau_i\circ\pi_i$
and
$\varphi_i=\tau_i\circ\pi_i$
and
![]() $\pi_i(A)''=M_i$
. We define the Wasserstein distance
$\pi_i(A)''=M_i$
. We define the Wasserstein distance
![]() $d_W(\varphi_1,\varphi_2)$
as the infimum of the quantity
$d_W(\varphi_1,\varphi_2)$
as the infimum of the quantity
![]() $\sum_{n=1}^\infty 2^{-n}\|\pi_1(a_n)-\pi_2(a_n)\|_{2,\tau}$
, over all tracial von Neumann algebras
$\sum_{n=1}^\infty 2^{-n}\|\pi_1(a_n)-\pi_2(a_n)\|_{2,\tau}$
, over all tracial von Neumann algebras
![]() $(M,\tau)$
such that
$(M,\tau)$
such that
![]() $M_i\subset M$
and
$M_i\subset M$
and
![]() $\tau_{|M_i}=\tau_i$
for every
$\tau_{|M_i}=\tau_i$
for every
![]() $i=1,2$
. The Wasserstein topology on
$i=1,2$
. The Wasserstein topology on
![]() $\text{T}(A)$
is the topology induced by
$\text{T}(A)$
is the topology induced by
![]() $d_W$
.
$d_W$
.
It is easy to see that
![]() $d_W$
is a well-defined metric (e.g., by adapting [Reference Biane and VoiculescuBV01, Theorem 1.3]), that the Wasserstein topology is independent of the choice of the sequence
$d_W$
is a well-defined metric (e.g., by adapting [Reference Biane and VoiculescuBV01, Theorem 1.3]), that the Wasserstein topology is independent of the choice of the sequence
![]() $(a_n)_{n=1}^\infty$
, and that the Wasserstein topology is stronger than the weak
$(a_n)_{n=1}^\infty$
, and that the Wasserstein topology is stronger than the weak
![]() $^*$
-topology on
$^*$
-topology on
![]() $\text{T}(A)$
. In general, the Wasserstein topology is strictly stronger than the weak
$\text{T}(A)$
. In general, the Wasserstein topology is strictly stronger than the weak
![]() $^*$
-topology. By [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22, Proposition 1.7], this holds if
$^*$
-topology. By [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22, Proposition 1.7], this holds if
![]() $A=C([-1,1])^{*m}$
is the free product of m copies of
$A=C([-1,1])^{*m}$
is the free product of m copies of
![]() $C([-1,1])$
for
$C([-1,1])$
for
![]() $m\geq 2$
. In fact,
$m\geq 2$
. In fact,
![]() $\text{T}(A)$
is not even separable in the Wasserstein topology [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22, Theorem 1.8]. Nevertheless, our density results apply even for this topology.
$\text{T}(A)$
is not even separable in the Wasserstein topology [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22, Theorem 1.8]. Nevertheless, our density results apply even for this topology.
Corollary D. Let A be any
![]() $C^*$
-algebra for which Theorem A, Corollary B, or Corollary C shows that
$C^*$
-algebra for which Theorem A, Corollary B, or Corollary C shows that
![]() $\text{T}(A)$
is a Poulsen simplex. Then
$\text{T}(A)$
is a Poulsen simplex. Then
![]() ${\partial_e\text{T}(A)}$
is dense in
${\partial_e\text{T}(A)}$
is dense in
![]() $\text{T}(A)$
in the Wasserstein topology.
$\text{T}(A)$
in the Wasserstein topology.
Prior to our work, this statement was only known for
![]() $A=C([-1,1])^{*m}$
, for every
$A=C([-1,1])^{*m}$
, for every
![]() $m\geq 2$
, by a result of Dabrowski [Reference DabrowskiDab10, Corollary 5]. The statement of Corollary D is new for all other
$m\geq 2$
, by a result of Dabrowski [Reference DabrowskiDab10, Corollary 5]. The statement of Corollary D is new for all other
![]() $C^*$
-algebras that we treat, including, notably,
$C^*$
-algebras that we treat, including, notably,
![]() $A=\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C)$
, for any
$A=\mathbb M_n(\mathbb C)*\mathbb M_n(\mathbb C)$
, for any
![]() $n\geq 2$
.
$n\geq 2$
.
1.3 Perturbations of von Neumann subalgebras
We next turn to our main technical result, Theorem E, from which we will deduce Theorem A. To motivate the former, we first outline our strategy for proving Theorem A.
Let
![]() $A=A_1*A_2$
be the free product of unital, separable
$A=A_1*A_2$
be the free product of unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, and let
$A_2$
, and let
![]() $\varphi\in\text{T}(A)$
. The GNS construction provides a tracial von Neumann algebra
$\varphi\in\text{T}(A)$
. The GNS construction provides a tracial von Neumann algebra
![]() $(M,\tau)$
and a
$(M,\tau)$
and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi:A\rightarrow M$
such that
$\pi:A\rightarrow M$
such that
![]() $\pi(A)''=M$
and
$\pi(A)''=M$
and
![]() $\varphi=\tau\circ\pi$
. Recall that
$\varphi=\tau\circ\pi$
. Recall that
![]() $\varphi$
is an extreme trace if and only if M is a factor. As in [Reference OrovitzOSV25], in order to conclude that
$\varphi$
is an extreme trace if and only if M is a factor. As in [Reference OrovitzOSV25], in order to conclude that
![]() $\text{T}(A)$
is a Poulsen simplex, it suffices to approximate
$\text{T}(A)$
is a Poulsen simplex, it suffices to approximate
![]() $\varphi$
by traces whose GNS von Neumann algebras are factors. To this end, we construct a
$\varphi$
by traces whose GNS von Neumann algebras are factors. To this end, we construct a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\widetilde\pi:A\rightarrow \widetilde M$
, for some tracial von Neumann algebra
$\widetilde\pi:A\rightarrow \widetilde M$
, for some tracial von Neumann algebra
![]() $(\widetilde M,\widetilde\tau)$
containing M and satisfying
$(\widetilde M,\widetilde\tau)$
containing M and satisfying
![]() $\widetilde\tau_{|M}=\tau$
, that is pointwise close to
$\widetilde\tau_{|M}=\tau$
, that is pointwise close to
![]() $\pi$
in
$\pi$
in
![]() $\|\cdot\|_2$
and such that
$\|\cdot\|_2$
and such that
![]() $\widetilde\pi(A)''$
is a factor. Once this is achieved, it follows that
$\widetilde\pi(A)''$
is a factor. Once this is achieved, it follows that
![]() $\varphi$
is close in the Wasserstein distance (and thus in the weak
$\varphi$
is close in the Wasserstein distance (and thus in the weak
![]() $^*$
-topology) to the extreme trace
$^*$
-topology) to the extreme trace
![]() $\widetilde\tau\circ\widetilde\pi$
.
$\widetilde\tau\circ\widetilde\pi$
.
In order to construct
![]() $\widetilde\pi$
, we exploit the free product structure of A by perturbing the image of
$\widetilde\pi$
, we exploit the free product structure of A by perturbing the image of
![]() $A_2$
while leaving
$A_2$
while leaving
![]() $A_1$
unchanged. Specifically, we consider small perturbations
$A_1$
unchanged. Specifically, we consider small perturbations
![]() $\widetilde\pi$
of
$\widetilde\pi$
of
![]() $\pi$
of the form
$\pi$
of the form
![]() $\widetilde\pi(a_1)=\pi(a_1)$
, for every
$\widetilde\pi(a_1)=\pi(a_1)$
, for every
![]() $a_1\in A_1$
, and
$a_1\in A_1$
, and
![]() $\widetilde\pi(a_2)=u\pi(a_2)u^*$
, for every
$\widetilde\pi(a_2)=u\pi(a_2)u^*$
, for every
![]() $a_2\in A_2$
, for some unitary
$a_2\in A_2$
, for some unitary
![]() $u\in\widetilde M$
with
$u\in\widetilde M$
with
![]() $\|u-1\|_2\approx 0$
. Denoting
$\|u-1\|_2\approx 0$
. Denoting
![]() $M_1=\pi(A_1)''$
and
$M_1=\pi(A_1)''$
and
![]() $M_2=\pi(A_2)''$
, the factoriality of
$M_2=\pi(A_2)''$
, the factoriality of
![]() $\widetilde\pi(A)''$
then amounts to the von Neumann algebra
$\widetilde\pi(A)''$
then amounts to the von Neumann algebra
![]() $M_1\vee uM_2u^*$
generated by
$M_1\vee uM_2u^*$
generated by
![]() $M_1$
and
$M_1$
and
![]() $uM_2u^*$
being a factor.
$uM_2u^*$
being a factor.
However, finding such a unitary u is not always possible: if there are minimal central projections
![]() $p_1\in M_1$
and
$p_1\in M_1$
and
![]() $p_2\in M_2$
with
$p_2\in M_2$
with
![]() $\tau(p_1)+\tau(p_2)>1$
, then
$\tau(p_1)+\tau(p_2)>1$
, then
![]() $p_1\wedge up_2u^*\in M_1\vee uM_2u^*$
is a non-zero minimal central projection for any unitary u, see also § 3.1. In other words, if
$p_1\wedge up_2u^*\in M_1\vee uM_2u^*$
is a non-zero minimal central projection for any unitary u, see also § 3.1. In other words, if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
have ‘large’ one-dimensional direct summands, then
$M_2$
have ‘large’ one-dimensional direct summands, then
![]() $M_1\vee uM_2u^*$
is never a factor. More generally, we show in Proposition 3.3 that the same conclusion can be reached if one of these direct summands is only assumed to be finite-dimensional, but not necessarily one-dimensional.
$M_1\vee uM_2u^*$
is never a factor. More generally, we show in Proposition 3.3 that the same conclusion can be reached if one of these direct summands is only assumed to be finite-dimensional, but not necessarily one-dimensional.
Theorem E shows that this is essentially the only obstruction to finding a unitary u with
![]() $\|u-1\|_2\approx 0$
such that
$\|u-1\|_2\approx 0$
such that
![]() $M_1\vee uM_2u^*$
is a factor. In order to capture the presence of a ‘large’ finite-dimensional direct summand, we define for a tracial von Neumann algebra
$M_1\vee uM_2u^*$
is a factor. In order to capture the presence of a ‘large’ finite-dimensional direct summand, we define for a tracial von Neumann algebra
![]() $(M,\tau)$
$(M,\tau)$
By convention, we define
![]() $\text{e}(M)=0$
, if M is diffuse.
$\text{e}(M)=0$
, if M is diffuse.
Theorem E. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra and
$(M,\tau)$
be a tracial von Neumann algebra and
![]() $M_1,M_2\subset M$
be von Neumann subalgebras. Assume that
$M_1,M_2\subset M$
be von Neumann subalgebras. Assume that
![]() $M_1\neq \mathbb C1,M_2\neq \mathbb C1$
,
$M_1\neq \mathbb C1,M_2\neq \mathbb C1$
,
![]() $\dim(M_1)+\dim(M_2)\geq 5$
, and
$\dim(M_1)+\dim(M_2)\geq 5$
, and
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
.
$\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
.
Then there exists a II
![]() $_1$
factor
$_1$
factor
![]() $(\widetilde M,\widetilde\tau)$
such that
$(\widetilde M,\widetilde\tau)$
such that
![]() $M\subset\widetilde M$
,
$M\subset\widetilde M$
,
![]() $\widetilde\tau_{|M}=\tau$
and for every
$\widetilde\tau_{|M}=\tau$
and for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $v_\varepsilon\in\mathcal U(\widetilde M)$
satisfying
$v_\varepsilon\in\mathcal U(\widetilde M)$
satisfying
![]() $\|v_\varepsilon-1\|_2<\varepsilon$
and
$\|v_\varepsilon-1\|_2<\varepsilon$
and
![]() $M_1\vee v_\varepsilon M_2 v_\varepsilon^*$
is a II
$M_1\vee v_\varepsilon M_2 v_\varepsilon^*$
is a II
![]() $_1$
factor.
$_1$
factor.
If
![]() $M_1$
or
$M_1$
or
![]() $M_2$
is diffuse, then Theorem E follows easily by applying [Reference Ioana, Peterson and PopaIPP08], see Corollary 4.4. However, in order to prove Theorem A, we need the general case of Theorem E.
$M_2$
is diffuse, then Theorem E follows easily by applying [Reference Ioana, Peterson and PopaIPP08], see Corollary 4.4. However, in order to prove Theorem A, we need the general case of Theorem E.
The main novelty of Theorem E lies in treating the most difficult case when
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are finite-dimensional. In fact, most of the proof of Theorem E is devoted to the case when
$M_2$
are finite-dimensional. In fact, most of the proof of Theorem E is devoted to the case when
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are finite-dimensional and abelian. In this case, the assumptions from Theorem E are inspired by Dykema’s work [Reference DykemaDyk93]. Specifically, [Reference DykemaDyk93, Theorem 2.3] implies that if
$M_2$
are finite-dimensional and abelian. In this case, the assumptions from Theorem E are inspired by Dykema’s work [Reference DykemaDyk93]. Specifically, [Reference DykemaDyk93, Theorem 2.3] implies that if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are finite-dimensional and abelian, then
$M_2$
are finite-dimensional and abelian, then
![]() $M_1*M_2$
is a II
$M_1*M_2$
is a II
![]() $_1$
factor if and only if
$_1$
factor if and only if
![]() $(\star$
)
$(\star$
)
![]() $M_1\neq \mathbb C1,M_2\neq \mathbb C1$
,
$M_1\neq \mathbb C1,M_2\neq \mathbb C1$
,
![]() $\dim(M_1)+\dim(M_2)\geq 5$
, and
$\dim(M_1)+\dim(M_2)\geq 5$
, and
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
. Identifying
$\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
. Identifying
![]() $M_1*M_2$
with
$M_1*M_2$
with
![]() $M_1\vee uM_2u^*$
, where u is a trace zero unitary which is freely independent from M, [Reference DykemaDyk93, Theorem 2.3] implies that if
$M_1\vee uM_2u^*$
, where u is a trace zero unitary which is freely independent from M, [Reference DykemaDyk93, Theorem 2.3] implies that if
![]() $(\star)$
holds, then
$(\star)$
holds, then
![]() $M_1$
and some unitary perturbation of
$M_1$
and some unitary perturbation of
![]() $M_2$
generate a II
$M_2$
generate a II
![]() $_1$
factor. Theorem E shows that if
$_1$
factor. Theorem E shows that if
![]() $(\star)$
holds, then
$(\star)$
holds, then
![]() $M_1$
and an arbitrarily small unitary perturbation of
$M_1$
and an arbitrarily small unitary perturbation of
![]() $M_2$
generate a II
$M_2$
generate a II
![]() $_1$
factor.
$_1$
factor.
We continue by illustrating the effectiveness of Theorem E with a consequence for the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A_{m,n}:=\mathbb C^m*\mathbb C^n\cong C^*({\mathbb Z}/{m\mathbb Z}*{\mathbb Z}/{n\mathbb Z})$
, where
$A_{m,n}:=\mathbb C^m*\mathbb C^n\cong C^*({\mathbb Z}/{m\mathbb Z}*{\mathbb Z}/{n\mathbb Z})$
, where
![]() $m,n\geq 2$
satisfy
$m,n\geq 2$
satisfy
![]() $m+n\geq 5$
. Traces on
$m+n\geq 5$
. Traces on
![]() $A_{m,n}$
have attracted considerable attention as they parameterize synchronous quantum correlations (see, e.g., [Reference Kim, Paulsen and SchafhauserKPS18]). Note that
$A_{m,n}$
have attracted considerable attention as they parameterize synchronous quantum correlations (see, e.g., [Reference Kim, Paulsen and SchafhauserKPS18]). Note that
![]() $\text{T}(A_{m,n})$
is not a Poulsen simplex, as follows from [Reference OrovitzOSV25, Theorem 1.4] (or Corollary B). Nevertheless, Theorem E allows to characterize the traces on
$\text{T}(A_{m,n})$
is not a Poulsen simplex, as follows from [Reference OrovitzOSV25, Theorem 1.4] (or Corollary B). Nevertheless, Theorem E allows to characterize the traces on
![]() $A_{m,n}$
which can be approximated by extreme traces.
$A_{m,n}$
which can be approximated by extreme traces.
Corollary F. Let
![]() $m,n\,\geq\, 2$
with
$m,n\,\geq\, 2$
with
![]() $m+n\,\geq\, 5$
. Write
$m+n\,\geq\, 5$
. Write
![]() $\mathbb C^m=\bigoplus_{i{\kern.5pt}={\kern.5pt}1}^m\mathbb Ce_i$
and
$\mathbb C^m=\bigoplus_{i{\kern.5pt}={\kern.5pt}1}^m\mathbb Ce_i$
and
![]() $\mathbb C^n=\bigoplus_{j{\kern.5pt}={\kern.5pt}1}^n\mathbb Cf_j$
for projections
$\mathbb C^n=\bigoplus_{j{\kern.5pt}={\kern.5pt}1}^n\mathbb Cf_j$
for projections
![]() $(e_i)_{i=1}^m$
and
$(e_i)_{i=1}^m$
and
![]() $(f_j)_{j=1}^n$
. Then the following conditions are equivalent for every
$(f_j)_{j=1}^n$
. Then the following conditions are equivalent for every
![]() $\varphi\in\textit{T}(A_{m,n})$
:
$\varphi\in\textit{T}(A_{m,n})$
:
-
(1)
 $\varphi\in\overline{\partial_{\textit{e}}\textit{T}(A_{m,n})}^{\mathrm{Wasserstein}}$
;
$\varphi\in\overline{\partial_{\textit{e}}\textit{T}(A_{m,n})}^{\mathrm{Wasserstein}}$
; -
(2)
 $\varphi\in\overline{\partial_{\textit{e}}\textit{T}(A_{m,n})}^{\mathrm{weak}^*}$
;
$\varphi\in\overline{\partial_{\textit{e}}\textit{T}(A_{m,n})}^{\mathrm{weak}^*}$
; -
(3)
 $\varphi(e_i)+\varphi(f_j)\leq 1$
, for every
$\varphi(e_i)+\varphi(f_j)\leq 1$
, for every
 $1\leq i\leq m$
and
$1\leq i\leq m$
and
 $1\leq j\leq n$
.
$1\leq j\leq n$
.
An immediate interesting consequence of Corollary F is that the closure of the extreme traces of
![]() $A_{m,n}$
is not a face of
$A_{m,n}$
is not a face of
![]() $\text{T}(A_{m,n})$
. Turning to the proof of Corollary, F, it is clear that (1)
$\text{T}(A_{m,n})$
. Turning to the proof of Corollary, F, it is clear that (1)
![]() $\Rightarrow$
(2). It is also easy to show that (3) holds if
$\Rightarrow$
(2). It is also easy to show that (3) holds if
![]() $\varphi\in\partial_{\text{e}}\text{T}(A_{m,n})$
(see the first paragraph of § 3.1). Thus, it also holds if
$\varphi\in\partial_{\text{e}}\text{T}(A_{m,n})$
(see the first paragraph of § 3.1). Thus, it also holds if
![]() $\varphi\in\overline{\partial_{\text{e}}\text{T}(A_{m,n})}^{\text{weak}^*}$
. Finally, the implication (3)
$\varphi\in\overline{\partial_{\text{e}}\text{T}(A_{m,n})}^{\text{weak}^*}$
. Finally, the implication (3)
![]() $\Rightarrow$
(1) is an immediate consequence of Theorem E in the case when
$\Rightarrow$
(1) is an immediate consequence of Theorem E in the case when
![]() $M_1\cong\mathbb C^m$
and
$M_1\cong\mathbb C^m$
and
![]() $M_2\cong\mathbb C^n$
.
$M_2\cong\mathbb C^n$
.
Next, we discuss in further detail the assumptions from Theorem E and propose an open question suggested by its statement. First, we note that the assumption that
![]() $\dim(M_1)+\dim(M_2)\geq 5$
is necessary. Indeed, if
$\dim(M_1)+\dim(M_2)\geq 5$
is necessary. Indeed, if
![]() $\dim(M_1)+\dim(M_2)<5$
, then since
$\dim(M_1)+\dim(M_2)<5$
, then since
![]() $M_1\neq \mathbb C1$
and
$M_1\neq \mathbb C1$
and
![]() $M_2\neq \mathbb C1$
, it follows that
$M_2\neq \mathbb C1$
, it follows that
![]() $\dim(M_1)=\dim(M_2)=2$
. In this case,
$\dim(M_1)=\dim(M_2)=2$
. In this case,
![]() $M_1\vee uM_2u^*$
is generated by two projections, and hence is a type I algebra and therefore not a II
$M_1\vee uM_2u^*$
is generated by two projections, and hence is a type I algebra and therefore not a II
![]() $_1$
factor, for any unitary u. Second, the assumption that
$_1$
factor, for any unitary u. Second, the assumption that
![]() $\text{e}(M_1)+\text{e}(M_2)\leq 1$
is also necessary if
$\text{e}(M_1)+\text{e}(M_2)\leq 1$
is also necessary if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are abelian. Indeed, if
$M_2$
are abelian. Indeed, if
![]() $\text{e}(M_1)+\text{e}(M_2)>1$
, then we can find minimal (and necessarily central) projections
$\text{e}(M_1)+\text{e}(M_2)>1$
, then we can find minimal (and necessarily central) projections
![]() $p_1\in M_1,p_2\in M_2$
with
$p_1\in M_1,p_2\in M_2$
with
![]() $\tau(p_1)+\tau(p_2)>1$
.
$\tau(p_1)+\tau(p_2)>1$
.
The II
![]() $_1$
factor
$_1$
factor
![]() $\widetilde M$
from Theorem E is obtained from M by applying iteratively various amalgamated free product constructions. It remains open whether
$\widetilde M$
from Theorem E is obtained from M by applying iteratively various amalgamated free product constructions. It remains open whether
![]() $\widetilde M$
can be taken of a specific form.
$\widetilde M$
can be taken of a specific form.
Question 1.2. Assume the setting of Theorem E.
-
(a) If M is a II
 $_1$
factor, does the conclusion of Theorem E hold for
$_1$
factor, does the conclusion of Theorem E hold for
 $\widetilde M=M$
?
$\widetilde M=M$
? -
(b) For general M, does the conclusion of Theorem E hold for
 $\widetilde M=M*\text{L}(\mathbb Z)$
and some
$\widetilde M=M*\text{L}(\mathbb Z)$
and some
 $v_\varepsilon\in\mathcal U(\widetilde M)$
such that
$v_\varepsilon\in\mathcal U(\widetilde M)$
such that
 $v_\varepsilon\in\text{L}(\mathbb Z)$
and
$v_\varepsilon\in\text{L}(\mathbb Z)$
and
 $\|v_\varepsilon-1\|_2\leq\varepsilon$
?
$\|v_\varepsilon-1\|_2\leq\varepsilon$
?
1.4 The Poulsen simplex as a closed face
A natural question arising from Theorem A is what happens when the equivalent conditions of Theorem A fail, i.e., when
![]() $\mathrm{T}(A)$
is not a Poulsen simplex. We show that although
$\mathrm{T}(A)$
is not a Poulsen simplex. We show that although
![]() $\mathrm{T}(A)$
might not be the Poulsen simplex, it always admits a closed face affinely homeomorphic to the Poulsen simplex, unless it is affinely homeomorphic to
$\mathrm{T}(A)$
might not be the Poulsen simplex, it always admits a closed face affinely homeomorphic to the Poulsen simplex, unless it is affinely homeomorphic to
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. We refer to Remark 6.10 for a description of the trace simplex of
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. We refer to Remark 6.10 for a description of the trace simplex of
![]() $\mathbb{C}^2\ast\mathbb{C}^2\cong C^*(\mathbb{Z}/2\mathbb{Z}\ast\mathbb{Z}/2\mathbb{Z})$
.
$\mathbb{C}^2\ast\mathbb{C}^2\cong C^*(\mathbb{Z}/2\mathbb{Z}\ast\mathbb{Z}/2\mathbb{Z})$
.
Theorem G. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $A_i$
be a unital, separable
$A_i$
be a unital, separable
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $\textit{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace. Let
$\textit{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace. Let
![]() $A=A_1*A_2$
be the free product. Then exactly one of the following holds:
$A=A_1*A_2$
be the free product. Then exactly one of the following holds:
-
(1)
 $\textit{T}(A)$
admits a closed face which is affinely homeomorphic to the Poulsen simplex; or
$\textit{T}(A)$
admits a closed face which is affinely homeomorphic to the Poulsen simplex; or -
(2)
 $A_i$
admits exactly two extreme traces, both of which are one-dimensional, for every
$A_i$
admits exactly two extreme traces, both of which are one-dimensional, for every
 $i\in\{1,2\}$
. Moreover, in this case,
$i\in\{1,2\}$
. Moreover, in this case,
 $\textit{T}(A)$
is affinely homeomorphic to
$\textit{T}(A)$
is affinely homeomorphic to
 $\textit{T}(\mathbb C^2*\mathbb C^2)$
.
$\textit{T}(\mathbb C^2*\mathbb C^2)$
.
Note that if
![]() $\text{T}(A)$
admits the Poulsen simplex as a closed face, then it admits any metrizable Choquet simplex as a closed face. This is in contrast to many
$\text{T}(A)$
admits the Poulsen simplex as a closed face, then it admits any metrizable Choquet simplex as a closed face. This is in contrast to many
![]() $C^*$
-algebras of interest, such as reduced
$C^*$
-algebras of interest, such as reduced
![]() $C^*$
-algebras of countable groups with trivial amenable radical [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17] that possess a unique trace. Note also that if A is a unital separable
$C^*$
-algebras of countable groups with trivial amenable radical [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17] that possess a unique trace. Note also that if A is a unital separable
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $\text{T}(A)$
admits the Poulsen simplex as a closed face, then the same is true for any unital separable
$\text{T}(A)$
admits the Poulsen simplex as a closed face, then the same is true for any unital separable
![]() $C^*$
-algebra B which admits A as a quotient (see [Reference Rørdam and MusatRM21], and also § 7).
$C^*$
-algebra B which admits A as a quotient (see [Reference Rørdam and MusatRM21], and also § 7).
The following corollary is an immediate consequence of Theorem G.
Corollary H. If
![]() $A=A_1*A_2$
is a free product of two finite-dimensional
$A=A_1*A_2$
is a free product of two finite-dimensional
![]() $C^*$
-algebras, then
$C^*$
-algebras, then
![]() $\textit{T}(A)$
admits the Poulsen simplex as a closed face if and only if
$\textit{T}(A)$
admits the Poulsen simplex as a closed face if and only if
![]() $A_1\neq\mathbb C\neq A_2$
and
$A_1\neq\mathbb C\neq A_2$
and
![]() $A_1\ast A_2\not\cong \mathbb{C}^2\ast\mathbb{C}^2$
.
$A_1\ast A_2\not\cong \mathbb{C}^2\ast\mathbb{C}^2$
.
If
![]() $G=G_1\ast G_2$
is a free product of two non-trivial countable discrete groups, then the space of traces of G admits the Poulsen simplex as a closed face if and only if
$G=G_1\ast G_2$
is a free product of two non-trivial countable discrete groups, then the space of traces of G admits the Poulsen simplex as a closed face if and only if
![]() $G\not\cong \mathbb{Z}/2\mathbb{Z}\ast \mathbb{Z}/2\mathbb{Z}$
.
$G\not\cong \mathbb{Z}/2\mathbb{Z}\ast \mathbb{Z}/2\mathbb{Z}$
.
Corollary H implies that the trace simplex of
![]() $\text{PSL}_2(\mathbb Z)\cong\mathbb Z/2\mathbb Z*\mathbb Z/3\mathbb Z$
admits the Poulsen simplex as a closed face. The same is therefore true for
$\text{PSL}_2(\mathbb Z)\cong\mathbb Z/2\mathbb Z*\mathbb Z/3\mathbb Z$
admits the Poulsen simplex as a closed face. The same is therefore true for
![]() $\text{SL}_2(\mathbb Z)$
since it has
$\text{SL}_2(\mathbb Z)$
since it has
![]() $\mathrm{PSL}_2(\mathbb{Z})$
as a quotient.
$\mathrm{PSL}_2(\mathbb{Z})$
as a quotient.
Next, we discuss [Reference OrovitzOSV25, Question 1.10], which asks whether the closed convex hull of the infinite-dimensional extreme traces always yields a Poulsen simplex. We answer this question in the negative, and show in Proposition 7.8 that this is in fact never the case. Moreover, we show that the closed convex hull of the infinite-dimensional extreme traces is in fact never a Choquet simplex, and, in particular, it is not a closed face. Nevertheless, despite this negative answer, the extreme points of this closed convex set are dense. Additionally, in Lemma 7.7, we identify a related natural maximal non-closed face of
![]() $\mathrm{T}(A)$
in which the extreme points are dense.
$\mathrm{T}(A)$
in which the extreme points are dense.
1.5 Infinite free products
Another question suggested by Theorem A is what happens for free products of more than two
![]() $C^*$
-algebras. Let
$C^*$
-algebras. Let
![]() $N\in\{2,3,\ldots\}\cup\{\infty\}$
and
$N\in\{2,3,\ldots\}\cup\{\infty\}$
and
![]() $\{A_i\}_{i=1}^N$
be unital separable
$\{A_i\}_{i=1}^N$
be unital separable
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $\text{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for every i. Denote
$\text{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for every i. Denote
![]() $A=*_{i=1}^N A_i$
. If
$A=*_{i=1}^N A_i$
. If
![]() $N\in\{2,3,\ldots\}$
, then Theorem A readily implies that the following conditions are equivalent:
$N\in\{2,3,\ldots\}$
, then Theorem A readily implies that the following conditions are equivalent:
-
(1)
 $\text{T}(A)$
is the Poulsen simplex;
$\text{T}(A)$
is the Poulsen simplex; -
(2) If
 $A_j$
has an isolated extreme one-dimensional trace, for every
$A_j$
has an isolated extreme one-dimensional trace, for every
 $j\in\{1,2,\ldots,N\}\setminus\{i\}$
, for some
$j\in\{1,2,\ldots,N\}\setminus\{i\}$
, for some
 $i\in\{1,2,\ldots,N\}$
, then
$i\in\{1,2,\ldots,N\}$
, then
 $A_i$
does not have an isolated extreme finite-dimensional trace;
$A_i$
does not have an isolated extreme finite-dimensional trace; -
(3) A does not have an isolated extreme finite-dimensional trace.
On the other hand, we show that if
![]() $N=\infty$
, then
$N=\infty$
, then
![]() $\text{T}(A)$
is always the Poulsen simplex.
$\text{T}(A)$
is always the Poulsen simplex.
Proposition I. For
![]() $i\geq 1$
, let
$i\geq 1$
, let
![]() $A_i$
be a unital separable
$A_i$
be a unital separable
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $\textit{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace. Let
$\textit{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace. Let
![]() $A=*_{i=1}^\infty A_i$
. Then
$A=*_{i=1}^\infty A_i$
. Then
![]() $\textit{T}(A)$
is the Poulsen simplex.
$\textit{T}(A)$
is the Poulsen simplex.
This result implies that if
![]() $G=*_{i=1}^\infty G_i$
is a free product of infinitely many non-trivial countable groups, then the trace space of G is the Poulsen simplex. This, in particular, applies when
$G=*_{i=1}^\infty G_i$
is a free product of infinitely many non-trivial countable groups, then the trace space of G is the Poulsen simplex. This, in particular, applies when
![]() $G_i$
are non-trivial finite groups, contrasting the fact that the trace space a free product of finitely many non-trivial finite groups is never Poulsen, as established by [Reference OrovitzOSV25, Theorem 1.4].
$G_i$
are non-trivial finite groups, contrasting the fact that the trace space a free product of finitely many non-trivial finite groups is never Poulsen, as established by [Reference OrovitzOSV25, Theorem 1.4].
Let B be a unital separable
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $\text{T}(B)$
is non-empty and does not consist of a single one-dimensional trace. Let
$\text{T}(B)$
is non-empty and does not consist of a single one-dimensional trace. Let
![]() $A=*_1^\infty B$
be the free product of infinitely many copies of B. It was shown in [Reference Dabrowski, Dykema and MukherjeeDDM14, Theorems 5.3 and 5.5] that a certain compact convex subset
$A=*_1^\infty B$
be the free product of infinitely many copies of B. It was shown in [Reference Dabrowski, Dykema and MukherjeeDDM14, Theorems 5.3 and 5.5] that a certain compact convex subset
![]() $\text{TQSS}(B)\subset\text{T}(A)$
(consisting of the tracial quantum symmetric states on A) is a closed face of
$\text{TQSS}(B)\subset\text{T}(A)$
(consisting of the tracial quantum symmetric states on A) is a closed face of
![]() $\text{T}(A)$
, which is the Poulsen simplex. Hence,
$\text{T}(A)$
, which is the Poulsen simplex. Hence,
![]() $\text{T}(A)$
admits the Poulsen simplex as a closed face. Strengthening this fact, Proposition I shows that
$\text{T}(A)$
admits the Poulsen simplex as a closed face. Strengthening this fact, Proposition I shows that
![]() $\text{T}(A)$
is in fact the Poulsen simplex.
$\text{T}(A)$
is in fact the Poulsen simplex.
1.6 An application to quantum information theory
There is a strong and interesting connection between traces on free products of
![]() $C^*$
-algebras and quantum information theory. Here, we describe one such instance and explain the implications of our results.
$C^*$
-algebras and quantum information theory. Here, we describe one such instance and explain the implications of our results.
In quantum communication, a quantum channel is modeled by a unital completely positive trace preserving (UCPT) map between matrix algebras
![]() $T:\mathbb{M}_n(\mathbb{C})\to \mathbb{M}_n(\mathbb{C})$
. Such a UCPT map T factorizes through a tracial von Neumann algebra
$T:\mathbb{M}_n(\mathbb{C})\to \mathbb{M}_n(\mathbb{C})$
. Such a UCPT map T factorizes through a tracial von Neumann algebra
![]() $(M,\tau)$
if there exist unital
$(M,\tau)$
if there exist unital
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\alpha,\beta:\mathbb{M}_n(\mathbb{C}) \to M$
, such that
$\alpha,\beta:\mathbb{M}_n(\mathbb{C}) \to M$
, such that
![]() $T=\beta^*\circ \alpha$
, where
$T=\beta^*\circ \alpha$
, where
![]() $\beta^*:M\to \mathbb{M}_n(\mathbb{C})$
is the adjoint map. This condition is equivalent to
$\beta^*:M\to \mathbb{M}_n(\mathbb{C})$
is the adjoint map. This condition is equivalent to
![]() $\text{tr}_n(T(x)y)=\tau(\alpha(x)\beta(y))$
, for every
$\text{tr}_n(T(x)y)=\tau(\alpha(x)\beta(y))$
, for every
![]() $x,y\in \mathbb M_n(\mathbb C)$
, where
$x,y\in \mathbb M_n(\mathbb C)$
, where
![]() $\text{tr}_n:\mathbb M_n(\mathbb C)\to \mathbb{C}$
is the normalized trace. The factorization is called surjective if
$\text{tr}_n:\mathbb M_n(\mathbb C)\to \mathbb{C}$
is the normalized trace. The factorization is called surjective if
![]() $\alpha(\mathbb M_n(\mathbb C))\vee\beta(\mathbb M_n(\mathbb C))=M$
. A UCPT map T is called factorizable if it admits a factorization through a tracial von Neumann algebra. We note that if
$\alpha(\mathbb M_n(\mathbb C))\vee\beta(\mathbb M_n(\mathbb C))=M$
. A UCPT map T is called factorizable if it admits a factorization through a tracial von Neumann algebra. We note that if
![]() $n = 2$
, then all UCPT maps are factorizable [Reference KummererKum85]. On the other hand, non-factorizable UCPT maps exist for all
$n = 2$
, then all UCPT maps are factorizable [Reference KummererKum85]. On the other hand, non-factorizable UCPT maps exist for all
![]() $n\geq 3$
[Reference Haagerup and MusatHM11].
$n\geq 3$
[Reference Haagerup and MusatHM11].
It was shown in [Reference Rørdam and MusatRM21] factorizable UCPT maps
![]() $\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)$
are parameterized by traces on the free product
$\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)$
are parameterized by traces on the free product
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathbb{M}_n(\mathbb{C})*\mathbb{M}_n(\mathbb{C})$
. This is exhibited by an explicit surjective continuous affine map from the trace space
$\mathbb{M}_n(\mathbb{C})*\mathbb{M}_n(\mathbb{C})$
. This is exhibited by an explicit surjective continuous affine map from the trace space
![]() $\mathrm{T}(\mathbb{M}_n(\mathbb{C})*\mathbb{M}_n(\mathbb{C}))$
onto the space of factorizable UCPT maps. Thus, in a similar fashion to [Reference OrovitzOSV25, Corollary 1.7], Corollary B has the following consequence.
$\mathrm{T}(\mathbb{M}_n(\mathbb{C})*\mathbb{M}_n(\mathbb{C}))$
onto the space of factorizable UCPT maps. Thus, in a similar fashion to [Reference OrovitzOSV25, Corollary 1.7], Corollary B has the following consequence.
Corollary J. Let
![]() $n\geq 2$
. Then any factorizable UCPT map
$n\geq 2$
. Then any factorizable UCPT map
![]() $T:\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)$
can be approximated arbitrarily well by UCPT maps factorizing surjectively through a II
$T:\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)$
can be approximated arbitrarily well by UCPT maps factorizing surjectively through a II
![]() $_1$
factor.
$_1$
factor.
Corollary J differs from [Reference OrovitzOSV25, Corollary 1.7] by showing that the approximating maps can be chosen to factorize surjectively through a II
![]() $_1$
factor rather than a (possibly finitely-dimensional) tracial factor. Furthermore, Corollary J also covers the cases
$_1$
factor rather than a (possibly finitely-dimensional) tracial factor. Furthermore, Corollary J also covers the cases
![]() $n=2$
and
$n=2$
and
![]() $n=3$
not covered in [Reference OrovitzOSV25]. On the finite-dimensional side, we point out that in the space of all factorizable UCPT maps, the density of UCPT maps which factor through finite-dimensional algebras is, by [Reference Haagerup and MusatHM15, Theorem 3.7], equivalent to a positive answer to the Connes embedding problem, a negative answer to which was announced in [Reference Ji, Natarajan, Vidick, Wright and YuenJNV+20].
$n=3$
not covered in [Reference OrovitzOSV25]. On the finite-dimensional side, we point out that in the space of all factorizable UCPT maps, the density of UCPT maps which factor through finite-dimensional algebras is, by [Reference Haagerup and MusatHM15, Theorem 3.7], equivalent to a positive answer to the Connes embedding problem, a negative answer to which was announced in [Reference Ji, Natarajan, Vidick, Wright and YuenJNV+20].
1.7 Organization of the paper
Besides § 1, this paper consists of six other sections. In § 2, we gather some definitions and notation, as well as a few elementary lemmas to be used throughout the paper. In § 3, we establish an obstruction to the trace simplex of a free product
![]() $C^*$
-algebra being a Poulsen simplex, and we prove Proposition I. In §§ 4 and 5, we prove Theorem E, and in § 6, we prove Theorem A. Finally, in § 7, we study what happens when the equivalent conditions of Theorem A fail and we prove Theorem G.
$C^*$
-algebra being a Poulsen simplex, and we prove Proposition I. In §§ 4 and 5, we prove Theorem E, and in § 6, we prove Theorem A. Finally, in § 7, we study what happens when the equivalent conditions of Theorem A fail and we prove Theorem G.
2. Preliminaries
2.1 Tracial von Neumann algebras
A tracial von Neumann algebra is a pair
![]() $(M,\tau)$
consisting of a von Neumann algebra M and a fixed faithful normal tracial state
$(M,\tau)$
consisting of a von Neumann algebra M and a fixed faithful normal tracial state
![]() $\tau:M\rightarrow\mathbb C$
. We start by recalling some terminology concerning tracial von Neumann algebras; see [Reference Anantharaman and PopaAP] for more information.
$\tau:M\rightarrow\mathbb C$
. We start by recalling some terminology concerning tracial von Neumann algebras; see [Reference Anantharaman and PopaAP] for more information.
Let
![]() $(M,\tau)$
be a tracial von Neumann algebra. Any unital embedding
$(M,\tau)$
be a tracial von Neumann algebra. Any unital embedding
![]() $M_0\subset M$
, where
$M_0\subset M$
, where
![]() $(M_0,\tau_0)$
is a tracial von Neumann algebra, will be assumed to be trace preserving, i.e., such that
$(M_0,\tau_0)$
is a tracial von Neumann algebra, will be assumed to be trace preserving, i.e., such that
![]() $\tau_0=\tau_{|M_0}$
. We denote by
$\tau_0=\tau_{|M_0}$
. We denote by
![]() $\mathrm{E}_{M_0}:M\rightarrow M_0$
the conditional expectation onto
$\mathrm{E}_{M_0}:M\rightarrow M_0$
the conditional expectation onto
![]() $M_0$
. For
$M_0$
. For
![]() $x\in M$
,
$x\in M$
,
![]() $\|x\|$
and
$\|x\|$
and
![]() $\|x\|_2:= \sqrt{\tau(x^*x)}$
denote the operator norm and 2-norm of x, respectively. We denote by
$\|x\|_2:= \sqrt{\tau(x^*x)}$
denote the operator norm and 2-norm of x, respectively. We denote by
![]() $\mathrm{L}^2(M)$
the Hilbert space obtained by completing M with respect to the 2-norm and by
$\mathrm{L}^2(M)$
the Hilbert space obtained by completing M with respect to the 2-norm and by
![]() $\mathcal U(M)$
the unitary group of M. A projection
$\mathcal U(M)$
the unitary group of M. A projection
![]() $p\in M$
is called minimal if
$p\in M$
is called minimal if
![]() $pMp\cong \mathbb{C} 1$
. We call M diffuse if it has no minimal projections.
$pMp\cong \mathbb{C} 1$
. We call M diffuse if it has no minimal projections.
The von Neumann algebra generated by a self-adjoint set
![]() $S\subset M$
with
$S\subset M$
with
![]() $1\in S$
is equal to its double commutant
$1\in S$
is equal to its double commutant
![]() $S'':= (S')'$
, where for
$S'':= (S')'$
, where for
![]() $S\subset \mathbb B(\mathcal H)$
we write
$S\subset \mathbb B(\mathcal H)$
we write
![]() $S':=\{x\in \mathbb B(\mathcal H)\mid xy=yx$
for all
$S':=\{x\in \mathbb B(\mathcal H)\mid xy=yx$
for all
![]() $y\in S\}$
. For von Neumann subalgebras
$y\in S\}$
. For von Neumann subalgebras
![]() $M_1,M_2\subset M$
, which we will always assume unital, we denote by
$M_1,M_2\subset M$
, which we will always assume unital, we denote by
![]() $M_1\vee M_2:= (M_1\cup M_2)''$
the von Neumann algebra generated by
$M_1\vee M_2:= (M_1\cup M_2)''$
the von Neumann algebra generated by
![]() $M_1$
and
$M_1$
and
![]() $M_2$
.
$M_2$
.
We denote by
![]() $\mathcal Z(M):= M'\cap M$
the center of M. Given a projection
$\mathcal Z(M):= M'\cap M$
the center of M. Given a projection
![]() $p\in M$
, we denote by
$p\in M$
, we denote by
![]() $z_M(p)$
the smallest projection
$z_M(p)$
the smallest projection
![]() $z\in\mathcal Z(M)$
with
$z\in\mathcal Z(M)$
with
![]() $z\geq p$
and call it the central support of p.
$z\geq p$
and call it the central support of p.
If
![]() $p,q\in M$
are projections, then
$p,q\in M$
are projections, then
![]() $\tau(p\wedge q)=\tau(p)+\tau(q)-\tau(p\vee q)\geq \tau(p)+\tau(q)-1$
. Here
$\tau(p\wedge q)=\tau(p)+\tau(q)-\tau(p\vee q)\geq \tau(p)+\tau(q)-1$
. Here
![]() $p\wedge q$
denotes the largest lower bound, i.e., the largest projection r satisfying
$p\wedge q$
denotes the largest lower bound, i.e., the largest projection r satisfying
![]() $r\leq p$
and
$r\leq p$
and
![]() $r\leq q$
, and
$r\leq q$
, and
![]() $p\vee q$
denotes the smallest upper bound, i.e., the smallest projection r satisfying
$p\vee q$
denotes the smallest upper bound, i.e., the smallest projection r satisfying
![]() $p\leq r$
and
$p\leq r$
and
![]() $q\leq r$
. We say that p and q are in general position if
$q\leq r$
. We say that p and q are in general position if
![]() $\tau(p\wedge q)=\max\{\tau(p)+\tau(q)-1,0\}$
.
$\tau(p\wedge q)=\max\{\tau(p)+\tau(q)-1,0\}$
.
We continue with two elementary lemmas.
Lemma 2.1. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra,
$(M,\tau)$
be a tracial von Neumann algebra,
![]() $p\in M\setminus\{0,1\}$
be a projection and
$p\in M\setminus\{0,1\}$
be a projection and
![]() $q_1,\ldots,q_n\in M\setminus\{1\}$
be pairwise orthogonal projections, for some
$q_1,\ldots,q_n\in M\setminus\{1\}$
be pairwise orthogonal projections, for some
![]() $n\geq 1$
. Assume that p and
$n\geq 1$
. Assume that p and
![]() $q_j$
are in general position, for every
$q_j$
are in general position, for every
![]() $1\leq j\leq n$
. Then
$1\leq j\leq n$
. Then
![]() $p-\sum_{j=1}^np\wedge q_j\neq 0$
.
$p-\sum_{j=1}^np\wedge q_j\neq 0$
.
Proof. Let
![]() $S=\{1\leq j\leq n\mid p\wedge q_j\neq 0\}$
. If
$S=\{1\leq j\leq n\mid p\wedge q_j\neq 0\}$
. If
![]() $S=\emptyset$
, the conclusion is immediate as
$S=\emptyset$
, the conclusion is immediate as
![]() $p\neq 0$
. If
$p\neq 0$
. If
![]() $|S|=1$
, let
$|S|=1$
, let
![]() $1\leq k\leq n$
such that
$1\leq k\leq n$
such that
![]() $S=\{k\}$
. Since
$S=\{k\}$
. Since
![]() $q_{k}\neq 1$
, we get that
$q_{k}\neq 1$
, we get that
![]() $\tau(p\wedge q_k)=\tau(p)+\tau(q_k)-1<\tau(p)$
, and hence
$\tau(p\wedge q_k)=\tau(p)+\tau(q_k)-1<\tau(p)$
, and hence
![]() $p-\sum_{1\leq j\leq n}p\wedge q_j=p-p\wedge q_k\neq 0$
. If
$p-\sum_{1\leq j\leq n}p\wedge q_j=p-p\wedge q_k\neq 0$
. If
![]() $|S|\geq 2$
, then as
$|S|\geq 2$
, then as
![]() $p\neq 1$
,
$p\neq 1$
,
![]() $(|S|-1)(\tau(p)-1)<0$
, and thus
$(|S|-1)(\tau(p)-1)<0$
, and thus
 $$\tau\bigg(\sum_{1\leq j\leq n}p\wedge q_j\bigg)=\sum_{j\in S} (\tau(p)+\tau(q_j)-1)=\tau(p)+ \bigg(\sum_{j\in S}\tau(q_j)-1\bigg)+(|S|-1)(\tau(p)-1)<\tau(p).$$
$$\tau\bigg(\sum_{1\leq j\leq n}p\wedge q_j\bigg)=\sum_{j\in S} (\tau(p)+\tau(q_j)-1)=\tau(p)+ \bigg(\sum_{j\in S}\tau(q_j)-1\bigg)+(|S|-1)(\tau(p)-1)<\tau(p).$$
This altogether implies that
![]() $p-\sum_{1\leq j\leq n}p\wedge q_j\neq 0$
.
$p-\sum_{1\leq j\leq n}p\wedge q_j\neq 0$
.
Lemma 2.2 [Reference DykemaDyk93]. Let M be a von Neumann algebra and
![]() $M_1, M_2\subset M$
be von Neumann subalgebras with
$M_1, M_2\subset M$
be von Neumann subalgebras with
![]() $M=M_1\vee M_2$
. Let
$M=M_1\vee M_2$
. Let
![]() $p\in \mathcal Z(M_1)$
be a projection and put
$p\in \mathcal Z(M_1)$
be a projection and put
![]() $N=(\mathbb Cp\oplus M_1(1-p))\vee M_2$
. Then:
$N=(\mathbb Cp\oplus M_1(1-p))\vee M_2$
. Then:
-
(1)
 $pMp=pNp\vee M_1p$
;
$pMp=pNp\vee M_1p$
; -
(2)
 $z_M(p)=z_N(p)$
.
$z_M(p)=z_N(p)$
.
This result is proved in [Reference DykemaDyk93, Theorem 1.2] when
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are freely independent, but the same arguments work in the more general context here. We recall the proof for the reader’s convenience.
$M_2$
are freely independent, but the same arguments work in the more general context here. We recall the proof for the reader’s convenience.
Proof. Since M is generated by N and
![]() $M_1p$
, and
$M_1p$
, and
![]() $p(N\vee M_1p)p\subset pNp\vee M_1p$
, part (1) follows. Since
$p(N\vee M_1p)p\subset pNp\vee M_1p$
, part (1) follows. Since
![]() $z_N(p)\geq p$
,
$z_N(p)\geq p$
,
![]() $z_N(p)$
commutes with
$z_N(p)$
commutes with
![]() $M_1p$
. Since
$M_1p$
. Since
![]() $z_N(p)$
also commutes with N, we deduce that
$z_N(p)$
also commutes with N, we deduce that
![]() $z_N(p)\in\mathcal Z(M)$
and thus
$z_N(p)\in\mathcal Z(M)$
and thus
![]() $z_N(p)\geq z_M(p)$
. Since we also have that
$z_N(p)\geq z_M(p)$
. Since we also have that
![]() $z_N(p)\leq z_M(p)$
, we conclude that
$z_N(p)\leq z_M(p)$
, we conclude that
![]() $z_N(p)=z_M(p)$
, which proves part (2).
$z_N(p)=z_M(p)$
, which proves part (2).
2.2 Minimal projections
Recall that for a tracial von Neumann algebra
![]() $(M,\tau)$
we denote
$(M,\tau)$
we denote
For instance,
![]() $\mathrm{e}(M)=0$
if M is diffuse, and
$\mathrm{e}(M)=0$
if M is diffuse, and
![]() $\mathrm{e}(M)=\max\{\tau(p_i)\mid 1\leq i\leq n\}$
if
$\mathrm{e}(M)=\max\{\tau(p_i)\mid 1\leq i\leq n\}$
if
![]() $M=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_n$
is finite-dimensional and abelian. Moreover, we see that
$M=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_n$
is finite-dimensional and abelian. Moreover, we see that
![]() $\mathrm{e}(M)=\mathrm{e}(A)$
, if
$\mathrm{e}(M)=\mathrm{e}(A)$
, if
![]() $A\subset M$
is a maximal abelian von Neumann subalgebra (MASA). The following lemma shows that whenever
$A\subset M$
is a maximal abelian von Neumann subalgebra (MASA). The following lemma shows that whenever
![]() $\mathrm{e}(M)\neq 0$
, we can in fact find a finite-dimensional abelian von Neumann subalgebra
$\mathrm{e}(M)\neq 0$
, we can in fact find a finite-dimensional abelian von Neumann subalgebra
![]() $A\subset M$
with
$A\subset M$
with
![]() $\mathrm{e}(M)=\mathrm{e}(A)$
.
$\mathrm{e}(M)=\mathrm{e}(A)$
.
Lemma 2.3. Let
![]() $(M,\tau)$
be a non-diffuse tracial von Neumann algebra with
$(M,\tau)$
be a non-diffuse tracial von Neumann algebra with
![]() $M\neq \mathbb C1$
. Then there exists a finite-dimensional abelian von Neumann subalgebra
$M\neq \mathbb C1$
. Then there exists a finite-dimensional abelian von Neumann subalgebra
![]() $A\subset M$
such that
$A\subset M$
such that
![]() $\mathrm{e}(A)=\mathrm{e}(M)$
. Moreover, if M is not isomorphic to either
$\mathrm{e}(A)=\mathrm{e}(M)$
. Moreover, if M is not isomorphic to either
![]() $\mathbb C^2$
or
$\mathbb C^2$
or
![]() $\mathbb M_2(\mathbb C)$
, then we can take A with
$\mathbb M_2(\mathbb C)$
, then we can take A with
![]() $\dim(A)\geq 3$
.
$\dim(A)\geq 3$
.
Proof. Let
![]() $\{p_i\}_{i=1}^N$
, for
$\{p_i\}_{i=1}^N$
, for
![]() $N\in\mathbb N\cup\{\infty\}$
, be a maximal family of non-zero pairwise orthogonal minimal projections of M. Moreover, we can arrange that
$N\in\mathbb N\cup\{\infty\}$
, be a maximal family of non-zero pairwise orthogonal minimal projections of M. Moreover, we can arrange that
![]() $\{\tau(p_i)\}_{i=1}^N$
is a decreasing sequence. Then
$\{\tau(p_i)\}_{i=1}^N$
is a decreasing sequence. Then
![]() $\mathrm{e}(M)=\tau(p_1)$
,
$\mathrm{e}(M)=\tau(p_1)$
,
![]() $p:= 1-\sum_{i=1}^Np_i\in\mathcal Z(M)$
and Mp is diffuse. If
$p:= 1-\sum_{i=1}^Np_i\in\mathcal Z(M)$
and Mp is diffuse. If
![]() $N\in\mathbb N$
, put
$N\in\mathbb N$
, put
![]() $K=N$
and
$K=N$
and
![]() $r=0$
; if
$r=0$
; if
![]() $N=\infty$
, choose
$N=\infty$
, choose
![]() $K\in\mathbb N$
such that
$K\in\mathbb N$
such that
![]() $K\geq 3$
and
$K\geq 3$
and
![]() $r=\sum_{i=K+1}^\infty p_i$
satisfies
$r=\sum_{i=K+1}^\infty p_i$
satisfies
![]() $\tau(r)\leq\tau(p_1)$
. Let
$\tau(r)\leq\tau(p_1)$
. Let
![]() $L\in\mathbb N$
with
$L\in\mathbb N$
with
![]() $L\geq 3$
and
$L\geq 3$
and
![]() $L\tau(p_1)\geq\tau(p)$
. Since Mp is diffuse, there are projections
$L\tau(p_1)\geq\tau(p)$
. Since Mp is diffuse, there are projections
![]() $q_1,\ldots,q_L\in Mp$
such that
$q_1,\ldots,q_L\in Mp$
such that
![]() $\sum_{j=1}^Lq_j=p$
and
$\sum_{j=1}^Lq_j=p$
and
![]() $\tau(q_j)\leq\tau(p_1)$
for every
$\tau(q_j)\leq\tau(p_1)$
for every
![]() $1\leq j\leq L$
. Then
$1\leq j\leq L$
. Then
![]() $A=(\bigoplus_{i=1}^K\mathbb Cp_i)\oplus\mathbb Cr\oplus(\bigoplus_{j=1}^L\mathbb Cq_j)$
satisfies
$A=(\bigoplus_{i=1}^K\mathbb Cp_i)\oplus\mathbb Cr\oplus(\bigoplus_{j=1}^L\mathbb Cq_j)$
satisfies
![]() $A\neq \mathbb C1$
and
$A\neq \mathbb C1$
and
![]() $\mathrm{e}(A)=\mathrm{e}(M)$
.
$\mathrm{e}(A)=\mathrm{e}(M)$
.
To prove the moreover assertion, assume that
![]() $\dim(A)\leq 2$
. Since
$\dim(A)\leq 2$
. Since
![]() $L\geq 3$
, and
$L\geq 3$
, and
![]() $K\geq 3$
if
$K\geq 3$
if
![]() $N=\infty$
, we deduce that in the above construction, we necessarily have
$N=\infty$
, we deduce that in the above construction, we necessarily have
![]() $p=0$
and
$p=0$
and
![]() $N\in\mathbb N$
. Thus, M is finite-dimensional and
$N\in\mathbb N$
. Thus, M is finite-dimensional and
![]() $A=\oplus_{i=1}^N\mathbb Cp_i$
is a MASA. Since
$A=\oplus_{i=1}^N\mathbb Cp_i$
is a MASA. Since
![]() $N=\dim(A)\leq 2$
, this forces M to be isomorphic to either
$N=\dim(A)\leq 2$
, this forces M to be isomorphic to either
![]() $\mathbb C^2$
or
$\mathbb C^2$
or
![]() $\mathbb M_2(\mathbb C)$
.
$\mathbb M_2(\mathbb C)$
.
We also record the following easy observation.
Lemma 2.4. Let
![]() $(\mathcal M,\tau)$
be a tracial von Neumann algebra and
$(\mathcal M,\tau)$
be a tracial von Neumann algebra and
![]() $M\subset\mathcal M$
be a von Neumann subalgebra. Assume that
$M\subset\mathcal M$
be a von Neumann subalgebra. Assume that
![]() $\{z_i\}_{i=1}^K\subset M'\cap \mathcal M$
, for some
$\{z_i\}_{i=1}^K\subset M'\cap \mathcal M$
, for some
![]() $K\in\mathbb N\cup\{\infty\},$
are projections such that
$K\in\mathbb N\cup\{\infty\},$
are projections such that
![]() $\sum_{i=1}^Kz_i=1$
. Then
$\sum_{i=1}^Kz_i=1$
. Then
![]() $\mathrm{e}(M)\leq\sum_{i=1}^K\mathrm{e}(Mz_i)$
.
$\mathrm{e}(M)\leq\sum_{i=1}^K\mathrm{e}(Mz_i)$
.
Proof. If
![]() $\mathrm{e}(M)=0$
, there is nothing to prove. Hence, we can assume
$\mathrm{e}(M)=0$
, there is nothing to prove. Hence, we can assume
![]() $\mathrm{e}(M)\neq 0$
. Let
$\mathrm{e}(M)\neq 0$
. Let
![]() $p\in M$
be a minimal projection with
$p\in M$
be a minimal projection with
![]() $\tau(p)=\mathrm{e}(M)$
. As
$\tau(p)=\mathrm{e}(M)$
. As
![]() $pz_i\in Mz_i$
is a minimal projection, we deduce that
$pz_i\in Mz_i$
is a minimal projection, we deduce that
![]() $\tau(pz_i)\leq\mathrm{e}(Mz_i)$
for every i. Therefore,
$\tau(pz_i)\leq\mathrm{e}(Mz_i)$
for every i. Therefore,
![]() $\mathrm{e}(M)=\tau(p)=\sum_{i=1}^K\tau(pz_i)\leq\sum_{i=1}^K\mathrm{e}(Mz_i)$
.
$\mathrm{e}(M)=\tau(p)=\sum_{i=1}^K\tau(pz_i)\leq\sum_{i=1}^K\mathrm{e}(Mz_i)$
.
2.3 Full free products of
 $C^*$
-algebras
$C^*$
-algebras
In this section we briefly recall the definition of the (unital full) free product of two unital
![]() $C^*$
-algebras, see also, e.g., [Reference Voiculescu, Dykema and NicaVDN92]. This is the co-product in the category of unital
$C^*$
-algebras, see also, e.g., [Reference Voiculescu, Dykema and NicaVDN92]. This is the co-product in the category of unital
![]() $C^*$
-algebras.
$C^*$
-algebras.
Definition 2.5. Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be two unital
$A_2$
be two unital
![]() $C^*$
-algebras. Their unital full free product
$C^*$
-algebras. Their unital full free product
![]() $A=A_1\ast A_2$
is the unique (up to isomorphism) unital
$A=A_1\ast A_2$
is the unique (up to isomorphism) unital
![]() $C^*$
-algebra A, together with unital
$C^*$
-algebra A, together with unital
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\psi_i:A_i\to A$
such that
$\psi_i:A_i\to A$
such that
![]() $\psi_1(A_1)$
and
$\psi_1(A_1)$
and
![]() $\psi_2(A_2)$
generate A, and the following condition holds: for any unital
$\psi_2(A_2)$
generate A, and the following condition holds: for any unital
![]() $C^*$
-algebra B and unital
$C^*$
-algebra B and unital
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\pi_i:A_i\to B$
, there exists a unique unital
$\pi_i:A_i\to B$
, there exists a unique unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi:A\to B$
such that
$\pi:A\to B$
such that
![]() $\pi\circ\psi_i = \pi_i$
, for every
$\pi\circ\psi_i = \pi_i$
, for every
![]() $i=1,2$
.
$i=1,2$
.
Remark 2.6.
-
(1) Many authors also use the notation
 $A_1\ast_\mathbb{C} A_2$
for the unital full free product of
$A_1\ast_\mathbb{C} A_2$
for the unital full free product of
 $A_1$
and
$A_1$
and
 $A_2$
. We use the notation
$A_2$
. We use the notation
 $A_1\ast A_2$
and terminology ‘free product’ throughout the paper, and we will always mean the unital full free product as defined in Definition 2.5.
$A_1\ast A_2$
and terminology ‘free product’ throughout the paper, and we will always mean the unital full free product as defined in Definition 2.5. -
(2) It is easy to see that the maps
 $\psi_i:A_i\to A$
are necessarily injective. Therefore, we will usually drop the notation
$\psi_i:A_i\to A$
are necessarily injective. Therefore, we will usually drop the notation
 $\psi_i$
and assume that
$\psi_i$
and assume that
 $A_1$
and
$A_1$
and
 $A_2$
are unital
$A_2$
are unital
 $C^*$
-subalgebras of A.
$C^*$
-subalgebras of A. -
(3) For an alternative description, one can also show that
 $A_1\ast A_2$
is the enveloping
$A_1\ast A_2$
is the enveloping
 $C^*$
-algebra of the
$C^*$
-algebra of the
 $*$
-algebra free product of
$*$
-algebra free product of
 $A_1$
and
$A_1$
and
 $A_2$
. In particular, this implies that words of the form
$A_2$
. In particular, this implies that words of the form
 $b_1c_1b_2c_2\cdots b_mc_m$
, where
$b_1c_1b_2c_2\cdots b_mc_m$
, where
 $b_1, \ldots, b_m\in A_1$
and
$b_1, \ldots, b_m\in A_1$
and
 $c_1,\ldots, c_m\in A_2$
, are dense in
$c_1,\ldots, c_m\in A_2$
, are dense in
 $A_1\ast A_2$
.
$A_1\ast A_2$
. -
(4) Given two discrete groups
 $G_1$
and
$G_1$
and
 $G_2$
, it is easy to show that
$G_2$
, it is easy to show that
 $C^*(G_1\ast G_2)\cong C^*(G_1)\ast C^*(G_2)$
.
$C^*(G_1\ast G_2)\cong C^*(G_1)\ast C^*(G_2)$
.
2.4 The trace space of a
 $C^*$
-algebra
$C^*$
-algebra
Let A be a unital, separable
![]() $C^*$
-algebra. We denote by
$C^*$
-algebra. We denote by
![]() $\mathrm{T}(A)$
the compact convex set of all traces on A endowed with the weak
$\mathrm{T}(A)$
the compact convex set of all traces on A endowed with the weak
![]() $^*$
-topology. We denote by
$^*$
-topology. We denote by
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
the set of extreme points of
$\partial_{\mathrm{e}}\mathrm{T}(A)$
the set of extreme points of
![]() $\mathrm{T}(A)$
. Then
$\mathrm{T}(A)$
. Then
![]() $\mathrm{T}(A)$
is a metrizable Choquet simplex, i.e., every
$\mathrm{T}(A)$
is a metrizable Choquet simplex, i.e., every
![]() $\varphi\in\mathrm{T}(A)$
is the barycenter of a unique Borel probability measure supported on
$\varphi\in\mathrm{T}(A)$
is the barycenter of a unique Borel probability measure supported on
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
.
$\partial_{\mathrm{e}}\mathrm{T}(A)$
.
A tracial representation of A is a triple
![]() $(M,\tau, \pi)$
where
$(M,\tau, \pi)$
where
![]() $(M,\tau)$
is a tracial von Neumann algebra and
$(M,\tau)$
is a tracial von Neumann algebra and
![]() $\pi:A\to M$
is a
$\pi:A\to M$
is a
![]() $*$
-homomorphism with
$*$
-homomorphism with
![]() $\pi(A)''=M$
. In such cases,
$\pi(A)''=M$
. In such cases,
![]() $\tau\circ\pi\in\mathrm{T}(A)$
. Two tracial representations
$\tau\circ\pi\in\mathrm{T}(A)$
. Two tracial representations
![]() $(M_1,\tau_1,\pi_1)$
and
$(M_1,\tau_1,\pi_1)$
and
![]() $(M_2,\tau_2,\pi_2)$
give rise to the same trace, namely
$(M_2,\tau_2,\pi_2)$
give rise to the same trace, namely
![]() $\tau_1\circ\pi_2 =\tau_2 \circ \pi_2$
, if and only if they are quasi-equivalent; namely, if there exists a
$\tau_1\circ\pi_2 =\tau_2 \circ \pi_2$
, if and only if they are quasi-equivalent; namely, if there exists a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\Psi:M_1 \rightarrow M_2$
such that
$\Psi:M_1 \rightarrow M_2$
such that
![]() $\tau_1=\tau_2\circ\Psi$
and
$\tau_1=\tau_2\circ\Psi$
and
![]() $\pi_2 = \Psi\circ \pi_1$
.
$\pi_2 = \Psi\circ \pi_1$
.
Conversely, given
![]() $\varphi\in\mathrm{T}(A)$
, there exists a unique (up to quasi-equivalence) tracial representation
$\varphi\in\mathrm{T}(A)$
, there exists a unique (up to quasi-equivalence) tracial representation
![]() $(M,\tau,\pi)$
of A such that
$(M,\tau,\pi)$
of A such that
![]() $\varphi=\tau\circ\pi$
. More precisely,
$\varphi=\tau\circ\pi$
. More precisely,
![]() $\pi$
is the GNS representation associated to
$\pi$
is the GNS representation associated to
![]() $\varphi$
. We say that
$\varphi$
. We say that
![]() $\varphi$
is finite-dimensional if
$\varphi$
is finite-dimensional if
![]() $\dim(M)<\infty$
. We denote by
$\dim(M)<\infty$
. We denote by
![]() $\mathrm{T}_{\mathrm{fin}}(A)$
the set of all finite-dimensional traces
$\mathrm{T}_{\mathrm{fin}}(A)$
the set of all finite-dimensional traces
![]() $\varphi\in\mathrm{T}(A)$
and let
$\varphi\in\mathrm{T}(A)$
and let
![]() $\mathrm{T}_{\infty}(A)=\mathrm{T}(A)\setminus\mathrm{T}_{\mathrm{fin}}(A)$
. Note that
$\mathrm{T}_{\infty}(A)=\mathrm{T}(A)\setminus\mathrm{T}_{\mathrm{fin}}(A)$
. Note that
![]() $\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
if and only if M is a factor (i.e.,
$\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
if and only if M is a factor (i.e.,
![]() $\pi(A)''$
is either a II
$\pi(A)''$
is either a II
![]() $_1$
factor or isomorphic to
$_1$
factor or isomorphic to
![]() $\mathbb M_n(\mathbb C)$
, for some
$\mathbb M_n(\mathbb C)$
, for some
![]() $n\in\mathbb N$
). We say that
$n\in\mathbb N$
). We say that
![]() $\varphi\in \partial_{\mathrm{e}}\mathrm{T}(A)$
is n-dimensional, for some
$\varphi\in \partial_{\mathrm{e}}\mathrm{T}(A)$
is n-dimensional, for some
![]() $n\in\mathbb N$
, if
$n\in\mathbb N$
, if
![]() $M\cong\mathbb M_n(\mathbb C)$
. Finally, we say that
$M\cong\mathbb M_n(\mathbb C)$
. Finally, we say that
![]() $\varphi$
is von Neumann amenable if M is an amenable von Neumann algebra.
$\varphi$
is von Neumann amenable if M is an amenable von Neumann algebra.
For future reference, we record the following useful known lemma concerning convergence of traces in the weak
![]() $^*$
-topology versus the Wasserstein topology.
$^*$
-topology versus the Wasserstein topology.
Lemma 2.7 [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22]. Let A be a unital, separable
![]() $C^*$
-algebra,
$C^*$
-algebra,
![]() $\varphi\in\mathrm{T}(A)$
and
$\varphi\in\mathrm{T}(A)$
and
![]() $(\varphi_n)_{n\in\mathbb N}\subset\mathrm{T}(A)$
be a sequence. Consider the following two conditions:
$(\varphi_n)_{n\in\mathbb N}\subset\mathrm{T}(A)$
be a sequence. Consider the following two conditions:
-
(1)
 $\varphi_n\rightarrow\varphi$
;
$\varphi_n\rightarrow\varphi$
; -
(2) there exist a II
 $_1$
factor
$_1$
factor
 $(M,\tau)$
,
$(M,\tau)$
,
 $*$
-homomorphisms
$*$
-homomorphisms
 $\pi:A\rightarrow M$
and
$\pi:A\rightarrow M$
and
 $\pi_n:A\rightarrow M$
such that
$\pi_n:A\rightarrow M$
such that
 $\tau\circ\pi=\varphi$
,
$\tau\circ\pi=\varphi$
,
 $\tau\circ\pi_n=\varphi_n$
for every
$\tau\circ\pi_n=\varphi_n$
for every
 $n\in\mathbb N$
, and
$n\in\mathbb N$
, and
 $\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
for every
$\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
for every
 $a\in A$
.
$a\in A$
.
Then (2)
![]() $\Rightarrow$
(1). Moreover, if
$\Rightarrow$
(1). Moreover, if
![]() $\varphi$
is von Neumann amenable, then (1)
$\varphi$
is von Neumann amenable, then (1)
![]() $\Rightarrow$
(2).
$\Rightarrow$
(2).
The main content of this lemma is the moreover assertion. This assertion can be deduced from [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22, Proposition 5.26] when A is a finitely generated
![]() $C^*$
-algebra. For the reader’s convenience we provide a short self-contained proof. Note that the moreover assertion in particular applies if
$C^*$
-algebra. For the reader’s convenience we provide a short self-contained proof. Note that the moreover assertion in particular applies if
![]() $\varphi\in\mathrm{T}_{\mathrm{fin}}(A)$
. Note also that condition (2) is equivalent to
$\varphi\in\mathrm{T}_{\mathrm{fin}}(A)$
. Note also that condition (2) is equivalent to
![]() $\varphi_n\rightarrow\varphi$
in the Wasserstein topology.
$\varphi_n\rightarrow\varphi$
in the Wasserstein topology.
Proof. Let
![]() $\pi,\pi_n:A\rightarrow M$
be tracial representations such that
$\pi,\pi_n:A\rightarrow M$
be tracial representations such that
![]() $\tau\circ\pi=\varphi$
and
$\tau\circ\pi=\varphi$
and
![]() $\tau\circ\pi_n=\varphi_n$
for every
$\tau\circ\pi_n=\varphi_n$
for every
![]() $n\in\mathbb N$
. Then
$n\in\mathbb N$
. Then
![]() $|\varphi_n(a)-\varphi(a)|=|\tau(\pi_n(a)-\pi(a))|\leq \|\pi_n(a)-\pi(a)\|_2$
for every
$|\varphi_n(a)-\varphi(a)|=|\tau(\pi_n(a)-\pi(a))|\leq \|\pi_n(a)-\pi(a)\|_2$
for every
![]() $a\in A$
and
$a\in A$
and
![]() $n\in\mathbb N$
. This shows that (2) implies (1).
$n\in\mathbb N$
. This shows that (2) implies (1).
For the moreover assertion, assume that
![]() $\varphi$
is von Neumann amenable and that (1) holds. Let
$\varphi$
is von Neumann amenable and that (1) holds. Let
![]() $\pi:A\rightarrow N$
and
$\pi:A\rightarrow N$
and
![]() $\rho_n:A\rightarrow N_n$
be tracial representations associated to
$\rho_n:A\rightarrow N_n$
be tracial representations associated to
![]() $\varphi$
and
$\varphi$
and
![]() $\varphi_n$
for every
$\varphi_n$
for every
![]() $n\in\mathbb N$
. Define
$n\in\mathbb N$
. Define
![]() $M=N*(*_{n\in\mathbb N}N_n)*\mathrm{L}(\mathbb F_2)$
and let
$M=N*(*_{n\in\mathbb N}N_n)*\mathrm{L}(\mathbb F_2)$
and let
![]() $\tau$
be its canonical trace. Then M is a II
$\tau$
be its canonical trace. Then M is a II
![]() $_1$
factor [Reference Anantharaman and PopaAP, Corollary 5.3.8]. Viewing N and
$_1$
factor [Reference Anantharaman and PopaAP, Corollary 5.3.8]. Viewing N and
![]() $N_n$
as subalgebras of M, we moreover have
$N_n$
as subalgebras of M, we moreover have
![]() $\varphi=\tau\circ\pi$
and
$\varphi=\tau\circ\pi$
and
![]() $\varphi_n=\tau\circ\rho_n$
for every
$\varphi_n=\tau\circ\rho_n$
for every
![]() $n\in\mathbb N$
.
$n\in\mathbb N$
.
We proceed with the following claim.
Claim. There exist
![]() $(u_n)_{n\in\mathbb N}\subset\mathcal U(M)$
such that
$(u_n)_{n\in\mathbb N}\subset\mathcal U(M)$
such that
![]() $\|u_n\rho_n(a)u_n^*-\pi(a)\|_2\rightarrow 0$
, for every
$\|u_n\rho_n(a)u_n^*-\pi(a)\|_2\rightarrow 0$
, for every
![]() $a\in A.$
$a\in A.$
Given the claim, it is clear that the maps
![]() $\pi_n:A\rightarrow M$
given by
$\pi_n:A\rightarrow M$
given by
![]() $\pi_n(a)=u_n\rho_n(a)u_n^*$
satisfy condition (2). Hence proving the claim will finish the proof of the lemma.
$\pi_n(a)=u_n\rho_n(a)u_n^*$
satisfy condition (2). Hence proving the claim will finish the proof of the lemma.
Proof of the claim. Let
![]() $(a_k)\subset (A)_1$
be a
$(a_k)\subset (A)_1$
be a
![]() $\|\cdot\|$
-dense sequence. For every
$\|\cdot\|$
-dense sequence. For every
![]() $n\in\mathbb N$
, let
$n\in\mathbb N$
, let
 $$\varepsilon_n:= \inf\bigg\{\sum_{k=1}^\infty2^{-k}\|u\rho_n(a_k)u^*-\pi(a_k)\|_2\mid u\in\mathcal U(M)\bigg\}.$$
$$\varepsilon_n:= \inf\bigg\{\sum_{k=1}^\infty2^{-k}\|u\rho_n(a_k)u^*-\pi(a_k)\|_2\mid u\in\mathcal U(M)\bigg\}.$$
The claim is equivalent to the statement that
![]() $\varepsilon_n\rightarrow 0$
. Assume by contradiction that this is false. Then we can find
$\varepsilon_n\rightarrow 0$
. Assume by contradiction that this is false. Then we can find
![]() $\delta>0$
and a subsequence
$\delta>0$
and a subsequence
![]() $(\varepsilon_{n_k})\subset(\varepsilon_n)$
such that
$(\varepsilon_{n_k})\subset(\varepsilon_n)$
such that
![]() $\varepsilon_{n_k}\geq \delta$
for every
$\varepsilon_{n_k}\geq \delta$
for every
![]() $k\in\mathbb N$
.
$k\in\mathbb N$
.
Let
![]() $\omega$
be a free ultrafilter on
$\omega$
be a free ultrafilter on
![]() $\mathbb N$
and
$\mathbb N$
and
![]() $M^{\omega}$
be the ultrapower von Neumann algebra together with its canonical trace given by
$M^{\omega}$
be the ultrapower von Neumann algebra together with its canonical trace given by
![]() $\tau^{\omega}((x_k)_{k\in\omega})=\lim_{k\rightarrow\omega}\tau(x_k)$
. Define
$\tau^{\omega}((x_k)_{k\in\omega})=\lim_{k\rightarrow\omega}\tau(x_k)$
. Define
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\widetilde\pi,\rho:A\rightarrow M^{\omega}$
by setting
$\widetilde\pi,\rho:A\rightarrow M^{\omega}$
by setting
![]() $\widetilde\pi(a)=(\pi(a))_{k\in\omega}$
and
$\widetilde\pi(a)=(\pi(a))_{k\in\omega}$
and
![]() $\rho(a)=(\rho_{n_k}(a))_{k\in\omega}$
for every
$\rho(a)=(\rho_{n_k}(a))_{k\in\omega}$
for every
![]() $a\in A$
. Then for every
$a\in A$
. Then for every
![]() $a\in A$
, we have
$a\in A$
, we have
Thus, there is a trace-preserving
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\theta:\widetilde\pi(A)''\rightarrow\rho(A)''$
such that
$\theta:\widetilde\pi(A)''\rightarrow\rho(A)''$
such that
![]() $\theta(\widetilde\pi(a))=\rho(a)$
for every
$\theta(\widetilde\pi(a))=\rho(a)$
for every
![]() $a\in A$
. Since
$a\in A$
. Since
![]() $\varphi$
is von Neumann amenable,
$\varphi$
is von Neumann amenable,
![]() $\widetilde\pi(A)''$
is amenable. By Connes’ theorem [Reference ConnesCon76],
$\widetilde\pi(A)''$
is amenable. By Connes’ theorem [Reference ConnesCon76],
![]() $\widetilde\pi(A)''$
is approximately finite-dimensional. Since M is a II
$\widetilde\pi(A)''$
is approximately finite-dimensional. Since M is a II
![]() $_1$
factor, a well-known fact (see, e.g., [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22, Lemma 5.23]) implies the existence of
$_1$
factor, a well-known fact (see, e.g., [Reference Gangbo, Jekel, Nam and ShlyakhtenkoGJNS22, Lemma 5.23]) implies the existence of
![]() $v=(v_k)_{k\in\omega}\in \mathcal U(M^\omega)$
, where
$v=(v_k)_{k\in\omega}\in \mathcal U(M^\omega)$
, where
![]() $v_k\in \mathcal U(M)$
for every
$v_k\in \mathcal U(M)$
for every
![]() $k\in\mathbb N$
, such that
$k\in\mathbb N$
, such that
![]() $\widetilde\pi(a)=v\rho(a)v^*$
for every
$\widetilde\pi(a)=v\rho(a)v^*$
for every
![]() $a\in A$
. In other words,
$a\in A$
. In other words,
![]() $\lim_{k\rightarrow\omega}\|\pi(a)-v_k\rho_{n_k}(a)v_k^*\|_2=0$
for every
$\lim_{k\rightarrow\omega}\|\pi(a)-v_k\rho_{n_k}(a)v_k^*\|_2=0$
for every
![]() $a\in A$
. This implies that
$a\in A$
. This implies that
![]() $\lim_{k\rightarrow\omega}\varepsilon_{n_k}=0$
, contradicting that
$\lim_{k\rightarrow\omega}\varepsilon_{n_k}=0$
, contradicting that
![]() $\varepsilon_{n_k}\geq\delta$
, for every
$\varepsilon_{n_k}\geq\delta$
, for every
![]() $k\in\mathbb N$
. This finishes the proof of the claim.
$k\in\mathbb N$
. This finishes the proof of the claim.
Thus, this also completes the proof of the lemma.
2.5 The tracial quotient of a
 $C^*$
-algebra
$C^*$
-algebra
Before continuing, we note that studying the trace space of a
![]() $C^*$
-algebra amounts to studying its tracial quotient.
$C^*$
-algebra amounts to studying its tracial quotient.
Definition 2.8. Let A be a unital, separable
![]() $C^*$
-algebra with
$C^*$
-algebra with
![]() $\mathrm{T}(A)\neq\emptyset$
. We define
$\mathrm{T}(A)\neq\emptyset$
. We define
![]() $A_{\mathrm{tr}}$
to be the quotient
$A_{\mathrm{tr}}$
to be the quotient
where
![]() $I_{\mathrm{tr}} = \{a\in A\mid \varphi(a^*a)=0 \text{ for all }\varphi\in\mathrm{T}(A)\}$
. We call
$I_{\mathrm{tr}} = \{a\in A\mid \varphi(a^*a)=0 \text{ for all }\varphi\in\mathrm{T}(A)\}$
. We call
![]() $A_{\mathrm{tr}}$
the tracial quotient of A.
$A_{\mathrm{tr}}$
the tracial quotient of A.
Remark 2.9. By construction,
![]() $\mathrm{T}(A)$
is affinely homeomorphic to
$\mathrm{T}(A)$
is affinely homeomorphic to
![]() $ \mathrm{T}(A_{\mathrm{tr}})$
. Furthermore, we could equivalently define
$ \mathrm{T}(A_{\mathrm{tr}})$
. Furthermore, we could equivalently define
![]() $A_{\mathrm{tr}}$
as the largest quotient
$A_{\mathrm{tr}}$
as the largest quotient
![]() $C^*$
-algebra of A that admits a faithful tracial state.
$C^*$
-algebra of A that admits a faithful tracial state.
We also note that the condition from Theorem A that
![]() $\mathrm{T}(A_i)$
does not consist of a single one-dimensional trace can be reformulated as
$\mathrm{T}(A_i)$
does not consist of a single one-dimensional trace can be reformulated as
![]() $A_{i,\mathrm{tr}}\not\cong \mathbb{C}$
(i.e.,
$A_{i,\mathrm{tr}}\not\cong \mathbb{C}$
(i.e.,
![]() $A_i$
is not ‘tracially equivalent’ to
$A_i$
is not ‘tracially equivalent’ to
![]() $\mathbb C$
).
$\mathbb C$
).
We record the following easy observation.
Lemma 2.10. Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. Then
$A_2$
. Then
![]() $\mathrm{T}(A)$
(or equivalently
$\mathrm{T}(A)$
(or equivalently
![]() $\mathrm{T}(A_{\mathrm{tr}})$
) is affinely homeomorphic to
$\mathrm{T}(A_{\mathrm{tr}})$
) is affinely homeomorphic to
![]() $\mathrm{T}(A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}})$
.
$\mathrm{T}(A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}})$
.
Proof. For
![]() $i=1,2$
, we have by construction a unital, surjective
$i=1,2$
, we have by construction a unital, surjective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi_i: A_i\to A_{i,\mathrm{tr}}$
such that any tracial representation
$\pi_i: A_i\to A_{i,\mathrm{tr}}$
such that any tracial representation
![]() $\rho_i:A_i\to M_i$
factors through
$\rho_i:A_i\to M_i$
factors through
![]() $\pi_i$
. Consider the unital, surjective
$\pi_i$
. Consider the unital, surjective
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\pi:A\to A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
determined by
$\pi:A\to A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
determined by
![]() $\pi_{|A_i} = \pi_i$
for
$\pi_{|A_i} = \pi_i$
for
![]() $i=1,2$
.
$i=1,2$
.
Let
![]() $\rho:A\to M$
be a tracial representation. Since
$\rho:A\to M$
be a tracial representation. Since
![]() $\rho_{|A_i}$
factors through
$\rho_{|A_i}$
factors through
![]() $\pi_i$
, we can find unital
$\pi_i$
, we can find unital
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\delta_i: A_{i,\mathrm{tr}}\to M$
such that
$\delta_i: A_{i,\mathrm{tr}}\to M$
such that
![]() $\rho_{|A_i} = \delta_i\circ \pi_i$
for
$\rho_{|A_i} = \delta_i\circ \pi_i$
for
![]() $i=1,2$
. Defining the unital
$i=1,2$
. Defining the unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\delta:A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}\to M$
by
$\delta:A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}\to M$
by
![]() $\delta_{|A_{i,\mathrm{tr}}} = \delta_i$
for
$\delta_{|A_{i,\mathrm{tr}}} = \delta_i$
for
![]() $i=1,2$
, we get that
$i=1,2$
, we get that
![]() $\rho = \delta\circ \pi$
.
$\rho = \delta\circ \pi$
.
This implies that the continuous affine injective map
![]() $\mathrm{T}(A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}})\ni \varphi\mapsto \varphi\circ \pi\in \mathrm{T}(A)$
is surjective, and is therefore an affine homeomorphism. This finishes the proof of the lemma.
$\mathrm{T}(A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}})\ni \varphi\mapsto \varphi\circ \pi\in \mathrm{T}(A)$
is surjective, and is therefore an affine homeomorphism. This finishes the proof of the lemma.
Remark 2.11. It is not clear to the authors whether for a free product
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $A=A_1\ast A_2$
, though it is true in general that
$A=A_1\ast A_2$
, though it is true in general that
![]() $(\star)$
$(\star)$
![]() $A_{\mathrm{tr}}\cong A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
. We note that by the proof of Lemma 2.10, every tracial representation of A factors through the quotient
$A_{\mathrm{tr}}\cong A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
. We note that by the proof of Lemma 2.10, every tracial representation of A factors through the quotient
![]() $A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
, and hence we have a natural surjective
$A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
, and hence we have a natural surjective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}} \to A_{\mathrm{tr}}$
. Since
$A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}} \to A_{\mathrm{tr}}$
. Since
![]() $A_{\mathrm{tr}}$
always has a faithful tracial state by construction, this implies that
$A_{\mathrm{tr}}$
always has a faithful tracial state by construction, this implies that
![]() $(\star)$
is equivalent to the statement that the free product of two unital, separable
$(\star)$
is equivalent to the statement that the free product of two unital, separable
![]() $C^*$
-algebras with a faithful tracial state, has a faithful tracial state. When
$C^*$
-algebras with a faithful tracial state, has a faithful tracial state. When
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are residually finite-dimensional (RFD), their free product is also RFD by [Reference Exel and LoringEL92, Theorem 3.2], and thus has a faithful trace. In particular, we conclude that
$A_2$
are residually finite-dimensional (RFD), their free product is also RFD by [Reference Exel and LoringEL92, Theorem 3.2], and thus has a faithful trace. In particular, we conclude that
![]() $A_{\mathrm{tr}}\cong A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
whenever
$A_{\mathrm{tr}}\cong A_{1,\mathrm{tr}}\ast A_{2,\mathrm{tr}}$
whenever
![]() $A_{1,\mathrm{tr}}$
and
$A_{1,\mathrm{tr}}$
and
![]() $A_{2,\mathrm{tr}}$
are RFD. We leave it open whether
$A_{2,\mathrm{tr}}$
are RFD. We leave it open whether
![]() $(\star)$
holds in general.
$(\star)$
holds in general.
3. An obstruction to the trace simplex being Poulsen
In this section, we prove one implication of Theorem A by establishing an obstruction to the trace simplex of a free product
![]() $C^*$
-algebra being a Poulsen simplex; see Corollary 3.5. This obstruction relies on the following general lemma, which shows that isolated extreme points in compact convex sets satisfy an a priori stronger condition on convergence of barycenter measures.
$C^*$
-algebra being a Poulsen simplex; see Corollary 3.5. This obstruction relies on the following general lemma, which shows that isolated extreme points in compact convex sets satisfy an a priori stronger condition on convergence of barycenter measures.
Lemma 3.1. Let C be a compact and convex set in a locally convex topological vector space, and denote by
![]() $\mathrm{bar} :\mathrm{Prob}(C)\to C$
the barycenter map. Let
$\mathrm{bar} :\mathrm{Prob}(C)\to C$
the barycenter map. Let
![]() $x\in\partial_{\mathrm{e}}C$
be an extreme point and suppose that it is an isolated point of
$x\in\partial_{\mathrm{e}}C$
be an extreme point and suppose that it is an isolated point of
![]() $\partial_{\mathrm{e}}C$
. Consider a sequence of Borel probability measures
$\partial_{\mathrm{e}}C$
. Consider a sequence of Borel probability measures
![]() $\mu_{n}\in\operatorname{Prob}(C)$
supported on
$\mu_{n}\in\operatorname{Prob}(C)$
supported on
![]() $\partial_{\mathrm{e}}C$
. Then
$\partial_{\mathrm{e}}C$
. Then
![]() $\operatorname{bar}\mu_{n}$
converges to x if and only if
$\operatorname{bar}\mu_{n}$
converges to x if and only if
![]() $\lim_n \mu_{n}(\{x\}) = 1$
.
$\lim_n \mu_{n}(\{x\}) = 1$
.
Proof. First, it is clear that if
![]() $\mu_{n}(\{x\})\to1$
, then
$\mu_{n}(\{x\})\to1$
, then
![]() $\operatorname{bar}\mu_{n}\to x$
. For the converse, let
$\operatorname{bar}\mu_{n}\to x$
. For the converse, let
![]() $\mu$
be any accumulation point of the sequence
$\mu$
be any accumulation point of the sequence
![]() $\mu_n$
in the weak-
$\mu_n$
in the weak-
![]() $^*$
compact space
$^*$
compact space
![]() $\operatorname{Prob}(C)$
. As the barycenter map is continuous, we have
$\operatorname{Prob}(C)$
. As the barycenter map is continuous, we have
![]() $ \operatorname{bar} \mu_n \to \operatorname{bar} \mu $
. But by assumption
$ \operatorname{bar} \mu_n \to \operatorname{bar} \mu $
. But by assumption
![]() $\operatorname{bar} \mu_n\to x$
, and so
$\operatorname{bar} \mu_n\to x$
, and so
![]() $\operatorname{bar}\mu =x$
. As x is an extreme point,
$\operatorname{bar}\mu =x$
. As x is an extreme point,
![]() $\mu$
must be the Dirac measure concentrated on x. In particular,
$\mu$
must be the Dirac measure concentrated on x. In particular,
![]() $\mu$
is supported on
$\mu$
is supported on
![]() $\partial_{\mathrm{e}} C$
, as is each
$\partial_{\mathrm{e}} C$
, as is each
![]() $\mu_n$
by assumption. Finally, as x is an isolated point of
$\mu_n$
by assumption. Finally, as x is an isolated point of
![]() $\partial_{\mathrm{e}}C$
, we can find a continuous function on f on C with
$\partial_{\mathrm{e}}C$
, we can find a continuous function on f on C with
![]() $f(x)=1$
and
$f(x)=1$
and
![]() $f(\partial_{\mathrm{e}}C\backslash \{x\})=0$
. Weak-
$f(\partial_{\mathrm{e}}C\backslash \{x\})=0$
. Weak-
![]() $*$
convergence then implies that
$*$
convergence then implies that
as desired.
In Theorem 3.4 we will see, in particular, that if
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
admit one-dimensional extreme traces which are isolated, then the free product
$A_2$
admit one-dimensional extreme traces which are isolated, then the free product
![]() $A=A_1*A_2$
admits a one-dimensional extreme trace which is isolated as well. Towards proving that, we will need the following corollary which is obtained from Lemma 3.1 when specializing to the trace simplex.
$A=A_1*A_2$
admits a one-dimensional extreme trace which is isolated as well. Towards proving that, we will need the following corollary which is obtained from Lemma 3.1 when specializing to the trace simplex.
Corollary 3.2. Let A be a unital, separable
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
be an extreme trace which is an isolated point in
$\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
be an extreme trace which is an isolated point in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
. Let
$\partial_{\mathrm{e}}\mathrm{T}(A)$
. Let
![]() $(\varphi_{n})_{n\in\mathbb N}\subset\mathrm{T}(A)$
be a sequence such that
$(\varphi_{n})_{n\in\mathbb N}\subset\mathrm{T}(A)$
be a sequence such that
![]() $\varphi_n\rightarrow\varphi$
. Then
$\varphi_n\rightarrow\varphi$
. Then
![]() $\mu_{n}(\{\varphi\})\to1$
where for every n,
$\mu_{n}(\{\varphi\})\to1$
where for every n,
![]() $\mu_{n}$
is the unique Borel probability measure on
$\mu_{n}$
is the unique Borel probability measure on
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
whose barycenter is
$\partial_{\mathrm{e}}\mathrm{T}(A)$
whose barycenter is
![]() $\varphi_{n}$
.
$\varphi_{n}$
.
3.1 An obstruction to diffuseness
Let
![]() $M_1,M_2$
be von Neumann subalgebras of a tracial von Neumann algebra
$M_1,M_2$
be von Neumann subalgebras of a tracial von Neumann algebra
![]() $(M,\tau)$
. Assume that there exist projections
$(M,\tau)$
. Assume that there exist projections
![]() $p\in \mathcal Z(M_1),q\in \mathcal Z(M_2)$
such that
$p\in \mathcal Z(M_1),q\in \mathcal Z(M_2)$
such that
![]() $M_1p=\mathbb Cp,M_2q=\mathbb Cq$
and
$M_1p=\mathbb Cp,M_2q=\mathbb Cq$
and
![]() $\tau(p)+\tau(q)>1$
. Then
$\tau(p)+\tau(q)>1$
. Then
![]() $M_1(p\wedge q)=(M_1p)(p\wedge q)=\mathbb C(p\wedge q)$
, and similarly
$M_1(p\wedge q)=(M_1p)(p\wedge q)=\mathbb C(p\wedge q)$
, and similarly
![]() $M_2(p\wedge q)=\mathbb C(p\wedge q)$
. These facts imply that
$M_2(p\wedge q)=\mathbb C(p\wedge q)$
. These facts imply that
![]() $p\wedge q\in \mathcal Z(M_1\vee M_2)$
and
$p\wedge q\in \mathcal Z(M_1\vee M_2)$
and
![]() $(M_1\vee M_2)(p\wedge q)=\mathbb C(p\wedge q)$
. Since
$(M_1\vee M_2)(p\wedge q)=\mathbb C(p\wedge q)$
. Since
![]() $\tau(p)+\tau(q)>1$
, it follows that
$\tau(p)+\tau(q)>1$
, it follows that
![]() $M_1\vee M_2$
has a one-dimensional direct summand.
$M_1\vee M_2$
has a one-dimensional direct summand.
We next generalize this fact by assuming that
![]() $M_2q$
is finite-(but not necessarily one-) dimensional.
$M_2q$
is finite-(but not necessarily one-) dimensional.
Proposition 3.3. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra and
$(M,\tau)$
be a tracial von Neumann algebra and
![]() $M_1,M_2\subset M$
be von Neumann subalgebras. Assume that there exist projections
$M_1,M_2\subset M$
be von Neumann subalgebras. Assume that there exist projections
![]() $p\in\mathcal Z(M_1),q\in\mathcal Z(M_2)$
and
$p\in\mathcal Z(M_1),q\in\mathcal Z(M_2)$
and
![]() $k\in\mathbb N$
such that
$k\in\mathbb N$
such that
![]() $M_1p=\mathbb Cp$
,
$M_1p=\mathbb Cp$
,
![]() $M_2q\cong\mathbb M_k(\mathbb C)$
and
$M_2q\cong\mathbb M_k(\mathbb C)$
and
![]() $\tau(p)+({\tau(q)}/{k^2})>1$
.
$\tau(p)+({\tau(q)}/{k^2})>1$
.
Then there exists a non-zero projection
![]() $p'\in\mathcal Z(M_1\vee M_2)$
such that
$p'\in\mathcal Z(M_1\vee M_2)$
such that
![]() $p'\leq p\wedge q$
,
$p'\leq p\wedge q$
,
![]() $Mp'\cong\mathbb M_k(\mathbb C)$
and
$Mp'\cong\mathbb M_k(\mathbb C)$
and
![]() $\tau(p')\geq k^2(\tau(p)+({\tau(q)}/{k^2})-1)$
.
$\tau(p')\geq k^2(\tau(p)+({\tau(q)}/{k^2})-1)$
.
Proof. Let
![]() $q_i\in M_2q\cong\mathbb M_k(\mathbb C)$
be minimal projections and
$q_i\in M_2q\cong\mathbb M_k(\mathbb C)$
be minimal projections and
![]() $v_{i,j}\in M_2q$
be partial isometries such that
$v_{i,j}\in M_2q$
be partial isometries such that
![]() $q_1+\cdots+q_k=q$
,
$q_1+\cdots+q_k=q$
,
![]() $v_{i,j}v_{i,j}^*=q_i$
,
$v_{i,j}v_{i,j}^*=q_i$
,
![]() $v_{i,j}^*v_{i,j}=q_j$
and
$v_{i,j}^*v_{i,j}=q_j$
and
![]() $v_{i,j}v_{j,l}=v_{i,l}$
for every
$v_{i,j}v_{j,l}=v_{i,l}$
for every
![]() $1\leq i,j,l\leq k$
.
$1\leq i,j,l\leq k$
.
Following the formula immediately before [Reference DykemaDyk93, Definition 3.3] we define
![]() $p'=\sum_{i=1}^kp_i$
, where
$p'=\sum_{i=1}^kp_i$
, where
Then
![]() $p_i=v_{i,j}p_jv_{i,j}^*$
, and hence
$p_i=v_{i,j}p_jv_{i,j}^*$
, and hence
![]() $p'v_{i,j}=p'q_iv_{i,j}=p_iv_{i,j}=v_{i,j}p_j=v_{i,j}q_jp'=v_{i,j}p'$
for every
$p'v_{i,j}=p'q_iv_{i,j}=p_iv_{i,j}=v_{i,j}p_j=v_{i,j}q_jp'=v_{i,j}p'$
for every
![]() $1\leq i,j\leq k$
. This implies that p' commutes with
$1\leq i,j\leq k$
. This implies that p' commutes with
![]() $M_2$
. Since
$M_2$
. Since
![]() $p'\leq p$
, p' also commutes with
$p'\leq p$
, p' also commutes with
![]() $M_1$
. Since
$M_1$
. Since
![]() $p'\in M_1\vee M_2$
, we derive that
$p'\in M_1\vee M_2$
, we derive that
![]() $p'\in \mathcal Z(M_1\vee M_2)$
. Since
$p'\in \mathcal Z(M_1\vee M_2)$
. Since
![]() $p_i\leq p\wedge q$
, for every
$p_i\leq p\wedge q$
, for every
![]() $1\leq i\leq k$
, we also get that
$1\leq i\leq k$
, we also get that
![]() $p'\leq p\wedge q$
.
$p'\leq p\wedge q$
.
To prove the lower bound for
![]() $\tau(p')$
, recall that for any projections
$\tau(p')$
, recall that for any projections
![]() $r\in M$
,
$r\in M$
,
![]() $e,f\in rMr$
we have
$e,f\in rMr$
we have
Let
![]() $1\leq i\leq k$
. By using repeatedly the last inequality, we get that
$1\leq i\leq k$
. By using repeatedly the last inequality, we get that
 \begin{align*}\tau(p_i)&\geq \sum_{j=1}^k\tau(p\wedge q_j)-(k-1)\tau(q_i)\\&\geq \sum_{j=1}^k(\tau(p)+\tau(q_j)-1)-(k-1)\tau(q_i)\\&=k\left(\tau(p)+\frac{\tau(q)}{k^2}-1\right)\!.\end{align*}
\begin{align*}\tau(p_i)&\geq \sum_{j=1}^k\tau(p\wedge q_j)-(k-1)\tau(q_i)\\&\geq \sum_{j=1}^k(\tau(p)+\tau(q_j)-1)-(k-1)\tau(q_i)\\&=k\left(\tau(p)+\frac{\tau(q)}{k^2}-1\right)\!.\end{align*}
Thus,
![]() $\tau(p')=\sum_{i=1}^k\tau(p_i)\geq k^2(\tau(p)+({\tau(q)}/{k^2})-1)$
, proving that
$\tau(p')=\sum_{i=1}^k\tau(p_i)\geq k^2(\tau(p)+({\tau(q)}/{k^2})-1)$
, proving that
![]() $p'\neq 0$
and the desired lower bound.
$p'\neq 0$
and the desired lower bound.
Since
![]() $M_1p'=\mathbb Cp'$
, we have
$M_1p'=\mathbb Cp'$
, we have
![]() $Mp'=M_2p'$
. As
$Mp'=M_2p'$
. As
![]() $p'\leq q$
is non-zero and
$p'\leq q$
is non-zero and
![]() $M_2q\cong\mathbb M_k(\mathbb C)$
is a factor, we get that
$M_2q\cong\mathbb M_k(\mathbb C)$
is a factor, we get that
![]() $Mp'\cong\mathbb M_k(\mathbb C)$
, which finishes the proof.
$Mp'\cong\mathbb M_k(\mathbb C)$
, which finishes the proof.
3.2 Finite-dimensional extreme traces
In this subsection, we use the foregoing results to establish an obstruction to the trace simplex of a free product
![]() $C^*$
-algebra being a Poulsen simplex. We also refer to Lemma 6.5 for a converse.
$C^*$
-algebra being a Poulsen simplex. We also refer to Lemma 6.5 for a converse.
Theorem 3.4. Let
![]() $A=A_1*A_2$
be the free product of two unital, separable
$A=A_1*A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. Assume that
$A_2$
. Assume that
![]() $A_1$
admits an extreme one-dimensional trace
$A_1$
admits an extreme one-dimensional trace
![]() $\varphi_1$
which is isolated in
$\varphi_1$
which is isolated in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A_1)$
, and
$\partial_{\mathrm{e}}\mathrm{T}(A_1)$
, and
![]() $A_2$
admits an extreme k-dimensional trace
$A_2$
admits an extreme k-dimensional trace
![]() $\varphi_2$
which is isolated in
$\varphi_2$
which is isolated in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A_2)$
for some
$\partial_{\mathrm{e}}\mathrm{T}(A_2)$
for some
![]() $k\in\mathbb N$
.
$k\in\mathbb N$
.
Then A admits an extreme k-dimensional trace
![]() $\varphi$
which is isolated in
$\varphi$
which is isolated in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
and satisfies
$\partial_{\mathrm{e}}\mathrm{T}(A)$
and satisfies
![]() $\varphi_{|A_1}=\varphi_1$
and
$\varphi_{|A_1}=\varphi_1$
and
![]() $\varphi_{|A_2}=\varphi_2$
.
$\varphi_{|A_2}=\varphi_2$
.
Proof. Let
![]() $\rho_1:A_1\rightarrow\mathbb C$
and
$\rho_1:A_1\rightarrow\mathbb C$
and
![]() $\rho_2:A_2\rightarrow\mathbb M_k(\mathbb C)$
be the tracial representations associated to
$\rho_2:A_2\rightarrow\mathbb M_k(\mathbb C)$
be the tracial representations associated to
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
. Let
$\varphi_2$
. Let
![]() $\rho:A\rightarrow\mathbb M_k(\mathbb C)$
be the tracial representation given by
$\rho:A\rightarrow\mathbb M_k(\mathbb C)$
be the tracial representation given by
![]() $\rho(a_1)=\rho_1(a_1)1$
and
$\rho(a_1)=\rho_1(a_1)1$
and
![]() $\rho(a_2)=\rho_2(a_2)$
, for every
$\rho(a_2)=\rho_2(a_2)$
, for every
![]() $a_1\in A_1$
and
$a_1\in A_1$
and
![]() $a_2\in A_2.$
We will prove that
$a_2\in A_2.$
We will prove that
![]() $\varphi=\mathrm{tr}_k\circ\rho\in \partial_{\mathrm{e}}\mathrm{T}(A)$
is isolated, where
$\varphi=\mathrm{tr}_k\circ\rho\in \partial_{\mathrm{e}}\mathrm{T}(A)$
is isolated, where
![]() $\mathrm{tr}_k:\mathbb M_k(\mathbb C)\rightarrow\mathbb C$
denotes the normalized trace, thereby proving the theorem.
$\mathrm{tr}_k:\mathbb M_k(\mathbb C)\rightarrow\mathbb C$
denotes the normalized trace, thereby proving the theorem.
Let
![]() $(\psi_n)_{n\in\mathbb{N}}\subset\partial_{\mathrm{e}}\mathrm{T}(A)$
be a sequence such that
$(\psi_n)_{n\in\mathbb{N}}\subset\partial_{\mathrm{e}}\mathrm{T}(A)$
be a sequence such that
![]() $\psi_n\rightarrow\varphi$
. For
$\psi_n\rightarrow\varphi$
. For
![]() $i\in\{1,2\}$
, let
$i\in\{1,2\}$
, let
![]() $\mu_{i,n}$
be the Borel probability measure on
$\mu_{i,n}$
be the Borel probability measure on
![]() $\partial_{\mathrm{e}}\mathrm{T}(A_i)$
whose barycenter is
$\partial_{\mathrm{e}}\mathrm{T}(A_i)$
whose barycenter is
![]() ${\psi_n}_{|A_i}$
. Since
${\psi_n}_{|A_i}$
. Since
![]() $\varphi_i=\varphi_{|A_i}\in\partial_{\mathrm{e}}\mathrm{T}(A_i)$
is isolated, Corollary 3.2 gives that
$\varphi_i=\varphi_{|A_i}\in\partial_{\mathrm{e}}\mathrm{T}(A_i)$
is isolated, Corollary 3.2 gives that
![]() $\lambda_{i,n}:= \mu_{i,n}(\{\varphi_i\})\rightarrow 1$
for every
$\lambda_{i,n}:= \mu_{i,n}(\{\varphi_i\})\rightarrow 1$
for every
![]() $i\in\{1,2\}$
.
$i\in\{1,2\}$
.
For
![]() $n\in\mathbb N$
, let
$n\in\mathbb N$
, let
![]() $\pi_n:A\rightarrow M_n$
be a tracial representation, where
$\pi_n:A\rightarrow M_n$
be a tracial representation, where
![]() $(M_n,\tau_n)$
is a tracial factor, such that
$(M_n,\tau_n)$
is a tracial factor, such that
![]() $\psi_n=\tau_n\circ\pi_n$
and
$\psi_n=\tau_n\circ\pi_n$
and
![]() $\pi_n(A)''=M_n$
. For
$\pi_n(A)''=M_n$
. For
![]() $i\in\{1,2\}$
, let
$i\in\{1,2\}$
, let
![]() $M_{i,n}=\pi_n(A_i)''$
. Then there exist projections
$M_{i,n}=\pi_n(A_i)''$
. Then there exist projections
![]() $p_{1,n}\in \mathcal Z(M_{1,n})$
,
$p_{1,n}\in \mathcal Z(M_{1,n})$
,
![]() $p_{2,n}\in \mathcal Z(M_{2,n})$
and a
$p_{2,n}\in \mathcal Z(M_{2,n})$
and a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\Psi:\mathbb M_k(\mathbb C)\rightarrow M_{2,n}p_{2,n}$
such that
$\Psi:\mathbb M_k(\mathbb C)\rightarrow M_{2,n}p_{2,n}$
such that
![]() $\tau_n(p_{1,n})=\lambda_{1,n}$
,
$\tau_n(p_{1,n})=\lambda_{1,n}$
,
![]() $\tau_n(p_{2,n})=\lambda_{2,n}$
,
$\tau_n(p_{2,n})=\lambda_{2,n}$
,
By Proposition 3.3, there exists a projection
![]() $p_n'\in \mathcal Z(M_n)$
such that
$p_n'\in \mathcal Z(M_n)$
such that
![]() $p_n'\leq p_{1,n}\wedge p_{2,n}$
and
$p_n'\leq p_{1,n}\wedge p_{2,n}$
and
![]() $\tau(p_n')\geq k^2(\tau(p_{1,n})+({\tau(p_{2,n})}/{k^2})-1)=k^2(\lambda_{1,n}+({\lambda_{2,n}}/{k^2})-1)$
. Then
$\tau(p_n')\geq k^2(\tau(p_{1,n})+({\tau(p_{2,n})}/{k^2})-1)=k^2(\lambda_{1,n}+({\lambda_{2,n}}/{k^2})-1)$
. Then
![]() $\tau(p_n')\rightarrow 1$
. Since
$\tau(p_n')\rightarrow 1$
. Since
![]() $M_n$
is a factor we conclude that
$M_n$
is a factor we conclude that
![]() $p_n'=1$
for n large enough. Hence
$p_n'=1$
for n large enough. Hence
![]() $p_{1,n}=p_{2,n}=1$
for n large enough.
$p_{1,n}=p_{2,n}=1$
for n large enough.
Let
![]() $a=b_1c_1\cdots b_mc_m$
, where
$a=b_1c_1\cdots b_mc_m$
, where
![]() $b_1,\ldots,b_m\in A_1$
and
$b_1,\ldots,b_m\in A_1$
and
![]() $c_1,\ldots,c_m\in A_2$
, for some
$c_1,\ldots,c_m\in A_2$
, for some
![]() $m\in\mathbb N$
. By using (3.1) we get that
$m\in\mathbb N$
. By using (3.1) we get that
![]() $\pi_n(a)=\rho_1(a_1)\Psi(\rho_2(a_2))=\Psi(\rho_1(a_1)\rho_2(a_2))=\Psi(\rho(a))$
, where
$\pi_n(a)=\rho_1(a_1)\Psi(\rho_2(a_2))=\Psi(\rho_1(a_1)\rho_2(a_2))=\Psi(\rho(a))$
, where
![]() $a_1=b_1\cdots b_m\in A_1$
and
$a_1=b_1\cdots b_m\in A_1$
and
![]() $a_2=c_1\cdots c_m\in A_2$
. As
$a_2=c_1\cdots c_m\in A_2$
. As
![]() $\mathbb M_k(\mathbb C)$
is a factor, and thus has a unique trace, we get that
$\mathbb M_k(\mathbb C)$
is a factor, and thus has a unique trace, we get that
![]() $\tau_n(\Psi(y))=\mathrm{tr}_k(y)$
for every
$\tau_n(\Psi(y))=\mathrm{tr}_k(y)$
for every
![]() $y\in\mathbb M_k(\mathbb C)$
. These facts imply that
$y\in\mathbb M_k(\mathbb C)$
. These facts imply that
Since the linear span of such
![]() $a\in A$
is norm dense in A, we conclude that
$a\in A$
is norm dense in A, we conclude that
![]() $\psi_n=\tau_n\circ\pi_n=\varphi$
for n large enough. This implies that
$\psi_n=\tau_n\circ\pi_n=\varphi$
for n large enough. This implies that
![]() $\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
is isolated.
$\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
is isolated.
Corollary 3.5. Let A be a
![]() $C^*$
-algebra satisfying the assumptions of Theorem 3.4 and assume that
$C^*$
-algebra satisfying the assumptions of Theorem 3.4 and assume that
![]() $|\mathrm{T}(A)|\geq 2$
. Then
$|\mathrm{T}(A)|\geq 2$
. Then
![]() $\mathrm{T}(A)$
is not a Poulsen simplex.
$\mathrm{T}(A)$
is not a Poulsen simplex.
Proof. If
![]() $\mathrm{T}(A)$
were a Poulsen simplex, then the set of its extreme points,
$\mathrm{T}(A)$
were a Poulsen simplex, then the set of its extreme points,
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
, would be connected. In fact, by [Reference Lindenstrauss, Olsen and SternfeldLOS78], the set of extreme points of the Poulsen simplex is homeomorphic to
$\partial_{\mathrm{e}}\mathrm{T}(A)$
, would be connected. In fact, by [Reference Lindenstrauss, Olsen and SternfeldLOS78], the set of extreme points of the Poulsen simplex is homeomorphic to
![]() $\ell_2$
(as well as to any other infinite-dimensional separable Banach space). However,
$\ell_2$
(as well as to any other infinite-dimensional separable Banach space). However,
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
has an isolated point by Theorem 3.4. Since
$\partial_{\mathrm{e}}\mathrm{T}(A)$
has an isolated point by Theorem 3.4. Since
![]() $|\mathrm{T}(A)|\geq 2$
, we also have that
$|\mathrm{T}(A)|\geq 2$
, we also have that
![]() $|\partial_{\mathrm{e}}\mathrm{T}(A)|\geq 2$
and thus
$|\partial_{\mathrm{e}}\mathrm{T}(A)|\geq 2$
and thus
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
is not connected.
$\partial_{\mathrm{e}}\mathrm{T}(A)$
is not connected.
3.3 Infinite free products of
 $C^*$
-algebras
$C^*$
-algebras
In this section, we prove Proposition I, showing that the obstructions established in the previous sections for finite free products disappear when considering infinite free products.
Proof of Proposition I. We will prove that
![]() $\partial_{\mathrm{e}}\text{T}(A)\cap \text{T}_\infty(A)$
is dense in
$\partial_{\mathrm{e}}\text{T}(A)\cap \text{T}_\infty(A)$
is dense in
![]() $\text{T}(A)$
, and thus
$\text{T}(A)$
, and thus
![]() $\text{T}(A)$
is a Poulsen simplex. To this end, let
$\text{T}(A)$
is a Poulsen simplex. To this end, let
![]() $\varphi\in\text{T}(A)$
and let
$\varphi\in\text{T}(A)$
and let
![]() $\pi:A\rightarrow M$
be the associated tracial representation.
$\pi:A\rightarrow M$
be the associated tracial representation.
Let
![]() $i\geq 1$
. We claim that there is a tracial representation
$i\geq 1$
. We claim that there is a tracial representation
![]() $\rho_i:A_i\rightarrow N_i=\rho_i(A_i)''$
such that any minimal projection of
$\rho_i:A_i\rightarrow N_i=\rho_i(A_i)''$
such that any minimal projection of
![]() $N_i$
has trace at most
$N_i$
has trace at most
![]() $\frac{1}{2}$
. If
$\frac{1}{2}$
. If
![]() $A_i$
admits a factorial tracial representation
$A_i$
admits a factorial tracial representation
![]() $\pi_i$
of dimension at least 2, we can take
$\pi_i$
of dimension at least 2, we can take
![]() $\rho_i=\pi_i$
. Otherwise, all factorial tracial representations of
$\rho_i=\pi_i$
. Otherwise, all factorial tracial representations of
![]() $A_i$
are one-dimensional. Since
$A_i$
are one-dimensional. Since
![]() $\text{T}(A_i)$
does not consist of a single one-dimensional trace, there are two distinct one-dimensional tracial representations
$\text{T}(A_i)$
does not consist of a single one-dimensional trace, there are two distinct one-dimensional tracial representations
![]() $\pi_i^1,\pi_i^2:A_i\rightarrow\mathbb C$
. Endow
$\pi_i^1,\pi_i^2:A_i\rightarrow\mathbb C$
. Endow
![]() $\mathbb C^2$
with the trace assigning
$\mathbb C^2$
with the trace assigning
![]() $\tfrac{1}{2}$
to (1, 0) and let
$\tfrac{1}{2}$
to (1, 0) and let
![]() $\rho_i=\pi_i^1\oplus\pi_i^2:A\rightarrow\mathbb C^2$
. Then any minimal projection in
$\rho_i=\pi_i^1\oplus\pi_i^2:A\rightarrow\mathbb C^2$
. Then any minimal projection in
![]() $\rho_i(A_i)''=\mathbb C^2$
has trace
$\rho_i(A_i)''=\mathbb C^2$
has trace
![]() $\tfrac{1}{2}$
.
$\tfrac{1}{2}$
.
For
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $M_n=M*(*_{i>n}N_i)$
and define a
$M_n=M*(*_{i>n}N_i)$
and define a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi_n:A\rightarrow M_n$
by letting
$\pi_n:A\rightarrow M_n$
by letting
![]() ${\pi_n}_{|A_i}=\pi_{|A_i}$
if
${\pi_n}_{|A_i}=\pi_{|A_i}$
if
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() ${\pi_n}_{|A_i}=\rho_i$
if
${\pi_n}_{|A_i}=\rho_i$
if
![]() $i>n$
. Denote
$i>n$
. Denote
![]() $\varphi_n:=\tau\circ\pi_n\in\text{T}(A)$
. Since
$\varphi_n:=\tau\circ\pi_n\in\text{T}(A)$
. Since
![]() $\pi_n(a)=\pi(a)$
, for every
$\pi_n(a)=\pi(a)$
, for every
![]() $a\in*_{i=1}^nA_i$
, we get that
$a\in*_{i=1}^nA_i$
, we get that
![]() $\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
, for every
$\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
, for every
![]() $a\in A$
. Thus,
$a\in A$
. Thus,
![]() $\varphi_n\rightarrow\varphi$
.
$\varphi_n\rightarrow\varphi$
.
In order to finish the proof, it is enough to argue that
![]() $\varphi_n\in\partial_{\mathrm{e}}\text{T}(A)\cap \text{T}_\infty(A)$
or, equivalently, that
$\varphi_n\in\partial_{\mathrm{e}}\text{T}(A)\cap \text{T}_\infty(A)$
or, equivalently, that
![]() $\pi_n(A)''$
is a II
$\pi_n(A)''$
is a II
![]() $_1$
factor for every
$_1$
factor for every
![]() $n\geq 1$
. Let
$n\geq 1$
. Let
![]() $n\geq 1$
and put
$n\geq 1$
and put
![]() $P_n=\pi(*_{i=1}^nA_i)''$
. By the construction of
$P_n=\pi(*_{i=1}^nA_i)''$
. By the construction of
![]() $\pi_n$
we have that
$\pi_n$
we have that
![]() $\pi_n(A)''=P_n*(*_{i=n+1}^\infty N_i)$
. Thus, letting
$\pi_n(A)''=P_n*(*_{i=n+1}^\infty N_i)$
. Thus, letting
![]() $Q_n=P_n*(*_{i=n+5}^\infty N_i)$
, we have
$Q_n=P_n*(*_{i=n+5}^\infty N_i)$
, we have
Since every minimal projection in
![]() $N_i$
has trace at most
$N_i$
has trace at most
![]() $\frac{1}{2}$
, [Reference DykemaDyk93] implies that
$\frac{1}{2}$
, [Reference DykemaDyk93] implies that
![]() $N_i*N_{i+1}$
is diffuse for every
$N_i*N_{i+1}$
is diffuse for every
![]() $i\geq 1$
. Indeed, each
$i\geq 1$
. Indeed, each
![]() $N_i$
is either a II
$N_i$
is either a II
![]() $_1$
factor, isomorphic to a matrix algebra
$_1$
factor, isomorphic to a matrix algebra
![]() $\mathbb{M}_n(\mathbb{C})$
for some
$\mathbb{M}_n(\mathbb{C})$
for some
![]() $n\geq 2$
, or isomorphic to
$n\geq 2$
, or isomorphic to
![]() $\mathbb{C}^2$
with each minimal projection of trace
$\mathbb{C}^2$
with each minimal projection of trace
![]() $\frac{1}{2}$
. If either
$\frac{1}{2}$
. If either
![]() $N_i$
or
$N_i$
or
![]() $N_{i+1}$
is a II
$N_{i+1}$
is a II
![]() $_1$
factor, and hence diffuse, then
$_1$
factor, and hence diffuse, then
![]() $N_i*N_{i+1}$
is obviously diffuse. In the remaining cases, the formulas in [Reference DykemaDyk93, Theorem 1.1, Proposition 3.2, Theorem 3.6] show that the free product
$N_i*N_{i+1}$
is obviously diffuse. In the remaining cases, the formulas in [Reference DykemaDyk93, Theorem 1.1, Proposition 3.2, Theorem 3.6] show that the free product
![]() $N_i*N_{i+1}$
is equal to a diffuse von Neumann algebra plus additional finite-dimensional direct summands with weights determined by the traces of the minimal projections in
$N_i*N_{i+1}$
is equal to a diffuse von Neumann algebra plus additional finite-dimensional direct summands with weights determined by the traces of the minimal projections in
![]() $N_i$
and
$N_i$
and
![]() $N_{i+1}$
. From these formulas it is immediate that all the finite-dimensional summands disappear if all these minimal projections have trace at most
$N_{i+1}$
. From these formulas it is immediate that all the finite-dimensional summands disappear if all these minimal projections have trace at most
![]() $\frac{1}{2}$
.
$\frac{1}{2}$
.
Finally, using the above fact, the free product decomposition (3.2) of
![]() $\pi_n(A)''$
, and [Reference PopaPop83] (or [Reference Ioana, Peterson and PopaIPP08, Theorem 1.1]) we get that
$\pi_n(A)''$
, and [Reference PopaPop83] (or [Reference Ioana, Peterson and PopaIPP08, Theorem 1.1]) we get that
![]() $\mathcal Z(\pi_n(A)'')\subset (N_{n+1}*N_{n+2})\cap (N_{n+3}*N_{n+4})=\mathbb C1$
. Indeed, [Reference Ioana, Peterson and PopaIPP08, Theorem 1.1] shows, in particular, that if
$\mathcal Z(\pi_n(A)'')\subset (N_{n+1}*N_{n+2})\cap (N_{n+3}*N_{n+4})=\mathbb C1$
. Indeed, [Reference Ioana, Peterson and PopaIPP08, Theorem 1.1] shows, in particular, that if
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are diffuse von Neumann algebras, then
$M_2$
are diffuse von Neumann algebras, then
![]() $M_1'\cap M_1*M_2\subset M_1$
and
$M_1'\cap M_1*M_2\subset M_1$
and
![]() $M_2'\cap M_1*M_2\subset M_2$
, which immediately yields the claim.
$M_2'\cap M_1*M_2\subset M_2$
, which immediately yields the claim.
We conclude that
![]() $\pi_n(A)''$
is a II
$\pi_n(A)''$
is a II
![]() $_1$
factor, as desired, thus finishing the proof.
$_1$
factor, as desired, thus finishing the proof.
4. Pairs of approximately factorial von Neumann subalgebras
This section is devoted to proving Theorem E. It is convenient to state the theorem using the following terminology.
Definition 4.1. Let
![]() $M_1,M_2$
be tracial von Neumann algebras.
$M_1,M_2$
be tracial von Neumann algebras.
-
(1) Let
 $(M,\tau)$
be a tracial von Neumann algebra which contains
$(M,\tau)$
be a tracial von Neumann algebra which contains
 $M_1$
and
$M_1$
and
 $M_2$
. We say that the triple
$M_2$
. We say that the triple
 $(M_1,M_2,M)$
is approximately factorial if for every
$(M_1,M_2,M)$
is approximately factorial if for every
 $\varepsilon>0$
, we can find a II
$\varepsilon>0$
, we can find a II
 $_1$
factor
$_1$
factor
 $M_\varepsilon$
and
$M_\varepsilon$
and
 $v_\varepsilon\in\mathcal U(M_\varepsilon)$
such that
$v_\varepsilon\in\mathcal U(M_\varepsilon)$
such that
 $M\subset M_\varepsilon$
,
$M\subset M_\varepsilon$
,
 $\|v_\varepsilon-1\|_2<\varepsilon$
and
$\|v_\varepsilon-1\|_2<\varepsilon$
and
 $M_1\vee v_\varepsilon M_2v_\varepsilon^*$
is a II
$M_1\vee v_\varepsilon M_2v_\varepsilon^*$
is a II
 $_1$
factor.
$_1$
factor. -
(2) We say that the pair
 $(M_1,M_2)$
is approximately factorial if the triple
$(M_1,M_2)$
is approximately factorial if the triple
 $(M_1,M_2,M)$
is approximately factorial for every tracial von Neumann algebra
$(M_1,M_2,M)$
is approximately factorial for every tracial von Neumann algebra
 $(M,\tau)$
which contains
$(M,\tau)$
which contains
 $M_1$
and
$M_1$
and
 $M_2$
.
$M_2$
.
With this terminology, Theorem E asserts that a pair
![]() $(M_1,M_2)$
is approximately factorial provided that
$(M_1,M_2)$
is approximately factorial provided that
![]() $M_1\neq \mathbb C1$
,
$M_1\neq \mathbb C1$
,
![]() $M_2\neq \mathbb C1$
,
$M_2\neq \mathbb C1$
,
![]() $\dim(M_1)+\dim(M_2)\geq 5$
and
$\dim(M_1)+\dim(M_2)\geq 5$
and
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
.
$\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
.
Before continuing, we make a few observations about Definition 4.1.
Remark 4.2.
-
(1) Since every tracial von Neumann algebra
 $(\mathcal M,\tau)$
embeds into a II
$(\mathcal M,\tau)$
embeds into a II
 $_1$
factor (e.g.,
$_1$
factor (e.g.,
 $\mathcal M*\mathrm{L}(\mathbb F_2)$
), taking
$\mathcal M*\mathrm{L}(\mathbb F_2)$
), taking
 $M_\varepsilon$
to be a tracial von Neumann does not change Definition 4.1(1).
$M_\varepsilon$
to be a tracial von Neumann does not change Definition 4.1(1). -
(2) We can take the II
 $_1$
factor
$_1$
factor
 $M_\varepsilon$
to be independent of
$M_\varepsilon$
to be independent of
 $\varepsilon$
in Definition 4.1(1). Indeed, if Definition 4.1(1) holds, then it still holds if we replace
$\varepsilon$
in Definition 4.1(1). Indeed, if Definition 4.1(1) holds, then it still holds if we replace
 $M_\varepsilon$
with
$M_\varepsilon$
with
 $*_{n\in\mathbb N, M}M_{\frac{1}{n}}$
for every
$*_{n\in\mathbb N, M}M_{\frac{1}{n}}$
for every
 $\varepsilon>0$
; see also the paragraph following the statement of Theorem E.
$\varepsilon>0$
; see also the paragraph following the statement of Theorem E. -
(3) If
 $M\subset \widetilde M$
are tracial von Neumann algebras which contain
$M\subset \widetilde M$
are tracial von Neumann algebras which contain
 $M_1$
and
$M_1$
and
 $M_2$
, then
$M_2$
, then
 $(M_1,M_2,M)$
is approximately factorial if and only if
$(M_1,M_2,M)$
is approximately factorial if and only if
 $(M_1,M_2,\widetilde M)$
is approximately factorial (for the ‘only if’ part, consider the push-out
$(M_1,M_2,\widetilde M)$
is approximately factorial (for the ‘only if’ part, consider the push-out
 $\widetilde M_\varepsilon =\widetilde{M} *_M M_\varepsilon$
). Consequently,
$\widetilde M_\varepsilon =\widetilde{M} *_M M_\varepsilon$
). Consequently,
 $(M_1,M_2,M)$
is approximately factorial if and only if
$(M_1,M_2,M)$
is approximately factorial if and only if
 $(M_1,M_2,M_1\vee M_2)$
is approximately factorial.
$(M_1,M_2,M_1\vee M_2)$
is approximately factorial. -
(4) A triple
 $(M_1,M_2,M)$
(respectively, a pair
$(M_1,M_2,M)$
(respectively, a pair
 $(M_1,M_2)$
) is approximately factorial if and only if
$(M_1,M_2)$
) is approximately factorial if and only if
 $(M_2,M_1,M)$
(respectively,
$(M_2,M_1,M)$
(respectively,
 $(M_2,M_1)$
) is approximately factorial.
$(M_2,M_1)$
) is approximately factorial. -
(5) If
 $M_1=\mathbb C1$
, then a triple
$M_1=\mathbb C1$
, then a triple
 $(M_1,M_2,M)$
(respectively, a pair
$(M_1,M_2,M)$
(respectively, a pair
 $(M_1,M_2)$
) is approximately factorial if and only if
$(M_1,M_2)$
) is approximately factorial if and only if
 $M_2$
is a II
$M_2$
is a II
 $_1$
factor.
$_1$
factor.
4.1 Perturbations in amalgamated free products
Definition 4.1 allows for perturbations within a larger von Neumann algebra
![]() $M_\varepsilon$
. We will construct this ambient von Neumann algebra
$M_\varepsilon$
. We will construct this ambient von Neumann algebra
![]() $M_\varepsilon$
as an iterated amalgamated free product, utilizing results from [Reference Ioana, Peterson and PopaIPP08] concerning relative commutants of subalgebras, to establish factoriality. The following lemma provides a criterion for when a particular type of perturbation within an amalgamated free product generates a II
$M_\varepsilon$
as an iterated amalgamated free product, utilizing results from [Reference Ioana, Peterson and PopaIPP08] concerning relative commutants of subalgebras, to establish factoriality. The following lemma provides a criterion for when a particular type of perturbation within an amalgamated free product generates a II
![]() $_1$
factor.
$_1$
factor.
We recall that an element u in a tracial von Neumann algebra
![]() $(M,\tau)$
is called a Haar unitary if u is unitary and it satisfies
$(M,\tau)$
is called a Haar unitary if u is unitary and it satisfies
![]() $\tau(u^n)=0$
for all
$\tau(u^n)=0$
for all
![]() $n\in \mathbb{Z}\backslash \{0\}$
. Additionally, for von Neumann subalgebras
$n\in \mathbb{Z}\backslash \{0\}$
. Additionally, for von Neumann subalgebras
![]() $P,Q\subset M$
, we write
$P,Q\subset M$
, we write
![]() $P\prec_M Q$
if a corner of P embeds into Q inside M in the sense of Popa, i.e., if there exist projections
$P\prec_M Q$
if a corner of P embeds into Q inside M in the sense of Popa, i.e., if there exist projections
![]() $p_0\in P$
,
$p_0\in P$
,
![]() $q_0\in Q$
, a
$q_0\in Q$
, a
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\psi:p_0Pp_0\to q_0Qq_0$
and a non-zero partial isometry
$\psi:p_0Pp_0\to q_0Qq_0$
and a non-zero partial isometry
![]() $v\in q_0Mp_0$
such that
$v\in q_0Mp_0$
such that
![]() $\psi(x)v=vx$
for all
$\psi(x)v=vx$
for all
![]() $x\in p_0Pp_0$
(see Theorem 2.1 and Corollary 2.3 in [Reference PopaPop06]). In particular, we point out that if P is diffuse, then
$x\in p_0Pp_0$
(see Theorem 2.1 and Corollary 2.3 in [Reference PopaPop06]). In particular, we point out that if P is diffuse, then
![]() $P\nprec_M \mathbb{C}1$
, and if P is type II
$P\nprec_M \mathbb{C}1$
, and if P is type II
![]() $_1$
and Q is type I, then
$_1$
and Q is type I, then
![]() $P\nprec_M Q$
.
$P\nprec_M Q$
.
Lemma 4.3. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra. Let
$(M,\tau)$
be a tracial von Neumann algebra. Let
![]() $A_1\subset M_1\subset M$
and
$A_1\subset M_1\subset M$
and
![]() $A_2\subset M_2\subset M$
be von Neumann subalgebras. Define
$A_2\subset M_2\subset M$
be von Neumann subalgebras. Define
![]() $\widetilde M=M*_{A_2}(A_2\overline{\otimes}\mathrm{L}(\mathbb Z))$
, let
$\widetilde M=M*_{A_2}(A_2\overline{\otimes}\mathrm{L}(\mathbb Z))$
, let
![]() $u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary and choose
$u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary and choose
![]() $h=h^*\in \mathrm{L}(\mathbb Z)$
such that
$h=h^*\in \mathrm{L}(\mathbb Z)$
such that
![]() $u=\exp(ih)$
. For
$u=\exp(ih)$
. For
![]() $t>0$
, set
$t>0$
, set
![]() $u_t=\exp(ith)$
. Assume that:
$u_t=\exp(ith)$
. Assume that:
-
(1)
 $M_1\vee A_2\nprec_M A_2$
;
$M_1\vee A_2\nprec_M A_2$
; -
(2)
 $A_1\vee A_2$
or
$A_1\vee A_2$
or
 $M_2$
is a factor;
$M_2$
is a factor; -
(3)
 $A_2\subsetneq M_2$
.
$A_2\subsetneq M_2$
.
Then
![]() $M_1\vee u_tM_2u_t^*$
is a II
$M_1\vee u_tM_2u_t^*$
is a II
![]() $_1$
factor for every
$_1$
factor for every
![]() $t>0$
.
$t>0$
.
Proof. Let
![]() $t>0$
and denote
$t>0$
and denote
![]() $N_t=M_1\vee u_tM_2u_t^*$
. Since
$N_t=M_1\vee u_tM_2u_t^*$
. Since
![]() $u_t\in\mathrm{L}(\mathbb Z)$
commutes with
$u_t\in\mathrm{L}(\mathbb Z)$
commutes with
![]() $A_2$
, we get that
$A_2$
, we get that
![]() $u_tA_2u_t^*=A_2$
. Thus,
$u_tA_2u_t^*=A_2$
. Thus,
![]() $N_t$
contains
$N_t$
contains
![]() $M_1\vee A_2$
. Since
$M_1\vee A_2$
. Since
![]() $M_1\vee A_2\nprec_M A_2$
by assumption (1), [Reference Ioana, Peterson and PopaIPP08, Theorem 1.1] implies that
$M_1\vee A_2\nprec_M A_2$
by assumption (1), [Reference Ioana, Peterson and PopaIPP08, Theorem 1.1] implies that
![]() $(M_1\vee A_2)'\cap \widetilde M\subset M$
. Hence,
$(M_1\vee A_2)'\cap \widetilde M\subset M$
. Hence,
![]() $N_t'\cap\widetilde M\subset M$
and so
$N_t'\cap\widetilde M\subset M$
and so
![]() $\mathcal Z(N_t)\subset M$
.
$\mathcal Z(N_t)\subset M$
.
Assume by contradiction that
![]() $N_t$
is not a II
$N_t$
is not a II
![]() $_1$
factor. Then there is a projection
$_1$
factor. Then there is a projection
![]() $p\in \mathcal Z(N_t)\setminus\{0,1\}$
; put
$p\in \mathcal Z(N_t)\setminus\{0,1\}$
; put
![]() $y=p-\mathrm{E}_{A_2}(p)$
. By assumption (2), there exists a factor P with
$y=p-\mathrm{E}_{A_2}(p)$
. By assumption (2), there exists a factor P with
![]() $A_2\subset P\subset N_t$
. This implies that
$A_2\subset P\subset N_t$
. This implies that
![]() $\mathrm{E}_{P}(p)\in\mathcal Z(P)=\mathbb{C} 1$
, and therefore
$\mathrm{E}_{P}(p)\in\mathcal Z(P)=\mathbb{C} 1$
, and therefore
![]() $\mathrm{E}_{A_2}(p)=\mathrm{E}_{A_2}(\mathrm{E}_{P}(p)) =\tau(p)$
. It follows that
$\mathrm{E}_{A_2}(p)=\mathrm{E}_{A_2}(\mathrm{E}_{P}(p)) =\tau(p)$
. It follows that
![]() $y=p-\tau(p)$
. From this we deduce that y commutes with
$y=p-\tau(p)$
. From this we deduce that y commutes with
![]() $u_t M_2 u_t^*$
(in fact with
$u_t M_2 u_t^*$
(in fact with
![]() $N_t$
) and that y is invertible. We will show that the existence of an element
$N_t$
) and that y is invertible. We will show that the existence of an element
![]() $y\in M$
with these two properties, along with the condition
$y\in M$
with these two properties, along with the condition
![]() $A_2\subsetneq M_2$
, leads to a contradiction.
$A_2\subsetneq M_2$
, leads to a contradiction.
Indeed, as
![]() $A_2\subsetneq M_2$
, we can find a non-zero element
$A_2\subsetneq M_2$
, we can find a non-zero element
![]() $x\in M_2$
with
$x\in M_2$
with
![]() $\mathrm{E}_{A_2}(x)=0$
. Since y commutes with
$\mathrm{E}_{A_2}(x)=0$
. Since y commutes with
![]() $u_tM_2u_t^*$
, we have
$u_tM_2u_t^*$
, we have
Put
![]() $v_t=u_t-\tau(u_t)$
, and let Q denote the orthogonal projection from
$v_t=u_t-\tau(u_t)$
, and let Q denote the orthogonal projection from
![]() $\mathrm{L}^2(\widetilde M)$
onto the
$\mathrm{L}^2(\widetilde M)$
onto the
![]() $\|\cdot\|_2$
-closure of the linear span of
$\|\cdot\|_2$
-closure of the linear span of
![]() $\{z_1z_2z_3z_4\mid z_1,z_3\in A_2\overline{\otimes}\mathrm{L}(\mathbb Z), z_2,z_4\in M \text{ and for all} 1\leq i\leq 4: \mathrm{E}_{A_2}(z_i)=0\}$
. It is immediate that
$\{z_1z_2z_3z_4\mid z_1,z_3\in A_2\overline{\otimes}\mathrm{L}(\mathbb Z), z_2,z_4\in M \text{ and for all} 1\leq i\leq 4: \mathrm{E}_{A_2}(z_i)=0\}$
. It is immediate that
![]() $Q(u_txu_t^*y)=v_txv_t^*y$
and
$Q(u_txu_t^*y)=v_txv_t^*y$
and
![]() $Q(yu_txu_t^*)=0$
, and (4.1) thus implies that
$Q(yu_txu_t^*)=0$
, and (4.1) thus implies that
![]() $v_txv_t^*y=0$
. Using that
$v_txv_t^*y=0$
. Using that
![]() $\mathrm{E}_{A_2}(x)=\mathrm{E}_{A_2}(y)=\mathrm{E}_{A_2}(v_t)=0$
,
$\mathrm{E}_{A_2}(x)=\mathrm{E}_{A_2}(y)=\mathrm{E}_{A_2}(v_t)=0$
,
![]() $\mathrm{E}_{A_2}(v_t^*v_t)=\mathrm{E}_{A_2}(v_tv_t^*)=\|v_t\|_2^2\cdot 1$
and
$\mathrm{E}_{A_2}(v_t^*v_t)=\mathrm{E}_{A_2}(v_tv_t^*)=\|v_t\|_2^2\cdot 1$
and
![]() $v_t\in A_2'\cap\widetilde M$
, we deduce that
$v_t\in A_2'\cap\widetilde M$
, we deduce that
 \begin{align*} 0=\|v_txv_t^*y\|_2^2=\tau(y^*v_tx^*v_t^*v_txv_t^*y)=&\|v_t\|_2^2\tau(y^*v_tx^*xv_t^*y)\\=&\|v_t\|_2^2\tau(y^*v_t\mathrm{E}_{A_2}(x^*x)v_t^*y) \\=&\|v_t\|_2^2\tau(y^*\mathrm{E}_{A_2}(x^*x)v_tv_t^*y)\\=&\|v_t\|_2^4\tau(y^*\mathrm{E}_{A_2}(x^*x)y).\end{align*}
\begin{align*} 0=\|v_txv_t^*y\|_2^2=\tau(y^*v_tx^*v_t^*v_txv_t^*y)=&\|v_t\|_2^2\tau(y^*v_tx^*xv_t^*y)\\=&\|v_t\|_2^2\tau(y^*v_t\mathrm{E}_{A_2}(x^*x)v_t^*y) \\=&\|v_t\|_2^2\tau(y^*\mathrm{E}_{A_2}(x^*x)v_tv_t^*y)\\=&\|v_t\|_2^4\tau(y^*\mathrm{E}_{A_2}(x^*x)y).\end{align*}
In the third equality we used that since
![]() $\mathrm{E}_{A_2}(x)=\mathrm{E}_{A_2}(y)=\mathrm{E}_{A_2}(v_t)=\mathrm{E}_{A_2}(v_t^*v_t-\|v_t\|_2^2\cdot 1)=0$
,
$\mathrm{E}_{A_2}(x)=\mathrm{E}_{A_2}(y)=\mathrm{E}_{A_2}(v_t)=\mathrm{E}_{A_2}(v_t^*v_t-\|v_t\|_2^2\cdot 1)=0$
,
![]() $x,y\in M$
and
$x,y\in M$
and
![]() $v_t,v_t^*v_t-\|v_t\|_2^2\cdot 1\in A_2\overline{\otimes}\text{L}(\mathbb Z)$
, the alternating word
$v_t,v_t^*v_t-\|v_t\|_2^2\cdot 1\in A_2\overline{\otimes}\text{L}(\mathbb Z)$
, the alternating word
![]() $y^*v_tx^*(v_t^*v_t-\|v_t\|_2^2\cdot 1)xv_t^*y$
has trace zero. Similarly, in the fourth and sixth equalities, we used that the alternating words
$y^*v_tx^*(v_t^*v_t-\|v_t\|_2^2\cdot 1)xv_t^*y$
has trace zero. Similarly, in the fourth and sixth equalities, we used that the alternating words
![]() $y^*v_t(x^*x-\text{E}_{A_2}(x^*x))v_t^*y$
and
$y^*v_t(x^*x-\text{E}_{A_2}(x^*x))v_t^*y$
and
![]() $(y^*\text{E}_{A_2}(x^*x))(v_tv_t^*-\|v_t\|_2^2\cdot 1)y$
have traces equal to zero.
$(y^*\text{E}_{A_2}(x^*x))(v_tv_t^*-\|v_t\|_2^2\cdot 1)y$
have traces equal to zero.
Since
![]() $v_t\neq 0$
, we derive that
$v_t\neq 0$
, we derive that
![]() $y^*\mathrm{E}_{A_2}(x^*x)y=0$
. Since y is invertible, it follows that
$y^*\mathrm{E}_{A_2}(x^*x)y=0$
. Since y is invertible, it follows that
![]() $\mathrm{E}_{A_2}(x^*x)=0$
and hence
$\mathrm{E}_{A_2}(x^*x)=0$
and hence
![]() $x=0$
, which is a contradiction. In conclusion,
$x=0$
, which is a contradiction. In conclusion,
![]() $N_t$
is a II
$N_t$
is a II
![]() $_1$
factor.
$_1$
factor.
Note that the above proof still works if we replace
![]() $u_t$
with any unitary from
$u_t$
with any unitary from
![]() $\text{L}(\mathbb Z)\setminus\mathbb C1$
. We nevertheless formulated Lemma 4.3 in this particular way which is more common in the free probability context.
$\text{L}(\mathbb Z)\setminus\mathbb C1$
. We nevertheless formulated Lemma 4.3 in this particular way which is more common in the free probability context.
We obtain the following immediate consequence of Lemma 4.3, establishing the special case of Theorem E when one of the algebras is diffuse.
Corollary 4.4. Let
![]() $M_1$
and
$M_1$
and
![]() $M_2$
be tracial von Neumann algebras such that
$M_2$
be tracial von Neumann algebras such that
![]() $M_1$
is diffuse and
$M_1$
is diffuse and
![]() $M_2\neq \mathbb C1$
. Then
$M_2\neq \mathbb C1$
. Then
![]() $(M_1,M_2)$
is approximately factorial.
$(M_1,M_2)$
is approximately factorial.
Proof. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra which contains
$(M,\tau)$
be a tracial von Neumann algebra which contains
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. Let
$M_2$
. Let
![]() $\widetilde M=M*\mathrm{L}(\mathbb Z)$
,
$\widetilde M=M*\mathrm{L}(\mathbb Z)$
,
![]() $u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary, and
$u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary, and
![]() $h=h^*\in \mathrm{L}(\mathbb Z)$
such that
$h=h^*\in \mathrm{L}(\mathbb Z)$
such that
![]() $u=\exp(ih)$
. For
$u=\exp(ih)$
. For
![]() $t>0$
, let
$t>0$
, let
![]() $u_t=\exp(ith)$
. Since
$u_t=\exp(ith)$
. Since
![]() $M_1$
is diffuse, we have that
$M_1$
is diffuse, we have that
![]() $M_1\nprec_M\mathbb C1$
. Applying Lemma 4.3 with
$M_1\nprec_M\mathbb C1$
. Applying Lemma 4.3 with
![]() $A_1=A_2=\mathbb C1$
immediately yields that
$A_1=A_2=\mathbb C1$
immediately yields that
![]() $M_1\vee u_tM_2u_t^*$
is a II
$M_1\vee u_tM_2u_t^*$
is a II
![]() $_1$
factor for every
$_1$
factor for every
![]() $t>0$
. Since
$t>0$
. Since
![]() $\|u_t-1\|_2<\varepsilon$
, for any small enough
$\|u_t-1\|_2<\varepsilon$
, for any small enough
![]() $t>0$
the conclusion follows.
$t>0$
the conclusion follows.
Using Lemma 4.3, we show next that the property of being approximately factorial is inherited from abelian subalgebras.
Proposition 4.5. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra and consider von Neumann subalgebras
$(M,\tau)$
be a tracial von Neumann algebra and consider von Neumann subalgebras
![]() $A_1\subset M_1\subset M$
and
$A_1\subset M_1\subset M$
and
![]() $A_2\subsetneq M_2\subset M$
. Assume that
$A_2\subsetneq M_2\subset M$
. Assume that
![]() $A_2$
is type I (e.g., abelian). If
$A_2$
is type I (e.g., abelian). If
![]() $(A_1,A_2,M)$
is approximately factorial, then
$(A_1,A_2,M)$
is approximately factorial, then
![]() $(M_1,M_2,M)$
is approximately factorial.
$(M_1,M_2,M)$
is approximately factorial.
Proof. Assume that the triple
![]() $(A_1,A_2,M)$
is approximately factorial. Then for any
$(A_1,A_2,M)$
is approximately factorial. Then for any
![]() $\varepsilon>0$
, there exist a II
$\varepsilon>0$
, there exist a II
![]() $_1$
factor
$_1$
factor
![]() $M_\varepsilon$
and
$M_\varepsilon$
and
![]() $v_\varepsilon\in \mathcal U(M_\varepsilon)$
such that
$v_\varepsilon\in \mathcal U(M_\varepsilon)$
such that
![]() $M\subset M_\varepsilon$
,
$M\subset M_\varepsilon$
,
![]() $\|v_\varepsilon-1\|_2<\varepsilon$
, and
$\|v_\varepsilon-1\|_2<\varepsilon$
, and
![]() $A_1 \vee v_\varepsilon A_2v_\varepsilon^*$
is a II
$A_1 \vee v_\varepsilon A_2v_\varepsilon^*$
is a II
![]() $_1$
factor.
$_1$
factor.
Fix
![]() $\varepsilon>0$
and define
$\varepsilon>0$
and define
![]() $\widetilde{M}_\varepsilon=M_{\varepsilon}*_{v_{\varepsilon} A_2v_{\varepsilon}^*}(v_{\varepsilon} A_2v_{\varepsilon}^*\overline{\otimes}\mathrm{L}(\mathbb Z))$
. Let
$\widetilde{M}_\varepsilon=M_{\varepsilon}*_{v_{\varepsilon} A_2v_{\varepsilon}^*}(v_{\varepsilon} A_2v_{\varepsilon}^*\overline{\otimes}\mathrm{L}(\mathbb Z))$
. Let
![]() $u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary and
$u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary and
![]() $h=h^*\in \mathrm{L}(\mathbb Z)$
with
$h=h^*\in \mathrm{L}(\mathbb Z)$
with
![]() $u=\exp(ih)$
. Let
$u=\exp(ih)$
. Let
![]() $t>0$
such that
$t>0$
such that
![]() $u_t=\exp(ith)$
satisfies
$u_t=\exp(ith)$
satisfies
![]() $\|u_t-1\|_2<\varepsilon-\|v_\varepsilon-1\|_2$
.
$\|u_t-1\|_2<\varepsilon-\|v_\varepsilon-1\|_2$
.
Since
![]() $A_1 \vee v_\varepsilon A_2v_\varepsilon^*$
is a II
$A_1 \vee v_\varepsilon A_2v_\varepsilon^*$
is a II
![]() $_1$
factor, we get that
$_1$
factor, we get that
![]() $M_1 \vee v_\varepsilon A_2v_\varepsilon^*$
is of type II
$M_1 \vee v_\varepsilon A_2v_\varepsilon^*$
is of type II
![]() $_1$
. Since
$_1$
. Since
![]() $A_2$
is of type I, we derive that
$A_2$
is of type I, we derive that
![]() $M_1 \vee v_\varepsilon A_2v_\varepsilon^*\nprec_{ M_\varepsilon} v_\varepsilon A_2v_\varepsilon^*$
. Since we also assume that
$M_1 \vee v_\varepsilon A_2v_\varepsilon^*\nprec_{ M_\varepsilon} v_\varepsilon A_2v_\varepsilon^*$
. Since we also assume that
![]() $A_2\subsetneq M_2$
, we derive from Lemma 4.3 that
$A_2\subsetneq M_2$
, we derive from Lemma 4.3 that
![]() $M_1 \vee u_tv_{\varepsilon}M_2v_{\varepsilon}^*u_t^*$
is a II
$M_1 \vee u_tv_{\varepsilon}M_2v_{\varepsilon}^*u_t^*$
is a II
![]() $_1$
factor. Since
$_1$
factor. Since
![]() $\|u_tv_\varepsilon-1\|_2\leq \|u_t-1\|_2+\|v_\varepsilon-1\|_2<\varepsilon$
, we conclude that the triple
$\|u_tv_\varepsilon-1\|_2\leq \|u_t-1\|_2+\|v_\varepsilon-1\|_2<\varepsilon$
, we conclude that the triple
![]() $(M_1,M_2,M)$
is approximately factorial.
$(M_1,M_2,M)$
is approximately factorial.
Last, we establish approximate factoriality in the presence of projections of trace
![]() $\frac{1}{2}$
and factoriality of one of the algebras.
$\frac{1}{2}$
and factoriality of one of the algebras.
Proposition 4.6. Let
![]() $M_1$
and
$M_1$
and
![]() $M_2$
be tracial von Neumann algebras, each admitting a projection of trace
$M_2$
be tracial von Neumann algebras, each admitting a projection of trace
![]() $\frac{1}{2}$
. Assume that at least one of
$\frac{1}{2}$
. Assume that at least one of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
is a factor. Then the pair
$M_2$
is a factor. Then the pair
![]() $(M_1,M_2)$
is approximately factorial.
$(M_1,M_2)$
is approximately factorial.
Proof. Assume without loss of generality that
![]() $M_2$
is a factor. Let
$M_2$
is a factor. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra containing
$(M,\tau)$
be a tracial von Neumann algebra containing
![]() $M_1$
and
$M_1$
and
![]() $M_2$
, and let
$M_2$
, and let
![]() $\varepsilon>0$
. Let
$\varepsilon>0$
. Let
![]() $p_1\in M_1$
and
$p_1\in M_1$
and
![]() $p_2\in M_2$
be projections with
$p_2\in M_2$
be projections with
![]() $\tau(p_1)=\tau(p_2)=\frac{1}{2}$
, and denote
$\tau(p_1)=\tau(p_2)=\frac{1}{2}$
, and denote
![]() $A_1=\mathbb{C} p_1\oplus \mathbb{C} (1-p_1)$
and
$A_1=\mathbb{C} p_1\oplus \mathbb{C} (1-p_1)$
and
![]() $A_2 = \mathbb{C} p_2 \oplus \mathbb{C} (1-p_2)$
.
$A_2 = \mathbb{C} p_2 \oplus \mathbb{C} (1-p_2)$
.
By Proposition 5.2 (see also [Reference Collins and KempCK14, Theorem 1.9]), there exist a II
![]() $_1$
factor
$_1$
factor
![]() $M_\varepsilon$
and
$M_\varepsilon$
and
![]() $v_\varepsilon\in \mathcal U(M_\varepsilon)$
such that
$v_\varepsilon\in \mathcal U(M_\varepsilon)$
such that
![]() $M\subset M_\varepsilon$
,
$M\subset M_\varepsilon$
,
![]() $\|v_\varepsilon-1\|_2<\varepsilon$
and
$\|v_\varepsilon-1\|_2<\varepsilon$
and
![]() $A_1\vee v_\varepsilon A_2v_\varepsilon^*$
is diffuse. Here, we used the fact that if two projections p,q of trace
$A_1\vee v_\varepsilon A_2v_\varepsilon^*$
is diffuse. Here, we used the fact that if two projections p,q of trace
![]() $\frac{1}{2}$
are such that each of the pairs of projections
$\frac{1}{2}$
are such that each of the pairs of projections
![]() $(p,q),(p,1-q),(1-p,q),(1-p,1-q)$
are in general position, then
$(p,q),(p,1-q),(1-p,q),(1-p,1-q)$
are in general position, then
![]() $p\wedge q=p\wedge (1-q)=(1-p)\wedge q=(1-p)\wedge (1-q)=0$
. This fact implies that
$p\wedge q=p\wedge (1-q)=(1-p)\wedge q=(1-p)\wedge (1-q)=0$
. This fact implies that
![]() $A_1\vee v_\varepsilon A_2v_\varepsilon^*$
has no one-dimensional summands and is thus diffuse by Proposition 5.2.
$A_1\vee v_\varepsilon A_2v_\varepsilon^*$
has no one-dimensional summands and is thus diffuse by Proposition 5.2.
Define
![]() $\widetilde{M}_\varepsilon=M_{\varepsilon}*_{v_{\varepsilon} A_2v_{\varepsilon}^*}(v_{\varepsilon} A_2v_{\varepsilon}^*\overline{\otimes}\mathrm{L}(\mathbb Z))$
. Let
$\widetilde{M}_\varepsilon=M_{\varepsilon}*_{v_{\varepsilon} A_2v_{\varepsilon}^*}(v_{\varepsilon} A_2v_{\varepsilon}^*\overline{\otimes}\mathrm{L}(\mathbb Z))$
. Let
![]() $u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary and
$u\in \mathrm{L}(\mathbb Z)$
be a Haar unitary and
![]() $h=h^*\in \mathrm{L}(\mathbb Z)$
such that
$h=h^*\in \mathrm{L}(\mathbb Z)$
such that
![]() $u=\exp(ih)$
. Let
$u=\exp(ih)$
. Let
![]() $t>0$
such that
$t>0$
such that
![]() $u_t=\exp(ith)$
satisfies
$u_t=\exp(ith)$
satisfies
![]() $\|u_t-1\|_2<\varepsilon-\|v_\varepsilon-1\|_2$
.
$\|u_t-1\|_2<\varepsilon-\|v_\varepsilon-1\|_2$
.
Since
![]() $A_1\vee v_\varepsilon A_2v_\varepsilon^*$
is diffuse and
$A_1\vee v_\varepsilon A_2v_\varepsilon^*$
is diffuse and
![]() $A_2$
is finite-dimensional, we get that
$A_2$
is finite-dimensional, we get that
![]() $M_1\vee v_\varepsilon A_2v_\varepsilon^*\nprec_{M_\varepsilon}v_\varepsilon A_2v_\varepsilon^*$
. Since
$M_1\vee v_\varepsilon A_2v_\varepsilon^*\nprec_{M_\varepsilon}v_\varepsilon A_2v_\varepsilon^*$
. Since
![]() $M_2$
is a factor,
$M_2$
is a factor,
![]() $A_2\subsetneq M_2$
and thus
$A_2\subsetneq M_2$
and thus
![]() $v_\varepsilon A_2v_\varepsilon^*\subsetneq v_\varepsilon M_2v_\varepsilon^*$
. Using that
$v_\varepsilon A_2v_\varepsilon^*\subsetneq v_\varepsilon M_2v_\varepsilon^*$
. Using that
![]() $M_2$
is a factor again, we may thus apply Lemma 4.3 and derive that
$M_2$
is a factor again, we may thus apply Lemma 4.3 and derive that
![]() $M_1\vee u_tv_{\varepsilon}M_2v_{\varepsilon}^*u_t^*$
is a II
$M_1\vee u_tv_{\varepsilon}M_2v_{\varepsilon}^*u_t^*$
is a II
![]() $_1$
factor. It is left to note that
$_1$
factor. It is left to note that
![]() $\|u_tv_\varepsilon-1\|_2\leq \|u_t-1\|_2+\|v_\varepsilon-1\|_2<\varepsilon$
, so we conclude that the triple
$\|u_tv_\varepsilon-1\|_2\leq \|u_t-1\|_2+\|v_\varepsilon-1\|_2<\varepsilon$
, so we conclude that the triple
![]() $(M_1,M_2,M)$
is approximately factorial.
$(M_1,M_2,M)$
is approximately factorial.
4.2 General position of von Neumann subalgebras
We continue with a technical result, given as Theorem 4.9, pertaining to von Neumann algebras of a specific form, and which we will rely on in the proof of Theorem E. We postpone its proof to the next section. In order to state the theorem, we first introduce the following notation.
Definition 4.7. Let
![]() $\mathcal C$
be the class of tracial von Neumann algebras
$\mathcal C$
be the class of tracial von Neumann algebras
![]() $(M,\tau)$
of the form
$(M,\tau)$
of the form
![]() $M=A\oplus B$
, where A is finite-dimensional abelian and B is diffuse. In other words, there exist projections
$M=A\oplus B$
, where A is finite-dimensional abelian and B is diffuse. In other words, there exist projections
![]() $p_1,\ldots,p_m,p\in\mathcal Z(M)$
such that
$p_1,\ldots,p_m,p\in\mathcal Z(M)$
such that
![]() $\sum_{i=1}^mp_i+p=1$
,
$\sum_{i=1}^mp_i+p=1$
,
![]() $M=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus Mp$
and Mp is diffuse.
$M=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus Mp$
and Mp is diffuse.
For algebras of class
![]() $\mathcal{C}$
, Theorem 4.9 establishes a more general version of Theorem E. To motivate its statement, note that, given von Neumann algebras
$\mathcal{C}$
, Theorem 4.9 establishes a more general version of Theorem E. To motivate its statement, note that, given von Neumann algebras
![]() $\mathbb{C}1\neq M_1,M_2\in\mathcal{C}$
with
$\mathbb{C}1\neq M_1,M_2\in\mathcal{C}$
with
![]() $\dim(M_1)+\dim(M_2)\geq 5$
, Theorem E would imply that we can find a unitary v close to 1 (in some II
$\dim(M_1)+\dim(M_2)\geq 5$
, Theorem E would imply that we can find a unitary v close to 1 (in some II
![]() $_1$
factor containing
$_1$
factor containing
![]() $M_1$
and
$M_1$
and
![]() $M_2$
) such that
$M_2$
) such that
![]() $M_1\vee vM_2v^*$
is a II
$M_1\vee vM_2v^*$
is a II
![]() $_1$
factor if the condition
$_1$
factor if the condition
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
is satisfied. If this condition fails, then that is never possible, since we will always have one-dimensional direct summands of the form
$\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
is satisfied. If this condition fails, then that is never possible, since we will always have one-dimensional direct summands of the form
![]() $\mathbb{C}(p\wedge q)$
for central projections
$\mathbb{C}(p\wedge q)$
for central projections
![]() $p\in\mathcal{Z}(M_1)$
and
$p\in\mathcal{Z}(M_1)$
and
![]() $q\in\mathcal{Z}(vM_2v^*)$
satisfying
$q\in\mathcal{Z}(vM_2v^*)$
satisfying
![]() $\tau(p)+\tau(q)>1$
(cf. the first paragraph of § 3.1). Nevertheless, Theorem 4.9 tells us that, even if
$\tau(p)+\tau(q)>1$
(cf. the first paragraph of § 3.1). Nevertheless, Theorem 4.9 tells us that, even if
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2) > 1$
, we can find a unitary v close to 1 such that those are the only one-dimensional direct summands of
$\mathrm{e}(M_1)+\mathrm{e}(M_2) > 1$
, we can find a unitary v close to 1 such that those are the only one-dimensional direct summands of
![]() $M_1\vee vM_2v^*$
, they have the minimal possible support projections, and the remaining direct summand is a II
$M_1\vee vM_2v^*$
, they have the minimal possible support projections, and the remaining direct summand is a II
![]() $_1$
factor. We formalize this in the next definition.
$_1$
factor. We formalize this in the next definition.
Recall that two projections p and q in a tracial von Neumann algebra
![]() $(M,\tau)$
are said to be in general position if
$(M,\tau)$
are said to be in general position if
![]() $\tau(p\wedge q) = \max\{\tau(p) + \tau(q) - 1, 0\}$
.
$\tau(p\wedge q) = \max\{\tau(p) + \tau(q) - 1, 0\}$
.
Definition 4.8. Let
![]() $M_1,M_2\in\mathcal C$
. Write
$M_1,M_2\in\mathcal C$
. Write
![]() $M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
,
$M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
,
![]() $M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
, where
$M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
, where
![]() $p_1,\ldots,p_m,p\in \mathcal Z(M_1), q_1,\ldots,q_n,q\in \mathcal Z(M_2)$
, are projections and
$p_1,\ldots,p_m,p\in \mathcal Z(M_1), q_1,\ldots,q_n,q\in \mathcal Z(M_2)$
, are projections and
![]() $M_1p,M_2q$
are diffuse.
$M_1p,M_2q$
are diffuse.
-
(a) Let
 $(M,\tau)$
be a tracial von Neumann algebra which contains
$(M,\tau)$
be a tracial von Neumann algebra which contains
 $M_1$
and
$M_1$
and
 $M_2$
.
$M_2$
.We say that the triple
 $(M_1,M_2,M)$
satisfies condition (B) if for every
$(M_1,M_2,M)$
satisfies condition (B) if for every
 $\varepsilon>0$
, we can find a II
$\varepsilon>0$
, we can find a II
 $_1$
factor
$_1$
factor
 $M_\varepsilon$
and
$M_\varepsilon$
and
 $v_\varepsilon\in\mathcal U(M_\varepsilon)$
such that
$v_\varepsilon\in\mathcal U(M_\varepsilon)$
such that
 $M\subset M_\varepsilon$
,
$M\subset M_\varepsilon$
,
 $\|v_\varepsilon-1\|_2<\varepsilon$
,
$\|v_\varepsilon-1\|_2<\varepsilon$
,-
(1)
 $p_i$
and
$p_i$
and
 $v_\varepsilon q_jv_\varepsilon^*$
are in general position for every
$v_\varepsilon q_jv_\varepsilon^*$
are in general position for every
 $1\leq i\leq m,1\leq j\leq n$
, and
$1\leq i\leq m,1\leq j\leq n$
, and -
(2)
 $M_1\vee v_\varepsilon M_2v_\varepsilon^*=\big({\kern-1pt}\bigoplus_{\substack{1\leq i\leq m \\ 1\leq j\leq n}}\mathbb C(p_i\wedge v_\varepsilon q_jv_{\varepsilon}^*)\big)\oplus B$
, where B is a II
$M_1\vee v_\varepsilon M_2v_\varepsilon^*=\big({\kern-1pt}\bigoplus_{\substack{1\leq i\leq m \\ 1\leq j\leq n}}\mathbb C(p_i\wedge v_\varepsilon q_jv_{\varepsilon}^*)\big)\oplus B$
, where B is a II
 $_1$
factor.
$_1$
factor.
-
-
(b) We say that the pair
 $(M_1,M_2)$
satisfies condition (B) if the triple
$(M_1,M_2)$
satisfies condition (B) if the triple
 $(M_1,M_2,M)$
satisfies condition (B) for every tracial von Neumann algebra
$(M_1,M_2,M)$
satisfies condition (B) for every tracial von Neumann algebra
 $(M,\tau)$
which contains
$(M,\tau)$
which contains
 $M_1$
and
$M_1$
and
 $M_2$
.
$M_2$
.
Theorem 4.9. Let
![]() $M_1, M_2\in\mathcal{C}$
be such that
$M_1, M_2\in\mathcal{C}$
be such that
![]() $M_1,M_2\neq \mathbb C1$
and
$M_1,M_2\neq \mathbb C1$
and
![]() $\dim(M_1)+\dim(M_2)\geq 5$
. Then
$\dim(M_1)+\dim(M_2)\geq 5$
. Then
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
For the proof of Theorem 4.9, we refer to § 5. In the remaining part of this section, we use Theorem 4.9 to establish Theorem E.
4.3 Proof of Theorem E
Before turning to the proof of Theorem E in full generality, we note that Theorem 4.9 immediately implies Theorem E when
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are finite-dimensional abelian.
$M_2$
are finite-dimensional abelian.
Corollary 4.10. Let
![]() $M_1$
and
$M_1$
and
![]() $M_2$
be finite-dimensional abelian tracial von Neumann algebras. Assume that
$M_2$
be finite-dimensional abelian tracial von Neumann algebras. Assume that
![]() $M_1\neq \mathbb C1,M_2\neq \mathbb C1$
,
$M_1\neq \mathbb C1,M_2\neq \mathbb C1$
,
![]() $\dim(M_1)+\dim(M_2)\geq 5$
and
$\dim(M_1)+\dim(M_2)\geq 5$
and
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
. Then the pair
$\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
. Then the pair
![]() $(M_1,M_2)$
is approximately factorial.
$(M_1,M_2)$
is approximately factorial.
Proof. Write
![]() $M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m$
and
$M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m$
and
![]() $M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n$
, where
$M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n$
, where
![]() $p_1,\ldots,p_m,q_1,\ldots,q_n$
are non-zero projections. Fix
$p_1,\ldots,p_m,q_1,\ldots,q_n$
are non-zero projections. Fix
![]() $\varepsilon>0$
and let M be a tracial von Neumann algebra containing
$\varepsilon>0$
and let M be a tracial von Neumann algebra containing
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. By Theorem 4.9, we can find a II
$M_2$
. By Theorem 4.9, we can find a II
![]() $_1$
factor
$_1$
factor
![]() $M\subset M_\varepsilon$
and
$M\subset M_\varepsilon$
and
![]() $v_\varepsilon\in\mathcal U(M_\varepsilon)$
with
$v_\varepsilon\in\mathcal U(M_\varepsilon)$
with
![]() $\left\|v_\varepsilon - 1\right\|_2<\varepsilon$
such that (1) and (2) in Definition (4.8)(a) hold. If
$\left\|v_\varepsilon - 1\right\|_2<\varepsilon$
such that (1) and (2) in Definition (4.8)(a) hold. If
![]() $1\leq i\leq m$
and
$1\leq i\leq m$
and
![]() $1\leq j\leq n$
, then
$1\leq j\leq n$
, then
![]() $\tau(p_i)+\tau(q_j)\leq\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
, thus
$\tau(p_i)+\tau(q_j)\leq\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
, thus
![]() $p_i\wedge v_\varepsilon q_jv_\varepsilon^*=0$
by (1). By (2) we thus get that
$p_i\wedge v_\varepsilon q_jv_\varepsilon^*=0$
by (1). By (2) we thus get that
![]() $M_1\vee v_\varepsilon M_2v_\varepsilon^*=B$
is a II
$M_1\vee v_\varepsilon M_2v_\varepsilon^*=B$
is a II
![]() $_1$
factor.
$_1$
factor.
Proof of Theorem E. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra, and let
$(M,\tau)$
be a tracial von Neumann algebra, and let
![]() $M_1,M_2\subset M$
be von Neumann subalgebras such that
$M_1,M_2\subset M$
be von Neumann subalgebras such that
![]() $M_1,M_2\neq \mathbb C1$
,
$M_1,M_2\neq \mathbb C1$
,
![]() $\mathrm{dim}(M_1)+\mathrm{dim}(M_2)\geq 5$
and
$\mathrm{dim}(M_1)+\mathrm{dim}(M_2)\geq 5$
and
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
. Our goal is to prove that the triple
$\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
. Our goal is to prove that the triple
![]() $(M_1,M_2,M)$
is approximately factorial.
$(M_1,M_2,M)$
is approximately factorial.
If
![]() $M_1$
or
$M_1$
or
![]() $M_2$
is diffuse, then Corollary 4.4 implies that
$M_2$
is diffuse, then Corollary 4.4 implies that
![]() $(M_1,M_2,M)$
is approximately factorial. Thus, we may assume that neither
$(M_1,M_2,M)$
is approximately factorial. Thus, we may assume that neither
![]() $M_1$
nor
$M_1$
nor
![]() $M_2$
is diffuse. By Lemma 2.3, we can thus find a finite-dimensional abelian von Neumann subalgebra
$M_2$
is diffuse. By Lemma 2.3, we can thus find a finite-dimensional abelian von Neumann subalgebra
![]() $A_i\subset M_i$
, for
$A_i\subset M_i$
, for
![]() $i=1,2$
, such that
$i=1,2$
, such that
![]() $A_i\neq \mathbb C1$
,
$A_i\neq \mathbb C1$
,
![]() $\mathrm{e}(A_i)=\mathrm{e}(M_i)$
. Moreover,
$\mathrm{e}(A_i)=\mathrm{e}(M_i)$
. Moreover,
![]() $\dim(A_i)\geq 3$
unless
$\dim(A_i)\geq 3$
unless
![]() $M_i$
is isomorphic to
$M_i$
is isomorphic to
![]() $\mathbb C^2$
or
$\mathbb C^2$
or
![]() $\mathbb M_2(\mathbb C)$
.
$\mathbb M_2(\mathbb C)$
.
In particular,
![]() $\mathrm{e}(A_1)+\mathrm{e}(A_2)=\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
, and since
$\mathrm{e}(A_1)+\mathrm{e}(A_2)=\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
, and since
![]() $A_1\neq \mathbb C1$
and
$A_1\neq \mathbb C1$
and
![]() $A_2\neq \mathbb C1$
, we get
$A_2\neq \mathbb C1$
, we get
![]() $\mathrm{dim}(A_1)+\mathrm{dim}(A_2)\geq 4$
. We finish the proof by considering the following two cases.
$\mathrm{dim}(A_1)+\mathrm{dim}(A_2)\geq 4$
. We finish the proof by considering the following two cases.
Case 1.
![]() $\mathrm{dim}(A_1)+\mathrm{dim}(A_2)\geq 5$
. In this case, Corollary 4.10 implies that the triple
$\mathrm{dim}(A_1)+\mathrm{dim}(A_2)\geq 5$
. In this case, Corollary 4.10 implies that the triple
![]() $(A_1,A_2,M)$
is approximately factorial. If
$(A_1,A_2,M)$
is approximately factorial. If
![]() $M_1=A_1$
and
$M_1=A_1$
and
![]() $M_2=A_2$
, then we get that
$M_2=A_2$
, then we get that
![]() $(M_1,M_2,M)$
is approximately factorial. Otherwise, we may assume, without loss of generality, that
$(M_1,M_2,M)$
is approximately factorial. Otherwise, we may assume, without loss of generality, that
![]() $A_2\subsetneq M_2$
. In this case, we obtain that the triple
$A_2\subsetneq M_2$
. In this case, we obtain that the triple
![]() $(M_1,M_2,M)$
is approximately factorial by applying Proposition 4.5.
$(M_1,M_2,M)$
is approximately factorial by applying Proposition 4.5.
Case 2.
![]() $\mathrm{dim}(A_{1})+\mathrm{dim}(A_{2})=4$
. In this case,
$\mathrm{dim}(A_{1})+\mathrm{dim}(A_{2})=4$
. In this case,
![]() $\mathrm{dim}(A_1)=\mathrm{dim}(A_2)=2$
. Thus,
$\mathrm{dim}(A_1)=\mathrm{dim}(A_2)=2$
. Thus,
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are isomorphic to either
$M_2$
are isomorphic to either
![]() $\mathbb C^2$
or
$\mathbb C^2$
or
![]() $\mathbb M_2(\mathbb C)$
. Since
$\mathbb M_2(\mathbb C)$
. Since
![]() $\mathrm{dim}(M_1)+\mathrm{dim}(M_2)\geq 5$
, at least one of
$\mathrm{dim}(M_1)+\mathrm{dim}(M_2)\geq 5$
, at least one of
![]() $M_1$
or
$M_1$
or
![]() $M_2$
is not isomorphic to
$M_2$
is not isomorphic to
![]() $\mathbb C^2$
. Thus, without loss of generality, we may assume that
$\mathbb C^2$
. Thus, without loss of generality, we may assume that
![]() $M_2 \cong \mathbb M_2(\mathbb C)$
.
$M_2 \cong \mathbb M_2(\mathbb C)$
.
Since
![]() $\mathrm{dim}(A_1)=\mathrm{dim}(A_2)=2$
, we have that
$\mathrm{dim}(A_1)=\mathrm{dim}(A_2)=2$
, we have that
![]() $A_1=\mathbb Cp_1\oplus\mathbb C(1-p_1)$
and
$A_1=\mathbb Cp_1\oplus\mathbb C(1-p_1)$
and
![]() $A_2=\mathbb Cp_2\oplus\mathbb C(1-p_2)$
for some projections
$A_2=\mathbb Cp_2\oplus\mathbb C(1-p_2)$
for some projections
![]() $p_1,p_2\in M$
with
$p_1,p_2\in M$
with
![]() $\tau(p_1)\geq\frac{1}{2}$
and
$\tau(p_1)\geq\frac{1}{2}$
and
![]() $\tau(p_2)\geq\frac{1}{2}$
. Since
$\tau(p_2)\geq\frac{1}{2}$
. Since
![]() $1\geq \mathrm{e}(A_1)+\mathrm{e}(A_2)=\tau(p_1)+\tau(p_2)$
, we conclude that
$1\geq \mathrm{e}(A_1)+\mathrm{e}(A_2)=\tau(p_1)+\tau(p_2)$
, we conclude that
![]() $\tau(p_1)=\tau(p_2)=\frac{1}{2}$
. We may thus proceed by applying Proposition 4.6 and conclude that the triple
$\tau(p_1)=\tau(p_2)=\frac{1}{2}$
. We may thus proceed by applying Proposition 4.6 and conclude that the triple
![]() $(M_1,M_2,M)$
is approximately factorial.
$(M_1,M_2,M)$
is approximately factorial.
5. General position of von Neumann subalgebras
In § 4 we proved Theorem E while relying on Theorem 4.9. The purpose of this section is to prove Theorem 4.9.
5.1 Pairs of two-dimensional algebras
Before turning to the proof of Theorem 4.9, we note that the assumption that
![]() $\dim(M_1)+\dim(M_2)\geq 5$
from Theorem 4.9 is necessary. Indeed, if
$\dim(M_1)+\dim(M_2)\geq 5$
from Theorem 4.9 is necessary. Indeed, if
![]() $M_1,M_2\neq\mathbb C1$
, having
$M_1,M_2\neq\mathbb C1$
, having
![]() $\dim(M_1)+\dim(M_2)<5$
forces that
$\dim(M_1)+\dim(M_2)<5$
forces that
![]() $\dim(M_1)=\dim(M_2)=2$
, i.e.,
$\dim(M_1)=\dim(M_2)=2$
, i.e.,
![]() $M_1 \cong \mathbb{C}^2 \cong M_2$
. In this case,
$M_1 \cong \mathbb{C}^2 \cong M_2$
. In this case,
![]() $M_1\vee vM_2v^*$
is a type I von Neumann algebra, and therefore has no type II
$M_1\vee vM_2v^*$
is a type I von Neumann algebra, and therefore has no type II
![]() $_1$
direct summand for any unitary v in any II
$_1$
direct summand for any unitary v in any II
![]() $_1$
factor containing
$_1$
factor containing
![]() $M_1$
and
$M_1$
and
![]() $M_2$
.
$M_2$
.
Nevertheless, the case
![]() $\dim(M_1)=\dim(M_2)=2$
will be the starting point in our approach to Theorem 4.9. To this end, in this section we prove a weaker version of Theorem 4.9 for this case; see Proposition 5.2. The weaker property we establish is essentially obtained by relaxing the requirement from Definition 4.8(a) that B should be a II
$\dim(M_1)=\dim(M_2)=2$
will be the starting point in our approach to Theorem 4.9. To this end, in this section we prove a weaker version of Theorem 4.9 for this case; see Proposition 5.2. The weaker property we establish is essentially obtained by relaxing the requirement from Definition 4.8(a) that B should be a II
![]() $_1$
factor, and only ask B to be diffuse.
$_1$
factor, and only ask B to be diffuse.
Definition 5.1. Let
![]() $M_1,M_2\in\mathcal C$
. Write
$M_1,M_2\in\mathcal C$
. Write
![]() $M_1=\mathbb Cp_1\oplus \cdots\oplus\mathbb Cp_m\oplus M_1p$
,
$M_1=\mathbb Cp_1\oplus \cdots\oplus\mathbb Cp_m\oplus M_1p$
,
![]() $M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
, where
$M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
, where
![]() $p_1,\ldots,p_m,p\in \mathcal Z(M_1), q_1,\ldots,q_n,q\in \mathcal Z(M_2)$
are projections and
$p_1,\ldots,p_m,p\in \mathcal Z(M_1), q_1,\ldots,q_n,q\in \mathcal Z(M_2)$
are projections and
![]() $M_1p,M_2q$
are diffuse.
$M_1p,M_2q$
are diffuse.
-
(a) Let
 $(M,\tau)$
be a tracial von Neumann algebra which contains
$(M,\tau)$
be a tracial von Neumann algebra which contains
 $M_1$
and
$M_1$
and
 $M_2$
.
$M_2$
.We say that the triple
 $(M_1,M_2,M)$
satisfies condition (C) if for every
$(M_1,M_2,M)$
satisfies condition (C) if for every
 $\varepsilon>0$
, we can find a II
$\varepsilon>0$
, we can find a II
 $_1$
factor
$_1$
factor
 $M_\varepsilon$
and
$M_\varepsilon$
and
 $v_\varepsilon\in\mathcal U(M_\varepsilon)$
such that
$v_\varepsilon\in\mathcal U(M_\varepsilon)$
such that
 $M\subset M_\varepsilon$
,
$M\subset M_\varepsilon$
,
 $\|v_\varepsilon-1\|_2<\varepsilon$
,
$\|v_\varepsilon-1\|_2<\varepsilon$
,-
(1)
 $p_i$
and
$p_i$
and
 $v_\varepsilon q_jv_\varepsilon^*$
are in general position, for every
$v_\varepsilon q_jv_\varepsilon^*$
are in general position, for every
 $1\leq i\leq m,1\leq j\leq n$
,
$1\leq i\leq m,1\leq j\leq n$
, -
(2)
 $M_1\vee v_\varepsilon M_2 v_\varepsilon^*=(\bigoplus_{\substack{1\leq i\leq m \\ 1\leq j\leq n}}\mathbb C(p_i\wedge v_\varepsilon q_jv_{\varepsilon}^*))\oplus B$
, where B is diffuse, and
$M_1\vee v_\varepsilon M_2 v_\varepsilon^*=(\bigoplus_{\substack{1\leq i\leq m \\ 1\leq j\leq n}}\mathbb C(p_i\wedge v_\varepsilon q_jv_{\varepsilon}^*))\oplus B$
, where B is diffuse, and -
(3)
 $\mathrm{E}_{\mathcal{Z}(B)}(p_i),\mathrm{E}_{\mathcal{Z}(B)}(v_\varepsilon q_jv_\varepsilon^*)\in\mathbb Cr$
, for every
$\mathrm{E}_{\mathcal{Z}(B)}(p_i),\mathrm{E}_{\mathcal{Z}(B)}(v_\varepsilon q_jv_\varepsilon^*)\in\mathbb Cr$
, for every
 $1\leq i\leq m,1\leq j\leq n$
, where we denote by
$1\leq i\leq m,1\leq j\leq n$
, where we denote by
 $r=1-\sum_{\substack{1\leq i\leq m\\1\leq j\leq n}}p_i\wedge v_\varepsilon q_jv_\varepsilon^*$
the unit projection of B.
$r=1-\sum_{\substack{1\leq i\leq m\\1\leq j\leq n}}p_i\wedge v_\varepsilon q_jv_\varepsilon^*$
the unit projection of B.
-
-
(b) We say that the pair
 $(M_1,M_2)$
satisfies condition (C) if the triple
$(M_1,M_2)$
satisfies condition (C) if the triple
 $(M_1,M_2,M)$
satisfies condition (C) for every tracial von Neumann algebra
$(M_1,M_2,M)$
satisfies condition (C) for every tracial von Neumann algebra
 $(M,\tau)$
which contains
$(M,\tau)$
which contains
 $M_1$
and
$M_1$
and
 $M_2$
.
$M_2$
.
Proposition 5.2. Let
![]() $M_1, M_2$
be tracial von Neumann algebras such that
$M_1, M_2$
be tracial von Neumann algebras such that
![]() $\dim(M_1)=\dim(M_2)=2$
. Then
$\dim(M_1)=\dim(M_2)=2$
. Then
![]() $(M_1,M_2)$
satisfies condition (C). Moreover, if M is a II
$(M_1,M_2)$
satisfies condition (C). Moreover, if M is a II
![]() $_1$
factor which contains
$_1$
factor which contains
![]() $M_1$
and
$M_1$
and
![]() $M_2$
, then in Definition 5.1(a), we can take
$M_2$
, then in Definition 5.1(a), we can take
![]() $M_\varepsilon=M$
, for every
$M_\varepsilon=M$
, for every
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Write
![]() $M_1=\mathbb Cp\oplus\mathbb C(1-p)$
and
$M_1=\mathbb Cp\oplus\mathbb C(1-p)$
and
![]() $M_2=\mathbb Cq\oplus\mathbb C(1-q)$
, for projections p,q and let M be a tracial von Neumann algebra which contains
$M_2=\mathbb Cq\oplus\mathbb C(1-q)$
, for projections p,q and let M be a tracial von Neumann algebra which contains
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. Before proving Proposition 5.2 we remark that one can deduce its main assertion from [Reference Collins and KempCK14, Theorem 1.9] if
$M_2$
. Before proving Proposition 5.2 we remark that one can deduce its main assertion from [Reference Collins and KempCK14, Theorem 1.9] if
![]() $\tau(p)=\tau(q)=\frac{1}{2}$
, and [Reference HamdiHam18, Theorem 1.1] in general.
$\tau(p)=\tau(q)=\frac{1}{2}$
, and [Reference HamdiHam18, Theorem 1.1] in general.
These results imply that Definition 5.1(a) holds for
![]() $M_\varepsilon=M*\mathrm{L}(\mathbb F_\infty)$
and
$M_\varepsilon=M*\mathrm{L}(\mathbb F_\infty)$
and
![]() $v_\varepsilon=u_{t_\varepsilon}$
for any
$v_\varepsilon=u_{t_\varepsilon}$
for any
![]() $t_\varepsilon>0$
with
$t_\varepsilon>0$
with
![]() $\|v_\varepsilon-1\|_2<\varepsilon$
, where
$\|v_\varepsilon-1\|_2<\varepsilon$
, where
![]() $(u_t)_{t\geq 0}\subset\mathcal U(\mathrm{L}(\mathbb F_\infty))$
is a free unitary Brownian motion that is free from M.
$(u_t)_{t\geq 0}\subset\mathcal U(\mathrm{L}(\mathbb F_\infty))$
is a free unitary Brownian motion that is free from M.
Below, we give a self-contained and elementary proof of Proposition 5.2 which additionally implies its moreover assertion. We point out, however, that the moreover assertion is not needed for our main results, and thus relying on [Reference Collins and KempCK14, Theorem 1.9] and [Reference HamdiHam18, Theorem 1.1] is sufficient. In preparation for the proof of Proposition 5.2, we introduce the following notation.
We denote
![]() $S^1=\{z\in\mathbb C\mid |z|=1\}$
. For
$S^1=\{z\in\mathbb C\mid |z|=1\}$
. For
![]() $t\in [0,1]$
and
$t\in [0,1]$
and
![]() $z\in S^1$
, put
$z\in S^1$
, put
Note that any projection of normalized trace
![]() $\frac{1}{2}$
in
$\frac{1}{2}$
in
![]() $\mathbb M_2(\mathbb C)$
is equal to
$\mathbb M_2(\mathbb C)$
is equal to
![]() $e_{t,z}$
for some
$e_{t,z}$
for some
![]() $(t,z)\in [0,1]\times S^1$
, and that
$(t,z)\in [0,1]\times S^1$
, and that
![]() $u_{t,z}\in\mathbb M_2(\mathbb C)$
is a unitary satisfying
$u_{t,z}\in\mathbb M_2(\mathbb C)$
is a unitary satisfying
![]() $e_{t,z}=u_{t,z}e_{0,1}u_{t,z}^*$
for every
$e_{t,z}=u_{t,z}e_{0,1}u_{t,z}^*$
for every
![]() $(t,z)\in [0,1]\times S^1$
. It is easy to check that
$(t,z)\in [0,1]\times S^1$
. It is easy to check that
The following elementary result will be needed in the proof of Proposition 5.2.
Lemma 5.3. Let A be a separable diffuse abelian von Neumann algebra and
![]() $p,q\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
be projections such that
$p,q\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
be projections such that
![]() $\mathrm{E}_{A\overline{\otimes}1}(p)=\mathrm{E}_{A\overline{\otimes} 1}(q)=\frac{1}{2}$
. Then for any
$\mathrm{E}_{A\overline{\otimes}1}(p)=\mathrm{E}_{A\overline{\otimes} 1}(q)=\frac{1}{2}$
. Then for any
![]() $\varepsilon>0$
, there exists a unitary
$\varepsilon>0$
, there exists a unitary
![]() $v\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
such that
$v\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
such that
![]() $\|v-1\|_2<\varepsilon$
and
$\|v-1\|_2<\varepsilon$
and
![]() $\{p,vqv^*\}''=A\overline{\otimes}\mathbb M_2(\mathbb C)$
.
$\{p,vqv^*\}''=A\overline{\otimes}\mathbb M_2(\mathbb C)$
.
Proof. Since A is separable, diffuse and abelian, we can identify it with
![]() $\mathrm{L}^\infty([0,1],\lambda)$
, where
$\mathrm{L}^\infty([0,1],\lambda)$
, where
![]() $\lambda$
is the Lebesgue measure on [0, 1]. Since
$\lambda$
is the Lebesgue measure on [0, 1]. Since
![]() $\mathrm{E}_{A\overline{\otimes}1}(p)=\frac{1}{2}$
, we may assume that
$\mathrm{E}_{A\overline{\otimes}1}(p)=\frac{1}{2}$
, we may assume that
![]() $p=1\otimes e_{0,1}$
. Since
$p=1\otimes e_{0,1}$
. Since
![]() $\mathrm{E}_{A\overline{\otimes} 1}(q)=\frac{1}{2}$
, we can find measurable functions
$\mathrm{E}_{A\overline{\otimes} 1}(q)=\frac{1}{2}$
, we can find measurable functions
![]() $f:[0,1]\rightarrow [0,1]$
and
$f:[0,1]\rightarrow [0,1]$
and
![]() $z:[0,1]\rightarrow S^1$
such that
$z:[0,1]\rightarrow S^1$
such that
![]() $q(t)=e_{f(t),z(t)}$
, for every
$q(t)=e_{f(t),z(t)}$
, for every
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
Let
![]() $\varepsilon\in (0,1)$
. We continue with the following claim.
$\varepsilon\in (0,1)$
. We continue with the following claim.
Claim 5.4. There is a measurable function
![]() $g:[0,1]\rightarrow (0,1)$
such that
$g:[0,1]\rightarrow (0,1)$
such that
![]() $\{g\}''=A$
and
$\{g\}''=A$
and
![]() $\|g-f\|_1<{\varepsilon^2}/{2}$
.
$\|g-f\|_1<{\varepsilon^2}/{2}$
.
Proof of Claim 5.4. First, we find
![]() $n\geq 1$
and pairwise distinct numbers
$n\geq 1$
and pairwise distinct numbers
![]() $\lambda_0,\ldots,\lambda_{n-1}\in (0,1)$
such that
$\lambda_0,\ldots,\lambda_{n-1}\in (0,1)$
such that
![]() $\|h-f\|_1<{\varepsilon^2}/{4}$
, where
$\|h-f\|_1<{\varepsilon^2}/{4}$
, where
![]() $h=\sum_{k=0}^{n-1}\lambda_k\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}$
. Let
$h=\sum_{k=0}^{n-1}\lambda_k\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}$
. Let
![]() $\delta\in (0,{\varepsilon^2}/{4})$
such that
$\delta\in (0,{\varepsilon^2}/{4})$
such that
![]() $\lambda_i+\delta<1$
for every i, and
$\lambda_i+\delta<1$
for every i, and
![]() $|\lambda_i-\lambda_j|>\delta$
for every
$|\lambda_i-\lambda_j|>\delta$
for every
![]() $i\neq j$
. Let
$i\neq j$
. Let
![]() $\zeta:[0,1]\rightarrow [0,1]$
be the identity function
$\zeta:[0,1]\rightarrow [0,1]$
be the identity function
![]() $\zeta(t)=t$
. Define
$\zeta(t)=t$
. Define
![]() $g=\sum_{k=0}^{n-1}(\lambda_k+\delta\zeta)\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}$
. Since
$g=\sum_{k=0}^{n-1}(\lambda_k+\delta\zeta)\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}$
. Since
![]() $\|g-h\|_1\leq\delta<{\varepsilon^2}/{4}$
, we get that
$\|g-h\|_1\leq\delta<{\varepsilon^2}/{4}$
, we get that
![]() $\|g-f\|_1<{\varepsilon^2}/{2}$
. Then for every
$\|g-f\|_1<{\varepsilon^2}/{2}$
. Then for every
![]() $0\leq k < n$
, we have
$0\leq k < n$
, we have
![]() $(\lambda_k+\delta\zeta)\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}=\boldsymbol{ 1}_{[\lambda_k,\lambda_k+\delta]}(g)g\in\{g\}''$
. Since
$(\lambda_k+\delta\zeta)\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}=\boldsymbol{ 1}_{[\lambda_k,\lambda_k+\delta]}(g)g\in\{g\}''$
. Since
![]() $(\lambda_k+\delta\zeta)\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}$
generates
$(\lambda_k+\delta\zeta)\boldsymbol{1}_{[{k}/{n},({k+1})/{n})}$
generates
![]() $\mathrm{L}^\infty([{k}/{n},({k+1})/{n}))$
as a von Neumann algebra, we get that
$\mathrm{L}^\infty([{k}/{n},({k+1})/{n}))$
as a von Neumann algebra, we get that
![]() $\mathrm{L}^\infty([{k}/{n},({k+1})/{n}))\subset \{g\}''$
for every
$\mathrm{L}^\infty([{k}/{n},({k+1})/{n}))\subset \{g\}''$
for every
![]() $0\leq k\leq n-1$
. This implies
$0\leq k\leq n-1$
. This implies
![]() $\{g\}''=A$
and finishes the proof of the claim.
$\{g\}''=A$
and finishes the proof of the claim.
Let g be the function given by Claim 5.4, and let
![]() $r\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
be the projection given by
$r\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
be the projection given by
![]() $r_t=e_{g(t),z(t)}$
for all
$r_t=e_{g(t),z(t)}$
for all
![]() $t\in [0,1]$
. Let
$t\in [0,1]$
. Let
![]() $v\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
be the unitary given by
$v\in A\overline{\otimes}\mathbb M_2(\mathbb C)$
be the unitary given by
![]() $v_t=u_{g(t),z(t)}u_{f(t),z(t)}^*$
for all
$v_t=u_{g(t),z(t)}u_{f(t),z(t)}^*$
for all
![]() $t\in [0,1]$
. Then
$t\in [0,1]$
. Then
![]() $v_te_{f(t),z(t)}v_t^*=e_{g(t),z(t)}$
for all
$v_te_{f(t),z(t)}v_t^*=e_{g(t),z(t)}$
for all
![]() $t\in [0,1]$
, and thus
$t\in [0,1]$
, and thus
![]() $vqv^*=r$
. Using (5.1) we get that
$vqv^*=r$
. Using (5.1) we get that
and therefore
![]() $\|v-1\|_2<\varepsilon$
.
$\|v-1\|_2<\varepsilon$
.
Put
![]() $B=\{p,vqv^*\}''=\{p,r\}''$
. Since
$B=\{p,vqv^*\}''=\{p,r\}''$
. Since
![]() $prp=(1-g)\otimes e_0$
,
$prp=(1-g)\otimes e_0$
,
![]() $(1-p)r(1-p)=g\otimes e_1$
and
$(1-p)r(1-p)=g\otimes e_1$
and
![]() $\{g\}''=A$
, we get that
$\{g\}''=A$
, we get that
![]() $pBp=A\otimes e_0$
and
$pBp=A\otimes e_0$
and
![]() $(1-p)B(1-p)=A\otimes e_1$
. As
$(1-p)B(1-p)=A\otimes e_1$
. As
and
![]() $g(t)\not\in\{0,1\}$
and
$g(t)\not\in\{0,1\}$
and
![]() $|z(t)|=1$
for all
$|z(t)|=1$
for all
![]() $t\in [0,1]$
, the partial isometry in the polar decomposition of
$t\in [0,1]$
, the partial isometry in the polar decomposition of
![]() $pr(1-p)$
is equal to
$pr(1-p)$
is equal to
![]() $1\otimes d$
, where
$1\otimes d$
, where
![]() $d=\big(\begin{smallmatrix} 0&\ \ 1\\[1.2pt]0&\ \ 0\end{smallmatrix}\big)$
. Thus
$d=\big(\begin{smallmatrix} 0&\ \ 1\\[1.2pt]0&\ \ 0\end{smallmatrix}\big)$
. Thus
![]() $1\otimes d\in B$
. Since
$1\otimes d\in B$
. Since
![]() $A\otimes e_0,A\otimes e_1$
and
$A\otimes e_0,A\otimes e_1$
and
![]() $1\otimes d$
generate
$1\otimes d$
generate
![]() $A\overline{\otimes}\mathbb M_2(\mathbb C)$
, we conclude that
$A\overline{\otimes}\mathbb M_2(\mathbb C)$
, we conclude that
![]() $B=A\overline{\otimes}\mathbb M_2(\mathbb C)$
, which finishes the proof of the lemma.
$B=A\overline{\otimes}\mathbb M_2(\mathbb C)$
, which finishes the proof of the lemma.
Proof of Proposition 5.2. Write
![]() $M_1=\mathbb Cp\oplus\mathbb C(1-p)$
and
$M_1=\mathbb Cp\oplus\mathbb C(1-p)$
and
![]() $M_2=\mathbb Cq\oplus\mathbb C(1-q)$
, where
$M_2=\mathbb Cq\oplus\mathbb C(1-q)$
, where
![]() $p\in M_1$
and
$p\in M_1$
and
![]() $q\in M_2$
are projections, both with trace at least
$q\in M_2$
are projections, both with trace at least
![]() $\frac{1}{2}$
. We assume without loss of generality that
$\frac{1}{2}$
. We assume without loss of generality that
![]() $\tau(p)\geq\tau(q)$
.
$\tau(p)\geq\tau(q)$
.
Consider a II
![]() $_1$
factor M containing
$_1$
factor M containing
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. Let
$M_2$
. Let
![]() $\varepsilon>0$
and put
$\varepsilon>0$
and put
![]() $N=\{p,q\}''$
. Then there are projections
$N=\{p,q\}''$
. Then there are projections
![]() $z_1,z_2\in \mathcal Z(N)$
such that
$z_1,z_2\in \mathcal Z(N)$
such that
![]() $z_1+z_2=1$
,
$z_1+z_2=1$
,
![]() $Nz_1$
is abelian and
$Nz_1$
is abelian and
![]() $Nz_2$
is of type
$Nz_2$
is of type
![]() $I_2$
. Moreover, writing
$I_2$
. Moreover, writing
![]() $Nz_2=C\overline{\otimes}\mathbb M_2(\mathbb C)$
, where C is an abelian von Neumann algebra, we claim that
$Nz_2=C\overline{\otimes}\mathbb M_2(\mathbb C)$
, where C is an abelian von Neumann algebra, we claim that
Indeed,
![]() $pz_2$
and
$pz_2$
and
![]() $qz_2$
are projections that generate
$qz_2$
are projections that generate
![]() $C\overline{\otimes} \mathbb{M}_2(\mathbb{C})\cong \int^\oplus_X \mathbb{M}_2(\mathbb{C}) \,\mathrm{d}\mu(x)$
, where we identify
$C\overline{\otimes} \mathbb{M}_2(\mathbb{C})\cong \int^\oplus_X \mathbb{M}_2(\mathbb{C}) \,\mathrm{d}\mu(x)$
, where we identify
![]() $C\cong L^\infty(X,\mu)$
for some standard probability space
$C\cong L^\infty(X,\mu)$
for some standard probability space
![]() $(X,\mu)$
. Disintegrating
$(X,\mu)$
. Disintegrating
![]() $pz_2 = \int^\oplus_X p_x \,\mathrm{d}\mu(x)$
, we see that each projection
$pz_2 = \int^\oplus_X p_x \,\mathrm{d}\mu(x)$
, we see that each projection
![]() $p_x\in\mathbb{M}_2(\mathbb{C})$
necessarily has trace 0,
$p_x\in\mathbb{M}_2(\mathbb{C})$
necessarily has trace 0,
![]() $\frac{1}{2}$
or 1. If the measure of
$\frac{1}{2}$
or 1. If the measure of
![]() $X_0:=\{x\in X\mid p_x=0\}$
is strictly positive, then
$X_0:=\{x\in X\mid p_x=0\}$
is strictly positive, then
![]() $\{pz_21_{X_0},qz_21_{X_0}\}'' = \{qz_21_{X_0}\}''\neq \mathrm{L}^\infty(X_0)\overline{\otimes}\mathbb{M}_2(\mathbb{C})$
, contradicting the fact that
$\{pz_21_{X_0},qz_21_{X_0}\}'' = \{qz_21_{X_0}\}''\neq \mathrm{L}^\infty(X_0)\overline{\otimes}\mathbb{M}_2(\mathbb{C})$
, contradicting the fact that
![]() $pz_2$
and
$pz_2$
and
![]() $qz_2$
generate
$qz_2$
generate
![]() $\mathrm{L}^\infty(X)\overline{\otimes}\mathbb{M}_2(\mathbb{C})$
. One can argue similarly for the points where
$\mathrm{L}^\infty(X)\overline{\otimes}\mathbb{M}_2(\mathbb{C})$
. One can argue similarly for the points where
![]() $p_x=1$
, and thus deduce that for almost every
$p_x=1$
, and thus deduce that for almost every
![]() $x\in X$
,
$x\in X$
,
![]() $\tau(p_x)=\frac{1}{2}$
. A similar argument holds for
$\tau(p_x)=\frac{1}{2}$
. A similar argument holds for
![]() $qz_2$
, yielding (5.2).
$qz_2$
, yielding (5.2).
Let
![]() $A_2\subset \mathbb M_2(\mathbb C)'\cap z_2Mz_2$
be a MASA containing C. Then
$A_2\subset \mathbb M_2(\mathbb C)'\cap z_2Mz_2$
be a MASA containing C. Then
![]() $Nz_2\subset A_2\overline{\otimes}\mathbb M_2(\mathbb C)$
and since we have
$Nz_2\subset A_2\overline{\otimes}\mathbb M_2(\mathbb C)$
and since we have
![]() $\mathrm{E}_{A_2\overline{\otimes}1}\circ\mathrm{E}_{C\overline{\otimes}\mathbb M_2(\mathbb C)}=\mathrm{E}_{C\overline{\otimes}1}$
, (5.2) implies that
$\mathrm{E}_{A_2\overline{\otimes}1}\circ\mathrm{E}_{C\overline{\otimes}\mathbb M_2(\mathbb C)}=\mathrm{E}_{C\overline{\otimes}1}$
, (5.2) implies that
Since M is diffuse,
![]() $A_2$
is diffuse. Thus, by applying Lemma 5.3, we can find a unitary
$A_2$
is diffuse. Thus, by applying Lemma 5.3, we can find a unitary
![]() $v_2\in z_2Mz_2$
such that
$v_2\in z_2Mz_2$
such that
Next, (5.2) implies that
![]() $\tau(pz_2)=\tau(qz_2)={\tau(z_2)}/{2}$
. Hence
$\tau(pz_2)=\tau(qz_2)={\tau(z_2)}/{2}$
. Hence
![]() $\tau(pz_1)\geq \tau(qz_1)\geq{\tau(z_1)}/{2}$
. Since
$\tau(pz_1)\geq \tau(qz_1)\geq{\tau(z_1)}/{2}$
. Since
![]() $Nz_1$
is abelian,
$Nz_1$
is abelian,
![]() $r\wedge s=rs$
for any projections
$r\wedge s=rs$
for any projections
![]() $r,s\in Nz_1$
. Therefore,
$r,s\in Nz_1$
. Therefore,
![]() $\tau(pqz_1)\geq\tau(pz_1)+\tau(qz_1)-\tau(z_1)\geq 0$
and
$\tau(pqz_1)\geq\tau(pz_1)+\tau(qz_1)-\tau(z_1)\geq 0$
and
![]() $\tau(p(1-q)z_1)\geq\tau(pz_1)-\tau(qz_1)\geq 0$
.
$\tau(p(1-q)z_1)\geq\tau(pz_1)-\tau(qz_1)\geq 0$
.
Since M is diffuse, there is a projection
![]() $z_3\in M$
such that
$z_3\in M$
such that
![]() $z_3\leq pz_1$
,
$z_3\leq pz_1$
,
![]() $z_3$
commutes with q,
$z_3$
commutes with q,
Since
![]() $z_3\leq p$
, we have that
$z_3\leq p$
, we have that
![]() $\tau(pz_3)+\tau(qz_3)-\tau(z_3)=\tau(qz_3)$
and
$\tau(pz_3)+\tau(qz_3)-\tau(z_3)=\tau(qz_3)$
and
![]() $\tau(pz_3)-\tau(qz_3)=\tau((1-q)z_3)$
. By combining this with (5.5), we get that
$\tau(pz_3)-\tau(qz_3)=\tau((1-q)z_3)$
. By combining this with (5.5), we get that
![]() $z_4=z_1-z_3$
satisfies
$z_4=z_1-z_3$
satisfies
![]() $\tau(pz_4)+\tau(qz_4)-\tau(z_4)=0$
and
$\tau(pz_4)+\tau(qz_4)-\tau(z_4)=0$
and
![]() $\tau(pz_4)-\tau(qz_4)=0$
. In other words, we have that
$\tau(pz_4)-\tau(qz_4)=0$
. In other words, we have that
Let
![]() $A_4=\mathrm{L}^\infty([0,1],\lambda)$
, where [0, 1] is endowed with its Lebesgue measure
$A_4=\mathrm{L}^\infty([0,1],\lambda)$
, where [0, 1] is endowed with its Lebesgue measure
![]() $\lambda$
. Since M is a II
$\lambda$
. Since M is a II
![]() $_1$
factor, we can find a unital trace preserving embedding
$_1$
factor, we can find a unital trace preserving embedding
![]() $A_4\overline{\otimes}\mathbb M_2(\mathbb C)\subset z_4Mz_4$
. Let
$A_4\overline{\otimes}\mathbb M_2(\mathbb C)\subset z_4Mz_4$
. Let
![]() $\tilde r\in A_4$
be a projection such that
$\tilde r\in A_4$
be a projection such that
![]() $\tau(\tilde r)=2\tau(pqz_4)$
and let
$\tau(\tilde r)=2\tau(pqz_4)$
and let
![]() $\tilde{p},\tilde{q}\in A_4\overline{\otimes}\mathbb M_2(\mathbb C)$
be given by
$\tilde{p},\tilde{q}\in A_4\overline{\otimes}\mathbb M_2(\mathbb C)$
be given by
![]() $\tilde{p}=1\otimes e_0$
and
$\tilde{p}=1\otimes e_0$
and
![]() $\tilde{q}=\tilde r\otimes e_0+(1-\tilde r)\otimes e_1$
. Then
$\tilde{q}=\tilde r\otimes e_0+(1-\tilde r)\otimes e_1$
. Then
![]() $\tau(\tilde{p})={\tau(z_4)}/{2}=\tau(pz_4), \tau(\tilde{q})={\tau(z_4)}/{2}=\tau(qz_4)$
and
$\tau(\tilde{p})={\tau(z_4)}/{2}=\tau(pz_4), \tau(\tilde{q})={\tau(z_4)}/{2}=\tau(qz_4)$
and
![]() $\tau(\tilde{p}\tilde{q})=\tau(\tilde{r} \otimes e_0)=\tau(pqz_4)$
. Using this and the fact that M is a II
$\tau(\tilde{p}\tilde{q})=\tau(\tilde{r} \otimes e_0)=\tau(pqz_4)$
. Using this and the fact that M is a II
![]() $_1$
factor, we can find a unitary
$_1$
factor, we can find a unitary
![]() $u\in z_4Mz_4$
such that
$u\in z_4Mz_4$
such that
![]() $pz_4=u\tilde{p}u^*$
and
$pz_4=u\tilde{p}u^*$
and
![]() $qz_4=u\tilde{q}u^*$
. Hence, after unitary conjugacy with u, we may assume that
$qz_4=u\tilde{q}u^*$
. Hence, after unitary conjugacy with u, we may assume that
![]() $pz_4=\tilde{p}$
and
$pz_4=\tilde{p}$
and
![]() $qz_4=\tilde{q}$
. Then
$qz_4=\tilde{q}$
. Then
and Lemma 5.3 gives a unitary
![]() $v_4\in z_4Mz_4$
such that
$v_4\in z_4Mz_4$
such that
Since
![]() $z_3+z_4=z_1$
, we have that
$z_3+z_4=z_1$
, we have that
![]() $z_2+z_3+z_4=1$
, and hence
$z_2+z_3+z_4=1$
, and hence
![]() $v_\varepsilon:= v_2+z_3+v_4\in M$
is a unitary. Furthermore, by using (5.4) and (5.8), we get that
$v_\varepsilon:= v_2+z_3+v_4\in M$
is a unitary. Furthermore, by using (5.4) and (5.8), we get that
![]() $\|v_\varepsilon-1\|_2\leq \|v_2-z_2\|_2+\|v_4-z_4\|_2<\varepsilon$
. We will prove that
$\|v_\varepsilon-1\|_2\leq \|v_2-z_2\|_2+\|v_4-z_4\|_2<\varepsilon$
. We will prove that
![]() $v_\varepsilon$
satisfies (1)–(3) from Definition 5.1(a).
$v_\varepsilon$
satisfies (1)–(3) from Definition 5.1(a).
First, let
![]() $p'\in\{p,1-p\}$
and
$p'\in\{p,1-p\}$
and
![]() $q'\in\{q,1-q\}$
. If two projections r,s generate a diffuse von Neumann algebra, then
$q'\in\{q,1-q\}$
. If two projections r,s generate a diffuse von Neumann algebra, then
![]() $r'\wedge s'=0$
for every
$r'\wedge s'=0$
for every
![]() $r'\in \{r,1-r\}$
and
$r'\in \{r,1-r\}$
and
![]() $s'\in\{s,1-s\}$
. Hence (5.4) and (5.8) imply that
$s'\in\{s,1-s\}$
. Hence (5.4) and (5.8) imply that
![]() $p'z_2\wedge v_2(q'z_2)v_2^*=0$
and
$p'z_2\wedge v_2(q'z_2)v_2^*=0$
and
![]() $p'z_4\wedge v_4(q'z_4)v_4^*=0$
. Thus
$p'z_4\wedge v_4(q'z_4)v_4^*=0$
. Thus
![]() $p'\wedge v_\varepsilon q'v_\varepsilon^*=p'z_3\wedge q'z_3=p'q'z_3$
. Since
$p'\wedge v_\varepsilon q'v_\varepsilon^*=p'z_3\wedge q'z_3=p'q'z_3$
. Since
![]() $z_3\leq p$
, we derive that
$z_3\leq p$
, we derive that
Since
![]() $\tau(pz_2)=\tau(qz_2)={\tau(z_2)}/{2}$
by (5.2), and
$\tau(pz_2)=\tau(qz_2)={\tau(z_2)}/{2}$
by (5.2), and
![]() $z_1+z_2=1$
, we get that
$z_1+z_2=1$
, we get that
![]() $\tau(pz_1)+\tau(qz_1)-\tau(z_1)=\tau(p)+\tau(q)-1$
and
$\tau(pz_1)+\tau(qz_1)-\tau(z_1)=\tau(p)+\tau(q)-1$
and
![]() $\tau(pz_1)-\tau(qz_1)=\tau(p)-\tau(q)$
. Using (5.5) and (5.10) we get that
$\tau(pz_1)-\tau(qz_1)=\tau(p)-\tau(q)$
. Using (5.5) and (5.10) we get that
This shows that p' and
![]() $v_\varepsilon q'v_\varepsilon^*$
are in general position, for every
$v_\varepsilon q'v_\varepsilon^*$
are in general position, for every
![]() $p'\in \{p,1-p\}$
and
$p'\in \{p,1-p\}$
and
![]() $q'\in\{q,1-q\}$
.
$q'\in\{q,1-q\}$
.
Second, let
![]() $N_\varepsilon := M_1\vee v_\varepsilon M_2 v_\varepsilon^*=\{p,v_\varepsilon qv_\varepsilon^*\}''$
. By (5.10), we deduce that
$N_\varepsilon := M_1\vee v_\varepsilon M_2 v_\varepsilon^*=\{p,v_\varepsilon qv_\varepsilon^*\}''$
. By (5.10), we deduce that
![]() $z_3=qz_3+(1-q)z_3\in N_\varepsilon$
. Since
$z_3=qz_3+(1-q)z_3\in N_\varepsilon$
. Since
![]() $z_3\leq p$
, by using (5.9) and (5.10) we get that
$z_3\leq p$
, by using (5.9) and (5.10) we get that
 $$N_\varepsilon z_3=\mathbb Cqz_3\oplus \mathbb C(1-q)z_3=\bigoplus_{\substack{p'\in\{p,1-p\}\\ q'\in\{q,1-q\}}} \mathbb{C} (p'\wedge v_\varepsilon q'v_\varepsilon^*).$$
$$N_\varepsilon z_3=\mathbb Cqz_3\oplus \mathbb C(1-q)z_3=\bigoplus_{\substack{p'\in\{p,1-p\}\\ q'\in\{q,1-q\}}} \mathbb{C} (p'\wedge v_\varepsilon q'v_\varepsilon^*).$$
Since
![]() $N_\varepsilon z_2=\{pz_2,v_2(qz_2)v_2^*\}''$
and
$N_\varepsilon z_2=\{pz_2,v_2(qz_2)v_2^*\}''$
and
![]() $N_\varepsilon z_4=\{pz_4,v_4(qz_4)v_4^*\}''$
, by (5.4) and (5.8) we derive that
$N_\varepsilon z_4=\{pz_4,v_4(qz_4)v_4^*\}''$
, by (5.4) and (5.8) we derive that
![]() $N_\varepsilon z_2$
and
$N_\varepsilon z_2$
and
![]() $N_\varepsilon z_4$
are diffuse. Thus
$N_\varepsilon z_4$
are diffuse. Thus
![]() $N_\varepsilon (z_2+z_4)$
is diffuse. Since
$N_\varepsilon (z_2+z_4)$
is diffuse. Since
![]() $z_2+z_3+z_4=1$
, this shows (2).
$z_2+z_3+z_4=1$
, this shows (2).
Finally, we check (3). By (5.4) and (5.8), we have
![]() $B:= N_\varepsilon (z_2+z_4) = \big(A_2\overline{\otimes} \mathbb{M}_2(\mathbb{C})\big) \oplus \big(A_4\overline{\otimes} \mathbb{M}_2(\mathbb{C})\big)$
, and the unit projection of B is
$B:= N_\varepsilon (z_2+z_4) = \big(A_2\overline{\otimes} \mathbb{M}_2(\mathbb{C})\big) \oplus \big(A_4\overline{\otimes} \mathbb{M}_2(\mathbb{C})\big)$
, and the unit projection of B is
![]() $r = z_2+z_4$
. In particular,
$r = z_2+z_4$
. In particular,
![]() $\mathcal{Z}(B) = (A_2\overline{\otimes} 1)\oplus (A_4\overline{\otimes} 1)$
, and thus by (5.3) and (5.7) we get
$\mathcal{Z}(B) = (A_2\overline{\otimes} 1)\oplus (A_4\overline{\otimes} 1)$
, and thus by (5.3) and (5.7) we get
and similarly for
![]() $1-p$
, q and
$1-p$
, q and
![]() $1-q$
. We conclude that all conditions from Definition 5.1(a) hold, finishing the proof of the proposition.
$1-q$
. We conclude that all conditions from Definition 5.1(a) hold, finishing the proof of the proposition.
5.2 Proof of Theorem 4.9
In [Reference DykemaDyk93, Theorem 2.3], Dykema showed that the free product of finite-dimensional abelian von Neumann algebras
![]() $M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m$
and
$M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m$
and
![]() $M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n$
is given by
$M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n$
is given by
![]() $M_1*M_2=(\bigoplus_{\substack{1\leq i\leq m\\1\leq j\leq n}}\mathbb C(p_i\wedge q_j))\oplus B$
for an interpolated free group factor B. The proof of Theorem 4.9 is inspired by the proof of [Reference DykemaDyk93, Theorem 2.3]. Paralleling [Reference DykemaDyk93], we will prove Theorem 4.9 by induction, building up from the case
$M_1*M_2=(\bigoplus_{\substack{1\leq i\leq m\\1\leq j\leq n}}\mathbb C(p_i\wedge q_j))\oplus B$
for an interpolated free group factor B. The proof of Theorem 4.9 is inspired by the proof of [Reference DykemaDyk93, Theorem 2.3]. Paralleling [Reference DykemaDyk93], we will prove Theorem 4.9 by induction, building up from the case
![]() $m=n=2$
treated in Proposition 5.2.
$m=n=2$
treated in Proposition 5.2.
The following lemma is the main technical part of the proof. It is formulated in a general way, so that it can be used repeatedly in various steps of the induction process.
Lemma 5.5. Let
![]() $M_1,M_2\in\mathcal C$
. Let
$M_1,M_2\in\mathcal C$
. Let
![]() $p_0\in \mathcal Z(M_1)$
be a projection. Write
$p_0\in \mathcal Z(M_1)$
be a projection. Write
![]() $M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
for projections
$M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
for projections
![]() $q_1,\ldots,q_n, q\in\mathcal Z(M_2)$
such that
$q_1,\ldots,q_n, q\in\mathcal Z(M_2)$
such that
![]() $\sum_{j=1}^nq_j+q=1$
and
$\sum_{j=1}^nq_j+q=1$
and
![]() $M_2q$
is diffuse. Assume that:
$M_2q$
is diffuse. Assume that:
-
(0)
 $p_0\neq 0$
,
$p_0\neq 0$
,
 $q_j\neq 1$
for every
$q_j\neq 1$
for every
 $1\leq j\leq n$
;
$1\leq j\leq n$
; -
(1) the pair
 $(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (C); and
$(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (C); and -
(2) the pair
 $(M_1p_0,L)$
satisfies condition (B) for any
$(M_1p_0,L)$
satisfies condition (B) for any
 $L\in\mathcal C$
with unit
$L\in\mathcal C$
with unit
 $p_0$
of the form
$p_0$
of the form
 $L=\mathbb Cr_1\oplus\cdots\oplus\mathbb Cr_n\oplus K$
, with
$L=\mathbb Cr_1\oplus\cdots\oplus\mathbb Cr_n\oplus K$
, with
 $r_j$
a projection of trace
$r_j$
a projection of trace
 $\max(\tau(p_0)+\tau(q_j)-1,0)$
for all
$\max(\tau(p_0)+\tau(q_j)-1,0)$
for all
 $1\leq j\leq n$
, and K diffuse.
$1\leq j\leq n$
, and K diffuse.
Then the pair
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Proof. If
![]() $p_0=1$
, there is nothing to prove, so we may assume that
$p_0=1$
, there is nothing to prove, so we may assume that
![]() $p_0\neq 1$
. Let
$p_0\neq 1$
. Let
![]() $(P,\tau)$
be any tracial von Neumann algebra containing
$(P,\tau)$
be any tracial von Neumann algebra containing
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. To prove the conclusion, we will show that the triple
$M_2$
. To prove the conclusion, we will show that the triple
![]() $(M_1,M_2,P)$
satisfies condition (B).
$(M_1,M_2,P)$
satisfies condition (B).
Let
![]() $\varepsilon>0$
, and write
$\varepsilon>0$
, and write
![]() $M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
for projections
$M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
for projections
![]() $p_1,\ldots,p_m,p\in\mathcal Z(M_1)$
such that
$p_1,\ldots,p_m,p\in\mathcal Z(M_1)$
such that
![]() $\sum_{i=1}^mp_i+p=1$
and
$\sum_{i=1}^mp_i+p=1$
and
![]() $M_1p$
is diffuse. Since
$M_1p$
is diffuse. Since
![]() $p_0\in \mathcal Z(M_1)$
, we may assume that
$p_0\in \mathcal Z(M_1)$
, we may assume that
![]() $p_0=\sum_{i=1}^kp_i+p'$
for some
$p_0=\sum_{i=1}^kp_i+p'$
for some
![]() $0\leq k\leq m$
and a projection
$0\leq k\leq m$
and a projection
![]() $p'\in\mathcal Z(M_1)p$
. Let
$p'\in\mathcal Z(M_1)p$
. Let
![]() $p''=p-p'$
. Note that we have
$p''=p-p'$
. Note that we have
![]() $\mathbb Cp_0\oplus M_1(1-p_0)=\mathbb Cp_0\oplus\mathbb Cp_{k+1}\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p''$
and
$\mathbb Cp_0\oplus M_1(1-p_0)=\mathbb Cp_0\oplus\mathbb Cp_{k+1}\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p''$
and
![]() $M_1p''$
is diffuse.
$M_1p''$
is diffuse.
Since the pair
![]() $(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (C) by assumption (1), so does the triple
$(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (C) by assumption (1), so does the triple
![]() $(\mathbb Cp_0\oplus M_1(1-p_0),M_2,P)$
. Thus, we can find a II
$(\mathbb Cp_0\oplus M_1(1-p_0),M_2,P)$
. Thus, we can find a II
![]() $_1$
factor
$_1$
factor
![]() $Q\supset P$
and
$Q\supset P$
and
![]() $y\in \mathcal U(Q)$
with
$y\in \mathcal U(Q)$
with
![]() $\|y-1\|_2<{\varepsilon}/{2}$
such that, denoting
$\|y-1\|_2<{\varepsilon}/{2}$
such that, denoting
![]() $\widetilde q_j=yq_jy^*$
,
$\widetilde q_j=yq_jy^*$
,
![]() $\widetilde M_2=yM_2y^*$
and
$\widetilde M_2=yM_2y^*$
and
![]() $N=(\mathbb Cp_0\oplus M_1(1-p_0))\vee \widetilde M_2$
, we have that
$N=(\mathbb Cp_0\oplus M_1(1-p_0))\vee \widetilde M_2$
, we have that
-
(a)
 $p_i$
and
$p_i$
and
 $\widetilde q_j$
are in general position for every
$\widetilde q_j$
are in general position for every
 $i\in\{0\}\cup\{k+1,\ldots, m\}$
and
$i\in\{0\}\cup\{k+1,\ldots, m\}$
and
 $1\leq j\leq n$
;
$1\leq j\leq n$
; -
(b)
 $N=\bigoplus_{\substack{i\in\{0\}\cup\{k+1,\ldots,m\}\\1\leq j\leq n}}\mathbb C(p_i\wedge \widetilde q_j)\oplus A$
, where A is diffuse; and
$N=\bigoplus_{\substack{i\in\{0\}\cup\{k+1,\ldots,m\}\\1\leq j\leq n}}\mathbb C(p_i\wedge \widetilde q_j)\oplus A$
, where A is diffuse; and -
(c)
 $\mathrm{E}_{\mathcal Z(A)}(p_i), \mathrm{E}_{\mathcal Z(A)}(\widetilde q_j)\in\mathbb Cr$
, for every
$\mathrm{E}_{\mathcal Z(A)}(p_i), \mathrm{E}_{\mathcal Z(A)}(\widetilde q_j)\in\mathbb Cr$
, for every
 $i\in\{0\}\cup\{k+1,\ldots,m\}$
and
$i\in\{0\}\cup\{k+1,\ldots,m\}$
and
 $1\leq j\leq n$
, where
$1\leq j\leq n$
, where
 $r=1-\sum_{\substack{i\in\{0\}\cup\{k+1,\ldots,m\}\\ 1\leq j\leq n}}p_i\wedge \widetilde q_j$
is the support projection of A.
$r=1-\sum_{\substack{i\in\{0\}\cup\{k+1,\ldots,m\}\\ 1\leq j\leq n}}p_i\wedge \widetilde q_j$
is the support projection of A.
Since
![]() $p_0\not\in\{0,1\}$
and
$p_0\not\in\{0,1\}$
and
![]() $q_j\neq 1$
, for every
$q_j\neq 1$
, for every
![]() $1\leq j\leq n$
, (a) and Lemma 2.1 together imply that
$1\leq j\leq n$
, (a) and Lemma 2.1 together imply that
![]() $p_0-\sum_{j=1}^np_0\wedge\widetilde q_j\neq 0$
. Thus,
$p_0-\sum_{j=1}^np_0\wedge\widetilde q_j\neq 0$
. Thus,
![]() $p_0r=p_0-\sum_{j=1}^np_0\wedge\widetilde q_j\neq 0$
and hence
$p_0r=p_0-\sum_{j=1}^np_0\wedge\widetilde q_j\neq 0$
and hence
![]() $\tau(p_0r)\neq 0$
. Since by (c) we have that
$\tau(p_0r)\neq 0$
. Since by (c) we have that
![]() $\mathrm{E}_{\mathcal Z(A)}(p_0)=({\tau(p_0r)}/{\tau(r)})r$
, (b) implies that
$\mathrm{E}_{\mathcal Z(A)}(p_0)=({\tau(p_0r)}/{\tau(r)})r$
, (b) implies that
 \begin{equation}z_N(p_0)=1-\sum_{\substack{k+1\leq i\leq m\\1\leq j\leq n}}p_i\wedge\widetilde q_j.\end{equation}
\begin{equation}z_N(p_0)=1-\sum_{\substack{k+1\leq i\leq m\\1\leq j\leq n}}p_i\wedge\widetilde q_j.\end{equation}
Furthermore, note that (b) implies that
Next, (a) gives that
![]() $\tau(p_0\wedge \widetilde q_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
$\tau(p_0\wedge \widetilde q_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
![]() $1\leq j\leq n$
. Assumption (2) therefore implies that the pair
$1\leq j\leq n$
. Assumption (2) therefore implies that the pair
![]() $(M_1p_0,p_0Np_0)$
, and thus the triple
$(M_1p_0,p_0Np_0)$
, and thus the triple
![]() $(M_1p_0,p_0Np_0,p_0Qp_0)$
satisfies condition (B). Since
$(M_1p_0,p_0Np_0,p_0Qp_0)$
satisfies condition (B). Since
![]() $M_1p_0= \mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_k\oplus M_1p'$
with
$M_1p_0= \mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_k\oplus M_1p'$
with
![]() $M_1p'$
is diffuse, using the symmetry of condition (B) with respect to swapping indices, we obtain II
$M_1p'$
is diffuse, using the symmetry of condition (B) with respect to swapping indices, we obtain II
![]() $_1$
factors C and
$_1$
factors C and
![]() $R\supset p_0Qp_0$
, where the latter is a unital inclusion, as well as
$R\supset p_0Qp_0$
, where the latter is a unital inclusion, as well as
![]() $w\in \mathcal U(R)$
such that
$w\in \mathcal U(R)$
such that
![]() $\|w-1\|_2<{\varepsilon}/{2}$
and, denoting
$\|w-1\|_2<{\varepsilon}/{2}$
and, denoting
![]() $\widetilde p_i=wp_iw^*$
, for
$\widetilde p_i=wp_iw^*$
, for
![]() $1\leq i\leq k$
:
$1\leq i\leq k$
:
-
(d)
 $\widetilde p_i$
and
$\widetilde p_i$
and
 $p_0\wedge\widetilde q_j$
are in general position for every
$p_0\wedge\widetilde q_j$
are in general position for every
 $1\leq i\leq k$
and
$1\leq i\leq k$
and
 $1\leq j\leq n$
;
$1\leq j\leq n$
; -
(e)
 $wM_1p_0w^*\vee p_0Np_0=\bigoplus_{\substack{1\leq i\leq k\\ 1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge (p_0\wedge \widetilde q_j))\oplus C$
.
$wM_1p_0w^*\vee p_0Np_0=\bigoplus_{\substack{1\leq i\leq k\\ 1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge (p_0\wedge \widetilde q_j))\oplus C$
.
Let
![]() $1\leq i\leq k$
and
$1\leq i\leq k$
and
![]() $1\leq j\leq n$
. Since
$1\leq j\leq n$
. Since
![]() $\widetilde p_i\leq p_0$
, we get that
$\widetilde p_i\leq p_0$
, we get that
![]() $\widetilde p_i\wedge (p_0\wedge \widetilde q_j)=\widetilde p_i\wedge \widetilde q_j$
. Using (a) and (d), we get that if
$\widetilde p_i\wedge (p_0\wedge \widetilde q_j)=\widetilde p_i\wedge \widetilde q_j$
. Using (a) and (d), we get that if
![]() $\widetilde p_i\wedge\widetilde q_j\neq 0$
, then
$\widetilde p_i\wedge\widetilde q_j\neq 0$
, then
![]() $\tau(\widetilde p_i\wedge \widetilde q_j)=\tau(\widetilde p_i)+\tau(p_0\wedge \widetilde q_j)-\tau(p_0)=\tau(\widetilde p_j)+\tau(\widetilde q_j)-1$
. Hence
$\tau(\widetilde p_i\wedge \widetilde q_j)=\tau(\widetilde p_i)+\tau(p_0\wedge \widetilde q_j)-\tau(p_0)=\tau(\widetilde p_j)+\tau(\widetilde q_j)-1$
. Hence
![]() $\widetilde p_i$
and
$\widetilde p_i$
and
![]() $\widetilde q_j$
are in general position. For
$\widetilde q_j$
are in general position. For
![]() $k+1\leq i\leq m$
, let
$k+1\leq i\leq m$
, let
![]() $\widetilde p_i=p_i$
. Then (a), (d) and (e) imply that:
$\widetilde p_i=p_i$
. Then (a), (d) and (e) imply that:
-
(f)
 $\widetilde p_i$
and
$\widetilde p_i$
and
 $\widetilde q_j$
are in general position for every
$\widetilde q_j$
are in general position for every
 $1\leq i\leq m$
and
$1\leq i\leq m$
and
 $1\leq j\leq n$
; and
$1\leq j\leq n$
; and -
(g)
 $wM_1p_0w^*\vee p_0Np_0=\bigoplus_{\substack{1\leq i\leq k\\ 1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge\widetilde q_j)\oplus C$
.
$wM_1p_0w^*\vee p_0Np_0=\bigoplus_{\substack{1\leq i\leq k\\ 1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge\widetilde q_j)\oplus C$
.
Since R and Q are II
![]() $_1$
factors and
$_1$
factors and
![]() $R\supset p_0Qp_0$
, we can find a II
$R\supset p_0Qp_0$
, we can find a II
![]() $_1$
factor S such that
$_1$
factor S such that
![]() $S\supset Q$
and
$S\supset Q$
and
![]() $p_0Sp_0=R$
. Let
$p_0Sp_0=R$
. Let
![]() $x\in\mathcal U(S)$
be given by
$x\in\mathcal U(S)$
be given by
![]() $x=w+(1-p_0)$
. Denote
$x=w+(1-p_0)$
. Denote
![]() $\widetilde M_1=xM_1x^*$
and
$\widetilde M_1=xM_1x^*$
and
![]() $M=\widetilde M_1\vee \widetilde M_2$
. Since
$M=\widetilde M_1\vee \widetilde M_2$
. Since
![]() $\widetilde M_1=w(M_1p_0)w^*\oplus M_1(1-p_0)$
, by Lemma 2.2(1) we get that
$\widetilde M_1=w(M_1p_0)w^*\oplus M_1(1-p_0)$
, by Lemma 2.2(1) we get that
![]() $p_0Mp_0$
is generated by
$p_0Mp_0$
is generated by
![]() $p_0[(\mathbb Cp_0\oplus\widetilde M_1(1-p_0)\vee\widetilde M_2]p_0=p_0[(\mathbb Cp_0\oplus M_1(1-p_0)\vee\widetilde M_2]p_0=p_0Np_0$
and
$p_0[(\mathbb Cp_0\oplus\widetilde M_1(1-p_0)\vee\widetilde M_2]p_0=p_0[(\mathbb Cp_0\oplus M_1(1-p_0)\vee\widetilde M_2]p_0=p_0Np_0$
and
![]() $\widetilde M_1p_0=w(M_1p_0)w^*$
. Thus, (g) can be rewritten as:
$\widetilde M_1p_0=w(M_1p_0)w^*$
. Thus, (g) can be rewritten as:
-
(h)
 $p_0Mp_0=\bigoplus_{\substack{1\leq i\leq k\\ 1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge\widetilde q_j)\oplus C$
.
$p_0Mp_0=\bigoplus_{\substack{1\leq i\leq k\\ 1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge\widetilde q_j)\oplus C$
.
Also, note that
![]() $\widetilde p_i=xp_ix^*$
for every
$\widetilde p_i=xp_ix^*$
for every
![]() $1\leq i\leq m$
. By combining Lemma 2.2(2) and (5.11), we get that
$1\leq i\leq m$
. By combining Lemma 2.2(2) and (5.11), we get that
![]() $z_M(p_0)=z_N(p_0)=1-\sum_{\substack{k+1\leq i\leq m\\1\leq j\leq n}}\widetilde p_i\wedge \widetilde q_j$
. Denote by
$z_M(p_0)=z_N(p_0)=1-\sum_{\substack{k+1\leq i\leq m\\1\leq j\leq n}}\widetilde p_i\wedge \widetilde q_j$
. Denote by
![]() $s=p_0-\sum_{\substack{1\leq i\leq k\\1\leq j\leq n}}\widetilde p_i\wedge\widetilde q_j$
the support projection of C. Since
$s=p_0-\sum_{\substack{1\leq i\leq k\\1\leq j\leq n}}\widetilde p_i\wedge\widetilde q_j$
the support projection of C. Since
![]() $\widetilde p_i\wedge \widetilde q_j\in\mathcal Z(M)$
for every
$\widetilde p_i\wedge \widetilde q_j\in\mathcal Z(M)$
for every
![]() $1\leq i\leq m,1\leq j\leq n$
, we get that
$1\leq i\leq m,1\leq j\leq n$
, we get that
 $$z_M(s)=z_M(p_0)-\sum_{\substack{1\leq i\leq k\\1\leq j\leq n}}\widetilde p_i\wedge\widetilde q_j=1-\sum_{\substack{1\leq i\leq m\\1\leq j\leq n}}\widetilde p_i\wedge \widetilde q_j.$$
$$z_M(s)=z_M(p_0)-\sum_{\substack{1\leq i\leq k\\1\leq j\leq n}}\widetilde p_i\wedge\widetilde q_j=1-\sum_{\substack{1\leq i\leq m\\1\leq j\leq n}}\widetilde p_i\wedge \widetilde q_j.$$
Thus
![]() $M(1-z_M(s))=\bigoplus_{\substack{1\leq i\leq m\\1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge\widetilde q_j)$
. Additionally, since
$M(1-z_M(s))=\bigoplus_{\substack{1\leq i\leq m\\1\leq j\leq n}}\mathbb C(\widetilde p_i\wedge\widetilde q_j)$
. Additionally, since
![]() $C=sMs$
is a II
$C=sMs$
is a II
![]() $_1$
factor, we get that
$_1$
factor, we get that
![]() $Mz_M(s)$
is also a II
$Mz_M(s)$
is also a II
![]() $_1$
factor. Finally, recall that
$_1$
factor. Finally, recall that
![]() $\widetilde M_1=xM_1x^*=\bigoplus_{1\leq i\leq m}\mathbb C\widetilde p_i\oplus x(M_1p)x^*$
and
$\widetilde M_1=xM_1x^*=\bigoplus_{1\leq i\leq m}\mathbb C\widetilde p_i\oplus x(M_1p)x^*$
and
![]() $\widetilde M_2=yM_2y^*=\bigoplus_{1\leq j\leq n}\mathbb C\widetilde q_j\oplus y(M_2q)y^*$
. Since
$\widetilde M_2=yM_2y^*=\bigoplus_{1\leq j\leq n}\mathbb C\widetilde q_j\oplus y(M_2q)y^*$
. Since
![]() $\|y^*x-1\|_2\leq \|x-1\|_2+\|y-1\|_2<\varepsilon$
, it follows that the triple
$\|y^*x-1\|_2\leq \|x-1\|_2+\|y-1\|_2<\varepsilon$
, it follows that the triple
![]() $(M_1,M_2,P)$
satisfies condition (B), which finishes the proof.
$(M_1,M_2,P)$
satisfies condition (B), which finishes the proof.
The following corollaries to Lemma 5.5 establish various cases of the induction process and will provide us with all the necessary ingredients for the proof of Theorem 4.9.
Corollary 5.6. Let
![]() $M_1,M_2\in\mathcal C$
be tracial von Neumann algebras. Assume that there are central projections
$M_1,M_2\in\mathcal C$
be tracial von Neumann algebras. Assume that there are central projections
![]() $p_0\in M_1\setminus\{0,1\}$
and
$p_0\in M_1\setminus\{0,1\}$
and
![]() $q_0\in M_2\setminus\{0,1\}$
such that:
$q_0\in M_2\setminus\{0,1\}$
such that:
-
(1)
 $M_1p_0$
is diffuse and
$M_1p_0$
is diffuse and
 $M_1(1-p_0)=\mathbb C(1-p_0)$
;
$M_1(1-p_0)=\mathbb C(1-p_0)$
; -
(2)
 $M_2q_0$
is either equal to
$M_2q_0$
is either equal to
 $\mathbb Cq_0$
or diffuse, and
$\mathbb Cq_0$
or diffuse, and
 $M_2(1-q_0)=\mathbb C(1-q_0)$
.
$M_2(1-q_0)=\mathbb C(1-q_0)$
.
Then the pair
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Proof. Assume first that
![]() $M_2q_0=\mathbb Cq_0$
, so
$M_2q_0=\mathbb Cq_0$
, so
![]() $M_2=\mathbb Cq_0\oplus\mathbb C(1-q_0)$
. Assume
$M_2=\mathbb Cq_0\oplus\mathbb C(1-q_0)$
. Assume
![]() $L\in\mathcal C$
has unit
$L\in\mathcal C$
has unit
![]() $p_0$
and is of the form
$p_0$
and is of the form
![]() $L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
, where
$L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
, where
![]() $r_1,r_2$
are projections with
$r_1,r_2$
are projections with
![]() $\tau(r_1)=\max(\tau(p_0)+\tau(q_0)-1,0)$
and
$\tau(r_1)=\max(\tau(p_0)+\tau(q_0)-1,0)$
and
![]() $\tau(r_2)=\max(\tau(p_0)+\tau(1-q_0)-1,0)$
, and K is diffuse. Since
$\tau(r_2)=\max(\tau(p_0)+\tau(1-q_0)-1,0)$
, and K is diffuse. Since
![]() $q_0\in M_2\setminus\{0,1\}$
, we have that
$q_0\in M_2\setminus\{0,1\}$
, we have that
![]() $\tau(r_1)<\tau(p_0)$
and
$\tau(r_1)<\tau(p_0)$
and
![]() $\tau(r_2)<\tau(p_0)$
; hence
$\tau(r_2)<\tau(p_0)$
; hence
![]() $L\neq \mathbb Cp_0$
. Since
$L\neq \mathbb Cp_0$
. Since
![]() $M_1p_0$
is diffuse, Corollary 4.4 implies that
$M_1p_0$
is diffuse, Corollary 4.4 implies that
![]() $(M_1p_0,L)$
satisfies condition (B). As the pair
$(M_1p_0,L)$
satisfies condition (B). As the pair
![]() $(\mathbb Cp_0\oplus M_1(1-p_0),M_2)=(\mathbb Cp_0\oplus\mathbb C(1-p_0),\mathbb Cq_0\oplus\mathbb C(1-q_0))$
satisfies condition (C) by Proposition 5.2, Lemma 5.5 implies that
$(\mathbb Cp_0\oplus M_1(1-p_0),M_2)=(\mathbb Cp_0\oplus\mathbb C(1-p_0),\mathbb Cq_0\oplus\mathbb C(1-q_0))$
satisfies condition (C) by Proposition 5.2, Lemma 5.5 implies that
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Second, assume that
![]() $M_2q_0$
is diffuse. Then
$M_2q_0$
is diffuse. Then
![]() $(\mathbb Cp_0\oplus\mathbb C(1-p_0),M_2)$
satisfies condition (B) and hence condition (C) by the above. Let
$(\mathbb Cp_0\oplus\mathbb C(1-p_0),M_2)$
satisfies condition (B) and hence condition (C) by the above. Let
![]() $L\in\mathcal C$
with unit
$L\in\mathcal C$
with unit
![]() $p_0$
and of the form
$p_0$
and of the form
![]() $L=\mathbb Cr\oplus K$
, where r is a projection with
$L=\mathbb Cr\oplus K$
, where r is a projection with
![]() $\tau(r)=\max(\tau(p_0)+\tau(1-q_0)-1,0)$
and K is diffuse. Since
$\tau(r)=\max(\tau(p_0)+\tau(1-q_0)-1,0)$
and K is diffuse. Since
![]() $q_0\in M_2\setminus\{0,1\}$
, we have that
$q_0\in M_2\setminus\{0,1\}$
, we have that
![]() $\tau(r)<\tau(p_0)$
, hence
$\tau(r)<\tau(p_0)$
, hence
![]() $L\neq \mathbb Cp_0$
. Since
$L\neq \mathbb Cp_0$
. Since
![]() $M_1p_0$
is diffuse, Corollary 4.4 again implies that
$M_1p_0$
is diffuse, Corollary 4.4 again implies that
![]() $(M_1p_0,L)$
satisfies condition (B). Lemma 5.5 thus implies that
$(M_1p_0,L)$
satisfies condition (B). Lemma 5.5 thus implies that
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Corollary 5.7. Let
![]() $M_1,M_2\in\mathcal C$
. Assume that
$M_1,M_2\in\mathcal C$
. Assume that
![]() $M_1=\mathbb Cp_1\oplus\mathbb Cp_2\oplus M_1p$
, for projections
$M_1=\mathbb Cp_1\oplus\mathbb Cp_2\oplus M_1p$
, for projections
![]() $p_1,p_2,p\in\mathcal Z(M_1)\setminus\{0\}$
, with
$p_1,p_2,p\in\mathcal Z(M_1)\setminus\{0\}$
, with
![]() $M_1p$
diffuse. Assume that
$M_1p$
diffuse. Assume that
![]() $\dim(M_2)=2$
. Then
$\dim(M_2)=2$
. Then
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Proof. Write
![]() $M_2=\mathbb Cq_1\oplus\mathbb Cq_2$
for projections
$M_2=\mathbb Cq_1\oplus\mathbb Cq_2$
for projections
![]() $q_1,q_2$
such that
$q_1,q_2$
such that
![]() $q_1+q_2=1$
and
$q_1+q_2=1$
and
![]() $\tau(q_1)\geq\tau(q_2)$
. Put
$\tau(q_1)\geq\tau(q_2)$
. Put
![]() $p_0=p_1+p_2$
. Since
$p_0=p_1+p_2$
. Since
![]() $M_1(1-p_0)=M_1p$
is diffuse and
$M_1(1-p_0)=M_1p$
is diffuse and
![]() $p\neq 0$
, Corollary 5.6 implies that
$p\neq 0$
, Corollary 5.6 implies that
Note that
![]() $\tau(p_1)+\tau(p_2)\in (0,1)=\bigcup_{n\geq1}(({n-1})/{n},{n}/({n+1})]$
. We will prove that
$\tau(p_1)+\tau(p_2)\in (0,1)=\bigcup_{n\geq1}(({n-1})/{n},{n}/({n+1})]$
. We will prove that
![]() $(M_1,M_2)$
satisfies condition (B) by induction on
$(M_1,M_2)$
satisfies condition (B) by induction on
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $\tau(p_1)+\tau(p_2)\in(({n-1})/{n},{n}/({n+1})]$
.
$\tau(p_1)+\tau(p_2)\in(({n-1})/{n},{n}/({n+1})]$
.
To prove the base case
![]() $n=1$
, assume that
$n=1$
, assume that
![]() $\tau(p_1)+\tau(p_2)\in(0,\frac{1}{2}]$
. Let
$\tau(p_1)+\tau(p_2)\in(0,\frac{1}{2}]$
. Let
![]() $L\in\mathcal C$
with support projection
$L\in\mathcal C$
with support projection
![]() $p_0$
be of the form
$p_0$
be of the form
![]() $L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
where
$L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
where
![]() $\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
$\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
![]() $1\leq j\leq 2$
, and K is diffuse. Since
$1\leq j\leq 2$
, and K is diffuse. Since
![]() $\tau(p_0)=\tau(p_1)+\tau(p_2)\leq \frac{1}{2}$
and
$\tau(p_0)=\tau(p_1)+\tau(p_2)\leq \frac{1}{2}$
and
![]() $\tau(q_2)\leq\frac{1}{2}$
, we get that
$\tau(q_2)\leq\frac{1}{2}$
, we get that
![]() $r_2=0$
; hence
$r_2=0$
; hence
![]() $L=\mathbb Cr_1\oplus K$
. Moreover, since
$L=\mathbb Cr_1\oplus K$
. Moreover, since
![]() $q_1\neq 1$
, we have that
$q_1\neq 1$
, we have that
![]() $r_1\neq p_0$
. By applying Corollary 34 if
$r_1\neq p_0$
. By applying Corollary 34 if
![]() $r_1\neq 0$
and Corollary 4.4 if
$r_1\neq 0$
and Corollary 4.4 if
![]() $r_1=0$
, we get that
$r_1=0$
, we get that
![]() $(M_1p_0,L)=(\mathbb Cp_1\oplus\mathbb Cp_2,\mathbb Cr_1\oplus K)$
satisfies condition (B). By combining this fact with (5.13), Lemma 5.5 implies that
$(M_1p_0,L)=(\mathbb Cp_1\oplus\mathbb Cp_2,\mathbb Cr_1\oplus K)$
satisfies condition (B). By combining this fact with (5.13), Lemma 5.5 implies that
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Assume that
![]() $n\geq 2$
is such that the inductive hypothesis holds for every
$n\geq 2$
is such that the inductive hypothesis holds for every
![]() $1\leq k\leq n-1$
. Assume that
$1\leq k\leq n-1$
. Assume that
![]() $\tau(p_1)+\tau(p_2)\in(({n-1})/{n},{n}/({n+1})]$
. Let
$\tau(p_1)+\tau(p_2)\in(({n-1})/{n},{n}/({n+1})]$
. Let
![]() $L\in\mathcal C$
with support projection
$L\in\mathcal C$
with support projection
![]() $p_0$
be of the form
$p_0$
be of the form
![]() $L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
where
$L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
where
![]() $\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
$\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
![]() $1\leq j\leq 2$
, and K is diffuse. If
$1\leq j\leq 2$
, and K is diffuse. If
![]() $r_2=0$
, then the same argument as in the case
$r_2=0$
, then the same argument as in the case
![]() $n=1$
implies that
$n=1$
implies that
![]() $(M_1p_0,L)$
satisfies condition (B). If
$(M_1p_0,L)$
satisfies condition (B). If
![]() $r_2\neq 0$
, then since
$r_2\neq 0$
, then since
![]() $\tau(r_2)\leq \tau(r_1)$
we also have
$\tau(r_2)\leq \tau(r_1)$
we also have
![]() $r_1\neq 0$
. Moreover, since
$r_1\neq 0$
. Moreover, since
![]() $\tau(p_0)=\tau(p_1)+\tau(p_2)\leq {n}/({n+1})$
, we get that
$\tau(p_0)=\tau(p_1)+\tau(p_2)\leq {n}/({n+1})$
, we get that
Since
![]() $\dim(M_1p_0)=2$
, the inductive hypothesis implies that
$\dim(M_1p_0)=2$
, the inductive hypothesis implies that
![]() $(M_1p_0,L)$
satisfies condition (B). By combining this fact with (5.13), Lemma 5.5 implies that
$(M_1p_0,L)$
satisfies condition (B). By combining this fact with (5.13), Lemma 5.5 implies that
![]() $(M_1,M_2)$
satisfies condition (B). By induction, this proves the conclusion.
$(M_1,M_2)$
satisfies condition (B). By induction, this proves the conclusion.
Corollary 5.8. Let
![]() $M_1,M_2\in\mathcal C$
. Assume that
$M_1,M_2\in\mathcal C$
. Assume that
![]() $M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
for projections
$M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
for projections
![]() $p_1,\ldots,p_m,p\in\mathcal Z(M_1)\setminus\{0\}$
, where
$p_1,\ldots,p_m,p\in\mathcal Z(M_1)\setminus\{0\}$
, where
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $M_1p$
is diffuse. Assume that
$M_1p$
is diffuse. Assume that
![]() $\dim(M_2)=2$
. Then
$\dim(M_2)=2$
. Then
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Proof. Write
![]() $M_2=\mathbb Cq_1\oplus\mathbb Cq_2$
for projections
$M_2=\mathbb Cq_1\oplus\mathbb Cq_2$
for projections
![]() $q_1,q_2$
. If
$q_1,q_2$
. If
![]() $m=0$
, then
$m=0$
, then
![]() $M_1$
is diffuse and the conclusion follows from Corollary 4.4. If
$M_1$
is diffuse and the conclusion follows from Corollary 4.4. If
![]() $m=1$
, the conclusion is a consequence of Corollary 5.6.
$m=1$
, the conclusion is a consequence of Corollary 5.6.
We will prove the conclusion for
![]() $m\geq 2$
by induction on m. If
$m\geq 2$
by induction on m. If
![]() $m=2$
, the conclusion follows from Corollary 5.7. If
$m=2$
, the conclusion follows from Corollary 5.7. If
![]() $m\geq 3$
, put
$m\geq 3$
, put
![]() $p_0=p_1+p_2$
. Since
$p_0=p_1+p_2$
. Since
![]() $\mathbb Cp_0\oplus M_1(1-p_0)=\mathbb Cp_0\oplus\mathbb Cp_2\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
,
$\mathbb Cp_0\oplus M_1(1-p_0)=\mathbb Cp_0\oplus\mathbb Cp_2\oplus\cdots\oplus\mathbb Cp_m\oplus M_1p$
,
![]() $\mathbb (\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (B) by the inductive hypothesis. Let
$\mathbb (\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (B) by the inductive hypothesis. Let
![]() $L\in\mathcal C$
with support projection
$L\in\mathcal C$
with support projection
![]() $p_0$
be of the form
$p_0$
be of the form
![]() $L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
where
$L=\mathbb Cr_1\oplus\mathbb Cr_2\oplus K$
where
![]() $\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
$\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
for every
![]() $1\leq j\leq 2$
, and K is diffuse. The proof of Lemma 2.1 implies that
$1\leq j\leq 2$
, and K is diffuse. The proof of Lemma 2.1 implies that
![]() $r_1+r_2\neq p_0$
. Since
$r_1+r_2\neq p_0$
. Since
![]() $\dim(M_1p_0)=2$
and the conclusion holds if
$\dim(M_1p_0)=2$
and the conclusion holds if
![]() $m\in\{0,1,2\}$
, we thus get by symmetry of condition (B) with respect to swapping indices that
$m\in\{0,1,2\}$
, we thus get by symmetry of condition (B) with respect to swapping indices that
![]() $(M_1p_0,L)$
satisfies condition (B). By Lemma 5.5 we conclude that
$(M_1p_0,L)$
satisfies condition (B). By Lemma 5.5 we conclude that
![]() $(M_1,M_2)$
satisfies condition (B), which finishes the proof of the corollary.
$(M_1,M_2)$
satisfies condition (B), which finishes the proof of the corollary.
Corollary 5.9. Let
![]() $M_1,M_2\in\mathcal C$
. Assume that
$M_1,M_2\in\mathcal C$
. Assume that
![]() $M_1=\mathbb Cp_1\oplus\cdots\oplus \mathbb Cp_m\oplus M_1p$
for projections
$M_1=\mathbb Cp_1\oplus\cdots\oplus \mathbb Cp_m\oplus M_1p$
for projections
![]() $p_1,\ldots,p_m,p\in\mathcal Z(M_1)\setminus\{0\}$
, where
$p_1,\ldots,p_m,p\in\mathcal Z(M_1)\setminus\{0\}$
, where
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $M_1p$
is diffuse. Assume
$M_1p$
is diffuse. Assume
![]() $M_2\neq \mathbb{C} 1$
. Then
$M_2\neq \mathbb{C} 1$
. Then
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Proof. Write
![]() $M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
, for some
$M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n\oplus M_2q$
, for some
![]() $n\geq 0$
, with
$n\geq 0$
, with
![]() $q_1, \ldots, q_n$
non-zero and
$q_1, \ldots, q_n$
non-zero and
![]() $M_2q$
diffuse. We note that, if
$M_2q$
diffuse. We note that, if
![]() $n=0$
, then
$n=0$
, then
![]() $M_2=M_2q$
is diffuse, and the result follows from Corollary 4.4. Thus, we may assume
$M_2=M_2q$
is diffuse, and the result follows from Corollary 4.4. Thus, we may assume
![]() $n\geq 1$
.
$n\geq 1$
.
First, assume
![]() $n=1$
, and thus necessarily
$n=1$
, and thus necessarily
![]() $q\neq 0$
. Corollary 5.8 implies that
$q\neq 0$
. Corollary 5.8 implies that
![]() $(M_1, M_2(1-q) \oplus \mathbb{C} q) = (M_1, \mathbb{C} (1-q) \oplus \mathbb{C} q)$
satisfies condition (B). Let
$(M_1, M_2(1-q) \oplus \mathbb{C} q) = (M_1, \mathbb{C} (1-q) \oplus \mathbb{C} q)$
satisfies condition (B). Let
![]() $L\in\mathcal{C}$
with support projection q be of the form
$L\in\mathcal{C}$
with support projection q be of the form
![]() $L = \mathbb{C} r_1\oplus\cdots\oplus \mathbb{C} r_m \oplus K$
with
$L = \mathbb{C} r_1\oplus\cdots\oplus \mathbb{C} r_m \oplus K$
with
![]() $r_i$
a projection of trace
$r_i$
a projection of trace
![]() $\max(\tau(p_i) + \tau(q) - 1, 0)$
for all
$\max(\tau(p_i) + \tau(q) - 1, 0)$
for all
![]() $1\leq i\leq m$
and K diffuse. Since
$1\leq i\leq m$
and K diffuse. Since
![]() $\tau(r_i)<\tau(q)$
, for all
$\tau(r_i)<\tau(q)$
, for all
![]() $1\leq i\leq m$
, we have that
$1\leq i\leq m$
, we have that
![]() $L\neq \mathbb Cq$
. Since
$L\neq \mathbb Cq$
. Since
![]() $M_2q$
is diffuse, Corollary 4.4 implies that
$M_2q$
is diffuse, Corollary 4.4 implies that
![]() $(L,M_2q)$
satisfies condition (B). Hence, Lemma 5.5 implies that
$(L,M_2q)$
satisfies condition (B). Hence, Lemma 5.5 implies that
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Next, if
![]() $n=2$
and
$n=2$
and
![]() $q=0$
, then the conclusion follows from Corollary 5.8.
$q=0$
, then the conclusion follows from Corollary 5.8.
We proceed by induction on k, where k is the number of non-zero projections appearing in the description of
![]() $M_2$
(i.e.,
$M_2$
(i.e.,
![]() $k=n$
if
$k=n$
if
![]() $q=0$
and
$q=0$
and
![]() $k=n+1$
otherwise). The base case
$k=n+1$
otherwise). The base case
![]() $k=2$
was proved above. Assume the conclusion holds for some
$k=2$
was proved above. Assume the conclusion holds for some
![]() $k\geq 2$
, and consider the case
$k\geq 2$
, and consider the case
![]() $k+1$
. Since
$k+1$
. Since
![]() $k+1\geq 3$
, we necessarily have
$k+1\geq 3$
, we necessarily have
![]() $n\geq 2$
. Define
$n\geq 2$
. Define
![]() $q_0 = q_1+q_2$
. Then by the induction hypothesis,
$q_0 = q_1+q_2$
. Then by the induction hypothesis,
![]() $(M_1, \mathbb{C} q_0\oplus M_2(1-q_0))$
satisfies condition (B). Moreover, since
$(M_1, \mathbb{C} q_0\oplus M_2(1-q_0))$
satisfies condition (B). Moreover, since
![]() $M_2q_0$
is two-dimensional, Corollary 5.8 implies that
$M_2q_0$
is two-dimensional, Corollary 5.8 implies that
![]() $(L,M_2q_0)$
satisfies condition (B) for every
$(L,M_2q_0)$
satisfies condition (B) for every
![]() $L\in \mathcal{C}$
with support projection
$L\in \mathcal{C}$
with support projection
![]() $q_0$
of the form
$q_0$
of the form
![]() $L = \mathbb{C} r_1\oplus\cdots\oplus \mathbb{C} r_m \oplus K$
with
$L = \mathbb{C} r_1\oplus\cdots\oplus \mathbb{C} r_m \oplus K$
with
![]() $r_i$
a projection of trace
$r_i$
a projection of trace
![]() $\max(\tau(p_i) + \tau(q_0) - 1, 0)$
for all
$\max(\tau(p_i) + \tau(q_0) - 1, 0)$
for all
![]() $1\leq i\leq m$
and K diffuse. Hence, Lemma 5.5 implies that
$1\leq i\leq m$
and K diffuse. Hence, Lemma 5.5 implies that
![]() $(M_1,M_2)$
satisfies condition (B). This finishes the inductive step and therefore the proof of the corollary.
$(M_1,M_2)$
satisfies condition (B). This finishes the inductive step and therefore the proof of the corollary.
We now have all the ingredients required for the proof of Theorem 4.9.
Proof of Theorem 4.9. When one of
![]() $M_1$
or
$M_1$
or
![]() $M_2$
has a non-zero diffuse direct summand, the result follows from Corollary 5.9. Hence we can assume that
$M_2$
has a non-zero diffuse direct summand, the result follows from Corollary 5.9. Hence we can assume that
![]() $M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m$
and
$M_1=\mathbb Cp_1\oplus\cdots\oplus\mathbb Cp_m$
and
![]() $M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n$
, for non-zero projections
$M_2=\mathbb Cq_1\oplus\cdots\oplus\mathbb Cq_n$
, for non-zero projections
![]() $p_1,\ldots,p_m,q_1,\ldots,q_n$
, where
$p_1,\ldots,p_m,q_1,\ldots,q_n$
, where
![]() $m,n\geq 2$
and
$m,n\geq 2$
and
![]() $m+n\geq 5$
.
$m+n\geq 5$
.
We will prove the conclusion by induction on
![]() $m+n$
. Assume without loss of generality that
$m+n$
. Assume without loss of generality that
![]() $m\geq 3$
and write
$m\geq 3$
and write
![]() $p_0=p_1+p_2$
. Let
$p_0=p_1+p_2$
. Let
![]() $L\in\mathcal C$
with support projection
$L\in\mathcal C$
with support projection
![]() $p_0$
be of the form
$p_0$
be of the form
![]() $L=\mathbb Cr_1\oplus\cdots\oplus\mathbb Cr_n \oplus K$
where
$L=\mathbb Cr_1\oplus\cdots\oplus\mathbb Cr_n \oplus K$
where
![]() $\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
, for every
$\tau(r_j)=\max(\tau(p_0)+\tau(q_j)-1,0)$
, for every
![]() $1\leq j\leq n$
, and K is diffuse. The proof of Lemma 2.1 implies that
$1\leq j\leq n$
, and K is diffuse. The proof of Lemma 2.1 implies that
![]() $r_1+\cdots+r_n\neq p_0$
. Since
$r_1+\cdots+r_n\neq p_0$
. Since
![]() $\mathrm{dim}(M_1p_0)=2$
, Corollary 5.8 implies that
$\mathrm{dim}(M_1p_0)=2$
, Corollary 5.8 implies that
![]() $(M_1p_0,L)$
satisfies condition (B).
$(M_1p_0,L)$
satisfies condition (B).
For the base case,
![]() $m+n=5$
, hence
$m+n=5$
, hence
![]() $m=3$
and
$m=3$
and
![]() $n=2$
. Thus
$n=2$
. Thus
![]() $\dim(\mathbb Cp_0\oplus M_1(1-p_0))=\dim(M_2)=2$
and therefore
$\dim(\mathbb Cp_0\oplus M_1(1-p_0))=\dim(M_2)=2$
and therefore
![]() $(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (C) by Proposition 5.2. Lemma 5.5 thus implies that
$(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (C) by Proposition 5.2. Lemma 5.5 thus implies that
![]() $(M_1,M_2)$
satisfies condition (B).
$(M_1,M_2)$
satisfies condition (B).
Now assume that the conclusion holds if
![]() $m+n=k$
, for some
$m+n=k$
, for some
![]() $k\geq 5$
. If
$k\geq 5$
. If
![]() $m+n=k+1$
, then the inductive hypothesis implies that
$m+n=k+1$
, then the inductive hypothesis implies that
![]() $(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (B). Hence Lemma 5.5 again implies that
$(\mathbb Cp_0\oplus M_1(1-p_0),M_2)$
satisfies condition (B). Hence Lemma 5.5 again implies that
![]() $(M_1,M_2)$
satisfies condition (B). This proves the inductive step and finishes the proof.
$(M_1,M_2)$
satisfies condition (B). This proves the inductive step and finishes the proof.
6. The Poulsen simplex as the trace simplex of a free product
In this section we will prove Theorem A, thereby characterizing exactly when the trace simplex of a free product
![]() $C^*$
-algebra is a Poulsen simplex.
$C^*$
-algebra is a Poulsen simplex.
Let
![]() $A_1, A_2$
be unital, separable
$A_1, A_2$
be unital, separable
![]() $C^*$
-algebras and put
$C^*$
-algebras and put
![]() $A=A_1*A_2$
. Any trace
$A=A_1*A_2$
. Any trace
![]() $\varphi\in\mathrm{T}(A)$
gives rise to a triple
$\varphi\in\mathrm{T}(A)$
gives rise to a triple
![]() $(M_1,M_2,M)$
, where
$(M_1,M_2,M)$
, where
![]() $\pi:A\rightarrow M$
is the tracial representation associated to
$\pi:A\rightarrow M$
is the tracial representation associated to
![]() $\varphi$
and
$\varphi$
and
![]() $M_i=\pi(A_i)''\subset M$
for
$M_i=\pi(A_i)''\subset M$
for
![]() $i\in\{1,2\}$
.
$i\in\{1,2\}$
.
Definition 6.1. We say that a trace
![]() $\varphi\in\mathrm{T}(A)$
is approximately factorial if the corresponding triple
$\varphi\in\mathrm{T}(A)$
is approximately factorial if the corresponding triple
![]() $(M_1,M_2,M)$
is approximately factorial, as defined in Definition 4.1. We denote by
$(M_1,M_2,M)$
is approximately factorial, as defined in Definition 4.1. We denote by
![]() $\mathrm{T}_{\mathrm{apf}}(A)$
the collection of approximately factorial traces.
$\mathrm{T}_{\mathrm{apf}}(A)$
the collection of approximately factorial traces.
We start with the following observation. Recall that
![]() $\mathrm{T}_\infty(A) = \mathrm{T}(A)\setminus \mathrm{T}_{\mathrm{fin}}(A)$
denotes the set of traces whose GNS von Neumann algebra is infinite-dimensional.
$\mathrm{T}_\infty(A) = \mathrm{T}(A)\setminus \mathrm{T}_{\mathrm{fin}}(A)$
denotes the set of traces whose GNS von Neumann algebra is infinite-dimensional.
Proposition 6.2. We have
![]() $\mathrm{T}_{\mathrm{apf}}(A)\subset\overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap \mathrm{T}_{\infty}(A)} \subset \overline{\partial_{\mathrm{e}}\mathrm{T}(A)}$
.
$\mathrm{T}_{\mathrm{apf}}(A)\subset\overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap \mathrm{T}_{\infty}(A)} \subset \overline{\partial_{\mathrm{e}}\mathrm{T}(A)}$
.
Proof. Let
![]() $\varphi\in\mathrm{T}_{\mathrm{apf}}(A)$
and
$\varphi\in\mathrm{T}_{\mathrm{apf}}(A)$
and
![]() $\pi:A\rightarrow M$
be the tracial representation associated to
$\pi:A\rightarrow M$
be the tracial representation associated to
![]() $\varphi$
. Denoting
$\varphi$
. Denoting
![]() $M_1=\pi(A_1)''$
and
$M_1=\pi(A_1)''$
and
![]() $M_2=\pi(A_2)''$
, we have by assumption that the triple
$M_2=\pi(A_2)''$
, we have by assumption that the triple
![]() $(M_1,M_2,M)$
is approximately factorial. As a result, for any
$(M_1,M_2,M)$
is approximately factorial. As a result, for any
![]() $n\in\mathbb N$
, we can find a II
$n\in\mathbb N$
, we can find a II
![]() $_1$
factor
$_1$
factor
![]() $P_n$
and
$P_n$
and
![]() $v_n\in\mathcal U(P_n)$
such that
$v_n\in\mathcal U(P_n)$
such that
![]() $M\subset P_n$
,
$M\subset P_n$
,
![]() $\|v_n-1\|_2<{1}/{n}$
, and
$\|v_n-1\|_2<{1}/{n}$
, and
![]() $M_1\vee v_nM_2v_n^*$
is a II
$M_1\vee v_nM_2v_n^*$
is a II
![]() $_1$
factor. Define the
$_1$
factor. Define the
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi_n:A\rightarrow P_n$
by letting
$\pi_n:A\rightarrow P_n$
by letting
![]() $\pi_n(a_1)=\pi(a_1)$
for every
$\pi_n(a_1)=\pi(a_1)$
for every
![]() $a_1\in A_1$
, and
$a_1\in A_1$
, and
![]() $\pi_n(a_2)=v_n\pi(a_2)v_n^*$
for every
$\pi_n(a_2)=v_n\pi(a_2)v_n^*$
for every
![]() $a_2\in A_2$
. Then clearly
$a_2\in A_2$
. Then clearly
![]() $\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
, for every
$\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
, for every
![]() $a\in A$
. Thus, if
$a\in A$
. Thus, if
![]() $\varphi_n:= \tau\circ\pi_n\in\mathrm{T}(A)$
, then
$\varphi_n:= \tau\circ\pi_n\in\mathrm{T}(A)$
, then
![]() $\varphi_n\rightarrow\varphi$
. Since
$\varphi_n\rightarrow\varphi$
. Since
![]() $\pi_n(A)''=M_1\vee v_nM_1v_n^*$
is a II
$\pi_n(A)''=M_1\vee v_nM_1v_n^*$
is a II
![]() $_1$
factor, we get that
$_1$
factor, we get that
![]() $\varphi_n\in \partial_{\mathrm{e}}\mathrm{T}(A)\cap \mathrm{T}_{\infty}(A)$
for every
$\varphi_n\in \partial_{\mathrm{e}}\mathrm{T}(A)\cap \mathrm{T}_{\infty}(A)$
for every
![]() $n\in\mathbb N$
. This finishes the proof.
$n\in\mathbb N$
. This finishes the proof.
In view of Proposition 6.2, in order to show that
![]() $\mathrm{T}(A)$
is a Poulsen simplex, it suffices to show that
$\mathrm{T}(A)$
is a Poulsen simplex, it suffices to show that
![]() $\mathrm{T}_{\mathrm{apf}}(A)$
is dense inside
$\mathrm{T}_{\mathrm{apf}}(A)$
is dense inside
![]() $\mathrm{T}(A)$
. For this, it will be useful to consider the class of traces whose corresponding triple satisfies the conditions of Theorem E.
$\mathrm{T}(A)$
. For this, it will be useful to consider the class of traces whose corresponding triple satisfies the conditions of Theorem E.
Definition 6.3. Let
![]() $A_1, A_2$
be unital, separable
$A_1, A_2$
be unital, separable
![]() $C^*$
-algebras and put
$C^*$
-algebras and put
![]() $A=A_1*A_2$
. We define
$A=A_1*A_2$
. We define
![]() $\mathrm{T}_{\mathrm{l}}(A)$
(
$\mathrm{T}_{\mathrm{l}}(A)$
(
![]() ${\mathrm{l}}$
standing for large) to be the set of traces
${\mathrm{l}}$
standing for large) to be the set of traces
![]() $\varphi\in\mathrm{T}(A)$
whose corresponding triple
$\varphi\in\mathrm{T}(A)$
whose corresponding triple
![]() $(M_1,M_2,M)$
satisfies
$(M_1,M_2,M)$
satisfies
![]() $M_1,M_2\neq \mathbb C1$
,
$M_1,M_2\neq \mathbb C1$
,
![]() $\mathrm{dim}(M_1)+\mathrm{dim}(M_2)\geq 5$
and
$\mathrm{dim}(M_1)+\mathrm{dim}(M_2)\geq 5$
and
![]() $\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
.
$\mathrm{e}(M_1)+\mathrm{e}(M_2)\leq 1$
.
We note that Theorem E implies that
![]() $\mathrm{T}_{\mathrm{l}}(A)\subset \mathrm{T}_{\mathrm{apf}}(A)$
.
$\mathrm{T}_{\mathrm{l}}(A)\subset \mathrm{T}_{\mathrm{apf}}(A)$
.
6.1 Perturbation of traces
The main result of this section is as follows.
Lemma 6.4. Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras. Assume that
$C^*$
-algebras. Assume that
![]() $\mathrm{T}(A_i)$
,
$\mathrm{T}(A_i)$
,
![]() $i=1,2$
, is non-empty and does not consist of a single one-dimensional trace. Assume that if
$i=1,2$
, is non-empty and does not consist of a single one-dimensional trace. Assume that if
![]() $A_1$
(respectively
$A_1$
(respectively
![]() $A_2$
) has an isolated extreme one-dimensional trace, then
$A_2$
) has an isolated extreme one-dimensional trace, then
![]() $A_2$
(respectively
$A_2$
(respectively
![]() $A_1$
) does not have an isolated extreme finite-dimensional trace. Then
$A_1$
) does not have an isolated extreme finite-dimensional trace. Then
![]() $\mathrm{T}(A)\subset\overline{\mathrm{T}_{\mathrm l}(A)}.$
$\mathrm{T}(A)\subset\overline{\mathrm{T}_{\mathrm l}(A)}.$
Proof. Let
![]() $\varphi\in\mathrm{T}(A)$
and
$\varphi\in\mathrm{T}(A)$
and
![]() $\pi:A\rightarrow M$
be the tracial representation associated to
$\pi:A\rightarrow M$
be the tracial representation associated to
![]() $\varphi$
. Denote
$\varphi$
. Denote
![]() $M_1=\pi(A_1)''$
and
$M_1=\pi(A_1)''$
and
![]() $M_2=\pi(A_2)''$
. Let
$M_2=\pi(A_2)''$
. Let
![]() $\mathcal M$
be a II
$\mathcal M$
be a II
![]() $_1$
factor containing M.
$_1$
factor containing M.
We treat three cases separately.
Case 1.
![]() $A_1$
has no isolated extreme finite-dimensional traces. For
$A_1$
has no isolated extreme finite-dimensional traces. For
![]() $n\in\mathbb{N}$
, we will define tracial representations
$n\in\mathbb{N}$
, we will define tracial representations
![]() $\pi_n:A\rightarrow \widetilde{\mathcal M}$
, where
$\pi_n:A\rightarrow \widetilde{\mathcal M}$
, where
![]() $\widetilde{\mathcal M}\supset \mathcal M$
, by first defining its restrictions to
$\widetilde{\mathcal M}\supset \mathcal M$
, by first defining its restrictions to
![]() $A_1$
and
$A_1$
and
![]() $A_2$
.
$A_2$
.
If
![]() $M_2\neq \mathbb C$
, we define
$M_2\neq \mathbb C$
, we define
![]() $\mathcal M_2=\mathcal M$
and
$\mathcal M_2=\mathcal M$
and
![]() $\pi_{n,2}:A_2\rightarrow\mathcal M_2$
by
$\pi_{n,2}:A_2\rightarrow\mathcal M_2$
by
![]() $\pi_{n,2}=\pi_{|A_2}$
for every n. Then we have
$\pi_{n,2}=\pi_{|A_2}$
for every n. Then we have
![]() $\pi_{n,2}(A_2)''=M_2\neq \mathbb C$
. If
$\pi_{n,2}(A_2)''=M_2\neq \mathbb C$
. If
![]() $M_2=\mathbb C$
, then
$M_2=\mathbb C$
, then
![]() $\varphi_{|A_2}\in\mathrm{T}(A_2)$
is a one-dimensional trace. Since
$\varphi_{|A_2}\in\mathrm{T}(A_2)$
is a one-dimensional trace. Since
![]() $\mathrm{T}(A_2)\neq \{\varphi_{|A_2}\}$
by assumption, we can find
$\mathrm{T}(A_2)\neq \{\varphi_{|A_2}\}$
by assumption, we can find
![]() $\psi\in\partial_{\mathrm{e}}\mathrm{T}(A_2)\setminus\{\varphi_{|A_2}\}$
. Let
$\psi\in\partial_{\mathrm{e}}\mathrm{T}(A_2)\setminus\{\varphi_{|A_2}\}$
. Let
![]() $\rho:A_2\rightarrow\mathcal N$
be the tracial representation associated to
$\rho:A_2\rightarrow\mathcal N$
be the tracial representation associated to
![]() $\psi$
. Let
$\psi$
. Let
![]() $p_n\in \mathcal M$
be a projection with
$p_n\in \mathcal M$
be a projection with
![]() $\tau(p_n)=1-\frac{1}{n}$
. We define
$\tau(p_n)=1-\frac{1}{n}$
. We define
![]() $\mathcal M_2=\mathcal M\overline{\otimes}\mathcal N$
and a
$\mathcal M_2=\mathcal M\overline{\otimes}\mathcal N$
and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi_{n,2}:A_2\rightarrow \mathcal M_2$
by letting
$\pi_{n,2}:A_2\rightarrow \mathcal M_2$
by letting
![]() $\pi_{n,2}(a_2)=\pi(a_2)p_n\otimes 1+(1-p_n)\otimes \rho(a_2)$
for every
$\pi_{n,2}(a_2)=\pi(a_2)p_n\otimes 1+(1-p_n)\otimes \rho(a_2)$
for every
![]() $a_2\in A_2$
. Since
$a_2\in A_2$
. Since
![]() $\varphi_{|A_2},\psi\in\partial_{\mathrm{e}}\mathrm{T}(A_2)$
are distinct,
$\varphi_{|A_2},\psi\in\partial_{\mathrm{e}}\mathrm{T}(A_2)$
are distinct,
![]() $\pi_{n,2}(A_2)''=\mathbb Cp_n\otimes 1\oplus (1-p_n)\otimes \mathcal N$
. In particular,
$\pi_{n,2}(A_2)''=\mathbb Cp_n\otimes 1\oplus (1-p_n)\otimes \mathcal N$
. In particular,
![]() $\pi_{n,2}(A_2)''\neq \mathbb C$
for every
$\pi_{n,2}(A_2)''\neq \mathbb C$
for every
![]() $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
.
In either case, we have that
![]() $\|\pi_{n,2}(a_2)-\pi(a_2)\|_2\rightarrow 0$
for every
$\|\pi_{n,2}(a_2)-\pi(a_2)\|_2\rightarrow 0$
for every
![]() $a_2\in A_2$
. Since
$a_2\in A_2$
. Since
![]() $\pi_{n,2}(A_2)''\neq \mathbb C$
, we have
$\pi_{n,2}(A_2)''\neq \mathbb C$
, we have
![]() $\mathrm{e}(\pi_{n,2}(A_2)'')<1$
. Put
$\mathrm{e}(\pi_{n,2}(A_2)'')<1$
. Put
![]() $\delta_n:= 1-\mathrm{e}(\pi_{n,2}(A_2)'')>0$
. Then we have that
$\delta_n:= 1-\mathrm{e}(\pi_{n,2}(A_2)'')>0$
. Then we have that
Next, we define representations
![]() $\pi_{n,1}:A_1\rightarrow\mathcal M_1$
, for
$\pi_{n,1}:A_1\rightarrow\mathcal M_1$
, for
![]() $n\in\mathbb{N}$
, for an appropriate von Neumann algebra
$n\in\mathbb{N}$
, for an appropriate von Neumann algebra
![]() $\mathcal{M}_1$
to be determined later. To this end, let
$\mathcal{M}_1$
to be determined later. To this end, let
![]() $\{z_k\}_{k=0}^K\subset \mathcal Z(M_1)$
, for some
$\{z_k\}_{k=0}^K\subset \mathcal Z(M_1)$
, for some
![]() $K\in\mathbb N\cup\{\infty\}$
, be (possibly zero) projections such that
$K\in\mathbb N\cup\{\infty\}$
, be (possibly zero) projections such that
![]() $\sum_{k=0}^K z_k=1$
,
$\sum_{k=0}^K z_k=1$
,
![]() $M_1z_0$
is diffuse and
$M_1z_0$
is diffuse and
![]() $M_1z_k\cong\mathbb M_{l_k}(\mathbb C)$
, for some
$M_1z_k\cong\mathbb M_{l_k}(\mathbb C)$
, for some
![]() $l_k\in\mathbb N$
, for every
$l_k\in\mathbb N$
, for every
![]() $1\leq k\leq K$
. For every
$1\leq k\leq K$
. For every
![]() $n\in\mathbb{N}$
, fix some
$n\in\mathbb{N}$
, fix some
![]() $L_n\in\mathbb N$
such that
$L_n\in\mathbb N$
such that
![]() $L_n\geq\max\{3,\frac{1}{\delta_n}\}$
.
$L_n\geq\max\{3,\frac{1}{\delta_n}\}$
.
Fix
![]() $1\leq k\leq K$
and let
$1\leq k\leq K$
and let
![]() $\psi_k\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
be given by
$\psi_k\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
be given by
![]() $\psi_k(a_1)=({\tau(\pi(a_1)z_k)}/{\tau(z_k)})$
for every
$\psi_k(a_1)=({\tau(\pi(a_1)z_k)}/{\tau(z_k)})$
for every
![]() $a_1\in A_1$
. Since
$a_1\in A_1$
. Since
![]() $\psi_k$
is
$\psi_k$
is
![]() $l_k$
-dimensional, it is not isolated in
$l_k$
-dimensional, it is not isolated in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A_1)$
by our assumption. Let
$\partial_{\mathrm{e}}\mathrm{T}(A_1)$
by our assumption. Let
![]() $\psi_{n,k}\in\partial_{\mathrm{e}}\mathrm{T}(A_1)\setminus\{\psi_k\}$
be a sequence such that
$\psi_{n,k}\in\partial_{\mathrm{e}}\mathrm{T}(A_1)\setminus\{\psi_k\}$
be a sequence such that
![]() $\psi_{n,k}\rightarrow\psi_k$
, as
$\psi_{n,k}\rightarrow\psi_k$
, as
![]() $n\rightarrow\infty$
. Moreover, we may assume that
$n\rightarrow\infty$
. Moreover, we may assume that
![]() $\psi_{n,k}\neq \psi_{n',k}$
whenever
$\psi_{n,k}\neq \psi_{n',k}$
whenever
![]() $n\neq n'$
. Defining
$n\neq n'$
. Defining
![]() $\eta_{n,k}=({1}/{L_n})\sum_{i=0}^{L_n-1}\psi_{n+i,k}\in\mathrm{T}(A_1)$
, we also have that
$\eta_{n,k}=({1}/{L_n})\sum_{i=0}^{L_n-1}\psi_{n+i,k}\in\mathrm{T}(A_1)$
, we also have that
![]() $\eta_{n,k}\rightarrow\psi_k$
, as
$\eta_{n,k}\rightarrow\psi_k$
, as
![]() $n\rightarrow\infty$
. Since
$n\rightarrow\infty$
. Since
![]() $\psi_k$
is finite-dimensional, Lemma 2.7 implies the existence of a tracial von Neumann algebra
$\psi_k$
is finite-dimensional, Lemma 2.7 implies the existence of a tracial von Neumann algebra
![]() $\mathcal N_k$
and
$\mathcal N_k$
and
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\rho_{n,k}:A_1\rightarrow \mathcal N_k$
such that
$\rho_{n,k}:A_1\rightarrow \mathcal N_k$
such that
![]() $M_1z_k\subset\mathcal N_k$
,
$M_1z_k\subset\mathcal N_k$
,
![]() $\|\rho_{n,k}(a_1)-\pi(a_1)z_k\|_2\rightarrow 0$
for every
$\|\rho_{n,k}(a_1)-\pi(a_1)z_k\|_2\rightarrow 0$
for every
![]() $a_1\in A_1$
, and
$a_1\in A_1$
, and
![]() $\tau\circ\rho_{n,k}=\eta_{n,k}$
for every
$\tau\circ\rho_{n,k}=\eta_{n,k}$
for every
![]() $n\in\mathbb N$
.
$n\in\mathbb N$
.
Note that
![]() $M_1= \bigoplus_{k=0}^K M_1z_k\subset M_1z_0\oplus(\bigoplus_{k=1}^K \mathcal N_k)$
and put
$M_1= \bigoplus_{k=0}^K M_1z_k\subset M_1z_0\oplus(\bigoplus_{k=1}^K \mathcal N_k)$
and put
![]() $\mathcal M_1=\mathcal M*_{M_1}(M_1z_0\oplus(\bigoplus_{k=1}^K\mathcal N_k))$
. For every
$\mathcal M_1=\mathcal M*_{M_1}(M_1z_0\oplus(\bigoplus_{k=1}^K\mathcal N_k))$
. For every
![]() $n\in\mathbb{N}$
, we define a
$n\in\mathbb{N}$
, we define a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi_{n,1}:A_1\rightarrow\mathcal M_1$
by letting
$\pi_{n,1}:A_1\rightarrow\mathcal M_1$
by letting
![]() $\pi_{n,1}(a_1)=\pi(a_1)z_0+\sum_{k=1}^K\rho_{n,k}(a_1)$
. Then, by construction,
$\pi_{n,1}(a_1)=\pi(a_1)z_0+\sum_{k=1}^K\rho_{n,k}(a_1)$
. Then, by construction,
![]() $\|\pi_{n,1}(a_1)-\pi(a_1)\|_2\rightarrow 0$
for every
$\|\pi_{n,1}(a_1)-\pi(a_1)\|_2\rightarrow 0$
for every
![]() $a_1\in A_1$
. We claim that for every
$a_1\in A_1$
. We claim that for every
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
Indeed, note that
![]() $\{z_k\}_{k=0}^K\subset \pi_{n,1}(A_1)'\cap\mathcal M_1$
. If
$\{z_k\}_{k=0}^K\subset \pi_{n,1}(A_1)'\cap\mathcal M_1$
. If
![]() $z_0\neq 0$
, then
$z_0\neq 0$
, then
![]() $\pi_{n,1}(A_1)''z_0=\pi(A_1)''z_0=M_1z_0$
is diffuse. Thus,
$\pi_{n,1}(A_1)''z_0=\pi(A_1)''z_0=M_1z_0$
is diffuse. Thus,
![]() $\mathrm{dim}(\pi_{n,1}(A_1)''z_0)=\infty$
and
$\mathrm{dim}(\pi_{n,1}(A_1)''z_0)=\infty$
and
![]() $\mathrm{e}(\pi_{n,1}(A_1)''z_0)=0$
. Otherwise, there is some
$\mathrm{e}(\pi_{n,1}(A_1)''z_0)=0$
. Otherwise, there is some
![]() $1\leq k\leq K$
such that
$1\leq k\leq K$
such that
![]() $z_k\neq 0$
. Then
$z_k\neq 0$
. Then
![]() $\pi_{n,1}(A_1)''z_k=\rho_{n,k}(A_1)''$
. Since
$\pi_{n,1}(A_1)''z_k=\rho_{n,k}(A_1)''$
. Since
![]() $\tau\circ\rho_{n,k}=\eta_{n,k}=({1}/{L_n})\sum_{i=0}^{L_n-1}\psi_{n+i,k}\in\mathrm{T}(A_1)$
, and
$\tau\circ\rho_{n,k}=\eta_{n,k}=({1}/{L_n})\sum_{i=0}^{L_n-1}\psi_{n+i,k}\in\mathrm{T}(A_1)$
, and
![]() $\psi_{n+i,k}\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
,
$\psi_{n+i,k}\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
,
![]() $0\leq i\leq L_n-1$
, are pairwise distinct, we get that
$0\leq i\leq L_n-1$
, are pairwise distinct, we get that
![]() $\dim(\rho_{n,k}(A_1)'')\geq L_n$
and
$\dim(\rho_{n,k}(A_1)'')\geq L_n$
and
![]() $\mathrm{e}(\rho_{n,k}(A_1)'')\leq({\tau(z_k)}/{L_n})$
. Consequently, we get that
$\mathrm{e}(\rho_{n,k}(A_1)'')\leq({\tau(z_k)}/{L_n})$
. Consequently, we get that
![]() $\dim(\pi_{n,1}(A_1)''z_k)\geq L_n$
and
$\dim(\pi_{n,1}(A_1)''z_k)\geq L_n$
and
![]() $\mathrm{e}(\pi_{n,1}(A_1)''z_k)\leq({\tau(z_k)}/{L_n})$
. Since these inequalities hold for every
$\mathrm{e}(\pi_{n,1}(A_1)''z_k)\leq({\tau(z_k)}/{L_n})$
. Since these inequalities hold for every
![]() $1\leq k\leq K$
with
$1\leq k\leq K$
with
![]() $z_k\neq 0$
, Lemma 2.4 implies that (6.2) holds.
$z_k\neq 0$
, Lemma 2.4 implies that (6.2) holds.
Define
![]() $\widetilde{\mathcal M}=\mathcal M_1*_\mathcal M\mathcal M_2$
and
$\widetilde{\mathcal M}=\mathcal M_1*_\mathcal M\mathcal M_2$
and
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\pi_n:A\rightarrow\widetilde{\mathcal M}$
, for
$\pi_n:A\rightarrow\widetilde{\mathcal M}$
, for
![]() $n\in\mathbb{N}$
, by letting
$n\in\mathbb{N}$
, by letting
![]() $\pi_n(a_1)=\pi_{n,1}(a_1)$
and
$\pi_n(a_1)=\pi_{n,1}(a_1)$
and
![]() $\pi_n(a_2)=\pi_{n,2}(a_2)$
for every
$\pi_n(a_2)=\pi_{n,2}(a_2)$
for every
![]() $a_1\in A_1$
and
$a_1\in A_1$
and
![]() $a_2\in A_2$
. Then
$a_2\in A_2$
. Then
![]() $\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
for every
$\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
for every
![]() $a\in A$
. Since
$a\in A$
. Since
![]() $\pi_n(A_1)=\pi_{n,1}(A_1),\pi_n(A_2)=\pi_{n,2}(A_2)$
, (6.1) and (6.2) imply that
$\pi_n(A_1)=\pi_{n,1}(A_1),\pi_n(A_2)=\pi_{n,2}(A_2)$
, (6.1) and (6.2) imply that
![]() $\dim(\pi_n(A_1)'')\geq 3,\dim(\pi_n(A_2))\geq 2$
and
$\dim(\pi_n(A_1)'')\geq 3,\dim(\pi_n(A_2))\geq 2$
and
![]() $\mathrm{e}(\pi_n(A_1)'')+\mathrm{e}(\pi_n(A_2)'')\leq 1$
. Thus
$\mathrm{e}(\pi_n(A_1)'')+\mathrm{e}(\pi_n(A_2)'')\leq 1$
. Thus
![]() $\varphi_n:= \tau\circ\pi_n\in\mathrm{T}_{\mathrm{l}}(A)$
. Since
$\varphi_n:= \tau\circ\pi_n\in\mathrm{T}_{\mathrm{l}}(A)$
. Since
![]() $\varphi_n\rightarrow\varphi$
, we conclude that
$\varphi_n\rightarrow\varphi$
, we conclude that
![]() $\varphi\in\overline{\mathrm{T}_{\mathrm{l}}(A)}$
, which finishes the proof of Case 1.
$\varphi\in\overline{\mathrm{T}_{\mathrm{l}}(A)}$
, which finishes the proof of Case 1.
Case 2.
![]() $A_1$
has an isolated extreme one-dimensional trace. In this case, by our assumption,
$A_1$
has an isolated extreme one-dimensional trace. In this case, by our assumption,
![]() $A_2$
has no isolated extreme finite-dimensional traces. Hence the proof of Case 1 gives the conclusion by swapping the roles of
$A_2$
has no isolated extreme finite-dimensional traces. Hence the proof of Case 1 gives the conclusion by swapping the roles of
![]() $A_1$
and
$A_1$
and
![]() $A_2$
.
$A_2$
.
Case 3.
![]() $A_1$
has an isolated extreme k-dimensional trace, for some
$A_1$
has an isolated extreme k-dimensional trace, for some
![]() $k\geq 2$
, but no isolated extreme one-dimensional traces. In this case, by our assumption,
$k\geq 2$
, but no isolated extreme one-dimensional traces. In this case, by our assumption,
![]() $A_2$
has no isolated extreme one-dimensional traces. In particular, neither
$A_2$
has no isolated extreme one-dimensional traces. In particular, neither
![]() $A_1$
nor
$A_1$
nor
![]() $A_2$
has an isolated extreme one-dimensional trace.
$A_2$
has an isolated extreme one-dimensional trace.
For
![]() $1\leq j\leq 2$
, let
$1\leq j\leq 2$
, let
![]() $\{z_{i,j}\}_{i=0}^{K_j}\subset \mathcal Z(M_j)$
be possibly zero projections such that
$\{z_{i,j}\}_{i=0}^{K_j}\subset \mathcal Z(M_j)$
be possibly zero projections such that
![]() $\sum_{i=0}^{K_j}z_{i,j}=1$
,
$\sum_{i=0}^{K_j}z_{i,j}=1$
,
![]() $M_jz_{0,j}$
has no one-dimensional direct summands, and
$M_jz_{0,j}$
has no one-dimensional direct summands, and
![]() $M_jz_{i,j}=\mathbb Cz_{i,j}$
for every
$M_jz_{i,j}=\mathbb Cz_{i,j}$
for every
![]() $1\leq i\leq K_j$
. By using that
$1\leq i\leq K_j$
. By using that
![]() $A_j$
has no isolated extreme one-dimensional traces and reasoning similarly to the proof of Case 1 (with
$A_j$
has no isolated extreme one-dimensional traces and reasoning similarly to the proof of Case 1 (with
![]() $L=3$
), we can find
$L=3$
), we can find
![]() $\mathcal M_j\supset \mathcal M$
and
$\mathcal M_j\supset \mathcal M$
and
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\pi_{n,j}:A_j\rightarrow\mathcal M_j$
such that
$\pi_{n,j}:A_j\rightarrow\mathcal M_j$
such that
![]() $\|\pi_{n,j}(a_j)-\pi(a_j)\|_2\rightarrow 0$
, as
$\|\pi_{n,j}(a_j)-\pi(a_j)\|_2\rightarrow 0$
, as
![]() $n\to\infty$
, for every
$n\to\infty$
, for every
![]() $a_j\in A_j$
, and for every
$a_j\in A_j$
, and for every
![]() $1\leq i\leq K_j$
with
$1\leq i\leq K_j$
with
![]() $z_{i,j}\neq 0$
we have that
$z_{i,j}\neq 0$
we have that
![]() $z_{i,j}\in \pi_{n,j}(A_j)'\cap\mathcal M_j$
,
$z_{i,j}\in \pi_{n,j}(A_j)'\cap\mathcal M_j$
,
![]() $\mathrm{dim}(\pi_{n,j}(A_j)''z_{i,j})\geq 3$
and
$\mathrm{dim}(\pi_{n,j}(A_j)''z_{i,j})\geq 3$
and
![]() $\mathrm{e}(\pi_{n,j}(A_j)''z_{i,j})\leq({\tau(z_{i,j})}/{3})$
, for every
$\mathrm{e}(\pi_{n,j}(A_j)''z_{i,j})\leq({\tau(z_{i,j})}/{3})$
, for every
![]() $n\in\mathbb N$
. Moreover, if
$n\in\mathbb N$
. Moreover, if
![]() $z_{0,j}\neq 0$
, then since
$z_{0,j}\neq 0$
, then since
![]() $\pi_{n,j}(A_j)''z_{0,j}=M_jz_{0,j}$
has no one-dimensional direct summands, we get that
$\pi_{n,j}(A_j)''z_{0,j}=M_jz_{0,j}$
has no one-dimensional direct summands, we get that
![]() $\mathrm{dim}(\pi_{n,j}(A_j)''z_{0,j})\geq 4$
and
$\mathrm{dim}(\pi_{n,j}(A_j)''z_{0,j})\geq 4$
and
![]() $\mathrm{e}(\pi_{n,j}(A_j)''z_{0,j})\leq({\tau(z_{0,j})}/{2})$
. Using that
$\mathrm{e}(\pi_{n,j}(A_j)''z_{0,j})\leq({\tau(z_{0,j})}/{2})$
. Using that
![]() $\sum_{i=0}^{K_j}z_{i,j}=1$
, Lemma 2.4 implies that
$\sum_{i=0}^{K_j}z_{i,j}=1$
, Lemma 2.4 implies that
![]() $\dim(\pi_{n,j}(A_j)'')\geq 3$
and
$\dim(\pi_{n,j}(A_j)'')\geq 3$
and
![]() $\mathrm{e}(\pi_{n,j}(A_j)'')\leq\frac{1}{2}$
for every
$\mathrm{e}(\pi_{n,j}(A_j)'')\leq\frac{1}{2}$
for every
![]() $n\in\mathbb N$
.
$n\in\mathbb N$
.
Define
![]() $\widetilde{\mathcal M}=\mathcal M_1*_\mathcal M\mathcal M_2$
and
$\widetilde{\mathcal M}=\mathcal M_1*_\mathcal M\mathcal M_2$
and
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\pi_n:A\rightarrow\widetilde{\mathcal M}$
by letting
$\pi_n:A\rightarrow\widetilde{\mathcal M}$
by letting
![]() $\pi_n(a_1)=\pi_{n,1}(a_1)$
and
$\pi_n(a_1)=\pi_{n,1}(a_1)$
and
![]() $\pi_n(a_2)=\pi_{n,2}(a_2)$
for every
$\pi_n(a_2)=\pi_{n,2}(a_2)$
for every
![]() $a_1\in A_1$
and
$a_1\in A_1$
and
![]() $a_2\in A_2$
. Then
$a_2\in A_2$
. Then
![]() $\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
, for every
$\|\pi_n(a)-\pi(a)\|_2\rightarrow 0$
, for every
![]() $a\in A$
. Since
$a\in A$
. Since
![]() $\pi_n(A_1)=\pi_{n,1}(A_1),\pi_n(A_2)=\pi_{n,2}(A_2)$
, we get that
$\pi_n(A_1)=\pi_{n,1}(A_1),\pi_n(A_2)=\pi_{n,2}(A_2)$
, we get that
![]() $\dim(\pi_n(A_1)'')\geq 3,\dim(\pi_n(A_2)'')\geq 3$
and
$\dim(\pi_n(A_1)'')\geq 3,\dim(\pi_n(A_2)'')\geq 3$
and
![]() $\mathrm{e}(\pi_n(A_1)'')+\mathrm{e}(\pi_n(A_2)'')\leq \frac{1}{2}+\frac{1}{2}=1$
. Thus
$\mathrm{e}(\pi_n(A_1)'')+\mathrm{e}(\pi_n(A_2)'')\leq \frac{1}{2}+\frac{1}{2}=1$
. Thus
![]() $\varphi_n:= \tau\circ\pi_n\in\mathrm{T}_{\mathrm{l}}(A)$
. Since
$\varphi_n:= \tau\circ\pi_n\in\mathrm{T}_{\mathrm{l}}(A)$
. Since
![]() $\varphi_n\rightarrow\varphi$
, we conclude that
$\varphi_n\rightarrow\varphi$
, we conclude that
![]() $\varphi\in\overline{\mathrm{T}_{\mathrm{l}}(A)}$
, which finishes the proof of Case 3, and therefore of the lemma.
$\varphi\in\overline{\mathrm{T}_{\mathrm{l}}(A)}$
, which finishes the proof of Case 3, and therefore of the lemma.
6.2 Isolated extreme finite-dimensional traces
We continue by establishing the equivalence of (2) and (3) in Theorem A by showing that the isolated extreme finite-dimensional traces of
![]() $A=A_1\ast A_2$
correspond exactly to the traces whose restrictions to
$A=A_1\ast A_2$
correspond exactly to the traces whose restrictions to
![]() $A_1$
and
$A_1$
and
![]() $A_2$
satisfy the negation of statement (2) in Theorem A.
$A_2$
satisfy the negation of statement (2) in Theorem A.
Lemma 6.5. Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
such that
$A_2$
such that
![]() $\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for
$\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for
![]() $i=1, 2$
. Assume
$i=1, 2$
. Assume
![]() $\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
. Then the following are equivalent:
$\varphi\in\partial_{\mathrm{e}}\mathrm{T}(A)$
. Then the following are equivalent:
-
(1)
 $\varphi$
is finite-dimensional and isolated in
$\varphi$
is finite-dimensional and isolated in
 $\partial_{\mathrm{e}}\mathrm{T}(A)$
;
$\partial_{\mathrm{e}}\mathrm{T}(A)$
; -
(2) Up to swapping indices, there exist an isolated extreme one-dimensional trace
 $\varphi_1\in \partial_{\mathrm{e}}\mathrm{T}(A_1)$
and an isolated extreme finite-dimensional trace
$\varphi_1\in \partial_{\mathrm{e}}\mathrm{T}(A_1)$
and an isolated extreme finite-dimensional trace
 $\varphi_2\in\partial_{\mathrm{e}}\mathrm{T}(A_2)$
such that
$\varphi_2\in\partial_{\mathrm{e}}\mathrm{T}(A_2)$
such that
 $\varphi_{|A_1} = \varphi_1$
and
$\varphi_{|A_1} = \varphi_1$
and
 $\varphi_{|A_2}=\varphi_2$
.
$\varphi_{|A_2}=\varphi_2$
.
To prove Lemma 6.5 we will need the following immediate consequence of Proposition 5.2.
Lemma 6.6. Let
![]() $(M,\tau)$
be a tracial von Neumann algebra and
$(M,\tau)$
be a tracial von Neumann algebra and
![]() $M_1\neq\mathbb C1,M_2\neq\mathbb C1$
be von Neumann subalgebras. Then there is
$M_1\neq\mathbb C1,M_2\neq\mathbb C1$
be von Neumann subalgebras. Then there is
![]() $t\in (0,1]$
such that for every
$t\in (0,1]$
such that for every
![]() $\varepsilon>0$
, we can find a II
$\varepsilon>0$
, we can find a II
![]() $_1$
factor
$_1$
factor
![]() $M_\varepsilon$
with
$M_\varepsilon$
with
![]() $M\subset M_\varepsilon$
,
$M\subset M_\varepsilon$
,
![]() $v_\varepsilon\in\mathcal U(M_\varepsilon)$
, and a projection
$v_\varepsilon\in\mathcal U(M_\varepsilon)$
, and a projection
![]() $z_\varepsilon\in\mathcal Z(M_1\vee v_\varepsilon M_2v_\varepsilon^*)$
such that
$z_\varepsilon\in\mathcal Z(M_1\vee v_\varepsilon M_2v_\varepsilon^*)$
such that
![]() $\|v_\varepsilon-1\|_2<\varepsilon$
,
$\|v_\varepsilon-1\|_2<\varepsilon$
,
![]() $\tau(z_\varepsilon)\geq t$
, and
$\tau(z_\varepsilon)\geq t$
, and
![]() $(M_1\vee v_\varepsilon M_2v_\varepsilon^*)z_\varepsilon$
is diffuse.
$(M_1\vee v_\varepsilon M_2v_\varepsilon^*)z_\varepsilon$
is diffuse.
Proof. For
![]() $i=1, 2$
, let
$i=1, 2$
, let
![]() $p_i\in M_i$
be a projection with
$p_i\in M_i$
be a projection with
![]() $\tau(p_i)\in [\frac{1}{2},1)$
and put
$\tau(p_i)\in [\frac{1}{2},1)$
and put
![]() $A_i=\mathbb Cp_i\oplus\mathbb C(1-p_i)\subset M_i$
. Assume without loss of generality that
$A_i=\mathbb Cp_i\oplus\mathbb C(1-p_i)\subset M_i$
. Assume without loss of generality that
![]() $\tau(p_2)\geq\tau(p_1)$
, put
$\tau(p_2)\geq\tau(p_1)$
, put
![]() $t=2(1-\tau(p_2))\in (0,1]$
and let
$t=2(1-\tau(p_2))\in (0,1]$
and let
![]() $\varepsilon>0$
. By applying Proposition 5.2 to
$\varepsilon>0$
. By applying Proposition 5.2 to
![]() $A_1,A_2\subset M$
, we can find a II
$A_1,A_2\subset M$
, we can find a II
![]() $_1$
factor
$_1$
factor
![]() $M_\varepsilon$
with
$M_\varepsilon$
with
![]() $M\subset M_\varepsilon$
and
$M\subset M_\varepsilon$
and
![]() $v_\varepsilon\in\mathcal U(M_\varepsilon)$
with
$v_\varepsilon\in\mathcal U(M_\varepsilon)$
with
![]() $\|v_\varepsilon-1\|_2<\varepsilon$
such that, denoting
$\|v_\varepsilon-1\|_2<\varepsilon$
such that, denoting
we have
![]() $q_\varepsilon\in \mathcal Z(A_1\vee v_\varepsilon A_2v_\varepsilon^*)$
and
$q_\varepsilon\in \mathcal Z(A_1\vee v_\varepsilon A_2v_\varepsilon^*)$
and
![]() $(A_1\vee v_\varepsilon A_2v_\varepsilon^*)q_\varepsilon$
is diffuse. Moreover, since
$(A_1\vee v_\varepsilon A_2v_\varepsilon^*)q_\varepsilon$
is diffuse. Moreover, since
![]() $\tau(p_2)\geq\tau(p_1)\geq\frac{1}{2}$
, we get that
$\tau(p_2)\geq\tau(p_1)\geq\frac{1}{2}$
, we get that
![]() $\tau(p_1\wedge v_\varepsilon p_2v_\varepsilon^*)=\tau(p_1)+\tau(p_2)-1$
,
$\tau(p_1\wedge v_\varepsilon p_2v_\varepsilon^*)=\tau(p_1)+\tau(p_2)-1$
,
![]() $\tau((1-p_1)\wedge v_\varepsilon p_2 v_\varepsilon^*)=\tau(p_2)-\tau(p_1)$
,
$\tau((1-p_1)\wedge v_\varepsilon p_2 v_\varepsilon^*)=\tau(p_2)-\tau(p_1)$
,
![]() $p_1\wedge v_\varepsilon(1-p_2)v_\varepsilon^*=0$
and
$p_1\wedge v_\varepsilon(1-p_2)v_\varepsilon^*=0$
and
![]() $(1-p_1)\wedge v_\varepsilon(1-p_2)v_\varepsilon^*=0$
. Thus
$(1-p_1)\wedge v_\varepsilon(1-p_2)v_\varepsilon^*=0$
. Thus
![]() $\tau(q_\varepsilon)=t$
.
$\tau(q_\varepsilon)=t$
.
Then
![]() $q_\varepsilon(M_1\vee v_\varepsilon M_2v_\varepsilon)q_\varepsilon$
is also diffuse. Thus, if
$q_\varepsilon(M_1\vee v_\varepsilon M_2v_\varepsilon)q_\varepsilon$
is also diffuse. Thus, if
![]() $z_\varepsilon\in \mathcal Z(M_1\vee v_\varepsilon M_2v_\varepsilon^*)$
is the central support of
$z_\varepsilon\in \mathcal Z(M_1\vee v_\varepsilon M_2v_\varepsilon^*)$
is the central support of
![]() $q_\varepsilon$
, then
$q_\varepsilon$
, then
![]() $(M_1\vee v_\varepsilon M_2v_\varepsilon^*)z_\varepsilon$
is diffuse and
$(M_1\vee v_\varepsilon M_2v_\varepsilon^*)z_\varepsilon$
is diffuse and
![]() $\tau(z_\varepsilon)\geq\tau(q_\varepsilon) = t$
.
$\tau(z_\varepsilon)\geq\tau(q_\varepsilon) = t$
.
![]() $(1)\Rightarrow (2)$
. Assume
$(1)\Rightarrow (2)$
. Assume
![]() $\varphi\in \partial_{\mathrm{e}}\mathrm{T}(A)$
is finite-dimensional and isolated. Let
$\varphi\in \partial_{\mathrm{e}}\mathrm{T}(A)$
is finite-dimensional and isolated. Let
![]() $\pi:A\to M$
be the tracial representation associated to
$\pi:A\to M$
be the tracial representation associated to
![]() $\varphi$
. Denote
$\varphi$
. Denote
![]() $M_1=\pi(A_1)''$
and
$M_1=\pi(A_1)''$
and
![]() $M_2=\pi(A_2)''$
.
$M_2=\pi(A_2)''$
.
If
![]() $\varphi\in \mathrm{T}_{\mathrm{l}}(A)$
, then by Theorem E and Proposition 6.2, it follows that
$\varphi\in \mathrm{T}_{\mathrm{l}}(A)$
, then by Theorem E and Proposition 6.2, it follows that
![]() $\varphi\in\overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_\infty(A)}$
, contradicting that
$\varphi\in\overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_\infty(A)}$
, contradicting that
![]() $\varphi$
is finite-dimensional and isolated. Hence
$\varphi$
is finite-dimensional and isolated. Hence
![]() $\varphi\not\in \mathrm{T}_{\mathrm{l}}(A)$
. We will prove the conclusion by treating two cases.
$\varphi\not\in \mathrm{T}_{\mathrm{l}}(A)$
. We will prove the conclusion by treating two cases.
Case 1.
![]() $M_1 = \mathbb{C} 1$
or
$M_1 = \mathbb{C} 1$
or
![]() $M_2 = \mathbb{C} 1$
. Assume without loss of generality that
$M_2 = \mathbb{C} 1$
. Assume without loss of generality that
![]() $M_1=\mathbb{C} 1$
. Then
$M_1=\mathbb{C} 1$
. Then
![]() $M_2=M$
, and hence
$M_2=M$
, and hence
![]() $\varphi_{|A_2}$
is an extreme finite-dimensional trace. We will argue by contradiction that both
$\varphi_{|A_2}$
is an extreme finite-dimensional trace. We will argue by contradiction that both
![]() $\varphi_1:=\varphi_{|A_1}\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
and
$\varphi_1:=\varphi_{|A_1}\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
and
![]() $\varphi_2:=\varphi_{|A_2}\in\partial_{\mathrm{e}}\mathrm{T}(A_2)$
are isolated, i.e., condition (2) holds.
$\varphi_2:=\varphi_{|A_2}\in\partial_{\mathrm{e}}\mathrm{T}(A_2)$
are isolated, i.e., condition (2) holds.
First, assume that
![]() $\varphi_2$
is not isolated in
$\varphi_2$
is not isolated in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A_2)$
. Then we can find a sequence of pairwise distinct traces
$\partial_{\mathrm{e}}\mathrm{T}(A_2)$
. Then we can find a sequence of pairwise distinct traces
![]() $\varphi_{n,2}\in \partial_{\mathrm{e}}\mathrm{T}(A_2)$
for
$\varphi_{n,2}\in \partial_{\mathrm{e}}\mathrm{T}(A_2)$
for
![]() $n\in\mathbb N$
such that
$n\in\mathbb N$
such that
![]() $\varphi_{n,2}\to \varphi_2$
. Denote by
$\varphi_{n,2}\to \varphi_2$
. Denote by
![]() $\rho_{n,2}$
the corresponding tracial representations of
$\rho_{n,2}$
the corresponding tracial representations of
![]() $A_2$
and define representations
$A_2$
and define representations
![]() $\rho_n$
of A by
$\rho_n$
of A by
![]() $\rho_n(a_1) = \varphi(a_1)1$
for
$\rho_n(a_1) = \varphi(a_1)1$
for
![]() $a_1\in A_1$
and
$a_1\in A_1$
and
![]() $\rho_n(a_2) = \rho_{n,2}(a_2)$
for
$\rho_n(a_2) = \rho_{n,2}(a_2)$
for
![]() $a_2\in A_2$
. Then
$a_2\in A_2$
. Then
![]() $\rho_n(A)'' = \rho_{n,2}(A_2)''$
are tracial factors, say with traces
$\rho_n(A)'' = \rho_{n,2}(A_2)''$
are tracial factors, say with traces
![]() $\tau_n$
, and the traces
$\tau_n$
, and the traces
![]() $\varphi_n:= \tau_n\circ \rho_n\in\partial_{\mathrm{e}}\text{T}(A)$
are distinct and converge to
$\varphi_n:= \tau_n\circ \rho_n\in\partial_{\mathrm{e}}\text{T}(A)$
are distinct and converge to
![]() $\varphi$
. This contradicts the fact that
$\varphi$
. This contradicts the fact that
![]() $\varphi$
is isolated in
$\varphi$
is isolated in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
.
$\partial_{\mathrm{e}}\mathrm{T}(A)$
.
Second, assume that
![]() $\varphi_1$
is not isolated in
$\varphi_1$
is not isolated in
![]() $\partial_{\mathrm{e}}\text{T}(A_1)$
. If
$\partial_{\mathrm{e}}\text{T}(A_1)$
. If
![]() $M_2 = \mathbb{C} 1$
, we can repeat the above argument to conclude; hence we can assume that
$M_2 = \mathbb{C} 1$
, we can repeat the above argument to conclude; hence we can assume that
![]() $M_2\neq \mathbb{C} 1$
. In particular,
$M_2\neq \mathbb{C} 1$
. In particular,
![]() $\dim(M_2)\geq 2$
and
$\dim(M_2)\geq 2$
and
![]() $\mathrm{e}(M_2)<1$
. Since
$\mathrm{e}(M_2)<1$
. Since
![]() $\varphi_1$
is not isolated, we can repeat the argument from Case 1 in the proof of Lemma 6.4 to conclude that there exist traces
$\varphi_1$
is not isolated, we can repeat the argument from Case 1 in the proof of Lemma 6.4 to conclude that there exist traces
![]() $\varphi_n\in\mathrm{T}_{\mathrm{l}}(A)$
such that
$\varphi_n\in\mathrm{T}_{\mathrm{l}}(A)$
such that
![]() $\varphi_n\to\varphi$
. By Theorem E and Proposition 6.2, it follows once more that
$\varphi_n\to\varphi$
. By Theorem E and Proposition 6.2, it follows once more that
![]() $\varphi\in \overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_\infty(A)}$
, contradicting that
$\varphi\in \overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_\infty(A)}$
, contradicting that
![]() $\varphi$
is finite-dimensional and isolated.
$\varphi$
is finite-dimensional and isolated.
Case 2.
![]() $M_1\neq\mathbb{C} 1$
and
$M_1\neq\mathbb{C} 1$
and
![]() $M_2\neq \mathbb{C} 1$
. By Lemma 6.6, there is
$M_2\neq \mathbb{C} 1$
. By Lemma 6.6, there is
![]() $t\in (0,1]$
such that for every
$t\in (0,1]$
such that for every
![]() $n\in\mathbb N$
, we can find a II
$n\in\mathbb N$
, we can find a II
![]() $_1$
factor
$_1$
factor
![]() $P_n$
with
$P_n$
with
![]() $M\subset P_n$
,
$M\subset P_n$
,
![]() $v_n\in\mathcal U(P_n)$
, and a projection
$v_n\in\mathcal U(P_n)$
, and a projection
![]() $z_n\in\mathcal Z(M_1\vee v_nM_2v_n^*)$
such that
$z_n\in\mathcal Z(M_1\vee v_nM_2v_n^*)$
such that
![]() $\|v_n-1\|_2<\frac{1}{n}$
,
$\|v_n-1\|_2<\frac{1}{n}$
,
![]() $(M_1\vee v_nM_2v_n^*)z_n$
is diffuse and
$(M_1\vee v_nM_2v_n^*)z_n$
is diffuse and
![]() $\tau(z_n)\geq t$
. Define representations
$\tau(z_n)\geq t$
. Define representations
![]() $\rho_n:A\to P_n$
by
$\rho_n:A\to P_n$
by
![]() $\rho_n(a_1) = \pi(a_1)$
for
$\rho_n(a_1) = \pi(a_1)$
for
![]() $a_1\in A_1$
and
$a_1\in A_1$
and
![]() $\rho_n(a_2) = v_n\pi(a_2)v_n^*$
for
$\rho_n(a_2) = v_n\pi(a_2)v_n^*$
for
![]() $a_2\in A_2$
.
$a_2\in A_2$
.
Then defining
![]() $\varphi_n:= \tau\circ\rho_n\in\text{T}(A)$
we have
$\varphi_n:= \tau\circ\rho_n\in\text{T}(A)$
we have
![]() $\varphi_n\to\varphi$
. Since
$\varphi_n\to\varphi$
. Since
![]() $\varphi$
is isolated, by Corollary 3.2 we get that
$\varphi$
is isolated, by Corollary 3.2 we get that
![]() $\mu_n(\{\varphi\})\to 1$
, where
$\mu_n(\{\varphi\})\to 1$
, where
![]() $\mu_n$
is the unique probability measure on
$\mu_n$
is the unique probability measure on
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
whose barycenter is
$\partial_{\mathrm{e}}\mathrm{T}(A)$
whose barycenter is
![]() $\varphi_n$
. For every
$\varphi_n$
. For every
![]() $n\in\mathbb N$
, we can thus find a central projection
$n\in\mathbb N$
, we can thus find a central projection
![]() $w_n\in\rho_n(A)''=M_1\vee v_nM_2v_n^*$
such that
$w_n\in\rho_n(A)''=M_1\vee v_nM_2v_n^*$
such that
![]() $\tau(w_n)=\mu_n(\{\varphi\})\rightarrow 1$
and
$\tau(w_n)=\mu_n(\{\varphi\})\rightarrow 1$
and
![]() $(M_1\vee v_nM_2v_n^*)w_n$
is isomorphic to
$(M_1\vee v_nM_2v_n^*)w_n$
is isomorphic to
![]() $\pi(A)''=M$
, and hence is finite-dimensional. Since
$\pi(A)''=M$
, and hence is finite-dimensional. Since
![]() $\tau(z_n)\geq t>0$
, for every
$\tau(z_n)\geq t>0$
, for every
![]() $n\in\mathbb N$
, we can find
$n\in\mathbb N$
, we can find
![]() $n\in\mathbb N$
such that
$n\in\mathbb N$
such that
![]() $z_nw_n\neq 0$
. Since
$z_nw_n\neq 0$
. Since
![]() $(M_1\vee v_nM_2v_n^*)z_nw_n$
would then be both diffuse and finite-dimensional, this is a contradiction.
$(M_1\vee v_nM_2v_n^*)z_nw_n$
would then be both diffuse and finite-dimensional, this is a contradiction.
Since Cases 1 and 2 either imply condition (2) or yield a contradiction, this finishes the proof of the lemma.
6.3 Proof of Theorem A and its corollaries
We now have all the ingredients to complete the proof of Theorem A.
Proof of Theorem A. Let
![]() $A=A_1 \ast A_2$
be the free product of two unital, separable
$A=A_1 \ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, satisfying that
$A_2$
, satisfying that
![]() $\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for every
$\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for every
![]() $1\leq i\leq 2$
.
$1\leq i\leq 2$
.
First of all, we note that Lemma 6.5 implies the equivalence of statements (2) and (3). We proceed by proving the equivalence of statements (1) and (2), and the moreover statement.
Assume that condition (2) in Theorem A holds. Note that Theorem E and Proposition 6.2 imply that
![]() $\mathrm{T}_{\mathrm{l}}(A)\subset \mathrm{T}_{\mathrm{apf}}(A)\subset \overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_{\infty}(A)}$
. From this and Lemma 6.4, it thus follows that
$\mathrm{T}_{\mathrm{l}}(A)\subset \mathrm{T}_{\mathrm{apf}}(A)\subset \overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_{\infty}(A)}$
. From this and Lemma 6.4, it thus follows that
Hence, the moreover statement of the theorem holds and
![]() $\mathrm{T}(A)\subset\overline{\partial_{\mathrm{e}}\mathrm{T}(A)}$
, meaning that
$\mathrm{T}(A)\subset\overline{\partial_{\mathrm{e}}\mathrm{T}(A)}$
, meaning that
![]() $\mathrm{T}(A)$
is a Poulsen simplex.
$\mathrm{T}(A)$
is a Poulsen simplex.
Conversely, assume that condition (2) in Theorem A fails. Without loss of generality, assume that
![]() $A_1$
admits an isolated extreme one-dimensional trace
$A_1$
admits an isolated extreme one-dimensional trace
![]() $\varphi$
and
$\varphi$
and
![]() $A_2$
admits an isolated extreme k-dimensional trace for some
$A_2$
admits an isolated extreme k-dimensional trace for some
![]() $k\in\mathbb{N}$
. By assumption,
$k\in\mathbb{N}$
. By assumption,
![]() $\varphi$
is not the only trace on
$\varphi$
is not the only trace on
![]() $A_1$
. In particular,
$A_1$
. In particular,
![]() $|\mathrm{T}(A_1)|\geq 2$
and therefore also
$|\mathrm{T}(A_1)|\geq 2$
and therefore also
![]() $|\mathrm{T}(A)|\geq 2$
. Hence Corollary 3.5 tells us that
$|\mathrm{T}(A)|\geq 2$
. Hence Corollary 3.5 tells us that
![]() $\mathrm{T}(A)$
is not a Poulsen simplex. This completes the proof of Theorem A.
$\mathrm{T}(A)$
is not a Poulsen simplex. This completes the proof of Theorem A.
Proof of Corollary B. Assume that
![]() $A_i$
, for every
$A_i$
, for every
![]() $1\leq i\leq 2$
, has no one-dimensional direct summand. Since
$1\leq i\leq 2$
, has no one-dimensional direct summand. Since
![]() $A_i$
is finite-dimensional, we get that
$A_i$
is finite-dimensional, we get that
![]() $\mathrm{T}(A_i)$
is non-empty and contains no one-dimensional trace for every
$\mathrm{T}(A_i)$
is non-empty and contains no one-dimensional trace for every
![]() $1\leq i\leq 2$
. Theorem A thus implies that
$1\leq i\leq 2$
. Theorem A thus implies that
![]() $\mathrm{T}(A)$
is Poulsen.
$\mathrm{T}(A)$
is Poulsen.
Conversely, assume that
![]() $\text{T}(A)$
is Poulsen. Since
$\text{T}(A)$
is Poulsen. Since
![]() $A_i$
is finite-dimensional, it admits an isolated extreme finite-dimensional trace, for every
$A_i$
is finite-dimensional, it admits an isolated extreme finite-dimensional trace, for every
![]() $1\leq i\leq 2$
. By Corollary 3.5 it follows that
$1\leq i\leq 2$
. By Corollary 3.5 it follows that
![]() $A_i$
does not admit a one-dimensional trace and thus has no one-dimensional direct summand for every
$A_i$
does not admit a one-dimensional trace and thus has no one-dimensional direct summand for every
![]() $1\leq i\leq 2$
.
$1\leq i\leq 2$
.
Finally, we turn to the proof of Corollary C. In order to do so, we first establish the following result which appears to be of independent interest. For a countable discrete group G, we denote by
![]() $\mathrm{Tr}(G)$
and
$\mathrm{Tr}(G)$
and
![]() $\mathrm{Ch}(G)$
the sets of traces and characters of G, respectively, and we identify
$\mathrm{Ch}(G)$
the sets of traces and characters of G, respectively, and we identify
![]() $\mathrm{Tr}(G)=\mathrm{T}(C^*G)$
and
$\mathrm{Tr}(G)=\mathrm{T}(C^*G)$
and
![]() $\mathrm{Ch}(G)=\partial_{\mathrm{e}}\mathrm{T}(C^*G)$
in the usual way. Recall that G is said to have property (ET) if the trivial character
$\mathrm{Ch}(G)=\partial_{\mathrm{e}}\mathrm{T}(C^*G)$
in the usual way. Recall that G is said to have property (ET) if the trivial character
![]() $1_G$
is isolated in
$1_G$
is isolated in
![]() $\mathrm{Ch}(G)$
.
$\mathrm{Ch}(G)$
.
Lemma 6.7. Let G be a countable discrete group. Assume that there exists a finite-dimensional character
![]() $\varphi\in\mathrm{Ch}(G)$
which is isolated in
$\varphi\in\mathrm{Ch}(G)$
which is isolated in
![]() $\mathrm{Ch}(G)$
. Then G has property (ET).
$\mathrm{Ch}(G)$
. Then G has property (ET).
Proof. To prove that G has property (ET), let
![]() $(\psi_n)_{n\in\mathbb N}\subset\mathrm{Ch}(G)$
be a sequence such that
$(\psi_n)_{n\in\mathbb N}\subset\mathrm{Ch}(G)$
be a sequence such that
![]() $\psi_n\rightarrow 1_G$
. Define
$\psi_n\rightarrow 1_G$
. Define
![]() $\varphi_n:= \varphi\psi_n\in\mathrm{Tr}(G)$
. Let
$\varphi_n:= \varphi\psi_n\in\mathrm{Tr}(G)$
. Let
![]() $\pi:G\rightarrow\mathcal U(k)$
be a homomorphism, for some
$\pi:G\rightarrow\mathcal U(k)$
be a homomorphism, for some
![]() $k\in\mathbb N$
, such that
$k\in\mathbb N$
, such that
![]() $\varphi=\mathrm{tr}_k\circ\pi$
and
$\varphi=\mathrm{tr}_k\circ\pi$
and
![]() $\pi(G)''=\mathbb M_k(\mathbb C)$
, where
$\pi(G)''=\mathbb M_k(\mathbb C)$
, where
![]() $\text{tr}_k:\mathbb M_k(\mathbb C)\rightarrow\mathbb C$
denotes the normalized trace. For
$\text{tr}_k:\mathbb M_k(\mathbb C)\rightarrow\mathbb C$
denotes the normalized trace. For
![]() $n\in\mathbb N$
, let
$n\in\mathbb N$
, let
![]() $P_n$
be a tracial factor and
$P_n$
be a tracial factor and
![]() $\rho_n:G\rightarrow\mathcal U(P_n)$
be a homomorphism such that
$\rho_n:G\rightarrow\mathcal U(P_n)$
be a homomorphism such that
![]() $\psi_n=\tau\circ\rho_n$
and
$\psi_n=\tau\circ\rho_n$
and
![]() $\rho_n(G)''=P_n$
. Define
$\rho_n(G)''=P_n$
. Define
![]() $\pi_n:G\rightarrow\mathcal U(\mathbb M_k(\mathbb C)\overline{\otimes}P_n)$
by letting
$\pi_n:G\rightarrow\mathcal U(\mathbb M_k(\mathbb C)\overline{\otimes}P_n)$
by letting
![]() $\pi_n(g)=\pi(g)\otimes\rho_n(g)$
, for every
$\pi_n(g)=\pi(g)\otimes\rho_n(g)$
, for every
![]() $g\in G$
. Then
$g\in G$
. Then
![]() $\tau\circ\pi_n=\varphi\psi_n=\varphi_n.$
$\tau\circ\pi_n=\varphi\psi_n=\varphi_n.$
Let
![]() $\mu_n$
be the unique Borel probability measure on
$\mu_n$
be the unique Borel probability measure on
![]() $\mathrm{Ch}(G)$
whose barycenter is
$\mathrm{Ch}(G)$
whose barycenter is
![]() $\varphi_n$
. Since
$\varphi_n$
. Since
![]() $\varphi_n\rightarrow\varphi$
and
$\varphi_n\rightarrow\varphi$
and
![]() $\varphi$
is isolated in
$\varphi$
is isolated in
![]() $\mathrm{Ch}(G)$
, Corollary 3.2 implies that
$\mathrm{Ch}(G)$
, Corollary 3.2 implies that
![]() $\lambda_n:= \mu_n(\{\varphi\})\rightarrow 1$
. Since
$\lambda_n:= \mu_n(\{\varphi\})\rightarrow 1$
. Since
![]() $\tau\circ\pi_n=\varphi_n$
, there is a projection
$\tau\circ\pi_n=\varphi_n$
, there is a projection
![]() $z_n\in\mathcal Z(\pi_n(G)'')$
such that
$z_n\in\mathcal Z(\pi_n(G)'')$
such that
![]() $\tau(z_n)=\lambda_n$
and
$\tau(z_n)=\lambda_n$
and
![]() $\tau(\pi_n(g)z_n)=\lambda_n\varphi(g)$
for every
$\tau(\pi_n(g)z_n)=\lambda_n\varphi(g)$
for every
![]() $g\in G$
.
$g\in G$
.
If
![]() $k=1$
, then
$k=1$
, then
![]() $\pi:G\rightarrow\mathcal U(1)=\mathbb T$
is a homomorphism. Thus
$\pi:G\rightarrow\mathcal U(1)=\mathbb T$
is a homomorphism. Thus
![]() $\varphi=\pi$
and
$\varphi=\pi$
and
![]() $\pi_n(g)=\varphi(g)\rho_n(g)$
. This implies that for every
$\pi_n(g)=\varphi(g)\rho_n(g)$
. This implies that for every
![]() $n\in\mathbb N$
and
$n\in\mathbb N$
and
![]() $g\in G$
we have that
$g\in G$
we have that
![]() $\lambda_n\varphi(g)=\tau(\pi_n(g)z_n)=\varphi(g)\tau(\rho_n(g)z_n)$
. Hence, for every
$\lambda_n\varphi(g)=\tau(\pi_n(g)z_n)=\varphi(g)\tau(\rho_n(g)z_n)$
. Hence, for every
![]() $n\in\mathbb N$
, we have
$n\in\mathbb N$
, we have
![]() $\tau(\rho_n(g)z_n)=\lambda_n=\tau(z_n)$
and thus
$\tau(\rho_n(g)z_n)=\lambda_n=\tau(z_n)$
and thus
![]() $\rho_n(g)z_n=z_n$
for every
$\rho_n(g)z_n=z_n$
for every
![]() $g\in G$
. This implies that
$g\in G$
. This implies that
![]() $z_n$
lies in the center of
$z_n$
lies in the center of
![]() $\rho_n(G)''=P_n$
. Since
$\rho_n(G)''=P_n$
. Since
![]() $P_n$
is a factor and
$P_n$
is a factor and
![]() $\tau(z_n)\rightarrow 1$
, we get that
$\tau(z_n)\rightarrow 1$
, we get that
![]() $z_n=1$
for large
$z_n=1$
for large
![]() $n\in\mathbb N$
. Hence,
$n\in\mathbb N$
. Hence,
![]() $\psi_n=\tau\circ\rho_n=1_G$
, for large
$\psi_n=\tau\circ\rho_n=1_G$
, for large
![]() $n\in\mathbb N$
. This shows that
$n\in\mathbb N$
. This shows that
![]() $1_G$
is isolated in
$1_G$
is isolated in
![]() $\text{Ch}(G)$
and so G has property (ET) if
$\text{Ch}(G)$
and so G has property (ET) if
![]() $k=1$
. For
$k=1$
. For
![]() $k\geq 2$
, we will need the following claim.
$k\geq 2$
, we will need the following claim.
Claim 6.8. If
![]() $p_n\in\pi_n(G)'\cap (\mathbb M_k(\mathbb C)\overline{\otimes}P_n)$
is a non-zero projection, for
$p_n\in\pi_n(G)'\cap (\mathbb M_k(\mathbb C)\overline{\otimes}P_n)$
is a non-zero projection, for
![]() $n\in\mathbb N$
, then
$n\in\mathbb N$
, then
![]() $\tau(p_n)\geq {1}/{k^2}$
.
$\tau(p_n)\geq {1}/{k^2}$
.
Proof of claim. Let
![]() $g\in G$
and note that
$g\in G$
and note that
![]() $\pi(g)\otimes 1$
commutes with
$\pi(g)\otimes 1$
commutes with
![]() $1\overline{\otimes}P_n$
and that
$1\overline{\otimes}P_n$
and that
![]() $1\otimes\rho_n(g)$
and
$1\otimes\rho_n(g)$
and
![]() $\pi_n(g)=\pi(g)\otimes\rho_n(g)$
normalize
$\pi_n(g)=\pi(g)\otimes\rho_n(g)$
normalize
![]() $1\overline{\otimes}P_n$
. Using these facts, we get that
$1\overline{\otimes}P_n$
. Using these facts, we get that
In other words,
![]() $\mathrm{E}_{1\overline{\otimes}P_n}(p_n)$
commutes with
$\mathrm{E}_{1\overline{\otimes}P_n}(p_n)$
commutes with
![]() $1\otimes \rho_n(g)$
for every
$1\otimes \rho_n(g)$
for every
![]() $g\in G$
. Since
$g\in G$
. Since
![]() $\rho_n(G)''=P_n$
and
$\rho_n(G)''=P_n$
and
![]() $P_n$
is a factor, we conclude that
$P_n$
is a factor, we conclude that
![]() $\mathrm{E}_{1\overline{\otimes}P_n}(p_n)=\tau(p_n)1$
. In contrast, for every tracial von Neumann algebra
$\mathrm{E}_{1\overline{\otimes}P_n}(p_n)=\tau(p_n)1$
. In contrast, for every tracial von Neumann algebra
![]() $(P,\tau)$
we have that
$(P,\tau)$
we have that
This inequality follows from [Reference Pimsner and PopaPP86, Proposition 2.1] when P is a II
![]() $_1$
factor, since in this case
$_1$
factor, since in this case
![]() $1\overline{\otimes}P\subset\mathbb M_k(\mathbb C)\overline{\otimes}P$
is an inclusion of II
$1\overline{\otimes}P\subset\mathbb M_k(\mathbb C)\overline{\otimes}P$
is an inclusion of II
![]() $_1$
factors of index
$_1$
factors of index
![]() $k^2$
. For general P, let Q be a II
$k^2$
. For general P, let Q be a II
![]() $_1$
factor which contains P and consider the natural inclusion
$_1$
factor which contains P and consider the natural inclusion
![]() $\mathbb M_k(\mathbb C)\overline{\otimes}P\subset\mathbb M_k(\mathbb C)\overline{\otimes}Q$
. If
$\mathbb M_k(\mathbb C)\overline{\otimes}P\subset\mathbb M_k(\mathbb C)\overline{\otimes}Q$
. If
![]() $x\in \mathbb M_k(\mathbb C)\overline{\otimes}P$
and
$x\in \mathbb M_k(\mathbb C)\overline{\otimes}P$
and
![]() $x\geq 0$
, then
$x\geq 0$
, then
![]() $\mathrm{E}_{1\overline{\otimes}P}(x)=\mathrm{E}_{1\overline{\otimes}Q}(x)\geq({1}/{k^2})x$
, which proves (6.3).
$\mathrm{E}_{1\overline{\otimes}P}(x)=\mathrm{E}_{1\overline{\otimes}Q}(x)\geq({1}/{k^2})x$
, which proves (6.3).
By applying (6.3), we get that
![]() $\tau(p_n)1=\mathrm{E}_{1\overline{\otimes}P_n}(p_n)\geq({1}/{k^2})p_n$
and hence
$\tau(p_n)1=\mathrm{E}_{1\overline{\otimes}P_n}(p_n)\geq({1}/{k^2})p_n$
and hence
![]() $p_n\leq k^2\tau(p_n)1$
. Since
$p_n\leq k^2\tau(p_n)1$
. Since
![]() $p_n$
is a non-zero projection, this implies that
$p_n$
is a non-zero projection, this implies that
![]() $k^2\tau(p_n)\geq 1$
and thus
$k^2\tau(p_n)\geq 1$
and thus
![]() $\tau(p_n)\geq{1}/{k^2}$
, as claimed.
$\tau(p_n)\geq{1}/{k^2}$
, as claimed.
Next, since
![]() $\tau(z_n)\rightarrow 1$
, we can find
$\tau(z_n)\rightarrow 1$
, we can find
![]() $N\in\mathbb N$
such that
$N\in\mathbb N$
such that
![]() $\tau(z_n)>1-{1}/{k^2}$
for every
$\tau(z_n)>1-{1}/{k^2}$
for every
![]() $n\geq N$
. Since
$n\geq N$
. Since
![]() $z_n\in\pi_n(G)'\cap (\mathbb M_k(\mathbb C)\overline{\otimes}P_n)$
, Claim 6.8 implies that
$z_n\in\pi_n(G)'\cap (\mathbb M_k(\mathbb C)\overline{\otimes}P_n)$
, Claim 6.8 implies that
![]() $z_n=1$
for every
$z_n=1$
for every
![]() $n\geq N$
. Thus,
$n\geq N$
. Thus,
![]() $\tau\circ\pi_n=\varphi$
and
$\tau\circ\pi_n=\varphi$
and
For
![]() $n\in\mathbb N$
, put
$n\in\mathbb N$
, put
![]() $H_n=\{g\in G\mid\psi_n(g)=1\}=\{g\in G\mid\rho_n(g)=1\}$
. Put
$H_n=\{g\in G\mid\psi_n(g)=1\}=\{g\in G\mid\rho_n(g)=1\}$
. Put
![]() $S=\{g\in G\mid \varphi(g)\neq 0\}$
and let
$S=\{g\in G\mid \varphi(g)\neq 0\}$
and let
![]() $H=\langle S\rangle<G$
be the subgroup generated by S. By (6.4) we get that
$H=\langle S\rangle<G$
be the subgroup generated by S. By (6.4) we get that
![]() $S\subset H_n$
, and since
$S\subset H_n$
, and since
![]() $H_n$
is a group, we deduce that
$H_n$
is a group, we deduce that
We claim that
![]() $[G:H]<\infty$
. Otherwise, we can find a sequence
$[G:H]<\infty$
. Otherwise, we can find a sequence
![]() $(g_i)_{i=1}^\infty\subset G$
such that
$(g_i)_{i=1}^\infty\subset G$
such that
![]() $g_j^{-1}g_i\not\in H$
for every
$g_j^{-1}g_i\not\in H$
for every
![]() $i\neq j$
. But then for every
$i\neq j$
. But then for every
![]() $i\neq j$
, we have
$i\neq j$
, we have
![]() $g_j^{-1}g_i\not\in S$
and thus
$g_j^{-1}g_i\not\in S$
and thus
![]() $0=\varphi(g_j^{-1}g_i)=\mathrm{tr}_k(\pi(g_j^{-1}g_i))$
. This would imply that the unitaries
$0=\varphi(g_j^{-1}g_i)=\mathrm{tr}_k(\pi(g_j^{-1}g_i))$
. This would imply that the unitaries
![]() $(\pi(g_i))_{i=1}^\infty\subset\mathbb M_k(\mathbb C)$
are pairwise orthogonal with respect to the scalar product
$(\pi(g_i))_{i=1}^\infty\subset\mathbb M_k(\mathbb C)$
are pairwise orthogonal with respect to the scalar product
![]() $\langle \xi,\eta\rangle=\text{tr}_k(\eta^*\xi)$
, contradicting that
$\langle \xi,\eta\rangle=\text{tr}_k(\eta^*\xi)$
, contradicting that
![]() $\mathbb M_k(\mathbb C)$
is finite-dimensional.
$\mathbb M_k(\mathbb C)$
is finite-dimensional.
Note that
![]() $H<G$
is a normal subgroup and let
$H<G$
is a normal subgroup and let
![]() $\zeta:G\rightarrow G/H$
be the quotient homomorphism. If
$\zeta:G\rightarrow G/H$
be the quotient homomorphism. If
![]() $n\geq N$
, then (6.5) gives that
$n\geq N$
, then (6.5) gives that
![]() $H\subset H_n$
and thus
$H\subset H_n$
and thus
![]() ${\psi_n}_{|H}=1_H$
. This implies that there exists
${\psi_n}_{|H}=1_H$
. This implies that there exists
![]() $\chi_n\in\mathrm{Ch}(G/H)$
such that
$\chi_n\in\mathrm{Ch}(G/H)$
such that
![]() $\psi_n=\chi_n\circ\zeta$
. Since
$\psi_n=\chi_n\circ\zeta$
. Since
![]() $\psi_n\rightarrow 1_G$
, we get that
$\psi_n\rightarrow 1_G$
, we get that
![]() $\chi_n\rightarrow 1_{G/H}$
. Since
$\chi_n\rightarrow 1_{G/H}$
. Since
![]() $G/H$
is a finite group,
$G/H$
is a finite group,
![]() $\mathrm{Ch}(G/H)$
is a finite set and thus
$\mathrm{Ch}(G/H)$
is a finite set and thus
![]() $1_{G/H}$
is isolated in
$1_{G/H}$
is isolated in
![]() $\mathrm{Ch}(G/H)$
. Hence, we can find
$\mathrm{Ch}(G/H)$
. Hence, we can find
![]() $N'\geq N$
such that
$N'\geq N$
such that
![]() $\chi_n=1_{G/H}$
and hence
$\chi_n=1_{G/H}$
and hence
![]() $\psi_n=1_G$
for every
$\psi_n=1_G$
for every
![]() $n\geq N'$
. This proves that
$n\geq N'$
. This proves that
![]() $1_G$
is isolated in
$1_G$
is isolated in
![]() $\mathrm{Ch}(G)$
, which means that G has property (ET).
$\mathrm{Ch}(G)$
, which means that G has property (ET).
Proof of Corollary C. The implications (1)
![]() $\Rightarrow$
(3) and (3)
$\Rightarrow$
(3) and (3)
![]() $\Rightarrow$
(2) follow from [Reference OrovitzOSV25, Proposition 7.9] and [Reference OrovitzOSV25, Proposition 7.4], respectively.
$\Rightarrow$
(2) follow from [Reference OrovitzOSV25, Proposition 7.9] and [Reference OrovitzOSV25, Proposition 7.4], respectively.
To justify the implication (2)
![]() $\Rightarrow$
(1), assume that
$\Rightarrow$
(1), assume that
![]() $G_{i_0}$
does not have property (ET) for some
$G_{i_0}$
does not have property (ET) for some
![]() $i_0\in\{1,2\}$
. Since
$i_0\in\{1,2\}$
. Since
![]() $G_{i_0}$
does not have property (ET), Lemma 6.7 implies that
$G_{i_0}$
does not have property (ET), Lemma 6.7 implies that
![]() $\mathrm{Ch}(G_{i_0})$
contains no isolated finite-dimensional characters. Equivalently,
$\mathrm{Ch}(G_{i_0})$
contains no isolated finite-dimensional characters. Equivalently,
![]() $\partial_{\mathrm{e}}\mathrm{T}(C^*G_{i_0})$
contains no isolated extreme finite-dimensional traces. Additionally, since
$\partial_{\mathrm{e}}\mathrm{T}(C^*G_{i_0})$
contains no isolated extreme finite-dimensional traces. Additionally, since
![]() $G_i$
is a non-trivial group, for
$G_i$
is a non-trivial group, for
![]() $i\in\{1,2\}$
,
$i\in\{1,2\}$
,
![]() $1_{G_i}$
and
$1_{G_i}$
and
![]() $\delta_e$
are distinct traces on
$\delta_e$
are distinct traces on
![]() $G_i$
, and therefore
$G_i$
, and therefore
![]() $|\mathrm{T}(C^*G_i)|=|\mathrm{Tr}(G_i)|\geq 2$
for
$|\mathrm{T}(C^*G_i)|=|\mathrm{Tr}(G_i)|\geq 2$
for
![]() $i\in\{1,2\}$
. Thus, by applying Theorem A to
$i\in\{1,2\}$
. Thus, by applying Theorem A to
![]() $C^*G=C^*G_1*C^*G_2$
, we conclude that
$C^*G=C^*G_1*C^*G_2$
, we conclude that
![]() $\mathrm{Tr}(G)=\mathrm{T}(C^*G)$
is a Poulsen simplex.
$\mathrm{Tr}(G)=\mathrm{T}(C^*G)$
is a Poulsen simplex.
Remark 6.9. Denoting by
![]() $\widehat G$
the space of irreducible representations of a group G equipped with the Fell topology, we recall the well-known fact that if G has property (T), i.e., the trivial representation is isolated in
$\widehat G$
the space of irreducible representations of a group G equipped with the Fell topology, we recall the well-known fact that if G has property (T), i.e., the trivial representation is isolated in
![]() $\widehat G$
, then automatically every finite-dimensional irreducible representation of G is isolated in
$\widehat G$
, then automatically every finite-dimensional irreducible representation of G is isolated in
![]() $\widehat G$
(see, for instance, [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.2.5]). Nevertheless, we note that the analogous statement for property (ET) fails, i.e., property (ET) does not imply that every finite-dimensional character is isolated in
$\widehat G$
(see, for instance, [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.2.5]). Nevertheless, we note that the analogous statement for property (ET) fails, i.e., property (ET) does not imply that every finite-dimensional character is isolated in
![]() $\mathrm{Ch}(G)$
. In other words, the converse to Lemma 6.7 fails.
$\mathrm{Ch}(G)$
. In other words, the converse to Lemma 6.7 fails.
Indeed, consider the groupFootnote
1
![]() $G=\mathbb{Z}/2\mathbb{Z} *\mathbb{Z}/2\mathbb{Z}$
. Then G has property (ET) by [Reference OrovitzOSV25, Proposition 7.4], but it admits a continuum of two-dimensional characters that are not isolated in
$G=\mathbb{Z}/2\mathbb{Z} *\mathbb{Z}/2\mathbb{Z}$
. Then G has property (ET) by [Reference OrovitzOSV25, Proposition 7.4], but it admits a continuum of two-dimensional characters that are not isolated in
![]() $\mathrm{Ch}(G)$
: since
$\mathrm{Ch}(G)$
: since
![]() $C^*G\cong\mathbb C^2*\mathbb C^2$
is the universal
$C^*G\cong\mathbb C^2*\mathbb C^2$
is the universal
![]() $C^*$
-algebra generated by two projections, say p and q, we can define the (two-dimensional) representations
$C^*$
-algebra generated by two projections, say p and q, we can define the (two-dimensional) representations
![]() $\pi_t:C^*G\to\mathbb{M}_2(\mathbb{C})$
, for
$\pi_t:C^*G\to\mathbb{M}_2(\mathbb{C})$
, for
![]() $t\in (0,1)$
, determined by
$t\in (0,1)$
, determined by
 \[ \pi_t(p) = \begin{pmatrix} 1 &\ \ 0 \\ 0 &\ \ 0\end{pmatrix} \quad\text{and}\quad \pi_t(q) = \begin{pmatrix} 1-t &\ \ \sqrt{t(1-t)} \\[2pt] \sqrt{t(1-t)}&\ \ t\end{pmatrix}. \]
\[ \pi_t(p) = \begin{pmatrix} 1 &\ \ 0 \\ 0 &\ \ 0\end{pmatrix} \quad\text{and}\quad \pi_t(q) = \begin{pmatrix} 1-t &\ \ \sqrt{t(1-t)} \\[2pt] \sqrt{t(1-t)}&\ \ t\end{pmatrix}. \]
Then
![]() $\|\pi_s(x)-\pi_{t}(x)\|_2\rightarrow 0$
, as
$\|\pi_s(x)-\pi_{t}(x)\|_2\rightarrow 0$
, as
![]() $s\rightarrow t$
, for every
$s\rightarrow t$
, for every
![]() $x\in C^*G$
. Thus, denoting
$x\in C^*G$
. Thus, denoting
![]() $\varphi_t:=\mathrm{tr}_2\circ\pi_t\in\text{Ch}(G)$
, we have that
$\varphi_t:=\mathrm{tr}_2\circ\pi_t\in\text{Ch}(G)$
, we have that
![]() $\varphi_s\rightarrow\varphi_t$
, as
$\varphi_s\rightarrow\varphi_t$
, as
![]() $s\rightarrow t$
. Hence,
$s\rightarrow t$
. Hence,
![]() $\varphi_t$
is not isolated in
$\varphi_t$
is not isolated in
![]() $\text{Ch}(G)$
, for every
$\text{Ch}(G)$
, for every
![]() $t\in (0,1)$
.
$t\in (0,1)$
.
Remark 6.10. In the notation of Remark 6.9, for
![]() $\varepsilon_1,\varepsilon_2\in\{0,1\}$
, let
$\varepsilon_1,\varepsilon_2\in\{0,1\}$
, let
![]() $\varphi_{\varepsilon_1,\varepsilon_2}:C^*G\rightarrow\mathbb C$
be the representation determined by
$\varphi_{\varepsilon_1,\varepsilon_2}:C^*G\rightarrow\mathbb C$
be the representation determined by
![]() $\varphi_{\varepsilon_1,\varepsilon_2}(p)=\varepsilon_1$
,
$\varphi_{\varepsilon_1,\varepsilon_2}(p)=\varepsilon_1$
,
![]() $\varphi_{\varepsilon_1,\varepsilon_2}(q)=\varepsilon_2$
, and view
$\varphi_{\varepsilon_1,\varepsilon_2}(q)=\varepsilon_2$
, and view
![]() $\varphi_{\varepsilon_1,\varepsilon_2}\in\text{Ch}(G)$
. Then we have
$\varphi_{\varepsilon_1,\varepsilon_2}\in\text{Ch}(G)$
. Then we have
![]() $\text{Ch}(G)=\{\varphi_t\mid t\in (0,1)\}\cup\{\varphi_{\varepsilon_1,\varepsilon_2}\mid\varepsilon_1,\varepsilon_2\in\{0,1\}\}.$
Moreover,
$\text{Ch}(G)=\{\varphi_t\mid t\in (0,1)\}\cup\{\varphi_{\varepsilon_1,\varepsilon_2}\mid\varepsilon_1,\varepsilon_2\in\{0,1\}\}.$
Moreover,
![]() $\{\varphi_{\varepsilon_1,\varepsilon_2}\mid\varepsilon_1,\varepsilon_2\in\{0,1\}\}$
are isolated points in
$\{\varphi_{\varepsilon_1,\varepsilon_2}\mid\varepsilon_1,\varepsilon_2\in\{0,1\}\}$
are isolated points in
![]() $\text{Ch}(G)$
and we have
$\text{Ch}(G)$
and we have
This implies that
![]() $\text{Tr}(G)$
is neither a Poulsen nor a Bauer simplex. Moreover, since we have that
$\text{Tr}(G)$
is neither a Poulsen nor a Bauer simplex. Moreover, since we have that
![]() $\overline{\text{Ch}(G)}=\text{Ch}(G)\cup\{\psi_0,\psi_1\}$
, it follows that
$\overline{\text{Ch}(G)}=\text{Ch}(G)\cup\{\psi_0,\psi_1\}$
, it follows that
![]() $\text{Tr}(G)$
does not contain the Poulsen simplex as a closed face. Indeed, if
$\text{Tr}(G)$
does not contain the Poulsen simplex as a closed face. Indeed, if
![]() $X\subset\text{Ch}(G)$
is a non-empty set satisfying
$X\subset\text{Ch}(G)$
is a non-empty set satisfying
![]() $\text{conv}(X)\subset\overline{X}$
, then X must be a singleton.
$\text{conv}(X)\subset\overline{X}$
, then X must be a singleton.
7. The Poulsen simplex as a closed face
Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. In this section, we investigate what happens when the conditions from Theorem A fail, i.e., when
$A_2$
. In this section, we investigate what happens when the conditions from Theorem A fail, i.e., when
![]() $\mathrm{T}(A)$
is not a Poulsen simplex. We start with proving Theorem G, which identifies the Poulsen simplex as a closed face of
$\mathrm{T}(A)$
is not a Poulsen simplex. We start with proving Theorem G, which identifies the Poulsen simplex as a closed face of
![]() $\mathrm{T}(A)$
, unless it is affinely homeomorphic to
$\mathrm{T}(A)$
, unless it is affinely homeomorphic to
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. We finish by answering in the negative [Reference OrovitzOSV25, Question 1.10].
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. We finish by answering in the negative [Reference OrovitzOSV25, Question 1.10].
7.1 The Poulsen simplex as a closed face of the trace simplex of a free product
In this subsection, we prove Theorem G. The proof uses the following observation made in [Reference Rørdam and MusatRM21]: a unital surjective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\gamma:A\to B$
between two unital, separable
$\gamma:A\to B$
between two unital, separable
![]() $C^*$
-algebras induces an affine continuous injection
$C^*$
-algebras induces an affine continuous injection
![]() $\mathrm{T}(B)\ni\varphi\mapsto\varphi\circ\gamma\in\mathrm{T}(A)$
whose image is a closed face. Thus, if
$\mathrm{T}(B)\ni\varphi\mapsto\varphi\circ\gamma\in\mathrm{T}(A)$
whose image is a closed face. Thus, if
![]() $\text{T}(B)$
is the Poulsen simplex or, more generally, admits the Poulsen simplex as a closed face, then
$\text{T}(B)$
is the Poulsen simplex or, more generally, admits the Poulsen simplex as a closed face, then
![]() $\text{T}(A)$
also contains the Poulsen simplex as a closed face. In particular, we get the following corollary.
$\text{T}(A)$
also contains the Poulsen simplex as a closed face. In particular, we get the following corollary.
Corollary 7.1. Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. Assume that
$A_2$
. Assume that
![]() $A_1$
admits an irreducible n-dimensional representation and
$A_1$
admits an irreducible n-dimensional representation and
![]() $A_2$
admits an irreducible k-dimensional representation for some
$A_2$
admits an irreducible k-dimensional representation for some
![]() $n,k\geq 2$
. Then
$n,k\geq 2$
. Then
![]() $\mathrm{T}(A)$
has a closed face which is affinely homeomorphic to the Poulsen simplex.
$\mathrm{T}(A)$
has a closed face which is affinely homeomorphic to the Poulsen simplex.
Proof. The assumptions imply the existence of a unital surjective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $A\to \mathbb{M}_n(\mathbb{C})\ast \mathbb{M}_k(\mathbb{C})$
. Since
$A\to \mathbb{M}_n(\mathbb{C})\ast \mathbb{M}_k(\mathbb{C})$
. Since
![]() $\mathrm{T}(\mathbb{M}_n(\mathbb{C})\ast\mathbb{M}_k(\mathbb{C}))$
is the Poulsen simplex by Corollary B, the desired result follows from the observation preceding the corollary.
$\mathrm{T}(\mathbb{M}_n(\mathbb{C})\ast\mathbb{M}_k(\mathbb{C}))$
is the Poulsen simplex by Corollary B, the desired result follows from the observation preceding the corollary.
In order to show that the trace simplexes of
![]() $\mathbb{C}^2\ast \mathbb{C}^n$
,
$\mathbb{C}^2\ast \mathbb{C}^n$
,
![]() $n\geq 3$
, and
$n\geq 3$
, and
![]() $\mathbb{C}^2\ast\mathbb{M}_n(\mathbb{C})$
,
$\mathbb{C}^2\ast\mathbb{M}_n(\mathbb{C})$
,
![]() $n\geq 2$
also admit the Poulsen simplex as a closed face, we first prove that these
$n\geq 2$
also admit the Poulsen simplex as a closed face, we first prove that these
![]() $C^*$
-algebras admit many quotients.
$C^*$
-algebras admit many quotients.
Lemma 7.2. Let A be a unital
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $n\geq 2$
be an integer.
$n\geq 2$
be an integer.
-
(1) [Reference VasilevskiVas98]. If A is generated by
 $n-1$
self-adjoint elements, then there is a unital surjective
$n-1$
self-adjoint elements, then there is a unital surjective
 $*$
-homomorphism
$*$
-homomorphism
 $\mathbb C^2*\mathbb C^n\rightarrow\mathbb M_n(\mathbb C)\otimes A$
.
$\mathbb C^2*\mathbb C^n\rightarrow\mathbb M_n(\mathbb C)\otimes A$
. -
(2) If A is generated by
 $n-1$
unitaries, then there is a unital surjective
$n-1$
unitaries, then there is a unital surjective
 $*$
-homomorphism
$*$
-homomorphism
 $\mathbb C^2*\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)\otimes A$
.
$\mathbb C^2*\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)\otimes A$
. -
(3) If A is generated by 2 self-adjoint elements, then there is a unital surjective
 $*$
-homomorphism
$*$
-homomorphism
 $\mathbb C^2*\mathbb M_2(\mathbb C)\rightarrow \mathbb M_2(\mathbb C)\otimes A$
.
$\mathbb C^2*\mathbb M_2(\mathbb C)\rightarrow \mathbb M_2(\mathbb C)\otimes A$
.
Proof.
-
(1) This is [Reference VasilevskiVas98, Corollary 4.5]. Indeed, [Reference VasilevskiVas98, Corollary 4.5] shows that
 $\mathbb M_n(\mathbb C)\otimes A$
is generated by projections
$\mathbb M_n(\mathbb C)\otimes A$
is generated by projections
 $p,q_1,\ldots,q_n$
such that
$p,q_1,\ldots,q_n$
such that
 $\sum_{i=1}^nq_i=1$
. Define unital
$\sum_{i=1}^nq_i=1$
. Define unital
 $*$
-homomorphisms
$*$
-homomorphisms
 $\alpha:\mathbb C^2\rightarrow \mathbb M_n(\mathbb C)\otimes A$
and
$\alpha:\mathbb C^2\rightarrow \mathbb M_n(\mathbb C)\otimes A$
and
 $\beta:\mathbb C^n\rightarrow\mathbb M_n(\mathbb C)\otimes A$
given by
$\beta:\mathbb C^n\rightarrow\mathbb M_n(\mathbb C)\otimes A$
given by
 $\alpha(s_1,s_2)=s_1p+s_2(1-p)$
and
$\alpha(s_1,s_2)=s_1p+s_2(1-p)$
and
 $\beta(t_1,\ldots,t_n)=\sum_{i=1}^nt_iq_i$
. Since the images of
$\beta(t_1,\ldots,t_n)=\sum_{i=1}^nt_iq_i$
. Since the images of
 $\alpha$
and
$\alpha$
and
 $\beta$
generate
$\beta$
generate
 $\mathbb M_n(\mathbb C)\otimes A$
, it follows that the unital
$\mathbb M_n(\mathbb C)\otimes A$
, it follows that the unital
 $*$
-homomorphism
$*$
-homomorphism
 $\gamma:\mathbb C^2*\mathbb C^n\rightarrow\mathbb M_n(\mathbb C)\otimes A$
determined by
$\gamma:\mathbb C^2*\mathbb C^n\rightarrow\mathbb M_n(\mathbb C)\otimes A$
determined by
 $\gamma_{|\mathbb C^2}=\alpha$
and
$\gamma_{|\mathbb C^2}=\alpha$
and
 $\gamma_{|\mathbb C^n}=\beta$
is surjective.
$\gamma_{|\mathbb C^n}=\beta$
is surjective. -
(2) Suppose that A is generated by unitaries
 $u_2, \ldots, u_n$
. The first part of the proof is the same as the first part of the proof of [Reference Rørdam and MusatRM21, Proposition 3.7(ii)]. For
$u_2, \ldots, u_n$
. The first part of the proof is the same as the first part of the proof of [Reference Rørdam and MusatRM21, Proposition 3.7(ii)]. For
 $1\leq i,j\leq n$
, denote by
$1\leq i,j\leq n$
, denote by
 $e_{ij}\in\mathbb M_n(\mathbb C)$
the elementary matrix with a 1 in the (i,j)-position and 0 elsewhere. Set
$e_{ij}\in\mathbb M_n(\mathbb C)$
the elementary matrix with a 1 in the (i,j)-position and 0 elsewhere. Set
 $f_{11} := e_{11}\otimes 1_A$
and
$f_{11} := e_{11}\otimes 1_A$
and
 $f_{1j} := e_{1j}\otimes u_j$
, for
$f_{1j} := e_{1j}\otimes u_j$
, for
 $2\leq j\leq n$
. Then
$2\leq j\leq n$
. Then
 $f_{1j}f_{1j}^* = e_{11}\otimes 1_\mathcal{A}$
and
$f_{1j}f_{1j}^* = e_{11}\otimes 1_\mathcal{A}$
and
 $f_{1j}^*f_{1j} = e_{jj}\otimes 1_\mathcal{A}$
for every
$f_{1j}^*f_{1j} = e_{jj}\otimes 1_\mathcal{A}$
for every
 $1\leq j\leq n$
. Setting
$1\leq j\leq n$
. Setting
 $f_{ij}:= f_{1i}^*f_{1j}$
for
$f_{ij}:= f_{1i}^*f_{1j}$
for
 $1\leq i,j\leq n$
, we get that
$1\leq i,j\leq n$
, we get that
 $\{f_{ij}\mid 1\leq i,j\leq n\}$
is a set of matrix units in
$\{f_{ij}\mid 1\leq i,j\leq n\}$
is a set of matrix units in
 $\mathbb{M}_n(\mathbb{C})\otimes A$
. Hence, there is a unital
$\mathbb{M}_n(\mathbb{C})\otimes A$
. Hence, there is a unital
 $*$
-homomorphism
$*$
-homomorphism
 $\beta:\mathbb{M}_n(\mathbb{C})\to \mathbb{M}_n(\mathbb{C})\otimes A$
determined by
$\beta:\mathbb{M}_n(\mathbb{C})\to \mathbb{M}_n(\mathbb{C})\otimes A$
determined by
 $\beta(e_{ij})=f_{ij}$
for
$\beta(e_{ij})=f_{ij}$
for
 $1\leq i,j\leq n$
. We note that, by construction,
$1\leq i,j\leq n$
. We note that, by construction,
 $e_{ii}\otimes 1_A\in\beta(\mathbb M_n(\mathbb C))$
for every
$e_{ii}\otimes 1_A\in\beta(\mathbb M_n(\mathbb C))$
for every
 $1\leq i\leq n$
.
$1\leq i\leq n$
.Next, let
 $p\in\mathbb M_n(\mathbb C)$
be the projection matrix whose every entry is equal to
$p\in\mathbb M_n(\mathbb C)$
be the projection matrix whose every entry is equal to
 ${1}/{n}$
, i.e.,
${1}/{n}$
, i.e.,
 $(p)_{i,j}={1}/{n}$
for every
$(p)_{i,j}={1}/{n}$
for every
 $1\leq i,j\leq n$
. Then the subalgebra V of
$1\leq i,j\leq n$
. Then the subalgebra V of
 $\mathbb{M}_n(\mathbb{C})$
generated by
$\mathbb{M}_n(\mathbb{C})$
generated by
 $\{p,e_{ii}\mid 1\leq i\leq n\}$
equals
$\{p,e_{ii}\mid 1\leq i\leq n\}$
equals
 $\mathbb{M}_n(\mathbb{C})$
. Indeed, given any
$\mathbb{M}_n(\mathbb{C})$
. Indeed, given any
 $1\leq i,j\leq n$
, we see that
$1\leq i,j\leq n$
, we see that
 $e_{ij} = ne_{ii}pe_{jj} \in V$
, which implies that
$e_{ij} = ne_{ii}pe_{jj} \in V$
, which implies that
 $V=\mathbb{M}_n(\mathbb{C})$
. Define a unital
$V=\mathbb{M}_n(\mathbb{C})$
. Define a unital
 $*$
-homomorphism
$*$
-homomorphism
 $\alpha: \mathbb{C}^2\to\mathbb{M}_n(\mathbb C) \otimes A$
by letting
$\alpha: \mathbb{C}^2\to\mathbb{M}_n(\mathbb C) \otimes A$
by letting
 $\alpha(s_1,s_2)=s_1 (p\otimes 1_A)+s_2((1-p)\otimes 1_A)$
.
$\alpha(s_1,s_2)=s_1 (p\otimes 1_A)+s_2((1-p)\otimes 1_A)$
.Finally, denote by
 $\gamma:\mathbb{C}^2\ast\mathbb{M}_n(\mathbb{C})\to \mathbb{M}_n(\mathbb{C})\otimes A$
the unital
$\gamma:\mathbb{C}^2\ast\mathbb{M}_n(\mathbb{C})\to \mathbb{M}_n(\mathbb{C})\otimes A$
the unital
 $*$
-homomorphism determined by
$*$
-homomorphism determined by
 $\gamma_{|\mathbb{C}^2}=\alpha$
and
$\gamma_{|\mathbb{C}^2}=\alpha$
and
 $\gamma_{|\mathbb M_n(\mathbb C)}=\beta$
. Then by construction,
$\gamma_{|\mathbb M_n(\mathbb C)}=\beta$
. Then by construction,
 $p\otimes 1_A$
and
$p\otimes 1_A$
and
 $e_{ii}\otimes 1_A$
are in the image of
$e_{ii}\otimes 1_A$
are in the image of
 $\gamma$
for every
$\gamma$
for every
 $1\leq i\leq n$
, and thus by the above,
$1\leq i\leq n$
, and thus by the above,
 $\mathbb{M}_n(\mathbb{C})\otimes 1_A\subset \gamma(\mathbb{C}^2\ast \mathbb{M}_n(\mathbb{C}))$
. Since we also have that
$\mathbb{M}_n(\mathbb{C})\otimes 1_A\subset \gamma(\mathbb{C}^2\ast \mathbb{M}_n(\mathbb{C}))$
. Since we also have that
 $f_{1j} = e_{1j}\otimes u_j\in \gamma(\mathbb{C}^2\ast \mathbb{M}_n(\mathbb{C}))$
, we deduce that
$f_{1j} = e_{1j}\otimes u_j\in \gamma(\mathbb{C}^2\ast \mathbb{M}_n(\mathbb{C}))$
, we deduce that
 $1\otimes u_j$
is contained in
$1\otimes u_j$
is contained in
 $\gamma(\mathbb{C}^2\ast \mathbb{M}_n(\mathbb{C}))$
for every
$\gamma(\mathbb{C}^2\ast \mathbb{M}_n(\mathbb{C}))$
for every
 $2\leq j\leq n$
. We conclude that
$2\leq j\leq n$
. We conclude that
 $\gamma$
is surjective, finishing the proof of (2).
$\gamma$
is surjective, finishing the proof of (2). -
(3) Suppose that A is generated by two self-adjoint elements. Then A is generated by a single element
 $z\in A$
with
$z\in A$
with
 $\|z\|\leq 1$
. Define, using continuous functional calculus,
$\|z\|\leq 1$
. Define, using continuous functional calculus,
 $p\in \mathbb M_2(\mathbb C)\otimes A=\mathbb M_2(A)$
by letting Since
$p\in \mathbb M_2(\mathbb C)\otimes A=\mathbb M_2(A)$
by letting Since $$p=\begin{pmatrix}\frac{1+\sqrt{1-z^*z}}{2}&\ z^*\\[6pt] z& \frac{1-\sqrt{1-zz^*}}{2} \end{pmatrix}.$$
$$p=\begin{pmatrix}\frac{1+\sqrt{1-z^*z}}{2}&\ z^*\\[6pt] z& \frac{1-\sqrt{1-zz^*}}{2} \end{pmatrix}.$$
 $z(z^*z)^n=(zz^*)^nz$
, for every
$z(z^*z)^n=(zz^*)^nz$
, for every
 $n\geq 0$
, it follows that
$n\geq 0$
, it follows that
 $z\sqrt{1-z^*z}=\sqrt{1-zz^*}z$
, which implies that p is a projection. Define unital
$z\sqrt{1-z^*z}=\sqrt{1-zz^*}z$
, which implies that p is a projection. Define unital
 $*$
-homomorphisms
$*$
-homomorphisms
 $\alpha:\mathbb C^2\rightarrow\mathbb M_2(\mathbb C)\otimes A$
and
$\alpha:\mathbb C^2\rightarrow\mathbb M_2(\mathbb C)\otimes A$
and
 $\beta:\mathbb M_2(\mathbb C)\rightarrow\mathbb M_2(\mathbb C)\otimes A$
by letting
$\beta:\mathbb M_2(\mathbb C)\rightarrow\mathbb M_2(\mathbb C)\otimes A$
by letting
 $\alpha(s_1,s_2)=s_1p+s_2(1-p)$
and
$\alpha(s_1,s_2)=s_1p+s_2(1-p)$
and
 $\beta(x)=x\otimes 1_A$
. Denote by
$\beta(x)=x\otimes 1_A$
. Denote by
 $\gamma:\mathbb{C}^2\ast\mathbb{M}_2(\mathbb{C})\to \mathbb{M}_2(\mathbb{C})\otimes A$
the unital
$\gamma:\mathbb{C}^2\ast\mathbb{M}_2(\mathbb{C})\to \mathbb{M}_2(\mathbb{C})\otimes A$
the unital
 $*$
-homomorphism determined by
$*$
-homomorphism determined by
 $\gamma_{|\mathbb{C}^2}=\alpha$
and
$\gamma_{|\mathbb{C}^2}=\alpha$
and
 $\gamma_{|\mathbb M_2(\mathbb C)}=\beta$
. Since z generates A, it follows that p and
$\gamma_{|\mathbb M_2(\mathbb C)}=\beta$
. Since z generates A, it follows that p and
 $\mathbb M_2(\mathbb C)\otimes 1_A$
generate
$\mathbb M_2(\mathbb C)\otimes 1_A$
generate
 $\mathbb M_2(\mathbb C)\otimes A$
. This implies that
$\mathbb M_2(\mathbb C)\otimes A$
. This implies that
 $\gamma$
is surjective.
$\gamma$
is surjective.
Lemma 7.3. The trace simplexes
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^3)$
and
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^3)$
and
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{M}_n(\mathbb{C}))$
, for
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{M}_n(\mathbb{C}))$
, for
![]() $n\geq 2$
, have a closed face which is affinely homeomorphic to the Poulsen simplex.
$n\geq 2$
, have a closed face which is affinely homeomorphic to the Poulsen simplex.
Proof. Let
![]() $A=C([0,1])*C([0,1])$
. Since A is generated by 2 self-adjoint elements, parts (1) and (3) of Lemma 7.2 provide unital surjective
$A=C([0,1])*C([0,1])$
. Since A is generated by 2 self-adjoint elements, parts (1) and (3) of Lemma 7.2 provide unital surjective
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\mathbb C^2*\mathbb C^3\rightarrow\mathbb M_3(\mathbb C)\otimes A$
and
$\mathbb C^2*\mathbb C^3\rightarrow\mathbb M_3(\mathbb C)\otimes A$
and
![]() $\mathbb C^2*\mathbb M_2(\mathbb C)\rightarrow\mathbb M_2(\mathbb C)\otimes A$
. Since
$\mathbb C^2*\mathbb M_2(\mathbb C)\rightarrow\mathbb M_2(\mathbb C)\otimes A$
. Since
![]() $\text{T}(A)$
is the Poulsen simplex by [Reference OrovitzOSV25, Theorem 1.5] (or Theorem A) and
$\text{T}(A)$
is the Poulsen simplex by [Reference OrovitzOSV25, Theorem 1.5] (or Theorem A) and
![]() $\text{T}(\mathbb M_k(\mathbb C)\otimes A)\cong\text{T}(A)$
, for
$\text{T}(\mathbb M_k(\mathbb C)\otimes A)\cong\text{T}(A)$
, for
![]() $k\geq 2$
, the conclusion for
$k\geq 2$
, the conclusion for
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^3)$
and
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^3)$
and
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{M}_2(\mathbb{C}))$
follows.
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{M}_2(\mathbb{C}))$
follows.
If
![]() $n\geq 3$
, then since
$n\geq 3$
, then since
![]() $C^*\mathbb F_{n-1}$
is generated by
$C^*\mathbb F_{n-1}$
is generated by
![]() $n-1$
unitaries, part (2) of Lemma 7.2 provides a unital surjective
$n-1$
unitaries, part (2) of Lemma 7.2 provides a unital surjective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\mathbb C^2*\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)\otimes C^*\mathbb F_{n-1}$
. Since
$\mathbb C^2*\mathbb M_n(\mathbb C)\rightarrow\mathbb M_n(\mathbb C)\otimes C^*\mathbb F_{n-1}$
. Since
![]() $\text{T}(C^*\mathbb F_{n-1})$
is the Poulsen simplex by [Reference OrovitzOSV25, Theorem 1.1] (or Theorem A) and
$\text{T}(C^*\mathbb F_{n-1})$
is the Poulsen simplex by [Reference OrovitzOSV25, Theorem 1.1] (or Theorem A) and
![]() $\text{T}(\mathbb M_n(\mathbb C)\otimes C^*\mathbb F_{n-1})\cong\text{T}(C^*\mathbb F_{n-1})$
, the conclusion also follows for
$\text{T}(\mathbb M_n(\mathbb C)\otimes C^*\mathbb F_{n-1})\cong\text{T}(C^*\mathbb F_{n-1})$
, the conclusion also follows for
![]() $\text{T}(\mathbb C^2*\mathbb M_n(\mathbb C))$
, for
$\text{T}(\mathbb C^2*\mathbb M_n(\mathbb C))$
, for
![]() $n\geq 3$
.
$n\geq 3$
.
Lemma 7.4. Let
![]() $A=A_1\ast A_2$
be the full free product of two unital, separable
$A=A_1\ast A_2$
be the full free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
such that
$A_2$
such that
![]() $\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for
$\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for
![]() $i=1, 2$
. Assume that
$i=1, 2$
. Assume that
![]() $\mathrm{T}(A_1)$
contains an infinite-dimensional extreme trace. Then
$\mathrm{T}(A_1)$
contains an infinite-dimensional extreme trace. Then
![]() $\mathrm{T}(A)$
has a closed face which is affinely homeomorphic to the Poulsen simplex.
$\mathrm{T}(A)$
has a closed face which is affinely homeomorphic to the Poulsen simplex.
Proof. Fix
![]() $\varphi_1\in\partial_{\mathrm{e}}\mathrm{T}(A_1)\cap\mathrm{T}_\infty(A_1)$
, and consider the set
$\varphi_1\in\partial_{\mathrm{e}}\mathrm{T}(A_1)\cap\mathrm{T}_\infty(A_1)$
, and consider the set
We will prove that X is a closed face of
![]() $\mathrm{T}(A)$
affinely homeomorphic to the Poulsen simplex, which will finish the proof.
$\mathrm{T}(A)$
affinely homeomorphic to the Poulsen simplex, which will finish the proof.
First, if
![]() $\phi,\chi\in X$
, then it is immediate that for every
$\phi,\chi\in X$
, then it is immediate that for every
![]() $\lambda\in [0,1]$
we have
$\lambda\in [0,1]$
we have
and hence X is convex. Similarly, if
![]() $\psi_n\in X$
is a sequence converging to some
$\psi_n\in X$
is a sequence converging to some
![]() $\psi\in\mathrm{T}(A)$
, then
$\psi\in\mathrm{T}(A)$
, then
![]() $\psi_{|A_1} = \lim_n \psi_{n|A_1} = \varphi_1$
, and hence X is closed.
$\psi_{|A_1} = \lim_n \psi_{n|A_1} = \varphi_1$
, and hence X is closed.
Next, assume that
![]() $\psi\in X$
satisfies
$\psi\in X$
satisfies
![]() $\psi = \lambda \phi +(1-\lambda) \chi$
, for some
$\psi = \lambda \phi +(1-\lambda) \chi$
, for some
![]() $\phi,\chi\in\text{T}(A)$
and
$\phi,\chi\in\text{T}(A)$
and
![]() $\lambda\in[0,1]$
. Then
$\lambda\in[0,1]$
. Then
Since
![]() $\phi_{|A_1},\chi_{|A_1}\in\mathrm{T}(A_1)$
and
$\phi_{|A_1},\chi_{|A_1}\in\mathrm{T}(A_1)$
and
![]() $\varphi_1\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
, we conclude that
$\varphi_1\in\partial_{\mathrm{e}}\mathrm{T}(A_1)$
, we conclude that
![]() $\phi_{|A_1} = \chi_{|A_1} = \varphi_1$
, i.e.,
$\phi_{|A_1} = \chi_{|A_1} = \varphi_1$
, i.e.,
![]() $\phi,\chi\in X$
. We conclude that X is a closed face of
$\phi,\chi\in X$
. We conclude that X is a closed face of
![]() $\mathrm{T}(A)$
.
$\mathrm{T}(A)$
.
Note that X contains at least two points. Indeed, if
![]() $\varphi_2\in\text{T}(A_2)$
is any trace which is not one-dimensional, then the traces
$\varphi_2\in\text{T}(A_2)$
is any trace which is not one-dimensional, then the traces
![]() $\varphi_1\otimes\varphi_2$
and
$\varphi_1\otimes\varphi_2$
and
![]() $\varphi_1*\varphi_2$
are distinct and belong to X.
$\varphi_1*\varphi_2$
are distinct and belong to X.
Finally, we show that the extreme points of X are dense in X. Since we already know that X is a closed face, is hence a simplex, and that X has at least two points, this will imply that X is affinely homeomorphic to the Poulsen simplex.
Fix
![]() $\psi\in X$
, and let
$\psi\in X$
, and let
![]() $\pi:A\to M$
be the associated tracial representation. Denote
$\pi:A\to M$
be the associated tracial representation. Denote
![]() $M_i = \pi(A_i)''$
. Note that by construction,
$M_i = \pi(A_i)''$
. Note that by construction,
![]() $\tau\circ \pi_{|A_1} = \psi_{|A_1} = \varphi_1$
; hence
$\tau\circ \pi_{|A_1} = \psi_{|A_1} = \varphi_1$
; hence
![]() $\pi_{|A_1}: A_1\to M_1$
is a tracial representation associated to
$\pi_{|A_1}: A_1\to M_1$
is a tracial representation associated to
![]() $\varphi_1$
. Since
$\varphi_1$
. Since
![]() $\varphi_1\in\partial_{\mathrm{e}}\mathrm{T}(A_1)\cap\mathrm{T}_\infty(A_1)$
, it follows that
$\varphi_1\in\partial_{\mathrm{e}}\mathrm{T}(A_1)\cap\mathrm{T}_\infty(A_1)$
, it follows that
![]() $M_1$
is a II
$M_1$
is a II
![]() $_1$
factor. If
$_1$
factor. If
![]() $M = M_1$
, then
$M = M_1$
, then
![]() $\psi$
is an extreme point and we are done. Otherwise, we necessarily have
$\psi$
is an extreme point and we are done. Otherwise, we necessarily have
![]() $M_2\neq \mathbb{C} 1$
, and thus applying Corollary 4.4, we get a von Neumann algebra
$M_2\neq \mathbb{C} 1$
, and thus applying Corollary 4.4, we get a von Neumann algebra
![]() $\widetilde{M}$
containing M, and unitaries
$\widetilde{M}$
containing M, and unitaries
![]() $u_n\in\widetilde{M}$
, with
$u_n\in\widetilde{M}$
, with
![]() $\left\|u_n - 1\right\|_2 \to 0$
as
$\left\|u_n - 1\right\|_2 \to 0$
as
![]() $n\to \infty$
, such that
$n\to \infty$
, such that
![]() $M_1\vee u_n M_2 u_n^*$
is a II
$M_1\vee u_n M_2 u_n^*$
is a II
![]() $_1$
factor for every
$_1$
factor for every
![]() $n\in\mathbb N$
. Define
$n\in\mathbb N$
. Define
![]() $\pi_n:A\to \widetilde{M}$
by
$\pi_n:A\to \widetilde{M}$
by
![]() $\pi_n(a_1) = \pi(a_1)$
for
$\pi_n(a_1) = \pi(a_1)$
for
![]() $a_1\in A_1$
, and
$a_1\in A_1$
, and
![]() $\pi_n(a_2)=u_n\pi(a_2)u_n^*$
for
$\pi_n(a_2)=u_n\pi(a_2)u_n^*$
for
![]() $a_2\in A_2$
. Then
$a_2\in A_2$
. Then
![]() $\psi_n:= \tau\circ \pi_n$
converges to
$\psi_n:= \tau\circ \pi_n$
converges to
![]() $\psi$
, as
$\psi$
, as
![]() $n\rightarrow\infty$
. Furthermore, we have by construction that
$n\rightarrow\infty$
. Furthermore, we have by construction that
![]() $\pi_n(A)''$
is a II
$\pi_n(A)''$
is a II
![]() $_1$
factor, and
$_1$
factor, and
![]() $\psi_{n|A_1} = \tau\circ \pi_{n|A_1} = \tau\circ \pi_{|A_1} = \psi_{|A_1} = \varphi_1$
; hence
$\psi_{n|A_1} = \tau\circ \pi_{n|A_1} = \tau\circ \pi_{|A_1} = \psi_{|A_1} = \varphi_1$
; hence
![]() $\psi_n\in \partial_{\mathrm{e}} X$
for every
$\psi_n\in \partial_{\mathrm{e}} X$
for every
![]() $n\in\mathbb{N}$
. We conclude that the extreme points of X are dense in X. This finishes the proof of the lemma.
$n\in\mathbb{N}$
. We conclude that the extreme points of X are dense in X. This finishes the proof of the lemma.
Proof of Theorem G. Recall that
![]() $A=A_1*A_2$
, where
$A=A_1*A_2$
, where
![]() $A_i$
is a unital, separable
$A_i$
is a unital, separable
![]() $C^*$
-algebra such that
$C^*$
-algebra such that
![]() $\text{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for every
$\text{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for every
![]() $i\in\{1,2\}$
. Assume that condition (1) of Theorem G fails, i.e., (
$i\in\{1,2\}$
. Assume that condition (1) of Theorem G fails, i.e., (
![]() $\star$
)
$\star$
)
![]() $\text{T}(A)$
does not admit a closed face which is affinely homeomorphic to the Poulsen simplex. We will prove that condition (2) holds.
$\text{T}(A)$
does not admit a closed face which is affinely homeomorphic to the Poulsen simplex. We will prove that condition (2) holds.
First, combining (
![]() $\star$
) and Lemma 7.4 implies that
$\star$
) and Lemma 7.4 implies that
![]() $A_i$
does not have an infinite-dimensional extreme trace, for every
$A_i$
does not have an infinite-dimensional extreme trace, for every
![]() $i\in\{1,2\}$
. In other words, all extreme traces of
$i\in\{1,2\}$
. In other words, all extreme traces of
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are finite-dimensional. Second, combining
$A_2$
are finite-dimensional. Second, combining
![]() $(\star)$
and Corollary 7.1 implies that at least one of
$(\star)$
and Corollary 7.1 implies that at least one of
![]() $A_1$
or
$A_1$
or
![]() $A_2$
, say
$A_2$
, say
![]() $A_1$
, has only one-dimensional extreme traces. But then
$A_1$
, has only one-dimensional extreme traces. But then
![]() $A_1$
must have at least two one-dimensional extreme traces, so we have a surjective unital
$A_1$
must have at least two one-dimensional extreme traces, so we have a surjective unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $A_1\rightarrow\mathbb C^2$
.
$A_1\rightarrow\mathbb C^2$
.
We claim that
![]() $A_2$
also only has one-dimensional extreme traces. Otherwise,
$A_2$
also only has one-dimensional extreme traces. Otherwise,
![]() $A_2$
admits a k-dimensional extreme trace for some
$A_2$
admits a k-dimensional extreme trace for some
![]() $k\geq 2$
. This would give a surjective unital
$k\geq 2$
. This would give a surjective unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $A_2\rightarrow M_k(\mathbb C)$
, and thus a surjective unital
$A_2\rightarrow M_k(\mathbb C)$
, and thus a surjective unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $A\rightarrow\mathbb C^2*\mathbb M_k(\mathbb C)$
. Since
$A\rightarrow\mathbb C^2*\mathbb M_k(\mathbb C)$
. Since
![]() $\text{T}(\mathbb C^2*\mathbb M_k(\mathbb C))$
has a closed face affinely homeomorphic to the Poulsen simplex by Lemma 7.3, this would contradict (
$\text{T}(\mathbb C^2*\mathbb M_k(\mathbb C))$
has a closed face affinely homeomorphic to the Poulsen simplex by Lemma 7.3, this would contradict (
![]() $\star$
).
$\star$
).
Hence, both
![]() $A_1$
and
$A_1$
and
![]() $A_2$
each have at least two extreme traces, all of which are one-dimensional. If
$A_2$
each have at least two extreme traces, all of which are one-dimensional. If
![]() $A_1$
or
$A_1$
or
![]() $A_2$
admits at least three extreme one-dimensional traces, we would get a surjective unital
$A_2$
admits at least three extreme one-dimensional traces, we would get a surjective unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $A\rightarrow\mathbb C^2*\mathbb C^3$
. However, by Lemma 7.3,
$A\rightarrow\mathbb C^2*\mathbb C^3$
. However, by Lemma 7.3,
![]() $\text{T}(\mathbb C^2*\mathbb C^3)$
has a face affinely homeomorphic to the Poulsen simplex, which would again contradict
$\text{T}(\mathbb C^2*\mathbb C^3)$
has a face affinely homeomorphic to the Poulsen simplex, which would again contradict
![]() $(\star)$
.
$(\star)$
.
Altogether, we conclude that
![]() $A_i$
admits exactly two extreme traces, both of which are one-dimensional, for every
$A_i$
admits exactly two extreme traces, both of which are one-dimensional, for every
![]() $i\in\{1,2\}$
. This implies that
$i\in\{1,2\}$
. This implies that
![]() $A_{i,\mathrm{tr}}\cong \mathbb{C}^2$
for
$A_{i,\mathrm{tr}}\cong \mathbb{C}^2$
for
![]() $i=1, 2$
. It then follows from Lemma 2.10 that
$i=1, 2$
. It then follows from Lemma 2.10 that
![]() $\mathrm{T}(A)$
is affinely homeomorphic to
$\mathrm{T}(A)$
is affinely homeomorphic to
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
, i.e., condition (2) holds.
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
, i.e., condition (2) holds.
Finally, since by Remark 6.10,
![]() $\text{T}(\mathbb C^2*\mathbb C^2)$
does not admit a closed face which is affinely homeomorphic to the Poulsen simplex, conditions (1) and (2) are mutually exclusive. This finishes the proof.
$\text{T}(\mathbb C^2*\mathbb C^2)$
does not admit a closed face which is affinely homeomorphic to the Poulsen simplex, conditions (1) and (2) are mutually exclusive. This finishes the proof.
7.2 The diffuse hull
In what follows, for a compact convex set C and a subset
![]() $X\subset C$
, we denote by
$X\subset C$
, we denote by
![]() $\overline{\mathrm{conv}}(X)\subset C$
the closed convex hull of X.
$\overline{\mathrm{conv}}(X)\subset C$
the closed convex hull of X.
For a free product of non-trivial finite groups, excluding
![]() $\mathbb{Z}/2\mathbb{Z}\ast\mathbb{Z}/2\mathbb{Z}$
, it was asked in [Reference OrovitzOSV25, Question 1.10] whether the closed convex hull of all the infinite-dimensional characters is a closed face affinely homeomorphic to the Poulsen simplex. One can ask the same question in the broader context of
$\mathbb{Z}/2\mathbb{Z}\ast\mathbb{Z}/2\mathbb{Z}$
, it was asked in [Reference OrovitzOSV25, Question 1.10] whether the closed convex hull of all the infinite-dimensional characters is a closed face affinely homeomorphic to the Poulsen simplex. One can ask the same question in the broader context of
![]() $C^*$
-algebras.
$C^*$
-algebras.
Question 7.5. Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
such that
$A_2$
such that
![]() $\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for
$\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace, for
![]() $i=1,2$
. Assume further that
$i=1,2$
. Assume further that
![]() $\mathrm{T}(A)$
is not affinely homeomorphic to
$\mathrm{T}(A)$
is not affinely homeomorphic to
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. Is
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. Is
![]() $\overline{\mathrm{conv}}(\partial_{\mathrm{e}} \mathrm{T}(A)\cap\mathrm{T}_\infty(A))$
a Poulsen simplex?
$\overline{\mathrm{conv}}(\partial_{\mathrm{e}} \mathrm{T}(A)\cap\mathrm{T}_\infty(A))$
a Poulsen simplex?
When A satisfies the equivalent conditions of Theorem A, then
![]() $\overline{\mathrm{conv}}(\partial_{\mathrm{e}} \mathrm{T}(A)\cap\mathrm{T}_\infty(A)) = \mathrm{T}(A)$
is the Poulsen simplex by Theorem A, and hence the answer is yes. However, we answer this question in the negative for every such A that does not satisfy the equivalent conditions of Theorem A. This in particular answers [Reference OrovitzOSV25, Question 1.10] in the negative. To this end, we introduce the following notation.
$\overline{\mathrm{conv}}(\partial_{\mathrm{e}} \mathrm{T}(A)\cap\mathrm{T}_\infty(A)) = \mathrm{T}(A)$
is the Poulsen simplex by Theorem A, and hence the answer is yes. However, we answer this question in the negative for every such A that does not satisfy the equivalent conditions of Theorem A. This in particular answers [Reference OrovitzOSV25, Question 1.10] in the negative. To this end, we introduce the following notation.
Definition 7.6. Let A be a
![]() $C^*$
-algebra. We denote by
$C^*$
-algebra. We denote by
![]() $\partial_{(\mathrm{fd})}\mathrm{T}(A)\subset \partial_{\mathrm{e}}\mathrm{T}(A)$
the set of extreme finite-dimensional traces of A that are isolated in
$\partial_{(\mathrm{fd})}\mathrm{T}(A)\subset \partial_{\mathrm{e}}\mathrm{T}(A)$
the set of extreme finite-dimensional traces of A that are isolated in
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
. We denote by
$\partial_{\mathrm{e}}\mathrm{T}(A)$
. We denote by
![]() $\mathrm{T}_{\mathrm{diff}}(A)\subset \mathrm{T}(A)$
the set of traces whose GNS von Neumann algebra is diffuse, and call its closure
$\mathrm{T}_{\mathrm{diff}}(A)\subset \mathrm{T}(A)$
the set of traces whose GNS von Neumann algebra is diffuse, and call its closure
![]() $\overline{\mathrm{T}_{\mathrm{diff}}(A)}$
the diffuse hull of
$\overline{\mathrm{T}_{\mathrm{diff}}(A)}$
the diffuse hull of
![]() $\mathrm{T}(A)$
.
$\mathrm{T}(A)$
.
Note that
![]() $\mathrm{T}_{\mathrm{diff}}(A)$
is a convex set, and hence the diffuse hull
$\mathrm{T}_{\mathrm{diff}}(A)$
is a convex set, and hence the diffuse hull
![]() $\overline{\mathrm{T}_{\mathrm{diff}}(A)}$
is a compact and convex set. It is also easy to see that
$\overline{\mathrm{T}_{\mathrm{diff}}(A)}$
is a compact and convex set. It is also easy to see that
![]() $\mathrm{T}_{\mathrm{diff}}(A)$
is a face of
$\mathrm{T}_{\mathrm{diff}}(A)$
is a face of
![]() $\text{T}(A)$
.
$\text{T}(A)$
.
Following the strategy from § 6, and in particular the proofs of Lemma 6.4 and Lemma 6.5, one can easily establish the following lemma which describes the diffuse hull of the trace simplex of a free product. We leave the details of the proof to the interested reader.
Lemma 7.7. Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
such that
$A_2$
such that
![]() $\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for
$\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for
![]() $i=1,2$
. Assume further that
$i=1,2$
. Assume further that
![]() $\mathrm{T}(A)$
is not affinely homeomorphic to
$\mathrm{T}(A)$
is not affinely homeomorphic to
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. Then
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
. Then
In particular, the extreme points of the diffuse hull of
![]() $\mathrm{T}(A)$
are dense.
$\mathrm{T}(A)$
are dense.
To a certain extent, Lemma 7.7 suggests a positive answer to Question 7.5. However, a closer look shows that, unless the diffuse hull is the whole simplex
![]() $\mathrm{T}(A)$
(which exactly occurs when the conditions of Theorem A hold), the diffuse hull is neither a face nor a simplex.
$\mathrm{T}(A)$
(which exactly occurs when the conditions of Theorem A hold), the diffuse hull is neither a face nor a simplex.
Proposition 7.8. Let
![]() $A=A_1\ast A_2$
be the free product of two unital, separable
$A=A_1\ast A_2$
be the free product of two unital, separable
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
such that
$A_2$
such that
![]() $\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for
$\mathrm{T}(A_i)$
is non-empty and does not consist of a single one-dimensional trace for
![]() $i=1,2$
. Assume that
$i=1,2$
. Assume that
![]() $A_1$
admits an isolated extreme one-dimensional trace
$A_1$
admits an isolated extreme one-dimensional trace
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $A_2$
admits an isolated extreme k-dimensional trace
$A_2$
admits an isolated extreme k-dimensional trace
![]() $\varphi_2$
, for some
$\varphi_2$
, for some
![]() $k\in\mathbb N$
. Assume further that
$k\in\mathbb N$
. Assume further that
![]() $\mathrm{T}(A)$
is not affinely homeomorphic to
$\mathrm{T}(A)$
is not affinely homeomorphic to
![]() $\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
.
$\mathrm{T}(\mathbb{C}^2\ast\mathbb{C}^2)$
.
Then the diffuse hull of
![]() $\mathrm{T}(A)$
is neither a face of
$\mathrm{T}(A)$
is neither a face of
![]() $\textit{T}(A)$
nor a Choquet simplex.
$\textit{T}(A)$
nor a Choquet simplex.
The proof will use free products of traces. For
![]() $i=1, 2$
, let
$i=1, 2$
, let
![]() $\varphi_i\in\text{T}(A_i)$
. Let
$\varphi_i\in\text{T}(A_i)$
. Let
![]() $(M_i,\tau_i)$
be a tracial von Neumann algebra and
$(M_i,\tau_i)$
be a tracial von Neumann algebra and
![]() $\pi_i:A_i\rightarrow M_i$
be a tracial representation with
$\pi_i:A_i\rightarrow M_i$
be a tracial representation with
![]() $\varphi_i=\tau_i\circ\pi_i$
. Let
$\varphi_i=\tau_i\circ\pi_i$
. Let
![]() $M=M_1*M_2$
endowed with the free product trace
$M=M_1*M_2$
endowed with the free product trace
![]() $\tau=\tau_1*\tau_2$
. Define
$\tau=\tau_1*\tau_2$
. Define
![]() $\pi:A\rightarrow M$
by letting
$\pi:A\rightarrow M$
by letting
![]() $\pi_{|A_i}=\pi_i$
for
$\pi_{|A_i}=\pi_i$
for
![]() $i=1,2$
. We call
$i=1,2$
. We call
![]() $\varphi=\tau\circ\pi\in\text{T}(A)$
the free product of
$\varphi=\tau\circ\pi\in\text{T}(A)$
the free product of
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
, and write
$\varphi_2$
, and write
![]() $\varphi=\varphi_1*\varphi_2$
.
$\varphi=\varphi_1*\varphi_2$
.
Proof. We will prove that
![]() $C=\overline{\mathrm{conv}}(\partial_{\mathrm{e}} \mathrm{T}(A)\cap\mathrm{T}_\infty(A))$
is neither a face of
$C=\overline{\mathrm{conv}}(\partial_{\mathrm{e}} \mathrm{T}(A)\cap\mathrm{T}_\infty(A))$
is neither a face of
![]() $\text{T}(A)$
nor a Choquet simplex. Since by Lemma 7.7, C is equal to the diffuse hull of
$\text{T}(A)$
nor a Choquet simplex. Since by Lemma 7.7, C is equal to the diffuse hull of
![]() $\text{T}(A)$
, this will prove the conclusion.
$\text{T}(A)$
, this will prove the conclusion.
As in the proof of Theorem 3.4, let
![]() $\varphi\in\partial_{(\mathrm{fd})}\mathrm{T}(A)$
be such that
$\varphi\in\partial_{(\mathrm{fd})}\mathrm{T}(A)$
be such that
![]() $\varphi_{|A_i}=\varphi_i$
for
$\varphi_{|A_i}=\varphi_i$
for
![]() $i=1,2$
. We begin by noticing that
$i=1,2$
. We begin by noticing that
![]() $\varphi\notin C$
. Indeed, assume that there exist diffuse traces
$\varphi\notin C$
. Indeed, assume that there exist diffuse traces
![]() $(\zeta_n)_n$
converging to
$(\zeta_n)_n$
converging to
![]() $\varphi$
. By Corollary 3.2, we have
$\varphi$
. By Corollary 3.2, we have
![]() $\mu_n(\{\varphi\})\to 1$
, where
$\mu_n(\{\varphi\})\to 1$
, where
![]() $\mu_n$
is the unique probability measure on
$\mu_n$
is the unique probability measure on
![]() $\partial_{\mathrm{e}}\mathrm{T}(A)$
whose barycenter is
$\partial_{\mathrm{e}}\mathrm{T}(A)$
whose barycenter is
![]() $\zeta_n$
. As
$\zeta_n$
. As
![]() $\varphi$
is finite-dimensional, this contradicts the diffuseness of
$\varphi$
is finite-dimensional, this contradicts the diffuseness of
![]() $\zeta_n$
.
$\zeta_n$
.
We next define
![]() $\psi_i\in\text{T}(A_i)$
, for
$\psi_i\in\text{T}(A_i)$
, for
![]() $i=1, 2$
, by considering three cases.
$i=1, 2$
, by considering three cases.
-
(1) Assume that
 $k=1$
and
$k=1$
and
 $|\partial_{\mathrm{e}}\text{T}(A_1)|=|\partial_{\mathrm{e}}\text{T}(A_2)|=2$
. Since
$|\partial_{\mathrm{e}}\text{T}(A_1)|=|\partial_{\mathrm{e}}\text{T}(A_2)|=2$
. Since
 $\partial_{\mathrm{e}}\text{T}(A_1)$
and
$\partial_{\mathrm{e}}\text{T}(A_1)$
and
 $\partial_{\mathrm{e}}\text{T}(A_2)$
cannot both consist of two one-dimensional traces, after possibly swapping indices, we may assume that there is
$\partial_{\mathrm{e}}\text{T}(A_2)$
cannot both consist of two one-dimensional traces, after possibly swapping indices, we may assume that there is
 $\psi_1\in \partial_{\mathrm{e}}\text{T}(A_1)$
of dimension at least 2. Let
$\psi_1\in \partial_{\mathrm{e}}\text{T}(A_1)$
of dimension at least 2. Let
 $\psi_2\in\partial_{\mathrm{e}}\text{T}(A_2)\setminus\{\varphi_2\}$
.
$\psi_2\in\partial_{\mathrm{e}}\text{T}(A_2)\setminus\{\varphi_2\}$
. -
(2) Assume that
 $k=1$
, and
$k=1$
, and
 $|\partial_{\mathrm{e}}\text{T}(A_1)|\geq 3$
or
$|\partial_{\mathrm{e}}\text{T}(A_1)|\geq 3$
or
 $|\partial_{\mathrm{e}}\text{T}(A_2)|\geq 3$
. After possibly swapping indices, we may assume that
$|\partial_{\mathrm{e}}\text{T}(A_2)|\geq 3$
. After possibly swapping indices, we may assume that
 $|\partial_{\mathrm{e}}\text{T}(A_1)|\geq 3$
. Let
$|\partial_{\mathrm{e}}\text{T}(A_1)|\geq 3$
. Let
 $\gamma,\delta$
be distinct elements of
$\gamma,\delta$
be distinct elements of
 $\partial_{\mathrm{e}}\text{T}(A_1)\setminus\{\varphi_1\}$
and put
$\partial_{\mathrm{e}}\text{T}(A_1)\setminus\{\varphi_1\}$
and put
 $\psi_1=\frac{1}{2}(\gamma+\delta)\in\text{T}(A_1)$
. Let
$\psi_1=\frac{1}{2}(\gamma+\delta)\in\text{T}(A_1)$
. Let
 $\psi_2\in\partial_{\mathrm{e}}\text{T}(A_2)\setminus\{\varphi_2\}$
.
$\psi_2\in\partial_{\mathrm{e}}\text{T}(A_2)\setminus\{\varphi_2\}$
. -
(3) Assume that
 $k\geq 2$
. Let
$k\geq 2$
. Let
 $\psi_1\in\partial_{\mathrm{e}}\text{T}(A_1)\setminus\{\varphi_1\}$
and put
$\psi_1\in\partial_{\mathrm{e}}\text{T}(A_1)\setminus\{\varphi_1\}$
and put
 $\psi_2=\varphi_2$
.
$\psi_2=\varphi_2$
.
We first show that C is not a face of
![]() $\text{T}(A)$
. Let
$\text{T}(A)$
. Let
![]() $\psi\in\mathrm{T}(A)$
be a trace satisfying
$\psi\in\mathrm{T}(A)$
be a trace satisfying
![]() $\psi_{|A_i}=\psi_i$
for
$\psi_{|A_i}=\psi_i$
for
![]() $i=1,2$
. For instance, we can take
$i=1,2$
. For instance, we can take
![]() $\psi$
to be the free product trace,
$\psi$
to be the free product trace,
![]() $\psi_1*\psi_2$
. Define
$\psi_1*\psi_2$
. Define
![]() $\chi=\frac{1}{2}(\varphi+\psi)\in\mathrm{T}(A)$
.
$\chi=\frac{1}{2}(\varphi+\psi)\in\mathrm{T}(A)$
.
We claim that
![]() $\chi\in C$
. Since
$\chi\in C$
. Since
![]() $\varphi\not\in C$
, this claim will imply that C is not a face of
$\varphi\not\in C$
, this claim will imply that C is not a face of
![]() $\text{T}(A)$
. To prove the claim, let
$\text{T}(A)$
. To prove the claim, let
![]() $\pi:A\rightarrow M$
be the tracial representation associated to
$\pi:A\rightarrow M$
be the tracial representation associated to
![]() $\chi$
and put
$\chi$
and put
![]() $M_i=\pi(A_i)''$
for
$M_i=\pi(A_i)''$
for
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $\chi_{|A_i}=\frac{1}{2}(\varphi_i+\psi_i)$
, for
$\chi_{|A_i}=\frac{1}{2}(\varphi_i+\psi_i)$
, for
![]() $i=1,2$
, it is easy to check that in any of the cases (1)–(3) we have
$i=1,2$
, it is easy to check that in any of the cases (1)–(3) we have
![]() $M_1,M_2\not=\mathbb C1$
,
$M_1,M_2\not=\mathbb C1$
,
![]() $\dim(M_1)+\dim(M_2)\geq 5$
and
$\dim(M_1)+\dim(M_2)\geq 5$
and
![]() $\text{e}(M_1)+\text{e}(M_2)\leq 1$
. Thus
$\text{e}(M_1)+\text{e}(M_2)\leq 1$
. Thus
![]() $\chi\in\mathrm{T}_{\mathrm{l}}(A)$
, and combining Theorem E and Proposition 6.2 gives that indeed
$\chi\in\mathrm{T}_{\mathrm{l}}(A)$
, and combining Theorem E and Proposition 6.2 gives that indeed
![]() $\chi\in C$
.
$\chi\in C$
.
To prove the stronger statement that C is not a Choquet simplex, we will need a more involved construction of traces on A. To this end, for
![]() $\alpha\in [\frac{1}{3},\frac{1}{2}]$
we define
$\alpha\in [\frac{1}{3},\frac{1}{2}]$
we define
![]() $\rho_\alpha\in\text{T}(A)$
by letting:
$\rho_\alpha\in\text{T}(A)$
by letting:
-
(a)
 $\rho_\alpha=\psi_1*(\alpha\varphi_2+(1-\alpha)\psi_2)$
in case (1);
$\rho_\alpha=\psi_1*(\alpha\varphi_2+(1-\alpha)\psi_2)$
in case (1); -
(b)
 $\rho_\alpha=(\frac{1}{3}\varphi_1+\frac{2}{3}\psi_1)*(\alpha\varphi_2+(1-\alpha)\psi_2)=(\frac{1}{3}\varphi_1+\frac{1}{3}\gamma+\frac{1}{3}\delta)*(\alpha\varphi_2+(1-\alpha)\psi_2)$
in case (2); and
$\rho_\alpha=(\frac{1}{3}\varphi_1+\frac{2}{3}\psi_1)*(\alpha\varphi_2+(1-\alpha)\psi_2)=(\frac{1}{3}\varphi_1+\frac{1}{3}\gamma+\frac{1}{3}\delta)*(\alpha\varphi_2+(1-\alpha)\psi_2)$
in case (2); and -
(c)
 $\rho_\alpha=(\alpha\varphi_1+(1-\alpha)\psi_1)*\varphi_2$
in case (3).
$\rho_\alpha=(\alpha\varphi_1+(1-\alpha)\psi_1)*\varphi_2$
in case (3).
We claim that
We will derive this claim as a consequence of the following particular case of [Reference UedaUed11, Theorem 4.1]:
![]() $(\star)$
if
$(\star)$
if
![]() $N_1,N_2\not=\mathbb C$
are tracial von Neumann algebras with
$N_1,N_2\not=\mathbb C$
are tracial von Neumann algebras with
![]() $\text{dim}(N_1)+\text{dim}(N_2)\geq 5$
, then their free product
$\text{dim}(N_1)+\text{dim}(N_2)\geq 5$
, then their free product
![]() $N_1*N_2$
is a II
$N_1*N_2$
is a II
![]() $_1$
factor if and only if for any projections
$_1$
factor if and only if for any projections
![]() $z_1\in\mathcal Z(N_1)$
and
$z_1\in\mathcal Z(N_1)$
and
![]() $z_2\in\mathcal Z(N_2)$
such that
$z_2\in\mathcal Z(N_2)$
such that
![]() $N_1z_1\cong \mathbb M_{k_1}(\mathbb C)$
and
$N_1z_1\cong \mathbb M_{k_1}(\mathbb C)$
and
![]() $N_2z_2\cong\mathbb M_{k_2}(\mathbb C)$
, for some
$N_2z_2\cong\mathbb M_{k_2}(\mathbb C)$
, for some
![]() $k_1,k_2\geq 1$
, we have that
$k_1,k_2\geq 1$
, we have that
![]() $({\tau(z_1)}/{k_1^2})+({\tau(z_2)}/{k_2^2})\leq 1$
.
$({\tau(z_1)}/{k_1^2})+({\tau(z_2)}/{k_2^2})\leq 1$
.
Let
![]() $\alpha\in [\frac{1}{3},\frac{1}{2}]$
and denote by N the GNS von Neumann algebra of
$\alpha\in [\frac{1}{3},\frac{1}{2}]$
and denote by N the GNS von Neumann algebra of
![]() $\rho_\alpha$
. In case (1), we have that
$\rho_\alpha$
. In case (1), we have that
![]() $N=N_1*N_2$
, where
$N=N_1*N_2$
, where
![]() $N_1\not=\mathbb C$
is a tracial factor and
$N_1\not=\mathbb C$
is a tracial factor and
![]() $N_2$
is a tracial von Neumann algebra whose minimal central projections have traces
$N_2$
is a tracial von Neumann algebra whose minimal central projections have traces
![]() $\alpha,1-\alpha$
. Since
$\alpha,1-\alpha$
. Since
![]() $\frac{1}{4}+\alpha\leq 1$
and
$\frac{1}{4}+\alpha\leq 1$
and
![]() $\frac{1}{4}+(1-\alpha)\leq 1$
,
$\frac{1}{4}+(1-\alpha)\leq 1$
,
![]() $(\star)$
implies that N is a II
$(\star)$
implies that N is a II
![]() $_1$
factor. Similarly, in case (3), using that
$_1$
factor. Similarly, in case (3), using that
![]() $\varphi_2\in\partial_{\text{e}}\text{T}(A_2)$
is k-dimensional for some
$\varphi_2\in\partial_{\text{e}}\text{T}(A_2)$
is k-dimensional for some
![]() $k\geq 2$
, it follows that N is a II
$k\geq 2$
, it follows that N is a II
![]() $_1$
factor. Finally, in case (2),
$_1$
factor. Finally, in case (2),
![]() $N=N_1*N_2$
, where
$N=N_1*N_2$
, where
![]() $N_1$
and
$N_1$
and
![]() $N_2$
are tracial von Neumann algebra whose minimal central projections have traces equal to
$N_2$
are tracial von Neumann algebra whose minimal central projections have traces equal to
![]() $\frac{1}{3}$
and
$\frac{1}{3}$
and
![]() $\alpha,1-\alpha$
, respectively. Since
$\alpha,1-\alpha$
, respectively. Since
![]() $\frac{1}{3}+\alpha\leq 1$
and
$\frac{1}{3}+\alpha\leq 1$
and
![]() $\frac{1}{3}+(1-\alpha)\leq 1$
,
$\frac{1}{3}+(1-\alpha)\leq 1$
,
![]() $(\star)$
again implies that N is a II
$(\star)$
again implies that N is a II
![]() $_1$
factor. Altogether, this proves that N is a II
$_1$
factor. Altogether, this proves that N is a II
![]() $_1$
factor in all cases (1)–(3), and thus (7.1) holds.
$_1$
factor in all cases (1)–(3), and thus (7.1) holds.
Next, for
![]() $\alpha\in [\frac{1}{3},\frac{1}{2}]$
, we put
$\alpha\in [\frac{1}{3},\frac{1}{2}]$
, we put
![]() $\beta_\alpha=({\frac{1}{2}-\alpha})/({1-\alpha})\in [0,\frac{1}{4}]$
. We claim that
$\beta_\alpha=({\frac{1}{2}-\alpha})/({1-\alpha})\in [0,\frac{1}{4}]$
. We claim that
To prove this claim we note that
![]() $\beta_\alpha+(1-\beta_\alpha)\alpha=\frac{1}{2}$
, and therefore:
$\beta_\alpha+(1-\beta_\alpha)\alpha=\frac{1}{2}$
, and therefore:
-
–
 $(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_1}=\beta_\alpha\varphi_1+(1-\beta_\alpha)\psi_1$
and
$(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_1}=\beta_\alpha\varphi_1+(1-\beta_\alpha)\psi_1$
and
 $(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_2}=\frac{1}{2}\varphi_2+\frac{1}{2}\psi_2$
in case (1);
$(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_2}=\frac{1}{2}\varphi_2+\frac{1}{2}\psi_2$
in case (1); -
–
 $(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_1}=(({2\beta_\alpha+1})/{3})\varphi_1+(({1-\beta_\alpha})/{3})\gamma+(({1-\beta_\alpha})/{3})\delta$
and
$(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_1}=(({2\beta_\alpha+1})/{3})\varphi_1+(({1-\beta_\alpha})/{3})\gamma+(({1-\beta_\alpha})/{3})\delta$
and
 $(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_2}=\frac{1}{2}\varphi_2+\frac{1}{2}\psi_2$
in case (2); and
$(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_2}=\frac{1}{2}\varphi_2+\frac{1}{2}\psi_2$
in case (2); and -
–
 $(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_1}=\frac{1}{2}\varphi_1+\frac{1}{2}\psi_1$
and
$(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_1}=\frac{1}{2}\varphi_1+\frac{1}{2}\psi_1$
and
 $(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_2}=\varphi_2$
in case (3).
$(\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha)_{|A_2}=\varphi_2$
in case (3).
Since
![]() $\psi_1\in\partial_{\text{e}}\text{T}(A_1)$
has dimension at least 2 in case (1),
$\psi_1\in\partial_{\text{e}}\text{T}(A_1)$
has dimension at least 2 in case (1),
![]() $({2\beta_\alpha+1}/{3})\leq\frac{1}{2}$
and
$({2\beta_\alpha+1}/{3})\leq\frac{1}{2}$
and
![]() $\varphi_2\in\partial_{\text{e}}\text{T}(A_2)$
has dimension at least 2 in case (3), it follows that in each of the cases (1)–(3) we have that
$\varphi_2\in\partial_{\text{e}}\text{T}(A_2)$
has dimension at least 2 in case (3), it follows that in each of the cases (1)–(3) we have that
![]() $\beta_\alpha \varphi+(1-\beta_\alpha)\rho_\alpha\in \text{T}_{\text{l}}(A)$
. Combining Theorem E and Proposition 6.2 gives that
$\beta_\alpha \varphi+(1-\beta_\alpha)\rho_\alpha\in \text{T}_{\text{l}}(A)$
. Combining Theorem E and Proposition 6.2 gives that
![]() $\beta_\alpha \varphi+(1-\beta_\alpha)\rho_\alpha\in \overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_\infty(A)}\subset C$
.
$\beta_\alpha \varphi+(1-\beta_\alpha)\rho_\alpha\in \overline{\partial_{\mathrm{e}}\mathrm{T}(A)\cap\mathrm{T}_\infty(A)}\subset C$
.
To show that C is not a Choquet simplex, assume by contradiction that C is a Choquet simplex. Choose
![]() $\alpha\not=\alpha'\in [\frac{1}{3},\frac{1}{2})$
. By (7.1),
$\alpha\not=\alpha'\in [\frac{1}{3},\frac{1}{2})$
. By (7.1),
![]() $\varphi,\rho_\alpha,\rho_{\alpha'}\in\partial_{\text{e}}\text{T}(A)$
are distinct extreme traces. Thus,
$\varphi,\rho_\alpha,\rho_{\alpha'}\in\partial_{\text{e}}\text{T}(A)$
are distinct extreme traces. Thus,
is a closed face of
![]() $\mathrm{T}(A)$
which is isomorphic to the two-dimensional simplex. Since C is assumed to be a simplex, the convex set
$\mathrm{T}(A)$
which is isomorphic to the two-dimensional simplex. Since C is assumed to be a simplex, the convex set
![]() $\Delta\cap C$
is also a simplex.
$\Delta\cap C$
is also a simplex.
Put
![]() $I=\text{conv}(\varphi,\rho_\alpha)$
. By (7.1), we get that
$I=\text{conv}(\varphi,\rho_\alpha)$
. By (7.1), we get that
![]() $\rho_\alpha\in C$
, and hence
$\rho_\alpha\in C$
, and hence
![]() $\rho_\alpha\in I\cap C$
. Since
$\rho_\alpha\in I\cap C$
. Since
![]() $\alpha<\frac{1}{2}$
, we get that
$\alpha<\frac{1}{2}$
, we get that
![]() $\beta_\alpha\not=0$
, and hence
$\beta_\alpha\not=0$
, and hence
![]() $\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha\not=\rho_\alpha$
. Hence, (7.2) implies that
$\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha\not=\rho_\alpha$
. Hence, (7.2) implies that
![]() $\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha\in (I\cap C)\setminus\{\rho_\alpha\}$
. Since
$\beta_\alpha\varphi+(1-\beta_\alpha)\rho_\alpha\in (I\cap C)\setminus\{\rho_\alpha\}$
. Since
![]() $\varphi\not\in C$
, we conclude that
$\varphi\not\in C$
, we conclude that
![]() $I\cap C$
is a non-degenerate interval which does not contain
$I\cap C$
is a non-degenerate interval which does not contain
![]() $\varphi$
. Similarly, if
$\varphi$
. Similarly, if
![]() $I'=\text{conv}(\varphi,\rho_{\alpha'})$
, then
$I'=\text{conv}(\varphi,\rho_{\alpha'})$
, then
![]() $I'\cap C$
is a non-degenerate interval which does not contain
$I'\cap C$
is a non-degenerate interval which does not contain
![]() $\varphi$
. However,
$\varphi$
. However,
![]() $ \Delta \cap C$
contains the quadrilateral prescribed by the endpoints of
$ \Delta \cap C$
contains the quadrilateral prescribed by the endpoints of
![]() $ I\cap C$
and
$ I\cap C$
and
![]() $ I'\cap C$
. However, any proper subset of
$ I'\cap C$
. However, any proper subset of
![]() $\Delta$
which contains such a quadrilateral cannot be a simplex. This gives the desired contradiction and finishes the proof.
$\Delta$
which contains such a quadrilateral cannot be a simplex. This gives the desired contradiction and finishes the proof.
Acknowledgements
The authors would like to thank Mikael Rørdam for asking us a question which led to Theorem G, and for pointing out the result from [Reference Exel and LoringEL92] in Remark 2.11. The second-named author would also like to thank Mikael Rørdam for fruitful conversations related to the contents of this paper, and both Mikael Rørdam and Magdalena Musat for useful discussions about the contents of [Reference Rørdam and MusatRM21] and [Reference OrovitzOSV25]. Additionally, the authors thank Raz Slutsky for his remarks on the manuscript and Dima Shlyakhtenko for pointing out the reference [Reference DabrowskiDab10]. Finally, the authors would like to thank the anonymous referee for their careful reading of the paper and for the useful comments which helped improve the exposition.
Conflicts of interest
None.
Financial support
AI was supported by NSF grants FRG-DMS-1854074 and DMS-2153805. PS was supported by MSCA Fellowship No. 101111079 from the European Union. IV was supported by NSF postdoctoral fellowship DMS-2402368.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.