Conditional flow matching for generative modelling of near-wall turbulence with quantified uncertainty

Abstract

Reconstructing near-wall turbulence from wall-based measurements is a critical yet inherently ill-posed problem in wall-bounded flows, where limited sensing and spatially heterogeneous flow–wall coupling challenge deterministic estimation strategies. To address this, we introduce a novel generative modelling framework based on conditional flow matching for synthesising instantaneous velocity fluctuation fields from wall observations, with explicit quantification of predictive uncertainty. Our method integrates continuous-time flow matching with a probabilistic forward operator trained using stochastic weight-averaging Gaussian, enabling zero-shot conditional generation without model re-training. We demonstrate that the proposed approach not only recovers physically realistic, statistically consistent turbulence structures across the near-wall region but also effectively adapts to various sensor configurations, including sparse, incomplete and low-resolution wall measurements. The model achieves robust uncertainty-aware reconstruction, preserving flow intermittency and structure even under significantly degraded observability. Compared with classical linear stochastic estimation and deterministic convolutional neural network methods, our stochastic generative learning framework exhibits superior generalisation for unseen realisations under same flow conditions and resilience under measurement sparsity with quantified uncertainty. This work establishes a robust semi-supervised generative modelling paradigm for data-consistent flow reconstruction and lays the foundation for uncertainty-aware, sensor-driven modelling of wall-bounded turbulence.

1. Introduction

Wall-bounded turbulence is fundamental to a wide range of engineering and natural systems, governing critical processes such as skin-friction drag, heat and mass transfer and the onset of flow instabilities. The near-wall region, including the viscous sublayer, buffer layer and lower logarithmic layer, plays a dominant role in the dynamics of wall-bounded flows, as this is where turbulent kinetic energy is both generated and dissipated at the highest rates (Townsend 1961; Pope 2001). Coherent structures in these regions, such as streamwise streaks and quasi-streamwise vortices, are known to mediate the transfer of momentum and energy across scales, and their spatiotemporal organisation governs the emergence of larger-scale turbulent motions farther from the wall (Adrian 2007; Hwang et al. 2016). Therefore, near-wall turbulence has long been the focus of flow-control strategies aimed at reducing drag, delaying transition or enhancing mixing (Kim 2007). However, implementing such strategies in practice demands high-fidelity instantaneous flow-field information, which remains challenging due to small spatial scales, high temporal variability and limited accessibility of measurements in this region.

Wall-mounted sensors, such as those measuring pressure or wall shear stress, are relatively easy to deploy, offering time-resolved, scalable and non-disruptive access to the surface signatures of near-wall turbulence (Löfdahl & Gad-el Hak 1999; Choi, Moin & Kim 1994). This practical advantage has naturally led to the question of whether it is possible to reconstruct the full, off-wall velocity field using only wall-based measurements. If successful, such reconstructions would enable closed-loop control, real-time flow monitoring and improved wall models for large-eddy simulations (LES) without requiring full-field sensing. The feasibility of this task is supported by the bidirectional coupling between near-wall and outer-layer structures (Zaki 2024). Large-scale motions in the logarithmic and outer regions of wall-bounded flows modulate the near-wall turbulence, leaving observable imprints on wall quantities (Abe, Kawamura & Choi 2004; Mathis, Hutchins & Marusic 2009; Hwang et al. 2016). Conversely, energetic near-wall events can propagate their influence outward and modulate the coherence of large-scale motions in the outer layer (Adrian 2007; Lozano-Durán & Jiménez 2014). These bidirectional interactions have inspired extensive efforts to infer inner velocity fields from wall measurements. Physics-based strategies often leverage data assimilation techniques to integrate wall observations into high-fidelity simulations such as direct numerical simulations (DNS) or LES, thereby reconstructing the full flow state (Colburn, Cessna & Bewley 2011; Suzuki & Hasegawa 2017; Wang & Zaki 2025). While these methods benefit from governing equations that enforce physical consistency, they remain computationally prohibitive for most practical settings. Alternatively, resolvent analysis provides a linearised, reduced-order mapping between wall forcing and flow response (Amaral et al. 2021). While insightful, these models rely on simplifying assumptions (e.g. linearisation around a mean flow) and cannot fully capture the nonlinear and intermittent nature of near-wall turbulence.

On the other hand, data-driven methods offer an attractive alternative for flow estimation and reconstruction, particularly in scenarios where repeated measurements are available, and the underlying physics are too complex to be modelled directly. Early work using linear stochastic estimation (LSE) (Adrian & Moin 1988; Marusic, Mathis & Hutchins 2010; Baars, Hutchins & Marusic 2016; Encinar & Jiménez 2019) and proper orthogonal decomposition (Towne, Schmidt & Colonius 2018) laid the foundation by extracting statistically dominant flow features and their correlations with wall signals. These techniques, however, are constrained by their linearity, and often fail to resolve the complex, multiscale turbulence structures. With the advent of deep learning, convolutional neural networks (CNNs) and their variants have emerged as powerful tools for nonlinear flow estimation from wall data (Güemes et al. 2019; Guastoni et al. 2021; Balasubramanian et al. 2023; Cuéllar et al. 2024a ; Yousif et al. 2023; Hora et al. 2024). These models have demonstrated promising results in reconstructing velocity fields at various wall-normal locations using wall shear stress or pressure as input. Despite these advances, most of the existing approaches remain fundamentally deterministic and do not account for the inherent uncertainty of the reconstruction task, which arises from spatially heterogeneous correlations and variability in wall measurement quality, such as practical imperfections, induced sensor noise, limited spatial resolution and intrusive measurement effects. In regions where wall-flow coherence is strong (e.g. within the viscous sublayer), deterministic models may perform well. However, as the correlation decays with wall-normal distance, especially across the buffer and logarithmic layers (Wang, Wang & Zaki 2022; Arranz & Lozano-Durán 2024), these models often fail to recover energetic but weakly observable flow features. Furthermore, practical limitations such as sensor sparsity, measurement noise and resolution constraints exacerbate this challenge, making the reconstruction problem increasingly ill-posed (Güemes et al. 2021; Cuéllar et al. 2024b ). As a result, deterministic models tend to produce overly smooth or biased estimates that suppress physically realistic variability. These limitations highlight the need for probabilistic modelling frameworks that not only generate physically consistent velocity features that are weakly correlated to wall quantities, but also quantify predictive uncertainty, enabling robust inference under imperfect or incomplete wall data.

Generative modelling, particularly when combined with Bayesian learning, offers a promising solution to these challenges. Rather than producing a single estimate, generative models learn the conditional distribution of turbulent velocity fields given wall measurements, enabling the synthesis of multiple physically plausible flow realisations that reflect both the informative and non-informative components of the flow with respect to wall data. Recent advances in generative AI, particularly diffusion-based models, have demonstrated impressive capabilities in synthesising high-fidelity flow realisations with accurate statistics (Rühling Cachay et al. 2023; Kohl, Chen & Thuerey 2023; Li et al. 2023; Shu, Li & Farimani 2023; Dong, Chen & Wu 2024; Du et al. 2024; Gao et al. 2024a , b ; Molinaro et al. 2024; Fan, Akhare & Wang 2025; Gao, Kaltenbach & Koumoutsakos 2025; Shehata, Holzschuh & Thuerey 2025; Zhuang, Cheng & Duraisamy 2025). Specifically, Wang and co-workers have developed a conditional neural field-based latent diffusion model, which has been successfully demonstrated in generating spatiotemporal wall-bounded turbulence in three dimensions that is both inhomogeneous and anisotropic, enabling applications such as synthetic inflow turbulence generation and zero-shot spatiotemporal flow reconstruction (Du et al. 2024; Liu et al. 2025). However, diffusion-based sampling remains computationally expensive due to its iterative nature and is sensitive to posterior conditioning. Recently, flow matching has emerged as a scalable alternative to diffusion, offering fast and stable sampling by learning continuous-time transport maps between simple base distributions and complex data distributions through direct supervision (Lipman et al. 2022).

In this work, we propose a novel generative learning framework for reconstructing near-wall turbulent velocity fields from wall-based measurements with quantified uncertainty. Specifically, we develop a conditional generative model that integrates conditional flow matching (Lipman et al. 2022) with Bayesian neural operators trained using stochastic weight-averaging Gaussian (SWAG) (Maddox et al. 2019). The conditional-flow-matching-based model enables efficient generation of diverse, physically consistent instantaneous velocity fluctuation fields across multiple wall-normal locations, while the SWAG-based operator serves as a probabilistic forward model that maps velocity fields to wall measurements with quantified epistemic uncertainty. At inference time, our framework performs zero-shot conditional generation by iteratively refining sampled velocity fields to satisfy wall measurements – whether sparse, noisy or partial – without requiring re-training, transfer learning or fine-tuning.

To the best of our knowledge, this work presents the first attempt to leverage flow matching to reconstruct inhomogeneous and anisotropic turbulent velocity fluctuations at pre-defined wall-normal locations. Moreover, it is the first to demonstrate zero-shot conditional flow generation with uncertainty quantification in this context. By explicitly modelling both flow variability and predictive uncertainty, our framework addresses the ill-posed nature of near-wall turbulence reconstruction and enables robust, data-consistent inference under realistic sensing conditions. The remainder of this paper is organised as follows. Section 2 details the methodology of the proposed generative modelling framework. Section 3 presents reconstruction results under varying sensor conditions, demonstrating the effectiveness of the proposed methods. Section 4 compares the performance of the proposed model against the state-of-the-art baseline methods and discusses each individual component of the proposed framework. Finally, § 5 summarises the key findings and outlines directions for future research.

2. Methodology

2.1. Problem formulation and analysis

This study tackles the challenge of reconstructing instantaneous velocity fluctuations at various wall-normal locations using only measurements acquired at the wall. The complexity of this task varies significantly across the near-wall region due to spatially heterogeneous correlations between wall measurements (e.g. wall shear stress) and turbulent structures in wall-bounded flows. Rather than focusing on a specific off-wall plane, our goal is to develop a general-purpose generative learning framework capable of synthesising physically realistic velocity fields throughout the entire near-wall region. Critically, the proposed framework explicitly quantifies predictive uncertainty, especially in regions where the coherence between wall signals and turbulent fluctuations is weak, or where wall measurements are sparse and contaminated by noise.

To better understand the inherent challenges associated with this reconstruction task, we first analyse the correlation between wall shear stress and velocity fluctuations across different wall-normal positions. As illustrated in figures 1(a) and 1(b), the correlation strength between wall shear stress and velocity fluctuations decreases sharply as the wall-normal distance ( $y^+$ ) increases. We note that this drop in correlation is slightly faster than that reported by Alfredsson et al. (1988) for two main reasons. First, our correlations are computed without incorporating any time lag, which is consistent with our entire framework. In contrast, Alfredsson et al. (1988) introduced a downstream displacement of approximately $50l^*$ (where $l^*$ is the viscous length scale) between the wall shear stress probe and the velocity measurement, thereby accounting for the convective delay of coherent structures. Recent work by Arranz & Lozano-Durán (2024) shows that including such a lag typically increases the measured correlations. Second, the relatively low Reynolds number ( $\textit{Re}_\tau =180$ ) considered in our study contributes to the more rapid decay. As seen in figure 1(b), at $y^+=100$ , the measurement point is already near the channel centre, where the influence of wall dynamics is weak and the correlation with wall shear stress naturally approaches zero. This reduction significantly limits the feasibility of accurately reconstructing instantaneous turbulent structures in outer regions using solely wall-based measurements (Suzuki & Hasegawa 2017; Wang et al. 2022). Nonetheless, large-scale flow structures in the outer region leave subtle yet detectable imprints on the wall through amplitude and wavelength modulation effects, indirectly encoding useful information within wall shear stress fluctuations (Arranz & Lozano-Durán 2024; Mathis et al. 2009). Recognising this indirect yet informative coupling motivates our generative model, which aims to reconstruct instantaneous velocity fluctuations at various off-wall locations, incorporating uncertainty quantification that reflects the progressive weakening of coherence, measurement sparsity and observational noise.

Figure 1. (a) Instantaneous streamwise velocity fluctuations $\boldsymbol{u}'$ of the turbulent channel flow ( $\textit{Re}_\tau = 180$ ) at three wall-normal locations ( $y^+ = 5, 20, 40$ ) alongside the corresponding wall shear stress field $\tau _{u}$ . (b) Correlation coefficients $C_{\tau _u, {u}'}$ between wall shear stress and velocity fluctuations as a function of $y^+$ . (c) Reconstruction concept: given wall input ${\boldsymbol{\varPhi }}_{w\textit{all}}$ , the model (parametrised by $\boldsymbol{\theta }$ ) predicts $\boldsymbol{u}'$ at different off-wall planes, with increasing uncertainty illustrated by blurred regions at higher $y^+$ .

Specifically, within the viscous sublayer, velocity fluctuations exhibit a nearly linear and direct relationship with wall measurements, characterised by a high correlation coefficient ( $C_{\tau _{u} u'} \approx 1$ ) (Wang et al. 2022). Due to this strong coupling, velocity fields in this region can be reconstructed accurately with minimal uncertainty, as illustrated conceptually in figure 1(c). Moving outward into the buffer layer, however, this direct coherence rapidly decays (Wang et al. 2022), even though this region is critical for turbulent kinetic energy production and hosts energetic coherent structures, such as streamwise streaks and hairpin vortices (Adrian 2007; Bae & Lee 2021). These dynamically important structures are only indirectly captured by wall signals due to modulation effects, significantly complicating their instantaneous reconstruction. Thus, while the deterministic models can perform well in terms of mean prediction accuracy, they cannot capture the variability and provide predictive uncertainty that are particularly important in the buffer layer. This limitation underscores the need for probabilistic modelling approaches that explicitly quantify the uncertainty arising from weakened correlations and indirect observability. Further away from the wall (logarithmic layer and beyond), large-scale turbulent motions, particularly low-speed streaks, persist and can extend significantly into the outer layer, sometimes reaching the boundary-layer edge (Adrian 2007; Encinar & Jiménez 2019). Although their instantaneous correlation with wall signals is generally low, these large-scale structures indirectly influence near-wall dynamics through modulation effects, leaving distinguishable but indirect signatures on wall quantities (Arranz & Lozano-Durán 2024; Mathis et al. 2009). Despite being less dominant energetically compared with smaller-scale structures nearer to the wall, accurately capturing their statistical features remains essential to realistically reconstruct turbulence characteristics. Deterministic methods relying solely on wall measurements often significantly underestimate fluctuations in this region, as they only recover weakly correlated, low-energy large-scale motions (Guastoni et al. 2021). Recognising this limitation, our framework not only predicts informative components directly from wall data, but also leverages generative learning to synthesise non-informative yet energetically crucial turbulence structures, thereby ensuring accurate statistical reconstructions.

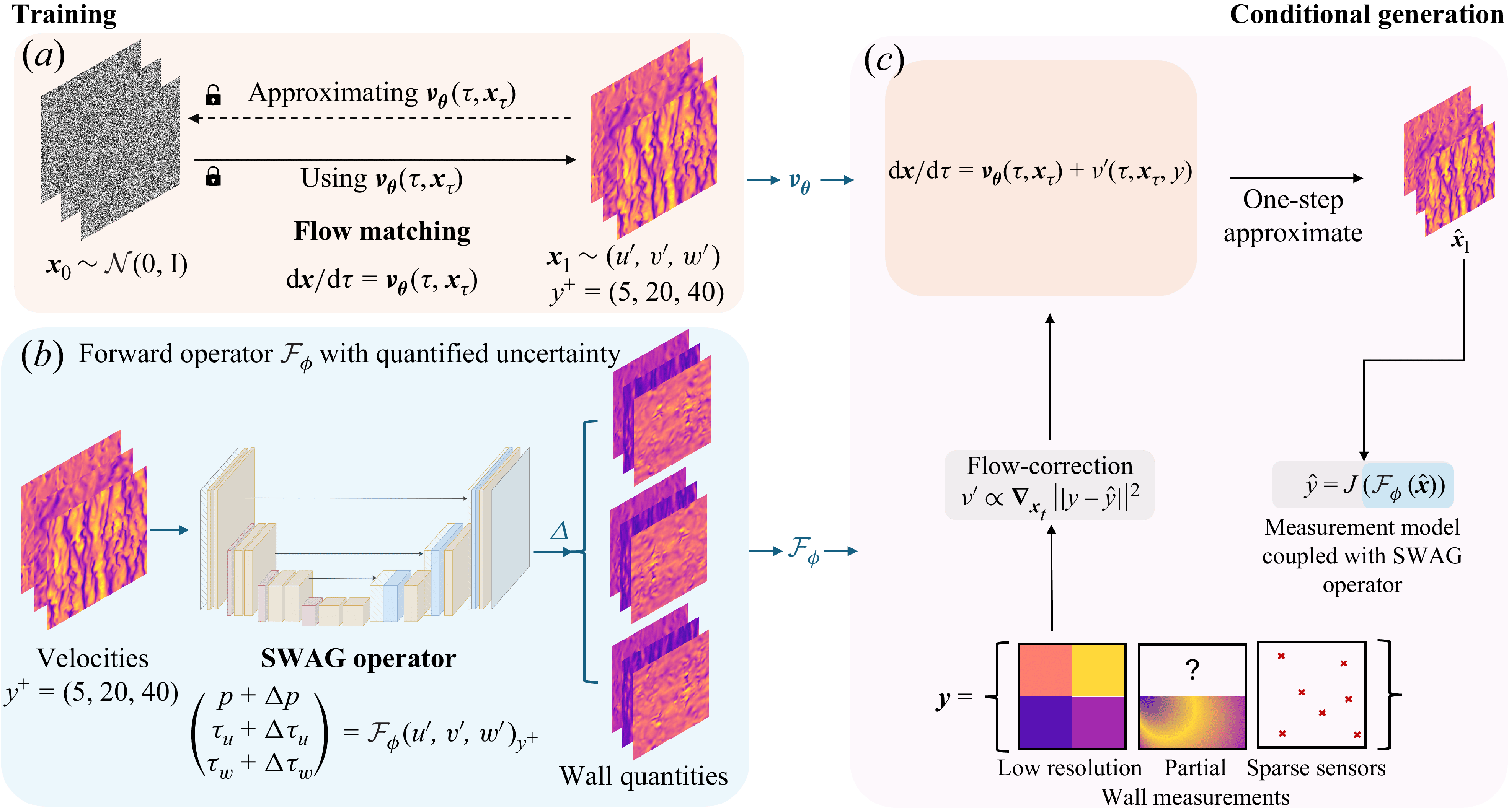
Figure 2. (a) Flow-matching-based generative model $\boldsymbol{\nu }_{\boldsymbol{\theta }}$ for synthesising novel instances of velocity fluctuations $(u',\ v',\ w')$ . (b) Forward operator with SWAG $\mathcal{F}_{\boldsymbol{\phi }}$ to quantify the epistemic uncertainty between velocity fluctuations $(u',\ v',\ w')$ and wall quantities $(p',\ \tau _u,\ \tau _w)$ . (c) Training-free conditional generation based on the predictor–corrector FM inference algorithm using conditional information $\boldsymbol{y}$ .

2.2. Overview of proposed generative modelling framework for near-wall turbulence

Building upon our analysis of spatially heterogeneous correlations between wall measurements and turbulent structures, we propose a generative modelling framework explicitly designed to reconstruct instantaneous velocity fluctuations across multiple wall-normal locations. Specifically, a representative wall-normal location from each of the viscous sublayer, buffer and logarithmic layers is chosen to systematically evaluate the data assimilation and uncertainty quantification capabilities of the proposed generative framework. The comprehensiveness of this test stems from assessing the framework’s performance in three distinct regimes based on the classification introduced in Arranz & Lozano-Durán (2024): the highly informative viscous sublayer ( $y^+=5$ ), the partially informative buffer layer ( $y^+=20$ ) and the almost non-informative logarithmic layer ( $y^+=40$ ). This approach provides a thorough analysis of the proposed framework across different operating conditions. The core idea of the framework leverages generative learning combined with probabilistic neural operators within a Bayesian framework to effectively handle the inherent uncertainties and indirect observability in wall-bounded turbulence. Figure 2 illustrates the three key components of our framework.

In the training phase (figure 2 a), a generative model based on flow matching (Lipman et al. 2022) is built to generate instantaneous full-field velocity fluctuation samples at pre-defined wall-normal positions ( $y^+ = 5, 20, 40$ ) by sampling from a standard Gaussian distribution, $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ . The trained model is able to randomly synthesise novel, physically plausible instantaneous velocity fluctuation fields consistent with the statistical features observed in turbulent channel flows. The details of the flow-matching training are further elaborated in § 2.3. Concurrently, as depicted in figure 2(b), a probabilistic neural operator is designed to predict wall quantities (e.g. wall shear stresses and pressures) from the velocity fluctuations with quantified uncertainties. This U-Net-based neural operator is trained probabilistically using SWAG (Maddox et al. 2019), a Bayesian learning technique enabling the quantification of epistemic uncertainty inherent in neural network predictions. The incorporation of the SWAG operator is critical as it allows our framework to explicitly learn the uncertainty arising from weak correlations, measurement sparsity and noise. As the generative model and the SWAG neural operator utilised in this work are based on CNNs, the current formulation requires access to the entire field of velocity fluctuations and wall measurements on a uniform grid during the training process.

In the inference stage, depicted in figure 2(c), our framework is able to perform conditional generation in a zero-shot manner (i.e. without re-training) using a predictor–corrector sampling approach. Specifically, given instantaneous wall measurements, the pre-trained generative model synthesises instantaneous velocity fluctuation fields that are consistent with these sensor data. This is accomplished through iterative refinement, where an initial prediction from the generative model is progressively updated using gradient-based corrections derived from discrepancies between predicted and actual wall data. The gradients are computed via the differentiable forward measurement model integrated with the probabilistic SWAG operator, thereby ensuring that the synthesised velocity fluctuations realistically reflect measurement uncertainties and the physical constraints imposed by available wall information. Further details are provided in § 2.4.

In summary, our proposed generative modelling framework uniquely integrates generative learning and scalable uncertainty quantification techniques, providing robust and physically consistent reconstructions of turbulent velocity fluctuations from limited wall-based measurements.

2.3. Flow matching for generative modelling of instantaneous velocity fluctuations

To model the complex, high-dimensional distribution of instantaneous velocity fluctuations in near-wall turbulence, we adopt the recently proposed flow matching (FM) framework (Lipman et al. 2022), which enables tractable and scalable training of continuous normalising flows by directly learning the velocity fields that transport probability mass from a simple base distribution to the target data distribution. Unlike conventional continuous normalising flows, which require density estimation via the change-of-variables formula and involve solving ordinary differential equations (ODEs) during training, FM bypasses these limitations by re-framing the generative modelling as a regression task over velocity fields that define transport paths between distributions. This makes FM particularly suitable for large-scale, high-dimensional turbulent flow data. In this work, we present the first use of FM to generate inhomogeneous, anisotropic turbulence by reconstructing the three velocity fluctuation components at the chosen wall-normal positions ( $y^+ = 5, 20, 40$ ).

Let $\boldsymbol{x}_1 \sim P_1(\boldsymbol{x})$ denote a sample drawn from the target data distribution, where each sample represents a snapshot of the instantaneous three-component velocity fluctuation field at a specified wall-normal location $y^+$ . Specifically, $\boldsymbol{x}_1 = [u'(x, z, t), v'(x, z, t), w'(x, z, t)]$ are defined on a discrete $(x, z)$ grid, where $x, z$ are wall-parallel coordinates and $t$ denotes physical time. We define the base distribution $P_0(\boldsymbol{x}) = \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ as a standard multivariate Gaussian in the same space as the target data. Our goal is to learn a transport neural velocity field $\boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau )$ , parametrised by neural network weights $\boldsymbol{\theta }$ , that smoothly transforms samples from $P_0$ into samples from $P_1$ along a continuous path indexed by a fictitious time variable $\tau \in [0, 1]$ . The generative process is defined by the flow ODE

(2.1) \begin{equation} \frac {{\rm d}\boldsymbol{x}_\tau }{{\rm d}\tau } = \boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau ), \end{equation}

where $\boldsymbol{x}_\tau$ denotes the sample at intermediate time $\tau$ along the transport trajectory from $P_0$ to $P_1$ .

To ensure probability conservation along the flow, the transport velocity field $\boldsymbol{\nu }(\tau , \boldsymbol{x}_\tau )$ must satisfy the continuity equation

(2.2) \begin{equation} \frac {\partial\! P_\tau }{\partial \tau } = - \boldsymbol{\nabla }\boldsymbol{\cdot }(P_\tau \boldsymbol{\nu }_\tau ), \end{equation}

where $P_\tau (\boldsymbol{x})$ denotes the intermediate distribution at time $\tau$ . If the true velocity field $\boldsymbol{\nu }(\tau , \boldsymbol{x}_\tau )$ is known, we can directly minimise the following loss:

(2.3) \begin{equation} \mathcal{L}(\boldsymbol{\theta }) := \mathbb{E}_{\tau \sim {U}[0,1], \boldsymbol{x}_\tau \sim P_\tau (\boldsymbol{x}_\tau )}\big \|\boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau ) - \boldsymbol{\nu }(\tau , \boldsymbol{x}_\tau )\big \|^2. \end{equation}

In practice, however, directly evaluating the true velocity $\boldsymbol{\nu }(\tau , \boldsymbol{x}_\tau )$ and sampling from $P_\tau (\boldsymbol{x}_\tau )$ is intractable. To address this, FM introduces a conditional formulation by introducing a latent variable $\boldsymbol{z} \sim q(\boldsymbol{z})$ that leads to conditional intermediate distributions $P_\tau (\boldsymbol{x}|\boldsymbol{z})$ and velocities $\boldsymbol{\nu }(\boldsymbol{x}_\tau |\boldsymbol{z})$ , such that

(2.4a) \begin{align} P_\tau (\boldsymbol{x}_\tau ) &= \int P_\tau (\boldsymbol{x}_\tau |\boldsymbol{z})q(\boldsymbol{z}){\rm d}\boldsymbol{z}, \end{align}

(2.4b) \begin{align} \boldsymbol{\nu }_\tau (\tau ,\boldsymbol{x}_\tau ) &= \int \frac {\boldsymbol{\nu }_\tau (\boldsymbol{x}_\tau |\boldsymbol{z}) P_\tau (\boldsymbol{x}_\tau |\boldsymbol{z})}{P_\tau (\boldsymbol{x}_\tau )}q(\boldsymbol{z}){\rm d}\boldsymbol{z} = \mathbb{E}_{q(\boldsymbol{z})}\bigg [ \frac {\boldsymbol{\nu }_\tau (\boldsymbol{x}_\tau |\boldsymbol{z}) P_\tau (\boldsymbol{x}_\tau |\boldsymbol{z})}{P_t(\boldsymbol{x}_\tau )}\bigg ]. \end{align}

Substituting (2.3) into the FM loss and swapping the gradient and expectation under suitable regularity conditions leads to the modified loss:

(2.5) \begin{equation} \tilde {\mathcal{L}}(\boldsymbol{\theta }) = \mathbb{E}_{\tau \sim \mathcal{U}[0,1], \boldsymbol{z} \sim q(\boldsymbol{z}), \boldsymbol{x}_\tau \sim P_\tau (\boldsymbol{x} | \boldsymbol{z})} \big \| \boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau ) - \boldsymbol{\nu }(\tau , \boldsymbol{x}_\tau | \boldsymbol{z}) \big \|^2. \end{equation}

Under certain assumptions on $q(\boldsymbol{z})$ and $P_\tau (\boldsymbol{x}_\tau |\boldsymbol{z})$ (Lipman et al. 2022), it can be proved that the gradient of the modified loss yields the same optimisation objective as the original FM loss, i.e.

(2.6) \begin{equation} \boldsymbol{\nabla} _{\boldsymbol{\theta }} \mathcal{L}(\boldsymbol{\theta }) = \boldsymbol{\nabla} _{\boldsymbol{\theta }} \tilde {\mathcal{L}}(\boldsymbol{\theta }). \end{equation}

Therefore, the neural velocity field can be trained based on the conditional formulation of the loss function, where both the conditional intermediate distributions and velocities are available. In practice, we use empirical samples from the data distribution as conditioning variables. Specifically, we let $q(\boldsymbol{z}) = (1/N) \sum _{i=1}^{N} \delta (\boldsymbol{z} - \boldsymbol{x}_1^{(i)})$ , where $\{\boldsymbol{x}_1^{(i)}\}_{i=1}^N$ are training velocity fluctuation data. Then we have the following tractable definitions for the conditional intermediate distribution and velocity:

(2.7a) \begin{align} P_\tau (\boldsymbol{x}_\tau | \boldsymbol{x}_1) &= \mathcal{N}\big (\tau \boldsymbol{x}_1, \big [1 - (1 - \sigma _{\textit{min}})\tau \big ]^2\boldsymbol{I}\big ), \end{align}

(2.7b) \begin{align} \boldsymbol{\nu }(\tau , \boldsymbol{x}_\tau | \boldsymbol{x}_1) &= \frac {\boldsymbol{x}_1 - (1 - \sigma _{\textit{min}})\boldsymbol{x}_\tau }{1 - (1 - \sigma _{\textit{min}})\tau }, \end{align}

which corresponds to an isotropic Gaussian interpolation with linearly evolving mean and covariance from $\mathcal{N}(0, \boldsymbol{I})$ to $\mathcal{N}(\boldsymbol{x}_1, \sigma _{\textit{min}}^2 \boldsymbol{I})$ . Here, the mean interpolates linearly from $\boldsymbol{0}$ to $\boldsymbol{x}_1$ , while the covariance linearly decays from $\boldsymbol{I}$ to $\sigma _{\textit{min}}^2 \boldsymbol{I}$ . This results in a simple and tractable sampling scheme, where both the intermediate samples $\boldsymbol{x}_\tau$ and their associated transport velocities $\boldsymbol{\nu }(\tau , \boldsymbol{x}_\tau | \boldsymbol{x}_1)$ are available in closed form for supervised training. Additionally, the neural velocity field $\boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau )$ is trained in a class-conditional way for the different wall-normal distances of $y^+=\{5,\, 20,\, 40\}$ considered in this study. The model learns a trainable neural embedding corresponding to each wall-normal distance. The details of network architectures are provided in Appendix A.

Once the FM model $\boldsymbol{\nu }_{\boldsymbol{\theta }}$ is trained, novel samples of the velocity fluctuations are generated by sampling from $P_0(\boldsymbol{x}_0)$ and solving the ODE in (2.1) by integrating $\boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau )$ over the fictitious time interval $\tau \in [0,1]$ . In this work, we employ a forward Euler scheme, and discretise the fictitious time domain into $250$ uniform steps.

2.4. Training-free conditional generation guided by wall measurements

The generative model described in § 2.3 enables efficient sampling of instantaneous velocity fluctuation fields from the learned distribution at specified wall-normal locations. While this unconditional generation captures the statistical structure of turbulent fluctuations, it does not incorporate any instance-specific observations. In practical settings, however, partial information about a specific turbulent flow realisation is often available, either in the form of direct but sparse velocity measurements within the domain or, more commonly, through indirect wall-based observations such as wall shear stress or pressure signals. These measurements $\boldsymbol{y}$ encode valuable information about the underlying flow state and can be leveraged during inference. This motivates the need for conditional generative inference that can synthesise velocity fields consistent with available observations, while retaining uncertainty quantification over unobserved regions.

A common strategy to condition generative models is to incorporate the observation vector $\boldsymbol{y}$ , whether wall measurements, sparse velocity probes, or both, into the sampling process. This is typically achieved by modifying the training objective to explicitly encode $\boldsymbol{y}$ as input, for example through input concatenation, modulation via feature-wise affine transformations, or injection via a hypernetwork $F_\phi (\boldsymbol{y})$ (Dhariwal & Nichol 2021; Fu et al. 2024; Jacobsen, Zhuang & Duraisamy 2025; Zhuang et al. 2025). However, these approaches require re-training the generative model for each new type of conditioning input and often scale poorly when the structure, modality or spatial extent of $\boldsymbol{y}$ varies across instances, as is the case in sensor-limited turbulence set-ups.

To overcome these limitations, we introduce a training-free conditional inference strategy that augments the unconditional FM model with a correction term derived from the conditioning measurements. Inspired by training-free conditional methods in diffusion models such as diffusion posterior sampling (Chung et al. 2022; Du et al. 2024) and Bayesian classifier guidance (Dhariwal & Nichol 2021; Gao et al. 2024a ), our approach adapts these ideas to the FM paradigm. Specifically, we define a guided sampling procedure in which the learned transport velocity $\boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau )$ is augmented during inference by a correction term $\boldsymbol{\nu }'(\tau , \boldsymbol{x}_\tau , \boldsymbol{y})$ that nudges the generative trajectory towards compatibility with the measurements:

(2.8) \begin{equation} \frac {{\rm d}\boldsymbol{x}}{{\rm d}\tau } = \boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau ) + \boldsymbol{\nu }'(\tau , \boldsymbol{x}_\tau , \boldsymbol{y}). \end{equation}

To derive this correction term, we first assess the discrepancy between the observations $\boldsymbol{y}$ and the predicted measurements $\hat {\boldsymbol{y}}$ derived from the current state $\boldsymbol{x}_\tau$ , and then propagate this discrepancy back to $\boldsymbol{x}_\tau$ . This process involves three components: (i) an efficient approximation of the terminal state $\hat {\boldsymbol{x}}_1$ from intermediate states $\boldsymbol{x}_\tau$ , (ii) a forward state-to-observable operator that maps the generated state to measurement space and (iii) a differentiable loss to quantify mismatch between predicted and observed measurements. In the first step, the target guidance field (2.7 b) defines a straight interpolation in data space between the noise sample and the data sample. Accordingly, we employ a one-step linear approximation of the terminal state (Lipman et al. 2022):

(2.9) \begin{equation} \hat {\boldsymbol{x}}_{1|\tau } = \boldsymbol{x}_\tau + (1-\tau )\boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau ), \end{equation}

which estimates the endpoint of the flow by extrapolating along the learned transport velocity. This is computationally efficient and justified by the nearly linear nature of the flow trajectory learned through conditional flow matching (§ 2.3). Next, we define the forward operator $\mathcal{F}$ that maps the predicted state $\hat {\boldsymbol{x}}_{1|\tau }$ to the observable domain. Depending on the context, $\mathcal{F}$ may represent a fixed linear mapping (e.g. extracting velocity values at sensor locations) or a learned neural operator that maps the off-wall flow states to indirect measurements (e.g. wall measurements). Considering measurement noises $\boldsymbol{\epsilon }$ , this operator is defined as

(2.10) \begin{align} \hat {\boldsymbol{y}} &= \mathcal{F}(\hat {\boldsymbol{x}}_{1|\tau }) + \boldsymbol{\epsilon }; \quad \boldsymbol{\epsilon } \sim \mathcal{N}(0, \varSigma _e) ,\end{align}

where $\varSigma _e = \sigma _e^2 \boldsymbol{I}$ captures the assumed level of aleatoric uncertainty. The aleatoric uncertainty is assumed to be a Gaussian distribution to model the measurement error of the sensors that commonly arises from the thermal or electronic noise.

The discrepancy $\mathscr{D}(\hat {\boldsymbol{y}}, \boldsymbol{y})$ between predicted and observed measurements is quantified via a loss function, typically the mean squared error. This loss is then differentiated with respect to $\boldsymbol{x}_\tau$ , yielding a gradient that points in the direction of greater alignment between the generated sample and the observations. We define the correction term as

(2.11) \begin{equation} \boldsymbol{\nu }'(\tau , \boldsymbol{x}_\tau , \boldsymbol{y}) = -b ||\boldsymbol{\nu }_{\boldsymbol{\theta }}(\tau , \boldsymbol{x}_\tau )|| \frac {\boldsymbol{\nabla} _{\boldsymbol{x}_\tau } \mathscr{D}(\hat {\boldsymbol{y}}, \boldsymbol{y})}{||\boldsymbol{\nabla} _{\boldsymbol{x}_\tau } \mathscr{D}(\hat {\boldsymbol{y}}, \boldsymbol{y})||}, \end{equation}

where $b$ is a scalar that controls the guidance strength, and is set to $1$ for all the experiments considered in this study. The correction direction is aligned with the normalised loss gradient, while the magnitude is scaled to match the norm of the current transport velocity, ensuring that the guidance term and learned flow are balanced in strength.

Importantly, this conditional sampling strategy is agnostic to the nature and modality of the measurement vector $\boldsymbol{y}$ . While in this paper we focus on wall-based observations, the framework can also accommodate sparse velocity probes, inpainting of partially known flow fields or any other differentiable observation models. In fact, the proposed corrector can be viewed as a variational approximation to the gradient of the log-posterior distribution $\boldsymbol{\nabla} _{\boldsymbol{x}} \log P(\boldsymbol{y} | \boldsymbol{x})$ , and thus relates conceptually to likelihood-based guidance in diffusion posterior sampling (Chung et al. 2022; Du et al. 2024; Gao et al. 2024a ). We demonstrate the flexibility and effectiveness of this approach through reconstruction experiments with wall-based and in-domain conditional signals in § 3, and further illustrate its applicability to sparse inpainting tasks in § 4.4.

2.5. Learning forward operators from velocity fields to wall measurements with uncertainty

As established in § 2.4, our conditional generation framework requires evaluating the discrepancy between synthesised velocity fields and observed flow measurements, which depends on a forward operator $\mathcal{F}$ that maps the generated velocity fluctuation field $\boldsymbol{u}'$ to predicted measurements $\hat {\boldsymbol{y}} = \mathcal{F}(\boldsymbol{u}')$ . In general, $\boldsymbol{y}$ may consist of direct velocity samples at sparse spatial locations or, more commonly, wall-based signals such as pressure or shear stress, which are nonlinearly related to the off-wall velocity field. While mapping from velocity to sparse velocity measurements can often be expressed as a linear masking operation, the velocity-to-wall mapping is inherently nonlinear and spatially non-local, reflecting the complex modulation mechanisms by which outer-layer motions influence near-wall quantities (Mathis et al. 2009; Arranz & Lozano-Durán 2024).

To enable training-free conditional inference using wall measurements, we need a forward observation operator, which should be differentiable and capable of quantifying predictive uncertainty, especially where the velocity–wall correlation is weak. This is particularly important because in regions such as the logarithmic layer, wall signals encode only indirect and noisy information about the flow. The forward operator must therefore propagate not only observations but also their epistemic confidence into the sampling process. To this end, we design a probabilistic forward operator $\mathcal{F}_{\boldsymbol{\phi }}$ , built as a convolutional U-Net, that learns to predict wall measurements $\boldsymbol{\varPhi }_{w\textit{all}} = [p, \tau _u, \tau _w]$ from input three-dimensional velocity fluctuations $\boldsymbol{u}' = [u', v', w']$ . A different forward operator is trained for each wall-normal distance. Crucially, to enable robust uncertainty-aware conditioning during inference, we train $\mathcal{F}_{\boldsymbol{\phi }}$ using the SWAG framework (Maddox et al. 2019), which approximates the posterior distribution over the network parameters and propagates uncertainty through the prediction. Specifically, we treat the operator’s parameters $\boldsymbol{\phi }$ as a distribution rather than a point estimate, modelling their posterior as a multivariate Gaussian with a diagonal plus low-rank covariance structure:

(2.12) \begin{equation} \boldsymbol{\phi } \sim \mathcal{N}\left (\boldsymbol{\phi }_{\textit{SWA}}, \frac {1}{2}\big (\varSigma _{\textit{diag}} + \varSigma _{\textit{low}\text{-}\textit{rank}}\big )\right )\!, \end{equation}

where $\boldsymbol{\phi }_{\textit{SWA}}$ is the running average of network weights collected over stochastic gradient descent trajectories after a burn-in period. The covariance matrices are computed as

(2.13a) \begin{align} \varSigma _{\textit{diag}} = {\text{diag}}(\overline {\boldsymbol{\phi }^2} - \boldsymbol{\phi }_{\textit{SWA}}^2), \end{align}

(2.13b) \begin{align} \varSigma _{\textit{low}\text{-}\textit{rank}} = \frac {1}{K - 1} \hat {H} \hat {H}^\top , \end{align}

where $\varSigma _{\textit{low}\text{-}\textit{rank}}$ is a low-rank approximation of the covariance using the last $K$ epochs, with $\hat {H} = [\boldsymbol{\phi }_{N-K+1} - \boldsymbol{\phi }_{\textit{SWA}}, \ldots , \boldsymbol{\phi }_N - \boldsymbol{\phi }_{\textit{SWA}}]$ .

During inference, the weights of the trained function $\mathcal{F}_{\boldsymbol{\phi }^*}$ are sampled from this posterior:

(2.14) \begin{equation} \boldsymbol{\phi }^* = \boldsymbol{\phi }_{\textit{SWA}} + \frac {1}{\sqrt {2}}\varSigma _{\textit{diag}}^{1/2}\boldsymbol{z}_1 + \frac {1}{\sqrt {2(K-1)}}\hat {H}\boldsymbol{z}_2, \end{equation}

where $\boldsymbol{z}_1$ and $\boldsymbol{z}_2$ are independently sampled from a multivariate standard normal distribution $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ . With the weight ensemble of size $m$ , the mean and epistemic uncertainty of wall quantity predictions are computed as

(2.15a) \begin{align} \overline {\boldsymbol{\varPhi }}_{w\textit{all}} &= \frac {1}{m}\sum _{i=1}^m \mathcal{F}_{\boldsymbol{\phi }^*_i}(\boldsymbol{u}'_i), \\[-12pt]\nonumber \end{align}

(2.15b) \begin{align} \boldsymbol{\sigma }_{\boldsymbol{\varPhi }_{w\textit{all}}} &= \sqrt {\frac {1}{m}\sum _{i=1}^m \big ( \mathcal{F}_{\boldsymbol{\phi }^*_i}(\boldsymbol{u}'_i) - \overline {\boldsymbol{\varPhi }}_{w\textit{all}}\big )^2}. \end{align}

Moreover, we adopt a patchwise training strategy: the operator is trained on small spatial subdomains of size $n_x \times n_z = 32$ , much smaller than the full domain size $N_x \times N_z$ . This localised learning strategy is inspired by the inherently local structure of near-wall turbulence, which increases the diversity of training examples, reduces memory usage and improves generalisation to unseen realisations of the flow at the trained wall-normal locations. An analysis of the effect of dataset size on the convergence of the SWAG operator is presented in Appendix D. The results confirm that the patchwise training strategy is essential for achieving convergence when learning this operator. Importantly, due to the fully convolutional nature of the U-Net, the trained model can be applied to full-domain velocity inputs during inference, leveraging translation invariance of convolution operations.

In summary, our patch-trained, SWAG-based forward operator $\mathcal{F}_{\boldsymbol{\phi }}$ provides a scalable, interpretable and uncertainty-aware mechanism to connect full-field turbulence predictions to surface measurements, and is essential to enabling flexible and rigorous conditional flow reconstruction in the proposed generative framework.

3. Results

In this section, we evaluate the performance of the proposed FM framework on reconstructing instantaneous velocity fluctuation fields from wall-based measurements in wall-bounded turbulent flow. The primary goal is to assess how well the model can synthesise physically realistic velocity fluctuations under varying wall measurement conditions, and to quantify the associated predictive uncertainty. The framework is tested on canonical turbulent channel flow at a friction Reynolds number of $\textit{Re}_\tau = 180$ . During training, the generative model is exposed to unconditional samples at wall-normal positions $y^+ = {5, 20, 40}$ , without access to any measurement-based conditioning information. Conditional inference is performed entirely at test time using the training-free guidance strategy described in § 2.4, which allows flexible assimilation of wall-based measurements across different levels of sparsity and noise.

3.1. The DNS case set-up, data generation and evaluation metrics

The dataset used for training and evaluation is generated via DNS of incompressible channel flow at $\textit{Re}_\tau = 180$ . The computational domain is defined as $[L_x, L_y, L_z] = [4\pi , 2, 2\pi ]$ in the streamwise ( $x$ ), wall-normal ( $y$ ) and spanwise ( $z$ ) directions, respectively. The simulation employs a uniform grid resolution of $[N_x, N_y, N_z] = [320, 400, 200]$ with periodic boundary conditions in $x$ and $z$ , and no-slip boundary conditions at the walls. The flow is driven by a constant mean pressure gradient in the streamwise direction. Snapshots of both the velocity field and wall quantities are recorded at intervals of $\Delta T^+ = 0.4$ in viscous time units.

To construct the dataset, statistical symmetry about the channel centreline is exploited by reflecting samples from the upper and lower halves of the domain, yielding a total of $43.8k$ snapshots. These snapshots span approximately 60 flow-through times. Each data sample comprises the velocity fluctuations $\boldsymbol{u}'_i = [u', v', w']$ at a given wall-normal location $y^+$ and the corresponding wall quantities $\boldsymbol{\varPhi }_{w\textit{all}} = [p, \tau _u, \tau _w]$ . The dataset is denoted as $\mathcal{D} = { (\boldsymbol{\varPhi }_{w\textit{all}}, \boldsymbol{u}'_i)}_{{y^+}}$ , where $y^+$ indexes the wall-normal planes and $i$ indexes the velocity fluctuation components.

For training the generative FM model, we use the full $\mathcal{D}$ but only the velocity fluctuation fields $\boldsymbol{u}'_i$ , since the training is entirely unsupervised. The forward operator $\mathcal{F}_{\boldsymbol{\phi }}$ , which maps $\boldsymbol{u}'_i$ to $\boldsymbol{\varPhi }_{w\textit{all}}$ with uncertainty quantification, is trained using approximately $9000$ velocity–wall data pairs randomly drawn from $\mathcal{D}$ . The training of the generative model and the forward operator is carried out with full-observability conditions of the velocity fluctuation fields and wall measurements. For evaluation, an entirely separate set of $500$ uncorrelated samples is generated with a larger sampling interval to ensure statistical independence from the training data. This evaluation set corresponds to approximately $7$ flow-through times. Such strict separation allows us to benchmark generalisation performance in fully unseen flow states. Thus, the training dataset enables the generative model to accurately learn the distribution of turbulent velocity fluctuations. A completely temporally independent testing set is then used for a robust statistical evaluation of the proposed framework. This robust evaluation is necessary due to the stochastic nature of generative models; in the current work, we assess performance by computing converged turbulent statistics. Additional details about the training and testing split are provided in Appendix E. A summary of the simulation set-up and dataset statistics is provided in table 1.

Table 1. Dataset of channel flow for training and testing the model.

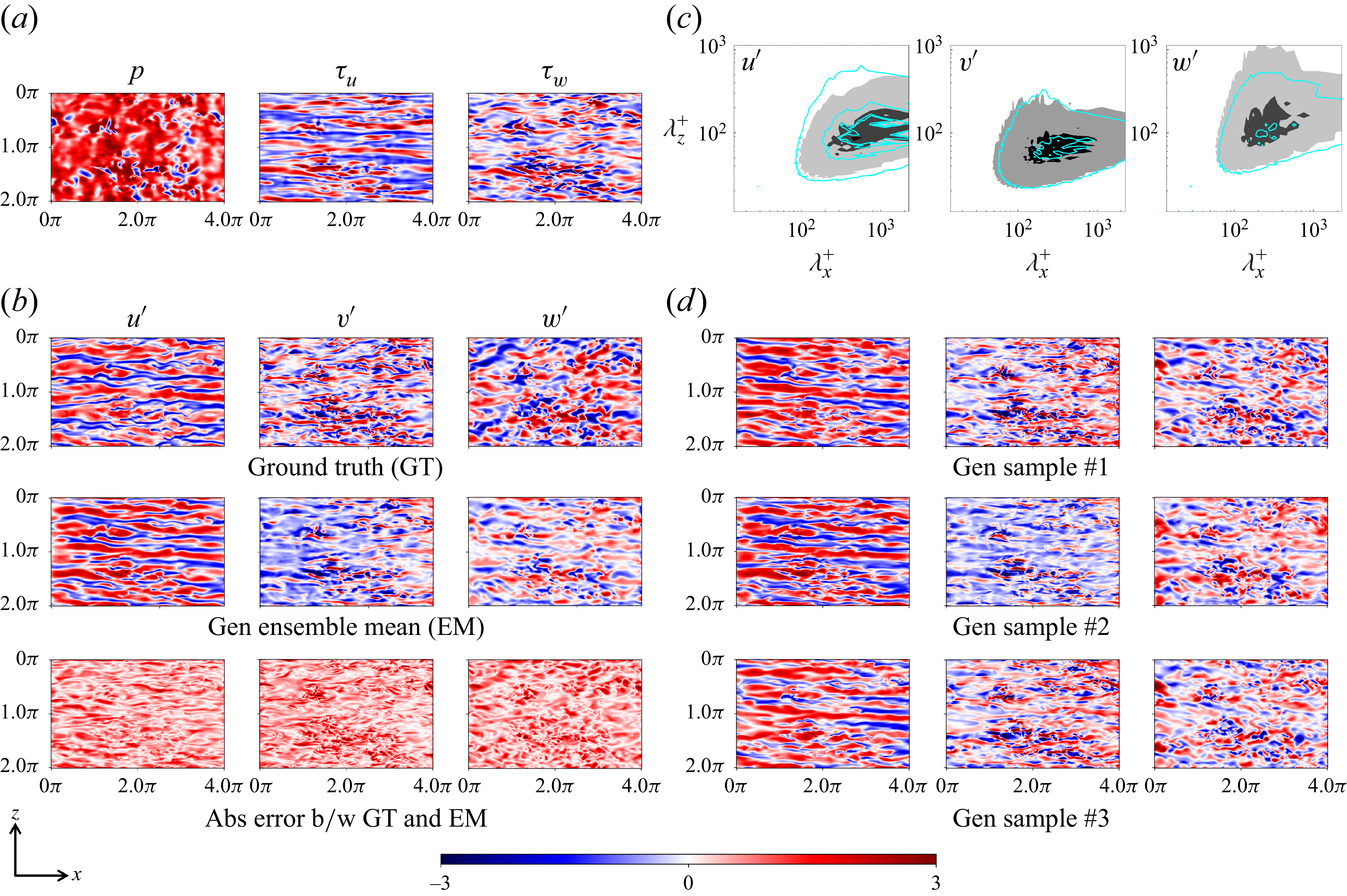
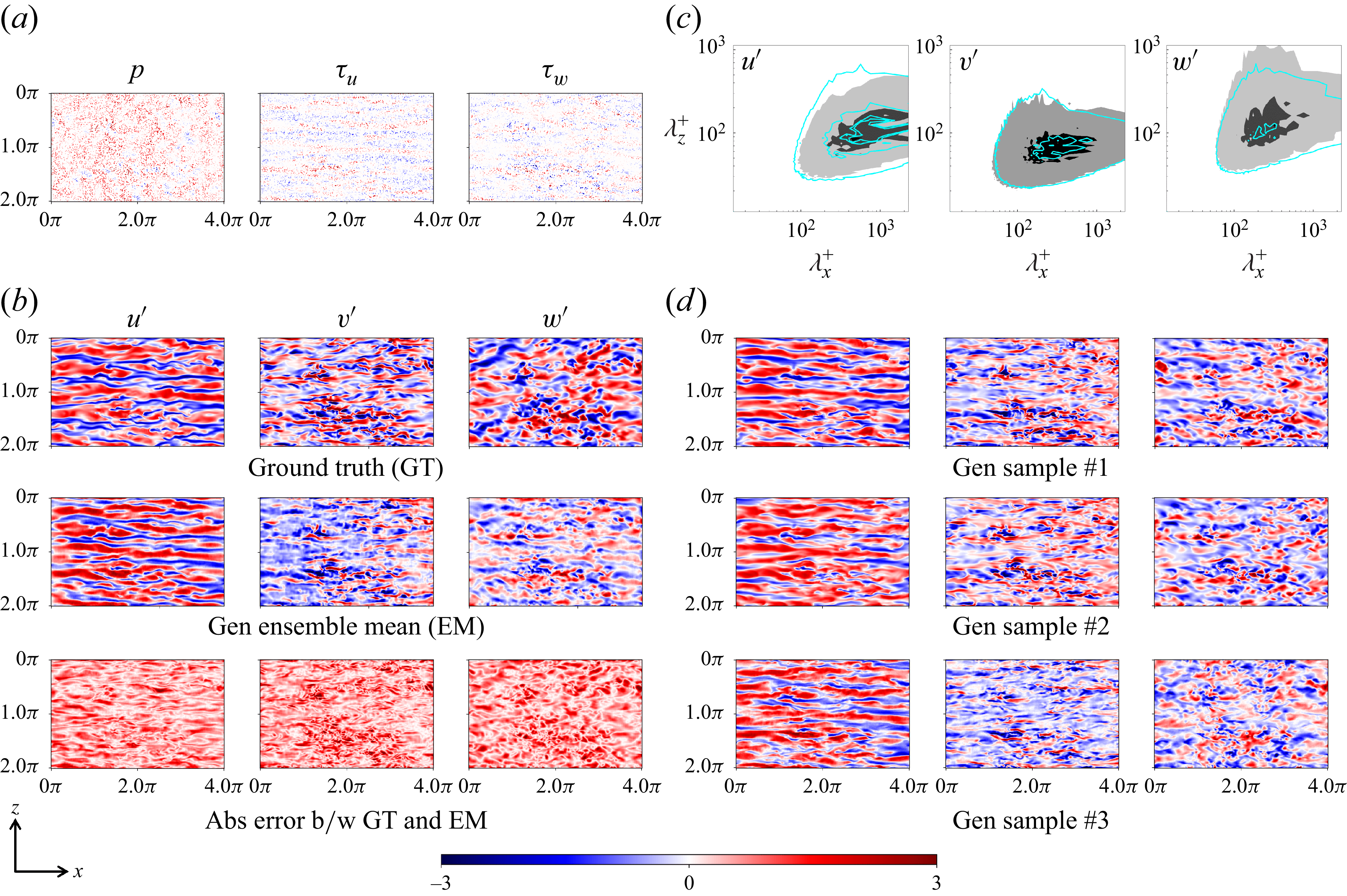
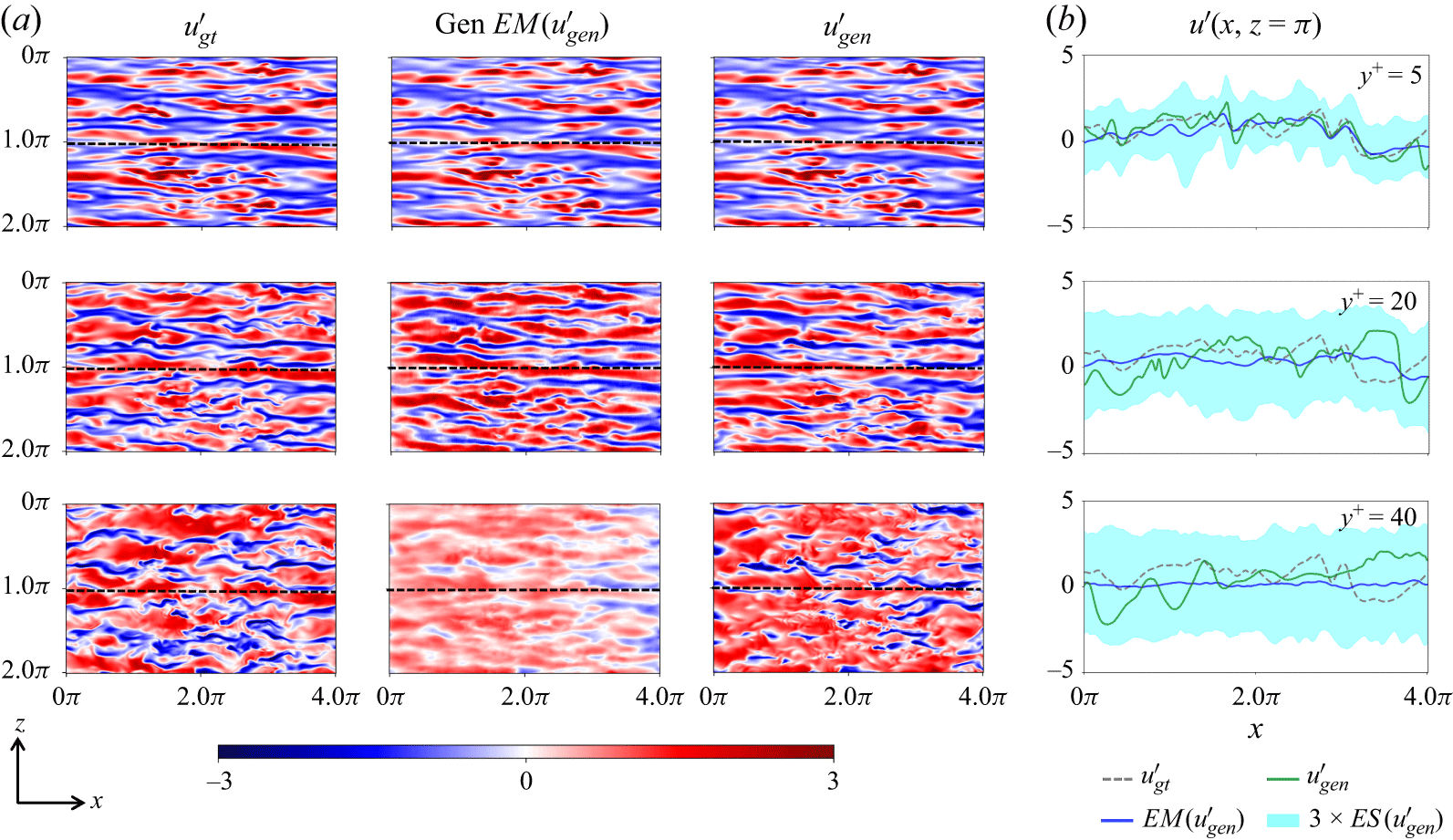
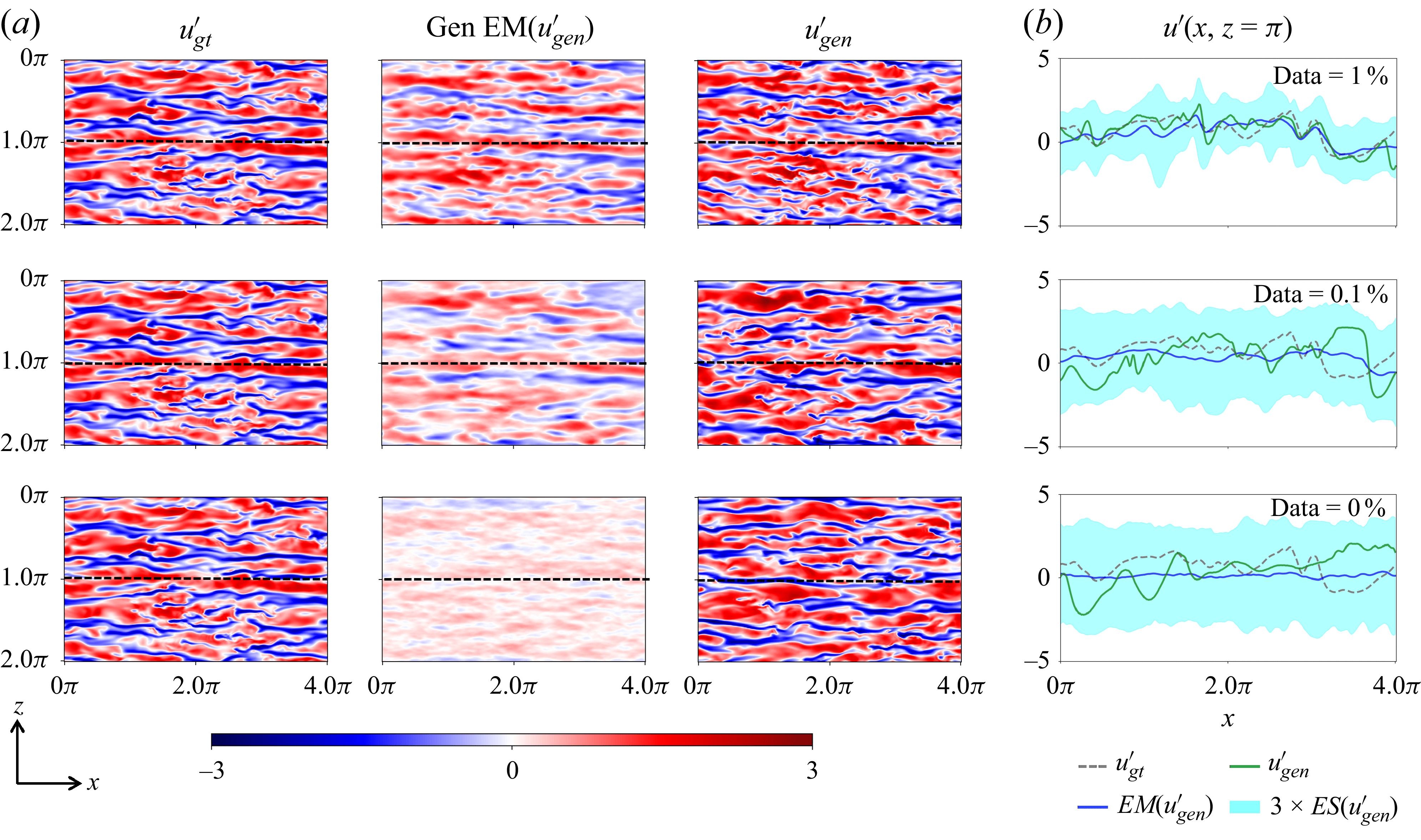
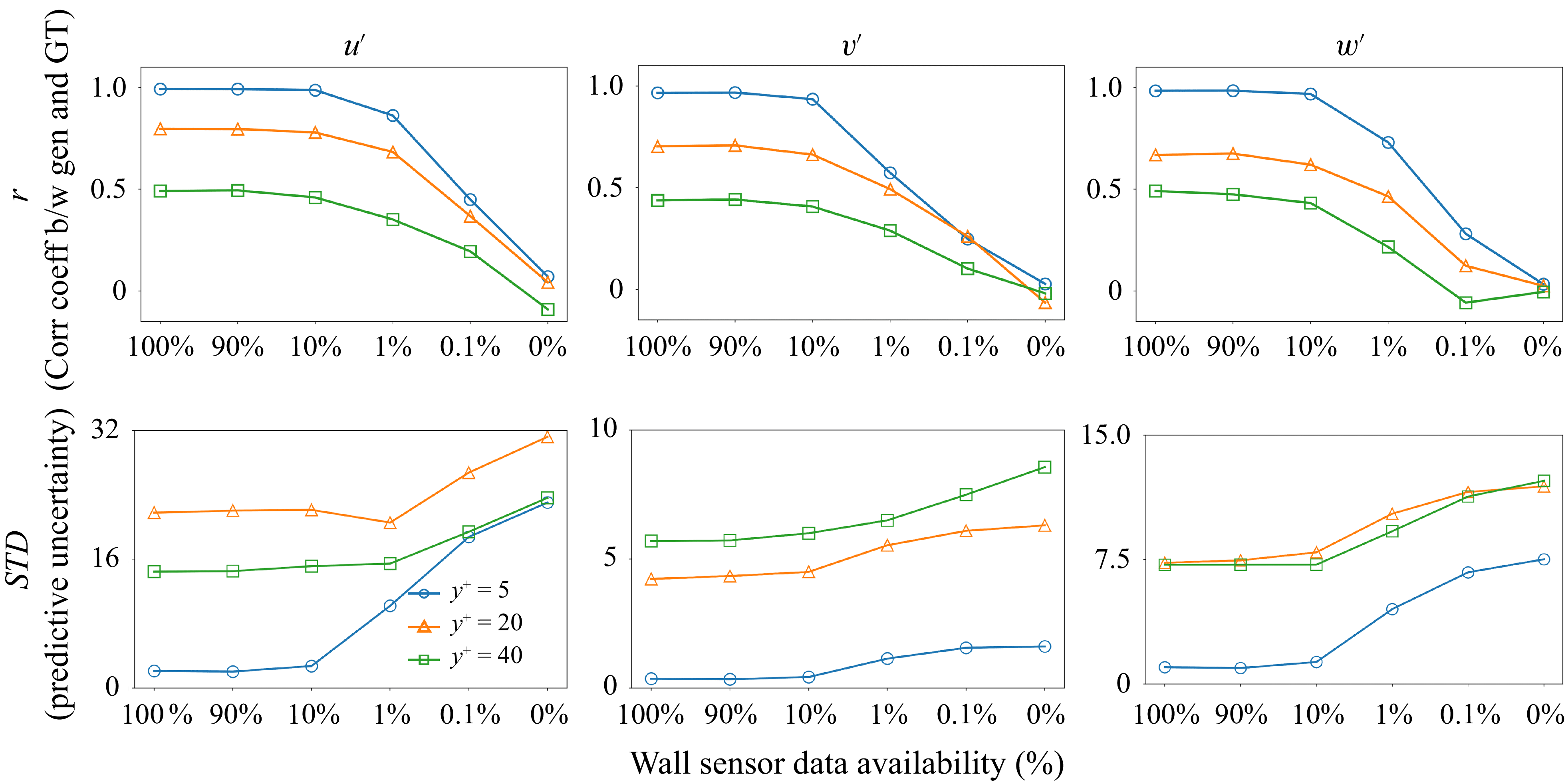
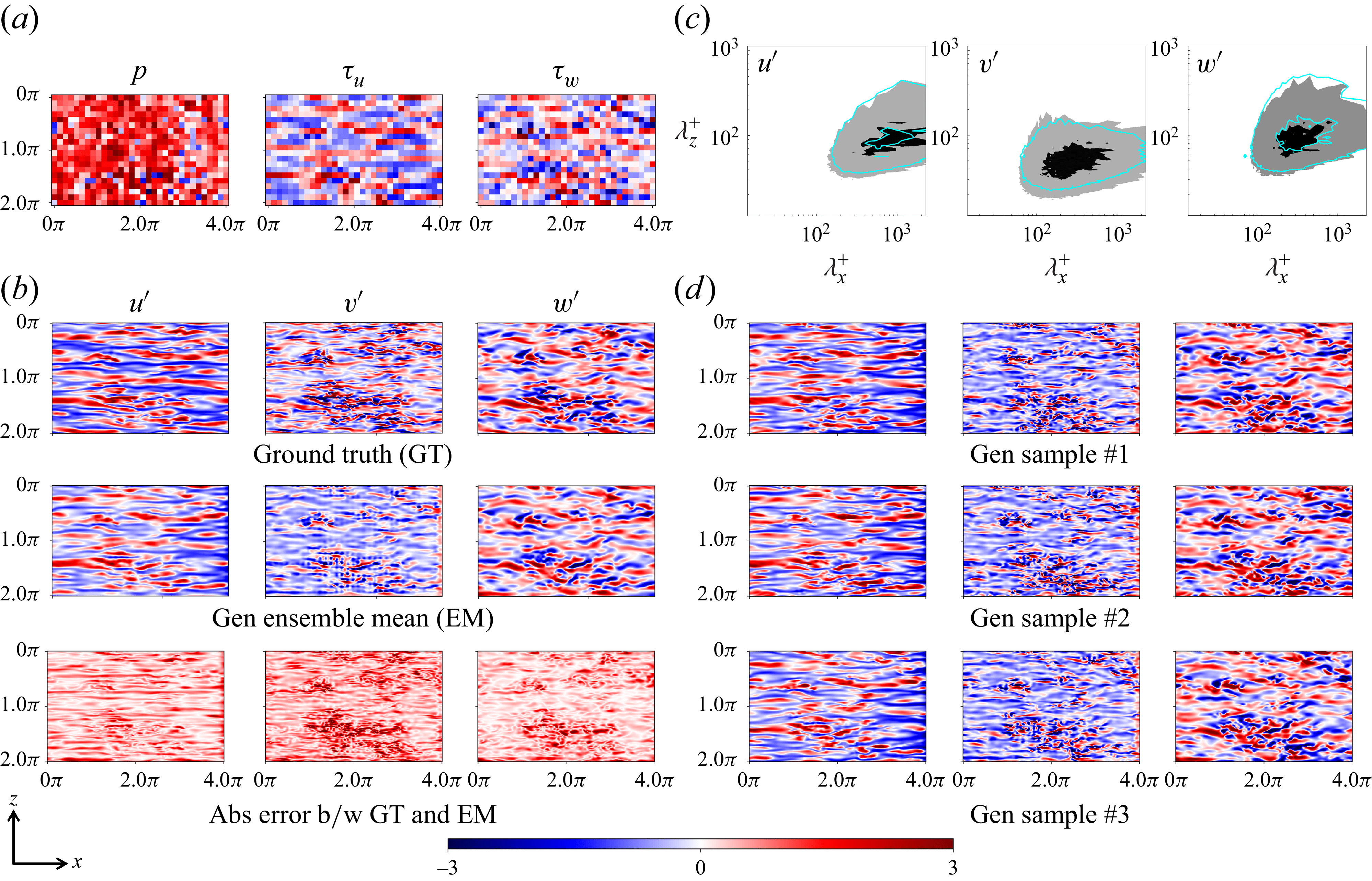
To demonstrate the effectiveness of the proposed framework, we evaluate its conditional generation capabilities under various wall measurement scenarios, including fully observed, partially masked and spatially downsampled sensor configurations. Both qualitative and quantitative analyses are conducted to assess how well the generated velocity fluctuation fields $\boldsymbol{u}'_i = [u', v', w']$ agree with the ground-truth flow and available wall-based observations. As qualitative assessment, we begin by visualising representative conditional samples generated under different wall measurement settings, allowing us to inspect the model’s ability to synthesise flow realisations that preserve the physical structure and intermittency of near-wall turbulence while adapting to available sensor data. The velocity fluctuation fields are normalised by the root-mean-squared value at their respective wall-normal locations to enable visualisation on a unified scale. For quantitative evaluation, we compute the ensemble mean (EM) and ensemble spread (ES) across multiple conditional samples. For example, the mean and standard deviation of $u'$ are defined as

(3.1) \begin{equation} \begin{aligned} \textit{EM}(u^{\prime}) &= \frac {1}{N_{\textit{ens}}}\sum ^{N_{\textit{ens}}}_{i=1} {u'}_{\textit{gen,i}},\\[3pt] \textit{ES}(u^{\prime}) &= \sqrt {\frac {\sum ^{N_{\textit{ens}}}_{i=1}|{u'}_{\textit{gen,i}} -\textit{EM}(u^{\prime})|^2}{N_{\textit{ens}}}}, \end{aligned} \end{equation}

where $N_{\textit{ens}}$ denotes the number of generated samples. Analogous definitions are used for $v'$ and $w'$ components. We further assess the accuracy of the ensemble mean by comparing it with the ground-truth DNS field using the Pearson correlation coefficient $r$ . After flattening the $x$ – $z$ plane into a one-dimensional vector, the correlation for $u'$ is calculated as follows:

(3.2) \begin{equation} r = \frac {\sum _{i}^{N_x \times N_z} \big ({u'}_{gt, i} - \overline {{u'}_{gt}}\big ) \big (\textit{EM}({u'}_{i}) - \overline {\textit{EM}({u'})}\big )}{\sqrt {\sum _{i}^{N_x \times N_z} \big ({u'}_{gt, i} - \overline {{u'}_{gt}}\big )^2 \sum _{i}^{N_x \times N_z} \big (\textit{EM}({u'}_{i}) - \overline {\textit{EM}({u'})}\big )^2}}, \end{equation}

where $\overline {(\boldsymbol{\cdot })}$ denotes spatial mean over the $x$ – $z$ plane. To quantify how well each generated sample matches the given wall measurements, we use the normalised pointwise $L_2$ error $\varDelta _{\boldsymbol{y}}(x,z)$ as proposed in Li et al. (2023) and Du et al. (2024):

(3.3) \begin{equation} \varDelta _{\boldsymbol{y}}(x, z) = \frac {1}{E_{\boldsymbol{y}}}\left |\boldsymbol{y}_{gen}(x,z) - \boldsymbol{y}_{gt}(x,z)\right |^2 \!, \end{equation}

where the normalisation factor $E_{\boldsymbol{y}}$ accounts for the spatial variability in both the generated and ground-truth wall measurements, and is given by $E_{\boldsymbol{y}} = \sigma ^{\textit{gen}}_{\boldsymbol{y}} \times \sigma ^{gt}_{\boldsymbol{y}}$ , where $\sigma ^{\textit{gen}}_{\boldsymbol{y}}$ denotes the ensemble-averaged spatial standard deviation of the generated wall measurements:

(3.4) \begin{equation} \sigma ^{\textit{gen}}_{\boldsymbol{y}} = \left \langle \frac {1}{A} \int |\boldsymbol{y}_{gen}|^2(x, z)\, {\rm d}x\,{\rm d}z\right \rangle ^{1/2} \end{equation}

and $\sigma ^{gt}_{\boldsymbol{y}}$ is defined analogously using the ground-truth measurements $\boldsymbol{y}_{{gt}}$ .

Finally, to further assess the physical realism of the generated samples, we perform a statistical turbulence analysis on an ensemble of 500 conditional realisations. Specifically, we evaluate the pre-multiplied two-dimensional energy spectra, $E_{u_i'u_i'}$ . This quantity is a standard diagnostic for characterising the energetic and structural fidelity of turbulent flows and is compared directly against the corresponding statistics computed from the DNS reference dataset. The pre-multiplied energy spectra are defined as

(3.5) \begin{equation} E_{u_i'u_i'}(k_x, k_z, y) = k_x k_z \big \langle \hat {u}_i (k_x, k_z, y) \hat {u}_i^* (k_x, k_z, y) \big \rangle ,\end{equation}

where $k_x$ and $k_z$ are the streamwise and spanwise wavenumbers, respectively; $i = 1, 2, 3$ corresponds to the streamwise, wall-normal and spanwise components of the velocity fluctuations; $\hat {u}_i$ denotes the Fourier transform of $u_i'$ in the horizontal plane; and $(\boldsymbol{\cdot })^*$ is the complex conjugate. The angle brackets $\langle \boldsymbol{\cdot }\rangle$ indicate averaging over both spatial directions and ensemble members.

For conciseness, this section presents results primarily at the buffer-layer height of $y^+ = 20$ , as this region presents a particularly illustrative test. It is a transitional zone containing a complex mixture of wall-correlated (informative) and independent (non-informative) structures, creating an intrinsic ambiguity that provides a stringent test of the model’s ability to generate physically plausible realisations while quantifying the resulting uncertainty. Additional results at $y^+ = 5$ and $y^+ = 40$ are included in Appendix F (figures 27–34).

3.2. Off-wall velocity generation conditioned on fully observed wall measurements

We begin our evaluation with an idealised scenario in which all wall quantities, i.e. streamwise and spanwise shear stress ( $\tau _u$ , $\tau _w$ ) and pressure ( $p$ ), are available across the entire surface. Although full-resolution wall measurements are rarely available in practice, this setting serves as a controlled benchmark to assess our generative model’s capacity to reconstruct physically realistic velocity fluctuations when provided with complete boundary information. It also allows us to examine how well the learned conditional FM framework captures the nonlinear, multiscale mapping from wall data to off-wall turbulent structures.

Figure 3 presents the results under this setting, where figure 3(a) displays one example of instantaneous wall measurements (i.e. wall shear stress and wall pressure fields) from one of the $500$ test cases. Given this conditioning input, our model generates an ensemble of $N_{\textit{ens}} = 50$ velocity fluctuation fields at $y^+ = 20$ . The choice of $N_{\textit{ens}}=50$ is based on a convergence analysis, the results of which are summarised in Appendix C. The ensemble mean of these samples, $EM(\boldsymbol{u}'_i)$ , is shown in the middle row of figure 3(b), while the top row presents the ground-truth DNS field. Qualitatively, the ensemble mean closely resembles the ground truth across all velocity components. For $u'$ , the large-scale streamwise streaks are clearly recovered with accurate orientation and spatial coherence. Similarly, high-amplitude fluctuations in $v'$ and $w'$ are faithfully reconstructed in both location and intensity. The bottom row in figure 3(b) displays the pointwise absolute error between the ensemble mean and the ground truth. Errors are concentrated in fine-scale regions and interstitial zones where flow structures are weakly correlated with wall data, consistent with expected limitations of wall-based observability. To further illustrate the diversity and realism of individual predictions, figure 3(d) displays three representative samples from the ensemble conditioned on the wall input in figure 3(a). These realisations exhibit certain spatial variability and small-scale structures while remaining consistent with the wall constraints. Compared with the ensemble mean, which smooths out fine-scale variations, these samples reflect the stochastic nature of the conditional velocity distribution, highlighting the model’s ability to capture multimodal uncertainty and preserve the intermittency of turbulent structures. This is a key strength of the proposed framework, enabling generation of multiple plausible flow states rather than a single deterministic estimate.

Figure 3. (a) An example of fully observed wall measurements $\boldsymbol{\varPhi }_{w\textit{all}} = [p, \tau _u, \tau _w]$ used as the condition for generating corresponding velocity fluctuations $\boldsymbol{u}'_i$ . (b) Comparison between the ground-truth velocity fluctuations (top row), the ensemble mean of $50$ conditionally generated samples (middle row) and the absolute error between the ensemble mean and ground truth (bottom row), for all three velocity components. (c) Pre-multiplied two-dimensional energy spectra of the generated samples ( lines) versus ground truth ( contours), computed from $500$ different test cases. Streamwise and spanwise wavelengths $\lambda _x^+$ and $\lambda _z^+$ are normalised by wall units; contours indicate $10\,\%$ , $50\,\%$ and $90\,\%$ of the maximum ground-truth energy. (d) Three representative samples from the ensemble, illustrating the diversity of generated flow realisations consistent with the wall measurements in (a).

To validate the statistical accuracy of the generated samples, we compute the pre-multiplied two-dimensional energy spectra $E_{u_i'u_i'}(\lambda _x^+, \lambda _z^+)$ for all 500 test cases and compare them with DNS reference statistics in figure 3(c). Here, $E_{u_i'u_i'}(\lambda _x^+, \lambda _z^+)$ is computed by averaging the spectra of individual instantaneous realisations ( $u'_{\textit{gen,i}}$ ), rather than from the spectrum of the ensemble mean. This approach is chosen because the generative framework is designed to produce full instantaneous flow-field realisations, not only mean predictions. Across all velocity components, the spectra of generated samples closely match the true spectra in both shape and magnitude. In particular, the dominant energetic scales in $u'$ and the anisotropic energy distributions in $v'$ and $w'$ are well preserved. This strong agreement confirms that the model not only reconstructs individual samples with realistic structure but also maintains consistency with the underlying energy distribution of wall-bounded turbulence.

Figure 4. (a) An example of sparse wall measurements ( $10\,\%$ data availability) ${\boldsymbol{\varPhi }}_{w\textit{all}}$ used as the condition for generating corresponding velocity fluctuations $\boldsymbol{u}'_i$ . (b) Comparison between the ground-truth velocity fluctuations (top row), ensemble mean of $50$ velocity fluctuation samples generated using the proposed method (middle row) and the absolute error between the ground truth and ensemble mean velocity fluctuations (bottom row). (c) Pre-multiplied two-dimensional energy spectra of the generated samples (top row) and the ensemble mean of $N_{\textit{ens}} = 50$ samples (bottom row) ( lines) versus ground truth ( contours), computed from $500$ different test cases. Streamwise and spanwise wavelengths $\lambda _x^+$ and $\lambda _z^+$ are normalised by wall units; contours indicate $10\,\%$ , $50\,\%$ and $90\,\%$ of the maximum ground-truth energy. (d) Two representative samples from the ensemble, illustrating the diversity of generated flow realisations consistent with the sparse wall measurements in (a).

3.3. Off-wall velocity generation conditioned on sparse wall measurements

We now consider a more practical and challenging scenario where the model is conditioned on only a sparse subset of the wall measurements. Specifically, we evaluate the reconstruction performance when just $10\,\%$ of the full-resolution wall data $\boldsymbol{\varPhi }_{w\textit{all}}$ are available. This set-up emulates practical sensing constraints in experiments, where sensor coverage is often sparse and non-uniform. The results, summarised in figure 4, follow the same structure as in the fully observed case. Figure 4(a) shows an example of the sparse wall measurements, constructed by randomly masking $90\,\%$ of the wall data. The effective measurement operator is defined as $\mathcal{F}(\boldsymbol{x}) = \mathcal{J}(\mathcal{F}_{\boldsymbol{\phi }}(\boldsymbol{x}))$ , combining the learned forward operator $\mathcal{F}_{\boldsymbol{\phi }}$ with a binary masking operator $\mathcal{J}$ that selects the observed entries. While the conditioning data contain substantially less information than in the full-measurement case, our model still performs well, because of the structured prior learned during training.

Figure 4(b) displays the reconstruction results at $y^+ = 20$ . The ensemble mean of the conditionally generated velocity fluctuation samples (middle row) remains in good agreement with the ground truth (top row), particularly for the streamwise component $u'$ , where large-scale streaks are reasonably reconstructed. Compared with the full-data case, the spatial error (bottom row) is slightly elevated and more spatially dispersed, especially in $v'$ and $w'$ . These differences are due to the increased epistemic uncertainty introduced by reduced wall-flow observability, particularly for velocity components less correlated with wall signals. This is further evidenced by the greater diversity observed in the conditionally generated samples shown in figure 4(d). Finally, we assess the statistical fidelity of the generated velocity fields in the top row of figure 4(c), which compares the pre-multiplied two-dimensional energy spectra of the generated and DNS velocity fluctuations for all $500$ test cases. While minor spectral attenuation is observed, particularly at smaller wavelengths where uncertainty is highest, the generated spectra remain in close agreement with the ground truth. This confirms that, even under sparse sensor deployment, the model maintains accuracy in the dominant energy-carrying modes, and preserves the global structural statistics of the flow. For comparison, the bottom row of figure 4(c) plots the spectrum of the ensemble mean ( $EM(\boldsymbol{u}'_i)$ ). This spectrum is, by definition, heavily attenuated at high wavenumbers, as the stochastic, out-of-phase structures present in individual samples (top row) are cancelled out by the averaging process.

3.4. Inference performance and uncertainty quantification analysis

We now examine how the predictive performance and associated uncertainty of the proposed framework vary across different wall-normal locations and levels of wall measurement sparsity. This analysis provides insight into the model’s robustness to decreasing wall-flow coherence and diminishing sensor coverage, two key challenges in real-world turbulence reconstruction. Specifically, we assess the accuracy of the conditional ensemble predictions and quantify the epistemic uncertainty arising from both physical observability limitations and the sparsity of wall data for conditioning.

Figure 5 addresses the first question by comparing conditional generation results at $y^+ = 5$ , $20$ and $40$ using the same $10\,\%$ sparse sensor configuration previously introduced in figure 4(a). To maintain clarity, we focus on the streamwise velocity component $u'$ ; results for $v'$ and $w'$ follow similar trends and are provided in Appendix F (figures 23–26). Figure 5(a) shows the ground truth $u'$ (first column), the ensemble mean ${EM}(u^{\prime})$ computed from 50 generated samples (second column) and one representative sample $u'_{{gen}}$ from the ensemble (third column). At $y^+=5$ , the ensemble mean closely matches the ground truth, with the representative sample exhibiting realistic variability. As $y^+$ increases, the quality of reconstruction gradually degrades. While large-scale streaks are still visible at $y^+=20$ , finer structures begin to deviate from the DNS reference. At $y^+=40$ , the ensemble mean becomes increasingly smooth and underestimates the true amplitude of fluctuations, an expected result due to the diminishing coherence between wall measurements and flow farther from the wall. However, each individual sample still maintains physically plausible small structures at all $y^+$ because of the generative module, even when theensemble mean smooths out.

Figure 5. (a) Comparison of streamwise velocity fluctuation $u'$ contours at $y^+=5$ (first row), $y^+=20$ (second row) and $y^+=40$ (third row), conditioned on sparse wall measurements ( $10\,\%$ data availability). The first column shows the ground truth, the second column is the ensemble mean of conditionally generated $N_{ens} =50$ samples and the third column displays one representative conditional sample. (b) Uncertainty quantification ( contour) of $u'$ at $y^+=5, \, 20, \, 40$ along $z=1.0\pi$ , with the ground truth (line), ensemble mean (line) and one sample ( line).

To quantify uncertainty and assess the variability of predictions, figure 5(b) shows one-dimensional profiles of $u'$ along the streamwise direction at fixed spanwise location $z = \pi$ , overlaid with $3\times {ES}(u^{\prime})$ confidence intervals. The shaded bands expand with increasing $y^+$ , reflecting greater epistemic uncertainty. Notably, the widest band occurs at $y^+=20$ , coinciding with the peak in turbulence intensity $u'_{{rms}}$ . This suggests that uncertainty is governed not just by wall proximity but also by intrinsic turbulence characteristics, particularly the chaotic amplification at buffer-layer heights. These observations are consistent with physical trends reported in prior works (Guastoni et al. 2021; Balasubramanian et al. 2023; Cuéllar et al. 2024a , b ), and they validate the model’s ability to capture non-monotonic patterns in prediction uncertainty.

We next investigate how data availability influences prediction fidelity and uncertainty. To this end, we fix the wall-normal location at $y^+ = 20$ and systematically reduce the sensor coverage from $10\,\%$ down to $0\,\%$ . While the $10\,\%$ sparse sensor case has already been shown in figure 4, we now present additional results for cases with less wall data availability. Figure 6(a) compares the ensemble mean, one representative sample and the ground truth under three increasingly sparse wall measurement scenarios: $1\,\%$ , $0.1\,\%$ and $0\,\%$ . As sensor coverage decreases, the ensemble mean predictions become progressively smoother and increasingly deviate from the ground truth, particularly in terms of amplitude attenuation. To quantify this effect, we evaluated the mean reconstruction error ${E}(\varDelta _{\boldsymbol{y}})$ as a function of sensor availability in Appendix F (figure 35). The degradation in predictive accuracy is further illustrated in figure 6(b), which presents streamwise profiles of $u'$ along $z = \pi$ , overlaid with shaded $3\times {ES}(u^{\prime})$ uncertainty bands. As the amount of available wall data decreases, these uncertainty intervals widen markedly, reflecting the model’s decreasing confidence in its predictions. In the extreme case of $0\,\%$ wall data (i.e. unconditional generation) the ensemble mean collapses to a smooth prior with negligible correlation to the ground truth. Nevertheless, individual samples remain physically plausible due to the inductive bias of the trained generative model, though they no longer reflect the specific realisation of the true flow field.

Figure 6. (a) Comparison of streamwise velocity fluctuation $u'$ contours conditioned on $1\,\%$ (first row), $0.1\,\%$ (second row) and $0\,\%$ (third row) wall data at $y^+=20$ . The first column represents the ground-truth DNS, the second column is the ensemble mean of conditionally generated $N_{ens} =50$ samples and the third column displays one representative conditional sample. (b) Uncertainty quantification ( contour) of $u'$ for $1\,\%, \, 0.1\,\%, \, 0\,\%$ wall data availability, with the ground truth ( line), ensemble mean (line) and one sample ( line).

To quantitatively summarise the trends observed in reconstruction accuracy and predictive uncertainty across wall-normal positions and sensor sparsity levels, figure 7 presents a set of scalar diagnostics across the full range of tested configurations. The top row reports the Pearson correlation coefficient $r$ between the ensemble mean of the generated samples and the DNS ground truth for $u'$ , $v'$ and $w'$ at three wall-normal distances: $y^+ = 5$ , $20$ and $40$ . The bottom row displays the corresponding global uncertainty level, computed as the scalar standard deviation $\textit{STD}$ of the predictive ensemble at each setting:

(3.6) \begin{align} \textit{STD} &= \sqrt {\sum ^{N_x}_{i} \sum ^{N_z}_{j}{(\textit{ES}(u'(i,j))}^2}. \end{align}

Figure 7. Effect of wall sensor data availability on reconstruction fidelity and predictive uncertainty at different wall-normal locations. (a) Pearson correlation coefficient $r$ between ensemble mean predictions and ground truth for streamwise ( $u'$ ), wall-normal ( $v'$ ) and spanwise ( $w'$ ) velocity fluctuations. (b) scalar ensemble standard deviation ( $STD$ ) quantifying predictive uncertainty for each velocity component. Calculations are performed by generating $N_{\textit{ens}} = 50$ samples for all the different measurement scenarios.

The correlation plots in the top row clearly demonstrate that reconstruction fidelity degrades with decreasing sensor availability, especially once coverage drops below $10\,\%$ . This trend holds consistently across all velocity components and wall-normal locations, though the impact is most pronounced for the wall-normal ( $v'$ ) and spanwise ( $w'$ ) fluctuations, which are more weakly coupled to wall data. For all three components, predictive accuracy is highest at $y^+ = 5$ , where near-wall coherence is strongest, and lowest at $y^+ = 40$ , where the flow becomes increasingly decoupled from the wall. These findings are consistent with the qualitative assessments presented earlier and further validate the model’s sensitivity to both wall distance and observability.

The bottom row captures how the model’s epistemic uncertainty evolves under the same conditions. As expected, $\textit{STD}$ increases as sensor coverage declines, reflecting reduced confidence in conditional predictions. Notably, the uncertainty growth is monotonic for each $y^+$ level and particularly steep between $10\,\%$ and $1\,\%$ data availability. Beyond this range, further increasing wall data leads to only marginal reductions in uncertainty, suggesting that the dominant source of epistemic uncertainty arises from the fundamental limitations of wall–flow coupling rather than sensor sparsity. Interestingly, the largest absolute uncertainty is observed around $y^+ = 20$ for $u'$ predictions, consistent with the peak turbulence intensity and the inherently greater variability in the buffer layer. This non-monotonic dependence on wall-normal location reinforces that predictive uncertainty is influenced not only by data sparsity but also by the intrinsic dynamics of wall-bounded turbulence.

3.5. Off-wall velocity generation with incomplete and low-resolution wall measurements

We now demonstrate the robustness of the proposed conditional generative framework under three practically relevant wall measurement scenarios: (i) incomplete spatial coverage, where only a portion of the wall is instrumented; (ii) partial observability, where only a subset of wall quantities (e.g. a single shear stress component) is accessible; and (iii) low-resolution sensing, where measurements are available across the full domain but are spatially downsampled due to acquisition constraints. These configurations reflect common limitations in real-world sensor deployments, enabling us to assess the model’s performance under degraded and incomplete wall information.

Figure 8. (a) An example of partial wall measurements ( $\tau _u$ over half of the domain) (left) and the corresponding ground-truth velocity fluctuations ( $u'$ ) at $y^+ =20$ (right). (b) Ensemble mean (top) and standard deviation (bottom) velocity fluctuations for $N_{\textit{ens}} = 50$ generated velocity fluctuation samples (c) Four randomly selected $u'$ velocity fluctuation samples given the wall measurements shown in (a). (d) Comparison of the distribution of pointwise normalised $L_2$ error ( $\varDelta _{\boldsymbol{y}}$ ) between measurements ( $\boldsymbol{y}$ ) of the unconditionally ( line) and conditionally generated ( line) velocity fluctuation samples corresponding to $500$ different test wall measurements.

Figure 8 shows the model’s performance when only the streamwise wall shear stress $\tau _u$ is measured over the downstream half of the domain ( $2\pi \leqslant x \leqslant 4\pi$ ). The wall observations (i.e. $\tau _u$ over the downstream half of the domain) and corresponding DNS ground truth for $u'$ at $y^+=20$ are shown in figure 8(a). From this partially available wall information, we generate an ensemble of $N_{\textit{ens}}=50$ velocity fluctuation samples. The ensemble mean (top) and standard deviation (bottom) fields are presented in figure 8(b). The mean field captures the prominent large-scale streaks observed in the ground truth, particularly in the region where wall data are available. The ensemble spread decreases markedly in the downstream region where wall measurements are available, confirming the model’s ability to quantify epistemic uncertainty. Figure 8(c) shows four representative ensemble samples, each preserving the spatial characteristics and intermittency of the flow across the transition between observed and unobserved wall zones ( $x=2\pi$ ). In regions with wall data, measurements enforce consistent streak patterns across realisations. In blanked regions, weaker correlation with the wall introduces variability in streak spacing and orientation, yet each sample remains physically self-consistent. This seamless blending highlights the model’s ability to infer plausible flow states while avoiding artefacts near sensor discontinuities. We also compute the distribution of pointwise normalised $L_2$ errors $\varDelta _{\boldsymbol{y}}$ over 500 independent test cases to evaluate measurement consistency. As shown in figure 8(d), the conditional samples exhibit a clear reduction in error magnitude compared with their unconditional counterparts. This shift towards lower $\varDelta _{\boldsymbol{y}}$ values confirms that the model effectively assimilates available wall information, even when spatially limited.

We next examine a low-resolution setting, where wall measurements are uniformly available across the entire domain of interest but lack spatial detail. This set-up reflects practical limitations in experimental acquisition systems, such as imaging or pressure-sensitive paint, which often capture wall quantities at coarse spatial resolutions. To mimic this constraint, we apply a $100\times$ downsampling operator $D$ , implemented via nearest-neighbour interpolation, on the original wall data $\varPhi _{w\textit{all}}$ , and visualise the resulting low-resolution streamwise shear stress $D(\tau _u)$ in figure 9(a). Conditioning on this degraded input, we generate an ensemble of $N_{\textit{ens}}=50$ conditional velocity samples. The ensemble mean and pointwise standard deviation fields $\textit{ES}(u^{\prime})$ are shown in figure 9(b). Despite the severe loss of spatial detail in the wall conditioning, the model reconstructs several dominant large-scale streaks observed in the ground-truth DNS field. However, the ensemble spread $\textit{ES}(u^{\prime})$ becomes high throughout the domain, indicating amplified epistemic uncertainty in the absence of high-resolution wall data. Figure 9(c) shows four representative samples drawn from the ensemble, which contain small-scale turbulent structures because of the FM module. These reflect the plausible diversity of flow fields consistent with coarse wall information, highlighting the expressiveness and adaptability of the generative framework. To quantify how well the generated samples honour the available wall data, we compute the distribution of pointwise normalised $L_2$ error $\varDelta _{\boldsymbol{y}}$ across 500 randomly selected test cases. Figure 9(d) shows that, even under low-resolution conditions, the conditional samples exhibit substantially lower errors than those generated unconditionally. This demonstrates the model’s ability to effectively leverage limited information while faithfully capturing the stochasticity and structure of wall-bounded turbulence.

Figure 9. (a) An example of (1 $\,\%$ ) low-resolution $\boldsymbol{y}_{LR}(x, z) = D({\boldsymbol{\varPhi }}_{w\textit{all}})$ , only $D(\tau _u)$ is illustrated (left), where $D$ is the nearest-neighbour interpolation downsampling operator and the corresponding ground-truth velocity fluctuations ( $u'$ ) at $y^+ =20$ (right). (b) Ensemble mean (top) and standard deviation (bottom) velocity fluctuations for $N_{\textit{ens}} = 50$ generated velocity fluctuation samples. (c) Four randomly chosen $u'$ velocity fluctuation samples generated for the prescribed wall measurements shown in (a). (d) Comparison of the distribution of pointwise normalised $L_2$ error ( $\varDelta _{\boldsymbol{y}}$ ) between measurements ( $\boldsymbol{y}$ ) of the unconditionally (line) and conditionally generated (line) velocity fluctuation samples corresponding to $500$ different test wall measurements.

4. Discussion

4.1. Comparison with deterministic data-driven baselines

To evaluate the effectiveness of our proposed stochastic generative model, we benchmark its performance against two widely used baseline methods: a CNN model (Guastoni et al. 2021) and the classical LSE method (Adrian 1979). Both methods are representative of state-of-the-art data-driven approaches for wall-based flow reconstruction. The CNN baseline adopts the fully CNN architecture introduced by Guastoni et al. (2021), which learns a nonlinear mapping from wall quantities to velocity fluctuations at a specified wall-normal location. The LSE method, on the other hand, estimates velocity fluctuations $\boldsymbol{u}'(\boldsymbol{x}, t)$ via a linear projection of wall measurements $\boldsymbol{\varPhi }_{w\textit{all}}(\boldsymbol{x}, t)$ using pre-computed correlation kernels:

(4.1) \begin{equation} \boldsymbol{u}' (\boldsymbol{x}, t) = \sum h (\boldsymbol{x}) {\boldsymbol{\varPhi }}_{w\textit{all}}(\boldsymbol{x}, t), \end{equation}

where $h$ is obtained by minimising the least-squares error over the training dataset. While LSE captures linear statistical correlations between wall and off-wall quantities, it cannot model nonlinear interactions or synthesise plausible flow structures in regions of weak observability. For both baselines considered in this work, we do not use the patchwise training strategy employed for the SWAG forward model. This limitation arises for the CNN architecture because of its usage of periodic padding to enforce a hard constraint of periodic boundary conditions across the full domain. On the other hand, the LSE method is built using global correlation kernels, and thus is not compatible with patchwise training. Additional implementation details for baselines are provided in Appendix B, while the information details about training dataset used for the baseline methods are summarised in Appendix E.

Figures 10 and 11 provide a comprehensive comparison between the proposed method and the baselines. For this baseline comparison, sparse sensor data are pre-processed using interpolation (e.g. nearest-neighbour, linear or cubic) before being passed to the pre-trained CNN and LSE models, as detailed in Appendix B. Figure 10 compares the pre-multiplied two-dimensional energy spectra of velocity fluctuations reconstructed by all methods at $y^+=20$ under $100\,\%$ , $90\,\%$ and $10\,\%$ wall measurement availability. For fair comparison with the deep-learning-based baseline, we highlight the performance of the CNN method using cubic interpolation. When complete wall information is available (figure 10 a), all models recover the dominant energy-containing structures and produce spectra in close agreement with DNS. Under mild sparsity (figure 10 b), the CNN baseline begins to lose fidelity, exhibiting significant deviations at smaller scales. In contrast, both our proposed model and the LSE model maintain strong spectral agreement with DNS, which is consistent with previous observations (Encinar & Jiménez 2019) indicating that LSE performs reasonably well in recovering wall-attached eddies within the viscous and buffer layers ( $y^+ \le 20$ ) when wall data are only moderately sparse and noise-free.

Figure 10. Comparison of pre-multiplied two-dimensional energy spectra between the proposed model and two baseline methods under varying availability of wall quantities at $y^+=20$ : (a) $100\,\%$ wall quantities, (b) $90\,\%$ wall quantities and (c) $10\,\%$ wall quantities. The sparse wall measurements are pre-processed using cubic interpolation for the CNN baseline method. The energy spectra are calculated over 500 test cases. Ground-truth DNS is shown as filled contours ( contours) and model predictions are shown as line plots. Streamwise and spanwise wavelengths $\lambda _x^+$ and $\lambda _z^+$ are normalised by wall units. The contour levels contain $10\,\%$ , $50\,\%$ and $90\,\%$ of the maximum energy spectra.

When the wall information is severely limited to $10\,\%$ coverage (figure 10 c), both deterministic baseline models fail to reconstruct the turbulent energy distribution accurately. The CNN baseline produces overly smoothed fields, and the LSE spectrum nearly vanishes due to underprediction of fluctuation amplitudes. In stark contrast, our model remains stable and physically realistic, preserving the large-scale streaks and the correct energy content across wavelengths. This robustness stems from two key features: (i) the use of a generative prior that synthesises statistically consistent flow fields in underdetermined regions (Duraisamy & Srivastava 2025) and (ii) explicit uncertainty quantification that allows the model to balance observed data with prior structure during sampling.

Figure 11. Comparison of instantaneous velocity fluctuations $u'$ at $y^+=20$ reconstructed from $10\,\%$ wall measurements using the proposed method, CNN and LSE. Comparison of the Pearson correlation coefficients between reconstructed and DNS velocity fluctuations $(u', v', w')$ for different methods under $100\,\%$ , $90\,\%$ and $10\,\%$ wall-sensor data availability.

To provide further qualitative and quantitative insight, figure 11 presents instantaneous contours of $u'$ at $y^+=20$ (for $10\,\%$ data) and a comprehensive table of Pearson correlation coefficients for all test cases. The $10\,\%$ contours show that our method produces sharp, structured flow fields that closely resemble the DNS ground truth. In contrast, the CNN (cubic) reconstruction is highly artefacted and grainy, while the LSE (cubic) prediction is overly smoothed and spatially decorrelated. The accompanying table details the reconstruction performance across all data availability scenarios and pre-processing strategies. It is clear that for extreme sparsity ( $10\,\%$ ), the performance of both baselines is remarkably poor. Furthermore, their results are highly sensitive to the chosen interpolation strategy, highlighting a lack of robustness. Our proposed method, which requires no such pre-processing, delivers strong reconstruction performance across all levels of data sparsity.

The results from both figures highlight critical, complementary failures in the baseline methods. The Pearson correlation table in figure 11 demonstrates that the LSE method fails the structural test: its correlation coefficients are near zero across all scenarios, indicating that its reconstructions are not physically coherent with the ground truth. This is true even though its energy spectrum appeared reasonable in figure 10(a,b). Conversely, the CNN baseline (with cubic interpolation) achieves high correlation coefficients when data are nearly complete ( $0.946$ at $100\,\%$ and $0.809$ at $90\,\%$ for $u'$ ). This suggests good structural alignment in high-data regimes. However, figure 10(b,c) reveals its simultaneous statistical failure, as it produces highly inaccurate spectra. In the extreme $10\,\%$ sparsity case, the baselines fail both tests, exhibiting poor correlation and inaccurate spectra. Our proposed method, in contrast, demonstrates unique robustness, delivering both high statistical fidelity (figure 10) and competitive structural correlation (figure 11) across all sparsity levels.

In summary, both baselines produce deterministic point estimates and offer no measure of confidence, making them less reliable in underdetermined or weakly observable regimes. In contrast, our framework not only delivers superior accuracy under sparse or degraded sensing, but also quantifies epistemic uncertainty – a critical capability for decision-making in wall modelling, sensor placement and active flow-control applications.

4.2. Advantages over probabilistic regression methods

Previous probabilistic learning approaches, such as Bayesian neural networks and other uncertainty-aware regressors (Goan & Fookes 2020), directly predict ensemble averages and variances from input data. While these methods can provide useful mean-field estimates with uncertainty bounds, they remain limited to moment-based approximations of the conditional distribution. By contrast, our framework generates distinct, physically plausible instantaneous realisations of the velocity fluctuation field, each consistent with wall observations. These realisations preserve intermittency and higher-order turbulence statistics that are typically lost in regression-based methods.

Specifically, the advantages of our approach over probabilistic regression are threefold. First, the inverse problem of reconstructing a flow field from sparse wall data is highly ill-posed, and the conditional posterior distribution $p(\boldsymbol{u}'|\boldsymbol{\varPhi }_{w\textit{all}})$ can be complex and multimodal. Regression methods usually provide only mean and variance under unimodal Gaussian assumptions, whereas our conditional FM framework learns a generative transport map, enabling sampling from the entire posterior and naturally capturing diversity and multimodality. Second, direct regressors smooth out intermittent, high-frequency features, producing over-smoothed fields. Our generative samples retain fine-scale structures and realistic turbulence dynamics, while ensemble statistics (e.g. spectra) remain consistent with DNS (figures 3 and 4). This capability is essential when structurally accurate, time-resolved fields are required. Third, our training is decoupled into two phases: an unsupervised FM model that learns the turbulence prior, and a probabilistic forward operator (trained with SWAG) that maps flow fields to wall quantities. This modularity, combined with our training-free inference strategy, is more stable and flexible than training a single, large, end-to-end Bayesian network to directly handle the high-dimensional mapping from wall data to flow fields. The latter can be more difficult to train and may suffer from issues such as posterior collapse. Our approach effectively regularises the inverse problem by leveraging a strong, separately learned physical prior.

In summary, the key advantage of our framework is that it provides access to the full conditional distribution of turbulence fields, yielding physically realistic instantaneous samples with multimodal uncertainty quantification, rather than being restricted to moment-based approximations.

4.3. The SWAG-based forward operator and implications for $w$ all modelling

The forward operator $\mathcal{F}_{\boldsymbol{\phi }}$ serves as measurement model in our conditional generation framework by mapping predicted velocity fluctuations to corresponding wall quantities. To determine the training dataset size for the SWAG forward model, we perform a convergence study and summarise our results in Appendix D. As it is used during the inference to guide conditional sampling, it must be both differentiable and capable of quantifying uncertainty, especially in regions where wall–flow coupling is weak. To this end, we adopt a Bayesian training strategy, enabling the operator to capture epistemic uncertainty in its predictions.

To evaluate the uncertainty quantification capability of the trained forward model, we apply it to $500$ temporally ordered test samples at three wall-normal distances ( $y^+ = 5$ , $20$ and $40$ ) and extract the reconstructed wall quantities $\boldsymbol{\varPhi }_{w\textit{all}}$ at the probe location $(x=2\pi , z=\pi )$ . Figure 12 shows the resulting time series of ensemble mean predictions and $3\sigma$ uncertainty intervals computed from $m = 50$ SWAG posterior weight samples. As $y^+$ increases, two trends are notable: (i) the ensemble mean becomes slightly less aligned with the ground truth and (ii) the uncertainty band of the prediction expands accordingly. This behaviour reflects the diminishing influence of velocity fluctuations on wall quantities with increasing distance from the wall, and confirms that the forward operator correctly captures epistemic uncertainty induced by weakening wall–flow coherence.

Figure 12. The SWAG-based forward operator predictions of wall quantities $\boldsymbol{\varPhi }_{w\textit{all}}$ for velocity inputs at $y^+ = 5$ (a), $20$ (b) and $40$ (c), evaluated along $x = 2\pi$ , $z = \pi$ over 500 time steps. Shaded bands show $\pm 3\sigma$ uncertainty intervals ( contour); lines show ensemble mean (line) and ground truth ( line).

We further assess our SWAG-based probabilistic neural operator $\mathcal{F}_{\boldsymbol{\phi }}$ by comparing its performance against a baseline CNN model adapted from Guastoni et al. (2021). Although originally developed to infer velocity fields from wall data, we reverse its input–output direction and re-train the model from scratch for a fair comparison, leveraging its purely data-driven nature. Figure 13 shows the one-dimensional pre-multiplied spectra of predicted wall quantities at $y^+ = 20$ for both models. Across all wall quantities, our SWAG-based model consistently outperforms the CNN baseline, particularly for pressure spectra in both streamwise and spanwise directions (figure 13 a,b) and across different wall-normal locations as highlighted in Appendix F (figures 36 and 37). The CNN significantly overestimates energy at high wavenumbers, suggesting the presence of spurious high-frequency artefacts, likely a result of overfitting and the absence of uncertainty regularisation. In contrast, our model produces smoother spectra that align closely with DNS, demonstrating improved multiscale fidelity. While both models show reduced accuracy at low wavenumbers, the gap is smaller in our model and likely reflects the intrinsic difficulty of recovering large-scale pressure structures rather than model capacity. For wall shear stress spectra in figure 13(c,d), both models recover the dominant energy content, though the SWAG-based operator again achieves better agreement with DNS across a broader range of scales. It is worth noting that the CNN baseline is trained on four times more data (36 000 samples versus 9000 samples for $\mathcal{F}_{\boldsymbol{\phi }}$ ), consistent with prior study (Guastoni et al. 2021; Güemes et al. 2021; Balasubramanian et al. 2023).

Figure 13. Comparison of statistics from different forward models for mapping velocities at $y^+=20$ to wall: (a) streamwise and (b) spanwise spectra of pressure fluctuations; (c) streamwise and (d) spanwise spectra of wall shear stresses $\tau _u$ and $\tau _w$ .

Beyond conditioning guidance, the forward operator also has potential use as a data-driven wall model in turbulence simulations. To evaluate this possibility, we conduct an a priori test, in comparison with a traditional algebraic wall model based on the Spalding function (Spalding et al. 1961), using input velocity fields at $y^+ = 20$ . Figure 14 shows that our operator produces predictions of wall shear stress that closely match DNS ground truth, while the Spalding-based model overpredicts $\tau _u$ by approximately $15\,\%$ , consistent with the well-documented logarithmic-layer mismatch observed in algebraic wall models (Yang, Park & Moin 2017). These results highlight the potential of $\mathcal{F}_{\boldsymbol{\phi }}$ as a differentiable, uncertainty-aware wall model. Its ability to learn from data while maintaining physical consistency makes it a promising candidate for hybrid Reynolds-averaged Navier–Stokes with LES or wall-modelled LES frameworks. More extensive a posteriori validation will be explored in future work.

Figure 14. Comparison of predicted instantaneous wall shear stress: (a) PDF of streamwise wall shear stress $\tau _u$ ; (b) PDF of spanwise wall shear stress $\tau _w$ . The input velocity field from $y^+=20$ .

4.4. Training-free conditional generation via flow matching

A key strength of the proposed framework lies in its ability to perform test-time conditional generation without re-training or modifying the learned generative model. This property is enabled by the proposed training-free conditional inference strategy for FM. In contrast to traditional supervised approaches, which require explicit re-training for each new sensor configuration, our approach flexibly assimilates conditioning data by incorporating it as a guidance term in the FM sampling dynamics. Importantly, our framework is modular: the generative model, which learns the high-dimensional distribution of turbulent flows, remains unchanged, while only the forward measurement operator mapping the flow state to the new wall measurements needs re-training. In contrast, traditional end-to-end supervised models typically require re-training the entire network from scratch when the inputs change, often involving extensive hyperparameter tuning to achieve comparable fidelity. This modularity preserves the high-fidelity nature of the generated fields and allows adaptation to new sensing modalities in a more efficient and targeted manner. This decoupling of model training and inference enables a unified generative framework for diverse inverse problems in turbulence modelling.

To illustrate this capability in a simplified setting, we consider an internal field recovery task in which the generative model is conditioned directly on partial measurements of the velocity fluctuation field $\boldsymbol{u}'_i$ . This setting serves as a conceptual analogue to classical inpainting tasks in computer vision and highlights the model’s behaviour under idealised but informative conditions. Here, the measurement operator $\mathcal{F}(\boldsymbol{u}'_i)$ is defined as a binary masking operator $\mathcal{J}(x,z)$ that zeroes out the velocity field at unobserved locations:

(4.2) \begin{equation} \boldsymbol{y}(x, z) = \mathcal{J}(x, z) \odot \boldsymbol{u}'_i(x, z), \end{equation}

where $\odot$ denotes elementwise multiplication and $\mathcal{J}(x,z) \in {0,1}$ indicates the sensor layout. We apply this masking operator to approximately $90\,\%$ of the streamwise velocity field at $y^+=20$ , leaving only sparse values available for conditioning (figure 15 a).

To generate posterior-consistent samples, we apply the FM ODE starting from Gaussian noise $\boldsymbol{x}_0 \sim \mathcal{N}(0, I)$ and compute a corrected trajectory using the training-free guidance method introduced in § 2.4. At each time step, an approximate one-step prediction $\hat {\boldsymbol{x}}_1$ is obtained using the learned velocity field $\boldsymbol{\nu }_\theta (t, \boldsymbol{x})$ , from which an estimated measurement $\hat {\boldsymbol{y}} = \mathcal{J} \odot \hat {\boldsymbol{x}}_1$ is constructed. The mismatch between $\hat {\boldsymbol{y}}$ and the true observation $\boldsymbol{y}$ defines the conditioning error, whose gradient is used to form the correction term $\boldsymbol{\nu }'(t, \boldsymbol{x}, \boldsymbol{y})$ as detailed in (2.11).

Figure 15. (a) An example of partial velocity fluctuation measurements ( $\boldsymbol{y}(x,z) = \mathcal{J}(x, z) \odot \boldsymbol{u}'_i(x, z)$ ) (left) and the corresponding ground-truth velocity fluctuations ( $u'$ ) at $y^+ =20$ (right). (b) Ensemble mean (top) and standard deviation (bottom) of $N_{\textit{ens}} = 50$ generated velocity fluctuation samples. (c) Four randomly chosen $u'$ velocity fluctuation samples generated for the prescribed wall measurements shown in (a). (d) Comparison of the distribution of pointwise normalised $L_2$ error ( $\varDelta _{\boldsymbol{y}}$ ) between measurements ( $\boldsymbol{y}$ ) of the unconditionally (line) and conditionally generated (line) velocity fluctuation samples corresponding to $500$ different wall measurements.

Figure 15(b) shows the ensemble mean and standard deviation computed from $N_{{ems}} = 50$ conditionally generated samples. The ensemble mean accurately reconstructs both the observed and nearby unobserved regions, reflecting spatial coherence in the generated fields. Importantly, the ensemble standard deviation adapts to the conditioning mask, exhibiting higher uncertainty in unobserved regions and lower variance near conditioned points. These results confirm that the model captures uncertainty in a physically consistent manner. Figure 15(c) visualises four representative conditional samples, each of which exhibits realistic turbulence structures with fine-scale variability and flow intermittency. The visual plausibility of the samples, despite strong underdetermination, demonstrates the inductive bias encoded by the generative model and the effectiveness of flow-based guidance in posterior exploration.

To quantify measurement consistency, figure 15(d) compares the distribution of the pointwise normalised $L_2$ error $\varDelta _{\boldsymbol{y}}$ for 500 test-time realisations. Samples generated with conditioning exhibit significantly lower errors compared with unconditional samples, confirming that the guided FM trajectory conforms to the measurement constraints.

In the tasks above, the training-free conditional generation for data assimilation on sparse sensors is applied during inference. An important limitation of the proposed formulation is that it cannot be trained directly on a scattered dataset. Designing architectures to alleviate this bottleneck presents an interesting research direction, as it would make the framework more easily extendable to experimental settings.

Together, these results highlight the effectiveness and robustness of the training-free inference strategy, enabling high-fidelity conditional generation under arbitrary sensor configurations without re-training the generative model.

4.5. Computational efficiency analysis

To further highlight the practicality of our framework for data assimilation, we evaluate its computational efficiency relative to traditional approaches. Our method requires approximately $6600$ seconds on a single NVIDIA L40 GPU to reversely generate $300$ conditional samples, corresponding to one flow-through time at $\textit{Re}_\tau =180$ . In contrast, conventional flow reconstruction (or data assimilation) methods treat the task as an inverse optimisation task, which is typically orders of magnitude more expensive.

Variational approaches, for example, often rely on tens to hundreds of forward and adjoint simulations to reconstruct flows from sparse measurements. A representative case is the adjoint-based 4DVar framework (Wang & Zaki 2025), which partitions the time horizon into windows and typically demands $\mathcal{O}(100)$ forward–adjoint iterations per window. For reference, a single forward DNS of the same duration using OpenFOAM on 16 AMD EPYC 7643 CPU cores already takes about $108{\,}000$ seconds, nearly an order of magnitude slower than our generative model. Since each adjoint run has a cost comparable to a forward DNS, the overall expense of 4DVar-based reconstruction can exceed $\sim 2000$ times that of our framework. Our generative approach eliminates the need for repeated forward–adjoint loops. Thus, compared with adjoint-based techniques, the proposed method provides a more computationally efficient pathway to producing uncertainty-aware reconstructions from sparse data. Nonetheless, the current computational cost remains a significant bottleneck, precluding its deployment for practical, real-time flow-control applications. We note, however, that these bottlenecks are being actively addressed in recent literature (Geng et al. 2025) through methods like one-step sampling, which suggests a viable path towards extending this framework to real-time flow estimation.

For the baselines considered in this work, the computational cost for reconstructing the velocity fluctuation fields over the same time span is approximately $1.5{-}2$ seconds on an NVIDIA L40 GPU. While this inference speed is vastly superior to that of our proposed method, the statistical and reconstruction performance of these models in sparse settings is severely limited. This poor performance under sparsity, as demonstrated in our comparative analysis, restricts their practical utility, despite their computational efficiency.

4.6. Separating the sources of stochasticity

Our framework incorporates two sources of stochasticity: (i) the intrinsic variability of the generative FM model and (ii) the epistemic uncertainty of the forward operator introduced through the SWAG formulation. The epistemic uncertainty, quantified by SWAG, captures variability in the forward operator’s trainable parameters, reflecting model-form error in the velocity-to-wall mapping. This is distinct from the intrinsic stochasticity of the generative process itself, which surrogates the distribution of turbulent fluctuations. To disentangle these contributions, we consider a controlled set-up in which velocity fluctuations are generated at $y^+=5$ using $640$ sensors located directly at this wall-normal position. In this case, the velocity fluctuations are used directly as conditioning data, eliminating epistemic uncertainty from the forward operator and isolating the stochasticity arising solely from the generative model. We then compare this baseline against a more realistic scenario using the same number of wall sensors, which are assimilated through the SWAG forward model.

Table 2. Predictive uncertainty of generated velocity fluctuations with and without the SWAG forward operator.

Figure 16. Comparison of generated velocity fluctuations with (right) and without (left) the SWAG forward operator for the reconstruction of velocity fluctuations at $y^+=5$ using $640$ sensors. The conditioning information for the case with the SWAG forward measurement model is the wall quantities $(p',\ \tau _u,\ \tau _w)$ , while for the case without the SWAG model the conditioning information is the velocity fluctuations $(u',\ v',\ w')$ .

In figure 16, ensembles of $N_{ens}=50$ samples are shown for both cases. As summarised in table 2, predictive uncertainty is noticeably larger when SWAG is used compared with the deterministic-forward baseline. When direct velocity measurements are available (left), the conditioning information is exact, and predictive uncertainty remains small, reflecting only the randomness of the FM generative process. By contrast, when conditioning relies on indirect wall quantities (right), the SWAG operator propagates its parameter uncertainty into the reconstructed velocity fields. This leads to wider uncertainty bands around the ensemble mean. Such behaviour is both expected and desirable: in data-assimilation tasks based on indirect observations, the framework should not only honour the generative variability but also faithfully represent the model-form uncertainty inherent in the data-driven forward operator.

5. Conclusion

In this work, we have proposed a data-driven generative framework for reconstructing near-wall turbulent velocity fluctuations from wall-based measurements, grounded in the theory of conditional FM and Bayesian neural operators. The method effectively decouples training from inference through a training-free conditional generation strategy, allowing flexible assimilation of wall data in various forms without the need for re-training across different sensor modalities. Our integration of FM with a SWAG-trained forward operator enables consistent propagation of both observations and their epistemic uncertainty into the generative sampling process.

To perform a rigorous analysis of our proposed novel strategy, we focus on the canonical case of turbulent channel flow at $\textit{Re}_\tau = 180$ . We have demonstrated that the model performs robustly on a temporally and statically independent testing set of the same friction Reynolds number across a range of wall measurement configurations, including fully observed, sparse, partial and low-resolution cases, and provides physically realistic reconstructions with quantified uncertainty. The results highlight how generative modelling can bridge data-driven inference and physically structured variability in turbulent flows. Compared with existing deterministic data-driven approaches such as CNNs and LSE, our proposed framework offers significantly improved robustness and fidelity, particularly under weak observability conditions. It accurately reconstructs fine-scale turbulent structures even at large wall-normal distances or with severely limited wall data, and crucially, it provides principled uncertainty quantification to capture the confidence of each prediction. This enables consistent, high-quality reconstruction of buffer-layer and logarithmic-layer turbulence where traditional methods often fail.

Looking forward, this framework opens several directions for future exploration. First, coupling with physics-based constraints (e.g. via differentiable solvers or spectral regularisation) may further enhance physical consistency. Second, integrating temporal dynamics via conditional generative trajectories and one-step sampling techniques could extend this work towards real-time state estimation and data assimilation. Another natural extension of this work is to generalise the proposed framework across different Reynolds number. This generalisation is critical for scaling the proposed methodology to practical data-assimilation tasks for out-of-training flow conditions. An additional critical direction of research is to extend the framework for continuous three-dimensional reconstruction along the wall-normal direction. This continuous parametrisation would be useful for providing improved uncertainty quantification by including additional physical constraints from the interactions between the wall-normal locations. An important limitation of the current formulation is that training requires full-field data on a uniform grid, which makes direct learning from sparse, non-uniformly distributed datasets challenging. A promising solution is to incorporate a two-stage strategy in which scattered data are first fitted with a continuous implicit representation that can then be queried on a structured grid for FM training. Finally, integrating the model with experimental measurements opens the door to practical applications in data-driven wall modelling, near-real-time flow control and the development of high-fidelity digital twin systems. A key challenge here is the domain gap between training on DNS data and real experimental measurements. While the SWAG operator can help identify out-of-distribution inputs, this gap could be more robustly addressed by adopting transfer-learning strategies such as those proposed by Guastoni et al. (2025), in which a generative prior pre-trained on DNS is fine-tuned with targeted experimental datasets. In summary, through its flexibility, uncertainty-awareness and sampling efficiency, this framework represents a significant step towards robust data-driven modelling of wall-bounded turbulence.